Геостационарная орбита – битва за пояс Кларка. Высота орбиты спутника

Реферат Геостационарный спутник

скачать

Реферат на тему:

План:

1 Точка стояния
2 Размещение спутников на орбите
3 Вычисление параметров геостационарной орбиты
- 3.1 Радиус орбиты и высота орбиты
- 3.2 Орбитальная скорость
- 3.3 Длина орбиты
4 Связь

Введение

Геостациона́рная орби́та (ГСО) — круговая орбита, расположенная над экватором Земли (0° широты), находясь на которой искусственный спутник обращается вокруг планеты с угловой скоростью, равной угловой скорости вращения Земли вокруг оси, и постоянно находится над одной и той же точкой на земной поверхности. Геостационарная орбита является разновидностью геосинхронной орбиты и используется для размещения искусственных спутников (коммуникационных, телетрансляционных и т. п.)

Спутник должен обращаться в направлении вращения Земли, на высоте 35 786 км над уровнем моря (вычисление высоты ГСО см. ниже). Именно такая высота обеспечивает спутнику период обращения, равный периоду вращения Земли относительно звёзд (сидерические сутки: 23 часа, 56 минут, 4,091 секунды).

Идея использования геостационарных спутников для целей связи высказывалась ещё[когда?] К. Э. Циолковским и словенским теоретиком космонавтики Германом Поточником[1] в 1928 г. Преимущества геостационарной орбиты получили широкую известность после выхода в свет научно-популярной статьи Артура Ч. Кларка в журнале «Wireless World» в 1945 году[2], поэтому на Западе геостационарная и геосинхронные орбиты иногда называются «орбитами Кларка», а «поясом Кларка» называют область космического пространства на расстоянии 36000 км над уровнем моря в плоскости земного экватора, где параметры орбит близки к геостационарной. Первым спутником, успешно выведенным на ГСО, был Syncom-2, запущенный NASA в июле 1963 года.

1. Точка стояния

Спутник, находящийся на геостационарной орбите, неподвижен относительно поверхности Земли[3], поэтому его местоположение на орбите называется точкой стояния. В результате, сориентированная на спутник и неподвижно закреплённая направленная антенна может сохранять постоянную связь с этим спутником длительное время.

2. Размещение спутников на орбите

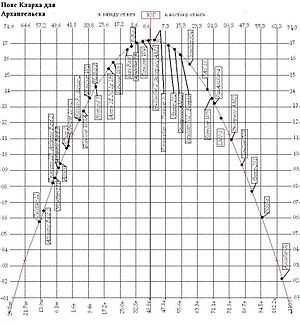
Для Архангельска максимально возможная высота спутника над горизонтом — 17,2°Наивысшая точка пояса Кларка всегда находится строго на юге. В нижней части графика градусы — меридианы, над которыми находятся спутники.По бокам — высоты спутников над горизонтом.Сверху — направление на спутник. Для наглядности можно растянуть по горизонтали в 7,8 раза и отразить слева направо. Тогда он будет выглядеть так же, как на небе.

Геостационарная орбита может быть точно обеспечена только на окружности, расположенной прямо над экватором, с высотой, очень близкой к 35 786 км.

Если бы геостационарные спутники были видны на небе невооружённым глазом, то линия, на которой они были бы видны, совпадала бы с «поясом Кларка» для данной местности. Геостационарные спутники, благодаря имеющимся точкам стояния, удобно использовать для спутниковой связи: единожды сориентированная антенна всегда будет направлена на выбранный спутник (если он не сменит позицию).

Для перевода спутников с низковысотной орбиты на геостационарную используются переходные геостационарные (геопереходные) орбиты (ГПО) — эллиптические орбиты с перигеем на низкой высоте и апогеем на высоте, близкой к геостационарной орбите.

После завершения активной эксплуатации на остатках топлива спутник должен быть переведён на орбиту захоронения, расположенную на 200—300 км выше ГСО.

3. Вычисление параметров геостационарной орбиты

3.1. Радиус орбиты и высота орбиты

На геостационарной орбите спутник не приближается к Земле и не удаляется от неё, и кроме того, вращаясь вместе с Землёй, постоянно находится над какой-либо точкой на экваторе. Следовательно, действующие на спутник силы гравитации и центробежная сила должны уравновешивать друг друга. Для вычисления высоты геостационарной орбиты можно воспользоваться методами классической механики и исходить из следующего уравнения:

Fu = FΓ,

где Fu — сила инерции, а в данном случае, центробежная сила; FΓ — гравитационная сила. Величину гравитационной силы, действующую на спутник, можно определить по закону всемирного тяготения Ньютона:

где mc — масса спутника, M3 — масса Земли в килограммах, G — гравитационная постоянная, а R — расстояние в метрах от спутника до центра Земли или, в данном случае, радиус орбиты.

Величина центробежной силы равна:

где a — центростремительное ускорение, возникающее при круговом движении по орбите.

Как можно видеть, масса спутника mc присутствует как множитель в выражениях для центробежной силы и для гравитационной силы, то есть высота орбиты не зависит от массы спутника, что справедливо для любых орбит[4] и является следствием равенства гравитационной и инертной массы. Следовательно, геостационарная орбита определяется лишь высотой, при которых центробежная сила будет равна по модулю и противоположна по направлению гравитационной силе, создаваемой притяжением Земли на данной высоте.

Центростремительное ускорение равно:

где ω — угловая скорость вращения спутника, в радианах в секунду.

Сделаем одно важное уточнение. В действительности, центростремительное ускорение имеет физический смысл только в инерциональной системе отсчета, в то время как центробежная сила является так называемой мнимой силой и имеет место исключительно в системах отсчета (координат), которые связаны с вращающимися телами. Центростремительная сила (в данном случае — сила гравитации) вызывает центростремительное ускорение. По модулю (по абсолютному численному значению) центростремительное ускорение в инерциальной системе отсчета равно центробежному в системе отсчета, связанной в нашем случае со спутником. Поэтому далее, с учетом сделанного замечания, мы можем употреблять термин «центростремительное ускорение» вместе с термином «центробежная сила».

Уравнивая выражения для гравитационной силы и центробежной силы с подстановкой центростремительного ускорения, получаем:

Сокращая mc, переводя R2 влево, а ω2 вправо, получаем:

или

Можно записать это выражение иначе, заменив на μ — геоцентрическую гравитационную постоянную:

Угловая скорость ω вычисляется делением угла, пройденного за один оборот ( радиан) на период обращения (время, за которое совершается один полный оборот по орбите: один сидерический день, или 86 164 секунды). Получаем:

рад/с

Полученный радиус орбиты составляет 42 164 км. Вычитая экваториальный радиус Земли, 6 378 км, получаем высоту 35 786 км.

3.2. Орбитальная скорость

Орбитальная скорость (скорость, с которой спутник летит в космосе), вычисляется умножением угловой скорости на радиус орбиты:

км/с или = 11052 км/ч

Можно сделать вычисления и иначе. Высота геостационарной орбиты — это такое удаление от центра Земли, где угловая скорость спутника, совпадающая с угловой скоростью вращения Земли, порождает орбитальную (линейную) скорость, равную первой космической скорости (для обеспечения круговой орбиты) на данной высоте. Решая данное простое уравнение мы, разумеется, получим те же значения, что и в расчетах через центробежную силу. Понятно также, почему геостационарные орбиты такие высокие. Требуется достаточно далеко отвести спутник от Земли, чтобы первая космическая скорость там была столь небольшой (примерно 3 км/с, ср. примерно 8 км/с на низких орбитах)

Важно также отметить, что геостационарная орбита должна быть именно круговой (и именно поэтому выше говорилось именно о первой космической скорости). Если скорость будет ниже первой космической (на данном удалении от Земли), то спутник будет снижаться, если скорость будет выше первой космической, то орбита будет эллиптической, и спутник не сможет равномерно вращаться синхронно с Землей.

3.3. Длина орбиты

Длина геостационарной орбиты: . При радиусе орбиты 42 164 км получаем длину орбиты 264 924 км.

Длина орбиты крайне важна для вычисления «точек стояния» спутников.

4. Связь

Связь через такого рода спутники характеризуется большими задержками в распространении сигнала. Даже один ход луча до спутника и обратно обходится почти в четверть секунды. Ping до другой точки на земле будет уже около половины секунды.

При высоте орбиты 35 786 км и скорости света около 300 000 км/с ход луча «Земля-спутник» требует 35786/300000 =~0,12 сек. Ход луча «Земля (передатчик) -> спутник -> Земля (приемник)» ~0,24 сек. Ping потребует ~0,48 сек

С учетом задержки сигнала в аппаратуре ИСЗ и аппаратуре наземных служб общая задержка сигнала на маршруте Земля -> спутник -> Земля может достигать 2-4 с. [1]

Поддержание спутника в точке стояния на геостационарной орбите требует энергетических и, соответственно, финансовых затрат. Связано это именно с тем, что орбита должна быть строго круговой, иметь строго определенную высоту и характеризоваться строго определенной скоростью (все три параметра взаимосвязаны). Поэтому геостационарные спутники достаточно быстро расходуют имеющийся у них запас топлива для коррекции скорости и высоты орбиты. Именно поэтому в настоящее время в основном используют не «висящие», а «восьмерочные» спутники, находящиеся на геосинхронных орбитах, которые, помимо прочего, могут быть значительно ниже геостационарной. Кроме того, «спарка» двух спутников на встречных эллиптических орбитах, расположенных под углом к плоскости экватора, в эксплуатации значительно дешевле одного геостационарного спутника.

Однако геостационарные спутники по-прежнему являются незаменимыми для многих военно-разведывательных целей, а также для целей так называемого космического прицеливания, то есть для ориентирования космических кораблей при выходе на орбиту и при переходе с орбиты на орбиту. Кроме того, в перспективе именно геостационарные спутники могут обеспечить работу так называемых космических лифтов.

wreferat.baza-referat.ru

Геостационарная орбита – битва за пояс Кларка

Немногие аспекты эпохи активного освоения космического пространства оказали настолько сильное воздействие на повседневную жизнь человечества, как концепция геостационарной орбиты, тесно сопряженная с изобретением спутника связи. Эти два фактора оказались настоящим технологическим и научным прорывом, придавшим грандиозный импульс развития не только телекоммуникационным технологиям, но и всей науке в целом, что позволило вывести жизнь людей на качественно новый уровень.

Это позволило покрыть всю планету густой паутиной устойчивого радиосигнала и соединить даже самые удаленные точки планеты способом, который еще совсем недавно был предметом мечтаний ученых и темой для писателей-фантастов. Сегодня можно свободно поговорить по телефону с полярниками Антарктиды или через Интернет мгновенно связаться с любым компьютером на поверхности земного шара. И все это благодаря геостационарной орбите и спутникам связи.

Геостационарная орбита – это круговая орбита, которая расположена точно над экватором планеты. Геостационарная орбита уникальна тем, что находящиеся на ней спутники имеют угловую скорость вращения вокруг Земли, равную скорости вращения самой планеты вокруг собственной оси, что дает им возможность постоянно «парить» над одной и той же точкой поверхности. Это и обеспечивает устойчивость и исключительное качество радиосигналов.

Геостационарная орбита, будучи разновидностью геосинхронной орбиты и обладая уникальными характеристиками, широко используется для размещения телекоммуникационных, телетрансляционных, метеорологических, научно-исследовательских и прочих спутников. Высота геостационарной орбиты составляет 35 785 километров над уровнем мирового океана. Именно эта точно рассчитанная высота и обеспечивает синхронность вращения с планетой. Искусственные спутники, расположенные на ГСО, вращаются в одном направлении с земным шаром. Это единственно возможное сочетание параметров, при котором достигается эффект синхронности движения спутника и планеты.

Геостационарная орбита имеет и альтернативное название – Пояс Кларка, по имени человека которому принадлежит львиная доля заслуг в развитии идеи и разработки концепции геостационарной и геосинхронной орбит. В 1945 году в своей публикации в журнале «Wireless World» он определил орбитальные характеристики этого узкого участка околоземного пространства и предложил обсуждение технических параметров, необходимых для системы связи Земля-спутник.

С бурным развитием телекоммуникационных и космических технологий геостационарная орбита превратилась в уникальную полосу космического пространства с невосполнимым и принципиально ограниченным ресурсом. Чрезвычайная загруженность этого участка разнообразными спутниками стала серьезной проблемой. По прогнозам экспертов, в 21-ом веке ожидается жесточайшее конкурентное экономическое и политическое противостояние за место на геостационарной орбите. Международными политическими соглашениями эту проблему не решить. Возникнет совершенно патовая ситуация. А в ближайшие два десятилетия, по компетентным прогнозам, геостационарная орбита в качестве наивыгоднейшего места для спутниковых систем полностью исчерпает свой ресурс.

Одним из наиболее вероятных решений может стать постройка на орбите тяжелых многоцелевых платформ-станций. При современных технологиях одна такая станция сможет успешно заменить десятки спутников. Эти платформы будут экономически выгоднее спутников и послужат информационному сближению стран.

fb.ru

обзор значимых высот и орбит — Naked Science

Высота Баумгартнера – 39 километров

14 октября 2012 года австрийский экстремал и парашютист Феликс Баумгартнер поднялся в стратосферу на высоту 38 969 метров над уровнем моря и совершил прыжок с парашютом. Это был совсем не обычный прыжок, и место, откуда он был совершен, тоже.

Герметизированная стеклопластиковая капсула, прикрепленная к воздушному шару, наполненному гелием, подняла Баумгартнера на высоту, выше которой не летают самолеты (до 20 км) и практически не поднимаются облака. Даже озоновый слой (а он на высоте от 20 до 30 км над Землей) остался под ним.

Феликс Баумгартнер / © felixbaumgartner.com

Уже на высоте 19 километров вода кипит при температуре человеческого тела, а начиная с 35 километров – при 0°C. Выше вода уже не может находиться в жидком состоянии. Дыхание без специальной аппаратуры невозможно, а по ярким звездам можно ориентироваться даже днем. Это стратосфера.

Почти космос. Хотя для кого-то уже. Американская компания World View Enterprises планирует отправлять туристов в стратосферу в ближайшее время. Подобные околокосмические путешествия рассматриваются как бюджетная альтернатива туристическим полетам в космос.

Конечно, покоряли стратосферу и до Баумгартнера. Предыдущий рекорд, продержавшийся почти 50 лет, был установлен советским парашютистом Евгением Андреевым 1 ноября 1962 года. Прыгал он тогда с высоты 25,5 километров.

А уже через 2 года после прыжка Баумгартнера, 24 октября 2014 года, вице-президент компании Google Алан Юстас поднялся на еще большую высоту – 41,42 км и совершил прыжок со стабилизирующим парашютом. Правда, в отличие от прыжка Баумгартнера, который в прямом эфире на YouTube смотрели более 8 миллионов человек, его прыжок не привлек столько внимания, так как не был столь разрекламирован.

Граница атмосферы / ©Wikipedia

Линия Кармана – 100 километров

Космос начинается там, где авиация становится невозможной. Руководствуясь этим принципом, Международная авиационная федерация установила условную границу между атмосферой и космосом на высоте 100 километров над уровнем моря.

Начиная с этой высоты использовать крылья для полета уже не имеет смысла. Для того чтобы создать подъемную силу и лететь, необходимо развить скорость, превышающую первую космическую, а это 7,9 км/с. Но достигнув этой скорости, любой объект выходит на околоземную орбиту и превращается в спутник Земли. Впервые определил эту высоту американский ученый Теодор фон Карман. В честь него ее и назвали. Строго говоря, атмосфера Земли продолжается и выше линии Кармана, но дальше она крайне разрежена и состоит в основном из атомов водорода.

Полеты к линии Кармана и выше недоступны простой авиации. 19 июля 1963 года летчик-испытатель NASA Джозеф Уокер на гиперзвуковом ракетоплане North American X-15 достиг высоты 106 км. А еще через месяц – 108 км.

Второй раз в истории гиперзвуковой летательный аппарат преодолел границу между атмосферой и космосом в 2004 году. В период с 21 июня по 4 октября 2004 года экипажем SpaceShipOne, боровшимся за Ansari X Prize, было совершено 3 таких полета, максимальная высота последнего из которых составила 112 км.

На высоте 120 километров уже начинаются орбиты спутников-шпионов. Низкая орбита удобна для видовой разведки, когда разведданные собираются с помощью фотосъемки поверхности. Но продолжительность жизни спутников на столь низких орбитах вследствие близости атмосферы колеблется от нескольких месяцев до нескольких лет.

МКС / ©NASA

«Обитаемый пояс» – 200–500 км

Высота орбиты Международной космической станции – 413–418 км, станции «Мир» – 354?374 км. Первая в мире пилотируемая орбитальная станция «Салют-1» 19 апреля 1971 года была выведена на орбиту 200–222 км.

Все орбиты в пределах 200–500 км.Такой выбор не случаен. Выше поднимать пилотируемую орбитальную станцию нельзя, так как это опасно для космонавтов. Начиная с высоты 500 километров повышается уровень радиации.

Ниже тоже нельзя. Космическая станция будет «цепляться» за атмосферу, которая хоть и разреженная, но все же оказывает аэродинамическое сопротивление космическим аппаратам на низких орбитах.

Ежедневно высота орбиты МКС, вследствие сопротивления атмосферы и под воздействием силы притяжения Земли, уменьшается на 150–200 метров. Не случайно каждый раз при посещении станции пилотируемыми и грузовыми кораблями ее орбиту поднимают выше.

Кроме того, более высокие орбиты были бы невыгодны по экономическим причинам, так как доставка грузов в этом случае обходилась бы дороже.

Van Allen Probes / ©NASA

Нижняя граница радиационного пояса – 500 км

Начиная с высоты 500 км возрастает интенсивность излучения радиационных поясов, удерживающих захваченные магнитным полем нашей планеты электроны и протоны солнечного ветра.

Предсказанные еще Николой Теслой, они были открыты с началом первых космических полетов.

Радиационные пояса защищают нашу планету, в том числе орбитальные станции, размещенные на низких орбитах, от космической радиации. Но одновременно являются серьезным препятствием на нашем пути в космос. Космонавты, пролетающие радиационные пояса, подвергаются действию радиации, а если прохождение поясов придется на время солнечных вспышек, то могут и погибнуть.

Сторонники теории лунного заговора называют непреодолимость радиационных поясов без вреда для здоровья астронавтов одной из причин невозможности полетов американцев на Луну.

Всегда считалось, что поясов два. Первый, находящийся на высоте в среднем 4 000 км над Землей, состоит в основном из протонов.

Второй, расположен выше – ориентировочно на высоте 17 000 км – и состоит в основном из электронов. Между первым и вторым имеется щель, расположенная в интервале от 2 до 3 радиусов Земли. Кроме того, нижняя граница внутреннего радиационного пояса располагается на разных высотах над поверхностью планеты. Над Атлантикой пояс может спускаться до высоты 500 км, а над Индонезией – до 1300 км

Не так давно NASA заявило об обнаружении третьего радиационного пояса. Расположился он между двумя уже обнаруженными и имеет, по-видимому, временный характер. Открыт пояс был зондами-близнецами Van Allen Probes, запущенными в августе 2012-го.

Космические аппараты названы так в честь Джеймса Ван Аллена – ученого, считающегося первооткрывателем радиационного пояса. Его именем в англоязычном мире пояса так и называют: пояса Ван Аллена.

Iridium-NEXT / ©Iridium Communications Inc.

Орбита «Иридиума» – 780 километров

Увидев яркую вспышку в ночном небе, чем-то похожую на след падающей звезды, кто-то поспешит загадать желание, но многие уже знают: не звезда это вовсе. Тысячи людей по всему миру выходят на улицу в определенное время, что бы увидеть то, что называется вспышкой «Иридиума».

Орбитальная группировка космических аппаратов спутниковой телефонной связи «Иридиум» начала создаваться в 90-х годах прошлого века. Первоначально планировалось запустить на орбиту 77 спутников, а так как это число соответствует атомному числу химического элемента иридия, то и кампанию было решено назвать «Иридиум».

В настоящий момент 66 спутников группировки расположены на орбите высотой 780 километров. Еще несколько запасных спутников (так называемый орбитальный запас) размещены на орбите 650 км и поднимаются на более высокую орбиту в случае отказа одного из основных.

Наблюдаемые с Земли яркие вспышки возникают вследствие отражения солнечного света гладкими поверхностями антенн спутников. Выглядит это как плавное нарастание и последующее затухание ярчайшей звезды, движущейся по ночному небосводу. Вспышка продолжается менее 10 секунд. Но за это время яркость вспыхнувшей «звездочки» достигает минус восьмой звездной величины. Для сравнения, звездная величина Венеры – минус 4,6.

Примечательно, что спутники системы «Иридиум» известны и в связи с первым случаем столкновения двух космических аппаратов. 10 февраля 2009 года выведенный из эксплуатации российский военный спутник «Космос-2251» не поделил орбиту с действующим спутником Iridium 33. В результате столкновения, произошедшего на высоте 788,6 километра над полуостровом Таймыр, оба космических аппарата разрушились. Образовавшиеся обломки, а это около 600 фрагментов размером более пяти сантиметров, хотя и остались на прежней орбите, но впоследствии, вероятно, будут снижаться, что создает угрозу для космических аппаратов, находящихся на более низких орбитах, в том числе для МКС.

Вывод на орбиту КА Galileo ракетой-носителем «Союз» / © ESA

Орбиты навигационных спутников – 19 400?23 222 км

Сейчас жизнь сложно представить без спутниковой навигации. Особенно если вы управляете автомобилем. Изначально предназначенная для военных целей спутниковая навигация повсеместно проникла в гражданскую жизнь. Как высоко навигационные спутники над нами?

Космические аппараты российской системы навигации ГЛОНАСС (Глобальная навигационная спутниковая система) занимают самую низкую среди других навигационных систем орбиту. Ее высота составляет 19 400 км.

Немного выше расположились спутники американской системы глобального позиционирования GPS (Global Positioning System) – 20 200 км.

Европейское космическое агентство выводит свои аппараты на высоту 23 222 км.

Стараются не отставать и другие страны. Ведь наличие своей такой системы – вопрос национальной безопасности. Так, Китай строит свою навигационную систему Beidou. 27 спутников планируется разместить на высоте 21 528 км – это так называемая средняя околоземная орбита. Как раз между орбитами американских и европейских спутников. Еще три спутника – на геосинхронной орбите, и пять – на геостационарной орбите.

Глобальные, охватывающие всю поверхность планеты навигационные системы не всем странам по карману. Поэтому некоторые строят свои региональные системы спутниковой навигации.

Японская QZSS (Quasi-Zenith Satellite System – «Квазизенитная спутниковая система») доступна только на территории этой страны. Но зато для ее строительства достаточно только трех спутников, выведенных на высокую эллиптическую орбиту. Квазизенитной она называется потому, что орбита позволяет спутнику держаться более 12 часов в день высоко в небе, то есть практически в зените. Высота в апогее – 42 164 км.

Индия, запустившая в апреле этого года очередной спутник региональной спутниковой системы навигации IRNSS (Indian Regional Navigation Satellite System), строит систему из семи спутников на геосинхронной орбите высотой 35 786 км, три из которых будут на геостационаре.

Космический лифт в представлении художника / ©Alan Chan

Геостационар – 35 786 километров

На высоте 35 786 км над экватором Земли расположена орбита, имеющая для нас незаменимую практическую ценность, – геостационарная. Спутник, находясь на этой орбите, обращается вокруг Земли с угловой скоростью, равной угловой скорости вращения нашей планеты вокруг своей оси. Он фактически зависает над одной точкой поверхности.

Для наблюдателя с Земли космический аппарат на геостационарной орбите находится все время в одной точке. Обратите внимание, что антенны для приема спутникового телевидения, так называемые «тарелки», всегда направлены на невидимую дугу в небе – геостационарную орбиту. А антенны одного оператора в одну точку.

На этой орбите находятся спутники, ведущие прямое телерадиовещание, дополняющие навигационные системы, коммуникационные спутники и другие. Это единственная орбита, использование которой регулируется международными правилами, так как количество мест, позиций, где можно разместить спутник так, чтобы он не создавал помех другим космическим аппаратам, ограничено.

Так как геостационарная орбита «не резиновая», то отработавшие свое время спутники, используя еще оставшееся в них топливо, поднимают на более высокую орбиту. Эта орбита, расположенная на 200–300 км выше геостационарной, называется орбитой захоронения, где эти спутники могут находиться до 2000 лет, пока мы не придумаем, что с ними делать дальше.

Интересной идеей, связанной с геостационарной орбитой, является концепция строительства космического лифта. Доставка грузов на околоземную орбиту по-прежнему дорога. Лифт в космос более привлекателен в этом плане по сравнению и с одноразовыми, и даже многоразовыми ракетами.

Основой лифта является трос (или лента, в зависимости от проекта), протянутый с поверхности планеты к орбитальной станции, расположенной на геостационарной орбите. По этому тросу будет передвигаться подъемник с грузом.

Подняться на геостационарную орбиту на таком лифте можно будет за неделю, но стоить это будет сравнительно недорого. Вот только материала достаточно легкого и прочного для создания такого троса пока еще не создано.

Фотография Земли, сделанная экипажем «Аполлон-8» с поверхности Луны / ©NASA

Луна. Расстояние до Земли – 384 467 км

А теперь сравним все эти орбиты с расстоянием до Луны. Среднее расстояние до нашего единственного естественного спутника – 384 467 км. Это примерно 30 земных диаметров, почти 10 геостационарных орбит, или 925 орбит МКС.

Но это расстояние сопоставимо с самой высокой точкой орбиты российского космического телескопа «Радиоастрон» (он же «Спектр-Р»). На момент запуска высота апогея эллиптической орбиты телескопа составляла 333 455 км. При этом перигей орбиты составил 600 км. Что, к примеру, сопоставимо с высотой низкой околоземной орбиты американского космического телескопа «Хаббл» (569 км).

Но орбита телескопа не постоянна. На него влияет гравитация нашего спутника. Предполагается, что за 5 лет притяжение Луны поднимет апогей орбиты телескопа до высоты 390 000 км.

Не является постоянной и орбита Луны. Наш спутник отдаляется от Земли на 4 сантиметра в год. Это позволяет некоторым ученым предполагать, что Луна рано или поздно покинет орбиту Земли и превратится в самостоятельную планету.

Но пока этого не случилось, надеемся, что человечество все-таки слетает к Луне еще раз, поднявшись на заветные 384 467 км.

naked-science.ru

Геостационарная орбита — википедия орг

Синхронная орбита

Вид Земли с высоты около 30 тысяч км (Аполлон-8)

Геостациона́рная орби́та (ГСО) — круговая орбита, расположенная над экватором Земли (0° широты), находясь на которой, искусственный спутник обращается вокруг планеты с угловой скоростью, равной угловой скорости вращения Земли вокруг оси. В горизонтальной системе координат направление на спутник не изменяется ни по азимуту, ни по высоте над горизонтом — спутник как бы «висит» в небе неподвижно. Поэтому спутниковая антенна, однажды направленная на такой спутник, всё время остаётся направленной на него. Геостационарная орбита является разновидностью геосинхронной орбиты и используется для размещения искусственных спутников (коммуникационных, телетрансляционных и т. п.).

Спутник должен обращаться в направлении вращения Земли, на высоте 35 786 км над уровнем моря (вычисление высоты ГСО см. ниже). Именно такая высота обеспечивает спутнику период обращения, равный периоду вращения Земли относительно звёзд (Звёздные сутки: 23 часа 56 минут 4,091 секунды).

Идея использования геостационарных спутников для целей связи высказывалась ещё словенским теоретиком космонавтики Германом Поточником[1] в 1928 году.

Преимущества геостационарной орбиты получили широкую известность после выхода в свет научно-популярной статьи Артура Кларка в журнале «Wireless World» в 1945 году[2], поэтому на Западе геостационарная и геосинхронные орбиты иногда называются «орбитами Кларка», а «поясом Кларка» называют область космического пространства на расстоянии 36000 км над уровнем моря в плоскости земного экватора, где параметры орбит близки к геостационарной. Первым спутником, успешно выведенным на ГСО, был Syncom-3[en], запущенный NASA в августе 1964 года.

Точка стояния

Спутник, находящийся на геостационарной орбите, неподвижен относительно поверхности Земли[3], поэтому его местоположение на орбите называется точкой стояния. В результате сориентированная на спутник и неподвижно закреплённая направленная антенна может сохранять постоянную связь с этим спутником длительное время.

Размещение спутников на орбите

Для Архангельска максимально возможная высота спутника над горизонтом — 17,2° Наивысшая точка пояса Кларка всегда находится строго на юге (для северного полушария). В нижней части графика градусы — меридианы, над которыми находятся спутники. По бокам — высоты спутников над горизонтом. Сверху — направление на спутник. Для наглядности можно растянуть по горизонтали в 7,8 раза и отразить слева направо. Тогда он будет выглядеть так же, как на небе.

Существуют каталоги объектов на геостационарной орбите.[4]

Вычисление параметров геостационарной орбиты

Радиус орбиты и высота орбиты

На геостационарной орбите спутник не приближается к Земле и не удаляется от неё, и кроме того, вращаясь вместе с Землёй, постоянно находится над какой-либо точкой на экваторе. Следовательно, действующие на спутник силы гравитации и центробежная сила должны уравновешивать друг друга. Для вычисления высоты геостационарной орбиты можно воспользоваться методами классической механики и, перейдя в систему отсчета спутника, исходить из следующего уравнения:

Fu=FΓ{\displaystyle F_{u}=F_{\Gamma }} ,

где Fu{\displaystyle F_{u}} — сила инерции, а в данном случае, центробежная сила; FΓ{\displaystyle F_{\Gamma }} — гравитационная сила. Величину гравитационной силы, действующую на спутник, можно определить по закону всемирного тяготения Ньютона:

FΓ=G⋅M3⋅mcR2{\displaystyle F_{\Gamma }=G\cdot {\frac {M_{3}\cdot m_{c}}{R^{2}}}} ,

где mc{\displaystyle m_{c}} — масса спутника, M3{\displaystyle M_{3}} — масса Земли в килограммах, G{\displaystyle G} — гравитационная постоянная, а R{\displaystyle R} — расстояние в метрах от спутника до центра Земли или, в данном случае, радиус орбиты.

Величина центробежной силы равна:

Fu=mc⋅a{\displaystyle F_{u}=m_{c}\cdot a} ,

где a{\displaystyle a} — центростремительное ускорение, возникающее при круговом движении по орбите.

Как можно видеть, масса спутника mc{\displaystyle m_{c}} присутствует как множитель в выражениях для центробежной силы и для гравитационной силы, то есть высота орбиты не зависит от массы спутника, что справедливо для любых орбит[5] и является следствием равенства гравитационной и инертной массы. Следовательно, геостационарная орбита определяется лишь высотой, при которой центробежная сила будет равна по модулю и противоположна по направлению гравитационной силе, создаваемой притяжением Земли на данной высоте.

Центростремительное ускорение равно:

a=ω2⋅R{\displaystyle a=\omega ^{2}\cdot R} ,

где ω{\displaystyle \omega } — угловая скорость вращения спутника, в радианах в секунду.

Сделаем одно важное уточнение. В действительности, центростремительное ускорение имеет физический смысл только в инерциальной системе отсчета, в то время как центробежная сила является так называемой мнимой силой и имеет место исключительно в системах отсчета (координат), которые связаны с вращающимися телами. Центростремительная сила (в данном случае — сила гравитации) вызывает центростремительное ускорение. По модулю центростремительное ускорение в инерциальной системе отсчета равно центробежному в системе отсчета, связанной в нашем случае со спутником. Поэтому далее, с учетом сделанного замечания, мы можем употреблять термин «центростремительное ускорение» вместе с термином «центробежная сила».

Уравнивая выражения для гравитационной и центробежной сил с подстановкой центростремительного ускорения, получаем:

mc⋅ω2⋅R=G⋅M3⋅mcR2{\displaystyle m_{c}\cdot \omega ^{2}\cdot R=G\cdot {\frac {M_{3}\cdot m_{c}}{R^{2}}}} .

Сокращая mc{\displaystyle m_{c}} , переводя R2{\displaystyle R^{2}} влево, а ω2{\displaystyle \omega ^{2}} вправо, получаем:

R3=G⋅M3ω2{\displaystyle R^{3}=G\cdot {\frac {M_{3}}{\omega ^{2}}}}

или

R=G⋅M3ω23{\displaystyle R={\sqrt[{3}]{\frac {G\cdot M_{3}}{\omega ^{2}}}}} .

Можно записать это выражение иначе, заменив G⋅M3{\displaystyle G\cdot M_{3}} на μ{\displaystyle \mu } — геоцентрическую гравитационную постоянную:

R=μω23{\displaystyle R={\sqrt[{3}]{\frac {\mu }{\omega ^{2}}}}}

Угловая скорость ω{\displaystyle \omega } вычисляется делением угла, пройденного за один оборот (360∘=2⋅π{\displaystyle 360^{\circ }=2\cdot \pi } радиан) на период обращения (время, за которое совершается один полный оборот по орбите: один сидерический день, или 86 164 секунды). Получаем:

ω=2⋅π86164=7,29⋅10−5{\displaystyle \omega ={\frac {2\cdot \pi }{86164}}=7,29\cdot 10^{-5}} рад/с

Линейная скорость спутника, движущегося с угловой скоростью ω{\displaystyle \omega } на расстоянии R{\displaystyle R} от центра вращения равна

vl=ω⋅R{\displaystyle v_{l}=\omega \cdot R}

Первая космическая скорость на расстоянии R{\displaystyle R} от объекта массой M{\displaystyle M} равна

vk=GMR;{\displaystyle v_{k}={\sqrt {G{\frac {M}{R}}}};}

Приравняв правые части уравнений друг к другу, приходим к полученному ранее выражению радиуса ГСО:

R=GMω23{\displaystyle R={\sqrt[{3}]{G{\frac {M}{\omega ^{2}}}}}}

Орбитальная скорость

Скорость движения по геостационарной орбите вычисляется умножением угловой скорости на радиус орбиты:

v=ω⋅R=3,07{\displaystyle v=\omega \cdot R=3{,}07} км/с

Это примерно в 2,5 раза меньше, чем первая космическая скорость, равная 8 км/с на околоземной орбите (с радиусом 6400 км). Так как квадрат скорости для круговой орбиты обратно пропорционален её радиусу,

v=GMR;{\displaystyle v={\sqrt {G{\frac {M}{R}}}};}

то уменьшение скорости по отношению к первой космической достигается увеличением радиуса орбиты более чем в 6 раз.

R≈6400⋅(83,07)2≈43000{\displaystyle R\approx \,\!{6400\cdot \left({\frac {8}{3{,}07}}\right)^{2}}\approx \,\!43000}

Длина орбиты

Длина геостационарной орбиты: 2⋅π⋅R{\displaystyle {2\cdot \pi \cdot R}} . При радиусе орбиты 42 164 км получаем длину орбиты 264 924 км.

Длина орбиты крайне важна для вычисления «точек стояния» спутников.

Удержание спутника в орбитальной позиции на геостационарной орбите

Спутник, обращающийся на геостационарной орбите, находится под воздействием ряда сил (возмущений), изменяющих параметры этой орбиты. В частности, к таким возмущениям относятся гравитационные лунно-солнечные возмущения, влияние неоднородности гравитационного поля Земли, эллиптичность экватора и т. д. Деградация орбиты выражается в двух основных явлениях:

1) Спутник смещается вдоль орбиты от своей первоначальной орбитальной позиции в сторону одной из четырёх точек стабильного равновесия, т. н. «потенциальных ям геостационарной орбиты» (их долготы 75,3°E, 104,7°W, 165,3°E, и 14,7°W) над экватором Земли;

2) Наклонение орбиты к экватору увеличивается (от первоначального 0) со скоростью порядка 0,85 градусов в год и достигает максимального значения 15 градусов за 26,5 лет.

Для компенсации этих возмущений и удержания спутника в назначенной точке стояния спутник оснащается двигательной установкой (химической или электроракетной). Периодическими включениями двигателей малой тяги (коррекция «север — юг» для компенсации роста наклонения орбиты и «запад — восток» для компенсации дрейфа вдоль орбиты) спутник удерживается в назначенной точке стояния. Такие включения производятся по нескольку раз в 10 — 15 суток. Существенно, что для коррекции «север — юг» требуется значительно большее приращение характеристической скорости (около 45 — 50 м/с в год), чем для долготной коррекции (около 2 м/с в год). Для обеспечения коррекции орбиты спутника на протяжении всего срока его эксплуатации (12 — 15 лет для современных телевизионных спутников) требуется значительный запас топлива на борту (сотни килограммов в случае применения химического двигателя). Химический ракетный двигатель спутника имеет вытеснительную подачу топлива (газ наддува — гелий), работает на долгохранимых высококипящих компонентах (обычно несимметричный диметилгидразин и диазотный тетраоксид). На ряде спутников устанавливаются плазменные двигатели. Их тяга существенно меньше по отношению к химическим, однако большая эффективность позволяет (за счёт продолжительной работы, измеряемой десятками минут для единичного манёвра) радикально снизить требуемую массу топлива на борту. Выбор типа двигательной установки определяется конкретными техническими особенностями аппарата.

Эта же двигательная установка используется при необходимости для манёвра перевода спутника в другую орбитальную позицию. В некоторых случаях (как правило, в конце срока эксплуатации спутника) для сокращения расхода топлива коррекция орбиты «север — юг» прекращается, а остаток топлива используется только для коррекции «запад — восток».

Запас топлива является основным лимитирующим фактором срока службы спутника на геостационарной орбите (кроме отказов компонентов самого спутника).

Недостатки геостационарной орбиты

Задержка сигнала

Связь через геостационарные спутники характеризуется большими задержками в распространении сигнала. При высоте орбиты 35 786 км и скорости света около 300 000 км/с ход луча «Земля — спутник» требует около 0,12 с. Ход луча «Земля (передатчик) → спутник → Земля (приемник)» ≈0,24 с. Полная задержка (измеряемая утилитой Ping) при использовании спутниковой связи для приема и передачи данных составит почти полсекунды. С учетом задержки сигнала в аппаратуре ИСЗ, в аппаратуре и в кабельных системах передач наземных служб общая задержка сигнала на маршруте «источник сигнала → спутник → приёмник» может достигать 2 — 4 секунд[6]. Такая задержка затрудняет применение спутников на ГСО в телефонии и делает невозможной применение спутниковой связи с использованием ГСО в различных сервисах реального времени (например в онлайн-играх)[7].

Невидимость ГСО с высоких широт

Так как геостационарная орбита не видна с высоких широт (приблизительно от 81° до полюсов), а на широтах выше 75° наблюдается очень низко над горизонтом (в реальных условиях спутники просто скрываются выступающими объектами и рельефом местности) и виден лишь небольшой участок орбиты (см. таблицу), то в высокоширотных районах Крайнего Севера (Арктики) и Антарктиды невозможна связь и телетрансляция с использованием ГСО[8]. К примеру, американские полярники на станции Амундсен-Скотт для связи с внешним миром (телефония, интернет) используют оптоволоконный кабель длиной 1670 километров до расположенной на 75° ю. ш. французской станции Конкордия, с которой уже видно несколько американских геостационарных спутников[9].

Таблица наблюдаемого сектора геостационарной орбиты в зависимости от широты местаВсе данные приведены в градусах и их долях.

Широтаместности Видимый сектор орбиты Теоретическийсектор Реальный(с уч. рельефа)сектор[10]

90	--	--
82	--	--
81	29,7	--
80	58,9	--
79	75,2	--
78	86,7	26,2
75	108,5	77
60	144,8	132,2
50	152,8	143,3
40	157,2	149,3
20	161,5	155,1
0	162,6	156,6

Из таблицы видно, например, что если на широте Санкт-Петербурга (~60°) видимый сектор орбиты (и, соответственно, количество принимаемых спутников) равен 84 % от максимально возможного (на экваторе), то на широте полуострова Таймыр (~75°) видимый сектор составляет 49 %, а на широте Шпицбергена и мыса Челюскина (~78°) — лишь 16 % от наблюдаемого на экваторе. В этот сектор орбиты в районе Сибири попадает 1 — 2 спутника (не всегда необходимого оператора).

Солнечная интерференция

Одним из самых неприятных недостатков геостационарной орбиты является уменьшение и полное отсутствие сигнала в ситуации, когда солнце и спутник находятся на одной линии с приёмной антенной (положение «солнце за спутником»). Данное явление присуще и другим орбитам, но именно на геостационарной, когда спутник «неподвижен» на небе, проявляется особенно ярко. В средних широтах северного полушария солнечная интерференция проявляется в периоды с 22 февраля по 11 марта и с 3 по 21 октября, с максимальной длительностью до десяти минут[11]. В такие моменты в ясную погоду солнечные лучи, сфокусированные светлым покрытием антенны могут даже повредить (расплавить или перегреть) приёмо-передающую аппаратуру спутниковой антенны[12].

Международно-правовой статус ГСО

Использование геостационарной орбиты ставит целый ряд не только технических, но и международно-правовых проблем. Значительный вклад в их разрешение вносит ООН, а также её комитеты и иные специализированные учреждения.

Некоторые экваториальные страны в разное время предъявляли претензии (например, Декларация об установлении суверенитета на участке ГСО, подписанная в Боготе Бразилией, Колумбией, Конго, Эквадором, Индонезией, Кенией, Угандой и Заиром 3 декабря 1976 г.[13]) на распространение их суверенитета на находящуюся над их территориями часть космического пространства, в которой проходят орбиты геостационарных спутников. Было, в частности, заявлено, что геостационарная орбита является физическим фактором, связанным с существованием нашей планеты и полностью зависящим от гравитационного поля Земли, а потому соответствующие части космоса (сегменты геостационарной орбиты) как бы являются продолжением территорий, над которыми они находятся. Соответствующее положение закреплено в Конституции Колумбии[14].

Эти притязания экваториальных государств были отвергнуты, как противоречащие принципу неприсвоения космического пространства. В Комитете ООН по космосу такие заявления подверглись обоснованной критике. Во-первых, нельзя претендовать на присвоение какой-либо территории или пространства, находящегося на таком значительном удалении от территории соответствующего государства. Во-вторых, космическое пространство не подлежит национальному присвоению. В-третьих, технически неправомочно говорить о какой-либо физической взаимосвязи между государственной территорией и столь отдаленным районом космоса. Наконец, в каждом отдельном случае феномен геостационарного спутника связан с конкретным космическим объектом. Если нет спутника, то нет и геостационарной орбиты.

См. также

Примечания

↑ Noordung, Hermann. The Problem With Space Travel. — DIANE Publishing, 1995. — P. 72.
↑ Extra-Terrestrial Relays — Can Rocket Stations Give Worldwide Radio Coverage? (англ.) (pdf). Arthur C. Clark (October 1945). Проверено 25 февраля 2010. Архивировано 23 августа 2011 года.
↑ Требование неподвижности спутников относительно Земли на своих орбитальных позициях на геостационарной орбите, а также большое количество спутников на этой орбите в разных её точках, приводят к интересному эффекту при наблюдении и фотографировании звёзд с помощью телескопа с использованием гидирования — удержания ориентации телескопа на заданной точке звёздного неба для компенсации суточного вращения Земли (задача, обратная геостационарной радиосвязи). Если наблюдать в такой телескоп звёздное небо вблизи небесного экватора, где проходит геостационарная орбита, то при определённых условиях можно видеть, как спутники друг за другом проходят на фоне неподвижных звёзд в пределах узкого коридора, как автомобили по оживлённой автотрассе. Особенно хорошо это заметно на фотографиях звёзд с длительными экспозициями, смотри, например: Babak A. Tafreshi. GeoStationary HighWay. (англ.). The World At Night (TWAN). Проверено 25 февраля 2010. Архивировано 23 августа 2011 года. Источник: Бабак Тафреши (Ночной мир). Геостационарная магистраль. (рус.). Астронет.ру. Проверено 25 февраля 2010. Архивировано 23 августа 2011 года.
↑ CLASSIFICATION OF GEOSYNCHRONOUS OBJECTS
↑ для орбит спутников, масса которых пренебрежимо мала по сравнению с массой притягивающего его астрономического объекта
↑ Орбиты искусственных спутников Земли. Вывод спутников на орбиту
↑ The Teledesic Network: Using Low-Earth-Orbit Satellites to Provide Broadband, Wireless, Real-Time Internet Access Worldwide
↑ Журнал «Вокруг Света».№ 9 Сентябрь 2009. Орбиты, которые мы выбираем
↑ Мозаика. Часть II
↑ взято превышение спутником горизонта в 3°
↑ Внимание! Настаёт период активной солнечной интерференции!
↑ Солнечная интерференция
↑ B.IV.1. Declaration of the First Meeting of Equatorial Countries ("Bogota Declaration") of December 3, 1976 // Space Law. Basic Legal Documents. Volume 1. / Karl-Heinz Böckstiegel, Marietta Benkö, Stephan Hobe. — Eleven International Publishing, 2005. — ISBN 9780792300915.
↑ Национальное законодательство и практика, имеющие отношение к определению и делимитации космического пространства

Ссылки

www-wikipediya.ru

Геостационарная орбита - это... Что такое Геостационарная орбита?

Геостациона́рная орби́та (ГСО) — круговая орбита, расположенная над экватором Земли (0° широты), находясь на которой искусственный спутник обращается вокруг планеты с угловой скоростью, равной угловой скорости вращения Земли вокруг оси. В горизонтальной системе координат направление на спутник не изменяется ни по азимуту ни по высоте над горизонтом, спутник «висит» в небе неподвижно. Геостационарная орбита является разновидностью геосинхронной орбиты и используется для размещения искусственных спутников (коммуникационных, телетрансляционных и т. п.).

Спутник должен обращаться в направлении вращения Земли, на высоте 35 786 км над уровнем моря (вычисление высоты ГСО см. ниже). Именно такая высота обеспечивает спутнику период обращения, равный периоду вращения Земли относительно звёзд (Звёздные сутки: 23 часа 56 минут 4,091 секунды).

Преимущества геостационарной орбиты получили широкую известность после выхода в свет научно-популярной статьи Артура Ч. Кларка в журнале «Wireless World» в 1945 году[2], поэтому на Западе геостационарная и геосинхронные орбиты иногда называются «орбитами Кларка», а «поясом Кларка» называют область космического пространства на расстоянии 36000 км над уровнем моря в плоскости земного экватора, где параметры орбит близки к геостационарной.

Первым спутником, успешно выведенным на ГСО, был Syncom-3, запущенный NASA в августе 1964 года.

Точка стояния

Размещение спутников на орбите

Для Архангельска максимально возможная высота спутника над горизонтом — 17,2° Наивысшая точка пояса Кларка всегда находится строго на юге. В нижней части графика градусы — меридианы, над которыми находятся спутники. По бокам — высоты спутников над горизонтом. Сверху — направление на спутник. Для наглядности можно растянуть по горизонтали в 7,8 раза и отразить слева направо. Тогда он будет выглядеть так же, как на небе.

Вычисление параметров геостационарной орбиты

Радиус орбиты и высота орбиты

где — сила инерции, а в данном случае, центробежная сила; — гравитационная сила. Величину гравитационной силы, действующую на спутник, можно определить по закону всемирного тяготения Ньютона:

где — масса спутника, — масса Земли в килограммах, — гравитационная постоянная, а — расстояние в метрах от спутника до центра Земли или, в данном случае, радиус орбиты.

Величина центробежной силы равна:

где — центростремительное ускорение, возникающее при круговом движении по орбите.

Как можно видеть, масса спутника присутствует как множитель в выражениях для центробежной силы и для гравитационной силы, то есть высота орбиты не зависит от массы спутника, что справедливо для любых орбит[4] и является следствием равенства гравитационной и инертной массы. Следовательно, геостационарная орбита определяется лишь высотой, при которых центробежная сила будет равна по модулю и противоположна по направлению гравитационной силе, создаваемой притяжением Земли на данной высоте.

Центростремительное ускорение равно:

где — угловая скорость вращения спутника, в радианах в секунду.

Сокращая , переводя влево, а вправо, получаем:

или

Можно записать это выражение иначе, заменив на — геоцентрическую гравитационную постоянную:

Угловая скорость вычисляется делением угла, пройденного за один оборот ( радиан) на период обращения (время, за которое совершается один полный оборот по орбите: один сидерический день, или 86 164 секунды). Получаем:

рад/с

Линейная скорость спутника, движущегося с угловой скоростью на расстоянии от центра вращения равна

Первая космическая скорость на расстоянии от объекта массой равна

Приравняв правые части уравнений друг другу, приходим к полученному ранее выражению радиуса ГСО:

Орбитальная скорость

Скорость движения по геостационарной орбите вычисляется умножением угловой скорости на радиус орбиты:

км/с

Это примерно в 2.5 раза меньше, чем первая космическая скорость равная 8 км/с на околоземной орбите (с радиусом 6400 км). Так как квадрат скорости для круговой орбиты обратно пропорционален её радиусу,

Длина орбиты

Длина геостационарной орбиты: . При радиусе орбиты 42 164 км получаем длину орбиты 264 924 км.

Длина орбиты крайне важна для вычисления «точек стояния» спутников.

Удержание спутника в орбитальной позиции на геостационарной орбите

1) Спутник смещается вдоль орбиты от своей первоначальной орбитальной позиции в сторону одной из четырех точек стабильного равновесия, т. н. «потенциальных ям геостационарной орбиты» (их долготы 75,3°E, 104,7°W, 165,3°E, и 14,7°W) над экватором Земли;

Для компенсации этих возмущений и удержания спутника в назначенной точке стояния спутник оснащается двигательной установкой (химической или электроракетной). Периодическими включениями двигателей малой тяги (коррекция «север-юг» для компенсации роста наклонения орбиты и «запад-восток» для компенсации дрейфа вдоль орбиты) спутник удерживается в назначенной точке стояния. Такие включения производятся по нескольку раз в несколько (10—15) суток. Существенно, что для коррекции «север-юг» требуется значительно большее приращение характеристической скорости (около 45—50 м/с в год), чем для долготной коррекции (около 2 м/с в год). Для обеспечения коррекции орбиты спутника на протяжении всего срока его эксплуатации (12—15 лет для современных телевизионных спутников) требуется значительный запас топлива на борту (сотни килограммов, в случае применения химического двигателя). Химический ракетный двигатель спутника имеет вытеснительную подачу топлива (газ наддува-гелий), работает на долгохранимых высококипящих компонентах (обычно несимметричный диметилгидразин и диазотный тетраоксид). На ряде спутников устанавливаются плазменные двигатели. Их тяга существенно меньше по отношению к химическим, однако большая эффективность позволяет (за счет продолжительной работы, измеряемой десятками минут для единичного маневра) радикально снизить потребную массу топлива на борту. Выбор типа двигательной установки определяется конкретными техническими особенностями аппарата.

Эта же двигательная установка используется, при необходимости, для маневра перевода спутника в другую орбитальную позицию. В некоторых случаях — как правило, в конце срока эксплуатации спутника, для сокращения расхода топлива коррекция орбиты «север-юг» прекращается, а остаток топлива используется только для коррекции «запад-восток».

Запас топлива является основным лимитирующим фактором срока службы спутника на геостационарной орбите.

Недостатки геостационарной орбиты

Задержка сигнала

Связь через геостационарные спутники характеризуется большими задержками в распространении сигнала. При высоте орбиты 35 786 км и скорости света около 300 000 км/с ход луча «Земля-спутник» требует около 0,12 с. Ход луча «Земля (передатчик) → спутник → Земля (приемник)» ≈0,24 с. Ping (ответ) составит полсекунды (точнее 0,48 с). С учетом задержки сигнала в аппаратуре ИСЗ и аппаратуре наземных служб общая задержка сигнала на маршруте «Земля → спутник → Земля» может достигать 2—4 секунд[5]. Такая задержка делает невозможной применение спутниковой связи с использованием ГСО в различных сервисах реального времени (например в онлайн-играх)[6].

Невидимость ГСО с высоких широт

Так как геостационарная орбита не видна с высоких широт (приблизительно от 81° до полюсов), а на широтах выше 75° наблюдается очень низко над горизонтом (в реальных условиях, спутники просто скрываются выступающими объектами и рельефом местности) и виден лишь небольшой участок орбиты (см. таблицу), то невозможна связь и телетрансляция с использованием ГСО в высокоширотных районах Крайнего Севера (Арктики) и Антарктиды[7]. К примеру, американские полярники на станции Амундсен-Скотт для связи с внешним миром (телефония, интернет) используют оптоволоконный кабель длиной 1670 километров до расположеной на 75° ю.ш. французской станции Конкордия, с которой уже видно несколько американских геостационарных спутников[8].

Широтаместности Видимый сектор орбиты Теоретическийсектор Реальный(с уч. рельефа)сектор[9]

90	--	--
82	--	--
81	29,7	--
80	58,9	--
79	75,2	--
78	86,7	26,2
75	108,5	77
60	144,8	132,2
50	152,8	143,3
40	157,2	149,3
20	161,5	155,1
0	162,6	156,6

Из вышележащей таблицы видно например, что если на широте С.-Петербурга (~60°) видимый сектор орбиты (и соответственно кол-во принимаемых спутников) равен 84 % от максимально возможного (на экваторе), то на широте по-ва Таймыр (~75°) видимый сектор составляет 49 %, а на широте Шпицбергена и мыса Челюскина (~78°) лишь 16 % от наблюдаемого на экваторе. В этот сектор орбиты в районе Сибири попадает 1-2 спутника (не всегда необходимой страны).

Солнечная интерференция

Одним из самых неприятных недостатков геостационарной орбиты, является уменьшение и полное отсутствие сигнала в ситуации, когда солнце и спутник-передатчик находятся на одной линии с приёмной антенной (положение «солнце за спутником»). Данное явление присуще и другим орбитам, но именно на геостационарной, когда спутник «неподвижен» на небе, проявляется особенно ярко. В средних широтах северного полушария солнечная интерференция проявляется в периоды с 22 февраля по 11 марта и с 3 по 21 октября, с максимальной длительностью до десяти минут[10]. В ясную погоду, сфокусированые светлым покрытием антенны солнечные лучи могут повредить (расплавить) приёмо-передающую аппаратуру спутниковой антенны[11].

См. также

Примечания

↑ Noordung Hermann The Problem With Space Travel. — DIANE Publishing, 1995. — P. 72. — ISBN 978-0788118494
↑ Extra-Terrestrial Relays — Can Rocket Stations Give Worldwide Radio Coverage? (англ.) (pdf). Arthur C. Clark (October 1945). Архивировано из первоисточника 23 августа 2011. Проверено 25 февраля 2010.
↑ Требование неподвижности спутников относительно Земли на своих орбитальных позициях на геостационарной орбите, а также большое количество спутников на этой орбите в разных её точках, приводят к интересному эффекту при наблюдении и фотографировании звёзд с помощью телескопа с использованием гидирования — удержания ориентации телескопа на заданной точке звёздного неба для компенсации суточного вращения Земли (задача, обратная геостационарной радиосвязи). Если наблюдать в такой телескоп звёздное небо вблизи небесного экватора, где проходит геостационарная орбита, то при определённых условиях можно видеть, как спутники друг за другом проходят на фоне неподвижных звёзд в пределах узкого коридора, как автомобили по оживлённой автотрассе. Особенно хорошо это заметно на фотографиях звёзд с длительными экспозициями, смотри, например: Babak A. Tafreshi. GeoStationary HighWay. (англ.). The World At Night (TWAN). Архивировано из первоисточника 23 августа 2011. Проверено 25 февраля 2010. Источник: Бабак Тафреши (Ночной мир). Геостационарная магистраль. (рус.). Астронет.ру. Архивировано из первоисточника 23 августа 2011. Проверено 25 февраля 2010.
↑ для орбит спутников, масса которых пренебрежимо мала по сравнению с массой притягивающего его астрономического объекта
↑ Орбиты искусственных спутников Земли. Вывод спутников на орбиту
↑ The Teledesic Network: Using Low-Earth-Orbit Satellites to Provide Broadband, Wireless, Real-Time Internet Access Worldwide
↑ Журнал «Вокруг Света».№ 9 Сентябрь 2009. Орбиты, которые мы выбираем
↑ Мозаика. Часть II
↑ взято превышение спутником горизонта в 3°
↑ Внимание! Настаёт период активной солнечной интерференции!
↑ Солнечная интерференция

Ссылки

biograf.academic.ru

Геостационарная орбита — Википедия РУ

Синхронная орбита

Вид Земли с высоты около 30 тысяч км (Аполлон-8)

Спутник должен обращаться в направлении вращения Земли, на высоте 35 786 км над уровнем моря (вычисление высоты ГСО см. ниже). Именно такая высота обеспечивает спутнику период обращения, равный периоду вращения Земли относительно звёзд (Звёздные сутки: 23 часа 56 минут 4,091 секунды).

Точка стояния

Спутник, находящийся на геостационарной орбите, неподвижен относительно поверхности Земли[3], поэтому его местоположение на орбите называется точкой стояния. В результате сориентированная на спутник и неподвижно закреплённая направленная антенна может сохранять постоянную связь с этим спутником длительное время.

Размещение спутников на орбите

Существуют каталоги объектов на геостационарной орбите.[4]

Вычисление параметров геостационарной орбиты

Радиус орбиты и высота орбиты

На геостационарной орбите спутник не приближается к Земле и не удаляется от неё, и кроме того, вращаясь вместе с Землёй, постоянно находится над какой-либо точкой на экваторе. Следовательно, действующие на спутник силы гравитации и центробежная сила должны уравновешивать друг друга. Для вычисления высоты геостационарной орбиты можно воспользоваться методами классической механики и, перейдя в систему отсчета спутника, исходить из следующего уравнения:

Fu=FΓ{\displaystyle F_{u}=F_{\Gamma }} ,

FΓ=G⋅M3⋅mcR2{\displaystyle F_{\Gamma }=G\cdot {\frac {M_{3}\cdot m_{c}}{R^{2}}}} ,

Величина центробежной силы равна:

Fu=mc⋅a{\displaystyle F_{u}=m_{c}\cdot a} ,

где a{\displaystyle a} — центростремительное ускорение, возникающее при круговом движении по орбите.

Центростремительное ускорение равно:

a=ω2⋅R{\displaystyle a=\omega ^{2}\cdot R} ,

где ω{\displaystyle \omega } — угловая скорость вращения спутника, в радианах в секунду.

mc⋅ω2⋅R=G⋅M3⋅mcR2{\displaystyle m_{c}\cdot \omega ^{2}\cdot R=G\cdot {\frac {M_{3}\cdot m_{c}}{R^{2}}}} .

Сокращая mc{\displaystyle m_{c}} , переводя R2{\displaystyle R^{2}} влево, а ω2{\displaystyle \omega ^{2}} вправо, получаем:

R3=G⋅M3ω2{\displaystyle R^{3}=G\cdot {\frac {M_{3}}{\omega ^{2}}}}

или

R=G⋅M3ω23{\displaystyle R={\sqrt[{3}]{\frac {G\cdot M_{3}}{\omega ^{2}}}}} .

R=μω23{\displaystyle R={\sqrt[{3}]{\frac {\mu }{\omega ^{2}}}}}

ω=2⋅π86164=7,29⋅10−5{\displaystyle \omega ={\frac {2\cdot \pi }{86164}}=7,29\cdot 10^{-5}} рад/с

vl=ω⋅R{\displaystyle v_{l}=\omega \cdot R}

Первая космическая скорость на расстоянии R{\displaystyle R} от объекта массой M{\displaystyle M} равна

vk=GMR;{\displaystyle v_{k}={\sqrt {G{\frac {M}{R}}}};}

Приравняв правые части уравнений друг к другу, приходим к полученному ранее выражению радиуса ГСО:

R=GMω23{\displaystyle R={\sqrt[{3}]{G{\frac {M}{\omega ^{2}}}}}}

Орбитальная скорость

Скорость движения по геостационарной орбите вычисляется умножением угловой скорости на радиус орбиты:

v=ω⋅R=3,07{\displaystyle v=\omega \cdot R=3{,}07} км/с

v=GMR;{\displaystyle v={\sqrt {G{\frac {M}{R}}}};}

R≈6400⋅(83,07)2≈43000{\displaystyle R\approx \,\!{6400\cdot \left({\frac {8}{3{,}07}}\right)^{2}}\approx \,\!43000}

Длина орбиты

Длина орбиты крайне важна для вычисления «точек стояния» спутников.

Удержание спутника в орбитальной позиции на геостационарной орбите

Недостатки геостационарной орбиты

Задержка сигнала

Невидимость ГСО с высоких широт

Широтаместности Видимый сектор орбиты Теоретическийсектор Реальный(с уч. рельефа)сектор[10]

90	--	--
82	--	--
81	29,7	--
80	58,9	--
79	75,2	--
78	86,7	26,2
75	108,5	77
60	144,8	132,2
50	152,8	143,3
40	157,2	149,3
20	161,5	155,1
0	162,6	156,6

Солнечная интерференция

Международно-правовой статус ГСО

См. также

Примечания

↑ Noordung, Hermann. The Problem With Space Travel. — DIANE Publishing, 1995. — P. 72.
↑ Extra-Terrestrial Relays — Can Rocket Stations Give Worldwide Radio Coverage? (англ.) (pdf). Arthur C. Clark (October 1945). Проверено 25 февраля 2010. Архивировано 23 августа 2011 года.
↑ Требование неподвижности спутников относительно Земли на своих орбитальных позициях на геостационарной орбите, а также большое количество спутников на этой орбите в разных её точках, приводят к интересному эффекту при наблюдении и фотографировании звёзд с помощью телескопа с использованием гидирования — удержания ориентации телескопа на заданной точке звёздного неба для компенсации суточного вращения Земли (задача, обратная геостационарной радиосвязи). Если наблюдать в такой телескоп звёздное небо вблизи небесного экватора, где проходит геостационарная орбита, то при определённых условиях можно видеть, как спутники друг за другом проходят на фоне неподвижных звёзд в пределах узкого коридора, как автомобили по оживлённой автотрассе. Особенно хорошо это заметно на фотографиях звёзд с длительными экспозициями, смотри, например: Babak A. Tafreshi. GeoStationary HighWay. (англ.). The World At Night (TWAN). Проверено 25 февраля 2010. Архивировано 23 августа 2011 года. Источник: Бабак Тафреши (Ночной мир). Геостационарная магистраль. (рус.). Астронет.ру. Проверено 25 февраля 2010. Архивировано 23 августа 2011 года.
↑ CLASSIFICATION OF GEOSYNCHRONOUS OBJECTS
↑ для орбит спутников, масса которых пренебрежимо мала по сравнению с массой притягивающего его астрономического объекта
↑ Орбиты искусственных спутников Земли. Вывод спутников на орбиту
↑ The Teledesic Network: Using Low-Earth-Orbit Satellites to Provide Broadband, Wireless, Real-Time Internet Access Worldwide
↑ Журнал «Вокруг Света».№ 9 Сентябрь 2009. Орбиты, которые мы выбираем
↑ Мозаика. Часть II
↑ взято превышение спутником горизонта в 3°
↑ Внимание! Настаёт период активной солнечной интерференции!
↑ Солнечная интерференция
↑ B.IV.1. Declaration of the First Meeting of Equatorial Countries ("Bogota Declaration") of December 3, 1976 // Space Law. Basic Legal Documents. Volume 1. / Karl-Heinz Böckstiegel, Marietta Benkö, Stephan Hobe. — Eleven International Publishing, 2005. — ISBN 9780792300915.
↑ Национальное законодательство и практика, имеющие отношение к определению и делимитации космического пространства

Ссылки

http-wikipediya.ru

definition of Геостационарная_орбита and synonyms of Геостационарная_орбита (Russian)

Геостациона́рная орби́та (ГСО) — круговая орбита, расположенная над экватором Земли (0° широты), находясь на которой искусственный спутник обращается вокруг планеты с угловой скоростью, равной угловой скорости вращения Земли вокруг оси. В горизонтальной системе координат направление на спутник не изменяется ни по азимуту ни по высоте над горизонтом, спутник «висит» в небе неподвижно. Геостационарная орбита является разновидностью геосинхронной орбиты и используется для размещения искусственных спутников (коммуникационных, телетрансляционных и т. п.).

Спутник должен обращаться в направлении вращения Земли, на высоте 35 786 км над уровнем моря (вычисление высоты ГСО см. ниже). Именно такая высота обеспечивает спутнику период обращения, равный периоду вращения Земли относительно звёзд (Звёздные сутки: 23 часа 56 минут 4,091 секунды).

Точка стояния

Размещение спутников на орбите

Вычисление параметров геостационарной орбиты

Радиус орбиты и высота орбиты

Величина центробежной силы равна:

где — центростремительное ускорение, возникающее при круговом движении по орбите.

Центростремительное ускорение равно:

где — угловая скорость вращения спутника, в радианах в секунду.

Сокращая , переводя влево, а вправо, получаем:

или

Можно записать это выражение иначе, заменив на — геоцентрическую гравитационную постоянную:

рад/с

Орбитальная скорость

км/с или км/ч

Длина орбиты

Длина геостационарной орбиты: . При радиусе орбиты 42 164 км получаем длину орбиты 264 924 км.

Длина орбиты крайне важна для вычисления «точек стояния» спутников.

Удержание спутника в орбитальной позиции на геостационарной орбите

2) Наклонение орбиты к экватору увеличивается (от первоначального 0) со скоростью порядка 0.85 градуса в год и достигает максимального значения 15 градусов за 26.5 лет.

Для компенсации этих возмущений и удержания спутника в назначенной точке стояния спутник оснащается двигательной установкой (химической или электроракетной). Периодическими включениями двигателей малой тяги (коррекция «север-юг» для компенсации роста наклонения орбиты и «запад-восток» для компенсации дрейфа вдоль орбиты) спутник удерживается в назначенной точке стояния. Такие включения производятся раз в несколько (10-15) суток. Существенно, что для коррекции «север-юг» требуется значительно большее приращение характеристической скорости (около 45-50 м/с в год), чем для долготной коррекции (около 2 м/с в год). Для обеспечения коррекции орбиты спутника на протяжении всего срока его эксплуатации (12-15 лет для современных телевизионных спутников) требуется значительный запас топлива на борту (сотни килограммов, в случае применения химического двигателя). Химический ракетный двигатель спутника имеет вытеснительную подачу топлива (газ наддува-гелий), работает на долгохранимых высококипящих компонентах (обычно несимметричный диметилгидразин и диазотный тетраоксид). На ряде спутников устанавливаются плазменные двигатели. Их тяга существенно меньше по отношению к химическим, однако большая эффективность позволяет (за счет продолжительной работы) радикально снизить потребную массу топлива на борту. Выбор типа двигательной установки определяется конкретными техническими особенностями аппарата.

Запас топлива является основным лимитирующим фактором срока службы спутника на геостационарной орбите.

Недостатки геостационарной орбиты

Задержка сигнала

Связь через геостационарные спутники характеризуется большими задержками в распространении сигнала. При высоте орбиты 35 786 км и скорости света около 300 000 км/с ход луча «Земля-спутник» требует около 0,12 с. Ход луча «Земля (передатчик) → спутник → Земля (приемник)» ≈0,24 с. Ping (ответ) составит полсекунды (точнее 0,48 с). С учетом задержки сигнала в аппаратуре ИСЗ и аппаратуре наземных служб общая задержка сигнала на маршруте «Земля → спутник → Земля» может достигать 2—4 секунд[5]. Такая задержка делает невозможной применение спутниковой связи с использованием ГСО в различных сервисах реального времени (например в онлайн-играх)[6].

Невидимость ГСО с высоких широт

Так как геостационарная орбита не видна с высоких широт (приблизительно от 81° до полюсов), а на широтах выше 75° наблюдается очень низко над горизонтом (в реальных условиях, спутники просто скрываются выступающими объектами и рельефом местности) и виден лишь небольшой участок орбиты, то невозможна связь и телетрансляция с использованием ГСО в высокоширотных районах Крайнего Севера (Арктики) и Антарктиды[7]. К примеру, американские полярники на станции Амундсен-Скотт для связи с внешним миром (телефония, интернет) используют оптоволоконный кабель длиной 1670 километров до расположеной на 75° ю.ш. французской станции Конкордия, с которой уже видно несколько американских геостационарных спутников[8].

Солнечная интерференция

Одним из самых неприятных недостатков геостационарной орбиты, является уменьшение и полное отсутствие сигнала в ситуации, когда солнце и спутник-передатчик находятся на одной линии с приёмной антенной (положение «солнце за спутником»). Данное явление присуще и другим орбитам, но именно на геостационарной, когда спутник «неподвижен» на небе, проявляется особенно ярко. В средних широтах северного полушария солнечная интерференция проявляется в периоды с 22 февраля по 11 марта и с 3 по 21 октября, с максимальной длительностью до десяти минут[9]. В ясную погоду, сфокусированые светлым покрытием антенны солнечные лучи могут повредить (расплавить) приёмо-передающую аппаратуру спутниковой антенны[10].

См. также

Примечания

↑ Noordung Hermann The Problem With Space Travel. — DIANE Publishing, 1995. — P. 72. — ISBN 978-0788118494
↑ Extra-Terrestrial Relays — Can Rocket Stations Give Worldwide Radio Coverage? (англ.) (pdf). Arthur C. Clark (October 1945). Архивировано из первоисточника 23 августа 2011. Проверено 25 февраля 2010.
↑ Требование неподвижности спутников относительно Земли на своих орбитальных позициях на геостационарной орбите, а также большое количество спутников на этой орбите в разных её точках, приводят к интересному эффекту при наблюдении и фотографировании звёзд с помощью телескопа с использованием гидирования — удержания ориентации телескопа на заданной точке звёздного неба для компенсации суточного вращения Земли (задача, обратная геостационарной радиосвязи). Если наблюдать в такой телескоп звёздное небо вблизи небесного экватора, где проходит геостационарная орбита, то при определённых условиях можно видеть, как спутники друг за другом проходят на фоне неподвижных звёзд в пределах узкого коридора, как автомобили по оживлённой автотрассе. Особенно хорошо это заметно на фотографиях звёзд с длительными экспозициями, смотри, например: Babak A. Tafreshi. GeoStationary HighWay. (англ.). The World At Night (TWAN). Архивировано из первоисточника 23 августа 2011. Проверено 25 февраля 2010. Источник: Бабак Тафреши (Ночной мир). Геостационарная магистраль. (рус.). Астронет.ру. Архивировано из первоисточника 23 августа 2011. Проверено 25 февраля 2010.
↑ для орбит спутников, масса которых пренебрежимо мала по сравнению с массой притягивающего его астрономического объекта
↑ Орбиты искусственных спутников Земли. Вывод спутников на орбиту
↑ The Teledesic Network: Using Low-Earth-Orbit Satellites to Provide Broadband, Wireless, Real-Time Internet Access Worldwide
↑ Журнал «Вокруг Света».№ 9 Сентябрь 2009. Орбиты, которые мы выбираем
↑ Мозаика. Часть II
↑ Внимание! Настаёт период активной солнечной интерференции!
↑ Солнечная интерференция

Ссылки

dictionary.sensagent.com