Копенгагенская интерпретация квантовой теории (стр. 1 из 3). Копенгагенская интерпретация квантовой механики

Копенгагенская интерпретация квантовой механики | LightCone

Квантовая механика настолько неинтуитивна, что было придумано несколько «интерпретаций» в терминах более доступных нашему мозгу для визуализации. Классической является «Копенгагенская интерпретация», переданная нам отцами-основателями: Вернер Гейзенберг, Вольфганг Паули, Пол Дирак, Нильс Бор и др.

Основные идеи Копенгагенской интерпретации довольно просты, но в то же время абстрактны:

Волновая функция (вектор состояния) следует унитарной эволюции во времени, описываемой уравнением Шредингера.
Физическим смыслом волновой функции является амплитуда вероятности, квадрат которой есть вероятность обнаружить систему при измерении в определенном состоянии. При измерении функция «коллапсирует», то есть сосредотачивается в точке, соответствующей результату измерения. Вся остальная информация об исходной функции теряется.

На счет первого пункта споров не идет. Унитарная эволюция является самым незыблемым фундаментальным физическим принципом на данный момент от которого в ближайшее время отказываться не собираются. Но вот по поводу второго пункта разногласия до сих пор не утихают. Отчасти потому что пункт 2 противоречит пункту 1. Коллапс волновой функции не является унитарной операцией! Он не подчиняется уравнению Шредингера. Казалось бы парадокс и несогласованность самой квантовой теории налицо.

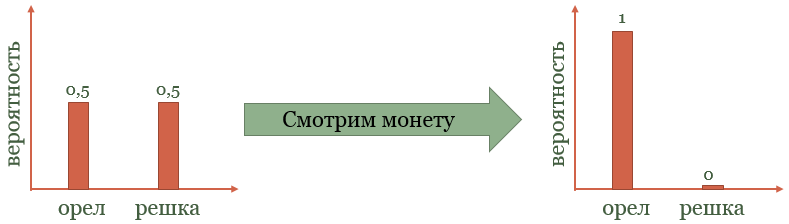
Тут есть один тонкий момент. Как нам показали отцы-основатели, роль наблюдателя в квантовой механике чрезвычайно важна. Квантовая механика субъективна. Все свои предсказания она выдает относительно наблюдателя — того субъекта кто ее использует. Экспериментатора. Тебя и меня. Поясним на примере. Представьте, что вы подкинули монетку и сейчас собираетесь посмотреть результат.

hands

До того как вы подняли руку, результат можно оценить только с помощью распределения вероятностей. Если монета честная, то с вероятностью 50% выпадет орел и с 50% решка. Это все, что вы можете в данный момент сказать о системе. Но как только вы подняли руку и увидели результат — распределение вероятностей «коллапсирует» в одну точку — в тот результат который действительно выпал. То есть сейчас вы со 100% вероятностью можете сказать, что выпал орел.

coin

Данный «коллапс» справедлив и для более сложных распределений вероятностей. Например, если подбрасывать два игральных кубика и смотреть вероятность выпадения того или иного числа (суммы выпавшего на первом и втором кубике — от 2 до 12), получим Гауссово распределение (выпадение семерки наиболее вероятно). Но когда мы реально смотрим на то что выпало в конкретном случае — это распределение коллапсирует в фактический результат (скажем в сумме выпало число шесть).

cube

Квантовую механику можно рассматривать как обобщение теории вероятностей по аналогии с тем как комплексные числа являются обобщением действительных. Волновая функция условно является неким «квадратным корнем» из функции распределения вероятности. Для того чтобы найти вероятность — волновую функцию необходимо возвести в квадрат. Кроме того она комплекснозначная. Амплитуда вероятности в общем случае является комплексным числом. В остальном идея «коллапса» как получение новых знаний о системе и неактуальности предыдущей информации остается такой же.

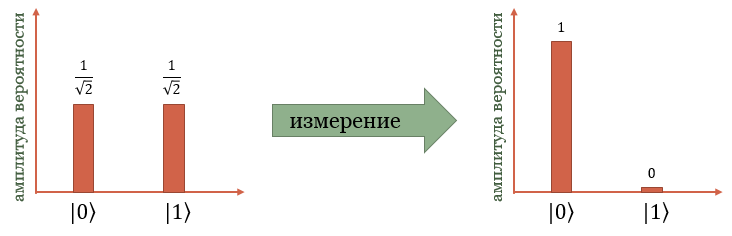
Возьмем кубит, находящийся в квантовой суперпозиции:

\( \displaystyle |\psi\rangle=\frac{1}{\sqrt{2}}|0\rangle+\frac{1}{\sqrt{2}}|1\rangle\)

При измерении происходит коллапс вектора состояния и мы получаем только одно из двух слагаемых. Либо при измерении мы получили ноль и вектор состояния коллапсирует в \( \displaystyle |\psi\rangle\rightarrow |0\rangle\), либо единицу и вектор переходит в \( \displaystyle |\psi\rangle\rightarrow |1\rangle\).

qubit

Отличие от классической теории вероятностей заключается еще и в том, что с монеткой мы подсознательно знаем, что она уже лежит или орлом или решкой до того как мы подняли руку чтобы посмотреть на результат. В случае квантовых объектов такое предполагать нельзя. Система приобретает классические свойства (характеристики) именно в момент субъективного измерения. Нельзя предполагать, что кубит до измерения был в состоянии \( \displaystyle |0\rangle\) или \( \displaystyle |1\rangle\). Он был именно в суперпозиции. Но эта суперпозиция ненаблюдаема. Поэтому слово был можно применять лишь условно. Вектор состояния не является объективной реальностью, как не является ею функция распределения вероятностей в классическом случае.

В этом и состоит разрешение парадокса кота Шредингера и других так называемых «парадоксов» в рамках Копенгагенской интерпретации — кот не является живым плюс мертвым. Это все равно что сказать: орел плюс решка, интерпретируя приведенную выше функцию распределения. cats Кот или жив или мертв. Мы ничего более не обнаружим при измерении. Просто квантовыя механика запрещает нам неявно делать какие-либо выводы до фактического измерения и описывает систему суперпозицией. То что нельзя измерить — не существует. То что можно измерить, но еще не измерено тоже не существует объективно.

Запутанные состояния, так волновавшие Эйнштейна, также интерпретируются с вероятностных позиций как квантовые корреляции. Пусть система из двух спинов находится в синглетном состоянии:

\( \displaystyle |S\rangle=\frac{1}{\sqrt{2}}(|\uparrow\downarrow\rangle-|\downarrow\uparrow\rangle)\)

При измерении мы всегда обнаружим корреляции: если спин одной частицы направлен вверх относительно какой-либо оси, то спин второй частицы обязательно окажется направленным вниз относительно той же оси. И наоборот. Можно опять провести аналогию с классической теорией вероятностей. Возьмем красную и синюю таблетки. Перемешаем их у себя за спиной и зажмем в каждый кулак по штуке. Не разжимая руки мы не можем сказать где находится синяя, а где красная. Можно построить график распределения вероятности аналогичный приведенному для монетки.

Но как только мы откроем один кулак и увидим, что там, например, синяя — мы мгновенно узнаем, что в другом кулаке красная. И наоборот. Это получение информации коллапсирует приведенный выше вектор состояния в одно из слагаемых. Таблетки могут быть разнесены на разные концы Вселенной и все равно статистические корреляции сохранятся. Очевидно, что тут не идет речь о сверхсветовой скорости передачи информации, простые корреляции.

Единственно новой вещью в квантовомеханическом случае является невозможность предположить, что в правой руке была синяя, а в левой красная до измерения. Теорема Белла или Загадка квантовых пирожков наиболее наглядно это разъясняют. Именно измерение данным наблюдателем какого-либо свойства (цвета в нашем случае) делает его реальным (объективным) для этого наблюдателя.

Квантовая механика субъективна. Она дает предсказания только для того кто ей пользуется. Только для него происходит субъективный коллапс вектора состояния, связанный с получением новой информации. Объективный мир существует только в его голове. Для всех других он такая же часть физического мира и подчиняется тем же самым квантовомеханическим законам с суперпозициями, комплексными числами и тому подобными вещами. Друг Вигнера является наглядной демонстрацией данного принципа.

Волновая функция (вектор состояния) ненаблюдаема. Это не классическое поле типа температуры или напряженности электрического поля. Эта функция скорее ближе к функции распределения вероятности, точнее ее можно рассматривать как некое ее обобщение. Саму квантовую механику можно рассматривать как обобщение теории информации + теории верояностей.

lightcone.ru

Что такое копенгагенская интерпретация?

Копенгагенская интерпретация – это объяснение квантовой механики, сформулированное Нильсом Бором и Вернером Гейзенбергом в 1927 году, когда ученые совместно работали в Копенгагене. Бор и Гейзенберг смогли усовершенствовать вероятностную интерпретацию функции, сформулированную М. Борном, и попробовали дать ответ на ряд вопросов, возникновение которых обусловлено корпускулярно-волновым дуализмом. В данной статье будут рассмотрены основные идеи копенгагенской интерпретации квантовой механики, и их влияние на современную физику.

Копенгагенская интерпретация

Проблематика

Интерпретациями квантовой механики называли философские воззрения на природу квантовой механики, как теории, которая описывает материальный мир. С их помощью можно было ответить на вопросы о сущности физической реальности, способе ее изучения, характере причинности и детерминизма, а также сущности статистики и ее месте в квантовой механике. Квантовую механику принято считать наиболее резонансной теорией в истории науки, однако консенсуса в ее глубинном понимании до сих пор не существует. Существует ряд интерпретаций квантовой механики, и сегодня мы познакомимся с наиболее популярной из них.

Основные идеи

Как известно, физический мир состоит из квантовых объектов и классических приборов для измерения. Изменение состояния измерительных приборов описывает необратимый статистический процесс изменения характеристик микрообъектов. Когда микрообъект вступает во взаимодействие с атомами измерительного прибора, суперпозиция сводится к одному состоянию, то есть происходит редукция волновой функции измерительного объекта. Уравнение Шредингера не описывает этот результат.

С точки зрения копенгагенской интерпретации, квантовая механика описывает не сами по себе микрообъекты, а их свойства, которые проявляются в макроусловиях, создающихся типичными измерительными приборами при наблюдении. Поведение атомных объектов нельзя отграничить от их взаимодействия с приборами для измерений, которые фиксируют условия происхождения явлений.

Копенгагенская интерпретация квантовой механики

Взгляд на квантовую механику

Квантовая механика является статической теорией. Это обусловлено тем, что измерение микрообъекта приводит к изменению его состояния. Так возникает вероятностное описание исходного положения объекта, описываемое волновой функцией. Комплексная волновая функция - центральное понятие квантовой механики. Волновая функция изменяется до нового измерения. Результат этого измерения зависит от волновой функции, вероятностным образом. Физическим значением обладает лишь квадрат модуля волновой функции, который подтверждает вероятность того, что изучаемый микрообъект находится в определенном месте пространства.

В квантовой механике закон причинности выполняется относительно волновой функции, изменяющейся во времени в зависимости от начальных условий, а не относительно координат скорости частиц, как в классической трактовке механики. Из-за того, что физическим значением наделен только квадрат модуля волновой функции, ее начальные значения нельзя определить в принципе, что приводит к некой невозможности получить точные знания о начальном состоянии системы квантов.

Философская основа

С философской точки зрения, основой копенгагенской интерпретации являются гносеологические принципы:

Наблюдаемости. Его суть состоит в исключении из физической теории тех утверждений, которые нельзя проверить посредством непосредственного наблюдения.
Дополнительности. Предполагает, что волновое и корпускулярное описание объектов микромира дополняют друг друга.
Неопределенности. Говорит о том, что координату микрообъектов и их импульс нельзя определить по отдельности, и с абсолютной точностью.
Статического детерминизма. Предполагает, что теперешнее состояние физической системы определяется ее предыдущими состояниями не однозначно, а лишь с долей вероятности осуществления тенденций изменения, заложенных в прошлом.
Соответствия. Согласно этому принципу, законы квантовой механики преобразуются в законы классической механики, когда есть возможность пренебречь величиной кванта действия.

Копенгагенская интерпретация квантовой механики (Гейзенберг, Бор)

Преимущества

В квантовой физике сведения об атомных объектах, полученные посредством экспериментальных установок, пребывают в своеобразном соотношении друг с другом. В соотношениях неопределенностей Вернера Гейзенберга просматривается обратная пропорциональность между неточностями фиксирования кинетических и динамических переменных, определяющих состояние физической системы в классической механике.

Весомым преимуществом копенгагенской интерпретации квантовой механики является тот факт, что она не оперирует детальными высказываниями непосредственно о физически ненаблюдаемых величинах. Кроме того, при минимуме предпосылок она выстраивает понятийную систему, исчерпывающим образом описывающую экспериментальные факты, имеющиеся на данный момент.

Смысл волновой функции

Согласно копенгагенской интерпретации, волновая функция может быть подвластна двум процессам:

Унитарной эволюции, которая описывается уравнением Шредингера.
Измерению.

Касательного первого процесса в научных кругах сомнений не возникло ни у кого, а второй процесс вызвал дискуссии и породил ряд толкований, даже в рамках самой копенгагенской интерпретации сознания. С одной стороны, есть все основания полагать, что волновая функция представляет собой не что иное, как реальный физический объект, и что она претерпевает коллапс во время второго процесса. С другой стороны, волновая функция может выступать не реальной сущностью, а вспомогательным математическим инструментом, единственное предназначение которой состоит в предоставлении возможности рассчитать вероятность. Бор сделал акцент на том, что единственное, что может быть предсказано – это результат физических опытов, поэтому все второстепенные вопросы должны относиться не к точной науке, а к философии. Он исповедовал в своих наработках философскую концепцию позитивизма, требующую, чтобы наука обсуждала только реально измеряемые вещи.

Копенгагенская интерпретация волновой функции

Двухщелевой опыт

В двухщелевом опыте свет, проходящий через две щели, падает на экран, на котором появляются две интерференционные полосы: темная и светлая. Этот процесс объясняется тем, что световые волны могут в одних местах взаимно усиливаться, а в других – взаимно гаситься. С другой стороны, эксперимент иллюстрирует, что свет обладает свойствами потока части, а электроны могут проявлять волновые свойства, давая при этом интерференционную картину.

Можно допустить, что опыт проводится с потоком фотонов (или электронов) настолько низкой интенсивности, что через щели каждый раз проходит только по одной частице. Тем не менее, при сложении точек попадания фотонов на экран, от накладывающихся волн получается такая же интерференционная картина, несмотря на то, что опыт касается якобы отдельных частиц. Это объясняется тем, что мы живем в «вероятностной» вселенной, в которой каждое будущее событие имеет переделенную степень возможности, а вероятность того, что в следующий момент времени случится нечто абсолютно непредвиденное, довольно мала.

Вопросы

Щелевой опыт ставит такие вопросы:

Каковыми будут правила поведения отдельных частиц? Законы квантовой механики указывают на место экрана, в котором окажутся частицы, статистически. Они позволяют рассчитать местоположение световых полос, в которых, скорее всего, окажется много частиц, и темных полос, куда, вероятно, попадет меньше частиц. Однако законы, которым подчиняется квантовая механика, не могут предсказать, где фактически окажется отдельная частица.
Что происходит с частицей в момент между испусканием и регистрацией? По результатам наблюдений, может создаться впечатление, что частица пребывает во взаимодействии с обеими щелями. Кажется, что это противоречит закономерностям поведения точечной частицы. Тем более что при регистрации частицы она становится точечной.
Под действием чего частица меняет свое поведение со статического на нестатическое, и наоборот? Когда частица проходит сквозь щели, ее поведение обуславливается нелокализованной волновой функцией, одновременно проходящей через обе щели. В момент регистрации частицы она всегда фиксируется как точечная, и никогда не получается размытого волнового пакета.

Копенгагенская интерпретация квантовой физики

Ответы

Копенгагенская теория квантовой интерпретации отвечает на поставленные вопросы следующим образом:

Принципиально невозможно устранить вероятностный характер предсказаний квантовой механики. То есть, он не может точно свидетельствовать об ограничении человеческих знаний о каких-либо скрытых переменных. Классическая физика ссылается на вероятность в тех случаях, когда нужно описать процесс типа подбрасывания игральных костей. То есть вероятность заменяет неполное знание. Копенгагенская интерпретация квантовой механики Гейзенберга и Бора напротив, утверждает, что результат измерений в квантовой механике принципиально недетерминирован.
Физика является наукой, изучающей результаты измерительных процессов. Размышлять о том, что происходит в их следствие, неправомерно. Согласно копенгагенской интерпретации, вопросы о том, где была частица до момента ее регистрации, и прочие подобные измышления бессмысленны, а значит, должны быть исключены из размышлений.
Акт измерения приводит к мгновенному коллапсу волновой функции. Следовательно, процесс измерения случайным образом выбирает лишь одну из возможностей, которые допускает волновая функция данного состояния. А чтобы отразить этот выбор, волновая функция должна мгновенно измениться.

Формулировки

Формулировка копенгагенской интерпретации в оригинальном виде породила несколько вариаций. Наиболее распространенная из них основывается на подходе непротиворечивых событий и таком понятии, как квантовая декогеренция. Декогеренция позволяет рассчитать нечеткую границу между макро- и микромирами. Остальные вариации разнятся по степени «реалистичности волнового мира».

Копенгагенская теория квантовой интерпретации

Критика

Полноценность квантовой механики (ответ Гейзенберга и Бора на первый вопрос) подверглась сомнению в мысленном эксперименте, проводимом Эйнштейном, Подольским и Розеном (ЭПР-парадокс). Таким образом ученые хотели доказать, что существование скрытых параметров необходимо для того, чтобы теория не приводила к мгновенному и нелокальному «дальнодействию». Однако во время проверки ЭПР-парадокса, которая стала возможной благодаря неравенствам Белла, было доказано, что квантовая механика верна, и различные теории скрытых параметров не имеют экспериментального подтверждения.

Но наиболее проблематичным стал ответ Гейзенберга и Бора на третий вопрос, который ставил измерительные процессы в особое положение, но не определял наличие в них отличительных черт.

Многие ученые, как физики, так и философы, наотрез отказывались принимать копенгагенскую интерпретацию квантовой физики. Первая тому причина заключалась в том, что толкование Гейзенберга и Бора было не детерминистическим. А вторая – в том, что оно вводило неопределенное понятие измерения, которое превращало вероятностные функции в достоверные результаты.

Эйнштейн был уверен, что описание физической реальности, даваемое квантовой механикой в толковании Гейзенберга и Бора, неполноценно. По словам Эйнштейна, он находил долю логики в копенгагенской интерпретации, но его научные инстинкты отказывались ее принимать. Поэтому Эйнштейн не мог отказаться от поисков более полной концепции.

В своем письме Борну Эйнштейн говорил: «Я уверен, что Бог не бросает кости!». Нильс Бор, комментируя эту фразу, сказал Эйнштейну, чтобы тот не указывал Богу, что делать. А в своем разговоре с Абрахамом Пайсом Эйнштейн восклицал: «Вы и впрямь думаете, что Луна существует только тогда, когда Вы на нее смотрите?».

Копенгагенская интерпретация сознания

Эрвин Шредингер придумал мысленный эксперимент с котом, посредством которого он хотел продемонстрировать неполноценность квантовой механики во время перехода от субатомных систем к микроскопическим. Вместе с тем, проблемным считался необходимый коллапс волновой функции в пространстве. Согласно теории относительности Эйнштейна, мгновенность и одновременность имеют смысл лишь для наблюдателя, находящегося в одной системе отсчета. Таким образом, не существует времени, которое могло бы стать единым для всех, а значит, мгновенный коллапс не может быть определен.

Распространение

Неофициальный опрос, проведенный в научных кругах в 1997 году, показал, что доминирующая ранее копенгагенская интерпретация, кратко рассмотренная выше, поддерживается менее чем половиной респондентов. Тем не менее, у нее больше приверженцев, нежели у других интерпретаций по отдельности.

Альтернатива

Многим физикам более близка другая интерпретация квантовой механики, которая получила название «никакая». Суть этого толкования исчерпывающе выражается в изречении Дэвида Мермина: «Заткнись и вычисляй!», которое часто приписывают Ричарду Фейнману или Полю Дираку.

fb.ru

Копенгагенская интерпретация | Наука | FANDOM powered by Wikia

Копенга́генская интерпрета́ция — это интерпретация (толкование) квантовой механики, которую сформулировали Нильс Бор и Вернер Гейзенберг во время совместной работы в Копенгагене около 1927 года. Бор и Гейзенберг усовершенствовали вероятностную интерпретацию волновой функции, данную М. Борном, и попытались ответить на ряд вопросов, возникающих вследствие свойственного квантовой механике корпускулярно-волнового дуализма, в частности на вопрос об измерении.

Распространенность среди ученых Править

Согласно опросу, проведённому на симпозиуме по квантовой механике в 1997 г., Копенгагенская интерпретация является наиболее признаваемой из всех. Сразу за ней идёт многомировая интерпретация. Несмотря на то, что на сегодняшний день появляется серьёзная конкуренция со стороны других интерпретаций, в XX столетии среди физиков была наиболее популярна именно копенгагенская.

Смысл волновой функции Править

Копенгагенская интепретация предполагает, что на волновую функцию могут влиять два процесса:

унитарная эволюция согласно уравнению Шрёдингера
процесс измерения

По поводу первого процесса не возникает разногласий ни у кого, а по поводу второго имеется ряд различных интерпретаций, даже в пределах самой копенгагенской интерпретации. С одной стороны, можно полагать, что волновая функция является реальным физическим объектом и что она во время второго процесса претерпевает коллапс, с другой стороны, можно считать, что волновая функция — лишь вспомогательный математический инструмент (а не реальная сущность), единственное предназначение которой — это давать нам возможность рассчитывать вероятности. Бор подчёркивал, что единственное, что можно предсказывать — это результаты физических опытов, поэтому дополнительные вопросы относятся не к науке, а к философии. Бор разделял философскую концепцию позитивизма, которая требует, чтобы наука говорила только о реально измеримых вещах.

В классическом двухщелевом опыте свет проходит через две щели и падает на экран, где появляются тёмные и светлые интерференционные полосы. Это можно объяснить тем, что в некоторых местах световые волны взаимно усиливаются, а в других — гасятся. С другой стороны, эксперимент показывает, что свет обладает и свойствами потока частиц, а такие объекты, как электроны могут проявлять и волновые свойства и тоже могут давать интерференционную картину.

Это ставит несколько интересных вопросов. Допустим, двухщелевой эксперимент проводится с настолько низкой интенсивностью потока фотонов (или электронов), что каждый раз через щели проходит только по одной частице. Однако, когда экспериментатор сложит точки попадания всех фотонов на экран, он получит ту же интерференционную картину от накладывающихся волн, несмотря на то, что вроде бы опыт касался отдельных частиц. Это показывает, что мы живём в «возможностной» вселенной — такой, что в ней с каждым будущим событием связана определённая степень возможности, а не в такой, что в каждый следующий момент может случиться всё что угодно.

Данный опыт ставит следующие вопросы:

Законы квантовой механики говорят о том, где частицы попадут в экран статистически и дают возможность рассчитать местоположение светлых полос, куда скорее всего попадёт много частиц и местоположение тёмных полос, куда скорее всего попадёт мало частиц. Однако, для отдельной частицы, законы квантовой механики не могут предсказать, где она фактически окажется. Каковы в таком случае правила поведения отдельных частиц?
Что происходит с частицей между моментом испускания и моментом регистрации? Создаётся впечатление, что частица претерпевает взаимодействие с обеими щелями и это кажется противоречащим тому, как может себя вести точечная частица, тем более, что когда частица регистрируется, она оказывается точечной.
Что заставляет частицу переключаться от статистического к нестатистическому поведению и обратно? Когда частица летит сквозь щели, её поведение описывается нелокализованной волновой функцией, которая одновременно проходит через обе щели. А когда частица регистрируется, никогда не получается размытый волновой пакет, а всегда получается точечная частица.

Копенгагенская интерпретация отвечает на эти вопросы так:

Вероятностный характер предсказаний квантовой механики принципиально неустраним, то есть, он вовсе не говорит о том, что наши знания ограничены, что мы не знаем значений каких-то скрытых переменных. В классической физике вероятность использовалась для описания результатов типа подбрасывания игральной кости, хотя фактически этот процесс считался детерминированным. То есть, вероятности использовались вместо неполного знания. Напротив, копенгагенская интерпретация утверждает, что в квантовой механике результат измерения принципиально недетерминирован.
Физика — это наука о результатах измерительных процессов. Измышления на тему того, что происходит за ними неправомерны. Копенгагенская интерпретация отбрасывает вопросы типа «где была частица до того, как я зарегистрировал её местоположение» как бессмысленные.
Акт измерения вызывает мгновенное схлопывание, «коллапс волновой функции». Это означает, что процесс измерения случайно выбирает в точности одну из возможностей, допустимых волновой функцией данного состояния, а волновая функция мгновенно изменяется, чтобы отразить этот выбор.

Оригинальная формулировка копегагенской интерпретации породила ряд вариаций; наиболее уважаемая основана на подходе непротиворечивых событий («Копенгаген прав?») и понятии квантовой декогеренции, которая позволяет рассчитывать нечёткую границу между «микро» и «макро» мирами. Другие вариации различаются степенью «реалистичности» волнового мира.

Полнота квантовой механики (тезис 1) была подвергнута сомнению в мысленном эксперименте Эйнштейна, Подольского и Розена (ЭПР-парадокс), который был предназначен для того, чтобы доказать, что скрытые параметры должны существовать, чтобы теория не приводила к нелокальному и мгновенному «дальнодействию». Однако, проверка ЭПР-парадокса на опыте при помощи неравенств Белла, показала, что квантовая механика верна и что различные теории локальных скрытых параметров не согласуются с экспериментом.

Из всех трёх тезисов, с физической точки зрения наиболее проблематичен последний, поскольку он ставит процессы измерения в особое положение, но не определяет ясно, что они такое, и не указывает на их отличительные черты.

Многие физики и философы не соглашаются с копенгагенской интерпретацией, как потому что она не детерминистична, так и потому, что она вводит неопределённое понятие измерения, которое превращает вероятностные функции в достоверные результаты измерений. Иллюстрируя это, Эйнштейн писал Бору, что «я убеждён, что Бог не бросает кости», а также восклицал в беседе с Абрахамом Пайсом: «Вы и вправду думаете, что Луна существует лишь когда Вы на неё смотрите?» Бор отвечал ему «Эйнштейн, не указывайте Богу, что делать». Эрвин Шрёдингер придумал знаменитый мысленный эксперимент про кота Шрёдингера, которым он хотел показать неполноту квантовой механики при переходе от субатомных систем к макроскопическим.

Аналогично вызывает проблемы необходимый «мгновенный» коллапс волновой функции во всем пространстве. Теория относительности Эйнштейна говорит, что мгновенность, одновременность, имеет смысл только для наблюдателей, находящихся в одной системе отсчёта. Не существует единого для всех времени, поэтому мгновенный коллапс тоже остаётся неопределён.

Многие физики склоняются к так называемой «никакой» интерпретации квантовой механики, ёмко выраженной в афоризме Дэвида Мермина: «Заткнись и считай!» (часто (видимо, по ошибке) приписываемом Ричарду Фейнману или Полю Дираку).

ru.science.wikia.com

Копенгагенская интерпретация - это... Что такое Копенгагенская интерпретация?

Копенга́генская интерпрета́ция — интерпретация (толкование) квантовой механики, которую сформулировали Нильс Бор и Вернер Гейзенберг во время совместной работы в Копенгагене около 1927 года[1]. Бор и Гейзенберг усовершенствовали вероятностную интерпретацию волновой функции, данную М. Борном, и попытались ответить на ряд вопросов, возникающих вследствие свойственного квантовой механике корпускулярно-волнового дуализма, в частности на вопрос об измерении.

Распространённость среди учёных

Весьма неофициальный опрос, сделанный в 1997 году на симпозиуме под эгидой UMBC (англ.)русск., показал[2], что некогда доминировавшая Копенгагенская интерпретация поддерживается менее чем половиной участников. В целом голоса участников опроса распределились следующим образом:

Смысл волновой функции

Копенгагенская интерпретация предполагает, что на волновую функцию могут влиять два процесса:

Это ставит несколько интересных вопросов. Допустим, двухщелевой эксперимент проводится с настолько низкой интенсивностью потока фотонов (или электронов), что каждый раз через щели проходит только по одной частице. Однако, когда экспериментатор сложит точки попадания всех фотонов на экран, он получит ту же интерференционную картину от накладывающихся волн, несмотря на то, что вроде бы опыт касался отдельных частиц. Это можно интерпретировать так, что мы живём в «возможностной» вселенной — такой, что в ней с каждым будущим событием связана определённая степень возможности, а не в такой, что в каждый следующий момент может случиться всё что угодно.

Следствия

Данный опыт ставит следующие вопросы:

Законы квантовой механики говорят о том, где частицы попадут в экран статистически и дают возможность рассчитать местоположение светлых полос, куда скорее всего попадёт много частиц и местоположение тёмных полос, куда скорее всего попадёт мало частиц. Однако для отдельной частицы законы квантовой механики не способны предсказать, где она окажется фактически. Каковы в таком случае правила поведения отдельных частиц?
Что происходит с частицей между моментом испускания и моментом регистрации? Создаётся впечатление, что частица претерпевает взаимодействие с обеими щелями. И это кажется противоречащим тому, как может себя вести точечная частица. Тем более что, когда частица регистрируется, она оказывается точечной.
Что заставляет частицу переключаться от статистического к нестатистическому поведению и обратно? Когда частица летит сквозь щели, её поведение описывается нелокализованной волновой функцией, которая одновременно проходит через обе щели. Когда же частица регистрируется, никогда не получается размытый волновой пакет, но всегда фиксируется точечная частица.

Копенгагенская интерпретация отвечает на эти вопросы так:

Вероятностный характер предсказаний квантовой механики принципиально неустраним, то есть он вовсе не говорит о том, что наши знания ограничены, что мы не знаем значений каких-то скрытых переменных. В классической физике вероятность использовалась для описания результатов типа подбрасывания игральной кости, хотя фактически этот процесс считался детерминированным. То есть вероятности использовались вместо неполного знания. Напротив, копенгагенская интерпретация утверждает, что в квантовой механике результат измерения принципиально недетерминирован.
Физика — это наука о результатах измерительных процессов. Измышления на тему того, что происходит за ними, неправомерны. Копенгагенская интерпретация отбрасывает вопросы типа «где была частица до того, как я зарегистрировал её местоположение» как бессмысленные.
Акт измерения вызывает мгновенное схлопывание, «коллапс волновой функции». Это означает, что процесс измерения случайно выбирает в точности одну из возможностей, допустимых волновой функцией данного состояния, а волновая функция мгновенно изменяется, чтобы отразить этот выбор.

Критика

Полнота квантовой механики (тезис 1) была подвергнута сомнению в мысленном эксперименте Эйнштейна, Подольского и Розена (ЭПР-парадокс), который был предназначен для того, чтобы доказать, что скрытые параметры должны существовать, чтобы теория не приводила к нелокальному и мгновенному «дальнодействию». Однако проверка ЭПР-парадокса на опыте при помощи неравенств Белла показала, что квантовая механика верна и что различные теории локальных скрытых параметров не согласуются с экспериментом.

Из всех трёх тезисов с физической точки зрения наиболее проблематичен последний, поскольку он ставит процессы измерения в особое положение, но не определяет ясно что они такое и не указывает на их отличительные черты.

Многие физики и философы не соглашаются с копенгагенской интерпретацией, как потому что она не детерминистична, так и потому, что она вводит неопределённое понятие измерения, которое превращает вероятностные функции в достоверные результаты измерений. Иллюстрируя это, Эйнштейн писал Бору, что «я убеждён, что Бог не бросает кости», а также восклицал в беседе с Абрахамом Пайсом: «Вы и вправду думаете, что Луна существует лишь когда вы на неё смотрите?». Бор отвечал ему: «Эйнштейн, не указывайте Богу что делать». Эрвин Шрёдингер придумал знаменитый мысленный эксперимент про кота Шрёдингера, которым он хотел показать неполноту квантовой механики при переходе от субатомных систем к макроскопическим.

Альтернативы

Многие физики склоняются к так называемой «никакой» интерпретации квантовой механики, ёмко выраженной в афоризме Дэвида Мермина: «Заткнись и вычисляй!» (ориг. англ. «Shut up and calculate»), часто (видимо, по ошибке) приписываемом Ричарду Фейнману или Полю Дираку[3].

Примечания

См. также

dic.academic.ru

Копенгагенская интерпретация квантовой теории

В. Гейзенберг

Копенгагенская интерпретация квантовой теории начинается с парадокса. Каждый физический эксперимент, безразлично относится ли он к явлениям повседневной жизни или к явлениям атомной физики, должен быть описан в понятиях классической физики. Понятия классической физики образуют язык, с помощью которого мы описываем наши опыты и результаты. Эти понятия мы не можем заменить ничем другим, а применимость их ограничена соотношением неопределенностей. Мы должны иметь в виду ограниченную применимость классических понятий, и не пытаться выходить за рамки этой ограниченности. А чтобы лучше понять этот парадокс, необходимо сравнить интерпретацию опыта в классической и квантовой физике.

Например, в ньютоновской небесной механике мы начинаем с того, что определяем положение и скорость планеты, движение которой собираемся изучать. Результаты наблюдения переводятся на математический язык благодаря тому, что из наблюдений выводятся значения координат и импульса планеты. Затем из уравнения движения, используя эти численные значения координат и импульса для данного момента времени, получают значения координат или какие-либо другие свойства системы для последующих моментов времени. Таким путем астроном предсказывает движение системы. Например, он может предсказать точное время солнечного затмения.

В квантовой теории все происходит по-иному. Допустим, нас интересует движение электрона в камере Вильсона, и мы посредством некоторого наблюдения определили координаты и скорость электрона. Однако это определение не может быть точным. Оно содержит по меньшей мере неточности, обусловленные соотношением неопределенностей, и, вероятно, кроме того, будет содержать еще большие неточности, связанные с трудностью эксперимента. Первая группа неточностей дает возможность перевести результат наблюдения в математическую схему квантовой теории. Функция вероятности, описывающая экспериментальную ситуацию в момент измерения, записывается с учетом возможных неточностей измерения. Эта функция вероятностей представляет собой соединение двух различных элементов: с одной стороны -- факта, с другой стороны -- степени нашего знания факта. Эта функция характеризует фактически достоверное, поскольку приписывает начальной ситуации вероятность, равную единице. Достоверно, что электрон в наблюдаемой точке движется с наблюдаемой скоростью. "Наблюдаемо" здесь означает -- наблюдаемо в границах точности эксперимента. Эта функция характеризует степень точности нашего знания, поскольку другой наблюдатель, быть может, определил бы положение электрона еще точнее. По крайней мере в некоторой степени экспериментальная ошибка или неточность эксперимента рассматривается не как свойство электронов, а как недостаток в нашем знании об электроне. Этот недостаток знания также выражается с помощью функции вероятности.

В классической физике в процессе точного исследования ошибки наблюдения также учитываются. В результате этого получают распределение вероятностей для начальных значений координат и скоростей, и это имеет некоторое сходство с функцией вероятности квантовой механики. Однако специфическая неточность, обусловленная соотношением неопределенностей, в классической физике отсутствует.

Если в квантовой теории из данных наблюдения определена функция вероятности для начального момента, то можно рассчитать на основании законов этой теории функцию вероятности для любого последующего момента времени. Таким образом, заранее можно определить вероятность того, что величина при измерении будет иметь определенное значение. Например, можно указать вероятность, что в определенный последующий момент времени электрон будет найден в определенной точке камеры Вильсона. Следует подчеркнуть, что функция вероятности не описывает само течение событий во времени. Она характеризует тенденцию события, возможность события или наше знание о событии. Функция вероятности связывается с действительностью только при выполнении одного существенного условия: для выявления определенного свойства системы необходимо произвести новые наблюдения или измерения. Только в этом случае функция вероятности позволяет рассчитать вероятный результат нового измерения. При этом снова результат измерения дается в понятиях классической физики. Поэтому теоретическое истолкование включает в себя три различные стадии. Во-первых, исходная экспериментальная ситуация переводится в функцию вероятности. Во-вторых, устанавливается изменение этой функции с течением времени. В-третьих, делается новое измерение, а ожидаемый результат его затем определяется из функции вероятности. Для первой стадии необходимым условием является выполнимость соотношения неопределенностей. Вторая стадия не может быть описана в понятиях классической физики; нельзя указать, что происходит с системой между начальным измерением и последующими. Только третья стадия позволяет перейти от возможного к фактически осуществляющемуся.

Мы разъясним эти три ступени на простом мысленном эксперименте. Уже отмечалось, что атом состоит из атомного ядра и электронов, которые двигаются вокруг ядра. Также было установлено, что понятие электронной орбиты в некотором смысле сомнительно. Однако вопреки последнему утверждению можно сказать, что все же, по крайней мере в принципе, можно наблюдать электрон на его орбите. Быть может, мы и увидели бы движение электрона по орбите, если бы могли наблюдать атом в микроскоп с большой разрешающей силой. Однако такую разрешающую силу нельзя получить в микроскопе, применяющем обычный свет, поскольку для этой цели будет пригоден только микроскоп, использующий г-лучи, с длиной волны меньшей размеров атома. Такой микроскоп до сих пор не создан, но технические затруднения не должны нас удерживать от обсуждения этого мысленного эксперимента. Можно ли на первой стадии перевести результаты наблюдения в функцию вероятности? Это возможно, если выполняется после опыта соотношение неопределенностей. Положение электрона известно с точностью, обусловленной длиной волны г-лучей. Предположим, что перед наблюдением электрон практически находится в покое. В процессе наблюдения по меньшей мере один квант г-лучей обязательно пройдет через микроскоп и в результате столкновения с электроном изменит направление своего движения. Поэтому электрон также испытает воздействие кванта. Это изменит его импульс и его скорость. Можно показать, что неопределенность этого изменения такова, что справедливость соотношения неопределенностей после удара гарантируется. Следовательно, первый шаг не содержит никаких трудностей. В то же время легко можно показать, что нельзя наблюдать движение электронов вокруг ядра. Вторая стадия -- количественный расчет функции вероятности -- показывает, что волновой пакет движется не вокруг ядра, а от ядра, так как уже первый световой квант выбивает электрон из атома. Импульс г-кванта значительно больше первоначального импульса электрона при условии, если длина волны г-лучей много меньше размеров атома. Поэтому уже достаточно первого светового кванта, чтобы выбить электрон из атома. Следовательно, нельзя никогда наблюдать более чем одну точку траектории электрона; следовательно, утверждение, что нет никакой, в обычном смысле, траектории электрона, не противоречит опыту. Следующее наблюдение -- третья стадия -- обнаруживает электрон, когда он вылетает из атома. Нельзя наглядно описать, что происходит между двумя следующими друг за другом наблюдениями. Конечно, можно было бы сказать, что электрон должен находиться где-то между двумя наблюдениями и что, по-видимому, он описывает какое-то подобие траектории, даже если невозможно эту траекторию установить. Такие рассуждения имеют смысл с точки зрения классической физики. В квантовой теории такие рассуждения представляют собой неоправданное злоупотребление языком. В настоящее время мы можем оставить открытым вопрос о том, касается ли это предложение формы высказывания об атомных процессах или самих процессов, то есть касается ли это гносеологии или онтологии. Во всяком случае, при формулировании положений, относящихся к поведению атомных частиц, мы должны быть крайне осторожны.

Фактически мы вообще не можем говорить о частицах. Целесообразно во многих экспериментах говорить о волнах материи, например о стоячей волне вокруг ядра. Такое описание, конечно, будет противоречить другому описанию, если не учитывать границы, установленные соотношением неопределенностей. Этим ограничением ликвидируется противоречие. Применив понятия "волна материи" целесообразно в том случае, если речь идет об излучении атома. Излучение, обладая определенной частотой и интенсивностью, дает нам информацию об изменяющемся распределении зарядов в атоме; при этом волновая картина ближе стоит к истине, чем корпускулярная. Поэтому Бор советовал применять обе картины. Их он назвал дополнительными. Обе картины, естественно, исключают друг друга, так как определенный предмет не может в одно и то же время быть и частицей (то есть субстанцией, ограниченной в малом объеме) и волной (то есть полем, распространяющимся в большом объеме). Но обе картины дополняют друг друга. Если использовать обе картины, переходя от одной к другой и обратно, то в конце концов получится правильное представление о примечательном виде реальности, который скрывается за нашими экспериментами с атомами.

Бор при интерпретации квантовой теории в разных аспектах применяет понятие дополнительности. Знание положения частицы дополнительно к знанию ее скорости или импульса. Если мы знаем некоторую величину с большой точностью, то мы не можем определить другую (дополнительную) величину с такой же точностью, не теряя точности первого знания. Но ведь, чтобы описать поведение системы, надо знать обе величины. Пространственно-временное описание атомных процессов дополнительно к их каузальному или детерминистскому описанию. Подобно функции координат в механике Ньютона, функция вероятности удовлетворяет уравнению движения. Ее изменение с течением времени полностью определяется квантово-механическими уравнениями, но она не дает никакого пространственно-временного описания системы. С другой стороны, для наблюдения требуется пространственно-временное описание. Однако наблюдение, изменяя наши знания о системе, изменяет теоретически рассчитанное поведение функции вероятности.

mirznanii.com

Концептуальные основания копенгагенской интерпретации квантовой механики | Философия науки (Физики) вики

Копенгагенская интерпретация— это интерпретация (толкование) квантовой механики, которую сформулировали Нильс Бор и Вернер Гейзенберг во время совместной работы в Копенгагене около 1927 года. То что взял из головы:

вероятностная сущность мира
вычисление волновой функции, которая позволяет предсказать исход данного события.Если в квантовой теории из данных наблюдения определена функциявероятности для начального момента, то можно рассчитать на основании законов этой теории функцию вероятности для любого последующего момента времени. Таким образом, заранее можно определить вероятность того, что величина при измерении будет иметь определенное значение.
особая роль наблюдателя. Никогда не сможем что-то измерить не нарушая квантовую систему.

В принципе, здесь можно много всего наговорить:

Корпускулярно-волновой дуализм.

Опыт с двумя щелями, что что Эрекаев расказывал. Электрон обладает волновой структурой.

Соотрношение неопределенностей.

Опыт Резерфорда (есть ядро у атома и у него положительный заряд).

Бор - планетарная модель атома, квантование орбит.

Что такое волновая функция? Плотность вероятности?

Физически измеряемым величинам ставятся в соответствие Эрмитовы операторы.

Один раз стоит прочитать!Править

Возникновение квантовой теории связано с известным явлением, которое вовсе не принадлежит к центральным разделам атомной физики. Любой кусок вещества, будучи нагрет, начинает светиться и при повышении температуры становится красным, а затем -- белым. Цвет почти не зависит от вещества и для черного тела определяется исключительно температурой. Был открыт закон теплового излучения Планка. Для Планка это открытие было только началом интенсивных теоретических исследований.

Стоял вопрос: какова правильная физическая интерпретация новой формулы? Так как Планк на основании своих более ранних работ легко мог истолковать эту формулу как утверждение об излучающем атоме (так называемом осцилляторе), он вскоре понял, что его формула имеет такой вид, как если бы осциллятор изменял свою энергию не непрерывно, а лишь отдельными квантами и если бы он мог находиться только в определенных состояниях или, как говорят физики, в дискретных состояниях энергии. Этот результат так отличался от всего, что знали в классической физике, что вначале Планк, по-видимому, отказывался в него верить. Но в период наиболее интенсивной работы, осенью 1900 года, он наконец пришел к убеждению, что уйти от этого вывода невозможно. Он объяснял, что чувствует -- либо он сделал открытие первого ранга, быть может, сравнимое только с открытиями Ньютона, либо он полностью ошибается. В это же время Планку стало ясно, что его формула затрагивает самые основы описания природы, что эти основы претерпят серьезное изменение и изменят свою традиционную форму на совершенно неизвестную. В декабре 1900 года он опубликовал свою квантовую гипотезу. Мысль о том, что энергия может испускаться и поглощаться лишь дискретными квантами энергии, была столь новой, что она выходила за традиционные рамки физики. Оказалась напрасной в существенных чертах попытка Планка примирить новую гипотезу со старыми представлениями об излучении.

Прошло около пяти лет, прежде чем в этом направлении был сделан следующий шаг. На этот раз именно молодой Альберт Эйнштейн, революционный гений среди физиков, не побоялся отойти еще дальше от старых понятий. Эйнштейн нашел две новые проблемы, в которых он успешно применил представления Планка. Первой проблемой был проблема фотоэлектрического эффекта. На базе прежней теории излучения это объяснить было нельзя. Однако Эйнштейн объяснил данные наблюдений, опираясь на гипотезу Планка, которую он интерпретировал с помощью предположения, что свет состоит из так называемых световых квантов, то есть из квантов энергии, которые движутся в пространстве подобно маленьким корпускулам. Энергия отдельного светового кванта, в согласии с гипотезой Планка, должна равняться частоте света, помноженной на постоянную Планка. Другой проблемой была проблема удельной теплоемкости твердых тел. Существовавшая теория удельной теплоемкости приводила к величинам, которые хорошо согласовывались с экспериментом в области высоких температур, но при низких температурах были много выше наблюдаемых величин. Эйнштейн снова сумел показать, что подобное поведение твердых тел можно понять благодаря квантовой гипотезе Планка, применяя ее к упругим колебаниям атомов в твердом теле. Эти два результата были большим шагом вперед на пути дальнейшего развития новой теории, в силу того что они обнаружили планковскую постоянную действия в различных областях, непосредственно не связанных с проблемой теплового излучения.

Эти результаты выявили и глубоко революционный характер новой гипотезы, ибо трактовка Эйнштейном квантовой теории привела к такому объяснению природы света, которое полностью отличалось от привычного со времени Гюйгенса объяснения на основе волнового представления. Следовательно, свет может быть объяснен или как распространение электромагнитных волн -- факт, который принимали на основе работ Максвелла и опытов Герца, -- или как нечто, состоящее из отдельных "световых квантов", или "энергетических пакетов", которые с большой скоростью движутся в пространстве. А может ли свет быть и тем и другим? Эйнштейн даже не пытался устранить внутренние противоречия своей интерпретации. Он принял противоречия как нечто такое, что, вероятно, может быть понято много позднее благодаря совершенно новому методу мышления.

Тем временем эксперименты Беккереля, Кюри и Резерфорда привели к несколько большей ясности в отношении строения атома. В 1911 году Резерфорд на основании наблюдений прохождения б-лучей через вещество предложил свою знаменитую модель атома. Атом состоит из атомного ядра, положительно заряженного и содержащего почти всю массу атома, и электронов, которые движутся вокруг ядра, подобно тому как планеты движутся вокруг Солнца. Химическая связь между атомами различных элементов объясняется взаимодействием между внешними электронами соседних атомов. Эта модель, правда, не могла объяснить одну из самых характерных черт атома, а именно его удивительную устойчивость. Никакая планетная система, которая подчиняется законам механики Ньютона, никогда после столкновения с другой подобной системой не возвратится в свое исходное состояние. В то время как,например, атом углерода остается атомом углерода и после столкновения с другими атомами или после того, как он, вступив во взаимодействие с другими атомами, образовал химическое соединение. Объяснение этой необычной устойчивости было дано в 1913 году Нильсом Бором путем применения квантовой гипотезы Планка к модели атома Резерфорда. Если атом может изменять свою энергию только прерывно, то это должно означать, что атом существует лишь в дискретных стационарных состояниях, низшее из которых есть нормальное состояние атома. Поэтому после любого взаимодействия атом в конечном счете всегда возвращается в это нормальное состояние. Бор, применяя квантовую теорию к модели атома, сумел не только объяснить устойчивость атома, но в некоторых простых случаях сумел также дать теоретическое объяснение линейных спектров, образующихся при возбуждении атомов посредством электрического разряда или теплоты. Его теория при описании движения электронов покоилась на соединении классической механики и квантовых условий, которые налагаются на классические законы движения для выделения дискретных стационарных состояний среди других состояний. Позднее Зоммерфельд дал точную математическую формулировку этих условий1. Бору было ясно, что квантовые условия в известном смысле разрушают внутреннюю прочность ньютоновской механики. В простейшем случае атома водорода на основании теории Бора можно рассчитать частоту излучаемого света, и согласие теоретических расчетов с наблюдениями оказывалось полным. В действительности эти частоты отличались от орбитальных частот электронов и высших гармоник этих частот, и это обстоятельство сразу показало, что теория еще полна противоречий. Несмотря на это, она, по всей вероятности, содержала большую долю истины. Она качественно объяснила химические свойства атомов и их линейные спектры. Существование дискретных стационарных состояний было непосредственно подтверждено и опытами: в экспериментах Франка и Герца, Штерна и Герлаха.

Таким образом, теория Бора открыла новую область исследований. Большое количество экспериментального материала, полученного спектроскопией в течение нескольких десятилетий, теперь при изучении квантовых законов движения электронов стало источником информации. Для той же самой цели могли быть использованы многие эксперименты химиков. Имея дело с этим экспериментальным материалом, физики постепенно научились ставить правильные вопросы. А ведь часть правильно поставленный вопрос означает больше чем наполовину решение проблемы. Каковы эти вопросы? Практически почти все они имели дело с явными и удивительными противоречиями в результатах различных опытов. Как может быть, что одно и то же излучение, которое образует интерференционную картину и доказывает тем самым существование лежащего в основе волнового движения, производит одновременно и фотоэлектрический эффект и потому должно состоять из движущихся световых квантов? Как может быть, что частота орбитального движения электронов в атоме не является также и частотой испускаемого излучения? Разве не означает это, что нет никакого орбитального движения? Но если представление об орбитальном движении неверно, то что в таком случае происходит с электроном внутри атома? Можно видеть те электроны, которые движутся в камере Вильсона; некоторые из них до этого являлись составной частью атома и были выбиты из атома. Почему, следовательно, внутри атома они не двигаются таким же образом? Можно было бы, пожалуй, представить себе, что в нормальном состоянии атома электроны покоятся. Но ведь имеются состояния с более высоким энергиями, в которых электроны обладают вращательным моментом, и поэтому в этих состояниях абсолютно исключено состояние покоя электронов. Можно перечислить много подобных примеров. Все отчетливее стали понимать, что попытка описать атомные процессы в понятиях обычной физики приводит к противоречиям. К началу 20-х годов физики постепенно освоились с этими трудностями. У них выработалась своего рода интуиция, правда не очень ясная, в отношении того, где, по всей вероятности, будут иметь место затруднения, и они научились избегать эти затруднения. Наконец, они узнали, какое в данном опыте описание атомных процессов приведет к правильному результату. Этого знания было недостаточно для того, чтобы дать общую непротиворечивую картину квантовых процессов, но оно так изменило мышление физиков, что они в некоторой степени прониклись духом квантовой теории. Уже в течение некоторого времени до того, как была дана строгая формулировка квантовой теории, знали более или менее точно, каков будет результат того или иного эксперимента. Часто обсуждали так называемые "мысленные эксперименты". Такие эксперименты изобретали для того, чтобы выяснить какой-либо особенно важный вопрос, вне зависимости от того, может ли быть проведен фактически этот эксперимент или нет. Конечно, важно было, чтобы эксперимент мог быть осуществим в принципе -- при этом экспериментальная техника могла быть любой сложности. Эти мысленные эксперименты оказались чрезвычайно полезными при выяснении некоторых проблем. Там, где в отношении вероятного результата такого эксперимента невозможно было добиться согласия между физиками, часто удавалось придумать подобный, но более простой эксперимент, который фактически можно было выполнить; экспериментальный результат значительно содействовал разъяснению квантовой теории. Удивительнейшим событием тех лет был тот факт, что по мере этого разъяснения парадоксы квантовой теории не исчезали, а, наоборот, выступали во все более явной форме и приобретали все большую остроту. Например, в то время был произведен опыт Комптона по рассеянию рентгеновских лучей. На основании прежних опытов по интерференции рассеянного света было совершенно очевидным, что рассеяние происходит в основном следующим образом: падающая световая волна выбивает из пучка электрон, колеблющийся с той же самой частотой; затем колеблющийся электрон испускает сферическую волну с частотой падающей волны и вызывает тем самым рассеянный свет. Однако в 1923 году Комптон обнаружил, что частота рассеянных рентгеновских лучей отличается от частоты падающих лучей 2. Это изменение частоты можно объяснить, предполагая, что рассеяние представляет собой столкновение кванта света с электроном. При ударе энергия светового кванта изменяется, а так как произведение частоты на постоянную Планка равняется энергии кванта света, частота также должна измениться. Но как в этом случае объяснить световые волны? Оба эксперимента -- один по интерференции рассеянного света, другой по изменению частоты рассеянного света - настолько противоречат друг другу, что, по-видимому, выход найти невозможно. В это время многие физики были уже убеждены в том, что эти явные противоречия принадлежат к внутренней природе атомной физики. Поэтому де Бройль во Франции в 1924 году попытался распространить дуализм волнового и корпускулярного описания и на элементарные частицы материи, в частности на электроны. Он показал, что движению электрона может соответствовать некоторая волна материи, так же как движению светового кванта соответствует световая волна. Конечно, в то время не было ясно, что означает в этой связи слово "соответствовать". Де Бройль предложил объяснить условия квантовой теории Бора с помощью представления о волнах материи. Волна, движущаяся вокруг ядра атома, по геометрическим соображениям может быть только стационарной волной; длина орбиты должна быть кратной целому числу длин волн. Тем самым де Бройль предложил перекинуть мост от квантовых условий, которые оставались чуждым элементом в механике электронов, к дуализму волн и частиц. Таким образом, в теории Бора различие между вычисленной орбитальной частотой электрона и частотой излучения показывало ограниченность понятия "электронная орбита". Ведь с самого начала это понятие вызывало большие сомнения. С другой стороны, в случае сильно возбужденных состояний, в которых электроны двигаются на большом расстоянии от ядра, нужно согласиться с тем, что электроны двигаются так же, как они двигаются, когда их видят в камере Вильсона. Следовательно, в этом случае можно употреблять понятие "электронная орбита". В силу этого представляется весьма удовлетворительным тот факт, что именно для сильно возбужденных состояний частота излучения приближается к орбитальной частоте (точнее говоря, к орбитальной частоте и высшим гармоническим составляющим этой частоты). Бор уже в одной из своих первых работ утверждал, что интенсивность спектральных линий излучения приблизительно должна согласовываться с интенсивностью соответствующих гармонических составляющих. Этот так называемый принцип соответствия оказался весьма полезным для приближенного расчета интенсивности спектральных линий. Таким образом, создалось впечатление, что теория Бора дает качественную, а не количественную картину того, что происходит внутри атома, и что по меньшей мере некоторые новые черты в поведении материи качественно могут быть выражены с помощью квантовых условий, которые со своей стороны как-то связаны с дуализмом волн и частиц. Точная математическая формулировка квантовой теории сложилась в конечном счете в процессе развития двух различных направлений. Одно направление было связано с принципом соответствия Бора. На этом направлении нужно было прежде всего отказаться от понятия "электронная орбита" и использовать его лишь приближенно в предельном случае больших квантовых чисел, то есть больших орбит. В этом последнем случае частота и интенсивность излучения некоторым образом соответствуют электронной орбите. Излучение соответствует тому, что математики называют "Фурье-представлением" орбиты электрона. Таким образом, вполне логична мысль, что механические законы следует записывать не как уравнения для координат и скоростей электронов, а как уравнения для частот и амплитуд их разложения Фурье. Исходя из таких представлений, возникает возможность перейти к математически представляемым отношениям для величин, которые соответствуют частоте и интенсивности излучения. Эта программа действительно могла быть осуществлена. Летом 1925 года она привела к математическому формализму, который был назван "матричной механикой", или, вообще говоря, квантовой механикой. Уравнения движения механики Ньютона были заменены подобными уравнениями для линейных алгебраических форм, которые в математике называются матрицами. Весьма удивительно, что многие из старых результатов механики Ньютона, как, например, сохранение энергии, остались и в новом формализме. Позднее исследования Борна, Иордана и Дирака показали, что матрицы, представляющие координаты и импульс электрона, не коммутируют друг с другом. На языке математики этот факт указывал на самое сильное из существенных различий между квантовой механикой и классической механикой. Другое направление исходило из идей де Бройля о волнах материи. Шредингер попытался записать волновое уравнение для стационарных волн де Бройля, окружающих атомное ядро. В начале 1926 года ему удалось вывести значения энергии для стационарных состояний атома водорода в качестве собственных значений своего волнового уравнения, и он сумел дать общее правило преобразования данных классических уравнений в соответствующие волновые уравнения, которые, правда, относятся к некоторому абстрактному математическому пространству, именно многомерному конфигурационному пространству. Позднее он показал, что его волновая механика математически эквивалентна более раннему формализму квантовой или матричной механики. Таким образом, мы получили наконец непротиворечивый математический формализм, который можно выразить двумя равноправными способами: или с помощью матричных соотношений, или с помощью волновых уравнений. Этот математический формализм дал верные значения энергии для атома водорода. Понадобилось меньше года, чтобы обнаружить, что верные результаты получаются и для атома гелия и в более сложном случае -- для тяжелых атомов. Однако собственно в каком смысле новый формализм описывает атомные явления? Ведь парадоксы корпускулярной и волновой картины еще не были решены, они только содержались в скрытом виде в математической схеме. В направлении действительного понимания квантовой теории первый и очень интересный шаг уже в 1924 году был сделан Бором, Крамерсом и Слэтером3. Они попытались устранить кажущееся противоречие между волновой и корпускулярной картинами с помощью понятия волны вероятности. Электромагнитные световые волны толковались не как реальные волны, а как волны вероятности, интенсивность которых в каждой точке определяет, с какой вероятностью в данном месте может излучаться и поглощаться атомом квант света. Это представление вело к заключению, что, по-видимому, законы сохранения энергии и динамических переменных в каждом отдельном случае могут не выполняться и речь идет, следовательно, о статистических законах; так что энергия сохраняется только в статистическом среднем. В действительности этот вывод был неверен, а взаимосвязь волновой и корпускулярной картин излучения позднее оказалась еще более сложной. Однако работа Бора, Крамера и Слэтера содержала уже существенную черту верной интерпретации квантовой теории. С введением волны вероятности в теоретическую физику было введено совершенно новое понятие, В математике или статистической механике волна вероятности означает суждение о степени нашего знания фактической ситуации. Бросая кость, мы не можем проследить детали движения руки, определяющие выпадение кости, и поэтому говорим, что вероятность выпадения отдельного номера равно одной шестой, поскольку кость имеет шесть граней. Но волна вероятности, по Бору, Крамерсу и Слэтеру, была чем-то гораздо большим. Она означала нечто подобное стремлению к определенному протеканию событий. Она означала количественное выражение старого понятия "потенция" аристотелевской философии. Она ввела странный вид физической реальности, который находится приблизительно посредине между возможностью и действительностью. Позднее, когда было закончено математическое оформление квантовой теории, Борн использовал эту идею волны вероятности и дал на языке формализма ясное определение математической величины, которую можно интерпретировать как волну вероятности. Волна вероятности являлась не трехмерной волной типа радиоволн или упругих волн, а волной в многомерном конфигурационном пространстве. Эта абстрактная математическая величина стала известной благодаря исследованиям Шредингера.

Даже в это время, летом 1926 года, еще не в каждом случае было ясно, как следует использовать математический формализм, чтобы дать описание данной экспериментальной ситуации. Правда, тогда уже знали, как описывать стационарные состояния, но не было еще известно, как объяснить гораздо более простые явления, например движение электрона в камере Вильсона. Когда летом 1926 года Шредингер показал, что формализм его волновой механики математически эквивалентен квантовой механике, он в течение некоторого времени совсем отказывался от представления о квантах и квантовых скачках и пытался заменить электроны в атоме трехмерными волнами материи. Поводом к такой попытке было то, что, по его теории, уровни энергии атома водорода являются собственными частотами некоторых стационарных волн. Поэтому Шредингер полагал, что будет ошибкой считать их значениями энергии; они являются частотами, а вовсе не энергией; однако во время дискуссии, которая происходила в Копенгагене осенью 1926 года между Бором и Шредингером и копенгагенской группой физиков, стало очевидным, что такая интерпретация недостаточна даже для объяснения планковского закона теплового излучения 4. В течение нескольких месяцев, последовавших за этой дискуссией, интенсивное изучение в Копенгагене всех вопросов, связанных с интерпретацией квантовой теории, привело наконец к законченному и, как считают многие физики, удовлетворительному объяснению всей ситуации. Однако оно не было тем объяснением, которое можно было легко принять. Я вспоминаю многие дискуссии с Бором, длившиеся до ночи и приводившие нас почти в отчаяние. И когда я после таких обсуждений предпринимал прогулку в соседний парк, передо мною снова и снова возникал вопрос, действительно ли природа может быть такой абсурдной, какой она предстает перед нами в этих атомных экспериментах. Окончательное решение пришло с двух сторон. Один из путей сводился к переформулировке вопроса. Вместо того чтобы спрашивать, как можно данную экспериментальную ситуацию описывать с помощью известной математической схемы, ставится другой вопрос: верно ли, что в природе встречается только такая экспериментальная ситуация, которая выражается в математическом формализме квантовой теории? Предположение, что это верная постановка вопроса, вело к ограничению применения понятий, со времени Ньютона составлявших основу классической физики. Правда, можно было говорить, как в механике Ньютона, о координате и скорости электрона. Эти величины можно и наблюдать и измерять. Но нельзя обе эти величины одновременно измерять с любой точностью. Оказалось, что произведение этих обеих неопределенностей не может быть меньше постоянной Планка (деленной на массу частицы, о которой втданном случае шла речь).

Подобные соотношения могут быть сформулированы для других экспериментальных ситуаций. Они называются соотношением неточностей или принципом неопределенности. Тем самым было установлено, что старые понятия не совсем точно удовлетворяют природе. Другой путь был связан с понятием дополнительности Бора. Шредингер описывал атом как систему, которая состоит не из ядра и электронов, а из атомного ядра и материальных волн. Несомненно, эта картина волн материи также содержит долю истины. Бор рассматривал обе картины -- корпускулярную и волновую -- как два дополнительных описания одной и той же реальности. Каждое из этих описаний может быть верным только отчасти. Нужно указать границы применения корпускулярной картины, так же как и применения волновой картины, ибо иначе нельзя избежать противоречий. Но если принять во внимание границы, обусловленные соотношением неопределенностей, то противоречия исчезают. Таким образом, в начале 1927 года пришли наконец к непротиворечивой интерпретации квантовой теории, которую часто называют копенгагенской интерпретацией. Эта интерпретация выдержала испытание на Сольвеевском конгрессе в Брюсселе осенью 1927 года. Те эксперименты, которые вели к досадным парадоксам, вновь дискутировались во всех подробностях, особенно Эйнштейном. Были найдены новые мысленные эксперименты с целью обнаружить оставшиеся внутренние противоречия теории, однако теория оказалась свободной от них и, по-видимому, удовлетворяла всем экспериментам, которые были известны к тому времени.

Детали этой копенгагенской интерпретации составляют предмет следующей главы. Быть может, следует указать на тот факт, что потребовалось более четверти века на то, чтобы продвинуться от гипотезы Планка о существовании кванта действия до действительного понимания законов квантовой теории. Отсюда понятно, как велики должны быть изменения в наших основных представлениях о реальности, для того чтобы можно было окончательно понять новую ситуацию.

ru.phylo.wikia.com

Копенгагенская интерпретация | Virtual Laboratory Wiki

Распространённость среди учёных Править

Смысл волновой функции Править

Копенгагенская интепретация предполагает, что на волновую функцию могут влиять два процесса:

Данный опыт ставит следующие вопросы:

Законы квантовой механики говорят о том, где частицы попадут в экран статистически и дают возможность рассчитать местоположение светлых полос, куда скорее всего попадёт много частиц и местоположение тёмных полос, куда скорее всего попадёт мало частиц. Однако, для отдельной частицы, законы квантовой механики не могут предсказать, где она фактически окажется. Каковы в таком случае правила поведения отдельных частиц?
Что происходит с частицей между моментом испускания и моментом регистрации? Создаётся впечатление, что частица претерпевает взаимодействие с обеими щелями и это кажется противоречащим тому, как может себя вести точечная частица, тем более, что когда частица регистрируется, она оказывается точечной.
Что заставляет частицу переключаться от статистического к нестатистическому поведению и обратно? Когда частица летит сквозь щели, её поведение описывается нелокализованной волновой функцией, которая одновременно проходит через обе щели. А когда частица регистрируется, никогда не получается размытый волновой пакет, а всегда получается точечная частица.

Копенгагенская интерпретация отвечает на эти вопросы так:

Вероятностный характер предсказаний квантовой механики принципиально неустраним, то есть, он вовсе не говорит о том, что наши знания ограничены, что мы не знаем значений каких-то скрытых переменных. В классической физике вероятность использовалась для описания результатов типа подбрасывания игральной кости, хотя фактически этот процесс считался детерминированным. То есть, вероятности использовались вместо неполного знания. Напротив, копенгагенская интерпретация утверждает, что в квантовой механике результат измерения принципиально недетерминирован.
Физика — это наука о результатах измерительных процессов. Измышления на тему того, что происходит за ними неправомерны. Копенгагенская интерпретация отбрасывает вопросы типа «где была частица до того, как я зарегистрировал её местоположение» как бессмысленные.
Акт измерения вызывает мгновенное схлопывание, «коллапс волновой функции». Это означает, что процесс измерения случайно выбирает в точности одну из возможностей, допустимых волновой функцией данного состояния, а волновая функция мгновенно изменяется, чтобы отразить этот выбор.

Многие физики склоняются к так называемой «никакой» интерпретации квантовой механики, ёмко выраженной в афоризме Поля Дирака: «Заткнись и считай!» (часто (видимо, по ошибке) приписываемом Ричарду Фейнману).

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Копенгагенская интерпретация. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

ru.vlab.wikia.com