Квантовая теория против гравитации: загадка наконец разгадана? Квантовая теория пули

«Бом-Бом»: подтверждена верность альтернативной квантовой теории | Futurist

Автор: Александра Алборова |  10 июня 2016, 11:40

Значительно уступая доминирующей копенгагенской интерпретации, механика Бома десятилетиями подвергалась критике как слишком упрощенный взгляд на квантовую механику. Детерминизм (причинно-следственная связь) этой интерпретации, которая была разработана еще в 1927 г., был описан математически, но на практике был назвал «сюрреалистичным». Несмотря на это, сторонники теории не оставляют попыток доказать ее состоятельность – эксперимент ученых университета Торонто может стать достойным ответом на критику и повысить популярность механики Бома.

Из многих противоречивых здравому смыслу особенностей квантовой механики, пожалуй, самым сложным для нашего представления является то, что частицы не имеют определенного местоположения, пока они не наблюдаются. Это именно то, что стандартное представление о квантовой механике, часто называемое копенгагенской интерпретацией, принимает за истину. Вместо четких позиций и движений ньютоновской физики, эта интерпретация квантовой механики представляет множество вероятностей, описываемых математической структурой, известной как волновая функция. Она же развивается с течением времени, и ее эволюция во времени регулируется четкими правилами, заданными уравнением Шредингера. Математические расчёты достаточно ясны, чего нельзя сказать о фактическом местонахождение частиц. Таким образом, до тех пор пока частица не наблюдается кем-либо, мы ничего не можем сказать о ее местонахождении. Одним из противников данного предположения являлся Альберт Эйнштейн, который задал ставший довольно известным в этом отношении вопрос: «Действительно ли вы считаете, что Луна существует только тогда, когда вы на нее смотрите?».

Но существует другой взгляд на квантовую механику — так называемая теория волны-пилота (или механика Бома). Она была впервые разработана в 1927 году Луи де Бройлем и вновь открыта в независимом от Бройля в исследовании Дэвида Бома в 1952 году, который продолжал совершенствовать ее до своей смерти в 1992 (из-за чего ее также называют теорией де Бройля-Бома). Однако ни 20-х, ни в 50-х теория не обрела популярности из-за доминирования копенгагенской интерпретации, с которой она расходилась. Согласно механике Бома, существует волновая функция, чья эволюция во времени задается уравнением Шредингера, а каждая частица всегда имеет определенное местоположение, даже когда она не измеряется кем-то. Изменения позиции частиц задаются другим уравнением, известным как уравнение волны-пилота (или управляющее уравнение). Данная теория основывается на понятии детерминизма – если вы знаете изначальные данные системы и имеете волновую функцию, вы можете определить положение любой частицы. Кроме того, механика Бома абсолютно нелокальная – траектория одной частицы напрямую зависит от положения и скорости других частиц, описанных той же волновой функцией. Границы системы этой функции не определены, то есть, теоретически, вся Вселенная может являться рассматриваемой системой. Это значит, что по сути, все элементы Вселенной взаимосвязаны, вне зависимости от расстояний.

«Волновая функция сочетает или связывает в себе удаленные друг от друга частицы в единую реальность,» — говорит Шелдон Голдштейн (Sheldon Goldstein), математик и физик университета Рутгерса.

Различия механики Бома и копенгагенской интерпретации можно пронаблюдать в ходе классического эксперимента с двумя щелями, в котором пучок частиц (например, электронов), проходит через барьер с двумя щелями и отображается на экране, где каждая частица фиксируется. Получаемая картина показывает интерференционные полосы, то есть электроны ведут себя как волны, происходящие из двух источников — щелей. Однако даже если электроны направляются по одному за раз, их отображение не меняется, что позволяет предположить, что один электрон проходит через две щели одновременно. Также, при одной закрытой щели никакой интерференционной картины мы не увидим.

Согласно копенгагенской интерпретации, в этом нет ничего удивительного — ведь мы не можем говорить о положении частицы до того как ее измерим.

Однако, если мы обратимся к механике Бома, то в ней электроны ведут себя как фактические частицы, их скорость в любой момент времени определена волной-пилотом, которая основывается на волновой функции. Таким образом, каждый электрон занимает определенное место, но при этом его движение подчиняется движению распространяемой волны, которая распределяется через оба отверстия, тогда как сами частицы проходят лишь через одно.

«Все, что нам надо сделать, чтобы понять квантовую механику в таком случае – это сказать себе «Когда мы говорим о частицах, мы действительно имеем в виду частицы». И все проблемы исчезнут», — говорит Голдштейн. — «У каждой вещи есть свое положение, все где-то находится. Если вы всерьез об этом задумаетесь, то это немедленно приведет вас к механике Бома. Эта теория квантовой механики намного легче».

Однако на протяжении своего существования теория серьезно оспаривалась, наиболее значимой критической работой стала «ESSW» (акроним по фамилиям авторов), в которой говорилось, что данная теория представляет упрощенную траекторию, по которой не могут следовать частицы. Авторы указывали, что если бы на каждом отверстии в ходе эксперимента находился датчик, записывающий каждую проходящую частицу, то, по механике Бома, фотон мог бы пройти через левое отверстие, но при этом быть зафиксирован проходящим через правое. Такая возможность показалась авторам «сюрреалистической».

Эфраим Штайнберг (Aephraim Steinberg) из университета Торонто (Канада) говорил, что доводы ESSW подорвали его увлечение механикой Бома. Однако он нашел способ вернуть интерес к теории. В статье, опубликованной в издании Science Advances, Штайнберг и его коллеги описали что произойдет при реальном проведении эксперимента ESSW. Они установили, что траектория фотонов не такая невероятная, как это представлялось, — точнее, она может показаться невероятной, только если не будет учитываться нелокальность, свойственная теории.

Эксперимент, который провела команда Штайнберга, являлся аналогом классического эксперимента с двумя щелями, однако вместо электронов использовались фотоны, которые проходили не через два отверстия, а через расщепитель луча, устройство, направляющее фотон по одному из двух путей в зависимости от его поляризации. В итоге, фотоны достигали однофотонной камеры (вместо экрана в оригинальном эксперименте), которая записывала их конечное положение.

Также ученые использовали пары запутанных фотонов (взаимозависимых), в результате чего они могли через один фотон получать информацию о другом. То есть, когда один фотон проходит по одному из двух путей, второй уже знает какой это был путь. Конечно, такие косвенные измерения имеют лишь приблизительное значение, но исследователям удалось усреднить получаемые данные для восстановления траектории первого фотона.

Как и говорилось в статье ESSW, фотон иногда появлялся в противоположной тому, какую траекторию предсказывала его пара, части экрана.

Однако Штайнберг и его коллеги пришли к выводу, что ответ на вопрос «По какой траектории двигается фотон?» зависит от того, когда он задан. Как только фотон проходит через расщепитель, его парный фотон передает крайне точную информацию о его траектории. Однако чем дальше первый фотон от второго, тем менее точной становится информация о нем – причиной этому является та сама нелокальность. Принцип локальности предполагает, что на объект влияет только его непосредственно близкое окружение. Но в эксперименте с квантово запутанными фотонами траектория первого фотона прямо влияет на поляризацию второго, который будет двигаться по той же траектории.

«Здесь нет никакого противоречия, – говорит Штайнберг. – Вы просто всегда должны помнить о нелокальности теории».

Некоторые физики не очень удивлены результатами Штайнберга, так как давно придерживались мнения о верности механики Бома. Однако результаты этого эксперимента должны дать старт серьезному обсуждению теории, считает Оуэн Марони (Owen Maroney), физик Оксфордского университета. В то же время, один из авторов ESSW Бертхолд-Джордж Энглерт (Berthold-Georg Englert) все еще считает, что их статья являлась «смертельным ударом» интерпретации Бома. По его мнению, эти траектории существуют как математические объекты, но «без физического значения».

Интересно, что Альберт Эйнштейн еще в 1952 году, после того, как Бом заново предложил теорию Бройля, в своем письме другому физику Максу Борну указывал, что данная интерпретация слишком упрощенная для того, чтобы быть реалистичной.

Однако даже для сторонников теории важным вопросом остается то, что механика Бома, таким образом, подразумевает коммуникацию между частицами быстрее, чем скорость света. Конечно, физики давно установили, что нелокальность квантовой запутанности не может допустить связи быстрее скорости света. Однако с ключевой ролью нелокальности в механике Бома, многие ученые считают, что необходимы пояснения взаимосвязи того что происходит «здесь» и того что может произойти «там».

Понравилась статья?

Поделись с друзьями!

  Поделиться 0   Поделиться 0   Твитнуть 0

Подпишись на еженедельную рассылку

futurist.ru

2. Теория «магической пули»

Первые представления о природе и силе массовой коммуника­ции. существовавшие в то время (Первая мировая война), фактически не были обобщены, но ретроспективно их стали называть теорией «магической пули». (Были и другие, не менее звучные н звания, например «теория инъекций» или «теория приводного ремня».) Основная мысль заключается в том, что сообщения масс- медиа принимаются всеми членами аудитории одинаково и такие стимулы вызывают мгновенные и непосредственные отклики.

Сегодня, когда о процессе массовой коммуникации известно намного больше, теория «магической пули» может показаться наи­вной и простодушной, но она полностью соответствовала теоре­тическим воззрениям в социологии и психологии того времени. Кроме того, был пример огромного воздействия военной пропа­ганды. Это казалось надежным доказательством того, что сила средств массовой коммуникации действительно так велика, как эмоционально описал Лассуэлл, назвав их «новыми молотом и наковальней социальной солидарности»3. Кроме того, якобы на ос­нове неоспоримых фактов о силе массовой рекламы того времени можно было сделать вывод о том, что медиа способны заставить людей покупать товары в неслыханном прежде количестве и ассор­тименте.

Пропаганда привлекла внимание первых теоретиков медиа, так как угрожала подорвать сами основы американской политической системы и демократического правления, где бы то ни было. К кон­цу 1930-х годов многие (если не большинство) американские ли­деры были убеждены, что демократия не выживет, если разре­шить свободное распространение экстремистской пропаганды. Нo запрет означал бы существенное ограничение самого важного прин­ципа западной демократии — свободы коммуникации. Теоретики пропаганды стремились понять и разрешить эту дилемму.

Вначале отдельные специалисты считали, что общественность можно научить противостоять пропаганде. В конце концов, про­паганда нарушает самые основные правила равноправной демок­ратической политической коммуникации. Она беззастенчиво пользуется ложью и обманом в целях убеждения. Если бы людей можно было научить критически оценивать пропагандистские сообщения, они знали бы, что эти сообщения надо отвергать как бесчестные и лживые.

Эти эксперты полагали, что демократию можно спасти путем просвещения народа. Но оптимизм по этому поводу исчезал по мере того, как в 1930-е годы в Америку из Европы стали про­никать новые веяния. Все больше и больше американцев, особенно иммигранты первого поколения, предпочитали слушать лидеров тоталитаризма, обещавших социальную справедливость и работу. Они вступали в общественные движения, которые базировались на пропаганде, более или менее откровенно заимствованной у Европы. На манифестациях в поддержку Гитлера и Сталина разда­вшись требования покончить с низшими расами и финансовыми воротилами с Уолл-стрит.

Специалисты в области пропаганды поняли, что даже если просвещение народа поможет противостоять пропаганде, этот про­цесс может оказаться слишком длительным. Поэтому теоретики пропаганды отказались от идеализма в пользу идей, которые, как они считали, реалистичны и основываются на научных фактах. С пропагандой нужно бороться всеми возможными средствами. Если бы найти способ использовать мощь пропаганды для распростра­нения идеалов доброты и справедливости, тогда можно было бы не только выдержать ее натиск, но и иметь инструмент создания более совершенного общественного порядка.

Именно это обещала стратегия использования положительных пропагандистских при­емов для борьбы с «плохой» пропагандой и содействия целям, которые элита считала хорошими, так называемая белая пропаганда. После Второй мировой войны эти приемы белой пропаган­ды легли в основу рекламных кампаний.

Наибольший интерес представляют теории пропаганды трех самых известных мыслителей своего времени — Гарольда Лассуэлла, Уолтера Липманна и Джона Дьюи. Почти все они в дальней­шем пересмотрели многие из своих идей, а от некоторых вовсе отказались.

studfiles.net

Теория «магической пули»

Первые представления о природе и силе массовой коммуника­ции, существовавшие в то время (Первая мировая война), факти­чески не были обобщены, но ретроспективно их стали называть теорией «магической пули». (Были и другие, не менее звучные названия, например «теория инъекций» или «теория приводного ремня».) Основная мысль заключается в том, что сообщения масс-медиа принимаются всеми членами аудитории одинаково и такие стимулы вызывают мгновенные и непосредственные отклики.

Сегодня, когда о процессе массовой коммуникации известно намного больше, теория «магической пули» может показаться наи­вной и простодушной, но она полностью соответствовала теоре­тическим воззрениям в социологии и психологии того времени. Кроме того, был пример огромного воздействия военной пропа­ганды. Это казалось надежным доказательством того, что сила средств массовой коммуникации действительно так велика, как эмоционально описал Лассуэлл, назвав их «новыми молотом и наковальней социальной солидарности»1. Кроме того, якобы на ос­нове неоспоримых фактов о силе массовой рекламы того времени можно было сделать вывод о том, что медиа способны заставить людей покупать товары в неслыханном прежде количестве и ассор­тименте. Это убеждение укрепляло уверенность в огромной силе ме­диа и усиливало кажущуюся достоверность теории «магической пули».

В основе теории «магической пули» лежали предположения, ко­торые теперь отвергаются теоретиками, и, как следствие, исследо­вателям масс-медиа пришлось весьма неохотно от нее отказаться. В конце 1920-х и начале 1930-х годов у ученых появился интерес к медиа как к предмету исследовании. Они перешли от простых рас­суждений об эффектах к систематическому изучению влияния кон­кретного содержания на определенные категории людей.

Пропаганда привлекла внимание первых теоретиков медиа, так как угрожала подорвать сами основы американской политической системы и демократического правления где бы то ни было. К кон­цу 1930-х годов многие (если не большинство) американские ли­деры были убеждены, что демократия не выживет, если разре­шить свободное распространение экстремистской пропаганды. Но запрет означал бы существенное ограничение самого важного прин­ципа западной демократии — свободы коммуникации. Теоретики пропаганды стремились понять и разрешить эту дилемму.

Вначале отдельные специалисты считали, что общественность можно научить противостоять пропаганде. В конце концов, про­паганда нарушает самые основные правила равноправной демок­ратической политической коммуникации. Она беззастенчиво пользуясь ложью и обманом в целях убеждения. Если бы людей можно было научить критически оценивать пропагандистские сообщения, они знали бы, что эти сообщения надо отвергать как бесчестные и лживые. Эти эксперты полагали, что демократию можно спасти путем просвещения народа. Но оптимизм по этому поводу исчезал по мере того, как в 1930-е годы в Америку из Европы стали про­никать новые веяния. Все больше и больше американцев, особенно иммигранты первого поколения, предпочитали слушать лидеров тоталитаризма, обещавших социальную справедливость и работу. Они вступали в общественные движения, которые базировались на пропаганде, более или менее откровенно заимствованной у Европы. На манифестациях в поддержку Гитлера и Сталина разда­вались требования покончить с низшими расами и финансовыми воротилами с Уолл-стрит.

Специалисты в области пропаганды поняли, что даже если про­свещение народа поможет противостоять пропаганде, этот про­цесс может оказаться слишком длительным. Поэтому теоретики пропаганды отказались от идеализма в пользу идей, которые, как они считали, реалистичны и основываются на научных фактах. С пропагандой нужно бороться всеми возможными средствами. Если бы найти способ использовать мощь пропаганды для распростра­нения идеалов доброты и справедливости, тогда можно было бы не только выдержать ее натиск, но и иметь инструмент создания более совершенного общественного порядка. Именно это обещала стратегия использования положительных пропагандистских при­емов для борьбы с «плохой» пропагандой и содействия целям, которые элита считала хорошими, так называемая белая пропа­ганда. После Второй мировой войны эти приемы белой пропаган­ды легли в основу рекламных кампаний.

Наибольший интерес представляют теории пропаганды трех самых известных мыслителей своего времени — Гарольда Лассуэлла, Уолтера Липманна и Джона Дьюи. Почти все они в дальней­шем пересмотрели многие из своих идей, а от некоторых вовсе отказались.

1Lasswell H. Op. cit. P. 221.

studfiles.net

Человек космический|Письма с границы между тенью и светом

Брайан Грин. Теория струн

Квантовая механика

Квантовая теория

Точно так же, как специальная и общая теории относительности потребовали решительного пересмотра нашего взгляда на мир для случая объектов, которые движутся очень быстро или имеют большую массу, квантовая механика установила, что наша Вселенная имеет такие же, если еще не более поразительные свойства, если исследовать ее в масштабе атомных и субатомных расстояний. В 1965 г. Ричард Фейнман, один из величайших специалистов в области квантовой механики, писал: «Было время, когда газеты сообщали, что только двенадцать человек понимают теорию относительности. Я не верю, что такое время когда-либо было. Могло быть время, когда ее понимал только один человек, который схватил ее суть перед тем, как написать свою статью. Но после того как люди прочитали его статью, масса людей стала так или иначе понимать теорию относительности, и уж точно число этих людей превышало двенадцать. С другой стороны, я думаю, что могу совершенно спокойно сказать, что квантовую механику не понимает никто.»

 

На кухне слишком жарко

Путь к квантовой механике начался в начале XX столетия с одной сбивающей с толку проблемы. Используя установленные в XIX веке законы термодинамики, физики рассчитали общее количество энергии, переносимой электромагнитным излучением в некоем замкнутом объеме (например, духовке), находящемся при заданной температуре. Получалось, что при любой заданной температуре общая энергия оказывалась бесконечной, что являлось очевидным нонсенсом – духовка может дать значительное количество энергии, но уж точно не бесконечное. В 1900 г. Планк высказал удивительную гипотезу, позволившую решить эту головоломку и принесшую ему Нобелевскую премию по физике.

Макс Планк предположил, что количество энергии, переносимой волной, изменяется порциями. Энергия может быть равно одному такому фундаментальному «номиналу энергии», или двум, или трем и т.д. – но это все. Согласно Планку, когда речь идет об энергии, доли недопустимы, точно так же, как вы не можете иметь монету в одну треть цента. Планк предположил, что энергетический номинал волны, т.е. минимальное количество энергии, которое она может нести, определяется ее частотой, точнее, что оно пропорционально ее частоте: большая частота (и более короткая длина волны) предполагает большую минимальную энергию, меньшая частота (и большая длина волны) – меньшую минимальную энергию. Он вывел коэффициент пропорциональности между частотой волны и минимальным количеством энергии – постоянная Планка. Ничтожно малая величина постоянной Планка означает, что размер порций энергии обычно очень мал. По этой причине нам, например, кажется, что мы заставляем энергию волны, создаваемой струной скрипки (и, следовательно, громкость звука), изменяться непрерывно. В действительности, однако, энергия волны изменяется дискретными шагами согласно формуле Планка, но размер этих шагов настолько мал, что дискретные скачки от одного уровня громкости к другому кажутся нам плавными переходами. По утверждению Планка, амплитуда этих скачков энергии растет по мере увеличения частоты волны (сопровождаемого уменьшением длины волны). Это тот основной момент, который разрешает парадокс бесконечной энергии. Однако квантовая гипотеза Планка пошла гораздо дальше и опрокинула многое из того, что мы считали само собой разумеющимся.

 

Что представляют собой порции

Планк не мог обосновать гипотезу дискретности энергии волн, играющую центральную роль в предложенном им решении. За исключением того, что это работает, ни у Планка, ни у кого-либо еще не было никакого рационального объяснения, почему все должно быть именно так. Как однажды заметил физик Георгий Гамов, это подобно тому, как если бы природа разрешала либо пить целый литр пива, либо не пить совсем, не допуская никаких промежуточных доз. В 1905 г. Эйнштейн нашел объяснение, за которое также получил Нобелевскую премию.

Эйнштейн показал, что гипотеза Планка о дискретности энергии на самом деле отражает фундаментальное свойство электромагнитных волн: они состоят из частиц – фотонов, которые представляют собой маленькие порции или кванты света. Дискретность энергии, заключенной в таких волнах, связана с тем, что они состоят из дискретных объектов.

Прозрение Эйнштейна представляло собой большой шаг вперед, однако история была не такой гладкой, как может показаться.

 

Волна или частица

Дело в том, что более трехсот лет назад Ньютон провозгласил, что свет представляет собой поток частиц, так что сама идея была не нова. Однако ряд коллег Ньютона, в частности, Гюйгенс, оспаривали это мнение, утверждая, что свет представляет собой волну. Долгое время этот вопрос был предметом ожесточенных дебатов, пока эксперименты, выполненные в начале XIX в. Томасом Юнгом, не показали, что Ньютон ошибался. 

 

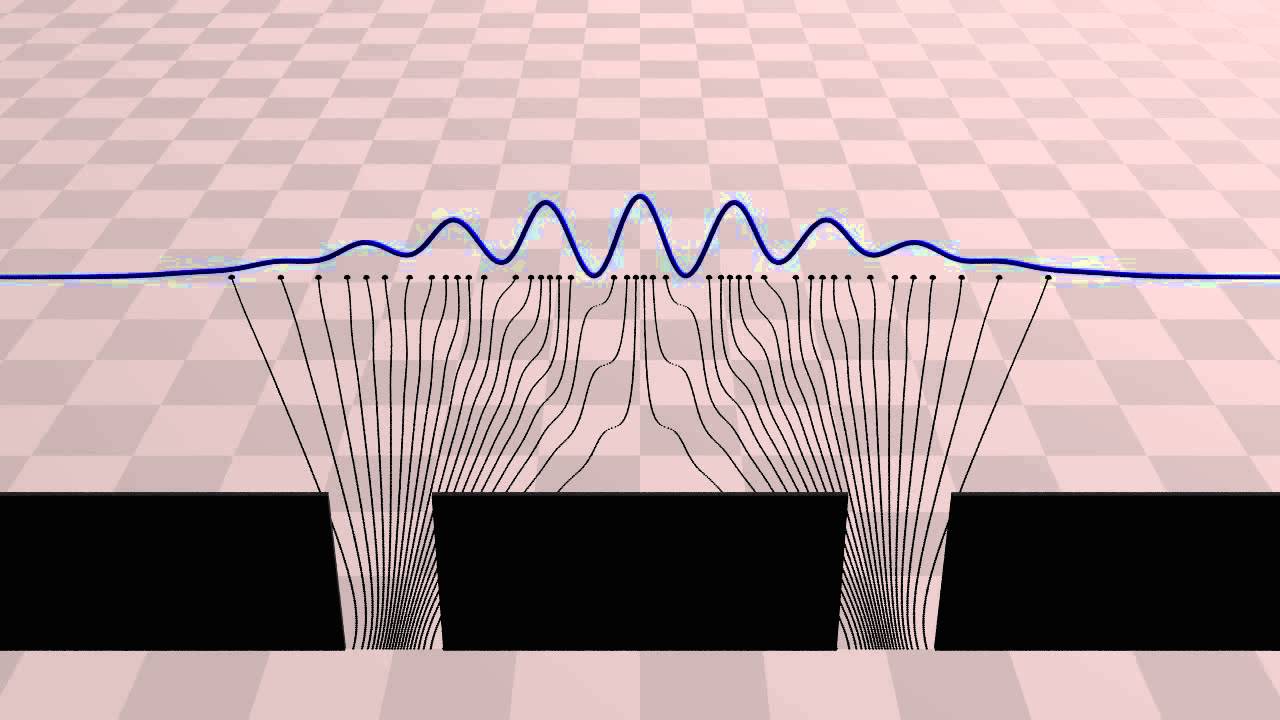
Вариант установки в эксперименте Юнга, известного под названием опыта с двумя щелями, схематически показан на рис. 4.3. Свет падает на сплошную преграду, в которой сделаны две щели. Свет, который прошел через щели, регистрируется на фотопластинке – более светлые места на фотографии указывают на те места, куда попало больше света. Если левая щель закрыта, а правая открыта, фотография будет выглядеть, как показано на рис. 4.4. Аналогично, если мы закроем правую щель, а левую оставим открытой, фотография будет выглядеть, как показано на рис. 4.5. Если открыты обе щели, то картина, предсказываемая ньютоновской корпускулярной моделью света должна выглядеть, как показано на рис. 4.6, представляющем собой комбинацию рис. 4.4 и 4.5. Однако эксперимент Юнга показал, что в действительности на фотографии появлялась интерференционная картина, показанная на рис. 4.8 – чередование светлых и темных полос, свидетельствующее о волновой природе света. 

 

Но Эйнштейн, низвергнувший заслуженную теорию гравитации Ньютона, похоже, возродил ньютоновскую корпускулярную модель света, введя понятие фотонов. Конечно, перед нами по-прежнему стоит вопрос: как объяснить интерференционную картину, показанную на рис. 4.8? На первый взгляд можно предложить следующее объяснение: вода состоит из молекул, «частиц» воды, однако когда огромные количества этих молекул движутся в одном потоке, они могут создавать волны на поверхности воды, с присущими этим волнам интерференционными свойствами. Можно предположить, что в корпускулярной модели света волновые эффекты, например, интерференционные картины, возникают благодаря взаимодействию огромного числа световых «частиц» - фотонов.

В действительности, однако, микромир устроен гораздо более тонко. Даже если интенсивность источника света на рис. 4.8 начнет уменьшаться вплоть до такого значения, когда в сторону преграды один за другим будут излучаться одиночные фотоны со скоростью, скажем, один фотон в десять секунд, результат на фотопластинке будет выглядеть точно так же, как показано на рис. 4.8. Если вы подождете достаточно долго, чтобы огромное число этих отдельных частиц света прошло через щели и оставило свой след в виде точек на фотопластинках, эти точки образуют показанную на рис. 4.8 интерференционную картину. Это поразительно. Как могут отдельные фотоны, последовательно проходящие через экран и независимо сталкивающиеся с фотопластинкой, «сговориться» и воспроизвести яркие и темные полосы интерференционной картины? Каким-то образом отдельные фотоны, разделенные во времени, смогли нейтрализовать друг друга. Подумайте о всей неординарности того, что произошло: фотоны, которые прошли через правую щель и попали на пленку, образуя светлую полосу на рис. 4.4, не смогли сделать этого при открытой левой щели на рис. 4.8 - поэтому пленка на этом месте осталась темной.

Эти эксперименты показали, что частицы света Эйнштейна довольно существенно отличаются от частиц Ньютона. Каким-то образом фотоны – хотя они являются частицами – обладают также и волновыми свойствами. Тот факт, что энергия этих частиц определяется параметром, используемым для описания волн, т.е. частотой, является первым признаком того, что это странное объединение имеет место. Свет обладает и волновыми и корпускулярными свойствами. Микромир требует, чтобы при попытке его описания мы отказались от наших интуитивных представлений о том, что любой объект представляет собой либо волну, либо частицу, и чтобы мы учитывали возможность того, что он может быть волной и частицей одновременно. Это один из тех случаев, когда высказывание Фейнмана о том, что «никто не понимает квантовую механику» особенно актуально. Мы можем произносить слова типа «корпускулярно-волновой дуализм», мы можем преобразовать эти слова в математическую модель, которая воспроизведет экспериментальные данные с поразительной точностью, но добиться глубокого, интуитивного понимания этой ошеломляющей особенности микромира необычайно трудно.

 

Частицы материи тоже являются волнами

В 1923 г. молодой французский аристократ Луи де Бройль предположил (и тоже получил Нобелевскую премию по физике :-))), что корпускулярно-волновой дуализм применим не только к свету, но и к веществу. Его аргументы, если опустить детали, состоят в том, что эйнштейновское уравнение E=mc2 связывает массу с энергией; но с другой стороны, Планк и Эйнштейн связали энергию с частотой волн. Объединяя эти два факта, можно прийти к выводу, что масса должна иметь и волновое воплощение.

Проведенные позднее эксперименты с электронами, пропускаемыми через две щели, показали, что электроны создают интерференционную картину, подобную показанной на рис. 4.8, что является неоспоримым признаком волн. Схожие эксперименты позволили сделать вывод о том, что все вещество имеет волновые свойства. Де Бройль предложил формулу для длины волны частиц вещества, которая показывает, что длина волны пропорциональна постоянной Планка. Поскольку постоянная Планка очень мала, длина волны является также очень малой по обычным масштабам. Именно по этой причине волновые характеристики материи становятся наблюдаемыми только в высокоточных микроскопических исследованиях. Точно так же, как большая величина скорости света скрывает истинные свойства пространства и времени, малая величина постоянной Планка маскирует волновые свойства материи в окружающем нас мире.

 

Волны чего?

Проведенные эксперименты реально продемонстрировали, что электроны подобны волнам. Но при этом возникает естественный вопрос: волнам чего? Одно из первых предположений на эту тему заключалось в том, что эти волны представляют собой «размазанные» электроны. Это предположение отчасти улавливало «сущность» электронной волны, но было слишком неточным. Когда вы размазываете что-нибудь, часть его находится здесь, а другая часть в другом месте. Однако никому и никогда не приходилось иметь дело с половиной, третью или четвертью электрона. В 1926 г. Макс Борн существенно уточнил предложенную Шредингером интерпретацию электронной волны, и именно этой интерпретацией, усиленной Бором и его коллегами, мы пользуемся и сегодня. Утверждение Борна касается одного из самых странных свойств квантовой теории, тем не менее, оно подтверждается огромным количеством экспериментальных данных. Согласно этому утверждению электронная волна должна интерпретироваться с точки зрения вероятности. В тех областях, где амплитуда волны больше, обнаружение электрона более вероятно; в местах, где амплитуда мала, вероятность обнаружить электрон меньше. Пример показан на рис. 4.9. 

 

Это действительно необычная идея. Мы привыкли к тому, что вероятность присуща лошадиным бегам, подбрасыванию монеты или игре в рулетку, но в этих случаях она просто является отражением неполноты нашего знания. Напротив, квантовая механика вводит понятие вероятности в устройство мироздания на гораздо более глубоком уровне. Согласно утверждению Борна наличие у материи волновых свойств подразумевает, что фундаментальное описание материи должно иметь вероятностный характер. Для больших объектов, таких как чашка кофе, волновые свойства практически ненаблюдаемыми, но на микроскопическом уровне мы, в лучшем случае, можем указать только вероятность того, что электрон будет обнаружен в любом заданном месте.

Таким образом, согласно квантовой механике Вселенная развивается в соответствии со строгими и точными математическими законами, но эти законы определяют только вероятность того, что может наступить то или иное конкретное будущее, и ничего не говорят о том, какое будущее наступит в действительности.

Тем не менее, споры о том, что же в действительности представляет собой квантовая механика, не утихают. Все согласны в том, как использовать уравнения квантовой механики для получения точных предсказаний. Нет согласия в вопросах о том, что же в действительности представляют собой волновые функции, каким образом частица «выбирает», какому из многих вариантов будущего ей следовать. Нет согласия даже в вопросе о том, действительно ли она выбирает или вместо этого разделяется, подобно разветвляющемуся руслу реки, и живет во всех возможных будущих, в вечно расширяющемся мире параллельных вселенных.

 

Точка зрения Фейнмана

Ричард Фейнман был одним из величайших физиков-теоретиков со времен Эйнштейна. Он полностью принял вероятностную интерпретацию квантовой механики, но предложил новый взгляд на эту теорию. С позиций численных предсказаний точка зрения Фейнмана полностью согласуется с тем, что было известно ранее. Но ее формулировка существенно отличается от общепринятой.

Проблема с интерпретацией рис. 4.8 возникает потому, что в нашем представлении электрон проходит либо через левую щель, либо через правую, и поэтому мы рассчитываем увидеть комбинацию картин рис. 4.4 и 4.5, показанную на рис. 4.6. Электрону, проходящему через правую щель, должно быть все равно, существует ли левая щель, и наоборот. Но каким-то образом он ее чувствует. Получаемая интерференционная картина требует взаимодействия между чем-то, чувствительным к обеим щелям, даже если электроны выстреливаются поодиночке. Шредингер, де Бройль и Борн объясняли этот феномен, приписывая каждому электрону волновую функцию. Подобно волнам на поверхности воды, волны функции плотности вероятности электрона «видят» обе щели и испытывают своего рода интерференцию при наложении. На тех участках, где вероятностная волна усиливается при наложении, обнаружение электрона вероятно, а там, где вероятностная волна ослабляется при наложении, обнаружение электрона маловероятно или невероятно. Электроны сталкиваются с фосфоресцирующим экраном один за другим, распределенные в соответствии с функцией плотности вероятности и, в конечном итоге, образуют интерференционную картину, схожую с той, которая показана на рис. 4.8.

Фейнман выбрал другой подход. Он усомнился в основном классическом предположении, согласно которому электрон проходит либо через левую щель, либо через правую. На первый взгляд это предположение настолько фундаментально, что сомневаться в нем нелепо. В конце концов, разве вы не можете заглянуть в область, расположенную между щелями и фосфоресцирующим экраном, и посмотреть, сквозь какую щель проходит каждый электрон? Да, вы можете. Но тем самым вы измените эксперимент. Электрон – ничтожно малая частица материи. Независимо от того, насколько осторожно вы будете определять щель, через которую он прошел, отражающиеся от электрона фотоны неизбежно повлияют на его последующее движение. А это изменение движения изменит результат нашего эксперимента. Квантовый мир гарантирует, что как только вы установили, через какую щель, правую или левую, прошел каждый электрон, интерференция между этими двумя щелями исчезнет.

Таким образом, хотя повседневный опыт говорит о том, что электрон должен проходить через одну из двух щелей, к концу 1920-х гг. физики поняли, что любая попытка проверить это якобы фундаментальное свойство неизбежно приведет к искажению результатов эксперимента.

Фейнман провозгласил, что каждый электрон, который проходит через преграду и попадает на фосфоресцирующий экран, проходит через обе щели. Это звучит дико, но вас ждут еще более сумасшедшие заявления. Фейнман высказал утверждение, что на отрезке от источника до некоторой точки на фосфоресцирующем экране каждый отдельно взятый электрон на самом деле перемещается по всем возможным траекториям одновременно; некоторые из этих траекторий показаны на рис. 4.10. Электрон вполне упорядоченным образом проходит через левую щель. Одновременно он столь же упорядоченно проходит через правую щель. Он направляется к левой щели, но вдруг меняет направление и устремляется к правой. Он петляет вперед и назад и, наконец, проходит сквозь левую щель. Он отправляется к туманности Андромеды, там он разворачивается, возвращается назад и проходит через левую щель на пути к экрану. Он движется и так, и этак – согласно Фейнману, электрон одновременно «рыщет» по всем возможным путям, соединяющим пункт отправления и пункт назначения. 

 

Фейнман показал, что каждому из этих путей можно поставить в соответствие некоторое число, и общее среднее этих чисел даст ту же вероятность, что и расчет с использованием волновой функции. Итак, с точки зрения Фейнмана, с электроном не нужно связывать никакой вероятностной волны. Вероятность того, что электрон, – который во всех отношениях проявляет себя частицей, - появится в некоторой заданной точке экрана, определяется суммарным эффектом от всех возможных путей, ведущих в эту точку. Этот подход к квантовой механике известен как фейнмановское «суммирование по путям».

Как показал Фейнман, для движения больших тел, таких как бейсбольные мячи, аэропланы или планеты, его правило определения весов различных траекторий гарантирует, что все траектории, кроме одной, взаимно сократятся при суммировании их вкладов. В действительности, когда дело касается движения классического тела, значение имеет только одна траектория из бесконечного их количества. И это именно та траектория, которая следует из ньютоновских законов движения. Вот почему в нашем повседневном мире нам кажется, что тела (такие как брошенный в воздух мяч) следуют вдоль единственной, уникальной и предсказуемой траектории из начальной точки в пункт назначения. Но для объектов микромира фейнмановское правило назначения весов траекториям показывает, что свой вклад в движение объекта могут вносить (и часто вносят) многочисленные возможные траектории. В микромире мы не можем гарантировать, что электрон пройдет только через одну щель или только через другую.

 

Соотношение неопределенностей

Квантовую механику трудно понять на интуитивном уровне, еще труднее, чем теорию относительности. Существует, однако, одно положение этой теории, которое может служить путеводителем для интуиции – это соотношение неопределенностей, открытое Вернером Гейзенбергом в 1927 г.

Это соотношение выросло из проблемы, с которой мы уже сталкивались выше. Мы установили, что процедура определения щели, через которую проходит каждый из электронов, неизбежно вносит возмущения в их последующее движение. Когда волна направляется на объект, она позволяет определить положение объекта с погрешностью, равной длине волны. Если мы используем высокочастотный свет (малой длины волны), мы можем с высокой точностью определить положение электрона. Но высокочастотные фотоны несут очень большое количество энергии и поэтому вносят большие возмущения в скорость движения электронов. Если мы используем низкочастотный свет (большой длины волны), мы минимизируем его влияние на движение электрона, поскольку фотоны, составляющие этот свет, имеют относительно низкую энергию, но в этом случае мы вынуждены пожертвовать точностью определения положения электрона. Гейзенберг установил, что эти величины обратно пропорциональны друг другу: большая точность в определении положения неизбежно ведет к большей погрешности в определении скорости, и наоборот.

В отличие от теорий Ньютона и даже Эйнштейна, в которых движущаяся частица описывается ее положением и скоростью, согласно квантовой механике на микроскопическом уровне вы не можете знать оба этих параметра с одинаковой точностью. Хотя мы ограничили наше описание электронами, то же самое относится ко всем составным элементам мироздания. Про электроны, как и про любые другие частицы, нельзя одновременно сказать, что они находятся в таком-то месте и имеют такую-то скорость. Если вы поместите электрон в большую коробку и затем начнете медленно сдвигать ее стенки, чтобы определить его положение с увеличивающейся точностью, вы обнаружите, что движение электрона будет становиться все более и более неистовым, отскакивая от стенок коробки со все возрастающей и непредсказуемой скоростью.

Соотношение неопределенностей лежит в основе еще одного потрясающего явления, известного под названием квантового туннелирования. Если вы выстрелите пластиковой пулей в бетонную стенку толщиной в десять футов, то результат будет один – пуля отскочит назад, поскольку у пули просто недостаточно энергии, чтобы пробить такое прочное препятствие. Однако если перейти на уровень фундаментальных частиц, то, как совершенно определенно показывает квантовая механика, в волновую функцию (вероятностную волну) каждой составляющей пулю частицы заложена небольшая вероятность того, что эта частица может пройти сквозь стену. Это означает, что существует маленькая, но ненулевая, вероятность того, что частица сможет пройти сквозь стену и оказаться на другой стороне. Причина снова содержится в соотношении неопределенностей Гейзенберга.

Чтобы понять это, представьте, что вы живете в полной нищете и вдруг узнаете, что ваш дальний родственник отошел в лучший мир, оставив вам огромное состояние. Единственная проблема состоит в том, что у вас нет денег для покупки авиабилета. Вы объясняете ситуацию своим друзьям: если они помогут вам преодолеть барьер между вами и наследством, одолжив деньги на билет, вы вернете им долг с процентами после возвращения. Но ни у кого нет денег, чтобы дать вам в долг. Ваш друг, работающий в авиакомпании, предлагает другое решение. Система учета в авиакомпании такова, что если вы вышлете деньги в уплату за билет телеграфным переводом в течение 24 часов с момента прибытия в пункт назначения, никто не узнает, что вы не уплатили их до вылета.

Показав, что существует компромисс между точностью измерения местоположения и скорости, Гейзенберг, кроме того, продемонстрировал существование компромисса между точностью измерения энергии и тем, сколько времени занимают эти измерения. Согласно квантовой механике вы не можете утверждать, что частица имеет в точности такую-то энергию в точно такой-то момент времени. За возрастающую точность измерения энергии приходится платить возрастающей продолжительностью проведения измерений. Грубо говоря, это означает, что энергия частицы может варьироваться в очень широких пределах, если измерения проводятся в течение достаточно короткого периода времени. Поэтому точно так же как система учета в авиакомпании «позволяет» вам занять «деньги» на билет при условии, что вы вернете их достаточно быстро, квантовая механика «позволяет» частице «занять» энергию при условии, что она может вернуть ее в течение промежутка времени, определяемого соотношением неопределенностей Гейзенберга.

Если говорить о микроскопических частицах, находящихся перед бетонной плитой, они имеют возможность занять достаточное количество энергии и иногда делают то, что с точки зрения классической физики является невозможным: они мгновенно проходят через область, для проникновения в которую у них раньше не хватало энергии. При переходе к более сложным объектам, состоящим из большего числа частиц, возможность квантового туннелирования сохраняется, но становится очень маловероятной, поскольку требует, чтобы все частицы совершили переход одновременно. Малость значения постоянной Планка в реальном мире означает, что если вы будете каждую секунду атаковать бетонную стену, вам придется потратить время, превышающее возраст Вселенной, прежде чем у вас появится сколько-нибудь заметный шанс пройти сквозь стену в одной из попыток. Однако имея бесконечное терпение (и такую же продолжительность жизни), рано или поздно вы можете оказаться с другой стороны.

Соотношение неопределенностей является сердцевиной квантовой механики. Свойства, которые кажутся нам обычно столь фундаментальными, что не вызывают никаких сомнений, - что объекты имеют определенное положение и скорость, и что в определенные моменты времени они имеют определенную энергию, - теперь представляются всего лишь следствием того, что постоянная Планка так мала в масштабах нашего повседневного мира.

 

К оглавлению >>

1. Предыстория и Основная идея >>

2. Теория относительности >> 3. Квантовая механика >> 4. Теория струн как разрешение конфликта >>

5. Свернутые измерения >> 6. Космология >> 7. Перспективы >>

 

nevada9.narod.ru

Теория одной пули

Теория одной пули

Jim Garrison (Kevin Costner) critiques the Single Bullet Theory: is this an accurate demonstration? 

Постепенно, мы переходим к самым интересным моментам фильма и параллельно проводимого мной расследования. Одна  из самых известных сцен в  JFK это монолог  окружного прокурора Джима Гаррисона о траектори пули поразившей, по версии Комиссии Уорена, Кеннеди и Коннелли семь раз. Джим Гаррисон приводит аргументы в пользу полной невозможности такого развития событий и анализируя пленку Запрудера пытается доказать, что выстрелов было гораздо больше. Сами выстрелы мы разберем в отдельнх разделах, а вот анализ ранений мы рассмотрим сейчас.

Итак, Джим Гаррисон говорит о том, что вывод Комиссии Уорена, о том, что семь ран Кеннеди и Коннелли могла нанести одна пуля абсолютно неверный и это невозможно. А раз это невозможно, то был как минимум еще один стрелок, а значит и заговор.  Давайте попробуем проанализировать и разобрать аргументы Гаррисона:

- Волшебная пуля входит в спину президента под углом в  17 градусов. рана номер один

Это один из показателей расчитаный достаточно давно и так же давно опровергнутый.  Дейл Майерз в отличной компьютерной реконструкции  фиксирует угол  21,4 градусов. (С учетом  наклона в 3 градуса вниз самой улицы  Вязов, Угол раны составляет около 18,4 град.) И входит не в спину, а в шею. Этот угол точно соответствует позиции Джонни Розелли в Дел Тексе.

- Затем пуля  движется вверх, что бы выйти из шеи Кеннеди спереди - рана номер два. . . . .

Абсолютно ошибочное утверждение, что пуля по "теории одной пули" должна идти вверх. Вот как выглядит схема этого ранения в отчете Комиссии Уорена.

На самом деле, это заблуждение было развенчано давольно давно. А пошло оно, из за пулевого отверстия в пиджаке и рубашке  президента. Отверстие в пиджаке и рубашке было действительно на уровне верхней части лопатки и если бы рана совпадала с отверстием на пиджаке, то пуля действительно потом должна была пойти вверх, что бы выйти из шей в том месте где рана.

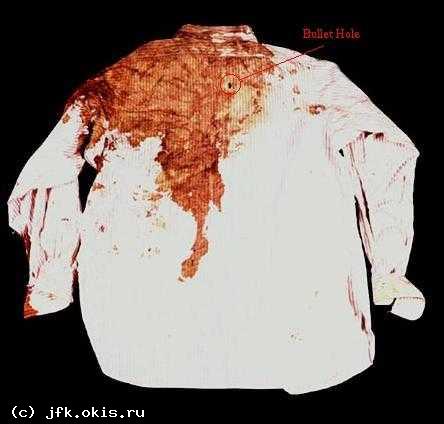
Рубашка Джона Кеннеди

Но дело в том, что отверстия не совпадают и по вполне объяснимой причине. У Кеннеди задрались кверху пиджак и рубашка, и несколько сбились в районе воротника. Это видно на очень многих фотографиях и видеозаписях сделаных в тот день. 

Гаррисон  продолжает:

. . . где она висит в воздухе  1.6 секунды. . . . .

 Абсолютно неверно. Это основано на утверждении, что Коннелли не был ранен  до кадра 236 фильме Запрудера. Действительно, лицо Коннели не выражает явной реакции на ранение до 236-го кадра, но тщательный анализ записи  неопровержимо доказывает, что губернатор был ранен между кадрами 223 и 224. Тогда же когда и Кеннеди получает ранение в шею. На записи даже видно, как меняется структура пиджака Коннели, в районе пятого ребра на кадре 224. Пиджак как бы взбухает на секунду. 

Governor Connally in Zapruder frames 223 and 224 

Так же анализ пленки ясно показывает, что Кеннеди и Коннели реагируют одновременно на этот выстрел и ранения. Обратите внимание на эти кадры. Реакция наступает одновременно между кадрами 224 и 226. Рука Кеннеди идет к шее синхронно с рукой Коннели в которой от держит свою шляпу.

JFK and Governor Connally in Zapruder frames 224-225 

JFK and Governor Connally in Zapruder frames 225-226 

А это полная запись этих кадров. Ясно видно что Кеннеди и Коннели ранены одновременно и никакой задержки пули на 1,6 секунды не было.

JFK and Governor Connally in Zapruder frames 222-262

Вернемся к монологу Гаррисона:

. . . . . . далее пуля поворачивает на право. . . . Абсолютно ложное утверждение. Оно основано на неверном представлении расположения кресел в лимузине. Дело в том, что Гаррисон развивает свою версию основываясь на том, что Кеннеди и Коннелли сидят как бы в линию, и Кеннеди сидит ровно позади губернатора. Однако это серьезная недоработка Гаррисона, так как специальные кресла, изначально предназначенные для сотрудников Секретной службы довольно сильно смещены к центру относительно положения пассажира на заднем сидении. Это смещение на 27 см, как раз и позволяет пуле нанести именно эти ранения. Далее следуют несколько компьютерных моделей, которые показывают реальное расположение пасажиров в салоне лимузина и траекторию полета пули по версии комиссии Уоррена.

Расположение кресел в лимузине

Гаррисон  продолжает:

. . . . . . пуля входит в тело Кеннелли сзади, под правой  подмышкой - рана номер три.

Это верно.

Затем пуля идет вниз под углом в 27 градусов и выходит в районе пятого ребра Коннелли . . . .

Почти точно. Новейшие исследования дают показания угла в 28,4 градуса.

. . . . .  из груди - раны, четыре и пять.

Правильно.

....далее пуля продолжает движение вниз в  правое запястье Коннели - рана номер  шесть.

Правильно.

.....Затем пуля попадает в левое бедро и ....

Правильно.

. . . . . . после этого, почти нетронутая, обнаруживается на носилках в больнице Парклэнда. 

Неверно. Во первых пуля не "почти не тронутая". Повреждения достаточно серьезные. Она согнута и сильно сплющена у основания и с одной стороны. Испытания подтвердили характер повреждений. А во вторых, пуля была извлечена из одежды Коннели когда его перегружали из лимузина на носилки. 

 И в последний раз обратимся к монологу Гаррисона:

- Эксперты Армии США провели несколько тестов и ни одна пуля не была похожа на эту. Вот Е 845. Пуля выпущенная в руку трупа. Всего одна кость и какие повреждения. А там. Семь ран. Крепкая кожа, твердые кости... Совершенно не соответствует действительности. Тестовые выстрелы проводились и все показали именно такой характер повреждений в тех условиях которые были на Дэйли Плаза. Более того, выстрелы велись из оружия теоретически возможного для охоты на слонов и гиппопотамов, а пуля способная пробить кожу этих животных вполне может остаться не сильно деформированой пройдя сквозь человека. Это вам подтвердит любой охотник. А Манлихер Каркано именно такое оружие.

Чарльз Николетти, один из стрелков на Дэйли Плаза вероятнее всего стрелял именно из Каркано, второго, который пристреливал Д. Фаилз. Первый он пристреливать не стал, из -за сбитого прицела и очень тугого курка. Именно этот, первый  Каркано и был подброшен в здание книгохранилища, что бы указать на Освальда.

"That's some bullet."

 

jfk.okis.ru

Гравитация и квантовая механика в теории струн

ТОП 10:

Единая схема, которую дает теория струн, очень привлекательна. Но истинную неотразимость придает ей возможность избавиться от вражды между гравитационным взаимодействием и квантовой механикой. Вспомним, что проблема при объединении общей теории относительности и квантовой механики возникает, когда основное понятие первой из них — плавно искривленная геометрическая структура пространства и времени — сталкивается с главной особенностью второй, что все во Вселенной, включая структуру пространства и времени, испытывает квантовые флуктуации, интенсивность которых растет при уменьшении масштаба исследований. На субпланковском масштабе расстояний квантовые флуктуации становятся столь сильными, что приводят к разрушению понятия гладкого искривленного геометрического пространства, и это означает нарушение принципов общей теории относительности. Теория струн смягчает неистовые квантовые флуктуации путем «размазывания» микроскопических характеристик пространства. На вопрос о том, что это значит в действительности и как это разрешает противоречие, есть два ответа: грубый и более точный. Мы поочередно рассмотрим каждый из них. Грубый ответ Хотя это звучит довольно наивно, один из способов, которым мы можем изучить структуру какого-либо объекта, состоит в том, чтобы бросать в него другие предметы и наблюдать за тем, как они отражаются от него. В качестве примера укажем, что мы способны видеть предметы потому, что наши глаза собирают, а наш мозг расшифровывает информацию, которую несут фотоны, отражающиеся от объектов, на которые мы смотрим. На этом же принципе основаны ускорители частиц: в них частицы материи, например, электроны и протоны, сталкиваются между собой и с другими объектами; затем Глава 6. Только музыка, или Суть теории суперструн 107 специальные детекторы анализируют разлетающиеся осколки для получения информации, позволяющей определить структуру объектов, участвующих в столкновениях. Общее правило при таких исследованиях состоит в том, что размер частиц, используемых для исследования, определяет нижний предел разрешающей способности измерительной установки. Чтобы лучше понять смысл этого важного утверждения, представим, что Слим и Джим решили приобщиться к культуре и записались в кружок по рисованию. По ходу занятий Джима начинают все более раздражать растущие художественные способности Слима, и он вызывает его на необычное состязание. Он предлагает, чтобы каждый взял косточку от персика, закрепил ее в тисках и изобразил наиболее точным образом. Необычность предложения Джима состоит в том, что ни ему, ни Слиму не разрешается смотреть на косточку. Вместо этого каждый из них может бросать в нее разные предметы (но не фотоны!), наблюдать за тем, как они отскакивают от косточки, и на этой основе определять размеры, форму и детали строения косточки (см. рис. 6.4). Тайком от Слима Джим заряжает его «стрелялку» крупными шариками (как на рис. 6.4а), а свою — пятимиллиметровыми пластиковыми пульками гораздо меньшего размера (как на рис. 6.4 б). Оба заводят свои орудия, и состязание начинается. Лучшее, что удалось изобразить Слиму, показано на рис. 6.4 а. Наблюдая за траекторией отскакивающих шариков, он смог установить, что размер косточки мал, и что она имеет твердую поверхность. Но это все, что ему удалось узнать. Шарики были слишком велики, чтобы на них оказывали влияние более мелкие детали строения персиковой косточки. Когда Слим бросил взгляд на рисунок Джима (рис. 6.45), он был поражен тем, что увидел. Однако быстрый взгляд на стрелялку Джима позволил ему понять, в чем дело: небольшие пульки, используемые Джимом, были достаточно малы, чтобы на угол, под которым они отражались, оказывали влияние некоторые крупные детали строения косточки. Таким образом, выстрелив в косточку большим количеством пятимиллиметровых пулек и наблюдая за их Рис. 6.4. Персиковая косточка закреплена в тисках. Для создания ее изображения используются только наблюдения за тем, как отскакивают предметы — «зонды», — брошенные в нее. 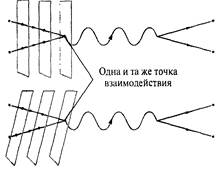Используя зонды все меньшего размера — шарики (а), пятимиллиметровые пульки (б), полумиллиметровые пульки (в), можно получать все более детальное изображение траекториями после отскока, Джим смог нарисовать более подробный рисунок. Чтобы не проиграть, Слим взял свою стрелялку, заполнил ее снарядами еще меньшего размера — полумиллиметровыми пульками, — которые так малы, что на характер их отражения будут оказывать влияние мельчайшие морщинки на поверхности косточки. Наблюдая за отскоком этих пулек, он смог нарисовать рисунок, который принес ему победу (рис. 6.4 в). Урок, который можно извлечь из этого маленького состязания, ясен: размер частиц-зондов не может существенно превышать размер изучаемых физических особенностей; в противном случае разрешающая способность исследования окажется недостаточной для изучения интересующих нас структур. Те же самые выводы относятся, конечно, и к случаю, когда мы захотим провести более глубокое исследование персиковой косточки, чтобы определить ее структуру на атомном и субатомном уровне. Полумиллиметровые пульки не дадут никакой полезной информации по этому вопросу; они явно слишком велики, чтобы исследовать структуру на атомном уровне. Именно по этой причине в ускорителях в качестве зондов 108 Часть III. Космическая симфония используются протоны или электроны: маленький размер этих частиц делает их гораздо более подходящими для этой цели. На субатомном уровне, где на смену классической логике приходят квантовые понятия, наиболее подходящей мерой разрешающей способности частиц является квантовая длина волны, которая определяет диапазон неопределенности местонахождения частиц. Этот факт является следствием приведенного в главе 4 обсуждения соотношения неопределенностей Гейзенберга. Там мы установили, что минимальная погрешность при использовании в качестве зонда точечных частиц (мы говорили о фотонных зондах, но сказанное применимо и ко всем другим частицам) примерно равна квантовой длине волны частицы, используемой в качестве зонда. Грубо говоря, разрешающая способность точечной частицы размазывается в результате действия квантовых флуктуации подобно тому, как точность скальпеля хирурга уменьшается, когда его руки дрожат. Вспомним, однако, что в главе 4 мы также отметили один важный факт, состоящий в том, что квантовая длина волны частицы обратно пропорциональна моменту количества движения, который, грубо говоря, определяется ее энергией. Таким образом, увеличивая энергию точечной частицы, можно делать ее квантовую длину волны все меньше и меньше, квантовое размазывание будет все более уменьшаться и, следовательно, мы сможем использовать эту частицу для изучения все более тонких структур. Интуитивно понятно, что частицы высокой энергии имеют большую проникающую способность и могут использоваться для изучения более мелких деталей строения. В этом смысле становится очевидным различие между точечными частицами и нитями струн. Как в примере с пластиковыми пульками для изучения структуры поверхности персиковой косточки, присущая струне пространственная протяженность не позволяет использовать ее для исследования объектов, размер которых существенно меньше размера струны, в нашем случае — объектов, характерные размеры которых меньше планковской длины. Если перейти к более точным формулировкам, в 1988 г. Дэвид Гросс, работавший в то время в Принстонском университете, и его студент Пол Менде показали, что если учитывать квантовую механику, то непрерывное увеличение энергии струны не приводит к непрерывному увеличению ее способности исследовать все более тонкие структуры, в отличие от того, что имело бы место для точечной частицы. Они установили, что при увеличении энергии струны сначала ее разрешающая способность растет так же, как у точечной частицы высокой энергии. Однако, когда энергия струны превышает значение, необходимое для изучения структур в масштабе планковской длины, дополнительная энергия перестает вызывать увеличение разрешающей способности. Вместо этого дополнительная энергия приводит к увеличению размера струны, тем самым уменьшая ее разрешающую способность. Типичный размер струны близок к планковской длине, но если накачать струну достаточной энергией, которую мы не можем даже представить, но которая могла существовать во время Большого взрыва, то можно было бы заставить струну вырасти до макроскопических размеров. Это был бы довольно топорный инструмент для изучения микромира! Все выглядит так, как будто струна, в отличие от точечной частицы, имеет два источника размазывания: квантовые флуктуации, как для точечной частицы, а также собственные пространственные размеры. Увеличение энергии струны уменьшает размазывание, связанное с первым источником, но, в конечном счете, увеличивает размазывание, обусловленное вторым. В результате, как бы вы ни старались, физические размеры струны не позволят вам использовать ее на субпланковском масштабе расстояний. Но ведь конфликт между обшей теорией относительности и квантовой механикой возникает благодаря свойствам структуры пространства, проявляющимся в субпланковском масштабе расстояний. Если элементарные компоненты Вселенной непригодны для исследований на субпланковских масштабах расстояний, это значит, что ни они, ни какие-либо объекты, состоящие из таких компонентов, не могут испытывать влияния этих кажущихся гибельных квантовых флуктуации на малых масштабах. Это похоже на то, что Глава 6. Только музыка, или Суть теории суперструн 109 произойдет, если мы проведем рукой по полированной гранитной поверхности. Хотя на микроскопическом уровне гранит является дискретным, зернистым и неровным, наши пальцы не смогут обнаружить эти микроскопические неровности, и поверхность покажется нам абсолютно гладкой. Наши толстые, длинные пальцы «смажут» микроскопическую дискретность. Подобно этому, поскольку струна имеет конечные пространственные размеры, существует нижний предел ее разрешающей способности. Струна не способна обнаружить изменения на суб-планковском масштабе расстояний. Подобно нашим пальцам на граните, струна смажет ультрамикроскопические флуктуации гравитационного поля. И хотя результирующие флуктуации по-прежнему остаются значительными, это смазывание сгладит их в степени, достаточной для преодоления несовместимости общей теории относительности и квантовой механики. В частности, теория струн ликвидирует обсуждавшиеся в предыдущей главе фатальные бесконечности, возникающие при попытке построить квантовую теорию гравитации на основе модели точечных частиц. Существенное различие между аналогией с гранитом и нашей реальной проблемой структуры пространства состоит в том, что существуют способы обнаружить микроскопическую дискретность поверхности гранита. Для этого могут использоваться более точные зонды, чем наши пальцы. Электронный микроскоп способен обнаружить поверхностные структуры, размер которых составляет менее одной миллионной доли сантиметра; этого достаточно, чтобы увидеть многочисленные неровности на поверхности. В противоположность этому, в теории струн нет способа обнаружить «неровности» в структуре пространства на субпланковском уровне. Во Вселенной, управляемой законами теории струн, уже не является истинной обычная точка зрения, согласно которой мы можем без ограничения делить объекты на все более и более мелкие части. Предел существует, он вступает в игру, когда мы сталкиваемся с разрушительной квантовой пеной, показанной на рис. 5.1. Следовательно, в определенном смысле, который станет яснее в последующих главах, можно утверждать, что бурные квантовые флуктуации на субпланковских расстояниях не существуют. Как выразился бы позитивист, объект или явление существует, только если мы можем — хотя бы в принципе — исследовать и измерить его. Поскольку предполагается, что струны являются наиболее фундаментальным объектом мироздания и имеют слишком большой размер, чтобы на них оказывали влияние флуктуации структуры пространства, происходящие на субпланковских расстояниях, эти флуктуации не могут быть измерены, и, следовательно, согласно теории струн они не существуют. Ловкость рук? Обсуждение, приведенное выше, может оставить у вас чувство неудовлетворенности. Вместо того чтобы показать, что теория струн укрощает субпланковские флуктуации структуры пространства, мы, похоже, использовали ненулевой размер струн для того, чтобы обойти всю проблему стороной. Решили ли мы вообще хоть что-нибудь? Решили. Следующие два соображения позволят нам лучше понять это. Прежде всего вывод, который можно сделать из предыдущего обсуждения, состоит в том, что предполагаемые флуктуации структуры пространства в масштабе субпланковских расстояний связаны исключительно с формулировкой общей теории относительности и квантовой механики в рамках модели, основанной на точечных частицах. Это означает, что центральное противоречие современной теоретической физики в определенном смысле является проблемой, которую породили мы сами. Поскольку мы ранее предположили, что все частицы вещества и все частицы, передающие взаимодействие, должны быть точечными объектами, практически не имеющими пространственной протяженности, мы были обязаны рассматривать свойства Вселенной на произвольно малых масштабах. И на самых малых расстояниях мы столкнулись с проблемой, выглядящей неразрешимой. Теория струн утверждает, что мы столкнулись с этой 110 Часть III. Космическая симфония проблемой только потому, что не поняли истинных правил игры: новые правила гласят, что существует предел тому, насколько глубоко можно исследовать Вселенную, — предел, определяющий, до какого уровня наше обычное понятие расстояния может применяться к ультрамикроскопической структуре мироздания. Становится понятно, что фатальные флуктуации структуры пространства возникают в наших теориях из-за неосведомленности об этих пределах: модель с точечными частицами далеко выходит за рамки физической реальности. Видя кажущуюся простоту этого решения, позволяющего разрешить конфликт, возникающий между общей теорией относительности и квантовой механикой, вы можете удивиться, почему прошло столько времени, пока ученые не осознали, что точечная модель частиц всего лишь идеализация, и что в реальном мире элементарные частицы имеют некоторые конечные размеры. Это второй момент, на который мы хотели бы обратить внимание. Уже давно некоторые из величайших умов теоретической физики, такие как Паули, Гейзенберг, Дирак и Фейнман, предполагали, что компоненты природы в действительности могут быть не точками, а маленькими, колеблющимися «капельками» или «ядрышками». Однако они, как и другие ученые, столкнулись с тем, что очень трудно построить теорию, фундаментальные компоненты которой не являются точечными частицами, и которая, в то же время, совместима с основополагающими физическими принципами, такими, как сохранение квантово-механической вероятности (согласно которому физические объекты не могут внезапно исчезать из Вселенной без всякого следа) и невозможность передачи информации со скоростью, превышающей скорость света. Снова и снова их исследования с разных точек зрения показывали, что отказ от парадигмы точечных частиц приводит к несоблюдению одного из этих принципов или их обоих. Поэтому в течение долгого времени казалось невозможным построить разумную квантовую теорию, основанную на чем либо ином, кроме точечных частиц. За двадцать с лишним лет глубоких исследований выяснилась поистине впечатляющая особенность теории струн: при всей непривычности некоторых понятий теория струн обладает всеми свойствами, которые должна иметь каждая разумная физическая теория. И, более того, благодаря наличию мод колебаний, реализующих гравитон, теория струн представляет собой квантовую теорию, включающую гравитацию. Более точный ответ Грубый ответ ухватывает сущность того, почему теория струн смогла добиться успеха там, где предшествующие теории, основанные на точечной модели частиц, потерпели неудачу. Поэтому без ущерба для понимания дальнейшего можно сразу перейти к следующему разделу. Однако, рассмотрев в главе 2 основные идеи специальной теории относительности, мы получили в свое распоряжение средства, позволяющие более точно описать, как теория струн борется с разрушительными квантовыми флуктуаииями. В более точном ответе мы будем использовать те же основные идеи, которые содержались в приближенном ответе, но выразим их непосредственно на языке струн. Мы увидим, как конечность размера струн «размазывает» информацию, которую можно было бы получить при зондировании с использованием точечных частиц, и тем самым, к нашему счастью, снимает проблему поведения пространства на ультрамикроскопических расстояниях, ответственную за центральную дилемму современной физики. Сначала рассмотрим, как происходило бы взаимодействие между точечными частицами, если бы они действительно существовали, и, соответственно, как можно было бы использовать их в качестве физических зондов. Наиболее важным является показанный на рис. 6.5 случай взаимодействия между частицами, движущимися по пересекающимся путям, приводящим к столкновению. Если бы эти частицы были бильярдными шарами, они могли бы столкнуться, после чего каждая из них начала бы двигаться по новой траектории. Квантовая теория Глава 6. Только музыка, или Суть теории суперструн 111 Рис.6.5. Две частицы взаимодействуют: они «сталкиваются между собой», и это приводит к изменению траектории каждой из них Рис.6.6. В квантовой теории поля частица и ее античастица могут мгновенно аннигилировать с образованием фотона. Затем этот фотон порождает другую частицу и античастицу, которые движутся по расходящимся траекториям поля с точечными частицами показывает, что то же самое происходит при столкновении элементарных частиц — они отскакивают друг от друга и продолжают свой путь по новым траекториям. — однако детали этого процесса отличаются. Для большей определенности и простоты представим себе, что одна из двух частиц является электроном, а другая — ее античастицей, позитроном. При столкновении частицы и античастицы они аннигилируют с выделением энергии в чистом виде, приводящим к образованию, например, фотона9). Чтобы отличать выходящую траекторию фотона от входящих траекторий электрона и позитрона, мы будем, следуя принятому в физике соглашению, изображать ее волнистой линией. Обычно фотон проходит небольшое расстояние, после чего высвобождает энергию, полученную от первоначальной электрон-позитронной пары, путем образования другой электрон-позитронной пары, показанной в правой части рис. 6.6. Эти две частицы испытывают электромагнитное взаимодействие и, в конце концов, разлетаются по расходящимся траекториям. Такая последовательность событий имеет определенное сходство с описанием бильярдных шаров. Нас интересуют детали взаимодействия, в частности, точка, где начальные электрон и протон аннигилируют с образованием фотона. Как станет ясно далее, главным является тот факт, что время и место этого события могут быть установлены однозначно и точно, как показано на рис. 6.6. Как изменится описание, приведенное выше, если после тщательного исследования объектов, которые мы считали нульмерными точками, они окажутся одномерными струнами? Основной процесс взаимодействия будет тем же самым, но теперь движущиеся по пути к столкновению объекты представляют собой осциллирующие петли, показанные на рис. 6.7. Для определенных колебаний струны ее моды будут как раз соответствовать протону и электрону, движущихся курсом на столкновение, как показано на рис. 6.6. Истинный струнный характер становится очевидным только при исследовании в ультрамикроскопическом масштабе, выходящем далеко за пределы современных экспериментальных возможностей. Как и в случае с точечными частицами, две струны сталкиваются и аннигилируют, превращаясь во вспышку, которая представляет собой фотон и сама по себе является струной, колеблющейся в определенной моде. Таким образом, две исходные струны взаимодействуют между собой, сливаясь и образуя третью струну, как показано на рис. 6.7. Как и в случае точечных частиц, эта струна проходит некоторое расстояние, после чего выделяет энергию, полученную от двух исходных струн, разделяясь на две новые струны, которые продолжают движение. Опять же, со всех точек зрения, кроме той, которая относится к микроскопическим масштабам, это будет выглядеть идентично взаимодействию между точечными частицами на рис. 6.6. Существует, однако, радикальное различие между этими двумя описаниями. Мы подчеркнули, что взаимодействие между точечными частицами происходит в однозначно идентифицируемой точке пространства и времени, в точке, с положением которой согласятся все наблюдатели. Как мы сейчас увидим, для взаимодействия между струнами это неверно. Мы продемонстрируем это, сравнив, как Джордж и Грейс, два наблюдателя, находящихся в относительном движении, могли бы описать это взаимодействие. Мы увидим, что они не придут к единому 112 Часть III. Космическая симфония мнению по вопросу о том, где и когда две струны впервые пришли в соприкосновение. Представим, что мы наблюдаем за взаимодействием двух струн с помощью фотокамеры, затвор которой остается открытым, и вся хронология процесса регистрируется на одном фрагменте пленки 10). На рис. 6.7 в показан результат: его называют мировой поверхностью. Путем «разрезания» мировой поверхности на параллельные части (примерно так же, как мы разрезаем на куски батон хлеба) можно восстановить, момент за моментом, историю взаимодействия струн. Пример такого разрезания показан на рис. 6.8. В частности, на рис. 6.8 а мы показали Джорджа, пристально наблюдающего за двумя сближающимися частицами, а также плоскость, которая вычленяет все события в пространстве, происходящие одновременно с его точки зрения. Как часто делалось в предыдущих главах, для наглядности мы отбросили на диаграмме одно пространственное измерение. На самом деле, конечно, существует трехмерный массив событий, которые происходили одновременно для любого наблюдателя. Рис. 6.7. а) Две струны, движущиеся курсом на столкновение, могут слиться и образовать третью струну, которая вслед за этим может разделиться на две струны, движущиеся по расходящимся траекториям. 6) Тот же процесс, что и на рис. а), но более явно прослеживающий движение струн, в) «Замедленная киносъемка» двух взаимодействующих струн дает мировую поверхность Рис. 6.8. Две исходные струны (с точки зрения Джорджа) в три последовательных момента времени. В моменты а) и б) струны сближаются, в момент в), с его точки зрения, они впервые соприкоснулись На рис. 6.8 б и 6.8 в приведены два последовательных моментальных снимка — два последовательных «среза» мировой поверхности, — показывающих, как Джордж видит две струны, приближающиеся друг к другу. Особую важность имеет отмеченный на рис. 6.8 в момент, когда, с точки зрения Джорджа, две струны войдут в соприкосновение и сольются, образовав третью струну. А теперь повторим все то же самое для Грейс. Как мы указывали в главе 2, относительное движение Джорджа и Грейс приведет к тому, что они не согласятся по вопросу о том, какие события являются одновременными. С точки зрения Грейс события в пространстве, являющиеся одновременными, лежат в другой плоскости, показанной на рис. 6.9. Иными словами, по мнению Грейс, для того чтобы момент за моментом восстановить процесс взаимодействия, мировая поверхность на рис. 6.7 в должна быть «нарезана» на куски под другим углом. На рис. 6.9 б и 6.9 в мы снова показали последовательные моменты времени, но теперь уже с точки зрения Грейс, включая Глава 6. Только музыка, или Суть теории суперструн 113 Рис. 6.9. Две исходные струны (с точки зрения Грейс) в три последовательных момента времени. В моменты о) и б) струны сближаются, в момент в), с ее точки зрения, они впервые соприкоснулись Рис. 6.11.Наблюдатели, находящиеся в относительном движении, придут к согласию о месте и времени взаимодействия между двумя частицами Рис. 6.10.Мнения Джорджа и Грейс по вопросу о месте, в котором произошло взаимодействие, разойдутся момент, когда две начальные струны по ее наблюдениям войдут в соприкосновение и образуют третью струну. Сравнивая рис. 6.8 в и 6.9 в (результат показан на рис. 6.10), мы видим, что мнения Джорджа и Грейс разделятся относительно того, где и когда две исходные струны впервые соприкоснулись, т. е. где они взаимодействовали. Поскольку струна является протяженным объектом, это означает, что не существует однозначного места в пространстве или момента во времени, когда струны начали взаимодействовать — эти характеристики зависят от того, как движется наблюдатель. Если применить те же самые рассуждения к взаимодействию точечных частиц, как показано на рис. 6.11, мы вновь придем к выводам, которые уже получили ранее: существуют определенная точка в пространстве и момент во времени, когда произошло взаимодействие частиц. Все взаимодействие точечных частиц происходит в одной определенной точке. Когда сила, связанная со взаимодействием, представляет собой гравитационную силу, т. е. когда частица, передающая взаимодействие, является гравитоном, а не фотоном, такая упаковка всей энергии взаимодействия в одну точку ведет к катастрофическим результатам, вроде упоминавшихся ранее бесконечных ответов. В противоположность этому струны «размазывают» место, в котором происходит взаимодействие. Поскольку разные наблюдатели регистрируют взаимодействие происходящим в разных точках левой части поверхности на рис. 6.10, это означает, что точка взаимодействия в действительности размазана по всей этой области. Это увеличивает область, в которой происходит взаимодействие, и в случае гравитационной силы такое размазывание существенно смягчает ультрамикроскопические свойства, настолько, что вычисления дают нормальные конечные результаты вместо получавшихся ранее бесконечностей. Это более точная версия того размазывания, о котором шла речь в грубом ответе в предыдущем разделе. Подчеркнем еще раз, что это размазывание приводит к сглаживанию ультрамикроскопических флуктуации 114 Часть III. Космическая симфония структуры пространства, когда субпланковские расстояния сливаются друг с другом. Субпланковские детали, которые были бы доступны для изучения с помощью точечных частиц, в теории струн смазываются и предстают в безобидном виде. Это подобно тому, что происходит, если смотреть на мир через слишком слабые или слишком сильные очки. Однако, если теория струн представляет собой окончательное описание мироздания, то в отличие от случая плохого зрения здесь уже не существует никаких «корректирующих линз», через которые смогли бы отчетливо проявиться предполагаемые субпланковские флуктуации. Несовместимости общей теории относительности и квантовой механики, проявляющейся только в масштабе субпланковских расстояний, можно избежать во Вселенной, где есть нижний предел для расстояний, которые доступны для исследований или которые существуют в обычном смысле этого слова. Такова Вселенная, описываемая теорией струн: в ней законы макромира и микромира могут быть без ущерба объединены, после того как мы покончили с воображаемой катастрофой, возникающей на ультрамикроскопических расстояниях. Не только струны? Струны имеют две важных особенности. Во-первых, несмотря на конечность пространственных размеров, они могут быть непротиворечиво описаны в рамках квантовой механики. Во-вторых, среди резонансных мод колебаний имеется мода, свойства которой в точности совпадают со свойствами гравитона: тем самым гарантируется, что гравитационное взаимодействие представляет собой неотъемлемую часть этой теории. Однако, как мы помним, теория струн показала, что принятое понятие нульмерной точечной частицы оказалось не более чем математической идеализацией, не имеющей отношения к действительности. Не может ли быть так, что бесконечно тонкая одномерная струна представляет собой такую же математическую идеализацию? Может быть, одномерная струна на самом деле имеет какую-то толщину, подобно внутренней поверхности двумерной велосипедной шины или, если быть более реалистичными, подобно тонкой трехмерной баранке? Но трудности, с которыми столкнулись Гейзенберг, Дирак и другие в попытках построить квантовую теорию трехмерных фундаментальных комочков, выглядели непреодолимыми и вновь и вновь ставили в тупик исследователей, старавшихся пойти столь естественным путем. Однако в середине 1990-х гг. специалисты по теории струн, используя косвенные и довольно сложные рассуждения, несколько неожиданно установили, что подобные фундаментальные объекты действительно играют важную и нетривиальную роль в самой теории струн. Исследователи постепенно осознали, что теория струн содержит не только струны. Важнейшее наблюдение, играющее центральную роль во второй революции в теории суперструн, начатой Виттеном и его коллегами в 1995 г., состоит в том, что теория суперструн в действительности включает в себя компоненты различной размерности: элементы, похожие на двумерные фрисби-диски, на трехмерные капли, и даже еще более экзотические конструкции. Эти новейшие достижения будут рассмотрены в главах 12 и 13. А пока будем следовать хронологии открытий и обсудим новые поразительные свойства Вселенной, состоящей не из нульмерных точечных частиц, а из одномерных струн. 

infopedia.su

Квантовая теория против гравитации: загадка наконец разгадана?

Как примирить два противоречивых столпа современной физики: квантовую теорию и гравитацию? Долгое время ученые считали, что рано или поздно наука признает ту или иную теорию господствующей, однако реальность как всегда оказалась намного интереснее. Новые исследования утверждают, что гравитация может возникать из-за случайных флуктуаций на квантовом уровне.

Василий Макаров

21 сентября 2017 15:25

Среди двух фундаментальных теорий, объясняющих окружающую нас реальность, квантовая теория апеллирует к взаимодействию между наименьшими частицами материи, а общая теория относительности обращается к гравитации и крупнейшим структурам во всей Вселенной. Со времен Эйнштейна физики пытались преодолеть разрыв между этими учениями, но с переменным успехом.

Один из способов согласования гравитации с квантовой механикой заключался в том, чтобы показать, что в основе гравитации лежат неделимые частицы материи, кванты. Этот принцип можно сравнить с тем, как сами кванты света, фотоны, представляют собой электромагнитную волну. До сих пор у ученых не было достаточно данных, чтобы подтвердить это предположение, но Антуан Тиллой (Antoine Tilloy) из Института квантовой оптики им. Макса Планка в Гархинге, Германия, попытался описать гравитацию принципами квантовой механики. Но как ему это удалось?

Квантовый мир

В квантовой теории состояние частицы описывается ее волновой функцией. Она, к примеру, позволяет рассчитать вероятность нахождения частицы в той или иной точке пространства. Перед самим измерением неясно не только то, где находится частица, но и то, существует ли она. Сам факт измерения буквально создает реальность, «разрушая» волновую функцию. Но квантовая механика редко обращается к измерениям — потому-то она и является одной из самых спорных областей физики. Вспомните парадокс Шредингера: вы не сможете разрешить его, пока не произведете измерение, открыв коробку и выяснив, жив кот или нет.

Одним из решений подобных парадоксов является так называемая модель GRW, которая была разработана в конце 1980-х годов. Эта теория включает в себя такое явление, как «вспышки» — спонтанные коллапсы волновой функции квантовых систем. Результат ее применения точно такой же, как если бы измерения были проведены без наблюдателей как таковых. Тиллой модифицировал ее, чтобы показать, как с ее помощью можно выйти на теорию гравитации. В его варианте вспышка, разрушающая волновую функцию и заставляющую частицу тем самым находиться в одном месте, также создает гравитационное поле в этот момент в пространстве-времени. Чем больше квантовая система — тем больше в ней частиц и тем чаще случаются вспышки, создавая тем самым флуктуирующее гравитационное поле.

Самое интересное, что среднее значение этих флуктуаций и является тем самым гравитационным полем, которое описывает теория гравитации Ньютона. Такой подход к объединению гравитации с квантовой механикой называется квазиклассическим: гравитация возникает из квантовых процессов, но остается классической силой. «Нет никакой реальной причины игнорировать квазиклассический подход, при котором гравитация является классической на фундаментальном уровне», говорит Тиллой.

Феномен гравитации

Клаус Хорнбергер из Университета Дуйсбург-Эссен в Германии, не принимавший участия в разработке теории, относится к ней с большой симпатией. Однако ученый указывает на то, что до того, как эта концепция ляжет в основу единой теории, объединяющей и объясняющей природу всех фундаментальных аспектов окружающего нас мира, необходимо будет решить еще целый ряд задач. К примеру, модель Тиллоя точно может быть использована для получения ньютоновской силы тяжести, а вот ее соответствие гравитационной теории еще нужно проверить с помощью математики.

Впрочем, ученый и сам согласен с тем, что его теория нуждается в доказательной базе. К примеру, он предсказывает, что гравитация будет вести себя по‑разному в зависимости от масштабов рассматриваемых объектов: для атомов и для сверхмассивных черных дыр правила могут сильно отличаться. Как бы то ни было, если тесты обнаружат, что модель Тиллроя и в самом деле отражает реальность, а гравитация и в самом деле является следствием квантовых флуктуаций, то это позволит физикам осмыслить окружающую нас действительность на качественно ином уровне.

www.popmech.ru

---

• 
  Квантовый телефон
• 
  Квантовая реальность
• 
  Новости квантовой физики 2018
• 
  Квантовый интернет
• 
  Квантовые часы
• 
  Что изучает квантовая физика
• 
  Кванты и волны вселенной
• 
  Квантовая физика что изучает
• 
  Квантовые технологии
• 
  Квантовый процессор
• 
  Квантовый мир