Спросите Итана: чего такого пугающего есть в квантовой запутанности? Квантовая запутанность картинки
чего такого пугающего есть в квантовой запутанности? / Хабр
Квантовая физика полна загадок, печально известных тем, что они противоречат нашей интуиции. Частицы, кажется, знают, смотрите ли вы на них, или нет, и демонстрируют различное поведение, в зависимости от того, наблюдаете вы за ними, или нет, проходя через двойную щель. Измерение одной величины, допустим, положения частицы, создаёт присущую ей неопределённость в дополняющей величине, к примеру, импульсе. А если вы измерите её спин в вертикальном направлении, то уничтожите информацию о спине в горизонтальном направлении. Но самым «пугающим» из всех квантовых явлений будет квантовая запутанность, когда одна частица, кажется, мгновенно «узнаёт», измерили ли спутанного с ней партнёра, даже если это проделают на другом конце Вселенной. На этой неделе мы рассмотрим вопрос читателя, заинтригованного тем, почему это вообще считается загадкой.
Для начала пройдёмся по вопросу запутанности. Эксперимент обычно проводят с фотонами: вы передаёте один квант света через специальный материал (рассеивающий кристалл), расщепляющий его на два фотона. Эти фотоны будут запутаны в определённом смысле, то есть, если у одного будет спин, внутренний момент импульса, +1, тогда у другого он будет -1. Но у какого какой, нам неизвестно. Можно даже проделать эксперименты, в которых после рассмотрения большого числа фотонов будет видно разницу между • статистическими результатами в случае, если спин +1, • статистическими результатами в случае, если спин -1, • и статистическими результатами в случае, если спин остался неопределённым.
Очень сложно визуализировать эти результаты, но в квантовой механике есть прекрасная аналогия: прохождение частицы через двойную щель.
Если пропускать электроны, фотоны или любые другие частицы через двойную щель, возникает картина интерференции. Но это происходит, только если вы не проверяете, через какую щель они проходят!
Если пропустить частицу через двойную щель – то есть, экран с двумя узкими щелями, находящимися очень близко друг от друга – и она пройдёт сквозь них, вместо того, чтобы быть задержанной экраном, вы легко можете определить, где она окажется с другой стороны. Если вы будете запускать множество частиц по одной через двойную зель, вы обнаружите, что прошедшие через щели частицы формируют интерференционную картину. Иначе говоря, каждая частица ведёт себя не так, будто она прошла через одну или другую щель; она ведёт себя так, будто она прошла через обе щели сразу, проинтерферировала сама с собой на манер волны, и продолжила движение.
Но этот рисунок, демонстрирующий странную квантовомеханическую природу всех частиц Вселенной, появляется, только если вы не определяете, через какую щель проходит частица.
Если вы определяете, через какую щель проходит частица, оставив весь остальной эксперимент без изменений, вы вообще не получаете интерференционную картину.
Если вы вместо этого вы измеряете частицу на проходе через одну из щелей – это можно сделать через установку счётчика – вы не получите интерференционную картину. Вы получите кучу частиц, соответствующую прохождению через щель 1, и кучу для щели 2.
Волновой рисунок электронов, проходящих через двойную щель по одному. Если вы измерите, через какую щель прошёл электрон, вы уничтожаете квантовую интерференционную картину. Отметим, что для создания такой картины требуется больше одного электрона.
Иначе говоря, проводя измерение, определяющее избранный частицей путь, вы меняете результат этого выбора! Для одной частицы вы сможете только определить вероятность прохождения через щель 1, щель 2, или интерференции с самой собой. Для открытия реального состояния вашего эксперимента потребуется больше статистики.
Квантовомеханический тест Белла для частиц с полуцелым спином
Вернёмся к запутанным фотонам. Или вообще к любым запутанным частицам. Вы создаёте две запутанные частицы, у которых вам известна общая сумма их свойств, но не свойства каждой из них. Простейшим примером будет спин – у двух фотонов он получится либо (+1 и -1), либо (-1 и +1), у двух электронов — (+½ и -½) или (-½ и +½) – и вы не знаете, у какого из них будет какой спин, пока не измерите. Вместо щелей можно отправлять их через поляризатор. И как только вы измеряете один, вы определяете другой. Иначе говоря, знаете это мгновенно.
Эксперимент квантового стирания, в котором две запутанных частицы разделяются и измеряются. Никакие действия с одной из частиц в точке назначения не влияют на другую.
«Пугающим» становится тот факт, что в физике ничто другое не происходит мгновенно. Самая большая скорость передачи любого сигнала будет равна с, скорости света в вакууме. Но эти две запутанные частицы можно разделить на метры, километры, астрономические единицы или световые года, и измерение одной из них мгновенно определяет состояние другой. Неважно, двигаются ли запутанные частицы со скоростью света или нет, обладают они массой или нет, много ли у них энергии, и изолируете ли вы их друг от друга, чтобы они не отправляли друг другу фотоны. Нет никаких лазеек, позволяющих скорости взаимодействия в любой системе отсчёта как-то это компенсировать. В конце 1990-х эксперименты с разделением и одновременным измерением этих частиц определили, что если какая-либо информация и передаётся между ними, то она двигается быстрее скорости света в 10000 раз.
Квантовая телепортация, которую часто путают с путешествием быстрее света. В реальности информация быстрее скорости света не передаётся.
Но этого не может быть! В реальности никакой информации не передаётся. Нельзя провести измерение частицы в одном месте и использовать это для передачи чего-либо частице, расположенной очень далеко. Было разработано множество хитроумных схем, задуманных так, чтобы, используя это свойство, передавать информацию быстрее света, но в 1993 году доказали, что этот механизм не допустит передачи информации. Тому есть простое объяснение:
• Если вы измерите «каково состояние имеющейся у меня частицы», вы узнаете состояние другой частицы, но с этой информацией нельзя ничего сделать до тех пор, пока либо вы доберётесь до другой частицы, либо она доберётся до нас, и передача сообщений должна будет идти со скоростью света или медленнее. • Если же вы заставите имеющуюся у вас частицу принять определённое состояние, это не изменит состояние запутанной частицы. Наоборот, это разрушит запутанность, так что вы не узнаете ничего о второй частице.
[Итан немного не до конца раскрыл суть проблемы. Всё вышеописанное может и не удивить вас, если представить себе аналогию с перчатками. Некто отправил вам одну перчатку из пары, а вашему другу – другую. И вы, открыв свою посылку, мгновенно узнаёте не только то, какую перчатку, левую или правую, вы получили, но и то, какую получил ваш друг. Однако в случае с запутанными частицами состояние «перчаток» изначально не определено. И мы его не просто не знаем или не умеем определять – оно на самом деле определяется случайным образом, и именно в момент измерения одной из «перчаток». Тогда другая «перчатка» мгновенно принимает противоположное состояние. Именно это Эйнштейн и называл «пугающим дальнодействием» / прим. перев.]
Если две частицы запутаны, свойства их волновых функций дополняют друг друга, и измерение одной из них определяет свойства другой. Но является ли волновая функция абстрактным математическим описанием, или же она лежит в основе более глубокой истины Вселенной и детерминистской, фундаментальной реальности – вопрос открытый.
Это философская проблема для реалистов. Это значит, что волновая функция частицы – или запутанная волновая функция нескольких частиц – представляет собой реальный, физический объект, существующий и эволюционирующий во Вселенной, но для этого требуется большое количество неудобных предположений. Нужно предположить, что существует бесконечное число возможных реальностей, и что мы живём только в одной из них, хотя никаких свидетельств о существовании других нет. Если вы инструменталист (как автор; это проще и практичнее), у вас нет этой философской проблемы. Вы просто принимаете, как данность, что волновая функция – это инструмент для расчётов.
Эйнштейн был убеждённым реалистом в вопросах квантовой механики, и это предубеждение он унёс с собой в могилу. Никаких свидетельств в поддержку его интерпретации квантовой механики обнаружено не было, хотя у неё до сих пор есть много приверженцев
Стивен Вайнберг, нобелевский лауреат, сооснователь Стандартной Модели и гениальный во многих областях физик-теоретик, недавно осудил подход инструментализма в журнале Science News, описывая его так:
Это так ужасно, представлять, что у нас нет знаний по поводу всего, что существует – мы можем сказать, что произошло, только проведя измерение.
Но вне зависимости от ваших философских увиливаний, квантовая механика работает, и волновая функция, запутывающая частицы, позволяет разрушать эту запутанность, даже на космических расстояниях. Это единственный мгновенный процесс во Вселенной, известный нам, и поэтому он действительно стоит особняком!
Итан Сигель – астрофизик, популяризатор науки, автор блога Starts With A Bang! Написал книги «За пределами галактики» [Beyond The Galaxy], и «Трекнология: наука Звёздного пути» [Treknology].
habr.com
Физики квантово запутали фотоны, одновременно не существующие
Похоже, они издеваются над нами. Физикам давно было известно, что квантовая механика позволяет создавать тонкую связь между двумя квантовыми частицами — запутанность. Это ситуация, в которой одна частица может мгновенно определять состояние другой — где бы та ни находилась. Теперь эксперименты показали, что возможно запутать два фотона, которые даже не существуют одновременно.
Парадоксы квантовой физики, не дающие физикам спать, тем не менее дают нам и практические результаты. Кто знает, возможно, квантовая запутанность однажды ляжет в основу элементарной телепортации?
«Вы знаете, это клево», — говорит Джереми О’Брайен, экспериментатор Университета Бристоля в Великобритании, не имеющий отношения к работе. Такое состояние запутанности, разделенное временем, предсказывается в рамках стандартной квантовой теории, однако «оно широко не распространялось, и я даже не знаю, было ли сформулировано четко до этого момента».
Запутанность это парадокс, который полностью спрятан в неопределенностях квантовой механики. Представьте: у вас есть квантовая частица света, или фотон. Ее можно расположить таким образом, что она будет вертеться вертикально или горизонтально. Квантовая механика любит неопределенности, и благодаря ей фотон может вертеться одновременно и по вертикали, и по горизонтали. Если потом вы измерите состояние фотона, вы обнаружите, что он вертится либо горизонтально, либо вертикально, поскольку двойственное состояние схлопнется в одно (коллапс волновой функции): только в одно. Только если измерите, конечно.
Запутанность появляется, когда вы берете два фотона. Каждый из них можно поставить в состояние неопределенной вертикальности или горизонтальности. Но поскольку фотоны запутываются, их состояние будет идентичным, даже если вы не измерите его. К примеру, вы измеряете первый фотон и обнаруживаете, что он поляризован горизонтально. В тот же момент вы понимаете, что второй фотон схлопывается и вертится в вертикальном положении — вне зависимости от того, как далеко он находится. И поскольку этот распад происходит моментально, сам Альберт Эйнштейн окрестил запутанность «жутким действием на расстоянии». Все это не противоречит общей теории относительности: вы не можете контролировать результаты измерения первого фотона, поэтому квантовая связь не может передавать сообщение, которое движется быстрее света. Впрочем, возможно ли движение быстрее света, мы уже выясняли.
На рисунке изображено следующее: запутывание с заменой (наверху), где состояние (синий цвет) передается фотонам 1 и 4 с произведением измерений на фотонах 2 и 3. В новом эксперименте (внизу) выяснилось, что схема работает, даже если фотон 1 уничтожается до того, как создается фотон 4.
Илий Мегидиш, Хагаи Айзенберг и коллеги из Еврейского университета Иерусалима запутали два фотона, которые не существовали в одно и то же время. Они начали со схемы, известной как запутывание с заменой. Для начала исследователи облучали лазером специальный кристалл несколько раз, чтобы создать две пары фотонов, 1-2 и 3-4. В начале фотоны 1 и 4 не были запутаны. Но они будут таковыми, если ученые произведут особый трюк с 2 и 3.
Суть в том, что измерение «проектирует» частицу в определенное положение — точно так же, как измерение фотона заставляет его коллапсировать в вертикальное или горизонтальное положение. Поэтому, даже если фотоны 2 и 3 начинают, не будучи запутанными, физики могут проделать «проектирующее измерение», которое установит запутанную связь между двумя разными парами. Это измерение запутает фотоны, даже путем поглощения и уничтожения их. Если ученые измерят только события, в которых запутанности фотонов 2 и 3 приходит конец, измерение также запутает фотоны 1 и 4. Эффект напоминает работу четырех цепных шестеренок: две внутренних задают связь внешним двум.
В последнее время физики работали в рамках обычного времени. К примеру, в прошлом году было показано, что запутывание с заменой будет работать даже после того, как состояния фотонов 1 и 4 будут измерены. Теперь же Айзенберг и его коллеги показали, что фотоны 1 и 4 могут вообще не существовать одновременно, о чем и поспешили сообщить в Physical Review Letters.
Чтобы проделать это, они сначала запутали пару 1 и 2, а после измерили поляризацию 1. Сразу после этого была создана запутанная пара 3 и 4, и выполнено проектирующее измерение. Наконец, ученые измерили поляризацию фотона 4. И хотя фотоны 1 и 4 никогда не существовали одновременно, измерения показали, что их поляризации в конечном счете запутались. Айзенберг подчеркнул, что хотя в теории относительности время измеряется по-разному наблюдателями, которые движутся с разной скоростью, ни один наблюдатель никогда не видел два фотона сосуществующими.
Эксперимент показал, что думать о природе запутанности как о физически осязаемой связи, совершенно неправильно.
«Там нет момента во времени, когда два фотона существуют одновременно», — говорит физик. — «А значит вы не можете сказать, что система запутана в этот или в тот момент».
Тем не менее, явление существует. Антон Цайлингер, физик из Венского университета, согласился с тем, что эксперимент показывает, насколько скользкой остается квантовая механика.
«Она неуловима, потому что демонстрирует в большей или меньшей мере, что квантовые события находятся за пределами наших повседневных представлений о пространстве и времени».
Чем же хорош этот эксперимент? Физики надеются создать квантовые сети, в которых протоколы с использованием запутывания с заменой помогут удаленным пользователям обрести невзламываемую шифрованную связь. Новые выводы позволяют предположить, что при совместном использовании запутанных пар фотонов в таких сетях пользователю не придется ждать, чтобы увидеть, что происходит с фотонами, которые «остались позади».
Кроме того, такие эксперименты открывают умы людей. Вдруг кому-нибудь придет в голову идея, как ее использовать.
hi-news.ru
Просто о квантовой запутанности / Хабр
Чарующей аурой загадочности окутано понятие квантовой запутанности, а также (каким-то образом) связанное с ним требование квантовой теории о необходимости наличия «многих миров». И, тем не менее, по сути своей это научные идеи с приземлённым смыслом и конкретными применениями. Я хотел бы объяснить понятия запутанности и множества миров настолько просто и ясно, насколько знаю их сам.
I
Запутанность считается явлением, уникальным для квантовой механики – но это не так. На самом деле, для начала будет более понятным (хотя это и необычный подход) рассмотреть простую, не квантовую (классическую) версию запутанности. Это позволит нам отделить тонкости, связанные с самой запутанностью, от других странностей квантовой теории.Запутанность появляется в ситуациях, в которых у нас есть частичная информация о состоянии двух систем. К примеру, нашими системами могут стать два объекта – назовём их каоны. «К» будет обозначать «классические» объекты. Но если вам очень хочется представлять себе что-то конкретное и приятное – представьте, что это пирожные.
Наши каоны будут иметь две формы, квадратную или круглую, и эти формы будут обозначать их возможные состояния. Тогда четырьмя возможными совместными состояниями двух каонов будут: (квадрат, квадрат), (квадрат, круг), (круг, квадрат), (круг, круг). В таблице указана вероятность нахождения системы в одном из четырёх перечисленных состояний.
Мы будем говорить, что каоны «независимы», если знание о состоянии одного из них не даёт нам информации о состоянии другого. И у этой таблицы есть такое свойство. Если первый каон (пирожное) квадратный, мы всё ещё не знаем форму второго. И наоборот, форма второго ничего не говорит нам о форме первого.
С другой стороны, мы скажем, что два каона запутаны, если информация об одном из них улучшает наши знания о другом. Вторая табличка покажет нам сильную запутанность. В этом случае, если первый каон будет круглым, мы будем знать, что второй тоже круглый. А если первый каон квадратный, то таким же будет и второй. Зная форму одного, мы однозначно определим форму другого.
Квантовая версия запутанности выглядит, по сути, также – это отсутствие независимости. В квантовой теории состояния описываются математическими объектами под названием волновая функция. Правила, объединяющие волновые функции с физическими возможностями, порождают очень интересные сложности, которые мы обсудим позже, но основное понятие о запутанном знании, которое мы продемонстрировали для классического случая, остаётся тем же.
Хотя пирожные нельзя считать квантовыми системами, запутанность квантовых систем возникает естественным путём – например, после столкновений частиц. На практике незапутанные (независимые) состояния можно считать редкими исключениями, поскольку при взаимодействии систем между ними возникают корреляции.
Рассмотрим, к примеру, молекулы. Они состоят из подсистем – конкретно, электронов и ядер. Минимальное энергетическое состояние молекулы, в котором она обычно и находится, представляет собой сильно запутанное состояние электронов и ядра, поскольку расположение этих составляющих частиц никак не будет независимым. При движении ядра электрон движется с ним.
Вернёмся к нашему примеру. Если мы запишем Φ■, Φ● как волновые функции, описывающие систему 1 в её квадратных или круглых состояниях и ψ■, ψ● для волновых функций, описывающих систему 2 в её квадратных или круглых состояниях, тогда в нашем рабочем примере все состояния можно описать, как:
Независимые: Φ■ ψ■ + Φ■ ψ● + Φ● ψ■ + Φ● ψ●
Запутанные: Φ■ ψ■ + Φ● ψ●
Независимую версию также можно записать, как:
(Φ■ + Φ●)(ψ■ + ψ●)
Отметим, как в последнем случае скобки чётко разделяют первую и вторую системы на независимые части.
Существует множество способов создания запутанных состояний. Один из них – измерить составную систему, дающую вам частичную информацию. Можно узнать, например, что две системы договорились быть одной формы, не зная при этом, какую именно форму они выбрали. Это понятие станет важным чуть позже.
Более характерные последствия квантовой запутанности, такие, как эффекты Эйнштейна-Подольского-Розена (EPR) и Гринберга-Хорна-Зейлингера (GHZ), возникают из-за её взаимодействия ещё с одним свойством квантовой теории под названием «принцип дополнительности». Для обсуждения EPR и GHZ позвольте мне сначала представить вам этот принцип.
До этого момента мы представляли, что каоны бывают двух форм (квадратные и круглые). Теперь представим, что ещё они бывают двух цветов – красного и синего. Рассматривая классические системы, например, пирожные, это дополнительное свойство означало бы, что каон может существовать в одном из четырёх возможных состояний: красный квадрат, красный круг, синий квадрат и синий круг.
Но квантовые пирожные – квантожные… Или квантоны… Ведут себя совсем по-другому. То, что квантон в каких-то ситуациях может обладать разной формой и цветом не обязательно означает, что он одновременно обладает как формой, так и цветом. Фактически, здравый смысл, которого требовал Эйнштейн от физической реальности, не соответствует экспериментальным фактам, что мы скоро увидим.
Мы можем измерить форму квантона, но при этом мы потеряем всю информацию о его цвете. Или мы можем измерить цвет, но потеряем информацию о его форме. Согласно квантовой теории, мы не можем одновременно измерить и форму и цвет. Ничей взгляд на квантовую реальность не обладает полнотой; приходится принимать во внимание множество разных и взаимоисключающих картин, у каждой из которых есть своё неполное представление о происходящем. Это и есть суть принципа дополнительности, такая, как её сформулировал Нильс Бор.
В результате квантовая теория заставляет нас быть осмотрительными в приписывании свойствам физической реальности. Во избежание противоречий приходится признать, что:
Не существует свойства, если его не измерили. Измерение – активный процесс, изменяющий измеряемую систему
II
Теперь опишем две образцовые, но не классические, иллюстрации странностей квантовой теории. Обе были проверены в строгих экспериментах (в реальных экспериментах люди меряют не формы и цвета пирожных, а угловые моменты электронов).Альберт Эйнштейн, Борис Подольский и Натан Розен (EPR) описали удивительный эффект, возникающий при запутанности двух квантовых систем. EPR-эффект объединяет особую, экспериментально достижимую форму квантовой запутанности с принципом дополнительности.
EPR-пара состоит из двух квантонов, у каждого из которых можно измерить форму или цвет (но не то и другое сразу). Предположим, что у нас есть множество таких пар, все они одинаковые, и мы можем выбирать, какие измерения мы проводим над их компонентами. Если мы измерим форму одного из членов EPR-пары, мы с одинаковой вероятностью получим квадрат или круг. Если измерим цвет, то с одинаковой вероятностью получим красный или синий.
Интересные эффекты, казавшиеся EPR парадоксальными, возникают, когда мы проводим измерения обоих членов пары. Когда мы меряем цвет обоих членов, или их форму, мы обнаруживаем, что результаты всегда совпадают. То есть, если мы обнаружим, что один из них красный и затем меряем цвет второго, мы также обнаруживаем, что он красный – и т.п. С другой стороны, если мы измеряем форму одного и цвет другого, никакой корреляции не наблюдается. То есть, если первый был квадратом, то второй с одинаковой вероятностью может быть синим или красным.
Согласно квантовой теории, мы получим такие результаты, даже если две системы будет разделять огромное расстояние и измерения будут проведены почти одновременно. Выбор типа измерений в одном месте, судя по всему, влияет на состояние системы в другом месте. Это «пугающее дальнодействие», как называл его Эйнштейн, по-видимому, требует передачу информации – в нашем случае, информации о проведённом измерении – со скоростью, превышающей скорость света.
Но так ли это? Пока я не узнаю, какой результат получили вы, я не знаю, чего ожидать мне. Я получаю полезную информацию, когда я узнаю ваш результат, а не когда вы проводите измерение. И любое сообщение, содержащее полученный вами результат, необходимо передать каким-либо физическим способом, медленнее скорости света.
При дальнейшем изучении парадокс ещё больше разрушается. Давайте рассмотрим состояние второй системы, если измерение первой дало красный цвет. Если мы решим мерить цвет второго квантона, мы получим красный. Но по принципу дополнительности, если мы решим измерить его форму, когда он находится в «красном» состоянии, у нас будут равные шансы на получение квадрата или круга. Поэтому, результат EPR логически предопределён. Это просто пересказ принципа дополнительности.
Нет парадокса и в том, что удалённые события коррелируют. Ведь если мы положим одну из двух перчаток из пары в коробки и отправим их в разные концы планеты, неудивительно, что посмотрев в одну коробку, я могу определить, на какую руку предназначена другая перчатка. Точно так же, во всех случаях корреляция пар EPR должна быть зафиксирована на них, когда они находятся рядом и потому они могут выдержать последующее разделение, будто бы имея память. Странность EPR-парадокса не в самой по себе возможности корреляции, а в возможности её сохранения в виде дополнений.
III
Дэниел Гринбергер, Майкл Хорн и Антон Зейлингер открыли ещё один прекрасный пример квантовой запутанности. ОН включает три наших квантона, находящихся в специально подготовленном запутанном состоянии (GHZ-состоянии). Мы распределяем каждый из них разным удалённым экспериментаторам. Каждый из них выбирает, независимо и случайно, измерять ли цвет или форму и записывает результат. Эксперимент повторяют многократно, но всегда с тремя квантонами в GHZ-состоянии.Каждый отдельно взятый экспериментатор получает случайные результаты. Измеряя форму квантона, он с равной вероятностью получает квадрат или круг; измеряя цвет квантона, он с равной вероятностью получает красный или синий. Пока всё обыденно.
Но когда экспериментаторы собираются вместе и сравнивают результаты, анализ показывает удивительный результат. Допустим, мы будем называть квадратную форму и красный цвет «добрыми», а круги и синий цвет – «злыми». Экспериментаторы обнаруживают, что если двое из них решили измерить форму, а третий – цвет, тогда либо 0, либо 2 результата измерений получаются «злыми» (т.е. круглыми или синими). Но если все трое решают измерить цвет, то либо 1 либо 3 измерения получаются злыми. Это предсказывает квантовая механика, и именно это и происходит.
Вопрос: количество зла чётное или нечётное? В разных измерениях реализовываются обе возможности. Нам приходится отказаться от этого вопроса. Не имеет смысла рассуждать о количестве зла в системе без связи с тем, как его измеряют. И это приводит к противоречиям.
Эффект GHZ, как описывает его физик Сидни Колман, это «оплеуха от квантовой механики». Он разрушает привычное, полученное из опыта ожидание того, что у физических систем есть предопределённые свойства, независимые от их измерения. Если бы это было так, то баланс доброго и злого не зависел бы от выбора типов измерений. После того, как вы примете существование GHZ-эффекта, вы его не забудете, а ваш кругозор будет расширен.
IV
Пока что мы рассуждаем о том, как запутанность не позволяет назначить уникальные независимые состояния нескольким квантонам. Такие же рассуждения применимы к изменениям одного квантона, происходящим со временем.Мы говорим об «запутанных историях», когда системе невозможно присвоить определённое состояние в каждый момент времени. Так же, как в традиционной запутанности мы исключаем какие-то возможности, мы можем создать и запутанные истории, проводя измерения, собирающие частичную информацию о прошлых событиях. В простейших запутанных историях у нас есть один квантон, изучаемый нами в два разных момента времени. Мы можем представить ситуацию, когда мы определяем, что форма нашего квантона оба раза была квадратной, или круглой оба раза, но при этом остаются возможными обе ситуации. Это темпоральная квантовая аналогия простейшим вариантам запутанности, описанным ранее.
Используя более сложный протокол, мы можем добавить чуть-чуть дополнительности в эту систему, и описать ситуации, вызывающие «многомировое» свойство квантовой теории. Наш квантон можно подготовить в красном состоянии, а затем измерить и получить голубое. И как в предыдущих примерах, мы не можем на постоянной основе присвоить квантону свойство цвета в промежутке между двумя измерениями; нет у него и определённой формы. Такие истории реализовывают, ограниченным, но полностью контролируемым и точным способом, интуицию, свойственную картинке множественности миров в квантовой механике. Определённое состояние может разделиться на две противоречащие друг другу исторические траектории, которые затем снова соединяются.
Эрвин Шрёдингер, основатель квантовой теории, скептически относившийся к её правильности, подчёркивал, что эволюция квантовых систем естественным образом приводит к состояниям, измерение которых может дать чрезвычайно разные результаты. Его мысленный эксперимент с «котом Шрёдингера» постулирует, как известно, квантовую неопределённость, выведенную на уровень влияния на смертность кошачьих. До измерения коту невозможно присвоить свойство жизни (или смерти). Оба, или ни одно из них, существуют вместе в потустороннем мире возможностей.
Повседневный язык плохо приспособлен для объяснения квантовой дополнительности, в частности потому, что повседневный опыт её не включает. Практические кошки взаимодействуют с окружающими молекулами воздуха, и другими предметами, совершенно по-разному, в зависимости от того, живы они или мертвы, поэтому на практике измерение проходит автоматически, и кот продолжает жить (или не жить). Но истории с запутанностью описывают квантоны, являющиеся котятами Шрёдингера. Их полное описание требует, чтобы мы принимали к рассмотрению две взаимоисключающие траектории свойств.
Контролируемая экспериментальная реализация запутанных историй – вещь деликатная, поскольку требует сбора частичной информации о квантонах. Обычные квантовые измерения обычно собирают всю информацию сразу – к примеру, определяют точную форму или точный цвет – вместо того, чтобы несколько раз получить частичную информацию. Но это можно сделать, хотя и с чрезвычайными техническими трудностями. Этим способом мы можем присвоить определённый математический и экспериментальный смысл распространению концепции «множественности миров» в квантовой теории, и продемонстрировать её реальность.
habr.com
Можно ли применить квантовую запутанность для коммуникаций быстрее света? (6 фото)
В прошлом месяце миллиардер Юрий Мильнер и астрофизик Стивен Хокинг объявили о проекте Breakthrough Starshot: невероятно амбициозном плане отправить первый сделанный людьми космический аппарат в другую звездную систему в нашей галактике. Гигантский лазерный массив мог бы запустить аппарат размером с микрочип к другой звезде на скорости в 20% от световой. Но непонятно, как это небольшое устройство сможет связаться с нами через огромное межзвездное пространство. Как насчет квантовой запутанности? Можно ли применить ее для такой связи?
Такая идея, безусловно, заслуживает внимания.
Представьте себе две монеты, каждая из которых может выпасть орлом или решкой. Одна монета у вас, другая у меня, а мы находимся чрезвычайно далеко друг от друга. Мы подбрасываем свои монетки в воздух, ловим их и шлепаем на стол. Перед тем как взглянуть на выпавшую фигуру, мы ожидаем, что решка выпадет с вероятностью в 50/50, и орел, конечно, также. В обычной, незапутанной Вселенной, ваш и мой результаты будут независимы друг от друга. Если у вас выпадет решка, моя монета с вероятностью в 50% упадет орлом или решкой. Но при определенных условиях эти результаты могут быть запутаны: если вы проводите этот эксперимент и получает решку, вы будете знать, что моя монета с вероятностью в 100% покажет орла, еще до того, как я вам об этом сообщу. Вы узнаете об этом мгновенно, даже если мы будем разделены световыми годами и не пройдет ни единой секунды.
В квантовой физике мы обычно запутываем не монеты, а отдельные частицы, вроде электронов и фотонов, где, например, каждый фотон может иметь спин +1 или -1. Если измерить спин одного фотона, вы мгновенно узнаете спин другого, даже если он будет за полвселенной от нас. Пока вы не измерите спин одного фотона, они оба существуют в неопределенном состоянии; но как только измерили один, вы сразу же узнаете о нем. На Земле мы проводили такой эксперимент, разделив два запутанных фотона многими километрами и измерив их спины в течение наносекунды. Оказалось, что если мы измеряем спин одного и он оказывается +1, мы узнаем о том, что спин другого -1 в 10000 раз быстрее, чем могла бы позволить нам скорость света.
И вот вопрос: могли бы мы использовать это свойство — квантовую запутанность — чтобы связаться с далекой звездной системой? Ответ: да, если считать проведение измерения в удаленном месте формой связи. Но когда вы говорите «связь», обычно вы хотите что-то узнать о том месте, с которым связываетесь. Вы можете, например, держать запутанную частицу в неопределенном состоянии, отправить ее на борту космического аппарата к ближайшей звезде и сказать ему искать признаки твердых планет в пределах обитаемой зоны этой звезды. Увидев такую, он проводит измерение, которое приводит к тому, что ваша частица окажется в состоянии +1, а если нет, то проведение измерения покажет, что ваша частица в состоянии -1.
Таким образом, предположите вы, частица на Земле должна быть в состоянии -1, когда вы измеряете ее, что скажет о том, что космический аппарат нашел планету в обитаемой зоне, или же в состоянии +1, что скажет о том, что аппарат планету не нашел. Если вы знаете о том, что измерение было проведено, вы сможете сделать собственное измерение и мгновенно узнать о состоянии другой частицы, даже если она за много световых лет от вас.
Волновой рисунок для электронов, проходящих через двойную щель. Если измерить, через какую щель проходит электрон, этим вы уничтожите рисунок квантовой интерференции.
План прекрасен. Но есть проблема: запутанность работает, только если вы спрашиваете частицу: в каком ты состоянии? Если вы помещаете запутанную частицу в определенное состояние, вы разрушаете запутанность, и измерение проводимое на Земле будет полностью независимым от измерения далекой звезды. Если вы просто измерили далекую частицу (и выяснили: +1 или -1), тогда ваше измерение на Земле тоже будет -1 или +1 (соответственно) и даст вам информацию о частице, расположенной за световые годы от вас. Если же вы погрузите частицу в состояние +1 или -1, то вне зависимости от результата ваша частица на Земле будет с 50% вероятностью +1 или -1 и ничего не скажет о частице за много световых лет.
Это одна из самых непонятных вещей в квантовой физике: запутанность можно использовать для получения информации о компоненте системы, когда вы знаете полное ее состояние и проводите измерение другого компонента (-ов), но не для создания и передачи информации из одной части запутанной системы в другую. Поэтому никакой возможности для связи быстрее света не появляется.
Квантовая запутанность — это удивительное свойство, которое мы можем использовать для кучи разных задач, вроде совершенной системы шифрования информации. Но связь быстрее света? Чтобы понять, почему это невозможно, нам нужно понять ключевое свойство квантовой физики: что насильственное погружение хотя бы части запутанной системы в одно состояние не позволяет вам получить информацию об этом погружении через измерение оставшейся части системы. Как однажды точно подметил Нильс Бор, «если квантовая механика еще глубоко не шокировала вас, вы это еще не поняли».
Вселенная играет с нами в кости постоянно, к большому огорчению Эйнштейна. Даже наши лучшие попытки схитрить в этой игре природа выявляет на корню.
Другие статьи:
nlo-mir.ru
Квантовые камеры впервые помогли ученым сделать фото "призраков"
Люди имеют разное представление о привидениях. Кто-то отказывается верить в их существование, кто-то представляет именно так, как их рисуют книги и мистические фильмы, а кто-то полагает, что призраков можно чувствовать и видеть.
Квантовые камеры спешат на помощь
Великий физик Альберт Эйнштейн в свое время пытался доказать теорию о существовании привидений. Однако, на свою беду, он не обладал тем техническим оснащением, которым обладают современные ученые. Теперь оболочку призрака можно будет «поймать» на пленку при помощи квантовой камеры.  Только для начала нам необходимо прояснить ситуацию: фотографии не могут запечатлеть блуждающие души умерших предков. Они скорее отображают образ, состоящий из фотонов, которые не видны в объективе обычной цифровой камеры.
Только для начала нам необходимо прояснить ситуацию: фотографии не могут запечатлеть блуждающие души умерших предков. Они скорее отображают образ, состоящий из фотонов, которые не видны в объективе обычной цифровой камеры.
Результат квантовой запутанности
Иногда на снимках видны посторонние объекты, которые не являются результатом некачественной печати. Дело в том, что иногда обычная фотокамера может захватывать объекты, которые не сразу видны в объектив. Получить изображение фантома сложно, ведь через него не преломляется свет. Однако помочь в этом деле может такое явление, как квантовая запутанность. При этом квантомеханическом явлении два или более объекта какое-то время сохраняют свою взаимозависимость. И это происходит вне зависимости от того, как далеко они удалены друг от друга.
Например, вы всегда можете получить такую пару фотонов, один из которых имеет положительный спин (вращение элементарных частиц), а другой отрицательный. Иными словами, на один фотон с положительной спинальностью всегда приходится другой. Измерения, выполненные в той же системе, непосредственно влияют на другие системы и переплетаются с ними. Однако никто до сих пор не знает, как это работает.
Как запечатлеть фантом на пленке?
Квантовые камеры оснащены двумя отдельными лазерными пучками с запутанными фотонами. И если один луч объектива устремлен на картинку, то другой воссоздает связи, не видимые объективу. По оценкам специалистов, это очень умное решение. В некотором смысле это волшебство, рожденное посредством квантовой оптики. Об этом говорит эксперт Национального института стандартов и технологий в Гейтерсберге (штат Мериленд) Пол Летт: «Все, что мы видим сейчас, это не новое слово в физике. Это аккуратная демонстрация физических возможностей на практике».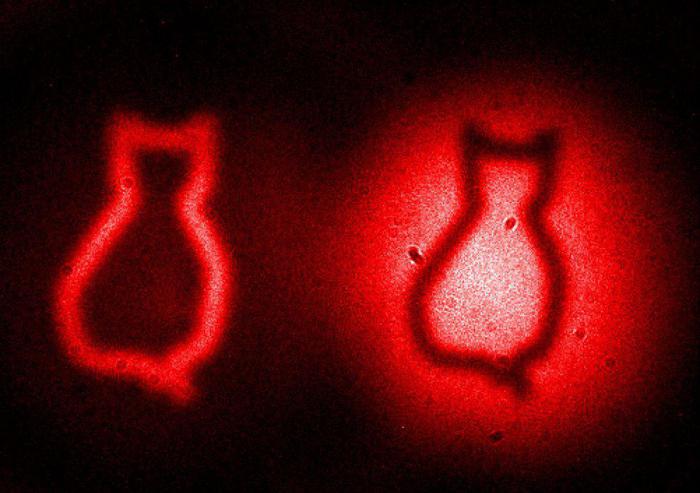
Фактический эксперимент
Как вы могли догадаться, с квантовой камерой был произведен фактический эксперимент. Его результаты были опубликованы в журнале Nature. Для этого исследователи использовали крошечные кошачьи трафареты и трезубец, выгравированный в кремнии. Было зафиксировано, что два луча света прошли сквозь отверстия на разных длинах волн. В итоге первый и второй лучи запутались, но один из них не попал в цель, а продолжал совершать путешествие на другой линии.
Заключение
По-настоящему удивительным результатом можно считать то, что второй луч света также участвовал в формировании объектов на снимке в то время, когда камера была сфокусирована на нем. И это несмотря на то, что он никогда не преломлялся через какой-либо из объектов. По мнению эксперта, это давняя экспериментальная идея, которая может привести к чему-то на практике. Например, в условиях медицинской визуализации.
fb.ru
Квантовая запутанность и червоточины могут быть тесно связаны
Когда Альберт Эйнштейн поражался «жуткой» дальнодействующей связи между частицами, он не думал о своей общей теории относительности. Вековая теория Эйнштейна описывает, как возникает гравитация, когда массивные объекты деформируют ткань пространства и времени. Квантовая запутанность, тот жуткий источник эйнштейновского испуга, как правило, затрагивает крошечные частицы, которые незначительно действуют на гравитацию. Пылинка деформирует матрас ровно так же, как субатомная частица искривляет пространство.
Тем не менее физик-теоретик Марк Ван Раамсдонк подозревает, что запутанность и пространство-время на самом деле связаны между собой. В 2009 году он рассчитал, что пространство без запутанности не смогло бы удержать себя. Он написал работу, из которой вытекало, что квантовая запутанность является иглой, которая сшивает воедино гобелен космического пространства-времени.
Многие журналы отказались публиковать его работу. Но спустя годы изначального скептицизма изучение идеи того, что запутанность формирует пространство-время, стало одной из самых горячих тенденций в области физики. «Выходя из глубоких основ физики, все указывает на то, что пространство должно быть связано с запутанностью», — говорит Джон Прескилл, физик-теоретик из Калтеха.
В 2012 году появилась еще одна провокационная работа, представляющая парадокс запутанных частиц внутри и снаружи черной дыры. Менее чем через год два эксперта в этой области предложили радикальное решение: запутанные частицы соединяются червоточинами — туннелями пространства-времени, представленными еще Эйнштейном, которые в настоящее время одинаково часто появляются на страницах журналов по физике и в научной фантастике. Если это допущение верно, запутанность не является жутким дальнодействующим соединением, о котором думал Эйнштейн — а вполне реальным мостом, связывающим удаленные точки в пространстве.
Многие ученые находят эти идеи достойными внимания. В последние годы физики, казалось бы, несвязанных специальностей сошлись на этом поле запутанности, пространства и червоточин. Ученые, которые когда-то были сосредоточены на создании безошибочных квантовых компьютеров, сегодня размышляют, не является ли сама Вселенная квантовым компьютером, который тихо программирует пространство-время в сложной сети запутанностей. «Все прогрессирует невероятным образом», — говорит Ван Раамсдонк из Университета Британской Колумбии в Ванкувере.
Физики возлагают большие надежды на то, куда их заведет это соединение пространства-времени с запутанностью. ОТО блестяще описывает, как работает пространство-время; новые исследования могут приоткрыть завесу над тем, откуда берется пространство-время и на что оно похоже на мельчайших масштабах, лежащих во власти квантовой механики. Запутанность может быть секретным ингредиентом, который объединит эти пока что несовместимые области в теорию квантовой гравитации, позволив ученым понять условия внутри черной дыры и состояние Вселенной в первые моменты после Большого Взрыва.
Голограммы и банки с супом
Прозрение Ван Раамсдонка в 2009 году не материализовалось из воздуха. Оно уходит корнями в голографический принцип, идею того, что граница, ограничивающая объем пространства, может содержать всю информацию, в нем заключенную. Если применить голографический принцип к повседневной жизни, то любопытный сотрудник может идеально реконструировать все, что находится в офисе, — кипы бумаг, семейные фотографии, игрушки в углу и даже файлы на жестком диске компьютера — просто глядя на внешние стены квадратного офиса. Эта идея противоречива, учитывая то, что стены имеют два измерения, а интерьер офиса три. Но в 1997 году Хуан Малдасена, струнный теоретик тогда из Гарварда, привел интригующий пример того, что голографический принцип мог бы раскрыть о Вселенной.
Он начал с анти-де-ситтеровского пространства, которое напоминает пространство-время, в котором преобладает гравитации, но обладает рядом странных атрибутов. Оно изогнуто таким образом, что вспышка света, излученного в определенном месте, в конечном счете вернется оттуда, где появилась. И хотя Вселенная расширяется, анти-де-ситтеровское пространство не растягивается и не сжимается. Из-за таких особенностей кусок анти-де-ситтеровского пространства с четырьмя измерениями (тремя пространственными и одним временным) может быть окружен трехмерной границей.
Малдасена обращался к цилиндру анти-де-ситтеровского пространства-времени. Каждый горизонтальный срез цилиндра представляет состояние его пространства в данный момент, тогда как вертикальное измерение цилиндра представляет время. Малдасена окружил свой цилиндр границей для голограммы; если бы анти-де-ситтеровское пространство было банкой супа, то граница была бы этикеткой.
На первый взгляд кажется, что эта граница (этикетка) не имеет ничего общего с наполнением цилиндра. Пограничная «этикетка», к примеру, соблюдает правила квантовой механики, а не гравитации. И все же гравитация описывает пространство внутри содержимого «супа». Малдасена показал, что этикетка и суп были одним и тем же; квантовые взаимодействия на границе отлично описывают анти-де-ситтеровское пространство, которое закрывает эта граница. «Две этих теории кажутся совершенно разными, но точно описывают одно и то же», — говорит Прескилл.
Малдасена добавил запутанность в голографическое уравнение в 2001 году. Он представил пространство в двух банках с супом, каждая из которых содержит черную дыру. Затем создал эквивалент самодельного телефона из стаканчиков, соединяющего черные дыры с помощью червоточины — туннеля через пространство-время, впервые предложенного Эйнштейном и Натаном Розеном в 1935 году. Малдасена искал способ создать эквивалент такой связи пространства-времени на этикетках банок. Хитрость, как он понял, была в запутанности.
Как и червоточина, квантовая запутанность связывает объекты, которые не имеют очевидных отношений. Квантовый мир — расплывчатое место: электрон может вращаться в обе стороны одновременно, будучи в состоянии суперпозиции, пока измерения не предоставят точный ответ. Но если два электрона запутаны, измерение спина одного позволяет экспериментатору узнать спин другого электрона — даже если партнерский электрон находится в состоянии суперпозиции. Эта квантовая связь остается даже если электроны будут разделять метры, километры или световые годы.
Малдасена показал, что с помощью запутывания частиц на одной этикетке с частицами на другой можно идеально квантово-механически описать соединение червоточиной банок. В контексте голографического принципа, запутанность эквивалентна физическому связыванию кусков пространства-времени вместе.
Вдохновленный этой связью запутанности с пространством-временем, Ван Раамсдонк задался вопросом, насколько большую роль запутанность может играть в формировании пространства-времени. Он представил самую чистую этикетку на банке с квантовым супом: белую, соответствующую пустому диску анти-де-ситтеровского пространства. Но он знал, что, согласно основам квантовой механики, пустое пространство никогда не будет полностью пустым. Оно заполнено парами частиц, которые всплывают и исчезают. И этим мимолетные частицы запутаны.
Поэтому Ван Раамсдонк нарисовал воображаемую биссектрису на голографической этикетке и затем математически разорвал квантовую запутанность между частицами на одной половине этикетке и частицами на другой. Он обнаружил, что соответствующий диск анти-де-ситтеровского пространства начал делиться пополам. Будто бы запутанные частицы были крючками, которые удерживают полотно пространства и времени на месте; без них пространство-времени разлетается на части. По мере того, как Ван Раамсдонк понижал степень запутанности, часть подключенного к разделенным регионам пространства становилась тоньше, подобно резиновой нити, тянущейся от жвачки. «Это навело меня на мысль, что присутствие пространства начинается с присутствия запутанности».
Это было смелое заявление, и потребовалось время, чтобы работа Ван Раамсдонка, опубликованная в General Relativity and Gravitation в 2010 году, привлекла серьезное внимание. Огонь интереса всполыхнул уже в 2012 году, когда четверо физиков из Калифорнийского университета в Санта-Барбаре написали работу, бросающую вызов общепринятым убеждениям о горизонте событий, точки невозврата черной дыры.
Истина, скрытая файрволом
В 1970-х годах физик-теоретик Стивен Хокинг показал, что пары запутанных частиц — тех же видов, которые Ван Раамсдонк позже анализировал в своей квантовой границе — могут распадаться на горизонте событий. Одна падает в черную дыру, а другая убегает вместе с так называемым излучением Хокинга. Этот процесс постепенно подтачивает массу черной дыры, в конечном итоге приводя к ее гибели. Но если черные дыры исчезают, вместе с ней должна исчезать и запись всего, что падало внутрь. Квантовая теория же утверждает, что информация не может быть уничтожена.
К 90-м годам несколько физиков-теоретиков, включая Леонарда Сасскинда из Стэнфорда, предложили решение этой проблемы. Да, сказали они, материя и энергия падает в черную дыру. Но с точки зрения внешнего наблюдателя, этот материал никогда не преодолевает горизонт событий; он словно балансирует на его грани. В результате горизонт событий становится голографической границей, содержащей всю информацию о пространстве внутри черной дыры. В конце концов, когда черная дыра испаряется, эта информация утекает в виде излучения Хокинга. В принципе, наблюдатель может собрать это излучение и восстановить всю информацию о недрах черной дыры.
В своей работе 2012 года физики Ахмед Альмхейри, Дональд Марольф, Джеймс Салли и Джозеф Полчинский заявили, что в этой картине что-то не так. Для наблюдателя, пытающегося собрать головоломку того, что находится внутри черной дыры, отметили одни, все отдельные части головоломки — частицы излучения Хокинга — должны быть запутаны между собой. Также каждая хокингова частица должна быть запутана со своим оригинальным партнером, который упал в черную дыру.
К сожалению, одной запутанности недостаточно. Квантовая теория утверждает, что для того, чтобы запутанность присутствовала между всеми частицами снаружи черной дыры, должна быть исключена запутанность этих частиц с частицами внутри черной дыры. Кроме того, физики обнаружили, что разрыв одной из запутанностей породил бы непроницаемую энергетическую стену, так называемый файрвол, на горизонте событий.
Многие физики усомнились в том, что черные дыры на самом деле испаряют все, что пытается проникнуть внутрь. Но сама возможность существования файрвола наводит на тревожные мысли. Ранее физики уже задумывались о том, как выглядит пространство внутри черной дыры. Теперь они не уверены в том, есть ли у черных дыр это «внутри» вообще. Все будто смирились, отмечает Прескилл.
Но Сасскинд не смирился. Он потратил годы, пытаясь доказать, что информация не исчезает внутри черной дыры; сегодня он так же убежден, что идея файрвола ошибочна, но доказать этого пока не смог. Однажды он получил загадочное письмо от Малдасены: «В нем было немного, — говорит Сасскинд. — Только ЭР = ЭПР». Малдасена, работающий сейчас в Институте продвинутых исследований в Принстоне, задумался о своей работе с банками супа 2001 года и заинтересовался, могут ли червоточины разрешить мешанину запутанности, порожденную проблемой файрвола. Сасскинд быстро подхватил эту идею.
В статье, опубликованной в немецком журнале Fortschritte der Physik в 2013 году, Малдасена и Сасскинд заявили, что червоточина — технически мост Эйнштейна-Розена, или ЭР — является пространственно-временным эквивалентом квантовой запутанности. (Под ЭПР понимают эксперимент Эйнштейна-Подольского-Розена, который должен был развеять мифологическую квантовую запутанность). Это означает, что каждая частица излучения Хокинга, независимо от того, как далеко она находится от начала, напрямую связана с недрами черной дыры посредством короткого пути через пространство-время. «Если двигать через червоточину, далекие вещи оказываются не такими уж и далекими», — говорит Сасскинд.
Сасскинд и Малдасена предложили собрать все частицы Хокинга и столкнуть их вместе, пока они не коллапсируют в черную дыру. Эта черная дыра была бы запутана, а значит соединена червоточиной с оригинальной черной дырой. Этот трюк превратил запутанную мешанину хокинговых частиц — парадоксально запутанных с черной дырой и между собой — в две черные дыры, соединенные червоточиной. Перегрузка запутанности разрешилась, и проблема файрвола была исчерпана.
Не все ученые прыгнули на подножку трамвая ЭР = ЭПР. Сасскинд и Малдасена признают, что им предстоит проделать еще много работы, чтобы доказать эквивалентность червоточин и запутанности. Но после обдумывания последствий парадокса файрвола, многие физики соглашаются, что пространство-время внутри черной дыры обязано своим существованием запутанности с излучением снаружи. Это важное прозрение, отмечает Прескилл, поскольку оно также означает, что вся ткань пространства-времени Вселенной, включая тот клочок, который занимаем мы, является продуктом квантового жуткого действия.
Космический компьютер
Одно дело сказать, что вселенная конструирует пространство-время посредством запутанности; совсем другое — показать, как вселенная это делает. Этой сложной задачей занялись Прескилл и коллеги, которые решили рассмотреть космос как колоссальный квантовый компьютер. Почти двадцать лет ученые работали над строительством квантовых компьютеров, которые используют информацию, зашифрованную в запутанных элементах, вроде фотонов или крошечных микросхем, чтобы решать проблемы, с которыми традиционные компьютеры справиться не могут. Команда Прескилла использует знание, полученное в результате этих попыток, чтобы предсказать, как отдельные детали внутри банки с супом могли бы отразиться на заполненной запутанностью этикетке.
Квантовые компьютеры работают, эксплуатируя компоненты, которые находятся в суперпозиции состояний, как носители данных — они могут быть нулями и единицами одновременно. Но состояние суперпозиции очень хрупкое. Избыток тепла, например, может разрушить состояние и всю заключенную в нем квантовую информацию. Эти потери информации, которые Прескилл сравнивает с рваными страницами в книге, кажутся неизбежными.
Но физики ответили на это, создав протокол квантовой коррекции ошибок. Вместо того чтобы полагаться на одну частицу для хранения квантового бита, ученые разделяют данные между несколькими запутанными частицами. Книга, написанная на языке квантовой коррекции ошибок, будет полна бреда, говорит Прескилл, но все ее содержимое можно будет восстановить, даже если половина страниц пропадет без вести.
Квантовая коррекция ошибок привлекла много внимания в последние годы, но теперь Прескилл и его коллеги подозревают, что природа придумала эту систему уже давно. В июне, в журнале Journal of High Energy Physics, Прескилл и его команда показали, как запутывание множества частиц на голографической границе идеально описывает одну частицу, притягиваемую гравитацией внутри куска анти-де-ситтеровского пространства. Малдасена говорит, что эта находка может привести к лучшему пониманию того, как голограмма кодирует все детали пространства-времени, которое окружает.
Физики признают, что их размышления должны пройти долгий путь, чтобы соответствовать реальности. В то время как анти-де-ситтеровское пространство предлагает физикам преимущество работы с хорошо определенной границей, у Вселенной нет такой четкой этикетки на банке с супом. Ткань пространства-времени космоса расширяется с момента Большого Взрыва и продолжает делать это в нарастающем темпе. Если вы отправите луч света в космос, он не развернется и не вернется; он будет лететь. «Непонятно, как определить голографическую теорию нашей Вселенной, — писал Малдасена в 2005 году. — Просто нет удобного места для размещения голограммы».
Тем не менее, как бы странно ни звучали все эти голограммы, банки с супом и червоточины, они могут стать перспективными дорожками, которые приведут к слиянию квантовых жутких действий с геометрией пространства-времени. В своей работе над червоточинами Эйнштейн и Розен обсудили возможные квантовые последствия, но не провели соединения со своими ранними работами по запутанности. Сегодня эта связь может помочь объединить квантовую механику ОТО в теорию квантовой гравитации. Вооружившись такой теорией, физики могли бы разобрать загадки состояния юной Вселенной, когда материя и энергия умещались в бесконечно малой точке пространства.
hi-news.ru
Квантовую запутанность можно будет увидеть невооруженным глазом
Светоделитель
Изображение: Wikimedia Commons
Физики из университетов Инсбрука, Женевы и Базеля предложили эксперимент, в котором можно будет наблюдать квантовую запутанность невооруженным взглядом. Несмотря на то, что это явление уже активно используется в лабораториях, в том числе и для передачи информации, это первый опыт, в котором человек может быть задействован напрямую — в роли детектора. Препринт опубликован на сервере arXiv.org, кратко о нем сообщает MIT Technology Review.
Экспериментальная установка представляет собой источник единичных запутанных фотонов, основанный на эффекте спонтанного параметрического рассеяния, и систему из лазеров и светоделителей. Фотоны разделяют на два пучка, каждый из которых направляют на свой соответствующий детектор. Перед детектором располагают еще один светоделитель, пропускающий лишь половину фотонов.
Напрямую увидеть глазом единичные фотоны невозможно — светочувствительные клетки сетчатки требуют по меньшей мере трех квантов света для того, чтобы запустить нервный импульс. Кроме того, лишь около 10 процентов всех фотонов доходят до сетчатки глаза. Поэтому для наблюдений запутанных фотонов физики использовали своеобразный усилитель, основанный на эффекте квантовой интерференции. Основой этого усилителя является светоделитель, стоящий перед детектором. По другую сторону относительно запутанного пучка физики предлагают разместить дополнительный лазер, испускающий такие же по поляризации, частоте и остальным параметрам фотоны, как и первоначальный.
Схема эксперимента
Изображение: Valentina Caprara Vivoli et al. / arXiv.org, 2016
Когда запутанный фотон попадает на светоделитель, происходит его взаимодействие с фотонами дополнительного лазера. В результате этого взаимодействия изменяется доля отраженных делителем фотонов дополнительного лазера. К примеру, большая их часть начинает отражаться в сторону детектора — человеческого глаза. Таким образом, единичный фотон оказывает влияние на свойства гораздо большего числа частиц, пучок которых уже возможно увидеть.
Чтобы зарегистрировать квантовую запутанность, необходимо собрать статистику «вспышек» (событий, когда вырастает интенсивность отраженного пучка) на двух детекторах. Запутанность приведет к тому, что «вспышки» или их отсутствие на двух детекторах будут регистрироваться одновременно: в момент, когда первый фотон из пары будет достигать усилителя, его состояние будет совпадать с состоянием второго фотона, а значит и влияние на отражающую способность светоделителя они будут оказывать одинаковое.
Хотя в изначальной постановке эксперимента предполагается использовать в роли второго детектора обыкновенную светочувствительную матрицу, точно также можно использовать в роли обоих детекторов двух волонтеров. Главный минус эксперимента — сбор статистики потребует тысячи или десятки тысяч повторов, что значительно утомит волонтеров. Как шутят авторы заметки на MIT Technology Review, с одной стороны, пары волонтеров могут узнать, каково это — быть квантово запутанными, но с другой стороны, по всей видимости, ответом будет «это отупляюще скучно».
Попытки поставить эксперименты, в которых человек может своими глазами увидеть проявления квантовой запутанности, ведутся с начала XX века. Одной из проблем является небольшая чувствительность человеческого глаза относительно современных матриц. Для того, чтобы увидеть вспышку, необходимо чтобы в пучок фотонов входило по меньшей мере десятки частиц. В современных экспериментах по запутыванию максимальное количество таких объектов не превышало 14.
Владимир Королёв
nplus1.ru