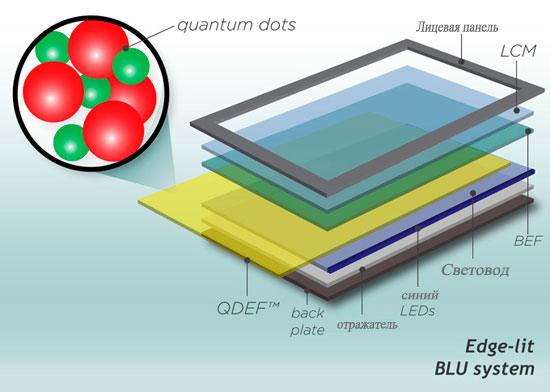
Актуальные проблемы квантовой механики (стр. 4 из 4). Математика квантовой механики 4 часть

Часть 4 Квантовая механика.

Количество просмотров публикации Часть 4 Квантовая механика. - 299

§1 Экспериментальные основы квантовой механики.

К началу 20го века основные физические явления были объяснены классической физикой за исключение нескольких явлений:

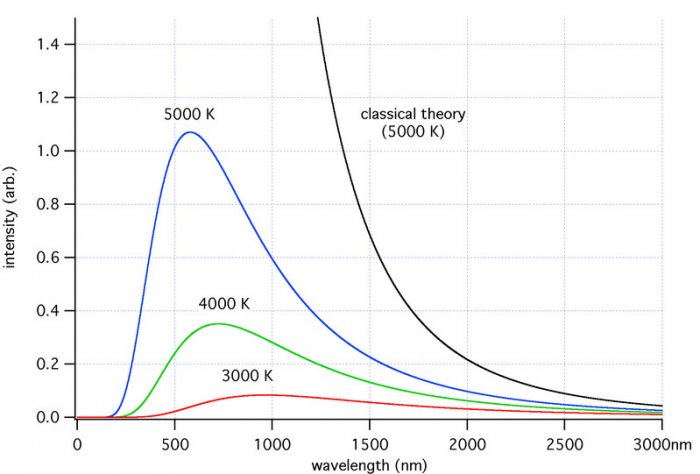
1) тепловое излучение тела. Как известно любая движущаяся с ускорением заряженная частица излучает электромагнитные волны. Так как все тела содержат заряженные частицы, то при температуре выше абсолютного 0 они двигаются. По этой причине любое тело при T>0 излучает электромагнитные волны частота которых от 0 до

Пусть энергия излучает электромагнитные волны за единицу времени приходящаяся на единицу поверхности в интервале частот от до будет

спектральная плотность излучения. С помощью классической электродинамики Максвелла можно получить зависимость

-закон Релея и Джинкса или ʼʼультрафиолетовой катастрофойʼʼ

2) Фотоэффект, который состоял в том, что электромагнитная волна вырывала с поверхности проводника электромагнит. Само это явление легко объясняется классической электродинамикой. Под действие электромагнитного поля электроны проводника начинают двигаться вдоль поверхности.

A на движение электронов со стороны со стороны магнитного поля направленного наружу и она приводит к выражению.

Столетов экспериментом установил, что увеличение амплитуды волны то есть энергии волны, скорость вылетевших электронов не меняется, а меняется их число, что невозможно объяснить классической физикой.

3) Опыты по дифракции электрона

1. Опыт с пулями

Будем описывать попадание пуль в мишень вероятность попадания P. В случае если открыть оба отверстия то вероятности попадания складываются.

2. Опыт с волнами

В случае если открыть одно отверстие то (§2.6) будем наблюдать дифракцию, в случае если второе-дифракцию

В случае если оба то интерференцию

3. Опыт с электронами

p- вероятность попадания в мишень.

Вероятности не складываются, а интерферируются

Электроны описывают вероятности как пули, а вероятности интерферируются как у волн.

referatwork.ru

Актуальные проблемы квантовой механики - часть 4

Транзактная интерпретация квантов утверждает, что частица посылает запрос в будущее (волна предложение) и получает ответ из будущего (волна подтверждение). Степень совпадения фаз определяет амплитуду. Квадрат амплитуды определяет вероятность события. Такой подход решает проблему наблюдателя (парадокс кота Шредингера, и мыши Эйнштейна).[4]

Кроме того, многие физики склоняются к так называемой «никакой» интерпретации квантовой механики, ёмко выраженной в афоризме Дэвида Мермина: «Заткнись и считай!»

Заключение

Несмотря на совершенно новый взгляд на многие природные явления, квантовую механику никак нельзя расценивать как полное опровержение классической физики. Последняя может рассматриваться как предельный случай квантовой механики или как первое и очень грубое приближение к ней. Как подчеркивал Поль Дирак, соответствие между квантовой и классической теориями состоит не только в их предельном согласии. Соответствие заключается прежде всего в том, что математические операции двух теорий во многих случаях подчиняются одним и тем же законам и описываются одной математической структурой. Отличия заключаются лишь в представлении (реализации) этих структур конкретными математическими объектами.

На данный момент квантовая механика является наиболее проверенной (и в то же время наиболее парадоксальной) теорией в истории науки. Каким же образом она работает, так никто до сих пор и не осознал, несмотря на многолетний мозговой штурм

Основной проблемой современной физики является попытка вывести «Теорию Всего», которая объединила бы квантовую физику с теорией относительности. Пока что эти попытки не привели к положительным результатам.

Среди возможных кандидатов на звание «Теории Всего» сейчас значатся несколько довольно сложных математических теорий, например Теория петлевой квантовой гравитации и, Теория струн. Впрочем, до окончательного решения проблемы еще довольно далеко. В итоге главный вопрос современности остается нерешённым.

Список литературы

1. Барвинский А.О., Каменщик А.Ю., Пономарёв В.Н. Фундаментальные проблемы интерпретации квантовой механики. Современный подход – М.: Изд-во МГПИ, 1988

2. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т.1, Механика – М.: Наука, 1988

3. Иванов П.Д. Мир Эйнштейна – М.: Логос, 2002

4. Пригожин И., Стенгерс И. Время, хаос, квант – М.: Прогресс, 1994

5. Торопин А. Общая теория квантовой механики – М.: Наука, 1992

[1] Ландау Л.Д., Лифшиц Е.М. Теоретическая физика с.52

[2] . Пригожин И., Стенгерс И. Время, хаос, квант, с.101

[3] Иванов П.Д. Мир Эйнштейна – М.: Логос, 2002, с.117

[4] Барвинский А.О., Каменщик А.Ю., Пономарёв В.Н. Фундаментальные проблемы интерпретации квантовой механики. Современный подход, с. 312

mirznanii.com

1. ОСОБЕННОСТИ КВАНТОВОЙ МЕХАНИКИ

Профессор

И.Н.Бекман

ЯДЕРНАЯ ФИЗИКА

Лекция 3. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ

Последовательная теория атома (равно как ядра и элементарных частиц) основана на законах квантовой механики.

Квантовая механика (волновая механика) – теория, устанавливающая способ описания и законы движения физических систем, для которых величины, характеризующие систему и имеющие размерность действия, оказываются сравнимыми с постоянной Планка h. Этому условию удовлетворяет, как правило, движение микрочастиц (электронов в атоме, атомов в молекулах, нуклонов в ядрах и т.д.). Однако в некоторых случаях специфическими квантовыми свойствами облают макроскопические системы как целое.

Квантовая механика представляет собой систему понятий и адекватный ей математический аппарат, необходимый и достаточный для описания всех наблюдаемых свойств соответствующих систем и их движения.

Квантовомеханическая теория объясняет устойчивость атома, необъяснимую в рамках классической физики, а также позволяет достаточно точно рассчитать для простейших атомов уровни энергии, вероятности переходов и т.д., с помощью различных приближённых можно рассчитывать характеристики сложных атомов. На основе квантовых представлений с единой точки зрения можно объяснить оптические, магнитные, электрические и химические свойства атома, а также периодическую систему элементов.

В данной лекции мы остановимся лишь на основных понятиях квантовой механики, знание которых позволяет лучше понять закономерности распада атомных ядер.

Для классической механики характерно описание частиц путём задания их координат и скоростей в зависимости от времени. Такому описанию соответствует движение частиц по вполне определённым траекториям. Однако опыт показал, что это описание не всегда справедливо в случае частиц с очень малой массой (микрочастиц). В этом состоит одно из ограничений применимости механики Ньютона. Более общее описание движения даёт квантовая механика, которая включает в себя как частный случай классическую механику. Квантовая механика делится на нерелятивистскую, справедливую при малых скоростях, и релятивистскую, удовлетворяющую требованиям специальной теории относительности.

Нерелятивистская квантовая механика (как и механика Ньютона для своей области применимости) – вполне законченная и логически непротиворечивая теория, способная в области своей применимости количественно описать любое физическое явление. Напротив, релятивистская квантовая механика за исключением отдельных частных задач не может считаться замкнутой теорией, а представляет собой составную часть квантовой теории поля (со всеми присущими ей трудностями). Это связано с тем, что при взаимодействии релятивистских частиц в игру неизбежно вовлекаются полевые степени свободы.

Соотношение между классической и квантовой механикой определяется универсальной мировой постоянной – постоянной Планка h=6,6210-27 эрг с (илиħ=h/2π=1,0510-27 эрг с), называется также квантом действия. Если в условиях данной задачи физические величины размерности действия значительно большеħ (так чтоħ считать очень малой величиной), то применима классическая механика,

- именно это условие и является критерием её применимости.

Рис. 1. Волна де Бройля в атоме при квантовом числеn=2.

2. КОРПУСКУЛЯРНО-ВОЛНОВОЙДУАЛИЗМ

Корпускулярно-волновой дуализм заключается в том, что любые микрочастицы материи (фотоны, электроны, протоны, атомы и др.) обладают свойствами и частиц (корпускул) и волн. Количественное выражениекорпускулярно-волновогодуализма – соотношения де Бройля.

Истоки корпускулярно-волновогодуализма связаны с экспериментальным обнаружением явления механического давления света, оказываемого им на освещаемую поверхность. В этих экспериментах (опыты П.Н.Лебедева, 1900) использовалась вертушка с лепестками из электропроводящих материалов. Классическое объяснение сводилось к взаимодействию поля магнитной индукцииВ с токами

проводимости, индуцированными электромагнитной волной в материале лепестков вертушки. Данное объяснение исчерпывающее и не нуждается в каких-либодополнениях. Однако сам факт наличия механического давления на отражающую поверхность подтолкнул физиков искать простую механистическую трактовку эффекта, проявившегося в данных опытах, и предположить аналогию электромагнитных волн с потоком неких корпускул - фотонов. Непосредственное же внедрениекорпускулярно-волновойдуализма связано с экспериментами по дифракции электронов, а так же с интерпретацией эффекта Комптона.

Французский ученый Луи де Бройль осознавая существующую в природе симметрию и развивая представления о двойственной корпускулярно-волновойприроде света, выдвинул в 1923 гипотезу об универсальностикорпускулярно-волновогодуализма. Он утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами. Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики - энергияE и импульс p, а с другой стороны - волновые характеристики - частота и длина волны.

Физической основой квантовой механики является корпускулярно-волновойдуализм – всеобщее и универсальное свойство материи, согласно котором не только любой волне с частотойν и волновым векторомk отвечает частица с энергиейЕ и импульсомр, соответственно равными:

Е=ħν,р=ħk,	(1)
С учётом известного уравнения Эйнштейна имеем:
mc2=ħν	(2)

В то же время, с любой частицей, обладающей энергией Е и импульсом р, связана волна, частотаν и волновой вектор которойk определяется соотношением (1). Наличие у частиц волновых свойств доказано в огромном числе экспериментов. Интерференция и дифракция наблюдались для электронов, нейтронов, атомных ядер, атомов, молекул. Волновые свойства нейтронов лежат в основе нейтронной оптики.

Замечание. Иногда говорят, что формулу де Бройля можно «вывести». При этом записывают постулаты ПланкаE=hν и ЭйнштейнаE=mc2=pc. Комбинируя оба равенства, можно «вывести» формулу де Бройля:mc2=hν. Но необходимо помнить, что как формула Планка, так и Эйнштейна, являются гипотезами.

Принципиального различия между описанием материи на языке волн или корпускул нет. Это – вопрос удобства расчётов конкретной ситуации. Например, в терминах частиц естественно описывать материю в терминах частиц при использовании величин импульсов, кинетических энергий, и т.д. Также естественно использовать волны для описания света. Однако, каждой материальной частице соответствует волновое описание, прочём длина волны (длина волны Де Бройля) задаётся как

где р – импульс частицы иh – постоянная Планка. (Заметим, что постоянная Планка очень малаh=6,6*10-34 Дж/с. Потому длина волны частицы важна только когда импульс экстремально мал, как это имеет место у электрона, масса которого9*10-31 кг). Выражение для длины волны Де Бройля можно записать в рациональных единицах:

		D =	h	(4)
		D =	p	(4)
			p
где h =	h	= 6,58212 10−22 МэВс.
где h =	2π	= 6,58212 10−22 МэВс.
	2π

Эти выражения относятся к классическим приближениям. В релятивистском приближении (при скоростях, близких к скорости света):

D =	hс	(5)
	Ek (Ek + 2m0c2 )

Значения типичных длин волн для некоторых частиц приведены в Табл. 1. Они даны в обычных ядерных размерах10-13 см.Табл. 1 демонстрирует энергии, при которых частицы будут иметь длины волны сравнимые или меньшие, размеров ядра. Приведённые здесь частицы можно использовать как зонды размеров ядер и их формы.

Табл. 1. Типичные величины длин волн Де Бройля.

Энергия,		Длина волны, см
МэВ
МэВ	Фотон		Электрон	Протон

0,1	1,2*10-9		3,7*10-10	9,0*10-12
1	1,2*10-10		8,7*10-11	2,9*10-12
10	1,2*10-11		1,2*10-11	0,9*10-12
100	1,2*10-12		1,2*10-12	2,8*10-13
1000	1,2*10-13		1,2*10-13	0,7*10-13

Аналогично можно описать фотон
λ =		с	=	hc	=	1,2397 *10−10	(см)	(6)
λ =	ν		=	Eγ	=	Eγ (МэВ)	(см)	(6)
	ν			Eγ		Eγ (МэВ)

Но часто приходится говорить о фотоне, как о частице, например, когда он поглощается ядром, или выделяется из него. Тогда

Рис. 2. Стоячие волны де Бройля, укладывающиеся вдоль круговой орбиты.Орбита показана тонкой линией, n –

число полных волн, укладывающихся вдоль нее.

Гипотеза де Бройля была подтверждена экспериментально опытами Лауэ, Фабриканта, Дэвиссона и Джермера, Томсона и Тартаковского по дифракции и интерференции индивидуальных микрообъектов: электронов, протонов и других частиц.

Рис. 3. Схема эксперимента по изучению дифракции электронов.

Дифракция частиц – рассеяние потока микрочастиц (электронов, нейтронов, атомов и молекул и др.) кристаллами или молекулами жидкостей и газов с образованием чередующихся максимумов и минимумов в интенсивности рассеянного пучка. Дифракция частиц аналогична дифракции света и является проявлениемкорпускулярно-волновогодуализма частиц; наблюдается для частиц, волна де Бройля для которых порядка расстояния между рассеивающими центрами. Дифракционная картина зависит от внутреннего строения рассеивающего объекта. На дифракции частиц основаны электронография и нейтронография.

Дифракционные явления проявляются наиболее отчетливо, когда размеры препятствия, на котором происходит дифракция вон, соизмеримы с длиной волны. Это относится к волнам любой физической природы и, в частности, к электронным волнам. Для волн де Бройля естественной дифракционной решеткой является упорядоченная структура кристалла с пространственным периодом порядка размеров атома (приблизительно 0,1 нм). Препятствие таких размеров (например, отверстие в непрозрачном экране) невозможно создать искусственно, но для уяснения природы волн де Бройля можно ставить мысленные эксперименты.

Рис.4. Картина дифракции электрона на щели.

Подтвержденная экспериментально гипотеза де Бройля о корпускулярно-волновом дуализме коренным образом изменила представления о свойствах микрообъектов.

Рис. 5. Распределение дифрагировавших электронов по фотопластинке

С точки зрения волновой теории, максимумы в картине дифракции электронов соответствуют наибольшей интенсивности волн де Бройля. В области максимумов, зарегистрированных на фотопластинке, попадает большое число электронов. Но процесс попадания электронов в различные места на фотопластинке не индивидуален. Принципиально невозможно предсказать, куда попадет очередной электрон после рассеяния, существует лишь определенная вероятность попадания электрона в то или иное место. Таким образом, описание состояния микрообъекта и его поведения может

быть дано только на основе понятия вероятности.

Рис. 6. Схема экспериментальной установки для наблюдения дифракции нейтронов (источник нейтронов – атомный реакторR (S – замедлитель нейтронов)

Это с неизбежностью ведёт к отказу от некоторых классических представлений, сформировавшихся в результате наблюдения движения макроскопических тел. В частности, наблюдение волновых явлений

несовместимо с представлением о движении частицы по определённой классической траектории. Здесь существенно, что соотношения (1), согласно которым с волной может быть сопоставлена частица, определяет лишь энергию и импульс этой частицы, не требуя её движения по какой-либоопределённой траектории.

Отказ от полностью детерминированного описания движения отдельной частицы и переход к вероятностному описанию, адекватному принципу суперпозиции состояний, позволяет совместить волновые и корпускулярные свойства материи. Вероятностное описание, таким образом, отвечает фундаментальным свойствам движения микрообъектов и не связано с какой-либонеполнотой сведений о них. Подчеркнём, однако, что в его основе лежит чуждое классической теории вероятностей понятие амплитуды вероятности, т.е. комплексного числа, у которого физический смысл имеет не только квадрат модуля (равный вероятности), но и фаза (точнее, разность фаз двух амплитуд, соответствующая разности фаз волн). Именно использование амплитуд вероятности позволяет отразить

волновые свойства объектов при их корпускулярном описании.

Рис. 7. Дифракционный максимум интенсивности нейтронов, отраженных от монокристалла CsHSeO4

Таким образом, в отличие от классической теории, все частицы выступают в квантовой механике как носители и корпускулярных, и волновых свойств, которые не исключают, а добавляют друг друга.

Волны де Бройля – проявление универсальногокорпускулярно-волновогодуализма материи: любой частице с энергией Е и импульсом р соответствует волна, названная волной де Бройля, с длинойλ=h/p и частотойν=Е/h, где h – постоянная Планка (1924). Волны де Бройля интерпретируются как волны вероятности: их существование подтверждается, например, дифракцией частиц.

studfiles.net

Фон Нейман против Дирака: математическая схема квантовой механики

Треки частиц в пузырьковой камере

На этом, в целом научно-популярном сайте встречаются статьи, которые у читателя без физ-мат образования могут вызвать затруднения (например http://extremal-mechanics.org/archives/2112). С данной публикацией дело обстоит еще хуже — она предполагает знакомство с квантовой механикой на уровне университетского курса (которое, впрочем, обычно является весьма поверхностным). Популярные сведения о ней, сводящиеся к формуле Планка и представлению об уровнях энергии атома, а также «квантовых скачках», для понимания этой статьи недостаточны. С другой стороны она поможет тем читателям, которые хотят разобраться в квантовой механике и готовы потратить на это время. Стоит предупредить их о том, что математическая изощренность данной науки (далее КМ) превосходит все остальные разделы физики, включая общую теорию относительности.

Последнее обстоятельство прямо связано с тем, что привычные для физиков изложения КМ, оперирующие дельта-функцией Дирака , кажутся выпускникам мех-матов возмутительно нестрогими. В самом деле, утверждения вроде того, что скалярное (точней эрмитово) произведение векторов состояния и

(1)

где при всех $x\in{\mathbb R}^n\setminus\{0\}$ , но (!), способны вызвать когнитивный диссонанс у правоверных математиков. Хотя теория обобщенных функций нашла место для «несобственной» дельта-функции Дирака, равенство (1) как бы числа и сингулярной обобщенной функции все же нуждается в формальных пояснениях.

Сразу после выхода в свет исходной версии книги [1] в 1930, которая подвела итог созданию КМ, такие пояснения были невозможны — теория обобщенных функций возникла лишь в 60-х. Поэтому блестящий математик Джон фон Нейман решительно взялся за «очищение» КМ от дельта-функции , выпустив в 1932 книгу [3]. Cегодня она считается каноническим и абсолютно строгим изложением КМ. Из предисловия:

«Книга Неймана является первым и до сих пор единственным доведенным до конца опытом изложения аппарата квантовой механики (на момент издания) с той последовательностью и строгостью, которой требуют обычно при построении математической теории. Поэтому только cуществованию этой книги мы обязаны нашей уверенностью в том, что квантовая механика представляет собой логически непротиворечивую схему.»

Фон Нейман «погрузил» КМ в функциональный анализ, приняв активное участие в его создании. Получилась математически безупречная, но технически громоздкая теория, которая далека от смелых и красивых рассуждений Дирака и Гейзенберга. Обычно рядом с ними вспоминают Йордана. Нильс Бор, конечно, был основоположником этой т.н. копенгагенской КМ. Вкратце теория фон Неймана состоит в следующем.

Вместилищем волновых функций считается гильбертово пространство функций с интегрируемым по Лебегу на квадратом модуля. Здесь $q\in{\mathbb R}^n$ и — число пространственных степеней свободы данной квантовой системы. Любые две функции из $L^2({\mathbb R}^n;\mathbb C)$ , отличающиеся лишь на множестве меры ноль, считаются равными элементами пространства . Эрмитово произведение .

Каждой физической величине данной квантовой системы соответствует эрмитов оператор $R:{\cal D}_R\to{\cal H}$ (также обозначаемый ), заданный на некотором всюду плотном в подмножестве . Оператор должен быть замкнутым, что означает следующее: для любого и любой последовательности , сходящейся к , существование предела влечет . Непрерывный оператор $R:{\cal D}_R\to{\cal H}$ является замкнутым в том и только том случае, когда . Также предполагается, что область определения не может быть расширена с сохранением свойств эрмитовости и замкнутости оператора. Такой оператор называется максимальным [3].

Примерами максимальных (эрмитовых и замкнутых), но не непрерывных операторов являются операторы координат и импульсов (где $j=1,\ldots, n$ ), действующие обычным образом

(2)

на те функции , которые после операций (2) остаются в $L^2({\mathbb R}^n;\mathbb C)$ (для применимости функция должна быть почти всюду дифференцируемой по q_j ). При этом области определения данных операторов, изначально не замкнутых, стандартным образом расширяются до таких, на которых они становятся замкнутыми и максимальными (подробности в [3]).

Двинемся дальше за фон Нейманом в заросли функционального анализа. Проектором называется такой непрерывный эрмитов оператор , что . Фактически это — оператор ортогональной проекции на некоторое замкнутое подпространство $Im(E)\subset\cal H$ ( означает образ оператора). Разбиением единицы, принадлежащим эрмитову оператору , называется отображение числовой оси в множество проекторов. Для каждого соответствующий проектор обозначается .

При этом для всех должно быть $Im(E(\lambda'))\subset Im(E(\lambda''))$ . В этом случае оператор является проектором на ортогональное дополнение $Im(E(\lambda'))$ до $Im(E(\lambda''))$ . Требуется, чтобы и (тождественный оператор), а также (непрерывность справа). Еще одно условие заключается в том, что для любых $f,g\in{\cal H}$ имеет место:

(3)

где интеграл считается по Стилтьесу и $h_{f,g}(\lambda)=\langle E(\lambda)(f)|g\rangle$ — комплекснозначная функция от , определяемая параметрами f,g . Выражение (3) называется спектральным разложением (эрмитова) оператора .

Известно, что для каждого непрерывного эрмитова оператора cуществует единственное разложение единицы c вышеуказаными свойствами. В этом заключается спектральная теорема, впервые доказанная Гильбертом. Что касается замкнутых эрмитовых операторов , не являющихся непрерывными и, таким образом, определенных на всюду плотных подмножествах , то о них известно лишь одно. Если такой оператор является максимальным (см. выше), то принадлежащее ему разбиение единицы не существует или существует и тогда оно единственно [3].

Единственность имеет принципиальное значение для того, чтобы спектральное разложение (3) имело физический смысл. Но вопрос о его существовании является, вообще говоря, открытым. Впрочем, для важнейших максимальных операторов и , не являющихся непрерывными, разложения единицы построены явным образом [3]. Максимальные операторы, для которых разбиение единицы существует фон Нейман назвал гипермаксимальными.

Ключевая гипотеза, связывающая весь этот функан с физикой, теперь выглядит так. Каждой физической величине данной квантовой системы соответствует гипермаксимальный эрмитов оператор $R:{\cal D}_R\to{\cal H}$ , заданный на некотором всюду плотном в подмножестве . Спектральное разложение (3) является основой для всех вычислений, связанных с величиной . Прежде всего определим ее возможные значения.

Спектром гипермаксимального оператора со спектральным разложением (3) называется множество тех точек , ни в какой окрестности которых оператор-функция не является постоянной. Таким образом спектр — замкнутое множество и каждый интеграл (3) вычисляется de’facto не по всей числовой оси, а только по спектру . Гипотеза о соответствии оператора физической величине уточняется утверждением о том, что ее всевозможные значения составляют спектр [3].

При этом собственные значения оператора определяются, как обычно — через равенство $R(f)=\lambda f$ при $f\neq 0$ . Собственными значениями являются те и только те точки , в которых оператор-функция имеет разрыв. Последнее означает, что . Тогда все собственные векторы со значением составляют замкнутое подпространство в , которое является ортогональным дополнением подпространства до $Im(E(\lambda))$ . Множество собственных значений может быть пустым (например, у операторов координат и импульсов), конечным или счетным. Других вариантов нет.

Для физической интерпретации своей теории фон Нейман ввел еще 2 постулата. Первый состоит в том, что любой вещественной функции F(r) от физической величины соответствует гипермаксимальный оператор F(R) . Тогда из (3) следует, что для любых $f,g\in{\cal H}$ имеет место:

Второй постулат утверждает, что мат. ожидание величины в произвольном состоянии равно (в силу эрмитовости это число вещественно). Точно такая аксиома есть в [1] и [2], но Дирак обозначает как . Из этих двух предположений фон Нейман выводит принципиально важное утверждение.

Пусть дан набор физических величин $r_1,\ldots,r_m$ с коммутирующими между собой операторами $R_1,\ldots, R_m$ . Обозначим E_j разбиение единицы, принадлежащее R_j . Пусть для всех $j=1,\ldots,m$ и $P_\psi(\lambda',\lambda'')$ есть вероятность того, что в состоянии данной квантовой системы с волновой функцией каждая величина r_j принимает значение из полуинтервала . Тогда

$P_\psi(\lambda';\lambda'')=\langle E_1(\lambda'_1;\lambda''_1)E_2(\lambda'_2;\lambda''_2)\ldots E_m(\lambda'_m;\lambda''_m)(\psi)|\psi\rangle$

где $E_j(\lambda'_j; \lambda''_j)=E_j(\lambda''_j)-E_j(\lambda'_j)$ (попарно коммутирующие проекторы). Отсюда, в частности, следует интерпретация Борна волновой функции , согласно которой есть плотность распределения случайных величин $q_1,\ldots,q_n$ (пространственных координат в данной системе).

Возможен случай, когда спектр состоит только из собственных значений. Тогда он не более, чем счетный. Примером служит оператор энергии (гамильтониан). В таком случае из (3) следует, что любой вектор разлагается по собственным векторам: , где $R(\psi_k)=\lambda_k\psi_k$ . Данный факт имеет фундаментальное значение в КМ, но для его доказательства не нужно разбиение единицы. Описанные выше, математические ухищрения понадобились фон Нейману для того, чтобы строго описать случай континуального спектра, во исполнение чего изгнать из КМ дельта-функцию вместе со следующим утверждением Дирака (которое с ней неразрывно связано).

Если множество собственных значений эрмитова оператора непрерывно, то всякий вектор состояния выражается в виде интеграла по спектру: , где $R(|\psi_{\lambda}\rangle)=\lambda|\psi_{\lambda}\rangle$ . Спектром оператора в книге [1] называется множество его собственных значений (вне всякой связи с разложением единицы).

Если убрать бра-кет обозначения Дирака и применить данное утверждение к функциям из гильбертова пространства , то оно станет ложным. Но в качестве пространства состояний квантовой системы Дирак, в действительности, рассматривал множество обобщенных функций на , которое содержит в качестве подпространства. А в разложение в интеграл от собственных векторов по непрерывному спектру из собственных значений в смысле Дирака может иметь место. Более того — в пространстве обобщенных функций не существует проблемы определенности эрмитовых операторов не всюду, которой фон Нейман посвятил много усилий. Подробности будут описаны в дальнейшем.

Таким образом, фон Нейман изгонял из КМ дельта-функцию напрасно. Возможно, хотя я не вполне в этом уверен, что основанная на спектральной теореме КМ не потеряла ничего по существу. Но она стала технически очень громоздкой! Чтобы почувствовать разницу достаточно сравнить изящные рассуждения Дирака в [1], связанные с излучением, поглощением и рассеиванием фотонов, с тем, как теория излучения излагается в [3]. Нет никаких сомнений в том, что на пути, который фон Нейман избрал для наведения математического порядка в квантовой механике, она бы не была открыта никогда. При этом порядок присутствовал в ней изначально. Просто гениальный Дирак намного опередил развитие математики, введя в обращение «несобственную» функцию [1].

Для понимания дальнейшего материала весьма желательно владеть понятием обобщенной функции на уровне книги [4]. Для этого достаточно прочитать в ней параграфы 5 — 9. Будет показано, что КМ может быть вполне строго изложена на исходном языке Дирака, в силу чего она не нуждается в теории фон Неймана. Весь остальной материал изложен в тексте http://extremal-mechanics.org/wp-content/uploads/2017/10/QM.pdf

1. П.А.М. Дирак, Принципы квантовой механики, 1960, М.: Физматгиз.

2. В. Гейзенберг, Физические принципы квантовой теории, 1932, М.: ГТТИ.

3. Дж. фон Нейман, Математические основы квантовой механики, М.: Наука, 1964.

4. В.С. Владимиров, Уравнения математической физики, М.:Наука, 1988.

Автор: д.ф.-м.н. Дмитрий Зотьев

Поделиться ссылкой:

extremal-mechanics.org

Часть 4 Квантовая механика. | Бесплатные курсовые, рефераты и дипломные работы

§1 Экспериментальные основы квантовой механики.

1) тепловое излучение тела. Как известно любая движущаяся с ускорением заряженная частица излучает электромагнитные волны. Так как все тела содержат заряженные частицы, то при температуре выше абсолютного 0 они двигаются. Поэтому любое тело при T>0 излучает электромагнитные волны частота которых от 0 до