Элементы квантовой физики. Строение атома и ядра. Основные положения квантовой физики
7. Основные положения квантовой механики
Двойственность свойств микрообъектов обусловливает невозможность описания их движения и взаимодействия в рамках классической механики. Потребовалась разработка новой механической теории - квантовой механики, основные принципы и законы которой установлены в конце 20-х годов ХХ в.
Принцип неопределенности В. Гейзенберга. Физическая интерпретация «неклассического» поведения микрообъектов была дана немецким ученым В. Гейзенбергом, который в 1927 г., исходя из созданного им математического аппарата квантовой механики, установил связь между предельными точностями определения («неопределенностями») координаты () и соответствующей проекции импульса () микрочастицы:
. (4.7)
Данное соотношение выражает принцип неопределенности Гейзенберга, который определяет фундаментальный предел возможности одновременного измерения пар определенных переменных. В частности, в случае движения электрона в атоме (∆х~10-10м) невозможно достаточно точно определить его ориентацию, что делает неприменимым к данному движению понятия «траектории».
Соотношение неопределенностей связывает также энергию (Е) и время (t):
. (4.8) Данное соотношение объясняет возможность виртуального состояния микрообъектов.
Следует подчеркнуть, что неопределенности обусловлены не техническими возможности определения точных значений данных параметров микрочастиц, а принципиальным «несуществованием» одновременно точных значений для данных пар параметров.
Эти соотношения свидетельствуют об объективно существующих ограничениях в возможности описания микрообъектов на языке классической механики.
Принцип дополнительности Н. Бора. Волновая функция. Н. Бор показал, что корпускулярная и волновая модели микрообъектов никогда не предстают одновременно: получение информации об одних характеристиках микрообъекта неизбежно связано с потерей информации о других, дополнительных к первым. В зависимости от эксперимента микрообъект проявляет либо свою корпускулярную природу, либо волновую, но не обе сразу. Эти две взаимоисключающие стороны природы микрообъекта следует рассматривать как диалектически дополнительные (единство противоположностей).
Описание микрообъектов не может быть дано на основе классической механики, в которой нет места корпускулярно-волновому дуализму. Однозначной характеристикой микрочастицы в квантовой механике является волновая функция величина, позволяющая определить параметры движения в заданных внешних условиях. Математически волновая функция описывает некоторый процесс, периодический во времени и в пространстве, длина волны которого определяется формулой де Бройля. Однако природа этого процесса не имеет аналогов в макромире, сама волновая функция - ненаблюдаемая величина, не имеющая физического смысла. В квантовой механике с ней связывают так называемые «волны вероятности», так как квадрат амплитуды волной функции является мерой вероятности обнаружения микрочастицы в какой-либо области пространства. Хотя основное уравнение квантовой механики позволяет однозначно определить зависимость волновой функции от координаты и времени в определенных условиях движения микрообъекта, оно фиксирует связь не осуществившихся событий, а потенциальных возможностей этих событий и выражающих их вероятностей. Поэтому однозначная причинно-следственная связь событий, проявляющаяся в классической механике, не свойственна микромиру, здесь эта связь включает и необходимое и случайное. Даже зная начальное состояние и условия движения микрообъекта, невозможно однозначно предсказать его последующее поведение. Описание его состояния с помощью волновой функции отражает изначально присущую микрообъектом вероятностность поведения. Ненаглядность создаваемых квантовой механикой моделей микромира не противоречит объективности даваемых ею знаний, но отражает качественное отличие свойств объектов микро- и макромира.
Особые свойства микрочастиц. Развитие релятивистской квантовой механики, описывающей движение микрообъектов со скоростями, сравнимыми со скоростью света, уже в конце двадцатых годов, привело к новым открытиям. В 1927 г. английский ученый Поль Дирак установил возможность существования у всех микрочастиц двойников – античастиц. Античастицы отличаются от частиц знаком электрического (или другого) заряда. Античастица электрона (е-) – позитрон (е+), имеющая положительный электрический заряд, была открыта в 1932 г. Взаимодействие частицы и античастицы приводит к аннигиляции (исчезновению) обеих и превращению их в кванты электромагнитного излучения:
е - +е + → 2γ (4.9)
Возможна и обратная реакция:
2γ → е - +е + (4.10)
Однако она становится реальной только в силовом поле ядра атома. В отсутствии такого поля электрон и позитрон появляются как виртуальные частицы.
В микро-мире могут возникать виртуальные частицы. В соответствии с принципом неопределенности в течение некоторого времени:
(4.11)
возможно существование частиц с полной энергией ΔЕ = mс2. Если это время слишком мало (меньше, чем 10-22 с), частицы невозможно экспериментально обнаружить, они виртуальны. Виртуальными являются все переносчики фундаментальных взаимодействий, фигурирующие в модели обменного взаимодействия.
Описание взаимодействия микрообъектов в настоящее время реализуется на основе развивающейся квантовой теории взаимодействий, которая является ядром всей современной физики. Она дает общий подход ко всем известным типам взаимодействий.
Физический вакуум. Одним из важнейших результатов такого подхода является представление о физическом вакууме.
Слово vacuum по латыни означает пустота. По обыденным житейским представлениям вакуум — это пространство, которое абсолютно ничего не содержит: ни молекул, ни атомов, ни элементарных частиц. Однако физики трактуют физический вакуум иначе. Чтобы пояснить что такое физический вакуум, проведем мысленный эксперимент. Допустим, мы имеем сосуд сферической формы с идеально изолирующими и идеально отражающими стенками. Пусть в исходном состоянии в сосуде не обнаруживаются (не регистрируются) ни частицы вещества, ни кванты электромагнитного излучения т.е. фотоны, и нам представляется, что в сосуде пустота, не содержащая в себе абсолютно ничего. Эксперимент начнем с того, что через очень малое прозрачное окошко в стенке сосуда начнем накачивать его электромагнитным излучением. Небольшая часть излучения после многократных отражений выйдет обратно из окошка, большая его часть останется внутри сосуда. Со временем количество фотонов в сосуде будет возрастать. В некоторый момент времени какой-нибудь фотон внутри сосуда столкнется с другим фотоном и появится электрон-позитронная пара (в соответствии с (4.10)). Теперь вакуум перестал быть пустым, теперь он содержит две частицы: электрон и позитрон. Откуда взялись эти частицы? Их не было в электромагнитном излучении. Следовательно, электрон и позитрон всегда находились в вакууме в каком-то нерегистрируемом виртуальном состоянии. Как уже указывалось, частицу можно зафиксировать, если время ее жизни более 10-22с. В «неподогретом» электромагнитным излучением вакууме пытающиеся появиться электрон и позитрон сразу исчезают в течение времени меньшем, чем 10-22 с., то есть умирают, не успев родиться. Обнаружить т.е детектировать их удалось лишь после того, как они получили энергию от фотонов и перешли из мерцающего, виртуального, в реальное состояние. Таким образом, физический вакуум можно представить себе как объект физического мира, в исходном состоянии которого не удается обнаружить приборами каких-либо частиц. Путем воздействия на физический вакуум, например, электромагнитным излучением можно увеличить его энергию (нагреть), и перевести его в возбужденное состояние, при котором из вакуума рождаются реальные частицы: электрон и позитрон. Если, посылая свет в окошко, продолжать увеличивать плотность электромагнитного излучения в сосуде, то фотоны начнут сталкиваться с электронами и позитронами. Вследствие такого воздействия рождаются более массивные положительно и отрицательно заряженные частицы: мюоны или мезоны. Дальнейшее «накачивание» сферического сосуда фотонами вызовет рождение частиц пионов или мезонов, а затем внутри сосуда начнут образовываться пары протон-антипротон и нейтрон-антинейтрон. Таким образом, в результате такого нарастающего энергетического воздействия фотонами на пустоту внутри сосуда можно получить все частицы, необходимые для построения атомных ядер и атомов Возникает вопрос: « А был ли вакуум пуст?» Если мы наблюдаем образование частиц из вакуума при его «разогреве», то они там были, но были в непроявленном, недетектируемом состоянии, следовательно, физический вакуум содержит плотно упакованный набор всех известных нам в природе частиц, находящихся в виртуальном состоянии. По выражению российского физика А.Б. Мигдала (1911 – 1991), физический вакуум можно представить себе как физический объект, который «кишит еще неродившимися» материальными частицами.
Свойства физического вакуума описывает квантовая теория поля, позволяющая понять механизм всех известных нам типов взаимодействий. Квантовая теория поля рассматривает физический вакуум как прародителя известного нам мира и дает его определение: физический вакуум — это низшее энергетическое состояние квантовых полей, характеризующееся отсутствием каких-либо реальных материальных частиц. В этом состоянии обращаются в нуль импульс, электрический заряд и другие характеристики частиц. В то же время физический вакуум не следует понимать как абсолютную пустоту. В нем постоянно происходят флуктуации (случайные всплески) энергии, приводящие к возникновению виртуальных частиц. Время жизни виртуальных частиц очень мало, не более 10-22с, и они не успевают вступить во взаимодействие с реальными частицами. Поэтому их можно считать чем-то вроде «призраков». Однако «призрачный туман» виртуальных частиц участвует в коллективных взаимодействиях с реальными объектами материального мира, например, с ансамблями реальных частиц. Известен целый ряд физических эффектов, обусловленных этим взаимодействием. Например, сдвиг энергетических уровней в спектре водорода, аномалии в величине магнитного момента электрона и др. Согласно современным космологическим теориям, в основе построения которых лежит концепция Большого Взрыва (подробнее об этом ниже), возникновение Вселенной явилось следствием фазового перехода физического квантового вакуума. В силу соотношений неопределенности В. Гейзенберга (3.8), в вакууме непрерывно происходят флуктуации энергии и спонтанные рождения и аннигиляции виртуальных частиц. Таким образом, физический вакуум не пуст, а насыщен всевозможными флуктуациями всевозможных полей и представляет собой физический объект, при коллективном взаимодействии с которым обнаруживают свои свойства все элементарные частицы (микрообъекты) реального мира.
Взаимодействие микрообъектов с вакуумом по современным воззрениям свидетельствует о целостности мира, о несведении его к отдельным элементам. Если согласно классической науке мир рассматривался как совокупность независимых отдельных частей, взаимодействующих по детерминистским законам, то в квантовой теории ни один объект не может быть полностью индивидуализирован. По словам Борна, Вселенная является неделимым целым, отдельные частицы которого имеют смысл абстракций или приближений, справедливых лишь в классическом пределе. Во второй половине XX в. основное внимание уделяется созданию единой квантово-релятивистской теории структуры материи и фундаментальных взаимодействий.
Взаимосвязь классической и квантовой механики. Согласно существующему в науке принципу соответствия, разные, но верные теории, относящиеся к одному кругу явлений, должны быть взаимосвязаны. В наличии такой связи мы убедились на примере релятивисткой и классической механики: вторая имеет более узкие рамки применимости и является частным случаем первой при выполнении условия (2.14). Аналогичная связь имеет место и в случае квантовой механики. Если произведение энергии объекта и времени соответствующего процесса слишком велико по сравнению с постоянной Планка
Е t >>h, (4.13)
волновые свойства объектов не проявляются, и соотношения квантовой механики переходят в формулы классической механики, которая является ее частным случаем. Наиболее общей теорией, имеющей самые большие границы применимости, является релятивистская квантовая механика. Выше названные три теории - ее частные случаи, которые реализуются при следующих условиях: при выполнении (2.14) – квантовая механика, при выполнении (4.11) – релятивистская, при выполнении обоих условий одновременно – классическая.
studfiles.net
Физики запутались в природе квантовой механики
Физики из Австрии и США опубликовали результаты опроса своих коллег по поводу того, как они понимают квантовую механику. Результаты оказались противоречивы — несмотря на то, что классическая копенгагенская интерпретация все еще чувствует себя довольно бодро, к ней постепенно подбирается теория квантовой информации. Гипотеза же многих миров сдает свои позиции.
Корни проблемы
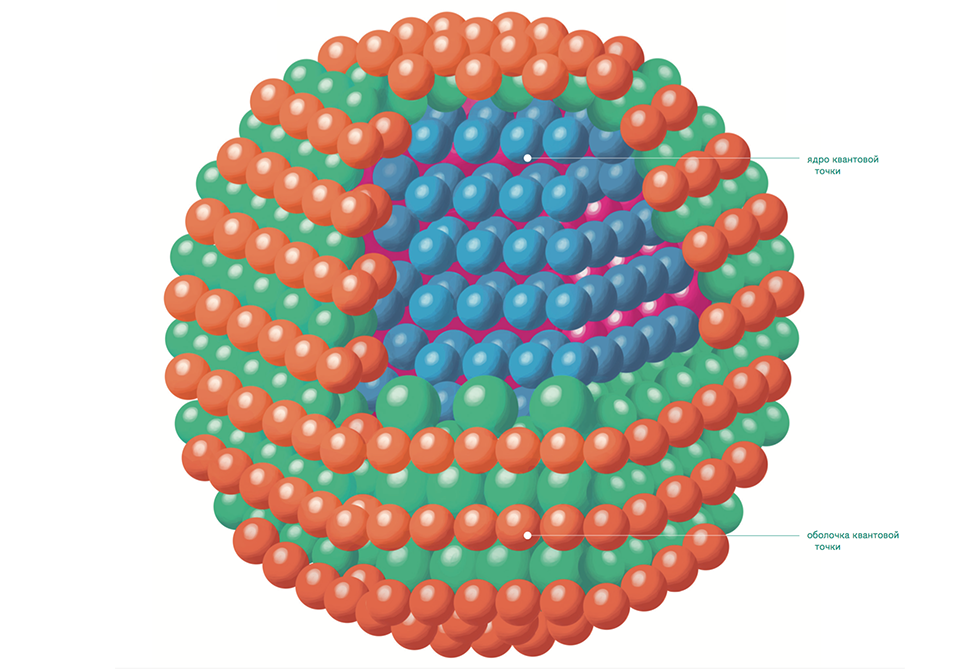
История квантовой механики начинается в конце XIX века, когда статистическая физика столкнулась с парадоксом, получившим название ультрафиолетовой катастрофы. Столкновение это был тем более неожиданным, что речь шла про, казалось бы, простую физическую задачу: описание излучения, связанного с нагревом тела, — будь то металл, камень или уголь в камине. Скажем, хорошо известно, что свечение нагретого металла с ростом температуры меняется от красного к светло-голубому. Почему это так?
Оказалось, что решение этой задачи сводится к изучению излучения так называемого абсолютно черного тела, абстракции, представляющей собой тело, которое поглощает все упавшее на него излучения. Название, как оказалось, было выбрано довольно неудачно — например, с достаточной степенью точности абсолютно черным телом можно считать Солнце.
И в этот момент физики столкнулись вот с чем: модель излучения, которая была у них на руках (так называемый закон Рэлея-Джинса) неплохо описывала излучение для длинных волн, но для коротких не работала совершенно. Более того, она давала невозможный результат: энергия, излучаемая телом, равна бесконечности. Этот парадокс и получил имя ультрафиолетовой катастрофы.
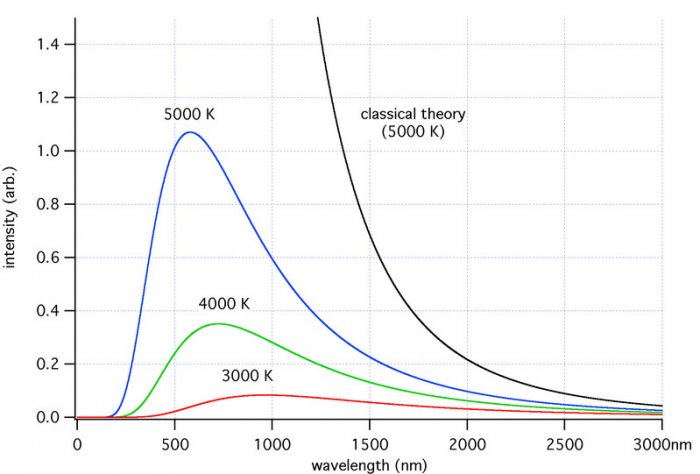 Рис. 1. Сравнение классического и квантового законов излучения для разных температур.
Рис. 1. Сравнение классического и квантового законов излучения для разных температур.
В 1900 году Макс Планк предложил совершенно неочевидное объяснение тому, что результаты экспериментов с короткими волнами противоречат теории — правда, сам термин «ультрафиолетовая катастрофа» появился только в 1911 году, а бесконечность энергии была обнаружена Рэлеем и Джинсом уже после появления планковского объяснения. Планк заявил, что
излучение испускается не непрерывно, как считалось ранее, а порциями (квантами). Энергия каждого кванта оказывается связана с частотой излучения простым линейным законом. На основе этих предположений он вывел свой закон излучения, который показал отличное согласование с экспериментальными данными и принес Планку нобелевскую премию по физике в 1918 году.
Обнаруженный закон невозможно было объяснить с точки зрения физики того времени, строго разделявшей две основные сущности — поля и частицы. Возник нетривиальный и, скорее, философский вопрос: если физика описывает нашу обычную действительность, то какую действительность описывают новые уравнения? Так вместе с квантовой механикой (именно с момента публикации работы Планка многие отсчитывают историю новой физической теории) появилась и проблема интерпретации квантовой механики.
Сначала, конечно, странность уравнений Планка не вызывала у физиков особого волнения — им казалось, что здание физики незыблемо, поэтому странные уравнения найдут объяснения в рамках классической теории (сами физики, конечно, свою физику классической еще не считали — тем же уравнениям Максвелла не было тогда и 20 лет). Более того, с порционностью физикам уже приходилось сталкиваться: идея существования мельчайшей неделимой порции электрического заряда, равной заряду электрона, на тот момент была общепризнанной.
Ситуация с квантами усугубилась в 1905 году. Дело в том, что в 90-х годах XIX века физики активно изучали фотоэффект — явление испускания электронов веществом под воздействием света. На основании экспериментов им удалось установить несколько эмпирических законов.
В 1905 году Альберт Эйнштейн предложил объяснение всем этим законам, распространив теорию порционного излучения Планка на свет. Получившаяся теория вновь давала прекрасное согласование с экспериментальными данными и вновь не помещалась в классическую картину мира.
Копенгагенская интерпретация
Спустя буквально 20 лет научный мир находился в состоянии непримиримого противостояния. Суть разногласий сводилась к вопросу о том, насколько хорошо квантовая теория описывает реальность (сами уравнения и тот факт, что они прекрасно работают, ни у кого возражений не вызывали). Противники молодой физики утверждали, что все эти корпускулярно-волновые дуализмы (свойства материи быть частицей и волной одновременно) и прочие противоречащие тогдашнему здравому физическому смыслу объекты являются просто следствием несовершенства математического аппарата. На стороне классиков сражались Эйнштейн, Планк, Шредингер. Последний, кстати, придумал своего кота как раз для того, чтобы продемонстрировать абсурдность новой теории.
В 1935 году Альберт Эйнштейн, Борис Подольский и Натан Розен опубликовали статью, в которой описали мысленный эксперимент, получивший название парадокса Эйнштейна-Подольского-Розена. Суть парадокса сводилась к тому, что в квантовом мире существует явление запутанности. Из-за этого в некотором случае измерение состояния одного объекта позволяет определить состояние другого, удаленного от первого на произвольное расстояние. При этом кажется, что нарушается причинно-следственная связь. Этот парадокс был предложен как доказательство неполноты квантовомеханического описания мира. Парадокс разрешается благодаря тому факту, что для передачи известной информации о втором объекте требуется канал связи, который не нарушает причинно-следственную связь. Позже явление запутанности неоднократно наблюдалось на практике.
Адепты же квантовой механики отстаивали реальность всех этих загадочных явлений (хотя позже стало понятно, что и среди этих ученых имеются серьезные разногласия). В период с 1924 по 1927 год Нильс Бор и Вернер Гейзенберг, одни из главных защитников «новой физики», сформулировали основные положения «реальности» в смысле квантовой механики. Эти положения были представлены широкой научной общественности в 1927 году, когда Гейзенберг прочитал серию лекций в Чикагском университете о том, что из себя представляет квантовая механика. Так на свет появилась копенгагенская интерпретация квантовой механики (и Бор, и Гейзенберг в ту пору работали в университете Копенгагена) — самая, пожалуй, распространенная и популярная интерпретация.
Главным отличием микромира от привычного нам макромира провозглашалась вероятностная природа происходящих там процессов. Материя демонстрирует корпускулярно-волновой дуализм. Основным объектом описания системы становилась волновая функция, которая характеризует амплиду вероятности обнаружить систему в том или ином состоянии в данной конкретной точке. Со временем волновая функция эволюционирует, и эта эволюция описывается так называемым уравнением Шредингера. По сути состояния системы оказываются «размазаны» по времени и пространству.
Традиционно это интерпретируется как нахождение квантовой системы в нескольких состояниях одновременно.
В случае измерения происходит коллапс волновой функции к одному из классических состояний. Это связано с тем, что все измерительные приборы и все измерения в физике считаются классическими. По этой причине, помимо прочего, невозможно получить всю возможную информацию о системе. Иллюстрацией последнего положения является знаменитый принцип неопределенности Гейезенберга, утверждающий, что произведение неопределенностей при измерении импульса и координата какой-нибудь механической системы всегда больше некоторого ненулевого значения. Наконец, последнее требование – для достаточно больших систем квантовое описание приближается к классическому.
Копенгагенская интерпретация позволила физике смириться с многими парадоксальными результатами наблюдений. Для примера можно рассмотреть так называемый двухщелевой опыт. Представим экран, который отгорожен от источника света светонепроницаемой поверхностью, в которой прорезаны две щели. Когда свет проходит через щели, на экране возникает последовательность светлых и темных полос — типичная интерференционная картина. Это связано с тем, что свет — волна и, проходя через щели, разделяется на пару волн, взаимодействующих между собой. При этом такая картина наблюдается и в случае пролета единичных фотонов.
Если у обеих щелей поставить детекторы, которые будут регистрировать проходящие через них фотоны, то срабатывать будет всегда только один из детекторов. Это и есть демонстрация корускулярно-волнового дуализма. Более того, если один из детекторов убрать и не фиксировать прохождение фотона, интерфереционная картина на экране все равно исчезает. С точки зрения копенгагенской интерпретации это является прямой демонстрацией того, что при измерении (пусть даже с отрицательным результатом) происходит коллапс волновой функции.
 Рис. 1. Сидят (слева направо): Вальтер Нернст, Эрнест Резерфорд, Вильгельм Вин, Джозеф Джон Томсон, Эмиль Варбург, Хендрик Лоренц, Марсель Бриллюэн, Вильям Барлоу, Хейке Камерлинг-Оннес, Роберт Вильямс Вуд, Луи Георг Гуи, Пьер Вейс. Стоят (слева направо): Фридрих Газенорль, Жюль Эмиль Вершафельт, Джеймс Хопвуд Джинс, Уильям Генри Брэгг, Макс фон Лауэ, Генрих Рубенс, Мария Кюри, Роберт Гольдшмидт, Арнольд Зоммерфельд, Эдуард Герцен, Альберт Эйнштейн, Фредерик Линдманн, Морис де Бройль, Вильям Поуп, Эдвард Грюнайзен, Мартин Кнудсен, Георг Хостлет, Поль Ланжевен.
Рис. 1. Сидят (слева направо): Вальтер Нернст, Эрнест Резерфорд, Вильгельм Вин, Джозеф Джон Томсон, Эмиль Варбург, Хендрик Лоренц, Марсель Бриллюэн, Вильям Барлоу, Хейке Камерлинг-Оннес, Роберт Вильямс Вуд, Луи Георг Гуи, Пьер Вейс. Стоят (слева направо): Фридрих Газенорль, Жюль Эмиль Вершафельт, Джеймс Хопвуд Джинс, Уильям Генри Брэгг, Макс фон Лауэ, Генрих Рубенс, Мария Кюри, Роберт Гольдшмидт, Арнольд Зоммерфельд, Эдуард Герцен, Альберт Эйнштейн, Фредерик Линдманн, Морис де Бройль, Вильям Поуп, Эдвард Грюнайзен, Мартин Кнудсен, Георг Хостлет, Поль Ланжевен.
Новые реальности
В середине XX века копенгагенская интерпретация считалась стандартным объяснением квантовой механики. Ситуация изменилась к концу века — в физике стали возникать вопросы, которые даже не приходили в голову классикам. Вот, например, волновая функция — это что? Удобный инструмент для описания или же некий реально существующий объект? Или, скажем, как быть с квантовой запутанностью?
В настоящее время вопрос интерпретации считается скорее философским, нежели физическим. Известный физик Ашер Перес — автор одноименного парадокса — считает, что интерпретации суть не более чем набор правил для оперирования экспериментальными данными, поэтому единственное требование, которое можно предъявить к интерпретациями — чтобы эти наборы правил были эквивалентны друг другу (среди прочего, это связано с тем фактом, что, как уже говорилось выше, математический аппарат у всех интерпретаций совершенно одинаковый).
В настоящее время помимо копенгагенской интерпретации существует несколько ранее считавшихся немного безумными или даже научно-фантастическими альтернатив, которые со временем уверенно подвинули классику. И это не считая типично инструменталистской интерпретации Дэвида Мермина, выраженной в знаменитом афоризме «Заткнись и считай».
Самой популярной из альтернатив является так называемая многомировая интерпретация, принадлежащая Хью Эверетту. Примечательно, что Эверетт оставил физику после нескольких работ, в том числе и из-за той критики, которой научное сообщество подвергло его взгляды. В основе многомировой интерпретации — отрицание реальности коллапса волновой функции, то есть разделения взаимодействий на классические и квантовые.
Для этого Эверетт ввел понятие квантовой декогеренции, суть которой, достаточно условно (пытаясь пояснить формулы словами, всегда сталкиваешься с некоторыми неизбежными упрощениями), заключается в том, что исследуемая система и наблюдатель — измерительный прибор — оказываются объединены в одну огромную (по меркам микромира) систему. Факт этого включения и приводит к кажущемуся ощущению «классичности» – ведь тезис о том, что большие системы должны быть похожи на классические, этой интерпретацией не отрицается. При этом каждый из возможных вариантов включения системы оказывается реализован. С точки зрения двухщелевого опыта, если за одной из щелей стоит детектор, то при подлете фотона к поверхности с прорезями Вселенная раздваивается. В результате в одной из реальностей наблюдатель регистрирует фотон, а в другой — нет.
При этом все бесчисленные Вселенные оказываются частью некоего глобального квантового мира, который никогда не теряет своей когеренции.
Помимо многомировой интерпретации, есть еще и информационная интерпретация — точнее, даже несколько интерпретаций такого рода. В их основе лежит идея о том, что при измерении наблюдатель извлекает из системы некоторую информацию. Эта информация, с одной стороны, воспринимается как результат наблюдения, с другой — меняет саму измеряемую квантовую систему, поскольку та информацию теряет. Эти идеи носят идеалистический характер, поскольку помещают в основу реальности информацию, а не материю.
Наконец, последней интерпретацией, которую стоит упомянуть (на самом деле их много больше), это интерпретация Пенроуза. В ней коллапс волновой функции признается объективной реальностью, то есть физическим процессом. Согласно этой теории, коллапс происходит случайно, а сам наблюдатель никакой роли в этом процессе не играет.
Разброд и шатание
В 1997 году известный физик и космолог Макс Тегмарк опросил 48 участников конференции «Фундаментальные проблемы в квантовой теории», чтобы выяснить, какая интерпретация этой самой теории кажется им предпочтительной. Несмотря на то, что опрос носил в целом неформальный характер, Тегмарк обнаружил, что
многомировая интерпретация квантовой механике уступила копенгагенской, но не слишком (13 голосов против восьми). Это довольно неожиданный результат, если учесть, что в свое время, как говорилось выше, автор теории многомировой интерпретации Эверетт был вынужден уйти из науки.
Теперь сразу три физика из Австрии и США повторили опрос Тегмарка. Местом его проведения была выбрана конференция «Квантовая механика и природа реальности», проходившая в июле 2011 года в Австрии. Каждому участнику съезда предлагалось выбрать из предложенных ответы к 16 вопросам. Сами исследователи признают, что, как и опрос Тегмарка, их исследование носило не слишком формальный характер. Ученым, например, разрешалось давать на один вопрос несколько ответов. Кроме этого в исследовании приняли участие 33 человека — то есть на 15 меньше, чем в предыдущем опросе.
 Рис. 3.
Рис. 3.
Оказалось, что 64 процента опрошенных уверены: случайность — это фундаментальное свойство природы. При этом 48 процентов заявили, что до измерения свойства объекта не определены. Это основные положения именно копенгагенской интерпретации. Что касается проблемы измерения — видимого и необратимого коллапса волновой функции — то тут мнения очень сильно разделились. Оказалось, что 27 процентов опрошенных считают ее псевдопроблемой (то есть математическим артефактом), еще 15 процентов полагают, что понятие декогеренции снимает вопрос об измерениях, 39 процентов думают, что эта проблема решена, и 24 процента — что эта проблема представляет серьезную трудность в квантовой картине мира. В сумме получается больше 100 процентов, но это именно потому, что можно было давать больше одного варианта ответа, а проценты считались как отношение количества ответов к количеству участников, помноженное на 100.
Наиболее интересными были ответы на воспросы о квантовой информации — оказалось, что 76 процентов опрошенных считают идею квантовой информации «глотком свежего воздуха» для основ квантовой механики. Довольно необычный сдвиг для физиков, известных своим прожженным материализмом. Еще у физиков спрашивали, когда появится квантовый компьютер, и 42 процента опрошенных заявили, что это произойдет через 10–25 лет.
Что касается самого главного вопроса: «какой интерпретации придерживаетесь вы?» — то тут результаты были следующими. Оказалось, что
- 42 процента поддерживают копенгагенскую интерпретацию,
- 24 процента — теорию квантовой информации и
- только 18 — многомировую интепретацию квантовой мезаники.
Еще 9 процентов придерживаются интерпретации Пенроуза об объективности коллапса волновой функции.
Вместо заключения
Здесь, конечно, следовало бы сделать вывод о неожиданном укреплении позиций классики, которое, судя по всему, вызвано постепенным спадом интереса к многомировой интерпретации. Также можно было бы отметить популярность квантовой информации, которая, разумеется в ближайшее время будет только расти — ведь многие называют этот подход перспективным.
Делать эти выводы, однако, бессмысленно. Похоже, такого же мнения придерживаются и сами ученые — на вопрос «будут ли через 50 лет проводиться конференции по основам квантовой механики?» 48 процентов опрошенных ответили «да» и еще 24 – «кто знает». Действительно, кто ж его знает?
Автор: Андрей Коняев.
www.nanonewsnet.ru
Основные положения квантовой механики.
ЭЛЕМЕНТЫ КВАНТОВОЙ ФИЗИКИ. СТРОЕНИЕ АТОМА И ЯДРА
Электронный учебник по физике
КГТУ-КХТИ. Кафедра физики. Казанцев С.А., Нефедьев Е.С., Старостина И.А.
Для перемещения по тексту электронного учебника можно использовать:
1- нажатие клавиш PgDn, PgUp,, ¯ для перемещения по страницам и строкам;
2- нажатие левой клавиши «мыши» по выделенному тексту для перехода в требуемый раздел;
3- нажатие левой клавиши «мыши» по выделенному значку @ для перехода в оглавление.
ОГЛАВЛЕНИЕ
Основные положения квантовой механики.
1.1.Противоречия классической физики: особенности строения атома, линейчатые спектры атомов, дифракция электронов, дифракция нейтронов.
1.2.Гипотеза Луи-де-Бройля о корпускулярно-волновом дуализме свойств микрочастиц. 1.3.Соотношение неопределенностей Гейзенберга
1.4.Постулаты квантовой механики. Вероятностный характер движения частиц.
Волновая функция, её статистический смысл. Задание состояния микрочастицы.
1.5.Уравнение Шредингера. Физические ограничения на вид волновой функции. Стационарное уравнение Шредингера, стационарные состояния.
1.6.Частица в одномерной бесконечно глубокой потенциальной яме. Квантование энергии частицы. Объяснение туннельного эффекта. Гармонический осциллятор.
Физика атома.
2.1.Электрон в атоме водорода. Энергетические уровни. Квантовые числа и их физический смысл.
2.2.Опыт Штерна и Герлаха.
2.3.Пространственное распределение электрона в атоме водорода.
2.4.Спин электрона.
2.5.Многоэлектронный атом. Правила распределения электронов по орбиталям. Принцип Паули.
2.6.Особенности структуры электронных уровней в сложных атомах. Связь распределения электронов по орбиталям с периодической таблицей Менделеева.
2.7.Элементарная квантовая теория испускания атомами электромагнитного излучения. 2.8.Спонтанное и вынужденное излучение фотонов. Принцип работы квантового генератора и их использование.
Атомное ядро.
3.1.Состав ядра. Характеристики ядра.
3.2.Модели ядра: капельная, оболочная. Ядерные силы.
3.3.Энергия связи ядра. Дефект массы.
3.4.Два типа ядерной реакции Энергия ядерной реакции.
3.5.Радиоактивность. Закон радиоактивного распада. Альфа, бета, гамма – излучения.
3.6.Цепная ядерная реакция деления.
3.7.Использования энергии ядерных цепных реакций. Атомная бомба. Ядерный реактор.
3.8.Проблемы развития атомной энергетики.
3.9.Управляемая реакция термоядерного синтеза.
3.10.Свойства и характеристики радиоактивных излучений.
3.11. Биологическое действие ионизирующих излучений.
Элементарные частицы.
4.1.Свойства элементарных частиц. Гравитационное, электромагнитное, слабое и сильное взаимодействия.
4.2.Классификация элементарных частиц.
4.3.Гипотеза строения элементарных частиц из кварков.
4.4.Гипотеза Великого объединения всех видов взаимодействия.
Основные положения квантовой механики.
1.1.Противоречия классической физики: особенности строения атома, линейчатые спектры атомов, дифракция электронов, дифракция нейтронов.@
Корпускулярно-волновой дуализм свойств, обнаруженный у электромагнитного излучения, вскоре был обнаружен и у микрочастиц (молекул, атомов, ядер атомов, электронов, протонов, нейтронов и др.). В начале ХХ века в ряде экспериментов с микрочастицами, были обнаружены явления, которые не могли быть объяснены классической механикой, созданной для макротел.
Первая серия таких явлений связана с экспериментами по рассеиванию альфа-частиц при прохождении их через вещество. Альфа-частицы являются ядрами атомов гелия и имеют положительный электрический заряд, так как состоят из двух протонов и двух нейтронов. Английский ученый Резерфорд, пропуская альфа-частицы с большой кинетической энергией через тонкие металлические пластинки, установил, что большая часть частиц отклоняются от первоначального направления на небольшие углы. Наряду с рассеиванием на малые углы, было обнаружено отклонение отдельных частиц и на большие углы, доходящие до 1800 (Рис.1). Такое рассеивание было обнаружено и при прохождении альфа-частиц через газы.
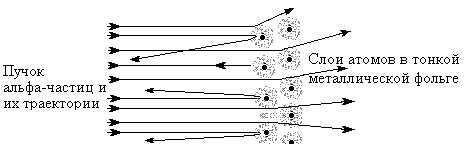 |
При анализе этих экспериментов было установлено, что отклонения происходят вследствие кулоновского отталкивания от положительного заряда, сосредоточенного в очень малом объеме внутри атома. До этого уже было известно (по экспериментам с ионизацией газов), что в составе атомов вещества также имеются элементарные частицы – электроны (с малой массой и отрицательным зарядом). Для объяснения результатов рассеивания Резерфорд в 1911г. предложил планетарную модель атома. Согласно этой модели атом построен по типу Солнечной системы - в центре атома в очень малой области (10-14 м) находится положительно заряженное ядро, в котором сосредоточена почти вся масса атома, а вокруг ядра под действием сил Кулоновского притяжения двигаются по замкнутым орбитам электроны (примерный радиус орбит -10-10м). При этом суммарный заряд электронов равен по величине заряду ядра, поэтому в целом атом нейтрален. При прохождении альфа-частиц через такой атом, только малая часть частиц будет сталкиваться с ядром и рассеиваться назад, основная их часть будет проходить на больших расстояниях от ядра и, вследствие малости Кулоновских сил, будут отклоняться на небольшие углы.
Таким образом, планетарная модель атома полностью объяснила эксперименты по рассеиванию. Однако, согласно классической электродинамике электрон, двигающийся по орбите вокруг ядра должен испускать электромагнитные волны непрерывного спектра частот. При этом он теряет свою энергию и через малый интервал времени (10-8 с) должен упасть на ядро, то есть такой атом нестабилен и имеет очень малое время жизни. Но, как известно, атомы отличаются большим временем жизни. Кроме того, из экспериментов по изучению частотного состава излучения (спектров) отдельных атомов в газах, известно, что атомы в невозбужденном (нормальном) состоянии не испускают электромагнитные волны, они излучают их только после передачи им энергии (при возбуждении), при зтом спектр частот имеет дискретный характер. Например, у атома водорода было обнаружено несколько серий частот излучения, наиболее известные описываются соотношениями:
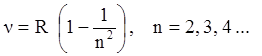 (1.1)
(1.1)
серия Лаймана для ультрафиолетового излучения,
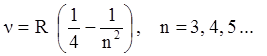 (1.2)
(1.2)
серия Бальмераа для видимого излучения
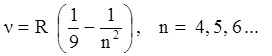 (1.3)
(1.3)
серия Пашена для инфракрасного излучения, здесь R-постоянная Ридберга, n – номер частоты (номер линии спектра излучения) в серии. Эксперименты по изучению спектра поглощения электромагнитного излучения для атома водорода показали, что спектр поглощения тоже имеет дискретный характер, описываемый соотношениями (1.1‑1.3). Подобная дискретность спектров была обнаружена у всех атомов. Таким образом, планетарная модель атома требовала серьезных доработок.
Для объяснения спектров излучения и поглощения атома водорода в 1913г. датский ученый Бор добавил к этой модели три ограничения (постулата), которые не соответствовали законам классической механики.
1. Атом может находиться в различных состояниях, в этих состояниях электрон двигается по определенным стационарным орбитам без излучения и без потери энергии. Эти орбиты называют Боровскими орбитами.
2. При движении по Боровским орбитам электрон имеет строго определенный (дискретный) момент импульса L (L равен произведению массы электрона, его скорости и радиуса орбиты). Его значение задается формулой квантования Бора
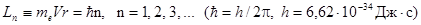 ,
,
где момент импульса связывается с постоянной Планка h и квантовым числом n.
Квантовое число n является номером состояния атома и номером Боровской орбиты электрона. В этих состояниях радиусы орбит электрона и его скорости различны, атом также имеет различные энергии. Обычно атом находится в основном или невозбужденном состоянии n=1 с наименьшим значением энергии, состояния с n = 2, 3, 4 имеют большие энергии и называются возбужденными.
3. При передаче атому энергии он переходит в какое-либо возбужденное состояние с n = 2, 3, 4… (если передача энергии производится с помощью электромагнитного излучения, то происходит поглощение атомом порции излучения), в возбужденном состоянии атом находится недолго (»10-8с), он испускает порцию (квант) электромагнитного излучения и переходит в какое-либо состояние с меньшим квантовым числом. При всех переходах, в соответствии с законом сохранения, энергия кванта e точно равна разности энергий атома e = En–Em.
При использовании этих постулатов, расчет полной энергии атома Е, которая складывается из кинетической энергии вращения электрона и потенциальной энергии электростатического взаимодействия электрона с ядром приводит к соотношению En= ‑hR/n2. Отсюда, используя формулу немецкого ученого Планка для кванта электромагнитного излучения e = hn и закон сохранения энергии в виде e = En‑Em , можно получить n = (En‑Em)/h = R(1/n2-1/n2), что полностью соответствует результатам экспериментов (1.1‑1.3). Таким образом, данная модель позволила рассчитывать и объяснять спектры атома водорода, за что в 1922 г. Бор был удостоен Нобелевской премии по физике. Изложенная выше теория была обобщена (Теория Бора-Зоммерфельда, 1915г.) и для описания "водородоподобных" атомов, содержащих один электрон, движущийся в поле ядра с положительным зарядом (таких как однократно ионизированный гелий, двукратно ионизированный литий, трехкратно ионизированный бериллий и т.д.), но для более сложных атомов она оказалась непригодной.
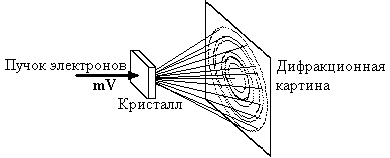
Вторая серия необычных явлений связана с прохождением элементарных частиц через неоднородные среды, при котором наблюдаются явления дифракции и интерференции. Например, при рассеянии электронов от поверхности монокристалла никеля получается отчетливая дифракционная картина (опыт Дэвиссона и Джермера). Дифракция пучка электронов при прохождении через тонкие слои металлов и кристаллов была обнаружена Томсоном (Рис.2). Позднее было обнаружено, что аналогичное явление дифракции наблюдается также для протонов, нейтронов и даже для молекул водорода при их попадании на кристалл.
 |
Обнаружена была и интерференция элементарных частиц. Например, если направить пучок электронов на две щели, то на экране из фотоимульсии после проявления можно наблюдать интерференционную картину в виде параллельных полос, расположенных на одинаковом расстоянии друг от друга (Рис.3). Интересно, что при малых интенсивностях электронных пучков, наблюдается постепенное формирование интерференционной картины (Рис.3.а – время пропускания мало, Рис.3.б – время пропускания большое), что доказывает корпускулярность электронов. Аналогичные результаты были получены и при интерференции других частиц.
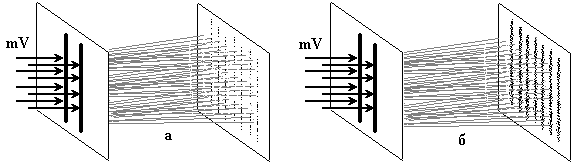 Рис.3. Схема экспериментов по интерференции электронов.
Рис.3. Схема экспериментов по интерференции электронов.
Таким образом, элементарные частицы в одних условиях проявляют свойства волн (явления дифракции, интерференции), в других же – свойства отдельных частиц‑корпускул (движение электронов в электронно-лучевой трубке, взаимодействие электрона и фотона при фотоэффекте и эффекте Комптона), что не может быть объяснено в рамках классической механики.
1.2.Гипотеза Луи-де-Бройля о корпускулярно-волновом дуализме свойств микрочастиц. @
Как известно, эксперименты с электромагнитными волнами показали, что в некоторых явлениях они проявляют свойства частиц (фотоэффект, эффект Комптона, тепловое излучение и др). Эти явления удалось описать, если предположить согласно теории Планка, что электромагнитное излучение является потоком частиц‑фотонов или квантов со следующими значениями энергии и импульса
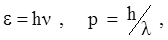 (1.4)
(1.4)
где n- частота, l- длина волны.
По аналогии, Луи де Бройль в 1923 году выдвинул гипотезу, что для объяснения волновых свойств микрочастиц им необходимо сопоставить особые волны, которые были названы волнами де Бройля. То есть, если микрочастице приписать некоторый волновой процесс с длиной волны
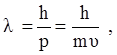 (1.5)
(1.5)
(где р, m, υ – импульс, масса и скорость частицы), то по формулам дифракции и интерференции для электромагнитных волн можно рассчитать эти явления и для пучков микрочастиц. Например, по известной формуле оптики для дифракционной решетки dSin(ak) = kl можно рассчитать положения максимумов и при дифракции микрочастиц. Эта гипотеза нашла полное подтверждение в вышеупомянутых экспериментах.
Эксперименты также показали, что распространение волн де Бройля не связано с распространением электромагнитных волн, а также каких-либо других волн, известных в классической физике. Наблюдаемое постепенное формирование интерференционной картины показывает, что волны де Бройля связаны со статистической природой движения микрочастиц и имеют вероятностное истолкование.
1.3.Соотношение неопределенностей Гейзенберга.@
Своеобразие движения микрочастиц, как оказалось, заключается также и в том, что ее траекторию нельзя характеризовать точными значениями координат и скорости (т.е. нельзя определить одновременно положение микрочастицы в пространстве и ее скорость с произвольной точностью). Немецкий ученый Гейзенберг в 1927г. установил, что неопределенности или погрешности измерения координаты Δх, Δy, Δz и импульса Δрх, Δрy, Δрz удовлетворяют соотношениям:
Δх Δрх ≥ h, Δy Δрy ≥ h, Δz Δрz ≥ h. (1.6)
Подобное соотношение имеется и для неопределенности измерения времени состояния микросистемы Δt и ее энергии ΔЕ
Δt ΔЕ≥h , (1.7)
все эти формулы называются соотношениями неопределенностей Гейзенберга.
Наличие этих соотношений объяснятся тем, что при измерении одного параметра микрочастицы, второй соответствующий параметр искажается измерительным прибором и чем точнее измеряется один, тем больше искажается второй. Это происходит и для макрообъектов, но вследствие их больших масс воздействие приборов оказывается несущественным. Например, при определении координат макрообъекта путем локации используют поток фотонов, которые испускаются локатором, они со скоростью света долетают до объекта, отражаются от него и возвращаются назад. Зная время движения фотона и его скорость можно легко определить расстояние до объекта, причем вследствие массивности макрообъекта, его скорость изменится незначительно. Если же использовать принцип локации для определения координаты микрочастицы, то при отражении от нее фотона он передаст ей импульс, сравнимый с импульсом частицы, что приведет к значительному изменению ее скорости. Подобные изменения соответствующих параметров происходят также при измерении скорости, энергии, времени.
Соотношения неопределенностей позволяют определить границы применимости понятий и законов классической механики к объектам, т.е. возможности одновременного использования понятий координаты и скорости при описании движения. Учитывая, что рх = mvx, можно получить Δх Δvх ≥ h/m, откуда следует, что чем больше масса частицы, тем меньше неопределенность ее координаты и скорости и, следовательно, с тем большей точностью можно применять к этой частице понятие траектории. Для пояснения рассмотрим два примера.
1. Рассмотрим пылинку массой m=10-12 кг и линейными размерами 10-6м и определим для нее неопределенность скорости (неопределенность определения ее координаты примерно равна сотой доли ее размера т.е. Δх = 10-8м). Согласно соотношениям неопределенностей Δvх = h/mΔx = 6,62∙10-34/(10-12∙10-8) = 6,62∙10-14м/с. В результате получается неопределенность измерения скорости, намного меньшая скорости, с которой пылинка может двигаться. Поэтому, в данном случае, скорость и импульс можно определить практически точно и поэтому для пылинки можно использовать понятие траектории и законы классической механики.
2. Рассмотрим электрон, движущийся в атоме водорода. Неопределенность его координаты порядка размера самого атома, т.е. Δx = 10-10м. Определим Δvх: Δvх = h/mΔx = 6,62∙10-34/(9, 1∙10-31∙10-10) = 7,3∙106м/с. Если рассчитать скорость электрона в атоме согласно классической механики, учитывая, что роль центростремительной силы играет сила Кулона, то скорость получается порядка 2∙106м/с и в данном случае неопределенность измерения скорости оказывается больше самой скорости. Поэтому нельзя говорить о движении электрона в атоме по определенной траектории.
1.4.Постулаты квантовой механики. Вероятностный характер движения частиц. Волновая функция, её статистический смысл. Задание состояния микрочастицы.@
Объяснить одновременное наличие корпускулярных и волновых свойств у микрочастиц удалось на основе идей Бора и Луи-де-Бройля в рамках новой теории, называемой волновой или квантовой механикой, созданной Гейзенбергом, Шредингером, Борном и многими другими учеными начала ХХ века. Квантовая механика базируется, как и любая другая физическая теория, на ряде постулатов. Основные постулаты можно представить упрощенно в следующем виде.
1.Движение микрочастиц в пространстве имеет вероятностный (стохастический) характер. Это относится не только к совокупности (ансамблю) частиц, но и к каждой отдельной частице. Согласно этому постулату, микрочастица, находясь в силовых полях или в вакууме (при отсутствии полей), испытывает такое воздействие, что нельзя в любой момент времени определить точно параметры ее движения. Например, нельзя одновременно характеризовать ее траекторию точными значениями координат и скорости или точными значениями энергии и времени какого-либо процесса у частицы.
2.Стохастический характер движения микрочастиц требует применения понятий математики теории вероятности для описания и расчета определенных значений параметров частиц в эксперименте. С точки зрения математики, отсюда следует, что движение таких частиц должно описываться с помощью некоторой «особой» волновой функции, которая должна характеризовать вероятностные особенности микрочастиц. Интерпретацию волновой функции дал в 1926г. немецкий физик Макс Борн следующим образом - волновая функция ψ (х, у, z) характеризует вероятность нахождения частицы в данный момент времени в некоторой точке пространства. Согласно Борну, физический смысл имеет не сама функция, а квадрат модуля волновой функции |ψ|2, который равен вероятности dP того, что частица будет обнаружена в пределах рассматриваемого малого объема dV. Формула связи этих понятий имеет вид
dP = |ψ|2 dV = |ψ|2dxdydz . (1.8)
Для совокупности частиц под вероятностью понимают отношение числа частиц в малом объеме к общему числу частиц, а для одной частицы – отношение времени пребывания частицы в малом объеме к общему времени рассмотрения движения частицы.
3.Волновая функция является основной характеристикой состояния микрообъекта, с помощью волновой функции можно рассчитать вероятность пребывания частицы в различных точках пространства в различные моменты времени, а также средние значения различных ее параметров. Соответственно вероятностному смыслу волновой функции и используя формулы теории вероятности, средние значения параметров находятся путем усреднения соответствующих операторов с помощью волновой функции. Например среднее значение для модуля радиуса-вектора частицы <r> можно найти по формуле
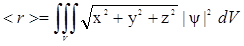 . (1.9)
. (1.9)
Так как в физических экспериментах определяются именно средние значения параметров частицы, то можно говорить, что состояние частицы полностью задается ее волновой функцией.
4.Вид волновой функции зависит от типа частицы и от внешних силовых полей, действующих на частицу. Вид функции находится с помощью специального дифференциального уравнения, называемого уравнением Шредингера.
5.Если в эксперименте наблюдается суперпозиция (объединение) микрочастиц, описываемых разными волновыми функциями, то объединенный ансамбль этих частиц будет описываться суммой их волновых функций. Например, если при интерференции микрочастиц на двух щелях, их можно по отдельности описать двумя функциями ψ1 и ψ2, тогда совокупность этих частиц в районе экрана должна описываться функцией ψ = ψ1+ψ2. Так как вероятность распределения частиц на экране dP определяется квадратом модуля волновой функции, то получаем dP » |ψ|2 = |ψ1|2 + 2|ψ1ψ2| + |ψ2|2. Отсюда следует, что распределение зависит не только от простого сложения вероятностей двух независимых ансамблей |ψ1|2 + |ψ2|2, но и от результата их специфичного квантового «взаимодействия» 2|ψ1ψ2|, вследствие чего и наблюдается интерференция частиц.
Имеется еще ряд постулатов, но они имеют более частный характер, о некоторых из них будет сказано далее.
1.5.Уравнение Шредингера. Физические ограничения на вид волновой функции. Стационарное уравнение Шредингера, стационарные состояния. @
Для расчета волновой функции необходимо иметь уравнение, которое позволяло бы для любого момента времени определить эту функцию с учетом действующих на частицу внешних силовых полей. Чтобы искомое уравнение учитывало волновые свойства микрочастиц, необходимо чтобы оно по форме было волновым уравнением, подобно тем, которые описывают звуковые или электромагнитные волны. Известно, что для плоской волны, распространяющейся вдоль оси х, волновое уравнение – это дифференциальное уравнение в частных производных, где независимыми переменными являются координаты и время. Учитывая такие аналогии, австрийский физик Эрвин Шредингер получил в 1926 г. основное уравнение квантовой механики для ψ (х, у, z, t)
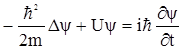 , (1.10)
, (1.10)
где m – масса частицы, i – мнимая единица, U – потенциальная энергия частицы, Δ‑оператор Лапласа, который представляет собой сумму вторых частных производных по координатам, т.е.
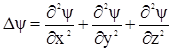 (1.11)
(1.11)
Из уравнения Шредингера следует, что конкретный вид волновой функции зависит от потенциальной энергии U, т.е. определяется характером сил, действующих на частицу. Уравнение Шредингера оказалось комплексным (включающим в себя мнимую единицу), поэтому и волновая функция также комплексная, при этом реальный физический смысл имеет квадрат модуля волновой функции (2.5, 2.6), который всегда действителен.
Уравнение Шредингера, будучи дифференциальным уравнением, может иметь множество решений. Из этих решений смысл имеют только те, в которых волновая функция будет однозначной, непрерывной и конечной, что соответствует физической реальности. Эти требования должны относиться и к частным производным от функции по времени и координатам, так как они тоже входят в уравнения Шредингера. Кроме этих требований на волновую функцию накладывается условие нормировки
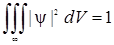 , (1.12)
, (1.12)
которое следует из того факта, что частица реально существует и обязательно находится где-либо в окружающем пространстве. Поэтому суммарная вероятность нахождения частицы во всем бесконечном пространстве равна единице, т.е. это достоверное событие. Смысл и назначение уравнения Шредингера заключается в том, что если известна волновая функция некоторой частицы в начальный момент времени и известно силовое поле, в котором она движется, то, решив это уравнение, можно найти волновую функцию и узнать характеристики состояния частицы в последующие моменты времени.
Если силовое поле, в котором движется частица, постоянно во времени, то U не зависит от времени и волновую функцию можно представить в виде  , где Е – полная энергия частицы. Если мы подставим такую функцию в уравнение Шредингера, проведем дифференцирование и сокращение, то получим уравнение
, где Е – полная энергия частицы. Если мы подставим такую функцию в уравнение Шредингера, проведем дифференцирование и сокращение, то получим уравнение
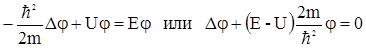 (1.13)
(1.13)
Это - уравнение Шредингера для, так называемых, стационарных состояний, находясь в которых частица имеет определенные, не меняющиеся со временем характеристики.
1.6.Частица в одномерной бесконечно глубокой потенциальной яме. Квантование энергии частицы. Объяснение туннельного эффекта. Гармонический осциллятор.@
Для выяснения особенностей решения уравнения Шредингера, рассмотрим поведение микрочастицы в одномерной бесконечно глубокой потенциальной «яме». Такой вид потенциала взаимодействия в природе не наблюдается, но он наиболее простой и может демонстрировать основные особенности решения (наиболее близок он к потенциалу, используемому при рассмотрении поведения электрона в металле). Такая потенциальная «яма» описывается следующими соотношениями для потенциальной энергии (рис.4):
U = ¥ в областях 1, 3 для x < 0 и x > a; U = 0 в области 2 для 0> x >a.
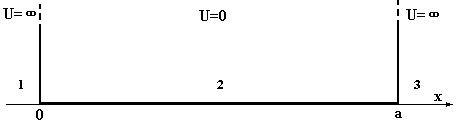
Рис.4. График потенциала одномерной бесконечно глубокой «ямы».
Запишем стационарное уравнение Шредингера для областей 1, 3 , где U=¥

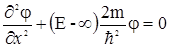 , (1.14)
, (1.14)
его единственно возможное решение j=0. Это означает, что вероятность нахождения частицы в этих областях равна нулю и частица туда проникнуть не может.
Для области 2 стационарное уравнение Шредингера имеет вид
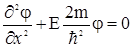 , (1.15)
, (1.15)
из теории дифференциальных уравнений следует, что его решение имеет вид
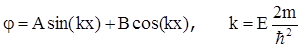 . (1.16)
. (1.16)
Вследствие требования непрерывности функции j, она должна быть равна нулю в точках x=0 и x=a, что следует из решения для областей 1, 3. Отсюда получается, что должны выполняться соотношения Asin(0)+Bcos(0)=0, Asin(ka)+Bcos(ka)=0 и, согласно математике, это будет при B=0 и ka=pn, где n-целое число. Необходимое также условие нормировки (1.12) в данной задаче имеет вид
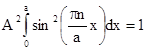 , (1.17)
, (1.17)
взяв этот интеграл, получаем 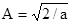 и в результате имеем конечное выражение для возможных решений уравнения Шредингера в поставленной задаче
и в результате имеем конечное выражение для возможных решений уравнения Шредингера в поставленной задаче
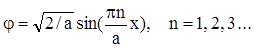 . (1.18)
. (1.18)
Данное решение показывает, что поведение микрочастицы в одномерной бесконечно глубокой потенциальной «яме» может быть различным в зависимости от значения числа n, его называют квантовым числом и рассматривают как номер возможного состояния микрочастицы.
Рассмотрим графики функции j2 (рис.5), которая согласно (1.8) определяет вероятность нахождения частицы в разных точках «ямы» для различных состояний.
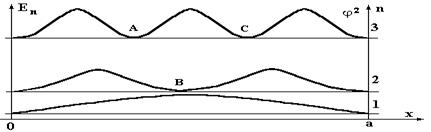
Рис.5. Графики вероятности нахождения частицы в бесконечно глубокой потенциальной «яме» для n = 1, 2, 3. Горизонтальные, тонкие линии соответствуют значениям энергий состояний (энергетическая диаграмма или уровни возможных энергий системы), толстые линии соответствуют функции j2.
Из рисунка 5 видно, что во втором и в третьем состояниях микрочастица не может находиться в некоторых точках «ямы» A,B,C, однако она может находиться между этими точками. Кроме этого, видно, что минимальное значение полной энергии Е1, которая в области 2 является кинетической энергией, не равна нулю, это означает что частица находится в непрерывном движении. Такое поведение микрочастицы существенно отличается от поведения макрочастиц и приводит к тому, что в квантовой механике не может быть использовано классическое понятие траектории.
Используя найденные соотношения ka = pn и (1.16), получим выражение для полной энергии частицы
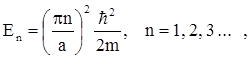 (1.19)
(1.19)
которое показывает, что энергия частицы в разных состояниях различна и строго определена (имеет дискретный спектр). Других значений энергии частица иметь не может, возможные дискретные значения называют квантовыми уровнями энергии. Подобное квантование у микрочастиц может происходить и с другими параметрами: импульсом, моментом импульса.
Если рассмотреть таким же образом более реальную ситуацию, когда частица находится в одномерной потенциальной «яме» конечной глубины (U = Uo в областях 1,3 для x < 0 и x > a; U = 0 в области 2 для 0 > x > a), то, в отличие от случая бесконечно глубокой ямы, функция j2 не будет равна нулю в областях 1, 3 даже при малых энергиях частицы (рис.6).

Рис.6. Графики вероятности нахождения частицы в потенциальной «яме» конечной глубины для n = 1, 2, 3.
Это означает, что частица может выйти за пределы потенциальной «ямы» даже в случае, когда ее энергия меньше Uo , чего в классической механике происходить не может. Подобное явление наблюдается и при рассмотрении поведения микрочастицы вблизи одномерного потенциального «барьера» (U = 0 в областях 1,3 для x < 0 и x > a; U = Uo в области 2 для 0 > x > a). Если решить уравнение Шредингера в этом случае, то можно обнаружить, что частица с энергией меньшей Uo может проходить сквозь этот «барьер».
Такие явления прохождения сквозь потенциальные барьеры частиц с малой энергией являются чисто квантовыми и называются «туннельными эффектами». Экспериментально эти явления наблюдаются с микрочастицами в различных ситуациях: автоэлектронная эмиссия – выход электронов за пределы металлов при малых температурах, автоионизация – выход электронов из атомов и молекул под действием слабого электрического поля, когда энергии поля бывает недостаточно для вырывания электрона с точки зрения классической механики. В физике элементарных частиц подобное явление наблюдается в радиоактивном излучении при выходе альфа частиц из ядер атомов.
Очень важным для атомной физики является рассмотрение поведения микрочастицы в силовом поле, когда потенциальная энергия зависит от координаты x в соответствии с законом 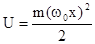 , этот случай соответствует в классической механике гармоническим колебаниям тела массой m с циклической частотой wo (гармонический осциллятор). Примерно такие колебания в мире микрочастиц происходят при движении атомов в молекуле, а также при колебаниях молекул около узлов кристаллической решетке в твердых телах.
, этот случай соответствует в классической механике гармоническим колебаниям тела массой m с циклической частотой wo (гармонический осциллятор). Примерно такие колебания в мире микрочастиц происходят при движении атомов в молекуле, а также при колебаниях молекул около узлов кристаллической решетке в твердых телах.
В классической механике гармонический осциллятор может иметь любую произвольную полную энергию Е, а его максимальное смещение от положения равновесия (амплитуда колебаний) xo ограничено и связано с энергией соотношением 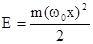 . В квантовой механике для анализа характеристик особенностей движения гармонического осциллятора необходимо решить уравнение Шредингера с данной потенциальной энергией
. В квантовой механике для анализа характеристик особенностей движения гармонического осциллятора необходимо решить уравнение Шредингера с данной потенциальной энергией

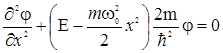 . (1.20)
. (1.20)
Решение такого дифференциального уравнения в аналитическом виде достаточно сложно, но качественные особенности аналогичны предыдущим случаям. На рисунке 7 представлены графики получаемого решения и возможные значения энергий.
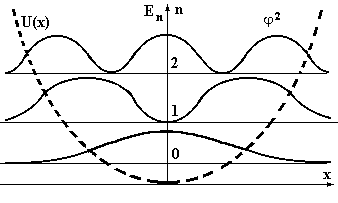
Рис.7. Графики вероятности нахождения гармонического осциллятора для n = 0, 1, 2. Горизонтальные, тонкие линии показывают значения энергий состояний (энергетическая диаграмма или уровни возможных энергий системы), толстые линии показывают j2, пунктирная – вид потенциала.
Возможные значения для полной энергии при решении определяются формулой
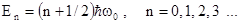 . (1.21)
. (1.21)
Из этой формулы видно, что полная энергия гармонического осциллятора тоже квантована, а ее минимальная величина при n = 0 отлична от нуля, также как и в предыдущих случаях. Наличие энергии нулевых колебаний – это чисто квантовый эффект, он говорит о том, даже в области нулевой потенциальной энергии у частицы имеется ненулевая кинетическая энергия и ненулевой импульс. Это означает, что микрочастица постоянно двигается и не может находиться в абсолютном покое.
Подтверждение наличия нулевых колебаний было получено в экспериментах по рассеиванию света в кристаллах. Согласно классической теории, при абсолютном нуле температуры по Кельвину колебаний атомов около узлов кристаллической решетки и соответственно рассеивания света, вызываемого этими колебаниями, не должно быть. Эксперименты показывают, что интенсивность рассеянного света при уменьшении температуры уменьшается, но даже при температурах очень близких к абсолютному нулю интенсивность рассеянного света не нулевая, что доказывает наличие нулевых колебаний.
Все выше приведенные варианты решений уравнения Шредингера и наличие в экспериментах эффектов, объясняемых рассмотренными примерами, указывают на необходимость использования квантово-механического описания поведения микрочастиц.
2 Физика атома.
2.1.Электрон в атоме водорода. Энергетические уровни. Квантовые числа и их физический смысл.@
Квантово-механическая теория атома, построенная на уравнении Шредингера, гораздо совершеннее полу‑классичекой теории атома Бора, построенной на ряде постулатов. Она сохраняет некоторые аспекты старой теории – например, электроны могут находиться в атоме только в состояниях с определенной дискретной энергией; при переходе электрона из одного состояния в другое испускается (или поглощается) фотон. Но квантовая механика не просто дополняет теорию Бора, она рисует совершенно иную картину строения атома. Согласно квантовой механике, не существует определенных круговых орбит у электронов, как в теории Бора. В силу волновой природы электрон «размазан» в пространстве, т.е. может с определенной вероятностью находится в любой точке пространства.
При рассмотрении атома водорода, движение его единственного электрона можно рассматривать как движение в электрическом поле ядра. По аналогии с задачей о движении частицы в потенциальной яме простой формы, здесь необходимо найти решения стационарного уравнения Шредингера в трехмерном пространстве с конкретным видом потенциальной энергии, описывающем его электростатическое взаимодействие с ядром
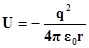 . (2.1)
. (2.1)
При решении уравнения Шредингера в данном случае используют специальные функции математической физики - сферические функции и сферическую систему координат, центр которой совпадает с центром ядра атома. Если записать уравнение Шредингера в сферических координатах (r, a, q), то его можно строго аналитически решить, это решение представляют в виде произведения трех функций
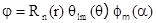 (2.2)
(2.2)
Важной особенностью решения является его зависимость от трех чисел n, l, m, называемых квантовыми числами. В квантовой механике каждому решению соответствует определенное состояние атома со своим распределением электрона вокруг ядра, которое задается соответствующей волновой функцией, зависящей от трех квантовых чисел: n, l, m.
poisk-ru.ru
Квантовая физика
| 1 | Классическая физика была создана в средние века. | Квантовая физика возникла в начале XX века. |
| 2 | В классической физике можно думать, что мы описываем природу как она есть сама по себе, независимо от используемых нами средств наблюдения. | В квантовой физике это не так, результат наблюдения принципиально зависит от того, каким прибором мы пользуемся. |
| 3 | В основе классической физики лежит механика, а в ее основе лежат законы Исаака Ньютона Основное уравнение классической механики F=m*a |
В основе квантовой механики лежит принцип суперпозиции состояний. Это означает, что если квантовая частица может быть в одном состоянии, и она может находиться и в другом состоянии, то она может находиться и в третьем состоянии, которое является суммой этих двух (линейная комбинация). Конечно же, это невозможно в классической физике. |
| 4 |
Законы Ньютона позволяют определить точное положение и скорость частицы в заданный момент времени в будущем
|
В квантовой механике можно определить лишь вероятность пребывания частицы в определённом месте пространства в заданный момент времени в будущем.
|
| 5 | Пример классического движения, мяч отскакивает от стен.  |
Если бы мы измеряли координаты движущегося мяча, то вероятностное распределение этих измерений изменялось бы со временем: Максимум вероятностного распределения перемещается вдоль траектории, предсказанной классической механикой. Это важно! Здесь очевидна взаимосвязь между вероятностью и законами классической механики. |
| 6 | Классическая физика является наукой детерминированной, случайность в ней обычно связывается с нашим незнанием. | В квантовой физике вероятность имеет фундаментальное значение и не связана с нашим незнанием. |
| 7 | В классической физике речь может идти либо о волне, либо о частице. | В квантовой физике существует понятие "корпускулярно-волновой дуализм"
|
| 8 | В классической механике частица может иметь любую энергию и любую скорость. В классической механике нет ни собственных значений, ни собственных состояний. |
В квантовой механике энергия и скорость могут быть квантованы. Это означает, что частица в квантовой системе может иметь только определённые значения энергии, и определённые значения скорости (и импульса). Они называются собственными значениями энергии и импульса квантовой системы. Каждому собственному значению соответствует собственное состояние. Собственные значения и собственные состояния квантовой системы – наиболее важные характеристики в квантовой механике. |
| 9 | В классической физике у частицы обновременно существуют координата и импульс. | В квантовой механике действует так называемый «Принцип неопределённости Гейзенберга». Согласно этому принципу, невозможно определить положение и скорость квантовой частицы с абсолютной точностью. Чем лучше известно положение частицы, тем меньше мы знаем о её скорости, и наоборот. Иногда он также объясняется таким образом, что измерение координаты обязательно влияет на импульс частицы. Более того, математический аппарат квантовой механики, использующий так называемые некоммутирующие операторы, приводит к тому, что координата и импульс не могут одновременно существовать у частицы. На практике, такой эффект заметен только когда речь идёт об очень маленьких объектах, например об атомах. Вот почему в повседневной жизни мы не замечаем влияние «Принципа неопределённости Гейзенберга». |
| 10 | Квантовомеханические системы могут иметь очень любопытные процессы, как например тунелирование или запутанность состояний. |
Нелокальность и индотерминизм
Как известно, в классической физике исследуемый объект находится лишь в каком-то одном или в другом состоянии. К примеру, учащийся может бегать на улице или кушать в столовой. Однако он не может быть в этих двух местах в одно и то же время, что могло бы соответствовать суперпозиции этих состояний. Тем не менее, в природе для микрочастиц имеет место и совершенно другая ситуация, когда объект находится в суперпозиции состояний. Иными словами, происходит наложение двух или большего числа состояний друг на друга без какого-либо взаимного влияния. Например, экспериментально доказано, что один объект, который мы по привычке называем частицей, может как бы одновременно проходить через две щели в непрозрачном экране. Частица, проходящая через первую щель, — это одно состояние, та же частица, проходящая через вторую, — другое. И эксперимент показывает, что наблюдается сумма этих состояний. В таком случае говорят о суперпозиции состояний, или о чисто-квантовом состоянии. Речь идет о квантовой суперпозиции (когерентной суперпозиции), то есть о суперпозиции состояний, которые не могут быть реализованы одновременно с классической точки зрения. Состояния квантовой частицы описываются посредством так называемой волновой функции, которую также называют вектором состояния. Можно сказать, что волновая функции описывает “программу” поведения электронов. Как в компьютере есть “железо” и программа, так и в квантовом мире электрон (частица) играет роль “железа”, а волновая функция - программы. Программа описывает, что можно делать электрону, а что нельзя. Существуют различные программы его поведения, они зависят от условий наших наблюдений. Когда меняется прибор наших наблюдений, меняется и программа. Можно сравнить это с воздействием красного или зеленого сигнала на автомобилиста. Это не физическое воздействие, однако, оно задаёт действие водителя. В соответствии с программой, которая задаётся водителю светофором, он едет дальше или останавливается.
Для того чтобы разобраться в этих понятиях, рассмотрим классический двухщелевой эксперимент.
Для начала возьмем пулемет и мысленно проведем эксперимент, показанный на рис. 1.
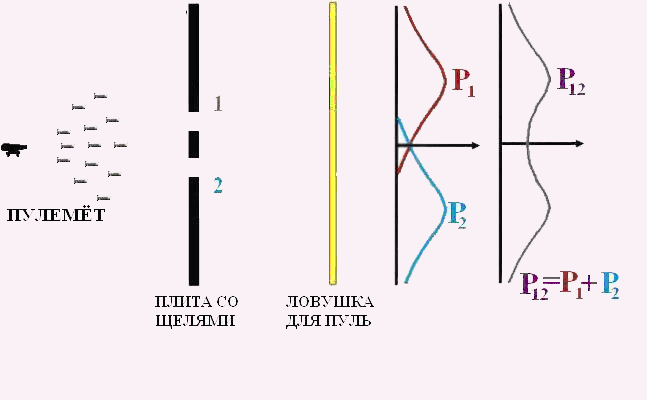 Рис. 1
Он не очень хорош, наш пулемет. Он выпускает пули, направление полета которых заранее неизвестно. То ли направо они полетят, то ли налево…. Перед пулеметом стоит броневая плита, а в ней проделаны две щели, через которые пули свободно проходят. Далее стоит «детектор» — любая ловушка, в которой застревают все попавшие в нее пули. По окончании эксперимента можно пересчитать число пуль, застрявших в ловушке, на единицу ее длины и разделить это число на общее количество выпущенных пуль. Или на время стрельбы, если скорость стрельбы считать постоянной. Эту величину — число застрявших пуль на единицу длины ловушки в окрестности некоторой точки Х, отнесенное к полному числу пуль, мы будем называть вероятностью попадания пули в точку Х. Заметим, что мы можем говорить только о вероятности — нельзя сказать определенно, куда попадет очередная пуля. И даже попав в дыру, она может срикошетить от ее края и уйти вообще неизвестно куда.
Мысленно проведем три опыта: первый — когда открыта первая щель, а вторая закрыта; второй — когда открыта вторая щель, а первая закрыта. И, наконец, третий опыт — когда обе щели открыты.
Результат нашего первого «эксперимента» показан на том же рисунке, на графиках. Ось вероятности в нем отложена вправо, а координата — снизу вверх. На первом графике показаны распределение вероятности P1 попавших в детектор пуль при открытой первой щели, и распределение вероятности P2 попавших в детектор пуль при открытой второй щели. На втором - вероятность попадания в детектор пуль P12 при обеих открытых щелях. Сравнив величины P1, P2 и P12, мы можем сделать вывод, что вероятности просто складываются,
P1 + P2 = P12.
Итак, для пуль воздействие двух одновременно открытых щелей складывается из воздействия каждой щели в отдельности.
Представим себе такой же опыт с электронами, схема которого показана на рис. 2.
Рис. 1
Он не очень хорош, наш пулемет. Он выпускает пули, направление полета которых заранее неизвестно. То ли направо они полетят, то ли налево…. Перед пулеметом стоит броневая плита, а в ней проделаны две щели, через которые пули свободно проходят. Далее стоит «детектор» — любая ловушка, в которой застревают все попавшие в нее пули. По окончании эксперимента можно пересчитать число пуль, застрявших в ловушке, на единицу ее длины и разделить это число на общее количество выпущенных пуль. Или на время стрельбы, если скорость стрельбы считать постоянной. Эту величину — число застрявших пуль на единицу длины ловушки в окрестности некоторой точки Х, отнесенное к полному числу пуль, мы будем называть вероятностью попадания пули в точку Х. Заметим, что мы можем говорить только о вероятности — нельзя сказать определенно, куда попадет очередная пуля. И даже попав в дыру, она может срикошетить от ее края и уйти вообще неизвестно куда.
Мысленно проведем три опыта: первый — когда открыта первая щель, а вторая закрыта; второй — когда открыта вторая щель, а первая закрыта. И, наконец, третий опыт — когда обе щели открыты.
Результат нашего первого «эксперимента» показан на том же рисунке, на графиках. Ось вероятности в нем отложена вправо, а координата — снизу вверх. На первом графике показаны распределение вероятности P1 попавших в детектор пуль при открытой первой щели, и распределение вероятности P2 попавших в детектор пуль при открытой второй щели. На втором - вероятность попадания в детектор пуль P12 при обеих открытых щелях. Сравнив величины P1, P2 и P12, мы можем сделать вывод, что вероятности просто складываются,
P1 + P2 = P12.
Итак, для пуль воздействие двух одновременно открытых щелей складывается из воздействия каждой щели в отдельности.
Представим себе такой же опыт с электронами, схема которого показана на рис. 2.

Рис. 2 Возьмем теперь не пулемёт, а источник электронов. Прошедшие через щели электроны можно регистрировать различными методами: с помощью сцинтиллирующего экрана, попадание электрона на который вызывает вспышку света, фотопленки или с помощью счетчиков различных типов, например, счетчика Гейгера. Результаты подсчетов в случае, когда одна из щелей закрыта, вполне предсказуемы и очень похожи на итоги пулеметной стрельбы (см. первый график). А вот в случае, когда обе щели открыты, мы получаем совершенно неожиданную кривую P12. Она явно не совпадает с суммой P1 и P2! Получившуюся кривую называют интерференционной картиной от двух щелей. Давайте попробуем разобраться, в чем тут дело. Если мы исходим из гипотезы, что электрон проходит либо через щель 1, либо через щель 2, то в случае двух открытых щелей мы должны получить сумму вкладов от одной и другой щели, как это имело место в опыте с пулеметной стрельбой. Вероятности независимых событий складываются, и в этом случае мы бы получили P1 + P2 = P12. Во избежание недоразумений отметим, что графики отражают вероятность попадания электрона в определенную точку детектора. Если пренебречь статистическими ошибками, эти графики не зависят от полного числа зарегистрированных частиц. Может, мы не учли какой-нибудь существенный эффект, и суперпозиция состояний (то есть одновременное прохождение электрона через две щели) здесь совсем не при чем? Может быть, у нас очень мощный поток электронов, и разные электроны, проходя через разные щели, как-то искажают движение друг друга? Для проверки этой гипотезы надо модернизировать источник электронов так, чтобы электроны вылетали из него достаточно редко. Скажем, не чаще, чем раз в полчаса. За это время каждый электрон уж точно пролетит все расстояние от источника до детектора и будет зарегистрирован. Так что никакого взаимного влияния летящих электронов друг на друга не будет! Сказано — сделано. Мы модернизировали источник электронов и полгода провели возле установки, проводя эксперимент и набирая необходимую статистику. Каков же результат? Он ничуть не изменился. Но, может быть, электроны каким-то образом блуждают от отверстия к отверстию и только потом достигают детектора? Это объяснение также не подходит: на кривой P12 при двух открытых щелях есть точки, в которые попадает значительно меньше электронов, чем при любой из открытых щелей. И наоборот, есть точки, вероятность попадания электронов в которые более чем вдвое превышает вероятность попадания электронов, прошедших через каждую щель по отдельности. Стало быть, утверждение о том, что электроны проходят либо сквозь щель 1, либо сквозь щель 2, неверно. Они проходят через обе щели одновременно. И очень простой математический аппарат, описывающий такой процесс, дает абсолютно точное согласие с экспериментом, показанным на втором графике. Если подойти к вопросу более строго, то утверждение, что электрон проходит одновременно через две щели, неверно. Понятие «электрон» можно соотнести только с локальным объектом («проявленным» в точке состоянием), здесь же мы имеем дело с квантовой суперпозицией различных компонент волновой функции. Дебройлевская волна каждого отдельного электрона проходит одновременно через оба отверстия. Как известно, поверхность, окружающая источник колебаний, все точки которой имеют одинаковые фазы колебаний, называется фронтом волны. В свою очередь все точки поверхности, через которые проходит фронт волны (щель один и щель два) в определённый момент времени, следует рассматривать как источник вторичных волн. В результате их наложения и возникает интерференция. Чем же отличаются пули от электронов? С точки зрения квантовой механики — ничем. Только, как показывают расчеты, интерференционная картина от рассеяния пуль характеризуется столь узкими максимумами и минимумами, что никакой детектор их зарегистрировать не в состоянии. Расстояния между этими минимумами и максимумами неизмеримо меньше размеров самой пули. Так что детекторы будут давать усредненную картину, показанную сплошной кривой на рис. 1. Давайте теперь внесем такие изменения в эксперимент, чтобы можно было «проследить» за электроном, то есть узнать, через какую щель он проходит. (рис. 3). Установим “прозрачный” детектор, который назван так, потому что не оказывает никакого влияния на движение электронов. В этом случае, если “прозрачный” детектор регистрирует прохождение электрона через щель 2, мы будем знать, что электрон прошел через эту щель, а если этот детектор не дает сигнала, а основной детектор электронов дает сигнал, то ясно, что электрон прошел через щель 1. Можно поставить и два прозрачных детектора — на каждую из щелей, но это никак не скажется на результатах нашего опыта. Конечно, любой детектор, так или иначе, исказит движение электрона, но будем считать это влияние не очень существенным. Для нас ведь куда более важен сам факт регистрации того, через какую из щелей проходит электрон!
 Рис. 3
Как вы думаете, какую картину мы увидим? Результат эксперимента показан на рис. 3, качественно он ничем не отличается от опыта с пулеметной стрельбой. Таким образом, мы выяснили, что, когда мы смотрим на электрон и фиксируем его состояние, то он проходит либо через одно отверстие, либо через другое. Суперпозиции этих состояний нет! А когда мы на него не смотрим, электрон одновременно проходит через две щели, и распределение частиц на экране совсем не такое, как тогда, когда мы на них смотрим! Так, электрон как бы “чувствует”, что за ним наблюдают, и перестаёт проявлять волновые свойства. Выходит, наблюдение как бы «вырывает» объект из совокупности неопределенных квантовых состояний и переводит его в проявленное, наблюдаемое, классическое состояние.
Может быть, все это не так, и дело только в том, что прозрачный детектор слишком сильно искажает движение электронов? Проведя дополнительные опыты с различными детекторами, по-разному искажающими движение электронов, мы заключаем, что роль этого эффекта не очень существенна. Существенным оказывается только сам факт фиксации состояния объекта!
Таким образом, если измерение, проведенное над классической системой, может и не оказать никакого влияния на ее состояние, для квантовой системы это не так. В связи с этим интересно разобрать другие задачи вместе со студентами, которые проиллюстрируют различия классического и квантового миров. Итак, любопытен следующий случай, предложенный Элитзуром и Вайдманом 2: Ниже представлен интерферометр, имеющий два оптических входа:
Рис. 3
Как вы думаете, какую картину мы увидим? Результат эксперимента показан на рис. 3, качественно он ничем не отличается от опыта с пулеметной стрельбой. Таким образом, мы выяснили, что, когда мы смотрим на электрон и фиксируем его состояние, то он проходит либо через одно отверстие, либо через другое. Суперпозиции этих состояний нет! А когда мы на него не смотрим, электрон одновременно проходит через две щели, и распределение частиц на экране совсем не такое, как тогда, когда мы на них смотрим! Так, электрон как бы “чувствует”, что за ним наблюдают, и перестаёт проявлять волновые свойства. Выходит, наблюдение как бы «вырывает» объект из совокупности неопределенных квантовых состояний и переводит его в проявленное, наблюдаемое, классическое состояние.
Может быть, все это не так, и дело только в том, что прозрачный детектор слишком сильно искажает движение электронов? Проведя дополнительные опыты с различными детекторами, по-разному искажающими движение электронов, мы заключаем, что роль этого эффекта не очень существенна. Существенным оказывается только сам факт фиксации состояния объекта!
Таким образом, если измерение, проведенное над классической системой, может и не оказать никакого влияния на ее состояние, для квантовой системы это не так. В связи с этим интересно разобрать другие задачи вместе со студентами, которые проиллюстрируют различия классического и квантового миров. Итак, любопытен следующий случай, предложенный Элитзуром и Вайдманом 2: Ниже представлен интерферометр, имеющий два оптических входа: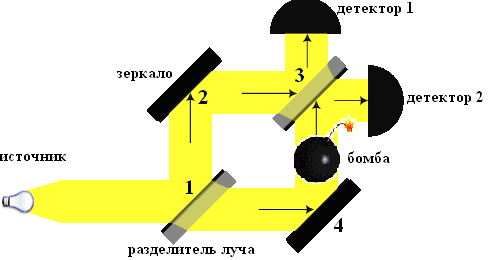 рис. 4
Фотон выстреливается в точку 1, где установлено полупрозрачное зеркало. Он может попасть в точку 3, пройдя по пути 123, либо 143. Если нет возможности проверить, по какому пути прошел фотон, то в точке 3 мы будем наблюдать интерференционную картину. Пусть при интерференции детектор 2, установленный вблизи точки 3, всегда даёт ответ “да”, а детектор 1 всегда даёт ответ “нет”.
Однако если каким-либо образом мы можем проследить, по какому пути прошел фотон, интерференция не наблюдается и тогда детектор 1 может дать ответ “да. Теперь представьте, что человек раздобыл две разные бомбы. Одна из них никогда не взорвется, если на её поверхности окажется фотон, а другая может взорваться, если фотон достигнет её поверхности.
Можем ли мы провести эксперименты с фотонами и понять, взорвётся ли одна из бомб, не взрывая её? С точки зрения классической физики это невозможно, однако какой ответ даёт квантовая физика? Проведём три эксперимента. Посмотрим, что будет происходить когда
I. - бомбы вообще нет.
II. - установлена бомба, которая не взрывается, если на её поверхности окажется фотон, он просто полетит сквозь неё.
III. - установлена бомба, которая взрывается, если на её поверхность попадает фотон.
Итак,
I. - Когда бомбы нет, мы сможем наблюдать интерференционную картину. Детектор 2 даст ответ “да”, а 1- “нет”.
Теперь установим бомбу на входе 143.
II. - В данном случае между бомбой и фотоном не будет взаимодействия, и мы будем наблюдать интерференционную картину. Детектор 2 даст ответ “да”, а детектор 1 всегда даёт ответ “нет”. Так, этот случай аналогичен первому.
III. - Теперь мы имеем дело с бомбой, которая взрывается от попадания фотона на её поверхность. Здесь следует принять во внимание, что для квантовой частицы важна сама вероятность взрыва (из-за того, что бомба может взорваться, мы можем знать путь, пройденный фотоном в интерферометре), и интерференционная картина исчезает. Существует любопытная вероятность отрицательного эксперимента, когда бомба, установленная в 143, может взорваться, но этого не происходит, так как фотон движется по пути 123! Тогда детектор 1 даёт ответ “да”. Интерференционная картина исчезает, и мы поймём, что оружие взорвется, если фотон коснётся его поверхности, не взрывая бомбы! Удивление состоит в том, что в классической физике мы не могли бы получить такую информацию. Квантовая частица, проходя по 123 как бы “чувствует” наличие бомбы в 143.
рис. 4
Фотон выстреливается в точку 1, где установлено полупрозрачное зеркало. Он может попасть в точку 3, пройдя по пути 123, либо 143. Если нет возможности проверить, по какому пути прошел фотон, то в точке 3 мы будем наблюдать интерференционную картину. Пусть при интерференции детектор 2, установленный вблизи точки 3, всегда даёт ответ “да”, а детектор 1 всегда даёт ответ “нет”.
Однако если каким-либо образом мы можем проследить, по какому пути прошел фотон, интерференция не наблюдается и тогда детектор 1 может дать ответ “да. Теперь представьте, что человек раздобыл две разные бомбы. Одна из них никогда не взорвется, если на её поверхности окажется фотон, а другая может взорваться, если фотон достигнет её поверхности.
Можем ли мы провести эксперименты с фотонами и понять, взорвётся ли одна из бомб, не взрывая её? С точки зрения классической физики это невозможно, однако какой ответ даёт квантовая физика? Проведём три эксперимента. Посмотрим, что будет происходить когда
I. - бомбы вообще нет.
II. - установлена бомба, которая не взрывается, если на её поверхности окажется фотон, он просто полетит сквозь неё.
III. - установлена бомба, которая взрывается, если на её поверхность попадает фотон.
Итак,
I. - Когда бомбы нет, мы сможем наблюдать интерференционную картину. Детектор 2 даст ответ “да”, а 1- “нет”.
Теперь установим бомбу на входе 143.
II. - В данном случае между бомбой и фотоном не будет взаимодействия, и мы будем наблюдать интерференционную картину. Детектор 2 даст ответ “да”, а детектор 1 всегда даёт ответ “нет”. Так, этот случай аналогичен первому.
III. - Теперь мы имеем дело с бомбой, которая взрывается от попадания фотона на её поверхность. Здесь следует принять во внимание, что для квантовой частицы важна сама вероятность взрыва (из-за того, что бомба может взорваться, мы можем знать путь, пройденный фотоном в интерферометре), и интерференционная картина исчезает. Существует любопытная вероятность отрицательного эксперимента, когда бомба, установленная в 143, может взорваться, но этого не происходит, так как фотон движется по пути 123! Тогда детектор 1 даёт ответ “да”. Интерференционная картина исчезает, и мы поймём, что оружие взорвется, если фотон коснётся его поверхности, не взрывая бомбы! Удивление состоит в том, что в классической физике мы не могли бы получить такую информацию. Квантовая частица, проходя по 123 как бы “чувствует” наличие бомбы в 143.
Данный эксперимент основан на принципе редукции волнового пакета (скачкообразном изменении волновой функции при измерении). Итак, есть волновая функция , которая описывает состояние фотона. Если
, которая описывает состояние фотона. Если 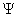 не меняется, значит есть интерференция.
Если же интерференции нет, то волновая функция меняется скачком.
не меняется, значит есть интерференция.
Если же интерференции нет, то волновая функция меняется скачком. 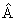 имеет два собственных значения:
имеет два собственных значения:  . Пусть собственное значение
. Пусть собственное значение  соответствует случаю, когда бомба не взрывается, а
соответствует случаю, когда бомба не взрывается, а  - когда взрывается. Тогда
- когда взрывается. Тогда 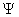 превращается либо в
превращается либо в  , либо в
, либо в 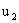 соответственно.
соответственно.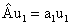
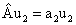
Также интересно рассмотреть отрицательный эксперимент Ренингера. Схема этого эксперимента изображена на рис. 5. Есть два сферических экрана, один из которых имеет отверстие. В центре находится источник электронов. Экраны покрыты сцинтиллирующим веществом, то есть когда на них попадают электроны, то они начинают светиться. Итак, происходит ?-распад и вылетает электрон. Он имеет импульс p. Если экран 1 светится, значит, электрон попал в него. Есл и же экран 1 не светится, значит, электрон пролетел через отверстие. Таким образом, мы располагаем информацией, что электрон не попал в экран 1, мы имеем отрицательное знание. Это наше отрицательное знание меняет волновую функцию (которая зависела от импульса). Следовательно, импульс стал другим. Импульс электрона изменился, несмотря на то, что ему не сообщили энергии, никакого взаимодействия не было. Это произошло, потому что мы что-то узнали. Такой эксперимент ещё не был поставлен, однако это можно сделать. Можно нанести на экран 2 сцинтиллирующее вещество, которое будет светиться, когда импульс электрона будет больше определённого значения. При этом импульс электрона в источнике должен быть меньше этого значения. Так, по вспышке на экране 2 мы определим, что импульс электрона стал больше.
и же экран 1 не светится, значит, электрон пролетел через отверстие. Таким образом, мы располагаем информацией, что электрон не попал в экран 1, мы имеем отрицательное знание. Это наше отрицательное знание меняет волновую функцию (которая зависела от импульса). Следовательно, импульс стал другим. Импульс электрона изменился, несмотря на то, что ему не сообщили энергии, никакого взаимодействия не было. Это произошло, потому что мы что-то узнали. Такой эксперимент ещё не был поставлен, однако это можно сделать. Можно нанести на экран 2 сцинтиллирующее вещество, которое будет светиться, когда импульс электрона будет больше определённого значения. При этом импульс электрона в источнике должен быть меньше этого значения. Так, по вспышке на экране 2 мы определим, что импульс электрона стал больше.
Данный эксперимент также основан на принципе редукции волнового пакета. Есть электрон в состоянии с определённым импульсом. Происходит бета-распад. 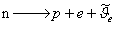 .
Волна де-Бройля
.
Волна де-Бройля 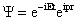 , где
, где 
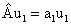
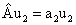
 имеет два собственных значения:
имеет два собственных значения:  . Пусть собственное значение
. Пусть собственное значение  соответствует случаю, когда возникает вспышка, а
соответствует случаю, когда возникает вспышка, а 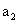 - когда вспышка не возникает. Тогда
- когда вспышка не возникает. Тогда 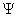 превращается либо в
превращается либо в 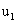 , либо в
, либо в  соответственно.
соответственно.
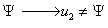
Некоторые положения квантовой механики изложенные математическим языком
I. Состояния квантовой системы описываются нормированными векторами гильбертова пространства. Гильбертово пространство — математическое понятие, обобщающее понятие евклидова пространства на бесконечномерный случай. При этом гильбертово пространство не обязательно является бесконечномерным. Это пространство предполагается комплекснозначным. Справедлив принцип суперпозиции: любой нормированный вектор гильбертова пространства 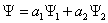 , где
, где 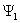 ,
,  — векторы, описывающие состояние системы, a1, a2 — комплексные числа, также описывают некоторое состояние системы.
Исключение представляют правила суперотбора для дискретного и непрерывного случаев. Например, суперпозиция состояний с разным электрическим зарядом ненаблюдаема и не есть состояние системы.
— векторы, описывающие состояние системы, a1, a2 — комплексные числа, также описывают некоторое состояние системы.
Исключение представляют правила суперотбора для дискретного и непрерывного случаев. Например, суперпозиция состояний с разным электрическим зарядом ненаблюдаема и не есть состояние системы.
II. Каждому наблюдаемому физическому свойству А соответствует эрмитов оператор  , действующий в гильбертовом пространстве состояний. Наблюдаемые A, E совместны, если соответствующие операторы
, действующий в гильбертовом пространстве состояний. Наблюдаемые A, E совместны, если соответствующие операторы  ,
, 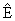 коммутируют.
коммутируют.
III Изменение наблюдаемой А даёт одно из собственных значений оператора  .
.
IV. Эволюция во времени вектора состояния  под действием внешних сил казуальна и линейна, т.е. по
под действием внешних сил казуальна и линейна, т.е. по  однозначно определяется
однозначно определяется 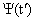 , так что если
, так что если 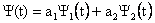 ,
То
,
То 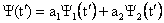 .
Эта эволюция описывается линейным уравнением Шредингера
.
Эта эволюция описывается линейным уравнением Шредингера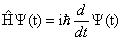 , (*)
Т.е.
, (*)
Т.е. 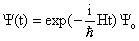
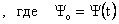 |t=to
|t=to
V. Постулат редукции волнового пакета и индотерминизм.
При изменении волновая функция 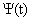 скачком (индетерминированно) превращается в собственную функцию оператора наблюдаемой
скачком (индетерминированно) превращается в собственную функцию оператора наблюдаемой 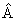 . То есть
. То есть
Если 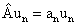 ,
То
,
То 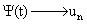 В случае измерений I рода повторное измерение с вероятностью I даёт результат an . Вероятность определённого результата измерения an и перехода в состояние un определяется как
В случае измерений I рода повторное измерение с вероятностью I даёт результат an . Вероятность определённого результата измерения an и перехода в состояние un определяется как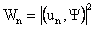 В частности, если наблюдатель “не посмотрел” на показания стрелки своего прибора, которому соответствует одно из чисел an , то он скажет, что Wn есть показания стрелки an . Такой обладающий неполной информацией о квантовой системе наблюдательбудет описывать систему уже не вектором в гильбертовом пространстве un, а матрицей плотности
В частности, если наблюдатель “не посмотрел” на показания стрелки своего прибора, которому соответствует одно из чисел an , то он скажет, что Wn есть показания стрелки an . Такой обладающий неполной информацией о квантовой системе наблюдательбудет описывать систему уже не вектором в гильбертовом пространстве un, а матрицей плотности 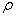 . Этой матрице сопоставляется статистический оператор
. Этой матрице сопоставляется статистический оператор  ,
где
,
где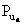 - проекторы на состояния un. Матрица
- проекторы на состояния un. Матрица 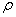 обладает свойствми:
а) эрмитовость
обладает свойствми:
а) эрмитовость  ,
б) нормировка
,
б) нормировка 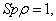 в) положительная определённость
в) положительная определённость 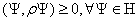 , где H – гильбертово пространство.
В случае измерения, проведенного с помощью прибора, но не зафиксированного наблюдателем, соответствующая матрица плотности
, где H – гильбертово пространство.
В случае измерения, проведенного с помощью прибора, но не зафиксированного наблюдателем, соответствующая матрица плотности  такова, что её собственные числа суть вероятности Wn
Итак, в случае неполной информации об изолированной квантовой системе возникает матрица плотности, описывающая “смесь состояний”: имеется либо состояние u1 c вероятностью W1, либо u2 с вероятностью W2, либо u3 c W3, и т.д.
Матрица плотности встречается ещё при описании подсистем квантовой системы, но эта матрица плотности вопреки довольно широко распространённому заблуждению не описывает смесь состояний. Д’Эспанья предлагает различать соответствующие ситуации, вводя термин “собственная смесь” и “несобственная смесь”.
Состояние, описываемоевектором в гильбертовом пространстве
такова, что её собственные числа суть вероятности Wn
Итак, в случае неполной информации об изолированной квантовой системе возникает матрица плотности, описывающая “смесь состояний”: имеется либо состояние u1 c вероятностью W1, либо u2 с вероятностью W2, либо u3 c W3, и т.д.
Матрица плотности встречается ещё при описании подсистем квантовой системы, но эта матрица плотности вопреки довольно широко распространённому заблуждению не описывает смесь состояний. Д’Эспанья предлагает различать соответствующие ситуации, вводя термин “собственная смесь” и “несобственная смесь”.
Состояние, описываемоевектором в гильбертовом пространстве 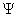 - чистое состояние- соответствует частному случаю матрицы плотности
- чистое состояние- соответствует частному случаю матрицы плотности  , такому, что статистический оператор есть
, такому, что статистический оператор есть  , а
, а 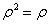 .
Постулат V редукции волнового пакета иногда формулируют как “превращение чистого состояния в смесь при измерении”. Действительно, можно сказать, что то обстоятельство – “посмотрел наблюдатель на стрелку прибора или не посмотрел” – связано с превращением неполной информации наблюдателя в полную, но постулат V предполагает некоторую особую математическую операцию, состоящую в следующем. Разложим волновую функцию
.
Постулат V редукции волнового пакета иногда формулируют как “превращение чистого состояния в смесь при измерении”. Действительно, можно сказать, что то обстоятельство – “посмотрел наблюдатель на стрелку прибора или не посмотрел” – связано с превращением неполной информации наблюдателя в полную, но постулат V предполагает некоторую особую математическую операцию, состоящую в следующем. Разложим волновую функцию  по ортогональному базису из собственных функций оператора
по ортогональному базису из собственных функций оператора 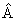
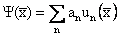 Функции
Функции  соответствует матрица плотности
соответствует матрица плотности 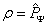 .
Постулат V означает превращение
.
Постулат V означает превращение 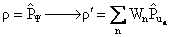 , (**)
Где
, (**)
Где 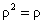 ,
,  ,
, 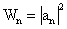 Итак, в квантовой механике существуют принципиально два различных способа изменения во времени вектора состояния:
Итак, в квантовой механике существуют принципиально два различных способа изменения во времени вектора состояния:
- детерминированный, согласно уравнению Шредингера (*),
- скачкообразный, согласно постулату редукции волнового пакета (**)
Сайт управляется системой uCoz
physicsforall.narod.ru
Элементы квантовой физики. Строение атома и ядра
Электронный учебник по физике
КГТУ-КХТИ. Кафедра физики. Казанцев С.А., Нефедьев Е.С., Старостина И.А.
Для перемещения по тексту электронного учебника можно использовать:
1- нажатие клавиш PgDn, PgUp,, для перемещения по страницам и строкам;
2- нажатие левой клавиши «мыши» по выделенному тексту для перехода в требуемый раздел;
3- нажатие левой клавиши «мыши» по выделенному значку @ для перехода в оглавление.
Оглавление
1. Основные положения квантовой механики.
1.1.Противоречия классической физики: особенности строения атома, линейчатые спектры атомов, дифракция электронов, дифракция нейтронов.
1.2.Гипотеза Луи-де-Бройля о корпускулярно-волновом дуализме свойств микрочастиц.1.3.Соотношение неопределенностей Гейзенберга
1.4.Постулаты квантовой механики. Вероятностный характер движения частиц.
Волновая функция, её статистический смысл. Задание состояния микрочастицы.
1.5.Уравнение Шредингера. Физические ограничения на вид волновой функции. Стационарное уравнение Шредингера, стационарные состояния.
1.6.Частица в одномерной бесконечно глубокой потенциальной яме. Квантование энергии частицы. Объяснение туннельного эффекта. Гармонический осциллятор.
2. Физика атома.
2.1.Электрон в атоме водорода. Энергетические уровни. Квантовые числа и их физический смысл.
2.2.Опыт Штерна и Герлаха.
2.3.Пространственное распределение электрона в атоме водорода.
2.4.Спин электрона.
2.5.Многоэлектронный атом. Правила распределения электронов по орбиталям. Принцип Паули.
2.6.Особенности структуры электронных уровней в сложных атомах. Связь распределения электронов по орбиталям с периодической таблицей Менделеева.
2.7.Элементарная квантовая теория испускания атомами электромагнитного излучения.2.8.Спонтанное и вынужденное излучение фотонов. Принцип работы квантового генератора и их использование.
3. Атомное ядро.
3.1.Состав ядра. Характеристики ядра.
3.2.Модели ядра: капельная, оболочная. Ядерные силы.
3.3.Энергия связи ядра. Дефект массы.
3.4.Два типа ядерной реакции Энергия ядерной реакции.
3.5.Радиоактивность. Закон радиоактивного распада. Альфа, бета, гамма – излучения.
3.6.Цепная ядерная реакция деления.
3.7.Использования энергии ядерных цепных реакций. Атомная бомба. Ядерный реактор.
3.8.Проблемы развития атомной энергетики.
3.9.Управляемая реакция термоядерного синтеза.
3.10.Свойства и характеристики радиоактивных излучений.
3.11. Биологическое действие ионизирующих излучений.
4. Элементарные частицы.
4.1.Свойства элементарных частиц. Гравитационное, электромагнитное, слабое и сильное взаимодействия.
4.2.Классификация элементарных частиц.
4.3.Гипотеза строения элементарных частиц из кварков.
4.4.Гипотеза Великого объединения всех видов взаимодействия.
1. Основные положения квантовой механики.
1.1.Противоречия классической физики: особенности строения атома, линейчатые спектры атомов, дифракция электронов, дифракция нейтронов.@
Корпускулярно-волновой дуализм свойств, обнаруженный у электромагнитного излучения, вскоре был обнаружен и у микрочастиц (молекул, атомов, ядер атомов, электронов, протонов, нейтронов и др.). В начале ХХ века в ряде экспериментов с микрочастицами, были обнаружены явления, которые не могли быть объяснены классической механикой, созданной для макротел.
Первая серия таких явлений связана с экспериментами по рассеиванию альфа-частиц при прохождении их через вещество. Альфа-частицы являются ядрами атомов гелия и имеют положительный электрический заряд, так как состоят из двух протонов и двух нейтронов. Английский ученый Резерфорд, пропуская альфа-частицы с большой кинетической энергией через тонкие металлические пластинки, установил, что большая часть частиц отклоняются от первоначального направления на небольшие углы. Наряду с рассеиванием на малые углы, было обнаружено отклонение отдельных частиц и на большие углы, доходящие до 1800(Рис.1). Такое рассеивание было обнаружено и при прохождении альфа-частиц через газы.
Рис.1. Схема опытов Резерфорда.
При анализе этих экспериментов было установлено, что отклонения происходят вследствие кулоновского отталкивания от положительного заряда, сосредоточенного в очень малом объеме внутри атома. До этого уже было известно (по экспериментам с ионизацией газов), что в составе атомов вещества также имеются элементарные частицы – электроны (с малой массой и отрицательным зарядом). Для объяснения результатов рассеивания Резерфорд в 1911г. предложил планетарную модель атома. Согласно этой модели атом построен по типу Солнечной системы - в центре атома в очень малой области (10-14м) находится положительно заряженное ядро, в котором сосредоточена почти вся масса атома, а вокруг ядра под действием сил Кулоновского притяжения двигаются по замкнутым орбитам электроны (примерный радиус орбит -10-10м). При этом суммарный заряд электронов равен по величине заряду ядра, поэтому в целом атом нейтрален. При прохождении альфа-частиц через такой атом, только малая часть частиц будет сталкиваться с ядром и рассеиваться назад, основная их часть будет проходить на больших расстояниях от ядра и, вследствие малости Кулоновских сил, будут отклоняться на небольшие углы.
Таким образом, планетарная модель атома полностью объяснила эксперименты по рассеиванию. Однако, согласно классической электродинамике электрон, двигающийся по орбите вокруг ядра должен испускать электромагнитные волны непрерывного спектра частот. При этом он теряет свою энергию и через малый интервал времени (10-8с) должен упасть на ядро, то есть такой атом нестабилен и имеет очень малое время жизни. Но, как известно, атомы отличаются большим временем жизни. Кроме того, из экспериментов по изучению частотного состава излучения (спектров) отдельных атомов в газах, известно, что атомы в невозбужденном (нормальном) состоянии не испускают электромагнитные волны, они излучают их только после передачи им энергии (при возбуждении), при зтом спектр частот имеет дискретный характер. Например, у атома водорода было обнаружено несколько серий частот излучения, наиболее известные описываются соотношениями:
(1.1)
серия Лаймана для ультрафиолетового излучения,
(1.2)
серия Бальмераа для видимого излучения
(1.3)
серия Пашена для инфракрасного излучения, здесь R-постоянная Ридберга, n– номер частоты (номер линии спектра излучения) в серии. Эксперименты по изучению спектра поглощения электромагнитного излучения для атома водорода показали, что спектр поглощения тоже имеет дискретный характер, описываемый соотношениями (1.1‑1.3). Подобная дискретность спектров была обнаружена у всех атомов. Таким образом, планетарная модель атома требовала серьезных доработок.
Для объяснения спектров излучения и поглощения атома водорода в 1913г. датский ученый Бор добавил к этой модели три ограничения (постулата), которые не соответствовали законам классической механики.
1. Атом может находиться в различных состояниях, в этих состояниях электрон двигается по определенным стационарным орбитам без излучения и без потери энергии.Эти орбиты называют Боровскими орбитами.
2. При движении по Боровским орбитам электрон имеет строго определенный (дискретный) момент импульса L (L равен произведению массы электрона, его скорости и радиуса орбиты). Его значение задается формулой квантования Бора
,
где момент импульса связывается с постоянной Планка hи квантовым числом n.
Квантовое число n является номером состояния атома и номером Боровской орбиты электрона. В этих состояниях радиусы орбит электрона и его скорости различны, атом также имеет различные энергии. Обычно атом находится в основном или невозбужденном состоянии n=1 с наименьшим значением энергии, состояния с n = 2, 3, 4 имеют большие энергии и называются возбужденными.
3. При передаче атому энергии он переходит в какое-либо возбужденное состояние с n = 2, 3, 4… (если передача энергии производится с помощью электромагнитного излучения, то происходит поглощение атомом порции излучения), в возбужденном состоянии атом находится недолго (10-8с), он испускает порцию (квант) электромагнитного излучения и переходит в какое-либо состояние с меньшим квантовым числом. При всех переходах, в соответствии с законом сохранения, энергия кванта точно равна разности энергий атома = En–Em.
При использовании этих постулатов, расчет полной энергии атома Е, которая складывается из кинетической энергии вращения электрона и потенциальной энергии электростатического взаимодействия электрона с ядром приводит к соотношениюEn = ‑hR/n2. Отсюда, используя формулу немецкого ученого Планка для кванта электромагнитного излучения = hи закон сохранения энергии в виде = En‑Em , можно получить =(En‑Em)/h = R(1/n2-1/n2), что полностью соответствует результатам экспериментов (1.1‑1.3). Таким образом, данная модель позволила рассчитывать и объяснять спектры атома водорода, за что в 1922 г. Бор был удостоен Нобелевской премии по физике. Изложенная выше теория была обобщена (Теория Бора-Зоммерфельда, 1915г.) и для описания "водородоподобных" атомов, содержащих один электрон, движущийся в поле ядра с положительным зарядом (таких как однократно ионизированный гелий, двукратно ионизированный литий, трехкратно ионизированный бериллий и т.д.), но для более сложных атомов она оказалась непригодной.
Вторая серия необычных явлений связана с прохождением элементарных частиц через неоднородные среды, при котором наблюдаются явления дифракции и интерференции. Например, при рассеянии электронов от поверхности монокристалла никеля получается отчетливая дифракционная картина (опыт Дэвиссона и Джермера). Дифракция пучка электронов при прохождении через тонкие слои металлов и кристаллов была обнаружена Томсоном (Рис.2). Позднее было обнаружено, что аналогичное явление дифракции наблюдается также для протонов, нейтронов и даже для молекул водорода при их попадании на кристалл.
Рис.2. Схема эксперимента Томпсона по дифракции электронов.
Обнаружена была и интерференция элементарных частиц. Например, если направить пучок электронов на две щели, то на экране из фотоимульсии после проявления можно наблюдать интерференционную картину в виде параллельных полос, расположенных на одинаковом расстоянии друг от друга (Рис.3). Интересно, что при малых интенсивностях электронных пучков, наблюдается постепенное формирование интерференционной картины (Рис.3.а – время пропускания мало, Рис.3.б – время пропускания большое), что доказывает корпускулярность электронов. Аналогичные результаты были получены и при интерференции других частиц.
Рис.3. Схема экспериментов по интерференции электронов.
Таким образом, элементарные частицы в одних условиях проявляют свойства волн (явления дифракции, интерференции), в других же – свойства отдельных частиц‑корпускул (движение электронов в электронно-лучевой трубке, взаимодействие электрона и фотона при фотоэффекте и эффекте Комптона), что не может быть объяснено в рамках классической механики.
studfiles.net
основные положения квантовой теории света? Заранее,спасибо), физика
03 июня 2016 г., 8:12:28 (2 года назад)
В основе идеи квантовой механики лежит представление о двойственности природы света. Если в классической теории электрону приписывают только корпускулярные свойства, а свет рассматривают как электромагнитную волну, то в квантовой механике электрон обладает как корпускулярными, так и волновыми свойствами.
Разногласия классической и квантовой теорий:
1) Фотоэффект, эффект Комптона. Фотоэффект бывает внутренний и внешний:
внешний фотоэффект – вырывание электронов с поверхности твердых и жидких тел в результате действия света;
2) Устойчивость атомов. С позиции классической физики электрон, вращающийся вокруг атомного ядра, должен непрерывно испускать энергию, терять скорость и падать на ядро. Т.е. стационарное состояние планетарной модели атома невозможно (частота обращения должна постоянно меняться), а совокупность атомов должна давать непрерывный спектр излучения.
В 1900 году Макс Планк высказал гипотезу: «Излучение и поглощение энергии материей происходит не непрерывно, а отдельными порциями – квантами». Величина каждого кванта E0=hn.
В 1907–1908 годах Эйнштейн высказал теорию, что свойство квантования энергии присуще не только процессам излучения и поглощения, но и вообще является свойством света.
Суть теории в том, что свет – это поток световых квантов – фотонов, летящих в пространстве со скоростью света:
Фотон не имеет массы покоя, в отличие от других частиц.
Фотон всегда и везде движется со скоростью света. Т.о. распространение света в веществе сопровождается процессами переизлучения фотонов: фотоны испускаются и практически тут же поглощаются и т.д. Связь между корпускулярными свойствами фотона и волновыми осуществляется через частоту излучения.
Взаимодействие фотонов с веществом при прохождении света через какую-либо оптическую систему (дифракционную решетку, например) ведет перераспределению фотонов в пространстве и возникновению интерференционной картины на экране, освещенность отдельных точек которого прямо пропорциональна суммарным энергиям фотонов, попадающих в эту точку за единицу времени.
Корпускулярные свойства обусловлены тем, что Э, p, m фотона или излучения локализованы в дискретных частицах, а волновые – статистическими закономерностями распределения фотонов в пространстве, т.е. закономерностями, определяющими вероятность нахождения фотона в определенных точках пространства.
В 1913 году Нильс Бор в теории о строении атома сформулировал два постулата:
1) Постулат стационарных орбит (состояний) – существуют определенные стационарные состояния атома, находясь в которых он не излучает энергию.
2) Постулат частот – при переходе из одного стационарного состояния в другое атом излучает/поглощает квант электромагнитной энергии – фотон.
Как у света, так и у микрочастиц мы не можем одновременно наблюдать проявление волновых и корпускулярных свойств.
Квантовые числа – целые или дробные числа, определяющие возможные дискретные значения физических величин, характеризующих квантовые системы (атомное ядро, атом, молекулу и т.д.) и отдельные элементарные частицы.
fizika.neznaka.ru



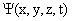 .
.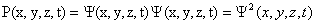 Волновая функция может быть комплексной, она может иметь вещественную и комплексную части. Тогда это уравнение преобразуется до:
Волновая функция может быть комплексной, она может иметь вещественную и комплексную части. Тогда это уравнение преобразуется до: