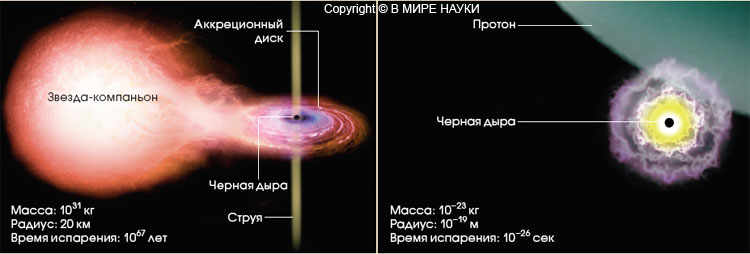
Большая Энциклопедия Нефти и Газа. Как строить квантовые ячейки
Квантовые ячейки, диаграмма - Справочник химика 21
При поглощении энергии в соответствии с формулой Планка (4.1) один или несколько электронов атома могут перейти на более высокие энергетические уровни. Такой атом называется возбужденным. В возбужденном атоме электроны занимают новые квантовые ячейки, уже не подчиняясь принципу минимальной энергии. Соответственно изменяются энергетические диаграммы и электронные формулы. Для примера на рис. 4.10 изображен переход атома углерода из основного состояния С— 8 2з 2р в возбужденное С —15 25 2р . [c.153]
Такая ячейка (зонную диаграмму см. рис. 38) содержит фотоанод из полупроводника п-типа и фотокатод из полупроводника р-типа. Площади обоих фотоэлектродов подбирают так, чтобы при их освещении фототоки (зависящие от коэффициента поглощения света, квантового выхода, скорости рекомбинации) были одинаковы по абсолютной величине. [c.73]
chem21.info
Квантовая ячейка - Большая Энциклопедия Нефти и Газа, статья, страница 1
Квантовая ячейка
Cтраница 1
Квантовые ячейки изображены со сдвигом по вертикали, чтобы наглядно показать возрастание энергии в ряду li -, 2j -, 2р - состояний. Соответствующие схемы в третьей - асти книги даны без сдвига ячеек. [1]
Квантовые ячейки изображены со сдвигом по вертикали, чтобы наглядно показать возрастание энергии в ряду 15, 2s, 2р - состояний. Соответствующие схемы в третьей части книги даны без сдвига ячеек. [2]
Квантовые ячейки изображены со сдвигом по вертикали, чтобы наглядно показать возрастание энергии в ряду Is, 2s, 2р - состояний. Соответствующие схемы в третьей части книги даны без сдвига ячеек. [3]
Квантовые ячейки изображены со сдвигом по вертикали, чтобы наглядно показать возрастание энергии в ряду Is -, 2s -, 2р - состояний. Соответствующие схемы в третьей: асти книги даны без сдвига ячеек. [4]
Число квантовых ячеек в подгруппе определяется магнитным квантовым числом и растет как ряд нечетных чисел. Пирамидальная схема ( рис. 1.2) может быть продолжена до бесконечности м оо. [5]
В квантовой ячейке Не, изображенной справа, направление спинов указано вертикальными стрелками. [6]
В квантовых ячейках с одинаковой энергией заселение электронами происходит так, чтобы атом имел наибольшее число неспаренных электронов. У каждого последующего элемента Периодической системы на один электрон больше по сравнению с предыдущим. Наиболее прост первый период Системы, состоящий лишь из двух элементов. У водорода единственный электрон заселяет наинизшую энергетическую орбиталь Is, а у гелия на этой же орбитали два электрона с антипараллельными спинами. Таким образом, атом гелия полностью формирует наиболее близкий к ядру Д - слой. [7]
При заполнении квантовых ячеек электронами необходимо руководствоваться правилом Гунда: в данном подуровне электроны стремятся занять свободные квантовые ячейки сначала по одному с параллельными спинами и затем только по второму с противоположным направлением спина. По принципу Паули в каждой ячейке может быть только два электрона с противоположными спинами. При таком способе заполнения квантовых ячеек одного подуровня данным числом электронов суммарный спин имеет наибольшее значение, что требует правило Гунда. [8]
При заполнении квантовых ячеек необходимо знать правило Гунда: устойчивому состоянию атома соответствует такое распределение электронов в пределах энергетического подуровня ( р, d, f), при котором абсолютное значение суммарного спина атома максимально. Так, если два электрона займут одну орбиталь п I I, то их суммарный спин будет равен нулю. Заполнение электронами двух орбиталей т IТI I даст суммарный спин, равный единице. [9]
Другими словами, квантовые ячейки подуровня заполняются сначала по одному электрону, а затем по второму с противоположно направленным спином. Так, у атома азота ( рис. 9) в трех / - ячейках разместятся три электрона по одному в каждой, в атоме три неспаренных электрона. Если же предположить иное размещение электронов, например, в одной ячейке 2, в другой 1 и третья пустая, то 2s 1 / 2 - 1 / 2 1 / 2 1 / 2, что противоречит правилу Гунда. [12]
Распределение электронов по квантовым ячейкам ( см. рис. 1.34) показывает, что в атоме фтора имеется только один неспаренный электрон, поэтому фтор одновалентен. [13]
Однако на рис. 19 квантовые ячейки для данного слоя ( квантовое число п постоянно) изображены на одной горизонтали, хотя в действительности существуют небольшие различия в энергиях разных орбиталей. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Квантовая ячейка - Большая Энциклопедия Нефти и Газа, статья, страница 3
Квантовая ячейка
Cтраница 3
Ниже приведено распределение электронов по квантовым ячейкам в некоторых октаэдрических комплексах в слабом и сильном полях. В тех случаях, когда число электронов в ионе комплексо-образователя больше, чем число орбиталей с низкой энергие имеют место различия. Эте связано с тем, что в случае слабого поля РД и электроны в квантовых ячейках распределяются в соответствии с правилом Гунда. Ион металла находится в состоянии с высоким спином. В случае сильного поля в пределах подуровня при распределении электронов соблюдается правило Гунда. [31]
Повышенная устойчивость электронных структур с полностью вакантными внешними квантовыми ячейками, а также наполовину заполненными электронами является следствием взаимного отталкивания друг от друга электронов, находящихся на одной и той же орбитали. [33]
Таким образом, распределяя электроны по квантовым ячейкам, можно выявлять число неспаренных электронов в атоме. [34]
Таким образом, размещая электроны по квантовым ячейкам, можно выявить число неспаренных электронов в атоме. [35]
Таким образом, распределяя электроны по квантовым ячейкам, можно выявить число неспаренных электронов в атоме. [36]
Таким образом, распределяя электроны по квантовым ячейкам, можно выявлять число неспаренных электронов в атоме. [37]
Таким образом, размещая электроны по квантовым ячейкам, можно выявить число неспаренных электронов в атоме. [38]
Как распределятся электроны в этом атоме по квантовым ячейкам. [39]
Структуру электронных оболочек изображают с помощью энергетических или квантовых ячеек. Каждая ячейка обозначается клеткой. [40]
Более полно описывает состояние электронов в атомах метод квантовых ячеек, использующий все четыре квантовых числа. Каждой ячейке отвечает определенная орбиталь, электрон изображается в виде стрелки, а направление последней олицетворяет спиновое квантовое число. Свободная ячейка означает свободную орбиталь, которую может занимать электрон при возбуждении атома. [41]
Очень часто структуру электронных оболочек изображают с помощью квантовых ячеек - это так называемые графические электронные формулы или схемы. Каждая такая ячейка обозначается клеткой: клетка - орбиталь, стрелка - электрон, направление стрелки - направление спина, свободная клетка - свободная орбиталь, которую может занимать электрон при возбуждении. [42]
В элементах VA, VIA и VILA подгрупп свободных квантовых ячеек уже не остается и начинается спари-электронов сначала в S -, а затем и в / - ячейках. [43]
Два электрона с противоположными спинами, занимающие одну квантовую ячейку, называют спаренными. Пользуясь этой терминологией, можно сказать, что, согласно теории Гейтлера и Лондона, водород способен к образованию молекулы Н2 потому, что в его атоме имеется один неспаренный электрон, а гелий не может образовать молекулу Не2 ввиду того, что оба электрона в атоме Не являются спаренными. [44]
Два электрона с противоположными спинами, занимающие одну квантовую ячейку, называют спаренными. Пользуясь этой терминологией, можно сказать, что согласно теории Гейтлера и Лондона водород способен к образованию молекулы Н2 потому, что в его атоме имеется один неспаренный электрон, а гелий не может образовать молекулу Не2 ввиду того, что оба электрона в атоме Не являются спаренными. [45]
Страницы: 1 2 3 4
Электронные конфигурации атомов и периодический закон
Рассмотрим строение атома гелия - простейшей одноядерной и двухэлектронной системы. Уравнение Шредингера записывается достаточно просто, только необходимо учитывать потенциальную энергию взаимодействия каждого из электронов с ядром и энергию отталкивания электронов между собой. При решении Уравнения Шредингера легко убедиться, что переменные не разделяются, и в аналитическом виде, как это было в случае с атомом водорода, решение получить не удается (возможны лишь приближенные решения на ЭВМ численными методами). Поэтому в квантовой механике постулируют, что в многоэлектронных системах каждый электрон характеризуется одним из наборов квантовых чисел, которые были получены для атома водорода.
Следующая особенность многоэлектронных атомов состоит в том, что электроны должны двигаться, проявляя свои волновые свойства, в ничтожно малом атомном объеме при действии на них чудовищных электростатических сил со стороны ядра и зарядов других электронов. Природа электронов такова, что для любого электрона в атоме имеется своя "орбиталь", предусмотрено свое особое пространственное существование. Формально это жесткое правило называют "Принципом запрета В.Паули": "В многоэлектронном атоме не может быть даже двух электронов, у которых все четыре квантовых числа были бы одинаковыми". То есть для каждого электрона имеется свое решение уравнения Шредингера, свой набор четырех квантовых чисел.
Если у атома водорода энергия электрона зависит от того, в каком электронном слое находится электрон (т.е. от значения главного квантового числа - n), то в многоэлектронном атоме в момент заполнения электронной оболочки энергия электрона тем меньше, чем меньше сумма n+l (главного и орбитального квантовых чисел). При их равенстве, например у орбиталей 3d (3+2=5) и 4p (4+1=5), меньшей энергией будет обладать электрон, у которого меньше n - это Правило Клечковского.
Электроны в многоэлектронном атоме не только притягиваются к ядру, но и отталкивают друг друга. Энергия электронной оболочки атома тем меньше, чем больше суммарный спин электронов, т.е. чем большее число электронов имеют одинаковую ориентацию собственных моментов количества движения (Правило Хунда).
Правило Клечковского и Правило Хунда иногда конкурируют между собой. Разобраться в этом сплетении правил позволяют атомные спектры, из которых достаточно легко определить, какое электронное состояние является у атома основным, наиболее устойчивым, т.е. обладает наименьшей энергией.
Принцип построения электронной оболочки многоэлектронного атома предельно простой: минимум энергии электронной системы при соблюдении Принципа запрета Паули.
Атом водорода. Заряд его ядра (протона) равен 1 и имеется один электрон. Основное электронное состояние - 1s. А как будет ориентирован спин у электрона? Дело в том, что протон также имеет собственный полуцелый спин и по Правилу Хунда спин электрона будет направлен в ту же сторону, что и спин ядра. При противоположной ориентации спина у электрона энергия атома на очень малую величину (21 см-1) будет больше, чем в первом случае. Наибольшее число фотонов во Вселенной имеют волновое число 21 см-1. Они образовались в результате перехода электрона из ориентации, противоположной направлению спина у ядра, в ориентацию с параллельными спинами электрона и ядра.
Атом гелия. Z = 2. Надо разместить два электрона. Емкость первого (ближайшего к ядру) электронного слоя равна 2. Дополнительный по сравнению с электронной конфигурацией атома водорода электрон вынужден иметь спин равный -1/2.
Атом лития. Z = 3. Его 2 электрона у атома гелия полностью заполнили ближайший к ядру первый электронный слой. Поэтому свой третий электрон атом Li размещает на орбитали 2s и полная электронная конфигурация атома лития записывается так: 1s2 2s.
Атом бериллия. Z = 4. Электронная конфигурация 1s2 2s2.
Атом бора. Z = 5. Электронная конфигурация 1s2 2s2 2p.
Атом углерода. Z = 6. Электронная конфигурация 1s22s22p2.
Сейчас полезно отойти от буквенно-цифровой и перейти к графической иллюстрации электронных оболочек многоэлектронных атомов. Прежде всего обсудим понятие "орбиталь" и ее графическое изображение в схемах для электронных оболочек атомов.
В планетарной Модели Резерфорда-Бора предполагалось, что электроны двигаются по "дозволенным" орбитам. В квантовой механике задача о движении электрона в атоме ставится и решается своеобразным способом. В Уравнение Шредингера для стационарных (обычных, устойчивых) состояний не входит время. В результате решения Уравнения Шредингера для атома водорода получают в аналитическом виде выражение для волновой функции. Волновая функция содержит в закодированном, зашифрованном виде информацию о всех свойствах электрона в атоме водорода, в том числе и о его пространственном существовании. Раз в волновую функцию не входит время, то описание с ее помощью движения электрона сводится к изображению усредненной картины результата движения электрона в околоядерном пространстве. Рассмотрим такую аналогию. Мы смотрим на экран работающего телевизора и видим текст какого-то объявления. Попробуем сфотографировать его с выдержкой 1/1000, 1/500, 1/250, 1/100 и 1/25 секунды. На фотографии экрана мы увидим соответственно 1/40, 1/20, 1/10/, 1/4 часть экрана и, наконец, весь экран. В действительности, благодаря строчной развертке, поток электронов за 1/25 секунды пробегает все 625 строк экрана. Если проводить скоростную съемку экрана, то можно добиться последовательного высвечивания каждой точки и проследить путь потока электронов, которые излучает катод. Человеческий глаз способен различить два события, которые отличаются одно от другого по времени более чем на 1/25 сек. Наши глаз и мозг всю информацию о свечении экрана подобно фотоаппарату усредняют с выдержкой 1/25 сек. То есть мы видим усредненную во времени картину движения электронного пучка. Точно также и волновая функция может передать только усредненную во времени картину движения электрона. В некоторых областях пространства электрон появлялся чаще и там плотность точек больше, говорят о большей вероятности нахождения электрона в этом объеме и т.д. Орбиталь и представляет собой изображение пространства, в котором, например, с вероятностью 95 % можно ожидать появление электрона при его движении в атоме.
В состояниях 1s, 2s, 3s и т.д. орбитальный момент количества движения электрона равен нулю, а так как l = 0, то и mеvr = 0. Масса электрона me не равна нулю, электрон не находится в ядре, и поэтому r не равно нулю. Следовательно, на s-орбиталях электрон в принципе не "вращается" вокруг ядра. Как же тогда он движется? Наверное падает на ядро, рассеивается им, удаляется от ядра в новом направлении, теряет свою скорость и вновь падает на ядро. Усредненной во времени картиной такого движения электрона будет шар, и чем ближе к центру этого шара мы будем смещаться, тем с большей вероятностью в единичном объеме можно будет встретить электрон. Для 2s- и 3s-орбиталей внутренняя структура шаров будет изменяться все более сложным образом. При рисовании s-орбиталей обычно ограничиваются изображением шара.
Для 2p- и 3p-орбиталей l = 1, т.е. наряду с движением электрона в направлении ядра происходит и его движение по окружности. Такую орбиталь обычно представляют в виде двух соприкасающихся шаров, в месте касания которых расположено ядро атома.
При изучении электронной конфигурации многоэлектронных атомов часто используют схематическую форму представления квантовых ячеек (орбиталей). Под квантовой ячейкой подразумевается ориентированная в пространстве орбиталь, которая характеризуется значениями сразу трех квантовых чисел: n, l и m. Поэтому емкость любой квантовой ячейки равна 2, т.е. в ней могут расположиться максимум два электрона, но при этом они, согласно Принципу Паули, обязательно должны иметь противоположные спины.
Мы уже рассмотрели построение электронных конфигураций атомов вплоть до бора. На рисунке этот процесс будет выглядеть так:
Для атомов азота, кислорода, фтора и неона схема заполнения квантовых ячеек электронами представлена на рисунке:
Распределение электронов по квантовым ячейкам у атомов углерода, азота и кислорода легко объяснить с помощью Правила Хунда.
Построение электронных конфигураций у элементов 3-го периода полностью повторяет ту последовательность, которую мы наблюдали у элементов 2-го периода.
У атомов K и Са (элементов 4-го периода) есть выбор: размещать новые электроны на 4s или 3d орбиталях? По правилу Клечковского в момент заполнения орбиталей меньшей энергией будут обладать электроны на 4s- (4+0=4), а не на 3d- (3+2=5) орбиталях, так как у 4s-орбитали меньше сумма квантовых чисел (n+l).
У атомов от Sc до Zn, т.е. у атомов переходных металлов возможен выбор между 4p-(4+1=5) и 3d-(3+2=5) орбиталями. При равенстве суммы n+l меньшей энергией электроны обладают на орбитали с меньшим n, т.е. у этих элементов идет заполнение 3d-орбиталей. Суммарная емкость 3d-орбиталей 10 электронов. Поэтому переходных металлов в Периодической системе в каждом большом периоде также 10. У атомов элементов от галлия до криптона идет заполнение электронами 4p-орбиталей.
У элементов 5-го периода (от Rb до Xe) построение электронных конфигураций полностью аналогично таковым у элементов 4-го периода. Только главное квантовое число орбиталей у них на единицу больше.
У элементов 6-го периода, начиная с лантана, впервые происходит заполнение электронами f-подуровней (в момент заполнения это третий снаружи электронный слой). Емкость f-подуровней 14 электронов. Мы видим 14 лантаноидов, которые помещаются в нижней части Периодической системы. После того как 4f-подуровень будет заполнен, заполнение электронной оболочки начинает происходить так же, как у элементов 4-го и 5-го периодов.
У элементов 7-го периода заполнение электронной обобочки идет так же, как у элементов 6-го периода. Заполнение 5f-подуровня начинается с актиния. 14 элементов 7-го периода называются актиноидами и помещаются в нижней части Периодической системы.
Строение электронных оболочек атомов химических элементов находит свое подтверждение не только при анализе их спектров, но и при рассмотрении таких характеристик атомов, как потенциалы ионизации, которые определяются той энергией, какую нужно затратить, чтобы удалить первый (первый потенциал ионизации), второй (2-ой потенциал ионизации), третий и т.д. электрон.
Электронное строение атомов и Периодический закон
Прежде всего изучение строения атомов на основе квантовой механики позволило по-новому сформулировать Периодический закон: "Свойства химических элементов, а также форма и свойства соединений находятся в периодической зависимости от заряда ядра". Наиболее полное и содержательное выражение Периодический закон находит в Периодической системе химических элементов. Отмеченные выше закономерности в строении электронных оболочек позволяют объяснить все особенности Периодической системы, как в короткой, так и в длинной форме.
На ближайшей к ядру 1s-орбитали могут разместиться всего два электрона (и в первом периоде Периодической системы химических элементов находятся всего два химических элемента: водород и гелий). Во втором от ядра электронном слое (n =2) могут расположиться 8 электронов (во втором периоде - 8 химических элементов). Емкость d-подуровня составляет 10 электронов (переходных металлов в 4-м,5-м и 6-м периодах тоже по десять). В каждом электронном слое, начиная с четвертого периода, могут находиться максимум 14 f-электронов (особое место в Периодической системе занимают два семейства из 14 элементов - лантаноиды и актиноиды). В целом имеется прекрасная корреляция между электронными конфигурациями атомов и общей структурой Периодической системы элементов Д.И.Менделеева. Даже кажущиеся несоответствия находят свое объяснение при использовании дополнительных правил и уточнений.
другие статьи:
- Агрегатные состояние вещества
- Строение атома - развитие моделей
- Квантовая механика и строение атома водорода
- Электронные конфигурации атомов и периодический закон
- Ядра атомов. Радиоактивность и изотопы
- Строение молекул. Типы химической связи
- Квантовая механика молекул и теория химической связи. Метод молекулярных орбиталей. Теория спин-валентности
- Окислительно-восстановительные реакции
- Химическая термодинамика
- Химическая кинетика и катализ
- Химическое равновесие. Обратимые и необратимые реакции
- Электрохимия. Свойства электролитов. Электролиз
www.himikatus.ru
5.2 СТРУКТУРА КРИСТАЛЛОВ
При таких углах кристалл в целом упаковывается в структуру, имеющую более высокую симметрию1, чем примитивный ромбоэдр. В частности, кристалл имеет три оси4-гопорядка, которых нет у ромбоэдра. Это видно на рис.5.2.4а, сравните объемоцентрированный куб и ромбоэдр.
ЯЧЕЙКА ВИГНЕРА-ЗЕЙТЦА,рис.5.2.4б, содержит, как и ромбоэдр, один атом. Но она ограничена плоскостями, перпендикулярными к центрам отрезков, соединяющих центральный узел изображенной ОЦКячейки с его ближайшими соседями. Таких соседей 8 в первойКООРДИНАЦИОННОЙ СФЕРЕ (в вершинах изображенного куба) и 6 во второй (в центрах соседних кубов). Получившаяся фигура, поверхность которой состоит из6-тиквадратов и8-миправильных шестиугольников (все
ребра равны c2 2 ), имеет все элементы симметрии решетки. Оси
симметрии 3-гои4-гопорядков, проходящие через центры шестиугольников и квадратов соответственно, показаны стрелками.
Объем ячейки равен c32 . Расстояния между параллельными шестиугольными гранями равно половине пространственной диагонали исходного куба, т.е. равноai , так что смещениями этой ячейки на те же элементарные векторы трансляции мы заполним все пространство.
Итак, ПРИМИТИВНАЯ ЭЛЕМЕНТАРНАЯ ЯЧЕЙКА КРИСТАЛЛИЧЕСКОЙ
РЕШЕТКИ – элементарная ячейка, содержащая один атом. Из соображений удобства она выбирается либо в форме параллелепипеда, либо в форме ячейкиВигнера-Зейтца.
Так или иначе, но, построив одну элементарную ячейку, мы в любом случае получаем представление обо всем кристалле. Просто надо бесконечное число раз приставить к нарисованной ячейке другие, точно такие же.
1 Операциями симметрии называются любые преобразования координат, приводящие к совпадению преобразованной структуры с исходной. Это – повороты, зеркальное отражение (изменение знака одной из координат), инверсия (изменение знака всех координат) и так далее. Трансляционной симметрией обладают только кристаллы и их одно- и двумерные аналоги, полимеры, поверхностные структуры. Понятия "высокая" или "низкая" симметрия качественны. Более высокой обычно считают симметрию с большим числом элементов симметрии и наличием осей более высокого порядка.
studfiles.net
Микроэлектроника переходит на квантовые точки // Нанофизика
На смену элементам электронных приборов, для которых применимо классическое описание, приходит элементная база наноэлектроники, где необходим последовательно квантовомеханический подход. Квантово-размерные наноструктуры важны не только для наноэлектроники, но и как основа информационных систем нового поколения, они могут применяться для создания магниточувствительных детекторов, на их основе в оптоэлектронике создаются сверхмалые лазерные источники.
Текст: Наталия Капуткина доктор физико-математических наук, НИТУ «МИСИС»Михаил Алтайский доктор физико-математических наук, Институт космических исследований РАН
Современная субмикронная технология позволяет создавать объекты, в которых движение электронов локализовано в плоскости. Такая ситуация имеет место в полупроводниковых гетероструктурах, на переходе металл-диэлектрик. При приложении достаточно высокого напряжения перпендикулярно слоям гетероструктуры электроны выходят на поверхность и ведут себя как двумерный электронный газ. Если к тому же потенциал ограничивает электроны в одном направлении в плоскости, то электроны могут свободно двигаться только в одном оставшемся — это одномерный газ (квантовые проволоки). Если же ограничивается движение электронов в обоих направлениях, мы получаем квантовую точку.
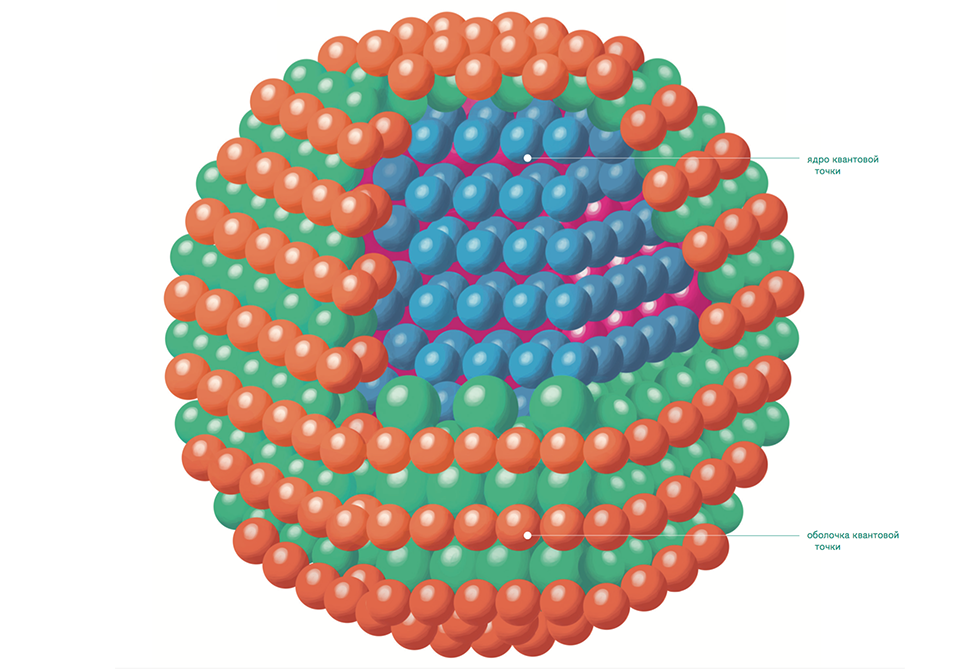Рис. 01 Строение трехмерной квантовой точки
ДекогеренцияДекогеренция — процесс нарушения когерентности, вызываемый взаимодействием квантовомеханической системы с окружающей средой. Можно сказать, что при декогеренции происходит потеря квантовых свойств системы.
Квантовые точки — искусственные атомы
Квантовые точки (КТ) — это гигантские (по сравнению с атомами) искусственные атомы с контролируемыми параметрами. Современные технологии позволяют получать и отдельные КТ, и массивы КТ с контролируемыми параметрами, такими как расположение, область локализации, число носителей заряда, крутизна удерживающего потенциала. Если мы сравним КТ и «обычные» атомы, то КТ перспективны из-за возможности управлять их свойствами с помощью магнитного поля таб. 01. Чтобы значимо изменить свойства обычных атомов, требуются поля, как в нейтронных звездах, а для квантовых точек — вполне доступные в земных лабораториях.
Системы же КТ могут рассматриваться как искусственные гигантские молекулы с контролируемо изменяемыми параметрам. Периодические и апериодические массивы КТ — искусственные кристаллы и квазикристаллы.
Таб. 01 Сравнение параметров квантовых точек и атомов
| параметр | атомы | квантовые точки |
| разность уровней энергии | 1 Эв | 10–4 Эв |
| энергия ионизации | 10 Эв | 10–4 Эв |
| управляющие магнитные поля | 104 Тл | 1–10 Тл |
Типичный размер квантовой точки — несколько десятков нанометров, однако размер занятой электронами области из-за внешнего потенциала может быть значительно меньше. В такой ситуации становится существенным квантование движения в плоскости границы, так что получается структура, подобная атому (с дискретными уровнями энергии), но роль атомного потенциала выполняет искусственно созданный потенциал квантовой точки, а число электронов может контролируемо изменяться от единиц до нескольких сотен.
В настоящее время наибольший интерес вызывают гетеронаноструктуры с квантовыми точками на основе арсенида галлия (GaAs) или его твердых растворов разного состава. Основное техническое применение квантово-размерных структур этого типа видится в настоящее время в разработках светоизлучающих приборов, прежде всего лазеров для волоконно-оптических линий связи. Также значительные возможности дает допирование структур на основе полупроводников переходными металлами.
Различие постоянных кристаллических решеток гетеропары, обычно считавшееся ее недостатком, оказалось весьма ценным свойством в технологии получения так называемых самоорганизованных квантовых точек. Под самоорганизацией понимается самопроизвольное возникновение упорядоченных макроскопических структур из менее упорядоченной среды. В основе процесса самоорганизации лежит свойство неравновесных физических систем при приближении к термодинамическому равновесию переходить в состояние, в котором свободная энергия системы минимальна.
Алгоритм ГровераКвантовый (то есть реализуемый на квантовом компьютере) алгоритм решения переборной задачи. Классические алгоритмы требуют экспоненциального времени, алгоритм Гровера эффективнее, он требует логарифмического времени. Автор — американский математик индийского происхождения Лов Гровер (Lov Kumar Grover).
Если на поверхности из материала А осажден тонкий однородный слой материала В, то при установлении термодинамического равновесия в слое В возникает атомная структура, и он имеет форму, при которой свободная энергия системы будет минимальна. Факторами, определяющими направление и конечный результат самоорганизации, являются рассогласование постоянных решеток материалов А и В, создающее упругие напряжения в системе и повышающее ее внутреннюю энергию, толщина слоя и некоторые другие. При одних значениях этих параметров может образоваться однородный слой материала В, повторяющий структуру подложки. При других значениях может оказаться более энергетически выгодным, чтобы материал В образовал массив напряженных кластеров определенных размеров и формы или собрался в один большой кластер.
Экспериментально уже давно установлено, что при осаждении из паровой фазы наблюдаются три типа начальной стадии роста слоя на подложке:
1) послойный (двумерный) рост. Он происходит, если материал В смачивает подложку и его постоянная решетки мало отличается от постоянной решетки материала А;
2) островковый (трехмерный) рост слоя. Он имеет место при плохом смачивании;
3) промежуточный механизм роста, при котором сначала происходит послойный рост слоя В, который затем сменяется островковым ростом. Этот механизм наблюдается при наличии смачивания и значительном рассогласовании решеток А и В.
Последний механизм используется для получения самоорганизующихся квантовых точек в системе InGaAs/GaAs. Самый важный результат изучения данного механизма — возможность получения массива однородных по размерам, бездефектных, напряженных нанокластеров InGaAs в матрице GaAs, обладающих свойствами квантовых точек.
Часто применяется получение массивов квантовых точек с помощью молекулярно-лучевой эпитаксии, основанное на использовании самосогласованного роста по механизму Странского-Крастанова. Но квантовые точки, полученные в таком процессе, оказываются значительно напряженными. Это приводит к существенным сдвигам спектра электронных состояний и к изменению управляющих параметров.
В зависимости от условий создания квантовых точек могут быть использованы различные виды представления удерживающего потенциала.
Для круглой квантовой точки возможно представление потенциала в виде:
Это достаточно адекватно для не слишком больших квантовых точек. Для больших квантовых точек адекватна модель «жестких стенок». Но и в том, и в другом случае получается дискретный энергетический спектр, как у атома.
Возможности управлять состоянием отдельных квантовых точек и систем квантовых точек и методы воздействия, схематически изображены на рисунке 03.
Квантовые точки активно применяются в различных полупроводниковых лазерах, детекторах излучения, дозиметрах, биосенсорах, солнечных батареях и т.д.
Рис. 03 Изменения состояния системы
Квантовые точки в квантовых компьютерах
В последнее время возрос интерес к квантовым точкам в качестве элементной базы наноэлектроники, для мало- и одноэлектронных транзисторов, элементов памяти, в том числе с возможностью иерархического доступа, кубитов и логических вентилей.
Идеи квантовой механики входят в теорию вычислительных систем двумя путями. Во-первых, квантовые вычислительные алгоритмы, благодаря заложенному в них параллелизму, основанному на суперпозиции квантовых состояний, могут решать классические неполиномиальные задачи за полиномиальное время. Во-вторых, миниатюризация элементной базы компьютеров приводит к необходимости учета конечной, но отличной от единицы, вероятности перехода отдельных битов между состояниями «0» и «1» и конечной вероятности влияния этих переходов на состояние соседних битов.
Кандидатом на роль квантовой ячейки памяти в наноэлектронных устройствах, стабильной на практически значимых временах миллисекундного порядка, может быть кубит на основе электронных состояний квантовой точки. Основное состояние спина электрона в изолированной КТ может быть надежно приготовлено с помощью оптической накачки, или же с помощью тепловой релаксации в магнитном поле. Время декогеренции спина в КТ имеет порядок микросекунд, и спиновый кубит на основе КТ является перспективным элементом хранения и обработки квантовой информации.
В реальных вычислительных устройствах и устройствах квантовой памяти необходимо манипулировать не с отдельным кубитом, а с регистром из кубитов. Такие регистры могут быть построены, например, в виде массива КТ, отделенных друг от друга расстоянием, меньшим оптической длины волны. Непосредственная адресация к отдельному кубиту в таком массиве меняет состояние других кубитов и приводит к декогеренции. Однако возможно применить (Altaisky, Kaputkina IJQI 10, (2012), 1250026; arxiv.org:1105.1464) алгоритм иерархической записи информации в блоки из кубитов, реализованных на основе КТ, не использующий адресации к отдельным кубитам, а изменяющий состояние регистра как целого.
Квантовый компьютерЭто компьютер, базовая ячейка которого имеет квантовую природу, то есть может находиться не в одном из N дискретных состояний (обычно N=2), а сразу в их суперпозиции. Идея квантовых вычислений была высказана в начале 1980-х советским математиком Юрием Маниным и американским физиком Ричардом Фейнманом (Richard Phillips Feynman). Квантовый компьютер требует для выполнения стандартных операций иных, чем у классического, алгоритмов.
Достоинствами КТ в качестве элементной базы наноэлектроники являются миниатюрность, возможности контроля уровней энергии, заряда и формы КТ, масштабируемость (наличие технологии, позволяющей собирать КТ в массивы), — а также возможность оптического приготовления/измерения состояний отдельных КТ. Недостатком КТ в качестве элементов сетевого квантового компьютера является неизбежность взаимодействия с фононами гетероструктуры, на которой реализованы КТ, и, как следствие, небольшие времена декогеренции. По этой причине известные алгоритмы сетевого квантового компьютинга — факторизация (разложение на простые множители) по Шору и поиск в неупорядоченной базе данных по Гроверу — пока реализованы на других квантовых системах — ионах в ловушках и системах с ядерным магнитным резонансом. Эти системы, в отличие от КТ, позволяют добиться почти полной изоляции от окружения, но требуют больших затрат и не являются масштабируемыми.
Ситуация качественно изменилась примерно с 2011 года, когда компания D-wave Systems Inc. выпустила на рынок первые адиабатические квантовые компьютеры D-wave 1 («Rainer») на 128 кубит и D-wave 2 («Vesuvius») на 512 кубит (Johnson et al. Nature 473, (2011), 194). Отличие адиабатического компьютера от сетевого компьютера состоит в том, что ключевым его элементом является не унитарная эволюция начального состояния системы кубитов через систему квантовых гейтов к конечному состоянию (решению задачи), а процесс квантового туннелирования из приготовленного начального состояния в состояние, реализующее минимум энергии некоторого гамильтониана. Фактически было реализовано квантовое решение задачи поиска минимума квадратичной формы. К данному типу относится огромный класс задач в теории автоматического управления, экономике, распознавании образов. Их решение на квантовом адиабатическом компьютере может быть получено за полиномиальное время, в то время как на обычных компьютерах требуется экспоненциальное. При этом использование процесса квантового туннелирования не накладывает жестких ограничений на взаимодействие с окружением и по сути позволяет проводить вычисления в открытой квантовой системе.
Алгоритм ШораАлгоритм факторизации целого числа (то есть разложения его на простые множители) при помощи квантового компьютера. Алгоритм требует полиномиального времени. Разработан американцем Питером Шором (Peter Shor) в 1994 году. Классический (то есть без квантового компьютера) алгоритм факторизации требует экспоненциального времени.
Квантовые точки в искусственном интеллекте
Квантовые нейронные сети привлекли к себе внимание, когда Google и NASA анонсировали использование процессоров D-wave Systems Inc. для задач искусственного интеллекта и классификации больших данных, с огромным финансированием соответствующих проектов. Создание квантовых систем искусственного интеллекта, безусловно, является приоритетным направлением исследований для любой индустриально развитой державы. По сути, такой интеллект должен заменить человека при принятии решений в многофакторных оптимизационных задачах, с которыми обычные компьютеры не могут справиться в силу экспоненциальных затрат времени. Прежде всего это относится к задачам автономного управления летательными аппаратами, задачам медицинской диагностики, управлению сложными техническими системами.
Квантовые точки могут оказаться полезными при создании квантовых нейронных сетей. Использование молекул квантовых точек на основе GaAs для построения квантовой нейронной сети было впервые предложено Элизабет Берман с соавторами в 2001 г. Данная идея в ее оригинальной форме, предполагавшей использование фононов подложки для управления сетью, практически нереализуема из-за сложностей, связанных с управлением спектром фононов и с его нестабильностью. Нами разрабатывается методика построения квантовой нейронной сети на основе квантовых точек с диполь-дипольным взаимодействием (Алтайский, Капуткина, Крылов ЭЧАЯ 45, (2014), 1824) и проводятся численные расчеты перепутывания состояний в такой системе при ненулевых температурах.
www.nanonewsnet.ru
Квантовый слой - Большая Энциклопедия Нефти и Газа, статья, страница 4
Квантовый слой
Cтраница 4
Следующие два электрона расположатся в ячейке - подуровня четвертого квантового слоя. [46]
Следующие два электрона расположатся в ячейке - подуровня шестого квантового слоя. Имеются еще незаполненный / - подуровень четвертого слоя, незаполненные подуровни пятого слоя, а очередные электроны спешат все дальше. Им соответствуют элементы VI периода главных подгрупп I и II групп: Cs и Ва. Следующий очередной электрон расположится в одной из ячеек / - подуровня пятого слоя: следовательно, ему должен соответствовать элемент побочной подгруппы. Следующие же 14 электронов расположатся в 7 ячейках / - подуровня четвертого квантового слоя. Им соответствуют 14 элементов VI периода ( № 58, Се - № 71, Lu), названных лантанидами. [47]
После того как все ячейки / - подуровня четвертого квантового слоя заполнятся электронами, очередные 9 электронов направятся в ячейки d - подуровня пятого квантового слоя. Очевидно, они должны породить элементы побочных подгрупп VI периода. И действительно, элементы № 72 ( Hf), - Та, - W, - Re, - Os, - Ir, - Pt, - Au, - № 80 ( Hg) находятся в VI периоде в побочных подгруппах. [48]
После того как все ячейки / - подуровня четвертого квантового слоя заполнятся электронами, очередные 9 электронов направятся в ячейки d - подуровня пятого квантового слоя. Очевидно, они должны породить элементы побочных подгрупп VI периода. И действительно, элементы № 72 ( Hf) - fa - W - Re - Os - Ir - Pt - Au - № 80 ( Hg) находятся в VI периоде в побочных подгруппах. [49]
В атомах элементов главной подгруппы III группы во внешнем квантовом слое находится три электрона - два на s - подуровне и один на р-подуровне. Структура предпоследнего квантового слоя рассматриваемых элементов неодинакова. [50]
Она характерна появлением еще одного квантового подслоя в квантовых слоях данного этапа. [51]
Электронная формула кальция показывает, что первый и второй квантовые слои заполнены до максимума, третий содержит пока 8 электронов и тем не менее началось формирование четвертого слоя. Стрелка указывает, куда поступил очередной ( 20 - й) электрон кальция; подчеркнуты валентные электроны; число их соответствует номеру той группы, где находится кальций. [52]
Обратите внимание: III период закончен, а третий квантовый слой еще не закончен. Здесь и в дальнейшем эти понятия уже не совпадают. [53]
У следующего за аргоном калия новый электрон поступает в четвертый квантовый слой, хотя в третьем еще свободны rf - орбитали. Or скандия ( Z 21) до цинка ( Z 30) электроны заполняют вакантные З - орбихали. Образующиеся десять элементов переходных металлов имеют во внешнем слое по два ( иногда по одному) - электрона. Недостроенный - подуровень лабилен, J-электроны легко участвуют в образовании химических связей наряду с внешними; д-электронами, с чем, в частности, связана способность переходных металлов к образованию комплексных соединений. [54]
Каждый период начинается элементом, в атоме которого появляется новый квантовый слой. Отсюда следует, что номер периода показывает, сколько квантовых слоев находится в электронной оболочке атома любого элемента данного периода. [55]
Вторые 2 электрона расположатся в ячейке - подуровня второго квантового слоя. Им соответствуют элементы II периода главных подгрупп I и II групп: Li и Be. Следующие 6 электронов расположатся в трех ячейках / - подуровня второго квантового слоя. Им соответствуют элементы II периода: расположенные в остальных шести главных подгруппах: В-С - N - О-F и Ne. В главе 3 отмечалось, что элементы главных подгрупп I и II групп несколько отличаются от элементов последующих шести главных подгрупп некоторыми особенностями в устройстве их электронной оболочки; какими - теперь ясно: первые относятся к s - семейству, вторые - к р-семейству. [56]
Первые два электрона располагаются в ячейке s - подуровня первого квантового слоя, ближайшего к ядру. Им соответствуют 2 элемента ( Н - водород и Не - инертный газ) первого периода. И слой и период закончены: здесь эти понятия совпадают. [57]
Следующие два электрона расположатся в ячейке s - подуровня пятого квантового слоя ( снова забегание вперед. Им соответствуют элементы V периода главных подгрупп I и II групп: Rbи Sr. Очевидно, они должны породить 10 элементов побочных подгрупп. И действительно, этим 10 электронам соответствуют элементы побочных подгрупп V периода: № 39 Y - Zr - Nb-Mo - Тс, - Ru, - Rh, - Pd, - Ag, - № 48 Cd. Четвертый квантовый слой еще и теперь не достроен: в нем остались незаполненными 7 ячеек / - подуровня. Тем не менее следующие 6 электронов направятся в 3 ячейки р-подуровня пятого квантового слоя. Им соответствуют элементы V периода остальных главных подгрупп: In-Sn-Sb - Те-J, - Хе. V период закончен, четвертый квантовый слой еще нет, пятый квантовый слой только начат. [58]
Объясняется это так называемым провалом одного s - электрона четвертого квантового слоя на d - подуровень третьего слоя. [59]
Первые два электрона располагаются в ячейке s - подуровня первого квантового слоя, ближайшего к ядру. Им соответствуют 2 элемента ( Н - водород и Не - инертный газ) гервого периода. И слой и период закончены: здесь эти понятия совпадают. [60]
Страницы: 1 2 3 4 5
www.ngpedia.ru
