«Проект по математике на тему «Удивительный мир чисел» (5 класс)». Мир больших чисел проект

Проект "В мире чисел" | Социальная сеть работников образования

Слайд 1

Выполнили обучающиеся кружка « Эрудит» Бутурлиновской средней общеобразовательной школы № 4 В мире чисел!

Слайд 2

Цель проекта: 1.Узнать как можно больше из истории чисел. 2. Исследовать влияние числа на судьбу человека. 3. Самим попробовать свои возможности в сочинении или другом творчестве.

Слайд 3

Как люди научились считать. У древних людей, кроме каменного топора и шкуры вместо одежды, ничего не было, поэтому считать им было нечего. Постепенно они стали приручать скот, возделывать поля; появилась торговля, и тут уж без счета никак не обойтись. Сначала считали на пальцах. Так, например, желая, обменять сделанное им копьё с каменным наконечником на пять шкурок , человек клал на землю руку и показывал, что против каждого пальца нужно положить шкурку.

Слайд 4

Одна пятерня означала 5, две – 10. Когда рук не хватало, в ход шли и ноги. Две руки и одна нога – 15, две руки и две ноги – 20.

Слайд 5

Как люди научились записывать цифры. Древние египтяне на очень длинных и дорогих папирусах писали вместо цифр очень сложные, громоздкие знаки.

Слайд 6

Египетские иероглифы:

Слайд 7

Мы попробовала египетским способом записать число 1289 и вот, что у нас получилось :

Слайд 8

Египетские иероглифы сохранились и на сфинксах, стоящих в Санкт –Петербурге на берегу Невы. Эти сфинксы (изображение царей в виде льва с человеческой головой) найдены при раскопках в Египте в 1819 году и привезены в Петербург в 1832году. Высечены они из самого прочного красного гранита, вынесли страшную жару Египта и холод Севера.

Слайд 10

Арабы были первыми, кто заимствовал цифры у индейцев, и привёз их в Европу. Чуть позже арабы упростили эти значки, они стали выглядеть вот так. Почти все похожи на наши цифры. У арабов нуль, или «пусто», называли «сифра». С тех пор и появилось слово «цифра». Правда, сейчас цифрами называются все десять значков для записи чисел, которыми мы пользуемся.

Слайд 11

Индейцы и народы Древней Азии при счете завязывали узелки на шнурках разной длины и цвета. У некоторых богатеев скапливалось по несколько метров этой веревочной «счетной книги», попробуй, вспомни через год, что означают четыре узелочка на красном шнурочке! Поэтому того, кто завязывал узелки, называли вспоминателем.

Слайд 12

Было очень неудобно хранить глиняные таблички, веревки с узелками и рулоны папируса. И это продолжалось до тех пор, пока древние индийцы не изобрели для каждой цифры свой знак. Вот как они выглядели

Слайд 13

Десятичную систему счисления ввели римляне. Римские цифры до сих пор используют в часах и для оглавления книг. І ІІ ІІІ ІV V VІ VІІ VІІІ ІХ Х.

Слайд 14

Для обозначения больших чисел славяне придумали свой оригинальный способ: Десять тысяч – тьма, десять тем – легион, десять легионов – леодр, десять леодров – ворон, десять воронов – колода. Такой способ обозначения чисел был очень неудобен.

Слайд 15

Поэтому Петр I ввел в России привычные для нас десять цифр, которыми мы пользуемся до сих пор.

Слайд 16

Слайд 17

«Магическое число» человека Мы узнали: древние ученые считали, что цифры имеют таинственный, магический смысл и влияют на судьбу человека. По верованиям древних, у каждого человека есть некое число, обладающее мистической силой, влияющее на характер и привычки. В нумерологии, науке о числах, используются первые 9 чисел от 1 до 9. И числа 11 и 22. Эти числа являются Мастер – числами. 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22.

Слайд 18

Значение чисел Число 1 – люди с числом один предпочитают быть лидерами, любят власть и всегда считают, что они правы. Идут к своей цели через головы людей. Проявляют агрессивность. Число 2 - число партнерства, дипломатии. Такие люди часто выступают в роли миротворцев. Двойки предпочитают, чтобы у них всё было как у всех, стараются нравиться всем без исключения. Число 3 - означает неустойчивость. Оно объединяет талант и весёлость и символизирует приспособляемость. Число 5 символизирует риск. Это число является и самым счастливым, и самым непредсказуемым.

Слайд 19

Число 6 - символ надёжности. Оно находится в гармонии с природой. Это идеальное число. Число 7 - число символизирует тайну, а так же изучение и знание. Число 8 - число материального успеха. Оно означает надёжность, доведённую до совершенства, равновесие. Число 9 - символ всеобщего успеха. Оно объединяет черты целой группы. Значение чисел

Слайд 20

У каждого человека есть свое главное число. Мы решили сосчитать «магические числа» для учеников нашего класса и провели маленькое исследование. Начала я с себя. Наше исследование. 1 2 3 4 5 6 7 8 9 11 22

Слайд 21

Свое «главное число», которое влияет на судьбу человека и определяет его характер и возможности можно вычислить по дню, месяцу и году своего рождения. Я родилась 22 декабря 2004 года (22.12.2004). Складываем между собой все эти числа: 2+2+1+2+2+4 Затем складываем цифры этого числа между собой и получается- 13. Складываем и эти цифры. Получилось – 4 Это и есть моё главное число. Если на каком нибудь этапе у вас получится 11 или 22, то эти числа складывать нельзя т. к. это особенные числа и они дают человеку определённые способности. Наше исследование

Слайд 22

Итак моё число 4. Это число трудоголика. 4 всегда доводят всё до конца. Любят порядок, работают неспешно и кропотливо. Я сравнила эту характеристику с тем, что указал мой классный руководитель.

Слайд 23

Характеристика классного руководителя Саша – человек ответственный аккуратный. Хорошо учится, старательна, но обидчива... Вывод: получается, что моя характеристика совпадает с числом судьбы. И тогда мы решили определить числа моих одноклассников и сравнить эти числа с чертами их характера. Вот, что у нас получилось.

Слайд 24

Влияние числа на судьбу человека. Ф.И. Дата рождения Число судьбы Филимоно- ва Варя 25.03.2005. 8. Романова Алёна 04.04.2005. 6. Шарова Настя 25.07.2005. 3. Шинкарен ко Лена 27.07.2005. 5.

Слайд 25

Соответствие числа – судьбы и характера. Ф. И. Число судьбы Характеристика Совпадение Шинкарен Ко Лена 5. Общительна, внимательна, доброжелательна, всегда спешит. + Шарова Настя 3. Любознательная,сочетание таланта, весёлости +

Слайд 26

Соответствие числа – судьбы и характера. Ф. И. Число судьбы Характеристика Совпадение Филимонова Варя 8. Надежность, равновесие, порядочность. + Романова Алёна 6. Любит рисовать, общительна, вспыльчива. +

Слайд 27

Вывод И из представленных таблиц видно, что характеристика человека совпадает с тем, что характерно для числа – судьбы. Моим проектом даже заинтересовались учителя и попросили определить их число.

Слайд 28

Мы вам рассказали о магии чисел и о том, как люди научились записывать цифры. А ещё мы решили поэкспериментировать с цифрами. Вот наши рисунки.

Слайд 34

Заключение. Работа над проектом позволила нам узнать многое из истории чисел. Но особенно нам понравилось работать над разделом проекта «Магия чисел». Для этого мы прочитали интересную книгу «Магическая нумерология». Автор Ричард Вебстер.

nsportal.ru

Проект по математике "Мир чисел"

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

Учебный проект по математике по теме: «Мир чисел» Авторы работы: учащиеся 6 класса– Мохонько Екатерина, Тахаева Милана, Чернышева Алина, Швецов Федор, Самигулин Сергей, Гугучкина Екатерина. Руководитель работы: Платова Юлия Александровна, учитель математики

2 слайд

Описание слайда:

Аннотация проекта Целью проекта является изучение основных видов чисел как в окружающей нас жизни, так и в математике. В связи с поставленной целью необходимо решить следующие учебные задачи: Рассмотреть основные виды чисел: натуральные, целые, рациональные числа. Узнать историю возникновения чисел в математике. Выяснить необходимость использования чисел как в профессиональной деятельности, так и в повседневной жизни. Проделав работу, дети будут владеть более широкой информацией о числах.

3 слайд

Описание слайда:

Иоганн Вольфганг Гёте Числа не управляют миром, но они показывают, как управляется мир.

4 слайд

Описание слайда:

оглавление Натуральные числа. Целые числа. Рациональные числа.

5 слайд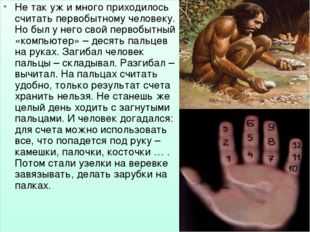

Описание слайда:

Не так уж и много приходилось считать первобытному человеку. Но был у него свой первобытный «компьютер» – десять пальцев на руках. Загибал человек пальцы – складывал. Разгибал – вычитал. На пальцах считать удобно, только результат счета хранить нельзя. Не станешь же целый день ходить с загнутыми пальцами. И человек догадался: для счета можно использовать все, что попадется под руку – камешки, палочки, косточки … . Потом стали узелки на веревке завязывать, делать зарубки на палках.

6 слайд

Описание слайда:

Около пяти тысяч лет назад люди догадались, что числа можно записывать не просто зарубками – единицами, а по разрядам. Это было очень важным открытием. Жизнь заставляла их учиться быстрее. Нужно было разбивать участки земли, отводить воду из рек, прорывать каналы в тех местах, где поля были выше реки, надо было поднимать воду наверх. Приходилось ломать голову над тем, как облегчить эту тяжелую работу. Постепенно из набора просто отдельных правил математика стала превращаться в науку.

7 слайд

Описание слайда:

Настоящей наукой математика стала только у древних греков. Это был удивительно талантливый народ, у которого есть чему поучиться даже сейчас, тысячи лет спустя. Каждое правило греческие математики старались объяснить, доказать, что оно действительно верное. Для этого они спорили друг с другом, рассуждали, старались найти в рассуждениях ошибки. Из правил складывались законы, из законов – наука математика.

8 слайд

Описание слайда:

Из какой страны к нам пришли цифры?

9 слайд

Описание слайда:

Страна Натуральных Чисел – это необыкновенная, замечательная страна, в которой живут, трудятся и властвуют натуральные числа. Интерес к изучению чисел возник у людей в глубокой древности, и вызван он был не только практической необходимостью. Привлекала необычайная магическая сила числа, которым можно выразить количество любых предметов. Натуральными числами обозначались и боги, и космос, и люди, и их взаимоотношения. Поэтому изучению натуральных чисел уделялось и сейчас уделяется особое внимание.

10 слайд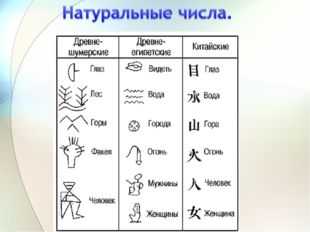

Описание слайда: 11 слайд

Описание слайда:

Целые числа – это отрицательные, положительные числа и ноль.

12 слайд

Описание слайда:

История возникновения отрицательных чисел начинается в VII веке в Китае и Индии. Только тогда они назывались не отрицательными числами, а были «долгами» или «недостачей». Математик из Индии уже в то время рассматривал их наравне с положительными. Но в этом он был одинок. Понимание того, что отрицательные числа нужны и полезны приходило постепенно. История чисел и систем счисления в общем довольна увлекательна . В Европе об отрицательных числах первым написал Леонард Пизанский в своей «Книге абака» в 1202 году. Изначально они также трактовались, как долг. Но даже несмотря на это в XVII такой знаменитый ученый как Паскаль считал, что если из ноля вычесть какое-либо положительное число, то в результате получится ноль.

13 слайд

Описание слайда:

История возникновения отрицательных чисел получила свое развитие с появлением аналитической геометрии. Теперь они на равнее с положительными были представлены на геометрической оси. В 1831 году Гаусс полно обосновал, что отрицательные числа абсолютно равнозначны по правам с положительными, а то что их можно применить не во всех случаях значения не имеет . История возникновения отрицательных чисел заканчивается в XIX веке когда Уильям Гамильтон и Герман Грассман создали полную теорию отрицательных чисел. С этого момента начинается история развития данного математического понятия.

14 слайд

Описание слайда:

Нуль бывает разный: - во-первых, нуль – это цифра, которая используется для обозначения пустого разряда; - во-вторых, нуль – это необычное число, так как на нуль делить нельзя и при умножении на нуль любое число становиться нулем; - в-третьих, нуль нужен для вычитания и сложения, иначе, сколько будет, если из 5 вычесть 5?

15 слайд

Описание слайда:

Нуль как математический символ впервые появляется у индийцев. Первые достоверные свидетельства о записи нуля относятся к 876 г.; в настенной надписи из Гвалиора (Индия) имеется число 270.

16 слайд

Описание слайда:

Нуль - это уникальный знак. Нуль – это чисто абстрактное понятие. Его нет в природе окружающей нас. Без нуля можно спокойно обойтись в устном счете, но невозможно обойтись для точной записи чисел. Нуль находится в противовесе всем остальным числам, и символизирует собой бесконечный мир. И если “все есть число”, то ничто есть все!

17 слайд

Описание слайда:

Рациональное число (лат. ratio — отношение, деление, дробь) — m/n число, представляемое обыкновенной дробью , числитель m — целое число, а знаменатель — n натуральное число.

18 слайд

Описание слайда:

Множество рациональных чисел Множество рациональных чисел обозначается и может быть записано в таком виде: При этом оказывается, что разные записи могут представлять одну и ту же дробь, например, и , (все дроби, которые можно получить друг из друга умножением или делением на одно и то же натуральное число, представляют одно и то же рациональное число). Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:

19 слайд

Описание слайда:

Терминология

20 слайд

Описание слайда:

Древнегреческие математики классической эпохи пользовались только целыми и дробными положительными числами. Эти числа получили название рациональных. В Древней Греции рациональные числа считались символом гармонии окружающего мира и проявлением божественного начала, а все отрезки, до некоторого времени, считались соизмеримыми, т.е. отношения их длин обязаны были выражаться рациональным числом. Термин рациональный происходит от латинского «ratio» - отношение, поэтому рациональные числа также называют относительными.

21 слайд

Описание слайда:

Числа целые, дробные (положительные и отрицательные) и нуль получили общее название рациональных чисел. Совокупность рациональных чисел обладает свойством замкнутости по отношению к четырем арифметическим действиям. Это значит, что сумма, разность, произведение и частное (кроме частного при делении на нуль, которое не имеет смысла) любых двух рациональных чисел является снова рациональным числом. Совокупность рациональных чисел упорядочена в отношении понятий «больше» и «меньше». Далее, совокупность рациональных чисел обладает свойством плотности: между любыми двумя различными рациональными числами находится бесконечно много рациональных чисел. Это даёт возможность при помощи рациональных чисел осуществлять измерение (например, длины отрезка в выбранной единице масштаба) с любой степенью точности.

Найдите материал к любому уроку,указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсемирная историяВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеДругоеДругойЕстествознаниеИЗО, МХКИзобразительное искусствоИностранные языкиИнформатикаИскусствоИспанский языкИсторияИстория РоссииИстория Средних вековИтальянский языкКлассному руководителюКультурологияЛитератураЛитературное чтениеЛогопедияМатематикаМировая художественная культураМузыкаМХКНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирОсновы безопасности жизнедеятельностиПриродоведениеРелигиоведениеРисованиеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФинский языкФранцузский языкХимияЧерчениеЧтениеШкольному психологуЭкология

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДБ-290827

Проект "В мире чисел"

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

Выполнили обучающиеся кружка « Эрудит» Бутурлиновской средней общеобразовательной школы № 4

2 слайд

Описание слайда:

3 слайд

Описание слайда:

4 слайд

Описание слайда:

5 слайд

Описание слайда:

6 слайд

Описание слайда:

Египетские иероглифы:

7 слайд

Описание слайда:

Мы попробовала египетским способом записать число 1289 и вот, что у нас получилось :

8 слайд

Описание слайда:

9 слайд

Описание слайда: 10 слайд

Описание слайда:

11 слайд

Описание слайда:

12 слайд

Описание слайда:

13 слайд

Описание слайда:

Десятичную систему счисления ввели римляне. Римские цифры до сих пор используют в часах и для оглавления книг.

14 слайд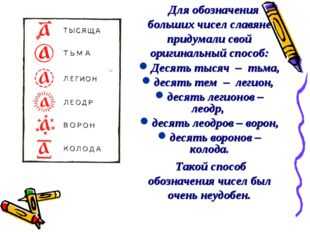

Описание слайда:

15 слайд

Описание слайда:

Поэтому Петр I ввел в России привычные для нас десять цифр, которыми мы пользуемся до сих пор.

16 слайд

Описание слайда:

В Америке объявлена премия автору, который напишет книгу: «Как человек без математики жил?» И что же? Премия до сих пор осталась не выданной. Ни один автор не сумел изобразить жизнь человека без математических знаний. Но в Южной Америке, на берегах реки Амазонки обнаружено индейское племя, которое знает из чисел только 1, 2 и 3. Причём последнее именуется ПОЭТТАРРАРОРИНКОАРОАК. Индейцы видимо боятся «сломать язык» и поэтому дальше они не считают. Им хватает и 3 – ки.

17 слайд

Описание слайда:

«Магическое число» человека Я узнала: древние ученые считали, что цифры имеют таинственный, магический смысл и влияют на судьбу человека. По верованиям древних, у каждого человека есть некое число, обладающее мистической силой, влияющее на характер и привычки. В нумерологии, науке о числах, используются первые 9 чисел от 1 до 9. И числа 11 и 22. Эти числа являются Мастер – числами.

18 слайд

Описание слайда:

19 слайд

Описание слайда:

20 слайд

Описание слайда:

У каждого человека есть свое главное число. Я решила сосчитать «магические числа» для всех учеников моего класса и провела маленькое исследование. Начала я с себя. Моё исследование.

21 слайд

Описание слайда:

Свое «главное число», которое влияет на судьбу человека и определяет его характер и возможности можно вычислить по дню, месяцу и году своего рождения. Я родилась 23 июля1999 года (23.07.99). Складываем между собой все эти числа: 23+7+1999= 2029 Затем складываем цифры этого числа между собой и получается- 13. Складываем и эти цифры. Получилось – 4 Это и есть моё главное число. Если на каком нибудь этапе у вас получится 11 или 22, то эти числа складывать нельзя т. к. это особенные числа и они дают человеку определённые способности. Наше исследование

22 слайд

Описание слайда:

23 слайд

Описание слайда:

Характеристика классного руководителя Настя – человек ответственный аккуратный. Хорошо учится, старательна, но обидчива... Вывод: получается, что моя характеристика совпадает с числом судьбы. И тогда я решила определить числа моих одноклассников и сравнить эти числа с чертами их характера. Вот, что у меня получилось.

24 слайд

Описание слайда:

Влияние числа на судьбу человека. Ф.И. Дата рождения Число судьбы Андреева Диана 27.12.1999. 5. Иванов Виталий 05.10.1999. 7. Кошелев Артем 02.02.1999. 5. Пегашова Мария 21.11.1999. 6.

25 слайд

Описание слайда:

Соответствие числа – судьбы и характера. Ф. И. Число судьбы Характеристика Совпадение Андреева Диана 5. Общительна, невнимательна, доброжелательна, всегда спешит. + Иванов Виталий 7. Любознательный, медлительный, рассеянный,. +

26 слайд

Описание слайда:

Соответствие числа – судьбы и характера. Ф. И. Число судьбы Характеристика Совпадение Кошелев Артем 5. Самоуверенный, вспыльчивый, нетерпеливый. + Пегашова Мария 6. Любит рисовать, общительна, вспыльчива. +

27 слайд

Описание слайда:

28 слайд

Описание слайда:

29 слайд

Описание слайда: 30 слайд

Описание слайда: 31 слайд

Описание слайда: 32 слайд

Описание слайда: 33 слайд

Описание слайда: 34 слайд

Описание слайда:

Найдите материал к любому уроку,указав свой предмет (категорию), класс, учебник и тему:

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДВ-096508

Доклад по теме"Числа великаны"

Две стихии господствуют в математике – числа и фигуры с их бесконечным многообразием свойств и взаимосвязей. Само возникновение понятия числа — одно из гениальнейших проявлений человеческого разума. Действительно, числами не только что-то измеряют, ими сравнивают, вычисляют, даже рисуют, проектируют, сочиняют, играют, делают умозаключения, выводы. Когда- то числа служили только для решения практических задач. А потом их стали изучать, узнавать их свойства.

Открытия в науке о числах делали Пифагор, Архимед, немецкий ученый Карл Гаусс, французские математики Алексис Клеро, Эверист Галуа, Шюке и др. Сначала люди умели называть лишь маленькие числа, а потом все больше и больше. Они создали разные системы исчисления, такие как двоичная, десятичная, шестидесятеричная.

Около 2.5- 3 тысяч лет до нашей эры египтяне придумали свою числовую систему. Своя система счисления была у римлян. В древности применялась и алфавитная система записи чисел. Любопытны были различные методы обозначения чисел. Но у всех этих методов был один недостаток: по мере увеличения чисел нужны были все новые и новые знаки.

Величайший ученый Древней Греции Архимед уже в III в. до н.э. написал книгу

« Исчисление песчинок», в которой он опровергает ложное мнение людей о том, будто бы число песчинок на земле столь велико, что его нельзя выразить, а числа больше этого и вообще якобы не существуют. Архимед доказывает, что если наполнить песчинками пространство всего мира, всю вселенную, которую он принимает за огромный шар с диаметром около 15000000000 километров, то число песчинок не превысит 1063. Это есть единица с 63 нулями. Таким образом, в «Псаммите» Архимед показал, что счёт можно продолжить неограниченно, то есть натуральный ряд бесконечен.

Впрочем, египтяне, римляне, греки с большими числами в своей практике не встречались. И когда древнегреческий математик Архимед научился называть громадные числа и изложил свое открытие в своей книге, на это никто не обратил внимание

Человечество развивалось и двигалось вперед. Люди пытались вычислить площадь земли, расстояние от земли до солнца, расстояние между звездами, изучали молекулы, атомы. Появилась необходимость в обозначении больших чисел. Ученые задумались: «Есть ли предел у числового ряда, как назвать и записать большое число?» В жизни мы эти числа почти не встречаем. Только в науке нужны большие числа.

Но изучение чисел и их свойств необходимо современному человеку для развития логического мышления, памяти, творческого решения задач. В школьном курсе «математика» не изучается тема «числа — великаны», но узнав, что существуют числа больше миллиарда, у нас возник интерес и желание больше узнать об этих числах. Безусловно, мало знать, как называются самые большие числа в мире, имеющие собственное название. Интересно узнать и посмотреть на то, как они записываются, где встречаются в жизни.

Это и обусловило выбор темы работы: «Числа — великаны».

Актуальность: расширить свой кругозор в употреблении чтения многозначных чисел- великанов в области астрономии, химии, физики.

Объект исследования: удивительный мир чисел

Предмет исследования: числа — великаны

Цель – знакомство с названием чисел — великанов, умение их читать.

Гипотеза «Если узнаем историю возникновения чисел, системы счисления и название классов, тогда легко будем читать и писать большие числа. Сможем избежать трудностей при чтении, сталкиваясь на практике с числами- великанами»

В истории математики сложилось так, что числа-великаны имеют свои названия и записи в двух вариантах. Их называют «длинная шкала» и «короткая шкала».

Например, число квинтиллион может быть записано таким образом:

1 000 000 000 000 000 000 = 1018 (согласно короткой шкале)

или так:

1 000 000 000 000 000 000 000 000 000 000 = 1030 (согласно длинной шкале)

Такое различие в значениях для одного и того числа начинается буквально с биллиона, – числа, записанного с помощью 9 нулей (по короткой шкале) и с 12 нулями (по длинной).

До биллиона (как видно из таблицы ниже) различия в записи чисел, являющихся степенями тысячи, нет.

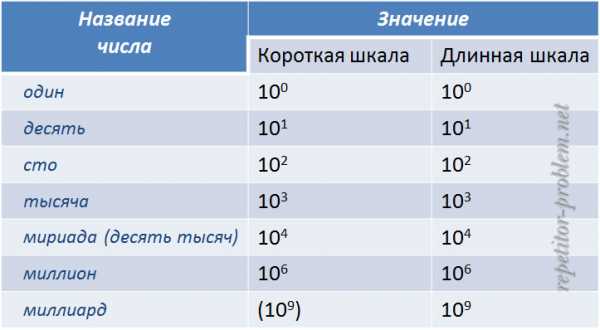
В чем разница наименования чисел-великанов в системе короткой шкалы и длинной шкалы?

Названия числа в системе короткой шкалы формируется так:

латинской числительное + «- иллион».

Например,

1) секстиллион = «sexta» (шестая) + «-иллион»:

1 000 000 000 000 000 000 000 = 10001 + 6 = 1000 * 10006 .

1) нониллион = «nona» (девятая) + «- иллион»:

1 000 000 000 000 000 000 000 000 000 000 = 10001 + 9 = 1000 * 10009 .

Исключение составляет название слова «миллион»; оно образовано от латинского «mille»( что означало «тысяча») + «-он» . То есть, миллион – это тысяча тысяч.

Система названий чисел-великанов по короткой шкале используется всего лишь в

нескольких странах: США, Великобритании, Канаде, России, Украине, Турции и

Греции.

Вот примеры значений чисел-великанов и их названий:

Обратите внимание, что некоторые из названных стран используют чаще слово «миллиард», нежели слово «биллион» (тысяча миллионов). А ведь «миллиард» уже по своему строению относится к системе с длинной шкалой.

Здесь названия чисел строятся по такому принципу: к латинскому числительному добавляется суффикс «-он», следующее за ним число ( то есть в 1000 раз большее) образуется из того же самого числительного по-латыни, но с окончанием «-ард».

Например, за триллионом в системе длинной шкалы идёт триллиард (тысяча триллионов), а только потом квадриллион, за ним идет квадриллиард (тысяча квадриллионов) и т. д.

В числах-великанах количество нулей определяется так: если в этой системе число оканчивается «-иллион», то оно вычисляется по такой формуле 6•x (где x — числительное латинское) . А если оканчивается на «-иллиард», то 6•x+3.

Например, квадриллион имеет 6•4 = 24 нуля (kvadra – четыре), а квадриллиард имеет

6•4 + 3 = 27 нулей

Название	Значение
	Короткаяшкала	Длиннаяшкала
тысяча	103	103
миллион	106	106
миллиард	(109)	109
биллион	109	1012
биллиард	—	1015
триллион	1012	1018
триллиард	—	1021
квадриллион	1015	1024
квадриллиард	—	1027
квинтиллион	1018	1030
квинтиллиард	—	1033
секстиллион	1021	1036
секстиллиард	—	1039
септиллион	1024	1042
септиллиард	—	1045
октиллион	1027	1048
октиллиард	—	1051
нониллион	1030	1054
нониллиард	—	1057
дециллион	1033	1060
дециллиард	—	1063

Произношение чисел, идущих далее, часто различается.

Название	Значение
	Короткаяшкала	Длиннаяшкала
ундециллион	1036	1066
додециллион	1039	1072
тредециллион	1042	1078
кваттуордециллион	1045	1084
квиндециллион	1048	1090
седециллион	1051	1096
септдециллион	1054	10102
октодециллион	1057	10108
новемдециллион	1060	10114
вигинтиллион	1063	10120
анвигинтиллион	1066	10126
довигинтиллион	1069	10132
тревигинтиллион	1072	10138
кватторвигинтиллион	1075	10144
квинвигинтиллион	1078	10150
сексвигинтиллион	1081	10156
септемвигинтиллион	1084	10162
октовигинтиллион	1087	10168
новемвигинтиллион	1090	10174
тригинтиллион	1093	10180
антригинтиллион	1096	10186
дуотригинтиллион	1099	10192
гугол[1]	10100	10100
септдециллиард	—	10105
октодециллиард	—	10111
новемдециллиард	—	10117
вигинтиллиард	—	10123
квадрагинтиллион	10123	10240
анвигинтиллиард	—	10129
дуовигинтиллиард	—	10135
тревигинтиллиард	—	10141
кватторвигинтиллиард	—	10147
квинвигинтиллиард

Интересные факты с числами-великанами.

Факт 1.

Суэцкий канал считается границей между Азией и Африкой. По нему могут проплыть самые крупные грузовые суда и танкеры, имеющие максимальную грузоподъемность 240.000 тонн. Сегодня его считают инженерным чудом: кораблям не нужно огибать Африку, чтобы например из Роттердама добраться в Токио. Суэцким каналом пользуются нефтяные танкеры и суда, перевозящие древесину, руду и зерно. В 2010 году через канал прошли 17993 корабля. Значит, к окончанию 2013 года их примерно было 17993 * 3 = 53979 и они перевезли грузов около 53979 * 240000 = 12 954 960 000 т, т.е. 13 миллиардов тонн или 13 триллионов кг груза.

Факт 2.

Фонтан Фахда в Джидде (Саудовская Аравия) внесен в Книгу рекордов Гиннеса как самый высокий фонтан в мире. Он находится в прибрежном заливе и извергает соленую воду, которую качает всего лишь 2 насоса. Он состоит из одного мощного столба воды, который устремляется вертикально в воздух со скоростью 374 км/час,

выбрасывая по 625 литров в секунду запасов Красного Моря на высоту 312 метров.

Масса воды в воздухе превышает 18 тонн.

Факт3

Солнеченая система

Масса Земли - 5 978 000 000 000 000 000 000 000 кг

Факт 4

Масса планет.

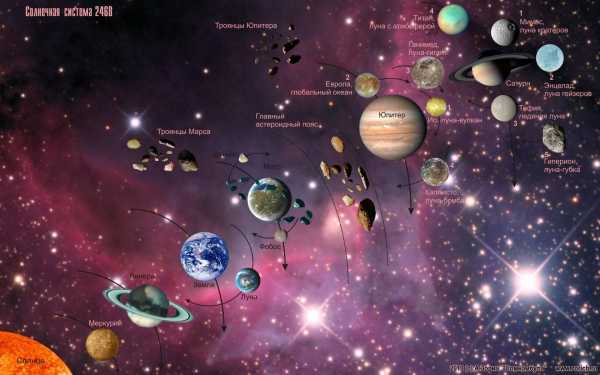
Масса Венеры 4.81068 · 1024 (Килограмм)Масса Земли 5.97600 · 1024 (Килограмм)Масса Луны 0.07350 · 1024 (Килограмм)Масса Марса 0.63345 · 1024 (Килограмм)Масса Меркурия 0.32868 · 1024 (Килограмм)

Масса Нептуна 101.59200 · 1024 (Килограмм)Масса Плутона 0.01195 · 1024 (Килограмм)Масса Сатурна 561.80376 · 1024 (Килограмм)Масса Солнца 1989000.00000 · 1024 (Килограмм)Масса Урана 86.05440 · 1024 (Килограмм)Масса Юпитера 1876.64328 · 1024 (Килограмм)

ФАКТ 5

Самый большой океан –Тихий, его площадь – 178 684 тыс.км2; Глубина тоже наибольшая – 4 281 метр .

Факт 6

Наибольшая высота суши над уровнем моря- горы Джомолунгма (Эверест) – 8848 метров. Сколько этажей имел бы дом высотой в эту гору, если считать, что расстояние между этажами 4 м? 8 848 : 4 = 2 212 (этажей).

Применение чисел — великанов в жизни

При исследовании проблемы среди учащихся 4-7, и 8-9 классов одной из школ было проведено анкетирование. Были представлены следующие вопросы:

- Какое число самое большое?

- Запишите число миллион, миллиард, триллион, квадриллион, и др.?

- Как называется число с 12 нулями?

- Существуют ли числа более чем с 12 нулями?

- Что больше биллион или миллиард?

Результаты следующие:

Из 36 опрошенных 10 учащихся самым большим числом назвали триллион, 21 учащихся — миллиард, а 3 ученика– квадриллион, 2 ученика – другие классы. 20 из опрошенных правильно записали числа миллион, миллиард, у четырех не хватает нулей, 10 учащихся правильно записали триллион, 2 квадриллион.

На вопрос «Как называется число с 12 нулями?» 19 учеников назвали правильный ответ. У других нет ответа.

На последний вопрос из опрошенных 19 учеников ответили – «да», 8 – «наверно», 8 учеников ответили «не знаю», 1 – нет.

В повседневной практике, даже при сложнейших вычислениях, редко используются числа больше миллиарда. Астрономы, физики и химики, имеющие дело с большими числами, предпочитают записывать числа с помощью степени числа десять. Мы с трудом ориентируемся в больших числах, даже миллион как следует, себе не представляем.

Как представить себе 1 000 000 учащихся? Чтобы это представить, посчитаем, на сколько километров протянулась бы шеренга в 1 000 000 учащихся, если бы каждые 2 из них заняли 1м. Почти от Москвы до Санкт-Петербурга протянулась бы эта шеренга. Каких размеров достигнет обыкновенный комар, увеличенный в миллион раз?

Длина комара приблизительно равна 5 мм. 5 мм x1 000 000 = 5 000 000мм = 5 км.

Рост человека, увеличенный в миллион раз, достигает 1700км.

Миллион можно назвать карликом по сравнению с таким числом, как миллиард. Если мы начнем считать подряд до миллиарда в 12 – летнем возрасте, то закончим счет глубоким стариком 100 – летнего возраста, работая ежедневно по 6 часов в сутки.

Миллиард – это не просто великан, а великанище. Ведь совсем небольшой промежуток времени – 1 минута. А миллиард таких минут – эта более 19 столетий. Секунда времени в сравнении с часом нам кажется мгновением. Но миллиард секунд – это около 32 лет.

Часто можно встретиться с числовыми великанами. Они присутствуют всюду вокруг и даже внутри нас самих — надо лишь уметь рассмотреть их. Небо над головой, песок под ногами, воздух вокруг нас, кровь в нашем теле — все скрывает в себе невидимых великанов из мира чисел.

Числовые исполины небесных пространств для большинства людей не являются неожиданными. Хорошо известно, что зайдет ли речь о числе звезд вселенной, об их расстояниях от нас и между собою, об их размерах, весе, возрасте — во всех случаях мы неизменно встречаемся с числами, подавляющими воображение своей огромностью. Недаром выражение «астрономическое число» сделалось крылатым. Многие, однако, не знают, что даже и те небесные тела, которые астрономы часто называют «маленькими», оказываются настоящими великанами, если применить к ним привычную земную мерку. Существуют в нашей солнечной системе планеты, которые, ввиду их незначительных размеров, получили у астрономов наименование «малых». Среди них имеются и такие, поперечник которых равен нескольким километрам. В глазах астронома, привыкшего к исполинским масштабам, они так малы, что, говоря о них, он пренебрежительно называет их «крошечными». Но они представляют собой «крошечные» тела только рядом с другими небесными светилами, еще более огромными: на обычную же человеческую мерку они далеко не миниатюрны. Возьмем такую «крошечную» планету с диаметром 3 км. По правилам геометрии легко рассчитать, что поверхность такого тела заключает 28 кв. км, или 28 000 000 кв. м. На 1 кв. м может поместиться стоя человек 7. Значит, на 28 миллионах кв. м найдется место для 196 миллионов человек.

Песок под нашими ногами также вводит нас в мир числовых исполинов. Недаром сложилось издавна выражение: «бесчисленны, как песок морской». Древние недооценивали многочисленность песка, считая ее одинаковой с многочисленностью звезд. В старину не было телескопов, а простым глазом мы видим на небе всего около 3500 звезд (в одном полушарии). Песок на морском берегу в миллионы раз многочисленнее, чем звезды, доступные невооруженному зрению.

Каждый кубический сантиметр окружающего нас воздуха (это примерно портновский наперсток) заключает в себе 27 квинтиллионов молекул, в крошечной капли крови плавает пять миллионов мелких телец красного цвета.

Практическая часть

Задачи с применением чисел- великанов

Мы можем решить такие задачи.

Задача 1.

Какой объем воды выкачали насосы фонтана Фахда с момента его открытия (1983г.) за 30 лет?

1) За 1 секунду: 625 л воды

2) За 1 час: 625 л * 3600 сек. = 2 250 000 л.

3) За 1 сутки: 2 250 000 л * 24 ч. = 54 000 000 л.

4) 1 год: 54 000 000 л. * 365 дн. = 19 710 000 000 л.

5) За 30 лет: 19 710 000 000 л. * 30 лет = 591 300 000 000 л.

Задача 2.

Объем воды Красного Моря составляет 251 тысячу кубометров. На сколько лет хватило бы беспрерывной работы фонтана Фахда, если бы вода не возвращалась назад в море?

1) Объем воды: 251 000 м3 = 251 000 000 л.

2) За 1 год фонтан выкачивает 19 710 000 000 л.

3) 19 710 000 000 л. больше, чем 251 000 000 л. Значит, запас воды в Красном Море закончился бы раньше, чем через год.

4) За 1 сутки фонтан извергает 54 000 000 л. воды. Тогда 251 000 000 л : 54 000 000 л ≈ 4,6 суток.

То есть, менее чем за 5 дней фонтан прекратил бы свою работу , а Красное Море было бы вычерпано до капельки.

Задача №3

Сколько времени потребуется человеку, чтобы сосчитать миллиард зерен, если он в минуту будет считать по 100 зерен.

Решение: По нашему условию, сосчитать до миллиарда человеку потребуется

1 000 000000:100=10 000 000 мин. Или (10 000 000:60=166 667), т. е. Примерно 170 000 ч. или (170000:24=7000) около 7000 суток, т. е. Более 16 лет беспрерывного счета.

Задача №4

В нашей стране проживают около 250 млн. человек. Если все люди встанут в одну шеренгу, то какой длины будет эта шеренга? (Пусть каждый человек занимает место длиной в 50см).

Решение: 250 000 000·50 =12 500 000 000см, т.е. 125 000 км

Список задач на тему «Числа великаны» см. Приложение.

Заключение

Проделанная исследовательская работа помогла узнать, как зародилась наука о числах, как она развивалось, какие трудности встречались на ее пути и какие ученые занимались изучением чисел и их свойств.Узнав историю возникновения чисел, систем счисления, название классов, расширили свой кругозор в области математики, а именно по вопросу числа- великаны.Были удивлены, что числа великаны и названия их появились давно. Оказывается, они окружают нас повсюду. Подробно изучив классы, можем называть и записывать числа- великаны, использовать знания при решении задач.

Через практическую деятельность – вычисления, сравнения попытались представить, насколько эти числа огромны. Полученные знания помогут в дальнейшем в изучении предметов физика, химия, астрономия.

Планируем продолжить изучение чисел их свойств. Зная, что существуют числа- великаны, хочется иметь представление о числах- карликах.

Литература

1. Депман И. Я.,Виленкин Н.Я. За страницами учебника математики: пособие для учащихся 5-6 классов средней школы.М.Просвещение,1989

2.Депман И. Я. Мир чисел. М.: Детская литература,1982

3.Кординский Б. А.,Ахадов Л. А.Удивительный мир чисел: книга для учащихся. М.Просвещение,1986

4.Литцман В. Великаны и карлики в мире чисел. М,1959.

5.Нагибин Ф. Ф., Канин Е. С.Математическая шкатулка. М.Просвещение,1988

6. Интернет ресурсы: http://yandex.ru/images; wikipedia.org; http://pandia.org.

План.

1.Вступление: Цель. Задачи работы.Гипотеза.

2.Исторические сведения возникновения чисел-великанов.

3. Обозначение чисел-великанов:

а) короткая шкала,

б) длинная шкала.

4. Интересные факты

5. Применение чисел-великанов.

6.Практическая часть (задачи).

7.Заключение.

8. Приложение

9.Литература.

Числа-великаны и их названия.

Выполнили: ученицы 5 «Г» класса

МБОУ «СОШ №48»

г. Астрахань

Ляликова Екатерина, Бакалым Анастасия

Учитель: Макеева Ю.К.

multiurok.ru

Удивительный мир чисел

МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«Средняя общеобразовательная школа №32»

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТАТема: «Удивительный мир чисел»

работу выполнил:

Шогенов Амрали Мухамедович

ученик 4 «А» класса

руководитель исследовательской работы:

Атмурзаева Лейла Тахировна

Нальчик 2016 г.

Введение

Невозможно представить себе мир без чисел. Без чисел - ни покупки не сделаешь, ни времени не узнаешь, ни номера телефона не наберешь. А космические корабли, лазеры и все другие технические средства и достижения. Они были бы попросту невозможны, если бы не наука о числах. Само возникновение понятия числа - одно из гениальных проявлений человеческого разума. Я выбрал именно эту тему потому, что очень люблю математику. В 3 классе мы изучали тему «Из истории чисел». Мне очень захотелось узнать о числах больше.

Число является одним из основных понятий математики. Понятие числа развивалось в тесной связи с изучением величин; эта связь сохраняется и теперь.

Самые древние по происхождению числа натуральные. Это числа, применяемые при счёте предметов. На уроках математики мы знакомились с четными и нечетными числами, Данный проект посвящен изучению удивительных особенностей некоторых чисел, их свойств и применению. Исследовали ряд натуральных чисел, обладающих любопытными особенностями.

Я провел опрос среди одноклассников и друзей и выяснил, что многие ребята слышали об этих числах, но подробную информацию знают единицы. 29 из 40 опрошенных учащихся хотели бы узнать об этих числах больше. В своей работе я хочу подробнее изучить числа.

Актуальность проекта.

Актуальность темы исследовательской работы проекта «Удивительный мир чисел» заключается в том, что мы встречаемся с числами в различных жизненных ситуациях в повседневной жизни: в школе, магазине, на почте, на улице, дома. Мир чисел загадочен, интересен, необходим. Данный проект позволяет понять нам значимость чисел в жизни человека, прививает интерес к науке математике. Дети узнают о старых единицах измерения, о первых вычислительных устройствах, знакомятся с великими математиками.

Современному человеку трудно представить себе математику без обозначений чисел и арифметических действий. Но ведь когда-то же этих обозначений не существовало. А тогда откуда они взялись? И почему именно такие, а не иначе? И вообще много ли их существовало? Ни для кого не секрет, что всюду и повсеместно каждое мгновение наша жизнь наполнена цифрами и числами: день недели, номер автомобиля, магазинный ценник, штрих-код на книжной обложке, количество калорий в пирожном и сколько дней осталось до каникул?.. Вся наша бытность состоит из арифметики, простой или сложной, у нас есть счастливые числа и памятные даты и мы не мыслим свою жизнь без количественной системы счисления. Мы никогда не задумываемся о значимости чисел в нашей культуре, общении и о том, что этим нехитрым знакам можно подчинить все на свете.

Тема: Удивительный мир чисел.

Цели исследования: Показать учащимся многообразие и разнообразие чисел. Рассмотреть влияние чисел на судьбу человека.

Задачи: изучить материал об истории возникновения чисел, магии чисел; провести опрос по теме работы среди одноклассников; научиться находить необходимую информацию в различных источниках.

Объект исследования: числа.

Предмет исследования: свойства чисел.

Гипотеза: Можно ли представить себе мир без чисел?

Если между числами и окружающим миром существует взаимосвязь, то мир не может существовать без чисел.

Методы исследования: изучение и анализ литературы по вопросу исследования, опрос одноклассников и друзей, систематизация и обобщение полученных результатов.

Часть 1. Магия чисел

Первоначальные представления о числе появились в эпоху каменного века, при переходе от простого собирания пищи к ее активному производству, примерно 100 веков до н. э. Числовые термины тяжело зарождались и медленно входили в употребление. Древнему человеку было далеко до абстрактного мышления, хватило того, что он придумал числа: "один" и "два". Остальные количества для него оставались неопределенными и объединялись в понятии "много". Росло производство пищи, добавлялись объекты, которые требовалось учитывать в повседневной жизни, в связи, с чем придумывались новые числа.

Число 5 - живая счетная машина

Цифра 5 является зеркальным омоглифом бирманской буквы «У» — .

Некоторые папуасские племена числительное «один» назвали «урапун», а числительное «два» - «окоза». А попробуйте сказать слово «сто» пользуясь этими названиями. И тут старые методы вытеснил новый – счет по пальцам.

Пальцы оказались настолько тесно связанными со счетом, что на древнегреческом языке понятие «считать» выражалось «пятерить». Да и в русском языке слово «пять» напоминает «пясть» - часть кисти руки. Для облегчения счета люди стали использовать пальцы сначала одной руки, затем обеих, а некоторых племенах и пальцы ног.

Счет на пальцах использовался очень долго. До сих пор ими пользуются отсталые народности и маленькие дти, постигающие понятие числа. Спросите у любого малыша до 4-5 лет «Сколько тебе лет?». Он не скажет, а покажет на пальцах руки.

Русский народ сложил немало пословиц с использованием цифры 5.

Дорогой – пять, а прямо десять.Как свои пять пальцев.Пятеро волов одной сохой пашут.Пятое колесо в телеге.У него шесть хитростей и пять обманов.

Число 7 – великолепная семерка

То, что число 7 – число особое, люди считали очень давно. Еще древних охотников и земледельцев привлекало на небе созвездие Большой медведицы – изображение семи звезд этого созвездия часто встречаются на древних изделиях.

Особенно чтили число 7 на Древнем Востоке. Шумеры выражали этим числом шесть главных направлений (вверх, вниз, вперед, назад, влево, вправо) да еще то место, от которого идет отсчет. В их храмах было тоже семь степеней, освещали храмы семисвечниками, они знали семь металлов и т.д.Древние греки насчитывали семь чудес света. В старину о непонятном говорили, что эта книжка "за семью печатями", знахарки в сказках давали больному "семь узелков с лекарственными травами, которые надо было настоять на семи водах в течение семи дней и принимать каждодневно по семь ложек".И сейчас числу 7 придают особое значение. Например, семь цветов радуги – красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый. Чтобы запомнить порядок цветов мы заучивали фразу «каждый охотник желает знать, где сидит фазан».

Очень много русских пословиц и поговорок с цифрой 7.

Семеро одного не ждут.Один с сошкой – семеро с ложкой.Семьраз отмерь – один раз отрежь.Семь бед – один ответ.Лук от семи недуг и т.д.

Мы в нашей жизни пользуемся семидневной неделей, у каждого дня есть свое название. А древние греки называли дни недели в честь богов, которые как они считали, были связаны с небесными светилами. Например, вторник – в честь бога войны Марса; четверг – в честь громовержца Юпитера. Воскресенье у очень многих народов называется «день Солнца».Семь и мое любимое число . Я родился 07.07.2007 г.

Число 10 – треугольное число

Число 10 пифагорейцы называли "священной четверицей", так как 10 = 1 + 2 + 3 + 4. Оно считалось священным числом и олицетворяла всю Вселенную. Пифагорейцы, комбинируя натуральные числа, составляли из них затейливые ряды, придавая элементам этих рядов то или иное геометрическое истолкование. Так возникли фигурные числа - это общее название чисел, геометрическое представление которых связано с той или иной геометрической фигурой.

Число 10 – фигурное, но в то же время, также как и числа 3 и 6, оно треугольное.10 – это основание десятичной системы счисления. Самая распространенная на сегодняшний день нумерация – это арабская, которой мы пользуемся в настоящее время: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.Применяемые в настоящее время цифры сложились в Индии около 400г.н.э. Арабы стали пользоваться подобной нумерациейоколо 800 г.н.э. В России арабская нумерация стала использоваться при Петре I.

Число 12 – дюжина

Число 12 стало соперником числа 10. При счете стали использовать дюжины – группы из двенадцати предметов. Во многих станах, в том числе и в России, некоторые товары продаются дюжинами. Например, столовые сервизы: 12 глубоких, 12 мелких и 12 маленьких тарелок.

Все мы в детстве прочли книгу Свифта «Приключения Гулливера». Так вот Гулливер был выше лилипутов в 12 раз и в 12 раз ниже великанов.

Древние люди, когда разделили год на 12 месяцев, называли каждую часть этого пути «домом Солнца», а звезды объединяли в созвездия. Так появились созвездия Зодиака.

В древних памятниках письменности число 12 встречается очень часто и в особой роли: 12 последователей у пророка; 12 подвигов Геракла; 12 основным богам преклонялись древние греки.

Часть II. Практические исследования

Мы провели опрос среди учащихся 5-6 классов школы.

Им было предложено ответить на следующие вопросы:

1. Все ли вы знаете о числах?

2. Какое число или цифра чаще встречается в повседневной жизни?

3. Какие удивительные особенности чисел вам известны?

В опросе приняли участие 47 учащихся 5-6 классов нашей школы. Проведя анализ вариантов их ответов, обобщив и систематизировав полученную информацию, мы представили все в виде диаграмм (Приложение 1).

Таким образом, благодаря проведённому исследованию, нам удалось узнать, что предвещало возникновению разных цифр и чисел, узнать мнения учащихся нашей школы по теме.

Заключение. В ходе нашего исследования мы нашли ответы на многие вопросы. Прочитали много статей в энциклопедиях, книгах и на сайтах всемирной паутины, узнали значение непонятных ранее слов, провели опрос среди учащихся по теме исследования, узнали из дополнительной литературы многое об истории возникновения чисел. Благодаря исследованию мы научились: анализировать и находить полезную информацию, делать выводы. Исследование позволило сделать вывод, что невозможно представить себе мир без чисел. Без чисел - ни покупки не сделаешь, ни времени не узнаешь, ни номера телефона не наберешь. А космические корабли, лазеры и все другие технические средства и достижения. Они были бы попросту невозможны, если бы не наука о числах. Само возникновение понятия числа - одно из гениальных проявлений человеческого разума Наша гипотеза, что числа и окружающий мир взаимосвязаны подтвердилась. Таким образом, можно сказать, что поставленные в данной работе цель и задачи выполнены. Нам очень понравилось изучать информацию по этой теме. Разве не интересно узнать, историю такого предмета как математика.

Список использованной литературы

Е. Карпеченко Тайны чисел. Математика/прил. к газете "Первое сентября" - №13-2007.

А.Н.Крылов. Числа и меры. Математика/прил. к газете "Первое сентября" - №7-1994

Г.И. Гейзер. История математики в школе/ пособие для учителей. – М.: Просвещение, 1981.

Я Познаю мир. Детская энциклопедия: Математика/ Я 11 Авт.-сост. А.П. Савин и др.: - М.: ООО "Издательство АСТ", 2001.Приложение 1

Все ли вы знаете о числах?

Да – 13

Нет – 17

Возможно – 11Не знаю - 6Какое число или цифра чаще встречается в повседневной жизни?

«1» - 2

«5» - 3

«7» – 9

«10» – 12

«12» – 12

«60» - 9Какие удивительные особенности чисел вам известны?

Простые - 4

Составные - 5

Натуральные - 19

Четные – 6

Нечетные-13

lablek.ru

Исследовательский проект "Удивительный мир чисел"

Слайд 1

Совершенные и дружественные числа

Слайд 2

Подготовила работу Алексеева Настя Цель работы : доказать, что в математике есть удивительные числа. Задачи: Выделить дружественные и совершенные числа чисел среди натуральных чисел; Установить свойства и закономерности этих чисел. Методы исследования : Работа с учебной и научно-популярной литературой, ресурсами сети Интернет. Систематизация данных. Предмет исследования : натуральные числа

Слайд 3

ИЗ ИСТОРИИ ЧИСЕЛ Число является одним из основных понятий математики. Существует большое количество определений понятию "число". О числах первый начал рассуждать Пифагор. Пифагору принадлежит высказывание "Всё прекрасно благодаря числу". По его учению число 2 означало гармонию, 5 – цвет, 6 –холод, 7 – разум, здоровье, 8 –любовь и дружбу. Первое научное определение числа дал Евклид в труде "Начала».

Слайд 4

СОВЕРШЕННОЕ ЧИСЛО Совершенным называется число, равное сумме всех своих делителей (включая 1, но исключая само число). Первым прекрасным совершенным числом, о котором знали математики Древней Греции, было число "6". На шестом месте, на званном пиру, возлежал самый уважаемый, самый почетный гость. В библейских преданиях утверждается, что мир был создан в шесть дней, ведь более совершенного числа, среди совершенных чисел, чем "6", нет, поскольку оно первое среди них. Рассмотрим число 6. Число имеет делители 1, 2, 3 и само число 6. Если сложить делители, отличные от самого числа 1 + 2 + 3 то мы получим 6. Значит, число 6 дружественно самому себе и является первым совершенным числом.

Слайд 5

ЭТО ИНТЕРЕСНО Следующим совершенным числом, известным древним, было "28". Мартин Гарднер усматривал в этом числе особый смысл. По его мнению, Луна обновляется за 28 суток, потому что число "28" – совершенное. В Риме в 1917 году при подземных работах было открыто странное сооружение: вокруг большого центрального зала расположены двадцать восемь келий. Это было здание неопифагорейской академии наук. В ней было двадцать восемь членов. 28

Слайд 6

ИЗ ИСТОРИИ СОВЕРШЕННЫХ ЧИСЕЛ До Евклида были известны только эти два совершенных числа, и никто не знал, существуют ли другие совершенные числа и сколько таких чисел вообще может быть. Благодаря своей формуле, Евклид сумел найти еще два совершенных числа: 496 и 8128. Почти полторы тысячи лет люди знали только четыре совершенных числа, и никто не знал, могут ли существовать еще числа, которые можно представить в евклидовской формуле, и никто не мог сказать, возможны ли совершенные числа, не удовлетворяющие формуле Евклида.

Слайд 7

СВОЙСТВА СОВЕРШЕННЫХ ЧИСЕЛ Формула Евклида позволяет без труда доказывать многочисленные свойства совершенных чисел. – Все совершенные числа треугольные . Это значит, что, взяв совершенные число шаров, мы всегда сможем сложить из них равносторонний треугольник. – Все совершенные числа, кроме 6, можно представить в виде частичных сумм ряда кубов последовательных нечетных чисел 1 3 + 3 3 + 5 3 … – Сумма обратных всем делителям совершенного числа, включая его самого, всегда равна 2. Кроме того, совершенство чисел тесно связано с двоичностью. Числа: 4=2×2, 8 = 2· 2· 2, 16 = 2 · 2 · 2 · 2 и т.д. называются степенями числа 2 и могут быть представлены в виде 2n, где n – число перемноженных двоек. – Все совершенные числа ( кроме 6) заканчиваются в десятичной записи на 16, 28, 36, 56, 76 или 96.

Слайд 8

Дру́жественные чи́сла — два различных натуральных числа , для которых сумма всех собственных делителей первого числа равна второму числу и наоборот, сумма всех собственных делителей второго числа равна первому числу.

Слайд 9

История изучения дружественных чисел Дружественные числа были открыты последователями Пифагора . Правда, пифагорейцы знали только одну пару дружественных чисел – 220 и 284. Только спустя много столетий Эйлер нашёл ещё 65 пар дружественных чисел. Одна из них – 17296 и 18416. Но общего способа нахождения таких пар нет до сих пор. Формулу, дающую три пары чисел, открыл, около 850 тыс. лет назад, арабский астроном и математик Табит ибн Кура (826 – 901). Неизвестно, конечно или бесконечно количество пар дружественных чисел. На сентябрь 2007 года известно 11994387пар дружественных чисел. Все они состоят из чисел одной чётности. Существует ли чётно-нечётная пара дружественных чисел, неизвестно. Также неизвестно, существуют ли взаимно простые дружественные числа. Но если такая пара дружественных чисел существует, то их произведение должно быть больше.

Слайд 10

Все пары дружественных чисел, значение которых меньше 100000. - Пара 220 и 284 открыта Пифагором, около 500 до н. э. - Пара 1184 и 1210 открыта Паганини в 1860 году. - Пара 2620 и 2924 открыта Эйлером в 1747 году. - Пара 5020 и 5564 (Эйлер, 1747г.) - Пара 6232 и 6368 (Эйлер, 1750) - Пара 10744 и 10856 (Эйлер, 1747) - Пара 12285 и 14595 открыта Брауном в 1939 году - Пара 17296 и 18416 открыта Аль-Банном , около 1300, Фариси , около 1300 и Пьером Ферма в 1636. - Пара 63020 и 76084 (Эйлер, 1747) - Пара66928 и 66992 (Эйлер, 1750) - Пара 67095 и 71145 (Эйлер, 1747) - Пара 69615 и 87633 (Эйлер, 1747) - Пара 79750 и 88730 открыта Рольфом ( Rolf ) в 1964 году.

Слайд 11

Среди всех интересных натуральных чисел, издавна изучаемых математиками, особое место занимают совершенные и близко связанные с ними дружественные числа. Из огромного многообразия натуральных чисел ученые выделили дружественные и совершенные числа, обладающие рядом очень интересных свойств. Мир полон тайн и загадок. Но разгадать их могут только пытливые. Современная наука встречается с величинами такой сложной природы, что для их изучения приходится изобретать все новые виды чисел. И мне бы хотелось продолжить изучение чисел, ведь я только знаю натуральные числа. Работа ученицы 6 класса Алексеевой Анастасии

nsportal.ru

«Проект по математике на тему «Удивительный мир чисел» (5 класс)»

Чтобы посмотреть презентацию с картинками, оформлением и слайдами, скачайте ее файл и откройте в PowerPoint на своем компьютере.Текстовое содержимое слайдов презентации: Удивительный мир чиселВыполнили:Водолазова ЮлияГлотова Елизавета МБОУ СОШ № 4г. Уссурийск, 2017 Проблемные вопросы:Как учились считать наши предки?Как люди научились записывать цифры?На что похожи цифры?Какова роль чисел в нашей жизни?

ЦифрыЦифры – это условные знаки для обозначения чисел.История возникновения чиселВ Древности у разных народов существовали свои способы счета. Майа использовали только три обозначения: точку, линию и эллипс и записывали ими любые цифры.Индейцы и народы Древней Азии при счете завязывали узелки на шнурках разной длины.

Шумеры изобрели клинописное письмо. Они пользовались всего двумя цифрами. Вертикальная палочка обозначала одну единицу, а угол из двух лежачих черточек - десять. В Древнем Египте использовали такую запись чисел: единица обозначалась палочкой, сотня - пальмовым листом, а сто тысяч - лягушкой.История возникновения чисел

Обозначение чисел у славянНаши предки-славяне использовали самую сложную запись чисел. Они их записывали буквами, над которыми ставили специальный значок «титло», чтобы отличить, где написали буквы, а где цифры, и значков у них было аж 27.Римские цифрыРимские цифры появились 500 лет до н.э. Римская система счисления была очень распространена в Европе и считалась на то время, пока не придумали арабские цифры, идеальной.I – 1V – 5X – 10L – 50C – 100D – 500M – 1000

В V веке в Индии появилась система записи, которую мы знаем как арабские цифры и активно используем сейчас. Это был набор из 9 цифр от 1 до 9. Арабы «нуль» или «пусто» называли «сифра». С тех пор появилось слово «цифра». Сейчас все десять знаков от 0 до 9 мы называем цифрами.Арабские цифры

Любимое число одноклассниковГлавное число одноклассников{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}ЧислоФ.И. одноклассникаЗначениеДевицина ОльгаСиненко ЛеонидТаратина ДианаСимвол единицы – корона. Она принадлежит тем, кто властвует, повелевает, командует. Эти люди никогда не сворачивают в сторону от избранного пути, не меняют свой характер и привычки. «Единицы» благородны, помогают тем, кто нуждается в их помощи. Главный недостаток - упрямство и привычка противоречить людям. Успеха они добиваются только при неустанной, тяжёлой работе, в результате которой могут стать маршалами, военными, лётчиками, директорами, учителями и журналистами. Главное число одноклассников{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}ЧислоФ.И. одноклассникаЗначениеВялков ДмитрийДанко ДанилПротасов ВячеславТоданова ЕкатеринаТурьянова Виолетта Двойка – символ любви и непостоянства. Люди этого числа находятся как бы между светом и мраком, добром и зло

schoolfiles.net