Инструкция: Создание нейронной сети без навыков программирования. Создаем нейронную сеть

Нейронные сети для начинающих. Часть 1 / Хабр

Привет всем читателям Habrahabr, в этой статье я хочу поделиться с Вами моим опытом в изучении нейронных сетей и, как следствие, их реализации, с помощью языка программирования Java, на платформе Android. Мое знакомство с нейронными сетями произошло, когда вышло приложение Prisma. Оно обрабатывает любую фотографию, с помощью нейронных сетей, и воспроизводит ее с нуля, используя выбранный стиль. Заинтересовавшись этим, я бросился искать статьи и «туториалы», в первую очередь, на Хабре. И к моему великому удивлению, я не нашел ни одну статью, которая четко и поэтапно расписывала алгоритм работы нейронных сетей. Информация была разрознена и в ней отсутствовали ключевые моменты. Также, большинство авторов бросается показывать код на том или ином языке программирования, не прибегая к детальным объяснениям.

Поэтому сейчас, когда я достаточно хорошо освоил нейронные сети и нашел огромное количество информации с разных иностранных порталов, я хотел бы поделиться этим с людьми в серии публикаций, где я соберу всю информацию, которая потребуется вам, если вы только начинаете знакомство с нейронными сетями. В этой статье, я не буду делать сильный акцент на Java и буду объяснять все на примерах, чтобы вы сами смогли перенести это на любой, нужный вам язык программирования. В последующих статьях, я расскажу о своем приложении, написанном под андроид, которое предсказывает движение акций или валюты. Иными словами, всех желающих окунуться в мир нейронных сетей и жаждущих простого и доступного изложения информации или просто тех, кто что-то не понял и хочет подтянуть, добро пожаловать под кат. Первым и самым важным моим открытием был плейлист американского программиста Джеффа Хитона, в котором он подробно и наглядно разбирает принципы работы нейронных сетей и их классификации. После просмотра этого плейлиста, я решил создать свою нейронную сеть, начав с самого простого примера. Вам наверняка известно, что когда ты только начинаешь учить новый язык, первой твоей программой будет Hello World. Это своего рода традиция. В мире машинного обучения тоже есть свой Hello world и это нейросеть решающая проблему исключающего или(XOR). Таблица исключающего или выглядит следующим образом:

a b c

0	0	0
0	1	1
1	0	1
1	1	0

Соответственно, нейронная сеть берет на вход два числа и должна на выходе дать другое число — ответ. Теперь о самих нейронных сетях.

Что такое нейронная сеть?

Нейронная сеть — это последовательность нейронов, соединенных между собой синапсами. Структура нейронной сети пришла в мир программирования прямиком из биологии. Благодаря такой структуре, машина обретает способность анализировать и даже запоминать различную информацию. Нейронные сети также способны не только анализировать входящую информацию, но и воспроизводить ее из своей памяти. Заинтересовавшимся обязательно к просмотру 2 видео из TED Talks: Видео 1, Видео 2). Другими словами, нейросеть это машинная интерпретация мозга человека, в котором находятся миллионы нейронов передающих информацию в виде электрических импульсов.

Какие бывают нейронные сети?

Пока что мы будем рассматривать примеры на самом базовом типе нейронных сетей — это сеть прямого распространения (далее СПР). Также в последующих статьях я введу больше понятий и расскажу вам о рекуррентных нейронных сетях. СПР как вытекает из названия это сеть с последовательным соединением нейронных слоев, в ней информация всегда идет только в одном направлении.

Для чего нужны нейронные сети?

Нейронные сети используются для решения сложных задач, которые требуют аналитических вычислений подобных тем, что делает человеческий мозг. Самыми распространенными применениями нейронных сетей является:

Классификация — распределение данных по параметрам. Например, на вход дается набор людей и нужно решить, кому из них давать кредит, а кому нет. Эту работу может сделать нейронная сеть, анализируя такую информацию как: возраст, платежеспособность, кредитная история и тд.

Предсказание — возможность предсказывать следующий шаг. Например, рост или падение акций, основываясь на ситуации на фондовом рынке.

Распознавание — в настоящее время, самое широкое применение нейронных сетей. Используется в Google, когда вы ищете фото или в камерах телефонов, когда оно определяет положение вашего лица и выделяет его и многое другое.

Теперь, чтобы понять, как же работают нейронные сети, давайте взглянем на ее составляющие и их параметры.

Что такое нейрон?

Нейрон — это вычислительная единица, которая получает информацию, производит над ней простые вычисления и передает ее дальше. Они делятся на три основных типа: входной (синий), скрытый (красный) и выходной (зеленый). Также есть нейрон смещения и контекстный нейрон о которых мы поговорим в следующей статье. В том случае, когда нейросеть состоит из большого количества нейронов, вводят термин слоя. Соответственно, есть входной слой, который получает информацию, n скрытых слоев (обычно их не больше 3), которые ее обрабатывают и выходной слой, который выводит результат. У каждого из нейронов есть 2 основных параметра: входные данные (input data) и выходные данные (output data). В случае входного нейрона: input=output. В остальных, в поле input попадает суммарная информация всех нейронов с предыдущего слоя, после чего, она нормализуется, с помощью функции активации (пока что просто представим ее f(x)) и попадает в поле output.Важно помнить, что нейроны оперируют числами в диапазоне [0,1] или [-1,1]. А как же, вы спросите, тогда обрабатывать числа, которые выходят из данного диапазона? На данном этапе, самый простой ответ — это разделить 1 на это число. Этот процесс называется нормализацией, и он очень часто используется в нейронных сетях. Подробнее об этом чуть позже.

Что такое синапс?

Синапс это связь между двумя нейронами. У синапсов есть 1 параметр — вес. Благодаря ему, входная информация изменяется, когда передается от одного нейрона к другому. Допустим, есть 3 нейрона, которые передают информацию следующему. Тогда у нас есть 3 веса, соответствующие каждому из этих нейронов. У того нейрона, у которого вес будет больше, та информация и будет доминирующей в следующем нейроне (пример — смешение цветов). На самом деле, совокупность весов нейронной сети или матрица весов — это своеобразный мозг всей системы. Именно благодаря этим весам, входная информация обрабатывается и превращается в результат.

Важно помнить, что во время инициализации нейронной сети, веса расставляются в случайном порядке.

Как работает нейронная сеть?

В данном примере изображена часть нейронной сети, где буквами I обозначены входные нейроны, буквой H — скрытый нейрон, а буквой w — веса. Из формулы видно, что входная информация — это сумма всех входных данных, умноженных на соответствующие им веса. Тогда дадим на вход 1 и 0. Пусть w1=0.4 и w2 = 0.7 Входные данные нейрона Н1 будут следующими: 1*0.4+0*0.7=0.4. Теперь когда у нас есть входные данные, мы можем получить выходные данные, подставив входное значение в функцию активации (подробнее о ней далее). Теперь, когда у нас есть выходные данные, мы передаем их дальше. И так, мы повторяем для всех слоев, пока не дойдем до выходного нейрона. Запустив такую сеть в первый раз мы увидим, что ответ далек от правильно, потому что сеть не натренирована. Чтобы улучшить результаты мы будем ее тренировать. Но прежде чем узнать как это делать, давайте введем несколько терминов и свойств нейронной сети.

Функция активации

Функция активации — это способ нормализации входных данных (мы уже говорили об этом ранее). То есть, если на входе у вас будет большое число, пропустив его через функцию активации, вы получите выход в нужном вам диапазоне. Функций активации достаточно много поэтому мы рассмотрим самые основные: Линейная, Сигмоид (Логистическая) и Гиперболический тангенс. Главные их отличия — это диапазон значений.

Линейная функция

Эта функция почти никогда не используется, за исключением случаев, когда нужно протестировать нейронную сеть или передать значение без преобразований.

Сигмоид

Это самая распространенная функция активации, ее диапазон значений [0,1]. Именно на ней показано большинство примеров в сети, также ее иногда называют логистической функцией. Соответственно, если в вашем случае присутствуют отрицательные значения (например, акции могут идти не только вверх, но и вниз), то вам понадобиться функция которая захватывает и отрицательные значения.

Гиперболический тангенс

Имеет смысл использовать гиперболический тангенс, только тогда, когда ваши значения могут быть и отрицательными, и положительными, так как диапазон функции [-1,1]. Использовать эту функцию только с положительными значениями нецелесообразно так как это значительно ухудшит результаты вашей нейросети.

Тренировочный сет

Тренировочный сет — это последовательность данных, которыми оперирует нейронная сеть. В нашем случае исключающего или (xor) у нас всего 4 разных исхода то есть у нас будет 4 тренировочных сета: 0xor0=0, 0xor1=1, 1xor0=1,1xor1=0.

Итерация

Это своеобразный счетчик, который увеличивается каждый раз, когда нейронная сеть проходит один тренировочный сет. Другими словами, это общее количество тренировочных сетов пройденных нейронной сетью.

Эпоха

При инициализации нейронной сети эта величина устанавливается в 0 и имеет потолок, задаваемый вручную. Чем больше эпоха, тем лучше натренирована сеть и соответственно, ее результат. Эпоха увеличивается каждый раз, когда мы проходим весь набор тренировочных сетов, в нашем случае, 4 сетов или 4 итераций.Важно не путать итерацию с эпохой и понимать последовательность их инкремента. Сначала n раз увеличивается итерация, а потом уже эпоха и никак не наоборот. Другими словами, нельзя сначала тренировать нейросеть только на одном сете, потом на другом и тд. Нужно тренировать каждый сет один раз за эпоху. Так, вы сможете избежать ошибок в вычислениях.

Ошибка

Ошибка — это процентная величина, отражающая расхождение между ожидаемым и полученным ответами. Ошибка формируется каждую эпоху и должна идти на спад. Если этого не происходит, значит, вы что-то делаете не так. Ошибку можно вычислить разными путями, но мы рассмотрим лишь три основных способа: Mean Squared Error (далее MSE), Root MSE и Arctan. Здесь нет какого-либо ограничения на использование, как в функции активации, и вы вольны выбрать любой метод, который будет приносить вам наилучший результат. Стоит лишь учитывать, что каждый метод считает ошибки по разному. У Arctan, ошибка, почти всегда, будет больше, так как он работает по принципу: чем больше разница, тем больше ошибка. У Root MSE будет наименьшая ошибка, поэтому, чаще всего, используют MSE, которая сохраняет баланс в вычислении ошибки.

MSE

Root MSEArctan Принцип подсчета ошибки во всех случаях одинаков. За каждый сет, мы считаем ошибку, отняв от идеального ответа, полученный. Далее, либо возводим в квадрат, либо вычисляем квадратный тангенс из этой разности, после чего полученное число делим на количество сетов.

Задача

Теперь, чтобы проверить себя, подсчитайте результат, данной нейронной сети, используя сигмоид, и ее ошибку, используя MSE.

Данные: I1=1, I2=0, w1=0.45, w2=0.78 ,w3=-0.12 ,w4=0.13 ,w5=1.5 ,w6=-2.3.

Решениеh2input = 1*0.45+0*-0.12=0.45 h2output = sigmoid(0.45)=0.61

h3input = 1*0.78+0*0.13=0.78 h3output = sigmoid(0.78)=0.69

O1input = 0.61*1.5+0.69*-2.3=-0.672 O1output = sigmoid(-0.672)=0.33

O1ideal = 1 (0xor1=1)

Error = ((1-0.33)^2)/1=0.45

Результат — 0.33, ошибка — 45%.

Большое спасибо за внимание! Надеюсь, что данная статья смогла помочь вам в изучении нейронных сетей. В следующей статье, я расскажу о нейронах смещения и о том, как тренировать нейронную сеть, используя метод обратного распространения и градиентного спуска.

Использованные ресурсы: — Раз — Два — Три

habr.com

Перевод «Создай свою нейросеть» — 1 – Нейронные сети

Всем привет!

Буквально вчера нашел книгу Тарика Рашида «Создай свою нейросеть». Книга является бестселлером (топ 1 продаж) в разделе «Искусственный интеллект». Книга свежая, вышла в прошлом году.

Впечатления от первых разделов замечательные. Одно из лучших введений в сферу нейросетей из всех мною виденных. Книга мне так понравилась, что я решил перевести ее на русский язык и выкладывать сюда в виде статей. Часть материала из книги пойдет на улучшение уже существующих глав, часть на следующие.

Перевел уже два первых раздела 1 главы. Вы можете скачать PDF версию этих разделов.

Читайте — наслаждайтесь!

Оглавление

1 Глава. Как они работают.

1.1 Легко для меня, тяжело для тебя

Все компьютеры являются калькуляторами в душе. Они умеют очень быстро считать.

Не стоит их в этом упрекать. Они отлично выполняют свою работу: считают цену с учетом скидки, начисляют долговые проценты, рисуют графики по имеющимся данным и так далее.

Даже просмотр телевизора или прослушивание музыки с помощью компьютера представляют собой выполнение огромного количества арифметических операций снова и снова. Это может прозвучать удивительно, но отрисовка каждого кадра изображения из нулей и единиц, полученных через интернет задействует вычисления, которые не сильно сложнее тех задач, которые мы все решали в школе.

Однако, способность компьютера складывать тысячи и миллионы чисел в секунду вовсе не является искусственным интеллектом. Человеку сложно так быстро складывать числа, но согласитесь, что эта работа не требует серьезных интеллектуальных затрат. Надо придерживаться заранее известного алгоритма по складыванию чисел и ничего более. Именно этим и занимаются все компьютеры — придерживаются четкого алгоритма.

С компьютерами все ясно. Теперь давайте поговорим о том, в чем мы хороши по сравнению с ними.

Посмотрите на картинки ниже и определите, что на них изображено:

Вы видите лица людей на первой картинке, морду кошки на второй и дерево на третьей. Вы распознали объекты на этих картинках. Заметьте, что вам хватило лишь взгляда, чтобы безошибочно понять, что на них изображено. Мы редко ошибаемся в таких вещах.

Мы мгновенно и без особого труда воспринимаем огромное количество информации, которое содержат изображения и очень точно определяем объекты на них. А вот для любого компьютера такая задача встанет поперек горла.

Проблема	Компьютер	Человек
Быстро оперировать множеством больших чисел	Легко	Сложно
Найти лица на фотографии с толпой людей	Сложно	Легко

У любого компьютера вне зависимости от его сложности и быстроты нет одного важного качества — интеллекта, которым обладает каждый человек.

Но мы хотим научить компьютеры решать подобные задачи, потому что они быстрые и не устают. Искусственный интеллект как раз занимается решением подобного рода задач.

Конечно компьютеры и дальше будут состоять из микросхем. Задача искусственного интеллекта — найти новые алгоритмы работы компьютера, которые позволят решать интеллектуальные задачи. Эти алгоритмы не всегда идеальны, но они решают поставленные задачи и создают впечатление, что компьютер ведет себя как человек.

Ключевые моменты

• Есть задачи легкие для обычных компьютеров, но вызывающие трудности и людей. Например, умножение миллиона чисел друг на друга.
• С другой стороны, существуют не менее важные задачи, которые невероятно сложны для компьютера и не вызывают проблем у людей. Например, распознавание лиц на фотографиях.

1.2 Простая предсказательная машина

Давайте начнем с чего-нибудь очень простого. Дальше мы будет отталкиваться от материала, изученного в этом разделе.

Представьте себе машину, которая получает вопрос, «обдумывает» его и затем выдает ответ. В примере выше вы получали картинку на вход, анализировали ее с помощью мозгов и делали вывод об объекте, который на ней изображен. Выглядит это как-то так:

Компьютеры на самом деле ничего не «обдумывают». Они просто применяют заранее известные арифметические операции. Поэтому давайте будем называть вещи своими именами:

Компьютер принимает какие-то данные на вход, производит необходимые вычисления и выдает готовый результат. Рассмотрим следующий пример. Если на вход компьютеру поступает выражение ​\( 3 \times 4 \)​, то оно преобразуется в более простую последовательность сложений. Как итог, получаем результат — 12.

Выглядит не слишком впечатляюще. Это нормально. С помощью этих тривиальных примеров вы увидите идею, которую реализуют нейросети.

Теперь представьте себе машину, которая преобразует километры в мили:

Теперь представьте, что мы не знаем формулу, с помощью которой километры переводятся в мили. Мы знаем только, что зависимость между двумя этими величинами линейная. Это означает, что если мы в два раза увеличим дистанцию в милях, то дистанция в километрах тоже увеличится в два раза. Это интуитивно понятно. Вселенная была бы очень странной, если бы это правило не выполнялось.

Линейная зависимость между километрами и милями дает нам подсказку, в какой форме надо преобразовывать одну величину в другую. Мы можем представить эту зависимость так:

\[ \text{мили} = \text{километры} \times C \]

В выражении выше ​\( C \)​ выступает в роли некоторого постоянного числа — константы. Пока мы не знаем, чему равно ​\( C \)​.

Единственное, что нам известно — несколько заранее верно отмеренных расстояний в километрах и милях.

Номер замера	Километры	Мили
1	0	0
2	100	62.137

И как же узнать значение ​\( C \)​? А давайте просто придумаем случайное число и скажем, что ему-то и равна наша константа. Пусть ​\( C = 0.5 \)​. Что же произойдет?

Принимая, что ​\( C = 0.5 \)​ мы из 100 километров получаем 50 миль. Это отличный результат принимая во внимания тот факт, что ​\( C = 0.5 \)​ мы выбрали совершенно случайно! Но мы знаем, что наш ответ не совсем верен, потому что согласно таблице верных замеров мы должны были получить 62.137 мили.

Мы промахнулись на 12.137 миль. Это наша погрешность — разница между полученным ответом и заранее известным правильным результатом, который в данном случае мы имеем в таблице.

\[ \begin{gather*} \text{погрешность} = \text{правильное значение} — \text{полученный ответ} \\ = 62.137 — 50 \\ = 12.137 \end{gather*} \]

Что же дальше? Теперь мы знаем, что допустили ошибку. Более того, нам известна величина этой ошибки. Не стоит впадать в отчаяние! Вместо этого лучше пересмотреть значение константы ​\( C \)​.

Вновь смотрим на погрешность. Полученное расстояние короче на 12.137. Так как формула по переводу километров в мили линейная (​\( \text{мили} = \text{километры} \times C \)​), то увеличение значения ​\( C \)​ увеличит и выходной результат в милях.

Давайте теперь примем, что ​\( C = 0.6 \)​ и посмотрим, что произойдет.

Так как ​\( C=0.6 \)​, то для 100 километров имеем ​\( 100 \times 0.6 = 60 \)​ миль. Это гораздо лучше предыдущей попытки (в тот раз было 50 миль)! Теперь наша погрешность очень мала — всего 2.137 мили. Вполне себе точный результат.

Теперь обратите внимание на то, как мы использовали полученную погрешность для корректировки значения константы ​\( C \)​. Нам нужно было увеличить выходное число миль и мы немного увеличили значение ​\( C \)​. Заметьте, что мы не используем алгебру для получения точного значения ​\( C \)​, а ведь мы могли бы. Почему? Потому что на свете полно задач, которые не имеют простой математической связи между полученным входом и выдаваемым результатом.

Именно для задач, которые практически не решаются простым подсчетом нам и нужны такие изощренные штуки, как нейронные сети.

Поехали дальше. Сейчас мы на выходе имеем 60 миль. Но это все равно меньше, чем правильный результат из таблицы. Пусть ​\( C = 0.7 \)​.

Боже мой! Мы хватанули слишком много и превысили правильный результат. Наша предыдущая погрешность равнялась 2.137, а теперь она равна -7.863. Минус означает, что наш результат оказался больше правильного ответа, так как погрешность вычисляется как правильный ответ — (минус) полученный ответ.

Получается, что при ​\( C=0.6 \)​ мы имеем гораздо более точный выход. На этом можно было бы и закончить. Но давайте все же увеличим ​\( C \)​, но не сильно! Пусть ​\( C=0.61 \)​.

Так-то лучше! Наша машина выдает 61 милю, что всего на 1.137 милю меньше, чем правильный ответ (62.137).

Из этой ситуации с превышением правильного ответа надо вынести важный урок. По мере приближения к правильному ответу параметры машины стоит менять все слабее и слабее. Это поможет избежать неприятных ситуаций, которые приводят к превышению правильного ответа.

Величина нашей корректировки ​\( C \)​ зависит от погрешности. Чем больше наша погрешность, тем более сильно мы меняем значение ​\( C \)​. Но когда погрешность становиться маленькой, необходимо менять ​\( C \)​ по чуть-чуть. Логично, не так ли?

Верьте или нет, но только что вы поняли самую суть работы нейронных сетей. Мы тренируем «машины» постепенно выдавать все более и более точный результат.

Важно понимать и то, как мы решали эту задачу. Мы не решали ее в один заход, хотя в данном случае так можно было бы поступить. Вместо этого, мы приходили к правильному ответу по шагам так, что с каждым шагом наши результаты становились лучше.

Не правда ли объяснения очень простые и понятные? Лично я не встречал более лаконичного способа объяснить, что такое нейросети.

Если вам что-то непонятно, задавайте вопросы на форуме.

Мне важно ваше мнение — оставляйте комментарии 🙂

neuralnet.info

Введение в построение нейронной сети прямого распространения (Feedforward)

Данная статья – это основа для практики, благодаря которой вы сможете построить рабочую нейросеть с нуля. Большая часть математических концепций и научных решений мы пропустим.

Вы научитесь программировать и создавать нейронную сеть прямого распространения (feedforward neural networks FNN или FF) уже сегодня при помощи PyTorch. Здесь изложена кодовая база jupyter для FNN.

FNN: https://github.com/yhuag/neural-network-labОтличная статья для старта: Шпаргалка по разновидностям нейронных сетей

Приступим к работе

1. Убедитесь, что на вашем компьютере установлены PyTorch и Python 3.6;

2. Проверьте корректность установки Python, используя данную команду в консоли:

На выходе должна быть версия Python 3.6.3 или выше.

3. Откройте хранилище (папку) и создайте свой первый файл нейросети:

mkdir fnn-tuto cd fnn-tuto touch fnn.py

mkdir fnn-tuto cd fnn-tuto touch fnn.py

Начинаем писать код

Все изложенные коды должны быть написаны в файле fnn.py

Импорт PyTorch

import torch import torch.nn as nn import torchvision.datasets as dsets import torchvision.transforms as transforms from torch.autograd import Variable

import torch import torch.nn as nn import torchvision.datasets as dsets import torchvision.transforms as transforms from torch.autograd import Variable

Так мы загрузим PyTorch в скрипт. Отлично! Мы уже на полпути.

Инициализация Гипер-параметров

Гипер-параметры – это мощные аргументы с предварительной настройкой и не будут обновляться в ходе изучения нейронной сети.

input_size = 784 # Размеры изображения = 28 x 28 = 784 hidden_size = 500 # Количество узлов на скрытом слое num_classes = 10 # Число классов на выходе. В этом случае от 0 до 9 num_epochs = 5 # Количество тренировок всего набора данных batch_size = 100 # Размер входных данных для одной итерации learning_rate = 0.001 # Скорость конвергенции

input_size = 784       # Размеры изображения = 28 x 28 = 784 hidden_size = 500      # Количество узлов на скрытом слое num_classes = 10       # Число классов на выходе. В этом случае от 0 до 9 num_epochs = 5         # Количество тренировок всего набора данных batch_size = 100       # Размер входных данных для одной итерации learning_rate = 0.001  # Скорость конвергенции

Загрузка набора данных MNIST

MNIST – это огромная база данных с тоннами прописанных чисел (т.е. от 0 до 9), которая направлена на обработку изображений.

train_dataset = dsets.MNIST( root='./data', train=True, transform=transforms.ToTensor(), download=True ) test_dataset = dsets.MNIST( root='./data', train=False, transform=transforms.ToTensor() )

train_dataset = dsets.MNIST(     root='./data',     train=True,     transform=transforms.ToTensor(),     download=True )   test_dataset = dsets.MNIST(     root='./data',     train=False,     transform=transforms.ToTensor() )

Загрузка набора данных. После загрузки MNIST, мы загружаем набор данных в наш код:

train_loader = torch.utils.data.DataLoader( dataset=train_dataset, batch_size=batch_size, shuffle=True ) test_loader = torch.utils.data.DataLoader( dataset=test_dataset, batch_size=batch_size, shuffle=False )

train_loader = torch.utils.data.DataLoader(     dataset=train_dataset,     batch_size=batch_size,     shuffle=True )   test_loader = torch.utils.data.DataLoader(     dataset=test_dataset,     batch_size=batch_size,     shuffle=False )

Обратите внимание: мы перемешиваем процесс загрузки train_dataset, чтобы процесс обучения не зависел от порядка данных, однако порядок test_loader остается неизменным, чтобы понять, когда мы можем обработать неопределенный порядок входов.

Создаем нейронную сеть Feedforward

Сейчас наши наборы данных готовы. Можно приступить к созданию нейронной сети. Можете взглянуть на изображение концепции работы нейросети внизу:

Структура модели нейросети

Нейронная сеть включает в себя два полностью соединенных слоя (т.е. fc1 и fc2) и нелинейный слой ReLU между ними. Как правило, мы называем эту структуру 1-скрытый слой нейросети, отбрасывая слой вывода (fc2).

Запустив следующий код, указанные изображения (х) могут пройти через нейронную сеть и сгенерировать вывод (out), показывая, как именно соответствие принадлежит каждому из 10 классов. Например, изображение кошки соответствует изображению собаки на 0.8, в то врем я как соответствие изображению самолета – 0.3.

class Net(nn.Module): def __init__(self, input_size, hidden_size, num_classes): super(Net, self).__init__() # Наследуемый родительским классом nn.Module self.fc1 = nn.Linear(input_size, hidden_size) # 1й связанный слой: 784 (данные входа) -> 500 (скрытый узел) self.relu = nn.ReLU() # Нелинейный слой ReLU max(0,x) self.fc2 = nn.Linear(hidden_size, num_classes) # 2й связанный слой: 500 (скрытый узел) -> 10 (класс вывода) def forward(self, x): # Передний пропуск: складывание каждого слоя вместе out = self.fc1(x) out = self.relu(out) out = self.fc2(out) return out

class Net(nn.Module):     def __init__(self, input_size, hidden_size, num_classes):         super(Net, self).__init__()                    # Наследуемый родительским классом nn.Module         self.fc1 = nn.Linear(input_size, hidden_size)  # 1й связанный слой: 784 (данные входа) -> 500 (скрытый узел)         self.relu = nn.ReLU()                          # Нелинейный слой ReLU max(0,x)         self.fc2 = nn.Linear(hidden_size, num_classes) # 2й связанный слой: 500 (скрытый узел) -> 10 (класс вывода)          def forward(self, x):                              # Передний пропуск: складывание каждого слоя вместе         out = self.fc1(x)         out = self.relu(out)         out = self.fc2(out)         return out

Демонстрация нейросети

Мы только что создали настоящую нейронную сеть по нашей структуре.

net = Net(input_size, hidden_size, num_classes)

net = Net(input_size, hidden_size, num_classes)

Включаем графический процессор (GPU)

Обратите внимание: вы можете включить эту строку для запуска кодов на GPU

net.cuda() # Вы можете прокомментировать (#) эту строку для отключения GPU

net.cuda() # Вы можете прокомментировать (#) эту строку для отключения GPU

Выбираем функцию потерь и оптимизатор

Функция потерь (критерий) выбирает, как выходные данные могут быть сопоставлены с классом. Это определяет, как хорошо или плохо работает нейросеть. Оптимизатор выбирает способ обновления веса, чтобы найти область, в которой будет найден лучшие параметры в конкретной нейросети.

criterion = nn.CrossEntropyLoss() optimizer = torch.optim.Adam(net.parameters(), lr=learning_rate)

criterion = nn.CrossEntropyLoss() optimizer = torch.optim.Adam(net.parameters(), lr=learning_rate)

Тренируем нейросеть

Этот процесс займет примерно 3-5 минут, в зависимости от работоспособности вашего компьютера. Подробные инструкции находятся в комментариях (после #) в следующих примерах.

for epoch in range(num_epochs): for i, (images, labels) in enumerate(train_loader): # Загрузка партии изображений с индексом, данными, классом images = Variable(images.view(-1, 28*28)) # Конвертация тензора в переменную: изменяем изображение с вектора, размером 784 на матрицу 28 x 28 labels = Variable(labels) optimizer.zero_grad() # Инициализация скрытых масс до нулей outputs = net(images) # Передний пропуск: определение выходного класса, данного изображения loss = criterion(outputs, labels) # Определение потерь: разница между выходным классом и предварительно заданной меткой loss.backward() # Обратный проход: определение параметра weight optimizer.step() # Оптимизатор: обновление параметров веса в скрытых узлах if (i+1) % 100 == 0: # Логирование print('Epoch [%d/%d], Step [%d/%d], Loss: %.4f' %(epoch+1, num_epochs, i+1, len(train_dataset)//batch_size, loss.data[0]))

for epoch in range(num_epochs):     for i, (images, labels) in enumerate(train_loader):   # Загрузка партии изображений с индексом, данными, классом         images = Variable(images.view(-1, 28*28))         # Конвертация тензора в переменную: изменяем изображение с вектора, размером 784 на матрицу 28 x 28         labels = Variable(labels)                  optimizer.zero_grad()                             # Инициализация скрытых масс до нулей         outputs = net(images)                             # Передний пропуск: определение выходного класса, данного изображения         loss = criterion(outputs, labels)                 # Определение потерь: разница между выходным классом и предварительно заданной меткой         loss.backward()                                   # Обратный проход: определение параметра weight         optimizer.step()                                  # Оптимизатор: обновление параметров веса в скрытых узлах                  if (i+1) % 100 == 0:                              # Логирование             print('Epoch [%d/%d], Step [%d/%d], Loss: %.4f'                  %(epoch+1, num_epochs, i+1, len(train_dataset)//batch_size, loss.data[0]))

Тестируем модель нейросети

Также как и с тренировкой нейронной сети, нам также нужно загрузить пачки тестируемых изображений и собрать выходные данные. Отличия теста от тренировки:

1. Проходит без подсчета потерь и веса;
2. Нет обновления веса;
3. Корректный расчет прогноза

correct = 0 total = 0 for images, labels in test_loader: images = Variable(images.view(-1, 28*28)) outputs = net(images) _, predicted = torch.max(outputs.data, 1) # Выбор лучшего класса из выходных данных: класс с лучшим счетом total += labels.size(0) # Увеличиваем суммарный счет correct += (predicted == labels).sum() # Увеличиваем корректный счет print('Accuracy of the network on the 10K test images: %d %%' % (100 * correct / total))

correct = 0 total = 0 for images, labels in test_loader:     images = Variable(images.view(-1, 28*28))     outputs = net(images)     _, predicted = torch.max(outputs.data, 1)  # Выбор лучшего класса из выходных данных: класс с лучшим счетом     total += labels.size(0)                    # Увеличиваем суммарный счет     correct += (predicted == labels).sum()     # Увеличиваем корректный счет        print('Accuracy of the network on the 10K test images: %d %%' % (100 * correct / total))

Мы сохраняем тренированную модель как pickle. Таким образом, ее можно будет загрузить и использовать в будущем.

torch.save(net.state_dict(), 'fnn_model.pkl')

torch.save(net.state_dict(), 'fnn_model.pkl')

Поздравляем! Вы создали вашу первую рабочую нейронную сеть прямого распространения (Feedforward).

Что дальше?

Сохраняем и закрываем файл. Запускаем файл в консоли:

Процесс тренировки будет выглядеть следующим образом:

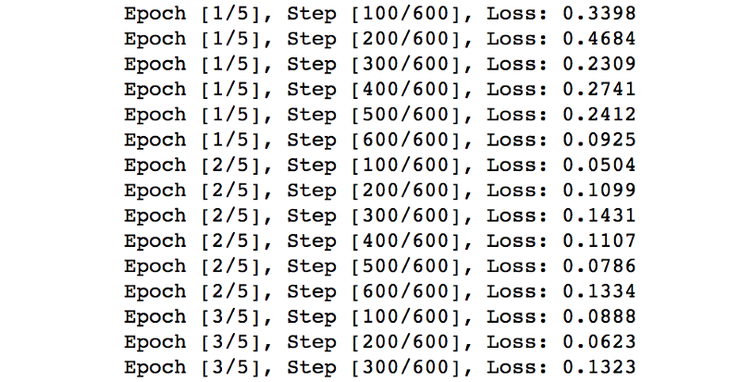
Спасибо, что уделили время. Надеюсь, вам понравилась данная статья. Весь код из статьи можно найти на github тут.

Данная статья была основана на разработки пользователя Yunjey у которого отличная библиотека примеров.

python-scripts.com

Пощупать нейросети или конструктор нейронных сетей / Хабр

Я давно интересовался нейросетями, но только с позиции зрителя – следил за новыми возможностями, которые они дают по сравнению с обычным программированием. Но никогда не лез ни в теорию, ни в практику. И вдруг (после сенсационной новости о AlphaZero) мне захотелось сделать свою нейросеть. Посмотрев несколько уроков по этой теме на YouTube, я немного врубился в теорию и перешёл к практике. В итоге я сделал даже лучше, чем свою нейросеть. Получился конструктор нейросетей и наглядное пособие по ним (то есть можно смотреть, что творится внутри нейросети). Вот как это выглядит:

А теперь немного подробнее. С помощью этого конструктора можно создавать сети прямого распространения (Feedforward neural network) до 8 скрытых слоёв (плюс слой входов и слой выходов, итого 10 слоёв (обычно 4-х слоёв более чем достаточно)) в каждом слое до 30 нейронов (ограничение связано с тем, что всё это одновременно отображается на экране, если будут просьбы в комментариях выпущу версию без ограничений и визуализации). Функция активации всех нейронов – сигмоид на основе логистической функции. Также можно обучать получившиеся сети методом обратного распространения ошибки градиентным спуском по заданным примерам. И, самое главное, можно посмотреть на каждый нейрон в каждом отдельном случае (какое значение он передаёт дальше, его смещение (поправку, bias) – нейроны с отрицательным смещением белые, с положительным – ярко-зелёные), связи нейронов в зависимости от их веса помечены красным – положительные, синим – отрицательные, а также отличаются по толщине – чем больше модуль веса, тем толще. А если навести мышку на нейрон, то можно ещё посмотреть какой сигнал на него приходит, и какое конкретно у него смещение. Это полезно, чтобы понять, как работает конкретная сеть или показать студентам принцип работы сетей прямого распространения. Но самое главное – свою сеть можно сохранить в файл и поделиться с миром.

Далее будут инструкции по пользованию программой, встраиванию созданных сетей в свои проекты, а также разбор нескольких сетей, идущих в комплекте.

Как пользоваться конструктором

Для начала скачайте архив отсюда.

Распакуйте в корень диска D:\

Запустите NeuroNet.exe

Можете попробовать «Загрузить» какую-нибудь сеть, посмотреть на неё, нажать «Обучение», увидеть её точность, потыкать стрелки влево, вправо (по бокам), чтобы посмотреть различные варианты входных (левый столбец нейронов) и выходных (правый) данных, нажать «Стоп» и попробовать ввести свои входные данные (разрешены любые значения от 0 до 1, учитывайте это при создании своих сетей и нормализуйте входные и выходные данные).

Теперь как строить свои сети. Первым делом необходимо задать архитектуру сети (количество нейронов в каждом слое через запятую), нажать «Построить» (или сначала «Снести», затем построить, если у Вас на экране уже отображается другая сеть), нажать «Обучающая выборка», «Удалить всё» и ввести свои обучающие примеры, согласно инструкции на экране. Также можно указать на вход и на выход маленькие квадратные картинки (максимум 5х5 пикселей), из которых будут определены нормализованные значения яркости пикселей (не учитывая их цвет), для чего нужно нажать на «in» и «out» соответственно. Нажать «Добавить пример», повторить процедуру нужное количество раз. Нажать «Готово», «Обучение» и как точность станет удовлетворительной (обычно 98%), нажать «Стоп», иконку в виде дискеты (сохранить), дать сети имя и радоваться, что Вы сами создали нейросеть. Дополнительно можете устанавливать скорость обучения ползунком «Точнее/Быстрее», а также визуализировать не каждый 50й шаг, а каждый 10й или 300й, как Вам угодно.

Интеграция созданных сетей в свои проекты

Чтобы использовать свои нейросети в собственных проектах, я создал отдельное приложение doNet.exe, которое нужно запускать с параметрами: «D:\NeuroNet\doNet.exe <название сети> <входные данные через пробел>», дождаться завершения работы приложения, после чего считать выходные данные из D:\NeuroNet\temp.txt

Для примера создано приложение 4-5.exe, использующее сеть «4-5» (об этой и других сетях ниже). В этом приложении подробно расписано как правильно запускать doNet.exe

Разбор сетей, идущих в комплекте

Начнём с классики – «XOR(Полусумматор)». Среди прочих, в частности, эту задачу – сложение по модулю 2 – в 1969 году приводили в качестве примера ограниченности нейросетей (а именно однослойных перцептронов). В общем, имеется два входа (со значениями либо 0, либо 1 у каждого), наша же задача — ответить 1, если значения входов разные, 0 – если одинаковые.

Далее «Количество-единиц». Три входа (0 либо 1 на каждом). Требуется посчитать, сколько было подано единиц. Реализовано как задача классификации – четыре выхода на каждый вариант ответа (0,1,2,3 единицы). На каком выходе максимальное значение, соответственно таков и ответ.

«Умножение» – Два входа (вещественные от 0 до 1), на выход их произведение.

«4-5» – На вход подаются нормализованные значения яркости пикселей картинки 4х4, на выходе имеем нормализованные значения яркости пикселей картинки 5х5.

Сеть задумывалась, как увеличение качества большой картинки на 25%, вышел же интересный фильтр для фото:

UPD: В архив добавлено приложение NeuroNet2.exe (тот же конструктор, но без визуализации (благодаря чему работает в 2 раза быстрее) и ограничений на количество нейронов в слое (до 1024 вместо 30), также в обучающей выборке на вход и выход можно подавать квадратные картинки до 32х32). Также добавлен график обучения. Нейросетями теперь могут пользоваться (и встраивать в свои проекты (даже на сервере)) и те, кто не знает их теории! В полуавтоматическом режиме (после обучения вручную подавать на вход значения и получать результат на экране) их можно использовать даже без знания программирования!

Вот собственно и всё, жду комментариев.

P.S. Если вылезает ошибка, попробуйте зарегистрировать от администратора с помощью regsvr32 файлы comdlg32, которые также есть в архиве.

habr.com

Нейронные сети для начинающих. Часть 2 / Хабр

Добро пожаловать во вторую часть руководства по нейронным сетям. Сразу хочу принести извинения всем кто ждал вторую часть намного раньше. По определенным причинам мне пришлось отложить ее написание. На самом деле я не ожидал, что у первой статьи будет такой спрос и что так много людей заинтересует данная тема. Взяв во внимание ваши комментарии, я постараюсь предоставить вам как можно больше информации и в то же время сохранить максимально понятный способ ее изложения. В данной статье, я буду рассказывать о способах обучения/тренировки нейросетей (в частности метод обратного распространения) и если вы, по каким-либо причинам, еще не прочитали первую часть, настоятельно рекомендую начать с нее. В процессе написания этой статьи, я хотел также рассказать о других видах нейросетей и методах тренировки, однако, начав писать про них, я понял что это пойдет вразрез с моим методом изложения. Я понимаю, что вам не терпится получить как можно больше информации, однако эти темы очень обширны и требуют детального анализа, а моей основной задачей является не написать очередную статью с поверхностным объяснением, а донести до вас каждый аспект затронутой темы и сделать статью максимально легкой в освоении. Спешу расстроить любителей “покодить”, так как я все еще не буду прибегать к использованию языка программирования и буду объяснять все “на пальцах”. Достаточно вступления, давайте теперь продолжим изучение нейросетей.

Перед тем как начать нашу основную тему, мы должны ввести понятие еще одного вида нейронов — нейрон смещения. Нейрон смещения или bias нейрон — это третий вид нейронов, используемый в большинстве нейросетей. Особенность этого типа нейронов заключается в том, что его вход и выход всегда равняются 1 и они никогда не имеют входных синапсов. Нейроны смещения могут, либо присутствовать в нейронной сети по одному на слое, либо полностью отсутствовать, 50/50 быть не может (красным на схеме обозначены веса и нейроны которые размещать нельзя). Соединения у нейронов смещения такие же, как у обычных нейронов — со всеми нейронами следующего уровня, за исключением того, что синапсов между двумя bias нейронами быть не может. Следовательно, их можно размещать на входном слое и всех скрытых слоях, но никак не на выходном слое, так как им попросту не с чем будет формировать связь. Нейрон смещения нужен для того, чтобы иметь возможность получать выходной результат, путем сдвига графика функции активации вправо или влево. Если это звучит запутанно, давайте рассмотрим простой пример, где есть один входной нейрон и один выходной нейрон. Тогда можно установить, что выход O2 будет равен входу h2, умноженному на его вес, и пропущенному через функцию активации (формула на фото слева). В нашем конкретном случае, будем использовать сигмоид.

Из школьного курса математики, мы знаем, что если взять функцию y = ax+b и менять у нее значения “а”, то будет изменяться наклон функции (цвета линий на графике слева), а если менять “b”, то мы будем смещать функцию вправо или влево (цвета линий на графике справа). Так вот “а” — это вес h2, а “b” — это вес нейрона смещения B1. Это грубый пример, но примерно так все и работает (если вы посмотрите на функцию активации справа на изображении, то заметите очень сильное сходство между формулами). То есть, когда в ходе обучения, мы регулируем веса скрытых и выходных нейронов, мы меняем наклон функции активации. Однако, регулирование веса нейронов смещения может дать нам возможность сдвинуть функцию активации по оси X и захватить новые участки. Иными словами, если точка, отвечающая за ваше решение, будет находиться, как показано на графике слева, то ваша НС никогда не сможет решить задачу без использования нейронов смещения. Поэтому, вы редко встретите нейронные сети без нейронов смещения.

Также нейроны смещения помогают в том случае, когда все входные нейроны получают на вход 0 и независимо от того какие у них веса, они все передадут на следующий слой 0, но не в случае присутствия нейрона смещения. Наличие или отсутствие нейронов смещения — это гиперпараметр (об этом чуть позже). Одним словом, вы сами должны решить, нужно ли вам использовать нейроны смещения или нет, прогнав НС с нейронами смешения и без них и сравнив результаты.

ВАЖНО знать, что иногда на схемах не обозначают нейроны смещения, а просто учитывают их веса при вычислении входного значения например:

input = h2*w1+h3*w2+b3 b3 = bias*w3

Так как его выход всегда равен 1, то можно просто представить что у нас есть дополнительный синапс с весом и прибавить к сумме этот вес без упоминания самого нейрона.

Ответ прост — нужно ее обучать. Однако, насколько бы прост не был ответ, его реализация в плане простоты, оставляет желать лучшего. Существует несколько методов обучения НС и я выделю 3, на мой взгляд, самых интересных:

• Метод обратного распространения (Backpropagation)
• Метод упругого распространения (Resilient propagation или Rprop)
• Генетический Алгоритм (Genetic Algorithm)

Об Rprop и ГА речь пойдет в других статьях, а сейчас мы с вами посмотрим на основу основ — метод обратного распространения, который использует алгоритм градиентного спуска. Это способ нахождения локального минимума или максимума функции с помощью движения вдоль градиента. Если вы поймете суть градиентного спуска, то у вас не должно возникнуть никаких вопросов во время использования метода обратного распространения. Для начала, давайте разберемся, что такое градиент и где он присутствует в нашей НС. Давайте построим график, где по оси х будут значения веса нейрона(w) а по оси у — ошибка соответствующая этому весу(e). Посмотрев на этот график, мы поймем, что график функция f(w) является зависимостью ошибки от выбранного веса. На этом графике нас интересует глобальный минимум — точка (w2,e2) или, иными словами, то место где график подходит ближе всего к оси х. Эта точка будет означать, что выбрав вес w2 мы получим самую маленькую ошибку — e2 и как следствие, самый лучший результат из всех возможных. Найти же эту точку нам поможет метод градиентного спуска (желтым на графике обозначен градиент). Соответственно у каждого веса в нейросети будет свой график и градиент и у каждого надо найти глобальный минимум.

Так что же такое, этот градиент? Градиент — это вектор который определяет крутизну склона и указывает его направление относительно какой либо из точек на поверхности или графике. Чтобы найти градиент нужно взять производную от графика по данной точке (как это и показано на графике). Двигаясь по направлению этого градиента мы будем плавно скатываться в низину. Теперь представим что ошибка — это лыжник, а график функции — гора. Соответственно, если ошибка равна 100%, то лыжник находиться на самой вершине горы и если ошибка 0% то в низине. Как все лыжники, ошибка стремится как можно быстрее спуститься вниз и уменьшить свое значение. В конечном случае у нас должен получиться следующий результат:

Представьте что лыжника забрасывают, с помощью вертолета, на гору. На сколько высоко или низко зависит от случая (аналогично тому, как в нейронной сети при инициализации веса расставляются в случайном порядке). Допустим ошибка равна 90% и это наша точка отсчета. Теперь лыжнику нужно спуститься вниз, с помощью градиента. На пути вниз, в каждой точке мы будем вычислять градиент, что будет показывать нам направление спуска и при изменении наклона, корректировать его. Если склон будет прямым, то после n-ого количества таких действий мы доберемся до низины. Но в большинстве случаев склон (график функции) будет волнистый и наш лыжник столкнется с очень серьезной проблемой — локальный минимум. Я думаю все знают, что такое локальный и глобальный минимум функции, для освежения памяти вот пример. Попадание в локальный минимум чревато тем, что наш лыжник навсегда останется в этой низине и никогда не скатиться с горы, следовательно мы никогда не сможем получить правильный ответ. Но мы можем избежать этого, снарядив нашего лыжника реактивным ранцем под названием момент (momentum). Вот краткая иллюстрация момента:

Как вы уже наверное догадались, этот ранец придаст лыжнику необходимое ускорение чтобы преодолеть холм, удерживающий нас в локальном минимуме, однако здесь есть одно НО. Представим что мы установили определенное значение параметру момент и без труда смогли преодолеть все локальные минимумы, и добраться до глобального минимума. Так как мы не можем просто отключить реактивный ранец, то мы можем проскочить глобальный минимум, если рядом с ним есть еще низины. В конечном случае это не так важно, так как рано или поздно мы все равно вернемся обратно в глобальный минимум, но стоит помнить, что чем больше момент, тем больше будет размах с которым лыжник будет кататься по низинам. Вместе с моментом в методе обратного распространения также используется такой параметр как скорость обучения (learning rate). Как наверняка многие подумают, чем больше скорость обучения, тем быстрее мы обучим нейросеть. Нет. Скорость обучения, также как и момент, является гиперпараметром — величина которая подбирается путем проб и ошибок. Скорость обучения можно напрямую связать со скоростью лыжника и можно с уверенностью сказать — тише едешь дальше будешь. Однако здесь тоже есть определенные аспекты, так как если мы совсем не дадим лыжнику скорости то он вообще никуда не поедет, а если дадим маленькую скорость то время пути может растянуться на очень и очень большой период времени. Что же тогда произойдет если мы дадим слишком большую скорость?

Как видите, ничего хорошего. Лыжник начнет скатываться по неправильному пути и возможно даже в другом направлении, что как вы понимаете только отдалит нас от нахождения правильного ответа. Поэтому во всех этих параметрах нужно находить золотую середину чтобы избежать не сходимости НС (об этом чуть позже). Вот мы и дошли до того момента, когда мы можем обсудить, как же все таки сделать так, чтобы ваша НС могла правильно обучаться и давать верные решения. Очень хорошо МОР визуализирован на этой гифке: А теперь давайте подробно разберем каждый этап. Если вы помните то в предыдущей статье мы считали выход НС. По другому это называется передача вперед (Forward pass), то есть мы последовательно передаем информацию от входных нейронов к выходным. После чего мы вычисляем ошибку и основываясь на ней делаем обратную передачу, которая заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значение весов будут меняться в ту сторону, которая даст нам наилучший результат. В моих вычисления я буду пользоваться методом нахождения дельты, так как это наиболее простой и понятный способ. Также я буду использовать стохастический метод обновления весов (об этом чуть позже).

Теперь давайте продолжим с того места, где мы закончили вычисления в предыдущей статье.

Данные задачи из предыдущей статьи Данные: I1=1, I2=0, w1=0.45, w2=0.78 ,w3=-0.12 ,w4=0.13 ,w5=1.5 ,w6=-2.3.

h2input = 1*0.45+0*-0.12=0.45 h2output = sigmoid(0.45)=0.61

h3input = 1*0.78+0*0.13=0.78 h3output = sigmoid(0.78)=0.69

O1input = 0.61*1.5+0.69*-2.3=-0.672 O1output = sigmoid(-0.672)=0.33

O1ideal = 1 (0xor1=1)

Error = ((1-0.33)^2)/1=0.45

Результат — 0.33, ошибка — 45%.

Так как мы уже подсчитали результат НС и ее ошибку, то мы можем сразу приступить к МОРу. Как я уже упоминал ранее, алгоритм всегда начинается с выходного нейрона. В таком случае давайте посчитаем для него значение δ (дельта) по формуле 1. Так как у выходного нейрона нет исходящих синапсов, то мы будем пользоваться первой формулой (δ output), следственно для скрытых нейронов мы уже будем брать вторую формулу (δ hidden). Тут все достаточно просто: считаем разницу между желаемым и полученным результатом и умножаем на производную функции активации от входного значения данного нейрона. Прежде чем приступить к вычислениям я хочу обратить ваше внимание на производную. Во первых как это уже наверное стало понятно, с МОР нужно использовать только те функции активации, которые могут быть дифференцированы. Во вторых чтобы не делать лишних вычислений, формулу производной можно заменить на более дружелюбную и простую формула вида: Таким образом наши вычисления для точки O1 будут выглядеть следующим образом.РешениеO1output = 0.33 O1ideal = 1 Error = 0.45

δO1 = (1 — 0.33) * ( (1 — 0.33) * 0.33 ) = 0.148

На этом вычисления для нейрона O1 закончены. Запомните, что после подсчета дельты нейрона мы обязаны сразу обновить веса всех исходящих синапсов этого нейрона. Так как в случае с O1 их нет, мы переходим к нейронам скрытого уровня и делаем тоже самое за исключение того, что формула подсчета дельты у нас теперь вторая и ее суть заключается в том, чтобы умножить производную функции активации от входного значения на сумму произведений всех исходящих весов и дельты нейрона с которой этот синапс связан. Но почему формулы разные? Дело в том что вся суть МОР заключается в том чтобы распространить ошибку выходных нейронов на все веса НС. Ошибку можно вычислить только на выходном уровне, как мы это уже сделали, также мы вычислили дельту в которой уже есть эта ошибка. Следственно теперь мы будем вместо ошибки использовать дельту которая будет передаваться от нейрона к нейрону. В таком случае давайте найдем дельту для h2:Решениеh2output = 0.61 w5 = 1.5 δO1 = 0.148

δh2 = ( (1 — 0.61) * 0.61 ) * ( 1.5 * 0.148 ) = 0.053

Теперь нам нужно найти градиент для каждого исходящего синапса. Здесь обычно вставляют 3 этажную дробь с кучей производных и прочим математическим адом, но в этом и вся прелесть использования метода подсчета дельт, потому что в конечном счете ваша формула нахождения градиента будет выглядеть вот так: Здесь точка A это точка в начале синапса, а точка B на конце синапса. Таким образом мы можем подсчитать градиент w5 следующим образом:Решениеh2output = 0.61 δO1 = 0.148

GRADw5 = 0.61 * 0.148 = 0.09

Сейчас у нас есть все необходимые данные чтобы обновить вес w5 и мы сделаем это благодаря функции МОР которая рассчитывает величину на которую нужно изменить тот или иной вес и выглядит она следующим образом: Настоятельно рекомендую вам не игнорировать вторую часть выражения и использовать момент так как это вам позволит избежать проблем с локальным минимумом.

Здесь мы видим 2 константы о которых мы уже говорили, когда рассматривали алгоритм градиентного спуска: E (эпсилон) — скорость обучения, α (альфа) — момент. Переводя формулу в слова получим: изменение веса синапса равно коэффициенту скорости обучения, умноженному на градиент этого веса, прибавить момент умноженный на предыдущее изменение этого веса (на 1-ой итерации равно 0). В таком случае давайте посчитаем изменение веса w5 и обновим его значение прибавив к нему Δw5.

РешениеE = 0.7 Α = 0.3 w5 = 1.5 GRADw5 = 0.09 Δw5(i-1) = 0

Δw5 = 0.7 * 0.09 + 0 * 0.3 = 0.063 w5 = w5 + Δw5 = 1.563

Таким образом после применения алгоритма наш вес увеличился на 0.063. Теперь предлагаю сделать вам тоже самое для h3.Решениеh3output = 0.69 w6 = -2.3 δO1 = 0.148 E = 0.7 Α = 0.3 Δw6(i-1) = 0

δh3 = ( (1 — 0.69) * 0.69 ) * ( -2.3 * 0.148 ) = -0.07

GRADw6 = 0.69 * 0.148 = 0.1

Δw6 = 0.7 * 0.1 + 0 * 0.3 = 0.07

w6 = w6 + Δw6 = -2.2

И конечно не забываем про I1 и I2, ведь у них тоже есть синапсы веса которых нам тоже нужно обновить. Однако помним, что нам не нужно находить дельты для входных нейронов так как у них нет входных синапсов.Решениеw1 = 0.45, Δw1(i-1) = 0 w2 = 0.78, Δw2(i-1) = 0 w3 = -0.12, Δw3(i-1) = 0 w4 = 0.13, Δw4(i-1) = 0 δh2 = 0.053 δh3 = -0.07 E = 0.7 Α = 0.3

GRADw1 = 1 * 0.053 = 0.053 GRADw2 = 1 * -0.07 = -0.07 GRADw3 = 0 * 0.053 = 0 GRADw4 = 0 * -0.07 = 0

Δw1 = 0.7 * 0.053 + 0 * 0.3 = 0.04 Δw2 = 0.7 * -0.07 + 0 * 0.3 = -0.05 Δw3 = 0.7 * 0 + 0 * 0.3 = 0 Δw4 = 0.7 * 0 + 0 * 0.3 = 0

w1 = w1 + Δw1 = 0.5 w2 = w2 + Δw2 = 0.73 w3 = w3 + Δw3 = -0.12 w4 = w4 + Δw4 = 0.13

Теперь давайте убедимся в том, что мы все сделали правильно и снова посчитаем выход НС только уже с обновленными весами.РешениеI1 = 1 I2 = 0 w1 = 0.5 w2 = 0.73 w3 = -0.12 w4 = 0.13 w5 = 1.563 w6 = -2.2

h2input = 1 * 0.5 + 0 * -0.12 = 0.5 h2output = sigmoid(0.5) = 0.62

h3input = 1 * 0.73 + 0 * 0.124 = 0.73 h3output = sigmoid(0.73) = 0.675

O1input = 0.62* 1.563 + 0.675 * -2.2 = -0.51 O1output = sigmoid(-0.51) = 0.37

O1ideal = 1 (0xor1=1)

Error = ((1-0.37)^2)/1=0.39

Результат — 0.37, ошибка — 39%.

Как мы видим после одной итерации МОР, нам удалось уменьшить ошибку на 0.04 (6%). Теперь нужно повторять это снова и снова, пока ваша ошибка не станет достаточно мала. Нейросеть можно обучать с учителем и без (supervised, unsupervised learning).

Обучение с учителем — это тип тренировок присущий таким проблемам как регрессия и классификация (им мы и воспользовались в примере приведенном выше). Иными словами здесь вы выступаете в роли учителя а НС в роли ученика. Вы предоставляете входные данные и желаемый результат, то есть ученик посмотрев на входные данные поймет, что нужно стремиться к тому результату который вы ему предоставили.

Обучение без учителя — этот тип обучения встречается не так часто. Здесь нет учителя, поэтому сеть не получает желаемый результат или же их количество очень мало. В основном такой вид тренировок присущ НС у которых задача состоит в группировке данных по определенным параметрам. Допустим вы подаете на вход 10000 статей на хабре и после анализа всех этих статей НС сможет распределить их по категориям основываясь, например, на часто встречающихся словах. Статьи в которых упоминаются языки программирования, к программированию, а где такие слова как Photoshop, к дизайну.

Существует еще такой интересный метод, как обучение с подкреплением (reinforcement learning). Этот метод заслуживает отдельной статьи, но я попытаюсь вкратце описать его суть. Такой способ применим тогда, когда мы можем основываясь на результатах полученных от НС, дать ей оценку. Например мы хотим научить НС играть в PAC-MAN, тогда каждый раз когда НС будет набирать много очков мы будем ее поощрять. Иными словами мы предоставляем НС право найти любой способ достижения цели, до тех пор пока он будет давать хороший результат. Таким способом, сеть начнет понимать чего от нее хотят добиться и пытается найти наилучший способ достижения этой цели без постоянного предоставления данных “учителем”.

Также обучение можно производить тремя методами: стохастический метод (stochastic), пакетный метод (batch) и мини-пакетный метод (mini-batch). Существует очень много статей и исследований на тему того, какой из методов лучше и никто не может прийти к общему ответу. Я же сторонник стохастического метода, однако я не отрицаю тот факт, что каждый метод имеет свои плюсы и минусы.

Вкратце о каждом методе:

Стохастический (его еще иногда называют онлайн) метод работает по следующему принципу — нашел Δw, сразу обнови соответствующий вес.

Пакетный метод же работает по другому. Мы суммируем Δw всех весов на текущей итерации и только потом обновляем все веса используя эту сумму. Один из самых важных плюсов такого подхода — это значительная экономия времени на вычисление, точность же в таком случае может сильно пострадать.

Мини-пакетный метод является золотой серединой и пытается совместить в себе плюсы обоих методов. Здесь принцип таков: мы в свободном порядке распределяем веса по группам и меняем их веса на сумму Δw всех весов в той или иной группе.

Гиперпараметры — это значения, которые нужно подбирать вручную и зачастую методом проб и ошибок. Среди таких значений можно выделить:

• Момент и скорость обучения
• Количество скрытых слоев
• Количество нейронов в каждом слое
• Наличие или отсутствие нейронов смещения

В других типах НС присутствуют дополнительные гиперпараметры, но о них мы говорить не будем. Подбор верных гиперпараметров очень важен и будет напрямую влиять на сходимость вашей НС. Понять стоит ли использовать нейроны смещения или нет достаточно просто. Количество скрытых слоев и нейронов в них можно вычислить перебором основываясь на одном простом правиле — чем больше нейронов, тем точнее результат и тем экспоненциально больше время, которое вы потратите на ее обучение. Однако стоит помнить, что не стоит делать НС с 1000 нейронов для решения простых задач. А вот с выбором момента и скорости обучения все чуточку сложнее. Эти гиперпараметры будут варьироваться, в зависимости от поставленной задачи и архитектуры НС. Например, для решения XOR скорость обучения может быть в пределах 0.3 — 0.7, но в НС которая анализирует и предсказывает цену акций, скорость обучения выше 0.00001 приводит к плохой сходимости НС. Не стоит сейчас заострять свое внимание на гиперпараметрах и пытаться досконально понять, как же их выбирать. Это придет с опытом, а пока что советую просто экспериментировать и искать примеры решения той или иной задачи в сети. Сходимость говорит о том, правильная ли архитектура НС и правильно ли были подобраны гиперпараметры в соответствии с поставленной задачей. Допустим наша программа выводит ошибку НС на каждой итерации в лог. Если с каждой итерацией ошибка будет уменьшаться, то мы на верном пути и наша НС сходится. Если же ошибка будет прыгать вверх — вниз или застынет на определенном уровне, то НС не сходится. В 99% случаев это решается изменением гиперпараметров. Оставшийся 1% будет означать, что у вас ошибка в архитектуре НС. Также бывает, что на сходимость влияет переобучение НС. Переобучение, как следует из названия, это состояние нейросети, когда она перенасыщена данными. Это проблема возникает, если слишком долго обучать сеть на одних и тех же данных. Иными словами, сеть начнет не учиться на данных, а запоминать и “зубрить” их. Соответственно, когда вы уже будете подавать на вход этой НС новые данные, то в полученных данных может появиться шум, который будет влиять на точность результата. Например, если мы будем показывать НС разные фотографии яблок (только красные) и говорить что это яблоко. Тогда, когда НС увидит желтое или зеленое яблоко, оно не сможет определить, что это яблоко, так как она запомнила, что все яблоки должны быть красными. И наоборот, когда НС увидит что-то красное и по форме совпадающее с яблоком, например персик, она скажет, что это яблоко. Это и есть шум. На графике шум будет выглядеть следующим образом. Видно, что график функции сильно колеблется от точки к точке, которые являются выходными данными (результатом) нашей НС. В идеале, этот график должен быть менее волнистый и прямой. Чтобы избежать переобучения, не стоит долго тренировать НС на одних и тех же или очень похожих данных. Также, переобучение может быть вызвано большим количеством параметров, которые вы подаете на вход НС или слишком сложной архитектурой. Таким образом, когда вы замечаете ошибки (шум) в выходных данных после этапа обучения, то вам стоит использовать один из методов регуляризации, но в большинстве случаев это не понадобиться. Надеюсь эта статья смогла прояснить ключевые моменты такого нелегко предмета, как Нейронные сети. Однако я считаю, что сколько бы ты статей не прочел, без практики такую сложную тему освоить невозможно. Поэтому, если вы только в начале пути и хотите изучить эту перспективную и развивающуюся отрасль, то советую начать практиковаться с написания своей НС, а уже после прибегать к помощи различных фреймворков и библиотек. Также, если вам интересен мой метод изложения информации и вы хотите, чтобы я написал статьи на другие темы связанные с Машинным обучением, то проголосуйте в опросе ниже за ту тему которую вам интересна. До встречи в будущих статьях :)

habr.com

Нейронные сети для начинающих. Часть 1

Привет всем читателям Habrahabr, в этой статье я хочу поделиться с Вами моим опытом в изучении нейронных сетей.

Мое знакомство с нейронными сетями произошло, когда вышло приложение Prisma. Оно обрабатывает любую фотографию, с помощью нейронных сетей, и воспроизводит ее с нуля, используя выбранный стиль. Заинтересовавшись этим, я бросился искать статьи и «туториалы», в первую очередь, на Хабре. И к моему великому удивлению, я не нашел ни одну статью, которая четко и поэтапно расписывала алгоритм работы нейронных сетей. Информация была разрознена и в ней отсутствовали ключевые моменты. Также, большинство авторов бросается показывать код на том или ином языке программирования, не прибегая к детальным объяснениям.

Поэтому сейчас, когда я достаточно хорошо освоил нейронные сети и нашел огромное количество информации с разных иностранных порталов, я хотел бы поделиться этим с людьми в серии публикаций, где я соберу всю информацию, которая потребуется вам, если вы только начинаете знакомство с нейронными сетями. В этой статье, я не буду делать сильный акцент на Java и буду объяснять все на примерах, чтобы вы сами смогли перенести это на любой, нужный вам язык программирования. В последующих статьях, я расскажу о своем приложении, написанном под андроид, которое предсказывает движение акций или валюты. Иными словами, всех желающих окунуться в мир нейронных сетей и жаждущих простого и доступного изложения информации или просто тех, кто что-то не понял и хочет подтянуть, добро пожаловать под кат.

Первым и самым важным моим открытием был плейлист американского программиста Джеффа Хитона, в котором он подробно и наглядно разбирает принципы работы нейронных сетей и их классификации. После просмотра этого плейлиста, я решил создать свою нейронную сеть, начав с самого простого примера. Вам наверняка известно, что когда ты только начинаешь учить новый язык, первой твоей программой будет Hello World. Это своего рода традиция. В мире машинного обучения тоже есть свой Hello world и это нейросеть решающая проблему исключающего или(XOR). Таблица исключающего или выглядит следующим образом:

a	b	c
0	0	0
0	1	1
1	0	1
1	1	0

Соответственно, нейронная сеть берет на вход два числа и должна на выходе дать другое число — ответ. Теперь о самих нейронных сетях.

Что такое нейронная сеть?

Нейронная сеть — это последовательность нейронов, соединенных между собой синапсами. Структура нейронной сети пришла в мир программирования прямиком из биологии. Благодаря такой структуре, машина обретает способность анализировать и даже запоминать различную информацию. Нейронные сети также способны не только анализировать входящую информацию, но и воспроизводить ее из своей памяти. Заинтересовавшимся обязательно к просмотру 2 видео из TED Talks: Видео 1, Видео 2). Другими словами, нейросеть это машинная интерпретация мозга человека, в котором находятся миллионы нейронов передающих информацию в виде электрических импульсов.

Какие бывают нейронные сети?

Пока что мы будем рассматривать примеры на самом базовом типе нейронных сетей — это сеть прямого распространения (далее СПР). Также в последующих статьях я введу больше понятий и расскажу вам о рекуррентных нейронных сетях. СПР как вытекает из названия это сеть с последовательным соединением нейронных слоев, в ней информация всегда идет только в одном направлении.

Для чего нужны нейронные сети?

Нейронные сети используются для решения сложных задач, которые требуют аналитических вычислений подобных тем, что делает человеческий мозг. Самыми распространенными применениями нейронных сетей является:

Классификация — распределение данных по параметрам. Например, на вход дается набор людей и нужно решить, кому из них давать кредит, а кому нет. Эту работу может сделать нейронная сеть, анализируя такую информацию как: возраст, платежеспособность, кредитная история и тд.

Предсказание — возможность предсказывать следующий шаг. Например, рост или падение акций, основываясь на ситуации на фондовом рынке.

Распознавание — в настоящее время, самое широкое применение нейронных сетей. Используется в Google, когда вы ищете фото или в камерах телефонов, когда оно определяет положение вашего лица и выделяет его и многое другое.

Теперь, чтобы понять, как же работают нейронные сети, давайте взглянем на ее составляющие и их параметры.

Что такое нейрон?

Нейрон — это вычислительная единица, которая получает информацию, производит над ней простые вычисления и передает ее дальше. Они делятся на три основных типа: входной (синий), скрытый (красный) и выходной (зеленый). Также есть нейрон смещения и контекстный нейрон о которых мы поговорим в следующей статье. В том случае, когда нейросеть состоит из большого количества нейронов, вводят термин слоя. Соответственно, есть входной слой, который получает информацию, n скрытых слоев (обычно их не больше 3), которые ее обрабатывают и выходной слой, который выводит результат. У каждого из нейронов есть 2 основных параметра: входные данные (input data) и выходные данные (output data). В случае входного нейрона: input=output. В остальных, в поле input попадает суммарная информация всех нейронов с предыдущего слоя, после чего, она нормализуется, с помощью функции активации (пока что просто представим ее f(x)) и попадает в поле output.

Важно помнить, что нейроны оперируют числами в диапазоне [0,1] или [-1,1]. А как же, вы спросите, тогда обрабатывать числа, которые выходят из данного диапазона? На данном этапе, самый простой ответ — это разделить 1 на это число. Этот процесс называется нормализацией, и он очень часто используется в нейронных сетях. Подробнее об этом чуть позже.

Что такое синапс?

Синапс это связь между двумя нейронами. У синапсов есть 1 параметр — вес. Благодаря ему, входная информация изменяется, когда передается от одного нейрона к другому. Допустим, есть 3 нейрона, которые передают информацию следующему. Тогда у нас есть 3 веса, соответствующие каждому из этих нейронов. У того нейрона, у которого вес будет больше, та информация и будет доминирующей в следующем нейроне (пример — смешение цветов). На самом деле, совокупность весов нейронной сети или матрица весов — это своеобразный мозг всей системы. Именно благодаря этим весам, входная информация обрабатывается и превращается в результат.

Важно помнить, что во время инициализации нейронной сети, веса расставляются в случайном порядке.

Как работает нейронная сеть?

В данном примере изображена часть нейронной сети, где буквами I обозначены входные нейроны, буквой H — скрытый нейрон, а буквой w — веса. Из формулы видно, что входная информация — это сумма всех входных данных, умноженных на соответствующие им веса. Тогда дадим на вход 1 и 0. Пусть w1=0.4 и w2 = 0.7 Входные данные нейрона Н1 будут следующими: 1*0.4+0*0.7=0.4. Теперь когда у нас есть входные данные, мы можем получить выходные данные, подставив входное значение в функцию активации (подробнее о ней далее). Теперь, когда у нас есть выходные данные, мы передаем их дальше. И так, мы повторяем для всех слоев, пока не дойдем до выходного нейрона. Запустив такую сеть в первый раз мы увидим, что ответ далек от правильно, потому что сеть не натренирована. Чтобы улучшить результаты мы будем ее тренировать. Но прежде чем узнать как это делать, давайте введем несколько терминов и свойств нейронной сети.

Функция активации

Функция активации — это способ нормализации входных данных (мы уже говорили об этом ранее). То есть, если на входе у вас будет большое число, пропустив его через функцию активации, вы получите выход в нужном вам диапазоне. Функций активации достаточно много поэтому мы рассмотрим самые основные: Линейная, Сигмоид (Логистическая) и Гиперболический тангенс. Главные их отличия — это диапазон значений.

Линейная функция

Эта функция почти никогда не используется, за исключением случаев, когда нужно протестировать нейронную сеть или передать значение без преобразований.

Сигмоид

Это самая распространенная функция активации, ее диапазон значений [0,1]. Именно на ней показано большинство примеров в сети, также ее иногда называют логистической функцией. Соответственно, если в вашем случае присутствуют отрицательные значения (например, акции могут идти не только вверх, но и вниз), то вам понадобиться функция которая захватывает и отрицательные значения.

Гиперболический тангенс

Имеет смысл использовать гиперболический тангенс, только тогда, когда ваши значения могут быть и отрицательными, и положительными, так как диапазон функции [-1,1]. Использовать эту функцию только с положительными значениями нецелесообразно так как это значительно ухудшит результаты вашей нейросети.

Тренировочный сет

Тренировочный сет — это последовательность данных, которыми оперирует нейронная сеть. В нашем случае исключающего или (xor) у нас всего 4 разных исхода то есть у нас будет 4 тренировочных сета: 0xor0=0, 0xor1=1, 1xor0=1,1xor1=0.

Итерация

Это своеобразный счетчик, который увеличивается каждый раз, когда нейронная сеть проходит один тренировочный сет. Другими словами, это общее количество тренировочных сетов пройденных нейронной сетью.

Эпоха

При инициализации нейронной сети эта величина устанавливается в 0 и имеет потолок, задаваемый вручную. Чем больше эпоха, тем лучше натренирована сеть и соответственно, ее результат. Эпоха увеличивается каждый раз, когда мы проходим весь набор тренировочных сетов, в нашем случае, 4 сетов или 4 итераций.

Важно не путать итерацию с эпохой и понимать последовательность их инкремента. Сначала n раз увеличивается итерация, а потом уже эпоха и никак не наоборот. Другими словами, нельзя сначала тренировать нейросеть только на одном сете, потом на другом и тд. Нужно тренировать каждый сет один раз за эпоху. Так, вы сможете избежать ошибок в вычислениях.

Ошибка

Ошибка — это процентная величина, отражающая расхождение между ожидаемым и полученным ответами. Ошибка формируется каждую эпоху и должна идти на спад. Если этого не происходит, значит, вы что-то делаете не так. Ошибку можно вычислить разными путями, но мы рассмотрим лишь три основных способа: Mean Squared Error (далее MSE), Root MSE и Arctan. Здесь нет какого-либо ограничения на использование, как в функции активации, и вы вольны выбрать любой метод, который будет приносить вам наилучший результат. Стоит лишь учитывать, что каждый метод считает ошибки по разному. У Arctan, ошибка, почти всегда, будет больше, так как он работает по принципу: чем больше разница, тем больше ошибка. У Root MSE будет наименьшая ошибка, поэтому, чаще всего, используют MSE, которая сохраняет баланс в вычислении ошибки.

MSE

Root MSE

Arctan

Принцип подсчета ошибки во всех случаях одинаков. За каждый сет, мы считаем ошибку, отняв от идеального ответа, полученный. Далее, либо возводим в квадрат, либо вычисляем квадратный тангенс из этой разности, после чего полученное число делим на количество сетов.

Задача

Теперь, чтобы проверить себя, подсчитайте результат, данной нейронной сети, используя сигмоид, и ее ошибку, используя MSE.

Данные:

I1=1, I2=0, w1=0.45, w2=0.78 ,w3=-0.12 ,w4=0.13 ,w5=1.5 ,w6=-2.3.

Решение

h2input = 1*0.45+0*-0.12=0.45

h2output = sigmoid(0.45)=0.61

h3input = 1*0.78+0*0.13=0.78

h3output = sigmoid(0.78)=0.69

O1input = 0.61*1.5+0.69*-2.3=-0.672

O1output = sigmoid(-0.672)=0.33

O1ideal = 1 (0xor1=1)

Error = ((1-0.33)^2)/1=0.45

Результат — 0.33, ошибка — 45%.

Большое спасибо за внимание! Надеюсь, что данная статья смогла помочь вам в изучении нейронных сетей. В следующей статье, я расскажу о нейронах смещения и о том, как тренировать нейронную сеть, используя метод обратного распространения и градиентного спуска.

Использованные ресурсы:

— Раз

— Два

— Три

webhamster.ru

Создание нейронной сети без навыков программирования — Selectel на vc.ru

Рассказываем, как за несколько шагов создать простую нейронную сеть и научить её узнавать известных предпринимателей на фотографиях.

Шаг 0. Разбираемся, как устроены нейронные сети

Проще всего разобраться с принципами работы нейронных сетей можно на примере Teachable Machine — образовательного проекта Google.

В качестве входящих данных — то, что нужно обработать нейронной сети — в Teachable Machine используется изображение с камеры ноутбука. В качестве выходных данных — то, что должна сделать нейросеть после обработки входящих данных — можно использовать гифку или звук.

Например, можно научить Teachable Machine при поднятой вверх ладони говорить «Hi». При поднятом вверх большом пальце — «Cool», а при удивленном лице с открытым ртом — «Wow».

Для начала нужно обучить нейросеть. Для этого поднимаем ладонь и нажимаем на кнопку «Train Green» — сервис делает несколько десятков снимков, чтобы найти на изображениях закономерность. Набор таких снимков принято называть «датасетом».

Теперь остается выбрать действие, которое нужно вызывать при распознании образа — произнести фразу, показать GIF или проиграть звук. Аналогично обучаем нейронную сеть распознавать удивленное лицо и большой палец.

Как только нейросеть обучена, её можно использовать. Teachable Machine показывает коэффициент «уверенности» — насколько система «уверена», что ей показывают один из навыков.

Кроткое видео о работе Teachable Machine

Шаг 1. Готовим компьютер к работе с нейронной сетью

Теперь сделаем свою нейронную сеть, которая при отправке изображения будет сообщать о том, что изображено на картинке. Сначала научим нейронную сеть распознавать цветы на картинке: ромашку, подсолнух, одуванчик, тюльпан или розу.

Для создания собственной нейронной сети понадобится Python — один из наиболее минималистичных и распространенных языков программирования, и TensorFlow — открытая библиотека Google для создания и тренировки нейронных сетей.

Устанавливаем Python

Если у вас Windows: скачиваем установщик с официального сайта Python и запускаем его. При установке нужно поставить галочку «Add Python to PATH».

На macOS Python можно установить сразу через Terminal:

brew install python

Для работы с нейронной сетью подойдет Python 2.7 или более старшая версия.

Устанавливаем виртуальное окружение

Открываем командную строку на Windows или Terminal на macOS и последовательно вводим несколько команд:

pip install --upgrade virtualenvvirtualenv --system-site-packages Названиеsource Название/bin/activate

На компьютер будет установлен инструмент для запуска программ в виртуальном окружении. Он позволит устанавливать и запускать все библиотеки и приложения внутри одной папки — в команде она обозначена как «Название».

Устанавливаем TensorFlow

Вводим команду:

pip install tensorflow

Всё, библиотека TensorFlow установлена в выбранную папку. На macOS она находится по адресу Macintosh HD/Users/Имя_пользователя/, на Windows — в корне C://.

Можно проверить работоспособность библиотеки последовательно вводя команды:

pythonimport tensorflow as tfhello = tf.constant('Hello, TensorFlow')sess = tf.Session()print(sess.run(hello))

Если установка прошла успешно, то на экране появится фраза «Hello, Tensorflow».

Шаг 2. Добавляем классификатор

Классификатор — это инструмент, который позволяет методам машинного обучения понимать, к чему относится неизвестный объект. Например, классификатор поможет понять, где на картинке растение, и что это за цветок.

Открываем страницу «Tensorflow for poets» на Github, нажимаем на кнопку «Clone or download» и скачиваем классификатор в формате ZIP-файла.

Затем распаковываем архив в созданную на втором шаге папку.

Шаг 3. Добавляем набор данных

Набор данных нужен для обучения нейронной сети. Это входные данные, на основе которых нейронная сеть научится понимать, какой цветок расположен на картинке.

Сначала скачиваем набор данных (датасет) Google с цветами. В нашем примере — это набор небольших фотографий, отсортированный по папкам с их названиями.

Содержимое архива нужно распаковать в папку /tf_files классификатора.

Шаг 4. Переобучаем модель

Теперь нужно запустить обучение нейронной сети, чтобы она проанализировала картинки из датасета и поняла при помощи классификатора, как и какой тип цветка выглядит.

Переходим в папку с классификатором

Открываем командную строку и вводим команду, чтобы перейти в папку с классификатором.

Windows:

cd C://Название/

macOS:

cd Название

Запускаем процесс обучения

python scripts/retrain.py --output_graph=tf_files/retrained_graph.pb --output_labels=tf_files/retrained_labels.txt --image_dir=tf_files/flower_photos

Что указано в команде:

• retrain.py — название Python-скрипта, который отвечает за запуск процесса обучения нейронной сети.
• output_graph — создаёт новый файл с графом данных. Он и будет использоваться для определения того, что находится на картинке.
• output_labels — создание нового файла с метками. В нашем примере это ромашки, подсолнухи, одуванчики, тюльпаны или розы.
• image_dir — путь к папке, в которой находятся изображения с цветами.

Программа начнет создавать текстовые файлы bottleneck — это специальные текстовые файлы с компактной информацией об изображении. Они помогают классификатору быстрее определять подходящую картинку.

Весь ход обучения занимает около 4000 шагов. Время работы может занять несколько десятков минут — в зависимости от мощности процессора.

После завершения анализа нейросеть сможет распознавать на любой картинке ромашки, подсолнухи, одуванчики, тюльпаны и розы.

Перед тестированием нейросети нужно открыть файл label_image.py, находящийся в папке scripts в любом текстовом редакторе и заменить значения в строках:

input_height = 299input_width = 299input_mean = 0input_std = 255input_layer = "Mul"

Шаг 5. Тестирование

Выберите любое изображение цветка, которое нужно проанализировать, и поместите его в папку с нейронной сетью. Назовите файл image.jpg.

Для запуска анализа нужно ввести команду:

python scripts/label_image.py --image image.jpg

Нейросеть проверит картинку на соответствие одному из лейблов и выдаст результат.

Например:

Это значит, что с вероятностью 72% на картинке изображена роза.

Шаг 6. Учим нейронную сеть распознавать предпринимателей

Теперь можно расширить возможности нейронной сети — научить её распознавать на картинке не только цветы, но и известных предпринимателей. Например, Элона Маска и Марка Цукерберга.

Для этого нужно добавить новые изображения в датасет и переобучить нейросеть.

Собираем собственный датасет

Для создания датасета с фотографиями предпринимателей можно воспользоваться поиском по картинкам Google и расширением для Chrome, которое сохраняет все картинки на странице.

Папку с изображениями Элона Маска нужно поместить в \tf_files\flower_photos\musk\. Аналогично все изображения с основателем Facebook — в папку \tf_files\flower_photos\zuckerberg\.

Чем больше фотографий будет в папках, тем точнее нейронная сеть распознает на ней предпринимателя.

Переобучаем и проверяем

Для переобучения и запуска нейронной сети используем те же команды, что и в шагах 4 и 5.

python scripts/retrain.py --output_graph=tf_files/retrained_graph.pb --output_labels=tf_files/retrained_labels.txt --image_dir=tf_files/flower_photos

python scripts/label_image.py --image image.jpg

Шаг 7. «Разгоняем» нейронную сеть

Чтобы процесс обучения не занимал каждый раз много времени, нейросеть лучше всего запускать на сервере с GPU — он спроектирован специально для таких задач.

Процесс запуска и обучения нейронной сети на сервере похож на аналогичный процесс на компьютере.

Создание сервера с Ubuntu

Нам понадобится сервер с операционной системой Ubuntu. Её можно установить самостоятельно, либо — если арендован сервер Selectel — через техподдержку компании.

Установка Python

sudo apt-get install python3-pip python3-dev

Установка TensorFlow

pip3 install tensorflow-gpu

Скачиваем классификатор и набор данных

Аналогично шагам 2 и 3 на компьютере, только архивы необходимо загрузить сразу на сервер.

Переобучаем модель

python3 scripts/retrain.py --output_graph=tf_files/retrained_graph.pb --output_labels=tf_files/retrained_labels.txt --image_dir=tf_files/flower_photos

Тестируем нейросеть

python scripts/label_image.py --image image.jpg

Заказать сервер для нейросети

#нейросети #инструкция

vc.ru

---

• 
  Ракета на марс
• 
  Сколько весит скафандр космонавта
• 
  Общая теория относительности кратко
• 
  Поверхности планет солнечной системы фото
• 
  Вулканы недействующие
• 
  Солнечные батареи прозрачные
• 
  Автомобили с автопилотом
• 
  Vfts 352
• 
  Новые технологии в россии
• 
  Новости космоса сегодня в яндекс новостях
• 
  Ледник ларсена на карте