Уже первые изобретатели «вечновращающихся колёс» обратили внимание на замечательное свойство жидкостей — достаточно придать дну сосуда хоть небольшой уклон, и жидкость сама перетекала в более низкую часть, собираясь там и увеличивая её вес. Это было очень удобно, и уже первая известная модель «вечного двигателя» использует это свойство жидкостей. Однако по мере развития науки и технологии выяснилось, что во многих случаях гораздо эффективнее вместо жидкостей использовать твёрдые шары, перекатывающиеся по жёстким направляющим. В результате все колёса с переливающимися жидкостями рано или поздно получили аналоги с перекатывающимися шарами (не путать с системами, где жидкость не переливается внутри колеса, а льётся по колесу, а потом возвращается обратно другим путём). Для нас же рабочие элементы с перекатывающимися шарами интересны тем, что расчёт моментов для них выполнить гораздо проще и нагляднее, чем для перетекающей жидкости — применение принципа мгновенной смены фаз здесь очень близко к реальному поведению шаров на малых скоростях вращения колеса. Колесо Бхаскары и колесо с шарами в наклонных спицах Колесо Бхаскары и колесо с шарами в наклонных спицах Первое упоминание в письменных источниках о «вечновращающемся колесе» относится к XII веку. Оно описано индийским поэтом, математиком и астрономом Бхаскарой Ачарья. В этом колесе наклонные полые спицы предлагалось заполнить ртутью наполовину. В первой фазе рабочего хода спица, находясь ещё значительно выше оси колеса, постепенно принимала горизонтальное положение и ртуть перетекала от центра колеса к его ободу, увеличивая вращающий момент. В первой фазе обратного хода та же спица, ещё находясь намного ниже оси колеса, начинала переворачиваться обратно, и ртуть снова возвращалась к центру колеса, уменьшая вращающий момент. Таким образом, на участке между горизонтальными положениями оси предполагалось наличие положительного вращающего момента, а на остальных участках моменты рабочего и обратного хода должны были взаимно компенсироваться, что позволило бы обеспечить суммарный положительный момент за полный цикл рабочего элемента. Расчётов, естественно, автор не проводил — компьютеров тогда не было, да и механики как точной науки тоже. О воплощении колеса в натуре сведений также не сохранилось, а работоспособность обосновывалась просто — оно будет вращаться, потому что это очевидно! Слева — колесо Бхаскары (Индия, ок.1150 г.), справа — его аналог с перекатывающимися шарами. Предполагаемая область положительного вращающего момента показана на ободе зелёным цветом. Жёлтым цветом отмечен рассчитываемый рабочий элемент, а жёлтым крестиком — начальное положение точки отсчёта. Но сейчас компьютеры есть, поэтому расчёт такой конструкции много времени не займёт. Глядя на аналог с шарами, можно заметить, что фаз всего две. При переходе в рабочее положение груз перемещается к ободу с радиуса R1 на радиус R2 и несколько опережает точку отсчёта, а в начале обратного хода возвращается на меньший радиус и вновь начинает вращаться синхронно с точкой отсчёта. Трение, сопротивление среды и прочее в первом приближении можно не учитывать. Масса груза в данном случае не изменяется. Для упрощения расчёта выберем точку отсчёта таким образом, чтобы в фазе обратного хода её угол поворота был равен углу поворота центра масс груза, и предположим тангенциальное размещение спиц по отношению к ступице. В этом случае, как видно из рисунка, R1 и R2 образуют прямоугольный треугольник, где R2 является гипотенузой, а R1— катетом. Для расчёта нам не хватает только угла опережения точки отсчёта во время рабочего хода, который как раз равен углу между R1 и R2 на рисунке.
Итак, при всех углах наклона спиц суммарная нормированная работа отрицательна, а это значит, что данная конструкция принципиально неработоспособна! При этом чем ближе положение спицы к нормальному (т.е. совпадающему с радиусом колеса), тем меньше потери. Сразу скажу, это потому, что мы предположили конечное время перехода груза из положения обратного хода в положение рабочего хода, равное времени поворота на один градус (R = R2 начиная с 1° и R = R1 начиная со 181°). Если мы предположим абсолютно мгновенное перемещение груза (R = R2 начиная с 0° и R = R1 начиная со 180°, а главное, также чуть раньше менялся бы и угол опережения), зависимость будет обратной, но всё равно все значения будут отрицательными, а если вдруг окажутся чуть-чуть положительными, то лишь из-за особенностей численных методов моделирования — желающие могут проверить самостоятельно, это несложно, — достаточно уменьшить шаг (скажем, до 0. И всё-таки, почему так получилось? Чтобы ответить на этот вопрос, необходимо проанализировать изменение текущего и суммарного моментов, например, для соотношения радиусов 50%. Текущий момент и суммарная нормированная работа одного элемента колеса Бхаскары при соотношении R1 / R2= 50%. На графиках наглядно видно, что когда груз находится в рабочем положении (возле обода), он успевает «отъесть» значительную часть полезной работы, прежде чем вернётся к ступице. В то же время, возвратившись к ступице, он «отматывает» назад и свой угол поворота, и если в рабочем положении, длящемся половину оборота колеса, он совершал как «полезную», так и «вредную» работу, то вторую половину оборота при обратном ходе он совершает только «вредную» работу, хотя и меньшую — из-за уменьшившегося момента, — но этого достаточно, чтобы «доесть» остатки полезной работы от первой половины оборота. Как с этим бороться? Во-первых, можно попытаться увеличить разность плеч рабочего и обратного ходов, то есть разность между R1 и R2. Однако при этом наклон спицы относительно радиуса уменьшается, и сокращается сектор, где предполагается получить положительную разность моментов, — достаточно взглянуть на рисунок колеса. В результате выигрыша нет, и расчёты это подтверждают. Второй путь — максимально расширить сектор с положительной разностью моментов. Однако при этом разница между R1 и R2 сокращается (таковы законы геометрии в нашем мире!), и, соответственно, уменьшается положительная разность моментов. Опять выигрыша нет! Замкнутый круг! И это не случайно — такой круг в той или иной форме будет всегда обнаруживаться во всех моделях тихоходных механических вечных двигателей… В числах изменение моментов представлено в подробной таблице пошагового изменения моментов — желающие могут сравнить с результатами собственных вычислений. Колесо со скошенными ящикамиНазвание несколько неуклюжее, зато достаточно точно отображает суть конструкции, показанной на рисунке. Общая идея всё та же — при неизменной массе груза плечо (расстояние от оси колеса до его центра масс) при рабочем ходе больше, чем при обратном, что и обеспечивает нужную разность вращающих моментов. В отличие от колеса Бхаскары, здесь нежелательный вращающий момент уменьшается уже в самом начале обратного хода, а увеличивается в самом начале рабочего хода. Поможет ли это получить выигрыш? Колесо со скошенными ящиками. Жёлтым цветом отмечен рассчитываемый рабочий элемент, а жёлтым крестиком — начальное положение точки отсчёта. Цифрами обозначены положения шара в ящике на разных фазах полного цикла работы элемента. Расчёт здесь более сложный — для этого нам придётся рассчитать 4 фазы движения. В качестве базового радиуса возьмём расстояние R от оси колеса до центра масс груза в первой фазе. Предположим, что стороны ящика скошены под углом 45°, при этом перемещение груза вдоль тангенциальной (параллельной ободу) стороны составляет 20% R, а при перевороте ящика центр масс груза смещается на 10% R от бывшего «дна» ящика.
Момент здесь превышает 100%, поскольку в данном случае в качестве эталона было выбрано не максимальное, а минимальное расстояние от оси, но на расчёт нормированной работы это не влияет — на то она и нормированная! В результате расчёта получаем следующую картину. Текущий момент и суммарная нормированная работа одного элемента в колесе со скошенными ящиками. Как и в случае колеса Бхаскары, здесь в первой половине графиков (рабочий ход) часть полезной работы уже «съедается» при поднятии шара из самого нижнего положения, в которое он попадает раньше, чем точка отсчёта пройдёт половину пути. В числах изменение моментов представлено в отдельной таблице пошагового изменения моментов. Кстати, если предположить, что высота ящиков так мала, что шар может кататься только вдоль тангенциальной стороны, то мы приходим к той же кинематике груза, что и в колесе Бхаскары при большом наклоне спиц (когда соотношение R1 / R2 приближается к 100%)! Колесо с качающейся направляющей Итак, в предыдущих конструкциях выигрыша получить не удалось, не в последнюю очередь из-за того, что часть полезной работы съедалась ещё во время рабочего хода. Три фазы рабочего цикла колеса с качающейся направляющей. Жёлтым крестиком отмечено начальное положение точки отсчёта, совпадающее с осью качания направляющей, зелёный цвет показывает открытое состояние фиксаторов, красный — закрытое. Здесь во время рабочего хода груз скатывается из центра колеса к его ободу, увеличивая вращающий момент, а немного погодя направляющая падает вниз, груз по ней возвращается обратно, и его вращающий момент становится минимальным ещё до начала обратного хода. Фиксаторы направляющей и груза легко реализуются с помощью защёлок и рычажков, выходящих на тыльную сторону колеса и переключаемых с помощью специальных направляющих, причём потери на трение и переключение будут незначительны — ведь в момент освобождения защёлок вес груза не давит на фиксаторы. В данном случае придётся рассчитать 3 фазы положения груза. Для расчёта предположим, что перемещение груза длится время, соответствующее повороту на 1°, а направляющая становится горизонтальной (шар начинает катиться), когда угол между вертикалью и направлением от оси вращения к грузу равен 45°. В этом случае минимальное расстояние от оси колеса до груза r = (R · tg(α / 2)) / ((tg(α / 2) + 1) · sin(45°)), где R — расстояние от оси колеса до оси качания направляющей, а α — полный угол качания направляющей. Если ось качания направляющей совпадает с центром масс груза в рабочем положении, то приняв плечо при рабочем ходе за 100%, а полный угол качания направляющей равным 30°, получаем следующую таблицу.
В результате расчёта видно, что полезной работы получить опять не удалось, и графики позволяют наглядно увидеть, почему это происходит. Текущий момент и суммарная нормированная работа одного элемента в колесе с качающейся направляющей. Всё дело в том, что, возвратившись к оси, груз существенно опережает точку отсчёта, и когда во время обратного хода направляющая возвращается в исходное положение, он дважды проходит очень существенный угол с отрицательным вращающим моментом, что и съедает весь небольшой выигрыш от положительной разности моментов на рабочем ходу. Конкретные численные значения приведены в отдельной таблице пошагового изменения моментов. Теперь попробуем максимально удлинить направляющую, так чтобы шар начинал движение тогда, когда он находится точно над осью. Здесь перемещение направляющей проходит через ось, однако технически это несложно реализовать, если закрепить колесо консольно — лишь за один конец оси, а другой конец оси упрятать заподлицо с той его поверхностью, по которой перемещается направляющая. Такое изменение конструкции очень упрощает расчёт, и, кстати, здесь становится абсолютно очевидной жесткая геометрическая связь между углом качания направляющей и плечом груза в положении обратного хода. В случае, если ось качания направляющей совпадает с центром масс груза в рабочем положении, r = R · sin(α / 2), где r — плечо в положении обратного хода, R — плечо при рабочем ходе, α — полный угол качания направляющей. Колесо с удлинённой качающейся направляющей. Как и в первом варианте, предположим, что перемещение груза длится время, соответствующее повороту на 1°, приняв плечо при рабочем ходе за 100%, а полный угол качания направляющей равным 30°.
Здесь положение ещё несколько ухудшилось, поскольку углы опережения и отставания груза возросли, а разность моментов увеличилась не так сильно. Конкретные численные значения приведены в отдельной таблице пошагового изменения моментов. Текущий момент и суммарная нормированная работа одного элемента в модифицированном колесе с качающейся направляющей. Результат снова неутешительный! При попытке изменить другие соотношения частей конструкции мы вновь попадаем в заколдованный круг — если мы увеличим угол, в течение которого имеем большой положительный вращающий момент, то неизбежно на столько же увеличим и отрицательный момент во время обратного хода! РезюмеИтак, все рассмотренные здесь конструкции со свободно катающимися шарами не дают выигрыша, причём основной причиной является опережение грузом точки отсчёта при рабочем ходе и необходимость возврата его в исходное положение на обратном ходу, когда некоторые участки траектории с отрицательным вращающим моментом груз, по сути, проходит дважды — именно это и съедает всю полезную работу, полученную во время рабочего хода. Кстати, обратите внимание на то, что все результаты в замкнутом цикле получаются не близкими к нулю, а с достаточно большими отрицательным значениями. И это не случайность и не погрешность расчёта — дело в том, что движение шаров во всех рассмотренных конструкциях начинается плавно, но завершается резкой остановкой с неупругим ударом о стенку или ограничитель. Может быть, поможет принудительное перемещение грузов на рычагах? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| последняя правка 03.11.2009 21:26:58
|
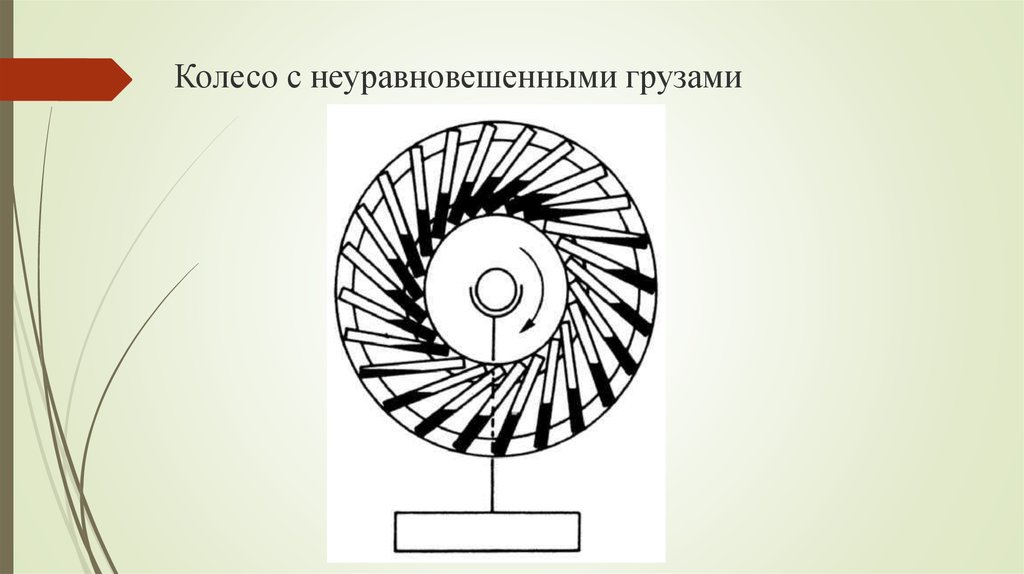
ВВЕДЕНИЕ «Вечным двигателем» называется такая воображаемая машина, которая, не заимствуя энергии извне, действовала бы безостановочно и совершала бы при том некоторую работу. Машина, которая поддерживала бы безостановочно только свое собственное движение, не производя никакой добавочной работы, не являлась бы «вечным двигателем» в строгом смысле этих слов. Осуществить «вечный двигатель» невозможно — это противоречило бы законам природы. Проследим, например, за пулей, пущенной вверх. Сопротивление воздуха и сила тяжести задерживают ее полет: пуля постепенно замедляет движение и, наконец, достигнув высшей точки своего пути, истощает всю свою скорость. Но исчезает ли при этом энергия пули, т. е. ее способность производить работу? Нет, потому что, во-первых, воздух, сдавливаемый летящей пулей, нагревается сам и нагревает пулю. Энергия движения пули частично переходит в тепловую энергию. Во-вторых, поднятая вверх пуля может теперь совершить при своем падении большую работу, чем когда она находилась внизу: ее «энергия положения» возросла. Мы видим, что запас энергии, первоначально сообщенный пуле, не исчез; он лишь преобразовался частью в тепловую энергию (воздух и пуля нагрелись), частью и энергию положения. Закон сохранения энергии не имеет ни одного исключения. Всякий раз, когда мы встречаемся с явлением, повидимому, противоречащим этому закону, при более внимательном рассмотрении обнаруживается ошибка в наблюдении или в рассуждении. Все проекты вечных двигателей, придуманные многочисленными изобретателями, заключают в себе какую-нибудь ошибку. Тем не менее, число искателей вечного двигателя еще и в настоящее время довольно велико. Не так давно была даже сделана в США бесплодная попытка осуществить вечный двигатель в промышленности; проект состоял в использовании энергии жидкого воздуха для приготовления другой порции жидкого воздуха в таком же количестве. В нашей книжечке описан десяток типичных проектов «вечного двигателя» и показана их несостоятельность. Разбор примеров мнимых «вечных двигателей» может предостеречь иных читателей от бесплодных попыток обойти закон сохранения энергии. Для понимания дальнейшего полезно остановиться предварительно на рассмотрении одного вопроса. Разберем, при каких условиях тело, могущее вращаться вокруг оси, придет во вращение под действием нескольких сил. Пусть (см. рис. стр. 6) к диску, насаженному на ось О, подвешены в точках а, b, с, d грузы А, В, С, D. Повернется ли диск и, если повернется, то в какую сторону? Чтобы узнать это, нужно — учит механика — вычислить так наз. «моменты» действующих на диск сил. Это значит, что надо найти произведение величины каждой силы на расстояние ее направления от оси вращения. В нашем случае: момент силы А = А × Oa1 » » В = В × Ob1 и т. Если сумма моментов всех сил, стремящихся повернуть диск вправо, равна сумме моментов сил, поворачивающих его влево, то — как учит механика, — диск вращаться не будет. Если же такого равенства нет, диск будет вращаться под действием избытка моментов сил. Эти соображения понадобятся нам при разборе некоторых проектов мнимых вечных двигателей. 1. Колесо с грузами При вращении этого колеса рычаги с грузами сами откидываются, занимая в левой половине колеса такое положение при котором грузы удалены от оси больше, чем в правой половине. По мнению изобретателя, левая сторона колеса должна всегда перевешивать правую; поэтому колесо будет непрерывно вращаться в направлении стрелки и может служить неисчерпаемым источником энергии. Что же произойдет с этим колесом в действительности? 2. Колесо с перекатывающимися шарами Тяжелые шарики, свободно перекатывающиеся в прорезах этого колеса, располагаются в правой его половине дальше от оси, нежели в левой; так будет при любом положении колеса. Изобретатель полагает поэтому, что такое колесо должно непрерывно вращаться в направлении стрелки и может служить неисчерпаемым источником энергии. Что же в действительности будет происходить с таким колесом? 3. На наклонных плоскостях Через трехгранную призму перекинута цепь из тяжелых шаров, свешивающаяся внизу гирляндой. Мы видим, что цепь тянут в левую сторону своим весом 4 шара, в правую — 2 шара Можно ожидать поэтому, что вся цепь будет увлекаться избытком силы в непрерывное движение и может служить неисчерпаемым источником энергии. Что же в действительности произойдет с этой цепью? 4. Самодвижущаяся цепь В правой части этого механизма цепь длиннее и потому тяжелее, чем в левой. Изобретатель полагает, что правая часть цепи будет всегда перевешивать левую; эта причина обусловить непрерывное движение цепи и колес в направлении стрелок, создав неисчерпаемый источник энергии. Что же произойдет с цепью в действительности? 5. Ведра на концах коромысла АВ, достигая попеременно дна верхнего бассейна, автоматически наполняются водой; опустившись же до уровня нижнего бассейна, они задевают за шесты С и D и опоражниваются. Этим поддерживается качание коромысла. Вода, выливающаяся из ведер, возвращается в верхний бассейн насосами E и F, которые приводятся в действие качанием коромысла. По мнению изобретателя, такая установка должна работать безостановочно и может служить неисчерпаемым источником энергии. Что же в действительности произошло бы с подобной установкой? 6. По закону Архимеда В стенке сосуда с жидкостью вставлено на оси колесо так, что жидкость не может просачиваться между колесом и стенкой. Часть колеса, находящаяся в жидкости, должна быть, по закону Архимеда, легче той части, которая находится вне сосуда. Изобретатель полагает, что так как наружная половина колеса при всех его положениях будет тяжелее, чем погруженная, то колесо должно находиться в непрерывном вращении и может служить неисчерпаемым источником энергий. |
Perpetual Motion Toy — Etsy.de
Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии.
Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.
Найдите что-нибудь памятное,
присоединяйтесь к сообществу, делающему добро.
(62 релевантных результата)
10 захватывающих попыток создания вечного двигателя
Вечный двигатель — это механизм, который после запуска не останавливается и не требует дополнительной энергии для продолжения работы. Это означает, что машину можно использовать как источник неограниченной бесплатной энергии. Это здорово, так почему бы нам просто не сделать его? Ну, это не из-за какой-то теории заговора в энергетическом секторе. Причина, по которой ни один из них никогда не был построен, заключается в том, что их на самом деле невозможно построить, поскольку вечный двигатель нарушает первые два закона термодинамики. Первый закон заключается в том, что энергия постоянна; его нельзя создать или уничтожить. Во-вторых, энтропия либо увеличится, либо останется неизменной. По сути, вы никогда не сможете получить больше выходной энергии, чем вводится, и энергия всегда будет уменьшаться с течением времени.
Это означает, что машину можно использовать как источник неограниченной бесплатной энергии. Это здорово, так почему бы нам просто не сделать его? Ну, это не из-за какой-то теории заговора в энергетическом секторе. Причина, по которой ни один из них никогда не был построен, заключается в том, что их на самом деле невозможно построить, поскольку вечный двигатель нарушает первые два закона термодинамики. Первый закон заключается в том, что энергия постоянна; его нельзя создать или уничтожить. Во-вторых, энтропия либо увеличится, либо останется неизменной. По сути, вы никогда не сможете получить больше выходной энергии, чем вводится, и энергия всегда будет уменьшаться с течением времени.
Хотя построить вечный двигатель может быть невозможно, с 1200-х годов его пытались создать изобретатели из самых разных слоев общества, и вот 10 самых интересных проектов.
10. Самотекущая колба Бойля
Одна из самых простых идей вечного двигателя принадлежит ирландскому химику и физику XVII века Роберту Бойлю. Его конструкция состоит в том, чтобы просто иметь бак с водой со шлангом на дне, по которому вода течет прямо из бака 9.0121 обратно в тот же бак. Конечно, эта система не работает, потому что гравитация так не работает. Чтобы вода вышла из бака, она должна стекать в емкость, которая ниже первоначальной. Если вы нам не верите, вы можете проверить это с материалами, которые есть у вас дома, или вы можете легко купить их в магазине за доллар.
Его конструкция состоит в том, чтобы просто иметь бак с водой со шлангом на дне, по которому вода течет прямо из бака 9.0121 обратно в тот же бак. Конечно, эта система не работает, потому что гравитация так не работает. Чтобы вода вышла из бака, она должна стекать в емкость, которая ниже первоначальной. Если вы нам не верите, вы можете проверить это с материалами, которые есть у вас дома, или вы можете легко купить их в магазине за доллар.
Но что, если бы можно было использовать химическую жидкость, которая постоянно реагировала и проталкивала жидкость через шланг? Например, на видео выше ютубер пробует пиво (хороший выбор!), и оно, по крайней мере, проталкивает жидкость через шланг. Проблема в том, что цикл остановится, когда пиво перестанет газироваться. Однако, опять же, найти химическое вещество, которое никогда не прекращает реагировать, так же невозможно, как и создать любой другой тип вечного двигателя.
9. Монополюсный магнит
» src=»https://www.youtube.com/embed/xR6Qait2JGY?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>
Магниты имеют два полюса, северный и южный, и противоположные полюса притягивают магниты друг к другу, а те же полюса раздвигают их. Но есть также гипотетические монопольные магнитные частицы, у которых будет только один полюс. В 2014 году исследователи создали синтетические монопольные магнитные частицы, спустя 85 лет после их появления. Несмотря на то, что они были обнаружены совсем недавно, некоторые ютуберы утверждают, что построили или купили их, и есть несколько магнитов, которые, как утверждается, являются монополиями на Alibaba. Конечно, мы должны сказать, покупатель остерегается.
Если бы мы могли построить монопольные магниты, они могли бы привести к свободной энергии. В видео к этой статье мужчина создает предполагаемую машину свободной энергии, используя материал стоимостью в несколько долларов из хозяйственного магазина и монопольный магнит, который он купил на eBay. Он забивает два гвоздя в доску и прорезает в гвоздях крошечные прорези, чтобы удерживать проволоку, образующую кольцо. Между двумя гвоздями и под кольцом он помещает магнит, который заставляет спиральную проволоку вращаться, создавая энергию.
Он забивает два гвоздя в доску и прорезает в гвоздях крошечные прорези, чтобы удерживать проволоку, образующую кольцо. Между двумя гвоздями и под кольцом он помещает магнит, который заставляет спиральную проволоку вращаться, создавая энергию.
Самая большая проблема с этим типом машин, помимо отсутствия научных доказательств того, что монопольные магниты реальны, заключается в том, что материалы испытывают слишком большое трение, поэтому их придется заменять, а это означает, что это никогда не будет настоящим вечным двигателем. машина.
8. Колесо с катящимся шариком
Эта попытка создать вечный двигатель была разработана немецким математиком, ученым и физиком Якобом Леупольдом, и ее дизайн был опубликован в его Theatrum Machinarum Generale Том.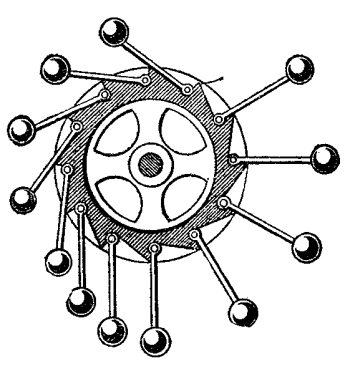 1 в 1724 году. В машине используется балансировочное колесо и катящиеся шарики.
1 в 1724 году. В машине используется балансировочное колесо и катящиеся шарики.
Идея состоит в том, что шарики всегда будут катиться, что смещает вес колеса, а гравитация просто берет верх. К сожалению, хотя может показаться, что это может работать в теории, это не так, потому что для продолжения работы требуется внешняя помощь.
7. Водяная мельница и насос
Считается, что конструкции водяной мельницы и вечного двигателя насоса, а также их варианты, существуют с 1600-х годов, а вполне возможно, и раньше. Идея состоит в том, что вода падает с верхней части машины, что заставляет вращаться водяную мельницу и, в конечном итоге, приводит в действие насос, который возвращает воду наверх, создавая цикл энергии.
Проблема в том, что в дизайне слишком много трения, и он фактически не работает вне компьютерных моделей. Итак, вернемся к старой чертежной доске? Боже, вы ожидаете большего от своих научных теоретиков 17-го века.
Итак, вернемся к старой чертежной доске? Боже, вы ожидаете большего от своих научных теоретиков 17-го века.
6. Зубчатое колесо Пауля Шеербарта с грузовым приводом
Пол Шеербарт, родившийся в Германии, не был математиком или инженером, как многие другие изобретатели из этого списка. Вместо этого он был писателем, известным своими произведениями в фантастическом жанре. Несмотря на отсутствие формального образования, Шеербарт провел два с половиной года, пытаясь построить вечный двигатель в прачечной своего дома. Его машина, которая выглядит странно знакомой, была наконец обнаружена в 1910 в своей книге Вечный двигатель: история одного изобретения .
В системе используется одно большое колесо, два набора роликов меньшего размера и груз. Проблема с его конструкцией, как и со многими другими вечными двигателями, заключается в том, что главному зубчатому колесу требуется внешняя энергия, чтобы поддерживать свой импульс. Тем не менее, это по-прежнему лучший вечный двигатель, созданный писателем-фантастом.
Проблема с его конструкцией, как и со многими другими вечными двигателями, заключается в том, что главному зубчатому колесу требуется внешняя энергия, чтобы поддерживать свой импульс. Тем не менее, это по-прежнему лучший вечный двигатель, созданный писателем-фантастом.
5. Магниты и гравитация
Физической постоянной на Земле является гравитация, что плохо, если вы ужасный, но преданный канатоходец, но это хорошая новость с точки зрения создания вечных двигателей, потому что это постоянный источник силы. Попыткой создать вечный двигатель, использующий эту силу, является вечное колесо, запатентованное в 1823 году. Это довольно простая конструкция: большое колесо вращается маленьким железным шариком, который притягивается к магниту.
Хотя видео выше может выглядеть так, как будто это осуществимо, на самом деле колесо не вращается так без посторонней помощи; также через некоторое время магниты размагничиваются, а это означает, что это не неограниченный источник энергии.
4. Сила гравитации Вечный двигатель
В этом так называемом вечном двигателе используются два вертикальных стержня. Стержень в центре прямой, а второй наклонен. Затем идут три горизонтальных стержня, которые пересекают два вертикальных стержня и соединяют оба вертикальных стержня. Наконец, к центральному стержню прикреплен груз. Это означает, что крутящий момент против часовой стрелки и крутящий момент по часовой стрелке равны, и, поскольку крутящие моменты одинаковы, вертикальный стержень сильнее давит на нижний рычаг, чем на верхний. Поскольку верхний и нижний стержни находятся на одинаковом расстоянии от вертикальных осей, крутящий момент толкает в одну сторону больше, чем в другую, что позволяет системе вращаться.
Поскольку верхний и нижний стержни находятся на одинаковом расстоянии от вертикальных осей, крутящий момент толкает в одну сторону больше, чем в другую, что позволяет системе вращаться.
Автор Wired проанализировал это конкретное видео и считает, что в машине есть скрытые двигатели. Если нет, то он считает, что вращение вызвано угловым моментом и крутящим моментом. Это означает, что он будет вращаться некоторое время, но не постоянно.
3. Неодимовые магниты
Самыми сильными коммерчески доступными батареями являются неодимовые магниты, которые были разработаны General Motors в 1982 году. Эта конструкция использует преимущества этих батарей и создает импульс путем размещения магнитов с одинаковыми полюсами друг против друга на рулевое колесо. Когда два магнита с одинаковыми полюсами встречаются, они отталкивают друг друга, и в этом случае колесо вращается.
Когда два магнита с одинаковыми полюсами встречаются, они отталкивают друг друга, и в этом случае колесо вращается.
Преимущество этой конструкции в том, что она не имеет трения, что является особенно большим преимуществом по сравнению с другими предлагаемыми вечными двигателями, поскольку трение приводит к энтропии, то есть машина в конечном итоге замедляется. Основная причина, по которой это не настоящий вечный двигатель, заключается в том, что магниты в конечном итоге перестанут работать и их необходимо будет заменить.
2. Perepiteia
Тейн Хейнс, бросивший колледж из Канады, работает над вечным двигателем под названием Perepiteia с 19 лет.85. Хайнс настолько предан машине, что говорит, что из-за нее потерял жену и опеку над двумя своими детьми. Так что, вы знаете, его приоритеты могут быть немного искажены.
Так что, вы знаете, его приоритеты могут быть немного искажены.
Тем не менее, Хайнс говорит, что он настолько предан делу, потому что он утверждает, что машина способна генерировать большое количество энергии от небольшого электрического входа, который считался невозможным. Что интересно, тесты показывают, что генератор каким-то образом превращает магнитное трение в магнитное ускорение, которое заставляет двигатель ускоряться, создавая петлю положительной обратной связи. Если тесты верны, это будет означать, что Перепития нарушает первый закон термодинамики. Это похоже на лампочку, которая питает себя, используя энергию собственного света.
В 2008 году Хайнс показал Перепитейю профессору Массачусетского технологического института Маркусу Зану, который является экспертом в области электромагнитных и электронных систем. Зан сказал, что Перепития изначально поставила его в тупик, и машина определенно заслуживает внимания. Но позже он пояснил, что это не вечный двигатель, потому что его нужно подключать к стене. Тем не менее, Зан говорит, что машина все еще может стать важным открытием, которое может улучшить двигатели. Несмотря на то, что есть много скептиков, Хайнс надеется, что его изобретение приведет к созданию электромобилей, которые сами будут питаться за счет ускорения и торможения.
Тем не менее, Зан говорит, что машина все еще может стать важным открытием, которое может улучшить двигатели. Несмотря на то, что есть много скептиков, Хайнс надеется, что его изобретение приведет к созданию электромобилей, которые сами будут питаться за счет ускорения и торможения.
1. Вечный двигатель Финсруда
https://www.youtube.com/watch?v=tlx2PgESXhs
Многие из предложенных машин довольно просты и используют минимальное количество деталей. На другом конце спектра находится предполагаемый вечный двигатель норвежского скульптора и математика Рейдара Финсруда. Это сложная система, в которой используются колесо, магниты и маятники. Его система гарантирует, что колесо всегда наклоняется, поэтому шарик, который притягивается магнитами, всегда катится по дорожке.
Предположительно, во время испытаний, проводившихся в течение трех дней, мяч сохранял постоянную скорость, измеряемую с точностью до 1/25 секунды. Инженер, изучавший машину, сказал, что она может поддерживать КПД 80-90%, в то время как большинство устройств, таких как двигатель внутреннего сгорания, имеют КПД только 30-50%.

.jpg)
 Следует подчеркнуть, что R1 и R2 — это не радиусы ступицы и обода, а расстояние от оси колеса до центра масс груза при обратном и рабочем ходе соответственно.
Следует подчеркнуть, что R1 и R2 — это не радиусы ступицы и обода, а расстояние от оси колеса до центра масс груза при обратном и рабочем ходе соответственно. Теперь можно выполнить расчёт для нескольких соотношений R1 и R2 в предположении, что перемещение груза длится один шаг после горизонтального положения спицы — рабочий ход начинается при повороте точки отсчёта на 1°, а обратный — начиная со 181°.
Теперь можно выполнить расчёт для нескольких соотношений R1 и R2 в предположении, что перемещение груза длится один шаг после горизонтального положения спицы — рабочий ход начинается при повороте точки отсчёта на 1°, а обратный — начиная со 181°.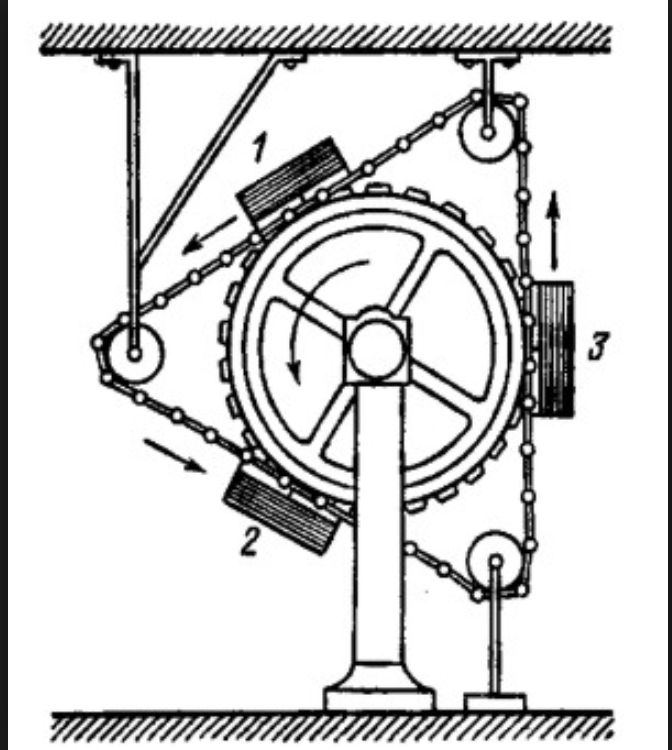 2°
2° 1°, 3600 шагов) и сразу же пропорционально уменьшится мнимый выигрыш!
1°, 3600 шагов) и сразу же пропорционально уменьшится мнимый выигрыш!

 Выбор точки отсчёта позволяет свести задачу к решению прямоугольных треугольников с известными катетами. Расстояние до центра в этом случае равно гипотенузе этого треугольника, а угол опережения — арктангенсу отношения меньшего катета a (тангенциального относительно обода) к большему b (ориентированному по нормали, т.е. перпендикулярно ободу). Предположив, что перемещение груза длится время, соответствующее повороту на 1°, получаем следующую таблицу.
Выбор точки отсчёта позволяет свести задачу к решению прямоугольных треугольников с известными катетами. Расстояние до центра в этом случае равно гипотенузе этого треугольника, а угол опережения — арктангенсу отношения меньшего катета a (тангенциального относительно обода) к большему b (ориентированному по нормали, т.е. перпендикулярно ободу). Предположив, что перемещение груза длится время, соответствующее повороту на 1°, получаем следующую таблицу. .45°
.45° Попробуем же создать конструкцию, где весь положительный вращающий момент сосредоточен в середине рабочего хода, а к началу обратного хода груз уже давно переместился на минимальное расстояние от оси вращения.
Попробуем же создать конструкцию, где весь положительный вращающий момент сосредоточен в середине рабочего хода, а к началу обратного хода груз уже давно переместился на минимальное расстояние от оси вращения.
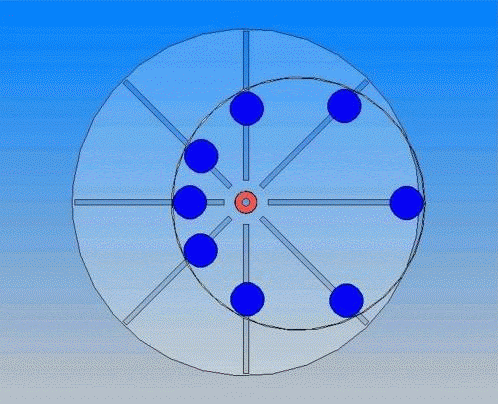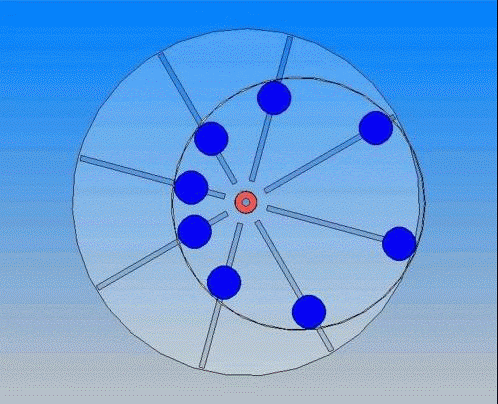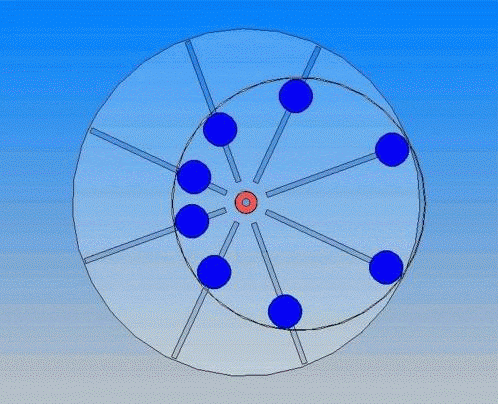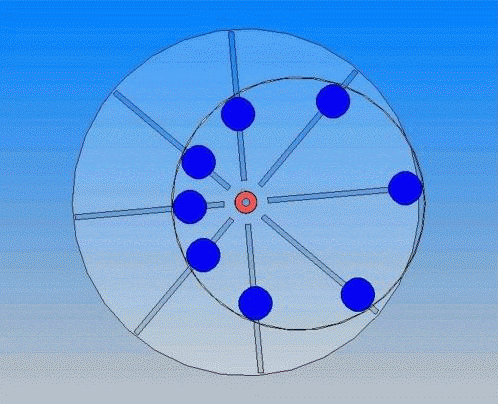 .75°
.75°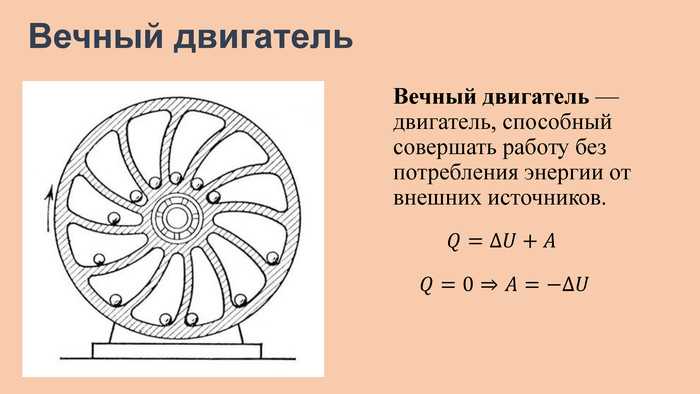
 Тогда получаем следующую таблицу.
Тогда получаем следующую таблицу.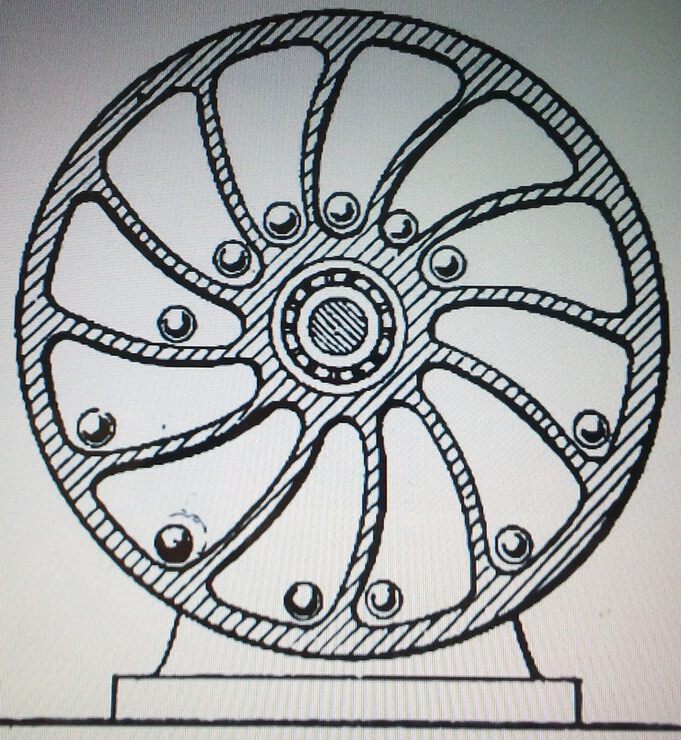
 При этом кинетическая энергия шара за счёт деформации материалов в момент удара превращается в тепловую, безвозвратно покидая «механический» цикл. Эти потери и обуславливают заметно отрицательный результат, хотя в расчётах этот фактор в явном виде нигде не учитывается!
При этом кинетическая энергия шара за счёт деформации материалов в момент удара превращается в тепловую, безвозвратно покидая «механический» цикл. Эти потери и обуславливают заметно отрицательный результат, хотя в расчётах этот фактор в явном виде нигде не учитывается! Нельзя создавать энергию ни из чего: энергия не создается, а лишь преобразуется из одного вида в другой. Таков основной закон всего естествознания, закон сохранения энергии, открытый в середине прошлого столетия Юлием Робертом Майером (стодвадцатипятилетие со дня рождения которого истекает в 1939 г.).
Нельзя создавать энергию ни из чего: энергия не создается, а лишь преобразуется из одного вида в другой. Таков основной закон всего естествознания, закон сохранения энергии, открытый в середине прошлого столетия Юлием Робертом Майером (стодвадцатипятилетие со дня рождения которого истекает в 1939 г.).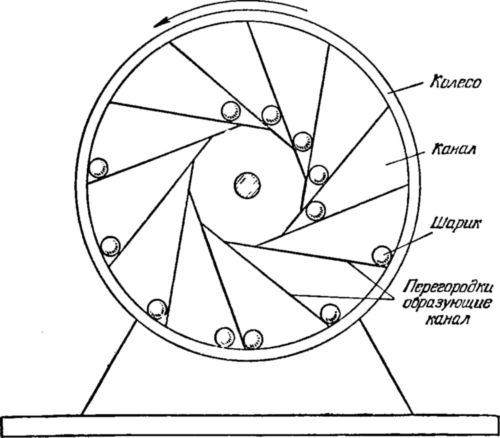 — Будем следить за пулей дальше. Достигнув высшей точки своего подъема, она начинает падать с возрастающей скоростью. Но энергий ее движения не создается при этом ни из чего: она получается здесь за счет уменьшения энергии положения, так как при падении с меньшей высоты пуля способна произвести и меньшую работу. Во время движения пули вверх и вниз первоначальный запас ее энергии меняет свою форму, но количественно остается неизменным. Так же происходит и во всех других случаях кажущегося исчезновения и появления энергии.
— Будем следить за пулей дальше. Достигнув высшей точки своего подъема, она начинает падать с возрастающей скоростью. Но энергий ее движения не создается при этом ни из чего: она получается здесь за счет уменьшения энергии положения, так как при падении с меньшей высоты пуля способна произвести и меньшую работу. Во время движения пули вверх и вниз первоначальный запас ее энергии меняет свою форму, но количественно остается неизменным. Так же происходит и во всех других случаях кажущегося исчезновения и появления энергии. Предприятие, разумеется, кончилось полным провалом.
Предприятие, разумеется, кончилось полным провалом. д.
д.
 Самодействующая водокачка
Самодействующая водокачка