ТЕХНОЛОГИИ, ИНЖИНИРИНГ, ИННОВАЦИИ. Возможности квантового компьютера

ТОП 10:

Осенью 1994 г. мне позвонил Джефф Кимбл, профессор физики Калифорнийского технологического института. Джефф прочел пару моих статей о квантовых вычислениях и хотел обсудить возможность создания квантовых логических элементов на основе фотонов.

Джефф Кимбл – долговязый техасец, который хорошо умеет обращаться с атомами и светом. Его представили мне как человека, который «так сильно сжал свет, как до него еще никому не удавалось», и если этот свет чувствовал себя так же, как моя рука после рукопожатия Джеффа, я склонен этому верить. Мы начали беседу, и я заметил две вещи. Во-первых, Джефф без всяких колебаний говорит то, что думает. Если он смотрит на ваше уравнение и произносит, со своим мягким техасским акцентом, что «есть проблема в Ривер-сити»[39], это значит, что вы в беде. Во-вторых, когда он описывает свои эксперименты, я понимаю примерно одно слово из трех.

Той осенью, неделю за неделей, я много общался с Джеффом и его студентами, и постепенно стал понимать, чем они занимаются. Джефф брал отдельные фотоны и заставлял их взаимодействовать с отдельными атомами. По сути, он помещал фотон в емкость с атомом и встряхивал их. Емкость представляла собой оптическую полость, состоящую из двух зеркал на расстоянии нескольких миллиметров друг от друга. Фотон десятки тысяч раз метался туда-сюда между зеркалами, пока, наконец, не вырывался на свободу. Джефф вводил в полость атомы цезия, в то же время освещая ее фотонами лазерного пучка, а потом смотрел, что получилось. Каждый фотон и каждый атом проводили в небольшом пространстве оптической полости существенную долю секунды, и у них было достаточно времени для взаимодействий друг с другом.

Атом очень маленький, его диаметр – одна десятимиллиардная метра, а фотон (как ни странно) может быть гораздо больше. Как мы помним, фотоны – это частицы света, возникающие из колебаний электромагнитного поля. Из-за принципа неопределенности Гейзенберга существует компромисс между скоростью, с которой колеблется электромагнитное поле, и объемом, который занимает фотон: чем лучше определена частота колебаний поля, тем больший объем пространства занимает фотон. Фотоны, которые Джефф Кимбл запускает в свои оптические полости, имеют очень хорошо определенную частоту, а поэтому они тощие и длинные – в сотню метров длиной! Но длина самой полости – всего несколько миллиметров. Как же нечто длиной в 100 метров может поместиться в таком маленьком пространстве? Мне потребовалось некоторое время, чтобы это уяснить. Оказывается, фотон входит в полость так же, как змея вползает в банку из-под кофе: он складывается вдоль тысячи раз. В результате такого сворачивания, сила электромагнитного поля, соответствующего отдельному фотону, внутри полости в тысячи раз выше, чем снаружи. Поэтому фотон в полости очень сильно взаимодействует с атомом, находящимся в ней в этот момент.

Джефф и его студенты Квентин Тюршетт, Кристина Худ и Хидео Мабути в это время проводили эксперименты, в которых запускали два фотона в оптическую полость, где в тот момент находился атом, и смотрели, что происходило с фотонами, когда они выходили из полости. Оба фотона сильно взаимодействовали с атомом, а поэтому сильно взаимодействовали и друг с другом. Но было ли это взаимодействие достаточным, чтобы создать квантовые логические элементы, например схему «условное не»? Когда мы начали эксперименты, Джефф не знал, как действуют квантовые логические элементы, а я не знал, как ведут себя фотоны. После окончания экспериментов я показал, что почти любого взаимодействия между фотонами достаточно для создания квантового логического элемента, а Джефф и его студенты смогли предъявить первые фотонные квантовые логические элементы.

В то же самое время Дейв Уайнленд и Крис Монро из Национального института стандартов и технологии (NIST) в Боулдере экспериментально реализовали предложения Игнасио Сирака и Петера Цоллера из Университета Инсбрука по поводу архитектуры квантовых компьютеров, основанной на том, чтобы улавливать ионы с помощью колеблющегося электромагнитного поля, а затем обстреливать их лазерами. Ионы – это атомы, лишенные электрона, у них суммарный заряд является положительным, благодаря чему их несложно «поймать». (Старый физический анекдот: два атома заходят в бар. Один атом осматривает себя и говорит: «Эй, я потерял электрон!» – «Ты уверен?» – спрашивает второй атом. «Положительно!» – отвечает первый атом.) Когда ионы «пойманы», их можно охладить до очень низкой температуры и обстреливать лазером, чтобы заставить взаимодействовать и выполнять квантовые логические операции.

Эксперименты Кимбла и Уайнленда были проведены на уже существующих, хотя и модернизированных экспериментальных установках. Относительная легкость, с которой были выполнены первые квантовые логические операции, позволила предположить, что квантовый компьютер действительно можно создать.

Когда я начал работать в Массачусетском технологическом институте в декабре 1994-го, я стал сотрудничать с учеными и инженерами со всех концов мира в попытке создать квантовый компьютер. Дэвид Кори, профессор ядерной техники Массачусетского технологического института, вместе со своими коллегами Тимом Хэвелом и Амиром Фами показал, как можно заставить ядерные спины вычислять с помощью обстрела атомов, описанного выше. В применении к ядерным спинам, эти методы называют «ядерным магнитным резонансом» (ЯМР).

Вскоре после этого и независимо от них Нейл Гершенфельд из Media Lab Массачусетского технологического института выяснил, как можно использовать ЯМР для вычисления, и я начал работать вместе с Нейлом и с Айзеком Чуаном над простыми квантовыми вычислениями с помощью ЯМР. Построив всего лишь двухбитовый квантовый компьютер, мы смогли продемонстрировать квантовый параллелизм, заставив его выполнять несколько задач одновременно. Позже Чуан стал разрабатывать квантовые компьютеры ЯМР-типа все больших и больших размеров, и несколько лет назад он создал компьютер на семи кубитах, способный реализовать простую версию алгоритма Шора. Чуан использовал этот компьютер, чтобы разложить на множители число 15. Конечно, предстоит еще очень много сделать, прежде чем появится квантовый компьютер, способный разложить на множители число из 400 цифр[40]!

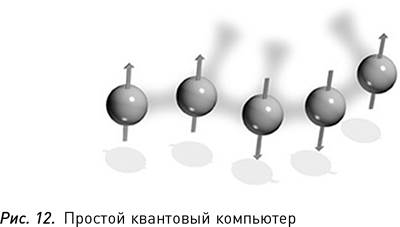
Простой квантовый компьютер можно собрать из цепочки ядерных спинов в молекуле. На рисунке ядерные спины имеют направления «вверх», «вверх», «вниз», «вниз», «вверх», иначе говоря, в них записаны квантовые биты 00110

Я продолжал сотрудничать с Джеффом Кимблом в области хранения и передачи квантовых битов на фотонах. Кроме того, я начал работать вместе с учеными из Массачусетского технологического института, чтобы заставить свет взаимодействовать с атомами. Джеффри Шапиро, Франко Вонг и Селим Шахрияр из Исследовательской лаборатории электроники изучали возможности квантовой связи, и вскоре мы написали предложение по созданию самого мощного в мире источника запутанных фотонов, а также описали метод, позволяющий «ловить» эти фотоны с помощью атомов, запертых в оптических полостях. Эта технология, как и сходные методы, предложенные Кимблом, Сираком и Цоллером, сформировали основу для попытки создать квантовый интернет – сеть квантовых компьютеров, оптически связанных друг с другом. (Сейчас я работаю над разработкой системы поиска в квантовом интернете с рабочим названием «Quoogle».)

В тот же период я начал сотрудничать с Хансом Моэем из Делфтского технологического университета. Мы искали возможность создания квантовых компьютеров с помощью сверхпроводящих систем. В сверхпроводнике электроны не испытывают почти никакого сопротивления при перемещении с места на место. Такой поток электронов в сверхпроводнике называют сверхтоком. Сверхпроводимость можно описать и иначе: атомам материала, в котором движутся электроны, трудно захватывать эти электроны. Это означает, что электроны могут двигаться сквозь материал, сохраняя при этом квантовую когерентность: они остаются запутанными. Ханс Моэй и другие ученые, изучающие сверхпроводимость, указывают, что это «скользкое» свойство электронов сверхпроводимости можно использовать для выполнения квантовых вычислений. Если создать петлю из сверхпроводящего материала и разорвать ее в подходящих местах очень тонкими участками материала, не являющегося сверхпроводящим (они называются переходами Джозефсона), то получившееся устройство способно поддерживать сверхтоки, текущие либо по часовой стрелке, либо против. Такое устройство легко может хранить один бит информации: просто определим сверхток, текущий против часовой стрелки, как состояние 0, а текущий по часовой стрелке – как состояние 1.

Такая сверхпроводниковая квантовая система может содержать не только биты, но и кубиты. Мы вычислили, что если очень тщательно разработать сверхпроводящий бит, сведя к абсолютному минимуму взаимодействия между сверхтоком и его окружением, то сверхток можно перевести в квантово-механическую суперпозицию циркуляции по часовой стрелке и против часовой стрелки. На некотором уровне способность сверхтока проявлять такую квантовую суперпозицию не должна нас удивлять; в конце концов, сверхток состоит из электронов, а отдельный электрон вполне может находиться в двух местах сразу. Но сверхток может состоять из миллиардов электронов, а контур, по которому он циркулирует по часовой стрелке и против нее одновременно, так велик, что почти доступен для невооруженного глаза. Такая макроскопическая квантовая когерентность по-настоящему удивительна, и исследователи уже много десятилетий пытались ее продемонстрировать, но безуспешно.

Мы с Терри Орландо из Массачусетского технологического института и Хансом Моэем создали исследовательскую группу, и несколькими годами позже она продемонстрировала квантовые биты, которые можно поместить в такую макроскопическую квантовую суперпозицию. Эту демонстрацию осуществил ученик Моэя Каспар ван дер Вал. (Группа Джеймса Льюкенса в Университете Стоуни-Брук продемонстрировала макроскопические квантовые суперпозиции независимо и почти одновременно с нами.) В последние несколько лет Моэй и другие исследователи придумали и реализовали на практике когерентное управление сверхпроводящими кубитами. Простые квантовые компьютеры, состоящие из нескольких соединенных друг с другом сверхпроводящих кубитов, в настоящее время создаются и тестируются. Сейчас я работаю в Японии с Цай Чжаошэнем, Ясунобу Накамурой и Цуёси Ямамото[41]из корпорации NEC и пытаюсь выполнить первые простые квантовые вычисления со сверхпроводящими кубитами.

В течение прошедшего десятилетия мне посчастливилось работать над созданием квантовых компьютеров и квантовых систем связи вместе с некоторыми из лучших ученых-экспериментаторов мира. Я не могу постичь степень понимания природы вещей этими людьми, уж не говоря о том, чтобы приблизиться к ней самому. Эти экспериментаторы обладают глубочайшим теоретическим пониманием квантовой механики – пониманием, необходимым для того, чтобы создавать совершенно новые способы общения с атомами и фотонами и убеждения делать их то, чего они никогда не делали прежде.

Глава 7

Универсальный компьютер

Моделирование Вселенной

Мы показали, как можно использовать законы физики для эффективного выполнения квантовых вычислений. Теперь давайте посмотрим, как квантовый компьютер может эффективно моделировать «работу» законов физики.

«Квантовое моделирование» – это процесс, в ходе которого квантовый компьютер моделирует другую квантовую систему. Из-за квантовых странностей разных типов классические компьютеры могут моделировать квантовые системы лишь громоздким и неэффективным образом. Но квантовый компьютер сам по себе является квантовой системой, способной демонстрировать полный спектр квантовых странностей, поэтому он может эффективно моделировать другие квантовые системы. Каждая из частей моделируемой квантовой системы отображается на набор кубитов в квантовом компьютере, и взаимодействия между этими частями становятся последовательностью квантовых логических операций. Такое моделирование может быть настолько точным, что поведение компьютера будет неотличимым от поведения самой моделируемой системы.

Вспомним, что, если две системы, обрабатывающие информацию, могут эффективно моделировать друг друга, они логически эквивалентны. Поскольку Вселенная может выполнять квантовые вычисления, а квантовый компьютер может моделировать Вселенную, Вселенная и квантовый компьютер обладают одной и той же мощностью обработки информации: по существу, они идентичны.

К настоящему времени квантовое моделирование является одной из самых замечательных экспериментальных демонстраций силы квантовых вычислений, а также их практическим применением, наиболее существенным для понимания идеи вычислительной Вселенной. Квантовые системы обычно делают много вещей сразу, поэтому их трудно моделировать классическим образом. Смоделировать один ядерный спин, который может делать две вещи квантово-параллельным образом, уже не так плохо, но 10 спинов могут выполнять 1024 дела сразу, 20 спинов могут сделать 1 048 576 дел сразу и т. д.

Как правило, чтобы проследить динамику квантовой системы, классический компьютер должен назначить отдельный расчет для каждой части квантовой волновой функции, но количество дел, которые выполняет квантовая система, растет очень быстро с ее размером. Смоделировать динамику даже относительно небольшой квантовой системы, состоящей из 300 ядерных спинов, как уже говорилось, совершенно невозможно.

Но квантовый компьютер не испытывает никаких затруднений, выполняя множество таких расчетов посредством квантового параллелизма. В 1982 г. Нобелевский лауреат Ричард Фейнман предложил гипотетическое устройство, которое он назвал универсальным квантовым имитатором. Чтобы смоделировать 300 ядерных спинов, универсальному квантовому имитатору потребовалось бы всего 300 квантовых битов. Если мы можем запрограммировать взаимодействия между 300 кубитами так, чтобы они имитировали взаимодействия между 300 спинами, то динамика кубитов сможет моделировать динамику спинов.

Фейнман просто указал на возможность существования универсального квантового имитатора; он не дал никаких ключей к тому, как его можно создать. В 1996 г. я показал, что обычные квантовые компьютеры как раз и являются универсальными квантовыми имитаторами; то есть любой желаемый набор квантово-механических взаимодействий можно запрограммировать на квантовом компьютере, и тогда можно выполнить квантовое моделирование путем многократного выполнения квантовых логических операций с кубитами компьютера[42]. (Методы квантового моделирования независимо от меня и примерно в это же время разработали Кристоф Залка из Бернского университета и Стивен Визнер из Тель-Авивского университета.)

Кроме того, я смог показать, что квантовое моделирование будет эффективным в том смысле, что, во-первых, количество кубитов, необходимых для моделирования, будет равно числу битов в моделируемой системе, а во-вторых, число операций, которые должен выполнить квантовый компьютер в процессе моделирования, будет пропорционально тем отрезкам времени, за которые система должна быть промоделирована.

Фейнман высказал догадку, а я доказал, что квантовые компьютеры могут функционировать как универсальные квантовые имитаторы, и их динамика может быть аналогом любой желаемой физической динамики. Квантовое моделирование происходит простым и непосредственным образом. Во-первых, отобразим части квантовой системы, которая будет промоделирована, на наборы квантовых битов; каждая часть моделируемой системы получает как раз достаточное количество кубитов для того, чтобы «схватить» ее динамику. Во-вторых, отобразим взаимодействия между частями системы на квантовые логические операции с кубитами, соответствующими частям системы. Универсальная природа квантовых логических операций гарантирует, что такие отображения способны выразить любую желаемую динамику.

Квантовое моделирование – не просто теоретическая концепция; оно было выполнено экспериментально, например в алгоритме поиска сомножителей Питера Шора. Однако в отличие от алгоритма Шора, который до сих пор позволил разложить на сомножители только число 15, квантовое моделирование было выполнено в масштабах, которые не может повторить классический компьютер. В течение нескольких последних лет группа Дэвида Кори в Массачусетском технологическом институте выполнила квантовое моделирование с миллиардами и миллиардами кубитов. Такими квантовыми имитаторами являются кристаллы фтористого кальция (мне нравится называть их «оружейной зубной пастой»). Их диаметр около сантиметра, они светло-пурпурного цвета, который придают этому веществу следовые количества атомов других типов. Каждый такой кристалл содержит больше миллиарда миллиардов атомов. Используя методы квантового ЯМР-вычисления для манипулирования ядерными спинами в кристаллах, Кори заставил эти спины вступать в самые разные взаимодействия, причем бо льшая их часть не встречается в природе. Чтобы смоделировать такую искусственную квантовую динамику на обычном классическом компьютере, потребовалось бы два в степени миллиард миллиардов элементарных расчетов. Таким образом, квантовые имитаторы Кори намного мощнее любого классического компьютера, существующего или в принципе возможного.

Квантовое моделирование Кори – на сегодня, бесспорно, наиболее впечатляющий пример квантовых вычислений. Но когда я впервые представил его результаты в своих лекциях, то был удивлен: многие слушатели стали возражать против того, чтобы назвать такое массивное квантовое моделирование вычислением. «Это не вычисление; это – эксперимент!» – утверждали они. Мне было нелегко понять такую реакцию. Конечно, Кори проводил эксперимент, а именно, эксперимент по квантовой обработке информации. По-видимому, это и смутило некоторых слушателей. Даже если они соглашались, что Кори выполнял вычисления, то считали, что это были аналоговые квантовые вычисления. Им было сложно воспринимать эти аналоговые квантовые вычисления как «цифровые» квантовые вычисления, вроде алгоритмов разложения на множители или поиска.

Чем отличаются аналоговые и цифровые компьютеры? Классический аналоговый компьютер манипулирует непрерывными переменными , например напряжением. Так происходит потому, что классические переменные, такие как положение, скорость, давление и объем, непрерывны, и чтобы моделировать классическую динамику, аналоговый компьютер тоже должен быть непрерывным. Классический цифровой компьютер имеет дело с дискретными величинами , ведь биты дискретны; он может иметь дело с непрерывными величинами, но только превратив их в дискретные.

Однако для квантового компьютера нет разницы между аналоговыми и цифровыми вычислениями. Кванты, по определению, дискретны, и их состояния могут быть отображены на состояния кубитов непосредственно, без аппроксимации. Но вместе с тем кубиты также и непрерывны, из-за своей волновой природы; их состояния могут быть непрерывными суперпозициями. И аналоговые квантовые компьютеры, и цифровые квантовые компьютеры состоят из кубитов; и аналоговые квантовые вычисления, и цифровые квантовые вычисления происходят посредством логических операций между этими кубитами. Наша классическая интуиция подсказывает, что аналоговые вычисления по сути своей непрерывны, а цифровые вычисления должны быть дискретными. Но когда дело касается квантовых вычислений, как, впрочем, и во многих других случаях, классическая интуиция нас подводит. Аналоговый квантовый компьютер и цифровой квантовый компьютер – это одно и то же устройство.

Моделирование и реальность

Вопрос о разнице между моделированием и реальностью возник очень давно. В VI в. до нашей эры в первых строках «Дао дэ цзин», «Книги пути и достоинства», Лао Цзы описал проблему, свойственную любому описанию реальности: «Путь, которым можно следовать, не есть истинный Путь. Имя, которое может быть названо, не есть истинное Имя». Оригинальный китайский текст «Дао дэ цзин» очень компактен и его можно толковать 10 000 способов, но Лао Цзы, кажется, полагает, что, давая вещам названия и для этого назначая словам то или иное значение, мы вводим искусственные различия, которые не могут охватить всю полноту Вселенной. (В виде автомобильной наклейки на бампер эта же мысль выглядит так: «Не говори об этом. Будь этим».) Философ Арчи Бам предложил менее буквальный перевод этого высказывания: «Природу невозможно описать полностью, ведь такое описание природы должно было бы в точности воспроизводить природу». Иначе говоря, совершенное описание Вселенной было бы неотличимо от самой Вселенной.

Давайте посмотрим, что произойдет, если применить изречение Лао Цзы к квантовому компьютеру, моделирующему Вселенную. Как мы увидим, Вселенная, по крайней мере доступная нам часть Вселенной, конечна в пространстве и времени. Все фрагменты доступной нам части Вселенной можно в принципе отобразить на конечное число кубитов. Аналогичным образом физическая динамика Вселенной, состоящая из взаимодействий между этими частями, может быть отображена на логические операции с этими кубитами.

Нельзя сказать, что мы точно знаем, как провести такое отображение. Мы знаем, как отобразить поведение элементарных частиц на кубиты и логические операции. Иначе говоря, мы знаем, как Стандартная модель физики элементарных частиц – модель, описывающая наш мир с поразительной точностью, – может быть отображена в квантовом компьютере. Но мы еще не знаем, как в квантовом компьютере может быть отображено поведение гравитации, по той простой причине, что физики еще не пришли к полной теории квантовой гравитации. Мы еще не знаем, как моделировать Вселенную, но, возможно, скоро узнаем.

Теперь вспомним «Дао дэ цзин». В квантовом компьютере, моделирующем Вселенную, будет столько же кубитов, сколько их во Вселенной, и логические операции с этими кубитами будут в точности моделировать динамику Вселенной. Такой квантовый компьютер был бы физическим воплощением демона маркиза Пьера-Симона де Лапласа: он моделировал бы поведение Вселенной в целом. Такое квантовое вычисление составило бы полное описание природы, и потому было бы неотличимо от самой природы. Так что, по сути, можно считать, что Вселенная выполняет квантовые вычисления. Точно так же, из-за того что поведение элементарных частиц может быть непосредственно отображено на поведение кубитов, взаимодействующих посредством логических операций, моделирование Вселенной квантовым компьютером неотличимо от самой Вселенной.

Обычный взгляд состоит в том, что Вселенная – это элементарные частицы, и ничего больше. Это так, но столь же верно было бы сказать, что Вселенная – это только биты, а скорее, только кубиты, и ничего больше. Поговорка гласит, что если нечто ходит как утка и крякает как утка, то это утка и есть. Так что с этой минуты и впредь мы примем, что если Вселенная хранит и обрабатывает информацию подобно квантовому компьютеру и для наблюдателя ее поведение неотличимо от поведения квантового компьютера, то Вселенная действительно является квантовым компьютером.