Многомировая интерпретация квантовой механики. Интерпретации квантовой механики

Многомировая интерпретация квантовой механики | LightCone

Квантовая механика является согласованной физической теорией, проверенной с беспрецедентной точностью. За 100 лет существования не было найдено ни единого отклонения экспериментальных данных от предсказаний теории. Между тем она оперирует абстрактными математическими объектами и их связь с наблюдаемой вокруг реальностью не очевидна. Предложенная отцами-основателями Копенгагенская интерпретация до сих пор является наиболее популярной среди профессиональных физиков-теоретиков. Но она сильно противоречит нашей интуиции, постулируя отсутствие объективно существующего (независимо от субъекта/наблюдателя) физического мира.

Многомировая интерпретация является сейчас второй по популярности и постулирует другую крайность — этих объективно существующих миров бесконечно много, постоянно рождаются бесконечности других, а мы просто живем в одной из эволюционных веток этой мультивселенной. Даже некоторые известные физики придерживаются данной точки зрения, например, Дэвид Дойч.

Как всегда, в квантовой механике ничего невозможно понять без математики, поэтому поясним на простейшей квантовомеханической системе — кубите, описываемом вектором состояния:\( \displaystyle |S\rangle=c_{0}|0\rangle+c_{1}|1\rangle\)Принцип суперпозиции утверждает, что в отличие от классического бита, который может быть либо нулем либо единицей, кубит в общем случае описывается приведенной суммой. Вместо векторов состояния \( \displaystyle |0\rangle\) и \( \displaystyle |1\rangle\) можно поставить что угодно: орел и решка, живой кот и мертвый кот и т.п.

Копенгагенская интерпретация говорит, что данная суперпозиция ненаблюдаема в принципе. Вектор состояния \( \displaystyle |S\rangle\)  и амплитуды вероятностей \( \displaystyle c_{0}\) и \( \displaystyle c_{1}\) не имеют объективной реальности. Их величины нельзя измерить как, например, электрическое поле. Это просто математический объект, который позволяет предсказывать результаты измерений.

При измерении кубита мы обнаружим ноль с вероятностью   \( \displaystyle |c_{0}|^{2}\) и единицу с вероятностью  \( \displaystyle |c_{1}|^{2}\). При этом исходный вектор состояния коллапсирует в одно из этих слагаемых.

\(\displaystyle |S\rangle\xrightarrow[]{измерение}|0\rangle\)

или

\(\displaystyle |S\rangle\xrightarrow[]{измерение}|1\rangle\)

Многомировая интерпретация постулирует объективное существование обоих слагаемых суперпозиции. Коллапса не происходит, вместо этого предполагается, что при измерении вселенная разветвляется: в одной из параллельных вселенных выпадет ноль, а в другой единица. Поскольку процесс измерения можно рассматривать как установление запутанного состояния между измеряемой системой и измерительным прибором, даже такое незначительное квантовое событие приводит к макроскопическим последствиям. Вектор состояния комбинированной системы (кубит и измеритель M) выглядит как:

\( \displaystyle |S\rangle=c_{0}|0\rangle|M_{0}\rangle +c_{1}|1\rangle|M_{1}\rangle\)

где за \( \displaystyle |M_{0}\rangle\) и \( \displaystyle |M_{1}\rangle\) обозначены состояния измерительного прибора, показавшего ноль и показавшего единицу в результате измерения.

Данную цепочку можно продолжать неограниченно: прибор показал результат, глаз увидел показания прибора, человек осознал результат измерения, он рассказал другу, результаты показали по телевидению и их увидели миллионы… Фактически две ветки становятся независимыми друг от друга даже на макроскопическом уровне.

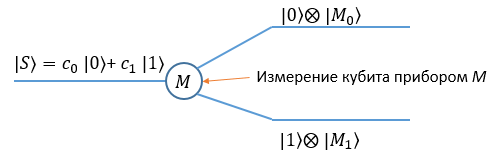
Оказавшись на одной из веток мы не увидим никаких логических противоречий или нарушений причинно-следственных связей. Если был измерен ноль, то все наблюдатели, ассоциированные с этой веткой согласятся с этим. Между тем, многомировая интерпретация утверждает, что объективно существует и вторая ветка, где была измерена единица.

Кубит является квантовомеханической системой всего с двумя состояниями. На практике даже в простейших физических ситуациях, слагаемых в суперпозиции может быть бесконечно много. Рассмотрим эффект дифракции. Если пропускать фотон (электрон или что угодно) через экран с отверстием, диаметр которого соизмерим с длиной волны фотона (де Бройлевой длиной волны электрона), то он может попасть практически в любую точку экрана  \( \displaystyle x_{1}…x_{N}\), а не только строго напротив отверстия. Вектор состояния такой системы выглядит как:

\( \displaystyle |S\rangle=c_{1}|x_{1}\rangle +c_{2}|x_{2}\rangle+c_{3}|x_{3}\rangle+…+c_{N}|x_{N}\rangle\)

Поскольку точек даже на конечном отрезке бесконечно много, согласно многомировой интерпретации при данном эксперименте образуется бесконечность новых вселенных в каждой из которых фотон попал в свою точку x. К тому же эти параллельные вселенные не равнозначны. Поясним на двухщелевом эксперименте.

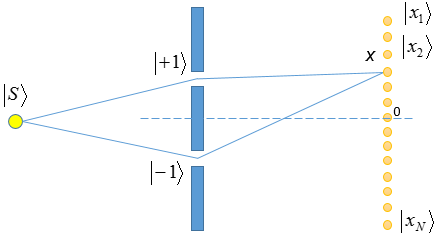
Для фотона, прошедшего первую и вторую щели можно записать выражения, аналогичные приведенному выше:

\( \displaystyle |+1\rangle=с_{1}|x_{1}\rangle +с_{2}|x_{2}\rangle+с_{3}|x_{3}\rangle+…+с_{N}|x_{N}\rangle\) \( \displaystyle =\sum_{i=1}^{N}c_{i}|x_{i}\rangle\)

\( \displaystyle |-1\rangle=b_{1}|x_{1}\rangle +b_{2}|x_{2}\rangle+b_{3}|x_{3}\rangle+…+b_{N}|x_{N}\rangle\) \( \displaystyle =\sum_{i=1}^{N}b_{i}|x_{i}\rangle\)

А полное состояние системы описывается их суммой:

\( \displaystyle (|+1\rangle+|-1\rangle)=\sum_{i=1}^{N}(c_{i}+b_{i})|x_{i}\rangle\)

Используя правило Борна мы можем найти вероятность попадания фотона в точку x возведя в квадрат соответствующую амплитуду вероятности:

\( \displaystyle |c+b|^2=(c^{*}+b^{*})(c+b)\)  \( \displaystyle =c^{*}c+b^{*}b+c^{*}b+b^{*}c\)

Слагаемое \( \displaystyle c^{*}c\) это вероятность попадания фотона в точку x, если бы была открыта только верхняя щель, а \( \displaystyle b^{*}b\) — только нижняя. Однако если открыты обе, добавляются интерференционные члены \( \displaystyle c^{*}b+b^{*}c\). Так, если рассмотреть вероятность попадания в точку в центре экрана (точка 0 на рисунке), из соображений симметрии \( \displaystyle c=b\) и вероятность равна \( \displaystyle 4c^{*}c\). В случае классических частиц мы бы получили только суммы вероятностей прохождения через первую и вторую щель, то есть \( \displaystyle 2c^{*}c\). Мы наблюдаем не что иное как интерференционный максимум.

Многомировая интерпретация не позволяет вывести правило Борна. Остается непонятным почему оказаться в одной вселенной более вероятно, чем в другой. А некоторые возможности вообще не осуществляются и соответствующие ветки мультивселенной отсутствуют (попадение в интерференционные минимумы). Все что гипотетически может произойти, действительно реализуется в той или иной ветке. Почему мы не находим себя в мирах где самые невероятные события обычны?

Поскольку объективного коллапса вектора состояния в многомировой интерпретации не происходит, то вся временная эволюция теоретически обратима. То есть ветки мультивселенной могут как делиться, так и объединяться. Например, процесс обратный показанному на первом рисунке также возможен. Таким механизмом и объясняются интерференционные эффекты в рамках многомировой интерпретации.

Джон Уилер был очень толерантен к чужим идеям и организовал встречу Хью Эверетта (автора многомировой интерпретации, второй справа) и Нильса Бора (в центре) — одного из отцов-основателей квантовой механики.

Встреча оказалась катастрофой. С точки зрения Бора парень так и не понял те нововведения, отделяющие классическую физику от квантовой. Отсутствие объективных свойств объекта до момента измерения, будь то координата попадания фотона на экран или значение кубита, является ключевым аспектом квантовой механики. Следуя Копенгагенской логике, нельзя рассуждать об объектах, которые непосредственно нельзя измерить. Даже понятие траектории частицы отбрасывается из-за невозможности одновременного измерения координаты и скорости (принцип неопределенности Гейзенберга). Постулирование бесконечностей новых миров, существование которых невозможно проверить даже в принципе, это уже чересчур.  К тому же эти вселенные не приносят ничего нового с практической точки зрения. Мы не можем отказаться от принципа суперпозиции и математического аппарата квантовой механики в целом если хотим производить конкретные расчеты. Бор видимо рассматривал многомировую интерпретацию как попытку отменить все новые открытия квантовой теории и вернуться в детерминированный интуитивный Ньютоновский мир в духе Эйнштейна или теории де Бройля-Бома.

Некоторые считают многомировую интерпретацию не интерпретацией, а целой теорией. То есть должны существовать эксперименты, дающие другие результаты по сравнению с Копенгагенской интерпретацией. Дэвид Дойч предложил построить искусственный интеллект на базе квантового компьютера, который может находиться в квантовой суперпозиции и спросить у него ощущает ли он эти суперпозиции. В Копенгагенской интерпретации до сознания доходит только классическая информация, а квантовые суперпозиции ненаблюдаемы.

Другой эксперимент известен как квантовое самоубийство или квантовое бессмертие. При ветвлении мультивселенной когда в одной ветке вы оказываетесь живым, а в другой мертвым, вы всегда будете оказываться в той где вы существуете. Сознание ведь не может ощущать себя мертвым. Попробовав выстрелить себе в голову или прыгнуть с девятого этажа вы всегда обнаружите невероятные случайности, которые помешали этому. С точки зрения многомировой интерпретации вы просто окажитесь в ветке где вы выжили. Фактически вы никогда не сможете умереть, поскольку всегда будут существовать ветки где вы есть. Но с точки зрения ваших близких во всех остальных вселенных вы умрете, так что не следует так экспериментировать!Только если вы окажетесь единственным на Земле дожившим лет до 150-ти, стоит всерьез задуматься над вопросом корректности многомировой интерпретации квантовой механики.

lightcone.ru

Проблема интерпретации квантовой механики

Поиск Лекций Одна из важнейших проблем философии квантовой механики – это проблема интерпретации этой теории. Дело в том, что первая значимая интерпретация этой теории, выдвинутая рядом её создателей – Н. Бором, В. Гейзенбергом, М. Борном, В Паули (копенгагенская интерпретация), порывала с классической установкой на объективное описание физической реальности. “Копенгагенская интерпретация, – писал В. Гейзенберг, – далеко увела физиков от простых материалистических воззрений, господствовавших в естествознании XIX столетия, …или, говоря на более общем философском языке, от онтологии материализма, т.е. от представления об объективном реальном мире, мельчайшие части которого существуют столь же объективно, что и камни и деревья” [4]. Высказанная в конце 20-х гг. копенгагенская интерпретация развивалась в двух направлениях. Во-первых, в плане физики: с копенгагенской точки зрения рассматривались различные мысленные эксперименты, существенные для понимания квантовой механики, анализировалась проблема измерения. Во-вторых, в плане философии: уточнялась философская позиция, которая в целом может быть охарактеризована как антиматериалистическая или во всяком случае нематериалистическая. При этом спектр философских квалификаций был достаточно широк: от феноменологии и неокантианства до позитивизма. Выяснение философских позиций позволяло более точно изложить всю интерпретацию в целом. Однако появился жанр “интерпретации интерпретации”. Это философские работы, построенные на подведении высказываний крупных физиков, интерпретировавших квантовую теорию, под ту или иную философскую концепцию, работы, не вникавшие в физическое содержание копенгагенской интерпретации. Этим вырождением философии квантовой механики в “интерпретацию интерпретации” отмечен ряд отечественных работ. В конце 40-х и в начале 50-х годов копенгагенская интерпретация подверглась нападкам, носящим политический характер. Однако в конце 60-х годов она не только становится вполне правомерной интерпретацией квантовой механики, но и “единственно правильной”. Этому способствовала позиция ряда крупных академических физиков (Л.Д. Ландау, И.Е. Тамм и др.), всегда поддерживавших копенгагенскую интерпретацию, а также изменение идеологической обстановки в стране. Марксизм-ленинизм становится более прагматическим и более служебным. Позиция же академических физиков в условиях милитаризированной науки становится весьма весомой. Перед советской философией науки (её обычно называли философскими вопросами естествознания) возникает задача адаптировать копенгагенскую интерпретацию. Целый ряд философов и физиков стал решать эту задачу. В работах П.С. Дышлевого, В.М. Свириденко [5] и И.С. Алексеева [6] была точно воспроизведена копенгагенская интерпретация в версии Бора. При этом П.С. Дышлевый, различая “объективную реальность” и “физическую реальность”, рассматриваемую в квантовой механике, определил эту последнюю как результат взаимодействия “объекта, субъекта и условий познания” [7]. И.С. Алексеев, следуя статье М.А. Маркова, опубликованной в 1947 г. [8], интерпретировал копенгагенскую интерпретацию как “мышление о мире в формах деятельности” [9]. Хотя П.С. Дышлевый, В.М. Свириденко и И.С. Алексеев выступали от имени диалектического материализма, они не следовали канонической онтологии материализма. В нашей философской литературе, однако, появились статьи и книги, нацеленные на то, чтобы интерпретировать копенгагенскую интерпретацию с позиций философского материализма. При такой “интерпретации интерпретации” искажались физические идеи, высказанные копенгагенской школой. Так, например, провозглашалось, что квантовая механика выражает “внутренне присущую процессам микромира объективную специфику”, которая проявляется “во всех квантовых процессах, независимо от их наблюдения и независимо от их макроскопического проявления” [10]. Между тем с копенгагенской точки зрения “шаг в сторону более существенного включения наблюдателя и условий опыта в физическое описание природы, сделанный в квантовой механике, является окончательным” [11].Это шаг в сторону вмешательства наблюдателя, который прерывает причинные связи. Н. Бор, правда, говорил о “рациональном обобщении” классического принципа причинности в его концепции дополнительности [12]. Но он же говорил и об “окончательном отказе от классического идеала причинности” [12]. Согласно Н. Бору, при описании квантовых явлений мы не можем отвлечься от “влияния условий опыта на поведение системы”. Ведь существенна “свобода выбора” как ставить опыт: “наблюдатель” останавливается на одной из двух дополнительных “экспериментальных манипуляций”. Он, например, ставит эксперимент либо с целью определить координату частицы, либо – с целью определить её импульс. Подгонка копенгагенской интерпретации под материализм, предпринятая рядом советских авторов, делает бессмысленной и непонятной ту идейную борьбу, которая развернулась вокруг этой интерпретации. Уже в 1927 г. с критикой той линии в интерпретации квантовой механики, которая затем была названа копенгагенской, выступил А. Эйнштейн, продолживший эти выступления и впоследствии. Эйнштейн выступал с позиции философского реализма. Копенгагенские представления также решительно критиковал один из создателей квантовой механики Э. Шрёдингер, предлагавший свои альтернативные интерпретации. Пример Эйнштейна и Шрёдингера вдохновил ряд других физиков. Нельзя не отметить и позицию профессиональных философов, среди которых находились как сторонники копенгагенской интерпретации, так и ее противники (например, К. Поппер). Причем полемика между ними порой носила весьма острый характер. Так, например, К. Поппер писал: “Большинство лидеров квантовой теории, кроме Эйнштейна и Шрёдингера, заняли позицию епископа инквизиции и кардинала, а не Галилея, Кеплера и Ньютона” [13]. Реализм, как он выражен Эйнштейном и Шрёдингером, это не просто философская позиция. Это способ понимания квантовой механики. В заметке 1927 г., адресованной пятой Сольвеевской конференции, Эйнштейн выдвинул то, что впоследствии было названо “скрытыми переменными”. В противовес Н. Бору, В. Гейзенбергу и их сторонникам, считавшим, что волновая функция представляет состояние одной частицы, он предложил статистический подход: волновая функция представляет состояние множества (“облака”) частиц, каждая из которых имеет определенную координату. Эта координата остается, однако, “скрытой”, т.е. вообще говоря неизвестной. Как и в классической статистической механике, измерение дает нам те значения динамических переменных (координата, импульс, энергия и т.д.), которые характеризуют весь ансамбль, а не каждую отдельную частицу. В отличие от классики, однако, “скрытость” здесь является принципиальной: в классической статистической физике мы все же можем найти средства, фиксирующие характеристики отдельных частиц, в квантовой же механике этому препятствуют соотношения неопределенностей. Впоследствии, правда, А. Эйнштейн дистанцировался от “скрытых переменных”. В 1935 г. он совместно с Б. Подольским и Н. Розеном опубликовал вышеупомянутую статью, обсуждение которой привело его к тому, что получило название дилеммы Эйнштейна: “квантовая механика либо неполна, либо нелокальна”. Неполнота означает то, что квантовая механика не способна адекватно выразить физическую реальность, относящуюся к её сфере приложения. Иными словами, квантовая механика не имеет статуса фундаментальной теории: она лишь приближение к более точной и глубокой теории, которая еще не сформулирована. Естественным развитием этой точки зрения была концепция “скрытых переменных”: предположение об еще недоступных измерению и наблюдению параметрах частиц, доопределяющих состояния этих частиц. Сами же эти переменные должны быть распределены по такому статистическому закону, который обеспечивал бы тот вероятностный характер, который свойственен квантово-механическим предсказаниям. Хотя сам Эйнштейн воздерживался от спекуляций на тему “скрытых переменных”, некоторые его последователи, например, упоминавшийся выше К. Поппер, прибегли к ним. Но ведь была вторая альтернатива “дилеммы Эйнштейна”: нелокальность. Эта альтернатива означает, что имеется некоторая разновидность дальнодействия: измерение, произведенное над одной из двух частиц, находившихся во взаимодействии, но удалившихся друг от друга на значительное расстояние, оказывается чувствительным для второй из этих частиц. Эйнштейн резко выступал против нелокальности. Он считал, что допущение нелокальности, как бы оно ни соотносилось с принципами теории относительности, подрывает саму идею физического эксперимента и оказывается чем-то родственным телепатии. Однако развитие идей в области интерпретации квантовой механики пошло по линии признания нелокальности. Более того, идея нелокальности была соединена с идеей “скрытых переменных”. Такой фундаментальной инновации способствовали размышления другого критика копенгагенской интерпретации – Э. Шрёдингера. Начав с волновой интерпретации, не выдержавшей критики, он пришел к истолкованию квантовой механики в терминах “возможность” и “виртуальность”. Восходящую к Аристотелю идею потенциальной возможности использовали при интерпретации волновой функции и В. Гейзенберг, примыкавший к копенгагенской интерпретации, и В.А. Фок, близкий к ней. Однако у них эта возможность обусловливалась (частичным) переходом в действительность. Переход от возможного к действительному, вызванный актом наблюдения, объяснял явление, обозначенное Гейзенбергом как “редукция волнового пакета”: при измерении волновая функция, представляющая состояние рассматриваемой системы, “редуцируется” в одно из собственных состояний измеряемой величины, тем самым реализуется одна из возможностей, соответствующих этой волновой функции. У Шрёдингера же возможность очерчивает границу “квантового мира”. Шрёдингер отвергал “редукцию волнового пакета” и считал переход возможного в действительное, привлекаемый для объяснения этой “редукции”, противоречащим динамике квантовой теории. При вариационном подходе к классической механике применяют образ бесконечного множества возможных траекторий, из которых одна оказывается реальной. Шрёдингер сохраняет этот образ и в квантовой механике, но подчеркивает, что это будут уже “фиктивные” траектории, “ни одна из которых не имеет преимущества быть осуществленной в каком-либо конкретном случае” [14]. То, что дается нам в наблюдении, объясняется всей совокупностью “траекторий”, а не превращением одной из них в “действительную”. Фиктивность усугубляется еще и тем обстоятельством, что множество траекторий – один из возможных вспомогательных образов. Этот “виртуализм” делал естественной холистскую точку зрения, строящуюся на отрицании “локальности. При этом нелокальность, наличествующая в индетерминистическом мире, отличается от той нелокальности, которую постулировали Н. Бор и другие представители копенгагенской школы. Шрёдингер с достаточной ясностью подчеркивал, что частицы в составе ЭПР пары находятся в “спутанном” состоянии, причем это состояние не уничтожается измерением, как то предполагается теми, кто придерживается концепции “редукции волнового пакета”. Согласно Бору, импульс у одной частицы мгновенно возникает при измерении импульса у удаленной второй частицы. Согласно Шрёдингеру, эти частицы изначально обладают коррелированными импульсами, которые проявляются при измерении. Разумеется, эта картина нуждалась в разработке, которая и была предпринята в дальнейшем. Можно отметить, что нелокальность, звучащая диссонансом при детерминистическом взгляде на мир, оказывается не такой уж противоестественной в мире возможностей, предполагаемом Шрёдингером. Можно привести пример: если поднял руку и где-то вдалеке пробили часы, то было бы мистицизмом утверждать, что между этими событиями существует связь. Однако если поднятие руки предшествует такому случайному событию, как распад атома радия, то связь уже не столь мистическая. Во всяком случае она менее мистическая, чем та, которую имеет ввиду игрок, поставивший на номер 16 рулетки и проигравший, поскольку выиграл номер 15. Разочарованный игрок думает, что если бы он поставил на 15, то выиграл бы. Истинно индетерминистический мир уникален в каждом из своих состояний, и даже такие ничтожные события, как поднятие руки и ставка в игре в рулетку, создают в нем новую ситуацию. Высказанные Шрёдингером виртуалистские идеи воплотились в двух современных интерпретациях квантовой механики – интерпретации относительных состояний Х. Эверетта – Б.С. Де Витта и модальной интерпретации.   Современные тенденции   Копенгагенский подход господствовал почти безраздельно вплоть до конца 60-х годов. Альтернативные интерпретации (волновая интерпретация Шрёдингера, статистическая интерпретация Поппера, выполненная в духе ранних идей Эйнштейна) не были влиятельными. Что же произошло в 60-е годы? Произошел ряд событий, из которых в первую очередь должны быть упомянуты работы Дж. Белла, изменившие сам стиль философии квантовой теории и повысившие интерес к проблеме “скрытых переменных”. В 1964 г. Дж. Белл вывел неравенство (неравенство Белла), показавшее, что философские проблемы физики можно решать, полагаясь на математический аппарат и эксперимент. Отсюда не следует, что эти проблемы исчезают. Они становятся тоньше и дифференцированнее, а философские утверждения становятся точно сформулированными посылками, используемыми при доказательствах теорем. Как отмечалось выше, копенгагенская интерпретация противостояла интерпретациям, допускающим “скрытые переменные”. Копенгагенские авторы при этом ссылались на теорему И. фон Неймана о полноте квантовой механики, запрещающей такие “переменные” (1932 г.). Эта теорема, однако, оказалась уязвимым звеном в копенгагенской аргументации. Дж. Белл и некоторые авторы до него подчеркивали, что эта теорема запрещает самые поверхностные и грубые “скрытые переменные”, она существенна лишь для тех концепций “скрытых переменных”, которые конфликтуют с соотношениями неопределенностей. Дж. Белл однажды назвал их “глупыми”. Более существенной преградой на пути “скрытых переменных” оказывается неравенство Белла, но и оно блокирует лишь класс “локальных скрытых переменных”. Еще в 50-е годы Д. Бом развил концепцию “скрытых переменных”, для которых неравенство Белла не стало преградой. Согласно Бому, квантовый мир состоит из частиц, которые всегда обладают точными пространственными координатами, и волновой функции, представляемой в виде “ведущего поля”, распространяющегося в конфигурационном пространстве в соответствии с уравнением Шрёдингера. Соотношения неопределенностей, однако, выполняются, поскольку взаимодействие с прибором “неконтролируемым образом” изменяет значения физических величин, характеризующих систему. Более того, такое изменение имеет место и при проведении косвенного измерения, описанного А. Эйнштейном, Б. Подольским и Н. Розаном, т.е. в том случае, когда система состоит из двух пространственно разделенных подсистем и прямому измерению подвергается одна из этих подсистем. “Ведущее поле” заставляет удаленную систему мгновенно реагировать на это измерение. Подытоживая неудачную борьбу копенгагенской интерпретации против “скрытых переменных”, ван Фраассен, один из создателей модальной интерпретации, заявил, что всякая интерпретация является интерпретацией со “скрытыми переменными”. Ведь всякая интерпретация вносит нечто дополнительное в теорию, не меняя её эмпирическое содержание. С точки зрения ван Фраассена и копенгагенская интерпретация грешит подключением “скрытой переменной”, только этой “скрытой переменной” оказывается “наблюдатель”. С другой стороны, “скрытые переменные”, введенные Бомом, были шагом назад к классике. Более перспективной философией оказался индетерминистический реализм К. Поппера, представление об объективной реальности случайного мира. Эта философия была изложена в “Постскриптуме к Логике научного исследования”, написанном во второй половине 50-х гг. и изданном в 1982 г., а также в ряде статей. Но впрямую философия Поппера не оказала воздействия на интерпретацию квантовой механики. Важными вехами здесь оказались многомировая интерпретация (1957 г.) и модальная интерпретация, получившая популярность в 90-е гг. В этих интерпретациях по-новому прозвучало центральное понятие квантовой механики – понятие состояния физической системы. В многомировой интерпретации, наряду с обычным квантовым состоянием, вводится “относительное состояние”. Как явствует из самого названия, это понятие характеризует состояние одного из компонентов физической системы в отношении состояния другого компонента. “Вообще говоря, – пишет Хью Эверетт, – не для одной подсистемы сложной системы не существует чего-то подобного индивидуальному состоянию. Подсистемы не имеют состояний, которые были бы независимы от состояний оставшейся части системы, так что состояния систем вообще говоря коррелируют друг с другом. Однако можно произвольно выбрать одно из состояний подсистемы и таким образом получить относительное состояние оставшейся части системы”. Однако, иллюзорен ли индетерминизм при многомировой интерпретации? Ван Фраассен прав в том отношении, что в каждом из “миров” протекает свой детерминистический процесс, который может быть прослежен вплоть до изменений в “сознании наблюдателя”, относящегося к данному “миру”. Однако “миры” согласованы лишь статистически и то, что происходит в “нашем мире”, не вытекает из того, что имеет место в совокупности “миров”, и в этом смысле, случайно. Выше отмечалась версия копенгагенской интерпретации, трактующая волновые функции как “потенциальные возможности”. Эта версия, однако, лишь внешне подобна модальной интерпретации, поскольку использует переход потенциальных возможностей в действительность при описании акта измерения. Модальная интерпретация более близка представлениям Шредингера, ограничивающим “мир” квантовой механики возможным или виртуальным. При модальной интерпретации (как, впрочем, и при многомировой) измерение не связано с переходом состояния системы в собственное состояние измеряемой величины. Измерение не создает то значение величины, которое является результатом измерения. Модальная интерпретация трактует измерение как обнаружение одного из возможных значений измеряемой величины, или, что тоже самое, одного из состояний-свойств рассматриваемой системы. Эти значения (свойства) существуют до измерения, но существуют как возможности. Квантовое состояние, выражаемое волновой функцией, никак не реагирует на акт измерения, оно лишь определяет (в логическом смысле слова) спектр возможных значений измеряемой величины. Обычно в физике под состоянием системы понимают такую совокупность ее параметров, которая определяет поведение этой системы. Например, пространственная координата и импульс задают состояние материальной точки, поскольку определяют поведение этой точки при условии отсутствия полей, действующих на нее. Это понятие состояния сохранено в модальной интерпретации в виде понятия квантового состояния. Но в физике присутствует и другое понятие состояния – понятие максимально информативного описания системы, скажем, описание газа с упоминанием его температуры, давления, электропроводности и т.д. Такое понятие состояние использовано в модальной интерпретации под именем состояния-свойства. Второй результат также очевиден – при модальной интерпретации появляются концептуальные средства, позволяющие трактовать состояния составных частей сложной системы. При обычных построениях квантовой механики эти концептуальные средства доставляются приближенными методами. Мы, например, вводим представление о состоянии электрона в многоэлектронном атоме, когда используем одноэлектронное приближение. Модальная интерпретация использует точную терминологию в отношении состояний составных частей системы, терминологию, развивающую и дополняющую математический аппарат квантовой теории. В некоторых версиях модальной интерпретации возникает идея особой стохастической динамики, дополняющей причинную динамику, выраженную уравнением Шрёдингера. Стохастическая динамика состояний-свойств – третий результат модальной интерпретации. Итак, модальная точка зрения – это не “интерпретация интерпретации”, а самостоятельная философская позиция, развивающая и обогащающая понятийный аппарат квантовой механики.   4. Сопоставление модальной интерпретации с ортодоксальной и статистической точками зрения.   При статистической интерпретации волновая функция соотносится не с одной частицей, а с ансамблем частиц. В изложении Мандельштама, волновая функция характеризует ансамбль мысленных или реальных опытов, в которых частицы (например, электроны) готовятся в одном и том же квантовом состоянии и производится измерение величин их свойств (координаты, импульса, спина и т.д.). Приготовить множество частиц в одном и том же состоянии значит задать совокупность макропараметров, определяющих “условия опыта”. Волновая функция, стало быть, соотносится с множеством опытов, определенных одной и той же совокупностью макропараметров. Каждый из опытов, однако, дает свой результат, обнаруживает свое “поведение” микрочастицы. Пусть, например, в эвакуированной трубке из накаленной нити, к которой приложено известное напряжение, летят электроны. Если зафиксированы такие макропараметры, как напряжение, температура нити, ее конфигурация, то совокупность электронов обладает определенным квантовомеханическим состоянием, представимым волновой функцией. В каждом из опытов, однако, электрон обнаруживает свое поведение, скажем, попадание в ту или иную точку анода или экрана [15]. Эвакуированная трубка иллюстрирует общий принцип статистической интерпретации. Разбирая теорию электронного микроскопа, Мандельштам рассматривает ансамбль опытов, в которых макроскопические параметры определяют состояние пары частиц – частицы, чью координату измеряют, и рассеянного на ней электрона. Пока не фиксируется попадание электрона на фотопластинку, мы имеем ансамбль, в котором присутствуют частицы с самыми разными координатами и импульсами [15]. Зафиксировав пятна на фотопластинке, мы отбираем из этого ансамбль подансамбль с определенными значениями координаты электрона и соответственно частицы. Электронный микроскоп служит измерителем координаты. Это значит, что он отбирает подансамбль пар частиц — рассеянных электронов с определенной координатой и, соответственно, тех частиц, на которых электроны рассеиваются и координата которых подлежит определению. Электронный микроскоп не измеряет импульс: в отобранном подансамбле – “импульсы любые” [15]. Модальная интерпретация как и копенгагенская, трактует квантовую механику как теорию, которая в своей основе является теорией не ансамбля, а одной физической системы. Координата и импульс частицы характеризуют ее состояние-свойство. В противоположность копенгагенской интерпретации, модальная интерпретация наделяет частицы динамическими характеристиками. Эти характеристики, однако, неопределенны: квантовое состояние определяет лишь вероятности тех значений, которые могут приобретать координата и импульс частиц. Фиксация пятна на фотопластинке не означает отбор подансамбля из ансамбля. Эта фиксация означает, что измерение дало определенную величину для состояния-свойства. Она означает, что мы нашли координату электрона и вычислили координату частицы, на которой электрон рассеян. Импульсы же электрона и этой частицы остаются по-прежнему неопределенными. Модальная интерпретация оказывается особенно удобной, когда рассматриваются приближенные измерения. Она хорошо выражает то обстоятельство, что в квантовой механике, в отличие от классики, приближенное знание физической величины – “не минус” [15]. Мандельштам не дает общего определения приближенного измерения. Он лишь модифицирует свою теорию электронного микроскопа, рассматривает микроскоп с конечной апертурой, дающий разброс пятнышек на фотопластинке – координат рассеянных электронов. Здесь уже невозможно однозначно рассчитать координату частицы, на которой происходит рассеяние. Можно, однако, воспользовавшись классической теорией вероятности, рассчитать вероятность того или иного значения этой координаты. Копенгагенский язык не вполне приспособлен для изложения вопроса о приближенных измерениях. Ведь с копенгагенской точки зрения, физическая величина характеризует частицу тогда и только тогда, когда производится измерение этой величины. Под измерением же имеется в виду процедура, дающая точное значение измеряемой величины. В модальной терминологии проблема измерения (речь идет не о рассеянии электронов на частице, координата которой подлежит измерению, а фиксации пятна на фотопластинке и расчете значения координаты) – это проблема состояний-свойств. Частица и электрон обладают не только квантовыми состояниями, но и состояниями свойствами. Они ими обладают до измерения и независимо от измерения. Если приближенно фиксируется координата рассеянного электрона, то приближенно фиксируется и искомая координата частицы. Приближенное измерение является “мягким”, так как мы, измерив координату частицы, можем приближенно фиксировать и ее импульс. В пределах соотношения неопределенностей частица обладает одновременно приближенной координатой и приближенным импульсом.



poisk-ru.ru

10 интерпретаций квантовой механики | Наука и жизнь

За многие годы были разработаны десятки интерпретаций квантовой механики. Большинство из них пытаются разрешить, что происходит, когда в квантовой системе производится наблюдение или измерение. Математическая формула, известная как волновая функция (или вектор состояния), описывает состояние системы, в которой происходит измерение, и многочисленные возможности «коллапсируют» в один результат. Квантовая «интерпретация» пытается объяснить, почему происходит коллапс и происходит ли он вообще. Некоторые интерпретации начинают с вопроса, является ли волновая функция физически реальной или остается чем-то сугубо математическим.

Предупреждение: вырезки ниже не отражают все тонкости различных интерпретаций, которые часто менялись с течением времени сторонниками или даже авторами. Мы просто пройдемся по ним. Как писал космолог Макс Тегмарк, «нет даже консенсуса на тему того, что называть интерпретацией».

10. Бомовская механика (Дэвид Бом)

Ее не очень любят, но у нее много поклонников и она заслуживает внимания. Разработанная в 1950-х годах Бомом, который взял за основу ранние взгляды Луи де Бройля, бомовская механика описывает полет частиц, управляемых «пилотными волнами». Эти волны говорят частицам, куда двигаться. Предполагается, что этот подход возвращает физику к детерминизму, игнорируя вероятности, которые осуждал Эйнштейн, говоря «Бог не играет в кости». Поскольку эксперимент исключает «скрытые переменные» в пользу детерминизма, бомовская механика требует некоторого действия на расстоянии (или нелокальности). Эйнштейну вообще ничего не понравилось. Также сложно усмотреть, как бомовская механика может предсказать любое экспериментальное различие между предсказаниями стандартной квантовой механики. Незадолго до своей смерти, Эйнштейн говорил, что не впечатлен бомовской интерпретацией. «Слишком дешево, как по мне», — писал Эйнштейн в письме физику Максу Борну.

9. Интерпретация стохастической эволюции

Эту интерпретацию, возможно, строго назвать интерпретацией квантовой механики нельзя, поскольку она меняет математику. В обычной квантовой механике волновая функция «эволюционирует», изменяется со временем весьма предсказуемым образом. Другими словами, шансы различных результатов могут меняться, а вы можете предсказать, как именно они изменятся, пока не сделаете измерение. Но некоторые физики предполагали на протяжении многих лет, что эволюция сама по себе может изменяться случайным (или стохастическим) образом, чтобы вызвать собственный коллапс. Предполагается, что этот коллапс происходит очень быстро для крупных (макроскопических) объектов и медленно для субатомных частиц. Нобелевский лауреат Стивен Вайнберг пристально изучает этот вариант.

8. Квантовое байесианство (Кристофер Фукс, Карлтон Кейвс, Рюдигер Шак)

Эта интерпретация, иногда называемая «кбизм» (QBism), принимает во внимание статистические изыскания Байеса, которые отражают личностный фактор в нахождении результатов — личные предположения. С этой точки зрения волновая функция — «личная», представляющая измерения индивидуальных знаний состояния системы, которые можно использовать для предсказания ее будущего.

7. Многомировая интерпретация (Хью Эверетт III)

Игнорируемая на протяжении многих лет с момента своего появления в 1957 году, многомировая интерпретация набрала популярность в последние десять лет. Интерпретация постулирует, что каждый раз, когда происходят измерения, все возможные результаты происходят в разных ответвлениях реальности, создавая множество параллельных вселенных. На самом деле, Эверетт думал о ней как о расщеплении наблюдателя на клоны, которые видят разные варианты измерений. В любом случае, это странно.

6. Космологическая интерпретация (Энтони Агирре и Макс Тегмарк)

Относительно новая. Работа появилась только в 2010 году. В принципе, Агирре и Тегмарк утверждают, что если вселенная бесконечна, то верна многомировая интерпретация, поскольку будет бесконечное количество параллельных вселенных, в которых могут произойти все возможные результаты измерений квантовомеханических процессов. Агирре и Тегмарк вычислили, что результаты будут возникать в тех же пропорциях, в которых предсказаны возможности, вычисленные в рамках квантовой математики. Таким образом, «волновая функция описывает фактическую пространственную коллекцию идентичных квантовых систем, и квантовая неопределенность объясняется неспособностью наблюдателя определить себя в этой коллекции».

5. Копенгагенская интерпретация

Копенгагенская интерпретация была сформулирована Нильсом Бором в конце 1920-х, на заре квантовой механики (и позже украшена Вернером Гейзенбергом). Бор считал, что измерения дают результаты, которые могут быть описаны только обычным языком классической физики, поэтому нет смысла интересоваться, что происходит в некой невидимой «квантовой» области. Вам нужно настроить экспериментальную установку, чтобы задать вопрос о природе вселенной, и вопрос, который вы задаете, подразумевает ответ,  который вы получите. Эта точка зрения включает принцип неопределенности Гейзенберга, который ограничивает не измерение, а саму природу реальности — одновременно положение частицы и ее скорость просто не существуют, когда происходит измерение. Измерение выбирает одну из множества возможностей (или потенциальных реальностей по Гейзенбергу). Бор объяснил предполагаемые парадоксы, вроде поведения частицы, как волны и волны как частицы, взаимоисключающими, но «комплементарными» аспектами природы.

4. Последовательные истории (Роберт Гриффитс)

Впервые предложенная Гриффитсом в 1984 году, интерпретация последовательных историй трактует классическую физику как приближенную к квантовой механике, и квантовая математика может рассчитать вероятности крупномасштабных явлений так же, как и субатомных. Вероятности относятся не к результатам измерений, а к физическому состоянию системы. Гриффитс особенно выделяет «несовместимость» множества возможных реальностей в квантовой физике. Вы можете сделать снимок горы с разных сторон, отмечает он, но фотографии должны быть объединены, чтобы сложить целую картину реальной горы. В квантовой физике вы можете выбрать, что будете измерять (скажем, скорость частицы или ее положение), но вы не можете совместить два измерения, чтобы составить цельную картинку частицы до измерения. До измерения реального положения и импульса просто не существует. Точно так же нет никакого реального физического состояния, в котором кот Шредингера будет одновременно живым и мертвым. Тот факт, что волновая функция может описать такое состояние, просто означает, что волновая функция ­— это математический конструкт для подсчета вероятностей последовательности событий или историй. В реальной жизни каждая последовательность событий расскажет последовательную историю.

3. Квантовый дарвинизм (Войцех Зурек)

Похожий в некоторых деталях на последовательные истории, квантовый дарвинизм Зурека подчеркивает роль декогеренции. Это процесс, при котором несколько возможных квантовых реалий устраняются, когда система взаимодействует с окружающей средой. По мере того, как молекулы или фотоны отскакивают от объекта, их траектории записывают позицию объекта; очень скоро только одна траектория останется связанной с информацией, записанной в окружающей среде. Такого рода природные взаимодействия производят своего рода «естественный отбор» свойств, которые записаны в среде, во множественных копиях, доступных наблюдателям. Так, наблюдателя могут согласовать конкретное расположение макроскопических объектов, вместо множественных расположений одновременно.

2. Декогерентные истории (Мюррей Гелл-Манн и Джеймс Хартл)

Разновидностью последовательных историй Гриффитса стала интерпретация Гелл-Манна и Хартла (1989 год), подчеркивающая декогеренцию, как и Журек с квантовым дарвинизмом. Но Гелл-Манн и Хартл утверждают, что вся вселенная может рассматриваться как квантовая система без внешней среды. Таким образом, декогеренция происходит внутри, производя то, что они называют «квазиклассическими доменами» — наборы последовательных историй, которые невозможно различить на фоне грубой зернистости, вызванной декогеренцией.

1. Интерпретация Томаса Зигфрида (Sciencenews.org)

Он полагает, что будет называть свою интерпретацию герменевтической. Работа еще идет. Ученый считает, что вместо создания интерпретации квантовой механики, он будет интерпретировать интерпретации, которые нуждаются в интерпретации.

Мар 4, 2018Геннадий

zhizninauka.info

А.А.Печенкин. Три классификации интерпретаций квантовой механики

 

А.А.Печенкин

 

Три классификации интерпретаций квантовой механики*

 

Название настоящей статьи – сколок названия известной брошюры М.А.Маркова[1]. Мы лишь заменили слово «интерпретации» на словосочетание «классификации интерпретаций». Эта замена, однако, существенна: посредством нее учитывается современная ситуация в философии квантовой механики, ситуация, которая может быть названа постмодернистской[2]. Копенгагенская интерпретация, выдвинутая Н.Бором, В.Гейзенбергом, В.Паули, поддержанная М.Борном, П.А.М.Дираком и многими другими крупными физиками, изложенная в авторитетнейших курсах – в томе «Теоретической физики» Л.Д.Ландау и Е.М.Лифшица и в двухтомнике А.Мессиа (ввиду этого ее также называют ортодоксальной), утратила свое монопольное положение. Эта интерпретация, ссылающаяся в стиле философского модернизма на субъекта (наблюдателя), производящего физические эксперименты и измерения, существует теперь в соседстве с множеством других интерпретаций, отчасти и до известных пределов возрождающих классический взгляд на мир. М.А.Марков в упоминавшейся брошюре аргументирует в конечном счете в пользу копенгагенской интерпретации. Настоящая статья исходит в оценке интерпретаций квантовой механики из принципа плюрализма.

 

 

 

– 165 –

 

Посвятив статью классификации интерпретаций квантовой механики, мы не претендуем на сколь-нибудь глубокий и тем более критический анализ тех интерпретаций, которые будут упомянуты ниже. Наша задача рассмотреть классификационные принципы, позволяющие систематизировать то многообразие интерпретаций, которое обозначено в физической и философской литературе. При этом будут заново изложены некоторые из идей и фактов, которые приводились в обзорных статьях и книгах[3]. Мы, однако, подчеркиваем не только множественность интерпретаций, но также множественность классификационных принципов, позволяющих упорядочить эти интерпретации. Мы показываем, что интерпретации квантовой механики не удается построить «в линейку». Здесь перед нами более сложная «многомерная» картина.

Прежде чем приступить к построению классификаций интерпретаций, надо, однако, уточнить само понятие интерпретации. Во всяком случае в дальнейшем изложении будут упоминаться интерпретации двух уровней: инструменталистские интерпретации и интерпретации ради понимания. Первые интерпретации – это интерпретации математической схемы физической теории на множестве наблюдаемых фактов, т.е. результатов измерения. Инструменталистские интерпретации квантовой механики состоят из двух правил – алгоритма «квантизации», устанавливающего, каким образом вычисляются результаты измерения физической величины Q, и статистического алгоритма, устанавливающего, как вычислить вероятности этих результатов и их математическое ожидание (среднее).

Если инструменталистские интерпретации не идут дальше «бруто-фактов», то интерпретации ради понимания обозначают физические идеи, скрывающиеся за математическими формулами, показывают, как выглядит природа с точки зрения квантовой механики. Инструменталистские интерпретации могут быть названы интерпретациями «для пользователей»: их достаточно для решения стандартных задач. Когда же решаются нестандартные задачи, важно знать, в чем специфика квантово-механического взгляда на мир, какие модели допустимы в этой теории, каковы ее идеальные объекты, словом, требуется интерпретация ради понимания.

Различая инструменталистские интерпретации и интерпретации ради понимания, мы имеем в виду два уровня физического опыта – уровень наблюдаемых фактов (результатов измерений

 

 

– 166 –

 

и реальных экспериментов) и уровень мысленных экспериментов, которые хотя и не выдают численные значения физических величин, но позволяют понять, что происходит на «самом деле».

Проблема классификации интерпретаций квантовой механики встает прежде всего в отношении интерпретаций ради понимания, которые весьма разнообразны и представляют широкий спектр метафизических позиций. Вопрос об инструменталистской интерпретации квантовой механики не столь дискуссионен. Тем не менее было выдвинуто несколько таких интерпретаций, не слишком, впрочем, отличающихся друг от друга. Расхождения в отношении инструменталистской интерпретации носят, так сказать, вторичный характер. Они отражают различия в позициях, формулируемых на уровне интерпретаций ради понимания.

 

1. «СТАТИСТИЧЕСКИЕ» (АНСАМБЛЕВЫЕ) И

«НЕСТАТИСТИЧЕСКИЕ»ИНТЕРПРЕТАЦИИ

Одна из основных классификаций делит интерпретации квантовой механики на два обширных класса: интерпретации, представляющие квантовую механику как в своей основе теорию одной индивидуальной физической системы (скажем, электрона), и интерпретации, при которых эта теория предстает как теория коллектива, ансамбля «приготовленных в некотором состоянии» физических систем (скажем, с помощью диафрагмы придается определенное направление электронам, испускаемым раскаленной нитью). Вторые интерпретации обычно называют «статистическими», или ансамблевыми (поскольку квантовая механика сама по себе статистическая теория, то используется также термин «чисто-статистические интерпретации»), первые, по контрасту, – «нестатистическими» (неансамблевыми).

Выше был использован термин «приготовление физических систем в некотором состоянии». Этот термин означает, что физические системы, над которыми проводятся какие-либо эксперименты и измерения, сперва помещаются в фиксированные макроусловия, позволяющие считать, что этим системам придано некоторое фиксированное состояние (представленное либо волновой функцией, либо матрицей плотности). Хотя понятие «приготовление состояния» было введено в 30-е гг. философами Генри Маргенау и Карлом Поппером, соответствующая идея

 

 

– 167 –

 

содержалась уже в «Чикагских лекциях» Вернера Гейзенберга (1928 г.), в том месте, где он рассмотрел разделенный на стадии «простейший мысленный эксперимент»[4]. К интерпретациям, трактующим квантовую механику как в своей основе теорию одной физической системы, принадлежит копенгагенская (ортодоксальная) интерпретация. При этой интерпретации предполагается, что волновая функция дает в максимально возможной степени полное описание физической системы. Кроме копенгагенской интерпретации к этому классу интерпретаций относятся некоторые интерпретации, допускающие «скрытые переменные», например интерпретация Д.Бома. Как пишет сам Д.Бом, «эта... интерпретация позволяет рассматривать каждую индивидуальную систему как находящуюся в некотором точно определенном состоянии, изменение которого со временем задается точными законами, похожими на классические уравнения движения (но не идентичными с ними). Представление о квантово-механических вероятностях рассматривается как вызванное практической необходимостью... Физические результаты, к которым приводит предлагаемая нами интерпретация, точно совпадают с обычными, коль скоро сохраняется уравнение Шредингера в его современной общей форме»[5]. Статистические (ансамблевые) интерпретации квантовой механики также распадаются на два класса. Следуя терминологии одного из недавних обзоров этих интерпретаций, назовем их классом минимальных интерпретаций и классом интерпретаций с презумпцией исходных значений физических величин, называемых в квантовой механике наблюдаемыми (например, координата, импульс, энергия) – pre-assigned initial values interpretations[6]. Минимальные ансамблевые интерпретации весьма близки к копенгагенской интерпретации. При этих интерпретациях (их проводили в своих работах Л.И.Мандельштам и Д.И.Блохинцев) элементам ансамбля не приписываются какие-либо «свои» свойства, ансамбль характеризуется лишь теми свойствами, которые наблюдаются при измерении, а именно – математическими ожиданиями (средними) физических величин и вероятностями того, что физическая величина примет то или иное значение. Значения физических величин, обнаруживаемые при измерении, относятся не к элементам ансамбля, а ко всему ансамблю в целом.

Ансамблевые интерпретации с презумпцией исходных значений физических величин предполагают, что каждый из элементов ансамбля характеризуется своими присущими именно

 

 

– 168 –

 

ему значениями физических величин, а именно – теми значениями, которые обнаруживаются при измерении. При этом каждый из элементов характеризуется «своими» свойствами, независимо от того, проводится ли в данный момент соответствующее измерение или нет, во всяком случае он характеризуется этими свойствами в момент времени, непосредственно предшествующий измерению.

Ансамблевая интерпретация с презумпцией исходных значений физических величин была высказана в 1927 г. А.Эйнштейном в его выступлении на 5-й Сольвеевской конференции. Рассматривая мысленный эксперимент с электронами, вылетающими из небольшого отверстия в экране, вокруг которого расположена в виде полусферы фотопленка, А.Эйнштейн использовал две интерпретации волновой функции: согласно первой, «чисто статистической», волновая функция соответствует «не одному электрону, а облаку электронов, распределенных в пространстве», и «дает информацию относительно бесконечного множества элементарных процессов», согласно же второй «квантовая теория претендует на полное описание отдельных процессов», однако каждая частица «не характеризуется положением и скоростью»[7]. А.Эйнштейн отдавал предпочтение первой интерпретации.

Последующие статьи Эйнштейна на эту тему уже не дают определенного ответа на вопрос, какой тип ансамблевого подхода он поддерживает. Поэтому классическим выразителем ансамблевой интерпретации с презумпцией исходных значений физических величин справедливо считают упоминавшегося выше К.Поппера. Касаясь соотношений неопределенностей, истолковываемых копенгагенцами как соотношения неточностей, К.Поппер пишет: «Статистические законы теории, включая формулы (1) и (2) (речь идет о формулах соотношений неопределенностей для энергии и времени и соответственно для координаты и импульса. – А.П.), …относятся к популяции частиц (если эксперименты проводятся с частицами), которые обладают координатой и импульсом (а также энергией и другими физическими свойствами, такими, как спин). Верно, что соотношения разброса говорят нам, что мы не можем приготовить опыты так, что можно было бы обойти при повторении опыта 1) рассеяние энергии, если мы устанавливаем узкий временной интервал, 2) рассеяние импульса, если мы устанавливаем узко ограниченную координату. Но это означает лишь, что имеются пределы статистической гомогенности наших экспериментальных результатов.

 

 

– 169 –

 

Однако не только возможно измерять энергию и время или импульс и координату с большей точностью, чем, казалось бы, позволяют формулы (1) и (2), но такие измерения необходимы для проверки разброса, предсказываемого этими самыми формулами»[8]. Поясняя эту цитату, заметим, что для Поппера проверка теории предполагает возможность ее опровержения. Чтобы квантовая теория была опровергаемой, эксперимент должен допускать принципиальную возможность наблюдать более узкие распределения, нежели те, которые предписывают соотношения неопределенностей. Поппер согласен с Гейзенбергом в том, что соотношения непределенностей «не относятся к прошлому, так как если сначала известна скорость электрона, а затем точно измерено положение, то возможно и для времени перед измерением положения точно вычислить его положение»[9]. Он, однако, не согласен с Гейзенбергом в том, что «это знание прошлого носит чисто умозрительный характер». Поппер истолковывает это высказывание Гейзенберга следующим образом: при описании экспериментов мы можем в принципе приписать каждой микрочастице координату и импульс (если бы это было невозможно, квантовая механика была бы неопровергаемой теорией, т.е. чистой идеологией), соотношения же неопределенностей относятся не к отдельным частицам, а к популяциям частиц. Упоминая интерпретации, трактующие квантовую механику как теорию индивидуальной физической системы, мы отметили интерпретацию, настаивающую на полноте этой теории (копенгагенскую интерпретацию), и интерпретации со «скрытыми переменными». Сохраняя эту терминологию, мы можем назвать минимальные ансамблевые интерпретации интерпретациями, исходящими из полноты этой теории, а интерпретации с презумпцией исходных значений физических величин интерпретациями, предполагающими возможность ее пополнения. Только под полнотой в данном случае надо понимать статистическую полноту теории, непополнимость ее статистических утверждений (см. один из недавних обзоров этой проблемы[10]). При минимальной ансамблевой интерпретации квантовая механика трактуется в соответствии с теоремой Й. фон Неймана о невозможности «скрытых параметров» (1932 г.): чистые ансамбли (представимые волновыми функциями) обязательно считаются гомогенными. При интерпретации с презумпцией исходных значений физических величин эта теорема (как, впрочем, и соотношения

 

 

– 170 –

 

неопределенностей) приобретает феноменологический характер. Пусть чисто умозрительно и философски, но эта интерпретация допускает продвижение к чистым бездисперсным ансамблям, запрещенным теоремой фон Неймана.

Как минимальные ансамблевые интерпретации (Л.И.Мандельштам, Д.И.Блохинцев и др.), так и интерпретации с презумпцией исходных значений физических величин (К.Поппер и др.) подчеркивают статистический (вероятностный) характер квантовой механики: они реализуют принцип Р. фон Мизеса, утверждающий, что «сперва должен быть налицо коллектив, тогда только можно говорить о вероятностях»[11]. Статистические интерпретации с презумпцией исходных значений физических величин вводят в квантовую механику, кроме того, дополнительную структурированность и тем самым позволяют обойти то, что с копенгагенской точки зрения считается неизбежным, а именно – ссылку на субъекта (наблюдателя). Однако эта структурированность имеет свою цену: как пишет Л.Баллентайн, один из активных сторонников такого рода интерпретаций, они «полностью открыты в отношении «скрытых переменных». Они не требуют их, но делают их поиск всецело осмысленным»[12]. Л.Баллентайн более осторожен в своих формулировках, чем Поппер: он, например, утверждает лишь то, что элементы ансамбля обнаруживают при измерении те значения физических величин, которыми они обладали непосредственно перед измерением. Его конфликт с теоремой фон Неймана проблематичен. Тем не менее и его версия ансамблевой интерпретации может быть истолкована так, что из нее следует статистическая неполнота квантовой механики.

Выше было отмечено, что дивергенция интерпретаций ради понимания отражается в разногласиях, касающихся инструменталисткой интерпретации. Вернемся в этой связи к основному для настоящего параграфа делению интерпретаций на ансамблевые и неансамблевые. Как отмечалось выше, инструменталистские интерпретации включают статистический алгоритм и, стало быть, используют понятие вероятности. М.Джеммер в своей фундаментальной книге по истории интерпретаций квантовой механики выделяет две инструменталистские интерпретации: первая использует классическое (лапласовское) понятие вероятности, определяющее эту величину как отношение числа благоприятных исходов какого-либо опыта к числу равновозможных исходов этого опыта, вторая – частотное понятие вероятности (вероятность – предел последовательности относительных

 

 

– 171 –

 

частот рассматриваемого результата при бесконечном увеличении числа испытаний)[13]. Используя классическое понятие вероятности, мы можем приписывать вероятность какому-либо единичному событию (например, локализации электрона в какой-либо точке). Ведь «благоприятность» и «равновозможность» могут трактоваться как априорные характеристики рассматриваемого эксперимента и экспериментального устройства. Частотное же определение вероятности предполагает рассмотрение не одного события, а коллектива. Формулируя статистический алгоритм, мы в этом случае имеем в виду ансамбль экспериментов (например, определяющих координату электрона), причем экспериментов с подобными приготовленными стадиями (приготовляющими физические системы в одном и том же состоянии).

М.Джеммер связывает первую инструменталистскую интерпретацию с именем М.Борна, который в 1926 г. предложил вероятностное истолкование волновой функции, а вторую – с именем А.Эйнштейна, который в 1927 г. выступил с ансамблевой интерпретацией квантовой механики. Последнее не вполне удачно, поскольку Эйнштейн в явном виде не использовал частотное понятие вероятности. Мы будем называть вторую инструменталистскую интерпретацию фонмизесовской, имея в виду, что Р. фон Мизес выдвинул в 1919 г. частотное определение вероятности и впоследствии применил его к квантовой механике.

Исторически копенгагенская интерпретация квантовой механики была связана с борновской инструменталистской интерпретацией. Понятия о неконтролируемом взаимодействии измерительного прибора и физической системы и дополнительности были выдвинуты в развитие этой интерпретации или во всяком случае были развиты с ее учетом. Эти понятия призваны обосновать принципиальную неустранимость вероятности из инструменталистской интерпретации.

Можно указать, однако, изложения копенгагенской интерпретации, в которых она связывается с фонмизесовской инструменталисткой интерпретацией[14]. При таких изложениях «неконтролируемое взаимодействие» и «дополнительность» несут добавочную нагрузку: они показывают, что квантовая механика, несмотря на ансамблевый характер проверяющих экспериментов, зафиксированный в инструменталистской интерпретации, остается в своей основе теорией единичной физической системы.

Статистические (ансамблевые) интерпретации в отличие от копенгагенской интерпретации исторически и логически связаны с фонмизесовской инструменталистской интерпретацией. Здесь

 

 

– 172 –

 

важно подчеркнуть следующее: это интерпретации ради понимания, вместе с ними мы покидаем «бруто-факты», учитываемые в инструменталистской интерпретации, и вступаем в область мысленных экспериментов, показывающих, что представляет собой физическая реальность. Это особенно важно подчеркнуть в отношении минимальной ансамблевой интерпретации, при которой принимаются во внимание только те свойства ансамбля, которые «работают» в инструменталистской интерпретации. Минимальная ансамблевая интерпретация – это тоже интерпретация ради понимания: она позволяет не только рассчитывать результаты экспериментов, но и теоретически моделировать различные экспериментальные ситуации, вводя образы чистого и смешанного ансамбля, «дополнительных» квантовых ансамблей, расщепления ансамбля на подансамбли.

Итак, мы рассмотрели классификацию интерпретаций квантовой механики, действующую не только на уровне интерпретаций ради понимания, но и на инструменталистском уровне. Это деление на интерпретации «нестатистические» и «статистические» (ансамблевые). Более дробная классификация, однако, касается только интерпретаций ради понимания. Это подразделение на интерпретации, предполагающие полноту квантовой теории и предполагающие, наоборот, ее пополнение.

 

2. ДОПОЛНИТЕЛЬНОСТЬ, ПРЕДРАСПОЛОЖЕННОСТЬ

И «СКРЫТЫЕ ПЕРЕМЕННЫЕ»

Разобранная в предыдущем параграфе классификация учитывает далеко не все интерпретации квантовой механики. Так, например, она не учитывает пропенситивную интерпретацию (от английского слова – propensity – предрасположенность, тенденция), развитую в 50-е годы К.Поппером (проводившем ранее тот статистический (ансамблевый) подход, о котором речь шла в предыдущем параграфе). Кроме того, в рамках вышеизложенной классификации остаются вопросы по поводу копенгагенской интерпретации и интерпретаций со «скрытыми переменными». Мы сказали, что при копенгагенской интерпретации квантово-механическое описание при помощи волновой функции считается в максимально возможной степени полным, а при интерпретациях со «скрытыми переменными» предполагается, что его можно пополнить. Однако что стоит здесь за словом «полнота»?

 

 

– 173 –

 

Чтобы ответить на этот вопрос, поставим другой, а именно: «Пусть система X не находится в собственном состоянии оператора Q, представляющего физическую величину Q. Что можно сказать о значении Q для данной системы?»[15].

В зависимости от ответа на этот вопрос мы получаем одну из трех интерпретаций квантовой механики – копенгагенскую, пропенситивную и интерпретацию со «скрытыми переменными». Копенгагенская интерпретация предполагает следующий ответ: «Ничего нельзя сказать о значении этой физической величины». Иными словами, сам вопрос признается неосмысленным. Только тогда, когда система находится в собственном состоянии оператора, представляющего некоторую физическую величину, мы можем утверждать, что рассматриваемая система обладает определенным значением данной величины. Это значение и будет собственным значением соответствующего оператора.

На языке физики сказанное означает, что определимость значения физической величины связана с ее измеримостью. Только в том случае, когда система находится в собственном состоянии какого-либо оператора, мы можем утверждать, что при измерении соответствующей физической величины будет с неизбежностью получено определенное значение этой величины – собственное значение соответствующего оператора. В курсе Л.Д.Ландау и Е.М.Лифшица такие измерения названы «предсказуемыми». «Определяемые предсказуемыми измерениями количественные характеристики состояния суть то, что в квантовой механике называют физическими величинами»[16]. Физическая величина, стало быть, является в квантовой механике в обличье своих «собственных значений». «Физически первичным оказывается не понятие самого оператора, а скорее понятие совокупности его собственных векторов с принадлежащими им собственными значениями»[17].

Здесь в игру вступает важное для копенгагенцев понятие дополнительности. В квантовой механике далеко не все физические величины могут быть одновременно измерены у данной физической системы. Следовательно, эта система не может быть столь же полно описана, сколь она описывается в классической физике. Однако она может быть охарактеризована классическим набором физических величин с учетом «дополнительности». В каждой конкретной ситуации мы можем выделить совокупности дополнительных (взаимоисключающих и предполагающих друг друга) «предсказуемых измерений» и, стало быть, физических величин, характеризующих физическую систему.

 

 

– 174 –

 

Вернемся к нашему вопросу: «Что мы можем сказать о значении физической величины Q, если система не находится в собственном состоянии соответствующего оператора?». Интерпретации со «скрытыми переменными» утверждают, что физическая величина и в этом случае имеет вполне определенное значение, но это значение остается нам неизвестным. Тем самым эти интерпретации предполагают пополнение концептуального аппарата квантовой механики: при стандартном изложении в аппарате квантовой механики нет концептуальных средств, способных выразить «определенные значения» физической величины у системы, не находящейся в собственном состоянии соответствующего оператора. При копенгагенской же интерпретации концептуальный аппарат стандартной квантовой механики предполагается полным.

Понятие «скрытой переменной» генетически восходит к известной теореме И. фон Неймана, устанавливающей полноту квантовой механики (см. выше). Однако эта теорема, в которой полнота теории связывается с невозможностью чистых бездисперсных состояний, «не ловит» большинство реально действующих концепций «скрытых переменных». Более жестким регулятивом, отсеивающим интерпретации со «скрытыми переменными», служит неравенство Дж.Белла (1964 г.). Это неравенство выведено при минимальных требованиях к «скрытым переменным», которые, однако, укладываются в рамки приведенного выше определения. Дж. Белл предположил, что все физические величины во всех состояниях физических систем имеют вполне определенные значения. Кроме того, он предположил, что эти значения локальны. Это означает, что они не могут измениться под влиянием удаленных экспериментов. Белл показал, что выведенное при указанных предпосылках неравенство нарушается квантовой механикой. Последующие исследования показали, что неравенство Белла скорее всего нарушается также и экспериментом.

Требование локальности, однако, является само по себе избыточным по отношению к концепции «скрытой переменной». В § 1 упоминалась концепция Бома, в которой вводится такое понятие «скрытых переменных», которое «не ловит» не только теорема фон Неймана, но и результат Белла. Эти «скрытые переменные» не являются локальными: волновая функция, представляющая состояние системы, оказывается у Бома также и объективно существующим y-полем, мгновенно реагирующим на измерения. Если волновая функция представляет состояние

 

 

– 175 –

 

пары удаленных друг от друга частиц (как в эксперименте Эйнштейна-Подольского-Розена), то измерение, выполненное над одной из них, сразу же затрагивает физические свойства другой.

Третий ответ на поставленный выше классифицирующий вопрос следующий: система, не находящаяся в собственном состоянии оператора, представляющего физическую величину, обладает нечетким, расплывчатым значением этой величины. Мы можем лишь утверждать предрасположенность (propensity) системы иметь то или иное количественное значение физической величины. Численной мерой этой предрасположенности служит вероятность, входящая в «статистический алгоритм».

Как отмечалось выше, пропенситивная интерпретация была выработана в 50-е годы К.Поппером, который ранее придерживался статистического (ансамблевого) подхода[18]. Поппер сам отмечает, что он следовал В.Гейзенбергу, интерпретировавшему в некоторых своих поздних работах волновую функцию как потенциальную возможность в стиле аристотелевской философии. Ему следовало бы упомянуть также В.А.Фока, который в своих послевоенных статьях рассматривал «совокупность потенциальных возможностей», вытекающих из «приготовительного опыта», как характеристику квантово-механического состояния, в которое этот опыт приводит физическую систему[19].

Поскольку предрасположенность характеризует не саму по себе физическую систему, а ее состояние, задаваемое экспериментальной установкой, возникает вопрос об отличии пропенситивной интерпретации от копенгагенской, в которой, как мы видели, понятие физической величины носит подчеркнуто операционалистский характер: физическая величина – это то, что фиксируется в «предсказуемом измерении». При пропенситивной интерпретации, однако, связь с измеримостью оказывается не столь жесткой. Хотя предрасположенность характеризует физическую систему вместе с ее экспериментальным окружением, она в силу своей «нечеткости» реализуется не только в «предсказуемых измерениях». В отличие от копенгагенцев Поппер ассоциирует физическую величину с соответствующим оператором, а не с его собственными значениями.

Возникает также вопрос: а не сводится ли пропенситивная интерпретация к инструменталистской? Ведь количественной мерой предрасположенности служит вероятность, входящая в статистический алгоритм. Однако предрасположенность – качественная характеристика состояния физической системы и как

 

 

– 176 –

 

таковая выходит за пределы «бруто-фактов» (показания измерительных приборов), которыми ограничена инструменталистская интерпретация. Ее статус в этом отношении похож на статус минимальной ансамблевой интерпретации: мы можем мысленно экспериментировать с предрасположенностями, как и с ансамблями, поясняя, какая реальность стоит за квантово-механическими расчетами и измерениями.

Итак, в дополнение к классификации, выделяющей статистические (ансамблевые) и нестатистические интерпретации, мы рассмотрели классификацию, построенную по принципу, как трактуется понятие физической величины. Эта классификация пересекается с первой: копенгагенская интерпретация и интерпретации со «скрытыми переменными» в ней уже упоминались. Вместе с тем она обогащает картину концептуальных ресурсов интерпретаций квантовой механики, четко определяя «скрытые переменные» и вводя понятие предрасположенности.

 

3. ДУАЛИСТИЧЕСКИЕ И МОНИСТИЧЕСКИЕ

(«АНТИКОЛЛАПСОВСКИЕ») ИНТЕРПРЕТАЦИИ

Классификационным принципом интерпретаций квантовой механики может служить отношение к «редукции волнового пакета», одной из самых острых интерпретационных проблем этой теории.

Идея редукции волнового пакета была высказана В.Гейзенбергом в 1927 г. при обсуждении измерения координаты электрона[20]. Эта идея была затем развита им же, а также П.А.М.Дираком и И. фон Нейманом в понятие некаузального изменения состояния системы при осуществлении измерения. В простейшем случае «идеального измерения», когда измерительный прибор действует как «идеальный фильтр», редукцией волнового пакета оказывается переход суперпозиции Ψ=∑сnφn, где φn – собственные состояния измеряемой величины, в одно из этих собственных состояний φn. Гейзенберг, Дирак и фон Нейман таким образом выделяют, наряду со стандартным каузальным изменением состояния системы в соответствии с уравнением Шредингера, «некаузальный прыжок» этого состояния, приходящийся на акт измерения.

Хотя в связи с понятием редукции волнового пакета среди сторонников копенгагенской интерпретации возникли разногласия, нельзя не признать, что это понятие достаточно органично

 

 

– 177 –

 

вписывается в аппарат этой интерпретации (кстати, о непринципиальном характере этих разногласий писал И.С.Алексеев[21]). Точнее, оно почти принудительно возникает, если копенгагенская точка зрения соединяется с точкой зрения на прибор как на квантово-механическую систему. Вспомним еще раз, что в рамках копенгагенской интерпретации физическая величина имеет определенное значение в том и только в том случае, когда система находится в собственном состоянии соответствующего оператора. Если мы в качестве физической величины рассматриваем «показание прибора», то, оставаясь на копенгагенских позициях, мы вынуждены связывать определенность этих показаний с переходом прибора в одно из собственных состояний оператора, представляющего эту «величину». Приведем основные формулы. Пусть физическая система I, у которой мы измеряем некоторую величину Q, первоначально находилась в состоянии |I,ψ〉, представимом в виде суперпозиции собственных состояний соответствующего оператора, т.е. в виде ∑cn|I,qn〉. Пусть прибор II первоначально находился в состоянии |II,0〉. В соответствии с законами квантовой механики измерение описывает следующая формула:

 

U|I,ψ〉 |II,0〉 = ∑сn|I,qn〉 |ll,αn〉, (1)

 

где U – оператор взаимодействия микросистемы с измерительным прибором, αn – показания прибора (непосредственные результаты измерения). Формула (1), однако, не описывает всего процесса измерения. Всякий раз с прибора снимают какое-либо одно показание αnи по нему определяют значение измеряемой физической величины qn. Чтобы осмыслить эту последнюю стадию, Гейзенберг, Дирак, фон Нейман, В.Паули и др. используют понятие редукции волнового пакета. Они постулируют переход суперпозиции, стоящей в правой части равенства (1) в один из ее членов, содержащий то значение αn, которое действительно наблюдалось. Иными словами, они постулируют следующее:

 

∑сn|I,qn〉 |ll,αn〉 ⇒ |I,qn〉 |ll,αn〉, (2)

 

В отличие от формулы (1) формула (2) выражает некаузальный скачок, про который мы можем лишь сказать, что его вероятность равна |сn|2.

«Редукция волнового пакета» сразу же встретила оппозицию. Именно против этого понятия выступил А.Эйнштейн на 5-ой Сольвеевской конференции, предложив статистическую интерпретацию волновой функции (см. первый параграф). «Скачком

 

 

– 178 –

 

теории» иронически называл «редукцию» Э.Шредингер. Он также предложил интерпретацию, исключающую понятие редукции из концептуального аппарата квантовой механики[22]. На волне этой критики возникли и другие «антиколлапсовские» интерпретации. Вместе с тем возникли интерпретации, сохраняющие введенный Гейзенбергом, Дираком и фон Нейманом дуализм, но придающие ему «рациональные» формы.

Остановимся в первую очередь на этих последних. В соединении с копенгагенской интерпретацией «редукция волнового пакета» окрашивается в тона крайнего субъективизма. Эта «редукция» происходит при единичном акте наблюдения: квантово-механическое состояние физической системы изменяет фиксация исследователем показаний прибора.

Хотя статистическая (ансамблевая) интерпретация в ее минималистской версии не позволяет как-то обойти понятие редукции волнового пакета, она делает это понятие менее субъективным, менее мистическим. Поскольку в рамках этой интерпретации физически осмысленным является лишь ансамбль микросистем и, стало быть, ансамбль измерений, то «редукция» оборачивается селекцией (отбором) подансамблей, целенаправленно осуществляемой исследователем (исследователями).

Возьмем случай идеального измерения (см. начало настоящего параграфа). Пусть зафиксировано N1 показаний, лежащих в окрестности q1 (собственное значение, соответствующее собственному состоянию φ1), N2 показаний, лежащих в окрестности q2 (собственное значение, соответствующее собственному состоянию φ2) и т.д.[23]. Тем самым уже осуществлена «редукция волнового пакета»: ансамбль результатов измерения и соответственно физических систем разбит на подансамбли. Вместо суперпозиции собственных состояний мы имеем смесь этих состояний (если заданы вероятности каждого из чистых (в частности, собственных) состояний, то такой ансамбль называется смешанным или просто смесью).

При пропенситивной интерпретации, развитой в послевоенные годы Поппером (см. предыдущий параграф), «редукция» предстает как переход потенциальной возможности в действительность, которая в свою очередь определяет новые возможности. Вспомним, что состояние микросистемы интерпретируется Поппером как предрасположенность этой системы вести себя в тех или иных обстоятельствах тем или иным образом, иными словами, состояние системы определяется не только этой системой,

 

 

– 179 –

 

но и тем экспериментальным процессом, который «приготовил» эту систему. Производя измерение, мы изменяем экспериментальную ситуацию, т.е. заново «готовим» эту систему для будущих опытов.

Поппер приводит здесь свой излюбленный пример: детский биллиард (уставленная иголками доска, по которой сверху скатывается металлический шарик, символизирующий физическую систему, – сам биллиард символизирует экспериментальное устройство). Когда шарик наверху биллиарда, мы имеем одну диспозицию, одну предрасположенность достичь какой-либо точки внизу доски. Если же мы зафиксировали шарик где-то в середине доски, мы изменили спецификацию эксперимента и получили новую предрасположенность. Квантово-механический индетерминизм сохраняется здесь в полном объеме: Поппер оговаривает, что биллиард не представляет собой механическую систему. Мы лишены возможности прослеживать траекторию шарика. Но «редукция волнового пакета» – это не акт субъективного наблюдения, это сознательное переопределение экспериментальной ситуации, сужение условий опыта.

Перейдем теперь к «антиколлапсовским» (монистическим) интерпретациям. Здесь особое место занимает многомировая интерпретация, выдвинутая в 1957 г. Г.Эвереттом (сам Эверетт называл эту интерпретацию интерпретацией относительных состояний)[24]. Чтобы понять эту интерпретацию, нам понадобится вышеприведенная формула (1) (формула (2), выражающая «редукцию волнового пакета», не находит в ней применения). Как отмечалось выше, формула (1) выражает то изменение, которое претерпевает при измерении комбинация физической системы, над которой производится измерение, и измерительного прибора, т.е. комбинация I и II.

Если предполагается «редукция волнового пакета», то предполагается и «факторизация» этой комбинации, превращение ее в совокупность произведений состояний системы, над которой производится измерение, и измерительного прибора. Иными словами, зафиксировав результаты измерений, мы имеем возможность отнести их непосредственно к системе, над которой проводилось измерение. При многомировой же интерпретации мы считаем осмысленным лишь относительное состояние этой системы, ее состояние, отнесенное к состоянию измерительного прибора. Если состояние комбинации I и II после измерения есть ∑сn|I,qn〉 |ll,αn〉, то относительное состояние I есть ее смешанное состояние (состояние смеси, выражаемое матрицей плотности, а не волновой функцией!), коррелированное с показанием αn измерительного прибора.

 

 

– 180 –

 

Кроме того, при многомировой интерпретации предполагается, что каждый элемент вышеприведенной суперпозиции (и каждое относительное состояние) приходится на свой мир, снабженный своим наблюдателем. Все эти элементы одинаково реальны, поскольку одинаково реальны все возможные результаты измерения. Квантовая механика таким образом трактуется как теория, не помещающаяся в один мир. Она описывает реальность, состоящую из множества сосуществующих миров.

Коэффициенты cn могут быть поняты в связи с вероятностными весами возможных миров. Если же наблюдатель в каждом из возможных миров одарен памятью, он может подсчитывать ∣cn∣2как относительные частоты появлений показаний прибора αnв своем мире.

Выше статистическая (ансамблевая) интерпретация в ее минималистской версии была охарактеризована как дуалистическая интерпретация, придающая, однако, «редукции волнового пакета» более рациональную окраску. Статистическая же интерпретация с презумпцией исходных значений физических величин относится к «антиколлапсовским» интерпретациям. С точки зрения этой интерпретации, то явление, которое названо «редукц

iphras.ru

Интерпретация квантовой механики — Википедия

Материал из Википедии — свободной энциклопедии

Интерпрета́ции ква́нтовой меха́ники — различные философские воззрения на сущность квантовой механики как физической теории, описывающей материальный мир. Они решают такие философские проблемы, как вопрос о природе физической реальности и способе её познания, о характере детерминизма и причинности, о сущности и месте статистики в квантовой механике. Квантовая механика считается «наиболее проверенной и наиболее успешной теорией в истории науки»[1], но консенсуса в понимании «её глубинного смысла» всё ещё нет.

Многие физики склоняются к так называемой «никакой» интерпретации квантовой механики, ёмко выраженной в афоризме Дэвида Мермина: «Заткнись и вычисляй!» (ориг. англ. «Shut up and calculate»), часто (видимо, по ошибке) приписываемом Ричарду Фейнману или Полю Дираку[2]. Критикуя подобный подход, Э. М. Чудинов заметил, что

У специалиста, работающего в области физики, часто возникает иллюзия полной независимости его научной деятельности от философии. Это происходит вследствие того, что он входит в уже готовое здание научной теории с присущим ей стилем научного мышления, и через стиль научного мышления воспринимает определенные философские принципы. Эти философские предпосылки научной теории не всегда ясно осознаются учеными, но от этого они не перестают быть философскими.[3]

М. Бунге отмечает, что отказ физиков от философии на словах означает фактическое принятие философии операционализма:

Современный физик отбрасывает устаревшие догматические системы...только для того, чтобы некритически воспринять некоторую альтернативную систему философских догм...операционализм.[4]

Исторические предпосылки

Понимание математических конструкций квантовой теории прошло в своём развитии через ряд стадий. Например, Шрёдингер сначала не понимал вероятностную природу волновой функции, связанной с электроном; это понимание привнёс Макс Борн, когда предложил рассматривать вероятностное распределение местоположения электрона в пространстве. Другие ведущие учёные, например Эйнштейн, также нелегко примирялись с положениями теории. Даже если эти трудности считать простыми проявлениями болезни роста, всё равно понятно, что они привели к работе по созданию интерпретаций.

Работа М. Борна по статистической интерпретации волновой функции получила высокую оценку, в 1954 году ему была присуждена Нобелевская премия по физике с формулировкой «за фундаментальное исследование в области квантовой механики, особенно за статистическую интерпретацию волновой функции».

Видео по теме

Интерпретации

Наиболее распространённые интерпретации

Малораспространённые интерпретации

Оценки

Неофициальный опрос, сделанный в 1997 году на симпозиуме под эгидой UMBC, показал[6], что некогда доминировавшая Копенгагенская интерпретация поддерживается менее чем половиной участников. В целом голоса участников опроса распределились следующим образом:

По словам философа Дэвида Чалмерса, все существующие в настоящее время интерпретации квантовой механики в определённой степени безумны. Чалмерс выделяет три главных интерпретации: вигнеровскую, бомовскую и эвереттовскую. Среди этих трёх интерпретаций на первое место по степени безумности он ставит концепцию Эверетта, на второе — концепцию Вигнера, на третье — концепцию Бома. Однако если использовать в качестве критерия их теоретическую ценность, то, с точки зрения Чалмерса, картина прямо противоположна: интерпретация Эверетта является наиболее простой, полностью локальной и напрямую совместимой с теорией относительности, интерпретация Вигнера достаточно элегантна, а интерпретация Бома чрезмерно сложна и искусственна[7].

См. также

Примечания

Литература

wikipedia.green

Интерпретация квантовой механики Википедия

Интерпрета́ции ква́нтовой меха́ники — различные философские воззрения на сущность квантовой механики как физической теории, описывающей материальный мир. Они решают такие философские проблемы, как вопрос о природе физической реальности и способе её познания, о характере детерминизма и причинности, о сущности и месте статистики в квантовой механике. Квантовая механика считается «наиболее проверенной и наиболее успешной теорией в истории науки»[1], но консенсуса в понимании «её глубинного смысла» всё ещё нет.

Многие физики склоняются к так называемой «никакой» интерпретации квантовой механики, ёмко выраженной в афоризме Дэвида Мермина: «Заткнись и вычисляй!» (ориг. англ. «Shut up and calculate»), часто (видимо, по ошибке) приписываемом Ричарду Фейнману или Полю Дираку[2]. Критикуя подобный подход, Э. М. Чудинов заметил, что

У специалиста, работающего в области физики, часто возникает иллюзия полной независимости его научной деятельности от философии. Это происходит вследствие того, что он входит в уже готовое здание научной теории с присущим ей стилем научного мышления, и через стиль научного мышления воспринимает определенные философские принципы. Эти философские предпосылки научной теории не всегда ясно осознаются учеными, но от этого они не перестают быть философскими.[3]

М. Бунге отмечает, что отказ физиков от философии на словах означает фактическое принятие философии операционализма:

Современный физик отбрасывает устаревшие догматические системы...только для того, чтобы некритически воспринять некоторую альтернативную систему философских догм...операционализм.[4]

Исторические предпосылки

Понимание математических конструкций квантовой теории прошло в своём развитии через ряд стадий. Например, Шрёдингер сначала не понимал вероятностную природу волновой функции, связанной с электроном; это понимание привнёс Макс Борн, когда предложил рассматривать вероятностное распределение местоположения электрона в пространстве. Другие ведущие учёные, например Эйнштейн, также нелегко примирялись с положениями теории. Даже если эти трудности считать простыми проявлениями болезни роста, всё равно понятно, что они привели к работе по созданию интерпретаций.

Работа М. Борна по статистической интерпретации волновой функции получила высокую оценку, в 1954 году ему была присуждена Нобелевская премия по физике с формулировкой «за фундаментальное исследование в области квантовой механики, особенно за статистическую интерпретацию волновой функции».

Интерпретации

Наиболее распространённые интерпретации

Малораспространённые интерпретации

Оценки

Неофициальный опрос, сделанный в 1997 году на симпозиуме под эгидой UMBC, показал[6], что некогда доминировавшая Копенгагенская интерпретация поддерживается менее чем половиной участников. В целом голоса участников опроса распределились следующим образом:

По словам философа Дэвида Чалмерса, все существующие в настоящее время интерпретации квантовой механики в определённой степени безумны. Чалмерс выделяет три главных интерпретации: вигнеровскую, бомовскую и эвереттовскую. Среди этих трёх интерпретаций на первое место по степени безумности он ставит концепцию Эверетта, на второе — концепцию Вигнера, на третье — концепцию Бома. Однако если использовать в качестве критерия их теоретическую ценность, то, с точки зрения Чалмерса, картина прямо противоположна: интерпретация Эверетта является наиболее простой, полностью локальной и напрямую совместимой с теорией относительности, интерпретация Вигнера достаточно элегантна, а интерпретация Бома чрезмерно сложна и искусственна[7].

См. также

Примечания

Литература

wikiredia.ru

Интерпретации квантовой механики Википедия

Интерпрета́ции ква́нтовой меха́ники — различные философские воззрения на сущность квантовой механики как физической теории, описывающей материальный мир. Они решают такие философские проблемы, как вопрос о природе физической реальности и способе её познания, о характере детерминизма и причинности, о сущности и месте статистики в квантовой механике. Квантовая механика считается «наиболее проверенной и наиболее успешной теорией в истории науки»[1], но консенсуса в понимании «её глубинного смысла» всё ещё нет.

Многие физики склоняются к так называемой «никакой» интерпретации квантовой механики, ёмко выраженной в афоризме Дэвида Мермина: «Заткнись и вычисляй!» (ориг. англ. «Shut up and calculate»), часто (видимо, по ошибке) приписываемом Ричарду Фейнману или Полю Дираку[2]. Критикуя подобный подход, Э. М. Чудинов заметил, что

У специалиста, работающего в области физики, часто возникает иллюзия полной независимости его научной деятельности от философии. Это происходит вследствие того, что он входит в уже готовое здание научной теории с присущим ей стилем научного мышления, и через стиль научного мышления воспринимает определенные философские принципы. Эти философские предпосылки научной теории не всегда ясно осознаются учеными, но от этого они не перестают быть философскими.[3]

М. Бунге отмечает, что отказ физиков от философии на словах означает фактическое принятие философии операционализма:

Современный физик отбрасывает устаревшие догматические системы...только для того, чтобы некритически воспринять некоторую альтернативную систему философских догм...операционализм.[4]

Исторические предпосылки

Понимание математических конструкций квантовой теории прошло в своём развитии через ряд стадий. Например, Шрёдингер сначала не понимал вероятностную природу волновой функции, связанной с электроном; это понимание привнёс Макс Борн, когда предложил рассматривать вероятностное распределение местоположения электрона в пространстве. Другие ведущие учёные, например Эйнштейн, также нелегко примирялись с положениями теории. Даже если эти трудности считать простыми проявлениями болезни роста, всё равно понятно, что они привели к работе по созданию интерпретаций.

Работа М. Борна по статистической интерпретации волновой функции получила высокую оценку, в 1954 году ему была присуждена Нобелевская премия по физике с формулировкой «за фундаментальное исследование в области квантовой механики, особенно за статистическую интерпретацию волновой функции».

Интерпретации

Наиболее распространённые интерпретации

Малораспространённые интерпретации

Оценки

Неофициальный опрос, сделанный в 1997 году на симпозиуме под эгидой UMBC, показал[6], что некогда доминировавшая Копенгагенская интерпретация поддерживается менее чем половиной участников. В целом голоса участников опроса распределились следующим образом:

По словам философа Дэвида Чалмерса, все существующие в настоящее время интерпретации квантовой механики в определённой степени безумны. Чалмерс выделяет три главных интерпретации: вигнеровскую, бомовскую и эвереттовскую. Среди этих трёх интерпретаций на первое место по степени безумности он ставит концепцию Эверетта, на второе — концепцию Вигнера, на третье — концепцию Бома. Однако если использовать в качестве критерия их теоретическую ценность, то, с точки зрения Чалмерса, картина прямо противоположна: интерпретация Эверетта является наиболее простой, полностью локальной и напрямую совместимой с теорией относительности, интерпретация Вигнера достаточно элегантна, а интерпретация Бома чрезмерно сложна и искусственна[7].

См. также

Примечания

Литература

wikiredia.ru

---

• 
  Квантовая механика рязанов
• 
  Квантовая механика и теория большого взрыва видео
• 
  Рязанов квантовая механика
• 
  Квантовая теория против гравитации
• 
  Теории квантовой
• 
  Новые открытия в квантовой физике 2018
• 
  Квантовая тень
• 
  Квантовые машины
• 
  Парадокс наблюдателя в квантовой физике
• 
  Квантовая механика теория всего или как мыслить позитивно
• 
  Что такое квантовый мир