Квантовая песочница: часть 2. Квантовое состояние это
Квантовый ликбез - 9. Квантовое состояние.
Предыдущие посты
После некоторого перерыва продолжаем наши блуждания в квантовых дебрях. Напоминаю, что вопросы, замечания и критика от заинтересованных лиц всячески приветствуются.
В этой части мы поговорим о том, что такое квантовое состояние, а заодно повторим и уточним некоторые важные моменты.
Если вы осилили предыдущие части, то некоторое представление о том, что такое квантовое состояние у вас уже имеется. Попробуем же превратить это смутное представление в чёткое понимание. Для начала уточним, что понимается под физическим состоянием в классической физике. Состояние – это некоторый набор значений физических величин, связанных с объектом. Обычно, говоря о физическом состоянии объекта, мы не рассматриваем все физические величины сразу. Например, если мы говорим о положении объекта в пространстве, то нам достаточно знать три числа, а именно, значения трёх физических величин: координат объекта X, Y, Z в заданной системе отсчёта. Во всяком случае, когда речь идёт об объекте типа «материальная точка». Или вообще нас может интересовать только одно число: значение координаты - X. Это будет «координатное представление» физического состояния.
В других задачах нас может интересовать не координата, а импульс частицы (импульс, напомню, это произведение скорости объекта на его массу). Тогда мы будем рассматривать состояние объекта в «импульсном представлении». Опять же, импульс в трёхмерном пространстве – это трёхмерный вектор. Он задаётся тремя числами: проекциями вектора импульса P на координатные оси X, Y, Z, но если мы говорим о движении точки вдоль оси X, то состояние в импульсном представлении полностью определяется одним числом – Px, то есть проекцией вектора импульса P на ось X. Или, если говорить компактнее – X-компонентой вектора P.
Надеюсь, понятно, но резюмирую. Состояние всегда рассматривается в каком-то представлении. Представление – это ограниченный набор физических величин. А состояние – это соответствующий набор конкретных значений этих величин. В классической физике обычно слово «представление» не используют. Просто говорят что-то вроде: «X = 10». Тут тебе и представление (координата X) и состояние (значение координаты X), как говорится, «в одном флаконе».
Теперь попробуем осилить «квантовое состояние». Мы говорили, что квантовая реальность – это бесконечная совокупность одновременно существующих виртуальных вариантов. Каждый отдельный виртуальный вариант можно рассматривать как виртуальное классическое состояние, стало быть, квантовое состояние – это совокупность бесконечного числа виртуальных классических состояний. Чтобы лучше уяснить смысл этого утверждения, давайте посмотрим, как выглядит квантовое состояние частицы в координатном представлении. Для простоты будем рассматривать только одну координату – X.
Классическое состояние в координатном представлении в какой-то момент времени можно представить себе как точку на координатной оси X. На рисунке 9.1 это точка x1.

Для наглядности на рисунке условно показан вариант (закрашенным синим кружочком), он «привязан» к точке x1. В классическом понимании это никакой не виртуальный, а единственный реальный вариант.
Важное замечание: здесь и дальше в этой части ликбеза мы говорим о «мгновенном» состоянии, то есть, о состоянии в определённый момент времени. Вот грубая, но наглядная аналогия: мы рассматриваем только «фотографию» состояния. А «кино» про состояние мы будем смотреть в следующей части. В смысле, будем разбираться, как квантовое состояние меняется во времени.
Теперь переходим от классического состояния к квантовому. Итак, квантовая реальность – это бесконечное количество виртуальных классических состояний. В нашем случае это означает, что частица расположена (виртуально) во всех точках пространства. Другими словами, частица обладает одновременно всеми значениями координаты X. Значит, в самом грубом приближении квантовое состояние в какой-то момент времени можно представить себе так:

Теперь синими кружочками (пустыми) показываем виртуальные варианты. Тут у нас нарисовано «квантовое состояние», включающее всего четыре виртуальных «классических» состояния. На самом деле их – бесконечность. На рисунке это показать нельзя, поэтому просто представьте, что эти синие кружочки бесконечно плотно расположены вдоль оси X. При этом пусть вас не пугает то, что кружочки будут налезать друг на друга. Напомню, кружочки – это у нас не разные частицы, а разные виртуальные варианты классического расположения одной и той же частицы.
Это, повторяю, очень грубое приближение. Уточним его. В пятой части мы ввели понятие «группа». Группа – это бесконечное множество виртуальных вариантов, приводящих к одному и тому же наблюдаемому результату. В нашем случае группа – это бесконечное число классических состояний с одним и тем же значением координаты X. Значит, ради приближения к истине, к каждой точке пространства мы должны нарисовать не один виртуальный вариант, а бесконечную группу вариантов.

На рисунке 9.3 я изобразил эти группы в виде таких «колод» виртуальных вариантов. Опять же прошу включить воображение и домыслить эту вынужденно убогую картинку до «настоящей квантовой реальности». Во-первых, представьте, что каждая из колод содержит бесконечное количество вариантов. Во-вторых, представьте, что все варианты одной группы на самом деле находятся в одной точке (что естественно, ведь у всех вариантов группы одинаковое значение координаты). И, в-третьих, представьте, что этих групп-колод не четыре, а бесконечное количество, по одной на каждую точку оси X.
Но и такого приближения тоже недостаточно. Третьим постулатом мы постановили, что каждый виртуальный вариант обладает специфической квантовой характеристикой: квантовым вектором. Значит, давайте в каждый кружочек на нашей картинке впишем красную стрелочку, которая будет символизировать направление квантового вектора. Варианты одной группы расположим теперь не «колодой», а «колонной», чтобы стрелочки было видно.

Вот эта картина (если её домыслить до бесконечностей) более-менее адекватно отражает то, что называют квантовым состоянием в координатном представлении. Надо только помнить, что направления квантовых векторов – это направления в условном математическом пространстве (для умников напомним – это вектора на комплексной плоскости). И они в общем случае не имеют ничего общего с направлениями координатных осей.
Итак, классическое состояние объекта в координатном представлении – это просто определённое значение координаты. Квантовое состояние в координатном представлении – это бесконечное количество групп вариантов, то есть, виртуальных классических состояний, отдельная группа для каждого значения координаты. При этом каждая группа – это бесконечное количество вариантов. И для каждого варианта – своё направление квантового вектора. Аналогично описывается квантовое состояние в любом другом представлении. Скажем, в импульсном представление – это бесконечное количество вариантов виртуальных классических состояний, для каждого варианта своё (одно!) значение импульса и своё (тоже одно!) направление квантового вектора.
Чтобы как-то математически оперировать с квантовым состоянием и решать практические задачи с квантовыми объектами, мы должны, казалось бы, знать направление квантового вектора каждого виртуального варианта, при том что этих вариантов бесконечное множество. Прикиньте сложность? К счастью, этого не требуется. Мы говорили раньше, что варианты одной группы находятся в состоянии суперпозиции. Квантовые вектора одной группы вариантов складываются и образуют единый квантовый вектор группы – амплитуду вероятности. Так вот, для решения практических задач с квантовыми объектами достаточно знать «всего лишь» амплитуды вероятности для каждой группы. Но и о виртуальных вариантах полезно помнить, потому что они придают абстрактной квантовой математике конкретный физический смысл. И вот что ещё: понятие о виртуальных вариантах нам ОЧЕНЬ пригодится, когда мы будем разбирать принцип действия квантового компьютера.
Давайте теперь изобразим наше квантовое состояние (рисунок 9.4) в амплитудах вероятности. Больше не будем рисовать кружочки – варианты, ограничимся стрелочками – векторами. Сложим квантовые вектора вариантов в каждой из четырёх показанных групп, и получится вот такая картина.

Смотрите, на рисунке 9.4 в группе, соответствующей координате x1, у каждого квантового вектора есть вектор «антипод» с противоположным направлением. Векторная сумма по группе x1 равна нулю. Все виртуальные варианты «нейтрализованы» деструктивной суперпозицией и не могут реализоваться. Это значит, что если мы захотим измерить координату частицы, находящейся в таком квантовом состоянии, то вероятность получить результат x1 равна нулю.
В группах x2, x3, xn векторная сумма не равна нулю. Это означает, что есть ненулевая вероятность обнаружить частицу в этих точках, если мы измерим координату X в данный момент времени. При этом наиболее вероятно обнаружить частицу в точке x3, поскольку длина вектора амплитуды вероятности в этой точке самая большая.
И опять попрошу вас самостоятельно домыслить этот рисунок «до бесконечностей». Представьте, что с каждым значением координаты X связан вектор амплитуды вектор амплитуды вероятности определённой длины и определённого направления. Надеюсь, вам поможет в этом рисунок 9.6.

Квантовое состояние показано в виде трёхмерного графика: одна пространственная координатная ось X, и две координатных оси условного пространства квантовых векторов. Выше уже упоминалось, что квантовые вектора и их суперпозиции – групповые амплитуды вероятности – математически эквивалентны комплексным числам. Соответственно, условное пространство амплитуд вероятности показано как комплексная плоскость с координатными осями «Re» (действительная часть комплексного числа) и «Im» (мнимая часть).
Так вот, в таком комбинированном ракурсе мгновенная «фотография» квантового состояния частицы в определённый момент времени (допустим, t1) выглядит как расширяющаяся, а затем сужающаяся спираль, которую вектор амплитуды вероятности описывает вокруг оси X. Вектора нарисованы для наглядности только для нескольких точек оси X, для остальных точек домыслите их самостоятельно. Если мы проследим, как ведёт себя вектор амплитуды вероятности с изменением координаты X от минус бесконечности до плюс бесконечности, то мы увидим, что он равномерно «вращается» вокруг оси X. При этом величина (длина вектора) амплитуды вероятности растёт от бесконечно малой величины, в какой-то точке достигает максимума (на рисунке это точка x3, где наибольший «диаметр» спирали), затем уменьшается обратно к бесконечно малой. Да, на всякий случай напомню, что мы тут нарисовали квантовое состояние «упрощённо», в групповых амплитудах вероятности. Полная картина квантового состояния должна была бы включать бесконечное множество разнонаправленных квантовых векторов единичной длины для каждой точки X. Но, повторяю, описание квантового состояния в амплитудах вероятности вполне достаточно для практического решения квантовых задач, поэтому таким описанием мы и будем пользоваться дальше.
Эта абстрактная картинка имеет вполне конкретный физический смысл Напоминаю, что относительная (нормированная) длина вектора амплитуды вероятности определяет вероятность получить соответствующий результат при измерении. Помним, да, что вероятность равна длине вектора амплитуды вероятности, возведённой в квадрат? В нашем случае, если мы в момент времени t1 измерим координату X, то с наибольшей вероятностью получим значение, близкое к x3, там, где длина амплитуды вероятности максимальна. Менее вероятно получить значения около x2 или x4. И уж совсем маловероятно обнаружить частицу в окрестностях точек x1 или x5, где амплитуда вероятности близка к нулю. Если нарисовать соответствующий график зависимости вероятности от координаты X, то он будет выглядеть примерно так:

трого говоря, в данной ситуации речь идёт не о вероятности, а о плотности вероятности, но сейчас это не принципиально.
Надо сказать, что форма «спирали» квантового состояния, а значит и форма графика вероятности, может быть различной. Вероятность может иметь ярко выраженный «пик» в окрестностях какой-то координаты x1, как на рисунке 9.8-а. В этом случае говорят о малой неопределённости, имея в виду, что при измерении координаты X мы определённо получим значение, близкое к x1. Или, наоборот, вероятность может быть «размазана» вдоль широкого диапазона значений оси X, как на рисунке 9.8-б. Это случай большой неопределённости координаты, когда различные результаты измерения более-менее равновероятны.

Ладно, отдельный разговор о неопределённостях у нас в перспективе. А также о том, от чего зависит вид этих графиков. Пока же заметим, что квантовое состояние можно рассматривать как векторную (комплексную) математическую функцию, выражающую зависимость длины и направления вектора амплитуды вероятности от координаты. А вероятность – это «обычная» действительная функция.
Конечно, всё сказанное верно и для любого другого представления. Например, если бы мы говорили об импульсном представлении квантового состояния, то мы подразумевали бы, что в квантовой реальности частица одновременно обладает всеми возможными виртуальными значениями импульса, от минус бесконечности до плюс бесконечности. В таком представлении квантовое состояние выглядело бы как функция амплитуды вероятности от импульса частицы. Кстати говоря, график этой функции выглядит аналогично: расширяющаяся, а затем сужающаяся спираль. Только координату X на рисунке 9.6 придётся заменить на «импульсную» координату Px. В других представлениях и/или в других физических ситуациях график амплитуды вероятности будет выглядеть по-другому. Но в любом случае это будет комплексная функция от соответствующей физической величины.
Здесь, пожалуй, уместно будет разобраться, откуда берутся бесконечные группы виртуальных вариантов. Мы выяснили, что квантовое состояние – это совокупность бесконечного числа виртуальных классических состояний. Иначе, это совокупность бесконечного количества различных виртуальных значений некоторой физической величины. Но ведь не существует таких физических объектов, которые характеризовались бы только одной физической величиной. Даже простейшая частица в пространстве «обладает», как минимум, тремя координатами и тремя компонентами импульса (проекциями вектора импульса на координатные оси). Я уже не говорю о всяких там угловых и магнитных моментах, зарядах и прочих физических величинах. Но достаточно рассмотреть в совокупности всего две физические величины, чтобы увидеть бесконечные группы виртуальных вариантов. Возьмём, например координату X и импульс Px.
Так, отставить. Сначала поиграем опять в карты. Вытаскиваем случайную карту из колоды в 36 карт. Заметим, что каждая карта характеризуется двумя «физическими величинами» – достоинством и мастью. Если наша задача - вытащить карту определённого достоинства, то у нас имеется 9 возможных результатов – от шестёрки до туза. То есть, 9 групп. Очевидно, что в каждой группе по 4 варианта, по количеству мастей. Можно сказать, что состояние колоды в представлении карточного достоинства включает 9 групп, по четыре варианта в каждой. Если же задача - вытащить карту определённой масти, то тут нас будет интересовать состояние колоды в представлении масти. Тогда наоборот, будет 4 группы, по 9 вариантов в каждой. Идея понятна? Тогда возвращаемся к нашей частице.
И в координатном, и в импульсном представлении квантового состояния частицы у нас бесконечное число вариантов. Это означает, что существует бесконечное число виртуальных классических состояний с одинаковым значением координаты X, например, X = x1, но разными значениями импульса Px. Это и будет бесконечная группа x1. И наоборот, бесконечную группу виртуальных состояний с одинаковым значением импульса Px составят состояния с различными значениями координаты X.
Короче, бесконечность числа виртуальных состояний, дающих один и тот же результат измерения, обусловлена двумя факторами: бесконечностью числа виртуальных значений любой физической величины (по-сути, это просто другая формулировка первого постулата) и тем обстоятельством, что с любым физическим объектом связано несколько (больше одной) физических величин.
Уф, эта часть получилась длинной. Но надо тут обсудить ещё вот какую вещь. Разговаривая о квантовой механике, мы пока что ни словом не упомянули собственно <кванты>. Вот теперь мы готовы к тому, чтобы поговорить о квантовании.
Выше уже говорилось о том, что форма зависимости амплитуды вероятности от значения измеряемой физической величины может быть различной. На рисунке 9.6 - это непрерывная «гладкая» функции. Но во многих физических ситуациях эта функция может быть дискретной, допустим, такой, как на следующем рисунке.

Если говорить о реальных физических примерах, то похоже выглядит квантовое состояние атома в «энергетическом представлении». Видно, что амплитуда вероятности не равна нулю только для нескольких определённых значений энергии атома. В переводе на русский язык это означает, что если мы измерим энергию атома, то мы получим какое-то одно значение из трёх: e1, e2, e3. Только варианты из этих трёх групп реализуемы, все остальные - нет. Эта дискретность возможных ркзультатов измерения и означает, что энергия атома «квантуется».
Вообще, квантование - это специфическое свойство некоторых физических величин и физических ситуаций. Например, координаты свободно движущегося электрона не квантуются. При измерении координаты такой частицы может быть получен любой результат, пусть и не с одинаковой вероятностью. В этом случае говорят, что измеряемая физическая величина имеет непрерывный спектр значений. А когда речь идёт об электроне на орбите атома, координата квантуется - электрон может быть <обнаружен> только на одной из нескольких определённых орбит. В этом случае спектр значений физической величины - дискретный.
Есть величины, которые квантуются в любой физической ситуации. Таков, например, спин частицы. Почему так? Это всё причуды суперпозиции. На уровне всех виртуальных вариантов никакого квантования нет, в квантовой реальности существуют все мыслимые значения физической величины. Но на уровне РЕАЛИЗУЕМЫХ виртуальных вариантов может сохраниться только несколько возможных значений, все остальные «сожрёт» деструктивная суперпозиция.
Ну и на десерт – чуточку философии. Крайним случаем «квантованности» является такой, когда реализуемой является только одна группа вариантов. Результат измерения может быть только один. Это такая ситуация, когда квантовая физика автоматически превращается в классическую. С другой стороны, можно классическую физику рассматривать как квантовую. В таком случае мы можем считать, что классическое физическое состояние – это бесконечная группа ОДИНАКОВЫХ виртуальных вариантов.
Впрочем, и квантовая физика сама по себе такие однозначные ситуации не исключает. Например, такая физическая величина, как масса покоя частицы, существует в единственном варианте. Точнее, в единственной группе вариантов. Короче, измерение массы покоя всегда даёт одно и то же значение. С точностью до ошибки измерения, конечно.
ПродолжениеTags: квантовый ликбез, физика
eslitak.livejournal.com
Квантовая песочница: часть 2 / Хабр
В данной статье постараемся ответить на эти вопросы и разобраться в сути квантовой механики. Цель: написать простую программу, «имитирующую» квантовую эволюцию, чтобы наконец можно было пощупать эти кубиты ручками.
- Часть I: Классическое состояние
- Часть II: Квантовое состояние
- Часть III: Кот
- Часть IV: Рой
Что такое обычное «состояние»? Этим термином пользуются так часто, что он начал восприниматься полностью интуитивно.
Вопрос №1: «Дана частица P, которую можно наблюдать вдоль отрезка . Что такое состояние частицы P?» Ответ: Классическое состояние частицы P — число из отрезка .Внимательного читателя привлечет слово «наблюдать» — как это вообще понимать? Оказалось, что все это время на участке были расположены какие-то «детекторы», которые «наблюдали», но почему мы о них ничего не сказали? И сколько их там вообще штук?
Мы сказали, что состояние частицы — число из отрезка . Мощность множества равна континууму — между нашими «границами» А и B находится бесконечно много чисел, причем они расположены бесконечно близко друг к другу — значит нам требуется бесконечно много детекторов для каждой точки? Звучит довольно затратно, не так ли?
А ведь, утверждая, что состояние есть число, мы, получается, подразумеваем именно это. Именно то, что у нас в наличии бесконечно много детекторов. Но ведь это не так. И такого не может быть в принципе.
На практике мы бы разбили отрезок на конечное число сегментов, а в пересечениях поставили бы детекторы, и каждый детектор был бы способен приближенно сообщить, есть ли частица в его окрестности или нет.
То, что было сделано выше называется квантованием. В данном случае мы провели квантование отрезка на сегменты. Квант — неделимая порция чего-либо в рамках используемой модели, абстрактный термин.
Самые интересные явления начинаются именно по той причине, что состояние частицы теперь перестало быть просто числом.
Вопрос №2: «Дана частица P, которую можно наблюдать только в окрестности некоторого числа детекторов на отрезке . Что такое состояние частицы P?» Ответ: ???Рассмотрим пример:
Дан отрезок и два детектора, расположенные в точках A и B.
Каждый детектор показывает какое-то определенное число, согласно которому мы можем определить, как далеко находится частица от данного детектора.
A — первый детектор, — его показания ( = 1, если частица попала прямо в А) B — второй детектор, — его показания ( = 1, если частица попала прямо в В)
Выдвинем предположение о частице, чтобы как-то ограничить круг наших исследований:
Предположение: Частица одна, она не может просто так взять и клонировать себя.
Из этого предположения следует, что если частица в А, то она не может быть в В, и наоборот.
Или, что то же самое, если = 1, то = 0 и наоборот.
Теперь рассмотрим «движение» частицы от детектора А к детектору В. Частица была в А ( = 1, = 0), затем она начала лететь к В. Показания детектора А начали уменьшаться ( < 1), а показания детектора В начали увеличиваться ( > 0). Затем частица достигла детектора В и его показания равны = 1, а детектор А оповещает нас, что частицы в нем нет = 0.
Таким образом, мы описываем состояние частицы с помощью самих детекторов и их показаний.
Это запись означает, что конфигурация X включает в себя детектор A, показывающий нам число c1, и детектор B, показывающий нам число c2.
Вопрос №2: «Дана частица P, которую можно наблюдать только в окрестности детекторов, расположенных в точках A и B, которые являются квантованием отрезка на один сегмент . Что такое состояние частицы P?» Предположение: Частица одна, она не может взять и просто так клонировать себя.Ответ: Квантовое состояние частицы P — вектор двумерного гильбертова пространства с базисными векторами A = {1, 0} и B = {0, 1}. При этом этот вектор нормирован на единицу (), а базисные векторы A и B являются классическими состояниями из вопроса 1. Такие частицы также называют кубитами в силу двумерности базиса. Когда базис трехмерный, частицы называются кутритами и т. д.Вопрос №2 (обобщенный): «Дана частица P, которую можно наблюдать только в окрестности конечного числа детекторов, расположенных в точках , которые являются квантованием отрезка на N — 1 сегмент . Что такое состояние частицы P?» Предположение: Частица одна, она не может взять и просто так клонировать себя.Ответ: Квантовое состояние частицы P — вектор N-мерного гильбертова пространства с базисными векторами . При этом этот вектор нормирован на единицу , а базисные векторы являются классическими состояниями из вопроса 1.Мы вплотную подошли к самым интересным проявлениям квантовой механики. Без сомнения каждый из читателей хоть краем уха слышал о таких терминах, как «квантовая суперпозиция» или «квантовая запутанность» — эти эффекты и другая подобная магия начинаются именно в тот момент, когда вы не будете делать тех умозаключений, которые не требуются.
У нас есть два определения состояния.
Определение №1: Классическое состояние частицы P — число из отрезка …Предположение: Частица одна, она не может взять и просто так клонировать себя.Определение №2: Квантовое состояние частицы P — вектор двумерного гильбертова пространства …Обычно из каких-то определений выводят следствия, здесь же нас будет интересовать то, что не следует из определения, но мы все равно назовем это следствиями для стройности.
Следствие №1: Из определения квантового состояния не следует, что частица находится в одной точке отрезка. Вообще ниоткуда никак не следует.То есть частица может находится сразу в двух точках! Например для частицы, которая находится в квантовом состоянии не следует, что она находится в одной точке. Да, может быть она где-то посередине, в какой-то точке M между A и B, но утверждая подобное, мы проявим необоснованную вольность.
Следствие №2: Из определения квантового состояния не следует, что частица разделилась на маленькие кусочки, одни кусочку полетели туда, а другие сюда.Как это вообще понимать? Как частица может находится сразу в двух точках и при этом оставаться неделимой? Мы же привыкли, что кот Шрёдингера и жив, и мертв одновременно, значит и частица тоже и здесь, и там одновременно. Но ведь она же неделима. Она что растянулась?
Введем понятие роя и экземпляра виртуальных частиц.
Определение №3: Экземпляр частицы — виртуальный объект, которому соответствует положение в пространстве в данный момент времени, траектория движения с течением времени, а также комплексное число (называемое амплитудой), обладающее модулем и аргументом, для которого справедливы все алгебраические правила: Определение №4: Рой — совокупность экземпляров.Определение №5: Частица — рой (при выполнении операции квантования пространства).Представим экземпляр как шарик, внутри которого есть стрелка, соответствующая комплексному числу в комплексной плоскости. Важно понимать, что шарик может иметь одно направление движения, а стрелка внутри него — другое, то есть эти направления разные.
Но почему разные? Дело в том, что процессы внутри элементарной частицы настолько сложно описать, что влияние этих процессов на движение самой частицы невозможно предсказать на фундаментальном уровне, поэтому и связи между стрелкой внутри шарика и направлением движения самого шарика для нас не существует.
Словесные манипуляция, которые мы сейчас совершили, бесполезны, если не определить законы изменения величин r, φ и закон движения, ведь в них все и упирается.
Закон изменения аргумента: φ постоянно равномерно увеличивается на величину dφ по мере движения экземпляра.Иными словами, наши комплексное стрелки постоянно крутятся в одном и том же направлении. Зачем это нужно? Чтобы система ни при каких обстоятельствах не перестала эволюционировать.
Закон сложения и умножения: По мере движения вдоль одной траектории амплитуды перемножаются. Амплитуды вдоль всевозможных траекторий складываются.Данный закон также известен как «принцип суперпозиции в квантовой механике»
Закон движения экземпляров в пространстве: Пусть дана частица в квантовом состоянии. Дан экземпляр, которые находится в какой-то клетке пространства (над которым была произведена операция квантования на клетки). Вокруг этой клетки пространства есть соседние клетки.- Данный экземпляр клонирует себя столько раз, сколько вокруг него существует соседних точек
- Каждый клон движется в ту соседнюю точку, которая ему соответствует
- Данный экземпляр-отец движется в произвольную точку
| 1. Внутри каждого шарика находится та самая комплексная стрелка, которая крутится на угол dφ после каждого перемещения экземпляра из одной клетки в другую. | 2. Таким образом у нас есть огромная динамическая система, которая постоянно клонирует себя. | 3. Направление движения самого первого экземпляра, в целом, определяет движения роя, но рой тем не менее распространяется во все стороны. Если же отследить движение любого отдельного экземпляра (не обращая внимание на клонов), то он будет двигаться по абсолютно случайной траектории. |
Формирование оператора энергии «по кусочкам ручками» будет рассмотрено в следующей статье.
Конструктивно, мы разобрались со следующими понятиями:
- Классическое состояние частицы как число (а не как что-либо еще)
- Квантовое состояние частицы как вектор (а не как «то, что находится сразу в нескольких местах»)
- Частица как рой (при выполнении операции квантования)
- Принцип суперпозиции роя, согласно которому амплитуды вдоль одной траектории перемножаются, а вдоль всевозможных траекторий складываются
- Закон движения экземпляров
Поскольку тема квантовой механики активно популяризируется в последнее время (начиная от соответствующих журналов, заканчивая целыми выставками, посвященными «квантовой запутанности»), мне кажется, что есть потребность в мониторинге актуального состояния, чтобы можно было зайти и проверить «а что там у нас с квантами?» Возможно, эта информация будет полезной — pleaded.ru
habr.com
Состояние (квантовая механика) - это... Что такое Состояние (квантовая механика)?
Квантовое состояние — любое возможное состояние, в котором может находиться квантовая система. Чистое квантовое состояние может быть описано:
Эти описания математически эквивалентны. В общем случае квантовое состояние (смешанное) принципиально не может быть описано волновой функцией и должно быть описано матрицей плотности, являющейся неотрицательным самосопряженным оператором с единичным следом. Квантовые состояния можно интерпретировать как статистические ансамбли с некоторыми фиксированными квантовыми числами.
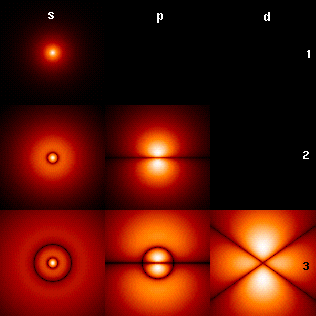
Распределение плотности вероятности для электрона в атоме водорода, находящемся в различных состояниях.Векторы состояний
Для описания возможных состояний заданной квантовой системы применяется математический аппарат гильбертова пространства , позволяющий практически полностью описать всё, что может происходить с системой.
Для описания квантового состояния в этом случае вводится так называемый вектор состояния, представляющий собой множество математических величин, которое полностью описывает квантовую систему. К примеру, множество 4 чисел{, , , } определяет состояние электрона в атоме водорода, и называются квантовыми числами электрона.
Подобная конструкция оказывается возможной благодаря экспериментально установленному[источник не указан 879 дней]принципу суперпозиции для квантовых систем. Он проявляется в том, что если существуют два возможных состояния квантовой системы, причём в первом состоянии некоторая наблюдаемая величина может принимать значения p1, p2, …, а во втором — q1, q2,… , то существует и состояние, называемое их суперпозицией, в котором эта величина может принимать любое из значений p1, p2, …, q1, q2,…. Количественное описание этого явления приведено ниже.
Обозначения бра-кет
Будем обозначать вектор состояния, соответствующий состоянию ψ, как . Сопряжённый вектор, соответствующий состоянию ψ, будем обозначать как . Скалярное произведение векторов и будем обозначать как , а образ вектора под действием оператора будем обозначать . Символ называется бра (англ. bra), а символ ψ, как — кет (англ. ket). Подобные обозначения в целом согласуются с обозначениями обычной линейной алгебры, но более удобны в квантовой механике, так как позволяют более наглядно и коротко называть используемые векторы. Такие обозначения были впервые введены Дираком. Названия векторов образованы разбиением слова bracket (скобка) на две звучные части — bra и ket.
Математический формализм
Всякий вектор из пространства , кроме нуля, соответствует некому состоянию. Однако, векторы, различающиеся лишь умножением на ненулевое комплексное число, отвечают одному физическому состоянию. Иногда полагают, что вектор состояния обязан быть «нормирован на единицу»: — любой ненулевой вектор приобретает это свойство, если разделить его на свою норму .
Если мы рассмотрим два различных состояния, то суперпозиции (всевозможные линейные комбинации) пары соответствующих им векторов дадут двумерное линейное комплексное пространство. Соответственное множество физических состояний будет представлять двумерную поверхность — сферу Римана.
При рассмотрении квантовой системы, состоящей из двух подсистем, пространство состояний строится в виде тензорного произведения. Подобные системы, помимо комбинаций состояний своих подсистем, имеют также и сцепленные (запутанные) состояния.
«Количество состояний»
Если система имеет хотя бы два физически различных состояния, то мощность множества возможных векторов состояния (даже с точностью до умножения на комплексное число), разумеется, бесконечна. Однако, под количеством состояний квантовой системы подразумевают количество линейно независимых состояний, то есть размерность пространства . Это вполне соответствует интуиции, поскольку описывает количество возможных исходов измерения; к тому же, при тензорном произведении (то есть, построении составной системы) размерность пространств перемножается.
В контексте рассмотрения замкнутой квантовой системы (то есть, решения уравнения Шрёдингера) под состояниями могут пониматься только стационарные состояния — собственные векторы гамильтониана, отвечающие различным уровням энергии. В случае конечномерного пространства и при отсутствии вырождения, число уровней энергии (и соответствующих им состояний) будет равно размерности пространства.
См. также
Литература
- Березин Ф. А., Шубин М. А. Уравнение Шредингера. М.: Изд-во МГУ, 1983. 392с.
- Боум А. Квантовая механика: основы и приложения. М.: Мир, 1990. — 720 c. Глава IV.
dic.academic.ru
квантовое состояние - это... Что такое квантовое состояние?
quantum state
Англо-русский словарь технических терминов. 2005.
- квантовая яма
- квантовое усиление
Смотреть что такое "квантовое состояние" в других словарях:
квантовое состояние — Одно из возможных дискретных стабильных состояний системы взаимодействующих частиц. [Сборник рекомендуемых терминов. Выпуск 79. Физическая оптика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Тематики физическая оптика… … Справочник технического переводчика
Квантовое состояние — У этого термина существуют и другие значения, см. Состояние. Квантовая механика … Википедия
квантовое состояние — kvantinė būsena statusas T sritis fizika atitikmenys: angl. quantum state vok. gequantelter Energiezustand, m; Quantenzustand, m rus. квантовое состояние, n; квантовое энергетическое состояние, n pranc. état quantique, m … Fizikos terminų žodynas
квантовое состояние — kvantinė būsena statusas T sritis chemija apibrėžtis Diskretiniu banginių funkcijų rinkiniu apibūdinama elektrono būsena atome. atitikmenys: angl. quantum state rus. квантовое состояние … Chemijos terminų aiškinamasis žodynas
КВАНТОВОЕ СОСТОЯНИЕ — первичное понятие квантовой механики. Единств, способ полностью охарактеризовать квантовую систему указать К. с., в к ром система находится. К. с. атомных ядер, атомов, молекул, кристаллов и т. п. квантовых систем считается заданным, если… … Химическая энциклопедия
возбужденное квантовое состояние — sužadintoji kvantinė būsena statusas T sritis chemija apibrėžtis Atomo (dalelės) būsena, kai elektronai yra perėję į aukštesnius energijos lygmenis. atitikmenys: angl. excited quantum state rus. возбужденное квантовое состояние … Chemijos terminų aiškinamasis žodynas
СОСТОЯНИЕ — (1) аморфное (рентгеноаморфное) состояние твёрдого вещества, в котором нет кристаллической структуры (атомы и молекулы расположены беспорядочно), оно изотропно, т. е. имеет одинаковые физ. свойства по всем направлениям и не имеет чёткой… … Большая политехническая энциклопедия
Состояние (квантовая механика) — У этого термина существуют и другие значения, см. Состояние. Квантовая механика Принцип неопределённости Гейзенберга … Википедия
квантовое энергетическое состояние — kvantinė būsena statusas T sritis fizika atitikmenys: angl. quantum state vok. gequantelter Energiezustand, m; Quantenzustand, m rus. квантовое состояние, n; квантовое энергетическое состояние, n pranc. état quantique, m … Fizikos terminų žodynas
Квантовое запутывание — Квантовая механика Принцип неопределённости Введение ... Математическая формулировка ... Основа … Википедия
Квантовое туннелирование — Квантовая механика Принцип неопределённости Введение ... Математическая формулировка ... Основа … Википедия
Книги
- Вибрационное целительство. Квантовое оздоровление сознания и тела, Проценко Тарас Анатольевич. Книга посвящена психической энергии, или жизненной силе человека, имеющей непосредственное отношение к самочувствию и здоровью. На фоне большого количества дилетантской литературы о… Подробнее Купить за 314 руб
- Вибрационное целительство. Квантовое оздоровление сознания и тела, Проценко Тарас Анатольевич. Книга посвящена психической энергии, или жизненной силе человека, имеющей непосредственное отношение к самочувствию и здоровью. На фоне большого количества дилетантской литературы о… Подробнее Купить за 279 руб
- Как сохранить энергетический иммунитет, Проценко Тарас Анатольевич. Проценко Тарас Анатольевич — профессиональный врач с большим стажем работы, терапевт, физиотерапевт, специалист в области нетрадиционной медицины и немедикаментозных методов лечения, автор… Подробнее Купить за 264 руб
dic.academic.ru
квантовое состояние - это... Что такое квантовое состояние?
Большой англо-русский и русско-английский словарь. 2001.
- квантово-механический туннельный эффект
- квантовое усиление
Смотреть что такое "квантовое состояние" в других словарях:
квантовое состояние — Одно из возможных дискретных стабильных состояний системы взаимодействующих частиц. [Сборник рекомендуемых терминов. Выпуск 79. Физическая оптика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Тематики физическая оптика… … Справочник технического переводчика
Квантовое состояние — У этого термина существуют и другие значения, см. Состояние. Квантовая механика … Википедия
квантовое состояние — kvantinė būsena statusas T sritis fizika atitikmenys: angl. quantum state vok. gequantelter Energiezustand, m; Quantenzustand, m rus. квантовое состояние, n; квантовое энергетическое состояние, n pranc. état quantique, m … Fizikos terminų žodynas
квантовое состояние — kvantinė būsena statusas T sritis chemija apibrėžtis Diskretiniu banginių funkcijų rinkiniu apibūdinama elektrono būsena atome. atitikmenys: angl. quantum state rus. квантовое состояние … Chemijos terminų aiškinamasis žodynas
КВАНТОВОЕ СОСТОЯНИЕ — первичное понятие квантовой механики. Единств, способ полностью охарактеризовать квантовую систему указать К. с., в к ром система находится. К. с. атомных ядер, атомов, молекул, кристаллов и т. п. квантовых систем считается заданным, если… … Химическая энциклопедия
возбужденное квантовое состояние — sužadintoji kvantinė būsena statusas T sritis chemija apibrėžtis Atomo (dalelės) būsena, kai elektronai yra perėję į aukštesnius energijos lygmenis. atitikmenys: angl. excited quantum state rus. возбужденное квантовое состояние … Chemijos terminų aiškinamasis žodynas
СОСТОЯНИЕ — (1) аморфное (рентгеноаморфное) состояние твёрдого вещества, в котором нет кристаллической структуры (атомы и молекулы расположены беспорядочно), оно изотропно, т. е. имеет одинаковые физ. свойства по всем направлениям и не имеет чёткой… … Большая политехническая энциклопедия
Состояние (квантовая механика) — У этого термина существуют и другие значения, см. Состояние. Квантовая механика Принцип неопределённости Гейзенберга … Википедия
квантовое энергетическое состояние — kvantinė būsena statusas T sritis fizika atitikmenys: angl. quantum state vok. gequantelter Energiezustand, m; Quantenzustand, m rus. квантовое состояние, n; квантовое энергетическое состояние, n pranc. état quantique, m … Fizikos terminų žodynas
Квантовое запутывание — Квантовая механика Принцип неопределённости Введение ... Математическая формулировка ... Основа … Википедия
Квантовое туннелирование — Квантовая механика Принцип неопределённости Введение ... Математическая формулировка ... Основа … Википедия
Книги
- Вибрационное целительство. Квантовое оздоровление сознания и тела, Проценко Тарас Анатольевич. Книга посвящена психической энергии, или жизненной силе человека, имеющей непосредственное отношение к самочувствию и здоровью. На фоне большого количества дилетантской литературы о… Подробнее Купить за 314 руб
- Вибрационное целительство. Квантовое оздоровление сознания и тела, Проценко Тарас Анатольевич. Книга посвящена психической энергии, или жизненной силе человека, имеющей непосредственное отношение к самочувствию и здоровью. На фоне большого количества дилетантской литературы о… Подробнее Купить за 279 руб
- Как сохранить энергетический иммунитет, Проценко Тарас Анатольевич. Проценко Тарас Анатольевич — профессиональный врач с большим стажем работы, терапевт, физиотерапевт, специалист в области нетрадиционной медицины и немедикаментозных методов лечения, автор… Подробнее Купить за 264 руб
dic.academic.ru
Квантовое состояние — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Состояние.Квантовое состояние — любое возможное состояние, в котором может находиться квантовая система. Чистое квантовое состояние может быть описано:
Эти описания математически эквивалентны. В общем случае квантовое состояние (смешанное) принципиально не может быть описано волновой функцией и должно быть описано матрицей плотности, являющейся неотрицательным самосопряженным оператором с единичным следом. Квантовые состояния можно интерпретировать как статистические ансамбли с некоторыми фиксированными квантовыми числами.
Векторы состояний
Для описания возможных состояний заданной квантовой системы применяется математический аппарат гильбертова пространства <math>\mathcal{H}</math>, позволяющий практически полностью описать всё, что может происходить с системой.
Для описания квантового состояния в этом случае вводится так называемый вектор состояния, представляющий собой множество математических величин, которое полностью описывает квантовую систему. К примеру, множество 4 чисел{<math>n \ </math>, <math>\ell \ </math>, <math>m_\ell \ </math>, <math>m_s</math>} определяет состояние электрона в атоме водорода, и называются квантовыми числами электрона.
Подобная конструкция оказывается возможной благодаря принципу суперпозиции для квантовых систем. Он проявляется в том, что если существуют два возможных состояния квантовой системы, причём в первом состоянии некоторая наблюдаемая величина может принимать значения p1, p2, …, а во втором — q1, q2,… , то существует и состояние, называемое их суперпозицией, в котором эта величина может принимать любое из значений p1, p2, …, q1, q2,…. Количественное описание этого явления приведено ниже.
Обозначения бра-кет
Будем обозначать вектор состояния, соответствующий состоянию <math>\psi</math>, как <math>\left|\psi\right\rangle</math>. Сопряжённый вектор, соответствующий состоянию <math>\psi</math>, будем обозначать как <math>\left\langle\psi\right|</math>. Скалярное произведение векторов <math>\left|\psi\right\rangle </math> и <math>\left|\phi\right\rangle </math> будем обозначать как <math>\left\langle\phi|\psi\right\rangle</math>, а образ вектора <math>\left|\psi\right\rangle</math> под действием оператора <math>\mathcal F</math> будем обозначать <math>\mathcal F\left|\psi\right\rangle</math>. Символ <math>\left\langle\psi\right|</math> называется бра (англ. bra), а символ <math>\psi</math>, как <math>\left|\psi\right\rangle</math> — кет (англ. ket). Подобные обозначения в целом согласуются с обозначениями обычной линейной алгебры, но более удобны в квантовой механике, так как позволяют более наглядно и коротко называть используемые векторы. Такие обозначения были впервые введены Дираком. Названия векторов образованы разбиением слова bracket (скобка) на две звучные части — bra и ket.
Математический формализм
Всякий ненулевой вектор из пространства <math>\mathcal{H}</math> соответствует некому чистому состоянию. Однако, векторы, различающиеся лишь умножением на ненулевое комплексное число, отвечают одному физическому состоянию. Иногда полагают, что вектор состояния <math>|\psi\rangle</math> обязан быть «нормирован на единицу»: <math>\langle\psi|\psi\rangle = 1</math> — любой ненулевой вектор приобретает это свойство, если разделить его на свою норму <math>\sqrt{\langle\psi|\psi\rangle}</math>.
Если мы рассмотрим два различных состояния, то суперпозиции (всевозможные линейные комбинации) пары соответствующих им векторов дадут двумерное линейное комплексное пространство. Соответственное множество физических состояний будет представлять двумерную поверхность — сферу Римана.
При рассмотрении квантовой системы, состоящей из двух подсистем, пространство состояний строится в виде тензорного произведения. Подобные системы, помимо комбинаций состояний своих подсистем, имеют также и сцепленные (запутанные) состояния.
«Количество состояний»
Если система имеет хотя бы два физически различных состояния, то мощность множества возможных векторов состояния (даже с точностью до умножения на комплексное число), разумеется, бесконечна. Однако, под количеством состояний квантовой системы подразумевают количество линейно независимых состояний, то есть размерность пространства <math>\mathcal{H}</math>. Это вполне соответствует интуиции, поскольку описывает количество возможных исходов измерения; к тому же, при тензорном произведении (то есть, построении составной системы) размерность пространств перемножается.
В контексте рассмотрения замкнутой квантовой системы (то есть, решения уравнения Шрёдингера) под состояниями могут пониматься только стационарные состояния — собственные векторы гамильтониана, отвечающие различным уровням энергии. В случае конечномерного пространства <math>\mathcal{H}</math> и при отсутствии вырождения, число уровней энергии (и соответствующих им состояний) будет равно размерности пространства.
Чистое состояние
Чистое состояние — это полностью указанное квантовое состояние. Если данный квантовый объект (например, какая-то элементарная частица) находится в чистом состоянии, это означает, что у нас есть вся информация о ней. Только чистые состояния полностью можно описать волновыми функциями.
См. также
Напишите отзыв о статье "Квантовое состояние"
Литература
- Березин Ф. А., Шубин М. А. Уравнение Шредингера. М.: Изд-во МГУ, 1983. 392с.
- Боум А. Квантовая механика: основы и приложения. М.: Мир, 1990. — 720 c. Глава IV.
- [eqworld.ipmnet.ru/ru/library/books/Dirak1979ru.djvu Дирак П. Принципы квантовой механики. 2-е изд. М.: Наука, 1979. — 480 с.]
- Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 4-е. — М.: Наука, 1989. — 768 с. — («Теоретическая физика», том III). — ISBN 5-02-014421-5.
Отрывок, характеризующий Квантовое состояние
Маленькая княгиня лежала на подушках, в белом чепчике. (Страдания только что отпустили ее.) Черные волосы прядями вились у ее воспаленных, вспотевших щек; румяный, прелестный ротик с губкой, покрытой черными волосиками, был раскрыт, и она радостно улыбалась. Князь Андрей вошел в комнату и остановился перед ней, у изножья дивана, на котором она лежала. Блестящие глаза, смотревшие детски, испуганно и взволнованно, остановились на нем, не изменяя выражения. «Я вас всех люблю, я никому зла не делала, за что я страдаю? помогите мне», говорило ее выражение. Она видела мужа, но не понимала значения его появления теперь перед нею. Князь Андрей обошел диван и в лоб поцеловал ее. – Душенька моя, – сказал он: слово, которое никогда не говорил ей. – Бог милостив. – Она вопросительно, детски укоризненно посмотрела на него. – Я от тебя ждала помощи, и ничего, ничего, и ты тоже! – сказали ее глаза. Она не удивилась, что он приехал; она не поняла того, что он приехал. Его приезд не имел никакого отношения до ее страданий и облегчения их. Муки вновь начались, и Марья Богдановна посоветовала князю Андрею выйти из комнаты. Акушер вошел в комнату. Князь Андрей вышел и, встретив княжну Марью, опять подошел к ней. Они шопотом заговорили, но всякую минуту разговор замолкал. Они ждали и прислушивались. – Allez, mon ami, [Иди, мой друг,] – сказала княжна Марья. Князь Андрей опять пошел к жене, и в соседней комнате сел дожидаясь. Какая то женщина вышла из ее комнаты с испуганным лицом и смутилась, увидав князя Андрея. Он закрыл лицо руками и просидел так несколько минут. Жалкие, беспомощно животные стоны слышались из за двери. Князь Андрей встал, подошел к двери и хотел отворить ее. Дверь держал кто то. – Нельзя, нельзя! – проговорил оттуда испуганный голос. – Он стал ходить по комнате. Крики замолкли, еще прошло несколько секунд. Вдруг страшный крик – не ее крик, она не могла так кричать, – раздался в соседней комнате. Князь Андрей подбежал к двери; крик замолк, послышался крик ребенка. «Зачем принесли туда ребенка? подумал в первую секунду князь Андрей. Ребенок? Какой?… Зачем там ребенок? Или это родился ребенок?» Когда он вдруг понял всё радостное значение этого крика, слезы задушили его, и он, облокотившись обеими руками на подоконник, всхлипывая, заплакал, как плачут дети. Дверь отворилась. Доктор, с засученными рукавами рубашки, без сюртука, бледный и с трясущейся челюстью, вышел из комнаты. Князь Андрей обратился к нему, но доктор растерянно взглянул на него и, ни слова не сказав, прошел мимо. Женщина выбежала и, увидав князя Андрея, замялась на пороге. Он вошел в комнату жены. Она мертвая лежала в том же положении, в котором он видел ее пять минут тому назад, и то же выражение, несмотря на остановившиеся глаза и на бледность щек, было на этом прелестном, детском личике с губкой, покрытой черными волосиками. «Я вас всех люблю и никому дурного не делала, и что вы со мной сделали?» говорило ее прелестное, жалкое, мертвое лицо. В углу комнаты хрюкнуло и пискнуло что то маленькое, красное в белых трясущихся руках Марьи Богдановны.Через два часа после этого князь Андрей тихими шагами вошел в кабинет к отцу. Старик всё уже знал. Он стоял у самой двери, и, как только она отворилась, старик молча старческими, жесткими руками, как тисками, обхватил шею сына и зарыдал как ребенок.
Через три дня отпевали маленькую княгиню, и, прощаясь с нею, князь Андрей взошел на ступени гроба. И в гробу было то же лицо, хотя и с закрытыми глазами. «Ах, что вы со мной сделали?» всё говорило оно, и князь Андрей почувствовал, что в душе его оторвалось что то, что он виноват в вине, которую ему не поправить и не забыть. Он не мог плакать. Старик тоже вошел и поцеловал ее восковую ручку, спокойно и высоко лежащую на другой, и ему ее лицо сказало: «Ах, что и за что вы это со мной сделали?» И старик сердито отвернулся, увидав это лицо.
Еще через пять дней крестили молодого князя Николая Андреича. Мамушка подбородком придерживала пеленки, в то время, как гусиным перышком священник мазал сморщенные красные ладонки и ступеньки мальчика. Крестный отец дед, боясь уронить, вздрагивая, носил младенца вокруг жестяной помятой купели и передавал его крестной матери, княжне Марье. Князь Андрей, замирая от страха, чтоб не утопили ребенка, сидел в другой комнате, ожидая окончания таинства. Он радостно взглянул на ребенка, когда ему вынесла его нянюшка, и одобрительно кивнул головой, когда нянюшка сообщила ему, что брошенный в купель вощечок с волосками не потонул, а поплыл по купели.
Участие Ростова в дуэли Долохова с Безуховым было замято стараниями старого графа, и Ростов вместо того, чтобы быть разжалованным, как он ожидал, был определен адъютантом к московскому генерал губернатору. Вследствие этого он не мог ехать в деревню со всем семейством, а оставался при своей новой должности всё лето в Москве. Долохов выздоровел, и Ростов особенно сдружился с ним в это время его выздоровления. Долохов больной лежал у матери, страстно и нежно любившей его. Старушка Марья Ивановна, полюбившая Ростова за его дружбу к Феде, часто говорила ему про своего сына. – Да, граф, он слишком благороден и чист душою, – говаривала она, – для нашего нынешнего, развращенного света. Добродетели никто не любит, она всем глаза колет. Ну скажите, граф, справедливо это, честно это со стороны Безухова? А Федя по своему благородству любил его, и теперь никогда ничего дурного про него не говорит. В Петербурге эти шалости с квартальным там что то шутили, ведь они вместе делали? Что ж, Безухову ничего, а Федя все на своих плечах перенес! Ведь что он перенес! Положим, возвратили, да ведь как же и не возвратить? Я думаю таких, как он, храбрецов и сынов отечества не много там было. Что ж теперь – эта дуэль! Есть ли чувство, честь у этих людей! Зная, что он единственный сын, вызвать на дуэль и стрелять так прямо! Хорошо, что Бог помиловал нас. И за что же? Ну кто же в наше время не имеет интриги? Что ж, коли он так ревнив? Я понимаю, ведь он прежде мог дать почувствовать, а то год ведь продолжалось. И что же, вызвал на дуэль, полагая, что Федя не будет драться, потому что он ему должен. Какая низость! Какая гадость! Я знаю, вы Федю поняли, мой милый граф, оттого то я вас душой люблю, верьте мне. Его редкие понимают. Это такая высокая, небесная душа!
wiki-org.ru
квантовое состояние - это... Что такое квантовое состояние?
- stationary state
- quantum state
квантовое состояниеОдно из возможных дискретных стабильных состояний системы взаимодействующих частиц. [Сборник рекомендуемых терминов. Выпуск 79. Физическая оптика. Академия наук СССР. Комитет научно-технической терминологии. 1970 г.]
Тематики
- физическая оптика
Обобщающие термины
- энергетические и спектральные характеристики оптического излучения
EN
- quantum state
- stationary state
DE
Русско-английский словарь нормативно-технической терминологии. academic.ru. 2015.
- квантовая эффективность фотокатода
- квантовые числа
Смотреть что такое "квантовое состояние" в других словарях:
квантовое состояние — Одно из возможных дискретных стабильных состояний системы взаимодействующих частиц. [Сборник рекомендуемых терминов. Выпуск 79. Физическая оптика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Тематики физическая оптика… … Справочник технического переводчика
Квантовое состояние — У этого термина существуют и другие значения, см. Состояние. Квантовая механика … Википедия
квантовое состояние — kvantinė būsena statusas T sritis fizika atitikmenys: angl. quantum state vok. gequantelter Energiezustand, m; Quantenzustand, m rus. квантовое состояние, n; квантовое энергетическое состояние, n pranc. état quantique, m … Fizikos terminų žodynas
квантовое состояние — kvantinė būsena statusas T sritis chemija apibrėžtis Diskretiniu banginių funkcijų rinkiniu apibūdinama elektrono būsena atome. atitikmenys: angl. quantum state rus. квантовое состояние … Chemijos terminų aiškinamasis žodynas
КВАНТОВОЕ СОСТОЯНИЕ — первичное понятие квантовой механики. Единств, способ полностью охарактеризовать квантовую систему указать К. с., в к ром система находится. К. с. атомных ядер, атомов, молекул, кристаллов и т. п. квантовых систем считается заданным, если… … Химическая энциклопедия
возбужденное квантовое состояние — sužadintoji kvantinė būsena statusas T sritis chemija apibrėžtis Atomo (dalelės) būsena, kai elektronai yra perėję į aukštesnius energijos lygmenis. atitikmenys: angl. excited quantum state rus. возбужденное квантовое состояние … Chemijos terminų aiškinamasis žodynas
СОСТОЯНИЕ — (1) аморфное (рентгеноаморфное) состояние твёрдого вещества, в котором нет кристаллической структуры (атомы и молекулы расположены беспорядочно), оно изотропно, т. е. имеет одинаковые физ. свойства по всем направлениям и не имеет чёткой… … Большая политехническая энциклопедия
Состояние (квантовая механика) — У этого термина существуют и другие значения, см. Состояние. Квантовая механика Принцип неопределённости Гейзенберга … Википедия
квантовое энергетическое состояние — kvantinė būsena statusas T sritis fizika atitikmenys: angl. quantum state vok. gequantelter Energiezustand, m; Quantenzustand, m rus. квантовое состояние, n; квантовое энергетическое состояние, n pranc. état quantique, m … Fizikos terminų žodynas
Квантовое запутывание — Квантовая механика Принцип неопределённости Введение ... Математическая формулировка ... Основа … Википедия
Квантовое туннелирование — Квантовая механика Принцип неопределённости Введение ... Математическая формулировка ... Основа … Википедия
Книги
- Вибрационное целительство. Квантовое оздоровление сознания и тела, Проценко Тарас Анатольевич. Книга посвящена психической энергии, или жизненной силе человека, имеющей непосредственное отношение к самочувствию и здоровью. На фоне большого количества дилетантской литературы о… Подробнее Купить за 314 руб
- Вибрационное целительство. Квантовое оздоровление сознания и тела, Проценко Тарас Анатольевич. Книга посвящена психической энергии, или жизненной силе человека, имеющей непосредственное отношение к самочувствию и здоровью. На фоне большого количества дилетантской литературы о… Подробнее Купить за 279 руб
- Как сохранить энергетический иммунитет, Проценко Тарас Анатольевич. Проценко Тарас Анатольевич — профессиональный врач с большим стажем работы, терапевт, физиотерапевт, специалист в области нетрадиционной медицины и немедикаментозных методов лечения, автор… Подробнее Купить за 264 руб
normative_ru_en.academic.ru















