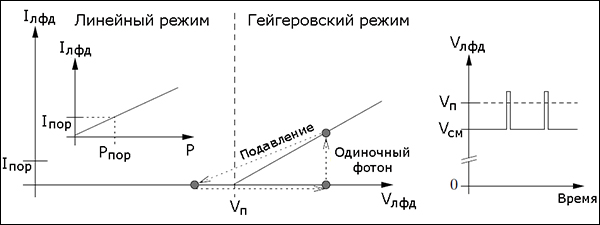
4.6. Концепции и методологические принципы квантовой механики. Понятие квантового микросостояния. Понятие квантового уровня
4.6. Концепции и методологические принципы квантовой механики. Понятие квантового микросостояния
Основные идеи, принципы и законы квантово-полевой картины мира в определённой степени отражены в предыдущей лекции №3 (см. схему 20).
Мы их концептуальную основу отразим на основе выделения основополагающих концепций и методологических принципов квантовой механики (см. схему 31).
Схема 31. Основополагающие концепции и методологические принципы квантовой механики.
| «Каждый элемент материи имеет свойства волны и частицы». |
| «Всё: материя, энергия, квантовые характеристики выступают дискретными величинами, и нельзя измерить ни одну из них, не изменив её». |
| |
| Принцип неопределённости в квантовой механике задаётся соотношениями неопределённостей В. Гейзенберга: и . и находит отражение в принципе дополнительности Н. Бора. |
| «Получение экспериментальной информации об одних физических величинах, описывающих состояние микрообъекта, неизбежно приводит к потере информации о других физических величинах, дополнительных к первым». В общенаучном плане принцип дополнительности можно сформулировать следующим образом: «Всякое истинное глубокое явление природы не может быть однозначно определено с помощью слов нашего языка и требует для своего определения по крайней мере двух взаимоисключающих дополнительных понятий». |
| |
| «Более простая теория обычно имеет «внешнее оправдание» (соответствие эксперименту, т.е. свою верификацию) и «внутреннее совершенство» (красоту теории в виде ограничений на возможные качества систем), более «фальсифицируема и в то же время более информативна.». |
Квантовое микросостояние одной микрочастицы включает в себя как характеристики частиц, так и ее окружения. Состояние микрочастицы задается волновой функцией (амплитудой вероятности состояния) , которая является комплексной величиной, определяемой во всех точках пространства и в каждый момент времени. Движение частицы носит стохастический характер и в волновой механике уравнением движения является уравнение Шредингера, которое в общем случае имеет следующий вид:
,
,
где - оператор Гамильтона.
Квадрат модуля волновой функции равен плотности вероятности, т.е. вероятности нахождения частицы в единице объема, .
Величина плотности вероятности является экспериментально наблюдаемой величиной, в то время как сама пси-функция, будучи комплексной, не доступна наблюдению.
Уравнение Шредингера можно применить и к квантовому микросостоянию системы частиц. Однако, в данном случае его решение всегда носит приближённый характер. При концептуальном анализе квантовой системы важную роль играют постулаты Бора (см. схему 32), квантовые статистики (см. схему 33) и квантовые числа микрочастиц (см. схему 34).
Схема 32. Обобщенные в рамках понятия квантовой системы постулаты Н. Бора.
| Энергетический спектр атома (квантовой системы) дискретен. |
| Частоты атомного излучения (электромагнитного излучения квантовой системы) связаны с энергетическими уровнями атома (квантовой системы). При переходе с уровня на уровень испускается квант излучения с частотой . При обратном переходе квант поглощается. . |
Вероятностный подход совместно с принципом тождественности, согласно которому состояния системы частиц, получающиеся друг из друга перестановкой тождественных частиц, нельзя различить ни в каком эксперименте, позволяют рассматривать такие состояния как одно физическое состояние. При этом принцип симметрии и асимметрии волновых функций при перестановке двух одинаковых микрочастиц позволяет ввести квантовые статистики Бозе-Эйнштейна и Ферми-Дирака (см. схему 33).
Схема 33. Основные свойства микрочастиц в рамках квантовых статистик.
| Название квантовой статистики | Свойства соответствующих классов микрочастиц | Тип симметрии волновой функции |
| Бозоны («коллективисты» имеют тенденцию скапливаться в одном квантовом состоянии. Элементарные частицы с целочисленными спинами, например, фотоны, фононы, пионы, тяжелые промежуточные бозоны, глюоны, гравитоны. | При перестановке двух одинаковых микрочастиц знак волновой функции не меняется. Симметричные волновые функции. | |
| Фермионы («индивидуалисты»). Согласно принципу Паули: «Два и более одинаковых фермиона не могут находиться в одном состоянии». Элементарные частицы с получисленными спинами, например, электроны, протоны, нейтроны, кварки, все лептоны. | При перестановке двух одинаковых микрочастиц меняется знак волновой функции. Антисимметричные волновые функции |
Как видно из схемы барионная вещественная материя создается из фермионов – протонов, нейтронов и электронов. При этом особое значение, по крайней мере, в объяснении физико-химических свойств химических элементов (совокупности атомов (изотопов) с одинаковым зарядом Z ядра) приобретает электронная структура, т.е. квантовое микросостояние электронов, определяемое набором соответствующих квантовых чисел (см. схему 34).
Схема 34. Квантовые числа и соответствующие условия квантования.
| Название квантового числа и задание его значений | Условия квантования и основные характеристики |
| =1, 2, 3… | Задает условие квантования энергии и характеризует уровни дискретных значений энергии атома, например, водородоподобного: . |
| 0, 1, 2, 3, …, . | Задает условие квантования момента импульса микрочастицы, например, электрона в атоме: |
| . | Задает условие квантования проекции момента импульса микрочастицы, например, электрона в атоме: . |
| Задает условие квантования собственного момента импульса микрочастицы, например, электрона в атоме: . Для электрона . | |
| Задает условие квантования проекции собственного момента импульса микрочастицы, например, электрона в атоме: . Характеризует спиновую степень свободы электрона. Для электрона . |
Итак, двигаясь от электромагнитной волны к понятию фотона и совершая внешне противоположное движение от электрона к его волне и наблюдению интерференции и дифракции электронов, мы осознали корпускулярно-волновой дуализм материи. Опираясь на корпускулярно-волновой дуализм и поняв вероятностный характер квантовой механики, мы ввели абстрактно-математическое описание квантового микросостояния одной микрочастицы на основе уравнения Шредингера, а также микросостояния системы тождественных частиц на основе квантовых статистик и квантовых чисел. Так мы получили новое видение электромагнитных взаимодействий и приблизились к квантовой электродинамике. Квантовая электродинамика – «это новое воззрение на взаимодействие между электронами и протонами, т.е. электромагнитная теория, но со всеми уточнениями, внесенными квантовой механикой». Как отмечает Р. Фейнман, «квантовая электродинамика – в принципе это теория всей химии, всех жизненных процессов, если жизнь сводится к химии, а, следовательно, и к физике». А так как электромагнитное взаимодействие доминирует в макромире, то «из квантовой электродинамики выводятся все известные механические, электрические и химические законы». Цивилизационная значимость квантовой механики в утилитарно-прикладном плане проявилась как в «физической экономике» индустриальной цивилизации, так и в кооперативном взаимодействии «информационной экономики» с «физической экономикой» в постиндустриальной цивилизации.
studfiles.net
5. Понятие волновой функции. Квантовые числа, их сущность. Понятие энергетического уровня, подуровня, орбитали. Электронное облако и его форма.
Понятие волновой функции.
Так как электрон обладает волновыми свойствами, поэтому характер его движения в вакууме описывается при помощи волновой функции (Ψ – пси), которая в свою очередь зависит от трех переменных: x,y,z; обладает замечательным свойством: квадрат волновой функции определяет относительную вероятность нахождения электрона в данной точке. С точки зрения квантовой механики электрон может находиться в любой точке пространства, но с разной вероятностью. Если бы нам удалось фотографировать электрон через малые промежутки времени, то при наложении этих фотографий мы бы получили картинку, кот называется электронным облаком. Чем плотнее расположены точки, тем больше плотность электронного облака, тем больше значение квадрата волновой функции и тем чаще встречается электрон в этих местах. Электронное облако не имеет четких границ, так как и на большом расстоянии от ядра есть вероятность обнаружить электрон. Поэтому электронным облаком принято называть ту область пространства, которой электрон отдает 90% своего времени. Учитывая волновые свойства электрона, используя два принципа квантовой механики, австрийский физик Шредингер дал математическое описание поведения электрона в вакууме. Но! Если в уравнение Шредингера поставить волновую функцию, описывающую определенное состояние электрона, то решением уравнения Шредингера будет энергия электрона в этом состоянии.
Квантовые числа и их сущность. Понятие энергетического уровня, подуровня, орбитали. Электронное облако и его форма.
Конкретный вид волновой функции задают с помощью трех величин: n, l, m – квантовые числа.
1. Главное квантовое число.
n=1, 2, 3, 4..
Определяет энергию электрона в атоме и его среднюю удаленность от ядра. Чем больше n тем больше энергия электрона. Чем меньше n тем меньше энергия электрона, тем меньше его энергия, тем сильнее он связан с ядром, тем меньше размер электронного облака.
Е Е=-А/n^2 (решение уравнение Шредингера для атома водорода)
С увеличением n увеличивается E
2.Второе квантовое число.
Второе квантовое число называется побочным и обозначается l. При данном n, l принимает следующие значения l=0,1,2,3,..,(n-1)(n значений).
Т.е. энергия электрона в атоме зависит не только от n, но и от l. Таким образом, при одном и том же n электрон может характеризоваться различными значениями l. Когда говорят об энергетических подуровнях значение энергии электронов, определяемое данным l. Число значений l при данном n определяет число подуровней уровня.
n=1 n=2 n=3 …………..
l=0 l=0,1 l=0,1,2……….
Численным значениям l соответствуют буквенные обозначения.
l=0,1,2,3……..(0-s,1-p,2-d,3-f……..)
Таким образом, побочное квантовое число определяет форму электронного облака.
s-сферические, симметричные облака; p-в форме гантелей или восьмерки;d-более сложной формы
3. Третье квантовое число.
Третье квантовое число называется магнитным. Обозначается m. При данном l, m принимает следующие значения: m=0, ±1, ±2, … ±l.Итого 2l+1 значений.
Магнитное квантовое число определяет ориентацию электронного облака в пространстве, то есть описывает поведение электрона во внешнем магнитном уровне.
Волновая функция определенная данным набором квантовых чисел, называется атомной электронной орбиталью.
Орбиталь в отличие от орбиты указывает на вероятностный характер описания электрона в атоме. АО-состояние электрона в атоме, характеризуемое значениями квантовых чисел, то есть определенными размерами, формой, расположением в пространстве электронных облаков. Графически атомная орбиталь изображается в виде квантовой ячейки. Число значений m при заданном l определяет число орбиталей в квантовом уровне.
4.Четвертое квантовое число.
Четвертое квантовое число - спиновое. Изучение атомных спектров показал, что электрон помимо орбитального момента количества движения обладает еще и собственным моментом количества движения, которое называется – спин. Это потребовало введения четвертого квантового числа которое называется спиновое.
Таким образом, для полной характеристики электрона в атоме необходимо введение четырех квантовых чисел. Первые три характеризуют пространственное состояние электрона, четвертое его собственная характеристика.
8. Периодический закон и его сущность. Периодическая система элементов. Зависимость между строением атома и химическими свойствами элементов. Энергия ионизации и сродства к электрону. Изменение этих величин в периодической системе. Горизонтальные, вертикальные, диагональные аналогии в периодической системе. Явление кайносимметрии.
Периодический закон и его сущность.
Периодический закон открыт в 1870 году Д.И. Менделеевым.
Свойства химических элементов, а также образованных ими простых и сложных формул (соединений) находятся в периодической зависимости от заряда ядра атома.
Периодическая система элементов.
Каждый период начинается со щелочного металла и заканчивается благородным газом.
При переходе от элемента к элементу, т.е. при увеличении порядкового номера происходит периодическое изменение структуры электронных оболочек.
Зависимость между строением атома и химическими свойствами элементов.
Начало каждого периода соответствует началу застройки нового энергетического уровня. Номер периода определяет номер внешнего уровня. Он является застраивающимся у элементов главных подгрупп. Т.е. s и p элементов. У d элементов идет заполнение первого с наружи уровня. У f- второго снаружи. Т.е. внешний и застраивающийся уровень не всегда совпадают. Т.к у d элементов заполняется первый снаружи уровень, а химические свойства в первую очередь определяются структурой внешнего энергетического уровня, то химические свойства этих элементов похожи между собой (например, все они металлы). У них отсутствует резкое изменение свойств при переходе от элемента к элементу. Как, например, у s и p элементов. Еще более похожи свойства f элементов (лантаноиды и актиноиды), поскольку у них заполняются еще более глубокие подуровни.
Энергия ионизации и сродства к электрону.
Энергия (потенциал) ионизации – это энергия необходимая для отрыва электрона с внешнего энергетического уровня атома.
Энергия сродства к электрону – энергия, которая выделяется или поглощается при присоединении электрона к нейтральному атому.
Изменение этих величин в периодической системе.
Рост потенциала ионизации происходит слева направо и связан с увеличением заряда ядра. Падение потенциалов ионизации атомов элементов третьего периода по отношению ко второму связано с тем, что не смотря на увеличение заряда ядра, внешние электроны расположены дальше от ядра, а внутренние препятствуют взаимодействию внешних с ядром.
Энергия сродства к электрону также изменяется периодически. Щелочные и щелочноземельные металлы имеют низкое сродство к электрону. У галогенов оно самое высокое. У бериллия, магния и благородных газов ЭСЭ <0.
Горизонтальные, вертикальные, диагональные аналогии в периодической системе.
При увеличении порядкового номера в периодах слева направо нарастают неметаллические (кислые) свойства. В группах нарастают металлические (основные свойства). Это приводит к тому, что вблизи диагонали проведенной из левого верхнего угла в правый нижний элементы образующие соединения амфотерного характера.
Друг под другом в таблице Менделеева расположены элементы с одинаковой структурой внешнего (застраивающегося) энергетического уровня. Это вертикальные аналоги. Первая группа – щелочные металлы, вторая – щелочноземельные (Sr, Ca, Ba), пятая – пниктогены, 6- халькогены, 7- благородные газы. Примером вертикальных аналогий в таблице Менделеева являются элементы одной и той же группы. Они образуют одинаковые по форме соединения, а их физические и химические свойства похожи между собой. Однако повторимость свойств вертикальных аналогов не является абсолютной. Это связано с двумя причинами: 1) увеличение металлических свойств в группах; 2)кайносимметрия
Явление кайносимметрии.
Еще Менделеев заметил, что элементы двух периодов резко отличаются по своим химическим свойствам от последователей. Он называл их типическими. В современной формулировке это элементы кайносимметрии (элементы с новой симметрией электронных облаков). Для элементов второго периода характерно появление p электронных облаков, что и приводит к отличию их свойств от элементов образующих группу. Аналогично легкие d элементы отличаются по свойствам от тяжелых d элементов (4d, 3d). Лантаноиды отличаются от актиноидов (4f, 5f). И совершенно уникальной является химия водорода. Кайносимметрия – явление резкого отличия химических свойств элементов с новой симметрией электронных облаков от их вертикальных аналогов.
9. Химическая связь, ее особенности, характеристика. Метод валентных связей, Q- и H- связи. Образование химической связи в молекулах h3, HCl, Cl2 с точки зрения метода валентных связей. Электроотрицательность элементов. Полярная химическая связь.
Химическая связь, ее особенности, характеристика. Полярная химическая связь.
Химическая связь – взаимодействие атомов, которое сопровождается уменьшением полной энергии системы, т.е. выделением энергии. При огромном разнообразии химических связей в основе их образования лежит перераспределение электронной плотности между двумя или несколькими центрами (ядрами). Если электроны принадлежат всем ядрам (обобществляются), то это наиболее общий случай ковалентной химической связи. Если связь образуется между одинаковыми атомами, то обобществленная электронная плотность в равной мере принадлежит им обоим, т.е. она расположена симметрично относительно оси связи. Это и есть неполярная ковалентная связь. Если же связываемые атомы различны, то это полярная ковалентная связь. Она характеризуется А симметрией в распределении электронной плотности, т.е. связывающее электронное облако смещено в сторону более электроотрицательного элемента. При этом он получает некоторый отрицательный заряд, а потом некоторый положительный. Эти заряды называются эффективными. Идеальным крайним случаем полярной ковалентной связи является ионная связь. Она соответствует полному переносу электронов от одного атома к другому. Однако, как и все идеальное, этот случай в природе недостижим. Даже в соединении сильных электроположительных элементов с фтором, степень ионности связи не превышает 80-90%. Таким образом, в реальных системах следует говорить о преимущественно ионном характере связи.
Метод валентных связей, Q- и H- связи. Образование химической связи в молекулах h3, HCl, Cl2 с точки зрения метода валентных связей.
Для квантово-химического описания молекул используется два метода: 1) метод валентных связей; 2) метод молекулярных орбиталей.
Основные положения метода валентных связей:
1. При описании связи молекул, считается, что взаимодействующие атомы обмениваются между собой электронами, которые образуют общие связывающие электронные пары. Обобществление происходит таким образом, что в пространстве между атомами возникает новая электронная плотность, которая обеспечивает их связь. Т.е. электронные облака атомов перекрываются, ядра при этом связываются.
2. Два обменивающихся электрона согласно принципу Паули должны иметь анти параллельные спины.
3. Валентная связь направлена в сторону максимального перекрывания облаков.
Различают сигма и пи связи.
Сигма – связь, обобществленное электронное облако которой имеет ось симметрии проходящую через центры атомов.
Пи – химическая связи, связывающиеся электронные облака которой имеют плоскость симметрии проходящую через центр ядер.
Электроотрицательность элементов.
Электроотрицательность характеризует способность атома находящегося в соединении присоединять электроны. Это не строго физическая величина, а условная характеристика, полученная на основе экспериментальных и расчетных данных.
Законы термохимии. Тепловой эффект химических реакций. Закон Гесса и его следствия.
В 1774 Лавуазье Лаплас. Экспериментально установил, что тепловые эффекты реакции идущих в прямом и обратном направлениях равны по величине и противоположны по знаку. Закон Лавуазье Лапласа носит частный характер.
Фундаментальный закон термохимии. Закон Гесса 1840г.
Тепловой эффект химической реакции зависит только от начального и конечного состояния системы (состояние исходных и конечных веществ) и не зависит от пути процесса (числа и последовательности промежуточных стадий).
Следствия закона Гесса.
1).Энтальпия образования вещества не зависит от способа его получения.
2).Тепловой эффект химической реакции равен разности между алгебраической суммой энтальпий образования продуктов реакции и алгебраической суммой энтальпии образования исходных веществ.
Энтальпия образования вещества.
Абсолютное значение энтальпии системы измерить невозможно, но для химии важен процесс изменения энтальпии. Слово изменение часто опускается.
Тепловой эффект образования более сложного вещества из простых называется энтальпией (теплотой) образования dHf.
Тепловой эффект образования сложного вещества из простых находящихся в стандартном состоянии, обозначается как стандартная энтальпия образования. Стандартное состояние – состояние с минимальной энтальпией и стандартными условиями. Станд. условия: 298К, 101кПа.
Энтальпия образования более устойчива при с.у. Аллотропная модификация простого вещества принимается равной 0.
18. Способы выражения состава растворов.
1. Массовая процентная концентрация (массовая доля).
Массовая доля – отношение массы растворенного вещества к массе всего раствора. Как следует из названия, процентная концентрация в 100 раз больше доли и выражается в процентах:
мас. % =м раств. вещ-ва/м раствора *100
м раствора – сумма масс всех компонентов раствора.
2. Объемная процентная концентрация (объемная доля).
Этот вид концентрации используется как количественная характеристика газовых растворов.
3. Мольная процентная концентрация (мольная доля). Мольная доля – отношение количества (числа молей) растворенного вещества к сумме количеств всех веществ в растворе.
4. Молярная концентрация (молярность).
Молярность - отношение количества растворенного вещества к объему раствора, выраженному в литрах. Обозначается См или М, моль/л. Т.к. объем зависит от температуры, то и молярность тоже зависит от температуры.
5. Нормальная концентрация (нормальность).
Нормальность – отношение числа эквивалентов (эквивалентных масс) к объему раствора, выраженному в литрах. Обозначается Сн или Н после числового значения. Если не указана конкретная химич. реакц. при расчете эквивалентной массы, то берется наименьшее значение.
6. Моляльная концентрация (моляльность).
Моляльность – отношение количества (числа молей) растворенного вещества к массе растворителя, выраженной в килограммах. Обозначается м, размерность моль/кг
Так ни число молей, ни масса не зависят от температуры, то и моляльность в отличие от молярности от температуры не зависит.
studfiles.net
4.6. Концепции и методологические принципы квантовой механики. Понятие квантового микросостояния
Основные идеи, принципы и законы квантово-полевой картины мира в определённой степени отражены в предыдущей лекции №3 (см. схему 20).
Мы их концептуальную основу отразим на основе выделения основополагающих концепций и методологических принципов квантовой механики (см. схему 31).
Схема 31. Основополагающие концепции и методологические принципы квантовой механики.
| «Каждый элемент материи имеет свойства волны и частицы». |
| «Всё: материя, энергия, квантовые характеристики выступают дискретными величинами, и нельзя измерить ни одну из них, не изменив её». |
| «Квантовая механика отказывается от стремления к точным предсказаниям того, что произойдёт при опредеоённых условиях. Мало того, это считается невозможным – единственное, что можно предсказать - это вероятность тех или иных событий. Так, что в квантовой механике мы должны удовлетвориться расчётом вероятностей, при этом считать, что такова природа на самом деле». |
| Принцип неопределённости в квантовой механике задаётся соотношениями неопределённостей В. Гейзенберга: и . и находит отражение в принципе дополнительности Н. Бора. |
| «Получение экспериментальной информации об одних физических величинах, описывающих состояние микрообъекта, неизбежно приводит к потере информации о других физических величинах, дополнительных к первым». В общенаучном плане принцип дополнительности можно сформулировать следующим образом: «Всякое истинное глубокое явление природы не может быть однозначно определено с помощью слов нашего языка и требует для своего определения по крайней мере двух взаимоисключающих дополнительных понятий». |
| «Любая новая более общая теория, являющаяся развитием предыдущих классических теорий, справедливость которых была экспериментально установлена для определенных групп явлений, не отвергает эти классические теории, а включает их в себя. В определенных случаях существует возможность предельного перехода новой теории в старую». |
| «Более простая теория обычно имеет «внешнее оправдание» (соответствие эксперименту, т.е. свою верификацию) и «внутреннее совершенство» (красоту теории в виде ограничений на возможные качества систем), более «фальсифицируема и в то же время более информативна.». |
Квантовое микросостояние одной микрочастицы включает в себя как характеристики частиц, так и ее окружения. Состояние микрочастицы задается волновой функцией (амплитудой вероятности состояния) , которая является комплексной величиной, определяемой во всех точках пространства и в каждый момент времени. Движение частицы носит стохастический характер и в волновой механике уравнением движения является уравнение Шредингера, которое в общем случае имеет следующий вид:
,
а в случае стационарных состояний вид его упрощается
,
где - оператор Гамильтона.
Квадрат модуля волновой функции равен плотности вероятности, т.е. вероятности нахождения частицы в единице объема, .
Величина плотности вероятности является экспериментально наблюдаемой величиной, в то время как сама пси-функция, будучи комплексной, не доступна наблюдению.
Уравнение Шредингера можно применить и к квантовому микросостоянию системы частиц. Однако, в данном случае его решение всегда носит приближённый характер. При концептуальном анализе квантовой системы важную роль играют постулаты Бора (см. схему 32), квантовые статистики (см. схему 33) и квантовые числа микрочастиц (см. схему 34).
Схема 32. Обобщенные в рамках понятия квантовой системы постулаты Н. Бора.
| Энергетический спектр атома (квантовой системы) дискретен. |
| Частоты атомного излучения (электромагнитного излучения квантовой системы) связаны с энергетическими уровнями атома (квантовой системы). При переходе с уровня на уровень испускается квант излучения с частотой . При обратном переходе квант поглощается. . |
Вероятностный подход совместно с принципом тождественности, согласно которому состояния системы частиц, получающиеся друг из друга перестановкой тождественных частиц, нельзя различить ни в каком эксперименте, позволяют рассматривать такие состояния как одно физическое состояние. При этом принцип симметрии и асимметрии волновых функций при перестановке двух одинаковых микрочастиц позволяет ввести квантовые статистики Бозе-Эйнштейна и Ферми-Дирака (см. схему 33).
Схема 33. Основные свойства микрочастиц в рамках квантовых статистик.
| Название квантовой статистики | Свойства соответствующих классов микрочастиц | Тип симметрии волновой функции |
| Бозоны («коллективисты» имеют тенденцию скапливаться в одном квантовом состоянии. Элементарные частицы с целочисленными спинами, например, фотоны, фононы, пионы, тяжелые промежуточные бозоны, глюоны, гравитоны. | При перестановке двух одинаковых микрочастиц знак волновой функции не меняется. Симметричные волновые функции. | |
| Фермионы («индивидуалисты»). Согласно принципу Паули: «Два и более одинаковых фермиона не могут находиться в одном состоянии». Элементарные частицы с получисленными спинами, например, электроны, протоны, нейтроны, кварки, все лептоны. | При перестановке двух одинаковых микрочастиц меняется знак волновой функции. Антисимметричные волновые функции |
Как видно из схемы барионная вещественная материя создается из фермионов – протонов, нейтронов и электронов. При этом особое значение, по крайней мере, в объяснении физико-химических свойств химических элементов (совокупности атомов (изотопов) с одинаковым зарядом Z ядра) приобретает электронная структура, т.е. квантовое микросостояние электронов, определяемое набором соответствующих квантовых чисел (см. схему 34).
Схема 34. Квантовые числа и соответствующие условия квантования.
| Название квантового числа и задание его значений | Условия квантования и основные характеристики |
| =1, 2, 3… | Задает условие квантования энергии и характеризует уровни дискретных значений энергии атома, например, водородоподобного: . |
| 0, 1, 2, 3, …, . | Задает условие квантования момента импульса микрочастицы, например, электрона в атоме: |
| . | Задает условие квантования проекции момента импульса микрочастицы, например, электрона в атоме: . |
| Задает условие квантования собственного момента импульса микрочастицы, например, электрона в атоме: . Для электрона . | |
| Задает условие квантования проекции собственного момента импульса микрочастицы, например, электрона в атоме: . Характеризует спиновую степень свободы электрона. Для электрона . |
Итак, двигаясь от электромагнитной волны к понятию фотона и совершая внешне противоположное движение от электрона к его волне и наблюдению интерференции и дифракции электронов, мы осознали корпускулярно-волновой дуализм материи. Опираясь на корпускулярно-волновой дуализм и поняв вероятностный характер квантовой механики, мы ввели абстрактно-математическое описание квантового микросостояния одной микрочастицы на основе уравнения Шредингера, а также микросостояния системы тождественных частиц на основе квантовых статистик и квантовых чисел. Так мы получили новое видение электромагнитных взаимодействий и приблизились к квантовой электродинамике. Квантовая электродинамика – «это новое воззрение на взаимодействие между электронами и протонами, т.е. электромагнитная теория, но со всеми уточнениями, внесенными квантовой механикой». Как отмечает Р. Фейнман, «квантовая электродинамика – в принципе это теория всей химии, всех жизненных процессов, если жизнь сводится к химии, а, следовательно, и к физике». А так как электромагнитное взаимодействие доминирует в макромире, то «из квантовой электродинамики выводятся все известные механические, электрические и химические законы». Цивилизационная значимость квантовой механики в утилитарно-прикладном плане проявилась как в «физической экономике» индустриальной цивилизации, так и в кооперативном взаимодействии «информационной экономики» с «физической экономикой» в постиндустриальной цивилизации.
studfiles.net
Концепции и методологические принципы квантовой механики. Понятие квантового микросостояния
Крушение классической физики и как следствие классического естествознания связано прежде всего со знаменитым немецким физиком-теоретиком Максом Планком, который связал хаотичность электромагнитного (светового) излучения атомных осцилляторов с их дискретностью и выдвинул идею квантового излучения энергии каждым осциллятором пропорционально частоте колебаний. Планк ввел коэффициент пропорциональности, новую фундаментальную константу 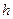 , имеющую размерность действия (энергия, умноженная на время), получившую название постоянной Планка:
, имеющую размерность действия (энергия, умноженная на время), получившую название постоянной Планка:
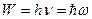 , где
, где  .
.
Квантовая гипотеза М. Планка сняла проблему «ультрафиолетовой катастрофы» теплового излучения, согласно которой, исходя из классических представлений о тепловом излучении, энергия излучения любого тела при любой температуре должна быть абсурдно бесконечной. А. Эйнштейн первым подхватил идею М. Планка, предположив, что электромагнитные волны не только излучаются, но и поглощаются квантами. Эта гипотеза позволила ему на основе формулы Планка и закона сохранения энергии получить в 1905 г. уравнение для внешнего фотоэффекта, подтвержденное в дальнейшем экспериментально рядом ученых и позволившее экспериментально определить постоянную Планка. Когда же было экспериментально продемонстрировано, что и процесс распространения света имеет квантовый характер (опыты В. Боте. Г. Гейгера, А. Комптона), стало ясно, что свет имеет двойственную корпускулярно-волновую природу. Так, свет при интерференции, дифракции, поляризации проявляет чисто волновые свойства, а при излучении нагретых тел, люминесценции, внешнем фотоэффекте, фотопроводимости – чисто корпускулярные свойства, т.е. как поток «частиц» (квантов), которые назвали фотонами.
Боровская теория водородоподобного атома, в основу которой Н. Бор в 1913 г. закладывает идею о квантовании величины действия при движении электрона по круговой орбите («планетарная модель атома Резерфорда-Бора»), подкрепляла возникший корпускулярно-волновой дуализм света.
И совершенно «безумная», но «революционная» в «драме идей» становления квантовой механики гипотеза была выдвинута Луи де Бройлем о том, что с двигающимся электроном связана некая волна, длина волны 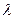 которой равна
которой равна 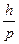 , где
, где  - импульс электрона. Он применил эту идею к интерпретации стационарных орбит боровской модели атома. Он считал, что в длине такой орбиты укладывается целое число длин волн электрона, и тогда волны электрона находятся в фазе сами с собой и не разрушаются собственной интерференцией. В 1924 г. де Бройль изложил эту идею в своей диссертации «Исследования по квантовой теории», которую поддержал А. Эйнштейн. Последний рекомендовал эту работу Эрвину Шредингеру, который на основе этой идеи создал одно из основных направлений квантовой механики – волновую механику.
- импульс электрона. Он применил эту идею к интерпретации стационарных орбит боровской модели атома. Он считал, что в длине такой орбиты укладывается целое число длин волн электрона, и тогда волны электрона находятся в фазе сами с собой и не разрушаются собственной интерференцией. В 1924 г. де Бройль изложил эту идею в своей диссертации «Исследования по квантовой теории», которую поддержал А. Эйнштейн. Последний рекомендовал эту работу Эрвину Шредингеру, который на основе этой идеи создал одно из основных направлений квантовой механики – волновую механику.
В 1927 г. эксперименты Дэвиссона и Джермера подтвердили «безумную» идею де Бройля в опытах по наблюдению дифракции электронов от кристалла никеля. В том же 1927 г. Дж. П. Томсон наблюдал дифракцию быстрых электронов на очень тонкой металлической фольге, изготовленной из поликристаллического материала с хаотическим расположением кристаллических осей.
В настоящее время корпускулярно-волновой дуализм распространяется на все элементарные частицы, а следовательно на все исходные принципы квантовой механики и их применения к материи, движению и фундаментальным взаимодействиям.
Эти исходные принципы квантовой механики в сжатой форме сформулировал Р. Фейнман в своих знаменитых лекциях по физике на основе рассмотрения прохождения щели электронами(см. рис. 5.1). Мы объединили в одном рисунке интерференцию электронных волн (б) со световым наблюдением за электронами (в). 
Теперь попробуем в сжатой форме прокомментировать результаты эксперимента на нашем электронном приборе. При этом мы изложим, следуя Р. Фейнмана, результаты в такой форме, чтобы они имели силу для всего класса аналогичных экспериментов. Для этого сформулируем определение идеального эксперимента: «Идеальным называется такой эксперимент, в котором все начальные и конечные условия полностью определены».
Теперь об общих выводах, которые приведем в краткой форме:
1. Вероятность некоего события в идеальном эксперименте, например, прохождения электронов через отверстие 1 или через отверстие 2 и их измерения с помощью щелчков на детекторе, равняется квадрату абсолютного значения комплексного числа  , именуемого амплитудой вероятности.
, именуемого амплитудой вероятности.
 вероятность,
вероятность, 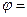 амплитуда вероятности,
амплитуда вероятности,  и тогда
и тогда 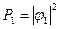 и
и 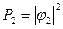 .
.
2. Если событие в эксперименте может осуществляться несколькими взаимно исключающими способами, т.е. когда, например, открыты оба отверстия (щели) и мы не фиксируем через какую щель проходит тот или иной электрон, то амплитуда вероятности для каждого отдельного события равняется сумме амплитуд вероятности для каждого отдельного способа. При этом «имеет место интерференция» (рис. 5.1, (б)).
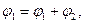
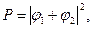 а
а  .
.
3. Если проводится эксперимент, дающий возможность определить, какой из этих двух взаимно исключающих способов осуществляется в действительности (в нашем случае контролем прохождения электронов с помощью сильного источника света), то вероятность события равна сумме вероятностей для каждого отдельного способа. Интерференция отсутствует.
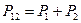 .
.
Основные идеи, принципы и законы квантово-полевой картины мира в определённой степени отражены в предыдущей лекции №3 (см. схему 21).
Мы их концептуальную основу отразим на основе выделения основополагающих концепций и методологических принципов квантовой механики (см. схему 33).
Схема 33. Основополагающие концепции и методологические принципы квантовой механики.
| v Концепция корпускулярно-волнового дуализма: «Каждый элемент материи имеет свойства волны и частицы». |
| v Концепция дискретности материи: «Всё: материя, энергия, квантовые характеристики выступают дискретными величинами, и нельзя измерить ни одну из них, не изменив её». |
| v Концепция вероятностного подхода: «Квантовая механика отказывается от стремления к точным предсказаниям того, что произойдёт при опредеоённых условиях. Мало того, это считается невозможным – единственное, что можно предсказать - это вероятность тех или иных событий. Так, что в квантовой механике мы должны удовлетвориться расчётом вероятностей, при этом считать, что такова природа на самом деле». |
v Принцип неопределённости:
Принцип неопределённости в квантовой механике задаётся соотношениями неопределённостей В. Гейзенберга:
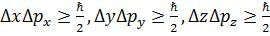 и и 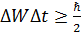 . и находит отражение в принципе дополнительности Н. Бора. . и находит отражение в принципе дополнительности Н. Бора.
|
| v Принцип дополнительности: «Получение экспериментальной информации об одних физических величинах, описывающих состояние микрообъекта, неизбежно приводит к потере информации о других физических величинах, дополнительных к первым». В общенаучном плане принцип дополнительности можно сформулировать следующим образом: «Всякое истинное глубокое явление природы не может быть однозначно определено с помощью слов нашего языка и требует для своего определения по крайней мере двух взаимоисключающих дополнительных понятий». |
| v Принцип соответствия: «Любая новая более общая теория, являющаяся развитием предыдущих классических теорий, справедливость которых была экспериментально установлена для определенных групп явлений, не отвергает эти классические теории, а включает их в себя. В определенных случаях существует возможность предельного перехода новой теории в старую». |
| v Принцип простоты. «Более простая теория обычно имеет «внешнее оправдание» (соответствие эксперименту, т.е. свою верификацию) и «внутреннее совершенство» (красоту теории в виде ограничений на возможные качества систем), более «фальсифицируема и в то же время более информативна.». |
Квантовое микросостояние одной микрочастицы включает в себя как характеристики частиц, так и ее окружения. Состояние микрочастицы задается волновой функцией (амплитудой вероятности состояния) 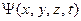 , которая является комплексной величиной, задаваемой во всех точках пространства и в каждый момент времени. Движение частицы носит стохастический характер и в волновой механике уравнением движения является уравнение Шредингера, которое в общем случае имеет следующий вид:
, которая является комплексной величиной, задаваемой во всех точках пространства и в каждый момент времени. Движение частицы носит стохастический характер и в волновой механике уравнением движения является уравнение Шредингера, которое в общем случае имеет следующий вид:
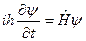 ,
,
а в случае стационарных состояний вид его упрощается
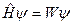 ,
,
где 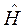 - оператор Гамильтона.
- оператор Гамильтона.
Квадрат модуля волновой функции 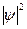 равен плотности вероятности, т.е. вероятности нахождения частицы в единице объема,
равен плотности вероятности, т.е. вероятности нахождения частицы в единице объема, 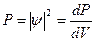 .
.
Величина плотности вероятности является экспериментально наблюдаемой величиной, в то время как сама пси-функция, будучи комплексной, не доступна наблюдению.
Уравнение Шредингера можно применить и к квантовому микросостоянию системы частиц. Однако, в данном случае его решение всегда носит приближённый характер. При концептуальном анализе квантовой системы важную роль играют постулаты Бора (см. схему 34), квантовые статистики (см. схему 35) и квантовые числа микрочастиц (см. схему 36).
Схема 34. Обобщенные в рамках понятия квантовой системы постулаты Н. Бора.
| v Первый постулат Бора. Энергетический спектр атома (квантовой системы) дискретен. |
v Второй постулат Бора
Частоты атомного излучения (электромагнитного излучения квантовой системы) связаны с энергетическими уровнями атома (квантовой системы). При переходе с уровня 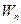 на уровень на уровень 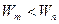 испускается квант излучения с частотой испускается квант излучения с частотой 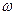 . При обратном переходе квант поглощается. . При обратном переходе квант поглощается.
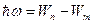 . .
|
Вероятностный подход совместно с принципом тождественности, согласно которому состояния системы частиц, получающиеся друг из друга перестановкой тождественных частиц, нельзя различить ни в каком эксперименте, позволяют рассматривать такие состояния как одно физическое состояние. При этом принцип симметрии и асимметрии волновых функций при перестановке двух одинаковых микрочастиц позволяет ввести квантовые статистики Бозе-Эйнштейна и Ферми-Дирака (см. схему 35).
Схема 35. Основные свойства микрочастиц в рамках квантовых статистик.
| Название квантовой статистики | Свойства соответствующих классов микрочастиц | Тип симметрии волновой функции |
| v Статистика Ш. Бозе и А. Эйнштейна (1924 г.) | Бозоны («коллективисты» имеют тенденцию скапливаться в одном квантовом состоянии. Элементарные частицы с целочисленными спинами, например, фотоны, фононы, пионы, тяжелые промежуточные бозоны, глюоны, гравитоны. | При перестановке двух одинаковых микрочастиц знак волновой функции не меняется. Симметричные волновые функции. |
| v Статистика Э.Ферми и П. Дирака (1926 г.) | Фермионы («индивидуалисты»). Согласно принципу Паули: «Два и более одинаковых фермиона не могут находиться в одном состоянии». Элементарные частицы с получисленными спинами, например, электроны, протоны, нейтроны, кварки, все лептоны. | При перестановке двух одинаковых микрочастиц меняется знак волновой функции. Антисимметричные волновые функции |
Как видно из схемы барионная вещественная материя создается из фермионов – протонов, нейтронов и электронов. При этом особое значение, по крайней мере, в объяснении физико-химических свойств химических элементов (совокупности атомов (изотопов) с одинаковым зарядом Z ядра) приобретает электронная структура, т.е. квантовое микросостояние электронов, определяемое набором соответствующих квантовых чисел (см. схему 36).
Схема 36. Квантовые числа и соответствующие условия квантования.
| Название квантового числа и задание его значений | Условия квантования и основные характеристики |
v 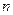 – главное квантовое число – главное квантовое число
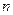 =1, 2, 3… =1, 2, 3…
| Задает условие квантования энергии и характеризует уровни дискретных значений энергии атома, например, водородоподобного:
 . .
|
v  - азимутальное квантовое число - азимутальное квантовое число
 0, 1, 2, 3, …, 0, 1, 2, 3, …, 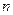 . .
| Задает условие квантования момента импульса микрочастицы, например, электрона в атоме:
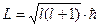 |
v  - магнитное квантовое число - магнитное квантовое число
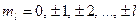 . .
| Задает условие квантования проекции момента импульса микрочастицы, например, электрона в атоме:
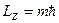 . .
|
v 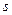 - спиновое квантовое число - спиновое квантовое число
 | Задает условие квантования собственного момента импульса микрочастицы, например, электрона в атоме:
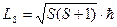 .
Для электрона .
Для электрона 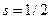 . .
|
v 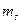 - магнитное спиновое число - магнитное спиновое число
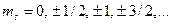 | Задает условие квантования проекции собственного момента импульса микрочастицы, например, электрона в атоме:
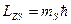 .
Характеризует спиновую степень свободы электрона. Для электрона .
Характеризует спиновую степень свободы электрона. Для электрона 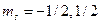 . .
|
Итак, двигаясь от электромагнитной волны к понятию фотона и совершая внешне противоположное движение от электрона к его волне и наблюдению интерференции и дифракции электронов, мы осознали корпускулярно-волновой дуализм материи. Опираясь на корпускулярно-волновой дуализм и поняв вероятностный характер квантовой механики, мы ввели абстрактно-математическое описание квантового микросостояния одной микрочастицы на основе уравнения Шредингера, а также микросостояния системы тождественных частиц на основе квантовых статистик и квантовых чисел. Так мы получили новое видение электромагнитных взаимодействий и приблизились к квантовой электродинамике. Квантовая электродинамика – «это новое воззрение на взаимодействие между электронами и протонами, т.е. электромагнитная теория, но со всеми уточнениями, внесенными квантовой механикой». Как отмечает Р. Фейнман, «квантовая электродинамика – в принципе это теория всей химии, всех жизненных процессов, если жизнь сводится к химии, а, следовательно, и к физике». А так как электромагнитное взаимодействие доминирует в макромире, то «из квантовой электродинамики выводятся все известные механические, электрические и химические законы». Цивилизационная значимость квантовой механики в утилитарно-прикладном плане проявилась как в «физической экономике» индустриальной цивилизации, так и в кооперативном взаимодействии «информационной экономики» с «физической экономикой» в постиндустриальной цивилизации.
megalektsii.ru
Квантовые уровни - Большая Энциклопедия Нефти и Газа, статья, страница 1
Квантовые уровни
Cтраница 1
Квантовые уровни Enl такого электрона определялись двумя квантовыми числами п, I. [1]
Найдем квантовые уровни и соответствующие им собственные функции системы связанных осцилляторов. [2]
Определение квантовых уровней не разбивается больше на два, по существу различных, этапа, а именно; 1) на нахождение всех динамически возможных траекторий и 2) на отбрасывание большинства полученных на первом этапе решений с выделением некоторых немногих, удовлетворяющих специальным требованиям; напротив, квантовые уровни определяются теперь сразу как собственные значения уравнения ( 18), при которых выполняются введенные выше естественные граничные условия. [3]
Открытие квантовых уровней атомов, затем их тонкой, и, наконец, сверхтонкой структуры ( разности энергий порядка 10 - 12, КГ15 и 10 18 эрг, соответственно), достигнутое развитием техники статистического эксперимента, может служить прекрасной иллюстрацией мощи этого метода и замечательным подтверждением ленинского тезиса о познаваемости материи и о неисчерпаемости ее свойств. [4]
Для расчета квантовых уровней атома гелия мы применим метод, который хотя и не является лучшим с точки зрения достигаемой точности расчетов, но зато отличается простотой и наглядностью. [5]
Волновые функции и квантовые уровни для такого движения известны, так как это есть движение в кулоновском поле. [6]
Замечательным образом наши квантовые уровни точно равны уровням, полученным по теории Гейзенберга. Формально при этом дело идет о старом вопросе нулевой энергии, вставшем уже ранее в связи с дилеммой: какое из истолкований планковской теории, первое или второе, считать правильным. [7]
Уровни Ландау - квантовые уровни электрона в магнитном поле, обусловленные движением электрона вокруг магнитных силовых линий. [8]
Исходя из расщепления квантовых уровней при сближении атомов, следует принимать во внимание не только квантовое состояние электрона в исходном атоме, но и его взаимодействие с атомами решетки и возникающими здесь электрическими полями. Указанные две точки зрения, два подхода к описанию энергетического спектра там, где они могут быть доведены до количественных выводов, не противоречат, а взаимно дополняют друг друга. [9]
Полученная формула для квантовых уровней Еп электрона, движущегося в кулоновском поле, найдена впервые Бором на основе полуклассической квантовой теории. [10]
Ядра атомов также имеют квантовые уровни энергии - нормальный и возбужденные - и переходы между этими уровнями ведут к возникновению коротковолнового электромагнитного излучения в виде у-лучей. [11]
Выведем условие, определяющее квантовые уровни энергии в квазиклассическом случае. [12]
Примером систем, имеющих квантовые уровни вида (109.26), могут служить молекулы и твердые тела. [13]
Выведем условие, определяющее квантовые уровни энергии в квазиклассическом случае. [14]
На рисунке изображена схема квантовых уровней атома. Как изменяется каждая из составляющих энергии электрона ( кинетическая и потенциальная) при переходе от нижних уровней к верхним. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Концепции и методологические принципы квантовой механики. Понятие квантового микросостояния
Основные идеи, принципы и законы квантово-полевой картины мира в определённой степени отражены в предыдущей лекции №3 (см. схему 20).
Мы их концептуальную основу отразим на основе выделения основополагающих концепций и методологических принципов квантовой механики (см. схему 31).
Схема 31. Основополагающие концепции и методологические принципы квантовой механики.
| v Концепция корпускулярно-волнового дуализма: «Каждый элемент материи имеет свойства волны и частицы». |
| v Концепция дискретности материи: «Всё: материя, энергия, квантовые характеристики выступают дискретными величинами, и нельзя измерить ни одну из них, не изменив её». |
| v Концепция вероятностного подхода: «Квантовая механика отказывается от стремления к точным предсказаниям того, что произойдёт при опредеоённых условиях. Мало того, это считается невозможным – единственное, что можно предсказать - это вероятность тех или иных событий. Так, что в квантовой механике мы должны удовлетвориться расчётом вероятностей, при этом считать, что такова природа на самом деле». |
| v Принцип неопределённости: Принцип неопределённости в квантовой механике задаётся соотношениями неопределённостей В. Гейзенберга: и . и находит отражение в принципе дополнительности Н. Бора. |
| v Принцип дополнительности: «Получение экспериментальной информации об одних физических величинах, описывающих состояние микрообъекта, неизбежно приводит к потере информации о других физических величинах, дополнительных к первым». В общенаучном плане принцип дополнительности можно сформулировать следующим образом: «Всякое истинное глубокое явление природы не может быть однозначно определено с помощью слов нашего языка и требует для своего определения по крайней мере двух взаимоисключающих дополнительных понятий». |
| v Принцип соответствия: «Любая новая более общая теория, являющаяся развитием предыдущих классических теорий, справедливость которых была экспериментально установлена для определенных групп явлений, не отвергает эти классические теории, а включает их в себя. В определенных случаях существует возможность предельного перехода новой теории в старую». |
| v Принцип простоты. «Более простая теория обычно имеет «внешнее оправдание» (соответствие эксперименту, т.е. свою верификацию) и «внутреннее совершенство» (красоту теории в виде ограничений на возможные качества систем), более «фальсифицируема и в то же время более информативна.». |
Квантовое микросостояние одной микрочастицы включает в себя как характеристики частиц, так и ее окружения. Состояние микрочастицы задается волновой функцией (амплитудой вероятности состояния) , которая является комплексной величиной, определяемой во всех точках пространства и в каждый момент времени. Движение частицы носит стохастический характер и в волновой механике уравнением движения является уравнение Шредингера, которое в общем случае имеет следующий вид:
,
а в случае стационарных состояний вид его упрощается
,
где - оператор Гамильтона.
Квадрат модуля волновой функции равен плотности вероятности, т.е. вероятности нахождения частицы в единице объема, .
Величина плотности вероятности является экспериментально наблюдаемой величиной, в то время как сама пси-функция, будучи комплексной, не доступна наблюдению.
Уравнение Шредингера можно применить и к квантовому микросостоянию системы частиц. Однако, в данном случае его решение всегда носит приближённый характер. При концептуальном анализе квантовой системы важную роль играют постулаты Бора (см. схему 32), квантовые статистики (см. схему 33) и квантовые числа микрочастиц (см. схему 34).
Схема 32. Обобщенные в рамках понятия квантовой системы постулаты Н. Бора.
| v Первый постулат Бора. Энергетический спектр атома (квантовой системы) дискретен. |
| v Второй постулат Бора Частоты атомного излучения (электромагнитного излучения квантовой системы) связаны с энергетическими уровнями атома (квантовой системы). При переходе с уровня на уровень испускается квант излучения с частотой . При обратном переходе квант поглощается. . |
Вероятностный подход совместно с принципом тождественности, согласно которому состояния системы частиц, получающиеся друг из друга перестановкой тождественных частиц, нельзя различить ни в каком эксперименте, позволяют рассматривать такие состояния как одно физическое состояние. При этом принцип симметрии и асимметрии волновых функций при перестановке двух одинаковых микрочастиц позволяет ввести квантовые статистики Бозе-Эйнштейна и Ферми-Дирака (см. схему 33).
Схема 33. Основные свойства микрочастиц в рамках квантовых статистик.
| Название квантовой статистики | Свойства соответствующих классов микрочастиц | Тип симметрии волновой функции |
| v Статистика Ш. Бозе и А. Эйнштейна (1924 г.) | Бозоны («коллективисты» имеют тенденцию скапливаться в одном квантовом состоянии. Элементарные частицы с целочисленными спинами, например, фотоны, фононы, пионы, тяжелые промежуточные бозоны, глюоны, гравитоны. | При перестановке двух одинаковых микрочастиц знак волновой функции не меняется. Симметричные волновые функции. |
| v Статистика Э.Ферми и П. Дирака (1926 г.) | Фермионы («индивидуалисты»). Согласно принципу Паули: «Два и более одинаковых фермиона не могут находиться в одном состоянии». Элементарные частицы с получисленными спинами, например, электроны, протоны, нейтроны, кварки, все лептоны. | При перестановке двух одинаковых микрочастиц меняется знак волновой функции. Антисимметричные волновые функции |
Как видно из схемы барионная вещественная материя создается из фермионов – протонов, нейтронов и электронов. При этом особое значение, по крайней мере, в объяснении физико-химических свойств химических элементов (совокупности атомов (изотопов) с одинаковым зарядом Z ядра) приобретает электронная структура, т.е. квантовое микросостояние электронов, определяемое набором соответствующих квантовых чисел (см. схему 34).
Схема 34. Квантовые числа и соответствующие условия квантования.
| Название квантового числа и задание его значений | Условия квантования и основные характеристики |
| v – главное квантовое число =1, 2, 3… | Задает условие квантования энергии и характеризует уровни дискретных значений энергии атома, например, водородоподобного: . |
| v - азимутальное квантовое число 0, 1, 2, 3, …, . | Задает условие квантования момента импульса микрочастицы, например, электрона в атоме: |
| v - магнитное квантовое число . | Задает условие квантования проекции момента импульса микрочастицы, например, электрона в атоме: . |
| v - спиновое квантовое число | Задает условие квантования собственного момента импульса микрочастицы, например, электрона в атоме: . Для электрона . |
| v - магнитное спиновое число | Задает условие квантования проекции собственного момента импульса микрочастицы, например, электрона в атоме: . Характеризует спиновую степень свободы электрона. Для электрона . |
Итак, двигаясь от электромагнитной волны к понятию фотона и совершая внешне противоположное движение от электрона к его волне и наблюдению интерференции и дифракции электронов, мы осознали корпускулярно-волновой дуализм материи. Опираясь на корпускулярно-волновой дуализм и поняв вероятностный характер квантовой механики, мы ввели абстрактно-математическое описание квантового микросостояния одной микрочастицы на основе уравнения Шредингера, а также микросостояния системы тождественных частиц на основе квантовых статистик и квантовых чисел. Так мы получили новое видение электромагнитных взаимодействий и приблизились к квантовой электродинамике. Квантовая электродинамика – «это новое воззрение на взаимодействие между электронами и протонами, т.е. электромагнитная теория, но со всеми уточнениями, внесенными квантовой механикой». Как отмечает Р. Фейнман, «квантовая электродинамика – в принципе это теория всей химии, всех жизненных процессов, если жизнь сводится к химии, а, следовательно, и к физике». А так как электромагнитное взаимодействие доминирует в макромире, то «из квантовой электродинамики выводятся все известные механические, электрические и химические законы». Цивилизационная значимость квантовой механики в утилитарно-прикладном плане проявилась как в «физической экономике» индустриальной цивилизации, так и в кооперативном взаимодействии «информационной экономики» с «физической экономикой» в постиндустриальной цивилизации.
5rik.ru
|
Поиск Лекций
Крушение классической физики и как следствие классического естествознания связано прежде всего со знаменитым немецким физиком-теоретиком Максом Планком, который связал хаотичность электромагнитного (светового) излучения атомных осцилляторов с их дискретностью и выдвинул идею квантового излучения энергии каждым осциллятором пропорционально частоте колебаний. Планк ввел коэффициент пропорциональности, новую фундаментальную константу , имеющую размерность действия (энергия, умноженная на время), получившую название постоянной Планка: , где . Квантовая гипотеза М. Планка сняла проблему «ультрафиолетовой катастрофы» теплового излучения, согласно которой, исходя из классических представлений о тепловом излучении, энергия излучения любого тела при любой температуре должна быть абсурдно бесконечной. А. Эйнштейн первым подхватил идею М. Планка, предположив, что электромагнитные волны не только излучаются, но и поглощаются квантами. Эта гипотеза позволила ему на основе формулы Планка и закона сохранения энергии получить в 1905 г. уравнение для внешнего фотоэффекта, подтвержденное в дальнейшем экспериментально рядом ученых и позволившее экспериментально определить постоянную Планка. Когда же было экспериментально продемонстрировано, что и процесс распространения света имеет квантовый характер (опыты В. Боте. Г. Гейгера, А. Комптона), стало ясно, что свет имеет двойственную корпускулярно-волновую природу. Так, свет при интерференции, дифракции, поляризации проявляет чисто волновые свойства, а при излучении нагретых тел, люминесценции, внешнем фотоэффекте, фотопроводимости – чисто корпускулярные свойства, т.е. как поток «частиц» (квантов), которые назвали фотонами. Боровская теория водородоподобного атома, в основу которой Н. Бор в 1913 г. закладывает идею о квантовании величины действия при движении электрона по круговой орбите («планетарная модель атома Резерфорда-Бора»), подкрепляла возникший корпускулярно-волновой дуализм света. И совершенно «безумная», но «революционная» в «драме идей» становления квантовой механики гипотеза была выдвинута Луи де Бройлем о том, что с двигающимся электроном связана некая волна, длина волны которой равна , где - импульс электрона. Он применил эту идею к интерпретации стационарных орбит боровской модели атома. Он считал, что в длине такой орбиты укладывается целое число длин волн электрона, и тогда волны электрона находятся в фазе сами с собой и не разрушаются собственной интерференцией. В 1924 г. де Бройль изложил эту идею в своей диссертации «Исследования по квантовой теории», которую поддержал А. Эйнштейн. Последний рекомендовал эту работу Эрвину Шредингеру, который на основе этой идеи создал одно из основных направлений квантовой механики – волновую механику. В 1927 г. эксперименты Дэвиссона и Джермера подтвердили «безумную» идею де Бройля в опытах по наблюдению дифракции электронов от кристалла никеля. В том же 1927 г. Дж. П. Томсон наблюдал дифракцию быстрых электронов на очень тонкой металлической фольге, изготовленной из поликристаллического материала с хаотическим расположением кристаллических осей. В настоящее время корпускулярно-волновой дуализм распространяется на все элементарные частицы, а следовательно на все исходные принципы квантовой механики и их применения к материи, движению и фундаментальным взаимодействиям. Эти исходные принципы квантовой механики в сжатой форме сформулировал Р. Фейнман в своих знаменитых лекциях по физике на основе рассмотрения прохождения щели электронами(см. рис. 5.1). Мы объединили в одном рисунке интерференцию электронных волн (б) со световым наблюдением за электронами (в). Теперь попробуем в сжатой форме прокомментировать результаты эксперимента на нашем электронном приборе. При этом мы изложим, следуя Р. Фейнмана, результаты в такой форме, чтобы они имели силу для всего класса аналогичных экспериментов. Для этого сформулируем определение идеального эксперимента: «Идеальным называется такой эксперимент, в котором все начальные и конечные условия полностью определены». Теперь об общих выводах, которые приведем в краткой форме: 1. Вероятность некоего события в идеальном эксперименте, например, прохождения электронов через отверстие 1 или через отверстие 2 и их измерения с помощью щелчков на детекторе, равняется квадрату абсолютного значения комплексного числа , именуемого амплитудой вероятности. вероятность, амплитуда вероятности, и тогда и . 2. Если событие в эксперименте может осуществляться несколькими взаимно исключающими способами, т.е. когда, например, открыты оба отверстия (щели) и мы не фиксируем через какую щель проходит тот или иной электрон, то амплитуда вероятности для каждого отдельного события равняется сумме амплитуд вероятности для каждого отдельного способа. При этом «имеет место интерференция» (рис. 5.1, (б)). а . 3. Если проводится эксперимент, дающий возможность определить, какой из этих двух взаимно исключающих способов осуществляется в действительности (в нашем случае контролем прохождения электронов с помощью сильного источника света), то вероятность события равна сумме вероятностей для каждого отдельного способа. Интерференция отсутствует. . Основные идеи, принципы и законы квантово-полевой картины мира в определённой степени отражены в предыдущей лекции №3 (см. схему 21). Мы их концептуальную основу отразим на основе выделения основополагающих концепций и методологических принципов квантовой механики (см. схему 33).
Схема 33. Основополагающие концепции и методологические принципы квантовой механики.
Квантовое микросостояние одной микрочастицы включает в себя как характеристики частиц, так и ее окружения. Состояние микрочастицы задается волновой функцией (амплитудой вероятности состояния) , которая является комплексной величиной, задаваемой во всех точках пространства и в каждый момент времени. Движение частицы носит стохастический характер и в волновой механике уравнением движения является уравнение Шредингера, которое в общем случае имеет следующий вид: , а в случае стационарных состояний вид его упрощается , где - оператор Гамильтона. Квадрат модуля волновой функции равен плотности вероятности, т.е. вероятности нахождения частицы в единице объема, . Величина плотности вероятности является экспериментально наблюдаемой величиной, в то время как сама пси-функция, будучи комплексной, не доступна наблюдению. Уравнение Шредингера можно применить и к квантовому микросостоянию системы частиц. Однако, в данном случае его решение всегда носит приближённый характер. При концептуальном анализе квантовой системы важную роль играют постулаты Бора (см. схему 34), квантовые статистики (см. схему 35) и квантовые числа микрочастиц (см. схему 36). Схема 34. Обобщенные в рамках понятия квантовой системы постулаты Н. Бора.
Вероятностный подход совместно с принципом тождественности, согласно которому состояния системы частиц, получающиеся друг из друга перестановкой тождественных частиц, нельзя различить ни в каком эксперименте, позволяют рассматривать такие состояния как одно физическое состояние. При этом принцип симметрии и асимметрии волновых функций при перестановке двух одинаковых микрочастиц позволяет ввести квантовые статистики Бозе-Эйнштейна и Ферми-Дирака (см. схему 35).
Схема 35. Основные свойства микрочастиц в рамках квантовых статистик.
Как видно из схемы барионная вещественная материя создается из фермионов – протонов, нейтронов и электронов. При этом особое значение, по крайней мере, в объяснении физико-химических свойств химических элементов (совокупности атомов (изотопов) с одинаковым зарядом Z ядра) приобретает электронная структура, т.е. квантовое микросостояние электронов, определяемое набором соответствующих квантовых чисел (см. схему 36).
Схема 36. Квантовые числа и соответствующие условия квантования.
Итак, двигаясь от электромагнитной волны к понятию фотона и совершая внешне противоположное движение от электрона к его волне и наблюдению интерференции и дифракции электронов, мы осознали корпускулярно-волновой дуализм материи. Опираясь на корпускулярно-волновой дуализм и поняв вероятностный характер квантовой механики, мы ввели абстрактно-математическое описание квантового микросостояния одной микрочастицы на основе уравнения Шредингера, а также микросостояния системы тождественных частиц на основе квантовых статистик и квантовых чисел. Так мы получили новое видение электромагнитных взаимодействий и приблизились к квантовой электродинамике. Квантовая электродинамика – «это новое воззрение на взаимодействие между электронами и протонами, т.е. электромагнитная теория, но со всеми уточнениями, внесенными квантовой механикой». Как отмечает Р. Фейнман, «квантовая электродинамика – в принципе это теория всей химии, всех жизненных процессов, если жизнь сводится к химии, а, следовательно, и к физике». А так как электромагнитное взаимодействие доминирует в макромире, то «из квантовой электродинамики выводятся все известные механические, электрические и химические законы». Цивилизационная значимость квантовой механики в утилитарно-прикладном плане проявилась как в «физической экономике» индустриальной цивилизации, так и в кооперативном взаимодействии «информационной экономики» с «физической экономикой» в постиндустриальной цивилизации.
|
|
poisk-ru.ru