История квантовой механики. Квантовую механику
Квантовая механика на пальцах. Часть II
ПЕРВЫЕ ШАГИ
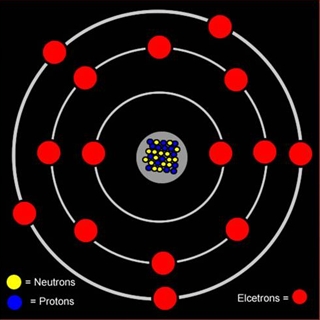
История квантовой механики очень интересна, но коротко о ней не расскажешь. Ограничусь парой ключевых этапов. В 1913 году датский физик Нильс Бор использовал квантовую модель света для объяснения спектра водорода. К тому времени физики хорошо знали, что атомы этого газа при нагреве испускают свет только строго определенных частот. Для этих частот была подобрана формула, которая отлично согласовывалась с опытом. Бор показал, что эту формулу можно получить теоретически, если допустить, что единственный электрон в атоме водорода обращается вокруг ядра только по некоторым разрешенным орбитам — первой, второй, третьей и так далее до бесконечности. Чем больше номер орбиты, тем она дальше от ядра и тем больше энергия электрона. Находясь на орбите, электрон ничего не излучает и потому не теряет энергию. Однако он может перескочить с какой-то из верхних орбит на какую-то из нижних (например, с третьей на первую или с четвертой на вторую). В этом случае он испустит световой квант, чья энергия будет равняться разности между энергиями верхней и нижней орбиты. Частота кванта будет равна этой энергии, поделенной на постоянную Планка.
Теория Бора отдавала дань ньютоновской механике, ведь он вполне традиционно считал, что электрон имеет на орбите определенный радиус и определенную скорость. Однако гипотеза о возможности только пронумерованных разрешенных орбит уже выходила за ее рамки. Согласно механике Ньютона и его же закону всемирного тяготения, планета может обращаться вокруг своей звезды по любому замкнутому эллипсу, не встречаясь ни с какими запретами (точно так же искусственный спутник можно вывести на любую околоземную орбиту). В модели Бора эти запреты возникают, причем разрешенные орбиты он определяет с помощью постоянной Планка. В общем, он явно отступает от ньютоновской механики, хотя пока не очень понятно, в какую сторону. Он также решительно рвет с общепринятой теорией электричества и магнетизма, созданной еще в середине девятнадцатого века. Согласно этой теории, так называемой классической электродинамике, любой орбитальный электрон должен излучать электромагнитные волны и потому обречен на потерю энергии и падение на ядро. А вот для боровских электронов это правило не действует!
В 1910-20-е годы физики еще не думали, что квантовая теория света станет предшественницей неньютоновской механики. Однако новые открытия все сильнее подталкивали к такому повороту. В 1922 году американский физик Артур Комптон экспериментально показал, что рентгеновские лучи при отражении от электронов ведут себя так, как если бы они состояли из отдельных частиц именно той энергии, которая дается формулой Планка. Тем самым он впервые напрямую подтвердил гипотезу Эйнштейна о существовании световых квантов.
В том же году впервые были произнесены слова «квантовая механика». В 1911 году голландский физик Хейке Камерлинг-Оннес обнаружил, что некоторые металлы (сначала ртуть, потом свинец и олово) при очень низких температурах перестают сопротивляться электрическому току. Это явление он назвал сверхпроводимостью. Его природа выглядела совершенно загадочной, объяснить ее тогдашняя физика была не в состоянии. В ходе обсуждения сверхпроводимости на научной конференции Эйнштейн отметил, что понять ее удастся только на основе квантовой механики. Так еще не существующая наука обрела имя, которое вскоре стало общепринятым.
ФИНИШ И НАЧАЛО
А потом события понеслись вскачь. Осенью 1923 года французский физик (тогда еще только аспирант) Луи де Бройль выдвинул совершенно сумасшедшую гипотезу, к которой он пришел, изучив эйнштейновскую теорию фотоэффекта и обдумав результаты Комптона. Он осознал, что если свет имеет свойства частиц, то «настоящие» частицы, и прежде всего электроны, должны обладать волновыми свойствами! Согласно де Бройлю, электрону можно приписать определенную длину волны, следовательно, и частоту, которая связана с его энергией формулой Планка. Отсюда следовало, что и волны, и частицы в равной мере подчиняются квантовым принципам.
Гипотеза де Бройля подтвердилась в эксперименте в 1927-28 годах. Физики из США и Англии независимо показали, что пучок электронов при прохождении через кристаллическое вещество ведет себя точно так же, как и пучок рентгеновских лучей. Оба пучка рисуют на фотопластинках концентрические окружности, чьи диаметры можно рассчитать по известным с начала девятнадцатого века правилам волновой оптики.
Из гипотезы де Бройля уже прямо вытекало, что ньютоновская механика не может описывать движение электронов. Требовались принципиально новые идеи, и они не замедлили появиться. В 1925-26 годах немецкий физик Вернер Гейзенберг и австриец Эрвин Шредингер независимо друг от друга и разными способами заложили фундамент квантовой механики. Их работы мгновенно продолжили и развили другие замечательные физики — Вольфганг Паули, Паскуаль Иордан, Макс Борн, Поль Дирак. Общими усилиями они изобрели математические средства, пригодные для описания тех физических величин, которые в принципе нельзя одновременно измерить (а это не только координаты и скорости!). Они также выяснили основное отличие квантовой механики от предшествующей доквантовой физики. Если прежняя физика в принципе позволяла однозначно предсказывать значения всех величин, которые можно наблюдать в эксперименте, то квантовая механика ограничивается только вероятностями. Например, она позволяет вычислить, с какой вероятностью можно обнаружить электрон в атоме водорода на том или ином расстоянии от ядра, но не дает возможность найти его траекторию (более того, с точки зрения квантовой механики ее просто не существует!).
К концу 1927 года математический аппарат квантовой механики был в основном создан. Правда, она возникла как "переработка" ньютоновской механики на основе квантовых принципов и потому не сочеталась с эйнштейновской теорией относительности. Однако уже в 1928 году Дирак построил квантовую теорию электрона, которая обобщала не ньютоновскую, а эйнштейновскую механику.
Работа Дирака стала важнейшей вехой в истории теоретической физики еще и по другой причине. До сих пор мы говорили только о том, что квантовая механика стала по-новому описывать физические величины, унаследованные у классической механики Ньютона. Именно это обстоятельство ставили во главу угла создатели этой науки, когда она только что возникла. Так, Поль Дирак в 1925 году отмечал, что квантовая механика «предполагает не то, что уравнения классической физики в каком-либо отношении ошибочны, а то, что необходимо изменить математические операции, посредством которых из этих уравнений выводятся физические результаты». Однако в том же году Сэмюэль Гаудсмит и Джордж Уленбек обнаружили у электрона совершенно новую, чисто квантовую характеристику, которая не имеет никаких классических аналогов — речь идет, конечно, о спине. Дираковская теория электрона показала, что существование спина есть необходимое следствие объединения квантовых принципов с принципами теории относительности. Позднее у объектов микромира было найдено много других неклассических свойств — например, четность, странность, очарование.
Квантовая механика быстро показала свое могущество. Уже к концу 1920-х годов с ее помощью физики в общих чертах выяснили, как устроены атомы различных химических элементов. Это позволило понять и таблицу Менделеева, поскольку химические свойства зависят от структуры электронного облака, окружающего атомное ядро. В 1930-е годы она позволила объяснить электрические свойства металлов и полупроводников, понять, почему железо, никель и еще некоторые металлы могут быть сильными постоянными магнитами, построить теорию атомного ядра и его распадов, и даже предсказать три новые частицы, позитрон, нейтрино и пи-мезон.
scientificrussia.ru
Квантовая механика - это... Что такое Квантовая механика?
Классическая механика, хорошо описывающая системы макроскопических масштабов, не способна описать явления на уровне молекул, атомов, электронов и фотонов. Квантовая механика адекватно описывает основные свойства и поведение атомов, ионов, молекул, конденсированных сред, и других систем с электронно-ядерным строением. Квантовая механика также способна описывать поведение электронов, фотонов, а также других элементарных частиц, однако более точное релятивистски инвариантное описание превращений элементарных частиц строится в рамках квантовой теории поля. Эксперименты подтверждают результаты, полученные с помощью квантовой механики.
Основными понятиями квантовой кинематики являются понятия наблюдаемой и состояния.
Основные уравнения квантовой динамики — уравнение Шрёдингера, уравнение фон Неймана, уравнение Линдблада, уравнение Гейзенберга и уравнение Паули.
Уравнения квантовой механики тесно связаны со многими разделами математики, среди которых: теория операторов, теория вероятностей, функциональный анализ, операторные алгебры, теория групп.
История
На заседании Немецкого физического общества, Макс Планк зачитал свою историческую статью «К теории распределения энергии излучения в нормальном спектре», в которой он ввёл универсальную постоянную h. Именно дату этого события, 14 декабря 1900 года, часто считают днем рождения квантовой теории.
Квантовая гипотеза Планка состояла в том, что для элементарных частиц, любая энергия поглощается или испускается только дискретными порциями (квантами). Эти порции состоят из целого числа квантов с энергией таких, что эта энергия пропорциональна частоте ν с коэффициентом пропорциональности, определённым по формуле:
где h — постоянная Планка, и .
В 1905 году, для объяснения явлений фотоэффекта, Альберт Эйнштейн, использовав квантовую гипотезу Планка, предположил, что свет состоит из квантов. Впоследствии, «кванты» получили название фотонов.
Для объяснения структуры атома, Нильс Бор предложил в 1913 году существование стационарных состояний электрона, в которых энергия может принимать лишь дискретные значения. Этот подход, развитый Арнольдом Зоммерфельдом и другими физиками, часто называют старой квантовой теорией (1900—1924 г.). Отличительной чертой старой квантовой теории является сочетание классической теории с противоречащими ей дополнительными предположениями.
В 1923 году Луи де Бройль выдвинул идею двойственной природы вещества, опиравшуюся на предположение о том, что материальные частицы обладают и волновыми свойствами, неразрывно связанными с массой и энергией. Движение частицы Л. де Бройль сопоставил с распространением волны, что в 1927 году получило экспериментальное подтверждение при исследовании дифракции электронов в кристаллах.
Высказанные в 1924 году идеи корпускулярно-волнового дуализма были в 1926 году подхвачены Э. Шрёдингером, развернувшим на их основе свою волновую механику.
В 1925—1926 годах были заложены основы последовательной квантовой теории в виде квантовой механики, содержащей новые фундаментальные законы кинематики и динамики. Первая формулировка квантовой механики содержится в статье Вернера Гейзенберга, датированной 29 июля 1925 года. Эту дату можно считать днем рождения нерелятивистской квантовой механики.
Развитие и формирование основ квантовой механики продолжается до сих пор. Оно связано, например, с исследованиями открытых и диссипативных квантовых систем, квантовой информатикой, квантовым хаосом и пр. Помимо квантовой механики, важнейшей частью квантовой теории является квантовая теория поля.
В 1927 году К. Дэвиссон и Л. Джермер в исследовательском центре Bell Labs демонстрируют дифракцию медленных электронов на никелевых кристаллах (независимо от Дж. Томсона). При оценке угловой зависимости интенсивности отраженного электронного луча, было показано её соответствие предсказанной на основании условия Вульфа — Брэгга для волн с длиной Де Бройля (см. Волны де Бройля). До принятия гипотезы де Бройля, дифракция расценивалась как исключительно волновое явление, а любой дифракционный эффект — как волновой. Когда длина волны де Бройля была сопоставлена с условием Вульфа — Брэгга, была предсказана возможность наблюдения подобной дифракционной картины для частиц. Таким образом экспериментально была подтверждена гипотеза де Бройля для электрона.
Подтверждение гипотезы де Бройля стало поворотным моментом в развитии квантовой механики. Подобно тому, как эффект Комптона показывает корпускулярную природу света, эксперимент Дэвиссона — Джермера подтвердил неразрывное «сосуществование» с частицей её волны, иными словами — присущность корпускулярной материи также и волновой природы. Это послужило оформлению идей корпускулярно-волнового дуализма. Подтверждение этой идеи для физики стало важным этапом, поскольку дало возможность не только характеризовать любую частицу, присваивая ей определённую индивидуальную длину волны, но также при описании явлений, полноправно использовать её в виде определённой величины в волновых уравнениях.
Математические основания квантовой механики
Существует несколько различных эквивалентных математических описаний квантовой механики:
Шрёдингеровское описание
Математический аппарат нерелятивистской квантовой механики строится на следующих положениях[1]:
где через обозначается скалярное произведение векторов и .
где — гамильтониан.
Основные следствия этих положений:
- При измерении любой квантовой наблюдаемой, возможно получение только ряда фиксированных её значений, равных собственным значениям её оператора — наблюдаемой.
- Наблюдаемые одновременно измеримы (не влияют на результаты измерений друг друга) тогда и только тогда, когда соответствующие им самосопряжённые операторы перестановочны.
Эти положения позволяют создать математический аппарат, пригодный для описания широкого спектра задач в квантовой механике гамильтоновых систем, находящихся в чистых состояниях. Не все состояния квантовомеханических систем, однако, являются чистыми. В общем случае состояние системы является смешанным и описывается матрицей плотности, для которой справедливо обобщение уравнения Шрёдингера — уравнение фон Неймана (для гамильтоновых систем). Дальнейшее обобщение квантовой механики на динамику открытых, негамильтоновых и диссипативных квантовых систем приводит к уравнению Линдблада.
Стационарное уравнение Шрёдингера
Пусть амплитуда вероятности нахождения частицы в точке М. Стационарное уравнение Шрёдингера позволяет ее определить.Функция удовлетворяет уравнению:
где —оператор Лапласа, а — потенциальная энергия частицы как функция .
Решение стационарного уравнения
Соотношение неопределённости возникает между любыми квантовыми наблюдаемыми, определяемыми некоммутирующими операторами.
Неопределенность между координатой и импульсом
Пусть — среднеквадратическое отклонение координаты частицы , движущейся вдоль оси , и — среднеквадратическое отклонение ее импульса. Величины и связаны следующим неравенством:
где — постоянная Планка, а Согласно соотношению неопределённостей, невозможно абсолютно точно определить одновременно координаты и скорость частицы. Например, чем больше точность определения координаты частицы, тем меньше точность определения ее скорости.
Неопределенность между энергией и временем
Пусть ΔЕ — среднеквадратическое отклонение энергии частицы, и Δt — время, требуемое для обнаружения частицы.Время Δt для обнаружения частицы с энергией E±ΔЕ определяется следующим неравенством:
Необычные явления, мысленные эксперименты и парадоксы квантовой механики
Разделы квантовой механики
В стандартных курсах квантовой механики изучаются следующие разделы
Интерпретации квантовой механики
Существует множество интерпретаций квантовой теории, которые иногда плохо согласуются друг с другом.
Интерпретации квантовой механики
Комментарии
- Обычно квантовая механика формулируется для нерелятивистских систем. Рассмотрение частиц с релятивистскими энергиями в рамках стандартного квантовомеханического подхода, предполагающего фиксированное число частиц в системе, сталкивается с трудностями, поскольку при достаточно большой энергии частицы могут превращаться друг в друга. Эти трудности устраняются в квантовой теории поля, которая и является самосогласованной теорией релятивистских квантовых систем.
- Важным свойством квантовой механики является принцип соответствия: в рамках квантовой механики доказывается, что в пределе больших величин действия (квазиклассический предел) и в случае, когда квантовая система взаимодействует с внешним миром (декогеренция), уравнения квантовой механики редуцируются в уравнения классической физики (см. Теорема Эренфеста). Таким образом, квантовая механика не противоречит классической физике, а лишь дополняет её на микроскопических масштабах.
- Некоторые свойства квантовых систем кажутся непривычными (невозможность одновременно измерить координату и импульс, несуществование определённой траектории частицы, вероятностное описание, дискретность средних значений наблюдаемых величин). Это вовсе не значит, что они неверны: это означает, что наша повседневная интуиция никогда не сталкивалась с таким поведением, т. е. в данном случае «здравый смысл» не может быть критерием, поскольку он годится только для макроскопических систем. Квантовая механика — самосогласованная математическая теория, предсказания которой согласуются с экспериментами. В настоящее время огромное число приборов, используемых в повседневной жизни, основываются на законах квантовой механики, как например — лазер или сканирующий туннельный микроскоп.
- Классическая механика оказалась неспособной объяснить движение электронов вокруг атомного ядра. Например, согласно классической электродинамике, электрон, вращающийся с большой скоростью вокруг атомного ядра, должен излучать энергию. Тогда его кинетическая энергия должна уменьшаться и он должен упасть на ядро. Для понимания процессов, происходящих на уровне элементарных частиц, потребовалась новая теория. Квантовая теория — это совершенно новый взгляд на систему, позволяющий с огромной точностью описать необычное поведение электронов и фотонов.[2]
См. также
Примечания
- ↑ Ф. А. Березин, М. А. Шубин. Уравнение Шрёдингера. — М.: Изд-во Моск. ун-та, 1983.
- ↑ Фейнман Р. КЭД-странная теория света и вещества — М: Наука, 1988. (Библиотечка «Квант»)
Литература
- Физический энциклопедический словарь. Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др. М.: Сов. Энциклопедия, 1984. — 944 с.
- Блохинцев Д. И. Основы квантовой механики. 5-е изд. Наука, 1976. — 664 с.
- Боум А. Квантовая механика: основы и приложения. М.: Мир, 1990. — 720 c.
- Джеммер М. Эволюция понятий квантовой механики. М.: Наука, 1985. — 384 с.
- Дирак П. Принципы квантовой механики. 2-е изд. М.: Наука, 1979. — 480 с.
- Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 6-е, исправленное. — М.: Физматлит, 2004. — 800 с. — («Теоретическая физика», том III). — ISBN 5-9221-0530-2
- Садбери А. Квантовая механика и физика элементарных частиц. М.: Мир, 1989. — 488 с.
- Фадеев Л. Д., Якубовский О. А. Лекции по квантовой механике для студентов-математиков. Ленинград, Изд-во ЛГУ, 1980. — 200 c.
- Фейнман Р., Лейтон Р., Сэндс М. Феймановские лекции по физике. Пер. с англ., Том. 8. Том 9., М., 1966—1967.
- К. Коэн-Таннуджи, Б. Диу, Ф. Лалоэ. Квантовая механика. Т.1. Екатеринбург: Изд-во Уральского ун-та, 2000. — 944 с.
- К. Коэн-Таннуджи, Б. Диу, Ф. Лалоэ. Квантовая механика. Т.2. Екатеринбург: Изд-во Уральского ун-та, 2000. — 800 с.
Ссылки
- Лорен Грэхэм «Естествознание, философия и науки о человеческом поведении в Советском Союзе, Глава X. Квантовая механика»
- Шрёдингер Э. Избранные труды по квантовой механике, — М..: Наука, 1976.
- Нейман И. Математические основы квантовой механики, — М.: Наука, 1964.
- Паули В. Общие принципы волновой механики, — М. — Л.: ГИТТЛ, 1947.
- Дирак П. А. М. Принципы квантовой механики (2-е издание), — М.: Наука, 1979.
- Фущич В. И., Никитин А. Г. Симметрия уравнений квантовой механики, — М.: Наука, 1990.
- Блохинцев Д. И. Принципиальные вопросы квантовой механики. М.: Наука, 1966.
- «Квантовая механика» — статья в Физической энциклопедии.
biograf.academic.ru
Квантовая механика - это... Что такое Квантовая механика?
Ква́нтовая меха́ника — раздел теоретической физики, описывающий физические явления, в которых действие сравнимо по величине с постоянной Планка. Предсказания квантовой механики могут существенно отличаться от предсказаний классической механики. Поскольку постоянная Планка является чрезвычайно малой величиной по сравнению с действием повседневных объектов, квантовые эффекты в основном проявляются только в микроскопических масштабах. Если физическое действие системы намного больше постоянной Планка, квантовая механика органически переходит в классическую механику. В свою очередь, квантовая механика является нерелятивистским приближением (то есть приближением малых энергий по сравнению с энергией покоя массивных частиц системы) квантовой теории поля.
Классическая механика, хорошо описывающая системы макроскопических масштабов, не способна описать явления на уровне молекул, атомов, электронов и фотонов. Квантовая механика адекватно описывает основные свойства и поведение атомов, ионов, молекул, конденсированных сред, и других систем с электронно-ядерным строением. Квантовая механика также способна описывать поведение электронов, фотонов, а также других элементарных частиц, однако более точное релятивистски инвариантное описание превращений элементарных частиц строится в рамках квантовой теории поля. Эксперименты подтверждают результаты, полученные с помощью квантовой механики.
Основными понятиями квантовой кинематики являются понятия наблюдаемой и состояния.
Основные уравнения квантовой динамики — уравнение Шрёдингера, уравнение фон Неймана, уравнение Линдблада, уравнение Гейзенберга и уравнение Паули.
Уравнения квантовой механики тесно связаны со многими разделами математики, среди которых: теория операторов, теория вероятностей, функциональный анализ, операторные алгебры, теория групп.
История
На заседании Немецкого физического общества, Макс Планк зачитал свою историческую статью «К теории распределения энергии излучения в нормальном спектре», в которой он ввёл универсальную постоянную h. Именно дату этого события, 14 декабря 1900 года, часто считают днем рождения квантовой теории.
Квантовая гипотеза Планка состояла в том, что для элементарных частиц, любая энергия поглощается или испускается только дискретными порциями (квантами). Эти порции состоят из целого числа квантов с энергией таких, что эта энергия пропорциональна частоте ν с коэффициентом пропорциональности, определённым по формуле:
где h — постоянная Планка, и .
В 1905 году, для объяснения явлений фотоэффекта, Альберт Эйнштейн, использовав квантовую гипотезу Планка, предположил, что свет состоит из квантов. Впоследствии, «кванты» получили название фотонов.
Для объяснения структуры атома, Нильс Бор предложил в 1913 году существование стационарных состояний электрона, в которых энергия может принимать лишь дискретные значения. Этот подход, развитый Арнольдом Зоммерфельдом и другими физиками, часто называют старой квантовой теорией (1900—1924 г.). Отличительной чертой старой квантовой теории является сочетание классической теории с противоречащими ей дополнительными предположениями.
В 1923 году Луи де Бройль выдвинул идею двойственной природы вещества, опиравшуюся на предположение о том, что материальные частицы обладают и волновыми свойствами, неразрывно связанными с массой и энергией. Движение частицы Л. де Бройль сопоставил с распространением волны, что в 1927 году получило экспериментальное подтверждение при исследовании дифракции электронов в кристаллах.
Высказанные в 1924 году идеи корпускулярно-волнового дуализма были в 1926 году подхвачены Э. Шрёдингером, развернувшим на их основе свою волновую механику.
В 1925—1926 годах были заложены основы последовательной квантовой теории в виде квантовой механики, содержащей новые фундаментальные законы кинематики и динамики. Первая формулировка квантовой механики содержится в статье Вернера Гейзенберга, датированной 29 июля 1925 года. Эту дату можно считать днем рождения нерелятивистской квантовой механики.
Развитие и формирование основ квантовой механики продолжается до сих пор. Оно связано, например, с исследованиями открытых и диссипативных квантовых систем, квантовой информатикой, квантовым хаосом и пр. Помимо квантовой механики, важнейшей частью квантовой теории является квантовая теория поля.
В 1927 году К. Дэвиссон и Л. Джермер в исследовательском центре Bell Labs демонстрируют дифракцию медленных электронов на никелевых кристаллах (независимо от Дж. Томсона). При оценке угловой зависимости интенсивности отраженного электронного луча, было показано её соответствие предсказанной на основании условия Вульфа — Брэгга для волн с длиной Де Бройля (см. Волны де Бройля). До принятия гипотезы де Бройля, дифракция расценивалась как исключительно волновое явление, а любой дифракционный эффект — как волновой. Когда длина волны де Бройля была сопоставлена с условием Вульфа — Брэгга, была предсказана возможность наблюдения подобной дифракционной картины для частиц. Таким образом экспериментально была подтверждена гипотеза де Бройля для электрона.
Подтверждение гипотезы де Бройля стало поворотным моментом в развитии квантовой механики. Подобно тому, как эффект Комптона показывает корпускулярную природу света, эксперимент Дэвиссона — Джермера подтвердил неразрывное «сосуществование» с частицей её волны, иными словами — присущность корпускулярной материи также и волновой природы. Это послужило оформлению идей корпускулярно-волнового дуализма. Подтверждение этой идеи для физики стало важным этапом, поскольку дало возможность не только характеризовать любую частицу, присваивая ей определённую индивидуальную длину волны, но также при описании явлений, полноправно использовать её в виде определённой величины в волновых уравнениях.
Математические основания квантовой механики
Существует несколько различных эквивалентных математических описаний квантовой механики:
Шрёдингеровское описание
Математический аппарат нерелятивистской квантовой механики строится на следующих положениях[1]:
где через обозначается скалярное произведение векторов и .
где — гамильтониан.
Основные следствия этих положений:
- При измерении любой квантовой наблюдаемой, возможно получение только ряда фиксированных её значений, равных собственным значениям её оператора — наблюдаемой.
- Наблюдаемые одновременно измеримы (не влияют на результаты измерений друг друга) тогда и только тогда, когда соответствующие им самосопряжённые операторы перестановочны.
Эти положения позволяют создать математический аппарат, пригодный для описания широкого спектра задач в квантовой механике гамильтоновых систем, находящихся в чистых состояниях. Не все состояния квантовомеханических систем, однако, являются чистыми. В общем случае состояние системы является смешанным и описывается матрицей плотности, для которой справедливо обобщение уравнения Шрёдингера — уравнение фон Неймана (для гамильтоновых систем). Дальнейшее обобщение квантовой механики на динамику открытых, негамильтоновых и диссипативных квантовых систем приводит к уравнению Линдблада.
Стационарное уравнение Шрёдингера
Пусть амплитуда вероятности нахождения частицы в точке М. Стационарное уравнение Шрёдингера позволяет ее определить.Функция удовлетворяет уравнению:
где —оператор Лапласа, а — потенциальная энергия частицы как функция .
Решение стационарного уравнения
Соотношение неопределённости возникает между любыми квантовыми наблюдаемыми, определяемыми некоммутирующими операторами.
Неопределенность между координатой и импульсом
Пусть — среднеквадратическое отклонение координаты частицы , движущейся вдоль оси , и — среднеквадратическое отклонение ее импульса. Величины и связаны следующим неравенством:
где — постоянная Планка, а Согласно соотношению неопределённостей, невозможно абсолютно точно определить одновременно координаты и скорость частицы. Например, чем больше точность определения координаты частицы, тем меньше точность определения ее скорости.
Неопределенность между энергией и временем
Пусть ΔЕ — среднеквадратическое отклонение энергии частицы, и Δt — время, требуемое для обнаружения частицы.Время Δt для обнаружения частицы с энергией E±ΔЕ определяется следующим неравенством:
Необычные явления, мысленные эксперименты и парадоксы квантовой механики
Разделы квантовой механики
В стандартных курсах квантовой механики изучаются следующие разделы
Интерпретации квантовой механики
Существует множество интерпретаций квантовой теории, которые иногда плохо согласуются друг с другом.
Интерпретации квантовой механики
Комментарии
- Обычно квантовая механика формулируется для нерелятивистских систем. Рассмотрение частиц с релятивистскими энергиями в рамках стандартного квантовомеханического подхода, предполагающего фиксированное число частиц в системе, сталкивается с трудностями, поскольку при достаточно большой энергии частицы могут превращаться друг в друга. Эти трудности устраняются в квантовой теории поля, которая и является самосогласованной теорией релятивистских квантовых систем.
- Важным свойством квантовой механики является принцип соответствия: в рамках квантовой механики доказывается, что в пределе больших величин действия (квазиклассический предел) и в случае, когда квантовая система взаимодействует с внешним миром (декогеренция), уравнения квантовой механики редуцируются в уравнения классической физики (см. Теорема Эренфеста). Таким образом, квантовая механика не противоречит классической физике, а лишь дополняет её на микроскопических масштабах.
- Некоторые свойства квантовых систем кажутся непривычными (невозможность одновременно измерить координату и импульс, несуществование определённой траектории частицы, вероятностное описание, дискретность средних значений наблюдаемых величин). Это вовсе не значит, что они неверны: это означает, что наша повседневная интуиция никогда не сталкивалась с таким поведением, т. е. в данном случае «здравый смысл» не может быть критерием, поскольку он годится только для макроскопических систем. Квантовая механика — самосогласованная математическая теория, предсказания которой согласуются с экспериментами. В настоящее время огромное число приборов, используемых в повседневной жизни, основываются на законах квантовой механики, как например — лазер или сканирующий туннельный микроскоп.
- Классическая механика оказалась неспособной объяснить движение электронов вокруг атомного ядра. Например, согласно классической электродинамике, электрон, вращающийся с большой скоростью вокруг атомного ядра, должен излучать энергию. Тогда его кинетическая энергия должна уменьшаться и он должен упасть на ядро. Для понимания процессов, происходящих на уровне элементарных частиц, потребовалась новая теория. Квантовая теория — это совершенно новый взгляд на систему, позволяющий с огромной точностью описать необычное поведение электронов и фотонов.[2]
См. также
Примечания
- ↑ Ф. А. Березин, М. А. Шубин. Уравнение Шрёдингера. — М.: Изд-во Моск. ун-та, 1983.
- ↑ Фейнман Р. КЭД-странная теория света и вещества — М: Наука, 1988. (Библиотечка «Квант»)
Литература
- Физический энциклопедический словарь. Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др. М.: Сов. Энциклопедия, 1984. — 944 с.
- Блохинцев Д. И. Основы квантовой механики. 5-е изд. Наука, 1976. — 664 с.
- Боум А. Квантовая механика: основы и приложения. М.: Мир, 1990. — 720 c.
- Джеммер М. Эволюция понятий квантовой механики. М.: Наука, 1985. — 384 с.
- Дирак П. Принципы квантовой механики. 2-е изд. М.: Наука, 1979. — 480 с.
- Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 6-е, исправленное. — М.: Физматлит, 2004. — 800 с. — («Теоретическая физика», том III). — ISBN 5-9221-0530-2
- Садбери А. Квантовая механика и физика элементарных частиц. М.: Мир, 1989. — 488 с.
- Фадеев Л. Д., Якубовский О. А. Лекции по квантовой механике для студентов-математиков. Ленинград, Изд-во ЛГУ, 1980. — 200 c.
- Фейнман Р., Лейтон Р., Сэндс М. Феймановские лекции по физике. Пер. с англ., Том. 8. Том 9., М., 1966—1967.
- К. Коэн-Таннуджи, Б. Диу, Ф. Лалоэ. Квантовая механика. Т.1. Екатеринбург: Изд-во Уральского ун-та, 2000. — 944 с.
- К. Коэн-Таннуджи, Б. Диу, Ф. Лалоэ. Квантовая механика. Т.2. Екатеринбург: Изд-во Уральского ун-та, 2000. — 800 с.
Ссылки
- Лорен Грэхэм «Естествознание, философия и науки о человеческом поведении в Советском Союзе, Глава X. Квантовая механика»
- Шрёдингер Э. Избранные труды по квантовой механике, — М..: Наука, 1976.
- Нейман И. Математические основы квантовой механики, — М.: Наука, 1964.
- Паули В. Общие принципы волновой механики, — М. — Л.: ГИТТЛ, 1947.
- Дирак П. А. М. Принципы квантовой механики (2-е издание), — М.: Наука, 1979.
- Фущич В. И., Никитин А. Г. Симметрия уравнений квантовой механики, — М.: Наука, 1990.
- Блохинцев Д. И. Принципиальные вопросы квантовой механики. М.: Наука, 1966.
- «Квантовая механика» — статья в Физической энциклопедии.
dikc.academic.ru
История квантовой механики — WiKi
История квантовой механики берёт своё начало 14 декабря 1900 г., когда Макс Планк предложил теоретический вывод соотношения между температурой тела и испускаемым этим телом излучением, вывод, который долгое время ускользал от других ученых. Как и его предшественники, Планк предположил, что излучение испускают атомные осцилляторы, но при этом считал, что энергия осцилляторов (и, следовательно, испускаемого ими излучения) существует в виде небольших дискретных порций, которые Эйнштейн назвал квантами. Энергия каждого кванта пропорциональна частоте излучения. Хотя выведенная Планком формула вызвала всеобщее восхищение, принятые им допущения оставались непонятными некоторое время, так как противоречили классической физике. В 1905 г. Альберт Эйнштейн воспользовался квантовой теорией для объяснения некоторых аспектов фотоэлектрического эффекта — испускания электронов поверхностью металла, на которую падает ультрафиолетовое излучение. Попутно Эйнштейн отметил кажущийся парадокс: свет, о котором на протяжении долгого времени было известно, что он распространяется как непрерывные волны, при поглощении и излучении проявляет дискретные свойства.
Примерно через восемь лет Нильс Бор распространил квантовую теорию на атом и объяснил частоты волн, испускаемых атомами, возбужденными в пламени или в электрическом разряде. Эрнест Резерфорд показал, что масса атома почти целиком сосредоточена в центральном ядре, несущем положительный электрический заряд и окруженном на сравнительно больших расстояниях электронами, несущими отрицательный заряд, вследствие чего атом в целом электрически нейтрален.
Бор предположил, что электроны могут находиться только на определенных дискретных орбитах, соответствующих различным энергетическим уровням, и что «перескок» электрона с одной орбиты на другую, с меньшей энергией, сопровождается испусканием фотона, энергия которого равна разности энергий двух орбит. Частота, по теории Планка, пропорциональна энергии фотона. Таким образом, модель атома Бора установила связь между различными линиями спектров, характерными для испускающего излучение вещества, и атомной структурой. Несмотря на первоначальный успех, модель атома Бора вскоре потребовала модификаций, чтобы избавиться от расхождений между теорией и экспериментом. Кроме того, квантовая теория на той стадии ещё не давала систематической процедуры решения многих квантовых задач. Однако стало ясно, что классическая физика неспособна объяснить тот факт, что движущийся с ускорением электрон не падает на ядро, теряя энергию при излучении электромагнитных волн.
Новая существенная особенность квантовой теории проявилась в 1924 г., когда Луи де Бройль выдвинул радикальную гипотезу о волновом характере материи: если электромагнитные волны, например свет, иногда ведут себя как частицы (что показал Эйнштейн), то частицы, например электрон при определенных обстоятельствах, могут вести себя как волны. Таким образом в микромире стёрлась граница между классическими частицами и классическими волнами. В формулировке де Бройля частота, соответствующая частице, связана с её энергией, как в случае фотона (частицы света), но предложенное де Бройлем математическое выражение было эквивалентным соотношением между длиной волны, массой частицы и её скоростью (импульсом). Существование электронных волн было экспериментально доказано в 1927 г. Клинтоном Дж. Дэвиссоном и Лестером Х. Джермером в Соединенных Штатах и Джорджем Паджетом Томсоном в Англии.
В свою очередь это открытие привело к созданию в 1933 г. Эрнстом Руской электронного микроскопа.
Под впечатлением от комментариев Эйнштейна по поводу идей де Бройля Эрвин Шрёдингер предпринял попытку применить волновое описание электронов к построению последовательной квантовой теории, не связанной с неадекватной моделью атома Бора. В известном смысле он намеревался сблизить квантовую теорию с классической физикой, которая накопила немало примеров математического описания волн. Первая попытка, предпринятая им в 1925 г., закончилась неудачей. Скорости электронов в теории Шрёдингера были близки к скорости света, что требовало включения в неё специальной теории относительности Эйнштейна и учёта предсказываемого ею значительного увеличения массы электрона при очень больших скоростях.
Одной из причин постигшей Шрёдингера неудачи было то, что он не учел наличия специфического свойства электрона, известного ныне под названием спина (вращение электрона вокруг собственной оси наподобие волчка, однако такое сравнение не совсем корректно), о котором в то время было мало известно. Следующую попытку Шрёдингер предпринял в 1926 г. Скорости электронов на этот раз были выбраны им настолько малыми, что необходимость в привлечении теории относительности отпадала сама собой. Вторая попытка увенчалась выводом волнового уравнения Шрёдингера, дающего математическое описание материи в терминах волновой функции. Шрёдингер назвал свою теорию волновой механикой. Решения волнового уравнения находились в согласии с экспериментальными наблюдениями и оказали глубокое влияние на последующее развитие квантовой теории. В настоящее время волновая функция лежит в основе квантовомеханического описания микросистем, подобно уравнениям Гамильтона в классической механике.
Незадолго до того Вернер Гейзенберг, Макс Борн и Паскуаль Иордан опубликовали другой вариант квантовой теории, получивший название матричной механики, которая описывала квантовые явления с помощью таблиц наблюдаемых величин. Эти таблицы представляют собой определенным образом упорядоченные математические множества, называемые матрицами, над которыми по известным правилам можно производить различные математические операции. Матричная механика также позволяла достичь согласия с наблюдаемыми экспериментальными данными, но в отличие от волновой механики не содержала никаких конкретных ссылок на пространственные координаты или время. Гейзенберг особенно настаивал на отказе от каких-либо простых наглядных представлений или моделей в пользу только таких свойств, которые могли быть определены из эксперимента, так как по его соображениям микромир имеет принципиально иное устройство, чем макромир в виду особой роли постоянной Планка, несущественной в мире больших величин.
Шрёдингер показал, что волновая механика и матричная механика математически эквивалентны. Известные ныне под общим названием квантовой механики, эти две теории дали долгожданную общую основу описания квантовых явлений. Многие физики отдавали предпочтение волновой механике, поскольку её математический аппарат был им более знаком, а её понятия казались более «физическими»; операции же над матрицами — более громоздкими.
Вскоре после того, как Гейзенберг и Шрёдингер разработали квантовую механику, Поль Дирак предложил более общую теорию, в которой элементы специальной теории относительности Эйнштейна сочетались с волновым уравнением. Уравнение Дирака применимо к частицам, движущимся с произвольными скоростями. Спин и магнитные свойства электрона следовали из теории Дирака без каких бы то ни было дополнительных предположений. Кроме того, теория Дирака предсказывала существование античастиц, таких, как позитрон и антипротон, — двойников частиц с противоположными по знаку электрическими зарядами.
ru-wiki.org
Квантовая механика
Ква́нтовая меха́ника (другие названия: волновая механика, матричная механика) — раздел теоретической физики, описывающий квантовые законы движения микроскопических частиц.
Основное уравнение квантовой механики — уравнение Шрёдингера, математический аппарат — теория матриц, теория групп, операторы, теория вероятностей.
История
Квантовая механика была создана в начале ХХ века трудами Шрёдингера, Гейзенберга, Дирака
Квантовая механика простыми словами
Комплексная вероятность
Квантовая (волновая) механика должна объяснять как корпускулярные, так и волновые свойства вещества (см. Корпускулярно-волновой дуализм). Любой волновой процесс (например, процесс колебаний маятника) полностью описывается его амплитудой и фазой, поэтому квантовая механика должна использовать именно такое описание. Так мы приходим к описанию системы комплексной волновой функцией, амплитуда и фаза которой полностью определяют состояние системы.
Такое описание позволяет естественным образом описывать волновые явления, такие, как интерференцию элементарных частиц или, скажем, дифракцию электронов на кристаллической решетке.
Как известно из теории поля, энергия волны квадратична по ее амплитуде, поэтому и вероятность обнаружить частицу в некотором состоянии равна квадрату модуля волновой функции. (Формально это легко понять: такая вероятность не должна зависеть от фазы волнового процесса в данной точке, поэтому может содержать волновую функцию только в комбинации ψψ*=|ψ|²)
Одно из отличий квантовой механики от обычной заключается в том, что вероятность обнаружить электрон в данном месте еще не полностью определяет его состояние. Для описания состояния электрона используется комплексная вероятность. Волновая функция и есть значение этой комплексной вероятности. Плотность вероятности обнаружения электрона в данной точке равна квадрату модуля комплексной вероятности. Комплексность приводит к эффекту интерференции: если комплексная вероятность электрона оказаться в точке A после прохождения через одну щель равна p, а комплексная вероятность электрона оказаться в точке A после прохождения через вторую щель равна -p, то если разрешить электрону проходить через обе щели эта вероятность станет равна 0 — то есть в этой точке электрон оказаться не может.
Практически интерференция наблюдалась для фотонов, электронов и некоторых атомов.
Соотношение неопределённостей
Другим необычным свойством электронного «облачка» является его неподатливость. Если мы со всех сторон начнём сдавливать это облачко, стремясь уменьшить его размеры, то оно станет оказывать всё большее и большее давление. И каковы бы ни были «тиски», сдавливающие электрон, рано или поздно электрон вырвется из них. Можно представить себе этот процесс, словно электрон начинает метаться по облачку, и чем меньше его размеры, тем сильнее он мечется, т. е. тем больше его кинетическая энергия.
Мы приходим к выводу: если мы пытаемся насильно избавить электрон от неопределённости в координате, то мы неизбежно увеличиваем неопределённость в импульсе электрона. Оказывается, произведение этих двух неопределённостей никогда не бывает меньше конкретной величины, постоянной Планка. Это соотношение называется соотношением неопределённостей. Аналогичные соотношения неопределённостей связывают и некоторые другие характеристики микрочастицы. Такие характеристики частицы называются дополнительными друг к другу.
Общее словесное описание этого закона таково:
улучшая наше знание о какой-либо одной характеристике частицы, мы ухудшаем наше знание о дополнительных её характеристиках.Важно понимать, что такое «квантовое дрожание» (обычно говорят нулевые колебания) локализованной микроскопической частицы неустранимо, и именно оно приводит к некоторым чисто квантовым явлениям. Например, даже при нулевой температуре, когда, согласно классической механике, никакого движения не должно быть, нулевые колебания по-прежнему остаются. Именно из-за этого жидкий гелий не затвердевает при нормальном давлении даже при нулевой температуре.
Наблюдение микрочастиц
Предыдущее свойство сразу же меняет понятие наблюдения за микрочастицей. Действительно, наблюдение — это процесс взаимодействия объекта с прибором, в результате которого на выходе прибора появляется какой-то определённый сигнал. Но всякое взаимодействие, а значит, и просто наблюдение, само по себе возмущает наблюдаемый объект, изменяет его свойства. И важно, что это возмущение нельзя сделать пренебрежимо малым.
Итак, при измерении какого-либо свойства частицы, и даже просто при её наблюдении, исходное состояние частицы, как правило, разрушается. Можно сказать, что какое-либо определённое квантовое состояние частицы — невероятно «хрупкая» вещь. Это важное свойство используется в квантовой телепортации и квантовой криптографии.
Квантование
Следующим важным свойством микрочастицы является тот факт, что она не всегда может находиться в произвольном состоянии. В частности, если она удерживается какими-либо силами в более-менее локализованном состоянии (то есть «не убегает на бесконечность»), то состояния частицы оказываются квантованными: т. е. частица может обладать только определённым дискретным набором энергий в поле связывающих сил. Это кардинально отличается от классической механики: в ней частица может обладать непрерывным набором энергий. С практической точки зрения, самым важным следствием этого является линейчатый (а не непрерывный) спектр излучения и поглощения атомов.
Математические основания квантовой механики
Математический аппарат квантовой механики — теория гильбертовых пространств и действующих в них операторов. Состояние изолированной квантовой системы — это вектор в гильбертовом пространстве, причем постулируется, что задание вектора состояния — это суть задание полной информации о квантовой системе. Наблюдаемым физическим величинам соответствуют определенные самосопряженные операторы в этом пространстве (См. Оператор физической величины), а результатам измерения соответствующей физической величины отвечают средние значения этих операторов по заданному вектору состояний. Эволюция квантовой системы со временем также определяется с помощью оператора эволюции, который, в свою очередь, выражается через гамильтониан системы.
В некоторых ситуациях, структура этого пространства и действующих в нём операторов выглядит существенно проще не в абстрактном виде, а в каком-либо представлении. Так, курсы квантовой механики стандартно начинаются с координатного представления, в котором вместо вектора состояния используется его разложение по базису координатного представления, т. е. волновая функция. Уравнение эволюции во времени в этом случае имеет вид дифференциального уравнения в частных производных и называется уравнением Шрёдингера.
Подчеркнём, что какой бы громоздкой ни казалась эта конструкция, она — единственная известная на сегодня теория, способная описать экспериментально наблюдаемое поведение микроскопических частиц.
Необычные явления, мысленные эксперименты и парадоксы квантовой механики
Разделы квантовой механики
В стандартных курсах квантовой механики изучаются следующие разделы
Комментарии
- Обычно квантовая механика формулируется для нерелятивистских систем. Попытка рассмотрения релятивистских частиц в рамках стандартного квантовомеханического подхода наталкивается на трудности, связанные с возможностью порождать новые частицы «из ничего». Эти трудности устраняются в квантовой теории поля, которая и является самосогласованной теорией релятивистских квантовых систем.
- Важным свойством квантовой механики является принцип соответствия: в рамках квантовой механики доказывается, что в пределе больших энергий (квазиклассический предел) и в случае, когда квантовая система взаимодействует с внешним миром (декогеренция), уравнения квантовой механики редуцируются в уравнения классической физики. Таким образом, квантовая механика не противоречит классической физике, а лишь дополняет её на микроскопических масштабах.
- Некоторые свойства квантовых систем кажутся нам непривычными (невозможность одновременно измерить координату и импульс, несуществование траектории частицы, вероятностное описание, дискретность наблюдаемых величин). Это вовсе не значит, что они неверны: это означает, что наша повседневная интуиция никогда не сталкивалась с таким поведением, т. е. в данном случае «здравый смысл» не может быть критерием, поскольку он годится только для макроскопических систем. Квантовая механика — самосогласованная математическая теория, предсказания которой согласуются с экспериментами. В настоящее время огромное число приборов, используемых в повседневной жизни, основываются на законах квантовой механики.
- Важно понимать, что квантовая механика не выводится из классической. Квантовая механика — это теория, построенная «с нуля», только при построении её требуется контролировать принцип соответствия. Грубо говоря, «квантование системы» — это не дополнительное видоизменение классических уравнений движения, а совершенно новый взгляд на систему. Впрочем, неоднократно делались попытки вывести квантовую механику из какой-то более глубокой, и, возможно, более простой, теории, т. е. понять, почему законы квантовой механики именно такие, а не другие. К этим попыткам можно отнести множество интерпретаций квантовой механики. Строго говоря, в настоящее время нет какой-либо одной общепринятой интерпретации квантовой механики. Консервативно настроенные физики предпочитают считать, что вопросы, связанные с интерпретацией квантовой механики, выходят за рамки физики.
Ссылки
См. также
mediaknowledge.ru
Квантовая механика — Традиция
Материал из свободной русской энциклопедии «Традиция»
Ква́нтовая меха́ника (другие названия: волновая механика, матричная механика) — раздел теоретической физики, описывающий квантовые системы и законы их движения.
Основными понятиями квантовой кинематики являются понятия наблюдаемой, состояния, среднего значения.
Основные уравнения квантовой динамики — уравнение Шрёдингера, уравнение фон Неймана, уравнение Линдблада, уравнение Гейзенберга.
Математический аппарат — теория операторов, теория вероятностей, функциональный анализ, операторные алгебры, теория групп.
На заседании Немецкого физического общества Макс Планк зачитал свою историческую статью “К теории распределения энергии излучения в нормальном спектре”, в которой он ввел универсальную постоянную h, изменившую ход развития теоретической физики. Именно дату этого события, 14 декабря 1900 года, часто считают днем рождения квантовой теории.
Квантовая гипотеза Макса Планка состояла в том, что любая энергия поглощается или испускается только дискретными порциями, которые состоят из целого числа квантов с энергией ε таких, что эта энергия пропорциональна частоте ν с коэффициентом пропорциональности, определённым по формуле: $$ \varepsilon = h \nu = \hbar \omega\, $$
где h — постоянная Планка.
В 1905 году для объяснения явлений фотоэффекта Альберт Эйнштейн, использовав квантовую гипотезу Планка, предположил, что свет состоит из квантов, которые впоследствии назвали фотонами.
Для объяснения структуры атома Нильс Бор в 1913 году предложил существование стационарных состояний электрона, в которых энергия может принимать лишь дискретные значения. Этот подход, развитый Арнольдом Зоммерфельдом и другими физиками, часто называют старой квантовой теорией (1900-1924). Отличительной чертой старой квантовой теории, является сочетание классической теории и противоречащими ей дополнительными предположениями.
В 1925-1926 годах была заложены основы последовательной квантовой теории, в виде квантовой механики, содержащей новые фундаментальные законы кинематики и динамики. Первая формулировка квантовой механики содержится в статье Вернера Гейзенберга, датированная 29 июля 1925 года. Эту дату можно считать днем рождения нерелятивистской квантовой механики. Отметим, что развитие и формирование основ квантовой механики продолжается до сих пор, и связано, например, с исследованиями открытых и диссипативных квантовых систем, квантовой информатикой, квантовым хаосом и др. Помимо квантовой механики, важнейшей частью квантовой теории является квантовая теория поля.
Математические основания квантовой механики[править]
Математический аппарат нерелятивистской квантовой механики строится на следующих положениях:[1]
- Чистые состояния системы описываются ненулевыми векторами \(~\psi\) комплексного сепарабельного гильбертова пространства \(~H\), причем векторы \(~\psi_1\) и \(~\psi_2\) описывают одно и то же состояние тогда и только тогда, когда \(~\psi_2=c\psi_1\), где \(~c\) — произвольное комплексное число. Каждой наблюдаемой однозначно сопоставляется линейный самосопряженный оператор.
- Наблюдаемые одновременно измеримы тогда и только тогда, когда соответствующие им самосопряженные операторы перестановочны (коммутируют).
- Эволюция чистого состояния гамильтоновой системы определяется уравнением Шредингера \(~i\hbar\frac{\partial \psi}{\partial t}= \hat{H}\psi , \) где \(~\hat{H}\) — гамильтониан.
- Каждому вектору \(~\psi\not=0\) из пространства \(~H\) отвечает некоторое чистое состояние системы, любой линейный самосопряженный оператор соответствует некоторой наблюдаемой.
Эти положения позволяют создать математический аппарат, пригодный для описания широкого спектра задач в квантовой механике гамильтоновых систем, находящихся в чистых состояниях. Дальнейшим развитием этого аппарата является уравнение Дирака, которое с хорошей точностью позволяет описать релятивистские эффекты. Для динамики открытых, негамильтоновых и диссипативных квантовых систем применяется уравнение Линдблада.
Необычные явления, мысленные эксперименты и парадоксы квантовой механики[править]
Разделы квантовой механики[править]
В стандартных курсах квантовой механики изучаются следующие разделы
- Обычно квантовая механика формулируется для нерелятивистских систем. Рассмотрение частиц с релятивистскими энергиями в рамках стандартного квантовомеханического подхода, предполагающего фиксированное число частиц в системе, наталкивается на трудности, т.к. при достаточно большой энергии частицы могут превращаться друг в друга. Эти трудности устраняются в квантовой теории поля, которая и является самосогласованной теорией релятивистских квантовых систем.
- Важным свойством квантовой механики является принцип соответствия: в рамках квантовой механики доказывается, что в пределе больших энергий (квазиклассический предел) и в случае, когда квантовая система взаимодействует с внешним миром (декогеренция), уравнения квантовой механики редуцируются в уравнения классической физики. Таким образом, квантовая механика не противоречит классической физике, а лишь дополняет её на микроскопических масштабах.
- Некоторые свойства квантовых систем кажутся нам непривычными (невозможность одновременно измерить координату и импульс, несуществование траектории частицы, вероятностное описание, дискретность наблюдаемых величин). Это вовсе не значит, что они неверны: это означает, что наша повседневная интуиция никогда не сталкивалась с таким поведением, т. е. в данном случае «здравый смысл» не может быть критерием, поскольку он годится только для макроскопических систем. Квантовая механика — самосогласованная математическая теория, предсказания которой согласуются с экспериментами. В настоящее время огромное число приборов, используемых в повседневной жизни, основываются на законах квантовой механики.
- Важно понимать, что квантовая механика не выводится из классической, хотя и может быть получена методами квантования из нее. Квантовая механика — это теория, построенная «с нуля», только при построении её требуется использовать принцип соответствия. Грубо говоря, «квантование системы» — это не дополнительное видоизменение классических уравнений движения, а совершенно новый взгляд на систему. Впрочем, неоднократно делались попытки вывести квантовую механику из какой-то более глубокой, и, возможно, более простой, теории, т. е. понять, почему законы квантовой механики именно такие, а не другие. К этим попыткам можно отнести множество интерпретаций квантовой механики. Строго говоря, в настоящее время нет какой-либо одной общепринятой интерпретации квантовой механики. Консервативно настроенные физики предпочитают считать, что вопросы, связанные с интерпретацией квантовой механики, выходят за рамки физики, смыкаясь с общими вопросами философии и методологии науки. Эту точку зрения выражает ироничный лозунг «Shut up and calculate!».
- Физический энциклопедический словарь. Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др. М.: Сов. Энциклопедия, 1984. — 944 с.
- Блохинцев Д. И. Основы квантовой механики. 5-ое изд. Наука, 1976. — 664 с.
- Боум А. Квантовая механика: основы и приложения. М.: Мир, 1990. — 720c.
- Джеммер М. Эволюция понятий квантовой механики. М.: Наука, 1985. — 384 с.
- Дирак П. Принципы квантовой механики. 2-ое изд. М.: Наука, 1979. — 480 с.
- Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 6-е, исправленное. — М.: Физматлит, 2004. — 800 с. — ISBN 5-9221-0530-2>
- Садбери А. Квантовая механика и физика элементарных частиц. М.: Мир, 1989. — 488 с.
- Фадеев Л. Д., Якубовский О.А. Лекции по квантовой механике для студентов-математиков. Ленинград, Изд-во ЛГУ, 1980. - 200 c.
- Фейнман Р., Лейтон Р., Сэндс М. Феймановские лекции по физике. Пер. с англ., Том. 8. Том 9., М., 1966—1967.
- ↑ Ф. А. Березин, М. А. Шубин. Уравнение Шрёдингера.. — М.: Изд-во Моск. ун-та, 1983.>
- Лорен Грэхэм «Естествознание, философия и науки о человеческом поведении в Советском Союзе, Глава X. Квантовая механика»
- Шрёдингер Э. Избранные труды по квантовой механике, — М..: Наука, 1976.
- Нейман И. Математические основы квантовой механики, — М.: Наука, 1964.
- Паули В. Общие принципы волновой механики, — М. : ГИТТЛ, 1947.
- Дирак П. А. М. Принципы квантовой механики (2-е издание), — М.: Наука, 1979.
- Фущич В. И., Никитин А. Г. Симметрия уравнений квантовой механики, — М.: Наука, 1990.
- Блохинцев Д. И. Принципиальные вопросы квантовой механики. М.: Наука, 1966.
- «Квантовая механика» — статья в Физической энциклопедии.
Электронные библиотеки[править]
При написании этой статьи использовались материалы страницы «Квантовая механика» Русской Википедии.
traditio.wiki
История квантовой механики - это... Что такое История квантовой механики?
История квантовой механики берёт своё начало 14 декабря 1900 г., когда Макс Планк предложил теоретический вывод о соотношении между температурой тела и испускаемым этим телом излучением, вывод, который долгое время ускользал от других ученых. Как и его предшественники, Планк предположил, что излучение испускают атомные осцилляторы, но при этом считал, что энергия осцилляторов (и, следовательно, испускаемого ими излучения) существует в виде небольших дискретных порций, которые Эйнштейн назвал квантами.
Энергия каждого кванта пропорциональна частоте излучения. Хотя выведенная Планком формула вызвала всеобщее восхищение, принятые им допущения оставались непонятными некоторое время, так как противоречили классической физике. В 1905 г. Альберт Эйнштейн воспользовался квантовой теорией для объяснения некоторых аспектов фотоэлектрического эффекта — испускания электронов поверхностью металла, на которую падает ультрафиолетовое излучение. Попутно Эйнштейн отметил кажущийся парадокс: свет, о котором на протяжении долгого времени было известно, что он распространяется как непрерывные волны, при поглощении и излучении проявляет дискретные свойства.Примерно через восемь лет Нильс Бор распространил квантовую теорию на атом и объяснил частоты волн, испускаемых атомами, возбужденными в пламени или в электрическом разряде. Эрнест Резерфорд показал, что масса атома почти целиком сосредоточена в центральном ядре, несущем положительный электрический заряд и окруженном на сравнительно больших расстояниях электронами, несущими отрицательный заряд, вследствие чего атом в целом электрически нейтрален.
Бор предположил, что электроны могут находиться только на определенных дискретных орбитах, соответствующих различным энергетическим уровням, и что «перескок» электрона с одной орбиты на другую, с меньшей энергией, сопровождается испусканием фотона, энергия которого равна разности энергий двух орбит. Частота, по теории Планка, пропорциональна энергии фотона. Таким образом, модель атома Бора установила связь между различными линиями спектров, характерными для испускающего излучение вещества, и атомной структурой. Несмотря на первоначальный успех, модель атома Бора вскоре потребовала модификаций, чтобы избавиться от расхождений между теорией и экспериментом. Кроме того, квантовая теория на той стадии ещё не давала систематической процедуры решения многих квантовых задач. Однако стало ясно, что классическая физика неспособна объяснить тот факт, что движущийся с ускорением электрон не падает на ядро, теряя энергию при излучении эл.-м. волн.
Новая существенная особенность квантовой теории проявилась в 1924 г., когда Луи де Бройль выдвинул радикальную гипотезу о волновом характере материи: если электромагнитные волны, например свет, иногда ведут себя как частицы (что показал Эйнштейн), то частицы, например электрон при определенных обстоятельствах, могут вести себя как волны. Таким образом в микромире стёрлась граница между классическими частицами и классическими волнами. В формулировке де Бройля частота, соответствующая частице, связана с её энергией, как в случае фотона (частицы света), но предложенное де Бройлем математическое выражение было эквивалентным соотношением между длиной волны, массой частицы и её скоростью (импульсом). Существование электронных волн было экспериментально доказано в 1927 г. Клинтоном Дж. Дэвиссоном и Лестером Х. Джермером в Соединенных Штатах и Джорджем Паджетом Томсоном в Англии.
В свою очередь это открытие привело к созданию в 1933 г. Эрнстом Руской электронного микроскопа.
Под впечатлением от комментариев Эйнштейна по поводу идей де Бройля Эрвин Шрёдингер предпринял попытку применить волновое описание электронов к построению последовательной квантовой теории, не связанной с неадекватной моделью атома Бора. В известном смысле он намеревался сблизить квантовую теорию с классической физикой, которая накопила немало примеров математического описания волн. Первая попытка, предпринятая им в 1925 г., закончилась неудачей. Скорости электронов в теории Шрёдингера были близки к скорости света, что требовало включения в неё специальной теории относительности Эйнштейна и учета предсказываемого ею значительного увеличения массы электрона при очень больших скоростях.
Одной из причин постигшей Шрёдингера неудачи было то, что он не учел наличия специфического свойства электрона, известного ныне под названием спина (вращение электрона вокруг собственной оси наподобие волчка, однако такое сравнение не совсем корректно), о котором в то время было мало известно. Следующую попытку Шрёдингер предпринял в 1926 г. Скорости электронов на этот раз были выбраны им настолько малыми, что необходимость в привлечении теории относительности отпадала сама собой. Вторая попытка увенчалась выводом волнового уравнения Шрёдингера, дающего математическое описание материи в терминах волновой функции. Шрёдингер назвал свою теорию волновой механикой. Решения волнового уравнения находились в согласии с экспериментальными наблюдениями и оказали глубокое влияние на последующее развитие квантовой теории. В настоящее время волновая функция лежит в основе квантовомеханического описания микросистем, подобно уравнениям Гамильтона в классической механике.
Незадолго до того Вернер Гейзенберг, Макс Борн и Паскуаль Иордан опубликовали другой вариант квантовой теории, получивший название матричной механики, которая описывала квантовые явления с помощью таблиц наблюдаемых величин. Эти таблицы представляют собой определенным образом упорядоченные математические множества, называемые матрицами, над которыми по известным правилам можно производить различные математические операции. Матричная механика также позволяла достичь согласия с наблюдаемыми экспериментальными данными, но в отличие от волновой механики не содержала никаких конкретных ссылок на пространственные координаты или время. Гейзенберг особенно настаивал на отказе от каких-либо простых наглядных представлений или моделей в пользу только таких свойств, которые могли быть определены из эксперимента, так как по его соображениям микромир имеет принципиально иное устройство, чем макромир в виду особой роли постоянной Планка, несущественной в мире больших величин.
Шрёдингер показал, что волновая механика и матричная механика математически эквивалентны. Известные ныне под общим названием квантовой механики, эти две теории дали долгожданную общую основу описания квантовых явлений. Многие физики отдавали предпочтение волновой механике, поскольку её математический аппарат был им более знаком, а её понятия казались более «физическими»; операции же над матрицами — более громоздкими.
Вскоре после того, как Гейзенберг и Шрёдингер разработали квантовую механику, Поль Дирак предложил более общую теорию, в которой элементы специальной теории относительности Эйнштейна сочетались с волновым уравнением. Уравнение Дирака применимо к частицам, движущимся с произвольными скоростями. Спин и магнитные свойства электрона следовали из теории Дирака без каких бы то ни было дополнительных предположений. Кроме того, теория Дирака предсказывала существование античастиц, таких, как позитрон и антипротон, — двойников частиц с противоположными по знаку электрическими зарядами.
См. также
Литература
- Гейзенберг В., Шредингер Э., Дирак П. А. М. Современная квантовая механика. Три нобелевских доклада. Л.-М.: Гостехиздат, 1934.
- Джеммер М. Эволюция понятий квантовой механики. М.: Наука, 1985. — 384с.
- Клайн Б. В поисках. Физики и квантовая теория. Пер с англ. М.: Атомиздат, 1971. — 288с.
- Уиттекер Э. История теории эфира и электричества. Современные теории 1900—1926. Пер с англ. Москва, Ижевск: Институт компьютерных исследований, 2004. — 464с. (Главы 3-4, 6, 8-9)
- Хунд Ф. История квантовой теории. Пер с нем. Киев: Наукова думка, 1980. — 244с.
Ссылки
dic.academic.ru