Случайный кубик Рубика • Николай Авилов • Научно-популярные задачи на «Элементах» • Математика
В ходе решения мы попутно выяснили, сколькими способами можно раскрасить куб в шесть данных цветов, если разные грани должны быть раскрашены разными красками (различными считаются те раскраски, которые не совмещаются при поворотах куба). Это сама по себе отдельная задача, которую сейчас обычно решают на кружках или в матклассах при знакомстве с основами комбинаторики.
Любопытно, что у нее есть своя история: эту задачу для первой Московской математической олимпиады предложил И. М. Гельфанд — один из крупнейших математиков XX века. Простая, на первый взгляд, задача оказалась весьма трудной для участников олимпиады: ее не решил ни один участник. Видимо, никому не удалось организовать системный перебор вариантов. В ответе лаконично указано, что существует 30 способов. По словам математика В. М. Тихомирова это «задача на все времена», поскольку обладает особой прелестью, в ней запрятано богатое содержание и предлагать ее можно кому угодно.
На рис. 2 наглядно показан процесс получения всех 30 способов раскраски граней куба и приведено дерево вариантов раскраски Т-образных разверток куба.
Перебор организован следующим образом. Если одну из граней покрасить, например, красным цветом, то противоположную ей грань можно покрасить одним из пяти оставшихся цветов. В центре рисунка изображены пять таких разверток. В каждом из этих случаев оставшиеся четыре цвета можно распределить шестью (\(1\cdot3\cdot2\cdot1\)) различными способами: третий цвет выбирается однозначно, четвертый цвет выбирается тремя различными способами, пятый цвет выбирается двумя различными способами, шестой цвет определяется однозначно. Таким образом, всего существует \(5\cdot6=30\) различных раскрасок куба. Развертки всех этих кубов расположены на периметре дерева вариантов, имеющего форму правильного пятиугольника.
У основной задачи есть интересный частный случай, в котором не используется переклеивание наклеек. Любители кубика Рубика знают, что нередко происходит непредвиденное: он рассыпается на мелкие составляющие (даже если не пытаться его ломать или разбирать). Из них можно собрать новый кубик 3×3×3, но при этом использовать детали в случайном порядке. Получившийся в итоге кубик будет на вид неотличим от настоящего, разница лишь в том, что его не всегда можно собрать. Возникает все тот же вопрос: какова вероятность собрать кубик Рубика в таком случае?
Из них можно собрать новый кубик 3×3×3, но при этом использовать детали в случайном порядке. Получившийся в итоге кубик будет на вид неотличим от настоящего, разница лишь в том, что его не всегда можно собрать. Возникает все тот же вопрос: какова вероятность собрать кубик Рубика в таком случае?
При решении этого варианта задачи надо помнить, что на поверхность кубика Рубика «выходят» единичные кубики трех видов (рис. 4):
а) Центральные, с одной цветной наклейкой (их 6 штук). При вращении граней эти кубики всегда остаются на месте, потому что они прикручены винтами к крестовине кубика Рубика.
б) Реберные, с двумя цветными наклейками (их 12 штук). При вращении граней каждый реберный кубик занимает место другого реберного кубика.
в) Угловые, с тремя цветными наклейками (их 8 штук). При вращении граней каждый угловой кубик занимает место другого углового кубика.
Посчитаем число всевозможных различных вариантов сборки этих деталей (единичных кубиков) в форме куба 3×3×3.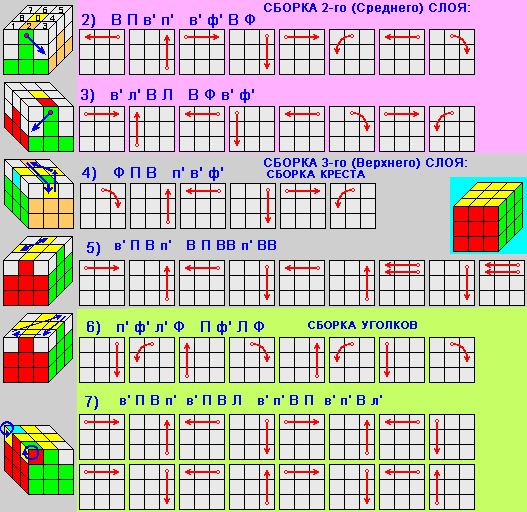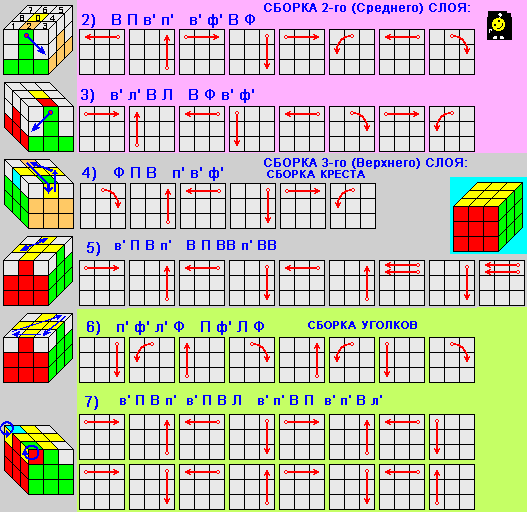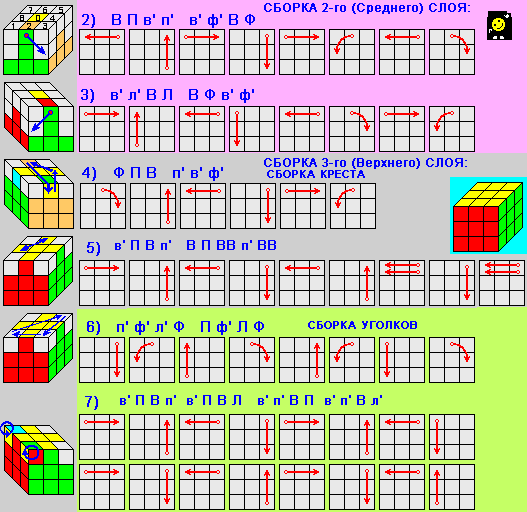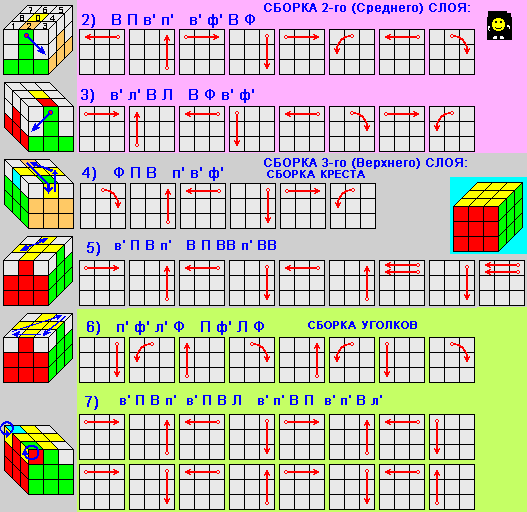 {11}}{2}\).
{11}}{2}\).
Тем самым вероятность сборки кубика Рубика в этом случае получается такой:
\[p=\dfrac{K}{n}=\dfrac1{12}.\]
Гораздо больше, чем в исходной задаче!
Специалисты по скоростной сборке кубика Рубика (спидкуберы) хорошо знают, как устроены «невозможные» состояния кубика, ведь именно у них нередко рассыпаются кубики во время сборки. Каждое из таких состояний при помощи поворота граней кубика можно привести к «базовому» состоянию с минимальным числом неправильных квадратиков. Все они приведены на рис. 7 (обозначены номерами 2–12).
Разберемся, как устроена эта картинка. Вверху расположен собранный кубик, как одна из возможных ситуаций. Во втором ряду расположены кубики с одной проблемой, из-за которой кубик Рубика не решается. В третьем ряду изображены кубики, в которых совмещены проблемы из кубиков второго ряда. Например, проблемная ситуация №7 получается совмещением простых проблемных ситуаций №2 и №4. Обратите внимание, что проблемные ситуации №2 и №3 несовместимы.
Одним из популярных методов скоростной сборки кубика Рубика является так называемый метод Джессики Фридрих, в котором весь процесс завершается сбором желтой грани и наведением порядка во всем слое с желтой гранью. По расположению трех последних кубиков этого слоя можно рассчитать вероятность сборки рассыпавшегося кубика Рубика совсем просто. Приведу рассуждение спидкубера Ивана Макачёва, участника чемпионата мира по скоростной сборке кубика Рубика. Угловой кубик правильно «садится» в свое гнездо с вероятностью 1/3 (рис. 8, верхний ряд). Реберный кубик правильно «садится» с вероятностью 1/2 (рис. 8, средний ряд). Не вдаваясь в подробности спидкуберской терминологии, скажем, что паритет по перестановке элементов возможен с вероятностью 1/2, поэтому он не попадается тоже с вероятностью 1/2. В итоге получается, что рассыпавшийся кубик, элементы которого случайным образом собраны в кубик 3×3×3, решается с вероятностью \(\frac13\cdot\frac12\cdot\frac12=\frac1{12}\).
Можно обсудить еще один вероятностный вопрос: какова вероятность случайно собрать кубик Рубика у необученного человека, если он будет крутить-вертеть кубик, не повторяя позиций?
Ответ на этот вопрос поможет дать число \(K=8!\cdot3^7\cdot\frac{12!}{2}\cdot2^{11} = 43\,252\,003\,274\,489\,856\,000\) всех достижимых различных состояний кубика Рубика 3×3×3. {10}\) лет, чтобы перепробовать все позиции!
{10}\) лет, чтобы перепробовать все позиции!
Y-метод — действительно простой способ собрать кубик Рубика / Хабр
Введение
В статье рассматривается «Y-метод» сборки кубика Рубика — его легко понять и запомнить. Он основан всего на одной последовательности, которая называется «Y-движение». Поняв этот алгоритм, вы навряд ли забудете как собрать кубик самостоятельно.
Если попытаться нагуглить инструкцию по сборке кубика Рубика, то найдётся много вариантов с описанием «простой сборки», в том числе на википедии. Которые, в целом, действительно достаточно простые к пониманию, но обладают существенным недостатком. Для того, чтобы собрать кубик, нужно знать порядка пяти или более нетривиальных последовательностей (алгоритмов) для перестановки отдельных кубиков, для сборки кубика Рубика по слоям. В связи с чем запомнить и воспроизвести самостоятельно эти инструкции затруднительно. Недавно я случайно наткнулся на упоминание алгоритма «The Ultimate Solution to Rubik’s Cube», о котором утверждалось, что его легко запомнить и понять, и в нём используются всего две последовательности. А когда стал выяснять подробнее, то нашёл также и другой алгоритм — «Y-метод», тоже простой и использующий всего одну последовательность.
А когда стал выяснять подробнее, то нашёл также и другой алгоритм — «Y-метод», тоже простой и использующий всего одну последовательность.
К сожалению, описания данного алгоритма на русском я не нашёл, поэтому я решил восполнить этот пробел. Также мне кажется, что главное в этом методе — понимание того как он работает. Поэтому тут я не предлагаю готовых наборов движений для конкретных ситуаций, а вместо этого я постарался подробнее описать что происходит.
Картинки в данной статье сгенерированы с помощью инструмента на сайте ruwix.com. Ссылки на картинках откроют этот инструмент с параметрами, соответствующими картинке. Это либо описываемое состояние кубика и вы сможете его повертеть мышкой, или, в некоторых случаях, там заданы описываемые движения, которые можно «проиграть» туда-обратно.
Y-движение
Основу данного алгоритма составляет Y-движение. И довольно важная составляющая алгоритма — это разобраться в механике этого движения.
Данная последовательность поворотов так называется из-за того, что кубики, которые она затрагивает, выглядят как буква «Y», составленная тремя рёбрами, выходящими из одного угла кубика.
Y-движение довольно простое и состоит из четырёх поворотов двух смежных граней, например правой и передней. В распространённой нотаци поворотов для кубика Рубика это выглядит так: R’ F R F’. Что можно описать следующим образом:
- правая грань против часовой стрелки на четверть оборота
- передняя грань по часовой стрелке на четверть оборота
- правая грань по часовой стрелке на четверть оборота
- передняя грань против часовой стрелки на четверть оборота
То есть грани сначала по очереди поворачиваются «на себя», а потом в обратном порядке «от себя».
Назовём этот вариант «правым Y-движением» (т.к. поворачивается сначала грань справа). В этом случае меняется положение кубиков на ребре, общем у данных граней и на верхних рёбрах. Если начинать повороты с передней грани, то будут затронуты те же самые кубики, такой вариант мы будем называть «левым Y-движением» (т.к. поворачивается сначала грань слева).
Если начинать повороты с передней грани, то будут затронуты те же самые кубики, такой вариант мы будем называть «левым Y-движением» (т.к. поворачивается сначала грань слева).
Также можно начинать с поворотов «от себя» — это будет то же самое, если бы мы перевернули кубик и начинали с поворотов «на себя», поэтому назовём такие варианты «правым и левым перевёрнутым Y-движением». При перевёрнутых Y-движениях будет также затронуто смежное ребро, а также уже не верхние, а нижние рёбра, соседние с ним.
Принципиальной разницы во всех этих движениях, конечно же, нет. Такое разнообразие нужно исключительно для удобства.
Перечислим некоторые свойства Y-движений:
- Правое и левое Y-движения обратны друг другу, т.е. последовательность правого и левого или левого и правого движений не изменят состояния кубика.
- Одно Y-движение приводит к тому, что меняются местами в паре два угловых кубика на смежной грани и два других угловых кубика. А три кубика находящиеся посередине рёбер (рёберные) перемещаются по кругу.

- Как можно догадаться, после двух движений угловые кубики возвращаются на свои места. Но при этом они оказываются повёрнутыми.
- И если выполнить три раза по два движения, то кубики повернутся три раза и в результате вернутся в исходное состояние.
- Рёберные кубики возвращаются в исходное состояние после цикла из трёх движений.
- Таким образом, если выполнить Y-движение шесть раз подряд, то состояние кубика вернётся в изначальное.
- После одного Y-движения рёберные кубики перемещаются в направлении первого поворота, при этом два кубика как бы поворачиваются вдоль соответствующих граней (вокруг их оси), а третий также поворачивается, но при этом переворачивается. Переворачивается тот кубик, который перемещается между верхними рёбрами, в случае обычного (не перевёрнутого) Y-движения. При работе с рёберными кубиками Y-движение вдоль одних и тех же рёбер можно производить повернув кубик в разных направлениях, тем самым добиваясь переворота нужного нам кубика.

Последовательность сборки кубика
Сначала собираются два нижних слоя кубика за исключением одного вертикального ребра, проходящего через эти слои. Это место мы оставляем себе как пространство для манёвра. Нижний крест и нижние угловые кубики собираются довольно просто, но если есть затруднения, то не так сложно приспособить Y-движение для этого или посмотреть одну из инструкций для простой послойной сборки кубика.
Далее нужно собрать средние кубики на вертикальных рёбрах (рёберные). Для этого нужно повернуть верхнюю грань с нужным кубиком, чтобы он оказался на одной из соседних с целевым ребром граней. А также временно (не забываем потом вернуть на место) повернуть нижнюю грань, чтобы на месте целевого ребра оказался кубик, который мы специально оставили несобранным. Теперь можно воспользоваться Y-движением, чтобы переместить кубик с верхней грани на нужное нам место. Y-движение нужно делать такое, чтобы этот рёберный кубик повернулся в нужном направлении в сторону ребра и если нужно, то перевернулся.
Если нужный кубик не находится на верхней грани, то нужно его предварительно, также Y-движением, «освободить» оттуда, не забывая опять же подставить несобранный угол на нижней грани.
Пока что мы собрали два нижних слоя без одного ребра. Далее нам нужно будет собрать два рёберных кубика на верхних рёбрах, которые не граничат с тем, что мы специально не собираем. После этого из рёберных кубиков останется только три несобранных, на рёбрах, которые формируют букву «Y»: вертикальное, которое мы не собирали, и два верхних ребра, соседних с ним.
И, конечно же, мы собираем их с помощью одного или нескольких Y-движений, переворачивая и ставя на нужные места. Тут только нужно учесть один момент с количеством перестановок, который описан чуть ниже.
При сборке последних пяти рёберных кубиков нам может понадобиться развернуть эту букву «Y», чтобы сделать Y-движение в другом направлении (поворачивая другие грани вдоль этих рёбер), таким образом добиваясь перемещения нужных нам кубиков на другие места с переворотом или без него.
К этому моменту у нас будет почти собранный кубик, в котором не собраны только угловые кубики на верхней грани и на вертикальном ребре, которое мы не собирали. Описанными ниже методами сначала переставляем углы друг с другом, чтобы они оказались на своих местах, возможно неправильно ориентированные. А потом разворачиваем их.
Ура, наш кубик собран!
Считаем перестановки
На что же нужно обратить внимание когда мы собираем пять последних рёберных кубиков. Когда их останется только три, то чтобы у всё получилось с перестановкой их в пределах буквы «Y», нужно чтобы либо они все находились на своих местах (возможно перевёрнутые) или же все были не на своих местах. Это связано с тем, что Y-движение переставляет три рёберных кубика одновременно. Если рассмотреть это с точки зрения попарных обменов кубиков местами на соседних рёбрах, то происходит два обмена (перестановки). Теперь должно быть понятно почему в случае, когда у нас ровно два кубика не на своих местах, то мы не сможем их собрать. Т.к. нам нужно совершить одну перестановку, а с помощью Y-движений мы можем сделать только чётное число перестановок.
Т.к. нам нужно совершить одну перестановку, а с помощью Y-движений мы можем сделать только чётное число перестановок.
Что же делать в таком случае? Обратим внимание, что если повернуть грань кубика, то мы поменяем местами одновременно четыре рёберных кубика, что будет эквивалентно трём перестановкам, т.е. нечётному числу, что нам и нужно. Из этого следует, что верхняя грань должна быть правильно ориентирована для того, чтобы мы могли собрать последние три рёберных кубика. Если так вышло, что последние три рёберных кубика требуют одной перестановки, то это значит, что нужно переставить на соседние места два рёберных кубика, уже собранные на верхней грани.
Кроме того, мы можем заранее, до сборки первых двух кубиков из этой пятёрки, подсчитать число перестановок, которые потребуются, чтобы поставить все пять рёберных кубиков на свои места. Если это число чётное, то верхняя грань ориентирована правильно. А если нечётное, то её нужно повернуть один раз в любую сторону. Таким образом, мы сразу сможем поставить те два кубика на нужные места.
Работа с угловыми кубиками
На последнем этапе сборки нам нужно переставлять угловые кубики местами и поворачивать их. Для этого воспользуемся перечисленными ранее свойствами Y-движения в отношении угловых кубиков. Т.к. удобнее работать с угловыми кубиками, расположенными на верхней грани, то для этого нам больше подойдёт перевёрнутое Y-движение (начинается с поворота «от себя»). В этом разделе будет использоваться именно эти варианты, без дополнительного уточнения. Обратим сразу внимание, что это движение меняет состояние только одного кубика на верхней грани — это угловой кубик на «смежном ребре».
Для перестановки угловых кубиков заметим, что одиночное Y-движение (как левое, так и правое) меняет местами пару угловых кубиков на «смежном ребре», а также что последовательное применение левого и правого Y-движения (или правого и левого) возвращает весь кубик в исходное состояние. Давайте подумаем, что произойдёт, если между этими движениями мы повернём верхнюю грань. Как мы уже обратили внимание, на верхней грани меняется только один угловой кубик, который переставляется с парным кубиком на ребре. В таком случае у нас произойдёт два обмена угловыми кубиками на ребре, но каждый раз сверху будет подставлен разный угол, а все остальные кубики останутся как были (конечно, нужно ещё не забыть повернуть верхнюю грань в исходное состояние). Таким образом, мы осуществили обмен местами трёх угловых кубиков — одного с нижней грани и двух с верхней.
Как мы уже обратили внимание, на верхней грани меняется только один угловой кубик, который переставляется с парным кубиком на ребре. В таком случае у нас произойдёт два обмена угловыми кубиками на ребре, но каждый раз сверху будет подставлен разный угол, а все остальные кубики останутся как были (конечно, нужно ещё не забыть повернуть верхнюю грань в исходное состояние). Таким образом, мы осуществили обмен местами трёх угловых кубиков — одного с нижней грани и двух с верхней.
Теперь разберёмся с поворотом кубиков. Для этого воспользуемся похожим трюком. Будем делать два последовательных Y-движения в одном направлении. В результате этого угловые кубики остаются на месте, но меняют свою ориентацию. Тут нас интересуют два варианта комбинации движений: три двойных движения в одном направлении (левые или правые) или двойное движение в одном направлении и двойное движение в обратном направлении. В каждом из этих вариантов весь кубик возвращается в исходное состояние. И мы опять будем между двойными движениями подставлять очередной нужный нам угол на место верхнего угла «смежного ребра». Таким образом мы можем повернуть либо три угловых кубика на одной грани в одном направлении, либо два угловых кубика на одной грани в разных направлениях, не меняя состояния остальных кубиков. Обратим внимание, что после двойного движения верхний кубик смежного ребра поворачивается в том же направлении, в котором осуществляется первое Y-движение.
Таким образом мы можем повернуть либо три угловых кубика на одной грани в одном направлении, либо два угловых кубика на одной грани в разных направлениях, не меняя состояния остальных кубиков. Обратим внимание, что после двойного движения верхний кубик смежного ребра поворачивается в том же направлении, в котором осуществляется первое Y-движение.
Заключение
Не знаю как будет в вашем случае, но для меня плюс данного алгоритма не только в том, что его легко запомнить и не нужно зубрить инструкцию по сборке. Но также и в том, что теперь, собирая кубик, я собираю его сам, понимая что происходит, вместо почти механического следования инструкции, а это намного приятнее. Чего и вам желаю!
И. Константинов — Сборка кубика Рубика читать онлайн
СОБРАТЬ КУБИК? ЭТО НЕСЛОЖНО!
Головоломка «Кубик Рубика» («Волшебный кубик», «Венгерский кубик» и даже просто «Рубик») привлекла внимание, как говорится, «всех групп населения» и получила широчайшее распространение, О достоинствах этой замечательной головоломки, в которую с удовольствием стали играть и школьники и академики, находя в ней достоинства, сообразные уровню учености, образования и склонности к исследованиям, мы уже писали (см. «Наука и жизнь» № 3, 1981 г. и № 2, 1982 г.) и даже приводили методы решения.
«Наука и жизнь» № 3, 1981 г. и № 2, 1982 г.) и даже приводили методы решения.
Но читательская почта заставляет нас вновь вернуться к опубликованным материалам. И не только к задачам-пасьянсам на кубике, ответов на которые мы еще не давали, но и к методу сборки.
Мы не будем касаться ни математической теории групп, ни квантовой физики, для определенных разделов которых кубик Рубика служит оригинальным наглядным пособием. Попытаемся рассказать о том, как привести в порядок перепутанный кубик, и тем читателям и читательницам, которые весьма и весьма далеки от математики и от физики вообще. Возможно, будет и некоторая польза в самообразовании, в расширении кругозора: ведь здесь придется познакомиться и с математическими символами и с чертежами, хотя и очень простыми. Надеемся, что желание собрать кубик пересилит их нелюбовь к точным наукам
Поэтому мы заранее просим прощения у более подготовленных читателей за «излишние» подробности в описании: уж очень много пришло писем с просьбой «рассказать так. чтобы было понятно всем, всем…».
чтобы было понятно всем, всем…».
Прежде всего напомним принятую в журнале систему обозначений. Грани куба обозначаются буквами Ф, Т, П, Л, В, Н — начальными буквами слов фасад, тыл, правая, левая, верх, низ. Какую грань куба посчитать фасадной — синюю, зеленую и т. п. — зависит от вас и от получившейся ситуации. В процессе сборки вам придется несколько раз принимать за фасадную ту или иную грань, удобную для данного случая. Центральные кубики определяют цвет грани, то есть можно сказать, что даже в полностью перепутанном кубике центральные кубики уже подобраны и к каждому из них остается присоединить по 8 кубиков того же цвета. Центральные кубики обозначаются одной буквой: ф, п. л, в, т, н.
Реберные кубики (их 12 штук) принадлежат двум граням и обозначаются двумя буквами, например фп, пв, фн и т. д.
Угловые кубики — тремя буквами по наименованию граней, например, фпв, флн и т. д.
Прописными буквами Ф, Т, П, Л, В, Н обозначаются элементарные операции поворота соответствующей грани (слоя, ломтика) куба иа 90° по часовой стрелке. Обозначения Ф’, Т’, П’, Л’, В’, Н’ соответствуют повороту граней на 90° против часовой стрелки. Обозначения Ф², П² и т. д. говорят о двойном повороте соответствующей грани (Ф²= ФФ).
Обозначения Ф’, Т’, П’, Л’, В’, Н’ соответствуют повороту граней на 90° против часовой стрелки. Обозначения Ф², П² и т. д. говорят о двойном повороте соответствующей грани (Ф²= ФФ).
Буквой С обозначают поворот среднего слоя. Подстрочный индекс показывает, со стороны какой грани следует проделать этот поворот. Например Сп— со стороны правой грани, Сн—со стороны нижней, С’л— со стороны левой, против часовой стрелки и т. д. Буква О— поворот (оборот) всего куба. Оф — со стороны фасадной грани по часовой стрелке и т. д.
Запись процесса (Ф’ П’) Н² (ПФ) означает: повернуть фасадную грань против часовой стрелки на 90°, то же — правую грань, повернуть нижнюю грань дважды (то есть на 180°), повернуть правую грань на 90° по часовой стрелке, повернуть фасадную грань.
Наряду с буквенной записью процессов применяется и матричная форма записи, где элементарные операции изображаются рисунком фасадной грани с соответствующими стрелками, обозначающими направления поворотов соответствующей грани (см.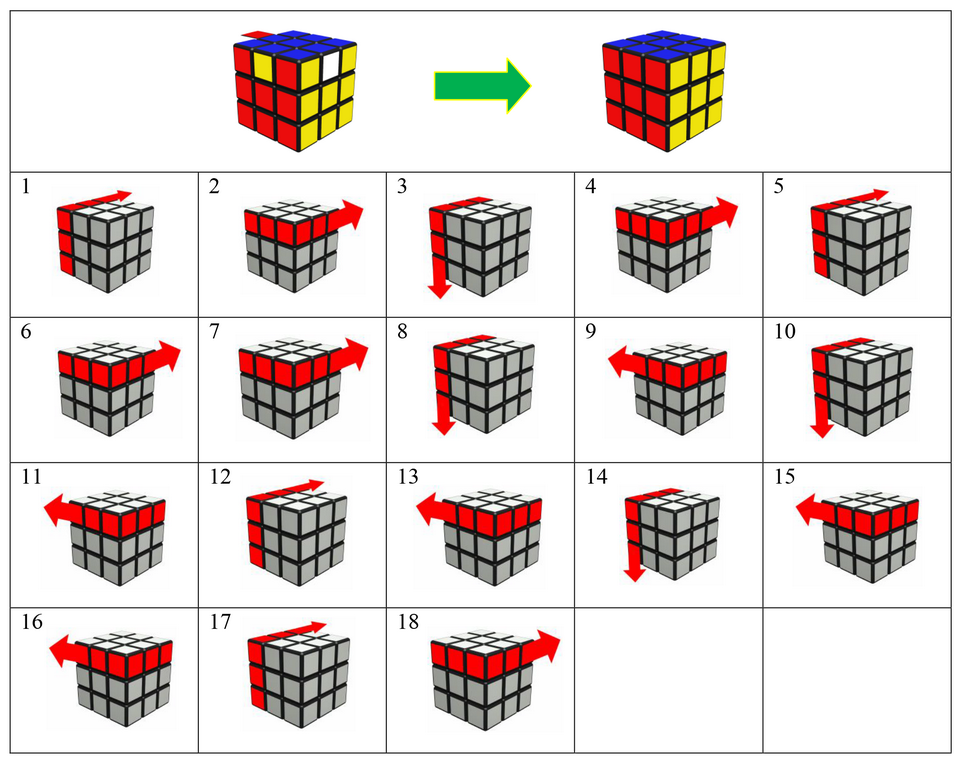 рис.).
рис.).
Теперь перейдем собственно к сборке куба. Есть несколько разных систем, но нам больше всего нравится послойная сборка, когда собирают сначала один слой, затем второй и, наконец, третий. Всего получается семь этапов.
Первый этап
Крест верхней грани. Нужный кубик опускается вниз поворотом соответствующей боковой грани (П, Т, Л) и выводится на фасадную грань операцией Н, Н’ или Н². Заканчивается операция выведения зеркальным поворотом (обратным) той же боковой грани, восстанавливающим первоначальное положение затронутого реберного кубика верхнего слоя После этого проводится операция а) или б) первого этана. В случае а) кубик вышел на фасадную грань так, что цвет его передней грани совпадает с цветом фасада. В случае б) кубик надо не только переместить наверх, но и развернуть его, чтобы он был правильно сориентирован, став на свое место. На рисунках точками отмечено место, на которое должен встать нужный кубик, выведенный предварительно на фасад нижней грани. Результат: собран крест верхней грани.
Результат: собран крест верхней грани.
Второй этап
Отыскивается нужный угловой кубик (имеющий цвета граней Ф, В, Л) и тем же приемом, который описан для первого этапа, выводится в левый угол избранной вами фасадной грани. Здесь могут быть три случая ориентации этого кубика. Сравните свой случай с рисунком и примените одну из операций второго этапа а), б) или в). Точками отмечено место, на которое должен стать нужный вам кубик. Отыщите на кубе остальные три угловых кубика и повторите описанный прием для перемещения их на свои места верхней грани. Результат: верхний слой подобран. Первые два этапа почти ни у кого не вызывают затруднений: довольно легко можно следить за своими действиями, так как все внимание обращено на один слон, а что делается в двух оставшихся — совсем неважно.
Третий этап
Пояс. Процессы, приведенные на рисунках, легко запоминаются, если применить мнемоническое правило. Для перемещения кубика, выведенного на фасадную грань, налево начало процесса совпадает с начальными буквами НЛ — НаЛево, а направо с начальными буквами НаП’раво. И здесь, как вы видите, нужный кубик отыскивается и сначала выводится вниз на фасадную грань. Если он внизу — простым поворотом нижней грани до совпадения с цветом фасада, а если он в среднем поясе, то его нужно сначала опустить вниз любой из операций а) или б), а потом совместить по цвету с цветом фасадной грани и проделать операцию третьего этапа а) или б). Результат: собрано два слоя.
И здесь, как вы видите, нужный кубик отыскивается и сначала выводится вниз на фасадную грань. Если он внизу — простым поворотом нижней грани до совпадения с цветом фасада, а если он в среднем поясе, то его нужно сначала опустить вниз любой из операций а) или б), а потом совместить по цвету с цветом фасадной грани и проделать операцию третьего этапа а) или б). Результат: собрано два слоя.
Четвертый этап
Крест нижней грани. К цели приводят операции, перемещающие бортовые кубики одной грани, не нарушающие в конечном счете порядка в собранных слоях. Один из процессов, позволяющий подобрать все бортовые кубики грани, дан на рисунке. Там же показано и что происходит при этом с другими кубиками грани Повторяя процесс, выбрав другую фасадную грань, можно поставить на место все четыре кубика. Результат: реберные кубики стоят на своих местах, но, как правило, два из них неверно ориентированы.
Читать дальше
Мегаминкс, пираминкс, додекаэдр… :: Петрозаводский государственный университет
Дмитрий Игоревич Балашов, директор Физико-технического института ПетрГУ, рассказал пресс-службе, когда у него появился первый кубик Рубика, сколько их сейчас в его коллекции, и помогает ли кубик Рубика в решении жизненных проблем.
– Игорь Дмитриевич, когда у Вас впервые появился кубик Рубика? И какие были первые впечатления?
– Самый первый Кубик Рубика у меня появился в далеком 1985 году. В то время я учился во 2-м классе школы. Отец был в командировке в Москве и оттуда привез замечательную игрушку – кубик Рубика. В то время даже в Москве купить данную головоломку было непросто, даже отстояв огромную очередь в магазине. Это был классический кубик Рубика 3х3х3 венгерского производства. Этот кубик находится в моей коллекции и сегодня. Единственное, изначальные цветные наклейки, которые были сделаны из самоклеящейся цветной пленки, на гранях куба сильно стерлись, и я приклеил другие, пластмассовые, наклейки. Но всё остальное в этом кубике осталось неизменным. Я с удовольствием им пользуюсь. Особенно радует его неповторимый, ни с чем не сравнимый хруст пластмассы при вращении граней.
Моё разочарование кубиком Рубика не заставило долго ждать. В то время я понял, что разобрать кубик легко, но чтобы его собрать – нужно приложить колоссальные усилия работы мозга. Мои родители тоже не смогли собрать кубик. Но, к счастью, мой отец вспомнил, что в одном из номеров журнала «Наука и жизнь» (а моя семья тогда выписывала этот журнал) была статья, посвященная алгоритму сборки кубика. Именно благодаря этому с немалыми усилиями отец первый раз в жизни собрал кубик Рубика. После него за это дело взялся я. Работа была нелегкой, но через какое-то время и мне это удалось. После этого кубик стал любимой игрушкой на несколько лет вперед.
Мои родители тоже не смогли собрать кубик. Но, к счастью, мой отец вспомнил, что в одном из номеров журнала «Наука и жизнь» (а моя семья тогда выписывала этот журнал) была статья, посвященная алгоритму сборки кубика. Именно благодаря этому с немалыми усилиями отец первый раз в жизни собрал кубик Рубика. После него за это дело взялся я. Работа была нелегкой, но через какое-то время и мне это удалось. После этого кубик стал любимой игрушкой на несколько лет вперед.
– И пришла идея начать собирать коллекцию?
– Идея начать собирать кубики пришла примерно в 2008 году. Именно тогда я заказал первые кубики Рубика из интернет-магазина Китая. Это были кубы размера 4х4х4 и 5х5х5. Именно тогда я понял, что классический куб 3х3х3 в плане сборки становится все менее интересным. После этого также в китайском интернет-магазине я приобрел нечто большее, чем простой куб – это был мегаминкс. Он представляет собой додекаэдр (десятигранник), грани которого имеют свою цветовую окраску. Несмотря на такую пугающую форму и количество граней, собирать его оказалось не сложнее классического кубика Рубика… только дольше. Затем появились и другие головоломки.
Несмотря на такую пугающую форму и количество граней, собирать его оказалось не сложнее классического кубика Рубика… только дольше. Затем появились и другие головоломки.
– А сколько сейчас в коллекции кубиков?
– Сейчас моя коллекция насчитывает более 40 различных головоломок по типу кубика Рубика. Это довольно скромная цифра, но практически каждый год коллекция пополняется новыми интересными головоломками. Также хочу отметить, что в коллекции есть и самый маленький кубик Рубика (действующая модель), размеры ребер которого не превышают 1 сантиметра.
– Это все кубики Рубика? Или какие-то головоломки?
– Это не только кубики, хотя кубиков здесь большинство. Это и другие головоломки, например, упомянутый уже мегаминкс и пираминкс-крислалл имеют формы додекаэдров. Также есть и классические пирамидки с различным количеством разбиений граней на отдельные элементы. Также есть октаэдр и другие головоломки.
Более того, есть такие кубы, которые сохраняют кубическую форму только в собранном виде. Но когда они разобраны, то их форма существенно изменяется, и на первый взгляд кажется, что собрать такую головоломку практически невозможно. Но если постараться, то, конечно же, всё получится.
Но когда они разобраны, то их форма существенно изменяется, и на первый взгляд кажется, что собрать такую головоломку практически невозможно. Но если постараться, то, конечно же, всё получится.
Также в последнее время часто встречаются кубики Рубика не просто цветные, а с различными изображениями на гранях. Это могут быть просто картинки или фотографии, например городов. Такие уже собирать намного сложнее, но интереснее. Среди подобных кубиков самым сложным, с моей точки зрения, является кубик в расцветке глобуса. Ведь для его успешной сборки необходимо еще знать географию.
Но тем не менее всё же, на мой взгляд, самыми интересными остаются кубы. Причем интересна не просто их классическая сборка, когда получаются все грани, окрашенные в одинаковые цвета. Интересной представляется сборка кубов, когда в результате нее на гранях появляется какой-либо узор или рисунок: точки, кресты, минусы, шахматы, а иногда и что-то посложнее, например гигантский мезон с вишнями. Именно сборка различных рисунков на кубах на сегодняшний день привлекает меня больше всего.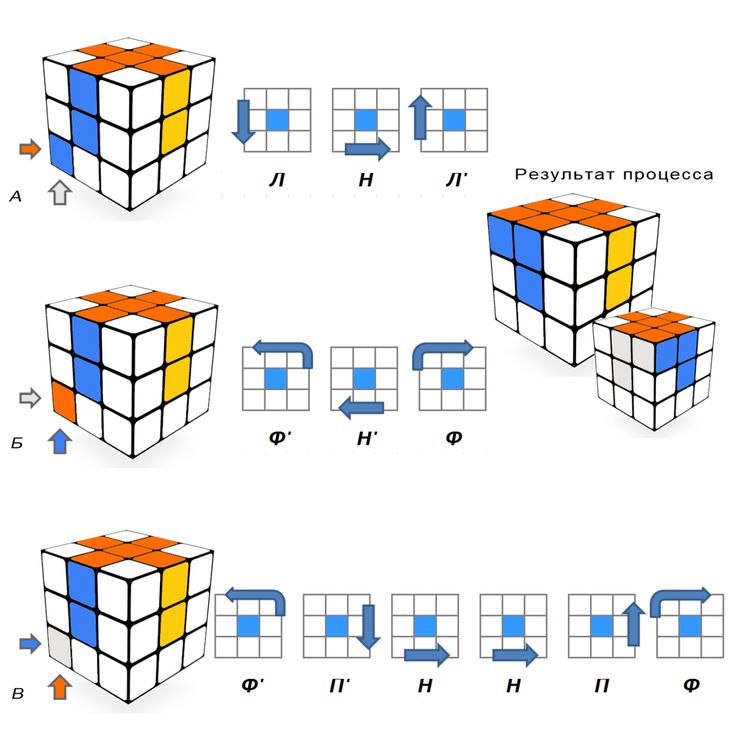
– Как коллекция пополняется? (Покупаете, дарят, следите за новинками?)
– Коллекция пополняется различными способами – недостающие интересные головоломки я заказываю в различных интернет-магазинах. Но в последнее время родные и друзья их часто дарят. При этом, конечно, есть вероятность того, что могут подарить головоломку, которая у меня уже есть. Но пока такого не случалось.
– За сколько Вы собираете кубик? Вы собираете на скорость?
– К сожалению, я не увлекаюсь спидкьюбингом (сборкой кубика на время). Но тем не менее процесс сборки классического кубика 3х3х3 не занимает много времени. Это 2–3 минуты. Если собирать хорошо смазанный куб, предназначенный для скоростной сборки, то можно успеть и за 1–2 минуты. Но чем больше элементов на гранях куба, тем больше времени требуется, чтобы его собрать. Так, кубик 9х9х9 я собираю за время от 1 до 2 часов.
– Как часто берете кубик в руки, чтобы собрать его?
– Сборкой кубиков нужно заниматься регулярно. То есть каждый день. Но ввиду высокой загруженности на работе, кубик беру в руки не так часто. По выходным точно беру. Иногда удается и на неделе позаниматься.
То есть каждый день. Но ввиду высокой загруженности на работе, кубик беру в руки не так часто. По выходным точно беру. Иногда удается и на неделе позаниматься.
– Для Вас кубик Рубика – это релакс или спорт?
– Кубик Рубика для меня – это, конечно же, релакс. Но релакс интеллектуальный.
– Есть ли у Вас секрет сборки кубика?
– По большому счету, больших секретов в сборке кубиков нет – большинство алгоритмов уже известны давно. Однако хочу сказать, что у каждого кубера есть свои нюансы выполнения тех или иных операций с кубом. Есть они и у меня.
– У Вас есть секрет, позволяющий собирать любые головоломки?
– Нет, такого секрета нет, поскольку разные головоломки собираются по различным алгоритмам…
– Помогает ли сборка кубика в решении каких-то трудных жизненных проблем? Может, есть примеры?
– Да. Очень часто при возникновении различных затруднительных ситуаций на работе или дома сборка кубика помогает правильно настроить интеллектуальную деятельность. Если обдумывать проблему и в это время собирать головоломку, то часто вместе со сборкой может прийти в голову и решение проблемы или выход из непростой жизненной ситуации.
Если обдумывать проблему и в это время собирать головоломку, то часто вместе со сборкой может прийти в голову и решение проблемы или выход из непростой жизненной ситуации.
– Участвуете ли в соревнованиях по сборке кубика?
– К сожалению, не участвую. Наверное, зря, но на это не хватает времени.
– Есть ли еще головоломка, которую не можете еще покорить?
– Да, на Новый год друг подарил сильно навороченную головоломку. Вот ее сборку пока я не освоил… Но это только пока не освоил.
Пресс-служба ПетрГУ
«Как собрать кубик Рубика?» — Яндекс Кью
Популярное
Сообщества
Стать экспертом Кью
ИгрушкиГоловоломки
Популярные вопросы из поиска
·
159,7 K
На Кью задали 4 похожих вопросаОтветитьУточнить
Первый
Алексей Вечканов
9
10 февр 2021
Конечно знаю. Уже собрал 3 на 3, мегаминкс, 2 на 2, в процессе 4 на 4.учился на указанном сайте, там кстати очень хорошая анимация. А если соберёшь 3 на 3 остальные собрать труда не составит нужно только терпение.
Уже собрал 3 на 3, мегаминкс, 2 на 2, в процессе 4 на 4.учился на указанном сайте, там кстати очень хорошая анимация. А если соберёшь 3 на 3 остальные собрать труда не составит нужно только терпение.
39,5 K
Комментировать ответ…Комментировать…
Первый
Константин
7
30 июл 2021
Собираю по алгоритму из «Науки и жизни». Была еще вторая статья с описанием перемещения угловых кубиков на третьем слое в 8 ходов вместо первоначальных 22, причем кубики таким способом можно «крутить», как в правую, так и в левую сторону, что значительно сокращает время сборки. Кроме того там рассматривались и другие комбинации для более быстрой замены кубиков на… Читать далее
Комментировать ответ…Комментировать…
Первый
Павел
4
7 февр 2021
Приблизительно знаю, делал бы по другой схеме, раз центральные кубики постоянны друг по отношению к другу, то их не трогаем вообще, или трогаем в последнюю очередь, далее по сложности идут кубики расположенные на боковых гранях (ребрах), и наконец самые сложные — расположенные по углам, главное сначала правильно сориентировать их не боясь разрушить предыдущие два.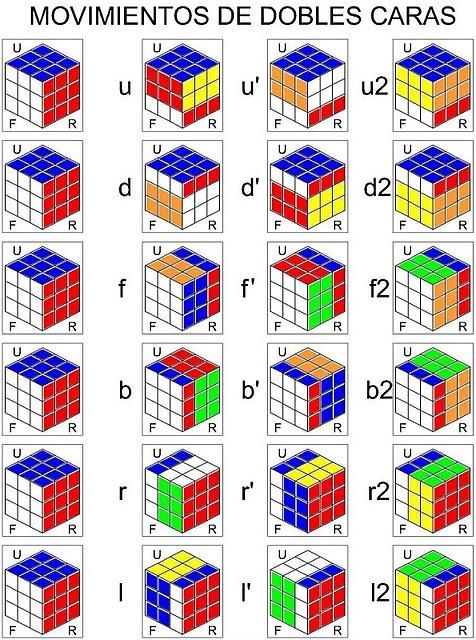 .. Читать далее
.. Читать далее
39,3 K
Роман Иванов
20 марта 2021
Был замечательный журнал, «Наука и жизнь». Давно, в конце 80-х или в начале 90-х очень подробно и очень доступно р… Читать дальше
Комментировать ответ…Комментировать…
Первый
Сергей Шабалин
3
29 июл 2021
Скажу просто береш и собираеш, с детства навыки остались 3*3 легко с большими приходится попыхтеть. В наше время была хорошая схема в журнале наука и жизнь вот год и номер не помню. .
Комментировать ответ…Комментировать…
Первый
Albachino1
2
30 июл 2021
40 лет назад я собрал кубик и сделал это за 3 суток.
Собирать кубик быстро это не сложно.
Сложно научиться набирать пасьянсы — упорядоченные узоры.
Комментировать ответ…Комментировать…
Первый
Диана Мурник
237
Тренер по спидкубингу, автор книги «Как собрать кубик?» · 16 дек 2019
Если отвечать на этот вопрос кратко, то нужно просто поставить на своё место каждую из 26 деталек кубика. Хорошая новость состоит в том, что одноцветные детальки кубика (центры, их 6 штук) уже и так всегда на своих местах. Осталось разобраться с остальными 20 детальками 🙂
И тут мы натыкаемся на самый главный миф о сборке кубика Рубика: большинство людей полагают, что… Читать далее
172,1 K
Андрей Беляев
22 января 2020
Круто все обьяснили. Спасибо. При случае попробую собрать)
Комментировать ответ…Комментировать…
Брунгильда
68
Читаю книги, есть время думать и размышлять, благо я на «вечных каникулах».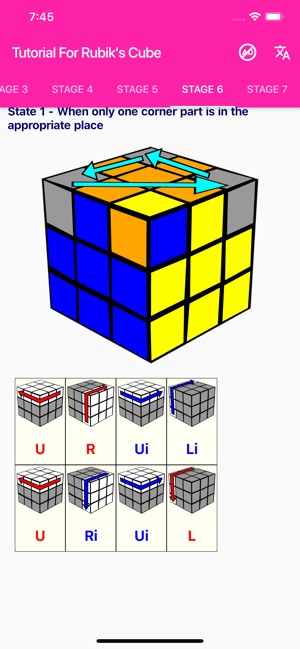 · 8 февр 2021
· 8 февр 2021
Главные понятия при сборке кубика Рубика это названия плоскостей кубика — верх, низ, право, лево, зад, перед. Движения — по часовой стрелке, против часовой стрелки. Два «этажа» собрать — просто. Формулы легко запоминаются, а руки сами автоматически крутят. Последний «этаж» — слишком длинные формулы для запоминания. В зависимости от расположения элементов кубика по… Читать далее
41,1 K
Комментировать ответ…Комментировать…
Первый
irik gabdullin
1
5 авг 2021
Собирал за 15 минут из любой комбинации. Журнал «Наука и техника» 1981г. №11 . Хотя номером могу и ошибаться. Третий и второй этажи собираю и сейчас-сложного там ничего нет. Первый заключительный этаж собирал по формуле из журнала, которые уже забыл.
Комментировать ответ…Комментировать…
zmey
59
31 мар 2021
Есть несколько способов, самый простой — именно слоями, как тут уже говорили. Правда тут в соседнем ответе чрезмерно подробно показано как собрать первый и самый простейший слой, но совсем ничего о дальнейшей сборке. А там совершенно разные алгоритмы для каждого слоя, и даже для каждой детальки, боковой или угловой. Я тоже не буду тут все это рассказывать, на схемах это… Читать далее
Правда тут в соседнем ответе чрезмерно подробно показано как собрать первый и самый простейший слой, но совсем ничего о дальнейшей сборке. А там совершенно разные алгоритмы для каждого слоя, и даже для каждой детальки, боковой или угловой. Я тоже не буду тут все это рассказывать, на схемах это… Читать далее
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
1 ответ скрыто(Почему?)
Ответы на похожие вопросы
Как научиться собирать Кубик Рубика? — 2 ответа, задан
Максим К.
5,1 K
Во всём по чуть-чуть: немного спорта и туризма, немного знаний в IT, немного разбираюсь в… · 20 февр 2018
Я бы советовал вам поискать схемы сборки кубика Рубика. Они не очень сложные. Запомнив их, вы без проблем сможете собирать кубик из любого состояния за считанные минуты или даже быстрее.
Они не очень сложные. Запомнив их, вы без проблем сможете собирать кубик из любого состояния за считанные минуты или даже быстрее.
Комментировать ответ…Комментировать…
Как собрать кубик Рубика (Журнал «Квант» 1983 год) — zna4koff.ru
Наверное, кубик Рубика уже не нуждается в представлении — только «Квант» посвятил ему четыре большие статьи, и даже по телевидению его показывали. А самое главное — наконец, он стал появляться в продаже. Теперь повсюду можно встретить людей (обычно весьма юных), пытающихся собрать кубик — упорно, но не всегда успешно. Вот мы и решили еще раз рассказать, а точнее — показать на картинках как это делается.
Повороты граней мы будем изображать с помощью стрелок в квадрате 3 на 3, изображающем переднюю грань кубика.
Рис. 0. Стрелочные и буквенные обозначения поворотов пяти граней (задняя грань нам не понадобится). Например, буква Ф обозначает поворот передней (Фасад) грани на 90° по часовой стрелке, Ф’ — ее поворот на 90° против часовой стрелки.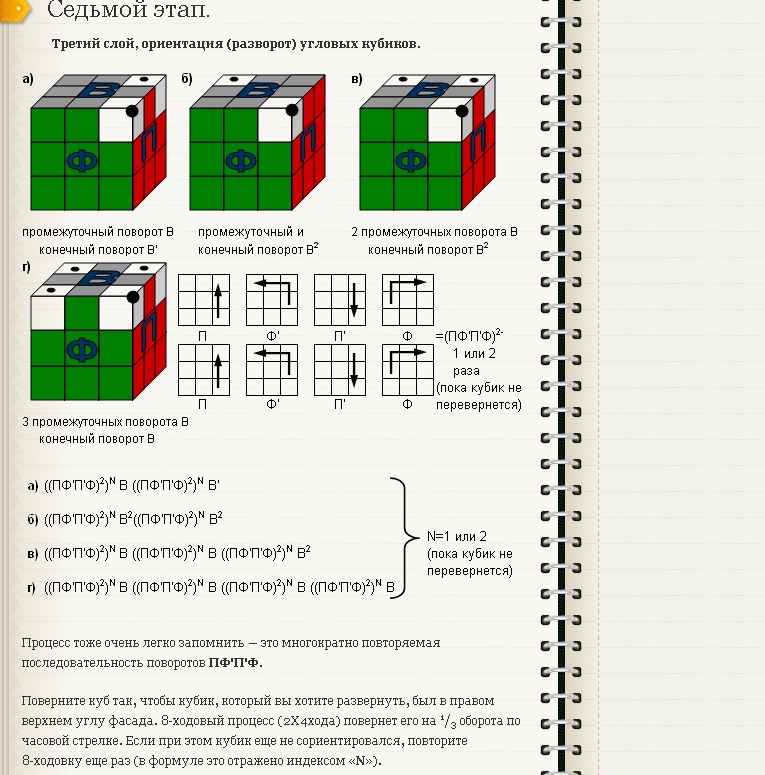 Ф2 — её поворот на 180°. На этом и следующих рисунках не закрашенные грани кубиков — это грани, цвет которых на данном рисунке мы не желаем фиксировать.
Ф2 — её поворот на 180°. На этом и следующих рисунках не закрашенные грани кубиков — это грани, цвет которых на данном рисунке мы не желаем фиксировать.
Каждый этап сборки задается рисунками, на которых показаны исходное положение кубичное, которые переставляются на этом этапе, последовательность поворотов этого этапа и вид кубика после его завершения.
Договоримся, что при сборке грань с синим центральным квадратом всегда будет у нас верхней. Центральный квадрат противоположной грани в разных экземплярах кубика бывает разным; для определенности будем считать его зеленым. Итак, в результате сборки верхняя грань кубика должна стать у нас синей, нижняя — зеленой. Передней гранью по ходу сборки может служить любая из четырех остальных (боковые) граней.
Если вы хоть немного крутили кубик, вы поняли, что центральные кубики всех граней сразу можно считать стоящими на своем месте (поскольку их взаимное расположение жестко установлено конструкцией кубика), а для каждого из остальных кубиков имеется вполне определенное окончательное положение: каждая грань кубика должна примыкать (по стороне или вершине) к центральному квадрату того же цвета.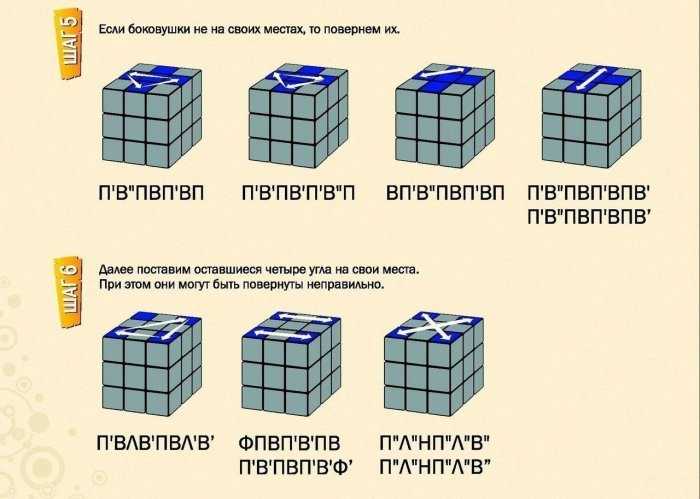
Кубик мы будем собирать послойно — сначала нижний слой (первые два шага), потом средний (третий шаг) и, наконец, верхний (последние четыре шага).
Итак, начинаем! Первый шаг.
Нижний крест: устанавливаем нижние реберные кубки. Выберите какой-нибудь реберный кубик с зеленой гранью, не стоящий в окончательном положении, и поворотом боковой грани, в которой он находится, переведите его в верхнюю грань. Пусть вторая грань выбранного кубика — желтая; поворотом кубика сделайте грань с желтым нейтральным квадратом передней и поворотом верхней грани приведите кубик в какое-то из двух исходных положении (рисунок ниже). Действуйте согласно рисунку — выбранный кубик окажется в нужном положении. Устанавливая каждый следующий реберный кубик, нельзя портить уже достигнутое (подумайте, как это сделать!).
Рис. 1. Первый шаг: установка нижнего реберного кубика.
В дальнейшем на всех рисунках мы тоже будем переднюю грань изображать желтой (то. есть с жёлтым центральным квадратом, правую — оранжевой, Но, разумеется, на каждом шаге, приводя кубик к исходному положению соответствующего рисунка, вам самим, придется соображать, какую грань принять за переднюю.
Рис. 2. Второй шаг: установка нижнего углового кубика.
Второй шаг.
Нижние углы: устанавливаем, нижние угловые кубик (рис, 2). Выберите какой-нибудь угловой кубик с зеленой гранью, находящийся в верхнем слое, и поворотом верхней грани поставьте его точно над его местом в нижнем слое. При этом выбранный кубик займет какое-то из трех исходных положений рисунка 2. Действуйте согласно рисунку — выбранный кубик окажется в нужном положении. Если и верхнем слое не осталось угловых кубиков с зеленой гранью, но в нижнем слое какой-то угловой кубик не стоит в окончательном положении, поверните кубик так, чтобы кубик оказался «передним-правым-нижним», и проделайте любую из операций рисунка 2 — он окажется в верхнем слое.
Рис. 3. Третий шаг: сборка среднего слоя Кубика Рубика.
Третий шаг.
Средний слой: устанавливаем средние реберные кубики (рис. 3). Выберите какой-нибудь реберный кубик без синих граней, находящийся в верхнем слое. Поворотом верхней грани приведите кубик в какое-то из двух исходных положений рисунка 3. Действуйте согласно рисунку — выбранный кубик окажется в нужном положении.
Поворотом верхней грани приведите кубик в какое-то из двух исходных положений рисунка 3. Действуйте согласно рисунку — выбранный кубик окажется в нужном положении.
Если в верхнем слое не осталось реберных кубиков без синих граней, но какой-то из средних реберных кубиков не находится в окончательном положении, поверните кубик так, чтобы этот кубик оказался «передним-правым», и продвигайте любую из операций рисунка 3 — он окажется в верхнем слое.
Рис. 4. Четвертый шаг: ориентирование двух верхних реберных кубиков. Красные стрелки показываю, как они при этом переставляются, что на этом этапе для нас не важно.
Четвертый шаг.
Ориентирование верхних реберных кубиков: устанавливаем верхние реберные кубинки синими гранями вверх (рис. 4). Неправильно повернутым и могут быть только два или четыре кубика — поэтому достаточно уметь переворачивать любую пару. В зависимости от того, хотите вы перевернуть пару соседних или пару противоположных кубиков, выполните одну из двух операций рисунка 4 -выбранные кубики перевернутся.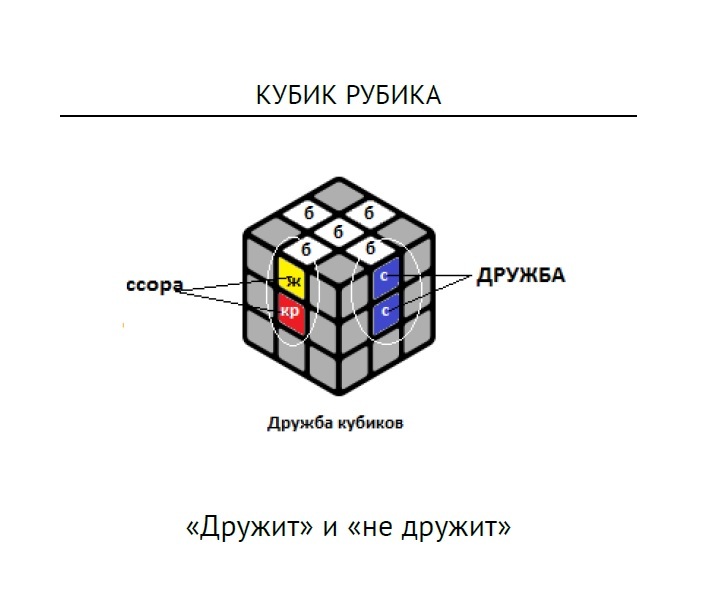 (При этом они еще и переставятся.)
(При этом они еще и переставятся.)
Рис. 5. Пятый шаг. Перестановка трех верхних реберных кубиков.
Пятый шаг.
Перестановка верхних реберных кубиков: расставляем верхние реберные кубики по своим местам, не переворачивая их (рис. 5). Если один из них уже стоит правильно, а три других надо переставить по направлению часовой стрелки (случай А), поместите кубик в исходное положение рисунка 5 и действуйте согласно рисунку — кубики расставятся по своим местом. В противном случае поверните верхнюю грань так, чтобы какие-то два ее реберных кубика встали правильно. (Это всегда возможно. Почему?) Если два других правильно не встанут, то дальше действуем в зависимости от того, являются ли «правильные» кубики соседними (случай Б или противоположными (случай В). В случае Б поверните верхнюю грань еще на 90° против часовой стрелки — получится случай А. В случае В действуйте согласно рисунку 5, приняв за переднюю любую боковую грань кубика; после этого, повернув верхнюю грань на 90° в нужном направлении, опять придем к А.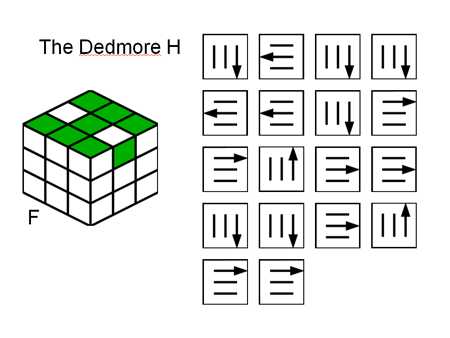 (Между прочим, случай В встречается в 5 раз реже случая Б — докажите!)
(Между прочим, случай В встречается в 5 раз реже случая Б — докажите!)
Рис. 6. Шестой шаг. Ориентирование трех верхних кубиков. (При выборе исходного положения кубика, красные стрелки игнорируются).
Остается уже немного. Шестой шаг.
Ориентирование верхних кубиков: устанавливаем верхние угловые кубики синими гранями вверх (рис. 6). После пятого шага неправильно повернутыми могут быть два, три или все четыре кубика, В случае трех «неправильных» кубиков поместите кубик в одно из двух исходных положений рисунка 6 и действуйте согласно рисунку — кубик повернется. При этом они еще и переставятся). Если надо перевернуть два иди четыре кубика, расположите, кубик так, чтобы левый верхний угол передней грани был синим и выполните операцию Т’ для случая двух кубиков или Т для четырех. После этого выполните операцию Т, приняв за переднюю соответствующую боковую грянь кубика.
Рис. 7. Седьмой шаг: установка трех верхних угловых кубика.
И, наконец.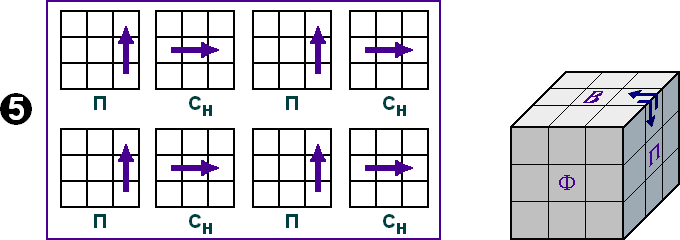 Седьмой шаг.
Седьмой шаг.
Перестановка верхних угловых кубиков: расставляем верхние узловые кубики по своим местам, не переворачивая их (рис. 7).
После шестого шага либо все верхние угловые кубики встанут правильно, либо один из них встанет правильно, а три других надо циклически переставить, либо асе они будут стоять неправильно. В первом случае асе в порядке — кубик Рубка собран. Во втором случае, в зависимости от того, надо ли переставить неправильные кубики против часовой стрелки или по часовой стрелке, выполните одну из двух операций рисунка 7 — кубики расставятся по своим местам. В третьем случае выполните любую из операций рисунка 7, приняв за переднюю любую боковую грань кубика, — один угловой кубик встанет правильно, и мы получим предыдущий случай).
Все. Можно вздохнуть с облегчением — кубик Рубика собран!
Журнал «Квант» 1983 год (Научно-популярный физико-математический журнал Академии наук СССР и Академии педагогические наук СССР)
Интернет магазин по продаже Кубиков Рубиков
Смотреть, как собрать кубик Рубика
В недавнем выпуске «Почти невозможно»,
я рассмотрел пределы спидкубинга,
соревнования, в котором люди соревнуются
, чтобы собрать кубик Рубика как можно быстрее.
И в ходе репортажа об этой статье,
я научился собирать кубик Рубика сам
с помощью Тайсона Мао,
соучредителя Всемирной ассоциации кубиков.
Менее чем за две недели, используя метод, которому меня научил Мао,
Я прошел путь от полной неспособности собрать куб,
, до того, что смог решить его последовательно
менее чем за минуту.
Некоторые из вас попросили нас опубликовать
пошаговое руководство по сборке куба,
и, возможно, вы также слышали,
, что достигается истинное мастерство в предмете
обучая этому кого-то другого.
Итак, в духе этой максимы,
я собираюсь показать вам метод, который я использовал
при обучении сборке кубика.
В этом видео,
, вы узнаете основы построения куба,
как держать куб и обращаться с ним,
как читать обозначения куба,
и как собирать куб за восемь шагов.
Все, что вам нужно, это перемешанный кубик.
Теперь, если вы решаете задачу впервые,
я бы выделил около часа, плюс-минус 15 минут,
, чтобы решить вашу первую задачу.
Я знаю, что это долго,
но чем больше времени вы тренируетесь,
тем быстрее эти времена сойдут,
и они действительно сойдут довольно быстро,
по крайней мере по моему опыту.
Наконец, есть много способов собрать куб,
это лишь один из них.
Это не самое быстрое, это не самое лучшее,
это далеко не самое простое.
Это просто метод, которому меня научил
один из основателей World Cube Association,
и метод, который я использовал
, чтобы сократить время до одной минуты.
Вы готовы?
Начнем.
Итак, прежде чем что-то двигать,
вот несколько идей, о которых следует помнить
которые облегчат сборку куба
чем больше вы будете практиковаться.
Номер один.
Собирая кубик, помните
, что вы собираете кубики, а не наклейки.
Что я имею в виду?
Большинство деталей куба на самом деле
имеют более одной наклейки.
Итак, если вы попытаетесь собрать куб, собирая только стикеры,
, вы быстро обнаружите, что если вы можете
собрать одну грань, то
другие грани не совпадут.
И это потому, что не все части куба одинаковы.
Есть три типа.
Кромки, подобные этой, имеют две наклейки.
Они выглядят так.
Угловые элементы, такие как этот,
имеют три наклейки, и они выглядят так.
И центральные части,
посередине каждой стороны три на три,
имеют по одной наклейке.
Эти центральные части прикреплены
к оси внутри головоломки, поэтому они никогда не двигаются.
На этом кубе, например,
белый центр всегда напротив желтого центра,
оранжевый центр всегда напротив красного центра,
и синий центр всегда напротив зеленого центра.
И это важно помнить,
потому что тот факт, что эти центры не перемещаются
означает, что они на самом деле диктуют, куда
должны двигаться все остальные части.
Эта концепция немного сбила меня с толку
когда я впервые ее услышала, но я обещаю,
чем больше времени вы будете проводить с кубом,
тем яснее и полезнее будет эта идея.
Наконец, многие думают, что куб
состоит из шести граней,
, но с другой точки зрения,
состоит в том, что он состоит из трех слоев:
— верх, середина и низ.
Сегодня мы сосредоточимся на сборке
куба по одному слою за раз.
Если вы уже забыли все, что я только что сказал,
это совершенно нормально.
Вы можете просто вернуться и пересмотреть его.
Пока достаточно этих идей
плавает у тебя в затылке.
Итак, имея в виду все это, давайте начнем.
Первым шагом в сборке первого слоя куба
является создание того, что куберы называют маргариткой.
Это называется изготовление маргаритки, потому что, когда вы закончите
, у вас должно получиться что-то похожее на это:
желтый центр, окруженный четырьмя белыми краями.
Итак, как нам добраться отсюда сюда?
Итак, вы начинаете с поиска желтого центра.
Цель этого шага состоит в том, чтобы окружить этот желтый центр
четырьмя краевыми элементами противоположного цвета,
, который в данном случае белый.
Если вы никогда раньше не собирали кубик,
очень заманчиво просто начать переворачивать грани наугад
в надежде поставить крайнюю часть туда, куда вы хотите,
но я хочу, чтобы вы сопротивлялись этому импульс.
Я дам вам два совета, которые
помогут вам логически расположить крайние части.
Первый совет: есть только
четыре белых края, вот и все.
Помните, что вы перемещаете фишки, а не наклейки,
и на этом кубе с белыми сторонами всего четыре грани
.
Чтобы найти их, все, что вам нужно сделать
, это осмотреть кубик в вашей руке.
Как только вы найдете его, сделайте паузу,
подумайте о поворотах, которые вам нужно будет переместить
, чтобы разместить его рядом с желтым центром.
Вот, например, белая кромка.
Чтобы разместить его рядом с желтым центром,
все, что мне нужно сделать, это
повернуть правую сторону на 90 градусов.
Вот еще один.
Чтобы получить его рядом с желтым центром,
Мне нужно повернуть его здесь, а затем вверх.
Поверьте мне, первые несколько раз, когда я собирал куб
этот процесс был совсем не интуитивным для меня,
но создание маргаритки становится второй натурой
тем быстрее, чем больше вы практикуетесь.
Второй совет: как только у вас будет
педаль к ромашке на месте,
на самом деле вам не нужно будет снимать ее
рядом с желтым центром
чтобы поставить любую из оставшихся педалей на место.
Это то, что я собираюсь сделать сейчас, и вы должны сделать то же самое.
Когда вы закончите, ваш желтый центр будет
окруженным со всех четырех сторон
белыми краями, как ромашка.
Не волнуйтесь, если у вас есть белый уголок,
мы доберемся до него через секунду.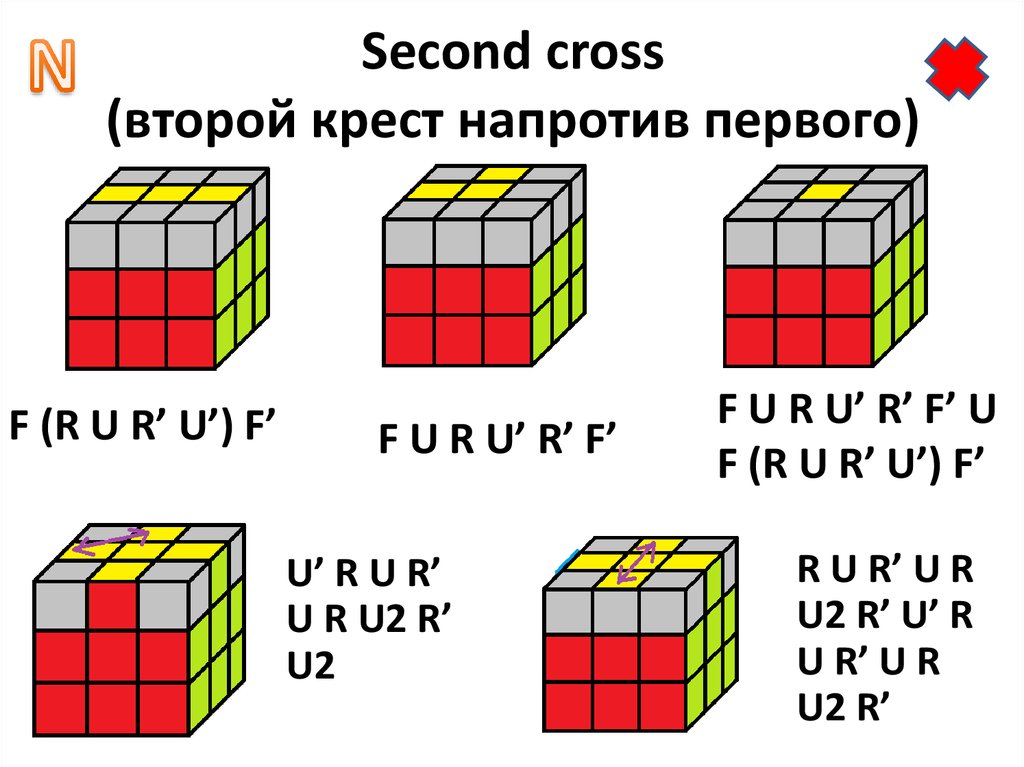
Вторым шагом решения первого слоя
является создание белого креста.
Когда вы закончите этот шаг,
у вас будет лицо с чем-то вроде белого креста,
или знаком плюса, в зависимости от того, как вы на него смотрите.
Начните с того, что посмотрите на свою ромашку.
Если у вас белые углы,
помните, просто игнорируйте их.
Сейчас мы сосредоточимся на четырех лепестках
, которые находятся на краях.
[легкая синтезаторная музыка]
На каждом из этих четырех краев есть две наклейки,
одна и две.
Вращая верхнюю грань куба,
соедините небелую наклейку каждой из краевых частей
с центральной частью того же цвета.
Так, например,
небелая наклейка на этой кромке оранжевая.
Я буду поворачивать верхнюю грань, пока оранжевая наклейка
не выровняется по оранжевому центру вот так.
После того, как вы сопоставите наклейку с одним и тем же цветовым центром,
поверните грань с соответствующим центром два раза,
переместите лепесток белой маргаритки
с верхней грани куба на нижнюю.
Теперь я повторю этот шаг еще три раза,
по одному разу для каждого оставшегося лепестка маргаритки.
Итак, у меня есть красный центр,
Я сопоставлю его с вот этим красным краем,
Поверните его дважды.
У меня есть эта зеленая кромка,
Я сопоставлю его с зеленым центром,
и поверну дважды.
И у меня есть этот синий край
, который я собираюсь совместить с синим центром,
, и повернуть его дважды.
Когда вы закончите, внизу куба появится белый крест
.
Как я уже говорил,
не волнуйтесь, если у вас также есть белые углы.
Сейчас вы просто ищете
эту конфигурацию прямо здесь.
Еще один совет.
Этот белый крест будет указывать вниз
до конца решения.
Наконец-то мы готовы решить
самый нижний слой куба.
Когда мы закончим этот шаг,
нижний слой куба будет решен.
И в качестве бонуса будет решена нижняя грань.
Но прежде чем мы начнем,
давайте остановимся на коротком уроке эргономики,
вот как держать куб и манипулировать им.
Белой стороной вниз
поместите большой палец левой руки на эти четыре квадрата
, а средний и безымянный пальцы
на четыре квадрата на противоположной стороне.
Теперь поместите средний и безымянный пальцы правой руки
на эти две наклейки вверху,
и большой палец правой руки на нижнюю сторону.
Держа куб таким образом, вы можете сделать две вещи.
Во-первых, он позволяет свободно и легко поворачивать правый циферблат.
И наоборот, смена положения рук
позволяет поворачивать и левое лицо.
И, во-вторых, он позволяет использовать указательные пальцы
для поворота верхней грани.
Когда вы соединяете эти вращения вместе
, вы получаете два самых фундаментальных движения в кубе.
Первая последовательность называется правым триггером,
и выглядит она так.
Правой рукой
поверните правую грань на 90 градусов от себя.
Указательным пальцем правой руки потяните
верхнюю поверхность на себя на 90 градусов.
Затем правой рукой поверните правую
сторону на 90 градусов назад к себе.
Левой рукой это выглядит так.
Левой рукой поверните левое лицо
от себя на 90 градусов.
Указательным пальцем левой руки потяните за верхнюю поверхность
к вам на 90 градусов.
Затем левой рукой поверните
левую сторону назад на 90 градусов к себе.
Мао называет эту последовательность из трех ходов левым триггером.
Правый и левый триггеры
самые основные движения в кубинге.
Чем больше вы их практикуете, тем быстрее вы становитесь.
Мы также будем часто использовать эти триггеры
до конца решения,
начиная прямо здесь, на третьем шаге.
Помните, цель этого шага состоит в том, чтобы решить
самый нижний слой куба,
и для этого мы будем искать белые наклейки
на верхнем слое, обращенные наружу.
Мы хотим решить части первого слоя
, которые еще не решены,
, которые являются углами с белыми наклейками.
Итак, мы будем искать эти
и размещать их по одному.
Теперь вы можете обнаружить, что куб, который вы держите,
имеет белую наклейку на верхней стороне вашего куба,
на самом деле, мы действительно видим это здесь, на этом.
У вас также может быть белая наклейка в этом нижнем слое.
Если вы увидите одну из этих вещей, не беспокойтесь об этом,
мы доберемся до них через секунду.
Пока просто сосредоточьтесь на белых наклейках
по бокам верхнего слоя.
Итак, у вас есть белая наклейка.
На угловом элементе.
Углы имеют три наклейки.
Игнорировать верхний.
Вместо этого укажите цвет
сбоку от белой наклейки.
В моем случае эта наклейка зеленая,
и она совмещена по диагонали с красным центром.
Теперь я хочу, чтобы вы повернули верхнюю грань
до тех пор, пока цвет рядом с вашей белой наклейкой,
, который в данном случае зеленый,
по диагонали не совпадет с центром того же цвета.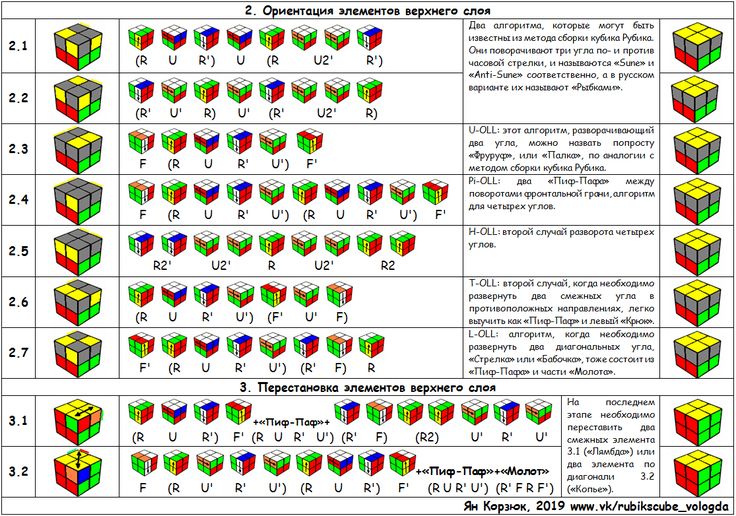
Если ваша угловая наклейка ориентирована
слева от центральной наклейки,
вы будете использовать левую руку
для выполнения левого триггера
повернув левую сторону от себя,
потянув левую сторону на себя левой рукой указательный палец,
, а затем поверните левую сторону к себе.
Если угловая наклейка ориентирована
справа от центральной наклейки,
вы будете использовать правую руку
для выполнения последовательности из трех движений
, повернув правую грань от себя,
потянув верхнюю грань к себе
указательным пальцем правой руки,
затем повернув правую грань к себе.
Ты снова сделаешь это движение.
Найдите верхний слой для обращенных наружу
белых наклеек, подобных этой.
Определите цвет рядом с ним,
выровняйте этот цвет, пока он не будет совпадать по диагонали
с центром того же цвета,
и выполните соответствующее правое
движение триггера левой рукой.
Здесь слева от центральной наклейки,
, поэтому я буду использовать левый триггер.
Здесь то же самое.
Слева.
Здесь то же самое.
Слева.
Теперь есть пара необычных ситуаций
, которые могут возникнуть на третьем шаге,
и они на самом деле не произошли
на кубе, который я использовал для решения,
поэтому я воспользуюсь демонстрацией куб, чтобы показать их вам здесь.
Первая белая наклейка
, обращенная наружу, на нижнем слое вместо верхнего.
Если вы столкнетесь с такой ситуацией,
просто найдите наклейку и определите,
справа или слева она находится
лица, на которое вы смотрите.
Если он справа,
выполните правый триггер, повернув
правую сторону на 90 градусов от себя,
потянув верхнюю часть на 90 градусов к себе,
, а затем повернуть правую грань назад
на 90 градусов к себе.
Это изменение положения белой наклейки
с внешней стороны нижнего слоя
на верхнюю часть первого слоя,
, который на самом деле является крайним случаем номер два.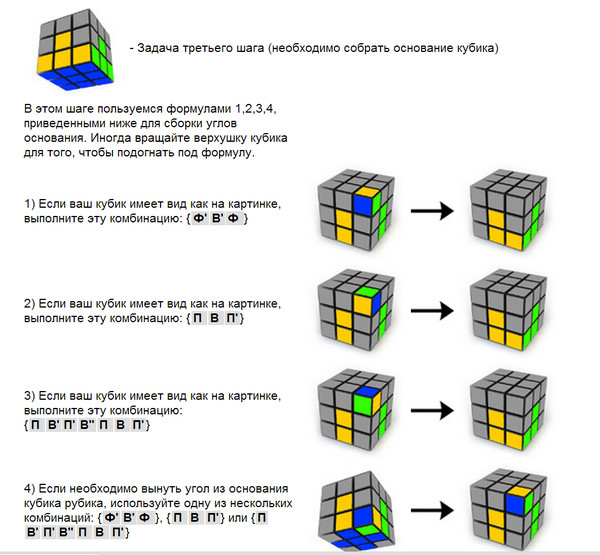
Если вы найдете белую наклейку на верхней грани,
поверните эту верхнюю грань, пока белая наклейка
не окажется прямо над ней, то есть напротив
небелой наклейки на нижней грани куба.
Чтобы помочь вам понять, как это выглядит, вот что я имею в виду.
Эта белая наклейка на верхней грани куба
в настоящее время находится прямо напротив другой белой наклейки
на нижней грани куба.
Вам это не нужно.
Вместо этого я хочу, чтобы вы повернули верхнюю грань
так, чтобы белая наклейка наверху
оказалась прямо напротив небелой наклейки внизу, в данном случае
, эта наклейка синего цвета.
Затем определите, находится ли белая наклейка
справа или слева от куба.
Если он с правой стороны, как здесь,
выполните соответствующее движение триггера,
но вместо того, чтобы сделать это только один раз, сделайте это дважды.
один раз,
два раза.
Теперь белая наклейка, которая была здесь
, находится на верхнем слое и обращена наружу.
И я могу решить эту проблему, сопоставив соседнюю наклейку
с ее цветным центром и выполнив
соответствующий ход триггера,
который в данном случае является правым триггером.
Продолжайте выполнять соответствующие ходы
, пока не останется белых угловых наклеек, которые нужно решить.
Сейчас я сделаю это на своем кубе.
У меня есть два, которые обращены вверх,
, так что я собираюсь сопоставить это с небелой стороной,
нажать на курок два раза,
переместить их в сторону.
Это сбоку от синей наклейки,
, который соответствует по диагонали справа от этого,
, поэтому я собираюсь выполнить правильный триггер.
Рядом с оранжевой наклейкой.
Подберу его к оранжевому центру.
Это слева, так что я собираюсь использовать левый триггер,
и все готово.
Когда вы закончите, весь нижний слой будет решен,
и в качестве бонуса будет решена нижняя грань.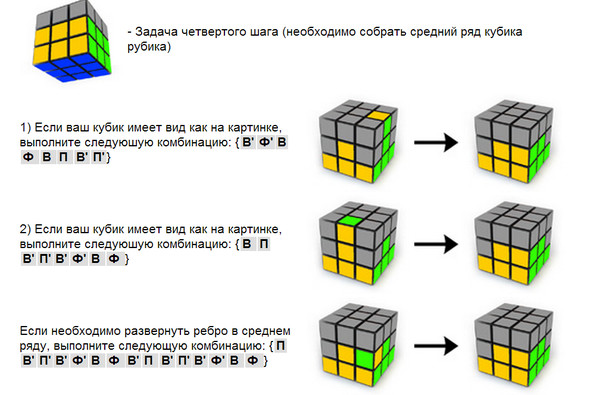
Переходим к четвертому шагу.
Цель этого шага — решить
второй слой куба.
Когда вы закончите, ваш куб будет выглядеть примерно так.
Эти первые два слоя полностью решены.
Сначала найдите в верхнем слое кромки
без желтых наклеек.
Как только вы его найдете,
соедините крайнюю часть, обращенную в сторону
, с центральной частью того же цвета.
Когда эта верхняя наклейка правильно подобрана,
у вас будет перевернутая Т.
Так, например,
это кромка без желтых наклеек.
Наклейка сбоку зеленого цвета.
Я буду вращать этот верхний слой, пока зеленая часть
не окажется в центре того же цвета.
У меня есть перевернутая Т,
, так что я посмотрю на наклейку
в верхней части этой кромки
и посмотрю, соответствует ли она
слева по центру или справа по центру.
В данном случае соответствует правому центру.
Итак, я собираюсь использовать правую руку, чтобы сначала потянуть
верхнюю сторону на 90 градусов,
затем выполнить правый триггер.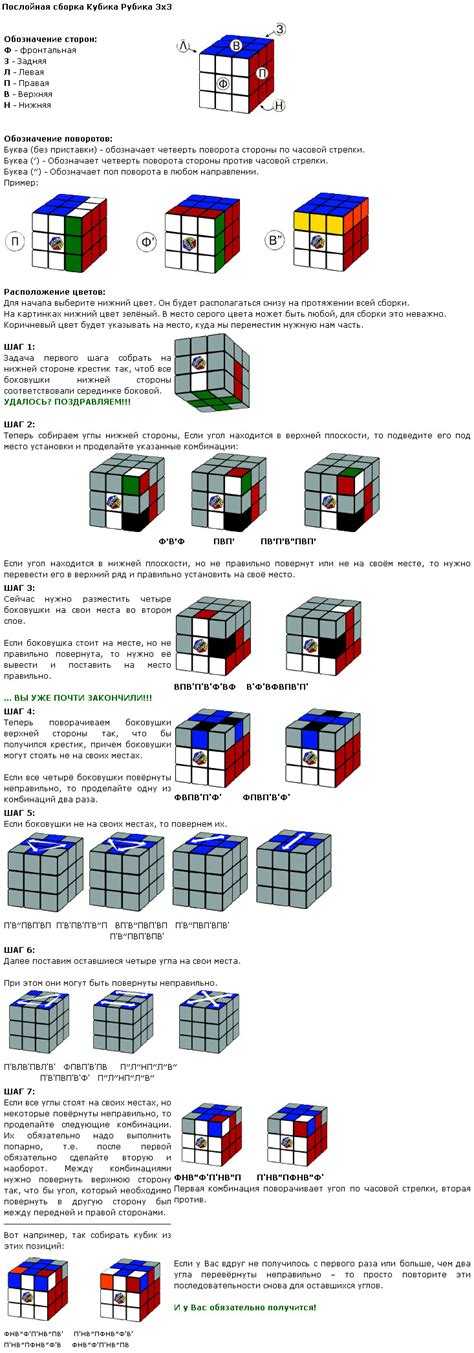
Я переместил белую наклейку,
, поэтому я буду использовать наклейку рядом с ней, оранжевую,
по диагонали совместить ее с центром того же цвета,
и поскольку она слева,
Я воспользуюсь левым триггером
, чтобы поместить его обратно на дно, как в третьем шаге.
Если в какой-либо момент наклейка на верхней части кромки
соответствует цвету наклейки на левой стороне,
вместо этого потяните левым указательным пальцем,
, затем нажмите левый триггер,
и зафиксируйте смещенную белую наклейку
, как в третьем шаге.
Продолжайте собирать кромки на верхнем слое
без желтых наклеек, пока
второй слой не будет полностью собран.
Иногда вы столкнетесь с краевым случаем, подобным этому
, где нет краев
в верхнем слое без желтых наклеек,
и еще средний слой не решен.
В таких случаях,
, вам нужно вытащить эти средние части
, нажав левый или правый триггер,
, а затем найти крайние части
без желтых наклеек, как обычно.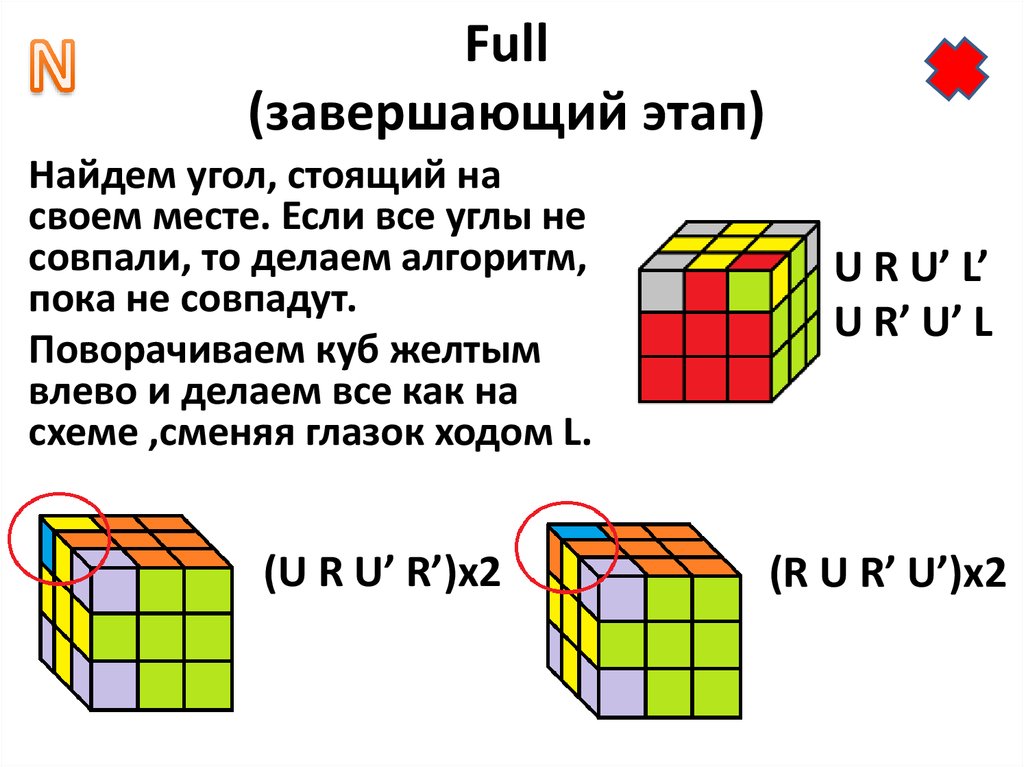
Вот как это выглядит.
В этом верхнем слое нет краев
без желтых наклеек,
и все же второй слой не решен.
Итак, нам нужно починить вот эту деталь.
Он находится на правой стороне куба,
, так что я воспользуюсь правым триггером, чтобы вытащить его.
Я собираюсь исправить белый элемент, который мы только что сместили
, совместив его по диагонали с красным центром здесь.
Он слева, так что я воспользуюсь левым триггером.
Теперь у меня должен быть край в верхнем слое
, у которого нет желтой стороны.
Вот этот.
Обратите внимание, это тот, который я только что выкинул.
Как и раньше, я возьму сторону, обращенную наружу
, и сопоставлю ее с тем же центром.
Перевернутый T.
Я посмотрю на верхнюю наклейку, она красная.
Красное на правом лице,
, так что я собираюсь использовать правую руку
, чтобы потянуть верхнюю часть один раз к себе,
, затем нажать правый триггер.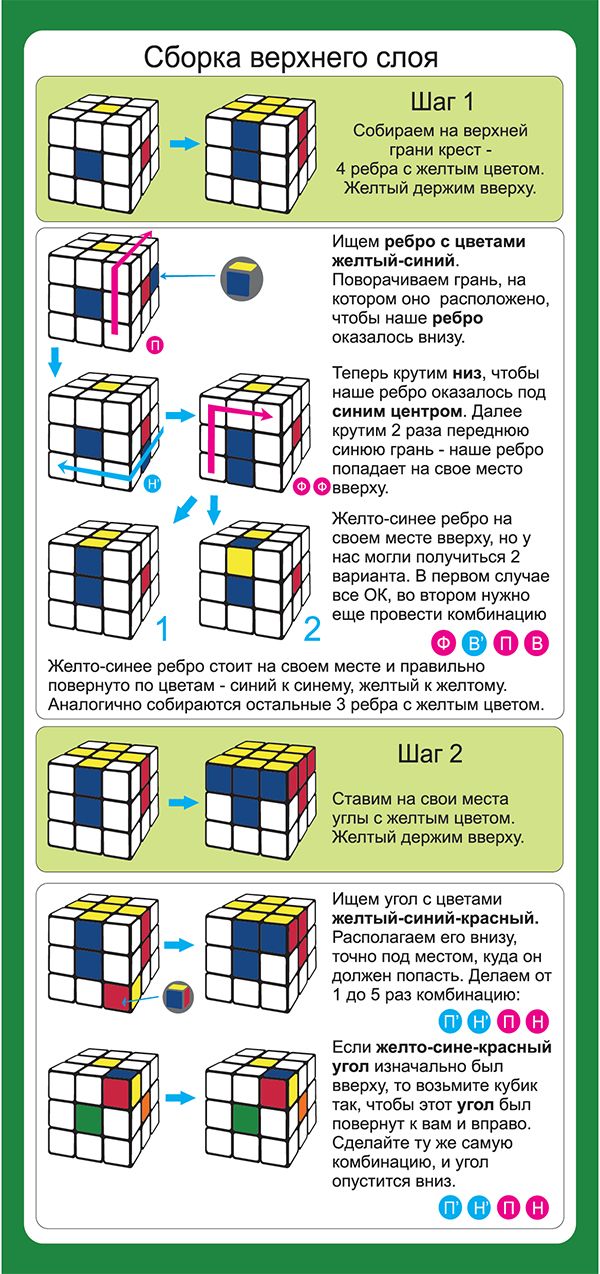
Опять же, я сдвинул эту белую фигуру,
, так что я собираюсь переместить красный, по диагонали, здесь,
, это слева.
Я нажму на левый триггер.
И теперь мой второй слой полностью решен.
Хорошо, это подводит нас к пятому шагу.
Целью пятого шага является создание
желтого креста на вершине куба.
Но прежде чем мы это сделаем, давайте остановимся на секунду
, чтобы обсудить кубическую нотацию.
Нотация куба — это то, что куберы используют для описания алгоритмов,
и алгоритмы — это заученные последовательности ходов
, которые они используют для быстрого решения куба.
F обозначает переднюю грань куба относительно вас.
B обозначает спинку.
L означает левый.
R означает право.
D означает вниз.
U означает вверх.
Если вы видите букву,
это значит повернуть соответствующую грань по часовой
на 90 градусов относительно перспективы
человека, смотрящего на это лицо в лоб.
Итак, это и это вращение по часовой
правой и левой граней соответственно.
Точно так же, если вы видите букву, за которой следует цифра два,
, это означает повернуть соответствующую грань два раза
, всего на 180 градусов.
Так, например, U2 означало бы два раза перевернуть
верхнюю грань.
Если за буквой следует апостроф,
, т. е. простой символ,
означает поворот соответствующей грани
против часовой стрелки на 90 градусов.
Например, L штрих означает повернуть левую грань
на 90 градусов против часовой стрелки вот так.
Я знаю, что все это звучит как много,
и это потому, что это так и есть,
, но с практикой чтение и использование обозначений
становится намного более простым.
Итак, теперь, когда вы знаете кубическую нотацию,
пришло время изучить алгоритм.
Обозначения для него следующие:
F, U, R, U простое, R простое, F простое.
Если вы ищете мнемонику,
вы можете назвать ее фурурф.
Цель пятого шага состоит в том, чтобы сделать желтый крест,
, и когда вы закончите, верхний
вашего куба должен выглядеть так.
Если у вас нет желтых краев, выполните фурурф.
F,
U,
R,
U прайм,
R прайм,
F прайм.
Если у вас есть две желтые кромки
так, чтобы они образовывали линию с центральной частью,
сориентируйте линию так, чтобы она смотрела вверх и вниз,
относительно вашей точки зрения,
и снова, выполните F,
U,
R,
U прайм,
R прайм,
F прайм.
Если у вас есть две желтые кромки
, образующие перевернутую букву L,
поворачивайте верхний слой, пока кромки
не окажутся на 12 и 9 позициях на часах,
и выполнить F,
U,
R,
U прайм,
R прайм,
F прайм.
На этом этапе у вас должен быть
желтый крест на верхней грани.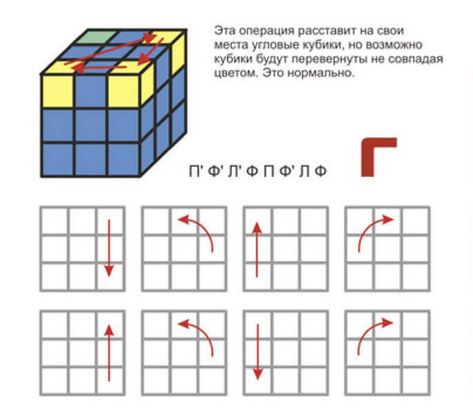
На следующий шаг.
Шестой шаг — решить всю желтую грань.
Начните этот шаг с осмотра верхней грани куба.
Сколько углов имеют желтые наклейки?
У тебя никогда не будет трех, но будет и то, и другое
ноль, один или два.
Если у вас есть ноль или два,
поверните верхнюю грань вашего куба, пока
на этом месте не появится желтая наклейка.
Если вы держите его в левой руке,
он находится в верхнем правом углу
левой стороны вот так.
Как только желтая наклейка окажется на месте,
выполните следующий алгоритм:
R,
U,
R Prime,
U,
R,
U2,
R простой.
Опять же, если у вас есть либо ноль
, либо две угловые наклейки, как здесь,
расположите этот верхний слой так, чтобы
была желтой наклейкой в верхнем правом углу
левого лица.
И снова выполняем алгоритм.
R,
U,
R Prime,
U,
R,
U2,
R Prime.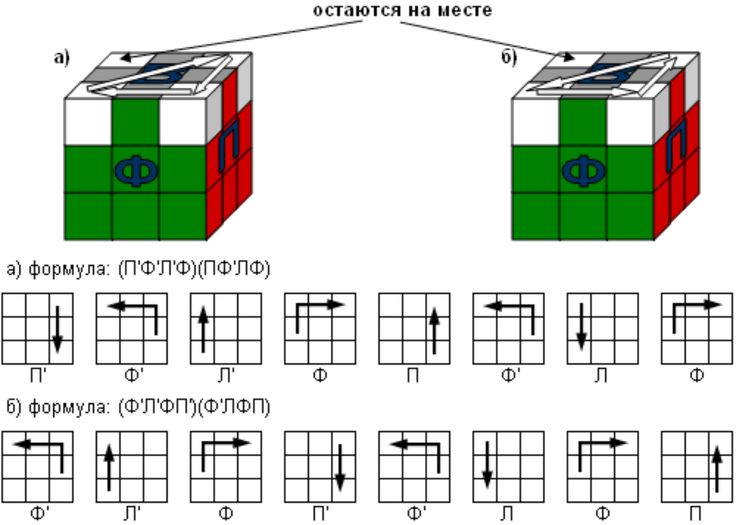
Если у вас есть желтый крест и только один желтый угол,
это будет выглядеть так, будто на верхней грани вашего куба изображена рыба.
Поверните эту верхнюю грань так, чтобы рот рыбы
был направлен вниз и влево,
относительно вашей перспективы,
и повторите алгоритм.
R,
U,
R Prime,
U,
R,
U2,
R Prime.
Возможно, вам придется сориентировать рыбу
и выполнить этот алгоритм в последний раз,
, но как только вы это сделаете, вы решите желтую сторону.
На седьмой шаг!
Целью шага sweven является
расположение углов куба.
Чтобы выполнить этот шаг, осмотрите верхний слой куба.
Вы хотите посмотреть на самые верхние
угловые части каждой грани.
Итак, здесь и здесь, здесь и здесь,
здесь и здесь, и здесь и здесь.
На седьмом шаге мы будем изучать новый алгоритм.
Я буду использовать этот куб для демонстрации.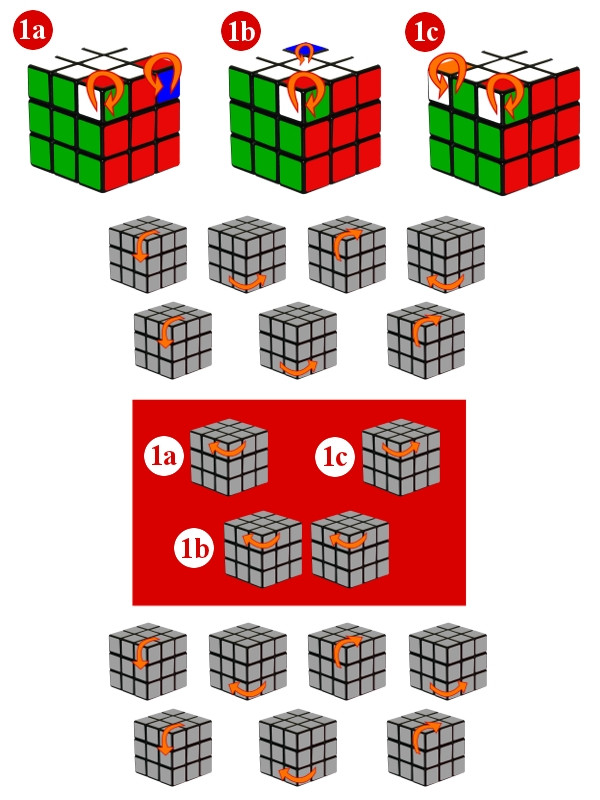
Это происходит так.
L Prime,
U,
R,
U Prime,
L,
U,
R Prime,
R,
U,
R Prime,
U,
R,
U2,
R простой.
Теперь вы заметите, что восьмой шаг этого алгоритма
на самом деле отменяет седьмой шаг, что странно,
, но на самом деле этот алгоритм легче запомнить.
И это потому, что вся вторая половина
точно такая же, как алгоритм, который мы изучили на шестом шаге.
Понял?
Хорошо.
Иногда вы можете обнаружить
, что ни на одной из ваших граней нет совпадающих угловых элементов,
, как на этом демонстрационном кубе,
, и если это так, просто выполните новый алгоритм.
L основной,
U,
R,
U основной,
L,
U,
R прайм,
R,
U,
R прайм,
U,
R,
U2,
R прайм.
Если на одном из ваших лиц есть совпадающие
угловые части, как здесь,
возьмите это лицо в левую руку и выполните алгоритм
L,
U,
R Prime,
R,
U,
R Prime,
U,
R,
U2,
R простой.
Теперь слушайте, у вас обязательно будет
чтобы запомнить все эти алгоритмы
если вы действительно хотите, чтобы ваше время действительно сократилось.
Но чем больше вы практикуетесь, тем менее неуклюжими
и тем более естественными они становятся.
На этом этапе все уголки должны совпадать.
Если они этого не сделают, вам может понадобиться выполнить
алгоритм седьмого шага еще раз.
Теперь поверните верхнюю грань так, чтобы уголки
совпали с остальными гранями куба.
Остался всего один шаг.
Ну вот и все, восьмой и последний шаг.
Целью этого шага является размещение ребер куба.
Если ни одна из сторон не решена, просто держитесь,
, и мы решим это через мгновение.
, а пока, если одна из сторон полностью решена,
, как у нас здесь, поверните ее от себя.
Теперь осмотрите края на оставшихся трех сторонах.
Они должны быть немного смещены.
Итак, например, эта оранжевая фигура очень хочет быть здесь,
эта зеленая фигура очень хочет быть здесь,
и эта синяя фигура очень хочет быть здесь.
Чтобы поменять местами эти три ребра по часовой стрелке,
вы будете выполнять новый алгоритм.
Это происходит так.
Ф2,
У,
R премьер,
L,
F2,
L премьер,
R,
U,
F2.
, чтобы поменять три края
в вращении против часовой стрелки. U премьер,
F2.
Хорошо, так что же делать
, если ни одна из ваших сторон не решена?
Просто, выполните алгоритм против часовой стрелки один раз,
переместите куб, а затем выполните его снова.
Выглядит так.
F2,
U Prime,
R Prime,
L,
F2,
L Prime,
R,
U Prime,
3 90.
Теперь у вас есть одно решенное лицо, наведите его от себя,
и выполните алгоритм против часовой стрелки во второй раз.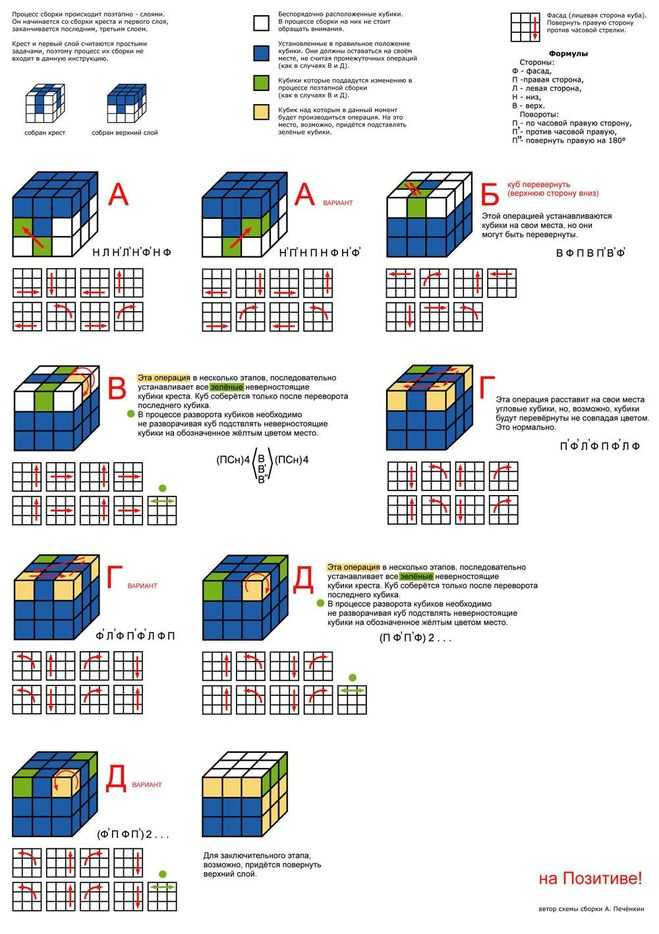
F2,
U премьер,
R премьер,
L,
F2,
L премьер,
R,
U премьер,
F2.
Теперь ваш куб должен быть собран.
И все!
Готово, вы собрали куб.
Как я уже сказал в начале,
это может быть что-то вроде
вам придется посмотреть несколько раз
и действительно попробовать несколько раз
, прежде чем вы действительно начнете вникать в это.
Но я бы сказал, что после первых полудюжины решений
вы сможете сделать это без просмотра видео.
И чем более последовательно вы будете решать ее после этого,
, тем быстрее начнет уменьшаться ваше время.
Решатель головоломок Статья по биологии для учащихся
БЫСТРЫЕ ПАЛЬЦЫ: Всемирная ассоциация кубиков ежегодно проводит около 200 соревнований, в ходе которых участники решают головоломки в стиле кубика Рубика так быстро, как только могут.
АЛЕКС ГУДЛЕТТ ДЛЯ NEW YORK TIMES/REDUX
Решатель головоломок
Познакомьтесь с действующим чемпионом по сборке кубика Рубика
ОСНОВНОЙ ВОПРОС: Как люди справляются с трудностями в своей жизни?
ПРЕДОСТАВЛЕНО КУБИКОМ РУБИКА/WWW. RUBIKS.COM
RUBIKS.COM
КУБИЧЕСКИЙ МАСТЕР: Макс Парк, 17 лет, один из лучших в мире спидкуберов.
В комнате тихо, пока 17-летний Макс Парк изучает головоломку в стиле кубика Рубика на столе перед ним. Каждая сторона игрушки состоит из четырех рядов по четыре квадрата, на которых изображена мешанина цветов. Когда Макс готов, он убирает руки со стола и берет куб. Таймер начинает отсчет, и его пальцы летают, крутя и переворачивая игрушку в молниеносном темпе. Макс бросает куб обратно на стол. Каждая сторона теперь показывает один сплошной цвет. Ему потребовалось всего 18,42 секунды — новый мировой рекорд.
Толпа, наблюдавшая за подвигом на прошлогоднем соревновании, разразилась аплодисментами. Отец Макса, Шван Парк, тоже хлопал рядом. Он гордился не только последним достижением своего сына, но и тем, как далеко продвинулся Макс. Это потому, что у Макса аутизм . Это состояние может затруднить общение, социализацию и восприятие окружающего мира ( см.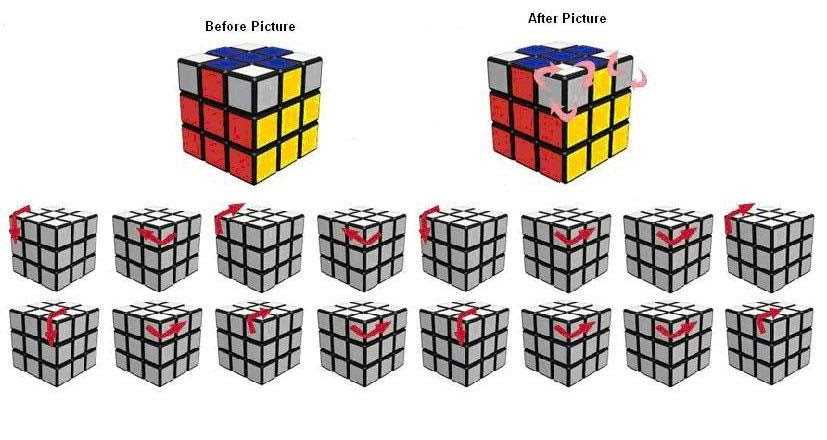 Понимание аутизма ).
Понимание аутизма ).
В комнате тихо. 17-летний Макс Парк изучает головоломку на столе перед ним. Головоломка выполнена в стиле кубика Рубика. Каждая сторона игрушки имеет четыре ряда по четыре квадрата разных цветов. Когда Макс готов, он берет куб. Таймер начинает отсчет, и его пальцы летают. Он крутит и крутит игрушку с молниеносной скоростью. Макс бросает куб обратно на стол. Каждая сторона теперь показывает один сплошной цвет. На решение у него ушло всего 18,42 секунды. Это новый мировой рекорд.
В прошлом году на это соревнование смотрела толпа. Они приветствовали и хлопали. Отец Макса, Шван, тоже хлопал. Он гордился последним подвигом своего сына, но он также гордился тем, как далеко продвинулся Макс. Это потому, что у Макса аутизм . Это состояние может затруднить общение, социализацию и восприятие окружающего мира ( см. Понимание аутизма ).
Парк и его жена Мики впервые осознали, что в Максе есть что-то особенное, когда ему было около 6 месяцев. Он не реагировал на громкие звуки и, казалось, жил в своем собственном мире. По мере того, как Макс рос, ему было трудно общаться с другими и устанавливать зрительный контакт. Он изо всех сил пытался понять невербальных сигналов , таких как указывание и выражение лица людей. Макс также с трудом справлялся с заданиями, требующими мелкой моторики , например, собирать монеты и класть их в копилку. Потом кто-то вручил ему кубик Рубика.
Он не реагировал на громкие звуки и, казалось, жил в своем собственном мире. По мере того, как Макс рос, ему было трудно общаться с другими и устанавливать зрительный контакт. Он изо всех сил пытался понять невербальных сигналов , таких как указывание и выражение лица людей. Макс также с трудом справлялся с заданиями, требующими мелкой моторики , например, собирать монеты и класть их в копилку. Потом кто-то вручил ему кубик Рубика.
Родители Макса думали, что манипуляции с игрушкой помогут улучшить ловкость их сына. Они и не подозревали, что это в конечном итоге изменит его жизнь. Сегодня Макс — один из лучших в мире спидкуберов — людей, посвятивших себя решению кубических головоломок как можно быстрее.
Пак и его жена Мики кое-что заметили, когда Максу было около 6 месяцев. Он не реагировал на громкие звуки и, казалось, жил в своем собственном мире. Когда Макс рос, ему было трудно разговаривать с другими и смотреть им в глаза. Он изо всех сил пытался понять невербальных сигналов , таких как указывание и выражение лиц людей. Максу тоже пришлось нелегко с мелкой моторикой . Например, подобрать монеты и положить их в копилку было непросто. Потом кто-то вручил ему кубик Рубика.
Максу тоже пришлось нелегко с мелкой моторикой . Например, подобрать монеты и положить их в копилку было непросто. Потом кто-то вручил ему кубик Рубика.
Родители Макса хотели, чтобы он взял игрушку в руки. Они думали, что это поможет улучшить его двигательные навыки. Но они не знали, что это изменит его жизнь. На сегодняшний день Макс является одним из лучших в мире спидкуберов . Эти люди работают над решением кубических головоломок как можно быстрее.
ИГРУШКА ДЛЯ РАЗМЫШЛЕНИЯ
RICK FINDLER/PA IMAGES/GETTY IMAGES
ШИРОКОЕ РАЗНООБРАЗИЕ: головоломки в виде кубиков бывают разных форм и размеров.
Кубик Рубика впервые стал популярным в 1980-х годах. Каждая сторона исходного куба содержала девять цветных квадратов в три ряда по три. Квадраты куба можно было переставить 43 квинтиллионами различных способов. (Это 43, за которыми следуют 18 нулей!) Неудивительно, что большинство людей, собиравших головоломку, быстро разочаровывались. Даже Эрнё Рубику, дизайнеру игрушки, понадобилось больше месяца, чтобы решить собственное изобретение ( см. Cube Creator ). Оставаясь причудой в течение нескольких лет, повальное увлечение кубиком Рубика закончилось. Но полностью игрушка не исчезла.
Даже Эрнё Рубику, дизайнеру игрушки, понадобилось больше месяца, чтобы решить собственное изобретение ( см. Cube Creator ). Оставаясь причудой в течение нескольких лет, повальное увлечение кубиком Рубика закончилось. Но полностью игрушка не исчезла.
Три десятилетия спустя кубики вернулись. Имея доступ к Интернету, люди могут выйти в Интернет, чтобы научиться угадывать кубики. Производители игрушек также разработали новые модели, которые вращаются быстрее, что повышает конкурентоспособность людей. И теперь они продают более сложные кубики разных размеров и форм. В результате соревнования по спидкубингу стали популярными.
Кубик Рубика стал популярным в 1980-х годах. В первом кубе было девять цветных квадратов в три ряда по три с каждой стороны. Квадраты куба можно было перемещать 43 квинтиллионами различных способов. (Это 43, за которыми следуют 18 нулей!) Многие люди взялись за головоломку, но большинство из них быстро сдались. Игрушку создал Эрнё Рубик, но на решение собственной головоломки у него ушло больше месяца ( см.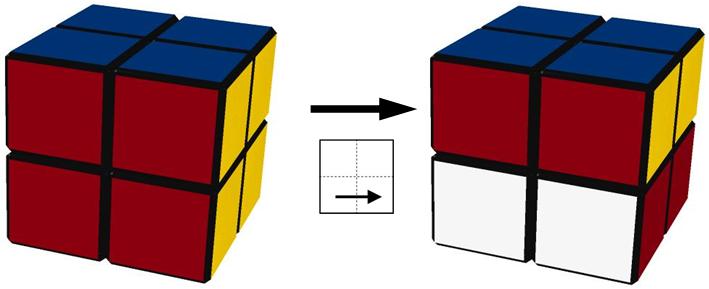 Cube Creator ). Кубик Рубика был увлечение в течение нескольких лет, а затем помешательство закончилось. Но полностью игрушка не исчезла.
Cube Creator ). Кубик Рубика был увлечение в течение нескольких лет, а затем помешательство закончилось. Но полностью игрушка не исчезла.
Три десятилетия спустя кубики вернулись. Теперь у людей есть доступ к интернету. Они могут выйти в интернет, чтобы узнать, как собирать кубики. Производители игрушек также создали новые модели, которые вращаются быстрее. Это заставляет людей конкурировать. И более хитрые кубики разных размеров и форм теперь продаются. В результате соревнования по спидкубингу стали популярными.
СОЗДАТЕЛЬ КУБИКА
Эрнё Рубик, профессор архитектуры из Венгрии, придумал кубик Рубика в 1974 году. дизайн своим ученикам. В 1980 году к нему обратилась компания по производству игрушек, заинтересованная в продаже пластиковой версии его изобретения. Это оказалось хитом. На сегодняшний день по всему миру продано 350 миллионов кубиков Рубика. «Если вам любопытно, вы найдете головоломки вокруг себя», — говорит Рубик.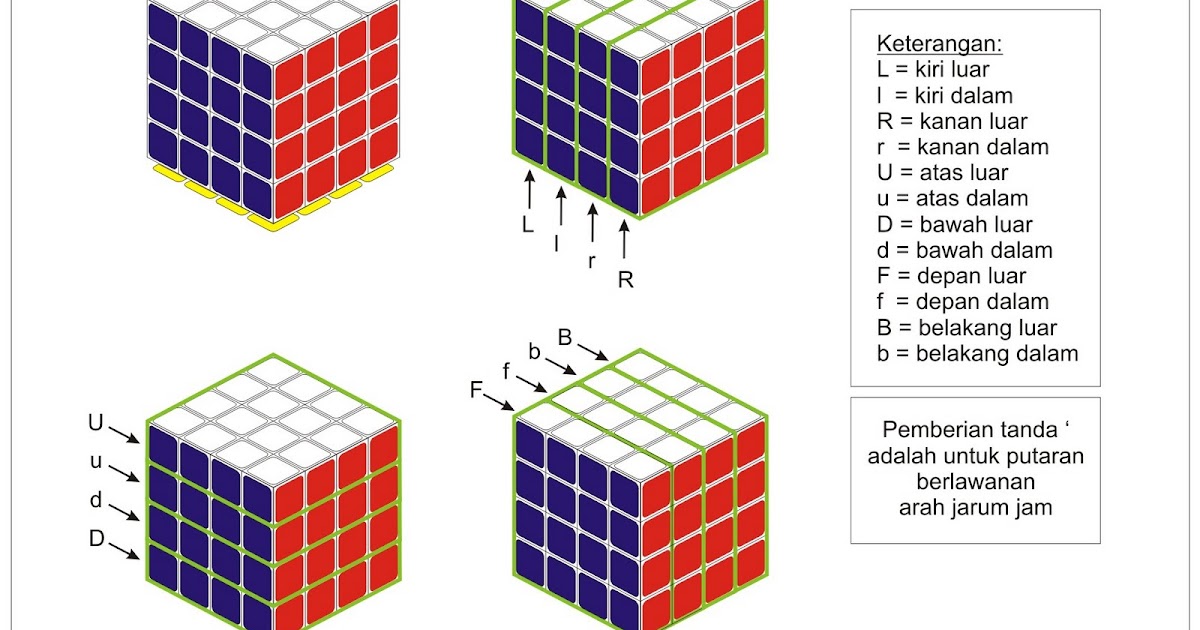 «Если вы полны решимости, вы решите их».
«Если вы полны решимости, вы решите их».
Эрнё Рубик, профессор архитектуры из Венгрии, придумал кубик Рубика в 1974 году. Он создал вращающийся куб размером 3 на 3 дюйма, сделанный из дерева, чтобы обучать своих студентов элементам трехмерного дизайна. . В 1980 году к нему обратилась компания по производству игрушек, заинтересованная в продаже пластиковой версии его изобретения. Это оказалось хитом. На сегодняшний день по всему миру продано 350 миллионов кубиков Рубика. «Если вам любопытно, вы найдете головоломки вокруг себя», — говорит Рубик. «Если вы полны решимости, вы решите их».
СОЗДАТЕЛЬ КУБИКА
Эрнё Рубик, профессор архитектуры из Венгрии, придумал кубик Рубика в 1974 году. дизайн своим ученикам. В 1980 году к нему обратилась компания по производству игрушек, заинтересованная в продаже пластиковой версии его изобретения. Это оказалось хитом. На сегодняшний день по всему миру продано 350 миллионов кубиков Рубика. «Если вам любопытно, вы найдете головоломки вокруг себя», — говорит Рубик. «Если вы полны решимости, вы решите их».
«Если вам любопытно, вы найдете головоломки вокруг себя», — говорит Рубик. «Если вы полны решимости, вы решите их».
Эрнё Рубик, профессор архитектуры из Венгрии, придумал кубик Рубика в 1974 году. Он создал вращающийся куб размером 3 на 3 дюйма, сделанный из дерева, чтобы обучать своих студентов элементам трехмерного дизайна. . В 1980 году к нему обратилась компания по производству игрушек, заинтересованная в продаже пластиковой версии его изобретения. Это оказалось хитом. На сегодняшний день по всему миру продано 350 миллионов кубиков Рубика. «Если вам любопытно, вы найдете головоломки вокруг себя», — говорит Рубик. «Если вы полны решимости, вы решите их».
ИГРА ВКЛЮЧЕНА
Макс увлекся спидкубингом после просмотра видео на YouTube. Он постоянно тренировался со своим кубиком Рубика. Потом, когда ему было 10, он попросился на свое первое соревнование. Его родители согласились. Они подумали, что это может стать прекрасной возможностью для их сына научиться взаимодействовать с другими людьми. «Нам было все равно, выиграет ли он, — говорит Пак. «Мы просто хотели, чтобы он потренировался стоять в очереди, ходить по очереди и слушать указания».
«Нам было все равно, выиграет ли он, — говорит Пак. «Мы просто хотели, чтобы он потренировался стоять в очереди, ходить по очереди и слушать указания».
На мероприятии родители Макса заметили, что он узнал лица спидкуберов, которых видел на YouTube. Он помнил, как они собирали кубики, и был взволнован, увидев их лично. Лучше всего то, что Макс, казалось, развлекался.
Макс смотрел видео спидкубинга на YouTube и был очарован. Он постоянно тренировался со своим кубиком Рубика. Когда ему было 10, он попросился принять участие в своем первом конкурсе. Его родители согласились. Они подумали, что для Макса это может стать отличным способом научиться взаимодействовать с другими. «Нам было все равно, выиграет ли он, — говорит Пак. «Мы просто хотели, чтобы он потренировался стоять в очереди, ходить по очереди и слушать указания».
На мероприятии родители Макса кое-что заметили. Макс видел этих спидкуберов на YouTube и теперь узнал их лица. Он помнил, как они собирали кубики, и был взволнован, увидев их лично. Лучше всего то, что Макс, казалось, развлекался.
Лучше всего то, что Макс, казалось, развлекался.
Когда Максу пришло время соревноваться, его родители не знали, чего ожидать. Ему нужно было решить пять запутанных головоломок как можно быстрее. Максу было дано 15 секунд, чтобы осмотреть каждую, прежде чем запустился таймер. Чтобы подсчитать его баллы, судьи отбрасывали его самое быстрое и самое медленное время и усредняли оставшиеся три. Макс принял вызов.
Когда он закончил, говорит Шван Парк, «мы спросили прохожего: «Хорошо ли его время?» Человек ответил: «100 лучших в мире». Его родители только пожали плечами. Возможно, в мире всего 100 человек этим занимаются, говорили они себе. На самом деле цифра приближается к 100 000. Огромная группа детей и взрослых по всему миру увлекается игрой в кубики, как и Макс.
Максу пора соревноваться. Его родители не знали, чего ожидать. Ему нужно было решить пять запутанных головоломок как можно быстрее. Макс мог потратить 15 секунд, чтобы посмотреть на каждую. Затем запустится таймер.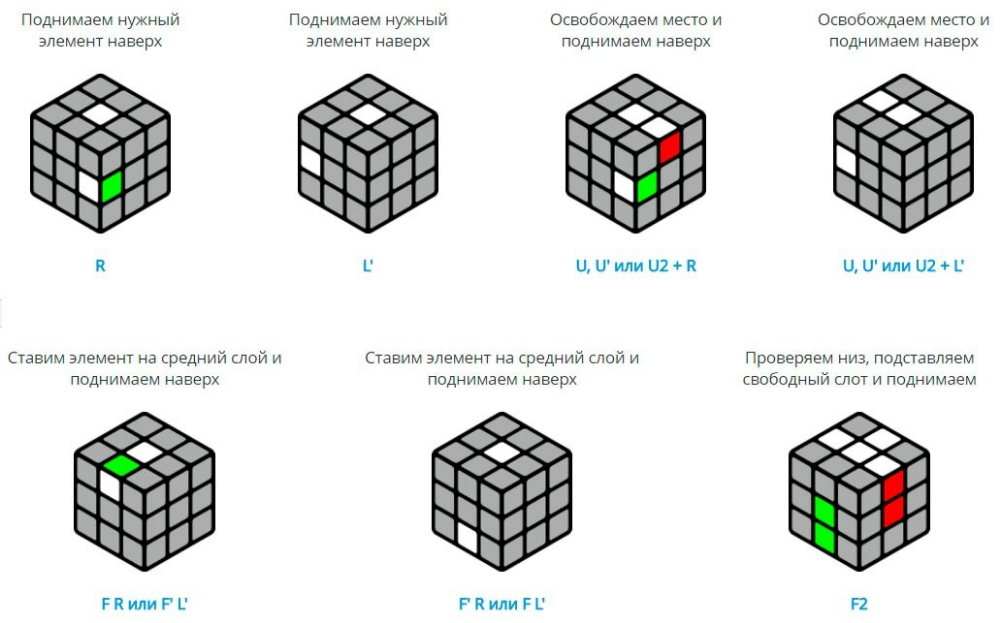 Чтобы сложить его баллы, судьи выбрасывали его самое быстрое и самое медленное время. Они усреднили бы остальные три. Макс принял вызов.
Чтобы сложить его баллы, судьи выбрасывали его самое быстрое и самое медленное время. Они усреднили бы остальные три. Макс принял вызов.
Шван Парк говорит, что, когда Макс закончил, «мы спросили прохожего: «Хорошо ли его время?» Человек ответил: «100 лучших в мире». Его родители только пожали плечами. Возможно, в мире этим занимается всего 100 человек, думали они. Но на самом деле цифра приближается к 100 000. Огромная группа детей и взрослых по всему миру увлекается игрой в кубики, как и Макс.
В следующий раз, когда родители Макса взяли его на соревнования, он занял второе место. Пять лет спустя он установил свой первый мировой рекорд. По последним подсчетам, Макс установил 29 рекордов в шести различных соревнованиях по спидкубингу. Они включают в себя самое быстрое среднее время для сборки четырех кубиков разного размера: 4 x 4, 5 x 5, 6 x 6 и 7 x 7. Он также является рекордсменом по самому быстрому среднему времени для решения традиционных кубиков 3 x 3. куб — одноручный.
Когда родители Макса взяли его на следующий конкурс, он занял второе место. Пять лет спустя он установил свой первый мировой рекорд. По последним подсчетам у Макса было 29рекорды в шести различных соревнованиях по спидкубингу. Они включают в себя самое быстрое среднее время для решения четырех кубов разных размеров. Это кубики 4 x 4, 5 x 5, 6 x 6 и 7 x 7. Он также является рекордсменом по исходному кубу 3 x 3. Это рекорд по самому быстрому среднему времени решения — одной рукой.
НАЙТИ СВОЕ МЕСТО
Родители Макса в восторге от того, что Макс наткнулся на то, что он любит делать и делает лучше, чем кто-либо другой в мире. Но что еще более важно, они в восторге от того, как спидкубинг помог ему чувствовать себя комфортно, просто здороваясь с людьми, которых он встречает.
Родители Макса в восторге. Макс нашел то, чем он любит заниматься, и делает это лучше, чем кто-либо другой в мире. Они рады, что спидкубинг помог ему чувствовать себя комфортно, просто здороваясь с людьми, которых он встречает. И это важнее.
И это важнее.
В окружении своих товарищей-спидкуберов Макс, кажется, нашел свой голос. Феликс Земдегс, австралийский рекордсмен по спидкуберу, впервые встретился с Максом на чемпионате мира по кубингу в 2017 году. «Аутизм Макса мешал поддерживать обычные разговоры, — вспоминает Земдегс. «Но казалось, что он может говорить о спидкубе целыми днями».
Родители Макса всегда надеялись, что их сын дойдет до этого момента. Пак говорит, что они перешли от того, что их сыну сказали, что у их сына аутизм и ему будет нужна помощь до конца жизни, к тому, что он показал им, что возможно: «Макс заставил нас все переосмыслить».
Кажется, Макс нашел свой голос среди других спидкуберов. Феликс Земдегс — австралийский спидкубер-рекордсмен. Впервые он встретил Макса на чемпионате мира по кубингу в 2017 году. «Из-за аутизма у Макса было сложно вести обычные разговоры, — вспоминает Земдегс. «Но казалось, что он может говорить о спидкубе целыми днями».
Родители Макса всегда надеялись, что их сын дойдет до этого момента. Пак помнит, как им сказали, что у их сына аутизм и ему всю оставшуюся жизнь будет нужна помощь. Теперь Макс показывает им, что возможно: «Макс заставил нас все переосмыслить».
Пак помнит, как им сказали, что у их сына аутизм и ему всю оставшуюся жизнь будет нужна помощь. Теперь Макс показывает им, что возможно: «Макс заставил нас все переосмыслить».
ПОНИМАНИЕ АУТИЗМА
ЧТО ТАКОЕ АУТИЗМ?
Расстройство аутистического спектра — это состояние, связанное с развитием мозга. Аутизм влияет на каждого человека по-разному и в разной степени. Как правило, у людей с аутизмом есть сенсорные проблемы, а также трудности в общении и социализации. Они также могут сосредоточиваться на определенных действиях и повторять определенные действия.
Расстройство аутистического спектра — это состояние, связанное с развитием мозга. Аутизм влияет на каждого человека по-разному и в разной степени. Как правило, у людей с аутизмом есть сенсорные проблемы, а также трудности в общении и социализации. Они также могут сосредоточиваться на определенных действиях и повторять определенные действия.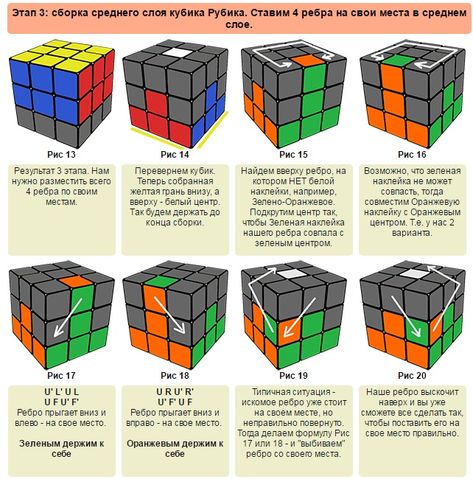
ЧТО ВЫЗЫВАЕТ АУТИЗМ?
В настоящее время причина неизвестна. Но исследования показывают, что генов , или единиц наследственного материала, и факторы окружающей среды оба вовлечены. Врачи совершенствуются в ранней диагностике аутизма, что позволяет им действовать раньше, чтобы уменьшить его симптомы.
В настоящее время причина неизвестна. Но исследования показывают, что генов , или единиц наследственного материала, и факторы окружающей среды оба вовлечены. Врачи совершенствуются в ранней диагностике аутизма, что позволяет им действовать раньше, чтобы уменьшить его симптомы.
У КОГО АУТИЗМ?
По оценкам, 3,5 миллиона человек в США страдают расстройствами аутистического спектра. По данным Центров по контролю и профилактике заболеваний, у 1 из 59 детей, родившихся в этом году, будет аутизм. Заболевание встречается во всех расовых, этнических и социальных группах. Но у мальчиков в четыре раза больше шансов диагностировать аутизм, чем у девочек.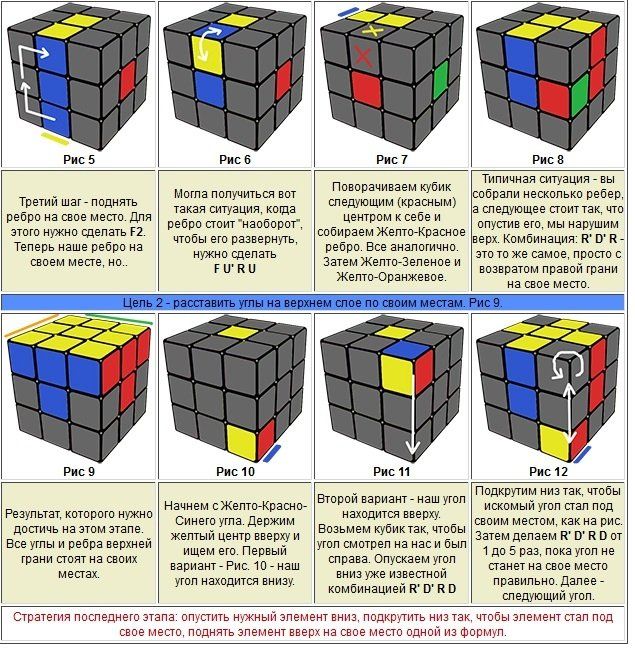
Приблизительно 3,5 миллиона человек в США страдают расстройствами аутистического спектра. По данным Центров по контролю и профилактике заболеваний, у 1 из 59 детей, родившихся в этом году, будет аутизм. Заболевание встречается во всех расовых, этнических и социальных группах. Но у мальчиков в четыре раза больше шансов диагностировать аутизм, чем у девочек.
ВОЗДЕЙСТВИЕ НА МОЗГ
Ученые изучают мозг, чтобы узнать об аутизме. Необходимы дополнительные исследования. Вот некоторые области, связанные с условием.
Ученые изучают мозг, чтобы узнать об аутизме. Необходимы дополнительные исследования. Вот некоторые области, связанные с условием.
КОРА МОЗГА: Внешний слой мозга участвует в социальном поведении и интерпретации сенсорных импульсов. Измененные структуры и нервные связи здесь могут повлиять на людей с аутизмом.
КОРА МОЗГА: Внешний слой мозга участвует в социальном поведении и интерпретации сенсорных импульсов. Измененные структуры и нервные связи здесь могут повлиять на людей с аутизмом.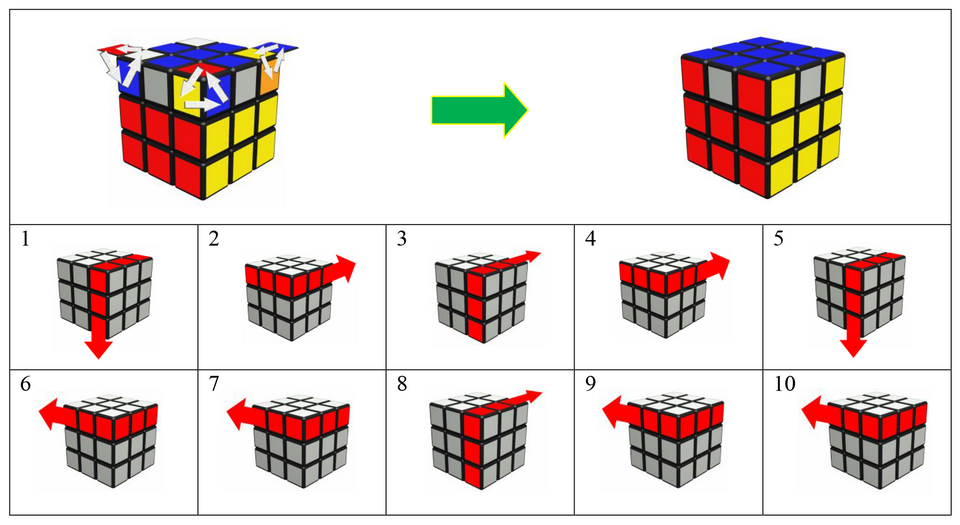
МИНДАЛА: Миндалевидное тело влияет на такие эмоции, как гнев и страх. У детей с аутизмом он часто бывает очень большим, что может влиять на то, как они воспринимают и регулируют свои чувства.
АМИГДАЛА: Миндалевидное тело влияет на такие эмоции, как гнев и страх. У детей с аутизмом он часто бывает очень большим, что может влиять на то, как они воспринимают и регулируют свои чувства.
ВИСОЧНАЯ ДОЛЯ: Височная доля представляет собой отдел коры головного мозга. Он играет роль в интерпретации того, что люди видят, включая выражение лица. У людей с аутизмом в этой области изменены нервные связи.
ВИСОЧНАЯ ДОЛЯ: Височная доля представляет собой часть коры головного мозга. Он играет роль в интерпретации того, что люди видят, включая выражение лица. У людей с аутизмом в этой области изменены нервные связи.
ГИППОКАМП: Гиппокамп играет ключевую роль в формировании воспоминаний. У многих людей с аутизмом он увеличен, что влияет на то, как они интерпретируют окружающий мир.
ГИППОКАМП: Гиппокамп играет ключевую роль в формировании воспоминаний. У многих людей с аутизмом он увеличен, что влияет на то, как они интерпретируют окружающий мир.
МОЗЖ: Эта часть мозга отвечает за равновесие и движения. У людей с аутизмом снижено количество специализированных нервных клеток, участвующих в моторном контроле в этой области.
Мозжечок: Эта часть мозга контролирует равновесие и движения. У людей с аутизмом снижено количество специализированных нервных клеток, участвующих в моторном контроле в этой области.
ПОНИМАНИЕ АУТИЗМА
ЧТО ТАКОЕ АУТИЗМ?
Расстройство аутистического спектра — это состояние, связанное с развитием мозга. Аутизм влияет на каждого человека по-разному и в разной степени. Как правило, у людей с аутизмом есть сенсорные проблемы, а также трудности в общении и социализации. Они также могут сосредоточиваться на определенных действиях и повторять определенные действия.
Они также могут сосредоточиваться на определенных действиях и повторять определенные действия.
Расстройство аутистического спектра — это состояние, связанное с развитием мозга. Аутизм влияет на каждого человека по-разному и в разной степени. Как правило, у людей с аутизмом есть сенсорные проблемы, а также трудности в общении и социализации. Они также могут сосредоточиваться на определенных действиях и повторять определенные действия.
ЧТО ВЫЗЫВАЕТ АУТИЗМ?
В настоящее время причина неизвестна. Но исследования показывают, что генов , или единиц наследственного материала, и факторы окружающей среды оба вовлечены. Врачи совершенствуются в ранней диагностике аутизма, что позволяет им действовать раньше, чтобы уменьшить его симптомы.
В настоящее время причина неизвестна. Но исследования показывают, что генов , или единиц наследственного материала, и факторы окружающей среды оба вовлечены. Врачи совершенствуются в ранней диагностике аутизма, что позволяет им действовать раньше, чтобы уменьшить его симптомы.
У КОГО АУТИЗМ?
По оценкам, 3,5 миллиона человек в США страдают расстройствами аутистического спектра. По данным Центров по контролю и профилактике заболеваний, у 1 из 59 детей, родившихся в этом году, будет аутизм. Заболевание встречается во всех расовых, этнических и социальных группах. Но у мальчиков в четыре раза больше шансов диагностировать аутизм, чем у девочек.
По оценкам, 3,5 миллиона человек в США страдают расстройствами аутистического спектра. По данным Центров по контролю и профилактике заболеваний, 1 из 59у детей, родившихся в этом году, будет аутизм. Заболевание встречается во всех расовых, этнических и социальных группах. Но у мальчиков в четыре раза больше шансов диагностировать аутизм, чем у девочек.
ВОЗДЕЙСТВИЕ НА МОЗГ
Ученые изучают мозг, чтобы узнать об аутизме. Необходимы дополнительные исследования. Вот некоторые области, связанные с условием.
Ученые изучают мозг, чтобы узнать об аутизме. Необходимы дополнительные исследования. Вот некоторые области, связанные с условием.
Вот некоторые области, связанные с условием.
КОРА МОЗГА: Внешний слой мозга участвует в социальном поведении и интерпретации сенсорных импульсов. Измененные структуры и нервные связи здесь могут повлиять на людей с аутизмом.
КОРА МОЗГА: Внешний слой мозга участвует в социальном поведении и интерпретации сенсорных импульсов. Измененные структуры и нервные связи здесь могут повлиять на людей с аутизмом.
АМИГДАЛА: Миндалевидное тело влияет на такие эмоции, как гнев и страх. У детей с аутизмом он часто бывает очень большим, что может влиять на то, как они воспринимают и регулируют свои чувства.
МИНДАЛА: Миндалевидное тело влияет на такие эмоции, как гнев и страх. У детей с аутизмом он часто бывает очень большим, что может влиять на то, как они воспринимают и регулируют свои чувства.
ВИСОЧНАЯ ДОЛЯ: Височная доля представляет собой отдел коры головного мозга. Он играет роль в интерпретации того, что люди видят, включая выражение лица. У людей с аутизмом в этой области изменены нервные связи.
У людей с аутизмом в этой области изменены нервные связи.
ВИСОЧНАЯ ДОЛЯ: Височная доля представляет собой отдел коры головного мозга. Он играет роль в интерпретации того, что люди видят, включая выражение лица. У людей с аутизмом в этой области изменены нервные связи.
ГИППОКАМП: Гиппокамп играет ключевую роль в формировании воспоминаний. У многих людей с аутизмом он увеличен, что влияет на то, как они интерпретируют окружающий мир.
ГИППОКАМП: Гиппокамп играет ключевую роль в формировании воспоминаний. У многих людей с аутизмом он увеличен, что влияет на то, как они интерпретируют окружающий мир.
Мозжечок: Эта часть мозга контролирует равновесие и движения. У людей с аутизмом снижено количество специализированных нервных клеток, участвующих в моторном контроле в этой области.
МОЗЖ: Эта часть мозга отвечает за равновесие и движения. У людей с аутизмом снижено количество специализированных нервных клеток, участвующих в моторном контроле в этой области.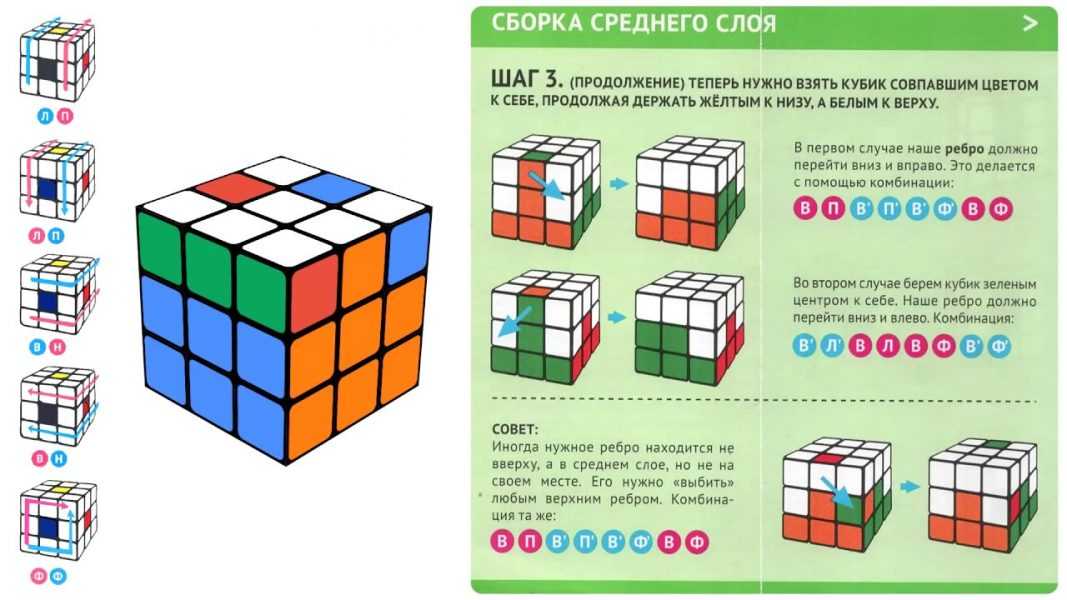
ОСНОВНОЙ ВОПРОС: Как спидкубинг помогает Максу справиться с некоторыми трудностями, с которыми он сталкивается?
ДОПОЛНИТЕЛЬНОЕ СОДЕРЖИМОЕ
видео
(1)
Таблицы навыков
(4)
Таблицы навыков
(4)
Таблицы навыков
(4)
Таблицы навыков
(4)
План урока
(2)
План урока
(2)
Текст в речь
Обычный
Медленный
Краткая история кубика Рубика | Инновация
Чтобы решить головоломку, вы должны крутить кубики так, чтобы в конце концов каждая сторона вернулась к своему первоначальному цвету: проблема заключается в поразительном количестве возможных вариантов — более 43 квинтиллионов из них.
Эндрю Спенсер / Автор
Весной 1974 года молодой венгерский архитектор по имени Эрно Рубик стал одержим поиском способа моделирования трехмерного движения для своих учеников. Потратив месяцы на возню с блоками кубиков — сделанными из дерева и бумаги, скрепленными резинками, клеем и скрепками — он, наконец, создал то, что назвал «Bűvös kocka», или «Волшебный куб».0003
Изобретение, впоследствии переименованное в кубик Рубика, станет самой популярной игрушкой-головоломкой в мире: по состоянию на 2018 год было продано более 350 миллионов штук. арены, где подростки соревнуются, чтобы собрать головоломку за минимальное время.
Но поначалу никто не был так ошеломлен безудержным успехом куба, как его создатель, как он объясняет в своей новой книге 9.1717 В кубе: загадка всех нас . Влияние куба было «гораздо более интересным, чем сам куб», — сказал Рубик в интервью Undark . По его словам, книга посвящена попытке понять ее популярность и «почему люди ее любят».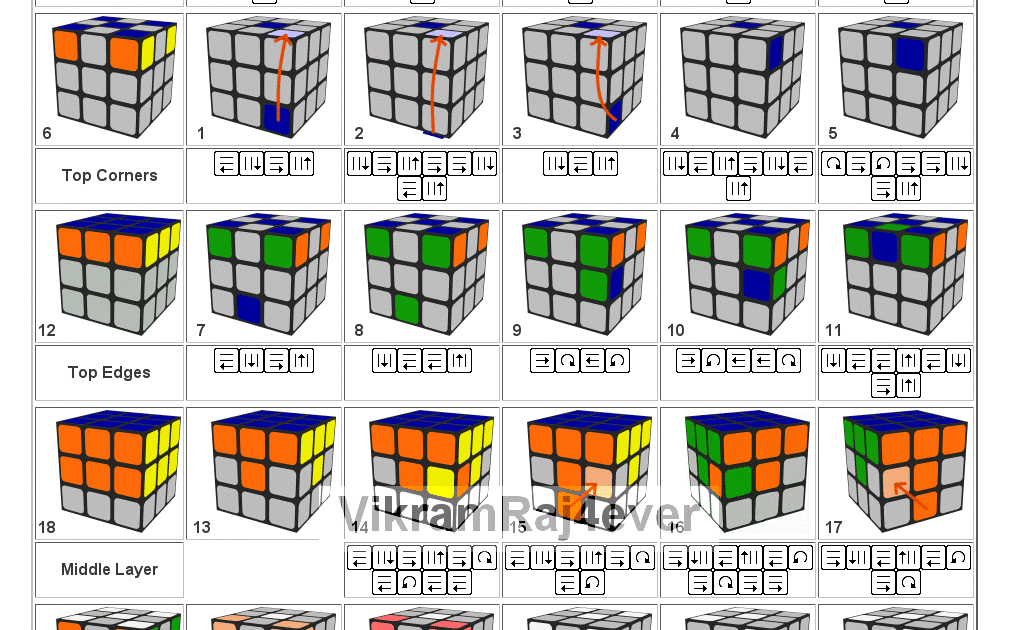
На первый взгляд куб кажется обманчиво простым, с каждой стороной по девять цветных квадратов. В исходном состоянии каждая сторона имеет однородный цвет — красный, зеленый, желтый, оранжевый, синий или белый. Чтобы решить головоломку, вы должны крутить кубики так, чтобы в конце концов каждая сторона вернулась к своему первоначальному цвету: задача состоит в поразительном количестве возможных вариантов — более 9.1717 г. 43 квинтиллиона из них.
Чтобы освоить куб, вы должны выучить последовательность движений, которые можно выполнять в последовательном порядке — предмет нескольких бестселлеров, а также онлайн-уроков. А эволюция куба — от формы три на три на три к более крупным кубам четыре на четыре на четыре и пять на пять на пять — предлагает различные сложные математические принципы теории групп. .
Рубик изначально полагал, что куб понравится тем, кто имеет образование в области естественных наук, математики или инженерии, и был потрясен, когда «нашел путь к людям, которых никто и представить не мог, что он может их привлечь», — пишет он.
В марте 1981 года Куб попал на обложку Scientific American , где лауреат Пулитцеровской премии ученый Дуглас Хофштадтер, автор книги «Гёдель, Эшер, Бах» (1979), назвал его «одной из самых удивительных вещей, когда-либо существовавших». изобретен для обучения математическим идеям».
Куб показался Хофштадтеру «парадоксальным», сказал он в телефонном интервью, поскольку его можно использовать в качестве инструмента для обучения теории групп или симметрии объектов. «Любой поворот любой грани (по часовой 90 градусов, против часовой 900 градусов или 180 градусов) — это групповой элемент, как и произвольные последовательности таких поворотов», — объяснил он позже по электронной почте.
Сидя во внутреннем дворике своего дома на холмах Будапешта, Рубик, которому сейчас 76 лет, возился с кубиком, вспоминая его «открытие» и случайный успех. (Он предпочитает использовать «открыл», а не «изобрел» — как будто существование объекта было каким-то образом предопределено).
После создания куба, объяснил он, он столкнулся со второй проблемой: как ее решить. В то время он понятия не имел, можно ли вернуть его куб на место, не говоря уже о том, как быстро — и ему потребовался целый месяц, чтобы решить собственную головоломку. Было чертовски трудно «найти обратный путь или найти цель — просто решить ее как комбинаторную задачу», — сказал он. «И у меня не было для этого никакого образования, потому что я был первым, кто попытался».
Cubed: головоломка для всех нас
Первая книга изобретателя-затворника самой знаменитой головоломки в мире — кубика Рубика. Эрно Рубик вдохновляет нас тем, чему он научился за всю жизнь творчества, любопытства и открытий.
Рубик описывает Кубик как произведение отшельника, который «выходит из тени». Он называет себя «конкретным и интуитивным мыслителем» и изобретателем-любителем, но, как и его изобретение, он не поддается категоризации. Его резюме включает в себя работу профессором, архитектором, дизайнером, редактором, а теперь и писателем.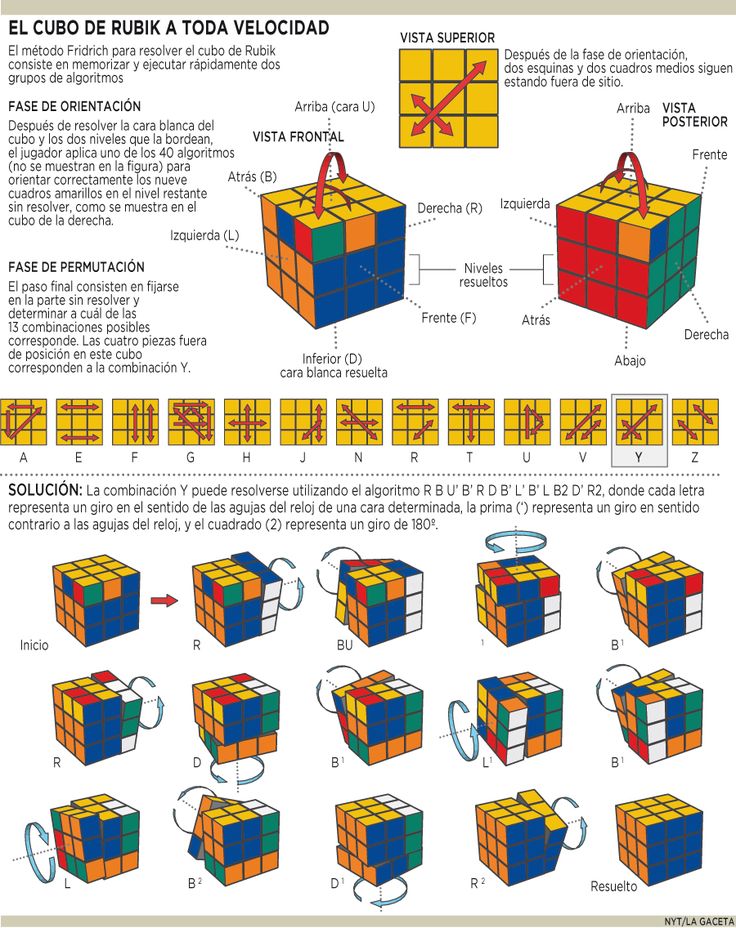 Рубик гордится своей способностью к самообучению и возмущается мыслью о том, что те, кто обладает властью, лучше всех могут делиться знаниями.
Рубик гордится своей способностью к самообучению и возмущается мыслью о том, что те, кто обладает властью, лучше всех могут делиться знаниями.
В его заявке, поданной в Венгерское патентное ведомство в 1975 году, куб назван «игрушкой пространственной логики». В то время Венгрия находилась за «железным занавесом» — до 1989 года она оставалась контролируемым коммунистами государством Восточного блока — и, как пишет Рубик, у страны «не было особого интереса к производству игрушек».
В то время пазлы были лишь небольшой частью общего рынка игрушек — их можно было найти только в сувенирных и специализированных магазинах — и представление о пазлах как об игрушках было новой концепцией. Он появился в венгерских магазинах игрушек в 1977, и была представлена на международных ярмарках игрушек, таких как Нюрнбергская ярмарка игрушек 1979 года, где ее заметил Том Кремер, маркетолог, который представил эту концепцию компании Ideal Toy Company в США. К началу 1980-х куб был показан в рекламных роликах и рекламе на американском телевидении, а в 1983 году стал звездой мультсериала под названием «Рубик, удивительный куб».
Успех куба оказался недолгим: в 1982 году газета New York Times заявила, что он «устарел» и назвала его «причудой», утверждение, которое не выдержало испытания временем. «Куб был слишком вечным, слишком удивительным сооружением, чтобы люди могли потерять к нему интерес», — сказал Хофштадтер. И хотя интерес к кубу упал, недавно он снова возродился, как показывает режиссер Сью Ким в своем новом документальном фильме «Куберы скорости».
Ким начала возить сына на соревнования по сборке кубиков и была очарована всемирной популярностью этой головоломки. Ким документирует то, как дети осваивают аналоговый инструмент, используя инструменты цифровой эпохи — учебные пособия на YouTube, статьи и многое другое — и создает онлайн-сообщества, посвященные их любви к кубу. «Я действительно думаю, что он нашел новую нишу в популярной культуре из-за своего погружения в цифровой ландшафт», — сказал Ким в видеочате.
Хофштадтер слышал о спидкуберах и считает вполне уместным, что объект выжил.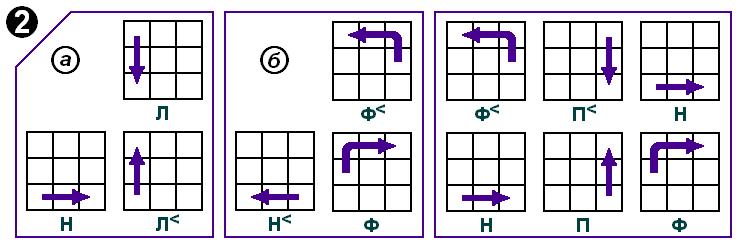 «Это абсолютно заслуженно», — сказал он. «Это чудесный объект, чудесное изобретение, прекрасное изобретение, глубокое изобретение».
«Это абсолютно заслуженно», — сказал он. «Это чудесный объект, чудесное изобретение, прекрасное изобретение, глубокое изобретение».
При всей своей привлекательности для математических навыков и логики, широкая популярность Куба может быть связана с почти безграничным числом возможных решений. «Это одно из самых загадочных его качеств», — пишет Рубик. «Конец превращается в новые начала».
Эта статья была первоначально опубликована на Undark Читать оригинал статьи
Рекомендуемые видео
Самый быстрый способ собрать кубик Рубика
Научные проекты
Реферат
Если вам нравится решать сложные головоломки, это может быть хорошим проектом для вас. В этом проекте вы исследуете различные методы сборки кубика Рубика, а затем проведете эксперимент, чтобы сравнить их друг с другом. Какой метод работает быстрее?
Краткое изложение
Чистая математика
Длинный (2-4 недели)
Для выполнения этого проекта вам должно нравиться решать головоломки и мыслить в трех измерениях.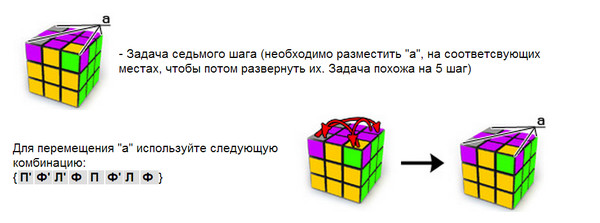
Всегда в наличии
Очень низкий (менее 20 долларов США)
Нет проблем
Эндрю Олсон, доктор философии, Science Buddies
Цель
Цель этого проекта — сравнить различные методы сборки кубика Рубика. Какой метод обеспечивает самое быстрое решение?
Введение
Кубик Рубика — интересная трехмерная головоломка, бросающая вызов вашему пространственному воображению и памяти. Цель состоит в том, чтобы расположить куб так, чтобы каждая сторона была сплошного цвета, как показано на рис. 1.
На рис. 1 также показаны обозначения, которые мы будем использовать для обозначения сторон куба. Шесть сторон названы попарно: вверх-вниз, спереди-сзади и слева-справа. Для обозначения определенной стороны мы будем использовать однобуквенные сокращения, показанные на рис. 1 (U, D, F, B, L, R).
Куб построен таким образом, что каждая сторона, строка и столбец могут вращаться (см. рис. 2). С помощью нескольких оборотов цвета могут быть тщательно перемешаны. Как вернуть все квадраты в исходное положение? Это настоящая головоломка, чтобы снова правильно расположить цвета!
рис. 2). С помощью нескольких оборотов цвета могут быть тщательно перемешаны. Как вернуть все квадраты в исходное положение? Это настоящая головоломка, чтобы снова правильно расположить цвета!
В этом проекте вы изучите как минимум два различных метода сборки кубика Рубика, а затем выясните, какой из них работает быстрее всего. . Кубик Рубика состоит из трех разных частей. Мы будем называть их центр , угол и край штук. Головоломка состоит из шести центральных частей, по одной в середине каждой грани. Каждая центральная часть имеет только одну видимую грань. В головоломке восемь угловых частей. Каждый угловой элемент имеет три видимые грани. Остальные двенадцать фигур являются краевыми фигурами, занимающими среднюю позицию вдоль каждого края куба. Каждая кромка имеет две видимые грани.
Для каждого шага в сборке куба пригодится определенная последовательность ходов. Чтобы эффективно суммировать последовательности ходов, мы будем использовать сокращенную запись, распространенную среди решателей кубика Рубика. Сокращенную запись легко выучить. Есть всего два правила, которые вам нужно знать.
Сокращенную запись легко выучить. Есть всего два правила, которые вам нужно знать.
- Когда сторона поворачивается по часовой стрелке на четверть оборота, сокращенное обозначение движения — это просто буква стороны. Например, если вы должны повернуть правую сторону на четверть оборота по часовой стрелке, сокращение будет 9.1568 р .
- Когда сторона поворачивается против часовой стрелки на четверть оборота, сокращенное обозначение движения представляет собой букву + апостроф (‘). Например, если вы должны повернуть правую сторону против часовой стрелки на четверть оборота, сокращение будет R’ .
Теперь, когда вы знакомы с основной терминологией, используемой для обозначения кубика Рубика, вы можете приступить к изучению различных методов решения. Вы можете использовать ресурсы в приведенной ниже библиографии, чтобы начать работу, но вы сможете найти много других ресурсов по кубику Рубика в Интернете.
Термины и понятия
Чтобы выполнить этот проект, вы должны провести исследование, которое позволит вам понять следующие термины и понятия:
- Кубик Рубика:
- Как он движется
- Терминология:
- Угловые элементы (8)
- Кромки (12)
- Центральные элементы (или боковые элементы, 6)
Вопросы
- Сколько видимых граней имеет ребро? Центральная часть? Угловой элемент?
г.
Библиография
- Вот несколько способов собрать кубик Рубика с пошаговыми инструкциями. Вы можете найти гораздо больше, выполнив поиск в Интернете.
- Beust, C., 2003. Решение кубика Рубика, которое легко запомнить. Проверено 3 января 2007 г.
- Lee, J., nd Сборка кубика Рубика для начинающих. Проверено 29 апреля 2009 г.
- Петрус Л. 1997. Сборка кубика Рубика на скорость. Проверено 3 января 2007 г.
- Youcandothecube.com. (н.д.). Вы МОЖЕТЕ собрать кубик Рубика. Проверено 23 ноября 2010 г.
.
.
.
г.
Материалы и оборудование
Для проведения эксперимента вам потребуются следующие материалы и оборудование:
- Кубик Рубика
- Таймер
Экспериментальная процедура
- Проведите предварительное исследование, чтобы ознакомиться с приведенными выше терминами, понятиями и вопросами.

- Если вы уже можете собрать кубик Рубика до выполнения этого проекта, вашим первым шагом должно быть измерение среднего времени решения. Засеките время для каждой из 5–10 попыток и рассчитайте среднее время решения. Куб должен быть хорошо рандомизирован для каждого испытания.
- Проведите фоновое исследование, чтобы определить первый метод сборки кубика Рубика.
- Потренируйтесь, используя каждый набор ходов на кубике Рубика.
- Убедитесь, что каждая последовательность работает, как описано.
- Достаточно хорошо изучите каждый набор ходов, чтобы вы могли пройти последовательность в своем воображении, не имея куба в руках.
- Потренируйтесь собирать куб, используя указанные выше движения.
- Засеките 10 или более попыток и посмотрите, сколько времени в среднем вам потребуется, чтобы решить головоломку. Куб должен быть хорошо рандомизирован для каждого испытания.
- Если бы вы смогли решить головоломку до того, как начали проект, улучшилось ли среднее время решения?
- Повторите процесс для второго метода сборки кубика Рубика.

- Изучите метод и убедитесь, что каждая последовательность работает, как описано.
- Достаточно хорошо изучите каждый набор ходов, чтобы вы могли пройти последовательность в своем воображении, не имея куба в руках.
- Потренируйтесь собирать куб. Выделите себе столько же времени на практику, как и в первом методе.
г.
- Выполните 10 или более попыток и посмотрите, сколько времени в среднем вам потребуется, чтобы решить головоломку с помощью нового метода. Куб должен быть хорошо рандомизирован для каждого испытания.
- Какой метод быстрее? Почему?
г.
г.
Задать вопрос эксперту
У вас есть конкретные вопросы о вашем научном проекте? Наша команда ученых-добровольцев может помочь. Наши эксперты не сделают всю работу за вас, но они сделают предложения, дадут рекомендации и помогут устранить неполадки.
Опубликовать вопрос
Варианты
- Проект по геометрическим узорам с помощью кубика Рубика см.
 в проекте Science Buddies Создание узоров с помощью кубика Рубика.
в проекте Science Buddies Создание узоров с помощью кубика Рубика. - Подробный эксперимент с кубиком Рубика см. в проекте Science Buddies «Разработка алгоритма сборки кубика Рубика».
Вакансии
Если вам нравится этот проект, вы можете изучить следующие родственные профессии:
- Руководство по проекту научной ярмарки
- Другие подобные идеи
- Идеи проекта «Чистая математика»
- Мои любимые
Лента новостей по этой теме
,
,
Цитировать эту страницу
Общая информация о цитировании представлена здесь. Обязательно проверьте форматирование, включая заглавные буквы, для используемого метода и при необходимости обновите цитату.
Стиль MLA
Сотрудники научных друзей.
«Какой самый быстрый способ собрать кубик Рубика?» Научные друзья ,
25 марта 2022 г. ,
,
https://www.sciencebuddies.org/science-fair-projects/project-ideas/Math_p023/pure-mathematics/what-is-the-fast-way-to-solve-rubiks-cube.
По состоянию на 28 сентября 2022 г.
APA Style
Сотрудники научных друзей.
(2022, 25 марта).
Какой самый быстрый способ собрать кубик Рубика?
Извлекаются из
https://www.sciencebuddies.org/science-fair-projects/project-ideas/Math_p023/pure-mathematics/what-is-the-fast-way-to-solve-rubiks-cube
Дата последнего редактирования: 25.03.2022
Ознакомьтесь с нашими научными видео
Смоделируйте легочную инфекцию
Как сделать винт Архимеда — Упражнение STEM
Насколько сильны ваши волосы? – STEM Activity
LEADERS Интервью с Полом Хоффманом, президентом и главным исполнительным директором Liberty Science Center
Интервью с Полом Хоффманом,
Президент и главный исполнительный директор,
Liberty Science Center
Примечание редактора
Пол Хоффман также является креативным директором Beyond Rubik’s Cube, а также журналистом и биографом. Он является автором 11 книг, последняя из которых — мемуары о мировом чемпионате по шахматам, «Королевский гамбит: сын, отец и самая опасная партия в мире». Первая биография Хоффмана «Человек, который любил только числа: история Пауля Эрдёша и поиски математической истины» стала международным бестселлером. Она была опубликована на 16 языках и получила приз Рона-Пуленка как лучшая научная книга года. Хоффман является лауреатом первой Национальной премии журналов за художественные статьи. Он долгое время был президентом и главным редактором журнала Discover, президентом и издателем Encyclopaedia Britannica, а совсем недавно — председателем редакции сайта видеоинтервью BigThink. Он является известным экспертом по общественному пониманию науки и консультировал НАСА и другие организации. Хоффман, избранный в Американскую академию искусств и наук, с отличием окончил Гарвардский колледж и получил степень Phi Beta Kappa. Он появился в «Поздней ночи с Дэвидом Леттерманом» и «Шоу Опры Уинфри». Он является совладельцем двух бруклинских ресторанов Rucola и BrisketTown, а также инвестором RockPaperRobot.
Он является автором 11 книг, последняя из которых — мемуары о мировом чемпионате по шахматам, «Королевский гамбит: сын, отец и самая опасная партия в мире». Первая биография Хоффмана «Человек, который любил только числа: история Пауля Эрдёша и поиски математической истины» стала международным бестселлером. Она была опубликована на 16 языках и получила приз Рона-Пуленка как лучшая научная книга года. Хоффман является лауреатом первой Национальной премии журналов за художественные статьи. Он долгое время был президентом и главным редактором журнала Discover, президентом и издателем Encyclopaedia Britannica, а совсем недавно — председателем редакции сайта видеоинтервью BigThink. Он является известным экспертом по общественному пониманию науки и консультировал НАСА и другие организации. Хоффман, избранный в Американскую академию искусств и наук, с отличием окончил Гарвардский колледж и получил степень Phi Beta Kappa. Он появился в «Поздней ночи с Дэвидом Леттерманом» и «Шоу Опры Уинфри». Он является совладельцем двух бруклинских ресторанов Rucola и BrisketTown, а также инвестором RockPaperRobot.
Краткий обзор организации
Центр науки Свободы (LSC.org) — это учебный центр площадью 300 000 квадратных футов, расположенный в парке штата Либерти на берегу Гудзона в Джерси-Сити, рядом со Статуей Свободы. В научном центре Liberty есть 12 музейных выставочных залов, коллекция живых животных со 110 видами, гигантские аквариумы, 3D-театр, крупнейший в мире купольный кинотеатр IMAX, операции с одновременной трансляцией в прямом эфире, симулятор ветра силы торнадо, классы и лаборатории K-12, а также программы развития учителей. Ежегодно Научный центр посещают более 650 000 учащихся, учителей и родителей, и еще десятки тысяч участвуют в программах Центра за пределами офиса и в онлайн-программах.
Каково наследие Научного центра Свободы и остается ли его миссия неизменной?
С тех пор, как мы открыли свои двери в 1993 году, наша миссия заключалась в том, чтобы вдохновлять следующее поколение ученых и инженеров, но в последнее время она изменилась. Наша миссия сейчас — вдохновлять следующее поколение ученых, инженеров и технологических предпринимателей.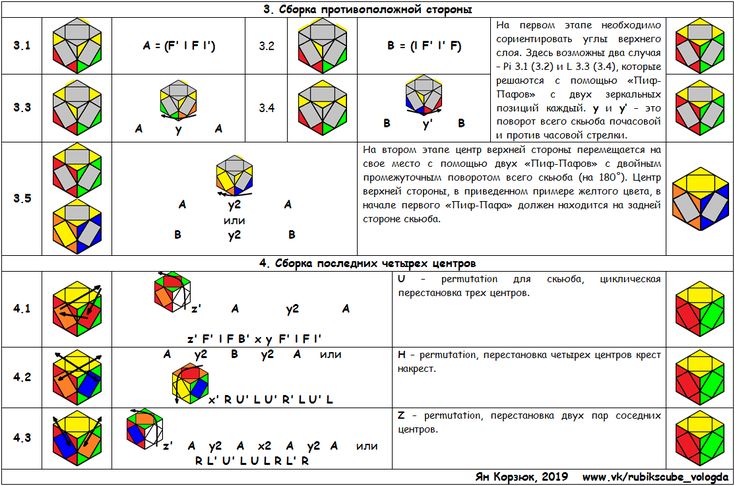 Наш мир стал интересным местом, где такие компании, как EY и JPMorgan, которые представлены в совете директоров Liberty Science Center и щедро поддерживают наши усилия, стали технологическими компаниями.
Наш мир стал интересным местом, где такие компании, как EY и JPMorgan, которые представлены в совете директоров Liberty Science Center и щедро поддерживают наши усилия, стали технологическими компаниями.
Весь мир теперь другой. Каждой компании нужны высококвалифицированные специалисты в области программирования, веб-дизайна и интеллектуального анализа данных. Даже если вы не фармацевтическая или энергетическая компания, вам необходимо иметь технически подкованных сотрудников.
Молодой студент в летнем лагере
Liberty Science Center
Какой подход вы используете при выполнении этой миссии?
Мы являемся крупнейшим культурным учреждением в Нью-Джерси по посещаемости: у нас более 650 000 гостей в год, и мы являемся крупнейшим интерактивным научным центром в столичном районе Нью-Йорка/Нью-Джерси.
Каждый ребенок рождается ученым, а это означает, что у него есть естественное любопытство к миру. К сожалению, что-то в нашей формальной системе образования и, возможно, в нашем обществе слишком часто подавляет это любопытство. Ученые и технологи с картами переносят это любопытство во взрослую жизнь и в конечном итоге работают в этих областях.
Ученые и технологи с картами переносят это любопытство во взрослую жизнь и в конечном итоге работают в этих областях.
В Научном центре Свободы мы пытаемся сохранить эту искру для младших детей. Например, по мере того, как мы добираемся до старшеклассников, мы напрямую знакомим их с возможными карьерами в области науки, технологий, инженерии, здравоохранения, компьютерного программирования и робототехники. Мы стараемся предоставить любое дополнительное наставничество, которое им может понадобиться, чтобы оставаться в процессе их карьеры.
Не уделяют ли этим программам должного внимания в школах, и можно ли сделать больше, чтобы вывести их на передний план?
Начинается делать больше. Ряд штатов объединились и создали Научные стандарты следующего поколения, которые сводятся к изучению науки путем ее занятия. Если я собираюсь научить ребенка, что такое гравитация, я не должен просто стоять перед аудиторией и проповедовать о том, как падают все предметы; Я должен бросить предмет.
Все науки лучше всего изучать, занимаясь ими; это стимулирует воображение и облегчает понимание концепций. Это не теоретические концепции; это концепции о том, как устроен реальный мир, поэтому мы должны изучать их, занимаясь реальной наукой.
Школьные системы, которые двигались в этом направлении, добились гораздо лучших результатов, и это наш хлеб с маслом в Liberty Science Center. У нас, вероятно, больше классных комнат и лабораторий, чем в любом другом научном центре США. 250 000 школьников K-12, которые ежегодно приезжают сюда, приходят не только для того, чтобы побегать по нашим выставочным залам; они приходят за управляемыми лабораторными экспериментами, основанными на запросах, которые соответствуют возрасту.
Даже детсадовцы занимаются здесь элементарными науками, в то время как старшеклассники занимаются очень сложными науками, и, поскольку они заняты, все больше детей открывают для себя, что наука увлекательна.
Насколько сложно разрабатывать программы для такого широкого возрастного диапазона?
В нашей работе много движущихся частей, но у нас есть специалисты, которые проводят программы, например, для детей дошкольного возраста. Мы также полагаемся на многих внешних экспертов из сообщества Нью-Джерси/Нью-Йорка из таких учреждений, как Stevens, Rutgers и Princeton, а также на врачей из Barnabas, Atlantic Health и Columbia Presbyterian. Многие люди поддерживают нашу миссию и приезжают сюда, чтобы работать со студентами.
Мы также полагаемся на многих внешних экспертов из сообщества Нью-Джерси/Нью-Йорка из таких учреждений, как Stevens, Rutgers и Princeton, а также на врачей из Barnabas, Atlantic Health и Columbia Presbyterian. Многие люди поддерживают нашу миссию и приезжают сюда, чтобы работать со студентами.
Вам приходится самим создавать многие выставки, чтобы удовлетворить ваше передовое, новаторское мышление?
Да. Самая большая выставка, которую мы создали в партнерстве с Google, называется Beyond Rubik’s Cube. Кубу-головоломке только что исполнилось 40 лет. Это большая выставка с роботами, которым посетители могут передавать кубики для сборки — не обязательно уметь собирать кубик Рубика самостоятельно.
Кубик Рубика — культурная икона. В мире их миллиард, поэтому мы устроили выставку, демонстрирующую математику и инженерию куба. Трудно угадать внутренний механизм Cube, который позволяет ему так плавно скручиваться, но не разваливаться.
Когда выставка открылась, Эмпайр Стейт Билдинг был освещен цветами кубика Рубика.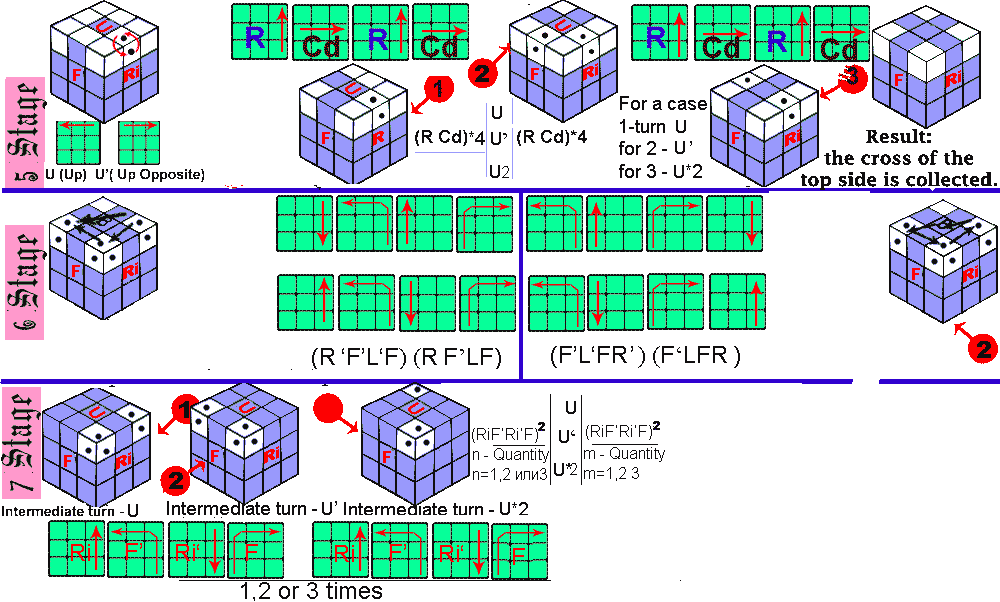 Сейчас этот экспонат на год передан в аренду нескольким музеям науки и искусства в Китае.
Сейчас этот экспонат на год передан в аренду нескольким музеям науки и искусства в Китае.
Выставочный дизайн – дело непростое. Наши экспонаты должны быть интерактивными и захватывающими — мы не музей, где на стене висят красивые артефакты. Наши выставки посещают 650 000 человек в год, поэтому они сильно изнашиваются.•
Жизнь учителя математики, рассказанная одаренными учениками, которых он наставлял
Джордж Берзеньи — профессор математики на пенсии, проживающий в округе Милуоки. Большинство людей никогда о нем не слышали.
Но Берзеньи оказал заметное влияние на американскую науку и математику. Он воспитал тысячи старшеклассников, в том числе тех, кто стал одним из лучших математиков и ученых в стране.
О Берзеньи я узнал из случайного разговора с ученым по имени Вамси Мутха.
В конце 1980-х, когда Мутха учился в старшей школе в Бомонте, штат Техас, он выиграл научную ярмарку. Через несколько дней на почту пришло письмо.
«В нем говорилось: «Дорогой Вамси, поздравляю с победой на Хьюстонской научной ярмарке, это большое достижение», — вспоминает Мутха.
«Но потом, когда я начал читать следующий абзац, у меня что-то сжалось в животе», — говорит Мута.
Далее в письме говорилось, что математическая задача, которую молодой Вамси решил выиграть на ярмарке, была решена сотни лет назад.
«Конечно, в письме продолжалось: «Вы не можете ожидать, что знаете это, потому что вы всего лишь второкурсник в старшей школе, и, возможно, у вас не было соответствующего наставничества … Если вам интересно в решении первоначальных проблем, почему бы вам не ответить мне».
Письмо было подписано «Георгий Берзеньи». В то время Берзеньи был профессором математики в Ламарском университете в Бомонте.
Мутха говорит, что письмо расстроило его, потому что он думал, что открыл что-то новое.
Но потом он заинтриговался. «Я сказал:« Знаешь что, я собираюсь принять его предложение и написать ему ответ ». »
Они встретились, и старший математик и юный вундеркинд нашли общий язык. Берзеньи давал Муте эти оригинальные задачи для решения . .. и ценил математику.
.. и ценил математику.
«Он также привил мне любовь к математике и любовь к изящной математике, которая имеет смысл», — говорит Мута.
Полдюжины или около того лет назад Мутха узнал, что его наставником является Джордж Берзеньи.
«Я делю офис с кем-то по имени Джоэл Хиршхорн, — говорит мне Мута. Хиршхорн — генетик из Гарварда и Института Броуда. Мута и Хиршхорн пытались решить математическую задачу, связанную с их работой.
«Джоэл сидит у доски и рисует уравнения, — вспоминает Мута. «После того, как мы поработали над задачей, мы просто вспоминаем наши школьные годы по математике». на самом деле мог закончить это предложение, он на самом деле спросил меня: «Подожди. Это письмо пришло от кого-то по имени Джордж Берзеньи? И я сказал: «Да, откуда ты знаешь?» И он сказал: «Раньше я также общался с Джорджем Берзеньи».
Хиршхорн присылал решения задач в математическом бюллетене под редакцией Берзеньи.
Совпадение было поразительным, а потом повторилось.
Две недели спустя Мутха рассказывает Себастьяну Сыну эту историю. Сын — нейробиолог, который в то время работал в Массачусетском технологическом институте. Прежде чем он успевает закончить рассказ, Мута говорит: «Себастьян прерывает меня и говорит: «Подождите, это был Джордж Берзеньи?» и я сказал: «Да, откуда ты знаешь?»
Мутха вскоре обнаружил, что Бержени повлиял на жизнь многих ведущих ученых и математиков.
В этот момент я понял, что должен встретиться с Берзеньи. Итак, я пошел встретиться с ним в его доме в округе Милуоки, где он живет со своей женой Кей.
Бержени сейчас 80 лет. Он родился в Венгрии. В старших классах он влюбился в математику. Венгрия превосходно бьет в тему. Страна произвела много известных математиков.
Берзеньи приехал в Америку и получил докторскую степень по математике.
Он присоединился к математическому факультету Ламара в Бомонте, где начал обучать талантливых школьников-математиков.
Он создал математический журнал по образцу KöMaL, который читал в Венгрии, когда учился в старшей школе.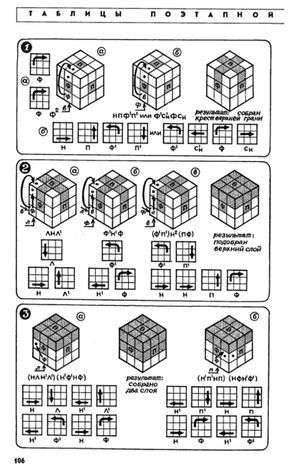 Журнал просуществовал всего несколько лет. Он надеется, что когда-нибудь кто-нибудь оживит его.
Журнал просуществовал всего несколько лет. Он надеется, что когда-нибудь кто-нибудь оживит его.
В журнале были сложные математические задачи. Когда студенты присылали решения, он отправлял комментарии.
Он был удивлен, насколько студенты были готовы работать с ним. Он понял, что восполняет неудовлетворенную потребность. Бержени сказал, что в большинстве средних школ нет опыта, чтобы помочь этим способным ученикам-математикам, а профессиональных математиков в целом это не беспокоит.
Берзеньи любил наблюдать за тем, как растут математические способности молодых людей.
«Несмотря на их молодость, я считал их математически в высшей степени зрелыми и обращался с ними таким образом… Я действительно восхищался ими», — говорит он.
На протяжении многих лет Берзени работал с тысячами детей. Он не ожидал, что все они станут математиками. Помимо математики, протеже Бержени занялись биологией, бизнесом и даже юриспруденцией.
Не видите рисунок выше? Кликните сюда.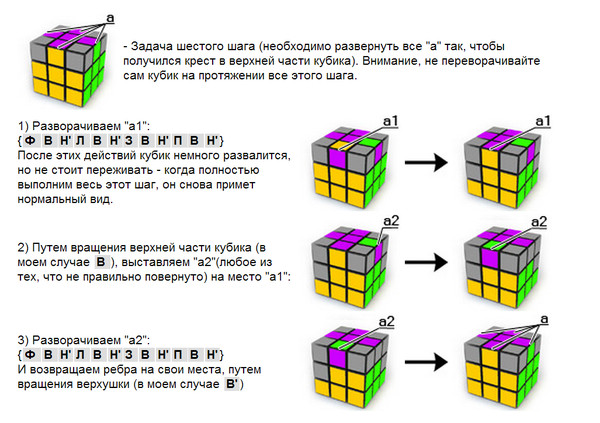
«Впервые я встретила доктора Берзени в рамках программ для молодых ученых в 1995 году, — говорит Ивонн Лай, доцент математики Университета Небраски в Линкольне. Она говорит, что Бержени создал программу как своего рода летний математический лагерь для старшеклассников.
Когда лагерь подходил к концу, Лай вспоминает: «Он дал нам группу из 10 математических задач в стиле соревнований, которые мы могли сдать в качестве итогового задания через 10 лет».
Группа поддерживала связь с помощью списка рассылки. И примерно десять лет спустя «кто-то написал список рассылки и сказал: «Прошло 10 лет, у нас есть проблема, которую необходимо решить», — смеется Лай.
Задание, которое нужно сдать через 10 лет, — это как раз та умная идея, которую Джордж Берзеньи использовал, чтобы увлечь студентов математикой.
Берзеньи гордится достижениями своих математических протеже. Феррелл Уилер занимается криптографией для Агентства национальной безопасности. Киран Кедлая работает над теорией чисел в Калифорнийском университете в Сан-Диего. Ноам Элкис стал штатным преподавателем математического факультета Гарварда, когда ему было всего 26 лет.
Ноам Элкис стал штатным преподавателем математического факультета Гарварда, когда ему было всего 26 лет.
Протеже одинаково благодарны за внимание Берзеньи.
«Благодаря программам, разработанным Джорджем Берзеньи, я думаю, что набрался смелости стать математиком», — говорит Лай.
«Его влияние на меня трудно описать, — говорит Уилер. «Он был мне как второй отец. И он мне очень помог».
«Трудно найти кого-то, кто так увлечен открытием будущего поколения талантов в любой области, но особенно в математике», — говорит Кедлая.
Из всех студентов, о которых Берзеньи рассказывал мне в те часы, когда мы разговаривали, один выделялся: Джимми Уилсон. «В конечном счете, Джимми, вероятно, стал моим главным открытием, — говорит Берзеньи.
Уилсон чуть не провалился. Когда он был первокурсником средней школы, Уилсон принял участие в математическом соревновании. Бержени случайно заглянул через плечо судьи, оценивая решение Уилсона одной из сложных задач соревнований.
«Решение проблемы, которое он предложил, было идеальным», — говорит Берзеньи. «Почему-то человек, который оценивал решение, не понял, что оно на самом деле решило проблему, и очень изящно».
Итак, Берзеньи отклонил решение первого судьи и поставил Уилсону высшую оценку.
Позже, в старших классах, Берзени взял Уилсона и группу других учеников на математическое соревнование на Восточном побережье.
Завершающим этапом соревнований стала игра Buzz.
«Ребенок никогда не слышал об этом раньше. Я никогда не слышал об этом раньше», — говорит Берзеньи.
Это счетная игра. Учащиеся встают в круг и по очереди считают, но существуют сложные правила, согласно которым вы заменяете числа такими словами, как «жужжание», «бах» или «удар». Скажешь неверное слово и вылетишь. Чертовски сложно соблюдать все правила, особенно если счет исчисляется сотнями.
В итоге осталось всего два ученика: прошлогодний чемпион и Уилсон.
«Это было просто невероятно, — вспоминает Берзеньи. «Очень методично, Джимми просто преуспел там, где другой ребенок не смог».
«Очень методично, Джимми просто преуспел там, где другой ребенок не смог».
Несмотря на всю свою естественную склонность к математике, Уилсон сначала плохо учился в колледже. Он бросил Техас A&M. Бержени говорит, что это произошло потому, что Уилсон на самом деле не научился учиться.
«В то время я не осознавал некоторых вещей, которые должен был делать», — говорит он. «Мне все еще плохо от этого».
«Я не думаю, что ему вообще нужно так себя чувствовать, — говорит Джимми Уилсон. Сегодня он идет Джим Уилсон. Теперь у него есть высшее образование. Он до сих пор живет в Бомонте, штат Техас. Большую часть своей взрослой жизни он работал педагогом в местной школьной системе.
Он гордится тем, что сделал на математическом соревновании Восточного побережья, гордится своими математическими способностями. Он особенно гордится тем днем, когда Джордж Берзеньи подарил ему кубик Рубика.
«Если вы можете это решить, вы можете оставить это себе», — вспоминает Уилсон слова Берзеньи.

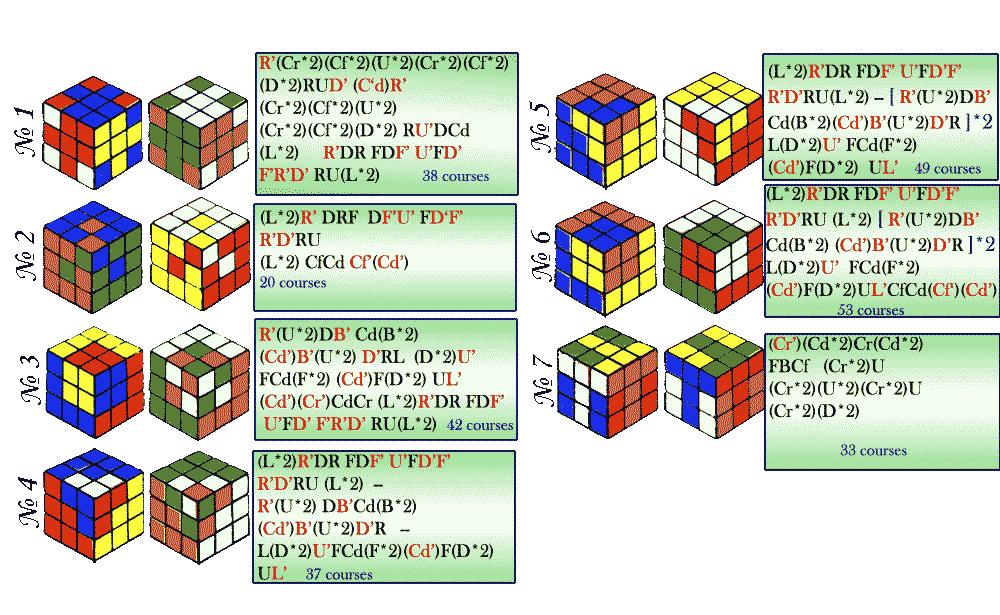
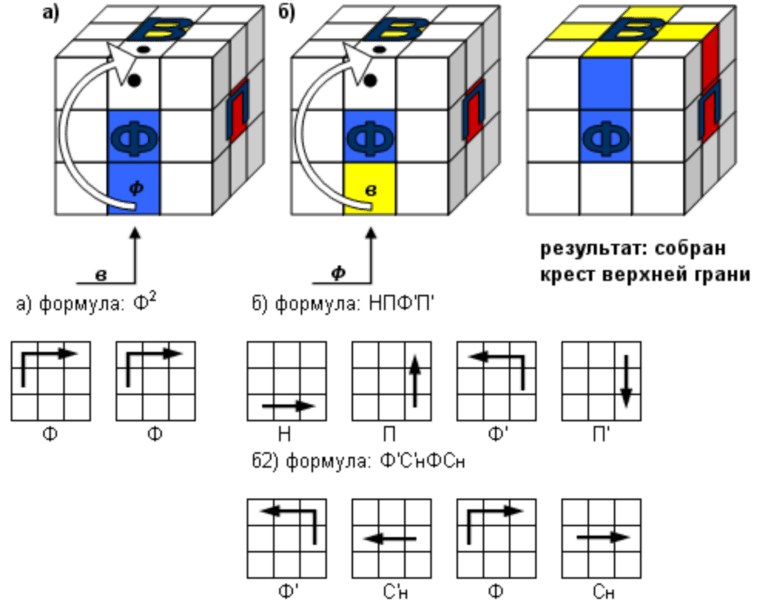
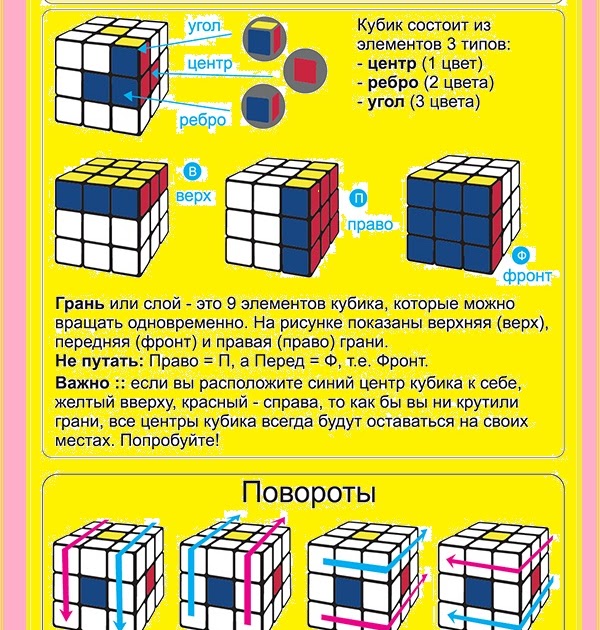

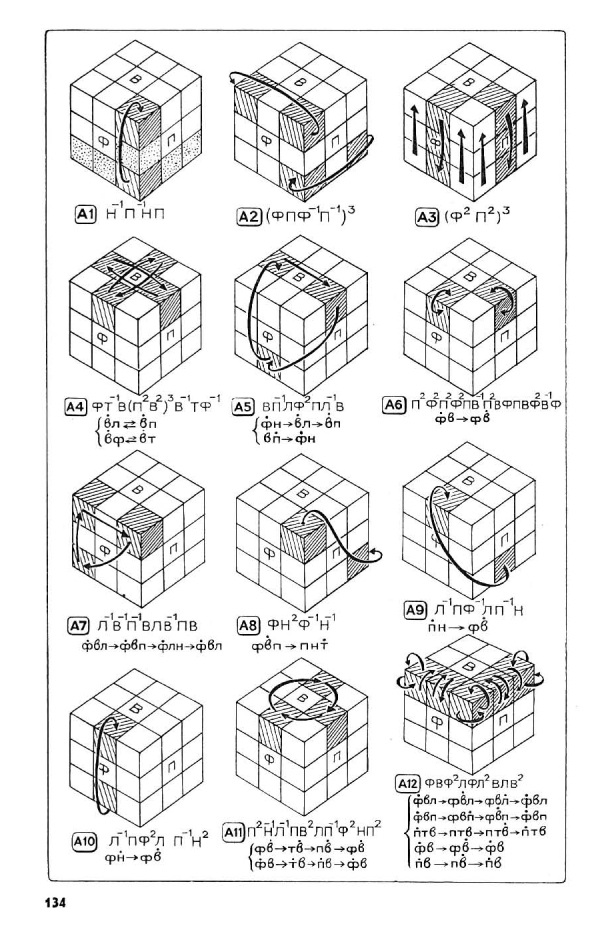 в проекте Science Buddies Создание узоров с помощью кубика Рубика.
в проекте Science Buddies Создание узоров с помощью кубика Рубика.