Содержание
Сергей Попов. «Все формулы мира. Как математика объясняет законы природы». Рецензия
По биологии и физике написано много хороших научно-популярных книг, но не так много — по математике. В самом деле, как популяризовать самую фундаментальную, но и самую абстрактную науку? Российский астрофизик Сергей Попов отчасти восполнил этот пробел. В книге «Все формулы мира» он повествует читателю о мире формул и уравнений, попутно проводя экскурс в астрофизику и космологию.
Качество и достоверность: 7/10
(0 — некачественно, 10 — очень качественно)
Лёгкость чтения: 6/10
(0 — очень сложно, 10 — легко)
Оригинальность: 8/10
(0 — похожих книг много, 10 — похожих книг нет)
Кому подойдет: людям с высшим (или неоконченным высшим) техническим или естественно-научным образованием.
Сергей Попов.
фейсбук Попова.
Сергей Попов — российский астрофизик, давно знакомый любителям популярной астрофизической литературы. Ещё в 2007 году он выпустил книгу «Звёзды: жизнь после смерти». Его книга «Суперобъекты: звезды размером с город» (2016) попала в лонг-лист премии «Просветитель» в 2016 году и была удостоена Беляевской премии. В 2018 году он порадовал читателей новой книгой «Вселенная. Краткий путеводитель по пространству и времени: от Солнечной системы до самых далеких галактик и от Большого взрыва до будущего Вселенной». А в 2020 году выпустил новую книгу — на этот раз не о звёздах и галактиках, а о формулах и математическом описании физических законов.
Ещё в 2007 году он выпустил книгу «Звёзды: жизнь после смерти». Его книга «Суперобъекты: звезды размером с город» (2016) попала в лонг-лист премии «Просветитель» в 2016 году и была удостоена Беляевской премии. В 2018 году он порадовал читателей новой книгой «Вселенная. Краткий путеводитель по пространству и времени: от Солнечной системы до самых далеких галактик и от Большого взрыва до будущего Вселенной». А в 2020 году выпустил новую книгу — на этот раз не о звёздах и галактиках, а о формулах и математическом описании физических законов.
В первых главах автор оживляет для читателя мир математики, который большинству из нас представляется серым и скучным. В самом начале он проводит параллель между формулами и естественным языком, затем — показывает, что формулы, как и живые организмы, могут эволюционировать. Это делает рассуждение понятным для гуманитариев и биологов. К теме эволюции математики автор ещё вернётся в главе 8 — на этот раз сравнивая её с искусством. Интересно Сергей Попов рассказывает и о научных идеях в математике: они могут не только кристаллизоваться, но менять агрегатное состояние (а для подробностей читайте главу 9). В итоге сложно сразу ответить на вопрос: о чём же эта книга? Зато понятно, что книга делает: она оживляет для читателя мир математики, обычно кажущийся серым и скучным.
В итоге сложно сразу ответить на вопрос: о чём же эта книга? Зато понятно, что книга делает: она оживляет для читателя мир математики, обычно кажущийся серым и скучным.
Целую половину от объёма книги составляют приложения. И вот в них больше конкретики — здесь автор относительно доступно объясняет, как в астрофизике можно получить многие величины и сделать предсказания при помощи не таких уж сложных расчётов. И если читателей гуманитарного склада эта половина способна напугать, то у обладателей хотя бы небольшого физико-математического бэкграунда на ней открывается настоящее второе дыхание.
Вопреки возможным страхам читателей, книга не перегружена формулами. Их в целом не так много. Правда, читателя могут слегка напугать «выскочившие из-за угла» пространства Калаби-Яу, теории струн и тому подобные вещи. Сергей Попов хорошо и доступно рассказывает про астрофизику, так что таких моментов минимум. Но они есть. Однако автор приводит довольно объёмные рассуждения, насыщенные философией и собственным взглядом на мир:
Книга природы написана на языке математики.
Кем? Неважно, кем конкретно, но ведь не сама же себя написала?
Сергей Попов. «Все формулы мира Как математика объясняет законы природы». Альпина нон-фикшн, 2019. — 288 с.
Не исключаю, что Льюису Кэрроллу понравился бы вопрос: «Чем математика похожа на глаз?» Мой ответ: «И то и другое удивительно, и в обоих случаях мы можем понять почему»
Сергей Попов. «Все формулы мира Как математика объясняет законы природы». Альпина нон-фикшн, 2019. — 288 с.
Такие рассуждения составляют изрядную часть книги, поэтому читателю придётся не только узнавать новое, но и философствовать вместе с автором. С какими-то его соображениями легко согласиться, но многие выглядят дискуссионными (или, по меньшей мере, фантастическими). Но, может, в том и ценность любой философии — даже если она преподносится в книге про математику?
…А в будущем дело может повернуться так, что никто из людей не сможет понять во всей полноте, что же и как доказал небелковый математик 1616FG#7687765 и в чём суть новой теории физика-теоретика 8747LD@8785780.
Тогда, по сути, всё собственно человеческое знание в естественно-научной (а также, возможно, математической) области станет «научно-популярным», т.е. неполным, упрощённым, адаптированным. <…> Популяризаторы тоже будут небелковыми. Люди же будут продолжать писать стихи и картины, играть на скрипке и в футбол.
Сергей Попов. «Все формулы мира Как математика объясняет законы природы». Альпина нон-фикшн, 2019. — 288 с.
Для иллюстрации рассказа о математике автор постоянно возвращается в свою основную специальность — астрофизику. Например, он рассказывает об обработке сильно зашумлённых данных математическими методами в контексте анализа данных о далёких звёздах и экзопланетах. И не только для иллюстрации — часть глав почти исключительно состоит из повествования об астрофизических гипотезах, пусть и с математическим уклоном (например, глава 11 «Воображаемые миры»). Но о чёрных дырах, ложном вакууме и мультивселенных Сергей Попов умеет рассказывать отлично. Так что эти главы книги читаются легко и с интересом.
Так что эти главы книги читаются легко и с интересом.
Пожалуй, в книге не хватает лишь одного: применения математических законов для описания не-астрофизических явлений. Даже физика не ограничивается астрофизикой (что хорошо обрисовано в книге Криса Вудфорда «Атомы у нас дома. Удивительная наука за повседневными вещами»), и в книге о формулах хотелось бы больше примеров из других разделов физики. Более того, математика давно является не только языком физики, но и языком биологии, геологии, метеорологии. И сейчас сфера её «нефизического» применения растёт: в науках о жизни всё сильнее становятся позиции системной биологии, тесно связанной с математической биологией. Да и наука о данных, проникающая во все отрасли, тесно связана с математикой, не говоря уже о программировании. В книге о математике как раз хотелось бы прочитать о том, как меняется математика, обретая такие грани? Этого во «Всех формулах мира» нет, и читатель из естественно-научной сферы после прочтения книги остаётся с большим количеством вопросов без ответа. Но надо понимать, что Сергей Попов — астрофизик, и рассказывает о тех явлениях, которые сам изучает и в которых является специалистом.
Но надо понимать, что Сергей Попов — астрофизик, и рассказывает о тех явлениях, которые сам изучает и в которых является специалистом.
Так что в целом можно охарактеризовать книгу как взгляд астрофизика на математику. Она довольно своеобразна для научно-популярной литературы: очень интересна, но для прочтения требует усилий и, более того, исходного уровня физико-математической подготовки. Поэтому мы рекомендуем браться за книгу людям с техническим или естественно-научным образованием.
«Все формулы мира». Глава из книги • С. Попов • Книжный клуб на «Элементах» • Опубликованные отрывки из книг
По мнению некоторых экспериментаторов, теоретики могут предлагать и публиковать все что угодно. Один наблюдатель мне так и сказал: «Вам легко: придумал идейку — написал статью, а тут человек спектры мерил!» Разумеется, не все думают столь прямолинейно, но бывает. Так вот, это не очень-то легко! Теоретики могут пробовать придумывать что угодно. Но потом приходится считаться с некоторыми ограничениями, а главное — нельзя опубликовать (в приличном месте) «просто идейку».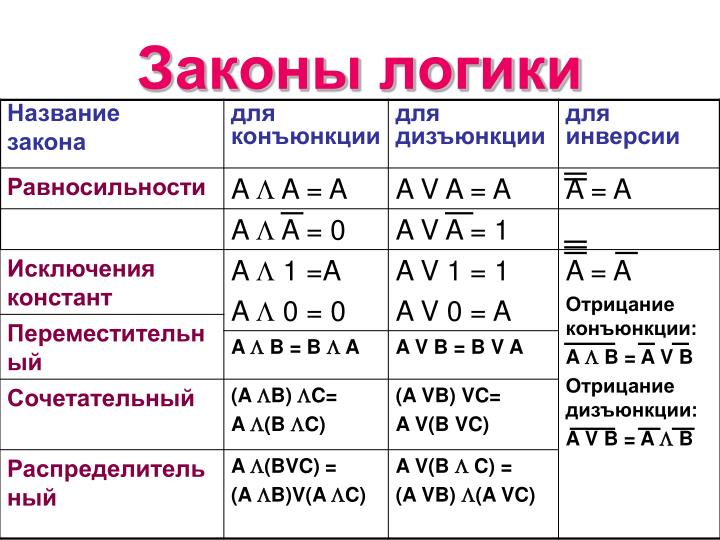
Во-первых, ограничения связаны с совокупностью известных данных экспериментов и наблюдений. Как говорится, «уродливый факт уничтожает прекрасную теорию». Но для многих областей это не слишком существенное ограничение. Ведь если фактов мало, то они не очень-то и мешают. И тогда на передний план выходит второй тип ограничений, связанный уже с внутренней кухней теоретических методов.
Эти внутренние ограничения условно можно разделить на физические и математические. Первые говорят о том, что, согласно нашему пониманию, нечто невозможно (или не реализуется) в нашем мире, а вторые — что это невозможно нигде.
Например, самые разнообразные наблюдения (космические лучи, фон неба в гамма-лучах и т. д.) свидетельствуют о том, что в нашей вселенной антивещества очень мало. Теоретический анализ говорит, что довольно трудно представить себе вселенную, в которой вещество и антивещество присутствуют примерно в равном количестве и скопления галактик из вещества соседствуют с конгломератами звездных систем из антивещества. Таким образом, с физической точки зрения у нас есть жесткое ограничение на количество антивещества в нашем мире и на возможную структуру миров с близкими долями обычного вещества и его антипартнера. Однако нет жесткого запрета на существование вселенных с антивеществом с точки зрения математики.
Таким образом, с физической точки зрения у нас есть жесткое ограничение на количество антивещества в нашем мире и на возможную структуру миров с близкими долями обычного вещества и его антипартнера. Однако нет жесткого запрета на существование вселенных с антивеществом с точки зрения математики.
Математика, т. е. решения уравнений физической теории, может в некотором смысле диктовать свойства объектов (или же утверждать, что наши уравнения недостаточно хороши для полного описания всех параметров). Здесь в качестве примера можно рассмотреть свойства черных дыр в общей теории относительности. Стандартным является утверждение о наличии сингулярности (в случае невращающейся черной дыры это точка в ее центре1). Этот вывод основан на решениях уравнений ОТО, т. е. на математической процедуре, а не на качественных (т. е. словесных) рассуждениях. В данном случае математика говорит нам, какими должны быть параметры объекта в рамках заданной модели. Мы понимаем, что в реальном мире это недостижимо: плотность не может достигать бесконечной величины. Но уравнения формально приводят к такому выводу. Значит, как минимум мы можем утверждать, что в недрах черной дыры формируется нечто очень плотное и компактное, и мы не можем это описать с помощью той физики, которую заложили. Иначе говоря, математика показывает нам ограниченность наших физических моделей.
Но уравнения формально приводят к такому выводу. Значит, как минимум мы можем утверждать, что в недрах черной дыры формируется нечто очень плотное и компактное, и мы не можем это описать с помощью той физики, которую заложили. Иначе говоря, математика показывает нам ограниченность наших физических моделей.
Другой пример «математического диктата». Возьмем четырехмерное пространство и попробуем рассчитать в нем орбиты планет, обращающихся вокруг звезд. В таком пространстве закон всемирного тяготения изменится. Теперь в знаменателе будет стоять не квадрат расстояния, а третья степень — куб. Вообще, показатель степени у расстояния в законах всемирного тяготения и Кулона равен размерности пространства минус единица. Это объясняется тем, что такую зависимость от радиуса имеет площадь сферы: на данном расстоянии воздействие как бы «размазано» по поверхности сферы (можно представлять себе, как уменьшается световой поток на единичную площадь при удалении от источника). Так вот, окажется, что существование устойчивых орбит, например круговых, в четырехмерном пространстве невозможно. Такой вывод не является следствием неполноты теории — это очень общее свойство, связанное именно с геометрией. Гравитация в мире с еще одним измерением будет спадать слишком быстро при росте расстояния между тяготеющими телами, и такое поведение не позволит получить стабильные орбиты. Значит, мы имеем дело именно со свойством решений уравнений. Таким образом, в данном случае математика жестко ограничивает фантазии теоретиков.
Такой вывод не является следствием неполноты теории — это очень общее свойство, связанное именно с геометрией. Гравитация в мире с еще одним измерением будет спадать слишком быстро при росте расстояния между тяготеющими телами, и такое поведение не позволит получить стабильные орбиты. Значит, мы имеем дело именно со свойством решений уравнений. Таким образом, в данном случае математика жестко ограничивает фантазии теоретиков.
От замысла до воплощения научная идея проходит ряд «агрегатных состояний». Часто это начинается со смутных идей, непродуманных гипотез. У нас есть пока лишь что-то эфемерное, «газообразное». Постепенно в процессе продумывания оно начинает сгущаться, и в какой-то момент происходит фазовый переход — «газ» превращается в «жидкость». В этот момент идея хорошо вербализована, ее можно начать обсуждать, но это еще не научная теория. Нужен еще один переход — «кристаллизация». Только теперь у нас есть математические формулировки. Мы получили уравнения, которые можно решать, а результаты сравнивать с наблюдениями и делать количественные предсказания.
Хочется сказать, что остановка на первом («газообразном») уровне соответствует поэтическому способу познания реальности, второй («жидкий») уровень — философии, а третий — науке. При этом именно последнему свойственны наиболее заметные ограничения. Газ и жидкость могут заполнить любой сосуд. Они аморфны — готовы принять форму тела, в котором находятся, особенно газ. А вот снежинки, несмотря на все свое многообразие, имеют вполне определенные симметрии2.
Если человек не может как следует придерживаться ограничений, связанных с современными методами исследований, или не пытается пройти всю цепочку «газ — жидкость — кристалл», то он не занимается наукой. Доведение идеи «до числа», позволяющее провести количественное сравнение с данными и сделать предсказания для проверки, — совершенно необходимый элемент работы ученого, по крайней мере в физике. Опубликовать «голую идею» в сколь-нибудь приличном журнале невозможно — необходимо представить развернутую аргументацию на количественном уровне и предложить методы количественной проверки.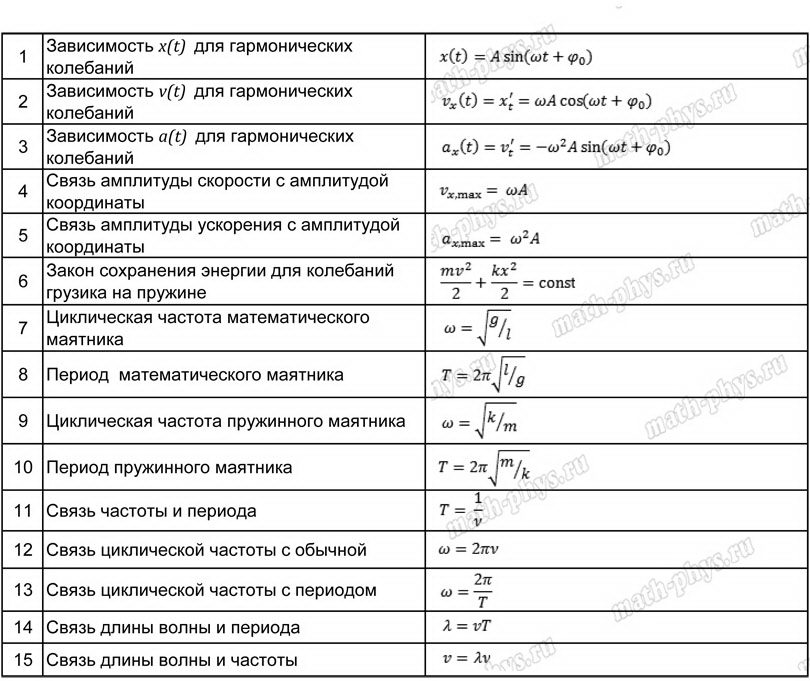 Аргументация должна быть основана в том числе на сравнении с имеющимися данными, а потому игнорирование даже части комплекса экспериментальных и наблюдательных результатов делает работу неполноценной. И, уж конечно, наличие проблем с математикой (т. е., попросту говоря, ошибок в расчетах) полностью ее обесценивает.
Аргументация должна быть основана в том числе на сравнении с имеющимися данными, а потому игнорирование даже части комплекса экспериментальных и наблюдательных результатов делает работу неполноценной. И, уж конечно, наличие проблем с математикой (т. е., попросту говоря, ошибок в расчетах) полностью ее обесценивает.
Парадокс «сумасшедших ученых», когда признанный специалист вдруг начинает упорно продвигать маргинальные идеи, на мой взгляд, чаще всего состоит именно в нежелании следовать этим ограничениям и требованиям. Как правило, речь идет об игнорировании значительной части известных данных, т. е. идея доводится «до числа», и проблем в расчетах нет, но при этом не обращается должного внимания на то, как идея вписывается в общий контекст. По сути, авторы сознательно игнорируют часть серьезных проблем, способных разрушить предлагаемую модель.
Можно предположить, что этот интересный эффект связан с тем, что многие (если не большинство) ученых приходят в науку с желанием совершить яркое большое открытие в духе тех, о которых мы в детстве читали в научно-популярных книгах. Им хочется воскликнуть: «Эврика!» В таких книгах (а особенно в фильмах) часто сам момент озарения считается ключевым. А это только фаза «газообразной» идеи или ее «конденсации». Про дальнейшую работу рассказывают реже, так как это «скучно». Следовательно, есть исходная селекция в пользу определенного склада характера.
Им хочется воскликнуть: «Эврика!» В таких книгах (а особенно в фильмах) часто сам момент озарения считается ключевым. А это только фаза «газообразной» идеи или ее «конденсации». Про дальнейшую работу рассказывают реже, так как это «скучно». Следовательно, есть исходная селекция в пользу определенного склада характера.
Попав в университет, человек постепенно начинает открывать для себя весь комплекс ограничений. Приходится учиться работать именно в таком консервативном ключе. Похоже на то, как какой-нибудь герой приключенческой книги внезапно оказывается «родовитым», попадает в светское общество, о котором всегда мечтал, но оказывается, что там много нудных правил, которым нужно неукоснительно следовать (по крайней мере, на публике). В результате наш герой может в какой-то момент все бросить и «уйти в разбойники или пираты». Такой образ многим близок. Не просто пират, а пират-дворянин. Похожими притягательными свойствами обладает и именитый ученый, вдруг начавший заниматься чем-то практически лженаучным или, по крайней мере, околонаучным или не совсем научным, но ярким и притягательным (НЛО, сверхъестественные явления). И, уж конечно, харизматичен образ знатного бунтаря. Известный ученый, начинающий все ниспровергать и покушаться на «священных коров», — просто находка для публики и журналистов. Кажется, чаще всего такой «бунт» и отрицание стандартных ограничений, являющихся основой нормального функционирования науки, происходит, когда человек достигает довольно высокого уровня, который он считает достаточным для себя. Теперь можно пренебречь правилами и вернуться к изначальным юношеским порывам, не удерживая их в слишком жестких рамках.
И, уж конечно, харизматичен образ знатного бунтаря. Известный ученый, начинающий все ниспровергать и покушаться на «священных коров», — просто находка для публики и журналистов. Кажется, чаще всего такой «бунт» и отрицание стандартных ограничений, являющихся основой нормального функционирования науки, происходит, когда человек достигает довольно высокого уровня, который он считает достаточным для себя. Теперь можно пренебречь правилами и вернуться к изначальным юношеским порывам, не удерживая их в слишком жестких рамках.
Но вернемся к нашей аналогии. Получив «снег и лед», мы можем двигаться дальше. Из снега можно что-то лепить, изо льда — высекать. Нельзя построить воздушный замок, а вот ледяной дворец — вполне реально. Конечно, можно сказать, что из лапласианов и синусов нельзя сложить слово «счастье», но никто к этому не стремился и этого не обещал.
Однако существенно, что кристаллы имеют определенные свойства, и это как раз соответствует внутренним ограничениям, накладываемым математикой. Если мы начали с паров воды, то получим вполне определенные кристаллы. Начав с некоторых физических рассуждений, мы получим, облекая их в форму уравнений, модели определенного типа. Здесь можно вспомнить, что в разных условиях и лед приобретает разные свойства (например, при высоком давлении в недрах планет). Это верно, и это можно уподобить тому, как наши физические модели дают разные предсказания для разных наборов параметров, а иногда при этом используется и разная структура уравнений — разная математика, как, к примеру, в случаях ньютоновской механики и общей теории относительности. Тем не менее нельзя получить что угодно. Раз уж мы упомянули физические свойства вещества в планетах, то приведем пример из этой области.
Если мы начали с паров воды, то получим вполне определенные кристаллы. Начав с некоторых физических рассуждений, мы получим, облекая их в форму уравнений, модели определенного типа. Здесь можно вспомнить, что в разных условиях и лед приобретает разные свойства (например, при высоком давлении в недрах планет). Это верно, и это можно уподобить тому, как наши физические модели дают разные предсказания для разных наборов параметров, а иногда при этом используется и разная структура уравнений — разная математика, как, к примеру, в случаях ньютоновской механики и общей теории относительности. Тем не менее нельзя получить что угодно. Раз уж мы упомянули физические свойства вещества в планетах, то приведем пример из этой области.
Планеты формируются в протопланетном диске, окружающем новорожденную звезду. Диски могут быть достаточно массивны (обычно порядка нескольких процентов от массы звезды), и в них содержится практически вся таблица Менделеева вплоть до урана. Значит, там могут образовываться какие угодно планеты? Конечно, нет.
Три основных ингредиента, из которых в той или иной пропорции могут состоять планеты, — это камни (сюда же будем включать все металлы), лед и газ. И пропорция не может быть любой. Основная причина в том, что, с одной стороны, газа намного больше, чем льда, а льдов3 — больше, чем каменных частиц. Кроме того, вещество достаточно хорошо перемешано. Поэтому, хотя в протопланетном диске может хватать, например, углерода для формирования планеты размером с Землю, такого не происходит в природе.
Более того, очень трудно (практически невероятно) создать планету массой в 20–30 земных и больше только из камней, потому что, как только планета в диске набирает такую массу, она начинает гравитационно захватывать газ, быстро превращаясь в газового гиганта, в основном состоящего из водорода и гелия (именно эти вещества доминируют в газовой составляющей диска, поскольку они — самые распространенные элементы во вселенной и именно из них в основном и состоят межзвездные облака и сами звезды). Альтернатива состоит в том, чтобы наращивать массу каменной планеты после исчезновения газового диска4, но тогда остается мало материала, который к тому же трудно собрать в единое тело. Остается один-единственный вариант: как-то лишить газового гиганта его массивной протяженной атмосферы. Это возможно в результате взаимодействия планеты со звездой. Такие гипотетические планеты называют хтоническими мирами. Однако очевидно, что если они и существуют, то это чрезвычайно редкие тела (встречающиеся в чрезвычайно экстремальных условиях).
Альтернатива состоит в том, чтобы наращивать массу каменной планеты после исчезновения газового диска4, но тогда остается мало материала, который к тому же трудно собрать в единое тело. Остается один-единственный вариант: как-то лишить газового гиганта его массивной протяженной атмосферы. Это возможно в результате взаимодействия планеты со звездой. Такие гипотетические планеты называют хтоническими мирами. Однако очевидно, что если они и существуют, то это чрезвычайно редкие тела (встречающиеся в чрезвычайно экстремальных условиях).
Таким образом, основные типы планет — это небольшие (в основном твердые, исключая в некоторых случаях внутреннее ядро) железно-каменные планеты, ледяные планеты (внутри которых лед находится в экзотическом жидком состоянии) и газовые гиганты (содержащие ядро из элементов тяжелее гелия, но вещество там обычно не находится в твердом состоянии из-за высокого давления). Примером первого типа являются четыре внутренние планеты Солнечной системы (Меркурий, Венера, Земля и Марс). Ледяные гиганты — это Нептун и Уран. Газовые — Юпитер и Сатурн. Кроме того, в Галактике распространен тип планет, называемый сверхземлями. Эти планеты, имеющие массу примерно 5–10 земных, могут состоять из железа и камней (т. е. являются массивными аналогами Земли) или льдов (таким образом, это мини-нептуны)*.
Ледяные гиганты — это Нептун и Уран. Газовые — Юпитер и Сатурн. Кроме того, в Галактике распространен тип планет, называемый сверхземлями. Эти планеты, имеющие массу примерно 5–10 земных, могут состоять из железа и камней (т. е. являются массивными аналогами Земли) или льдов (таким образом, это мини-нептуны)*.
Итак, распространенность элементов во вселенной, особенности процесса звездообразования и физики протопланетных дисков определяют ключевые свойства планет, их типы и распространенность каждого из них. Несмотря на то что каждая планетная система образуется независимо и в Галактике их сотни миллиардов, наличие единых правил и общность начальных условий не приводят к появлению большого разнообразия планет. В фантастическом романе можно описать планету из чистого железа или воды, но в реальности это невозможно. В естественных условиях осуществляется далеко не все, что можно себе представить. И мы лучше начинаем это понимать, когда доводим наши идеи до количественных характеристик.
Три «агрегатных состояния идей» сильно отличаются друг от друга. Конечно, нельзя сказать, что «лед лучше пара и воды». Лед лучше для того, чтобы построить дом (пусть в нем и прохладно). Но для многих других целей больше подойдут жидкость или газ. Как сказал поэт, «хочется пить, но не выпить твердую воду». Мы не сумеем дышать без газов, жизнь была бы невозможна без жидкой воды (или ее заменителя в качестве универсального растворителя). В мире идей и фантазий тоже не все сводится к науке, к счастью. Но и заменить научный метод ничто не может.
Для меня лично в этих «фазовых переходах идей» есть элемент творческого чуда, когда мысли, пока существующие лишь в виде слов или образов, обретают плоть (и одновременно каркас) в виде формул (для меня это почти всегда так или иначе готовые формулы, я их не изобретаю — только использую). Это похоже на внезапную кристаллизацию. Именно в данный момент идея становится научной. Из воды получается лед, из пуха — нить, и ясно, что с этим можно дальше работать.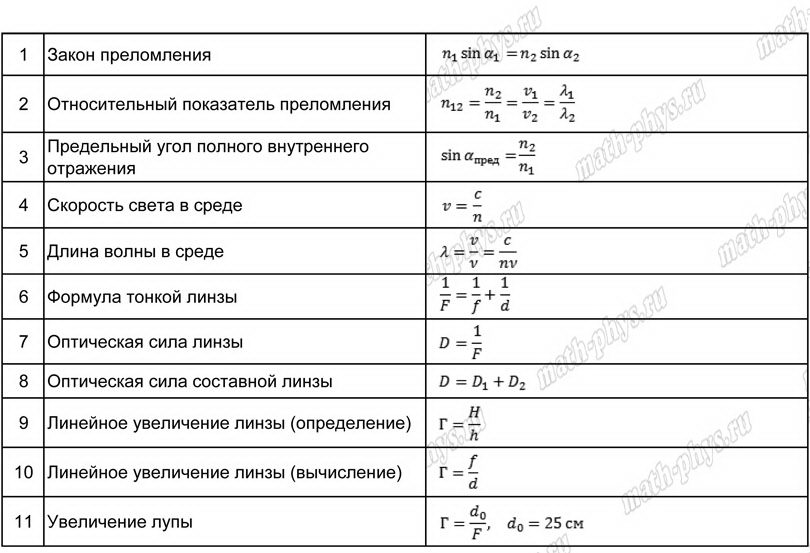 Из нитей делать ткань. Кристалл может продолжать расти. В частности, получив «теоретическую снежинку», ее можно сравнивать с настоящими. Если совпадение есть, значит, идея правильная или, по крайней мере, имеет право на существование.
Из нитей делать ткань. Кристалл может продолжать расти. В частности, получив «теоретическую снежинку», ее можно сравнивать с настоящими. Если совпадение есть, значит, идея правильная или, по крайней мере, имеет право на существование.
* Большинство сверхземель должно иметь также довольно плотную атмосферу, которая, однако, по своей массе намного уступает основной части планеты.
1 Популярное изложение многих современных идей об устройстве сингулярности можно найти в книге К. Торна «Интерстеллар: наука за кадром» (М.: Манн, Иванов и Фербер, 2015).
2 О роли симметрии в физике, в первую очередь о квантовой механике, можно почитать в сборнике статей Ю. Вигнера «Этюды о симметрии» (М.: Мир, 1971).
3 В данном случае под словом «лед» подразумевается не только водяной лед, но и замерзший метан, аммиак, угарный газ и многие другие соединения с похожими свойствами.
4 Газовый диск рассеивается за несколько миллионов лет. В основном это происходит за счет ультрафиолетового излучения звезды, поэтому газовые гиганты должны формироваться относительно быстро. Железно-каменные планеты могут наращивать массу в течение десятков миллионов лет за счет столкновений друг с другом и с небольшими твердыми телами — планетезималями.
В основном это происходит за счет ультрафиолетового излучения звезды, поэтому газовые гиганты должны формироваться относительно быстро. Железно-каменные планеты могут наращивать массу в течение десятков миллионов лет за счет столкновений друг с другом и с небольшими твердыми телами — планетезималями.
«Все формулы мира. Как математика объясняет законы природы»
Математический анализ помогает совершать естественно-научные открытия. С математическими расчетами сопряжено создание любой сложной конструкции. Весь наш мир вполне успешно можно описать с помощью математических методов. Как перестать бояться формул и полюбить математику? Почему она так эффективна в естественных науках? На эти и другие вопросы в книге «Все формулы мира. Как математика объясняет законы природы» (издательство Альпина нон-фикшн) пробует ответить астрофизик и популяризатор науки Сергей Попов. N + 1 предлагает своим читателям ознакомиться с отрывком, рассказывающим о том, что такое антропный принцип, в чем разница между его слабой и сильной разновидностями, а также почему для науки важно создавать модели, не имеющие отношения к наблюдаемой реальности.
Снежинки теорий
Снежинки являются символом уникальности. Любопытно, что это разнообразие форм существует, невзирая на строгие законы, связанные со свойствами молекул воды. Более 400 лет назад Иоганн Кеплер написал небольшой трактат «О шестиугольных снежинках». Наука того времени не располагала возможностью достаточно полно объяснить правила, определяющие вид этих объектов. Однако многие считают, что именно эта работа лежит в основе современной кристаллографии, поскольку в ней впервые на достаточно хорошем уровне была сделана попытка объяснить свойства кристаллов, используя не только качественные рассуждения, но и математику. Кеплер, разумеется, ничего не знал о молекулах воды, поэтому было бы удивительно, если бы он смог найти полностью правильный ответ на вопрос о форме снежинок. Тем не менее в его книге изложено много любопытных идей, причем не только о кристаллах. Это очень интересный (и доступный, практически научно-популярный) пример того, как логика и математика помогали работать с гипотезами о свойствах природных явлений на заре возникновения современной физики.
Представим цивилизацию, обитающую на планете, где в естественных условиях снежинки не образуются, к тому же пусть вообще жизнь на этой планете основана не на воде. Межпланетная станция исследовала холодный спутник близкой планеты и прислала фотографию снежинки. Теперь ученые в лаборатории пытаются воспроизвести ее форму. Поняв, что снежинка состоит из молекул воды, они довольно быстро научатся делать самые разнообразные снежинки, которые будут похожи на оригинал, но не будут в точности его воспроизводить. Ученые установят, что существуют различные типы снежинок, возникающие при разных комбинациях параметров (влажность, температура и т. д.), но воссоздать их точную форму можно будет только путем манипулирования с отдельными молекулами, а не воспроизводя естественные условия: слишком много вариантов. Важно, что исследователи поймут, почему снежинки шестиугольные (и не бывает пяти- или семиугольных). Может быть, им удастся установить, что снежинки из других видов льда (неводяного) будут иметь другую симметрию, но опять-таки не всё возможно. И вероятно, в течение долгого времени нерешенным останется вопрос о деталях происхождения воды на этом небесном теле.
И вероятно, в течение долгого времени нерешенным останется вопрос о деталях происхождения воды на этом небесном теле.
Такая ситуация похожа на то, как физики-теоретики пытаются понять мир. Физическая реальность — некая уникальная реализация множества физических параметров, но она подчинена каким-то единым физическим законам, которые в полной мере нам пока неизвестны. Однако мы знаем уже довольно много. Это позволяет строить все более реалистичные модели. Некоторые из них ухватывают глобальные черты «снежинки», а некоторые пытаются точно воспроизвести отдельные «лучики».
Здесь хочется сделать один важный комментарий. Занимаясь конструированием «снежинок», не совпадающих с оригиналом, ученый не работает впустую. Хотя он и не изучает непосредственно исходную «снежинку» (реальный мир), но он исследует снег, воду, взаимодействие молекул. Иными словами, даже создавая модели, явно не имеющие отношения к наблюдаемой реальности, теоретик может заниматься важной, осмысленной деятельностью, связанной с изучением физики (и, возможно, математики). Таким образом, потенциальные возможности физики в некотором смысле превосходят конкретную реализацию в виде нашей наблюдаемой части вселенной.
Таким образом, потенциальные возможности физики в некотором смысле превосходят конкретную реализацию в виде нашей наблюдаемой части вселенной.
В фильме «В ожидании волн и частиц» Сергей Троицкий, физик-теоретик из Института ядерных исследований в Москве, высказывает интересную мысль: «Теоретик должен заниматься тем, что не существует, но что могло бы существовать. То, что существует, экспериментаторы и так откроют». Разумеется, это высказывание отчасти шуточное. Но лишь отчасти! Изучение нереализованных в природе возможностей (проводимое в соответствии с довольно строгими правилами и ограничениями, о которых мы говорили выше) — важная составляющая исследовательской работы.
Почему же мы наблюдаем некоторую реализацию из ряда возможностей? Почему именно эту? С одной стороны, мы можем надеяться найти прямой и детальный ответ на этот вопрос. Правда, сделать это будет нелегко, так как почти наверняка для достоверности результата нам придется научиться исследовать другие варианты не только теоретически, но и экспериментально (или убедительно доказать, что наша наблюдаемая вселенная — единственная). Но часть вариантов мы можем отбросить, используя довольно оригинальный подход, наиболее четко впервые сформулированный Брендоном Картером вначале в препринте, опубликованном в 1967 г., а затем в докладе на симпозиуме Международного астрономического союза в 1973 г., проходившем в Польше и посвященном 500-летию со дня рождения Коперника. На основании этих идей Картером была написана классическая статья, опубликованная в 1974 г. в журнале Classical and Quantum Gravity. Именно на симпозиуме в Кракове им был предложен и прижившийся термин «антропный принцип»*.
Но часть вариантов мы можем отбросить, используя довольно оригинальный подход, наиболее четко впервые сформулированный Брендоном Картером вначале в препринте, опубликованном в 1967 г., а затем в докладе на симпозиуме Международного астрономического союза в 1973 г., проходившем в Польше и посвященном 500-летию со дня рождения Коперника. На основании этих идей Картером была написана классическая статья, опубликованная в 1974 г. в журнале Classical and Quantum Gravity. Именно на симпозиуме в Кракове им был предложен и прижившийся термин «антропный принцип»*.
*Наиболее детальное описание идеи антропного принципа можно найти в книге: Barrow, John D.; Tipler, Frank J. The Anthropic Cosmological Principle. — Oxford University Press, 1988. Также стоит отметить редакторский комментарий Джорджа Эллиса к классической статье Брендона Картера. Статья Картера 1967 г. также была впоследствии размещена в Архиве. Другие важные статьи по этой теме, наличествующие в открытом доступе на сайте arXiv. org, можно найти по ключевому слову «антропный» у меня на сайте.
org, можно найти по ключевому слову «антропный» у меня на сайте.
Поделиться
В самой простой формулировке принцип звучит так: мы наблюдаем такой мир, потому что в других (сильно отличающихся) мирах нет наблюдателей, подобных нам. Разумеется, в той или иной степени подобные мысли возникали задолго до рубежа 60-х и 70-х гг. XX века у разных людей. Но эти идеи не выстраивались в некую целостную концепцию, которую можно развивать и пытаться приложить к объяснению реальных данных. Развитие происходит на стыке физики и философии, что накладывает свой отпечаток. На сегодняшний день существует несколько вариантов формулировки антропного принципа.
В первую очередь важно разделение на так называемые слабый и сильный антропные принципы. Приведенная выше формулировка в большей степени относится к слабому. Его идея до некоторой степени даже банальна. В самом деле, мы знаем довольно много, для того чтобы утверждать, что не при всех комбинациях физических параметров может существовать жизнь в высокоразвитой форме (а для появления разумного наблюдателя это необходимо; исключим из рассмотрения так называемый больцмановский мозг). Жизнь вряд ли появится в мирах с двумя или четырьмя пространственными измерениями (здесь речь о макроскопических, т. е. некомпактифицированных*, измерениях. Таким образом, пространство может быть и 10-, и 11-мерным, но дополнительные измерения «свернуты» и в макромире не проявляются непосредственно: например, орбитальное движение планет или даже движение электронов в атоме происходят в трехмерии).
Жизнь вряд ли появится в мирах с двумя или четырьмя пространственными измерениями (здесь речь о макроскопических, т. е. некомпактифицированных*, измерениях. Таким образом, пространство может быть и 10-, и 11-мерным, но дополнительные измерения «свернуты» и в макромире не проявляются непосредственно: например, орбитальное движение планет или даже движение электронов в атоме происходят в трехмерии).
*Во многих современных теориях (в том числе в теории струн) существуют дополнительные пространственные измерения, однако их роль начинает проявляться лишь на очень малых масштабах, поскольку глобальная топология пространства такова, что дополнительные измерения оказываются «свернутыми» или, как говорят, «компактифицированными». Популярное изложение этих идей можно найти, например, в книге Лизы Рэндалл «Закрученные пассажи: проникая в тайны скрытых размерностей пространства» (М.: Либроком, 2011).
Поделиться
Если жизнь в гипотетическом мире основана на наборе частиц, похожем на наш (протоны, нейтроны, электроны), то возникает ряд ограничений на их свойства, например на соотношения масс. Есть и более тонкие «настройки». Известен пример с энергией одного из уровней возбуждения ядра атома углерода, предсказанный Фредом Хойлом. Если бы энергии частиц в так называемой тройной альфа-реакции (синтез ядра углерода из трех альфа-частиц, т. е. ядер гелия*) не были особым образом согласованы, то термоядерный синтез в звездах практически не приводил бы к образованию углерода. А без него не могла бы существовать наша форма жизни. Оттолкнувшись от факта ее существования, Хойл предсказал наличие такого согласования параметров. Таким образом, если мы представим себе мир, где массы протонов и нейтронов чуть-чуть отличаются от наших, то там такого совпадения не будет, а значит, там нет и большого количества углерода, т. е. отсутствует жизнь, подобная земной. Отметим, что в нашей вселенной углерод занимает четвертое место по распространенности, а в первую тройку, напомним, кроме гелия, входят водород и кислород, составляющие вместе воду. Иначе говоря, углерод и вода — основа нашей жизни — чрезвычайно распространены.
Есть и более тонкие «настройки». Известен пример с энергией одного из уровней возбуждения ядра атома углерода, предсказанный Фредом Хойлом. Если бы энергии частиц в так называемой тройной альфа-реакции (синтез ядра углерода из трех альфа-частиц, т. е. ядер гелия*) не были особым образом согласованы, то термоядерный синтез в звездах практически не приводил бы к образованию углерода. А без него не могла бы существовать наша форма жизни. Оттолкнувшись от факта ее существования, Хойл предсказал наличие такого согласования параметров. Таким образом, если мы представим себе мир, где массы протонов и нейтронов чуть-чуть отличаются от наших, то там такого совпадения не будет, а значит, там нет и большого количества углерода, т. е. отсутствует жизнь, подобная земной. Отметим, что в нашей вселенной углерод занимает четвертое место по распространенности, а в первую тройку, напомним, кроме гелия, входят водород и кислород, составляющие вместе воду. Иначе говоря, углерод и вода — основа нашей жизни — чрезвычайно распространены.
*Тройная альфа-реакция происходит в ядрах достаточно массивных звезд после исчерпания водорода в качестве термоядерного горючего в их недрах. Наше Солнце примерно через 5–6 млрд лет (после своего превращения в красный гигант) перейдет на стадию горения гелия в ядре. Столкновение сразу трех частиц крайне маловероятно, поэтому для эффективного протекания реакции нужно согласование параметров ядер гелия, бериллия и углерода. Бериллий образуется на промежуточной стадии в результате слияния двух альфа-частиц. За счет того что вступающие в реакцию ядра бериллия и гелия имеют энергию, крайне близкую к энергии возбужденного ядра углерода, вероятность всей реакции резко повышается.
Поделиться
История с возбужденным уровнем ядра углерода считается примером успешного применения антропного принципа: исходя из факта нашего существования удалось предсказать реальные свойства физических объектов. Правда, это не только наиболее яркий пример, но и практически единственный*. Тем не менее и этого достаточно, чтобы более серьезно отнестись к идее, на первый взгляд кажущейся слишком банальной или слишком философской.
Тем не менее и этого достаточно, чтобы более серьезно отнестись к идее, на первый взгляд кажущейся слишком банальной или слишком философской.
*Другой интересный пример можно найти в статье Эндрю Гулда. Речь идет о свойствах ядра трития в сравнении с гелием-3.
Поделиться
Итак, слабый антропный принцип говорит нам, что сам факт нашего существования требует отбросить такие варианты устройства вселенной, при реализации которых нас бы не было. Заметим, что это не дает никакого ответа на вопрос о том, «почему же все-таки так получилось». Поэтому многие ученые не считают антропный принцип частью науки. Иными словами, все равно важно искать ответы на вопросы, почему измерений именно три, почему массы частиц именно такие и т. д. Ведь в физике мы всегда стремимся добраться до сути, понять механизмы явлений.
Сильный антропный принцип выглядит несколько более странно и является куда как более спорным утверждением. Одна из формулировок гласит: «Свойства вселенной должны быть таковы, чтобы в ней могла появиться разумная жизнь». Звучит вполне как тезис какой-нибудь религии. Для многих так оно и есть. Существуют и более наукообразные формулировки, например связанные с некоторыми вариантами интерпретации квантовой механики: «Наблюдатели необходимы, чтобы вселенная реально существовала». В таком подходе в отсутствие наблюдателя «нет реальности» (дерево в лесу падает беззвучно, если этого никто не слышит). Наконец, еще один вариант связан с возможностью существования мультивселенных. В этой формулировке под словом «Вселенная» понимается вся совокупность миров: «Рано или поздно во Вселенной появляется разумный наблюдатель». Если верен сильный принцип, то автоматически верен и слабый.
Звучит вполне как тезис какой-нибудь религии. Для многих так оно и есть. Существуют и более наукообразные формулировки, например связанные с некоторыми вариантами интерпретации квантовой механики: «Наблюдатели необходимы, чтобы вселенная реально существовала». В таком подходе в отсутствие наблюдателя «нет реальности» (дерево в лесу падает беззвучно, если этого никто не слышит). Наконец, еще один вариант связан с возможностью существования мультивселенных. В этой формулировке под словом «Вселенная» понимается вся совокупность миров: «Рано или поздно во Вселенной появляется разумный наблюдатель». Если верен сильный принцип, то автоматически верен и слабый.
Аргументы в пользу сильного антропного принципа очень косвенные и часто, скорее, «философские», даже если они связаны с интерпретацией квантовой механики. Зато такой подход потенциально претендует на объяснение исключительности набора физических параметров в нашей вселенной. И слабый, и сильный варианты призваны помочь понять, почему наша «снежинка» именно такая. Однако сами по себе эти подходы похожи не на снежинки, а, скорее, на капли воды.
Однако сами по себе эти подходы похожи не на снежинки, а, скорее, на капли воды.
Понимание того, что наш мир в принципе мог бы быть другим (пусть в нем не было бы нас самих), дает простор фантазии. Причем фантазировать можно, рассматривая все уровни: газообразный, жидкий и твердый. Иначе говоря, можно сделать конструирование миров предметом искусства, философских рассуждений или даже рассмотрений в рамках теоретической физики. Ведь если мы не могли бы появиться и/или жить в какой-то вселенной, это еще не значит, что мы не можем ее полностью описать с помощью формул.
Мы можем наслаждаться созданием «снежинки» — теории и ее конкретной формой как творением человеческого разума, вдохновленного реальными вопросами устройства мира. С определенной точки зрения это «игра в бисер», но важно помнить, что методы и задачи теоретической физики не являются отвлеченными от актуальных вопросов науки, включая и прикладные. Скорее уж, это похоже на проектирование фантастических городов, которые никогда не будут построены, но архитектура и инфраструктура которых просчитываются достаточно детально.
В последние десятилетия появились научные аргументы в пользу осмысленности такого подхода, а также возможность подвести основу под антропный принцип. В частности, некоторые из них связаны с теорией струн и так называемым струнным ландшафтом, о которых мы поговорим в следующей главе.
Подробнее читайте:
Попов, С. Все формулы мира. Как математика объясняет законы природы / Сергей Попов. — М.: Альпина нон-фикшн, 2019. — 288 с
Формулы стихии — Поиск — новости науки и техники
Раскрыть секреты океанской кухни помогает математическое моделирование
На компьютерном мониторе – земной шар. Неподвижные темные континенты и пульсирующий, переливающийся живой Мировой океан, занимающий 2/3 поверхности планеты, больше всех континентов вместе взятых. Желтые, красные точки обозначают уровень водной поверхности по отношению к берегам, а клубок мерцающих красных точек в районе Флоридского пролива – это Гольфстрим. Ученые знают едва ли не все, что творится на «океанской кухне». Им по силам создать портрет Мирового океана в разрезе благодаря возможностям математического моделирования. Рассказывает заведующий лабораторией Института океанологии им. П.П.Ширшова РАН, член-корреспондент РАН Сергей ГУЛЕВ.
Им по силам создать портрет Мирового океана в разрезе благодаря возможностям математического моделирования. Рассказывает заведующий лабораторией Института океанологии им. П.П.Ширшова РАН, член-корреспондент РАН Сергей ГУЛЕВ.
– Глобальная циркуляция Мирового океана – механизм наисложнейший. А математические модели помогают понять, как он устроен и как работает. На первый взгляд, водная стихия мало чем отличается от воздушной, как мы говорим, это такая же сплошная жидкая среда. Чтобы смоделировать ее поведение с помощью уравнений, нужно описать постоянное и разно-образное движение течений и вихрей, а также сил, заставляющих перемещаться морскую воду. Получится картина состояния океана от поверхности до дна, подчас глубиной в километры. Но в отличие от атмосферы моделирование океана – задача более сложная. Мало того что океаны разделены континентами, по сравнению с атмосферой мы знаем о них гораздо меньше. В первую очередь это касается их глубин. Сегодня спутниковые наблюдения дают огромный объем информации. Однако динамику океана на глубинах увидеть из космоса невозможно – есть лишь информация о его поверхности. Смоделировать подводную стихию позволяют гидродинамические уравнения. Это известные из школьного курса физики фундаментальные законы движения: второй закон Ньютона и некоторые другие. Они трансформируются в достаточно сложные уравнения, для их решения требуются сверхмощные компьютеры и большие программы (компьютерные коды).
Однако динамику океана на глубинах увидеть из космоса невозможно – есть лишь информация о его поверхности. Смоделировать подводную стихию позволяют гидродинамические уравнения. Это известные из школьного курса физики фундаментальные законы движения: второй закон Ньютона и некоторые другие. Они трансформируются в достаточно сложные уравнения, для их решения требуются сверхмощные компьютеры и большие программы (компьютерные коды).
– Составить их – дело очень трудоемкое?
– Модели – далеко не самые простые компьютерные программы, предусматривающие уйму операций. На бумаге издание было бы не толще энциклопедического словаря. Строит современную гидродинамическую модель группа из нескольких специалистов (иногда пяти, иногда двадцати), где каждый отвечает за свой раздел. И на это ей потребуется несколько лет напряженного труда. Одна из признанных в мире и наиболее удачных моделей – NEMO, созданная в конце 2000-х, – постоянно эволюционирует. Сегодня это семейство моделей, решающее различные задачи: от оперативного прогноза океана до исследования его климатических изменений. Авторы действующей системы – большая группа специалистов со всего мира, включая сотрудников нашей лаборатории. В последние годы консорциум возглавляют французские ученые во главе с профессором Бернаром Барнье из Института природной среды (примерно так можно перевести его название) в Гренобле, моим старым товарищем. Модель циркуляции океана – живой организм, он развивается и совершенствуется. После серьезных модификаций новая версия становится самостоятельным продуктом и часто носит имя авторов-исполнителей. Так, региональная версия NEMO, особым образом описывающая взаимодействие Арктики и Атлантики, будет носить имя сотрудницы нашей лаборатории Полины Вереземской.
Авторы действующей системы – большая группа специалистов со всего мира, включая сотрудников нашей лаборатории. В последние годы консорциум возглавляют французские ученые во главе с профессором Бернаром Барнье из Института природной среды (примерно так можно перевести его название) в Гренобле, моим старым товарищем. Модель циркуляции океана – живой организм, он развивается и совершенствуется. После серьезных модификаций новая версия становится самостоятельным продуктом и часто носит имя авторов-исполнителей. Так, региональная версия NEMO, особым образом описывающая взаимодействие Арктики и Атлантики, будет носить имя сотрудницы нашей лаборатории Полины Вереземской.
– Самый, наверное, важный вопрос, как работают модели?
– Есть несколько задач для океанского моделирования. Едва ли не самая серьезная – понять механизмы циркуляции океана, как она меняется и почему и, главное, как стихия влияет на климат. Для этого нужно создать такую же сложную модель атмосферы, работающую совместно с океанской. Это позволит моделировать климат, дать его прогноз, разобраться в его «характере». В современных климатических моделях океанский блок представлен достаточно упрощенными моделями, в которых, как правило, нет вихрей или они описываются параметрически. По-другому пока нельзя – слишком дорого стоит. Чтобы рассчитать годовые характеристики, получить объемный трехмерный «портрет» океана с учетом скорости течений, изменений температуры, других данных с высоким разрешением в 1/12 градуса, даже на самых современных суперкомпьютерах потребуется около недели, а если на 100 лет, то почти два года. Но тогда мы узнаем, например, как реагирует Гольфстрим на охлаждение в результате таяния арктического льда, какие массы атлантической воды попадают в Арктику или как процессы переноса воды на экваторе влияют на характер и поведение среднеширотных течений. Вопросов уйма, а дают ответы модели.
Это позволит моделировать климат, дать его прогноз, разобраться в его «характере». В современных климатических моделях океанский блок представлен достаточно упрощенными моделями, в которых, как правило, нет вихрей или они описываются параметрически. По-другому пока нельзя – слишком дорого стоит. Чтобы рассчитать годовые характеристики, получить объемный трехмерный «портрет» океана с учетом скорости течений, изменений температуры, других данных с высоким разрешением в 1/12 градуса, даже на самых современных суперкомпьютерах потребуется около недели, а если на 100 лет, то почти два года. Но тогда мы узнаем, например, как реагирует Гольфстрим на охлаждение в результате таяния арктического льда, какие массы атлантической воды попадают в Арктику или как процессы переноса воды на экваторе влияют на характер и поведение среднеширотных течений. Вопросов уйма, а дают ответы модели.
Как уже говорилось, главный сдерживающий фактор их построения не столько отсутствие данных или ошибки в понимании физических процессов. Все упирается в состояние вычислительных мощностей. В 70-80-х годах прошлого века, когда начали разрабатывать первые модели, компьютеры позволяли проводить расчеты с разрешением в 100-200 км. И картина получалась неправдоподобная. Океан – среда турбулентная. Ведь Гольфстрим, хоть и называется «рекой в океане», состоит из множества вихрей, взаимодействующих между собой. Да, спутники видят вихри, но необходимо узнать, какова их структура на глубине. Поэтому для построения моделей необходимы суперкомпьютеры. Стоят они дорого, но еще дороже обходится их постоянное поддержание в рабочем состоянии. Учитывая важность создания математических моделей с высоким разрешением, Минобрнауки выделило нам трехлетний грант. В 2019-м он закончился, но нам продлили его еще на год. Безусловно, 30 миллионов ежегодно – сумма большая. Но и потребности немалые. Мы не только оплатили работу примерно 20 человек (включая совместителей), главное – приобрели оборудование: переоснастили наш кластер, персональные компьютеры и программное обеспечение.
Все упирается в состояние вычислительных мощностей. В 70-80-х годах прошлого века, когда начали разрабатывать первые модели, компьютеры позволяли проводить расчеты с разрешением в 100-200 км. И картина получалась неправдоподобная. Океан – среда турбулентная. Ведь Гольфстрим, хоть и называется «рекой в океане», состоит из множества вихрей, взаимодействующих между собой. Да, спутники видят вихри, но необходимо узнать, какова их структура на глубине. Поэтому для построения моделей необходимы суперкомпьютеры. Стоят они дорого, но еще дороже обходится их постоянное поддержание в рабочем состоянии. Учитывая важность создания математических моделей с высоким разрешением, Минобрнауки выделило нам трехлетний грант. В 2019-м он закончился, но нам продлили его еще на год. Безусловно, 30 миллионов ежегодно – сумма большая. Но и потребности немалые. Мы не только оплатили работу примерно 20 человек (включая совместителей), главное – приобрели оборудование: переоснастили наш кластер, персональные компьютеры и программное обеспечение. Благодаря мегагранту и помощи института, подчеркну этот факт, теперь у нас есть пусть и небольшой, но суперкомпьютер. И все же многие расчеты приходится выполнять в зарубежных вычислительных центрах.
Благодаря мегагранту и помощи института, подчеркну этот факт, теперь у нас есть пусть и небольшой, но суперкомпьютер. И все же многие расчеты приходится выполнять в зарубежных вычислительных центрах.
По условиям мегагранта организовали лабораторию, скажем так, с международным участием. Ее руководители – Бернар Барнье и я, сотрудники – в основном молодежь. Как и любая область науки, моделирование ее очень интересует.
– Тем более что направление перспективное и успешно развивается.
– Это расхожее мнение. Считаю, что каждая наука, ставящая перед собой разумные задачи, привлекательна для молодежи. Если молодой ученый действительно увлечен наукой, то сам выдвинет выбранную область на передний край, что недавно и подтвердилось.
Я каждый год читаю лекции в Гренобле в рамках магистерской программы по механике сплошной среды. Она собирает студентов из разных стран,
включая Россию. По окончании мастер-программы они должны подготовить дипломную работу. Несколько лет назад на курсе была студентка из России Настя Домина, выпускница мехмата Новосибирского госуниверситета. Когда мы обсуждали с ней ее диплом, она сказала, что хочет проанализировать возможности получения энергии из океанских течений (чем-то это напоминает приливные электростанции). Меня, честно говоря, ее идея не взволновала: мы ведем фундаментальные исследования, а она предлагала сугубо прикладной проект. Так я ей и сказал, предложив несколько тем на выбор. Настя – человек увлеченный и упорный – наотрез отказалась: она будет заниматься только этим. Я познакомил ее с Барнье, другими французскими специалистами, и вместе мы стали обдумывать возможность моделирования эффекта установки турбин в областях сильных океанских течений. Нужно было понять, что из этого может выйти. Изменят ли турбины характер океанских течений, ведь через какое-то время они начнут стороной обходить расставленные Настей турбины? Хватит ли полученной энергии, чтобы снабдить ею, скажем, небольшой прибрежный город? В итоге мы вместе написали статью для журнала Nature Energy (его импакт-фактор даже выше, чем у «главы семейства» самого Nature).
Когда мы обсуждали с ней ее диплом, она сказала, что хочет проанализировать возможности получения энергии из океанских течений (чем-то это напоминает приливные электростанции). Меня, честно говоря, ее идея не взволновала: мы ведем фундаментальные исследования, а она предлагала сугубо прикладной проект. Так я ей и сказал, предложив несколько тем на выбор. Настя – человек увлеченный и упорный – наотрез отказалась: она будет заниматься только этим. Я познакомил ее с Барнье, другими французскими специалистами, и вместе мы стали обдумывать возможность моделирования эффекта установки турбин в областях сильных океанских течений. Нужно было понять, что из этого может выйти. Изменят ли турбины характер океанских течений, ведь через какое-то время они начнут стороной обходить расставленные Настей турбины? Хватит ли полученной энергии, чтобы снабдить ею, скажем, небольшой прибрежный город? В итоге мы вместе написали статью для журнала Nature Energy (его импакт-фактор даже выше, чем у «главы семейства» самого Nature). Публикация только что вышла, уверен, она вызовет отклики. А все потому, что у девушки есть идея и она способна за нее побороться. (Сейчас она работает по контракту в частной английской фирме.)
Публикация только что вышла, уверен, она вызовет отклики. А все потому, что у девушки есть идея и она способна за нее побороться. (Сейчас она работает по контракту в частной английской фирме.)
– Удалось ли вам за эти годы предсказать изменения климата?
– А это не совсем наша задача. Океанские модели работают вместе с расчетами других компонентов климатической системы, в первую очередь атмосферы, поскольку в каждодневных и краткосрочных прогнозах роль океана незначительна. Но это не значит, что он не должен присутствовать вовсе, просто его состояние необязательно меняется в течение нескольких суток (время прогноза погоды). Водная стихия консервативна по сравнению с атмосферой: теплоемкость океана в четыре раза ее больше, а плотность – аж в 800. Но когда надо заглянуть вперед на годы и десятилетия, роль океана возрастает многократно. Так что пока мы строим динамические модели с максимально возможной детализацией. В частности, смоделировали процессы конвекции в субполярной Атлантике и обмен водами между Северной Атлантикой и Арктикой. Это важно. Отдельно занимаемся высокоразрешающим атмосферным моделированием. Вместе с расчетами атмосферных процессов наши модели дают метеорологам и океанологам возможность заглянуть на океанскую кухню. Понять, как происходящие там процессы влияют на климат в Арктике и состояние льда, – в перспективе это позволит давать более точные, научно обоснованные прогнозы погоды едва ли не для всего земного шара. Отдельно занимаемся высокоразрешающим атмосферным моделированием. Недавно завершили длительный численный эксперимент по исследованию динамики атмосферы над Северной Атлантикой. Отмечу, что такой огромный массив данных очень высокого разрешения получен впервые в мире. Он нужен для понимания процессов, происходящих в атмосфере и океане, и объясняет их связь. Наверняка поможет намного точнее прогнозировать погоду. Наша статья об этом принята к печати журналом Journal of Applied Meteоrology and Climatology.
Это важно. Отдельно занимаемся высокоразрешающим атмосферным моделированием. Вместе с расчетами атмосферных процессов наши модели дают метеорологам и океанологам возможность заглянуть на океанскую кухню. Понять, как происходящие там процессы влияют на климат в Арктике и состояние льда, – в перспективе это позволит давать более точные, научно обоснованные прогнозы погоды едва ли не для всего земного шара. Отдельно занимаемся высокоразрешающим атмосферным моделированием. Недавно завершили длительный численный эксперимент по исследованию динамики атмосферы над Северной Атлантикой. Отмечу, что такой огромный массив данных очень высокого разрешения получен впервые в мире. Он нужен для понимания процессов, происходящих в атмосфере и океане, и объясняет их связь. Наверняка поможет намного точнее прогнозировать погоду. Наша статья об этом принята к печати журналом Journal of Applied Meteоrology and Climatology.
Понимание происходящих на океанской кухне перемен важно, конечно, не само по себе – оно помогает совершенствованию прогнозов. Сегодня их достоверность на 5-7 суток выросла настолько, что соответствует точности суточных прогнозов погоды 1979 года. Прогресс налицо, но достигнут он не столько благодаря совершенству методов сбора данных, сколько возможностям их обработки, то есть эффективности компьютеров. И хотя в нашей области фактически нет фундаментальных физических открытий, теперь о прогнозировании погоды мы знаем намного больше.
Сегодня их достоверность на 5-7 суток выросла настолько, что соответствует точности суточных прогнозов погоды 1979 года. Прогресс налицо, но достигнут он не столько благодаря совершенству методов сбора данных, сколько возможностям их обработки, то есть эффективности компьютеров. И хотя в нашей области фактически нет фундаментальных физических открытий, теперь о прогнозировании погоды мы знаем намного больше.
Юрий ДРИЗЕ
Знаменитую формулу Эйнштейна знают все, но мало кто ее понимает
В Американском музее естественной истории в Нью-Йорке открылась выставка, посвященная жизни и творчеству Альберта Эйнштейна. В экспозиции выставки представлены оригинальные рукописи и личные вещи великого физика, которые раньше никогда и нигде не выставлялись.
Гвоздем выставки являются поразительные по качеству интерактивные экспонаты, которые, возможно, потрясли бы самого Эйнштейна. Вот, например, огромная видеоустановка, которая искривляет зрительные образы посетителей, иллюстрируя положение Эйнштейна о том, что свет отдаленных звезд искривляется, попав в поле тяготения нашего солнца.
Другой экспонат позволяет посетителям изменять на экране размеры черной дыры — маленького небесного тела, которое, согласно теории, образуется при коллапсе звезд.
А вот еще одна установка, позволяющая следить за элементарными частицами — мюонами. «Мы видим на дне резервуара слой тумана, — поясняет куратор выставки Гретхен Уокер. — Проходя через резервуар, космические лучи нагревают туман и оставляют нечто похожее на инверсионный след самолета. Эти космические лучи — мюоны — движутся с околосветовой скоростью, поэтому течение времени для них резко замедляется. Реальный срок существования мюонов — всего две микросекунды, но по нашим понятиям они живут несколько часов».
Специальная теория относительности Эйнштейна, выражением которой является знаменитая формула эквивалентности массы и энергии E = mc², представляет собой краеугольный камень экспозиции и современной науки. Физик-теоретик Ханох Гутфройнд, которой консультировал кураторов музея при организации экспозиции, говорит, что выставка, которая в начале будущего года отправится в поездку по странам мира, насыщает легендарную формулу реальным содержанием. Знаменитую формулу, говорит он, можно увидеть на спичечных коробках и в рекламных видеоклипах, но очень мало кто понимает, что она значит. Любой посетитель, у которого хватит терпения задержаться на несколько минут у стенда, на котором объясняется эта формула, поймет ее смысл.
Знаменитую формулу, говорит он, можно увидеть на спичечных коробках и в рекламных видеоклипах, но очень мало кто понимает, что она значит. Любой посетитель, у которого хватит терпения задержаться на несколько минут у стенда, на котором объясняется эта формула, поймет ее смысл.
Специальная теория относительности Эйнштейна заложила основы теории и практики использования энергии атомного ядра. Его открытия в области фотоэлектронной эмиссии повели к появлению электронно-вакуумных приборов и микропроцессов, проложив путь к компьютерной революции. Его прозрения в отношении размера и конфигурации молекул помогли раскрыть тайны ДНК.
И все эти великие достижения отражены в данной выставке — самой крупной в истории. Но экспозиция также отдает дань и незаконченным трудам Эйнштейна, указывает куратор выставки Майкл Шара: «Альберт Эйнштейн потратил последние 30 лет своей жизни, пытаясь создать единую теорию поля, которая свела бы воедино законы существования микро- и макромира — как элементарных частиц, так и космических тел. Ему это не удалось, и он считал, что эта часть его жизни была потрачена зря. Однако сегодня мы понимаем, насколько успешным и плодотворным был этот период в его научном творчестве, ибо он подтолкнул теоретическую физику в сторону единой теории поля. Сегодня это одно из самых перспективных направлений науки — и все благодаря ему».
Ему это не удалось, и он считал, что эта часть его жизни была потрачена зря. Однако сегодня мы понимаем, насколько успешным и плодотворным был этот период в его научном творчестве, ибо он подтолкнул теоретическую физику в сторону единой теории поля. Сегодня это одно из самых перспективных направлений науки — и все благодаря ему».
В 1921-м году Эйнштейну была присуждена Нобелевская премия по физике. Двенадцать лет спустя он уехал из нацистской Германии в США, где до конца своих дней преподавал в Принстонском университете. Гордость экспозиции — блокнот Эйнштейна с его вычислениями, которые он вел в попытке объединить все законы физики в рамках единой теории до самой своей смерти в 1955 году.
Экспонаты выставки отдают дань и жизни Альберта Эйнштейна и за пределами науки. В числе экспонатов — школьный табель с его отметками, чайный сервиз, набор его трубок, принадлежавший ему компас. Тут же выставлено письмо Эйнштейна от 1939 года президенту Франклину Рузвельту с предупреждением, что нацисты, по всей видимости, пытаются создать атомную бомбу на основе урана. А рядом письмо самому Эйнштейну от посла Израиля в США Абы Эбана с предложением занять пост президента еврейского государства.
А рядом письмо самому Эйнштейну от посла Израиля в США Абы Эбана с предложением занять пост президента еврейского государства.
Научный консультант выставки Ханох Гуттфройнд указывает, что все эти экспонаты — неотъемлемая часть коллекции, ибо без них невозможно понять истинные масштабы колоссальной фигуры Эйнштейна. «Он обязан своей славой научным достижениям, — говорит Гуттфройнд. — Но Эйнштейн выражал свои взгляды практически по всем вопросам культурной и политической жизни своего времени. Он говорил о проблемах войны и мира, религии, прав человека, национализма и так далее, причем зачастую весьма откровенно и нелицеприятно. Компромиссов и половинчатых мнений он не признавал. Иногда его взгляды отличались наивностью, но не прислушаться к ним было невозможно».
В экспозицию включена подборка писем, которые писали Эйнштейну его поклонники со всего света. Одно письмо от маленького мальчика из пенсильванского городка Бристоль отражает необычайные масштабы непреходящей славы Альберта Эйнштейна. В нем говорится: «Дорогой доктор Эйнштейн. Я хочу знать, что находится по ту сторону неба. Мама говорит, что только вы это знаете. С глубоким уважением, Фрэнк Феллерман».
В нем говорится: «Дорогой доктор Эйнштейн. Я хочу знать, что находится по ту сторону неба. Мама говорит, что только вы это знаете. С глубоким уважением, Фрэнк Феллерман».
Читать «Все формулы мира» — Попов Сергей Борисович — Страница 1
Сергей Попов
Все формулы мира. Как математика объясняет законы природы
Научный редактор Игорь Иванов, канд. физ. – мат. наук
Редактор Полина Суворова
Руководитель проекта А. Шувалова
Корректоры И. Астапкина, Е. Сметанникова
Компьютерная верстка А. Фоминов
Арт-директор Ю. Буга
Иллюстрации на обложке и в блоке Р. Тавасиев
Фото автора на обложке И. Соловей
Фото художника на обложке Г. Собченко
© Попов С., 2019
© Тавасиев Р., иллюстрации, 2019
© ООО «Альпина нон-фикшн», 2019
Все права защищены. Данная электронная книга предназначена исключительно для частного использования в личных (некоммерческих) целях. Электронная книга, ее части, фрагменты и элементы, включая текст, изображения и иное, не подлежат копированию и любому другому использованию без разрешения правообладателя. В частности, запрещено такое использование, в результате которого электронная книга, ее часть, фрагмент или элемент станут доступными ограниченному или неопределенному кругу лиц, в том числе посредством сети интернет, независимо от того, будет предоставляться доступ за плату или безвозмездно.
Электронная книга, ее части, фрагменты и элементы, включая текст, изображения и иное, не подлежат копированию и любому другому использованию без разрешения правообладателя. В частности, запрещено такое использование, в результате которого электронная книга, ее часть, фрагмент или элемент станут доступными ограниченному или неопределенному кругу лиц, в том числе посредством сети интернет, независимо от того, будет предоставляться доступ за плату или безвозмездно.
Копирование, воспроизведение и иное использование электронной книги, ее частей, фрагментов и элементов, выходящее за пределы частного использования в личных (некоммерческих) целях, без согласия правообладателя является незаконным и влечет уголовную, административную и гражданскую ответственность.
* * *
Предисловие автора
Меня всегда удивляли фразы, в которых встречалось выражение «наука и культура». Звучит как «литература и культура» или «искусство и культура». Такое разделение и даже противопоставление лишено смысла, ведь, безусловно, наука – неотъемлемая часть современной культуры. Также меня всегда расстраивало противопоставление «двух культур» – гуманитарной и естественно-научной, о котором писал еще Чарльз Сноу в своей знаменитой работе. Кажется, что такое разделение – а оно до сих пор заметно – основано в первую очередь на взаимном непонимании, свойственном многим людям и с той и с другой стороны. Чтобы лучше понять друг друга, надо больше общаться. Отчасти предлагаемая читателю книга является попыткой такого общения. Соответственно, основной ее адресат – человек, считающий себя в большей степени «гуманитарием», что в первую очередь подразумевает нелюбовь ко «всяким формулам».
Также меня всегда расстраивало противопоставление «двух культур» – гуманитарной и естественно-научной, о котором писал еще Чарльз Сноу в своей знаменитой работе. Кажется, что такое разделение – а оно до сих пор заметно – основано в первую очередь на взаимном непонимании, свойственном многим людям и с той и с другой стороны. Чтобы лучше понять друг друга, надо больше общаться. Отчасти предлагаемая читателю книга является попыткой такого общения. Соответственно, основной ее адресат – человек, считающий себя в большей степени «гуманитарием», что в первую очередь подразумевает нелюбовь ко «всяким формулам».
В некотором смысле книга состоит из трех частей, и важнейшая из них связана с набором иллюстраций, созданных Ростаном Тавасиевым. С самого начала идея проекта вращалась вокруг визуальных образов, которые могли бы по-своему выразить роль математики в познании и описании мира, а также ее связь с другими подходами. Поэтому иллюстративный ряд – не просто дополнение к тексту, а самостоятельная сущность, у которой есть создатель, своими методами выражающий собственную точку зрения на мысли и образы, представленные в основной – текстовой – части книги.
В 15 главах, составляющих эту часть, формул практически нет. Целью был разговор о математическом методе описания мира с точки зрения ученого, который им активно пользуется, но сам его не развивает, создание некоего внятного образа, подкрепленного разнообразными аналогиями (с которыми, разумеется, можно не соглашаться) и примерами, которые я брал в первую очередь из физики и астрофизики. Мне хотелось, чтобы читатель понял, что математика – не способ все запутать, а единственная возможность понять очень и очень многое из того, что мы узнали и узнаем о мире, в первую очередь в результате физических исследований. Кроме того, математика – метод не только (и не столько) представления и описания, но еще и исследований природы, поскольку оказалось, что множество новых результатов удается вначале получить с помощью анализа уравнений (а иногда даже создания нового математического аппарата), а эксперимент или наблюдения впоследствии их лишь подтверждают.
Однако многим продвинутым читателям покажется, что слов недостаточно, – надо и уравнения выписывать. Рассказывать о математических методах в физике без помощи формул – все равно что говорить о живописи без иллюстраций или показа картин. Поэтому появилась третья часть книги – приложения, куда вынесен ряд примеров, призванных непосредственно продемонстрировать, как математика применяется в физике и астрономии. Там формулы присутствуют в большом количестве, правда, сложных выражений среди них нет. Фактически приложения – это ряд независимых научно-популярных статей разного объема, посвященных самым разным методам, процессам и объектам. Стандартного курса нетехнического вуза по высшей математике и физике (или даже естествознанию) будет вполне достаточно, чтобы во всем разобраться. Не возникнет сложностей и у старшеклассников из физико-математических школ или астрономических кружков.
Рассказывать о математических методах в физике без помощи формул – все равно что говорить о живописи без иллюстраций или показа картин. Поэтому появилась третья часть книги – приложения, куда вынесен ряд примеров, призванных непосредственно продемонстрировать, как математика применяется в физике и астрономии. Там формулы присутствуют в большом количестве, правда, сложных выражений среди них нет. Фактически приложения – это ряд независимых научно-популярных статей разного объема, посвященных самым разным методам, процессам и объектам. Стандартного курса нетехнического вуза по высшей математике и физике (или даже естествознанию) будет вполне достаточно, чтобы во всем разобраться. Не возникнет сложностей и у старшеклассников из физико-математических школ или астрономических кружков.
Особняком стоят два последних больших приложения, одно из которых посвящено гипотезам в астрофизике, а второе – практической пользе фундаментальных исследований вообще и астрономических в частности. Читатель, все-таки желающий формул избежать, может, пропустив первые девять приложений, смело браться за два последних, не боясь столкнуться с «математическими монстрами».
Предисловие художника
Предложение Сергея Попова иллюстрировать книгу про математические формулы застало меня врасплох. Как иллюстрировать то, чего не понимаешь? Но я решил довериться удивительному дару Сергея Борисовича объяснять непостижимое.
В школе мир цифр казался ужасно скучным. Клетку в тетради воспринимал как средство ограничения свободы воображения. И боролся за эту свободу заполняя тетрадки рисунками. Рисовал и в учебниках, визуализируя условия задач и украшая буденновскими усами портреты великих математиков.
И вот теперь мои рисунки снова встретились с математикой на страницах этой книги. Подозреваю, что стал тем максимально не подготовленным «гуманитарием», на котором автор тестировал свой текст. Если поймет этот художник, то, вероятно, и другие тоже поймут.
Издательство попросило пояснить в этом коротком вступлении, как устроены иллюстрации. Они состоят из трех основных элементов: клякса, чертеж (или карандашный рисунок) и орнамент. Клякса, след падения капли акварели на белом листе, – естественное физическое явление. Чертеж этой кляксы – попытка человека измерить и понять это физическое явление. Орнамент – один из первых доступных человеку способов описать через рисунок и ритм окружающий мир.
Чертеж этой кляксы – попытка человека измерить и понять это физическое явление. Орнамент – один из первых доступных человеку способов описать через рисунок и ритм окружающий мир.
Собранные из этих элементов иллюстрации я отправлял Сергею Борисовичу на благословение. В ответ получал наставительные комментарии и исправлял рисунки. Так, шаг за шагом, приближался к пониманию смысла каждой главы. Теперь эта книга у вас в руках. И вы даже уже прочитали предисловие.
Ростан Тавасиев
Часть I
Новый язык
А. ЗАКОНАМИ ПРИРОДЫ МЫ НАЗЫВАЕМ НАДЕЖНО УСТАНОВЛЕННЫЕ ЗАКОНОМЕРНОСТИ, ОПИСЫВАЮЩИЕ ПРОЦЕССЫ В РЕАЛЬНОМ МИРЕ. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ПОМОГАЮТ НЕ ТОЛЬКО ЧЕТЧЕ ФОРМУЛИРОВАТЬ ЭТИ ЗАКОНЫ, НО И ИСПОЛЬЗОВАТЬ ПРОВЕРЕННЫЕ АЛГОРИТМЫ И ПРАВИЛА КАК ДЛЯ РАСЧЕТОВ РЕЗУЛЬТАТА ИХ ДЕЙСТВИЯ, ТАК И ДЛЯ ПОЛУЧЕНИЯ НОВЫХ СООТНОШЕНИЙ, Т.Е. НОВЫХ ЗАКОНОВ ПРИРОДЫ.
Б. «НЕПОСТИЖИМАЯ ЭФФЕКТИВНОСТЬ МАТЕМАТИКИ» СОСТОИТ В ПЕРВУЮ ОЧЕРЕДЬ В ТОМ, ЧТО ЗАКОНЫ И ПРАВИЛА, СФОРМУЛИРОВАННЫЕ И ДОКАЗАННЫЕ ДЛЯ ИДЕАЛЬНЫХ МАТЕМАТИЧЕСКИХ ОБЪЕКТОВ, ОКАЗЫВАЮТСЯ С ВЫСОКОЙ ТОЧНОСТЬЮ ПРИМЕНИМЫ К РЕАЛЬНЫМ ОБЪЕКТАМ И ПРОЦЕССАМ.
Глава 1
Формулы и законы природы
Самый глобальный процесс – расширение вселенной[1] – описывается формулой всего лишь из трех символов: v = Hr. Это закон Хаббла. Здесь r – так называемое собственное расстояние до объекта («нормальное» расстояние «в метрах» в данный момент времени), v – скорость изменения этого собственного расстояния со временем по часам наблюдателя (так называемое cosmic time), связанная с расширением. Наконец, H – постоянная Хаббла. Это коэффициент пропорциональности, характеризующий, насколько быстро происходит расширение в данную эпоху. Закон Хаббла можно сформулировать и словами (вообще, чем проще уравнение, тем, как правило, легче это сделать): скорость удаления галактики за счет расширения вселенной прямо пропорциональна расстоянию до нее. Однако весь контекст лучше проявляется именно при формульной записи даже в таком простом случае. И сам закон выводится с очевидной неизбежностью именно на языке формул (см. приложение 1).
приложение 1).
Полный список всех физических формул
Изучение физики заключается в применении концепций для решения задач. В этой статье представлен исчерпывающий список физических формул, который будет служить готовым справочником при решении физических задач. Вы даже можете использовать этот список для быстрого повторения перед экзаменом.
Физика — самая фундаментальная из всех наук. Это также одна из самых сложных наук для освоения. Изучение физики — это, по сути, изучение фундаментальных законов, управляющих нашей Вселенной. Я бы сказал, что нужно выяснить гораздо больше, чем просто запомнить и разобрать физические формулы. Попытайтесь понять, что формула говорит и означает, и какое физическое отношение она объясняет. Если вы понимаете физические понятия, лежащие в основе этих формул, вывести их или запомнить несложно. В этой статье ScienceStruck перечислены некоторые физические формулы, которые вам понадобятся для решения основных физических задач.
Формулы физики
- Механика
- Трение
- Момент инерции
- Ньютоновская гравитация
- Движение снаряда
- Простой маятник
- Электричество
- Термодинамика
- Электромагнетизм
- Оптика
- Квантовая физика
Выведите все эти формулы один раз, прежде чем начать их использовать. Изучайте физику и смотрите на нее как на возможность оценить скрытую красоту природы, выраженную через естественные законы. Помощь по физике предоставляется здесь в виде готовых к использованию формул. Физика имеет репутацию сложной, и в какой-то степени это правда из-за задействованной математики.
Изучайте физику и смотрите на нее как на возможность оценить скрытую красоту природы, выраженную через естественные законы. Помощь по физике предоставляется здесь в виде готовых к использованию формул. Физика имеет репутацию сложной, и в какой-то степени это правда из-за задействованной математики.
Если вы не хотите думать самостоятельно и применять основные принципы физики, решать физические задачи всегда будет сложно. Наш список формул по физике призван помочь вам в решении задач. Радость самостоятельного решения физической задачи стоит всех затраченных усилий! Понимание концепций физики бросает вызов вашему воображению и мыслительному потенциалу, при этом, если вы визуализируете проблему, вы можете найти решение. Итак, вот обещанный список, который поможет вам.
Механика
Механика — старейший раздел физики. Механика имеет дело со всеми видами и сложностями движения. Он включает в себя различные приемы, которые могут упростить решение механической задачи.
Движение в одном измерении
Формулы для движения в одном измерении (также называемые кинематическими уравнениями движения) следующие. (Здесь «u» — начальная скорость, «v» — конечная скорость, «a» — ускорение, t — время):
(Здесь «u» — начальная скорость, «v» — конечная скорость, «a» — ускорение, t — время):
- с = ut + ½ в 2
- v = u + at
- v 2 = u 2 + 2as
- v av (Средняя скорость) = (v+u)/2
Импульс, сила и импульс
Формулы для импульса, импульса и силы относительно частицы, движущейся в трех измерениях, следующие (Здесь сила, импульс и скорость являются векторами):
- Импульс является произведением массы и скорости тело. Импульс рассчитывается по формуле: P = m (масса) x v (скорость)
- Сила может быть определена как то, что вызывает изменение импульса тела. Сила определяется знаменитым законом движения Ньютона: F = m (масса) x a (ускорение)
- Импульс — это большая сила, приложенная за очень короткий промежуток времени. Удар молотка – это импульс. Импульс определяется выражением I = m(v-u)
Давление
Давление определяется как сила на единицу площади:
| Давление ( P ) = | Сила ( Ф ) Зона ( А ) |
Плотность
Плотность – это масса, содержащаяся в теле на единицу объема.
Формула плотности:
| Плотность ( D ) = | Масса ( М ) Том ( В ) |
Угловой момент
Угловой момент – это величина, аналогичная линейному импульсу, при котором тело совершает вращательное движение. Формула для углового момента (J) определяется как:
J = r x p
, где J обозначает угловой момент, r — радиус-вектор, а p — линейный импульс.
Крутящий момент
Крутящий момент можно определить как момент силы. Крутящий момент вызывает вращательное движение. Формула для крутящего момента: τ = r x F , где τ — крутящий момент, r — радиус-вектор, а F — линейная сила.
Круговое движение
Формулы для кругового движения объекта массы «m», движущегося по окружности радиуса «r» с тангенциальной скоростью «v», следующие:
| Центростремительная сила ( F ) = | мв 2 р |
| Центростремительное ускорение ( a ) = | в 2 р |
Центр масс
Общая формула для центра масс твердого тела:
| Ч = | Σ N i = 1 m i r i Σ N i = 1 м i |
где R — вектор положения центра масс, r — общий вектор положения всех частиц объекта, а N — общее количество частиц.
Приведенная масса для двух взаимодействующих тел
Физическая формула приведенной массы (μ):
| мк = | м 1 м 2 м 1 + м 2 |
где m 1 – масса первого тела, m 2 – масса второго тела.
Работа и энергия
Формулы для работы и энергии в случае одномерного движения следующие:
Вт (выполненная работа) = F (сила) x D (перемещение) типы, потенциальная энергия и кинетическая энергия. В случае гравитационной силы потенциальная энергия определяется выражением
PE (гравитация) = m (масса) x g (ускорение свободного падения) x h (высота)
Переходная кинетическая энергия выражается как ½ m (масса) x v 2 (квадрат скорости)
Мощность
Мощность равна работе, совершаемой в единицу времени. Формула мощности задается как
Формула мощности задается как
| Мощность ( P ) = | В 2 Р | = I 2 Р |
где P=мощность, W=работа, t=время.
Трение
Трение можно разделить на два вида: статическое трение и динамическое трение.
Статическое трение:
Статическое трение характеризуется коэффициентом статического трения μ . Коэффициент статического трения определяется как отношение приложенной тангенциальной силы (F), которая может вызвать скольжение, к нормальной силе между поверхностями, соприкасающимися друг с другом. Формула для расчета этого статического коэффициента выглядит следующим образом:
| мк = | Приложенная тангенциальная сила ( F ) Нормальная сила ( N ) |
Величина силы, необходимой для скольжения твердого тела, покоящегося на плоской поверхности, зависит от коэффициента статического трения и определяется по формуле: ускорение)
Динамическое трение:
Динамическое трение также характеризуется тем же коэффициентом трения, что и статическое трение, поэтому формула для расчета коэффициента динамического трения также такая же, как и выше. Только динамический коэффициент трения, как правило, ниже статического, поскольку приложенная сила, необходимая для преодоления нормальной силы, меньше.
Только динамический коэффициент трения, как правило, ниже статического, поскольку приложенная сила, необходимая для преодоления нормальной силы, меньше.
Момент инерции
Вот некоторые формулы для моментов инерции различных объектов. (M означает массу, R — радиус и L — длину):
| Объект | Ось | Момент инерции |
| Диск | Ось, параллельная диску, проходящая через центр | MR 2 /2 |
| Диск | Ось, проходящая через центр и перпендикулярная диску | MR 2 /2 |
| Тонкий стержень | Ось, перпендикулярная стержню и проходящая через центр | МЛ 2 /12 |
| Твердая сфера | Ось, проходящая через центр | 2MR 2 /5 |
| Твердая оболочка | Ось, проходящая через центр | 2MR 2 /3 |
Ньютоновское тяготение
Вот несколько важных формул, связанных с ньютоновским тяготением:
Закон всемирного тяготения Ньютона:
| F г = | Gm 1 m 2 r 2 |
где
- m 1 , m 2 являются массами двух тел
- G — универсальная гравитационная постоянная, имеющая значение 6,67300 × 10-11 м3 кг-1 с-2
- r — расстояние между двумя телами
Формула для скорости убегания (v esc ) = (2GM / R) 1/2 где,
- M — масса центрального гравитирующего тела
- R — радиус центрального тела
Движение снаряда
Вот две важные формулы, относящиеся к движению снаряда:
(v = скорость частицы, v 0 = начальная скорость, g — ускорение свободного падения, θ — угол проекции, h — максимальная высота l — дальность полета снаряда. )
)
| Максимальная высота снаряда ( ч ) = | v 0 2 sin 2 θ 2 г |
Горизонтальный диапазон снаряда (L) = V 0 2 SIN 2θ / G
Простой майку
Формула физики для периода простого пенделума (T) 9013
Формула физики для периода простого Pendulum (T) = 9015. (л/г) где
- l длина маятника
- g это ускорение свободного падения
Конический маятник
Период конического маятника (T) = 2π √(lcosθ/g)
где
- l длина маятника
- g это ускорение свободного падения
- Половина угла конического маятника
Электричество
Вот несколько формул, связанных с электричеством.
Закон Ома
Закон Ома дает зависимость между приложенным напряжением и током, протекающим по твердому проводнику:
В (Напряжение) = I (Ток) x R (Сопротивление)
Мощность
В случае замкнутой электрической цепи с приложенным напряжением V и сопротивлением R, через которую протекает ток I,
| Мощность ( P ) = | В 2 Р |
= I 2 Р. . . (поскольку V = IR, закон Ома)
. . (поскольку V = IR, закон Ома)
Закон напряжения Кирхгофа
для каждой циклы в электрической цепи:
σ I V I = 0
, где V I — все, что прилагается на v. I .
Текущий закон Кирчоффа
на каждом узле электрической цепи:
σ I I I = 0
, где I I
Сопротивление
Физические формулы для эквивалентного сопротивления в случае параллельного и последовательного соединения следующие: 1 + R 2 + R 3
R 1 + R 93 2
For n number of resistors, R 1 , R 2 …R n , the formula will be:
1/ R eq = 1/ R 1 + 1/ R 2 + 1/ R 3 …+ 1/ R n
Конденсаторы
Конденсатор накапливает электрическую энергию, если его поместить в электрическое поле. Типичный конденсатор состоит из двух проводников, разделенных диэлектриком или изоляционным материалом. Вот наиболее важные формулы, относящиеся к конденсаторам. Единицей измерения емкости является фарад (Ф), а ее значения обычно указываются в мФ (микрофарад = 10 -6 Ф).
Типичный конденсатор состоит из двух проводников, разделенных диэлектриком или изоляционным материалом. Вот наиболее важные формулы, относящиеся к конденсаторам. Единицей измерения емкости является фарад (Ф), а ее значения обычно указываются в мФ (микрофарад = 10 -6 Ф).
Емкость (C) = Q / V
Энергия, запасенная в конденсаторе (E крышка ) = 1/2 CV 2 = 1/2 (Q 2 / C) = 1/2 (QV)
Ток, протекающий через конденсатор I = C (DV / DT)
Эквивалентная емкость для конденсаторов N ‘, подключенных в параллели:
C Уравнение (параллель) = C 1 + C 2 + C 3 …+ C N + C 3 … C N 2 + C 3 … C N 2 + C 3 … C N 2 + C 3 … C N 2 + C 3 … C N 2 = Σ i=1 to n C i
Эквивалентная емкость для n последовательно соединенных конденсаторов:
1 / C eq (Серия) = 1 / C 1 + 1 / C 2 …+ 1 / C n = Σ i=от 1 до n (1 / C i 9 0)
Здесь
- C — емкость
- Q — заряд, накопленный на каждом проводнике конденсатора
- В — разность потенциалов на конденсаторе
.
Формула плоскопараллельного конденсатора:
C = kε 0 (A/d)
Где
- k = диэлектрическая проницаемость (k = 1 в вакууме)
- ε 0 = Диэлектрическая проницаемость свободного пространства (= 8,85 × 10 -12 C 2 / Нм 2 )
- A = Площадь пластины (в квадратных метрах)
- d = Расстояние между пластинами (в метрах)
Формула цилиндрического конденсатора:
C = 2π kε 0 [L / ln(b / a)]
Где
- k = диэлектрическая проницаемость (k = 1 в вакууме)
- ε 0 = Диэлектрическая проницаемость свободного пространства (= 8,85 × 10 -12 C 2 / Н·м 2 )
- L = Длина конденсатора
- a = Внутренний радиус проводника
- b = Внешний радиус проводника
Формула сферического конденсатора:
C = 4π kε 0 [(ab)/(b-a)]
Где
- k = диэлектрическая проницаемость (k = 1 в вакууме)
- ε 0 = Диэлектрическая проницаемость свободного пространства (= 8,85 × 10 -12 C 2 / Нм 2 )
- a = радиус внутреннего проводника
- b = Внешний радиус проводника
Катушки индуктивности
Катушка индуктивности представляет собой электрический компонент, который сопротивляется потоку электронов или электрическому току через него. Это свойство индуктивности в этих устройствах обусловлено электродвижущей силой, создаваемой индуцируемым в них магнитным полем. Единицей индуктивности является Генри. Вот несколько важных формул, связанных с катушками индуктивности.
Это свойство индуктивности в этих устройствах обусловлено электродвижущей силой, создаваемой индуцируемым в них магнитным полем. Единицей индуктивности является Генри. Вот несколько важных формул, связанных с катушками индуктивности.
Энергия, запасенная в индукторе (E , сохраненная ) = 1/2 (LI 2 )
Где L — индуктивность, а I — ток, протекающий через индуктор.
Индуктивность цилиндрического воздушного сердечника катушки (L) = (м 0 кН 2 А/л)
Где
- L — индуктивность, измеренная в генри
- Н — число витков на катушке
- А — площадь поперечного сечения катушки
- м 0 является проницаемостью свободного пространства (= 4π × 10 -7 Гн/м)
- К — коэффициент Нагаоки
- л — длина рулона
Индукторы в серии сети
для индукторов, L 1 , L 2 … L N Подключены последовательно,
L EQ = L 1 + L 2 EQ = L 1 + L 2 . + L n (L — индуктивность)
+ L n (L — индуктивность)
Катушки индуктивности в параллельной сети
Для катушек индуктивности, L 1 , L 2 …L
8
8 n
8 n
8соединенные параллельно,
1 / L eq = 1 / L 1 + 1 / L 2 …+ 1 / L n
поведения материи в массе. Это область, ориентированная на изучение материи и энергии во всех их проявлениях. Вот некоторые из наиболее важных формул, связанных с классической термодинамикой и статистической физикой.
Первый закон термодинамики
dU = dQ + dW
где dU — изменение внутренней энергии, dQ — теплота, поглощаемая системой, а dW — работа, совершаемая системой.
Термодинамические потенциалы
Все термодинамические явления можно понять с точки зрения изменений пяти термодинамических потенциалов при различных физических ограничениях. Это внутренняя энергия (U), энтальпия (H), свободная энергия Гельмгольца (F), свободная энергия Гиббса (G), Ландау или большой потенциал (Φ). Каждая из этих скалярных величин представляет способность термодинамической системы совершать работу различного рода при различных типах ограничений на ее физические параметры.
Каждая из этих скалярных величин представляет способность термодинамической системы совершать работу различного рода при различных типах ограничений на ее физические параметры.
| Термодинамический потенциал | Определяющее уравнение |
|
| Внутренняя энергия (U) | dU = TdS − pdV + µdN | |
| Энтальпия (H) | H = U + pV dH = TdS + Vdp + µdN | |
| Свободная энергия Гиббса (G) | G = U – TS + pV = F + pV = H – TS dG = -SdT + Vdp + µdN | |
| Свободная энергия Гельмгольца (F) | F = U – TS dF = – SdT – pdV + µdN | |
| Ландау или Гранд Потенциал | Φ = F – µN dΦ = – SdT – pdV – Ndµ |
Уравнения идеального газа
Идеальный газ — это физическая концепция идеального газа, состоящего из невзаимодействующих частиц, которые легче анализировать по сравнению с реальными газами, которые намного сложнее и состоят из взаимодействующих частиц. Полученные уравнения и законы идеального газа согласуются с природой реальных газов при определенных условиях, хотя и не позволяют точно предсказывать из-за неучтенной интерактивности молекул. Вот некоторые из наиболее важных физических формул и уравнений, связанных с идеальными газами. Начнем с основных законов идеального газа и уравнения состояния идеального газа.
Полученные уравнения и законы идеального газа согласуются с природой реальных газов при определенных условиях, хотя и не позволяют точно предсказывать из-за неучтенной интерактивности молекул. Вот некоторые из наиболее важных физических формул и уравнений, связанных с идеальными газами. Начнем с основных законов идеального газа и уравнения состояния идеального газа.
| Право | Уравнение |
|
| Закон Бойля | PV = константа или P 1 В 1 = P 2 В 2 (при постоянной8 температуре) 9008 | |
| Закон Чарльза | V / T = константа или V 1 / T 1 = V 2 / T 2 ( при постоянном давлении ) | |
| Закон давления-температуры Амонтона | P/T = константа или P 1 / T 1 = P 2 / T 2 ( При постоянном объеме ) | |
| Уравнение состояния идеального газа | PV = nRT = NkT |
Кинетическая теория газов
Основываясь на первичных предположениях о том, что объем атомов или молекул пренебрежимо мал по сравнению с объемом контейнера, а силы притяжения между молекулами пренебрежимо малы, кинетическая теория описывает свойства идеальных газов. Вот наиболее важные физические формулы, относящиеся к кинетической теории одноатомных газов.
Вот наиболее важные физические формулы, относящиеся к кинетической теории одноатомных газов.
Давление (P) = 1/3 (Нм v 2 )
Здесь P — давление, N — число молекул, а v 2 — среднеквадратическая скорость частиц.
Внутренняя энергия (U) = 3/2 (NKT)
Тепловые возможности
Тепловая вместимость при постоянном давлении (C P ) = 5/2 NK = C В + NK
= C V + NK
= C V + NK
Теплоемкость при постоянном объеме (C v ) = 3/2 Nk
Отношение теплоемкостей (γ) = C p / C v = 5/3
Формулы скорости
Средняя молекулярная скорость (V означает ) = [(8kT)/(πm)] 19004 2
Среднеквадратичная скорость молекулы (V rms ) = (3kT/m) 1/2
Наиболее вероятная скорость молекулы (V prob ) = (20kT0/m6) /2
Средний свободный пробег молекулы (λ) = (kT)/√2πd 2 P ( Здесь P в Паскалях )
Здесь N — число молекул, k — постоянная Больцмана, P — давление, d — диаметр молекулы, m — масса молекулы, T — температура газа.
Электромагнетизм
Вот некоторые из основных формул электромагнетизма.
Кулоновская сила между двумя покоящимися зарядами равна
| ( Ф ) = | q 1 q 2 4πε 0 r 2 |
Здесь,
- q 1 , q 2 являются сборами
- ε 0 это диэлектрическая проницаемость свободного пространства
- r — расстояние между двумя зарядами
Сила Лоренца
Сила Лоренца — это сила, с которой электрическое и/или магнитное поле действует на заряженную частицу.
(сила Лоренца) F = q (E + v x B)
где
- q — заряд частицы
- E и B — векторы электрического и магнитного поля
Релятивистская механика
Вот некоторые из наиболее важных формул релятивистской механики. Переход от классической к релятивистской механике вовсе не гладок, так как он сливает пространство и время в одно целое, убирая ньютоновское представление об абсолютном времени. Если вы знаете, что такое специальная теория относительности Эйнштейна, то следующие формулы будут вам понятны.
Переход от классической к релятивистской механике вовсе не гладок, так как он сливает пространство и время в одно целое, убирая ньютоновское представление об абсолютном времени. Если вы знаете, что такое специальная теория относительности Эйнштейна, то следующие формулы будут вам понятны.
Преобразования Лоренца
Преобразования Лоренца можно воспринимать как вращения в четырехмерном пространстве. Точно так же, как вращения в трехмерном пространстве смешивают пространственные координаты, преобразование Лоренца смешивает временные и пространственные координаты. Рассмотрим две, трехмерные системы отсчета S(x,y,z) и S'(x’,y’,z’), совпадающие друг с другом.
Теперь рассмотрим, что система S’ начинает двигаться с постоянной скоростью v относительно системы S. В релятивистской механике время относительно! Таким образом, временная координата для кадра S будет t’, а для кадра S будет t.
Учитывать
| γ = | 1 √(1 – v 2 / c 2 ) |
Преобразования координат между двумя системами отсчета известны как преобразования Лоренца и задаются следующим образом:
Преобразования Лоренца пространства и времени
– vt)
y = y’
z= z’
t = γ(t’ + vx’/c 2 ) и t’ = γ(t – vx/c 2 )
Релятивистские преобразования скорости
В тех же двух кадрах S и S’ преобразования для компонент скорости будут следующими (Здесь (U x , U y , U z ) и (U x ‘, U y ‘, U z ‘) — компоненты скорости в S и S’ кадрах соответственно):
8 U x = (U x ‘ + v) / (1 + U x ‘v / c 2 )
U y = (U y ‘) / γ(1 + U x ‘v / c 2 )
U z = (U z’1)900 x ‘V / C 2 ) и
U x ‘ = (U x — V) / (1 — U x В / с 2 )
U Y ‘ = (U y ) / γ(1 – U x v / c 2 )
U z ‘ = (U z ) / γ(1 – U x 0 v 2 )
Преобразования импульса и энергии в релятивистской механике
Рассмотрим те же две системы координат (S, S’), что и в случае преобразования координат Лоренца выше. S’ движется со скоростью ‘v’ вдоль оси x. Здесь снова γ — фактор Лоренца. В кадре S (P x , P y , P z ) и в кадре S’ (P x ’, P y ’, P z ’) компоненты импульса. Теперь рассмотрим формулы для преобразования импульса и энергии частицы между этими двумя системами отсчета в релятивистском режиме.
S’ движется со скоростью ‘v’ вдоль оси x. Здесь снова γ — фактор Лоренца. В кадре S (P x , P y , P z ) и в кадре S’ (P x ’, P y ’, P z ’) компоненты импульса. Теперь рассмотрим формулы для преобразования импульса и энергии частицы между этими двумя системами отсчета в релятивистском режиме.
Компонент мудрый импульс преобразования и преобразования энергии
P x = γ (стр x ‘ + ve’ / c 2 )
P y = P Y ‘
P Z = = y ‘
P Z = y ‘
P Z = P Y ‘
P P Z ‘
E = γ (E’ + VP x )
и
P x ‘= γ (стр x — VE / C 2 )
P y. ‘ = P y
P z ‘ = P z
E’ = γ(E – vP x )
Физические формулы для величин в релятивистской динамике
Все известные величины в классической механике модифицируются, когда мы переходим к релятивистской механике, основанной на специальной теории относительности. Вот формулы величин в релятивистской динамике.
Вот формулы величин в релятивистской динамике.
Релятивистский импульс p = γm 0 v
, где m 0 – масса покоя частицы.
Энергия массы покоя E = m 0 c 2
Суммарная энергия (релятивистская) E = √(p 2 c 2 + m 0 2 c 4 ))
Оптика — одна из древнейших ветвей физики
7 9 Существует много важных формул оптической физики, которые нам часто нужны при решении физических задач. Вот некоторые из важных и часто используемых оптических формул.
Закон Снеллиуса
| Син и Син р | = | n 2 n 1 | = | v 1 v 2 |
- где i угол падения
- r — угол преломления
- n 1 показатель преломления среды 1
- n 2 показатель преломления среды 2
- v 1 , v 2 – скорости света в среде 1 и среде 2 соответственно
Формула линзы Гаусса: 1/u + 1/v = 1/f
где
- u – расстояние до объекта
- v – расстояние до изображения
- f – Фокусное расстояние объектива
Уравнение производителя линз
Наиболее фундаментальным свойством любой оптической линзы является ее способность сводить или расходить лучи света, что измеряется ее фокусным расстоянием. Вот формула производителя объектива, которая поможет вам рассчитать фокусное расстояние объектива по его физическим параметрам.
Вот формула производителя объектива, которая поможет вам рассчитать фокусное расстояние объектива по его физическим параметрам.
1 / f = [n-1][(1 / R 1 ) – (1 / R 2 ) + (n-1) d / nR 1 R 2 )]
Здесь
- n — показатель преломления материала линзы
- R 1 радиус кривизны поверхности линзы, обращенной к источнику света
- R 2 радиус кривизны поверхности линзы, обращенной в сторону от источника света
- d — толщина линзы
Если линза очень тонкая по сравнению с расстояниями – R 1 и R 2 приведенная выше формула может быть аппроксимирована следующим образом:
(Приближение тонкой линзы) 1 / f ≈ (n-1) [1 / R 1 – 1 / R 2
9 ]
8 5
Составные линзы
Суммарное фокусное расстояние (f) двух тонких линз с фокусным расстоянием f 1 и f 2 , соприкасающихся друг с другом:
1 / f = 1 / f 1 + 1 / f 2
Если две тонкие линзы разнесены на расстояние d, их общее фокусное расстояние определяется по формуле:
1 / F = 1 / F 1 + 1 / F 2 — (D / F 1 — F 2 ) )
Newton’s Rings Formulas
Вот важные формы для Ньютона. эксперимент с кольцами, иллюстрирующий дифракцию.
эксперимент с кольцами, иллюстрирующий дифракцию.
n th Dark ring formula: r 2 n = nRλ
n th Bright ring formula: r 2 n = (n + ½) Rλ
where
- n -й радиус кольца
- Радиус кривизны линзы
- Длина волны падающего света
Квантовая физика
Квантовая физика — один из самых интересных разделов физики, описывающий атомы и молекулы, а также атомную субструктуру. Вот некоторые формулы, относящиеся к самым основам квантовой физики, которые могут вам часто понадобиться.
Волна Де Бройля
Длина волны Де Бройля:
| λ = | ч р |
где, λ- длина волны де Бройля, h – постоянная Планка, p – импульс частицы.
Закон дифракции Брэгга : 2a Sin θ = nλ
где
- a – расстояние между атомными плоскостями
- н – Порядок дифракции
- θ – угол дифракции
- λ – Длина волны падающего излучения
Соотношение Планка
Соотношение Планка дает связь между энергией и частотой электромагнитной волны:
| E = hv = | ч ω 2π |
где h – постоянная Планка, v частота излучения и ω = 2π v
Принцип неопределенности
Принцип неопределенности является основой, на которой основана квантовая механика. Он раскрывает неотъемлемое ограничение, которое природа накладывает на то, насколько точно может быть измерена физическая величина. Соотношение неопределенностей имеет место между любыми двумя некоммутирующими переменными. Ниже приведены два специальных соотношения неопределенностей.
Он раскрывает неотъемлемое ограничение, которое природа накладывает на то, насколько точно может быть измерена физическая величина. Соотношение неопределенностей имеет место между любыми двумя некоммутирующими переменными. Ниже приведены два специальных соотношения неопределенностей.
Неопределенность положения-импульса
Соотношение неопределенности положения-импульса говорит о том, что вы не можете предсказать, где находится частица и как быстро она движется, с произвольной точностью. Чем точнее вы определите положение, тем более неуверенными вы будете в отношении импульса частицы, и наоборот. Математическая формулировка этого отношения выглядит следующим образом:
| Δ x .Δ p ≥ | ч 2π |
где Δx — неопределенность положения, а Δp — неопределенность импульса.
Неопределенность энергии и времени
Это соотношение неопределенности между энергией и временем. Это соотношение приводит к некоторым поразительным результатам, таким как создание виртуальных частиц на сколь угодно короткие промежутки времени! Математически это выражается следующим образом:
Это соотношение приводит к некоторым поразительным результатам, таким как создание виртуальных частиц на сколь угодно короткие промежутки времени! Математически это выражается следующим образом:
| Δ Е .Δ т ≥ | ч 2π |
где ΔE — неопределенность по энергии, а Δt — погрешность по времени.
На этом я завершаю обзор некоторых важных физических формул. Этот список является лишь репрезентативным и далеко не полным. Физика является основой всех наук, и поэтому ее область распространяется на все науки. Каждая область теории физики изобилует бесчисленными формулами. Если вы прибегнете к тому, чтобы просто замазать все эти формулы, вы можете сдать экзамены, но вы не будете заниматься настоящей физикой. Если вы усвоите теорию, лежащую в основе этих формул, физика упростится. Чтобы рассматривать физику через формулы и законы, вы должны хорошо разбираться в математике. Убежать от него невозможно. Математика — это язык природы!
Убежать от него невозможно. Математика — это язык природы!
Чем больше мы узнаем о природе, тем больше слов нам нужно для ее описания. Это привело к усилению жаргонизации науки с созданием полей и подполей. Вы можете обратиться к глоссарию научных терминов и научных определений для любого жаргона, который находится за пределами вашего понимания.
Если вы действительно хотите понять, что значит быть физиком, и получить представление о взглядах физика на вещи, прочитайте «Фейнмановские лекции по физике», которые настоятельно рекомендуется прочитать всем, кто любит физику. Она написана одним из величайших физиков всех времен, профессором Ричардом Фейнманом. Читайте и учитесь у мастера. Решите как можно больше задач самостоятельно, чтобы получить четкое представление о предмете.
5 самых важных научных уравнений всех времен
Что в уравнении? Буквы, цифры и странные символы — но также и новый взгляд на взаимосвязь между фундаментальными составляющими нашей физической реальности. Все уравнения кристаллизуют что-то важное во вселенной, будь то отношение между массой и энергией, гравитационное притяжение между двумя телами или стороны треугольника.
Все уравнения кристаллизуют что-то важное во вселенной, будь то отношение между массой и энергией, гравитационное притяжение между двумя телами или стороны треугольника.
Самая важная часть любого уравнения — это знак равенства в его основе. Эти две горизонтальные линии говорят нам, что когда мы изменим одну вещь, мы увидим соответствующее изменение в другой, по-видимому, отдельной вещи. Таким образом, уравнения выявляют связи между внешне различными величинами или свойствами. Соединив вместе, эти вновь открытые отношения могут служить основой для будущих открытий.
Выбрать наиболее важные уравнения — почти безнадежная задача. Важность любых отношений будет сильно различаться в зависимости от контекста. Например, если вы падаете с самолета, закон всемирного тяготения покажется вам гораздо более значимым, чем уравнение Шредингера. Точно так же уравнения имеют разное значение для ученых в зависимости от области, в которой они работают.
Но можно выделить несколько уравнений, которые оказали огромное влияние на то, как мы видим мир. Хотя это не исчерпывающий список, все эти пять уравнений суммируют что-то совершенно новое — будь то новые отношения между вещами или просто новый взгляд на мир. И однажды записанные на бумаге, все эти уравнения сделали возможными будущие прорывы, поскольку поколения мыслителей использовали свои способности для совершения новых открытий. 92
Хотя это не исчерпывающий список, все эти пять уравнений суммируют что-то совершенно новое — будь то новые отношения между вещами или просто новый взгляд на мир. И однажды записанные на бумаге, все эти уравнения сделали возможными будущие прорывы, поскольку поколения мыслителей использовали свои способности для совершения новых открытий. 92
(Источник: BrainCityArts/Shutterstock)
Для начала возьмем, пожалуй, самое известное уравнение. Уравнение Альберта Эйнштейна 1905 года, связывающее массу и энергию, одновременно элегантно и внешне противоречит здравому смыслу. В нем говорится, что энергия равна массе объекта в его системе покоя, умноженной на квадрат скорости света. При этом Эйнштейн обнаружил, что массу и энергию можно считать эквивалентными друг другу, объединяющими то, что до этого было двумя отдельными областями.
Из уравнения Эйнштейна видно, что изменение массы объекта также изменит содержащуюся в нем энергию, и наоборот. Это становится ужасно очевидным во время ядерного взрыва, когда крошечные изменения в массе радиоактивных элементов соответствуют огромному количеству энергии.
Существует распространенное заблуждение, что уравнение показывает, что масса может быть преобразована в энергию и обратно. На самом деле это не то, что имел в виду Эйнштейн. Вместо этого он просто показал, что изменение массы должно привести к изменению энергии, хотя и очень большому.
Теорема Пифагора
(Источник: imagestockdesign/Shutterstock)
Существенная связь между двумя катетами прямоугольного треугольника и его гипотенузой названа в честь греческого философа Пифагора, хотя он не обязательно был первым, кто ее придумал.
Теорема показывает, что для любого прямоугольного треугольника мы можем сложить два его более коротких катета в квадрате и получить длину его самого длинного катета в квадрате. Это понимание объединило дисциплины геометрии и алгебры, и это хороший ранний пример использования отношений между формами для получения основных наблюдений о числах. Последующие открытия в этом духе продолжают жить и сегодня в области топологии, и, говоря более прозаически, мы полагаемся на теорему каждый раз, когда GPS триангулирует для нас положение.
Второй закон термодинамики
(Источник: Фуад А. Саад/Shutterstock)
Законы термодинамики возникли в результате наблюдений за движением энергии. Первый закон гласит, что энергия всегда должна сохраняться — важное открытие само по себе. Но второй закон, первоначально описывавший, как тепло передается в системе, имел чрезвычайно далеко идущие последствия.
Этот закон можно сформулировать по-разному, в зависимости от ситуации, но основное его наблюдение заключается в том, что тепло — а, следовательно, и энергия — естественным образом течет только в одном направлении, от горячего к холодному. Хотя мы можем что-то нагреть, затрачивая энергию, это всего лишь временное решение.
Это то, что мы видим каждый день, но значение огромно. Эта необратимость лежит в основе таких пьянящих концепций, как стрела времени и энтропия. В конечном итоге это приводит к неизбежности тепловой смерти Вселенной — когда масса и энергия настолько тонко и равномерно рассредоточены по космосу, что больше ничего не может произойти.
Исчисление
(Источник: Undrey/Shutterstock)
Исчисление включает множество различных уравнений, но все началось с одного прорыва. Два мыслителя XVII века, Исаак Ньютон и Готфрид Лейбниц, независимо друг от друга нашли способ формализовать сходимость бесконечных рядов по мере их приближения к определенному пределу. Частично это возникло из-за проблемы вычисления наклона кривой в любой заданной точке. Это вопрос, на который математики частично ответили раньше, но никогда так элегантно и полно, как это сделали Лейбниц и Ньютон.
Их работа привела к производной и интегралу, двум краеугольным камням исчисления. Производные дают нам скорость мгновенного изменения функции, а интегралы дают площадь под кривой на графике. Сегодня исчисление является частью инженерии, физики, экономики и многих других научных дисциплин.
Два математика ожесточенно спорили о том, кого следует считать истинным отцом исчисления. Сегодня обоим мужчинам приписывают изобретение его независимо друг от друга. Однако мы можем поблагодарить Лейбница за сам термин «исчисление». Если бы у Ньютона был свой путь, сегодня мы вместо этого ссылались бы на «Метод флюксий».
Однако мы можем поблагодарить Лейбница за сам термин «исчисление». Если бы у Ньютона был свой путь, сегодня мы вместо этого ссылались бы на «Метод флюксий».
Универсальный закон всемирного тяготения
Хотя Ньютон должен разделить заслуги в расчетах, он может в одностороннем порядке требовать признания своего Универсального закона всемирного тяготения. Уравнение основано на работах таких ученых, как Галилей и Иоганн Кеплер, которые утверждают, что каждая частица материи во Вселенной оказывает притягивающее действие на любую другую частицу материи. Эта сила увеличивается с массой и экспоненциально убывает с расстоянием.
Работы Ньютона объединили наблюдения Галилея за движением объектов на Земле с исследованиями Кеплера за движением астрономических тел. В результате было получено уравнение, которое показало, что одни и те же правила управляют движением как планет, так и пушечных ядер, что не обязательно было задано в его время.
Сегодня законы Ньютона были заменены теорией относительности Эйнштейна, которая, среди прочего, объясняет объекты, расположенные очень близко друг к другу или очень тяжелые. Но наблюдения Ньютона по-прежнему справедливы для большинства взаимодействий, которые мы наблюдаем вокруг себя. Неплохо для кого-то в 17 веке.
Но наблюдения Ньютона по-прежнему справедливы для большинства взаимодействий, которые мы наблюдаем вокруг себя. Неплохо для кого-то в 17 веке.
9 уравнений, которые изменили мир
Математические уравнения открывают уникальные окна в мир. Они придают смысл реальности и помогают нам увидеть вещи, которые раньше не замечались. Поэтому неудивительно, что новые достижения в математике часто идут рука об руку с достижениями в нашем понимании Вселенной. Здесь мы рассмотрим девять уравнений из истории, которые произвели революцию в нашем взгляде на все, от крошечных частиц до огромного космоса. 92, и известно по меньшей мере 3700 лет , со времен древних вавилонян.
Греческому математику Пифагору приписывают запись версии уравнения, используемого сегодня, согласно Университету Сент-Эндрюс в Шотландии. Наряду с нахождением применения в строительстве, навигации, составлении карт и других важных процессах, теорема Пифагора помогла расширить само понятие чисел. В пятом веке до нашей эры математик Гиппас из Метапонта заметил, что у равнобедренного прямоугольного треугольника, длина двух сторон которого равна 1 единице, гипотенуза равна квадратному корню из 2, что равно 9.1471 иррациональное число . (До этого момента никто в письменной истории не встречал таких чисел.) Говорят, что за свое открытие Гиппас был брошен в море, потому что последователи Пифагора (включая Гиппаса) были настолько обеспокоены возможностью чисел, что продолжался вечно после запятой без повторения, в соответствии со статьей Кембриджского университета.
В пятом веке до нашей эры математик Гиппас из Метапонта заметил, что у равнобедренного прямоугольного треугольника, длина двух сторон которого равна 1 единице, гипотенуза равна квадратному корню из 2, что равно 9.1471 иррациональное число . (До этого момента никто в письменной истории не встречал таких чисел.) Говорят, что за свое открытие Гиппас был брошен в море, потому что последователи Пифагора (включая Гиппаса) были настолько обеспокоены возможностью чисел, что продолжался вечно после запятой без повторения, в соответствии со статьей Кембриджского университета.
F = ма и закон всемирного тяготения
(Изображение предоставлено: Фон: Эскай Лим / EyeEm через Getty Images) 92, где m1 и m2 — массы двух объектов, r — расстояние между ними. G — фундаментальная константа, значение которой должно быть обнаружено экспериментальным путем. С тех пор эти концепции использовались для понимания многих физических систем, включая движение планет в Солнечной системе и средства перемещения между ними с помощью ракет.
Волновое уравнение
(Изображение предоставлено: Фон: Эскай Лим / EyeEm через Getty Images)
Используя относительно новые законы Ньютона, ученые 18-го века начали анализировать все вокруг себя. Согласно статье, опубликованной в 2020 году в журнале 9, в 1743 году французский эрудит Жан-Батист ле Ронд д’Аламбер вывел уравнение, описывающее колебания колеблющейся струны или движение волны.2
В этом уравнении v — скорость волны, а остальные части описывают смещение волны в одном направлении. Волновое уравнение, расширенное до двух или более измерений, позволяет исследователям предсказывать движение воды, сейсмических и звуковых волн и является основой для таких вещей, как уравнение Шредингера в квантовой физике, которое лежит в основе многих современных компьютерных устройств.
Уравнения Фурье
(Изображение предоставлено: Neslihan Gorucu/istock/Getty Images Plus)
Даже если вы не слышали о французском бароне Жане-Батисте Жозефе Фурье, его работа повлияла на вашу жизнь. Это потому, что математические уравнения, которые он записал в 1822 году, позволили исследователям разбить сложные и беспорядочные данные на комбинации простых волн, которые гораздо легче анализировать. Преобразование Фурье, как известно, было радикальным понятием в свое время, и многие ученые отказывались верить, что сложные системы могут быть сведены к такой элегантной простоте, согласно статье в журнале 9.1471 Йельский научный . Но преобразования Фурье — рабочие лошадки во многих современных областях науки, включая обработку данных, анализ изображений, оптику, связь, астрономию и инженерию.
Это потому, что математические уравнения, которые он записал в 1822 году, позволили исследователям разбить сложные и беспорядочные данные на комбинации простых волн, которые гораздо легче анализировать. Преобразование Фурье, как известно, было радикальным понятием в свое время, и многие ученые отказывались верить, что сложные системы могут быть сведены к такой элегантной простоте, согласно статье в журнале 9.1471 Йельский научный . Но преобразования Фурье — рабочие лошадки во многих современных областях науки, включая обработку данных, анализ изображений, оптику, связь, астрономию и инженерию.
Уравнения Максвелла
(Изображение предоставлено: ClaudeLux/istock/Getty Image Plus)
Электричество и магнетизм были еще новыми концепциями в 1800-х годах, когда ученые исследовали, как улавливать и использовать эти странные силы. Шотландский ученый Джеймс Клерк Максвелл значительно расширил наше понимание обоих явлений в 1864 году, когда он опубликовал список из 20 уравнений, описывающих, как электричество и магнетизм функционируют и взаимосвязаны. Уравнения Максвелла, позже доведенные до четырех, теперь преподаются первокурсникам студентов-физиков в колледжах и служат основой для всего электронного в нашем современном технологическом мире. 92, мы бы не поняли, как работают звезды или Вселенная, и не знали бы, как строить гигантские ускорители частиц, такие как Большой адронный коллайдер , чтобы исследовать природу субатомного мира.
Уравнения Максвелла, позже доведенные до четырех, теперь преподаются первокурсникам студентов-физиков в колледжах и служат основой для всего электронного в нашем современном технологическом мире. 92, мы бы не поняли, как работают звезды или Вселенная, и не знали бы, как строить гигантские ускорители частиц, такие как Большой адронный коллайдер , чтобы исследовать природу субатомного мира.
Уравнения Фридмана
(Изображение предоставлено Минди Вайсбергер)
Кажется высокомерием думать, что вы можете создать набор уравнений, которые определяют весь космос, но именно это русский физик Александр Фридман сделал в 1920-х годах. Используя теории относительности Эйнштейна, Фрейдман показал, что характеристики расширяющейся Вселенной можно выразить, начиная с Большого взрыва, с помощью двух уравнений.
Они сочетают в себе все важные аспекты космоса, включая его кривизну, количество вещества и энергии, которые он содержит, и скорость его расширения, а также ряд важных констант, таких как скорость света, гравитационная постоянная и . постоянная Хаббла , отражающая ускоряющееся расширение Вселенной. Известно, что Эйнштейну не нравилась идея расширяющейся или сжимающейся Вселенной, которая, как предполагала его общая теория относительности, происходила из-за эффектов гравитации. Он попытался добавить к результату переменную , обозначенную греческой буквой лямбда, которая действовала против гравитации, делая космос статичным. Хотя позже он назвал это своей величайшей ошибкой, спустя десятилетия от этой идеи сняли пыль и показали, что она существует в форме таинственной субстанции темной энергии , которая вызывает ускоренное расширение Вселенной.
постоянная Хаббла , отражающая ускоряющееся расширение Вселенной. Известно, что Эйнштейну не нравилась идея расширяющейся или сжимающейся Вселенной, которая, как предполагала его общая теория относительности, происходила из-за эффектов гравитации. Он попытался добавить к результату переменную , обозначенную греческой буквой лямбда, которая действовала против гравитации, делая космос статичным. Хотя позже он назвал это своей величайшей ошибкой, спустя десятилетия от этой идеи сняли пыль и показали, что она существует в форме таинственной субстанции темной энергии , которая вызывает ускоренное расширение Вселенной.
(Изображение предоставлено: Фон: Эскай Лим / EyeEm через Getty Images)
Большинство людей знакомы с 0 и 1, которые составляют компьютерные биты. Но эта важная концепция не стала бы популярной без новаторской работы американского математика и инженера Клода Шеннона. В важном 19В статье 48 Шеннон изложил уравнение, показывающее максимальную эффективность, с которой может передаваться информация, часто определяемое как C = B * 2log(1+S/N). В формуле C — достижимая пропускная способность конкретного информационного канала, B — ширина полосы пропускания линии, S — средняя мощность сигнала и N — средняя мощность шума. (Отношение S к N дает знаменитое отношение сигнал/шум в системе.) Результат уравнения выражается в битах в секунду. В статье 1948 года Шеннон приписывает идею бита математику Джону У. Тьюки как сокращению фразы «двоичная цифра».
В формуле C — достижимая пропускная способность конкретного информационного канала, B — ширина полосы пропускания линии, S — средняя мощность сигнала и N — средняя мощность шума. (Отношение S к N дает знаменитое отношение сигнал/шум в системе.) Результат уравнения выражается в битах в секунду. В статье 1948 года Шеннон приписывает идею бита математику Джону У. Тьюки как сокращению фразы «двоичная цифра».
Логистическая карта мая
(Изображение предоставлено фоном: Eskay Lim / EyeEm через Getty Images)
Иногда очень простые вещи могут привести к невообразимо сложным результатам. Этот трюизм может показаться не таким уж радикальным, но только в середине 20-го века ученые полностью оценили вес этой идеи. Когда в то время бурно развивалась теория хаоса, исследователи начали разбираться в том, как системы, состоящие всего из нескольких частей, которые обратятся друг к другу, могут давать случайное и непредсказуемое поведение. Австралийский физик, математик и эколог Роберт Мэй написал статью, опубликованную в журнале Nature в 1976 году под названием «Простые математические модели с очень сложной динамикой», в котором популяризировалось уравнение xn+1 = k * xn(1 – xn).
Xn представляет некоторую величину в системе в настоящее время, которая возвращается сама к себе через часть, обозначенную (1 – xn). K — константа, а xn+1 показывает систему в следующий момент времени. Несмотря на то, что это довольно просто, различные значения k приведут к сильно отличающимся результатам, в том числе со сложным и хаотичным поведением. Карта Мэя использовалась для объяснения динамики популяций в экологических системах и для генерации случайных чисел для компьютерного программирования.
Адам Манн — независимый журналист с десятилетним стажем, специализирующийся на астрономии и физике. Он имеет степень бакалавра астрофизики Калифорнийского университета в Беркли. Его работы публиковались в New Yorker, New York Times, National Geographic, Wall Street Journal, Wired, Nature, Science и многих других изданиях. Он живет в Окленде, штат Калифорния, где любит кататься на велосипеде.
17 уравнений, изменивших ход истории : ScienceAlert
Математика окружает нас повсюду, и она во многом повлияла на наше понимание мира. В 2013 году математик и писатель Ян Стюарт опубликовал книгу о 17 уравнений, изменивших мир . Недавно мы наткнулись на эту удобную таблицу в твиттер-аккаунте Пола Коксона, написанную репетитором по математике и блогером Ларри Филлипсом, которая обобщает уравнения. (Наше объяснение каждого приведено ниже):
В 2013 году математик и писатель Ян Стюарт опубликовал книгу о 17 уравнений, изменивших мир . Недавно мы наткнулись на эту удобную таблицу в твиттер-аккаунте Пола Коксона, написанную репетитором по математике и блогером Ларри Филлипсом, которая обобщает уравнения. (Наше объяснение каждого приведено ниже):
Вот еще немного об этих замечательных уравнениях, которые сформировали математику и историю человечества:
1. Теорема Пифагора
понимание геометрии. Он описывает отношение между сторонами прямоугольного треугольника на плоской плоскости: возведите в квадрат длины коротких сторон, a и b, сложите их вместе, и вы получите квадрат длины длинной стороны, c.
Это соотношение, в некотором роде, действительно отличает нашу нормальную, плоскую, евклидову геометрию от криволинейной, неевклидовой геометрии. Например, прямоугольный треугольник, нарисованный на поверхности сферы, не обязательно должен следовать теореме Пифагора.
2. Логарифмы
Логарифмы обратны или противоположны экспоненциальным функциям. Логарифм по конкретному основанию говорит вам, в какую степень нужно возвести это основание, чтобы получить число. Например, логарифм 1 по основанию 10 равен log(1) = 0, поскольку 1 = 10 0 ; log(10) = 1, так как 10 = 10 1 ; и log(100) = 2, так как 100 = 10 2 .
Уравнение на графике log(ab) = log(a) + log(b) показывает одно из наиболее полезных применений логарифмов: они превращают умножение в сложение.
До появления цифровых компьютеров это был наиболее распространенный способ быстрого умножения больших чисел, значительно ускоряющий вычисления в физике, астрономии и технике.
3. Исчисление
Приведенная здесь формула является определением производной в исчислении. Производная измеряет скорость изменения величины. Например, мы можем думать о скорости или скорости как о производной от положения: если вы идете со скоростью 3 мили (4,8 км) в час, то каждый час вы меняете свое положение на 3 мили.
Естественно, большая часть науки заинтересована в том, чтобы понять, как вещи изменяются, а производная и интеграл — другая основа исчисления — лежат в основе того, как математики и ученые понимают изменение.
4. Закон всемирного тяготения
Закон тяготения Ньютона описывает силу притяжения между двумя объектами, F, через универсальную постоянную, G, массы двух тел, m1 и m2, и расстояние между объектами, r. Закон Ньютона — замечательная часть научной истории — он почти идеально объясняет, почему планеты движутся именно так, а не иначе. Также примечателен ее универсальный характер — гравитация работает не только на Земле или в нашей Солнечной системе, но и где угодно во Вселенной.
Гравитация Ньютона прекрасно держалась в течение 200 лет, и только общая теория относительности Эйнштейна заменила ее.
5. Квадратный корень из -1
Математики всегда расширяли представление о том, что на самом деле представляют собой числа, переходя от натуральных чисел к отрицательным числам, к дробям, к действительным числам. Квадратный корень из -1, обычно записываемый как i, , завершает этот процесс, приводя к комплексным числам.
Квадратный корень из -1, обычно записываемый как i, , завершает этот процесс, приводя к комплексным числам.
С математической точки зрения комплексные числа в высшей степени элегантны. Алгебра работает совершенно так, как мы этого хотим — любое уравнение имеет решение в виде комплексных чисел, ситуация, которая неверна для действительных чисел: x 2 + 4 = 0 не имеет решения в виде действительных чисел, но имеет комплексное решение : квадратный корень из -2. Исчисление можно распространить на комплексные числа, и, сделав это, мы обнаружим некоторые удивительные симметрии и свойства этих чисел. Эти свойства делают комплексные числа незаменимыми в электронике и обработке сигналов.
6. Формула многогранников Эйлера
Многогранники — это трехмерные версии многоугольников, как куб справа. Углы многогранника называются его вершинами, линии, соединяющие вершины, — его ребрами, а многоугольники, покрывающие его, — его гранями.
Куб имеет 8 вершин, 12 ребер и 6 граней. Если я сложу вершины и грани вместе и вычту ребра, я получу 8 + 6 – 12 = 2.
Формула Эйлера утверждает, что если ваш многогранник ведет себя хорошо, если вы сложите вершины и грани вместе, и вычтите ребра, вы всегда получите 2. Это будет верно независимо от того, имеет ли ваш многогранник 4, 8, 12, 20 или любое количество граней.
Наблюдение Эйлера было одним из первых примеров того, что сейчас называется топологическим инвариантом — некоторым числом или свойством, общим для класса фигур, похожих друг на друга. Весь класс «хороших» многогранников будет иметь V + F — E = 2. Это наблюдение, наряду с решением Эйлера проблемы Кенигсбургских мостов, проложило путь к развитию топологии, раздела математики, необходимого для современная физика.
7. Нормальное распределение
Нормальное распределение вероятностей со знакомой колоколообразной кривой слева используется в статистике повсеместно.
Нормальная кривая используется в физике, биологии и социальных науках для моделирования различных свойств. Одна из причин, по которой нормальная кривая появляется так часто, заключается в том, что она описывает поведение больших групп независимых процессов.
8. Волновое уравнение
Это дифференциальное уравнение, или уравнение, описывающее изменение свойства во времени с точки зрения производной этого свойства, как указано выше. Волновое уравнение описывает поведение волн — вибрация гитарной струны, рябь в пруду после брошенного камня или свет, исходящий от лампы накаливания. Волновое уравнение было ранним дифференциальным уравнением, и методы, разработанные для решения уравнения, открыли дверь для понимания и других дифференциальных уравнений.
9. Преобразование Фурье
Преобразование Фурье необходимо для понимания более сложных волновых структур, таких как человеческая речь. Учитывая сложную беспорядочную волновую функцию, такую как запись разговора человека, преобразование Фурье позволяет нам разбить беспорядочную функцию на комбинацию ряда простых волн, что значительно упрощает анализ.
Учитывая сложную беспорядочную волновую функцию, такую как запись разговора человека, преобразование Фурье позволяет нам разбить беспорядочную функцию на комбинацию ряда простых волн, что значительно упрощает анализ.
Преобразование Фурье лежит в основе современной обработки и анализа сигналов, а также сжатия данных.
10. Уравнения Навье-Стокса
Подобно волновому уравнению, это дифференциальное уравнение. Уравнения Навье-Стокса описывают поведение текучих сред — воды, движущейся по трубе, потока воздуха над крылом самолета или дыма, поднимающегося от сигареты. Хотя у нас есть приблизительные решения уравнений Навье-Стокса, которые позволяют компьютерам довольно хорошо моделировать движение жидкости, все еще остается открытым вопрос (с призом в миллион долларов), можно ли построить математически точные решения уравнений.
11. Уравнения Максвелла
Этот набор из четырех дифференциальных уравнений описывает поведение и связь между электричеством (E) и магнетизмом (H).
Уравнения Максвелла относятся к классическому электромагнетизму так же, как законы движения Ньютона и закон всемирного тяготения к классической механике — они лежат в основе нашего объяснения того, как электромагнетизм работает в повседневном масштабе. Однако, как мы увидим, современная физика опирается на квантово-механическое объяснение электромагнетизма, и теперь ясно, что эти элегантные уравнения — всего лишь приближение, которое хорошо работает в человеческом масштабе.
12. Второй закон термодинамики
Это утверждает, что в закрытой системе энтропия (S) всегда постоянна или возрастает. Термодинамическая энтропия — это, грубо говоря, мера того, насколько неупорядочена система. Система, которая изначально находится в упорядоченном, неравномерном состоянии — скажем, горячая область рядом с холодной областью — всегда будет иметь тенденцию к выравниванию, когда тепло будет течь из горячей области в холодную до тех пор, пока не будет равномерно распределено.
Второй закон термодинамики — один из немногих случаев в физике, где время имеет такое значение. Большинство физических процессов обратимы — мы можем вычислить уравнения в обратном порядке, ничего не напутав. Однако второй закон работает только в этом направлении. Если мы кладем кубик льда в чашку с горячим кофе, мы всегда видим, как кубик льда тает, и никогда не видим, как кофе замерзает.
13. Относительность
Эйнштейн радикально изменил курс физики своими специальной и общей теориями относительности. Классическое уравнение E = mc 2 утверждает, что материя и энергия эквивалентны друг другу. Специальная теория относительности привнесла такие идеи, как скорость света, являющаяся универсальным пределом скорости, и течение времени, различное для людей, движущихся с разной скоростью.
Общая теория относительности описывает гравитацию как искривление и складывание пространства и времени как таковых, и это была первая крупная перемена в нашем понимании гравитации со времен закона Ньютона. Общая теория относительности необходима для нашего понимания происхождения, структуры и конечной судьбы Вселенной.
Общая теория относительности необходима для нашего понимания происхождения, структуры и конечной судьбы Вселенной.
14. Уравнение Шрёдингера
Это основное уравнение квантовой механики. Поскольку общая теория относительности объясняет нашу Вселенную в ее самых больших масштабах, это уравнение управляет поведением атомов и субатомных частиц.
Современная квантовая механика и общая теория относительности — две самые успешные научные теории в истории — все экспериментальные наблюдения, которые мы сделали на сегодняшний день, полностью согласуются с их предсказаниями. Квантовая механика также необходима для большинства современных технологий — ядерная энергетика, полупроводниковые компьютеры и лазеры построены вокруг квантовых явлений.
15. Теория информации
Приведенное здесь уравнение относится к информационной энтропии Шеннона. Как и в случае термодинамической энтропии, приведенной выше, это мера беспорядка. В этом случае он измеряет информационное содержание сообщения — книги, изображения в формате JPEG, отправленного в Интернет, или чего-либо, что может быть представлено символически. Энтропия Шеннона сообщения представляет собой нижнюю границу того, насколько это сообщение может быть сжато без потери части его содержимого.
В этом случае он измеряет информационное содержание сообщения — книги, изображения в формате JPEG, отправленного в Интернет, или чего-либо, что может быть представлено символически. Энтропия Шеннона сообщения представляет собой нижнюю границу того, насколько это сообщение может быть сжато без потери части его содержимого.
Измерение энтропии Шеннона положило начало математическому изучению информации, и его результаты играют центральную роль в том, как мы сегодня общаемся по сетям.
16. Теория хаоса
Это уравнение представляет собой логистическую карту Мэя. Он описывает процесс, развивающийся во времени — x t+1 , уровень некоторой величины x в следующий период времени — задается формулой справа и зависит от xt, уровня x в данный момент. k – выбранная константа. Для определенных значений k карта показывает хаотическое поведение: если мы начнем с некоторого определенного начального значения x, процесс будет развиваться в одном направлении, но если мы начнем с другого начального значения, даже очень близкого к первому, процесс будет развиваться совершенно по другому пути.
Мы наблюдаем хаотичное поведение — поведение, чувствительное к начальным условиям — подобное этому во многих областях. Погода является классическим примером: небольшое изменение атмосферных условий в один день может привести к совершенно другим погодным системам через несколько дней, что чаще всего отражается в идее бабочки, взмахивающей крыльями на одном континенте, вызывающей ураган на другом континенте.
17. Уравнение Блэка-Шоулза
Другое дифференциальное уравнение Блэка-Шоулза описывает, как финансовые эксперты и трейдеры находят цены на деривативы. Деривативы — финансовые продукты, основанные на некотором базовом активе, таком как акции, — являются важной частью современной финансовой системы.
Уравнение Блэка-Шоулза позволяет специалистам по финансам рассчитать стоимость этих финансовых продуктов на основе свойств производного инструмента и базового актива.
Эта статья была первоначально опубликована Business Insider.
Дополнительная информация от Business Insider:
Топ-10 величайших формул мира
Несколько лет назад британский научный журнал «Physics World» попросил читателей проголосовать за «величайшую формулу».
В десятку самых известных формул списка вошли как неизвестная 1 + 1 = 2, так и знаменитая E = MC²;
Существуют как простые формулы окружности, так и сложные формулы Эйлера…
Эти формулы являются не только кристаллизацией мудрости математиков и физиков, но и концентрированным выражением человеческой цивилизации.
Каждая формула глубоко повлияла на преобразование человеческого общества и даже сформировала человеческое мышление.
Некоторые из этих формул будут вам знакомы, а некоторые из вас могут быть с ними не знакомы.
Нам, людям, необходимо понимать эти формулы и мыслительный процесс человека.
Инженеры-электронщики должны лучше всего понимать и осваивать преобразование Фурье и уравнения Максвелла.
Сегодня мы собрали эти 10 известных формул из Интернета и поделились ими с вами:
Содержание
№10 Длина окружности
Основатель: Древние
Значение: A математическое выражение красоты природы.
Эта потрясающая формула – мы учили ее еще в средней школе.
В настоящее время людям удалось получить 206,1 миллиарда цифр числа пи. Все равно как-то скучно.
Достаточно дюжины значений числа пи, используемых в современной науке и технике.
Если вы используете 35-битное значение пи для вычисления длины окружности, которая может охватывать Солнечную систему, ошибка составит менее одной миллионной диаметра протона.
Сейчас большинство людей вычисляют число Пи для проверки вычислительной мощности компьютера и ради интереса.
No.9 Преобразование Фурье
Основатель: Жан Баптис Жозеф Фурье
Значение: Любой нерегулярный сигнал может быть выражен как бесконечная суперпозиция правильных синусоидальных волн.
Это важный метод в области цифровой обработки сигналов.
Это очень профессионально, и большинство людей вообще этого не понимают.
Короче говоря, без этой формулы сегодня нет компьютера, так что мы должны благодарить за эту совершенно непонятную формулу. Кроме того, хотя Фурье и носит фамилию Фу, он француз.
№ 8 Отношения де Бройля
Основатель: Луи Виктор Де Бройль
Значение: Де Бройль считает, что любое вещество является одновременно и твердым, и летучим, или что любое вещество можно также рассматривать как волну , включая самого человека.
Человек существует не только как субстанция, но и в некотором смысле как волна.
Эта штука тоже очень классная.
Многие понятия от школьной физики до оптики являются дальними родственниками.
Короче говоря, ДеБройль считает, что электрон — это не только частица, но и волна, у него тоже есть «длина волны».
Итак, у нас есть уравнение материальной волны, которое выражает отношение между длиной волны, энергией и так далее.
Он также получил Нобелевскую премию по физике 1929 года.
№7 1+1=2
Эта формула не требует ни названия, ни перевода, ни объяснения.
No.6 Уравнение Шрёдингера
Основатель: Эрвин Шредингер
Значение: В квантовой механике состояние объекта не может быть описано перемещением, скоростью и т. д., как в классической механике, а только функцией физической величины.
Эта физическая величина является уже не определенным значением, а вероятностью, распределенной во времени.
Каждой микросистеме соответствует уравнение Шрёдингера.
Значение уравнения Шрёдингера в квантовой механике такое же, как и второго закона Ньютона в классической механике.
Он также совершенно неизвестен большинству людей.
Поэтому я привожу официальную оценку: «Уравнение Шрёдингера является наиболее широко используемой и влиятельной формулой в мировой литературе по атомной физике».
За выдающийся вклад в квантовую механику Шредингер получил Нобелевскую премию по физике 1933 года.
Кроме того, Шредингер — австриец.
№ 5 Массово-энергетическая эквивалентность
Основатель: Альберт Эйнштейн
Значение: Уравнение массы и энергии глубоко раскрывает взаимосвязь между массой и энергией.
До этого не было сомнений, что масса есть масса, а энергия есть энергия, и между ними не было никакой связи.
Именно открытие уравнения массы и энергии привело к взрыву атомных и водородных бомб.
Что более важно в этом уравнении, так это то, что оно полностью ниспровергает присущее человечеству мышление и способствует прогрессу человеческой цивилизации.
Кажется, формула в научном сообществе никогда не имела такого широкого значения.
В «чудесный год» физики в 1905 году ее предложил молодой человек по имени Эйнштейн.
В том же году он также опубликовал «Об электродинамике движущихся объектов», широко известную как специальная теория относительности.
Эта формула говорит нам, что Эйнштейн превосходен, а энергия и масса взаимозаменяемы.
Побочный продукт: Атомная бомба.
No.4 Теорема Пифагора
Основатель: Пифагор (Некоторые считают, что теорема Пифагора также появилась при династии Шан в Китае и доказала ее)
Значение: Теорема Пифагора является типичным методом решения задачи математическими методами.
В настоящее время существует более 400 форм доказательств.
3:4:5 треугольник находится глубоко в сердце каждого земного человека.
No.3 Второй закон движения Ньютона
Основатель: Исаак Ньютон
Значение: Второй закон Ньютона лежит в основе классической физики и применим ко всем аспектам нашей повседневной жизни.
Это положило начало исследованиям настоящей физики.
Без Ньютона человеческая цивилизация провела бы гораздо больше времени в темном мире.
Один из величайших ученых всех времен, основной закон одного из величайших научных шедевров всех времен «Математические принципы натуральной философии» считается одним из величайших в классической физике.
Все основные уравнения мощности могут быть выведены из него с помощью исчисления.
No.2 Тождество Эйлера
Основатель: Леонард Эйлер
Значение: многие математические формулы были открыты Эйлером, поэтому формула Эйлера не является единой формулой.
Формула Эйлера широко распространена в различных разделах математики.
Государственный секретарь Швейцарии по вопросам образования и исследований Шарль Кляйбер сказал: «Без многих научных открытий Эйлера мы сегодня будем жить совершенно другой жизнью».
Французский математик Лаплас считает, что: прочитав Эйлера, он учитель всех.
Была ли эта формула написана Богом?
В последних творениях все боги.
Эйлер — самый плодовитый математик в истории и ученый с наибольшим количеством книг во всех областях (включая все разделы математики и механики, оптику, акустику, водное хозяйство, астрономию, химию, медицину и т. д.).
История математики называет восемнадцатый век «эпохой Эйлера».
Эйлер родился в Швейцарии. Он потерял зрение на правый глаз в 31 год и ослеп в 59 лет. Однако он оптимистичен, обладает потрясающей памятью и концентрацией внимания.
Всю свою жизнь он был скромным и редко называл то, что нашел.
Тем не менее, одна из самых важных констант названа – e.
О е, раньше был анекдот:
В психиатрической больнице пациент весь день говорил другим: «Я различаю вас, я различаю вас».
Я не знаю почему, у этих пациентов простое понятие исчисления. Они думали, что однажды они продифференцируются до нуля и исчезнут, как обычные полиномиальные функции.
Однако однажды он встретил неподвижного человека. Он был удивлен, и человек сказал ему легкомысленно: «Я — икс в степени е».
Прелесть этой формулы в том, что в ней нет никакого дополнительного содержания.
Он помещает самые основные e, i и pie в математике в одну формулу, а также добавляет математику, которая является наиболее важными 0 и 1 в философии.
Соединитесь с помощью простого знака плюс.
Гаусс однажды сказал: «Если человек впервые увидит эту формулу, не почувствовав ее прелести, он не сможет стать математиком».
No.1 Уравнения Максвелла
Основатель: Джеймс Кларк Максвелл
Значение: Органически объединяет электрические и магнитные поля в полное электромагнитное поле. И создал теорию электромагнитного поля, и без электромагнитной теории сегодня не было бы социальной цивилизации.
интегро
дифференциал
Кто может понять эти формулы, тот обязательно почувствует, что за ними стоит прохладный ветер — если Бога нет, то как объяснить такое совершенное уравнение?
Этот набор формул объединяет закон электричества Гаусса, закон магнетизма Гаусса, закон Фарадея и закон Ампера.
Более скромная оценка: «Вообще любое электромагнитное явление во Вселенной можно объяснить этой системой уравнений».
Позже Максвелл предсказал существование электромагнитных волн на основе этого набора формул только путем вычислений на бумаге.
Разве мы не всегда любим писать истории, например, когда Эйнштейн был ребенком, он встал на путь усердной учебы и служения Родине из-за определенного стимула?
На самом деле этот стимул представляет собой систему уравнений, которую вы видите.
Именно потому, что эта система уравнений идеально объединяет все электромагнитное поле, Эйнштейн всегда хотел таким же образом объединить гравитационное поле и подвести макро- и микросилы к одному и тому же набору формул: знаменитая «большая объединенная теория.
Эйнштейн не выходил из туннеля до самой смерти, и если он выйдет, мы увидим самого Бога на другом конце туннеля.
Точка зрения редактора: Теория относительности Эйнштейна основана на постоянной скорости света и доказана геометрическими методами. А уравнение Максвелла как раз и содержит принцип постоянной скорости света. Следовательно, краеугольным камнем теории относительности Эйнштейна является уравнение Максвелла!
Следовательно, краеугольным камнем теории относительности Эйнштейна является уравнение Максвелла!
Основные формулы физики и примечания для конкурсных экзаменов
Вы когда-нибудь задумывались, почему небо голубое или как действует гравитация? Физика по существу изучает, как взаимодействуют фундаментальные составляющие нашей Вселенной. Включая обязательную часть программы многих конкурсных экзаменов , организованных для приема на инженерно-технические программы, эта дисциплина представляет собой широкий спектр подполей, от квантовой физики до ядерной физики. Этот блог призван предоставить вам исчерпывающий список основных формул по физике, которые вы должны знать, чтобы успешно сдать выбранный вами конкурсный экзамен.
Выписка: Английский для конкурсных экзаменов
Этот блог включает в себя:
- Список основных формул физики
- Популярные формулы базовой физики
- Примечания по базовой физике
- Практические вопросы
Основные формулы физики PDF Download
Список основных формул физики для некоторых основных экзаменов по физике
| Основные формулы физики | Концепция | Формула |
| Формула средней скорости | Используется для расчета средней скорости (S) движущегося тела для пройденного расстояния (D), а также продолжительности времени (T). | S = д/т |
| Формула ускорения | Ускорение относится к скорости изменения скорости по отношению к изменению времени. Обозначается символом а. | а =(v-u)/t |
| Формула плотности | Эта формула отображает плотность материала в определенной заданной области. | Р=м/В |
| Формула силы | Способность выполнять действие известна как Энергия. С другой стороны, энергия, затрачиваемая на выполнение деятельности (работы) в течение определенного периода времени, называется мощностью. | P=Вт/т |
| Второй закон Ньютона | Используя формулу, силу можно выразить произведением массы на ускорение тела. | Ж = ма |
| Весовая формула | Формула измеряет силу, с которой объект падает под действием силы тяжести. | Вт=мг |
| Формула давления | Давление относится к величине силы, прикладываемой к единице площади объекта. | П=Ж/А |
| Формула закона Ома | Закон Ома гласит, что ток, проходящий через материал проводника, прямо пропорционален разности потенциалов между двумя концами проводника. | В= I × R |
| Формула кинетической энергии | Кинетическая энергия – это энергия, которой обладает тело благодаря своему состоянию движения. | E = 1/2 мВ² |
| Формула частоты | Частота относится к числу оборотов, совершаемых в секунду, или к числу волновых циклов. | F = v/λ |
| Формула маятника | Это уравнение вычисляет, как долго маятник качается вперед и назад в секундах | Т = 2π√Lg |
| Формула Фаренгейта | Это формула преобразования температуры. | F = (9/5× °С) + 32 |
| Рабочая формула | Формула работы измеряет произведение величины смещения d и составляющей силы. | Вт = F × d × cosθ |
| Формула крутящего момента | Крутящий момент — это сила вращения или вращательный эффект. Он измеряет величину Он измеряет величину | Т = F × r × sinθ |
| Формула смещения | Относится к изменению положения объекта с его начального положения на его конечное положение. | D = Xf–Xi = ΔX |
| Массовая формула | Эта формула представляет собой отношение между силой и массой. Здесь F = сила, m = масса и a = ускорение. | F = мА или м = F/м |
Популярные формулы базовой физики
- Формула средней скорости
Используя эту формулу физики, мы можем рассчитать среднюю скорость (S) движущегося тела для пройденного расстояния (D), а также продолжительность времени (T).
Формула средней скорости
- Формула плотности
Эта формула показывает плотность материала в определенной заданной области.
Формула плотности
- Формула ускорения
Ускорение — это скорость изменения скорости по отношению к изменению во времени.
Формула ускорения
- Формула мощности
Способность выполнять действие известна как Энергия. С другой стороны, энергия, затрачиваемая на выполнение деятельности (работы) в течение определенного периода времени, называется мощностью.
Формула мощности
- Формула давления
Величина силы, приложенной к единице площади, называется давлением объекта.
Формула давления
- Формула закона Ома
Среди популярных физических формул закон Ома объясняется тем, что ток (I), проходящий через некоторый материал проводника, прямо пропорционален разности потенциалов (V) между двумя концами проводника.
Формула закона Ома
Изучение формул физики? Ознакомьтесь с Тригонометрические формулы для количественного раздела конкурсных экзаменов
Примечания по основам физики
Чтобы сдать любой конкурсный экзамен, первостепенное значение имеет ознакомление с программой и образцом экзамена. Учитывая огромное количество абитуриентов каждый год, нельзя отрицать тот факт, что, чтобы получить дразнящий балл, вы должны изучить тонкости на ваших подсказках. Часто важные концепции готовятся всеми, но дополнительные оценки получают за знание мельчайших концепций предметов. Хотя вы должны укрепить свои основные формулы по физике, также необходимо пройти через фундаментальные концепции по этому предмету. Чтобы помочь вам укрепить различные концепции физики, мы объяснили некоторые из часто задаваемых тем в рамках этой дисциплины.
Учитывая огромное количество абитуриентов каждый год, нельзя отрицать тот факт, что, чтобы получить дразнящий балл, вы должны изучить тонкости на ваших подсказках. Часто важные концепции готовятся всеми, но дополнительные оценки получают за знание мельчайших концепций предметов. Хотя вы должны укрепить свои основные формулы по физике, также необходимо пройти через фундаментальные концепции по этому предмету. Чтобы помочь вам укрепить различные концепции физики, мы объяснили некоторые из часто задаваемых тем в рамках этой дисциплины.
Выписка: Аналитическое обоснование для конкурсных экзаменов
Единицы СИ
Вопросы, касающиеся единиц СИ, часто задают на многих инженерных экзаменах. Вот ключевые указатели, которые вы должны помнить в единицах СИ, а также основные физические формулы, упомянутые выше. Единицам СИ как понятию придается меньшее значение, но они занимают очень значительное место в контрольных работах различных экзаменов. Ниже приведены некоторые из важных SI, которые вы должны помнить и применять в своих основных физических формулах.
Ниже приведены некоторые из важных SI, которые вы должны помнить и применять в своих основных физических формулах.
| Наименование количества | Единица СИ | Наименование подразделения |
| Масса | Килограмм | кг |
| Время | Второй | с |
| Длина | Метр | м |
| Термодинамический/температурный | Кельвин | К |
| Электрический ток | Ампер | А |
| Светящийся | Кандела | CD |
| Количество вещества | Крот | Крот |
| Электрическое сопротивление | Ом | Ом |
| Мощность | Вт | Вт |
| Длина волны света | Ангстрем | Å |
| Магнитная индукция | Гаусс | Гс |
| Электрический заряд | Кулон | С |
| Атмосферное давление | Бар | бар |
| Энергия | Джоуль | Дж |
| Магнитный поток | Максвелл | Мх |
| Давление | Паскаль | Па |
| Сила | Ньютон | № |
Важные инструменты и устройства
Большинство из них знают только об обычных устройствах или инструментах, используемых в различных экспериментах по физике. Эти инструменты могут быть включены в различные вопросы, чтобы оценить понимание учащимся основных понятий и формул физики. Взгляните на следующее, в котором перечислены эти инструменты и устройства, а также их упрощенные определения.
Эти инструменты могут быть включены в различные вопросы, чтобы оценить понимание учащимся основных понятий и формул физики. Взгляните на следующее, в котором перечислены эти инструменты и устройства, а также их упрощенные определения.
Читайте также: LCM и HCF для конкурсных экзаменов
| Инструменты | Функции |
| Спидометр | Устройство, используемое для измерения и отображения скорости транспортного средства. |
| Акселерометр | Это устройство, которое измеряет ускорение. |
| Динамометр | Обычно этот прибор используется для измерения крутящего момента, силы а также мощности тела. |
| Анемометр | С помощью этого устройства мы можем измерить скорость ветра. |
| Гальванометр | Это электромеханический прибор, который используется для обнаружения и индикации электрического тока.  |
| Барометр | Барометр — это научный прибор, который применяется в метеорологии и используется для расчета атмосферного давления. |
| Вискозиметр | С помощью этого устройства мы можем рассчитать вязкость жидкости. |
| Сейсмометр | Этот прибор помогает в оценке и измерении случайных движений внутри земной коры, вызванных землетрясением или извержением вулкана и т. д. |
| Вольтметр | Используя вольтметр, мы можем измерить электрический потенциал разницы между двумя заданными точками |
Практические вопросы
- Ширина двери 40 см. Если его освободить, приложив усилие 2 Н к его краю (от шарниров). Вычислите крутящий момент, при котором дверь открывается.
- Длина маятника 4 метра. Он совершает один полный цикл 0,25 раза в секунду. Максимальное смещение, которого достигает маятник, составляет 0,1 метра от центра.
 Узнать период колебаний? А какое водоизмещение через 0,6 секунды?
Узнать период колебаний? А какое водоизмещение через 0,6 секунды? - Маятник имеет период 1,9о от горизонтальной плоскости. Кроме того, сила имеет величину 900 Н. Значит, если он толкнет косилку на 30 м. Затем рассчитайте работу, которую совершил человек, чтобы переместить газонокосилку.
- Волна имеет частоту 50 Гц. Он также имеет длину волны 10 м. Узнать скорость волны?
- Предположим, Гита уезжает из Дели, чтобы навестить Рохита в Дели. Она решает путешествовать на поезде и преодолевает 350 километров на север. Затем трасса поворачивает обратно на юг на 125 километров. Рассчитать полное перемещение Гиты по формуле перемещения?
- Ящик массой 250 Н покоится на полу. Если давление, оказываемое коробкой на пол, равно 25 000 Па, на какой площади коробка соприкасается с полом?
- Масса предмета равна 1 кг. Кроме того, на него действует сила в 2 ньютона. Определите величину и направление ускорения тела.
- Масса человека составляет 70 кг, а сила тяжести на Земле составляет 9,8 м/с2.


 Кем? Неважно, кем конкретно, но ведь не сама же себя написала?
Кем? Неважно, кем конкретно, но ведь не сама же себя написала?