Доказательства круглой земли: Как с помощью квадрокоптера доказать, что Земля круглая?

10 простых доказательств того, что Земля круглая

Люди давно знают, что Земля круглая, и находят все новые и новые способы показать, что наш мир не плоский. И все же, даже в 2016 году, на планете довольно много людей, которые твердо уверены в том, что Земля не круглая. Это страшные люди, они, как правило, верят в теории заговора, и с ними трудно спорить.

Но они существуют. Как и «Общество плоской Земли». Смешно становится при одной мысли об их возможных аргументах. Но история нашего вида была интересной и изворотливой, опровергались даже твердо устоявшиеся истины. Вам не придется прибегать к сложным формулам, чтобы развеять теорию заговора плоской Земли.

Достаточно взглянуть вокруг и десять раз проверить: Земля однозначно, неизбежно, совершенно и абсолютно не плоская на 100%.

Луна

Сегодня люди уже знают, что Луна — это не кусочек сыра и не игривое божество, а явления нашего спутника хорошо объясняет современная наука. Но древние греки понятия не имели, что это такое, и в поисках ответа сделали несколько проницательных наблюдений, которые позволили людям определить форму нашей планеты.

Аристотель (который сделал довольно много наблюдений о сферической природе Земли) заметил, что во время лунных затмений (когда орбита Земли помещает планету точно между Солнцем и Луной, порождая тень) тень на лунной поверхности — круглая. Эта тень и есть Земля, а отбрасываемая ей тень прямо указывает на сферическую форму планеты.

Поскольку Земля вращается (поищите информацию на тему эксперимента с «маятником Фуко», если сомневаетесь), овальная тень, которая рождается в ходе каждого лунного затмения, говорит не только о том, что Земля круглая, но и не плоская.

Корабли и горизонт

Если вы недавно были в порту или просто прогуливались по пляжу, вглядываясь в горизонт, вы могли заметить очень интересное явление: приближающиеся корабли не просто «появляются» из горизонта (как должны были бы, будь мир плоским), а скорее выходят из моря. Причина того, что корабли буквально «выходят из волн», в том, что наш мир не плоский, а круглый.

Представьте себе муравья, который идет по поверхности апельсина.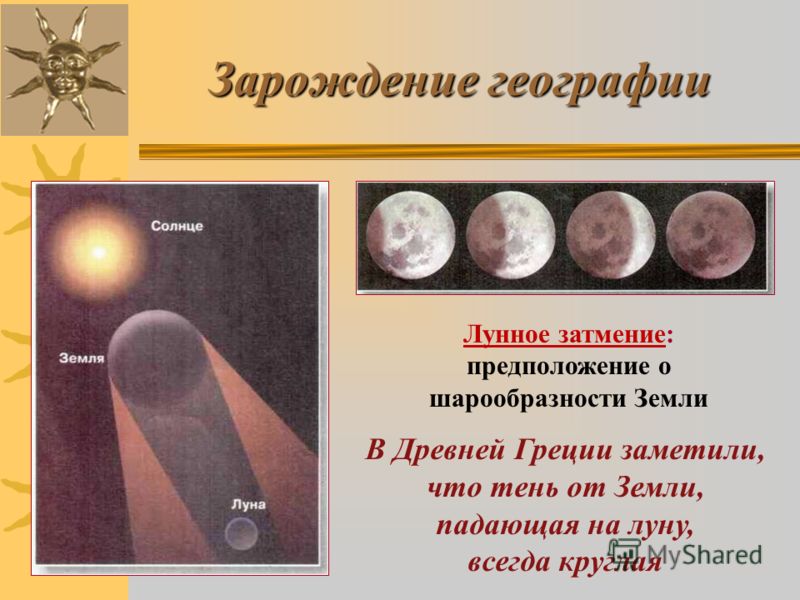 Если смотреть на апельсин с близкого расстояния, нос к плоду, вы увидите, как тело муравья медленно поднимается над горизонтом ввиду кривизны поверхности апельсина. Если проделать этот эксперимент с длинной дорогой, эффект будет другой: муравей будет медленно «материализоваться» в поле зрения, в зависимости от того, насколько острое у вас зрение.

Смена созвездий

Это наблюдение первым сделал Аристотель, который объявил Землю круглой, наблюдая за сменой созвездий при пересечении экватора.

Вернувшись из поездки в Египет, Аристотель заметил, что «в Египте и на Кипре наблюдаются звезды, которых не видели в северных регионах». Это явление можно объяснить лишь тем, что люди смотрят на звезды с круглой поверхности. Аристотель продолжал и заявил, что сфера Земли «небольших размеров, ведь в противном случае эффект такой легкой перемены местности не проявился бы так скоро».

Чем дальше вы от экватора, тем далее «известные» созвездия уходят к горизонту, сменяясь другими звездами. Этого не происходило бы, будь мир плоским.

Тени и палочки

Если вы воткнете палочку в землю, она даст тень. Тень движется по мере течения времени (на основе этого принципа древние люди изобрели солнечные часы). Если бы мир был плоским, две палочки в разных местах производили бы одну и ту же тень.

Но этого не происходит. Потому что Земля круглая, а не плоская.

Эратосфен (276–194 гг. до н. э.) использовал этот принцип, чтобы рассчитать окружность Земли с хорошей точностью.

Чем выше, тем дальше видно

Стоя на плоском плато, вы смотрите в сторону горизонта от вас. Вы напрягаете свои глаза, затем достаете любимый бинокль и смотрите через него, насколько могут видеть глаза (с помощью бинокулярных линз).

Затем вы взбираетесь на ближайшее дерево — чем выше, тем лучше, главное — не уронить бинокль. И снова смотрите, напрягая глаза, через бинокль за горизонт.

Чем выше вы заберетесь, тем дальше будет видно. Обычно мы склонны связывать это с препятствиями на Земле, когда за деревьями не видно леса, а за каменными джунглями — свободы. Но если вы будете стоять на идеально чистом плато, без каких-либо препятствий между вами и горизонтом, вы увидите намного больше свысока, чем с земли.

Все дело в кривизне Земли, конечно, и этого не было бы, будь Земля плоской.

Полет на самолете

Если вы когда-либо вылетали из страны, особенно куда подальше, вы должны были заметить два интересных факта о самолетах и Земле:

Самолеты могут лететь по относительно прямой линии очень долго и не падают за край мира. Они также могут летать вокруг Земли без остановки.

Если вы посмотрите в окно во время трансатлантического перелета, вы в большинстве случаев увидите кривизну земли на горизонте. Лучший вид кривизны был на «Конкорде», но этого самолета давно уж нет. С нового самолета Virgin Galactic горизонт должен быть абсолютно изогнутым.

Взгляните на другие планеты!

Земля отличается от других, и это бесспорно. В конце концов, у нас есть жизнь, и мы не находили пока планет с жизнью. Однако все планеты обладают схожими характеристиками, и было бы логично предположить, что если все планеты ведут себя определенным образом или демонстрируют конкретные свойства — особенно если планеты разделены расстоянием или сложились при различных обстоятельствах — то и наша планета аналогична.

Другими словами, если существует так много планет, которые образовались в разных местах и в разных условиях, но обладают схожими свойствами, вероятнее всего, и наша планета будет таковой. Из наших наблюдений стало ясно, что планеты круглые (а поскольку мы знали, как они образовались, мы знаем и почему у них такая форма). Нет никакой причины думать, что наша планета не будет такой же.

В 1610 году Галилео Галилей наблюдал вращение спутников Юпитера. Он описал их как маленькие планеты, вращающиеся вокруг большой планеты — и это описание (и наблюдение) не понравилось церкви, поскольку бросало вызов геоцентрической модели, в которой все вертелось вокруг Земли. Это наблюдение показало также и то, что планеты (Юпитер, Нептун, а позже и Венера) сферические и вращаются вокруг Солнца.

Плоскую планету (нашу или любую другую) будет настолько невероятно наблюдать, что перевернет практически все, что мы знаем о формировании и поведении планет. Это не только изменит все, что мы знаем о формировании планет, но и о формировании звезд (поскольку наше Солнце должно вести себя по-другому, приноравливаясь к теории плоской Земли), о скорости и движении космических тел. Короче, мы не просто подозреваем, что наша Земля круглая — мы это знаем.

Существование часовых поясов

В Пекине сейчас 12 ночи, полночь, солнца нет. В Нью-Йорке 12 пополудни. Солнце в зените, хотя его и трудно разглядеть под облаками. В Аделаиде, Австралия, час тридцать утра. Солнце взойдет очень нескоро.

Это можно было бы объяснить лишь тем, что Земля круглая и вращается вокруг собственной оси. В определенный момент, когда солнце светит на одной части Земли, на другом конце темно, и наоборот. Отсюда появляются часовые пояса.

Другой момент. Если бы солнце было «прожектором» (его свет прямо падал на конкретную область), а мир был плоским, мы видели бы солнце, даже если бы оно не светило над нами. Примерно так же вы можете увидеть свет прожектора на сцене театра, сами оставаясь в тени. Единственный способ создать два совершенно раздельных часовых пояса, один из которых будет всегда в темноте, а другой на свету, — это обзавестись сферическим миром.

Центр тяжести

Есть интересный факт о нашей массе: она притягивает вещи. Сила притяжения (гравитация) между двумя объектами зависит от их массы и от расстояния между ними. Проще говоря, гравитация будет притягивать в сторону центра масс объектов. Чтобы найти центр массы, нужно изучить объект.

Представьте сферу. Ввиду формы сферы, где бы вы ни стояли, под вами будет все то же количество сферы. (Представьте себе муравья, идущего по стеклянному шару. С точки зрения муравья, единственным признаком передвижения будет перемещение ног муравья. Форма поверхности не будет меняться совершенно). Центр массы сферы находится в центре сферы, то есть гравитация притягивает все, что на поверхности, в направлении центра сферы (прямо вниз), независимо от местоположения объекта.

Рассмотрим плоскость. Центр массы плоскости находится в центре, поэтому сила гравитации будет притягивать все, что на поверхности, к центру плоскости. Это значит, если вы будете на краю плоскости, гравитация будет тянуть вас в сторону центра, а не вниз, как мы привыкли.

И даже в Австралии яблоки падают сверху вниз, а не сбоку набок.

Снимки из космоса

За последние 60 лет освоения космоса мы запустили много спутников, зондов и людей в космос. Некоторые из них вернулись, некоторые продолжают оставаться на орбите и передавать прекрасные снимки на Землю. И на всех фотографиях Земля (внимание) круглая.

Если ваш ребенок будет спрашивать, откуда мы знаем, что Земля круглая, потрудитесь объяснить.

Источник

Как древние греки доказали, что Земля круглая

Zefirka > Наука и технологии > Как древние греки доказали, что Земля круглая

В последнее время появляется все больше приверженцев теории плоской Земли, которые ставят под сомнение общеизвестный факт, что наша планета круглая. А ведь еще в Древней Греции сумели доказать, что Земля имеет сферическую форму.

1.

Предположение Пифагора
В 500 году до н.э древнегреческий философ Пифагор предположил, что Земля круглая. Возможно, информацию о шарообразности земли он получил от египетских жрецов и захотел ее обосновать. Он пытался опровергнуть теорию плоской земли и заявлял, что она не имеет опоры.

Пифагор заметил, что звёзды, Солнце и Луна ежедневно заходят за Землю и появляются с другой стороны, обходя ее вокруг. Свободное движение небесных тел вокруг Земли Пифагор объяснил тем, что планета имеет сферическую форму. Однако его предположение было осмеяно.

Доказательства Аристотеля
Первым, кто привел доказательство того, что Земля круглая, был мыслитель Аристотель. В трактате «О небесах», написанном в 350 году до н.э, он рассказал, что наблюдения за звездами наводят его на мысли о том, что Земля круглая и имеет большие размеры. Аристотель заметил, что многие звезды не видны в северных широтах, тогда как в южных их можно увидеть. На основании этого и был сделан вывод о том, что Земля имеет форму шара. Ведь если бы она была плоской, то одно и те же звезды можно было бы видеть из любой точки Земли.

2.

Аристотель – древнегреческий философ. Ученик Платона. С 343 года до н. э. – воспитатель Александра Македонского.

Также Аристотель часто наблюдал за лунными затмениями и заметил, что тень на Луне, отбрасываемая Землей, круглая. Это также прямо указывало на форму планеты.

Теорию плоской земли Аристотель отвергал. Ее сторонники были уверены, что Солнце на закате отсекается прямой, а не дугообразной линией, а мыслитель считал это ни чем иным, как оптической иллюзией.

Доказательства Эратосфена
«Отец географии» и астроном Эратосфен понял, что Земля круглая, наблюдая за тенями во время летнего солнцестояния. Это произошло примерно в 250 году до н.э. Эратосфен заметил, что в одном населенном пункте в полдень предметы не отбрасывают тени, а в другом тени от предметов длинные и вытянутые.

Он задумался, почему так происходит. Эратосфен рассуждал, если лучи от Солнца, попадающие на Землю, относительно параллельны, значит, и тени должны быть везде одинаковые. Однако это было не так и, опираясь на свои наблюдения, он пришел к выводу, что планета не может быть плоской.

Ему даже удалось вычислить угол лучей в 7 градусов и на основании этого высчитать приблизительный размер Земли, которая, по убеждению Эратосфена, была круглой. Также именно он ввел понятие широты и долготы, которые хорошо известно и сегодня и изобрел первые географические карты, опираясь на теорию сферической планеты.

Наука и технологии
23 октября, 2020
995 просмотров

Даже ребенок может доказать, что Земля круглая: вот как

Космос поддерживается аудиторией. Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот почему вы можете доверять нам.

Этот вид горизонта Земли был сделан членом экипажа 7-й экспедиции на борту Международной космической станции 13 июня 2003 года.
(Изображение предоставлено НАСА)

Эта статья была первоначально опубликована по адресу  The Conversation.  Статья опубликована в Live Science’s Голоса экспертов: комментарии и идеи .

Могут ли 2000 лет веры быть ошибочными? Действительно ли мы живем на диске, а не на глобусе? Один верующий из Общества Плоской Земли полон решимости выяснить это. «Безумный» Майк Хьюз собирается построить собственную ракету, чтобы лично убедиться в том, что Земля плоская.

В течение последних 50 лет мы могли просматривать фотографии Земли из космоса, которые могут показаться достаточным доказательством того, что наша планета на самом деле круглая. Но осознание того, как легко изображения можно подделать, и рост теорий заговора в Интернете, по-видимому, способствовали возрождению веры в плоскую Землю.

В то же время отсутствует понимание науки, которая уже давно используется для демонстрации того, что мы живем на земном шаре, не покидая его. Я желаю Хьюзу удачи в его усилиях, поскольку он, по крайней мере, был готов попытаться доказать свою теорию. Возможно, если бы больше людей действительно могли увидеть доказательства своими глазами, мы могли бы обратить вспять эту тревожную тенденцию.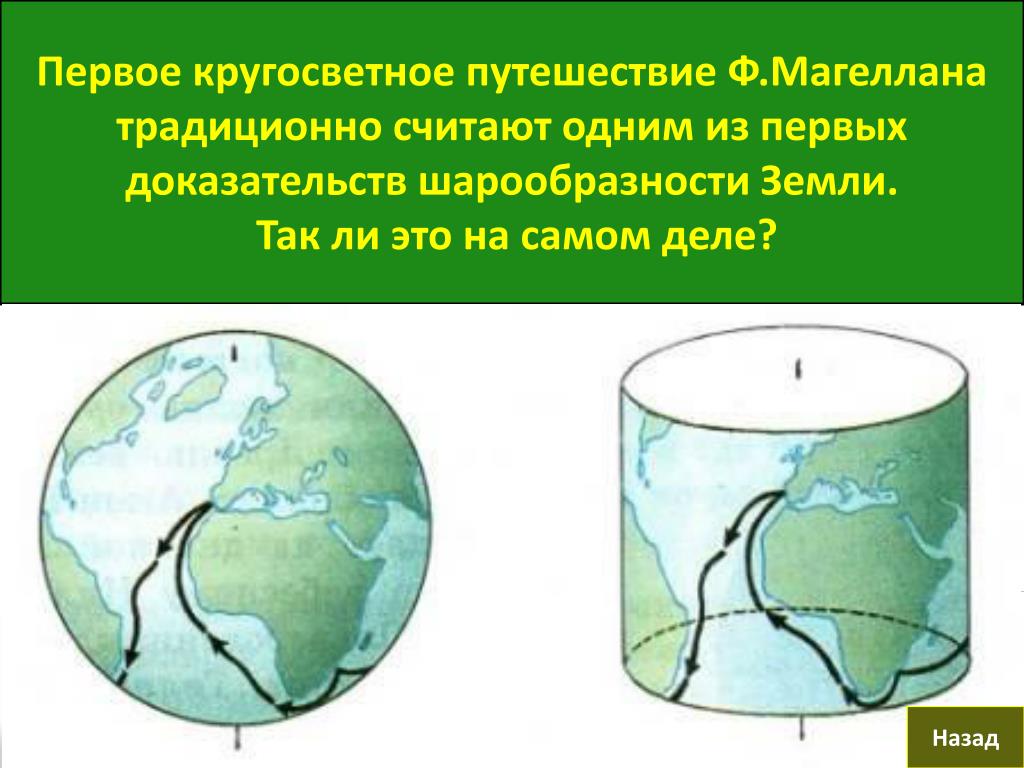 Хорошо бы начать с того, чтобы у детей была возможность попробовать простые эксперименты в школе.

Один из наиболее задокументированных методов определения округлости Земли был впервые применен (насколько нам известно) древними греками. Этого удалось добиться путем сравнения теней от палочек в разных местах. Когда солнце было прямо над головой в одном месте, палка не отбрасывала тени. В то же время в городе примерно в 500 милях к северу палка отбрасывала тень.

Если бы Земля была плоской, то обе палочки должны давать одинаковую тень (или ее отсутствие), потому что они были бы расположены под одним и тем же углом к ​​солнцу. Древние греки обнаружили, что тени были другими, потому что Земля искривлена, и поэтому палочки располагались под разными углами. Затем они использовали разницу этих углов для расчета окружности Земли. Им удалось получить его с точностью до 10% от истинного значения — неплохо для примерно 250 г. до н.э.

Другим свидетельством наличия глобуса является разница между ночным небом в северном и южном полушариях. Вид совершенно другой, потому что Земля под вами указывает в другом направлении. Если бы Земля была плоской, вид был бы таким же. Это можно сделать еще проще, просто сравнив, когда в каждой стране наступает ночь и день.

Вы также можете наблюдать за планетами. Все они вращаются, и наблюдение в течение нескольких дней дает четкое представление о том, что они сферические, а не плоские. Вероятность того, что большинство планет имеют сферическую форму, а Земля плоская, кажется очень маловероятной.

Но когда научные эксперименты проводятся неправильно, может показаться, что они дают противоположный результат. Если ими поделиться через социальные сети, эти ложные идеи могут быстро распространиться, и никто не укажет на их недостатки. Одним из распространенных примеров является эксперимент уровня Бедфорда, форма которого была впервые проведена в 1838 году и использовалась для «доказательства» того, что Земля плоская в течение более 30 лет, прежде чем было найдено объяснение.

Этот эксперимент заключался в размещении маркера на заданной высоте на обоих концах канала длиной около шести миль. Если Земля круглая, то при одновременном наблюдении в телескоп один маркер должен казаться ниже другого, потому что самый дальний маркер отпал бы из-за кривизны Земли. Но сообщалось, что маркеры имеют одинаковую высоту, что говорит о том, что Земля на самом деле плоская. Современные теоретики плоской Земли до сих пор цитируют этот эксперимент.

Проблема в том, что здесь не учитывается оптический эффект воздуха на промежуточную воду, который искривляет или «преломляет» свет на пути от маркера к телескопу и создает впечатление, что они имеют одинаковую высоту. . Решение состоит в использовании нескольких маркеров по длине канала, которые при наблюдении оказываются на разной высоте (откроется в новой вкладке).

Возможно, самый впечатляющий эксперимент, который сегодня могут провести даже школы, — отправить камеру на высотном воздушном шаре. На кадрах будет видно, что с достаточно высокой точки обзора можно увидеть кривизну Земли. Это то, что Майк Хьюз обнаружит, если когда-нибудь заставит свою ракету работать.

В конце концов, споры в Интернете — не лучший путь для любой научной деятельности. Нам нужно предоставить людям средства для проверки этих теорий и понимания полученных ими результатов.

Ян Уиттакер, лектор, Университет Ноттингем Трент

Первоначально эта статья была опубликована на The Conversation. Прочитайте оригинальную статью.

Присоединяйтесь к нашим космическим форумам, чтобы продолжать обсуждать последние миссии, ночное небо и многое другое! А если у вас есть новость, исправление или комментарий, сообщите нам об этом по адресу: [email protected].

Доктор Ян Уитакер — старший преподаватель физики в Ноттингемском Трентском университете в Ноттингеме, Англия, Соединенное Королевство. Он получил степень магистра физики в области космической науки и техники в Лестерском университете в 2006 году и защитил докторскую диссертацию. по космической физике из Уэльского университета в Аберистуите в 2010 году при изучении взаимодействия Солнца с верхними слоями атмосферы Венеры. Ян читает лекции в Университете Ноттингем Трент с 2017 года и проявляет особый интерес к популяризации космической науки. В дополнение к своим лекционным обязанностям Ян является автором журнала The Conversation, где он пишет о широком круге вопросов, связанных с исследованием космоса и наукой.

Калькулятор плоской и круглой Земли

Создано Стивеном Вудингом

Отзыв от Bogna Szyk

Последнее обновление: 22 ноября 2022 г. эксперимент

Как лучше всего познавать мир? Предложить теорию и вознамериться доказать ее наблюдениями (наукой)? Или просто выдумываете и игнорируете очевидные факты (ерунда)? Здесь, в Omni, мы склонны думать, что первый вариант работает довольно хорошо. Это привело нас на Луну, не так ли? — Между прочим, это действительно так.

Чтобы отпраздновать Всемирный день науки за мир и развитие , который проводится 10 ноября, мы создали калькулятор, который поможет вам бороться с чушью, полуправдой и чепухой, а также за науку, наблюдательность и непредубежденность. .

Калькулятор плоской и круглой Земли Omni включает эксперименты, которые помогают доказать, что Земля действительно круглая. Не волнуйся; вы не будете строить свою собственную ракету, чтобы отправиться в открытый космос, чтобы проверить (или рассчитать ее импульс и импульс или ее кинетическую энергию).

У нас есть три относительно простых эксперимента, которые вы можете попробовать:

• Тени палочки — Используйте длины теней, отбрасываемых палкой в ​​разных местах, чтобы оценить окружность Земли.
• Закат дважды — Изменив точку обзора над землей, вы сможете увидеть закат дважды. Наш калькулятор подскажет, сколько второго заката вы увидите.
• Исчезающие объекты — Скройте объекты за кривизной Земли, изменив высоту точки обзора. Этот калькулятор покажет вам, какой высоты объект вы можете заставить исчезнуть.

Прежде чем мы перейдем к экспериментам, давайте кратко рассмотрим, почему люди верят в плоскую Землю и в модель мира, которую они выдвигают.

Вера в плоскую Землю

Удивительно, но в самой богатой, самой технологически развитой стране мира каждый шестой житель не уверен, что Земля круглая 🤔. Конечно, страна — это США , и вера в плоскую Землю может проистекать из ее крайне индивидуалистической культуры и недоверия к властям, институтам и экспертам.

Сообщение Общества плоской Земли в Facebook

Плоскоземельцы, кажется, смотрят на мир самостоятельно, без ссылки на колодец за 2000 лет человеческих открытий . Вау, они упускают. Они также крайне недоверчивы к любым фактам, которые не проверили на себе лично.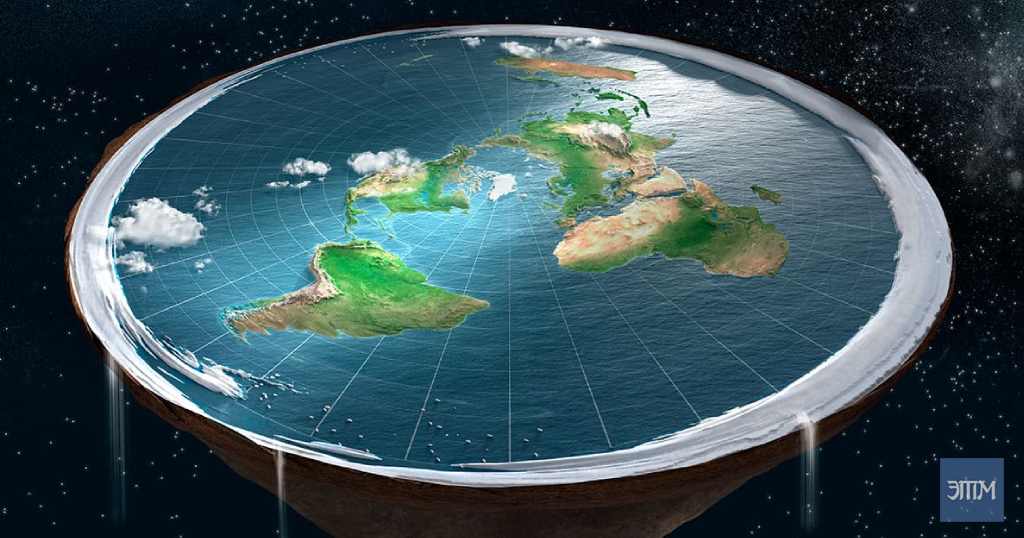 Поговорите о проблемах с доверием.

Затем они берутся за невероятные испытания, чтобы доказать, что Земля плоская, когда есть простые вещи, которые они могут сделать, чтобы доказать, что Земля круглая. Вот несколько примеров:

• «Безумный» Майк Хьюз построил свои собственные паровые ракеты, чтобы летать на высоту 1800 футов (550 м), чтобы сфотографировать отсутствие кривизны пустыни Мохаве. К сожалению, вам нужно подняться на высоту не менее 35 000 футов (11 000 м), чтобы увидеть кривизну Земли. К сожалению, он скончался в феврале 2020 года в результате неудачного полета ракеты.
• Звезда YouTube Логан Пол собирается посетить Антарктиду, чтобы найти край плоской Земли. Ему лучше собрать много припасов, так как до другой стороны Антарктиды около 3000 миль (5000 км).
• Рэпер B.o.B пытался собрать средства на запуск собственного спутника, чтобы проверить плоскость Земли. Ему удалось собрать только 6 883 доллара из своей цели в 1 миллион долларов. Ну да ладно. Может быть, вместо этого он мог бы попробовать наши простые, недорогие эксперименты.

Этот мультфильм Тома Фондера очень хорошо описывает сторонников плоской Земли.

Мультфильм Тома Фондера.

Модель плоской Земли

В модели плоской Земли мир представляет собой диск (похожий на шестерни, используемые для редукторов) с северным полюсом в центре. По краю диска лед и снег «южного полюса». Затем он образует ледяной барьер, по-видимому, для того, чтобы вода океанов не падала с диска в космос.

Карта физического мира в трехосной бореальной проекции Хеллерик, которую сторонники плоской Земли используют в качестве модели плоской Земли.

Толщина плоского земного диска не ясна. Однако задействованная масса должна быть намного меньше круглой Земли, поэтому Земля не сможет удержать свою атмосферу. Может быть, есть прозрачный купол над Землей, не дающий ей убежать.

Традиционная модель плоской Земли имеет солнце, расположенное над диском, кружащимся по небу, как мобильник ребенка, и на гораздо более близком расстоянии. Тогда это не объясняет закаты и рассветы. Для здравого смысла представим, что диск вращается, как монета, относительно солнца. Это, по крайней мере, вернуло бы наш восход и закат (то, что могли бы наблюдать даже простейшие животные). Однако не было бы часовых поясов, поскольку восход и закат были бы в одно и то же время по всему миру.

🔎 💻 Вы можете испытать, каково это жить на плоской Земле, используя компьютерную модель, созданную Брюсом Шервудом. Он показывает, что солнце никогда не садится и его видимый размер меняется в течение дня, а также многие другие вещи, которые мы просто не наблюдаем в реальности.

Это основная проблема модели плоской Земли. Он полон несоответствий и необъяснимых наблюдений. Например, почему холодно и в центре, и на краю диска?

Вернемся к более научному мышлению и представим первый эксперимент.

Двойной эксперимент «Закат»

Этот первый эксперимент может быть очень простым. Двигайтесь вверх достаточно быстро, чтобы опередить тень, отбрасываемую горизонтом. После этого вы сможете дважды увидеть часть заката! Если вы заметите это, то Земля действительно круглая. Этот эксперимент подсчитает, сколько секунд вы могли бы видеть закат и как долго вы могли бы продлить закат.

Что бы вы увидели, если бы Земля была плоской? Нет второго заката 😭. Неважно, как высоко или быстро вы поднялись с поверхности плоской Земли; ты не увидишь солнца снова до рассвета.

Для круглой Земли, когда солнце садится, представьте тень, отбрасываемую земным горизонтом, приближающуюся к вам и движущуюся вверх по вашему телу. Если вы сможете опередить эту тень, двигаясь вверх достаточно быстро, вы снова сможете увидеть закат. Давайте посмотрим на математику.

В этой статье дается уравнение, связывающее время с высотой тени:

t = 8 × √h ,

где t — время, за которое тень поднимается вверх на величину ч . Мы можем связать ч с разницей высот между двумя высотами и t со временем, которое требуется для движения вверх. Поскольку мы не можем мгновенно переместиться с более низкой высоты на более высокую, нам необходимо учитывать время в пути. Наконец, чтобы найти количество секунд заката, которое мы можем увидеть снова, нам нужно знать продолжительность заката. Затем у нас есть это уравнение для процента заката два, который вы будете наблюдать снова:

процент заката два = 100 × (1 - ((продолжительность заката - t - время в пути) / продолжительность заката)))

Направления, как дважды увидеть закат

Есть несколько способов снова увидеть солнце сразу после его захода, в той или иной степени. Калькулятор плоской и круглой Земли Omni подскажет, сколько секунд заката вы сможете наблюдать. Давайте рассмотрим три идеи, которые мы придумали.

1. Лечь, встать

Эта идея самая простая с точки зрения оборудования. Вам просто нужно место, где вы можете видеть закат солнца в море или на очень плоской земле (например, в пустыне). Поможет и красивое безоблачное небо.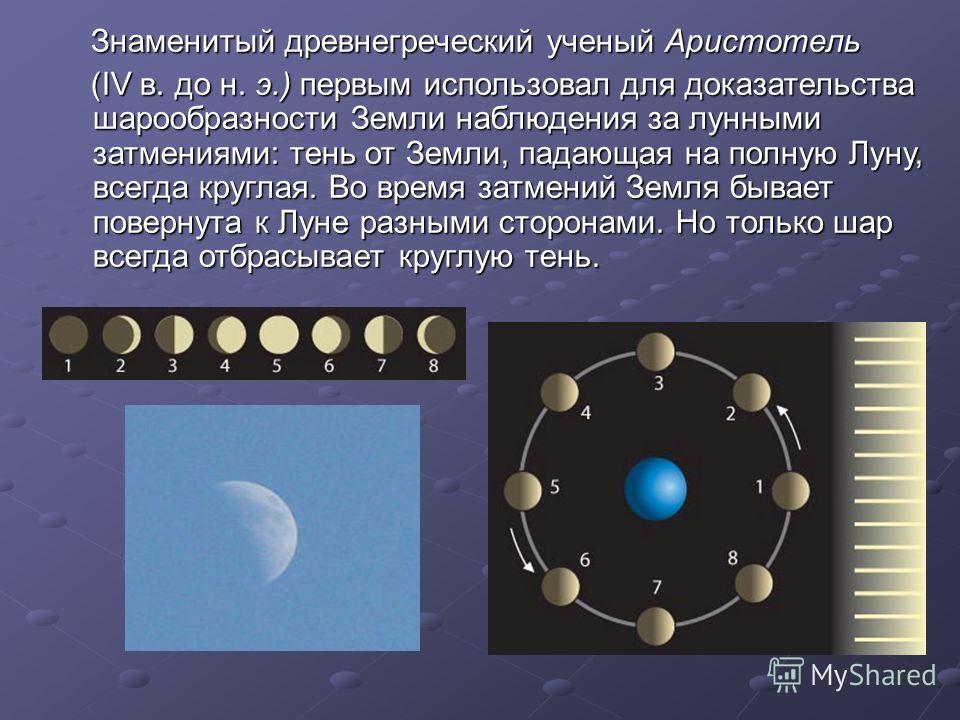 Все, что вам нужно сделать, это смотреть на закат лежа. Как только вы больше не сможете видеть Солнце, немедленно встаньте так быстро, как только сможете. Вы должны снова увидеть небольшую часть верхней части солнца.

Вот как использовать калькулятор для точного подсчета.

1. Выберите ближайшее к вам место или вручную введите продолжительность заката там, где вы находитесь.
2. Введите нижнюю начальную высоту вашего уровня глаз. В данном случае лежа. Мы рекомендуем около 8 дюймов (20 см).
3. Введите, сколько времени вам потребуется, чтобы подняться на большую высоту. Мы рассчитываем примерно на полсекунды, но давайте перепроверим время.
4. Введите окончательную высоту вашего уровня глаз, когда вы стоите. Вы можете измерить это, вычтя расстояние от макушки головы до глаз из вашего роста.
5. Затем вы увидите процент солнца, которое вы снова сможете увидеть заходящим. Хочу увидеть больше? Попробуйте изменить значения в калькуляторе или перейдите к более сложным вариантам эксперимента ниже.

С помощью этого метода вы сможете увидеть около 5% второго заката.

2. Быстро подняться на небоскреб

Чтобы увидеть больше второго заката, вам придется подниматься выше и быстрее, чтобы опередить тень горизонта. Небоскреб с быстрым лифтом — один из вариантов. Это явление наблюдалось в отеле Buri Khalifa в Дубае.

Чтобы выбрать входные значения для этого небоскреба, выберите «Небесный подъемник — отель Бури Халифа» из списка идей. Если вы хотите попробовать это в другом здании, измените входные значения соответствующим образом.

Вы снова сможете увидеть массивный 88% закат, и его продолжительность почти удвоится. Если вы любитель заката, это то, что нужно сделать.

3. Дрон с камерой

Еще одна идея — использовать качественный дрон с камерой для прямой трансляции. Мы нашли один беспилотник, который может подняться на высоту 3300 футов (1000 м) за 200 секунд. Если вы выберете «Дрон» из списка идей, вы увидите, что должны снова увидеть около трети заката этим методом.

Проверьте, насколько быстро и высоко может летать ваш дрон, и соответствующим образом скорректируйте значения в калькуляторе.

Эксперимент с исчезающим объектом

В этом эксперименте мы скроем часть объекта за кривизной Земли. Вам нужно будет найти водоем, где дальний берег находится на расстоянии не менее мили с четвертью (2 км), и это должен быть хороший безветренный день.

Кроме того, чтобы избежать светового эффекта миража [преломления]), проведите эксперимент утром, когда прохладно. Вот почему мы не рекомендуем использовать пустыню — эффект миража будет означать, что вы не сможете достаточно четко видеть объекты на дальнем берегу.

В этом видео на YouTube парень заставил грузовик в 4 милях (7 км) исчезнуть на дальнем берегу озера, опустив камеру ближе к земле.

Смотреть это на YouTube

В качестве альтернативы, морская ветряная электростанция также является хорошим вариантом, как показано на этой фотографии:

Морские ветряные мельницы исчезают за кривизной Земли, у берегов Бельгии. Оффшорные ветряные мельницы, исчезающие за кривизной Земли у берегов Бельгии (Атрибуция: Lieven, CC BY-SA 4.0, через Wikimedia Commons).

Обратите внимание, чем дальше ветряная мельница, тем больше она скрыта. Вот о чем этот эксперимент — вычисление того, какую часть удаленного объекта вы можете скрыть за кривизной Земли.

💡 Кривизна Земли была измерена как 8 дюймов на милю (12 см на километр). Это означает, что на каждую милю, которую вы удаляете от объекта, 8 дюймов нижней части объекта скрыты кривизной Земли. Однако это предполагает, что вы смотрите на объект с нулевой высотой, что не очень практично.

Как кривизна Земли скрывает часть удаленного объекта.

В этом эксперименте мы начнем с высокой точки обзора, а затем спустимся на более низкую точку обзора, чтобы скрыть удаленный объект . Говоря математическим языком, мы находим, сколько скрыто при высоких и низких просмотрах, и вычисляем разницу.

Чтобы рассчитать скрытую высоту, нам сначала нужно знать расстояние до горизонта. Это определяется следующим уравнением:

a = √[(r + h)² - r²]

, где:

• a это расстояние до горизонта,
• h — уровень точки обзора над землей, а
• r — радиус Земли, равный 3959 миль или 6371 км.

Затем мы вводим результат во второе уравнение, которое вычисляет, какая часть объекта затемнена, x , если смотреть с нулевой высоты:

x = √(a² - 2ad + d² + r²) - r

Разница между двумя значениями x — это высота объекта, который мы можем заставить исчезнуть, изменив точку обзора.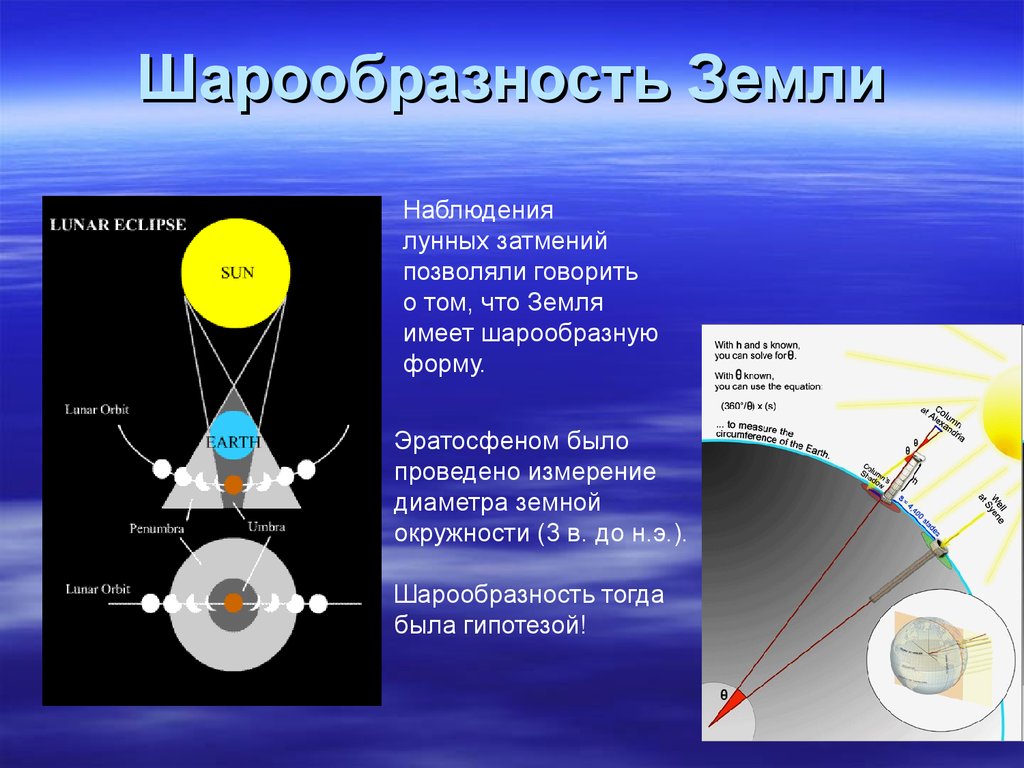

Инструкции по сокрытию объекта за кривизной Земли

Итак, вы нашли отличное место, например, озеро с берегом в нескольких милях от вас. Чтобы увидеть какие-либо объекты на дальнем берегу, вам понадобится хороший бинокль . А еще лучше видеокамера с мощным зум-объективом. Это также позволит вам записать эксперимент, как на видео выше.

Чтобы получить четкий обзор через бинокль или камеру, установите их на штатив рекомендуется. Использование штатива также позволяет точно измерить две высоты.

Вот как с помощью калькулятора вычислить объект какого размера вы могли бы скрыться за кривизной Земли.

1. Измерьте расстояние до дальнего берега озера. Для этого вы можете использовать бумажную карту или функцию измерения на Google Maps. Введите расстояние в переменную «Расстояние до объекта» в калькуляторе.
2. Измерьте высоту над землей на уровне ваших глаз, когда вы стоите, или камеры, когда она находится в верхнем положении. Введите эту высоту в следующее поле ввода.
3. Сделайте то же самое, когда вы лежите или ваша камера находится в низком положении. Чтобы добиться максимального эффекта, постарайтесь опуститься как можно ниже до уровня воды.
4. Затем вы увидите, что высота объекта, скрытого из-за кривизны Земли, рассчитывается для вас. Если он кажется слишком маленьким, чтобы его можно было увидеть, попробуйте увеличить большую высоту и уменьшить нижнюю.

Если бы Земля была плоской, вы не увидели бы никакой разницы в объектах на дальнем берегу озера, как бы низко вы ни смотрели на них.

Эксперимент с тенью палки

Этот эксперимент не только доказывает, что Земля круглая, вы также можете оценить окружность Земли. Именно это и сделал греческий математик Эратосфен в Александрии примерно в  240 году до н. э.  года. Он знал, что в Асуане, примерно в 500 милях к югу, есть колодец, где солнечный свет достигает дна в полдень летнего солнцестояния. В то же время он измерил тень, отбрасываемую палкой в ​​Александрии.

Предполагая, что Земля круглая, а Солнце находится далеко, и используя математику, которую мы рассмотрим ниже, он пришел к выводу, что окружность Земли примерно в 50 раз превышает расстояние между Александрией и Асуаном. это в пределах 10% от правильного ответа . Фантастический результат для такого простого эксперимента, проведенного более 2000 лет назад.

💡 Окружность Земли — это расстояние вокруг Земли. Измеряя вокруг полюсов, это 24 860 миль (40 008 км). По экватору это 24 901 миля (40 075 км). Небольшая разница между двумя измерениями связана с тем, что Земля вращается.

Палки на разных широтах отбрасывают тени разной длины.

Глядя на треугольник, образованный палкой и тенью, мы можем использовать тригонометрическую функцию арктангенса, чтобы вычислить угол между палкой и солнечным лучом, используя уравнение:

θ = арктангенс (длина тени / высота палочки)

Итак, мы делаем это для двух мест. Как эти два угла связаны с окружностью Земли? Рисунок ниже поможет нам ответить на этот вопрос.

Показывает, как углы тени палочки соотносятся с углом в центре Земли между двумя точками А и В.

Используя некоторую геометрию, мы можем показать, что угол α между линиями, проходящими через точки А и В, и центром Земли, разница углов тени от палочки:

α = θ₂ - θ₁

Теперь мы знаем длину дуги (расстояние по поверхности Земли) между A и B и угол α. Это позволяет нам просто увеличить расстояние до полной окружности Земли, используя уравнение:

Окружность Земли = Расстояние A → B × (360° / α)

Важно отметить, что расстояние от A до B должно быть расстояние, если бы вы могли путешествовать только на север или юг (расстояние север-юг). Нам нужно это расстояние, поскольку только когда вы движетесь на север, тень, отбрасываемая палкой, становится длиннее.

Карта США, показывающая расстояние с севера на юг между точками A и B.

Предполагая, что точка A находится к югу от точки B, начертите на карте линию строго на север от точки A. Затем проведите линию строго на восток от точки B. Расстояние с севера на юг — это длина от точки А до пересечения двух начерченных вами линий.

Инструкции по измерению размера Земли с помощью теней от палочек

Есть два основных способа провести этот эксперимент. Вы можете либо путешествовать на значительное расстояние на север или юг (более 100 миль, но чем дальше, тем лучше), либо сотрудничать с кем-то, кто живет далеко, чтобы помочь вам.

Начнем с путешествия. Лучше всего делать это в самый короткий или самый длинный день в году, так как продолжительность дня относительно стабильна. Это уменьшит ошибки измерения угла тени в двух точках. Вот пошаговые инструкции:

1. Измерьте длину вашей палки . Вам нужно будет ввести это в первое поле ввода калькулятора. Если часть палки находится в земле, укажите только длину над землей.
2. Измерьте длину тени в точке А в полдень по местному времени. Если это не солнечный день, подождите, пока он не появится. Введите длину тени в калькулятор, и угол тени будет рассчитан для вас.
3. Отправляйтесь в локацию B и сделайте то же самое, что и в шаге 2.
4. Используя карту, измерьте расстояние с севера на юг между двумя точками и введите это число в калькулятор (см. инструкции выше).
5. Затем вы получите ответ на измеренную оценку окружности Земли и то, насколько близко вы подошли к реальному ответу.

Если у вас есть друг в другом месте, чтобы помочь вам, шаги в основном такие же. Убедитесь, что две палочки имеют одинаковую длину и что вы измеряете тень в полдень по местному времени того же дня. Этот вариант намного проще и может выполняться в любой солнечный день в году.

Пример расчета эксперимента с тенью палки

Например, давайте отправимся на север из Флориды в Пенсильванию (от А до Б), преодолев расстояние с севера на юг около 1000 миль (1609км). Палка имеет длину 3 фута (0,91 м), и мы измеряем длину тени 3 фута в точке А. Это означает угол тени 45°. Затем мы отправляемся в точку B и измеряем тень длиной 5,2 фута, что означает, что угол тени здесь составляет около 60°.

Введите все эти цифры в калькулятор, и мы получим результат 24 000 миль (38 624 км) . Это в пределах 4% от реальной окружности, измеренной между полюсами на расстоянии 24 860 миль (40 008 км).

Что происходит в эксперименте с тенью палки, если Земля плоская?

Давайте на мгновение представим, что плоскоземельцы правы. Как приведенный выше пример работает в модели плоской Земли?

Диаграмма показывает, что происходит без эксперимента с тенью палки в модели плоской Земли.

В модели плоской Земли палочки по-прежнему будут отбрасывать тени разной длины. Однако результат выполнения некоторой тригонометрии приводит к странному результату. Ссылаясь на приведенную выше диаграмму и применяя указанную тригонометрию, мы можем сказать, что:

d = h × (tan θ₂ - tan θ₁)

Используя углы 45° и 60° и 1000 миль для d, мы видим, что расстояние до Солнца h равно

h = 1000 / (1,73 - 1) = 1370 миль

Это делает кажутся очень близкими. Однако модель плоской Земли может сказать, что Солнце намного меньше, чем считает наука.

Теперь мы можем рассчитать два других расстояния до Солнца из двух точек:

R₁ = h / cos θ₁ = 1370 / cos(45°) = 1937 миль

R₂ = h / cos θ₂ = 1370 / cos(60°) = 2740 миль

Этот результат означает, что, пройдя на юг 1000 миль, солнце должно было стать меньше примерно на 40% . На самом деле, как вы можете убедиться сами, солнце не становится меньше по мере вашего продвижения на юг.

Следовательно, можно сделать вывод, что модель плоской Земли неверна. Это не согласуется с наблюдением. Это ключевое свойство любой научной модели. Он должен согласовываться с экспериментальными результатами.

Стивен Вудинг

Выберите эксперимент

Если Земля круглая 🌎, вы сможете дважды увидеть часть заходящего солнца! Вы делаете это, двигаясь вверх быстрее, чем тень, отбрасываемая горизонтом. Давайте подсчитаем, сколько секунд вы должны увидеть закат.

Инструкции:

1. Выберите свое местоположение или введите продолжительность заката, где вы находитесь.
2. Выберите способ набрать высоту или введите пользовательскую начальную высоту, время и конечную высоту.
3. Если калькулятор говорит, что вы снова можете увидеть часть второго заката, а вы это сделали, вы только что доказали, что Земля круглая!

Нужна дополнительная помощь? Кликните сюда!

Закат

Местоположение 📍

Продолжительность заката 🌅

Продолжительность заката зависит от того, насколько севернее или южнее находится место.

Набрать высоту, чтобы поймать второй закат

Метод

Начальная высота

Время в пути ⏱️

Конечная высота

2-й закат

Количество, которое вы сможете увидеть снова

Дополнительное время заката 🌞

Общая продолжительность

Этот результат означает, что Земля действительно кажется круглой 🌎 .