Двухщелевой эксперимент: Двухщелевой опыт Юнга — все самое интересное на ПостНауке

Квантовый ликбез — 18-1. Двухщелевой эксперимент

03:54 pm: Квантовый ликбез — 18-1. Двухщелевой эксперимент
Предыдущие посты

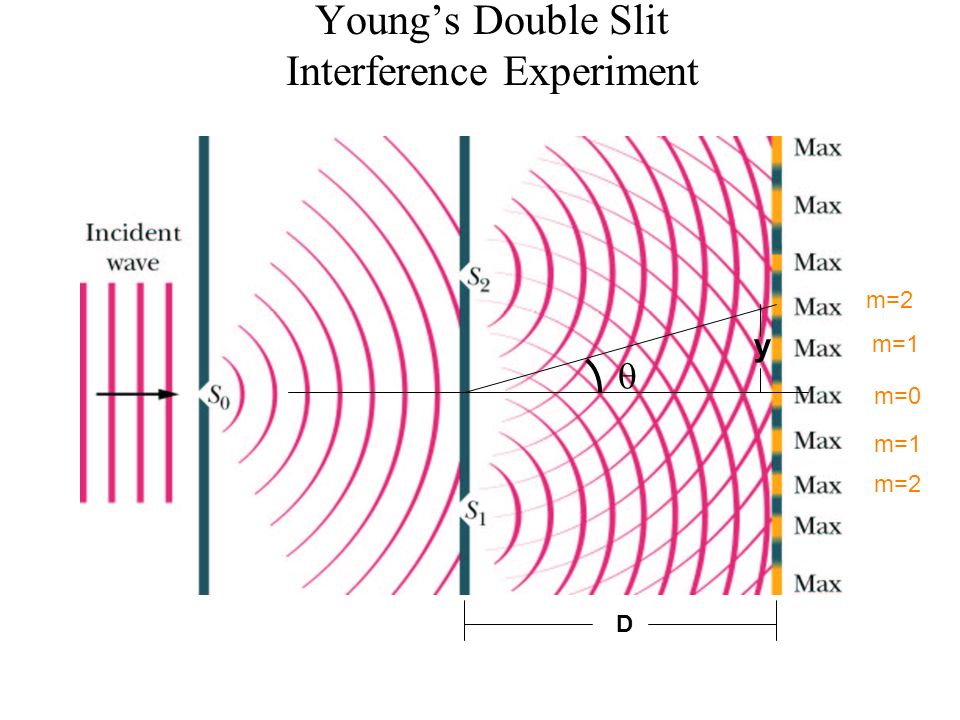
Восемнадцатую часть ликбеза мы посвятим разбору физических опытов, наиболее ярко проявляющих квантовую природу мира. И первым номером в программе будет, конечно же, двухщелевой эксперимент.

Вспомним для начала, что получается, когда мы запускаем частицы через одну щель. Результат такого опыта показан на рисунке 18.1.1.

Попадания, вместо того, чтобы сформировать узкое пятно напротив щели, распределяются по регистрирующему экрану (вдоль координаты X) широкой полосой. График распределения показан на рисунке красной кривой. Причину такой дифракции частиц на щели мы уже выяснили в десятой части.

А что получится, если прорезать в первом экране не одну, а две щели? Казалось бы, распределения от обеих щелей должны сложиться и образовать примерно такую картину попаданий, какая показана на рисунке 18. 1.2.

Однако на деле получается совершенно другой результат, такой, как на рисунке 18.1.3.

Попадания, как видим, распределяются по экрану не равномерно, образуя явные максимумы и минимумы. Как это объяснить? Если бы мы выпускали сразу множество частиц, то это было просто: достаточно предположить, что частицы, прошедшие через разные щели, как то взаимодействуют друг с другом. Но штука в том, что такое же «полосатое» распределение получается даже в том случае, если выпускать частицы строго по одной штуке за выстрел. Для объяснения этого странного факта физики придумали корпускулярно-волновой дуализм. Мол, при распространении частица ведёт себя как размазанная в пространстве волна, а при регистрации – как точечный объект. Соответственно, частица в виде волны проходит через обе щели одновременно. На щелях происходит волновая дифракция, а дальше – интерференция волн от двух щелей. Таким образом в области экрана образуются участки максимальной и минимальной амплитуды волны.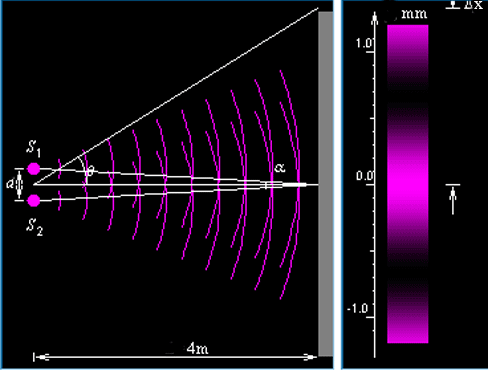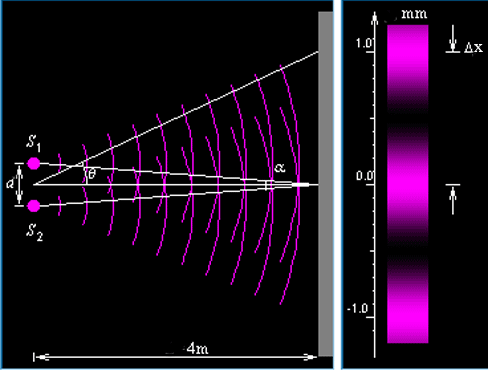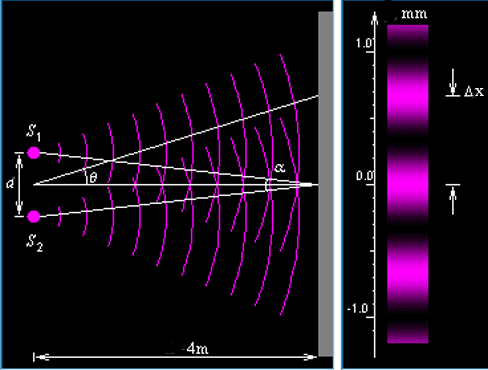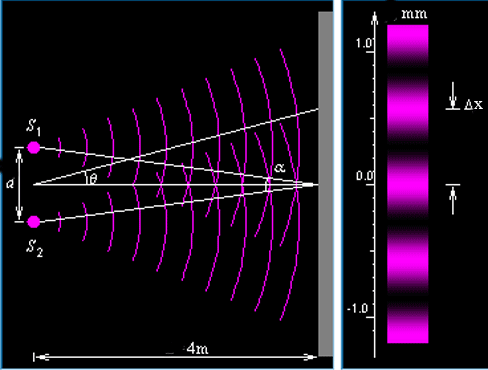

В принципе, так оно и есть. Но мы, владея концепцией множественности виртуальных вариантов, можем разобраться глубже и понять, откуда на самом деле берутся эти «волны».

В девятой части у нас была картинка, показывающая квантовое состояние свободной частицы в координатном представлении. Изобразим её ещё раз, но более красочно (верхняя часть рисунка 18.1.4).

Напомню вкратце, что здесь изображено. Квантовое состояние в координатном представлении мы рассматриваем как бесконечный набор групп виртуальных вариантов, каждая из которых «привязана» к одному значению координаты. Каждая группа обладает собственной амплитудой вероятности. Амплитуда вероятности представляется вектором на комплексной плоскости и выражается, стало быть, комплексным числом. На верхнем графике рисунка 18.1.4 как раз показана зависимость этого комплексного числа от координаты X. Для нескольких значений координаты X в целях наглядности показаны также соответствующие вектора амплитуд вероятности. Верхний график нарисован в «комбинированных» координатах: вглубь рисунка уходит реальная координатная ось X, а в плоскости рисунка — координатные оси Re и Im комплексного пространства квантовых векторов.

График этот, как видите, представляет собой этакую веретенообразную спираль вокруг оси X. С ростом координаты X абсолютное значение амплитуды вероятности плавно растёт от бесконечно малой величины, достигает максимума, а затем плавно падает обратно к бесконечно малой. Направление вектора амплитуды вероятности с изменением X равномерно меняется, вектор как бы вращается вокруг оси X. Длина шага этого вращения вектора амплитуды вероятности, обозначенная на рисунке как λ (лямбда), соответствует длине волны де Бройля для исследуемой частицы.

Для удобства дальнейшего понимания направления векторов амплитуды вероятности «закодированы» цветами:

— синий — вектор вверх;
— красный — вектор влево.
— желтый — вектор вниз;
— зелёный — вектор вправо.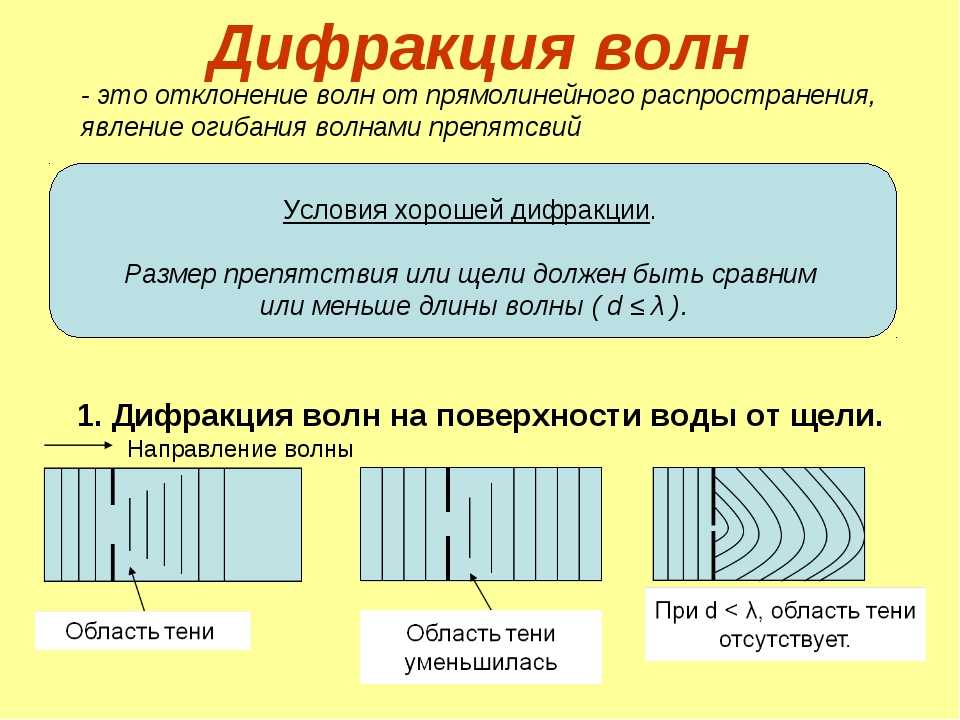

Промежуточные цвета соответствуют промежуточным же направлениям вектора амплитуды вероятности. Например, фиолетовый цвет означает, что вектор направлен на «пол-одинадцатого».

В нижней части рисунка 18.1.4 показано то же самое состояние, но уже не в комбинированных, а в обычных пространственных координатах. Конкретнее — в «разрезе» по плоскости XY. Цвет, как мы условились, соответствует направлению вектора амплитуды вероятности в той или иной точке пространства. А интенсивность раскраски соответствует абсолютному значению, то есть, длине вектора амплитуды вероятности.

Что, вы спрашиваете, почему вдоль оси X цвет (направление вектора) меняется, а вдоль оси Y остаётся постоянным? Отвечаю: мы просто произвольно решили, что частица движется только вдоль оси X, как, например, на рисунках 18.1.1 – 18.1.3 между излучателем и щелевым экраном. Следовательно, частица обладает значительным импульсом вдоль оси X, и близким к нулю импульсом вдоль оси Y. А поскольку длина волны де Бройля обратно пропорциональна импульсу частицы, то вдоль оси X длина волны относительно короткая — направление вектора амплитуды вероятности меняется часто. А вдоль оси Y длина волны близка к бесконечной — направление вектора не меняется.

Это была, ещё раз подчёркиваю, мгновенная, статичная картина квантового состояния. В динамике, если мы рассматриваем движение частицы вдоль оси X, перемещается, на самом деле, никакая не частица, а вот это квантовое «веретено» различных значений амплитуд вероятности, которое в части 10 мы обозвали роем или облаком виртуальных вариантов. Теперь, вспомнив, как выглядит тонкая структура этого виртуального облака, мы легко объясним результаты двухщелевого эксперимента. В этом нам поможет следующая анимация.

Надо, наверное, дать некоторые пояснения к мультфильму. Он демонстрирует динамику поведения амплитуд вероятности в двухщелевом эксперименте. В плоскости, образованной координатными осями XY (см. рисунок 8.1.3).

Слева — источник частиц. Вот он срабатывает, и к экранам движется виртуальное облако реализуемых вариантов. Это облако, вообще-то, по форме похоже на веретено, а в разрезе — на сильно вытянутый ивовый лист, как на рисунке 18.1.4. Но мы упростили картину и изобразили это «веретено в разрезе» как разноцветный прямоугольник.

На щелях облако подвергается дифракции. И дальше, к регистрирующему экрану, виртуальные варианты распространяются уже расходящимися от щелей кольцами, как волны от брошенного в воду камня. В каждом кольце своё направление вектора амплитуды вероятности, поэтому кольца показаны разными цветами.

Дальше две системы расширяющихся колец накладываются друг на друга, образуя динамическую интерференционную картину. В каких-то областях пространства наложения колец нет. В тех областях, где кольца пересекаются, вектора амплитуд вероятности, порождённые разными щелями, вступают в суперпозицию, проще говоря — суммируются. Абсолютное значение суммарного вектора амплитуды вероятности в каждой области разное, ведь оно определяется взаимным направлением векторов в пересекающихся кольцах.

Напоминаю, видя определённый цвет, вы должны мысленно представлять себе вектор амплитуды вероятности на комплексной плоскости определённого же направления, о соответствии цветов и направлений мы чуть выше договорились. Так вот, там, где пересекаются кольца с противоположными направлениями векторов (наложение синего и желтого либо красного и зелёного), абсолютное значение результирующего вектора равно нулю, такие области у нас закрашены белым цветом.

Области, где вектора перпендикулярны, (наложение соседствующих цветов: синий-красный, красный-желтый, желтый-зелёный, зелёный-синий), показаны смешанными цветами.

Области, где вектора направлены в одну сторону (цвета колец одинаковы), показаны более насыщенным основным цветом. В таких областях абсолютное значение суммарных амплитуд вероятности максимально.

И ещё в анимации учтено то обстоятельство, что длина вектора амплитуды вероятности уменьшается от центра (напротив щели) к краям экрана вне зависимости от интерференции.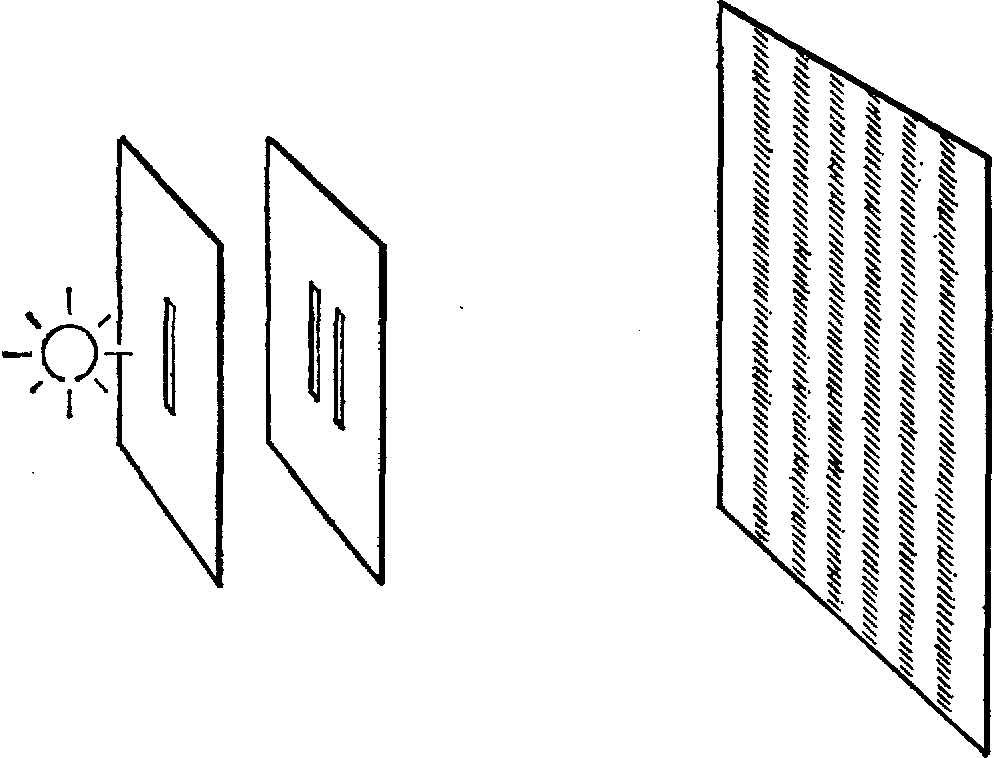 Поэтому в центре все цвета в целом более насыщены, чем по краям.

Вот эти виртуальные волны с разными абсолютными значениями амплитуд вероятности «бьются» в регистрирующий экран и вносят больший или меньший вклад в формирование вероятности попадания частицы в ту или иную его точку. Нарастающая диаграмма справа показывает, как в ходе опыта формируется эта вероятность. Например, в центре экрана, где сосредотачиваются области с удвоенной амплитудой, вероятность реализации попадания получается максимальной. Выше и ниже, там, куда приходят виртуальные варианты с нулевой амплитудой вероятности, наблюдаются минимумы вероятности. Ещё дальше от центра, где сходятся волны с промежуточными цветами, вероятность попадания опять нарастает. Таким образом, после множества «выстрелов» экран становится полосатым, что мы и наблюдаем на опыте (см. рисунок 8.1.3).

Да, прошу ещё учесть, что этот мультфильм содержит ряд существенных упрощений реальной картины.

Во-первых, про прямоугольник вместо «листа» уже сказано выше.

Во-вторых, показана суперпозиция не всех, а только четырёх основных направлений векторов амплитуды вероятности. Поэтому интерференционная картина в целом получилась несколько угловатой, так сказать, в стиле кубизма. В реальности (виртуальной) она гладкая, как интерференция волн на водной поверхности.

В-третьих, у нас тут длина волны де Бройля сильно преувеличена. На самом деле она обычно
многократно меньше размеров экспериментальной установки. Например, длина волны электрона, летящего со скоростью 1000 м/с, составляет порядка одного микрометра. А количество периодов волны, укладывающихся в длину облака реализуемых вариантов, наоборот, занижено. В анимации показано всего два периода, тогда как в реальности (виртуальной, опять же) их много больше. Скажем, если импульс излучаемой частицы определён с точностью до одного процента, тогда на длину вылетающего из источника облака уложится порядка сотни волновых периодов (ох я бы замучился это рисовать, а вы – разглядывать).

Но, думаю, несмотря на все эти условности, у вас в голове сложилось теперь правильное понимание результатов двухщелевого эксперимента.

Следующим постом мы будем изучать «квантовое видение в темноте».

Продолжение

Tags: квантовый ликбез, физика

7 комментариев | Оставить комментарий

Двухщелевой эксперимент . Программируя Вселенную. Квантовый компьютер и будущее науки

Двухщелевой эксперимент демонстрирует волновую природу частиц. Волны накладываются друг на друга, иными словами, интерферируют. Если моя дочь Эмма, сидя в одном конце ванны, отправляет волну своей сестре Зое, сидящей в другом конце ванны, а Зоя одновременно оправляет волну Эмме, то, когда эти волны встретятся посередине, произойдет столкновение, и вода выплеснется на меня. Световые волны при столкновении интерферируют точно таким же образом. Если направить луч света на преграду, в которой проделаны две щели, и посмотреть на картину, которую свет создает на стене позади преграды, то мы увидим перемежающиеся светлые и темные полосы. Это – так называемая интерференционная картина. Подобно тому, как волны воды проходят сквозь ряд свай, световые волны проходят через обе щели сразу; каждая волна при этом делится на две, а потом они собираются уже на стене. Полосы света возникают в тех местах, где пики и впадины волны от одной щели совпадают с пиками и впадинами волны от другой щели, а потому волны усиливаются. Это явление называют «положительной интерференцией». Темные полосы возникают там, где пики волны от одной щели совпадают с впадинами волны от другой щели. Две волны как бы уравновешивают друг друга – происходит «отрицательная интерференция». Если закрыть одну из щелей, интерференционная картина исчезнет, потому что не будет второй волны, которая бы накладывалась на волну, проходящую через оставшуюся прорезь. Чтобы возникла интерференция, волна обязательно должна пройти через обе щели сразу.

Двухщелевой эксперимент можно провести и над частицами! Направим пучок частиц, скажем электронов, на преграду с двумя щелями и поместим на стену за ним фотографическую пластину, чтобы зарегистрировать места, куда попадут частицы. Каждая частица оставляет след на фотографической пластине. Если закрыть левую щель, чтобы электроны проходили только через правую, то мы получим одну картину следов на фотопластинке.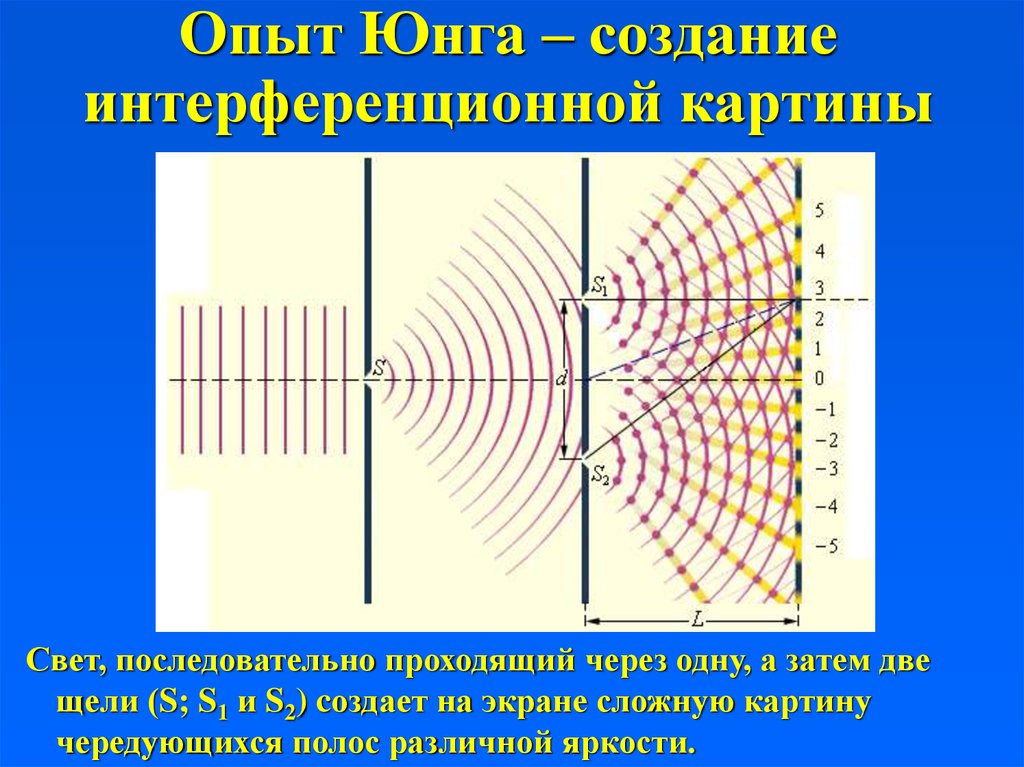 Если закрыть правую щель, чтобы электроны проходили только через левую, мы получим другую картину.

В двухщелевом эксперименте частицы сначала проходят через одну щель, а затем через пару щелей, прежде чем попасть на экран. Картина, которую частицы создают на экране, – это типичная интерференционная картина, свидетельство волновой природы частиц

Теперь откроем обе щели. Что мы ожидаем увидеть? Классическая логика говорит нам, что каждый электрон пройдет либо через одну, либо через другую щель. Распределение следов на фотографической пластинке поэтому должно представлять собой простое наложение двух распределений, полученных ранее от каждой из щелей. Никакой интерференции быть не должно, потому что каждая из частиц проходит только через одну щель. Интерференционная картина – это ведь волновой феномен: он возникает потому, что волны могут проходить и проходят через обе щели сразу. Но частица – это частица: она не может пройти через обе щели сразу.

Здорово, а теперь все-таки проведем эксперимент с пропусканием частиц через пару щелей. Что же мы видим? Интерференционную картину! Следы, оставленные отдельными частицами, ложатся на фотографическую пластинку в виде серии полос! Когда же мы закрываем одну из щелей, интерференционная картина исчезает. Нагляднее некуда: частицы ведут себя как волны!

Как это может быть? Быть может, электроны, проходящие через одну щель, сталкиваются с электронами, проходящими через другую щель, и это создает столь неожиданную картину? Хорошо, давайте уменьшим число электронов в пучке, чтобы свести к минимуму их столкновения. Интерференционная картина остается на месте. Ладно, тогда будем стрелять по экрану одиночными электронами. Удивительно: интерференционная картина все равно остается! Различие в том, что теперь она как бы управляет вероятностью попадания электронов в то или иное место на фотографической пластинке, и электроны преимущественно оставляют следы там, где уже есть полоса следов. Итак, наша интерференционная картина не может быть результатом интерференции множества электронов друг на друга. Всего лишь один электрон каким-то непонятным образом умудряется вести себя так, будто он – волна! Наш эксперимент однозначно доказывает, что одна частица проходит через обе щели сразу, а это значит, что электрон, протон, фотон, атом могут находиться в двух местах одновременно.

Двухщелевой эксперимент иллюстрирует тот факт, что частица не обязательно должна быть или «здесь», или «там». Благодаря присущей ей волновой природе частица может быть и «здесь», и «там» одновременно. Эта способность вещей находиться во многих местах сразу и обеспечивает ту мощь квантовых вычислений, с которой мы познакомимся позже.

экспериментов с двумя щелями

экспериментов с двумя щелями

Эксперимент с двумя щелями — ключ к пониманию микроскопического мира

Волновые свойства света были продемонстрированы знаменитым эксперимент, впервые проведенный Томасом Янгом в начале девятнадцатого века. век. В оригинальном эксперименте точечный источник света освещает два узкие соседние щели в экране и изображение проходящего света через щели наблюдается на втором экране.

, если мы уменьшим интенсивность света или поток электронов (электрический ток), мы сможем увидеть каждый фотон попадает на экран каждый фотон образует точку на экране, но где интерференционная картина?

Однако обратите внимание, что электроны действуют как частицы, как и фотоны.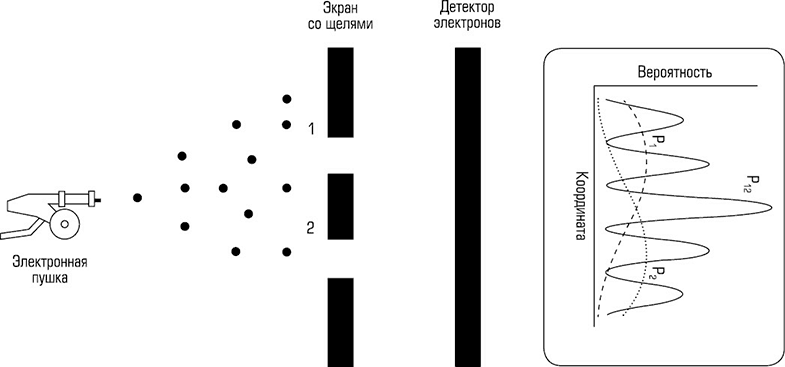 За Например, они наносят одиночный удар по экрану электронно-лучевой трубки. Итак, если мы снизить количество электронов в пучке, скажем, до одного в секунду. Делает интерференционная картина исчезнет?

интерференционная картина все еще существует, просто требуется некоторое время, чтобы достаточное количество фотонов или электронов ударьте по экрану, чтобы создать узнаваемый узор интерференция, или волновое явление, все еще происходит, даже если мы пропускаем только фотоны или электроны через один за раз Так чему же мешают отдельные частицы? видимо сами

Ответ — нет, мы видим отдельные электроны (и фотоны) ударяют по экрану, и со временем интерференционная картина выстраивается. Обратите внимание, что при такой низкой скорости каждый фотон (или электрон) не взаимодействует с другими фотонами, создавая интерференционную картину. 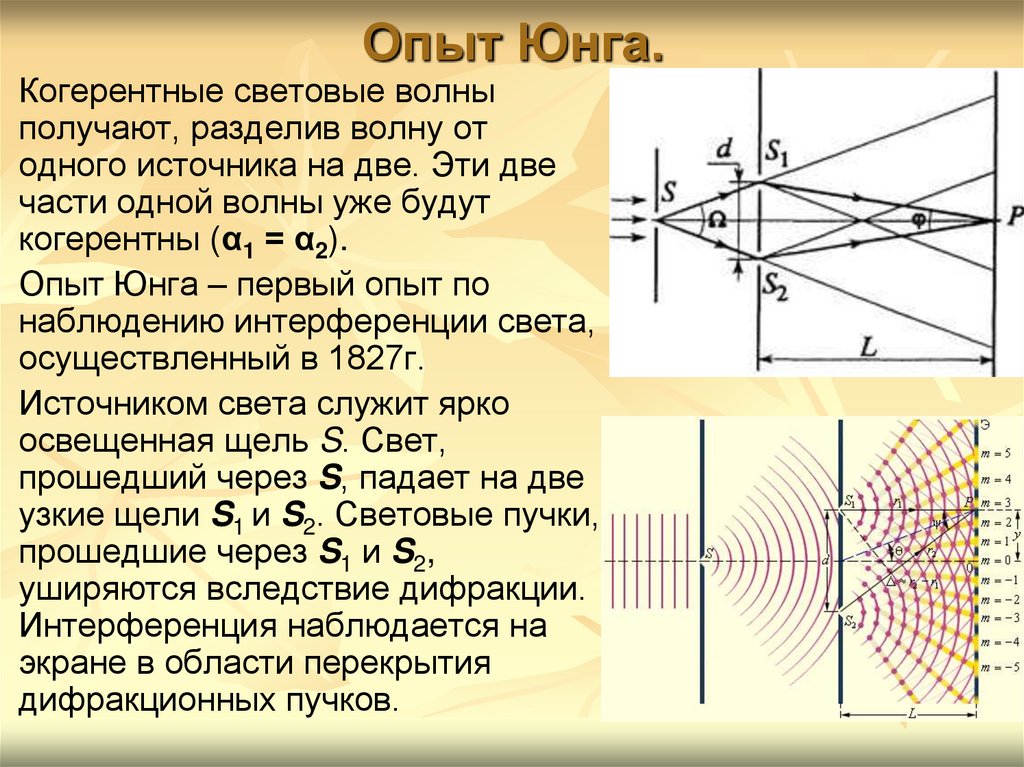В на самом деле фотоны взаимодействуют сами с собой, внутри своей собственной волны пакеты для создания помех.

Роль наблюдателя :

, так как квантовый мир нельзя наблюдать напрямую, мы вынуждены использовать инструменты как расширения нашего чувства Однако квантовые объекты настолько малы, что даже контакт с одним фотоном меняет их положение и импульс = проблема измерения 1-й намек на то, что наблюдатель является важной частью любого квантового эксперимента, не может изолировать наблюдателя или их эффекты

Квантовый мир можно воспринимать не напрямую, а через использование инструментов. А, значит, есть проблема с тем, что акт измерения нарушает энергию и положение субатомных частиц. Это называется проблемой измерения.

Эксперимент с двумя щелями — хорошая проверка роли наблюдателя в квантовой сфере. любой экспериментальный план, который пытается определить, через какую щель прошел фотон (тест на его корпускулярная природа) разрушает интерференционную картину (ее волновую природу) это нарушение объективной реальности каждая квантовая сущность обладает двойными потенциальными свойствами, которые становятся реальной характеристикой, если и когда она наблюдается

Таким образом, мы начинаем видеть сильную связь свойств квантового объект и акт измерения этих свойств. Вопрос о реальность квантовых свойств остается нерешенной. Все квантово-механические принципы должны сводиться к ньютоновским принципам на макроскопическом уровне (есть преемственность между квантовой и ньютоновской механикой). 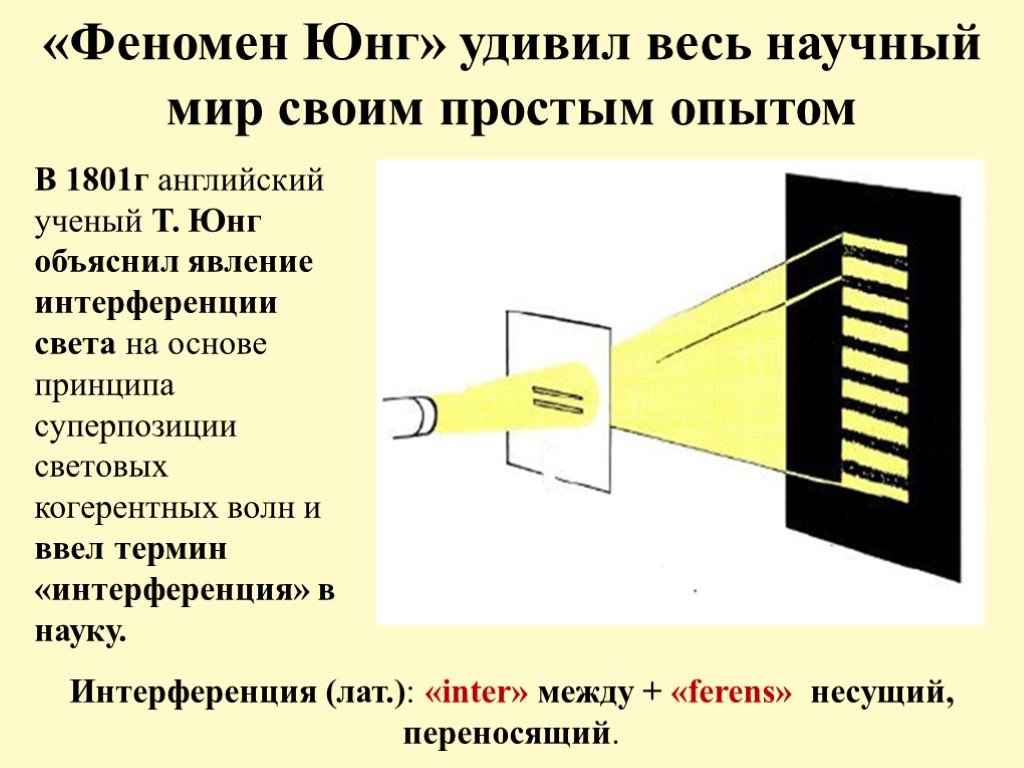Как роль наблюдателя влияет на волновую и корпускулярную природу квантовый мир? Один тест состоит в том, чтобы вернуться к эксперименту с двумя щелями и попытайтесь определить, через какую щель проходит фотон. Если фотон является частицей, то она должна пройти через одну или другую щель. Делает этот эксперимент приводит к исчезновению интерференционной картины. Волна природа света устраняется, остается только природа частиц и частицы не могут создавать интерференционные картины. Ясно, что эксперименты с двумя щелями впервые в физике указывают на что существует гораздо более глубокая связь между наблюдателем и явление, по крайней мере, на субатомном уровне. Это экстремальный перерыв из идеи объективной реальности или такой, в которой законы природы имеют особое, платоническое существование. Если физик ищет частицу (использует детекторы частиц), то частица найдена. Если физик ищет волну (использует волну детектор), то обнаруживается волновая картина. Квантовая сущность имеет двойное потенциальная природа, но его актуальная (наблюдаемая) природа одна или другой.

Квантовая волновая функция :

волновая функция выражает вероятность *до* измерения

Ключевым моментом волновой функции является то, что положение частицы зависит только от выражается как правдоподобие или вероятность до тех пор, пока не будет выполнено измерение. 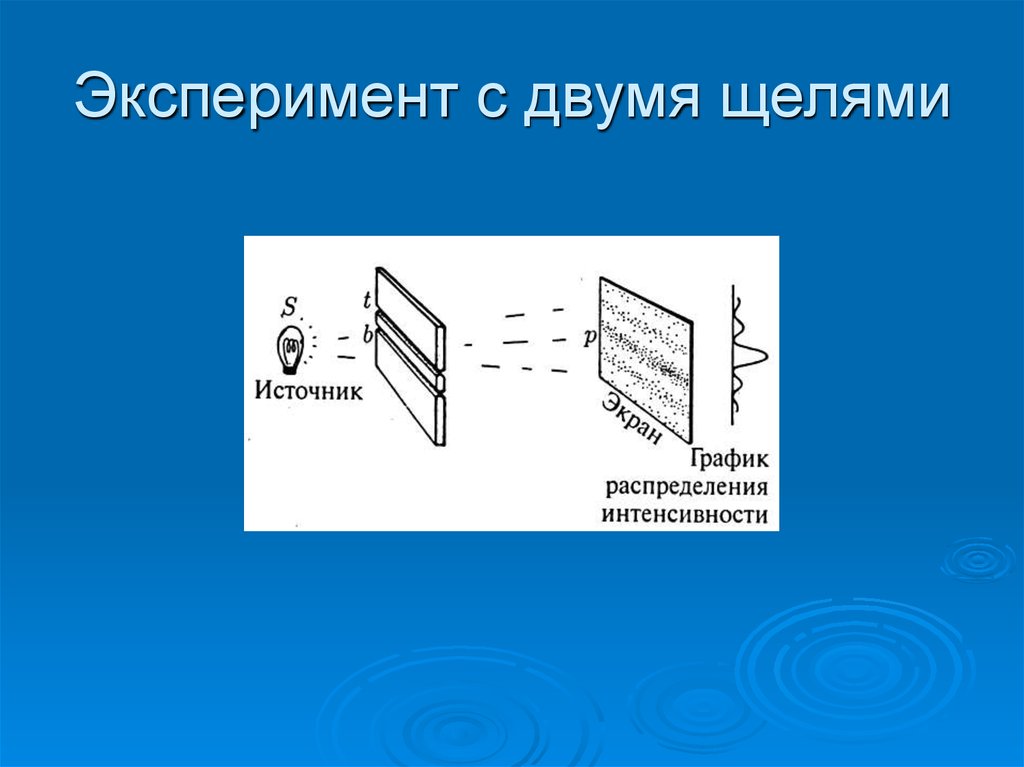За например, попадание фотона в электрон приводит к измерению положения, и мы говорят, что волновая функция «схлопнулась» (т.е. волновая природа электрона преобразована в частицу).

Суперпозиция :

квантовая физика — это наука о возможностях, а не о точности ньютоновской физики квантовые объекты и величины становятся реальными при наблюдении ключевым доказательством квантовых суперпозиций является явление квантового туннелирования

Тот факт, что квантовые системы, такие как электроны и протоны, неопределенные аспекты означают, что они существуют как возможности, а не актуальность. Это дает им свойство быть вещами, которые могли бы быть или может произойти, а не то, что есть. это в резком В отличие от ньютоновской физики, где вещи есть или их нет, существует отсутствие неопределенности, кроме тех, которые вызваны плохими данными или ограничениями данных собирательное оборудование. 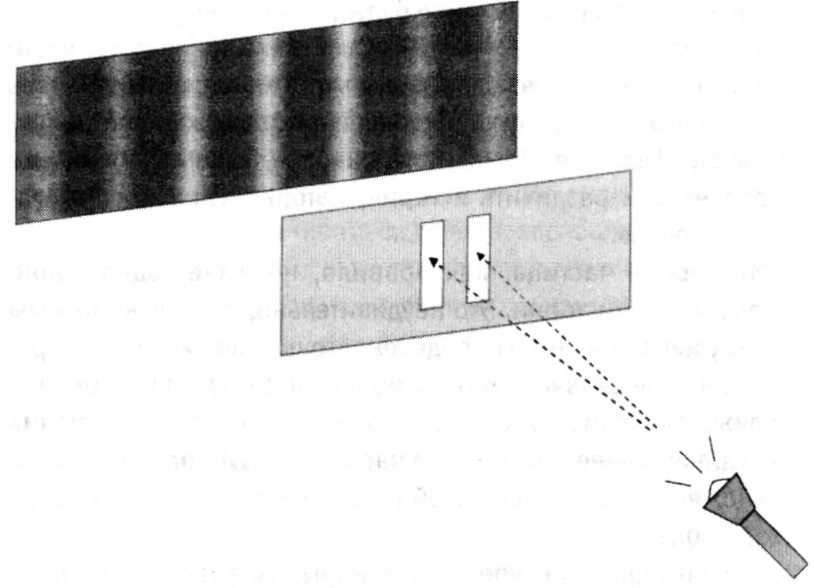Дальнейшие эксперименты показали, что реальность на квантовом (микроскопическом) уровне уровень состоит из двух видов реальности, актуальной и потенциальной. действительность — это то, что мы получаем, когда видим или измеряем квантовую сущность, потенциал – это состояние, в котором объект находился до того, как измерено. В результате квантовая сущность (фотон, электрон, нейтрон и т. д.) существует во множестве возможностей реальностей, известных как суперпозиции. Суперпозиция возможных положений электрона может быть продемонстрировано наблюдаемым явлением, называемым квантовым туннелированием.

положение электрона, волновая функция, действительно рассредоточено, а не неопределенно наблюдение приводит к коллапсу волновой функции до фактического

Обратите внимание, что единственное объяснение квантового туннелирования состоит в том, что положение электрона действительно рассредоточено, а не просто скрыто или не измерено. 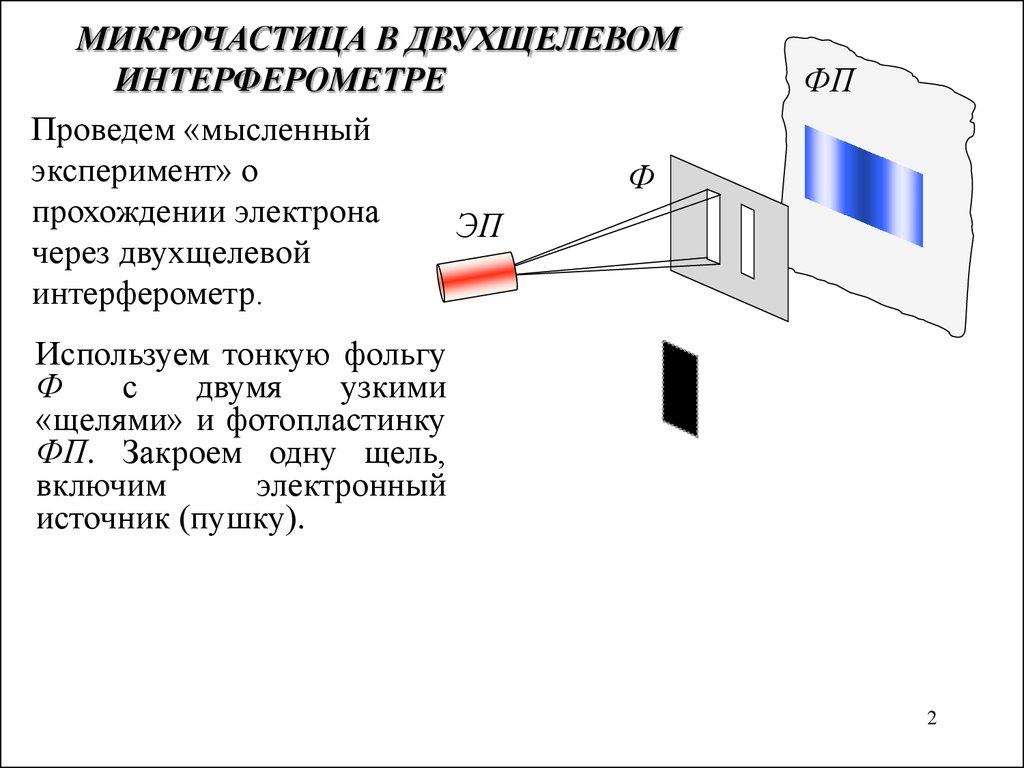Это сырое неопределенность позволяет волновой функции преодолевать барьер. Этот является подлинным индетерминизмом, а не просто неизвестной величиной, пока кто-нибудь измеряет это. Важно отметить, что только суперпозиция возможностей происходит до того, как сущность будет замечена. После того, как наблюдение сделано (т. измеряется положение, определяется масса, определяется скорость), то суперпозиция превращается в фактическую. Или, говоря на квантовом языке, мы говорим волновая функция схлопнулась.

квантовое существование привязано к окружающей среде, в отличие от независимости макроскопических объектов

Коллапс волновой функции при наблюдении — это переход от многого к единому, от возможности к действительности. Личность и существование квантовых объектов связаны с его общим среды (это называется контекстуализм). Подобно омонимам, слова, зависит от контекста, в котором они используются, сдвиги квантовой реальности его природа в соответствии с его окружением. 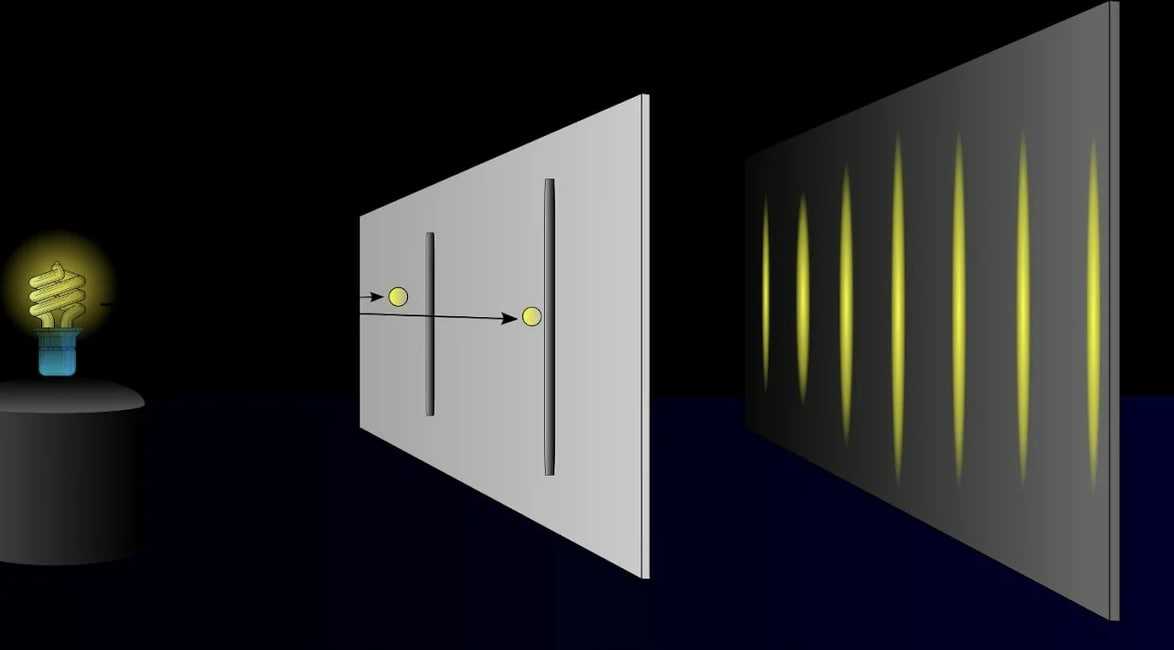В макроскопическом мире, которым правит классическая физика, вещи таковы, что они есть. В микроскопическом мире, где правит квантовая физика, представляет собой экзистенциальный диалог между частицей, ее окружением и человек, изучающий его.

Двухщелевой эксперимент | Brilliant Math & Science Wiki

Содержание

• Волны против частиц
• Двухщелевой эксперимент с электронами
• Моделирование двухщелевого эксперимента
• использованная литература

Чтобы понять, почему важен эксперимент с двумя щелями, полезно понять сильные различия между волной и частицей, которые делают дуальность волна-частица такой интригующей.

Волны описывают колебания значений физической величины, которые подчиняются волновому уравнению. Их обычно описывают суммами функций синуса и косинуса, так как любую периодическую (осциллирующую) функцию можно разложить в ряд Фурье. Когда две волны проходят друг через друга, результирующая волна является суммой двух первоначальных волн. это называется суперпозиция , так как волны располагаются («-позиция») друг над другом («супер-«). Суперпозиция — один из фундаментальных принципов квантовой механики. Общая квантовая система не обязательно должна находиться в том или ином состоянии, но может находиться в суперпозиции двух, где есть некоторая вероятность измерения квантовой волновой функции в том или ином состоянии.

Слева: пример наложенных волн, конструктивно интерферирующих. Справа: наложенные волны деструктивно интерферируют. ^[2]

Если одна волна имеет вид A(x)=sin⁡(2x)A(x) = \sin (2x)A(x)=sin(2x), а другая – B(x)=sin ⁡(2x)B(x) = \sin (2x)B(x)=sin(2x), то они складываются вместе, чтобы получить A+B=2sin⁡(2x)A + B = 2 \sin (2x)A +B=2sin(2x). Сложение двух волн для формирования волны большей амплитуды обычно известно как конструктивная интерференция , поскольку интерференция приводит к большей волне.

Если одна волна имеет вид A(x)=sin⁡(2x)A(x) = \sin (2x)A(x)=sin(2x), а другая – B(x)=sin⁡(2x+π )B(x) = \sin (2x + \pi)B(x)=sin(2x+π), то они складываются вместе, чтобы получить A+B=0A + B = 0A+B=0 (\big(( поскольку sin⁡(2x+π)=−sin⁡(2x)).\sin (2x + \pi) = — \sin (2x)\big).sin(2x+π)=−sin(2x)). Это известно как деструктивная интерференция в общем случае при сложении двух волн получается волна меньшей амплитуды. На рисунке выше приведены примеры как конструктивной, так и деструктивной интерференции.

а) только

а) и б)

б) и в)

в) только

Два динамика воспроизводят звуки с одинаковой фазой, амплитудой и длиной волны. Две звуковые волны могут создавать конструктивную интерференцию, как показано выше слева. Или они могут сделать деструктивное вмешательство, как указано выше. Если мы хотим выяснить точное место, где два звука создают деструктивную интерференцию, что из следующего нам нужно знать?

а) длина волны звуковых волн
б) расстояние от двух динамиков
в) скорость звука, генерируемого двумя динамиками

Такое поведение волны совершенно не похоже на поведение частиц. Классически частицы — это объекты с одним определенным положением и одним определенным импульсом. Частицы не образуют интерференционных картин с другими частицами в детекторах независимо от того, проходят ли они через щели или нет. Они взаимодействуют только путем упругого столкновения, то есть посредством электромагнитных сил на коротких расстояниях. До открытия квантовой механики предполагалось, что волны и частицы представляют собой две различные модели объектов и что любую реальную физическую вещь можно описать только как частицу или волну, но не то и другое одновременно.

В более современной версии эксперимента с двумя щелями с использованием электронов электроны с таким же импульсом выбрасываются из «электронной пушки», такой как те, что внутри ЭЛТ-телевизоров, к экрану с двумя щелями. После того, как каждый электрон проходит через одну из щелей, наблюдается его попадание в одну точку на детектирующем экране в явно случайном месте. По мере того, как все больше и больше электронов проходят по одному, они образуют общую картину из светлых и темных интерференционных полос. Если бы каждый электрон был действительно точечной частицей, тогда было бы только два кластера наблюдений: один для электронов, проходящих через левую щель, и один для правого. Однако, если электроны состоят из волн, они интерферируют друг с другом и проходят через обе щели одновременно. Именно это и наблюдается при проведении двухщелевого эксперимента с использованием электронов. Следовательно, должно быть верно, что электрон интерферирует сам с собой, поскольку каждый электрон проходит только по одному — других электронов, которые могли бы ему интерферировать, не было! 9{-5} r_{B}4×10−5rB​, вы должны дать −5.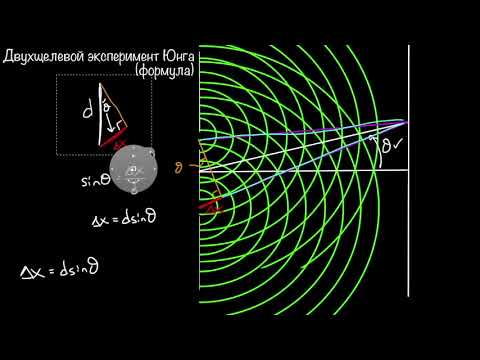 -5.−5.

Изображение предоставлено Flickr drcliffordchoi.

В то время как соотношение де Бройля было постулировано для массивной материи, оно в равной степени применимо и к свету. Имея свет с определенной длиной волны, импульс и энергию этого света можно найти с помощью формулы де Бройля. Это обобщает наивную формулу p=mvp = m vp=mv, которую нельзя применить к свету, поскольку свет не имеет массы и всегда движется с постоянной скоростью ccc независимо от длины волны.

Приведенное ниже воспроизводится из вики Amplitude, Frequency, Wave Number, Phase Shift.

В эксперименте Юнга с двумя щелями фотоны, соответствующие свету с длиной волны λ\lambdaλ, испускаются на барьер с двумя тонкими щелями, разделенными расстоянием d,d,d, как показано на диаграмме ниже. Пройдя через щели, они ударяются об экран на расстоянии DDD с D≫d,D \gg d,D≫d, и измеряется точка попадания. Примечательно, что и эксперимент, и теория квантовой механики предсказывают, что количество фотонов, измеренное в каждой точке экрана, следует сложной серии пиков и впадин, называемых интерференционная картина , как показано ниже. Фотоны должны каким-то образом проявлять волновое поведение относительного фазового сдвига, чтобы быть ответственными за это явление. Ниже выводится условие, при котором максимумы интерференционной картины появляются на экране.

Слева: реальная экспериментальная интерференционная картина фотонов с двумя щелями, демонстрирующая множество небольших пиков и впадин. Справа: схема эксперимента, как описано выше. ^[3]

Поскольку D≫dD \gg dD≫d, угол от каждой из щелей примерно одинаков и равен θ\thetaθ. Если yyy — это вертикальное смещение интерференционного пика от средней точки между щелями, то, следовательно, верно, что тета = y.Dtanθ≈Dsinθ≈Dθ=y.

Кроме того, существует разность хода ΔL\Delta LΔL между двумя щелями и интерференционным пиком. Свет от нижней щели должен пройти ΔL\Delta LΔL дальше, чтобы достичь любой конкретной точки на экране, как показано на диаграмме ниже:

Свет от нижней щели должен проходить дальше, чтобы достичь экрана в любой заданной точке выше средней точки, вызывая интерференционную картину.

Условием конструктивной интерференции является то, что разность хода ΔL\Delta LΔL точно равна целому числу длин волн. Фазовый сдвиг света, проходящего через целое число nnn длин волн, составляет ровно 2πn2\pi n2πn, что равносильно отсутствию фазового сдвига и, следовательно, конструктивной интерференции. Из приведенной выше диаграммы и базовой тригонометрии можно написать

ΔL=dsin⁡θ≈dθ=nλ.\Delta L = d\sin\theta \приблизительно d\theta = n\lambda.ΔL=dsinθ≈dθ=nλ.

Первое равенство всегда верно; второе — условие конструктивного вмешательства.

Теперь, используя θ=yD\theta = \frac{y}{D}θ=Dy​, можно увидеть, что условие максимума интерференционной картины, соответствующее конструктивной интерференции, равно

nλ=dyD,n\ lambda = \frac{dy}{D},nλ=Ddy​,

т.е. максимумы приходятся на вертикальные смещения

y=nλDd.y = \frac{n\lambda D}{d}.y=dnλD​.

Аналогичная экспериментальная установка и математическое моделирование с использованием электронов вместо фотонов идентичны, за исключением того, что длина волны де Бройля электронов λ=hp\lambda = \frac{h}{p}λ=ph​ используется вместо буквальной длины волны света.