Содержание
Почему ракетка кувыркается в воздухе и как это связано с квантовой физикой
Александр
Шереметьев
новостной редактор
Александр
Шереметьев
новостной редактор
Раскручивая гайку в невесомости, советский космонавт обнаружил необычный эффект. Она начинала кувыркаться в космосе. «Хайтек» рассказывает, что стоит за этим явлением, как его наблюдать на Земле и где еще применяют эффект Джанибекова.
Читайте «Хайтек» в
В 1980 году профессор факультета статистики Чикагского университета Стивен Мак Стиглер сформулировал закон Стиглера об эпонимии. Он говорит, что «никакое научное открытие не было названо в честь первооткрывателя» (No scientific discovery is named after its original discoverer).
Чтобы показать, что это не просто слова, сам Стиглер приписывает первоначальное открытие этого закона американскому социологу Роберту Мортону.
Пять лет спустя советский космонавт Владимир Джанибеков, наблюдая за поведением гайки в невесомости, заметил необычный эффект. Словно бы в подтверждение закона Стиглера он получит название эффекта Джанибекова, хотя на самом деле является следствием ключевых постулатов классической механики, сформулированных задолго до этого.
Что увидел космонавт?
Доставленный на орбиту груз, как правило, закрывается с помощью специальных барашковых гаек или бабочек. Это такая конструкция с небольшими ушками, которая не требует специального инструмента, чтобы ее раскрутить. В невесомости достаточно ударить по одному «ушку» бабочки и она сама раскрутится. При этом на орбите, соскочив со стержня, гайка продолжит движение, вращаясь в воздухе.
Во время спасательной операции космической станции «Салют-7» Владимир Джанибеков заметил: если не трогать гайку, то, пролетев небольшое расстояние, она самостоятельно развернется в воздухе на 180° и продолжит лететь.
Спустя еще какое-то время это повторится снова.
Космонавт провел множество экспериментов, но всякий раз результаты оказывались одними и теми же. Вращающаяся в воздухе гайка постоянно делала развороты на 180° через равные расстояния. Проведя эксперимент с другими предметами, например, с обычной гайкой, к которой прикрепили шарик из пластилина, Джанибеков убедился, что не только гайка-бабочка демонстрирует необычное поведение.
Демонстрация эффекта Джанибекова в невесомости. Видео: NASA
Как это объяснить?
Первая публикация, объясняющая странное поведение объекта, вращающегося в невесомости, появилась в 1991 году. Но сам эффект был известен задолго до этого. Еще в 1834 году Луи Пуансо в своей работе «Новая теория вращения тел» показал, что вращение тела вокруг промежуточной (средней) главной оси инерции носит неустойчивый характер. В то время как вращение вокруг двух других осей — устойчивое. Общие принципы, описывающие вращение твердого тела, еще раньше сформулировал математик Леонард Эйлер в теореме вращения Эйлера.
Напомним, главными осями инерции тела называются такие оси координат в декартовой системе, относительно которых центробежный момент инерции равен нулю. Главные оси инерции, проходящие через центр тяжести тела, называются главными центральными осями инерции тела. Через любую точку тела можно провести три главные оси, при этом все они будут взаимно перпендикулярны.
Необычные кульбиты в воздухе объясняют небольшими отклонениями, которые возникают при вращении. Если закрутить тело строго вокруг средней главной центральной оси (той, момент инерции которой занимает промежуточное положение), ничего не произойдет. Но в реальных условиях вращение происходит не только вокруг одной оси. Небольшие колебания приводят к тому, что тело начинает вращаться вокруг всех трех осей.
Вращение твердого тела в системе координат, связанной с самим телом, описывается уравнениями Эйлера. Если применить их к твердому телу с тремя разными моментами инерции, можно увидеть, что при вращении вокруг средней оси инерции угловая скорость вокруг меньшей из осей будет возрастать, что и приведет к перевороту.
В двух других случаях побочные эффекты в процессе вращения убывают.
Визуализация нестабильности средней оси. Величина углового момента и кинетическая энергия вращающегося объекта сохраняются. В результате вектор угловой скорости остается на пересечении двух эллипсоидов. Изображение: Student298, CC BY-SA 4.0, via Wikimedia Commons
Как можно наблюдать?
Наблюдать эффект Джанебекова можно не только в космосе в условиях невесомости, но и на Земле. Для этого достаточно теннисной ракетки. Нужно взять ракетку за ручку так, чтобы ее плоскость была расположена горизонтально. Если подбросить ее таким образом, чтобы она совершила полный оборот вокруг горизонтальной оси, перпендикулярной ручке, а потом поймать ракетку, то окажется, что она также совершила пол-оборота вокруг вертикальной оси.
Вращение теннисной ракетки в полете. Изображение: Steffen Glaser, TUM
Напротив, если, подбрасывая ракетку, придать ей вращение вокруг одной из двух других осей (проходящих вокруг оси рукоятки или вертикальной оси), то вращение будет осуществляться только вокруг них.
Тот же эксперимент можно повторить с любым твердым телом, у которого есть три разных главных момента вращения. Например, подойдет книга или смартфон. Хотя эксперименты с последним чреваты разбитым экраном и мы их не рекомендуем, эффект Джанибекова будет работать. В обоих случаях средней будет ось, перпендикулярная длинной стороне книги или телефона.
Вращение теннисной ракетки. Изображение: Cmglee, CC BY-SA 4.0, via Wikimedia Commons
Просто красивая математика?
Эффект Джанибекова — это не просто забавный факт, который интересно наблюдать. Случайные вращения могут изменить траекторию космического корабля или спутника. При этом не стоит переживать за вращение Земли или спутников. В этих случаях на вращение влияют другие силы, например, приливные, которые способны рассеивать энергию вращения вокруг других осей, в результате чего тело стабильно вращается вокруг оси с наибольшим моментом вращения.
Кроме того, эффект Джанибекова нашел применение в квантовой физике.
Кванты также обладают угловым моментом, известным как спин. На него можно воздействовать, применяя электромагнитное поле. В работе, опубликованной в журнале Scientific Reports, ученые обнаружили, что изменения поведения спина можно описать, используя те же математические формулы, которые объясняют теорему вращающейся ракетки.
Эту теорию можно применять, чтобы целенаправленно изменить ориентацию спина, тем самым сводя к минимуму ошибки, вызванные небольшими возмущениями. Это помогает оптимизировать электромагнитное управления квантовыми состояниями.
Иллюстрация теоремы вращающейся ракетки для квантов. Изображение: Van Damme et al., Scientific Reports
Читать далее:
Ученые приблизились к разгадке тайн пирамид: как древние люди смогли их построить
Раскрыт механизм сохранения здоровья печени в пожилом возрасте
Физики объяснили «космическую нестыковку» Хокинга: как это изменит науку
Эффект Джанибекова. Ось Земли — может переворачиваться.
: dmitgu — LiveJournal
Эффект Джанибекова – интересное открытие нашего времени. Дважды герой Советского Союза, генерал-майор авиации Владимир Александрович Джанибеков заслуженно считается самым опытным космонавтом СССР. Он совершил наибольшее количество полетов – пять, причем все в качестве командира корабля. Владимиру Александровичу принадлежит открытие одного любопытного эффекта, названного его именем – т.н. эффекта Джанибекова, который был обнаружен им в 1985 году, во время своего пятого полета на корабле «Союз Т-13» и орбитальной станции «Салют-7» (6 июня – 26 сентября 1985 года).
Эффект Джанибекова состоит в странном поведении летящего вращающегося тела в невесомости. После его открытия, как обычно, появились десятки различных объяснений эффекта Джанибекова.
Давайте узнаем правильное объяснение этого эффекта :
Для начала узнаем, как это обнаружилось.
Когда космонавты распаковывали доставленный на орбиту груз, то им приходилось откручивать так называемые «барашки» – гайки с ушками.
Стоит ударить по ушку «барашка», и он сам раскручивается. Затем, раскрутившись до конца и соскочив с резьбового стержня, гайка продолжает, вращаясь, лететь по инерции в невесомости (примерно как летящий вращающийся пропеллер). Так вот, Владимир Александрович заметил, что пролетев примерно 40 сантиметров ушками вперед, гайка вдруг совершает внезапный переворот на 180 градусов и продолжает лететь в том же направлении, но уже ушками назад и вращаясь в другую сторону. Затем, опять пролетев сантиметров 40, гайка снова делает кувырок на 180 градусов и продолжает лететь снова ушками вперед, как в первый раз и так далее. Джанибеков неоднократно повторял эксперимент, и результат неизменно повторялся. В общем, вращающаяся гайка, летящая в невесомости, совершает резкие 180-градусные периодические перевороты каждые 43 сантиметра. Также он пробовал вместо гайки использовать другие предметы, например, пластилиновый шарик с прилепленной к нему обычной гайкой, который точно так же, пролетев некоторое расстояние, совершал такие же внезапные перевороты.
Эффект, действительно, любопытен. После его открытия, как обычно, появились десятки различных объяснений эффекта Джанибекова. Не обошлось и без устрашающих апокалиптических прогнозов. Многие стали говорить о том, что наша планета – это по сути такой же вращающийся пластилиновый шарик или «барашек», летящий в невесомости. И что Земля периодически совершает подобные кульбиты. Кто-то даже назвал период времени: переворот земной оси происходит раз в 12 тысяч лет. И что, мол, последний раз планета совершила кувырок в эпоху мамонтов и скоро намечается очередной такой переворот – может завтра, а может через несколько лет – в результате которого на Земле произойдет смена полюсов и начнутся катаклизмы.
Правильное объяснение эффекта Джанибекова состоит в следующем. Дело в том, что скорость вращения «барашка» сравнительно невелика, поэтому он находится в неустойчивом состоянии (в отличие от гироскопа, который вращается быстрее и поэтому имеет стабильную ориентацию в пространстве и кувырки ему не грозят).
Гайка, помимо основной оси вращения, также вращается и вокруг двух других пространственных осей со скоростями на порядок ниже (второстепенные движения). В результате влияния этих второстепенных движений, со временем постепенно происходит изменение наклона основной оси вращения (усиливается прецессия), и когда он (т.е. угол наклона) достигает критического значения, система делает кувырок (подобно маятнику, изменившему направление колебания).
Грозят ли Земле подобные апокалиптические кульбиты? Скорее всего, нет. Во-первых, центр тяжести «барашка», как и пластилинового шарика с гайкой, значительно смещен по оси вращения, чего нельзя сказать о нашей планете, которая хоть и не является идеальным шаром, но более-менее уравновешена. И, во-вторых, значение величин моментов инерции Земли и величины прецессии Земли (колебания оси вращения) позволяют ей быть устойчивой как гироскоп, а не кувыркающейся как гайка Джанибекова.
(Прецессия земной оси равна примерно 50 секундам (1 угловая секунда = 1/3600 градуса) – этого крайне недостаточно, чтобы кувыркаться в пространстве).
Почему же столь важное открытие умалчивалось? Дело в том, что обнаруженный эффект позволил отбросить в сторону все ранее выдвинутые гипотезы и подойти к проблеме совсем с иных позиций. Ситуация уникальная — экспериментальное доказательство появилось раньше, чем была выдвинута сама гипотеза. Для создания надежной теоретической базы российские ученые вынуждены были пересмотреть ряд законов классической и квантовой механики. Над доказательствами работал большой коллектив специалистов из Института проблем механики, Научно-технического центра ядерной и радиационной безопасности и Международного научно-технического центра полезных нагрузок космических объектов. Ушло на это более десяти лет. И все десять лет ученые отслеживали, не заметят ли подобного эффекта зарубежные астронавты. Но иностранцы, вероятно, гаек в космосе не закручивают, благодаря чему мы не только имеем приоритеты в открытии этой научной проблемы, но и почти на два десятилетия опережаем весь мир в ее изучении.
Какое-то время считалось, что феномен имеет лишь научный интерес. И лишь с того момента, когда удалось теоретически доказать его закономерность, открытие обрело свое практическое значение. Было доказано, что изменения оси вращения Земли являются не загадочными гипотезами археологии и геологии, а закономерными событиями в истории планеты. Изучение проблемы помогает рассчитывать оптимальные временные рамки стартов и полётов космических кораблей. Стала более понятной природа таких катаклизмов, как тайфуны, ураганы, потопы и наводнения, связанные с глобальными смещениями атмосферы и гидросферы планеты. Открытие эффекта Джанибекова послужило толчком к развитию абсолютно новой области науки, которая занимается псевдоквантовыми процессами, то есть квантовыми процессами, которые происходят в макромире. Ученые всегда говорят о каких-то непонятных скачках, если речь заходит о квантовых процессах. В обычном макромире вроде бы все происходит плавно, пусть даже иногда очень быстро, но последовательно.
А в лазере или в различных цепных реакциях процессы происходят скачком. То есть до их начала все описывается одними формулами, после — уже совсем другими, а о самом процессе — ноль информации. Считалось, что все это присуще только микромиру.
Руководитель департамента прогнозирования природных рисков Национального комитета экологической безопасности, Виктор Фролов и заместитель директора НИИЭМ МГЩ член совета директоров того самого центра полезных космических нагрузок, который занимался теоретической базой открытия, Михаил Хлыстунов, обнародовали совместный доклад. В этом докладе об эффекте Джанибекова сообщили всей мировой общественности. Сообщили из морально-этических соображений. Скрывать от человечества возможность катастрофы было бы преступлением. Но теоретическую часть наши ученые держат за «семью замками». И дело не только в возможности торговать самим ноу-хау, но и в том, что оно напрямую связано с удивительными возможностями прогнозирования природных процессов.
[источники]
источники
http://www.orator.ru/int_19.html
http://intelogic.ru/news/perevorot_zemli_ehffekt_dzhanibekova/2010-10-02-47
Давайте вспомним еще какие нибудь интересные и сперва непонятные эффекты, вот например Эффект Кулиджа, а вот Эффект Мпембы и Эффект Рингельмана. Не забудем еще про Эффект Линденфроста и например про Эффект Иисуса Навина вместе с Эффектом прыгающей капли
Оригинал статьи находится на сайте ИнфоГлаз.рф Ссылка на статью, с которой сделана эта копия — http://infoglaz.ru/?p=65955
Вращение в космосе
1 февраля 2012 г.
Вращение в космосе
Профессор Кэролин Кроуфорд
Введение
Вращение является свойством целого ряда космических объектов. Мы наблюдаем, как звезды, планеты, черные дыры и галактики вращаются, некоторые с феноменальной скоростью.
Но почему ротация так распространена? Как мы можем сказать, что астрономические тела вращаются? Почему одни вещи крутятся, а другие нет? И что мы можем узнать из наблюдений за этим вращением?
В этой лекции я рассмотрю два типа движения, которые обычно называют «вращением»:
Вращение — это действие объекта, движущегося вокруг центра, например Земля, вращающаяся вокруг своей оси;
Революция — это действие по вращению вокруг внешней точки, такой как Луна, вращающаяся вокруг Земли.
Однако фундаментальный вопрос, с которого стоит начать, самый простой: почему что-то во Вселенной вообще вращается? Ответ основан на введении очень важного понятия углового момента.
Угловой момент
Угловой момент, или вращательный момент, является неотъемлемым свойством вращающихся тел, которое определяет направление и скорость их вращения. Трудно объяснить, тем не менее, это то, с чем мы все интуитивно хорошо знакомы. Подобно энергии или линейному импульсу, угловой момент тела или системы является сохраняющейся величиной; это означает, что количество углового момента объекта такое, какое оно всегда будет иметь в будущем, и может быть изменено только приложением к нему внешней крутящей силы (крутящего момента).
Угловой момент является векторной величиной, а это означает, что для полного описания требуется информация как о величине, так и о направлении. Одним из упрощений является то, что для тела, вращающегося вокруг определенной оси (будь то велосипедное колесо, волчок или целая планета), физическая величина, являющаяся произведением
(масса) x (скорость вращения) x (радиус)2
всегда сохраняется относительно этой оси. Это означает, что для данной массы с определенным угловым моментом, если мы изменим его радиус, объект должен изменить свою скорость вращения, чтобы количество углового момента оставалось постоянным. Увеличение радиуса замедляет скорость вращения, а уменьшение ускоряет вращение. Это обычно иллюстрируется тем, как фигурист будет вращаться быстрее, когда он сильнее притянет свое тело к оси вращения. Другой пример — ныряльщик, совершающий сальто, который сжимает свое тело, чтобы быстро вращаться, и выполняет несколько сальто, прежде чем распрямить свое тело, замедляя вращение, прежде чем он плюхнется в воду.
[Использовано видео:]
Наталья Канунникова установила мировой рекорд Гиннеса по самому быстрому вращению на коньках в Рокфеллер-центре, Нью-Йорк
http://www.youtube.com/watch?v=AQLtcEAG9v0
Олимпийский дайвер Марк Лензи во время выступления 21 /2 Прыжок с обратным сальто
http://www.youtube.com/watch?v=EAhNlWkWun0
Какое отношение это имеет к астрономии?
Все астрономические объекты сформированы тем, как гравитация сближает материю; присущее этому процессу резкое уменьшение размеров. Если космическое тело возникло из чего-либо, что изначально имело наименьшее количество вращательного движения, эта скорость вращения будет только значительно увеличиваться по мере того, как оно схлопывается. Вещи ускоряются, когда они разрушаются под действием силы тяжести.
Представьте себе большое облако молекулярного газа и пыли, которое вот-вот схлопнется под действием силы тяжести, чтобы сформировать звезду, или огромное гало горячего газа, которое сожмется, чтобы создать галактику.
Если это облако имеет даже самое незначительное вращательное движение в самом начале — такое, которое может быть вызвано легким притяжением с одной стороны из-за гравитационного притяжения соседнего облака или звезды — сохранение углового момента означает, что конечная звезда (или галактика), образовавшаяся в результате коллапса этого облака, будет вращаться в том же направлении, только намного, намного быстрее. На самом деле вращаются все звезды, в том числе и наше Солнце.
Вращение Солнца
Солнце не твердое тело, а состоит из газа. Он вращается вокруг вертикальной оси, смещенной только примерно на 7 ° от вертикали, но имеет дифференциальное вращение в том смысле, что скорость вращения меняется в зависимости от широты. Он вращается быстрее всего на экваторе, и эта скорость уменьшается с увеличением широты, пока в полярных регионах один оборот не занимает на 10 дней больше, чем на экваторе. Откуда нам это знать? Астрономы рассматривают два периода вращения наблюдаемого объекта.
Во-первых, это звездное вращение, которое показывает, сколько времени на самом деле требуется телу, чтобы повернуться. Вторым, и, возможно, более легким для наблюдения, является синодическое вращение, которое измеряет, сколько времени требуется неподвижному элементу на поверхности тела, чтобы повернуться в то же видимое положение, как если бы оно наблюдалось с Земли. Для Солнца, например, последний немного длиннее первого, так как за время, которое потребовалось Солнцу для завершения сидерического вращения, требуется некоторое дополнительное время, чтобы компенсировать орбитальное движение Земли вокруг Солнца в промежуточный период. Мы вернемся к этой идее позже.
Солнечные пятна
Наиболее очевидными особенностями, используемыми для отслеживания вращения Солнца, являются солнечные пятна на его диске. Это темные области неправильной формы, периодически возникающие на разных широтах на поверхности Солнца. Типичные солнечные пятна имеют диаметр от нескольких десятков тысяч километров (сравнимых с размером Земли) и существуют от нескольких часов до нескольких месяцев.
Они кажутся темнее, чем их окружение, так как они примерно на 1500° холоднее. Солнечные пятна связаны с областями интенсивных магнитных полей (и часто являются источником массовых выбросов плазмы), поэтому их количество и расположение являются полезными индикаторами уровня активности Солнца. Галилей был первым, кто подробно изучил их, и он определил, что Солнце совершает один оборот примерно за 4 недели, отслеживая их перемещение по солнечному диску летом 1612 года.0003
Сегодня мы также используем гелиосейсмологию — то, как звуковые волны проходят через внутреннюю часть Солнца и заставляют его колебаться (см. мою последнюю лекцию о звуках Вселенной), — чтобы показать, что внутренняя часть Солнца не вращается. точно так же, как и его поверхность. Самые внутренние области, такие как ядро и непосредственно окружающая его радиационная зона, вращаются больше как твердое тело, чем внешние слои, несущие солнечные пятна.
Вращение звезд
Другие звезды также являются магнитоактивными, с похожими темными «звездными пятнами» на их поверхности, которые можно использовать для определения скорости их вращения.
В отличие от Солнца, отдельные пятна не могут быть различимы, но об их присутствии можно судить по тому, как они временно уменьшают яркость звезды на микроскопическую величину при движении по звездному диску. Однако этот сигнал может быть спутан как наличием каких-либо транзитных планет, так и присущей звезде изменчивостью.
Лучшим методом является анализ ширины темных абсорбционных деталей в спектре звезды, которые размываются, чтобы казаться шире, чем ожидалось, если вращение звезды благоприятно ориентировано по отношению к нашему лучу зрения. Это связано с тем, что спектр включает вклад как света, смещенного в голубую сторону от края звезды, движущегося к нам, так и света, смещенного в красную сторону от другого края, удаляющегося от нас. Величина этих сдвигов связана со скоростью, с которой движутся конечности звезды, и, следовательно, со скоростью вращения звезды.
Планетарные системы
Маловероятно, что звезда сформируется изолированно, так как не вся материя во вращающемся коллапсирующем облаке будет включена в совершенно новую звезду в центре.
Некоторая часть облачного материала еще не аккрецируется на ядре до того, как будут достигнуты достаточно высокие температуры и начнется ядерный синтез, отмечающий рождение протозвезды. Вместо этого оставшийся материал оседает в виде концентрированного непрозрачного пыльного диска материи, известного как проплид (сокращение от «протопланетарный диск»), который может достигать радиуса примерно в 50 раз (или более) расстояния между Солнцем и Плутоном.
Но почему материал принимает форму диска? Вещи сглаживаются, когда они рушатся. Облако частиц будет естественным образом сплющиваться, если в системе есть какое-либо чистое направление вращения. По мере того, как облако сжимается, оно становится более плотным, что увеличивает количество столкновений между частицами, которые усредняют все случайные движения частиц внутри облака, оставляя только системное вращательное движение.
Представьте себе большое облако движущихся частиц, каждая из которых следует по орбите, случайным образом наклоненной по отношению к другим, хотя существует небольшой общий уклон в сторону движения большинства частиц либо по часовой стрелке, либо против нее.
По мере увеличения плотности облака каждая частица будет испытывать последовательность столкновений с другими. Каждое из этих столкновений приведет к тому, что два ударника разделят свою среднюю скорость после события. Любые частицы, изначально вращающиеся «не в ту сторону», столкнутся с лобовыми ударами, чтобы в конечном итоге либо развернуться, либо полностью рассыпаться в пыль. Конечным результатом является то, что все вертикальные компоненты движения будут усреднены, и частицы будут следовать по все менее наклонным орбитам. Таким образом, система довольно быстро превращается в тонкий диск, где все частицы движутся в одном направлении с примерно одинаковой скоростью, стремясь столкнуть своих соседей, а не столкнуться с сильными столкновениями. Любые частицы-отступники, оставшиеся на наклонных орбитах, должны будут проходить через диск дважды на каждой орбите и, таким образом, будут подвергаться регулярным столкновениям, которые быстро приведут их в складку.
Таким образом, за удивительно короткое время все наклоненные частицы потеряют свое наклонение или будут уничтожены.
Таким образом вращающиеся ансамбли частиц образуют плоский диск. Примеры варьируются от колец Сатурна, которые образовались из ледяных обломков маленького спутника, разбившегося около 100 миллионов лет назад, до гигантских спиральных галактик, образующих большой плоский диск газа вокруг центральной выпуклости. Оставшееся сырье для звездообразования аналогичным образом сплющивается в протопланетные диски, и именно внутри этих пыльных проплидов продолжающееся скопление материи образует планетарные массы, которые затем сами сталкиваются и развиваются (в конечном итоге) в окружающую планетную систему. Поэтому в Солнечной системе это неудивительно:
Все орбиты планет лежат в плоской плоскости вокруг Солнца;
Все планеты движутся по этим орбитам вокруг Солнца в одном и том же направлении, то есть так же, как Солнце вращается вокруг своей оси;
Что отдельные планеты вращаются вокруг своих осей;
И что многочисленные лунные системы вращаются вокруг своих газовых гигантов-хозяев, каждая из которых (как заметил Галилей) очень похожа на Солнечную систему в миниатюре.
Все эти тела имеют одинаковое направление вращения, потому что все они образовались из одного и того же вращающегося облака газа
Исключения из правила
Конечно, не все так однозначно. Исключения, однако, раскрывают кое-что интересное об истории Солнечной системы. Например, Уран вращается почти на боку относительно своей орбиты. Считается, что она начала вращаться в том же направлении, что и другие планеты, но, скорее всего, она была отброшена в сторону в результате крупного столкновения с большим планетоземлем в начале своей истории. Венера вращается очень медленно с полностью ретроградным движением, т.е. она вращается назад (или вращается вперед, но только вверх дном…?) так, что если смотреть с ее поверхности, то Солнце будет восходить на западе, а не на востоке. Почему Венера ведет себя так, неизвестно. Теории состоят в том, что он тоже мог подвергнуться крупному удару несколько миллиардов лет назад или вызвать кумулятивные приливные эффекты между гравитационным притяжением Солнца и Земли, которые могли каким-то образом перевернуть его по оси.
Таким образом, даже в группе спутников вокруг газового гиганта любое отклонение от общего системного движения — например, маленькая Феба, которая вращается вокруг Сатурна в очень наклонной плоскости и в неправильном направлении — оказывается поздним приобретением, таким как захваченное астероид, а не были сформированы вместе с другими лунами.
На экзопланетах
Конечно, наша собственная Солнечная система теперь не единственная планетарная система, доступная для изучения. К сожалению, поведение (экзо-)планет вокруг других звезд, похоже, представляет некоторые проблемы для нашего понимания. В частности, было обнаружено довольно много экзопланет, вращающихся в направлении, полностью противоположном вращению их родительской звезды, что является полной противоположностью того, что можно ожидать от теории и того, что наблюдается в Солнечной системе. Но, во-первых, как мы можем это сказать? Представьте себе экзопланету, которая движется по орбите, совпадающей с линией нашего обзора, так что она проходит транзитом (т.
е. пересекает прямо перед) своей родительской звездой. Мы можем сказать, в каком направлении она движется по сравнению с вращением звезды, по порядку, в котором различные смещенные в синий/красный цвет компоненты линий поглощения в звездном спектре уменьшаются, поскольку силуэт планеты блокирует свет от первого конца звезды и затем другой.
Многие из этих экзопланет являются гигантскими объектами, больше Юпитера. Считается, что такие планеты сформировались в дальних внешних регионах проплида, мигрируя внутрь ближе к своему хозяину в течение нескольких миллионов лет. Это движение обусловлено комбинированным гравитационным взаимодействием с пылевым диском, из которого они образовались. Открытие такого большого количества ретроградных экзопланет предполагает, что требуется гораздо более медленная эволюция через пылевой диск, а также гравитационное влияние ближайших звезд, которое может вытянуть гигантскую планету на чрезвычайно наклонную и ретроградную орбиту, с которой она теряет энергию, чтобы медленно двигаться по спирали.
в. Кажется, нам предстоит многое узнать о формировании планетных систем.
Следует отметить некоторые интересные следствия вращения и обращения планет в нашей Солнечной системе.
Законы движения планет Кеплера
Планета вращается по своей орбите, потому что она постоянно отклоняется от прямой траектории гравитационным притяжением Солнца. Скорость, с которой он вращается, определяется гравитацией, то есть массой Солнца и расстоянием от него до планеты. Первый закон движения планет Кеплера состоит в том, что планеты не следуют строго круговым орбитам, а движутся по эллипсам с Солнцем в одном из двух фокусов. Эллиптическая траектория означает, что существует изменение расстояния планеты от Солнца с должными последствиями для скорости их вращения из-за сохранения углового момента. На тех участках своей орбиты, где она находится дальше от Солнца, планета движется медленнее; во втором законе Кеплера это выражается в том, что воображаемая линия между планетой и Солнцем заметает равные площади за равные промежутки времени.
Это изменение скорости вокруг орбиты также имеет значение, когда мы измеряем время по прохождению Солнца.
Хронометраж на Земле
Нас учат определять полдень как точку каждого дня, когда Солнце находится над головой. Однако за время, за которое Земля совершает один оборот вокруг своей оси (звездное вращение), она также проделала короткий путь по своей орбитальной траектории вокруг Солнца. Следовательно, требуется немного большее вращение Земли, прежде чем Солнце снова окажется полностью над головой. Чистый эффект заключается в том, что Солнце не находится точно над головой в полдень каждый день в году; на самом деле солнечные часы показывают точное время только четыре дня в году. Поправка между положением Солнца и официальным временем на часах известна как уравнение времени.
Несоответствие усугубляется, когда Земля находится ближе всего к Солнцу, поэтому (из-за второго закона Кеплера и сохранения углового момента) движется быстрее всего по своей орбите. Это происходит зимой в Северном полушарии, во время самого короткого дня.
По обе стороны от зимнего солнцестояния закаты начинают задерживаться примерно на 2-3 недели до того, как произойдет последний восход солнца. В этой точке орбиты Земля продвинулась вперед больше всего за один звездный период вращения и, таким образом, должна повернуться дальше всего, прежде чем Солнце снова окажется прямо над головой. Таким образом, уравнение времени меняется быстрее всего в середине декабря, в результате чего дни наименее симметричны около полудня. Ситуация усугубляется тем, что Земля вращается вокруг наклонной оси, а значит, этот эффект еще более выражен на более низких широтах, чем в Англии.
На Меркурии
Один оборот вокруг Солнца мы считаем годом, а один оборот вокруг нашей оси — сутками, но еще сложнее на маленькой планете Меркурий, лежащей ближе всего к Солнцу. Меркурию требуется всего 88 (земных) дней, чтобы совершить один оборот вокруг Солнца, и 58 (земных) дней, чтобы совершить один оборот вокруг своей оси (что составляет две трети его года). Но в то время как его звездные сутки (сколько времени на самом деле требуется для одного оборота) составляют всего 58 (земных) дней, требуется 176 (земных) дней — два года Меркурия — прежде чем Солнце снова окажется прямо над головой.
Как это может быть? К тому времени, как Меркурий сделает один оборот вокруг своей оси, он сделает 2/3 своего оборота вокруг Солнца; после меркурианского года планета обращена в противоположную сторону, так что сейчас полночь. Только после трех и двух оборотов Солнце снова оказывается над головой.
Коллапс звезды
Существуют и другие космические объекты, у которых гравитационный коллапс приводит к очень высокой скорости вращения. Когда массивная звезда (более чем в 10 раз больше массы нашего Солнца) достигает конца своей жизни, она больше не может поддерживать ядерный синтез в своем ядре, чтобы противодействовать собственной гравитации. При последующем взрыве сверхновой внешние слои звезд выбрасываются в космос, в результате чего центральное ядро сжимается под действием внутренней гравитации, образуя очень компактный объект.
Нейтронные звезды
В этом процессе образуются нейтронные звезды, при этом ядро звезды уменьшается в размерах примерно в 100 000 раз — с нескольких миллионов километров до нескольких десятков километров, что приводит к феноменальному увеличению скорости вращения.
Быстрое повторение радиосигнала от пульсаров (см. «Звуки Вселенной») показывает, что скорость вращения достигает более 700 раз в секунду.
Черные дыры
Еще более массивные звезды (более чем в 25 раз больше, чем наше Солнце) продолжают коллапсировать за пределами точки, в которой могла бы быть создана нейтронная звезда, что приводит к еще более плотным областям массы и экстремальной гравитации, известным как черные дыры. Мы можем измерить массу черной дыры, наблюдая ее гравитационное воздействие на соседнее светящееся вещество. Определить его скорость вращения намного сложнее; Теория относительности предсказывает, что существует последняя «стабильная» орбита, которую вещество может занять вокруг черной дыры, прежде чем оно полностью поглотится. Размер этой орбиты связан со вращением черной дыры, и измерение ее протяженности является одним из передовых достижений современной рентгеновской астрофизики.
Аккреционные диски
Сильное гравитационное притяжение, создаваемое белыми карликами, черными дырами и нейтронными звездами, позволяет им накапливать материю из своего непосредственного окружения, особенно когда компактный объект сформировался из одного члена того, что изначально было двойной звездной системой.
Однако материал не может быть прикреплен непосредственно к компактному объекту, если он имеет угловой момент; любая падающая масса должна потерять свой угловой момент, прежде чем она сможет аккрецироваться. Это приводит к образованию плоского диска вокруг аккрецирующего объекта, который может перераспределять любой угловой момент наружу от центра. Чтобы объяснить: представьте два соседних кольца внутри аккреционного диска вокруг компактного объекта, где внутреннее кольцо будет вращаться быстрее, чем внешнее. Два кольца не полностью не пересекаются, но в некоторых местах некоторая связь или вязкость вдоль их общего края означает, что более быстрое внутреннее кольцо заставит материал во внешнем двигаться быстрее, а это означает, что при той же массе и радиусе внешнее кольцо увеличилось. угловой момент. В свою очередь, внутреннее кольцо немного замедляется внешним, а это значит, что оно теряет угловой момент. Поскольку этот процесс затем происходит повсюду в диске, конечным результатом является то, что угловой момент перемещается от центра к самым краям диска.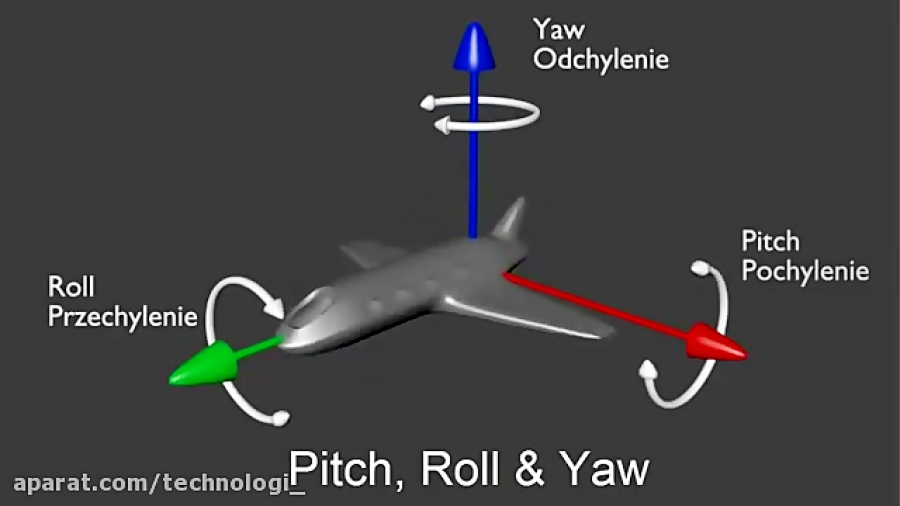
Весь диск будет медленно увеличиваться в размерах, поскольку, хотя большая часть массы теряет достаточно углового момента, чтобы упасть на центральный объект, крошечное количество материи в конечном итоге перенесет весь угловой момент очень далеко. Такие аккреционные диски обнаруживаются не только вокруг черных дыр звездного размера в нашем Млечном Пути, но и вокруг очень активных сверхмассивных черных дыр, лежащих в сердцах гигантских галактик.
Мы можем проанализировать спектр рентгеновского излучения внутреннего аккреционного диска и использовать его для измерения как массы, так и вращения черной дыры. Однако эти структуры слишком малы, чтобы их можно было разрешить с помощью визуализирующих наблюдений даже с использованием самых больших телескопов. Вращательное движение вещества на орбите вокруг гигантской массы сверхмассивной черной дыры может быть разрешено в масштабах, гораздо более широких, чем аккреционный диск. Один из таких примеров находится в ядре нашей «ближайшей» гигантской эллиптической галактики, M87, где в пределах центрального светового года наблюдается большой диск ионизированного газа (по его сине-красному смещению), который вращается со скоростью до до 1000 км/с, показывая, что он реагирует на гравитационное притяжение 9Черная дыра с массой в миллиард солнечных масс в ее центре.
Спиральные галактики
Крупнейшие явно вращающиеся астрономические объекты — это сплющенные диски спиральных галактик. Легко определить, в какую сторону вращается такая галактика, поскольку спиральные рукава отслеживают направление вращения; во Вселенной видны галактики, вращающиеся как по часовой стрелке, так и против часовой стрелки в равном количестве. Наш собственный Млечный Путь — одна из таких систем, около 100 000 световых лет в поперечнике; Солнцу (и сопутствующим планетам) требуется около 220 миллионов лет, чтобы совершить один оборот вокруг центра, а это означает, что с момента образования Солнца мы совершили всего около 20 оборотов. Мы можем измерить структуру вращения как нашей собственной Галактики, так и других спиральных галактик помимо нашей, наблюдая синие/красные смещения в спектрах далеких звезд и газовых облаков.
Масса спиральной галактики
Астрономы используют соотношение между скоростью вращения и радиусом звезд и газовых облаков в диске спиральной галактики, чтобы определить ее общую массу.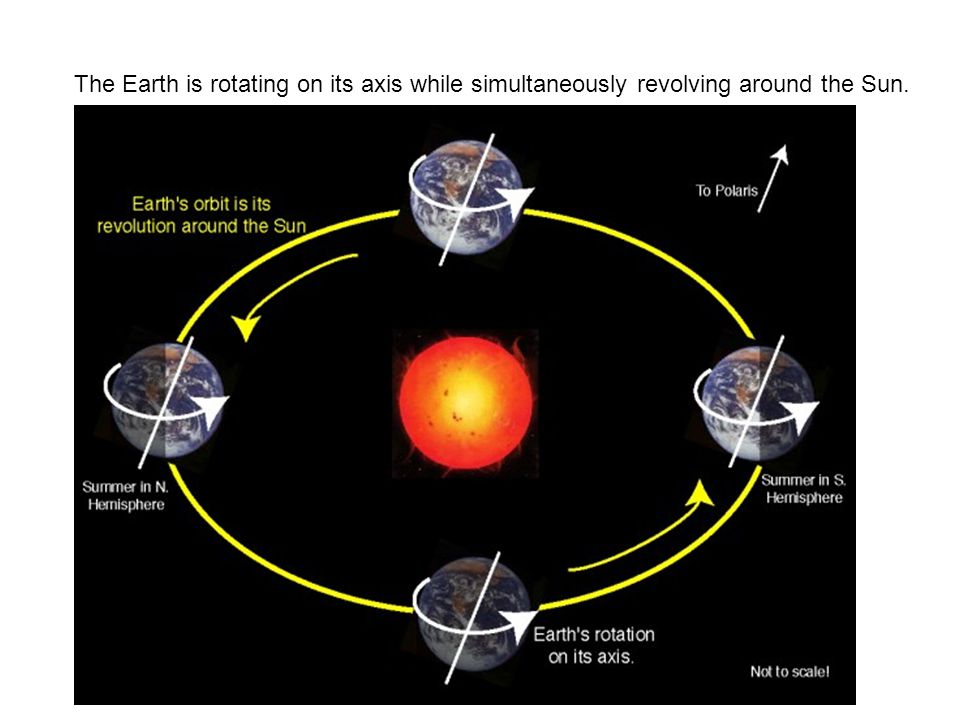
Точно так же, как скорость, с которой планеты вращаются по своим орбитам, зависит от силы гравитационного притяжения, которое они испытывают от Солнца, скорость, с которой движется объект в галактике, зависит от совокупной гравитации всей массы, содержащейся на его орбите. Таким образом, «кривую вращения» галактики можно использовать для отслеживания распределения материи в галактике. Удивительный результат заключается в том, что звезды и газ на внешних краях спиральной галактики вращаются слишком быстро, чтобы оставаться на связи — даже Солнце, находящееся всего лишь на полпути от центра к краю Млечного Пути, проходит около 70 км/ч. быстрее, чем нужно. Единственный способ объяснить наблюдения — это сказать, что должно быть больше массы, т. е. больше гравитации, чем кажется, если суммировать массы всех видимых компонентов. Это одна из основных линий доказательств темной материи; что должен быть основной компонент массы спиральной галактики, обладающий гравитацией, но не излучающий и не поглощающий свет ни в одном диапазоне волн.
Из кривых вращения астрономы делают вывод, что видимая часть спиральной галактики заключена в (слегка сплющенном) сферическом ореоле этой темной материи, который простирается далеко за пределы, над и под наблюдаемый диск. Типичная спиральная галактика содержит примерно в десять раз больше темной материи, чем светящейся — настолько много, что именно гравитация темной материи, а не звезд, удерживает галактику вместе и заставляет ее вращаться.
А темная материя — это тема, к которой мы вернемся на следующей лекции в марте, когда я буду говорить о скоплениях галактик.
Благодарность: Приношу благодарность доктору Анне Куидер за то, что она позволила мне убежать с ее первоначальной идеей.
для создания имитации гравитации отклонение Кориолиса может мешать выполнению простых задач и, в крайнем случае, вызывать укачивание.
В качестве примера эффекта, с которым вы можете столкнуться, я разместил следующую пару диаграмм:
Первая показывает траекторию упавшего мяча при наблюдении из за пределами вращающейся среды обитания (направление вращения отмечено синяя стрелка), при этом мяч и экспериментатор отмечены в четырех последовательных положениях, которые они занимают, пока мяч падает.
Мяч движется прямолинейно со скоростью, определяемой скоростью вращения среды обитания в точке его выпуска. Тем временем пол (и экспериментатор) движутся по кривой траектории, и они проходят немного дальше, чем мяч во время своего полета.
Результат, наблюдаемый экспериментатором, вращающимся вместе со средой обитания, показан на втором изображении — кажется, что мяч отклоняется вправо при падении. Чтобы объяснить это отклонение, экспериментатор прибегает к псевдосиле Кориолиса, которую я объяснял более подробно в прошлый раз. Это отклонение движущихся объектов вправо происходит во всех системах отсчета, вращающихся против часовой стрелки (влево — в системах отсчета, вращающихся по часовой стрелке).
Подготовив эти две диаграммы, я задумался о диапазоне возможных траекторий, с которыми можно столкнуться, подбрасывая мяч во вращающейся центрифуге. Из любопытства я собрал код для наброска результирующих траекторий для объектов, запущенных под любым углом и с любой скоростью.
Результаты, которые я покажу, достаточно обобщаемы — оказывается, траектория зависит только от скорости старта как пропорции к скорости вращения среды обитания. Интересные вещи происходят, когда скорость сравнима со скоростью вращения дна среды обитания — при более высоких скоростях траектории становятся все более пологими (и для наших целей более скучными).
Сначала немного терминологии. Еще в 1970 году Ларри Нивен придумал два полезных слова в своем научно-фантастическом романе «Мир-кольцо », в котором речь шла об (очень большом!) вращающемся космическом пространстве. Нивен назвал направление, в котором вращалась его среда обитания, против вращения , а противоположное направление против вращения . Таким образом, в случае объекта, который просто упал в среду обитания, как в ситуации, показанной на диаграмме выше, мы можем сказать, что объект всегда будет падать на пол в направлении, противоположном вращению точки его высвобождения.
Это означает, что вам нужно придать объекту небольшую скорость вращения, чтобы он упал на пол прямо под точкой запуска.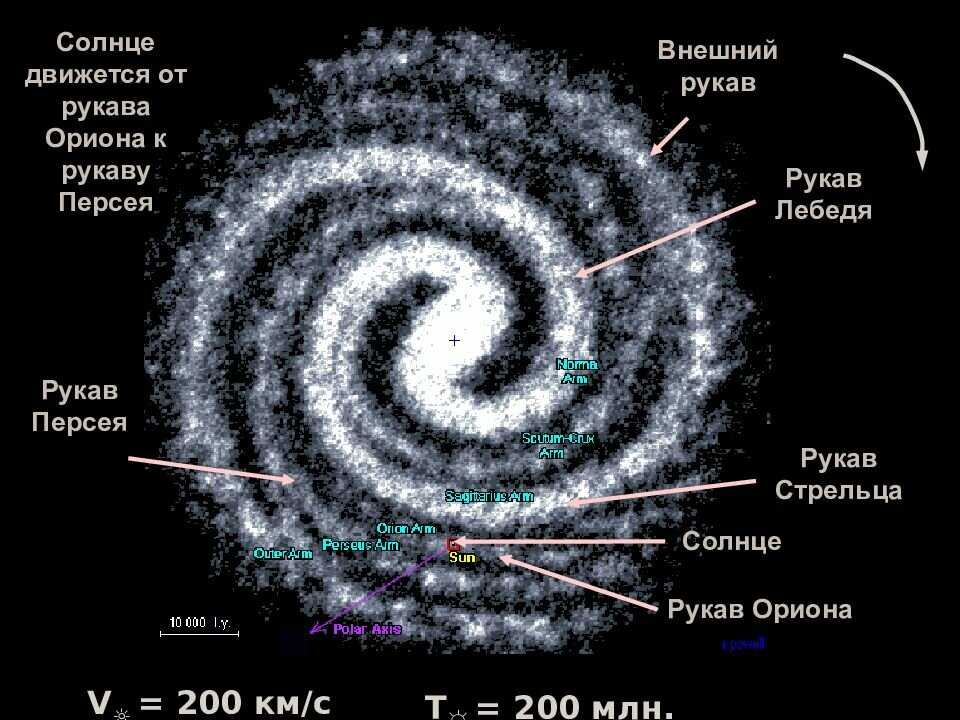
Вот набор спиновых траекторий, наблюдаемых во вращающейся системе отсчета среды обитания, при этом каждый объект запускается «горизонтально» (то есть параллельно той части изогнутого пола, на которой стоит наш экспериментатор):
Нажмите, чтобы увеличить
Кривая, помеченная «0», представляет собой запуск без горизонтальной скорости — просто простое падение, как показано ранее. Кривая с пометкой «1» — это траектория объекта, брошенного с дополнительной скоростью, равной скорости вращения среды обитания на высоте пуска. Красные кривые до «5» — это объекты, брошенные с удвоенной, трехкратной, четырехкратной и пятикратной локальной скоростью вращения, а синие кривые делят диапазон от «0» до «1» на десять равных приращений. При более высоких скоростях объект падает на пол по кривой, которая не кажется слишком нелогичной по сравнению со стандартным гравитационным полем.
Но если наш экспериментатор повернется в другую сторону и бросит предметы против направления вращения, произойдет нечто более интересное:
Нажмите, чтобы увеличить
Кривая, обозначенная цифрой «0», имеет ту же траекторию, что и раньше.
Синие линии представляют собой те же приращения скорости запуска, что и на предыдущей диаграмме, но в этом направлении отклонение Кориолиса вправо служит для подъема 90 129 на 90 130 по каждой траектории, поэтому объект летит дальше и пролетает 90 129 вокруг 90 130 кривой среды обитания перед он ударяется об пол. Зеленая траектория со скоростью запуска 0,9.раз превышает местную скорость вращения, это замечательно. Он не просто исчезает из поля зрения против направления вращения, он снова появляется в направлении вращения и совершает более чем полный круг вокруг среды обитания, прежде чем упадет на пол.
Для ясности я сохранил красные траектории со скоростями от 1 до 5 для другой диаграммы:
Нажмите, чтобы увеличить
Траектория, отмеченная цифрой 1, просто постоянно остается на одной и той же высоте, в принципе огибая среду обитания в течение всегда с той же скоростью, поддерживаемой силой Кориолиса. (Конечно, если в нашей среде обитания есть воздух, он фактически замедлится и упадет на пол из-за сопротивления воздуха.
) Траектории с более высокими скоростями запуска становятся все более плоскими, но по-прежнему имеют восходящие кривые.
Так что же происходит с Траекторией 1? Этот объект был запущен со скоростью, которая в точности компенсирует скорость вращения среды обитания. Для стороннего наблюдателя такой объект просто висит в пространстве, неподвижно, в то время как среда обитания вращается вокруг него, многократно перенося экспериментатора мимо объекта, один раз за оборот. Для того же стороннего наблюдателя все объекты с синей или зеленой траекторией, направленной против вращения, на моей диаграмме на самом деле медленно плывут к вращению , поскольку их скорость вращения частично, но не полностью удалена, а потому, что среда обитания и экспериментатор движутся быстрее по вращению. , объекты на этих медленных траекториях удаляются на против вращения во вращающейся системе отсчета.
Диаграмма может помочь проиллюстрировать это. Вот как невращающийся наблюдатель видит ситуацию, когда объект брошен против вращения со скоростью, меньшей местной скорости вращения:
Нажмите, чтобы увеличить
Нажмите, чтобы увеличить
Теперь вернемся к тому, о чем я упоминал ранее.
Чтобы объект приземлился на пол прямо под точкой запуска, его нужно немного подтолкнуть, чтобы он вращался во время отпускания. Чем ближе наш экспериментатор к оси среды обитания (чем выше над ее полом), тем сильнее требуется толчок объекту и тем шире кривая траектория, по которой он движется. Вот траектории объектов, запускаемых с разных высот в пределах среды обитания:
Щелкните, чтобы увеличить
Каждый из них плавно изгибается вправо, сначала двигаясь по направлению вращения, а затем возвращаясь против направления вращения.
То же самое происходит, если запустить объект «вертикально» (то есть, нацелившись прямо на ось вращения). Для каждой высоты над полом среды обитания существует уникальная скорость запуска, которая позволит Кориолису искривить траекторию так, чтобы он ударился о пол прямо под точкой запуска:
Нажмите, чтобы увеличить
Интересно, скорость запуска, необходимая в ситуация сначала возрастает по мере того, как наш экспериментатор приближается к оси вращения, но затем снова уменьшает на радиусах менее 0,3 радиуса пола.
Но, как и прежде, траектории становятся все шире по мере того, как экспериментатор приближается к оси вращения.
Следствием всех этих кривых вращения является то, что если вы хотите подбросить объект вверх и поймать его, вам нужно бросить его немного против вертикали. Его траектория изгибается прямо на пути вверх и вниз и вернется в вашу руку по замкнутому циклу, если вы бросите его правильно. Чем большую скорость вы сообщаете, тем больше против вращения вам нужно направить свой бросок, поэтому у нас есть семейство возможных кривых, которые вернут брошенный объект в исходную точку:
Нажмите, чтобы увеличить
Если вы ошибетесь и бросите объект слишком далеко против направления вращения, то петля над головой все еще может возникнуть, но объект не вернется в вашу руку, как показано на зеленой траектории ниже:
Нажмите, чтобы увеличить
Все траектории на этой диаграмме имеют одинаковую скорость запуска, но разные направления запуска. Синяя траектория — идеальная петля для броска и ловли.
Зеленая траектория все еще зацикливается, но объект падает против направления вращения. Красная траектория соответствует критическому углу запуска, при котором петля просто исчезает, оставляя объект на мгновение неподвижным во вращающейся системе отсчета, как раз на пике его траектории. При углах запуска более пологих, чем критический, мы получаем что-то вроде черной траектории, по которой объект просто поднимается, а затем снова падает, без каких-либо причудливых прикрас. Важно отметить, что все эти траектории включают объекты, которые были запущены с антиспиновыми скоростями меньшей величины, чем локальная скорость вращения в точке запуска. Таким образом, для невращающегося внешнего наблюдателя они все еще движутся по направлению вращения , но медленнее, чем вращаются среда обитания и экспериментатор, поэтому они движутся против вращения во вращающейся системе отсчета экспериментатора и среды обитания.
Что происходит с красной траекторией, так это то, что экспериментатор, выбрав восходящую траекторию, продвинул объект на небольшое радиальное расстояние в пределах среды обитания, до точки, где более медленная скорость вращения точно соответствует медленной скорости вращения объекта.
Таким образом, когда он проходит через эту точку, объект на мгновение становится неподвижным относительно вращающейся среды обитания.
На зеленой траектории объект подброшен выше, и его медленная скорость вращения теперь превышает скорость вращения в области, близкой к оси вращения. Таким образом, хотя он движется против вращения по отношению к вращающейся среде обитания, когда он находится близко к полу, он движется по направлению вращения относительно среды обитания, когда он близок к оси — отсюда и петлевая траектория во вращающейся системе координат среды обитания.
Возможно, это немного сложно визуализировать, поэтому вот картина того, как выглядит распределение скоростей вращения во вращающейся среде обитания:
Нажмите, чтобы увеличить
Итак, если экспериментатор подбрасывает что-то вверх, оно попадает в области с более низкой скоростью вращения, потому что они ближе к оси вращения.
И снова, как и в случае простых горизонтальных бросков, траектория брошенного предмета определяется суммированием скорости вращения экспериментатора и скорости броска, например:
В этом случае вращающийся экспериментатор подбрасывает предмет вверх и против вращения, но результирующая скорость в невращающейся системе отсчета направлена вверх и по направлению вращения.
Обратите внимание, что экспериментатор изначально движется по вращению быстрее, чем брошенный объект, поэтому он увидит, как он отступает в сторону, противоположную вращению. Но для внешнего, невращающегося наблюдателя ситуация выглядит так:
Нажмите, чтобы увеличить
На пике своей траектории объект может опережать вращение среды обитания и поэтому снова ненадолго перемещается к экспериментатору , создавая петлю, которую мы видели во вращающейся системе отсчета.
Итак, это теория. Но будут ли эти траектории наблюдаться в любых возможных вращающихся космических средах обитания?
Они бы. Мои диаграммы на самом деле примерно соответствуют масштабу небольшой центрифуги Discovery , которая фигурирует в романе и фильме 9.0129 2001: Космическая одиссея .
Как я уже говорил в предыдущем посте о центробежной силе, эта структура, 35 футов в поперечнике, вероятно, настолько мала, насколько может быть космическая центрифуга, не вызывая серьезного укачивания у ее обитателей из-за эффекта Кориолиса.
В романе Артура Кларка он вращался со скоростью 6 об/мин, создавая центробежный эквивалент лунной гравитации. В фильме Стэнли Кубрика обязательно было показано, что она создает эквивалент земной гравитации, что требует от нее вращения со скоростью около 13 об/мин. Но оказывается, что скорость вращения не имеет значения, потому что центробежный эффект и эффект Кориолиса масштабируются одинаково с угловой скоростью, поэтому траектории остаются прежними. Если один из 9Астронавты 0129 Discovery сбрасывали объект с метра над полом центрифуги, он двигался по кривой, подобной той, что я проиллюстрировал выше, приземляясь примерно в 75 сантиметрах против вращения от точки выброса. Единственная разница будет заключаться в том, что в центрифуге, которая вращается медленно, он будет падать медленнее.
Эффект также невосприимчив к изменениям линейного масштаба — если мы увеличим центрифугу в два раза и бросим объект с удвоенной высоты, форма его траектории будет такой же, и он приземлится в два раза дальше против направления вращения.
Это постоянство с масштабированием также применимо к траекториям, которые включают в себя бросание объекта — до тех пор, пока скорость запуска сохраняет ту же пропорцию к скорости вращения, траектория будет той же формы.
Для центрифуги Discovery скорость вращения на уровне пола составляет 3,2 м/с (семь миль в час) в версии, описанной в романе, и 7,2 м/с (16 миль в час) в версии фильма. Таким образом, астронавты могли очень легко бросать объекты по различным траекториям, которые я показал. Для 2001 , более крупная космическая станция, показанная на изображении в начале этого поста, окружная скорость составляет 15 м/с (34 миль/ч) для лунно-гравитационной версии в романе и 37 м/с (84 миль/ч). ) для версии 1 г в фильме. Таким образом, требовалось довольно сильное запястье или ручная катапульта, чтобы запустить объект так, чтобы он скрылся из виду по длинному кольцевому коридору, показанному в фильме. Если вы уроните объект с высоты метра в такой среде, он упадет всего на восемь сантиметров против направления вращения.
*
И есть проблема — по мере того, как среда обитания становится больше, человеческий масштаб становится пропорционально меньше, поэтому эффекты Кориолиса становятся менее заметными. В масштабе среды обитания О’Нила, километров в диаметре, отклонение Кориолиса при падении на один метр на краю составляет всего сантиметр, и его становится трудно увидеть; а скорость вращения у обода измеряется сотнями метров в секунду, поэтому запуск объектов по интересным траекториям становится проблематичным. В этих крупномасштабных средах интересные вещи происходят только вблизи оси (где скорости вращения малы) или на больших масштабах (например, если объект падает с большой высоты).
К сожалению, красивый фонтан Кориолиса Тай-Ян «Джордж» Йе может украшать только самые маленькие вращающиеся среды обитания.
(Источник)
Постскриптум: В ответ на некоторые вопросы, которые я получил, я написал дополнительную статью, в которой обсуждается, что происходит с объектами, которые движутся параллельно оси вращения среды обитания, а также описывается эффект Кориолиса на объектах.
которые катятся по поверхности , а не летят по воздуху. Вы можете найти это здесь.
Пост-постскриптум: Если вы относитесь к тому типу людей, которые находят этот пост интересным, вас также могут заинтересовать мои посты о воздействии вакуума на человека, части первая (теория) и вторая (экспериментальные данные).
Примечание: Просто чтобы перенести свои точки отсчета в 21-й век, я укажу, что центрифуги, которые использовались в космическом корабле Endurance из фильма Interstellar (2014) и Hermes от Марсианин (2015) занимает промежуточное положение между двумя центробежными средами обитания, использованными в 2001: Космическая одиссея , которые я использовал в качестве примеров. Таким образом, мы могли бы ожидать, что эффекты Кориолиса будут достаточно заметно проявляться в любой среде.
Все эти выдуманные центрифуги в какой-то степени нереалистичны, по крайней мере, в краткосрочной перспективе, потому что они требуют большой массы, которую необходимо вывести на орбиту, а затем перемещать в космосе.