Если бы земля была плоская то тени отбрасываемые предметами в одно и тоже: Выводы по результатам работы с картой Древнего Египта (вставьте пропущенные слова) Если бы Земля была плоская, то нети,

Плоская Земля, эффект Доплера и гидростатический парадокс

• Наука
• / Физика

25 октября 2018 г. | Автор: Матвей Багров

5 физических опытов: Плоская Земля, эффект Доплера и гидростатический парадокс

Наука — дело тонкое. Одно дело, вывести теорию, другое — её доказать, причём правильным путём. Сколько великолепных идей ожидает своего часа (взять ту же знаменитую Теорию струн) из-за несоответствия наших возможностей с планами. Мы расскажем о 5 любопытных опытах, проводившихся в разное время — от древних веков до наших дней, с помощью которых учёные смогли вписать свои имена в историю.

Эта статья была опубликована в журнале OYLA №6. Оформить подписку на печатную и онлайн-версию можно здесь.

1. Три кита и большая черепаха

Существует миф, что в древности люди поголовно верили в то, что Земля плоская. На самом деле это не так: греческим учёным давно была известна форма нашей планеты. Первым учёным, который смог это доказать, стал математик и астроном Эратосфен Киренский. Дело происходило в III веке до нашей эры. Путешествуя по разным городам, Эратосфен заметил, что длина теней, которые отбрасывают предметы, в одно и то же время бывает разной. 

Решив выяснить, в чём дело, Эратосфен выявил, чему равен радиус Земли. Учёный знал, что из-за громадного расстояния от Земли до Солнца, лучи последнего достигают и Сиены, и Александрии (города, которые он взял для изучения) параллельными лучами. Если бы Земля была плоской, то тени исчезали бы на ней повсеместно 21 июня. Но так как Земля искривлена,— рассуждал он,— то в Александрии, удалённой от Сиены на 500 миль, местные стены и колонны будут стоять под определённым углом относительно сиенских. 

В полдень первого дня лета Эратосфен измерил длину тени, отбрасываемую колонной. Уже зная высоту колонны, он смог легко вычислить длину линии, соединяющей вершину и конец тени, ведь получился прямоугольный треугольник. С помощью теоремы Пифагора учёный нашёл, что угол отклонения колонны от солнечного луча составляет чуть больше 7 градусов. Так как в Сиене вертикальные предметы не отбрасывали тени, то угол между ними и солнечным лучом составлял ноль градусов. Это значило, что Александрия «отклоняется» от Сиены на 7 градусов. Такой угол между городами — это 1/50 часть окружности (как мы помним, окружность содержит 360 градусов, а разделив 360 на 7, мы получим примерно 50). Эратосфен умножил расстояние между Сиеной и Александрией — 500 миль на 50, и получил значение окружности Земли. Оно оказалось равным 25 тысячам миль. Погрешность этого расчёта составляет всего лишь 5%.

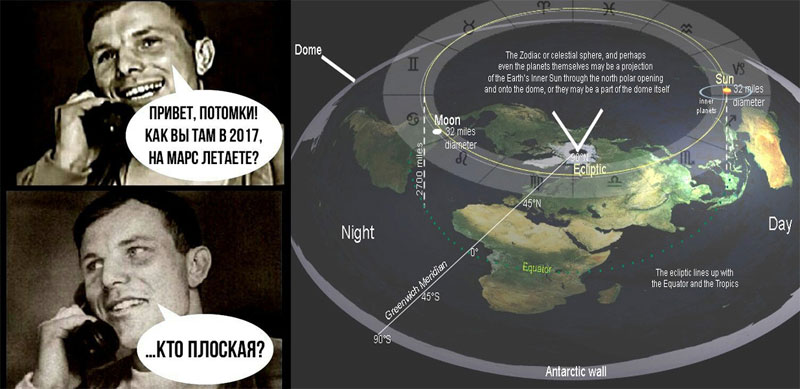
2. Плоская Земля

Впрочем, и в ХХI веке есть те, кто упорно отрицает факт округлой формы планеты. Сейчас этих людей (например, Общество плоской Земли) уже никто не воспринимает всерьёз, но в 1870 году ещё были сомнения. Джон Хэмден, автор книги о плоской Земле, дал объявление в газете, что заплатит 500 фунтов тому, кто сможет с помощью несложного опыта доказать, что планета имеет форму шара. Первым вызвался учёный, географ и натуралист Альфред Рассел Уоллес.

Альфред нашёл прямой канал длиной 6 миль, в конце и начале которого были установлены мосты. На одном из них и был установлен в горизонтальном положении пятидесятикратный телескоп. А ровно между мостами, в реке, была установлена жердь с чёрным кругом на конце. На противоположном мосту была повешена доска, с чёрной горизонтальной полосой. Все предметы опыта находились на одном уровне.

Если Земля — диск, то, глядя в телескоп, наблюдатель должен был увидеть совпадение круга и чёрной полосы. Разумеется, в реальности круг оказался выше линии, потому что Земля выпуклая.

На эксперимент Хэмден даже не приехал, отправив секретаря. Выплачивать выигрыш он также отказался, но Рассел подал в суд и в итоге он выиграл. Правда, думается, что судебные издержки обошлись учёному дороже, чем в 500 фунтов.

3. Дубовая бочка и гидростатический парадокс

Процессы, происходящие в жидкостях, досконально не изучены по сей день. К примеру, уравнение Навье-Стокса о движении вязких ньютоновских жидкостей является одной из задач тысячелетия, за решение которой математический институт Клэя дает награду в 1 миллион долларов. Кстати, наш соотечественник, профессор Мухтарбай Отелбаев уже несколько лет бьётся над решением этой проблемы, но пока что терпит неудачи.

Но даже уже в изученных отраслях гидродинамики можно отыскать интригующие до сих пор явления. К примеру, эксперимент французского учёного Блеза Паскаля, открывшего гидростатический парадокс.

Для эксперимента Паскалю понадобилось всего три предмета — дубовая бочка (обычно такие использовались для хранения вина), узкая трубка длиной пару метров и чашка для чая. Наполнив бочку до краёв, учёный вставил трубку в отверстие сверху под прямым углом ко дну, после чего поднялся на второй этаж и влил в трубку чашку воды. Крепкая дубовая бочка, обшитая железом, треснула под напором.

Причина гидростатического парадокса состоит в том, что жидкость давит не только на дно, но и на стенки сосуда. Вес жидкости в сосуде будет равен сумме высотных составляющих напора по всей внутренней площади сосуда. Если, к примеру, сосуд имеет участки внутренней поверхности, давление на которые направлено вверх, эти участки внесут вклад в вес со знаком минус. Так, если мы возьмём трубку диаметром 1 см и длиной 10 метров, то в неё поместится всего 3 литра воды. Однако, поставив эту трубку с водой вертикально и воткнув её в обычную литровую бутылку (предварительно тоже заполненную водой), мы обнаружим, что вода давит на дно такой бутылки с силой около 80 кг.

4. Космическая линейка

Сегодня один из стандартных способов измерения длинны расстояний — это эхолокация. Прибор посылает сигнал, дожидается его возвращения и замеряет время, за которое сигнал прошёл расстояние. Но со звёздами эта штука не прокатывает. Причина проста — звёзды находятся на слишком большом расстоянии от нас. Электромагнитный сигнал движется всего лишь со скоростью света, а этого мало, учитывая объекты, которые находятся от нас в нескольких тысячах световых лет (для сравнения, Солнце расположено от нас в 8 световых минутах).

Один из первых удачных опытов с использованием новой методики провёл в ХIХ веке российский учёный Василий Струве. Название этой методики — параллакс.

Все мы замечали, что объекты, находящиеся на разном расстоянии от нас, визуально движутся с разной скоростью: те, что дальше — плетутся, а те, что поближе — проносятся мимо. Измерив, насколько визуально переместился такой объект, и точно зная, насколько переместились мы сами, довольно легко геометрически вычислить расстояние до него.

Но как понять, что нужная нам звезда вообще сдвинулась с места? Должна быть точка отсчёта, относительно которой мы будем делать все замеры. Очевидно, что на Земле её искать бессмысленно, так как Земля довольно быстро перемещается.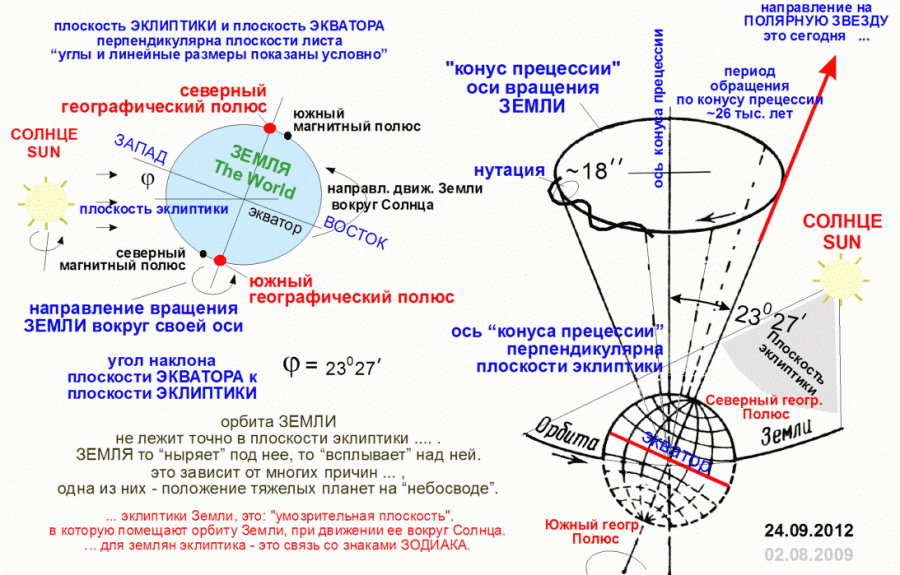 Лучше всего для этих целей подходят сверхдалёкие звёзды, они так далеко, что даже если и двигаются, мы этого не замечаем, а потому можем считать, что они неподвижны. Их в космосе очень много.

Вторая проблема заключается в том, что чем больше расстояние до объекта, тем он меньше визуально смещается. Когда вы едете на машине, то не замечаете смещения Солнца, хотя, как вы помните, оно сравнительно близко. Логично подумать, что в таких ситуациях единственный выход — сильнее передвинуться самим.

Как уже упоминалось, в случае со звёздами расстояния на нашей крохотной планете не подойдут. Даже десятки тысяч километров — все ещё слишком мало. Зато наша планета движется сама — вращается вокруг Солнца. Делая половину оборота, она как бы перемещается вбок на 300 млн км — вполне достаточно. Таким образом, одно измерение будет занимать, по меньшей мере, полгода: сначала мы «запоминаем» звёзды в одной крайней точке на орбите, по которой Земля вращается вокруг Солнца, потом ждём, когда она переместится в противоположную точку, и смотрим на небо снова. И ещё нужно постараться избежать ошибок, а то быстро повторить опыт будет довольно проблематично.

5. Трубачи и эффект Доплера

Всем, кто смотрел «Теорию Большого Взрыва» должен быть известен эффект Доплера: в костюме с диаграммой эффекта Доплера Шелдон решил пойти на Хэллоуин. Это эффект, при котором звуки от объекта, приближающегося к нам, кажутся более высокими, нежели звуки от такого же объекта, отдаляющегося от нас. Это происходит потому, что высота звука зависит от частоты звуковых волн, а сама частота — от того, как близко друг к другу находятся отдельные «гребни» волны: чем ближе, тем выше частота, потому что за единицу времени наше ухо улавливает большее количество «гребней».

Теперь представим себе объект, который звучит — то есть посылает звуковые волны во все стороны от себя с одинаковой скоростью. Если объект начинает двигаться, то волны, которые идут вперёд, находятся ближе друг к другу, поскольку предыдущая волна не успевает отойти слишком далеко от следующей, ведь её «догоняет» движущийся объект.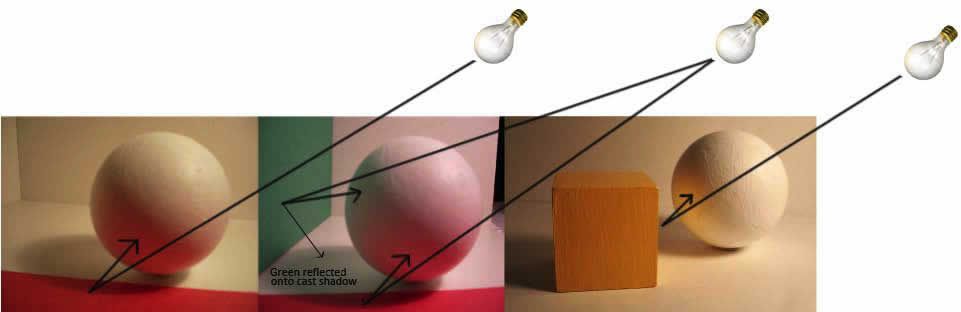 Расстояния между такими волнами меньше, их частота больше, и слышимый нами звук становится выше. Если же волны идут назад, дистанция между ними, наоборот, увеличивается, их частота снижается, и звук тоже становится для нашего уха более низким.

В 1845 году голландский химик и метеоролог Христофор Бейс-Баллот решил проверить эту теорию на практике. Строго говоря, то, что он сделал, не является полноценным научным опытом, потому что не проводилось никаких точных замеров. Тем не менее, изучить его обязательно стоит.

Учёный нанял паровоз с прицепом, на который посадил двух трубачей. Бейс-Баллот хотел получить непрерывный звук определённой высоты, поэтому приказал музыкантам по очереди играть одну ноту (один играл, пока другой восстанавливал дыхание, и наоборот).

На платформе находились наблюдатели с идеальным музыкальным слухом, задачей которых было определить изменение высоты производимых звуков. Паровоз двигался с разной скоростью назад и вперёд мимо платформы. Проверка проводилась в течение двух дней, на смену одним музыкантам регулярно вызывались другие.

В результате эффект Доплера был подтверждён.

Тэги:

физикадоказательствоэксперимент

Эратосфен и земная окружность. Призма и маятник. Десять самых красивых экспериментов в истории науки

В третьем веке до нашей эры греческий ученый Эратосфен Киренский (ок. 276 – ок. 195 до н. э.) произвел первое известное в истории измерение размеров Земли. Его инструменты были очень просты: он следил за тенью, отбрасываемой гномоном (центральным стержнем солнечных часов), делая довольно естественные предположения и проводя очень простые измерения. Эксперимент был произведен настолько изящно, что его результаты на протяжении нескольких столетий приводились в качестве наиболее авторитетных. Этот простой и поучительный опыт и поныне, 2500 лет спустя, ежегодно воспроизводят школьники по всему миру. Принцип данного измерения так элегантен, что стоит понять его, как у вас тут же возникает желание измерять тени всего вокруг.

Эксперимент Эратосфена вдохновлялся двумя идеями принципиальной значимости. Первая состояла в том, чтобы представить космос в виде набора объектов (Земля, Солнце, планеты и звезды) внутри обычного трехмерного пространства. Это может показаться нам чем-то вполне тривиальным, но не совсем соответствовало тогдашним представлениям. Огромным вкладом греческой культуры в науку была догадка, что в основе бесконечного множества постоянно меняющихся видов движения на Земле и на ночном небе лежит безличный и неизменный порядок, космическая архитектура, которая может быть описана и объяснена в терминах геометрии. Вторая идея состояла в том, чтобы в целях лучшего понимания размеров и масштаба этой космической архитектуры применить обычные измерительные практики. Соединив две упомянутые идеи, Эратосфен выступил с довольно дерзким для своего времени предположением, что те же самые методы, которые были уже разработаны для строительства домов и мостов, для прокладывания дорог и межевания полей, для прогнозирования ливней и наводнений, можно использовать для получения информации о размерах Земли и других небесных тел.

Эратосфен исходил из предположения, что Земля представляет собой некое подобие шара. Хотя и в наше время иногда приходится слышать, что Колумб отправился в свое путешествие в первую очередь затем, чтобы доказать, что Земля не плоская, однако уже многие древние греки, всерьез задумывавшиеся об устройстве мироздания, приходили к выводу не только о том, что Земля круглая, но и о том, что она имеет весьма незначительные размеры по сравнению со всей остальной Вселенной. Среди таких ученых был Аристотель, в сочинении которого «О небе», написанном примерно за столетие до Эратосфена, выдвигался ряд различных аргументов в пользу того, что Земля представляет собой шар. Среди этих аргументов были как логические построения, так и опытные наблюдения. Аристотель отмечал, к примеру, что во время затмений тень, отбрасываемая Землей на Луну, всегда искривлена, что может иметь место только в том случае, если Земля круглая. Он также упоминает о том, что путешественники, оказавшиеся далеко на севере и на юге, видят разные звезды (что было бы крайне маловероятно, будь Земля плоской) и что определенные звезды, видимые в Египте и на Кипре, не видны в более северных странах, в то время как другие звезды, которые всегда видны на севере, восходят и заходят на юге, как если бы на них смотрели с поверхности круглого объекта. «Судя по этому, тело Земли должно быть не только шарообразным, – писал Аристотель, – но и небольшим по сравнению с величиной других звезд»11.

Но великий мыслитель предложил и более хитроумные аргументы. Из сообщений путешественников и участников военных экспедиций ему было известно, что слоны водятся в отдаленных землях как в Африке, так и в Азии. Из этого он сделал вывод, что названные части света, по-видимому, соединены, – вполне логичное, хоть и не совсем конкретное заключение. Другие греческие ученые выдвигали и другие аргументы в пользу шарообразности Земли, которые включали разницу во времени восхода и заката в разных странах и то, что отплывающие корабли постепенно скрываются из виду, как бы опускаясь за горизонт.

Однако ни одно из приведенных доказательств не отвечало на главный вопрос: насколько велика эта круглая Земля? И возможно ли вообще узнать ее размеры, не обойдя ее по всей окружности с измерительными приборами?

До Эратосфена на сей счет существовали только догадки.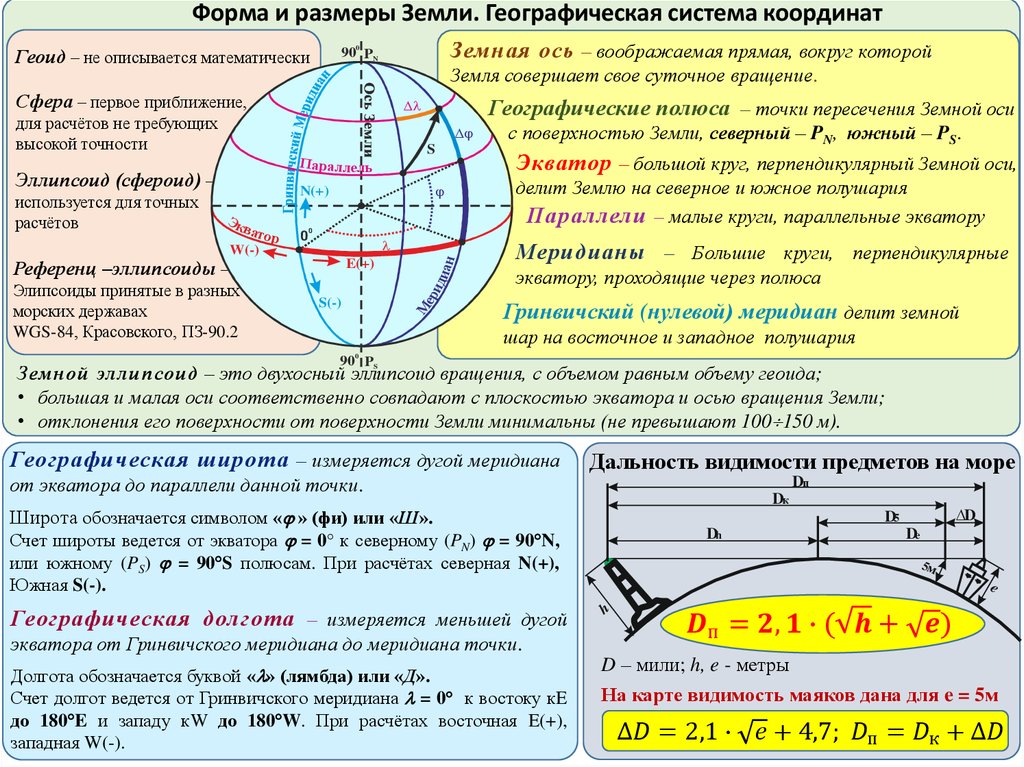 Самая ранняя из них принадлежит Аристотелю, который писал, что «те математики, которые берутся вычислять величину [земной] окружности, говорят, что она составляет около четырехсот тысяч [стадиев]»12. Однако он не сообщает ни источников данной цифры, ни ее оснований. Кроме того, эти данные невозможно точно перевести в современные меры длины. Стадий соотносился с протяженностью греческого скакового круга, который различался от города к городу. Используя приблизительные соответствия с современными мерами длины, ученые приходят к выводу, что Аристотель оценивал длину земной окружности более чем в 40 000 миль (в реальности она составляет примерно 24 900 миль). Архимед, создавший модель космоса, в которой небесные тела вращались друг вокруг друга, давал несколько меньшее число, чем Аристотель, – 300 000 стадий (более 30 000 миль). Но он, равно как и его предшественник, никак не обосновывает свои оценки.

И вот появляется Эратосфен. Младший современник Архимеда, Эратосфен родился в Северной Африке и получил образование в Афинах. Эрудиция его была почти безгранична, он был знатоком во многих областях – от литературной критики и поэзии до географии и математики. Но он ни в чем не достиг первенства, из-за чего современники присвоили Эратосфену саркастическое прозвище Бета (вторая буква греческого алфавита) с намеком на то, что он во всем был только вторым. Несмотря на подобные насмешки, его таланты и блестящие познания были широко известны, a в середине третьего столетия до нашей эры царь Египта Птолемей III пригласил Эратосфена учителем к своему сыну, а позднее назначил его руководителем знаменитой Александрийской библиотеки.

Это была первая и крупнейшая библиотека такого рода, созданная царями из правившей в Египте династии Птолемеев в ходе строительства Александрии, культурной столицы эллинистического мира. Библиотека стала местом встречи ученых всех стран, а Александрия превратилась в важнейший интеллектуальный центр. Здесь, к примеру, жил и преподавал Евклид. В Александрии библиотекари собрали обширную коллекцию рукописей по широчайшему диапазону тем, и ею мог воспользоваться любой ученый. (Помимо всего прочего, Александрийская библиотека была первым известным учреждением подобного рода, в котором рукописи были упорядочены по имени автора в алфавитном порядке [2] .)

Эратосфен написал два сочинения по географии, очень важные для античного мира. Трехтомник «Географика» представлял собой первую попытку картографирования мира с использованием параллелей (линий, параллельных экватору) и меридианов (линий, которые проходят через оба полюса и данную точку на карте). Его «Измерения мира» содержали первые известные описания способов измерения размеров Земли. К несчастью, обе работы утеряны, и нам приходится восстанавливать логику рассуждений Эратосфена на основании замечаний других древних авторов, знакомых с его работами13. На наше счастье, таковых было довольно много.

Эратосфен начал свои рассуждения с предположения, что если Земля – небольшое шарообразное тело в огромной Вселенной, то другие составные части Вселенной, такие как Солнце, располагаются довольно далеко – так далеко, что его лучи можно считать параллельными независимо от того, в каком месте они падают на Землю.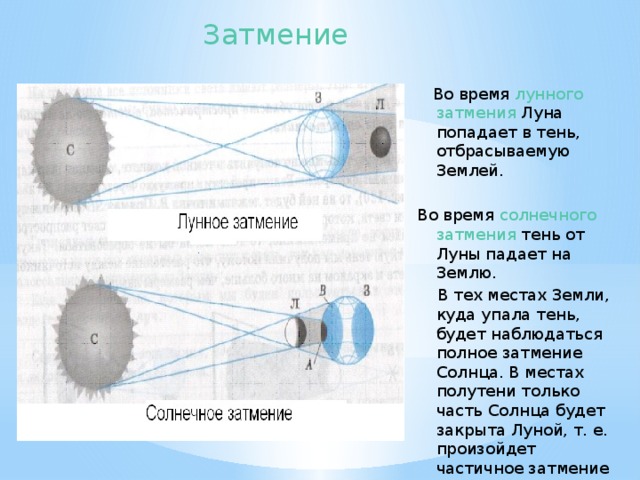 Эратосфену также было известно, что по мере того, как солнце поднимается вверх по небосводу, тени становятся короче, а из рассказов путешественников он знал, что во время летнего солнцестояния в городе Сиена (современный Асуан) солнце в полдень достигает зенита и находится прямо над головой и тогда исчезают тени у всех вертикальных предметов – будь то колонны, столбы и даже гномоны солнечных часов, главная функция которых как раз и состоит в отбрасывании тени. На несколько мгновений солнечные лучи даже достигают дна городского колодца, освещая всю его поверхность, «подобно пробке, идеально подходящей к отверстию», как сообщает один древний источник14. (Я, конечно, немного неточен: тени не исчезали полностью, а просто падали прямо под предметами, в другое же время они падают сбоку от них.)

Помимо этого, Эратосфену было известно, что Александрия располагается к северу от Сиены и примерно на том же меридиане. Благодаря царским землемерам, которых египетское правительство ежегодно – после сезонных разливов Нила – посылало измерять и наносить на карту границы полей, ученый знал, что оба города находятся на расстоянии пяти тысяч стадиев друг от друга (это число было, конечно, приблизительным, поэтому использовать упомянутую информацию для установления точного соответствия между стадиями и современными мерами длины невозможно).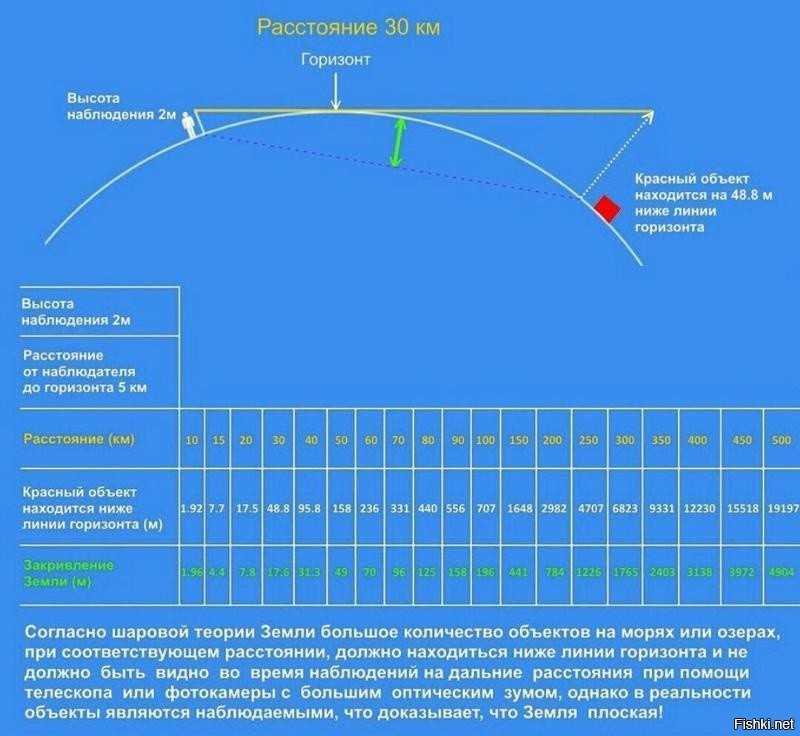

В сегодняшних терминах Сиена располагалась на Тропике Рака, воображаемой линии, опоясывающей мир и проходящей через северную Мексику, южный Египет, Индию и южный Китай (ее можно увидеть на большинстве глобусов). Для всех точек на ней характерна одна необычная особенность: солнце находится прямо над головой только один раз в году, в самый долгий световой день – 21 июня, день летнего солнцестояния. Те, кто живет к северу от Тропика Рака, никогда не видят солнце непосредственно над головой, и предметы всегда отбрасывают тени. Те же, кто живет в Северном полушарии к югу от Тропика Рака, видят солнце прямо над головой дважды в год: один раз – перед днем летнего солнцестояния и один раз – после. Непосредственная дата зависит от того, где расположена данная местность. Причина упомянутого явления заключается в положении Земли, ось которой наклонена по отношению к плоскости орбиты ее обращения вокруг Солнца.

Однако совсем другое занимало сейчас мысли Эратосфена. Для него главным было то, что в момент, когда солнце стоит прямо над головой в Сиене, оно не находится в зените ни в одном другом месте к северу и к югу от нее, включая и Александрию. Во всех остальных местах гномон солнечных часов отбрасывает тень. Длина же тени должна зависеть от кривизны земной поверхности. Чем больше кривизна, тем длиннее будет тень в таком месте, как, например, Александрия.

Эратосфен обладал достаточными познаниями в геометрии, чтобы разработать весьма изящный эксперимент, на основе которого он смог вычислить меру названной кривизны и, исходя из этого, определить протяженность земной окружности.

Чтобы оценить красоту данного эксперимента, нет нужды знать что-либо конкретное о том, как Эратосфен проводил его. Это очень удачное обстоятельство, так как нам практически ничего неизвестно об условиях его проведения. Эксперимент известен нам лишь по далеко не полным описаниям современников и учеников Эратосфена, многие из которых, очевидно, даже не до конца понимали то, что именно они описывают. Нет необходимости знать что-либо о логике рассуждений ученого: что непосредственно пробудило его интерес к данной проблеме, какими были его первые шаги в разработке будущего эксперимента, встречал ли он какие-либо препятствия на своем пути, как он реализовал свой проект и к каким дальнейшим научным изысканиям это привело.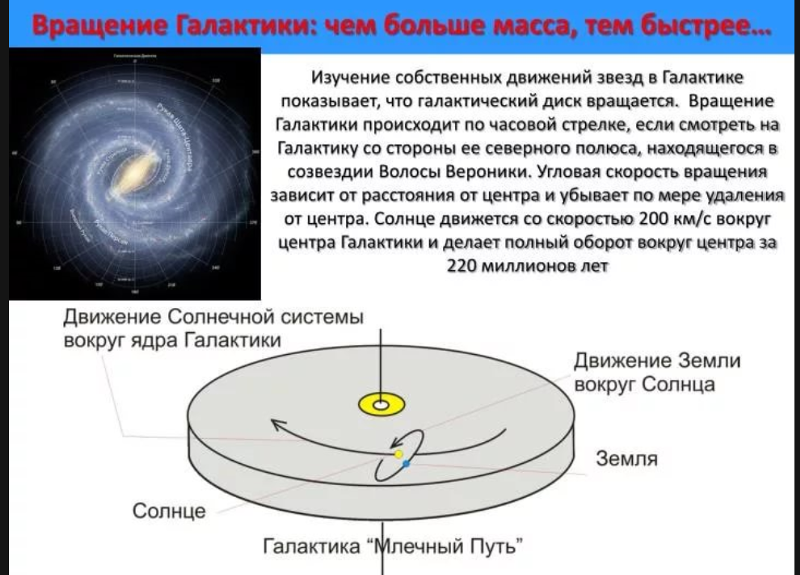 Конечно, можно лишь сожалеть о подобном недостатке информации, так как может сложиться впечатление, что идея пришла к Эратосфену в виде некого озарения, как гром среди ясного неба. Но как бы то ни было, отсутствие всех этих деталей не мешает нашему пониманию сути эксперимента. У нас не возникает необходимости предаваться интеллектуальным спекуляциям, углубляться в сложные математические вычисления или строить догадки, основанные на сомнительных эмпирических данных. Красота эксперимента Эратосфена состоит в том, что он доказал возможность производить измерения космического масштаба, измеряя длину крошечной тени.

Поразительную простоту и элегантность иллюстрируют две диаграммы на рис. 2 и 3.

Во время солнцестояния, когда солнце в Сиене находится прямо над головой ( А ), тени исчезают – они падают по направлению прямо к центру Земли (линия АВ ). Тени в Александрии ( Е ) в этот момент также падают в том же самом направлении ( CD ), так как солнечные лучи условно параллельны друг другу.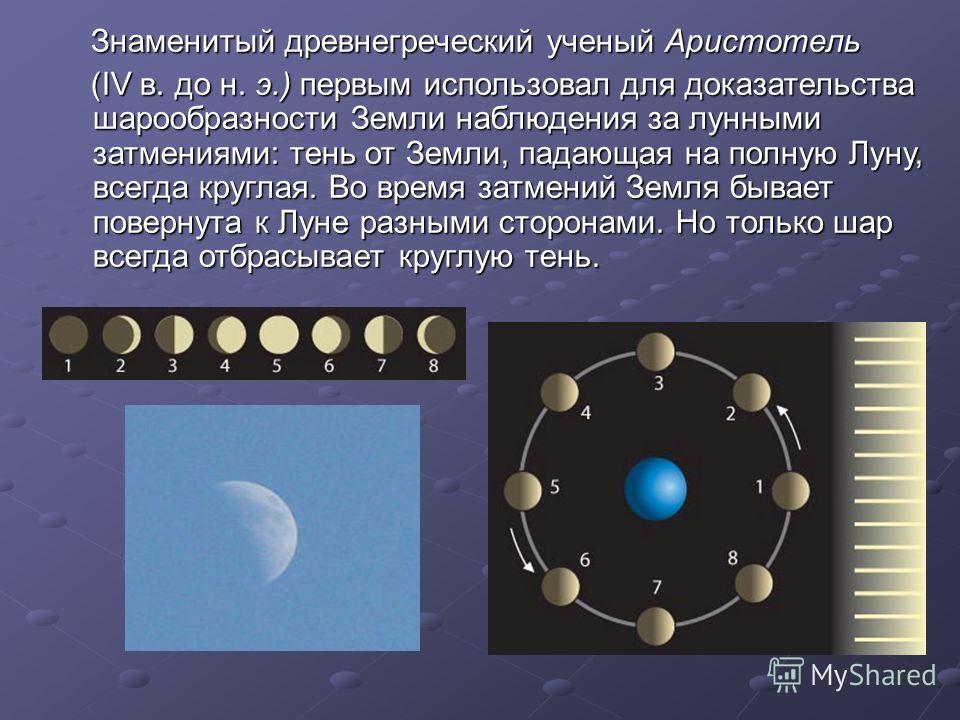 Но так как земная поверхность искривлена, они падают под небольшим углом, который мы назовем х . Небольшой угол (короткая тень) означал бы, что земная поверхность относительно плоская и что, следовательно, Земля имеет очень большую окружность. Большой угол (или длинная тень) будет означать сильное искривление и, соответственно, небольшую окружность. Однако существует ли способ точного измерения длины земной окружности по длине тени? Такой способ дает геометрия.

Рис. 2. Угол между лучом солнца в тот момент, когда оно находится в зените в Александрии, и вертикальным шестом (гномоном) в Сиене (х) равен углу между земными радиусами (y), проведенными к Александрии и Сиене. Следовательно, отношение длины дуги окружности EF к полному кругу таково же, что и отношение длины дуги AE (расстояние от Сиены до Александрии) к окружности Земли

Евклид доказал, что внутренние накрест лежащие углы, образуемые прямой, пересекающей две параллельные прямые, равны.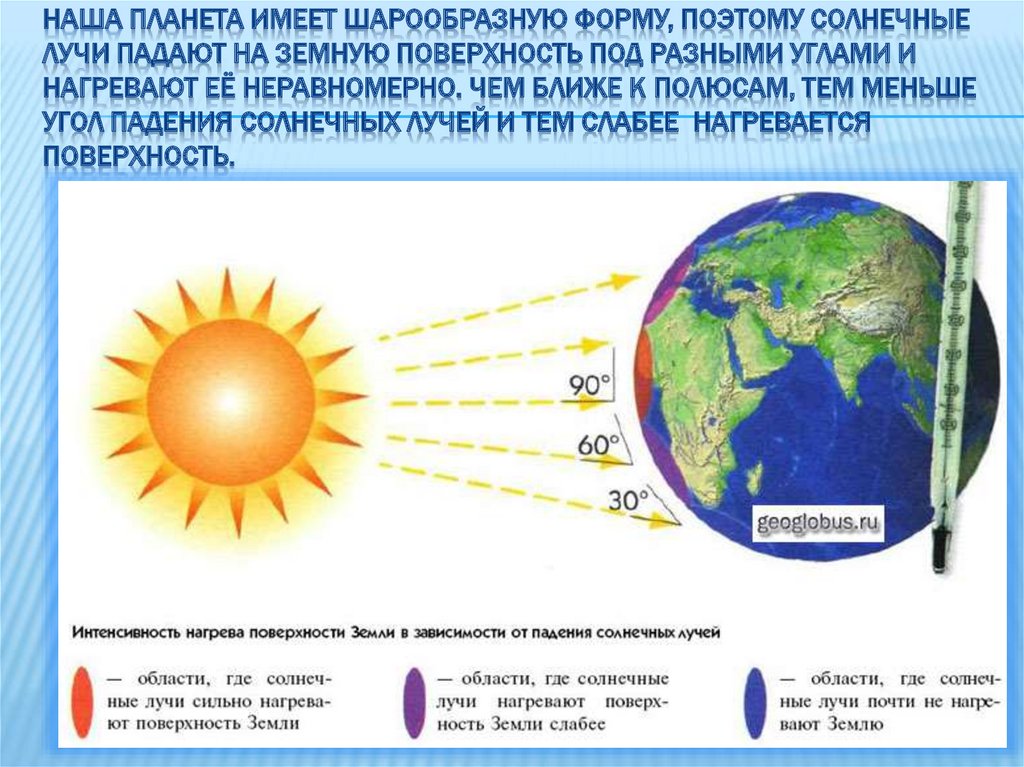 Таким образом, угол х , образуемый тенями в Александрии, равен углу у с вершиной в центре Земли, образуемому двумя лучами, проходящими через Александрию и Сиену ( ВС и ВА ). Это, в свою очередь, означает, что соотношение между длиной дуги гномона ( FE ) и полной окружности вокруг гномона (см. рис. 2) такое же, как и соотношение между расстоянием от Сиены до Александрии и длиной земной окружности. Эратосфен пришел к выводу, что если измерить названное относительно небольшое расстояние, то можно вычислить длину земной окружности. Хотя Эратосфен мог произвести свои измерения целым рядом разных способов, историки науки уверены, что он проделал их с помощью греческой разновидности солнечных часов, так как дуга их тени достаточно четко видна. Солнечные часы, или скафис, представляли собой бронзовую чашу с закрепленной в центре иглой – гномоном, тень которого медленно скользила вдоль линий на внутренней поверхности чаши, соответствующих часам. Однако Эратосфен воспользовался часами необычным способом. Его интересовало не положение тени на часовых отметках, а угол тени, отбрасываемой гномоном в полдень в день летнего солнцестояния. Вначале он измерил, какую часть этот угол составляет в полной окружности (измерение окружности с помощью деления ее на 360 равных частей, называемых градусами, вошло в общую практику лишь примерно столетие спустя после Эратосфена). Или, что практически то же самое, он мог измерить отношение длины дуги, отбрасываемой гномоном на поверхности сосуда, к длине всей окружности сосуда.

Рис. 3. Вероятно, Эратосфен измерял, какую часть всей окружности солнечных часов составляет длина тени (EF), то есть какую часть полного угла составляет угол (х) между лучом и отвесной линией

В полдень того же дня Эратосфен выяснил, что сектор, занимаемый тенью, составляет 1/50 полной окружности (мы бы сейчас сказали: составляет 7,2 градуса). Таким образом, расстояние между Александрией и Сиеной равнялось пятидесятой части протяженности всего меридиана.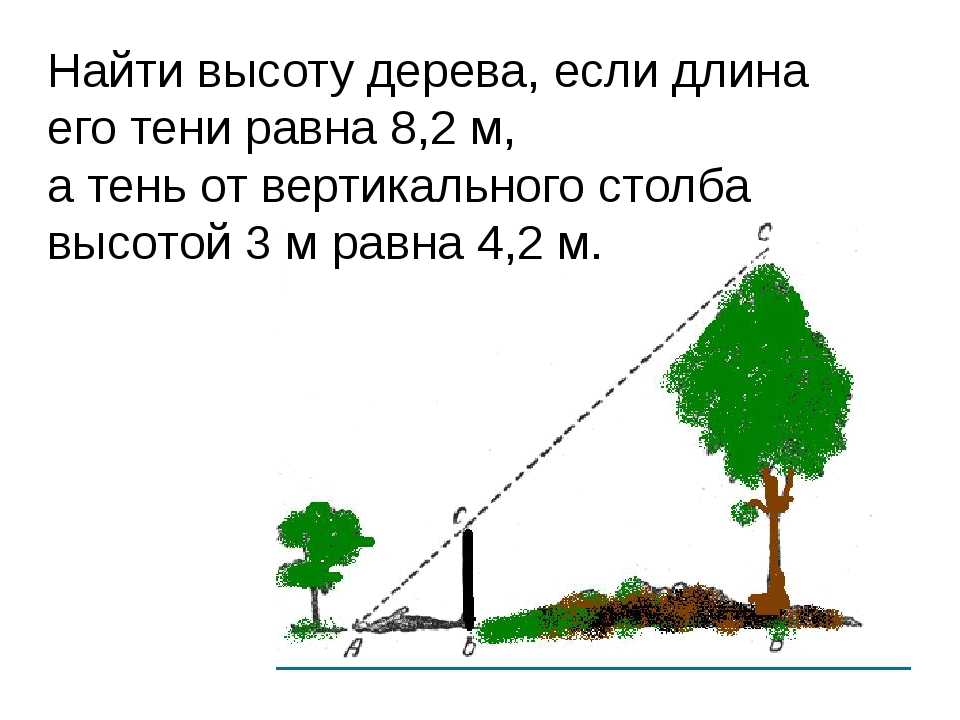 Умножив 5000 стадий на 50, он получил 250 000 стадий для длины земной окружности. Позже, внеся некоторые уточнения, Эратосфен увеличил цифру до 252 000 стадий (в переводе на современные меры длины и то и другое число – это чуть больше 25 000 миль). Причина, по которой Эратосфен внес данное уточнение, не совсем ясна, но, скорее всего, это как-то связано с его стремлением упростить расчет географических расстояний.

Эратосфен делил круг на шестьдесят частей, и на каждую такую часть приходилось по равному количеству в 4200 стадий при общей протяженности земной окружности в 252 000 стадий. Но какую бы из двух названных величин мы ни использовали, 250 000 или 252 000 стадий (при том что, как мы уже знаем, не существует абсолютно точной формулы перевода стадий в современные меры длины), результат, полученный Эратосфеном, лишь незначительно отличается от величины, которая считается правильной сегодня, – 24 900 миль.

Важнейшим условием успешности эксперимента Эратосфена была его картина Вселенной. Без нее он не смог бы прийти к своей идее. К примеру, в древнекитайском картографическом тексте «Хуайнаньцзы» («Философы из Хуайнани») тоже отмечается, что гномоны одинаковой высоты, но находящиеся на разных (север – юг) расстояниях друг от друга, в одно и то же время отбрасывают тени различной длины15. Исходя из предположения, что Земля плоская, автор трактата объясняет названную разницу тем, что гномон, отбрасывающий более узкую тень, находится ближе к положению солнца на небе, и приходит к выводу, что разницу в длине теней можно использовать для расчета высоты неба!

Данные Эратосфена и его вычисления были достаточно приблизительными. Возможно, он знал, что Сиена расположена не совсем на той линии, которую мы сейчас называем Тропиком Рака. И что находится она не прямо к югу от Александрии. И что расстояние между обоими городами не равняется в точности пяти тысячам стадий. А так как солнце на небе представляет собой не световую точку, а небольшой диск (примерно в половину градуса шириной), свет от одной стороны диска падает на гномон не совсем под тем же углом, что и свет от другой его стороны, таким образом слегка смазывая тень.

Но если исходить из уровня развития науки и техники во времена Эратосфена, то его эксперимент был проведен блестяще. Полученный им результат в 252 000 стадий в течение нескольких столетий рассматривался как вполне достоверная оценка протяженности земной окружности. В первом веке нашей эры римский автор Плиний называл Эратосфена «великим ученым, особенно славным» в вопросе длины земной окружности, и характеризовал его эксперимент как «дерзкий», рассуждения – как «тонко обоснованные», а полученный результат – как «общепризнанный»16.

Примерно через сто лет после Эратосфена другой греческий ученый попытался на основании разницы между углом, под которым из Александрии была видна яркая звезда Канопус, и углом, под которым она же была видна с Родоса (где, как считалось, эта звезда находится прямо на горизонте), измерить протяженность земной окружности, но его результат оказался ненадежным. Даже целое тысячелетие спустя арабские астрономы не смогли улучшить результат Эратосфена, несмотря на то, что пытались сделать это, измеряя земной горизонт, видимый с вершины горы известной высоты, и высоту звезды над горизонтом из двух различных точек одновременно.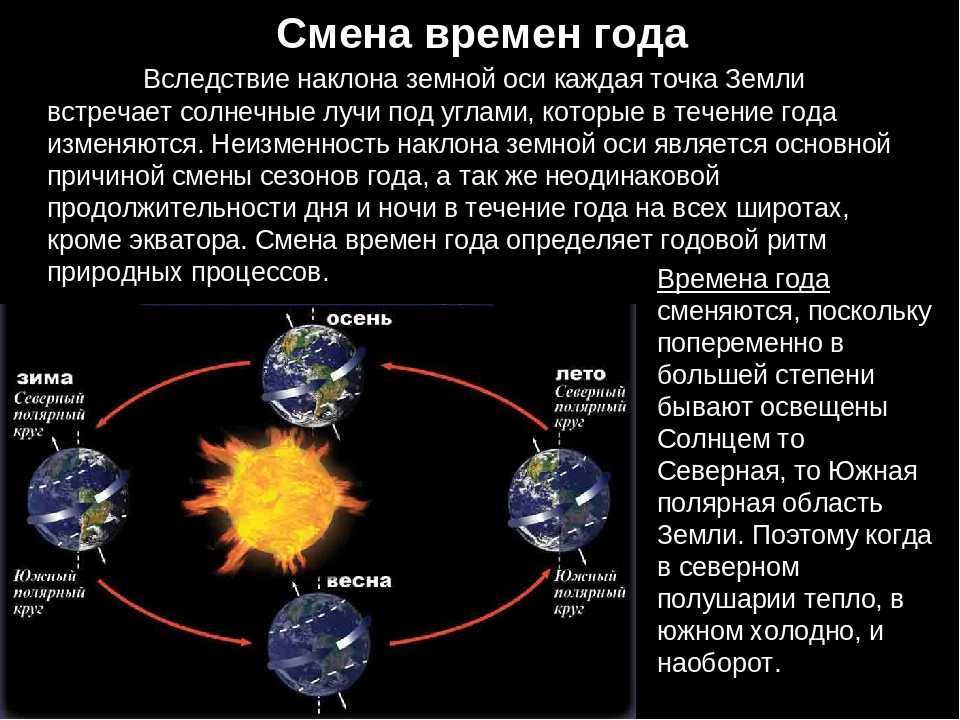 Результаты Эратосфена сумели улучшить лишь в наше время, когда стали доступны более точные данные о положении небесных тел.

Эксперимент Эратосфена стал причиной настоящего переворота в географии и астрономии. Во-первых, теперь любой географ мог определить расстояние между любыми двумя точками на земной поверхности известной широты, например между Афинами и Карфагеном или между Карфагеном и дельтой Нила. Эратосфен определил размеры и положение известной ему обитаемой части Земли, а его преемники получили в свое распоряжение измерительную методику для определения космических расстояний – например, расстояний до Луны, Солнца и звезд. Короче говоря, благодаря эксперименту Эратосфена полностью преобразились представления тогдашнего человечества о Земле, ее положении во Вселенной (или, по крайней мере, в Солнечной системе) и о месте человека во всем этом.

Эксперимент Эратосфена не требует каких-либо особых условий и может быть проведен многими различными способами. Именно поэтому он и явился значительным вкладом в человеческую культуру. Его составляющие просты и знакомы каждому: тень, измерительный инструмент и элементарные правила геометрии. Для его проведения необязательно отправляться в Александрию или иметь в своем распоряжении греческие солнечные часы. Даже совсем необязательно дожидаться дня летнего солнцестояния. Сотни школ по всему миру включают эксперимент Эратосфена в свои программы в качестве обязательного. Некоторые при его проведении используют солнечные часы собственного изготовления, другие – флагштоки или башни. В последнее время подобные эксперименты часто проводятся совместно несколькими школами – по электронной почте и с использованием различных картографических интернет-ресурсов. Подобные воспроизведения эксперимента Эратосфена не похожи, скажем, на реконструкции старинных сражений (такие реконструкции часто устраивают любители истории). В ходе такой реконструкции основной целью является историческая достоверность или, по крайней мере, игровое уподобление прототипу. Что касается эксперимента Эратосфена, то учащиеся не копируют и не реконструируют его, они просто проводят его, словно в первый раз, и эксперимент демонстрирует тот же результат снова и снова – с прямотой и ясностью, в которой невозможно усомниться.

Эксперимент Эратосфена является ярчайшей иллюстрацией самих основ процесса экспериментирования в целом. Каким образом ученые могут узнать протяженность земной окружности без непосредственного ее измерения? Оказывается, мы совсем не беспомощны и нам нет нужды ждать, пока кто-нибудь изготовит для нас рулетку в несколько десятков тысяч миль длиной. Умно организованный эксперимент с использованием доступных и, в принципе, весьма элементарных инструментов может заставить даже такую эфемерную и неуловимую вещь, как тень, раскрыть для нас самые сокровенные и неизменные тайны небес. Эксперимент Эратосфена дает нам метод упорядочения того, что, на первый взгляд, представляется хаосом, с помощью простейших инструментов нашего собственного изготовления.

Красота эксперимента Эратосфена проистекает из его невероятной, немыслимой широты. Некоторые эксперименты привносят порядок в хаос с помощью анализа, выделения или расчленения вещей в окружающем нас мире. Рассматриваемый эксперимент ведет нас совершенно в другом направлении. С его помощью измеряются огромные расстояния, отраженные в малом. Он расширяет наше восприятие мира, учит нас по-новому смотреть на очень простые вещи и отвечать на элементарный вопрос: «Что есть тень и как она возникает?»

Благодаря этому эксперименту мы начинаем понимать, что размеры тени, которая лежит у нас под ногами, связаны с шарообразностью Земли, с размерами Солнца и с расстоянием до него, с постоянно изменяющимся положением двух этих небесных тел по отношению друг к другу. В эксперименте Эратосфена громадное расстояние, отделяющее нас от Солнца, циклический ход времени и шарообразность Земли становятся почти физически ощутимыми. Таким образом, он воздействует на качество нашего восприятия и понимания действительности.

Бытует мнение, что физические эксперименты заставляют человека чувствовать себе более ничтожным во Вселенной. Иногда кажется, что естественные науки лишают человека его привилегированного положения в природе, и многие, чтобы как-то восполнить эту воображаемую утрату, заменяют науку магией, начинают фантазировать, что Солнце, планеты и звезды каким-то образом мистически связаны с нашей судьбой. Но эксперимент Эратосфена, на первый взгляд совершенно абстрактный, более эффективно гуманизирует мир, наделяя нас реалистическим чувством того, кем мы являемся и в какой именно Вселенной находимся. В то время как многое в современном мире пытается возвеличить свой масштаб, силу и власть, данный эксперимент заставляет нас по достоинству оценить огромные возможности, заложенные в малом и временном, и осознать то, насколько связаны между собой вещи самого разного масштаба.

Science A-Z

Science A-Z гарантирует, что у учителей есть ресурсы, необходимые им для развития научных знаний и практики учащихся, а также поддержка основных навыков грамотности.

• Тысячи ресурсов для обучения основным научным идеям и практикам
• Многоуровневые учебники для дифференцированного обучения чтению
• Практические эксперименты и проекты по применению научных концепций

Получить больше информацииНачать бесплатную пробную версиюЗаказать сейчас

Дифференцированные уроки и занятия по естествознанию для учащихся K-6

Science A-Z — это отмеченный наградами учебный ресурс, который предоставляет надежную библиотеку многоуровневых информационных текстов, практических экспериментов и других увлекательных возможностей обучения.

• Дифференцируйте обучение многоуровневыми материалами для чтения, предлагаемыми для трех классов (K-2, 3-4 и 5-6).
• Применение науки на практике с интересными научными мероприятиями и проектами, которые поощряют любопытство и исследования.
• Расширьте понимание учащихся с помощью дополнительных текущих событий и ресурсов, ориентированных на STEM.

Подробнее

Бесплатные образцы
Бесплатная пробная версия
Заказать сейчас

Настраиваемые уроки и информационные тексты

в четырех научных областях

Наука от А до Я предлагает преподавателям и учащимся множество ресурсов, предлагаемых в комплексных единицах по четырем научным областям: жизнь, Земля и космос, физика и наука о процессах.

• Ресурсы по наукам о жизни рассказывают учащимся об окружающем их живом мире и о том, как организмы взаимодействуют друг с другом.
• Ресурсы по науке о Земле и космосе рассказывает учащимся об особенностях, материалах и процессах на Земле и в космосе.
• Ресурсы по физическим наукам обучают учащихся природе и свойствам энергии, сил и материи.
• Ресурсы по науке о процессах обучают учащихся навыкам и инструментам, необходимым для проведения исследований и поиска ответов.

Подробнее

Бесплатные образцы
Бесплатная пробная версия
Заказать сейчас

Многоуровневые тексты, органично сочетающие науку и чтение

Science AZ предоставляет библиотеку контента, подходящего для развития, чтобы обучать учащихся научным концепциям, навыкам грамотности и практическим приемам науки и техники с помощью печатных и цифровых книг и других ресурсов.

• Удовлетворяйте требованиям стандартов по естественным наукам и учебной программе ELA благодаря увлекательному контенту, предлагаемому для трех классов.
• Дополнение к инструкции с сотнями вспомогательных текстов, рабочих листов и дополнений к урокам, которые расширяют понимание учащихся.
• Улучшите связь между домом и школой с помощью привлекательных многоуровневых электронных книг, к которым учащиеся могут получить доступ в любое время и в любом месте.

Подробнее

Бесплатные образцы
Бесплатная пробная версия
Заказать сейчас

Практический опыт для учащихся K-6

Наука лучше всего изучается на практическом опыте. Наука от А до Я предлагает обширную коллекцию увлекательных заданий, управляемых экспериментов и открытых проектов, которые позволяют учащимся думать и исследовать, как ученые и инженеры.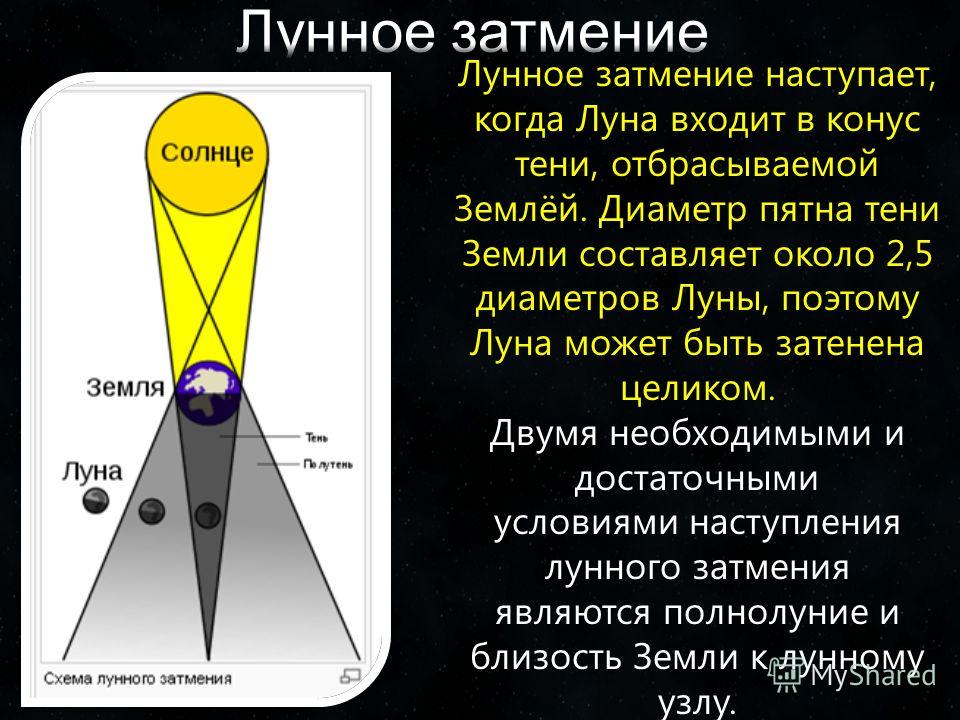

• Применяйте науку на практике с увлекательными экспериментами и действиями, в которых используются предметы повседневного обихода для расширения концепций единиц
• Содействуйте сотрудничеству и обучению на основе запросов с открытыми задачами, которые требуют от учащихся применения методов STEM.
• Поощряйте творчество и инновации с помощью ресурсов, необходимых для проведения научной ярмарки.

Узнать больше

Бесплатные образцы
Бесплатная пробная версия
Заказать сейчас

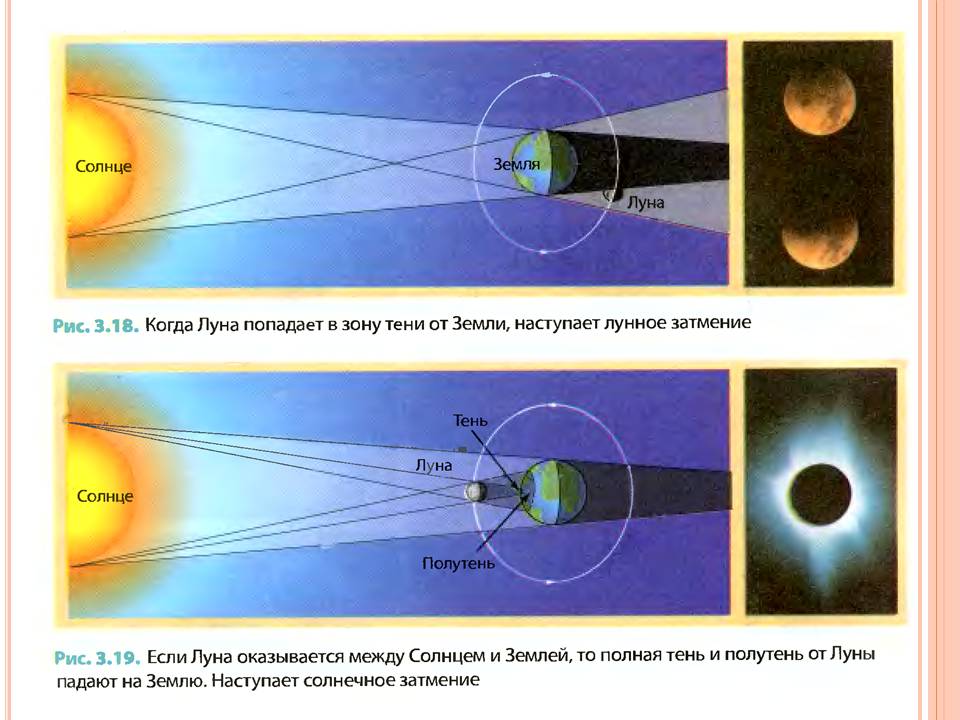
Как сторонники плоской Земли объясняют полные лунные затмения

Кроваво-красный цвет Луны во время полного лунного затмения может быть трудно объяснить без базового понимания орбитальной механики, но сторонники теории плоской Земли придумали способ обойти научные факты и создать творческое объяснение явление.

900:02 Во время Луны Супер Кровавого Волка в эти выходные (20-21 января) наблюдатели за небом в большей части Западного полушария видели, как Луна прошла прямо через тень Земли. Наш естественный спутник кажется красным во время лунных затмений по той же причине, по которой рассветы и закаты здесь, на Земле, кажутся такими темными: потому что солнечный свет рассеивается, проходя через атмосферу.

По мнению сторонников теории заговора плоской Земли, это астрономическое явление, известное как полное лунное затмение, на самом деле было редкой возможностью мельком увидеть загадочный «теневой объект», который вращается вокруг Солнца и иногда проходит перед Луной из наша точка зрения здесь, на Земле, якобы имеющей форму пиццы. [Удивительные фотографии Луны Супер Кровавого Волка 2019 года!] 

Хотя сторонники плоской Земли считают, что наша планета плоская, как блин, они неожиданно пришли к единому мнению, что Солнце и Луна являются сферическими объектами. Однако эти теоретики утверждают, что и Солнце, и Луна вращаются вокруг северного полюса Земли, зависая прямо над блином и никогда не переходя на другую сторону. Однако если бы это было правдой, то лунные затмения, какими мы их знаем, не могли бы происходить, потому что для того, чтобы такое событие произошло, Луна должна находиться на противоположной стороне Земли от Солнца. Итак, плоскоземельцы придумали новое объяснение тени, видимой на Луне во время затмения.

В сообщении на The Flat Earth Wiki, веб-сайте Общества плоской Земли, сторонники теории заговора не предлагают описания так называемого «теневого объекта» — никаких подробностей о его размере, форме, составе или происхождении. Но писатели утверждают, что эта таинственная призрачная фигура является причиной всех лунных затмений. О, и он совершенно невидим, когда не находится перед луной.

Что делает луну темной и красной? Узнайте в полной инфографике SPACE.com здесь. (Изображение предоставлено Карлом Тейтом, автором SPACE.com)

«Теневой объект никогда не виден в небе, потому что он вращается близко к Солнцу», — говорится в вики The Flat Earth. Несмотря на то, что крошечную, самую внутреннюю планету Меркурий можно увидеть рядом с Солнцем (а иногда и перед ним), The Flat Earth Wiki ложно утверждает, что «нам никогда не дается мельком увидеть небесные тела, которые появляются вблизи Солнца в течение дня. »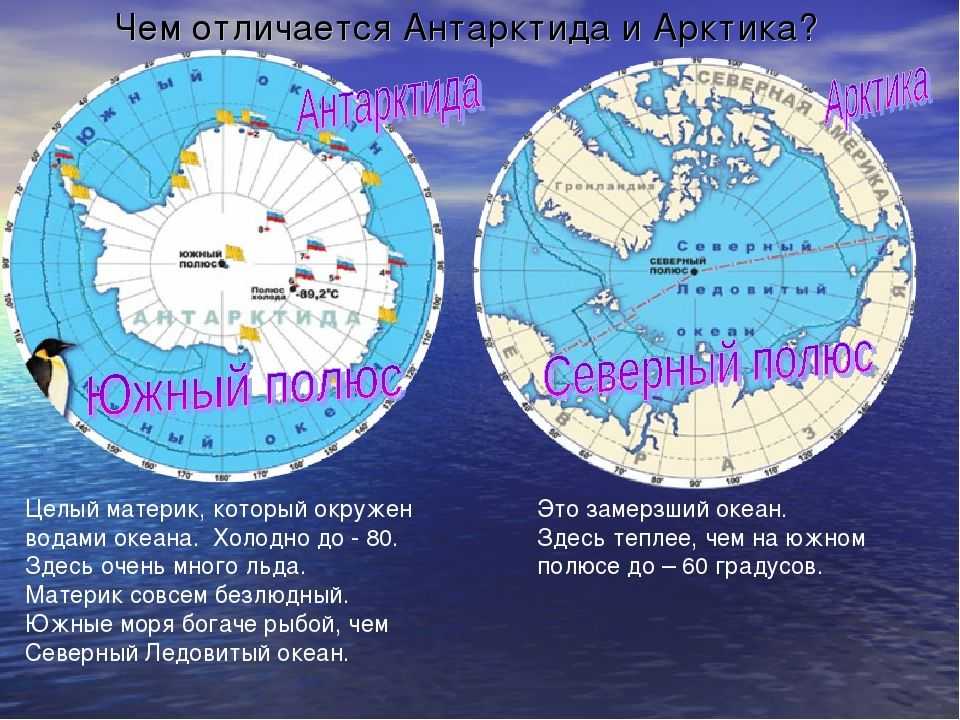

Во всяком случае, The Flat Earth Wiki дает описание орбиты таинственного предполагаемого объекта, заявляя, что он наклонен примерно на 5,15 градуса к плоскости орбиты Солнца. По совпадению, на самом деле это угол, на который орбита Луны наклонена по отношению к орбите Земли. Общество плоской Земли не представило математических расчетов, с помощью которых оно пришло к этому числу, которое, по-видимому, было скорее «заимствовано» из расчетов реальных астрономов, чем получено с нуля.

Вики дополнительно заявляет, что «существует также вероятность того, что Теневой Объект является известным небесным телом, которое вращается вокруг Солнца; но потребуются дополнительные исследования, чтобы отслеживать положения Меркурия, Венеры и астероидных спутников Солнца и соотносить их с уравнения для лунного затмения, прежде чем можно будет сделать какой-либо вывод».

Астрономы уже нанесли на карту орбиты всех планет в обозримом будущем, и ни одна из них не окажется между Землей и Луной в ближайшее время (или когда-либо).

Совершенно очевидно, что объяснение лунного затмения Обществом плоской Земли абсолютно неверно. Вы можете прочитать больше об удивительной математике и физике лунных и солнечных затмений здесь. И не волнуйтесь, если вы пропустили Супер Луну Кровавого Волка; вот когда произойдут следующие затмения.

Напишите Ханнеке Вейтеринг по адресу [email protected] или подпишитесь на ее @hannekescience. Следите за нами в Твиттере @Spacedotcom и на Facebook. Оригинальная статья на Space.com.

Присоединяйтесь к нашим космическим форумам, чтобы продолжать обсуждать последние миссии, ночное небо и многое другое! А если у вас есть новость, исправление или комментарий, сообщите нам об этом по адресу: [email protected].

Ханнеке Вейтеринг — редактор Space.com с 10-летним опытом научной журналистики. Ранее она писала для журналов Scholastic Classroom, MedPage Today и Объединенного института вычислительных наук в Окриджской национальной лаборатории.