Генетический алфавит в информатике: Генетический код 2.0 / Хабр

Генетический код 2.0 / Хабр

Открыт новый подход к использованию генетического материала, который позволит создавать белки со свойствами, невиданными в естественной среде. Открытие может когда-нибудь привести к созданию новой либо «улучшенной» формы жизни, которая вберет в себя эти новые материалы.

Во всех существующих формах жизни, четыре «буквы» генетического кода, называемые нуклеотидами, читаются триплетами, так что три нуклеотида кодируют аминокислоту.

Но так было раньше… Джейсон Чин и его коллеги в Кембриджском университете перепроектировали клеточные механизмы так, чтобы они читали генетический код квадруплетами (проще говоря по 4).

В генетическом коде, который жизнь использовала по сей день, есть 64 возможных комбинации триплетов из 4-х букв-нуклеотидов. Эти генетические «слова» называются кодоны. Каждый кодон либо кодирует аминокислоту либо говорит клетке остановить производство протеиновой цепи. Теперь же команда Чина создала 256 пустых четырёхбуквенных кодона, которые могут быть «назначены» на аминокислоты, которые еще даже не существуют. ( Прим. переводчика: следует понимать, что нуклеотиды кодируют аминокислоты не потому, что связываются химически, а потому, что рибосома, словно компилятор, «знает» все 64 кода и умеет создавать аминокислоту, соответствующую коду. Поэтому новые 256 комбинаций — «пустые». Нормальная рибосома не знает что делать по этим кодам. Их надо «назначить»)

Чтобы достичь этого результата, команде пришлось перестроить несколько клеточных механизмов по производству белков. Но они не остановились на получении работающей системы. Чтобы доказать, что конечный генетический код работает, они «назначили» двум «неприродным» аминокислотам квадриплетные кодоны и включили их в реальную белковую цепь.

По заявлению Чина: «Это начало параллельного генетического кода».

Однако, что более интересно — эти две аминокислоты могут реагировать друг с другом, формируя разные типы химических связей, в том числе и те, которые обычно соединяют белки при формировании их трёхмерной структуры.

Обычный тип связей — дисульфидные — можно разорвать изменяя температуру или кислотность, вследствие чего белки теряют свою трёхмерную форму. Например куриное яйцо изменяет текстуру и цвет при приготовлении именно вследствие этого процесса: альбумин в белке (яичном белке) теряет свою трёхмерную структуру и его физические характеристики меняются.

Но новые аминокислоты создают более прочные связи и поэтому белки, сформированные из них, могут работать в гораздо более широком спектре температур и сред, что, например, может помочь создать лекарства, которые не будут разрушаться в нецелевых местах желудочно-кишечного тракта.

«Это большой прорыв, который открывает новые теоретические горизонты в синтетической биологии», — заявил один из первооткрывателей Крейг Вентер, который сам возглавляет институт в Роквиле и в данный момент работает над созданием синтетического организма с чистого листа.

Лекция 2 — Информатика и ИКТ

Тема:
Подходы к понятию информации и измерению информации

Термин
информация имеет множество определений. «Информация» происходит от латинского
слова «informatio», что означает разъяснение, изложение, осведомление.
Информация всегда представляется в виде сообщения. Сообщение – это форма
представления каких-либо сведений в виде речи, текста, изображения, цифровых
данных, графиков, таблиц и т.д. В широком смысле информация – это сведения,
совокупность каких-либо данных, знаний. Наряду с понятие информация в
информатике часто употребляется понятие данные. Данные – это результаты
наблюдений над объектами и явлениями, которые по каким-то причинам не
используются, а только хранятся. Как только данные начинают использовать в
каких-либо практических целях, они превращаются в
информацию.

1. Представление
и кодирование информации с помощью знаковых систем.

 С древних времен знаки используются
человеком для долговременного хранения информации и ее передачи на большие
расстояния.

Форма
знаков.
В соответствии со способом восприятия знаки можно разделить на зрительные,
слуховые, осязательные, обонятельные и вкусовые, причем в человеческом общении
используются знаки первых трех типов.

К
зрительным знакам, воспринимаемым с помощью зрения, относятся буквы и цифры,
которые используются в письменной речи, знаки химических элементов, музыкальные
ноты, дорожные знаки и т. д.

К
слуховым знакам, воспринимаемым с помощью слуха, относятся звуки, которые
используются в устной речи, а также звуковые сигналы, которые производятся с
помощью звонка, колокола, свистка, гудка, сирены и т. д.

Для
слепых разработана азбука Брайля, которая использует осязательный способ
восприятия текстовой информации.

В
коммуникации многих видов животных особую роль играют обонятельные знаки.
Например, медведи и другие дикие животные помечают место обитания клочьями
шерсти, сохраняющей запах, чтобы отпугнуть чужака и показать, что данная
территория уже занята.

Для
долговременного хранения знаки записываются на носители
информации.

Для
передачи информации на большие расстояния используются знаки в форме сигналов.
Всем известны световые сигналы светофора, звуковые сигналы школьного звонка
оповещают о начале или конце урока, электрические сигналы передают информацию по
телефонным и компьютерным сетям, электромагнитные волны передают сигналы радио и
телевидения.

Значение
знаков.
Знаки отображают объекты окружающего мира или понятия, т. е. имеют определенное
значение (смысл).

Знаки
различаются по способу связи между их формой и значением. Иконические знаки
позволяют догадаться об их смысле, так как они имеют форму, похожую на
отображаемый объект. Примером таких знаков являются значки на Рабочем столе
операционной системы компьютера, например, значок Мой
компьютер.

Символами
называются знаки, для которых связь между формой и значением устанавливается по
общепринятому соглашению. Примером таких знаков являются символы химических
элементов, отображающие атомы химических веществ (табл.
2).

Если
неизвестно соглашение о связи формы и значения символов, то ничего нельзя
сказать о смысле информации, записанной такими знаками. Существуют найденные
археологами и до сих пор нерасшифрованные тексты на древних языках, так как
неизвестно значение знаков, которыми они записаны.

Таблица
2. Иконические знаки и символы

В
современном мире широко применяется шифрование, которое использует секретный
ключ в качестве соглашения о связи формы символов с их значениями. Если
секретный ключ неизвестен, то содержание передаваемого текста понять
невозможно.

Один
и тот же символ может иметь различное значение в разных знаковых системах.
Например, знак «О» используется в качестве:

—
буквы «О» в русском алфавите;

—
буквы «О» [ou] в английском алфавите;

—
цифры 0 в системах счисления;

—
символа химического элемента «О» (кислорода) в таблице Д. И.
Менделеева.

Знаковые
системы
являются наборами знаков определенного типа. С некоторыми знаковыми системами вы
хорошо знакомы и постоянно ими пользуетесь (языки и системы счисления), с
другими познакомитесь в этом пункте.

Каждая
знаковая система строится на основе определенного алфавита (набора знаков) и
правил выполнении операций над знаками.

Естественные
языки.
Человек широко использует для представления информации знаковые системы, которые
называются языками. Естественные языки начали формироваться еще в древнейшие
времена в целях обеспечения обмена информацией между людьми. В настоящее время
существуют сотни естественных языков (русский, английский, китайский и
др.).

В
устной речи, которая используется как средство коммуникации при непосредственном
общении людей, в качестве знаков языка используются различные звуки
(фонемы).

В
основе письменной речи лежит алфавит, т. е. набор знаков (букв), которые человек
различает по их начертанию. В большинстве современных языков буквы соответствуют
определенным звукам устной речи. Алфавит русского языка называется кириллицей и
содержит 33 знака, английский язык использует латиницу и содержит 26
знаков.

На
основе алфавита по правилам грамматики образуются основные объекты языка —
слова. Правила, согласно которым из слов данного языка строятся предложения,
называются синтаксисом. Необходимо отметить, что в естественных языках
грамматика и синтаксис языка формулируются с помощью большого количества правил,
из которых существуют исключения, так как такие правила складывались
исторически.

Формальные
языки.
В процессе развития науки были разработаны формальные языки (системы счисления,
алгебра, языки программирования и др.), основное отличие которых от естественных
языков состоит в существовании строгих правил грамматики и
синтаксиса.

Например,
десятичную систему счисления можно рассматривать как формальный язык, имеющий
алфавит (цифры) и позволяющий не только именовать и записывать объекты (числа),
но и выполнять над ними арифметические операции по строго определенным
правилам.

Существуют
формальные языки, в которых в качестве знаков используют не буквы и цифры, а
другие символы, например, музыкальные ноты, изображения элементов электрических
или логических схем, дорожные знаки, точки и тире (код азбуки
Морзе).

Физическая
реализация знаков в естественных и формальных языках может быть различной.
Например, текст и числа могут быть напечатаны на бумаге, высвечены на экране
монитора компьютера, записаны на магнитном или оптическом
диске.

Генетический
алфавит.
Генетический алфавит является «азбукой», на которой строится единая система
хранения и передачи наследственной информации живыми
организмами.

Как
слова в языках образуются из букв, так и гены состоят из знаков генетического
алфавита. В процессе эволюции от простейших организмов до человека количество
генов постоянно возрастало, так как было необходимо закодировать все более
сложное строение и функциональные возможности живых
организмов.

Генетическая
информация хранится в клетках живых организмов в специальных молекулах. Эти
молекулы состоят из двух длинных скрученных друг с другом в спираль цепей,
построенных из четырех различных молекулярных   фрагментов (рис. 1.6). Фрагменты
образуют генетический алфавит и обычно обозначаются латинскими прописными
буквами {A, G, С, Т}.

Рис
1. Модель молекулы генетического кода

Двоичная
знаковая система. В процессах хранения, обработки и передачи информации в
компьютере используется двоичная знаковая система, алфавит которой состоит всего
из двух знаков {0, 1}. Физически знаки реализуются в форме электрических
импульсов (нет импульса — 0, есть импульс — 1), а также состояний ячеек
оперативной памяти и участков поверхностей носителей информации (одно состояние
— 0, другое состояние — 1).

Именно
двоичная знаковая система используется в компьютере, так как существующие
технические устройства могут надежно сохранять и распознавать только два
различных состояния (знака).

В
60-е годы XX века в СССР учеными Московского государственного университета была
разработана и запущена в производство ЭВМ «Сетунь» (всего было произведено 50
экземпляров) (рис. 1.7). «Сетунь» использовала троичное кодирование информации
и, соответственно, состояла из устройств, способных находиться в одном из трех
возможных состояний.

Рис.
2. ЭВМ «Сетунь»

2. Двоичное
кодирование текстовой, графической и звуковой
информации.

Код — это набор условных обозначений
(или сигналов) для записи (или передачи) некоторых заранее определенных
понятий.

           
Кодирование информации – это
процесс формирования определенного представления информации. В более узком
смысле под термином «кодирование» часто понимают переход от одной формы
представления информации к другой, более удобной для хранения, передачи или
обработки.

           
Обычно каждый образ при кодировании (иногда говорят — шифровке)
представлении отдельным знаком.

           
Знак — это элемент конечного
множества отличных друг от друга элементов.

           
В более узком смысле под термином «кодирование» часто понимают переход от
одной формы представления информации к другой, более удобной для хранения,
передачи или обработки.

           
Компьютер может обрабатывать только информацию, представленную в числовой
форме. Вся другая информация (например, звуки, изображения, показания приборов и
т. д.) для обработки на компьютере должна быть преобразована в числовую форму.
Например, чтобы перевести в числовую форму музыкальный звук, можно через
небольшие промежутки времени измерять интенсивность звука на определенных
частотах, представляя результаты каждого измерения в числовой форме. С помощью
программ для компьютера можно выполнить преобразования полученной информации,
например, «наложить» друг на друга звуки от разных источников.

           
Аналогичным образом на компьютере можно обрабатывать текстовую
информацию. При вводе в компьютер каждая буква кодируется определенным числом, а
при выводе на внешние устройства (экран или печать) для восприятия человеком по
этим числам строятся изображения букв. Соответствие между набором букв и числами
называется кодировкой символов.

           
Как правило, все числа в компьютере представляются с помощью нулей и
единиц (а не десяти цифр, как это привычно для людей). Иными словами, компьютеры
обычно работают в двоичной системе счисления, поскольку при этом устройства для
их обработки получаются значительно более простыми. Ввод чисел в компьютер и
вывод их для чтения человеком может осуществляться в привычной десятичной форме,
а все необходимые преобразования выполняют программы, работающие на компьютере.

           
Способы кодирования
информации.

           
Одна и та же информация может быть представлена (закодирована) в
нескольких формах. C появлением компьютеров возникла необходимость кодирования
всех видов информации, с которыми имеет дело и отдельный человек, и человечество
в целом. Но решать задачу кодирования информации человечество начало задолго до
появления компьютеров. Грандиозные достижения человечества — письменность и
арифметика — есть не что иное, как система кодирования речи и числовой
информации. Информация никогда не появляется в чистом виде, она всегда как-то
представлена, как-то закодирована.

           
Двоичное кодирование – один
из распространенных способов представления информации.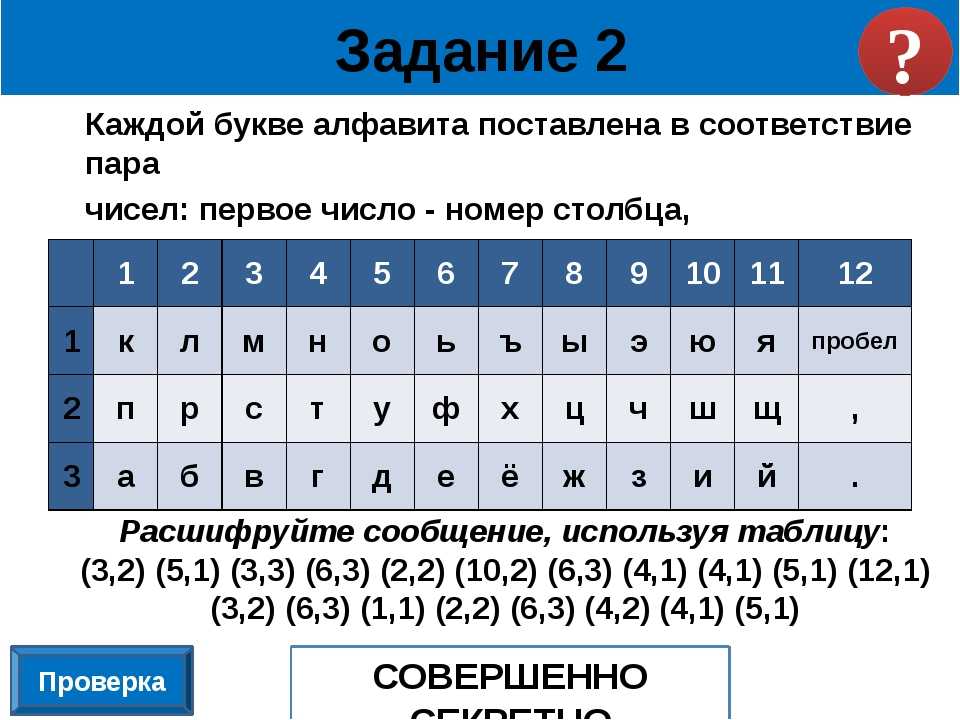 В вычислительных машинах,
в роботах и станках с числовым программным управлением, как правило, вся
информация, с которой имеет дело устройство, кодируется в виде слов двоичного
алфавита.

           
Кодирование символьной
(текстовой) информации.

           
Основная операция, производимая над отдельными символами текста —
сравнение символов.

           
При сравнении символов наиболее важными аспектами являются уникальность
кода для каждого символа и длина этого кода, а сам выбор принципа кодирования
практически не имеет значения.

           
Для кодирования текстов используются различные таблицы перекодировки.
Важно, чтобы при кодировании и декодировании одного и того же текста
использовалась одна и та же таблица.

           
Таблица перекодировки — таблица, содержащая упорядоченный некоторым
образом перечень кодируемых символов, в соответствии с которой происходит
преобразование символа в его двоичный код и обратно.

           
Наиболее популярные таблицы перекодировки: ДКОИ-8, ASCII, CP1251,
Unicode.

Можно
поступить следующим образом: измерять амплитуду сигнала через равные промежутки
времени и записывать полученные числовые значения в память
компьютера.

3.
Представление числовой информации с помощью систем
счисления.

Для
записи информации о количестве объектов используются числа. Числа записываются с
использованием особых знаковых систем, которые называются системами счисления.
Алфавит систем счисления состоит из символов, которые называются цифрами.
Например, в десятичной системе счисления числа записываются с помощью десяти
всем хорошо известных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Система
счисления —
это знаковая система, в которой числа записываются по определенным правилам с
помощью символов некоторого алфавита, называемых цифрами.

Все
системы счисления делятся на две большие группы: позиционные и непозиционные системы
счисления. В позиционных системах счисления значение цифры зависит от ее
положения в числе, а в непозиционных — не зависит.

Римская
непозиционная система счисления. Самой
распространенной из непозиционных систем счисления является римская. В качестве
цифр в ней используются: I (1), V (5), X (10), L (50), С (100), D (500), М
(1000).

Значение
цифры не зависит от ее положения в числе. Например, в числе XXX (30) цифра X
встречается трижды и в каждом случае обозначает одну и ту же величину — число
10, три числа по 10 в сумме дают 30.

Величина
числа в римской системе счисления определяется как сумма или разность цифр в
числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа
— прибавляется. Например, запись десятичного числа 1998 в римской системе
счисления будет выглядеть следующим образом:

MCMXCVIII
= 1000 + (1000 — 100) + (100 -10)+ 5 + 1 + 1 + 1.

Позиционные
системы счисления.  Первая
позиционная система счисления была придумана еще в Древнем Вавилоне, причем
вавилонская нумерация была шестидесятеричной, то есть в ней использовалось
шестьдесят цифр! Интересно, что до сих пор при измерении времени мы используем
основание, равное 60 (в 1 минуте содержится 60 секунд, а в 1 часе — 60
минут).

В
XIX веке довольно широкое распространение получила двенадцатеричная система
счисления. До сих пор мы часто употребляем дюжину (число 12): в сутках две
дюжины часов, круг содержит тридцать дюжин градусов и так
далее.

В позиционных
системах счисления количественное значение цифры зависит от ее позиции
в числе.

Наиболее
распространенными в настоящее время позиционными системами счисления являются
десятичная, двоичная, восьмеричная и шестнадцатеричная. Каждая позиционная
система имеет определенный алфавит цифр и основание.

В позиционных
системах счисления основание системы равно количеству цифр (знаков в ее
алфавите) и определяет, во сколько раз различаются значения одинаковых цифр,
стоящих в соседних позициях числа.

Десятичная
система счисления имеет алфавит цифр, который состоит из десяти всем известных,
так называемых арабских, цифр, и основание, равное 10, двоичная — две цифры и
основание 2, восьмеричная — восемь цифр и основание 8, шестнадцатеричная —
шестнадцать цифр (в качестве цифр используются и буквы латинского алфавита) и
основание 16 (табл. 3).

Десятичная
система счисления.  Рассмотрим
в качестве примера десятичное число 555. Цифра 5 встречается трижды, причем
самая правая цифра 5 обозначает пять единиц, вторая справа — пять десятков и,
наконец, третья справа — пять сотен.

Позиция
цифры в числе называется разрядом. Разряд числа возрастает
справа налево, от младших разрядов к старшим. В десятичной системе цифра,
находящаяся в крайней справа позиции (разряде), обозначает количество единиц,
цифра, смещенная на одну позицию влево, — количество десятков, еще левее —
сотен, затем тысяч и так далее. Соответственно имеем разряд единиц, разряд
десятков и так далее.

Число
555 записано в привычной для нас свернутой форме. Мы
настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем
цифры числа на различные степени числа 10.

В развернутой форме записи
числа такое умножение записывается в явной форме. Так, в развернутой форме
запись числа 555 в десятичной системе будет выглядеть следующим
образом:

555₁₀ =
5 × 10² + 5 × 10¹ +
5 × 10⁰.

Как
видно из примера, число в позиционной системе счисления записывается в виде
суммы числового ряда степеней основания (в данном случае
10), в качестве коэффициентов которых выступают цифры данного
числа.

Для
записи десятичных дробей используются отрицательные значения степеней основания.
Например, число 555,55 в развернутой форме записывается следующим
образом:

555,55₁₀ =
5 × 10² + 5 × 10¹ +
5 × 10⁰ + 5 × 10^-1 +
5 × 10^-2 .

В
общем случае в десятичной системе счисления запись числа А₁₀, которое
содержит n целых разрядов числа и m дробных разрядов числа, выглядит
так:

A₁₀ =
a_n-1 × 10^n-1 + … +
a₀ × 10⁰ +
a_-1 × 10^-1 + … +
a_-m × 10^-m

Коэффициенты
a_i в этой записи являются цифрами десятичного числа, которое в
свернутой форме записывается так:

А₁₀ =
a_n-1 a_n-2 . .. a₀,
a_-1 … a_-m.

Из
вышеприведенных формул видно, что умножение или деление десятичного числа на 10
(величину основания) приводит к перемещению запятой, отделяющей целую часть от
дробной, на один разряд соответственно вправо или влево.
Например:

555,55₁₀ × 10
= 5555,5₁₀; 
555,55₁₀ : 10 =
55,555₁₀.

Двоичная
система счисления. В
двоичной системе счисления основание равно 2, а алфавит состоит из двух цифр (0
и 1). Следовательно, числа в двоичной системе в развернутой форме записываются в
виде суммы степеней основания 2 с коэффициентами, в качестве которых выступают
цифры 0 или 1.

Например,
развернутая запись двоичного числа может выглядеть так:

А₂ =
1 × 2² + 0 × 2¹ +
1 × 2⁰ + 0 × 2^-1 +
1 × 2^-2.

Свернутая
форма этого же числа:

А₂ =
101,01₂.

В
общем случае в двоичной системе запись числа А₂, которое содержит n
целых разрядов числа и m дробных разрядов числа, выглядит
так:

А₂ =
a_n-1 × 2^n-1 +
a_n-2 × 2^n-2 + … +
a₀ × 2⁰ +
a_-1 × 2^-1 + … +
a_-m × 2^-m

Коэффициенты
а_i в этой записи являются цифрами (0 или 1) двоичного числа,
которое в свернутой форме записывается так:

А₂ =
а_n-1 а_n-2 … а₀,
а_-1 а_-2 … а_-m

Из
вышеприведенных формул видно, что умножение или деление двоичного числа на 2
(величину основания) приводит к перемещению запятой, отделяющей целую часть от
дробной на один разряд соответственно вправо или влево.
Например:

101,01₂ × 2
= 1010,1₂; 
101,01₂ : 2 =
10,101₂.

Позиционные
системы счисления с произвольным основанием. Возможно
использование множества позиционных систем счисления, основание которых равно
или больше 2. В системах счисления с основанием q (q-ичная система счисления)
числа в развернутой форме записываются в виде суммы степеней основания q с
коэффициентами, в качестве которых выступают цифры 0, 1, q —
1:

A_q =
a_n-1 × q^n-1 +
a_n-2 × q^n-2 + … +
a₀ × q⁰ +
a_-1 × q^-1 + … +
a_-m × q^-m

Коэффициенты
а_i в этой записи являются цифрами числа, записанного в q-ичной
системе счисления.

Так,
в восьмеричной системе основание равно восьми (q = 8). Тогда записанное в
свернутой форме восьмеричное число А₈ = 673,2₈ в
развернутой форме будет иметь вид:

А₈ =
6 × 8² + 7 × 8¹ +
3 × 8⁰ +
2 × 8^-1.

В
шестнадцатеричной системе основание равно шестнадцати (q = 16), тогда записанное
в свернутой форме шестнадцатеричное число А₁₆ =
8A,F₁₆ в развернутой форме будет иметь
вид:

А₁₆ =
8 × 16¹ + А × 16⁰ +
F × 16^-1.

Если
выразить шестнадцатеричные цифры через их десятичные значения (А=10, F=15), то
запись числа примет вид:

А₁₆ =
8 × 16¹ +
10 × 16⁰ +
15 × 16^-1.

Ученые только что добавили четыре новые буквы в генетический код

Алфавит из четырех букв может показаться ограниченным, но это все, что нужно природе, чтобы написать инструкции для всей жизни на планете. Новость о том, что исследователи добавили четыре буквы в генетический алфавит, открывает дверь к новым возможностям синтетической биологии, хранения данных и даже поиска жизни за пределами нашей планеты.

Генетический код, лежащий в основе всех живых существ, элегантно прост. Каждая половина знаменитой структуры двойной спирали построена из четырех небольших молекул, называемых основаниями: аденина, тимина, цитозина и гуанина (ATCG). Порядок, в котором они появляются, определяет, что кодирует ДНК, точно так же, как последовательность нулей и единиц в сердце компьютера.

Но теперь ученые из Фонда прикладной молекулярной эволюции во Флориде успешно добавили четыре новых основания для создания того, что они называют «ДНК хати-модзи» (восьмибуквенная ДНК на японском языке), удвоив потенциальную информационную плотность генетического кода.

Это не первая попытка расширения генетического кода. В 2014 году ученые из Исследовательского института Скриппса в Калифорнии представили ДНК с двумя дополнительными основаниями, а в 2017 году показали, что могут заставить бактерии использовать этот код для создания белков, не существующих в природе. Но новая работа не только добавляет две дополнительные основы, но и более точно соответствует схеме, используемой природой.

Двойная спираль ДНК удерживается вместе водородными связями между комплементарными основаниями — пары А с Т и пары С с G. В исследовании Скриппса использовались водоотталкивающие молекулы, которые слипаются, но отталкивают другие основания. Эти базы должны быть зажаты между естественными базами, поэтому невозможно иметь протяженные участки неестественных баз, ограничивающие то, что они могут кодировать.

В ДНК хати-модзи, как и в природной ДНК, используются водородные связи для связывания двух новых пар — S с B и P с Z — и основания также могут располагаться рядом друг с другом. Поскольку ДНК читается в триплетах оснований, называемых кодонами, каждое из которых кодирует определенную аминокислоту, это значительно увеличивает количество потенциальных кодонов по сравнению с предыдущим подходом: 512 по сравнению с 64 в обычной ДНК.

Эксперименты также показывают, что ДНК хачи-модзи сохраняет все ключевые характеристики, необходимые для поддержки дарвиновской эволюции, что имеет решающее значение для поддержания жизни. Основания надежно спариваются, структура остается стабильной независимо от последовательности оснований, и они продемонстрировали, что ее можно скопировать в РНК.

Это очень важно, потому что, хотя ДНК содержит чертежи организма, чтобы клетки могли что-то делать с этой информацией, она должна быть преобразована в мобильную одноцепочечную молекулу РНК, которая может действовать как инструкции для белковых фабрик, называемых рибосомами. или может помочь регулировать гены.

С точки зрения потенциального использования новых букв, возможности широки. Вся сложность природы была создана из 20 аминокислот, которые может производить обычная ДНК (несколько кодонов кодируют одну и ту же аминокислоту). Новые кодоны позволяют кодировать новые аминокислоты с новыми свойствами, которые могут помочь во всем, от более мощных лекарств и промышленных катализаторов до более диковинных идей, таких как электропроводящие белки.

Это потребует огромной работы над инструментами, которые могут использовать преимущества нового кода, однако ученые, стоящие за исследованием, признали Проводной . Потенциально ближайшая цель может состоять в том, чтобы воспользоваться преимуществами дополнительной плотности информации, чтобы активизировать усилия, направленные на то, чтобы рассматривать ДНК как сверхкомпактную и стабильную форму долгосрочного хранения данных.

Возможно, самым большим вкладом исследования является то, что оно дает нам представление о возможных формах жизни. Новый код далек от поддержки самоподдерживающихся организмов — исследователям еще предстоит продемонстрировать, что код может быть воспроизведен клетками, и он зависит от поставок лабораторных строительных блоков, которых нет в природе.

Но тот факт, что вы можете воспроизвести форму и функцию ДНК с очень разными составными частями, предполагает, что жизнь за пределами Земли может быть не похожа ни на что, что мы видели раньше. Исследование финансировалось НАСА, и представители сообщили CNN , что они надеются, что это поможет им расширить масштабы поиска внеземной жизни.

ДНК-вычисления | информатика

Похожие темы:

компьютер

Просмотреть весь связанный контент →

Сводка

Прочтите краткий обзор этой темы

ДНК-вычисления , выполнение вычислений с использованием биологических молекул, а не традиционных кремниевых чипов. Идея о том, что отдельные молекулы (или даже атомы) можно использовать для вычислений, восходит к 1959 году, когда американский физик Ричард Фейнман представил свои идеи о нанотехнологиях. Однако вычисления ДНК не были физически реализованы до 1994 года, когда американский ученый-компьютерщик Леонард Адлеман показал, как можно использовать молекулы для решения вычислительной задачи.

Решение задач с молекулами ДНК

Вычисление можно рассматривать как выполнение алгоритма, который сам по себе может быть определен как пошаговый список четко определенных инструкций, которые принимают некоторые входные данные, обрабатывают их и выдают результат. В вычислениях ДНК информация представляется с использованием четырехсимвольного генетического алфавита (A [аденин], G [гуанин], C [цитозин] и T [тимин]), а не двоичного алфавита (1 и 0), используемого традиционными методами. компьютеры. Это достижимо, потому что короткие молекулы ДНК любой произвольной последовательности могут быть синтезированы на заказ. Таким образом, ввод алгоритма представлен (в простейшем случае) молекулами ДНК с определенными последовательностями, инструкции выполняются лабораторными операциями над молекулами (такими как их сортировка по длине или отсечение нитей, содержащих определенную подпоследовательность), а результат определяется как некоторое свойство конечного набора молекул (например, наличие или отсутствие определенной последовательности).

Эксперимент Адлемана заключался в поиске маршрута через сеть «городов» (обозначенных от «1» до «7»), соединенных «дорогами» с односторонним движением. В задаче указано, что маршрут должен начинаться и заканчиваться в определенных городах и посещать каждый город только один раз. (Математикам она известна как проблема гамильтоновой траектории, двоюродная сестра более известной задачи коммивояжера.) Адлеман воспользовался свойством комплементарности ДНК по Уотсону-Крику: А и Т слипаются попарно, как и G и C (так что последовательность AGCT идеально подходит для TCGA). Он разработал короткие нити ДНК для представления городов и дорог таким образом, чтобы нити дорог скрепляли нити городов вместе, образуя последовательности городов, которые представляли маршруты (например, фактическое решение, которое оказалось «1234567»). Большинство таких последовательностей представляли собой неверные ответы на задачу («12324» посещает город более одного раза, а «1234» не посещает каждый город), но Адлеман использовал достаточное количество ДНК, чтобы быть достаточно уверенным, что правильный ответ будет представлен в его исходном коде. горшок из прядей. Проблема заключалась в том, чтобы извлечь это уникальное решение. Он добился этого, сначала сильно амплифицируя (используя метод, известный как полимеразная цепная реакция [ПЦР]) только те последовательности, которые начинались и заканчивались в нужных городах. Затем он отсортировал набор нитей по длине (используя технику, называемую гель-электрофорезом), чтобы убедиться, что он сохранил только нити правильной длины. Наконец, он неоднократно использовал молекулярную «удочку» (аффинную очистку), чтобы убедиться, что каждый город по очереди представлен в последовательностях-кандидатах. Затем нити, которые остались у Адлемана, были секвенированы, чтобы выявить решение проблемы.

Хотя Адлеман стремился только установить возможность вычислений с помощью молекул, вскоре после его публикации некоторые представили его эксперимент как начало соревнования между компьютерами на основе ДНК и их кремниевыми аналогами. Некоторые люди верили, что молекулярные компьютеры однажды смогут решить проблемы, которые заставят существующие машины бороться из-за присущего биологии массивного параллелизма. Поскольку маленькая капля воды может содержать триллионы нитей ДНК и поскольку биологические операции воздействуют на все из них — эффективно — параллельно (а не по одной за раз), утверждалось, что однажды ДНК-компьютеры смогут представлять (и решать) сложные задачи, выходящие за рамки «обычных» компьютеров.

Однако в большинстве сложных задач количество возможных решений растет экспоненциально с размером задачи (например, количество решений может удваиваться для каждого добавленного города). Это означает, что даже относительно небольшие проблемы потребуют неуправляемых объемов ДНК (порядка больших ванн), чтобы представить все возможные ответы. Эксперимент Адлемана имел большое значение, поскольку в нем проводились мелкомасштабные вычисления с биологическими молекулами. Однако, что еще более важно, это открыло возможность непосредственно запрограммированных биохимических реакций.

Информационные технологии на основе биохимии

Программируемая информационная химия позволит создавать новые типы биохимических систем, которые могут ощущать свое собственное окружение, действовать в соответствии с решениями и, возможно, даже общаться с другими подобными формами. Хотя химические реакции происходят в наномасштабе, так называемые информационные технологии, основанные на биохимии (био/химические ИТ), отличаются от нанотехнологий из-за зависимости первых от относительно крупномасштабных молекулярных систем.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас

Хотя в современных био/химических информационных технологиях используется множество различных типов (био) химических систем, ранние работы по программируемым молекулярным системам в основном основывались на ДНК. Американский биохимик Надриан Симан был одним из первых пионеров нанотехнологии на основе ДНК, которая изначально использовала эту конкретную молекулу исключительно как наноразмерный «каркас» для манипулирования и контроля над другими молекулами. Американский ученый-компьютерщик Эрик Уинфри работал с Симаном, чтобы показать, как двумерные «листы» из «плиток» на основе ДНК (фактически прямоугольники, состоящие из переплетенных нитей ДНК) могут самостоятельно собираться в более крупные структуры. Затем Уинфри вместе со своим учеником Полом Ротемундом показал, как можно спроектировать эти плитки таким образом, чтобы процесс самосборки мог выполнять определенные вычисления. Позже Ротемунд расширил эту работу своим исследованием «ДНК-оригами», в котором одна нить ДНК многократно складывается в двухмерную форму, чему помогают более короткие нити, которые действуют как «скобы».