Содержание
Sasapost (Египет): познакомьтесь с мусульманским ученым, который объявил Землю круглой задолго до Европы
Материалы ИноСМИ содержат оценки исключительно зарубежных СМИ и не отражают позицию редакции ИноСМИ
Арабский мир называет Захарию аль-Казвини «средневековым Геродотом» и «арабским Птолемеем». Его вклад в различные научные направления невозможно переоценить, но, к сожалению, о нем мало кому известно. Аль-Казвини доказал, что Земля имеет форму шара задолго до европейцев, а его научные труды изобилуют мифическими и сказочными персонажами.
Фатима Нади (فاطمة نادي)
«Закария аль-Казвини по прозвищу «восточный Плиний» (1203-1283) — один из самых выдающихся арабских историков естествознания. Аль-Казвини подробно описывал специфику различных явлений, как делал после него Буффон». Так пишет Густав Лебон в книге «История арабской цивилизации».
Одни называют Закарию аль-Казвини «средневековым Геродотом», другие — «арабским Плинием». Его считают одной из самых выдающихся фигур XIII столетия, чье появление способствовало обогащению научного наследия арабов. Имад ад-Дин Абу Яхья Закария ибн Мухаммед ибн Махмуд аль-Казвини — один из самых выдающихся арабских ученых и историков средневековой эпохи. Какова история его жизни? Какой основной вклад он внес в развитие науки? Какие сочинения он оставил миру?
Имад ад-Дин Абу Яхья Закария ибн Мухаммед ибн Махмуд аль-Казвини — один из самых выдающихся арабских ученых и историков средневековой эпохи. Какова история его жизни? Какой основной вклад он внес в развитие науки? Какие сочинения он оставил миру?
От иранского Каспия до Дамаска и Багдада
«Вначале задача арабского естествознания состояла лишь в том, чтобы объяснить труды Аристотеля, но вскоре арабы решили учиться у природы, а не по книгам. Это привело к тому, что арабы написали множество интересных сочинений по зоологии, ботанике, минералогии, палеонтологии и так далее» (Густав Лебон, «История арабской цивилизации».
Закария аль-Казвини родился в 1208 году в городе Казвин, который находится между Рештом и Тегераном. Предки аль-Казвини были родом из Хиджаза, поэтому он считал себя потомком ансаров, а среди своих предков называл Анаса ибн Малика. Он провел детство в Казвине, а затем уехал в Дамаск, где попал под влияние известного мистика Мухиддина ибн Араби.
Аль-Казвини долгое время жил в Ираке, где занимал должность кади районов Васита и Хиллы (мусульманский судья-чиновник, назначаемый правителем и вершащий правосудие на основе шариата — прим. ред.) во время правления последнего аббасидского халифа аль-Мустасима, а также работал в школе Шарабия до взятия Багдада монголами в 1258 году. Он прожил большую часть жизни в Багдаде и Дамаске и был свидетелем важных исторических событий, таких как: восстание монголов, взятие Багдада, битва при Айн-Джалуте и падение Севильи, которое привело к тому, что в руках арабов остался только Гранадский эмират.
Стоит отметить, что аль-Казвини проявлял интерес не только к преподавательской деятельности и судебной практике, но и к другим различным областям науки: географии, астрономии, естествознанию, паранормальным и мистическим явлениям, а также он питал страсть к природе и биологии. И хотя аль-Казвини изучал различные науки, его величайшие труды были посвящены метеорологии и астрономии.
Ученый-энциклопедист: вклад аль-Казвини в различные отрасли науки
Закария аль-Казвини — один из выдающихся деятелей в области астрономии и метеорологии.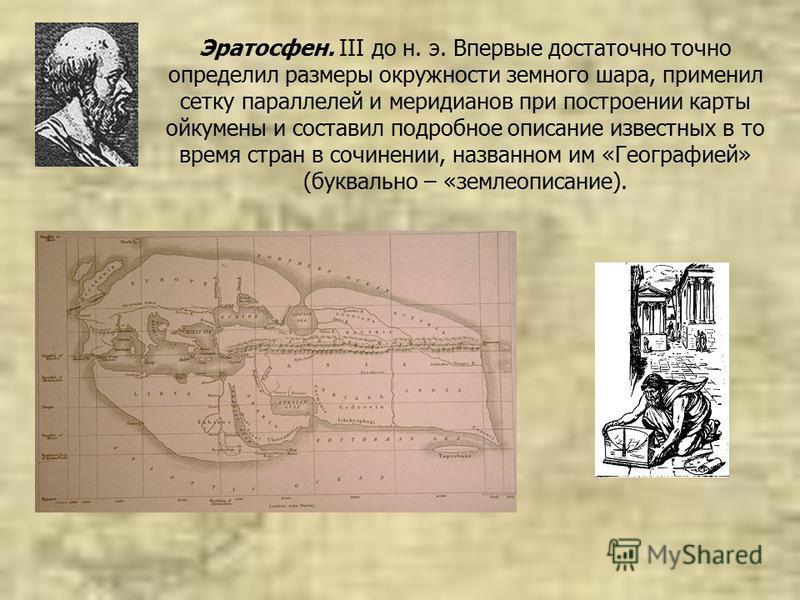 Он был первым, кто нашел способ определять время по звездам, а его теории заложили основу для метеорологии. Аль-Казвини первым заговорил о классификации звезд по спектру излучения, видимом движении планет и о том, как узнать время по звездам. Он предложил классификацию ветров и облаков и выдвинул гипотезу о том, как они образуются, а также о том, почему дождь выпадает в виде капель. Аль-Казвини посвятил первую часть своей книги «Чудеса сотворенного и диковинки существующего» астрономии и звёздам. В ней же он рассказал об арабском, римском и персидском календарях, а также о связанных с ними праздниками и событиями.
Он был первым, кто нашел способ определять время по звездам, а его теории заложили основу для метеорологии. Аль-Казвини первым заговорил о классификации звезд по спектру излучения, видимом движении планет и о том, как узнать время по звездам. Он предложил классификацию ветров и облаков и выдвинул гипотезу о том, как они образуются, а также о том, почему дождь выпадает в виде капель. Аль-Казвини посвятил первую часть своей книги «Чудеса сотворенного и диковинки существующего» астрономии и звёздам. В ней же он рассказал об арабском, римском и персидском календарях, а также о связанных с ними праздниками и событиями.
Кроме того, значительную часть своей книги он посвятил географии, в том числе климатическим поясам, слоям атмосферы, образованию облаков и дождя, появлению ветров. Он интересовался соотношением засушливых регионов и воды, тепловыми поясами и задавался вопросом почему в тропиках высокие температуры, а в полярных регионах сильный холод. Аль-Казвини подробно рассказал о горах, реках, морях и озерах, которые были известны в то время и причинах их возникновения с геологической точки зрения.
Аль-Казвини оставил свой след в геологии, а его идеи стали пользоваться популярностью среди западных ученых. Стоит отметить, что они оказали большое влияние на геолога Чарльза Лайеля, который упомянул аль-Казвини во введении к «Основам геологии» в 1830 году. Французский философ Гюстав Лебон также высоко оценил достижения аль-Казвини в области геологии, сказав: «Теория глобальной эволюции Земли, движения водных масс и трансформации земель набирает популярность в арабском мире благодаря книги по естествознанию аль-Казвини».
Вместе с тем не стоит забывать о большом вкладе аль-Казвини в историю, медицину и фармацевтику, химию, физику, естественные науки, психологию, ботанику, зоологию и живопись. Перевод его работ на европейские языки способствовал появлению астролябий в западных странах. Интересно, что бедуинские племена и кочевники полагаются на сочинения аль-Казвини, чтобы определить скорость ветра, дождь и смену времен года. Все эти знания помогают им в сельском хозяйстве и разведении овец.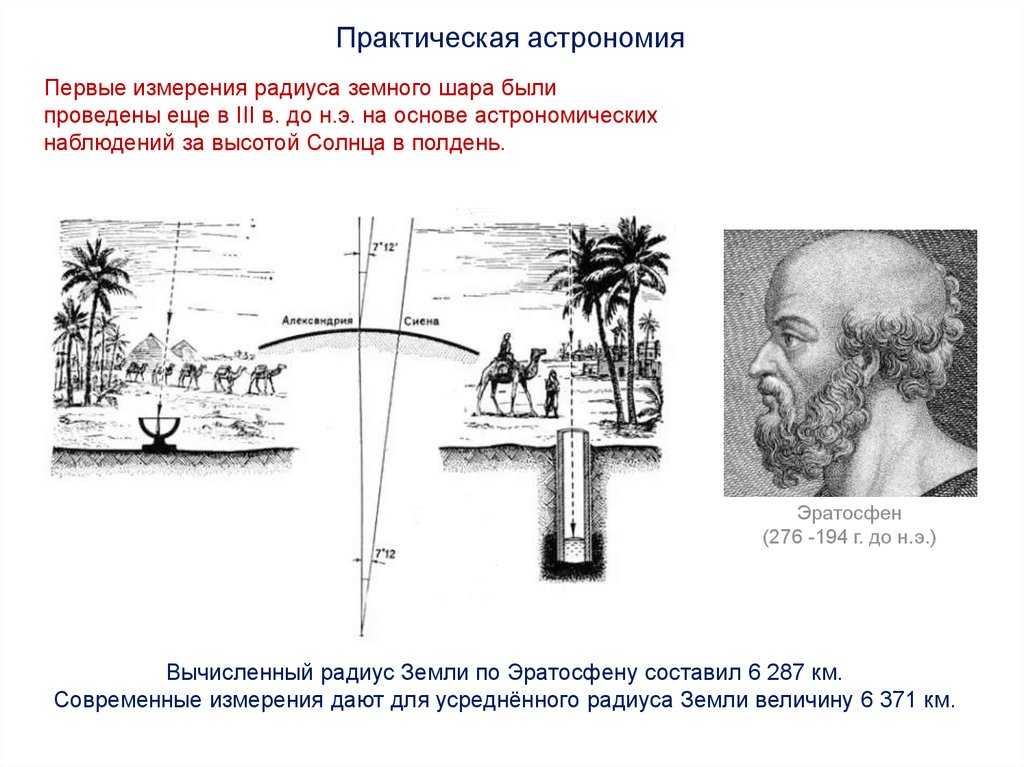
Глобальное восприятие мира: «Чудеса сотворенного и диковинки существующего»
«Стремись к справедливости и однажды запиши все, что знаешь для всех людей, а не только для элиты. И объедини свои знания о жизни и Вселенной со своей религией, тогда Аллах благословит все то, что ты пишешь, сын мой. Слово останется после тебя, помни об этом» (часть завещания отца аль-Казвин).
Аль-Казвини много размышлял о детских поездках с отцом к портам на Каспийском море, которые очаровали молодого человека своим культурным разнообразием. Когда пришли монголы, семья аль-Казвини бежала в Багдад, и, несмотря на то, что он обладал знаниями, которые позволяли ему работать судьей, молодой аль-Казвини почувствовал непреодолимое желание написать книгу, которая опередит время.
Он попросил у отца разрешение на 10-летнюю поездку из Багдада до границ Китая, в ходе которой посетил Аравию, Левант и Египет. Так дух путешественника слился с миром. После возвращения в Багдад аль-Казвини работал кади, женился и оставался в Ираке на протяжении 15 лет, читая книги и узнавая о мире все больше. В то время арабо-исламская цивилизация достигла своего пика, что позволило аль-Казвини погружаться в сочинения Аристотеля, Птолемея, аль-Бируни, ибн Сины и аль-Фараби. Кроме того, аль-Казвини решил исследовать новые горизонты и узнать больше о Хорасане, Афганистане, Турции, Хорезме, Армении и Азербайджане.
В то время арабо-исламская цивилизация достигла своего пика, что позволило аль-Казвини погружаться в сочинения Аристотеля, Птолемея, аль-Бируни, ибн Сины и аль-Фараби. Кроме того, аль-Казвини решил исследовать новые горизонты и узнать больше о Хорасане, Афганистане, Турции, Хорезме, Армении и Азербайджане.
Во время своего путешествия он увидел потрясающие чудеса на суше и в воде, разноцветные минералы, различные виды растений, животных, птиц и людей, что привело к публикации книги «Чудеса сотворенного и диковинки существующего», в которой аль-Казвини описал вселенную, созвездия, планеты и их движение и влияние на Землю, а также множество странных и паранормальных явлений.
«Чудеса сотворенного и диковинки существующего» — естественнонаучная и географическая энциклопедия, в которой содержится огромное количество информации, где одна часть основывается на личном опыте автора, а другая на знаниях различных народов и цивилизаций. Таким образом, можно сказать, что эта книга представляет собой сборник знаний человечества о природных явлениях и существах, известных во времена аль-Казвини, а также отражает взгляд на то, что человек знает о природе и на то, что скрыто от его глаз.
Книга разделена на введение и два раздела: небесный и земной миры. В первом разделе, посвященном небесному миру, рассказывается о небесных телах: Солнце, Луне, звездах, а также о небесных жителях — ангелах. Кроме того, в нем есть арабский и сирийский календари и связанные с ними праздники и события. Второй раздел посвящен Земле, природным явлениям и четырем элементам: огню, воздуху, воде и земле. Аль-Казвини описывает разделение Земли на семь материков, причины землетрясений, образования гор, появления рек, озер и морей.
Затем следует описание трех природных царств: минерального, растительного и животного. Кроме того, аль-Казвини пишет об еще одном царстве — человеческом, где рассказывает об особенностях характера, анатомии, органических веществах, а также о других созданиях, включая джиннов, огров и фениксов. В книге есть главы, посвященные Красному мору и взаимодействию воздуха и моря. Также есть главы, посвященные птицам, которых обучают, а затем используют на охоте. Аль-Казвини даже перечисляет некоторые виды птиц: турул, кобчик, сойка и ястреб.
В книге «Чудеса сотворенного и диковинки существующего» аль-Казвини выдвинул теорию о том, что Земля круглая, а не квадратная, цилиндрическая или плоская, как считали в то время, а доказательством послужил тот факт, что лунное затмение видно из разных стран, а это означает, что восход луны и закат солнца происходят в разное время в разных местах, о чем свидетельствует стих в Коране: «Он покрывает ночью день и покрывает днем ночь (сура аз-Зумар)».
По мнению аль-Казвини, Земля вращается вокруг своей оси с запада на восток, а не находится в центре Вселенной, как считал Птолемей. Все живые существа находятся на ней благодаря силе притяжения и силе вращения. Тоже самое касается слоев Земли, паров, газов и минералов. Кроме того, он объяснил, почему ландшафт земли меняется каждые несколько тысяч лет.
В книге присутствует дух народных сказок с сильным религиозным окрасом, а также суры Корана, иллюстрации и притчи. Но вместе с тем, в ней сохраняется дух историка, который хотел обобщить знания своего времени, чтобы сохранить их для будущих поколений в нестабильное время, которое угрожало положить конец арабо-мусульманской цивилизации.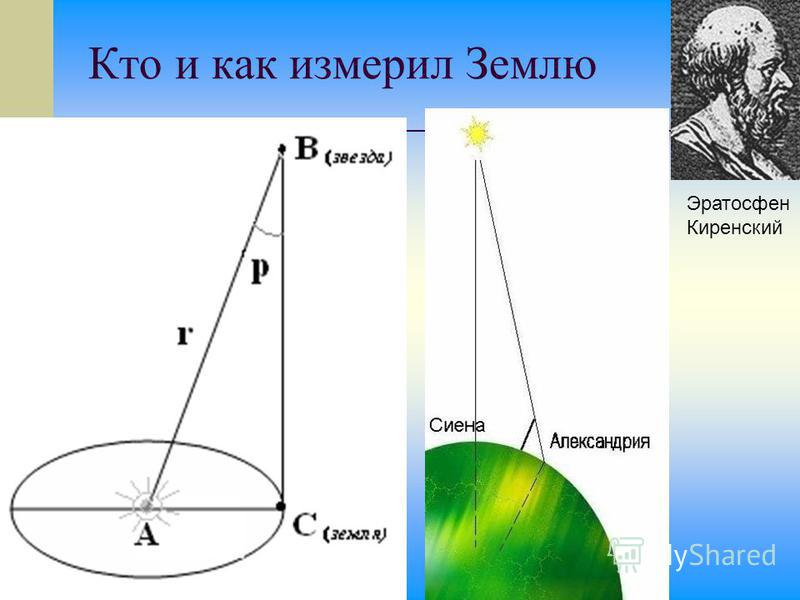
«Космография» аль-Казвини упростила понимание науки
Некоторые исследователи и ученые считают аль-Казвини величайшим космографом, чей вклад упростил восприятие науки для общественности. «Космография» аль-Казвини — выдающееся сочинение своего времени. Благодаря ему ученые часто сравнивают аль-Казвини с «отцом истории» Геродотом и Плинием Великим, написавшим энциклопедию природных и искусственных предметов и явлений.
Еще одно сочинение аль-Казвини пользуется большой популярностью — «Достопамятности стран и сообщения о рабах Аллаха», которое еще известно под названием «Чудеса стран». В географическом сочинении аль-Казвини подробно описывает разделение земли на семь материков, различные регионы, города, горы, острова, озера и реки. Вместе с тем в нем присутствуют некоторые исторические сводки, включая биографии известных людей того времени.
Книга включает в себя три части. Первая часть проливает свет на необходимость создания городов и деревень. Во второй части приводятся характеристики стран и описывается влияние окружающей среды на население, минералы, растения и животных. А в третьей части приводится описание различных земель, известных в то время. Кроме того, в книге есть информация о народах, переводы ученых, писателей и султанов, а также в ней присутствуют описания торнадо, летающего дракона, гейзеров и так далее.
А в третьей части приводится описание различных земель, известных в то время. Кроме того, в книге есть информация о народах, переводы ученых, писателей и султанов, а также в ней присутствуют описания торнадо, летающего дракона, гейзеров и так далее.
Аль-Казвини поделился своими впечатлениями о Леванте и Ираке, а также о том, что он слышал, видел или читал в различных книгах, включая «Выдержки из новостей Андалусии» Ибн Хайяна аль-Куртуби и «Сокровища достоинств жителей полуострова» Ибн Бассама аш-Шантарини. Кроме того, он вставил в книгу выдержки из путевых заметок путешественников, среди которых путешествие Абу Далфа аль-Хазраджи в Китай и Индию. К слову, книга «Чудеса стран» была издана немецким востоковедом Фердинандом Вюстенфельдом во второй половине XIX века.
Все книги аль-Казвини снабжены не только астрономическими формулами и таблицами, но и небольшими рисунками, а в его в рукописях даже есть круглая карта мира. Аль-Казвини покинул этот мир в 1283 году, но он успел оставить бесценное научное наследие миру.
«Как доказать, что земля шар?» — Яндекс Кью
Андрей Кулаков · ·
62,2 K
Илья Левин
Программирование
программист, предприниматель · 4 янв 2017
Первым это сделал Аристотель, сделав очень простое наблюдение. Всякий раз, когда Земля отбрасывает тень на Луну, эта тень имеет круглую форму. Единственное тело, способное оставлять последовательно круглую тень — сфера. Ч.т.д.
Второй довольно простой вариант — понаблюдать за парусниками, удаляющимися в море (парусниками, потому, что у них мачты высокие).
Ну и еще много способов наблюдения.
37 оценили
·
16,2 K
Александр Боронников
21 февр 2020
Плоскоземельцам, которые не обладают знаниями в области физики, доказать ничего невозможно. Любой аругмент будет… Читать дальше
Любой аругмент будет… Читать дальше
Комментировать ответ…Комментировать…
Антон Фурс
Физика
программист, интересны квантовая механика, теория… · 21 июн 2020
Это доказал ещё Эратосфен в древней Греции с помощью отбрасываемой палкой тени. Более того, он достаточно неплохо сумел вычислить размеры Земли, не сильно ошибся. А вы не можете? О_о. Как сильно скатились знания людей со времён… Читать далее
23 оценили
·
7,9 K
Константин
1 окт 2020
Чем больше палок, тем больше людей😊🤭 которые так же будут задавать эти вопросы подобны нашим. Вот она теория)
Комментировать ответ…Комментировать…
Андрей Ларионов
Топ-автор
пользователь TheQuestion. · 4 янв 2017
Если не летать в космос, то возможен такой эксперимент:
Как можно доказать, что Земля круглая, кроме как посмотреть на неё из космоса?
4 оценили
·
702
Алиса из сегодня
10 сент 2020
По-моему, что Земля круглая, можно определить по расстоянию до горизонта. Ведь мы не видим дальше горизонта, не… Читать дальше
Ведь мы не видим дальше горизонта, не… Читать дальше
Комментировать ответ…Комментировать…
Виктор Брыксин
пенсионер
· 11 мая 2021
Уже доказано, что Земля не шар в точном математическом смысле. Земля в нулевом приближении шар. Это обнаружили уже древние. В настоящее время для целей геодезии, картографии и космонавтики принята модель шарообразной Земли… Читать далее
3 оценили
·
219
Комментировать ответ…Комментировать…
Борис Попов
интеллектуал. дизайнер. меломан. мизантроп. · 4 янв 2017
Самые «очевидные» доказательства — это суточный цикл (по причине вращения Земли вокруг собственной оси) и годовой цикл (по причине наклона оси Земли относительно эклиптики). Правда, они становятся очевидными уже после… Читать далее
5 оценили
·
751
Тяптяп Тяптяп
4 янв 2017
Как сумерки доказывают шарообразность Земли?
Комментировать ответ…Комментировать…
Green Wood
Green Wood · 8 окт 2020
Прямых доказательств нет. А на основе имеющейся теории этого сделать практически невозможно — всегда остаётся масса вопросов, как в случае с гироскопом, например, или дальностью прямой видимости…
А на основе имеющейся теории этого сделать практически невозможно — всегда остаётся масса вопросов, как в случае с гироскопом, например, или дальностью прямой видимости…
12 оценили
·
559
Александр Боронников
24 нояб 2020
> А на основе имеющейся теории этого сделать практически невозможно
Если ты не знаешь, как это сделать так и пиши… Читать дальше
Комментировать ответ…Комментировать…
Eugene Pankovets
Химик · 4 янв 2017
А еще, на всякий случай, Земля не шар, а немного эллипс.
Доказательства этому можно узнать в школьном курсе географии, где даются теории различных времен о строении мира.
5 оценили
·
642
Борис Попов
4 янв 2017
Тогда уж эллипсоид. 8)
8)
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
3 ответа скрыто(Почему?)
Переосмысление Эратосфена | Ответы в Бытие
В дискуссиях о том, плоская ли земля, часто всплывает работа Эратосфена. Как я уже отмечал ранее, многие люди неправильно понимают знаменитый эксперимент Эратосфена. Это распространенное заблуждение, что Эратосфен доказал, что Земля является шаром. Во времена Эратосфена на Западе уже было общеизвестно, что Земля есть шар. Эратосфен использовал это знание для измерения окружности Земли и, следовательно, ее радиуса.
Хотя существует некоторая неопределенность в отношении единицы измерения, которую использовал Эратосфен, его измерение размера Земли близко к современному принятому значению.
Как Эратосфен сделал это? Угол, который любой объект в небе образует с горизонтом, называется высотой .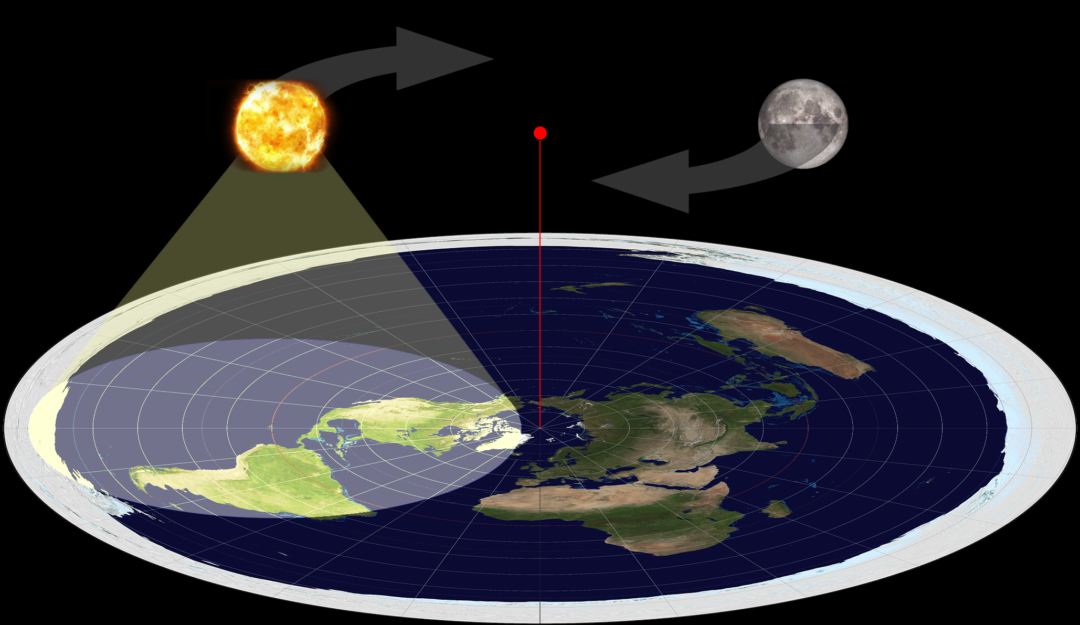 Высота колеблется от 0° (на горизонте) до 90° (в зените, точка прямо над головой). С другой стороны, мы могли бы выразить это понятие как зенитный угол 9000° астрономического тела , дополнение его высоты. Если Земля представляет собой шар, то высота солнца в полдень в определенный день будет зависеть от того, насколько далеко на север или на юг он находится. Следовательно, если в один и тот же день измерить высоту (или зенитное расстояние) полуденного солнца в двух точках, разнесенных в направлении север-юг, можно вычислить размер Земли при условии, что известно расстояние между двумя точками. Именно это и сделал Эратосфен. Хотя существует некоторая неопределенность в отношении единицы измерения, которую использовал Эратосфен, его измерение размера Земли близко к современному принятому значению.
Высота колеблется от 0° (на горизонте) до 90° (в зените, точка прямо над головой). С другой стороны, мы могли бы выразить это понятие как зенитный угол 9000° астрономического тела , дополнение его высоты. Если Земля представляет собой шар, то высота солнца в полдень в определенный день будет зависеть от того, насколько далеко на север или на юг он находится. Следовательно, если в один и тот же день измерить высоту (или зенитное расстояние) полуденного солнца в двух точках, разнесенных в направлении север-юг, можно вычислить размер Земли при условии, что известно расстояние между двумя точками. Именно это и сделал Эратосфен. Хотя существует некоторая неопределенность в отношении единицы измерения, которую использовал Эратосфен, его измерение размера Земли близко к современному принятому значению.
Поскольку Эратосфен уже знал, что Земля представляет собой шар, сторонники плоской Земли правы, когда утверждают, что Эратосфен не доказал, что Земля является шаром. Плоскоземельцы также часто говорят, что эксперимент Эратосфена можно объяснить на плоской Земле. Это тоже верно. Но это объяснение имеет последствия. Если Земля представляет собой шар, то эксперимент Эратосфена можно использовать для измерения размеров Земли. Но если земля плоская, эксперимент Эратосфена можно использовать для измерения того, насколько высоко над плоской землей находится солнце. Давайте сравним результаты.
Это тоже верно. Но это объяснение имеет последствия. Если Земля представляет собой шар, то эксперимент Эратосфена можно использовать для измерения размеров Земли. Но если земля плоская, эксперимент Эратосфена можно использовать для измерения того, насколько высоко над плоской землей находится солнце. Давайте сравним результаты.
Оригинальный эксперимент Эратосфена
Эратосфен жил в Александрии, Египет, 22 века назад. Он работал в расположенной там знаменитой Великой библиотеке. Александрия была логичным выбором для размещения Великой библиотеки, потому что в то время она была центром греческой культуры и образования. Эратосфен однажды путешествовал в Сиену на юге Египта, так назывался в то время современный город Асуан. Эратосфен заметил, что солнце было прямо над головой в полдень июньского солнцестояния. Это потому, что Сиена/Асуан находится на тропике Рака, самом северном краю тропиков. Солнце находится прямо над головой в местный полдень июньского солнцестояния во всех местах тропика Рака. Поскольку Александрия находится примерно в 500 милях от тропиков, солнце там никогда не бывает над головой. Эратосфен понял, что это наблюдение дало возможность измерить размеры Земли. Вернувшись в Александрию, Эратосфен построил гномон, вертикальный шест известной высоты над плоской поверхностью. В следующем году Эратосфен измерил длину тени гномона в местный полдень июньского солнцестояния (рис. 1). Если бы гномон имел высоту ×, а тень имела длину y , тогда зенитный угол θ был равен арктангенсу ( y / x ). Эратосфен обнаружил, что зенитный угол солнца составляет 1/50 окружности, или 7,2°.
Поскольку Александрия находится примерно в 500 милях от тропиков, солнце там никогда не бывает над головой. Эратосфен понял, что это наблюдение дало возможность измерить размеры Земли. Вернувшись в Александрию, Эратосфен построил гномон, вертикальный шест известной высоты над плоской поверхностью. В следующем году Эратосфен измерил длину тени гномона в местный полдень июньского солнцестояния (рис. 1). Если бы гномон имел высоту ×, а тень имела длину y , тогда зенитный угол θ был равен арктангенсу ( y / x ). Эратосфен обнаружил, что зенитный угол солнца составляет 1/50 окружности, или 7,2°.
Рисунок 1
На рисунке 2 показано, как Эратосфен использовал эту информацию для определения окружности Земли. Мало того, что люди во времена Эратосфена знали, что Земля представляет собой шар, но они также понимали, что расстояние до Солнца намного больше, чем радиус Земли. Поэтому Эратосфен предположил, что солнце находится достаточно далеко, чтобы направление на солнце в одном месте на земле было почти параллельно направлению на солнце в любом другом месте. Плоскоземельцы, вероятно, возразят, что линии не параллельны, и таким образом опровергнут результат Эратосфена. Давайте рассмотрим это утверждение. Если солнце 93 миллиона миль, то угол между двумя линиями, направленными к солнцу из двух точек на поверхности земли, находящихся на расстоянии 500 миль друг от друга, не превышает 0,0003°. Эратосфен не мог измерить такой маленький угол. Угол, который он измерил, был в 24 000 раз больше этого. Предположение, что линии параллельны, внесло ошибку 0,004%. Поэтому данное возражение является необоснованным.
Плоскоземельцы, вероятно, возразят, что линии не параллельны, и таким образом опровергнут результат Эратосфена. Давайте рассмотрим это утверждение. Если солнце 93 миллиона миль, то угол между двумя линиями, направленными к солнцу из двух точек на поверхности земли, находящихся на расстоянии 500 миль друг от друга, не превышает 0,0003°. Эратосфен не мог измерить такой маленький угол. Угол, который он измерил, был в 24 000 раз больше этого. Предположение, что линии параллельны, внесло ошибку 0,004%. Поэтому данное возражение является необоснованным.
Рисунок 2
Из рисунка 2 видно, что, поскольку направления на солнце из двух мест практически параллельны, зенитный угол, θ , также должен быть углом между Александрией (точка A) и Сиеной (точка B), измеренным в центре Земли. Мы бы сказали, что этот угол представляет собой разницу в широте между двумя городами. Поскольку θ составляет 1/50 окружности, то длина дуги s между двумя городами должна составлять 1/50 окружности Земли. Следовательно, длина окружности Земли должна быть 50×s. Эратосфен был отцом географии, поэтому он знал расстояние s между двумя городами. Он использовал греческую единицу измерения расстояния, называемую стадионом, но мы можем использовать современное расстояние между двумя городами, 500 миль. Умножив 50 на 500 миль, мы получим 25 000 миль окружности Земли. Это находится в пределах 0,5% от современного принятого значения окружности земли.
Следовательно, длина окружности Земли должна быть 50×s. Эратосфен был отцом географии, поэтому он знал расстояние s между двумя городами. Он использовал греческую единицу измерения расстояния, называемую стадионом, но мы можем использовать современное расстояние между двумя городами, 500 миль. Умножив 50 на 500 миль, мы получим 25 000 миль окружности Земли. Это находится в пределах 0,5% от современного принятого значения окружности земли.
Переосмысление результата Эратосфена
Теперь давайте переинтерпретируем эксперимент Эратосфена, предполагая, что Земля плоская (рис. 3). Если солнце находится на высоте ч над землей, и если ч не слишком велико по сравнению с размером Земли, то высота солнца будет разной при измерении в одно и то же время в разных местах. Как и раньше, Александрия находится в точке А, а Сиена — в точке В, расстояние между ними s. Солнце находится прямо над головой в точке B, и солнце будет иметь зенитный угол θ в точке А.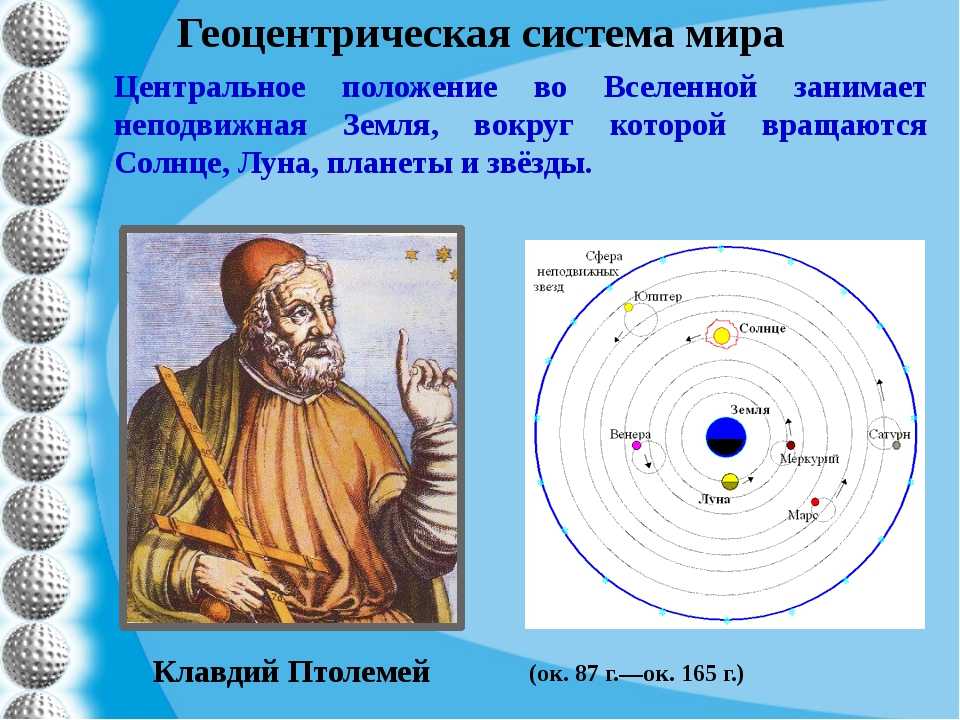 Пусть ч будет высотой солнца над плоской землей. Затем
Пусть ч будет высотой солнца над плоской землей. Затем
Рисунок 3
Подставляя значения, получаем, что ч = 3958 миль. Выраженное тремя значащими цифрами, это 3960 миль; до двух значащих цифр это 4000 миль. Я обнаружил, что современные плоскоземельцы избегают каких-либо мнений относительно высоты солнца, но если они высказывают мнение, то цифра в диапазоне 3 000–4 000 миль является обычной. Эта цифра, вероятно, связана с этой новой интерпретацией эксперимента Эратосфена. .
Мой собственный эксперимент типа Эратосфена
В полдень по местному времени в среду, 9 декабря, я провел эксперимент типа Эратосфена, за исключением того, что я сделал это незадолго до декабрьского солнцестояния, до которого оставалось менее двух недель. Ближе к любому солнцестоянию склонение солнца2 не сильно меняется каждый день. Например, во время моего эксперимента склонение солнца составляло около -22° 53′, что находится в пределах 33′ (0,55°) от минимального склонения солнца в декабрьское солнцестояние 12 дней спустя. Поскольку ежедневные изменения склонения Солнца в период солнцестояния так малы, проведение эксперимента типа Эратосфена вблизи одного из солнцестояний более снисходительно, чем в любое другое время года. Поэтому наиболее целесообразно проводить такого рода эксперименты вблизи одного из солнцестояний. В Северном полушарии преимущество делать это ближе к декабрьскому солнцестоянию, а не к июньскому солнцестоянию, заключается в том, что с более длинными тенями можно с большей точностью измерить зенитное расстояние.
Поскольку ежедневные изменения склонения Солнца в период солнцестояния так малы, проведение эксперимента типа Эратосфена вблизи одного из солнцестояний более снисходительно, чем в любое другое время года. Поэтому наиболее целесообразно проводить такого рода эксперименты вблизи одного из солнцестояний. В Северном полушарии преимущество делать это ближе к декабрьскому солнцестоянию, а не к июньскому солнцестоянию, заключается в том, что с более длинными тенями можно с большей точностью измерить зенитное расстояние.
Склонение солнца во время моего эксперимента очень хорошо округляется до 23°. Это означает, что солнце было прямо над головой в полдень на 23° южной широты, когда я проводил свой эксперимент. Обратите внимание, что это верно независимо от того, плоская земля или шар. Очевидно, я не смог подтвердить, действительно ли солнце было над головой на 23° южной широты в полдень в тот день, но я уверен, что это так, и я уверен, что большинство плоскоземельцев согласится с этим. Вопрос в следующем. , каково расстояние между 39-й -й параллели, где я живу, и 23-й южной параллели? Обычно считается, что между каждым градусом разницы широты 69 статутных миль. Следовательно, расстояние от того места, где я живу, и ближайшего места, где солнце было прямо над головой в полдень того дня, составляет (39 + 23) × 69 миль = 4278 миль. Если плоскоземельцы захотят оспорить, что на каждый градус широты приходится 69 миль, то я буду счастлив пересчитать свои результаты для любого преобразования, которое они предпочитают.
Вопрос в следующем. , каково расстояние между 39-й -й параллели, где я живу, и 23-й южной параллели? Обычно считается, что между каждым градусом разницы широты 69 статутных миль. Следовательно, расстояние от того места, где я живу, и ближайшего места, где солнце было прямо над головой в полдень того дня, составляет (39 + 23) × 69 миль = 4278 миль. Если плоскоземельцы захотят оспорить, что на каждый градус широты приходится 69 миль, то я буду счастлив пересчитать свои результаты для любого преобразования, которое они предпочитают.
На рисунке 4 показано мое оборудование. Я прикрепил линейку к боковой части деревянного ящика и поставил ящик на ровную поверхность. Это устройство удерживало линейку перпендикулярно земле. Я использовал рулетку, чтобы записать длину тени линейки в местный полдень (рис. 5). Как видите, длина тени составила 65,5 дюймов. Чтобы убедиться, что это минимальная длина тени в течение дня, я провел измерения в течение более получаса около полудня по местному времени (также с учетом уравнения времени). Высота солнца, θ, представляет собой арктангенс 36/65,5 = 28,8 градуса. Следовательно, зенитный угол солнца в местный полдень составлял 61,2 градуса. Используя те же рассуждения, что и Эратосфен, окружность Земли равна (360/61,2) × 4 278 миль = 25 162 мили. С точностью до двух значащих цифр это 25 000 миль, что соответствует результату Эратосфена. С точностью до трех значащих цифр это 25 200 миль. Это находится в пределах 1% от значения Эратосфена и в пределах 1,2% от современной окружности земли. Учитывая вероятные ошибки моего измерения, это хорошее совпадение.
Высота солнца, θ, представляет собой арктангенс 36/65,5 = 28,8 градуса. Следовательно, зенитный угол солнца в местный полдень составлял 61,2 градуса. Используя те же рассуждения, что и Эратосфен, окружность Земли равна (360/61,2) × 4 278 миль = 25 162 мили. С точностью до двух значащих цифр это 25 000 миль, что соответствует результату Эратосфена. С точностью до трех значащих цифр это 25 200 миль. Это находится в пределах 1% от значения Эратосфена и в пределах 1,2% от современной окружности земли. Учитывая вероятные ошибки моего измерения, это хорошее совпадение.
Рисунок 4
Рисунок 5
Какая высота солнца приводит к новой интерпретации моего результата, если предположить, что Земля плоская? Как и при новой интерпретации первоначального эксперимента Эратосфена, высота Солнца будет
. При s = 4278 миль и θ = 28,8° мы находим, что h = 2352 мили. Выраженное до трех значащих цифр, это 2350 миль; до двух значащих цифр это 2400 миль. Обратите внимание, что это на 1600 миль меньше, чем результат оригинального эксперимента Эратосфена, переосмысленного с точки зрения плоской Земли, разница составляет 40%. Сравните это с очень небольшой разницей в измерении размеров Земли, предполагая, что Земля представляет собой шар. Когда возникают большие отклонения между экспериментальными результатами, это происходит потому, что существует фундаментальная проблема. Наиболее вероятное объяснение состоит в том, что Земля не плоская. Поскольку эксперимент дает непротиворечивые результаты, предполагая, что Земля представляет собой шар, этот эксперимент является подтверждением модели шара. Обратите внимание, что один эксперимент типа Эратосфена не может быть использован в качестве доказательства того, что Земля является шаром, но несколько тестов, проведенных на разных расстояниях, являются доказательством того, что Земля является шаром.
Сравните это с очень небольшой разницей в измерении размеров Земли, предполагая, что Земля представляет собой шар. Когда возникают большие отклонения между экспериментальными результатами, это происходит потому, что существует фундаментальная проблема. Наиболее вероятное объяснение состоит в том, что Земля не плоская. Поскольку эксперимент дает непротиворечивые результаты, предполагая, что Земля представляет собой шар, этот эксперимент является подтверждением модели шара. Обратите внимание, что один эксперимент типа Эратосфена не может быть использован в качестве доказательства того, что Земля является шаром, но несколько тестов, проведенных на разных расстояниях, являются доказательством того, что Земля является шаром.
История плоскоземельных измерений высоты Солнца
Рисунок 6
Сэмюэл Роуботам был основателем движения плоской Земли. В 1865 году, писавший под псевдонимом Параллакс, Роуботэм сделал попытку своего первого измерения высоты солнца над землей. Роуботэм утверждал: «Таким образом, расстояние будет значительно меньше 4000 миль». Роуботэм не привел расчетов для этого вывода, хотя это достаточно легко сделать. Рисунок 6 представляет собой адаптацию рисунка 26 Роуботама. Солнце находится прямо над 9-м горизонтом.0007 подсолнечной точки C. В тот же момент, когда солнце находится над точкой C, измерьте высоту солнца θ 1 в точке A и высоту солнца θ 2 в точке B. Пусть d — расстояние между точками A и B, пусть s — расстояние между точками B и C, а h — высота солнца над землей. Если известны углы θ 1 и θ 2 и расстояние d , затем h и s — единственные неизвестные. С помощью базовой тригонометрии и алгебры можно решить для обоих неизвестных. Так как в точке C прямой угол, то
Роуботэм не привел расчетов для этого вывода, хотя это достаточно легко сделать. Рисунок 6 представляет собой адаптацию рисунка 26 Роуботама. Солнце находится прямо над 9-м горизонтом.0007 подсолнечной точки C. В тот же момент, когда солнце находится над точкой C, измерьте высоту солнца θ 1 в точке A и высоту солнца θ 2 в точке B. Пусть d — расстояние между точками A и B, пусть s — расстояние между точками B и C, а h — высота солнца над землей. Если известны углы θ 1 и θ 2 и расстояние d , затем h и s — единственные неизвестные. С помощью базовой тригонометрии и алгебры можно решить для обоих неизвестных. Так как в точке C прямой угол, то
и
Исключить h , приравняв эти два уравнения, а затем решить для s :
Решив третье уравнение для s , значение s можно подставить в любое из первых двух уравнений, чтобы найти h .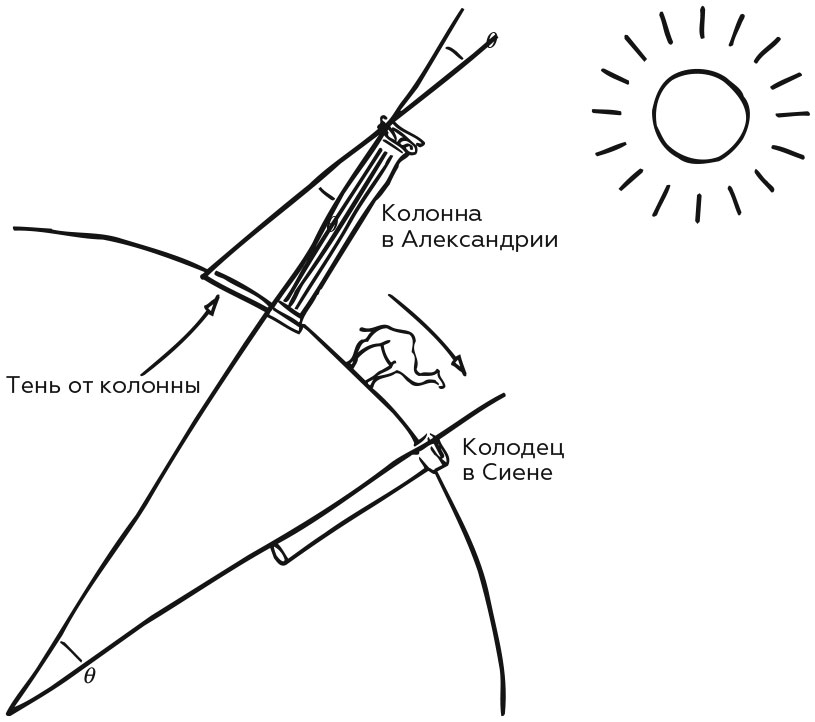
Роуботэм предположил, что если такой эксперимент провести в Лондоне и в 51 миле к югу в Брайтоне, то «высота солнца окажется значительно меньше 4000 миль». Роуботэм, по-видимому, не проводил этот эксперимент, поскольку не предоставил никаких данных. Однако он предоставил данные таких измерений, проведенных Ordnance Survey (национальным картографическим агентством Великобритании) в двух других местах (Лондон и Акворт, 151 миля к северу от Лондона) в неустановленный день и время:0133
θ 1 = 53° 02′
θ 2 = 55° 13′
d = 151 миля
Подставляя соответствующие значения в третье уравнение выше, я нахожу s = 1806 миль. Подставив это обратно в любое из первых двух уравнений, мы получим ч = 2600 миль. Конечно, это «менее 4000 миль», но почему Роуботэм вместо этого не сказал, что это было менее 3000 миль? Так выразилось бы большинство людей. Характеризовать 2600 миль как «менее 4000 миль» в лучшем случае вводит в заблуждение.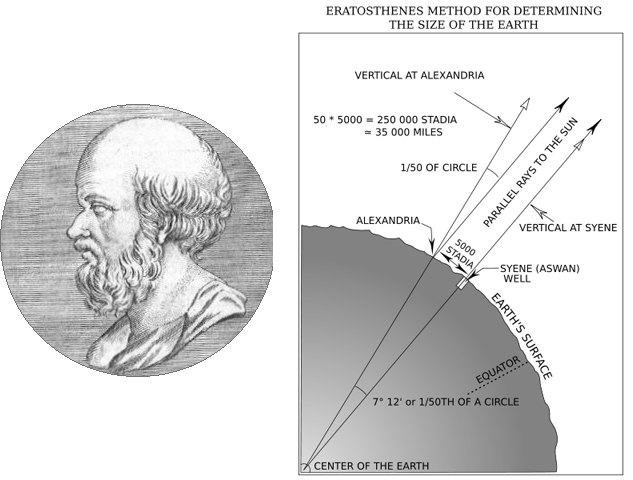 Могло ли случиться так, что Роуботам переосмыслил эксперимент Эратосфена, как это сделал я выше, и хотел, чтобы его новые вычисления соответствовали этому результату? Если да, то почему он не сказал об этом?
Могло ли случиться так, что Роуботам переосмыслил эксперимент Эратосфена, как это сделал я выше, и хотел, чтобы его новые вычисления соответствовали этому результату? Если да, то почему он не сказал об этом?
Роуботэм привел еще один пример с данными, снова предоставленными Управлением боеприпасов:
θ 1 = 38°
θ 2 = 45°
d = 800 миль
Обратите внимание, что этим измерениям не хватает точности предыдущего набора данных. Используя эти измерения в трех приведенных выше уравнениях, я получаю ч и с , равные 2858 милям. Это на 9,5% отличается от первого примера. Роуботэм снова пришел к выводу, что результат «менее 4000 миль».
В своей второй книге, теперь уже под своим именем, Роуботэм вернулся к своему гипотетическому эксперименту между Лондоном и Брайтоном, проведенному в полдень 13 июля 1870 года, и пришел к выводу, что Солнце находится на высоте 700 миль над землей5. Роуботэм предоставил эти измерения: 90 133
Лондон: θ 1 = 61°
Брайтон: θ 2 = 64°
d = 50 миль
Обратите внимание, что Роуботэм изменил расстояние с 51 мили на 50 миль, но это незначительная разница. В отличие от своей предыдущей книги, Роуботэм объяснил, как он измерил ч и с . Он решил путем построения, сделав масштабную диаграмму (его рисунок 58) и измерив эти длины. Почему Роуботэм не использовал тригонометрию и алгебру, как это сделал я выше? Сразу приходят на ум два варианта. Возможно, Роуботэму не хватало этих математических навыков, а может быть, он боялся, что его читателям не хватает этих навыков. Используя измерения Роуботама, я нахожу s = 366 миль. Это расстояние от Брайтона до подсолнечной точки. Поскольку расстояние между Лондоном и Брайтоном составляет 50 миль, подсолнечная точка находится на расстоянии 366 миль + 50 миль = 416 миль от Лондона. Роуботэм сказал, что это расстояние составляло 400 миль, ошибка всего 3,8%. Учитывая, что он решил задачу построением и возможностью округления с его стороны, это хорошее согласие. Для высоты солнца ч , я проехал 751 милю, что близко к 700 милям Роуботама. Это ошибка 6,8%, но, опять же, учитывая, что Роуботэм решил построением и включением округления, это хорошее совпадение.
В отличие от своей предыдущей книги, Роуботэм объяснил, как он измерил ч и с . Он решил путем построения, сделав масштабную диаграмму (его рисунок 58) и измерив эти длины. Почему Роуботэм не использовал тригонометрию и алгебру, как это сделал я выше? Сразу приходят на ум два варианта. Возможно, Роуботэму не хватало этих математических навыков, а может быть, он боялся, что его читателям не хватает этих навыков. Используя измерения Роуботама, я нахожу s = 366 миль. Это расстояние от Брайтона до подсолнечной точки. Поскольку расстояние между Лондоном и Брайтоном составляет 50 миль, подсолнечная точка находится на расстоянии 366 миль + 50 миль = 416 миль от Лондона. Роуботэм сказал, что это расстояние составляло 400 миль, ошибка всего 3,8%. Учитывая, что он решил задачу построением и возможностью округления с его стороны, это хорошее согласие. Для высоты солнца ч , я проехал 751 милю, что близко к 700 милям Роуботама. Это ошибка 6,8%, но, опять же, учитывая, что Роуботэм решил построением и включением округления, это хорошее совпадение. Поэтому мы можем быть уверены, что Роуботэм правильно определил s и h на основе своих данных. Далее Роуботэм высказал мнение, что рассмотрение атмосферной рефракции позволяет «совершенно безопасно утверждать, что нижний край Солнца находится значительно меньше, чем 700 статутных миль над землей», хотя он не обосновал этот вывод. Далее Роуботэм утверждал, что, основываясь на других, неуказанных экспериментах, Луна находится ниже этой отметки и что звезды находятся не более чем в 1000 миль над Землей.
Поэтому мы можем быть уверены, что Роуботэм правильно определил s и h на основе своих данных. Далее Роуботэм высказал мнение, что рассмотрение атмосферной рефракции позволяет «совершенно безопасно утверждать, что нижний край Солнца находится значительно меньше, чем 700 статутных миль над землей», хотя он не обосновал этот вывод. Далее Роуботэм утверждал, что, основываясь на других, неуказанных экспериментах, Луна находится ниже этой отметки и что звезды находятся не более чем в 1000 миль над Землей.
Роуботэм правильно нашел значения s и h, но насколько разумен его результат?
Роуботам правильно нашел значения s и h , но насколько разумен его результат? Эксперимент Роуботама поместил подсолнечную точку в 400 милях к югу от Лондона. Но 400 миль к югу от Лондона — это небольшое расстояние к северо-востоку от Бордо, Франция, около 45 й северной параллели. Это более чем на 20° к северу от тропиков, поэтому солнце там никогда не бывает прямо над головой. Очевидно, что измерения высоты солнца Роуботама были неправильными. На дату, указанную Роуботэмом, я ожидаю, что в Лондоне полуденное солнце будет иметь высоту около 60°, что близко к заявленным Роуботэмом 61°. Однако, поскольку Брайтон находится всего в 50 милях к югу от Лондона, я ожидаю, что высота солнца в полдень там будет меньше, чем на градус, чем высота солнца в полдень в Лондоне, а не на 64°. Таким образом, измерения Роуботама в Брайтоне явно были ошибочными. Тот факт, что рассчитанное Роуботамом расстояние между Лондоном и подсолнечной точкой было смехотворно слишком коротким, должен был указывать на то, что он ошибался. Однако нет никаких доказательств того, что Роуботэм это видел. Будут ли современные плоскоземельцы считать это проблемой?
Очевидно, что измерения высоты солнца Роуботама были неправильными. На дату, указанную Роуботэмом, я ожидаю, что в Лондоне полуденное солнце будет иметь высоту около 60°, что близко к заявленным Роуботэмом 61°. Однако, поскольку Брайтон находится всего в 50 милях к югу от Лондона, я ожидаю, что высота солнца в полдень там будет меньше, чем на градус, чем высота солнца в полдень в Лондоне, а не на 64°. Таким образом, измерения Роуботама в Брайтоне явно были ошибочными. Тот факт, что рассчитанное Роуботамом расстояние между Лондоном и подсолнечной точкой было смехотворно слишком коротким, должен был указывать на то, что он ошибался. Однако нет никаких доказательств того, что Роуботэм это видел. Будут ли современные плоскоземельцы считать это проблемой?
Несколько других плоскоземельцев эпохи Роуботама предоставили свои собственные оценки высоты солнца. Например, в 1893 году Александр Глисон пришел к выводу, что и Солнце, и Полярная звезда находятся на высоте 1725 миль над землей. Глисон сделал это, используя очень запутанную методологию, но он не сомневался в ее правильности. Как путается? Глисон заявил, что существует «60 миль на градус». Это относится к морским милям, но не к статутным милям (на градус приходится 69 статутных миль, при этом одна морская миля равна 1,1528 статутных миль). Большинство людей, читающих книгу Глисона, думают об статутных милях, а не о морских милях, так что это в лучшем случае сбивает с толку. Если не указано иное или в морском контексте, обычно понимается, что термин «миля» относится к статутным милям, а не к морским милям. Подозреваю, что Глисон не заметил разницы. С этого момента аргументация Глисона пошла под откос, и я не мог ее следовать. Например, на Рисунке 25 Глисона, по-видимому, 2 × 1725 миль = 3450 миль между экватором и Северным полюсом, но, поскольку он уже сказал, что на градус приходится 60 миль, а на экваторе 90 градусов от Северного полюса, то это расстояние должно быть 90 × 60 миль = 5400 миль. Преобразование между морскими и статутными милями не может исправить это.
Глисон сделал это, используя очень запутанную методологию, но он не сомневался в ее правильности. Как путается? Глисон заявил, что существует «60 миль на градус». Это относится к морским милям, но не к статутным милям (на градус приходится 69 статутных миль, при этом одна морская миля равна 1,1528 статутных миль). Большинство людей, читающих книгу Глисона, думают об статутных милях, а не о морских милях, так что это в лучшем случае сбивает с толку. Если не указано иное или в морском контексте, обычно понимается, что термин «миля» относится к статутным милям, а не к морским милям. Подозреваю, что Глисон не заметил разницы. С этого момента аргументация Глисона пошла под откос, и я не мог ее следовать. Например, на Рисунке 25 Глисона, по-видимому, 2 × 1725 миль = 3450 миль между экватором и Северным полюсом, но, поскольку он уже сказал, что на градус приходится 60 миль, а на экваторе 90 градусов от Северного полюса, то это расстояние должно быть 90 × 60 миль = 5400 миль. Преобразование между морскими и статутными милями не может исправить это.
Глисон продолжал:
Некоторые зететики давали высоту солнца 2500, 3500, а некоторые даже меньше, чем я дал. С помощью какого процесса они пришли к различным результатам, я не знаю, но я не знаю никакого другого геометрического процесса, кроме последнего из приведенных здесь.
Противоречивые результаты должны были свидетельствовать о том, что в действиях Глисона и других плоскоземельцев того времени было что-то ужасно неправильное.
Как я уже сказал, Глисон, казалось, не сомневался в правильности своего метода, но он даже не стал объяснять, почему существует большой разброс в оценках высоты Солнца в рамках модели плоской Земли. . Опять же, противоречивые результаты должны были указывать на то, что в том, что делали Глисон и другие плоскоземельцы того времени, было что-то ужасно неправильное.
В 1899 году Томас Уиншип использовал метод, аналогичный методу Глисона, для измерения высоты солнца. Уиншип правильно заявил, что в дни равноденствия солнце находится прямо над головой в полдень на экваторе и что солнце находится на высоте 45° на экваторе.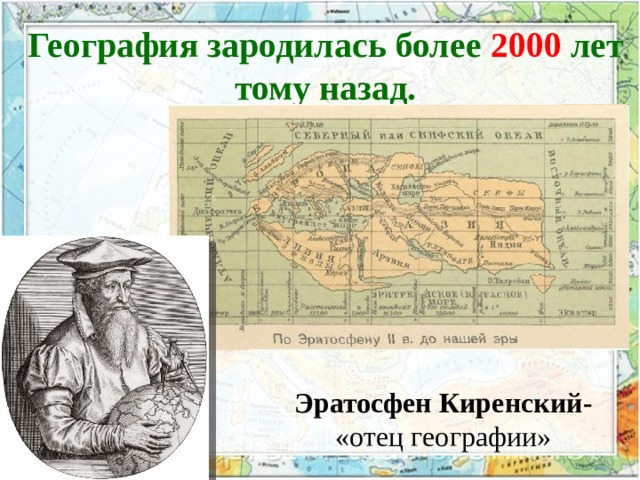 полдень в местах на 45° северной широты и 45° южной широты. Это то, что ожидается, если Земля представляет собой шар, а Солнце находится намного дальше, чем радиус Земли. Однако, как и в случае с экспериментом Эратосфена, можно интерпретировать это наблюдение с точки зрения плоской Земли, как это сделал Уиншип. Уиншип рассудил, что если Земля плоская, то расстояние от 45 -й , параллельный экватору, является одной стороной треугольника 45-45-90, а другая сторона является высотой солнца. Стороны треугольника 45-45-90 имеют одинаковую длину, поэтому высота солнца должна быть равна расстоянию между 45-й параллели и экватором. Утверждая, что «60 географических миль = 1 градус», Уиншип пришел к выводу, что Солнце находится на высоте 45 × 60 географических миль = 2700 географических миль над землей. «Географическая миля» — это альтернативный термин для морской мили, поэтому расчеты Winship таковы, что солнце находится на высоте 3113 статутных миль над землей. Мы можем округлить это до 3110 или 3100 миль.
полдень в местах на 45° северной широты и 45° южной широты. Это то, что ожидается, если Земля представляет собой шар, а Солнце находится намного дальше, чем радиус Земли. Однако, как и в случае с экспериментом Эратосфена, можно интерпретировать это наблюдение с точки зрения плоской Земли, как это сделал Уиншип. Уиншип рассудил, что если Земля плоская, то расстояние от 45 -й , параллельный экватору, является одной стороной треугольника 45-45-90, а другая сторона является высотой солнца. Стороны треугольника 45-45-90 имеют одинаковую длину, поэтому высота солнца должна быть равна расстоянию между 45-й параллели и экватором. Утверждая, что «60 географических миль = 1 градус», Уиншип пришел к выводу, что Солнце находится на высоте 45 × 60 географических миль = 2700 географических миль над землей. «Географическая миля» — это альтернативный термин для морской мили, поэтому расчеты Winship таковы, что солнце находится на высоте 3113 статутных миль над землей. Мы можем округлить это до 3110 или 3100 миль.
Шаг вперед по методу Уиншипа
Было бы интересно, если бы Уиншип применил это рассуждение к одному из солнцестояний, а не только к равноденствиям (таким образом, делая эксперимент типа Эратосфена, как я сделал выше). Например, в полдень июньского солнцестояния солнце будет иметь высоту 68,4° на 45° северной широты. Между тем, солнце будет находиться прямо над головой в полдень на 23,4° северной широты. Это разница в расстоянии (45 – 23,4) × 60 морских миль = 1,29.6 морских миль. Высота Солнца составит 1296 морских миль × тангенс (68,4°) = 3273 морских мили = 3773 статутных мили. Это на 660 статутных миль больше, чем заявлено Winship. Если рассмотреть тот же эксперимент в полдень декабрьского солнцестояния на 45° южной широты, то ситуация будет такой же с тем же вычислением высоты солнца.
Но что, если мы проделаем тот же эксперимент на 45° с противоположным солнцестоянием? То есть, что, если бы мы провели этот эксперимент в полдень в день декабрьского солнцестояния на 45° северной широты или в день июньского солнцестояния на 45° южной широты? Солнце будет иметь высоту 21,6 °, а разница в расстоянии составит (45 + 23,4) × 60 морских миль = 4 104 морских мили. Это приводит к тому, что высота солнца составляет 4104 морских мили × тангенс (21,6°) = 1625 морских миль = 1873 статутных мили, что на 1240 миль меньше результата Уиншипа.
Это приводит к тому, что высота солнца составляет 4104 морских мили × тангенс (21,6°) = 1625 морских миль = 1873 статутных мили, что на 1240 миль меньше результата Уиншипа.
Конечно, я не измерял высоту солнца на 45° широты ни в день солнцестояния, но имейте в виду, что Winship фактически не измерял высоту солнца. Вместо этого я вычислил высоту солнца по времени, дате и широте, используя модель земного шара. Это было равносильно предсказанию модели земного шара, которое может проверить каждый, и я призываю других, особенно плоскоземельцев, проверить мои предсказания, сделав эти наблюдения.
А пока давайте воспользуемся высотой солнца, полученной Уиншипом, чтобы предсказать, какой должна быть высота солнца в полдень в день декабрьского солнцестояния на 45° северной широты. Расстояние между 45 ° северной широты и тропиком Козерога, где солнце находится над головой в полдень в день декабрьского солнцестояния, составляет (45 + 23,4) × 60 морских миль = 4104 морских мили. Если высота солнца составляет 2700 морских миль, то высота солнца будет арктангенсом (2700/4104) = 33,4°. Напомним, что я измерил полуденную высоту солнца на 39° северной широты около декабрьского солнцестояния и составил 28,8°. Как получается, что в полдень дня, близкого к декабрьскому солнцестоянию, солнце может быть на 4,5° выше в небе в месте, на 6° севернее того места, где я живу? Очевидный ответ: нельзя. Следовательно, с моделью Winship что-то ужасно не так. Земля не плоская.
Напомним, что я измерил полуденную высоту солнца на 39° северной широты около декабрьского солнцестояния и составил 28,8°. Как получается, что в полдень дня, близкого к декабрьскому солнцестоянию, солнце может быть на 4,5° выше в небе в месте, на 6° севернее того места, где я живу? Очевидный ответ: нельзя. Следовательно, с моделью Winship что-то ужасно не так. Земля не плоская.
Заключение
Непоследовательные результаты измерения высоты солнца указывают на то, что Земля не плоская.
Я продемонстрировал, что интерпретация различных измерений высоты солнца в предположении, что Земля плоская, приводит к сильно различающимся высотам солнца над землей. Сами плоскоземельцы получили широкий диапазон измерений высоты Солнца. Непоследовательные результаты высоты солнца указывают на то, что Земля не плоская. С другой стороны, непротиворечивые результаты измерений радиуса Земли в предположении, что Земля имеет шаровидную форму, подтверждают гипотезу о шарообразности Земли. Следовательно, шар Земли установлен наукой, в то время как наука опровергает представление о том, что Земля плоская.
Следовательно, шар Земли установлен наукой, в то время как наука опровергает представление о том, что Земля плоская.
В отличие от плоскоземельцев более века назад, современные плоскоземельцы избегают определять положение на высоте солнца над землей, потому что многие из них понимают, что если они это сделают, их высота над солнцем может быть использована для проверяемых предсказаний. . Плоскоземельцы рекламируют эксперименты, дающие результаты, которые, по их мнению, подтверждают, что Земля плоская, тем самым в их сознании доказывая, что их модель верна. Но они чрезвычайно избирательны, концентрируясь на нескольких экспериментах, которые им нравятся, и одновременно игнорируя многие другие результаты, противоречащие тому, во что они решили верить. Это не то, как работает наука.
Предыдущая статья
Эффект Кориолиса, маятник Фуко и движение плоской Земли
Следующая статья
Что происходит в 2021 году
5.4: Измерение Земли с Эратосфеном
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 31557
- Дэниел Э.
 Барт
Барт - Университет Арканзаса, Фейетвилл
Древнегреческий астроном по имени Эратосфен был первым человеком, который точно измерил размер Земли. Его метод был очень прост: он измерил угол, под которым тень отбрасывает вертикальную палку в двух разных городах в один и тот же день и время. С помощью другого учителя вы можете воссоздать эксперимент Эратосфена, а ваши ученики смогут сами измерить размер Земли! Все, что вам понадобится, это две линейки, транспортир, магнитный компас и кусок веревки.
Академические стандарты
Научная и инженерная практика
- Задавать вопросы и формулировать проблемы.
- Планирование и проведение расследований.
- Анализ и интерпретация данных.
- Использование математики.
- Построение объяснений.
- Аргумент из улик.
- Получайте, оценивайте и сообщайте информацию.

Сквозные концепции
- Масштаб, пропорции и количество.
- Системы и модели систем.
Научные стандарты следующего поколения
- Проектирование и проектирование (K-5, 6-8, 9-12).
- Система Земля-Луна (6-8, 9-12).
Для преподавателей
Факты, которые вам необходимо знать
- Окружность Земли была впервые точно измерена более 2200 лет назад греческим астрономом по имени Эратосфен.
- Метод Эратосфена был очень прост; он измерил длину тени от вертикальной палки известной высоты в двух городах в один и тот же день. Соотношение между расстоянием с севера на юг между двумя городами и измеренными углами дало соотношение, которое позволило Эратосфену рассчитать размер Земли.
Преподавание и педагогика
Это замечательный пример практической геометрии и мощное знакомство с древними культурами; это занятие не только STEM, но и межпредметное. Это распространенное заблуждение, что только потому, что культуры были древними, они должны были быть примитивными или упрощенными. Мы часто путаем технологическую сложность с обучением и знаниями. Деятельность, где учащиеся фактически работают вместе с детьми из другой школы, является живым доказательством того, что это не так.
Это распространенное заблуждение, что только потому, что культуры были древними, они должны были быть примитивными или упрощенными. Мы часто путаем технологическую сложность с обучением и знаниями. Деятельность, где учащиеся фактически работают вместе с детьми из другой школы, является живым доказательством того, что это не так.
Это упражнение также является еще одним примером практического применения математики. Математика не должна быть сложной или полностью оторванной от реальности; дети на самом деле реагируют и учатся лучше, когда математика представлена в реальной концепции. Я не могу придумать более драматического ответа на извечный вопрос: «Для чего мы все равно будем использовать этот математический хлам?» чем сказать: «Сегодня мы измерим размер Земли!»
Результаты учащихся
Что откроет ученик?
- Это прекрасный проект по многим причинам; как и в упражнениях № 10 и № 11, учащиеся могут использовать простые методы, чтобы делать удивительные вещи, в данном случае измерять всю Землю.

- Эратосфен измерил Землю с точностью до 2% от современного измеренного значения. С помощью палочки, транспортира и веревки вы легко сможете это сделать.
Что ваши ученики узнают о науке?
- Наука — это совместное предприятие. Без помощи студентов-ученых из другой школы эта деятельность невозможна. Несмотря на то, что само действие чрезвычайно просто (измерьте один угол в определенное время суток), без сотрудничества ничего не получится.
Проведение мероприятия
Материалы
- Метровый стержень
- Веревка или шпагат
- Точный транспортир
Измерение Земли с помощью Эратосфена
- Первый шаг — связаться с другим учителем того же уровня, что и вы, который живет не менее чем в 100 милях к северу или югу от вас — чем дальше друг от друга, тем лучше для этого эксперимента. Для этого также важна прямая линия север-юг между городами, вам нужно будет как можно точнее знать, сколько миль к северу или югу от вас находится другая школа, в отличие от прямого расстояния между городами.
 Посмотрите на карту и выберите подходящий город, найдите их школы в Интернете, свяжитесь с кем-нибудь по электронной почте и отправьте им приглашение присоединиться к вашему классу в этом увлекательном проекте. Это может занять одну или две попытки, но держу пари, вы сможете найти партнера без особых трудностей!
Посмотрите на карту и выберите подходящий город, найдите их школы в Интернете, свяжитесь с кем-нибудь по электронной почте и отправьте им приглашение присоединиться к вашему классу в этом увлекательном проекте. Это может занять одну или две попытки, но держу пари, вы сможете найти партнера без особых трудностей! - Когда наступит большой день, отправьте утром электронное письмо, чтобы убедиться, что в обоих городах будет солнечная погода. За несколько минут до полудня установите дворовые палки на детской площадке. Одну палочку нужно держать вертикально, (для этого используйте небольшой столярный уровень). С помощью компаса разложите вторую линейку на земле так, чтобы она указывала точно на север. Вы сделали простые солнечные часы! Наблюдайте, как тень движется по часовой стрелке; когда тень лежит прямо на плоской линейке, измерьте и запишите положение, куда падает кончик тени. В зависимости от вашего местонахождения и времени года тень может простираться за конец плоской линейки — ничего страшного, просто отметьте ее положение тротуарным мелом.

- Теперь, когда вы отметили кончик тени, протяните кусок веревки от вершины вертикальной линейки вниз до того места, где кончик тени коснулся земли. Измерьте углом между вертикальной палкой и нитью транспортиром как можно точнее и запишите его. Отправьте эту информацию друг другу по электронной почте — это будет разница между углами , которая будет важна для этой деятельности!
- Эратосфен считал, что Земля круглая, и поэтому угол наклона Солнца в небе будет разным в зависимости от того, насколько далеко на север вы находитесь от экватора — и он был прав! Установив простое соотношение и пропорцию между разницей двух углов и расстоянием между городами, он смог впервые точно измерить окружность Земли около 2300 лет назад. Расчет Эратосфена для размера Земли был точным с точностью до 2% от нашего современного значения, насколько близко могут подобраться ваши ученики? Настройте свой расчет, как показано ниже!
5. Фактическая окружность Земли составляет 24 900 миль. Приведенный выше пример был сделан моими собственными учениками несколько лет назад и показывает значение в пределах 4% от истинного размера Земли — довольно хорошо для детей, использующих веревку и транспортир! Насколько близки будут ваши ученики!
Приведенный выше пример был сделан моими собственными учениками несколько лет назад и показывает значение в пределах 4% от истинного размера Земли — довольно хорошо для детей, использующих веревку и транспортир! Насколько близки будут ваши ученики!
Вопросы для обсуждения
- У Эратосфена явно не было ни телефона, ни интернета, как вы думаете, как ему удавалось заниматься этим в Древнем Египте? (Египет тогда был частью греко-македонской империи.)
- Ответ: Эратосфен не делал оба измерения в один и тот же день! Астроном измерил солнечный угол в городе Сиена на юге Египта в день летнего солнцестояния. Затем он отправился в город Александрию на севере Египта, тщательно измерил расстояние по пути и снова измерил солнечный угол в день летнего солнцестояния в следующем году.
- Иногда мы думаем о древних народах как о «примитивных» или даже «невежественных». Что вы думаете о древнегреческой культуре Эратосфена теперь, когда вы знаете, что люди в эту эпоху могли измерить размер Земли и Луны и даже точно измерить расстояние между ними?
- Ответ: Не все древние культуры были невежественными или примитивными! Во многих культурах были «темные века», когда обучение не было развито, но древние культуры были во многих отношениях удивительно развиты!
Дополнительные материалы
Углубляясь
Понимание того, что происходит, когда мы измеряем солнечный угол в двух разных местах, и как это помогает нам измерять Землю, является шедевром научного мышления. Иногда силу простого эксперимента или аргумента трудно понять.
Иногда силу простого эксперимента или аргумента трудно понять.
Один из способов понять мышление Эратосфена — нарисовать Землю и Солнце, показав углы между ядром Земли и линиями, представляющими лучи Солнца. Посмотрим, сможешь ли ты таким образом понять идеи Эратосфена!
В Интернете есть много рисунков идей Эратосфена, которые помогут вам!
Быть астрономом
Измерение солнечного угла с помощью палки, веревки и транспортира — еще одно упражнение, которое может показать, как небо меняется в зависимости от времени года. Если ваши ученики смогут измерять солнечный угол раз в неделю и вести постоянную запись результатов, вы обнаружите, что солнечный угол заметно меняется в зависимости от времени года.
Можете ли вы найти связь между солнечным углом и временем года?
Быть ученым:
Климатические изменения — горячая тема в исследованиях и политических дебатах в наши дни, но климат меняется не просто медленно на протяжении веков. Климатические изменения сезонной погоды, вызванные изменением солнечного угла, являются одновременно мощными и измеримыми.
Если ваши учащиеся будут вести постоянную запись как угла наклона солнца, так и средней высокой температуры каждую неделю, вы обнаружите интересную взаимосвязь.
Создайте два графика, один из которых показывает изменение угла наклона солнца с течением времени, а другой — среднее значение высокой температуры за неделю с течением времени. Сравните два графика; что вы находите?
Солнце является самым мощным фактором климатических изменений. Сравнивая солнечный угол с колебаниями температуры, мы можем найти мощную связь между тем, сколько солнечного света мы получаем, и нашей местной температурой.
Продолжение
Древние ученые, такие как Эратосфен, Пифагор, Аристотель и многие другие, внесли свой вклад в наши современные научные знания. Взгляните на некоторые идеи и открытия этих древних мастеров и посмотрите, что вы можете найти!
Эта страница под названием 5.4: Измерение Земли с помощью Эратосфена распространяется под лицензией CC BY-NC-SA 4.

 Барт
Барт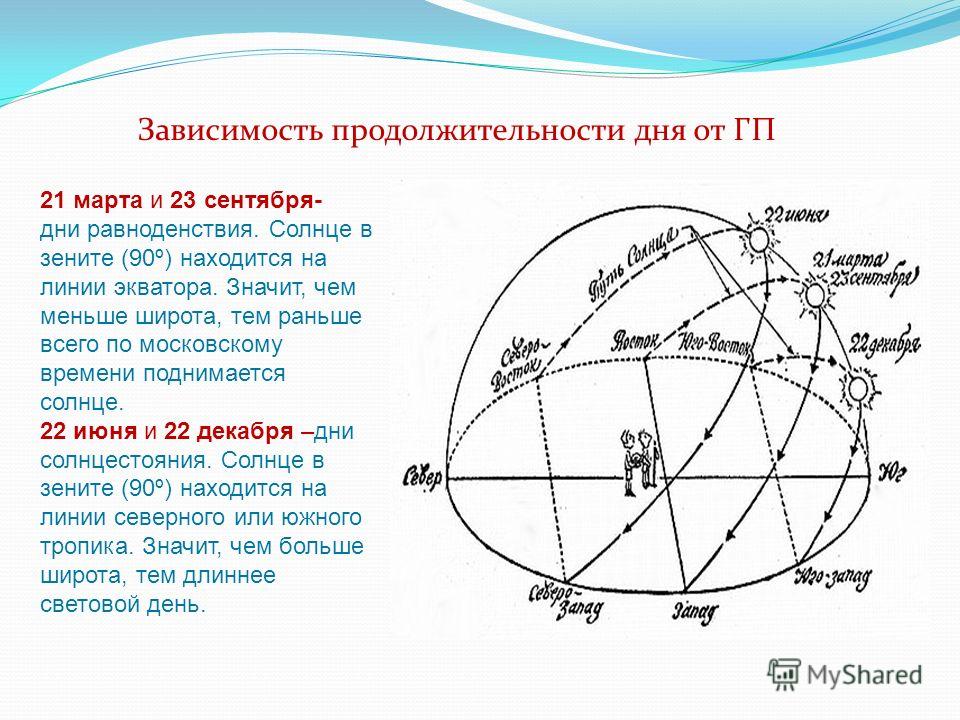

 Посмотрите на карту и выберите подходящий город, найдите их школы в Интернете, свяжитесь с кем-нибудь по электронной почте и отправьте им приглашение присоединиться к вашему классу в этом увлекательном проекте. Это может занять одну или две попытки, но держу пари, вы сможете найти партнера без особых трудностей!
Посмотрите на карту и выберите подходящий город, найдите их школы в Интернете, свяжитесь с кем-нибудь по электронной почте и отправьте им приглашение присоединиться к вашему классу в этом увлекательном проекте. Это может занять одну или две попытки, но держу пари, вы сможете найти партнера без особых трудностей!