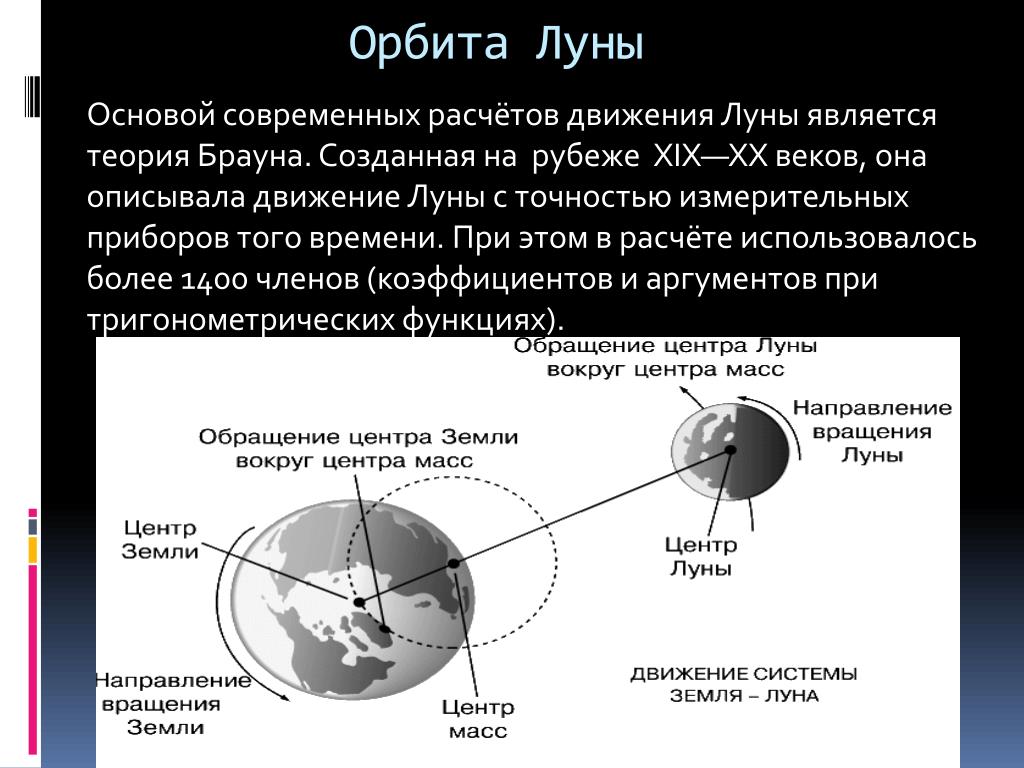
Содержание
Какая сила удерживает спутник земли. Почему спутники не сходят с орбиты? Высокая эллиптическая орбита
Как известно, геостационарные спутники висят неподвижно над землёй над одной и той же точкой. Почему они не падают? На той высоте не действует сила притяжения?
Ответ
Геостационарный искусственный спутник Земли представляет собой аппарат, который движется вокруг планеты в восточном направлении (в том же, в каком вращается сама Земля), по круговой экваториальной орбите с периодом обращения, равным периоду собственного вращения Земли.
Таким образом, если смотреть с Земли на геостационарный спутник, мы будем видеть его неподвижно висящим на одном и том же месте. Из-за этой неподвижности и большой высоты около 36 000 км, с которой видна почти половина поверхности Земли, на геостационарную орбиту выводят спутники-ретрансляторы для телевидения, радио и коммуникаций.
Из того, что геостационарный спутник висит постоянно над одной и той же точкой поверхности Земли, некоторые делают неверный вывод, что на геостационарный спутник не действует сила притяжения к Земле, что сила тяготения на определённом расстоянии от Земли исчезает, т. е. они опровергают самого Ньютона. Конечно это не так. Сам запуск спутников на геостационарную орбиту рассчитывается именно по закону всемирного тяготения Ньютона.
е. они опровергают самого Ньютона. Конечно это не так. Сам запуск спутников на геостационарную орбиту рассчитывается именно по закону всемирного тяготения Ньютона.
Геостационарные спутники, как и все остальные спутники, на самом деле падают на Землю, но не достигают её поверхности. На них действует сила притяжения к Земле (гравитационная сила), направленная к её центру, а в обратном направлении на спутник действует отталкивающая от Земли центробежная сила (сила инерции), которые уравновешивают друг друга — спутник не улетает от Земли и не падает на неё точно так же, как ведро, раскручиваемое на верёвке, остаётся на своей орбите.
Если бы спутник совсем не двигался, то он упал бы на Землю под действием притяжения к ней, но спутники движутся, в том числе и геостационарные (геостационарные — с угловой скоростью равной угловой скорости вращения Земли, т. е. один оборот за сутки, а у спутников нижележащих орбит угловая скорость больше, т. е. за сутки они успевают совершить вокруг Земли несколько оборотов). Линейная скорость, сообщаемая спутнику параллельно поверхности Земли при непосредственном выводе на орбиту сравнительно большая (на низкой околоземной орбите — 8 километров в секунду, на геостационарной орбите — 3 километра в секунду). Если бы не было Земли, то спутник с такой скоростью летел бы по прямой, но наличие Земли заставляет спутник падать на неё под действием силы притяжения, искривляя траекторию по направлению к Земле, но поверхность Земли не плоская, она искривлена. На сколько спутник приближается к поверхности Земли, на столько поверхность Земли уходит из-под спутника и, таким образом, спутник постоянно находится на одной и той же высоте, двигаясь по замкнутой траектории. Спутник всё время падает, но никак не может упасть.
Линейная скорость, сообщаемая спутнику параллельно поверхности Земли при непосредственном выводе на орбиту сравнительно большая (на низкой околоземной орбите — 8 километров в секунду, на геостационарной орбите — 3 километра в секунду). Если бы не было Земли, то спутник с такой скоростью летел бы по прямой, но наличие Земли заставляет спутник падать на неё под действием силы притяжения, искривляя траекторию по направлению к Земле, но поверхность Земли не плоская, она искривлена. На сколько спутник приближается к поверхности Земли, на столько поверхность Земли уходит из-под спутника и, таким образом, спутник постоянно находится на одной и той же высоте, двигаясь по замкнутой траектории. Спутник всё время падает, но никак не может упасть.
Итак, все искусственные спутники Земли падают на Землю, но — по замкнутой траектории. Спутники находятся в состоянии невесомости, как все падающие тела (если лифт в небоскрёбе сорвётся и начнёт свободно падать, то люди внутри тоже будут находиться в состоянии невесомости). Космонавты внутри МКС находятся в невесомости не потому, что на орбите не действует сила притяжения к Земле (она там почти такая же как и на поверхности Земли), а потому, что МКС свободно падает на Землю — по замкнутой круговой траектории.
Космонавты внутри МКС находятся в невесомости не потому, что на орбите не действует сила притяжения к Земле (она там почти такая же как и на поверхности Земли), а потому, что МКС свободно падает на Землю — по замкнутой круговой траектории.
Подобно тому, как места в театре позволяют по-разному взглянуть на представление, различные орбиты спутников дают перспективу, каждая из которых имеет свое назначение. Одни кажутся висящими над точкой поверхности, они обеспечивают постоянный обзор одной стороны Земли, в то время как другие кружат вокруг нашей планеты, за день проносясь над множеством мест.
Типы орбит
На какой высоте летают спутники? Различают 3 типа околоземных орбит: высокие, средние и низкие. На высокой, наиболее удаленной от поверхности, как правило, находятся многие погодные и некоторые спутники связи. Сателлиты, вращающиеся на средней околоземной орбите, включают навигационные и специальные, предназначенные для мониторинга конкретного региона. Большинство научных космических аппаратов, в том числе флот системы наблюдения за поверхностью Земли НАСА, находится на низкой орбите.
От того, на какой высоте летают спутники, зависит скорость их движения. По мере приближения к Земле гравитация становится все сильнее, и движение ускоряется. Например, спутнику НАСА Aqua требуется около 99 минут, чтобы облететь вокруг нашей планеты на высоте около 705 км, а метеорологическому аппарату, удаленному на 35 786 км от поверхности, для этого потребуется 23 часа, 56 минут и 4 секунды. На расстоянии 384 403 км от центра Земли Луна завершает один оборот за 28 дней.
Аэродинамический парадокс
Изменение высоты спутника также изменяет его скорость движения по орбите. Здесь наблюдается парадокс. Если оператор спутника хочет повысить его скорость, он не может просто запустить двигатели для ускорения. Это увеличит орбиту (и высоту), что приведет к уменьшению скорости. Вместо этого следует запустить двигатели в направлении, противоположном направлению движения спутника, т. е. совершить действие, которое на Земле бы замедлило движущееся транспортное средство. Такое действие переместит его ниже, что позволит увеличить скорость.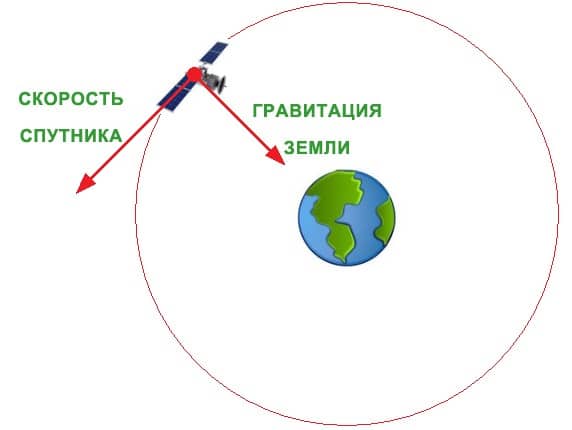
Характеристики орбит
В дополнение к высоте, путь движения спутника характеризуется эксцентриситетом и наклонением. Первый относится к форме орбиты. Спутник с низким эксцентриситетом движется по траектории, близкой к круговой. Эксцентричная орбита имеет форму эллипса. Расстояние от космического аппарата до Земли зависит от его положения.
Наклонение — это угол орбиты по отношению к экватору. Спутник, который вращается непосредственно над экватором, имеет нулевой наклон. Если космический аппарат проходит над северным и южным полюсами (географическими, а не магнитными), его наклон составляет 90°.
Все вместе — высота, эксцентриситет и наклонение — определяют движение сателлита и то, как с его точки зрения будет выглядеть Земля.
Высокая околоземная
Когда спутник достигает ровно 42164 км от центра Земли (около 36 тыс. км от поверхности), он входит в зону, где его орбита соответствует вращению нашей планеты. Поскольку аппарат движется с той же скоростью, что и Земля, т. е. его период обращения равен 24 ч, кажется, что он остается на месте над единственной долготой, хотя и может дрейфовать с севера на юг. Эта специальная высокая орбита называется геосинхронной.
е. его период обращения равен 24 ч, кажется, что он остается на месте над единственной долготой, хотя и может дрейфовать с севера на юг. Эта специальная высокая орбита называется геосинхронной.
Спутник движется по круговой орбите прямо над экватором (эксцентриситет и наклонение равны нулю) и относительно Земли стоит на месте. Он всегда расположен над одной и той же точкой на ее поверхности.
Орбита «Молния» (наклонение 63,4°) используется для наблюдения в высоких широтах. Геостационарные спутники привязаны к экватору, поэтому они не подходят для дальних северных или южных регионов. Эта орбита весьма эксцентрична: космический аппарат движется по вытянутому эллипсу с Землей, расположенной близко к одному краю. Так как спутник ускоряется под действием силы тяжести, он движется очень быстро, когда находится близко к нашей планете. При удалении его скорость замедляется, поэтому он больше времени проводит на вершине орбиты в самом дальнем от Земли краю, расстояние до которого может достигать 40 тыс. км. Период обращения составляет 12 ч, но около двух третей этого времени спутник проводит над одним полушарием. Подобно полусинхронной орбите сателлит проходит по одному и тому же пути через каждые 24 ч. Используется для связи на крайнем севере или юге.
км. Период обращения составляет 12 ч, но около двух третей этого времени спутник проводит над одним полушарием. Подобно полусинхронной орбите сателлит проходит по одному и тому же пути через каждые 24 ч. Используется для связи на крайнем севере или юге.
Низкая околоземная
Большинство научных спутников, многие метеорологические и космическая станция находятся на почти круговой низкой околоземной орбите. Их наклон зависит от того, мониторингом чего они занимаются. TRMM был запущен для мониторинга осадков в тропиках, поэтому имеет относительно низкое наклонение (35°), оставаясь вблизи экватора.
Многие из спутников системы наблюдения НАСА имеют почти полярную высоконаклонную орбиту. Космический аппарат движется вокруг Земли от полюса до полюса с периодом 99 мин. Половину времени он проходит над дневной стороной нашей планеты, а на полюсе переходит на ночную.
По мере движения спутника под ним вращается Земля. К тому времени, когда аппарат переходит на освещенный участок, он находится над областью, прилегающей к зоне прохождения своей последней орбиты. За 24-часовой период полярные спутники покрывают большую часть Земли дважды: один раз днем и один раз ночью.
За 24-часовой период полярные спутники покрывают большую часть Земли дважды: один раз днем и один раз ночью.
Солнечно-синхронная орбита
Подобно тому как геосинхронные спутники должны находиться над экватором, что позволяет им оставаться над одной точкой, полярно-орбитальные имеют способность оставаться в одном времени. Их орбита является солнечно-синхронной — при пересечении космическим аппаратом экватора местное солнечное время всегда одно и то же. Например, спутник Terra пересекает его над Бразилией всегда в 10:30 утра. Следующее пересечение через 99 мин над Эквадором или Колумбией происходит также в 10:30 по местному времени.
Солнечно-синхронная орбита необходима для науки, так как позволяет сохранять солнечного света на поверхность Земли, хотя он будет меняться в зависимости от сезона. Такое постоянство означает, что ученые могут сравнивать изображения нашей планеты одного времени года в течение нескольких лет, не беспокоясь о слишком больших скачках в освещении, которые могут создать иллюзию изменений. Без солнечно-синхронной орбиты было бы сложно отслеживать их с течением времени и собирать информацию, необходимую для изучения изменений климата.
Без солнечно-синхронной орбиты было бы сложно отслеживать их с течением времени и собирать информацию, необходимую для изучения изменений климата.
Путь спутника здесь очень ограничен. Если он находится на высоте 100 км, орбита должна иметь наклон 96°. Любое отклонение будет недопустимым. Поскольку сопротивление атмосферы и сила притяжения Солнца и Луны изменяют орбиту аппарата, ее необходимо регулярно корректировать.
Выведение на орбиту: запуск
Запуск спутника требует энергии, количество которой зависит от расположения места старта, высоты и наклона будущей траектории его движения. Чтобы добраться до удаленной орбиты, требуется затратить больше энергии. Спутники со значительным наклоном (например, полярные) более энергозатратны, чем те, которые кружат над экватором. Выведению на орбиту с низким наклоном помогает вращение Земли. движется под углом 51,6397°. Это необходимо для того, чтобы космическим челнокам и российским ракетам было легче добраться до нее. Высота МКС — 337-430 км. Полярные спутники, с другой стороны, от импульса Земли помощи не получают, поэтому им требуется больше энергии, чтобы подняться на такое же расстояние.
Полярные спутники, с другой стороны, от импульса Земли помощи не получают, поэтому им требуется больше энергии, чтобы подняться на такое же расстояние.
Корректировка
После запуска спутника необходимо приложить усилия, чтобы удержать его на определенной орбите. Поскольку Земля не является идеальной сферой, ее гравитация в некоторых местах сильнее. Эта неравномерность, наряду с притяжением Солнца, Луны и Юпитера (самой массивной планеты Солнечной системы), изменяет наклон орбиты. На протяжении всего своего срока службы положение спутников GOES корректировалось три или четыре раза. Низкоорбитальные аппараты НАСА должны регулировать свой наклон ежегодно.
Кроме того, на околоземные спутники оказывает воздействие атмосфера. Самые верхние слои, хотя и достаточно разрежены, оказывают достаточно сильное сопротивление, чтобы притягивать их ближе к Земле. Действие силы тяжести приводит к ускорению спутников. Со временем они сгорают, по спирали опускаясь все ниже и быстрее в атмосферу, или падают на Землю.
Атмосферное сопротивление сильнее, когда Солнце активно. Так же, как воздух в воздушном шаре расширяется и поднимается при нагревании, атмосфера поднимается и расширяется, когда Солнце дает ей дополнительную энергию. Разреженные слои атмосферы поднимаются, а их место занимают более плотные. Поэтому спутники на орбите Земли должны изменять свое положение примерно четыре раза в год, чтобы компенсировать сопротивление атмосферы. Когда солнечная активность максимальна, положение аппарата приходится корректировать каждые 2-3 недели.
Космический мусор
Третья причина, вынуждающая менять орбиту — космический мусор. Один из коммуникационных спутников Iridium столкнулся с нефункционирующим российским космическим аппаратом. Они разбились, образовав облако мусора, состоящее из более чем 2500 частей. Каждый элемент был добавлен в базу данных, которая сегодня насчитывает свыше 18000 объектов техногенного происхождения.
НАСА тщательно отслеживает все, что может оказаться на пути спутников, т. к. из-за космического мусора уже несколько раз приходилось менять орбиты.
к. из-за космического мусора уже несколько раз приходилось менять орбиты.
Инженеры отслеживают положение космического мусора и сателлитов, которые могут помешать движению и по мере необходимости тщательно планируют маневры уклонения. Эта же команда планирует и выполняет маневры по регулировке наклона и высоты спутника.
Или почему спутники не падают? Орбита спутника представляет собой хрупкий баланс между инерцией и гравитацией. Сила тяжести непрерывно притягивает спутник к Земле, в то время как инерция спутника стремится поддерживать его движение прямолинейным. Если бы не было силы тяжести, инерция спутника отправила бы его прямо с земной орбиты в открытый космос. Однако в каждой точке орбиты сила тяжести держит спутник на привязи.
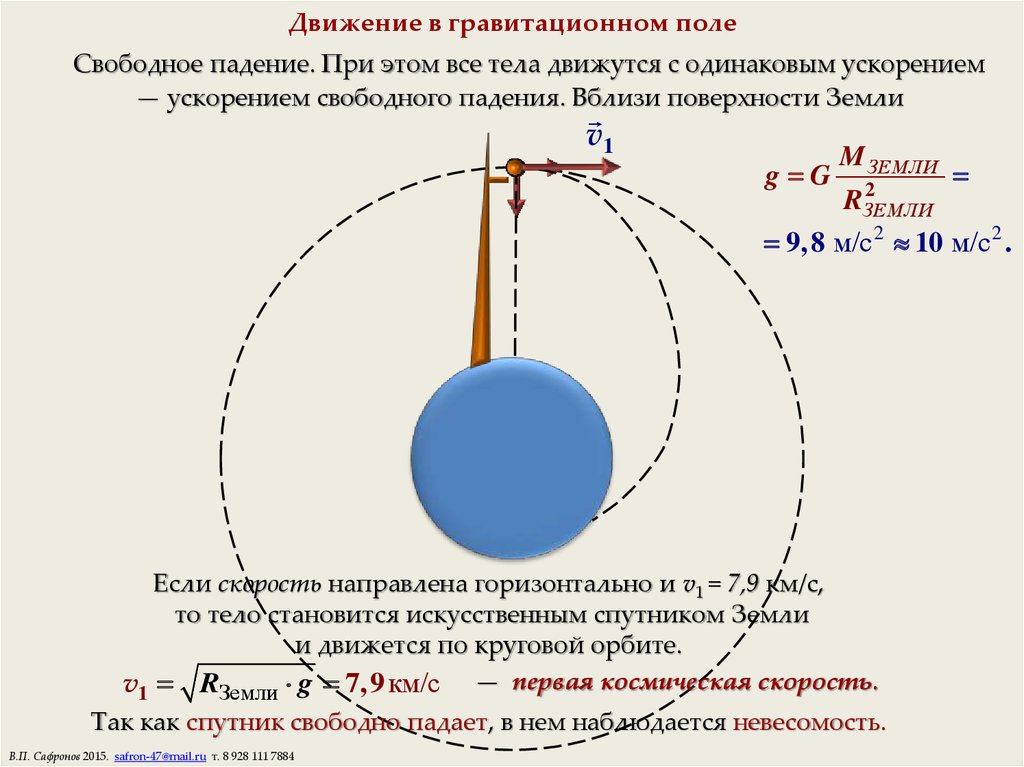
Чтобы достичь равновесия между инерцией и силой тяжести, спутник должен иметь строго определенную скорость. Если он летит слишком быстро, инерция преодолевает силу тяжести и спутник покидает орбиту. (Вычисление так называемой второй космической скорости, позволяющей спутнику покидать околоземную орбиту, играет важную роль в запуске межпланетных космических станций. ) Если спутник движется слишком медленно, сила тяжести победит в борьбе с инерцией и спутник упадет на Землю. Именно это случилось в 1979 году, когда американская орбитальная станция Скайлэб начала снижаться в результате растущего сопротивления верхних слоев земной атмосферы. Попав в железные клещи гравитации, станция вскоре упала на Землю.
) Если спутник движется слишком медленно, сила тяжести победит в борьбе с инерцией и спутник упадет на Землю. Именно это случилось в 1979 году, когда американская орбитальная станция Скайлэб начала снижаться в результате растущего сопротивления верхних слоев земной атмосферы. Попав в железные клещи гравитации, станция вскоре упала на Землю.
Скорость и расстояние
Поскольку земное притяжение ослабевает с расстоянием, скорость, необходимая для удержания спутника на орбите, изменяется с высотой над уровнем моря. Инженеры могут вычислять, как быстро и как высоко спутник должен вращаться на орбите. Например, геостационарный спутник, расположенный всегда над одной и той же точкой земной поверхности, должен совершать один виток за 24 часа (что соответствует времени одного оборота Земли вокруг своей оси) на высоте 357 километров.
Сила тяжести и инерция
Балансирование спутника между силой тяжести и инерцией может быть сымитировано вращением груза на привязанной к нему веревке. Инерция груза стремится переместить его подальше от центра вращения, в то время как натяжение веревки, выполняющее роль гравитации, удерживает груз на круговой орбите. Если веревку перерезать, груз улетит по прямолинейной траектории перпендикулярно радиусу своей орбиты.
Инерция груза стремится переместить его подальше от центра вращения, в то время как натяжение веревки, выполняющее роль гравитации, удерживает груз на круговой орбите. Если веревку перерезать, груз улетит по прямолинейной траектории перпендикулярно радиусу своей орбиты.
Для вывода спутника на околоземную орбиту надо придать ему начальную скорость, равную первой космической скорости или несколько превышающую последнюю. Это происходит не сразу, а постепенно. Несущая спутник многоступенчатая ракета плавно набирает скорость. Когда скорость ее полета достигнет расчетного значения, спутник отделяется от ракеты и начинает свое свободное движение по орбите. От приданной ему начальной скорости и ее направления зависит форма орбиты: ее размеры и эксцентриситет.
Если бы не было сопротивления среды и возмущающих притяжений Луны и Солнца, а Земля имела бы шаровую форму, то орбита спутника не претерпевала бы никаких измений, а сам спутник двигался бы по ней вечно. Однако в действительности орбита каждого спутника изменяется под действием различных причин.
Главная сила, изменяющая орбиту спутника,- это торможение, возникающее вследствие сопротивления разреженной среды, сквозь которую пролетает спутник. Посмотрим, как она влияет на его движение. Так как орбита спутника обычно эллиптическая, то его расстояние от Земли периодически изменяется. Он снижается к перигею и достигает максимального удаления в апогее. Плотность земной атмосферы быстро уменьшается по мере увеличения высоты, и потому спутник встречает наибольшее сопротивление вблизи перигея. Затратив часть кинетической энергии на преодоление этого, хотя и небольшого, сопротивления, спутник уже не может подняться на прежнюю высоту, и его апогей постепенно снижается. Снижение перигея тоже происходит, но гораздо медленнее, чем снижение апогея. Таким образом, постепенно уменьшаются размеры орбиты и ее эксцентриситет: эллиптическая орбита приближается к круговой. Спутник движется вокруг Земли по медленно свертывающейся спирали и в конце концов заканчивает свое существование в плотных слоях земной атмосферы, разогреваясь и испаряясь подобно метеорному телу. При больших размерах он может долететь и до поверхности Земли.
При больших размерах он может долететь и до поверхности Земли.
Интересно отметить, что торможение спутника не уменьшает его скорости, а наоборот, увеличивает ее. Сделаем простые вычисления.
Из третьего закона Кеплера следует, что
где С — постоянная, М — масса Земли, m — масса спутника, Р — период его обращения и а — большая полуось орбиты. Пренебре-
гая массой спутника в сравнении с массой Земли получим
Примем для простоты расчетов орбиту спутника за круговую. Двигаясь с постоянной скоростью υ, спутник за полный оборот проходит по орбите расстояние υ Р = 2 πа, откуда Р = 2πa/υ. Подставив это значение Р в формулу (9.1) и выполнив преобразования, найдем
Итак, с уменьшением размеров орбиты а скорость спутника v возрастает: кинетическая энергия спутника растет за счет быстрого уменьшения потенциальной энергии.
Вторая сила, изменяющая форму орбиты спутника,- это давление солнечного излучения, т. е. света и корпускулярных потоков (солнечного ветра). На спутники малых размеров эта сила практически не влияет, но для таких спутников, как «Пагеос», она очень существенна.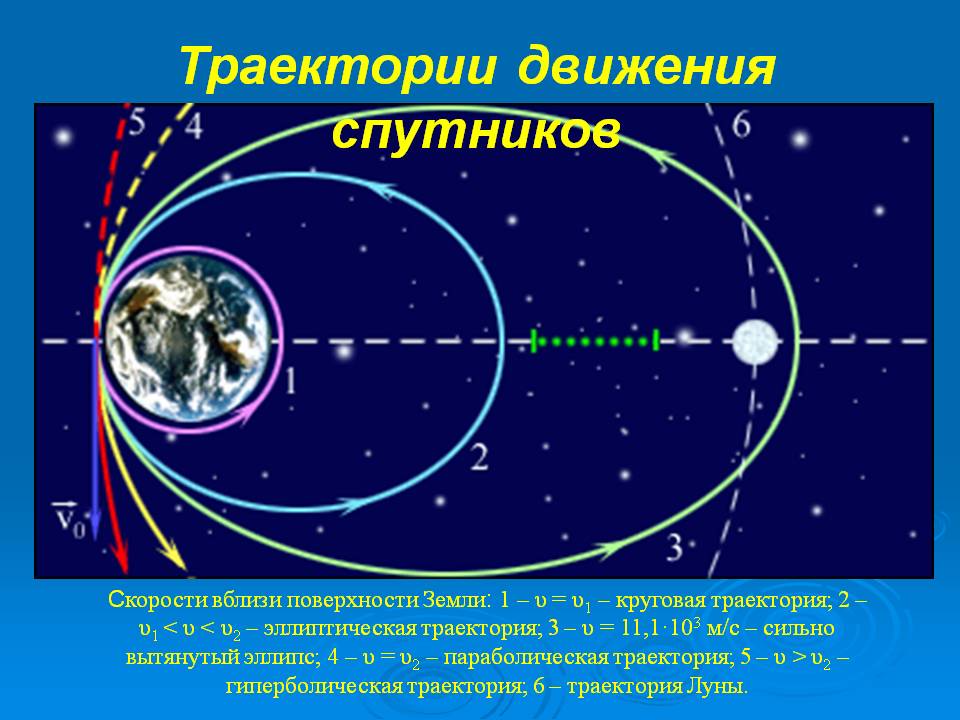 При запуске «Пагеос» имел круговую орбиту, а через два года она стала очень вытянутой эллиптической.
При запуске «Пагеос» имел круговую орбиту, а через два года она стала очень вытянутой эллиптической.
На движение спутника влияет также и магнитное поле Земли, так как спутник может приобрести некоторый электрический заряд и при его движении в магнитном поле должны возникнуть изменения в траектории.
Однако все эти силы являются возмущающими. Главная же сила, удерживающая спутник на его орбите,- сила земного притяжения. И тут мы встречаемся с некоторыми особенностями. Мы знаем, что в результате осевого вращения фигура Земли отличается от шаровой и что земное притяжение не направлено точно к центру Земли. На очень далеких объектах это не сказывается, но находящийся поблизости от Земли спутник реагирует на наличие у Земли «экваториальных вздутий». Плоскость его орбиты медленно, но вполне регулярно поворачивается вокруг оси вращения Земли. Такое явление хорошо заметно из наблюдений, проведенных на протяжении одной недели. Все эти изменения орбит представляют большой научный интерес, и потому за движением искусственных спутников проводятся систематические наблюдения.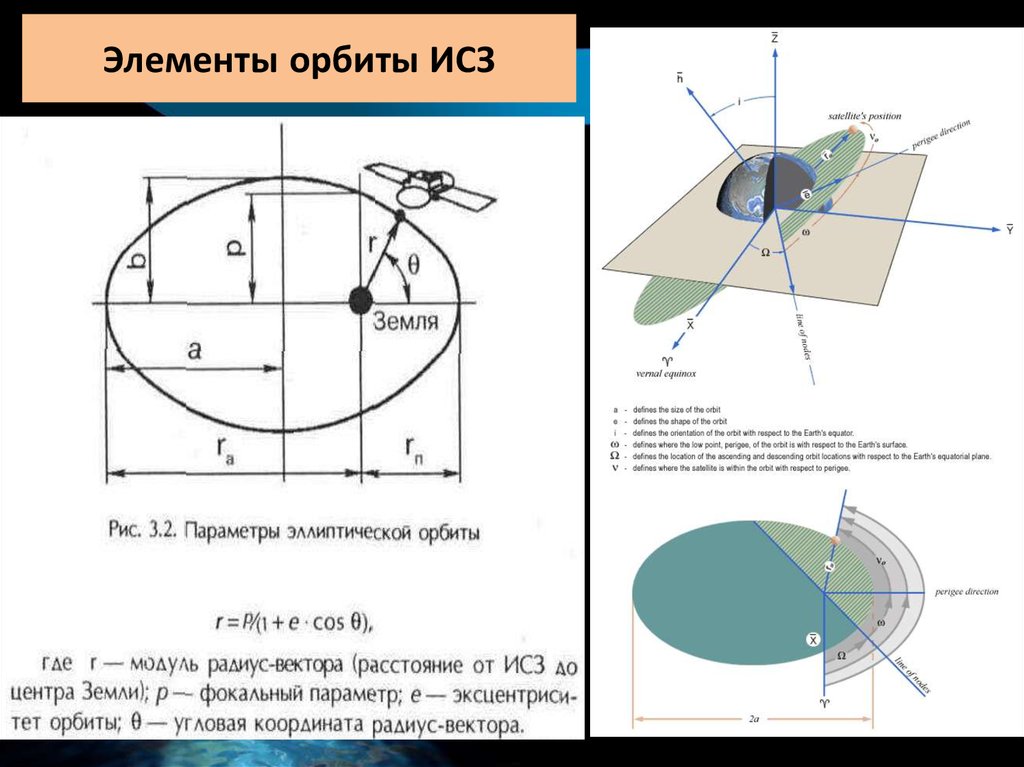
Что собой представляет геостационарная орбита? Это круговое поле, которое расположилось над экватором Земли, по нему искусственный спутник обращается с угловой скоростью вращения планеты вокруг оси. Он не изменяет свое направление в горизонтальной системе координат, а неподвижно висит в небе. Геостационарная орбита Земли (ГСО)представляет собой разновидность геосинхронного поля и применяется для размещения коммуникационных, телетрансляционных и других спутников.
Идея использования искусственных аппаратов
Само понятие геостационарной орбиты инициировано русским изобретателем К. Э. Циолковским. В своих работах он предлагал заселить космос с помощью орбитальных станций. Зарубежные ученые также описывали работы космических полей, например, Г. Оберт. Человеком, который развил концепцию использования орбиты для связи, является Артур Кларк. Он в 1945 году поместил статью в журнале «Wireless World», где описал преимущества работы геостационарного поля. За активный труд в данной области в честь ученого орбита получила свое второе название — «пояс Кларка». Над проблемой осуществления качественной связи думали многие теоретики. Так, Герман Поточник в 1928 году высказал мысль о том, как можно применять геостационарные спутники.
Над проблемой осуществления качественной связи думали многие теоретики. Так, Герман Поточник в 1928 году высказал мысль о том, как можно применять геостационарные спутники.
Характеристика «пояса Кларка»
Чтобы орбита была названа геостационарной, она должна отвечать ряду параметров:
1. Геосинхронность. К такой характеристике относится поле, которое имеет период, соответствующий периоду обращения Земли. Геосинхронный спутник заканчивает оборот вокруг планеты за сидерический день, который равен 23 часам 56 минутам и 4 секундам. То же время необходимо Земле для выполнения одного оборота в фиксированном пространстве.
2. Для поддержания спутника на определенной точке геостационарная орбита должна быть круговой, с нулевым наклонением. Эллиптическое поле приведет к смещению либо к востоку, либо к западу, так как аппарат движется в определенных точках орбиты по-разному.
3. «Точка зависания» космического механизма должна находиться на экваторе.
4. Расположение спутников на геостационарной орбите должны быть таким, чтобы небольшое количество частот, предназначенных для связи, не привело к наложению частот разных аппаратов при приеме и передаче, а также для исключения их столкновения.
5. Достаточное количество топлива для поддержания неизменного положения космического механизма.
Геостационарная орбита спутника уникальна тем, что только при сочетании ее параметров можно добиться неподвижности аппарата. Еще одной особенностью является возможность видеть Землю под углом в семнадцать градусов из расположенных на космическом поле спутников. Каждый аппарат отхватывает примерно одну третью часть поверхности орбиты, поэтому три механизма способны обеспечить охват почти всей планеты.
Искусственные спутники
Летательный аппарат вращается вокруг Земли по геоцентрическому пути. Для его вывода используют многоступенчатую ракету. Она представляет собой космический механизм, который приводит в действие реактивная сила двигателя. Для движения по орбите искусственные спутники Земли должны иметь начальную скорость, которая соответствует первой космической. Их полеты осуществляются на высоте не меньше нескольких сотен километров. Период обращения аппарата может составлять несколько лет. Искусственные спутники Земли могут запускаться с бортов других аппаратов, например, орбитальных станций и кораблей. Беспилотники имеют массу до двух десятков тонн и размер до нескольких десятков метров. Двадцать первый век ознаменовался рождением аппаратов со сверхмалым весом — до несколько килограммов.
Период обращения аппарата может составлять несколько лет. Искусственные спутники Земли могут запускаться с бортов других аппаратов, например, орбитальных станций и кораблей. Беспилотники имеют массу до двух десятков тонн и размер до нескольких десятков метров. Двадцать первый век ознаменовался рождением аппаратов со сверхмалым весом — до несколько килограммов.
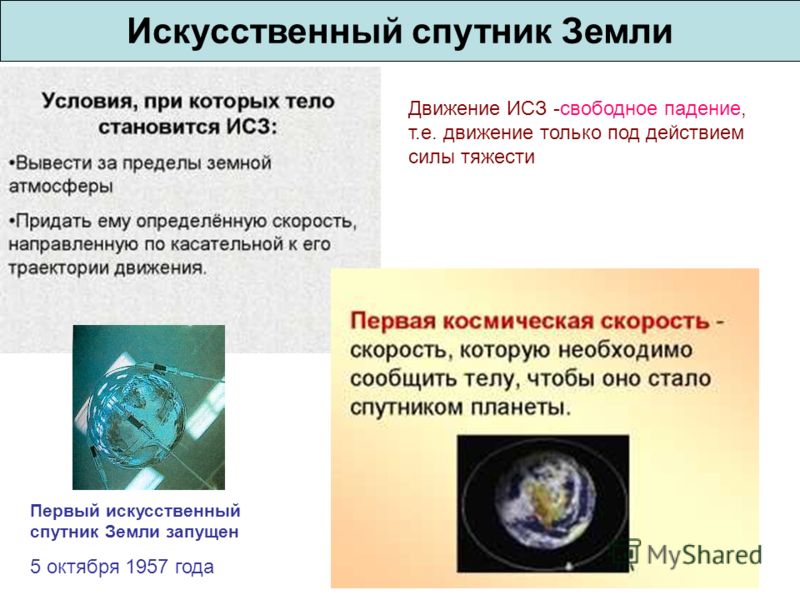
Спутники запускались многими странами и компаниями. Первый в мире искусственный аппарат был создан в СССР и полетел в космос 4 октября 1957 года. Он носил имя «Спутник-1». В 1958 году США запустила второй аппарат — «Эксплорер-1». Первый спутник, который был выведен NASA в 1964 году, носил имя Syncom-3. Искусственные аппараты в основном невозвратные, но есть те, которые возвращаются частично или полностью. Их используют для проведения научных исследований и решения различных задач. Так, существуют военные, исследовательские, навигационные спутники и другие. Также запускаются аппараты, созданные сотрудниками университетов или радиолюбителями.
«Точка стояния»
Геостационарные спутники располагаются на высоте 35786 километров над уровнем моря. Такая высота обеспечивает период обращения, который соответствует периоду циркуляции Земли по отношению к звездам. Искусственный аппарат неподвижен, поэтому его местоположение на геостационарной орбите называется «точкой стояния». Зависание обеспечивает постоянную длительную связь, однажды сориентированная антенна всегда будет направлена на нужный спутник.
Передвижение
Спутники можно переводить с низковысотной орбиты на геостационарную с помощью геопереходных полей. Последние представляют собой эллиптический путь с точкой на низкой высоте и пиком на высоте, которая близка к геостационарному кругу. Спутник, который стал непригодным для дальнейшей работы, отправляется на орбиту захоронения, расположенную на 200-300 километров выше ГСО.
Высота геостационарной орбиты
Спутник на данном поле держится на определенном расстоянии от Земли, не приближаясь и не удаляясь. Он всегда находится над какой-либо точкой экватора. Исходя из данных особенностей следует вывод, что силы гравитации и центробежная сила уравновешивают друг друга. Высота геостационарной орбиты рассчитывается методами, в основе которых лежит классическая механика. При этом учитывается соответствие гравитационных и центробежных сил. Значение первой величины определяется с помощью закона всемирного тяготения Ньютона. Показатель центробежной силы рассчитывается путем произведения массы спутника на центростремительное ускорение. Итогом равенства гравитационной и инертной массы является заключение о том, что высота орбиты не зависит от массы спутника. Поэтому геостационарная орбита определяется только высотой, при которой центробежная сила равна по модулю и противоположна по направлению гравитационной силе, создающейся притяжением Земли на данной высоте.
Он всегда находится над какой-либо точкой экватора. Исходя из данных особенностей следует вывод, что силы гравитации и центробежная сила уравновешивают друг друга. Высота геостационарной орбиты рассчитывается методами, в основе которых лежит классическая механика. При этом учитывается соответствие гравитационных и центробежных сил. Значение первой величины определяется с помощью закона всемирного тяготения Ньютона. Показатель центробежной силы рассчитывается путем произведения массы спутника на центростремительное ускорение. Итогом равенства гравитационной и инертной массы является заключение о том, что высота орбиты не зависит от массы спутника. Поэтому геостационарная орбита определяется только высотой, при которой центробежная сила равна по модулю и противоположна по направлению гравитационной силе, создающейся притяжением Земли на данной высоте.
Из формулы расчета центростремительного ускорения можно найти угловую скорость. Радиус геостационарной орбиты определяется также по этой формуле либо путем деления геоцентрической гравитационной постоянной на угловую скорость в квадрате. Он составляет 42164 километра. Учитывая экваториальный радиус Земли, получаем высоту, равную 35786 километрам.
Он составляет 42164 километра. Учитывая экваториальный радиус Земли, получаем высоту, равную 35786 километрам.
Вычисления можно провести другим путем, основываясь на утверждении, что высота орбиты, представляющая собой удаление от центра Земли, с угловой скоростью спутника, совпадающей с движением вращения планеты, рождает линейную скорость, которая равна первой космической на данной высоте.
Скорость на геостационарной орбите. Длина
Данный показатель рассчитывается путем умножения угловой скорости на радиус поля. Значение скорости на орбите равно 3,07 километра в секунду, что намного меньше первой космической скорости на околоземном пути. Чтобы уменьшить показатель, необходимо увеличить радиус орбиты более чем в шесть раз. Длина рассчитывается произведением числа Пи на радиус, умноженным на два. Она составляет 264924 километра. Показатель учитывается при вычислении «точек стояния» спутников.
Влияние сил
Параметры орбиты, по которой обращается искусственный механизм, могут изменяться под действием гравитационных лунно-солнечных возмущений, неоднородности поля Земли, эллиптичности экватора. Трансформация поля выражается в таких явлениях, как:
Трансформация поля выражается в таких явлениях, как:
- Смещение спутника от своей позиции вдоль орбиты в сторону точек стабильного равновесия, которые носят название потенциальных ям геостационарной орбиты.
- Угол наклона поля к экватору растет с определенной скоростью и достигает 15 градусов один раз за 26 лет и 5 месяцев.
Для удержания спутника в нужной «точке стояния» его оснащают двигательной установкой, которую включают несколько раз в 10-15 суток. Так, для восполнения роста наклонения орбиты используют коррекцию «север-юг», а для компенсации дрейфа вдоль поля — «запад-восток». Для регулирования пути спутника в течение всего срока его работы необходим большой запас топлива на борту.
Двигательные установки
Выбор приспособления определяется индивидуальными техническими особенностями спутника. Например, химический ракетный двигатель имеет вытеснительную подачу топлива и функционирует на долго хранимых высококипящих компонентах (диазотный тетроксид, несимметричный диметилгидразин). Плазменные устройства имеют существенно меньшую тягу, но за счет продолжительной работы, которая измеряется десятками минут для единичного передвижения, способны значительно снизить потребляемое количество топлива на борту. Такой тип двигательной установки используется для маневра перевода спутника в другую орбитальную позицию. Основным ограничивающим фактором срока службы аппарата является запас топлива на геостационарной орбите.
Плазменные устройства имеют существенно меньшую тягу, но за счет продолжительной работы, которая измеряется десятками минут для единичного передвижения, способны значительно снизить потребляемое количество топлива на борту. Такой тип двигательной установки используется для маневра перевода спутника в другую орбитальную позицию. Основным ограничивающим фактором срока службы аппарата является запас топлива на геостационарной орбите.
Недостатки искусственного поля
Существенным пороком во взаимодействии с геостационарными спутниками являются большие запоздания в распространении сигнала. Так, при скорости света 300 тысяч километров в секунду и высоте орбиты 35786 километров движение луча «Земля — спутник» занимает около 0,12 секунды, а «Земля — спутник — Земля» — 0,24 секунды. Учитывая задержку сигнала в аппаратуре и кабельных системах передач наземных служб общее запоздание сигнала «источник — спутник — приемник» достигает примерно 2-4 секунд. Такой показатель существенно затрудняет применение аппаратов на орбите в телефонии и делает невозможным использование спутниковой связи в системах реального времени.
Еще одним недостатком является невидимость геостационарной орбиты с высоких широт, что мешает проводимости связи и телетрансляций в районах Арктики и Антарктиды. В ситуациях, когда солнце и спутник-передатчик находятся на одной линии с приемной антенной, наблюдается уменьшение, а порой и полное отсутствие сигнала. На геостационарных орбитах за счет неподвижности спутника такое явление проявляется особенно ярко.
Эффект Допплера
Этот феномен заключается в изменении частот электромагнитных вибраций при взаимном продвижении передатчика и приемника. Явление выражается изменением расстояния во времени, а также движением искусственных аппаратов на орбите. Эффект проявляется как малоустойчивость несущей частоты колебаний спутника, которая прибавляется к аппаратурной нестабильности частоты бортового ретранслятора и земной станции, что осложняет прием сигналов. Эффект Допплера содействует изменению частоты модулирующих вибраций, что невозможно контролировать. В случае, когда на орбите используются спутники связи и непосредственного телевизионного вещания, данное явление практически устраняется, то есть не наблюдается изменений уровня сигналов в точке приема.
Отношение в мире к геостационарным полям
Космическая орбита своим рождением создала много вопросов и международно-правовых проблем. Их решением занимается ряд комитетов, в частности, Организация Объединенных Наций. Некоторые страны, расположенные на экваторе, предъявляли претензии на распространение их суверенитета на находящуюся над их территорией часть космического поля. Государства заявляли, что геостационарная орбита представляет собой физический фактор, который связан с существованием планеты и зависит от гравитационного поля Земли, поэтому сегменты поля являются продолжением территории их стран. Но такие притязания были отвергнуты, так как в мире существует принцип неприсвоения космического пространства. Все проблемы, связанные с работой орбит и спутников, разрешаются на мировом уровне.
Тест: Сила тяжести. Сила упругости. Вес тела. Единицы силы
Вопрос №
1
Весом тела называют силу, с которой. ..
..
Тело притягивается к Земле
Тело вследствие притяжения к Земле действует на опору или подвес
Тело действует на другое тело, вызывающее деформацию
Нет правильного ответа
Вопрос №
2
Силой упругости называют силу, с которой…
Тело притягивается к Земле
Тело вследствие притяжения к Земле действует на опору или подвес
Тело действует на другое тело, вызывающее деформацию
Нет правильного ответа
Вопрос №
3
Какая сила удерживает спутник на орбите?
Нет правильного ответа
Сила тяжести.
Сила упругости
Вес тела.
Вопрос №
4
На рисунке изображены силы, действующие на доску и лежащий на ней груз.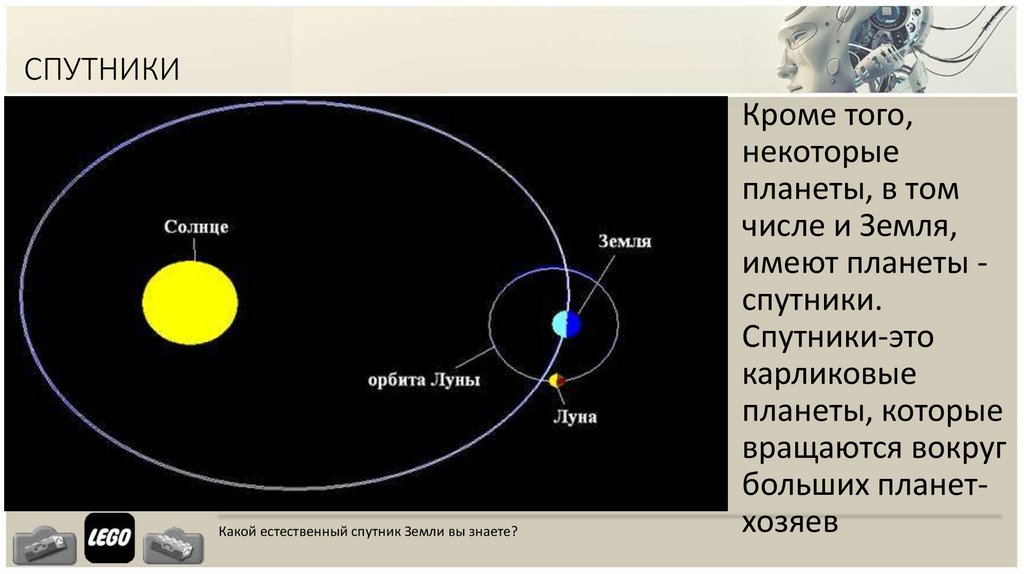 Как называется сила F2?
Как называется сила F2?
Вес тела
Силой упругости
Силой тяжести
Силой давления
Вопрос №
5
На гирю, лежащую на столе, действуют ..(1). . Эти силы .(2).. по модулю и имеют (3)… направления.
(1)сила тяжести и вес тела …(2) не равны ..(3) одинаковые
(1)сила упругости и вес тела …(2) равны … (3)противоположные …
(1)сила тяжести и вес тела … (2)равны … (3)одинаковые …
(1)сила тяжести и сила упругости …(2) равны … (3)противоположные … .
Вопрос №
6
На книгу, лежащую на столе, со стороны стола действует …
Сила тяжести.
Сила упругости.
Вес тела.
Нет правильного ответа
Вопрос №
7
Пружина под действием подвешенной к ней гири растянулась (см.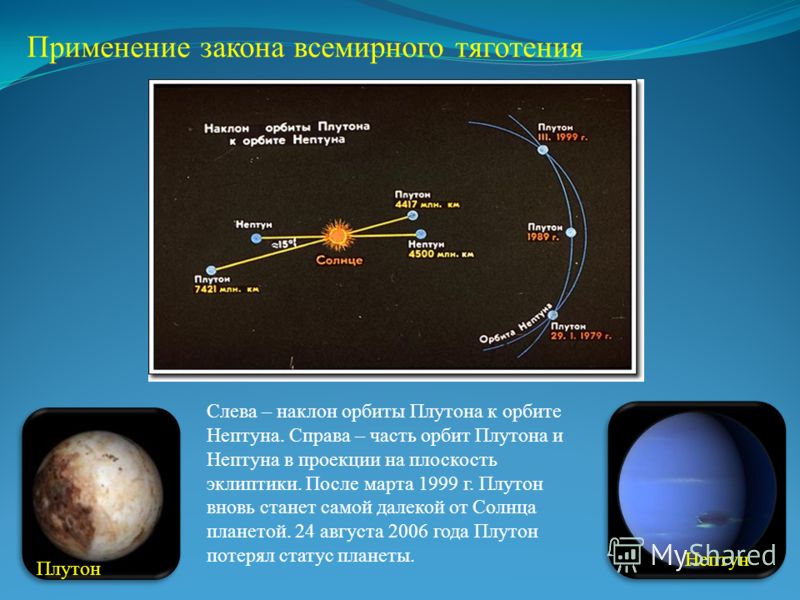 рисунок). Какая сила вызвала растяжение пружины?
рисунок). Какая сила вызвала растяжение пружины?
Нет правильного ответа
Сила тяжести.
Сила упругости.
Вес тела.
Вопрос №
8
Сила — причина …
постоянной скорости движения тела
движения тела.
покоя тела
изменения скорости движения тела
Вопрос №
9
Зависит ли сила тяжести от массы тела?
Сила тяжести обратно пропорциональна массе тела.
Сила тяжести прямо пропорциональна массе тела
Чем больше масса тела, тем меньше сила тяжести, с которой оно притягивается к Земле
Не зависит.
Вопрос №
10
Сила тяжести действует .(1).., а вес этого тела действует . (2)..
(2)..
(1)на опору — (2)на подвес
(1)на опору или подвес … (2)на само тело
(1)на само тело … (2)на опору или подвес
Вопрос №
11
В каких единицах измеряется вес тела?
Килограмм (кг) и грамм (г)
Ньютон (Н)
Метр в секунду (м/с).
грамм (г)
килоньютон (кН)
километр в час (км/ч)
Вопрос №
12
Переведите 0,1 кН в Н
1Н
10Н
100Н
0,0001Н
Вопрос №
13
Чему равна сила тяжести, действующая на тело массой 50 кг?
0,49Н
4,9Н
49Н
490Н
4900Н
Вопрос №
14
1 Ньютон — это сила, которая . ..
..
за 1 с изменяет скорость тела массой 1 кг на 1 м/с.
за 1 с сообщает телу массой 1 кг скорость 1 м/с
за 1 с изменяет скорость тела на 1 м/с
равна силе тяжести действующей на тело массой 1 кг
Вопрос №
15
Переведите 25Н в кН
25000Н
2500Н
250Н
0,25Н
0,025Н
Вопрос №
16
Тело имеет массу 0,5 кг. Каков вес этого тела, если оно неподвижно и находится на горизонтальной опоре?
4,9 Н.
490 Н.
4900 Н.
49 Н.
0,49 Н.
Вопрос №
17
На сколько изменится масса и вес человека, если он выпьет стакан воды вместимостью 0,2 л?
Масса на 20 кг, а вес на 1,96 Н
Масса на 0,2 кг, а вес на 1,96 Н
Масса на 2 кг, а вес на 19,6 Н
Масса на 0,2 кг, а вес на 19,6 Н
Вопрос №
18
1 ньютон приблизительно равен силе тяжести, действующей на тело массой . ..
..
1/8,9 кг
0,1 кг.
1/9,8 кг
9,8 кг
8,9 кг.
Вопрос №
19
Тело, выпущенное из рук, падает на землю. Какая сила вызывает падение тел
Сила тяжести.
Сила упругости.
Вес тела.
Вопрос №
20
На линейку, лежащую на двух опорах, поставили гирю, и линейка прогнулась. Как называется сила, с которой гиря действует на линейку?
Сила тяжести.
Сила упругости.
Вес тела.
Вопрос №
21
Может ли тело находится в движении, если на него не действуют другие тела?
Может, но скоро остановится
Если тело двигалось, то скорость его движения сохранится
Не может
Вопрос №
22
Пружина под действием подвешенной к ней гири растянулась (см. рисунок). Какая сила вызвала растяжение пружины?
рисунок). Какая сила вызвала растяжение пружины?
Сила тяжести.
Сила упругости.
Вес тела.
Вопрос №
23
На стол, со стороны лежащей на нем книги, действует …
Вес тела.
Сила тяжести.
Сила упругости.
Вопрос №
24
На рисунке изображены силы, действующие на доску и лежащий на ней груз. Как называется сила F3?
Силой давления
Вес тела
Силой тяжести.
Силой упругости
Вопрос №
25
Чему примерно равна масса тела, если его вес 800Н?
8 кг
80 кг
800 кг
0,8 кг
Сила. Явление тяготения.
 Сила тяжести. Сила упругости. Вес тела. 7 класс
Сила тяжести. Сила упругости. Вес тела. 7 класс
Получите готовые материалы учителя на весь учебный год для работы в классе и удалённо! Подробнее…
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Выбрать материалы
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Вашему вниманию будет предложен тест из 14-ти вопросов. Внимательно читайте каждый вопрос, потому что иногда возникает ощущение, что вам дают одинаковые вопросы. Это не совсем так: просто одно и то же явление рассматривается с разных точек зрения. В этом тесте не предусмотрены подсказки, но посмотреть правильные ответы после написания теста, Вы сможете.
Это не совсем так: просто одно и то же явление рассматривается с разных точек зрения. В этом тесте не предусмотрены подсказки, но посмотреть правильные ответы после написания теста, Вы сможете.
Вопрос 1
На линейку, лежащую на двух опорах, поставили гирю, и линейка прогнулась (см. рисунок). Как называется сила, с которой гиря действует на линейку?
Варианты ответов
- Силой тяжести
- Весом тела
- Силой упругости
Вопрос 2
Пружина под действием подвешенной к ней гири растянулась (см. рисунок). Какая сила вызвала растяжение пружины?
Варианты ответов
- Сила упругости
- Вес тела
- Сила тяжести
Вопрос 3
На гирю, лежащую на столе, действуют . .. . Эти силы … по модулю и имеют … направления.
.. . Эти силы … по модулю и имеют … направления.
Варианты ответов
- сила упругости и вес тела … равны … противоположные … .
- сила тяжести и сила упругости … равны … противоположные … .
- сила тяжести и вес тела … не равны … одинаковые … .
Вопрос 4
Если на движущееся тело не действует другое тело, то скорость его …
Варианты ответов
- увеличивается
- уменьшается
- не изменяется.
Вопрос 5
Зависит ли сила тяжести от массы тела?
Варианты ответов
- Чем больше масса тела, тем меньше сила тяжести, с которой оно притягивается к Земле
- Не зависит.

- Сила тяжести прямо пропорциональна массе тела
Вопрос 6
Какая сила удерживает тело на поверхности Земли?
Варианты ответов
- Вес тела.
- Сила тяжести.
- Сила упругости.
Вопрос 7
Какая сила удерживает спутник на орбите?
Варианты ответов
- Сила тяжести.
- Сила упругости.
- Вес тела.
Вопрос 8
Силой упругости называют силу, с которой. …
…
Варианты ответов
- тело притягивается к Земле.
- тело действует на другое тело, вызывающее деформацию.
- тело, вследствие притяжения к Земле, действует на опору или подвес.
Вопрос 9
Весом тела называют силу, с которой….
Варианты ответов
- тело, вследствие притяжения к Земле, действует на опору или подвес.
- тело действует на другое тело, вызывающее деформацию.
- тело притягивается к Земле.
Вопрос 10
На рисунке изображены силы, действующие на доску и лежащий на ней груз.
Как называется сила F3?
Варианты ответов
- Весом тела.
- Силой упругости.
- Силой тяжести.
Вопрос 11
Может ли тело находится в движении, если на него не действуют другие тела?
Варианты ответов
- Если тело двигалось, то скорость его движения сохранится.
- Может, но скоро остановится.
- Не может.
Вопрос 12
Тело, выпущенное из рук, падает на землю. Какая сила вызывает падение тел?
Варианты ответов
- Сила тяжести
- Вес тела
- Сила упругости.

Вопрос 13
Сила — причина …
Варианты ответов
- изменение скорости движения тела.
- движения тела.
- постоянной скорости движения тела.
Вопрос 14
Сила тяжести действует …, а вес этого тела действует …
Варианты ответов
- на опору или подвес … на само тело.
- на опору — на подвес.
- на само тело … на опору или подвес.
Пройти тест
Сохранить у себя:
© 2020,
Пономарчук Анастасия Сергеевна
1022
ньютоновская механика — Какая сила требуется спутнику, вращающемуся вокруг Земли?
Спросил
Изменено
5 лет, 10 месяцев назад
Просмотрено
7к раз
$\begingroup$
Поскольку центростремительная сила — это направленная внутрь сила, необходимая для поддержания движения объекта с постоянной скоростью по круговой траектории, а центробежная сила — это кажущаяся сила, которая тянет объект от его центра или оси вращения.
Итак… спутник, вращающийся вокруг Земли, удерживается на своей орбите как центростремительной, так и центробежной силой? Или только центростремительная сила
Как меня еще в школе учили, что для спутника нужна и центробежная и центростремительная сила, но лично я считаю, что должна быть только центростремительная сила, так как спутник все равно вращается вокруг земли, так причем тут центробежная сила Войдите?. Потому что единственная причина, по которой спутник может оторваться от своей оси вращения, — это удар астероида или какие-то другие причины.
- ньютоновская механика
- силы
- системы отсчета
- центростремительная сила
- центробежная сила
$\endgroup$
2
$\begingroup$
Какая сила требуется спутнику, вращающемуся вокруг Земли?
В контексте принятой в настоящее время теории гравитации, общей (теории) относительности, ответ сила не требуется .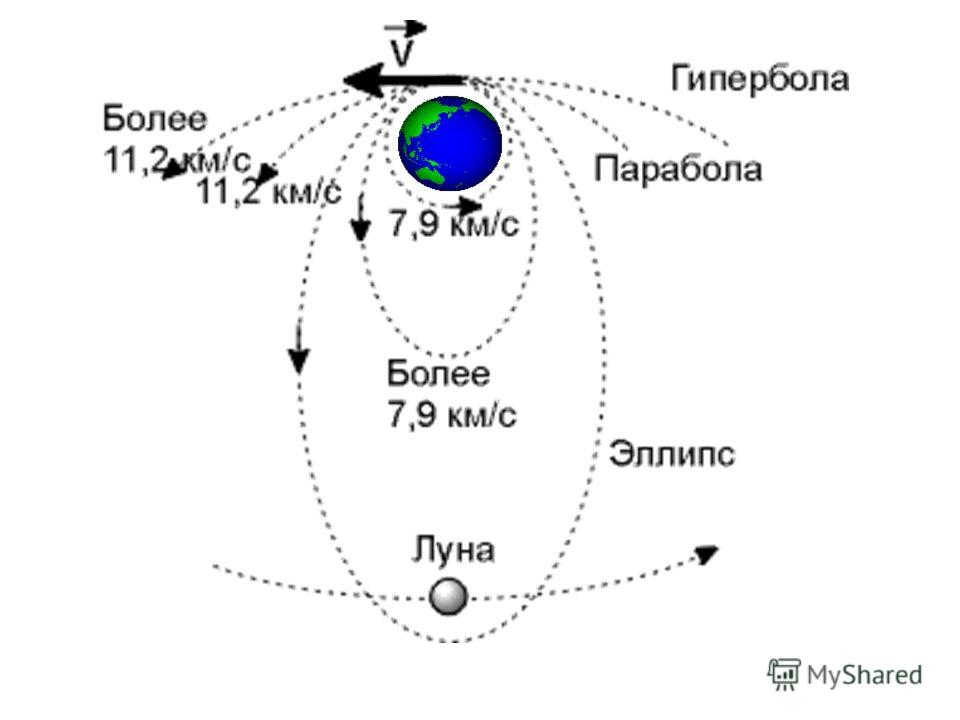
Рассмотрим случай, когда мяч вынужден совершать равномерное круговое движение благодаря веревке. Согласно акселерометру, прикрепленному к мячу, существует ускорение постоянной величины, направленное к центру круговой траектории; это центростремительное ускорение, необходимое для равномерного кругового движения. Центростремительная сила, отвечающая за ускорение, возникает из-за натяжения струны.
Теперь рассмотрим акселерометр, прикрепленный к шару на круговой орбите вокруг Земли. Можно было бы ожидать, что акселерометр на мяче показывает центростремительное ускорение, но на самом деле акселерометр (в идеале) показывает ноль! Очевидно, что на вращающийся шар не действует результирующая сила. Почему же тогда мяч движется по круговой траектории?
С точки зрения ОТО мяч движется по неускоренной траектории (геодезической) в пространстве-времени, искривленной массой Земли (пространство-время говорит материи, как двигаться; материя сообщает пространству-времени, как искривляться).
$\endgroup$
$\begingroup$
Правда в том, что для вращения спутника вокруг Земли необходимы как центростремительные, так и центробежные силы. Потому что, пока тело движется по круговой траектории, его скорость в точке находится вдоль линии, проведенной из этой точки, что порождает центробежную силу, а в случае спутника центростремительная сила определяется гравитацией Земли, а центробежная сила равна определяется его скоростью. И если бы не было центробежной силы, то спутник должен был бы упасть на землю.
$\endgroup$
1
$\begingroup$
Правда, есть только центростремительная сила, то есть гравитационная сила, удерживающая тело на орбите. Тело постоянно падает из-за силы, но оно также имеет импульс, перпендикулярный радиальному направлению, поэтому оно вращается по орбите (я полагаю, вы знаете эти подробности).
Центробежная сила добавляется в анализ, если вы находитесь в системе отсчета тела или в системе отсчета, где оно движется по прямой линии. Тогда это неинерциальная (ускоряющая) система отсчета, которая не следует системе Ньютона. второй закон, т.е. на тело действует центростремительная сила, но оно не движется к нему (в его системе отсчета)! Чтобы противостоять этому, добавляется фиктивная сила, равная и противоположная реальной центростремительной силе, и это центробежная сила.
Случай аналогичен тому, как направление вращения циклонов объясняется силой Кориолиса в земной системе отсчета. Это удобнее, чем брать реальную внутреннюю систему отсчета и явно изучать вращение Земли.
$\endgroup$
$\begingroup$
Проще говоря, центростремительная сила удерживает спутник на орбите.
Но давайте еще немного разберемся в терминологии. Спутник находится в космосе, и его притягивает гравитация Земли. Направление этой гравитационной силы, действующей со стороны Земли на спутник, равно поиск центра , и мы называем эту силу центростремительной (что означает поиск центра) силой.
Направление этой гравитационной силы, действующей со стороны Земли на спутник, равно поиск центра , и мы называем эту силу центростремительной (что означает поиск центра) силой.
Но если ты на спутнике, то чувствуешь себя невесомым. Вы смотрите и видите Землю. Вы говорите: «Хм, там есть Земля, значит, там должна быть и гравитация». Итак, будучи хорошим ньютоновским физиком, вы рисуете диаграмму свободного тела. Но вы понимаете, что единственный способ стать невесомым — это наличие направленной наружу силы, называемой центробежной силой, которая нейтрализует гравитационную силу. Но причина этой силы неизвестна, если она вообще существует. Получается, что нахождение в ускоряющемся спутнике означает, что вы не находитесь в инерциальной системе отсчета, а эта центробежная сила — сила фиктивная.
Когда использовать какую терминологию, зависит от вашей системы отсчета. Вы должны очень четко понимать, в какой системе отсчета вы работаете, но лично я просто придерживаюсь интерпретации центростремительной силы.
$\endgroup$
Почему спутники не падают с неба?
Изображение через Pixabay.
Спутники могут оставаться на орбите Земли благодаря идеальному взаимодействию сил между гравитацией и их скоростью. Тенденция спутника улетать в космос компенсируется гравитационным притяжением Земли, так что он находится в идеальном равновесии. Это тот же принцип, который объясняет, как естественные спутники, такие как Луна, застревают на орбите планеты.
Но некоторым очень умным людям пришлось проделать очень сложную математику, чтобы спроектировать идеальный запуск спутника. Если спутник движется слишком быстро, он улетает в космос. Слишком медленно, и ему суждено врезаться в атмосферу.
При правильном расстоянии, скорости и траектории объект может довольно долго противостоять гравитационному притяжению Земли. На самом деле гравитация — та же самая сила, которая пытается вытащить их на поверхность — является жизненно важной силой, удерживающей спутники на орбите вокруг нашей планеты.
РЕКЛАМА
А чтобы было интересно, начнем с американских горок.
Бесконечное падение
Если вы когда-нибудь катались на американских горках, то вам знакомо это странное ощущение в животе на поворотах или подъемах. С физической точки зрения это ощущение создается по инерции; хотя тележка меняет направление, ваше тело сопротивляется этому сдвигу. Вы надежно привязаны к тележке, но ваши внутренние органы могут свободно двигаться. Итак, в течение нескольких мгновений они, по сути, продолжают двигаться по старой траектории, в то время как остальная часть вашего тела движется по новой.
Этот процесс четко описан в первом законе движения: объект, движущийся прямолинейно или находящийся в состоянии покоя, будет сохранять это состояние до тех пор, пока на него не подействуют внешние силы. «Внешняя сила» здесь может означать очень многое, от сопротивления воздуха до гравитации и удара битой по летящему мячу.
Искусственные и естественные спутники полагаются на этот закон, чтобы оставаться над облаками. Поскольку в космосе нет сопротивления воздуха, когда тело начинает двигаться, практически ничто не может его замедлить. Он не теряет кинетическую энергию (импульс), поэтому может двигаться вечно.
Поскольку в космосе нет сопротивления воздуха, когда тело начинает двигаться, практически ничто не может его замедлить. Он не теряет кинетическую энергию (импульс), поэтому может двигаться вечно.
РЕКЛАМА
Спутники, которые мы строим сегодня, получают энергию от ракет, которые выводят их на орбиту. У них есть внутренние запасы топлива и двигатели, но они не используются для поддержания скорости. Они нужны для таких маневров, как уход от обломков или смещение орбиты. Ракеты передают спутникам, которые они несут, довольно много энергии, поскольку им необходимо двигаться со скоростью не менее 17 600 миль в час (28 330 км/ч), чтобы избежать гравитации Земли. После отделения от спутника остается достаточно энергии, чтобы удерживать этот спутник на орбите вокруг Земли в течение нескольких десятилетий, даже нескольких столетий.
Тем не менее, цель спутника — оставаться рядом (условно говоря), чтобы он мог транслировать наши сообщения в социальных сетях по всему миру. Но из того, что мы видели до сих пор, не должны ли они просто вечно путешествовать в космос? Да.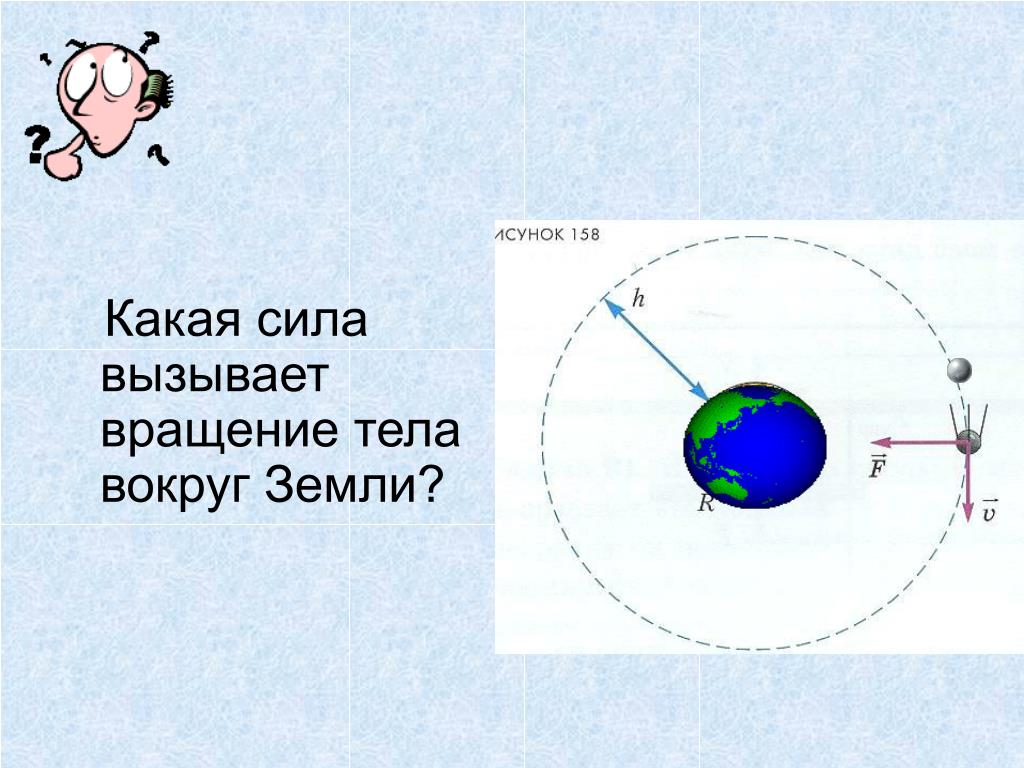 Но здесь действует еще одна сила — гравитация. В то время как импульс заставляет спутники двигаться, гравитация — это то, что удерживает их на нашей орбите.
Но здесь действует еще одна сила — гравитация. В то время как импульс заставляет спутники двигаться, гравитация — это то, что удерживает их на нашей орбите.
Если наполнить ведро водой и очень быстро его раскрутить, то вы увидите, что вода из него не выльется. Его прижимает ко дну ведра инерция (в данном случае центробежная сила), но ведро и ваша рука действуют против этой силы. В конце концов они выравниваются: вода не может пройти через дно ведра, она не может выйти через край, поэтому она как бы остается на одном месте.
Для спутников гравитация Земли действует как рука и ковш в приведенном выше примере. Один действительно простой способ понять этот процесс — представить спутник как ракету, которая всегда движется вперед, привязанная очень длинной цепью к центру нашей планеты — она просто будет двигаться по кругу.
Здесь важно правильно подобрать расстояние. Во-первых, вы хотите, чтобы ваш спутник находился за пределами атмосферы планеты, чтобы избежать сопротивления воздуха и поддерживать постоянную скорость. Но вы не хотите быть слишком далеко, потому что сила тяжести обратно пропорциональна квадрату расстояния между двумя объектами. Таким образом, если вы удвоите расстояние между спутником и Землей, гравитация будет притягивать его только на четверть меньше. Если вы утроите его, это будет только одна девятая силы. Другими словами, поднесите спутник слишком близко к Земле, и он упадет. Поместите его слишком далеко, и он убежит в космос.
Но вы не хотите быть слишком далеко, потому что сила тяжести обратно пропорциональна квадрату расстояния между двумя объектами. Таким образом, если вы удвоите расстояние между спутником и Землей, гравитация будет притягивать его только на четверть меньше. Если вы утроите его, это будет только одна девятая силы. Другими словами, поднесите спутник слишком близко к Земле, и он упадет. Поместите его слишком далеко, и он убежит в космос.
По сути, инженеры, выводя спутник на орбиту, пытаются заставить его упасть навсегда. Мы поставили его достаточно высоко, чтобы трение о воздух было почти нулевым (в идеале нулевым). Затем мы толкаем его очень быстро в одном направлении. Наконец, мы полагаемся на гравитацию Земли, которая тянет ее вниз, пока она движется вперед, так что в результате получается круговое движение. Поскольку он движется вперед, а планета круглая, он постоянно набирает высоту. Но, поскольку он одновременно падает, он постоянно теряет высоту. Лучше всего, чтобы он постоянно улетал в космос так же быстро, как падает на Землю.
Если математика сделана правильно, и фаза развертывания пройдет правильно, эти два нейтрализуют друг друга, и мы получим спутник на орбите. На практике никогда не достигает идеального , вот почему эти устройства снабжены топливом и двигателями, чтобы они могли выполнять крошечные корректировки направления своего движения или высоты и удерживать их на орбите.
Хорошим примером того, что произошло бы без этих двигателей, является Луна. Наш верный и отличительный ночной спутник не находится на стабильной орбите — он медленно ускользает от гравитационного притяжения Земли. Из-за специфики того, как гравитационное поле Земли взаимодействует с Луной, наша планета очень медленно ускоряет ее на более высокую орбиту. Продолжая приведенный выше пример, это делает силу «побега в космос» немного более мощной, чем силу «падения на Землю». Как следствие, Луна, вероятно, сойдет с орбиты вместе с Землей в будущем, но здесь мы говорим о миллиардах лет.
В качестве альтернативы у нас есть (была?) космическая станция «Мир» в качестве примера. Эта российская установка завершила свою миссию в марте 2001 года и была выведена на более низкую орбиту — «уведена с орбиты». Здесь трение о воздух неуклонно замедляло его. Из-за этого гравитация начала брать верх, и Мир в конце концов сгорел в атмосфере, вращаясь вокруг земного шара, все ближе и ближе к поверхности.
Эта российская установка завершила свою миссию в марте 2001 года и была выведена на более низкую орбиту — «уведена с орбиты». Здесь трение о воздух неуклонно замедляло его. Из-за этого гравитация начала брать верх, и Мир в конце концов сгорел в атмосфере, вращаясь вокруг земного шара, все ближе и ближе к поверхности.
Физика того, как тела взаимодействуют в космосе, всегда увлекательна, по крайней мере, для меня, и обычно имеет странную причуду, которая оживляет любой сценарий. Мысль о том, что что-то может продолжать падать вечно, фактически не приближаясь к земле, безусловно, причудлива, и она завораживала меня с тех пор, как я впервые столкнулся с ней. Позже научная фантастика привела меня к таким концепциям, как гравитационные рогатки, которые очень похожи на то, что мы обсуждали здесь, но на самом деле они помогают вам отправиться в космос 9.0043 быстрее . Прохладный.
Из нашего обсуждения весь этот процесс кажется простым, и в теории это так и есть. Но очень многим умным людям пришлось проделать чрезвычайно сложную математику, чтобы сделать это возможным, и многие до сих пор это делают, чтобы спутники вращались вокруг наших голов. Несмотря на то, что падение навсегда звучит как волшебство, оно основано на бесчисленных часах интеллектуальной работы, а в наши дни — на очень мощных компьютерах, круглосуточно выполняющих вычисления.
Несмотря на то, что падение навсегда звучит как волшебство, оно основано на бесчисленных часах интеллектуальной работы, а в наши дни — на очень мощных компьютерах, круглосуточно выполняющих вычисления.
Метки: землягравитацияЛунаспутники
13.4 Спутниковые орбиты и энергия
Цели обучения
К концу этого раздела вы сможете:
- Описать механизм круговых орбит
- Найти периоды обращения и скорости спутников
- Определить, связаны ли объекты гравитацией
Луна вращается вокруг Земли. В свою очередь, Земля и другие планеты вращаются вокруг Солнца. Пространство непосредственно над нашей атмосферой заполнено искусственными спутниками на орбите. Мы исследуем простейшую из этих орбит, круговую орбиту, чтобы понять взаимосвязь между скоростью и периодом движения планет и спутников по отношению к их положению и телам, вокруг которых они вращаются.
Круговые орбиты
Как отмечалось в начале этой главы, Николай Коперник впервые предположил, что Земля и все другие планеты вращаются вокруг Солнца по кругу. Он также отметил, что орбитальные периоды увеличиваются с расстоянием от Солнца. Более поздний анализ Кеплера показал, что эти орбиты на самом деле являются эллипсами, но орбиты большинства планет Солнечной системы почти круговые. Орбитальное расстояние Земли от Солнца изменяется всего на 2%. Исключением является эксцентрическая орбита Меркурия, орбитальное расстояние которой варьируется почти на 40%.
Он также отметил, что орбитальные периоды увеличиваются с расстоянием от Солнца. Более поздний анализ Кеплера показал, что эти орбиты на самом деле являются эллипсами, но орбиты большинства планет Солнечной системы почти круговые. Орбитальное расстояние Земли от Солнца изменяется всего на 2%. Исключением является эксцентрическая орбита Меркурия, орбитальное расстояние которой варьируется почти на 40%.
Определение орбитальной скорости и орбитального периода спутника намного проще для круговых орбит, поэтому мы делаем это предположение в последующем выводе. Как мы описали в предыдущем разделе, объект с отрицательной полной энергией связан гравитацией и поэтому находится на орбите. Наш расчет для частного случая круговых орбит подтвердит это. Мы ориентируемся на объекты, вращающиеся вокруг Земли, но наши результаты можно обобщить и на другие случаи.
Рассмотрим спутник массой 9{2}}{р}. [/latex]
Рис. 13.12 Спутник массой m вращается на орбите с радиусом r от центра Земли.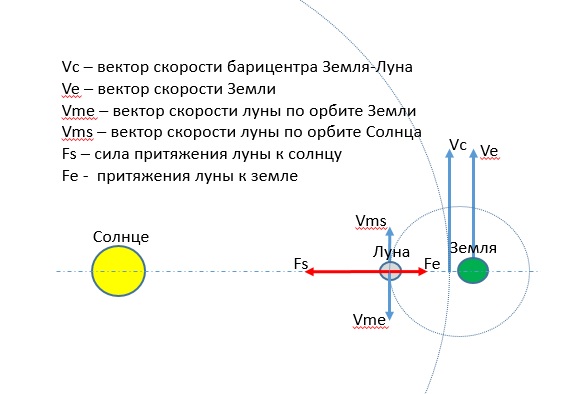 Сила гравитации обеспечивает центростремительное ускорение.
Сила гравитации обеспечивает центростремительное ускорение.
Решаем скорость орбиты, учитывая, что м отменяет, чтобы получить орбитальную скорость
[латекс] {v} _ {\ text {орбита}} = \ sqrt {\ frac {G {M} _{\текст{Е}}}{г}}. [/latex]
В соответствии с тем, что мы видели на (Рисунок) и (Рисунок), m не появляется на (Рисунок). Значение g скорость убегания и орбитальная скорость зависят только от расстояния до центра планеты, а не от массы объекта, на который воздействуют. Обратите внимание на сходство уравнений для [латекс] {v}_{\text{орбита}} [/латекс] и [латекс] {v}_{\текст{esc}} [/латекс]. Скорость убегания ровно в [латекс] \sqrt{2} [/латекс] раз больше, примерно на 40%, чем орбитальная скорость. Это сравнение отмечено на (Рисунок) и верно для спутника любого радиуса. 9{3}}{G{M}_{\text{E}}}}. [/latex]
В следующем разделе мы увидим, что это представляет третий закон Кеплера для случая круговых орбит. Это также подтверждает наблюдение Коперника о том, что период планеты увеличивается с удалением от Солнца. Нам нужно только заменить [латекс] {M}_{\text{E}} [/латекс] на [латекс] {M}_{\текст{Солнце}} [/латекс] в (Рисунок).
Нам нужно только заменить [латекс] {M}_{\text{E}} [/латекс] на [латекс] {M}_{\текст{Солнце}} [/латекс] в (Рисунок).
Мы завершаем этот раздел, возвращаясь к нашему более раннему обсуждению астронавтов на орбите, которые кажутся невесомыми, как будто они свободно падают на Землю. По сути, они находятся в свободном падении. Рассмотрим траектории, показанные на (рис.). (Эта цифра основана на рисунке Ньютона в его Principia , а также появлялась ранее в «Движении в двух и трех измерениях».) Все показанные траектории, достигающие поверхности Земли, имеют скорость меньше орбитальной. Астронавты будут ускоряться к Земле по показанным некруговым траекториям и чувствовать себя невесомыми. (На самом деле астронавты готовятся к жизни на орбите, летая на самолетах, которые свободно падают по 30 секунд за раз.) Но при правильной орбитальной скорости поверхность Земли изгибается от них точно с той же скоростью, с какой они падают на Землю. Разумеется, на том же расстоянии от поверхности находится точка круговой орбиты.
Рис. 13.13 Круговая орбита является результатом выбора тангенциальной скорости таким образом, что поверхность Земли изгибается с той же скоростью, с которой объект падает на Землю.
Мы можем обобщить наше обсуждение орбитальных спутников в следующей стратегии решения проблем.
Стратегия решения задач: орбиты и сохранение энергии
- Определите, применимы ли уравнения для скорости, энергии или периода к рассматриваемой задаче. Если нет, начните с первых принципов, которые мы использовали для вывода этих уравнений.
- Чтобы начать с первых принципов, нарисуйте диаграмму свободного тела и примените закон всемирного тяготения Ньютона и второй закон Ньютона.
- Наряду с определениями скорости и энергии примените второй закон Ньютона к интересующим вас телам.
Пример
Международная космическая станция
Определите орбитальную скорость и период для Международной космической станции (МКС). {2}\text{км} [/латекс]. Мы используем (Рисунок) и (Рисунок), чтобы найти орбитальную скорость и период соответственно. 9{3}\,\text{s} [/latex]
{2}\text{км} [/латекс]. Мы используем (Рисунок) и (Рисунок), чтобы найти орбитальную скорость и период соответственно. 9{3}\,\text{s} [/latex]
, что составляет чуть более 90 минут.
Значение
МКС считается находящейся на низкой околоземной орбите (НОО). Почти все спутники находятся на НОО, включая большинство метеорологических спутников. Спутники GPS на расстоянии около 20 000 км считаются средней околоземной орбитой. Чем выше орбита, тем больше энергии требуется, чтобы вывести его туда, и тем больше энергии нужно, чтобы добраться до него для ремонта. Особый интерес представляют спутники на геостационарной орбите. Все стационарные спутниковые тарелки на земле, направленные в небо, например антенны для приема телевизионных сигналов, направлены на геостационарные спутники. Эти спутники размещены на точном расстоянии и чуть выше экватора, так что их период обращения составляет 1 день. Они остаются в фиксированном положении относительно поверхности Земли.
Проверьте правильность понимания
Во сколько раз должен измениться радиус, чтобы орбитальная скорость спутника уменьшилась вдвое? Во сколько раз это изменит период?
Показать решение
Пример
Определение массы Земли
Определите массу Земли по орбите Луны. {6}\,\текст{с} [/латекс], а 9{24}\,\text{kg} [/latex], которые мы получили на (рис.), используя значение g на поверхности Земли. Хотя эти значения очень близки (~ 0,8%), в обоих расчетах используются средние значения. Величина г изменяется от экватора к полюсам примерно на 0,5%. Но Луна имеет эллиптическую орбиту, на которой значение r варьируется чуть более чем на 10%. (Видимый размер полной Луны на самом деле варьируется примерно на эту величину, но это трудно заметить при случайном наблюдении, поскольку время от одной крайности до другой составляет много месяцев.)
{6}\,\текст{с} [/латекс], а 9{24}\,\text{kg} [/latex], которые мы получили на (рис.), используя значение g на поверхности Земли. Хотя эти значения очень близки (~ 0,8%), в обоих расчетах используются средние значения. Величина г изменяется от экватора к полюсам примерно на 0,5%. Но Луна имеет эллиптическую орбиту, на которой значение r варьируется чуть более чем на 10%. (Видимый размер полной Луны на самом деле варьируется примерно на эту величину, но это трудно заметить при случайном наблюдении, поскольку время от одной крайности до другой составляет много месяцев.)
Проверьте свое понимание
Есть еще одно соображение относительно этого последнего расчета [латекс] {M}_{\text{E}} [/латекс]. Мы получили (рисунок), предполагая, что спутник вращается вокруг центра астрономического тела с тем же радиусом, который используется в выражении для гравитационной силы между ними. Какое предположение делается для обоснования этого? Земля примерно в 81 раз массивнее Луны. Луна вращается вокруг точного центра Земли?
Луна вращается вокруг точного центра Земли?
Показать решение
Пример
Галактическая скорость и период
Вернемся к (рисунок). Предположим, что галактики Млечный Путь и Андромеда вращаются по круговой орбите друг вокруг друга. Какова будет скорость каждого из них и каков будет их орбитальный период? Предположим, что масса каждого из них составляет 800 миллиардов солнечных масс, а их центры разделены 2,5 миллионами световых лет.
Стратегия
Мы не можем использовать (Рисунок) и (Рисунок) напрямую, потому что они были получены в предположении, что объект массой m вращалась вокруг центра гораздо большей планеты с массой M . Мы определили гравитационную силу на (рис.) с помощью закона всемирного тяготения Ньютона. Мы можем использовать второй закон Ньютона, примененный к центростремительному ускорению любой галактики, чтобы определить их тангенциальную скорость. Из этого результата мы можем определить период орбиты. {9{2}. [/latex]
{9{2}. [/latex]
Так как галактики находятся на круговой орбите, они имеют центростремительное ускорение. Если мы проигнорируем влияние других галактик, то, как мы узнали из раздела «Линейный импульс, столкновения и вращение с фиксированной осью», центры масс двух галактик останутся фиксированными. Следовательно, галактики должны вращаться вокруг этого общего центра масс. Для равных масс центр масс находится ровно посередине между ними. Таким образом, радиус орбиты [латекс] {г}_{\текст{орбита}} [/латекс] не равен расстоянию между галактиками, а составляет половину этого значения, или 1,25 миллиона световых лет. . Эти два разных значения показаны на (Рисунок).
Рисунок 13.14 Расстояние между двумя галактиками, которое определяет гравитационную силу между ними, равно r и отличается от [латекс] {г}_{\текст{орбита}} [/латекс], который является радиусом орбиты для каждого. Для равных масс [латекс] {r}_{\text{орбита}}=1\текст{/}2r [/латекс]. (кредит: модификация работы Марка Ван Нордена)
Используя выражение для центростремительного ускорения, мы имеем
[латекс] \begin{array}{ccc}\hfill {a}_{\text{c}}& = \hfill & \frac{{v}_{\text{орбита}}^{2}}{{r}_{\text{орбита}}}\hfill \\ \hfill 1. 9{18}\,\text{s} [/latex], около 50 миллиардов лет.
9{18}\,\text{s} [/latex], около 50 миллиардов лет.
Значение
Орбитальная скорость 47 км/с на первый взгляд может показаться высокой. Но эта скорость сравнима со скоростью убегания от Солнца, которую мы рассчитали в более раннем примере. Чтобы дать еще большую перспективу, этот период почти в четыре раза больше, чем время существования Вселенной.
Фактически, нынешнее относительное движение этих двух галактик таково, что они, как ожидается, столкнутся примерно через 4 миллиарда лет. Хотя плотность звезд в каждой галактике делает маловероятным прямое столкновение любых двух звезд, такое столкновение окажет драматическое влияние на форму галактик. Примеры таких столкновений хорошо известны в астрономии.
Проверьте свое понимание
Галактики не являются отдельными объектами. Как гравитационная сила одной галактики, действующая на «ближние» звезды другой галактики, сравнивается с более удаленными? Как это повлияет на форму самих галактик?
Показать решение
См. страницу Sloan Digital Sky Survey для получения дополнительной информации о сталкивающихся галактиках.
страницу Sloan Digital Sky Survey для получения дополнительной информации о сталкивающихся галактиках.
Энергия на круговых орбитах
В разделе «Потенциальная гравитационная энергия» и «Общая энергия» мы утверждали, что объекты гравитационно связаны, если их полная энергия отрицательна. Аргумент был основан на простом случае, когда скорость была направлена прямо от планеты или к ней. Теперь мы исследуем полную энергию для круговой орбиты и покажем, что полная энергия действительно отрицательна. Как и раньше, мы начнем со второго закона Ньютона, примененного к круговой орбите, 9{}}. [/latex]
Мы видим, что полная энергия отрицательна и имеет ту же величину, что и кинетическая энергия. Для круговых орбит величина кинетической энергии составляет ровно половину величины потенциальной энергии. Примечательно, что этот результат применим к любым двум массам, движущимся по круговым орбитам вокруг их общего центра масс на расстоянии r друг от друга. Доказательство этого оставлено в качестве упражнения. В следующем разделе мы увидим, что очень похожее выражение применимо и к эллиптическим орбитам.
В следующем разделе мы увидим, что очень похожее выражение применимо и к эллиптическим орбитам.
Пример
Энергия, необходимая для выхода на орбиту
На (рисунке) мы рассчитали энергию, необходимую для простого подъема 9000-килограммового корабля «Союз » массой от поверхности Земли на высоту МКС, 400 км над поверхностью. Другими словами, мы нашли его изменение потенциальной энергии. Теперь зададимся вопросом, какое полное изменение энергии требуется в корабле «Союз », чтобы поднять его с поверхности Земли и вывести на орбиту с МКС для сближения ((Рисунок))? Сколько из этой полной энергии составляет кинетическая энергия?
Рис. 13.15 «Союз» на сближении с МКС. Обратите внимание, что эта диаграмма не в масштабе; Союз очень мал по сравнению с МКС, и его орбита намного ближе к Земле. (кредит: модификация работ НАСА)
Стратегия
Требуемая энергия — это разница в общей энергии «Союз » на орбите и на поверхности Земли. Мы можем использовать (Рисунок), чтобы найти полную энергию Союз на орбите МКС. Но полная энергия на поверхности — это просто потенциальная энергия, поскольку она начинается из состояния покоя. [Обратите внимание, что мы не используйте (рисунок) на поверхности, так как мы не находимся на орбите на поверхности.] Кинетическая энергия может быть найдена из разницы между изменением полной энергии и изменением потенциальной энергии, найденным на (рисунке). В качестве альтернативы мы можем использовать (Рисунок), чтобы найти [латекс] {v}_{\text{орбита}} [/латекс] и вычислить кинетическую энергию непосредственно из этого. Тогда полная требуемая энергия равна кинетической энергии плюс изменение потенциальной энергии, найденное на (рис.).
Мы можем использовать (Рисунок), чтобы найти полную энергию Союз на орбите МКС. Но полная энергия на поверхности — это просто потенциальная энергия, поскольку она начинается из состояния покоя. [Обратите внимание, что мы не используйте (рисунок) на поверхности, так как мы не находимся на орбите на поверхности.] Кинетическая энергия может быть найдена из разницы между изменением полной энергии и изменением потенциальной энергии, найденным на (рисунке). В качестве альтернативы мы можем использовать (Рисунок), чтобы найти [латекс] {v}_{\text{орбита}} [/латекс] и вычислить кинетическую энергию непосредственно из этого. Тогда полная требуемая энергия равна кинетической энергии плюс изменение потенциальной энергии, найденное на (рис.).
Раствор
9{11}\,\text{J.} [/latex]
Значение
Кинетическая энергия корабля «Союз » почти в восемь раз превышает изменение его потенциальной энергии, или 90% от общей энергии, необходимой для сближения. с МКС. И важно помнить, что эта энергия представляет собой только ту энергию, которую необходимо отдать «Союзу ». С нашей современной ракетной технологией масса двигательной установки (ракетного топлива, его контейнера и системы сгорания) намного превышает массу полезной нагрузки, и этой массе необходимо передать огромное количество кинетической энергии. Таким образом, фактическая стоимость энергии во много раз превышает изменение энергии самой полезной нагрузки.
с МКС. И важно помнить, что эта энергия представляет собой только ту энергию, которую необходимо отдать «Союзу ». С нашей современной ракетной технологией масса двигательной установки (ракетного топлива, его контейнера и системы сгорания) намного превышает массу полезной нагрузки, и этой массе необходимо передать огромное количество кинетической энергии. Таким образом, фактическая стоимость энергии во много раз превышает изменение энергии самой полезной нагрузки.
Резюме
- Орбитальные скорости определяются массой тела, находящегося на орбите, и расстоянием от центра этого тела, а не массой гораздо меньшего объекта на орбите.
- Период обращения также не зависит от массы объекта на орбите.
- Тела с сопоставимыми массами вращаются вокруг своего общего центра масс, а их скорости и периоды должны определяться из второго закона Ньютона и закона всемирного тяготения.
9{2} [/латекс]. С кем вы согласны и почему?
Многие спутники размещены на геостационарных орбитах. Что особенного в этих орбитах? Сколько таких спутников потребуется для глобальной сети связи?
Что особенного в этих орбитах? Сколько таких спутников потребуется для глобальной сети связи?
Показать решение
Задачи
Если бы по орбите Земли двигалась планета, масса которой в 1,5 раза больше массы Земли, каков был бы ее период?
Две планеты на круговых орбитах вокруг звезды имеют скорости v и 2 v . а) Каково отношение радиусов орбит планет? б) Каково соотношение их периодов?
Показать решение
Используя среднее расстояние Земли от Солнца и период обращения Земли, (а) найдите центростремительное ускорение Земли при ее движении вокруг Солнца. (b) Сравните это значение с центростремительным ускорением на экваторе из-за вращения Земли.
Каков радиус орбиты спутника Земли с периодом 1 час? б) Что неразумного в этом результате? 9{7} [/latex] лет вместо этого, какова масса галактики? Такие расчеты используются, чтобы предположить существование другой материи, такой как очень массивная черная дыра в центре Млечного Пути.
(a) Чтобы маленький спутник не дрейфовал на соседний астероид, его выводят на орбиту с периодом 3,02 часа и радиусом 2,0 км. Какова масса астероида? (b) Кажется ли эта масса приемлемой для размера орбиты?
Показать решение
Луна и Земля вращаются вокруг своего общего центра масс, который находится примерно в 4700 км от центра Земли. (это 169{4} [/latex] световых лет. (Световой год — это расстояние, пройденное светом за 1 год.) Вычислите центростремительное ускорение Солнца на его галактической орбите. Подтверждает ли ваш результат утверждение о том, что на Солнце может быть расположена почти инерциальная система отсчета? б) Вычислите среднюю скорость движения Солнца по его галактической орбите. Ответ вас удивляет?
Показать решение
Геосинхронный спутник Земли — это спутник с периодом обращения ровно 1 день. Такие орбиты полезны для связи и наблюдения за погодой, потому что спутник остается над одной и той же точкой на Земле (при условии, что он вращается в экваториальной плоскости в том же направлении, что и вращение Земли).