Кто доказал: Британский математик доказал гипотезу Римана

Британский математик доказал гипотезу Римана

Наука

Британский математик доказал гипотезу Римана — одну из «задач тысячелетия», вознаграждение за решение которых составляет $1 млн. Он получит деньги, если доказательство будет подтверждено научным сообществом. Пока что эта награда присуждалась только российскому математику Григорию Перельману, но он от нее отказался.

Знаменитый британский математик Майкл Атья, профессор Оксфордского, Кембриджского и Эдинбургского институтов и лауреат почти десятка престижных премий в области математики, представил доказательство гипотезы Римана, одной из «задач тысячелетия». Доказательство занимает всего 15 строк, а вместе с введением и списком литературы — пять страниц. Текст Атья выложил на сервисе Google Drive.

Гипотеза о распределении нулей дзета-функции Римана была сформулирована математиком Бернхардом Риманом в 1859 году.

Она описывает, как расположены на числовой прямой простые числа.

В то время как не найдено какой-либо закономерности, описывающей распределение простых чисел среди натуральных, Риман обнаружил, что количество простых чисел, не превосходящих x, — функция распределения простых чисел, обозначаемая π(x) — выражается через распределение так называемых «нетривиальных нулей» дзета-функции.

Гипотеза Римана утверждает, что все нетривиальные нули дзета-функции лежат на вертикальной линии Re=0,5 комплексной плоскости. Гипотеза Римана важна не только для чистой математики — дзета-функция постоянно всплывает в практических задачах, связанных с простыми числами, например, в криптографии.

По словам Атьи, решение он нашел, экспериментируя с постоянной тонкой структуры — фундаментальной физической постоянной, характеризующей силу электромагнитного взаимодействия. Она определяет размер очень малого изменения величины (расщепления) энергетических уровней атома и, следовательно, образования тонкой структуры — набора узких и близких частот в его спектральных линиях.

Гипотеза Римана входит в список семи «задач тысячелетия», за решение каждой из которых Математический институт Клэя в США обязывается выплатить награду в один миллион долларов США.

Incidentally, here is the proof. You’re welcome. #HLF18 pic.twitter.com/cXe2mPyFfB

— Markus Pssel (@mpoessel) 24 сентября 2018 г.

Если доказательство будет подтверждено, Атья получит награду.

Также Атья в 2016 году предложил решение одной из главных проблем дифференциальной геометрии — вопроса о существовании комплексной структуры на шестимерной сфере, однако подтверждения этого доказательства со стороны научного сообщества до сих пор не последовало.

На сегодняшний день найдено решение только одной задачи тысячелетия — гипотезы Пуанкаре. Она заключается в том, что всякое односвязное компактное трехмерное многообразие без края гомеоморфно трехмерной сфере. Доказать гипотезу смог российский математик Григорий Перельман. От вознаграждения он отказался.

«Если говорить совсем коротко, то главная причина — это несогласие с организованным математическим сообществом. Мне не нравятся их решения, я считаю их несправедливыми», — заявил Перельман. Он также добавил, что считает ничуть не меньшим своего вклад в доказательство гипотезы Пуанкаре со стороны американского математика Ричарда Гамильтона.

Математический институт Клэя объявил о своем решении отдать премию Перельману 19 марта 2010 года. Работы, за которые математик удостоился награды, были написаны им в 2002 году, причем они были выложены в архив электронных препринтов, а не напечатаны в рецензируемом научном журнале. В своих выкладках Перельман завершил доказательство гипотезы геометризации Терстона, которая прямо связана с гипотезой Пуанкаре.

В 2005 году за эти работы Перельману была присуждена Филдсовская премия, которую часто называют Нобелевской премией для математиков. От этой награды российский математик также отказался.

В 2014 году математик из Казахстана Мухтарбай Отелбаев заявил, что решил еще одну из «задач тысячелетия» — нашел условия системы уравнений Навье — Стокса, при которых для каждого набора параметров имеется единственное решение. Уравнения Навье — Стокса — система дифференциальных уравнений в частных производных, описывающая движение вязкой ньютоновской жидкости. Уравнения Навье — Стокса являются одними из важнейших в гидродинамике и применяются в математическом моделировании многих природных явлений и технических задач.

Для того чтобы признать решение Отелбаева верным, научное сообщество должно его проверить. Пока что результаты проверки неизвестны.

В 2010 году американский математик индийского происхождения Винай Деолаликар заявил, что решил еще одну из задач тысячелетия — нашел доказательство неравенства классов сложности P и NP.

Данная проблема состоит в следующем: если положительный ответ на какой-то вопрос можно быстро проверить (за полиномиальное время), то правда ли, что ответ на этот вопрос можно быстро найти (за полиномиальное время и используя полиномиальную память), то есть действительно ли задачу легче проверить, чем решить?

Данных о том, что научное сообщество признало доказательство верным, пока что нет.

Теорему Ферма снова «доказали» — Российская газета

Завистники утверждают, что французский математик Пьер Ферма вписал свое имя в историю всего одной фразой. На полях рукописи с формулировкой знаменитой теоремы в 1637 году он сделал пометку: «Я нашел удивительное решение, но здесь маловато места, чтобы его поместить». Тогда и началась удивительная математическая гонка, в которую наряду с выдающимися учеными включилась армия дилетантов.

В чем коварство задачи Ферма? На первый взгляд, она понятна даже школьнику.

В основе — известная каждому теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: х2 + у2 = z2. Ферма утверждал: уравнение при любых степенях больше двух не имеет решения в целых числах.

Казалось бы, просто. Протяни руку, и вот ответ. Неудивительно, что академии разных стран, научные институты, даже редакции газет были завалены десятками тысяч доказательств. Их число беспрецедентно, уступает разве что проектам «вечных двигателей». Но если эти сумасшедшие идеи серьезная наука давно не рассматривает, то работы «фермистов» честно и заинтересованно изучает. И, увы, находит ошибки. Говорят, что за три с лишним века образовалось целое математическое кладбище решений теоремы.

Не зря говорят: близок локоть, а не укусишь. Проходили года, десятилетия, века, и задача Ферма представлялась все более удивительной и заманчивой. Вроде бы простенькая, она оказалась не по зубам стремительно наращивающему мускулы прогрессу. Человек уже расщепил атом, добрался до гена, ступил на Луну, а Ферма не давался, продолжая манить потомков ложными надеждами.

Однако попытки одолеть научную вершину не прошли даром. Первый шаг сделал великий Эйлер, доказав теорему для четвертой степени, затем для третьей. В конце XIX века немец Эрнст Куммер довел число степеней до ста. Наконец, вооружившись компьютерами, ученые увеличили эту цифру до 100 тысяч. Но Ферма-то говорил о любых степенях. В этом состояла вся загвоздка.

Конечно, мучились ученые над задачей не из-за спортивного интереса. Знаменитый математик Давид Гильберт говорил, что теорема — это пример, как вроде бы малозначительная проблема может оказать на науку огромное влияние. Работая над ней, ученые открыли совершенно новые математические горизонты, например, были заложены фундаменты теории чисел, алгебры, теории функций.

И все же Великая теорема была в 1995 году покорена. Ее решение представил американец из Принстонского университета Эндрю Уайлс, и оно официально признано научным сообществом. Более семи лет жизни отдал он, чтобы найти доказательство. По мнению ученых, эта выдающаяся работа свела воедино труды многих математиков, восстановив утраченные связи между разными ее разделами.

— Итак, вершина взята, и наука ответ получила, — сказал корреспонденту «РГ» ученый секретарь Отделения математики Российской академии наук, доктор технических наук Юрий Вишняков. — Теорема доказана, пусть и не простейшим способом, на чем настаивал сам Ферма. А теперь желающие могут печатать свои варианты.

Однако семейство «фермистов» вовсе не собирается признавать доказательство Уайлса. Нет, они не опровергают решение американца, ведь оно очень сложное, а потому понятно лишь узкому кругу специалистов. Но не проходит недели, чтобы в Интернете ни появилось новое откровение очередного энтузиаста, «наконец-то поставившего точку в многолетней эпопее».

Кстати, буквально вчера в редакцию «РГ» позвонил один из старейших в нашей стране «фермистов» Всеволод Ярош: «А вы знаете, что теорему Ферма я доказал еще до Уайлса. Более того, потом нашел у него ошибку, о чем написал выдающемуся нашему математику академику Арнольду с просьбой напечатать об этом в научном журнале. Теперь жду ответа. Переписываюсь по этому поводу и с французской академией наук».

И вот только что, как сообщается в ряде СМИ, с «легким изяществом раскрыл великую тайну математики», еще один энтузиаст — бывший генеральный конструктор ПО «Полет» из Омска, доктор технических наук Александр Ильин. Решение оказалось настолько простым и коротким, что поместилось на маленьком участке газетной площади одного из центральных изданий.

Редакция «РГ» обратилась в ведущий в стране Институт математики им. Стеклова РАН с просьбой оценить это решение. Ученые были категоричны: нельзя комментировать газетную публикацию. Но после долгих уговоров и учитывая повышенный интерес к знаменитой задаче, согласились. По их словам, в опубликованном очередном доказательстве допущено несколько принципиальных ошибок. Кстати, их вполне мог бы заметить даже студент математического факультета.

И все же редакция хотела получить информацию из первых рук. Тем более что вчера в академии авиации и воздухоплавания Ильин должен был представить свое доказательство. Однако оказалось, что о такой академии мало кто знает даже среди специалистов. А когда все-таки с величайшим трудом удалось разыскать телефон ученого секретаря этой организации, то, как выяснилось, он даже не подозревал, что именно у них должно состояться столь историческое событие. Словом, корреспонденту «РГ» стать свидетелем мировой сенсации так и не удалось.

Что же доказал Григорий Перельман?

Сергей Дужин,
доктор физ. -мат. наук, старший научный сотрудник Санкт-Петербургского отделения Математического института РАН
«Троицкий вариант» №10(104), 22 мая 2012 года

Последним великим достижением чистой математики называют доказательство петербуржцем Григорием Перельманом в 2002–2003 годах гипотезы Пуанкаре, высказанной в 1904 году и гласящей: «всякое связное, односвязное, компактное трехмерное многообразие без края гомеоморфно сфере S3».

В этой фразе имеется несколько терминов, которые я постараюсь объяснить так, чтобы их общий смысл стал понятен нематематикам (я предполагаю, что читатель закончил среднюю школу и кое-что из школьной математики еще помнит).

Начнем с понятия гомеоморфизма, центрального в топологии. Вообще, топологию часто определяют как «резиновую геометрию», т. е. как науку о свойствах геометрических образов, которые не меняются при плавных деформациях без разрывов и склеек, а точнее, при возможности установить между двумя объектами взаимно-однозначное и взаимно-непрерывное соответствие.

Главную идею проще всего объяснить на классическом примере кружки и бублика. Первую можно превратить во второй непрерывной деформацией.

Эти рисунки наглядно показывают, что кружка гомеоморфна бублику, причем этот факт верен как для их поверхностей (двумерных многообразий, называемых тором), так и для заполненных тел (трехмерных многообразий с краем).

Приведем толкование остальных терминов, фигурирующих в формулировке гипотезы.

  1. Трехмерное многообразие без края. Это такой геометрический объект, у которого каждая точка имеет окрестность в виде трехмерного шара. Примерами 3-многообразий может служить, во-первых, всё трехмерное пространство, обозначаемое R3 , а также любые открытые множества точек в R3 , к примеру внутренность полнотория (бублика). Если рассмотреть замкнутое полноторие, т. е. добавить и его граничные точки (поверхность тора), то мы получим уже многообразие с краем — у краевых точек нет окрестностей в виде шарика, но лишь в виде половинки шарика.
  2. Связное. Понятие связности здесь самое простое. Многообразие связно, если оно состоит из одного куска, или, что то же самое, любые две его точки можно соединить непрерывной линией, не выходящей за его пределы.
  3. Односвязное. Понятие односвязности сложнее. Оно означает, что любую непрерывную замкнутую кривую, расположенную целиком в пределах данного многообразия, можно плавно стянуть в точку, не покидая этого многообразия. Например, обычная двумерная сфера в R3 односвязна (кольцевую резинку, как угодно приложенную к поверхности яблока, можно плавной деформацией стянуть в одну точку, не отрывая резинки от яблока). С другой стороны, окружность и тор неодносвязны.
  4. Компактное. Многообразие компактно, если любой его гомеоморфный образ имеет ограниченные размеры. Например, открытый интервал на прямой (все точки отрезка, кроме его концов) некомпактен, так как его можно непрерывно растянуть до бесконечной прямой. А вот замкнутый отрезок (с концами) является компактным многообразием с краем: при любой непрерывной деформации концы переходят в какие-то определенные точки, и весь отрезок обязан переходить в ограниченную кривую, соединяющую эти точки.

Размерность многообразия — это число степеней свободы у точки, которая на нем «живет». У каждой точки есть окрестность в виде диска соответствующей размерности, т. е. интервала прямой в одномерном случае, круга на плоскости в двумерном, шара в трехмерном и т. д. Одномерных связных многообразий без края с точки зрения топологии всего два: это прямая и окружность. Из них только окружность компактна.

Примером пространства, не являющегося многообразием, может служить, например, пара пересекающихся линий — ведь у точки пересечения двух линий любая окрестность имеет форму креста, у нее нет окрестности, которая была бы сама по себе просто интервалом (а у всех других точек такие окрестности есть). Математики в таких случаях говорят, что мы имеем дело с особым многообразием, у которого есть одна особая точка.

Двумерные компактные многообразия хорошо известны. Если рассматривать только ориентируемые1 многообразия без края, то они с топологической точки зрения составляют простой, хотя и бесконечный, список: и так далее. Каждое такое многообразие получается из сферы приклеиванием нескольких ручек, число которых называется родом поверхности.

На рисунке изображены поверхности рода 0, 1, 2 и 3. Чем выделяется сфера из всех поверхностей этого списка? Оказывается, односвязностью: на сфере любую замкнутую кривую можно стянуть в точку, а на любой другой поверхности всегда можно указать кривую, которую стянуть в точку по поверхности невозможно.

Любопытно, что и трехмерные компактные многообразия без края можно в некотором смысле классифицировать, т. е. выстроить в некоторый список, хотя не такой прямолинейный, как в двумерном случае, а имеющий довольно сложную структуру. Тем не менее, трехмерная сфера S3 выделяется в этом списке точно так же, как двумерная сфера в списке, приведенном выше. Тот факт, что любая кривая на S3 стягивается в точку, доказывается столь же просто, как и в двумерном случае. А вот обратное утверждение, а именно, что это свойство уникально именно для сферы, т.  е. что на любом другом трехмерном многообразии есть нестягиваемые кривые, очень трудное и в точности составляет содержание гипотезы Пуанкаре, о которой мы ведем речь.

Важно понимать, что многообразие может жить само по себе, о нем можно мыслить как о независимом объекте, никуда не вложенном. (Представьте себе жизнь двумерных существ на поверхности обычной сферы, не подозревающих о существовании третьего измерения.) К счастью, все двумерные поверхности из приведенного выше списка можно вложить в обычное пространство R3, что облегчает их визуализацию. Для трехмерной сферы S3 (и вообще для любого компактного трехмерного многообразия без края) это уже не так, поэтому необходимы некоторые усилия для того, чтобы понять ее строение.

По-видимому, простейший способ объяснить топологическое устройство трехмерной сферы S3 — это при помощи одноточечной компактификации. А именно, трехмерная сфера S3 представляет собой одноточечную компактификацию обычного трехмерного (неограниченного) пространства R3.

Поясним эту конструкцию сначала на простых примерах. Возьмем обычную бесконечную прямую (одномерный аналог пространства) и добавим к ней одну «бесконечно удаленную» точку, считая, что при движении по прямой вправо или влево мы в конце концов попадаем в эту точку. С топологической точки зрения нет разницы между бесконечной прямой и ограниченным открытым отрезком (без концевых точек). Такой отрезок можно непрерывно изогнуть в виде дуги, свести поближе концы и вклеить в место стыка недостающую точку. Мы получим, очевидно, окружность — одномерный аналог сферы.

Подобным же образом, если я возьму бесконечную плоскость и добавлю одну точку на бесконечности, к которой стремятся все прямые исходной плоскости, проходимые в любом направлении, то мы получим двумерную (обычную) сферу S2 . Эту процедуру можно наблюдать при помощи стереографической проекции, которая каждой точке P сферы, за исключением северного полюса N, ставит в соответствие некоторую точку плоскости P’.

Таким образом, сфера без одной точки — это топологически все равно, что плоскость, а добавление точки превращает плоскость в сферу.

В принципе, точно такая же конструкция применима и к трехмерной сфере и трехмерному пространству, только для ее осуществления необходим выход в четвертое измерение, и на чертеже это не так просто изобразить. Поэтому я ограничусь словесным описанием одноточечной компактификации пространства R3.

Представьте себе, что к нашему физическому пространству (которое мы, вслед за Ньютоном, считаем неограниченным евклидовым пространством с тремя координатами x, y, z) добавлена одна точка «на бесконечности» таким образом, что при движении по прямой в любом направлении вы в нее попадаете (т. е. каждая пространственная прямая замыкается в окружность). Тогда мы получим компактное трехмерное многообразие, которое и есть по определению сфера S3.

Легко понять, что сфера S3 односвязна. В самом деле, любую замкнутую кривую на этой сфере можно немного сдвинуть, чтобы она не проходила через добавленную точку. Тогда мы получим кривую в обычном пространстве R3, которая легко стягивается в точку посредством гомотетий, т.  е. непрерывного сжатия по всем трем направлениям.

Для понимания, как устроено многообразие S3, весьма поучительно рассмотреть его разбиение на два полнотория. Если из пространства R3 выбросить полноторие, то останется нечто не очень понятное. А если пространство компактифицировать в сферу, то это дополнение превращается тоже в полноторие. То есть сфера S3 разбивается на два полнотория, имеющих общую границу — тор.

Вот как это можно понять. Вложим тор в R3 как обычно, в виде круглого бублика, и проведем вертикальную прямую — ось вращения этого бублика. Через ось проведем произвольную плоскость, она пересечет наше полноторие по двум кругам, показанным на рисунке зеленым цветом, а дополнительная часть плоскости разбивается на непрерывное семейство красных окружностей. К их числу относится и центральная ось, выделенная более жирно, потому что в сфере S3 прямая замыкается в окружность. Трехмерная картина получается из этой двумерной вращением вокруг оси. Полный набор повернутых окружностей заполнит при этом трехмерное тело, гомеоморфное полноторию, только выглядящее необычно.

В самом деле, центральная ось будет в нем осевой окружностью, а остальные будут играть роль параллелей — окружностей, составляющих обычное полноторие.

Чтобы было с чем сравнивать 3-сферу, я приведу еще один пример компактного 3-многообразия, а именно трехмерный тор. Трехмерный тор можно построить следующим образом. Возьмем в качестве исходного материала обычный трехмерный куб:

В нем имеется три пары граней: левая и правая, верхняя и нижняя, передняя и задняя. В каждой паре параллельных граней отождествим попарно точки, получающиеся друг из друга переносом вдоль ребра куба. То есть будем считать (чисто абстрактно, без применения физических деформаций), что, например, A и A’ — это одна и та же точка, а B и B’ — тоже одна точка, но отличная от точки A. Все внутренние точки куба будем рассматривать как обычно. Сам по себе куб — это многообразие с краем, но после проделанных склеек край замыкается сам на себя и исчезает. В самом деле, окрестностями точек A и A’ в кубе (они лежат на левой и правой заштрихованных гранях) служат половинки шаров, которые после склейки граней сливаются в целый шарик, служащий окрестностью соответствующей точки трехмерного тора.

Чтобы ощутить устройство 3-тора исходя из обыденных представлений о физическом пространстве, нужно выбрать три взаимно перпендикулярных направления: вперед, влево и вверх — и мысленно считать, как в фантастических рассказах, что при движении в любом из этих направлений достаточно долгое, но конечное время, мы вернемся в исходную точку, но с противоположного направления. Это тоже «компактификация пространства», но не одноточечная, использованная раньше для построения сферы, а более сложная.

На трехмерном торе есть нестягиваемые пути; например, таковым является отрезок AA’ на рисунке (на торе он изображает замкнутый путь). Его нельзя стянуть, потому что при любой непрерывной деформации точки A и A’ обязаны двигаться по своим граням, оставаясь строго друг напротив друга (иначе кривая разомкнется).

Итак, мы видим, что бывают односвязные и неодносвязные компактные 3-многообразия. Перельман доказал, что односвязное многообразие ровно одно.

Исходной идеей доказательства является использование так называемого «потока Риччи»: мы берем односвязное компактное 3-многообразие, наделяем его произвольной геометрией (т. е. вводим некоторую метрику с расстояниями и углами), а затем рассматриваем его эволюцию вдоль потока Риччи. Ричард Гамильтон, который высказал эту идею в 1981 году, надеялся, что при такой эволюции наше многообразие превратится в сферу. Оказалось, что это неверно, — в трехмерном случае поток Риччи способен портить многообразие, т. е. делать из него немногообразие (нечто с особыми точками, как в приведенном выше примере пересекающихся прямых). Перельману путем преодоления неимоверных технических трудностей, с использованием тяжелого аппарата уравнений с частными производными, удалось внести поправки в поток Риччи вблизи особых точек таким образом, что при эволюции топология многообразия не меняется, особых точек не возникает, а в конце концов, оно превращается в круглую сферу. Но нужно объяснить, наконец, что же такое этот поток Риччи. Потоки, использованные Гамильтоном и Перельманом, относятся к изменению внутренней метрики на абстрактном многообразии, и это объяснить довольно трудно, поэтому я ограничусь описанием «внешнего» потока Риччи на одномерных многообразиях, вложенных в плоскость.

Представим себе гладкую замкнутую кривую на евклидовой плоскости, выберем на ней направление и рассмотрим в каждой точке касательный вектор единичной длины. Тогда при обходе кривой в выбранном направлении этот вектор будет поворачиваться с какой-то угловой скоростью, которая называется кривизной. В тех местах, где кривая изогнута круче, кривизна (по абсолютной величине) будет больше, а там, где она более плавная, кривизна будет меньше.

Кривизну будем считать положительной, если вектор скорости поворачивает в сторону внутренней части плоскости, разбитой нашей кривой на две части, и отрицательной, если он поворачивает вовне. Это соглашение не зависит от направления обхода кривой. В точках перегиба, где вращение меняет направление, кривизна будет равна 0. Например, окружность радиуса 1 имеет постоянную положительную кривизну, равную 1 (если считать ее в радианах).

Теперь забудем про касательные векторы и к каждой точке кривой прикрепим, наоборот, перпендикулярный ей вектор, по длине равный кривизне в данной точке и направленный вовнутрь, если кривизна положительна, и вовне, если отрицательна, а затем заставим каждую точку двигаться в направлении соответствующего вектора со скоростью, пропорциональной его длине. Вот пример:

Оказывается, что любая замкнутая кривая на плоскости ведет себя при такой эволюции подобным же образом, т. е. превращается, в конце концов, в окружность. Это и есть доказательство одномерного аналога гипотезы Пуанкаре при помощи потока Риччи (впрочем, само утверждение в данном случае и так очевидно, просто способ доказательства иллюстрирует, что происходит в размерности 3).

Заметим в заключение, что рассуждение Перельмана доказывает не только гипотезу Пуанкаре, но и гораздо более общую гипотезу геометризации Тёрстона, которая в известном смысле описывает устройство всех вообще компактных трехмерных многообразий. Но этот предмет лежит уже за рамками настоящей элементарной статьи.

1 За неимением места, я не буду говорить о неориентируемых многообразиях, примером которых может служить известная бутылка Клейна — поверхность, которую нельзя вложить в пространство без самопересечений.

Говард Робертсон – человек, доказавший ошибочность Эйнштейна

В 1936 г. ведущий американский журнал по физике Physical Review получил интригующую статью под названием Существуют ли гравитационные волны? от Альберта Эйнштейна и его коллеги Натана Розена.

Статья стала продолжением исторического прорыва Эйнштейна в 1915 году, когда он представил уравнения, показывающие, как масса и энергия вызывают искривление пространства-времени и как масса и энергия реагируют на это искривление – другими словами, общая теория относительности. . В 1916 Эйнштейн дополнил теорию предсказанием существования гравитационных волн, распространяющихся со скоростью света.

Оливер Хевисайд, который в 1893 году выдвинул теорию о существовании гравитационных волн.

Эйнштейн был не первым, кто предположил существование гравитационных волн — они были впервые предложены 25 годами ранее Оливером Хевисайдом, который провел аналогию с теорией электромагнитных волн Джеймса Клерка Максвелла, чтобы открыть волновые уравнения для гравитации. (Именно Хевисайд сформулировал форму векторного исчисления уравнений Максвелла, которую мы используем сегодня.)

В 1917 году Эйнштейн сказал, что наша Вселенная статична — она не расширяется и не сжимается. Он открыл эту вселенную как решение собственных уравнений относительности. Дразнящая красота этих уравнений заключается в том, что они на самом деле имеют любое количество решений, каждое из которых описывает отдельную вселенную. Вскоре Виллем де Ситтер, Александр Фридман и Жорж Леметр открыли альтернативные вселенные, которые также удовлетворяли уравнениям Эйнштейна.

Виллем де Ситтер, Александр Фридман и Жорж Леметр. Де Ситтер и Леметр открыли расширяющиеся вселенные в уравнениях Эйнштейна. Фридман обнаружил возможность как расширения, так и сжатия.

Вернемся к статье Эйнштейна и Розена Существуют ли гравитационные волны? , который они представили в 1936 году в Physical Review . В нем они объявили о своем открытии нового увлекательного решения уравнений Эйнштейна, описывающего вселенную с симметрией цилиндра и гравитационными волнами, которые, казалось, пробегали по нему. Эйнштейн и Розен решили, что эти волны были фикцией, порожденной математическими процедурами, и не были физически реальными.

Вместо публикации статьи 9Редактор 0005 Physical Review Джон Тейт отправил его анонимному рецензенту, которым, как мы теперь знаем, был Говард Робертсон.

Уважаемый профессор Эйнштейн, подумайте еще раз

Робертсон прочитайте Существуют ли гравитационные волны? и сообщил Тейт на 10 машинописных страницах, что Эйнштейн и Розен ошиблись. Он сказал, что гравитационные волны, описанные в их статье, были настоящими физическими волнами, а не математическими причудами. Он попросил авторов подумать еще раз.

Эйнштейн прожил в Америке три года. В Европе он привык к тому, что его статьи публикуются без вопросов, и его раздражала просьба пересмотреть его работу. Он быстро отправил письмо редактору Physical Review Джону Тейту:

«Мы отправили вам нашу рукопись для публикации и не уполномочивали вас показывать ее специалистам до того, как она будет напечатана. Не вижу смысла обращаться к — во всяком случае ошибочным — комментариям вашего анонимного эксперта. На основании этого инцидента я предпочитаю опубликовать статью в другом месте».

Альберт Эйнштейн, 1936

 

Эйнштейн сдержал свое слово, отправив статью в Журнал Института Франклина под новым названием О гравитационных волнах .

Вскоре после этого досадного инцидента помощник Эйнштейна Леопольд Инфельд, сменивший Натана Розена, столкнулся с Говардом Робертсоном. Не зная, что Робертсон был анонимным рецензентом, который предложил своему боссу еще раз подумать о гравитационных волнах, они начали болтать о космологии в целом и о гравитационных волнах в частности.

Робертсон убедил Инфельда, что Эйнштейн и Розен ошибались, что их статью нужно переформулировать и что гравитационные волны физически реальны. Инфилд вернулся к Мастеру, который теперь беспристрастно выслушал те самые аргументы, которые он отверг, когда ему прислали Physical Review . Затем Говард Робертсон поговорил с Эйнштейном, в результате чего статья Эйнштейна и Розена была:

«…полностью переработана, потому что я тем временем смог убедить его, что она доказывает обратное тому, что он думал».

Письмо Говарда Робертсона Джону Тейту, редактору Physical Review , февраль 1937 г.

В отредактированной статье Эйнштейн признал, что он и Розен изначально неправильно интерпретировали свои результаты, и добавил примечание с благодарностью человеку, который доказал его неправоту:

«… моему коллеге профессору Робертсону за его дружескую помощь в разъяснении исходной ошибки».

Альберт Эйнштейн, 1936

 

Эйнштейн так и не узнал, что Говард Робертсон был анонимным рецензентом журнала Physical Review. Поразмыслив, Эйнштейн, должно быть, понял, что рефери дал ему хороший совет. Тем не менее, он, кажется, так и не простил Physical Review и никогда не подавал туда ни одной статьи.

Хотя физики долгое время были уверены, что гравитационные волны должны существовать, понадобилось 122 года, чтобы обнаружить их после первого предположения Хевисайда. За это достижение Райнер Вайс, Кип Торн и Барри Бариш разделили Нобелевскую премию по физике 2017 года.

Кем был Говард Робертсон?

Говард Перси Робертсон родился 27 января 1903 года в Хокиаме, штат Вашингтон, США. Его отец, Джордж Дункан Робертсон, был инженером. Его мать, Анна Маклеод, была медсестрой.

Робертсон окончил Вашингтонский университет в Сиэтле со степенью бакалавра наук. по математике в 1922 г., а год спустя со степенью магистра. по математике и физике.

Он переехал на юг, в Калифорнийский технологический институт, где получил степень доктора философии. по математике и физике, автор диссертации на тему: О динамических пространствах-временах, содержащих конформное евклидово трехмерное пространство .

Göttingen

Робертсон проводил свои постдокторские исследования в Германии, в основном в Геттингенском университете, который в то время был мировым центром математики. В Геттингене он познакомился с некоторыми из величайших математиков и физиков мира, включая Давида Гильберта, Альберта Эйнштейна, Вернера Гейзенберга, Эрвина Шредингера, Джона фон Неймана и Юджина Вигнера.

Профессор

Вернувшись в Калифорнийский технологический институт Робертсон был назначен доцентом в 1928 лет, прежде чем переехать в Принстон в 1931 году в качестве адъюнкт-профессора. Он был назначен профессором в 1938 году.

Виртуоз в области квантовой механики, общей теории относительности и космологии, Робертсон утверждал, что мы живем в расширяющейся Вселенной.

Работа во время войны

После того, как Америка вступила во Вторую мировую войну, Робертсон переехал в столицу Великобритании, Лондон, где работал над методами шифрования сигналов вражеских радаров. За свою работу он был удостоен высшей гражданской награды Соединенных Штатов — Медали за заслуги.

Калифорнийский технологический институт и НЛО

В 1947 году Робертсон вернулся в Калифорнийский технологический институт, где провел остаток своей карьеры.

В 1953 году он возглавлял Группу Робертсона, которая исследовала большое количество сообщений об НЛО, сделанных в то время, и пришла к выводу, что, по всей вероятности, все сообщения можно объяснить как природные явления или ошибочные интерпретации повседневных воздушных объектов.

Конец

Ховард Робертсон умер в возрасте 58 лет 26 августа 1961 года. У него остались жена Анджела (урожденная Турински) и их дети Джордж и Мариетта.

Рекламные объявления

Дополнительная литература
Оливер Хевисайд
Гравитационная и электромагнитная аналогия, часть 1
Электрик, том. 31, стр. 281–282, 1893

Оливер Хевисайд
Гравитационная и электромагнитная аналогия, часть 2
Электрик, том. 31, с. 359, 1893

А. Эйнштейн, Н. Розен
О гравитационных волнах
Journal of the Franklin Institute, Vol. 223, № 1, стр. 43–54, январь 1937 г.

Дэниел Кеннефик
Einstein Versus the Physical Review
Physics Today, сентябрь 2005 г.

John D. Barrow
Книга вселенных: исследование пределов космоса
W.W. Norton & Company, июнь 2012 г.

Репортеры, доказавшие, что журналистика сильнее Чем Трамп

Но призыв к фундаментальному переосмыслению журналистики — аргументировать, что многие традиционные представления о профессионализме провоцируют робость и препятствуют сообщению правды, — достиг своего расцвета в годы правления Трампа.

Что касается стиля, утверждается, что новый и раскрепощенный вид журналистики будет избегать ласковых слов и мягкого нейтралитета. Вместо этого он с гордостью возвысит свой голос, разоблачая ложь и демагогию. Что касается вопросов существа, журналисты должны перестать беспокоиться о ложных обвинениях в предвзятости и дать понять, что они не нейтральны в экзистенциальных вопросах, таких как будущее демократии в США. Это момент для принятия какой-либо стороны, а не пассивного репортажа со стороны.

Эта критика объясняет многочисленные голоса тревоги по поводу планов нового генерального директора CNN Криса Лихта вернуть сеть к журналистскому традиционализму — от сенсационного тона, предпочитаемого его предшественником, от дерзких выражений, которые могут звучать как комментарии, а не нейтральные репортажи, подальше от контента, который может заставить критиков заявить, что у сети есть идеологическая повестка дня.

Я нахожусь в непростом положении, когда дело доходит до дебатов между традиционалистами и агитаторами. Я помог основать POLITICO почти 16 лет назад именно потому, что считал многие старые журналистские условности устаревшими. К ним относятся пророческий тон голоса Бога, который обычно пронизывал освещение в традиционных СМИ, и то, как жесткие правила презентации часто означали, что репортеры были более интересны в беседе за обедом или пивом — полные юмора, проницательности и возмущения — чем они были опубликованы. рассказы.

В то же время классическая критика справа по поводу предвзятости и новая критика слева по поводу ложной эквивалентности часто кажутся мне легкомысленными. Они часто могут понять какой-то конкретный предмет — Ой, должен признать, это довольно хороший момент — но в совокупности, кажется, упускают важный момент.

Дело, на мой взгляд, в том, что сила журналистики не проистекает главным образом из выбора слова. ( Не называйте это «искажением», когда на самом деле это «ложь».) Не вытекает из тонального представления. (Более полувека назад вице-президент Ричарда Никсона Спиро Агнью сказал, что сетевые комментаторы выдавали свою предвзятость «по выражению лиц, тону вопросов, сарказму ответов».) Дело в том, что власть журналистики исходит из примата r репортажей — из сообщения своей аудитории вещей, которые люди, находящиеся у власти, предпочли бы, чтобы они не знали.

Согласно этому стандарту, мне кажется, что журналисты, сформированные на основе ценностей и мировоззрения традиционной журналистики, по-прежнему демонстрируют большую власть — большую силу, чем представители нового и более откровенно идеологического направления журналистики.

Некоторые из самых заслуживающих освещения в печати историй Вашингтона 2022 года вышли в виде трех книг. Это не пройдет , из весны, Александр Бернс и Джонатан Мартин разоблачили лицемерие и слабость лидера республиканцев в Палате представителей Кевина Маккарти, в частном порядке поклявшись противостоять Трампу в отрицании выборов — «У меня было это с этим парнем» — прежде чем публично вернуться к подобострастной поддержке. Этой осенью соавторы Питер Бейкер и Сьюзен Б. Глассер опубликовали статью The Divider , многочисленные разоблачения которой включают в себя то, как даже предполагаемые сторонники Трампа, такие как его госсекретарь Майк Помпео, говорили соратникам, что «сумасшедшие захватили власть» в Белом доме. Палата представителей после того, как Трамп отказался признать, что он проиграл выборы 2020 года. На следующей неделе Мэгги Хаберман выпустит свою долгожданную девятку.0159 Confidence Man , основанная на ее десятилетиях освещения Трампа. Он уже освещал смыв официальных документов Трампа в унитаз Белого дома и ее откровение о том, что президент в приступе досады был близок к тому, чтобы использовать Twitter, чтобы уволить свою дочь Иванку Трамп и зятя Джареда Кушнера из аппарата Белого дома. .

В дополнение к этим книгам, которые основаны на образцовых репортажах, которые эти журналисты сделали для своих основных новостных платформ, позвольте мне добавить пример, близкий к дому. В том, что считается одним из самых экстраординарных эксклюзивов на памяти, журналисты POLITICO Джош Герштейн и Александр Уорд в мае сообщили о внутреннем проекте Верховного суда, отменяющем Roe v. Wade , точно предсказавший историческое решение о правах на аборт, когда оно стало достоянием общественности семь недель спустя.

За исключением Уорда, который присоединился к POLITICO в прошлом году, я знаю всех этих репортеров много лет, а в некоторых случаях и десятилетия, — достаточно хорошо, чтобы иметь представление о том, что делает их журналистами несколько бывших сотрудников Politico). Они разные по личному стилю и интересам. Но есть важные сходства. Младшие члены этой группы — Бернс, Мартин и Уорд — не начинали свою карьеру в традиционных отделах новостей, как это сделали Бейкер, Герштейн и Глассер (и я). Тем не менее, все они формируются в соответствии с тем, что я считаю традиционными новостными ценностями. Одним из них является вера в первичность общих фактов как обязательное условие для интеллектуально честных аргументов. Другой — профессиональная скромность, позволяющая признать, что журналисты никогда не владеют всеми соответствующими фактами.

Самое главное их сходство — мания репортажей, намного превосходящая типичный журналист. Сообщается, что Герштейн, будучи студентом колледжа, контролировал полицейский радиосканер даже в часы простоя. Он известен среди коллег своим вниманием к деталям и ревностным использованием Закона о свободе информации. Когда я поделился с Бейкером битой Белого дома в Washington Post, он имел обыкновение звонить незнакомым чиновникам за их рабочие места, просто чтобы посмотреть, чем это может кончиться. Как и другие упомянутые здесь, он из тех репортеров, которые могут заставить коллег задуматься, правильно ли мы работаем.

Джонатан Мартин, национальный политический корреспондент New York Times, выступает на сцене во время Саммита Concordia Lexington 2022 года в Lexington Marriott City Center, 8 апреля 2022 года в Лексингтоне, штат Кентукки.
|
Джон Черри / Getty Images для Concordia

Вся работа здесь включала в себя установление доверия и доверия к десяткам источников с различными мотивами и политическими ориентациями. В значительной степени им это удалось, потому что у этих источников были все основания доверять их традиционным профессиональным стандартам. У всех авторов книги были интервью с Трампом, который не мог устоять перед возможностью высказаться в проектах, которые, как он знал, привлекут широкое внимание.

Но вот что отличает работу этих журналистов — мягкость или нежелание делать резкие интерпретационные суждения. Существует скудное свидетельство того, что кто-либо из них наносит удары в обмен на доступ. Каждый журналист, которого я здесь упомянул, — и десятки других, которых я мог бы легко назвать, — с большим отрывом прошел пороговое испытание: они рассказывали своей аудитории истории, которые влиятельные люди хотели бы, чтобы им не рассказывали.

Естественно, у разных репортеров разные стили. Бейкер сказал, что не голосует на выборах, чтобы быть уверенным, что его разум остается открытым. Глассер, его супруга, а также соавтор, открыто высказывается в социальных сетях и других местах о своей тревоге по поводу того, как Трамп подрывает демократические нормы. Ее не смягчает и его личная аура. Описывая опыт интервьюирования экс-президента, Глассер, выросший с родителями, которые руководили местной газетой, сказал Punchbowl News: «Этот человек не очарователен. Он эгоцентричный, бессвязный, самовлюбленный старик, которого не волнуют ваши вопросы».

Это миф, что традиционная журналистика когда-либо требовала продуманного нейтралитета. Журналисты не являются нейтральными и не должны быть нейтральными в элементарных вопросах демократии. Мы предпочитаем раскрытие информации секретности, честность пропаганде, подотчетность и общественные интересы лжи, демократию авторитаризму.

Журналистика всегда должна развиваться, чтобы по-новому встречать и обслуживать свою аудиторию. Но достижение этих желаемых целей не требует полного переосмысления проверенных временем ценностей. Оказывается, старые способы все еще имеют много жизни.

Сэр Роджер Пенроуз: Человек, который доказал, что черные дыры не были «невозможными»

  • Опубликовано

Источник изображения, Антони Хоуарт/Наука. Роджер изображен в Оксфорде в 1980 году. Он применил свой ум во многих областях науки

Джонатан Амос

Корреспондент Би-би-си по науке

Если у вас когда-либо были проблемы с математикой в ​​школе, вы были в хорошей компании. Сэр Роджер Пенроуз, получивший во вторник Нобелевскую премию по физике, тоже чесал затылок в классе.

«Я всегда был очень медлительным. Я был хорош в математике, да, но я не всегда хорошо справлялся со своими тестами», — вспоминал лауреат из Колчестера (1931).

«Но учитель понял, что если он уделит мне достаточно времени, у меня все получится. По сути, мне приходилось все делать, исходя из первых принципов.»

Кем бы ни был этот учитель – а уроки проходили в Канаде в годы войны – у нас есть основания благодарить его за терпение к юному ученику.

Сэр Роджер впоследствии стал звездой математики, сначала в Университетском колледже Лондона, а затем в Кембриджском университете, где он защитил докторскую диссертацию.

  • Послушайте передачу BBC The Life Scientific: Сэр Роджер Пенроуз
  • Открытие черных дыр принесло Нобелевскую премию по физике
  • Черная дыра, вошедшая в историю, совершила шимми

Сэр Роджер интересовался топологией — математикой, описывающей свойства геометрических объектов при их скручивании или растяжении. И именно этот раздел математики он применил к проблеме черных дыр — тех необычных областей пространства, где материя коллапсирует сама в себя, и где гравитация настолько сильна, что ничто, даже свет, не может найти путь. вне.

Сегодня мы считаем само собой разумеющимся способность телескопов отображать черные дыры или, по крайней мере, их окрестности. И надо сказать, мы немного пресытились, когда лазерные интерферометры «слышат», как еще одна пара черных дыр сталкивается друг с другом и сливаются. И все же, вернемся всего на несколько десятилетий назад, и споры о реальности черных дыр были очень жаркими.

Это был котел, в который прыгнул сэр Роджер, когда начал применять некоторые из принципов топологии к черным дырам. До его основополагающих 1965, модели могли описывать, как могут формироваться эти объекты, но их часто отвергали как идеализированные ситуации с идеальной симметрией, которые вряд ли могли бы произойти в «реальном мире».

Источник изображения, сотрудничество LIGO-VIRGO

Подпись к изображению,

Сегодня у нас есть лазерные лаборатории, где мы можем «слушать» черные дыры, когда они сталкиваются в космосе показать, что сингулярность или состояние бесконечной плотности и давления было бы общим ожиданием, независимо от симметрии, если бы у вас было достаточно материи, слипшейся вместе.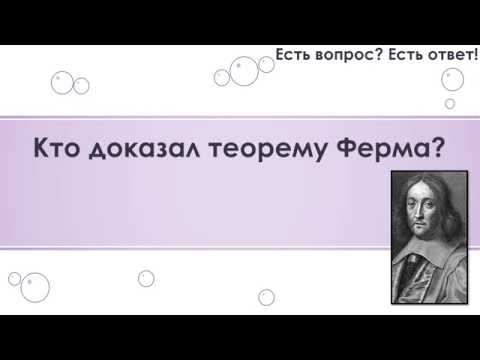

«Я думал о геометрии того, что происходит (внутри этих вещей, которые мы теперь называем черными дырами) — как ведут себя световые лучи, что они делают, когда начинают фокусироваться, и можно ли остановить их фокусировку и тому подобное, » он объяснил.

«И у меня были общие аргументы, которые были чисто математическими, топологическими аргументами — не из тех вещей, которые люди использовали. И это была идея, которую я позже назвал захваченной поверхностью, которая является характеристикой того, когда ваш коллапс достиг предела. точка невозврата, грубо говоря, но это не зависело от симметрии или чего-то подобного. Это была просто общая характеристика, которая могла сказать вам, что что-то пошло не так».

Если бы астрономы вышли и поискали в нужных местах, они бы нашли доказательства, решил сэр Роджер. От остатков взорвавшихся звезд до гигантских объектов, скрывающихся в ядрах большинства галактик.

«Хотя общая теория относительности Эйнштейна предсказывает существование черных дыр, сам Эйнштейн не верил, что они действительно существуют», — сказал профессор Джим Аль-Халили, который брал интервью у сэра Роджера для программы BBC The Life Scientific в 2016 году. «Пенроуз первым доказал математически, в 1965, что они являются естественным следствием теории относительности, а не только научной фантастики». В конце 60-х и 70-х годах они работали над одними и теми же проблемами после того, как их собрал научный руководитель Хокинга Деннис Скиама.

Их жизни шли параллельно в течение многих лет.0003

Для Хокинга именно «Краткая история времени» позволила ему прорваться. А для сэра Роджера именно «Новый разум императора» и «Дорога к реальности» установили его связь с непрофессионалами. Хотя Хокинг воздерживался от использования уравнений в своих книгах, сэр Роджер любил разбрасывать по страницам всего несколько уравнений.

«Я думаю, это зависит от того, какого читателя вы ищете; я думаю, что мои книги, возможно, привлекают определенную читательскую аудиторию, которая немного отличается», — признал он.

Источник изображения, EHT

Подпись к изображению,

Гигантская черная дыра в центре галактики M87

  • Черная дыра — это область пространства, в которой материя коллапсирует сама в себя
  • Гравитационное притяжение настолько сильно, что ничто, даже свет, не может ускользнуть
  • Черные дыры возникнут в результате взрывной гибели некоторых крупных звезд
  • Но некоторые из них действительно гигантские, в миллиарды раз больше массы нашего Солнца
  • Как эти монстры, найденные в центрах галактик, сформировались неизвестно
  • Черные дыры обнаруживаются по тому, как они влияют на свое окружение
  • Они производят наблюдаемые гравитационные волны, когда они скручиваются друг с другом

Где многие люди, не интересующиеся наукой, узнают, что сэр Роджер будет в так называемом » Лестница Пенроуза», или «Невозможная лестница». Это забавная оптическая иллюзия, которая изображает постоянно нисходящую или восходящую серию ступенек.

Сэр Роджер был очарован художником М. С. Эшером после того, как увидел некоторые из его работ на математическом конгрессе в Амстердаме в 1950-х — и пытался лепить собственные иллюзии.

«Я пытался нарисовать схемы с дорогами, реками, поездами и прочим, что было невозможно. А потом я как бы упростил это до того, что я считал сутью, и это было то, что они называют трибаром. Это просто треугольник из трех стержней, соединенных невозможным образом. И я показал это отцу, и он увлекся этим и начал строить здания, которые были невозможны, и, наконец, придумал лестницу ».

Отец и сын поделились этой идеей с голландским художником, который прославил иллюзию благодаря литографии «Восхождение и нисхождение», выпущенной в 1960 году. бар и невозможная лестница

Нобелевская премия по физике — это венец достижений сэра Роджера, на счету которого уже множество наград.