Общая теория относительности кратко: Теория относительности • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Теория относительности. Кратко

Теория относительности — это физическая теория, в которой объединены пространство и время. С ее появлением стало ясно, что классическая механика Ньютона — только часть более обширной теории, объясняющей устройство мира, и выполняется лишь для скоростей, далеких от скорости света (около 300 000 км/с), для размеров, которые значительно превышают размеры атомов и молекул, и тогда, когда скорость распространения гравитации является бесконечной.

Мемориал Альберта Эйнштейна (1879—1955) в Вашингтоне

Существуют две теории относительности — специальная и общая. Специальная теория относительности (СТО) изучает процессы, при исследовании которых можно пренебречь полями тяготения; общая теория относительности представляет собой теорию гравитации и обобщает ньютоновскую физику.

Начало специальной теории относительности — это 1905 г., когда Альберт Эйнштейн опубликовал статью «К электродинамике движущихся тел». Эйнштейн предположил, что физические процессы, в том числе скорость света, не зависят от скорости движения наблюдателя.

Кротовая кора, или червоточина, — гипотетический «туннель» в пространстве, через который можно попадать в невообразимо отдаленные области. Его существование предполагает общая теория относительности

Эйнштейн объяснил, как следует интерпретировать движения различных инерциальных систем отсчета, то есть объектов, которые движутся относительно друг друга с постоянной скоростью. При этом ни один из них не принимается как абсолютная система отсчета. Возьмем, например, два корабля. Один из них движется, другой неподвижен относительно первого. Человек в движущемся корабле направляет луч света вертикально в потолок. Для человека, который находится в неподвижном корабле, свет будет направлен по диагонали и пройдет большее расстояние, пока не отразится от потолка. Следовательно, и время для пассажиров второго корабля окажется другим. Это эффект замедления времени.

Специальная теория относительности показывает также, что масса тела увеличивается с приближением скорости его движения к скорости света.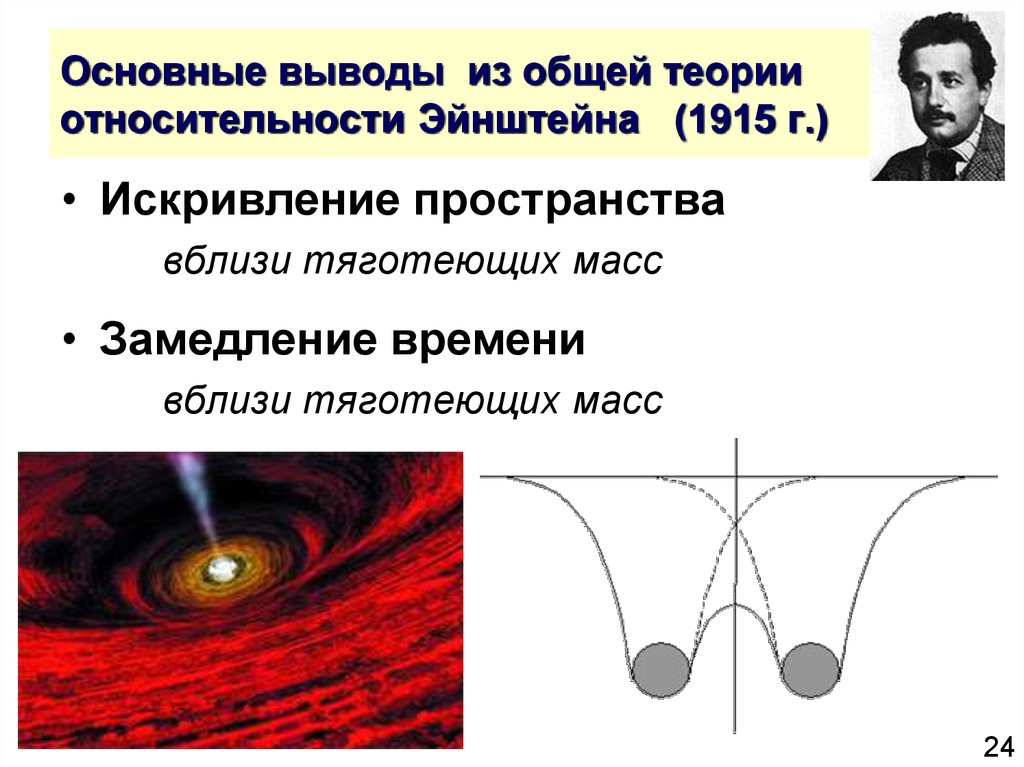 А чем больше масса, тем большее ускорение требуется придать телу, чтобы оно продолжало двигаться. Если достигается скорость света, то масса тела становится бесконечной, как и его энергия.

Отсюда Эйнштейн вывел свою знаменитую формулу:

Е = mc²,

где Е—энергия, m — масса, c — скорость света.

Специальная теория относительности, объединив энергию и массу, расширила современную физику, в частности, физику элементарных частиц, и дала многое для развития науки.

Любое тело, обладающее массой, искривляет и деформирует пространство-время

Общую теорию относительности Эйнштейн предложил в 1915—1918 гг. Она развивает специальную теорию относительности и постулирует, что гравитационные эффекты обусловлены деформацией пространства-времени. Благодаря общей теории относительности оказалось возможным предсказать существование черных дыр, гравитационных волн и нейтронных звезд.

Основные принципы специальной теории относительности

1. Принцип относительности: физические процессы протекают одинаково в инерциальных системах отсчета, независимо от того, неподвижны ли системы или находятся в состоянии прямолинейного и равномерного движения относительно друг друга.
2. Принцип скорости света: скорость света в вакууме, измеренная в любой инерциальной системе отсчета, остается неизменной для всех наблюдателей, независимо от их скорости по отношению к источнику света.

Из второго принципа следует, что движение быстрее скорости света невозможно.

Формула специальной теории относительности, объединяющая энергию, массу и ускорение

Парадокс близнецов

Иногда парадоксом близнецов называется следующая ситуация. Существуют два брата-близнеца. Первый остается на Земле, второй улетает к далекой звезде со скоростью, близкой к скорости света. Из-за этого его часы должны сильно отстать, и он постареет меньше. Но это так и есть, и никакого парадокса на самом деле здесь нет. Настоящий парадокс в другом. Оставшийся брат двигается вместе с Землей, следовательно, часы должны отстать у него, и сильнее постареть должен космонавт. Так по-разному течет время или нет?

И где оно течет быстрее? Однако это противоречие можно разрешить. Брат-космонавт, который возвращается, должен изменить свою скорость, двигаться с ускорением. Значит, его система отсчета окажется неинерциальной.

А согласно специальной теории относительности, только инерциальные системы оказываются равноправными. Следовательно, системы космонавта и оставшегося на Земле брата неравноправны, несимметричны, и время у них будет течь по-разному, причем сильнее постареет оставшийся на Земле близнец.

Поделиться ссылкой

5. Общая теория относительности. Теория относительности для миллионов

5. Общая теория относительности

В начале гл. 2 мы указывали, что есть два пути обнаружить абсолютное движение: измерять движение по отношению к пучку света и использовать явление инерции, возникающее при ускорении предмета. Опыт Майкельсона — Морли показал, что первый путь непригоден. И специальная теория относительности Эйнштейна объяснила причину этого.

В этой главе мы возвращаемся ко второму методу: использованию явлений инерции как ключа к абсолютному движению.

Когда ускоряется космический корабль, космонавт внутри корабля гигантской силой прижимается к спинке своего кресла. Это обычное явление инерции, вызванное ускорением ракеты. Доказывает ли это явление, что ракета движется? Для доказательства относительности всех движений, включая и ускоренное движение, необходимо, чтобы и ракету можно было принять за неподвижную систему отсчета. В этом случае Земля и все космическое пространство должны будут казаться движущимися назад, прочь от ракеты. Но, посмотрев на создавшееся положение с этой точки зрения, можно ли объяснить силы, действующие на космонавта? Сила, которая прижимает его к креслу, показывает, без всякого сомнения, что движется ракета, а не космос.

Другой подходящий пример представляет вращающаяся Земля. Центробежная сила, инерционное явление, сопровождающее вращение, вызывает растяжение земного экватора, так что Земля сплющивается. Если всякое движение относительно, то нельзя ли принять Землю за неподвижную систему отсчета и считать космос вращающимся вокруг нее? Конечно, это можно вообразить, но что же тогда растягивает земной экватор? Это растяжение показывает, что вращается сама Земля, а не Вселенная. Кстати, астрономы не договорились еще, растягивают центробежные силы и сейчас экватор Земли или растяжение возникло в прошедшие геологические эпохи, когда вещество Земли было более пластичным, а теперь стало характерной чертой твердой Земли, чертой, которая сохранится, даже если прекратится вращение Земли. Все согласны, однако, что центробежная сила ответственна за это растяжение.

Цепь размышлений, приведших Ньютона к мысли о том, что движение не относительно, точно такая же. Он ссылался как на доказательство на тот факт, что во вращающемся вокруг вертикальной оси ведре центробежная сила искривляет поверхность воды и даже может привести к выплескиванию воды через край. Невозможно представить себе, что вращающаяся Вселенная может так влиять на воду, следовательно, утверждает Ньютон, необходимо признать, что вращение ведра абсолютно.

В течение десяти лет, последовавших за опубликованием специальной теории относительности, Эйнштейн размышлял над этой задачей. Большинство физиков не рассматривало ее как задачу вообще.

Почему бы, говорили они, равномерному движению не быть относительным (как это утверждает специальная теория относительности), а ускоренному — абсолютным? Такое положение дел Эйнштейна не удовлетворяло. Он чувствовал, что если равномерное, прямолинейное движение относительно, то таким же должно быть и ускоренное движение. Наконец, в 1916 г., через 11 лет после создания специальной теории относительности, он опубликовал свою общую теорию относительности. Эта теория названа общей, так как она является обобщением, расширением специальной теории. Она включает в себя специальную теорию как частный случай.

Общая теория является значительно более крупным научным достижением, чем специальная теория.

Если бы не Эйнштейн впервые сформулировал специальную теорию, то нет сомнения, что эта теория вскоре была бы создана другими физиками. Пуанкаре был одним из тех, кто почти вплотную подошел к ней. В своей замечательной речи, произнесенной в 1904 г., Пуанкаре предсказал возникновение «совершенно новой механики», в которой никакая скорость не может достигать скорости света, подобно тому, как никакая температура не может опуститься ниже абсолютного нуля. Будет установлен, говорил он, «принцип относительности, согласно которому законы физических явлений должны быть одинаковы, независимо от того, покоится наблюдатель или находится в равномерном и прямолинейном движении; у нас не будет способа различать, находимся мы в состоянии покоя или в таком движении». Пуанкаре не видел того решающего шага, который необходимо было сделать для выполнения этой программы, но интуитивно он понял сущность специальной теории. В то время Эйнштейн еще не сознавал, насколько мысли Пуанкаре, Лоренца и других были близки его собственным. Несколькими годами позже он чрезвычайно высоко оценил выдающийся вклад этих людей.

С общей теорией относительности положение совершенно отличное. Она была, по выражению Теллера, «прекрасной неожиданностью»; работой такой изумительной оригинальности, такой необычности, что она вызвала в научном мире нечто похожее на то, что произошло в танцевальных залах США, когда в 1962 г. в них вторгся новый танец, крик моды, твист. Эйнштейн изменил[3] древние ритмы танцев времени и пространства. В удивительно короткое время каждый физик или танцевал новый твист, не скрывая охватившего его ужаса перед ним, или жаловался на старость, мешающую научиться новому танцу. Если бы не родился Эйнштейн, то нет сомнения, что другие ученые дали бы физике такой же твист, но могло бы пройти столетие или больше, прежде чем это бы произошло. В истории науки немного основополагающих теорий, в такой степени являющихся делом рук одного человека.

«Ньютон, прости меня», — писал Эйнштейн в конце жизни. «В твое время ты нашел тот единственный путь, который был пределом возможного для человека величайшего ума и творческой силы». Это трогательная дань уважения гениальнейшего ученого нашего времени своему гениальному предшественнику.

Центральным стержнем общей теории Эйнштейна является то, что получило название принципа эквивалентности.

Принцип эквивалентности не что иное, как ошеломляющее утверждение (Ньютон счел бы Эйнштейна безумцем), что тяжесть и инерция одно и то же. Это не просто похожие явления.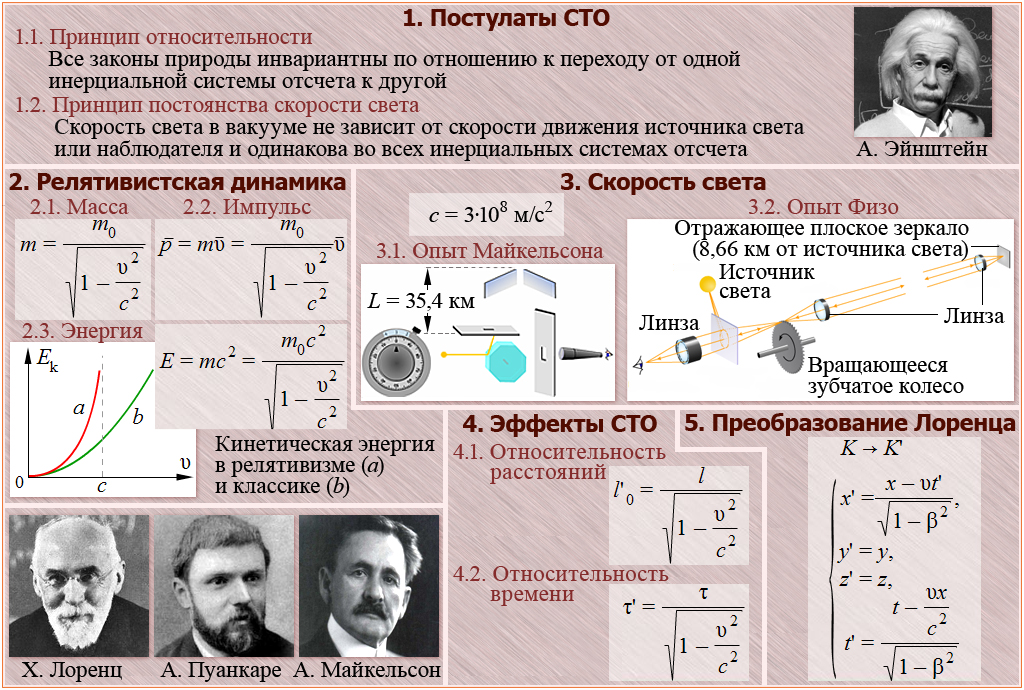 Тяжесть и инерция — два различных слова для одного и того же явления.

Эйнштейн был не первый ученый, которого поразило странное сходство между гравитационным и инерционными явлениями. Представим себе, что пушечное ядро и маленький деревянный шарик падают с одной и той же высоты. Допустим, что вес ядра в сто раз больше, чем вес деревянного шарика. Это означает, что на ядро действует сила тяжести, в сто раз большая, чем сила, действующая на деревянный шарик. Легко понять причину, по которой враги Галилея не могли поверить, что эти шарики достигнут Земли одновременно. Мы теперь, конечно, знаем, что если пренебречь сопротивлением воздуха, то шары будут падать бок о бок. Чтобы объяснить это явление, Ньютон должен был предположить нечто очень удивительное. В той же степени, с какой тяжесть тянет вниз ядро, инерция ядра, сопротивляемость силе, его сдерживает. Действительно, на ядро действует сила тяжести в сто раз большая, чем на деревянный шарик, но инерция сдерживает ядро ровно в сто раз сильнее!

Физики часто выражают это другими словами.

Сила тяжести, действующая на предмет, всегда пропорциональна инерционной массе этого предмета.

Бели предмет А вдвое тяжелее предмета Б, его инерция также вдвое больше. Вдвое большая сила необходима для ускорения предмета А до той же конечной скорости, что и у предмета Б. Если бы это было не так, то предметы разного веса падали бы с разными ускорениями.

Очень легко вообразить себе мир, в котором нет пропорциональности между этими силами (инерции и тяготения). И действительно, во времена от Аристотеля до Галилея ученые представляли себе мир именно таким! Мы очень хорошо чувствовали бы себя в таком мире. Изменились бы условия в падающем лифте, но ведь мы не часто в нем оказываемся.

Как бы там ни было, мы имеем счастье жить в мире, где эти две силы пропорциональны. Впервые это показал Галилей. Удивительно точные опыты, подтвердившие открытие Галилея, были выполнены около 1900 г. венгерским физиком бароном Роландом фон Этвешем. Наиболее точная всесторонняя проверка была сделана несколько лет назад группой ученых Принстонского университета. С той точностью, которой они могли достигнуть, гравитационная масса (вес) всегда оказывалась пропорциональной инертной массе.

Ньютон, конечно, знал об этой удивительной связи между тяжестью и инерцией, связи, которая заставляет все предметы падать с одинаковым ускорением, но он никак не мог это объяснить. Для него эта связь казалась необычайным совпадением. За счет такого совпадения можно использовать инерцию таким образом, что гравитационное поле будет возникать и исчезать. В первой главе было рассказа но об искусственном поле тяжести, которое может быть создано в космическом корабле тороидальной формы (в виде бублика) простым вращением корабля как колеса. Центробежная сила будет прижимать предметы к внешнему краю. Вращая корабль с определенной постоянной скоростью, можно получить внутри корабля поле сил инерции с таким же действием, как и поле тяжести Земли. Прогуливающийся космонавт будет чувствовать себя как бы на кривом полу. Брошенные предметы будут падать на этот пол.

Дым будет подниматься к потолку. Все явления будут такими же, как и в обычном поле тяжести. Для иллюстрации этого положения Эйнштейн предложил следующий мысленный эксперимент.

Вообразите в космосе лифт, двигающийся вверх с постоянно нарастающей скоростью. Если ускорение постоянно и в точности равно ускорению падающего на землю предмета, то человек внутри лифта будет чувствовать себя так же, как и в гравитационном поле, в точности равном земному. Этим способом можно не только промоделировать тяжесть, но и нейтрализовать ее. В падающем лифте, например, ускорение вниз полностью ликвидирует влияние тяжести внутри кабины. Состояние с g = 0 (отсутствие тяготения) существует внутри космического корабля все то время, пока он находится в состоянии свободного падения, т. е. когда он движется только под действием сил тяжести. Невесомость, которую ощущали советские и американские космонавты в полетах вокруг Земли, объясняется тем, что их корабли находились в состоянии свободного падения, обращаясь вокруг Земли. Все время, пока ракетные двигатели космического корабля выключены, внутри корабля будет состояние с g = 0.

Замечательное соответствие между тяжестью и инерцией оставалось иеобъясненным до тех пор, пока Эйнштейн не создал общую теорию относительности.

Как и в специальной теории относительности, он предложил наипростейшую, наиболее смелую гипотезу. Вспомните, в специальной теории относительности Эйнштейн предположил, что причина, по которой мы не замечаем эфирного ветра, состоит в том, что нет никакого эфирного ветра. В общей теории относительности он сказал: тяжесть и инерция кажутся одним и тем же потому, что они являются одним и тем же.

Неправильно говорить, что внутри свободно падающего лифта притяжение Земли нейтрализуется.

Тяготение не нейтрализуется, оно ликвидируется.

Тяготение действительно исчезает. Аналогично этому неправильно говорить, что тяготение во вращающемся космическом корабле или в поднимающемся с ускорением лифте моделируется. И в этом случае тяготение не моделируется, оно создается. Гравитационное поле, созданное этим способом, имеет иную математическую форму, чем гравитационные поля, окружающие большие небесные тела, например Землю, но тем не менее это обычное гравитационное поле.

Как и в специальной теории, математическое описание природы усложняется в общей теории, но окончательный результат оправдывает это усложнение.

Вместо двух различных сил оставлена только одна.

Более того, теория приводит к новым предсказаниям, которые могут быть проверены на опыте.

Принцип эквивалентности Эйнштейна — эквивалентности тяготения и инерции — дает возможность рассматривать все движения, в том числе и ускоренные, как относительные. Когда воображаемый лифт Эйнштейна с нарастающей скоростью движется в космосе, внутри него можно наблюдать явления инерции. Но теоретически лифт можно рассматривать как неподвижную, фиксированную систему отсчета.

Тогда вся Вселенная со всеми ее галактиками окажется движущейся вниз мимо лифта с нарастающей скоростью. Это ускоренное движение Вселенной создает гравитационное поле, которое заставляет все предметы в лифте прижиматься к полу. Можно сказать, что эти явления не инерционные, а гравитационные.

Но что же происходит в действительности? Движется лифт, и его движение создает инерционные явления, или движется Вселенная, создавая гравитационное поле? Это неправильный вопрос. Нет никакого «действительного», абсолютного движения. Существует лишь относительное движение лифта и Вселенной. Это относительное движение создает силовое поле, описываемое уравнениями поля общей теории.

Силовое поле может называться гравитационным или инерционным в зависимости от выбора системы отсчета. Если системой отсчета служит лифт, то поле называется гравитационным. Если же системой отсчета является космос, то поле называется инерционным. Инерция и тяготение — всего лишь два различных слова, примененных к одному и тому же явлению. Естественно, много проще и более удобно рассматривать Вселенную покоящейся. В этом случае никто не попытается назвать поле внутри лифта гравитационным. Общая теория относительности говорит, однако, что это поле может быть названо гравитационным, если выбрана подходящая система отсчета.

Ни один эксперимент, выполненный внутри этого лифта, не сможет доказать «ложность» такого представления.

Когда говорят, что наблюдатель внутри лифта не может сказать, является поле, прижимающее его к полу, инерционным или гравитационным, то это не означает, что он не может найти разницу между этим полем и гравитационным полем, окружающим большие количества вещества, скажем планету. Гравитационное поле вокруг Земли, например, обладает сферической симметрией и такое поле нельзя точно воспроизвести ускорением лифта в пространстве. Если два яблока разнести на метр, а затем сбросить с большой высоты на Землю, то, падая, они будут сближаться, так как каждое яблоко падает по прямой линии, направленной к центру Земли. В движущемся лифте, однако, все предметы падают по параллельным линиям. Это различие между двумя полями может быть найдено опытами внутри лифта, но этими опытами нельзя найти различия между инерцией и тяготением. В опытах можно различить только поля различной математической структуры.

Подобное положение возникает и на вращающейся Земле. Древний спор о том, вращается Земля или небеса вокруг нее (так думал Аристотель), оказывается не более чем спором о выборе самой простой системы отсчета. Конечно, наиболее удобно выбрать систему отсчета, связанную со Вселенной. Мы говорим, что относительно Вселенной Земля вращается и инерция сплющивает Землю, растягивая ее экватор.

Ничто, кроме неудобства, не мешает нам выбрать Землю в качестве фиксированной системы отсчета.

В последнем случае мы скажем, что космос вращается вокруг Земли, создавая гравитационное поле, воздействующее на ее экватор. И снова это поле будет иметь математически иную структуру, чем гравитационное поле вокруг планеты, и тем не менее оно справедливо может быть названо гравитационным.

Если мы выберем Землю за неподвижную систему отсчета, нам даже не придется изменять нашу повседневную речь. Мы говорим, что Солнце всходит по утрам и заходит вечером, что Большая Медведица вращается вокруг Полярной Звезды. Какая же точка зрения «правильна»? Вращаются небеса или вращается Земля? Этот вопрос лишен смысла. С тем же основанием официантка могла бы спросить клиента, желает он мороженое на пироге или пирог под мороженым.

Вообразите себе космос вскруженным некими «захватами» для каждого предмета в нем. (В гл. 7 рассматривается вопрос о происхождении этих захватов. ) Необычайность этих захватов состоит в том, что, пока предмет движется по Вселенной прямолинейно и равномерно, Вселенная не препятствует его движению. Но стоит только попытаться заставить предмет двигаться неравномерно (ускоренно), захват сожмется. Если за неподвижную систему отсчета принята Вселенная, то захват называется инерцией предмета, его сопротивляемостью изменению движения. Если за неподвижную систему отсчета принят предмет, захват называется тяготением, попыткой Вселенной сдержать неравномерное движение предмета относительно нее.

Часто общую теорию относительности резюмируют следующим образом. Ньютон разъяснил, что если наблюдатель находится в состоянии равномерного и прямолинейного движения, то нет ни одного механического опыта, с помощью которого он мог бы отличить свое состояние от покоя. Специальная теория относительности распространила это заключение и на оптические опыты. Общая теория является следующим по порядку сообщением — обобщением специальной теории на неравномерное движение. Ни один эксперимент, говорит общая теория, какого бы вида он ни был, не поможет наблюдателю, в каком бы движении тот ни находился, равномерном или неравномерном, отличить свое состояние от состояния покоя.

Сущность общей теории относительности иногда формулируется и так: все законы природы инвариантны (одинаковы) для любого наблюдателя. Это означает, что независимо от того, как движется наблюдатель, он может описать все законы природы (как они ему представляются) одинаковыми математическими уравнениями. Он может быть ученым, работающим в земной лаборатории, или на Луне, или в огромном космическом корабле, медленно ускоряющемся на пути к далекой звезде. Общая теория относительности дает ему ряд уравнений, с помощью которых можно выразить все законы природы, прояв- ляющиеся в любом выполнимом эксперименте. Эти уравнения будут точными независимо от того, находится наблюдатель в покое или в равномерном либо ускоренном движении по отношению к любому другому предмету.

В следующей главе мы подробнее рассмотрим теорию тяготения Эйнштейна и ее связь с новым важным понятием, известным под названием пространства — времени.

4. Общая теория относительности

4. Общая теория относительности
Остановимся теперь в нескольких словах на общей теории относительности. Вначале теория относительности была создана Эйнштейном лишь для инерционных систем координат, т е. для систем координат, движущихся прямолинейно и равномерно

Общая теория относительности и ее экспериментальная проверка

Общая теория относительности и ее экспериментальная проверка
Общая теория относительности пытается сформулировать физические законы для всех систем координат. Фундаментальная проблема теории относительности есть проблема тяготения. Теория относительности сделала

«Спойлер арифметики» и общая теория относительности

«Спойлер арифметики» и общая теория относительности
В 1949 г. Эйнштейна обеспокоило открытие одного из его близких друзей и коллег, венского математика Курта Гёделя из Института перспективных исследований в Принстоне, где работал и Эйнштейн. Гёдель нашел внушающее

Теория относительности

Теория относительности
С изобретением прибора, названного масс-спектрографом появилась возможность измерить массу отдельных атомных ядер с такой точностью, чтобы обнаружить несостоятельность закона сохранения массы. Прибор был сконструирован английским физиком

Глава 1. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ

Глава 1. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Какими бы ни были воспоминания о школьных годах, в них всегда есть одна общая деталь: в каждом классе всегда находилась горстка детей — самых «крутых», — пылающих неутолимой страстью высмеивать все и вся вокруг. Вот почему

12.

Теория относительности — тормоз в науке

12. Теория относительности — тормоз в науке
Изложение теории относительности всегда отличалось и отличается запутанностью, неясностью, разъяснением второстепенных, не имеющих отношения к существу дела деталей. Поддерживается миф о том, что смысл теории недоступен

Глава 5 Специальная теория относительности

Глава 5
Специальная теория относительности
Установив исходные факты, мы начнем строить, основываясь на них, нашу теорию и попытаемся определить, какие моменты в данном деле можно считать узловыми.
Конан Дойль «Записки Шерлока Холмса»
Принципы построения
Попытки решить

Глава 6 Общая теория относительности

Глава 6
Общая теория относительности
Каждый из магов имеет свой предел… [они] могут, скажем, останавливать время, но только в римановом пространстве и ненадолго.
Аркадий Стругацкий, Борис Стругацкий «Понедельник начинается в субботу»
Предпосылки построения ОТО
Наконец,

4. Специальная теория относительности. Часть II

4. Специальная теория относительности. Часть II
Длина и время, как было показано в предыдущей главе, являются относительными понятиями.Если один космический корабль пролетает мимо другого с постоянной скоростью, то наблюдатели на каждом из кораблей найдут, что

5. Общая теория относительности

5. Общая теория относительности
В начале гл. 2 мы указывали, что есть два пути обнаружить абсолютное движение: измерять движение по отношению к пучку света и использовать явление инерции, возникающее при ускорении предмета. Опыт Майкельсона — Морли показал, что первый

Теория относительности

Теория относительности
Теория относительности, которая произвела революцию в наших представлениях о времени и пространстве, и которая приводит к очень важным следствиям, до 1918 г. (до конца конец Первой мировой войны) оставалась неизвестной широким кругам, за исключением

Глава 1 Специальная теория относительности

Глава 1
Специальная теория относительности
Что будет, если посмотреть на себя в зеркало, когда путешествуешь со скоростью света?
Какими бы ни были воспоминания о школьных годах, в них всегда есть одна общая деталь: в каждом классе всегда находилась горстка детей – самых

Краткий очерк развития теории относительности

[Перевод д-ра Роберта У. Лоусона.] ЕСТЬ что-то привлекательное в представлении эволюции последовательности идей в как можно более краткой форме, и все же с полнота, достаточная для сохранения на протяжении всей непрерывности развития. Мы попытаемся сделать это для теории относительности и показать, что все восхождение состоит из маленьких, почти самоочевидных шагов мысли.

Все развитие начинается с идеи Фарадея и Максвелла, согласно которой все физические процессы предполагают непрерывное действие (в отличие от действия на расстоянии), или, говоря языком математики, они выражаются уравнениями в частных производных. Максвеллу удалось это сделать для электромагнитных процессов в покоящихся телах посредством представления о магнитном действии вакуумного тока смещения вместе с постулатом об идентичности природы электродинамических полей, создаваемых индукцией, и электростатическое поле.

Распространение электродинамики на случай движущихся тел выпало на долю преемников Максвелла. Г. Герц пытался решить проблему, приписывая пустому пространству (эфиру) физические свойства, весьма сходные с теми, которыми обладает весомая материя; в частности, подобно весомой материи, эфир должен иметь в каждой точке определенную скорость. Как и в покоящихся телах, электромагнитная или магнитоэлектрическая индукция должна определяться скоростью изменения электрического или магнитного потока соответственно при условии, что эти скорости изменения относятся к поверхностным элементам, движущимся вместе с телом. Но теории Герца противостоял фундаментальный опыт Физо по распространению света в текущих жидкостях. Наиболее очевидное распространение теории Максвелла на случай движущихся тел было несовместимо с результатами эксперимента.

В этот момент на помощь пришел Г. А. Лоренц. Ввиду своей безоговорочной приверженности атомной теории материи Лоренц чувствовал себя неспособным рассматривать последнюю как вместилище непрерывных электромагнитных полей. Таким образом, он представлял эти поля как состояния æ, которые считались непрерывными. Лоренц считал æ внутренне независимым от материи как с механической, так и с физической точки зрения. æ не принимали участия в движениях материи, и взаимность между æ и материей можно было предполагать лишь постольку, поскольку последняя считалась носителем присоединенных электрических зарядов. Великая ценность теории Лоренца заключалась в том, что вся электродинамика покоящихся и движущихся тел сводилась к уравнениям Максвелла пустого пространства. Эта теория не только превзошла теорию Герца с методической точки зрения, но и с ее помощью Г. А. Лоренцу удалось также выдающимся образом объяснить экспериментальные факты.

Теория оказалась неудовлетворительной только в одном принципиально важном пункте. Оказалось, что она отдает предпочтение одной системе координат определенного состояния движения (в покое относительно æ) всем другим системам координат в движении по отношению к этой. В этом отношении теория, казалось, находилась в прямом противоречии с классической механикой, в которой все инерциальные системы, находящиеся в равномерном движении относительно друг друга, в равной степени оправданы как системы координат (специальный принцип относительности). В связи с этим весь опыт в области электродинамики (в частности опыт Майкельсона) поддерживал идею эквивалентности всех инерциальных систем 9 .0011, т.е. , было в пользу специального принципа относительности.

Специальная теория относительности обязана своим происхождением этой трудности, которая из-за ее фундаментального характера считалась невыносимой. Эта теория возникла как ответ на вопрос: действительно ли специальный принцип относительности противоречит уравнениям поля Максвелла для пустого пространства? Ответ на этот вопрос оказался утвердительным. В самом деле, если эти уравнения справедливы по отношению к системе координат К и мы вводим новую систему координат К’ в соответствии с — по всей видимости, легко устанавливаемыми — уравнениями преобразования

K j

xf=x —

,~~y KПреобразование Галилея),? -? j J

, то уравнения поля Максвелла больше не действуют в новых координатах ( x′ y′, z′, t′ ). Но внешность обманчива. Более тщательный анализ физического значения пространства и времени сделал очевидным, что преобразование Галилея основано на произвольных предположениях и, в частности, на предположении, что утверждение об одновременности имеет смысл, не зависящий от состояния движения системы. используемых координат. Было показано, что уравнения поля для vacuo удовлетворяют специальному принципу относительности при условии, что мы используем приведенные ниже уравнения преобразования:

(преобразование Лоренца).

В? — v2lc

В этих уравнениях x, y, z представляют собой координаты, измеренные с помощью мерных стержней, которые находятся в состоянии покоя относительно системы координат, а t представляет собой время, измеренное соответствующим образом отрегулированными часами. одинаковой конструкции, находящиеся в состоянии покоя.

Теперь, чтобы мог выполняться специальный принцип относительности, необходимо, чтобы все уравнения физики не изменяли своей формы при переходе от одной инерциальной системы к другой, когда мы используем преобразование Лоренца для вычисления это изменение. Говоря языком математики, все системы уравнений, выражающие физические законы, должны быть ковариантны по отношению к преобразованию Лоренца. Таким образом, с точки зрения метода специальный принцип относительности сравним с принципом Карно о невозможности вечного двигателя второго рода, ибо, как и последний, он дает нам общее условие, которому должны удовлетворять все законы природы. .

Позднее Г. Минковски нашел особенно элегантное и выразительное выражение для этого условия ковариантности, которое выявляет формальную связь между евклидовой геометрией трех измерений и пространственно-временным континуумом физики.

Евклидова геометрия трех измерений.

Для двух соседних точек в пространстве существует числовая мера (расстояние ds ), которая соответствует уравнению

DS ² = DX ₁ ² + DX ₂ ² + DX _{3 .}

Не зависит от выбранной системы координат и может быть измерена с помощью единичной измерительной рейки.

Допустимые преобразования имеют такой характер, что выражение для ds ² является инвариантным, т. е. допустимы линейные ортогональные преобразования.

По отношению к этим преобразованиям законы евклидовой геометрии инвариантны.

Специальная теория относительности.

Двум соседним точкам пространства-времени (точечным событиям) соответствует числовая мера (расстояние ds ), которая удовлетворяет уравнению + дх ₃ ² + дх ₄ ² .

Он не зависит от выбранной инерциальной системы и может быть измерен с помощью измерительного стержня и стандартных часов. x ₁ , x ₂ , x ₃ — здесь прямоугольные координаты, а 4=VTcf — это время, умноженное на воображаемую единицу и на скорость света.

Допустимые преобразования имеют такой характер, что выражение для ds ² является инвариантным, т. е. допустимы те линейные ортогональные замены, которые сохраняют видимость реальности x ₂ , x ₃ , x 0 4 , x ₃ Эти замены являются преобразованиями Лоренца.

По отношению к этим преобразованиям законы физики инвариантны.

Отсюда следует, что по своей роли в уравнениях физики, хотя и не по своему физическому значению, время эквивалентно пространственным координатам (независимо от отношений действительности). С этой точки зрения физика есть как бы евклидова геометрия четырех измерений или, вернее, статика в четырехмерном евклидовом континууме.

Развитие специальной теории относительности состоит из двух основных этапов, а именно: адаптации «метрики» пространства-времени к электродинамике Максвелла и адаптации остальной физики к этой измененной «метрике пространства-времени». .» Первый из этих процессов дает относительность одновременности, влияние движения на измерительные стержни и часы, модификацию кинематики и, в частности, новую теорему сложения скоростей. Второй процесс дает нам модификацию закона движения Ньютона для больших скоростей, а также информацию фундаментального значения о природе инертной массы.

Выяснилось, что инерция не является фундаментальным свойством материи и даже непреодолимой величиной, а является свойством энергии. Если телу сообщить некоторое количество энергии, инерционная масса тела увеличится на величину E/ c ² , где c — скорость света в вакууме . С другой стороны, тело массой м следует рассматривать как запас энергии величиной мс ² .

Кроме того, вскоре оказалось невозможным естественным образом связать науку о гравитации со специальной теорией относительности. В связи с этим меня поразил тот факт, что сила тяготения обладает фундаментальным свойством, отличающим ее от электромагнитных сил. Все тела падают в поле тяготения с одинаковым ускорением, или — что является лишь другой формулировкой того же факта — гравитационная и инертная массы тела численно равны друг другу. Это числовое равенство предполагает тождество в характере. Могут ли гравитация и инерция быть идентичными? Этот вопрос ведет непосредственно к общей теории относительности. Не могу ли я считать Землю свободной от вращения, если я представляю себе центробежную силу, действующую на все тела, покоящиеся относительно Земли, как «реальное» поле тяготения или как часть такого поля? поле? Если эту идею удастся осуществить, то мы действительно докажем тождество тяготения и инерции. Для того же свойства, которое рассматривается как инерция с точки зрения системы, не участвующей во вращении, может быть интерпретирована как гравитация , если рассматривать ее по отношению к системе, разделяющей вращение. По Ньютону, такая интерпретация невозможна, так как по закону Ньютона центробежное поле нельзя рассматривать как создаваемое материей, и потому что в теории Ньютона нет места «реальному» полю типа «поля Кориолиса». Но, может быть, закон поля Ньютона можно было бы заменить другим, согласующимся с полем, справедливым по отношению к «вращающейся» системе координат? Мое убеждение в тождестве инертной и гравитационной масс вызвало во мне чувство абсолютной уверенности в правильности этой интерпретации. В связи с этим меня воодушевила следующая идея. Мы знакомы с «кажущимися» полями, действующими по отношению к системам координат, обладающим произвольным движением по отношению к инерциальной системе. С помощью этих специальных полей мы должны быть в состоянии изучить закон, которому вообще удовлетворяют поля тяготения. В связи с этим нам придется принять во внимание, что весомые массы будут определяющим фактором в создании поля или, согласно основному результату специальной теории относительности, плотности энергии — величине, имеющей трансформационный характер тензора.

С другой стороны, соображения, основанные на метрических результатах специальной теории относительности, привели к тому, что евклидовы метрики уже не могут быть справедливы по отношению к ускоренным системам координат. Хотя это задержало развитие теории на несколько лет, эта огромная трудность была смягчена нашим знанием того, что евклидовы метрики справедливы для малых областей. Вследствие этого величина ds , которая до сих пор физически определялась в специальной теории относительности, сохранила свое значение и в общей теории относительности. Но сами координаты утратили свое прямое значение и выродились просто в числа, лишенные физического смысла, единственным назначением которых была нумерация точек пространства-времени. Таким образом, в общей теории относительности координаты выполняют ту же функцию, что и гауссовы координаты в теории поверхностей. Неизбежным следствием предыдущего является то, что в таких общих координатах измеримая величина ds должна иметь возможность представления в виде0003

ds2 =2

где символы gu _v являются функциями пространственно-временных координат. Из вышеизложенного также следует, что характер пространственно-временной вариации факторов gu _v определяет, с одной стороны, пространственно-временную метрику, а с другой — гравитационное поле, управляющее механическим поведением материальных точек. .

Закон гравитационного поля определяется главным образом следующими условиями: во-первых, он справедлив при произвольном выборе системы координат; во-вторых, он должен определяться тензором энергии материи; в-третьих, он не должен содержать высших дифференциальных коэффициентов факторов gu _v чем второй, и должен быть линейным в этих. Таким образом был получен закон, который, хотя и принципиально отличался от закона Ньютона, но настолько точно соответствовал последнему в выводах, которые из него вытекали, что можно было найти лишь очень немного критериев, на которых теория могла быть решительно проверена на опыте.

Ниже перечислены некоторые важные вопросы, ожидающие решения в настоящее время. Действительно ли электрические и гравитационные поля настолько различны по своему характеру, что нет формальной единицы, к которой их можно было бы свести? Играют ли гравитационные поля какую-то роль в строении материи и следует ли рассматривать континуум внутри атомного ядра как существенно неевклидову? Последний вопрос относится к космологической проблеме. Следует ли сводить инерцию к взаимодействию с удаленными массами? И в связи с последним: конечна ли пространственная протяженность Вселенной? В этом мое мнение расходится с мнением Эддингтона. У Маха я чувствую, что утвердительный ответ необходим, но пока ничего нельзя доказать. Только после того, как будет проведено динамическое исследование больших систем неподвижных звезд с точки зрения границ применимости ньютоновского закона тяготения для огромных областей пространства, возможно, будет возможно получить в конце концов точную основу для решения этого увлекательного вопроса.

Общая теория относительности | Относительность: очень краткое введение

Фильтр поиска панели навигации

Oxford AcademicRelativity: A Very Short IntroductionVery Short IntroductionsCosmologyRelativity and GravitationBooksJournals
Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации

Oxford AcademicRelativity: A Very Short IntroductionVery Short IntroductionsCosmologyRelativity and GravitationBooksJournals
Термин поиска на микросайте

Расширенный поиск

• 
  Иконка Цитировать
  
  Цитировать

• Разрешения

• Делиться

  • Твиттер
  • Подробнее

CITE

Stannard, Russell,

‘General Relativity’

,

Относительность относительности: очень короткое введение

, очень короткие введения

(

Oxford,

8 Oxford Academic

, 24 сентября 2013 г.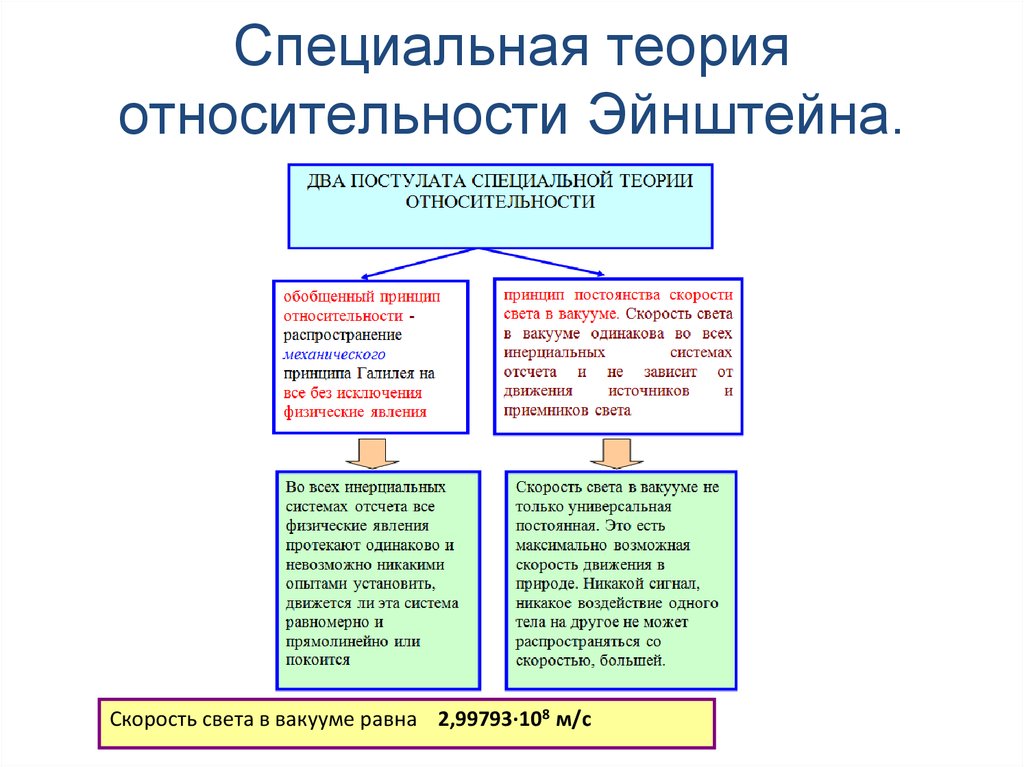

), https://doi.org/10.1093/actrade/9780199236220.003.0002,

по состоянию на 29 декабря 2022 г.

Выберите формат
Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Фильтр поиска панели навигации

Oxford AcademicRelativity: A Very Short IntroductionVery Short IntroductionsCosmologyRelativity and GravitationBooksJournals
Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации

Oxford AcademicRelativity: A Very Short IntroductionVery Short IntroductionsCosmologyRelativity and GravitationBooksJournals
Термин поиска на микросайте

Advanced Search

Abstract

«Общая теория относительности» объясняет общую теорию относительности Эйнштейна, которая включает гравитацию и ускорение в специальную теорию относительности. Галилей открыл универсальность свободного падения, а Эйнштейн объяснил это явление, используя принцип эквивалентности, который гласит, что любое поведение под действием гравитации идентично поведению под ускорением. Принцип эквивалентности позволяет легко предсказать влияние гравитации в задачах специальной теории относительности, например, в парадоксе близнецов. Эффекты гравитационных полей также искривляют свет, вызывая гравитационное линзирование. Эйнштейн утверждал, что вблизи гравитирующих тел пространство, а значит, и время искажаются. Это означает, что материя — и свет — больше не движутся по прямой линии, а по геодезической кривой. Эта кривизна обычно конечна. Однако если масса конденсируется в область нулевого объема и бесконечной плотности, кривизна становится бесконечной, и образуется черная дыра. Общая теория относительности может предсказать существование гравитационных волн, которые, как наблюдалось, исходят от квазаров. Как эта теория применима ко Вселенной? Космологический принцип гласит, что пространство может быть либо плоским, либо иметь отрицательную или положительную кривизну. Универсальная кривизна возникает из-за плотности энергии, но видимой материи недостаточно, чтобы вызвать наблюдаемую нами кривизну. Это указывает на существование темной материи и темной энергии.

Ключевые слова:
черная дыра, космологический принцип, темная энергия, гравитационные волны, теория относительности, парадокс близнецов

Предмет

Относительность и гравитационная космология

Серия

Краткие введения

В настоящее время у вас нет доступа к этой главе.

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Нажмите Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа в систему.
3. Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.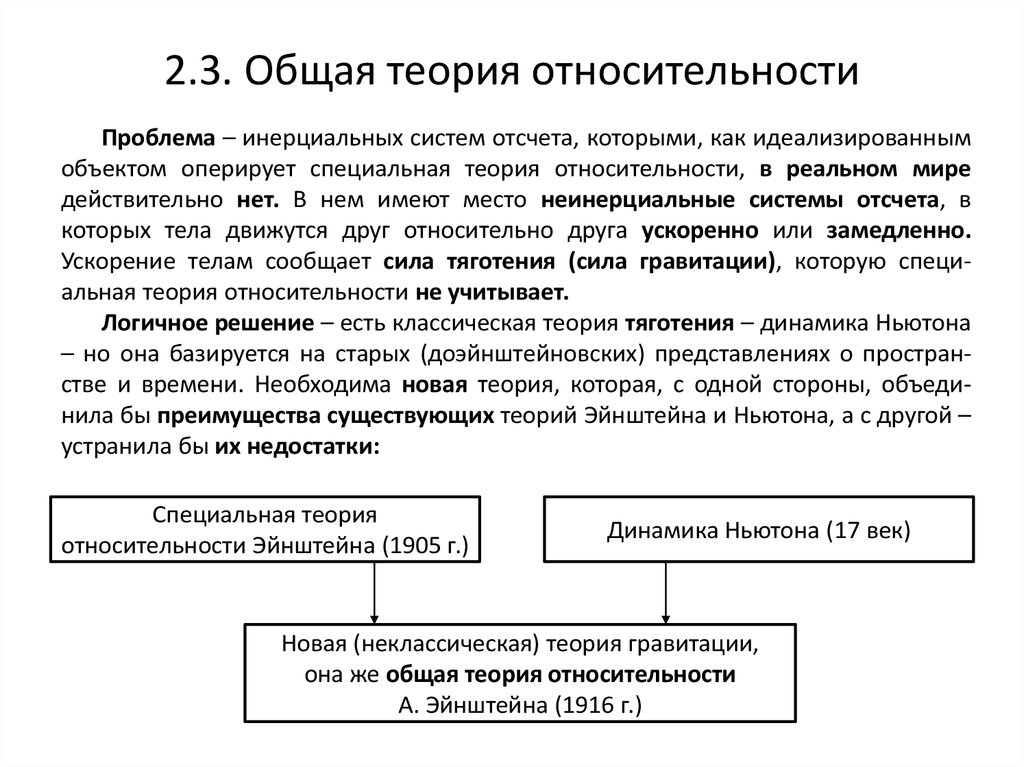

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Вход через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи, в которой выполнен вход, и доступ к функциям управления учетной записью.
• Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции.