Почему простые числа разного цвета: Почему в таблице простых чисел (смотри обложку учебника) некоторые простые числа выделены другим цветом? Что это такое

Содержание

888. В таблице простых чисел на форзаце учебника синим цветом выделены числа-близнецы. 6 класс математика Мордкович – Рамблер/класс

888. В таблице простых чисел на форзаце учебника синим цветом выделены числа-близнецы. 6 класс математика Мордкович – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

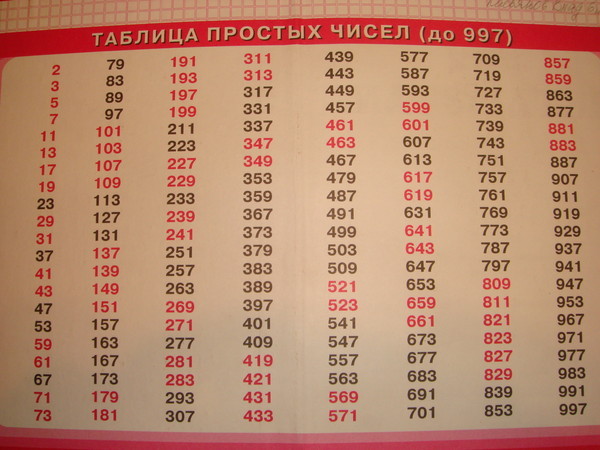
888. В таблице простых чисел на форзаце учебника синим цветом
выделены числа-близнецы — простые числа, между которыми в на-
туральном ряду чисел находится только одно число.
а) Выпишите три любые пары чисел-близнецов.
б) Укажите последнюю пару чисел-близнецов первой тысячи
натуральных чисел.

ответы

Ответ:
а) 281; 283. 269; 271; 659; 661.
б) 881; 883

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

Психология

3 класс

5 класс

Репетитор

похожие вопросы 5

Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра

10. При каких значениях р уравнение -х 2 + 6х — 2 = р:
а) не имеет корней;
б) имеет один корень; (Подробнее. ..)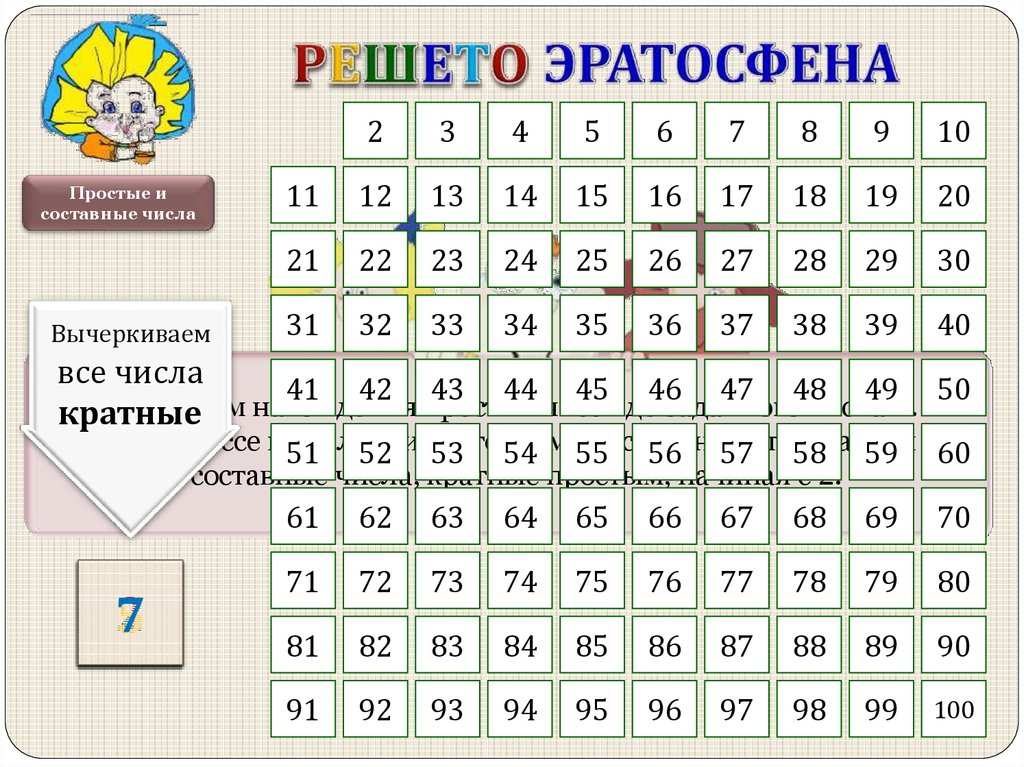

ГДЗМордкович А.Г.Алгебра8 класс

Приветик! Кто решил? № 411 Математика 6 класс Виленкин.

Выполните вычисления с помощью микрокалькулятора и резуль-
тат округлите до тысячных:
3,281 ∙ 0,57 + 4,356 ∙ 0,278 — 13,758 (Подробнее…)

ГДЗМатематика6 классВиленкин Н.Я.

Помогите установить соответствие между неравенствами. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.

Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.

Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Исследовательская работа по математике «Эти непростые «простые числа»

Ленинский район

МБОУ СОШ № 160

Секция «Математика»

Горбунов Александр

4В класс

Эти непростые «простые числа»

Руководитель:

Плешивцева Алёна Николаевна,

учитель начальных классов

Новосибирск

2018

Содержание

I Введение

II Теоритическая часть

Из истории вопроса
Алгоритм «решето Эратосфена»
Моё исследование
Самое большое простое число
Узоры простых чисел

III Заключение

Приложение

Всякий, кто изучает простые числа, бывает очарован и одновременно ощущает собственное бессилие. Определение простых чисел так просто и очевидно; найти очередное простое число так легко; разложение на простые сомножители — такое естественное действие. Почему же простые числа столь упорно сопротивляются нашим попыткам постичь порядок и закономерности их расположения? Может быть, в них вообще нет порядка, или же мы так слепы, что не видим его?

Ч. Узерелл «Этюды для программистов»

Введение

Однажды на уроке мы говорили о «признаках делимости» и я услышал про простые и составные числа. Мне захотелось подробнее изучить эту тему. Какие числа называются простыми? Так ли они просты на самом деле? Простые числа с давних времен привлекают внимание математиков. Простые числа следуют одно за другим по закону, который еще не найден. Хорошо было бы, если все простые числа можно было сосчитать! Но эта проблема до сих пор остается нерешенной.

Цель:

исследование множества простых чисел.

Задачи:

исследовать «решето Эратосфена»
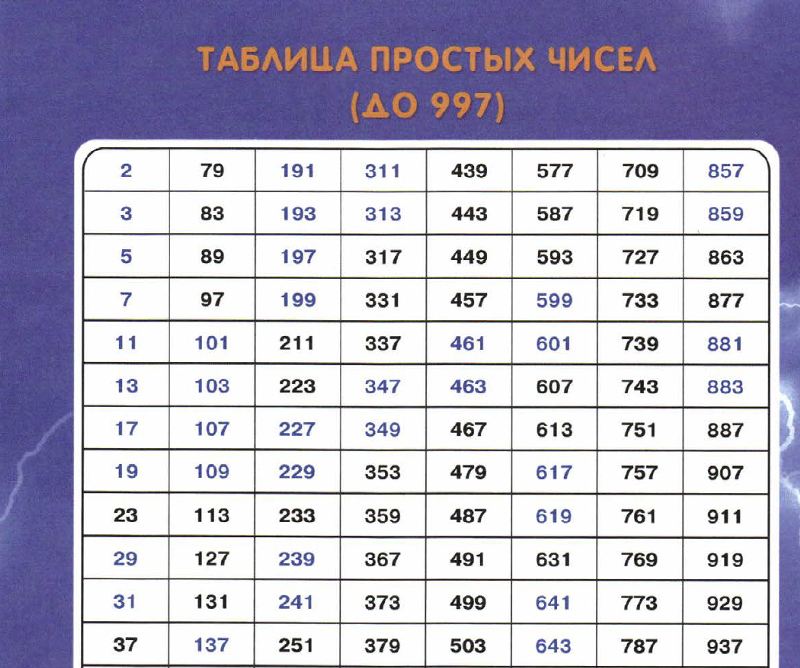
самостоятельно составить таблицу простых чисел до 1000
выяснить, существует ли самое большое простое число и имеет ли ряд простых чисел конец?
подробнее узнать о применении простых чисел

Гипотеза: если простые числа так просты, как это кажется, то математики давно их изучили, и тогда про них должно быть все известно.

Методы исследования:

работа с учебной и научно-популярной литературой, ресурсами сети Интернет
метод «решето Эратосфена».
наблюдение, сравнение, анализ

Объект исследования: простые числа

Из истории вопроса

Изучением свойств простых чисел занимается теория чисел.

Просто́е число́ — это натуральное число, которое имеет ровно 2 натуральных делителя (только 1 и самого себя).

Составное число́ — натуральное число большее 1, не являющееся простым.1(единица) – особое число, оно не является ни простым, ни составным.Таким образом, все натуральные числа, за исключением единицы, разбиваются на простые и составные.

Евклид — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Биография, сведения о нем крайне скудны. Его научная деятельность протекала в Александрии в 3 веке до н. э. Евклид — первый математик александрийской школы. Его главная работа «Начала» содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел. В ней он подвёл итог предшествующему развитию греческой математики и создал фундамент дальнейшего развития математики. Евклид — автор работ по математике, астрономии, оптике, музыке и др.

Евклид доказал, что простых чисел бесконечно много. Можно также сказать, что среди простых чисел нет самого большого числа.

Эратосфен Киренский — древнегреческий математик (276-194 до нашей эры), заведовал Александрийской библиотекой и заложил основы математической географии, вычислив с большой точностью величину земного шара. Он был первым составителем таблицы простых чисел.

Для нахождения простых чисел Эратосфен придумал следующий способ. Название «решето» метод получил потому, что, согласно легенде, Эратосфен писал числа на дощечке, покрытой воском, и прокалывал дырочки в тех местах, где были написаны составные числа. Поэтому дощечка являлась неким подобием решета, через которое «просеивались» все составные числа, а оставались только числа простые.

Решето́ Эратосфе́на — алгоритм нахождения всех простых чисел до некоторого целого числа n. Как и во многих случаях, здесь название алгоритма говорит о принципе его работы, то есть решето подразумевает фильтрацию, в данном случае фильтрацию всех чисел за исключением простых. По мере прохождения списка нужные числа остаются, а ненужные исключаются.

Алгоритм «Решето Эратосфена»

Эратосфен родился в 276 году до нашей эры, то есть этому методу уже около 2200 лет. Но он настолько прост и изящен,что можно объяснить его любому ребёнку. Итак, в чем суть метода и как его применять.

Предположим для примера,что нужно вычислить все простые числа меньшие 40.

Берем числовую последовательность натуральных чисел, начиная с 2

2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12

И удаляем все числа кратные 2.

Для этого умножаем числа натурального ряда, по порядку на 2 и результат

умножения вычеркиваем.

2×2=4, вычеркиваем 4,

2х3=6, вычеркиваем 6 и т.д.

Таким образом, исключаем все четные, больше 2.

Два — простое число, так как имеет, всего два натуральных делителя 1 и 2.

Получаем.

2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12…

Затем вычеркиваем числа кратные трем (умножаем на 3 все числа, также по

порядку ):

2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15…

Потом, вычеркиваем числа кратные пяти и т.д.

В итоге получим последовательность не зачеркнутых чисел, которые и

есть простые.

Сам Эратосфен построил таблицу простых чисел до 1000.

Сейчас, найдены огромные простые числа, но процесс все еще идет.

Моё исследование

Я решил сам составить таблицу простых чисел по методу «решето Эратосфена».

В итоге я составил 10 таблиц и выяснил, что количество простых чисел до 1000 равно 168.

Простые числа от 1 до 100: 25 чисел

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67,71, 73, 79, 83, 89, 97

Простые числа от 101 до 200: 21 число

101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199

Простые числа от 201 до 300: 16 чисел

211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293

Простые числа от 301 до 400: 16 чисел

307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397

Простые числа от 401 до 500: 17 чисел

401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499

Простые числа от 501 до 600: 14 чисел

503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599

Простые числа от 601 до 700: 16 чисел

601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691

Простые числа от 700 до 800: 14 чисел

701,709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797

Простые числа от 800 до 900: 15 чисел

809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887

Простые числа от 900 до 1000: 14 чисел

907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997

Я пришёл к выводу:количество простых чисел постепенно уменьшается.

Самое большое простое число.

Итак, по мере продвижения от малого числа к большему в натуральном ряду простые числа встречаются всё реже. Поэтому одним из первых вопросов был такой: существует ли последнее простое число, то есть, имеет ли ряд простых чисел конец?

Согласно теореме Евклида, количество простых чисел бесконечно. Следовательно, количество простых чисел, превышающих наибольшее известное, тоже бесконечно. Представим, что количество простых чисел конечно. Перемножим их и прибавим единицу. Полученное число не делится ни на одно из конечного набора простых чисел, потому что остаток от деления на любое из них даёт единицу. Значит, число должно делиться на некоторое простое число, не включённое в этот набор.

Многие учёные-математики, а также любители, занимаются поиском рекордных по величине простых чисел, за нахождение которых организацией ElectronicFrontierFoundationбыло предложено несколько наград в зависимости от величины числа. Так, в 2009 году была вручена премия в 100 000 долларов США, назначенная сообществом ElectronicFrontierFoundation за нахождение простого числа, десятичная запись которого содержит не менее 10 миллионов цифр.

Издавна ведутся записи, отмечающие наибольшие известные на то время простые числа. Один из рекордов поставил в 1772 году математик Эйлер, найдя простое число 231 — 1 = 2 147 483 647[2].

26 декабря 2017 года наибольшим известным простым числом стало число 277 232 917 − 1, которое содержит 23 249 425 десятичных цифр[1]. Открытие сделал JonathanPace в рамках проекта GIMPS.

Узоры простых чисел

Иногда своего рода формула возникает как результат наблюдения визуальных закономерностей. Одну из таких закономерностей случайно открыл Станислав Улам, американский математик, поляк по происхождению.

Сидя как-то на скучной лекции, он, ни о чем не думая, начал рисовать решетку из горизонтальных и вертикальных линий. В одной из полученных таким образом клеток он поставил 1 и стал нумеровать остальные клетки по спирали, расходящейся от первой клетки:

5 4 3

6 1 2

7 8 9

Когда спираль совершила уже несколько оборотов, Улам начал обводить кружками простые числа, не преследуя никакой определенной цели. Однако вскоре заметил, как на его глазах возникает довольно любопытная закономерность. Откуда ни возьмись, стали появляться прямые линии. Улам, конечно, сразу понял, что такие линии говорят о закономерности, которую можно облечь в формулу для простых чисел.

Компьютерная распечатка, дублирует то, что Улам сделал от руки. На компьютерном графике составные числа представлены маленькими белыми

квадратиками, а простые — черными. Выделяющиеся тёмные линии – это залежи простых чисел.

Улама заинтересовало, как же будет выглядеть его спираль, если её продолжить до нескольких тысяч простых чисел. Разработав программу, Улам получил рисунок для чисел от 1 до 65 000 (иногда его называют «скатертью Улама»), из которого видно, что даже у края картины простые числа продолжают послушно укладываться на прямые.

Фрагмент спирали Улама — простейшая иллюстрация закономерности в распределении простых чисел.

Чтобы отмеченная закономерность проявилась, не обязательно начинать спираль с единицы. Например, простые числа выстраиваются по диагоналям у спирали, начинающейся с числа 41 и заканчивающейся числом 41.

Заключение

В работе «Эти непростые «простые числа» я изучил историю, закономерности и свойства простых чисел. Убедился, что указать самое большое простое число невозможно, т.к. они бесконечны.

В процессе работы над исследованием, я сделал следующие выводы:

Можно сказать, что простые числа представляют собой как бы кирпичики, из которых строятся все остальные числа.
Для простых чисел не существует формулы, по которой их можно вычислить.
Не существует самого большого простого числа, последовательность простых чисел бесконечна.
Многие ученые на протяжении многих веков вносили свой вклад в изучение темы «Простые числа»
В настоящее время исследование темы продолжается, ученые делают и будут делать новые открытия!

Казалось бы, простые числа – чего уж может быть проще. А, оказывается, можно сделать еще столько открытий, и столько проблем ждут своего доказательства.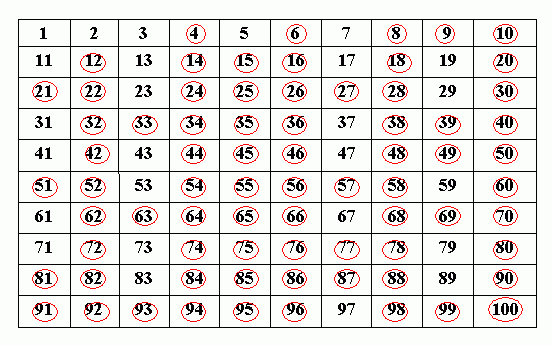

Математикам всего мира до сих пор хочется найти формулу, позволяющую хотя бы указать точное число простых чисел на любом интервале числовой оси, но, сколько ни бились математики, им так и не удалось найти желанную формулу. Существуют миллионы простых чисел, имеющих ровно 100 цифр, но пока ни одно такое число не обнаружено.

Итак, в наше время изучение простых чисел продолжается… Меня очень заинтересовали вопросы практического применения простых чисел в науке и технике, в криптографии и шифровании. Я думаю, что обязательно в 5 или 6 классе продолжу изучение этой темы.

«Простые числа не так просты,

как это кажется с первого взгляда!»

Фома Евграфович Топорищев,

писатель-философ

Приложение 1

Удивительные сказки

«Сказка о простых числах»

Жил да был на свете один мальчик. Звали его Кирилл. Однажды он в 4 классе со своим учителем поспорил, что простые числа человеку не нужны.

-Ну, есть они и пусть будут, но нам от этого ни какой пользы нет.

Учитель ему и говорит:

-Раз ты так считаешь то приведи пример.

-Сейчас… ну… эм…

-Ну-ну, молодой человек.

— Я дома найду почему нам от этого нет никакой пользы.

Думал Кирилл, думал и тут, у него дома начались новости. И диктор сказала:

-Срочно — на человека упала надпись с магазина…

И тут Кирилла осенило, что вот они могут убить человека.

Пришёл он в класс и говорит:

-Алена Николаевна, по новостям вчера сказали, что на человека упала надпись с магазина.

-Да-да, было такое!Эх, бедный человек!

-И вот упала цифра 3, это ведь простое число!

— Это работники плохо прикрепили, вот она и упала.

Кирилл продолжал думать, потом пошёл спать. И ему приснился странный сон, как он попал в мир простых чисел. К Кириллу подошла цифра 7 и говорит:

-Добро пожаловать, человек, в наш мир – Мир Простых чисел.

— От вас всё равно нет никакой пользы, — перебил Кирилл.

Подходит к нему учитель и Кирилл подумал, что он заснул на уроке:.

-Так Курочкин к доске! — сказала Алена Николаевна.

Кирилл вышел к доске. Учительница указала на 1.

-Скажи, простое это число или нет?

-Да,- ответил Кирилл.

-Нет. Неправильно, оно не простое и не составное. «2» за урок!

Потом он проснулся, пришёл в школу и сказал:

— Я понял, для чего нужны простые числа.

-Для чего?

-Для того, что бы не получать двойки за урок…

Практическое применение простых чисел.

Поиск простых чисел — по крайней мере, больших простых чисел — довольно сложная задача, потому что еще никому не удалось найти формулу или алгоритм, позволяющий генерировать любые простые числа. Но может возникнуть логичный вопрос: «Для чего нужно генерировать простые числа?»

На этот вопрос можно дать два ответа. Первый из них имеет теоретическое значение. Попытки генерации простых чисел ведут к появлению новых интересных инструментов для расчетов, особенно для компьютерных вычислений. Кроме того, наличие большого списка простых чисел позволяет проверять теоремы, которые еще не доказаны. Если кто-то выдвигает гипотезу относительно простых чисел, но оказывается, что одно из миллионов чисел нарушает ее, то вопрос снимается. Это стимулирует поиск простых чисел различных видов: простых чисел Мерсенна, чисел-близнецов и так далее. Иногда такой поиск превращается в соревнование, в котором устанавливаются мировые рекорды и за победы присуждаются большие призы.

Но есть и другая, более практическая причина, связанная с так называемым шифрованием. Электронная почта, банковские операции, кредитные карты и мобильная телефонная связь — все это защищено секретными кодами, непосредственно основанными на свойствах простых чисел.

Криптография и простые числа

В 1975 г. УитфилдуДиффи и Мартину Хеллману, в то время работавшим в Стэнфордском университете, пришла в голову идея асимметричного шифрования, или «шифрования с открытым ключом». Эта система основана на специальных математических функциях, называемых «односторонними функциями с потайным входом», которые позволяют зашифровывать текст, но делают расшифровку практически невозможной без знания используемого кода. Идея состоит в том, что каждый пользователь имеет пару ключей: открытый и закрытый. Если мы хотим отправить кому-то сообщение, мы зашифровываем это сообщение с помощью открытого ключа — то есть ключа, известного всем. Но только человек, имеющий соответствующий закрытый ключ, может расшифровать это сообщение. Одним из преимуществ такого метода является то, что закрытый ключ никогда не передается и поэтому его не нужно постоянно менять в целях безопасности. Идея метода не совсем проста, но мы можем пояснить ее с помощью аналогии. Представьте себе большой магазин, где продаются сотни тысяч банок с краской разного цвета. Возьмем две любые банки и смешаем краску в разных количествах. Пока все просто. Теперь, если мы покажем кому-нибудь получившийся цвет и попросим «расшифровать», какое количество каких красок использовалось изначально, на такой вопрос будет очень трудно ответить.

Именно так работают односторонние функции с потайным входом, которые легко применить в одном направлении, но практически невозможно — в обратном.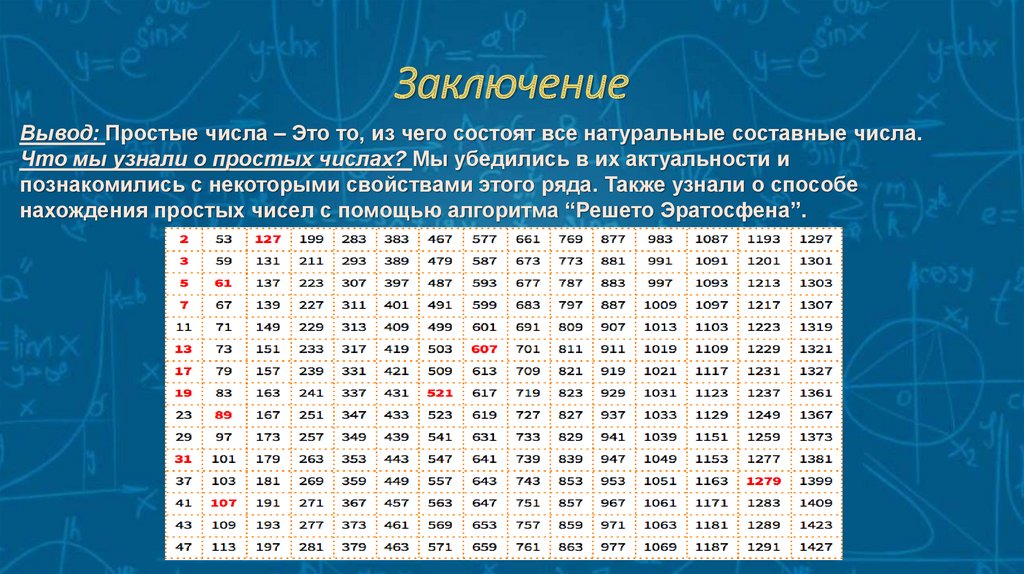

Схема, иллюстрирующая алгоритм Диффи — Хеллмана. Имеются два абонента, Алиса и Боб, желающие общаться втайне. Они открыто договариваются о двух числах (простое число р и другое число g, имеющие определенные свойства). И Алиса, и Боб выполняют некоторые операции с этими числами и с еще одним целым числом, которое они держат в секрете, а затем открыто посылают друг другу результаты. Теперь и Алиса, и Боб выполняют с полученным результатом еще одну операцию и получают один и тот же ответ, который будет для них секретным кодом. Потенциальный шпион, перехвативший результаты, посланные Алисой и Бобом, не может сгенерировать секретный код, имея лишь эту информацию.

Предположим теперь, что вместо банок с краской в магазине находятся простые числа. Возьмем любые два, например, 7 и 13, и перемножим их (аналогично смешиванию краски). В результате мы получим 7 х 13 = 91.

Тогда возникает вопрос: можно ли узнать, какие простые числа были перемножены, чтобы в результате получилось 91? Для ответа на него надо взять список простых чисел и проделать несколько проверок.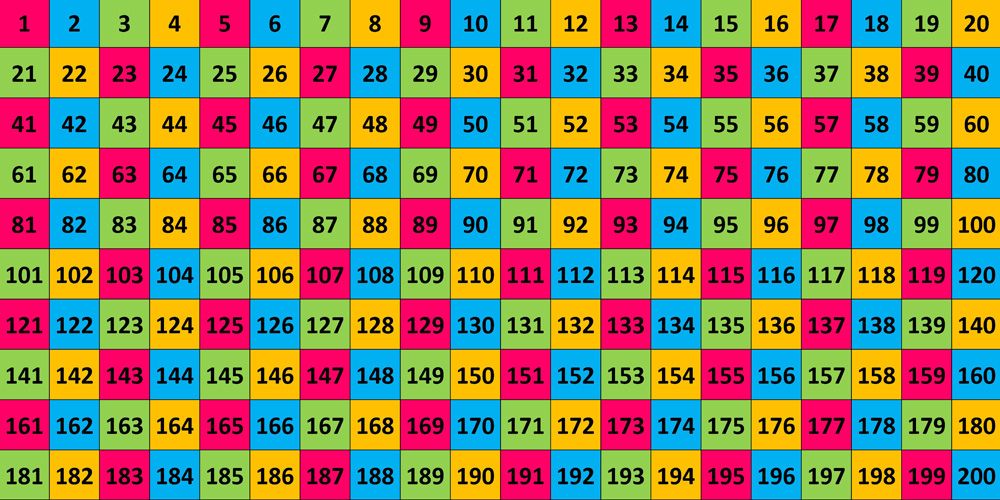 Казалось бы, простое решение, как и в случае определения цвета красок, если в магазине было всего около десятка основных цветов.Но с простыми числами все намного сложнее.

Например, ни у кого не хватит терпения проверить, что число 1409 305 684 859 является результатом умножения простых чисел 705 967 и 1996 277, особенно если учесть, что эти два простых числа взяты из списка простых чисел между 1 и 2000000, а там таких «всего лишь» 148933. Однако мы живем в эпоху высоких технологий, и, конечно, эту задачу можно довольно быстро решить с помощью хорошей программы и мощного компьютера. Хотя все зависит от того, насколько большой этот магазин красок. Не следует также забывать, что количество простых чисел не просто очень большое, а бесконечное.

Пара простых чисел в приведенном выше примере содержит лишь несколько цифр. Если мы возьмем простые числа, каждое из которых содержит сотни цифр, то время, которое потребуется компьютерной программе на простой перебор всех возможных вариантов — метод «грубой силы», как говорят криптографы, — будет больше, чем предполагаемое время существования Земли.

Простые числа повсеместно используются в нашей повседневной жизни, например, в кредитных картах и персональных компьютерах, поэтому постоянно существует потребность в новых простых числах (чем больше, тем лучше) для генерации секретных кодов. Таким образом, имеется спрос на простые числа, но контроль качества так же важен, как и их производство. Чтобы большому числу присвоить статус простого, его должна проверить специальная организация.

Шифр RSA был опубликован в 1978 г., но повсеместно начал использоваться в качестве метода шифрования лишь в конце 1990 гг. в связи с ростом сети интернет. Поиск больших простых чисел прежде требовал специального программного обеспечения, которое, как правило, можно было купить лишь в специализированных фирмах или в университетах, занимающихся такими исследованиями. Однако экспоненциальный рост вычислительных мощностей и появление более совершенных алгоритмов изменили рынок простых чисел и сделали их гораздо более доступными.

Простые числа в науке и технике.

Шифрование – это не единственная область применения простых чисел на практике. Простые числа используются в компьютерном моделировании различных процессов. Так же без них не обойтись и в машиностроении – на пример количество лопаток турбин реактивных самолётов должно составлять простое число. Если этим правилом пренебречь, то возникает резонанс, разрушающий лопатки турбины.

Самое большое простое число в веб-цветах RGB

Значок поискаУвеличительное стекло. Это означает: «Нажмите, чтобы выполнить поиск».
Логотип InsiderСлово «Инсайдер».

Рынки США Загрузка…

ЧАС
М
С

В новостях

Значок шевронаОн указывает на расширяемый раздел или меню, а иногда и на предыдущие/следующие параметры навигации. ДОМАШНЯЯ СТРАНИЦА

957 885 161 минус 1.

Интернет был очень взволнован этим и возился с числом. Вот новое применение для них: пользователь Flicker pbump решил превратить цифры в искусство:

Я взял необработанные числовые данные из нового 17-миллионного простого числа, разбил их на 6-значные фрагменты, преобразовал их в цвета RGB. , и сделал образ.

Веб-код RBG идентифицирует цвета по шестизначному числу, поэтому каждый шестизначный фрагмент обозначает цвет. Вот все 17 миллионов цифр:

пбамп

А вот отдельные фрагменты шестизначных чисел, превращенные в цвета, крупным планом:

Подпишитесь на уведомления от Insider! Будьте в курсе того, что вы хотите знать.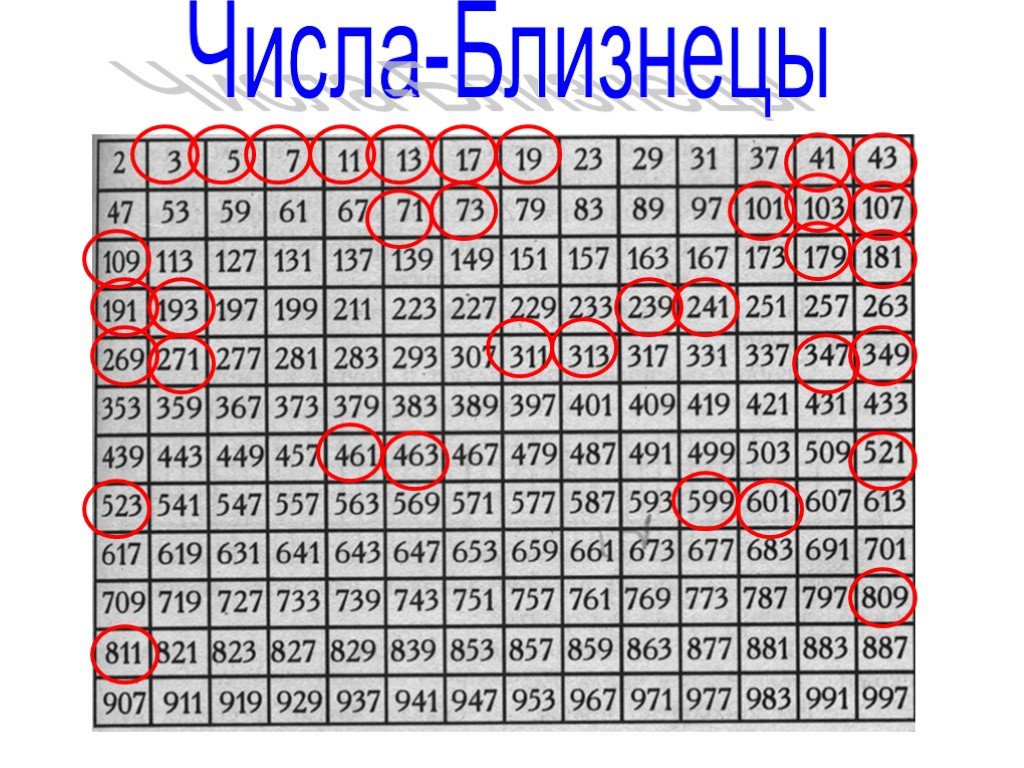

Подписаться на push-уведомления

LoadingЧто-то загружается.

Спасибо за регистрацию!

Получайте доступ к своим любимым темам в персонализированной ленте, пока вы в пути.

Математика
Цвет

график сотен Prime Climb — Чудо математики

Это шестой в серии сообщений о моем курсе «Развитие математического мышления», факультативном математическом материале для будущих учителей начального и среднего уровня математики. Все посты из этой серии здесь.

Это последний пост с подробным описанием того, как я представил «Уведомление и удивление» своим учителям до начала работы. Мы использовали его для придания смысла. Затем мы просмотрели фотографии окружающего мира и провели мозговой штурм, увидев и задаваясь вопросом. Студенты позже сделали свои собственные фотографии и идентифицировали математические идеи, которые они видели. (Фотографии и размышления было очень интересно рассматривать!) Затем мы перенесли наши навыки «Замечать и удивляться» в более математические условия, включая одну из математических задач Дэна Мейера в трех действиях, «Зубочистки». Теперь я расскажу вам о консолидирующем задании, в котором я попросил студентов рассказать мне, что они замечают и удивляются в изображении, переполненном математическими идеями.

Обновление от 6 августа 2017 г.: В этом посте описывается еще один способ включения «Notice and Wonder» в график сотен Prime Climb.

Примечание. Хотя это выглядит как длинное сообщение, первые 200 слов являются введением; последние 1500 слов представляют собой краткое изложение идей учащихся.

Таблица сотен Prime Climb

Prime Climb — красивая настольная игра, в которой игроки углубляют свое понимание арифметики посредством игрового процесса. Честно говоря, я никогда не играл! Но это не помешало мне оценить великолепную диаграмму сотен, которая сопровождает игру. Версия ниже; вы можете купить это изображение на потрясающем плакате здесь.

Эта диаграмма сотен заставляет нас замечать и удивляться. Найдите минутку и проведите мозговой штурм для себя. (Дэн Финкель, создатель игры Prime Climb, рассказывает об этом изображении в своем замечательном выступлении на TED «Пять принципов экстраординарного преподавания математики». На просмотр стоит потратить примерно 15 минут.) от моих учеников

Я попросил свою группу из почти пятидесяти учителей до начала работы рассказать мне о пяти вещах, которые они заметили, и об одной вещи, которая их удивила. Как группа, это потенциально 250 различных вещей, которые они замечают, и 50 вещей, которым они удивляются! Вот сопоставленный список из примерно 100 их идей (с небольшими поправками к неправильной терминологии), небрежно сгруппированных по моим собственным заголовкам разделов. Я попросил их сделать это как индивидуально. Я уверен, что в групповом обсуждении они развили бы и расширили идеи друг друга. В следующий раз!

Приятного чтения; Я, конечно, сделал.

I

уведомление что …

Цвет и структура

Круги пронумерованы от 1 до 100.
Диаграмма организована по системе 10×10.
Числа возрастают.
Числа в каждом столбце увеличиваются на десять по мере продвижения вниз по списку.
Цвет как-то связан с числом, и наоборот.
Есть разные цвета: синий, оранжевый, желтый, красный, зеленый.
Некоторые круги имеют только один цвет.
За исключением целых красных кругов, каждый другой цвет появляется как целый круг только один раз.
Каждый круг состоит из одного или нескольких цветов.
Цвет используется для демонстрации отношений между числами.
В каждом втором числе есть оранжевый (и аналогичные утверждения о других цветах).
Все четные числа окрашены в желтый/оранжевый цвет.
Дружественные числа (5 и 10) выделены синим цветом.
Круги с синим концом в 5 или 0.
Много красных кругов/цифр.
Есть 21 сплошной красный кружок/цифра.
Красный — самый заметный цвет.
Фиолетовый – наименее используемый цвет.
Полностью зеленые числа кратны 3 (и аналогичные утверждения о других цветах).
Кольца разбиты на части, которые варьируются от целого до 1/6.
В некоторых красных секциях есть маленькие белые цифры.
Все маленькие белые числа, которые появляются «случайно» в нижней части кругов, являются нечетными числами.
Красные полные кружки появляются только на нечетных числах.
Числа с оранжевым цветом (кратные 2) расположены по вертикали, как и числа с синим цветом (кратные 5). Но числа с зеленым цветом (кратные 3) расположены по диагонали (справа налево), если смотреть сверху вниз.
Если вы поместите палец на цифру с фиолетовым цветом, затем переместите палец вверх на одну строку, а затем переместите его на три столбца вправо, вы окажетесь на другой цифре с фиолетовым цветом (работает с большинством фиолетовых чисел, если это не слишком близко к край).
Наибольшее количество цветных секторов вокруг числа равно шести.
Наибольшее количество различных цветов, содержащихся в секторах, окружающих любое число, равно трем.
Ни один номер/круг не имеет всех цветов.
Кажется, что в цветах нет узора.

Число 1

Число 1 не имеет цвета, потому что оно не является ни простым, ни составным числом.
Число 1 имеет собственный цвет и не является частью какого-либо определенного рисунка на графике. Каждое целое число имеет делитель 1,
1 не является простым числом, поэтому оно не окрашено.

Простые числа

Полноцветные кружки — это простые числа.
Все простые числа имеют одну сплошную окружность.
97 — наибольшее простое число меньше 100.
Простые числа имеют свой особый цвет до значения 7.
Числа в красных кружках также являются простыми числами от 11 и выше.
Все простые числа от 1 до 100, кроме 2, являются нечетными.
Существует 25 простых чисел от 1 до 100.
Если внизу круга написано меньшее число, обозначающее большее число, то это означает, что большее число делится на простое число. Например, у числа 92 внизу круга написано маленькое число 23, это означает, что 92 делится на простое число 23.
Между 91 и 100 есть только одно простое число. Во всех остальных блоках по 10 есть как минимум два простых числа.
В столбце «3» больше всего простых чисел от 1 до 100.

Составные числа

Непростые числа представляют собой смесь цветов. Например, 15 — это 5×3, где 5 — синий, а 3 — зеленый, поэтому 15 — это наполовину синий и наполовину зеленый.
Все числа, кратные 6, должны быть оранжевого (2) и зеленого (3) цвета.
Любое число, оканчивающееся на 4,6,8 или 0, не является простым числом.
Некоторые непростые числа состоят из множителей, которые являются просто (только) простыми числами.

Квадратные числа

Все квадратные числа состоят из нескольких частей одного цвета.
Сумма всех квадратных чисел равна 385.

Ориентирован на умножение

Мы можем использовать цвета вокруг каждого числа и перемножать их «представляющие числа» вместе, чтобы получить число в середине.
Фрагменты круга символизируют, сколько раз произошло умножение. Например, число 8 состоит из трех фрагментов желтого круга, обозначающих 2×2×2.
Цвета каждого круга представляют собой числа, на которые можно разделить большее число. Например, число 95 окрашено в синий и красный цвета. Эти цвета представляют 5 и простое число 19. При умножении их сумма равна 95.

Делитель и множитель

На этой диаграмме есть только 2 числа, которые представлены кружком, разделенным на шестые. Им 64 и 96.
Для составления чисел до 100 требуется не более шести множителей.
Нечетные числа чаще всего имеют делители, являющиеся простыми числами.
Круги делятся на секции в зависимости от того, сколько у них делителей.
Множители каждого числа очевидны по раскраске.
Различные цветные части круга означают, что число делится более чем на одно число.
Нечетные числа обычно имеют меньше делителей, даже если они не простые.

Простые множители

Цвета, окружающие число, представляют собой простые множители числа. Например, число 96 состоит из пяти оранжевых сегментов и одного зеленого сегмента, что предполагает, что простые множители числа 96 равны 2×2×2×2×2×3.

Другое

Все числа, делящиеся на 11, имеют цифру 11 в нижнем индексе и располагаются на диагональной линии.
Рассмотрите числа с одинаковыми цифрами (11, 22, …). Сумма цифр – все четные числа.
Нет явных инструкций или «ключа», объясняющего, что на самом деле показывает диаграмма.
Сумма первых девяти простых чисел равна 100.
Если вы прищуритесь, вы начнете видеть цветовые узоры, а не числа, как я заметил некоторые из моих предыдущих пунктов.

Интересно…

Цвет и структура

Почему 1 – единственная цифра серого цвета?
Почему на некоторых кругах есть лишние цифры белого цвета?
Что означают сечения кругов?
Почему разные числа делятся на разные «дроби»? Есть ли в этом основная причина?
Почему некоторые числа имеют части своего цвета, даже если эти части одного цвета? Например, число 64 состоит из шести частей оранжевого цвета, а оранжевый ассоциируется только с двумя.
Как им удалось разделить внешний круг числа 24 на четыре сегмента? И почему три из них оранжевые, а один зеленый?
Какой цвет используется чаще всего?
Было бы легче читать диаграмму, если бы все простые числа имели свой цвет, а не первые 10?
Почему числа 96 и 64 имеют больше всего делений?
Есть ли несколько «решений» этой проблемы?

Выкройки

Если есть выкройка? А если бы я разобрался?
Есть ли закономерность между числами и количеством частей в их цветном круге, которую можно использовать для вычисления любого числа?
Почему они не написали, сколько раз конкретное число входит в большое число внутри соответствующей цветовой секции?
Почему числа окрашены случайным образом (без определенного шаблона)?
Можете ли вы использовать эту числовую таблицу и расширить ее, чтобы найти каждое простое число без ручных и утомительных вычислений?
Существует ли систематический способ определения наибольшего количества секторов или различных цветов, которые могут окружать любое число в наборе (например, от 1 до 1 000 000), без необходимости садиться и умножать простые числа?

Расширение диаграммы

Если бы число увеличилось до 1000, какое число имело бы наибольшее количество различных цветов?
Если бы это число увеличилось до 1000, стали бы мы видеть все больше и больше красного цвета по сравнению с другими цветами?
Интересно, как будут выглядеть следующие 100 чисел, разложенные таким образом на простые множители? Я бы предположил, что количество видимого красного уменьшится.