Содержание
ЗАСТЫВШИЕ ЭМБРИОНЫ ЗВЕЗД | Наука и жизнь
Наука получила пока еще самые первые сведения о спутниках далеких звезд. Вот некоторые данные. Цифры обозначают массу спутника по сравнению с массой Юпитера.
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
‹
›
Открыть в полном размере
С 1995 года, когда шведские астрономы М. Мейор и Д. Гуелоз открыли первую планету, принадлежащую не Солнечной системе, а далекой звезде, было найдено еще более 50 таких же небесных тел. Все они представляют собой гигантские газовые шары размером с Юпитер, а некоторые даже много больше. Присутствие жизни на таких планетах полностью исключено. Что-либо похожее на нашу Землю до сих пор не попало в поле зрения телескопов, хотя астрономы теперь уже располагают несколькими методами обнаружения спутников далеких звезд.
В конце января 2001 года в Сан-Диего (США) проходил съезд членов Американского астрономического общества, где основной темой стала дискуссия о планетах-спутниках, принадлежащих звездам. Общее внимание привлекла открытая совсем недавно планета, вращающаяся вокруг звезды Глизе 876 в созвездии Водолея. Главное здесь в том, что это уже вторая планета, обнаруженная у одной и той же звезды. Первую увидели в 1998 году. Она вдвое превышает по массе Юпитер, свою орбиту проходит примерно за 60 дней. Вторая планета, о существовании которой узнали совсем недавно, меньше первой, и период ее обращения вдвое короче. Ее масса по отношению к Юпитеру пока точно не определена. Но открытие двух спутников у одной звезды дает астрономам редкую возможность определить абсолютную величину каждого из этих небесных тел (благодаря гравитационному взаимодействию планет на их орбитах.) Одинокая планета позволяет вычислить только ее наименьшую возможную массу и размер орбиты.
Общее внимание привлекла открытая совсем недавно планета, вращающаяся вокруг звезды Глизе 876 в созвездии Водолея. Главное здесь в том, что это уже вторая планета, обнаруженная у одной и той же звезды. Первую увидели в 1998 году. Она вдвое превышает по массе Юпитер, свою орбиту проходит примерно за 60 дней. Вторая планета, о существовании которой узнали совсем недавно, меньше первой, и период ее обращения вдвое короче. Ее масса по отношению к Юпитеру пока точно не определена. Но открытие двух спутников у одной звезды дает астрономам редкую возможность определить абсолютную величину каждого из этих небесных тел (благодаря гравитационному взаимодействию планет на их орбитах.) Одинокая планета позволяет вычислить только ее наименьшую возможную массу и размер орбиты.
Больше половины из всех известных ныне спутников звезд открыли два американских астронома — Д. Марси из университета в Беркли и Р. Батлер из Института Карнеги. Они ведут многолетние наблюдения за 120 звездами, расположенными недалеко от Солнца и похожими на наше светило.
Свое сообщение на съезде эти астрономы посвятили удивительному объекту, открытому ими в созвездии Змеи около звезды HD 168443. Три года назад они обнаружили там планету, которая по меньшей мере равна семи массам Юпитера. И вот теперь они же обнаружили там вторую планету, очень большую — в семнадцать раз больше Юпитера. Это рекордный размер среди известных астрономам планет. Однако астрофизики уже давно предполагали, что в космосе существует большое число объектов примерно с такой массой.
«Но является ли это тело планетой? — поставил вопрос Д. Марси. — Или это что-то новое в нашей науке о небе?»
Сейчас их природу ученые видят таким образом. Подобно истинным звездам, они рождаются из облаков межзвездного газа, которые «слепляются» в шарообразные тела под действием собственной гравитации. Но если возникает шар, меньший, чем 60 масс Юпитера, то внутри его не развивается давление, необходимое для начала ядерной реакции, подобной той, что раскаляет наше Солнце. И тем не менее давления в центре такого шара достаточно, чтобы находящийся в газе дейтерий вспыхивал хотя бы временами. Вместо сияющей звезды рождается темно-красный тлеющий водородный шар. Обнаружить его в небе столь же сложно, как и холодную планету далекой звезды. Такие обитатели Вселенной получили название «коричневый карлик». Его можно сравнить с эмбрионом звезды, так и не достигшей полной зрелости.
И тем не менее давления в центре такого шара достаточно, чтобы находящийся в газе дейтерий вспыхивал хотя бы временами. Вместо сияющей звезды рождается темно-красный тлеющий водородный шар. Обнаружить его в небе столь же сложно, как и холодную планету далекой звезды. Такие обитатели Вселенной получили название «коричневый карлик». Его можно сравнить с эмбрионом звезды, так и не достигшей полной зрелости.
Но чем отличаются такие тела от истинных планет?
По мнению одних ученых, главную роль здесь играет их происхождение. «Коричневые карлики» подобно настоящим звездам рождаются, как уже говорилось, из газовых облаков, а планеты — из протопланет ного облака, окружающего юную звезду. Близкие к ней планеты бывают «слеплены» из более тяжелых атомов, тогда как легкие элементы — газы световым давлением звезды вытесняются на периферию системы. Там они собираются в шары, подобные нашему Юпитеру. По расчетам сторонников такого сценария развития, тело, имеющее массу меньше 17 масс Юпитера, следует отнести к планетам. Сторонники другой точки зрения считают, что вспышки дейтерия возможны при величине небесного тела не меньше 13 масс Юпитера.
Сторонники другой точки зрения считают, что вспышки дейтерия возможны при величине небесного тела не меньше 13 масс Юпитера.
Загадкой пока остается, как возникают системы, в которых одновременно существуют и звезда, и истинные планеты, и «коричневые карлики»».
МАССЫ НЕБЕСНЫХ ТЕЛ • Большая российская энциклопедия
МА́ССЫ НЕБЕ́СНЫХ ТЕЛ (методы определения). Определение М. н. т. стало возможным в 17 в., после открытия всемирного тяготения закона.
Массы Земли и других планет
Одна из первых оценок массы Земли получена Г. Кавендишем после проведения опыта по эксперим. определению универсальной гравитац. постоянной. Измеряя с помощью крутильных весов силу притяжения между массивным свинцовым шаром и подвешенным вблизи него небольшим металлич. шариком, Кавендиш сравнил величину этой силы с силой притяжения шарика Землёй и сумел вычислить, во сколько раз масса Земли превышает массу свинцового шара. 3$. По параметрам орбит Земли и Луны была проведена оценка массы Солнца – примерно в 333 000 раз больше массы Земли.
3$. По параметрам орбит Земли и Луны была проведена оценка массы Солнца – примерно в 333 000 раз больше массы Земли.
Массы Меркурия и Венеры, у которых отсутствуют естеств. спутники, этим способом определить невозможно. Единственный и гораздо более трудный путь состоит в использовании возмущений (всегда являющихся функциями возмущающей массы), которые планета вызывает в движении др. тел Солнечной системы. Значительно более трудную задачу представляет определение массы Луны. Являясь ближайшим к Земле небесным телом, Луна не может, строго говоря, считаться спутником нашей планеты, т. к. Солнце притягивает её в 2,5 раза сильнее, чем Земля. Вокруг Солнца обращается т. н. барицентр (центр масс) двойной планеты Земля–Луна, в то время как обе они описывают относительно барицентра эллиптич. орбиты с периодом в 1 месяц. Поэтому массу Луны можно вычислить по величине месячного смещения Земли относительно барицентра. В точных астрономич. наблюдениях долготы Солнца проявляется т. н. лунное неравенство, свидетельствующее о том, что центр Земли в течение месяца описывает эллипс с большой полуосью, равной примерно 3/4 радиуса Земли. Последнее означает, что барицентр системы Земля–Луна всегда располагается внутри Земли и никогда не выходит за пределы её поверхности. Определённая по этим данным масса Луны составляет ок. 1/81 массы Земли.
В точных астрономич. наблюдениях долготы Солнца проявляется т. н. лунное неравенство, свидетельствующее о том, что центр Земли в течение месяца описывает эллипс с большой полуосью, равной примерно 3/4 радиуса Земли. Последнее означает, что барицентр системы Земля–Луна всегда располагается внутри Земли и никогда не выходит за пределы её поверхности. Определённая по этим данным масса Луны составляет ок. 1/81 массы Земли.
Массы всех планет Солнечной системы входят в число фундам. астрономич. постоянных, значения которых регулярно уточняются на основе всей совокупности астрономич. наблюдений и утверждаются Междунар. астрономич. союзом.
Массы звёзд
Третий закон Кеплера в его обобщённой форме позволяет также определить суммарную массу двойной звезды по известному значению её годичного параллакса. 2$. Напр., для двойной звёздной системы Сириус А и Сириус B соответствующие значения составляют $a″$=7,57″, $π$=0,37″ и $P$ = 50 лет, соответственно суммарная масса этой двойной звёздной системы оценивается в 3,4$M_☉$.
2$. Напр., для двойной звёздной системы Сириус А и Сириус B соответствующие значения составляют $a″$=7,57″, $π$=0,37″ и $P$ = 50 лет, соответственно суммарная масса этой двойной звёздной системы оценивается в 3,4$M_☉$.
В том случае, когда удаётся измерить положения визуально-двойных звёзд относительно их барицентра, возникает возможность определить отношение масс обоих компонентов. Такие измерения требуют знания точных положений компонентов системы относительно далёких звёзд (т. н. звёзд фона) на достаточно длительных интервалах времени. Продолжит. наблюдения одиночной звезды в течение мн. лет показывают, что если она имеет собственное движение относительно звёздного фона, то её перемещение происходит по дуге большого круга небесной сферы. Но если звезда – визуально-двойная, то по дуге большого круга смещается её барицентр, а оба компонента системы движутся по криволинейным барицентрич.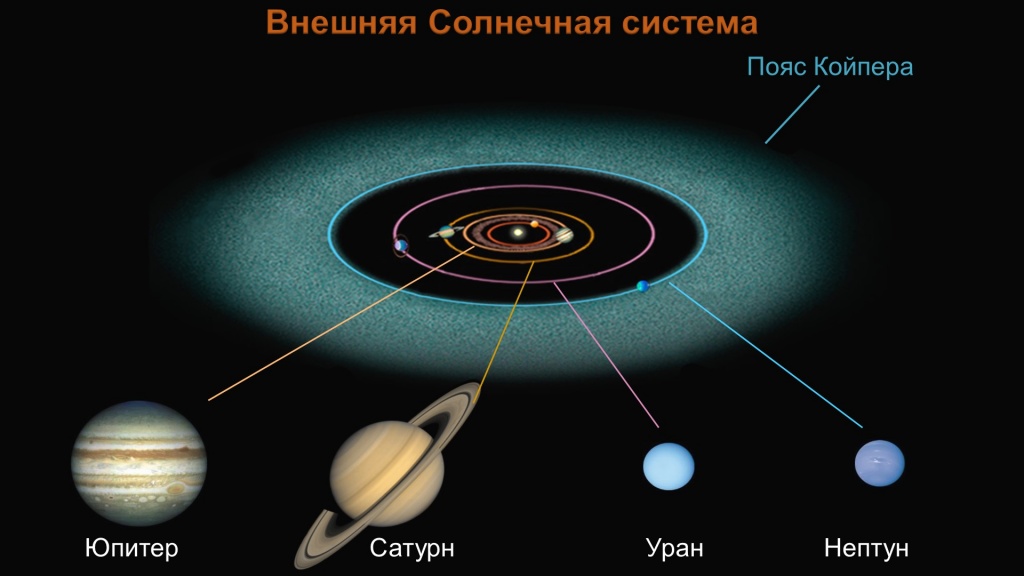 траекториям. Точные астрометрич. измерения положений компонентов двойной системы позволяют проследить траекторию центра масс, а затем и индивидуальные орбиты отд. компонентов. Если $α_1$ и $α_2$ – выраженные в секундах дуги угловые расстояния от гл. звезды с массой $M_1$ и звезды-спутника с массой $M_2$ до видимого положения центра масс двойной системы, то тогда, по определению центра масс, $M_1α_1=M_2α_2$, откуда следует формула для отношения масс компонентов визуально-двойной звезды: $M_1/M_2=α_2/α_1$.
траекториям. Точные астрометрич. измерения положений компонентов двойной системы позволяют проследить траекторию центра масс, а затем и индивидуальные орбиты отд. компонентов. Если $α_1$ и $α_2$ – выраженные в секундах дуги угловые расстояния от гл. звезды с массой $M_1$ и звезды-спутника с массой $M_2$ до видимого положения центра масс двойной системы, то тогда, по определению центра масс, $M_1α_1=M_2α_2$, откуда следует формула для отношения масс компонентов визуально-двойной звезды: $M_1/M_2=α_2/α_1$.
Знание суммарной массы двойной звезды и отношения масс её компонентов позволяет без труда вычислить массы обеих звёзд. Типичные значения масс звёзд, полученные по наблюдениям визуально-двойных звёзд, лежат в пределах (0,1–20)$M_☉$. Более половины звёзд нашей Галактики входят в состав двойных, тройных звёзд или звёздных систем большей кратности. Именно исследования двойных звёзд позволили получить данные о звёздных массах и послужили основой для установления соотношения масса – светимость (см. Масса – светимость зависимость). Это соотношение широко используется в звёздной астрономии и астрофизике в качестве незаменимого средства оценки масс звёзд по их светимостям.
Именно исследования двойных звёзд позволили получить данные о звёздных массах и послужили основой для установления соотношения масса – светимость (см. Масса – светимость зависимость). Это соотношение широко используется в звёздной астрономии и астрофизике в качестве незаменимого средства оценки масс звёзд по их светимостям.
Согласно совр. представлениям, массы звёзд заключены в пределах (0,08–100)$M_☉$. Масса отд. звезды в среднем близка к $M_☉$, в то время как звёзды с массами, в десятки раз бóльшими массы Солнца, встречаются достаточно редко: это гл. обр. звёзды ранних спектральных классов O и B.
Массы звёздных скоплений и галактик
Массу $M$ шарового звёздного скопления радиуса $R$ можно оценить по величине круговой скорости $V$ звезды, движущейся на границе скопления, считая, что центростремит. ускорение звезды вызвано притяжением всех звёзд шарового скопления. 2R/G$, где $G$ – гравитац. постоянная. Более точная оценка массы звёздного скопления получается при использовании некоторых усреднённых значений скоростей звёзд и их ср. удалённости от центра скопления.
2R/G$, где $G$ – гравитац. постоянная. Более точная оценка массы звёздного скопления получается при использовании некоторых усреднённых значений скоростей звёзд и их ср. удалённости от центра скопления.
Наличие у галактики одного спутника (играющего роль пробного тела) позволяет оценить массу галактики с помощью аналогичной формулы, но точность такой оценки очень невысока. В качестве пробного тела может рассматриваться др. галактика, шаровое скопление, расположенное на периферии галактики, и даже облако межзвёздного газа. Если у галактики имеется неск. спутников (или др. пробных тел), то можно предположить, что распределение положений и скоростей спутников имеет случайный характер. Это предположение реализуется тем точнее, чем больше имеется пробных тел (напр., в галактике М31 в созвездии Андромеды ок. 400 шаровых скоплений). Тогда в приведённой формуле можно использовать видимые расстояния и скорости пробных тел, усреднённые за промежуток времени, значительно превышающий их орбитальные периоды. Массы спиральных галактик можно оценивать с помощью облаков межзвёздного газа на круговых орбитах в галактич. плоскости. Изложенный метод измерения масс галактик (метод Ньютона) базируется на законе всемирного тяготения. Более перспективным считается метод Эйнштейна, в котором массивные галактики рассматриваются в качестве гравитац. линзы (см. Гравитационная фокусировка).
Тогда в приведённой формуле можно использовать видимые расстояния и скорости пробных тел, усреднённые за промежуток времени, значительно превышающий их орбитальные периоды. Массы спиральных галактик можно оценивать с помощью облаков межзвёздного газа на круговых орбитах в галактич. плоскости. Изложенный метод измерения масс галактик (метод Ньютона) базируется на законе всемирного тяготения. Более перспективным считается метод Эйнштейна, в котором массивные галактики рассматриваются в качестве гравитац. линзы (см. Гравитационная фокусировка).
В оценке суммарной массы галактики с учётом всех её составляющих (звёзд, газа, пыли и др.) существенную роль играет круговая скорость пробного тела. Эта скорость при удалении от центра галактики должна уменьшаться по определённому закону. Однако по результатам наблюдений удалось установить, что этот закон выполняется только во внутр. области галактики. На периферии любой галактики круговая скорость почти всегда выше значения, полученного в предположении, что вся масса галактики заключена в её звёздах и газе. Чаще всего скорость вращения звёзд не уменьшается с расстоянием от центра галактики, а остаётся постоянной или даже растёт при приближении к видимому краю галактики. Для объяснения такого феномена было выдвинуто предположение о существовании в галактиках скрытой массы, повышающей величину напряжённости гравитац. поля галактики вдали от её центра. Вопрос о границах галактик и их полных массах на нач. 21 в. не решён: несветящиеся части галактик могут простираться на порядок дальше видимой границы их звёздных дисков.
области галактики. На периферии любой галактики круговая скорость почти всегда выше значения, полученного в предположении, что вся масса галактики заключена в её звёздах и газе. Чаще всего скорость вращения звёзд не уменьшается с расстоянием от центра галактики, а остаётся постоянной или даже растёт при приближении к видимому краю галактики. Для объяснения такого феномена было выдвинуто предположение о существовании в галактиках скрытой массы, повышающей величину напряжённости гравитац. поля галактики вдали от её центра. Вопрос о границах галактик и их полных массах на нач. 21 в. не решён: несветящиеся части галактик могут простираться на порядок дальше видимой границы их звёздных дисков.
естественных спутников — На каком расстоянии от Солнца могут существовать планетарные спутники?
Краткий ответ:
Существует внутренний предел того, как класс palnet может вращаться вокруг своей звезды и удерживать лунную орбиту вокруг нее. Но я не знаю, как его рассчитать. Насколько мне известно, не существует внешнего предела тому, насколько далеко планета может находиться от своей звезды и иметь луны. Планета-изгой в межзвездном пространстве вдали от звезды может иметь спутники.
Но я не знаю, как его рассчитать. Насколько мне известно, не существует внешнего предела тому, насколько далеко планета может находиться от своей звезды и иметь луны. Планета-изгой в межзвездном пространстве вдали от звезды может иметь спутники.
Длинный ответ:
Каждая планета, вращающаяся вокруг звезды, имеет внутреннее и внешнее расстояние, между которыми должны вращаться любые луны.
Внутреннее расстояние частично зависит от характеристик конкретной луны. Это называется радиусом Роша или пределом Роша. Любой объект, который удерживается вместе в основном за счет своей гравитации, такой как звезда, планета или луна, который проходит с пределом Роша более массивного объекта, будет разорван на части приливными силами. Предел Роша зависит от относительной плотности двух тел и от того, является ли меньший объект твердым или жидким.
Луна не может образоваться из более мелких объектов, если она находится в пределах предела Роша своей планеты, и если луна проходит в пределах предела Роша своей планеты, она распадается. Так что не должно быть лун в пределах Роша их планет.
Так что не должно быть лун в пределах Роша их планет.
Формулы для расчета пределов Роша для астрономических тел можно найти по адресу:
https://en.wikipedia.org/wiki/Roche_limit[1]
Внешний предел, на котором Луна может вращаться вокруг планеты, называется Радиус холма или сфера холма. Размер сферы холма зависит от масс планеты и ее звезды и расстояния между ними, так как чем сильнее гравитация звезды относительно планеты, тем меньше будет сфера холма планеты.
Существуют формулы для расчета сферы холма объекта по адресу:
https://en.wikipedia.org/wiki/Hill_sphere[2]
Однако оказывается, что луна, вращающаяся во внешних частях сферы Хилла, не будет иметь стабильной орбиты в течение длительных периодов астрономического времени.
Сфера Хилла является лишь приближением, и другие силы (например, радиационное давление или эффект Ярковского) могут в конечном итоге вывести объект из сферы. Этот третий объект также должен иметь достаточно малую массу, чтобы не создавать дополнительных сложностей из-за собственной гравитации.
Подробные численные расчеты показывают, что орбиты на сфере Хилла или только внутри нее не являются стабильными в долгосрочной перспективе; оказывается, что стабильные спутниковые орбиты существуют только в пределах от 1/2 до 1/3 радиуса Хилла. Область устойчивости для ретроградных орбит на большом расстоянии от главной звезды больше, чем область для прямых орбит на большом расстоянии от главной. Считалось, что это объясняет преобладание ретроградных спутников вокруг Юпитера; однако у Сатурна более равномерное сочетание ретроградных и прямоходящих спутников, поэтому причины более сложны.3
https://en.wikipedia.org/wiki/Hill_sphere#True_region_of_stability[3]
Сфера холма Земли простирается примерно на 1 500 000 километров, поэтому область действительно стабильных орбит вокруг Земли простирается только на расстояние от 500 000 до 750 000 километров. с Земли.
Предел Роша для Земли составляет 1,49 радиуса для твердых объектов и 2,88 радиуса для жидких объектов. Поскольку радиус Земли составляет 6 371 км, предел Роша для твердых объектов составляет 9 492,79 км, а для жидких объектов — 18 348,48 км.
Поскольку радиус Земли составляет 6 371 км, предел Роша для твердых объектов составляет 9 492,79 км, а для жидких объектов — 18 348,48 км.
Чем больше и массивнее планета, тем больше будут радиусы ее предела Роша и сферы Хилла. Чем дальше планета от своей звезды, тем больше будет радиус ее сферы Хилла.
Меркурий и Венера менее массивны, чем Земля, поэтому их пределы Роша меньше, что хорошо для того, чтобы не разрушать близкие спутники. Они ближе к Солнцу, чем Земля, поэтому гравитация Солнца сильнее там, где они вращаются, и поскольку они менее массивны, чем Земля, их массы и расстояния от Солнца в совокупности делают их сферы Хилл намного меньше, чем у Земли, что плохо для удержания лун.
Сфера Хилла Меркурия имеет радиус всего 175 300 километров, поэтому истинная область стабильности должна иметь внешний край только на расстоянии от 58 432 до 87 650 километров.
Высота холма Венеры составляет 1 004 200 километров, поэтому истинная область стабильности должна иметь внешний край только на расстоянии от 334 733,3 до 502 100 километров, что намного больше, чем у Меркурия, но меньше, чем у Земли.
Но есть и другие проблемы с спутниками Меркурия и Венеры. Орбита луны вокруг этой планеты будет постоянно меняться по мере того, как луна будет приближаться к планете или удаляться от нее. Таким образом, если луна начинается между пределом Роша и сферой Хилла своей планеты, она может выйти из зоны, где возможны стабильные орбиты.
Если планета и ее луна образовались вместе, у луны будет прямая орбита. Большинство объектов Солнечной системы вращаются в том же направлении, в котором они вращаются вокруг Солнца, что называется прямой орбитой. Если вместе с планетой образуется луна, то, что называется обычной луной, она будет вращаться вокруг планеты в том же направлении, что и планета, то есть прямо относительно планеты. Поскольку большинство планет вращаются в прямом направлении относительно своей орбиты, большинство обычных лун, сформированных с их планетами, вращаются в прямом направлении относительно орбиты растения вокруг Солнца.
Планеты также могут захватывать проходящие объекты и делать их своими спутниками. Процесс захвата может привести либо к прямой орбите, либо к орбите в противоположном направлении, ретроградной орбите. В Солнечной системе есть несколько захваченных лун, некоторые из которых имеют прямые орбиты, а некоторые — ретроградные.
Процесс захвата может привести либо к прямой орбите, либо к орбите в противоположном направлении, ретроградной орбите. В Солнечной системе есть несколько захваченных лун, некоторые из которых имеют прямые орбиты, а некоторые — ретроградные.
Все ретроградные спутники испытывают приливное замедление в той или иной степени. Единственный спутник в Солнечной системе, для которого этим эффектом нельзя пренебречь, — это спутник Нептуна Тритон. Все остальные ретроградные спутники находятся на дальних орбитах, и приливные силы между ними и планетой пренебрежимо малы.
https://en.wikipedia.org/wiki/Retrograde_and_prograde_motion#Natural_satellites_and_rings[4]
Обращение Тритона вокруг Нептуна превратилось в почти идеальный круг с почти нулевым эксцентриситетом. Считается, что вязкоупругое демпфирование только за счет приливов не способно сделать орбиту Тритона круговой за время, прошедшее с момента образования системы, и сопротивление газа от движущегося вперед диска обломков, вероятно, сыграло существенную роль.
Приливные взаимодействия также вызывают изменение орбиты Тритона. который уже ближе к Нептуну, чем Луна к Земле, чтобы постепенно распадаться; прогнозы таковы, что через 3,6 миллиарда лет Тритон пройдет в пределах предела Роша Нептуна. Это приведет либо к столкновению с атмосферой Нептуна, либо к распаду Тритона, сформировав новую систему колец, подобную той, что обнаружена вокруг Сатурна.[25]
https://en.wikipedia.org/wiki/Triton_(moon)#Orbit_and_rotation[5]
Таким образом, если бы Меркурий или Венера захватили луну на ретроградной по отношению к их вращению орбите, эта луна постепенно опустилась бы по спирали в пределах Roche ограничивают и уничтожают через миллионы или миллиарды лет.
Луны, движущиеся по прямой орбите вокруг своих планет, будут либо удаляться от планет, либо приближаться к своим планетам.
Если луна находится на прямой орбите выше уровня синхронной орбиты, она будет удаляться от планеты из-за приливного ускорения. Таким образом, через миллионы или миллиарды или, возможно, триллионы лет, он может выйти за пределы сферы Хилла планеты и выйти на орбиту вокруг своей звезды. МО лун — это орбиты Солнечной системы дальше, чем синхронные орбиты их планет, и поэтому они постепенно удаляются от них.
МО лун — это орбиты Солнечной системы дальше, чем синхронные орбиты их планет, и поэтому они постепенно удаляются от них.
https://en.wikipedia.org/wiki/Tidal_acceleration#Other_cases_of_tidal_acceleration[6]
Некоторые луны вращаются вокруг своих планет ниже уровня синхронной орбиты. Их орбитальные периоды меньше, чем одни сутки планеты. Эти луны испытывают приливное замедление и медленно движутся по спирали внутрь к своим планетам, в конечном итоге достигая пределов Роша своих планет и распадаясь.
https://en.wikipedia.org/wiki/Tidal_acceleration#Tidal_deceleration[7]
Звездные сутки, период, за который они совершают оборот на 360 градусов относительно далеких звезд Меркурия и Венеры, составляют 58,646 земных суток. и 243,0226 земных суток соответственно. Таким образом, любые луны, вращающиеся вокруг Меркурия и Венеры на синхронных орбитах, будут вращаться очень далеко от своих планет.
Считается, что у Меркурия и Венеры нет спутников, главным образом потому, что любой гипотетический спутник давно бы испытал торможение и врезался бы в планеты из-за очень низких скоростей вращения обеих планет; кроме того, Венера также имеет ретроградное вращение.
https://en.wikipedia.org/wiki/Tidal_acceleration#Tidal_deceleration[7]
Долгое время астрономы считали, что Меркурий и, возможно, Венера приливно привязаны к Солнцу с периодами вращения, равными их орбитальным периодам. , так что день был бы равен году, и одна сторона планеты всегда была бы обращена к Солнцу, а другая сторона всегда была бы обращена от Солнца. Это называется резонансом 1:1. Теперь известно, что Меркурий и Венера не имеют резонансов 1:1, но их периоды вращения очень велики по сравнению с их годами 87,9.7 земных дней и 224,7 земных дня.
Когда гравитация звезды слишком сильна на орбите планеты — что зависит от массы звезды и орбитального расстояния планеты от звезды — эта планета станет приливно-приливной связью со Звездой, либо с Резонанс 1:1 или резонанс с простыми целыми числами, такой как резонанс 3:2 планеты Меркурий — Меркурий совершает три оборота за два меркурианских года — или какой-то другой простой резонанс.
Таким образом, если планета находится слишком глубоко в гравитационном колодце своей звезды, вращение планеты будет сильно замедлено, а синхронная орбита планеты будет очень далеко от планеты, возможно, за пределами сферы Хилла. Таким образом, луна за пределами сферы Хилла будет потеряна в космосе, а луна ниже синхронной орбиты будет иметь затухающую орбиту и в конечном итоге достигнет предела вращения планеты.
Таким образом, луна за пределами сферы Хилла будет потеряна в космосе, а луна ниже синхронной орбиты будет иметь затухающую орбиту и в конечном итоге достигнет предела вращения планеты.
Таким образом, если известна масса звезды, можно рассчитать расстояние, на котором планета будет двигаться значительно медленнее, что сделает для нее трудным или невозможным сохранение своей луны(ей).
И, конечно же, еще одна проблема для любых потенциальных спутников — более короткие годы, когда планеты вращаются вокруг своих звезд.
Было показано, что максимально возможная продолжительность дня спутника, совместимая с устойчивостью Хилла, составляет около P∗p/9, где P∗p — период обращения планеты вокруг звезды (Киппинг, 2009 г.).а)
https://arxiv.org/ftp/arxiv/papers/1209/1209.5323.pdf[8]
И источник указан как:
https://academic.oup.com/mnras/article/392 /1/181/1071655[9]
Таким образом, это утверждает, что луна не может иметь устойчивую орбиту вокруг своих планет, если только орбита луны не меньше одной девятой (0,111111) периода обращения планеты вокруг звезды.
Чем больше масса звезды, тем короче будет год планет, вращающихся вокруг нее на определенном расстоянии, поскольку повышенная гравитация звезды означает, что планета должна вращаться быстрее, чтобы оставаться на орбите. Чем ближе планета обращается к звезде, тем быстрее она должна будет вращаться из-за более сильной гравитации на таком расстоянии, и тем короче будет ее год.
Таким образом, чем ближе к орбите планеты находится звезда и чем массивнее звезда, тем короче будет год планеты.
Самый короткий орбитальный период или год среди всех известных экзопланет, обращающихся вокруг звезды главной последовательности, — это, по-моему, K2-137b, который составляет всего 4,31 часа.
https://academic.oup.com/mnras/article/474/4/5523/4604789[10]
Таким образом, если бы спутник K2-137b имел стабильную орбиту вокруг себя, эта орбита, вероятно, должна была бы быть менее примерно 0,4788 часа. Который должен быть намного ниже предела Роша для K2-137b и, вероятно, также намного ниже поверхности K2-137b.
Таким образом, должна быть возможность создать формулу, показывающую, насколько близко планета может подойти к звезде определенной массы и при этом сохранить луну.
Конечно, нет предела тому, насколько далеко планета с луной может удалиться от своей звезды.
.
Земля удаляется от Солнца, как и все планеты
Ларри Макниш, RASC Калгари
3 января 2019 года Земля достигла точки на своей орбите, в которой она максимально сближается с Солнцем: перигелия. Каждый объект, вращающийся вокруг одной массы (например, наше Солнце), образует эллипс, содержащий точку наибольшего сближения, уникальную для этой конкретной орбиты, известную как перицентр. За последние 4,5 миллиарда лет Земля вращалась вокруг Солнца по эллипсу, точно так же, как и все другие планеты, вращающиеся вокруг своих звезд во всех других зрелых солнечных системах по всей галактике и Вселенной.
За последние 4,5 миллиарда лет Земля вращалась вокруг Солнца по эллипсу, точно так же, как и все другие планеты, вращающиеся вокруг своих звезд во всех других зрелых солнечных системах по всей галактике и Вселенной.
Но кое-что, чего вы, возможно, не ожидаете или не понимаете, тем не менее происходит: орбитальный путь Земли не остается неизменным с течением времени, а закручивается наружу. В этом, 2019 году, наш перигелий был на 1,5 сантиметра дальше, чем в прошлом году, который был дальше, чем годом ранее, и т. д. Это касается не только Земли; каждая планета дрейфует от своей родительской звезды. Вот наука почему.
Рис Тейлор
Сила, отвечающая за движение каждой планеты вокруг каждой солнечной системы во Вселенной, одна и та же: универсальный закон гравитации. Если вы посмотрите на это с точки зрения Ньютона, где каждая масса притягивает любую другую массу во Вселенной, или с точки зрения Эйнштейна, где масса и энергия искривляют ткань пространства-времени, через которую движутся другие массы, наибольшая масса доминирует на орбите. всего, на что он влияет.
Если бы центральная масса была неизменной и была бы единственным действующим фактором, сила гравитации оставалась бы неизменной во времени. Каждая орбита всегда будет продолжаться по идеальному замкнутому эллипсу и никогда не изменится.
NCSA, Калифорнийский университет в Лос-Анджелесе / Кек, группа А. Гез; Визуализация: С. Леви и Р. Паттерсон / UIUC
Конечно, так не бывает. В каждой солнечной системе есть и другие массы: планеты, луны, астероиды, кентавры, объекты пояса Койпера, спутники и многое другое. Эти массы возмущают орбиты, вызывая их прецессию. Это означает, что точка наибольшего сближения — перицентр вообще или перигелий для орбиты по отношению к нашему Солнцу — со временем вращается.
Орбитальная механика различными способами влияет на прецессию равноденствий. У Земли, например, перигелий и декабрьское солнцестояние совпали всего 800 лет назад, но они медленно расходятся. С периодом в 21 000 лет наш перигелий прецессирует таким образом, что изменяет не только точку наибольшего сближения на нашей орбите, но и положение наших полярных звезд.
Грег Бенсон на Wikimedia Commons
Существуют и другие факторы, которые изменяют нашу орбиту, в том числе:
- дополнительное искривление пространства-времени из-за Общей теории относительности, из-за которого планеты с большой массой подвергаются дополнительной прецессии,
- присутствие частиц материи на плоскости Солнечной системы, вызывающее сопротивление планет и создающее вдохновляющее явление,
- и создание гравитационных волн, что происходит, когда любая масса (например, планета) проходит через область, где изменяется кривизна пространства-времени (например, вблизи звезды), что также вызывает инспирацию.
Последние два эффекта, однако, важны только в экстремальных условиях, например, очень близко к большой, компактной массе или на ранних стадиях формирования солнечной системы, когда протопланетные диски присутствуют и все еще массивны.
С. М. Эндрюс и др. и сотрудничество DSHARP, arXiv:1812.04040
Сегодня Земля (и все планеты) находятся так далеко от Солнца и окружены таким редким количеством материи, что шкала времени на вдохе в триллионы-квадриллионы раз длиннее нынешнего возраста Вселенной. Поскольку около 4,5 миллиардов лет назад протопланетный диск полностью испарился, почти не осталось ничего, что могло бы рассеять наш угловой момент. Самый большой эффект, способствующий нашей спирали, — это излучение солнечного ветра, т.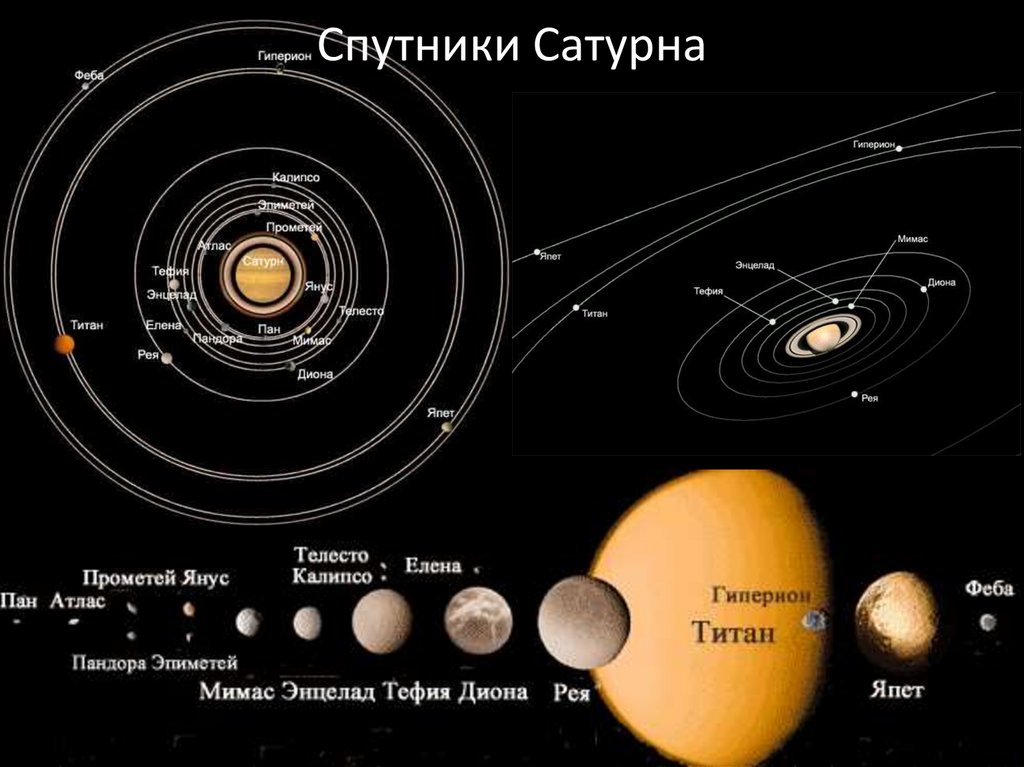 е. частиц Солнца, которые врезаются в нашу планету и прилипают, заставляя нас немного терять угловой момент.
е. частиц Солнца, которые врезаются в нашу планету и прилипают, заставляя нас немного терять угловой момент.
В целом, Земля даже не движется по спирали к Солнцу; это спираль наружу, прочь от него. Как и все планеты Солнечной системы. С каждым годом мы оказываемся лишь немного — на 1,5 сантиметра, или 0,00000000001 % расстояния между Землей и Солнцем — дальше от Солнца, чем годом ранее.
Причина в самом Солнце.
Пользователь Wikimedia Commons Kelvinsong
Глубоко внутри Солнца происходит процесс ядерного синтеза. Каждую секунду Солнце излучает около 3,846 × 10 90 189 26 90 190 джоулей энергии, которые высвобождаются в результате преобразования массы в энергию в ядре. Эйнштейновское E = mc 2 является первопричиной, ядерный синтез — процессом, а непрерывное излучение энергии Солнцем — результатом. Эта энергия является основным процессом, который приводит в действие практически все биологически интересные процессы, происходящие на Земле.
Эйнштейновское E = mc 2 является первопричиной, ядерный синтез — процессом, а непрерывное излучение энергии Солнцем — результатом. Эта энергия является основным процессом, который приводит в действие практически все биологически интересные процессы, происходящие на Земле.
Но недооценивается то, что со временем преобразование материи в энергию приводит к тому, что Солнце теряет значительную часть массы. За 4,5 миллиарда лет истории Солнечной системы наше Солнце из-за процесса ядерного синтеза потеряло примерно 0,03% своей первоначальной массы: сопоставимо с массой Сатурна.
НАСА
Ежегодно Солнце теряет около 4,7 миллиона тонн вещества, что уменьшает гравитационное притяжение каждого объекта в нашей Солнечной системе. Именно это гравитационное притяжение заставляет наши орбиты вести себя так, как мы их знаем.
Если бы сила притяжения осталась неизменной, из-за трения, столкновений и гравитационного излучения образовалась бы очень, очень медленная внутренняя спираль. Но с изменениями, которые мы на самом деле переживаем, Земля, как и все планеты, вынуждена медленно дрейфовать и двигаться по спирали наружу от Солнца. Хотя эффект невелик, это изменение на 1,5 сантиметра в год легко вычисляется и является однозначным.
Совфото/UIG через Getty Images
Однако мы не смогли измерить это изменение расстояния напрямую. Мы знаем, что это должно произойти; мы знаем, какой должна быть его величина; мы знаем, что удаляемся от Солнца по спирали; мы знаем, что это происходит со всеми планетами.
Но то, что мы хотели бы сделать, это измерить его напрямую, как еще одну проверку законов физики, какими мы их знаем. Вот как развивается физика:
- предсказывая то, что мы ожидаем наблюдать на основе всех накопленных нами знаний и наших лучших теорий,
- путем проведения эксперимента/наблюдения, которое измеряет результаты такого теста с требуемой точностью,
- и сравнить то, что мы видим, с тем, что мы ожидаем.
Когда все сходится, наши теории подтверждаются; когда они этого не делают, это указывает на то, что мы, возможно, находимся на пороге научной революции.
ALMA (ESO/NAOJ/NRAO)/М. Меркер и др.
Однако в случае с Солнечной системой было бы шоком, если бы Земля и все планеты не отклонялись от Солнца по спирали. История о том, почему мы должны удаляться от Солнца по спирали, настолько проста и убедительна, что ее невозможно игнорировать.
Солнце излучает энергию, которую мы наблюдаем, что позволяет нам рассчитать скорость потери массы по формуле Эйнштейна E = mc 2 .
Масса Солнца, наряду с параметрами орбит наших планет, определяет путь и форму их вращения вокруг Солнца.
Если мы изменим эту массу, орбиты изменятся на величину, которую легко вычислить, даже используя простую ньютоновскую физику.
Когда мы делаем эти расчеты, мы обнаруживаем, что Земля мигрирует от Солнца примерно на 1,5 сантиметра в год.
Space Place НАСА
Потеря массы Солнца в результате сжигания его ядерного топлива гарантирует, что каждая масса, вращающаяся по орбите в нашей Солнечной системе, с течением времени медленно движется наружу по спирали. Около 4,5 миллиардов лет назад наша планета была примерно на 50 000 километров ближе к Солнцу, чем сегодня, и будет отдаляться все быстрее по мере того, как Солнце продолжает развиваться.

 Подробные численные расчеты показывают, что орбиты на сфере Хилла или только внутри нее не являются стабильными в долгосрочной перспективе; оказывается, что стабильные спутниковые орбиты существуют только в пределах от 1/2 до 1/3 радиуса Хилла. Область устойчивости для ретроградных орбит на большом расстоянии от главной звезды больше, чем область для прямых орбит на большом расстоянии от главной. Считалось, что это объясняет преобладание ретроградных спутников вокруг Юпитера; однако у Сатурна более равномерное сочетание ретроградных и прямоходящих спутников, поэтому причины более сложны.3
Подробные численные расчеты показывают, что орбиты на сфере Хилла или только внутри нее не являются стабильными в долгосрочной перспективе; оказывается, что стабильные спутниковые орбиты существуют только в пределах от 1/2 до 1/3 радиуса Хилла. Область устойчивости для ретроградных орбит на большом расстоянии от главной звезды больше, чем область для прямых орбит на большом расстоянии от главной. Считалось, что это объясняет преобладание ретроградных спутников вокруг Юпитера; однако у Сатурна более равномерное сочетание ретроградных и прямоходящих спутников, поэтому причины более сложны.3 Приливные взаимодействия также вызывают изменение орбиты Тритона. который уже ближе к Нептуну, чем Луна к Земле, чтобы постепенно распадаться; прогнозы таковы, что через 3,6 миллиарда лет Тритон пройдет в пределах предела Роша Нептуна. Это приведет либо к столкновению с атмосферой Нептуна, либо к распаду Тритона, сформировав новую систему колец, подобную той, что обнаружена вокруг Сатурна.[25]
Приливные взаимодействия также вызывают изменение орбиты Тритона. который уже ближе к Нептуну, чем Луна к Земле, чтобы постепенно распадаться; прогнозы таковы, что через 3,6 миллиарда лет Тритон пройдет в пределах предела Роша Нептуна. Это приведет либо к столкновению с атмосферой Нептуна, либо к распаду Тритона, сформировав новую систему колец, подобную той, что обнаружена вокруг Сатурна.[25]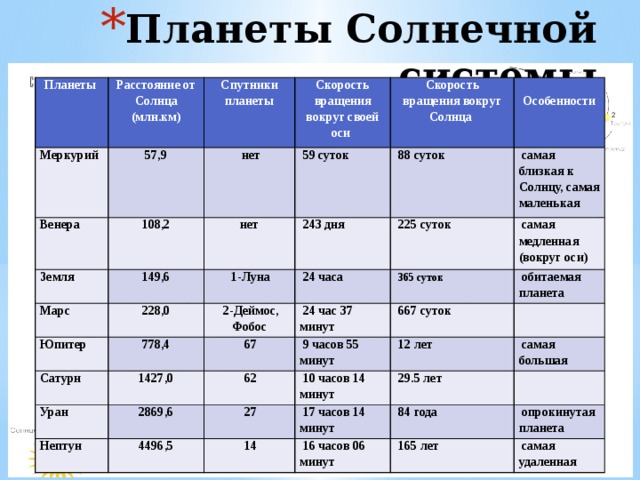

 Меркурий прецессирует со скоростью 43 дюйма (где 1 дюйм равен 1/3600 градуса) за столетие; меньшая черная дыра в OJ 287 прецессирует со скоростью 39 градусов за 12-летнюю орбиту.
Меркурий прецессирует со скоростью 43 дюйма (где 1 дюйм равен 1/3600 градуса) за столетие; меньшая черная дыра в OJ 287 прецессирует со скоростью 39 градусов за 12-летнюю орбиту.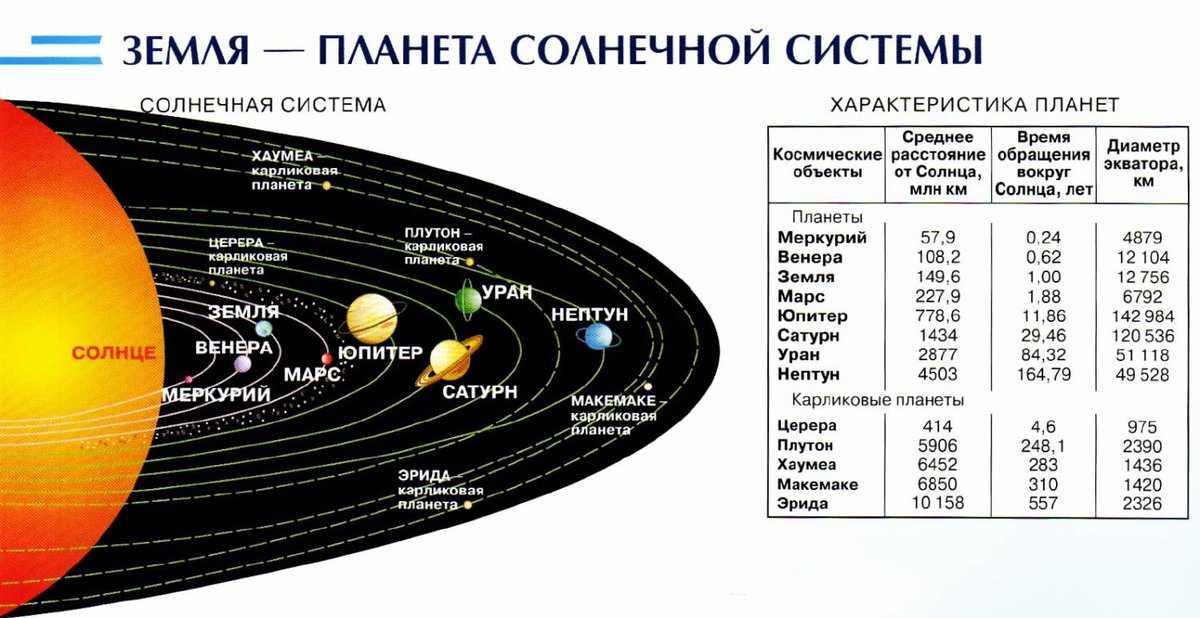

 .. [+] неожиданную спиральную структуру в веществе вокруг старой звезды R Sculptoris. Эта особенность никогда раньше не наблюдалась и, вероятно, вызвана скрытой звездой-компаньоном, вращающейся вокруг звезды, что является одним из многих неожиданных научных результатов, полученных с помощью ALMA. В общем, неожиданные результаты могут быть предвестниками новой физики или физических систем и часто являются самыми интересными результатами, которые может предложить природа.
.. [+] неожиданную спиральную структуру в веществе вокруг старой звезды R Sculptoris. Эта особенность никогда раньше не наблюдалась и, вероятно, вызвана скрытой звездой-компаньоном, вращающейся вокруг звезды, что является одним из многих неожиданных научных результатов, полученных с помощью ALMA. В общем, неожиданные результаты могут быть предвестниками новой физики или физических систем и часто являются самыми интересными результатами, которые может предложить природа.