Содержание
Электронный справочник по математике для школьников арифметика простые и составные числа разложение на множители
| Справочник по математике | Арифметика | Делимость и деление с остатком |
Содержание
| Простые и составные числа |
| Разложение натуральных чисел на множители (каноническое разложение натуральных чисел) |
| Бесконечность множества простых чисел |
Простые и составные числа
ОПРЕДЕЛЕНИЕ 1. Простым числом называется натуральное число, отличное от 1 и такое, которое делится только на 1 и на самого себя.
Поскольку на 1 и на самого себя делится любое натуральное число, то из этого определения вытекает, что у простого числа других делителей нет.
ОПРЕДЕЛЕНИЕ 2. Составным числом называется натуральное число, отличное от 1 и не являющееся простым.
Следовательно, у составного числа существует, по крайней мере, один делитель, отличный от 1 и самого числа.
ОПРЕДЕЛЕНИЕ 3. Делители составного числа, отличные от 1 и самого числа, называют множителями.
Например, числа 2 , 3 , 5 , 7 , 11 , 13 , 17 и т.д. являются простыми. Числа 4 , 6 , 8 , 9 , 10 , 12 и т.д. являются составными.
ЗАДАЧА. Доказать, что полусумма двух последовательных простых чисел, больших 2, является составным числом.
РЕШЕНИЕ. Поскольку все простые числа большие 2 являются нечетными числами, то их сумма будет четным числом, а полусумма — натуральным числом.
Это натуральное число будет больше, чем меньшее из заданных последовательных простых чисел, и меньше, чем большее из них.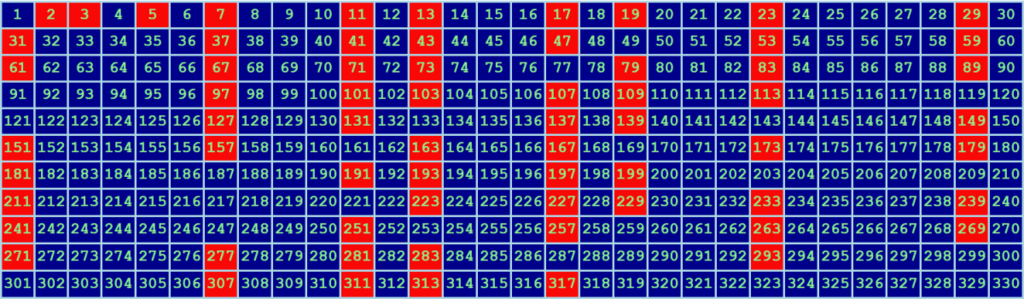
Так как заданные простые числа являются последовательными простыми числами, то между ними не может быть других простых чисел, а, значит, их полусумма является составным числом.
ЗАМЕЧАНИЕ. Чтобы выяснить, является ли данное число a простым или составным, достаточно проверить, делится ли это число на простые числа, не превосходящие числа .
Разложение натуральных чисел на множители (каноническое разложение натуральных чисел)
ТЕОРЕМА. Любое натуральное число, отличное от 1 , можно представить в виде произведения множителей, являющихся простыми числами, причем единственным образом.
Иногда эту теорему формулируют так: любое натуральное число, отличное от 1 , можно единственным образом разложить на простые множители.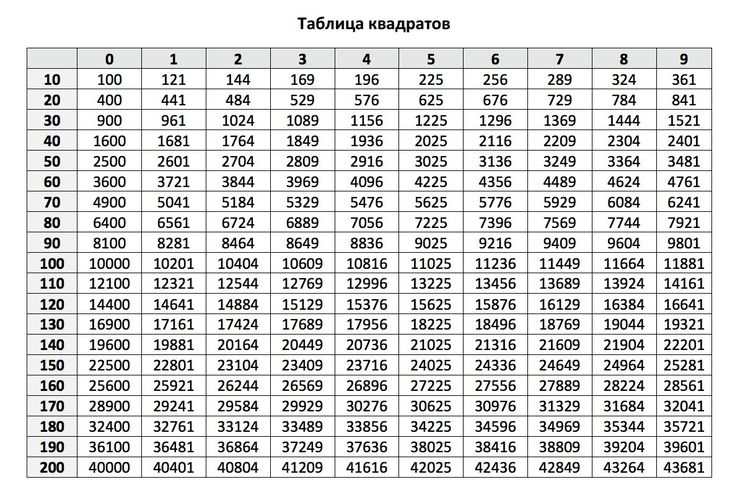
ПРИМЕР. Разложить на множители число 816 .
РЕШЕНИЕ.
Равенство
и есть единственное разложение числа 816 на простые множители. Простыми множителями в данном примере являются числа 2 , 3 и 17 .
Бесконечность множества простых чисел
ТЕОРЕМА. Множество простых чисел бесконечно.
ДОКАЗАТЕЛЬСТВО. Будем доказывать эту теорему от противного, предположив, что множество простых чисел конечно.
Тогда рассмотрим число, равное произведению всех простых чисел плюс 1 . Это число не делится ни на одно из простых чисел, поэтому его разложение на простые множители с одной стороны должно существовать, а с другой стороны не может содержать ни одного из множителей, являющихся простым числом.
Полученное противоречие доказывает, множество простых чисел должно быть бесконечным.
ЗАМЕЧАНИЕ. В нашем справочнике приведена таблица простых чисел от 1 до 10000 .
Зачем математики ищут простые числа с миллионами знаков?
Простые числа — это больше, чем числа, которые делятся на себя и на единицу. Это математическая загадка, которую математики пытаются разгадать с тех самых пор, когда Евклид доказал, что им нет конца. Проект Great Internet Mersenne Prime Search, перед которым стоит задача поиска большого числа простых чисел особо редкого вида, недавно открыл самое большое простое число, известное на сегодняшний день. В нем 23 249 425 цифр — это достаточно, чтобы заполнить книгу из 9000 страниц. Для сравнения: количество атомов во всей наблюдаемой Вселенной оценивается в число с не более чем сотней знаков.
Новое число, которое записывается как 2⁷⁷²³²⁹¹⁷-1 (два в 77 232 917-й степени минус один), было обнаружено волонтером, который посвятил 14 лет вычислительного времени этому поиску.
Возможно, вас удивит, зачем нам знать число, которое растягивается на 23 миллиона знаков? Ведь самые важные числа для нас — это те, которые мы используем для количественного описания нашего мира? Так, да не так. Нам нужно знать о свойствах различных чисел, чтобы не только развивать технологии, от которых мы зависим, но и сохранять их безопасность.
Безопасность простых чисел
Одно из самых распространенных применений простых чисел — система шифрования RSA. В 1978 году Рональд Ривести, Ади Шамир и Леонард Адлеман взяли за основу простейшие известные факты о числах и создали RSA. Разработанная ими система позволяла передавать информацию в зашифрованном виде — вроде номера кредитной карточке — и через Интернет.
Первым ингредиентом алгоритма стали два больших простых числа. Чем больше эти числа, тем безопаснее шифрование. Числа, которые используются для счета, один, два, три, четыре и так далее — известные также как натуральные числа — также чрезвычайно полезны для этого процесса. Но простые числа лежат в основе всех натуральных чисел и поэтому более важны.
Но простые числа лежат в основе всех натуральных чисел и поэтому более важны.
Возьмем, к примеру, число 70. Оно делится на 2 и 35. Далее, 35 — произведение 5 и 7. 70 — это произведение трех меньших чисел: 2, 5 и 7. На этом все, потому что они уже не разбиваются. Мы нашли первичные компоненты, составляющие 70, осуществили его факторизацию.
Перемножение двух чисел, даже очень больших, — это утомительная, но простая задача. Факторизация же целого числа, с другой стороны, — это сложно, поэтому система RSA использует это преимущество.
Допустим, Алиса и Боб хотят секретно пообщаться в Интернете. Им нужна система шифрования. Если они сначала встретятся лично, они могут оговорить метод шифрования и дешифрования, который будет известен только им, но если же первый разговор состоится в онлайне, им придется сперва открыто обсудить систему шифрования — а это риск.
Однако если Алиса выберет два больших числа, рассчитает их произведение и сообщит об этом открыто, определить первоначальные простые числа будет очень сложно, потому что только она знает факторы.
Поэтому Алиса сообщает свое произведение Бобу, сохраняя в тайне факторы. Боб использует произведение для шифрования своего послания Алисе, которое можно расшифровать только при помощи известных ей факторов. Если Ева захочет подслушать, она никогда не сможет расшифровать сообщение Боба, если не заполучит факторы Алисы, а Алиса, конечно, будет против. Если Ева попытается разложить произведение — даже при помощи самого быстрого суперкомпьютера — у нее это не получится. Просто не существует такого алгоритма, который справился бы с этой задачей за время жизни Вселенной.
В поиске простых
Большие простые числа также используются в других криптосистемах. Чем быстрее компьютеры, тем больше числа, которые они могут взломать. Для современных приложений достаточно простых чисел, содержащих сотни цифр. Эти числа незначительны по сравнению с недавно обнаруженным гигантом. На самом деле новое простое число настолько большое, что в настоящее время ни один возможный технологический прогресс в скорости вычислений не может привести к необходимости использовать его для криптографической безопасности. Вполне вероятно, что даже риски, обусловленные появлением квантовых компьютеров, не потребуют использования таких монстров для безопасности.
Вполне вероятно, что даже риски, обусловленные появлением квантовых компьютеров, не потребуют использования таких монстров для безопасности.
Тем не менее не поиск более безопасных криптосистем и не улучшающиеся компьютеры стали причиной последнего открытия Мерсенна. Это математики одержимы поиском драгоценностей внутри сундука с надписью «простые числа». Эта жажда началась со счета «один, два, три…» и до сих пор ведет нас дальше. А то, что вместе с тем произошла революция в области Интернета, это случайность.
Известный британский математик Годфри Гарольд Харди сказал: «Чистая математика в целом значительно более полезна, чем применяется. Полезным ее делает техника, а математическая техника учится по большей части у чистой математики». Станут ли гигантские простые числа полезными, непонятно. Но поиск таких знаний утоляет интеллектуальную жажду человеческого рода, которая началась с евклидового доказательства бесконечности простых чисел.
Научные экспериментыСуперкомпьютеры
Для отправки комментария вы должны или
Названия больших чисел — Простая английская Википедия, бесплатная энциклопедия
Назвать очень большие числа относительно легко. Существует два основных способа наименования числа: экспоненциальное обозначение и наименование по группировке. Например, число 500 000 000 000 000 000 000 может быть записано как 5 x 10 20 в экспоненциальном представлении, поскольку после 5 стоит 20 нулей. Если число названо по группировке, оно равно пятистам квинтиллионам (американское) или 500 триллионов (европейское).
Существует два основных способа наименования числа: экспоненциальное обозначение и наименование по группировке. Например, число 500 000 000 000 000 000 000 может быть записано как 5 x 10 20 в экспоненциальном представлении, поскольку после 5 стоит 20 нулей. Если число названо по группировке, оно равно пятистам квинтиллионам (американское) или 500 триллионов (европейское).
Когда в больших числах много разных десятичных знаков, например 642 500 000 000, присвоение им экспоненциального представления примерно то же самое, но с одним отличием. Еще подсчитывая количество чисел после первого числа (в данном случае после 6 идет 11 чисел) нужно включить в формулу те, которые не нулевые, а после запятой. Таким образом, 642 500 000 000 будет 6,425 x 10 11 . При именовании по группировке каждая группа является именем группы. С таким же числом можно сказать, что это 642 миллиарда 500 миллионов (США) или 642 миллиарда 500 миллионов (Евро).
| Номер | Научное обозначение | Группировка |
|---|---|---|
| 600 000 000 000 000 000 000 000 000 | 6 х 10 26 | 600 септиллион (квадриллион) |
| 765 476 250 000 000 | 7,6547625 x 10 14 | 765 триллионов, 476 миллиардов, 250 миллионов |
| 145 000 | 1,45 x 10 5 | 145 тысяч |
Американский способ или «краткая форма» для наименования больших чисел отличается от европейского способа или «полной формы» для наименования больших чисел. Это в основном из-за американских финансов. Нумерация в краткой форме основана на тысячах, а в длинной — на миллионах. Из-за этого в краткой форме миллиард составляет одну тысячу миллионов (10 9 ), а в длинной форме — один миллион миллионов (10 12 ). Переход в Соединенном Королевстве на краткую нумерацию произошел в 1974 году. Сегодня краткая форма чаще всего используется в большинстве англоязычных стран.
Это в основном из-за американских финансов. Нумерация в краткой форме основана на тысячах, а в длинной — на миллионах. Из-за этого в краткой форме миллиард составляет одну тысячу миллионов (10 9 ), а в длинной форме — один миллион миллионов (10 12 ). Переход в Соединенном Королевстве на краткую нумерацию произошел в 1974 году. Сегодня краткая форма чаще всего используется в большинстве англоязычных стран.
| Научное обозначение | американское имя (краткая форма) | Старое европейское имя (полная форма) | Старобританское имя | Символ СИ | Метрический префикс |
|---|---|---|---|---|---|
| 1 | Один | Один | Один | ||
| 10 1 | Десять | Десять | Десять | дн. | Дека- |
| 10 2 | Сотня | Сотня | Сотня | ч | гекто- |
| 10 3 | Тысяча | Тысяча | Тысяча | К | Кило- |
| 10 4 | Десять тысяч | Десять тысяч | Десять тысяч | мой (устарело) | Myria- (устарело) |
| 10 5 | Сотни тысяч | Сотни тысяч | Сотни тысяч | ||
| 10 6 | млн. | млн. | млн. | М | Мега- |
| 10 9 | миллиарда | Миллиард | тысяч миллионов | Г | Гига- |
| 10 12 | трлн | миллиарда | миллиарда | Т | Тера- |
| 10 15 | Квадриллион | Бильярд | тысяч миллиардов | П | Пета- |
| 10 18 | Квинтиллион | трлн | трлн | Э | Экса- |
| 10 21 | Секстиллион | Триллиард | тысяч триллионов | З | Зетта- |
| 10 24 | септиллион | Квадриллион | Квадриллион | Д | Йотта- |
| 10 27 | Октиллион | Квадрильярд | Тысяча квадриллионов | ||
| 10 30 | Нониллион | Квинтилион | Квинтиллион | ||
| 10 33 | Дециллион | Квинтильярд | Тысяча квинтиллионов | ||
| 10 36 | Ундециллион | Секстиллион | Секстиллион | ||
| 10 39 | Дуодециллион | Секстильярд | Тысяча секстиллионов | ||
| 10 42 | Тредециллион | септиллион | септиллион | ||
| 10 45 | Кваттуордециллион | Септиллиард | Тысяча септиллион | ||
| 10 48 | Квиндециллион | Октиллион | Октиллион | ||
| 10 51 | Сексдециллион | Октильярд | Тысяча октиллионов | ||
| 10 54 | Септендециллион | Нониллион | Нониллион | ||
| 10 57 | Октодециллион | Нониллард | Тысяча нониллионов | ||
| 10 60 | Новемдециллион | Дециллион | Дециллион | ||
| 10 63 | Вигинтиллион | Дециллиард | Тысяча дециллионов | ||
| 10 66 | Унвигинтиллион | Ундециллион | Ундециллион | ||
| 10 69 | Дуовигинтиллион | Ундецильярд | Тысяча ундециллионов | ||
| 10 72 | Тревинтиллион | Дуодециллион | Дуодециллион | ||
| 10 75 | Кваттуорвигинтиллион | Дуодециллиард | Тысяча дуодециллионов | ||
| 10 78 | Квинвигинтиллион | Тредециллион | Тредециллион | ||
| 10 81 | Сексвигинтиллион | Тредецильярд | Тысяча тредециллионов | ||
| 10 84 | Септенвигинтиллион | Кваттуордециллион | Кваттуордециллион | ||
| 10 87 | Октовигинтиллион | Кваттуордецильярд | Тысяча кватт или дециллион | ||
| 10 90 | Новэмвигинтиллион | Квиндециллион | Квиндециллион | ||
| 10 93 | Тригинтиллион | Квиндециллиард | Тысяча квиндециллионов | ||
| 10 96 | Унтригинтиллион | Сексдециллион | Сексдециллион | ||
| 10 99 | Дуотригинтиллион | Сексдециллиард | Тысяча сексдециллионов | ||
| 10 100 | Гугол | Гугол | Гугол | ||
| 10 102 | Третригинтиллион | Септендециллион | Септендециллион | ||
| 10 105 | Кварттуртригинтиллион | Сентябрьский | Тысяча септедециллионов | ||
| 10 108 | Квинтригинтиллион | Октодециллион | Октодециллион | ||
| 10 111 | Секстригинтиллион | Октодециллиард | Тысяча октодециллионов | ||
| 10 114 | сентемтригинтиллион | Новемдециллион | Новемдециллион | ||
| 10 117 | Октотригинтиллион | Новемдесильярд | Тысяча новемдециллион | ||
| 10 120 | Новемтригинтиллион | Вигинтиллион | Вигинтиллион | ||
| 10 123 | Квадрагинтиллион | Квинквагинтильярд | .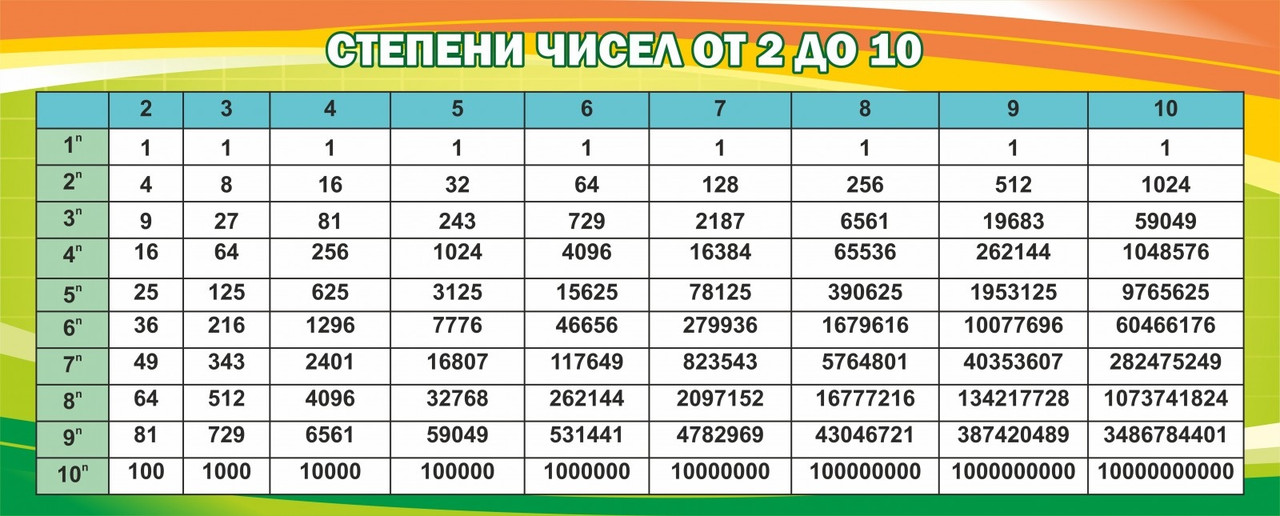 | ||
| 10 126 | Унквадрагинтиллион | миллиона | миллиона | Септингентиллард | |
| 10 303 | Центиллион | Квинквагинтильярд | . |
Существует также № Googol , который составляет 1 с 100 нулей (10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000), а число 9 0003 000 0004 000 000 000 000 000 000 000 000), а число 9 0003 000 000 — 9 0004 000 000 000 000 000 000 000 000 000 — 9 0003 000 000 000 000 000 000 000 000 000 000 000 000 000 — 9 0003 000 000 000 000 000 000 000 000 000 000 000 000 000 000.0726 Googol of Zeros позади него (10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 0006666) (10 10 100 ). А также число гуголплексиан , 1 с гуголплексным числом нулей за ним. Гуголплексианплекс или гуголплексианплексиан все еще являются теоретическими числами, но они могут иметь некоторое применение в реальной жизни.
Гуголплексианплекс или гуголплексианплексиан все еще являются теоретическими числами, но они могут иметь некоторое применение в реальной жизни.
Название центиллион было придумано в 19го века для 100-го «миллиона», что составляет 10 303 в краткой форме и 10 600 в полной форме.
- Порядок величины
- лакх
- крор
- Большие числа
- Считаю, ДЕЙСТВИТЕЛЬНО, ДЕЙСТВИТЕЛЬНО, ДЕЙСТВИТЕЛЬНО Высокий
- Именование больших чисел
Названия больших чисел — Простая английская Википедия, бесплатная энциклопедия
Называть очень большие числа относительно легко. Существует два основных способа наименования числа: экспоненциальное обозначение и наименование по группировке. Например, число 500 000 000 000 000 000 000 можно назвать 5 х 10 20 в экспоненциальном представлении, поскольку за цифрой 5 стоит 20 нулей. Если число названо по группировке, оно равно пятистам квинтиллионам (американское) или 500 триллионам (европейское).
Когда в больших числах много разных десятичных знаков, например 642 500 000 000, присвоение им имени в экспоненциальном представлении примерно такое же, но с одним отличием. Еще подсчитывая количество чисел после первого числа (в данном случае после 6 идет 11 чисел) нужно включить в формулу те, которые не нулевые, а после запятой. Итак, 642 500 000 000 будет 6,425 х 10 11 . При именовании по группировке каждая группа является именем группы. С таким же числом можно сказать, что это 642 миллиарда 500 миллионов (США) или 642 миллиарда 500 миллионов (Евро).
| Номер | Научное обозначение | Группировка |
|---|---|---|
| 600 000 000 000 000 000 000 000 000 | 6 х 10 26 | 600 септиллион (квадриллион) |
| 765 476 250 000 000 | 7,6547625 х 10 14 | 765 триллионов, 476 миллиардов, 250 миллионов |
| 145 000 | 1,45 x 10 5 | 145 тысяч |
Американский способ или «краткая форма» для обозначения больших чисел отличается от европейского способа или «полной формы» для обозначения больших чисел. Это в основном из-за американских финансов. Нумерация в краткой форме основана на тысячах, а в длинной — на миллионах. Из-за этого в краткой форме миллиард равен одной тысяче миллионов (10 9 ), а в длинной форме это один миллион миллионов (10 12 ). Переход в Соединенном Королевстве на краткую нумерацию произошел в 1974 году. Сегодня краткая форма чаще всего используется в большинстве англоязычных стран.
Это в основном из-за американских финансов. Нумерация в краткой форме основана на тысячах, а в длинной — на миллионах. Из-за этого в краткой форме миллиард равен одной тысяче миллионов (10 9 ), а в длинной форме это один миллион миллионов (10 12 ). Переход в Соединенном Королевстве на краткую нумерацию произошел в 1974 году. Сегодня краткая форма чаще всего используется в большинстве англоязычных стран.
| Научное обозначение | американское имя (краткая форма) | Старое европейское имя (полная форма) | Старобританское имя | Символ СИ | Метрический префикс |
|---|---|---|---|---|---|
| 1 | Один | Один | Один | ||
| 10 1 | Десять | Десять | Десять | дн. | Дека- |
| 10 2 | Сотня | Сотня | Сотня | ч | гекто- |
| 10 3 | Тысяча | Тысяча | Тысяча | К | Кило- |
| 10 4 | Десять тысяч | Десять тысяч | Десять тысяч | мой (устарело) | Myria- (устарело) |
| 10 5 | Сотни тысяч | Сотни тысяч | Сотни тысяч | ||
| 10 6 | млн. | млн. | млн. | М | Мега- |
| 10 9 | миллиарда | Миллиард | тысяч миллионов | Г | Гига- |
| 10 12 | трлн | миллиарда | миллиарда | Т | Тера- |
| 10 15 | Квадриллион | Бильярд | тысяч миллиардов | П | Пета- |
| 10 18 | Квинтиллион | трлн | трлн | Э | Экса- |
| 10 21 | Секстиллион | Триллиард | тысяч триллионов | З | Зетта- |
| 10 24 | септиллион | Квадриллион | Квадриллион | Д | Йотта- |
| 10 27 | Октиллион | Квадрильярд | Тысяча квадриллионов | ||
| 10 30 | Нониллион | Квинтилион | Квинтиллион | ||
| 10 33 | Дециллион | Квинтильярд | Тысяча квинтиллионов | ||
| 10 36 | Ундециллион | Секстиллион | Секстиллион | ||
| 10 39 | Дуодециллион | Секстильярд | Тысяча секстиллионов | ||
| 10 42 | Тредециллион | септиллион | септиллион | ||
| 10 45 | Кваттуордециллион | Септиллиард | Тысяча септиллион | ||
| 10 48 | Квиндециллион | Октиллион | Октиллион | ||
| 10 51 | Сексдециллион | Октильярд | Тысяча октиллионов | ||
| 10 54 | Септендециллион | Нониллион | Нониллион | ||
| 10 57 | Октодециллион | Нониллард | Тысяча нониллионов | ||
| 10 60 | Новемдециллион | Дециллион | Дециллион | ||
| 10 63 | Вигинтиллион | Дециллиард | Тысяча дециллионов | ||
| 10 66 | Унвигинтиллион | Ундециллион | Ундециллион | ||
| 10 69 | Дуовигинтиллион | Ундецильярд | Тысяча ундециллионов | ||
| 10 72 | Тревинтиллион | Дуодециллион | Дуодециллион | ||
| 10 75 | Кваттуорвигинтиллион | Дуодециллиард | Тысяча дуодециллионов | ||
| 10 78 | Квинвигинтиллион | Тредециллион | Тредециллион | ||
| 10 81 | Сексвигинтиллион | Тредецильярд | Тысяча тредециллионов | ||
| 10 84 | Септенвигинтиллион | Кваттуордециллион | Кваттуордециллион | ||
| 10 87 | Октовигинтиллион | Кваттуордецильярд | Тысяча кватт или дециллион | ||
| 10 90 | Новэмвигинтиллион | Квиндециллион | Квиндециллион | ||
| 10 93 | Тригинтиллион | Квиндециллиард | Тысяча квиндециллионов | ||
| 10 96 | Унтригинтиллион | Сексдециллион | Сексдециллион | ||
| 10 99 | Дуотригинтиллион | Сексдециллиард | Тысяча сексдециллионов | ||
| 10 100 | Гугол | Гугол | Гугол | ||
| 10 102 | Третригинтиллион | Септендециллион | Септендециллион | ||
| 10 105 | Кварттуртригинтиллион | Сентябрьский | Тысяча септедециллионов | ||
| 10 108 | Квинтригинтиллион | Октодециллион | Октодециллион | ||
| 10 111 | Секстригинтиллион | Октодециллиард | Тысяча октодециллионов | ||
| 10 114 | сентемтригинтиллион | Новемдециллион | Новемдециллион | ||
| 10 117 | Октотригинтиллион | Новемдесильярд | Тысяча новемдециллион | ||
| 10 120 | Новемтригинтиллион | Вигинтиллион | Вигинтиллион | ||
| 10 123 | Квадрагинтиллион | Квинквагинтильярд | .
|
