{- 1} \; {\ rm {Mpc}}}.
Принимая значение h = 0,7, мы получаем около 4,3 гигапарсека , или около 14 миллиардов световых лет .
Связь между размером наблюдаемой Вселенной и радиусом Хаббла зависит от рассматриваемой космологической модели . Например, в сценарии типа Большого взрыва без космологической постоянной размер наблюдаемой Вселенной немного меньше двух хаббловских лучей (см. Космологический горизонт ). При наличии космологической постоянной эта цифра увеличивается. Когда параметр плотности космологической постоянной достигает 0,7 (общепринятое значение для нашей Вселенной), тогда размер наблюдаемой Вселенной составляет порядка 3,2 радиуса Хаббла, то есть с предыдущими числами радиус 45 миллиардов световых лет. Такая цифра априори парадоксальна: удивительно, что размер наблюдаемой Вселенной больше, чем ее возраст (от 13,5 до 14 миллиардов лет), помноженный на скорость света. Однако достаточно учитывать, что цифра в 45 миллиардов световых лет выражает тот факт, что самые далекие регионы наблюдаемой Вселенной сегодня находятся на расстоянии 45 миллиардов световых лет от нас. С другой стороны, они были значительно ближе к нам, когда излучали тот свет, который мы видим сегодня.
С другой стороны, они были значительно ближе к нам, когда излучали тот свет, который мы видим сегодня.
Содержание
Примечания и ссылки
- (ru) Запись «Радиус Хаббла» в Яне Ридпате , Астрономический словарь , Оксфорд и Нью-Йорк, Oxford University Press , сб. «Оксфордская книга в мягкой обложке»,, VII-534 с. ( ISBN 978-0-19-960905-5 , OCLC 756278923 , читать онлайн ), стр. 224 ( читайте онлайн в Oxford Reference )
Смотрите также
- Объем Хаббла
- Постоянная Хаббла
- Время Хаббла
<img src=»https://fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Что такое сфера Хаббла и как изменяется расстояние до неё?
наивные вопросы
Спрашивает редакция культурно-просветительского центра «АРХЭ»
Отвечает Сергей Попов, доктор физико-математических наук, профессор РАН, ведущий научный сотрудник Государственного астрономического института им. П.К. Штернберга МГУ, лауреат премии «За верность науке–2015» Министерства образования и науки РФ в категории «Популяризатор года», лауреат Беляевской премии 2017 года, лектор «АРХЭ»
Хаббловской сферой называют поверхность, расстояние до которой определяется как d=c/H. То есть в данный момент времени галактики, находящиеся на сфере Хаббла, удаляются от нас из-за расширения Вселенной со скоростью, равной скорости света. Здесь d — собственное расстояние (то, которое растёт по мере расширения), а H — постоянная Хаббла.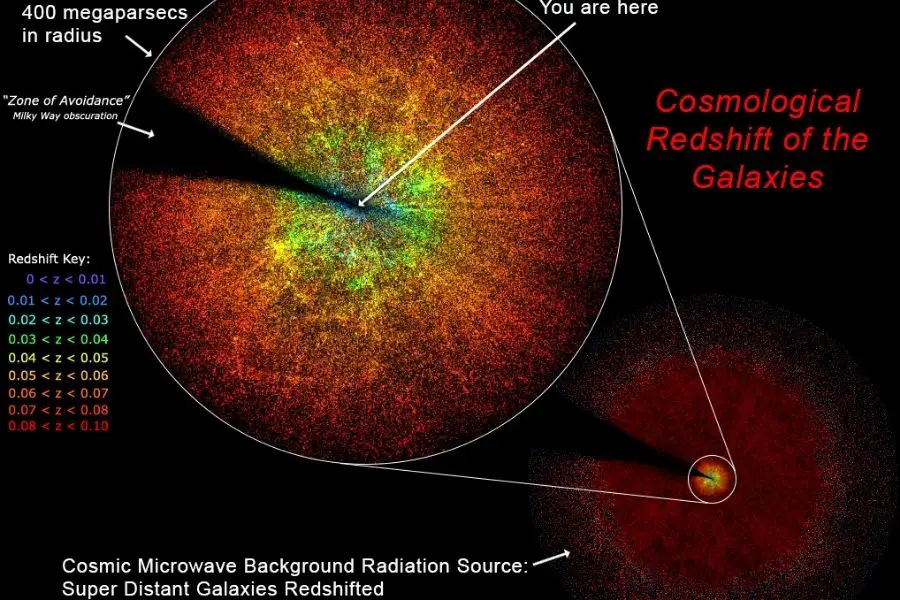
Постоянная Хаббла меняется со временем (зато она одинакова во всех местах в данный момент времени). В нашей Вселенной в течение всей её истории по окончании стадии инфляции постоянная Хаббла уменьшается. Соответственно, поскольку скорость света постоянна, собственное расстояние до хаббловской сферы в настоящее время растёт (то есть в метрах, сантиметрах и т.д. расстояние возрастает).
Вопрос в том, с какой скоростью растёт расстояние до сферы Хаббла. В ускоренно расширяющейся Вселенной это расстояние растёт со скоростью меньше световой, а в замедленно расширяющейся — быстрее. Точная формула для этой скорости c(1+q), где q — так называемый параметр замедления; этот параметр меньше нуля во Вселенной, расширяющейся с ускорением (у нас сейчас он равен примерно – 0.55), и больше нуля — в противоположном случае. Знак параметра замедления обратен знаку второй производной так называемого масштабного фактора. Масштабный фактор (обычно его обозначают буквой «a») показывает, во сколько раз выросли расстояния во Вселенной по мере течения времени.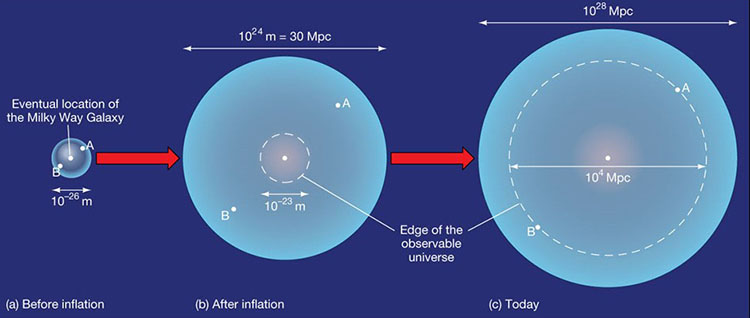 Эта величина всегда растёт, соответственно её первая производная положительна. А вот вторая как раз отражает, происходит ли рост расстояний все быстрее и быстрее (ускоренно расширяющаяся Вселенная) или нет.
Эта величина всегда растёт, соответственно её первая производная положительна. А вот вторая как раз отражает, происходит ли рост расстояний все быстрее и быстрее (ускоренно расширяющаяся Вселенная) или нет.
Но можно говорить о другом виде расстояния — сопутствующем. Это расстояние по определению не меняется по мере расширения Вселенной. По сути, оно как бы «нумерует» галактики. Если обозначит сопутствующее расстояние как r, то собственное будет равно d=ar. В ускоренно расширяющейся Вселенной галактики «вылетают» за сферу Хаббла, поскольку «чуть за» сферой Хаббла их скорость больше световой (не надо бояться сверхсветовых скоростей в космологии), и сфера от них отстаёт, поскольку движется с меньшей скоростью. Это можно описать как «продвижение» сферы Хаббла в нашу сторону, если говорить о сопутствующем расстоянии. Таким образом, сопутствующее расстояние до сферы Хаббла уменьшается. Во Вселенной, расширяющейся с замедлением, ситуация обратная.
Замечу, что в космологии можно говорить о разных определениях расстояний, скоростей и времени. Если это не уточняется, то может возникать путаница. Например, в Википедии написано без уточнений, что расстояние до хаббловской сферы в ускоренно расширяющейся Вселенной уменьшается, а в расширяющейся с замедлением — растёт (речь идёт как раз о сопутствующем расстоянии).
В качестве подробного популярного объяснения могу посоветовать серию наших статей с космологом Алексеем Топоренским. Начать можно вот с этой. Затем можно почитать статью про горизонты в космологии, чтобы понять, что сфера Хаббла в общем случае с ними не совпадает.
И наконец — этот текст.
Уважаемые читатели! Свои вопросы и вопросы ваших детей присылайте на адрес: [email protected]. Будем рады на них ответить.
общая теория относительности — космологический горизонт на радиусе Хаббла?
Проблема в том, что ваши расчеты не имеют реального физического смысла. Сравнивать две величины имеет смысл только в одной и той же инерциальной системе отсчета. Но нет глобальной инерциальной системы отсчета, которая соединяет нас с сопутствующей галактикой на хаббловском радиусе: такая галактика покоится в своей собственной локальной космологической инерциальной системе отсчета (игнорируя локальные пекулярные движения). Итак, в силу Космологического Принципа, его собственное космическое время подобно нашему.
Сравнивать две величины имеет смысл только в одной и той же инерциальной системе отсчета. Но нет глобальной инерциальной системы отсчета, которая соединяет нас с сопутствующей галактикой на хаббловском радиусе: такая галактика покоится в своей собственной локальной космологической инерциальной системе отсчета (игнорируя локальные пекулярные движения). Итак, в силу Космологического Принципа, его собственное космическое время подобно нашему.
Чтобы получить значимую информацию, нам нужно проанализировать свет этой галактики, как мы его наблюдаем. И, как вы указываете в своем собственном ответе, радиус Хаббла не является космологическим горизонтом с точки зрения световых путей.
Итак, давайте рассмотрим Стандартную ΛCDM-модель более подробно. Расширение Вселенной может быть выражено через масштабный фактор $a(t)$ и его производные, при этом сегодня $a=1$. Из уравнений Фридмана можно показать, что параметр Хаббла 92Н(а)},
$$
где $a_\text{em} = a(t_\text{em})$ и $a_\text{ob} = a(t_\text{ob})$ — масштабные коэффициенты в моменты излучения и наблюдения. 1\text{d}a = D_\text{H},
1\text{d}a = D_\text{H},
$$
отсюда следует, что радиус Хаббла меньше горизонта частиц и, следовательно, является частью наблюдаемой Вселенной. Фактически, $D_\text{ph}\примерно 46,2\;\text{Gly}$. 92} = Д_\текст{Н},
$$
так что радиус Хаббла также меньше горизонта событий: галактика на радиусе Хаббла все еще может посылать нам сигналы (или мы им). $D_\text{eh}\примерно 16,7\;\text{Gly}$.
Ситуация отображается на этих графиках (нажмите на «просмотреть изображение», чтобы увеличить его): первый — с координатами сопутствующего движения, второй — с правильными координатами.
Сплошные черные линии показывают наше текущее положение. Синяя линия — горизонт частиц во времени, красная линия — горизонт событий, зеленая область — сфера Хаббла. Черная пунктирная линия — это движущаяся вместе галактика, которая в настоящее время находится в радиусе Хаббла. Его фотоны, которые мы наблюдаем сегодня, путешествовали по голубому пути (они были испущены при $t=4,3\;\text{Gy}$). {t_\text{em} + \delta t_\text{em}}\frac{c\,\text{d} t}{a(t)}.
{t_\text{em} + \delta t_\text{em}}\frac{c\,\text{d} t}{a(t)}.
$$
на этих малых интервалах подынтегральные выражения остаются постоянными, так что
$$
\ frac {\ delta t_ \ text {ob}} {a (t_ \ text {ob})} = \ frac {\ delta t_ \ text {em}} {a (t_ \ text {em})}
$$
а также
$$
1 + z = \frac{a(t_\text{ob})}{a(t_\text{em})}.
$$
Свет сопутствующей галактики с текущим хаббловским радиусом, который мы наблюдаем сегодня, был испущен, когда $a(t_\text{em})=0,403$, так что $z=1,48$, и наблюдаемые события от этой галактики замедлено по времени в $2,48$. И свет, который она излучает сегодня, будет наблюдаться, когда $a(t_\text{ob})=8,07$, с красным смещением $z=7,07$.
Такое замедление времени действительно наблюдалось: мы буквально видим, как далекие сверхновые взрываются в замедленной съемке!
космология — Заблуждения о Вселенной — Сфера Хаббла
Итак, я наконец добрался до сути этого. По сути, путаница возникает из-за того, что значит говорить, что Вселенная ускоряется, так что давайте проясним это.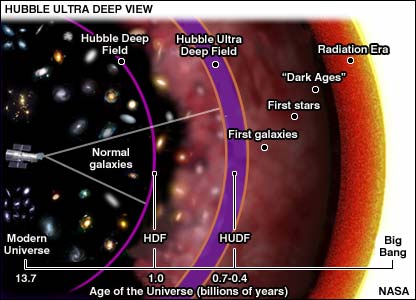 Параметр Хаббла определяется как $H(t)=\dot a(t) /a(t)$, где $a(t)$ — масштабный коэффициент . Когда мы говорим, что расширение Вселенной ускоряется, мы имеем в виду, что $\ddot a$ больше нуля. Это абсолютно точно не , однако расскажите нам что-нибудь о $H(t)$. $H(t)$ может увеличиваться, может уменьшаться или даже оставаться постоянным.
Параметр Хаббла определяется как $H(t)=\dot a(t) /a(t)$, где $a(t)$ — масштабный коэффициент . Когда мы говорим, что расширение Вселенной ускоряется, мы имеем в виду, что $\ddot a$ больше нуля. Это абсолютно точно не , однако расскажите нам что-нибудь о $H(t)$. $H(t)$ может увеличиваться, может уменьшаться или даже оставаться постоянным.
Модель де Ситтера , например, описывает вселенную, в которой параметр Хаббла, $H(t)$, фактически постоянен во времени. То есть $\dot a(t) /a(t)=H_0$, имеющая экспоненциальное решение для $a(t)$, но по большей части $H(t)$ может убывать или возрастать, несмотря на $ \ddot a$ больше нуля.
Как я могу это увидеть?
Представьте себе две разъезжающиеся машины, между которыми протянут бесконечно эластичный кусок ленты. На них есть некоторые отметки, которые вы можете представить себе как галактики (или с сопутствующими координатами ). Я нарисовал три набора картинок и объясню их по очереди.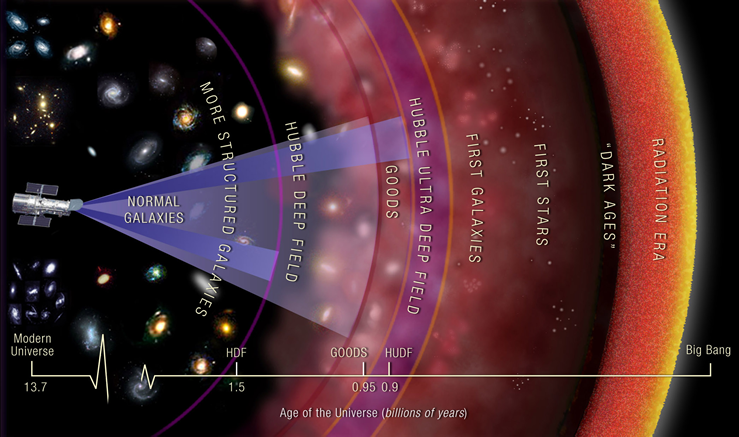
Изображение первое
Сначала рассмотрим две машины, разъезжающиеся со скоростью $3c$ (не обращайте внимания на нереалистичность этого утверждения — я приму $c$ за $10$/ч) с нами в центре. Эти машины не разгоняются. Эти автомобили разъезжаются со скоростью 30 долларов в час в противоположных направлениях. Где-то на ленте есть сфера Хаббла, где сопутствующие галактики удаляются со скоростью $c$ (или 10$ в час). Я отметил его зеленым цветом. Мы можем нарисовать график скорости рецессии, $v_{rec}$, относительно правильного расстояния, $d$, и увидеть, что между ними существует линейная зависимость. То есть предметы, находящиеся на расстоянии 2 км от нас, движутся в два раза быстрее, чем предметы, находящиеся на расстоянии 1 км от нас. Параметр Хаббла $H(t)$ — это градиент.
Фото 2
Имейте в виду, что эти автомобили не ускоряются, и давайте посмотрим чуть позже. Помните, они тоже не замедляются. Все развалилось, и Сфера Хаббла отправилась в путь. Подумайте об этом — если автомобили по-прежнему движутся со скоростью 30 долларов в час, то наша сфера Хаббла все еще находится на одной трети пути по ленте от нас. Важно отметить, что если сфера Хаббла растет, она может начать захват фотонов, которые когда-то были за пределами сферы Хаббла, и, как только эти фотоны окажутся внутри, они смогут начать свое путешествие к нам. Мы увидим эти фотоны. Обратите внимание, что градиент нашего графика $v_{rec}-d$ уменьшился по мере расширения сферы Хаббла.
Подумайте об этом — если автомобили по-прежнему движутся со скоростью 30 долларов в час, то наша сфера Хаббла все еще находится на одной трети пути по ленте от нас. Важно отметить, что если сфера Хаббла растет, она может начать захват фотонов, которые когда-то были за пределами сферы Хаббла, и, как только эти фотоны окажутся внутри, они смогут начать свое путешествие к нам. Мы увидим эти фотоны. Обратите внимание, что градиент нашего графика $v_{rec}-d$ уменьшился по мере расширения сферы Хаббла.
Рисунок 3
Хорошо, добавим ускорение, которое математически можно записать как $\ddot a(t)>0$. Что происходит? Ну, это зависит от того, насколько сильно машины разгоняются . В моем примере я заставил машины разогнаться до всего лишь до достаточно сильно, чтобы сфера Хаббла сохраняла постоянный размер. Обратите внимание, что градиент остается постоянным на диаграмме справа (которая описывает вселенную де Ситтера ). В этом случае фотоны снаружи набиваются.
