Простые и Составные Числа
Числа бывают натуральные целые, простые и составные — и это то, что очень нам пригодится при решении разных задач. Этим и займемся: просто и без воды.
Основные определения
Натуральные числа больше единицы бывают простые и составные.
Простое число — это натуральное число больше 1, у которого есть всего два делителя: единица и само число.
Например:
- 11, 13, 17, 19 — список простых чисел.
- 11 — делится только на 1 и 11.
- 13 — делится на 1 и 13.
- 17 — делится на 1 и 17.
Составное число — похоже на простое. Это точно такое же натуральное число больше единицы, которое делится на единицу, на само себя и еще хотя бы на одно натуральное число.
Например:
- 9, 10, 12, 14 — примеры из списка составных чисел.
- 9 — делится на 1, на 3 и на 9.
- 10 — делится на 1, на 2, на 5 и на 10.
- 12 — делится на 1, на 2, 3, 4, 6 и на 12.
Число 1 — не является ни простым, ни составным числом, так как у него только один делитель — 1. Именно этим оно отличается от всех остальных натуральных чисел. Число 2 — первое наименьшее простое, единственное четное, простое число. Все остальные — нечетные. Число 4 — первое наименьшее составное число. |
В математике есть первые простые и составные числа, но последних таких чисел не существует.
А еще не существует простых чисел, которые оканчиваются на 4, 6, 8 или 0. В числе простых есть только одно число, которое заканчивается на 2 — и это само число 2. Из оканчивающихся на 5 — число 5. Все остальные оканчиваются на 1, 3, 7 или 9, за исключением 21, 27, 33 и 39.
В числе простых есть только одно число, которое заканчивается на 2 — и это само число 2. Из оканчивающихся на 5 — число 5. Все остальные оканчиваются на 1, 3, 7 или 9, за исключением 21, 27, 33 и 39.
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
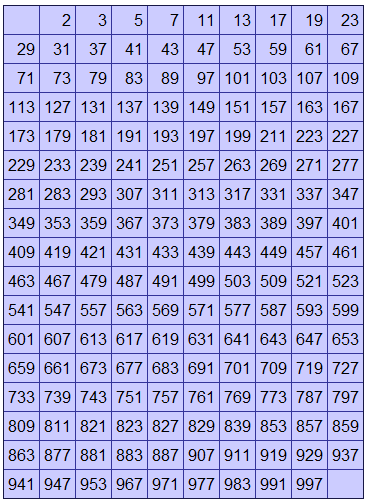
Таблица простых чисел до 1000
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 |
| 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 |
| 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 |
| 257 | 263 | 269 | 271 | 277 | 281 | 283 | 293 | 307 |
| 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 | 419 |
| 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 |
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 |
| 647 | 653 | 659 | 661 | 673 | 677 | 683 | 691 | 701 |
| 709 | 719 | 727 | 733 | 739 | 743 | 751 | 757 | 761 |
| 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 |
| 887 | 907 | 911 | 919 | 929 | 937 | 941 | 947 | 953 |
| 967 | 971 | 977 | 983 | 991 | 997 |
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Шпаргалки по математике родителей
Все формулы по математике под рукой
Таблица простых чисел от 1 до 10000. Таблица простых чисел от 1 до 1000
Таблица простых чисел от 1 до 10000. Таблица простых чисел от 1 до 1000
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица простых чисел от 1 до 10000. Таблица простых чисел от 1 до 1000. Простые числа список. Поделиться: |
Вы сейчас находитесь в каталоге: Таблица простых чисел от 1 до 10000. Таблица простых чисел от 1 до 1000. Простые числа список. |
|
Ниже приведена таблица простых чисел от 2 до 10000 (1229 штук).
Таблица простых чисел от 2 до 1000. Таблица простых чисел от 2 до 1000 выделена серым. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
«>
|
Справка проекта:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Простые и составные числа 6 класс онлайн-подготовка на Ростелеком Лицей
Игра
Рассмотрим рисунок 1, на нем выписан натуральный ряд чисел.
Рис. 1. Числа от 1 до 100 (Источник)
Правила игры
1. Берем число, а потом вычеркиваем все числа, которые на него делятся. Начинаем с 2.
Так, каждое второе число будет делиться на два (рис. 2).
Рис. 2. Вычеркивание всех чисел, которые делятся на 2
2. Берем следующее незачеркнутое число и обводим его кружочком. Вычеркиваем числа, которые делятся на три.
Рис. 3. Вычеркивание чисел, которые делятся на 3
3. Следующее незачеркнутое число – пять. Вычеркиваем все числа, делящиеся на пять (рис. 4).
Рис. 4. Вычеркивание чисел, которые делятся на 5
4. Берем число семь и продолжаем зачеркивать числа (рис. 5).
Рис. 5. Вычеркивание чисел, которые делятся на 7
5. Посмотрим, что получилось: зачеркнуты почти все числа. После того как мы подумаем над тем, что объединяет все зачеркнутые числа, ответим: они все на что-то делились. Те числа, которые остались незачеркнутыми (рис. 4), ни на что, кроме себя и единицы, не делятся.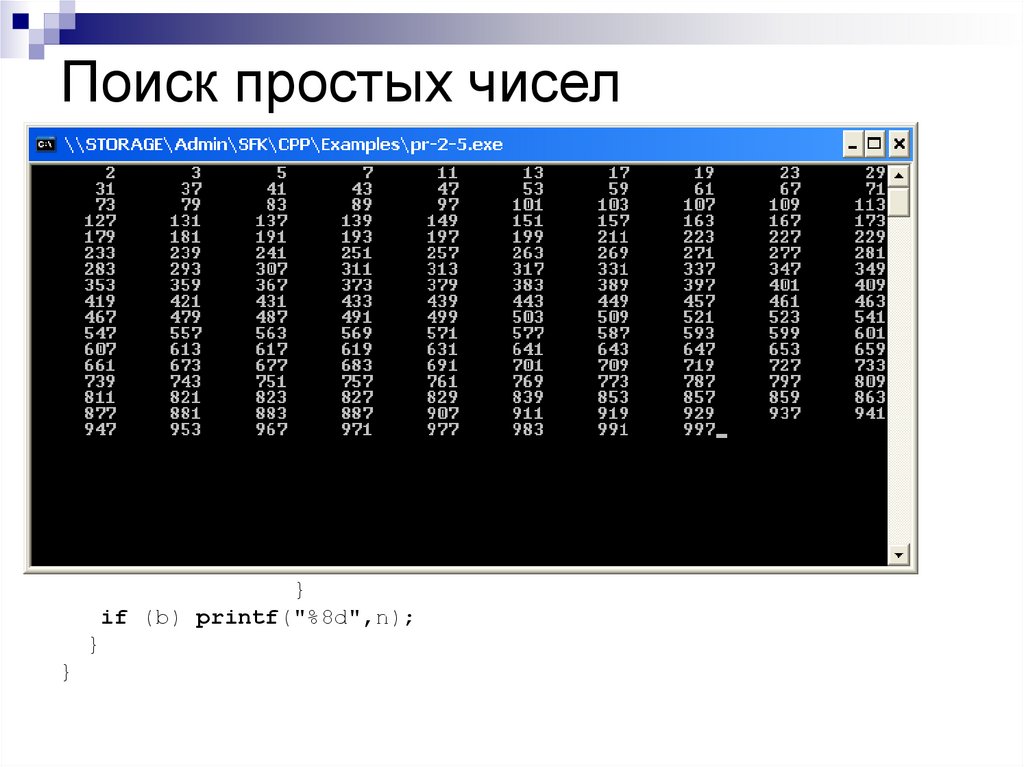
Данное действие называется решето Эратосфена – просеивание натурального ряда в поисках простых чисел. Простые числа – это такие числа, которые делятся на себя и на единицу (например: 2, 3, 5, 7 и т. д.). Те числа, которые делятся не только на себя и на единицу, имеют больше двух делителей, называются составными.
Есть интересное число, которое делится только на себя (имеет один делитель). Это единица, она не является ни простым, ни составным.
Группы натуральных чисел
Все натуральные числа – числа, которые мы используем при счете, можно разделить на три группы.
1. Простые – имеют только два делителя: единицу и само себя, например: 2, 3, 5, 7, 11, 17, 19, 23 и т. д.
2. Составные числа – имеют больше двух делителей, например: 4, 6, 8,10,15, 22 и т. д.
3. Единица (1) имеет только один делитель.
Простые числа
Если посмотрим на таблицу простых чисел (рис. 6), то заметим, что все числа, кроме двойки, нечетные. Самое маленькое простое число – два. А самое большое из ныне найденных простых чисел содержит семнадцать миллионов четыреста двадцать пять тысяч сто семьдесят цифр: 17 425 170 цифр.
6), то заметим, что все числа, кроме двойки, нечетные. Самое маленькое простое число – два. А самое большое из ныне найденных простых чисел содержит семнадцать миллионов четыреста двадцать пять тысяч сто семьдесят цифр: 17 425 170 цифр.
Рис. 6. Таблица некоторых простых чисел (Источник)
Основная теорема арифметики
Любое натуральное число можно разложить в произведение простых чисел единственным образом с точностью до порядка сомножителей.
1. Например, число 6 можно получить, если 3 умножить на 2 или 2 умножить на 3.
2. Аналогично раскладываем на простые множители число 48.
Обратите внимание: каждый раз мы выделяли простой множитель, а потом второй множитель раскладывали на множители и так, пока не получили все простые.
3. Теперь для разложения с помощью основной теоремы арифметики возьмем 122. Данное число делится на два, получаем 61. Так как шестьдесят один – это простое число, то разложение числа 122 на простые множители:
4. Если разложим число 462 на простые множители, получим:
Если разложим число 462 на простые множители, получим:
В простых числах интересно то, что иногда они стоят через один (подряд простые числа стоять не могут, потому что каждое второе делится на 2, исключением является пара 2 и 3), например 3 и 5 или 71 и 73, или 461 и 463, такие числа называют «близнецами». Иногда простые числа очень далеко расположены друг от друга и найти каждое следующее простое число с каждым разом все сложнее.
Определение
Криптограф – специалист по расшифровке и зашифровыванию информации.
Так, криптографы используют большие простые числа, для того чтобы создавать коды, которые очень сложно взламывать.
В последующих уроках нам потребуются знания о простых числах, чтобы вычислять НОД – наибольший общий делитель и НОК – наименьшее общее кратное.
Список литературы
1. Математика. 6 класс. Учеб. для общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013. – 288 с.: ил.
Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013. – 288 с.: ил.
2. Зубарева И.И., Мордкович А.Г. Математика, 6 класс. – М.: Мнемозина.
3. Истомина Н.Б., Математика, 6 класс. – М.: Ассоциация ХХI век.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет портал «Научная библиотека» (Источник)
2. Интернет портал «Clever Students» (Источник)
3. Интернет портал «Школьный помощник» (Источник)
Домашнее задание
1. Математика. 6 класс. Учеб. для общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013., ст. 17 § 4, № 95, 98, 104.
2. Что такое натуральные числа?
3. Какие группы натуральных чисел вы знаете?
4.*Разложите на простые множитель такие числа, воспользовавшись основной теоремой арифметики:
а) 335 б) 892 в) 647 г) 995 д) 44 е) 220
Какое самое маленькое простое число? Четное ли это число.
 ..
..
Перейти к
- Игра с числами. Упражнение 2.1.
- Игра с числами. Упражнение 2.8.
- Игра с числами. Упражнение 2.2.
- Игра с числами. Упражнение 2.3.
- Игра с числами. Упражнение 2.4.
- Игра с числами. Упражнение 2.5.
- Игра с числами.
 Упражнение 2.6.
Упражнение 2.6. - Игра с числами. Упражнение 2.7.
- Игра с числами. Упражнение 2.9.
- Игра с числами. Упражнение 2.10.
- Игра с числами. Упражнение 2.11.
- Зная свои числа
- Игра с числами
- Целые числа
- Действия над целыми числами
- Отрицательное число и целые числа
- Фракции
- Десятичные
- Введение в алгебру
- Соотношение, пропорция и унитарный метод
- Основные геометрические понятия
- Углы
- Треугольники
- Круги
- Пара прямых и поперечная
- Понимание трехмерных форм
- Симметрия
- Основные геометрические инструменты
- Геометрические построения
- Измерение
- Обработка данных Представление данных
- Обработка данных – II
- Гистограммы обработки данных
Главная >
РД Шарма Решения
Класс 6
Математика
>
Глава 2. Игра с числами
Игра с числами
>
Игра с числами. Упражнение 2.3.
>
Вопрос 3
Вопрос 3 Игра с числами Упражнение 2.3
Какое самое маленькое простое число? Это четное число?
Ответ:
2 — наименьшее простое число.
Мы знаем, что 2 — четное простое число, поскольку оно делится на 2.
Похожие вопросы
Что такое простые числа? Перечислите все простые числа от 1 до 30.
Запишите все простые числа между: (i) 10 и 50 (ii) 70 и 90(iii)40 и 85(iv)60 и 100
Какое наименьшее нечетное простое число? Всякое ли нечетное число является простым числом? Если нет, то приведите пример ода…
Что такое составные числа? Может ли составное число быть нечетным? Если да, напишите наименьшее нечетное составное. ..
..
Что такое простые числа-близнецы? Запишите все пары простых чисел-близнецов от 50 до 100.
Что такое со-премьеры? Приведите примеры пяти пар взаимно простых чисел. Всегда ли взаимные простые числа являются простыми? Если нет, то рис…
Фейсбук
Копировать ссылку
Было ли это полезно?
Упражнения
игра с номерами Упражнение 2.1
Игра с номерами Упражнение 2.8
Игра с номерами Упражнение 2.2
Игра с номерами Упражнение 2.3
Игра с числа 2.6
Игра с числами Упражнение 2. 7
7
Игра с числами Упражнение 2.9
Игра с числами Упражнение 2.10
Игра с числами Упражнение 2.11
Главы
Знание ваших номеров
Игра с номерами
целые числа
Операции на целых числах
Отрицательные числа и целые числа
Фракции
Decimals
Введение в Algebra
. Основные геометрические понятия
Углы
Треугольники
Окружности
Пара прямых и поперечная
Понимание трехмерных фигур
Симметрия
Основные геометрические инструменты
Геометрические построения
Измерение
Обработка данных Представление данных
Обработка данных – II
Обработка данных Гистограммы
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
1000 наименьших простых чисел
1000 самых маленьких простых чисел
Понимание математики
по
Питер Альфельд,
кафедра математики,
Университет Юты
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83
89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167
173 179 181 191 193 197 199 211 223 227 229233 239 241 251 257
263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353
359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449
457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563
569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653
659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761
769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877
881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991
997 1009 1013 1019 1021 1031 1033 1039 1049 1051 1061 1063 1069
1087 1091 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163 1171
1181 1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277
1279 1283 1289 1291 1297 1301 1303 1307 1319 1321 1327 1361 1367
1373 1381 1399 1409 1423 1427 1429 1433 1439 1447 1451 1453 1459
1471 1481 1483 1487 1489 1493 1499 1511 1523 1531 1543 1549 1553
1559 1567 1571 1579 1583 1597 1601 1607 16091613 1619 1621 1627
1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723 1733 1741
1747 1753 1759 1777 1783 1787 1789 1801 1811 1823 1831 1847 1861
1867 1871 1873 1877 1879 1889 1901 1907 1913 1931 1933 1949 1951
1973 1979 1987 1993 1997 1999 2003 2011 2017 2027 2029 2039 2053
2063 2069 2081 2083 2087 2089 2099 2111 2113 2129 2131 2137 2141
2143 2153 2161 2179 2203 2207 2213 2221 2237 2239 2243 2251 2267
2269 2273 2281 2287 2293 2297 23092311 2333 2339 2341 2347 2351
2357 2371 2377 2381 2383 2389 2393 2399 2411 2417 2423 2437 2441
2447 2459 2467 2473 2477 2503 2521 2531 2539 2543 2549 2551 2557
2579 2591 2593 2609 2617 2621 2633 2647 2657 2659 2663 2671 2677
2683 2687 2689 2693 2699 2707 2711 2713 2719 2729 2731 2741 2749
2753 2767 2777 2789 2791 2797 2801 2803 2819 2833 2837 2843 2851
2857 2861 2879 2887 2897 2903 2909 2917 2927 2939 2953 2957 2963
2969 2971 2999 3001 3011 30193023 3037 3041 3049 3061 3067 3079
3083 3089 3109 3119 3121 3137 3163 3167 3169 3181 3187 3191 3203
3209 3217 3221 3229 3251 3253 3257 3259 3271 3299 3301 3307 3313
3319 3323 3329 3331 3343 3347 3359 3361 3371 3373 3389 3391 3407
3413 3433 3449 3457 3461 3463 3467 3469 3491 3499 3511 3517 3527
3529 3533 3539 3541 3547 3557 3559 3571 3581 3583 3593 3607 3613
3617 3623 3631 3637 3643 3659 3671 3673 3677 3691 3697 3701 3709
3719 3727 3733 37393761 3767 3769 3779 3793 3797 3803 3821 3823
3833 3847 3851 3853 3863 3877 3881 3889 3907 3911 3917 3919 3923
3929 3931 3943 3947 3967 3989 4001 4003 4007 4013 4019 4021 4027
4049 4051 4057 4073 4079 4091 4093 4099 4111 4127 4129 4133 4139
4153 4157 4159 4177 4201 4211 4217 4219 4229 4231 4241 4243 4253
4259 4261 4271 4273 4283 4289 4297 4327 4337 4339 4349 4357 4363
4373 4391 4397 4409 4421 4423 4441 4447 4451 4457 4463 4481 4483
4493 4507 4513 4517 45194523 4547 4549 4561 4567 4583 4591 4597
4603 4621 4637 4639 4643 4649 4651 4657 4663 4673 4679 4691 4703
4721 4723 4729 4733 4751 4759 4783 4787 4789 4793 4799 4801 4813
4817 4831 4861 4871 4877 4889 4903 4909 4919 4931 4933 4937 4943
4951 4957 4967 4969 4973 4987 4993 4999 5003 5009 5011 5021 5023
5039 5051 5059 5077 5081 5087 5099 5101 5107 5113 5119 5147 5153
5167 5171 5179 5189 5197 5209 5227 5231 5233 5237 5261 5273 5279
5281 5297 5303 53095323 5333 5347 5351 5381 5387 5393 5399 5407
5413 5417 5419 5431 5437 5441 5443 5449 5471 5477 5479 5483 5501
5503 5507 5519 5521 5527 5531 5557 5563 5569 5573 5581 5591 5623
5639 5641 5647 5651 5653 5657 5659 5669 5683 5689 5693 5701 5711
5717 5737 5741 5743 5749 5779 5783 5791 5801 5807 5813 5821 5827
5839 5843 5849 5851 5857 5861 5867 5869 5879 5881 5897 5903 5923
5927 5939 5953 5981 5987 6007 6011 6029 6037 6043 6047 6053 6067
6073 60796089 6091 6101 6113 6121 6131 6133 6143 6151 6163 6173
6197 6199 6203 6211 6217 6221 6229 6247 6257 6263 6269 6271 6277
6287 6299 6301 6311 6317 6323 6329 6337 6343 6353 6359 6361 6367
6373 6379 6389 6397 6421 6427 6449 6451 6469 6473 6481 6491 6521
6529 6547 6551 6553 6563 6569 6571 6577 6581 6599 6607 6619 6637
6653 6659 6661 6673 6679 6689 6691 6701 6703 6709 6719 6733 6737
6761 6763 6779 6781 6791 6793 6803 6823 6827 6829 6833 6841 6857
6863 68696871 6883 6899 6907 6911 6917 6947 6949 6959 6961 6967
6971 6977 6983 6991 6997 7001 7013 7019 7027 7039 7043 7057 7069
7079 7103 7109 7121 7127 7129 7151 7159 7177 7187 7193 7207 7211
7213 7219 7229 7237 7243 7247 7253 7283 7297 7307 7309 7321 7331
7333 7349 7351 7369 7393 7411 7417 7433 7451 7457 7459 7477 7481
7487 7489 7499 7507 7517 7523 7529 7537 7541 7547 7549 7559 7561
7573 7577 7583 7589 7591 7603 7607 7621 7639 7643 7649 7669 7673
7681 7687 7691 7699 7703 7717 7723 7727 7741 7753 7757 7759 7789
7793 7817 7823 7829 7841 7853 7867 7873 7877 7879 7883 7901 7907
7919
Список 10 000 наименьших простых чисел.
Мелкий шрифт, ваши комментарии, больше ссылок, Питер Альфельд,
PA1UM
[16 августа 1996 г.]
Если a — наименьшее простое число больше 21, а b — это • PrepScholar GRE
Перейти к содержимому
Если $a$ — наименьшее простое число больше $21$, а $b$ — наибольшее простое число меньше $16$, то $ab=$
- 299 $
- $323$
- $330$
- $345$
- $351$
Итак, вы пытались быть хорошим сдающим экзамен и практиковаться для GRE с помощью PowerPrep онлайн. Нуууу, тогда у вас были вопросы по разделу «Количество», в частности по вопросу 12 раздела 6 практического теста 1. Эти вопросы проверяли наши знания по Целые числа могут быть довольно сложными, но не бойтесь, PrepScholar прикроет вас!
Изучите вопрос
Давайте поищем в задаче подсказки относительно того, что она будет тестировать, так как это поможет переключить наши мысли на мысли о том, какой тип математических знаний мы будем использовать для решения этого вопроса. Обратите внимание на любые слова, которые относятся к математике, и на что-нибудь особенное в отношении того, как выглядят числа, и отметьте их на бумаге.
Обратите внимание на любые слова, которые относятся к математике, и на что-нибудь особенное в отношении того, как выглядят числа, и отметьте их на бумаге.
Этот вопрос касается простых чисел , которые являются особым типом целых чисел, поэтому этот вопрос, вероятно, проверяет наши математические способности. Давайте держать в уме то, что мы узнали об этом навыке, когда мы подходим к этому вопросу.
Что мы знаем?
Давайте внимательно прочитаем вопрос и составим список вещей, которые мы знаем.
- Мы хотим найти произведение $ab$, поэтому нам нужны $a$ и $b$
- $a$ — наименьшее простое число больше $21$
- $b$ — наибольшее простое число меньше $16$
Разработайте план
Чтобы получить $ab$, нам нужны $a$ и $b$. Итак, давайте начнем с поиска $a$. Поскольку $a$ — это наименьшее простое число больше $21$, мы можем начать с $22$ и продолжать увеличивать одно целое число, пока не найдем простое число.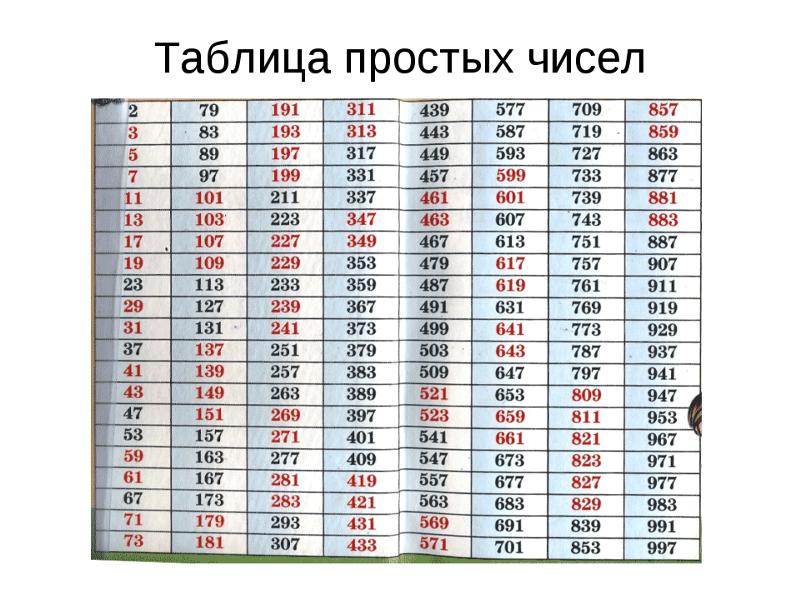 Точно так же, чтобы найти $b$, поскольку это самое большое простое число меньше $16$, мы можем начать с $15$ и продолжать уменьшать одно целое число за раз, пока не найдем простое число. Затем мы можем перемножить $a$ и $b$ вместе, чтобы получить $ab$. Чтобы определить, является ли число простым, мы сначала проверим, находится ли оно на нашей 9-долларовой шкале.Таблица умножения ×9$, которую мы запомнили. Если нет, мы будем использовать правила делимости для $2, 3, \ и 5$, чтобы дополнительно проверить, не является ли это простым числом. Давайте также быстро рассмотрим простые числа, прежде чем мы займемся этим вопросом. Конечно, мы можем пропустить это повторение, если нам удобно работать с простыми числами.
Точно так же, чтобы найти $b$, поскольку это самое большое простое число меньше $16$, мы можем начать с $15$ и продолжать уменьшать одно целое число за раз, пока не найдем простое число. Затем мы можем перемножить $a$ и $b$ вместе, чтобы получить $ab$. Чтобы определить, является ли число простым, мы сначала проверим, находится ли оно на нашей 9-долларовой шкале.Таблица умножения ×9$, которую мы запомнили. Если нет, мы будем использовать правила делимости для $2, 3, \ и 5$, чтобы дополнительно проверить, не является ли это простым числом. Давайте также быстро рассмотрим простые числа, прежде чем мы займемся этим вопросом. Конечно, мы можем пропустить это повторение, если нам удобно работать с простыми числами.
Освежение понятий – простые числа
простым числом является любое число, которое делится только на $1$ и само на себя. Если целое число не является простым числом, то мы называем его числом 9.0219 составной номер . «Делится» означает, что при делении на определенное число остатка нет. Например,
Например,
$12$ делится на $3 без остатка, потому что $3$ входит в $12$ четыре раза без остатка. Однако 14$ не делятся на 3$ без остатка, потому что 3$ входят в 14$ четыре раза, а в остатке остаются 2$.
$2$ — первое простое число. Оно также имеет честь быть единственным четным простым числом. Следующие несколько простых чисел: $3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41$. Список можно продолжать и продолжать. Итак, как лучше всего распознавать простые числа? Два лучших совета по распознаванию простых чисел: 1) Изучение 9 долларов.Таблица умножения ×9$ и 2) Изучение правил делимости для $2, 3, \и 5$.
Хорошо изучив таблицу умножения $9×9$, мы сразу же распознаем многие числа как НЕ простые числа. Например, если мы знаем, что $63=9·7$, то мы сразу распознаем $63$ как НЕ простое число.
Число делится на $2$, если оно четное. То есть, если его разряд единиц (тот, что слева от десятичной точки) равен $0, 2, 4, 6, \или 8$. Так, например, $16$ делится на $2$, потому что его цифра единиц равна $6$, но $17$ НЕ делится на $2$.
Число делится на $3$, если сумма его цифр делится на $3$. Например, $57$ делится на $3$, потому что $5+7=12$, а $12$ делится на $3$. Это правило поможет нам распознать множество довольно больших чисел, которые НЕ являются простыми числами, но также не встречаются в нашей таблице умножения $9×9$.
Число делится на $5$, если его разряд единиц равен $0 \или 5$. Так, например, $65$ делится на $5$, но $66$ НЕ делится на $5$. Теперь, когда мы рассмотрели простые числа, давайте вернемся к нашему вопросу!
Решите вопрос
Хорошо, сначала получите $a$. Сначала давайте проверим $22$. $22$ — четное число, поэтому оно делится на $2$. Дальше $23$. Мы не узнаем его по нашей таблице умножения $9×9$, а $23$ не делится на $2$, $3$ или $5$. $23$ — простое число, а наименьшее простое число больше $21$ .
Теперь за $b$. Сначала давайте проверим $15$. Из нашей таблицы умножения $9×9$ мы узнали, что $15=3·5$. Далее, мы знаем, что $14$ делится на $2$, так как оно четное.

 Единица не включена, извините. Некоторые считают, что единица не включена поскольку… она и не может там быть. «Простым числом называются числа имеющие два делителя: единицу и само число.» А число 1 имеет только один делитель, оно не относится ни к простым, ни к составным числам. (толковое замечание от Ольги 21.09.12) Мы, тем не менее помним, что простые числа вводятся иногда и так: «Простым числом называются числа которые делятся нацело на единицу и само себя.» В этом случае единица, очевидно, является простым числом.
Единица не включена, извините. Некоторые считают, что единица не включена поскольку… она и не может там быть. «Простым числом называются числа имеющие два делителя: единицу и само число.» А число 1 имеет только один делитель, оно не относится ни к простым, ни к составным числам. (толковое замечание от Ольги 21.09.12) Мы, тем не менее помним, что простые числа вводятся иногда и так: «Простым числом называются числа которые делятся нацело на единицу и само себя.» В этом случае единица, очевидно, является простым числом. Упражнение 2.6.
Упражнение 2.6.