Содержание
Простые и Составные Числа
Поможем понять и полюбить математику
Начать учиться
Числа бывают натуральные целые, простые и составные — и это то, что очень нам пригодится при решении разных задач. Этим и займемся: просто и без воды.
Основные определения
Натуральные числа больше единицы бывают простые и составные.
Простое число — это натуральное число больше 1, у которого есть всего два делителя: единица и само число.
Например:
- 11, 13, 17, 19 — список простых чисел.
- 11 — делится только на 1 и 11.
- 13 — делится на 1 и 13.
- 17 — делится на 1 и 17.
Составное число — похоже на простое. Это точно такое же натуральное число больше единицы, которое делится на единицу, на само себя и еще хотя бы на одно натуральное число.
Например:
- 9, 10, 12, 14 — примеры из списка составных чисел.
- 9 — делится на 1, на 3 и на 9.
- 10 — делится на 1, на 2, на 5 и на 10.
- 12 — делится на 1, на 2, 3, 4, 6 и на 12.
Число 1 — не является ни простым, ни составным числом, так как у него только один делитель — 1. Именно этим оно отличается от всех остальных натуральных чисел. Число 2 — первое наименьшее простое, единственное четное, простое число. Все остальные — нечетные. Число 4 — первое наименьшее составное число. |
В математике есть первые простые и составные числа, но последних таких чисел не существует.
А еще не существует простых чисел, которые оканчиваются на 4, 6, 8 или 0. В числе простых есть только одно число, которое заканчивается на 2 — и это само число 2. Из оканчивающихся на 5 — число 5. Все остальные оканчиваются на 1, 3, 7 или 9, за исключением 21, 27, 33 и 39.
В числе простых есть только одно число, которое заканчивается на 2 — и это само число 2. Из оканчивающихся на 5 — число 5. Все остальные оканчиваются на 1, 3, 7 или 9, за исключением 21, 27, 33 и 39.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Таблица простых чисел до 1000
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 |
| 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 |
| 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 |
| 257 | 263 | 269 | 271 | 277 | 281 | 283 | 293 | 307 |
| 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 | 419 |
| 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 |
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 |
| 647 | 653 | 659 | 661 | 673 | 677 | 683 | 691 | 701 |
| 709 | 719 | 727 | 733 | 739 | 743 | 751 | 757 | 761 |
| 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 |
| 887 | 907 | 911 | 919 | 929 | 937 | 941 | 947 | 953 |
| 967 | 971 | 977 | 983 | 991 | 997 |
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Шпаргалки по математике родителей
Все формулы по математике под рукой
«Какое простое число самое большое?» — Яндекс Кью
Популярное
Сообщества
Математика
Анонимный вопрос
·
10,5 K
ОтветитьУточнить
Надежда Шихова
Математика
8,5 K
Редактор, автор и переводчик книг по математике · 31 июл 2019 ·
problemaday
Самого большого простого числа не существует, потому что простых чисел бесконечно много.
Считается, что первое доказательство этого факта построил Евклид. Он доказал его от противного.
И правда, пусть среди простых чисел есть самое большое. Тогда их конечное количество и мы можем перенумеровть все по порядку:
Тогда их конечное количество и мы можем перенумеровть все по порядку:
p_1 — самое маленькое, p_n — самое большое.
Теперь перемножим все эти числа и прибавим к произведению 1, получится ооочень большое число. Обозначим его Х. Подумаем: это простое число или нет?
Оно явно больше всех простых чисел из списка, так что простым быть не может.
Придется ему быть составным и делиться на какое-нибудь простое число из списка. Этого тоже быть не может, потому что при делении Х на каждое простое число получится остаток 1.
Вот мы и получили, что Х не может быть ни простым, ни составным, а такого не бывает. Значит, исходное предположение быо неверным: среди простых чисел самого большого нет.
Александр Анатольевич Пономарев Пономарев
16 декабря 2019
Здорово! и ещё интересно!
Комментировать ответ…Комментировать…
Богдан Дмитриев
59
Интересуюсь архитектурой и историей эвм. · 26 нояб 2019
· 26 нояб 2019
Ответа на данный вопрос не существует по определению. Не существует ни самого маленького числа, ни самого большого числа. Числовой ряд бесконечен. Знак бесконечности-это не число, а условное обозначение бесконечности.
Комментировать ответ…Комментировать…
Термо топ
5
Компания Termo-Top, осуществляет:
продажу, обслуживание, ремонт оборудования Webasto… · 21 мая 2020 · termo-top.ru
Отвечает
Termo Top
Число с собственным, а не составным названием больше 103003 получить невозможно. Однако числа больше миллеиллиона известны – это внесистемные числа.
Самое маленькое внесистемное число носит название мириада. Означает сотню сотен, т.е. 10000.
Далее идет гугол. Это десять в сотой степени — 1010100. Единица со ста нулями. О гуголе впервые написали в 1938 году. Американский… Читать далее
Американский… Читать далее
Комментировать ответ…Комментировать…
Иса Фараджов
-6
27 нояб 2019
Самое большое которое можно составить это 9 в 9степени = 9*9*9*9*9*9*9*9*9= 387 420 489 Согласитесь ну уж ооооооочень большие числа из вродебы двух девяток. Удачи и пока.
Комментировать ответ…Комментировать…
Olga Talantova
1,4 K
Писатель и путешественник. Мечтаю написать настоящую книгу и совершить кругосветное… · 13 авг 2019
Наибольшее известное простое число — 2(степень 28 589 933)− 1. Оно было открыто Патриком Ларошем в рамках проекта GIMPS7.12.2018г. и содержит 24 862 048десятичных цифр. Об открытии этого числа была официально заявлено 21.12.2018г.
Виталий Матин
15 октября 2019
не 28 589 933 а 82 589 933
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Определение простейшей формулы и примеры
Эта запись была опубликована автором Anne Helmenstine (обновлено )
Простейшая формула — это наименьшее отношение элементов целого числа. Молекулярная формула представляет собой фактическое целочисленное соотношение элементов.
В химии простейшая формула — это химическая формула соединения, которое показывает наименьшее целочисленное соотношение элементов. Формула состоит из символов элементов, за которыми следуют нижние индексы, обозначающие количество атомов. Если есть один атом элемента, опустите нижний индекс. Другое название простейшей формулы — эмпирическая формула. Напротив, молекулярная формула кратна самой простой или эмпирической формуле и дает фактическое соотношение целых чисел элементов в соединении.
Примеры простейших формул
Например, простейшая формула воды H 2 O. На каждый моль кислорода в воде приходится два моля водорода. В этом случае простейшая формула и молекулярная формула совпадают.
Напротив, простейшая и молекулярная формулы глюкозы отличаются друг от друга. Простейшая формула — CH 2 O, а молекулярная формула — C 6 H 12 O 6 . Обратите внимание, что молекулярная формула кратна самой простой формуле, в которой вы умножаете каждый нижний индекс на 6.
Пример задачи: Простейшая формула из состава в процентах по массе
Задача
Одним из распространенных применений этой концепции является нахождение простейшей формулы соединения из его состава в процентах по массе. Например, найдите простейшую формулу для витамина С, учитывая массовые проценты элемента: есть 100 грамм образца. Таким образом, значения массовых процентов в сумме дают то же число (100 %), что и масса образца (100 граммов).
Затем используйте периодическую таблицу и найдите атомные массы элементов:
- H равно 1,01
- C равно 12,01
- O равно 16,00
Зная атомные массы, вы получите количество молей в граммах. фактор общения. Рассчитайте количество молей каждого элемента:
фактор общения. Рассчитайте количество молей каждого элемента:
- C = 40,9 г C x 1 моль C / 12,01 г C = 3,41 моль C
- H = 4,58 г H x 1 моль H / 1,01 г H = 4,53 моль H
- O = 54,5 г O x 1 моль O / 16,00 г O = 3,41 моль O
Осталось только найти наименьшее целочисленное отношение элементов. Сделайте это, разделив количество молей каждого элемента на малое число. В этом случае наименьшее число составляет 3,41 моля (как для C, так и для O).
- C: 3,41 / 3,41 = 1,00
- H: 4,53 / 3,41 = 1,33
- O: 3,41 / 3,41 = 1,00
Отношение целых чисел не равно 1:1:1,3. Надеюсь, вы понимаете, что 1,33 примерно равно дроби 4/3. Если нет, вы научитесь распознавать обыкновенные дроби, немного потренировавшись. Запишите соотношение элементов 1 C: 4/3 H: 1 O. Наконец, умножьте каждое число на знаменатель дроби (3), чтобы очистить дробь и получить целые числа. Это дает вам 3 C: 4 H: 3 O. Превратите это в химическую формулу, превратив числа отношений в нижние индексы.
Простейшая формула витамина С: C 3 H 4 O 3 .
Ссылки
- Берроуз, Эндрю. (2013). Химия: введение в неорганическую, органическую и физическую химию (2-е изд.). Оксфорд. ISBN 978-0-19-969185-2.
- Хилл, Эдвин А. (1900). «О системе индексации химической литературы; Принято Отделом классификации Патентного ведомства США». Варенье. хим. соц. 22 (8): 478–494. дои: 10.1021/ja02046a005
- Петруччи, Ральф Х.; Харвуд, Уильям С.; Селедка, Ф. Джеффри (2002). Общая химия: принципы и современные приложения (8-е изд.). Река Аппер-Сэдл, Нью-Джерси: Prentice Hall. ISBN 978-0-13-014329-7.
Упрощение калькулятора — CalcuNation.com
Приведите дроби к простейшей форме с помощью этого калькулятора Simplify Calculator.
Числитель дроби (верхнее число)
Знаменатель дроби
(нижний номер)
Вычислить простейшую форму дроби.
Как упростить дроби?
Пример: Для дроби 33 / 99 число 33 является числителем, а
99 — знаменателем.
Сначала найдите наибольший общий делитель двух чисел.
GCF = 33
Калькулятор GCF
Во-вторых, разделите и числитель, и знаменатель на GCF.
Числитель получен из 33/33 = 1
Знаменатель получен из 99/33 = 3
Дробь 33 / 99 , приведенная к простейшему виду, равна 1 / 3 .
Калькулятор простых дробей
Другой пример: на этот раз мы рассмотрим дробь 6 / 10 . Число 6 — числитель, а 10 — знаменатель.
Довольно легко увидеть, что и числитель, и знаменатель — четные числа. Итак, мы знаем, что они оба делятся на 2. Давайте разделим и числитель, и
знаменатель на 2.
Это дает нам числитель 3 и знаменатель 10.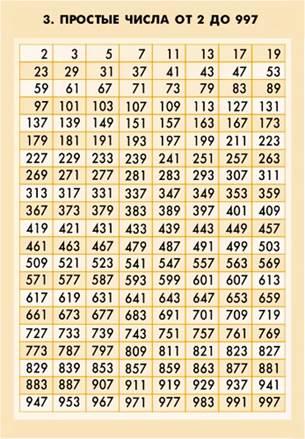 Это была бы самая простая форма для того факта, что одно из чисел является простым числом и не делится
Это была бы самая простая форма для того факта, что одно из чисел является простым числом и не делится
дальше.
Дробь 6 / 10 приведенная к простейшей форме равна 3 / 5 .
Упрощение дроби, делящейся на 4
Для следующего примера преобразуем дробь 12 / 20 в простейшую форму. В числителе 12, а в знаменателе 20.
Как и в предыдущем примере, числитель и знаменатель — четные числа. Как и в предыдущем случае, и числитель, и
знаменатель четный и делится на 2. Но вы можете заметить, что они также делятся на 4. Поскольку 4 — больший множитель, давайте разделим оба на это число.
Наши новые числа 3 и 5. Это самая простая форма. Хотя бы одно из чисел простое и дальше не делится. И 3, и 5 — простые числа.
Дробь 12 / 20 приведенная к простейшей форме равна 3 / 5 .
Упрощение дроби на 5
Для следующей дроби переведем дробь 15 / 20 в простейшей форме.
