Содержание
Астрофизик собрал версии того, что происходит внутри черной дыры
«Самое страшное в черных дырах — то, что на самом деле мы не знаем, что там внутри».
Пол Саттер, астрофизик, ведущий научно-популярных программ и автор книги «Как умереть в космосе», рассказал о разных версиях происходящего внутри черной дыры.
Сингулярность в центре черной дыры — это абсолютная нейтральная зона: место, где материя сжимается до бесконечно крошечной точки, а все представления о времени и пространстве полностью рушатся. Что-то должно заменить сингулярность, и ученые предлагают различные версии этого, рассказал Пол Саттер в статье на Live Science.
Планковская звезда
Когда материя сжимается под огромным гравитационным весом коллапсирующей звезды, она встречает сопротивление. Дискретность пространства-времени не позволяет материи достичь размера менее длины Планка (около 1,68 x 10-35 м). Весь материал, который когда-либо попадал в черную дыру, сжимается в шар не намного больше этого. Совершенно микроскопический, но определенно не бесконечно маленький.
Весь материал, который когда-либо попадал в черную дыру, сжимается в шар не намного больше этого. Совершенно микроскопический, но определенно не бесконечно маленький.
Это сопротивление продолжающемуся сжатию в конечном итоге заставляет материал взорваться, делая черные дыры лишь временными объектами. Но из-за экстремальных эффектов замедления времени вокруг черных дыр, с нашей точки зрения, во внешней Вселенной требуются миллиарды, даже триллионы лет, прежде чем они взорвутся.
Гравастар
Еще одна попытка искоренить сингулярность, не опирающаяся на теорию квантовой гравитации, известна как гравастар. Разница между черной дырой и гравастаром в том, что вместо сингулярности гравастар заполнен темной энергией. Темная энергия пронизывает пространство-время, заставляя его расширяться с ускорением.
Когда материя падает на гравастар, она не может фактически проникнуть за горизонт событий (из-за темной энергии внутри) и поэтому просто висит на поверхности.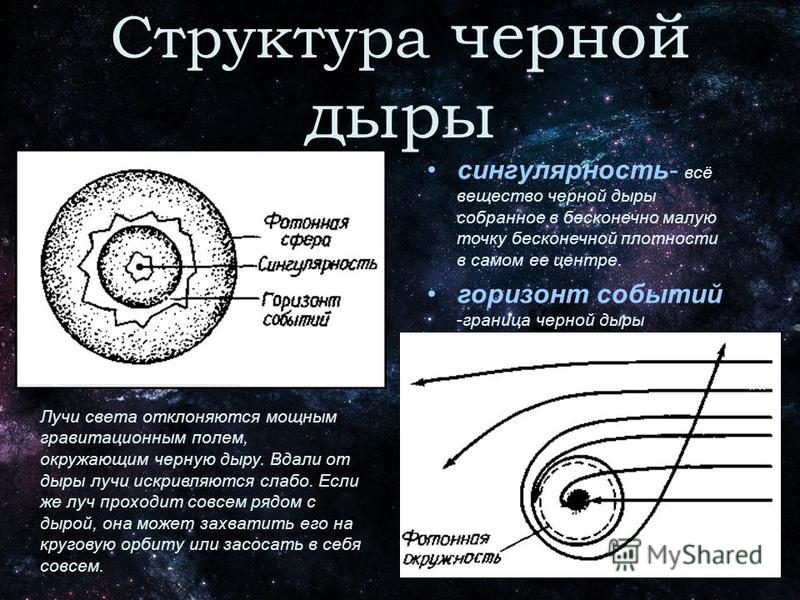 Но за пределами этой поверхности гравастары выглядят и действуют как обычные черные дыры.
Но за пределами этой поверхности гравастары выглядят и действуют как обычные черные дыры.
Вращение
Идея единой точки бесконечной плотности исходит из нашей концепции неподвижных черных дыр. Настоящие черные дыры — гораздо более интересные персонажи, особенно когда они вращаются.
Вращение вращающейся черной дыры вытягивает сингулярность в кольцо. И согласно общей теории относительности Эйнштейна, как только вы проходите через сингулярность кольца, вы входите в червоточину и вылетаете через белую дыру (полярная противоположность черной дыры, куда ничего не может войти и материя устремляется со скоростью света) в совершенно новый и захватывающий участок Вселенной.
Ранее астрофизики ответили на шесть занимательных вопросов о черных дырах.
На сайте могут быть использованы материалы интернет-ресурсов Facebook и Instagram, владельцем которых является компания Meta Platforms Inc., запрещённая на территории Российской Федерации
Расскажите друзьям
East News
Кто мы и откуда: за что в этом году присудили Нобелевскую премию по медицине и физиологии
Песчаные дюны.
 Зимний иней покрывает более холодную, обращенную на север половину каждой дюны
Зимний иней покрывает более холодную, обращенную на север половину каждой дюныNASA/JPL-Caltech/University of Arizona
В НАСА показали, как из космоса выглядит зима на Марсе
Современный карликовый крокодил
Shutterstock
Обнаружены еще два вида вымерших крокодилов, которые охотились на предков человека
Shutterstock
Исследование показало, что котики не только милые — котик может изобличить преступника
Shutterstock
Генетики описали механику «тикающих часиков» — почему с возрастом снижается фертильность
Хотите быть в курсе последних событий в науке?
Оставьте ваш email и подпишитесь на нашу рассылку
Ваш e-mail
Нажимая на кнопку «Подписаться», вы соглашаетесь на обработку персональных данных
Бездна в яблоке
Принято считать, что в центре черной дыры находится сингулярность. За доказательство этого факта в прошлом году дали Нобелевскую премию по физике — что удивило некоторых ученых, потому что эмпирически его не проверить. Из-за этой принципиальной невозможности заглянуть за пределы горизонта событий вокруг сингулярности высвечивается ореол трансцендентного. Но понять, как устроены сингулярности, можно и не выходя из дома — достаточно взять в руки яблоко или открыть водопроводный кран.
За доказательство этого факта в прошлом году дали Нобелевскую премию по физике — что удивило некоторых ученых, потому что эмпирически его не проверить. Из-за этой принципиальной невозможности заглянуть за пределы горизонта событий вокруг сингулярности высвечивается ореол трансцендентного. Но понять, как устроены сингулярности, можно и не выходя из дома — достаточно взять в руки яблоко или открыть водопроводный кран.
Слово «сингулярность» в зависимости от того, кто его говорит, может обозначать довольно разные явления. Для футуролога сингулярность — момент, когда человек теряет контроль над технологическим прогрессом, а для климатолога — вообще локальное изменение погоды в определенные дни, не продиктованное сезонными изменениями (например, оттепель). В зависимости от контекста этот термин может означать любые резкие и исключительные переходы, развороты или зарождения новых явлений.
Так или иначе, все эти «сингулярности» порождены математикой, но чем дальше и дольше путешествовал термин, тем больше размывалась строгость его определения. У физиков и математиков «сингулярности», впрочем, своего значения не потеряли, хотя смысл у них может очень разным.
У физиков и математиков «сингулярности», впрочем, своего значения не потеряли, хотя смысл у них может очень разным.
В русском математическом языке вместо термина «сингулярность» используют другое слово — «особенность». Это точка, в которой функция имеет разрыв или у нее нет однозначно определенной производной. Если эта функция описывает какую-то физическую величину, то в особой точке ее значение будет, например, бесконечным.
Пожалуй, самый известный пример физической сингулярности — черная дыра. В ней в бесконечность обращаются кривизна и плотность пространства-времени. Сложность с черной дырой в том, что находится она за пределами видимости, даже теоретическими. Если какая-то информация попала в черную дыру, то вернуться обратно из-за горизонта событий она уже не сможет. А тепловое излучение Хокинга, которое черная дыра испускает из-за квантовых эффектов, информации не несет. Поэтому взглянуть на сингулярность, удостовериться, что она действительно там есть, и увидеть, что она из себя представляет, невозможно.
Именно из-за невозможности наблюдения черных дыр многие ученые скептически восприняли присуждение Нобелевской премии по физике 2020 года Роджеру Пенроузу. Он доказал, что в черной дыре обязательно должна быть сингулярность, но проверить этот факт невозможно. Увидеть, что происходит с фотонами около черной дыры, — можно: фотография тени черной дыры стала одним из научных прорывов 2019 года. Но изображение этой области вокруг черной дыры, в которой из-за искривления траекторий фотонов и отсутствия стабильных орбит сильно снижается яркость свечения, ничего не говорит о том, как фотоны ведут себя за горизонтом событий.
Впрочем, столкнуться с сингулярностями можно и на Земле. А некоторые — даже подержать в руках. С точки зрения избыточной потенциальной энергии и механической устойчивости быть круглым (или хотя бы гладким) лучше, чем угловатым: на изломах концентрируется напряжение, поэтому там проще ломаться. Но в материальном мире сингулярности повсюду — в воде, траве, животных.
Сингулярная вода
Почему так — не очень понятно. Одна из семи Задач тысячелетия — не просто поиск общего решения уравнений Навье–Стокса, описывающих механику вязких жидкостей, но и доказательство или опровержение гладкости их возможных частных решений. Математики ищут ответ на вопрос, может ли в гидродинамике естественным образом рождаться сингулярность или нет.
При этом самые наглядные примеры естественных сингулярностей связаны как раз с течением воды. Например, сингулярность возникает в тот момент, когда от поверхности воды отделяется капля или из трубки на дне заполненного сосуда вылетает пузырек газа. Если на этот процесс смотреть в замедленной съемке, то можно увидеть, как сначала между поверхностью и каплей образуется шейка, которая истончается и затем рвется. В момент разрыва на обеих его сторонах неизбежно возникают особенности.
Тогда же уравнение, которое описывало весь объем воды, должно расщепиться на два: для капли и для родившей его поверхности.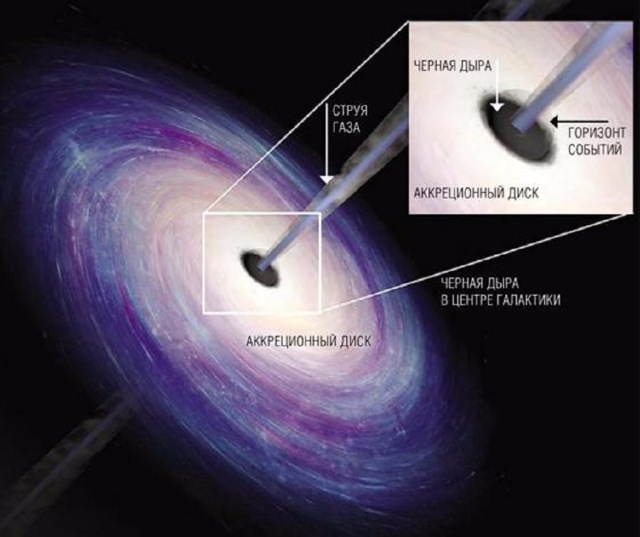 При этом «новорожденные» уравнения в первое мгновение своего существования должны в тех же условиях давать то же решение, что и «материнское». Но при этом они содержат еще и сингулярности.
При этом «новорожденные» уравнения в первое мгновение своего существования должны в тех же условиях давать то же решение, что и «материнское». Но при этом они содержат еще и сингулярности.
Еще один наглядный пример сингулярности в гидродинамике — сток воды. В зависимости от объема и вязкости жидкости и размера сливного отверстия, в такой системе можно увидеть два вида сингулярностей, одна из которых перетекает в другую. Первая возникает на верхней поверхности жидкости. Если жидкость достаточно вязкая, а отверстие — достаточно маленькое по сравнению с толщиной слоя, то в какой-то момент поверхность теряет свою гладкость. Вторая сингулярность появляется в центре сливного отверстия. Если жидкость не очень вязкая, а сток достаточно широкий, то в его центре скорость жидкости формально становится бесконечной. Похожая сингулярность возникает в центре вихревых потоков, например в торнадо или в кружке с чаем, в которой ложечкой размешивают сахар.
Переход от ламинарного течения к турбулентному — тоже, возможно, следствие сингулярности (это не точно, потому что хорошей теории для описания турбулентного течения до сих пор нет). В любом случае, если сингулярность там есть, то ее, как и той, что находится в центре черной дыры, не видно — она возникает на уровне решений уравнений. При устремлении числа Рейнольдса к бесконечности решения для ламинарных потоков должны смениться на решения совсем другого вида. И эта смена режима должна проходить через особенность.
В любом случае, если сингулярность там есть, то ее, как и той, что находится в центре черной дыры, не видно — она возникает на уровне решений уравнений. При устремлении числа Рейнольдса к бесконечности решения для ламинарных потоков должны смениться на решения совсем другого вида. И эта смена режима должна проходить через особенность.
Математика с особенностями
Сингулярности в непрерывных средах — воплощенные решения дифференциальных уравнений в частных производных. Для воды это уравнения Навье–Стокса. Решая их, можно получить функции, в которых и на уровне математики возникают особенности.
У математиков для описания и исследования этих решений есть отдельная дисциплина — теория особенностей (или теория сингулярностей). В изначальном варианте, который предложил американский математик Хасслер Уитни, теория изучает гладкие отображения — например, проекции гладких поверхностей на плоскость. Уитни обнаружил, что на таких проекциях может быть два вида устойчивых особенностей: складки и сборки.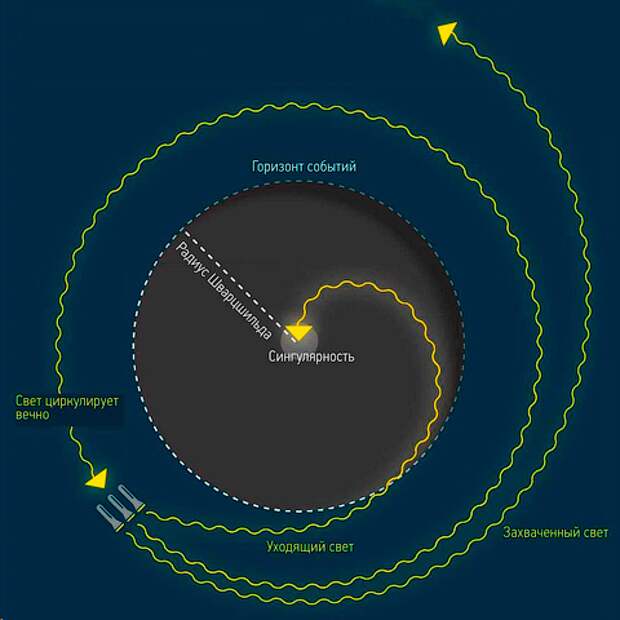 Складка образуется при проекции замкнутого тела (например сферы) на плоскость, сборка — при проекции на плоскость «волнистой» поверхности.
Складка образуется при проекции замкнутого тела (например сферы) на плоскость, сборка — при проекции на плоскость «волнистой» поверхности.
Складка делит плоскость на две области: внутри у каждой точки на плоскости два прообраза на поверхности, снаружи — ни одного, на границе — один. В случае сборки проекция тоже делит плоскость на две области. На большей части каждая точка проекции соответствует одной точки поверхности, а на меньшей — трем. Две эти области разделяет полукубическая парабола, состоящей из двух симметричных ветвей, которые сходятся в точке возврата (она же острие, она же касп).
Все другие особенности (сингулярности) гладких отображений — сводятся малыми шевелениями поверхности к складкам и сборкам. Взаимной однозначности у этих отображений нет (то есть одной точке проекции может соответствовать несколько точек поверхности), но именно эти особенности — устойчивые и не разваливаются при небольших движениях поверхности. Все остальные особенности гладких отображений можно свести к этим двум. В итоге двумя гладкими — без особенностей — поверхностями порождаются кривые с особыми точками. Единственная точка, в которой эти кривые не гладкие, — это точка сингулярности. Движение по гладкой кривой не предвещает никаких сложностей. Сингулярность наступает внезапно — а вместе с ней появляются сложности.
В итоге двумя гладкими — без особенностей — поверхностями порождаются кривые с особыми точками. Единственная точка, в которой эти кривые не гладкие, — это точка сингулярности. Движение по гладкой кривой не предвещает никаких сложностей. Сингулярность наступает внезапно — а вместе с ней появляются сложности.
Здесь сходятся два решения с разными производными и функция становится нйеодмиефуфреирценнецриерфуфеимдоейн
нйеодмиефуфреирценнецриерфуфеимдоейн ястивонатс яицкнуф и имындовзиорп имынзар с яинешер авд ястядохс ьседЗ
На другой стороне сингулярности — снова гладкая функция. Но уже не совсем такая, как была.
Как эта сингулярная математика просачивается в реальный мир, легче всего увидеть даже не в гидродинамических явлениях, а в оптических. Например, при распространении волнового фронта после рассеяния света на стакане с водой. Для описания точек, где интенсивность света максимальна, используют каустики — особые линии, огибающие для всех лучей, которые расходятся от стакана.
Например, при распространении волнового фронта после рассеяния света на стакане с водой. Для описания точек, где интенсивность света максимальна, используют каустики — особые линии, огибающие для всех лучей, которые расходятся от стакана.
Каустики могут быть разной формы, но практически все содержат сингулярности. Нефроида, кардиоида, циклоида — на всех этих кривых есть особые точки. Уравнения для каждой из них свои, но у сингулярностей они очень близки к полукубической параболе. При этом те же уравнения подходят не только для оптических, но и других естественных сингулярностей, поэтому большинство статических особых точек в естественной среде можно точно описать с помощью теории особенностей (или теории сингулярностей).
Сингулярный мозг
Рассматривая, как вода утекает в сливное отверстие или как стакан с водой рассеивает свет, можно лучше понять, как устроена черная дыра, чем просто смотря на графики функций. Но помимо них, в природе есть множество тел с устойчивыми особыми точками — их можно не только рассмотреть, но и пощупать.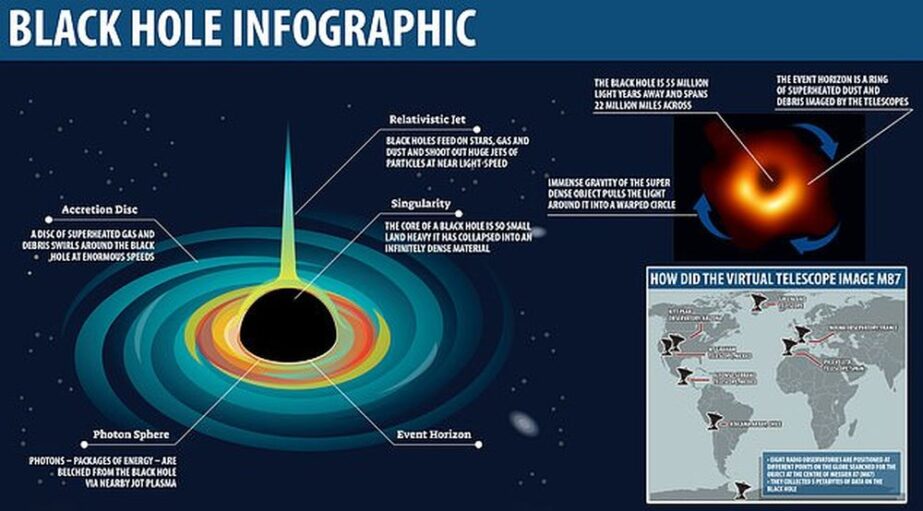 И описать с помощью теории особенностей, решив соответствующие дифференциальные уравнения.
И описать с помощью теории особенностей, решив соответствующие дифференциальные уравнения.
Например, складки или морщины на теле — результат того, что разные ткани растут (или наоборот — уменьшаются в объеме) с разной скоростью. Когда механическое внутреннее напряжение в ткани становится слишком большим, то поверхность складывается — так образуется морщина. Иногда с ними оказывается даже удобнее, и такие нарушения устойчивости при развитии закрепляются в ходе эволюции — так организмы начали выращивать на себе сингулярности. Извилины на головном мозге — пример таких преднамеренных сингулярностей. У всех людей главные извилины расположены одинаково, и процесс их образования управляется физическими механизмами, хотя и кажется, что нарушение устойчивости должно быть случайным процессом.
Чтобы разобраться, почему живым организмам удается управлять этим сложным и сильно нелинейным процессом, у математиков есть еще одна теория, тоже построенная вокруг сингулярностей. Для описания динамических процессов ученые используют теорию бифуркаций.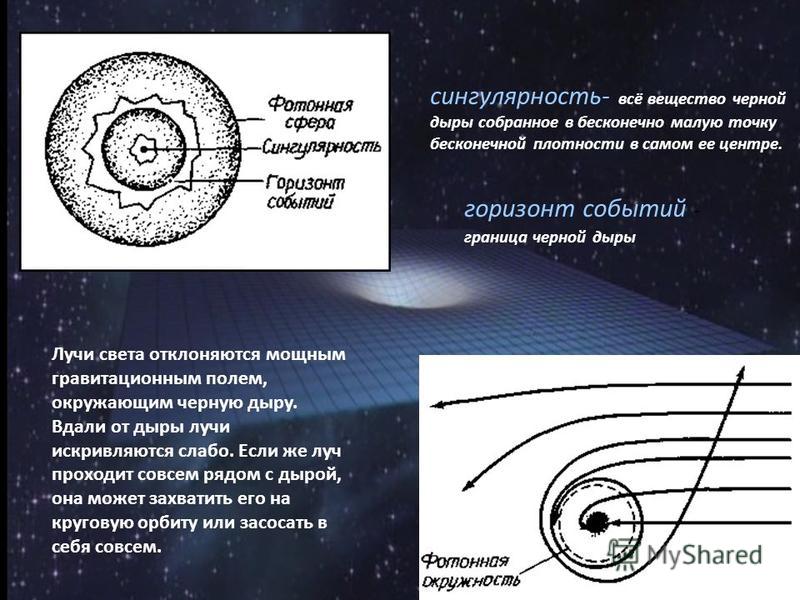 Те же самые складки и сборки в этой теории описывают особые точки, линии или поверхности, на которых система из-за плавного изменения одной из характеристик системы резко меняет свое состояние. В случае с извилинами — из-за плавного увеличения внутреннего механического напряжения растущая кора из гладкого состояния резко переходит к морщинистому. В точке бифуркации (это сингулярность) оба состояния равновероятны, но после ее прохождении выбор в пользу складок уже сделан.
Те же самые складки и сборки в этой теории описывают особые точки, линии или поверхности, на которых система из-за плавного изменения одной из характеристик системы резко меняет свое состояние. В случае с извилинами — из-за плавного увеличения внутреннего механического напряжения растущая кора из гладкого состояния резко переходит к морщинистому. В точке бифуркации (это сингулярность) оба состояния равновероятны, но после ее прохождении выбор в пользу складок уже сделан.
В таких системах сингулярность — результат роста в ограниченном пространстве гиперупругого неогуковского тела, у которых напряжение и деформация связаны нелинейно. Морщина появляется вынужденно из-за избыточной деформации (это происходит примерно при 45-процентной деформации), но после прохождения точки бифуркации она становится устойчивой. Например, если вынуть мозг из черепа, извилины не распрямятся.
То, что такая конфигурация двумерных сингулярностей действительно устойчива, воспроизводима и определяется геометрическими ограничениями, ученые проверяют не только общими математическими уравнениями, но и в реальных физических экспериментах, на реальных моделях из полидиметилсилоксана — эластомера с нелинейными механическими свойствами.
При этом из-за физических эффектов воспроизводимость системы сингулярных складок выполняется не только для больших деформаций, когда точка бифуркации уже пройдена, но и для маленьких. Например, недавно физики установили, что из-за адгезии и пининга краевой линии после распрямления поверхности на ней остаются «шрамы». Из-за чего процесс сгибания–разгибания материала становится асимметричным, а место складки — буквально впечатывается в его память.
Сингулярные яблоки
Сингулярности в извилинах и морщинах двумерны. В особой точке в одном измерении кривизна действительно бесконечная, но в другом — наоборот, нулевая. Значит ли это, что в трехмерном мире эти сингулярности будто бы не совсем полноценны? Нарисованные на бумаге графики парабол с особенностями и каустики, которые видны на плоских проекциях, — примеры сингулярностей на одномерных линиях. Извилины головного мозга, морщины или водопад на широкой реке — сингулярности в двумерных системах. И те, и другие примеры точно помогают чуть лучше представить, что происходит в черной дыре — сингулярности в четырехмерном пространстве-времени. Но любая трехмерная особенность, особенно если ее можно подержать в руках, должна помочь лучше.
И те, и другие примеры точно помогают чуть лучше представить, что происходит в черной дыре — сингулярности в четырехмерном пространстве-времени. Но любая трехмерная особенность, особенно если ее можно подержать в руках, должна помочь лучше.
Трехмерные сингулярности растут практически на каждом дереве. Например в той точке, за которую яблоко подвешено к ветке, возникают осесимметричные особенности, очень похожие на полукубические параболы. С точки зрения геометрии это почти полные аналоги гидродинамических сингулярностей — с отрывом капли или стеканием жидкости в круглое отверстие. Выдавливая из себя яблоко через трубку плодоножки, ветка яблони превращает точку, на которой висит плод, в своеобразный сингулярный слив.
Физики из Гарвардского университета внимательно изучили, как эта сингулярность меняется во время роста яблока и почему она получается именно такой формы. Оказалось, что поверхность яблока, вздувшаяся вблизи плодоножки, действительно хорошо описывается теорией сингулярности, а дуги его поверхности вблизи особой точки описываются параболой.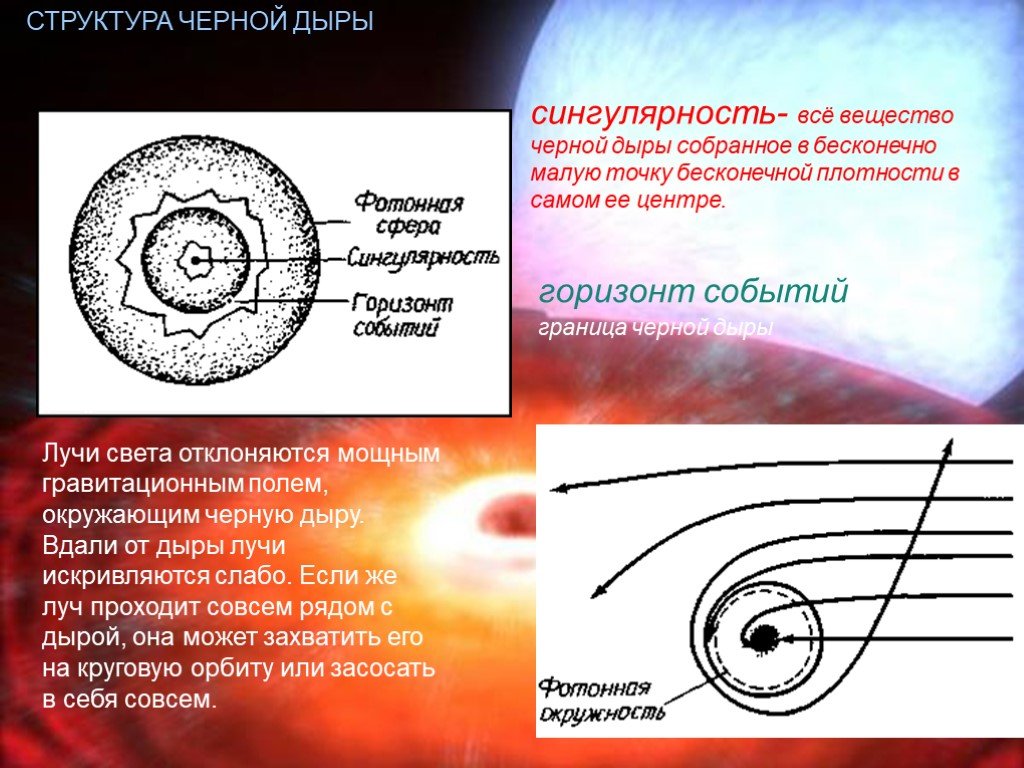
Ученые выяснили, что если рассматривать рост яблока как равномерное движение его фронта во всех направлениях, то когда в одном конкретном направлении этому росту препятствует какой-то ингибитор, в этой точке возникает сингулярность. И форма яблока на каждой стадии его развития оказывается не сферой, а задается уравнением эйконала. Это уравнение из оптики, которое описывает распространение световых лучей при заданных граничных условиях, связывая фазу светового поля с оптической длиной пути. Для яблока в первые моменты после начала роста решение этого уравнения будет гладким даже при наличии точки ингибирования, но в определенный момент в нем действительно появляется касп (он же острие, он же точка возврата).
И это решение универсально — оно чисто геометрическое и не зависит от химического состава, типа клеток или физической природы явления. Согласно ему будет меняться форма и яблока, и чего угодно, что растет как яблоко.
Так же, как и извилины головного мозга, касп в яблоке образуется по законам механики.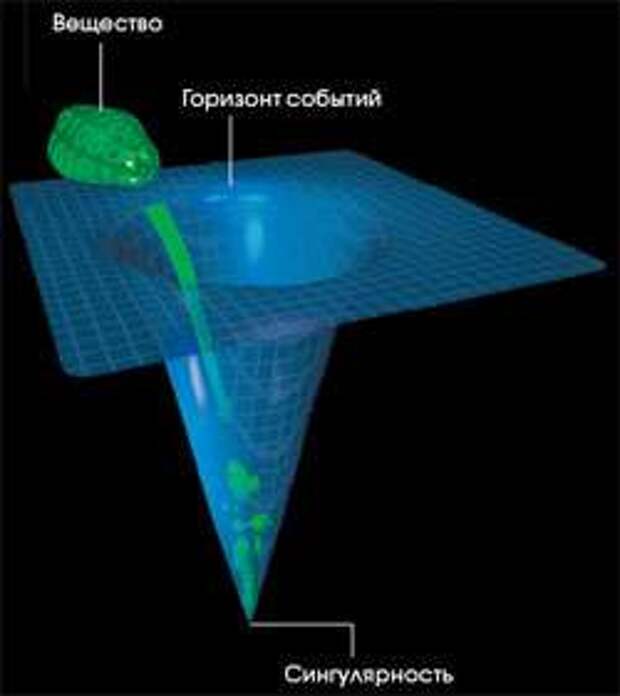 Поэтому его можно точно так же проверить с помощью моделирования и на реальной модели.
Поэтому его можно точно так же проверить с помощью моделирования и на реальной модели.
Эти эксперименты уже провели: и они не только подтверждают механизм возникновения сингулярности на яблоке, но и позволяют изучить более тонкие эффекты. Так, если яблоко висит на слишком толстой плодоножке, то сингулярность перестает быть осесимметричной, и на ее берегах возникают сингулярности второго порядка — дополнительные складки, которые делят плод на хорошо заметные доли. Чем толще плодоножка, тем больше долей будет у сингулярности. Такой же эффект можно увидеть и, например, на помидорах.
Физика с особенностями
Здесь математика сталкивается с чувственным опытом. Рассматривая яблоко, мы не видим бесконечности. Математические бездны не умещаются в наблюдаемый мир.
Но математика абстрактна. Сама по себе она не отвечает, почему при решении уравнений, в которых физики не сомневаются, возникает бесконечность, а максимальная кривизна оказывается выгоднее гладкости. В дифференциальных уравнениях, которые описывают физический мир, решения с особыми точками возникают сами собой. Это происходит, если процесс, который эти уравнения пытаются описать, оказывается для них слишком тонким. Тогда задача становится мультимасштабной и сильно нелинейной, и модель перестает справляться с ней до конца. Извне решение выглядит правильным, но как только мы попадаем в особую точку, выясняется, что никакой физической сингулярности здесь нет, это просто уравнения дают сбой. Бесконечность — артефакт модели, она означает переход на новый уровень, где работают другие формальные законы.
В дифференциальных уравнениях, которые описывают физический мир, решения с особыми точками возникают сами собой. Это происходит, если процесс, который эти уравнения пытаются описать, оказывается для них слишком тонким. Тогда задача становится мультимасштабной и сильно нелинейной, и модель перестает справляться с ней до конца. Извне решение выглядит правильным, но как только мы попадаем в особую точку, выясняется, что никакой физической сингулярности здесь нет, это просто уравнения дают сбой. Бесконечность — артефакт модели, она означает переход на новый уровень, где работают другие формальные законы.
Если мы посмотрим на эту же точку иначе — например, возьмем квантовую физику вместо классической или дискретную модель вместо континуальной, — то сингулярность перестанет быть бесконечным падением и станет чем-то конечным и доступным для понимания.
Поэтому в каждом отдельном случае: с текущей водой, растущим яблоком или бесконечным сжатием материи в черной дыре — надо разобраться, какое именно допущение перестало соблюдаться в особой точке.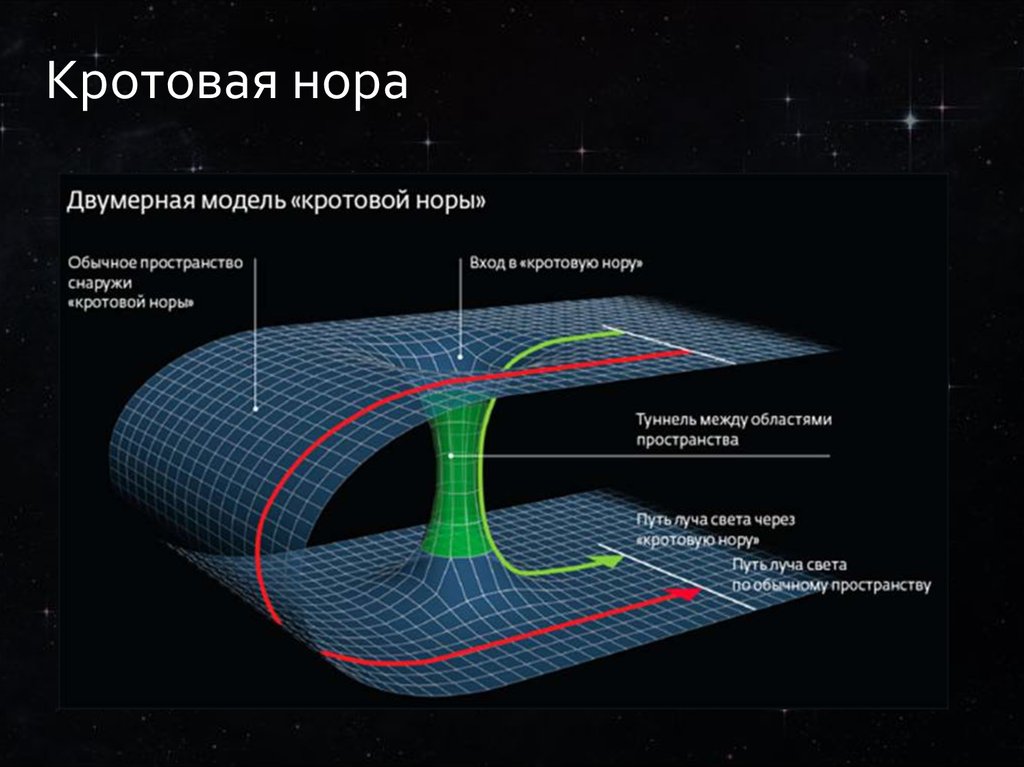 И как надо поменять свой взгляд на проблему, чтобы избавиться от сингулярности.
И как надо поменять свой взгляд на проблему, чтобы избавиться от сингулярности.
Взгляд в черную дыру для нас чем-то похож на попытку увидеть с поверхности яблока, куда упирается плодоножка. Подойдешь слишком близко — и бездна исчезнет. А найти подходящую точку зрения, не поломав при этом привычную картину мира, — (пока) невозможно.
Александр Дубов
Черные дыры «звенят» после слияния, как колокола — и это может быть ключом к тому, чтобы заглянуть внутрь них
Иллюстрация двух сливающихся черных дыр
(Изображение предоставлено ЕКА)
Черные дыры — одни из самых загадочных объектов во Вселенной. Отчасти это связано с тем, что уравнения общей теории относительности, которые мы используем для их понимания, нарушаются при изучении черных дыр в сверхплотных центрах. Тем не менее, новая статья показывает, как астрономы однажды смогут преодолеть эту проблему, используя гравитационные волны, чтобы «заглянуть» внутрь сливающихся черных дыр и узнать, из чего они на самом деле сделаны.
В общей теории Эйнштейна относительности черные дыры — это объекты, которые препятствуют выходу света из-за их чрезвычайно сильной гравитации. Граница черной дыры известна как горизонт событий — если вы преодолеете этот порог, вы никогда не выберетесь наружу. Теория относительности также предсказывает, что центры черных дыр представляют собой точки с бесконечно высокой плотностью, известные как сингулярности.
Наличие особенностей означает, что сами уравнения нарушаются; в математике начинают появляться бесконечности, которые мешают дальнейшим вычислениям. Итак, мы знаем, что общая теория относительности неполна. Должна существовать более фундаментальная теория, вероятно, связанная с квантовой физикой субатомных масштабов, которая могла бы правильно описать то, что происходит в центре черной дыры.
У нас пока нет полной квантовой теории гравитации, но есть несколько кандидатов. Например, существует теория струн , которая предсказывает, что все частицы во Вселенной на самом деле состоят из ультратонких вибрирующих струн. Существует также петлевая квантовая гравитация, согласно которой само пространство-время состоит из крошечных неделимых кусочков, подобных пикселям на экране компьютера.
Существует также петлевая квантовая гравитация, согласно которой само пространство-время состоит из крошечных неделимых кусочков, подобных пикселям на экране компьютера.
Оба этих подхода могут заменить традиционную сингулярность в центре черной дыры чем-то другим. Но когда вы заменяете сингулярность, вы обычно также устраняете горизонт событий. Это потому, что горизонт событий вызван бесконечным гравитационным притяжением сингулярности. Без сингулярности гравитационное притяжение просто невероятно сильное, но не бесконечное, поэтому вы всегда можете покинуть окрестности черной дыры, если бежите с достаточной скоростью.
В некоторых вариантах теории струн сингулярность и горизонты событий заменены переплетенными сетями запутанных узлов пространства-времени. В петлевой квантовой гравитации сингулярность становится чрезвычайно маленьким и чрезвычайно плотным самородком экзотической материи. В других моделях вся черная дыра заменяется тонкой оболочкой материи или сгустками новых видов спекулятивных частиц.
Гравитационные микроскопы
Тайна черной дыры
С ближайшими известными черными дырами тысячи световых года на расстоянии , трудно проверить эти модели. Но иногда черные дыры посылают нам важную информацию, особенно когда они сливаются вместе. Когда они это делают, они выпускают потоки гравитационных волн, которые представляют собой рябь в пространстве-времени, которую можно обнаружить с помощью чувствительных инструментов на Земле , таких как Лазерный интерферометр Гравитационно-волновая обсерватория (LIGO) и эксперименты VIRGO.
Пока что все наблюдения слияний черных дыр согласуются с моделью ванильных черных дыр, предсказанной общей теорией относительности. Но это может измениться в будущем, когда новые поколения гравитационно-волновых обсерваторий появятся в сети, говорится в статье, опубликованной 30 ноября в журнале препринтов 9.0003 arXiv предлагает.
Согласно статье, ключ не в гравитационных волнах, излучаемых во время самого слияния, а в тех, которые излучаются сразу после него. Когда слияние закончилось и две черные дыры стали единым объектом, новая объединенная масса вибрирует с интенсивным количеством энергии, как удар колокола. Эта фаза «звонка вниз» имеет отчетливую сигнатуру гравитационной волны.
Когда слияние закончилось и две черные дыры стали единым объектом, новая объединенная масса вибрирует с интенсивным количеством энергии, как удар колокола. Эта фаза «звонка вниз» имеет отчетливую сигнатуру гравитационной волны.
Изучая эти сигнатуры, исследователи однажды смогут сказать, какие теории о черных дырах верны, а какие нет. Каждая модель черной дыры предсказывает различия в гравитационных волнах, излучаемых во время фазы звонка, которые возникают из-за различий во внутренней структуре черной дыры. С разной структурой черных дыр возникают разные виды гравитационных волн.
Астрономы надеются, что следующее поколение детекторов гравитационных волн будет достаточно чувствительным, чтобы обнаружить эти предсказанные крошечные изменения в сигнатуре кольца. Если они это сделают, они радикально изменят наше представление о черных дырах и продвинут нас вперед в распутывании их глубочайших тайн.
Пол М. Саттер — профессор-исследователь в области астрофизики в Университете Стоуни-Брук Университета штата Нью-Йорк и Институте Флэтайрон в Нью-Йорке. Он регулярно появляется на телевидении и в подкастах, в том числе «Спросите космонавта». Он является автором двух книг: «Твое место во Вселенной» и «Как умереть в космосе», а также регулярно публикуется на Space.com, Live Science и других ресурсах. Пол получил докторскую степень по физике в Университете Иллинойса в Урбана-Шампейн в 2011 году и провел три года в Парижском институте астрофизики, после чего прошел стажировку в Триесте, Италия.
Он регулярно появляется на телевидении и в подкастах, в том числе «Спросите космонавта». Он является автором двух книг: «Твое место во Вселенной» и «Как умереть в космосе», а также регулярно публикуется на Space.com, Live Science и других ресурсах. Пол получил докторскую степень по физике в Университете Иллинойса в Урбана-Шампейн в 2011 году и провел три года в Парижском институте астрофизики, после чего прошел стажировку в Триесте, Италия.
Каждая ли черная дыра содержит сингулярность?
Категория: Космос Опубликовано: 13 сентября 2013 г.
Художественное изображение черной дыры. Изображение общественного достояния, источник: Кристофер С. Бэрд.
В реальной Вселенной не черных дыр содержат сингулярности. В общем, сингулярности — это нефизический математический результат ошибочной физической теории. Когда ученые говорят о сингулярностях черных дыр, они говорят об ошибках, которые появляются в наших современных теориях, а не о реально существующих объектах. Когда ученые и не ученые говорят о сингулярностях так, как будто они действительно существуют, они просто демонстрируют свое невежество.
Когда ученые и не ученые говорят о сингулярностях так, как будто они действительно существуют, они просто демонстрируют свое невежество.
Сингулярность — это точка в пространстве, в которой находится масса с бесконечной плотностью. Это привело бы к пространству-времени с бесконечной кривизной. Наличие сингулярностей в черных дырах предсказывает общая теория относительности Эйнштейна, которая замечательно справилась с сопоставлением экспериментальных результатов. Проблема в том, что в реальном мире никогда не существует бесконечности. Всякий раз, когда из теории выскакивает бесконечность, это просто признак того, что ваша теория слишком проста для обработки крайних случаев.
Например, рассмотрим простейшую физическую модель, которая точно описывает, как волны распространяются по гитарной струне. Если вы двигаете такую струну на ее резонансной частоте, простейшая модель предсказывает, что вибрация струны будет экспоненциально возрастать со временем, даже если вы двигаете ее осторожно. Строка действительно делает это… до определенного момента. Проблема в том, что экспоненциальная функция быстро стремится к бесконечности. Таким образом, модель предсказывает, что гитарная струна, работающая на своей резонансной частоте, со временем будет вибрировать мимо Луны, мимо звезд, в бесконечность, а затем обратно. Действительно ли струна бесконечно вибрирует только потому, что так говорит модель? Конечно, нет. Струна рвется задолго до того, как вибрирует на Луне. Таким образом, появление бесконечности в модели указывает на то, что модель достигла своих ограничений. Простая модель волн на струне верна, пока вибрации малы. Чтобы избежать бесконечности в уравнениях, вам нужно построить лучшую теорию. Для вибрирующих гитарных струн все, что вам нужно сделать, это добавить в модель описание того, когда гитарные струны рвутся.
Строка действительно делает это… до определенного момента. Проблема в том, что экспоненциальная функция быстро стремится к бесконечности. Таким образом, модель предсказывает, что гитарная струна, работающая на своей резонансной частоте, со временем будет вибрировать мимо Луны, мимо звезд, в бесконечность, а затем обратно. Действительно ли струна бесконечно вибрирует только потому, что так говорит модель? Конечно, нет. Струна рвется задолго до того, как вибрирует на Луне. Таким образом, появление бесконечности в модели указывает на то, что модель достигла своих ограничений. Простая модель волн на струне верна, пока вибрации малы. Чтобы избежать бесконечности в уравнениях, вам нужно построить лучшую теорию. Для вибрирующих гитарных струн все, что вам нужно сделать, это добавить в модель описание того, когда гитарные струны рвутся.
В качестве другого примера рассмотрим тонкий стеклянный кубок для питья. Если певец поет ноту правильной высоты, кубок начинает трястись все сильнее и сильнее.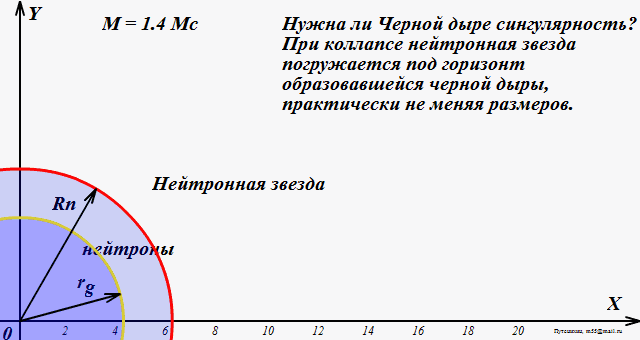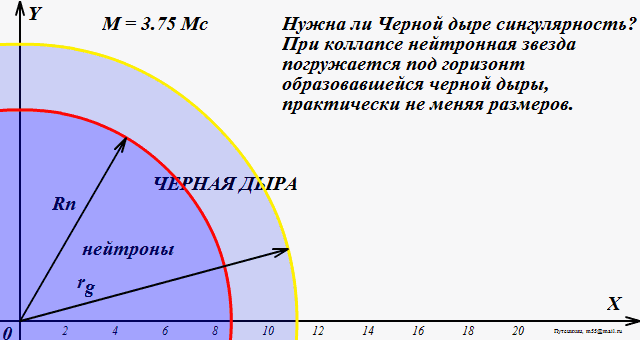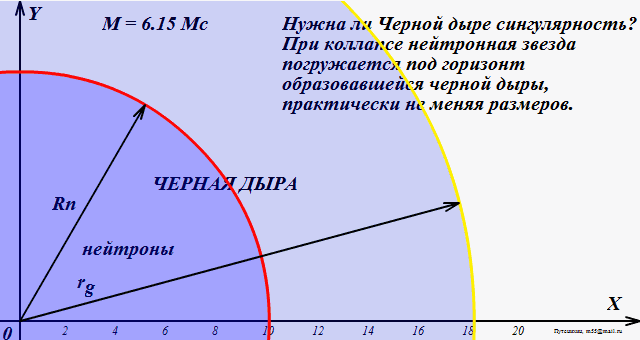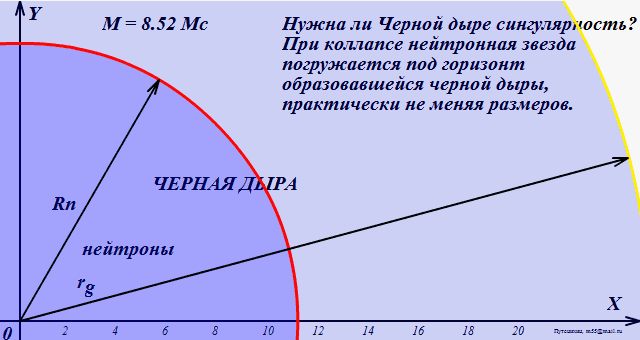 Простейшая модель предсказывает, что со временем кубок будет бесконечно трястись. В реальной жизни так не бывает. Вместо этого пение заставляет кубок разбиться на куски, когда тряска становится слишком сильной.
Простейшая модель предсказывает, что со временем кубок будет бесконечно трястись. В реальной жизни так не бывает. Вместо этого пение заставляет кубок разбиться на куски, когда тряска становится слишком сильной.
Каждая научная теория имеет свои ограничения. В пределах своей применимости хорошая теория очень хорошо соответствует экспериментальным результатам. Но выходите за пределы теории, и она начинает давать неточные или даже бессмысленные прогнозы. Физики надеются когда-нибудь разработать теорию всего, которая не имеет ограничений и будет точной во всех ситуациях. Но у нас пока этого нет. В настоящее время лучшими физическими теориями являются квантовая теория поля и общая теория относительности Эйнштейна. Квантовая теория поля очень точно описывает физику от размеров человека до мельчайших частиц. В то же время квантовая теория поля терпит неудачу в планетарных и астрономических масштабах и, по сути, вообще ничего не говорит о гравитации. Напротив, общая теория относительности точно предсказывает гравитационные эффекты и другие эффекты в астрономическом масштабе, но ничего не говорит об атомах, электромагнетизме или чем-либо в мелком масштабе. Использование общей теории относительности для предсказания орбиты электрона вокруг атомного ядра даст вам удручающе плохие результаты, и использование квантовой теории поля для предсказания орбиты Земли вокруг Солнца также даст вам плохие результаты. Но пока ученые и инженеры используют правильную теорию в правильных условиях, они в основном получают правильные ответы в своих исследованиях, расчетах и прогнозах.
Использование общей теории относительности для предсказания орбиты электрона вокруг атомного ядра даст вам удручающе плохие результаты, и использование квантовой теории поля для предсказания орбиты Земли вокруг Солнца также даст вам плохие результаты. Но пока ученые и инженеры используют правильную теорию в правильных условиях, они в основном получают правильные ответы в своих исследованиях, расчетах и прогнозах.
Хорошо, что общая теория относительности не сильно пересекается с квантовой теорией поля. Для большинства астрономических и гравитационных вычислений можно обойтись только общей теорией относительности и игнорировать квантовую теорию поля. Точно так же для мелкомасштабных и электромагнитных расчетов можно обойтись квантовой теорией поля и игнорировать общую теорию относительности. Например, вы используете только квантовую теорию поля, чтобы описать, что делают атомы на солнце, но используете только общую теорию относительности, чтобы описать, что делает солнце в целом.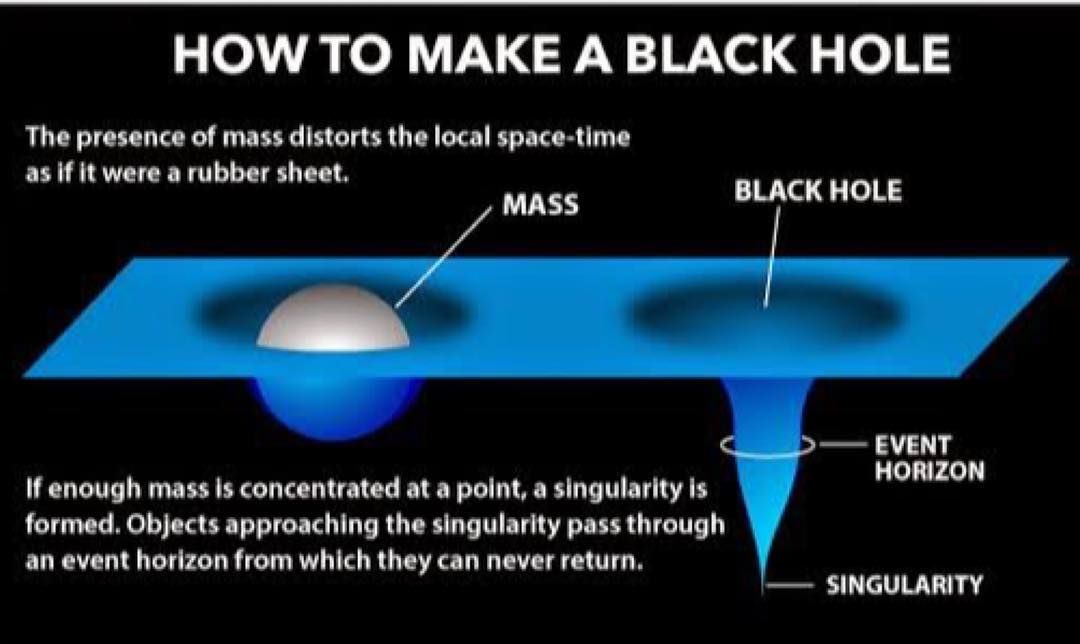 Предпринимаются многочисленные попытки последовательно объединить квантовую теорию поля и общую теорию относительности в одну законченную теорию, но ни одна из этих попыток не была полностью закреплена или подтверждена экспериментами. Пока не появится успешная теория всего, физики в большинстве случаев могут обходиться использованием как общей теории относительности, так и релятивистской квантовой теории лоскутным одеялом. Этот подход в основном работает, потому что сферы достоверности обеих теорий не сильно пересекаются. Но этот подход не работает, когда астрономический объект коллапсирует до квантовых размеров, что и представляет собой черная дыра.
Предпринимаются многочисленные попытки последовательно объединить квантовую теорию поля и общую теорию относительности в одну законченную теорию, но ни одна из этих попыток не была полностью закреплена или подтверждена экспериментами. Пока не появится успешная теория всего, физики в большинстве случаев могут обходиться использованием как общей теории относительности, так и релятивистской квантовой теории лоскутным одеялом. Этот подход в основном работает, потому что сферы достоверности обеих теорий не сильно пересекаются. Но этот подход не работает, когда астрономический объект коллапсирует до квантовых размеров, что и представляет собой черная дыра.
Черная дыра образуется, когда у массивной звезды заканчивается топливо, необходимое для уравновешивания гравитации, и она коллапсирует под действием собственной гравитации до очень малых размеров. Общая теория относительности предсказывает, что звезда коллапсирует в бесконечно маленькую точку с бесконечной плотностью. Но, как теперь должно быть ясно, такого зверя на самом деле не существует в реальном мире.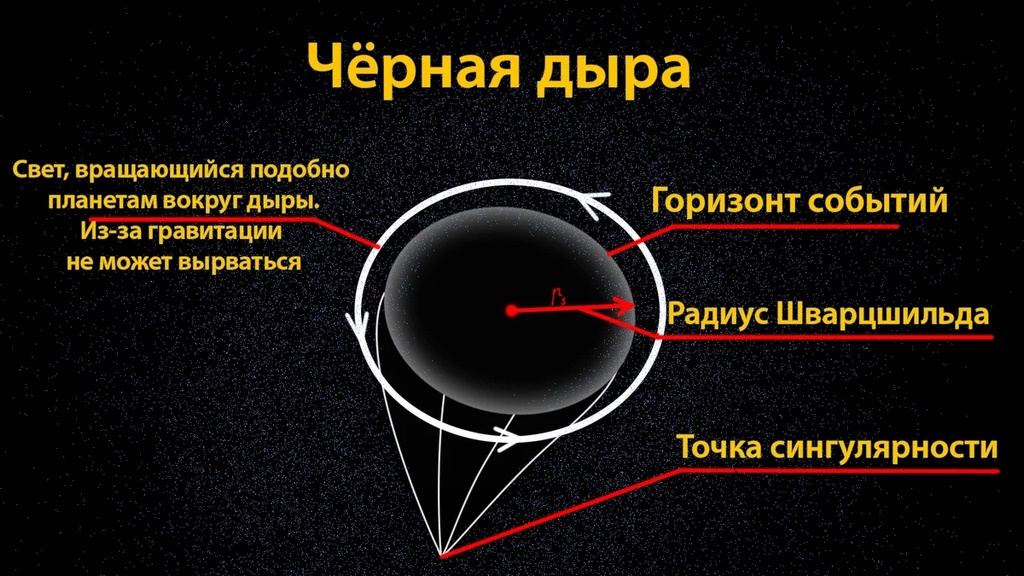 Появление сингулярности черной дыры в ОТО просто указывает на то, что ОТО неточна при очень малых размерах, о которых мы уже знали. Вам нужна квантовая теория поля для описания объектов малых размеров. Но квантовая теория поля не включает гравитационные эффекты, которые являются главной особенностью черной дыры. Этот факт означает, что мы не будем точно знать, что происходит в черной дыре, пока ученые не смогут успешно создать новую теорию, точно описывающую небольшие размеры и сильные гравитационные эффекты одновременно. Что бы в итоге ни сказала нам новая теория, она совершенно точно не скажет, что в черных дырах есть сингулярности. Если бы это было так, то результат просто указывал бы на то, что новая теория так же плоха, как и старая. На самом деле одно из требований к будущей теории всего состоит в том, чтобы она не предсказывала сингулярности в черных дырах. В этом смысле внутренности черных дыр — последний рубеж теоретической физики. Почти все остальное во Вселенной можно точно описать (по крайней мере, в принципе) с помощью наших современных теорий.
Появление сингулярности черной дыры в ОТО просто указывает на то, что ОТО неточна при очень малых размерах, о которых мы уже знали. Вам нужна квантовая теория поля для описания объектов малых размеров. Но квантовая теория поля не включает гравитационные эффекты, которые являются главной особенностью черной дыры. Этот факт означает, что мы не будем точно знать, что происходит в черной дыре, пока ученые не смогут успешно создать новую теорию, точно описывающую небольшие размеры и сильные гравитационные эффекты одновременно. Что бы в итоге ни сказала нам новая теория, она совершенно точно не скажет, что в черных дырах есть сингулярности. Если бы это было так, то результат просто указывал бы на то, что новая теория так же плоха, как и старая. На самом деле одно из требований к будущей теории всего состоит в том, чтобы она не предсказывала сингулярности в черных дырах. В этом смысле внутренности черных дыр — последний рубеж теоретической физики. Почти все остальное во Вселенной можно точно описать (по крайней мере, в принципе) с помощью наших современных теорий.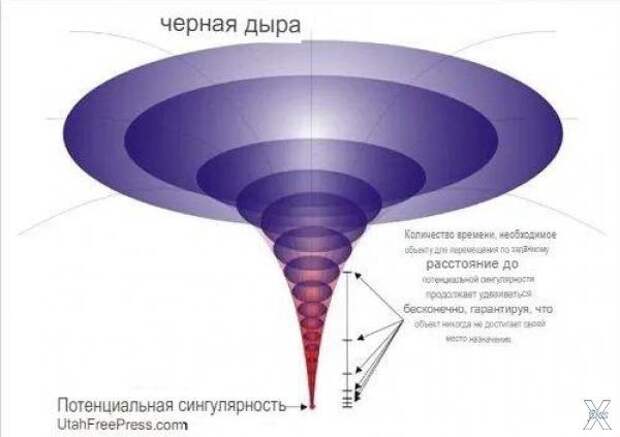

 Зимний иней покрывает более холодную, обращенную на север половину каждой дюны
Зимний иней покрывает более холодную, обращенную на север половину каждой дюны