Сто эйнштейна: 4.1. Постулаты СТО |

Содержание

Физические основы механики

Достижения предшественников были осмыслены и приведены в стройную систему благодаря работам А. Пуанкаре и А. Эйнштейна.

Рис. 6.5. А. Эйнштейн

К 1905 г. была создана специальная теория относительности. Специальная теория относительности (СТО) представляет собой современную физическую теорию пространства и времени, в которой, как и в классической ньютоновской механике, предполагается, что время однородно, а пространство однородно и изотропно. СТО основана на двух постулатах.

Принцип относительности:

Никакие опыты (механические, электрические, оптические), проведенные внутри данной инерциальной системы, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой.

Принцип инвариантности скорости света:

Скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.

Первый постулат является обобщением механического принципа относительности Галилея на все явления природы. Согласно второму постулату, постоянство скорости света — фундаментальное свойство природы, которое констатируется как опытный факт. Выше мы использовали этот постулат в форме уравнений движения светового импульса

Из этих постулатов следует необходимость замены преобразований Галилея преобразованиями Лоренца.

Непосредственное следствие преобразований Лоренца: не может быть объектов, движущихся быстрее света. С такими объектами можно было бы связать систему отсчета, а при V > c для координат и времен получатся мнимые значения. Выходит, что скорость света играет роль предельно возможной скорости распространения сигнала.

Инвариантность интервала. Пусть даны два события: одно произошло в момент времени t₁ в точке с координатами x₁, y₁, z₁, а второе — в момент времени t₂ в точке с координатами x₂, y₂, z₂.

Интервалом между событиями называется величина

Поставив над координатами и временами штрихи, мы получим величину интервала s’₁₂ между этими же событиями в другой системе отсчета. Из преобразований Лоренца находим:

откуда следует:

Таким образом,

Величина интервала является инвариантом относительно преобразований Лоренца.

В классической механике таким свойством обладали по отдельности временной интервал

и пространственное расстояние

В релятивистской физике (от англ. relativity — относительность) этим свойством обладает только интервал между событиями

Замедление времени. Пусть в начале координат системы К’ закреплены часы: их координаты равны тогда х’ = у’ = z’ = 0, a t’ — показываемое ими время (то есть время в системе отсчета К’). Подставляя эти значения в уравнения преобразований Лоренца, находим обычные выражения для координат этих часов в системе К: х = Vt, у = z = 0 (то есть в системе К часы движутся со скоростью V вдоль оси х).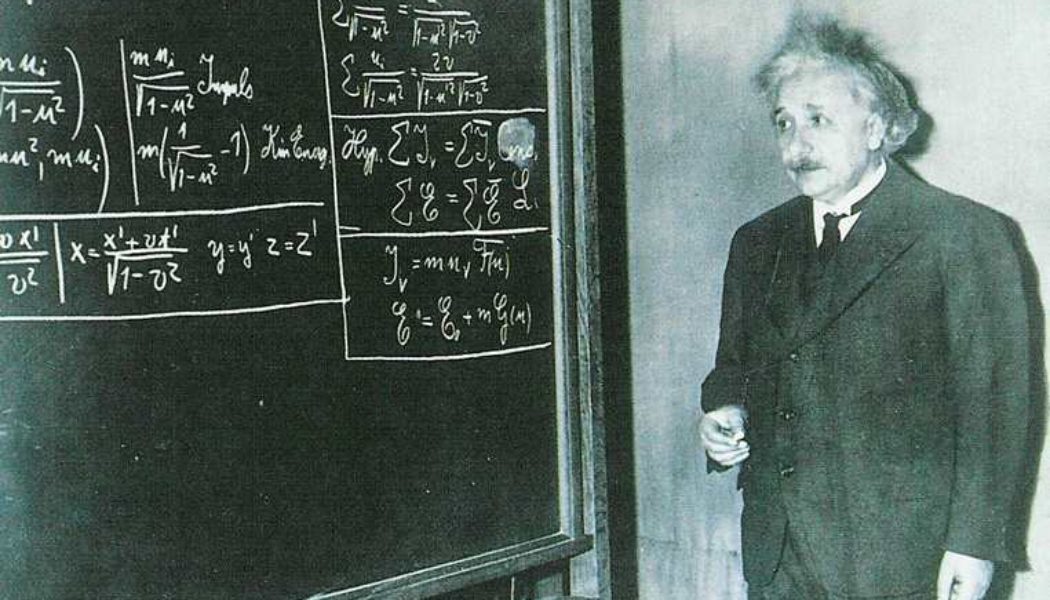 Удивительным является последнее уравнение — преобразование времени:

или

Время t’, отсчитываемое часами в системе К’, меньше времени t, отсчитываемого часами системы К.

Рис. 6.6. Согласование показаний часов у наблюдателей А и В

Время t’, показываемое часами в системе отсчета, где они покоятся, называется собственным временем.

Конкретное устройство часов здесь не играет никакой роли: речь идет о том, что временной интервал не является больше инвариантом и различен для разных систем отсчета. Это демонстрирует следующий пример.

Пример 1. Время жизни τ₀ покоящегося мюона (одной из элементарных частиц) равно 2,2 мкс. От точки рождения до детектора, зарегистрировавшего его распад, мюон пролетел расстояние l = 6 км. Определим, с какой скоростью v (в долях скорости света) летел мюон.

В системе отсчета К’, связанной с мюоном, его время жизни равно τ₀. В лабораторной системе К, согласно полученному соотношению, от рождения мюона до распада пройдет время

За это время мюон преодолеет расстояние

откуда находим

Величина

подставляя cτ₀ и l в (6.4.1), получаем

Если бы время жизни мюона относительно лабораторной системы К было таким же как и в той системе отсчета, где он покоится, то в лабораторной системе отсчета он пролетел бы расстояние L

которое более чем в девять раз меньше действительного. Даже если бы он летел не со своей действительной скоростью (6.4.2), а с предельной скоростью c, что невозможно для частицы с отличной от нуля массой, он пролетел бы всего ct₀ = 660 м, но никак не 6 км.

Многочисленные наблюдения за элементарными частицами, покрывающими гораздо большие расстояния, чем им позволяет классическая механика, — прямое доказательство реальности эффекта замедления времени.

Рис. 6.7. Распад пи-мезона на мюон и нейтрино

Сокращение длины. Пусть в движущейся системе отсчета вдоль оси 0x закреплена линейка, длина которой (собственная длина) равна l₀. Если один конец линейки находится в начале координат (x’₁ = 0), а ее другой конец находится в точке с координатой x’₂=l₀, то из преобразований Лоренца непосредственно следуют координаты концов линейки в системе отсчета К :

Разность этих координат дает длину линейки в системе отсчета К :

Движущаяся линейка становится короче линейки покоящейся. Этот факт также находится в согласии с утверждением, что в релятивистской механике инвариантом является интервал s₁₂, а не пространственные расстояния. Полученное сокращение длины движущегося объекта напоминает сокращение Фитцджеральда-Лоренца. Но с той разницей, что никакой эфир на объект не действует и никаких механических напряжений в линейке не возникает. Просто длина в движущейся и неподвижной системе отсчета различается, как различаются временные интервалы между двумя событиями. Эти оба эффекта — сокращение длины и замедление времени — связаны друг с другом.

Пример 2. Рассмотрим события, описанные в предыдущем примере, с точки зрения наблюдателя, «сидящего» на мюоне.

В момент рождения мюона детектор, регистрирующий его распад, находился с точки зрения наблюдателя в лаборатории на расстоянии l. С точки зрения наблюдателя на мюоне детектор приближается к мюону со скоростью v, причем начальное расстояние L до него будет меньше:

Детектор приблизится к мюону за время

Это время совпадает со временем жизни мюона, который распадется в детекторе, как это видел и неподвижный наблюдатель. Описания событий разные, но оба наблюдателя зафиксируют один и тот же физический факт — распад мюона в детекторе.

Одновременность событий. Пусть имеются два события 1 и 2. Место и время совершения первого из них выберем за начало отсчета соответствующих координат: x₁ = 0, t₁ = 0. Пусть событие 2 происходит одновременно или позже первого

в точке на оси 0x, удаленной на расстояние L. Посмотрим, каковы координаты и моменты времени совершения этих событий с точки зрения наблюдателя, движущегося в положительном направлении оси 0x со скоростью V. Из преобразований Лоренца следует, что x’₁ = 0, t’₁ = 0, то есть координаты и время совершения первого события не изменяются. Второе же событие произойдет в точке x’₂ в момент времени t’₂, где

Знак координаты x’₂ будет таким же, как и в классической механике. Если наблюдатель не успеет долететь до места совершения события к моменту, когда оно произойдет (Vt₂ < L), то событие случится у него впереди по курсу (x’₂ > 0), если же успеет (Vt₂ > L), — то событие 2 произойдет сзади него (x’₂ < 0). Но вот то, что происходит с моментом совершения события 2, не имеет аналога в классической физике. В самом деле, относительно неподвижного наблюдателя событие 2 произошло позже события 1. Но при достаточно большой скорости

знак у t’₂ становится отрицательным, то есть порядок событий меняется!

Но всегда ли это возможно? Ведь события 1 и 2 могут быть причинно связаны друг с другом. Например, событие 1 — рождения отца, а событие 2 — рождение его ребенка. Разве не было бы абсурдным, если бы нашелся наблюдатель, для которого ребенок родился бы прежде отца (нарушилась бы, как говорят, причинно-следственная связь)? Конечно, это невозможно. Давайте сформулируем условие, при котором события 1 и 2 могут быть связаны друг с другом. Так как максимально возможная скорость распространения любого сигнала не превышает c, то события могут находиться в причинно-следственной связи, если они не слишком удалены друг от друга:

Только тогда «сообщение» о первом событии достигнет второго до его совершения. Но если

то для изменения порядка событий наблюдатель должен двигаться со скоростью

А это, как мы видели, невозможно.

Таким образом, события, которые могут в принципе зависеть друг от друга, имеют тот же временной порядок для всех наблюдателей.

Если же события происходят настолько далеко друг от друга, что они не могут быть связаны никаким сигналом

то порядок совершения этих событий зависит от скорости движения наблюдателя и при

порядок событий будет иным, нежели в неподвижной системе отсчета. В частности, одновременные события (t₁ = t₂), происходящие в неподвижной системе отсчета на любом расстоянии друг от друга, не могут быть причинно-связанными (для этого нужны были бы сигналы с бесконечно большой скоростью). Из формулы для преобразования времени получаем при t₂ = 0:

Значит, при любой скорости наблюдателя, движущегося в положительном направлении оси 0x, событие 2 происходит раньше события 1. При движении в обратном направлении (V < 0) событие 2 происходит позже.

Рис. 6.8. События могут быть одновременными, с точки зрения некоего наблюдателя, если ds² > 0

Проиллюстрируем сказанное на следующем примере. Пусть движется поезд А’В’, в концы которого ударяют две молнии, оставляющее на рельсах отметки А и В (рис. 6.9).

Рис. 6.9. К понятию относительности одновременности

Отметим в поезде среднюю точку 0’, а на полотне — соответственно 0. Свяжем с железнодорожным полотном систему отсчета 0х, а с поездом — систему отсчета 0х’. Пусть в точку 0 вспышки света происходят одновременно. Тогда в неподвижной системе отсчета х оба события (удары молнии) происходят одновременно.

Поскольку поезд движется вправо, и, следовательно, в момент прихода вспышек в середину поезда точка 0’ находится правее 0, то вспышка из точки А’ в точку 0’ придет позже, чем из точки B’. Это означает, что в системе х’ удар молнии в точке В’ происходит раньше, чем в точке А’.

Мы убедились, что наряду с относительностью временных интервалов и пространственных расстояний даже одновременность событий не имеет абсолютного значения. Все они относительны, то есть зависят от движения наблюдателя. В классической физике относительными были, например, скорости тел, их кинетические энергии. Теперь список подобных величин пополнился, только и всего.

Рис. 6.10. Кинематические преобразования физических величин в СТО

Задачи по специальной теории относительности (СТО) с решением

Специальную теорию относительности мало кто понимает в полной мере. Тем не менее, решать простейшие задачи по СТО может научиться каждый. Приведем в этой статье несколько примеров задач по специальной теории относительности с решением.

Подпишитесь на наш телеграм, там много полезной и интересной информации. А если хотите получить скидку на заказ, ищите ее на нашем втором канале для клиентов.

Нужна помощь?

Доверь свою работу кандидату наук!

Задачи на специальную теорию относительности с решением

Если не знаете, с чего начать решение физических задач, повторите памятку по решению и держите под рукой полезные формулы.

Задача №1 на СТО Эйнштейна

Условие

Чему равна длина космического корабля, движущегося со скоростью 0,9с? Длина покоящегося корабля 100 м.

Решение

Для решения этой простейшей задачи нужно использовать преобразования Лоренца:

l=l01-v2c2l=1001-0,9с2с2=43,5 м

Ответ: 43,5 м

Задача №2 на СТО Эйнштейна

Условие

Ускоритель сообщил радиоактивному ядру скорость 0,4с (0,4 от скорости света в вакууме). В момент вылета из ускорителя ядро выбросило в направлении своего движения β — частицу со скоростью 0,75с относительно ускорителя.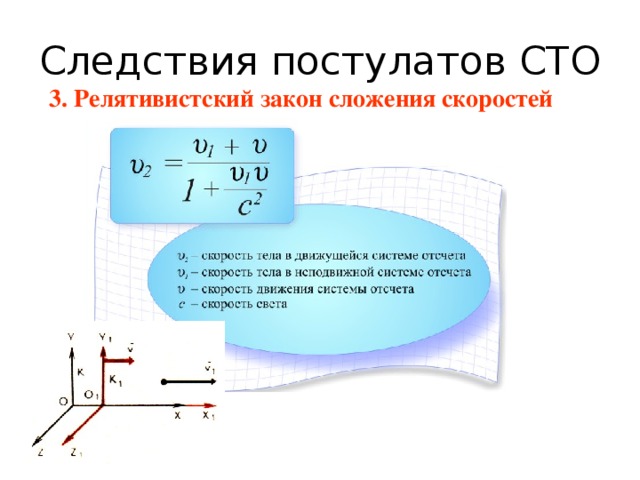 Определите скорость частицы относительно ядра. Ответ дать в мегаметрах за секунду.

Решение

Для решения этой задачи нужно использовать релятивистский закон сложения скоростей:

vx=vx’+v1+vx’·vc2

Здесь vx — скорость частицы в системе отсчета, связанной с ускорителем, vx’ — c скорость частицы в системе отсчета, связанной с ядром, v — скорость одной системы отсчета относительно другой.

Тогда скорость частицы относительно ядра будет равна:

vx’=vx-v1-vx·vc2vx’=0,75с-0,4с1-0,75с·0,4сс2=с2=1,5·108 мс=150 М мс

Ответ: 150 М мс.

Задача №3 на СТО Эйнштейна

Условие

На сколько процентов полная энергия протона, вылетающего из ускорителя со скоростью 0,8с, больше его энергии покоя?

Решение

Для решения этой задачи найдем энергию покоя протона W0, его полную релятивистскую энергию W, а затем вычислим их соотошение ∆WW0, где ∆W=W-W0.

Получаем:

∆WW0=W-W0W0=WW0-1

W0=mc2

W=mc21-v2c2

∆WW0=mc2mc21-v2c2-1=11-v2c2-1

∆WW0=11-0,8с2с2-1=11-0,64-1=0,67

Ответ: полная энергия больше энергии покоя на 67%.

Задача №4 на СТО Эйнштейна

Условие

Чему равна будет масса космонавта, движущегося в космическом корабле со скоростью 0,8с? Масса покоящегося космонавта 90 кг.

Решение

Для решения задачи используем преобразования Лоренца для массы:

m=m01-v2c2

m=901-0,8с2с2=900,6=150 кг

Ответ: 150 кг.

Задача №5 на СТО Эйнштейна

Условие

С космического корабля, удаляющегося от Земли со скоростью 0,7с, стартует ракета в направлении движения корабля. Скорость ракеты относительно Земли 0,96с. Чему равна скорость ракеты относительно Земли?

Решение

Обозначим v – скорость движения корабля относительно Земли, v1 – скорость ракеты относительно космического корабля, v2 – скорость ракеты относительно Земли. Тогда v=0,7с, v2=0,96с.

На основании релятивистского закона сложения скоростей имеем:

v2=v1+v1+v1vc2v1+v=v21+v1vc2v1c2+vc2=v2c2+v·v1v1=c2v-v2vv1-c2=c20,7с-0,96с0,7с·0,96с-с2=0,8с

Ответ: 0,8с

Вопросы по теме СТО

Вопрос 1. Что такое специальная теория относительности? Какие задачи она решает?

Ответ. Теория относительности – физическая теория пространства и времени. В частной (специальной) теории относительности рассматриваются только инерциальные системы отсчета. Явления, описываемые теорией относительности, называются релятивистскими (от лат. «относительный») и проявляются при скоростях, близких к скорости света в вакууме (эти скорости тоже принято называть релятивистскими).

Вопрос 2. Сфомулируйте принцип относительности Эйнштейна

Ответ. Принцип относительности Эйнштейна гласит:

«Никакими физическими экспериментами (механическими, электрическими, оптическими) невозможно определить в любой инерциальной системе отсчета, движется ли эта система равномерно и прямо, или она находится в покое».

Не только механические, но и все физические законы одинаковы во всех инерциальных системах отсчета.

Нужно больше вопросов по физике? Загляните в наш блог!

Вопрос 3. В основе специальной теорит относительности лежат два постулата, выдвинутых Эйнштейном. Сформулируйте их.

Ответ.

Первый постулат является естественным обобщением принципа относительности Галилея с механических на все в отсутствие исключения явления природы и может быть сформулирован как утверждение о невозможности наблюдателю, находящемуся в замкнутой системе отсчета, с помощью какого-либо физического (а значит и любого другого) опыта установить, покоится ли его система отсчета или находится в состоянии равномерного прямолинейного движения.
Вторым постулатом Эйнштейна является утверждение о постоянстве скорости света и ее инвариантности во всех системах отсчета. Этот факт неоднократно проверялся в точных экспериментах.

Вопрос 4. Какие выводы делаются из постулатов относительности?

Ответ. На основе сформулированных постулатов Эйнштейна пересматриваются все коренные положения классической механики (кинематики). Понятия одновременности событий, длительности временного промежутка и длины отрезка перестают носить абсолютный характер, становясь зависимыми от выбора системы отсчета, в которой ведется наблюдение.

В рамках специальной теории относительности классическая механика Ньютона является приближением при низких скоростях.

Вопрос 5. В чем смысл преобразований Лоренца?

Ответ. При скоростях, близких к скорости света, преобразования Лоренца приходят на смену классическим преобразованиям Галилея.

Посмотри примеры работ и убедись, что мы поможем на совесть!

Нужна помощь в решении задач по физике и выполнении других заданий? Обращайтесь за ней в профессиональный сервис для учащихся в любое время.

физиков — Действительно ли Эйнштейн сказал: «Если бы я ошибался, то потребовался бы только один».

спросил
6 лет, 10 месяцев назад

Изменено
11 месяцев назад

Просмотрено
13 тысяч раз

$\begingroup$

Рассказывают, что Эйнштейну показали немецкую газету, в которой говорилось: «Сто немецких физиков утверждают, что теория относительности Эйнштейна неверна». Предположительно, ответ Эйнштейна был: «Если бы я был неправ, то потребовался бы только один раз». Я искал и искал эту историю, и я не могу найти ее нигде. Я только что мечтал об этом?

физика
эйнштейн
физики
цитата

$\endgroup$

$\begingroup$

От The Ultimate Quotable Einstein p. 170:

Если бы я ошибался, то хватило бы и одного [автора]!
^{Возражение Эйнштейна по поводу его теории, когда он услышал, что книга под названием 100 авторов против Эйнштейна был опубликован в Германии. Цитируется по Стивену Хокингу, Краткая история времени (Лондон: Bantam, 1988), 178}

$\endgroup$

$\begingroup$

Возвращаясь к этому старому вопросу с хотя бы частичным ответом: действительно существовала книга под названием «Hundert Autoren gegen Einstein»; Вы можете прочитать это здесь:

https://archive. org/details/HundertAutorenGegenEinstein

Он был опубликован в 1931 году, за два года до прихода к власти нацистов, и несколько авторов, в том числе тот, кто назван первым на титульном листе, на самом деле были евреями. Я не могу найти современный источник для ответа Эйнштейна, но это, безусловно, пример «se non è vero, è ben trovato».

$\endgroup$

$\begingroup$

«Когда Эйнштейна попросили прокомментировать это осуждение теории относительности столькими учеными, он ответил, что для победы над теорией относительности нужно не слово 100 ученых, а достаточно одного факта».0005

Британская энциклопедия
Соединять
https://www.britannica.com/biography/Albert-Einstein/Nazi-backlash-and-coming-to-America

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Альберт Эйнштейн | Биография, образование, открытия и факты

Альберт Эйнштейн

Смотреть все СМИ

Дата рождения:: 14 марта 1879 г.
Ульм
Германия

Умер:: 18 апреля 1955 г. (76 лет)
Принстон
Нью-Джерси

Награды и награды:: Медаль Копли (1925 г.)
Нобелевская премия (1921 г.)

Предметы изучения:: Соотношение массы и энергии Эйнштейна
гравитационная волна
эквивалентность массы-энергии
фотоэлектрический эффект
единая теория поля

Просмотреть весь связанный контент →

Прочтите краткий обзор этой темы

Альберт Эйнштейн , (родился 14 марта 1879, Ульм, Вюртемберг, Германия — умер 18 апреля 1955, Принстон, Нью-Джерси, США), физик немецкого происхождения, который разработал специальную и общую теории относительности и выиграл Нобелевская премия по физике в 1921 году за объяснение фотоэлектрического эффекта. Эйнштейна обычно считают самым влиятельным физиком 20 века.

Родители Эйнштейна были светскими евреями из среднего класса. Его отец, Герман Эйнштейн, сначала был продавцом перин, а позже управлял электрохимическим заводом с умеренным успехом. Его мать, бывшая Полина Кох, вела домашнее хозяйство. У него была сестра Мария (которую звали Майя), родившаяся через два года после Альберта.

Эйнштейн писал, что два «чуда» глубоко повлияли на его ранние годы. Первым было его знакомство с компасом в возрасте пяти лет. Он был озадачен тем, что невидимые силы могут отклонить иглу. Это привело бы к пожизненному увлечению невидимыми силами. Второе чудо пришло в 12 лет, когда он обнаружил книгу по геометрии, которую проглотил, назвав ее своей «священной маленькой книгой по геометрии».

Эйнштейн стал глубоко религиозным в 12 лет, он даже сочинил несколько песен, восхваляющих Бога, и распевал религиозные песни по дороге в школу. Однако это начало меняться после того, как он прочитал научные книги, противоречащие его религиозным убеждениям. Этот вызов существующей власти оставил глубокое и неизгладимое впечатление. В гимназии Луитпольда Эйнштейн часто чувствовал себя не на своем месте и стал жертвой образовательной системы прусского типа, которая, казалось, душила оригинальность и творчество. Один учитель даже сказал ему, что он никогда ничего не добьется.

Еще одно важное влияние на Эйнштейна оказал молодой студент-медик Макс Талмуд (позже Макс Талми), который часто обедал в доме Эйнштейна. Талмуд стал неформальным наставником, познакомившим Эйнштейна с высшей математикой и философией. Поворотный момент произошел, когда Эйнштейну было 16 лет. Ранее Талмуд познакомил его с серией детских научных книг Аарона Бернштейна, Naturwissenschaftliche Volksbucher (1867–68; Popular Books on Physical Science 9).0032), в котором автор представил себе, как он едет рядом с электричеством, движущимся по телеграфному проводу. Затем Эйнштейн задал себе вопрос, который будет доминировать в его мыслях в течение следующих 10 лет: как бы выглядел луч света, если бы вы могли бежать рядом с ним? Если бы свет был волной, то луч света должен казаться неподвижным, как застывшая волна. Однако даже в детстве он знал, что стационарные световые волны никогда не наблюдались, так что это был парадокс. Эйнштейн также написал свою первую «научную работу» в то время («Исследование состояния эфира в магнитных полях»).

Образование Эйнштейна было прервано неоднократными неудачами его отца в бизнесе. В 1894 году, после того как его компании не удалось получить важный контракт на электрификацию города Мюнхена, Герман Эйнштейн переехал в Милан, чтобы работать с родственником. Эйнштейна оставили в пансионе в Мюнхене и ожидали, что он закончит свое образование. Одинокий, несчастный и отталкиваемый перспективой военной службы, когда ему исполнилось 16 лет, Эйнштейн сбежал шесть месяцев спустя и оказался на пороге своих удивленных родителей. Его родители осознавали огромные проблемы, с которыми он столкнулся, когда бросил школу и уклонился от призыва, не имея навыков, необходимых для трудоустройства. Его перспективы не выглядели многообещающими.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас

К счастью, Эйнштейн мог подать заявление непосредственно в Eidgenössische Polytechnische Schule («Швейцарская федеральная политехническая школа»); в 1911 году, после расширения в 1909 году до полного статуса университета, она была переименована в Eidgenössische Technische Hochschule, или «Швейцарский федеральный технологический институт». ») в Цюрихе без эквивалента аттестата средней школы, если он сдаст жесткие вступительные экзамены. Его оценки показали, что он преуспевал в математике и физике, но провалился во французском, химии и биологии. Из-за его исключительных результатов по математике его допустили в политехнический институт при условии, что он сначала закончит формальное образование. Он пошел в специальную среднюю школу, которой руководил Йост Винтелер в Аарау, Швейцария, и окончил ее в 189 году.6. В то время он также отказался от своего немецкого гражданства. (Он был лицом без гражданства до 1901 года, когда ему было предоставлено швейцарское гражданство.) Он на всю жизнь подружился с семьей Винтелер, с которой жил на пансионе. (Дочь Винтелера, Мария, была первой любовью Эйнштейна; сестра Эйнштейна, Майя, в конце концов вышла замуж за сына Винтелера Пауля, а его близкий друг Мишель Бессо женился на их старшей дочери Анне.)

Эйнштейн вспоминал, что его годы в Цюрихе из самых счастливых лет своей жизни. Он познакомился со многими студентами, которые впоследствии стали его верными друзьями, например, с Марселем Гроссманном, математиком, и Бессо, с которым ему нравились продолжительные беседы о пространстве и времени.