Содержание
История ракетно-космической промышленности СССР. Досье
4 октября 2017, 11:27
ТАСС-ДОСЬЕ. 4 октября 2017 года исполняется 60 лет со дня запуска первого в мире искусственного спутника Земли. С этого космического аппарата, созданного Советским Союзом, началось освоение космического пространства человечеством.
Редакция ТАСС-ДОСЬЕ подготовила материал об истории советской ракетно-космической программы.
Циолковский и первые ракеты в СССР
Первым идею полетов в космос высказал основоположник практической космонавтики, русский ученый Константин Циолковский (1857-1935).
Читайте также
Космические пророчества Циолковского
В своем труде «Грезы о земле и небе и эффекты всемирного тяготения» (1895) он писал: «Еще с юных лет я нашел путь к космическим полетам. Это — центробежная сила и быстрое движение». Впоследствии в своих работах он подробно описал теорию полета и конструкцию ракет, предложенных им для исследования атмосферы.
Идеи Циолковского начали воплощаться в 1933 году, когда инженеры московской Группы изучения реактивного движения (ГИРД) под руководством Сергея Королева провели испытания экспериментальной ракеты на гибридном топливе ГИРД-09 (конструкции Михаила Тихонравова). Она поднялась на высоту 400 м, всего находилась в полете 18 секунд. В 1938 году работы по ракетам на жидком топливе в СССР были прерваны в связи с арестом Королева. К созданию баллистических ракет он вернулся только в 1945 году.
Она поднялась на высоту 400 м, всего находилась в полете 18 секунд. В 1938 году работы по ракетам на жидком топливе в СССР были прерваны в связи с арестом Королева. К созданию баллистических ракет он вернулся только в 1945 году.
Становление ракетно-космической промышленности
После окончания Великой Отечественной войны среди советских трофеев оказались комплектующие немецких баллистических ракет «Фау-2» (V-2, сокращение от Vergeltungswaffe-2 — «Оружие возмездия — 2»), а также их завод по производству близ города Нордхаузен. Первоначально завод был занят американскими военными, которые вывезли оттуда все собранные ракеты, но затем был передан в Советскую зону оккупации Германии в обмен на Западный Берлин.
Кроме того, в плену у советских войск оказались около ста немецких ученых-ракетчиков. При этом основной разработчик «Фау-2» Вернер фон Браун сдался в плен американцам, захватив с собой всю документацию. Уже летом 1945 года специальная группа, руководить которой назначили освобожденного из заключения незадолго до этого Королева, приступила к изучению немецких ракет.
13 мая 1946 года вышло секретное постановление Совета министров СССР №1017-419сс «Вопросы реактивного вооружения». Документ предусматривал создание при Совмине СССР специального комитета по реактивной технике во главе с заместителем председателя Совета министров Георгием Маленковым, а также научно-исследовательских институтов (НИИ), конструкторских бюро (КБ) и полигонов по этой тематике.
Читайте также
Человечество отмечает 60 лет с начала космической эры
В их число входило специальное конструкторского бюро НИИ-88, при котором в августе того же года был образован отдел №3 для разработки баллистических ракет дальнего действия под руководством Королева. В апреле 1950 года отдел был преобразован в особое конструкторское бюро №1 (ОКБ-1) НИИ-88. В августе 1956 года ОКБ-1 вместе с опытным заводом №88 было выделено из состава НИИ-88 и стало самостоятельной организацией (впоследствии — ЦКБЭМ, НПО «Энергия», ныне — Ракетно-космическая корпорация «Энергия» им. С. П. Королева).
Специалистами ОКБ-1 на основе узлов и агрегатов немецкой «Фау-2» была собрана баллистическая ракета и 18 октября 1947 года произведен ее запуск. Копия «Фау-2» пролетела 247 км, поднявшись на высоту 86 км.
Конструкторским бюро Королева из отечественных материалов на базе немецкой ракеты была разработана ракета Р-1. С 1950 года, изучив все недостатки немецкой конструкции, коллектив Королева, с участием таких ученых, как Валентин Глушко, Николай Пилюгин и др., занялся ее коренной переработкой. В 1949 году начались испытания Р-2, чья дальность увеличилась с 300 до 600 км. В 1955 году впервые стартовала советская стратегическая баллистическая ракета Р-5М (8К51), а в 1957 году — межконтинентальная Р-7 (8К71).
Несмотря на то, что первоначально у американцев было преимущество в виде команды фон Брауна, и их ракетная программа до середины 1950-х годов опережала советскую, руководство США совершило ряд просчетов. Так, баллистическая ракета Jupiter-C, сравнимая по классу с «семеркой», была запущена почти на год раньше, в сентябре 1956 года, однако президент Дуайт Эйзенхауэр запретил использовать ее для запуска спутника.
Специально разработанная для космических полетов облеченная ракета Vanguard оказалась крайне ненадежной. В результате американцам пришлось возобновлять программу по космическому запуску с помощью ракеты Jupiter-C, четырехступенчатая модификация которой под названием Juno 1 смогла вывести на орбиту спутник Explorer 1 лишь 1 февраля 1958 года.
Начало космической эры
4 октября 1957 года с помощью переоборудованной МБР Р-7 (получила индекс 8К71ПС) в космос был выведен первый искусственный спутник Земли. Запуск был осуществлен с 5-го Научно-исследовательского испытательного полигона Минобороны СССР (ныне — космодром Байконур).
Читайте также
Спутник один. История первого космического устройства
Космический аппарат получил название «Спутник-1». Чтобы не раскрывать индексы стоящей на вооружении баллистической ракеты, ее также назвали «Спутник».
Запуск первого искусственного спутника Земли позволил СССР захватить преимущество в космической гонке. В 1959 году советский аппарат «Луна-3» первым запечатлел обратную сторону Луны; в 1961 году первым человеком в космосе стал Юрий Гагарин.
На базе Р-7 были созданы ряд модификаций, которые использовались в космических запусках. Это «Спутник-3» (индекс 8А91), «Полет» (11А59), «Луна» или «Восток-Л» (8К72), серия «Восток» («Восток-К», «Восток-2», «Восток-2М» — 8К72К, 8А92, 8А92М), «Молния» и «Молния-М» (8К78 и 8К78М), «Восход» (11К57), а также «Союз» (11А511) — первая ракета одного из самых многочисленных семейств советских и российских ракет-носителей. Всего с 1957 года в космос было запущено свыше 1800 ракет, входящих в семейство Р-7.
Как летает космическая ракета? (Продолжение) / Хабр
Здравствуйте, дорогие любители острых космических ощущений (хабровчане)!
В предыдущей своей публикации я посчитал траекторию космической ракеты «РН Союз», сравнив результаты с телеметрией из видеоролика на Ютуб. Расчёты были произведены без учёта силы сопротивления атмосферы, что в итоге привело к существенным расхождениям с реальностью (если конечно же верить той самой телеметрии из видеоролика). Разумеется, мне стало интересно, а что если учесть это сопротивление? Как оно повлияет на траекторию и другие параметры полёта космической ракеты? Попробуем по порядку в этом разобраться.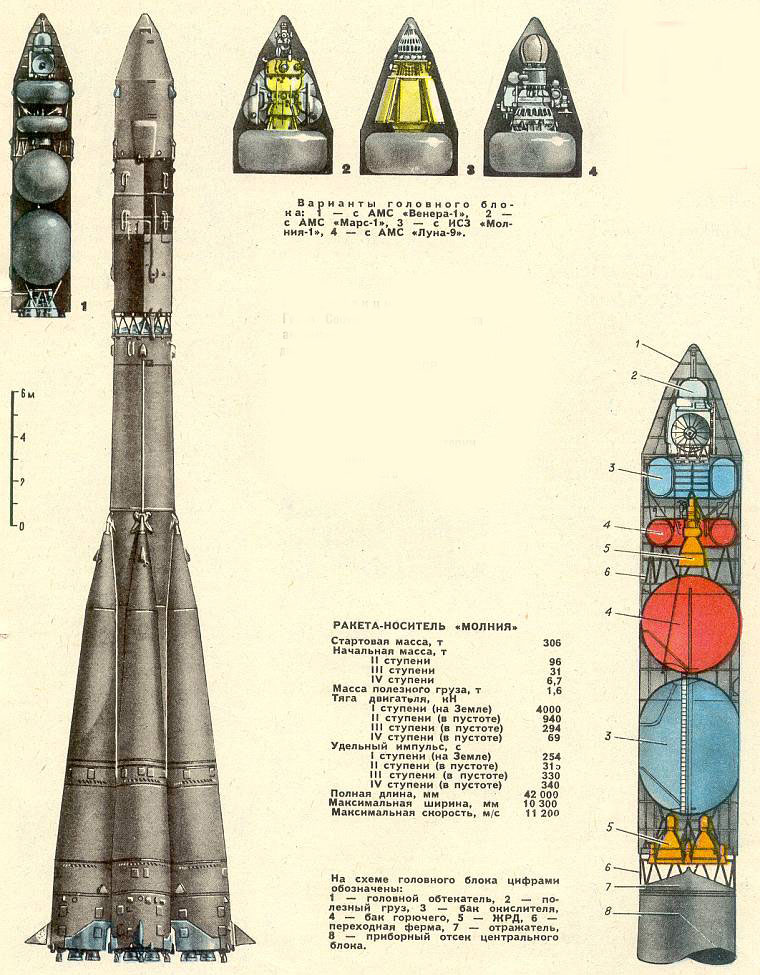
Благодарю пользователя в комментариях, это дополнительно послужило мотивацией к данному исследованию, спасибо!
Если коротко, то моё исследование можно описать так — увяз коготок, вся птичка пропала. Хотелось обойтись какими-нибудь упрощёнными вычислениями, но, как уж получилось.
Для тех, кто не прочитал начало, оно тут https://habr.com/ru/post/649961/
Постановка задачи
Физическая модель, системы координат и допущения, принятые в предыдущей публикации остаются справедливыми и для текущих расчётов, за исключением сопротивления атмосферы. Напомню, ракета имеет три ступени. Соответственно, полёт разделяется на три этапа: полёт с момента старта до отстыковки первой ступени, с момента отстыковки первой ступени до момента отстыковки второй ступени, и с момента отстыковки второй ступени до момента отстыковки третьей ступени. Изменения в вычислениях коснутся только первого этапа полёта, то есть от старта до момента отстыковки первой ступени. На этом участке полёта ракета преодолевает наиболее плотные слои атмосферы и испытывает вместе с этим наибольшее сопротивление трения. Забегая вперёд, из вычислений получилось, что в конце работы первой ступени сила сопротивления атмосферы, действующая на ракету (высота 45 км, скорость 1700 м/с), составляет около 5 тонн-сил!
Забегая вперёд, из вычислений получилось, что в конце работы первой ступени сила сопротивления атмосферы, действующая на ракету (высота 45 км, скорость 1700 м/с), составляет около 5 тонн-сил!
Напишем уравнение динамики с учётом силы сопротивления:
где m — масса ракеты, — вектор ускорения, — вектор силы тяги двигателей, — вектор силы тяжести, — сила сопротивления атмосферы.
Разделив обе части на массу ракеты и сделав необходимые подстановки (см. первую публикацию), получим:
Аэродинамическое сопротивление
Теперь давайте разберёмся, что такое .
Аэродинамическое сопротивление вычисляется по формуле:
где — коэффициент лобового аэродинамического сопротивления, — плотность атмосферы, — скорость движения в среде, — характерная площадь.
Сначала разберёмся с плотностью атмосферы.
Как известно, плотность атмосферы вслед за давлением убывает с высотой. Но не всё так просто. Плотность атмосферы также зависит и от температуры, которая тоже убывает с высотой. Но и это ещё не всё. Мы собираемся лететь так высоко, что будем пересекать такие слои атмосферы, где температура не изменяется или даже возрастает.
Но и это ещё не всё. Мы собираемся лететь так высоко, что будем пересекать такие слои атмосферы, где температура не изменяется или даже возрастает.
Теперь в правильных терминах.
Введём параметр — градиент температуры. Не надо пугаться, в нашем случае это просто положительное или отрицательное число, которое характеризует быстроту и направление изменения температуры в i — том слое атмосферы. Нумерация слоёв начинается с самого нижнего слоя — тропосферы. Если градиент отрицательный, то температура атмосферы убывает, если положительный — возрастает. Атмосфера Земли хорошо изучена и градиенты температуры слоёв измерены и известны. Вот они:
Номер слоя | Диапазон высот, км | Градиент температуры, | Температура в начале слоя , K | Давление в начале слоя , гПа |
1 | 0 — 11 | -6,5 | 288 | 1030 |
2 | 11 — 20 | 0,0 | 216 | 229,8 |
3 | 20 — 32 | +1,0 | 216 | 55,3 |
4 | 32 — 47 | +2,8 | 227 | 8,7 |
5 | 47 — 51 | 0,0 | 270 | 1,1 |
6 | 51 — 71 | -2,8 | 270 | 0,6 |
7 | 71 — 85 | -2,0 | 216 | 0,03 |
Таким образом, зная эту таблицу, можем вычислить температуру на любой высоте по следующей формуле:
где — высота начала слоя (например, для первого слоя ).
Изобразим эту зависимость графически:
Давление для каждого слоя соответственно вычисляется по формулам:
если градиент температуры
если градиент температуры
Плотность есть некоторая функция температуры и давления , где температура и давление в свою очередь являются функциями высоты. Плотность вычисляется по формуле:
где — молярная масса воздуха, — универсальная газовая постоянная.
Зависимость плотности от высоты будет выглядеть следующим образом:
Итак, с плотностью воздуха разобрались. Теперь вернёмся к формуле аэродинамического сопротивления и посмотрим на ещё один интересный параметр — — аэродинамический коэффициент сопротивления. Наш полёт происходит на разной высоте, с разной скоростью. Поэтому этот коэффициент так же как и плотность воздуха не может считаться константой. Если рассматривать большой диапазон скорости летательного аппарата, например от близких к нулю значений, до нескольких Махов, а это как раз наш случай, то окажется, что коэффициент значительно изменяется, и мы не можем этого не учитывать. В данном случае этот коэффициент будет зависеть от числа Маха, то есть от скорости полёта ракеты. Число Маха, в свою очередь, зависит от скорости звука, а скорость звука зависит от температуры среды, в которой он распостраняется. А, как мы выяснили раньше, температура среды изменяется с высотой. Давайте попробуем это записать:
В данном случае этот коэффициент будет зависеть от числа Маха, то есть от скорости полёта ракеты. Число Маха, в свою очередь, зависит от скорости звука, а скорость звука зависит от температуры среды, в которой он распостраняется. А, как мы выяснили раньше, температура среды изменяется с высотой. Давайте попробуем это записать:
Разберём по порядку все зависимости. Для начала займёмся функцией — зависимостью коэффициента сопротивления от числа Маха. После продолжительных исследований литературы на эту тему я решил найти готовый, наиболее подходящий под задачу полёта ракеты вариант, нежели самому проводить расчёты этой зависимости. Коэффициент сопротивления сильно зависит от формы обтекаемого газом тела, его геометрических параметров, плюс отдельно считаются боковые блоки, элементы аэродинамики и т. д. Методика таких расчётов довольно объёмна и муторна, приводить её здесь я посчитал излишним. Поэтому привожу то, что нашёл уже посчитанным для реальной ракеты. Вот оно:
Интересно то, что при приближении скорости к числу Маха и его пересечении коэффициент сопротивления резко возрастает.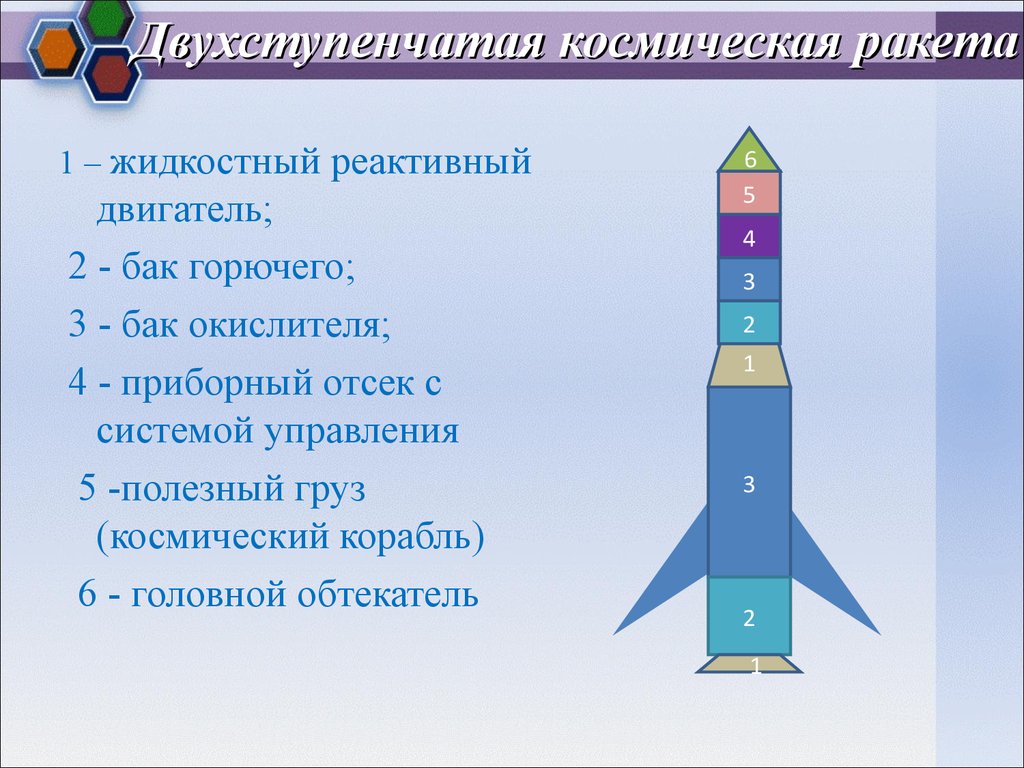 Происходит так называемый скачок уплотнения. После этого при дальнейшем возрастании скорости коэффициент несколько уменьшается.
Происходит так называемый скачок уплотнения. После этого при дальнейшем возрастании скорости коэффициент несколько уменьшается.
Со следующей зависимостью — всё просто: число Маха есть отношение скорости движения в среде к скорости звука — .
Зависимость скорости звука в воздухе от температуры тоже известна, её можно найти в любом справочнике по физике:
Теперь напишем формулу для вычисления силы сопротивления воздуха с учётом всех выше приведённых расчётов:
Подставим силу сопротивления в основное уравнение динамики и распишем его на оси координат:
Или в производных:
Таким образом, задача сводится к решению системы дифференциальных уравнений вида:
что мы и сделаем численным методом с помощью программы.
Входные данные
Параметры ракеты (в основном, массовые характеристики) были уточнены. Поэтому есть расхождения между траекториями без учёта сопротивления воздуха в предыдущей публикации и в этой. В данный момент они являются более точными. Ссылки на источники будут ниже.
Ссылки на источники будут ниже.
Результаты вычислений
Результаты весьма интересны. Честно говоря, они меня впечатлили. Я не думал что атмосфера настолько сильно влияет на траекторию полёта и конечные орбитальные параметры. Разницу траекторий без учёта силы сопротивления и с учётом этой силы Вы можете видеть на этом изображении:
Давайте сравним полученные данные.
В момент перед отстыковкой первой ступени:
Параметры телеметрии | Расчёты программы с учётом R | Расчёты программы без учёта R | |
Высота, км | 45 | 44 | 51 |
Дальность, км | 48 | 47 | 51 |
Скорость, км/ч | 6312 | 6198 | 6785 |
Перегрузка, g | 4 | 3,95 | 3,99 |
В момент перед отстыковкой второй ступени:
Параметры телеметрии | Расчёты программы с учётом R | Расчёты программы без учёта R | |
Высота, км | 154 | 153 | 185 |
Дальность, км | 452 | 459 | 480 |
Скорость, км/ч | 13732 | 13864 | 14266 |
Перегрузка, g | 2,3 | 2,3 | 2,3 |
В момент перед отстыковкой третьей ступени:
Параметры телеметрии | Расчёты программы с учётом R | Расчёты программы без учёта R | |
Высота, км | 202 | 204 | 281 |
Дальность, км | 1675 | 1725 | 1770 |
Скорость, км/ч | 26737 | 27120 | 27386 |
Перегрузка, g | 2,9 | 2,8 | 2,8 |
Хотел бы привести ещё один график, который мы немного проанализируем:
Это зависимость сопротивления атмосферы от высоты.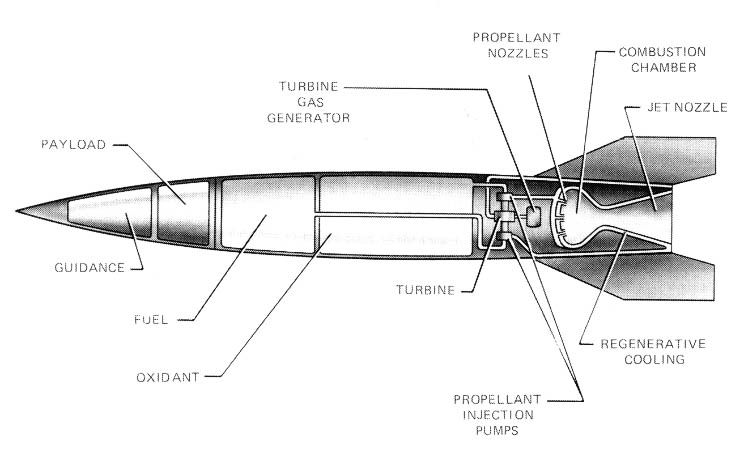
Ну во-первых, сразу бросается в глаза значение максимума — 740 кН, это 75 тонн-сил! Да, уже на высоте чуть больше 10 км ракета набирает такую скорость, что сила сопротивления воздуха составляет такую большую величину, даже с учётом того, что атмосфера на этой высоте значительно разреженная. Для сравнения, когда ракета стартует, избыток тяги (разница между тягой двигателей и весом ракеты) составляет 1130 кН. То есть сила сопротивления на максимуме составляет две трети от тяги на старте!
Также интересно, насколько быстро нарастает сила сопротивления, но это и не удивительно. Ракета — тело переменной массы. Ракета теряет массу, ускорение стремительно возрастает. Эффекта добавляет здесь ещё тот факт, что двигатели существенно прибавляют мощности с ростом высоты (тяга в ваккууме больше, чем на уровне моря).
Ещё один интересный результат — сопротивление атмосферы в момент отстыковки первой ступени. Казалось бы, высота уже 45 км, атмосфера крайне разреженная. Но не тут то было, получите: 46 кН (4,7 тонн-сил)! Неожиданно, правда? Но если учесть, что в этот момент ракета летит со скоростью 1722 м/с, что уже является даже не сверхзвуковой, а гиперзвуковой скоростью (> 5 Маха), то можно в это поверить. К тому же если сравнить с тягой двигателя в этот момент, а осталась у нас только вторая ступень, вполне приемлемо:
К тому же если сравнить с тягой двигателя в этот момент, а осталась у нас только вторая ступень, вполне приемлемо:
95% тяги остаётся, потери на сопротивление всего 5%, и оно продолжает уменьшаться, мы же взлетаем.
Ну и в завершении обратим внимание на то место, которое обозначено красным овалом. Там явно прослеживается излом. Давайте посмотрим, что в этот момент происходит со скоростью:
Зелёный график — зависимость скорости от высоты, чёрный — зависимость силы сопротивления от высоты. Ось абсцисс выдержана в одном масштабе. а ось ординат теперь это значение скорости. Отсюда видно, что в момент излома скорость составляет почти 400 м/с. Что это за скорость? Вычислим число Маха для данной высоты. На высоте, соответствующей излому (~8 км) скорость звука составляет примерно 308 м/с
Теперь обратимся к графику зависимости аэродинамического коэффициента сопротивления от числа Маха:
Данное зачение числа Маха соответствует резкому прекращению возрастания коэффициента сопротивления. Физически это означает, что ракета в данный момент закончила преодолевать трансзвуковой барьер (0,8 < M < 1,2).
Физически это означает, что ракета в данный момент закончила преодолевать трансзвуковой барьер (0,8 < M < 1,2).
На этом всё, спасибо за внимание!
Ссылка на программу здесь, бранч soyz
Использованные источники:
Параметры РН Союз
Аэродинамический коэффициент сопротивления
Параметры атмосферы
Зависимость скорости звука от температуры: справочник по физике.
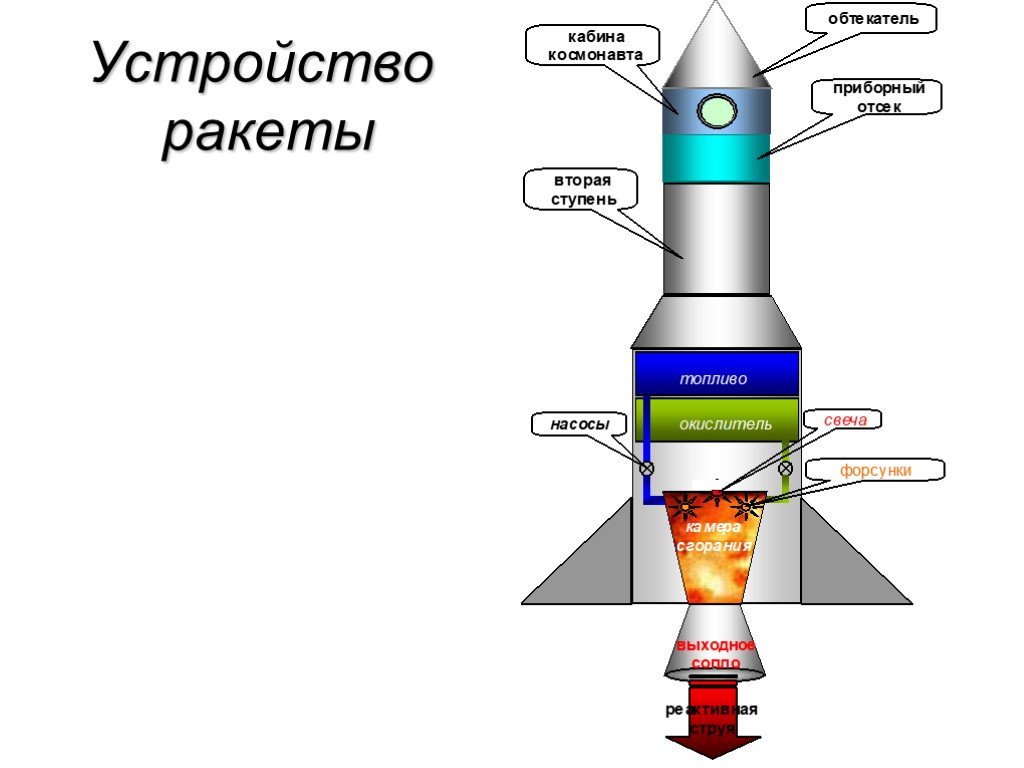
Изучение ракет – отличный способ для школьников Структурная система или рама аналогична Система полезной нагрузки ракеты зависит от миссии ракеты. Система наведения ракеты может включать очень сложные Как видно на рисунке, большая часть полного масштаба Различные части ракеты, описанные выше, были сгруппированы по функции . Экскурсии с гидом
Деятельность: Похожие сайты: |
Забавные факты
Забавные факты о ракетах
Типичная ракета производит более миллиона фунтов тяги, что позволяет ей нести более 6000 фунтов на скорости свыше 22000 миль в час.
 Это эквивалентно мощности, генерируемой 13 плотинами Гувера, которые несут вес восьми лошадей и движутся со скоростью, в 15 раз превышающей скорость летящей пули!
Это эквивалентно мощности, генерируемой 13 плотинами Гувера, которые несут вес восьми лошадей и движутся со скоростью, в 15 раз превышающей скорость летящей пули!Вместе ракеты Atlas и Delta запустили более 1300 миссий
Гонка на Луну зависела от очень успешных полетов Atlas. В 1962 году Джон Гленн стал первым американцем, вышедшим на орбиту, когда Атлас запустил свой космический корабль «Дружба-7».
В январе 2006 года Atlas V установил новый мировой рекорд во время запуска миссии «Новые горизонты» для самого быстрого космического корабля во время выхода из атмосферы Земли — более 36 000 миль в час. При такой скорости потребуется всего 41 минута 44 секунды, чтобы обойти земной экватор, что составляет 24,902 мили. Космический корабль достиг максимальной скорости 47 000 миль в час. При такой скорости полет из Денвера в Нью-Йорк займет всего 2 минуты 16 секунд.
Delta II может запустить спутник, вес которого эквивалентен седану Mercedes S500 (примерно 4200 фунтов).
 Atlas V или Delta IV могут запустить спутник, вес которого эквивалентен Humvee (примерно 6500 фунтов). Будучи самой крупной ракетой-носителем, Delta IV Heavy может запустить спутник, вес которого эквивалентен полуприцепу (примерно 29 кг).000 фунтов).
Atlas V или Delta IV могут запустить спутник, вес которого эквивалентен Humvee (примерно 6500 фунтов). Будучи самой крупной ракетой-носителем, Delta IV Heavy может запустить спутник, вес которого эквивалентен полуприцепу (примерно 29 кг).000 фунтов).На сегодняшний день надежной Delta II запущено более 220 отдельных космических аппаратов.
За всю свою 25-летнюю историю, начиная с первого запуска 14 февраля 1989 года, Delta II имеет почти 99-процентный показатель успешности миссии. ракета от установки вертикальной интеграции (ВИФ) до стартовой площадки весит 1,34 миллиона фунтов. MLP требуется около 30 минут, чтобы пройти 1800 футов от VIF до площадки.
Еще в версии IIAS автомобиль Atlas содержал структурные детали, сделанные из дерева. Направляющие, представляющие собой трубчатые опоры по бокам бустерного бака, были изготовлены из пихты, сорта древесины, на который распространяется спецификация Mil.
Производственные площади ULA в Декейтере, штат Алабама, составляют 1,6 миллиона квадратных футов.





 Это эквивалентно мощности, генерируемой 13 плотинами Гувера, которые несут вес восьми лошадей и движутся со скоростью, в 15 раз превышающей скорость летящей пули!
Это эквивалентно мощности, генерируемой 13 плотинами Гувера, которые несут вес восьми лошадей и движутся со скоростью, в 15 раз превышающей скорость летящей пули!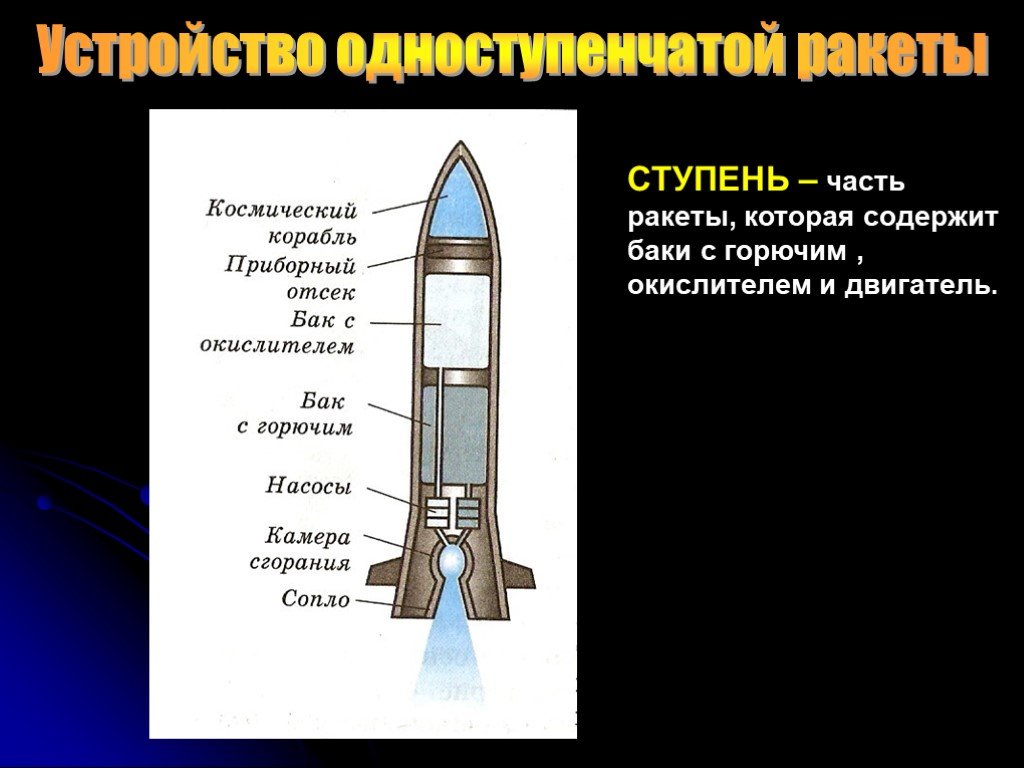 Atlas V или Delta IV могут запустить спутник, вес которого эквивалентен Humvee (примерно 6500 фунтов). Будучи самой крупной ракетой-носителем, Delta IV Heavy может запустить спутник, вес которого эквивалентен полуприцепу (примерно 29 кг).000 фунтов).
Atlas V или Delta IV могут запустить спутник, вес которого эквивалентен Humvee (примерно 6500 фунтов). Будучи самой крупной ракетой-носителем, Delta IV Heavy может запустить спутник, вес которого эквивалентен полуприцепу (примерно 29 кг).000 фунтов).