Телепортация фотона: Впервые фотон телепортировали с одного чипа на другой / Хабр

Стала ли телепортация реальностью? — BBC News Русская служба

• Том Спендер,
• Би-би-си

17 июля 2017

Подпишитесь на нашу рассылку ”Контекст”: она поможет вам разобраться в событиях.

Автор фото, Getty Images

Подпись к фото,

Как долго кадры из «Звездного пути» останутся чистой фантастикой?

Китайские физики сообщили, что им удалось телепортировать фотон с наземной станции на спутник, находящийся на орбите, в 1400 км от лаборатории.

Однако у большинства из нас слово «телепортация» вызывает несколько другие, более экзотические, ассоциации. Раньше о ней упоминали исключительно в контексте научной фантастики — можно ли говорить, что теперь она стала реальностью?

В некотором смысле, да. Однако вряд ли мы сможем мгновенно переноситься на работу или на пляж на Багамах — во всяком случае, уж точно не в самое ближайшее время. Увы.

Как это работает?

Грубо говоря, телепортацией называется факт передачи на расстояние не самого физического объекта, а его состояния.

Некоторые физики приводят в качестве примера факс-машину — ведь она отправляет информацию о расположении знаков на листе бумаге, а не собственно сам лист. Принимающий аппарат получает эту информацию и соответствующим образом располагает знаки на уже присутствующем там чистом листе.

Это, конечно, не та телепортация, которая в ранних книгах братьев Стругацких называется «нуль-транспортировкой», а мировую известность получила благодаря американскому телесериалу «Звездный путь». Там речь шла о мгновенной передаче материи, и даже живого организма, из одного места в другое.

На самом деле в сообщении китайских ученых речь идет о физическом явлении под названием «квантовая запутанность».

Автор фото, AFP/Getty

Подпись к фото,

Китайский спутник оснащен высокочувствительным детекторов фотонов

Явление это состоит в том, что в одной точки пространства и времени возникают две частицы, фактически имеющие одно существование.

Запутанность продолжается даже после того, как частицы — в данном случае фотоны — разделяют друг от друга. Это означает, что если изменяется состояние одного из фотонов, его «фотон-близнец» в другой точке пространства меняется точно так же.

• Ученые объяснили, какую телепортацию внедряют в России
• Ученые научились телепортации на 600 метров

Профессор Санду Попеску из Бристольского университета изучает явление квантовой запутанности с 1990-х годов.

«Уже тогда люди, конечно, сразу начинали думать о телепортации, известной нам по «Звездному пути». Но на самом деле пока речь идет о передаче состояния единственной частицы, а не миллиардов частиц, из которых состоит человек», — объясняет профессор.

Как телепортировать частицу?

Пропустить Подкаст и продолжить чтение.

Подкаст

Что это было?

Мы быстро, просто и понятно объясняем, что случилось, почему это важно и что будет дальше.

эпизоды

Конец истории Подкаст

Давайте вернемся к двум запутанным частицам. Если с запутанной парой начинает взаимодействовать третья частица, то изменения, которые происходят в одной из них, зеркально отражаются в ее «близнеце».

Получается, что этот «близнец» также несет в себе информацию о третьей частице — и реагирует на ее воздействие.

Отлично, так в чем тогда проблема?

До сих пор было невозможно разнести запутанные частицы на большое расстояние друг от друга, потому что такой запутанный фотон может пройти по оптоволоконному кабелю лишь около 150 км до своего поглощения.

Ученые давно указывали на возможность создания спутникового квантового канала, потому что фотонам намного проще путешествовать в вакууме, однако в земной атмосфере их передача может быть затруднена погодными условиями.

Так чего добились китайские физики?

Они сумели наладить генерацию 4000 пар квантозапутанных фотонов в секунду в своей лаборатории в Тибете, и переслать по одному фотону из каждой пары с помощью луча света, направленного на приемное устройства спутника «Мо-Цзы», названного так в честь древнекитайского философа.

На этом спутнике установлено сверхчувствительный детектор, способный регистрировать квантовые состояния отдельных фотонов, поступающих с Земли. В публикации китайских физиков говорится, что им впервые удалось создать «надежный и устойчивый канал сверхдальней квантовой телепортации».

«Это очень элегантный эксперимент — я не ожидал, что всё сработает так быстро и так гладко», — говорит профессор Антон Цайлингер из Венского университета, студентом которого был китайский физик и автор публикации Пань Цзяньвэй.

Так если людей телепортировать нельзя, то какой в этом толк?

Основной целью квантовой телепортацией в настоящее время является создание абсолютно неуязвимых для перехвата сетей связи.

Автор фото, Science Photo Library

Подпись к фото,

Квантовые каналы связи обладают высокой устойчивостью к перехвату

«Законы природы предоставляют такую защиту, — объясняет профессор Попеску. — Если кто-то попытается перехватить информацию в такой сети, этого нельзя не заметить, потому что сам факт наблюдения за такой квантовой системой меняет ее состояние».

В китайском городе Цзинань уже начались испытания системы связи, в основе которой лежит квантовая технология; ведутся также работы по созданию такого канала между Пекином и Шанхаем, где через каждые 100 км установлены так называемые «доверенные узлы», в которых квантовый сигнал измеряется и посылается дальше.

«Это первый квантовый интернет. Пока что скорость передачи данных по нему крайне невелика, и практической пользы от такой сети нет. Но для квантового шифрования сигналов связи это просто находка», — говорит профессор Цайлингер.

Профессор Иэн Уолмсли из Оксфордского университета указывает, что подобные квантовые сети могут использоваться для защиты финансовой информации или базы данных избирателей.

«Еще предстоит преодолеть значительные барьеры, но именно так начинаются революционные перемены», — говорит он.

Что такое телепортация и где она уже применяется

Рассказываем, что такое кротовые норы, как работает квантовая телепортация, какие фейки о ней существуют и где она используется уже сегодня

⏰ Время на чтение: 7–9 минут

Что такое телепортация

Телепортация (от греческого «далеко» и латинского «нести») — гипотетическое мгновенное перемещение объекта на любое расстояние со скоростью быстрее скорости света. Этот термин ввел в употребление американский публицист, исследователь «непознанного», Чарльз Хой Форт после публикации в 1931 году книги «Вулканы небес» о парапсихологии и сверхъестественном. Правда тогда понятие имело мало общего с наукой.

Когда мы думаем о способах телепортации, первое, что приходит в голову — кротовые норы (они же червоточины), которые не отрицает теория относительности. Согласно ней, наша Вселенная изгибается в четвертом пространственном измерении, и в некоторых местах возможны пограничные зоны, где пространство удалено друг от друга, но при этом приближается довольно близко друг к другу сквозь четвертое измерение. При определенных условиях две разные точки трехмерного пространства сольются в одну через дополнительное измерение, образуя тоннель. Шагнул в такое — и переместился мгновенно на миллиарды световых лет. Казалось бы, все просто, но для того, чтобы человека в этом тоннеле не «размазало», его стенки нужно укрепить специальной материей, которая и будет держать их в стабильном состоянии. А такой материи у людей пока нет.

Кротовая нора

(Фото: wikipedia.org)

Второй способ телепортации — квантовый. Доказал, что она возможна, создатель теории относительности Альберт Эйнштейн, который, однако, пытался заявление о возможности телепортации опровергнуть. О том, что такое квантовая телепортация и как она работает, поговорим подробнее.

Квантовая телепортация

Квантовая телепортация означает возможность мгновенной передачи состояния с одной частицы на другую независимо от того, как далеко друг от друга они находятся. Обязательным условием для проведения квантовой телепортации является наличие набора одинаковых атомов в точке отправления состояния и в точки получения состояния. То есть квантовая телепортация не имеет ничего общего с материальным перемещением объекта.

Профессор физфака МГУ Сергей Вятчанин — о квантовой телепортации и квантовой запутанности

Эйнштейн открыл это явление в 1935 году в соавторстве с физиками Борисом Подольским и Натаном Розеном. Ученые доказали, что состояние двух частиц А и Б, однажды провзаимодейстовавших и разлетевшихся в разные направления после соударения, зависит друг от друга на любом расстоянии и эта зависимость проявляется мгновенно. Например, у нас есть две частицы А и Б, они однажды были во взаимодействии, и мы знаем, что сумма их спинов (моментов импульса) всегда равна нулю, при этом спин частицы А направлен вверх, а спин Б — вниз. Как бы далеко мы не разнесли эти частицы, при изменении спина частицы А вниз, спин частицы Б будет мгновенно направляться вверх.

Примеры телепортации

В мире есть много нашумевших примеров телепортации, которые на деле оказались фейками. Один из самых громких примеров — телепортация матки муравьев атта. Данное явление было открыто натуралистом Айвеном Сандерсоном. Он проводил серию опытов — помещал женскую особь насекомого, отмеченную красной краской, в бункер. Когда бункер был открыт, особь оставалась в нем, но как только бункер закрывали, матка тут же исчезала и ученые находили ее в нескольких метрах от места опыта. Впрочем, современная наука не допускает возможности телепортации макроскопических тел; физики не подтвердили опыты Сандерсона.

Еще один пример — телепортация американского военного корабля. По легенде, в 1943 году ВМС США проводил эксперимент с эсминцем «Элдридж», который вначале находился в американском городе Норфолке и в этот же день «телепортировался» на 320 км в Филадельфию. Факт проведения эксперимента по телепортации ВМС США опровергли, а «мгновенное» перемещение корабля мореплаватели объяснили наличием канала, по которому эсминец мог быстро добраться из одного города в другой.

Но есть и реальные случаи телепортации — квантовой, — возможность которых доказана и объяснена физиками. В 1997 году под руководством Антона Цайлингера из Инсбрукского университета и Франческо де Мартини из Римского университета прошла первая в мире экспериментальная квантовая телепортация поляризационного состояния фотона. А уже в 2004 году физики Венского университета телепортировали фотоны на расстояние 600 м через Дунай.

Путешествие через кротовую нору в представлении художника NASA, 1998 год

(Фото: wikipedia.org)

Возможна ли телепортация?

Отсюда ответ на главный вопрос — да, телепортация сегодня возможна, но ограничена законами физики.

«Несмотря на многообещающее название, квантовая телепортация — это всего лишь процедура, в результате которой получатель в ходе согласованного классического сеанса связи с отправителем может восстановить на своей стороне квантовое состояние, которое было у отправителя. Исходное квантовое состояние отправителя при этом уничтожается. То есть возможна лишь передача квантовой информации, а не макрообъектов», — объясняет сотрудник лаборатории квантовой информатики Университета ИТМО Роман Гончаров.

Как объясняет Гончаров, есть ряд проблем с осуществлением квантовой телепортации, чаще всего связанных с несовершенством оборудования, и не позволяющих в полной мере переложить теорию на эксперимент. «Отсюда и возникают ограничения, например, по расстоянию. И хотя различные научные группы активно работают над усовершенствованием текущих схем и ищут новые подходы, в ближайшие несколько лет навряд ли получится приблизиться к серьезным изменениям. Оборудование может быть «идеальным» только в простых теоретических моделях», — добавляет ученый.

Что касается мгновенного перемещения живых существ, то руководитель научной группы «Квантовая оптика» в Российском квантовом центре и профессор Оксфордского университета Александр Львовский объясняет: теоретически наука не опровергает возможность квантовой телепортации человека, т. к. мы сами состоим из кислорода, водорода и углерода с небольшой добавкой других химических веществ.

«Если мы соберем нужное количество атомов нужных элементов, а затем с помощью телепортации приведем их в состояние, идентичное их состоянию в теле телепортируемого человека — получится тот самый человек. Я, конечно, предельно утрирую — от телепортации человека нас отделяет целая вечность. Однако суть вопроса именно в этом: идентичные квантовые частицы встречаются везде, а вот привести их в нужное квантовое состояние совсем непросто», — заявил он изданию N+1.

Но телепортировать живого человека у ученых едва ли получится и через века — как отмечает Гончаров из ИТМО, «оригинал при телепортации уничтожается».

Телепортация в России и в мире сегодня

Опрошенные эксперты утверждают: у квантовой телепортации есть колоссальный технологический потенциал, и лежит он, в основном, в области связи и вычислительной техники. По словам руководителя научной группы «Квантовые информационные технологии» в Российском квантовом центре Алексея Федорова, одно из направлений, которым сегодня занимаются физики — увеличение расстояния для квантовых коммуникаций. Ученым это необходимо для создания криптографических ключей, которые используются для интернет-соединения и в мобильных банках.

«Сегодня для выработки криптографических ключей используются определенные классы математических алгоритмов, однако такой способ будет неустойчивым для атак с квантовым компьютером. Когда появится квантовый компьютер достаточной мощности, мы не сможем использовать нынешнее поколение математических алгоритмов, а вот квантовое распределение ключей абсолютно устойчивое», — говорит Федоров.

Одно из технических ограничений для использования квантового распределения ключей — это расстояние, на которое ключ может быть передан. «Сейчас максимальное расстояние распределения ключей с разумной скоростью составляет 100-200 км, и связано это с затуханием в канале передачи квантовых состояний (например, оптоволокне), то есть часть фотонов просто теряется. Чтобы это предотвратить, нужны квантовые повторители, которые могут строиться на основе квантовой телепортации. Поэтому эксперименты с квантовой телепортацией могут помочь нам увеличить расстояние для квантового распределения криптографических ключей», — объясняет Федоров.

За последние десятилетия ученые в мире регулярно делают новые открытия в квантовых коммуникациях. В конце 2019 года исследователи из Бристольского университета в Великобритании и Датского технического университета впервые смогли передать состояние между двумя чипами. Эти чипы, по заявлению ученых, способны кодировать квантовую информацию в свете и обрабатывать ее с высокой эффективностью и низким уровнем шума. Изобретение поможет человечеству создавать более сложные схемы для квантовых вычислений и коммуникаций.

Одним из научных центров в России, где сегодня изучают квантовую телепортацию, является Российский квантовый центр; там исследования ведутся группой ученых под руководством Александра Львовского. Схожие эксперименты проходят в лаборатории квантовой оптики Московского государственного университета.

На мировом уровне квантовой телепортацией занимается группа Юджина Ползика в институте Нильса Бора в Копенгагене, группа Антона Цайлингера в Австрии, Михаила Лукина в Гарвардском университете и группа Цзянь-Вэй Пана в Китае. Последней принадлежит рекорд по расстоянию передачи квантовой телепортации на 1 200 км.

КВАНТОВАЯ ТЕЛЕПОРТАЦИЯ ФОТОНОВ

Ключевое исследование, доказывающее принципиальную возможность квантовой телепортации фотонов.
Это необходимо для фундаментального физического обоснования принципиальной возможности дистантной трансляции генетико-метаболической информации с помощью поляризованных (спинирующих) фотонов. Доказательство, применимое как для трансляции in vitro (с помощью лазера), так и in vivo, т.е. в самой биосистеме между клетками.
ЭКСПЕРИМЕНТАЛЬНАЯ КВАНТОВАЯ ТЕЛЕПОРТАЦИЯЭкспериментально продемонстрирована квантовая телепортация – передача и восстановление на любой произвольной дистанции состояния квантовой системы. В процессе телепортации первичный фотон поляризуется, и эта поляризация является передаваемым дистантно состоянием. При этом пара спутанных фотонов является объектом измерения, в котором второй фотон спутанной пары может находиться произвольно далеко от начального. Квантовая телепортация будет ключевым элементом в сетях квантового компьютинга.

Мечта о телепортации – это мечта о способности к путешествию путем простого появления на некотором расстоянии. Объект телепортации может быть полностью охарактеризован по своим свойствам классической физикой путем измерений. Для того, чтобы на некотором расстоянии сделать копию этого объекта нет необходимости передавать туда его части или фрагменты. Все, что необходимо для такой передачи – это снятая с объекта полная информация о нем, которая может использоваться для воссоздания объекта. Но насколько точна должна быть эта информация для генерации точной копии оригинала? Что если эти части и фрагменты будут представлены электронами, атомами и молекулами? Что произойдет с их индивидуальными квантовыми свойствами, которые, в соответствии с принципом неопределенности Гейзенберга, не могут быть измерены с произвольной точностью? Беннет и др. [1] доказали, что возможна передача квантового состояния одной частицы на другую, т. е. процесс квантовой телепортации, которая не обеспечивает передачу любой информации об этом состоянии в процессе передачи. Эта трудность может быть устранена, если использовать принцип спутывания (entanglement), как особого свойства квантовой механики [2]. Оно отображает корреляции между квантовыми системами существенно более строго, чем это могут делать любые классические корреляции. Возможность передачи квантовой информации – одна из базовых структур волновой квантовой коммуникации и квантового компьютинга [3]. Хотя и существует быстрый прогресс в описании квантового информационного процессинга, трудности в управлении квантовыми системами не позволяют делать адекватные подвижки в экспериментальной реализации новых предложений. Не обещая быстрых успехов в квантовой криптографии (первичные соображения по передаче секретных данных), ранее мы только успешно доказали возможность квантового плотного кодирования [5], как пути квантово-механического усиления сжатия данных. Основная причина такого медленного экспериментального прогресса в том, что хотя и существуют методы генерации пар спутанных фотонов [6], спутанные состояния для атомов только начинают изучаться [7] и они не более возможны, чем спутанные состояния для двух квантов. Здесь мы публикуем первую экспериментальную проверку квантовой телепортации. Путем создания пар спутанных фотонов с помощью процесса параметрической даун-конверсии, а также путем двухфотонной интерферометрии для анализа процесса спутывания, мы можем передать квантовые свойства (в нашем случае состояние поляризации) с одного фотона на другой. Методы, развитые в этом эксперименте, будут иметь большое значение как для исследований в области квантовой коммуникации, так и для будущих экспериментов по фундаментальным основам квантовой механики. Проблема Для более ясного понимания проблемы передачи квантовой информации, допустим, что Алиса имеет некоторую частицу с квантовым состоянием |Ψ|, и она хочет передать Бобу, находящемуся на некоторой дистанции, ту же частицу в том же состоянии. Ясно, что существует возможность послать Бобу частицу прямо. Но предположим, что канал сообщений между Алисой и Бобом не очень хорош для сохранения необходимой квантовой когерентности, или допустим, что передача займет слишком много времени и это явится причиной того, что |Ψ| обретет состояние более сложного или массивного объекта. Итак, каково должно быть стратегическое поведение Алисы и Боба? Как отмечено выше, не существует таких измерений, которые могла бы провести Алиса по параметру |Ψ|, которые были бы достаточны для воссоздания их Бобу, поскольку состояние квантовой системы не может быть полностью детерминировано путем измерений. Квантовые системы так неуловимы, поскольку они могут быть в суперпозиции нескольких состояний в одно время. Измерение квантовой системы будет точным только в одном из этих состояний, и это будет одним из основных положений предлагаемой модели. Мы можем продемонстрировать это важное квантовое свойство, беря одиночный фотон, который может иметь горизонтальную или вертикальную поляризацию, помеченные состояниями |↔| и | |. Он даже может иметь поляризацию общей суперпозиции этих двух состояний. (1) |Ψ|=α|↔|+β| | где α и β есть два комплексных числа, удовлетворяющих |α|²+|β|²=1 Учитывая этот пример в более общем случае, мы можем заменять состояния |↔| и | | в уравнении (1) на |0| и |1| , которые соответствуют состояниям любой квантовой системы в режиме двух состояний. Суперпозиции |0| и |1| названы кубитами (qubits), они обладают важными новыми возможностями, введенными квантовой физикой в информационную науку [8]. Если фотон в состоянии |Ψ> проходит через поляризационный расщепитель пучка (устройство для отражения горизонтально или вертикально поляризованных фотонов), он будет найден в отраженном (переданном) луче с вероятностью |α|²(|β|²). Затем дифференцировку общего состояния |Ψ| можно прогнозировать как путь на |↔| , так и на путь | | в зависимости от измерения. Мы считаем, что законы квантовой механики, в особенности постулат (projection) прогноза такого рода, делает невозможным для Алисы точное измерение |↔|, т.е. невозможно получение всей информации, которая необходима для реконструкции состояния. Концепция квантовой телепортации Хотя постулат прогноза в квантовой механике кажется достаточным для попыток Алисы обеспечить правильный переход Боба в состояние |↔| (как эквивалент приема телепортационной информации от Алисы к Бобу (П.Г.)), однако, практически это стало возможным после работы Беннета и др. [1], которые смогли точно прогнозировать телепортацию состояния |↔| от Алисы к Бобу. В ходе телепортации Алиса будет разрушать (собственное? П.Г.) квантовое состояние в момент приема Бобом (нового П.Г.) квантового состояния (посланного ею? П.Г.), и в то же время ни Боб, ни Алиса не обладают точной информацией о состоянии |↔|. Ключевую роль в схеме телепортации играют дополнительные спутанные пары частиц, которыми вначале оперируют Алиса и Боб. Предположим, частица 1, которую Алиса желает телепортировать, находится в состоянии |Ψ|1=α|↔|1+β| |1 (Рис.1а), а спутанные пары частиц 2 и 3, которыми манипулируют Алиса и Боб, обладают состоянием (2) |Ψ-|2 3=1/√2 |↔|2 | |3 – | |2 |↔|3 Такая смешанная пара в единой квантовой системе эквивалентна суперпозиции состояний |↔|2 | |3 и | |2 |↔|3. Смешанное состояние не содержит никакой информации об индивидуальных частицах; оно лишь указывает, что частицы будут находиться в противоположных состояниях. Важное свойство смешанной пары заключается в том, что как только измеряется состояние одной частицы, скажем поляризация оказывается в состоянии |↔|, другая частица будет поляризована (ортогонально П. Г.) | |, и наоборот. Каким образом измерение одной частицы немедленно влияет на состояние другой частицы, которая может находиться неопределенно далеко? Эйнштейн среди многих достижений физиков не признавал это «действие привидений на расстоянии». Но обсуждаемое свойство спутанного состояния продемонстрировано сейчас многочисленными экспериментами [см. обзоры 9,10]. Схема телепортации работает следующим образом. Алиса имеет частицу 1 в начальном состоянии |Ψ|1 и частицу 2. Частица 2 спутана с частицей 3, которая идет к Бобу. Особый момент – это специальное измерение на частицах 1 и 2, которое переводит их в спутанное состояние: (3) |Ψ-|1 2=1/√2 |↔|2 | |3 – | |2 |↔|3 Это только одно из возможных максимально спутанных состояний, в которые две частицы могут быть переведены. Прогнозирование неопределенного состояния двух частиц на основе их (вероятных? П.Г.) четырех состояний называется Белловское измерение состояния (Bell-state measurement). Состояние, даваемое в уравнении (3), обнаруживает себя из трех других максимально спутанных состояний тем, что его изменение базируется на промежуточных изменениях частицы 1 и частицы 2. Это уникальное антисимметрическое свойство |Ψ-|1 2 будет играть важную роль в экспериментальной идентификации, то есть в измерении этого состояния. Квантовая физика предсказывает [1], что если частицы 1 и 2 прогнозируются в состояние |Ψ-|1 2, то частица 3 немедленно переходит в начальное состояние частицы 1. Причина для этого следующая. Поскольку мы наблюдаем частицы 1 и 2 в состоянии |Ψ-|1 2, то мы знаем, что при каком-то состоянии частицы 1, частица 2 будет в противоположном состоянии, то есть в состоянии ортогональном состоянию частицы 1. Но мы сразу перевели частицы 2 и 3 в состояние |Ψ-|2 3, а это означает, что частица 2 также ортогональна частице 3. Это возможно только, если частица 3 находится в том же состоянии, что и частица 1 изначально. Конечное состояние частицы 3 поэтому: (4) |Ψ|3=α|↔|3 + β| |3 Заметим, что в ходе Белловского измерения частица 1 утрачивает самоидентичность, поскольку начинает спутываться с частицей 2. Поэтому в процессе телепортации состояние |Ψ|1 у Алисы утрачивается.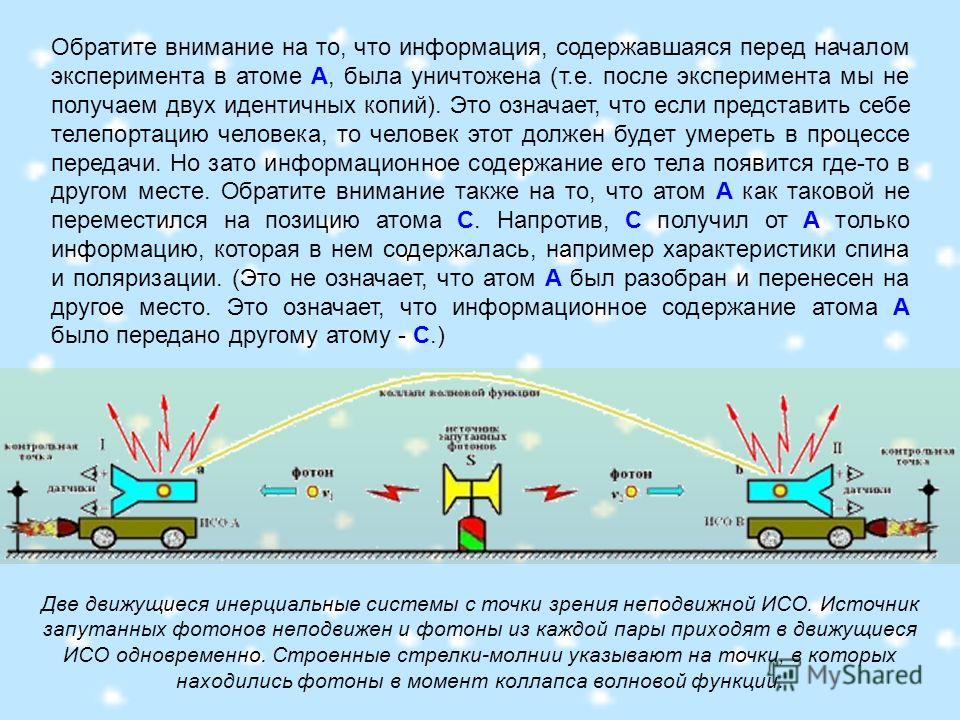 Этот результат (уравнение (4)) заслуживает некоторых комментариев. Передача квантовой информации от частицы 1 к частице 3 может произойти на любом расстоянии, что и является телепортацией. Экспериментально показано [11], что квантовое спутывание сохраняется на расстояниях более 10 км. Характерно также, что в схеме телепортации нет необходимости, чтобы Алиса знала где находится Боб. Более того, начальное состояние частицы 1 может быть абсолютно неизвестно не только Алисе, но и кому бы то ни было. Такая квантово-механическая полная неопределенность может происходить даже в том случае, когда имеет место Белловское измерение состояния. Это происходит тогда, как уже отмечали Беннет и соавторы [1], когда сама частица 1 является членом спутанной пары и поэтому не имеет четко определенных свойств. Это в итоге приводит к затягиванию в запутанность [12,13]. Также важно подчеркнуть, что Белловское измерение состояния не выявляют никакой информации о свойствах каких-либо частиц. Понятно, почему квантовая телепортация работает с использованием когерентных ансамблей из пар суперпозиционных частиц, в то время как любые измерения на единичных суперпозиционных частицах будут обречены на неудачу. То, что абсолютно никакая информация не приобретается от любой частицы – также причина почему квантовая телепортация избегает вердикта аналога какой-либо теоремы [14]. После успешной телепортации частица 1 уже более недоступна в своем естественном состоянии, и поэтому частица 3 не является аналогом, она – результат реальной телепортации (и переноса свойств с 1 на 3 (П.Г.)). Полное Белловское измерение состояния может дать не только результат, что две частицы 1 и 2 находятся в антисимметрическом состоянии, но с вероятностью 25% мы можем найти их в любом из трех других спутанных состояниях. Когда это случается, частица 3 входит в одно из трех различных состояний. Затем оно переводится Бобом в исходное состояние частицы 1 в соответствии с выбранным преобразованием, независимым от состояния частицы 1. Это происходит после приема через классический канал связи информации, которую Алиса получила по результатам анализа Белловского состояния. Наконец, особо отметим, что даже если бы мы захотели идентифицировать только одно из четырех Белловских состояний, как обсуждалось выше, телепортация будет успешной, хотя только в четверти случаев. Экспериментальное подтверждение Телепортация тесным образом связана как с генерацией так и с измерением спутанных фотонов; Они являются важнейшими задачами для любого экспериментального подтверждения. До сих пор существовали только немногие экспериментальные установки, с помощью которых можно добиться образования спутанных состояний, и не существует экспериментально подтвержденных данных для того, чтобы определить все четыре Белловских состояний для любого вида квантовых систем. Однако, спутанные пары фотонов можно легко получить, и они могут прогнозироваться по крайней мере в два из четырех Белловских состояний. Мы получили спутанные фотоны 2 и 3 путем параметрической даун-конверсии. В этом методе, внутри нелинейного кристалла, вошедший путем накачки фотон может спонтанно распадаться на два фотона, которые в случае 2-го типа параметрической Даун-конверсии находятся в состоянии, данном в уравнении (2) (Рис.2) [6]. Чтобы достичь прогнозирования фотонов 1 и 2 в Белловское состояние, мы должны сделать их неразличимыми. Чтобы и достигнуть этой неразличимости, эти два фотона мы переводим в суперпозицию в расщепителе пучка (Рис.1b). Если они падают каждый со своей стороны, как получается, что каждый из них все же появляется на тех самых сторонах? Ясно, что это может произойти, если они или отражаются, или превращаются. В квантовой физике мы должны иметь суперпозицию амплитуд для этих двух вероятностей. Единичные импульсы, амплитуды которых были отражены, получили путем сложения минусовых сигналов. Тем не менее, кажется, что эти два процесса исключают друг друга. Однако, это подходит только симметричного входного состояния. Для антисимметричного состояния эти две возможности получают другим связанным минусовым сигналом, и следовательно, они полностью интерферируют [15,16]. Это удовлетворяет прогнозированию фотонов 1 и 2 в антисимметричное состояние |Ψ|1 2 с целью помещения детекторов в каждый из выходов расщепителя и для одновременной регистрации (совпадений) [17-19]. Чтобы быть быть уверенным в том, что фотоны 1 и 2 неразличимы ко времени их прибытия, их генерирут, используя импульсный луч накачки, и направляют через фильтры с узкой полосой пропускания, дающими время когерентности много большее, чем длина импульса накачки [20]. В эксперименте импульсная накачка имела длительность 200 fs с частотой повторения 76 MHz. Анализ даун-конвертированных фотонов с длиной волны 788 nm при ширине щели 4 nm показал, что их время когерентности составляло 520 fs. Это следует понимать таким образом, что поскольку фотон 1 также продуцируется как часть спутанной пары, его партнер может служить в качестве индикатора возникновения фотона 1. Каким образом можно единственным экспериментом доказать, что неизвестное квантовое состояние может телепортироваться? Во-первых он должен в полной мере продемонстрировать, что телепортация работает в режиме установления единственных известных состояний, при которых любые другие состояния исчезают. Главное в поляризационных состояниях именно их две компоненты, и в принципе, мы можем узнавать горизонтальную или вертикальную поляризации по излучению источника. Но и это все еще не показывает, что телепортация работает для любой общей суперпозиции, поскольку эти два направления предпочтительны в наших экспериментах. Поэтому в первом эксперименте мы выбираем в качестве основы телепортации два состояния линейной поляризации -450 и +450, в которых уже имеется суперпозиция горизонтальной и вертикальной поляризации. Во-вторых, эксперимент должен доказать, что телепортация работает на суперпозициях этих двух основных состояний. Поэтому мы также демонстрируем телепортацию для круговой поляризации. Результаты В первом эксперименте фотон 1 был поляризован на 450. Телепортация срабатывала как только фотоны 1 и 2 определялись в состоянии |Ψ|1 2, которое наблюдается в 25% всех возможных случаев. Состояние |Ψ|1 2 определялось записью совпадения между двумя детекторами f1 и f2 , помещенными позади расщепителя пучка (Рис.1b). Если мы определили совпадение f1f2 (между детекторами f1 и f2), тогда фотон 3 также будет поляризован на 450 . Поляризация фотона 3 анализируется по прохождению его через поляризационный расщепитель пучка, разделяющий -450 и +450 поляризации. Для демонстрации телепортации (при выходе пучка из поляризующего расщепителя) подает звуковой сигнал (регистрация обнаружения) только детектор d2 на 450 и однократно детекторы f1 и f2. Детектор d1 при -450 на выходе из поляризационного расщепителя пучка не детектирует фотон. Поэтому запись трех-кратного совпадения d2f1f2 (+450 анализ) вместе с отсутствием трех-кратного совпадения d1f1f2 (-450 анализ) является доказательтвом того, что поляризованный фотон 1 телепортируется на фотон 3. Чтобы выполнить условие временного перекрытия, мы изменяем на небольших шагах время прибытия фотона 2, регулируя задержку между первой и второй даун-конверсией посредством обратноотражающего зеркала (Рис 1b). Таким путем мы сканируем район временного перекрытия на расщепителе пучка с тем, чтобы добиться наблюдения телепортации. Вне области телепортации каждый из фотонов 1 и 2 будут идти в f1 или f2 независимо друг от друга. Вероятность совпадения между f1 и f2 поэтому 50%, которая вдвое выше области телепортации. Фотон 3 не имеет определенной поляризации, будучи составной частью спутанной пары. Поэтому d1 и d2 оба имеют 50% шансов получить фотон 3. Этим и объясняется 25% вероятности для обоих случаев -450 анализа (совпадения d1f1f2) и для +450 анализа (совпадения d2f1f2) вне области телепортации. Рис.3. суммирует предсказания как функцию задержки. Успешность телепортации +450 поляризационного состояния доказывается также уменьшением до нуля в -450 анализе (Рис.3а) и неизменным состоянием для +450 анализа (Рис.3b). Теоретическое предсказание Рис.3 может быть точно истолковано, если учесть, что время задержки уменьшает на половину совпадения для двух детекторов в Белловских анализаторах состояний f1 и f2, в сравнении с областью вне телепортации. Поэтому, если поляризация фотона 3 никак не коррелирует с другими поляризациями, то это также указывает на то, что 3-х кратные совпадения уменьшаются вдвое. На правильную телепортацию состояний фотона указывает факт падения кривой до нуля на Рис.3а и плоская кривая на Рис. 3b. Заметим, что одинаково вероятна как продукция фотонов 1, 2 и 3, так и эмиссия одиночным источником двух пар даун-конвертированных фотонов. Хотя и нет фотона, пришедшего из первого источника (фотон1 отсутствует), вклад в трех-кратный показатель совпадений все еще будет значимым. Эти совпадения не имеют значения для телепортации и могут толковаться как показатель блокирования прохождения фотона 1. Вероятность случайных 2-х и 3-х кратных совпадений для этих процессов может рассчитываться из экспериментальных результатов. Экспериментально определенное значение для 3-х кратных случайных совпадений составляет 68%1%. На экспериментальных графах Рис.4 мы вычли опытным путем определенные случайные совпадения. Экспериментальные результаты для фотонов, поляризованных на +450, показаны в левой колонке Рис.4; Рис.4a и b должны быть сопоставлены с теоретическим предсказанием на Рис.3. Сильное уменьшение сигнала в -450 анализе и постоянный уровень сигнала в +450 анализе показывает, что фотон 3 поляризован вдоль направления (along the direction) фотона 1, и это подтверждает телепортацию. Таб. 1. Реальность телепортации в 3-х кратных совпадениях _________________________________________________ Поляризация⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕Реальность (Visibility) _________________________________________________ +450⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕0,630,02 _________________________________________________ -450⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕0,640,02 _________________________________________________ 00⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕0,660,02 _________________________________________________ 900⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕0,610,02 _________________________________________________ Круговая⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕⁕0,570,02 __________________________________________________________________________________________________ Результаты для фотона 1, поляризованного на -450, демонстрируют, что телепортация работает на полномасштабной базе поляризационных состояний (правая колонка Рис. 4). Мы провели дополнительные исследования, чтобы исключить любое классическое объяснение наших экспериментальных результатов и подтвердить их. В этой части работы мы телепортировали фотоны с линейной поляризацией 00 и 900, а также телепортировали фотоны с круговой поляризацией. Эти результаты суммированы в Табл.1, где мы демонстрируем реальность достоверность по 3-х кратным совпадениям, которые наблюдаются в ортогональном анализе при наведении поляризации. Как указывалось выше, значения достоверности получены после вычитания случайных 3-х кратных совпадений. Это может быть экспериментально исключено созданием условий для 3-х кратных совпадений при детекции фотона 4, который реально переходит в фотон 1 как в состояние одной частицы. Мы замерили это 4-х кратное совпадение в случае +450 и +900 поляризационных состояний, также как и для 2-х не ортогональных состояний. Следующие шаги В наших экспериментах мы использовали пары поляризованных спутанных фотонов, которые получаются за счет методов импульсной даун-конверсии и двухфотонной интерферометрии для перевода поляризационных состояний фотонов из одного состояния в другое. Но телепортация не означает, что могут работать только такие системы. Кроме пар спутанных фотонов или спутанных атомов в качестве работающих можно представить себе спутанные фотоны с атомами или фотоны с ионами и т.д. Затем можно допустить транспорт таких состояний, как например, быстрая декогеренция и коротко живущие частицы, на некоторые более стабильные системы. Это открывает перспективы квантовой памяти, где информация, пеносимая фотонами, запасается в ионных ловушках, тщательно экранированных от среды. В дальнейшем, используя очистку спутыванием [22] – метод улучшения качества спутывания при наличии нежелательной декогеренции в ходе запасания или передачи частиц через зашумленные каналы – становится возможным телепортировать квантовое состояние частицы в определенное место, даже если доступные квантовые каналы очень плохого качества и поэтому посылаемые частицы будут с большой вероятностью терять свое хрупкое квантовое состояние. Возможность защиты квантовых состояний в неблагоприятных условиях имеет огромное значение в области квантового компьютинга. Схема телепортации, может также использоваться для обеспечения связей между квантовыми компьютерами. Квантовая телепортация – это не только важный компонент в квантово-информационных задачах; она также позволяет ставить новые типы экспериментов и исследований в фундаментальной квантовой механике. Как любое квантовое состояние может быть телепортировано, так и, наоборот, оно может полностью стать неопределенным для частицы – члена спутанной пары. Аналогично передается состояние спутывания между частицами. Это позволяет нам осуществлять не только цепь передачи квантовых состояний на расстояние, где декогеренция уже устранена состоянием комплементарности (пар частиц, П.Г.), но также позволяет нам проверить теорему Белла для частиц, которые не воздействуют каким-либо образом на прошлое. Схема квантовой телепортации Это следующий шаг в будущих исследованиях квантовой механики. Последнее, но не менее важное. Споры относительно локальной точности понимания природы могут прекратиться, если будущие эксперименты используют генерацию спутывания более чем на двух пространственно разделенных частицах. Рис.1. Схема, показывающая принципы работы квантовой телепортации (a) и экспериментальная установка (b). a, Алиса имеет квантовую систему, частицу 1, в начальном состоянии, которое она хочет передать Бобу. Алиса и Боб также владеют дополнительной парой спутанных фотонов 2 и 3, излучаемых источником Эйнштейна-Подольского-Розена (EPR). Алиса затем проводит комбинированный (joint) Анализ Белловского Состояния (Bell-state measurement, BSM) начального фотона и одного из дополнительных, предназначенных также для перевода с спутанное состояние. После этого она посылает результат своего измерения как классическую информацию Бобу, он проводит унитарный перевод (U) на другой дополнительный фотон, принимающий при этом состояние частицы 1. b, Импульсное ультрафиолетовое излучение, проходящее через нелинейный кристалл, создает дополнительную пару фотонов 2 и 3. При обратном отражении, после его второго прохода через кристалл, создаются другие пары фотонов, один из которых будет переведен в начальное состояние фотона 1 телепортацией, другой же служит в качестве триггера, указывающего, что фотон должен быть телепортирован другим путем. Алиса затем отслеживает совпадения после расщепителя пучка (BS), где начальный фотон и один из дополнительных суперпозиционируются (superposed). Боб, после приема классической информации, которую Алиса получила по совпадениям отсчетов в детекторах f1 и f2, идентифицирующих Белловское состояние |Ψ-|1 2, знает, что его фотон 3 идентичен по начальному состоянию фотону 1. Боб может проверить это, используя поляризационный анализ с поляризующим расщепителем пучка (PBS) и детекторами d1 и d2. Детектор p дает информацию, что фотон 1 на другом пути (under way). http://www.wavegenetic.ru/Shema-kvantovoy-teleportatsii.png Фотоны, возникающие по типу II даун-конверсии (см. текст) на Рис. 2. Фотография перпендикулярна направлению их распространения. Фотоны продуцируются парными. Фотон (верхний круг) поляризован горизонтально, в то время как другой фотон (нижний круг) поляризован вертикально. В точках пересечений этих кругов поляризация фотонов неопределенна и все, что известно о них – это то, что они различаются и то, что такое их состояние есть результат их спутывания. Рис.3. Теоретическое предсказание вероятности 3-х кратного совпадения между двумя детекторами Белловского состояния (f1,f2) и один из них регистрирует состояние телепортации. Отметка телепортации состояния поляризации фотона в +450 является падение до нуля на нулевой задержке в 3-х кратном совпадении с детектором, анализирующим -450 (d1f1f2) (a) и постоянное значение для детектора, анализирующего +450 (d2f1f2) (b). Заштрихованная область обозначает границы телепортаци Рис.4. Экспериментальные результаты. Замер значений 3-х кратного совпадения d1f1f2 (-450) и d2f1f2 (+450) в случае телепортации состояния поляризации при +450 (a и b) или при -450 (c и d). Значения совпадений нанесены как функция запаздывания прихода фотонов 1 и 2 на расщепитель пучка Алисы (см. Рис.1b). 3-х кратное совпадение значений нанесено после вычитания случайного 3-х кратного вклада (см. текст). Эти данные, в сравнении с Рис.3, вместе со сходными результатами для других поляризаций (Табл.1) подтверждают телепортацию для произвольного состояния. 5 Рис.5. Значения 4-х кратного совпадения (без вычитания фона). Условия для 3-х кратных совпадений аналогичны Рис.4 при регистрации фотона 4 (см. Рис.1b) с вычитанием 3-х кратных фоновых зачений. a и b показывают значения 4-х кратного совпадения в случае телепортации +450 поляризационного состояния. Видно, что совпадения при такой поляризации телепортируемых фотонов получены без какого-либо вычитания фона и составляют 70%3%. Эти результаты по телепортации двух не ортогональных состояний доказывают, что мы получили телепортацию квантового состояния одиночного фотона. Experimental quantum teleportation. Dik Bouwmeester, Jian-Wei Pan, Klaus Mattle, Manfred Eibl, Harald Weinfurter & Anton Zeilinger. Nature, v.390, N11, pp.575-579, December 1997. (перевод П.П.Гаряева, ИПУ РАН)

Поделится в соц сетях

Квантовая телепортация между чипами и многофотонная запутанность в кремнии

Abstract

Интегрированная оптика обеспечивает универсальную платформу для обработки и передачи квантовой информации с помощью фотонов ^{1,2,3,4,5,6,7,8} . Для реализации квантовых протоколов требуется возможность генерировать несколько высококачественных одиночных фотонов и обрабатывать фотоны с помощью нескольких высокоточных операторов ^9,10,11 . Однако предыдущие экспериментальные демонстрации столкнулись с серьезными проблемами при реализации достаточно качественных многофотонных источников и многокубитных операторов в единой интегрированной системе 9.0005 4,5,6,7,8 , и полностью основанные на чипах реализации многокубитных квантовых задач остаются серьезной проблемой ^1,2,3 . Здесь мы сообщаем о демонстрации квантовой телепортации между чипами и настоящей многокомпонентной запутанности, основных функциональных возможностей квантовых технологий, на кремниево-фотонной схеме. Четыре одиночных фотона с высокой чистотой и неразличимостью производятся в массиве микрорезонаторных источников, не требующих какой-либо спектральной фильтрации. До четырех кубитов обрабатываются в перепрограммируемой линейно-оптической квантовой схеме, которая облегчает проекцию Белла и операцию синтеза. Генерация, обработка, прием и измерение многофотонных многокубитных состояний выполняются в кремниевых чипах микрометрового размера, изготовленных с помощью комплементарного процесса металл-оксид-полупроводник. Наша работа закладывает основу для крупномасштабных интегрированных фотонных квантовых технологий для связи и вычислений.

Это предварительный просмотр содержимого подписки, доступ через ваше учреждение

Соответствующие статьи

Статьи открытого доступа со ссылками на эту статью.

• Квантовые перспективы гибридного тонкопленочного ниобата лития на кремниевой фотонике

  • Джереми С. Адкок
  • и Юнхун Дин

  Границы оптоэлектроники
  Открытый доступ
  11 апреля 2022 г.

• Ультракомпактная нанофотоника: излучение света и манипулирование метаповерхностями

  • Ю-Хэн Хун
  • , Вэнь-Чэн Хсу
  •  … Хао-Чунг Куо

  Письма об исследованиях в области наноразмеров
  Открытый доступ
  02 апреля 2022 г.

• Программируемый квантовый процессор на основе кудита

  • Юйлинь Чи
  • , Цзешань Хуан
  •  … Цзяньвэй Ван

  Природные коммуникации
  Открытый доступ
  04 марта 2022 г.

Варианты доступа

Подписка на журнал

Получить полный доступ к журналу на 1 год

99,00 €

всего 8,25 € за выпуск

Подписаться

Расчет налогов будет завершен во время оформления заказа.

Купить артикул

Получите ограниченный по времени или полный доступ к статье на ReadCube.

32,00 $

Купить

Все цены указаны без учета стоимости.

Рис. 1: Многофотонные многокубитные квантовые устройства с микрорезонаторным усилением в кремнии. Рис. 2: Генерация пар фотонов в массиве микрорезонаторных нелинейных источников. Рис. 3: Программируемые линейно-оптические квантовые схемы для проекции Белла и операции синтеза. Рис. 4. Квантовая телепортация между чипами и многофотонная многокубитная запутанность.

Доступность данных

Данные, представленные на рис. 2–4 доступны в качестве исходных данных в дополнительной информации. Все другие данные, подтверждающие графики в этой статье и другие результаты этого исследования, можно получить у соответствующего автора по обоснованному запросу.

Наличие кода

Компьютерный код, используемый для анализа данных, можно получить по запросу у соответствующего автора.

История изменений

• 24 февраля 2020 г.

  Опубликовано исправление к этому документу: https://doi.org/10.1038/s41567-020-0840-x

Ссылки

1. Полити, А., Крайан, М. Дж., Рэрити, Дж. Г., Ю, С. и О’Брайен, Дж. Л. Квантовые схемы волновода «кремний на кремнии». Наука 320 , 646–649 (2008).

   ОБЪЯВЛЕНИЯ
   Статья

   Google ученый

2. «>

   Меткалф, Б. Дж. и др. Квантовая телепортация на фотонном чипе. Нац. Фотон. 8 , 770–774 (2014).

   ОБЪЯВЛЕНИЯ
   Статья

   Google ученый

3. Harris, N.C. et al. Моделирование квантового переноса в программируемом нанофотонном процессоре. Нац. Фотон. 11 , 447–452 (2017).

   ОБЪЯВЛЕНИЯ
   Статья

   Google ученый

4. Сильверстоун, Дж. В. и др. Запутанность кубитов между источниками пары фотонов кольцевого резонатора на кремниевом чипе. Нац. коммун. 6 , 7948 (2015).

   ОБЪЯВЛЕНИЯ
   Статья

   Google ученый

5. Reimer, C. et al. Генерация многофотонных запутанных квантовых состояний с помощью интегральных частотных гребенок. Наука 351 , 1176–1180 (2016).

   ОБЪЯВЛЕНИЯ
   Статья

   Google ученый

6. «>

   Ван, Дж. и др. Многомерная квантовая запутанность с крупномасштабной интегрированной оптикой. Наука 360 , 285–291 (2018).

   ОБЪЯВЛЕНИЯ
   MathSciNet
   Статья

   Google ученый

7. Чжан, М. и др. Генерация многофотонных запутанных квантовых состояний с помощью одной кремниевой нанопроволоки. Легкие науки. заявл. 8 , 41 (2019).

   ОБЪЯВЛЕНИЯ
   Статья

   Google ученый

8. Adcock, JC, Vigliar, C., Santagati, R., Siverstone, J. & Thompson, M. Программируемые состояния четырехфотонного графа на кремниевой микросхеме. Нац. коммун. 10 , 3528 (2019).

   ОБЪЯВЛЕНИЯ
   Статья

   Google ученый

9. Книл Э., Лафламм Р. и Милберн Г. Дж. Схема эффективных квантовых вычислений с линейной оптикой. Природа 409 , 46–52 (2000).

   ОБЪЯВЛЕНИЯ
   Статья

   Google ученый

10. Нильсен, М. А. Оптические квантовые вычисления с использованием кластерных состояний. Физ. Преподобный Летт. 93 , 040503 (2004).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

11. Пирандола С., Эйзерт Дж., Видбрук К., Фурусава А. и Браунштейн С.Л. Достижения в области квантовой телепортации. Нац. Фотон. 9 , 641–652 (2015).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

12. Валиварти, Р. и др. Квантовая телепортация по оптоволоконной сети города. Нац. Фотон. 10 , 676–680 (2016).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

13. Рен, Ж.-Г. и другие. Квантовая телепортация земля-спутник. Природа 549 , 70–73 (2017).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

14. Готтесман Д. и Чуанг И. Л. Демонстрация жизнеспособности универсальных квантовых вычислений с использованием телепортации и операций с одним кубитом. Природа 402 , 390–393 (1999).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

15. Венер, С., Элкусс, Д. и Хэнсон, Р. Квантовый интернет: взгляд на будущее. Наука 362 , eaam9288 (2018).

    ОБЪЯВЛЕНИЯ
    MathSciNet
    Статья

    Google ученый

16. Wang, J. et al. Интегрированные фотонные квантовые технологии. Нац. Фотон. https://doi.org/10.1038/s41566-019-0532-1 (2019).

17. Грайс В., У’Рен А. и Уолмсли И. Устранение частотных и пространственно-временных корреляций в многофотонных состояниях. Физ. Ред. A 64 , 063815 (2001 г.).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

18. Paesani, S. et al. Генерация и выборка квантовых состояний света в кремниевом чипе. Нац. физ. 15 , 925–929 (2019).

    Артикул

    Google ученый

19. Вернон З. и др. По-настоящему незапутанные пары фотонов без спектральной фильтрации. Опц. лат. 42 , 3638–3641 (2017).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

20. Вернон, З., Лисцидини, М. и Сайп, Дж. Э. Бесплатных обедов не будет: компромисс между скоростью и эффективностью заявленных источников одиночных фотонов на основе микрорезонаторов. Опц. лат. 41 , 788–791 (2016).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

21. «>

    Грассани, Д. и др. Интегрированный кремниевый источник фотонов, запутанных во времени и энергии, микрометрового масштаба. Optica 2 , 88–94 (2015).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

22. Фарук, И. И., Синклер, Г., Бонно, Д., Рэрити, Дж. Г. и Томпсон, М. Г. Квантовая интерференция на кристалле с заявленными фотонами от двух независимых микрокольцевых резонаторных источников в кремниевой фотонике. Опц. Экспресс 26 , 20379–20395 (2018).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

23. Бергамаско, Н., Менотти, М., Сайп, Дж. Э. и Лискидини, М. Генерация закодированных по пути состояний Гринбергера-Хорна-Цайлингера. Физ. Преподобный заявл. 8 , 054014 (2017).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

24. «>

    Дин, Ю., Пешере, К., Оу, Х. и Ивинд, К. Полностью протравленный аподизированный решетчатый ответвитель на платформе КНИ с эффективностью связи -0,58 дБ. Опц. лат. 39 , 5348–5350 (2014).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

25. Wang, J. et al. Квантовое фотонное соединение между чипами за счет взаимного преобразования поляризации пути. Optica 3 , 407–413 (2016).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

26. Гринбергер Д. М., Хорн М. А., Шимони А. и Цайлингер А. Теорема Белла без неравенств. 900:31 утра. Дж. Физ. 58 , 1131–1143 (1990).

    ОБЪЯВЛЕНИЯ
    MathSciNet
    Статья

    Google ученый

27. Буреннан, М. и др. Экспериментальное обнаружение многочастичной запутанности с помощью операторов-свидетелей. Физ. Преподобный Летт. 92 , 087902 (2004 г.). (8).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

28. млн лет, З.-Х. и другие. Мера подлинной многодольной запутанности с вычислимыми нижними оценками. Физ. Ред. A 83 , 062325 (2011 г.).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

29. Бавареско, Дж. и др. Измерений в двух базах достаточно для подтверждения многомерной запутанности. Нац. физ. 14 , 1032–1037 (2018).

    Артикул

    Google ученый

30. Канеда, Ф. и Пол, К. Высокоэффективная однофотонная генерация с помощью широкомасштабного активного мультиплексирования во времени. Науч. Доп. 5 , eaaw8586 (2019).

    ОБЪЯВЛЕНИЯ
    Статья

    Google ученый

31. «>

    Тот, Г. и Апелланиз, И. Квантовая метрология с точки зрения квантовой информатики. J. Phys. А 47 , 424006 (2014).

    ОБЪЯВЛЕНИЯ
    MathSciNet
    Статья

    Google ученый

Ссылки на скачивание

Благодарности

Мы благодарим Г.Дж. Mendoza и D. Bonneau за полезные обсуждения. Мы благодарим У. А. Мюррея, М. Лутита, Э. Джонстона, Дж. У. Сильверстоуну и Л. Клингу за помощь в проведении экспериментов. Мы признательны за поддержку со стороны Национальной ключевой программы исследований и разработок Китая (2019YFA0308700, 2018YFB1107205), Фонда естественных наук Китая (№№ 61975001, 61590933, 11527901 и 11825402), Пекинского фонда естественных наук (Z1^{), Пекинской академии квантовых информационных наук (Y18G21 ) и Ключевая программа исследований и разработок провинции Гуандун (2018B030329001). Д.Л., И.И.Ф., Дж.Г.Р. и М.Г.Т. выражаем благодарность Британскому центру квантовых технологий за поддержку квантовых коммуникационных технологий, финансируемых EPSRC: EP/M013472/1; программа гранта нет. ЕР/L024020/1. Ю.Д. выражает благодарность за поддержку со стороны Дании SPOC (DNRF123), Villum Fonden, QUANPIC (00025298). И.И.Ф. выражает благодарность Сети первоначального обучения Марии Кюри FP7 PICQUE (608062). М.Х. выражает благодарность Австрийскому научному фонду (FWF) в рамках проекта START (Y879-N27) и совместного чешско-австрийского проекта MultiQUEST (I 3053-N27, GF17-33780L). М.М. выражает благодарность Исследовательскому совету по инженерным и физическим наукам (EPSRC; EP/P024114/1) и совместному фонду QuantERA ERA-NET (проект FWF I3773-N36). К.Р. признает поддержку от QuantERA. Джей Ло отмечает награду Королевского общества Вольфсона за заслуги и кафедру Королевской инженерной академии в области новых технологий. М.Г.Т. признает поддержку стартового гранта Европейского исследовательского совета (ERC) (ERC-2014-STG 640079) и стипендию EPSRC для ранней карьеры (EP/K033085/1).}

Информация об авторе

Примечания автора

1. Эти авторы внесли равный вклад: Daniel Llewellyn, Yunhong Ding, Imad I. Faruque.

Авторы и филиалы

1. Лаборатория квантовых инженерных технологий, Физическая лаборатория Х. Х. Уиллса и факультет электротехники, Бристольский университет, Бристоль, Великобритания

   Даниэль Ллевеллин, Имад И. Фарук, Стефано Паэсани, , Гэри Ф. Синклер, Джон Г. Рэрити, Цзяньвэй Ван и Марк Г. Томпсон

2. Кафедра фотоники, Датский технический университет, Люнгбю, Дания

   Юнхонг Дин, Дэвид Бакко, Карстен Роттвитт и Лейф К. Оксенлоу

3. Центр кремниевой фотоники для оптических коммуникаций (SPOC), Дания, Lyngby, Дания

   Yunhong Ding, Davide Bacco, Karsten Rottwitt и Leif K. Oxenlowe

4. Государственная ключевая лаборатория мезоскопической физики, Школа физики, Пекинский университет, Пекин, Китай

   Yan-Jun Qian, Yan Li, Yun-Feng Xiao, Qihuang Gong и Jianwei Wang

5. Frontiers Science Center for Nano-optoelectronics & Collaborative Innovation Center of Quantum Matter, Пекинский университет, Пекин, Китай

   Yan Li, Юн-Фэн Сяо, Цихуан Гонг и Цзяньвэй Ван

6. Пекинская академия квантовых информационных наук, Пекин, Китай

   Юн-Фэн Сяо, Цихуан Гонг и Цзяньвэй Ван

7. Институт квантовой информации и оптики (QIO) , Австрийская академия наук, Вена, Австрия

   Маркус Хубер

8. Институт фотоники и квантовых наук (IPaQS), Университет Хериот-Ватт, Эдинбург, Великобритания

   Мехул Малик

9. Государственная ключевая лаборатория оптоэлектронных материалов и технологий, Школа физики им. Университет Сена, Гуанчжоу, Китай

   Сяоци Чжоу

10. Факультет физики, Университет Западной Австралии, Перт, Западная Австралия, Австралия

    Джереми Л. О’Брайен

Авторы

1. Daniel Llewellyn

   Просмотр публикаций автора

   Вы также можете искать этого автора в
   PubMed Google Scholar

2. Yunhong Ding

   Просмотр публикаций автора

   Вы также можете искать этого автора в
   PubMed Google Scholar

3. Imad I. Faruque

   Просмотр публикаций автора

   Вы также можете искать этого автора в
   PubMed Google Академия

4. Stefano Paesani

   Посмотреть публикации автора

   Вы также можете искать этого автора в
   PubMed Google Scholar

5. Davide Bacco

   Просмотр публикаций автора

   Вы также можете искать этого автора в
   PubMed Google Scholar

6. Raffaele Santagati

   Просмотр публикаций автора

   Вы также можете искать этого автора в
   PubMed Google Scholar

7. Yan-Jun Qian

   Посмотреть публикации автора

   Вы также можете искать этого автора в
   PubMed Google Scholar

8. Yan Li

   Просмотр публикаций автора

   Вы также можете искать этого автора в
   PubMed Google Scholar

9. Yun-Feng Xiao

   Просмотр публикаций автора

   Вы также можете искать этого автора в
   PubMed Google Scholar

10. Маркус Хубер

    Просмотр публикаций автора

    Вы также можете искать этого автора в
    PubMed Google Scholar

11. Mehul Malik

    Просмотр публикаций автора

    Вы также можете искать этого автора в
    PubMed Google Scholar

12. Gary F. Sinclair

    Просмотр публикаций автора

    Вы также можете искать этого автора в
    PubMed Google Scholar

13. Xiaoqi Zhou

    Посмотреть публикации автора

    Вы также можете искать этого автора в
    PubMed Google Scholar

14. Karsten Rottwitt

    Просмотр публикаций автора

    Вы также можете искать этого автора в
    PubMed Google Scholar

15. Jeremy L. O’Brien

    Просмотр публикаций автора

    Вы также можете искать этого автора в
    PubMed Google Scholar

16. John G. Rarity

    Посмотреть публикации автора

    Вы также можете искать этого автора в
    PubMed Google Scholar

17. Qihuang Gong

    Просмотр публикаций автора

    Вы также можете искать этого автора в
    PubMed Google Scholar

18. Leif K. Oxenlowe

    Просмотр публикаций автора

    Вы также можете искать этого автора в
    PubMed Google Scholar

19. Jianwei Wang

    Просмотр публикаций автора

    Вы также можете искать этого автора в
    PubMed Google Академия

20. Mark G. Thompson

    Просмотр публикаций автора

    Вы также можете искать этого автора в
    PubMed Google Scholar

Contributions

Все авторы участвовали в обсуждении и развитии проекта. Дж. В. разработал концепцию эксперимента. Ю.Д. спроектировал и изготовил устройство. Д.Л., Ю.Д., И.И.Ф., Дж.В., С.П., Д.Б. и Р.С. провел эксперимент. J.W., D.L., Y.D., I.I.F., Y.-J.Q., Y.L., Y.-F.X., M.H., M.M., G.F.S. и Х.З. провел теоретический анализ. К.Р., Дж.Л.О., Дж.Г.Р., К.Г., Л.К.О., Ю.Д., Дж.В. и М.Г.Т. руководил проектом. Рукопись написана J.W., D.L., Y.D. и I.I.F., при участии всех других авторов.

Автор, ответственный за переписку

Цзяньвэй Ван.

Декларации этики

Конкурирующие интересы

M.T. участвует в разработке квантово-фотонных технологий в корпорации PsiQuantum.

Дополнительная информация

Примечание издателя Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и ​​институциональной принадлежности.

Дополнительная информация

Дополнительная информация

Дополнительная информация Рис. 1–12 и обсуждение.

Исходные данные

Исходные данные рис. 2

Исходные данные рис. 2

Исходные данные рис. 3

Исходные данные рис. 3

Исходные данные рис.

Права и разрешения

Перепечатка и разрешения

Об этой статье

Дополнительная литература

• Ультракомпактная нанофотоника: излучение света и манипулирование метаповерхностями

  • Ю-Хэн Хун
  • Вэнь-Чэн Хсу
  • Хао-Чунг Куо

  Письма об исследованиях в области наноразмеров (2022)

• Квантовая интерференция идентичных фотонов от удаленных квантовых точек GaAs

  • Лян Чжай
  • Джанг Н. Нгуен
  • Ричард Дж. Уорбертон

  Природа Нанотехнологии (2022)

• Квантовая телепортация одним классическим битом

  • Абхишек Парах

  Научные отчеты (2022)

• Топологически защищенные излучатели квантовой запутанности

  • Тяньсян Дай
  • Ютянь АО
  • Цзяньвэй Ван

  Природа Фотоника (2022)

• Потенциал и глобальные перспективы интегрированной фотоники для квантовых технологий

  • Эмануэле Пелуччи
  • Йоргос Фагас
  • Клаус Д. Йонс

  Nature Reviews Physics (2022)

Элегантная квантовая телепортация с помощью всего одного фотона

Ученым из MPQ впервые удалось телепортировать квантовую информацию, закодированную в атомном кубите, в лабораторию на расстоянии 60 метров, используя всего один фотон в качестве ресурса.

У большинства людей телепортация ассоциируется со «Звездным путем», где одним нажатием кнопки материя мгновенно перемещается из одного места в другое. Хотя эта фикция физически невозможна, квантовая телепортация описывает совершенно другую, четкую и, тем не менее, значительно более реалистичную процедуру: передачу квантовой информации, такой как спиновое состояние атома, другому удаленному атому. Таким образом, квантовая телепортация не переносит материю — атомы остаются на своих местах — а только хранящуюся в них информацию.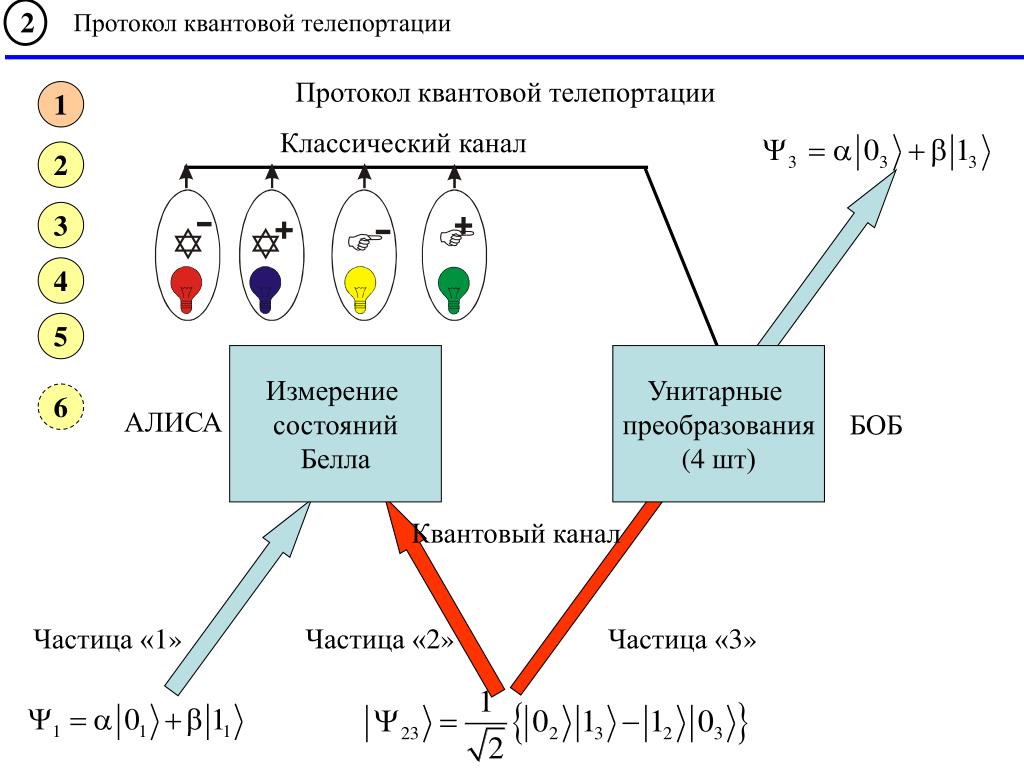 Ученые из Института квантовой оптики Макса Планка (MPQ) разработали новый и простой метод для этого процесса, который требует только одного фотона в качестве ресурса для передачи. Работа опубликована в журнале Physical Review Letters.

Для передачи квантовой информации на большие расстояния не обязательно нужна квантовая телепортация. Передача может просто происходить следующим образом: кубит — небольшая квантовая информационная память — кодируется в направлении колебания фотона. Затем фотон проходит через оптическое волокно и, таким образом, в принципе может передавать квантовую информацию туда и обратно между двумя удаленными точками. Этот процесс сам по себе очень прост, но у него есть проблема: фотоны очень хрупкие и легко теряются по пути, а значит, исчезает и хранимая в них квантовая информация.

«В начале 1990-х Шарль Беннет, Жиль Брассар и их коллеги предложили элегантное решение этой проблемы, позволяющее передавать квантовую информацию без потерь: квантовую телепортацию», — объясняет профессор Герхард Ремпе, директор группы квантовой динамики в Макс. Институт квантовой оптики им. Планка. «Но квантовая телепортация сложна», добавляет он, «она требует, чтобы у вас были две запутанные частицы заранее, которые служат ресурсом для телепортации. Этот ресурс обычно трудно произвести и требует усилий.» Таким образом, Стефан Вельте, Стефан Лангенфельд и их коллеги из группы профессора Ремпе задались вопросом, как можно было бы реализовать квантовую телепортацию с более доступным ресурсом, а именно с одним-единственным фотоном в качестве вспомогательной частицы.

Совершенно новый метод квантовой телепортации

Для этой цели ученые использовали одиночные охлажденные атомы и принципы резонаторной квантовой электродинамики и продемонстрировали совершенно новый метод квантовой телепортации. Этот метод позволяет одному фотону телепортировать спиновое состояние одного атомного кубита ко второму атому на расстоянии 60 м без потери квантовой информации. Ученые реализовали телепортацию следующим образом (см. рисунок): Есть кубит, который нужно телепортировать. Этот кубит закодирован в одном атоме (а), пойманном в оптический резонатор. В 60 метрах в соседней лаборатории есть второй атом (б), тоже в резонаторе. Цель состоит в том, чтобы передать информацию от одного атома (а) к другому (б). Для этого ученые последовательно отражают один фотон от двух резонаторов, в которых находятся два атома. Фотон летит по оптоволокну, соединенному с двумя резонаторами. Затем измеряются фотон и спиновое состояние атома (а). В конце концов, сигнал обратной связи, основанный на двух измерениях, отправляется на атом (b). Этот сигнал обратной связи представляет собой лазерный импульс, который облучается атомом (b) и свойства которого зависят от измерения фотона и атома (a).

Этот протокол позволяет телепортировать информацию от одного атома к другому. Запутывание двух атомов происходит без дополнительных усилий, так сказать, как естественный побочный эффект.

Концептуально просто, но очень элегантно

Квантовая телепортация — явление не новое; это было реализовано экспериментально с конца 1990-х годов. Однако в этом эксперименте впервые удалось осуществить квантовую телепортацию, используя в качестве ресурса только один-единственный фотон. Единственный фотон — это абсолютный минимум ресурсов, поэтому передача информации теперь может осуществляться простейшими средствами. «Это концептуально простой и очень элегантный эксперимент, который также отлично работает на практике», — радостно говорит исследователь с докторской степенью Стефан Велте.

Особое значение имеет то, что используемые физические принципы применимы на многих экспериментальных платформах. «Таким образом, продемонстрированный протокол можно также реализовать с помощью масштабируемых твердотельных систем, которые в настоящее время разрабатываются во многих лабораториях по всему миру», — добавляет аспирант Стефан Лангенфельд. Эта платформа может обеспечить массовое и экономичное производство систем атомных резонаторов, что будет иметь большое значение для последующих приложений в крупномасштабной квантовой сети.

Теперь ученые планируют расширить эксперимент. «Далее мы хотим захватить несколько атомов в каждый из резонаторов, которые затем все могут взять на себя роль кубитов и сформировать универсальный узел в квантовой сети», — говорит исследователь с докторской степенью Эмануэле Дистанте, который также участвовал в эксперименте. . В сети, состоящей из множества таких узлов, новый протокол телепортации представляет собой чрезвычайно полезный инструмент для обмена квантовой информацией между всеми ее узлами.

Квантовая телепортация распространяется за пределы соседних узлов — Physics World

Идет телепортация Исследователи QuTech в Нидерландах проводят эксперимент по квантовой телепортации. (Предоставлено QuTech)

Физики из Нидерландов впервые продемонстрировали, что квантовая информация может надежно телепортироваться между узлами сети, которые не связаны друг с другом напрямую. По словам исследователей, создавших первую в мире квантовую сеть с тремя узлами в QuTech (сотрудничество Делфтского технологического университета и TNO) в 2021 году, последняя работа знаменует собой еще один шаг на пути к масштабируемому квантовому Интернету.

Квантовые сети предлагают сверхзащищенный способ передачи информации между различными точками или узлами. Хотя эти узлы могут быть соединены с помощью обычных оптических волокон, потери фотонов внутри волокон ограничивают качество или точность соединения: когда фотон теряется, его квантовая информация также теряется. Использование квантовой запутанности для телепортации информации напрямую с одного узла на другой устраняет этот механизм потерь, что делает его желательным для будущего квантового Интернета.

Сеть с тремя узлами, продемонстрированная на QuTech в 2021 году, использовала квантовые биты или кубиты, сделанные из центров азотных вакансий (NV), которые являются дефектами в алмазной решетке атомов углерода. Каждый узел содержал кубит связи, а один узел также включал кубит памяти (сделанный из соседнего атома углерода), который мог хранить квантовую информацию узла. Таким образом, строительные блоки для запутывания трех узлов уже присутствовали, но система была далека от надежной в постоянном телепортировании.

Квантовая телепортация

Первым шагом в телепортации квантовой информации от отправителя к получателю является установление запутанности между их соответствующими кубитами. Выполнение так называемого измерения состояния Белла (BSM) на кубите-отправителе приводит к телепортации его квантового состояния — это означает, что он исчезает из узла-отправителя и появляется в зашифрованном виде в узле-получателе. Затем квантовое состояние можно расшифровать, используя результат BSM, который отправляется получателю по классическому каналу (например, по оптоволокну).

Раньше это делалось только с двумя соседними сетевыми точками, традиционно называемыми Алисой и Бобом. Добавление третьей точки, Чарли, — непростая задача, поскольку запутанность между Алисой и Чарли должна быть создана через Боба, промежуточного узла. Также требуется высокая точность, чтобы телепортация работала.

Этапы оптимизации

Чтобы добиться такой высокой точности, исследователи QuTech выполнили несколько обновлений. В их предыдущей системе «предвещающие» сигналы, указывающие на запутывание, исходили от тех же фотодетекторов, которые регистрировали фотоны, используемые для запутывания. Это, однако, может привести к ложным предупреждающим сигналам из-за различных нежелательных процессов, генерирующих второй фотон. Чтобы избежать этого, команда настроила дополнительный путь обнаружения, который помечает ложные предвестники, ловя второй фотон.

Кубиты вблизи: центры азотных вакансий в образце алмаза используются в качестве кубитов в эксперименте по телепортации. (Предоставлено QuTech)

Еще одна проблема, которую решили решить исследователи, — это спектральная диффузия, из-за которой кубиты выходят из фазы, снижая точность передачи. Этот процесс оказывает большее влияние на фотоны, испускаемые в более позднее время, поэтому команда сократила окно обнаружения.

Последний набор улучшений касается памяти, используемой для хранения квантовой информации. Во-первых, команда защитила кубит памяти от взаимодействия с соседними ядерными спинами. Для этого они интегрировали импульс магнитного поля в запутывающую последовательность, которая переворачивает кубит памяти через заданные промежутки времени, тем самым усредняя эффекты этих нежелательных взаимодействий. Они также улучшили свою способность читать кубит памяти. Поскольку одно из состояний кубита памяти имеет более благоприятную точность, его считывание не является симметричным. Повторяя процесс считывания, команда отфильтровала «плохие» показания, в конечном итоге повысив точность.

Поднимите меня по лучу

После этих улучшений исследователи смогли телепортировать квантовую информацию между несмежными узлами Чарли и Алисы. Во-первых, они перепутали кубит Алисы и Чарли через кубит Боба. Затем Чарли сохранил часть запутанного состояния в своем кубите памяти и подготовил квантовое состояние для телепортации. Применение BSM к Чарли телепортирует состояние к Алисе. Затем исследователи отправили результат BSM Алисе и получили состояние с точностью 71% — выше классической границы ⅔, доказав, что телепортация прошла успешно.

Рональд Хэнсон, исследователь QuTech, руководивший исследованием, говорит, что следующим шагом команды будет увеличение количества кубитов памяти, что позволит запускать более сложные протоколы. Другая цель состоит в том, чтобы заставить технологию работать за пределами лабораторной среды, например, используя уже развернутые оптические волокна в реальной сети. «Мы также сотрудничаем с учеными-компьютерщиками для разработки стека управления квантовой сетью — аналогичного стека уровней управления, которые в настоящее время управляют Интернетом, который мы все используем сегодня», — говорит он.0767 Мир физики.

Хьюг де Ридматтен, исследователь ICFO в Барселоне, Испания, который не участвовал в исследовании, говорит, что квантовая телепортация через несоседние узлы является важной вехой. По его мнению, самым большим достижением команды было объединение нескольких сложных экспериментов, каждый из которых необходимо полностью оптимизировать для достижения требуемой точности квантовой телепортации, в одну демонстрацию.