Содержание
происхождение и судьба Вселенной», Стивен Хокинг – ЛитРес
Перевод оригинального издания:
Stephen Hawking
The Theory of Everything
Печатается с разрешения Waterside Productions Inc и литературного агентства «Синопсис».
Оригинальное издание опубликовано Phoenix Books and Audio.
© Phoenix Books and Audio, 2006
© ООО «Издательство АСТ», 2017 (перевод на русский язык)
Введение
В этой серии лекций я постараюсь в общих чертах рассказать о наших представлениях об истории Вселенной от Большого взрыва до образования черных дыр. Первая лекция посвящена краткому обзору идей о строении Вселенной, которых придерживались в прошлом, и рассказу о том, как была построена современная картина мира. Эту часть можно назвать историей развития представлений об истории Вселенной.
Во второй лекции я опишу, как теории гравитации Ньютона и Эйнштейна привели к пониманию того, что Вселенная не может быть неизменной – она должна либо расширяться, либо сжиматься. Из этого, в свою очередь, следует вывод, что в какое-то время в интервале от 10 до 20 млрд лет назад плотность Вселенной была бесконечной. Эта точка на оси времени называется Большим взрывом. По-видимому, этот момент и был началом существования Вселенной.
Из этого, в свою очередь, следует вывод, что в какое-то время в интервале от 10 до 20 млрд лет назад плотность Вселенной была бесконечной. Эта точка на оси времени называется Большим взрывом. По-видимому, этот момент и был началом существования Вселенной.
В третьей лекции я расскажу о черных дырах. Они образуются, когда массивная звезда или более крупное космическое тело коллапсирует под действием собственной гравитации. Согласно общей теории относительности Эйнштейна, каждый, кто окажется достаточно глуп, чтобы угодить в черную дыру, останется там навсегда. Никто не сможет оттуда выбраться. В сингулярности истории существования любого объекта приходит конец. Однако общая теория относительности – это теория классическая, то есть в ней не учитывается квантовомеханический принцип неопределенности.
В четвертой лекции я объясню, как квантовая механика позволяет энергии ускользать из черной дыры. Черные дыры не так уж черны, «как их малюют».
В пятой лекции я расскажу о применении идей квантовой механики к решению вопросов, связанных с Большим взрывом и происхождением Вселенной.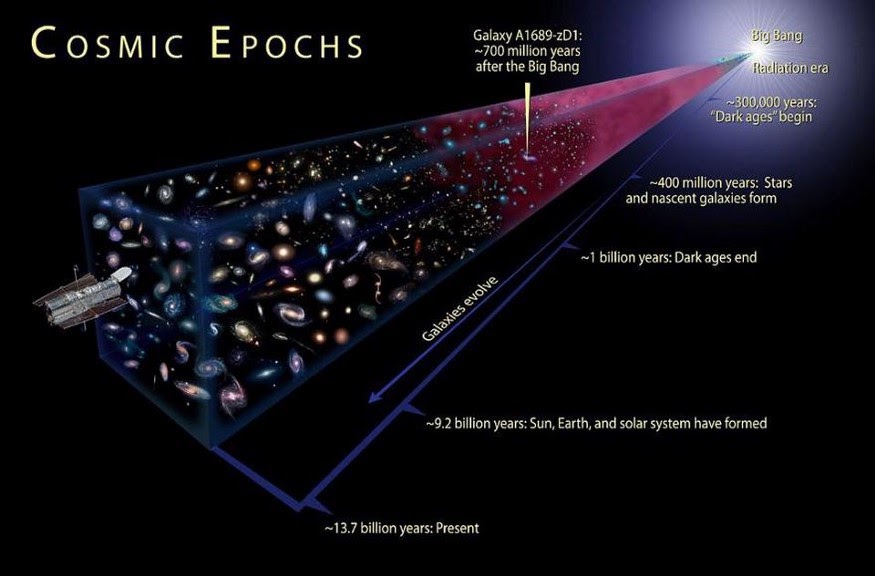 Это подведет нас к пониманию того, что пространство-время может быть конечным, но не иметь границы или края. Это напоминает поверхность Земли, но с добавлением еще двух измерений.
Это подведет нас к пониманию того, что пространство-время может быть конечным, но не иметь границы или края. Это напоминает поверхность Земли, но с добавлением еще двух измерений.
В шестой лекции я покажу, как на основе этого нового предположения о границе можно объяснить, почему прошлое так сильно отличается от будущего, хотя законы физики симметричны относительно времени.
Наконец, в седьмой лекции я расскажу о попытках сформулировать единую теорию, охватывающую квантовую механику, гравитацию и все остальные физические взаимодействия. Если нам это удастся, мы действительно сможем понять Вселенную и свое место в ней.
Лекция первая
Представления о Вселенной
Еще в 340 г. до н. э. Аристотель в своем трактате «О небе» сформулировал два веских довода в пользу того, что Земля имеет форму шара, а не является плоской, как тарелка. Во-первых, он понял, что лунные затмения вызваны прохождением Земли между Солнцем и Луной. Тень Земли на Луне – всегда круглая, а это возможно, только если Земля имеет сферическую форму.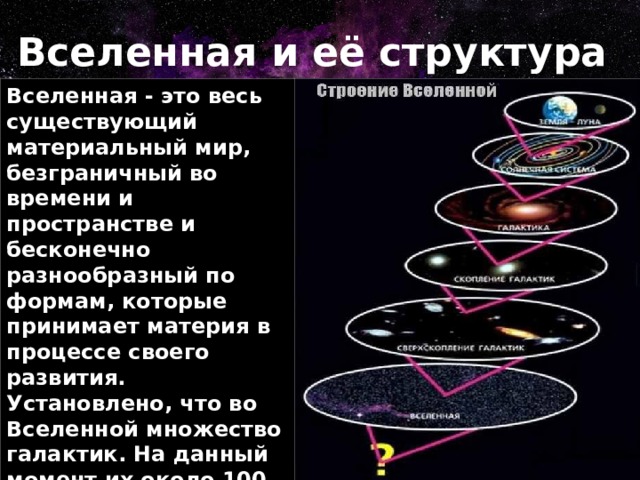 Если бы Земля представляла собой плоский диск, тень была бы вытянутой и имела бы форму эллипса, за исключением тех случаев, когда в момент затмения Солнце находится точно над центром диска.
Если бы Земля представляла собой плоский диск, тень была бы вытянутой и имела бы форму эллипса, за исключением тех случаев, когда в момент затмения Солнце находится точно над центром диска.
Во-вторых, из опыта своих путешествий греки знали, что в южных районах Полярная звезда находится ниже над горизонтом, чем в более северных. Опираясь на разницу видимых положений Полярной звезды в Египте и Греции, Аристотель даже приводит оценку длины окружности Земли – 400 тыс. стадиев. Чему равен один стадий – точно не известно (возможно, около 180 метров). Тогда оценка Аристотеля почти в два раза превосходит значение, принятое в настоящее время.
У древних греков был еще и третий аргумент в пользу того, что Земля должна иметь форму шара: иначе почему на горизонте сначала появляются паруса приближающегося корабля и только потом становится виден его корпус? Аристотель думал, что Земля неподвижна, а Солнце, Луна, планеты и звезды движутся по круговым орбитам вокруг нее. Он так считал, поскольку в силу мистических соображений был убежден, что Земля – центр Вселенной, а круговое движение – самое совершенное.
Аристотель считал, что Земля неподвижна, а Солнце, Луна, планеты и звезды движутся по круговым орбитам вокруг нее.
В I веке н. э. эта идея была развита Птолемеем в целостную космологическую модель. Земля располагается в центре, ее окружают восемь сфер, несущих на себе Луну, Солнце, звезды и пять планет, известных в то время: Меркурий, Венеру, Марс, Юпитер и Сатурн. Планеты движутся по окружностям меньших радиусов, которые связаны с соответствующими сферами. Это требовалось, чтобы объяснить их достаточно сложные наблюдаемые траектории движения по небу. На внешней сфере расположены так называемые неподвижные звезды, которые сохраняют свои положения относительно друг друга, но все вместе совершают круговое движение по небу. Что находится за пределами внешней сферы – оставалось неясным, но эта часть Вселенной, несомненно, была недоступна для наблюдений.
Модель Птолемея давала возможность достаточно точно предсказывать положения небесных тел на небе. Но для этого Птолемею пришлось допустить, что иногда Луна подходит вдвое ближе к Земле, чем в другие моменты своего движения по предсказанной траектории. Это означало, что периодически Луна должна казаться вдвое больше обычного. Птолемей знал об этом недостатке, но, несмотря на это, его модель была принята большинством, хотя и не всеми. Она получила одобрение христианской церкви, как картина мира, согласующаяся со Священным писанием. Ведь эта модель обладала огромным преимуществом, поскольку оставляла за сферой неподвижных звезд достаточно места для рая и ада.
Но для этого Птолемею пришлось допустить, что иногда Луна подходит вдвое ближе к Земле, чем в другие моменты своего движения по предсказанной траектории. Это означало, что периодически Луна должна казаться вдвое больше обычного. Птолемей знал об этом недостатке, но, несмотря на это, его модель была принята большинством, хотя и не всеми. Она получила одобрение христианской церкви, как картина мира, согласующаяся со Священным писанием. Ведь эта модель обладала огромным преимуществом, поскольку оставляла за сферой неподвижных звезд достаточно места для рая и ада.
Старинный рисунок, на котором изображены разные космологические модели, объяснявшие движение планет. На центральной схеме представлена гелиоцентрическая (в центре находится Солнце) модель движения шести известных в то время планет, их спутников и других небесных тел, обращающихся вокруг Солнца. Со второго века доминирующей моделью стала геоцентрическая (в центре находится Земля) система Птолемея (вверху слева). На смену ей пришла гелиоцентрическая система Коперника, опубликованная в 1543 г. (внизу справа). В египетской модели (внизу слева) и модели Тихо Браге (вверху справа) предпринимались попытки сохранить представление о неподвижной Земле как центре Вселенной. Подробные сведения об орбитах планет приведены слева и справа.
(внизу справа). В египетской модели (внизу слева) и модели Тихо Браге (вверху справа) предпринимались попытки сохранить представление о неподвижной Земле как центре Вселенной. Подробные сведения об орбитах планет приведены слева и справа.
Из «Иллюстрированного атласа» Иоганна Георга Хека, 1860 г.
Однако в 1514 г. польский священник Николай Коперник предложил гораздо более простую модель. Сначала, опасаясь обвинений в ереси, он опубликовал свою модель анонимно. Он считал, что в центре находится неподвижное Солнце, а Земля и планеты движутся вокруг него по круговым орбитам. К несчастью для Коперника, прошло почти сто лет, прежде чем его идеи были приняты всерьез. Тогда два астронома – немец Иоганн Кеплер и итальянец Галилео Галилей – публично выступили в поддержку теории Коперника несмотря на то, что орбиты, предсказанные на основе этой теории, несколько отличались от наблюдаемых. Конец господству теории Аристотеля-Птолемея был положен в 1609 г., когда Галилео Галилей начал изучать ночное небо с помощью недавно изобретенного телескопа.
В 1609 г. Галилео Галилей начал изучать ночное небо с помощью недавно изобретенного телескопа.
Наблюдая Юпитер, Галилей заметил, что планету сопровождают несколько небольших спутников (лун), которые обращаются вокруг нее. Это означало, что не все небесные тела должны обращаться вокруг Земли, как думали Аристотель и Птолемей. Конечно, по-прежнему можно было считать, что Земля неподвижна и находится в центре Вселенной, а спутники Юпитера движутся по крайне сложным траекториям вокруг Земли, так что создается видимость их обращения вокруг Юпитера. Однако теория Коперника была гораздо проще.
В это же время Кеплер развил теорию Коперника, предположив, что планеты движутся не по круговым орбитам, а по эллиптическим. Теперь предсказания теории окончательно совпали с наблюдениями. Что касается Кеплера, эллиптические орбиты были лишь искусственной гипотезой, причем весьма досадной, поскольку эллипс считался менее совершенной фигурой, чем круг. Обнаружив (почти случайно), что эллиптические орбиты хорошо соответствуют наблюдениям, он не мог согласовать это со своей идеей о том, что планеты обращаются вокруг Солнца под действием магнитных сил.
Объяснение было найдено гораздо позднее, в 1687 г., когда Ньютон опубликовал свой труд «Математические начала натуральной философии». Это, возможно, самый важный из когда-либо опубликованных трудов по физике. В нем Ньютон не только предложил теорию движения тел в пространстве и времени, но также разработал математический аппарат для анализа этого движения. Кроме того, он сформулировал закон всемирного тяготения. Этот закон гласит, что все тела во Вселенной притягиваются друг к другу с силой, которая тем больше, чем больше массы тел и чем ближе друг к другу они расположены. Это та же сила, которая заставляет объекты падать на землю. История с упавшим на Ньютона яблоком почти наверняка является вымышленной. Сам Ньютон упоминал лишь о том, что идея гравитации пришла ему в голову, когда он пребывал в созерцательном настроении и заметил падение яблока.
Ньютон не только предложил теорию движения тел в пространстве и времени, но также разработал математический аппарат для анализа этого движения.

Затем Ньютон показал, что, согласно его закону, гравитация заставляет Луну двигаться по эллиптической орбите вокруг Земли, а Землю и другие планеты – следовать по эллиптическим траекториям вокруг Солнца. Коперниканская модель избавилась от небесных сфер Птолемея, а заодно и от представлений о том, что Вселенная имеет естественную границу. Так называемые неподвижные звезды не меняют свои видимые взаимные положения в процессе движения Земли вокруг Солнца. Поэтому естественно было предположить, что это такие же объекты, как наше Солнце, но расположенные гораздо дальше. Это рождало вопросы. Ньютон понимал, что, согласно его теории гравитации, звезды должны притягиваться друг к другу. То есть они не могут оставаться абсолютно неподвижными. Не упадут ли они все вместе в одну точку?
В письме, написанном в 1691 г. Ричарду Бентли, другому выдающемуся мыслителю того времени, Ньютон утверждал, что такое действительно случилось бы, будь число звезд конечным. С другой стороны, если в бесконечном пространстве более-менее равномерно распределено бесконечное число звезд, этого не произойдет, поскольку нет никакой центральной точки, в которую они могли бы упасть. Этот аргумент – пример ловушки, в которую можно угодить, рассуждая о бесконечности.
Этот аргумент – пример ловушки, в которую можно угодить, рассуждая о бесконечности.
В бесконечной Вселенной каждая точка может считаться центром, поскольку по любую сторону от нее находится бесконечное число звезд. Как стало ясно намного позднее, правильный подход заключается в том, чтобы рассматривать конечную область, в которой все звезды «падают» друг на друга. Возникает вопрос: что изменится, если добавить в рассмотрение другие звезды, практически равномерно распределенные за пределами этой области? По закону Ньютона, добавление звезд никак не повлияет на исходные звезды – они будут приближаться друг к другу с прежней скоростью. Мы можем добавить сколько угодно звезд, но коллапса не избежать. Теперь мы знаем, что невозможно построить модель бесконечной стационарной Вселенной, в которой гравитация всегда связана с притяжением.
Что интересно, до XX века общий образ мыслей был таков, что никто не предполагал, что Вселенная может расширяться или сжиматься. Считалось, что либо Вселенная существовала всегда в неизменном виде, либо была создана в определенный момент в прошлом примерно такой, какой мы видим ее сегодня. Отчасти это объясняется склонностью людей верить в вечные истины, а также находить утешение в мысли, что, хотя мы стареем и умираем, Вселенная всегда остается неизменной.
Отчасти это объясняется склонностью людей верить в вечные истины, а также находить утешение в мысли, что, хотя мы стареем и умираем, Вселенная всегда остается неизменной.
До XX века никто не предполагал, что Вселенная может расширяться или сжиматься.
Даже те, кто понимал, что в соответствии с теорией гравитации Ньютона Вселенная не может быть стационарной, не решались предположить, что она может расширяться. Вместо этого они пытались подправить теорию, приписывая силе гравитации свойство отталкивания на очень больших расстояниях. Это почти не сказывалось на прогнозах движения планет, но позволяло бесконечному числу звезд находиться в равновесии, поскольку силы притяжения между близко расположенными звездами уравновешивались бы силами отталкивания между далекими.
Когда-то люди считали, что бесконечное число звезд может находиться в равновесии, поскольку силы притяжения между близкими звездами уравновешиваются силами отталкивания между далекими. Однако сегодня мы понимаем, что такое равновесие было бы неустойчивым. Скопление Квинтоль, одно из крупнейших молодых звездных скоплений в нашей Галактике Млечный Путь, разрушится всего через несколько миллионов лет под действием гравитационных приливных сил в ядре Галактики. Но в течение короткого периода своего существования оно сияет ярче всех остальных звездных скоплений нашей Галактики.
Однако сегодня мы понимаем, что такое равновесие было бы неустойчивым. Скопление Квинтоль, одно из крупнейших молодых звездных скоплений в нашей Галактике Млечный Путь, разрушится всего через несколько миллионов лет под действием гравитационных приливных сил в ядре Галактики. Но в течение короткого периода своего существования оно сияет ярче всех остальных звездных скоплений нашей Галактики.
Однако сегодня мы понимаем, что такое равновесие не могло быть устойчивым. Если звезды в некоторой области хотя бы немного приблизятся друг к другу, притяжение между ними станет сильнее и будет преобладать над отталкиванием. Это означает, что звезды продолжат сближаться. С другой стороны, если звезды слегка отдалятся друг от друга, возобладают силы отталкивания и звезды будут удаляться друг от друга.
Еще одно возражение против идеи бесконечной стационарной Вселенной обычно приписывают немецкому философу Генриху Ольберсу. На самом деле многие современники Ньютона обращали внимание на эту проблему, и статья Ольберса, опубликованная в 1823 г. , не была первой из работ, содержащих убедительные рассуждения на эту тему. Однако она первой получила широкую известность. Трудность заключается в том, что в бесконечной стационарной Вселенной почти любой луч зрения должен упираться в поверхность звезды. Из этого следует, что все небо должно светиться так же ярко, как Солнце, даже ночью. Тогда Ольберс высказал мысль, что свет далеких звезд ослабляется из-за поглощения веществом, находящимся на его пути. Однако в таком случае межзвездное вещество со временем должно было бы нагреться и засиять так же ярко, как звезды.
, не была первой из работ, содержащих убедительные рассуждения на эту тему. Однако она первой получила широкую известность. Трудность заключается в том, что в бесконечной стационарной Вселенной почти любой луч зрения должен упираться в поверхность звезды. Из этого следует, что все небо должно светиться так же ярко, как Солнце, даже ночью. Тогда Ольберс высказал мысль, что свет далеких звезд ослабляется из-за поглощения веществом, находящимся на его пути. Однако в таком случае межзвездное вещество со временем должно было бы нагреться и засиять так же ярко, как звезды.
Звезды в бесконечной стационарной Вселенной.
В бесконечной стационарной Вселенной почти любой луч зрения должен упираться в поверхность какой-нибудь звезды.
Избежать вывода о том, что ночное небо должно сиять так же ярко, как поверхность Солнца, можно только в том случае, если предположить, что звезды не светят вечно, а зажглись в какой-то определенный момент в прошлом. В таком случае, возможно, межзвездное вещество еще не успело нагреться или свет самых далеких звезд пока нас не достиг. И это подводит нас к вопросу о том, что заставило звезды зажечься.
В таком случае, возможно, межзвездное вещество еще не успело нагреться или свет самых далеких звезд пока нас не достиг. И это подводит нас к вопросу о том, что заставило звезды зажечься.
Зарождение Вселенной
Разумеется, люди издревле размышляли о зарождении Вселенной. Во многих древних учениях о Вселенной, относящихся к еврейской, христианской или мусульманской традиции, Вселенная возникла в определенный конечный момент времени не так давно в прошлом. Одним из доводов в пользу такого начала было убеждение, что для существования Вселенной необходима первопричина.
Еще один довод выдвинул Блаженный Августин в своем труде «О граде Божьем». Он обратил внимание на развитие цивилизации и на то, что мы помним, кто совершил определенное деяние или создал какое-то изобретение. Значит, человечество, а также, возможно, и Вселенная существуют не так давно. Иначе мы бы ушли по пути прогресса гораздо дальше.
Вселенная бесконечна? Об устройстве места, в котором мы живём.
 Новости общества
Новости общества
04 октября 2018, 11:32
5198
Фото Натальи Малыхиной
Новость
4 октября начинается Всемирная неделя космоса. «БелПресса» собрала семь интересных фактов о том, как устроена Вселенная, чем занимаются астрономы, зачем нужна Теория всего и есть ли цивилизация за пределами Земли.
Из чего появилась Вселенная
Из одной точки. 13,7 млрд лет назад из бесконечно кривого пространства и времени образовался наш дом – Вселенная. Стивен Хокинг в книге «Кратчайшая история времени» называет молодую Вселенную «бесконечно горячей». За несколько секунд после Большого взрыва Вселенная расширилась (и делает это до сих пор) и остыла. Когда всё вещество остыло до 1 млрд градусов по Цельсию, стали образовываться первые во Вселенной молекулы – тяжёлого водорода (дейтерия) и гелия. Из этих элементов сложились более тяжёлые, а из них – звёзды и другие космические тела. Так как водород и гелий (их больше всего) лёгкие, для их синтеза условия во Вселенной сложились в первую очередь. Синтез более тяжёлых элементов происходит сложнее. Кроме того, даже человек состоит из звёздной пыли: очень тяжёлые элементы (тяжелее железа), которые входят в состав живых организмов, образовались при взрыве звёзд. Для появления таких элементов нужна колоссальная энергия.
За несколько секунд после Большого взрыва Вселенная расширилась (и делает это до сих пор) и остыла. Когда всё вещество остыло до 1 млрд градусов по Цельсию, стали образовываться первые во Вселенной молекулы – тяжёлого водорода (дейтерия) и гелия. Из этих элементов сложились более тяжёлые, а из них – звёзды и другие космические тела. Так как водород и гелий (их больше всего) лёгкие, для их синтеза условия во Вселенной сложились в первую очередь. Синтез более тяжёлых элементов происходит сложнее. Кроме того, даже человек состоит из звёздной пыли: очень тяжёлые элементы (тяжелее железа), которые входят в состав живых организмов, образовались при взрыве звёзд. Для появления таких элементов нужна колоссальная энергия.
Бесконечное расширение
Однозначного ответа, бесконечна ли Вселенная, нет, потому что она расширяется и мы не успеваем догнать её границы (даже если они есть). То, что Вселенная растёт, предположил российский учёный Александр Фридман. Из‑за постоянного расширения Вселенной телескопы с нашей планеты видят только то, что к нам успело дойти, потому что свет не распространяется мгновенно (у него тоже есть конечная скорость – 300 тыс. км/с). Кроме того, расширение происходит в любой точке. Находясь на Земле, которая располагается в галактике Млечный Путь, мы наблюдаем, как убегают от нас другие галактики. Но и из другой галактики мы бы увидели то же самое.
км/с). Кроме того, расширение происходит в любой точке. Находясь на Земле, которая располагается в галактике Млечный Путь, мы наблюдаем, как убегают от нас другие галактики. Но и из другой галактики мы бы увидели то же самое.
Астроном не звездочёт
Для многих будет шоком, что астрономы уже давно не открывают звёзды. За них это делают телескопы и компьютеры. Работа астронома заключается в том, чтобы работать с большим массивом данных, которые предоставляют ему телескопы. Из этих данных с помощью специальных программ можно выяснить, что происходит в галактиках и как они образуются. Благодаря этим наблюдениям учёные открывают законы, по которым живёт Вселенная.
Теория всего
Эта теория должна объяснить всё и соединить несоединимое – теорию относительности, которая объясняет все свойства гравитации, и квантовую теорию поля, объясняющую поведение частиц. Обе теории работают хорошо в своих масштабах: первая – в макромире (с космическими телами), вторая – в микромире (с частицами). Но если эти теории применить в одном масштабе, то возникнет противоречие. Именно разработкой масштабной теории, которая сможет устранить противоречие, занимаются передовые астрофизики.
Но если эти теории применить в одном масштабе, то возникнет противоречие. Именно разработкой масштабной теории, которая сможет устранить противоречие, занимаются передовые астрофизики.
На её место претендовала теория суперструн. На маленьких пространствах, меньше протона, есть колебания поля – эти волны и назвали струнами. Они несут энергию, которая эквивалентна массе (это и есть согласование с теорией относительности). Чтобы эта теория сошлась и с теорией квантового поля, четырёхмерного пространства было недостаточно – учёным в математической модели пришлось сделать его одиннадцатимерным. К сожалению, теория оказалась настолько гибкой, что фактически любая Вселенная может существовать в её рамках. Чересчур много вариантов не позволяет учёным предсказывать что‑либо с её помощью. Так что работа над Теорией всего продолжается.
Тёмное нечто
Это вещество, которое мы не видим, но оно повсюду. Кроме того, его больше, чем обычного вещества. Когда учёные изучали галактики, они выяснили, что на их краях, где звёзд значительно меньше, масса оставалась достаточно высокой. Это натолкнуло их на мысль, что есть какое‑то вещество, которое мы не видим. Более того, его в разы больше обычного. По современным подсчётам тёмная материя составляет 22 % всей Вселенной.
Когда учёные изучали галактики, они выяснили, что на их краях, где звёзд значительно меньше, масса оставалась достаточно высокой. Это натолкнуло их на мысль, что есть какое‑то вещество, которое мы не видим. Более того, его в разы больше обычного. По современным подсчётам тёмная материя составляет 22 % всей Вселенной.
К слову, газ, звёзды и другие тела – это всего 4 %. Остальные 74 % – тёмная энергия. Это гипотетический вид энергии, благодаря которому можно объяснить ускоряющееся расширение Вселенной.
В 2011 году три астронома: Сол Перлмуттер, Брайан Шмидт и Адам Рисс – получили Нобелевскую премию за то, что математически доказали существование тёмной энергии. Её сравнивают с океаном, в котором плавает материя – галактики со звёздами, газом и другими космическими телами. Про этот океан учёные могут только сказать, что у него низкая плотность и он взаимодействует с обычной материей только посредством гравитации.
Кротовые норы
Чтобы объяснить, что это такое и как это связано с путешествием во времени и пространстве, Хокинг приводит сравнение с горой, которую надо перейти. Но вместо подъёма учёный предлагает прорыть туннель через гору. Идея кротовых нор состоит в том, что, возможно, существуют такие туннели, которые могут переместить нас из Солнечной системы, например, в Туманность Андромеды, соседнюю галактику. Существование таких мостов допускал даже Эйнштейн, но их до сих пор не обнаружили. Путешествовать по таким норам достаточно сложно: предположительно они очень маленькие и нестабильные. Но учёные предполагают, что, если их удастся найти, человечество, возможно, сможет удерживать их открытыми для перемещения во времени и пространстве.
Но вместо подъёма учёный предлагает прорыть туннель через гору. Идея кротовых нор состоит в том, что, возможно, существуют такие туннели, которые могут переместить нас из Солнечной системы, например, в Туманность Андромеды, соседнюю галактику. Существование таких мостов допускал даже Эйнштейн, но их до сих пор не обнаружили. Путешествовать по таким норам достаточно сложно: предположительно они очень маленькие и нестабильные. Но учёные предполагают, что, если их удастся найти, человечество, возможно, сможет удерживать их открытыми для перемещения во времени и пространстве.
Внеземные цивилизации
Немного самонадеянно думать, что в огромной Вселенной мы одни разумные существа. В одной нашей галактике около 300 млрд звёзд, предполагаемое количество галактик – 200 млрд. Все эти цифры здесь для того, чтобы показать, насколько мала вероятность, что мы одиноки во Вселенной. Кроме того, учёные давно ведут поиски внеземных цивилизаций. Знаменитый радиосигнал Wow, полученный Джерри Эйманом в 1977 году, сначала считался сигналом от пришельцев. Однако позже выяснили, что такие сигналы могут давать и кометы.
Однако позже выяснили, что такие сигналы могут давать и кометы.
Ещё одна интересная история о надежде встретить инопланетян связана с космическим аппаратом «Вояджер-1». Именно на его борту прикреплена золотая пластинка, на которой записано местонахождение Земли, изображения и звуки, характеризующий наш мир. Если инопланетяне найдут этот аппарат, то смогут узнать, как связаться с нами.
Наталья Малыхина
Бесконечность | Определение, символ и факты
концентрические окружности и бесконечность
Смотреть все медиа
- Ключевые люди:
- Георг Кантор
Ричард Дедекинд
Зенон из Элеи
Бернхард Больцано
- Похожие темы:
- математика
бесконечное множество
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
бесконечность , концепция чего-то безграничного, бесконечного, безграничного. Общий символ бесконечности ∞ был изобретен английским математиком Джоном Уоллисом в 1655 году. Можно выделить три основных типа бесконечности: математический, физический и метафизический. Математические бесконечности встречаются, например, как количество точек на непрерывной линии или как размер бесконечной последовательности счетных чисел: 1, 2, 3,…. Пространственные и временные концепции бесконечности возникают в физике, когда кто-то спрашивает, существует ли бесконечно много звезд и будет ли Вселенная существовать вечно. В метафизическом обсуждении Бога или Абсолюта возникают вопросы о том, должна ли конечная сущность быть бесконечной и могут ли меньшие вещи также быть бесконечными.
Общий символ бесконечности ∞ был изобретен английским математиком Джоном Уоллисом в 1655 году. Можно выделить три основных типа бесконечности: математический, физический и метафизический. Математические бесконечности встречаются, например, как количество точек на непрерывной линии или как размер бесконечной последовательности счетных чисел: 1, 2, 3,…. Пространственные и временные концепции бесконечности возникают в физике, когда кто-то спрашивает, существует ли бесконечно много звезд и будет ли Вселенная существовать вечно. В метафизическом обсуждении Бога или Абсолюта возникают вопросы о том, должна ли конечная сущность быть бесконечной и могут ли меньшие вещи также быть бесконечными.
Древние греки выражали бесконечность словом apeiron , которое имело коннотации неограниченного, неопределенного, неопределенного и бесформенного. Одно из первых проявлений бесконечности в математике касается соотношения между диагональю и стороной квадрата. Пифагор (ок. 580–500 гг. до н. э.) и его последователи изначально считали, что любой аспект мира может быть выражен последовательностью, включающей только целые числа (0, 1, 2, 3,…), но они были удивлены, обнаружив, что диагональ и сторона квадрата несоизмеримы, то есть их длины не могут одновременно быть выражены целым числом, кратным какой-либо общей единице (или мерной линейке). В современной математике это открытие выражается в том, что это отношение иррационально и что оно является пределом бесконечного неповторяющегося десятичного ряда. В случае квадрата со стороной 1 диагональ представляет собой квадратный корень из √2, записанный как 1,414213562…, где многоточие (…) указывает на бесконечную последовательность цифр без шаблона.
э.) и его последователи изначально считали, что любой аспект мира может быть выражен последовательностью, включающей только целые числа (0, 1, 2, 3,…), но они были удивлены, обнаружив, что диагональ и сторона квадрата несоизмеримы, то есть их длины не могут одновременно быть выражены целым числом, кратным какой-либо общей единице (или мерной линейке). В современной математике это открытие выражается в том, что это отношение иррационально и что оно является пределом бесконечного неповторяющегося десятичного ряда. В случае квадрата со стороной 1 диагональ представляет собой квадратный корень из √2, записанный как 1,414213562…, где многоточие (…) указывает на бесконечную последовательность цифр без шаблона.
И Платон (428/427–348/347 до н. э.), и Аристотель (384–322 до н. э.) разделяли общее отвращение греков к понятию бесконечности. Аристотель оказал влияние на последующую мысль более чем на тысячелетие своим отказом от «актуальной» бесконечности (пространственной, временной или числовой), которую он отличал от «потенциальной» бесконечности способности считать без конца. Чтобы избежать использования фактической бесконечности, Евдокс Книдский (ок. 400–350 до н. э.) и Архимед (ок. 285–212/211 до н. э.) разработали технику, позже известную как метод исчерпания, с помощью которого площадь вычислялась делением вдвое измерительный блок на последовательных этапах до тех пор, пока оставшаяся площадь не станет ниже некоторого фиксированного значения (оставшаяся область «исчерпается»).
Чтобы избежать использования фактической бесконечности, Евдокс Книдский (ок. 400–350 до н. э.) и Архимед (ок. 285–212/211 до н. э.) разработали технику, позже известную как метод исчерпания, с помощью которого площадь вычислялась делением вдвое измерительный блок на последовательных этапах до тех пор, пока оставшаяся площадь не станет ниже некоторого фиксированного значения (оставшаяся область «исчерпается»).
Проблема бесконечно малых чисел привела к открытию исчисления в конце 1600-х годов английским математиком Исааком Ньютоном и немецким математиком Готфридом Вильгельмом Лейбницем. Ньютон представил свою собственную теорию бесконечно малых чисел, или бесконечно малых, для обоснования вычисления производных или наклонов. Чтобы найти наклон (то есть изменение х по сравнению с изменением х ) линии, касающейся кривой в заданной точке ( х , y ), он счел полезным взглянуть на отношение между d y и d x , где d y есть бесконечно малое изменение, производимое перемещением y . d x из x . Бесконечно малые числа подвергались резкой критике, и большая часть ранней истории анализа вращалась вокруг попыток найти альтернативную, строгую основу для предмета. Использование бесконечно малых чисел, наконец, получило прочную основу с развитием нестандартного анализа немецким математиком Авраамом Робинсоном в XIX веке.60-е годы.
d x из x . Бесконечно малые числа подвергались резкой критике, и большая часть ранней истории анализа вращалась вокруг попыток найти альтернативную, строгую основу для предмета. Использование бесконечно малых чисел, наконец, получило прочную основу с развитием нестандартного анализа немецким математиком Авраамом Робинсоном в XIX веке.60-е годы.
Более прямое использование бесконечности в математике связано с попытками сравнить размеры бесконечных множеств, таких как множество точек на линии (действительные числа) или множество счетных чисел. Математики быстро поражаются тем фактом, что обычные представления о числах вводят в заблуждение, когда речь идет о бесконечных размерах. Средневековые мыслители знали о парадоксальном факте, что отрезки прямой различной длины, по-видимому, имеют одинаковое количество точек. Например, нарисуйте две концентрические окружности, одна из которых в два раза больше радиуса (и, следовательно, в два раза больше окружности), чем другая, как показано на рисунке. Удивительно, но каждый пункт P на внешнем круге можно соединить с уникальной точкой P ′ на внутреннем круге, проведя линию от их общего центра O до P и обозначив ее пересечение с внутренним кругом P ′. Интуиция подсказывает, что внешний круг должен иметь в два раза больше точек, чем внутренний круг, но в этом случае бесконечность кажется такой же, как удвоенная бесконечность. В начале 1600-х годов итальянский ученый Галилео Галилей обратился к этому и подобному неинтуитивному результату, который теперь известен как парадокс Галилея. Галилей продемонстрировал, что множество счетных чисел может быть поставлено во взаимно однозначное соответствие с гораздо меньшим набором их квадратов. Точно так же он показал, что набор счетных чисел и их двойников (т. Е. Набор четных чисел) можно соединить в пары. Галилей пришел к выводу, что «мы не можем говорить о бесконечных количествах как о том, что одно больше или меньше другого или равно ему».
Удивительно, но каждый пункт P на внешнем круге можно соединить с уникальной точкой P ′ на внутреннем круге, проведя линию от их общего центра O до P и обозначив ее пересечение с внутренним кругом P ′. Интуиция подсказывает, что внешний круг должен иметь в два раза больше точек, чем внутренний круг, но в этом случае бесконечность кажется такой же, как удвоенная бесконечность. В начале 1600-х годов итальянский ученый Галилео Галилей обратился к этому и подобному неинтуитивному результату, который теперь известен как парадокс Галилея. Галилей продемонстрировал, что множество счетных чисел может быть поставлено во взаимно однозначное соответствие с гораздо меньшим набором их квадратов. Точно так же он показал, что набор счетных чисел и их двойников (т. Е. Набор четных чисел) можно соединить в пары. Галилей пришел к выводу, что «мы не можем говорить о бесконечных количествах как о том, что одно больше или меньше другого или равно ему». Такие примеры побудили немецкого математика Рихарда Дедекинда в 1872 году предложить определение бесконечного множества как множества, которое можно поставить во взаимно-однозначное отношение с некоторым собственным подмножеством.
Такие примеры побудили немецкого математика Рихарда Дедекинда в 1872 году предложить определение бесконечного множества как множества, которое можно поставить во взаимно-однозначное отношение с некоторым собственным подмножеством.
Путаница с бесконечными числами была разрешена немецким математиком Георгом Кантором в 1873 году. Первый Кантор строго продемонстрировал, что множество рациональных чисел (дробей) имеет тот же размер, что и счетные числа; следовательно, они называются исчисляемыми или исчисляемыми. Конечно, это не стало настоящим шоком, но позже в том же году Кантор доказал удивительный результат, что не все бесконечности равны. Используя так называемый «диагональный аргумент», Кантор показал, что размер счетных чисел строго меньше размера действительных чисел. Этот результат известен как теорема Кантора.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Чтобы сравнить множества, Кантор сначала провел различие между конкретным множеством и абстрактным понятием его размера или мощности. В отличие от конечного множества, бесконечное множество может иметь ту же мощность, что и его собственное подмножество. Кантор использовал диагональный аргумент, чтобы показать, что мощность любого набора должна быть меньше мощности его набора мощности, т. Е. Набора, который содержит все возможные подмножества данного набора. В общем набор с n элементов имеют набор мощности с 2 n элементов, и эти две мощности различны, даже когда n бесконечно. Кантор называл размеры своих бесконечных множеств «трансфинитными кардиналами». Его аргументы показали, что существуют трансфинитные кардиналы бесконечного множества различных размеров (например, кардиналы множества счетных чисел и множества действительных чисел).
В отличие от конечного множества, бесконечное множество может иметь ту же мощность, что и его собственное подмножество. Кантор использовал диагональный аргумент, чтобы показать, что мощность любого набора должна быть меньше мощности его набора мощности, т. Е. Набора, который содержит все возможные подмножества данного набора. В общем набор с n элементов имеют набор мощности с 2 n элементов, и эти две мощности различны, даже когда n бесконечно. Кантор называл размеры своих бесконечных множеств «трансфинитными кардиналами». Его аргументы показали, что существуют трансфинитные кардиналы бесконечного множества различных размеров (например, кардиналы множества счетных чисел и множества действительных чисел).
Трансфинитные кардиналы включают алеф-нуль (размер набора целых чисел), алеф-единица (следующая большая бесконечность) и континуум (размер действительных чисел). Эти три числа также записываются как ℵ 9.0091 0 , ℵ 1 и c соответственно. По определению ℵ 0 меньше ℵ 1 , а по теореме Кантора ℵ 1 меньше или равно c . Наряду с принципом, известным как аксиома выбора, метод доказательства теоремы Кантора может быть использован для обеспечения бесконечной последовательности трансфинитных кардиналов, продолжающихся от ℵ 1 до таких чисел, как ℵ 2 и ℵ ℵ 0 .
По определению ℵ 0 меньше ℵ 1 , а по теореме Кантора ℵ 1 меньше или равно c . Наряду с принципом, известным как аксиома выбора, метод доказательства теоремы Кантора может быть использован для обеспечения бесконечной последовательности трансфинитных кардиналов, продолжающихся от ℵ 1 до таких чисел, как ℵ 2 и ℵ ℵ 0 .
Проблема континуума — это вопрос о том, какой из алефов равен мощности континуума. Кантор предположил, что с = ℵ 1 ; это известно как гипотеза континуума Кантора (CH). CH также можно рассматривать как утверждение, что любой набор точек на линии должен либо быть счетным (размер меньше или равен ℵ 0 ), либо должен иметь размер, равный всему пространству (иметь размер c ).
В начале 1900-х годов была разработана основательная теория бесконечных множеств. Эта теория известна как ZFC, что означает теорию множеств Цермело-Френкеля с аксиомой выбора. Известно, что CH неразрешим на основе аксиом ZFC. В 1940 логик австрийского происхождения Курт Гёдель смог показать, что ZFC не может опровергнуть CH, а в 1963 году американский математик Пол Коэн показал, что ZFC не может доказать CH. Теоретики множеств продолжают исследовать способы разумного расширения аксиом ZFC, чтобы решить CH. Недавняя работа предполагает, что CH может быть ложным и что истинный размер c может быть большей бесконечностью ℵ 2 .
Известно, что CH неразрешим на основе аксиом ZFC. В 1940 логик австрийского происхождения Курт Гёдель смог показать, что ZFC не может опровергнуть CH, а в 1963 году американский математик Пол Коэн показал, что ZFC не может доказать CH. Теоретики множеств продолжают исследовать способы разумного расширения аксиом ZFC, чтобы решить CH. Недавняя работа предполагает, что CH может быть ложным и что истинный размер c может быть большей бесконечностью ℵ 2 .
Бесконечность — красивая концепция, и она разрушает физику
Бесконечность соблазнила меня в раннем возрасте. Доказательство диагональности Георга Кантора о том, что одни бесконечности больше других, очаровало меня, а его бесконечная иерархия бесконечностей поразила меня. Предположение, что в природе существует что-то действительно бесконечное, лежит в основе каждого курса физики, который я когда-либо читал в Массачусетском технологическом институте, да и вообще всей современной физики. Но это непроверенное предположение, которое вызывает вопрос: правда ли это на самом деле?
Кризис в физике
На самом деле существует два отдельных предположения: «бесконечно большое» и «бесконечно малое». Под бесконечно большим я подразумеваю, что пространство может иметь бесконечный объем, что время может продолжаться вечно и что может быть бесконечно много физических объектов. Под бесконечно малым я подразумеваю континуум — идею о том, что даже литр пространства содержит бесконечное число точек, что пространство можно растянуть до бесконечности, и ничего плохого не произойдет, и что в природе существуют величины, которые могут непрерывно изменяться.
Под бесконечно большим я подразумеваю, что пространство может иметь бесконечный объем, что время может продолжаться вечно и что может быть бесконечно много физических объектов. Под бесконечно малым я подразумеваю континуум — идею о том, что даже литр пространства содержит бесконечное число точек, что пространство можно растянуть до бесконечности, и ничего плохого не произойдет, и что в природе существуют величины, которые могут непрерывно изменяться.
Эти два предположения тесно связаны, потому что инфляция, наиболее популярное объяснение нашего Большого Взрыва, может создать бесконечный объем, бесконечно растягивая непрерывное пространство. Теория инфляции оказалась впечатляюще успешной и является главным претендентом на Нобелевскую премию. Она объясняет, как субатомная частица материи превратилась в массивный Большой взрыв, создав огромную, плоскую, однородную вселенную с крошечными флуктуациями плотности, которые в конечном итоге превратились в современные галактики и космическую крупномасштабную структуру — все это прекрасно согласуется с точными измерениями, полученными в результате экспериментов. такие как эксперименты Planck и BICEP2. Но, предсказывая, что пространство не просто велико, но действительно бесконечно, инфляция также привела к так называемой проблеме меры, которую я рассматриваю как величайший кризис, стоящий перед современной физикой.
такие как эксперименты Planck и BICEP2. Но, предсказывая, что пространство не просто велико, но действительно бесконечно, инфляция также привела к так называемой проблеме меры, которую я рассматриваю как величайший кризис, стоящий перед современной физикой.
Физика занимается предсказанием будущего по прошлому, но инфляция, кажется, саботирует это. Когда мы пытаемся предсказать вероятность того, что произойдет что-то конкретное, инфляция всегда дает один и тот же бесполезный ответ: бесконечность, деленная на бесконечность. Проблема в том, что какой бы эксперимент вы ни проводили, инфляция предсказывает, что будет бесконечно много ваших копий, далеко в нашем бесконечном пространстве, получающих каждый физически возможный результат; и, несмотря на годы скрежетания зубами в космологическом сообществе, не возникло единого мнения о том, как извлечь разумные ответы из этих бесконечностей. Так что, строго говоря, мы, физики, уже вообще ничего не можем предсказать!
Это означает, что лучшие сегодняшние теории нуждаются в серьезной встряске, отказавшись от неверного предположения. Который из? Вот мой главный подозреваемый: ∞.
Который из? Вот мой главный подозреваемый: ∞.
Бесконечности не существует
Резиновую ленту нельзя растягивать бесконечно, потому что, хотя она кажется гладкой и непрерывной, это просто удобное приближение. Он действительно состоит из атомов, и если его слишком сильно растянуть, он лопнет. Если мы аналогичным образом откажемся от идеи, что пространство само по себе является бесконечно растянутым континуумом, то своего рода большой щелчок не позволит инфляции создать бесконечно большое пространство, и проблема измерения исчезнет. Без бесконечно малого инфляция не может сделать бесконечно большим, поэтому вы избавляетесь от обеих бесконечностей одним махом — вместе со многими другими проблемами, преследующими современную физику, такими как бесконечно плотные сингулярности черных дыр и бесконечности, возникающие, когда мы пытаемся квантовать гравитацию.
В прошлом многие маститые математики скептически относились к бесконечности и континууму. Легендарный Карл Фридрих Гаусс отрицал, что нечто бесконечное действительно существует, говоря: «Бесконечность — это просто способ говорить» и «Я протестую против использования бесконечной величины как чего-то законченного, что никогда не допустимо в математике». Однако в прошлом столетии бесконечность стала математическим мейнстримом, и большинство физиков и математиков были настолько очарованы бесконечностью, что редко подвергают ее сомнению. Почему? В основном потому, что бесконечность — чрезвычайно удобное приближение, для которого мы не нашли удобных альтернатив.
Однако в прошлом столетии бесконечность стала математическим мейнстримом, и большинство физиков и математиков были настолько очарованы бесконечностью, что редко подвергают ее сомнению. Почему? В основном потому, что бесконечность — чрезвычайно удобное приближение, для которого мы не нашли удобных альтернатив.
Возьмем, к примеру, воздух перед собой. Отслеживание позиций и скоростей октиллионов атомов было бы безнадежно сложным. Но если вы проигнорируете тот факт, что воздух состоит из атомов, и вместо этого аппроксимируете его как континуум — гладкую субстанцию, которая имеет плотность, давление и скорость в каждой точке — вы обнаружите, что этот идеализированный воздух подчиняется прекрасному простому уравнению, объясняющему почти все, что нас волнует: как строить самолеты, как мы слышим их с помощью звуковых волн, как составлять прогнозы погоды и так далее. Тем не менее, несмотря на все это удобство, воздух, конечно же, не является непрерывным. Думаю, то же самое и с пространством, временем и всеми остальными строительными блоками нашего физического мира.
Нам не нужно бесконечное
Посмотрим правде в глаза: несмотря на их соблазнительную привлекательность, у нас нет прямых наблюдательных данных ни о бесконечно большом, ни о бесконечно малом. Мы говорим о бесконечных объемах с бесконечным количеством планет, но наша наблюдаемая Вселенная содержит всего около 1089 объектов (в основном фотонов). Если пространство является истинным континуумом, то для описания даже такой простой вещи, как расстояние между двумя точками, требуется бесконечное количество информации, определяемой числом с бесконечным числом знаков после запятой. На практике нам, физикам, никогда не удавалось измерить что-либо с точностью более семнадцати знаков после запятой. Тем не менее, действительные числа с их бесконечным числом десятичных знаков заполонили почти все уголки и закоулки физики, от напряженности электромагнитных полей до волновых функций квантовой механики. Мы описываем даже один бит квантовой информации (кубит), используя два действительных числа, содержащих бесконечно много десятичных знаков.

