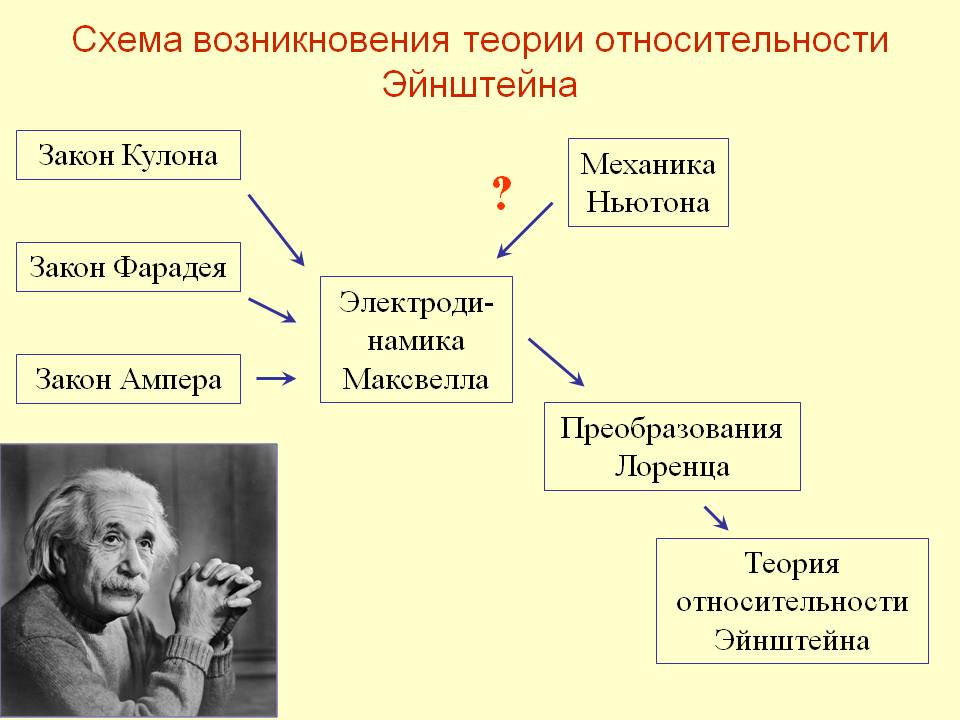
Содержание
Теория относительности Эйнштейна, объясняем и читаем краткими понятными словами. Теория относительности для чайников
Содержание
- 1 Теория относительности Эйнштейна кратко
- 2 По теме
- 2.1 18-ти летний тинейджер снял короткое видео про СТО и выиграл $400 тысяч от Марка Цукерберга
- 2.2 Скорость света оказалась меньше, чем считалось?
- 3 Чем отличается специальная теория относительности от общей теории относительности?
- 4 Объединение массы и энергии
- 5 Двоякость измерений
Теория относительности Эйнштейна кратко
Эйнштейн и еще один ученый, Хендрик Лоренц выяснили, что есть только один способ объяснить, как все это может быть. Это возможно только в том случае, если время замедляется.
Представьте, что произойдет, если время замедлится для вас, а вы при этом не знаете, что двигаетесь медленнее.Вам будет казаться, что все остальное происходит быстрее, всё вокруг вас будут двигаться, как в фильме в быстрой перемотке.
Читайте также: Альберт Эйнштейн краткая биография
Итак, теперь давайте представим, что вы снова при ливне с ветром. Как такое возможно, что дождь будет воздействует на вас одинаково, даже если вы бежите? Выходит если бы вы пытались убежать от дождя, то ваше время бы замедлилось, а дождь — ускорился. Капли дождя попадали бы вам на спину с такой же скоростью. Ученые называют это расширение времени. Независимо от того, насколько быстро вы двигаетесь, ваше время замедляется, по крайней мере для скорости света это выражение справедливо.
По теме
ПоказатьСвернуть
18-ти летний тинейджер снял короткое видео про СТО и выиграл $400 тысяч от Марка Цукерберга
12.11.2015
Редакция Naked Science
Скорость света оказалась меньше, чем считалось?
27.06.2014
Редакция Naked Science
Чем отличается специальная теория относительности от общей теории относительности?
- Специальная теория относительности (СТО была создана в 1905 году): существуют одни и те же законы природы для всех систем отсчёта, которые движутся с постоянной скоростью; эта теория исследует физические процессы равномерно движущихся тел.
 2.
2.©deviantART/ RowanPhoenix
Согласно теории великого физика, когда скорость материального тела увеличивается, приближаясь к скорости света, увеличивается и его масса. Т.е. чем быстрее движется объект, тем тяжелее он становится. В случае достижения скорости света, масса тела, равно как и его энергия, становятся бесконечными. Чем тяжелее тело, тем сложнее увеличить его скорость; для ускорения тела с бесконечной массой требуется бесконечное количество энергии, поэтому для материальных объектов достичь скорости света невозможно.
- Как собрать кубик Рубика, не сломав голову
Как вы, наверное, уже знаете, несколько дней назад был побит мировой рекорд по скоростной сборке кубика Рубика. Голландский спидкубер Матс Валк на чемпионате Jawa Timur Open 2016 в Индонезии смог с…
naked-science.ru
До Эйнштейна концепции массы и энергии в физике рассматривались по отдельности. Гениальный ученый доказал, что закон сохранения массы, как и закон сохранения энергии, являются частями более общего закона массы-энергии.

Благодаря фундаментальной связи между этими двумя понятиями, материю можно превратить в энергию, и наоборот – энергию в материю.
Нашли опечатку? Выделите фрагмент и нажмите Ctrl + Enter.Закладка
Скопировать ссылку
Email
Печать
Twitter
VK
Telegram С точки зрения науки # материя # ОТО # СТО # теория относительности # физика # эйнштейн Партнерский материал Выбор редакции Подписывайтесь на нас в Telegram, Яндекс.Новостях и VKTelegram
Дзен
VK
Создано зеркало, которое показывает внутренние органы человека06.05.2014
Предыдущая статья
Космическая рокировка06.05.2014Следующая статьяПредстоящие мероприятия Все Лекция12Дек700 ₽ Кроманьонцы заселяют Землю
Центр «Архэ»Москва Лекция12Дек600 ₽ Последующие периоды онтогенеза поведения собак
Центр «Архэ»
ОнлайнЛекция13Дек500 ₽ Колосс Родосский
Центр «Архэ»Санкт-Петербург Лекция14Дек700 ₽Внегалактическая астрономия и основы космологии
Центр «Архэ»Москва Лекция15ДекБесплатно Где водятся хоббиты
ВДНХМосква Лекция15ДекБесплатно Дистанционное зондирование Земли
Твой сектор космосаМосква Лекция16Дек400 ₽ Главное растение планеты
Центр «Архэ»
ОнлайнЛекция17ДекБесплатно Простоматика: что же такое математика?
Культурный центр ЗИЛМосква Лекция17ДекБесплатно Из истории русского алфавита
Центр славянской письменности «Слово»Москва
Двоякость измерений
Другое, что Эйнштейн и Лоренц выяснили, это то, что два человека при разных обстоятельствах могут получить разные расчетные значения и самое странное, что они оба будут правы.
 Это еще один побочный эффект того, что свет всегда движется с одинаковой скоростью.
Это еще один побочный эффект того, что свет всегда движется с одинаковой скоростью.Проведем мысленный эксперимент
Представьте, что вы стоите в центре своей комнаты, и вы установили лампу прямо посередине комнаты. Теперь представьте, что скорость света очень медленна, и вы можете видеть, как он распространяется, представьте, что вы включили лампу.
Как только вы включите лампу, свет начнет расходится и освещать. Поскольку обе стены находятся на одном и том же расстоянии, свет достигнет обе стены одновременно.
Теперь представьте, что в вашей комнате есть большое окно, и ваш знакомый проезжает мимо. Он увидит уже другое. Для него это будет выглядеть так, как будто ваша комната движется вправо и когда вы включите лампу, он увидит, что левая стена движется к свету. а правая стена отодвигается от света. Он увидит, что свет сначала попал в левую стену, а потом на правую. Ему покажется, что свет не осветил обе стены одновременно.
Согласно теории относительности Эйнштейна, обе точки зрения будут правы.
 С вашей точки зрения, свет попадает в обе стены одновременно. С точки зрения вашего знакомого это не так. В этом нет ничего плохого.
С вашей точки зрения, свет попадает в обе стены одновременно. С точки зрения вашего знакомого это не так. В этом нет ничего плохого.Вот почему ученые говорят, что «одновременность относительна». Если вы измеряете две вещи, которые должны произойти одновременно, то тот, кто движется с другой скоростью или в другом направлении, не сможет их измерить одинаково с вами.
Нам это кажется очень странным, потому что скорость света для нас мгновенная, и мы двигаемся очень медленно по сравнению с ней. Поскольку скорость света настолько велика, мы не замечаем скорость распространения света, до тех пор пока не будем проводить специальные эксперименты.
- https://oldinvent.ru/teoriya-otnositelnosti-ejnshtejna-ob/
- https://naked-science.ru/article/nakedscience/einsteins-special-relativity
- https://www.uznaychtotakoe.ru/teoriya-otnositelnosti/
Специальная теория относительности Эйнштейна / 100 великих событий XX века
Немецко-швейцарско-американский физик Альберт Эйнштейн родился в Ульме (земля Баден-Вюртенберг в Германии), в семье Германа Эйнштейна и Паулины Эйнштейн, урождённой Кох.
 Вырос он в Мюнхене, где у его отца и дяди был небольшой электрохимический завод. Эйнштейн был тихим, рассеянным мальчиком, который питал склонность к математике, но терпеть не мог школу с её механической зубрёжкой и казарменной дисциплиной.
Вырос он в Мюнхене, где у его отца и дяди был небольшой электрохимический завод. Эйнштейн был тихим, рассеянным мальчиком, который питал склонность к математике, но терпеть не мог школу с её механической зубрёжкой и казарменной дисциплиной.В юные годы, проведённые в мюнхенской гимназии Луитпольда, Эйнштейн самостоятельно читал книги по философии, математике, космологии, научно-популярную литературу. После того как дела отца в 1895 году пришли в упадок, семья переселилась в Милан. Эйнштейн оставил гимназию, так и не получив аттестата.
Шестнадцатилетнего Эйнштейна поразила та атмосфера свободы и культуры, которую он нашёл в Италии. Отец настаивал на том, чтобы сын избрал инженерное поприще и в будущем смог поправить шаткое финансовое положение семьи. Эйнштейн попытался сдать вступительные экзамены в Федеральный технологический институт в Цюрихе, для поступления в который не требовалось свидетельства об окончании средней школы. Не обладая достаточной подготовкой, он провалился на экзаменах, но директор училища, оценив математические способности Эйнштейна, направил его в Аарау, в двадцати милях к западу от Цюриха, чтобы тот закончил там гимназию.

Через год, летом 1896 года, Эйнштейн успешно выдержал вступительные экзамены в Федеральный технологический институт. В Аарау он расцвёл, наслаждаясь тесным контактом с учителями и либеральным духом, царившим в гимназии. Всё прежнее вызывало у него настолько глубокое неприятие, что он подал официальное прошение о выходе из германского подданства, на что его отец согласился весьма неохотно.
В Цюрихе Эйнштейн изучал физику, больше полагаясь на самостоятельное чтение, чем на обязательные курсы. Сначала он намеревался преподавать физику, но после окончания Федерального института в 1901 году и получения швейцарского гражданства не смог найти постоянной работы. В 1902 году Эйнштейн стал экспертом Швейцарского патентного бюро в Берне, в котором прослужил семь лет. Для него это были счастливые и продуктивные годы. Он опубликовал одну работу о капиллярности (о том, что происходит с поверхностью жидкости, если её заключить в узкую трубку). Хотя жалованья едва хватало, работа в патентном бюро оставляла Эйнштейну достаточно сил и времени для теоретических исследований.
 Его первые работы были посвящены силам взаимодействия между молекулами и приложениям статистической термодинамики. Одна из них — «Новое определение размеров молекул» — была принята в качестве докторской диссертации Цюрихским университетом, и в 1905 году Эйнштейн стал доктором наук. В том же году он опубликовал небольшую серию работ, которые изменили лицо всей физики.
Его первые работы были посвящены силам взаимодействия между молекулами и приложениям статистической термодинамики. Одна из них — «Новое определение размеров молекул» — была принята в качестве докторской диссертации Цюрихским университетом, и в 1905 году Эйнштейн стал доктором наук. В том же году он опубликовал небольшую серию работ, которые изменили лицо всей физики.Одна из этих работ была посвящена объяснению броуновского движения — хаотического зигзагообразного движения частиц, взвешенных в жидкости. Эйнштейн связал движение частиц, наблюдаемое в микроскоп, со столкновениями этих частиц с невидимыми молекулами; кроме того, он предсказал, что наблюдение броуновского движения позволяет вычислить массу и число молекул, находящихся в данном объёме. Через несколько лет это было подтверждено Жаном Перреном.
В другой работе предлагалось объяснение фотоэлектрического эффекта — испускания электронов металлической поверхностью под действием электромагнитного излучения в ультрафиолетовом или каком-либо другом диапазоне.
 Филипп де Ленард высказал предположение, что свет выбивает электроны с поверхности металла. Предположил он и то, что при освещении поверхности более ярким светом электроны должны вылетать с большей скоростью. Но эксперименты показали, что прогноз Ленарда неверен. Между тем в 1900 году Максу Планку удалось описать излучение, испускаемое горячими телами. Он принял радикальную гипотезу о том, что энергия испускается не непрерывно, а дискретными порциями — квантами. Физический смысл квантов оставался неясным, но величина кванта равна произведению некоторого числа (постоянной Планка) и частоты излучения.
Филипп де Ленард высказал предположение, что свет выбивает электроны с поверхности металла. Предположил он и то, что при освещении поверхности более ярким светом электроны должны вылетать с большей скоростью. Но эксперименты показали, что прогноз Ленарда неверен. Между тем в 1900 году Максу Планку удалось описать излучение, испускаемое горячими телами. Он принял радикальную гипотезу о том, что энергия испускается не непрерывно, а дискретными порциями — квантами. Физический смысл квантов оставался неясным, но величина кванта равна произведению некоторого числа (постоянной Планка) и частоты излучения.Идея Эйнштейна состояла в том, чтобы установить соответствие между фотоном (квантом электромагнитной энергии) и энергией выбитого с поверхности металла электрона. Каждый фотон выбивает один электрон. Кинетическая энергия электрона (энергия, связанная с его скоростью) равна энергии, оставшейся от энергии фотона за вычетом той её части, которая израсходована на то, чтобы вырвать электрон из металла.
 Чем ярче свет, тем больше фотонов и больше число выбитых с поверхности металла электронов, но не их скорость. Более быстрые электроны можно получить, направляя на поверхность металла излучение с большей частотой, так как фотоны такого излучения содержат больше энергии.
Чем ярче свет, тем больше фотонов и больше число выбитых с поверхности металла электронов, но не их скорость. Более быстрые электроны можно получить, направляя на поверхность металла излучение с большей частотой, так как фотоны такого излучения содержат больше энергии.Эйнштейн выдвинул ещё одну смелую гипотезу, предположив, что свет обладает двойственной природой. Как показывают проводившиеся на протяжении веков оптические эксперименты, свет ведёт себя как волна, но, как свидетельствует фотоэлектрический эффект, может вести себя и как поток частиц. Правильность предложенной Эйнштейном интерпретации фотоэффекта была многократно подтверждена экспериментально, причём не только для видимого света, но и для рентгеновского и гамма-излучения.
Необходимо отметить, что в изучении фотоэффекта самое непосредственное участие принимала жена Эйнштейна, талантливый физик-экспериментатор.
В 1924 году Луи де Бройль сделал ещё один шаг в преобразовании физики, предположив, что волновыми свойствами обладает не только свет, но и материальные объекты, например электроны.
 Идея де Бройля также нашла экспериментальное подтверждение и заложила основы квантовой механики. Работы Эйнштейна позволили объяснить флуоресценцию, фотоионизацию и загадочные вариации удельной теплоёмкости твёрдых тел при различных температурах.
Идея де Бройля также нашла экспериментальное подтверждение и заложила основы квантовой механики. Работы Эйнштейна позволили объяснить флуоресценцию, фотоионизацию и загадочные вариации удельной теплоёмкости твёрдых тел при различных температурах.Третья, поистине замечательная работа Эйнштейна, опубликованная всё в том же 1905 году, — специальная теория относительности, революционизировавшая все области физики. В то время большинство физиков полагало, что световые волны распространяются в эфире — загадочном веществе, которое, как принято было думать, заполняет всю Вселенную. Однако обнаружить эфир экспериментально никому не удавалось.
Поставленный в 1887 году Альбертом А. Майкельсоном и Эдвардом Морли эксперимент по обнаружению различия в скорости света, распространяющегося в гипотетическом эфире вдоль и поперёк направления движения Земли, дал отрицательный результат. Если бы эфир был носителем света, который распространяется по нему в виде возмущения, как звук по воздуху, то скорость эфира должна была бы прибавляться к наблюдаемой скорости света или вычитаться из неё, подобно тому как река влияет, с точки зрения стоящего на берегу наблюдателя, на скорость лодки, идущей на вёслах по течению или против течения.

В основу специальной теории относительности Эйнштейна были положены два универсальных допущения, делавших излишней гипотезу о существовании эфира: все законы физики одинаково применимы для любых двух наблюдателей, независимо от того, как они движутся относительно друг друга, свет всегда распространяется в свободном пространстве с одной и той же скоростью, независимо от движения его источника.
Выводы, сделанные из этих допущений, изменили представления о пространстве и времени: ни один материальный объект не может двигаться быстрее света; с точки зрения стационарного наблюдателя, размеры движущегося объекта сокращаются в направлении движения, а масса объекта возрастает; чтобы скорость света была одинаковой для движущегося и покоящегося наблюдателей, движущиеся часы должны идти медленнее. Даже понятие стационарности подлежит тщательному пересмотру.
Движение или покой определяются всегда относительно некоего наблюдателя. Наблюдатель, едущий верхом на движущемся объекте, неподвижен относительно данного объекта, но может двигаться относительно какого-либо другого наблюдателя.
 Поскольку время становится такой же относительной переменной, как и пространственные координаты x, y, z, понятие одновременности также становится относительным. Два события, кажущихся одновременными одному наблюдателю, могут быть разделены во времени с точки зрения другого. Из других выводов, к которым приводит специальная теория относительности, заслуживает внимание эквивалентность массы и энергии. Масса m представляет собой своего рода «замороженную» энергию E, с которой связана соотношением E = mc2, где c — скорость света. Таким образом, испускание фотонов света происходит ценой уменьшения массы источника.
Поскольку время становится такой же относительной переменной, как и пространственные координаты x, y, z, понятие одновременности также становится относительным. Два события, кажущихся одновременными одному наблюдателю, могут быть разделены во времени с точки зрения другого. Из других выводов, к которым приводит специальная теория относительности, заслуживает внимание эквивалентность массы и энергии. Масса m представляет собой своего рода «замороженную» энергию E, с которой связана соотношением E = mc2, где c — скорость света. Таким образом, испускание фотонов света происходит ценой уменьшения массы источника.Релятивистские эффекты, как правило, пренебрежимо малые при обычных скоростях, становятся значительными только при больших скоростях, характерных для атомных и субатомных частиц. Потеря массы, связанная с испусканием света, чрезвычайно мала и обычно не поддаётся измерению даже с помощью самых чувствительных химических весов. Однако специальная теория относительности позволила объяснить такие особенности процессов, происходящих в атомной и ядерной физике, которые до того оставались непонятными.

Почти через сорок лет после создания теории относительности физики, работавшие над созданием атомной бомбы, сумели вычислить количество выделяющейся при её взрыве энергии на основе дефекта (уменьшения) массы при расщеплении ядер урана.
После публикации статей в 1905 году к Эйнштейну пришло академическое признание. В 1909 году он стал адъюнкт-профессором Цюрихского университета, в следующем году профессором Немецкого университета в Праге, а в 1912 году — цюрихского Федерального технологического института. В 1914 году Эйнштейн был приглашён в Германию на должность профессора Берлинского университета и одновременно директора Физического института кайзера Вильгельма (ныне Институт Макса Планка). Германское подданство Эйнштейна было восстановлено, и он был избран членом Прусской академии наук.
После напряжённых усилий Эйнштейну удалось в 1915 году создать общую теорию относительности, выходившую далеко за рамки специальной теории, в которой движения должны быть равномерными, а относительные скорости постоянными.
 Общая теория относительности охватывала все возможные движения, в том числе и ускоренные (т. е. происходящие с переменной скоростью).
Общая теория относительности охватывала все возможные движения, в том числе и ускоренные (т. е. происходящие с переменной скоростью).Господствовавшая ранее механика, берущая начало из работ Исаака Ньютона (XVII–XVIII веков), становилась частным случаем, удобным для описания движения при относительно малых скоростях. Эйнштейну пришлось заменить многие из введённых Ньютоном понятий. Такие аспекты ньютоновской механики, как, например, отождествление гравитационной и инертной масс, вызывали у него беспокойство. По Ньютону, тела притягивают друг друга, даже если их разделяют огромные расстояния, причём сила притяжения, или гравитация, распространяется мгновенно. Гравитационная масса служит мерой силы притяжения. Что же касается движения тела под действием этой силы, то оно определяется инертной массой тела, которая характеризует способность тела ускоряться под действием данной силы. Эйнштейна заинтересовало, почему эти две массы совпадают.
Он произвёл так называемый «мысленный эксперимент».
 Допустим, один наблюдатель находится в кабине лифта небоскрёба, другой снаружи. Внезапно канат, поддерживающий кабину, обрывается, и она свободно падает. Экспериментатор в кабине проводит следующий опыт: вынимает из своего кармана платок и часы и выпускает их из рук. Относительно небоскрёба падает экспериментатор, часы и платок.
Допустим, один наблюдатель находится в кабине лифта небоскрёба, другой снаружи. Внезапно канат, поддерживающий кабину, обрывается, и она свободно падает. Экспериментатор в кабине проводит следующий опыт: вынимает из своего кармана платок и часы и выпускает их из рук. Относительно небоскрёба падает экспериментатор, часы и платок.Посмотрим, каким путём оба наблюдателя, внутренний и внешний, описывают то, что происходит в лифте.
Внутренний наблюдатель-экспериментатор. Пол лифта медленно начинает уходить из-под ног. Часы с платком медленно движутся вверх относительно экспериментатора. Платок движется вверх быстрее, чем часы. Экспериментатор делает вывод: все тела к земле движутся с разным ускорением. Самое большее ускорение у лифта, затем у него самого, потом следуют часы, и медленнее всех падает платок. Вывод — система неинерциальная (в инерциальной системе тело, на которое не действуют никакие силы, находится в покое или движется равномерно и прямолинейно).
Внешний наблюдатель.
 Все четыре тела: лифт, экспериментатор, часы и платок падают с различным ускорением к земле. Его вывод также совпадает с мнением внутреннего наблюдателя — система неинерциальная.
Все четыре тела: лифт, экспериментатор, часы и платок падают с различным ускорением к земле. Его вывод также совпадает с мнением внутреннего наблюдателя — система неинерциальная.Внутренний и внешний наблюдатель Эйнштейна рассуждает иначе: «Внешний наблюдатель замечает движение лифта и всех тел в нём, и находит его соответствующим закону тяготения Ньютона. Для него движение является не равномерным, а ускоренным, вследствие поля тяготения Земли.
Однако физик рождённый и воспитанный в лифте, рассуждал бы совершенно иначе. Он был бы уверен в том, что обладает инерциальной системой, и относил бы все законы природы к своему лифту, заявляя с уверенностью, что законы принимают особенно простую форму в его системе координат. Для него было бы естественным считать свой лифт покоящимся и свою систему координат — инерциальной.
Один из друзей Эйнштейна заметил по поводу такой ситуации, что человек в лифте не мог бы отличить, находится ли он в гравитационном поле или движется с постоянным ускорением.
 Эйнштейновский принцип эквивалентности, утверждающий, что гравитационные и инерциальные эффекты неотличимы, объяснил совпадение гравитационной и инертной массы в механике Ньютона. Затем Эйнштейн расширил картину, распространив ее на свет. Если луч света пересекает кабину лифта «горизонтально», в то время как лифт падает, то выходное отверстие находится на большем расстоянии от пола, чем входное, так как за то время, которое требуется лучу, чтобы пройти от стенки к стенке, кабина лифта успевает продвинуться на какое-то расстояние. Наблюдатель в лифте увидел бы, что световой луч искривился. Для Эйнштейна это означало, что в реальном мире лучи света искривляются, когда проходят на достаточно малом расстоянии от массивного тела.
Эйнштейновский принцип эквивалентности, утверждающий, что гравитационные и инерциальные эффекты неотличимы, объяснил совпадение гравитационной и инертной массы в механике Ньютона. Затем Эйнштейн расширил картину, распространив ее на свет. Если луч света пересекает кабину лифта «горизонтально», в то время как лифт падает, то выходное отверстие находится на большем расстоянии от пола, чем входное, так как за то время, которое требуется лучу, чтобы пройти от стенки к стенке, кабина лифта успевает продвинуться на какое-то расстояние. Наблюдатель в лифте увидел бы, что световой луч искривился. Для Эйнштейна это означало, что в реальном мире лучи света искривляются, когда проходят на достаточно малом расстоянии от массивного тела.Общая теория относительности Эйнштейна заменила ньютоновскую теорию гравитационного притяжения тел пространственно-временным математическим описанием того, как массивные тела влияют на характеристики пространства вокруг себя. Согласно этой точке зрения тела не притягивают друг друга, а изменяют геометрию пространства-времени, которая и определяет движение проходящих через него тел.

Но в тот период Эйнштейн работал не только над теорией относительности. Например, в 1916 году он ввёл в квантовую теорию понятие индуцированного излучения. В 1913 году Нильс Бор разработал модель атома, в которой электроны вращаются вокруг центрального ядра (открытого несколькими годами ранее Эрнестом Резерфордом) по орбитам, удовлетворяющим определённым квантовым условиям. Согласно модели Бора, атом испускает излучение, когда электроны, перешедшие в результате возбуждения на более высокий уровень, возвращаются на более низкий. Разность энергии между уровнями равна энергии, поглощаемой или испускаемой фотонами.
Возвращение возбуждённых электронов на более низкие энергетические уровни представляет собой случайный процесс. Эйнштейн предположил, что при определённых условиях электроны в результате возбуждения могут перейти на определённый энергетический уровень, затем, подобно лавине, возвратиться на более низкий. Этот процесс лежит в основе действия современных лазеров.
Хотя и специальная, и общая теории относительности были слишком революционны, чтобы снискать немедленное признание, они вскоре получили ряд подтверждений.
 Одним из первых было объяснение прецессии орбиты Меркурия, которую не удавалось полностью понять в рамках ньютоновской механики. Во время полного солнечного затмения в 1919 году астрономам удалось наблюдать звезду, скрытую за кромкой Солнца. Это свидетельствовало о том, что лучи света искривляются под действием гравитационного поля Солнца. Всемирная слава пришла к Эйнштейну, когда сообщения о наблюдении солнечного затмения 1919 года облетели весь мир. Относительность стала привычным словом.
Одним из первых было объяснение прецессии орбиты Меркурия, которую не удавалось полностью понять в рамках ньютоновской механики. Во время полного солнечного затмения в 1919 году астрономам удалось наблюдать звезду, скрытую за кромкой Солнца. Это свидетельствовало о том, что лучи света искривляются под действием гравитационного поля Солнца. Всемирная слава пришла к Эйнштейну, когда сообщения о наблюдении солнечного затмения 1919 года облетели весь мир. Относительность стала привычным словом.В 1920 году Эйнштейн стал приглашённым профессором Лейденского университета. Однако в самой Германии он подвергался нападкам из-за своих антимилитаристских взглядов и революционных физических теорий, названных некоторыми его коллегами «еврейской физикой».
В 1922 году Эйнштейну была вручена Нобелевская премия по физике 1921 года «за заслуги перед теоретической физикой, и особенно за открытие закона фотоэлектрического эффекта».
В то время как большинство физиков начало склоняться к принятию квантовой теории, Эйнштейна все более не удовлетворяли следствия, к которым она приводила.
 В 1927 году он выразил своё несогласие со статистической интерпретацией квантовой механики, предложенной Нильсом Бором и Максом Борном. Согласно этой интерпретации, принцип причинно-следственной связи неприменим к субатомным явлениям. Эйнштейн был глубоко убеждён, что статистика является не более чем средством и что фундаментальная физическая теория не может быть статистической по своему характеру. По словам Эйнштейна, «Бог не играет в кости» со Вселенной.
В 1927 году он выразил своё несогласие со статистической интерпретацией квантовой механики, предложенной Нильсом Бором и Максом Борном. Согласно этой интерпретации, принцип причинно-следственной связи неприменим к субатомным явлениям. Эйнштейн был глубоко убеждён, что статистика является не более чем средством и что фундаментальная физическая теория не может быть статистической по своему характеру. По словам Эйнштейна, «Бог не играет в кости» со Вселенной.До конца жизни он стремился построить единую теорию поля, которая могла бы выводить квантовые явления из релятивистского описания природы. Осуществить эти замыслы Эйнштейну так и не удалось.
Теория относительности Эйнштейна. Объяснил максимально просто, но нет… | Panda the Red
На основе фотографии под названием «Альберт Эйнштейн, автор Дорис Ульманн». Источник: Викисклад. Всеобщее достояние.
«Все должно быть сделано как можно проще, но не проще».
Обновление от 20 апреля 2020 г.
 : Вышло продолжение этой статьи: Релятивистское мышление .
: Вышло продолжение этой статьи: Релятивистское мышление . Специальная теория относительности, без сомнения, является одним из самых важных открытий в истории науки и уступает только открытию законов механики Ньютоном по своему значению для физики. Несмотря на это, специальная теория относительности плохо изучена, и в Интернете и в средствах массовой информации существует множество дезинформации по этому вопросу. Этому не способствует в основном незаслуженная репутация слишком сложной для понимания большинства людей.
На самом деле основные идеи не так уж сложны для понимания. В этой статье мы объясним некоторые из этих основных идей, пройдя прямой путь через историю физики со времен Галилея, показав, почему законы физики, как они понимались в 19 веке, должны были быть скорректированы, показав, как в результате этой корректировки возникла специальная теория относительности. и изучение некоторых следствий этой новой теории.
Системы отсчета, ковариация и теория относительности Галилея
Основная идея теории относительности заключается в том, что два разных наблюдателя, движущихся относительно друг друга, должны согласиться с законами физики.
 Когда два разных наблюдателя находятся в относительном движении, говорят, что они находятся в разных системах отсчета, а когда их относительная скорость постоянна, эти системы отсчета называются инерциальными. Когда все наблюдатели во всех инерциальных системах отсчета соглашаются с физической теорией, говорят, что эта теория ковариант . Мы будем рассматривать только инерциальные системы отсчета.
Когда два разных наблюдателя находятся в относительном движении, говорят, что они находятся в разных системах отсчета, а когда их относительная скорость постоянна, эти системы отсчета называются инерциальными. Когда все наблюдатели во всех инерциальных системах отсчета соглашаются с физической теорией, говорят, что эта теория ковариант . Мы будем рассматривать только инерциальные системы отсчета.Предположим, что наблюдатель, покоящийся относительно системы координат S, стоит в начале системы координат (x,y,z), а наблюдатель, покоящийся относительно системы координат S′, стоит в начале координат система координат (x′,y′,z′). Если наблюдатель в S видит, что начало координат S’ движется вправо с постоянной скоростью V, то говорят, что две системы отсчета находятся в стандартной конфигурации : 9.0004 Источник: Викисклад. Всеобщее достояние.
Мы всегда будем предполагать, что S и S’ находятся в стандартной конфигурации.
Предположим, что наблюдатель в S отмечает, что событие происходит в точке P в момент времени T₀ и что другое событие происходит в точке Q в момент времени T₁, и пусть L — расстояние между P и Q и ΔT=T₁-T₀.
 Предположим, что одни и те же события наблюдает наблюдатель в S’, разделенный расстоянием L’, и второе событие происходит через ΔT’ секунд после первого. До Эйнштейна были сделаны следующие предположения:
Предположим, что одни и те же события наблюдает наблюдатель в S’, разделенный расстоянием L’, и второе событие происходит через ΔT’ секунд после первого. До Эйнштейна были сделаны следующие предположения:- Расстояние абсолютное: L=L′
- Время абсолютное: ΔT=ΔT′
Длины определяются по теореме Пифагора: L²=(Δx)²+(Δy)²+(Δz)², где Δx , Δy и Δz — смещения в направлениях x, y и z. Величины, которые принимают одно и то же числовое значение во всех инерциальных системах отсчета, называются -инвариантными.
Пусть x, y, z и t будут координатами положения и времени системы координат, присоединенной к S, а x’, y’, z’, и t’ координатами положения и времени системы координат, прикрепленной к S ‘. Эти предположения о расстояниях и временных интервалах подразумевают, что эти системы координат связаны следующим правилом:
Это называется преобразованием Галилея . Галилеевская теория относительности — это теория, согласно которой законы физики ковариантны по отношению к преобразованию Галилея.
 Проверим, верно ли это для ньютоновской физики. Предположим, что известно, что закон Ньютона верен в системе отсчета S′:
Проверим, верно ли это для ньютоновской физики. Предположим, что известно, что закон Ньютона верен в системе отсчета S′:. Мы игнорируем координаты y′ и z′ для простоты.
Здесь F′(x′,t′) – произвольная сила, измеренная экспериментально, а F(x,t) – выражение той же силы согласно системе S. Предположим, что наблюдатель в S′ определил F′ (x′,t′) путем проверки числовых значений x′ и t′. Чтобы найти F(x,t), наблюдатель в S проверяет те же числовые значения для x и t. Поскольку это одна и та же сила, а также поскольку S не испытывает никакого ускорения относительно S’, наблюдатель в S должен получить те же результаты, F(x,t)=F'(x’,t’). Подставляя x′=x-Vt и t′=t в производную, мы получаем:
Отсюда следует, что:
Итак, ньютоновская физика ковариантна по отношению к преобразованию Галилея. Но верно ли это для всех законов физики?
Рассмотрим уравнения Максвелла в области пространства, свободной от зарядов или токов:
Возьмите изгиб третьей линии и используйте тождество векторного исчисления ∇⨯(∇⨯ E )=∇(∇⋅ E )- ∇² E = -∇² E , потому что ∇⋅ E = 0.
 Тогда вектор электрического поля E подчиняется волновому уравнению:
Тогда вектор электрического поля E подчиняется волновому уравнению:С помощью того же процесса можно показать, что вектор магнитного поля B также подчиняется волновому уравнению. Это уравнение предсказывает, что возмущение электрического поля будет распространяться с постоянной скоростью c , скоростью света. Рассмотрим электрическое поле, единственная составляющая которого находится в направлении x и которое не зависит от y или z. Предположим, что в системе S′ выполняется волновое уравнение:
Нам нужно это преобразовать в:
Давайте посмотрим, произойдет ли это с преобразованием Галилея.
Производные преобразуются в соответствии с цепным правилом:
И это означает, что при преобразовании Галилея волновое уравнение, как оно видно из системы S’, при взгляде из S’ превращается в следующее:
Это представляет проблему: наблюдатели в разных инерциальные системы отсчета не согласятся с законом, управляющим распространением луча света.
 Чтобы решить эту проблему, у нас нет другого выбора, кроме как заключить, что по крайней мере одно из следующих утверждений верно:
Чтобы решить эту проблему, у нас нет другого выбора, кроме как заключить, что по крайней мере одно из следующих утверждений верно:- Уравнения Максвелла неверны.
- Существует только одна особая система отсчета, в которой верны уравнения Максвелла, а именно система покоя так называемого светоносного эфира.
- Преобразование Галилея неверно, а следовательно, и лежащие в его основе предположения о пространстве и времени неверны.
Первое предложение можно сразу отбросить. Уравнения Максвелла — это экспериментальные факты реальности. Второй можно отбросить в свете нескольких десятилетий во второй половине XIX века, в течение которых физики безуспешно пытались обнаружить эфир. Остается только третий вариант.
Преобразование Лоренца и теория относительности Эйнштейна
В 1892 году Хендрик Лоренц опубликовал статью, в которой показал, что преобразование, при котором уравнения Максвелла являются ковариантными, имеет вид:
Где γ называется фактором Лоренца:
Законы Ньютона также ковариантен относительно этого преобразования с соответствующей модификацией, но об этом мы поговорим в продолжении этой статьи.

Это называется преобразованием Лоренца. К сожалению, Лоренц не дал правильной физической интерпретации, так как неправильно приписал ее движению Земли относительно светоносного эфира.
Эйнштейн дал правильную интерпретацию в своей статье 1905 года «Об электродинамике движущихся тел» , и эта интерпретация является основой того, что сейчас называется специальной теорией относительности. Он начал со следующих двух постулатов:
- Законы физики одинаковы во всех инерциальных системах отсчета.
- Скорость света имеет одинаковое значение во всех инерциальных системах отсчета, то есть является инвариантом .
Мы можем использовать их для получения преобразования Лоренца, но для этого потребуется внести некоторые изменения в то, как мы понимаем пространство и время.
Замедление времени
Пусть S′ будет кадром покоя поезда в стандартной конфигурации с S, кадром покоя человека, стоящего на платформе. На поезде проводится эксперимент, в котором в течение интервала времени Δt′ происходит какой-либо физический процесс.
 Мы покажем, что наблюдатель на платформе увидит, что тот же самый физический процесс происходит в течение интервала времени Δt, где Δt и Δt′ связаны соотношением:
Мы покажем, что наблюдатель на платформе увидит, что тот же самый физический процесс происходит в течение интервала времени Δt, где Δt и Δt′ связаны соотношением:Поскольку γ>1, это называется замедлением времени . Предположим, что, по словам человека, проводившего эксперимент в поезде, лазерный импульс покидает точку А’, движется прямо вверх, затем отражается от зеркала в точке В’, а затем возвращается к детектору в точке С’, которая находится рядом с к А’.
Общее расстояние, пройденное лазерным импульсом, составило 2 часа, а скорость c , поэтому:
Теперь давайте подумаем о том, что видит наблюдатель на платформе. Пока лазерный импульс движется с постоянной скоростью от излучателя к зеркалу, а затем обратно к детектору, поезд также движется вправо. Для наблюдателя на платформе путь лазерного импульса представляет собой треугольник:
Не в масштабе.
По теореме Пифагора длина прямой AB равна:
Общая длина пути в два раза больше этой величины, а также, поскольку скорость света одинакова в обеих системах отсчета, общая длина пути должна быть равна cΔt, поэтому:
Теперь найдем Δt через Δt ′ путем исключения h.
 Из формулы для Δt′ мы получаем h=cΔt′/2, поэтому, подставив это и возведя в квадрат обе части формулы для Δt, мы получим:
Из формулы для Δt′ мы получаем h=cΔt′/2, поэтому, подставив это и возведя в квадрат обе части формулы для Δt, мы получим:Это показывает, что, поскольку скорость света должна быть неизменной, время расширяется между системами отсчета. Это объясняет, почему движущиеся часы кажутся медленнее: если часы в поезде тикают каждую секунду, то интервал между тактами увеличивается в зависимости от того, кто наблюдает за ними с пути.
Демонстрация: распад мюона
Мюон — субатомная частица, идентичная электрону во всех отношениях, кроме массы: мюон примерно в 207 раз тяжелее. Слабое взаимодействие (одно из четырех фундаментальных взаимодействий) заставляет мюон распадаться на электрон и две другие частицы, называемые электронным антинейтрино и мюонным нейтрино: выборке из 100 мюонов потребуется около 2,2 микросекунды, чтобы половина из них распалась на электроны.
Мюоны образуются в верхних слоях атмосферы, когда космические лучи сталкиваются с молекулами газа на высоте около 15 километров.
 Детекторы мюонов на уровне моря обычно обнаруживают один мюон на квадратный сантиметр в минуту, а их средняя скорость при обнаружении на уровне моря составляет около 0,995 с. Если пренебречь теорией относительности, мы обнаружим, что время, необходимое мюону для достижения уровня моря, составляет 15 000 м/0,995 c~ 50 микросекунд, или около 23 периодов полураспада. Поскольку поток мюонов на уровне моря составляет 1/с∙см², это означает, что количество мюонов, производимых на высоте, будет 2²³/с∙см², что не очень реалистично.
Детекторы мюонов на уровне моря обычно обнаруживают один мюон на квадратный сантиметр в минуту, а их средняя скорость при обнаружении на уровне моря составляет около 0,995 с. Если пренебречь теорией относительности, мы обнаружим, что время, необходимое мюону для достижения уровня моря, составляет 15 000 м/0,995 c~ 50 микросекунд, или около 23 периодов полураспада. Поскольку поток мюонов на уровне моря составляет 1/с∙см², это означает, что количество мюонов, производимых на высоте, будет 2²³/с∙см², что не очень реалистично.Но давайте посмотрим, что произойдет, если мы рассмотрим специальную теорию относительности. Когда дело доходит до распада частиц, для вас, наблюдателя, не имеет значения, сколько времени проходит. Важно то, сколько времени проходит для частиц, и если эти частицы движутся намного быстрее, чем вы, то из-за замедления времени, когда для вас истекает временной интервал Δt, для частицы.
Для V=0,995c, γ~10. Итак, хотя вам кажется, что мюонам требуется около 50 микросекунд, чтобы достичь уровня моря, для мюонов требуется всего около 5 микросекунд, или около 2,3 периода полураспада.
 Это означает, что если поток мюонов на уровне моря составляет 1/с∙см², то поток мюонов, производимых на расстоянии 15 км, составляет около 4,5/с∙см², что является гораздо более разумным числом.
Это означает, что если поток мюонов на уровне моря составляет 1/с∙см², то поток мюонов, производимых на расстоянии 15 км, составляет около 4,5/с∙см², что является гораздо более разумным числом.Мюоны, со своей стороны, видят землю, движущуюся к ним со скоростью 0,995 c. Мюоны увидят, как они достигают земли (или, так сказать, земля достигает их) всего через 5 микросекунд, но как они могли пройти 15 000 метров за 5 микросекунд со скоростью всего 0,995c? Ответ заключается в том, что они этого не сделали.
Сокращение длины
Наблюдатель, находящийся в состоянии покоя в системе S, видит, как частица со скоростью V x проходит мимо столба в точке A в момент времени t=0, а затем в момент времени Δt он видит, как частица проходит мимо столба в точке B, с обеими точками на оси x, разделенными длиной L. Система покоя частицы S ‘, а в S ‘частица неподвижна, а два столба, разделенные длиной L ‘, приближаются к частице со скоростью -V х .
 Первый столб проходит частицу в момент времени t′=0, а второй – в момент времени Δt′=Δt/γ. Поскольку L=VΔt и L′=VΔt′, мы видим, что L′=L/γ. Это означает, что в подвижной системе отсчета длина сокращается.
Первый столб проходит частицу в момент времени t′=0, а второй – в момент времени Δt′=Δt/γ. Поскольку L=VΔt и L′=VΔt′, мы видим, что L′=L/γ. Это означает, что в подвижной системе отсчета длина сокращается.Это отвечает на вопрос, заданный в конце предыдущего раздела: мюонам не обязательно преодолевать расстояние в 15 000 метров, которое видит наблюдатель с Земли. В остальных кадрах мюонов расстояние составляет всего 1500 метров.
Это относится к сужению пространства по мнению наблюдателя в системе покоя движущегося объекта. Существует также обратная версия этого принципа, согласно которой движущиеся объекты кажутся сжатыми. Пусть S′ будет системой покоя стержня, который движется со скоростью V x в соответствии с кадром наблюдения S. Наблюдатель не имеет возможности узнать, движется ли он относительно стержня или стержень движется относительно него. Если бы она двигалась относительно стержня, то она увидела бы, что пространство сжимается, поэтому стержень кажется короче, чем его длина в состоянии покоя.
 Это в точности эквивалентно утверждению, что стержень кажется короче, потому что он движется, поскольку у нее нет возможности узнать, движется ли он или стержень.
Это в точности эквивалентно утверждению, что стержень кажется короче, потому что он движется, поскольку у нее нет возможности узнать, движется ли он или стержень.Преобразование Лоренца
Теперь мы можем доказать, что преобразование Лоренца связывает системы координат двух систем отсчета в стандартной конфигурации. Мы покажем, что:
Поскольку скорость S’ относительно S постоянна и полностью в направлении x, по симметрии должно быть верно, что y’=y и z’=z.
Чтобы продолжить, определим новую величину, называемую пространственно-временным интервалом (Δs)²:
Имейте в виду, что для знаков минус существуют другие соглашения.
Мы покажем, что пространственно-временной интервал инвариантен, что означает, что (Δs)²=(Δs′)² для всех пар систем отсчета S и S′.
Предположим, что человек, стоящий неподвижно в кадре S, посылает лазерный импульс, который проходит расстояние L за время Δt, и относительно кадра S’ импульс проходит расстояние L’ за время Δt’.
 Тогда c² =(L/Δt)²=(L′/Δt′)² из инвариантности c . Тогда мы имеем:
Тогда c² =(L/Δt)²=(L′/Δt′)² из инвариантности c . Тогда мы имеем:Остальная часть вывода преобразования Лоренца следует выводу, который использовал Эйнштейн в своей популярной книге по теории относительности. Отбросьте дельта-символы во второй строке выше, и, поскольку y′=y и z′=z, эти члены исключаются из уравнения. Тогда мы можем написать:
Мы можем использовать это, чтобы написать:
Добавьте второе уравнение к первому, чтобы получить уравнение для x’ и вычтите первое уравнение из второго, чтобы получить уравнение для c t’:
Затем сделайте следующее присваивания:
Итак, мы получаем линейную систему для x’ и c t’:
Начало системы координат со штрихом имеет скорость V x , и поэтому мы можем установить его вектор положения как (Vt,0,0 ), поэтому пусть x′=0 совпадает с x=Vt. Тогда первое уравнение дает:
Теперь система уравнений принимает вид:
Чтобы найти a , подставьте их в выражение инвариантности пространственно-временного интервала c²(t′)²-(x′)²=c²t²-x²:
Это означает, что:
Тогда мы получим преобразование Лоренца, если подставим это в формулы, которые мы нашли для x’ и ct’:
Итак, мы успешно получили преобразование Лоренца из физических принципов.

Демонстрация: классический предел
Преобразование Лоренца сильно отличается от преобразования Галилея. Как физики могли так долго ошибаться?
Рассмотрим реактивный истребитель, летящий на скорости чуть выше скорости звука относительно наблюдателя в ближайшей диспетчерской вышке с V=350 м/с. Тогда V²/ c ²~1,4×10⁻¹². Лучший способ приблизить значение γ для малых значений V²/ c ² — это использовать биномиальное приближение, которое говорит, что:
Это дает хорошую оценку для γ:
Таким образом, для скорости, близкой к скорости Здравая, нерелятивистская физика имеет точность до триллионных долей (12 знаков после запятой). И конечно, даже эта «низкая» скорость была практически недоступна для тех, кто проводил эксперименты до 20-го века и уж точно никогда не встречалась бы никому в их повседневной жизни, так что нетрудно понять, почему со времени начала XX века прошло почти 300 лет. Галилей, прежде чем кто-либо заметил, что что-то не так.

Пространство-время
Нельзя достаточно сильно подчеркнуть, что замедление времени и сокращение длины являются свойствами самих пространства и времени. Они не являются результатом действия сил, заставляющих часы идти медленнее в зависимости от того, кто на них смотрит, и движение с релятивистской скоростью не вызывает сил, растягивающих или сжимающих объекты. Это также не результат ошибки измерения или оптической иллюзии, из-за которой наблюдатели в разных кадрах неправильно оценивают длину объекта или скорость хода часов. Когда наблюдатели в разных системах отсчета сообщают о разной длине измерительных стержней или о разной частоте хода часов, все они верны, потому что длины и временные интервалы не являются инвариантными, и именно так работают пространство и время.
Классическая физика сформулирована в трехмерном евклидовом пространстве, E₃, наборе всех упорядоченных троек действительных чисел (x,y,z) в сочетании с достаточной топологической структурой, чтобы такие вещи, как «расстояние» и «точка», имели смысл , а также функцию, называемую евклидовой метрикой , которая говорит, что расстояние между двумя точками P₁=(x₁,y₁,z₁) и P₂=(x₂,y₂,z₂) равно:
Итак, в классической физике, если событие происходит в точке P₁ в момент времени t₁, а затем второе событие происходит в точке P₂ в момент времени t₂, где P₁ и P₂ разделены расстоянием L и временем Δt=t₂-t₁, лучшее, что мы можем сказать, это то, что два события произошли разместите на расстоянии L метров друг от друга, а второе произошло через Δt секунд после первого.
 Вот что имеется в виду, когда мы говорим, что пространство и время в классической физике «отделимы»: нет последовательного способа присвоить единое число «расстоянию» между двумя событиями в классическом пространстве-времени.
Вот что имеется в виду, когда мы говорим, что пространство и время в классической физике «отделимы»: нет последовательного способа присвоить единое число «расстоянию» между двумя событиями в классическом пространстве-времени.Действительно ли мы живем в евклидовом пространстве? Мы не. Если бы пространство-время было евклидовым, то преобразование Галилея было бы правильным соотношением между координатами разных систем отсчета, поэтому расстояния были бы инвариантны по отношению к изменению системы отсчета. Но это неверно из-за сокращения длины. Это ставит вопрос о том, в каком пространстве мы на самом деле живем.
Рассмотрим множество всех точек пространства-времени (x,y,z,t), но на этот раз предположим, что «расстояние» между двумя точками есть интервал пространства-времени. . Если событие s₁ происходит в позиции (x₁,y₁,z₁) и момент времени t₁, а другое событие s₂ происходит в позиции (x₂,y₂,z₂) в момент времени t₂, то «расстояние» между ними определяется как:
Имя функции, определяющей пространственно-временной интервал между двумя событиями, — метрика Минковского , в честь Германа Минковского.
 Минковский, который на самом деле был одним из профессоров Эйнштейна в колледже, фактически формализовал концепцию пространства-времени. Таким образом, вместо трехмерного евклидова пространства с одним «дополнительным» измерением времени мы живем в четырехмерном пространстве-времени Минковского. Последствия этого огромны, и некоторым из них придется ждать продолжения этой статьи. Но чтобы закрыть эту статью, давайте поговорим о самом известном из них.
Минковский, который на самом деле был одним из профессоров Эйнштейна в колледже, фактически формализовал концепцию пространства-времени. Таким образом, вместо трехмерного евклидова пространства с одним «дополнительным» измерением времени мы живем в четырехмерном пространстве-времени Минковского. Последствия этого огромны, и некоторым из них придется ждать продолжения этой статьи. Но чтобы закрыть эту статью, давайте поговорим о самом известном из них.Демонстрация: Эквивалентность массы и энергии, E=mc²
Одним из самых известных следствий специальной теории относительности является то, что масса покоя эквивалентна энергии. Масса покоя частицы — это ее масса, измеренная в системе отсчета, в которой частица не движется. Этот раздел предназначен для предоставления обоснования, но не формального доказательства этого утверждения.
Сначала я буду утверждать, исходя из физических принципов, что частица может двигаться со скоростью света тогда и только тогда, когда у нее нет массы покоя.
 Фактическое доказательство придется ждать после этой статьи, которая будет посвящена некоторым приложениям релятивистской физики.
Фактическое доказательство придется ждать после этой статьи, которая будет посвящена некоторым приложениям релятивистской физики.Предположим, что частица движется со скоростью света в системе отсчета S и преодолевает расстояние L за время Δt, так что c Δt=L, поэтому (Δs)²=( c Δt)²-L² =0. Но в силу неизменности пространственно-временного интервала (Δs′)²=(Δs)², поэтому в любой другой системе отсчета S′ (Δs′)²=( c Δt′)²-(L′)² =0, поэтому L′/Δt′= c , поэтому скорость частицы составляет c в на каждые инерциальных систем отсчета. Это означает, что у него нет системы покоя, и поэтому физически бессмысленно говорить, что у него есть масса покоя. Это удовлетворяет части утверждения «только если».
Теперь предположим, что имеется система отсчета, в которой частица покоится и имеет нулевую массу. Тогда частица может также и не существовать: она покоится, поэтому у нее нет импульса, чтобы передать ее другим частицам, и у нее нет массы, поэтому никакая другая частица не может передать ей импульс, поэтому для этого нет никакого способа.
 частица для взаимодействия с чем-либо во Вселенной. Поскольку нас интересуют только частицы, существование которых имеет физический смысл, мы можем сказать, что не существует системы отсчета, в которой безмассовая частица покоится, поэтому все безмассовые частицы должны двигаться со скоростью света. Это удовлетворяет части «если» утверждения.
частица для взаимодействия с чем-либо во Вселенной. Поскольку нас интересуют только частицы, существование которых имеет физический смысл, мы можем сказать, что не существует системы отсчета, в которой безмассовая частица покоится, поэтому все безмассовые частицы должны двигаться со скоростью света. Это удовлетворяет части «если» утверждения.В дальнейшем мы увидим, что теория относительности заставляет импульс и энергию работать не так, как мы привыкли думать о них, но основные законы сохранения остаются в силе: импульс и энергия по-прежнему сохраняются в каждой системе отсчета.
Позитрон — субатомная частица, античастица электрона. Он идентичен электрону во всех отношениях, за исключением того, что имеет противоположный заряд. Из опыта известно, что когда частица и античастица сталкиваются друг с другом, они аннигилируют друг с другом и производят излучение. Формула для этого:
Где e⁺ означает позитрон, e⁻ означает электрон, а γ означает фотон, поэтому получается два фотона.
 Рассмотрим случай, когда электрон и позитрон покоятся и находятся в контакте друг с другом за мгновение до того, как произойдет аннигиляция. Общая масса системы равна 2mₑ, что в два раза больше массы электрона, а полный импульс системы равен нулю. Но после аннигиляции полная масса покоя равна нулю, потому что образовавшиеся фотоны движутся со скоростью света. Куда уходит масса и откуда берется энергия?
Рассмотрим случай, когда электрон и позитрон покоятся и находятся в контакте друг с другом за мгновение до того, как произойдет аннигиляция. Общая масса системы равна 2mₑ, что в два раза больше массы электрона, а полный импульс системы равен нулю. Но после аннигиляции полная масса покоя равна нулю, потому что образовавшиеся фотоны движутся со скоростью света. Куда уходит масса и откуда берется энергия?Поскольку импульс сохраняется, после аннигиляции общий импульс по-прежнему равен нулю, поэтому два фотона имеют импульс с одинаковой величиной p и противоположными направлениями. Хотя у фотонов нет массы покоя, у них все же есть кинетическая энергия, которую мы можем записать как E = пк .
Эксперименты показали, что после аннигиляции полная кинетическая энергия двух фотонов составляет около 1,637×10⁻¹³ Джоулей. Суммарная масса покоя двух электронов составляет около 1,829×10⁻³⁰ кг. Когда эта общая масса покоя умножается на c², мы получаем (2mₑ) c ²=1,644×10⁻¹³ Джоулей, что соответствует общей выделившейся энергии с точностью до ошибки округления.
 Такое же соотношение между энергией и массой покоя возникает, когда этот эксперимент повторяется с протонами и антипротонами, нейтронами и антинейтронами, мюонами и антимюонами и так далее.
Такое же соотношение между энергией и массой покоя возникает, когда этот эксперимент повторяется с протонами и антипротонами, нейтронами и антинейтронами, мюонами и антимюонами и так далее.Поскольку энергия сохраняется, до аннигиляции в системе должно было быть столько же энергии, сколько и после. Это означает, что мы можем предположить, что энергия перед аннигиляцией была запасена как масса электрона и позитрона, при этом количество накопленной энергии равно E=m c ², и что процесс аннигиляции превратил эту энергию в кинетическую энергию фотонов. Это могло бы объяснить как появление кинетической энергии в системе, в которой изначально ее не было, так и исчезновение массы покоя в системе, но нам все еще нужно доказать это на самом деле, что будет сделано в следующей статье.
Обновление от 20 апреля 2020 г .: Вышло продолжение: Релятивистское мышление .
Заключение и авторские материалы
Любые изображения, которые не были процитированы, являются моей собственной оригинальной работой.
 Некоторые из примеров, которые я использовал, основаны на примерах, описанных в учебнике «Современная физика для ученых и инженеров», 2-е издание Тейлора, Дубсона и Зафиратоса.
Некоторые из примеров, которые я использовал, основаны на примерах, описанных в учебнике «Современная физика для ученых и инженеров», 2-е издание Тейлора, Дубсона и Зафиратоса.Специальная теория относительности Эйнштейна – манекены
В 1905 году Альберт Эйнштейн опубликовал специальную теорию относительности , , которая объясняет, как интерпретировать движение между различными инерциальными системами отсчета — то есть места, которые движутся с постоянными скоростями относительно друг друга.
Эйнштейн объяснил, что когда два объекта движутся с постоянной скоростью, как относительное движение между двумя объектами, вместо обращения к эфиру как к абсолютной системе отсчета, определяющей происходящее. Если вы и какой-нибудь астронавт Эмбер двигаетесь на разных космических кораблях и хотите сравнить свои наблюдения, важно только то, как быстро вы и Эмбер движетесь друг относительно друга.
Специальная теория относительности включает только частный случай (отсюда и название), когда движение является равномерным.
 Движение, которое он объясняет, происходит только в том случае, если вы движетесь по прямой с постоянной скоростью. Как только вы ускоряетесь или изгибаетесь — или делаете что-либо, что каким-либо образом меняет характер движения — специальная теория относительности перестает применяться. Вот тут-то и появляется общая теория относительности Эйнштейна, потому что она может объяснить общий случай любого вида движения.
Движение, которое он объясняет, происходит только в том случае, если вы движетесь по прямой с постоянной скоростью. Как только вы ускоряетесь или изгибаетесь — или делаете что-либо, что каким-либо образом меняет характер движения — специальная теория относительности перестает применяться. Вот тут-то и появляется общая теория относительности Эйнштейна, потому что она может объяснить общий случай любого вида движения.Теория Эйнштейна основывалась на двух ключевых принципах:
Принцип относительности: Законы физики не меняются даже для объектов, движущихся в инерциальных (с постоянной скоростью) системах отсчета.
Принцип скорости света: Скорость света одинакова для всех наблюдателей, независимо от их движения относительно источника света. (Физики записывают эту скорость, используя символ c. )
Гениальность открытий Эйнштейна в том, что он смотрел на эксперименты и предполагал, что результаты верны.
 Это было полной противоположностью тому, что, казалось, делали другие физики. Вместо того, чтобы предположить, что теория верна и что эксперименты потерпели неудачу, он предположил, что эксперименты были правильными, а теория потерпела неудачу.
Это было полной противоположностью тому, что, казалось, делали другие физики. Вместо того, чтобы предположить, что теория верна и что эксперименты потерпели неудачу, он предположил, что эксперименты были правильными, а теория потерпела неудачу.Во второй половине 19-го века физики искали таинственную вещь под названием эфир — среду, которая, по их мнению, существовала для распространения световых волн. По мнению Эйнштейна, вера в эфир привела к беспорядку, поскольку он ввел среду, которая заставляла определенные законы физики работать по-разному в зависимости от того, как наблюдатель двигался относительно эфира. Эйнштейн только что полностью удалил эфир и предположил, что законы физики, включая скорость света , работали одинаково независимо от того, как вы двигались — именно так, как показали эксперименты и математика!
Объединение пространства и времени
Специальная теория относительности Эйнштейна установила фундаментальную связь между пространством и временем.
 Вселенную можно рассматривать как имеющую три пространственных измерения — вверх/вниз, влево/вправо, вперед/назад — и одно временное измерение. Это 4-мерное пространство называется пространственно-временным континуумом .
Вселенную можно рассматривать как имеющую три пространственных измерения — вверх/вниз, влево/вправо, вперед/назад — и одно временное измерение. Это 4-мерное пространство называется пространственно-временным континуумом . Если вы перемещаетесь в пространстве достаточно быстро, то наблюдения, которые вы делаете о пространстве и времени, несколько отличаются от наблюдений других людей, которые движутся с другой скоростью.
Вы можете себе это представить, разобравшись с мысленным экспериментом, изображенным на этом рисунке. Представьте, что вы находитесь на космическом корабле и держите в руках лазер, который выпускает луч света прямо вверх, попадая в зеркало, которое вы разместили на потолке. Затем световой луч возвращается вниз и попадает на детектор.
(Вверху) Вы видите, как луч света поднимается вверх, отражается от зеркала и падает прямо вниз. (Внизу) Эмбер видит, как луч движется по диагонали.
Однако космический корабль движется с постоянной скоростью, равной половине скорости света (0,5 c, , как написали бы физики).
 Согласно Эйнштейну, для вас это не имеет значения — вы даже не можете сказать, что движетесь. Однако если бы астронавт Эмбер шпионила за вами, как показано на рисунке внизу, это была бы другая история.
Согласно Эйнштейну, для вас это не имеет значения — вы даже не можете сказать, что движетесь. Однако если бы астронавт Эмбер шпионила за вами, как показано на рисунке внизу, это была бы другая история.Эмбер увидит, как ваш луч света движется вверх по диагонали, попадает на зеркало, а затем движется вниз по диагонали, прежде чем попасть в детектор. Другими словами, вы и Эмбер увидите 90 319 различных 90 320 путей света, и, что более важно, эти пути даже не будут одинаковой длины. Это означает, что время прохождения луча от лазера к зеркалу и детектору также должно быть разным для вас и Эмбер, чтобы вы оба согласились со скоростью света.
Это явление известно как замедление времени , , когда время на корабле, движущемся очень быстро, кажется медленнее, чем на Земле.
Как ни странно, этот пример (и многие другие) демонстрирует, что в теории относительности Эйнштейна пространство и время тесно связаны друг с другом. Если вы примените уравнения преобразования Лоренца, они сработают так, что скорость света будет идеально согласована для обоих наблюдателей.

Это странное поведение пространства и времени становится очевидным только тогда, когда вы путешествуете со скоростью, близкой к скорости света, поэтому никто никогда не наблюдал этого раньше. Эксперименты, проведенные после открытия Эйнштейна, подтвердили, что это правда — время и пространство воспринимаются по-разному, именно так, как описал Эйнштейн, для объектов, движущихся со скоростью, близкой к скорости света.
Объединение массы и энергии
Самая известная работа в жизни Эйнштейна также датируется 1905 годом (для него это был напряженный год), когда он применил идеи своей статьи по теории относительности, чтобы вывести уравнение E = mc 2 , которое представляет соотношение между массой (м) и энергия (Е).
Короче говоря, Эйнштейн обнаружил, что по мере того, как объект приближается к скорости света, с, масса объекта увеличивается. Объект движется быстрее, но и становится тяжелее. Если бы он действительно мог двигаться в c, масса и энергия объекта были бы бесконечны.

- Как собрать кубик Рубика, не сломав голову

 2.
2.
 Это еще один побочный эффект того, что свет всегда движется с одинаковой скоростью.
Это еще один побочный эффект того, что свет всегда движется с одинаковой скоростью. С вашей точки зрения, свет попадает в обе стены одновременно. С точки зрения вашего знакомого это не так. В этом нет ничего плохого.
С вашей точки зрения, свет попадает в обе стены одновременно. С точки зрения вашего знакомого это не так. В этом нет ничего плохого. Вырос он в Мюнхене, где у его отца и дяди был небольшой электрохимический завод. Эйнштейн был тихим, рассеянным мальчиком, который питал склонность к математике, но терпеть не мог школу с её механической зубрёжкой и казарменной дисциплиной.
Вырос он в Мюнхене, где у его отца и дяди был небольшой электрохимический завод. Эйнштейн был тихим, рассеянным мальчиком, который питал склонность к математике, но терпеть не мог школу с её механической зубрёжкой и казарменной дисциплиной.
 Его первые работы были посвящены силам взаимодействия между молекулами и приложениям статистической термодинамики. Одна из них — «Новое определение размеров молекул» — была принята в качестве докторской диссертации Цюрихским университетом, и в 1905 году Эйнштейн стал доктором наук. В том же году он опубликовал небольшую серию работ, которые изменили лицо всей физики.
Его первые работы были посвящены силам взаимодействия между молекулами и приложениям статистической термодинамики. Одна из них — «Новое определение размеров молекул» — была принята в качестве докторской диссертации Цюрихским университетом, и в 1905 году Эйнштейн стал доктором наук. В том же году он опубликовал небольшую серию работ, которые изменили лицо всей физики. Филипп де Ленард высказал предположение, что свет выбивает электроны с поверхности металла. Предположил он и то, что при освещении поверхности более ярким светом электроны должны вылетать с большей скоростью. Но эксперименты показали, что прогноз Ленарда неверен. Между тем в 1900 году Максу Планку удалось описать излучение, испускаемое горячими телами. Он принял радикальную гипотезу о том, что энергия испускается не непрерывно, а дискретными порциями — квантами. Физический смысл квантов оставался неясным, но величина кванта равна произведению некоторого числа (постоянной Планка) и частоты излучения.
Филипп де Ленард высказал предположение, что свет выбивает электроны с поверхности металла. Предположил он и то, что при освещении поверхности более ярким светом электроны должны вылетать с большей скоростью. Но эксперименты показали, что прогноз Ленарда неверен. Между тем в 1900 году Максу Планку удалось описать излучение, испускаемое горячими телами. Он принял радикальную гипотезу о том, что энергия испускается не непрерывно, а дискретными порциями — квантами. Физический смысл квантов оставался неясным, но величина кванта равна произведению некоторого числа (постоянной Планка) и частоты излучения. Чем ярче свет, тем больше фотонов и больше число выбитых с поверхности металла электронов, но не их скорость. Более быстрые электроны можно получить, направляя на поверхность металла излучение с большей частотой, так как фотоны такого излучения содержат больше энергии.
Чем ярче свет, тем больше фотонов и больше число выбитых с поверхности металла электронов, но не их скорость. Более быстрые электроны можно получить, направляя на поверхность металла излучение с большей частотой, так как фотоны такого излучения содержат больше энергии. Идея де Бройля также нашла экспериментальное подтверждение и заложила основы квантовой механики. Работы Эйнштейна позволили объяснить флуоресценцию, фотоионизацию и загадочные вариации удельной теплоёмкости твёрдых тел при различных температурах.
Идея де Бройля также нашла экспериментальное подтверждение и заложила основы квантовой механики. Работы Эйнштейна позволили объяснить флуоресценцию, фотоионизацию и загадочные вариации удельной теплоёмкости твёрдых тел при различных температурах.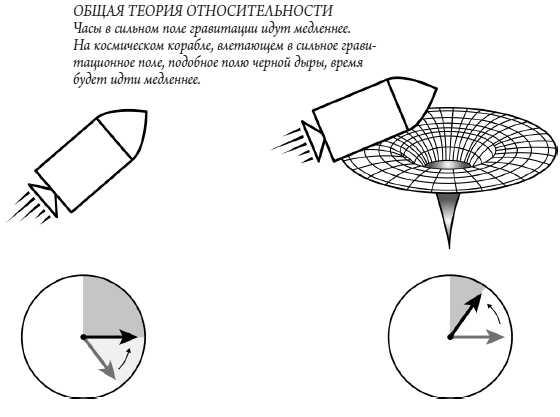
 Поскольку время становится такой же относительной переменной, как и пространственные координаты x, y, z, понятие одновременности также становится относительным. Два события, кажущихся одновременными одному наблюдателю, могут быть разделены во времени с точки зрения другого. Из других выводов, к которым приводит специальная теория относительности, заслуживает внимание эквивалентность массы и энергии. Масса m представляет собой своего рода «замороженную» энергию E, с которой связана соотношением E = mc2, где c — скорость света. Таким образом, испускание фотонов света происходит ценой уменьшения массы источника.
Поскольку время становится такой же относительной переменной, как и пространственные координаты x, y, z, понятие одновременности также становится относительным. Два события, кажущихся одновременными одному наблюдателю, могут быть разделены во времени с точки зрения другого. Из других выводов, к которым приводит специальная теория относительности, заслуживает внимание эквивалентность массы и энергии. Масса m представляет собой своего рода «замороженную» энергию E, с которой связана соотношением E = mc2, где c — скорость света. Таким образом, испускание фотонов света происходит ценой уменьшения массы источника.
 Общая теория относительности охватывала все возможные движения, в том числе и ускоренные (т. е. происходящие с переменной скоростью).
Общая теория относительности охватывала все возможные движения, в том числе и ускоренные (т. е. происходящие с переменной скоростью). Допустим, один наблюдатель находится в кабине лифта небоскрёба, другой снаружи. Внезапно канат, поддерживающий кабину, обрывается, и она свободно падает. Экспериментатор в кабине проводит следующий опыт: вынимает из своего кармана платок и часы и выпускает их из рук. Относительно небоскрёба падает экспериментатор, часы и платок.
Допустим, один наблюдатель находится в кабине лифта небоскрёба, другой снаружи. Внезапно канат, поддерживающий кабину, обрывается, и она свободно падает. Экспериментатор в кабине проводит следующий опыт: вынимает из своего кармана платок и часы и выпускает их из рук. Относительно небоскрёба падает экспериментатор, часы и платок. Все четыре тела: лифт, экспериментатор, часы и платок падают с различным ускорением к земле. Его вывод также совпадает с мнением внутреннего наблюдателя — система неинерциальная.
Все четыре тела: лифт, экспериментатор, часы и платок падают с различным ускорением к земле. Его вывод также совпадает с мнением внутреннего наблюдателя — система неинерциальная. Эйнштейновский принцип эквивалентности, утверждающий, что гравитационные и инерциальные эффекты неотличимы, объяснил совпадение гравитационной и инертной массы в механике Ньютона. Затем Эйнштейн расширил картину, распространив ее на свет. Если луч света пересекает кабину лифта «горизонтально», в то время как лифт падает, то выходное отверстие находится на большем расстоянии от пола, чем входное, так как за то время, которое требуется лучу, чтобы пройти от стенки к стенке, кабина лифта успевает продвинуться на какое-то расстояние. Наблюдатель в лифте увидел бы, что световой луч искривился. Для Эйнштейна это означало, что в реальном мире лучи света искривляются, когда проходят на достаточно малом расстоянии от массивного тела.
Эйнштейновский принцип эквивалентности, утверждающий, что гравитационные и инерциальные эффекты неотличимы, объяснил совпадение гравитационной и инертной массы в механике Ньютона. Затем Эйнштейн расширил картину, распространив ее на свет. Если луч света пересекает кабину лифта «горизонтально», в то время как лифт падает, то выходное отверстие находится на большем расстоянии от пола, чем входное, так как за то время, которое требуется лучу, чтобы пройти от стенки к стенке, кабина лифта успевает продвинуться на какое-то расстояние. Наблюдатель в лифте увидел бы, что световой луч искривился. Для Эйнштейна это означало, что в реальном мире лучи света искривляются, когда проходят на достаточно малом расстоянии от массивного тела.
 Одним из первых было объяснение прецессии орбиты Меркурия, которую не удавалось полностью понять в рамках ньютоновской механики. Во время полного солнечного затмения в 1919 году астрономам удалось наблюдать звезду, скрытую за кромкой Солнца. Это свидетельствовало о том, что лучи света искривляются под действием гравитационного поля Солнца. Всемирная слава пришла к Эйнштейну, когда сообщения о наблюдении солнечного затмения 1919 года облетели весь мир. Относительность стала привычным словом.
Одним из первых было объяснение прецессии орбиты Меркурия, которую не удавалось полностью понять в рамках ньютоновской механики. Во время полного солнечного затмения в 1919 году астрономам удалось наблюдать звезду, скрытую за кромкой Солнца. Это свидетельствовало о том, что лучи света искривляются под действием гравитационного поля Солнца. Всемирная слава пришла к Эйнштейну, когда сообщения о наблюдении солнечного затмения 1919 года облетели весь мир. Относительность стала привычным словом. В 1927 году он выразил своё несогласие со статистической интерпретацией квантовой механики, предложенной Нильсом Бором и Максом Борном. Согласно этой интерпретации, принцип причинно-следственной связи неприменим к субатомным явлениям. Эйнштейн был глубоко убеждён, что статистика является не более чем средством и что фундаментальная физическая теория не может быть статистической по своему характеру. По словам Эйнштейна, «Бог не играет в кости» со Вселенной.
В 1927 году он выразил своё несогласие со статистической интерпретацией квантовой механики, предложенной Нильсом Бором и Максом Борном. Согласно этой интерпретации, принцип причинно-следственной связи неприменим к субатомным явлениям. Эйнштейн был глубоко убеждён, что статистика является не более чем средством и что фундаментальная физическая теория не может быть статистической по своему характеру. По словам Эйнштейна, «Бог не играет в кости» со Вселенной. : Вышло продолжение этой статьи: Релятивистское мышление .
: Вышло продолжение этой статьи: Релятивистское мышление .  Когда два разных наблюдателя находятся в относительном движении, говорят, что они находятся в разных системах отсчета, а когда их относительная скорость постоянна, эти системы отсчета называются инерциальными. Когда все наблюдатели во всех инерциальных системах отсчета соглашаются с физической теорией, говорят, что эта теория ковариант . Мы будем рассматривать только инерциальные системы отсчета.
Когда два разных наблюдателя находятся в относительном движении, говорят, что они находятся в разных системах отсчета, а когда их относительная скорость постоянна, эти системы отсчета называются инерциальными. Когда все наблюдатели во всех инерциальных системах отсчета соглашаются с физической теорией, говорят, что эта теория ковариант . Мы будем рассматривать только инерциальные системы отсчета. Предположим, что одни и те же события наблюдает наблюдатель в S’, разделенный расстоянием L’, и второе событие происходит через ΔT’ секунд после первого. До Эйнштейна были сделаны следующие предположения:
Предположим, что одни и те же события наблюдает наблюдатель в S’, разделенный расстоянием L’, и второе событие происходит через ΔT’ секунд после первого. До Эйнштейна были сделаны следующие предположения: Проверим, верно ли это для ньютоновской физики. Предположим, что известно, что закон Ньютона верен в системе отсчета S′:
Проверим, верно ли это для ньютоновской физики. Предположим, что известно, что закон Ньютона верен в системе отсчета S′: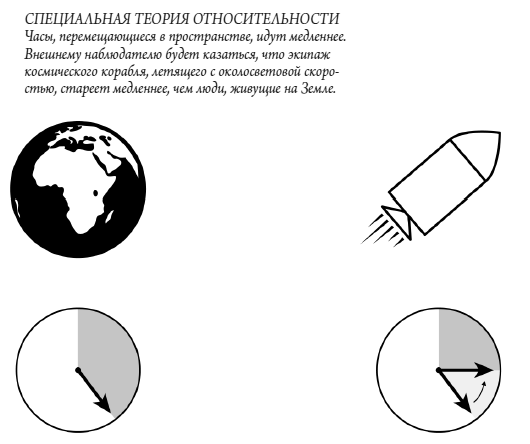 Тогда вектор электрического поля E подчиняется волновому уравнению:
Тогда вектор электрического поля E подчиняется волновому уравнению: Чтобы решить эту проблему, у нас нет другого выбора, кроме как заключить, что по крайней мере одно из следующих утверждений верно:
Чтобы решить эту проблему, у нас нет другого выбора, кроме как заключить, что по крайней мере одно из следующих утверждений верно:
 Мы покажем, что наблюдатель на платформе увидит, что тот же самый физический процесс происходит в течение интервала времени Δt, где Δt и Δt′ связаны соотношением:
Мы покажем, что наблюдатель на платформе увидит, что тот же самый физический процесс происходит в течение интервала времени Δt, где Δt и Δt′ связаны соотношением: Из формулы для Δt′ мы получаем h=cΔt′/2, поэтому, подставив это и возведя в квадрат обе части формулы для Δt, мы получим:
Из формулы для Δt′ мы получаем h=cΔt′/2, поэтому, подставив это и возведя в квадрат обе части формулы для Δt, мы получим: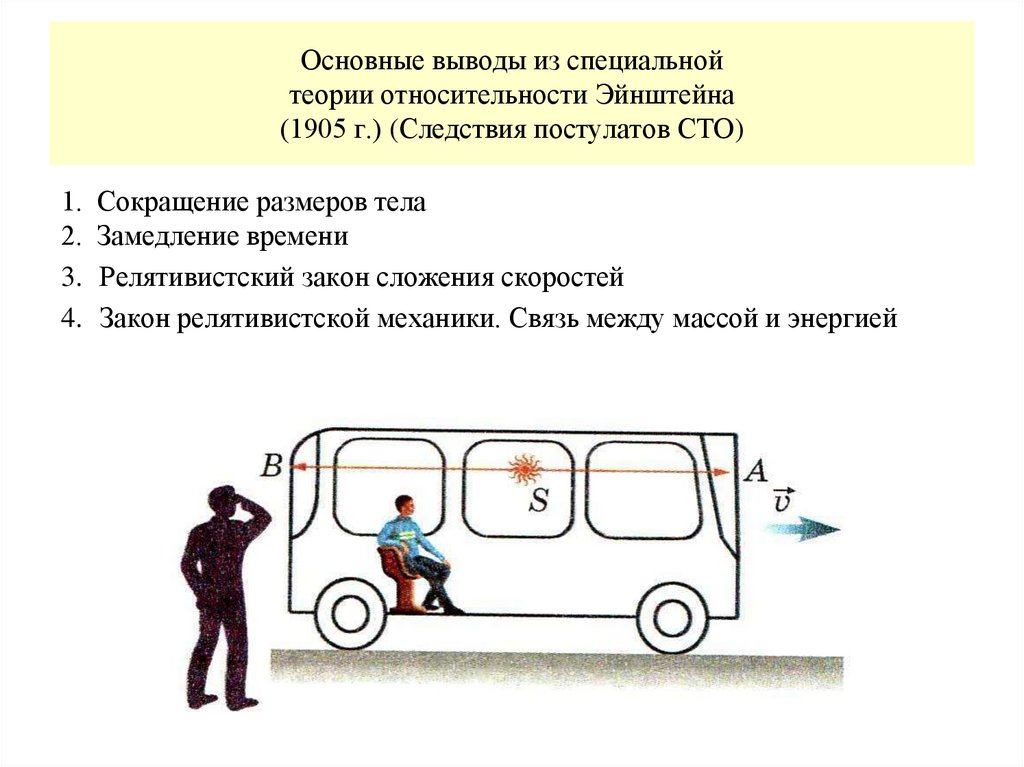 Детекторы мюонов на уровне моря обычно обнаруживают один мюон на квадратный сантиметр в минуту, а их средняя скорость при обнаружении на уровне моря составляет около 0,995 с. Если пренебречь теорией относительности, мы обнаружим, что время, необходимое мюону для достижения уровня моря, составляет 15 000 м/0,995 c~ 50 микросекунд, или около 23 периодов полураспада. Поскольку поток мюонов на уровне моря составляет 1/с∙см², это означает, что количество мюонов, производимых на высоте, будет 2²³/с∙см², что не очень реалистично.
Детекторы мюонов на уровне моря обычно обнаруживают один мюон на квадратный сантиметр в минуту, а их средняя скорость при обнаружении на уровне моря составляет около 0,995 с. Если пренебречь теорией относительности, мы обнаружим, что время, необходимое мюону для достижения уровня моря, составляет 15 000 м/0,995 c~ 50 микросекунд, или около 23 периодов полураспада. Поскольку поток мюонов на уровне моря составляет 1/с∙см², это означает, что количество мюонов, производимых на высоте, будет 2²³/с∙см², что не очень реалистично. Это означает, что если поток мюонов на уровне моря составляет 1/с∙см², то поток мюонов, производимых на расстоянии 15 км, составляет около 4,5/с∙см², что является гораздо более разумным числом.
Это означает, что если поток мюонов на уровне моря составляет 1/с∙см², то поток мюонов, производимых на расстоянии 15 км, составляет около 4,5/с∙см², что является гораздо более разумным числом. Первый столб проходит частицу в момент времени t′=0, а второй – в момент времени Δt′=Δt/γ. Поскольку L=VΔt и L′=VΔt′, мы видим, что L′=L/γ. Это означает, что в подвижной системе отсчета длина сокращается.
Первый столб проходит частицу в момент времени t′=0, а второй – в момент времени Δt′=Δt/γ. Поскольку L=VΔt и L′=VΔt′, мы видим, что L′=L/γ. Это означает, что в подвижной системе отсчета длина сокращается. Это в точности эквивалентно утверждению, что стержень кажется короче, потому что он движется, поскольку у нее нет возможности узнать, движется ли он или стержень.
Это в точности эквивалентно утверждению, что стержень кажется короче, потому что он движется, поскольку у нее нет возможности узнать, движется ли он или стержень. Тогда c² =(L/Δt)²=(L′/Δt′)² из инвариантности c . Тогда мы имеем:
Тогда c² =(L/Δt)²=(L′/Δt′)² из инвариантности c . Тогда мы имеем:

 Вот что имеется в виду, когда мы говорим, что пространство и время в классической физике «отделимы»: нет последовательного способа присвоить единое число «расстоянию» между двумя событиями в классическом пространстве-времени.
Вот что имеется в виду, когда мы говорим, что пространство и время в классической физике «отделимы»: нет последовательного способа присвоить единое число «расстоянию» между двумя событиями в классическом пространстве-времени. Минковский, который на самом деле был одним из профессоров Эйнштейна в колледже, фактически формализовал концепцию пространства-времени. Таким образом, вместо трехмерного евклидова пространства с одним «дополнительным» измерением времени мы живем в четырехмерном пространстве-времени Минковского. Последствия этого огромны, и некоторым из них придется ждать продолжения этой статьи. Но чтобы закрыть эту статью, давайте поговорим о самом известном из них.
Минковский, который на самом деле был одним из профессоров Эйнштейна в колледже, фактически формализовал концепцию пространства-времени. Таким образом, вместо трехмерного евклидова пространства с одним «дополнительным» измерением времени мы живем в четырехмерном пространстве-времени Минковского. Последствия этого огромны, и некоторым из них придется ждать продолжения этой статьи. Но чтобы закрыть эту статью, давайте поговорим о самом известном из них. Фактическое доказательство придется ждать после этой статьи, которая будет посвящена некоторым приложениям релятивистской физики.
Фактическое доказательство придется ждать после этой статьи, которая будет посвящена некоторым приложениям релятивистской физики. частица для взаимодействия с чем-либо во Вселенной. Поскольку нас интересуют только частицы, существование которых имеет физический смысл, мы можем сказать, что не существует системы отсчета, в которой безмассовая частица покоится, поэтому все безмассовые частицы должны двигаться со скоростью света. Это удовлетворяет части «если» утверждения.
частица для взаимодействия с чем-либо во Вселенной. Поскольку нас интересуют только частицы, существование которых имеет физический смысл, мы можем сказать, что не существует системы отсчета, в которой безмассовая частица покоится, поэтому все безмассовые частицы должны двигаться со скоростью света. Это удовлетворяет части «если» утверждения. Рассмотрим случай, когда электрон и позитрон покоятся и находятся в контакте друг с другом за мгновение до того, как произойдет аннигиляция. Общая масса системы равна 2mₑ, что в два раза больше массы электрона, а полный импульс системы равен нулю. Но после аннигиляции полная масса покоя равна нулю, потому что образовавшиеся фотоны движутся со скоростью света. Куда уходит масса и откуда берется энергия?
Рассмотрим случай, когда электрон и позитрон покоятся и находятся в контакте друг с другом за мгновение до того, как произойдет аннигиляция. Общая масса системы равна 2mₑ, что в два раза больше массы электрона, а полный импульс системы равен нулю. Но после аннигиляции полная масса покоя равна нулю, потому что образовавшиеся фотоны движутся со скоростью света. Куда уходит масса и откуда берется энергия? Такое же соотношение между энергией и массой покоя возникает, когда этот эксперимент повторяется с протонами и антипротонами, нейтронами и антинейтронами, мюонами и антимюонами и так далее.
Такое же соотношение между энергией и массой покоя возникает, когда этот эксперимент повторяется с протонами и антипротонами, нейтронами и антинейтронами, мюонами и антимюонами и так далее. Некоторые из примеров, которые я использовал, основаны на примерах, описанных в учебнике «Современная физика для ученых и инженеров», 2-е издание Тейлора, Дубсона и Зафиратоса.
Некоторые из примеров, которые я использовал, основаны на примерах, описанных в учебнике «Современная физика для ученых и инженеров», 2-е издание Тейлора, Дубсона и Зафиратоса. Движение, которое он объясняет, происходит только в том случае, если вы движетесь по прямой с постоянной скоростью. Как только вы ускоряетесь или изгибаетесь — или делаете что-либо, что каким-либо образом меняет характер движения — специальная теория относительности перестает применяться. Вот тут-то и появляется общая теория относительности Эйнштейна, потому что она может объяснить общий случай любого вида движения.
Движение, которое он объясняет, происходит только в том случае, если вы движетесь по прямой с постоянной скоростью. Как только вы ускоряетесь или изгибаетесь — или делаете что-либо, что каким-либо образом меняет характер движения — специальная теория относительности перестает применяться. Вот тут-то и появляется общая теория относительности Эйнштейна, потому что она может объяснить общий случай любого вида движения. Это было полной противоположностью тому, что, казалось, делали другие физики. Вместо того, чтобы предположить, что теория верна и что эксперименты потерпели неудачу, он предположил, что эксперименты были правильными, а теория потерпела неудачу.
Это было полной противоположностью тому, что, казалось, делали другие физики. Вместо того, чтобы предположить, что теория верна и что эксперименты потерпели неудачу, он предположил, что эксперименты были правильными, а теория потерпела неудачу. Вселенную можно рассматривать как имеющую три пространственных измерения — вверх/вниз, влево/вправо, вперед/назад — и одно временное измерение. Это 4-мерное пространство называется пространственно-временным континуумом .
Вселенную можно рассматривать как имеющую три пространственных измерения — вверх/вниз, влево/вправо, вперед/назад — и одно временное измерение. Это 4-мерное пространство называется пространственно-временным континуумом . 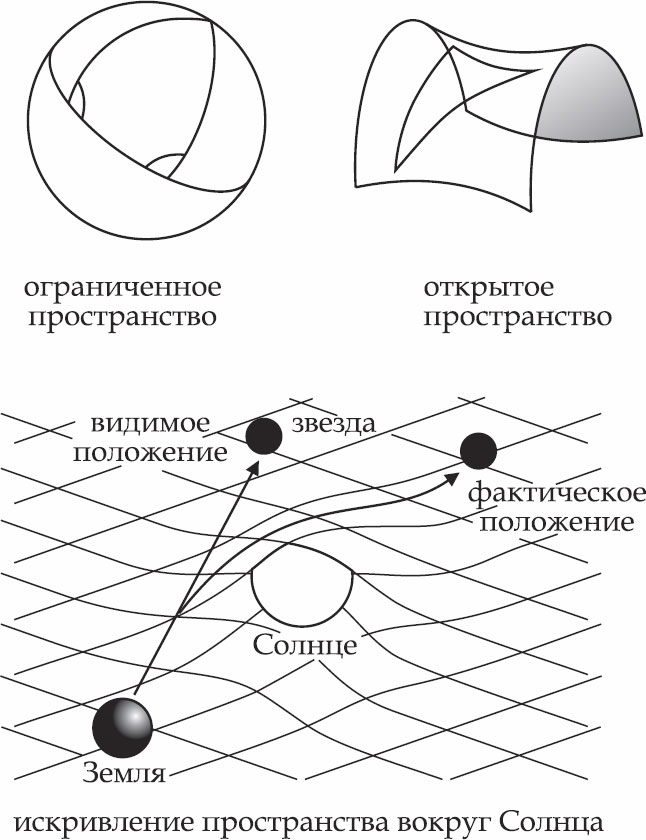 Согласно Эйнштейну, для вас это не имеет значения — вы даже не можете сказать, что движетесь. Однако если бы астронавт Эмбер шпионила за вами, как показано на рисунке внизу, это была бы другая история.
Согласно Эйнштейну, для вас это не имеет значения — вы даже не можете сказать, что движетесь. Однако если бы астронавт Эмбер шпионила за вами, как показано на рисунке внизу, это была бы другая история.