Содержание
Общая Теория Относительности на пальцах™: sly2m — LiveJournal
Одной из жемчужин научной мысли в тиаре знаний человечества с которой мы вошли в 21й век является Общая Теория Относительности (далее ОТО). Данная теория подтверждена бесчисленными опытами, скажу больше, нет ни одного эксперимента, где наши наблюдения хоть на чуть–чуть, хоть на кропалюшечку отличались бы от предсказаний Общей Теории Относительности. В пределах ее применимости, естественно.
Сегодня я хочу рассказать вам, что же это за зверь такой Общая Теория Относительности. Почему она такая сложная и почему на самом деле она такая простая. Как вы уже поняли, объяснение пойдет на пальцах™, посему прошу не судить слишком строго за весьма вольные трактовки и не вполне корректные аллегории. Я хочу, чтобы прочитав данное объяснение любой гуманитарий, без багажа знаний дифференциального исчисления и интегрирования по поверхности, смог уяснить себе основы ОТО. В конце концов исторически это одна из первых научных теорий, начинающих уходить вдаль от привычного повседневного человеческого опыта. С ньютоновской механикой все просто, на ее объяснение хватит и трех пальцев — вот сила, вот масса, вот ускорение. Вот яблоко на голову падает (все видели как яблоки падают?), вот ускорение его свободного падения, вот силы на него действующие.
С ньютоновской механикой все просто, на ее объяснение хватит и трех пальцев — вот сила, вот масса, вот ускорение. Вот яблоко на голову падает (все видели как яблоки падают?), вот ускорение его свободного падения, вот силы на него действующие.
С ОТО не все так просто — искривления пространства, гравитационные замедления времени, черные дыры — все это должно вызывать (и вызывает!) у неподготовленного человека массу смутных подозрений — а не по ушам ли ты мне ездишь, чувачок? Какие–такие искривления пространства? Кто их видел эти искривления, откуда они берутся, как подобное вообще можно себе представить?
Попробуем разобраться.
Как можно понять из названия Общей Теории Относительности, суть ее в том, что в общем–то все в мире относительно. Шутка. Хотя и не очень.
Скорость света это та величина, относительно которой относительны все остальные вещи в мире. Любые системы отсчета равноправны, куда бы они ни двигались, что бы они ни делали, даже крутились бы на месте, даже двигались бы с ускорением (что есть серьезный удар под дых Ньютону с Галилеем, которые думали, что только равномерно и прямолинейно двигающиеся системы отсчета могут быть относительными и равноправными, да и то, лишь в рамках элементарной механики) — все равно, всегда можно найти хитрый трюк (по–научному это называется преобразование координат), при помощи которого можно будет безболезненно переходить из одной системы отсчета в другую, практически ничего не теряя по пути.
Сделать такой вывод Эйнштейну помог постулат (напомню — логическое утверждение, принимаемое на веру без доказательств в силу своей очевидности) «о равенстве гравитации и ускорения». (внимание, здесь происходит сильное упрощение формулировок, но в общих чертах все верно — эквивалентность эффектов равноускоренного движения и гравитации находится в самом сердце ОТО).
Доказать сей постулат, или хотя бы мысленно его попробовать на вкус весьма просто. Пожалуйте в «лифт Эйнштейна».
Идея сего мысленного эксперимента в том, что если вас заперли в лифте без окон и дверей, то нет ни малейшего, совершенно ни единого способа узнать, в какой ситуации вы находитесь: или лифт продолжает стоять как и стоял на уровне первого этажа, и на вас (и все остальное содержимое лифта) действует обычная сила притяжения, т.е. сила гравитации Земли, или же всю планету Земля убрали у вас из–под ног, а лифт стал подниматься вверх, с ускорением равным ускорению свободного падения g=9.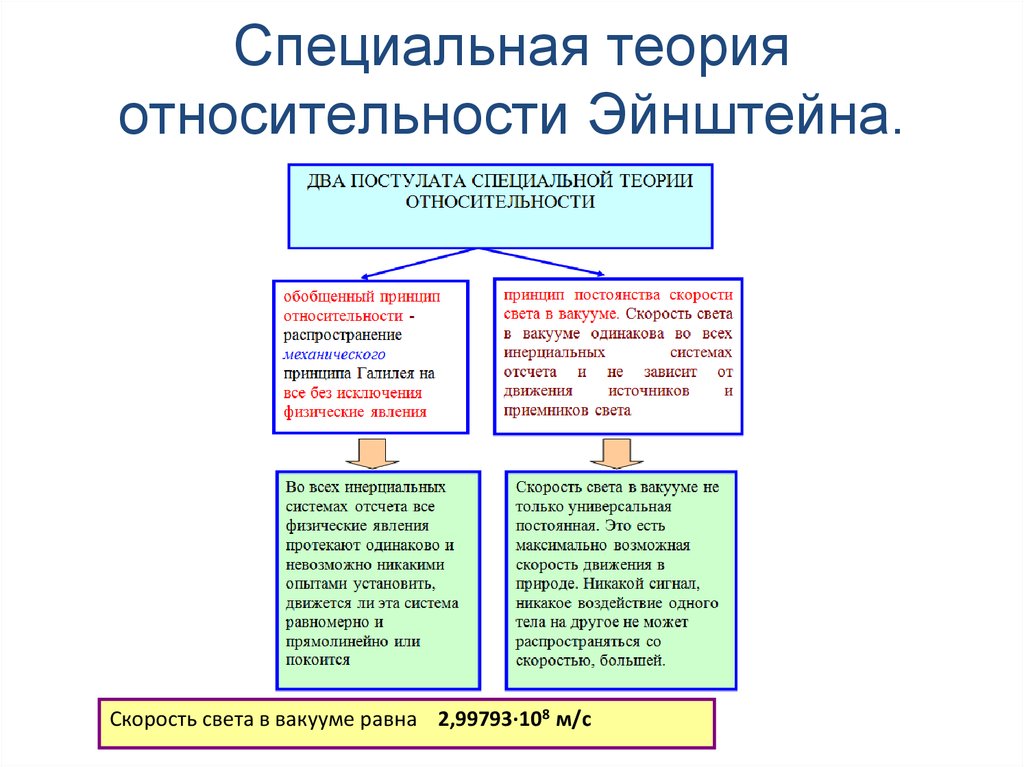 8м/с2.
8м/с2.
Что бы вы ни делали, какие бы опыты ни ставили, какие бы измерения окружающих предметов и явлений ни производили — различить эти две ситуации невозможно, и в первом и во втором случае все процессы в лифте будут проходить совершенно одинаково.
Читатель со звездочкой(*) наверняка знает один хитрый выход из этого затруднения. Приливные силы. Если лифт очень (очень–очень) большой, километров 300 в поперечнике, теоретически можно отличить гравитацию от ускорения, измерив силу гравитации (или величину ускорения, мы же пока еще не знаем что есть что) в разных концах лифта. Такой огромный лифт будет чуть–чуть сжиматься приливными силами в поперечнике и чуть–чуть вытягиваться ими же в продольной плоскости. Но это уже пошли хитрости. Если лифт достаточно мал, никаких приливных сил вы обнаружить не сможете. Так что не будем о грустном.
Итого, в достаточно маленьком лифте можно считать, что гравитация и ускорение это одно и то же. Казалось бы мысль очевидная, и даже тривиальная. Чего тут такого нового или сложного, скажете вы, это же и ребенку должно быть понятно! Да, в принципе, ничего сложного. Вовсе не Эйнштейн это придумал, такие вещи были известны гораздо раньше.
Чего тут такого нового или сложного, скажете вы, это же и ребенку должно быть понятно! Да, в принципе, ничего сложного. Вовсе не Эйнштейн это придумал, такие вещи были известны гораздо раньше.
Эйнштейн же решил выяснить как будет вести себя луч света в подобном лифте. А вот у этой мысли оказались очень далеко идущие последствия, о которых до 1907го года никто всерьез не задумывался. В смысле, задумывались, если честно, многие, но так глубоко заморочиться решился только один.
Представим себе, что мы посветили в нашем мысленном лифте Эйнштейна фонариком. Луч света вылетел из одной стенки лифта, из точки 0) и полетел параллельно полу в сторону противоположной стенки. Покуда лифт стоит на месте, логично предположить, что луч света ударится в противоположную стенку аккурат напротив начальной точки 0), т.е. прилетит в точку 1). Лучи света же по прямой линии распространяются, в школу все ходили, в школе все это учили и юный Альбертик тоже.
Несложно догадаться, что если лифт поехал вверх, то за время покуда луч летел по кабине, она успеет сместиться чуточку вверх.
И если лифт будет двигаться с равномерным ускорением, то луч попадет на стенку в точке 2), то есть при взгляде со стороны будет казаться, что свет двигался как бы по параболе.
Ну, понято, что на самом деле никакой параболы нет. Луч как летел прямо, так и летит. Просто покуда он летел по своей прямой, лифт успел уехать чуточку наверх, вот нам и кажется, что луч по параболе двигался.
Все утрировано и преувеличенно, конечно. Эксперимент мысленный, от чего свет у нас летает медленно, а лифты ездят быстро. Тут пока все еще ничего особо крутого, это все тоже должно быть понятно любому школьнику. Подобный эксперимент можно провести у себя дома. Только нужно найти «очень медленные лучи» и годные, быстрые лифты.
Но Эйнштейн был реально гений. Сегодня многие его ругают, типа он вообще никто и ничто, сидел в своем патентном бюро, плел свои еврейские заговоры и тырил идеи у настоящих физиков. Большинство из заявляющих такое вообще не понимают кто такой Эйнштейн и что он сделал для науки и человечества.
Эйнштейн же сказал — раз «гравитация и ускорение эквивалентны» (еще раз повторю, он не совсем так сказал, я сознательно утрирую и упрощаю), значит в присутствии поля гравитации (например около планеты Земля) свет тоже полетит не по прямой, а по кривой. Гравитация искривит луч света.
Что само по себе было абсолютной ересью для того времени. Любой крестьянин должен знать, что фотоны — безмассовые частицы. Значит свет ничего «не весит». А потому на гравитацию свету должно быть пофиг, он не должен «притягиваться» Землей, как притягиваются камни, мячики и горы. Если кто помнит формулу Ньютона, гравитация обратно пропорциональна квадрату расстояния между телами и прямо пропорциональна их массам. Если у луча света нет массы (а ее у света действительно нет), значит никакого притяжения быть не должно! Тут современники начали коситься на Эйнштейна с подозрением.
А он, зараза, еще дальше попер. Говорит — не будем ломать крестьянам голову. Поверим древним грекам (привет, древние греки!), пусть свет распространяется как и раньше строго по прямой. Давайте лучше предположим, что само пространство вокруг Земли (и любого тела обладающего массой) гнется. Причем не просто трехмерное пространство, а сразу четырехмерное пространство–время.
Давайте лучше предположим, что само пространство вокруг Земли (и любого тела обладающего массой) гнется. Причем не просто трехмерное пространство, а сразу четырехмерное пространство–время.
Т.е. свет как летел по прямой, так и летит. Только эта прямая теперь нарисована не на плоскости, а лежит на как–бы скомканном полотенце. Да еще и в 3D. А комкает это полотенце как раз близкое присутствие массы. Ну, точнее присутствие энергии–импульса, если быть абсолютно точным.
Все ему — «Альбертик, ты гонишь, завязывай–ка поскорее с опиумом! Потому что ЛСД все еще не изобрели, а на трезвую голову такое точно не выдумаешь! Какое гнутое пространство, что ты мелешь?»
А Эйнштейн такой — «Я вам еще покажу!»
Заперся в своей белой башне (в смысле в патентном бюро) и давай математику под идейки подгонять. 10 лет подгонял, пока не родил вот это:
Точнее это квинтэссенция того, что он родил. В более развернутом варианте там 10 независимых формул, а в полном — две страницы математических символов мелким шрифтом.
Если вы решили взять настоящий курс Общей Теории Относительности, здесь вводная часть заканчивается и далее должны последовать два семестра изучения сурового матана. А чтобы подготовиться к изучению этого матана, нужны еще как минимум три года высшей математики, учитывая, что вы закончили среднюю школу и уже знакомы с дифференциальным и интегральным исчислением.
Положа руку на сердце, матан там не столько сложный, сколько нудный. Тензорное исчисление в псевдоримановом пространстве не сильно замороченная тема для восприятия. Это вам не квантовая хромодинамика, или, упаси Бог, не теория струн. Тут все четко, все логично. Вот вам пространство Римана, вот вам многообразие без разрывов и складок, вот метрический тензор, вот невырожденная матрица, сиди себе формулы выписывай, да индексы балансируй, следя чтобы ковариантные и контравариантные представления векторов с обеих сторон уравнения соответствовали друг другу. Это не сложно. Это долго и нудно.
Но не будем забираться в такие дали и вернемся к нашим пальцам™. По–нашему, по–простецки формула Эйнштейна означает примерно следующее. Слева от знака «равно» в формуле стоят тензор Эйнштейна плюс ковариантный метрический тензор и космологическая постоянная (Λ). Эта лямбда есть по сути своей темная энергия, которую мы сегодня до сих пор нифига не знаем, но любим и уважаем. А Эйнштейн об этом еще даже и не догадывается. Тут своя интересная история, достойная целого отдельного поста.
По–нашему, по–простецки формула Эйнштейна означает примерно следующее. Слева от знака «равно» в формуле стоят тензор Эйнштейна плюс ковариантный метрический тензор и космологическая постоянная (Λ). Эта лямбда есть по сути своей темная энергия, которую мы сегодня до сих пор нифига не знаем, но любим и уважаем. А Эйнштейн об этом еще даже и не догадывается. Тут своя интересная история, достойная целого отдельного поста.
В двух словах, все, что стоит слева от знака «равно» показывает, как изменяется геометрия пространства, т.е. как оно гнется и скручивается под действием силы гравитации.
А справа, кроме обычных постоянных вроде π, скорости света c и гравитационной постоянной G находится буковка Т — тензор энергии–импульса. В ламмерских терминах можно считать, что это конфигурация того, как распределена в пространстве масса (точнее энергия, ибо что масса, что энергия, все равно эмце квадрат) для того, чтобы создавать гравитацию и гнуть ею пространство, дабы соответствовать левой части уравнения.
Вот, в принципе, и вся Общая Теория Относительности на пальцах™.
Теория относительности в картинках / Хабр
В своей статье я хотел бы рассказать о теории относительности. Эта теория не требуется в представлении. С самого своего создания она была окутана ореолом тайны, поскольку полностью подрывает наши привычные представления о пространстве и времени. Все мы в школе учили формулы теории относительности, но мало кто действительно понимал их. И это не удивительно, ведь человеку, чтобы по-настоящему понять какую-то теорию во всей её красоте, полноте и непротиворечивости, не достаточно знать формулы. Нужно иметь какой-то визуальный ориентир, нужна динамика, чтобы было что-то, что можно повертеть в руках. Я решил восполнить этот пробел и написал небольшую программку, в которой можно «повертеть в руках» пространство-время. Мы, как настоящие исследователи, с помощью небольших экспериментов попытаемся выяснить основные свойства этой загадочной материи.
Под катом много картинок (и ни одной формулы).
Сразу следует прояснить, что существует две теории относительности:
— специальная теория относительности (СТО) рассматривает механику движения тел в пустом (не искривленном) пространстве-времени.
— общая теория относительности (ОТО) изучает явления гравитации и искривление пространства-времени объектами, обладающими массой.
Все описанное ниже относится к первой из них.
Прежде, чем рассматривать пространство-время, давайте вспомним, что такое обычное евклидово пространство.
И так, у нас имеется плоскость. В этой плоскости имеются некоторые геометрические фигуры: точки, отрезки. Так же у нас имеются две операции: параллельный перенос, и поворот. Давайте внимательно рассмотрим эти две операции.
Далее перейдем к рассмотрению так называемого пространства Минковского. В нем мы оставили параллельный перенос, но операцию поворота заменили на другую операцию. Как видите, при «повороте» каждая точка движется вдоль сереньких кривых. В результате все точки вытягиваются либо вдоль одной желтой прямой, либо вдоль другой.
Как видите, при «повороте» каждая точка движется вдоль сереньких кривых. В результате все точки вытягиваются либо вдоль одной желтой прямой, либо вдоль другой.
При таком «повороте» отрезки сохраняют свою форму и переходят в отрезки.
Собственно, это и есть пространство-время. Давайте, будем считать, что горизонтальная ось — это пространство, а вертикальная — время. Будем считать, что время идет снизу вверх. Точка в пространстве-времени — это некоторое событие, которое произошло в некотором месте в некоторое время. А отрезок — это некоторый процесс. Например, если объект движется, то будем обозначать его движение отрезком.
Чтобы Вы немного сориентировались, поставим первый эксперимент.
Первым делом будем рассматривать объекты движущиеся с небольшими скоростями (много меньше скорости света).
Допустим, имеется некоторый неподвижный объект, например дерево. Нарисуем его с помощью вертикального отрезка.
Так же у нас имеется некоторый движущийся объект — автомобиль. Мы видим, что автомобиль едет навстречу дереву.
Нарисуем еще один движущийся объект. В результате получаем картину:
Обратите внимание, что чем сильнее наклон, тем скорость объекта больше.
Так выглядит наша картина из неподвижной системы отсчета. А что мы увидим, если будем сидеть в автомобиле? Для этого нам нужно немножко «перекосить» нашу плоскость.
Все правильно. Автомобиль теперь неподвижен, а дерево и человек движутся нам навстречу.
Точно так же мы можем перейти в систему отсчета, связанную с человеком. Для этого нам нужно «перекосить» пространство-время в другую сторону. В целом процесс перехода от одной системы отсчета в другую выглядит следующим образом:
Такое преобразование называется «преобразованием Галилея». При этом каждая точка движется вдоль горизонтальной прямой. Это значит, что время одинаково во всех системах отсчета (время абсолютно).
Давайте теперь перейдем к бОльшим масштабам, «сжав» нашу ось X.
На самом деле, переход от одной системы отсчета в другую есть ни что иное, как «поворот» в пространстве Минковского, а преобразования Галилея — это всего лишь предельный случай для маленьких скоростей.
Мы видим, что точки теперь движутся не горизонтально. Т.е. время не является абсолютной величиной, а зависит от выбранной системы отсчета.
Допустим имеются два наблюдателя, один неподвижный, другой летит на своем космическом корабле от него с некоторой скоростью.
Отметки на отрезке показывают, как идет время внутри объекта. Мы видим, что время неподвижного наблюдателя движется быстрее, чем у подвижного (один час у движущегося наблюдателя наступает позже, чем у неподвижного).
Но точно такую же картину видит и второй наблюдатель.
Вот так одна система отсчета переходит в другую
Получается странная ситуация — два наблюдателя смотрят друг на друга, и они друг другу кажутся «заторможенными».
Чтобы выяснить, кто же из них на самом деле «тормоз», второй наблюдатель разворачивает свой космический корабль и летит обратно.
Вместе они сверяют часы и выясняют, что у неподвижного наблюдателя прошло 5 единиц времени, а у подвижного — чуть больше 4. Т.е. наблюдатель, который «сделал крюк» в пространстве-времени потратил меньше своего внутреннего времени, чем неподвижный наблюдатель.
Но то же самое, только с точностью до наоборот, произошло бы, если бы первый наблюдатель полетел на встречу второму.
Вывод: у неподвижного наблюдателя время всегда идет быстрее, чем у движущегося.
Допустим, у нас имеется неподвижная космическая станция. От неё отстыковался некоторый корабль.
Перейдем в систему отсчета этого корабля. Далее от этого корабля отстыковался другой корабль.
Затем от второго корабля отстыковался третий.
и так далее.
Таким образом я пытался изобразить процесс ускорения. Очевидно, что каждый следующий корабль будет двигаться с большей скоростью, чем предыдущий. Давайте теперь вернемся к первому кораблю и посмотрим.
Очевидно, что каждый следующий корабль будет двигаться с большей скоростью, чем предыдущий. Давайте теперь вернемся к первому кораблю и посмотрим.
Напомню Вам, что наклон определяет скорость. Желтая линия, а точнее её наклон, показывает скорость света.
По картинке видно, что каждый следующий корабль приближается к скорости света, но не может превысить её. Так же видно, что внутреннее время с увеличением скорости все больше замедляется. Из этого мы делаем вывод, что ничто не может двигаться со скоростью, превышающей скорость света.
Пусть теперь каждый корабль выпускает луч света.
Мы видим, что свет в любой системе отсчета движется со скоростью света.
Две желтые линии очерчивают фигуру, называемую «световой конус». Световой конус разделяет пространство-время на две области, которые я отметил красным и зеленым цветами.
Если какое-то событие находится в красной области, то мы будем говорить, что событие находится в пределах светового конуса. Это означает, что свет из начала координат успевает долететь до нашей точки.
Это означает, что свет из начала координат успевает долететь до нашей точки.
Если событие находится в зеленой области, то мы говорим, что событие находится за пределами светового конуса, и свет из начала координат не успевает долететь до этого события.
Рассмотрим следующий пример. Имеется три одновременных события
Давайте посмотрим, что произойдет, если мы будем менять систему отсчета.
Мы видим, что в другой системе отсчета события вовсе не являются одновременными. Теперь события не просто смещаются во времени, они еще меняют свой хронологический порядок. Событие, которое произошло раньше некоторого события, в другой системе отсчета может произойти позже. Но как такое может быть? Не является ли это нарушением причинно-следственных связей?
Напомню, что если событие находится за пределами светового конуса, это значит, что свет не может долететь до этого события за отведенное время. А поскольку ничто (никакой объект или сигнал) не может двигаться быстрее скорости света, получается, что событие, произошедшее в точке А, никак не может повлиять на событие в точке Б.
То же самое справедливо и в обратную сторону. Событие в точке Б никак не может повлиять на событие в точке А.
Про такие события говорят, что они не связаны причинно-следственными связями. Получается, что событие, находящееся за пределом светового конуса относительно данного, не связано с ним причинно-следственными связями.
Все космические объекты: солнечные системы, галактики — находятся на гигантских расстояниях друг от друга. И даже двигаясь со скоростью света, нам потребуется очень много времени, чтобы преодолеть эти расстояния. Например, ближайшая к нам звезда (альфа-Центавра) находится на расстоянии 4 световых года, а ближайшая галактика (Большое Магелланово Облако) — уже 160 тысяч световых лет. Если до альфа-Центавра мы еще можем слетать «туда и обратно», то слетать «туда и обратно» в соседнюю галактику уже не получится. Точнее, улететь-то мы сможем, а вот когда вернемся, на Земле пройдет уже 320 тысяч лет (напомню, что внутри объекта, движущегося со скоростью света, время практически стоит на месте). Что же делать?
Что же делать?
Писатели-фантасты в своих произведениях очень ловко обходят это ограничение. Чего-только они не напридумывали: сверхскоростные двигатели, гипер-пространства, мультиплексы, искривление пространства-времени, прыжки через червоточины, черные дыры и т.д. На самом деле, проблема гораздо глубже, чем может показаться. Заключается она в том, что за пределами светового конуса НЕ МОГУТ существовать причинно-следственные связи. Иначе мы неизбежно придем к противоречиям.
Рассмотрим пример. Мы сидим на своей планете. В один прекрасный момент наши ученые изобретают «супер-телепортатор» способный телепортировать нас на любое расстояние за минимальное количество времени. Ну мы взяли и телепортировались в соседнюю галактику. Посидев в другой галактике, мы отправились на дальнейшее исследование космоса.
Если мы теперь перейдем в систему отсчета, связанную с нашим кораблем, то увидим следующее.
Мы видим, что наша исходная точка (планета Земля) сместилась в будущее. А поскольку законы природы во всех системах отсчета работают одинаково, то мы можем снова воспользоваться нашим «супер-телепортатором» и вернуться в собственное прошлое.
А поскольку законы природы во всех системах отсчета работают одинаково, то мы можем снова воспользоваться нашим «супер-телепортатором» и вернуться в собственное прошлое.
Получается, что движение со сверх-световой скоростью, эквивалентно перемещению во времени, а оно тянет за собой кучу парадоксов. Таким образом, проблема космических путешествий не в том, что мы не умеем искривлять пространство-время или строить сверх-световые двигатели, а в том, что даже теоретическая возможность таких перемещений подрывает все причинно-следственные связи.
На этом в общем-то и все. Самое основное, кажется, рассказал. Надеюсь, было понятно.
При написании статьи была использована программка (Ссылка на github)
Теория относительности: что это простыми словами, разница между СТО и ОТО
Существует две теории относительности Альберта Эйнштейна:
- Специальная теория относительности (СТО, 1905 г.
 ): суть этой теории в том, что законы физики одинаковы для всех неускоряющихся наблюдателей и что скорость света в вакууме не зависит от движения наблюдателей (вообще никого, кто является частью действия/эксперимента).
): суть этой теории в том, что законы физики одинаковы для всех неускоряющихся наблюдателей и что скорость света в вакууме не зависит от движения наблюдателей (вообще никого, кто является частью действия/эксперимента). - Общая теория относительности (ОТО, 1915 г.): массивные объекты вызывают искажение пространства-времени, что ощущается гравитацией; ускорение является частью этой теории, которая математически намного сложнее предыдущей.
Специальная теория относительности
СТО основана на том, что скорость света постоянна для всех. В 1905 году Эйнштейн понял это, когда провёл эксперименты и пришёл к выводу, что скорость света не меняется, когда Земля вращается вокруг Солнца.
СТО объясняет, как пространство и время связаны между собой для объектов, которые движутся с постоянной скоростью по прямой.
Особое внимание заостряется на объектах, движущихся со скоростью света. Когда объект приближается к скорости света, его масса становится бесконечной, и он не может двигаться быстрее света. Поскольку человечество всегда стремилось к путешествиям на огромные расстояния, это ограничение скорости было предметом многочисленных дискуссий и в физике, и в научной фантастике.
Поскольку человечество всегда стремилось к путешествиям на огромные расстояния, это ограничение скорости было предметом многочисленных дискуссий и в физике, и в научной фантастике.
Своей теорией учёный представил новую основу для всей физики и предложил новые концепции пространства и времени.
Пример СТО: вы сидите в поезде (который едет со скоростью 100 км/ч) и бросаете теннисный мячик своему другу (со скоростью 10 км/час). С какой скоростью пролетел мячик?
Невозможно дать с уверенностью ответ на этот вопрос, т.к. ответ зависит от того, кто наблюдатель.
Для вас и людей внутри поезда теннисный мячик пролетел со скоростью 10 км/час, но для людей вне поезда он пролетел со скоростью 110 км/ч (100 + 10).
Формула Специальной теории относительности (E = mc²)
В СТО Эйнштейн представил самое известное уравнение из когда-либо написанных: E = mc²
Формула Эйнштейна E = mc²
Где:
E — энергия
m — масса
c — скорость света (равняется примерно 300 000 км/с). 16 джоулей (это 1кг × (300.000.000 м/с)²).
16 джоулей (это 1кг × (300.000.000 м/с)²).
Эта формула устанавливает количественную эквивалентность (равноценность) превращения материи в энергию и наоборот.
В этом уравнении связываются и взаимозаменяются масса и энергия.
Относительность времени в специальной теории относительности
Интервал времени неподвижной системы (наблюдателя) всегда меньше системы, что находится в движении.
Промежуток времени между двумя событиями зависит от системы отсчёта, поэтому они (промежутки времени) могут быть разными, т. е. промежуток времени является относительным.
Представьте, что вы наблюдаете за каким-то явлением, происходящим в космосе. Если вы наблюдаете и замеряете время:
- находясь на движущемся объекте (например, находитесь на движущемсякосмическом корабле), это будут одни данные,
- но если вы находитесь на неподвижном объекте (например, ваш космический корабль не движется), вы увидите совершенно другие данные — время завершения этого действия будет значительно меньше.

Этот эффект также называется релятивистское замедление времени.
Общая теория относительности
После СТО Эйнштейн проработал ещё 10 лет над общей теорией, которая включает ускорение. В этой работе он определил, что массивные объекты вызывают искажение пространства-времени и оно ощущается как гравитация.
ОТО представила концепцию четырёхмерности мира (или пространственно-временной континуум): 3 пространственные измерения (длина, ширина, высота) и время. ОТО применяется ко всем системам отсчёта, в то время как СТО применялась лишь к движущимся с постоянной скоростью относительно друг друга. ОТО (общая) включает в себя СТО (специальную).
Пример ОТО: вы находитесь в падающем лифте, вы будете свободно парить в этом лифте, т.к. падаете вместе с этим лифтом (свободное падение). Другая ситуация: вы находитесь внутри ракеты и парите в невесомости вдали от источников гравитации. Если ракета начнёт движение, то вы опуститесь в сторону, противоположную движению ракеты (если она полетит наверх, то вы упадёте вниз).
Существует эквивалент между ускоренным движением и гравитационным притяжением; т.е. ОТО утверждает, что ускорение очень похоже на гравитационное поле.
Чем отличается специальная теория относительности от общей теории относительности?
- Специальная теория относительности (СТО была создана в 1905 году): существуют одни и те же законы природы для всех систем отсчёта, которые движутся с постоянной скоростью; эта теория исследует физические процессы равномерно движущихся тел.
- Общая теория относительности (ОТО была создана в 1915 году): тот же принцип, что у специальной, но включая любые системы отсчёта даже те, что движутся с ускорением; эта теория исследует ускоряющиеся тела и описывает возникновение гравитации.
Система отсчёта — это совокупность тела отсчёта, системы координат и отсчёта времени (они связаны с телом, и относительно него рассматривается движение или равновесие других тел или точек).
Движение тел и материи должно находиться в пределах параметров времени и пространства.
Принцип относительности Галилея
Этот принцип гласит: во всех инерциальных системах отсчёта все механические явления протекают одинаково. Был установлен великим итальянским учёным Галилеем в 1636 г.
Узнайте также про Теорию струн и Фотон.
Дата обновления 26/03/2021.
Другие значения и понятия, которые могут вас заинтересовать
- Космология
- Сингулярность
- Теория струн
- Теория Дарвина
- Теория вероятностей
- Фотон
- Искусственный интеллект
- Марксизм
- Поколение Z
- Агностицизм
Как понять уравнение Эйнштейна для общей теории относительности
Хотя Эйнштейн — легендарная фигура в науке по большому количеству причин — E = mc², фотоэлектрический эффект и представление о том, что скорость света постоянна для всех — его наиболее устойчивое открытие также является наименее понятым: его теория гравитации, общая теория относительности. До Эйнштейна мы думали о гравитации в ньютоновских терминах: все во Вселенной, имеющее массу, мгновенно притягивает любую другую массу в зависимости от величины их масс, гравитационной постоянной и квадрата расстояния между ними. Но концепция Эйнштейна была совершенно иной, она основывалась на идее, что пространство и время объединены в ткань, пространство-время, и что кривизна пространства-времени указывает не только материи, но и энергии, как двигаться в нем.
До Эйнштейна мы думали о гравитации в ньютоновских терминах: все во Вселенной, имеющее массу, мгновенно притягивает любую другую массу в зависимости от величины их масс, гравитационной постоянной и квадрата расстояния между ними. Но концепция Эйнштейна была совершенно иной, она основывалась на идее, что пространство и время объединены в ткань, пространство-время, и что кривизна пространства-времени указывает не только материи, но и энергии, как двигаться в нем.
Эта фундаментальная идея — что материя и энергия сообщают пространству-времени, как искривляться, а искривленное пространство-время, в свою очередь, сообщает материи и энергии, как двигаться, — представляла собой революционно новый взгляд на вселенную. Выдвинутая в 1915 году Эйнштейном и подтвержденная четырьмя годами позже во время полного солнечного затмения — когда искривление звездного света, исходящего от источников света позади Солнца, совпало с предсказаниями Эйнштейна, а не Ньютона — общая теория относительности прошла все наблюдательные и экспериментальные проверки, которые мы когда-либо придумывали.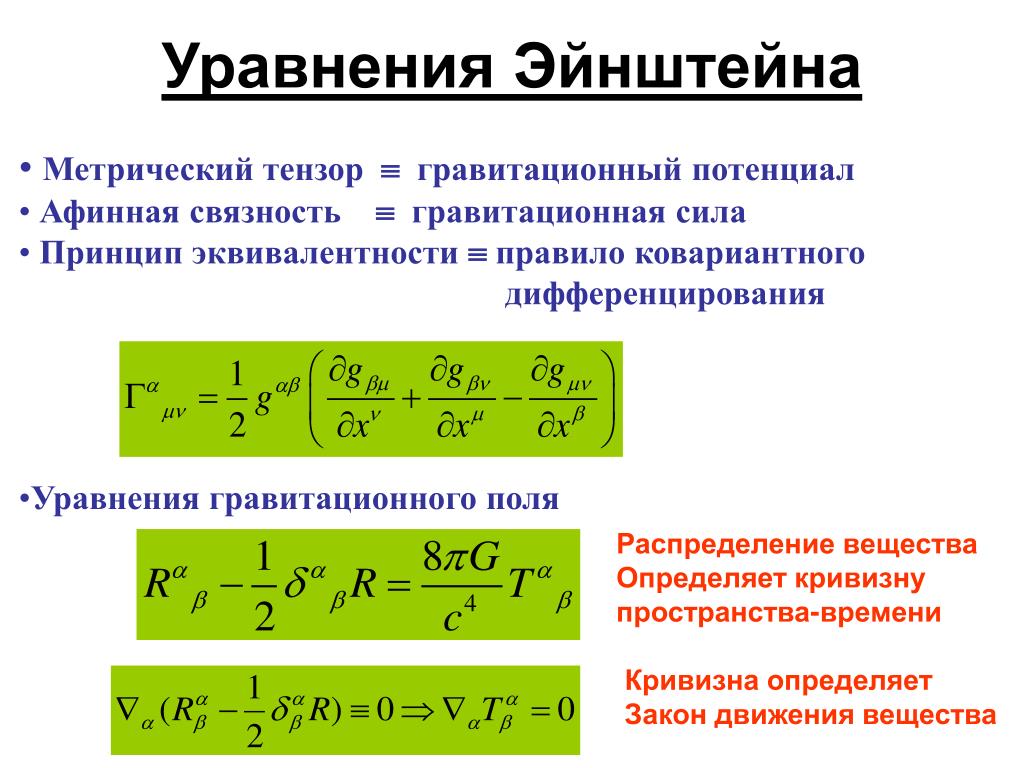 . Тем не менее, несмотря на его успех на протяжении более 100 лет, почти никто не понимает, что на самом деле представляет собой одно уравнение, лежащее в основе общей теории относительности. Вот, на простом английском языке, что это на самом деле означает.
. Тем не менее, несмотря на его успех на протяжении более 100 лет, почти никто не понимает, что на самом деле представляет собой одно уравнение, лежащее в основе общей теории относительности. Вот, на простом английском языке, что это на самом деле означает.
Исходное уравнение Эйнштейна связывает кривизну пространства-времени с энергией напряжения системы (вверху). Можно добавить член космологической постоянной (в середине) или, что то же самое, его можно сформулировать как темную энергию (внизу), еще одну форму плотности энергии, вносящую вклад в тензор энергии-импульса. Предоставлено: © Токийский университет, 2014; Kavli IPMU
Это уравнение выглядит довольно просто, так как присутствует всего несколько символов. Но это довольно сложно.
- Первый, G μν , известен как тензор Эйнштейна и представляет кривизну пространства.

- Второй, Λ, космологическая постоянная: количество энергии, положительной или отрицательной, присущей самой ткани пространства.
- Третий член, g μν , известен как метрика, которая математически кодирует свойства каждой точки в пространстве-времени.
- Четвертый член, 8πG/c 4 , является просто произведением констант и известен как гравитационная постоянная Эйнштейна, аналог ньютоновской гравитационной постоянной (G), с которой большинство из нас более знакомо.
- Пятый член, T μν , известен как тензор энергии-импульса и описывает локальную (в непосредственной близости) энергию, импульс и напряжение в этом пространстве-времени.
Этих пяти терминов, связанных друг с другом через то, что мы называем уравнениями поля Эйнштейна, достаточно, чтобы связать геометрию пространства-времени со всей материей и энергией в нем: отличительный признак общей теории относительности.
..»> Фреска с изображением уравнений поля Эйнштейна с иллюстрацией света, огибающего затменное солнце, наблюдения, впервые подтвердившие общую теорию относительности еще в 19 году.19. Тензор Эйнштейна показан слева в разложении на тензор Риччи и скаляр Риччи. Кредит: Высоцкий / Wikimedia Commons
Вам может быть интересно, что со всеми этими нижними индексами — этими странными комбинациями греческих букв «μν», которые вы видите в нижней части тензора Эйнштейна, метрики и тензора энергии-импульса. . Чаще всего, когда мы пишем уравнение, мы пишем скалярное уравнение, то есть уравнение, которое представляет собой только одно равенство, где сумма всего в левой части равна всему в правой. Но мы также можем записать системы уравнений и представить их одной простой формулировкой, которая кодирует эти отношения.
E = mc² является скалярным уравнением, потому что энергия (E), масса (m) и скорость света (c) имеют только одно уникальное значение. Но F = m a Ньютона — это не одно уравнение, а три отдельных уравнения: F x = ma x для направления «x», F y = ma y для направления «y». «, и F z = ma z для направления «z». В общей теории относительности тот факт, что у нас есть четыре измерения (три пространственных и одно время), а также два нижних индекса, которые физики называют индексами, означает, что нет ни одного уравнения, ни даже трех или четырех. Вместо этого у нас есть каждое из четырех измерений (t, x, y, z), влияющее на каждое из четырех других (t, x, y, z), всего 4 × 4 или 16 уравнений.
Но F = m a Ньютона — это не одно уравнение, а три отдельных уравнения: F x = ma x для направления «x», F y = ma y для направления «y». «, и F z = ma z для направления «z». В общей теории относительности тот факт, что у нас есть четыре измерения (три пространственных и одно время), а также два нижних индекса, которые физики называют индексами, означает, что нет ни одного уравнения, ни даже трех или четырех. Вместо этого у нас есть каждое из четырех измерений (t, x, y, z), влияющее на каждое из четырех других (t, x, y, z), всего 4 × 4 или 16 уравнений.
Вместо пустой трехмерной сетки размещение массы приводит к тому, что линии, которые были бы «прямыми», вместо этого изгибаются на определенную величину. В общей теории относительности пространство и время непрерывны, и все формы энергии вносят свой вклад в искривление пространства-времени. Кредит: Кристофер Витале из Networkologies и Института Пратта
Кредит: Кристофер Витале из Networkologies и Института Пратта
Зачем нам нужно так много уравнений только для описания гравитации, тогда как Ньютону нужно было только одно?
Потому что геометрия — сложный зверь, потому что мы работаем в четырех измерениях, и потому что то, что происходит в одном измерении или даже в одном месте, может распространяться наружу и влиять на все места во Вселенной, если только вы дадите достаточно времени, чтобы проходить. Наша вселенная с тремя пространственными измерениями и одним временным измерением означает, что геометрию нашей вселенной можно математически рассматривать как четырехмерное многообразие.
В римановой геометрии, где многообразия не обязательно должны быть прямыми и жесткими, но могут быть произвольно изогнуты, вы можете разбить эту кривизну на две части: части, искажающие объем объекта, и части, искажающие форму объекта. Часть «Риччи» искажает объем, и это играет роль в тензоре Эйнштейна, поскольку тензор Эйнштейна состоит из тензора Риччи и скаляра Риччи с добавлением некоторых констант и метрики. Часть «Вейля» искажает форму и, как это ни парадоксально, не играет никакой роли в уравнениях поля Эйнштейна.
Часть «Вейля» искажает форму и, как это ни парадоксально, не играет никакой роли в уравнениях поля Эйнштейна.
Уравнения поля Эйнштейна — это не просто одно уравнение, а скорее набор из 16 различных уравнений: по одному для каждой из комбинаций «4 × 4». При изменении одного компонента или аспекта Вселенной, например пространственной кривизны в любой точке или в любом направлении, любой другой компонент также может измениться в ответ. Эта структура во многом выводит концепцию дифференциального уравнения на новый уровень.
Дифференциальное уравнение — это любое уравнение, в котором можно сделать следующее:
- вы можете указать начальные условия вашей системы, например, что присутствует, где и когда она находится и как она движется,
- затем вы можете подставить эти условия в ваше дифференциальное уравнение,
- и уравнение расскажет вам, как эти вещи развиваются во времени, двигаясь вперед к следующему моменту,
- , где вы можете включить эту информацию обратно в дифференциальное уравнение, где оно затем расскажет вам, что произойдет впоследствии, в следующее мгновение.

Это чрезвычайно мощная структура, и именно поэтому Ньютону понадобилось изобрести исчисление, чтобы такие вещи, как движение и гравитация, стали понятными научными областями.
Когда вы размещаете в пространстве-времени даже одну точку массы, в результате вы искривляете ткань пространства-времени повсюду. Уравнения поля Эйнштейна позволяют связать кривизну пространства-времени с материей и энергией, в принципе, для любого выбранного вами распределения. Кредит: ДжонсонМартин / Pixabay
Только когда мы начинаем иметь дело с общей теорией относительности, это не просто одно уравнение или даже ряд независимых уравнений, которые все распространяются и развиваются в своем собственном измерении. Вместо этого, поскольку то, что происходит в одном направлении или измерении, влияет на все остальные, у нас есть 16 связанных, взаимозависимых уравнений, и по мере того, как объекты движутся и ускоряются в пространстве-времени, меняется энергия напряжения и кривизна пространства.
Однако эти «16 уравнений» не совсем уникальны! Во-первых, тензор Эйнштейна симметричен, а это означает, что существует связь между каждым компонентом, связывающим одно направление с другим. В частности, если ваши четыре координаты для времени и пространства (t, x, y, z), то:
- компонент «tx» будет эквивалентен компоненту «xt»,
- компонент «ty» будет эквивалентен компоненту «yt»,
- компонент «tz» будет эквивалентен компоненту «zt» компонент,
- компонент «yx» будет эквивалентен компоненту «xy»,
- компонент «zx» будет эквивалентен компоненту «xz»,
- и компонент «zy» будет эквивалентен компоненту » yz».
Вдруг уникальных уравнений не 16, а всего 10.
Кроме того, есть четыре отношения, которые связывают воедино кривизну этих разных измерений: Тождества Бьянки. Из 10 оставшихся уникальных уравнений только шесть являются независимыми, поскольку эти четыре соотношения еще больше уменьшают общее количество независимых переменных. Сила этой части дает нам свободу выбора любой системы координат, которая нам нравится, что буквально является силой относительности: каждый наблюдатель, независимо от его положения или движения, видит одни и те же законы физики, такие как одни и те же правила общей теории относительности. .
Сила этой части дает нам свободу выбора любой системы координат, которая нам нравится, что буквально является силой относительности: каждый наблюдатель, независимо от его положения или движения, видит одни и те же законы физики, такие как одни и те же правила общей теории относительности. .
Иллюстрация гравитационного линзирования и искривления звездного света из-за массы. Искривление пространства может быть настолько сильным, что свет может следовать несколькими путями из одной точки в другую. Авторы и права: NASA / STScI
У этого набора уравнений есть и другие чрезвычайно важные свойства. В частности, если вы возьмете дивергенцию тензора энергии-импульса, вы всегда, всегда получите ноль не только в целом, но и для каждой отдельной компоненты. Это означает, что у вас есть четыре симметрии: нет дивергенции во временном измерении или любом пространственном измерении, и каждый раз, когда у вас есть симметрия в физике, у вас также есть сохраняющаяся величина.
В общей теории относительности эти сохраняющиеся величины переводятся в энергию (для временного измерения), а также в импульс в направлениях x, y и z (для пространственных измерений). Точно так же, по крайней мере локально в непосредственной близости от вас, и энергия, и импульс сохраняются для отдельных систем. Несмотря на то, что в общей теории относительности невозможно определить такие вещи, как «глобальная энергия», для любой локальной системы в рамках общей теории относительности и энергия, и импульс остаются неизменными во все времена; это требование теории.
Когда массы движутся в пространстве-времени относительно друг друга, они вызывают излучение гравитационных волн: рябь сквозь ткань самого пространства. Эти пульсации математически закодированы в метрическом тензоре. Авторы и права: ESO / L. Calçada
Еще одно свойство общей теории относительности, которое отличается от большинства других физических теорий, заключается в том, что общая теория относительности нелинейна. Если у вас есть решение вашей теории, например, «на что похоже пространство-время, когда я опускаю одну точечную массу», у вас может возникнуть искушение сделать утверждение вроде: «Если я положу две точечные массы, то я смогу скомбинировать их». решение для массы № 1 и массы № 2 и получить другое решение: решение для обеих масс вместе».
Если у вас есть решение вашей теории, например, «на что похоже пространство-время, когда я опускаю одну точечную массу», у вас может возникнуть искушение сделать утверждение вроде: «Если я положу две точечные массы, то я смогу скомбинировать их». решение для массы № 1 и массы № 2 и получить другое решение: решение для обеих масс вместе».
Это верно, но только если у вас есть линейная теория. Ньютоновская гравитация — это линейная теория: гравитационное поле — это гравитационное поле каждого объекта, сложенного вместе и наложенного друг на друга. Электромагнетизм Максвелла аналогичен: электромагнитное поле двух зарядов, двух токов или заряда и тока можно рассчитать по отдельности и сложить вместе, чтобы получить чистое электромагнитное поле. Это справедливо даже для квантовой механики, поскольку уравнение Шредингера также является линейным (по волновой функции).
Но уравнения Эйнштейна нелинейны, а это значит, что вы не можете этого сделать. Если вы знаете кривизну пространства-времени для одной точечной массы, а затем записываете вторую точечную массу и спрашиваете: «Как сейчас искривлено пространство-время?» мы не можем записать точное решение. На самом деле, даже сегодня, более чем через 100 лет после того, как общая теория относительности была впервые выдвинута, в теории относительности все еще известно всего около 20 точных решений, и пространство-время с двумя точечными массами все еще не является одним из них.
На самом деле, даже сегодня, более чем через 100 лет после того, как общая теория относительности была впервые выдвинута, в теории относительности все еще известно всего около 20 точных решений, и пространство-время с двумя точечными массами все еще не является одним из них.
Фотография Итана Сигела у гиперстены Американского астрономического общества в 2017 году вместе с первым уравнением Фридмана справа — которое иногда называют самым важным уравнением во Вселенной и одним из редких точных решений в общей теории относительности. Авторы и права: Harley Thronson / Perimeter Institute)
Первоначально Эйнштейн сформулировал общую теорию относительности только с первым и последним членами уравнений, то есть с тензором Эйнштейна с одной стороны и тензором энергии-импульса (умноженным на гравитационная постоянная Эйнштейна) с другой стороны. Он только добавил космологическую постоянную, по крайней мере, согласно легенде, потому что не мог переварить последствия Вселенной, которая была вынуждена либо расширяться, либо сжиматься.
И тем не менее, сама по себе космологическая постоянная была бы революционным дополнением, даже если бы в природе не оказалось ненулевой единицы (в виде сегодняшней темной энергии) по простой, но увлекательной причине. Космологическая постоянная с математической точки зрения — буквально единственная «дополнительная» вещь, которую вы можете добавить к общей теории относительности, не меняя коренным образом природу отношений между материей и энергией и кривизну пространства-времени.
Однако сердцевиной общей теории относительности является не космологическая постоянная, которая представляет собой просто один конкретный тип «энергии», который вы можете добавить, а два других более общих термина. Тензор Эйнштейна, G μν говорит нам, какова кривизна пространства, и она связана с тензором энергии-импульса, T μν , который говорит нам, как распределены материя и энергия во Вселенной.
..»> Квантовая гравитация пытается объединить общую теорию относительности Эйнштейна с квантовой механикой. Квантовые поправки к классической гравитации визуализируются в виде петлевых диаграмм, как показано здесь белым цветом. Предоставлено: SLAC National Accelerator Lab
В нашей вселенной мы почти всегда делаем приближения. Если бы мы проигнорировали 15 из 16 уравнений Эйнштейна и просто сохранили «энергетическую» составляющую, вы бы восстановили теорию, которую она заменила: закон всемирного тяготения Ньютона. Если вместо этого вы сделаете Вселенную симметричной во всех пространственных измерениях и не позволите ей вращаться, вы получите изотропную и однородную Вселенную, управляемую уравнениями Фридмана (и, следовательно, требующую расширения или сжатия). В самых больших космических масштабах это фактически описывает вселенную, в которой мы живем.
Но вы также можете указать любое распределение материи и энергии, а также любой набор полей и частиц, который вам нравится, и если вы сможете это записать, уравнения Эйнштейна свяжут геометрию вашего пространства-времени с тем, как сама Вселенная искривлена в соответствии с тензором энергии-импульса, который представляет собой распределение энергии, импульса и напряжения.
Если на самом деле существует «теория всего», описывающая как гравитацию, так и квантовую вселенную, необходимо будет рассмотреть фундаментальные различия между этими концепциями, включая принципиально нелинейный характер теории Эйнштейна. В нынешнем виде, учитывая их сильно отличающиеся свойства, объединение гравитации с другими квантовыми силами остается одной из самых амбициозных мечтаний всей теоретической физики.
Общая теория относительности – Гиперучебник по физике
[закрыть]
своего рода введение для неорганизованной секции
В былые времена.
Я не буду определять время, пространство, место и движение, как всем известные.
Исаак Ньютон, 1689
Добро пожаловать в очередной сдвиг парадигмы.
Пробел говорит материи, как двигаться. Материя говорит пространству, как искривляться.
Джон Арчибальд Уилер, 1973 (платная ссылка)
Принцип эквивалентности …
- Отсутствие гравитационного поля (истинная невесомость) неотличимо от ускорения свободного падения в гравитационном поле (кажущаяся невесомость).

- Ускоренное движение в отсутствие гравитационного поля (кажущийся вес) неотличимо от неускоренного движения в присутствии гравитационного поля (истинный вес). Локальные эффекты гравитации такие же, как и при нахождении в ускоряющейся системе отсчета.
В основном…
- Кривые масса-энергия пространство-время — новая версия закона Гука.
- Объекты очерчивают мировые линии, которые являются геодезическими (путями наименьшего действия в искривленном пространстве-времени), если на них не действует чистая внешняя сила — новая версия закона инерции.
Гравитация — это не сила, это искривление пространства-времени, вызванное наличием массы-энергии.
| ут натяжение, | по сравнению с | |||
| штамм | ∝ | стресс | ||
| пространство-время кривизна | ∝ | масса-энергия напряжение | ||
Уравнения поля Эйнштейна…
| R μν − ½ Rg μν = | 8π Г | Т мкν |
| с 4 |
где…
| R мкν = | кривизна тензора Риччи |
| Р = | Скалярная кривизна Риччи |
| г мкν = | метрический тензор |
| T мкν = | тензор энергии-импульса |
| с = | скорость света в вакууме |
| Г = | универсальная гравитационная постоянная |
| π = | знаменитая константа из геометрии |
Правильно, я использовал форму множественного числа — уравнений .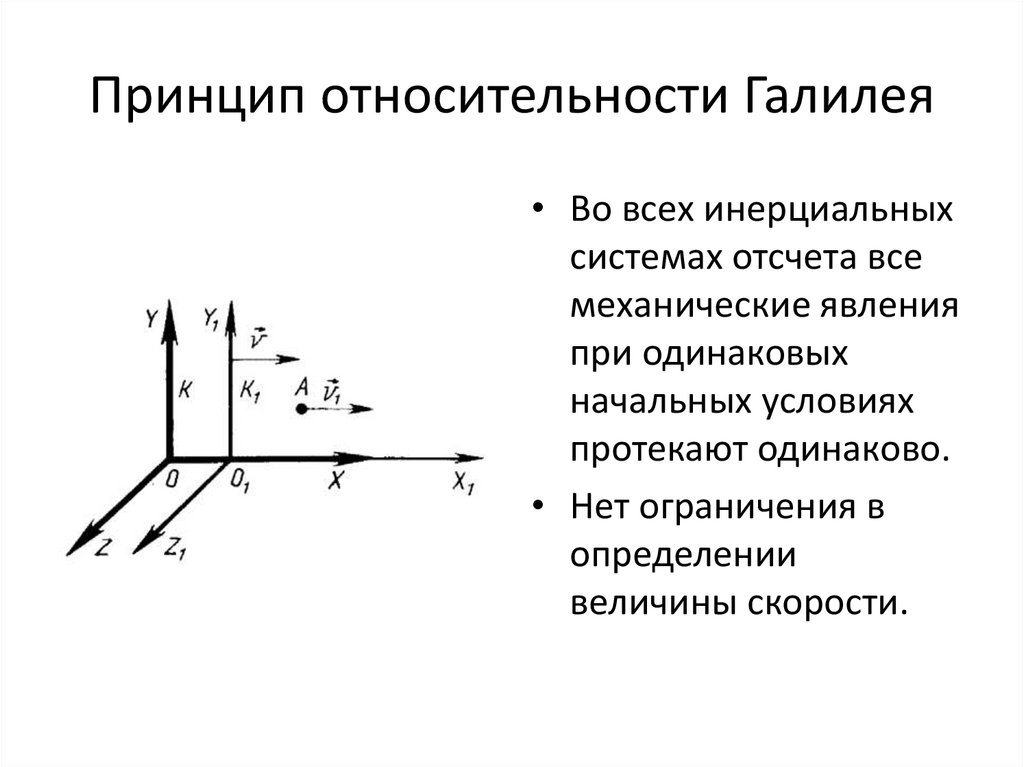 То, что выглядит как одно уравнение, на самом деле представляет собой набор из десяти связанных нелинейных дифференциальных уравнений в частных производных. В обратном порядке прилагательных эти уравнения равны дифференциальный , потому что они имеют дело со скоростью изменения (скоростью изменения), частичный , потому что задействовано несколько переменных (множество частей), нелинейный , потому что некоторые операции повторяются (скорость изменения скорости изменения ), и связаны с , потому что они не могут быть решены по отдельности (каждое уравнение имеет по крайней мере одну особенность, найденную в другом).
То, что выглядит как одно уравнение, на самом деле представляет собой набор из десяти связанных нелинейных дифференциальных уравнений в частных производных. В обратном порядке прилагательных эти уравнения равны дифференциальный , потому что они имеют дело со скоростью изменения (скоростью изменения), частичный , потому что задействовано несколько переменных (множество частей), нелинейный , потому что некоторые операции повторяются (скорость изменения скорости изменения ), и связаны с , потому что они не могут быть решены по отдельности (каждое уравнение имеет по крайней мере одну особенность, найденную в другом).
- Заявление об очевидном: Решение этих уравнений оказывается трудным.
- Удивительное заявление: эти уравнения могут быть разбиты на более простые уравнения теми, кто обладает большими навыками. Некоторые из этих более простых уравнений подходят для уровня этой книги, а это значит, что вы можете научиться делать некоторые общие теории относительности.
 Однако они будут получены с минимальным доказательством или без него.
Однако они будут получены с минимальным доказательством или без него.
космологическая постоянная
Пространство-время — это больше, чем просто набор значений для идентификации событий. Пространство-время само по себе. Космологическая постоянная — это величина, используемая в общей теории относительности для описания некоторых свойств пространства-времени. Вот как это происходит.
Возможно, гравитация — это искривление пространства-времени, вызванное массой-энергией материи внутри него плюс энергия самого пространства.
| R мкν − ½ Rg мкν | = |
| − | Λ г мкν | |||
| пространство-время кривизна | = | стресс от вещей в пространстве-времени | − | стресс от пустоты само пространство-время |
Или, может быть, гравитация — это искривление пространства-времени, вызванное массой-энергией сверх искривления самого пространства-времени.
| R мкν − ½ Rg мкν | + | Λ г мкν | = |
| |||
| кривизна из материала в пространстве-времени | + | кривизна самого пространства-времени | = | масса-энергия напряжение |
Странный выбор Эйнштейном знака может иметь больше смысла, если вычесть метрический тензор из левой части уравнения. Космологическая постоянная была изобретена как способ сдерживать гравитацию, чтобы статическая Вселенная не коллапсировала. (Кстати, эта цепочка рассуждений оказывается ошибочной, но это ошибка, которая в конце концов окупается.)
| R μν − (½ R − Λ) г μν = | 8π Г | Т мкν |
| с 4 |
Эйнштейн предполагал, что Вселенная статична и неизменна. Он думал, что это правда, потому что астрономы того времени думали, что видят именно это, когда смотрят в свои телескопы. Статическая Вселенная была бы нестабильной, если бы гравитация была только притягивающей. Каждая частица материи будет притягиваться друг к другу, и любой небольшой дисбаланс в распределении заставит все это в конечном итоге сжаться в себя. Эйнштейн добавил к своим уравнениям космологическую постоянную (технически он вычел ее из скалярной кривизны), чтобы сдержать гравитацию, чтобы его уравнения имели решение, согласующееся со статической моделью.
Он думал, что это правда, потому что астрономы того времени думали, что видят именно это, когда смотрят в свои телескопы. Статическая Вселенная была бы нестабильной, если бы гравитация была только притягивающей. Каждая частица материи будет притягиваться друг к другу, и любой небольшой дисбаланс в распределении заставит все это в конечном итоге сжаться в себя. Эйнштейн добавил к своим уравнениям космологическую постоянную (технически он вычел ее из скалярной кривизны), чтобы сдержать гравитацию, чтобы его уравнения имели решение, согласующееся со статической моделью.
Напишите еще.
Темная энергия абсолютно плавно распространяется по Вселенной.
неорганизованные мысли
- прецессия замкнутых (и открытых) орбит
- В 1859 году Урбен Леверье (1811–1877) Франция, директор Парижской обсерватории, опубликовал свои наблюдения аномалии на орбите Меркурия. Прецессия перигелия Меркурия (точка наибольшего сближения с Солнцем) прецессировала со скоростью 574 угловых секунды за столетие.
 Думая, что это произошло из-за воздействия других планет, он рассчитал скорость прецессии, используя законы Ньютона, в 531 секунду за столетие, оставив неучтенными 43 секунды. Можно сказать «маленький».
Думая, что это произошло из-за воздействия других планет, он рассчитал скорость прецессии, используя законы Ньютона, в 531 секунду за столетие, оставив неучтенными 43 секунды. Можно сказать «маленький».
- В 1859 году Урбен Леверье (1811–1877) Франция, директор Парижской обсерватории, опубликовал свои наблюдения аномалии на орбите Меркурия. Прецессия перигелия Меркурия (точка наибольшего сближения с Солнцем) прецессировала со скоростью 574 угловых секунды за столетие.
- гравитационное искривление света
- Подтверждено Артуром Эддингтоном (1882–1944) Англия в 1919 году. Общая теория относительности заменяет ньютоновскую теорию всемирного тяготения как наиболее полную теорию тяготения. Ньютон и Эддингтон были англичанами. Эйнштейн был немцем. 1919 год был первым годом после Первой мировой войны. В Европе все еще были высоки антинемецкие настроения. Подтверждение Эддингтоном теории Эйнштейна показало, что наука стоит выше культуры и политики. Эйнштейн стал знаменитостью.
- Крест Эйнштейна
- гравитационное линзирование
- увеличение удаленных объектов
- Гравитационный зонд А (1976 г.)
- Полет на атомно-водородном мазере на ракете «Скаут», запущенной на высоту 10 000 км.
 Мазер похож на лазер для микроволн. Он производит микроволны точной частоты. Измерьте доплеровский сдвиг из-за гравитации и движения и сравните с предсказанными значениями (ошибка = 70 частей на миллион = 0,007%)
Мазер похож на лазер для микроволн. Он производит микроволны точной частоты. Измерьте доплеровский сдвиг из-за гравитации и движения и сравните с предсказанными значениями (ошибка = 70 частей на миллион = 0,007%)
- Полет на атомно-водородном мазере на ракете «Скаут», запущенной на высоту 10 000 км.
- Гравитационный зонд B (2004–2005 гг.)
- Проверено на перетаскивание кадров.
Пространство никогда ничего не делало в ньютоновской механике. Просто был космос. В теории относительности Эйнштейна пространство и время стали вещью — вещью, которая могла делать такие вещи, как расширяться, сжиматься, сдвигаться и деформироваться (или изгибаться, или искривляться).
эволюция вселенной
Уравнение Фридмана (1923). Стандартная модель космологии. Одно обыкновенное дифференциальное уравнение, которое получается из десяти связанных нелинейных уравнений в частных производных Эйнштейна.
| 1 | ⎛ ⎜ ⎝ | от | ⎞ 2 ⎟ ⎠ | = | ⎛ ⎜ ⎝ | 8π G ρ | + | Λ | ⎞ ⎟ ⎠ | а 2 — к | |
| с 2 | дт | 3 с 2 | 3 |
где…
| и = | масштабный коэффициент (размер характерного куска Вселенной, может быть любого размера) |
| да / дт = | скорость изменения масштабного коэффициента (измеряется по красному смещению) |
| ρ = | плотность массы-энергии Вселенной (плотность материи-излучения Вселенной) |
| к = | кривизна Вселенной (+1 замкнутая, 0 плоская, −1 открытая) |
| Λ = | космологическая постоянная (энергетическая плотность самого пространства, пустого пространства) |
| с = | скорость света в вакууме |
| Г = | универсальная гравитационная постоянная |
| π = | знаменитая константа из геометрии |
Постоянная Хаббла, параметр Хаббла, скорость расширения
| Н = | da / DT |
| и |
Снова уравнение Фридмана.
| 1 | ⎛ ⎜ ⎝ | от | ⎞ 2 ⎟ ⎠ | = | ⎛ ⎜ ⎝ | 8π G ρ | + | Λ | ⎞ ⎟ ⎠ | а 2 — к | |
| с 2 | дт | 3 с 2 | 3 |
| ⎛ ⎜ ⎝ | дата/дата | ⎞ 2 ⎟ ⎠ | = | ⎛ ⎜ ⎝ | 8π G ρ | + | Λ с 2 | ⎞ ⎟ ⎠ | − | кс 2 |
| и | 3 | 3 | а 2 |
| Н 2 = | 8π G ρ | + | Λ с 2 | − | кс 2 |
| 3 | 3 | и 2 |
Критическая плотность.
| ρ c = | 3 Н 2 |
| 8π Г |
Параметр плотности.
| Ом = | р |
| р с |
Большой взрыв. Жорж Леметр.
2-е уравнение Фридмана.
| 1 | г 2 а | = − | 4π Г | ⎛ ⎜ ⎝ | ρ + | 3 р | ⎞ ⎟ ⎠ | + | Λ с 2 | ||
| и | дт 2 | 3 | с 2 | 3 |
замедление времени
Время для движущегося объекта идет медленнее, чем для неподвижного. Это следствие специальной теории относительности Эйнштейна известно как замедление времени и работает оно следующим образом…
Это следствие специальной теории относительности Эйнштейна известно как замедление времени и работает оно следующим образом…
| т ′ = | т |
| √(1 − v 2 / c 2 ) |
где…
| т = | продолжительность события в подвижной системе отсчета |
| т ′ = | продолжительность одного и того же события относительно стационарной системы отсчета |
| v = | скорость движущейся движущейся системы отсчета |
| с = | скорость света в вакууме (универсальная и, по-видимому, неизменная постоянная) |
Чем больше скорость движущегося наблюдателя, тем ближе соотношение v 2 / c 2 к единице, чем ближе знаменатель √(1 − v 2 / c 2) 90 , увеличивается или расширяется. С точки зрения стационарного наблюдателя, все события в системе отсчета, движущейся со скоростью света, происходят за бесконечное количество времени. Никакие события не могут произойти. Ничего не может случиться. Время перестает существовать.
С точки зрения стационарного наблюдателя, все события в системе отсчета, движущейся со скоростью света, происходят за бесконечное количество времени. Никакие события не могут произойти. Ничего не может случиться. Время перестает существовать.
Время также течет медленнее в гравитационном поле. Это следствие общей теории относительности Эйнштейна, известное как гравитационное замедление времени . Это работает так…
| т ′ = | т |
| √(1 − 2 В г / c 2 ) |
, где В г — гравитационный потенциал, связанный с гравитационным полем в некотором месте. Если вы читали в этой книге раздел о гравитационной потенциальной энергии, то, возможно, помните, что…
| В г = — | Гм |
| р |
Если вы не читали этот раздел, просто послушайте меня сейчас, когда я скажу, что из-за этого уравнения (и игнорируя знак минус) гравитационное замедление времени работает следующим образом…
| т ′ = | т |
| √(1 − 2 Gm / rc 2 ) |
где…
| т = | продолжительность события в гравитационном поле какого-либо объекта (планеты, солнца, черной дыры) |
| т ′ = | продолжительность одного и того же события, если смотреть с бесконечно большого расстояния (гипотетическое место, где гравитационное поле равно нулю) |
| м = | масса гравитирующего объекта |
| р = | расстояние от гравитирующего объекта до места, где происходит событие (их разделение) |
| с = | скорость света в вакууме (универсальная и, по-видимому, неизменная постоянная) |
| Г = | универсальная гравитационная постоянная (еще одна универсальная и, по-видимому, неизменная постоянная) |
Это уравнение говорит, что чем ближе событие происходит к гравитирующему телу, тем медленнее течет время; чем больше масса тяготеющего тела, тем медленнее течет время; чем сильнее гравитация, тем медленнее течет время.
Для небольших изменений высоты, когда гравитационное поле достаточно постоянно, это приближение работает нормально.
| т ′ ≈ | т |
| √(1 − 2 г ∆ ч / с 2 ) |
И это еще более приблизительное приближение тоже неплохо.
| т ′ ≈ т | ⎛ ⎜ ⎝ | 1 + | г ∆ ч | ⎞ ⎟ ⎠ |
| с 2 |
где…
| т = | продолжительность события в гравитационном поле какого-либо объекта (планеты, солнца, черной дыры) |
| т ′ = | продолжительность одного и того же события, если смотреть немного выше |
| г = | местное гравитационное поле (местное ускорение под действием силы тяжести) |
| ∆ ч = | разница высот между событием и наблюдателем |
| с = | скорость света в вакууме |
- Часы на самолетах Experiment
Prediction Abstract: В октябре 1971 года четыре цезиевых атомных часа дважды совершали регулярные полеты вокруг света на коммерческих реактивных самолетах, один раз на восток и один раз на запад, чтобы проверить теорию относительности Эйнштейна с помощью макроскопических часов. Исходя из фактических траекторий каждого рейса, теория предсказывает, что летающие часы по сравнению с эталонными часами в Военно-морской обсерватории США должны были отставать на 40 ± 23 наносекунды во время полета на восток и увеличиваться на 275 ± 21 наносекунду во время полета на запад. путешествие. Резюме результатов: 19 октября четыре цезиевых часа совершили кругосветное путешествие на коммерческих реактивных самолетах.71, один раз на восток и один раз на запад, зафиксировали разницу во времени, зависящую от направления, что хорошо согласуется с предсказаниями традиционной теории относительности. По отношению к шкале атомного времени Военно-морской обсерватории США летающие часы потеряли 59 ± 10 наносекунд во время полета на восток и увеличили 273 ± 7 наносекунд во время полета на запад, где ошибки представляют собой соответствующие стандартные отклонения. Эти результаты обеспечивают однозначное эмпирическое разрешение знаменитого «парадокса» часов с макроскопическими часами.
Исходя из фактических траекторий каждого рейса, теория предсказывает, что летающие часы по сравнению с эталонными часами в Военно-морской обсерватории США должны были отставать на 40 ± 23 наносекунды во время полета на восток и увеличиваться на 275 ± 21 наносекунду во время полета на запад. путешествие. Резюме результатов: 19 октября четыре цезиевых часа совершили кругосветное путешествие на коммерческих реактивных самолетах.71, один раз на восток и один раз на запад, зафиксировали разницу во времени, зависящую от направления, что хорошо согласуется с предсказаниями традиционной теории относительности. По отношению к шкале атомного времени Военно-морской обсерватории США летающие часы потеряли 59 ± 10 наносекунд во время полета на восток и увеличили 273 ± 7 наносекунд во время полета на запад, где ошибки представляют собой соответствующие стандартные отклонения. Эти результаты обеспечивают однозначное эмпирическое разрешение знаменитого «парадокса» часов с макроскопическими часами. - Часы, поднятые на 33 см — треть метра, чуть выше фута США, примерно на две ступени вверх по типичной лестнице.
 Прогнозируемое дробное изменение 3,6 × 10 −17 . Измеренное относительное изменение (4,1 ± 1,6) × 10 −17 . Потребуется около миллиарда лет, чтобы эта разница накопилась до одной секунды.
Прогнозируемое дробное изменение 3,6 × 10 −17 . Измеренное относительное изменение (4,1 ± 1,6) × 10 −17 . Потребуется около миллиарда лет, чтобы эта разница накопилась до одной секунды. - GPS
гравитационный эффект Доплера
Допплер движения (специальная теория относительности)
| λ | = | ф 0 | = √ | ⎛ ⎜ ⎝ | 1 + v / c | ⎞ ⎟ ⎠ |
| λ 0 | ф | 1 − v / c |
Гравитационный допплер (общая теория относительности)
| ф | = e −∆ В г / с 2 |
| ф 0 |
| ф | = 1 − | В г | + | В г 2 | − | В г 3 | + | В г 4 | − … |
| ф 0 | с 2 | 2 с 4 | 6 с 6 | 24 с 8 |
| ф | ≈ 1 − | В г |
| ф 0 | с 2 |
| Δ f | ≈ | Δ В г |
| ф 0 | с 2 |
| ф | ≈ 1 − | Гм |
| ф 0 | с 2 р |
| ф | ≈ 1 − | г ∆ ч |
| ф 0 | с 2 |
- 1959 Эксперимент Гарвардской Башни.
 Паунд, Ребка и Снайдер. Физическая лаборатория Джефферсона, Гарвард. Подтверждено экспериментом, проведенным в шахте лифта (?) Гарвардского университета Робертом Паундом (1919–2010) и Гленом Ребкой (1931–2015) в 1959 году. Источник гамма-излучения был помещен наверху шахты, а детектор внизу. Источник излучал гамма-лучи с определенной частотой, а детектор был разработан для обнаружения только гамма-лучей с этой конкретной частотой. В процессе «падения» вниз по шахте гамма-лучи синего цвета смещались в более высокую частоту. Паунд и Ребка поместили источник на вибрирующий динамик. Когда динамик двигался вверх с нужной скоростью, гравитационное синее смещение компенсировалось движущимся красным смещением, и детектор обнаруживал гамма-лучи. Двигайтесь с любой другой скоростью, и заметка будет обнаружена. Измерьте скорость источника, локальное гравитационное поле, высоту детектора над излучателем и скорость света; поставить числа в уравнение; проверьте, равны ли обе стороны в пределах ошибки эксперимента (~10%, Паунд и Снайдер уменьшили это до ~1% в 1964).
Паунд, Ребка и Снайдер. Физическая лаборатория Джефферсона, Гарвард. Подтверждено экспериментом, проведенным в шахте лифта (?) Гарвардского университета Робертом Паундом (1919–2010) и Гленом Ребкой (1931–2015) в 1959 году. Источник гамма-излучения был помещен наверху шахты, а детектор внизу. Источник излучал гамма-лучи с определенной частотой, а детектор был разработан для обнаружения только гамма-лучей с этой конкретной частотой. В процессе «падения» вниз по шахте гамма-лучи синего цвета смещались в более высокую частоту. Паунд и Ребка поместили источник на вибрирующий динамик. Когда динамик двигался вверх с нужной скоростью, гравитационное синее смещение компенсировалось движущимся красным смещением, и детектор обнаруживал гамма-лучи. Двигайтесь с любой другой скоростью, и заметка будет обнаружена. Измерьте скорость источника, локальное гравитационное поле, высоту детектора над излучателем и скорость света; поставить числа в уравнение; проверьте, равны ли обе стороны в пределах ошибки эксперимента (~10%, Паунд и Снайдер уменьшили это до ~1% в 1964).
- Эксперимент с ракетой-разведчиком, 1976 г. Смитсоновская астрофизическая обсерватория. Первым таким экспериментом был эксперимент Национального управления по аэронавтике и исследованию космического пространства / Смитсоновской астрофизической обсерватории (NASA-SAO) Rocket Redshift Experiment, который состоялся в июне 1976 года. по сравнению с аналогичными часами на земле. На этой высоте часы должны идти на 4,5 части из 10 10 быстрее, чем на Земле. В течение двух часов свободного падения с максимальной высоты ракета передавала синхронизирующие импульсы от мазера-генератора, который действовал как часы и сравнивался с аналогичными часами на земле. Этот результат подтвердил гравитационное замедление времени с точностью до 0,01%.
горизонт событий
Что бы ни приближало 2 Gm / rc 2 к единице, доминатор √(1 − 2 Gm / rc 2 ) приближается к нулю, а время события растягивается до бесконечности . Это происходит, когда событие приближается на следующее расстояние от гравитирующего тела…
Это происходит, когда событие приближается на следующее расстояние от гравитирующего тела…
| р с = | 2 Гм |
| с 2 |
Это расстояние известно как радиус Шварцшильда. Другой способ записать уравнение гравитационного замедления времени — использовать это число…
.
| т ′ = | т |
| √(1 − r s / r ) |
Радиус Шварцшильда делит пространство-время на две области, разделенные горизонтом событий. Горизонт на Земле делит поверхность Земли на две области — видимую и невидимую. Горизонт событий делит пространство-время на две области: внешнюю, куда информация течет в любом направлении, и внутреннюю, куда информация может поступать, но не выходить. На Земле горизонт связан с наблюдателем. В пространстве-времени горизонт событий связан с источником экстремальной гравитации.
| пробел | время | имя | описание |
|---|---|---|---|
| r > r s | т ′ > т | снаружи | время замедляется, события на этом расстоянии происходят дольше, если смотреть из мест, находящихся дальше от |
| р = р с | т ′ = ∞ | горизонт событий | время останавливается, все события происходят бесконечно долго, если смотреть извне |
| r < r с | т ′ = бит т | внутри | время математически мнимо, время становится пространственноподобным, пространство становится времениподобным ( bi мнимое число, составленное из действительного коэффициента b умножить на мнимую единицу i , где i 2 = −1) |
| r = 0 | т ′ = 0 | сингулярность | время не имеет значения, все события происходят одновременно, нужна новая физика |
Большинство объектов не имеют горизонта событий. Это расстояние, которое не может существовать. Все объекты, с которыми мы сталкиваемся в повседневной жизни, и большинство объектов во Вселенной значительно больше своего радиуса Шварцшильда. Нельзя подойти так близко к Земле, чтобы время остановилось. Его радиус Шварцшильда равен 9мм, а его фактический радиус составляет 6400 км. Не думайте, что вы сможете остановить время, прокопав туннель в ядро Земли. Гравитация внутри Земли уменьшается до нуля в ее центре. Вы не ближе к Земле в ее центре, вы внутри нее. Когда вы находитесь на поверхности Земли, как сейчас, гравитация в целом тянет вас в одну сторону — вниз. Если бы вы могли отправиться к центру Земли, гравитация тянула бы вас наружу во всех направлениях, что равносильно отсутствию направления. Гравитация, которая не тянет ни в каком направлении, не может быть сильной.
Это расстояние, которое не может существовать. Все объекты, с которыми мы сталкиваемся в повседневной жизни, и большинство объектов во Вселенной значительно больше своего радиуса Шварцшильда. Нельзя подойти так близко к Земле, чтобы время остановилось. Его радиус Шварцшильда равен 9мм, а его фактический радиус составляет 6400 км. Не думайте, что вы сможете остановить время, прокопав туннель в ядро Земли. Гравитация внутри Земли уменьшается до нуля в ее центре. Вы не ближе к Земле в ее центре, вы внутри нее. Когда вы находитесь на поверхности Земли, как сейчас, гравитация в целом тянет вас в одну сторону — вниз. Если бы вы могли отправиться к центру Земли, гравитация тянула бы вас наружу во всех направлениях, что равносильно отсутствию направления. Гравитация, которая не тянет ни в каком направлении, не может быть сильной.
Давайте попробуем более крупный объект с большей гравитацией — Солнце. Шварцшильдовский радиус Солнца составляет 3 км, но его реальный радиус составляет 700 000 км. Это не намного лучше. Попробуйте самую тяжелую из известных звезд — RMC 136a1. Он в 315 раз массивнее, но только в 30 раз больше в поперечнике. Его радиус Шварцшильда составляет 930 км, что все же намного меньше его радиуса.
Это не намного лучше. Попробуйте самую тяжелую из известных звезд — RMC 136a1. Он в 315 раз массивнее, но только в 30 раз больше в поперечнике. Его радиус Шварцшильда составляет 930 км, что все же намного меньше его радиуса.
Проблема (которая на самом деле не является проблемой) заключается в том, что все объекты вокруг нас и большинство небесных тел, таких как планеты, луны, астероиды, кометы, туманности и звезды, невозможно сделать достаточно маленькими. Солнце однажды умрет, и его ядро сожмется за миллиарды лет до размеров Земли, но на этом все и закончится. Земля может разлететься вдребезги из-за высвобождающегося газа умирающего солнца, но она никогда не будет симметрично раздавлена в шарикоподшипник. По сути, нет никакого способа увеличить радиус Солнца до 3 км или Земли до 9 км.мм. Однако RMC 136a1 — это совсем другая история.
Звезды — это миазмы раскаленной плазмы, как поется в песне. Они нагреваются изнутри за счет слияния легких элементов с более тяжелыми. Это тепло поддерживает их в определенном смысле надутыми. Когда они исчерпывают свое топливо, они теряют это тепло и начинают сжиматься. В таких звездах, как Солнце, водород превращается в гелий в ядре, где давление достаточно велико. Когда все ядро превратилось в гелий, звезда теряет энергию, необходимую для поддержания ее накачки, и начинает сжиматься.
Это тепло поддерживает их в определенном смысле надутыми. Когда они исчерпывают свое топливо, они теряют это тепло и начинают сжиматься. В таких звездах, как Солнце, водород превращается в гелий в ядре, где давление достаточно велико. Когда все ядро превратилось в гелий, звезда теряет энергию, необходимую для поддержания ее накачки, и начинает сжиматься.
Солнце будет сжиматься до тех пор, пока пространство между атомами не станет настолько маленьким, насколько это возможно. Такая звезда называется белым карликом. Представьте, что Солнце уменьшилось до размеров Земли. Мы все еще в 1000 раз или на 3 порядка больше, чем горизонт событий.
В процессе сжатия Солнце также сбросит большую часть своих внешних слоев. Это создает туманное облако раскаленного газа, окружающее ядро белого карлика, называемое планетарной туманностью. Это неудачный термин, поскольку он не имеет прямого отношения к формированию планет.
Более крупные звезды ведут более сложный образ жизни. Некоторые из них могут извлекать ядерную энергию путем слияния трех ядер гелия с образованием одного ядра углерода. Некоторые присоединяют к этому углероду дополнительные ядра гелия, образуя кислород, неон, магний, кремний, серу, аргон и так далее вплоть до железа. Такие звезды могут умереть одним из двух способов. Оба связаны с коллапсом ядра и осыпанием внешних слоев. Такая умирающая звезда называется сверхновой, и этот процесс происходит гораздо быстрее, чем смерть таких звезд, как Солнце, — за часы, а не за тысячелетия. Остаток ядра может образовать белый карлик, если будет выброшено слишком много материала с поверхности, но более вероятным результатом будет нейтронная звезда или черная дыра.
Некоторые из них могут извлекать ядерную энергию путем слияния трех ядер гелия с образованием одного ядра углерода. Некоторые присоединяют к этому углероду дополнительные ядра гелия, образуя кислород, неон, магний, кремний, серу, аргон и так далее вплоть до железа. Такие звезды могут умереть одним из двух способов. Оба связаны с коллапсом ядра и осыпанием внешних слоев. Такая умирающая звезда называется сверхновой, и этот процесс происходит гораздо быстрее, чем смерть таких звезд, как Солнце, — за часы, а не за тысячелетия. Остаток ядра может образовать белый карлик, если будет выброшено слишком много материала с поверхности, но более вероятным результатом будет нейтронная звезда или черная дыра.
Нейтронная звезда — это остаток звездного ядра с достаточной массой, чтобы ее гравитационное поле было достаточно сильным, чтобы преодолеть давление вырождения электронов — квантово-механический эквивалент электростатической силы отталкивания между электронами. Это вдавливает вращающиеся электроны в ядро, где они соединяются с протонами, образуя нейтроны. Такая звезда фактически представляет собой гигантский шар нейтронов. Представьте себе звездное ядро, в 2 или 3 раза превышающее массу Солнца, раздавленное до размеров города, скажем, 10 км в радиусе. Радиус Шварцшильда объекта массой 3 солнечных составляет 9км. Мы почти там.
Такая звезда фактически представляет собой гигантский шар нейтронов. Представьте себе звездное ядро, в 2 или 3 раза превышающее массу Солнца, раздавленное до размеров города, скажем, 10 км в радиусе. Радиус Шварцшильда объекта массой 3 солнечных составляет 9км. Мы почти там.
Когда некоторые действительно большие звезды коллапсируют, их остаточные ядра содержат достаточную массу, чтобы гравитация в конечном итоге преодолела давление вырождения нейтронов — аспект сильного ядерного взаимодействия, которое удерживает нейтроны и протоны на приличном расстоянии друг от друга. Теперь нечему противодействовать гравитации, и ядро сжимается до нулевого радиуса и объема. Не просто очень маленький, а настоящий математический ноль. Такой объект называется черной дырой, потому что ничто, даже свет, не может вырваться из ее гравитационного захвата.
Вернуться к RMC 136a1?
Вспомним, что в разделе этой книги, посвященном гравитационной потенциальной энергии, радиус Шварцшильда был получен именно так — как расстояние от массивного компактного объекта, на котором скорость убегания равнялась бы скорости света. К этому мы только что добавили еще одну функцию. Это место, где останавливается время.
К этому мы только что добавили еще одну функцию. Это место, где останавливается время.
гравитационные волны
- двойных пульсаров, сходящихся друг с другом по спирали
- косвенное свидетельство
- Джозеф Тейлор и Рассел Халс
- подвесной алюминиевый цилиндр
- ложноположительный
- действительно обнаружено в 2015 г., заявлено в 2016 г.
- интерферометр
- LIGO (Лазерно-интерферометрическая гравитационно-волновая обсерватория), Advanced LIGO
Лазерно-интерферометрическая гравитационно-волновая обсерватория (LIGO) — это объект, предназначенный для обнаружения космических гравитационных волн и использования этих волн для научных исследований. Он состоит из двух широко разнесенных объектов в Соединенных Штатах — одного в Хэнфорде, штат Вашингтон, и другого в Ливингстоне, штат Луизиана, — которые работают одновременно как единая обсерватория 9.0018 - Virgo, Advanced Virgo
Детектор гравитационных волн Virgo состоит в основном из лазерного интерферометра Майкельсона, состоящего из двух ортогональных плеч, каждое из которых имеет длину 3 километра. Многократные отражения между зеркалами, расположенными на концах каждого плеча, увеличивают эффективную оптическую длину каждого плеча до 120 километров. Virgo находится на территории EGO, Европейской гравитационной обсерватории, базирующейся в Кашине, недалеко от Пизы, на равнине реки Арно. Частотный диапазон Девы простирается от 10 до 6000 Гц. Этот диапазон, а также высокая чувствительность должны позволить обнаруживать гравитационное излучение сверхновых и слияния двойных систем в Млечном Пути и во внешних галактиках, например, от скопления Девы.
Многократные отражения между зеркалами, расположенными на концах каждого плеча, увеличивают эффективную оптическую длину каждого плеча до 120 километров. Virgo находится на территории EGO, Европейской гравитационной обсерватории, базирующейся в Кашине, недалеко от Пизы, на равнине реки Арно. Частотный диапазон Девы простирается от 10 до 6000 Гц. Этот диапазон, а также высокая чувствительность должны позволить обнаруживать гравитационное излучение сверхновых и слияния двойных систем в Млечном Пути и во внешних галактиках, например, от скопления Девы. - LISA (космическая антенна с лазерным интерферометром) предполагаемая дата запуска 2018–2020 гг.
LISA состоит из трех идентичных космических аппаратов, положения которых отмечают вершины равностороннего треугольника со стороной пять миллионов километров на орбите вокруг Солнца. LISA можно рассматривать как гигантский интерферометр Майкельсона в космосе. Разделение космических аппаратов устанавливает диапазон частот GW, которые может наблюдать LISA (от 0,03 мГц до более 0,1 Гц). Центр треугольника LISA описывает земную орбиту в плоскости эклиптики, на расстоянии одной астрономической единицы от Солнца, но на 20 градусов позади Земли. Плоскость треугольника наклонена под углом 60 градусов к эклиптике. Естественные орбиты свободного падения трех космических кораблей вокруг Солнца поддерживают эту треугольную форму, при этом кажется, что треугольник вращается вокруг своего центра один раз в год.
Центр треугольника LISA описывает земную орбиту в плоскости эклиптики, на расстоянии одной астрономической единицы от Солнца, но на 20 градусов позади Земли. Плоскость треугольника наклонена под углом 60 градусов к эклиптике. Естественные орбиты свободного падения трех космических кораблей вокруг Солнца поддерживают эту треугольную форму, при этом кажется, что треугольник вращается вокруг своего центра один раз в год.
- LIGO (Лазерно-интерферометрическая гравитационно-волновая обсерватория), Advanced LIGO
Что такое общая теория относительности? | plus.maths.org
Когда физики говорят об уравнении Эйнштейна, они не
обычно имеют в виду знаменитое E=mc 2 , но другое
Формула, которая заключает в себе знаменитую общую теорию
относительность. Эйнштейн опубликовал эту теорию сто лет назад в
1915. Чтобы отпраздновать столетие, мы попросили физика Дэвида Тонга из
Кембриджский университет, чтобы объяснить, что такое общая теория относительности и как
Уравнение Эйнштейна выражает это. Вы можете посмотреть его объяснение в видео
ниже или читайте дальше.
Начните с Ньютона
Общая теория относительности описывает силу
сила тяжести. Эйнштейн не был первым, кто выдвинул такую теорию.
Еще в 1686 году Исаак Ньютон сформулировал свой знаменитый закон обратных квадратов .
гравитация . Закон Ньютона отлично работает на небольших масштабах: мы можем использовать его, чтобы вычислить, насколько быстро объект
выпавший из высотного здания рванет на землю и даже пошлет
людей на Луну. Но когда
расстояния и скорости очень велики, или речь идет об очень массивных объектах, закон Ньютона
становится неточным. Это хорошее место для начала, так как это проще
описать, чем теория Эйнштейна.
Предположим, у вас есть два объекта, скажем, Солнце и Земля, с массой и соответственно. Запишите расстояние между двумя объектами. Тогда закон Ньютона говорит, что гравитационная сила между ними равна
где — фиксированное число, известное как постоянная Ньютона.
Формула интуитивно понятна: она говорит нам, что гравитация ослабевает на больших расстояниях (чем больше, тем меньше ) и что гравитационная сила сильнее между более массивными объектами (чем больше один из и тем больше ).
Другая сила, та же формула
Есть еще одна формула, которая выглядит очень похожей, но описывает
разная сила. В 1785 году французский физик Шарль-Огюстен
де Кулон вывел уравнение для описания электростатической силы, действующей между двумя заряженными частицами с зарядами:
Здесь обозначает расстояние между двумя частицами и константа, определяющая силу электромагнетизма. (У него причудливое название диэлектрическая проницаемость свободного пространства .)
Проблема с Ньютоном
Формулы Ньютона и Кулона хороши и аккуратны, но есть
проблема. Возвращаясь к закону Ньютона, предположим, что вы взяли Землю и
Солнце и очень быстро отдалили их друг от друга. Это сделало бы
Это сделало бы
сила, действующая между ними, слабее, но, согласно формуле,
ослабление силы произойдет сразу же, как только вы переместите
два тела друг от друга. То же самое относится и к закону Кулона: перемещение заряженного
очень быстрое разделение частиц привело бы к немедленному ослаблению
электростатическая сила между ними.
Но этого не может быть. специальная теория относительности Эйнштейна,
предложенный за десять лет до общей теории в 1905 году, говорит, что
ничто во Вселенной не может двигаться быстрее света — даже
«сигнал», сообщающий о том, что два объекта разошлись и
сила должна стать слабее.
Зачем нужны поля
Это одна из причин, по которой классическая идея силы нуждается в замене в современной физике. Вместо этого нам нужно мыслить в категориях чего-то — нового.
объекты — которые передают силу между одним объектом и
еще один. Это был большой вклад британского ученого Майкла
Фарадея к теоретической физике. Фарадей понял, что распространился по всему
Вселенной есть объекты, которые мы сегодня называем поля , которые
участвуют в передаче силы. Примеры
Примеры
электрические и магнитные поля, с которыми вы, вероятно, знакомы
из школы.
Альберт Эйнштейн (1879-1955) в 1921 году.
Заряженная частица создает электрическое поле, которое
«почувствовал»
другая частица (имеющая собственное электрическое поле). Один
частица будет двигаться в ответ на чужое электрическое поле — вот что
мы называем силой. Когда одна частица быстро удаляется от другой, то это
вызывает пульсации в электрическом поле первой частицы. Рябь путешествует по пространству, на
со скоростью света и, в конечном счете, повлияют на другую частицу. Фактически,
движущаяся частица также создает магнитное поле и излучает
электромагнитное излучение. Конечным результатом является сложное взаимодействие пульсирующих полей.
— но дело в том, что сила на самом деле представляет собой одну частицу,
воздействуют рябью, распространяющейся через поле другого.
Ученым потребовалось много времени, чтобы полностью разработать эту картину поля
электромагнетизма. Основная заслуга принадлежит шотландскому ученому Джеймсу Клерку.
Максвелл, который не только понял, что электрические и магнитные
силы были двумя аспектами единой силы электромагнетизма, но
также заменил простой закон электростатики Кулона на четыре
уравнения, которые описывают, как электрические и магнитные поля реагируют на
движущиеся заряженные частицы. Четыре формулы Максвелла — одни из самых удивительных уравнений в
физики, потому что они охватывают все, что нужно знать об электричестве.
и магнетизм.
Гравитация и пространство-время
А как насчет гравитации? Так же, как и в случае с электромагнетизмом, необходимо
быть полем, порождающим то, что мы воспринимаем как гравитационную силу
действует между двумя телами.
Великое озарение Эйнштейна заключалось в том, что
это поле состоит из чего-то, о чем мы уже знаем: пространства и времени.
Представьте себе тяжелое тело, подобное Солнцу, сидящее в пространстве. Эйнштейн
понял, что пространство не просто пассивный наблюдатель, но отвечает на
тяжелый предмет сгибанием. Другое тело, похожее на Землю, движется
в вмятину, созданную более тяжелым предметом, будет отвлечен этим
вмятина.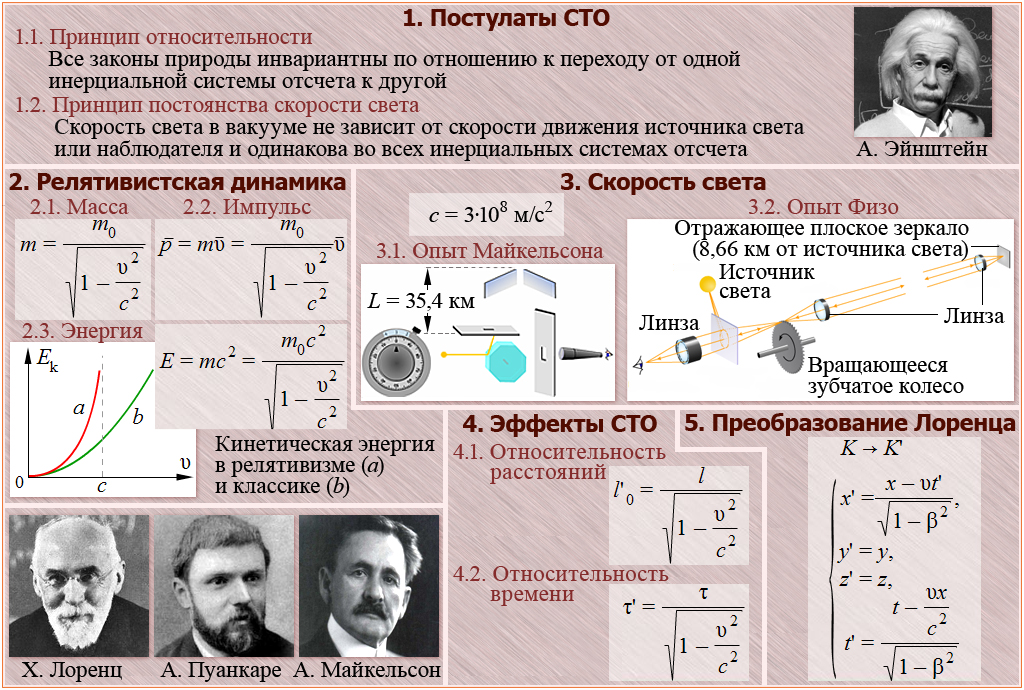 Вместо того, чтобы продолжать движение по прямой линии, он начнет
Вместо того, чтобы продолжать движение по прямой линии, он начнет
вращается вокруг более тяжелого объекта. Или, если он достаточно медленный,
врезаться в него. (Эйнштейну понадобилось много лет борьбы, чтобы прийти к
его теория — см. это
статью, чтобы узнать больше.)
Еще один урок
Теория Эйнштейна состоит в том, что пространство и время могут переходить друг в друга.
они неразрывно связаны и время тоже может быть искажено массивными
объекты. Вот почему мы говорим не только об искривлении пространства,
а насчет искривления пространства-времени .
Уравнение
Общая теория относительности представлена обманчиво простым уравнением:
По существу уравнение говорит нам, как заданное количество массы и энергии искажает пространство-время. Левая часть уравнения:
описывает искривление пространства-времени, действие которого мы воспринимаем как гравитационную силу. Это аналог члена в левой части уравнения Ньютона.
Это аналог члена в левой части уравнения Ньютона.
Массивные объекты искривляют пространство-время. Изображение предоставлено НАСА.
Член в правой части уравнения описывает все, что нужно знать о том, как масса, энергия, импульс и давление распределяются по Вселенной. Это то, что стало с членом в уравнении Ньютона, но все гораздо сложнее. Все это необходимо, чтобы понять, как искривляются пространство и время. называется техническим термином тензор энергии-импульса . Константа, которая появляется в правой части уравнения, снова является константой Ньютона и представляет собой скорость света.
А как насчет греческих букв, которые появляются в виде нижних индексов? Чтобы понять, что они означают, сначала обратите внимание на то, что пространство-время имеет четыре измерения. Есть три измерения пространства (соответствующие трем направлениям влево-вправо, вверх-вниз и вперед-назад пространства) и одно измерение времени (которое имеет только одно направление). Если вы хотите понять, как движущаяся частица массы влияет на пространство-время, вам нужно понять, как она влияет на каждое из этих четырех измерений и их различные комбинации.
Если вы хотите понять, как движущаяся частица массы влияет на пространство-время, вам нужно понять, как она влияет на каждое из этих четырех измерений и их различные комбинации.
(В качестве аналогии подумайте о том, как вы описали бы объект, движущийся с постоянной скоростью по прямой линии в классической ньютоновской физике. Вам нужны две части информации: направление и скорость движения. Направление задано тремя числами, каждое из которых говорит вам, насколько объект перемещается в каждом из трех направлений пространства. Следовательно, движение описывается в общей сложности четырьмя числами, три из которых относятся к пространству, а одно — к скорости. Поскольку скорость — это пройденное расстояние в единицу времени нам нужно три бита информации, относящихся к пространству, и один — ко времени, чтобы описать движение.)
Не одно уравнение
В уравнении Эйнштейна греческие буквы и — это метки, каждая из которых может принимать значения 0, 1, 2 или 3. Так что на самом деле приведенное выше уравнение скрывает целый набор уравнений, соответствующих возможным комбинациям значений, которые может принимать и:
и так далее.
Значение 0 соответствует времени, а значения 1, 2 и 3 — трем измерениям пространства.
Уравнение
Таким образом,
относится ко времени и 1-направлению пространства. Термин в правой части описывает импульс (скорость и массу) материи, движущейся в 1-направлении пространства. Движение заставляет время и 1-направление пространства смешиваться и деформироваться друг в друга — этот эффект описывается левой частью уравнения. (Аналог подходит для уравнения с и равным 2 или 3.)
Если в уравнении есть только единицы, двойки или тройки, например,
то это относится только к космосу. Член в правой части теперь измеряет давление , которое материя оказывает в соответствующем направлении пространства. Левая сторона говорит вам, как эта материя заставляет пространство растягиваться в этом направлении.
Левая сторона говорит вам, как эта материя заставляет пространство растягиваться в этом направлении.
Если и оба принимают значение 0, то уравнение
относится только ко времени. Теперь этот термин означает энергию, которая заставляет время ускоряться или замедляться. Левая часть уравнения описывает это изменение течения времени.
Поскольку каждое из и может принимать четыре значения, всего получается 4 x 4 = 16 уравнений. Однако оказывается, что уравнение с и (при и каждое равно одному из 0, 1, 2 или 3) такое же, как уравнение с и Это сокращает общее количество уравнений до десяти.
Художественное представление черной дыры. Изображение: Роберт Херт, NASA/JPL-Caltech.
Теоретически уравнения Эйнштейна позволяют точно определить, как
массивные объекты, такие как планеты, звезды, галактики или даже черные дыры, влияют на
пространство-время, в котором они находятся. Однако на практике все обстоит не так
Однако на практике все обстоит не так
простой. Уравнения Эйнштейна невероятно сложно решить —
суперкомпьютеры необходимы для поиска решений, а разработка новых решений является активной областью
теоретическая физика. Одна из больших текущих задач — выяснить, что происходит с пространством-временем, когда сталкиваются два очень тяжелых объекта, таких как черные дыры.
Откуда мы знаем, что теория Эйнштейна верна? В сотне
Спустя годы после публикации теория прошла все испытания, которые она проводила.
подвергался. Несмотря на слегка эзотерический характер, это очень важно.
в вещах, на которые большинство из нас полагаются каждый день, таких как функции GPS в нашем
смартфоны и устройства Satnav в наших автомобилях. Теория действительно открывается
некоторые новые вопросы, вот почему некоторые физики считают, что это необходимо
изменить (см. эту статью). Но будь то или
не то это действительно оказывается нужным, можно не сомневаться, что
Общая теория относительности — одно из самых удивительных достижений в
история науки.

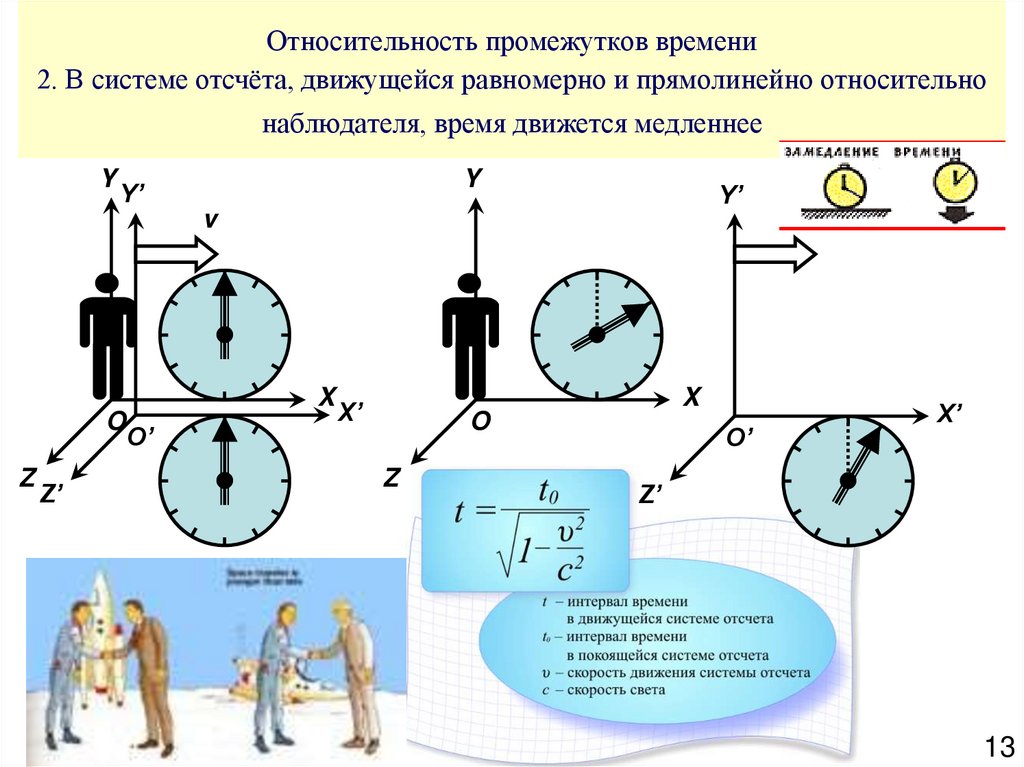 ): суть этой теории в том, что законы физики одинаковы для всех неускоряющихся наблюдателей и что скорость света в вакууме не зависит от движения наблюдателей (вообще никого, кто является частью действия/эксперимента).
): суть этой теории в том, что законы физики одинаковы для всех неускоряющихся наблюдателей и что скорость света в вакууме не зависит от движения наблюдателей (вообще никого, кто является частью действия/эксперимента).



 Однако они будут получены с минимальным доказательством или без него.
Однако они будут получены с минимальным доказательством или без него. Думая, что это произошло из-за воздействия других планет, он рассчитал скорость прецессии, используя законы Ньютона, в 531 секунду за столетие, оставив неучтенными 43 секунды. Можно сказать «маленький».
Думая, что это произошло из-за воздействия других планет, он рассчитал скорость прецессии, используя законы Ньютона, в 531 секунду за столетие, оставив неучтенными 43 секунды. Можно сказать «маленький». Мазер похож на лазер для микроволн. Он производит микроволны точной частоты. Измерьте доплеровский сдвиг из-за гравитации и движения и сравните с предсказанными значениями (ошибка = 70 частей на миллион = 0,007%)
Мазер похож на лазер для микроволн. Он производит микроволны точной частоты. Измерьте доплеровский сдвиг из-за гравитации и движения и сравните с предсказанными значениями (ошибка = 70 частей на миллион = 0,007%) Исходя из фактических траекторий каждого рейса, теория предсказывает, что летающие часы по сравнению с эталонными часами в Военно-морской обсерватории США должны были отставать на 40 ± 23 наносекунды во время полета на восток и увеличиваться на 275 ± 21 наносекунду во время полета на запад. путешествие. Резюме результатов: 19 октября четыре цезиевых часа совершили кругосветное путешествие на коммерческих реактивных самолетах.71, один раз на восток и один раз на запад, зафиксировали разницу во времени, зависящую от направления, что хорошо согласуется с предсказаниями традиционной теории относительности. По отношению к шкале атомного времени Военно-морской обсерватории США летающие часы потеряли 59 ± 10 наносекунд во время полета на восток и увеличили 273 ± 7 наносекунд во время полета на запад, где ошибки представляют собой соответствующие стандартные отклонения. Эти результаты обеспечивают однозначное эмпирическое разрешение знаменитого «парадокса» часов с макроскопическими часами.
Исходя из фактических траекторий каждого рейса, теория предсказывает, что летающие часы по сравнению с эталонными часами в Военно-морской обсерватории США должны были отставать на 40 ± 23 наносекунды во время полета на восток и увеличиваться на 275 ± 21 наносекунду во время полета на запад. путешествие. Резюме результатов: 19 октября четыре цезиевых часа совершили кругосветное путешествие на коммерческих реактивных самолетах.71, один раз на восток и один раз на запад, зафиксировали разницу во времени, зависящую от направления, что хорошо согласуется с предсказаниями традиционной теории относительности. По отношению к шкале атомного времени Военно-морской обсерватории США летающие часы потеряли 59 ± 10 наносекунд во время полета на восток и увеличили 273 ± 7 наносекунд во время полета на запад, где ошибки представляют собой соответствующие стандартные отклонения. Эти результаты обеспечивают однозначное эмпирическое разрешение знаменитого «парадокса» часов с макроскопическими часами. Прогнозируемое дробное изменение 3,6 × 10 −17 . Измеренное относительное изменение (4,1 ± 1,6) × 10 −17 . Потребуется около миллиарда лет, чтобы эта разница накопилась до одной секунды.
Прогнозируемое дробное изменение 3,6 × 10 −17 . Измеренное относительное изменение (4,1 ± 1,6) × 10 −17 . Потребуется около миллиарда лет, чтобы эта разница накопилась до одной секунды. Паунд, Ребка и Снайдер. Физическая лаборатория Джефферсона, Гарвард. Подтверждено экспериментом, проведенным в шахте лифта (?) Гарвардского университета Робертом Паундом (1919–2010) и Гленом Ребкой (1931–2015) в 1959 году. Источник гамма-излучения был помещен наверху шахты, а детектор внизу. Источник излучал гамма-лучи с определенной частотой, а детектор был разработан для обнаружения только гамма-лучей с этой конкретной частотой. В процессе «падения» вниз по шахте гамма-лучи синего цвета смещались в более высокую частоту. Паунд и Ребка поместили источник на вибрирующий динамик. Когда динамик двигался вверх с нужной скоростью, гравитационное синее смещение компенсировалось движущимся красным смещением, и детектор обнаруживал гамма-лучи. Двигайтесь с любой другой скоростью, и заметка будет обнаружена. Измерьте скорость источника, локальное гравитационное поле, высоту детектора над излучателем и скорость света; поставить числа в уравнение; проверьте, равны ли обе стороны в пределах ошибки эксперимента (~10%, Паунд и Снайдер уменьшили это до ~1% в 1964).
Паунд, Ребка и Снайдер. Физическая лаборатория Джефферсона, Гарвард. Подтверждено экспериментом, проведенным в шахте лифта (?) Гарвардского университета Робертом Паундом (1919–2010) и Гленом Ребкой (1931–2015) в 1959 году. Источник гамма-излучения был помещен наверху шахты, а детектор внизу. Источник излучал гамма-лучи с определенной частотой, а детектор был разработан для обнаружения только гамма-лучей с этой конкретной частотой. В процессе «падения» вниз по шахте гамма-лучи синего цвета смещались в более высокую частоту. Паунд и Ребка поместили источник на вибрирующий динамик. Когда динамик двигался вверх с нужной скоростью, гравитационное синее смещение компенсировалось движущимся красным смещением, и детектор обнаруживал гамма-лучи. Двигайтесь с любой другой скоростью, и заметка будет обнаружена. Измерьте скорость источника, локальное гравитационное поле, высоту детектора над излучателем и скорость света; поставить числа в уравнение; проверьте, равны ли обе стороны в пределах ошибки эксперимента (~10%, Паунд и Снайдер уменьшили это до ~1% в 1964).
 Многократные отражения между зеркалами, расположенными на концах каждого плеча, увеличивают эффективную оптическую длину каждого плеча до 120 километров. Virgo находится на территории EGO, Европейской гравитационной обсерватории, базирующейся в Кашине, недалеко от Пизы, на равнине реки Арно. Частотный диапазон Девы простирается от 10 до 6000 Гц. Этот диапазон, а также высокая чувствительность должны позволить обнаруживать гравитационное излучение сверхновых и слияния двойных систем в Млечном Пути и во внешних галактиках, например, от скопления Девы.
Многократные отражения между зеркалами, расположенными на концах каждого плеча, увеличивают эффективную оптическую длину каждого плеча до 120 километров. Virgo находится на территории EGO, Европейской гравитационной обсерватории, базирующейся в Кашине, недалеко от Пизы, на равнине реки Арно. Частотный диапазон Девы простирается от 10 до 6000 Гц. Этот диапазон, а также высокая чувствительность должны позволить обнаруживать гравитационное излучение сверхновых и слияния двойных систем в Млечном Пути и во внешних галактиках, например, от скопления Девы. Центр треугольника LISA описывает земную орбиту в плоскости эклиптики, на расстоянии одной астрономической единицы от Солнца, но на 20 градусов позади Земли. Плоскость треугольника наклонена под углом 60 градусов к эклиптике. Естественные орбиты свободного падения трех космических кораблей вокруг Солнца поддерживают эту треугольную форму, при этом кажется, что треугольник вращается вокруг своего центра один раз в год.
Центр треугольника LISA описывает земную орбиту в плоскости эклиптики, на расстоянии одной астрономической единицы от Солнца, но на 20 градусов позади Земли. Плоскость треугольника наклонена под углом 60 градусов к эклиптике. Естественные орбиты свободного падения трех космических кораблей вокруг Солнца поддерживают эту треугольную форму, при этом кажется, что треугольник вращается вокруг своего центра один раз в год.