Сверхпроводники второго рода. Вихри Абрикосова. Вихри абрикосова

Сверхпроводники второго рода. Вихри Абрикосова

Выше мы говорили о выталкивании магнитного поля из объема сверхпроводника при Т<ТС и переходе его в нормальное состояние в сильном магнитном поле при Н>НС. Все эти физические особенности относятся к так называемым сверхпроводникам первого рода, к которым принадлежат почти все чистые металлы. Они характеризуются низкой температурой перехода и невысоким значением критического тока, что ограничивает их практическое применение.

В работах А.А. Абрикосова создана теория сверхпроводников второго рода, которые имеют два критических поля HC1 и HC2, и верхнее критическое поле HC2 может достигать очень больших значений, критические токи очень высоки (табл. 1.3), магнитное поле в смешанном состоянии проникает внутрь сверхпроводника в виде двухмерной решетки вихревых линий.

Таблица 1.3

Сверхпроводники второго рода

Соединение	ТС, К	j, А/см (Тл) при 4,2 К	BC2, Тл (Т, К)
Nb3Sn	18,1 – 18,5	(1 – 8)*105 (0)	24,5 – 28 (0)
Nb Ti	9,5 – 10,5	(3 – 8)*104 (5)	12 (4,2)
Nb N	14,5 – 17,8	(2 – 5)*107 (18)	8 – 13 (4,2)

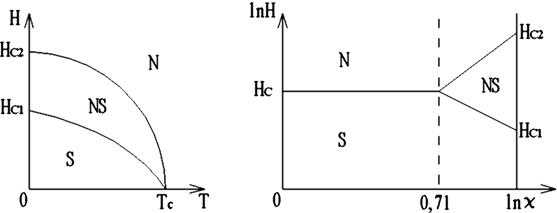
Фазовая диаграмма сверхпроводника второго рода показана на рис. 1.7, а (сравните с рис. 1.5). Она включает в себя кроме N – нормального, S – сверхпроводящего состояний, еще NS – смешанное состояние, представляющее собой сверхпроводящий образец, через который проникают тонкие нитевидные области нормального состояния с магнитным полем. Такие области получили название вихри Абрикосова. При рассмотрении сверхпроводящих состояний важную роль играет поверхностная энергия границ раздела между нормальными и сверхпроводящими областями. Такие границы могут возникать в магнитном поле.

а) б)

Рис. 1.7. Фазовые диаграммы сверхпроводника второго рода

Возможны два варианта. Если энергия поверхности положительная и увеличивает энергию системы, образование границы не выгодно. Переход из сверхпроводящего в нормальное состояние происходит непосредственно. Так ведут себя сверхпроводники первого рода.

Во втором случае поверхностная энергия отрицательна и уменьшает энергию системы. Переход S à N осуществляется через смешанное состояние, где вихри Абрикосова содержат границы раздела. Это сверхпроводник второго рода.

Критерием знака поверхностной энергии может служить соотношение между глубиной проникновения χ и длиной когерентности ξ. Из теории Гинзбурга-Ландау следует:

, (1.11)

где VФ – скорость электрона на уровне Ферми;

Δ – полуширина энергетической щели.

Для сверхпроводников второго рода λ >> ξ.

К этой группе относятся металлы с примесями, интерметаллические соединения и высокотемпературные сверхпроводники (см. ниже). На рис. 1.7, б приведена фазовая диаграмма с учетом критерия χ=λ/ξ.

Особый интерес представляет смешанное состояние – состояние Шубникова. Рассмотрим проникновение магнитного поля в сверхпроводник второго рода. Поверхностная энергия в этом случае отрицательна – выгодно образование большого числа нормальных областей как можно меньших размеров – нитей. Диаметр нити по порядку величины равен длине когерентности ξ, так как концентрация сверхпроводящих электронов изменяется на длине r ≈ ξ. Необходимо отметить, что условие убывания поля (1.6) для сверхпроводников действует и в случае вихря Абрикосова (рис. 1.8).

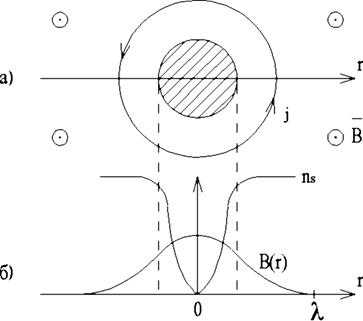
Рис. 1.8. Вихрь Абрикосова: а – сверхпроводящий ток j; б – распределение индукции поля и концентрации СП электронов

В этой области вокруг нити циркулирует сверхпроводящий ток, связанный с магнитным полем по закону Максвелла. Такое распределение магнитного поля называется вихрем. Нормальная сердцевина вихря представляет собой аналог полости в сверхпроводящем кольце, и поэтому поток вихря должен быть квантован согласно (1.9). Если бы вихрь имел несколько квантов потока, он бы разбился на несколько вихрей согласно принципу минимума свободной энергии. Поэтому вихрь характеризуется одним квантом потока Ф0. Анализ энергетического состояния вихря позволяет оценить его энергию. Опуская соответствующие выкладки, приведем оценку энергии единицы длины вихря:

. (1.12)

В отсутствие поля (Н=0) энергия положительна, т.е. образование вихрей невыгодно. Они смогут образоваться, когда с ростом поля энергия обратится в нуль и станет отрицательной. Приравняв (1.13) к нулю, найдем оценку НС1:

НС1~ . (1.13)

С ростом магнитного поля число вихрей растет. Однако вихри обладают одинаковой ориентацией поля и будут отталкиваться, если расстояние между ними будет меньше . Поэтому максимальная концентрация вихрей сопровождается их упорядочением в правильную треугольную решетку. Предельная концентрация вихрей соответствует расстоянию между ними порядка ξ, после чего они сливаются и сверхпроводник переходит в нормальное состояние (рис. 1.7) при Н=НС2. Оценка верхнего критического поля дает зависимость:

. (1.14)

Магнитное поле транспортного тока, превышающее НС1, тоже вызывает образование вихрей в сверхпроводнике второго рода. Круговые токи вихрей и транспортные токи взаимодействуют между собой. В однородном сверхпроводнике возникает движение вихрей. Это движение является вязким, сопровождается диссипацией энергии, следовательно, в сверхпроводнике возникает сопротивление. Рассмотренное состояние называют резистивным. Если в сверхпроводнике второго рода существуют включения нормальной фазы или поры размером не менее ξ, эти дефекты играют роль потенциальных ям для вихрей. В этом случае возникает пиннинг – закрепление вихрей на дефектах и торможение всей вихревой решетки.

В практическом использовании сверхпроводников второго рода возможны два направления. В первом – криоэлектронные устройства используют интегральные свойства, например, переход S ↔ N и возникающие в процессе перехода вихри являются побочным паразитным явлением. Во втором направлении – вихри Абрикосова являются носителями информации. Для того, чтобы магнитные вихри могли возникать, перемещаться и аннигилировать, выполняя определенные информационные задачи, сверхпроводник должен иметь необычные свойства – быть беспиннинговым. В этом случае решетка вихрей будет иметь треугольную структуру.

Вихри могут зарождаться и исчезать только на краю сверхпроводника. Если сравнить такой магнитный вихрь с пакетом неосновных носителей заряда в приборах с зарядовой связью (ПЗС), то для перемещения вихря вдоль поверхности сверхпроводника (или СП пленки) требуется внешнее поле, выполняющее такие же функции, что и поле электродов при переносе зарядов в ПЗС.

Вихри Абрикосова - это... Что такое Вихри Абрикосова?

Вихрь Абрикосова, абрикосовский вихрь (англ. Abrikosov vortex) — вихрь сверхпроводящего тока (сверхтока), циркулирующий вокруг нормального (несверхпроводящего) ядра (нити вихря), индуцирующий магнитное поле с магнитным потоком, эквивалентным кванту магнитного потока.[1]

А. А. Абрикосовым в 1957 году в своей работе «О магнитных свойствах сверхпроводников второй группы» было теоретически показано, что проникновение магнитного поля в сверхпроводник 2 рода происходит в виде квантованных вихревых нитей (такая система энергетически «выгодна»). Каждая такая нить (вихрь) имеет нормальную (несверхпроводящую) сердцевину с радиусом порядка длины когерентности сверхпроводника ξ. Вокруг этого нормального цилиндра в области с радиусом порядка глубины проникновения магнитного поля λ течет вихревой незатухающий ток куперовских пар (сверхток), ориентированный так, что создаваемое им магнитное поле направлено вдоль нормальной сердцевины, то есть совпадает с направлением внешнего магнитного поля. При этом каждый вихрь несет один квант потока .[1]

Описание

В теории сверхпроводимости вихрями Абрикосова называют вихри сверхтока в сверхпроводниках второго рода.

Сверхток циркулирует вокруг нормального (несврехпроводящего) домена, представляющего собой цилиндр, вытянутый вдоль направления внешнего магнитного поля, образуя вихрь. Радиус основания этого цилиндра определяется длиной когерентности (один из основных параметров теории Гинзбурга-Ландау). Сверхток исчезает в домене на расстоянии порядка (Лондоновской длины проникновения от края — характерный параметр для каждого конкретного сверхпроводящего материала). Циркулирующий сверхток порождает магнитное поле, величина которого определяется квантом магнитного потока . Поэтому вихри Абрикосова называют иногда флюксонами.

Распределение магнитного поля в одиночном вихре на расстоянии, большем характерного размера ядра определяется соотношением:

где — функция Бесселя нулевого порядка. При поле определяется следующим соотношением:

где κ = λ/ξ — известный параметр теории Гинзбурга-Ландау, который должен удовлетворять соотношению в сверхпроводниках второго рода.

Вихри, проникнув в сверхпроводник, располагаются друг от друга на расстоянии порядка , образуя в поперечном сечении правильную треугольную решётку, возникает так называемое смешанное состояние. При увеличении внешнего магнитного поля плотность вихрей становится настолько большой, что расстояние между ближайшими вихрями становится порядка , вихри соприкасаются своими нормальными областями и происходит фазовый переход второго рода сверхпроводника в нормальное состояние.

См. также

Примечания

Литература

Абрикосов А. А., О магнитных свойствах сверхпроводников второй группы, «ЖЭТФ», 1957, т. 32, с. 1442;
Сан Жам Д., Сарма Г., Томас Е., Сверхпроводимость второго рода, пер. с англ., М., 1970. Н. Б. Копнин.

Ссылки

dic.academic.ru

Вихри Абрикосова — Википедия Переиздание // WIKI 2

Вихрь Абрикосова, абрикосовский вихрь, вихри Абрикосова-Нильсена-Олесена[1] (англ. Abrikosov vortex) — вихрь сверхпроводящего тока (сверхтока), циркулирующий вокруг нормального (несверхпроводящего) ядра (нити вихря), индуцирующий магнитное поле с магнитным потоком, эквивалентным кванту магнитного потока.[2]

Открыт физиком А. А. Абрикосовым в 1957 году. В своей работе «О магнитных свойствах сверхпроводников второй группы» было теоретически показано, что проникновение магнитного поля в сверхпроводник 2 рода происходит в виде квантованных вихревых нитей (такая система энергетически «выгодна»). Каждая такая нить (вихрь) имеет нормальную (несверхпроводящую) сердцевину с радиусом порядка длины когерентности сверхпроводника ξ{\displaystyle \xi }. Вокруг этого нормального цилиндра в области с радиусом порядка глубины проникновения магнитного поля λ{\displaystyle \lambda } течёт вихревой незатухающий ток куперовских пар (сверхток), ориентированный так, что создаваемое им магнитное поле направлено вдоль нормальной сердцевины, то есть совпадает с направлением внешнего магнитного поля. При этом каждый вихрь несёт один квант потока Φ0=h/(2e){\displaystyle {\Phi _{0}}=h/(2e)}.[2]

Описание

В теории сверхпроводимости вихрями Абрикосова называют вихри сверхтока в сверхпроводниках второго рода. Сверхток циркулирует вокруг нормального (несверхпроводящего) домена, представляющего собой цилиндр, вытянутый вдоль направления внешнего магнитного поля, образуя вихрь. Радиус основания этого цилиндра определяется длиной когерентности ∼ξ{\displaystyle \sim \xi } (один из основных параметров теории Гинзбурга — Ландау). Сверхток исчезает в домене на расстоянии порядка λ{\displaystyle \lambda } (Лондоновской глубины проникновения от края — характерный параметр для каждого конкретного сверхпроводящего материала). Циркулирующий сверхток порождает магнитное поле, величина которого определяется квантом магнитного потока Φ0{\displaystyle \Phi _{0}}. Поэтому вихри Абрикосова называют иногда флюксонами.

Распределение магнитного поля в одиночном вихре на расстоянии, большем характерного размера ядра, определяется соотношением:

B(r)=Φ02πλ2K0(rλ)≈λrexp⁡(−rλ),{\displaystyle B(r)={\frac {\Phi _{0}}{2\pi \lambda ^{2}}}K_{0}\left({\frac {r}{\lambda }}\right)\approx {\sqrt {\frac {\lambda }{r}}}\exp \left(-{\frac {r}{\lambda }}\right),}

где K0(z){\displaystyle K_{0}(z)} — функция Бесселя нулевого порядка. При r≲ξ{\displaystyle r\lesssim \xi } поле определяется следующим соотношением:

B(0)≈Φ02πλ2ln⁡κ,{\displaystyle B(0)\approx {\frac {\Phi _{0}}{2\pi \lambda ^{2}}}\ln \kappa ,}

где κ=λ/ξ{\displaystyle \kappa =\lambda /\xi } — известный параметр теории Гинзбурга — Ландау, который должен удовлетворять соотношению κ>1/2{\displaystyle \kappa >1/{\sqrt {2}}} в сверхпроводниках второго рода.

Вихри, проникнув в сверхпроводник, располагаются друг от друга на расстоянии порядка λ{\displaystyle \lambda }, образуя в поперечном сечении правильную треугольную решётку, возникает так называемое смешанное состояние. При увеличении внешнего магнитного поля плотность вихрей становится настолько большой, что расстояние между ближайшими вихрями становится порядка ξ{\displaystyle \xi }, вихри соприкасаются своими нормальными областями и происходит фазовый переход второго рода сверхпроводника в нормальное состояние.

См. также

Примечания

Литература

Абрикосов А. А. О магнитных свойствах сверхпроводников второй группы // ЖЭТФ, 1957, т. 32, с. 1442;
Сан Жам Д., Сарма Г., Томас Е. Сверхпроводимость второго рода / Пер. с англ. Н. Б. Копнин. — М., 1970.

Ссылки

Эта страница в последний раз была отредактирована 17 мая 2018 в 19:42.

wiki2.org

Физики сложили вихри Абрикосова в буквы с помощью лазерного пинцета — Naked Science

В статье, опубликованной в Nature Communications, учёные говорят о возможности создания новых квантовых логических элементов для суперкомпьютеров.

Явление сверхпроводимости, или отсутствия электрического сопротивления, наблюдается во многих материалах при низких температурах: от −273о до −70о по Цельсию. Переход в сверхпроводящее состояние сопровождается вытеснением магнитного поля из объёма сверхпроводника. Вытеснение может быть как полным (магнитное поле внутри тела равно нулю), так и неполным.

Справа — одиночные вихри, слева — аббревиатура «Abrikosov Vortices».

Эффект неполного вытеснения был объяснён в 1957 году Алексеем Абрикосовым, за что в 2003 году он был удостоен Нобелевской премии. Материалы, в которых вытеснение является неполным, получили название сверхпроводников второго рода. Помимо этого Абрикосов показал, что проникновение поля возможно только небольшими порциями — квантами магнитного потока. Увеличение магнитного поля сопровождается рождением в сверхпроводнике кольцевых токов — вихрей Абрикосова.

«Сверхпроводники второго рода используются повсеместно: это и медицина, и энергетика, и многие другие отрасли промышленности. «Вихревая материя» в свою очередь определяет свойства сверхпроводников. Поэтому контроль над ней и её изучение — важнейшие задачи современной физики», — говорит сотрудник лаборатории топологических квантовых явлений в сверхпроводящих системах МФТИ Иван Вещунов, один из авторов статьи.

Для передвижения вихрей учёные использовали сфокусированный лазерный пучок. Вихри Абрикосова имеют тенденцию смещаться в зоны с более высокой температурой — таковыми являлись прогретые лазером области тонких плёнок ниобия, охлаждённых до температуры −268 градусов по Цельсию. Важным моментом является тот факт, что при перегреве сверхпроводимость в образце разрушается, поэтому необходимо очень точно регулировать интенсивность лазерного излучения.

Так как вихри являются носителями элементарного кванта магнитного потока, с их помощью можно создавать различные конфигурации магнитного поля для физических исследований. Одну из таких конфигураций использует сама природа: при определённом магнитном поле вихри сами выстраиваются в виде треугольной решётки. Сдвигая вихри, можно получить новые типы решёток или вихревых линз.

По словам авторов, одной из областей применения исследованного процесса может стать разработка оптических систем управления быстрой одноквантовой логикой (БОК-логикой). Она представляет одно из направлений развития квантовых компьютеров. Эта технология считается самой перспективной кандидатурой для создания сверхбыстрой памяти для квантовых компьютеров. На данный момент элементы БОК-логики используются в цифро-аналоговых и аналого-цифровых преобразователях, сверхточных магнитометрах, элементах памяти. Существуют и прототипы вычислительных машин, например американский компьютер FLUX-1. Однако управление схемами БОК-логики в них в основном реализуется с помощью импульсов электрического тока. Переход к оптическому управлению — одно из направлений, в котором будут развиваться сверхпроводящие системы.

То, что сделали учёные, на профессиональном сленге называется «proof of concept» — проверка того, что данный метод может быть использован для последующего изучения вихрей Абрикосова. Физикам ещё предстоит выяснить, как повышение температуры приводит к срыву вихрей с места, исследовать свойства решёток, которые они образуют, разобраться в их динамических свойствах. Все эти аспекты являются определяющими для понимания физики сверхпроводников и для возможности конструирования принципиально новых элементов микроэлектроники на их основе.

naked-science.ru

Вихри Абрикосова — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

А. А. Абрикосовым в 1957 году в своей работе «О магнитных свойствах сверхпроводников второй группы» было теоретически показано, что проникновение магнитного поля в сверхпроводник 2 рода происходит в виде квантованных вихревых нитей (такая система энергетически «выгодна»). Каждая такая нить (вихрь) имеет нормальную (несверхпроводящую) сердцевину с радиусом порядка длины когерентности сверхпроводника ξ. Вокруг этого нормального цилиндра в области с радиусом порядка глубины проникновения магнитного поля λ течёт вихревой незатухающий ток куперовских пар (сверхток), ориентированный так, что создаваемое им магнитное поле направлено вдоль нормальной сердцевины, то есть совпадает с направлением внешнего магнитного поля. При этом каждый вихрь несет один квант потока <math>{\Phi_0} = h/(2e)</math>.[1]

Описание

В теории сверхпроводимости вихрями Абрикосова называют вихри сверхтока в сверхпроводниках второго рода. Сверхток циркулирует вокруг нормального (несверхпроводящего) домена, представляющего собой цилиндр, вытянутый вдоль направления внешнего магнитного поля, образуя вихрь. Радиус основания этого цилиндра определяется длиной когерентности <math>\sim\xi</math> (один из основных параметров теории Гинзбурга-Ландау). Сверхток исчезает в домене на расстоянии порядка <math>\lambda</math> (Лондоновской глубины проникновения от края — характерный параметр для каждого конкретного сверхпроводящего материала). Циркулирующий сверхток порождает магнитное поле, величина которого определяется квантом магнитного потока <math>\Phi_0</math>. Поэтому вихри Абрикосова называют иногда флюксонами.

<math> B(r) = \frac{\Phi_0}{2\pi\lambda^2}K_0\left(\frac{r}{\lambda}\right) \approx \sqrt{\frac{\lambda}{r}} \exp\left(-\frac{r}{\lambda}\right), </math>

где <math>K_0(z)</math> — функция Бесселя нулевого порядка. При <math>r\lesssim\xi</math> поле определяется следующим соотношением:

<math> B(0)\approx \frac{\Phi_0}{2\pi\lambda^2}\ln\kappa, </math>

где κ = λ/ξ — известный параметр теории Гинзбурга-Ландау, который должен удовлетворять соотношению <math>\kappa>1/\sqrt{2}</math> в сверхпроводниках второго рода.

Вихри, проникнув в сверхпроводник, располагаются друг от друга на расстоянии порядка <math>\lambda</math>, образуя в поперечном сечении правильную треугольную решётку, возникает так называемое смешанное состояние. При увеличении внешнего магнитного поля плотность вихрей становится настолько большой, что расстояние между ближайшими вихрями становится порядка <math>\xi</math>, вихри соприкасаются своими нормальными областями и происходит фазовый переход второго рода сверхпроводника в нормальное состояние.

См. также

Напишите отзыв о статье "Вихри Абрикосова"

Примечания

↑ 1 2 Солдатов Евгений Сергеевич. [thesaurus.rusnano.com/wiki/article24392 Вихрь Абрикосова в словаре нанотехнологичных терминов]. Роснано. Проверено 26 ноября 2011. [www.webcitation.org/69r5pNyVn Архивировано из первоисточника 12 августа 2012].

Литература

Абрикосов А. А. О магнитных свойствах сверхпроводников второй группы // ЖЭТФ, 1957, т. 32, с. 1442;
Сан Жам Д., Сарма Г., Томас Е. Сверхпроводимость второго рода / Пер. с англ. Н. Б. Копнин. — М., 1970.

Ссылки

Козлов В. А., Самохвалов А. В. [www.phys.nsu.ru/vestnik/catalogue/2008/01/Vestnik_NSU_08T3V1_p100_p104.pdf Замкнутые вихри Абрикосова в сверхпроводниках второго рода]. Письма в ЖЭТФ. [www.webcitation.org/67eShg9q6 Архивировано из первоисточника 14 мая 2012].
Гл. ред. А.М. Прохоров. [femto.com.ua/articles/part_2/3445.html Решетка вихрей Абрикосова]. — Физическая энциклопедия. — М.: Советская энциклопедия, 1988. — Т. 1. — 389 с.

Отрывок, характеризующий Вихри Абрикосова

– Там наши? – спросил Пьер. – Да, а вон подальше и французы, – сказал офицер. – Вон они, вон видны. – Где? где? – спросил Пьер. – Простым глазом видно. Да вот, вот! – Офицер показал рукой на дымы, видневшиеся влево за рекой, и на лице его показалось то строгое и серьезное выражение, которое Пьер видел на многих лицах, встречавшихся ему. – Ах, это французы! А там?.. – Пьер показал влево на курган, около которого виднелись войска. – Это наши. – Ах, наши! А там?.. – Пьер показал на другой далекий курган с большим деревом, подле деревни, видневшейся в ущелье, у которой тоже дымились костры и чернелось что то. – Это опять он, – сказал офицер. (Это был Шевардинский редут.) – Вчера было наше, а теперь его. – Так как же наша позиция? – Позиция? – сказал офицер с улыбкой удовольствия. – Я это могу рассказать вам ясно, потому что я почти все укрепления наши строил. Вот, видите ли, центр наш в Бородине, вот тут. – Он указал на деревню с белой церковью, бывшей впереди. – Тут переправа через Колочу. Вот тут, видите, где еще в низочке ряды скошенного сена лежат, вот тут и мост. Это наш центр. Правый фланг наш вот где (он указал круто направо, далеко в ущелье), там Москва река, и там мы три редута построили очень сильные. Левый фланг… – и тут офицер остановился. – Видите ли, это трудно вам объяснить… Вчера левый фланг наш был вот там, в Шевардине, вон, видите, где дуб; а теперь мы отнесли назад левое крыло, теперь вон, вон – видите деревню и дым? – это Семеновское, да вот здесь, – он указал на курган Раевского. – Только вряд ли будет тут сраженье. Что он перевел сюда войска, это обман; он, верно, обойдет справа от Москвы. Ну, да где бы ни было, многих завтра не досчитаемся! – сказал офицер. Старый унтер офицер, подошедший к офицеру во время его рассказа, молча ожидал конца речи своего начальника; но в этом месте он, очевидно, недовольный словами офицера, перебил его. – За турами ехать надо, – сказал он строго. Офицер как будто смутился, как будто он понял, что можно думать о том, сколь многих не досчитаются завтра, но не следует говорить об этом. – Ну да, посылай третью роту опять, – поспешно сказал офицер. – А вы кто же, не из докторов? – Нет, я так, – отвечал Пьер. И Пьер пошел под гору опять мимо ополченцев. – Ах, проклятые! – проговорил следовавший за ним офицер, зажимая нос и пробегая мимо работающих. – Вон они!.. Несут, идут… Вон они… сейчас войдут… – послышались вдруг голоса, и офицеры, солдаты и ополченцы побежали вперед по дороге. Из под горы от Бородина поднималось церковное шествие. Впереди всех по пыльной дороге стройно шла пехота с снятыми киверами и ружьями, опущенными книзу. Позади пехоты слышалось церковное пение. Обгоняя Пьера, без шапок бежали навстречу идущим солдаты и ополченцы. – Матушку несут! Заступницу!.. Иверскую!.. – Смоленскую матушку, – поправил другой. Ополченцы – и те, которые были в деревне, и те, которые работали на батарее, – побросав лопаты, побежали навстречу церковному шествию. За батальоном, шедшим по пыльной дороге, шли в ризах священники, один старичок в клобуке с причтом и певчпми. За ними солдаты и офицеры несли большую, с черным ликом в окладе, икону. Это была икона, вывезенная из Смоленска и с того времени возимая за армией. За иконой, кругом ее, впереди ее, со всех сторон шли, бежали и кланялись в землю с обнаженными головами толпы военных. Взойдя на гору, икона остановилась; державшие на полотенцах икону люди переменились, дьячки зажгли вновь кадила, и начался молебен. Жаркие лучи солнца били отвесно сверху; слабый, свежий ветерок играл волосами открытых голов и лентами, которыми была убрана икона; пение негромко раздавалось под открытым небом. Огромная толпа с открытыми головами офицеров, солдат, ополченцев окружала икону. Позади священника и дьячка, на очищенном месте, стояли чиновные люди. Один плешивый генерал с Георгием на шее стоял прямо за спиной священника и, не крестясь (очевидно, пемец), терпеливо дожидался конца молебна, который он считал нужным выслушать, вероятно, для возбуждения патриотизма русского народа. Другой генерал стоял в воинственной позе и потряхивал рукой перед грудью, оглядываясь вокруг себя. Между этим чиновным кружком Пьер, стоявший в толпе мужиков, узнал некоторых знакомых; но он не смотрел на них: все внимание его было поглощено серьезным выражением лиц в этой толпе солдат и оиолченцев, однообразно жадно смотревших на икону. Как только уставшие дьячки (певшие двадцатый молебен) начинали лениво и привычно петь: «Спаси от бед рабы твоя, богородице», и священник и дьякон подхватывали: «Яко вси по бозе к тебе прибегаем, яко нерушимой стене и предстательству», – на всех лицах вспыхивало опять то же выражение сознания торжественности наступающей минуты, которое он видел под горой в Можайске и урывками на многих и многих лицах, встреченных им в это утро; и чаще опускались головы, встряхивались волоса и слышались вздохи и удары крестов по грудям.

wiki-org.ru

Решётка вихрей абрикосова - Физическая энциклопедия

РЕШЁТКА ВИХРЕЙ АБРИКОСОВА - двумерная решётка квантованных вихрей в сверхпроводниках второго рода (СВР). Теоретически предложена А. А. Абрикосовым (1957) для объяснения магн. свойств СВР. Вихри, образующие Р. в. А., характеризуются остовом с радиусом порядка длины когерентности. В центре остова (на оси вихря) плотность сверхпроводящих электронов равна нулю. Вокруг остова на расстояниях порядка глубины проникновения магн. поля циркулирует сверхпроводящий ток, распределённый так, что создаваемый им магн. поток равен кванту магн. потока (см. Квантование магнитного потока ).Схематич. поведение магн. поля и плотности сверхпроводящих электронов изолиров. вихря изображено на рис. 1. В интервале полей HС1 < H < HС2 (см. Критическое магнитное поле)такие вихри в результате взаимодействия друг с другом (отталкивания) образуют регулярную (в однородном материале) решётку. Минимуму свободной энергии отвечает треугольная решётка, однако в нек-рых сверхпроводящих материалах, обладающих тетрагональной симметрией, можно наблюдать также квадратную решётку. Характерное расстояние между вихрями определяется приложенным магн. полем. По мере приближения Н к HС2 остовы вихрей сближаются, начинают перекрываться и сверхпроводимость подавляется, пока полностью не разрушится при Н = HС2. Р. в. А. обладает жёсткостью, значения модулей упругости Р. в. А. выражаются через параметры кривой намагничивания сверхпроводника. Причиной электрич. сопротивления СВР является движение Р. в. А. Регулярность Р. в. А. может нарушаться за счёт дефектов структуры материала, приводящих к пиннингу вихревых нитей (см. Критический ток ),захвату магн. потока в образце и необратимости процесса намагничивания СВР. Р. в. А. можно непосредственно наблюдать по рассеянию нейтронов, а также в электронном микроскопе с помощью техники декорирования ферромагн. порошком (рис. 2).

Рис. 1. Распределение плотности сверхпроводящих электронов ns и магнитного поля изолированного вихря в зависимости от расстояния до оси вихря r.

Рис. 2. Воспроизведение структуры решётки Абрикосова в сплаве Рb - 6,3 ат. % In, Н 80 Э.

Лит.: Абрикосов А. А., О магнитных свойствах сверхпроводников второй группы, «ЖЭТФ», 1957, т. 32, с. 1442; Сан Ж а м Д., С а р м а Г., Томас Е., Сверхпроводимость второго рода, пер. с англ., М., 1970. Н. Б. Копнин.

Предметный указатель >>

www.femto.com.ua

Сверхпроводимость: время понимания

Алексей Левин«Популярная механика» №9, 2011

После окончания Войны исследования сверхпроводимости возобновились. Большинство теорий прожили недолго, хотя среди их авторов были и такие звезды теоретической физики, как Макс Борн и Вернер Гейзенберг. Но в 1950 году были опубликованы две модели, которые оказались важными вехами на пути к осмыслению сверхпроводимости. Они обобщали теорию братьев Лондонов, которые не вывели свои уравнения из каких-то фундаментальных законов, а фактически изобрели их (такие теории называют феноменологическими).

Одну из моделей предложил английский физик Брайан Пиппард. В ходе своих экспериментов он пришел к выводу, что сверхпроводящая зона у поверхности образца распространяется на иную глубину, чем магнитное поле. Для описания этой глубины он ввел новый параметр — длину когерентности (ее называют также длиной корреляции). В модели Пиппарда состояние сверхпроводника в конкретной точке зависит от величины магнитного поля не только в ней самой, как у Лондонов, но также в ее окрестности, масштабы которой определяет длина когерентности. Из этого следует, что в основе сверхпроводимости лежат нелокальные взаимодействия, связывающие пространственно разделенные электроны. Впервые такую мысль высказал в 1935 году Фриц Лондон, а Пиппард выразил ее математически. Эта идея оказалась весьма плодотворной, но ее физический смысл в полной мере выявился лишь спустя несколько лет.

Другим обобщением теории Лондонов стала модель, предложенная будущими академиками и нобелевскими лауреатами Виталием Гинзбургом и Львом Ландау. Она основана на феноменологической теории фазовых переходов второго рода, сформулированной Ландау в 1937 году. Эта теория актуальна и по сей день — правда, в несколько откорректированном виде. Ландау понял, что фазовый переход второго рода представляет собой изменение внутренней симметрии (или, что то же самое, степени внутренней упорядоченности) физической системы. Например, если нагреть ферромагнетик до температуры Кюри, атомные магнитные моменты лишатся прежней параллельной ориентации — это и есть фазовый переход второго рода. Ландау предложил для описания таких переходов особую величину – параметр порядка (для ферромагнетиков это магнитный момент единицы объема). Согласно его теории, в фазе с меньшей упорядоченностью среднее значение параметра порядка равно нулю, а в более упорядоченной фазе отлично от нуля и по мере увеличения степени упорядоченности возрастает по абсолютной величине.

Гинзбург и Ландау интерпретировали возникновение сверхпроводящего состояния в отсутствие магнитного поля как фазовый переход второго рода. В качестве параметра порядка они ввели комплексную функцию, квадрат модуля которой пропорционален плотности носителей сверхпроводящего тока. При температурах выше критической эта плотность равна нулю, при более низких возрастает и достигает максимума при абсолютном нуле. Гинзбург и Ландау написали систему из двух уравнений, связывающих параметр порядка с плотностью электрического тока и магнитным полем. Эти уравнения не объясняют причин сверхпроводимости, но хорошо описывают поведение сверхпроводника вблизи критической температуры. В модели Гинзбурга и Ландау фигурирует заряд носителей сверхпроводящего тока, который эта теория не определяет. Ландау полагал его равным заряду электрона, Гинзбург в этом сомневался, но до поры до времени вопрос остался открытым.

Вихри Абрикосова

При решении уравнений Гинзбурга–Ландау появляются две величины, имеющие размерность длины. Первая — это лондоновская глубина проникновения магнитного поля, вторая же практически совпадает с пиппардовской длиной корреляции. Оказалось, что свойства сверхпроводника существенным образом зависят от параметра, приблизительно равного отношению этих величин при нулевой температуре. Если этот параметр меньше примерно 0,7, сверхпроводник ведет себя в магнитном поле как идеальный диамагнетик и полностью подчиняется эффекту Мейсснера–Оксенфельда. В противном случае возникают осложнения, физический смысл которых тогда не был понятен. Однако Гинзбург и Ландау решили, что такой режим не стоит рассматривать, поскольку фактически этот параметр всегда много меньше единицы. Правда, к тому времени экспериментаторы уже выяснили, что это вовсе не обязательно, но до Гинзбурга с Ландау эти сведения еще не дошли.

Следующий шаг сделал коллега Ландау по теоретическому отделу Института физических проблем Алексей Абрикосов. Он показал, что рассматривать другой вариант все-таки стоит, поскольку в этом случае сверхпроводник может снизить внутреннюю энергию, пропустив вглубь внешнее магнитное поле. Для этого необходимо, чтобы напряженность поля превысила нижнее критическое значение Hc1, определенное группой Шубникова (см. «ПМ» №8'2011). Абрикосов выделил такие сверхпроводники в особое семейство и назвал их сверхпроводниками второй группы (или, как говорят сейчас, второго рода). Из его уравнений следует, что внешнее магнитное поле проникает в сверхпроводник второго рода в виде нитей, которые называют вихрями Абрикосова. Каждый вихрь несет единственный квант магнитного потока, предсказанный еще Фрицем Лондоном. Сердцевина вихря представляет собой трубку радиусом порядка длины когерентности, и вещество в ней находится не в сверхпроводящем, а в нормальном состоянии. Трубку охватывают вихревые токи, текущие внутри слоя толщиной примерно с лондоновскую глубину проникновения, которые экранируют от магнитного поля сверхпроводящие зоны между вихрями. В результате возникает смешанное состояние (тоже термин Абрикосова), в котором сверхпроводник пронизан вкраплениями нормальной фазы.

Плотность вихрей увеличивается по мере нарастания магнитного поля. Если оно лишь немного превосходит Hc1, вихри выстраиваются далеко друг от друга и почти не взаимодействуют между собой. При увеличении поля токи соседних вихрей перекрываются, и между вихрями возникают силы отталкивания. Из-за этого вихри формируют нечто вроде кристаллической решетки, которая в однородных сверхпроводниках состоит из треугольных ячеек. При возрастании поля ячейки стягиваются, и по достижении Нс2 нормальные сердцевины соседних вихрей сливаются друг с другом. Объемная сверхпроводимость разрушается, и внешнее магнитное поле полностью проникает внутрь образца. Таким образом, теория Абрикосова объяснила экспериментальные результаты харьковских физиков. А смешанное состояние сверхпроводника второго рода нередко называют шубниковской фазой.

Как рассказал «Популярной механике» сам Алексей Абрикосов, который сейчас работает в США в Аргоннской национальной лаборатории, Ландау долго не признавал его выводов, поскольку возникновение вихрей не стыковалось с теорией Лондонов: «То, что лондоновские уравнения теряют силу в масштабах межатомных расстояний, было понято не сразу». Эксперименты подтвердили выводы Абрикосова лишь в середине 1960-х, а в 2003 году он одновременно с Виталием Гинзбургом был удостоен Нобелевской премии.

Сверхпроводимость на три буквы

В 1950 году, почти одновременно с появлением моделей Пиппарда и Гинзбурга–Ландау, американские физики-экспериментаторы Чарльз Рейнольдс и Бернард Серин и их соотечественник Эммануэль Максвелл обнаружили, что у изотопов ртути критическая температура перехода в сверхпроводящее состояние изменяется обратно пропорционально квадратному корню из атомного веса. Это прямо указывало, что сверхпроводимость возникает при участии колебаний кристаллической решетки, частота которых подчиняется такой же зависимости. Незадолго до этого к такому же выводу пришел и профессор теоретической физики Ливерпульского университета Герберт Фрёлих. Модель Фрёлиха не объяснила эффекта Мейсснера–Оксенфельда, однако подкрепила подозрения, что сверхпроводящее состояние возникает на стыке между атомами и электронами.

Тогда же сверхпроводимостью занялся и Джон Бардин, один из создателей транзистора. Он задумывался о ней еще в предвоенные годы, а после открытия изотопического эффекта вернулся к этой проблеме. В 1951 году в Университете Иллинойса Бардин всерьез занялся сверхпроводимостью. Его первая модель, разработанная совместно с Дэвидом Пайнсом, оказалась не слишком удачной, но все же учитывала взаимодействие между электронами и колебаниями кристаллической решетки. В 1955 году Бардин привлек себе в помощь блестящих молодых теоретиков Леона Купера и Роберта Шриффера. Результатом сотрудничества стала удивительно красивая модель, вошедшая в историю физики как БКШ-теория (по первым буквам фамилий).

Начало ей положил Леон Купер. В 1956году он теоретически показал, что вблизи абсолютного нуля электроны проводимости в металле в принципе способны формировать пары, объединяющие частицы с равными и противоположно направленными импульсами. Для этого нужно, чтобы между электронами существовало притяжение, пусть сколь угодно слабое. Поскольку в результате спаривания полная энергия системы уменьшается, такое состояние обладает определенным запасом прочности и само по себе не разрушается.

Но откуда взяться притяжению, коль скоро электроны отталкиваются по закону Кулона? Как догадался еще Фрёлих, его может создать кристаллическая решетка, состоящая из положительных ионов. Поскольку движущийся электрон притягивает близлежащие ионы, они смещаются в его сторону и создают локальный избыток положительного заряда. Поляризованный участок решетки, в свою очередь, может притянуть другой электрон, который сдвинется по направлению к первому. Конечно, для этого необходимо, чтобы опосредованное решеткой притяжение электронов преобладало над кулоновским отталкиванием. Это объясняет, почему лучшие проводники, такие как серебро и медь, не превращаются в сверхпроводники: их электроны проводимости слишком слабо взаимодействуют с ионами решетки.

В теории твердого тела упругие колебания кристаллической решетки описываются как движение фононов — квантов звуковых волн. В этих терминах спаривание электронов возникает благодаря обмену фононами, или, как говорят физики, электрон-фононному взаимодействию. Можно сказать, что электроны притягиваются, испуская и поглощая фононы. Именно этот механизм заложен в основу теории БКШ. Однако исходная модель Купера имеет более общий характер, поскольку указывает на возможность спаривания электронов под воздействием любого эффективного притяжения, вовсе не обязательно обусловленного обменом фононами. Такие альтернативные механизмы сверхпроводимости, по всей вероятности, существуют, но их реальность еще окончательно не доказана.

Нормальное электрическое сопротивление возникает из-за рассеивания носителей тока на тепловых колебаниях решетки (иначе говоря, фононах), а также на атомах примесей и иных неоднородностях. Если ток переносят отдельные электроны, то сопротивление не может быть нулевым, поскольку они рассеиваются при любых энергиях. Иное дело, если в этом качестве выступают куперовские пары (несущие, естественно, двойной электронный заряд). Спаренный электрон может претерпеть рассеяние, только разорвав связь с партнером. Поэтому для разрушения сверхпроводимости средняя скорость, которую набирают электроны во внешнем электрическом поле, должна превысить определенный предел, пропорциональный энергии связи электронных пар. Эта предельная скорость соответствует критической плотности тока. Парные связи должны разрываться и при взаимодействии с фононами достаточно высоких энергий, что и происходит при повышении температуры выше критической. Ниже этой границы куперовские пары при встрече с фононами чаще всего не рвутся, а просто переходят в новые состояния.

Теория БКШ объясняет и эффект Мейсснера. Поскольку спаренные электроны движутся с противоположными импульсами, в магнитном поле на них действуют силы, направленные в разные стороны и потому работающие на разрыв пары. Если напряженность поля невелика, сверхпроводнику выгодней вытолкнуть его на поверхность и удержать куперовские пары в связанном состоянии. Хотя такое выталкивание требует расхода энергии, он с лихвой компенсируется ее экономией при сохранении куперовских пар. Теория БКШ также позволяет понять физический смысл длины когерентности, которая соответствует средней дистанции между спаренными электронами. Эта длина примерно равна 10–5 см и потому в тысячи раз превышает межатомные расстояния.

В 1957 году журнал Physical Review опубликовал короткое письмо Бардина, Купера и Шриффера «Микроскопическая теория сверхпроводимости», за которым вскоре последовала 20-страничная статья «Теория сверхпроводимости». Эти две работы объясняли, почему и как вещество превращается в сверхпроводник. Интересно, что в том же году в ЖЭТФ появилась и статья Абрикосова «О магнитных свойствах сверхпроводников второй группы».

Затишье перед бурей

В 1959 году коллега Абрикосова Лев Горьков показал, что вблизи критической температуры уравнения Гинзбурга–Ландау являются следствием теории БКШ. А в 1972 году микроскопическая теория сверхпроводимости принесла своим авторам Нобелевскую премию.

Однако эта теория имеет серьезное ограничение — она не позволяет предсказать свойства новых сверхпроводников. Американский физик Бернд Маттиас, в 1950–1970-х годах открывший сотни сверхпроводящих материалов, остроумно заметил, что теория БКШ «объясняет все, но не позволяет найти ничего». Впрочем, нет правил без исключений. В 1962 году на базе теории БКШ был сделан удивительный прогноз, вскоре подтвержденный в эксперименте. Все куперовские пары движутся как единое целое и потому описываются единой волновой функцией. В силу квантового туннельного эффекта эта функция способна «просочиться» сквозь энергетический барьер. В данном случае барьером может быть тонкий слой диэлектрика, разделяющий два сверхпроводника. Первую действующую схему со сверхпроводящим туннельным контактом собрал сотрудник исследовательской лаборатории корпорации General Electric Айвар Джайевер в 1960 году. Однако подлинный прорыв был достигнут два года спустя, когда английский физик Брайан Джозефсон теоретически показал, что сквозь диэлектрик туннелируют сверхпроводящие токи, которые обладают уникальными свойствами чисто квантовой природы. За открытие этого эффекта Джозефсон (вместе с Джайевером и Лео Эсаки) в 1973 году получил Нобелевскую премию. Сейчас этот эффект широко применяется — в частности, на его основе работают сквиды, сверхчувствительные сверхпроводящие магнитометры.

elementy.ru

Сверхпроводники второго рода. Вихри Абрикосова. Вихри абрикосова