Содержание
КОСМОС ЛИЧНОГО ПОЛЬЗОВАНИЯ | Наука и жизнь
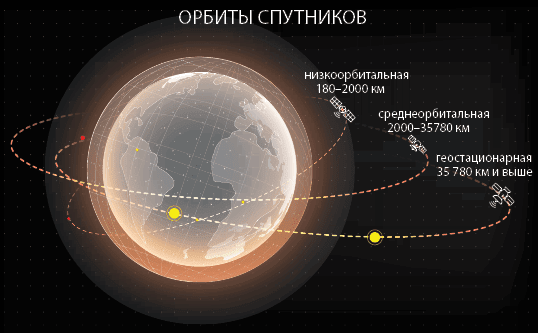
В последнее время космос основательно «персонализировался», и услугами космических систем может воспользоваться любой человек. Телевидение и телефонная связь, интернет и навигация без спутников сейчас практически немыслимы. В создании глобальных систем связи и навигации участвует и Россия. И с каждым годом всё активнее.
Наука и жизнь // Иллюстрации
Чтобы вывести в заданные точки спутники связи «Экспресс-АМ44» и «Экспресс-МД1» и при этом сэкономить топливо, пришлось четыре раза включать двигатель разгонного блока, меняя таким образом параметры орбиты.
В российской группировке телекоммуникационных спутников сейчас насчитывается одиннадцать аппаратов.
Западные штаты США и Новая Зеландия пока остаются вне зоны действия российских спутников.
Спутники системы глобальной навигации движутся группами по трём орбитам, расположенным под примерно одинаковыми углами одна к другой.
‹
›
Открыть в полном размере
ЛЕТЕТЬ, ЧТОБЫ ОСТАВАТЬСЯ НА МЕСТЕ
Шахматная королева из «Алисы в Зазеркалье» говорит, что в их стране, чтобы оставаться на месте, нужно бежать со всех ног. Конечно, Л. Кэрролл не мог предвидеть появления спутников связи, но писал словно о них.
Эти космические аппараты несутся вокруг Земли с огромной скоростью по круговым геостационарным орбитам для того, чтобы всего лишь оставаться над одной точкой земной поверхности. Геостационарные орбиты находятся в экваториальной плоскости нашей планеты. Двигаясь по ним, спутник делает оборот ровно за то время, за которое Земля обращается вокруг своей оси. Поэтому он «висит» всё время над одной и той же точкой. Это чрезвычайно удобно для ретрансляции радиосигналов: не нужно регулировать положение «тарелок», направляя их на «убегающий» спутник.
Чтобы вывести спутник связи на геостационарную орбиту, баллистикам приходится решать очень непростую задачу, требующую высочайшей точности функционирования носителя. «С ходу» запустить спутник на геостационарную орбиту можно только с космодрома на экваторе (см. «Наука и жизнь» № 4, 2009 г.). Если корабль стартует из средних широт, где расположены Байконур и тем более Плесецк, то приходится несколько раз менять параметры орбиты — её высоту и положение в пространстве. С Земли носитель со спутником выводится на опорную орбиту, затем на промежуточную и переходную (у всех у них есть общее название — «орбита выведения»), с которой попадает на геостационарную орбиту.
«С ходу» запустить спутник на геостационарную орбиту можно только с космодрома на экваторе (см. «Наука и жизнь» № 4, 2009 г.). Если корабль стартует из средних широт, где расположены Байконур и тем более Плесецк, то приходится несколько раз менять параметры орбиты — её высоту и положение в пространстве. С Земли носитель со спутником выводится на опорную орбиту, затем на промежуточную и переходную (у всех у них есть общее название — «орбита выведения»), с которой попадает на геостационарную орбиту.
Лучше всего проводить коррекцию в апогее орбиты выведения, где скорость минимальна и на изменение траектории требуется меньший импульс и соответственно меньше топлива. Но воспользоваться таким экономным способом коррекции орбиты не всегда получается, поскольку спутник нужно доставить не просто на геостационарную орбиту, а в строго заданную на ней точку.
Подобных трудностей можно было бы избежать, будь Земля идеальной сферой. Тогда её гравитационное поле было бы равномерным (такое поле называют центральным) и спутник связи мог бы находиться в любой точке геостационарной орбиты.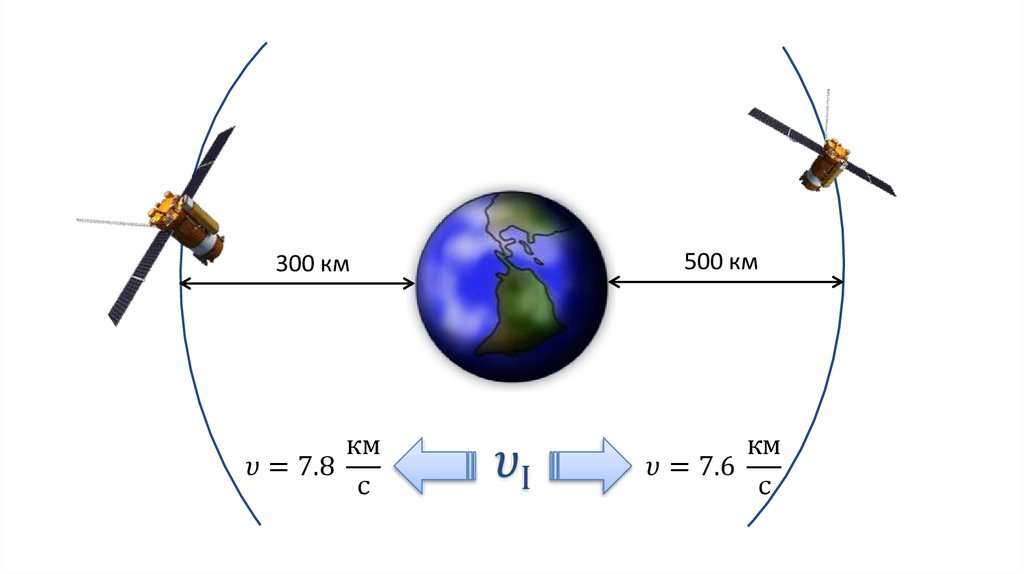 На самом деле наша планета имеет более сложную форму, и в её гравитационном поле имеются неравномерности, которые возмущают движение спутника, немного ускоряя или замедляя его. В некоторых точках геостационарной орбиты, называемых точками стояния, образуются как бы гравитационные ямки. Именно в этой точке спутник должен быть отделён от носителя. Число точек стояния ограничено, сейчас вычислена долгота 400 с лишним таких точек и во многих уже находятся спутники связи.
На самом деле наша планета имеет более сложную форму, и в её гравитационном поле имеются неравномерности, которые возмущают движение спутника, немного ускоряя или замедляя его. В некоторых точках геостационарной орбиты, называемых точками стояния, образуются как бы гравитационные ямки. Именно в этой точке спутник должен быть отделён от носителя. Число точек стояния ограничено, сейчас вычислена долгота 400 с лишним таких точек и во многих уже находятся спутники связи.
Оказавшись возле гравитационной ямки, спутник «скатывается» в неё, совершая сложные движения относительно земной поверхности, и, пока он совсем не «успокоится», может пройти довольно много времени. Зато потом в течение нескольких лет гравитационное поле Земли «тащит» спутник за собой, сделав его квазинеподвижным (двигающимся по круговой орбите, но не меняющим своего положения относительно земной поверхности). Весь этот срок он исправно ретранслирует радиосигналы.
С течением времени равновесие всё же нарушается и спутник начинает дрейфовать, постепенно удаляясь от точки стояния. С поверхности земли этот дрейф выглядит как постоянно увеличивающаяся «восьмёрка». Следить за ним становится трудно, и спутник снимают с орбиты, заменяя его новым.
С поверхности земли этот дрейф выглядит как постоянно увеличивающаяся «восьмёрка». Следить за ним становится трудно, и спутник снимают с орбиты, заменяя его новым.
СВЯЗЬ ЧЕРЕЗ МАТЕРИКИ И ОКЕАН
В феврале 2009 года ракета-носитель «Протон-М», оборудованная разгонным блоком «Бриз-М» (см. «Наука и жизнь» № 4, 2004 г.) и дополнительным топливным баком, вывела сразу два спутника: тяжёлый «Экспресс-АМ44» (2560 кг) и малый «Экспресс-МД1» (1140 кг). Запуск стал уникальным, поскольку общая масса спутников составляет 3,7 т и предельна для «Протонов».
Корабль перешёл на геостационарную орбиту в точке 11 градусов западной долготы, где от него отделился «Экспресс-АМ44». Затем корабль переместился восточнее и в точке 80 градусов восточной долготы «освободился» от «Экспресса-МД1».
Спутники построены на российских предприятиях, а их начинка — транспондеры — устройства, которые ретранслируют сигнал с изменением его частоты, — на французском и итальянском предприятиях. В «Экспрессе-АМ44» смонтированы работающие в диапазоне СВЧ 10 транспондеров с полосой по 40 МГц, 16 транспондеров с полосой по 54 МГц и один транспондер с полосой 1 МГц. Обладая такими характеристиками, спутник способен передавать информацию со скоростью 1265 Мбит/с.
В «Экспрессе-АМ44» смонтированы работающие в диапазоне СВЧ 10 транспондеров с полосой по 40 МГц, 16 транспондеров с полосой по 54 МГц и один транспондер с полосой 1 МГц. Обладая такими характеристиками, спутник способен передавать информацию со скоростью 1265 Мбит/с.
В «Экспрессе-МД1» аппаратуры поменьше — там работают восемь транспондеров с полосой по 40 МГц и один транспондер с полосой 1 МГц, которые обеспечивают скорость передачи 321 Мбит/с.
В составе группировки теперь будет 11 спутников, которые охватят практически всю обитаемую поверхность Земли, за исключением западных областей Северной Америки и Океании.
КОСМИЧЕСКАЯ КАРУСЕЛЬ
Создатели космической техники продолжают работу над совершенствованием российской системы спутниковой навигации ГЛОНАСС. Сейчас на орбитах, расположенных в трёх плоскостях, которые находятся под примерно одинаковыми углами относительно друг друга, движутся 20 спутников «ГЛОНАСС-М»: 19 рабочих и один резервный. Они могут обеспечить навигационной информацией всё население России и стран СНГ. Только над Москвой в любой момент видно созвездие из восьми спутников, которые позволяют надёжно определять местоположение объекта, несмотря на плотную многоэтажную застройку, мешающую прохождению радиосигналов (чтобы узнать координаты объекта, в пределах прямой видимости должны находиться не менее трёх навигационных спутников).
Они могут обеспечить навигационной информацией всё население России и стран СНГ. Только над Москвой в любой момент видно созвездие из восьми спутников, которые позволяют надёжно определять местоположение объекта, несмотря на плотную многоэтажную застройку, мешающую прохождению радиосигналов (чтобы узнать координаты объекта, в пределах прямой видимости должны находиться не менее трёх навигационных спутников).
В течение этого года планируется довести состав группировки до штатного. В каждой орбитальной плоскости вокруг Земли будут обращаться по 10 спутников «ГЛОНАСС-М», из которых по два будут находиться в резерве или на техобслуживании.
По утверждению начальника Управления космических систем навигации, связи и наземных комплексов управления Федерального космического агентства А. Е. Шилова, мы достигли точности определения координат 10,5 м, то есть уже вплотную приблизились к американской системе GPS, которая гарантирует точность 10 м, хотя в реальности она у них немного выше. Более того, в следующем году во время запуска одного из российских навигационных спутников в комбинации с ним будет выведен на орбиту спутник «ГЛОНАСС-К», позволяющий намного более точно определять место. И если американцы не модернизируют к тому времени свои аппараты, то по точности мы будем первыми.
Более того, в следующем году во время запуска одного из российских навигационных спутников в комбинации с ним будет выведен на орбиту спутник «ГЛОНАСС-К», позволяющий намного более точно определять место. И если американцы не модернизируют к тому времени свои аппараты, то по точности мы будем первыми.
У «ГЛОНАСС-К» есть ещё одно большое достоинство: он не имеет герметичного корпуса, а значит, будет легче предшественников и вывод его на орбиту обойдётся дешевле.
РОССИЯ ПЕРЕНЕСЛА СИСТЕМУ КООРДИНАТ
В общем, будущее космических объектов ГЛОНАСС особых беспокойств не вызывает. Больше возникает вопросов о том, на какие приёмники будут приходить сигналы со спутников. По нормативам выпускающиеся в России приёмники должны быть мультисистемными, как, например, современные телевизоры, которые дают нормальную картинку и в Европе (PAL), и в России (SECAM), и в США и Японии (NTSC). Навигационные приёмники должны расшифровывать сигналы спутников ГЛОНАСС и GPS. Благо различия в показаниях обеих систем сейчас устранены. Причина разночтений состояла в том, что в основе американской системы координат WGS-84 и российской системы ПЗ-90 лежали геоиды (геометрические фигуры, поверхность которых совпадает со сглаженной поверхностью Земли), близкие по форме, но с несовпадающими началами координат (см. «Наука и жизнь» № 4, 2007 г.). Поэтому в одной и той же точке приёмники, настроенные на сигналы со спутников ГЛОНАСС и GPS, показывали разницу координат в десятки метров.
Благо различия в показаниях обеих систем сейчас устранены. Причина разночтений состояла в том, что в основе американской системы координат WGS-84 и российской системы ПЗ-90 лежали геоиды (геометрические фигуры, поверхность которых совпадает со сглаженной поверхностью Земли), близкие по форме, но с несовпадающими началами координат (см. «Наука и жизнь» № 4, 2007 г.). Поэтому в одной и той же точке приёмники, настроенные на сигналы со спутников ГЛОНАСС и GPS, показывали разницу координат в десятки метров.
В 2007 году в соответствии с постановлением Правительства Российской Федерации была введена система координат ПЗ-90.02, у которой точка отсчёта смещена по осям X, Y, Z соответственно на –36, +8 и +18 см. После коррекции параметров аппаратуры на спутниках ГЛОНАСС различия в показаниях практически исчезли. Имея двухсистемный приёмник, остаётся только выбрать одну из них — а именно ту, у которой видно больше спутников, — и определить своё местонахождение.
Редакция благодарит профессора Л. Н. Лысенко (МГТУ им. Н. Э. Баумана) за помощь и консультации при подготовке материала.
Н. Лысенко (МГТУ им. Н. Э. Баумана) за помощь и консультации при подготовке материала.
Орбиты, которые мы выбираем | Публикации
Статьи журнала «Вокруг света»
Фото: NASA
Мы редко задумываемся, как организовано движение в околоземном пространстве. Например, о том, что от Земли до космической станции — рукой подать, меньше чем от Москвы до Питера, а принятый спутниковой тарелкой сигнал проделал больший путь, чем средний автомобиль проходит за пять лет. К тому же каждому запуску предшествует тщательное проектирование орбиты, по которой аппарат будет двигаться в космическом пространстве. Орбиты, которые мы выбираем
Когда в 1961 году специалисты королёвского ОКБ-1 приступили к созданию первого советского спутника связи «Молния-1» для телевизионной системы «Орбита», перед ними встала проблема выбора целевой орбиты для своего детища. Самой эффективной, на первый взгляд, казалась геостационарная орбита высотой 36 тысяч километров. Находящийся на ней спутник круглосуточно пребывает в прямой видимости примерно для 1/3 поверхности Земли.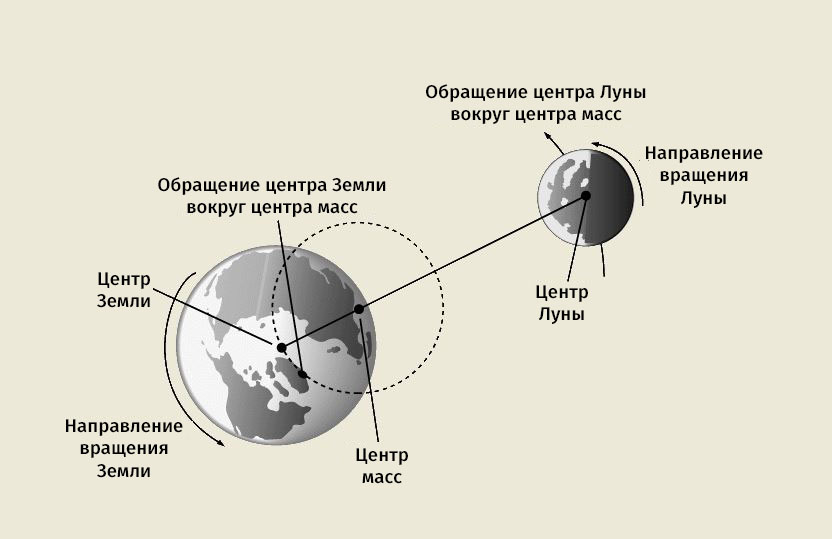 Однако с такой орбиты невозможно обеспечить связь в высоких широтах и телевещание в районах Крайнего Севера. Кроме того, Советский Союз не располагал тогда носителями для вывода тяжелых спутников на геостационарную орбиту.
Однако с такой орбиты невозможно обеспечить связь в высоких широтах и телевещание в районах Крайнего Севера. Кроме того, Советский Союз не располагал тогда носителями для вывода тяжелых спутников на геостационарную орбиту.
Выход нашли баллистики, придумавшие орбиту, на которую спутник связи можно было выводить ракетой, уже находившейся в разработке. Это была сильно вытянутая орбита с минимальной высотой (перигеем) 500 километров, а максимальной (апогеем) — 40 000 километров. Период обращения составлял 12 часов, причем в соответствии с законами небесной механики большую часть времени спутник проводил в районе апогея. Наклонение орбиты (63,4°) было выбрано так, чтобы в этот период спутник был виден с большей части территории СССР. Благоприятные условия для связи длились восемь часов, после чего спутник уходил на другую сторону Земли, а на следующем витке проходил апогей над Северной Америкой. Вновь он становился доступен для ретрансляции телевидения только через 16 часов.
Успешно вывести на эту орбиту спутник связи «Молния-1» удалось с третьей попытки 23 апреля 1965 года, и уже на следующий день состоялся первый в Советском Союзе сеанс космической связи между Москвой и Владивостоком. Для круглосуточного телевещания приходилось держать в космосе одновременно три спутника «Молния», а на Земле строить сложные антенны. Большие параболические «зеркала» отслеживали замысловатую траекторию спутника в небе: он быстро восходил на западе, поднимался в зенит, переваливал через него, потом начинал двигаться в обратную сторону, снова разворачивался и, ускоряясь, спускался к восточному горизонту. Еще одним осложняющим фактором были значительные изменения скорости при движении по вытянутой орбите, в результате чего из-за эффекта Доплера постоянно менялась частота принимаемого на Земле сигнала.
Для круглосуточного телевещания приходилось держать в космосе одновременно три спутника «Молния», а на Земле строить сложные антенны. Большие параболические «зеркала» отслеживали замысловатую траекторию спутника в небе: он быстро восходил на западе, поднимался в зенит, переваливал через него, потом начинал двигаться в обратную сторону, снова разворачивался и, ускоряясь, спускался к восточному горизонту. Еще одним осложняющим фактором были значительные изменения скорости при движении по вытянутой орбите, в результате чего из-за эффекта Доплера постоянно менялась частота принимаемого на Земле сигнала.
Траектория, выбранная для первого советского спутника связи, позднее получила название орбита «Молния». Ее развитием с появлением более мощных ракет стала высокоэллиптическая орбита «Тундра» с перигеем 500 километров, апогеем 71 000 и периодом обращения 24 часа. Орбиты с таким периодом называют геосинхронными, поскольку, двигаясь по ним, космический аппарат всегда проходит апогей над одним и тем же районом Земли.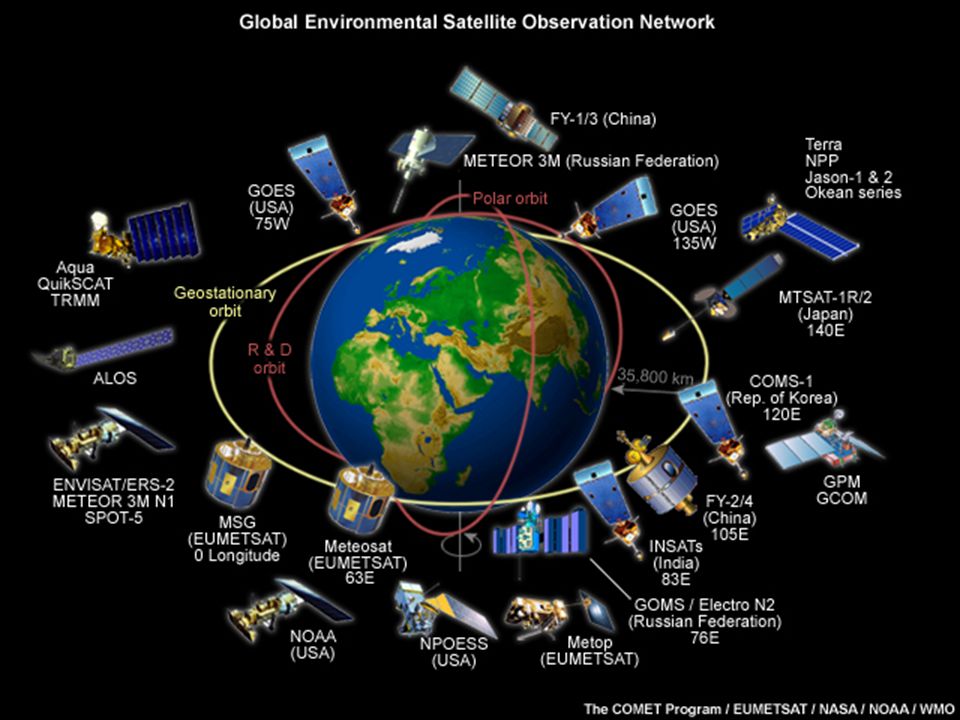 Эффективность использования спутников на орбите «Тундра» значительно повышается, так как они могут обслуживать выбранную территорию более 12 часов на каждом витке, а для организации круглосуточной связи достаточно двух аппаратов. Однако наземное оборудование по-прежнему остается сложным, ведь геосинхронные спутники постоянно меняют свое положение на небе, и за ними приходится следить.
Эффективность использования спутников на орбите «Тундра» значительно повышается, так как они могут обслуживать выбранную территорию более 12 часов на каждом витке, а для организации круглосуточной связи достаточно двух аппаратов. Однако наземное оборудование по-прежнему остается сложным, ведь геосинхронные спутники постоянно меняют свое положение на небе, и за ними приходится следить.
Спутники «Молния» на высокоэллиптических орбитах доставляли телевизионный сигнал в самые отдаленные районы СССР, однако для использования этого сигнала требовались капитальные приемные сооружения системы «Орбита». Фото: ИТАР-ТАСС
Зависшие в небе
Приемное оборудование радикально упрощается, если спутник остается неподвижным относительно Земли. Из всего множества геосинхронных орбит это достигается только на одной круговой, расположенной строго над экватором (наклонение 0°). Эта орбита называется геостационарной, поскольку на ней спутник словно бы зависает над выбранной точкой экватора на высоте 35 786 километров.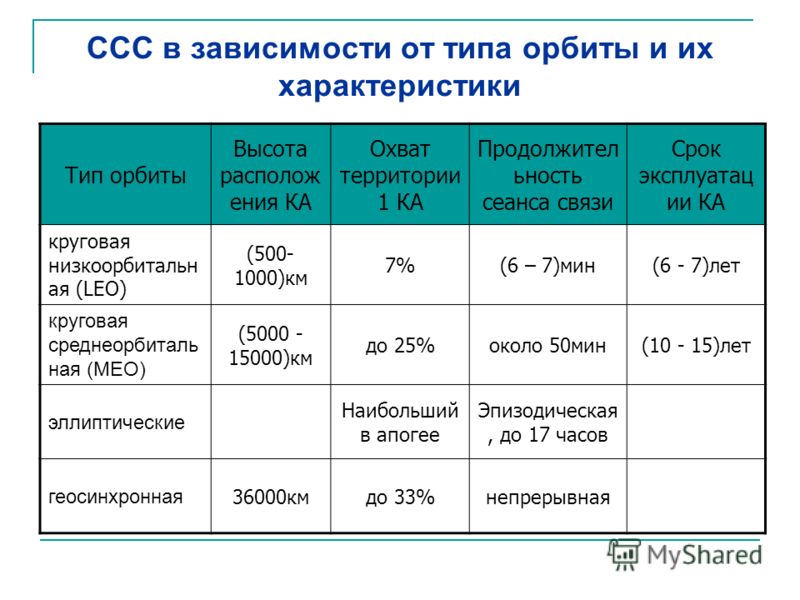
Американцы первыми запустили геостационарный спутник, но удалось им это не сразу. Первые две попытки в 1963 году окончились неудачей, и только 10 сентября 1964 года на ГСО вышел спутник «Синком-3». Интересно, что в космос он стартовал еще 19 августа, и почти месяц с помощью собственного двигателя подкрадывался к выбранной для него точке стояния. Первый отечественный геостационарный спутник «Радуга-1» был запущен лишь 22 декабря 1975 года. С тех пор ГСО постоянно пополняется, и сегодня на ней расположено более 400 спутников и еще 600 аппаратов движутся вблизи нее.
Строго говоря, из-за различных возмущений и погрешностей выведения геостационарный спутник не «висит» совсем неподвижно над экватором, а совершает колебательное движение относительно своей точки стояния. В проекции на земную поверхность его траектория напоминает небольшую восьмерку. Вдобавок из-за гравитационных возмущений аппарат может «дрейфовать» вдоль орбиты. Чтобы удержаться в выбранной точке стояния и не выйти из створа наземных антенн, аппарат должен регулярно корректировать свою орбиту. Для этого на борту имеется запас топлива. Именно от него порой зависит срок службы геостационарного спутника.
Для этого на борту имеется запас топлива. Именно от него порой зависит срок службы геостационарного спутника.
Несложные геометрические построения показывают, что на широтах выше 81° геостационарные спутники находятся под горизонтом, а значит, связь с их помощью в полярных районах невозможна. На практике мобильная связь через геостационарный спутник ограничивается широтой 65—70°, а фиксированная — 70—75°. Связь через ГСО имеет и еще один серьезный недостаток. По пути к спутнику и обратно радио сигнал преодолевает более 70 тысяч километров, затрачивая на это четверть секунды. С учетом времени на обработку сигнала и его передачу по наземным линиям связи задержка может заметно превышать полсекунды. В результате интернет-сервисы через спутник откликаются медленно, а телефонное общение становится некомфортным, поскольку даже современные средства «эхоподавления» не всегда справляются с большими задержками. Чтобы избавиться от этих недостатков, приходится уменьшать высоту спутников.
Элементы орбиты
Слово «орбита» по-латыни означает «колея» или «путь». Околоземную орбиту характеризует ряд параметров: наименьшая и наибольшая высота (перигей и апогей, которые также определяют период обращения), наклонение (угол между плоскостью орбиты и плоскостью земного экватора), долгота восходящего узла, задающая, «в какую сторону» (вокруг какой линии в плоскости экватора) наклонена орбита, и аргумент перигея, указывающий, как повернута эллиптическая орбита в своей собственной плоскости. Гравитационные возмущения со стороны других планет, давление солнечного излучения, несферическая форма Земли, ее магнитное поле и атмосфера приводят к тому, что орбиты спутников могут заметно меняться во времени. Поэтому в ходе эксплуатации спутника регулярно проводятся траекторные измерения, и при необходимости его орбита корректируется.
Околоземную орбиту характеризует ряд параметров: наименьшая и наибольшая высота (перигей и апогей, которые также определяют период обращения), наклонение (угол между плоскостью орбиты и плоскостью земного экватора), долгота восходящего узла, задающая, «в какую сторону» (вокруг какой линии в плоскости экватора) наклонена орбита, и аргумент перигея, указывающий, как повернута эллиптическая орбита в своей собственной плоскости. Гравитационные возмущения со стороны других планет, давление солнечного излучения, несферическая форма Земли, ее магнитное поле и атмосфера приводят к тому, что орбиты спутников могут заметно меняться во времени. Поэтому в ходе эксплуатации спутника регулярно проводятся траекторные измерения, и при необходимости его орбита корректируется.
Созвездие Iridium
На сравнительно невысоких орбитах формируются коммерческие и правительственные системы спутников связи. Технически эти траектории нельзя назвать удобными для связи, поскольку спутники на них большую часть времени видны низко над горизонтом, что негативно сказывается на качестве приема, а при гористом рельефе может сделать его невозможным.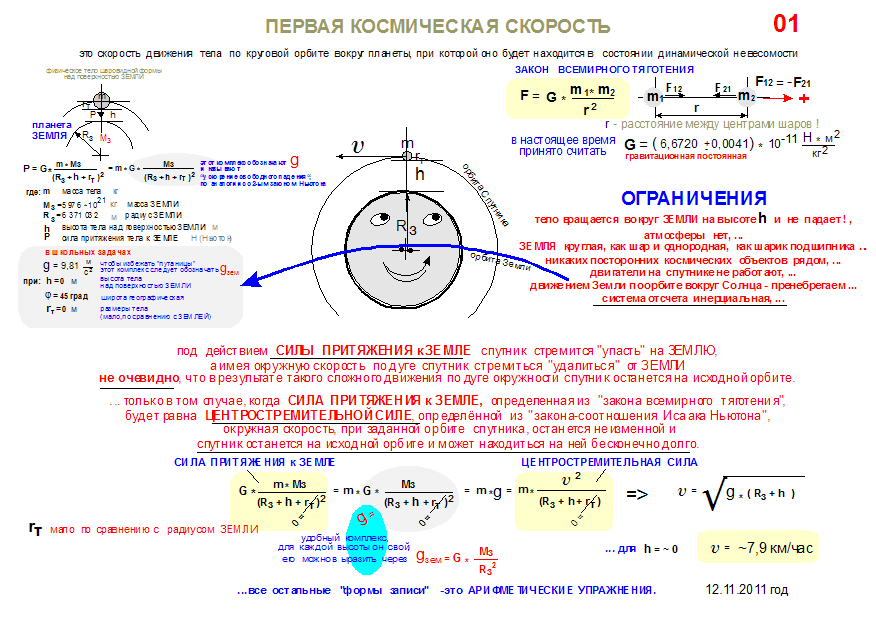 Поэтому чем ниже орбита, тем больше спутников должно быть в системе. Если для глобальной системы связи на ГСО достаточно трех спутников, то на орбитах средней высоты (5000—15 000 километров) требуется уже от 8 до 12 космических аппаратов. А для высот 500—2000 километров нужно более полусотни спутников.
Поэтому чем ниже орбита, тем больше спутников должно быть в системе. Если для глобальной системы связи на ГСО достаточно трех спутников, то на орбитах средней высоты (5000—15 000 километров) требуется уже от 8 до 12 космических аппаратов. А для высот 500—2000 километров нужно более полусотни спутников.
И все же к концу 1980-х годов сложились предпосылки для реализации низкоорбитальных систем связи. Во-первых, на ГСО спутникам становилось все теснее. «Парковочные места» на этой орбите подлежат международной регистрации, причем расположенные по соседству спутники не должны работать на одних и тех же радиочастотах, чтобы не создавать друг другу помех. Во-вторых, прогресс в области радиоэлектроники позволил создавать недорогие (а главное — легкие) спутники с достаточно широкими возможностями. Ракета, способная вывести на ГСО всего один большой спутник связи, могла забросить на низкую орбиту целую «пачку» таких аппаратов. В-третьих, завершение «холодной войны» и процесс разоружения высвобождали сотни межконтинентальных баллистических ракет, которые могли по «бросовым ценам» использоваться для запуска небольших спутников.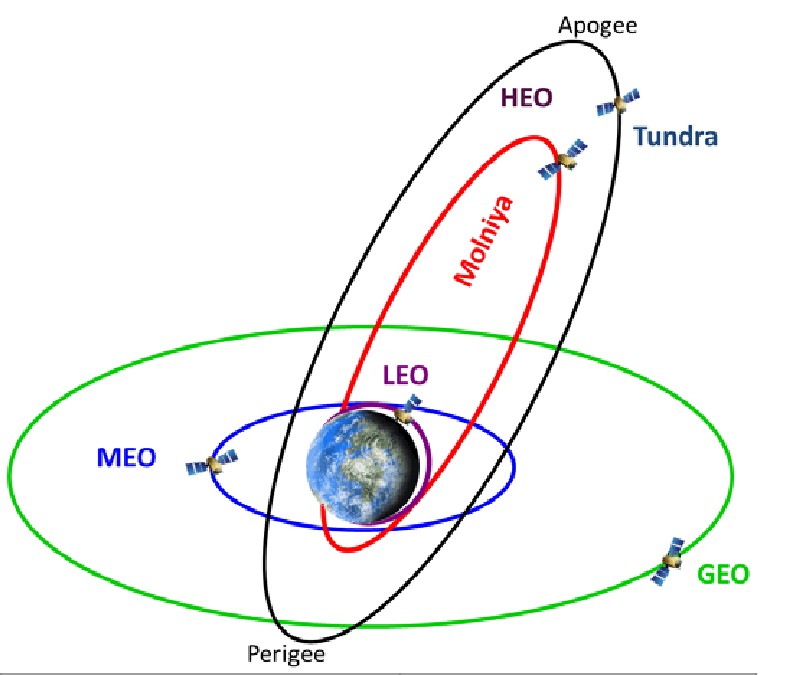 И наконец, именно в эти годы стал быстро расти спрос на мобильную связь, для которой характерно использование маломощных ненаправленных антенн, «не добивающих» до ГСО. Все эти факторы делали запуск даже очень большого числа недорогих низкоорбитальных спутников выгоднее создания группировки из нескольких тяжелых геостационарных аппаратов.
И наконец, именно в эти годы стал быстро расти спрос на мобильную связь, для которой характерно использование маломощных ненаправленных антенн, «не добивающих» до ГСО. Все эти факторы делали запуск даже очень большого числа недорогих низкоорбитальных спутников выгоднее создания группировки из нескольких тяжелых геостационарных аппаратов.
Среди первых низкоорбитальных систем связи были Orbcomm (США) и «Гонец» (Россия). Они не обеспечивали передачу голоса, а предназначались для отправки текстовых сообщений и сбора информации с различных датчиков, например метеорологических. На сегодня Orbcomm включает 29 спутников массой 42 килограмма на орбитах высотой 775 километров. Система «Гонец» первоначально содержала всего 6 спутников, из-за чего время доставки сообщений могло затягиваться на несколько часов. Сейчас в ней сменяется уже третье поколение спутников, число работающих аппаратов достигло девяти, но в перспективе должно быть доведено до 45 — по девять штук на пяти почти полярных орбитах (наклонение 82,5°) высотой 1500 километров.
Полярными называют орбиты, которые проходят над Северным и Южным полюсами Земли, то есть располагаются перпендикулярно экватору. В поле зрения спутника на полярной орбите периодически попадает любой участок земной поверхности. Если использовать несколько таких орбит, повернутых под углом друг к другу, и по каждой с равными интервалами запустить несколько спутников, можно непрерывно обозревать всю поверхность Земли. Именно так работает сеть спутниковой телефонии Iridium. В ней используются полярные орбиты с наклонением 86,4° и высотой 780 километров. Первоначально на них размещалось 77 спутников, откуда и возникло название системы: иридий — 77-й элемент Периодической системы Менделеева. Однако через девять месяцев после запуска, в ноябре 1998 года, компания Iridium обанкротилась. Цена разговора, доходившая до семи долларов в минуту, оказалась слишком высокой для потребителей, отчасти из-за того, что система Iridium обеспечила по-настоящему глобальную связь — от полюса до полюса. Стартовавшая чуть позже система GlobalStar ради экономии использует вместо полярных орбиты с наклонением 52°, что ограничивает связь 70-й параллелью (примерно на широте Ямала).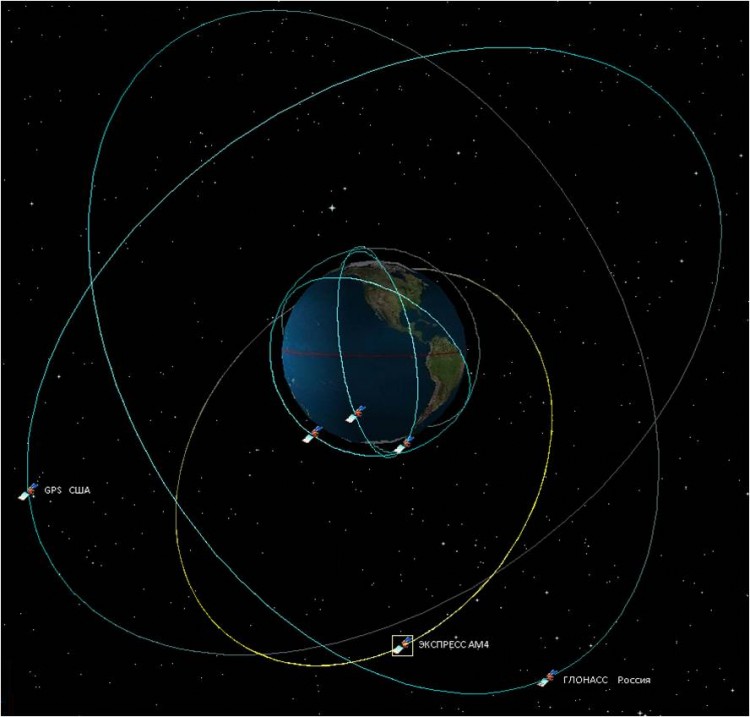 Зато для работы хватает 48 спутников (плюс четыре запасных), а стоимость связи в том же 1999 году составляла не более двух долларов в минуту.
Зато для работы хватает 48 спутников (плюс четыре запасных), а стоимость связи в том же 1999 году составляла не более двух долларов в минуту.
Спутники Iridium уже готовились свести с орбиты и сжечь в плотных слоях атмосферы, когда всю систему выкупило американское министерство обороны. По сей день Iridium остается единственной спутниковой системой связи, которая непрерывно обеспечивает телефонную связь по всему земному шару. Например, через нее с 2006 года обеспечивается постоянное подключение к Интернету полярной станции Амундсен-Скотт на Южном полюсе. Скорость соединения составляет 28,8 килобит в секунду, как на старом телефонном модеме.
Использование околоземного пространства
В первом приближении орбиты спутников делятся на низкие (до 2000 километров от Земли), средние (ниже геостационарной орбиты) и высокие. Пилотируемые полеты совершаются не выше 600 километров, поскольку космические корабли не должны входить в окружающие нашу планету радиационные пояса. Энергичные протоны внутреннего радиационного пояса создают опасность для жизни космонавтов.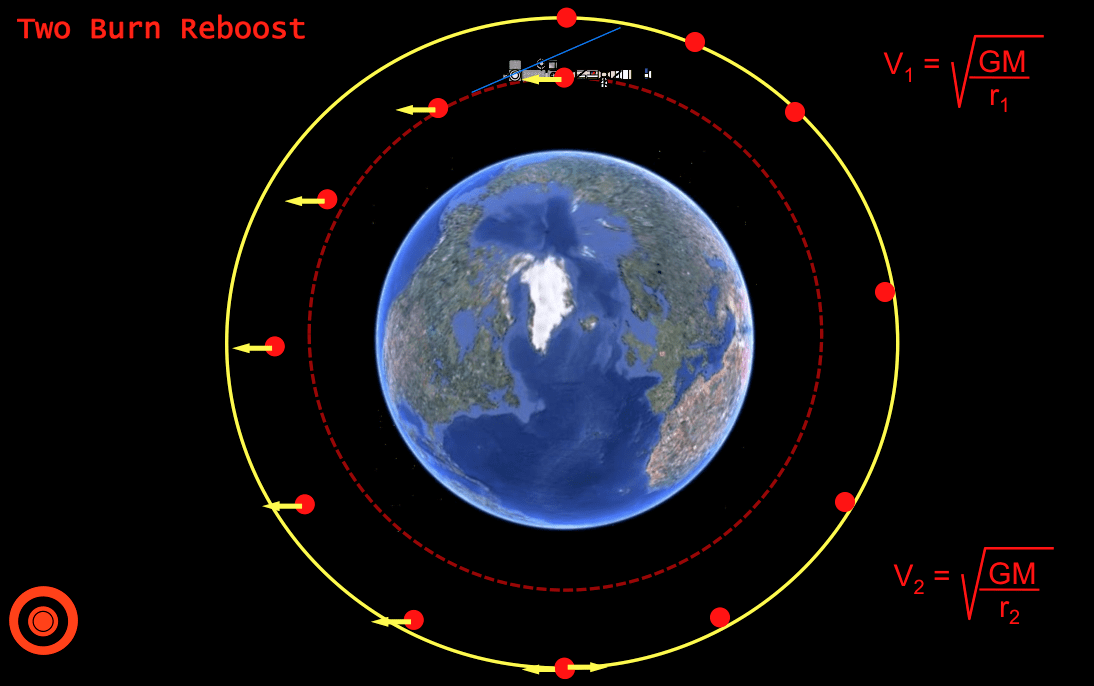 Максимальная интенсивность облучения достигается на высоте около 3000 километров, которой избегают все космические аппараты. Внешний электронный пояс не так опасен. Его максимум лежит где-то между зонами навигационных и геостационарных спутников. Еще выше обычно поднимаются спутники, работающие на сильно вытянутых эллиптических орбитах. Таковы, например, рентгеновская обсерватория «Чандра» (США), которая во избежание помех наблюдает вдали от радиационных поясов, и будущая российская обсерватория «Радиоастрон», данные которой тем точнее, чем больше расстояние от работающих с ней в паре земных радиотелескопов. Самые высокие околоземные орбиты, которые в равной мере можно считать околосолнечными, лежат на высоте 1,5 миллиона километров вблизи так называемых точек Лагранжа.
Максимальная интенсивность облучения достигается на высоте около 3000 километров, которой избегают все космические аппараты. Внешний электронный пояс не так опасен. Его максимум лежит где-то между зонами навигационных и геостационарных спутников. Еще выше обычно поднимаются спутники, работающие на сильно вытянутых эллиптических орбитах. Таковы, например, рентгеновская обсерватория «Чандра» (США), которая во избежание помех наблюдает вдали от радиационных поясов, и будущая российская обсерватория «Радиоастрон», данные которой тем точнее, чем больше расстояние от работающих с ней в паре земных радиотелескопов. Самые высокие околоземные орбиты, которые в равной мере можно считать околосолнечными, лежат на высоте 1,5 миллиона километров вблизи так называемых точек Лагранжа.
В прямой видимости из любой точки Земли всегда находится хоть один спутник низкоорбитальной системы связи Iridium. Но в помещения их сигналы почти не проникают. Так что дозвониться до обладателя спутниковой трубки можно не всегда
Вместе с солнцем
К полярным близок еще один важный класс орбит, называемых солнечносинхронными (ССО), которые всегда имеют постоянную ориентацию относительно Солнца. На первый взгляд кажется, что это противоречит законам небесной механики, согласно которым плоскость орбиты остается постоянной, а значит, в ходе движения Земли вокруг Солнца она должна поворачиваться к нему то одной, то другой стороной. Но если учесть, что Земля имеет приплюснутую форму, то оказывается, что плоскость орбиты испытывает прецессию, то есть немного поворачивается от витка к витку. Правильно подобрав высоту и наклонение, можно добиться того, чтобы поворот плоскости орбиты как раз соответствовал дуге, пройденной Землей вокруг Солнца. Например, для высоты орбиты 200 километров наклонение должно составлять чуть больше 96° градусов, а для 1000 километров — уже более 99° (цифры более 90° соответствуют движению по орбите против суточного вращения Земли).
На первый взгляд кажется, что это противоречит законам небесной механики, согласно которым плоскость орбиты остается постоянной, а значит, в ходе движения Земли вокруг Солнца она должна поворачиваться к нему то одной, то другой стороной. Но если учесть, что Земля имеет приплюснутую форму, то оказывается, что плоскость орбиты испытывает прецессию, то есть немного поворачивается от витка к витку. Правильно подобрав высоту и наклонение, можно добиться того, чтобы поворот плоскости орбиты как раз соответствовал дуге, пройденной Землей вокруг Солнца. Например, для высоты орбиты 200 километров наклонение должно составлять чуть больше 96° градусов, а для 1000 километров — уже более 99° (цифры более 90° соответствуют движению по орбите против суточного вращения Земли).
Ценность ССО состоит в том, что, двигаясь по ней, спутник пролетает над земными объектами всегда в одно и то же время суток, что важно для проведения космической съемки. Кроме того, благодаря близости ССО к полярным орбитам с них можно следить за всей земной поверхностью, что важно для метеорологических, картографических и разведывательных спутников, которые собирательно называются спутниками дистанционного зондирования Земли (ДЗЗ).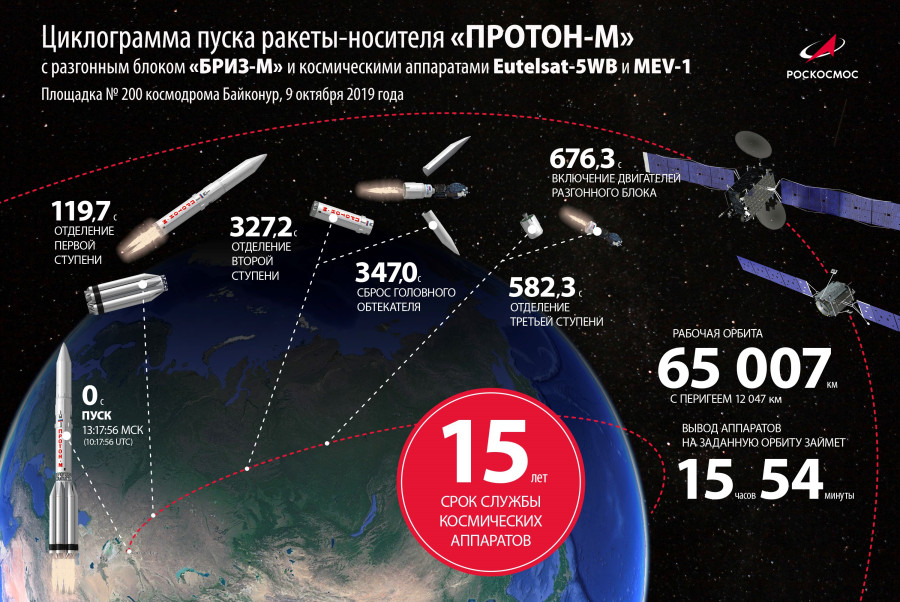 Определенный выбор параметров ССО позволяет спутнику никогда не уходить в тень Земли, всегда оставаясь на солнце вблизи границы дня и ночи. Спутник при этом не испытывает перепадов температуры, а солнечные батареи непрерывно обеспечивают его энергией. Такие орбиты удобны для радарного картирования земной поверхности.
Определенный выбор параметров ССО позволяет спутнику никогда не уходить в тень Земли, всегда оставаясь на солнце вблизи границы дня и ночи. Спутник при этом не испытывает перепадов температуры, а солнечные батареи непрерывно обеспечивают его энергией. Такие орбиты удобны для радарного картирования земной поверхности.
Гражданские спутники ДЗЗ, от которых требуется различать предметы размером порядка метра, обычно работают на высотах 500—600 километров. Для военных спутников-разведчиков с разрешением съемки в 10—30 сантиметров такие высоты слишком велики. Поэтому их орбиты часто выбирают так, чтобы перигей лежал над точкой съемки. Если «объект внимания» не один, разведчику приходится менять форму орбиты с помощью двигателя, иногда совершая «нырки» к верхним слоям атмосферы, снижаясь до высот около 150 километ ров. Необходимость «подбираться» как можно ближе к Земле имеет существенный недостаток — сопротивление атмосферы резко сокращает срок пребывания спутника в космосе. Чуть зазеваешься — и атмосфера утащит спутник в свою пучину, где он неизбежно сгорит.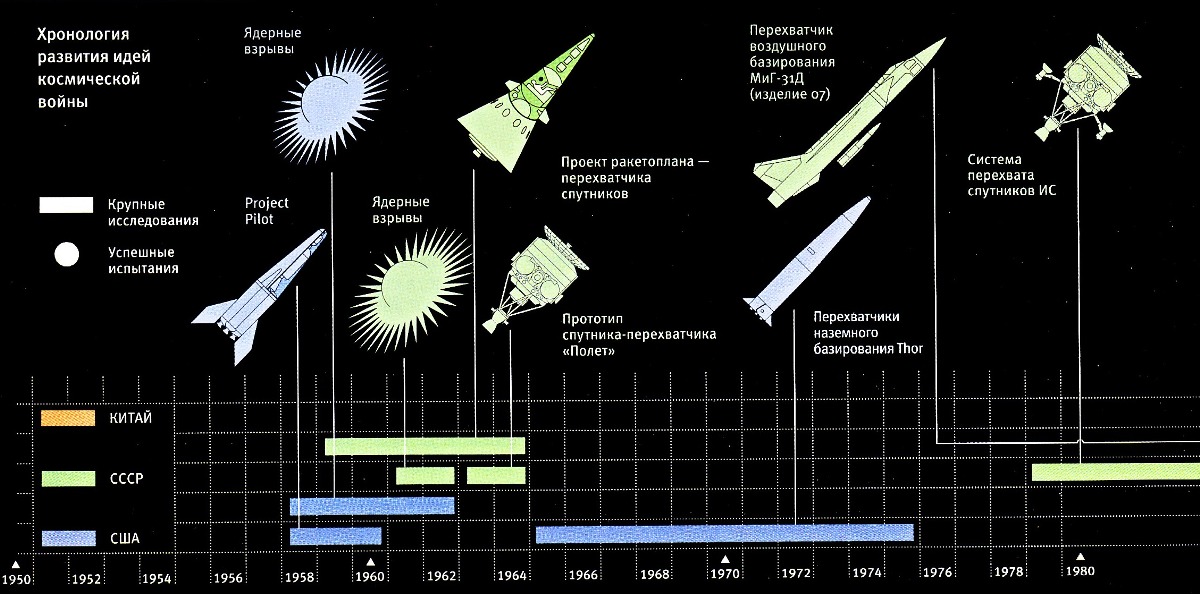 Из-за этого на борту низкоорбитальных «шпионов» приходится держать большие запасы топлива для коррекции орбиты и периодического подъема высоты. Например, из 18 тонн стартовой массы американского фоторазведчика KH-11 на топливо приходится примерно 40%. Таким образом, выбранная орбита может непосредственно влиять на конструкцию, а иногда и на внешний вид аппарата.
Из-за этого на борту низкоорбитальных «шпионов» приходится держать большие запасы топлива для коррекции орбиты и периодического подъема высоты. Например, из 18 тонн стартовой массы американского фоторазведчика KH-11 на топливо приходится примерно 40%. Таким образом, выбранная орбита может непосредственно влиять на конструкцию, а иногда и на внешний вид аппарата.
Особенно ярко эта зависимость проявилась в конструкции европейского научного аппарата GOCE, запущенного недавно с российского космодрома Плесецк. Он имеет необычную стреловидную форму, непохожую на угловатые контуры большинства современных спутников, и даже вызывает ассоциации со скоростным самолетом. Дело в том, что для спутника, изучающего гравитационное поле Земли, выбрана низкая ССО высотой 240—250 километров. Она оптимальна с точки зрения точности измерений, но чтобы противостоять тормозящему действию атмосферы, спутнику придали форму с минимальным поперечным сечением. Кроме того, в кормовой части аппарата установлены ионные электроракетные двигатели для коррекции траектории.
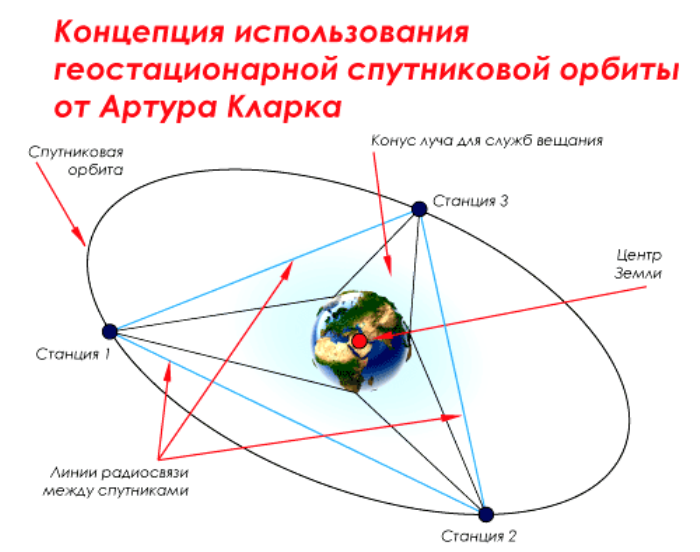
«Орбита Кларка»
Вероятно, первыми о возможности геостационарных спутников заговорили Константин Эдуардович Циолковский и Герман Поточник, теоретик космонавтики из Словении, более известный как Герман Ноордунг. Однако широкое распространение идея их использования для связи получила с подачи известного британского ученого и писателя-фантаста Артура Кларка. В 1945 году он опубликовал в журнале Wireless World научно-популярную статью с описанием спутников связи на геостационарной орбите (ГСО), которую теперь нередко называют «Орбитой Кларка».
Глобальный взгляд
Но не всем спутникам ДЗЗ требуется высокое разрешение. Что проку от возможности обнаружить объект размером 30 сантиметров, если задача аппарата — отслеживать региональные или глобальные перемещения воздушных масс и тепловые режимы крупных регионов. Для ее осуществления гораздо важнее широта охвата. При глобальном метеорологическом мониторинге спутники обычно размещают на ГСО или высокой ССО, а при региональном — на орбите сравнительно небольшой высоты (500—1000 километров) с наклонением, позволяющим регулярно проводить съемку выбранного района.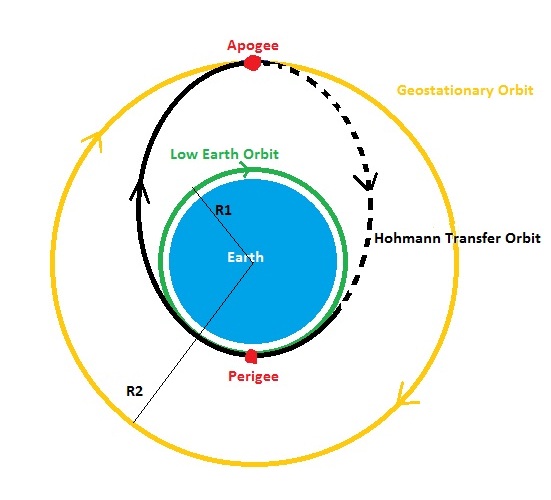 К примеру, перспективный российский спутник
К примеру, перспективный российский спутник
В околоземном пространстве движется около 10 тысяч спутников и не меньшее число их фрагментов. В основном они сконцентрированы на малых высотах и вблизи гео стационарной орбиты, «парковочные места» на которой уже приходится тщательно распределять. Фото: CHEEJU.FILES.WORDPRESS.COM
«Метеор-М» должен проводить мониторинг гидрометеорологической ситуации в глобальном масштабе с ССО высотой 830 километров. А для аппарата «Электро-Л» была выбрана ГСО, поскольку его основным назначением будет съемка всего диска Земли в видимом и инфракрасном диапазонах. Кроме того, ГСО в данном случае оптимальна для получения информации о глобальных атмосферных процессах, протекающих в приэкваториальной зоне.
Именно потому, что с ГСО можно обозревать значительную часть земной поверхности, ее «заселяют» не только аппараты связи и метеоспутники, но и системы предупреждения о ракетном нападении. Их основная задача — обнаруживать пуски баллистических ракет, для чего в состав аппаратуры включается инфракрасный телескоп, способный засечь факел работающего двигателя.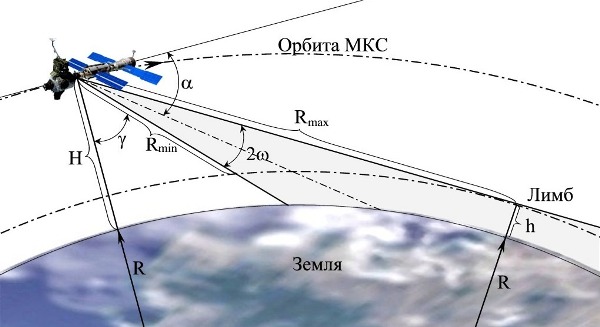 Недостатки ГСО в данном случае роли не играют — ведь спутнику не надо передавать информацию на Северный или Южный полюс, зато треть земной поверхности как на ладони.
Недостатки ГСО в данном случае роли не играют — ведь спутнику не надо передавать информацию на Северный или Южный полюс, зато треть земной поверхности как на ладони.
Весьма непростым оказался выбор параметров орбиты для спутников глобальных навигационных систем GPS и ГЛОНАСС. Хотя сама идея (по задержке сигнала измерять расстояние до спутников с хорошо известными координатами) была очевидна, ее реализация затянулась на десятилетия. В СССР исследования в этом направлении начались еще в 1958 году. Через пять лет стартовала работа над первой спутниковой навигационной системой «Цикада», которую сдали в эксплуатацию только через 16 лет. Четыре ее навигационных спутника работали на низких круговых орбитах высотой 1000 километров с наклонением 83°. Плоскости их орбит были равномерно распределены вдоль экватора. Примерно раз в полтора-два часа потребитель мог войти в радиоконтакт с одним из спутников «Цикада» и после 5—6 минут связи определить свои широту и долготу. Разумеется, военных заказчиков спутниковой навигации такой режим работы не устраивал. Им требовалось в произвольный момент и в любой точке Земли определять три пространственные координаты, вектор скорости и точное время. Для этого необходимо одновременно принимать сигналы не менее четырех спутников. На низких орбитах для этого потребовалось бы разместить сотни космических аппаратов, что было бы не только безумно дорого, но и попросту неосуществимо. Дело в том, что срок эксплуатации советских спутников не превышал одного-двух лет (а чаще — нескольких месяцев), и получилось бы, что вся ракетно-космическая промышленность работала бы исключительно на изготовление и запуск навигационных спутников. Вдобавок низкоорбитальные спутники испытывают значительные возмущения из-за влияния земной атмосферы, что сказывается на точности определяемых по ним координат.
Им требовалось в произвольный момент и в любой точке Земли определять три пространственные координаты, вектор скорости и точное время. Для этого необходимо одновременно принимать сигналы не менее четырех спутников. На низких орбитах для этого потребовалось бы разместить сотни космических аппаратов, что было бы не только безумно дорого, но и попросту неосуществимо. Дело в том, что срок эксплуатации советских спутников не превышал одного-двух лет (а чаще — нескольких месяцев), и получилось бы, что вся ракетно-космическая промышленность работала бы исключительно на изготовление и запуск навигационных спутников. Вдобавок низкоорбитальные спутники испытывают значительные возмущения из-за влияния земной атмосферы, что сказывается на точности определяемых по ним координат.
Исследования показали, что необходимые параметры навигационной системы обеспечиваются при размещении спутников на круговых траекториях высотой 19 000—20 000 километров (для ГЛОНАСС выбрана высота 19 100 километров) с наклонением около 64°. Влияние атмосферы здесь уже незначительно, а гравитационные возмущения со стороны Луны и Солнца еще не приводят к быстрым изменениям орбиты.
Влияние атмосферы здесь уже незначительно, а гравитационные возмущения со стороны Луны и Солнца еще не приводят к быстрым изменениям орбиты.
Кладбище спутников
В последние 20 лет все больше стран обзаводились собственными телекоммуникационными, метеорологическими и военными спутниками на геостационарной орбите. В результате на ГСО стало тесно. Среднее расстояние между спутниками составляет около 500 километров, а на некоторых ее участках тяжелые аппараты «висят» всего в нескольких десятках километров друг от друга. Это может вызывать помехи при связи и даже приводить к столкновениям. Возвращать спутники с высокой орбиты на Землю слишком дорого. Поэтому для расчистки ГСО было решено, что после завершения активной эксплуатации они должны на остатках топлива переводиться на «орбиту захоронения», расположенную на 200—300 километров выше. Это «кладбище спутников» пока гораздо свободнее рабочей орбиты.
Теоретически на такой высоте достаточно 18 спутников в трех орбитальных плоскостях, чтобы из любой точки на Земле было видно не менее четырех аппаратов одновременно. Но на самом деле для повышения точности определения местоположения самих космических аппаратов группировку ГЛОНАСС придется расширить до 24 работающих спутников, а с учетом резерва в системе надо иметь 27—30 спутников. Примерно на таких же принципах строятся и остальные навигационные системы — GPS (США), Galileo (Европа) и «Бэйдоу» (Китай). Их спутниковые группировки располагаются на круговых орбитах высотой 20 000—23 500 километров с наклонением 55—56°.
Но на самом деле для повышения точности определения местоположения самих космических аппаратов группировку ГЛОНАСС придется расширить до 24 работающих спутников, а с учетом резерва в системе надо иметь 27—30 спутников. Примерно на таких же принципах строятся и остальные навигационные системы — GPS (США), Galileo (Европа) и «Бэйдоу» (Китай). Их спутниковые группировки располагаются на круговых орбитах высотой 20 000—23 500 километров с наклонением 55—56°.
GOCE — редкий случай, когда в конструкции спутника приходится учитывать аэродинамику. Гравиметрические измерения требуют лететь как можно ближе к Земле. Ионный двигатель периодически включается, чтобы компенсировать торможение в атмосфере. Фото: ESA
Трассы для пилотов
Орбиты пилотируемых аппаратов выбираются особо. Так, при строительстве Международной космической станции (МКС) учитывались удобство запуска к ней новых модулей и космических кораблей, безопасность экипажа, расход топлива на поддержание высоты. В результате станция была выведена на орбиту высотой около 400 километров. Это немного ниже границы радиационного пояса Земли, в котором под действием магнитного поля нашей планеты накапливаются заряженные частицы солнечного ветра. Длительное нахождение внутри радиационного пояса подвергало бы экипаж опасному облучению или потребовало бы мощных средств радиационной защиты орбитальной станции. Существенно ниже опустить орбиту тоже нельзя, иначе из-за значительного аэродинамического сопротивления станция будет тормозиться и потребуется много топлива для поддержания ее высоты. Наклонение орбитальной плоскости (51,6°) определяется условиями запусков с Байконура, самого северного космодрома, откуда осуществляются пилотируемые полеты.
Это немного ниже границы радиационного пояса Земли, в котором под действием магнитного поля нашей планеты накапливаются заряженные частицы солнечного ветра. Длительное нахождение внутри радиационного пояса подвергало бы экипаж опасному облучению или потребовало бы мощных средств радиационной защиты орбитальной станции. Существенно ниже опустить орбиту тоже нельзя, иначе из-за значительного аэродинамического сопротивления станция будет тормозиться и потребуется много топлива для поддержания ее высоты. Наклонение орбитальной плоскости (51,6°) определяется условиями запусков с Байконура, самого северного космодрома, откуда осуществляются пилотируемые полеты.
Сходными соображениями продиктован выбор орбиты для космического телескопа Хаббла, поскольку с самого начала предполагалось, что его будут периодически посещать астронавты. Потому наклонение орбиты 28,5° было выбрано по широте американского космодрома Канаверал. В результате орбиты МКС и телескопа расположены под значительным углом друг к другу, и космический челнок не может посетить их в одном полете, ведь смена плоскости орбиты — один из самых «дорогих» маневров, у шаттла для него просто недостаточно топлива.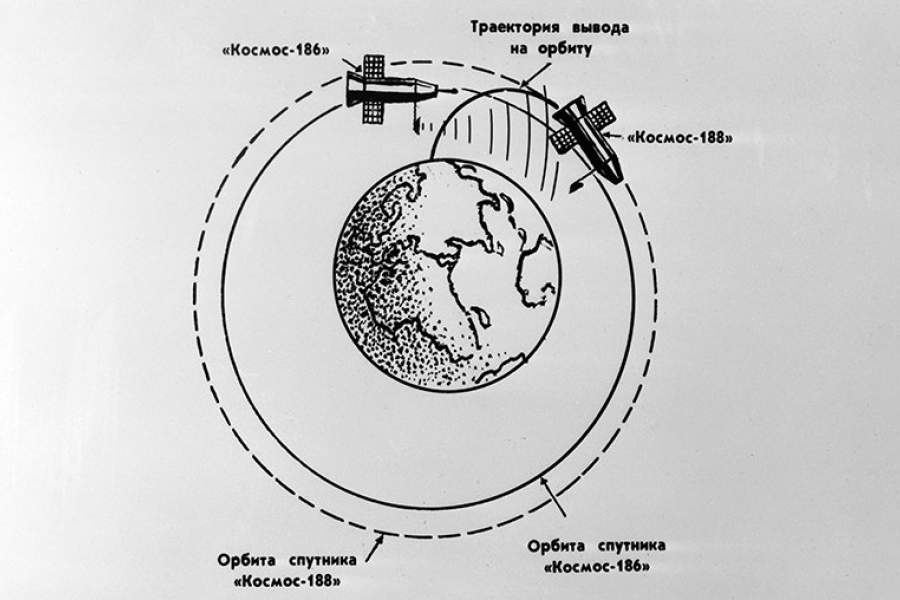 Из-за этого работа космического телескопа едва не завершилась преждевременно. После катастрофы шаттла «Колумбия» в 2003 году было решено, что астронавты должны иметь возможность укрыться на МКС, если в полете будут обнаружены серьезные повреждения корабля. Полет к телескопу Хаббла исключал такую возможность и едва не был отменен. В итоге его все-таки одобрили, и после серьезной модернизации в 2009 году «Хаббл», который находился на грани выхода из строя, сможет проработать еще лет пять, пока ему на смену не придет новый телескоп имени Джеймса Вебба. Правда, тот будет запущен уже не на околоземную орбиту, а гораздо дальше — в точку Лагранжа на высоте 1,5 миллиона километров, где период обращения в точности равен году, и телескоп будет постоянно прятаться от Солнца позади Земли. Туда пилотируемые полеты пока не осуществляются.
Из-за этого работа космического телескопа едва не завершилась преждевременно. После катастрофы шаттла «Колумбия» в 2003 году было решено, что астронавты должны иметь возможность укрыться на МКС, если в полете будут обнаружены серьезные повреждения корабля. Полет к телескопу Хаббла исключал такую возможность и едва не был отменен. В итоге его все-таки одобрили, и после серьезной модернизации в 2009 году «Хаббл», который находился на грани выхода из строя, сможет проработать еще лет пять, пока ему на смену не придет новый телескоп имени Джеймса Вебба. Правда, тот будет запущен уже не на околоземную орбиту, а гораздо дальше — в точку Лагранжа на высоте 1,5 миллиона километров, где период обращения в точности равен году, и телескоп будет постоянно прятаться от Солнца позади Земли. Туда пилотируемые полеты пока не осуществляются.
Мы описали целый ряд разных орбит, но на этом их многообразие отнюдь не исчерпывается. Для любого типа орбит существуют вариации, призванные усилить их положительные и ослабить отрицательные свойства. Например, некоторые спутники движутся вблизи геостационарной орбиты с наклонением до 10°. Это позволяет им периодически «заглядывать» в высокие широты, но наземным антеннам при этом требуется умение наклоняться вверх-вниз, отслеживая колебания спутника. Важную роль играют различные переходные траектории, соединяющие две орбиты. С распространением ионных двигателей малой тяги в околоземном пространстве стали использоваться сложные спиральные пути. Выбором траектории космического аппарата занимаются баллистики. Есть даже термин «баллистическое проектирование», означающий совместную разработку оптимальной траектории полета аппарата, его облика и основных проектных параметров. Иначе говоря, орбита разрабатывается вместе со спутником и ракетой, которая его выводит.
Например, некоторые спутники движутся вблизи геостационарной орбиты с наклонением до 10°. Это позволяет им периодически «заглядывать» в высокие широты, но наземным антеннам при этом требуется умение наклоняться вверх-вниз, отслеживая колебания спутника. Важную роль играют различные переходные траектории, соединяющие две орбиты. С распространением ионных двигателей малой тяги в околоземном пространстве стали использоваться сложные спиральные пути. Выбором траектории космического аппарата занимаются баллистики. Есть даже термин «баллистическое проектирование», означающий совместную разработку оптимальной траектории полета аппарата, его облика и основных проектных параметров. Иначе говоря, орбита разрабатывается вместе со спутником и ракетой, которая его выводит.
Игорь Афанасьев
Математика движения спутников
Движение объектов подчиняется законам Ньютона. Те же самые простые законы, которые управляют движением объектов на Земле, также распространяются на небес , управляя движением планет, лун и других спутников. Математика, описывающая движение спутника, та же математика, что и для кругового движения, представленная в Уроке 1. В этой части Урока 4 нас будут интересовать разнообразные математические уравнения, описывающие движение спутников.
Математика, описывающая движение спутника, та же математика, что и для кругового движения, представленная в Уроке 1. В этой части Урока 4 нас будут интересовать разнообразные математические уравнения, описывающие движение спутников.
Уравнение орбитальной скорости
Рассмотрим спутник с массой M sat , вращающийся вокруг центрального тела с массой M Central . Центральным телом может быть планета, солнце или какая-то другая большая масса, способная вызвать достаточное ускорение менее массивного близлежащего объекта. Если спутник движется по окружности, то результирующая центростремительная сила, действующая на этот орбитальный спутник, определяется соотношением
Эта результирующая центростремительная сила является результатом гравитационной силы, которая притягивает спутник к центральному телу, и может быть представлена как
Поскольку F grav = F net , приведенные выше выражения для центростремительной силы и силы тяжести можно приравнять друг другу.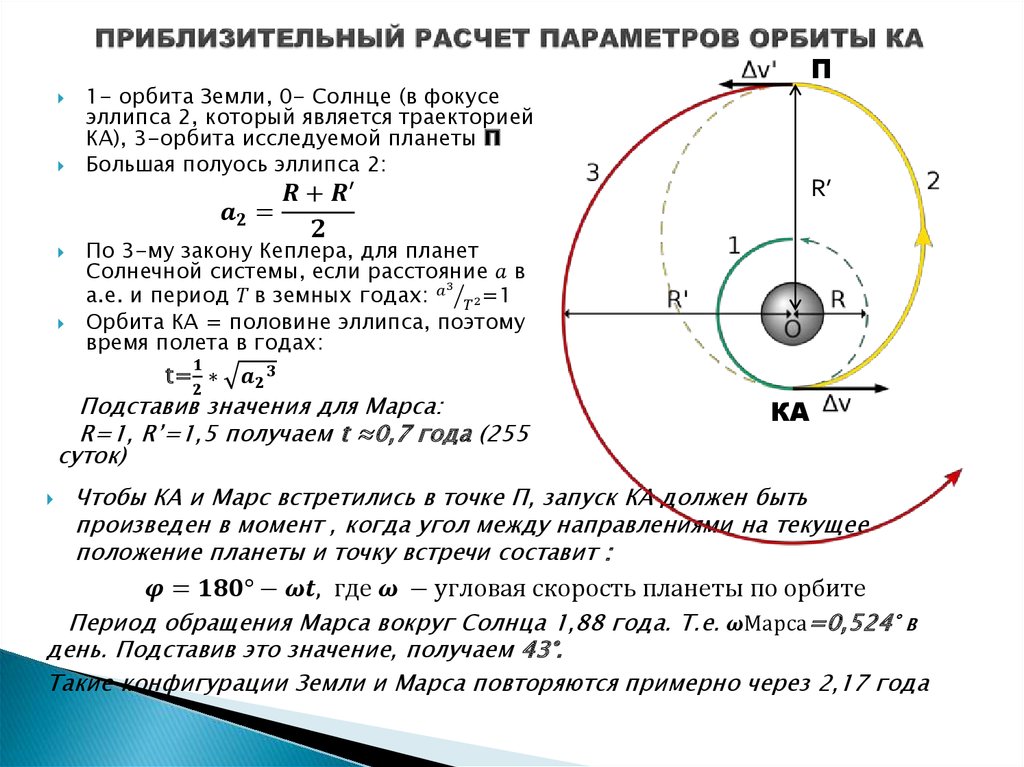 Таким образом,
Таким образом,
Заметим, что масса присутствует с обеих сторон спутника уравнение; таким образом, его можно отменить, разделив на M sat . Затем обе части уравнения можно умножить на R , получив следующее уравнение.
Извлекая квадратный корень из каждой стороны, получаем следующее уравнение для скорости спутника, движущегося вокруг центрального тела при круговом движении:
, где G равно 6,673 x 10 -11 Н•м 2 / кг 2 , M центральный — масса центрального тела, вокруг которого вращается спутник, а R — радиус орбиты спутника.
Уравнение ускорения
Аналогичные рассуждения можно использовать для определения уравнения ускорения нашего спутника, которое выражается через массы и радиус орбиты. Значение ускорения спутника равно ускорению свободного падения спутника в любом месте, где он вращается. На уроке 3 уравнение ускорения свободного падения было дано как
Значение ускорения спутника равно ускорению свободного падения спутника в любом месте, где он вращается. На уроке 3 уравнение ускорения свободного падения было дано как
Таким образом, ускорение спутника, совершающего круговое движение вокруг некоторого центрального тела, определяется следующим уравнением
, где 6,673 x 10 -11 Н•м 2 /кг 2 , M центральная — масса центрального тела, вокруг которого вращается спутник, а R — средний радиус орбиты для спутниковое.
Уравнение орбитального периода
Последнее уравнение, полезное для описания движения спутников, представляет собой ньютоновскую форму третьего закона Кеплера. Поскольку логика развития уравнения была представлена в другом месте, здесь будет представлено только уравнение.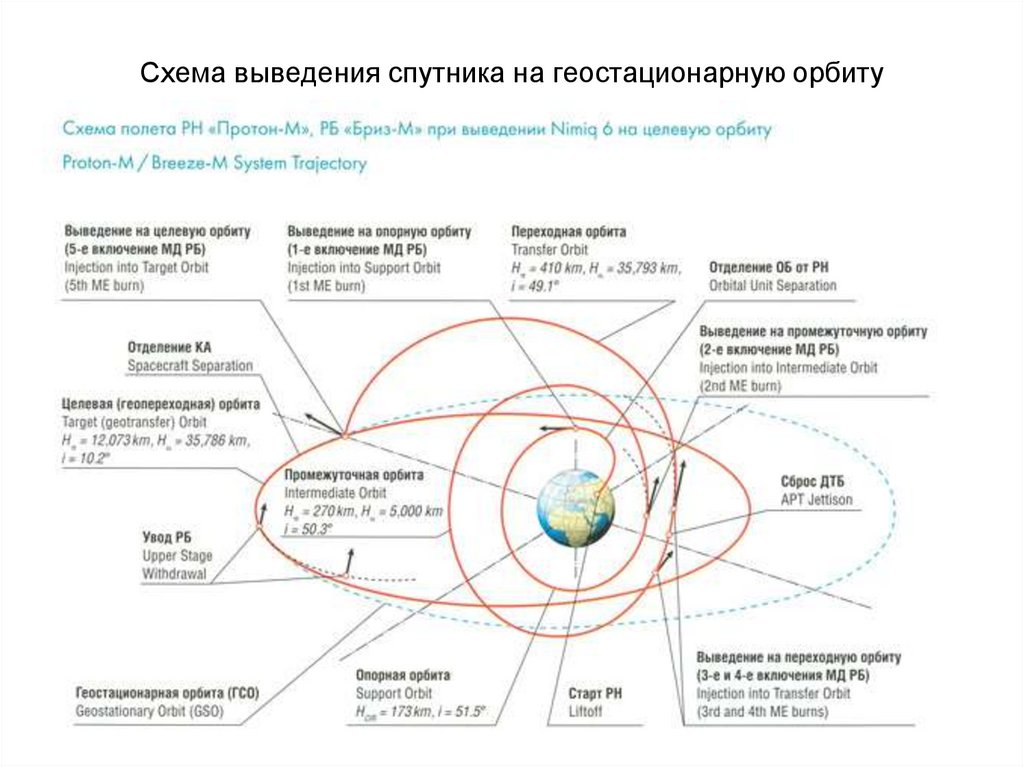 Период спутника ( T ) и среднее расстояние от центрального тела ( R ) связаны следующим уравнением:
Период спутника ( T ) и среднее расстояние от центрального тела ( R ) связаны следующим уравнением:
, где T — период спутника, R — средний радиус орбиты спутника (расстояние от центра центральной планеты), а G — 6,673 x 10 -11 Н•м 2 /кг 2 .
Во всех трех уравнениях очевидна важная концепция: период, скорость и ускорение спутника, находящегося на орбите, не зависят от массы спутника.
Ни в одном из этих трех уравнений нет переменной M спутник в них. Период, скорость и ускорение спутника зависят только от радиуса орбиты и массы центрального тела, вокруг которого вращается спутник. Как и в случае движения снарядов по земле, масса снаряда не влияет на ускорение по направлению к земле и скорость в любой момент. Когда сопротивление воздуха незначительно и присутствует только сила тяжести, масса движущегося объекта перестает быть фактором.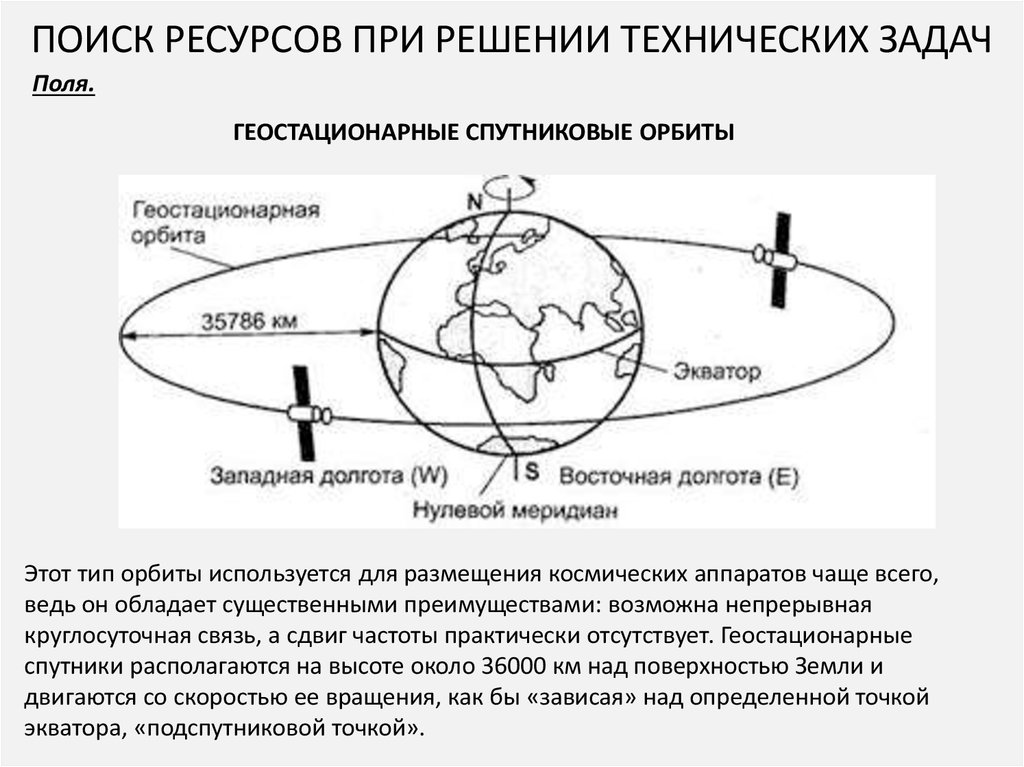 Так обстоит дело с орбитальными спутниками.
Так обстоит дело с орбитальными спутниками.
Примеры задач
Чтобы проиллюстрировать полезность приведенных выше уравнений, рассмотрим следующие практические задачи.
Спутник хочет выйти на орбиту Земли на высоте 100 км (приблизительно 60 миль) над поверхностью Земли. Определить скорость, ускорение и период обращения спутника. (Дано: M земля = 5,98 x 10 24 кг, R земля = 6,37 x 10 6 м) |
Как и большинство задач в физике, эта задача начинается с определения известной и неизвестной информации и выбора подходящего уравнения, способного решить неизвестное. Для этой задачи известные и неизвестные перечислены ниже.
Р = Р земля + высота = 6,47 x 10 6 м M земля = 5,98×10 24 кг G = 6,673 x 10 -11 Н·м 2 /кг 2 | v = ??? а = ??? Т = ??? |
Обратите внимание, что радиус орбиты спутника можно определить, зная радиус Земли и высоту спутника над Землей.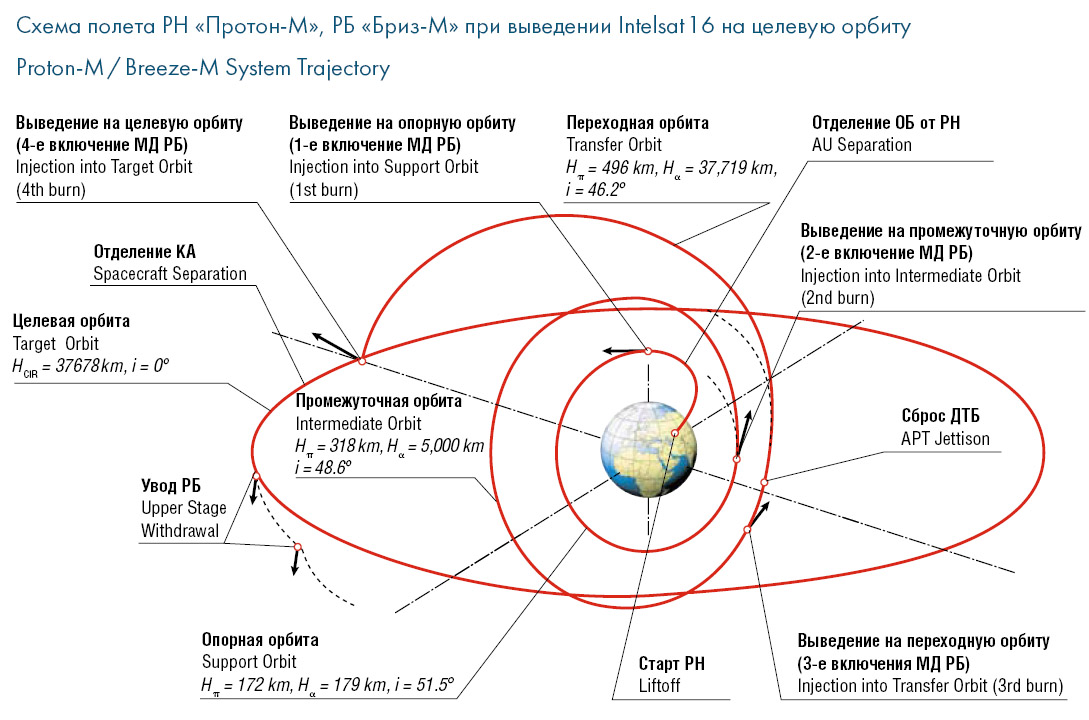 Как показано на диаграмме справа, радиус орбиты спутника равен сумме радиуса Земли и высоты над землей. Эти две величины можно сложить, чтобы получить радиус орбиты. В этой задаче 100 км нужно сначала преобразовать в 100 000 м, прежде чем прибавить к радиусу Земли. Уравнения, необходимые для определения неизвестного, перечислены выше. Мы начнем с определения орбитальной скорости спутника, используя следующее уравнение:
Как показано на диаграмме справа, радиус орбиты спутника равен сумме радиуса Земли и высоты над землей. Эти две величины можно сложить, чтобы получить радиус орбиты. В этой задаче 100 км нужно сначала преобразовать в 100 000 м, прежде чем прибавить к радиусу Земли. Уравнения, необходимые для определения неизвестного, перечислены выше. Мы начнем с определения орбитальной скорости спутника, используя следующее уравнение:
Замена и решение следующие: 2 ) • (5,98 x 10 24 кг) / (6,47 x 10 6 м) ]
v = 7,85 x 10 3 м/с
Ускорение можно найти с помощью одного из следующих уравнений:
Уравнение (1) было получено выше.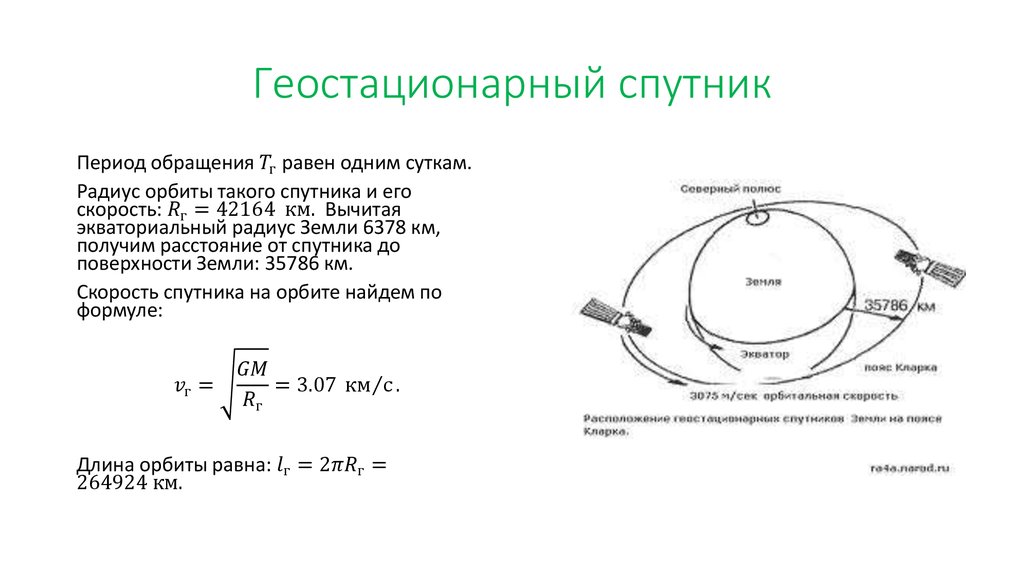 Уравнение (2) является общим уравнением для кругового движения. Любое уравнение может быть использовано для расчета ускорения. Здесь будет продемонстрировано использование уравнения (1).
Уравнение (2) является общим уравнением для кругового движения. Любое уравнение может быть использовано для расчета ускорения. Здесь будет продемонстрировано использование уравнения (1).
a = (6,673 x 10 -11 Н·м 2 /кг 2 ) • (5,98 x 10 24 кг) / (6,47 x 10 6 м) 2
1
а = 9,53 м/с 2
Обратите внимание, что это ускорение немного меньше значения 9,8 м/с 2 , ожидаемого на поверхности земли. Как обсуждалось в Уроке 3, увеличение расстояния от центра Земли снижает значение g.
Наконец, период можно рассчитать с помощью следующего уравнения: 9Уравнение можно преобразовать в следующий вид следующим образом:
Т = 5176 с = 1,44 часа
Период Луны составляет примерно 27,2 дня (2,35 х 10 6 с). |
Как и практическая задача № 2, эта задача начинается с определения известных и неизвестных значений. Они показаны ниже.
Т = 2,35 х 10 6 с M земля = 5,98 x 10 24 кг G = 6,673 x 10 -11 Н·м 2 /кг 2 | Р = ??? v = ??? |
Радиус орбиты можно рассчитать с помощью следующего уравнения:
Уравнение можно преобразовать в следующий вид: ) / (4 • pi 2 ) ]
Подстановка и решение таковы:
R 3 = 5,58 x 10 25 м 3
By taking the cube root of 5. 58 x 10 25 m 3 , the radius can be determined as follows:
58 x 10 25 m 3 , the radius can be determined as follows:
The orbital speed of the satellite можно вычислить из любого из следующих уравнений:
Уравнение (1) было получено выше. Уравнение (2) является общим уравнением для кругового движения. Любое уравнение можно использовать для расчета орбитальной скорости; использование уравнения (1) будет продемонстрировано здесь. Подстановка значений в это уравнение и решение следующие:
v = 1,02 x 10 3 м/с
Геосинхронный спутник — это спутник, обращающийся вокруг Земли с периодом обращения 24 часа, что совпадает с периодом вращения Земли. |
Как и в предыдущей задаче, решение начинается с отождествления известных и неизвестных величин. Это показано ниже.
Т = 86400 с M земля = 5,98×10 24 кг R земля = 6,37 x 10 6 м G = 6,673 x 10 -11 Н·м 2 /кг 2 | ч = ??? |
Неизвестным в этой задаче является высота ( h ) спутника над поверхностью земли.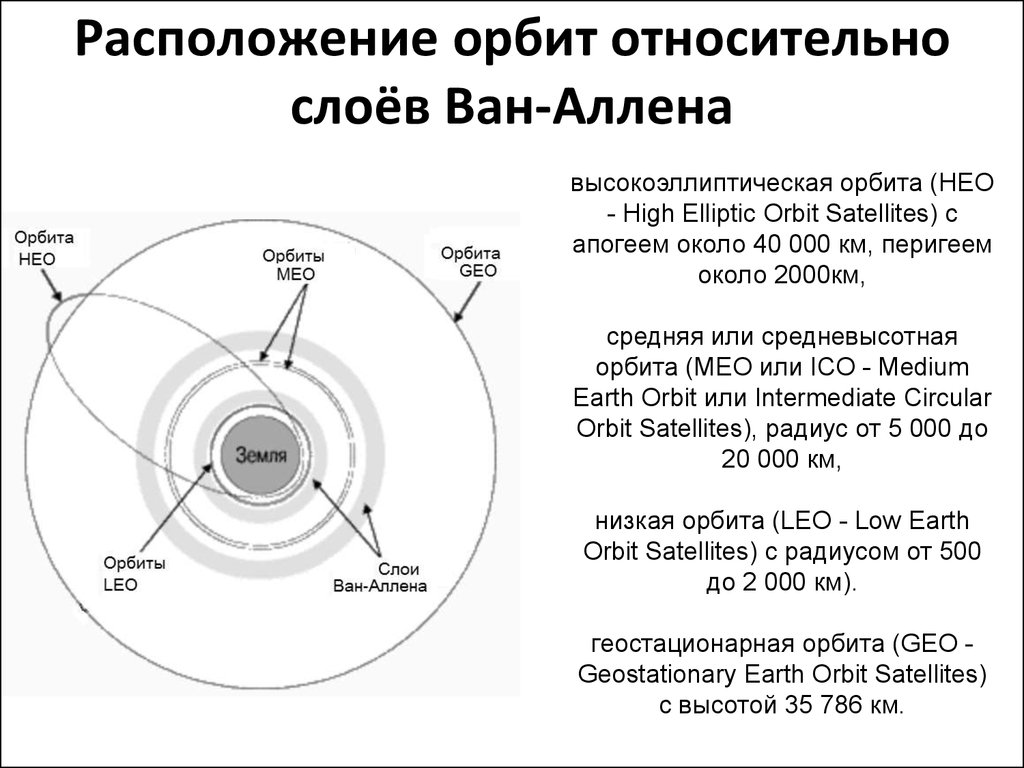 Но нет уравнения с переменной ч . Затем решение включает в себя сначала определение радиуса орбиты и использование этого значения R и R земли для определения высоты спутника над землей. Как показано на диаграмме справа, радиус орбиты спутника равен сумме радиуса Земли и высоты над землей. Радиус орбиты можно найти с помощью следующего уравнения:
Но нет уравнения с переменной ч . Затем решение включает в себя сначала определение радиуса орбиты и использование этого значения R и R земли для определения высоты спутника над землей. Как показано на диаграмме справа, радиус орбиты спутника равен сумме радиуса Земли и высоты над землей. Радиус орбиты можно найти с помощью следующего уравнения:
Уравнение можно преобразовать в следующий вид
Подстановка и решение следующие: x 10 -11 Н·м 2 /кг 2 ) • (5,98×10 24 кг) ) / (4 • (3,1415) 2 ) ]
R 3 = 7,54 x 10 22 м 3
Извлекая кубический корень из 7,54 x 10 22 м 3 , радиус можно определить равным
Радиус орбиты показывает расстояние, на котором спутник находится от центра Земли. Теперь, когда радиус орбиты найден, можно вычислить высоту над землей. Поскольку земная поверхность находится на расстоянии 6,37 x 10 6 м от ее центра (это радиус Земли), спутник должен иметь высоту
Теперь, когда радиус орбиты найден, можно вычислить высоту над землей. Поскольку земная поверхность находится на расстоянии 6,37 x 10 6 м от ее центра (это радиус Земли), спутник должен иметь высоту
над поверхностью земли. Итак, высота спутника 3,59 х 10 7 м .
Расследуй!
Вокруг Земли вращаются сотни искусственных спутников. Список геостационарных спутников можно найти на http://www.satsig.net/sslist.htm. Используйте виджет Satellite Information ниже, чтобы изучить различные свойства — скорость, высоту, орбитальный путь и т. д. — любого существующего спутника. Просто введите название (правильно) спутника и нажмите на кнопку 9.0712 Кнопка «Получить информацию» .
Проверьте свое понимание
1. Спутник вращается вокруг Земли. Какая из следующих переменных повлияет на скорость спутника?
Спутник вращается вокруг Земли. Какая из следующих переменных повлияет на скорость спутника?
а. масса спутника
б. высота над земной поверхностью
в. масса земли
2. Используйте приведенную ниже информацию и соотношение выше для расчета T 2 /R 3 соотношение планет относительно Солнца, Луны относительно Земли и спутников Сатурна относительно планеты Сатурн. Значение G равно 6,673 x 10 -11 Н•м 2 /кг 2 .
а.
T 2 /R 3 для планет вокруг солнца
б. T 2 /R 3 для Луны о Земле
в. T 2 /R 3 для спутников Сатурна
3. Один из спутников Сатурна называется Мимас. Среднее орбитальное расстояние Мимаса составляет 1,87 x 10 8 м. Средний период обращения Мимаса составляет примерно 23 часа (8,28×10 4 с). Используйте эту информацию для оценки массы планеты Сатурн.
4. Рассмотрим спутник, который находится на низкой орбите вокруг Земли на высоте 220 км над поверхностью Земли. Определите орбитальную скорость этого спутника. Используйте информацию, приведенную ниже.
M Земля = 5,98 x 10 24 кг R земля = 6,37 x 10 6 м |
5. Предположим, что космический челнок находится на орбите вокруг Земли на высоте 400 км над ее поверхностью. Используйте информацию, приведенную в предыдущем вопросе, чтобы определить орбитальную скорость и период обращения космического корабля «Шаттл».
Предположим, что космический челнок находится на орбите вокруг Земли на высоте 400 км над ее поверхностью. Используйте информацию, приведенную в предыдущем вопросе, чтобы определить орбитальную скорость и период обращения космического корабля «Шаттл».
Следующий раздел:
Калькулятор орбиты Земли
Автор Джухи Радж, кандидат наук
Отзыв Стивена Вудинга
Последнее обновление: 21 декабря 2022 г.
Содержание:
- Что такое спутники Земли?
- Как рассчитать орбитальную скорость спутника с помощью калькулятора околоземной орбиты
- Как рассчитать период вращения спутника Земли?
- Пример использования этого калькулятора околоземной орбиты
- Часто задаваемые вопросы
Этот калькулятор околоземной орбиты поможет вам определить орбитальную скорость и период обращения спутников Земли на заданной высоте над средним земным уровнем моря.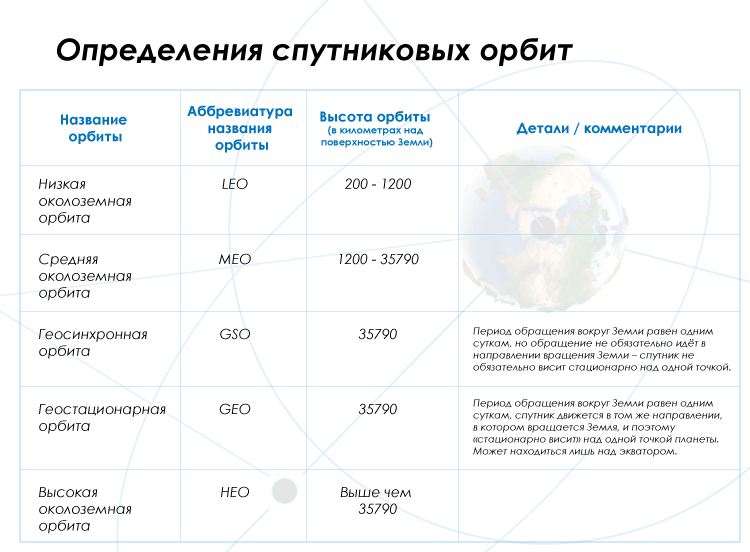 Фундаментальные законы, управляющие движением спутников Земли вокруг Земли, применимы к движению планет, Луны, единственного естественного спутника Земли и других спутников в небе. Читайте дальше, чтобы узнать о том, как различные атрибуты вращения спутника определяются его расстоянием от поверхности Земли.
Фундаментальные законы, управляющие движением спутников Земли вокруг Земли, применимы к движению планет, Луны, единственного естественного спутника Земли и других спутников в небе. Читайте дальше, чтобы узнать о том, как различные атрибуты вращения спутника определяются его расстоянием от поверхности Земли.
Что такое спутники Земли?
Спутник — это небольшой объект, вращающийся вокруг другого более крупного объекта. Земля является спутником, потому что она вращается вокруг Солнца. Мы считаем Луну спутником, потому что она вращается вокруг Земли. Однако большинство людей думают об искусственном спутнике , когда говорят о спутнике . Эти космические корабли выводятся на орбиту вокруг Земли или любого другого небесного тела. Спутник-1 был первым искусственным спутником Земли. Он был выведен на эллиптическую низкую околоземную орбиту высотой 939 км. Он находился на орбите три недели, пока его батареи не разрядились.
Вокруг Земли вращаются десятки тысяч искусственных спутников.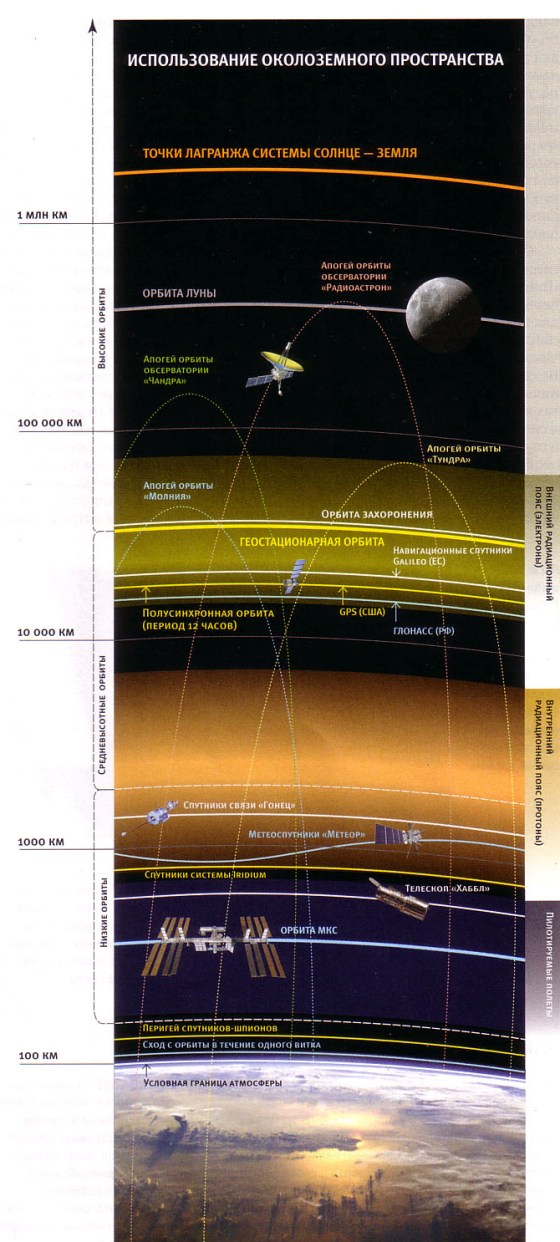 Одни фотографируют наш земной шар, другие — другие планеты, солнце и другие небесные тела. Эти изображения помогают ученым в изучении Земли, Солнечной системы и Вселенной. Другие спутники транслируют телевидение и осуществляют телефонные звонки по всему миру.
Одни фотографируют наш земной шар, другие — другие планеты, солнце и другие небесные тела. Эти изображения помогают ученым в изучении Земли, Солнечной системы и Вселенной. Другие спутники транслируют телевидение и осуществляют телефонные звонки по всему миру.
Этот калькулятор орбиты Земли имеет две функции, которые помогут вам рассчитать орбитальную скорость и период вращения спутника Земли, запущенного на определенной высоте от поверхности земли.
Как рассчитать орбитальную скорость спутника с помощью этого калькулятора орбиты Земли
Согласно Николаю Копернику, Земля и другие планеты вращаются вокруг Солнца по кругу. Он также обнаружил, что по мере увеличения расстояния от Солнца увеличивается и период обращения. Позже Кеплер обнаружил, что эти орбиты представляют собой эллипсы, но орбиты большинства планет Солнечной системы примерно круглые. Орбитальное расстояние Земли от Солнца колеблется всего на 2%. Исключением является эксцентрическая орбита Меркурия, орбитальное расстояние которой изменяется примерно на 40%.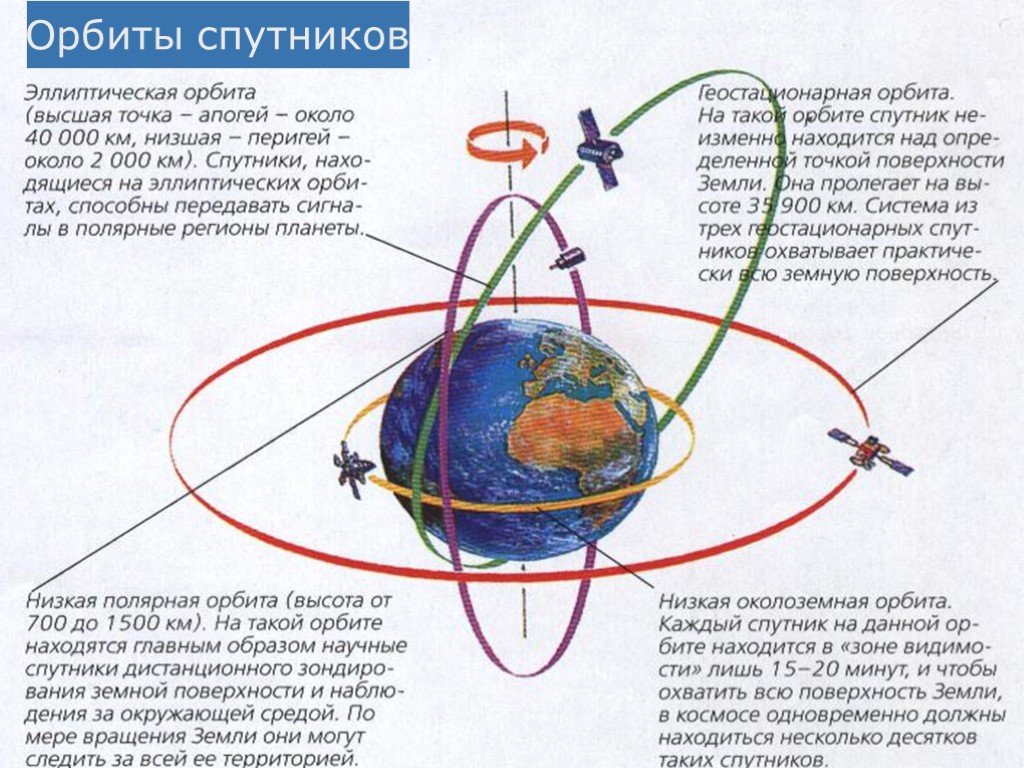
Определение орбитальной скорости и периода спутника значительно проще на круговых орбитах. Мы используем это упрощение в следующих расчетах. Этот инструмент фокусируется на объектах, вращающихся вокруг Земли, но вы можете применить наши выводы и к другим ситуациям. Следовательно, орбитальная скорость (см. Калькулятор орбитальной скорости) спутника Земли определяется следующим образом:
орбитальная скорость=G⋅ME(RE+h)\small
\text{орбитальная скорость} = \sqrt{\frac{G \cdot M_{E}}{(R_{E}+h)}}орбитальная скорость=(RE+h)G⋅ME
где:
- GGG – гравитационная постоянная Земли;
- MEM_EME – масса Земли;
- RER_ERE – радиус Земли; и
- ччч – расстояние от спутника до поверхности земли по перпендикуляру.
Вы можете просто рассчитать это с помощью этого калькулятора орбиты Земли, выбрав опцию Скорость спутника , введя высоту объекта, вращающего Землю, и вуаля, у вас есть орбитальная скорость спутника Земли!
Вам нужна определенная скорость, чтобы выйти на орбиту (и остаться на ней): узнайте, как рассчитать ее с помощью нашего калькулятора дельта-ввв!
Как можно оценить период вращения спутника Земли?
Подобно орбите Земли, все спутники Земли вращаются вокруг Земли на определенной высоте с постоянным периодом вращения.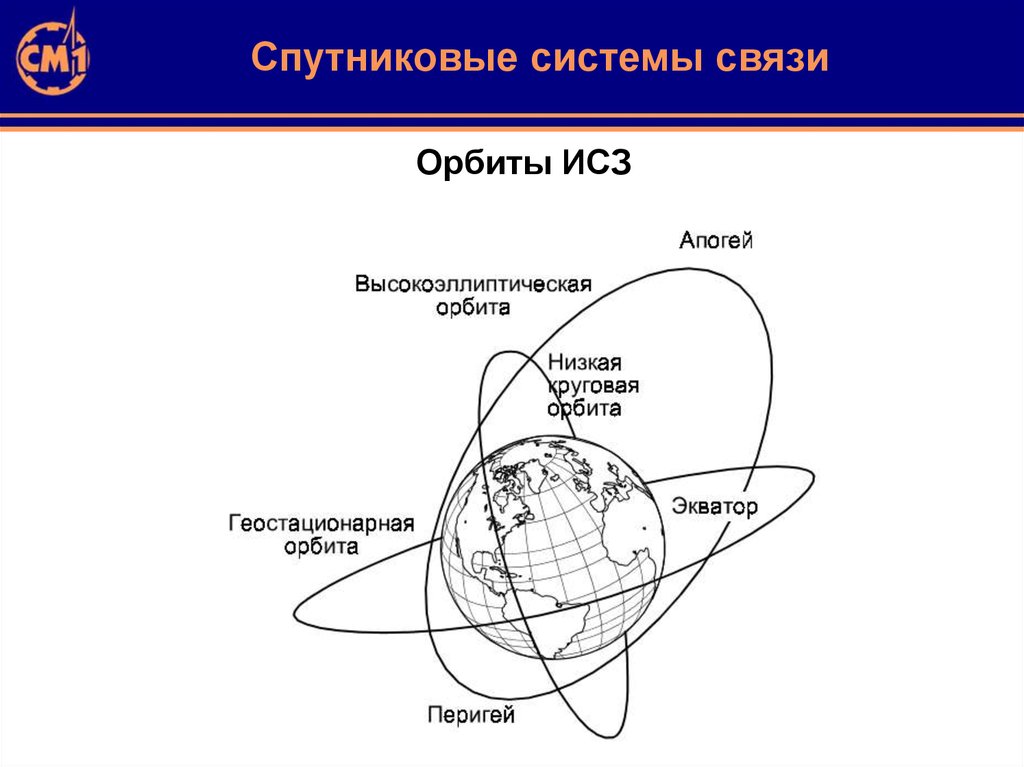 3}{G \cdot M_{E}}}орбитальный период=2πG⋅ME(RE+h) 3
3}{G \cdot M_{E}}}орбитальный период=2πG⋅ME(RE+h) 3
Период обращения
Узнайте больше о том, как рассчитать период обращения, используя наш специальный инструмент по этому вопросу.
Можно выбрать опцию Период вращения спутника ; введите высоту объекта, вращающего землю; теперь вы знаете период обращения спутника Земли!
Пример использования этого калькулятора околоземной орбиты
Попробуем определить орбитальную скорость и период для Международной космической станции (МКС)
Поскольку МКС вращается на высоте 400 км над поверхностью Земли , радиус ее обращения равен R E + 400 км .
Вы можете просто подставить высоту МКС с поверхности земли как 400 км , и калькулятор вычислит период обращения 1,54 часа и орбитальную скорость как 7,672 км/с .
Часто задаваемые вопросы
Как рассчитать орбитальную скорость спутника Земли?
Чтобы рассчитать орбитальную скорость спутника Земли, вам необходимо знать гравитационную постоянную (G), массу Земли (M), радиус Земли (R) и высоту вращения спутника (h).
Орбитальная скорость рассчитывается как:
- √((G × M) / (R + h))
От чего зависит период обращения спутника?
Период обращения спутника зависит от массы планеты, вокруг которой он вращается, и расстояния спутника от центра планеты.
Мы можем получить период обращения спутника T из ньютоновской формы третьего закона Кеплера.
- T 2 = 4 π a 3 / ГМ
, где G — гравитационная постоянная, а M — масса Земли.
Джухи Радж, кандидат наук
Select
Высота
Период обращения
Высота спутника над Землей.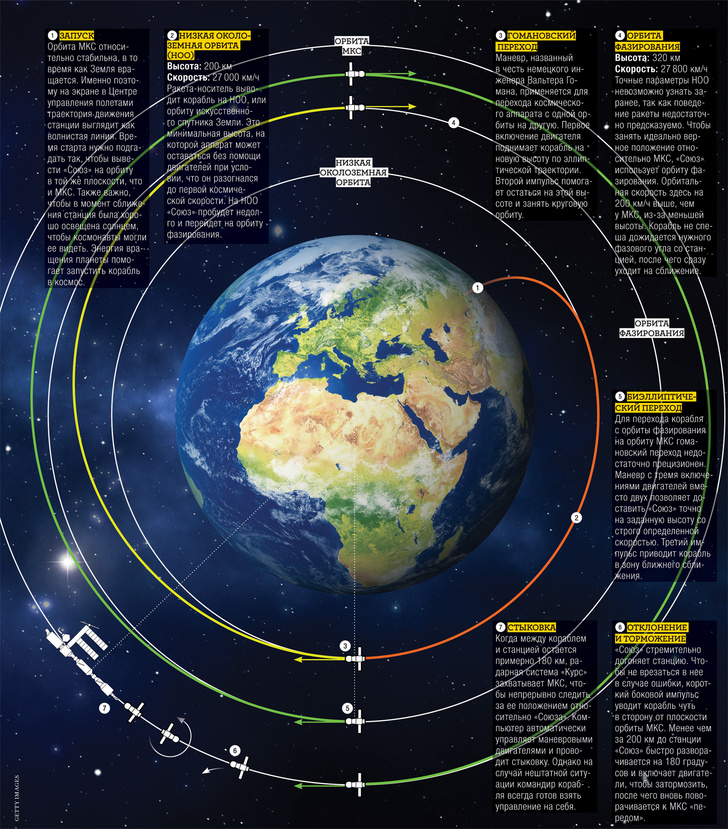

 Определите радиус орбиты Луны и орбитальную скорость Луны. (Дано: M земля = 5,98 x 10 24 кг, R земля = 6,37 x 10 6 м)
Определите радиус орбиты Луны и орбитальную скорость Луны. (Дано: M земля = 5,98 x 10 24 кг, R земля = 6,37 x 10 6 м)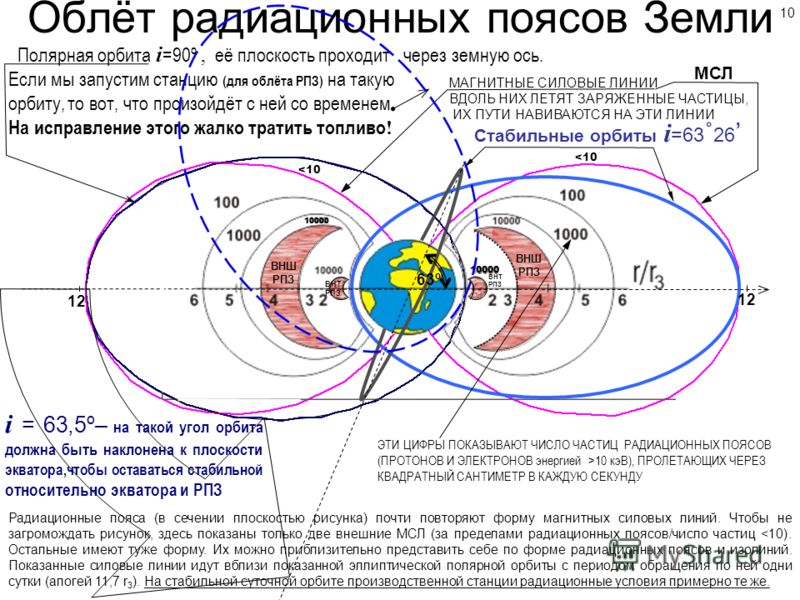 Особым классом геосинхронных спутников являются геостационарные спутники. Геостационарный спутник совершает оборот вокруг Земли за 24 часа по орбитальной траектории, параллельной воображаемой плоскости, проведенной через земной экватор. Такой спутник кажется постоянно закрепленным над одним и тем же местом на Земле. Если геостационарный спутник хочет совершить оборот вокруг Земли за 24 часа (86 400 с), то на какой высоте над земной поверхностью он должен находиться? (Дано: М земля = 5,98×10 24 кг, R земля = 6,37 x 10 6 м)
Особым классом геосинхронных спутников являются геостационарные спутники. Геостационарный спутник совершает оборот вокруг Земли за 24 часа по орбитальной траектории, параллельной воображаемой плоскости, проведенной через земной экватор. Такой спутник кажется постоянно закрепленным над одним и тем же местом на Земле. Если геостационарный спутник хочет совершить оборот вокруг Земли за 24 часа (86 400 с), то на какой высоте над земной поверхностью он должен находиться? (Дано: М земля = 5,98×10 24 кг, R земля = 6,37 x 10 6 м) T 2 /R 3 для планет вокруг солнца
T 2 /R 3 для планет вокруг солнца