Запутанные фотоны: Просто о квантовой запутанности / Хабр

Содержание

Просто о квантовой запутанности / Хабр

Квантовая запутанность – одно из самых сложных понятий в науке, но основные её принципы просты. А если понять её, запутанность открывает путь к лучшему пониманию таких понятий, как множественность миров в квантовой теории.

Чарующей аурой загадочности окутано понятие квантовой запутанности, а также (каким-то образом) связанное с ним требование квантовой теории о необходимости наличия «многих миров». И, тем не менее, по сути своей это научные идеи с приземлённым смыслом и конкретными применениями. Я хотел бы объяснить понятия запутанности и множества миров настолько просто и ясно, насколько знаю их сам.

I


Запутанность считается явлением, уникальным для квантовой механики – но это не так. На самом деле, для начала будет более понятным (хотя это и необычный подход) рассмотреть простую, не квантовую (классическую) версию запутанности. Это позволит нам отделить тонкости, связанные с самой запутанностью, от других странностей квантовой теории.

Запутанность появляется в ситуациях, в которых у нас есть частичная информация о состоянии двух систем. К примеру, нашими системами могут стать два объекта – назовём их каоны. «К» будет обозначать «классические» объекты. Но если вам очень хочется представлять себе что-то конкретное и приятное – представьте, что это пирожные.

Наши каоны будут иметь две формы, квадратную или круглую, и эти формы будут обозначать их возможные состояния. Тогда четырьмя возможными совместными состояниями двух каонов будут: (квадрат, квадрат), (квадрат, круг), (круг, квадрат), (круг, круг). В таблице указана вероятность нахождения системы в одном из четырёх перечисленных состояний.

Мы будем говорить, что каоны «независимы», если знание о состоянии одного из них не даёт нам информации о состоянии другого. И у этой таблицы есть такое свойство. Если первый каон (пирожное) квадратный, мы всё ещё не знаем форму второго. И наоборот, форма второго ничего не говорит нам о форме первого.

С другой стороны, мы скажем, что два каона запутаны, если информация об одном из них улучшает наши знания о другом. Вторая табличка покажет нам сильную запутанность. В этом случае, если первый каон будет круглым, мы будем знать, что второй тоже круглый. А если первый каон квадратный, то таким же будет и второй. Зная форму одного, мы однозначно определим форму другого.

Квантовая версия запутанности выглядит, по сути, также – это отсутствие независимости. В квантовой теории состояния описываются математическими объектами под названием волновая функция. Правила, объединяющие волновые функции с физическими возможностями, порождают очень интересные сложности, которые мы обсудим позже, но основное понятие о запутанном знании, которое мы продемонстрировали для классического случая, остаётся тем же.

Хотя пирожные нельзя считать квантовыми системами, запутанность квантовых систем возникает естественным путём – например, после столкновений частиц. На практике незапутанные (независимые) состояния можно считать редкими исключениями, поскольку при взаимодействии систем между ними возникают корреляции.

Рассмотрим, к примеру, молекулы. Они состоят из подсистем – конкретно, электронов и ядер. Минимальное энергетическое состояние молекулы, в котором она обычно и находится, представляет собой сильно запутанное состояние электронов и ядра, поскольку расположение этих составляющих частиц никак не будет независимым. При движении ядра электрон движется с ним.

Вернёмся к нашему примеру. Если мы запишем Φ■, Φ● как волновые функции, описывающие систему 1 в её квадратных или круглых состояниях и ψ■, ψ● для волновых функций, описывающих систему 2 в её квадратных или круглых состояниях, тогда в нашем рабочем примере все состояния можно описать, как:

Независимые: Φ■ ψ■ + Φ■ ψ● + Φ● ψ■ + Φ● ψ●

Запутанные: Φ■ ψ■ + Φ● ψ●

Независимую версию также можно записать, как:

(Φ■ + Φ●)(ψ■ + ψ●)

Отметим, как в последнем случае скобки чётко разделяют первую и вторую системы на независимые части.

Существует множество способов создания запутанных состояний. Один из них – измерить составную систему, дающую вам частичную информацию. Можно узнать, например, что две системы договорились быть одной формы, не зная при этом, какую именно форму они выбрали. Это понятие станет важным чуть позже.

Более характерные последствия квантовой запутанности, такие, как эффекты Эйнштейна-Подольского-Розена (EPR) и Гринберга-Хорна-Зейлингера (GHZ), возникают из-за её взаимодействия ещё с одним свойством квантовой теории под названием «принцип дополнительности». Для обсуждения EPR и GHZ позвольте мне сначала представить вам этот принцип.

До этого момента мы представляли, что каоны бывают двух форм (квадратные и круглые). Теперь представим, что ещё они бывают двух цветов – красного и синего. Рассматривая классические системы, например, пирожные, это дополнительное свойство означало бы, что каон может существовать в одном из четырёх возможных состояний: красный квадрат, красный круг, синий квадрат и синий круг.

Но квантовые пирожные – квантожные… Или квантоны… Ведут себя совсем по-другому. То, что квантон в каких-то ситуациях может обладать разной формой и цветом не обязательно означает, что он одновременно обладает как формой, так и цветом. Фактически, здравый смысл, которого требовал Эйнштейн от физической реальности, не соответствует экспериментальным фактам, что мы скоро увидим.

Мы можем измерить форму квантона, но при этом мы потеряем всю информацию о его цвете. Или мы можем измерить цвет, но потеряем информацию о его форме. Согласно квантовой теории, мы не можем одновременно измерить и форму и цвет. Ничей взгляд на квантовую реальность не обладает полнотой; приходится принимать во внимание множество разных и взаимоисключающих картин, у каждой из которых есть своё неполное представление о происходящем. Это и есть суть принципа дополнительности, такая, как её сформулировал Нильс Бор.

В результате квантовая теория заставляет нас быть осмотрительными в приписывании свойствам физической реальности. Во избежание противоречий приходится признать, что:

Не существует свойства, если его не измерили.

Измерение – активный процесс, изменяющий измеряемую систему

II


Теперь опишем две образцовые, но не классические, иллюстрации странностей квантовой теории. Обе были проверены в строгих экспериментах (в реальных экспериментах люди меряют не формы и цвета пирожных, а угловые моменты электронов).

Альберт Эйнштейн, Борис Подольский и Натан Розен (EPR) описали удивительный эффект, возникающий при запутанности двух квантовых систем. EPR-эффект объединяет особую, экспериментально достижимую форму квантовой запутанности с принципом дополнительности.

EPR-пара состоит из двух квантонов, у каждого из которых можно измерить форму или цвет (но не то и другое сразу). Предположим, что у нас есть множество таких пар, все они одинаковые, и мы можем выбирать, какие измерения мы проводим над их компонентами. Если мы измерим форму одного из членов EPR-пары, мы с одинаковой вероятностью получим квадрат или круг. Если измерим цвет, то с одинаковой вероятностью получим красный или синий.

Интересные эффекты, казавшиеся EPR парадоксальными, возникают, когда мы проводим измерения обоих членов пары. Когда мы меряем цвет обоих членов, или их форму, мы обнаруживаем, что результаты всегда совпадают. То есть, если мы обнаружим, что один из них красный и затем меряем цвет второго, мы также обнаруживаем, что он красный – и т.п. С другой стороны, если мы измеряем форму одного и цвет другого, никакой корреляции не наблюдается. То есть, если первый был квадратом, то второй с одинаковой вероятностью может быть синим или красным.

Согласно квантовой теории, мы получим такие результаты, даже если две системы будет разделять огромное расстояние и измерения будут проведены почти одновременно. Выбор типа измерений в одном месте, судя по всему, влияет на состояние системы в другом месте. Это «пугающее дальнодействие», как называл его Эйнштейн, по-видимому, требует передачу информации – в нашем случае, информации о проведённом измерении – со скоростью, превышающей скорость света.

Но так ли это? Пока я не узнаю, какой результат получили вы, я не знаю, чего ожидать мне. Я получаю полезную информацию, когда я узнаю ваш результат, а не когда вы проводите измерение. И любое сообщение, содержащее полученный вами результат, необходимо передать каким-либо физическим способом, медленнее скорости света.

При дальнейшем изучении парадокс ещё больше разрушается. Давайте рассмотрим состояние второй системы, если измерение первой дало красный цвет. Если мы решим мерить цвет второго квантона, мы получим красный. Но по принципу дополнительности, если мы решим измерить его форму, когда он находится в «красном» состоянии, у нас будут равные шансы на получение квадрата или круга. Поэтому, результат EPR логически предопределён. Это просто пересказ принципа дополнительности.

Нет парадокса и в том, что удалённые события коррелируют. Ведь если мы положим одну из двух перчаток из пары в коробки и отправим их в разные концы планеты, неудивительно, что посмотрев в одну коробку, я могу определить, на какую руку предназначена другая перчатка. Точно так же, во всех случаях корреляция пар EPR должна быть зафиксирована на них, когда они находятся рядом и потому они могут выдержать последующее разделение, будто бы имея память. Странность EPR-парадокса не в самой по себе возможности корреляции, а в возможности её сохранения в виде дополнений.

III


Дэниел Гринбергер, Майкл Хорн и Антон Зейлингер открыли ещё один прекрасный пример квантовой запутанности. ОН включает три наших квантона, находящихся в специально подготовленном запутанном состоянии (GHZ-состоянии). Мы распределяем каждый из них разным удалённым экспериментаторам. Каждый из них выбирает, независимо и случайно, измерять ли цвет или форму и записывает результат. Эксперимент повторяют многократно, но всегда с тремя квантонами в GHZ-состоянии.

Каждый отдельно взятый экспериментатор получает случайные результаты. Измеряя форму квантона, он с равной вероятностью получает квадрат или круг; измеряя цвет квантона, он с равной вероятностью получает красный или синий. Пока всё обыденно.

Но когда экспериментаторы собираются вместе и сравнивают результаты, анализ показывает удивительный результат. Допустим, мы будем называть квадратную форму и красный цвет «добрыми», а круги и синий цвет – «злыми». Экспериментаторы обнаруживают, что если двое из них решили измерить форму, а третий – цвет, тогда либо 0, либо 2 результата измерений получаются «злыми» (т. е. круглыми или синими). Но если все трое решают измерить цвет, то либо 1 либо 3 измерения получаются злыми. Это предсказывает квантовая механика, и именно это и происходит.

Вопрос: количество зла чётное или нечётное? В разных измерениях реализовываются обе возможности. Нам приходится отказаться от этого вопроса. Не имеет смысла рассуждать о количестве зла в системе без связи с тем, как его измеряют. И это приводит к противоречиям.

Эффект GHZ, как описывает его физик Сидни Колман, это «оплеуха от квантовой механики». Он разрушает привычное, полученное из опыта ожидание того, что у физических систем есть предопределённые свойства, независимые от их измерения. Если бы это было так, то баланс доброго и злого не зависел бы от выбора типов измерений. После того, как вы примете существование GHZ-эффекта, вы его не забудете, а ваш кругозор будет расширен.

IV


Пока что мы рассуждаем о том, как запутанность не позволяет назначить уникальные независимые состояния нескольким квантонам. Такие же рассуждения применимы к изменениям одного квантона, происходящим со временем.

Мы говорим об «запутанных историях», когда системе невозможно присвоить определённое состояние в каждый момент времени. Так же, как в традиционной запутанности мы исключаем какие-то возможности, мы можем создать и запутанные истории, проводя измерения, собирающие частичную информацию о прошлых событиях. В простейших запутанных историях у нас есть один квантон, изучаемый нами в два разных момента времени. Мы можем представить ситуацию, когда мы определяем, что форма нашего квантона оба раза была квадратной, или круглой оба раза, но при этом остаются возможными обе ситуации. Это темпоральная квантовая аналогия простейшим вариантам запутанности, описанным ранее.

Используя более сложный протокол, мы можем добавить чуть-чуть дополнительности в эту систему, и описать ситуации, вызывающие «многомировое» свойство квантовой теории. Наш квантон можно подготовить в красном состоянии, а затем измерить и получить голубое. И как в предыдущих примерах, мы не можем на постоянной основе присвоить квантону свойство цвета в промежутке между двумя измерениями; нет у него и определённой формы. Такие истории реализовывают, ограниченным, но полностью контролируемым и точным способом, интуицию, свойственную картинке множественности миров в квантовой механике. Определённое состояние может разделиться на две противоречащие друг другу исторические траектории, которые затем снова соединяются.

Эрвин Шрёдингер, основатель квантовой теории, скептически относившийся к её правильности, подчёркивал, что эволюция квантовых систем естественным образом приводит к состояниям, измерение которых может дать чрезвычайно разные результаты. Его мысленный эксперимент с «котом Шрёдингера» постулирует, как известно, квантовую неопределённость, выведенную на уровень влияния на смертность кошачьих. До измерения коту невозможно присвоить свойство жизни (или смерти). Оба, или ни одно из них, существуют вместе в потустороннем мире возможностей.

Повседневный язык плохо приспособлен для объяснения квантовой дополнительности, в частности потому, что повседневный опыт её не включает. Практические кошки взаимодействуют с окружающими молекулами воздуха, и другими предметами, совершенно по-разному, в зависимости от того, живы они или мертвы, поэтому на практике измерение проходит автоматически, и кот продолжает жить (или не жить). Но истории с запутанностью описывают квантоны, являющиеся котятами Шрёдингера. Их полное описание требует, чтобы мы принимали к рассмотрению две взаимоисключающие траектории свойств.

Контролируемая экспериментальная реализация запутанных историй – вещь деликатная, поскольку требует сбора частичной информации о квантонах. Обычные квантовые измерения обычно собирают всю информацию сразу – к примеру, определяют точную форму или точный цвет – вместо того, чтобы несколько раз получить частичную информацию. Но это можно сделать, хотя и с чрезвычайными техническими трудностями. Этим способом мы можем присвоить определённый математический и экспериментальный смысл распространению концепции «множественности миров» в квантовой теории, и продемонстрировать её реальность.

Физики построили первый универсальный генератор запутанных фотонов

Физика
Физики смогли

Сложность
6.1

Hui Wang et al. / Physical Review Letters, 2019

Китайские физики построили первый генератор запутанных фотонов, который удовлетворяет четырем ключевым критериям: работает только «по требованию», создает фотоны с высокой степенью запутанности, неразличимости и эффективности. До этого ученым удавалось добиться только трех из этих критериев. Статья опубликована в Physical Review Letters, кратко о ней сообщает Physics, препринт работы выложен на сайте arXiv. org.

Запутанные фотоны — пара частиц, которые находятся в скоррелированных квантовых состояниях, — играют в современной физике очень важную роль. С одной стороны, благодаря запутанным фотонам удалось доказать нелокальность квантовой механики, то есть отсутствие «скрытых параметров», предложенных Альбертом Эйнштейном. С другой стороны, без запутанных пар практически невозможно реализовать квантовую связь и квантовую телепортацию, а также построить квантовые компьютеры, соединенные с квантовым интернетом. Кроме того, с помощью запутанных частиц можно повысить точность измерений и ускорить сбор информации о системе (эти возможности изучает квантовая метрология).

Для всех этих целей важно качество запутанных фотонов, которое определяется следующими четырьмя факторами. Во-первых, генератор должен производить фотоны, квантовое состояние которых совпадает с максимально запутанным состоянием Белла. Степень этого совпадения измеряется параметром «верности» (fidelity): для запутанных состояний этот параметр равен единице, для абсолютно случайных состояний — нулю. Во-вторых, генератор должен генерировать фотоны «по требованию» (on-demand generation), то есть испускать только одну запутанную пару за раз и включаться только в те моменты, когда это нужно для опыта. В-третьих, все испущенные фотоны должны быть извлечены из источника и собраны с высокой степенью эффективности. Другими словами, они не должны поглощаться и теряться внутри генератора. Наконец, запутанные фотоны, испущенные генератором в разные моменты времени, должны быть абсолютно неразличимыми. Если какое-то из этих условий нарушено, физикам приходится искусственно его восстанавливать, отсеивая лишние фотоны. Это усложняет установку и уменьшает число эффективно производимых запутанных пар.

К сожалению, до последнего времени не существовало генератора запутанных фотонов, который удовлетворял бы всем четырем требованиям. Более того, генератор, который удовлетворяет хотя бы трем из четырех требований, удалось построить только в прошлом году. Для этого группа физиков под руководством Цзянь-Вэй Паня (Jian-Wei Pan) использовала процесс спонтанного параметрического рассеяния (подробности можно найти в методичке Алексея Калачёва). Настраивая параметры среды, ученым удалось добиться сравнительно высокой «верности» (57 процентов), эффективности (97 процентов) и неразличимости (96 процентов). К сожалению, в ходе спонтанного параметрического рассеяния запутанные пары рождаются случайно, а не «по требованию», и сопровождаются большим потоком нежелательных незапутанных пар. Поэтому в тот раз исследователи не смогли выполнить второе условие.

В новой же статье группа Паня впервые описывает генератор запутанных фотонов, которые удовлетворяют всем четырем необходимым условиям. На этот раз ученые генерировали фотоны с помощью квантовой точки, помещенной в оптическую полость — «яблочко» круглой мишени диаметром порядка десяти микрометров. Квантовая точка — это область полупроводника, в которой носители заряда (электроны или дырки) ограничены по трем направлениям; более подробно про квантовые точки можно узнать из рассказа физика Михаила Киселева. В данной работе полупроводником выступал арсенид галлия-индия InGaAs.

Микрофотография установки (a), схема прибора, вид сбоку (b) и распределение интенсивности электромагнитного поля, собираемого линзой (c)

Hui Wang et al. / Physical Review Letters, 2019

Поделиться

Преимущество квантовых точек перед другими генераторами запутанных фотонов заключается в том, что они практически сразу удовлетворяют трем из четырех критериев. В самом деле, квантовая точка испускает пару запутанных фотонов за счет распада возбужденного состояния, которое предварительно нужно создать, посветив на точку лазером. Следовательно, управлять производством запутанных пар сравнительно легко. Кроме того, «верность» и неразличимость фотонов, производимых таким путем, сравнительно высока: например, в прошлом году группа физиков под руководством Даниэля Хубера (Daniel Huber) получила для этих параметров значения 98 и 93 процента соответственно. Единственный параметр, который оставалось «докрутить» ученым — это эффективность извлечения запутанных фотонов. Для этого физики положили под квантовую точку золотое зеркало, поместили ее в «яблочко» круглой мишени, составленной из полимерных колец, и поместили над точкой собирающую линзу. Согласно расчетам ученых, такая конструкция должна довести эффективность извлечения фотонов до 90 процентов. Кроме того, она должна в 20 раз увеличить скорость генерации запутанных фотонов, что тоже важно для практических применений.

Построенная учеными установка генерировала фотоны с «верностью» и неразличимостью порядка 90 процентов, эффективностью извлечения 62 процента и скоростью генерации 59 процентов (то есть создавала запутанные пары только «по требованию»). Стоит отметить, что ни одно из этих чисел не является рекордным, однако добиться таких высоких результатов одновременно ранее никому не удавалось. Таким образом, разработанный физиками генератор — первый генератор, который удовлетворяет всем четырем ключевым критериям.

С каждым годом физики все больше и больше совершенствуют генераторы запутанных фотонов. Например, в июне 2018 исследователи из Технического университета Делфта (Нидерланды) впервые построили квантовую сеть, которая непрерывно генерировала и передавала запутанные состояния со скоростью, превышающей скорость их декогеренции (разрушения). По словам ученых, это открытие — первый шаг на пути к квантовому интернету. А в июле 2018 австрийские физики заставили квантовую точку излучать запутанные фотоны с рекордно высоким значением «верности» f ≈ 0,98, не прибегая к постобработке сигнала. В новой статье группа Паня развивала именно этот подход.

О том, как физики изучают нелокальность квантовой механики и «телепортируют» состояния частиц с помощью запутанных фотонов, подробно рассказывают материалы «Квантовая азбука: Нелокальность» и «Квантовая азбука: Телепортация». А узнать, как устроена первая в России линия квантовой связи, по которой передают запутанные фотоны, можно в материале «Выдергиваете и сжигаете».

Дмитрий Трунин

Читайте также

Привязанность к смартфону связали с поиском смысла жизни

SpaceX и NASA изучат возможность полета корабля Dragon к телескопу «Хаббл»

Нобелевскую премию по физиологии или медицине присудили за изучение древних людей

Человек, который собрал древних

Кто такой Сванте Паабо, лауреат Нобелевской премии по физиологии и медицине 2022 года

квантовая запутанность — Телеканал «Наука»

«Бог не играет в кости» — «Не указывайте Богу, что ему делать». Квантовая запутанность породила спор Эйнштейна и Бора.

Запутанность — пожалуй, самое интересное свойство, отличающее квантовый мир от классического. Оно лежит в основе доказательства принципиальной неопределенности событий в квантовом мире, и на нем основаны современные квантовые технологии, такие как квантовая связь, квантовые вычисления и сверхточные квантовые измерительные приборы.

Буквально на днях американские физики изобрели сверхточные атомные часы на базе квантово-запутанных атомов, а группа китайских ученых продемонстрировала оптический квантовый вычислитель, работающий во много раз быстрее самого быстрого классического суперкомпьютера.

Само понятие «запутывание» ввел Эрвин Шредингер в 1935 году — тот самый физик-теоретик, который «мучил» воображаемого кота. Однако в широкое употребление понятие вошло лишь в 1990-е годы, с появлением первых систем квантовой связи и прототипов квантовых компьютеров.

Что же такое квантовая запутанность? Мы побеседовали о ней с Константином Катамадзе, кандидатом физико-математических наук, старшим научным сотрудником лаборатории физики квантовых компьютеров ФТИАН РАН и лаборатории квантовых оптических технологий физического факультета МГУ.

— Константин, можно ли просто и понятно объяснить, что такое квантовая запутанность?

— Давайте для начала поясним, что такое запутанное состояние (или перепутанное, сцепленное, связанное, переплетенное — в русском языке есть много вариантов перевода термина entangle). Начнем с того, что квантовая запутанность — это всегда история о двухчастичной системе — один атом или фотон не может быть перепутанным. Система может быть и многочастичной, но тогда для определения ее запутанности все равно нужно разделить ее на две подсистемы и рассматривать их корреляции.

Чтобы частицы были перепутанными, они должны были когда-то провзаимодействовать. Если они никогда не взаимодействовали, значит, они не перепутаны. Как пример: две частицы образовались в результате распада одной частицы. Но дальше они физически не взаимодействуют, никаких сил между ними нет. Просто их состояние таково, что они проявляют корреляции в разных измерениях, которые нельзя описать с точки зрения классической физики.

— Математически это выражается в каком-то уравнении?

— Квантовые состояния описываются волновой функцией. Соответственно, если у нас есть две системы, то они описываются совместной волновой функцией Ψ (x1, x2), которая зависит от параметров первой системы (x1) и второй системы (x2). И если эту совместную волновую функцию нельзя представить в виде произведения волновых функций ее подсистем, то такое состояние называется запутанным. Физически это означает, что параметры этих систем связаны друг с другом. И если я измеряю параметр одной системы, то я сразу получаю информацию о параметре другой системы.

Важно отличать перепутанные состояния от состояний, проявляющих классические корреляции. Приведу простой пример классических корреляций. У нас есть пьяный стрелок с двуствольным ружьем. Он случайным образом палит во все стороны. И понятно, что каждая пуля — независимо от того, из какого дула она вышла, — может попасть в любую сторону. Но поскольку стрелок одновременно выпускает две пули, то куда пошла одна пуля, туда же примерно пойдет и другая. Эти пули друг с другом более-менее связаны, и если я измерю координаты одной, то примерно смогу понять, куда попала другая.

Еще пример классической корреляции. У меня есть пара сапог из одной коробки. Я случайным образом кладу один в одну коробку, другой — в другую. Один отправляется коллеге на Марс, другой — на Венеру. Они получают их, открывают коробки и видят: «Ага, у меня сапог левый, значит, у него правый». И наоборот: «Ага, у меня правый, значит, у него левый!» То есть, измерив состояние сапога в своей коробке, они могут понять состояние сапога у коллеги на другой планете.

— Понятно. А что же такое неклассические корреляции, которые проявляются при перепутанности?

— Представьте, что мы с сапогами можем проводить некий другой тип измерения, который одинаково — что для правого, что для левого — давал бы с равной вероятностью разные результаты. Например, я могу брать сапог, подбрасывать и смотреть, куда он упадет: направо или налево — так раньше гадали. И вот мои экспериментаторы на Марсе и Венере так же сапоги подбрасывают, и если их сапоги падают в одну и ту же сторону, то получается, что результаты их измерений связаны независимо от того, какой тип измерений они проводят. Вот такие неклассические корреляции и называются запутанностью.

— Зачем вся эта запутанность вообще была нужна и что она порождает?

— Начнем с фундаментальной истории, которая называется «проверка нарушений неравенства Белла». Что это такое? Существует глубокий философский вопрос о том, предсказуем наш мир или нет, принцип детерминизма. Можно ли определить, как все дальше будет развиваться, или это невозможно и есть принципиальная неопределенность? Долгое время разные ученые и философы считали, что мир предсказуем. Грубо говоря, еще в школе нас учили: если мы кинем шар под углом к горизонту с такой-то скоростью, траекторию можно посчитать. А когда человечество столкнулось с квантовой физикой, выяснилось, что квантовая теория не дает ответа на вопрос, как будет вести себя результат измерения в каждом конкретном эксперименте.

Допустим, фотон летит на светоделитель (полупрозрачную пластинку). С вероятностью 50% он отразится, с вероятностью 50% пройдет. Но квантовая физика не дает ответа на вопрос, как он поведет себя в каждом конкретном эксперименте. И многие отцы-основатели квантовой физики были с этим не согласны, считали, что это какой-то косяк этой теории. В частности, Эйнштейн считал, что это неполнота теории, что эта теория плохая и скоро придумают «нормальную» теорию, которая будет все хорошо описывать. То, что теория не может ответить, что будет в каждом конкретном случае, — это бред какой-то, так быть не может! У Эйнштейна была большая полемическая переписка с Нильсом Бором. Он писал: «Бог не играет в кости», на что Бор отвечал: «Не указывайте Богу, что ему делать».

И этот вопрос глубоко философский, на самом деле. Оказывается, его можно решить, как раз проводя эксперименты над перепутанными состояниями. И такой эксперимент называется «проверка нарушений неравенства Белла». Этот эксперимент показывает, что мир не детерминирован. Впервые такой эксперимент был проведен в 1972 году, но с тех пор разные ученые продолжают спорить о его результатах, искать возможные дыры в методике его проведения, и последний масштабный эксперимент такого рода, в котором вроде бы все известные дыры были закрыты, был проведен в 2015 году.

— Как практически можно применять квантовую запутанность?

— Если говорить про прикладные применения запутанности, то это квантовая метрология, квантовая связь и квантовые вычисления. В разных метрологических приложениях использование перепутанных частиц позволяет точнее измерять время, расстояние, электрические и гравитационные поля и пр.

Перепутанность является ресурсом в квантовых вычислениях. Дело в том, что если у нас есть многочастичная (например, многофотонная) система, то в общем случае состояние такой системы будет перепутано. Оказывается, что для описания такого состояния нужно очень много информации. Если я увеличиваю число квантовых битов, у меня количество коэффициентов будет расти как 2n. То есть это очень быстрый экспоненциальный рост. (Сейчас в связи с ковидной пандемией мы все усвоили, что такое экспоненциальный рост, когда количество зараженных раз в две-три недели удваивалось.) Таким образом, если у меня будет хотя бы 50–60 квантовых битов, то мне никакого компьютера не хватит, чтобы записать туда их состояние.

Если я не могу рассчитать квантовую систему, значит, я могу делать с этой системой что-то, что не может обычный компьютер. Это лежит в основе квантового вычисления. Сейчас разрабатываются разные квантовые вычислители — пока у них довольно ограниченное число квантовых бит, несколько десятков, но, когда их будет несколько сотен или тысяч, тогда уже это будут системы, на которых можно будет решать определенный круг важных задач.

Буквально две недели назад группа китайских ученых продемонстрировала квантовый симулятор, у которого был стоканальный интерферометр, и там на входе были такие хитрые сжатые состояния света (состояния, которые содержат только четное число фотонов). Ученые измеряли число фотонов на его выходах и показали, что получить аналогичные результаты с помощью обычного компьютера невозможно. Даже у суперкомпьютера это займет десятки и сотни лет. Это то, что называется квантовым превосходством.

Впервые аналогичный эксперимент, демонстрирующий квантовое превосходство, провела компания Google, но они использовали не фотоны, а сверхпроводящие кубиты.

Тут, конечно, нужно понимать, что пока такой квантовый симулятор решает лишь одну задачу — симулирует сам себя. Но это первый шаг к квантовым симуляторам, которые смогут решать задачи квантовой химии, логистики и другие полезные задачи.

— Еще всех, конечно же, интересует криптография — передача информации без возможности ее перехватить. Расскажите о квантовой связи: как она работает?

— Суть квантовой связи состоит в том, что, если мы кодируем информацию квантовыми системами и если кто-то хотел бы ее по дороге послушать и считать, он проведет измерения над этой квантовой системой и неизбежно ее возмутит, изменит ее состояние, и таким образом это прослушивание будет вскрыто.

— Как именно происходит квантовое распределение ключа? Один фотон шифрует сообщение при передаче, а с помощью другого происходит дешифрация на приемнике?

— Смысл процедуры в том, чтобы у Алисы и Боба (так традиционно называют пользователей криптографических систем) была одинаковая последовательность нулей и единиц — ключ. Имея такой ключ, Алиса может зашифровать информацию, передать ее Бобу по открытому информационному каналу, а Боб, имея такой же ключ, сможет ее расшифровать. Доказано, что если длина ключа равна длине сообщения, то расшифровать информацию без ключа невозможно.

Квантовое распределение ключа — это процедура, в результате которой Алиса и Боб получают эту самую последовательность нулей и единиц, которой точно никто другой не обладает. Один из способов ее получить — это проводить измерения над перепутанными фотонами. Тогда результаты измерений фактически и будут представлять собой эту последовательность. Чтобы убедиться, что процедура распределения ключа происходила правильно, что никто по дороге ничего не подслушивал, Алиса и Боб часть ключа сверяют по открытому каналу и смотрят на процент ошибок. Если ошибок нет, значит, никто ничего не подслушивал, и оставшуюся часть ключа можно использовать для кодирования полезной информации.

К сожалению, пока что системы квантового распределения ключа ограничены по дальности, поскольку квантовые состояния нельзя усилить. Есть идея «квантовых повторителей», но технически они пока что не реализованы.

— Были ли примеры удачной квантовой связи на расстоянии?

— Самый масштабный эксперимент такого рода был поставлен несколько лет назад китайцами. Они со спутника распределяли пары перепутанных фотонов: один фотон летел в один город, другой — в другой город. Расстояние между городами было более 1000 км. В этих двух городах проводили измерения над этими фотонами, и результаты были коррелированы, их можно было использовать дальше для кодирования информации и передачи секретных сообщений. Но это, конечно, демонстрационный эксперимент. А коммерчески доступные системы квантовой криптографии на сегодня ограничены дальностью около 100 км.

— В научно-популярных роликах нередко говорят о взаимовлиянии одной частицы на другую из запутанной пары. Может ли быть такое, что мы, воздействуя на один фотон, на дальнем расстоянии воздействуем и на другой, если они перепутаны?

— Это распространенное заблуждение. Никакого дальнодействия между перепутанными частицами нет, и никакого взаимодействия — тоже.

Есть такое понятие «квантовая нелокальность». Термин может ввести людей в заблуждение. Обычно нелокальность понимается так: когда я что-то делаю в одной точке, то моментально что-то меняется в другой точке. Вспомним пример с сапогами: я открыл сапог на Венере и узнал, какой сапог на Марсе. До моего измерения состояние сапога на Марсе не было определено, а после я точно знаю, что он правый. Это является моментальным нелокальным изменением его состояния? Конечно, нет! Измерение сапога на Венере никак не повлияло на результат измерения сапога на Марсе — просто результаты этих измерений будут противоположны друг другу. Даже если у меня есть перепутанные частицы, я не могу сделать что-то в точке А, что приведет к каким-то изменениям в точке B. То есть я не могу передавать информацию быстрее скорости света, как многие думают. Я не меняю состояние системы, но результаты моих измерений коррелированы с результатами измерений в другой точке.

С другой стороны, такая квантовая нелокальность существует «на бумаге». Дело в том, что измерение, проводимое над квантовой системой, изменяет ее квантовое состояние, ее волновую функцию. И если две системы описываются общей волновой функцией, то измерение, проведенное над одной из них, меняет общую волновую функцию и таким образом меняет и волновую функцию второй системы. Но, как говорил известный ученый Ашер Перес, квантовые явления происходят не в пространстве волновых функций, а в лаборатории, и вот в лаборатории никакой нелокальности не наблюдается.

— А что такое квантовая телепортация? Сам термин звучит интригующе — в духе научной фантастики.

— Как мы говорили, в квантовой физике ключевую роль играет неопределенность.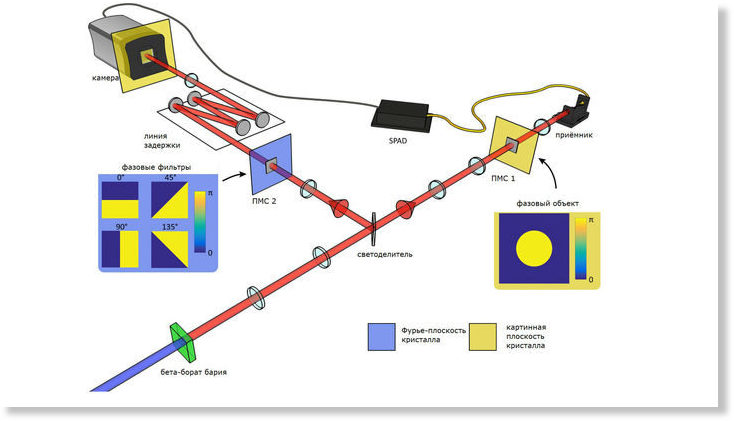 Я не могу заранее предсказать, как поведет себя квантовый объект при том или ином измерении. Поэтому, чтобы точно мое квантовое состояние померить, мне нужно взять много-много копий одного и того же состояния, провести над ними много разных измерений, и тогда я могу определить вероятность, с которой они в разных случаях дают те или иные результаты измерений. Но за один раз я квантовое состояние померить не могу.

А теперь представьте, что у меня есть задача телепортировать какой-то объект из точки А в точку В. Если это классический объект (например, я хочу телепортировать стул), я его измеряю, смотрю, из чего он состоит, строю чертежи, пересылаю в точку В, там находят такой же материал и по моему чертежу делают такой же стул. Элементарно! А если стул квантовый, то возникает проблема: я не могу свой квантовый стул измерить. А я хочу, чтобы в точке В появился стул ровно такой же. И на этот счет есть специальная процедура квантовой телепортации, которая позволяет мне перенести состояние одной системы на состояние другой системы.

Допустим, у меня есть два атома. Один находится в ловушке в точке А, второй — в точке В. Я хочу состояние атома в точке А скопировать и перенести на состояние атома в точке В. Это я могу сделать. Для этого можно использовать запутанные фотоны: когда я над своим атомом и фотоном произвожу совместное измерение, о результатах этого измерения сообщаю своему коллеге, и он проводит определенные манипуляции со своим фотоном и атомом. И в результате он получает, что его атом в таком же состоянии, в котором был атом у меня до того, как я провел свои измерения. При этом мой атом вследствие моих манипуляций уже перешел в другое состояние. Это квантовая телепортация.

«Квантовая физика дает надежду на то, что судьбы нет»

Все переплетено, но не предопределено

Нобелевскую премию по физике получил выдающийся автор безумных идей

На сайте могут быть использованы материалы интернет-ресурсов Facebook и Instagram, владельцем которых является компания Meta Platforms Inc. , запрещённая на территории Российской Федерации

  • Физика всего

  • Остальные теги

Расскажите друзьям

    • Хтоническое

    Геофизики предсказывают обратное слияние континентов

    • Живое
    • Устройство человека

    Ученые выяснили, по каким признакам можно определить наличие «генов долголетия»

    • Что было раньше

    Невероятно реалистичные реконструкции лиц средневековых женщины, священника и епископа

    • Околонаука

    Нобелевскую премию по физиологии и медицине присудили Сванте Паабо

    • Околонаука

    Стартовал второй сезон конкурса детского научно-популярного видео «Знаешь? Научи!» 

  • Shoji Takeuchi

    Создан первый в мире робопалец с живой кожей

  • Челябинский метеорит, кристаллы

    Sergey Taskaev et al. /European Physical Journal Plus, 2022

    В пыли Челябинского метеорита нашли невиданные ранее кристаллы

  • Shutterstock

    Тайны Черного моря

  • Хомо футурис. Каким будет человек будущего?

  • University of Michigan

    Химический анализ бивня мастодонта рассказал о поведении вымершего животного

Хотите быть в курсе последних событий в науке?

Оставьте ваш email и подпишитесь на нашу рассылку

Ваш e-mail

Нажимая на кнопку «Подписаться», вы соглашаетесь на обработку персональных данных

Запутанные фотоны что это

Квантовая запутанность остаётся объектом пристального внимания учёных уже многие десятилетия.

Принципиальная схема визуализации квантовой запутанности фотонов.

Изображения, прошедшие различные фазовые фильтры, демонстрируют, что камера регистрировала фотоны с изменённой фазой.

Квантовая запутанность – одно из самых удивительных явлений в квантовом мире. Новое исследование впервые позволило человечеству буквально увидеть его.

«Вести.Наука» (nauka.vesti.ru) подробно рассказывали о квантовой запутанности. Напомним в двух словах, о чём речь. Когда два объекта (обычно используются фотоны) запутаны друг с другом, изменение в состоянии одного мгновенно отражается на состоянии другого, какое бы расстояние их ни разделяло. При этом никаких физических взаимодействий между двумя запутанными частицами нет. Волшебство? Наука.

В новом эксперименте физики создавали пары запутанных фотонов. Для этого они облучали кристалл бета-бората бария ультрафиолетом. Испускаемый кристаллом свет попадал на светоделитель, разделяющий световой луч надвое. При этом фотоны первого луча оказывались запутанными с фотонами второго. Каждый луч проходил через собственный пространственный модулятор света (ПМС).

Помимо этого первый луч встречал на своём пути так называемый фазовый объект, который менял фазу фотонов.

Далее первый луч поступал на приёмник. По оптоволокну фотоны добирались от него до однофотонного лавинного диода (single-photon avalanche diode, или SPAD). Этот прибор порождал кратковременный, но заметный электрический ток даже в ответ на приход одного фотона.

Ток, порождаемый SPAD, включал сверхчувствительную камеру. Камера была установлена так, чтобы в её объектив падал второй луч.

Но второй луч не встречал на своём пути устройства, меняющего фазу. Зато он проходил через фазовые фильтры, пропускающие только фотоны с определённой фазой.

Чтобы не потеряться в этом обилии терминов и процессов, поясним разницу между первой и второй ситуацией «на пальцах». Вообразим, что луч света – это поток не фотонов, а людей. На пути первого потока стоит сумасшедший модельер, который насильно всех переодевает (это изменение фазы). Второй поток встречается со строгими охранниками, которые никого не переодевают, но пропускают лишь тех, кто соответствует заявленному дресс-коду (это фазовый фильтр). При этом охранникам можно дать инструкцию пропускать (или, наоборот, задерживать) лишь тех, кто одет согласно вкусу модельера. Благодаря этому можно судить о том, подвергся ли влиянию безумного модельера тот поток людей, что не встречался с ним самим.

Возвращаясь к физике, можно сказать, что фазовые фильтры помогают понять, изменилась ли фаза фотонов второго луча (которые не встречались с меняющим фазу объектом), однако известно, что это делали запутанные с ними «близнецы» из первого луча.

Первый фотон из пары инициировал включение камеры как раз тогда, когда до неё добирался второй фотон из пары (если его пропускали фазовые фильтры). Для этого путь второго луча был удлинён специальной линией задержки, состоящей из четырёх зеркал.

Камера фиксировала, достиг ли её второй фотон, то есть пропустили ли его фазовые фильтры.

Эксперимент подтвердил, что первый фотон менял фазу синхронно со вторым, несмотря на то, что он не проходил через меняющий фазу объект. Так и должно было быть, поскольку фотоны в первом и втором лучах были запутаны между собой, и изменение в состоянии одного моментально отражалось на состоянии другого.

«Изображение, которое нам удалось запечатлеть, является элегантной демонстрацией фундаментального свойства природы, впервые зафиксированного в форме изображения. Это захватывающий результат, который можно использовать для развития новой области квантовых вычислений и создания новых типов визуализации [квантовых явлений]», – объясняет первый автор статьи Поль-Антуан Моро (Paul-Antoine Moreau) из Университета Глазго.

К слову, ранее «Вести.Наука» рассказывали о том, как свет древнейших квазаров подтвердил реальность квантовой запутанности, и об эксперименте по выявлению возможного влияния гравитации на этот феномен.

Здравствуйте, дорогие читатели! Добро пожаловать на блог!

Что такое квантовая запутанность простыми словами? Телепортация – возможно ли это? Доказана ли экспериментально возможность телепортации? Что такое кошмар Энштейна? В этой статье Вы получите ответы на эти вопросы.

Вступление

Мы в фантастических фильмах и книгах часто встречаемся с телепортацией. Вы задумывались, почему то, что придумали писатели, со временем становится нашей реальностью? Как им удаётся предсказывать будущее? Думаю, это не случайность. Часто писатели-фантасты обладают обширными знаниями по физике и другим наукам, что в сочетании с их интуицией и незаурядной фантазией помогает им построить ретроспективный анализ прошлого и смоделировать события будущего.

Из статьи Вы узнаете:

  • Что такое квантовая запутанность?
  • Спор Энштейна с Бором. Кто прав?
  • Теорема Белла. Спор разрешён?
  • Подтверждена ли телепортация экспериментально?

Понятие «квантовая запутанность» появилось из теоретического предположения, вытекающего из уравнений квантовой механики. Оно означает вот что: если 2 квантовые частицы (ими могут быть электроны, фотоны) оказываются взаимозависимыми (запутанными), то связь сохраняется, даже если их разнести в разные части Вселенной

Открытие квантовой запутанности в некоторой степени объясняет теоретическую возможность телепортации.

Если получить пару фотонов одновременно, то они окажутся связанными (запутанными). А если замерить спин одного из них и он окажется положительным, то спин 2-го фотона – будьте уверены – мгновенно станет отрицательным. И, наоборот. Что такое Квантовая физика и Спин можете узнать из Квантовая физика простыми словами. А если Вам интересно узнать о практическом применении квантовой физики, читайте статью Что такое квантовый компьютер? Просто о сложном.

Если коротко, то спином квантовой частицы (электрона, фотона) называется ёё собственный угловой момент. Спин можно представить в виде вектора, а саму квантовую частицу – в виде микроскопического магнитика.

Важно понять, что когда за квантом, например, электроном никто не наблюдает, то он имеет все значения спина одновременно. Это фундаментальное понятие квантовой механики называется «суперпозицией».

Представьте, что Ваш электрон вращается одновременно по часовой стрелке и против часовой стрелки. То есть он сразу в обоих состояниях спина (вектор спина вверх/вектор спина вниз). Представили? ОК. Но как только появляется наблюдатель и измеряет его состояние, электрон сам определяет, какой вектор спина ему принять – вверх или вниз.

Хотите узнать, как измеряют спин электрона? Его помещают в магнитное поле: электроны со спином против направления поля, и со спином по направлению поля отклонятся в разные стороны. Спины фотонов измеряют, направляя в поляризационный фильтр. Если спин (или поляризация) фотона «-1», то он не проходит через фильтр, а если «+1», то проходит.

Резюме. Как только Вы измерили состояние одного электрона и определили, что его спин «+1», то связанный или «запутанный» с ним электрон принимает значение спина «-1». Причём моментально, даже если он находится на Марсе. Хотя до измерения состояния 2-го электрона, он имел оба значения спина одновременно («+1» и «-1»).

Этот парадокс, доказанный математически, очень не нравился Энштейну. Потому что он противоречил его открытию, что нет скорости больше, чем скорость света. Но понятие запутанных частиц доказывало: если одна из запутанных частиц будет находиться на Земле, а 2-я – на Марсе, то 1-я частица в момент замера ёё состояния мгновенно (быстрее скорости света) передаёт 2-й частице информацию, какое значение спина ей принять. А именно: противоположное значение.

Спор Энштейна с Бором. Кто прав?

Энштейн называл «квантовую запутанность» SPUCKHAFTE FERWIRKLUNG (нем.) или пугающим, призрачным, сверхъестественным действием на расстоянии.

Энштейн не соглашался с интерпретацией Бора о квантовой запутанности частиц. Потому что это противоречило его теории, что информация не может передаваться со скоростью больше скорости света. В 1935 году он опубликовал статью с описанием мысленного эксперимента. Этот эксперимент назвали «Парадоксом Эйнштейна — Подольского — Розена».

Энштейн соглашался, что связанные частицы могут существовать, но придумал другое объяснение мгновенной передачи информации между ними. Он сказал, что «запутанные частицы» скорее напоминают пару перчаток. Представьте, что у Вас пара перчаток. Левую Вы положили в один чемодан, а правую – во второй. 1-й чемодан Вы отправили другу, а 2-й – на Луну. Когда друг получит чемодан, он будет знать, что в чемодане либо левая, либо правая перчатка. Когда же он откроет чемодан и увидит, что в нём левая перчатка, то он мгновенно узнает, что на Луне – правая. И это не означает, что друг повлиял на то, что в чемодане левая перчатка и не означает, что левая перчатка мгновенно передала информацию правой. Это только означает то, что свойства перчаток были изначально такими с момента, как их разделили. Т.е. в запутанные квантовые частицы изначально заложена информация об их состояниях.

Так кто же был прав Бор, который считал, что связанные частицы передают друг другу информацию мгновенно, даже если они разнесены на огромные расстояния? Или Энштейн, который считал, что никакой сверхъестественной связи нет, и всё предопределено задолго до момента измерения.

Этот спор на 30 лет переместился в область философии. Разрешился ли спор с тех времён?

Теорема Белла. Спор разрешён?

Джон Клаузер, будучи ещё аспирантом Колумбийского университета, в 1967 отыскал забытую работу ирландского физика Джона Белла. Это была сенсация: оказывается Беллу удалось вывести из тупика спор Бора и Энштейна. Он предложил экспериментально проверить обе гипотезы. Для этого он предложил построить машину, которая бы создавала и сравнивала много пар запутанных частиц. Джон Клаузер принялся разрабатывать такую машину. Его машина могла создавать тысячи пар запутанных частиц и сравнивать их по разным параметрам. Результаты экспериментов доказывали правоту Бора.

А вскоре французский физик Ален Аспе провёл опыты, один из которых касался самой сути спора между Энштейном и Бором. В этом опыте измерение одной частицы могло прямо повлиять на другую только в случае, если сигнал от 1-й ко 2-й прошёл бы со скоростью, превышающей скорость света. Но сам Энштейн доказал, что это невозможно. Оставалось только одно объяснение – необъяснимая, сверхъестественная связь между частицами.

Результаты опытов доказали, что теоретическое предположение квантовой механики – верно. Квантовая запутанность – это реальность (Квантовая запутанность Википедия). Квантовые частицы могут быть связанными несмотря на огромные расстояния. Измерение состояния одной частицы влияет на состояние далеко расположенной от нёё 2-й частицы так, как если бы расстояния между ними не существовало. Сверхъестественная связь на расстоянии происходит в действительности.

Остаётся вопрос, возможна ли телепортация?

Подтверждена ли телепортация экспериментально?

Японские учёные ещё в 2011 году впервые в мире телепортировали фотоны! Мгновенно переместили из пункта А в пункт Б пучок света.

Для этого Нориюки Ли со своими коллегами разложили свет на частицы – фотоны. Один фотон был «квантово запутанным» с другим фотоном. Фотоны были взаимосвязанными, хотя находились в разных точках. Учёные уничтожили 1-й фотон в точке А, но он был мгновенно воссоздан в точке Б благодаря их «квантовой запутанности». До телепортации Кота Шрёдингера ещё, конечно, далеко, но 1-й шаг уже сделан. Кстати, хотите узнать, что означает парадокс «Кота Шрёдингера»? — читайте статью Кот Шредингера простыми словами. Суть эксперимента.

Хотите, чтобы за 5 минут всё, что Вы прочитали о квантовой запутанности, разложилось по полочкам – посмотрите это видео замечательное видео.

До скорых встреч!

Желаю всем интересных, вдохновляющих проектов!

Новый способ запутывать фотоны оказался эффективнее всех прочих.

Квантовая физика знаменита своей неинтуитивностью: концентрация парадоксов в ней кладёт на лопатки теорию относительности и космологию вместе взятые. Наиболее обсуждаемые в наши дни разделы квантовой физики, в которых парадоксальность воплотилась во всей полноте – это квантовая информация и квантовая оптика.

Квантовая защита информации – святой Грааль для технологии безопасной передачи данных. В основе так называемой квантовой криптографии лежит удивительное квантовое явление – запутанность фотонов (элементарных частиц, переносящих электромагнитное взаимодействие и, в частности, свет).

Суть его в том, что два определённым образом полученных фотона оказываются связаны между собой, так что изменение состояния одного из них вызывает мгновенное изменение в состоянии другого, даже если они находятся на большом расстоянии друг от друга. Запутанность можно использовать для безопасной передачи данных: если некое третье лицо попробует скопировать информацию, о том мгновенно станет известно ее настоящим владельцам. Однако запутать фотоны и потом еще сохранить их запутанность при неизбежном взаимодействии с окружающим миром – задача весьма и весьма непростая.

Станислав Страупе из МГУ рассказывает об этом так: «Перепутанные состояния вообще типичны и повсеместны. Проблема только в том, что для большинства частиц взаимодействие с окружением быстро разрушает перепутывание. Фотоны же практически ни с чем не взаимодействуют, поэтому они являются очень удобным объектом для экспериментов в этой области».

Большая часть источников света, с которыми мы сталкиваемся в жизни – Солнце, лампы накаливания, лазеры, светодиоды – называют классическими: испускаемые ими фотоны подчиняются некоторому статистическому распределению. В неклассическом свете из источника вылетает один или два фотона в единицу времени, и создать такой источник довольно сложно. Для этого можно, например, изолировать одиночный атом или квантовую точку и регистрировать одиночные фотоны, испускаемые в результате возбуждения.

Чтобы получить запутанные фотоны, чаще всего используют эффект спонтанного параметрического рассеяния света в нелинейных кристаллах. Для этого кристалл с определёнными оптическими свойствами облучают так называемым лазером накачки. Фотон из лазерного пучка, попадая в кристалл, распадается на два фотона, энергия которых в сумме равна энергии фотона накачки. В силу законов сохранения фотоны оказываются коррелированы, или запутаны, однако главная проблема такого способа запутывания заключается в низкой эффективности и необходимости фильтровать фотоны на выходе, чтобы получить пары с необходимыми свойствами.

Станислава Страупе и его коллеги предложили новый метод создания пространственного перепутывания, который более эффективен, чем прочие. По словам Егора Ковлакова, в своих экспериментах они получают пучки фотонов, которые оказываются коррелированы по так называемой пространственной форме. Ключевое отличие нового подхода заключается в том, что форма и тип пучка накачки подбираются так, чтобы оптимизировать эффективность испускания запутанных фотонов, избавляя экспериментаторов от необходимости фильтровать выходящее из нелинейного кристалла излучение. Полностью результаты исследователей опубликованы в Physical Review Letters .

Метод можно использовать не только в квантовой криптографии, хотя на данный момент это наиболее развитая область применения фотонной запутанности. «В отличии от классических систем связи, где неважно, какой именно алфавит используется для кодирования сообщения и достаточно использовать бинарный код (0 и 1), в квантовой связи все сложнее. Оказывается, что повышение размерности алфавита не только увеличивает количество информации, кодируемое в одном фотоне, но и увеличивает секретность связи. Поэтому системы квантовой связи, основанные в том числе и на кодировании информации в пространственной форме фотонов, интересны как физикам, так и индустрии», – отмечает Станислав Страупе.

Возможно, новый способ запутывать фотонов позволит создать оптический канал со спутником на орбите, куда нельзя протянуть оптическое волокно.

22 факта о квантовой механике, запутанных фотонах и удачном эксперименте японских ученых

Объясняем квантовую запутанность с помощью забавных корги.

Квантовая запутанность – это явление в квантовой физике, состояние двух фотонов (связанных частиц света), которое позволяет предсказать поведение первого фотона на основании известного состояния второго. Простыми словами, если измерить характеристику первого фотона, которая описывает условное вращение частицы вокруг своей оси (иначе – спин), то спин второго – будет иметь противоположное значение.

И если раньше провести эксперимент можно было на расстоянии не более 100 км, то в 2017 году группе китайских ученых удалось доказать, что эта закономерность сохраняется на гораздо больших расстояниях. Они смогли разнести запутанные частицы на 1200 км. Это в 10 раз больше, чем предыдущий рекорд!

Getty Images: Марк Гарлик / Научная Фотобиблиотека

Для этого китайские ученые запустили на орбиту спутник Micius, который создал в космосе пару запутанных фотонов и отправил их обратно в разные точки земной поверхности. Результаты своего исследования они опубликовали в научном журнале «Science».

EZUMELIMAGES / ISTOCKPHOTO / gizmodo.com.au

«Это поразительный и довольно красивый эксперимент», — поделился своими впечатлениями профессор физики в Университете Сассекса Джейкоб Даннингем, добавив, что это был «огромный скачок» в изучении квантовой запутанности в глобальных масштабах. «Это большой шаг вперед в квантовой технологии», — сказал он.

Вполне нормально, если вы не до конца поняли, что представляет из себя квантовая запутанность. Поэтому мы решили разложить все на тезисы, сопроводив материал гифками милых помощников.

youtube. com

1. В очень малых масштабах физика ведет себя немного иначе – не так, как мы привыкли. Законы, которые описывают это поведение, называют квантовой механикой.

Facebook: 355558944642122

Предсказания квантовой механики могут разительно отличаться от положений классической механики.

2. Одна важная вещь, которую вы должны знать из квантовой механики, заключается в следующем: материя ведет себя и как частица, и как волна.

Facebook: LiloTheCorgi

3. Еще один момент: когда дело касается квантовой механики, стоит попрощаться с уверенностью. Ведь если частица действует как волна, мы не можем знать наверняка, где именно она находится.

captain-fluffy-llama.tumblr.com

Смотрите также

5 научных мифов о космосе, в которые не нужно верить

4. До того момента, пока мы ее не измерим. Но вот в чем загвоздка: если мы узнаем ее местоположение, то не сможем узнать скорость.

И наоборот: вычислив скорость, не сможем распознать местоположение.  

arockettopigfarts.tumblr.com

5. В 1935 году три физика – Альберт Эйнштейн, Борис Подольский и Натан Розен – пытались доказать неполноту модели квантовой механики, когда впервые описали пример квантовой запутанности.

instagram: @threecorgis

6. Но сам термин «запутанность» был впервые выведен Эрвином Шредингером в том же году.

reddit.com

Смотрите также

Будут ли светить фары автомобиля на скорости света: теоретические рассуждения

7. Он назвал это «характерной чертой квантовой механики, той, которая обеспечивает ее отход от классического мышления».

vine.co

8. Эйнштейн не очень обрадовался квантовому запутыванию и назвал его «жутким действием на расстоянии».

youtube.com

9. Основная идея квантовой запутанности заключается в следующем: если две частицы вступают в тесный контакт друг с другом, они становятся связанными.

youtube.com

10. Теперь судьбы этих частиц переплетены. Поэтому мы и называем их запутанными.

imgur.com

Смотрите также

Американским ученым удалось сфотографировать скорость света

11. Мы можем переместить эти две запутанные частицы далеко друг от друга, но они все равно останутся связанными.

youtube.com

12. Поскольку они ведут себя странным, квантовым образом, мы не знаем, каковы свойства частиц, пока не посмотрим на них.

youtube.com

13. И как только мы взглянем на одну из частиц, то тут же узнаем, в каком состоянии находится другая.

youtube.com

14. Эта закономерность соблюдается, даже если вторая частица находится на другом конце Вселенной.

Facebook: juniehouse.petshop

15. Это большое открытие, которое означает, что в какой-то степени мы взаимодействуем со второй частицей быстрее скорости света.

youtube.com

16. Естественно, на практике все оказывается куда сложнее (впрочем, как и всегда).

corgiaddict.com

17. Ведь мы не можем просто запутать две частицы, а затем отправить одну из них в дальний уголок Вселенной.

Facebook: Corgioverload

18. Существует два способа передачи запутанных фотонов: через оптические волокна и через открытое пространство.

youtube.com

19. Но на большом расстоянии оптоволокно может поглотить фотоны, что исказит результаты исследования.

youtube.com

20. Однако, создав запутанные частицы в космосе и отправив их на Землю, ученые смогли обойти прежние препятствия.

vine.co

21. Возможность размещать запутанные фотоны на большом расстоянии имеет решающее значение, если в будущем мы хотим использовать запутывание для безопасного общения, квантовых компьютеров или квантовой телепортации.

Facebook: lokithecorgi

22. Но если вам все еще трудно понять, что такое квантовая запутанность, просто вспомните, что однажды сказал американский ученый Ричард Фейнман: «Я думаю, что могу с уверенностью сказать, что никто не понимает квантовую механику».

Facebook: lokithecorgi

 

Обложка: EZUMELIMAGES / ISTOCKPHOTO / youtube.com

Эффективно запутанные фотоны

Новый метод запутывать фотоны был действеннее всех других.

Квантовая физика известна собственной неинтуитивностью: концентрация парадоксов в ней кладёт на лопатки космологию и теорию относительности совместно забранные. Самый обсуждаемые Сейчас разделы квантовой физики, в которых парадоксальность воплотилась во всей полноте – это квантовая информация и квантовая оптика.

Пучки фотонов, заснятые посредством ПЗС-матрицы. Цвета соответствуют интенсивности: от тёмного (минимальной) до белого (большой). (Фото: Егор Ковлаков. )

Квантовая защита информации – святой Грааль для разработки надёжной передачи данных. В базе так называемой квантовой криптографии лежит необычное квантовое явление – запутанность фотонов (элементарных частиц, переносящих электромагнитное сотрудничество и, например, свет).

Сущность его в том, что два определённым образом взятых фотона выясняются связаны между собой, так что изменение состояния одного из них приводит к мгновенному изменению в состоянии другого, даже если они находятся на громадном расстоянии друг от друга. Запутанность возможно применять для надёжной передачи данных: в случае если некое третье лицо попытается скопировать данные, о том мгновенно станет известно ее настоящим обладателям. Но запутать фотоны и позже еще сохранить их запутанность при неизбежном сотрудничестве с окружающим миром – задача очень и очень непростая.

Станислав Страупе из МГУ говорит об этом так: «Перепутанные состояния по большому счету обычны и повсеместны. Неприятность лишь в том, что для большинства частиц сотрудничество с окружением скоро разрушает перепутывание. Фотоны же фактически ни с чем не взаимодействуют, исходя из этого они являются весьма эргономичным объектом для опытов в данной области».

Большинство источников света, с которыми мы сталкиваемся в жизни – Солнце, лампы накаливания, лазеры, светодиоды – именуют хорошими: испускаемые ими фотоны подчиняются некоему статистическому распределению. В неклассическом свете из источника вылетает один либо два фотона в единицу времени, и создать таковой источник достаточно сложно. Для этого возможно, к примеру, изолировать одиночный атом либо квантовую точку и регистрировать одиночные фотоны, испускаемые в следствии возбуждения.

Чтобы получить запутанные фотоны, значительно чаще применяют эффект спонтанного параметрического рассеяния света в нелинейных кристаллах. Для этого кристалл с определёнными оптическими особенностями облучают так называемым лазером накачки. Фотон из лазерного пучка, попадая в кристалл, распадается на два фотона, энергия которых в сумме равна энергии фотона накачки.

В силу законов сохранения фотоны выясняются коррелированы, либо запутаны, но основная неприятность для того чтобы метода запутывания содержится в необходимости и низкой эффективности фильтровать фотоны на выходе, для получения паров с нужными особенностями.

Станислава Страупе и его сотрудники предложили новый способ создания пространственного перепутывания, что более действен, чем другие. По словам Егора Ковлакова, в собственных опытах они приобретают пучки фотонов, каковые оказываются коррелированы по так называемой пространственной форме. Главное отличие нового подхода содержится в том, что тип и форма пучка накачки подбираются так, дабы оптимизировать эффективность испускания запутанных фотонов, избавляя экспериментаторов от необходимости фильтровать выходящее из нелинейного кристалла излучение. Всецело результаты исследователей размещены в Physical Review Letters .

Способ возможно применять не только в квантовой криптографии, не смотря на то, что сейчас это самая развитая область применения фотонной запутанности. «В отличии от хороших совокупностей связи, где не имеет значение, какой как раз алфавит употребляется для кодирования сообщения и достаточно применять двоичный код (0 и 1), в квантовой связи все сложнее. Выясняется, что увеличение размерности алфавита не только увеличивает количество информации, кодируемое в одном фотоне, но и увеличивает секретность связи. Исходя из этого совокупности квантовой связи, основанные среди них и на кодировании информации в пространственной форме фотонов, занимательны как физикам, так и индустрии», – отмечает Станислав Страупе.

Быть может, новый метод запутывать фотонов разрешит создать оптический канал со спутником на орбите, куда нельзя протянуть оптическое волокно.

Создатель: Аня Грушина

Источник: жизнь и Наука, nkj.ru

Случайные записи:
  • Госдума решила судьбу российской науки
  • Почему кошки привередливы в еде

Взаимосвязь свойств двух частиц во Времени (Квантовая запутанность)


Похожие статьи, которые вам понравятся:

  • Физики заставили фотоны взаимодействовать друг с другом

    Канадские ученые в первый раз смогли передать данные о состоянии с единичного фотона на другие фотоны – данный эффект возможно использован в будущих…

  • Создана квантовая запутанность между одним фотоном и триллионом атомов

    Физики Университета Варшавы создали многомерное состояние запутанности единственного фотона и триллиона раскаленных атомов рубидия, пролив свет на…

  • Создан источник фотонов для квантовых компьютеров

    Совместная несколько исследователей из Китая, Германии и Великобритании сказала о том, что ей удалось взять самый высококачественный из когда-либо…

  • Эффект джозефсона для фотонов можно увидеть

    Сотрудничество света с веществом постоянно будоражило умы неспециалистов и очень интересовало ученых – физиков. Сейчас техника опыта, соответствующая…

Поляризационная корреляция запутанных фотонов, полученная без использования нелокальных взаимодействий

1. Введение

В 1935 г. Эйнштейн и др. [1] инициировал дискуссию о том, является ли квантовая механика полной или нет. В последующие годы не удавалось найти конкретных указаний на появление скрытых переменных. В 1964 г. Белл [2] на примере двух частиц со спином 1/2 показал, что локальные реалистические теории принципиально не могут воспроизвести результаты квантовой механики. В 1969 г. Clauser и соавт. [3] предложили эксперимент для проверки локальных теорий скрытых переменных с запутанными фотонами. Уже через 3 года Фридман и Клаузер представили первые измерения, доказавшие, что локальные реалистические теории не в состоянии описать экспериментальные результаты [4].

Более сложные эксперименты по поляризационной корреляции запутанных фотонов [5–12] показали, что экспериментальные результаты полностью воспроизводятся квантовой механикой.

Все эксперименты, дающие данные о корреляции поляризации с хорошей статистикой, выполняются таким образом, чтобы процессы обнаружения двух удаленных наблюдателей были пространственно разделены. Таким образом, публикации об этих экспериментах обычно предполагают, что результаты могут быть вызваны только сверхсветовыми сигналами между наблюдателями. Особенно Саларт и др. [9] подчеркивают, что нарушение неравенства Белла, кажется, доказывает, что квантовая механика использует нелокальные взаимодействия.

Расхождения между результатами локальных реалистических теорий и квантовой механики обсуждаются также для более сложных квантовых систем с более чем двумя частицами [13]. Многие из этих публикаций намекают на то, что возможна связь со скоростью, превышающей скорость света. Недостаток всех этих попыток доказать существование нелокальных взаимодействий состоит в том, что до сих пор не удавалось представить никаких конкретных результатов, воспроизводящих экспериментальные данные.

В последние несколько лет несколько признанных физиков пытаются доказать, что квантовая механика не использует нелокальные взаимодействия [14–21]. Авторы показывают, что некоторые математические операции, такие как редукция квантового состояния, по-видимому, имеют нелокальные последствия. При ближайшем рассмотрении эти операции вызывают лишь изменения знаний наблюдателя о квантовом состоянии. Таким образом, изменения происходят не в физическом пространстве, а только в информационном пространстве.

На самом деле, результаты экспериментов с параметрическими источниками фотонов с понижающей конверсией могут быть получены из волновых оптических и квантовых статистических соображений без использования сверхсветовых сигналов. Имеются веские основания полагать, что эксперименты Аспекта и его сотрудников с запутанными фотонами, возникающими из специфического каскада распада кальция [5, 6], также могут быть объяснены без использования нелокальных взаимодействий. Однако дополнительные тесты на статус поляризации фотонов были бы полезны, чтобы окончательно ответить на вопрос.

2. Фотонные пары, возникающие из источников с понижающей конверсией

За последние 22 года было проведено несколько экспериментов по корреляции поляризации с параметрическими источниками с понижающей конверсией [7–12]. При необходимости экспериментальные подробности взяты из докторской диссертации Вейса [22]. В кристалле BBO ультрафиолетовые фотоны преобразуются в двухфазные поляризованные по кругу зеленые фотоны с равными энергиями.

Волновые пакеты с круговой поляризацией немедленно разлагаются на два линейно поляризованных волновых пакета с ортогональными направлениями поляризации. Обычный луч имеет вертикальную поляризацию. Необыкновенный луч имеет горизонтальную поляризацию. Из-за разного направления распространения конусы излучения обыкновенного и необыкновенного луча выглядят на плоскости выхода в виде двух смещенных от центра окружностей, пересекающихся в двух точках (см. рис. 1). После прохождения компенсационной пластины повторно собранные волновые пакеты с круговой поляризацией почти не изменяют две зоны пересечения.

Рисунок 1 . Схематическая диаграмма простой экспериментальной установки, подходящей для определения поляризационных корреляций. В правом верхнем углу показан источник BBO, который обеспечивает запутанные фотоны, вращающиеся в одном направлении. Системы координат наблюдателей Алисы и Боба, показанные в левом нижнем углу, являются правыми. Углы α и β указывают направления линейных поляризаций, которые ищут Алиса и Боб соответственно. Тонкие линии между источником и наблюдателями обозначают оптические волокна. Расстояние между Алисой и Бобом обычно выбирается достаточно большим, чтобы гарантировать, что два связанных процесса обнаружения фотонов пространственно разделены.

В экспериментах по корреляции поляризации с параметрическими источниками с понижающей конверсией изучалась только так называемая синглетная конфигурация. В этой конфигурации плоскости поляризации связанных фотонов вращаются в одном направлении. В среднем около половины фотонных пар вращаются по часовой стрелке, а другая половина — против часовой стрелки.

3. Обнаружение поляризованных фотонов Алисой и Бобом

Фотоны, выходящие из двух выходов источника, направляются к наблюдателям по оптическим волокнам. Покинув оптические волокна, волновые пакеты проходят через электрооптический модулятор, расположенный между двумя соответствующим образом ориентированными четвертьволновыми пластинами. В сочетании три оптически активных элемента закручивают линейно поляризованные волны на произвольно выбираемый угол, пропорциональный приложенному напряжению. Детекторный блок фиксируется в пространстве. Закрутка плоских волн электрооптическим модулятором имитирует виртуальную закрутку детекторного блока. Для удобства в дальнейшем будем предполагать, что узлы закручивания опущены и что детекторы действительно закручены в пространстве.

С помощью призм Волластона Алиса и Боб разделили входящие волновые пакеты на две равные по размеру составляющие с ортогональными направлениями поляризации. Линейно поляризованные компоненты попадают в общей сложности на четыре детектора, которые должны быть высокочувствительными, чтобы обнаруживать почти все входящие фотоны [11, 12]. При тщательной настройке прибора скорость счета детекторов уже не должна зависеть от направления поляризации.

В четырех каналах детектора каждый зарегистрированный импульс сохраняется вместе с индивидуальной меткой времени. После завершения измерения четыре списка данных сравниваются, чтобы определить четыре степени совпадения, а именно 9.0035 I (α, β), I (α, β+90°), I (α+90°, β), I (α+90°, β+90°). Пусть I 0 будет коэффициентом совпадений, когда фильтры выбора удалены с обеих сторон эксперимента. Если потери в фильтрах пренебрежимо малы, то I 0 также является суммой коэффициентов совпадений по четырем каналам. Две степени совпадения I (α, β) и I (α, β +90°) в сумме дают I 0 /2. То же самое верно и для коэффициентов совпадения I (α+90°, β) и I (α+90°, β+90°). При этом следует иметь в виду, что коэффициенты совпадений демонстрируют статистическую неопределенность.

В этой статье будут рассмотрены корпускулярные и волновые аспекты, поскольку корреляция фотонов, обнаруженных Алисой и Бобом, зависит от относительной фазы волновых пакетов с круговой поляризацией, сопровождающих фотоны. Вывод поляризационной корреляции в основном основан на волновых аргументах, но при необходимости также будут учитываться аспекты частиц.

Термины «волна» и «свет» часто используются для удобства. Фактически под световым лучом всегда будем понимать поток независимых волновых пакетов с ограниченной длиной когерентности. Только пары волновых пакетов, включающие запутанные пары фотонов, строго связаны по фазе, когда они покидают источник фотонов. В эксперименте Вейса [22, с. 63] длина когерентности оценивается примерно в 0,1 м. Таким образом, волновые пакеты, покидающие источник фотонов, очень короткие по сравнению с расстоянием между Алисой и Бобом, что исключает нелокальные взаимодействия между наблюдателями на основе волн.

4. Формальный вывод поляризационной корреляции

В волновой оптике и квантовой механике часто требуется фазовое соотношение интерферирующих волн в плоскости обнаружения, чтобы получить интерференционную картину. Однако в корреляционных экспериментах необходимо запрашивать соотношение фаз двух связанных волновых пакетов в источнике. Относительная фаза в источнике проявляется в интеграле перекрытия двух нормированных волновых пакетов.

Два волновых пакета, одновременно покидающих выходы A и B, имеют фазовый сдвиг ±90° в источнике. Знак показывает, какой из волновых пакетов лидирует. На рисунке 1 фазовый сдвиг показан скрученными векторами вращения. Если α≠β, необходимо учитывать дополнительный фазовый сдвиг ±(α−β). Знак зависит от направления вращения двух волновых пакетов с круговой поляризацией. Таким образом, полный фазовый сдвиг двух линейно поляризованных парциальных волн, искомый двумя наблюдателями, составляет

φ=±90°±(α-β). (1)

Пренебрегая функцией огибающей, необходимо вычислить интеграл перекрытия двух нормированных функций

f(t)=ω/π sin(ωt)g(t)=ω/π sin(ωt±90°±(α-β)). (2)

Вторую функцию, деленную на нормирующий множитель, можно преобразовать, дважды используя тригонометрические теоремы сложения

sin(ωt±90°±(α-β))=sin(ωt)cos(±90°±(α -β))+cos(ωt)sin(±90°±(α-β))=±sin(ωt)sin(α-β)±cos(ωt)cos(α-β)    (3)

с помощью определенных интегралов

ωπ∫02π/ωsin(ωt)sin(ωt)dt=1ωπ∫02π/ωsin(ωt)cos(ωt)dt=0    (4)

нетрудно вычислить интеграл перекрытия

∫ 02π/ωf(t)g(t)dt=±sin(α-β). (5)

Квадрат (абсолютного) интеграла перекрытия двух нормализованных фазово-связанных волновых пакетов пропорционален частоте совпадений. Как объяснялось в предыдущей главе, коэффициенты совпадений I (α, β) и I (α, β +90°) в сумме дают I 0 /2. Следовательно, коэффициент пропорциональности должен быть равен I 0 /2.

Таким образом, частота совпадений определяется как

I(α,β)=I0 sin2(α-β)/2    (6)

, а корреляция определяется как

C(α,β)=I(α,β)I(α,β)+I(α,β+90°)=sin2(α-β). (7)

При таком довольно простом соображении были полностью воспроизведены экспериментально обнаруженные корреляции запутанных фотонов.

5. Разработка квантово-статистических аспектов

Квантовая статистика станет намного яснее, если каждый из двух циркулярно поляризованных световых лучей A и B, выходящих из источника, будет формально разделен на два соизмеримых линейно поляризованных луча с ортогональными направлениями поляризации. Волну с круговой поляризацией всегда можно понимать как суперпозицию двух линейно поляризованных парциальных волн одинакового размера с ортогональными направлениями поляризации. Две парциальные волны сдвинуты по фазе относительно друг друга на ±90°. Направления линейных поляризаций ϑ и ϑ+90° можно выбирать произвольно.

Фотоны, содержащиеся в двух парциальных лучах, образуют две непересекающиеся группы. Если фотон был назначен парциальному лучу с линейной поляризацией, он всегда останется в этом луче. Между двумя группами фотонов на пути от источника к наблюдателям не происходит перемешивания, даже если фотоны и сопровождающие их волновые пакеты пересекают электрооптические модуляторы и четвертьволновые пластины.

Все современные эксперименты планируются таким образом, чтобы процессы отбора и обнаружения, осуществляемые двумя наблюдателями, были пространственно разделены. Поэтому расщепление выполняется прямо перед детекторами. Достаточно поздняя фиксация углов α и β касается даже фотонов, вылетающих из источника намного раньше. Таким образом, разделение лучей с круговой поляризацией, по общему признанию, требует нелокальной информации, но, конечно же, не требует нелокального взаимодействия, потому что два потока фотонов, распространяющихся к Алисе и Бобу, не модифицируются повторным изменением углов обнаружения. Прежде чем фотоны достигнут соответствующей призмы Волластона, процедура расщепления является чисто математическим, а не физическим процессом.

Из-за общего происхождения пары запутанных фотонов имеют фазовую связь, когда покидают источник. В случае параметрических процессов преобразования с понижением частоты два запутанных фотона находятся в фазе, но два связанных волновых пакета с круговой поляризацией сдвинуты по фазе на ±90°.

Поскольку оптические пути от источника к Алисе и Бобу, как правило, не сбалансированы, информацию об исходной фазе нельзя восстановить, просто сравнивая время прихода запутанных фотонов. Это было бы просто невозможно из-за ограниченного временного разрешения внешних часов и дрожания электроники обнаружения.

К счастью, два луча оснащены синхронизированными внутренними часами, которые легко считываются наблюдателями. За один волновой цикл плоскость поляризации совершает полный оборот. Таким образом, относительная фаза фотонов в источнике вплоть до кратных 180° может быть восстановлена ​​по разнице углов поляризации, которую ищут два наблюдателя. Член по модулю 180 ° происходит от 180-градусной периодичности коэффициента пропускания поляризатора.

Корреляция поляризации с учетом аспекта частиц будет получена в два этапа. Сначала будет рассмотрен случай α = β. Этот шаг охватывает ключевой момент в цепи аргументов, объясняющих, почему запутанные фотоны статистически распределены только по двум из четырех возможных каналов совпадения.

Два частичных луча A (α) и B (α+90°) находятся в фазе (или противоположны по фазе) в источнике. То же самое верно для частичных лучей A (α+90°) и B (α). Поскольку в источнике фотоны находятся в фазе, они должны находиться либо в канале совпадения A (α)/ B (α+90°), либо в канале совпадения A (α+90°)/ В (α). Поскольку два канала совпадения эквивалентны, вероятности найти запутанные пары фотонов в этих двух каналах совпадения должны быть равными.

Напротив, парциальные лучи A (α) и B (α) сдвинуты по фазе в источнике на ± 90°. Это означает, что они ортогональны друг другу. То же самое верно для частичных лучей A (α+90°) и B (α+90°). Поэтому совпадений в этих двух каналах совпадений не будет.

Для каждого угла α коэффициенты совпадений в четырех возможных каналах, таким образом, определяются как

I(α,β=α+90°)=I0/2I(α,β=α)=0I(α+90°, β=α)=I0/2I(α+90°,β=α+90°)=0. (8)

Корреляции C (α, β = α), C (α, β = α+90°), C (α+90°, β = α+90°) и C (α+90°, β = α) равны нулю или единице. Это означает, что запутанные фотоны строго антикоррелированы. Это утверждение справедливо для каждой отдельной пары запутанных фотонов, а не только для статистического ансамбля пар запутанных фотонов.

Приведенные выше рассуждения доказывают, что оба запутанных фотона содержатся либо в парциальной волновой паре A (α) и B (α+90°) или в парциальной паре волн A (α+90°) и B (α). Обнаруживается ли фотон детектором A (α) или детектором A (α+90°), чисто случайно. Нельзя предсказать, в какой детектор попадут отдельные фотоны. Однако после обнаружения первого фотона пары фотонов, например, на стороне Алисы будет ясно, в какой из двух детекторов на стороне Боба попадет второй фотон.

Предопределена только антикорреляция запутанных фотонов, но не поляризация отдельных фотонов [23]. Вот почему направление поляризации не следует рассматривать как элемент реальности.

Соотношение фаз парциальных лучей в источнике, таким образом, приводит к сильной поляризационной корреляции, хотя информация о состоянии поляризации не является скрытым свойством фотонов. Эйнштейн и др. [1] утверждал, что свойство, одинаково обнаруживаемое в двух больше не взаимодействующих квантовых состояниях, должно быть элементом реальности. Ярко выраженная поляризационная корреляция запутанных фотонов кажется контрпримером.

Неправильная оценка Эйнштейна и его сотрудников повлекла за собой ошибочный подход Белла [2], который предположил, что направления поляризации являются реальными свойствами фотонов. На самом деле фазовая связь предопределяет только взаимосвязь, но не само свойство. Следовательно, неравенства Белла не имеют значения.

Распространение рассмотрения на случай α≠β довольно тривиально и основывается исключительно на оптическом законе, открытом Этьеном Луи Малюсом в 1810 г. Закон Малюса гласит: Если свет, линейно поляризованный в направлении γ, проходит через поляризационный фильтр с его поляризацией оси, ориентированной в направлении δ, его интенсивность уменьшается в 9 раз0005

cos2(γ-δ).

Нельзя предсказать, какой из фотонов пройдет через поляризационный фильтр, поскольку закон Малюса носит чисто статистический характер. Закон справедлив не только для света, выходящего из классического источника света, но и для лазерного света. Это означает, что он не зависит от свойств когерентности второго порядка фотонного потока. Это также экспериментально доказано в случае малой интенсивности, когда интенсивность пучка измеряется детекторами одиночных фотонов. Брукнер и Цайлингер явно показывают, что закон Малюса справедлив и в квантовом режиме [24]. В одной из своих недавних публикаций Хренников также использовал закон Малюса, когда вывел поляризационную корреляцию запутанных фотонов, исходя из квантово-механических соображений [16, с. 3].

Первое из уравнения (8) означает, что если один из запутанных фотонов был зарегистрирован детектором A (α), то связанный с ним фотон обязательно будет содержаться в парциальном луче B (α+90°). Следовательно, нужно применить закон Малюса для γ = α + 90° и δ = β. Это означает, что частота совпадений I 0 /2 уменьшается на коэффициент cos 2 (α+90°−β) = sin 2 (α−β). При этом коэффициент совпадения I (α, β) определяется как

I(α,β)=I0sin2(α-β)/2. (9)

в соответствии с уравнением (6).

Роли Алисы и Боба можно поменять местами. Если лучи с круговой поляризацией разделить на парциальные лучи с линейной поляризацией в направлениях β и β+90°, будут воспроизведены представленные выше результаты.

Для α ≠ β закон Малюса с присущим ему статистическим характером должен применяться на стороне Алисы или на стороне Боба. В этом случае корреляция C (α, β) больше нуля и меньше единицы. Таким образом, корреляция определяется не для одной пары запутанных фотонов, а только для достаточно большой группы пар запутанных фотонов.

Как было доказано выше, источником информации, ответственным за появление ярко выраженной корреляции, является фазовый сдвиг двух ассоциированных волновых пакетов при их выходе из источника. Традиционно квантовая механика строго учитывает разности фаз волновых функций, содержащихся в матричном элементе. Поэтому можно с уверенностью предположить, что разность фаз двух запутанных фотонов также будет учитываться в квантовой механике.

Неважно, решается ли проблема корреляции классически или квантово-механически. Имеет значение только то, используется ли фазовая информация или нет.

Расчеты на основе локальных реалистических теорий не учитывают фазовые соотношения. Они только пытаются воспроизвести корреляцию поляризации, предполагая, что направления поляризации запутанных фотонов закодированы в фотонах как скрытые переменные. При объяснении сильной поляризационной корреляции запутанных фотонов имеет значение только их относительная фаза в источнике.

6. Общие замечания

Ярко выраженная корреляция запутанных фотонов не является ни сверхъестественной, ни таинственной. Это зависит исключительно от начального фазового сдвига волн с круговой поляризацией, сопровождающих запутанные фотоны. Нужно только убедиться, что направления поляризации α и β, которые ищут два наблюдателя, связаны с соответствующими углами поляризации в источнике. Это условие выполняется в каждом из экспериментов. При этом не имеет значения, в какое время были выбраны направления поляризации. Чисто концептуальное разделение двух частичных лучей и обнаружение фотонов не влияет на процесс параметрического преобразования с понижением частоты. Внутри источника зафиксирована относительная фаза запутанных фотонов. Наблюдатели только решают, какие направления поляризации им искать. Нет необходимости в сверхсветовой передаче информации между наблюдателями. Расстояние между наблюдателями абсолютно не имеет значения.

Относительную фазу запутанных фотонов в источнике можно было бы объявить скрытой переменной, окончательно раскрываемой в процессе обнаружения совпадений. Скрытые переменные этого типа могут быть связаны только с волновыми пакетами, но не с частицами. Решающим моментом аргументации является то, что интенсивность волны и, следовательно, также частота совпадений пропорциональны (абсолютному) квадрату амплитуды рассеяния. Свойства проявляются только после возведения в квадрат интеграла перекрытия. В рассмотрении, основанном на частицах, свойства непосредственно влияют на скорость счета.

Неравенство Белла вводит в заблуждение, поскольку оно приписывает такие свойства, как направление поляризации, частицам, а не волнам. Поэтому Белл не может учесть разность фаз запутанных фотонов. В дальнейшем следует игнорировать нарушения теоремы Белла, поскольку рассуждения Белла неадекватны для описания волновых явлений.

7. Корреляция фотонных пар в триплетной конфигурации

Ярко выраженная корреляция запутанных фотонов должна наблюдаться и в триплетной конфигурации. Это означает, что две волны с круговой поляризацией вращаются в противоположных направлениях. В этом случае корреляцию нельзя вывести так же просто, как в синглетном случае. Можно понять, что триплетная конфигурация возникает из синглетной конфигурации путем отражения одной из волн с круговой поляризацией в вертикальной плоскости. Это может быть выполнено с помощью полуволновой пластины с оптической осью, ориентированной в вертикальном направлении. Если волновые пакеты с круговой поляризацией сдвинуты по фазе на ±90° корреляция должна быть

C(α,β)=sin2(α+β). (10)

Таким образом, начало углов α и β должно лежать в вертикальной плоскости. Предварительные измерения Вейса [22, с. 72] подтверждают этот результат. Например, если оба наблюдателя ищут направления поляризации, параллельные 45°, степень совпадения максимальна.

В предыдущей публикации [25] в корреляционном уравнении для триплетной конфигурации вместо плюса стоял знак минус. Смена знака связана с тем, что система координат Боба в предыдущей статье была левосторонней. В приведенном выше рассмотрении обе системы координат правые.

8. Свойства фотонных пар, возникающих из атомных источников

В экспериментах с параметрическими источниками с понижающей конверсией два волновых пакета с круговой поляризацией сдвинуты по фазе на ±90°, что приводит к строгой антикорреляции линейных поляризаций. Напротив, в экспериментах Aspect et al. [5, 6] два волновых пакета с круговой поляризацией находятся в фазе или противоположны по фазе. Таким образом, корреляция определяется как

C(α,β)=cos2(α-β). (11)

Два фотона, произведенных каскадом распада кальция, имеют разные частоты. Только при равенстве частот вращения можно определить фазовый сдвиг. Таким образом, в будущих экспериментах следует проверить, равны ли частоты вращения двух запутанных фотонов. Что касается вращательного движения, то время когерентности двух фотонов должно быть больше, чем время жизни промежуточного состояния каскада распада.

9. Помогает ли постулирование нелокальных взаимодействий?

Действительно ли полезно постулировать новое взаимодействие, которое находится в серьезном противоречии со специальной теорией относительности? Постулирование передачи информации быстрее скорости света влечет за собой множество новых проблем. Мгновенное влияние на расстоянии требует, чтобы одновременность могла быть строго определена для удаленных местоположений, в отличие от соответствующих утверждений специальной теории относительности.

Даже если игнорировать такие принципиальные возражения, возникает много практических проблем. Как такое предполагаемое взаимодействие могло привести к правильным результатам? В корреляционных экспериментах отношение скоростей совпадений в двух комплементарных каналах I (α, β) и I (α, β+90°) должны быть точно определены. Новое постулируемое взаимодействие должно перенаправлять точно определенный процент стохастически прибывающих фотонов из одного канала в другой. Ожидаемое соотношение совпадений в двух каналах зависит от разности направлений поляризации α и β? Как постулируемое взаимодействие получает информацию об углах? В экспериментах углы закручивания α и β создаются путем подачи напряжения на электрооптические модуляторы. Как может какая-либо теория связать напряжение с углом? Коэффициент пропорциональности зависит от материала, ориентации оси кристалла и множества других экспериментальных деталей.

На самом деле в оптических волокнах возникают паразитные эффекты двойного лучепреломления, которые компенсируются вручную. Как постулируемое новое взаимодействие может узнать, хорошо ли приспособлен аппарат или нет? Кстати, все процессы скручивания частотно-зависимы. Только свет, состоящий из фотонов, подобных тем, которые использовались в эксперименте, может получить информацию о состоянии настройки и об углах α и β.

Эксперимент Salart et al. [9, с. 863] показывает, что предполагаемое «призрачное» взаимодействие должно быть как минимум в 50 000 раз быстрее скорости света. Если длины оптических волокон заметно отличаются друг от друга, то сверхсветовому сигналу приходится выжидать довольно длительный, но чрезвычайно четко определенный интервал времени, прежде чем он перенаправит отдельные импульсы с одного выхода на другой. Встроить такую ​​запаздывающую реакцию в серьезную физическую теорию будет крайне сложно.

Заявление о доступности данных

Все наборы данных, созданные для этого исследования, включены в статью/дополнительный материал.

Вклад авторов

Автор подтверждает, что является единственным автором этой работы и одобрил ее публикацию.

Конфликт интересов

Автор заявляет, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.

Благодарности

Благодарю Андрея Хренникова за любезное прочтение моей рукописи. Я попытался учесть его озабоченность по поводу квантовой статистики.

Литература

1. Эйнштейн А., Подольский Б., Розен Н. Можно ли считать квантово-механическое описание физической реальности полным? Phys Rev. (1935) 47:777–80.

Google Scholar

2. Bell JS. О парадоксе Эйнштейна-Подольского-Розена. Физика. (1964) 1: 195–200.

Google Scholar

3. Clauser JF, Horne MA, Shimony A, Holt RA. Предлагаемый эксперимент для проверки локальных теорий скрытых переменных. Phys Rev Letter. (1969) 23:880–4.

Google Scholar

4. Фридман С.Дж., Клаузер Дж.Ф. Экспериментальная проверка локальных теорий скрытых переменных. Phys Rev Letter. (1972) 28:938–41.

Google Scholar

5. Аспект А., Гранжье П., Роджер Г. Экспериментальные проверки реалистичных локальных теорий с помощью теоремы Белла. Phys Rev Letter. (1981) 47:460–3.

Google Scholar

6. Аспект А., Гранжье П., Роджер Г. Экспериментальная реализация Эйнштейна-Подольского-Розен-Бома Умозрительный эксперимент : новое нарушение неравенств Белла. Phys Rev Letter. (1982) 49:91–4.

Google Scholar

7. Tittel W, Brendel J, Gisin B, Herzog T, Zbinden H, Gisin N. Экспериментальная демонстрация квантовых корреляций на расстоянии более 10 км. Phys Rev A. (1998) 57:3229–32.

Google Scholar

8. Титтель В., Брендель Дж., Збинден Х., Гизин Н. Нарушение неравенств Белла фотонами на расстоянии более 10 км друг от друга. Phys Rev Letter. (1998) 81:3563–6.

Google Scholar

9. Salart D, Baas A, Branciard C, Gisin N, Zbinden H. Проверка скорости «жутких действий на расстоянии». Природа. (2008) 454:861–4. doi: 10.1038/nature07121

PubMed Abstract | Полный текст перекрестной ссылки | Академия Google

10. Weihs G, Jennewein J, Simon C, Weinfurter H, Zeilinger A. Нарушение неравенства Белла при строгих условиях локальности Эйнштейна. Phys Rev Letter. (1998) 81:5039–43.

Google Scholar

11. Giustina M, Versteegh MAM, Wengerowsky S, Handsteiner J, Hochrainer A, Phelan K, et al. (2015) Проверка теоремы Белла без существенных лазеек с запутанными фотонами. Phys Rev Letter. (2015) 115:250401. doi: 10.1103/PhysRevLett.115.250401

PubMed Abstract | Полный текст перекрестной ссылки | Академия Google

12. Shalm L, Meyer-Scott E, Christensen BG, Bierhorst P, Wayne MA, Stevens MJ, et al. Сильный тест на местный реализм без лазеек. Phys Rev Letter. (2015) 115:250402. doi: 10.1103/PhysRevLett.115.250402

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

13. Пан Дж. В., Боумистер Д., Даниэль М., Вайнфуртер Х., Цайлингер А. Экспериментальная проверка квантовой нелокальности в трехфотонной запутанности Гринбергера-Хорна-Цайлингера. Природа. (2000) 403: 515–9. doi: 10.1038/35000514

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

14. Хренников А. Избавьтесь от нелокальности в квантовой физике. Энтропия. (2019) 21:806. doi: 10.3390/e21080806

Полный текст CrossRef | Google Scholar

15. Хренников А. Квант против классической запутанности: устранение проблемы квантовой нелокальности. Найдено физ. (2020) doi: 10.1007/s10701-020-00319-7

CrossRef Полный текст | Академия Google

16. Хренников А. Двуликий Янус квантовой нелокальности. Энтропия. (2020) 22:303. doi: 10.3390/e22030303

Полный текст CrossRef | Google Scholar

17. Купчински М. Закрытие двери для квантовой нелокальности. Энтропия. (2018) 20:877. doi: 10.3390/e20110877

Полный текст CrossRef | Google Scholar

18. Гесс К. Теорема Белла и мгновенное влияние на расстоянии. J Мод.физ. (2018) 9:1573–90. дои: 10.4236/jmp.2018.98099

Полнотекстовая перекрестная ссылка | Google Scholar

19. Гесс К. Категории нелокальности в теориях ЭПР и справедливость принципа разделения Эйнштейна, а также теоремы Белла. J Мод.физ. (2019) 10:1209–21. doi: 10.4236/jmp.2019.1010080

Полный текст CrossRef | Google Scholar

20. Боун С. Понимание теоремы Белла и квантовой нелокальности. Найдено физ. (2017) 47: 640–57. doi: 10.1007/s10701-017-0083-6

CrossRef Полный текст | Академия Google

21. Гриффитс РБ. Требования нелокальности несовместимы с квантовой механикой гильбертова пространства. Phys Rev A. (2020) 101:022117. doi: 10.1103/PhysRevA.101.022117

CrossRef Полный текст | Google Scholar

22. Weihs G. Ein Experiment zum Test der Bellschen Ungleichung unter Einsteinscher Lokalität (диссертация), Universität Wien (1999). Доступно в Интернете по адресу: https://www.uibk.ac.at/exphys/photonik/people/gwdiss.pdf (по состоянию на 1 марта 2020 г.).

Google Scholar

23. Хренников А. К разрешению дилеммы: нелокальность или необъективность. Int J Theor Phys. (2012) 51:2488–502. doi: 10.1007/s10773-012-1129-3

CrossRef Полный текст | Google Scholar

24. Брукнер Ш., Цайлингер А. Закон Малуса и квантовая информация. Acta Phys Slov. (1999) 49:647–52.

Google Scholar

25. Юнг К. Нарушение неравенства Белла: действительно ли нужно отказаться от местности Эйнштейна? J Phys Conf Ser. (2017) 880:1–8. doi: 10.1088/1742-6596/880/1/012065

CrossRef Full Text | Google Scholar

Запутанные фотоны, сделанные на заказ — ScienceDaily

Чтобы эффективно использовать квантовый компьютер, для выполнения вычислительных операций требуется большее количество специально подготовленных — с технической точки зрения: запутанных — основных строительных блоков. Группа физиков из Института квантовой оптики Макса Планка в Гархинге впервые продемонстрировала эту задачу с фотонами, испускаемыми одним атомом. Следуя новой методике, исследователи генерировали до 14 запутанных фотонов в оптическом резонаторе, которые можно целенаправленно и очень эффективно преобразовывать в определенные квантово-физические состояния. Новый метод может облегчить создание мощных и надежных квантовых компьютеров и обеспечить безопасную передачу данных в будущем.

Явления квантового мира, которые часто кажутся странными с точки зрения обычного повседневного мира, уже давно нашли свое применение в технике. Например, запутанность: квантово-физическая связь между частицами, которая странным образом связывает их на сколь угодно больших расстояниях. Его можно использовать, например, в квантовом компьютере — вычислительной машине, которая, в отличие от обычного компьютера, может выполнять множество математических операций одновременно. Однако, чтобы использовать квантовый компьютер с выгодой, большое количество запутанных частиц должно работать вместе. Это базовые элементы для вычислений, так называемые кубиты.

«Фотоны, частицы света, особенно хорошо подходят для этого, потому что они прочны по своей природе и ими легко манипулировать», — говорит Филип Томас, докторант Института квантовой оптики Макса Планка (MPQ) в Гархинге недалеко от Мюнхена. . Вместе с коллегами из отдела квантовой динамики под руководством профессора Герхарда Ремпе ему удалось сделать важный шаг к тому, чтобы сделать фотоны пригодными для технологических приложений, таких как квантовые вычисления: впервые команда сгенерировала до 14 запутанных фотонов в определенным образом и с высокой эффективностью.

Один атом как источник фотонов

«Хитрость этого эксперимента заключалась в том, что мы использовали один атом, чтобы испускать фотоны и переплетать их очень специфическим образом», — говорит Томас. Для этого исследователи Макса Планка поместили атом рубидия в центр оптического резонатора — своего рода эхо-камеры для электромагнитных волн. С помощью лазерного излучения определенной частоты можно было точно определить состояние атома. Используя дополнительный управляющий импульс, исследователи также специально вызвали испускание фотона, связанного с квантовым состоянием атома.

«Мы повторили этот процесс несколько раз и заранее определенным образом», — сообщает Томас. В промежутке атомом манипулировали определенным образом — на техническом жаргоне: вращали. Таким образом можно было создать цепочку до 14 частиц света, которые запутывались друг с другом за счет вращения атомов и приводились в нужное состояние. «Насколько нам известно, 14 взаимосвязанных световых частиц представляют собой наибольшее количество запутанных фотонов, которые до сих пор генерировались в лаборатории», — подчеркивает Томас.

Детерминированный процесс генерации

Но не только количество запутанных фотонов является важным шагом на пути к разработке мощных квантовых компьютеров — способ их генерации также сильно отличается от традиционных методов. «Поскольку цепочка фотонов возникла из одного атома, ее можно было произвести детерминированным образом», — объясняет Томас. Это означает: в принципе, каждый управляющий импульс действительно доставляет фотон с нужными свойствами. До сих пор запутывание фотонов обычно происходило в специальных нелинейных кристаллах. Недостаток: там частицы света создаются случайным образом и не поддаются контролю. Это также ограничивает количество частиц, которые могут быть объединены в коллективное состояние.

С другой стороны, метод, используемый командой Гархинга, позволяет генерировать практически любое количество запутанных фотонов. Кроме того, метод особенно эффективен — еще одна важная мера для возможных технических применений в будущем: «Измеряя образующуюся фотонную цепочку, мы смогли доказать эффективность почти 50 процентов», — говорит Филип Томас. Это означает, что почти каждое второе «нажатие кнопки» на атоме рубидия доставляло пригодную для использования легкую частицу — гораздо больше, чем было достигнуто в предыдущих экспериментах. «В целом наша работа устраняет давнее препятствие на пути к масштабируемым квантовым вычислениям, основанным на измерениях», — резюмирует результаты директор департамента Герхард Ремпе.

Больше места для квантовой связи

Ученые MPQ хотят устранить еще одно препятствие. Например, сложные вычислительные операции потребуют по крайней мере двух атомов в качестве источников фотонов в резонаторе. Квантовые физики говорят о двумерном кластерном состоянии. «Мы уже работаем над решением этой задачи, — рассказывает Филип Томас. Исследователь Макса Планка также подчеркивает, что возможные технические приложения выходят далеко за рамки квантовых вычислений: «Другим примером применения является квантовая связь» — передача информации с защитой от перехвата, например, с помощью света в оптическом волокне. Там свет испытывает неизбежные потери во время своего распространения из-за оптических эффектов, таких как рассеяние и поглощение, что ограничивает расстояние, на которое могут передаваться данные. Используя метод, разработанный в Гархинге, квантовая информация может быть упакована в запутанные фотоны, а также может выдерживать определенную потерю света и обеспечивать безопасную связь на больших расстояниях.

Источник истории:

Материалы предоставлены Max-Planck-Gesellschaft . Примечание. Содержимое можно редактировать по стилю и длине.

Запутанные фотоны теперь могут выходить в сети

Dragon никогда не перепродавался — странная судьба одной из наиболее исторически значимых NFT. Новые NFT, такие как
«Слияние», произведение цифрового искусства, которое было продано за сумму, эквивалентную 92 миллионам долларов, оставило позади Dragon, поскольку рынок NFT подскочил до рекордных продаж, составив примерно 18 миллиардов долларов в 2021 году. Может, мир просто перешел к более новым блокчейн-проектам? Или это судьба, которая ожидает все NFT?

Блокчейны, смарт-контракты и кошачьи гены

Чтобы понять медленную смерть
CryptoKitties , вы должны начать с самого начала. Технология блокчейн
возможно, началось с статьи 1982 года ученого-компьютерщика Дэвида Чаума, но оно привлекло всеобщее внимание благодаря успеху Биткойн, криптовалюты, созданной анонимным лицом или людьми, известными как Сатоши Накамото. По своей сути блокчейн — это простая книга транзакций, размещенных одна за другой, — мало чем отличающаяся от очень длинной электронной таблицы Excel.

Сложность заключается в том, как блокчейны обеспечивают стабильность и безопасность реестра без центрального органа; детали того, как это делается, различаются в зависимости от блокчейна. Биткойн, хотя и популярен как актив и полезен для денежных транзакций, имеет ограниченную поддержку для чего-либо еще. Новые альтернативы, такие как
Эфириум приобрел популярность, поскольку позволяет создавать сложные «умные контракты» — исполняемый код, хранящийся в блокчейне.

«До
CryptoKitties , если бы вы сказали «блокчейн», все бы предположили, что вы говорите о криптовалюте», — Брайс Блэдон.

CryptoKitties был одним из первых проектов, использующих смарт-контракты путем присоединения кода к конструкциям данных, называемым токенами, в блокчейне Ethereum. Каждый фрагмент игрового кода (называемый «геном») описывает атрибуты цифрового кота. Игроки покупают, собирают, продают и даже разводят новых кошек. Так же, как отдельные токены Ethereum и биткойны, код кота также гарантирует, что токен, представляющий каждого кота, уникален, и именно здесь появляется невзаимозаменяемый токен, или NFT. Взаимозаменяемый товар, по определению, может быть заменен товаром. идентичный предмет — один биткойн так же хорош, как и любой другой биткойн. NFT, напротив, имеет уникальный код, который не применяется ни к какому другому NFT.

Есть еще одна последняя часть головоломки блокчейна, которую вам нужно понять: «газ». Некоторые блокчейны, в том числе Ethereum, взимают плату за вычислительную работу, которую сеть должна выполнить для проверки транзакции. Это создает препятствие для перегрузки сети блокчейна. Высокий спрос означает высокие комиссии, побуждающие пользователей дважды подумать, прежде чем совершать транзакцию. В результате снижение спроса защищает сеть от перегрузки, а время транзакций не становится чрезмерно долгим. Но это может быть слабостью, когда игра NFT становится вирусной.

Взлет и падение CryptoKitties

Запущен 28 ноября 2017 года после пятидневного закрытого бета-тестирования.
Популярность CryptoKitties резко возросла благодаря заманчивому слогану:
первая в мире игра Ethereum.

«Как только он был запущен, он сразу же стал вирусным», — говорит
Брайс Блэдон, один из основателей команды, создавшей CryptoKitties . «Это было невероятно сбивающее с толку время».

Объем продаж вырос с 1500 невзаимозаменяемых кошек в день запуска до более 52 000 10 декабря 2017 года, согласно nonfungible.com, при этом многие CryptoKitties продаются по цене в сотни или тысячи долларов. Ценность кошек, сгенерированных алгоритмами в игре, получила освещение в сотнях публикаций.

Что такое CryptoKitty?

Каждый CryptoKitty — это токен, набор данных в блокчейне Ethereum. В отличие от криптовалют Ethereum и Bitcoin, эти токены не взаимозаменяемы; то есть они не взаимозаменяемы.

Уникальный идентификатор
 Удостоверение личности матери, удостоверение личности отца
 Гены
Уникальный идентификатор делает CryptoKitty невзаимозаменяемым токеном.Жетон содержит родословную котенка и другие данные. Гены котенка определяют его уникальный внешний вид.

Dapper Labs

Более того, игра, возможно, способствовала успеху Ethereum, блокчейна, используемого в игре.
Ethereum взлетел как ракета в тандеме с выпуском CryptoKitties , поднявшись с чуть менее 300 долларов за токен в начале ноября 2017 года до чуть более 1360 долларов в январе 2018 года.

Рост Ethereum продолжился с запуском
десятки новых блокчейн-игр, основанных на криптовалюте, до конца 2017 и 2018 гг. Ethermon , Ethercraft , Ether Goo , CryptoCountries , CryptoCelebrities и CryptoCities являются одними из наиболее известных примеров. Некоторые прибыли в течение нескольких недель после CryptoKitties .

Это был прорыв, которого ждали поклонники Ethereum. Тем не менее, что стало бы зловещим признаком для здоровья блокчейн-игр,
CryptoKitties споткнулись, когда Ethereum рванул вверх.

Ежедневные продажи достигли пика в начале декабря 2017 года, затем снизились в январе и к марту составили в среднем менее 3000 штук. Стоимость самих NFT снижалась медленнее, а это признак того, что у игры была база преданных поклонников, таких как Рабоно, которые купили Dragon задолго до пика игры. Их активность установила рекорды стоимости NFT до 2018 года. Это позволило сохранить игру в новостях, но не привлекло новых игроков.

Сегодня,
CryptoKitties повезло совершить 100 продаж в день, а общая стоимость часто составляет менее 10 000 долларов. Крупные сделки, такие как продажа
Основатель Cat # 71 за 60 эфиров (примерно 170 000 долларов США) 30 апреля 2022 года все еще происходит, но только раз в несколько месяцев. Большинство невзаимозаменяемых меховых младенцев продаются за крошечные доли 1 эфира, что в июле 2022 года стоит всего несколько десятков долларов.

CryptoKitties ’ погружение в безвестность вряд ли будет отменено. Dapper Labs, которой принадлежит CryptoKitties перешел к таким проектам, как NBA Top Shot, платформе, которая позволяет фанатам баскетбола покупать «моменты» NFT — по сути, видеоклипы — из игр NBA. Dapper Labs не ответила на запросы об интервью о CryptoKitties . Блэйдон покинул Dapper в 2019 году.

Что пошло не так?

Один ключ к кончине игры можно найти в последнем посте на
игровой блог (4 июня 2021 г.), посвященный разведению 2-миллионного CryptoKitty. Разведение, основная механика игры, позволяет владельцам объединять свои существующие NFT для создания алгоритмически сгенерированного потомства. Это придавало NFT неотъемлемую ценность в игровой экосистеме. Каждый NFT мог генерировать больше NFT, которые игроки могли затем перепродавать с прибылью. Но этот игровой механизм также насытил рынок. Сяофань Лю, доцент кафедры СМИ и коммуникаций Городского университета Гонконга, соавтор статьи о CryptoKitties ’ взлеты и падения, считает это недостатком, который игра никогда не сможет преодолеть.

«Цена котенка зависит в первую очередь от редкости, а это зависит от генетической стороны. И второе измерение — это количество котят на рынке», — говорит Лю. «Чем больше людей, тем больше котят».

Больше игроков означало больший спрос, но это также означало больше возможностей для создания предложения за счет разведения новых кошек. Это быстро уменьшило редкость каждого NFT.

Блэдон согласен с этой оценкой механизма размножения. «Я думаю, что критика справедлива», — говорит он, объясняя, что она должна была вызвать чувство открытия и волнения. Он также надеялся, что это побудит игроков удерживать NFT, а не сразу продавать их, поскольку разведение теоретически обеспечивает непреходящую ценность.

Огромный объем
CryptoKitties вызвал другую, более неотложную проблему: он функционально сломал блокчейн Ethereum, который является второй по величине криптовалютой в мире по рыночной капитализации (после биткойна). Как объяснялось ранее, Ethereum использует комиссию, называемую газом, для оценки стоимости транзакций. Любой всплеск транзакций — покупка, создание и т. д. — вызовет всплеск платы за газ, и это именно то, что произошло, когда CryptoKitties отправились на Луну.

«Все, что символизировало
CryptoKitties — успех был обманут. Все, что не было видно сразу, в основном игнорировалось», — Брайс Блэдон.

«Игроки, которые хотели купить
CryptoKitties несли высокие сборы за газ».
Об этом заявил в интервью Михай Викол, рыночный аналитик Newzoo. «Эти сборы за газ составляли от 100 до 200 долларов за транзакцию. Вы должны были заплатить цену CryptoKitty плюс плата за газ. Это серьезная проблема».

Высокие гонорары были проблемой не только для
КриптоКотики . Это была проблема для всего блокчейна. Любой, кто по какой-либо причине хотел совершать транзакции в Ethereum, должен был платить больше за газ, поскольку игра становилась все более успешной.

Эта динамика остается проблемой для Ethereum и сегодня. 30 апреля 2022 г., когда Yuga Labs
выпустила Otherdeeds — NFT, которые обещают владельцам недвижимость в метавселенной — она подняла плату за газ Ethereum в стратосферу. Средняя цена на газ ненадолго превысила эквивалент 450 долларов по сравнению с примерно 50 долларами накануне.

Несмотря на то что
CryptoKitties ’ требования к сети снизились, когда игроки ушли, газ, вероятно, станет последним гвоздем в гроб игры. Средняя цена CryptoKitty за последние три месяца составляет около 0,04 эфира, или от 40 до 50 долларов, что часто меньше газа, необходимого для завершения транзакции. Даже те, кто хочет случайно владеть и разводить недорогих CryptoKitties для развлечения, не могут сделать это, не потратив сотни долларов.

Блокчейн-игры: два шага вперед, один шаг назад

Взлет и падение
CryptoKitties был драматичным, но дал его преемникам — которых сотни — возможность учиться на своих ошибках и преодолевать их. Многие не усвоили уроки: современные игровые хиты с блокчейном, такие как
Axie Infinity и BinaryX имели аналогичный первоначальный всплеск цены и активности, за которым последовала длинная нисходящая спираль.

«Все, что символизировало
CryptoKitties — успех был обманут. Все, что не было сразу видно, в основном игнорировалось», — говорит Блэдон. А оказывается многие из CryptoKitties ’ трудности не были видны публике. «Дело в том, что проект CryptoKitties действительно споткнулся. У нас было много отключений. Нам приходилось иметь дело со многими людьми, которые никогда раньше не использовали блокчейн. У нас была ошибка, которая привела к утечке эфира на десятки тысяч долларов». Подобные проблемы преследовали более поздние проекты NFT, часто в гораздо большем масштабе.

Лю не уверен, как игры с блокчейном могут решить эту проблему. «Короткий ответ: я не знаю», — говорит он. «Длинный ответ заключается в том, что это проблема не только игр с блокчейном».

World of Warcraft , например, большую часть жизни игры сталкивался с безудержной инфляцией. Это вызвано постоянным притоком золота от игроков и постоянно растущей стоимостью новых предметов, вводимых дополнениями. Постоянная потребность в новых игроках и предметах связана с другой ключевой проблемой современных игр с блокчейном: зачастую они слишком просты.

«Я думаю, что самая большая проблема блокчейн-игр сейчас заключается в том, что они неинтересны, а если они неинтересны, люди не хотят вкладывать деньги в саму игру», — говорит Викол из Newzoo. «Каждый, кто тратит деньги, хочет выйти из игры с большим количеством денег, чем они потратили».

Это, возможно, нереальное желание становится невыполнимым, как только начинается нисходящая спираль. Игроки, не чувствуя никакой другой привязанности к игре, кроме роста инвестиций, быстро убегают и не возвращаются.

В то время как некоторые игры с блокчейном, по-видимому, игнорировали опасности
CryptoKitties ’ быстрый рост и длительный спад, другие узнали из нагрузки, которую он оказал на сеть Ethereum. В большинстве игр с блокчейном теперь используется сайдчейн, блокчейн, который существует независимо, но подключается к другому, более заметному «родительскому» блокчейну. Цепочки соединены мостом, который облегчает передачу токенов между каждой цепочкой. Это предотвращает рост комиссий на основном блокчейне, поскольку вся игровая активность происходит на сайдчейне.

Тем не менее, даже эта новая стратегия сопряжена с проблемами, потому что боковые цепи оказываются менее безопасными, чем родительский блокчейн. Атака на Ronin, сайдчейн, используемый
Акси Бесконечность ,
пусть хакеры сойдут с рук с суммой, эквивалентной 600 миллионам долларов. Polygon, еще один сайдчейн, часто используемый играми с блокчейном, должен был исправить эксплойт, который поставил под угрозу 850 миллионов долларов, и выплатить награду за ошибку в размере 2 миллионов долларов хакеру, обнаружившему проблему. Игроки, владеющие NFT в сайдчейне, теперь с осторожностью следят за его безопасностью.

Помните дракона

Криптовалютный кошелек, в котором находится котенок Дракон стоимостью почти миллион долларов, теперь содержит эфир едва на 30 долларов и не торговал NFT в течение многих лет. Кошельки анонимны, поэтому вполне возможно, что человек, стоящий за кошельком, перешел на другой. Тем не менее, трудно не рассматривать бездействие кошелька как признак того, что для Rabono веселье длилось недолго.

Неважно, взлетят ли игры на блокчейне и NFT до небес или упадут до нуля, Bladon по-прежнему гордится тем, что
CryptoKitties выполнено, и мы надеемся, что это подтолкнуло индустрию блокчейнов в более доступном направлении.

«До
CryptoKitties , если бы вы сказали «блокчейн», все бы предположили, что вы говорите о криптовалюте», — говорит Блэдон. «Больше всего я горжусь тем, что это было что-то действительно новое. Были настоящие технические инновации и, казалось бы, реальное влияние на культуру».

Эта статья была исправлена ​​11 августа 2022 года, чтобы указать правильную дату ухода Брайса Бладона из Dapper Labs.

Эта статья появилась в печатном выпуске за сентябрь 2022 года под названием «Впечатляющий крах CryptoKitties».

Как создать квантовую запутанность?

Однажды утром на прошлой неделе я прибыл в кампус одновременно с коллегой с исторического факультета, изучающим историю физики. Когда мы шли от парковки к центру кампуса, он задал главный вопрос этого поста: «Как создать квантовую запутанность?» Он отметил, что читал множество научно-популярных статей, рассказывающих о странных аспектах физики, которые возникают, когда у вас есть две запутанные частицы, но они, как правило, слегка пропускают детали того, как вы запутать их в первую очередь.

Мы мило поговорили об этом на прогулке, и я сохранил это как тему для сообщения в блоге. Я подумал, что если мой коллега был смущен этим, то, вероятно, и куча других людей тоже. И хотя я, конечно, много писал здесь о запутанности (на первой странице результатов Google по запросу «запутанность orzel forbes» даются одна, две, три, четыре, пять, шесть, семь, восемь, девять ссылок, и это еще не все из них ), верно и то, что я не вдавался в подробности создания запутанности. Что оказывается проще, чем вы могли бы подумать, исходя из обработки поп-физики, подчеркивающей ее странность, и это отличный повод для публикации в блоге.

Прежде чем мы это сделаем, важно установить основные параметры того, что мы подразумеваем под «квантовой запутанностью». Центральная идея очень проста: у вас есть две частицы, каждая из которых может находиться в одном из двух состояний, и поместить их в состояние, в котором их состояния неопределенны, но коррелированы. Если вы измерите их по отдельности, вы получите случайное распределение ответов «0» и «1», но если вы повторите измерения много раз для многих одинаково подготовленных пар, вы обнаружите, что полученные списки из «0» и «1» измерений идентичны. Состояние одной из двух частиц зависит от состояния другой, и эта корреляция сохранится, даже если они разделены.

Вот краткое описание четырех способов, которыми вы можете взять два объекта и поместить их в такое запутанное квантовое состояние:

Схема третьего эксперимента Аспекта, проверяющего квантовую нелокальность. Запутанные фотоны из… [+] источника направляются на два быстрых переключателя, которые направляют их на поляризационные детекторы. Переключатели меняют настройки очень быстро, эффективно изменяя настройки детектора для эксперимента, пока фотоны находятся в полете. (Рисунок Чада Орзеля)

1) Запутанность с момента рождения: В подавляющем большинстве экспериментов по квантовой запутанности на сегодняшний день в качестве запутанных частиц используются фотоны по той простой причине, что запутать два фотона очень легко. И большинство способов, с помощью которых людям приходится запутывать фотоны, с самого начала просто дают вам запутанное состояние.

Исторический способ сделать это — использовать «каскадный» переход, как это было сделано Аленом Аспектом и его коллегами в классической серии экспериментов еще в начале 19 века.80-х, а несколько раньше Фридманом и Клаузером. В этих экспериментах они поместили группу атомов кальция на высоковозбужденный энергетический уровень, где электрон не может вернуться в основное состояние, испустив один фотон. Вместо этого они распадаются, испуская 90 483 двух 90 484 фотонов, проходя через промежуточное состояние с коротким временем жизни. За испусканием одного фотона в течение нескольких наносекунд следует испускание второго, поэтому, если вы видите один фотон, вы знаете, что другой должен быть где-то рядом. И хотя эти фотоны излучаются в случайных направлениях, когда случается, что они излучаются в противоположных направлениях, то сохранение углов требует, чтобы их поляризации были коррелированы друг с другом: то есть они должны быть в запутанном состоянии.

Каскадные источники работают, но они довольно медленные, потому что каждый атом испускает фотоны в случайных направлениях, поэтому отправка двух фотонов в правильном направлении для попадания в ваши детекторы может занять некоторое время. Бизнес квантовой запутанности произвел революцию благодаря разработке источников «параметрического преобразования с понижением частоты», в которых используются нелинейные оптические кристаллы для преобразования одиночных фотонов высокой энергии в пары фотонов с вдвое меньшей начальной энергией. Фиолетовый лазер, падающий на один из этих кристаллов (наиболее часто используемый материал — «бета-борат бария» или «BBO»), производит небольшое количество пар фотонов ближнего инфракрасного диапазона. В этом процессе все еще присутствует некоторая случайность, но для сохранения импульса требуется, чтобы пары выходили на противоположных сторонах конуса вокруг исходного лазерного луча, что позволяет разместить два детектора точно в нужном месте для улавливания фотонов. А при правильном расположении кристалла (на самом деле это два тонких кристалла, правильно склеенных вместе) поляризации двух фотонов будут коррелировать именно так, как вам нужно, чтобы продемонстрировать запутанность.

Эти параметрические источники преобразования с понижением частоты обеспечивают гораздо более высокую скорость счета, позволяя экспериментам достигать действительно нелепых уровней статистической значимости. Базовая система также достаточно проста, чтобы ее можно было использовать в лабораторных экспериментах для студентов; в последние годы у нас было несколько студентов, которые делали свои выпускные диссертации по параметрическому преобразованию с понижением частоты (пока не с запутанностью, но у меня есть несколько летних студентов, которые выстроились в очередь, чтобы поработать над этим). Это также ключевые источники для экспериментов по квантовой телепортации и многих экспериментов с квантовой информацией. Если вы читаете новость, в заголовке которой содержится ссылка на ироничное описание Эйнштейном запутанности, «жутких взаимодействий на расстоянии», вероятно, примерно 75% вероятности, что в нем описываются эксперименты, в которых каким-то образом используется параметрическое преобразование с понижением частоты.

Изображение схемы квантовых вычислений с ионной ловушкой. От группы Монро в JQI: http://iontrap.umd.edu/

2) Запутанность второго поколения. Фотоны отлично подходят для демонстрации запутанности и передачи информации, но мир состоит не только из фотонов, и у них есть существенные недостатки. Главным из них является то, что их довольно сложно удержать, поскольку по определению они всегда куда-то движутся со скоростью света. Для многих целей было бы лучше запутать материальные частицы, потому что их легче удерживать в течение длительного периода времени.

Один из самых простых способов представить себе это — просто взять пару фотонов, созданных в запутанном состоянии, и направить их, скажем, на пару атомов, которые могут поглотить рассматриваемые фотоны. Конечное состояние поглощения фотонов будет зависеть от поляризации фотонов, поэтому, поскольку поляризации неопределенны, но коррелированы, вы получите два атома, состояния которых неопределенны, но коррелированы.

На практике это довольно сложно, поскольку виды запутанных фотонов, которые вы можете легко генерировать, не сразу соединяются с атомными состояниями, которые существуют долгое время. Однако, если вы сообразительны, вы можете найти способы сделать что-то подобное и преобразовать запутанность фотонов в запутанность атомов, которые поглощают эти фотоны.

3) Случайное запутывание. Этот метод представляет собой хитрый трюк, который выворачивает предыдущий метод наизнанку. То есть все начинается с пары атомов в разных местах, которые излучают фотоны. Правильное объединение фотонов может запутать состояния двух фотонов таким образом, что это приведет к запутыванию исходных атомов.

Впервые я узнал об этом в экспериментах группы Криса Монро в Мэриленде (ссылка на статью в другом моем блоге), где они использовали ионы иттербия, удерживаемые в отдельных ионных ловушках. Ионы возбуждались до состояния, из которого они могли распадаться одним из двух способов, испуская фотон с одной из двух поляризаций. Они собирают излучаемые фотоны и объединяют их на светоделителе с двумя фотодетекторами, размещенными на двух выходах светоделителя.

В этой конфигурации примерно в 25% случаев, когда два фотона достигают светоделителя, они регистрируют по одному фотону на каждом выходе. Из квантовой оптики мы знаем, что когда это происходит, два фотона имеют противоположную поляризацию, а это означает, что два иона оказываются в двух разных состояниях. Но у них нет способа узнать, какой ион испустил какой фотон. Таким образом, два иона оказываются запутанными: если вы измеряете отдельные состояния, вы получаете случайные результаты, но если вы сравниваете списки результатов для каждого иона за множество повторений, вы обнаружите, что они идеально коррелируют.

Это по своей сути вероятностный процесс, а первоначальные эксперименты в 2009 году (приблизительно) были очень медленными. Они внесли некоторые усовершенствования в базовую схему, но это все еще не такой удобный источник запутанных пар, как при параметрическом преобразовании с понижением частоты. Однако это исключительно крутой трюк, потому что два иона никогда не находятся близко друг к другу — они захвачены в совершенно разных вакуумных камерах на разных частях лазерного стола. Единственное, что сходится, — это излучаемый ими свет, но этого достаточно, чтобы запутать ионы со всеми вытекающими из этого странными последствиями.

Схема блокады Ридберга. Слева: два атома в основном состоянии не влияют друг на друга, и… [+] можно возбудить лазером (зеленая стрелка). Посередине: как только один атом возбуждается, он сдвигает энергетические уровни другого, блокируя лазерное возбуждение. Справа: запутанное состояние, возникающее в результате помещения первого атома в суперпозицию и последующей попытки возбудить второй. (Рисунок Чада Орзеля)

4) Запутанность взаимодействием. Самая крутая часть предыдущего метода — то, что ионы всегда разделены — указывает на окончательный метод создания запутанности, который состоит в том, чтобы просто свести их вместе и позволить им взаимодействовать таким образом, чтобы конечные состояния двух частицы зависят друг от друга. В конце концов, в этом и состоит основной смысл того, чем является запутанное состояние.

Существует множество способов сделать это, в основном связанных с различными схемами квантовых вычислений, но проще всего представить это с помощью схемы «блокады Ридберга». Идея здесь в том, что если у вас есть два атома в основном состоянии, разделенные небольшим расстоянием, они не влияют друг на друга, но если вы возбудите эти атомы до состояния с очень высокой энергией («состояние Ридберга» на жаргоне атомной физики ), они взаимодействуют на больших расстояниях и, таким образом, могут сдвигать энергетические уровни друг друга.

Если все устроить правильно, возбуждение одного атома в ридберговское состояние сдвинет энергетические уровни другого настолько, что его нельзя будет возбудить тем же лазером. Итак, вы используете лазерный импульс, чтобы поместить один в суперпозицию основного состояния и ридберговского состояния, затем пытаетесь возбудить второй атом, он оказывается в суперпозиции, которая совершенно антикоррелирует с первым атомом: часть первый атом, находящийся в основном состоянии, соединяется с частью второго атома, находящейся на ридберговском уровне, и наоборот. Другими словами, два атома теперь запутаны.

Это простой пример взаимодействия, которое приводит к неопределенным, но коррелирующим конечным состояниям, но он передает ключевую идею. Каждый раз, когда вы можете объединить две системы таким образом, что конечное состояние одной частицы зависит от входного состояния другой, вы можете создать запутанное состояние, сделав это входное состояние квантовой суперпозицией. Это обязательно приведет к паре частиц, каждая из которых находится в неопределенном состоянии, и любые возможные измерения этих состояний будут полностью коррелированы (или антикоррелированы). Это мощная идея, и она занимает центральное место практически в каждой схеме квантовых вычислений.

Здесь стоит отметить, что все эти схемы имеют общую черту, а именно то, что запутанность создается локальным образом. То есть в схемах либо участвуют запутанные частицы, находящиеся в одном и том же месте в какой-то точке (запутанные фотоны исходят от одного и того же атома или входного фотона, и взаимодействующие атомы обязательно находятся близко друг к другу), либо они взаимодействуют через что-то, проходящее между ними ни при каких обстоятельствах. больше, чем скорость света (пара запутанных фотонов, движущихся к отдельным атомам, или фотоны от двух ионов, движущиеся к светоделителю). Это критическая особенность для сдерживания странности запутанности — вы не можете просто произвольно запутать две частицы, у которых нет общей истории, что исключает большинство попыток оправдать паранормальные явления, ссылаясь на квантовую запутанность.

Эти методы создания запутанности очень общие, и я пропускаю множество технических деталей их реализации в конкретных системах. Тем не менее, они должны помочь донести общие идеи, поэтому в следующий раз, когда вы будете читать научно-популярную статью о квантовой запутанности, у вас будет лучшее представление о том, откуда она взялась.

Исследователи Стивенса создают запутанные фотоны в 100 раз эффективнее, чем это было возможно ранее

0005

Исследования и инновации

Быстрый источник сверхъярких фотонов делает масштабируемую квантовую фотонику доступной

Юпин Хуанг и его коллеги из Технологического института Стивенса демонстрируют квантовую схему, которую можно легко интегрировать с другими оптическими компонентами, прокладывая путь для высокоскоростных, реконфигурируемых и многогранных квантовых устройств.

(Хобокен, Нью-Джерси – 17 декабря 2020 г.) — Сверхбыстрые квантовые компьютеры и устройства связи могут произвести революцию во многих аспектах нашей жизни, но сначала исследователям нужен быстрый и эффективный источник запутанных пар фотонов, таких как системы используют для передачи и обработки информации. Исследователи из Технологического института Стивенса сделали именно это, создав источник фотонов на основе чипа, в 100 раз более эффективный, чем это было возможно ранее. Эта работа делает возможной масштабную интеграцию квантовых устройств.

«Давно предполагалось, что это возможно в теории, но мы первые, кто продемонстрировал это на практике», — сказал Юпин Хуан, доцент кафедры физики Галлахера в Стивенсе и директор Центра квантовой науки и техники.

Чтобы создать пары фотонов, исследователи улавливают свет в тщательно вылепленных наноразмерных микрополостях; когда свет циркулирует в полости, его фотоны резонируют и распадаются на запутанные пары. Но есть одна загвоздка: в настоящее время такие системы крайне неэффективны, им требуется поток входящего лазерного излучения, состоящий из сотен миллионов фотонов, прежде чем одна запутанная пара фотонов неохотно просочится на другом конце.

Хуан и его коллеги из Stevens разработали новый источник фотонов на основе чипа, который в 100 раз эффективнее любого предыдущего устройства и позволяет создавать десятки миллионов запутанных пар фотонов в секунду с помощью одного лазерного луча мощностью микроватт.

«Это огромная веха для квантовых коммуникаций», — сказал Хуан, чья работа опубликована сегодня в выпуске Physical Review Letters от 17 декабря.

Работая с аспирантами Стивенса Чжаохуэй Ма и Цзяян Ченом, Хуан опирался на предыдущие исследования своей лаборатории, чтобы вырезать чрезвычайно высококачественные микрополости в чешуйках кристалла ниобата лития. Полости в форме беговой дорожки внутренне отражают фотоны с очень небольшой потерей энергии, что позволяет свету циркулировать дольше и взаимодействовать с большей эффективностью.

Путем точной настройки дополнительных факторов, таких как температура, команда смогла создать беспрецедентно яркий источник запутанных пар фотонов. На практике это позволяет производить пары фотонов в гораздо больших количествах для заданного количества входящего света, что значительно снижает энергию, необходимую для питания квантовых компонентов.

Команда уже работает над дальнейшим совершенствованием своего процесса и говорит, что вскоре они надеются получить настоящий Святой Грааль квантовой оптики: систему, которая может превращать один входящий фотон в запутанную пару исходящих фотонов с практически не тратьте энергию по пути. «Это определенно достижимо», — сказал Чен. «На данный момент нам просто нужны постепенные улучшения».

До тех пор команда планирует продолжать совершенствовать свою технологию и искать способы использования источника фотонов для управления логическими вентилями и другими компонентами квантовых вычислений или связи. «Поскольку эта технология уже основана на чипах, мы готовы начать масштабирование, интегрируя другие пассивные или активные оптические компоненты», — пояснил Хуанг.

Конечная цель, по словам Хуанга, состоит в том, чтобы сделать квантовые устройства настолько эффективными и дешевыми в эксплуатации, чтобы их можно было интегрировать в обычные электронные устройства. «Мы хотим вывести квантовую технологию из лаборатории, чтобы она могла принести пользу каждому из нас», — пояснил он. «Когда-нибудь в ближайшее время мы хотим, чтобы у детей в рюкзаках были квантовые ноутбуки, и мы прилагаем все усилия, чтобы сделать это реальностью».

— Stevens —

О Технологическом институте Стивенса

Технологический институт Стивенса — ведущий частный исследовательский университет, расположенный в Хобокене, штат Нью-Джерси. С момента нашего основания в 1870 году технологические инновации были отличительной чертой образования и исследований Стивенса. В трех школах университета и одном колледже 7300 студентов и аспирантов тесно сотрудничают с преподавателями в междисциплинарной, ориентированной на студентов предпринимательской среде. Академические и исследовательские программы, охватывающие бизнес, вычислительную технику, инженерию, искусство и другие дисциплины, активно расширяют границы науки и используют технологии для решения наших самых насущных глобальных проблем. Поскольку Стивенс празднует свое 150-летие, университет по-прежнему неизменно входит в число лидеров страны по карьерным услугам, заработной плате выпускников после выпуска и окупаемости инвестиций в обучение.

Директор по связям с общественностью : Thania Benios, [email protected], 917-930-5988

 

Узнать больше об исследованиях на факультете физики→

Исследователи предлагают новый способ создания источника света из запутанных фотонов

Шерил Пирс, Университет Пердью

Кредит: Pixabay/CC0 общественное достояние

Запутанность — это странное явление в квантовой физике, когда две частицы неразрывно связаны друг с другом независимо от расстояния между ними. Когда одно измеряется, другое измерение мгновенно становится заданным. Исследователи из Университета Пердью предложили новый, нетрадиционный подход к созданию специального источника света, состоящего из запутанных фотонов. 6 сентября 2022 года они опубликовали свои выводы в Physical Review Research 9.0036 .

Команда предложила метод генерации запутанных фотонов в экстремальных ультрафиолетовых (XUV) длинах волн, где в настоящее время такого источника не существует. Их работа представляет собой дорожную карту того, как генерировать эти запутанные фотоны и использовать их для отслеживания динамики электронов в молекулах и материалах в невероятно коротких временных масштабах аттосекунд.

«Запутанные фотоны в нашей работе гарантированно прибудут в заданное место в течение очень короткого периода аттосекунд, пока они проходят одинаковое расстояние», — говорит доктор Ниранджан Шиварам, доцент кафедры физики и астрономии. «Эта корреляция во времени их прихода делает их очень полезными для измерения сверхбыстрых событий. Одним из важных приложений является аттосекундная метрология, чтобы раздвинуть границы измерения явлений с самым коротким временем. Этот источник запутанных фотонов также можно использовать в квантовой визуализации и спектроскопии. , где было показано, что запутанные фотоны улучшают способность получать информацию, но теперь в XUV и даже в рентгеновском диапазоне длин волн».

Авторы публикации под названием «Аттосекундные запутанные фотоны в результате двухфотонного распада метастабильных атомов: источник для аттосекундных экспериментов и не только» принадлежат к факультету физики и астрономии Университета Пердью и работают с Purdue Quantum Science and Инженерный институт (PQSEI). Это доктор Имэн Ван, недавний выпускник Университета Пердью; Сиддхант Пандей, доктор философии. кандидат в области экспериментальной сверхбыстрой спектроскопии; Доктор Крис Х. Грин, заслуженный профессор физики и астрономии Альберта Оверхаузера; и доктор Шиварам.

«Кафедра физики и астрономии Университета Пердью имеет мощную программу по атомной, молекулярной и оптической (АМО) физике, которая объединяет экспертов в различных областях АМО», — говорит Шиварам. «Экспертные знания Криса Грина в области теоретической атомной физики в сочетании с опытом Ниранджана в относительно молодой области экспериментальной аттосекундной науки привели к этому совместному проекту. наука АМО».

Каждый исследователь сыграл важную роль в этом продолжающемся исследовании. Первоначально Грин предложил идею использования фотонов, испускаемых атомами гелия, в качестве источника запутанных фотонов, а Шиварам предложил приложения к аттосекундной науке и предложил экспериментальные схемы. Затем Ван и Грин разработали теоретическую основу для расчета испускания запутанных фотонов атомами гелия, в то время как Панди и Шиварам сделали оценки скоростей испускания/поглощения запутанных фотонов и проработали детали предложенных аттосекундных экспериментальных схем.

Публикация знаменует собой начало исследования Шиварама и Грина. В данной публикации авторы предлагают идею и прорабатывают теоретические аспекты эксперимента. Шиварам и Грин планируют продолжить сотрудничество в области экспериментальных и теоретических идей. Лаборатория Шиварама, Ultrafast Quantum Dynamics Group, в настоящее время строит аппарат для экспериментальной демонстрации некоторых из этих идей. По словам Шиварама, есть надежда, что другие исследователи аттосекундной науки начнут работать над этими идеями. Согласованные усилия многих исследовательских групп могли бы еще больше увеличить влияние этой работы. В конце концов, они надеются уменьшить временную шкалу запутанных фотонов до зептосекунд, 10 -21 секунд.

«Обычно эксперименты с аттосекундными шкалами времени проводятся с использованием аттосекундных лазерных импульсов в качестве «стробов» для «изображения» электронов. Текущие ограничения на эти импульсы составляют около 40 аттосекунд. Предлагаемая нами идея использования запутанных фотонов может сократить это время до нескольких аттосекунды или зептосекунды», — говорит Шиварам.

Чтобы понять синхронизацию, нужно понять, что электроны играют фундаментальную роль в определении поведения атомов, молекул и твердых материалов. Временная шкала движения электронов обычно измеряется фемтосекундами (одна миллионная миллиардной доли секунды — 10 -15 секунд) и аттосекундной (одна миллиардная миллиардной доли секунды, или 10 -18 секунд) шкалы. По словам Шиварама, важно понять динамику электронов и отслеживать их движение в этих сверхкоротких временных масштабах.

«Цель области сверхбыстрой науки состоит в том, чтобы создавать такие «кинофильмы» электронов, а затем использовать свет для управления поведением этих электронов для организации химических реакций, создания материалов с новыми свойствами, создания устройств молекулярного масштаба и т. д. ,» он говорит. «Это взаимодействие света и материи на самом базовом уровне, и возможностей для открытий много. Одна зептосекунда составляет 10 -21 секунд. Тысяча зептосекунд — это аттосекунда. Исследователи только сейчас начинают изучать зептосекундные явления, хотя экспериментально это недостижимо из-за отсутствия зептосекундных лазерных импульсов. Наш уникальный подход к использованию запутанных фотонов вместо фотонов в лазерных импульсах может позволить нам достичь зептосекундного режима. Это потребует значительных экспериментальных усилий и, вероятно, возможно в течение пяти лет».

Узнать больше

Высокояркие аттосекундные рентгеновские лазеры на свободных электронах на основе управления волновым фронтом

Дополнительная информация:
Yimeng Wang et al, Аттосекундно запутанные фотоны от двухфотонного распада метастабильных атомов: источник для аттосекундных экспериментов и не только, Physical Review Research (2022). DOI: 10.1103/PhysRevResearch.4.L032038

Предоставлено
Университет Пердью

Цитата :
Исследователи предлагают новый способ создания источника света из запутанных фотонов (9 сентября 2022 г.