Вечный двигатель на воде: PhysBook:Электронный учебник физики — PhysBook

PhysBook:Электронный учебник физики — PhysBook

Содержание


  • 1 Учебники


  • 2 Механика


    • 2.1 Кинематика


    • 2.2 Динамика


    • 2.3 Законы сохранения


    • 2.4 Статика


    • 2.5 Механические колебания и волны


  • 3 Термодинамика и МКТ


    • 3.1 МКТ


    • 3. 2 Термодинамика


  • 4 Электродинамика


    • 4.1 Электростатика


    • 4.2 Электрический ток


    • 4.3 Магнетизм


    • 4.4 Электромагнитные колебания и волны


  • 5 Оптика. СТО


    • 5.1 Геометрическая оптика


    • 5.2 Волновая оптика


    • 5. 3 Фотометрия


    • 5.4 Квантовая оптика


    • 5.5 Излучение и спектры


    • 5.6 СТО


  • 6 Атомная и ядерная


    • 6.1 Атомная физика. Квантовая теория


    • 6.2 Ядерная физика


  • 7 Общие темы


  • 8 Новые страницы

Здесь размещена информация по школьной физике:

  1. материалы из учебников, лекций, рефератов, журналов;

  2. разработки уроков, тем;

  3. flash-анимации, фотографии, рисунки различных физических процессов;

  4. ссылки на другие сайты

и многое другое.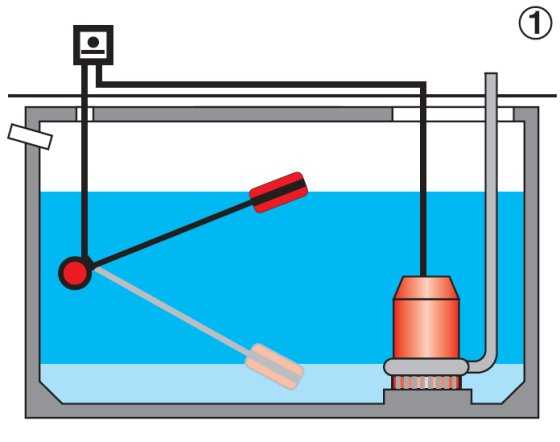

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

3. Вопреки законам гидромеханики и молекулярной физики . Возможен ли вечный двигатель?

Изобретатели, создавая вечный двигатель, нередко пытались, кроме силы тяжести, использовать другие явления природы. В частности, они пробовали применить для этого потерю веса тел, погружённых в жидкость (закон Архимеда).

Первый вечный двигатель, основанный на использовании закона Архимеда, был предложен швейцарцем Германом Леонард из Сент-Галена в 1865 году. Свою идею он воплотил в конструкции, показанной на рисунке 14.

Рис. 14. Поплавковый вечный двигатель, предложенный Германом Леонард (XIX век).


Бесконечная цепь из жестяных поплавков проходит правой половиной сквозь сосуд Б с водой. По мысли автора, поплавки, стремясь всплыть, будут вращать колесо В, через которое эта цепь переброшена.

Однако даже беглый взгляд на эту конструкцию показывает, что колесо не станет вращаться в предположенном направлении. В самом деле, поплавок, проходя через трубку А в днище, должен прилегать к ней настолько плотно, чтобы из сосуда не вытекала вода. Но тогда трение между стенкой отверстия А и поплавком будет настолько велико, что вечного движения всё же не получится. А трение никакими ухищрениями уничтожить нельзя.



«Усовершенствование» этого двигателя представлено другим, оставшимся неизвестным, изобретателем (рис. 15).

Рис. 15. Вечный двигатель со складывающимися поплавками (XIX век).


В сосуде, наполненном жидкостью, находится бесконечная цепь со складывающимися поплавками. С левой стороны поплавки в сжатом состоянии, а с правой, находясь в воде, наполняются воздухом. Поплавки в правой части, стремясь всплыть, будут вращать колесо вечно. Так полагал изобретатель. Но он не указал, как наполнять под водой поплавки воздухом. К тому же для этого требуется преодолеть давление воды и трение в деталях механизма раскрывающихся поплавков, на что необходима значительно большая работа, чем та, которая получается от их всплывания.

Таким образом, и этого изобретателя вечного двигателя постигла неудача.

Ещё с времён Герона Александрийского (около I века до нашей эры) для переливания жидкостей самотёком из верхнего сосуда в нижний часто применялся так называемый сифон (рис.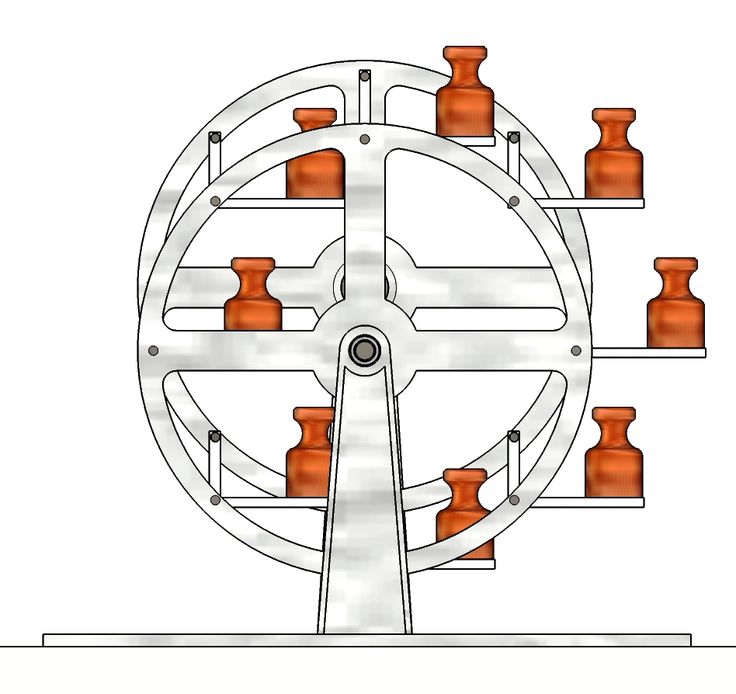  16).

Рис. 16. Сифон.


Действие его основано на разности уровней жидкости в этих сосудах. Чем больше эта разница Н, тем сильнее напор жидкости, а следовательно, и больше скорость перетекания жидкости из верхнего сосуда в нижний. Однако по законам гидравлики верхняя точка сифонной трубы должна располагаться при этом над уровнем жидкости в верхнем сосуде на определённой высоте. В противном случае струя жидкости в сифонной трубе обрывается. Например, для переливания воды при нормальном атмосферном давлении и температуре 15 °C предельная высота верхней точки сифонной трубы над уровнем жидкости в верхнем сосуде не может быть более 10 метров.

Две тысячи лет тому назад, и много позже, принцип действия сифона представляли чрезвычайно смутно. Поэтому иногда возникало множество самых абсурдных предложений практического использования его.

Современник Галилея, итальянец Порта, например, предлагал подавать сифоном воду в случае необходимости через горы. Понятно, это неосуществимо, так как верхняя точка сифонной трубы была бы в этом случае расположена над уровнем жидкости больше чем на 10 метров.

Использовали сифон и в изобретениях вечного двигателя.

Городской архитектор г. Падуи (Италия), Витторио Зонка, предложил невозможное — использовать сифон для перемещения воды из водоёма в него же, используя поток её для вращения турбины с жёрновом на валу. Чтобы возместить отсутствие разности высот между уровнями жидкости у входного и выходного отверстий сифонной трубы, он предлагал выходную часть её сделать большего диаметра (рис. 17).

Рис. 17. Сифонный вечный двигатель Витторио Зонка (XVI век).


В XVII веке инженер и архитектор Г. Анрей Бёклер издал своё сочинение, в котором представил проект вечного двигателя для точки ножей под громким названием «Искусство верчения и кручения с двойной передачей». Такой «двигатель», между прочим, был известен задолго до Г. А. Бёклера.  В 1575 году его предлагал итальянский механик Страада-Старший.

Конструкция вечного двигателя, предложенная Страадой-Старшим и А. Бёклером, представлена на рисунке 18 и состоит из следующих основных деталей: верхнего и нижнего водоёмов; рабочего вала Б с наглухо насаженным на него точилом; маховика Г; червячной шестерни В; водяного колеса; коронной шестерни Е, приводимой во вращение червячной шестернёй В, промежуточного вала Ж с маховиком и шестернёй И; двух шестерён К, наглухо насаженных на вал З. Левая шестерня входит в зацепление с шестернёй на валу архимедова винта, предназначенного поднимать воду из нижнего водоёма в верхний.

Рис. 18. «Искусство верчения и кручения с двойной передачей», вечный двигатель для точки ножей (XVI–XVII век).


По предположению изобретателей, их машина должна действовать следующим образом. Вода из верхнего водоёма вытекает по двум трубам А и Д. Из трубы Д она падает на точило, а из трубы А падает на водяное колесо и стекает в нижний водоём.

Под силой падающей из трубы А воды водяное колесо вращается и приводит в движение вал с находящимися на нём точилом, маховиком и червячной шестерней В, которая приводит во вращение коронную шестерню Е, валы Ж и 3 и через шестерню К архимедов винт.

Архимедов винт подаёт воду из нижнего водоёма в верхний.

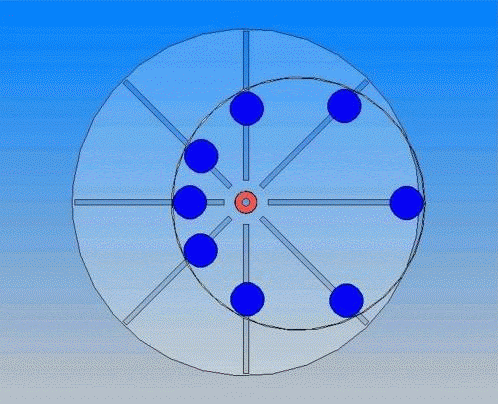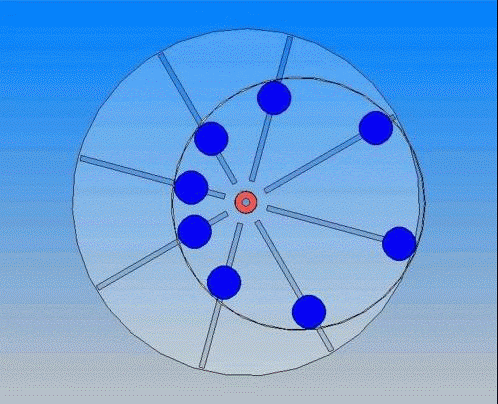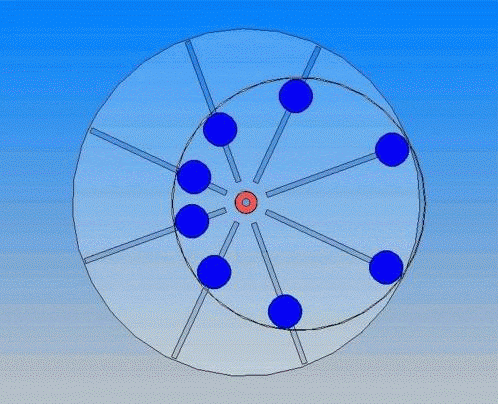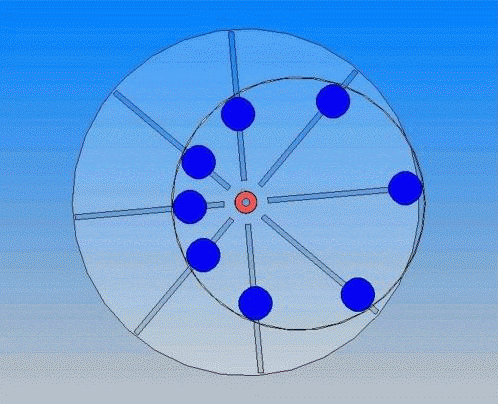
Несмотря на сложность и кажущуюся надёжность этого вечного двигателя, он оказался не способным совершать работу. Причины этого станут ясны, если вспомнить вечный двигатель, изображённый на рисунке 9, в котором вместо воды применены шарики. Но сущность действия, вернее бездействия, одинакова.

«Усовершенствованием» сифонного вечного двигателя можно считать сифонно-капиллярный вечный двигатель (рис. 19), предложенный Синклером в XVIII веке.

Рис. 19. Сифонно-капиллярный вечный двигатель (XVIII век).


Изобретатель предполагал, что вода из верхнего сосуда, перелившись по сифону в нижний, будет возвращаться в верхний по другим трубкам очень малого диаметра, так называемым капиллярным трубкам. Однако ожидаемого передвижения воды по ним не происходило. Почему так получалось, мы разберём, ознакомившись ещё с одним жидкостным, также оказавшимся бездействующим, вечным двигателем (рис. 20).

Рис. 20. Капиллярно-фитильный вечный двигатель (XIX век).


По предположению изобретателя вода или масло из нижнего сосуда будет подниматься вверх по обыкновенному фитилю и стекать в верхний сосуд. Отсюда жидкость, попав на колесо, приведёт его в движение. А затем из нижнего сосуда она беспрерывно поднимается по фитилю вверх. Однако двигатель не работал.

Какие же физические явления пытались использовать изобретатели, создавая последние два вечных двигателя?

Всем нам достаточно хорошо известна керосиновая лампа. В ней керосин действительно, вопреки силе тяжести, поднимается из резервуара на 10–15 см вверх по фитилю. Почему же не работали только что описанные вечные двигатели?

Чтобы понять причины этого, возьмём сосуд с водой и на её поверхность осторожно уложим стальную иглу или проволочную спираль, смазанные жиром. Оказывается, что игла и спираль не потонут. Они будут плавать на поверхности. Внимательно всмотревшись, мы обнаружим, что поверхность воды под иглой или спиралью изогнулась словно резина под тяжёлым грузом. Следовательно, в поверхностном слое жидкости действуют какие-то силы, поддерживающие свободную поверхность в напряженном состоянии, подобно растянутой тонкой плёнке из резины. Что это именно так, можно убедиться, проделав следующий опыт. Возьмём проволочное кольцо, затянутое мыльной плёнкой, и положим на неё петлю из нити. Петля останется лежать в том случайном положении, в каком оказалась в момент укладывания (рис. 21, слева). Разрушим внутри нитяной петли плёнку, прикоснувшись к ней разогретой иглой. Петля немедленно растягивается в круг (рис. 21, справа).



Рис. 21. Пример действия сил поверхностного натяжения.


Произошло это под действием натяжения плёнки, сохранившейся вокруг петли. Нечто подобное происходит и с кисточкой для рисования, когда её вынимают из воды: все её волоски как бы слипаются вместе.

Учёные установили, что силы, удерживающие стальную иглу и спираль на поверхности жидкости, растягивающие петлю в кольцо и стягивающие волоски кисточки, всегда направлены перпендикулярно к контуру, на который они действуют. Называют эти силы силами поверхностного натяжения.

Почему же возникает поверхностное натяжение?

Рассмотрим внимательно рисунок 22, на котором условно изображены отдельно две молекулы жидкости: одна внутри жидкости, а другая — у её поверхности.

Рис. 22. Схема действия межмолекулярных сил на молекулу внутри жидкости и у поверхности.


На каждую из них действуют по-разному силы притяжения соседних молекул. Молекулу, находящуюся под поверхностью жидкости, окружают со всех сторон другие молекулы. Межмолекулярные силы притягивают эту молекулу со всех сторон одинаково, в результате чего она находится в равновесии. По-иному действуют межмолекулярные силы на молекулу, находящуюся на поверхности жидкости. Верхняя половина этой молекулы испытывает ничтожное притяжение со стороны молекул газов воздуха; практически оно отсутствует совсем. Такая молекула оказывается лишь под действием нижележащих молекул жидкости, стремящихся втянуть её внутрь, а также соседних молекул, лежащих в одном с нею слое и увлекающих её в разные стороны в горизонтальной плоскости. Поверхность жидкости в сосуде вследствие этого подобна коже, натянутой на корпус барабана, — непосредственно на поверхности жидкости образуется упругая плёнка.

Подсчитано, что поверхностное натяжение в этой плёнке толщиной несколько больше одной молекулы давит на нижележащий слой жидкости с огромной силой. Под влиянием поверхностного натяжения плёнки внутреннее молекулярное давление достигает, например, для воды 10 000 атмосфер, для эфира 1400 атмосфер, для спирта 2400 атмосфер.

От поверхностного натяжения, оказывается, зависит и «поведение» жидкости в различных сосудах. Поверхностное натяжение ртути и керосина, например, резко различается между собою. Это можно заметить, рассматривая положение (форму) свободной поверхности их в сосудах (рис. 23).

Рис. 23. Явление капиллярности.


Поверхность ртути слегка выпуклая, её края у стенок сосуда опущены ниже всей поверхности. Поверхность керосина, наоборот, вогнутая, её края у стенки сосуда приподняты выше всей поверхности.

Положение поверхности жидкости по отношению к стенкам сосуда называется мениском (от греческого слова — менискос, что означает лунный серп, луночка).

В широких сосудах мениск наблюдается только у самых стенок, вся остальная часть поверхности — плоская. Нередко мениск бывает трудно заметить. В трубках же с очень малым диаметром, так называемых капиллярах, мениск захватывает всю поверхность жидкости, его легко заметить.

В капилляре, опущенном в сосуд с керосином, например, мениск окажется вогнутым, а в сосуд с ртутью, наоборот, выпуклым. Кроме того, уровень керосина или любой другой жидкости с вогнутым мениском в капилляре окажется значительно выше её уровня в сосуде, а уровень ртути или какой-либо другой жидкости с выпуклым мениском, наоборот, ниже, чем в сосуде (рис. 23). В стеклянной трубке диаметром 1 мм при 20 °C и 760 мм ртутного столба вода, например, поднимется на 30, спирт на 12, а эфир на 10 мм выше общего уровня в сосуде, куда опущен капилляр.

Выпуклый мениск образуется у жидкостей, не смачивающих стенки сосуда, а вогнутый — у смачивающих. Смачиваемость или несмачиваемость стенок сосуда зависит от свойств жидкости и материала, из которого изготовлены стенки сосуда. Между молекулами жидкости и стенок сосуда возникают силы притяжения или отталкивания. Если силы притяжения со стороны молекул стенки больше межмолекулярных сил жидкости, то те молекулы её, которые соприкасаются со стенками сосуда, поднимаются по стенке сосуда выше всей поверхности. Происходит смачивание стенок сосуда жидкостью, в этом случае образуется вогнутый мениск. Если же межмолекулярные силы жидкости больше сил притяжения молекул стенки или если молекулы стенки сосуда и жидкости отталкиваются друг от друга — образуется выпуклый мениск. В этом случае жидкость не смачивает стенок сосуда.

В капилляре с вогнутым мениском давление поверхностной плёнки на нижележащую жидкость меньше, чем в широком сосуде. Поэтому уровень жидкости в капилляре поднимается выше общего уровня её в большом сосуде (рис. 23, справа). При выпуклом мениске давление поверхностной плёнки в капилляре на нижележащую жидкость больше, чем в широком сосуде. Поэтому уровень жидкости в капилляре окажется ниже общего уровня её в большом сосуде (рис. 23, слева). Теперь нам понятна ошибка изобретателей сифонно-капиллярного и фитильного вечных двигателей. У сифонно-капиллярного вечного двигателя (рис. 19) жидкость поднимется по капилляру лишь до верхнего сосуда при условии, что сосуд пустой.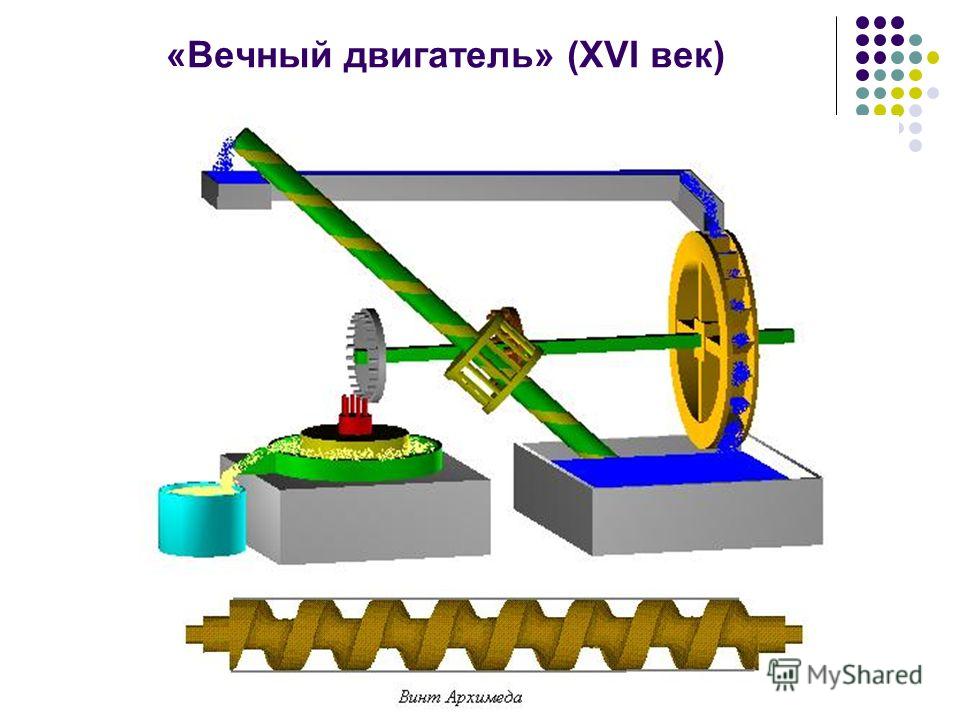  Здесь в месте расширения капилляра давление поверхностной плёнки на жидкость станет таким же, как и в обычном сосуде. Движение жидкости вверх прекратится. И система, созданная воображением изобретателя, действовать не будет. Если же в верхнем сосуде будет хотя бы небольшой запас жидкости, то капиллярная трубочка окажется просто дополнительным каналом, по которому жидкость будет перетекать из верхнего сосуда в нижний.

Фитильный вечный двигатель (рис. 20), являясь как бы усовершенствованием предыдущего, также не будет действовать.

Изобретатель фитильного вечного двигателя полагал, что жидкость, поднявшись по капиллярам фитиля из нижнего сосуда, начнёт стекать в верхний. Но этого не произойдёт. В данном случае те силы взаимодействия между молекулами жидкости и стенок капилляра в фитиле, благодаря которым она поднялась вверх вопреки силе тяжести, удержат её от падения с фитиля на дно верхнего сосуда. Больше того, если этот сосуд наполнить жидкостью, то она устремится вниз по образовавшемуся капиллярному сифону. Таким образом, в действительности получится не то, чего хотел добиться изобретатель этого вечного двигателя.

Упорно стремясь создать вечный двигатель, изобретатели пытались использовать и многие другие явления природы. В частности, они пытались использовать явление осмоса. Осмос — слово греческое, по-русски оно означает: толчок, давление.

Под действием осмоса, например, влага из почвы проникает в семена растений. Давления, возникающие при этом, огромны и возрастают по мере уменьшения влажности почвы. Так, при влажности почвы 35 % влага проникает в семена под влиянием осмотического давления в 35 атмосфер, а при влажности почвы 6 % — под влиянием осмотического давления в 400 атмосфер.



Осмотический вечный двигатель пытались построить следующим образом.

В сосуд с чистой водой погружали трубку, нижнее отверстие которой затянуто животным пузырём (рис. 24).

Рис. 24. Вечный двигатель с раствором сахара.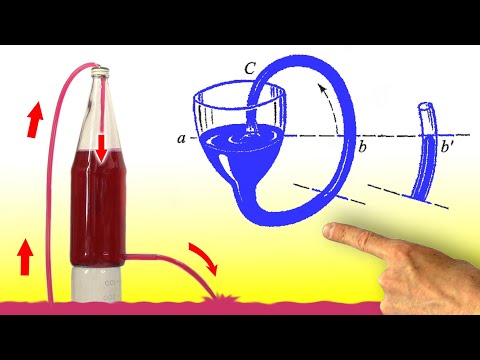


Трубка наполнялась водным раствором сахара (170–180 г сахара на 100 г воды). Через некоторое время объём раствора сахара увеличивался, его уровень становился значительно выше уровня воды. Причём, если трубка недостаточно высока, то раствор переливался через её верхний конец. Это объясняется тем, что из сосуда чистая вода проникает под влиянием осмотического давления через перегородку, непроницаемую для водного раствора сахара. В результате трубка переполняется, и разбавленный раствор сахара переливается в сосуд с водой. Но это происходит до выравнивания концентрации раствора сахара в трубке и сосуде. Как только концентрация сахара станет одинаковой, движение жидкости прекратится.

Поток сахарного сиропа через верх трубки представлялся изобретателям как средство создания вечного двигателя. Известный учёный Иоганн Бернулли (1667–1748 гг.) видел в явлении осмоса возможность создания вечного двигателя.

Однако из. рассказанного нетрудно понять, почему изобретатели осмотического вечного двигателя не смогли достигнуть успеха. Ведь вместо раствора сахара, непрерывно текущего через край трубки, в неё из сосуда через полупроницаемую перегородку поступает чистая вода. Но как только концентрация сахара в сосуде и в трубке станет одинаковой, поступление воды через перегородку прекратится. Чтобы этого не произошло, чтобы поддерживать осмотическое давление, необходимо добавлять в трубку концентрированный раствор сахара взамен вытекающего, а в сосуде сменять раствор чистой водой. Но это уже не вечный двигатель, создающий энергию из ничего.



вода — Капиллярный вечный двигатель

спросил

Изменено
7 месяцев назад

Просмотрено
4к раз

$\begingroup$

Кто-нибудь может понять, что не так с этим вечным двигателем? Какая его часть нарушает физику? Я нашел это на веб-сайте некоторое время назад, и я не мог понять, что с ним не так. Спасибо и наслаждайтесь!

Кстати, вот сайт: https://www.lockhaven.edu/~dsimanek/museum/capillar.htm

  • вода
  • поверхностное натяжение
  • вечное движение
  • 0 капиллярный

$\endgroup$

3

$\begingroup$

Ответ очень прост.
При увеличенном диаметре капиллярной трубки капиллярность теряется/уменьшается в зависимости от диаметра. Вода больше не будет подниматься до большего диаметра в верхней части капиллярной трубки, и сифон не может работать, если его входной конец не будет погружен в воду.

$\endgroup$

$\begingroup$

Вот кое-что, что я нашел, потому что в настоящее время изучал этот вопрос. Насколько нам известно, вечный двигатель нарушил бы первый и второй законы термодинамики, сказал Симанек Live Science. Проще говоря, Первый закон термодинамики гласит, что энергия не может быть создана или уничтожена, а только преобразована из одной формы в другую. Вечный двигатель должен был бы производить работу без затрат энергии. Второй закон термодинамики гласит, что изолированная система будет двигаться к состоянию беспорядка. Кроме того, чем больше энергии трансформируется, тем больше ее тратится впустую. Вечный двигатель должен иметь энергию, которая никогда не тратится впустую и никогда не переходит в неупорядоченное состояние. Если вы все еще не в курсе, то вот сайты, которые мне помогли.
https://www.livescience.com/55944-вечные-движения-машины.html
[https://www.britannica.com/science/thermodynamics/Isothermal-and-adiabatic-processes#ref510518
Надеюсь, это было полезно

$\endgroup$

2

$\begingroup$

Я выкачиваю жидкое мыло из бочек с помощью шлангов и электрических насосов, так что мне нетрудно разобраться.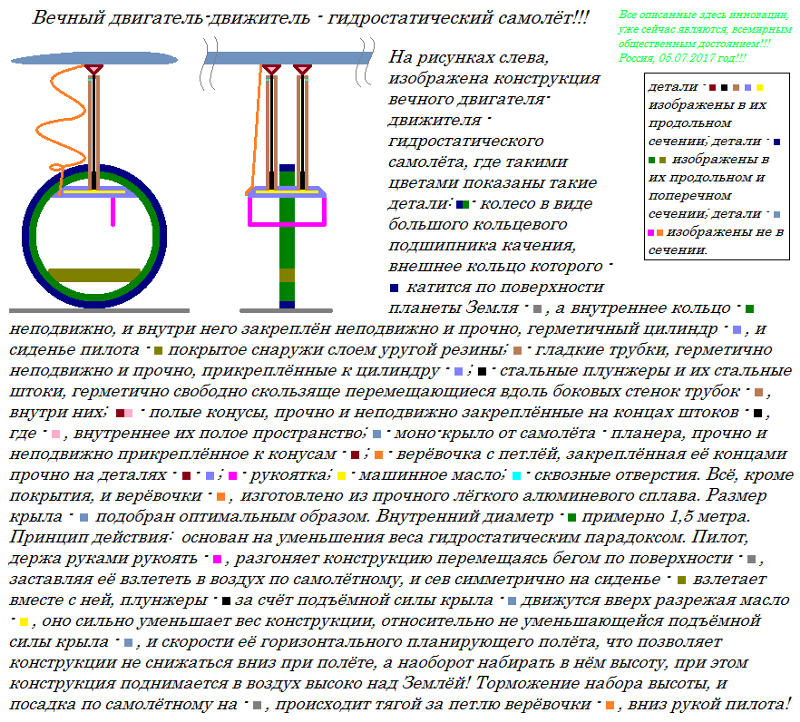 Конец сифона должен быть ниже источника, который он откачивает. Вы можете просто перекачивать из A в B, поскольку B ниже, чем A, но соединение A с C приводит к тому, что B становится выше, а соединение двух фактически приведет к тому, что более высокий пул будет перекачиваться назад к нижнему. Когда мне нужно получить точный вес на весах, я использую электродвигатель, чтобы накачать дополнительное мыло, и как только я его выключаю, он начинает перекачивать назад, пока я не закрываю клапан. Представьте себе небольшой бассейн, представляющий собой контейнер, который я наполняю, используя бассейн на дне в качестве бочки, А — это электродвигатель, а на участке между А и С есть запорный клапан. Если моторы не форсируют вверх, гравитация толкает его обратно вниз.

$\endgroup$

$\begingroup$

A, B и C являются частью одного водоема.

  • B перекачает в C через A под действием силы тяжести
  • C поднимется до A благодаря капиллярному действию

Поток в сифоне больше, чем в капилляре, поэтому B будет сливаться в C через A, пока B не окажется ниже впускной трубы, и поток прекратится.

$\endgroup$

$\begingroup$

У вас есть стрелки назад, чтобы это был сифон с вечным двигателем.
Трубопровод должен быть закрыт, а линия A должна быть прямой, чтобы сифон мог течь из B в C.
Аристотель учил нас, что вода будет искать свой собственный уровень.
Вода будет продолжать течь, поскольку она ищет уровень от C до B.
Уровень воды B выше, чем C, позволяет сифону течь под действием силы тяжести на более низкий уровень, пока C и B не станут равными.
Если бы B снабжался постоянным источником, таким как река, а C оставался открытым для перелива при заполнении или питании притоков, эта конфигурация могла бы работать непрерывно.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

потенциальной энергии — Почему этот вечный двигатель на основе испарения не работает?

спросил

Изменено
2 года, 7 месяцев назад

Просмотрено
300 раз

$\begingroup$

Сегодня утром меня посетила странная мысль:

  1. Гидроэлектростанции получают энергию, сбрасывая воду с высоты. Чем больше разница в высоте между верхом и низом, тем больше энергии можно получить.
  2. Для испарения 1 грамма кипящей жидкости требуется постоянное количество энергии.
  3. После испарения газообразное вещество поднимется в воздух как можно выше благодаря плавучести (ну, если предположить, что оно менее плотное, чем воздух). Другими словами, для его поднятия не требуется дополнительной энергии.

Сложите эти три вместе, поиграйте с веществами, которые вы используете для «воздуха» и «жидкости», и вы сможете поднять испарившуюся жидкость достаточно высоко, чтобы после конденсации наверху и падения вниз она производила больше энергии, чем было необходимо его выпарить в первую очередь.

Очевидно, что это не сработает, потому что вечный двигатель не может работать, но я не знаю, какое из моих предположений неверно или какие другие факторы могут сделать это невозможным.

  • потенциальная энергия
  • испарение
  • вечное движение

$\endgroup$

1

$\begingroup$

Сценарий, который вы описываете, более или менее примерно соответствует тому, как работают гидроэлектростанции, но они используют источник энергии — солнце — для выполнения работы по испарению и создания ветров, которые перемещают влажный воздух.

Если бы не было поступления солнечной энергии, прекратились бы испарение и глобальная циркуляция атмосферы, прекратились бы дожди, а гидроэлектростанции остановились бы, как только их резервуары иссякли бы.

Это демонстрирует, что вечный двигатель на основе испарения не может работать.

$\endgroup$

1

$\begingroup$

После испарения газообразное вещество поднимется в воздух как можно выше благодаря плавучести (ну, если предположить, что оно менее плотное, чем воздух). Другими словами, для его поднятия не требуется дополнительной энергии.

Это, кажется, ключевая ошибка. Неправильно, что столбец может быть произвольной высоты. Поскольку имеет значение только давление паров рабочей жидкости, мы можем избавиться от воздуха и сосредоточиться только на рабочей жидкости. Я назову это водой, но принципы справедливы и для других жидкостей.

В гидростатическом случае давление пара определяется весом пара выше. Пар, как и все, что имеет массу, падает под действием силы тяжести, если его не поддерживает давление внизу. Поэтому высота, на которую он может подняться, ограничена высотой столба водяного пара. Вес столба водяного пара ограничивает высоту, на которую он может подняться, а также определяет давление на дне.

Давление на дне важно, поскольку часть энтальпии испарения представляет собой работу $P\Delta V$, совершаемую при расширении жидкости в паровую фазу на дне. Эта работа представляет собой механическую работу, которая поднимает столб пара обратно на его первоначальную высоту до конденсации.

Механическая работа, совершаемая при падении жидкой воды на дно, равна механической работе $P\Delta V$, необходимой на дне (поскольку центр масс один и тот же до и после). Поскольку это всего лишь часть энтальпии испарения, общий процесс потребует больше энергии, чем вырабатывается, даже на максимальной высоте.

$\endgroup$

$\begingroup$

Вот концептуальная причина, почему без математики используются крайности.

Сначала несколько утверждений, затем рассуждения:
Во Вселенной нет полностью изолированных систем, и каждая система теряет положительное количество энергии в виде тепла в окружающую среду. Тепло течет от более горячего к более холодному, и всегда есть более холодные регионы, пока Вселенная не достигнет теплового равновесия (игнорируя флуктуации), чего не произойдет в течение триллионов лет. Энтропия теплоизолированной системы не может уменьшаться и постоянна тогда и только тогда, когда все процессы обратимы. Поскольку не существует идеально теплоизолированных систем, вы видите поток тепла и, следовательно, увеличение энтропии во Вселенной. Но обратимые системы допускают обратный поток тепла и энтропии, поэтому нам нужно установить хотя бы один необратимый процесс. Когда она у нас есть, все вышеперечисленное объединяется, чтобы дать энтропийную стрелу времени, и таким образом, мы можем сказать, что каждый процесс или система отдает энергию Вселенной как целому . Таким образом, вам нужно вводить энергию в систему, чтобы поддерживать ее равновесие (с собой, а не с окружающей средой).

По необратимым процессам. Это очень интересная тема, и я уже задавал вопросы по SE для уточнения. Пока не получу ответа, буду апеллировать к мнению Сасскинда о том, что без мультивселенной необратимых процессов не бывает. Даже в ускоряющейся, расширяющейся Вселенной, такой как наша, у нас все еще есть повторения из-за конечности нашей «коробки»/горизонта. Это гарантирует обратную стрелу времени в каком-то далеком будущем. Так что у нас не было бы настоящей, полной необратимости. Введите аргумент Сасскинда о том, что процессы Колемана-Де Люччиа, связанные с формированием и схлопыванием вселенных-пузырей в рамках вечной инфляции, порождают действительно полный необратимый процесс. Мое понимание его рассуждений состоит в том, что скорость порождения вселенных настолько велика в такой мультивселенной, что она превышает количество вселенных, которые в настоящее время повторяются, поэтому мы можем использовать самовыборку, чтобы сказать, почему мы не видим ни одной.