Квантовые вычисления. Квантовые системы
Квантовая система
Квантовая система
Для объяснения многих свойств микрочастиц (фотонов, электронов и др.) требуются специальные законы и подходы квантовой механики. Квантовые свойства микромира проявляются через свойства макросистем. Микрообъекты составляют определенную физическую систему, которая называется квантовой. Примерами квантовых систем могут служить: фотонный газ, электроны в металлах. Под терминами квантовая система, квантовая частица следует понимать материальный объект, который описывается с помощью специального аппарата квантовой механики.
Квантовая механика исследует свойства и явления мира микрочастиц, которые не может трактовать классическая механика. Такими особенностями, например, стали: корпускулярно-волновой дуализм, дискретность, существование спинов. Методы классической механики не могут описать поведение частиц микромира. Имеющиеся одновременно волновые и корпускулярные свойства у микрочастицы не дают возможности определить состояние частицы с классической точки зрения.
Данный факт отразился в соотношении неопределенности Гейзенберга ($1925г.$):
где $\triangle x$ -- неточность в определении координаты, $\triangle p$ -- погрешность в определении импульса микрочастицы. Подобное соотношение можно записать в виде:
где $\triangle E$ -- неопределенность в величине энергии, $\triangle t$ -- неопределенность по времени. Соотношения (1) и (2) указывают на то, что если одна из величин в этих соотношениях определены с высокой точностью, то другой параметр имеет большую погрешность в определении. В этих соотношениях $\hbar =1,05\cdot {10}^{-34}Дж\cdot с$. Так, состояние микрочастицы в квантовой механике, нельзя описать, одномоментно используя координат и импульс, что является возможным в классической механики. Аналогичная ситуация относится к энергии в данный момент времени. Состояния с конкретным значением энергии можно получить только в стационарных случаях (то есть в случаях, которые не имеют точного определения во времени).
Имея корпускулярные и одновременно волновые свойства, микрочастица не обладает точной координатой, а является «размазанной» в некоторой области пространства. В случае присутствия в некоторой области пространства двух и более частиц не возможно их отличить друг от друга, так как нельзя отследить за движением каждой. Из вышесказанного следует тождественность частиц в квантовой механике.
Некоторые параметры, относящиеся к микрочастицам, принимают дискретные значения, что классическая механика объяснить не может. В соответствии с положениями и законами квантовой механики, помимо энергии системы, дискретными могут быть момент количества движения системы:
где $l=0,1,2,\dots $
спин может принимать значения:
где $s=0,\ \frac{1}{2},\ 1,\ \frac{3}{2},\dots $
Проекция магнитного момента на направление внешнего поля принимает значения:
где $m_z$ -- магнитное квантовое число, которое принимает значения: $2s+1: s, s-1,...0,...,-(s-1), -s.$
${\mu }_B$ -- магнетон Бора.
С целью математического описания квантовых особенностей физических величин в соответствие каждой величине ставят оператор. Так, в квантовой механике физические величины отображаются операторами, при этом их значения определяются средними по собственным значениям операторов.
Состояние квантовой системы
Любое состояние в квантовой системе описывается при помощи волновой функции. Однако данная функция прогнозирует параметры будущего состояния системы с некоторой долей вероятности, а не достоверно, то является принципиальным отличием от классической механики. Таким образом, для параметров системы волновая функция определяет вероятностные значения. Такая неопределенность, неточность предсказаний более всего вызывала споры в среде ученых.
Измеряемые параметры квантовой системы
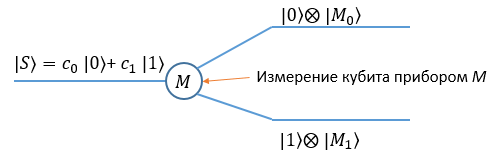
Самые глобальные различия между классической и квантовой механикой заключены в роли измерения параметров изучаемой квантовой системы. Проблема измерений в квантовой механике заключается в том, что при попытках провести измерения параметров микросистемы исследователь действует на систему макроприбором, чем изменяет состояние самой квантовой системы. Так, при попытке точно измерить параметр микрообъекта (координату, импульс, энергию), мы сталкиваемся с тем, что сам процесс измерения изменяет параметры, которые мы пытаемся измерить, причем существенно. Провести точные измерения в микромире невозможно. Всегда будет иметь место ошибки в соответствии с принципом неопределенности.
В квантовой механике динамические переменные представляют операторы, поэтому говорить о числовых значениях не имеет смысла, так как оператор определяет действие на вектор состояния. Результат представлен, так же вектором пространства Гильберта, а не числом.
Замечание 1
Только в том случае, если вектор состояния - собственный вектор оператора динамической переменной, то его действие на вектор можно свести к умножению на число без изменения состояния. В таком случае оператору динамической переменной можно сопоставить единственное число, которое равно собственному значению оператора. При этом можно считать, что динамическая переменная имеет определенное численное значение. Тогда динамическая переменная имеет количественное значение независимое от измерения.
В том случае, если вектор состояния не собственный вектор оператора динамической переменной, то результат измерения не становится однозначным и говорят только о вероятности того или иного значения получаемого в измерении.
Результатами теории, которые проверяемы эмпирически служат вероятности получения в измерении динамической переменной при большом количестве измерений для одного и того же вектора состояния.
Основной характеристикой квантовой системы является волновая функция, которая введена М. Борном. Физический смысл чаще всего определяют не для самой волновой функции, а квадрат ее модуля, который определяет вероятность того, что квантовая система в указанный момент времени находится в данной точке пространства. Основа микромира -- вероятность. Помимо знания волновой функции для описания квантовой системы необходима информация о других параметрах, например о параметрах поля, с которым система взаимодействует.
Процессы, которые происходят в микромире лежат за пределами чувственного восприятия человека. Следовательно, понятия и явления, которые использует квантовая механика, лишены наглядности.
Пример 1
Задание: Какова минимальная ошибка, с которой можно определить скорость электрона и протона, если координаты частиц известны с неопределенностью $1$ мкм.
Решение:
В качестве основы для решения задачи используем соотношение неопределенностей Гейзенберга в виде:
\[\triangle p_x\triangle x\ge \hbar \left(1.1\right),\]где $\triangle x$ -- неопределенность координаты, $\triangle p_x$ -- неопределенность проекции импульса частицы на ось X. Величину неопределенности импульса можно выразить как:
\[\triangle p_x=m\triangle v_x\left(1.2\right).\]Подставим правую часть выражения (1.2) вместо неопределенности проекции импульса в выражении (1.1), имеем:
\[m\triangle v_x\triangle x\ge \hbar \left(1.3\right).\]Из формулы (1.3) выразим искомую неопределенность скорости:
\[\triangle v_x\ge \frac{\hbar }{m\triangle x}\left(1.4\right).\]Из неравенства (1.4) следует, что минимальная погрешность при определении скорости частицы равна:
\[\triangle v_x=\frac{\hbar }{m\triangle x}.\]Зная массу электрона $m_e=9,1\cdot {10}^{-31}кг,$ проведем вычисления:
\[\triangle v_{ex}=\frac{1,05\cdot {10}^{-34}}{9,1\cdot {10}^{-31}\cdot {10}^{-6}}=1,1\cdot {10}^2(\frac{м}{с}).\]масса протона равна $m_p=1,67\cdot {10}^{-27}кг$, вычислим погрешность в измерении скорости протона при заданных условиях:
\[\triangle v_{px}=\frac{1,05\cdot {10}^{-34}}{1,67\cdot {10}^{-27}\cdot {10}^{-6}}=0,628\cdot {10}^{-1}(\frac{м}{с}).\]Ответ: $\triangle v_{ex}=1,1\cdot {10}^2\frac{м}{с},$ $\triangle v_{px}=0,628\cdot {10}^{-1}\frac{м}{с}.$
Пример 2
Задание: Какова минимальная погрешность в измерении кинетической энергии электрона, если он находится в области, размер которой l.
Решение:
В качестве основы для решения задачи используем соотношение неопределенностей Гейзенберга в виде:
\[\triangle p_xl\ge \hbar \to \triangle p_x\ge \frac{\hbar }{l}\left(2.1\right).\]Из неравенства (2.1) следует, что минимальная погрешность импульса равна:
\[\triangle p_x=\frac{\hbar }{l}\left(2.2\right).\]Погрешность кинетической энергии можно выразить как:
\[\triangle E_k=\frac{{\left(\triangle p_x\right)}^2}{2m}=\frac{{\left(\hbar \right)}^2}{{\left(l\right)}^22\cdot m_e}.\]Ответ: $\triangle E_k=\frac{{\left(\hbar \right)}^2}{{\left(l\right)}^22\cdot m_e}.$
spravochnick.ru
Открытая система (квантовая механика) — WiKi
Открытая система в квантовой механике — квантовая система, которая может обмениваться энергией и веществом с внешней средой. В определенном смысле всякая квантовая система может рассматриваться как открытая система, поскольку измерение любой динамической величины (наблюдаемой) связано с конечным необратимым изменением квантового состояния системы. Поэтому в отличие от классической механики, в которой измерения не играют существенной роли, теория открытых квантовых систем должна включать в себя теорию квантовых измерений.
Открытые системы в статистической механике и в квантовой механике могут быть гамильтоновыми и негамильтоновыми. Эволюция гамильтоновых систем целиком определяется её гамильтонианом. Например, в равновесной статистической механике системы с переменным числом частиц, которые можно считать открытыми, описываются большим каноническим распределением Гиббса. Важным классом открытых систем является класс негамильтоновых систем. Именно в негамильтоновых системах возможны процессы самоорганизации. Среди негамильтоновых систем выделяются диссипативные, аккретивные, обобщенно диссипативные системы.
Динамика гамильтоновой квантовой системы, описывается однопараметрической группой унитарных операторов. В качестве уравнений движения используются уравнение фон Неймана и уравнение Гейзенберга. Эволюция негамильтоновой системы, подверженной внешним воздействиям, будь то процесс установления равновесия с окружающей средой или взаимодействие с измерительным прибором, обычно описывается вполне положительными отображениями. Динамика негамильтоновых открытых квантовых систем, обладающих свойством марковости, задается уравнение Линдблада.
Исследования открытых квантовых негамильтоновых систем восходят к работам польского физика А. Коссаковского[1], и связаны с введением понятия квантовой динамической полугруппы[2][3], затем развитого Г. Линдбладом[4].
ru-wiki.org
Квантовые вычисления - это... Что такое Квантовые вычисления?
3 кубита квантового регистра против 3 битов обычного
Квантовый компьютер — гипотетическое[1]вычислительное устройство, которое путем выполнения квантовых алгоритмов существенно использует при работе квантовомеханические эффекты, такие как квантовый параллелизм и квантовая запутанность.
Содержание понятия «квантовый параллелизм» может быть раскрыто так: «Данные в процессе вычислений представляют собой квантовую информацию, которая по окончании процесса преобразуется в классическую путём измерения конечного состояния квантового регистра. Выигрыш в квантовых алгоритмах достигается за счет того, что при применении одной квантовой операции большое число коэффициентов суперпозиции квантовых состояний, которые в виртуальной форме содержат классическую информацию, преобразуется одновременно» [1].
Под квантовой запутанностью, которую называют также «квантовой суперпозицией», обычно понимается следующее: "Вообразите атом, который мог бы подвергнуться радиоактивному распаду в определенный промежуток времени. Или не мог бы. Мы можем ожидать, что у этого атома есть только два возможных состояния: «распад» и «не распад», /…/ но в квантовой механике у атома может быть некое объединенное состояние — «распада — не распада», то есть ни то, ни другое, а как бы между. Вот это состояние и называется «суперпозицией» [2].
Базовые характеристики квантовых компьютеров в теории позволяют им преодолеть некоторые ограничения, возникающие при работе классических компьютеров.
Теория
Кубиты
Идея квантовых вычислений, впервые высказанная Ю. И. Маниным[3] и Р. Фейнманом[4] состоит в том, что квантовая система из L двухуровневых квантовых элементов (кубитов) имеет 2L линейно независимых состояний, а значит, вследствие принципа квантовой суперпозиции, 2L-мерное гильбертово пространство состояний. Операция в квантовых вычислениях соответствует повороту в этом пространстве. Таким образом, квантовое вычислительное устройство размером L кубит может выполнять параллельно 2L операций.
Предположим, что имеется один кубит. В таком случае после измерения, в так называемой классической форме, результат будет 0 или 1. В действительности кубит — квантовый объект и поэтому, вследствие принципа неопределённости, может быть и 0, и 1 с определенной вероятностью. Если кубит равен 0 (или 1) со стопроцентной вероятностью, его состояние обозначается с помощью символа |0> (или |1>) — в обозначениях Дирака. |0> и |1> — это базовые состояния. В общем случае квантовое состояние кубита находится между базовыми и записывается, в виде , где |a|² и |b|² — вероятности измерить 0 или 1 соответственно; ; |a|² + |b|² = 1. Более того, сразу после измерения кубит переходит в базовое квантовое состояние, аналогичное классическому результату.
Пример:
Имеется кубит в квантовом состоянии В этом случае, вероятность получить при измерении| 0 | составляет | (4/5)²=16/25 | = 64 %, |
| 1 | (-3/5)²=9/25 | = 36 %. |
Приведем для объяснения два примера из квантовой механики: 1) фотон находится в состоянии суперпозиции двух поляризаций; измерение раз и навсегда коллапсирует состояние фотона в таковое с определенной поляризацией; 2) радиоактивный атом имеет определенный период полураспада; измерение может выявить то, что он еще не распался, но это не значит, что он никогда не распадется.
Перейдем к системе из двух кубитов. Измерение каждого из них может дать 0 или 1. Поэтому у системы 4 классических состояния: 00, 01, 10 и 11. Аналогичные им базовые квантовые состояния: |00>, |01>, |10> и |11>. И наконец, общее квантовое состояние системы имеет вид . Теперь |a|² — вероятность измерить 00 и т. д. Отметим, что |a|²+|b|²+|c|²+|d|²=1 как полная вероятность.
В общем случае, системы из L кубитов у неё 2L классических состояний (00000…(L-нулей), …00001(L-цифр), … , 11111…(L-единиц)), каждое из которых может быть измерено с вероятностями 0—100 %.
Таким образом, одна операция над группой кубитов затрагивает все значения, которые она может принимать, в отличие от классического бита. Это и обеспечивает беспрецедентный параллелизм вычислений.
Вычисление
Упрощённая схема вычисления на квантовом компьютере выглядит так: берется система кубитов, на которой записывается начальное состояние. Затем состояние системы или её подсистем изменяется посредством базовых квантовых операций. В конце измеряется значение, и это результат работы компьютера.
Оказывается, что для построения любого вычисления достаточно двух базовых операций. Квантовая система дает результат, только с некоторой вероятностью являющийся правильным. Но за счет небольшого увеличения операций в алгоритме можно сколь угодно приблизить вероятность получения правильного результата к единице.
С помощью базовых квантовых операций можно симулировать работу обычных логических элементов, из которых сделаны обычные компьютеры. Поэтому любую задачу, которая решена сейчас, квантовый компьютер решит, и почти за такое же время. Следовательно, новая схема вычислений будет не слабее нынешней.
Чем же квантовый компьютер лучше классического? Большая часть современных ЭВМ работают по такой же схеме: n бит памяти хранят состояние и каждый такт времени изменяются процессором. В квантовом случае система из n кубитов находится в состоянии, являющимся суперпозицией всех базовых состояний, поэтому изменение системы касается всех 2n базовых состояний одновременно. Теоретически новая схема может работать намного (в экспоненциальное число раз) быстрее классической. Практически (квантовый) алгоритм Гровера поиска в базе данных показывает квадратичный прирост мощности против классических алгоритмов. Пока в природе их не существует.
Алгоритмы
- Алгоритм Гровера позволяет найти решение уравнения за время .
- Алгоритм Шора позволяет разложить натуральное число n на простые множители за полиномиальное от log(n) время.
- Алгоритм Дойча — Джоза позволяет «за одно вычисление» определить, является ли функция двоичной переменной f(n) постоянной (f1(n) = 0, f2(n) = 1 независимо от n) или «сбалансированной» (f3(0) = 0, f3(1) = 1; f4(0) = 1, f4(1) = 0).
Было показано, что не для всякого алгоритма возможно «квантовое ускорение».
Квантовая телепортация
Алгоритм телепортации реализует точный перенос состояния одного кубита (или системы) на другой. В простейшей схеме используются 4 кубита: источник, приёмник и два вспомогательных. Отметим, что в результате работы алгоритма первоначальное состояние источника разрушится — это пример действия общего принципа невозможности клонирования — невозможно создать точную копию квантового состояния, не разрушив оригинал. На самом деле, довольно легко создать одинаковые состояния на кубитах. К примеру, измерив 3 кубита, мы переведем каждый из них в базовые состояния (0 или 1) и хотя бы на двух из них они совпадут. Не получится скопировать произвольное состояние, и телепортация — замена этой операции.
Телепортация позволяет передавать квантовое состояние системы с помощью обычных классических каналов связи. Таким образом, можно, в частности, получить связанное состояние системы, состоящей из подсистем, удаленных на большое расстояние.
Применение квантовых компьютеров
Специфика применения
Может показаться, что квантовый компьютер — это разновидность аналоговой вычислительной машины. Но это не так: по своей сути это цифровое устройство, но с аналоговой природой.
Основные проблемы, связанные с созданием и применением квантовых компьютеров:
- необходимо обеспечить высокую точность измерений;
- внешние воздействия могут разрушить квантовую систему или внести в неё искажения.
Приложения к криптографии
Благодаря огромной скорости разложения на простые множители, квантовый компьютер позволит расшифровывать сообщения, зашифрованные при помощи популярного асимметричного криптографического алгоритма
Применение идей квантовой механики уже открыли новую эпоху в области криптографии, так как методы квантовой криптографии открывают новые возможности в области передачи сообщений[5]. Прототипы систем подобного рода находятся на стадии разработки[6].
Реализации
Канадская компания D-Wave заявила в феврале 2007 года о создании образца квантового компьютера, состоящего из 16 кубит (устройство получило название Orion). Однако информация об этом устройстве не отвечала строгим требованиям точного научного сообщения; новость не получила научного признания. Более того, дальнейшие планы компании (создать уже в ближайшем будущем 1024-кубитный компьютер) вызвали скепсис у членов экспертного сообщества[7].
В ноябре 2007 года та же компания D-Wave продемонстрировала работу образца 28-кубитного компьютера онлайн на конференции, посвященной суперкомпьютерам[8]. Данная демонстрация также вызвала определенного рода скепсис.
В декабре 2008 года компания организовала проект Распределенных вычислений AQUA@home(Adiabatic QUantum Algorithms) [9], в котором тестируются алгоритмы, оптимизирующие вычисления на адиабатических сверхпроводящих квантовых компьютерах D-Wave.
См. также
Примечания
Литература
Ссылки
- Квантовый ликбез
- Квантовый компьютер и его полупроводниковая элементарная база
- Кафедра квантовой информатики факультета ВМК МГУ
- Лаборатория физики квантовых компьютеров Физикотехнологического института РАН
- Китаев,А., Шень, А., Вялый, М. Классические и квантовые вычисления
- QWiki(англ.) и Quantiki(англ.) — Wiki-ресурсы по квантовой информатике
- Язык программирования QCL для квантовых компьютеров(англ.)
- Курс «Современные задачи теоретической информатики» (лекции по квантовым вычислениям: введение, суперплотное кодирование, квантовая телепортация, алгоритмы Саймона и Шора)
- Gilles Brassard, Isaac Chuang, Seth Lloyd and Christopher Monroe. Quantum computing
- Beyond Bits: The Future of Quantum Information Processing Andrew M. Steane, Eleanor G. Rieffel
- InFuture.ru: Будущее квантовых компьютеров — в троичных вычислениях
- Валиев К. А. «Квантовые компьютеры и квантовые вычисления» УФН 175 3 (2005)
- Страничка проекта AQUA@home на сайте команды «Russia»
Wikimedia Foundation. 2010.
dic.academic.ru
квантовая система — с русского
См. также в других словарях:
Квантовая система — Квантовая механика Принцип неопределённости Введение ... Математическая формулировка ... Основа … Википедия
квантовая система — Отдельные частицы вещества или совокупности частиц, процессы в которых подчиняются законам квантовой механики. [ГОСТ 15093 90] Тематики лазерное оборудование … Справочник технического переводчика
квантовая система — kvantinė sistema statusas T sritis fizika atitikmenys: angl. quantum system vok. Quantensystem, n rus. квантовая система, f pranc. système quantique, m … Fizikos terminų žodynas
Квантовая механика — Квантовая механика … Википедия
Квантовая телепортация — Квантовая телепортация передача квантового состояния на расстояние при помощи разъединённой в пространстве сцепленной(запутанной) пары и классического канала связи, при которой состояние разрушается в точке отправления при проведении… … Википедия
Квантовая теория открытых систем — Открытая система в квантовой механике квантовая система, которая может обмениваться энергией и веществом с внешней средой. В определенном смысле всякая квантовая система может рассматриваться как открытая система, поскольку измерение любой… … Википедия
КВАНТОВАЯ МЕХАНИКА — (волновая механика), теория, устанавливающая способ описания и законы движения микрочастиц (элем. ч ц, атомов, молекул, ат. ядер) и их систем (напр., кристаллов), а также связь величин, характеризующих ч цы и системы, с физ. величинами,… … Физическая энциклопедия
Квантовая теория поля — Квантовая теория поля квантовая теория систем с бесконечным числом степеней свободы (полей физических (См. Поля физические)). К. т. п., возникшая как обобщение квантовой механики (См. Квантовая механика) в связи с проблемой описания… … Большая советская энциклопедия
КВАНТОВАЯ ТЕОРИЯ ПОЛЯ — (КТП), релятивистская квант. теория физ. систем с бесконечным числом степеней свободы. Пример такой системы эл. магн. поле, для полного описания к рого в любой момент времени требуется задание напряжённостей электрич. и магн. полей в каждой точке … Физическая энциклопедия
КВАНТОВАЯ ТЕОРИЯ ПОЛЯ. — КВАНТОВАЯ ТЕОРИЯ ПОЛЯ. Содержание:1. Квантовые поля ................. 3002. Свободные поля и корпускулярно волновой дуализм .................... 3013. Взаимодействие полей .........3024. Теория возмущений ............... 3035. Расходимости и… … Физическая энциклопедия
Квантовая криптография — Квантовая криптография метод защиты коммуникаций, основанный на принципах квантовой физики. В отличие от традиционной криптографии, которая использует математические методы, чтобы обеспечить секретность информации, квантовая криптография… … Википедия
translate.academic.ru
Квантовая система — с русского
См. также в других словарях:
Квантовая система — Квантовая механика Принцип неопределённости Введение ... Математическая формулировка ... Основа … Википедия
квантовая система — Отдельные частицы вещества или совокупности частиц, процессы в которых подчиняются законам квантовой механики. [ГОСТ 15093 90] Тематики лазерное оборудование … Справочник технического переводчика
квантовая система — kvantinė sistema statusas T sritis fizika atitikmenys: angl. quantum system vok. Quantensystem, n rus. квантовая система, f pranc. système quantique, m … Fizikos terminų žodynas
Квантовая механика — Квантовая механика … Википедия
Квантовая телепортация — Квантовая телепортация передача квантового состояния на расстояние при помощи разъединённой в пространстве сцепленной(запутанной) пары и классического канала связи, при которой состояние разрушается в точке отправления при проведении… … Википедия
Квантовая теория открытых систем — Открытая система в квантовой механике квантовая система, которая может обмениваться энергией и веществом с внешней средой. В определенном смысле всякая квантовая система может рассматриваться как открытая система, поскольку измерение любой… … Википедия
КВАНТОВАЯ МЕХАНИКА — (волновая механика), теория, устанавливающая способ описания и законы движения микрочастиц (элем. ч ц, атомов, молекул, ат. ядер) и их систем (напр., кристаллов), а также связь величин, характеризующих ч цы и системы, с физ. величинами,… … Физическая энциклопедия
Квантовая теория поля — Квантовая теория поля квантовая теория систем с бесконечным числом степеней свободы (полей физических (См. Поля физические)). К. т. п., возникшая как обобщение квантовой механики (См. Квантовая механика) в связи с проблемой описания… … Большая советская энциклопедия
КВАНТОВАЯ ТЕОРИЯ ПОЛЯ — (КТП), релятивистская квант. теория физ. систем с бесконечным числом степеней свободы. Пример такой системы эл. магн. поле, для полного описания к рого в любой момент времени требуется задание напряжённостей электрич. и магн. полей в каждой точке … Физическая энциклопедия
КВАНТОВАЯ ТЕОРИЯ ПОЛЯ. — КВАНТОВАЯ ТЕОРИЯ ПОЛЯ. Содержание:1. Квантовые поля ................. 3002. Свободные поля и корпускулярно волновой дуализм .................... 3013. Взаимодействие полей .........3024. Теория возмущений ............... 3035. Расходимости и… … Физическая энциклопедия
Квантовая криптография — Квантовая криптография метод защиты коммуникаций, основанный на принципах квантовой физики. В отличие от традиционной криптографии, которая использует математические методы, чтобы обеспечить секретность информации, квантовая криптография… … Википедия
translate.academic.ru
квантовая система - это... Что такое квантовая система?
квантовая системаОтдельные частицы вещества или совокупности частиц, процессы в которых подчиняются законам квантовой механики.[ГОСТ 15093-90]
Тематики
- лазерное оборудование
Справочник технического переводчика. – Интент. 2009-2013.
- квантовая радиофизика
- квантовая точка
Смотреть что такое "квантовая система" в других словарях:
Квантовая система — Квантовая механика Принцип неопределённости Введение ... Математическая формулировка ... Основа … Википедия
квантовая система — kvantinė sistema statusas T sritis fizika atitikmenys: angl. quantum system vok. Quantensystem, n rus. квантовая система, f pranc. système quantique, m … Fizikos terminų žodynas
Квантовая механика — Квантовая механика … Википедия
Квантовая телепортация — Квантовая телепортация передача квантового состояния на расстояние при помощи разъединённой в пространстве сцепленной(запутанной) пары и классического канала связи, при которой состояние разрушается в точке отправления при проведении… … Википедия
Квантовая теория открытых систем — Открытая система в квантовой механике квантовая система, которая может обмениваться энергией и веществом с внешней средой. В определенном смысле всякая квантовая система может рассматриваться как открытая система, поскольку измерение любой… … Википедия
КВАНТОВАЯ МЕХАНИКА — (волновая механика), теория, устанавливающая способ описания и законы движения микрочастиц (элем. ч ц, атомов, молекул, ат. ядер) и их систем (напр., кристаллов), а также связь величин, характеризующих ч цы и системы, с физ. величинами,… … Физическая энциклопедия
Квантовая теория поля — Квантовая теория поля квантовая теория систем с бесконечным числом степеней свободы (полей физических (См. Поля физические)). К. т. п., возникшая как обобщение квантовой механики (См. Квантовая механика) в связи с проблемой описания… … Большая советская энциклопедия
КВАНТОВАЯ ТЕОРИЯ ПОЛЯ — (КТП), релятивистская квант. теория физ. систем с бесконечным числом степеней свободы. Пример такой системы эл. магн. поле, для полного описания к рого в любой момент времени требуется задание напряжённостей электрич. и магн. полей в каждой точке … Физическая энциклопедия
КВАНТОВАЯ ТЕОРИЯ ПОЛЯ. — КВАНТОВАЯ ТЕОРИЯ ПОЛЯ. Содержание:1. Квантовые поля ................. 3002. Свободные поля и корпускулярно волновой дуализм .................... 3013. Взаимодействие полей .........3024. Теория возмущений ............... 3035. Расходимости и… … Физическая энциклопедия
Квантовая криптография — Квантовая криптография метод защиты коммуникаций, основанный на принципах квантовой физики. В отличие от традиционной криптографии, которая использует математические методы, чтобы обеспечить секретность информации, квантовая криптография… … Википедия
technical_translator_dictionary.academic.ru
квантовые системы - это... Что такое квантовые системы?
Makarov: quantum systems
Универсальный русско-английский словарь. Академик.ру. 2011.
- квантовые роторы
- квантовые скачки
Смотреть что такое "квантовые системы" в других словарях:
КВАНТОВЫЕ ЧИСЛА — целые или дробные числа, к рые определяют возможные значения физ. величин, характеризующих квант. системы (ат. ядро, атом, молекулу и др.), отд. элем. ч цы, гипотетич. ч цы кварки и глюоны. К. ч. были впервые введены в физику для описания… … Физическая энциклопедия
КВАНТОВЫЕ ЧИСЛА — целые или дробные числа, определяющие возможные дискретные значения физических величин, характеризующих квантовые системы (атомное ядро, атом, молекулу и др.) и отдельные элементарные частицы … Большой Энциклопедический словарь
Квантовые числа — целые (0, 1, 2,...) или полуцелые (1/2, 3/2, 5/2,...) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы.… … Большая советская энциклопедия
квантовые числа — целые или дробные числа, определяющие возможные дискретные значения физических величин, характеризующих квантовые системы (атомное ядро, атом, молекулу и др.) и отдельные элементарные частицы. * * * КВАНТОВЫЕ ЧИСЛА КВАНТОВЫЕ ЧИСЛА, целые или… … Энциклопедический словарь
КВАНТОВЫЕ СТАНДАРТЫ ЧАСТОТЫ — устройства для точного измерения частоты колебаний или для генерирования колебаний с весьма стабильной частотой, в к рых используются квант. переходы (атомов, молекул, ионов) из одного энергетич. состояния в другое. Рис. 1. Схема атомно лучевой… … Физическая энциклопедия
КВАНТОВЫЕ НЕРАЗРУШАЮЩИЕ ИЗМЕРЕНИЯ — (квантовые невозмущающие измерения; КНИ) измерения, не изменяющие состояния исследуемой системы, если оно является собственным для оператора измеряемой величины. КНИ представляет собой реализацию идеального квантового измерения, описываемого… … Физическая энциклопедия
КВАНТОВЫЕ ОСЦИЛЛЯЦИИ — в магнитном поле осцилляторная зависимость термодинамич. и кинетич. характеристик металлов и вырожденных полупроводников от магн. поля. К. о. обусловлены вырождением системы носителей заряда и квантованием их энергии при периодич. движении по… … Физическая энциклопедия
Квантовые торпеды — Дефайент ведёт огонь квантовыми торпедами Квантовые торпеды (англ. Quantum torpedo) фантастическая технология из вселенной «Звёздного пути», энергетическая форма торпед особо разрушительного … Википедия
КВАНТОВЫЕ ЧАСЫ — (атомные часы), устройство для точного измерения времени, основной частью к рого является квантовый стандарт частоты. Ход К. ч. регулирует частота излучения атомов при их квант. переходах из одного энергетич. состояния в другое. Эта частота столь … Физическая энциклопедия
КВАНТОВЫЕ ПЕРЕХОДЫ — КВАНТОВЫЕ ПЕРЕХОДЫ, скачкообразные переходы квантовой системы (атома, молекулы, атомного ядра, кристалла) из одного возможного состояния в другое. Квантовые переходы могут быть излучательными и безызлучательными. Излучательные квантовые переходы… … Современная энциклопедия
КВАНТОВЫЕ РАЗМЕРНЫЕ ЭФФЕКТЫ — изменение термодинамич. и кинетич. свойств кристалла, когда хотя бы один из его геом. размеров становится соизмеримым с длиной волны де Бройля l Б электронов. К. р. э. обусловлены квантованием движения электрона в направлении, в к ром размер… … Физическая энциклопедия
universal_ru_en.academic.ru