Квантовая криптография. Квантовые вычисления и квантовая криптография

Квантовая криптография - это... Что такое Квантовая криптография?

Квантовая криптография — метод защиты коммуникаций, основанный на принципах квантовой физики. В отличие от традиционной криптографии, которая использует математические методы, чтобы обеспечить секретность информации, квантовая криптография сосредоточена на физике, рассматривая случаи, когда информация переносится с помощью объектов квантовой механики. Процесс отправки и приёма информации всегда выполняется физическими средствами, например, при помощи электронов в электрическом токе, или фотонов в линиях волоконно-оптической связи. А подслушивание может рассматриваться, как измерение определённых параметров физических объектов — в нашем случае, переносчиков информации.

Технология квантовой криптографии опирается на принципиальную неопределённость поведения квантовой системы — невозможно одновременно получить координаты и импульс частицы, невозможно измерить один параметр фотона, не исказив другой. Это фундаментальное свойство природы в физике известно как принцип неопределённости Гейзенберга, сформулированный в 1927 г.

Используя квантовые явления, можно спроектировать и создать такую систему связи, которая всегда может обнаруживать подслушивание. Это обеспечивается тем, что попытка измерения взаимосвязанных параметров в квантовой системе вносит в неё нарушения, разрушая исходные сигналы, а значит, по уровню шума в канале легитимные пользователи могут распознать степень активности перехватчика.

История возникновения

Впервые идея защиты информации с помощью квантовых объектов была предложена Стивеном Визнером в 1970 году. Спустя десятилетие Ч. Беннет (фирма IBM) и Ж. Брассард (Монреальский университет), знакомые с работой Визнера, предложили передавать секретный ключ с использованием квантовых объектов. В 1984 году они предположили возможность создания фундаментально защищённого канала с помощью квантовых состояний. После этого ими была предложена схема (BB84), в которой легальные пользователи (Алиса и Боб) обмениваются сообщениями, представленными в виде поляризованных фотонов, по квантовому каналу.

Злоумышленник (Ева), пытающийся исследовать передаваемые данные, не может произвести измерение фотонов без искажения текста сообщения. Легальные пользователи по открытому каналу сравнивают и обсуждают сигналы, передаваемые по квантовому каналу, тем самым проверяя их на возможность перехвата. Если ими не будет выявлено никаких ошибок, то переданную информацию можно считать случайно распределённой, случайной и секретной, несмотря на все технические возможности, которые может использовать криптоаналитик.

Первое устройство квантовой криптографии

Первая квантово-криптографическая схема. Система состоит из квантового канала и специального оборудования на обоих концах схемы.

Первая работающая квантово-криптографическая схема была построена в 1989 году в Исследовательском центре компании IBM, все теми же Беннетом и Брассардом. Данная схема представляла собой квантовый канал, на одном конце которого был передающий аппарат Алисы, на другом принимающий аппарат Боба. Оба аппарата размещены на оптической скамье длиной около 1 м, в светонепроницаемом кожухе размерами 1,5х0,5х0,5 м. Управление происходило с помощью компьютера, в который были загружены программные представления легальных пользователей и злоумышленника.

Сохранность тайны передаваемых данных напрямую зависит от интенсивности вспышек света, используемых для передачи. Слабые вспышки, хоть и делают трудным перехват сообщений, все же приводят к росту числа ошибок у легального пользователя, при измерении правильной поляризации. Повышение интенсивности вспышек значительно упрощает перехват путем расщепления начального одиночного фотона (или пучка света) на два: первого по-прежнему направленному легальному пользователю, а второго анализируемого злоумышленником. Легальные пользователи могут исправлять ошибки с помощью специальных кодов, обсуждая по открытому каналу результаты кодирования.

Но все-таки при этом часть информации попадает к криптоаналитику. Тем не менее, легальные пользователи Алиса и Боб, изучая количество выявленных и исправленных ошибок, а также интенсивность вспышек света, могут дать оценку количеству информации, попавшей к злоумышленнику.

Простейший алгоритм генерации секретного ключа (BB84)

Схема ВВ84 работает следующим образом. Вначале отправитель (Алиса) производит генерацию фотонов со случайной поляризацией, выбранной из 0, 45, 90 и 135°. Получатель (Боб) принимает эти фотоны, затем для каждого выбирает случайным образом способ измерения поляризации, диагональный или перпендикулярный. Затем по открытому каналу сообщает о том, какой способ он выбрал для каждого фотона, не раскрывая при этом самих результатов измерения. После этого Алиса по тому же открытому каналу сообщает, правильный ли был выбран вид измерений для каждого фотона. Далее Алиса и Боб отбрасывают те случаи, когда измерения Боба были неверны. Если не было перехвата квантового канала, то секретной информацией или ключом и будут оставшиеся виды поляризации. На выходе будет последовательность битов: фотоны с горизонтальной или 45°-й поляризацией принимаются за двоичный «0», а с вертикальной или 135°-й поляризацией — за двоичную «1». Этот этап работы квантово-криптографической системы называется первичной квантовой передачей.

Алиса посылает фотоны, имеющие одну из четырёх возможных поляризаций, которую она выбирает случайным образом.

Для каждого фотона Боб выбирает случайным образом тип измерения: он изменяет либо прямолинейную поляризацию (+), либо диагональную (х).

Боб записывает результаты изменения и сохраняет в тайне.

Боб открыто объявляет, какого типа измерения он проводил, а Алиса сообщает ему, какие измерения были правильными.

Алиса и Боб сохраняют все данные, полученные в тех случаях, когда Боб применял правильное измерение. Эти данные затем переводятся в биты (0 и 1), последовательность которых и является результатом первичной квантовой передачи.

Следующим этапом очень важно оценить попытки перехватить информацию в квантово-криптографическом канале связи. Это производится по открытому каналу Алисой и Бобом путем сравнения и отбрасывания подмножеств полученных данных случайно ими выбранных. Если после такого сравнения будет выявлен перехват, то Алиса и Боб должны будут отбросить все свои данные и начать повторное выполнение первичной квантовой передачи. В противном случае они оставляют прежнюю поляризацию. Согласно принципу неопределённости, криптоаналитик (Ева) не может измерить как диагональную, так и прямоугольную поляризацию одного и того же фотона. Даже если им будет произведено измерение для какого-либо фотона и затем этот же фотон будет переслан Бобу, то в итоге количество ошибок намного увеличится, и это станет заметно Алисе. Это приведет к тому, что Алиса и Боба будут полностью уверены в состоявшемся перехвате фотонов. Если расхождений нет, то биты, использованные для сравнения, отбрасываются, ключ принимается. С вероятностью 1 — 2-k (где k — число сравненных битов) канал не прослушивался.

Впрочем, если недоброжелатель может не только прослушивать основной канал Алиса->Боб, но и может фальсифицировать работу открытого канала Боб->Алиса, то вся схема рушится (Man-In-The-Middle).

Описанный алгоритм носит название протокола квантового распределения ключа BB84. В нём информация кодируется в ортогональные квантовые состояния. Помимо использования ортогональных состояний для кодирования информации, можно использовать и неортогональные состояния (например, протокол B92).

Недостаток этого подхода уже в самом его принципе.

Так, при данном алгоритме Еве не обязательно даже измерять квантовую последовательность. Она перехватывает последовательность от Алисы и заменяет её своей. Затем подслушивает разговор Алисы и Боба и определяет, какие именно кванты будут использованы для ключа; так Еве становится известен ключ полностью, при этом Алиса и Боб пока ни о чём не догадываются. Боб посылает Алисе зашифрованное сообщение, которое Ева тут же дешифрует. Алиса, получив сообщение, не поддающееся дешифровке (ключ Алисы не совпадает с ключом шифрования, так как Боб использовал ключ Евы), понимает, что сообщение перехвачено, но к этому времени уже поздно, так как Ева знает его содержание.

Для любых тестов и проверок необходимо повторное установление связи, а значит все начинается сначала. Таким образом решаются сразу две задачи: перехват сообщений и нарушение связи противника. Отсюда можно сделать вывод, что такой способ связи хорош исключительно только для дезинформации, но тогда он не рентабелен и смысл его использования падает до нуля, так как Ева знает, что он только для дезинформации.

Алгоритм Беннета

В 1991 году Ч. Беннетом был предложен следующий алгоритм для выявления искажений в переданных по квантовому каналу данных:

Отправитель и получатель заранее оговаривают произвольность расположения битов в строках, что определяет произвольный характер положения ошибок.
Все строки разбиваются на блоки длины k. Где k выбирается так, чтобы минимизировать вероятность ошибки.
Отправитель и получатель определят четность каждого блока, и сообщают её друг другу по открытому каналу связи. После этого в каждом блоке удаляют последний бит.

Если четность двух каких-либо блоков оказалось различной, отправитель и получатель производят итерационный поиск неверных битов и исправляют их.
Затем весь алгоритм выполняется заново для другого (большего) значения k. Это делается для того, чтобы исключить ранее незамеченные кратные ошибки.
Чтобы определить все ли ошибки были обнаружены, проводится псевдослучайная проверка. Отправитель и получатель открыто сообщают о произвольной перестановке половины бит в строках, а затем вновь открыто сравнивают четности (Если строки различны, четности обязаны не совпадать с вероятностью 0,5). Если четности отличаются, отправитель и получатель производят двоичный поиск и удаляют неверные биты.
Если различий не наблюдается, после n итераций отправитель и получатель будут иметь одинаковые строки с вероятностью ошибки 2-n.

Физическая реализация системы[1]

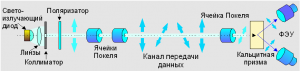
Рассмотрим схему физической реализации квантовой криптографии. Её иллюстрация представлена на рисунке (где рисунок???). Слева находится отправитель, справа — получатель. Для того, чтобы передатчик имел возможность импульсно варьировать поляризацию квантового потока, а приёмник мог анализировать импульсы поляризации, используются ячейки Покеля. Передатчиком формируется одно из четырёх возможных состояний поляризации. На ячейки данные поступают в виде управляющих сигналов. Для организации канала связи обычно используется волокно, а в качестве источника света берут лазер.

На стороне получателя после ячейки Покеля расположена кальцитовая призма, которая должна расщеплять пучок на две составляющие, улавливаемые двумя фотодетекторами (ФЭУ), а те в свою очередь измеряют ортогональные составляющие поляризации. Вначале необходимо решить проблему интенсивности передаваемых импульсов квантов, возникающую при их формировании. Если в импульсе содержится 1000 квантов, существует вероятность того, что 100 из них будут отведены криптоаналитиком на свой приёмник. После чего, проводя анализ открытых переговоров, он сможет получить все необходимые ему данные. Из этого следует, что идеален вариант, когда в импульсе количество квантов стремится к одному. Тогда любая попытка перехватить часть квантов неизбежно изменит состояние всей системы и соответственно спровоцирует увеличение числа ошибок у получателя. В этой ситуации следует не рассматривать принятые данные, а заново повторить передачу. Однако, при попытках сделать канал более надёжным, чувствительность приёмника повышается до максимума, и перед специалистами встает проблема «темнового» шума. Это означает, что получатель принимает сигнал, который не был отправлен адресантом. Чтобы передача данных была надёжной, логические нули и единицы, из которых состоит двоичное представление передаваемого сообщения, представляются в виде не одного, а последовательности состояний, что позволяет исправлять одинарные и даже кратные ошибки.

Для дальнейшего увеличения отказоустойчивости квантовой криптосистемы используется эффект EPR (Einstein-Podolsky-Rosen), возникающий в том случае, если сферическим атомом были излучены в противоположных направлениях два фотона. Начальная поляризация фотонов не определена, но в силу симметрии их поляризации всегда противоположны. Это определяет тот факт, что поляризацию фотонов можно узнать только после измерения. Криптосхема на основе эффекта ERP, гарантирующая безопасность пересылки, была предложена Экертом. Отправителем генерируется несколько фотонных пар, после чего один фотон из каждой пары он откладывает себе, а второй пересылает адресату. Тогда если эффективность регистрации около единицы и на руках у отправителя фотон с поляризацией «1», то у получателя будет фотон с поляризацией «0» и наоборот. То есть легальные пользователи всегда имеют возможность получить одинаковые псевдослучайный последовательности. Но на практике оказывается, что эффективность регистрации и измерения поляризации фотона очень мала.

Практические реализации системы

1989 г. Беннет и Брассар в Исследовательском центре IBM построили первую работающую квантово-криптографическую систему. Она состояла из квантового канала, содержащего передатчик Алисы на одном конце и приёмник Боба на другом, размещённые на оптической скамье длиной около метра в светонепроницаемом полутораметровом кожухе размером 0,5×0,5 м. Собственно квантовый канал представлял собой свободный воздушный канал длиной около 32 см. Макет управлялся от персонального компьютера, который содержал программное представление пользователей Алисы и Боба, а также злоумышленника.
1989 г. передача сообщения посредством потока фотонов через воздушную среду на расстояние 32 см с компьютера на компьютер завершилась успешно. Основная проблема при увеличении расстояния между приёмником и передатчиком — сохранение поляризации фотонов. На этом основана достоверность способа.

Созданная при участии Женевского университета компания GAP-Optique под руководством Николаса Гисина совмещает теоретические исследования с практической деятельностью. Первым результатом этих исследований стала реализация квантового канала связи с помощью оптоволоконного кабеля длинной 23 км, проложенного по дну озера и соединяющего Женеву и Нион. Тогда был сгенерирован секретный ключ, уровень ошибок которого не превышал 1,4 %. Но все-таки огромным недостатком этой схемы была чрезвычайно малая скорость передачи информации. Позже специалистам этой фирмы удалось передать ключ на расстояние 67 км из Женевы в Лозанну с помощью почти промышленного образца аппаратуры. Но и этот рекорд был побит корпорацией Mitsubishi Electric, передавшей квантовый ключ на расстояние 87 км, правда, на скорости в один байт в секунду.
Активные исследования в области квантовой криптографии ведут IBM, GAP-Optique, Mitsubishi, Toshiba, Национальная лаборатория в Лос-Аламосе, Калифорнийский технологический институт, молодая компания MagiQ и холдинг QinetiQ, поддерживаемый британским министерством обороны. В частности, в национальной лаборатории Лос-Аламоса была разработана и начала широко эксплуатироваться опытная линия связи, длиной около 48 километров. Где на основе принципов квантовой криптографии происходит распределение ключей, и скорость распределения может достигать несколько десятков кбит/с.

2001 г. доктор Эндрю Шилдс и его коллеги из TREL и Кембриджского университета создали диод, способный испускать единичные фотоны. В основе нового светодиода лежит «квантовая точка» — миниатюрный кусочек полупроводникового материала диаметром 15 нм и толщиной 5 нм, который может при подаче на него тока захватывать лишь по одной паре электронов и дырок. Это дало возможность передавать поляризованные фотоны на большее расстояние. В ходе экспериментальной демонстрации удалось передать зашифрованные данные со скоростью 75 Кбит/с — при том, что более половины фотонов терялось.
В Оксфордском университете ставятся задачи повышения скорости передачи данных. Создаются квантово-криптографические схемы, в которых используются квантовые усилители. Их применение способствует преодолению ограничения скорости в квантовом канале и, как следствие, расширению области практического применения подобных систем.
В университете Дж. Хопкинса (США) на квантовом канале длиной 1 км построена вычислительная сеть, в которой каждые 10 минут производится автоматическая подстройка. В результате этого, уровень ошибки снижен до 0,5 % при скорости связи 5 кбит/с.
Министерством обороны Великобритании поддерживается исследовательская корпорация QinetiQ, являющаяся частью бывшего британского агентства DERA (Defence Evaluation and Research Agency), которая специализируется на неядерных оборонных исследованиях и активно совершенствует технологию квантового шифрования.

Исследованиями в области квантовой криптографии занимается молодая американская компания Magiq Technologies из Нью-Йорка, выпустившая прототип коммерческой квантовой криптотехнологии собственной разработки. Основной продукт Magiq — средство для распределения ключей (quantum key distribution, QKD), которое названо Navajo (По имени индейцев Навахо, язык которых во время Второй мировой войны американцы использовали для передачи секретных сообщений, поскольку за пределами США его никто не знал). Navajo способен в реальном времени генерировать и распространять ключи средствами квантовых технологий и предназначен для обеспечения защиты от внутренних и внешних злоумышленников.
В октябре 2007 года на выборах в Швейцарии были повсеместно использованы квантовые сети, начиная избирательными участками и заканчивая датацентром ЦИК. Была использована техника, которую ещё в середине 90-х в Университете Женевы разработал профессор Николас Гисин. Также одним из участников создания такой системы была компания Id Quantique.
В 2011 году в Токио прошла демонстрация проекта «Tokyo QKD Network», в ходе которого разрабатывается квантовое шифрование телекоммуникационных сетей. Была проведена пробная телеконференция на расстоянии в 45 км. Связь в системе идёт по обычным оптоволоконным линиям. В будущем предполагается применение для мобильной связи.

Квантовый криптоанализ

Частотный спектр в оптическом канале квантово-криптографической системы.

Широкое распространение и развитие квантовой криптографии не могло не спровоцировать появление квантового криптоанализа, который обладает неоспоримыми преимуществами и экспоненциально перед обычным. Рассмотрим, например, всемирно известный и распространенный в наши дни алгоритм шифрования RSA (Rivest, Shamir, Adleman, 1977). В основе этого шифра лежит идея того, что на простых компьютерах невозможно решить задачу разложения очень большого числа на простые множители, ведь данная операция потребует астрономического времени и экспоненциально большого числа действий. Поэтому, для решения этой задачи, и был разработан квантовый алгоритм, позволяющий найти за конечное и приемлемое время все простые множители больших чисел, и, как следствие, взломать шифр RSA. Поэтому создание квантовой криптоаналитической системы является плохой новостью для RSA и любого другого шифра, ведь квантовый криптоанализ может быть применён ко всем классическим шифросистемам. Необходимо только создание квантового компьютера, способного развить достаточную мощность.

Взлом квантовой системы[2][3]

В 2010 году учёные успешно опробовали один из возможных способов необнаружимой атаки, показав принципиальную уязвимость двух криптографических систем, разработанных компаниями ID Quantique и MagiQ Technologies. И уже в 2011 году работоспособность метода была проверена в реальных условиях эксплуатации, на развёрнутой в Национальном университете Сингапура системе распространения ключей, которая связывает разные здания отрезком оптоволокна длиной в 290 м.

В эксперименте использовалась физическая уязвимость четырёх однофотонных детекторов (лавинных фотодиодов), установленных на стороне получателя (Боба). При нормальной работе фотодиода приход фотона вызывает образование электронно-дырочной пары, после чего возникает лавина, а результирующий выброс тока регистрируется компаратором и формирователем импульсов. Лавинный ток «подпитывается» зарядом, хранимым небольшой ёмкостью (≈ 1,2 пФ), и схеме, обнаружившей одиночный фотон, требуется некоторое время на восстановление (~ 1 мкс).

Если на фотодиод подавать такой поток излучения, когда полная перезарядка в коротких промежутках между отдельными фотонами будет невозможна, амплитуда импульса от одиночных квантов света может оказаться ниже порога срабатывания компаратора.

В условиях постоянной засветки лавинные фотодиоды переходят в «классический» режим работы и выдают фототок, пропорциональный мощности падающего излучения. Поступление на такой фотодиод светового импульса с достаточно большой мощностью, превышающей некое пороговое значение, вызовет выброс тока, имитирующий сигнал от одиночного фотона. Это и позволяет криптоаналитику (Еве) манипулировать результатами измерений, выполненных Бобом: она «ослепляет» все его детекторы с помощью лазерного диода, который работает в непрерывном режиме и испускает свет с круговой поляризацией, и по мере надобности добавляет к этому линейно поляризованные импульсы. При использовании четырёх разных лазерных диодов, отвечающих за все возможные типы поляризации (вертикальную, горизонтальную, ±45˚), Ева может искусственно генерировать сигнал в любом выбранном ею детекторе Боба.

Опыты показали, что схема взлома работает очень надёжно и даёт Еве прекрасную возможность получить точную копию ключа, переданного Бобу. Частота появления ошибок, обусловленных неидеальными параметрами оборудования, оставалась на уровне, который считается «безопасным».

Однако, устранить такую уязвимость системы распространения ключей довольно легко. Можно, к примеру, установить перед детекторами Боба источник одиночных фотонов и, включая его в случайные моменты времени, проверять, реагируют ли лавинные фотодиоды на отдельные кванты света.

Подключай и работай (Plug & Play)

Практически все квантово-оптические криптографические системы сложны в управлении с каждой стороны канала связи требуют постоянной подстройки. На выходе канала возникают беспорядочные колебания поляризации ввиду воздействия внешней среды и двойного лучепреломления в оптоволокне. Но недавно была сконструирована такая реализация системы, которую смело можно назвать plug and play («подключай и работай»). Для такой системы не нужна подстройка, а только синхронизация. Система построена на использовании зеркала Фарадея, которое позволяет избежать двойного лучепреломления и как следствие не требует регулировки поляризации. Это позволяет пересылать криптографические ключи по обычным телекоммуникационным системам связи. Для создания канала достаточно лишь подключить приёмный и передающий модули, провести синхронизацию и можно начинать передачу. Поэтому такую систему можно назвать plug and play.

Перспективы развития

Сейчас одним из самых важных достижений в области квантовой криптографии является то, что ученые смогли показать возможность передачи данных по квантовому каналу со скоростью до 1 Мбит/с. Это стало возможно благодаря технологии разделения каналов связи по длинам волн и их единовременного использования в общей среде. Что кстати позволяет одновременное использование как открытого, так и закрытого канала связи. Сейчас в одном оптическом волокне возможно создать около 50 каналов. Экспериментальные данные позволяют сделать прогноз на достижение лучших параметров в будущем:

1) Достижение скорости передачи данных по квантовому каналу связи в 50 Мбит/с, при этом единовременные ошибки не должны будут превышать 4 %.

2) Создание квантового канала связи длиной более 100 км.

3) Организация десятков подканалов при разделении по длинам волн.

На данном этапе квантовая криптография только приближается к практическому уровню использования. Диапазон разработчиков новых технологий квантовой криптографии охватывает не только крупнейшие мировые институты, но и маленькие компании, только начинающие свою деятельность. И все они уже способны вывести свои проекты из лабораторий на рынок. Все это позволяет сказать, что рынок находится на начальной стадии формирования, когда в нём могут быть на равных представлены и те и другие.

Безусловно, квантовая криптография — очень перспективная часть криптографии, ведь технологии, используемые там, позволяют вывести безопасность информации на высочайший уровень. Осталось немного подождать, и уже очень скоро квантовая криптография обеспечит ещё один слой безопасности для нуждающихся в этом организаций.

Литература

↑ Семёнов Ю. А. «Телекоммуникационные технологии»;
↑ Nature Communicaion «Perfect eavesdropping on a quantum cryptography system» : [1];
↑ Nature Communicaion «Full-field implementation of a perfect eavesdropper on a quantum cryptography system, June 2011» : [2];

Килин С. Я., Хорошко Д. Б., Низовцев А. П. «Квантовая криптография: идеи и практика»;
Килин С. Я. «Квантовая информация / Успехи Физических Наук.» — 1999. — Т. 169. — C. 507—527. [3];
Robert Malaney . «Технологии, основанные на принципе ULV (unconditional location verification)» : [4], [5];
Computerworld Россия , № 37, 2007 [6];
Красавин В. «Квантовая криптография».

См. также

biograf.academic.ru

Квантовые вычисления, криптография и запутанность

запутанность, спросите науку Для квантовых физиков запутывание квантовых систем является одной из текущих ежедневных задач. Запутанность является ключевым ресурсом для будущих квантовых компьютеров и симуляторов. Физики в Инсбруке и Женеве разработали новый, надежный способ проверки состояний запутанности в лаборатории с использованием минимального набора измерительных приборов.

Их результаты были опубликована в Nature Physics.

Квантовые вычисления, квантовая связь и квантовая криптография часто требуют запутанности. Для многих из этих будущих квантовых технологий, запутанность - труднопонимаемый, нелогичный аспект квантового мира - является ключевым элементом. Физикам-экспериментаторам часто нужно проверить запутанность их систем. "Два года назад нам удалось проверить запутанность между 14 ионами," - говорит Томас Монц. Он работает в группе Райнер Блатт в Институте экспериментальной физики, в Инсбруке. Эта команда все еще держит мировой рекорд по самому большому количеству запутанных частиц. "Для того, чтобы проверить запутанность, мы должны сделать некоторые экспериментальные предположения по калибровке. Но предположения все-таки получаются недостаточными", объясняет Монц. Вместе с Хулио Барейро, который недавно перешел в Институт Макса Планка, физиками и внедрен новый метод проверки запутанности между несколькими объектами.

Представленный аппаратно-независимый метод основан на предположении: "Мы всегда применяем одинаковый набор операций на квантовых объектах, и операции не зависят друг от друга", объясняет Хулио Барейро. "Детали каждой операции мы не знаем." Этот подход - называемый аппаратно-независимым (Device Independent) - позволяет им обойти несколько потенциальных источников ошибок, а впоследствии - неправильную интерпретацию полученных результатов. "В конце концов, мы исследуем корреляцию между настройками и полученные результаты. Если на выходе корреляции соответствуют определенному порогу, мы знаем, что объекты запутались». В реальном эксперименте вряд ли можно избежать помех, но швейцарский теоретик Жан-Даниэль Банкл сумел определить порог наихудшего сценария. «Когда этот порог будет преодолен, мы сможем в большой вероятностью утверждать, что система запутана".

Для физиков процедуры, основанные на ограниченном числе предположений, очень интересны, так как они в основном зависят от системы. "Предположения всегда являются уязвимыми, эдакой ахиллесовой пятой - будь они для теоретической работы или лабораторных данных", подчеркивает Томас Монц. "Нам удалось свести количество предположений для проверки запутанности к минимуму. Наш метод обеспечивает надежное указание на запутанность системы". Фактически, физики в Инсбруке смогли проверить запутывание до 6 ионов. Этот новый метод может быть применен и для больших систем. Количество технических требований, однако, также соответственно увеличится.

Есть мнение:

Квантовая запутанность является ключом к квантовым вычислениям, криптографии и многим другим приложениям квантовой механики.

Два объекта запутанные, если их физические свойства не определены, но связаны, даже тогда, когда два объекта разделены большим расстоянием.

Системы из нескольких частиц будут иметь тенденцию находиться близко к обычному состоянию – состоянию, в котором ни одна из внутренних частиц не переплетена друг с другом. Частицы такой системы не покажут по существу никаких признаков своей запутанности. Вы можете создать состояние нескольких частиц, в котором частицы запутаны, но эти состояния довольно необычны.

Если вы рассматриваете большие системы, то квантовое описание по существу то же самое. Теперь обычные состояния составляют очень небольшую часть возможных квантовых состояний, и, как следствие, более вероятное поведение – когда части системы переплетены друг с другом.

Команда под руководством Szarek в этом году рассмотрела запутывание подсистем в запутанной системе. Если выбрать две частицы из системы, вероятность того, что они запутались, очень мала. Если же разделить систему на две части, эти половины почти наверняка будут запутанными друг с другом.

Анализ показывает, что в системах с большим числом частиц пара небольших подсистем, менее 1/5 от общего числа частиц в системе, скорее всего не будет запутанной друг с другом. Но пара больших подсистем, как правило, запутана. Резкое изменение в поведении запутанности характерно для геометрии многомерных пространств.

i-nauka.ru

Квантовая криптография - это... Что такое Квантовая криптография?

История возникновения

Первое устройство квантовой криптографии

Простейший алгоритм генерации секретного ключа (BB84)

Боб записывает результаты изменения и сохраняет в тайне.

Недостаток этого подхода уже в самом его принципе.

Алгоритм Беннета

Отправитель и получатель заранее оговаривают произвольность расположения битов в строках, что определяет произвольный характер положения ошибок.
Все строки разбиваются на блоки длины k. Где k выбирается так, чтобы минимизировать вероятность ошибки.
Отправитель и получатель определят четность каждого блока, и сообщают её друг другу по открытому каналу связи. После этого в каждом блоке удаляют последний бит.
Если четность двух каких-либо блоков оказалось различной, отправитель и получатель производят итерационный поиск неверных битов и исправляют их.
Затем весь алгоритм выполняется заново для другого (большего) значения k. Это делается для того, чтобы исключить ранее незамеченные кратные ошибки.
Чтобы определить все ли ошибки были обнаружены, проводится псевдослучайная проверка. Отправитель и получатель открыто сообщают о произвольной перестановке половины бит в строках, а затем вновь открыто сравнивают четности (Если строки различны, четности обязаны не совпадать с вероятностью 0,5). Если четности отличаются, отправитель и получатель производят двоичный поиск и удаляют неверные биты.
Если различий не наблюдается, после n итераций отправитель и получатель будут иметь одинаковые строки с вероятностью ошибки 2-n.

Физическая реализация системы[1]

Практические реализации системы

1989 г. Беннет и Брассар в Исследовательском центре IBM построили первую работающую квантово-криптографическую систему. Она состояла из квантового канала, содержащего передатчик Алисы на одном конце и приёмник Боба на другом, размещённые на оптической скамье длиной около метра в светонепроницаемом полутораметровом кожухе размером 0,5×0,5 м. Собственно квантовый канал представлял собой свободный воздушный канал длиной около 32 см. Макет управлялся от персонального компьютера, который содержал программное представление пользователей Алисы и Боба, а также злоумышленника.
1989 г. передача сообщения посредством потока фотонов через воздушную среду на расстояние 32 см с компьютера на компьютер завершилась успешно. Основная проблема при увеличении расстояния между приёмником и передатчиком — сохранение поляризации фотонов. На этом основана достоверность способа.
Созданная при участии Женевского университета компания GAP-Optique под руководством Николаса Гисина совмещает теоретические исследования с практической деятельностью. Первым результатом этих исследований стала реализация квантового канала связи с помощью оптоволоконного кабеля длинной 23 км, проложенного по дну озера и соединяющего Женеву и Нион. Тогда был сгенерирован секретный ключ, уровень ошибок которого не превышал 1,4 %. Но все-таки огромным недостатком этой схемы была чрезвычайно малая скорость передачи информации. Позже специалистам этой фирмы удалось передать ключ на расстояние 67 км из Женевы в Лозанну с помощью почти промышленного образца аппаратуры. Но и этот рекорд был побит корпорацией Mitsubishi Electric, передавшей квантовый ключ на расстояние 87 км, правда, на скорости в один байт в секунду.
Активные исследования в области квантовой криптографии ведут IBM, GAP-Optique, Mitsubishi, Toshiba, Национальная лаборатория в Лос-Аламосе, Калифорнийский технологический институт, молодая компания MagiQ и холдинг QinetiQ, поддерживаемый британским министерством обороны. В частности, в национальной лаборатории Лос-Аламоса была разработана и начала широко эксплуатироваться опытная линия связи, длиной около 48 километров. Где на основе принципов квантовой криптографии происходит распределение ключей, и скорость распределения может достигать несколько десятков кбит/с.
2001 г. доктор Эндрю Шилдс и его коллеги из TREL и Кембриджского университета создали диод, способный испускать единичные фотоны. В основе нового светодиода лежит «квантовая точка» — миниатюрный кусочек полупроводникового материала диаметром 15 нм и толщиной 5 нм, который может при подаче на него тока захватывать лишь по одной паре электронов и дырок. Это дало возможность передавать поляризованные фотоны на большее расстояние. В ходе экспериментальной демонстрации удалось передать зашифрованные данные со скоростью 75 Кбит/с — при том, что более половины фотонов терялось.
В Оксфордском университете ставятся задачи повышения скорости передачи данных. Создаются квантово-криптографические схемы, в которых используются квантовые усилители. Их применение способствует преодолению ограничения скорости в квантовом канале и, как следствие, расширению области практического применения подобных систем.
В университете Дж. Хопкинса (США) на квантовом канале длиной 1 км построена вычислительная сеть, в которой каждые 10 минут производится автоматическая подстройка. В результате этого, уровень ошибки снижен до 0,5 % при скорости связи 5 кбит/с.
Министерством обороны Великобритании поддерживается исследовательская корпорация QinetiQ, являющаяся частью бывшего британского агентства DERA (Defence Evaluation and Research Agency), которая специализируется на неядерных оборонных исследованиях и активно совершенствует технологию квантового шифрования.

Исследованиями в области квантовой криптографии занимается молодая американская компания Magiq Technologies из Нью-Йорка, выпустившая прототип коммерческой квантовой криптотехнологии собственной разработки. Основной продукт Magiq — средство для распределения ключей (quantum key distribution, QKD), которое названо Navajo (По имени индейцев Навахо, язык которых во время Второй мировой войны американцы использовали для передачи секретных сообщений, поскольку за пределами США его никто не знал). Navajo способен в реальном времени генерировать и распространять ключи средствами квантовых технологий и предназначен для обеспечения защиты от внутренних и внешних злоумышленников.
В октябре 2007 года на выборах в Швейцарии были повсеместно использованы квантовые сети, начиная избирательными участками и заканчивая датацентром ЦИК. Была использована техника, которую ещё в середине 90-х в Университете Женевы разработал профессор Николас Гисин. Также одним из участников создания такой системы была компания Id Quantique.
В 2011 году в Токио прошла демонстрация проекта «Tokyo QKD Network», в ходе которого разрабатывается квантовое шифрование телекоммуникационных сетей. Была проведена пробная телеконференция на расстоянии в 45 км. Связь в системе идёт по обычным оптоволоконным линиям. В будущем предполагается применение для мобильной связи.

Квантовый криптоанализ

Частотный спектр в оптическом канале квантово-криптографической системы.

Взлом квантовой системы[2][3]

Подключай и работай (Plug & Play)

Перспективы развития

2) Создание квантового канала связи длиной более 100 км.

3) Организация десятков подканалов при разделении по длинам волн.

Литература

↑ Семёнов Ю. А. «Телекоммуникационные технологии»;
↑ Nature Communicaion «Perfect eavesdropping on a quantum cryptography system» : [1];
↑ Nature Communicaion «Full-field implementation of a perfect eavesdropper on a quantum cryptography system, June 2011» : [2];

Килин С. Я., Хорошко Д. Б., Низовцев А. П. «Квантовая криптография: идеи и практика»;
Килин С. Я. «Квантовая информация / Успехи Физических Наук.» — 1999. — Т. 169. — C. 507—527. [3];
Robert Malaney . «Технологии, основанные на принципе ULV (unconditional location verification)» : [4], [5];
Computerworld Россия , № 37, 2007 [6];
Красавин В. «Квантовая криптография».

См. также

dikc.academic.ru

Квантовые вычисления - это... Что такое Квантовые вычисления?

3 кубита квантового регистра против 3 битов обычного

Квантовый компьютер — гипотетическое[1]вычислительное устройство, которое путем выполнения квантовых алгоритмов существенно использует при работе квантовомеханические эффекты, такие как квантовый параллелизм и квантовая запутанность.

Содержание понятия «квантовый параллелизм» может быть раскрыто так: «Данные в процессе вычислений представляют собой квантовую информацию, которая по окончании процесса преобразуется в классическую путём измерения конечного состояния квантового регистра. Выигрыш в квантовых алгоритмах достигается за счет того, что при применении одной квантовой операции большое число коэффициентов суперпозиции квантовых состояний, которые в виртуальной форме содержат классическую информацию, преобразуется одновременно» [1].

Под квантовой запутанностью, которую называют также «квантовой суперпозицией», обычно понимается следующее: "Вообразите атом, который мог бы подвергнуться радиоактивному распаду в определенный промежуток времени. Или не мог бы. Мы можем ожидать, что у этого атома есть только два возможных состояния: «распад» и «не распад», /…/ но в квантовой механике у атома может быть некое объединенное состояние — «распада — не распада», то есть ни то, ни другое, а как бы между. Вот это состояние и называется «суперпозицией» [2].

Базовые характеристики квантовых компьютеров в теории позволяют им преодолеть некоторые ограничения, возникающие при работе классических компьютеров.

Теория

Кубиты

Идея квантовых вычислений, впервые высказанная Ю. И. Маниным[3] и Р. Фейнманом[4] состоит в том, что квантовая система из L двухуровневых квантовых элементов (кубитов) имеет 2L линейно независимых состояний, а значит, вследствие принципа квантовой суперпозиции, 2L-мерное гильбертово пространство состояний. Операция в квантовых вычислениях соответствует повороту в этом пространстве. Таким образом, квантовое вычислительное устройство размером L кубит может выполнять параллельно 2L операций.

Предположим, что имеется один кубит. В таком случае после измерения, в так называемой классической форме, результат будет 0 или 1. В действительности кубит — квантовый объект и поэтому, вследствие принципа неопределённости, может быть и 0, и 1 с определенной вероятностью. Если кубит равен 0 (или 1) со стопроцентной вероятностью, его состояние обозначается с помощью символа |0> (или |1>) — в обозначениях Дирака. |0> и |1> — это базовые состояния. В общем случае квантовое состояние кубита находится между базовыми и записывается, в виде , где |a|² и |b|² — вероятности измерить 0 или 1 соответственно; ; |a|² + |b|² = 1. Более того, сразу после измерения кубит переходит в базовое квантовое состояние, аналогичное классическому результату.

Пример:

Имеется кубит в квантовом состоянии В этом случае, вероятность получить при измерении

0	составляет	(4/5)²=16/25	= 64 %,
1		(-3/5)²=9/25	= 36 %.

В данном случае, при измерении мы получили 0 с 64 % вероятностью. Тогда кубит перескакивает в новое квантовое состояние 1*|0>+0*|1>=|0>, то есть, при следующем измерении этого кубита мы получим 0 со стопроцентной вероятностью. Это обусловлено тем, что дираковский вектор состояния не зависит от времени, то есть раскладывается в сумму векторов базисных состояний с независящими от времени коэффициентами.

Приведем для объяснения два примера из квантовой механики: 1) фотон находится в состоянии суперпозиции двух поляризаций; измерение раз и навсегда коллапсирует состояние фотона в таковое с определенной поляризацией; 2) радиоактивный атом имеет определенный период полураспада; измерение может выявить то, что он еще не распался, но это не значит, что он никогда не распадется.

Перейдем к системе из двух кубитов. Измерение каждого из них может дать 0 или 1. Поэтому у системы 4 классических состояния: 00, 01, 10 и 11. Аналогичные им базовые квантовые состояния: |00>, |01>, |10> и |11>. И наконец, общее квантовое состояние системы имеет вид . Теперь |a|² — вероятность измерить 00 и т. д. Отметим, что |a|²+|b|²+|c|²+|d|²=1 как полная вероятность.

В общем случае, системы из L кубитов у неё 2L классических состояний (00000…(L-нулей), …00001(L-цифр), … , 11111…(L-единиц)), каждое из которых может быть измерено с вероятностями 0—100 %.

Таким образом, одна операция над группой кубитов затрагивает все значения, которые она может принимать, в отличие от классического бита. Это и обеспечивает беспрецедентный параллелизм вычислений.

Вычисление

Упрощённая схема вычисления на квантовом компьютере выглядит так: берется система кубитов, на которой записывается начальное состояние. Затем состояние системы или её подсистем изменяется посредством базовых квантовых операций. В конце измеряется значение, и это результат работы компьютера.

Оказывается, что для построения любого вычисления достаточно двух базовых операций. Квантовая система дает результат, только с некоторой вероятностью являющийся правильным. Но за счет небольшого увеличения операций в алгоритме можно сколь угодно приблизить вероятность получения правильного результата к единице.

С помощью базовых квантовых операций можно симулировать работу обычных логических элементов, из которых сделаны обычные компьютеры. Поэтому любую задачу, которая решена сейчас, квантовый компьютер решит, и почти за такое же время. Следовательно, новая схема вычислений будет не слабее нынешней.

Чем же квантовый компьютер лучше классического? Большая часть современных ЭВМ работают по такой же схеме: n бит памяти хранят состояние и каждый такт времени изменяются процессором. В квантовом случае система из n кубитов находится в состоянии, являющимся суперпозицией всех базовых состояний, поэтому изменение системы касается всех 2n базовых состояний одновременно. Теоретически новая схема может работать намного (в экспоненциальное число раз) быстрее классической. Практически (квантовый) алгоритм Гровера поиска в базе данных показывает квадратичный прирост мощности против классических алгоритмов. Пока в природе их не существует.

Алгоритмы

Алгоритм Гровера позволяет найти решение уравнения за время .
Алгоритм Шора позволяет разложить натуральное число n на простые множители за полиномиальное от log(n) время.
Алгоритм Дойча — Джоза позволяет «за одно вычисление» определить, является ли функция двоичной переменной f(n) постоянной (f1(n) = 0, f2(n) = 1 независимо от n) или «сбалансированной» (f3(0) = 0, f3(1) = 1; f4(0) = 1, f4(1) = 0).

Было показано, что не для всякого алгоритма возможно «квантовое ускорение».

Квантовая телепортация

Алгоритм телепортации реализует точный перенос состояния одного кубита (или системы) на другой. В простейшей схеме используются 4 кубита: источник, приёмник и два вспомогательных. Отметим, что в результате работы алгоритма первоначальное состояние источника разрушится — это пример действия общего принципа невозможности клонирования — невозможно создать точную копию квантового состояния, не разрушив оригинал. На самом деле, довольно легко создать одинаковые состояния на кубитах. К примеру, измерив 3 кубита, мы переведем каждый из них в базовые состояния (0 или 1) и хотя бы на двух из них они совпадут. Не получится скопировать произвольное состояние, и телепортация — замена этой операции.

Телепортация позволяет передавать квантовое состояние системы с помощью обычных классических каналов связи. Таким образом, можно, в частности, получить связанное состояние системы, состоящей из подсистем, удаленных на большое расстояние.

Применение квантовых компьютеров

Специфика применения

Может показаться, что квантовый компьютер — это разновидность аналоговой вычислительной машины. Но это не так: по своей сути это цифровое устройство, но с аналоговой природой.

Основные проблемы, связанные с созданием и применением квантовых компьютеров:

необходимо обеспечить высокую точность измерений;
внешние воздействия могут разрушить квантовую систему или внести в неё искажения.

Приложения к криптографии

Благодаря огромной скорости разложения на простые множители, квантовый компьютер позволит расшифровывать сообщения, зашифрованные при помощи популярного асимметричного криптографического алгоритма

Применение идей квантовой механики уже открыли новую эпоху в области криптографии, так как методы квантовой криптографии открывают новые возможности в области передачи сообщений[5]. Прототипы систем подобного рода находятся на стадии разработки[6].

Реализации

Канадская компания D-Wave заявила в феврале 2007 года о создании образца квантового компьютера, состоящего из 16 кубит (устройство получило название Orion). Однако информация об этом устройстве не отвечала строгим требованиям точного научного сообщения; новость не получила научного признания. Более того, дальнейшие планы компании (создать уже в ближайшем будущем 1024-кубитный компьютер) вызвали скепсис у членов экспертного сообщества[7].

В ноябре 2007 года та же компания D-Wave продемонстрировала работу образца 28-кубитного компьютера онлайн на конференции, посвященной суперкомпьютерам[8]. Данная демонстрация также вызвала определенного рода скепсис.

В декабре 2008 года компания организовала проект Распределенных вычислений AQUA@home(Adiabatic QUantum Algorithms) [9], в котором тестируются алгоритмы, оптимизирующие вычисления на адиабатических сверхпроводящих квантовых компьютерах D-Wave.

См. также

Примечания

Литература

Ссылки

Квантовый ликбез
Квантовый компьютер и его полупроводниковая элементарная база
Кафедра квантовой информатики факультета ВМК МГУ
Лаборатория физики квантовых компьютеров Физикотехнологического института РАН
Китаев,А., Шень, А., Вялый, М. Классические и квантовые вычисления
QWiki(англ.) и Quantiki(англ.) — Wiki-ресурсы по квантовой информатике
Язык программирования QCL для квантовых компьютеров(англ.)
Курс «Современные задачи теоретической информатики» (лекции по квантовым вычислениям: введение, суперплотное кодирование, квантовая телепортация, алгоритмы Саймона и Шора)
Gilles Brassard, Isaac Chuang, Seth Lloyd and Christopher Monroe. Quantum computing
Beyond Bits: The Future of Quantum Information Processing Andrew M. Steane, Eleanor G. Rieffel
InFuture.ru: Будущее квантовых компьютеров — в троичных вычислениях
Валиев К. А. «Квантовые компьютеры и квантовые вычисления» УФН 175 3 (2005)
Страничка проекта AQUA@home на сайте команды «Russia»

Wikimedia Foundation. 2010.

dvc.academic.ru

Квантовые вычисления - это... Что такое Квантовые вычисления?

3 кубита квантового регистра против 3 битов обычного

Теория

Кубиты

Пример:

Имеется кубит в квантовом состоянии В этом случае, вероятность получить при измерении

0	составляет	(4/5)²=16/25	= 64 %,
1		(-3/5)²=9/25	= 36 %.

Вычисление

Алгоритмы

Алгоритм Гровера позволяет найти решение уравнения за время .
Алгоритм Шора позволяет разложить натуральное число n на простые множители за полиномиальное от log(n) время.
Алгоритм Дойча — Джоза позволяет «за одно вычисление» определить, является ли функция двоичной переменной f(n) постоянной (f1(n) = 0, f2(n) = 1 независимо от n) или «сбалансированной» (f3(0) = 0, f3(1) = 1; f4(0) = 1, f4(1) = 0).

Было показано, что не для всякого алгоритма возможно «квантовое ускорение».

Квантовая телепортация

Применение квантовых компьютеров

Специфика применения

Основные проблемы, связанные с созданием и применением квантовых компьютеров:

необходимо обеспечить высокую точность измерений;
внешние воздействия могут разрушить квантовую систему или внести в неё искажения.

Приложения к криптографии

Реализации

См. также

Примечания

Литература

Ссылки

Квантовый ликбез
Квантовый компьютер и его полупроводниковая элементарная база
Кафедра квантовой информатики факультета ВМК МГУ
Лаборатория физики квантовых компьютеров Физикотехнологического института РАН
Китаев,А., Шень, А., Вялый, М. Классические и квантовые вычисления
QWiki(англ.) и Quantiki(англ.) — Wiki-ресурсы по квантовой информатике
Язык программирования QCL для квантовых компьютеров(англ.)
Курс «Современные задачи теоретической информатики» (лекции по квантовым вычислениям: введение, суперплотное кодирование, квантовая телепортация, алгоритмы Саймона и Шора)
Gilles Brassard, Isaac Chuang, Seth Lloyd and Christopher Monroe. Quantum computing
Beyond Bits: The Future of Quantum Information Processing Andrew M. Steane, Eleanor G. Rieffel
InFuture.ru: Будущее квантовых компьютеров — в троичных вычислениях
Валиев К. А. «Квантовые компьютеры и квантовые вычисления» УФН 175 3 (2005)
Страничка проекта AQUA@home на сайте команды «Russia»

Wikimedia Foundation. 2010.

biograf.academic.ru

Квантовые вычисления - это... Что такое Квантовые вычисления?

3 кубита квантового регистра против 3 битов обычного

Теория

Кубиты

Пример:

Имеется кубит в квантовом состоянии В этом случае, вероятность получить при измерении

0	составляет	(4/5)²=16/25	= 64 %,
1		(-3/5)²=9/25	= 36 %.

Вычисление

Алгоритмы

Алгоритм Гровера позволяет найти решение уравнения за время .
Алгоритм Шора позволяет разложить натуральное число n на простые множители за полиномиальное от log(n) время.
Алгоритм Дойча — Джоза позволяет «за одно вычисление» определить, является ли функция двоичной переменной f(n) постоянной (f1(n) = 0, f2(n) = 1 независимо от n) или «сбалансированной» (f3(0) = 0, f3(1) = 1; f4(0) = 1, f4(1) = 0).

Было показано, что не для всякого алгоритма возможно «квантовое ускорение».

Квантовая телепортация

Применение квантовых компьютеров

Специфика применения

Основные проблемы, связанные с созданием и применением квантовых компьютеров:

необходимо обеспечить высокую точность измерений;
внешние воздействия могут разрушить квантовую систему или внести в неё искажения.

Приложения к криптографии

Реализации

См. также

Примечания

Литература

Ссылки

Квантовый ликбез
Квантовый компьютер и его полупроводниковая элементарная база
Кафедра квантовой информатики факультета ВМК МГУ
Лаборатория физики квантовых компьютеров Физикотехнологического института РАН
Китаев,А., Шень, А., Вялый, М. Классические и квантовые вычисления
QWiki(англ.) и Quantiki(англ.) — Wiki-ресурсы по квантовой информатике
Язык программирования QCL для квантовых компьютеров(англ.)
Курс «Современные задачи теоретической информатики» (лекции по квантовым вычислениям: введение, суперплотное кодирование, квантовая телепортация, алгоритмы Саймона и Шора)
Gilles Brassard, Isaac Chuang, Seth Lloyd and Christopher Monroe. Quantum computing
Beyond Bits: The Future of Quantum Information Processing Andrew M. Steane, Eleanor G. Rieffel
InFuture.ru: Будущее квантовых компьютеров — в троичных вычислениях
Валиев К. А. «Квантовые компьютеры и квантовые вычисления» УФН 175 3 (2005)
Страничка проекта AQUA@home на сайте команды «Russia»

Wikimedia Foundation. 2010.

dal.academic.ru

Квантовые вычисления - это... Что такое Квантовые вычисления?

3 кубита квантового регистра против 3 битов обычного

Теория

Кубиты

Пример:

Имеется кубит в квантовом состоянии В этом случае, вероятность получить при измерении

0	составляет	(4/5)²=16/25	= 64 %,
1		(-3/5)²=9/25	= 36 %.

Вычисление

Алгоритмы

Алгоритм Гровера позволяет найти решение уравнения за время .
Алгоритм Шора позволяет разложить натуральное число n на простые множители за полиномиальное от log(n) время.
Алгоритм Дойча — Джоза позволяет «за одно вычисление» определить, является ли функция двоичной переменной f(n) постоянной (f1(n) = 0, f2(n) = 1 независимо от n) или «сбалансированной» (f3(0) = 0, f3(1) = 1; f4(0) = 1, f4(1) = 0).

Было показано, что не для всякого алгоритма возможно «квантовое ускорение».

Квантовая телепортация

Применение квантовых компьютеров

Специфика применения

Основные проблемы, связанные с созданием и применением квантовых компьютеров:

необходимо обеспечить высокую точность измерений;
внешние воздействия могут разрушить квантовую систему или внести в неё искажения.

Приложения к криптографии

Реализации

См. также

Примечания

Литература

Ссылки

Квантовый ликбез
Квантовый компьютер и его полупроводниковая элементарная база
Кафедра квантовой информатики факультета ВМК МГУ
Лаборатория физики квантовых компьютеров Физикотехнологического института РАН
Китаев,А., Шень, А., Вялый, М. Классические и квантовые вычисления
QWiki(англ.) и Quantiki(англ.) — Wiki-ресурсы по квантовой информатике
Язык программирования QCL для квантовых компьютеров(англ.)
Курс «Современные задачи теоретической информатики» (лекции по квантовым вычислениям: введение, суперплотное кодирование, квантовая телепортация, алгоритмы Саймона и Шора)
Gilles Brassard, Isaac Chuang, Seth Lloyd and Christopher Monroe. Quantum computing
Beyond Bits: The Future of Quantum Information Processing Andrew M. Steane, Eleanor G. Rieffel
InFuture.ru: Будущее квантовых компьютеров — в троичных вычислениях
Валиев К. А. «Квантовые компьютеры и квантовые вычисления» УФН 175 3 (2005)
Страничка проекта AQUA@home на сайте команды «Russia»

Wikimedia Foundation. 2010.

3dic.academic.ru