Содержание
Самое большое число в мире: как называется
Содержание
Считается, что концепция чисел впервые возникла, когда доисторические люди начали использовать свои пальцы для подсчета чего-либо. С тех пор человечество прошло долгий путь. Теперь мы используем калькуляторы и компьютеры для подсчета самых больших чисел. И даже появились названия для чисел, которые настолько велики, что их с трудом можно представить.
Бесконечность счетных чисел
Казалось бы, ответ на вопрос о том, каково самое большое число в математике — очень прост. Бесконечность, верно? Но это не совсем правильно. Ведь бесконечность — вовсе не число, а концепция. Идея.
Бесконечность (infinitum) — это понятие, которое в переводе с латинского означает «без границ». Определение бесконечности в математике гласит, что независимо от того, насколько велико число, вы всегда можете добавить к нему 1, и оно станет больше.
Поэтому, строго говоря, не существует такого понятия, как самое большое число в мире. Можно лишь назвать наибольшее число, которому дали конкретное название.
Можно лишь назвать наибольшее число, которому дали конкретное название.
Вот некоторые наиболее известные названия больших чисел:
| Число нулей | Название | Название на английском |
|---|---|---|
| 3 | тясяча | thousand |
| 6 | миллион | million |
| 9 | миллиард (биллион) | billion |
| 12 | триллион | trillion |
| 15 | квадриллион | quadrillion |
| 18 | квинтиллион | quintillion |
| 21 | секстиллион | sextillion |
| 24 | септиллион | septillion |
| 27 | октиллион | octillion |
| 30 | нониллион | nonillion |
| 33 | дециллион | decillion |
| 36 | ундециллион | undecillion |
| 39 | дуодециллион | duodecillion |
| 42 | тредециллион | tredecillion |
| 45 | кватуордециллион | quattuordecillion |
| 48 | квиндециллион | quindecillion |
| 51 | сексдециллион | sexdecillion |
| 54 | септендециллион | septendecillion |
| 57 | октодециллион | octodecillion |
| 60 | новемдециллион | novemdecillion |
| 63 | вигинтиллион | vigintillion |
| 66 | унвигинтиллион | unvigintillion |
| 69 | дуовигинтиллион | duovigintillion |
| 72 | тревигинтиллион | trevigintillion |
| 75 | кватуорвигинтиллион | quattuorvigintillion |
| 78 | квинвигинтиллион | quinvigintillion |
| 81 | сексвигинтиллион | sexvigintillion |
| 84 | септенвигинтиллион | septenvigintillion |
| 87 | октовигинтиллион | octovigintillion |
| 90 | новемвигинтиллион | novemvigintillion |
| 93 | тригинтиллион | trigintillion |
| 96 | унтригинтиллион | untrigintillion |
| 99 | дуотригинтиллион | duotrigintillion |
| 102 | третригинтиллион | trestrigintillion |
| 105 | кватортригинтиллион | quattuortrigintillion |
| 108 | квинтригинтиллион | quintrigintillion |
| 111 | секстригинтиллион | sextrigintillion |
| 114 | септентригинтиллион | septentrigintillion |
| 117 | октотригинтиллион | octotrigintillion |
| 120 | новемтригинтиллион | novemtrigintillion |
| 123 | квадрагинтиллион | quadragintillion |
| 126 | унквадрагинтиллион | unquadragintillion |
| 129 | дуоквадрагинтиллион | duoquadragintillion |
| 132 | треквадрагинтиллион | trequadragintillion |
| 135 | кваторквадрагинтиллион | quattuorquadragintillion |
| 138 | квинквадрагинтиллион | quinquadragintillion |
| 141 | сексквадрагинтиллион | sexquadragintillion |
| 144 | септенквадрагинтиллион | septenquadragintillion |
| 147 | октоквадрагинтиллион | octoquadragintillion |
| 150 | новемквадрагинтиллион | novemquadragintillion |
| 153 | квинквагинтиллион | quinquagintillion |
| 156 | унквинкагинтиллион | unquinquagintillion |
| 159 | дуоквинкагинтиллион | duoquinquagintillion |
| 162 | треквинкагинтиллион | trequinquagintillion |
| 165 | кваторквинкагинтиллион | quattuorquinquagintillion |
| 168 | квинквинкагинтиллион | quinquinquagintillion |
| 171 | сексквинкагинтиллион | sexquinquagintillion |
| 174 | септенквинкагинтиллион | septenquinquagintillion |
| 177 | октоквинкагинтиллион | octoquinquagintillion |
| 180 | новемквинкагинтиллион | novemquinquagintillion |
| 183 | сексагинтиллион | sexagintillion |
| 186 | унсексагинтиллион | unsexagintillion |
| 189 | дуосексагинтиллион | duosexagintillion |
| 192 | тресексагинтиллион | tresexagintillion |
| 195 | кваторсексагинтиллион | quattuorsexagintillion |
| 198 | квинсексагинтиллион | quinsexagintillion |
| 201 | секссексагинтиллион | sexsexagintillion |
| 204 | септенсексагинтиллион | septensexagintillion |
| 207 | октосексагинтиллион | octosexagintillion |
| 210 | новемсексагинтиллион | novemsexagintillion |
| 213 | септагинтиллион | septuagintillion |
| 216 | унсептагинтиллион | unseptuagintillion |
| 219 | дуосептагинтиллион | duoseptuagintillion |
| 222 | тресептагинтиллион | treseptuagintillion |
| 225 | кваторсептагинтиллион | quattuorseptuagintillion |
| 228 | квинсептагинтиллион | quinseptuagintillion |
| 231 | секссептагинтиллион | sexseptuagintillion |
| 234 | септенсептагинтиллион | septenseptuagintillion |
| 237 | октосептагинтиллион | octoseptuagintillion |
| 240 | новемсептагинтиллион | novemseptuagintillion |
| 243 | октогинтиллион | octogintillion |
| 246 | уноктогинтиллион | unoctogintillion |
| 249 | дуооктогинтиллион | duooctogintillion |
| 252 | треоктогинтиллион | treoctogintillion |
| 255 | кватороктогинтиллион | quattuoroctogintillion |
| 258 | квиноктогинтиллион | quinoctogintillion |
| 261 | сексоктогинтиллион | sexoctogintillion |
| 264 | септоктогинтиллион | septoctogintillion |
| 267 | октооктогинтиллион | octooctogintillion |
| 270 | новемоктогинтиллион | novemoctogintillion |
| 273 | нонагинтиллион | nonagintillion |
| 276 | уннонагинтиллион | unnonagintillion |
| 279 | дуононагинтиллион | duononagintillion |
| 282 | тренонагинтиллион | trenonagintillion |
| 285 | кваторнонагинтиллион | quattuornonagintillion |
| 288 | квиннонагинтиллион | quinnonagintillion |
| 291 | секснонагинтиллион | sexnonagintillion |
| 294 | септеннонагинтиллион | septennonagintillion |
| 297 | октононагинтиллион | octononagintillion |
| 300 | новемнонагинтиллион | novemnonagintillion |
| 303 | центиллион | centillion |
Как называется самое большое простое число
Простое число — то, которое делится только на себя и на единицу. В конце 2018 года американец Патрик Лярош представил научному миру самое большое простое число.
В конце 2018 года американец Патрик Лярош представил научному миру самое большое простое число.
- Длина его — 24 862 048 символов. Для сравнения: в эпохальном произведении Л.Н. Толстого «Война и мир» около 6-7 миллионов символов, если учитывать знаки препинания и пробелы.
- Это число можно записать следующим образом: 282589933-1
- А читается оно так: два в степени 82589933 минус один.
- Существует целый онлайн-проект GIMPS, нацеленный как раз на поиск самых больших простых чисел. В нем принимают участие математики из разных стран. Поэтому новые рекордсмены появляются часто. Работают ученые, что называется, не за страх, а за деньги. Ведь тому, кто откроет следующее наибольшее простое число Мерсенна достанется 3000 долларов.
Какое самое большое число в мире
В 1980 году в Книгу рекордов Гиннеса вошло число Грэма (оно же G64 или G), названное в честь американского математика Рональда Грэма. Оно является наибольшим числом, которое когда-либо использовалось в важном математическом доказательстве. Речь идет про теорию Франка Рамсея.
Речь идет про теорию Франка Рамсея.
Кратко об этой теории: представим себе N-мерный куб, его вершины в случайном порядке соединены красными или синими отрезками-линиями. А наша задача — понять, до какого значения N возможно (если по-разному закрашивать ребра куба), избежать ситуации, при которой одна плоскость в кубе будет окрашена одним цветом. То есть у нас не должен получиться одноцветный «конвертик».
Математики позакрашивали кубик и так и эдак, получилось, что до шестимерного куба можно исхитриться и сделать, чтобы линии одного цвета, соединяющие четыре вершины, не лежали в одной плоскости. А вот с семимерным, как выяснили Грэм и Ротшильд, такой фокус уже не провернешь. И с восьмимерным. И… «и так далее», которое, впрочем, не бесконечно, а заканчивается фантастически гигантским числом. Вот его-то и именуют числом Грэма. Кстати, в настоящее время решение Грэма и Ротшильда устарело. Математики выяснили, что 6-7-8-9-10-11-12-мерные кубы все же можно покрасить без «конвертов». Но где-то в промежутке между 13 и числом Грэма гарантированно есть число выше которого «конверты» в любом случае будут.
Но где-то в промежутке между 13 и числом Грэма гарантированно есть число выше которого «конверты» в любом случае будут.
Число Грэма получило всемирное признание в 1977 году, когда известный популяризатор науки Мартин Гарднер написал об этом в Scientific American.
И хотя с тех пор в математической науке были и другие кандидаты на титул самого большого числа, «детище» Грэма является самым распиаренным и общеизвестным. И если вы слышали про «гугольное семейство»:
- гугол — 10100;
Или: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - гуголплекс — 10гугол,
то знайте, что этими числами в математике лишь «разминаются», а число Грэма в немыслимое количество раз больше, чем они. И даже больше, чем число Скьюза, находящееся между 1019 и 1,3971672·10316 и приблизительно равное e727,951336108.
Любопытно, что придумав гугол американский математик Эдвард Казнер хотел показать студентам разницу между невероятно большим числом и бесконечностью. Тогда число Грэма может просто «взорвать мозг».
Тогда число Грэма может просто «взорвать мозг».
Возможно ли представить и записать число за гранью понимания
Математики не смогут назвать вам точное количество цифр в числе Грэма, не говоря уже о том, чтобы досчитать до него. Известны лишь последние 50 цифр самого большого числа в мире — это …03222348723967018485186439059104575627262464195387.
А вот цифры, с которых начинается G64 неизвестны, и вряд ли когда-либо будут.
Давайте сравним трех монстров: гугол, гуголплекс и число Грэма.
- Гугол — это количество песчинок, которые могут поместиться во вселенной, умноженное на 10 миллиардов. Итак, представьте себе вселенную, заполненную мелкими песчинками — на десятки миллиардов световых лет над Землей, под ней, перед ней, позади нее — бесконечный песок.
Теперь представьте, что в какой-то момент вы берете одну песчинку, чтобы рассмотреть ее под мощным микроскопом. И видите, что на самом деле это не единственное зерно, а 10 миллиардов микроскопических зерен, а все вместе они размером с песчинку.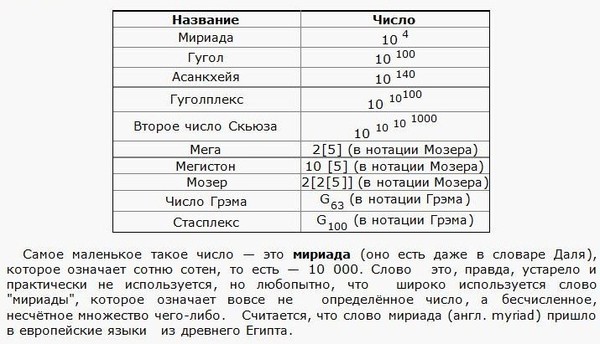 Если бы это было так для каждой отдельной песчинки в этой гипотетической вселенной, то общее количество этих микроскопических зерен было бы гуголом.
Если бы это было так для каждой отдельной песчинки в этой гипотетической вселенной, то общее количество этих микроскопических зерен было бы гуголом.
- Для количественной оценки гуголплекса астроном и астрофизик Карл Саган привел пример заполнения всего объема наблюдаемой вселенной мелкими частицами пыли размером приблизительно 1,5 микрометра. Исходя из этого, общее количество различных комбинаций, в которых эти частицы могут быть расположены, будет равно примерно одному гуголплексу.
- А теперь представим, что гуголплекс — это даже не песчинка, а крохотная точка, которую можно рассмотреть лишь в самый мощный микроскоп. И у нас вся вселенная заполнена такими крохотными точками. Так вот, даже это не идет ни в какое сравнение с числом Грэма. Но что, если мы хотим использовать все пространство наблюдаемой вселенной для его записи (предположим, что запись каждой цифры занимает как минимум объём Планка)? Увы, у нас это не выйдет! Но всегда можно пойти другим путем.
Как записать G64 с помощью метода Кнута
В 1976 году американский ученый Дональд Кнут предложил понятие сверхстепеней или нотацию Кнута. Это метод, позволяющий при помощи стрелочек, направленных вверх, записывать очень большие числа. Возведение в степень обозначается одной стрелкой вверх: ↑.
Это метод, позволяющий при помощи стрелочек, направленных вверх, записывать очень большие числа. Возведение в степень обозначается одной стрелкой вверх: ↑.
Вот как выглядит эта нотация: a ↑ b = ab = a × a × a × …, и так b раз.
- Например 3↑3 = 3³.
- Гугол записывается так 10↑10↑2.
- А гуголплекс — 10↑10↑10↑2
Важной особенностью стрелок вверх является то, что они растут очень быстро. Экспонентация растет гораздо быстрее, чем умножение. 2 × 10 — это всего лишь 20, но 2↑10 = 1024. Таким же образом, каждый новый уровень стрелок растет намного быстрее, чем предыдущий уровень.
Если мысленно представить себе степенную башню из троек 3↑↑↑4 то получится конструкция, размером от Земли до Марса. А ведь мы еще даже не дошли до «нижней ступеньки», ведущей нас к числу Грэма.
Мы можем описать число Грэма огромным набором этих стрелок вверх.
Проще всего думать об этом как об итерационном процессе. Мы начинаем снизу с g 1 = 3 ↑↑↑↑ 3, а затем создаем вторую строку (назовем ее g 2) с g 1 стрелками между тройками.
Тогда g 3 — это две тройки, разделенные g 2 стрелками вверх и так далее, пока g 64 с g 63 стрелками между тройками не будет числом Грэма.
Если выбрать продолжительность жизни, равную числу Грэма вместо бессмертия, то результат будет практически одинаков. Даже если предположить, что условия во Вселенной, в Солнечной системе и на Земле вечно останутся неизменными, человеческий мозг никак не мог бы выдержать столь длинный промежуток времени без пагубных изменений.
Самое большое число — 24СМИ
Содержание
- Самое большое число
- Внесистемные числа
Из школьного курса известно, что наибольшего числа не существует. Ведь если к самому большому числу прибавить хотя бы единицу, то получим еще большее число. Школьник с легкостью скажет, что, например, самое большое двузначное число — 99, а трехзначное — 999 и т.д.
Ведь если к самому большому числу прибавить хотя бы единицу, то получим еще большее число. Школьник с легкостью скажет, что, например, самое большое двузначное число — 99, а трехзначное — 999 и т.д.
Существует два алгоритма наименования чисел – английский и американский.
В американском названия больших чисел строятся следующим образом: сначала идет латинское порядковое числительное, а затем добавляется суффикс «иллион». Исключение – миллион. Далее получаются числа: триллион, квадриллион, квинтиллион. После идут секстиллион, септиллион, октиллион, нониллион и дециллион. Такой способ используют в США, Канаде, России и Франции.
Американский алгоритм наименования чисел
Английский алгоритм используют в Испании и Великобритании, а так же в ряде бывших колоний. Здесь названия строятся так: к латинскому числительному прибавляют суффикс «иллион», к следующему числу (которое больше в 1000 раз) уже добавляют суффикс «иллиард». После триллиона идет триллиард, после квадриллион, квадриллиард и т. д. Получается, что по английскому и американскому алгоритму одни и те же большие числа называются по-разному.
д. Получается, что по английскому и американскому алгоритму одни и те же большие числа называются по-разному.
Читайте по теме: Самое маленькое число
В русский язык из английской системы пришел только миллиард (109), который американцы называют биллионом. Иногда в России употребляют слово триллиард, т.е. 1000 триллионов или квадриллион.
Самое большое число
Самое большое простое число в мире – 274207281 – 1, которое содержит 22 338 618 десятичных цифр (простое число Мерсенна). Значение нашли в 2015 году в ходе проекта по распределенному поиску простых чисел Мерсенна GIMPS. Поясним, что простыми называются натуральные (целые положительные) числа, имеющие только два делителя — единицу и само себя. Например, 2, 3, 5, 7 — простые числа. Список продолжают 11, 13, 17, 19… Кроме двойки все числа нечетные, иначе бы делились не только на единицу и себя, но и на два. Значит, найденное простое число еще и самое большое из нечетных.
Маренн Марсен и самое большое простое число
По утверждению Евклида, простых чисел бесконечное множество, значит, наибольшего простого числа нет. Ученые до сих пор ищут числа-рекордсмены. И тому есть разумное объяснение. Всемирная организация Electronic Frontier Foundation учредила награды за подобные открытия: чем больше найденное число, тем выше награда.
Ученые до сих пор ищут числа-рекордсмены. И тому есть разумное объяснение. Всемирная организация Electronic Frontier Foundation учредила награды за подобные открытия: чем больше найденное число, тем выше награда.
Есть специальный способ проверки простоты чисел, который называется тест Люка-Лемера. Правда, предназначен он исключительно для чисел Мерсенна. Что же это за числа? Это вид натуральных чисел, расположенных в определенной последовательности. Имя им дал французский математик Мерсенн Марен. Вид числа Мерсенна такой:
Mn = 2n – 1,
где n — натуральное число.
При n = 1, 2, 3, 4, … числа Мерсенна образуют последовательность, начинающуюся с 1, 3, 7, 15. Затем идут 31, 63, 127. Продолжают ряд 255, 511, 1023, 2047 и т.д.
Такие числа используют в криптографии, например, для усовершенствования банковских кодов.
Внесистемные числа
Кроме чисел, которые записаны при помощи английской или американской систем, известны внесистемные числа. У них есть собственные названия, в которых нет латинских префиксов. Для понимания сначала рассмотрим запись латинскими числительными.
Для понимания сначала рассмотрим запись латинскими числительными.
Единица – это 100, десять — 101 и так далее: миллиард — 109, триллион — 1012, квадриллион — 1015, квинтиллион — 1018, секстиллион — 1021, септиллион — 1024, октиллион — 1027, нониллион — 1030, дециллион — 1033.
С помощью приставок можно и дальше выводить числа: андециллион, дуодециллион, тридециллион и так далее. Но нужны собственные названия чисел, а тут только составные названия. Поэтому по этой системе собственных имен еще только три — вигинтиллион — 1063, центиллион — 10303, миллеиллион — 103003.
В миллеиллионе 3003 нуля
Число с собственным, а не составным названием больше 103003 получить невозможно. Однако числа больше миллеиллиона известны – это внесистемные числа.
Самое маленькое внесистемное число носит название мириада. Означает сотню сотен, т.е. 10000.
Далее идет гугол. Это десять в сотой степени — 1010100. Единица со ста нулями. О гуголе впервые написали в 1938 году. Американский математик Эдвард Каснер сказал, что назвать большое число таким образом предложил племянник. А популярным это название стало после того, как в честь него назвали поисковик «Google».
А популярным это название стало после того, как в честь него назвали поисковик «Google».
Число гугол
Далее встречается число асанкхейя. Это 1010140. Следом идет число гуголплекс. Его придумал тот же Каснер с племянником. Означает 10 в степени 10 в степени 100. Или единица с гуголом нулей.
Еще больше гуголплекса число Скьюза. Его предложил Скьюз в 1933 году во время доказательства гипотезы Риманна о простых числах.
Обозначается — Sk1.
Есть второе число Скьюза. Обозначается как Sk2. Вводится, если гипотеза Риманна не справедлива. Второе число Скьюза равно
Но и это число не предел. Самое большое число, которое применяется в математическом доказательстве, это число Грэма. Его использовали впервые в 1977 году в доказательстве оценки в теории Рамсея.
Число выражено в 64-уровневой схеме, вывел которую Кнут в 1978 году. Ученый придумал понятие сверхстепень и предложил записывать ее стрелками вверх. В итоге число Грэма G63, или просто G, — самое большое число в мире. 80
80
Десять в восьмидесятой степени — 1 с 80 нулями — это довольно массивное число, обозначающее примерное число элементарных частиц в известной вселенной, и, говоря элементарные частицы, мы не имеем в виду микроскопические частицы — мы говорим о куда меньших вещах вроде кварков и лептонов — о субатомных частицах. Это число в США и современной Великобритании называют «сто квинквавигинтиллионов». Вроде бы, несложно понять, что это число обозначает количество мельчайших частиц в нашей Вселенной, однако это самое маленькое и простое число в нашем списке.
Один гугол
Слово гугол, несколько измененное, стало часто используемым в современности, благодаря популярной поисковой системе. У этого числа есть интересная история — достаточно просто погуглить. Термин был придуман Милтоном Сироттой в 1938 году, когда ему было 9 лет. И хотя это относительно абстрактное число, и его существование объясняется необходимостью технического существования, ему все-таки нашли применение.
Алексис Лемер поставил мировой рекорд, рассчитав корень тринадцати из стозначного числа. 43,112,609 – 1
43,112,609 – 1
Третье по величине число в этом списке — это число всех планковых объемов во Вселенной, и в нем 185 цифр. А в этом числе почти 13 миллионов цифр. Чем это число важно? Это самое большое из известных сегодня простых чисел. Его обнаружили в августе 2008 года в ходе Great Internet Messene Prime Search (GIMPS).
Гуголплекс
Вы наверняка слышали это слово, хотя бы в фильме «Назад в будущее», когда доктор Эммет Браун бормотал «она одна на миллион, одна на миллиард, одна на гуголплекс». Что такое гуголплекс? Помните длину гугола? Единица и сто нулей. А гуголплекс — это десять в степени гугол. Это больше, чем число всех частиц в известной нам части вселенной.
Вы можете отметить, что можно возводить десять в степень гуголплекс и будет еще больше, и так далее, и окажетесь совершенно правы.
Числа Скьюза
Число Скьюза — это верхний предел для математической задачи π(x) > Li(x), хоть и просто выглядящей, но крайне сложной на самом деле. По существу, число Скьюза доказывает, что число x существует и нарушает это правило, если предположить, что гипотеза Римана верна, а число x меньше, чем 10^10^10^36, первое число Скьюза. n3. Лучший способ его представить — разложить по полочкам. Первый слой — это 3↑↑↑↑3, что уже невероятно много. Следующий слой — это множество стрелок между тройками. Возьмите эти стрелки и поместите между следующими тройками. Это умножается в 64 раза. Даже сам Грэм не знает первое число, но последние десять вот: 2464195387. Вся наблюдаемая вселенная слишком мала, чтобы вместить в себя обыкновенную десятичную запись числа Грэма.
n3. Лучший способ его представить — разложить по полочкам. Первый слой — это 3↑↑↑↑3, что уже невероятно много. Следующий слой — это множество стрелок между тройками. Возьмите эти стрелки и поместите между следующими тройками. Это умножается в 64 раза. Даже сам Грэм не знает первое число, но последние десять вот: 2464195387. Вся наблюдаемая вселенная слишком мала, чтобы вместить в себя обыкновенную десятичную запись числа Грэма.
∞. Бесконечность
Это число известно всем и каждому, оно часто используется для преувеличений — как какой-нибудь «многоллион». Однако это число намного сложнее, чем большинство может представить, и если вы могли представить числа, идущие до этого пункта, именно это число очень странное и противоречивое. Согласно правилам бесконечности, есть бесконечное число нечетных и четных чисел в бесконечности, однако только половина от всех чисел может быть четной. Бесконечность плюс один равна бесконечности, бесконечность минус один равна бесконечности, бесконечность плюс бесконечность равна бесконечности, деленная пополам — тоже бесконечность, бесконечность минус бесконечность — никто не знает, бесконечность, деленная на бесконечность, будет, скорее всего, 1. 80 субатомных частиц, но это только известная вселенная. Некоторые предполагают, что вселенная бесконечна. Если это так, то математически достоверно, что есть другая Земля где-то там, где каждый атом складывается таким же образом, как и мы, и наша Земля. Шанс того, что копия Земли существует, невероятно мал, но в бесконечной вселенной это не только может произойти, но и бесконечно много раз.
80 субатомных частиц, но это только известная вселенная. Некоторые предполагают, что вселенная бесконечна. Если это так, то математически достоверно, что есть другая Земля где-то там, где каждый атом складывается таким же образом, как и мы, и наша Земля. Шанс того, что копия Земли существует, невероятно мал, но в бесконечной вселенной это не только может произойти, но и бесконечно много раз.
В бесконечность верят не все. Израильский профессор математики Дорон Зильбергер утверждает, что по его мнению, числа не будут продолжаться вечно, и найдется настолько большое число, что когда вы добавите к нему единицу, вы придете к нулю. И хотя это число едва ли когда будет обнаружено и едва ли кто сможет его вообразить, бесконечность является важной частью математической философии.
∞ + 1
Простите, но этот пункт здесь очень важен.
Самое большое число в мире или самая большая величина
Сейчас появились числа, которые настолько велики, что их с трудом можно представить. А когда-то люди считали на пальцах! Рассказываем про самые большие и самые маленькие числа.
А когда-то люди считали на пальцах! Рассказываем про самые большие и самые маленькие числа.
Сложно сказать, как давно люди научились считать. Скорее всего, для счета наши первобытные предки сначала использовали свои пальцы, объекты окружающего мира и тому подобное. С тех пор математика прошла долгий путь. И даже появились названия для чисел, которые настолько велики, что их с трудом можно представить. Каковы же самая большая и маленькая величины?
Бесконечность
Многих мучил вопрос, что в математике самое большое. На ум сразу приходит бесконечность. Но бесконечность — не число, а концепция. Определение бесконечности в математике гласит, что независимо от того, насколько велико число, вы всегда можете добавить к нему 1, и оно станет больше.
Поэтому, строго говоря, не существует такого понятия, как самое большое число в мире или самая большая величина. Можно лишь назвать наибольшее число, которому дали конкретное название.
«Миллиард», например, уже понятен для нас. В западных странах миллиард еще называют «биллионом». Этими большими числами мы активно оперируем, например, обсуждая бюджетные ассигнования. Вселенная возникла из Большого взрыва всего 13,4 миллиарда лет назад. А вот для людей несколько веков назад миллиард был, по всей видимости, каким-то фантастическим, запредельным числом.
В западных странах миллиард еще называют «биллионом». Этими большими числами мы активно оперируем, например, обсуждая бюджетные ассигнования. Вселенная возникла из Большого взрыва всего 13,4 миллиарда лет назад. А вот для людей несколько веков назад миллиард был, по всей видимости, каким-то фантастическим, запредельным числом.
Триллион — число с 12 нулями, квадриллион — с 15, в секстиллионе количество нулей — уже 21. Существует даже название для впечатляющего по величине числа с 300 нулями — новемнонагинтиллион. Такое множество уже современные человек представить не может даже приблизительно. Да, числа, скорее всего, бесконечны, но есть определенный порог, за которым числа становятся настолько большими, что в них нет смысла, кроме того, что технически они могут существовать.
Самое маленькое число
Точно также не существует самое маленькое число — как бы вы его не уменьшали, всегда возможен N-1.
Для удобства подсчета в математике принята система цифр и чисел. Цифра — это знак от 0 до 9. Числа складываются из цифр. Они бывают однозначные, двузначные, трехзначные и так далее. Однозначные числа состоят из одной цифры. Принято считать, что самое маленькое однозначное число — это ноль. Его еще называют границей между отрицательным и положительным рядом.
Цифра — это знак от 0 до 9. Числа складываются из цифр. Они бывают однозначные, двузначные, трехзначные и так далее. Однозначные числа состоят из одной цифры. Принято считать, что самое маленькое однозначное число — это ноль. Его еще называют границей между отрицательным и положительным рядом.
Число Грэма
Рональд Льюис Грэм — американский математик, оказавший заметное влияние на развитие дискретной математики во второй половине XX века, автор ряда важных работ по планированию выполнения задач, вычислительной геометрии, теории Рамсея
В 1980 году в Книгу рекордов Гиннеса попало число Грэма (оно же G64 или G), названное в честь американского математика. Так называется самое большое число, которое когда-либо использовалось в важном математическом доказательстве. Речь идет про теорию Франка Рамсея.
Кратко об этой теории: представим себе N-мерный куб, его вершины в случайном порядке соединены красными или синими отрезками-линиями. А наша задача — понять, до какого значения N возможно (если по-разному закрашивать ребра куба), избежать ситуации, при которой одна плоскость в кубе будет окрашена одним цветом. То есть у нас не должен получиться одноцветный «конвертик».
То есть у нас не должен получиться одноцветный «конвертик».
Математики позакрашивали кубик и так и эдак, получилось, что до шестимерного куба можно исхитриться и сделать, чтобы линии одного цвета, соединяющие четыре вершины, не лежали в одной плоскости. А вот с семимерным, как выяснили Грэм и Ротшильд, такой фокус уже не провернешь. И с восьмимерным. И… «и так далее», которое, впрочем, не бесконечно, а заканчивается фантастически гигантским числом. Вот его-то и именуют числом Грэма. Кстати, в настоящее время решение Грэма и Ротшильда устарело. Математики выяснили, что 6-7-8-9-10-11-12-мерные кубы все же можно покрасить без «конвертов». Но где-то в промежутке между 13 и числом Грэма гарантированно есть число, выше которого «конверты» в любом случае будут.
Это число имеет настолько большой размер, что вся наблюдаемая вселенная слишком мала, чтобы вместить в себя обыкновенную десятичную запись числа Грэма.
Гугол
Эдвард Казнер — американский математик, профессор. Около 1920 года Казнер решил придумать хорошее, заразительное название для большого числа. Когда он ходил с племянниками Милтоном (Milton Sirotta, 1911—1980) и Эдвином Сироттами в Палисейдс (Нью-Джерси), Казнер попросил их подумать о хороших названиях. Милтон сказал «googol».
Около 1920 года Казнер решил придумать хорошее, заразительное название для большого числа. Когда он ходил с племянниками Милтоном (Milton Sirotta, 1911—1980) и Эдвином Сироттами в Палисейдс (Нью-Джерси), Казнер попросил их подумать о хороших названиях. Милтон сказал «googol».
Гугол — это число с сотней нулей. Оно традиционно входит в топ-10 самых известных больших чисел. Термин был придуман Милтоном Сироттой в 1938 году, когда тому было 9 лет. И хотя это относительно абстрактное число, ему все-таки нашли применение.
Алексис Лемер поставил мировой рекорд, рассчитав корень тринадцати из стозначного числа. Также предполагается, что от одного до полутора гугол лет с момента Большого Взрыва взорвется самая массивная черная дыра. И тогда Вселенная вступит в так называемую «темную эпоху» — конец того мира, каким мы его знаем.
Самая маленькая величина
В 1899 году (в некоторых источниках — в 1900-м) немецкий физик и по совместительству основоположник квантовой теории Макс Планк предложил особую меру измерения — планковские единицы. -35 метра). Если теория квантовой механики верна, то это расстояние определяет максимальную точность, с которой мы можем определить положение в пространстве. Причем эта точность является фундаментальной и проистекает из физических законов, а не из уровня развития техники или точности измерительных приборов. Следовательно, расстояния меньше планковской длины физически не имеют смысла.
-35 метра). Если теория квантовой механики верна, то это расстояние определяет максимальную точность, с которой мы можем определить положение в пространстве. Причем эта точность является фундаментальной и проистекает из физических законов, а не из уровня развития техники или точности измерительных приборов. Следовательно, расстояния меньше планковской длины физически не имеют смысла.
Это одна из единиц универсальных постоянных в физике, наряду с планковскими массой временем и температурой (физики часто называют их «единицами Бога»). Это численные значения некоторой величины, которые вообще не зависят от каких-либо внешних параметров и не меняются со временем. Предполагается, что на этом уровне господствуют квантовые явления, а гравитация, пространство и время перестают существовать.
Измерение расстояния
Световой год равняется расстоянию, проходимому светом за год, а это приблизительно 9 460 730 472 580 километров
В метрической системе самая маленькая единица измерения — ангстрем. Он равен десятимиллиардной доле метра.
Он равен десятимиллиардной доле метра.
Мера длины, которая является самой большой, — это километр. Но все очень относительно. Если мы, например, обратимся к единицам измерения расстояния, применяемым в астрономии, то найдем и другие определения. Например, световой год. Световой год равняется расстоянию, проходимому светом за год, а это приблизительно 9 460 730 472 580 километров. Еще одна астрономическая единица, измеряющая расстояния, парсек, равна 31 триллиону километров, или 3,26 световых лет. В начале XX века активно использовалась самая большая величина измерения расстояния — сириометр. Он равен 149 597 870 700 000 км. Однако со временем его вытеснил парсек.
На сайте могут быть использованы материалы интернет-ресурсов Facebook и Instagram, владельцем которых является компания Meta Platforms Inc., запрещённая на территории Российской Федерации.
математика
число
рекорд
величина
Самый глубокий в мире бассейн открыли в Дубае
Самый глубокий в мире бассейн открыли в Дубае
Это целый подводный мир на 14 млн л пресной воды
11 июля 2021
Марианская впадина: Эверест наоборот
Марианская впадина: Эверест наоборот
Представьте, что на каждый сантиметр вашего тела поставили автомобиль. Примерно такое же вы испытаете в Марианской впадине. Поэтому людей здесь побывало меньше, чем на Луне. «Моя Планета» «спустилась» в Марианскую впадину
Примерно такое же вы испытаете в Марианской впадине. Поэтому людей здесь побывало меньше, чем на Луне. «Моя Планета» «спустилась» в Марианскую впадину
28 июля 2022
331386
10 снов, которые потрясли мир
10 снов, которые потрясли мир
Какие сны были вещими, а какие — изменили историю?
11 января 2016
Семья гепардов и левитация: объявлены победители конкурса на лучшее черно-белое фото года
22 сентября 2022
В Дубае планируют построить для туристов 200-метровую Луну
22 сентября 2022
Выяснилось, как всего один час на природе влияет на мозг человека
22 сентября 2022
Мама-туристка рассказала, как сделать перелет с детьми спокойнее
22 сентября 2022
Откуда на крыльях бабочек рисунок?
Наш мир «не нашими» глазами
Почему слоны боятся мышей
Самые большие леса на земле
Рекорды скорости
Кто живет в пустыне
Почему у человека нет брачного сезона?
Наибольшее известное простое число — frwiki.
 {82 \, 589 \, 933} -1}
{82 \, 589 \, 933} -1}
Это число из 24 862 048 цифр, записанное по основанию десять . Это было обнаружено нав Великой Интернет Мерсенна Поиск (GIMPS), и подтвердил ,.
Евклид уже продемонстрировал , что не существует простое число , которое больше , чем все остальные; что означает, что существует бесконечное количество простых чисел. Несмотря на эту безграничность или из-за нее, многие математики, даже любители, продолжают искать большие простые числа.
С 1992 года все самые большие простые числа, известные на данную дату, являются простыми числами Мерсенна . В, восемнадцать наибольших известных простых чисел (в этом смысле) принадлежат Мерсенну, а девятнадцатое — многочлену чисел Мерсенна.
Быстрое преобразование Фурье реализован с тестом на простоту Lucas-Лехмер для чисел Мерсены быстро по сравнению с другими известными тестами на простоту для других типов номеров. Эта относительная скорость объясняет большое количество чисел Мерсенна среди самых больших известных простых чисел.
Эта относительная скорость объясняет большое количество чисел Мерсенна среди самых больших известных простых чисел.
Резюме
- 1 Рекорд
- 2 награды
- 3 История
- 4 Примечания и ссылки
- 4.1 Примечания
- 4.2 Ссылки
- 5 См. Также
- 5.1 Библиография
- 5.2 Статьи по теме
Запись
Рекорд принадлежит 2 82 589 933 — 1, число Mersenne, испытанное первым Патриком Ларошем в рамках программы GIMPS ,.
Это число, записанное по основанию 10, состоит из 24 862 048 цифр, что почти на миллион цифр больше по сравнению со старой записью, датированной (см. ниже ).
Его первые десять цифр — 1488944457 …, а последние 10 — … 5217902591.
Цена
Программа Great Internet Mersenne Prime Search (GIMPS) в настоящее время предлагает вознаграждение в размере трех тысяч долларов участникам, которые загружают и запускают свое бесплатное программное обеспечение и чей компьютер обнаруживает новое простое число Мерсенна с менее чем 100 миллионами цифр.
Фонд Electronic Frontier Foundation предлагает несколько призов за открытие простых чисел. GIMPS также координирует свои долгосрочные усилия по созданию простых чисел, состоящих из более чем 100 миллионов цифр, с Electronic Frontier Foundation с целью получения вознаграждения в размере 150 000 долларов США для победившего участника.
История
Сравнительная хронология вычислений десятичных знаков числа π и простых чисел.
Рекорд самого большого известного простого числа почти всегда находился среди чисел Мерсенна.
В литературе и в таблице ниже простые числа Мерсенна обозначаются следующими обозначениями:
- M n , где присоединенное число n представляет ранг в возрастающей последовательности простых чисел Мерсенна;
- M p , где индекс p указывает на простой показатель степени 2 в выражении 2 p — 1 числа Мерсенна.
Число, удерживавшее рекорд, было M 19 = 524 287 за 144 года.
До 1456 г. нет никаких свидетельств .
| Датировано | Первооткрыватель | Машина | Тип | Обозначение | Значение или количество цифр в десятичной системе счисления | ||
|---|---|---|---|---|---|---|---|
| До XVI — го века , это не представляется возможным точно определить расчетные записей наибольшее простое число. Документы, которые дошли до нас для обоснования расчетов, отсутствуют или являются неполными. | |||||||
| 1456 | анонимный | — | Числа Мерсенна | M4 = M 13 | 8 191 | ||
| 1460 | анонимный | — | M5 = M 17 | 131 071 | |||
| 1588 | Пьетро катальди | — | M7 = M 19 | 524 287 | |||
1732 г. {64} +1} {274177}}} {64} +1} {274177}}} | 67 280 421 310 721 | ||||||
| 1876 г. | Эдвард Лукас | — | Число Мерсенна | M12 = M 127 | 170 141 183 460 469 230 000 000 000 000 000 000 000 | ||
| 1951 г. | Эме Феррье | — | — | 2 148 + 1/17 | 20 988 936 657 440 586 000 000 000 000 000 000 000 000 000 000 000 | ||
| 1951 г. | Миллер ( выходит ) и Уиллер | EDSAC1 из Кембриджа | Многочлен числа Мерсенна | 180 × (М 127 ) 2 + 1 | 79 цифр | ||
| Робинсон | SWAC | Числа Мерсенна | M13 = M 521 | 157 цифр | |||
| Робинсон | SWAC | M14 = M 607 | 183 цифры | ||||
| Робинсон | SWAC | M15 = M 1279 | 386 цифр | ||||
| Робинсон | SWAC | M16 = M 2203 | 664 цифры | ||||
| Робинсон | SWAC | M17 = M 2281 | 687 цифр | ||||
| Ризель | БЕСК (ru) | M18 = M 3217 | 969 цифр | ||||
| Гурвиц | IBM 7090 | M20 = M 4423 | 1332 цифры | ||||
| Гиллис (ru) | ИЛЛИАК 2 | M21 = M 9689 | 2917 цифр | ||||
| Гиллис | ИЛЛИАК 2 | M22 = M 9941 | 2993 цифры | ||||
| Гиллис | ИЛЛИАК 2 | M23 = M 11213 | 3376 цифр | ||||
| Такерман (ru) | IBM 360/91 | M24 = M 19937 | 6002 цифры | ||||
| Noll (en) и никель | CDC Cyber 174 | M25 = M 21701 | 6533 цифры | ||||
| Нолл | CDC Cyber 174 | M26 = M 23209 | 6 987 цифр | ||||
| Нельсон (en) и Словински (en) | Крей -1 | M27 = M 44497 | 13 395 цифр | ||||
| Словински | Крей-1 | M28 = M 86243 | 25 962 цифры | ||||
| Словински | Cray X-MP | M30 = M 132049 | 39 751 цифра | ||||
| Словински | Крей X-MP / 24 | M31 = M 216091 | 65 050 цифр | ||||
1989 г. | Amdahl 6 | Амдал 1200 | Полиномиальные числа Мерсенна | × М триста девяносто одна тысяча пятьсот восемьдесят один 756839 + 391580 = 391 581 × 2 756 839 — 1 | 65 087 цифр | ||
| Словински, Гейдж и др. | Крей-2 | Числа Мерсенна | M32 = M 756839 | 227 832 цифр | |||
| Словински и Гейдж | Cray C90 | M33 = M 859433 | 258 716 цифр | ||||
| Словински и Гейдж | Cray T94 | M34 = M 1257787 | 378 632 цифр | ||||
| Joël Armengaud, Woltman et al. (Проект GIMPS) | Pentium (90 МГц ) | M35 = M 1398269 | 420 921 цифра | ||||
| Гордон Спенс, Вольтман и др. (Проект GIMPS) | Pentium (100 МГц ) | M36 = M 2976221 | 895 932 цифр | ||||
Кларксон, Вольтман, Куровски и др. (Проект GIMPS) (Проект GIMPS) | Pentium (200 МГц ) | M37 = M 3021377 | 909 526 цифр | ||||
| Хайратвала, Вольтман, Куровски и др. (Проект GIMPS) | Pentium (350 МГц ) | M38 = M 6972593 | 2,098,960 цифр | ||||
| Кэмерон, Вольтман, Куровски и др. (Проект GIMPS) | AMD T-Bird (800 МГц ) | M39 = M 13466917 | 4 053 946 цифр | ||||
| Шафер, Вольтман, Куровски и др. , МГУ (Проект GIMPS) | Pentium (2 ГГц ) | M40 = M 20996011 | 6 320 430 цифр | ||||
| Финдли, Вольтман, Куровски и др. (Проект GIMPS) | Pentium 4 (2,4 ГГц ) | M41 = M 24036583 | 7 235 733 цифр | ||||
Новак, Вольтман, Куровски и др. (Проект GIMPS) (Проект GIMPS) | Pentium 4 (2,4 ГГц ) | M42 = M 25964951 | 7816230 цифр | ||||
| К. Купер , С. Бун, Г. Вольтман, С. Куровски и др. , UCM (en) (проект GIMPS) | Pentium 4 (с 2 ГГц до 3 ГГц ) | M43 ?? = M 30402457 | 9152052 цифры | ||||
К. Купер, С. Бун, Г. Вольтман, С. Куровски и др. , UCM (Проект GIMPS) , UCM (Проект GIMPS) | Pentium 4 (3 ГГц ) | M44 ?? = M 32582657 | 9 808 358 цифр | ||||
| Эдсон Смит, Джордж Вольтман, Скотт Куровски и др. , UCLA (проект GIMPS) | Intel Core 2 Duo E6600 процессор (2,4 ГГц ) | M47 ?? = M 43112609 | 12 978 189 цифр | ||||
| К. Купер, Г. Вольтман, С. Куровски и др. , UCM (Проект GIMPS) | M 57885161 | 17 425 170 цифр | |||||
| К. Купер, Г. Вольтман, С. Куровски, А. Блоссер и др. , UCM (Проект GIMPS) | M 74207281 | 22 338 618 цифр | |||||
| J. Pace, G. Woltman, S. Kurowski, A. Blosser, et al. (Проект GIMPS) | Процессор Intel i5-6600 | M 77232917 | 23 249 425 цифр | ||||
| Патрик Ларош (Проект GIMPS) | Intel i5-4590T | M 82589933 | 24 862 048 цифр | ||||
Примечания и ссылки
Заметки
(fr) Эта статья частично или полностью взята из статьи в англоязычной Википедии под названием « Самое большое известное простое число » ( см. простые числа 82589933-1 — Прайм! » , На www.mersenne.org ,(по состоянию на 24 декабря 2018 г. )
82589933-1 — Прайм! » , На www.mersenne.org ,(по состоянию на 24 декабря 2018 г. ) org GIMPS: поиск мировых рекордных премий с 1996 года.
org GIMPS: поиск мировых рекордных премий с 1996 года.
 Точно так же 46- й (M 42643801 ) был обнаружен через девять месяцев после 47- го (M 43112609 ).
Точно так же 46- й (M 42643801 ) был обнаружен через девять месяцев после 47- го (M 43112609 ). ) Веб-сайт Лэндона Курта Нолла 2 43,112,609 — 1 является простым.
) Веб-сайт Лэндона Курта Нолла 2 43,112,609 — 1 является простым.Смотрите также
Библиография
Статьи по Теме
Задано формулой комбинаторный многочлен экспоненциальный Принадлежность к сюите Имея замечательное свойство Наличие базового зависимого свойства Свойства, включающие несколько номеров одиночка кортеж после  Д.)
Д.)Классификация по размеру Обобщения ( квадратичное целое число ) Составное число Связанный номер Тест на первичность Гипотезы и теоремы теории чисел Константы, относящиеся к простым числам
<img src=»//fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Простые числа и их использование в криптографии
Простые числа и их использование в криптографии
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Мусохранов М.М. 1
1МБОУ «Лицея №9 имени К.Э. Циолковского г. Калуги
Рылова И.Г. 1
1МБОУ «Лицея №9 имени К.Э. Циолковского г. Калуги
Автор работы награжден дипломом победителя II степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Предлагаемая вашему вниманию исследовательская работа посвящена простым числам и использованию их в кодировании.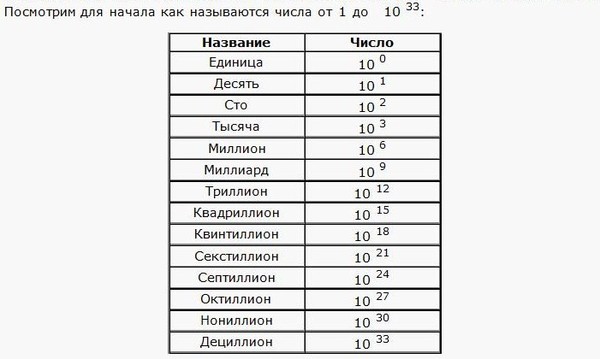 Данная тема заинтересовала меня, когда я стал изучать простые числа. Больше всего меня удивил тот факт, что ученые всего мира до сих пор активно ищут их. Так проект Great Internet Mersenne Prime Search, перед которым стоит задача поиска большого числа простых чисел особо редкого вида, недавно открыл самое большое простое число, известное на сегодняшний день. В нем 23 249 425 цифр — это достаточно, чтобы заполнить книгу из 9000 страниц. Для сравнения: количество атомов во всей наблюдаемой Вселенной оценивается в число с не более чем сотней знаков. Новое число, которое записывается как 2⁷⁷²³²⁹¹⁷-1 (два в 77 232 917-й степени минус один), было обнаружено волонтером, который посвятил 14 лет вычислительного времени этому поиску! Но зачем нам знать число, которое растягивается на 23 миллиона знаков? Ведь самые важные числа для нас — это те, которые мы используем для количественного описания нашего мира? Так, да не так. На сегодняшний день большие простые числа повсеместно используются в нашей повседневной жизни, например, в кредитных картах и персональных компьютерах, поэтому постоянно существует потребность в новых простых числах (чем больше, тем лучше) для генерации секретных кодов.
Данная тема заинтересовала меня, когда я стал изучать простые числа. Больше всего меня удивил тот факт, что ученые всего мира до сих пор активно ищут их. Так проект Great Internet Mersenne Prime Search, перед которым стоит задача поиска большого числа простых чисел особо редкого вида, недавно открыл самое большое простое число, известное на сегодняшний день. В нем 23 249 425 цифр — это достаточно, чтобы заполнить книгу из 9000 страниц. Для сравнения: количество атомов во всей наблюдаемой Вселенной оценивается в число с не более чем сотней знаков. Новое число, которое записывается как 2⁷⁷²³²⁹¹⁷-1 (два в 77 232 917-й степени минус один), было обнаружено волонтером, который посвятил 14 лет вычислительного времени этому поиску! Но зачем нам знать число, которое растягивается на 23 миллиона знаков? Ведь самые важные числа для нас — это те, которые мы используем для количественного описания нашего мира? Так, да не так. На сегодняшний день большие простые числа повсеместно используются в нашей повседневной жизни, например, в кредитных картах и персональных компьютерах, поэтому постоянно существует потребность в новых простых числах (чем больше, тем лучше) для генерации секретных кодов. Эта информация меня поразила, поэтому и стала темой моего исследования.
Эта информация меня поразила, поэтому и стала темой моего исследования.
Актуальность темы моей работы определяется тем, что в современном мире наука криптография имеет большое значение, поскольку настоящее время – это время информационных войн. Ведь как сказал Натан Ротшильд: «Кто владеет информацией – тот владеет миром». На сегодняшний день без шифрования информации не обходится ни одно государство, организация или предприятие, а средства криптографической защиты применяются повсеместно, в том числе, и для защиты коммерческой информации: электронная почта, банковские операции, кредитные карты и мобильная телефонная связь — все это защищено секретными кодами, непосредственно основанными на свойствах простых чисел. Поэтому всем нам нужно знать особенности простых чисел и способы применения их в шифровании, чтобы не только развивать технологии, от которых мы зависим, но и сохранять их безопасность.
Цель исследований: выяснить, почему простые числа так важны в современном мире и необходимы для криптографии.
Задачи исследования: для достижения поставленной цели нам необходимо решить следующие задачи:
Изучить найденную литературу по данному вопросу.
Выяснить значение терминов «простое число», «криптография», «RSA»
Найти примеры и изучить применение простых чисел в кодировании.
Приобрести навыки научно-исследовательской работы.
Распространить свой опыт кодирования с помощью простых чисел среди учащихся 5 классов.
Гипотеза: простые числа являются основой современной криптографии. Большинство обычных учеников средней школы пользуются кодами с простыми числами каждый день, даже не задумываясь об этом.
Определение простого числа.
Простые числа представляют собой одно из самых интересных математических явлений, которое привлекает к себе внимание ученых и простых граждан на протяжении уже более двух тысячелетий. Несмотря на то, что сейчас мы живем в век компьютеров и самых современных информационных программ, многие загадки простых чисел не решены до сих пор, есть даже такие, к которым ученые не знают, как подступиться [2].
Несмотря на то, что сейчас мы живем в век компьютеров и самых современных информационных программ, многие загадки простых чисел не решены до сих пор, есть даже такие, к которым ученые не знают, как подступиться [2].
Простые числа — это, как известно еще из курса элементарной арифметики, те натуральные числа, которые делятся без остатка только на единицу и самое себя. Простые числа называют «кирпичами» в здании математики, «атомами» математики и «генетическим кодом» числа, потому что любое составное число может быть представлено в виде единственно возможного произведения простых чисел. Эта теорема была сформулирована Евклидом и известна как «основная теорема арифметики». Следовательно, простые числа являются первичными элементами, из которых построены все числа. Так же как атомы образуют молекулы. Простые числа образуют составные числа. Интересные факты. Во-первых, число 1 имеет только один делитель: само это число. Поэтому его не относят ни к составным числам, ни к простым. Во-вторых, единственным четным числом, относящимся к простым, является, естественно, двойка. Любое другое четное число сюда попасть попросту не может, так как кроме себя и единицы, делится еще и на два.
Во-вторых, единственным четным числом, относящимся к простым, является, естественно, двойка. Любое другое четное число сюда попасть попросту не может, так как кроме себя и единицы, делится еще и на два.
Имеет ли этот ряд конец? Этот вопрос поставлен в IX книге «Начал» Евклид и там же дает ответ на него — «За каждым простым числом может быть указано еще одно, большее простое число – ряд простых чисел бесконечен» [1].
Способы нахождения простых чисел.
Выделение простых чисел является сложной задачей математики. Ученые на протяжении многих веков пытаются найти формулу, которая позволила бы из множества натуральных чисел выписать простые. Первый, кто занимался этой задачей, был великий математик древности Эратосфен (рис. 1), живший почти 2 300 лет назад [4].
Рис. 1. Великий математик древности Эратосфен
Он придумал такой способ: записал все числа от единицы до какого-то числа, а потом вычеркнул единицу, которая не является ни простым, ни составным числом, затем вычеркивал через одно все числа, идущие после 2 (числа, кратные двум, т. е. 4,6,8 и т.д.). Первым оставшимся числом после 2 было 3. Далее вычеркивались через два все числа, идущие после трех (числа, кратные 3, т.е. 6, 9, 12, и т.д.), в конце концов оставались невычеркнуыми только простые числа: 2, 3, 5, 7, 11, 13,… Поскольку во времена Эратосфена писали на восковых дощечках, а вместо того, чтобы числа вычеркивать, дощечку в нужном месте прокалывали, то способ получил название “решето Эратосфена”.
е. 4,6,8 и т.д.). Первым оставшимся числом после 2 было 3. Далее вычеркивались через два все числа, идущие после трех (числа, кратные 3, т.е. 6, 9, 12, и т.д.), в конце концов оставались невычеркнуыми только простые числа: 2, 3, 5, 7, 11, 13,… Поскольку во времена Эратосфена писали на восковых дощечках, а вместо того, чтобы числа вычеркивать, дощечку в нужном месте прокалывали, то способ получил название “решето Эратосфена”.
В приведенной таблице 1, полученной с помощью решета Эратосфена, можно видеть простые числа из первой тысячи натуральных чисел.
С первого взгляда видно, что простые числа совершенно непредсказуемы. Например, между 1 и 100 простых чисел больше, чем между 101 и 200. Всего в первой тысяче 168 простых чисел. Можно предположить, что если продолжить нашу таблицу, то с каждой тысячей количество простых чисел будет увеличиваться. Но это не так. Уже известно, что, например, среди тысячи чисел между 10100 и 10100 + 1000 находится лишь два простых числа. И эти числа состоят более чем из ста цифр!
И эти числа состоят более чем из ста цифр!
Таблица 1
Простые числа из первой тысячи натуральных чисел
|
2
|
3
|
5
|
7
|
11
|
13
|
17
|
19
|
23
|
29
|
31
|
37
|
41
|
43
|
47
|
53
|
59
|
61
|
67
|
71
|
|
73
|
79
|
83
|
89
|
97
|
101
|
103
|
107
|
109
|
113
|
127
|
131
|
137
|
139
|
149
|
151
|
157
|
163
|
167
|
173
|
|
179
|
181
|
191
|
193
|
197
|
199
|
211
|
223
|
227
|
229
|
233
|
239
|
241
|
251
|
257
|
263
|
269
|
271
|
277
|
281
|
|
283
|
293
|
307
|
311
|
313
|
317
|
331
|
337
|
347
|
349
|
353
|
359
|
367
|
373
|
379
|
383
|
389
|
397
|
401
|
409
|
|
419
|
421
|
431
|
433
|
439
|
443
|
449
|
457
|
461
|
463
|
467
|
479
|
487
|
491
|
499
|
503
|
509
|
521
|
523
|
541
|
|
547
|
557
|
563
|
569
|
571
|
577
|
587
|
593
|
599
|
601
|
607
|
613
|
617
|
619
|
631
|
641
|
643
|
647
|
653
|
659
|
|
661
|
673
|
677
|
683
|
691
|
701
|
709
|
719
|
727
|
733
|
739
|
743
|
751
|
757
|
761
|
769
|
773
|
787
|
797
|
809
|
|
811
|
821
|
823
|
827
|
829
|
839
|
853
|
857
|
859
|
863
|
877
|
881
|
883
|
887
|
907
|
911
|
919
|
929
|
937
|
941
|
|
947
|
953
|
967
|
971
|
977
|
983
|
991
|
997
|
Рис. 2. Древнегреческий математик Евклид
2. Древнегреческий математик Евклид
Теорема Евклида: «Первых простых чисел существует больше любого указанного числа их».
Конечно, способ Эратосфена не смог удовлетворить ученых, и они пытались найти формулу простых чисел. На протяжении многих столетий это сделать не удавалось. В ряду простых чисел были найдены многие интересные закономерности, но поставленная задача оставалась без ответа. Над поиском максимально больших простых чисел в своё время бились Катальди, Декарт, Ферма, Мерсенн, Лейбниц, Эйлер и многие другие математики. В математике широко известен термин простые числа Мерсенна. Простые числа Мерсена являются простыми числами специального вида
Mp = 2p — 1
где р — другое простое число.
До 1750 года было найдено всего 8 простых чисел Мерсенна: М2, М3, М5, М7, М13, М17, М19, М31. То, что М31 — простое число, доказал в 1750 году Л. Эйлер. В 1876 году французский математик Эдуард Люка установил, что число М127=170141183460469231731687303715884105727 — простое. В 1883 г. сельский священник Пермской губернии И.М.Первушин доказал, что число М61=2305843009213693951 является простым. Позднее было установлено, что числа М89 и М107 простые. 12 простых чисел Мерсена были вычислены с помощью только карандаша и бумаги, а для вычисления следующих уже использовались механические настольные счетные машины.
Эйлер. В 1876 году французский математик Эдуард Люка установил, что число М127=170141183460469231731687303715884105727 — простое. В 1883 г. сельский священник Пермской губернии И.М.Первушин доказал, что число М61=2305843009213693951 является простым. Позднее было установлено, что числа М89 и М107 простые. 12 простых чисел Мерсена были вычислены с помощью только карандаша и бумаги, а для вычисления следующих уже использовались механические настольные счетные машины.
Масштабный проект по поиску простых чисел GIMPS был запущен в 1997 году, и ныне считается самым длительным непрерывным процессом распределённых вычислений в истории человечества: он продолжается уже почти 20 лет. Сейчас в пиковые моменты в GIMPS участвует 360.000 процессоров с суммарной производительностью 150 трлн операций в секунду. За время работы GIMPS участники этого проекта нашли 14 простых чисел Мерсенна. Последнее из них 274 207 281-1 было обнаружено 07 января 2016 года. Всего на данный момент известно 49 простых чисел Мерсена. В списке самых больших простых чисел, известных на сегодняшний день, десять первых мест занимают числа Мерсенна.
В списке самых больших простых чисел, известных на сегодняшний день, десять первых мест занимают числа Мерсенна.
Поиск простых чисел — по крайней мере больших простых чисел — довольно сложная задача, потому что еще никому не удалось найти точную формулу или алгоритм, позволяющий генерировать любые простые числа.
Применение простых чисел в криптографии.
Актуальны ли простые числа сегодня? Еще как! Простые числа являются основой современной криптографии, так что большинство людей пользуются ими каждый день, даже не задумываясь об этом. Любой процесс аутентификации, например, регистрация телефона в сети, банковские платежи и прочее, требуют криптографических алгоритмов.
В 1975 г. Уитфилду Диффи и Мартину Хеллману, в то время работавшим в Стэнфордском университете, пришла в голову идея асимметричного шифрования, или «шифрования с открытым ключом». Эта система основана на специальных математических функциях, называемых «односторонними функциями с потайным входом», которые позволяют зашифровывать текст, но делают расшифровку практически невозможной без знания используемого кода. Идея состоит в том, что каждый пользователь имеет пару ключей: открытый и закрытый. Если мы хотим отправить кому-то сообщение, мы зашифровываем это сообщение с помощью открытого ключа — то есть ключа, известного всем. Но только человек, имеющий соответствующий закрытый ключ, может расшифровать это сообщение. Одним из преимуществ такого метода является то, что закрытый ключ никогда не передается и поэтому его не нужно постоянно менять в целях безопасности. Идея метода не совсем проста, но мы можем пояснить ее с помощью аналогии. Представьте себе большой магазин, где продаются сотни тысяч банок с краской разного цвета. Возьмем две любые банки и смешаем краску в разных количествах. Пока все просто. Теперь, если мы покажем кому-нибудь получившийся цвет и попросим «расшифровать», какое количество каких красок использовалось изначально, на такой вопрос будет очень трудно ответить. Именно так работают односторонние функции с потайным входом, которые легко применить в одном направлении, но практически невозможно — в обратном.
Идея состоит в том, что каждый пользователь имеет пару ключей: открытый и закрытый. Если мы хотим отправить кому-то сообщение, мы зашифровываем это сообщение с помощью открытого ключа — то есть ключа, известного всем. Но только человек, имеющий соответствующий закрытый ключ, может расшифровать это сообщение. Одним из преимуществ такого метода является то, что закрытый ключ никогда не передается и поэтому его не нужно постоянно менять в целях безопасности. Идея метода не совсем проста, но мы можем пояснить ее с помощью аналогии. Представьте себе большой магазин, где продаются сотни тысяч банок с краской разного цвета. Возьмем две любые банки и смешаем краску в разных количествах. Пока все просто. Теперь, если мы покажем кому-нибудь получившийся цвет и попросим «расшифровать», какое количество каких красок использовалось изначально, на такой вопрос будет очень трудно ответить. Именно так работают односторонние функции с потайным входом, которые легко применить в одном направлении, но практически невозможно — в обратном.
Алгоритм шифрования RSA
В августе 1977 г. знаменитый американский писатель и популяризатор науки Мартин Гарднер озаглавил свою колонку по занимательной математике в журнале Scientific American так: «Новый вид шифра, на расшифровку которого потребуются миллионы лет» [3]. После объяснения принципа системы шифрования с открытым ключом он показал само зашифрованное сообщение и открытый ключ N, используемый в этом шифре:
Гарднер призвал читателей попробовать расшифровать сообщение, используя предоставленную информацию, и даже дал подсказку: для решения необходимо разложить число N на простые множители р и q. Более того, Гарднер назначил приз в размере $100 (приличная сумма на тот момент) тому, кто первым получит правильный ответ. Каждый, кто захочет побольше узнать о шифре, писал Гарднер, может обратиться к создателям шифра — Рону Ривесту, Ади Шамиру и Лену Адлеману из Лаборатории информации Массачусетского технологического института. Правильный ответ был получен лишь через 17 лет. Он стал результатом сотрудничества более чем 600 человек. Ключами оказались р = 32769132993266 709549961988190834461413177642967992942539798288533 и q = 3490529510847650949147849619903898133417764638493387843990820577, а зашифрованная фраза звучала так: «Волшебные слова — это брезгливый ягнятник».
Правильный ответ был получен лишь через 17 лет. Он стал результатом сотрудничества более чем 600 человек. Ключами оказались р = 32769132993266 709549961988190834461413177642967992942539798288533 и q = 3490529510847650949147849619903898133417764638493387843990820577, а зашифрованная фраза звучала так: «Волшебные слова — это брезгливый ягнятник».
Алгоритм, представленный Гарднером, известен как RSA — буквенная аббревиатура от фамилий Rivest (Ривест), Shamir (Шамир) и Adleman (Адлеман). Это первое практическое применение придуманной Диффи системы шифрования с открытым ключом, которая повсеместно используется и по сей день. Надежность ее практически гарантирована, потому что процесс расшифровки является невероятно сложным, почти невозможным делом.
На сегодняшний день разложить числа, состоящие из тысячи и более цифр, за соизмеримое с человеческой жизнью время, способны только суперкомпьютеры! Именно с их помощью ученные находят все новые и новые, наибольшие из известных, простые числа.
Представим, что один человек, зашифровав важную информацию, установил на нее пароль (P) равный одному из простых делителей числа (А), сказав другому человеку, что число (А) содержит только два простых делителя и дав ему ключ для расшифровки – число (B), являющееся вторым делителем числа (А). Не трудно понять, что для расшифровки необходимо разделить А на B, чтобы получить пароль Р. Например в элементарном варианте А=111, ключ B=3 тогда пароль равен А/B=37.
Допустим, число А попало к злоумышленнику, и он знает условие о том, что А состоит из 2-х простых делителей. При условии, что А=111 злоумышленнику не составит особого труда даже в уме взломать пароль. Теперь представим ситуацию, когда число А состоит из 2 простых чисел, каждое из которых состоит из тысячи цифр… Если злоумышленник не знает ключа (одного из делителей), для факторизации числа А, состоящего из двух тысяч цифр, ему потребуется, как минимум, суперкомпьютер и большое количество времени его работы!!! Если попытаться попытается разложить произведение — даже при помощи самого быстрого суперкомпьютера — это не получится. Просто не существует такого алгоритма, который справился бы с этой задачей за время жизни Вселенной.
Просто не существует такого алгоритма, который справился бы с этой задачей за время жизни Вселенной.
Для применения алгоритма RSA требуется построить открытый и секретный ключи следующим образом.
1. Выбрать два больших простых числа, p и q.
2. Найти их произведение n = p • q и значение ϕ =(р-1)-(q-1)
3. Выбрать число e (1 < e < ϕ), которое не имеет общих делителей с ϕ .
4. Найти число d, которое удовлетворяет условию d • е = k⋅ϕ + 1 для некоторого целого k.
5. Пара значений (e, n) — это открытый ключ RSA (его можно свободно публиковать), а пара (d, n) — это секретный ключ.
Передаваемое сообщение нужно сначала представить в виде последовательности чисел в интервале от 0 до n -1. Для шифрования используют формулу
C = Тe mod n
где Т — число исходного сообщения,
(e, n) — открытый ключ,
С — число закодированного сообщения, а запись С e mod n обозначает остаток от деления x e на n.
Расшифровка сообщения выполняется по формуле
Т = Cd mod n
Это значит, что зашифровать сообщение может каждый (открытый ключ общеизвестен), а прочитать его — только тот, кто знает секретный показатель степени d.
В 2009 году группа ученых из разных стран в результате многомесячных расчетов на сотнях компьютеров смогла расшифровать сообщение, зашифрованное алгоритмом. Если будет построен работающий квантовый компьютер, взлом алгоритма RSA будет возможен за очень небольшое время. При использовании симметричных шифров всегда возникает проблема: как передать ключ, если канал связи ненадежный? Ведь, получив ключ, противник сможет расшифровать все дальнейшие сообщения. Для алгоритма RSA этой проблемы нет, сторонам достаточно обменяться открытыми ключами, которые можно показывать всем желающим.
Где применяют алгоритм RSA на практике? Криптосистема RSA используется в самых различных продуктах, на различных платформах и во многих отраслях. В настоящее время криптосистема RSA встраивается во многие коммерческие продукты, число которых постоянно увеличивается. Также ее используют операционные системы Microsoft, Apple, Sun и Novell. В аппаратном исполнении RSA алгоритм применяется в защищенных телефонах, на сетевых платах Ethernet, на смарт-картах, широко используется в криптографическом оборудовании. Кроме того, алгоритм входит в состав всех основных протоколов для защищенных коммуникаций Internet, в том числе S/MIME, SSL и S/WAN, а также используется во многих учреждениях, например, в правительственных службах, в большинстве корпораций, в государственных лабораториях и университетах. На осень 2000 года технологии с применением алгоритма RSA были лицензированы более чем 700 компаниями.
В настоящее время криптосистема RSA встраивается во многие коммерческие продукты, число которых постоянно увеличивается. Также ее используют операционные системы Microsoft, Apple, Sun и Novell. В аппаратном исполнении RSA алгоритм применяется в защищенных телефонах, на сетевых платах Ethernet, на смарт-картах, широко используется в криптографическом оборудовании. Кроме того, алгоритм входит в состав всех основных протоколов для защищенных коммуникаций Internet, в том числе S/MIME, SSL и S/WAN, а также используется во многих учреждениях, например, в правительственных службах, в большинстве корпораций, в государственных лабораториях и университетах. На осень 2000 года технологии с применением алгоритма RSA были лицензированы более чем 700 компаниями.
Технологию шифрования RSA BSAFE используют около 500 миллионов пользователей всего мира. Так как в большинстве случаев при этом используется алгоритм RSA, то его можно считать наиболее распространенной криптосистемой общего (public) ключа в мире и это количество имеет явную тенденцию к увеличению по мере роста Internet.
На начало 2001 года криптосистема RSA являлась наиболее широко используемой асимметричной криптосистемой (криптосистемой открытого (public) ключа) и зачастую называется стандартом де факто. Вне зависимости от официальных стандартов существование такого стандарта чрезвычайно важно для развития электронной коммерции и вообще экономики. Единая система открытого (public) ключа допускает обмен документами с электронно-цифровыми подписями между пользователями различных государств, использующими различное программное обеспечение на различных платформах; такая возможность насущно необходима для развития электронной коммерции. Распространение системы RSA дошло до такой степени, что ее учитывают при создании новых стандартов. При разработке стандартов цифровых подписей, в первую очередь в 1997 был разработан стандарт ANSI X9.30, поддерживающий Digital Signature Standard (стандарт Цифровой подписи). Годом позже был введен ANSI X9.31, в котором сделан акцент на цифровых подписях RSA, что отвечает фактически сложившейся ситуации, в частности, для финансовых учреждений.
Проведение анкетирования
Для того, чтобы выяснить знают ли ученики 5-х классов о применение простых чисел в кодирование, об алгоритме RSA, а также выявить количество учеников, использующих ежедневно технологию шифрования RSA, я решил провести опрос. Опрос проводился посредством анкетирования. В опросе приняли участие 21 учащийся из 5-х классов МБОУ «Лицей №9 имени К.Э. Циолковского» г. Калуги.
Респондентам были заданы вопросы, представленные в таблице 2.
Таблица 2
Вопросы для проведения анкетирования
|
№
|
Вопрос
|
Ответы
| |
|
1.
|
Пользуетесь ли вы Internet?
|
ДА
|
НЕТ
|
|
2.
|
Совершает ли ваша семья покупки в сети Internet?
|
ДА
|
НЕТ
|
|
3.
|
Встречалось ли вам понятие – электронная подпись?
|
ДА
|
НЕТ
|
|
4.
|
Знаете ли вы что такое технологию шифрования RSA?
|
ДА
|
НЕТ
|
|
5.
|
Знаете ли вы, где применяются шифрование RSA?
|
ДА
|
НЕТ
|
Результаты анкетирования представлены ниже.
Рис. 3. Диаграмма опроса учеников 5 класса,
где ось ординат — это количество опрошенных учеников, ось абсцисс – это вопросы представленные в табл.2.
Как видно из результатов анкетирования, представленных на рис.3, подавляющее большинство учеников 5-х классов являются активными пользователями Internet, практикуют в кругу семьи покупки через сеть Internet, но при этом не имеют представление о шифровании с помощью алгоритма RSA. Все вышесказанное доказывает, что большинство обычных учеников средней школы пользуются кодами с простыми числами каждый день, даже не задумываясь об этом.
Шифрование с помощью алгоритма RSA
С целью повышения осведомленности учеников 5-х классов о применении простых чисел в кодировании, я решил попробовать зашифровать с помощью алгоритма RSA фразу «Приветствую участников конференции» (вычисления сведены в таблицу 3) и познакомить одноклассников с алгоритмом шифрования:
Выбираю два простых числа p и q, p = 7 и q = 13
Вычисляю произведение n = p*q = 7*13 = 91
Вычисляю функцию Эйлера φ(n)= (p-1)*(q-1) = (7-1)*(13-1) = 72
Выбираю произвольное целое e: 0 < e < n взаимно простое с значением функции Эйлера φ(n). Пусть e = 5. Пара чисел (e, n) объявляется открытым ключом шифра.
В моем примере (e, n) = (5, 91).
Вычисляю целое число d из соотношения
(d*e) mod φ(n) = 1
(Операция mod вычисляет остаток от целочисленного деления двух чисел).
Это соотношение означает, что результатом деления произведения чисел e и d на значение функции Эйлера должно быть число 1. Поэтому d можно рассчитать по формуле:
d = (k* φ(n) +1) / e.
Придавая k последовательно значения 1, 2, 3,.. до тех пор, пока не будет получено целое число d.
Подбор k я проводил в табличном процессоре Excel.
Вычисляю число d:
d = (k* 72 +1) / 5,
при k = 1, d – не целое, при k = 2, d = 29. Получаю закрытый ключ шифра (d, n) = (29, 91).
Получаю закрытый ключ шифра (d, n) = (29, 91).
Процедуры шифрования и дешифрования выполняются по следующим формулам:
C = Тe mod n = Т5 mod 91
Т = Cd mod n = C29 mod 91
где Т, C — числовые эквиваленты символов открытого и шифрованного сообщения (см. табл.4).
Таблица 3
Сводная таблица процедуры создания ключей
|
Простые числа
|
Произведение простых чисел
|
Функция Эйлера
|
Произвольное целое e <p
|
Открытый ключ
|
Секретный ключ
|
Закрытый ключ
| |
|
p
|
q
|
n
|
φ
|
е
|
(e, n)
|
d
|
(d, n)
|
|
7
|
13
|
91
|
72
|
5
|
(5, 91)
|
29
|
(29, 91)
|
Таблица 4
|
Числовые эквиваленты русских букв, цифр и символа пробелаX1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
|
А
|
Б
|
В
|
Г
|
Д
|
Е
|
Ё
|
Ж
|
З
|
И
|
Й
|
К
|
Л
|
М
|
Н
|
О
|
П
|
Р
|
С
|
Т
|
У
|
Ф
|
Х
|
|
X24
|
25
|
26
|
27
|
28
|
29
|
30
|
31
|
32
|
33
|
34
|
35
|
36
|
37
|
38
|
39
|
40
|
41
|
42
|
43
|
44
|
|
Ц
|
Ч
|
Ш
|
Щ
|
Ъ
|
Ы
|
Ь
|
Э
|
Ю
|
Я
|
пробел
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
Кодирование фразы «Приветствую участников конференции».
Буквы в фразе «Приветствую участников конференции» заменены на числовые эквиваленты из таблицы 3.
Расчеты проводил с помощью электронных таблицExcel и занесены в таблицу 5.
Таблица 5
Вычисление шифрограммы
|
Текст сообщения
|
П
|
р
|
и
|
в
|
е
|
т
|
с
|
т
|
в
|
у
|
ю
| |
|
Код символа
|
17
|
18
|
10
|
3
|
6
|
20
|
19
|
20
|
3
|
21
|
32
|
34
|
|
Зашифрованный код Т5 mod 91
|
75
|
44
|
82
|
61
|
41
|
76
|
80
|
76
|
61
|
21
|
2
|
34
|
|
Расшифрованное сообщение C29 mod 91
|
17
|
18
|
10
|
3
|
6
|
20
|
19
|
20
|
3
|
21
|
32
|
34
|
|
Текст сообщения
|
у
|
ч
|
а
|
с
|
т
|
н
|
и
|
к
|
о
|
в
| |
|
Код символа
|
21
|
25
|
1
|
19
|
20
|
15
|
10
|
12
|
16
|
3
|
34
|
|
Зашифрованный код Т5 mod 91
|
21
|
51
|
1
|
80
|
76
|
71
|
82
|
38
|
74
|
61
|
34
|
|
Расшифрованное сообщение C29 mod 91
|
21
|
25
|
1
|
19
|
20
|
15
|
10
|
12
|
16
|
3
|
34
|
|
Текст сообщения
|
к
|
о
|
н
|
ф
|
е
|
р
|
е
|
н
|
ц
|
и
|
и
|
|
Код символа
|
12
|
16
|
15
|
22
|
6
|
18
|
6
|
15
|
24
|
10
|
10
|
|
Зашифрованный код Т5 mod 91
|
38
|
74
|
71
|
29
|
41
|
44
|
41
|
71
|
33
|
82
|
82
|
|
Расшифрованное сообщение C29 mod 91
|
12
|
16
|
15
|
22
|
6
|
18
|
6
|
15
|
24
|
10
|
10
|
Нужно отметить, что кодирование с помощью алгоритма RSA было довольно сложно в понимании для учеников 5-го класса, но при этом вызвало неподдельный интерес.
В ходе выполнения данной исследовательской работы мне удалось обобщить и систематизировать изученный материал по выбранной теме, а также изучить различные способы практического применения простых чисел в кодировании. В процессе написания работы я выяснил степень осведомленности по данному вопросу своих ровесников, что было очень познавательно. Так же я приобрел опыт кодирования с помощью алгоритма RSA и попробовал передать полученные знания ученикам своего класса. Очень радует, что своей работой я смог заинтересовать ровесников и донести до них новую информацию.
Исследование в корне изменило мое представление о простых числах и их значении в современном мире. Полученные знания о простых числах как основы современной криптографии заставили по-новому взглянуть на способы шифрования информации. В перспективе мне было бы интересно более подробно изучить и другие способы шифрования и защиты.
Думаю, что данное исследование может быть полезно и интересно учащимся школ, которые увлекаются математикой и информатикой. Результаты исследования могут быть использованы учителями при подготовке уроков, конкурсов, викторин.
Результаты исследования могут быть использованы учителями при подготовке уроков, конкурсов, викторин.
Список литературы
Гальперин Г. Просто о простых числах // Квант, 1987. – №4. С. 9-14.
Мир математики: в 40 т. Т.2: Жуан Гомес. Математики, шпионы и хакеры. Кодирование и криптография. / Пер. с англ. – М.: Де Агостини, 2014. – 144 с.
Мир математики: в 40 т. Т.3: Грисан Энрике. Простые числа. Долгая дорога к бесконечности. / Пер. с англ. – М.: Де Агостини, 2014с144 с.
Росанова К. А., Воронцова Я. О., Гаврилова А. М., Шмелева О. В. Эти сложные простые числа! // Юный ученый. — 2016. — №6.1. — С. 40-41.
Просмотров работы: 4321
Самое большое число во Вселенной
Публикация от 10.11.2012Время прочтения: 6 минут
Гугол . это
большое количество, невообразимо
большой. Легко записать в экспоненциальном формате: 10 100 , чрезвычайно компактный
метод, чтобы легко представить самые большие числа (а также
самые маленькие числа). Приложив минимум усилий, вы также можете представить его в полном формате:
Приложив минимум усилий, вы также можете представить его в полном формате:
«единица», за которой следуют сто «ноликов». Однако в экспоненциальном формате это может быть
легко читается; в полном формате, вы можете потерять счет количества
раз вам нужно использовать термин «миллиард» в «десяти миллиардах миллиардов
из миллиардов миллиардов …. так далее.». В любом случае, мы не можем даже начать ценить
степень. Даже имея всего один гугол, мы сталкиваемся с
число, которое больше, чем все, что используется для описания Вселенной
что мы понимаем. Наша Галактика, например, состоит из
около ста миллиардов звезд. В экспоненциальной форме около 10 11 звезд. Масса Солнца
составляет 2×10 33 грамм. Используя это измерение как
среднюю массу звезды, мы можем вычислить, что масса (видимая) нашей Галактики равна
поэтому примерно 10 45 грамм. Во Вселенной существуют
несколько сотен миллиардов галактик, число, сравнимое с числом
звезд нашей Галактики. Поэтому вместе мы собрали
около 10 56 -10 57 граммов вещества. Этот
Этот
вещество в основном состоит из барионов (протонов и нейтронов), связанных
к ядрам атомов, которые, начиная от водорода и заканчивая ураном (среди прочего), составляют часть
наша Вселенная. При расчете массы электроны, которые весят примерно один
двухтысячных нуклонов можно легко не принимать во внимание.
Учитывая, что масса протона (и нейтрона) равна 1,7 х 10 -24 г, мы можем вычислить, что количество
барионов, присутствующих во Вселенной, составляет примерно 10 80 . Большое количество, но существенно
меньше гугола; если быть точным, сотая миллиардная часть
миллиард гуголов. Нейтрино и фотонов больше, но даже
их количество значительно меньше, чем у гугола. К
превышает гугол, мы должны обратиться к самому большому контейнеру, который мы
знать и его наименьшую относительную часть.
Наименьшая длина, с точки зрения физики, известная нам, — это планковская длина. Он равен 1,6 х 10 -33 сантиметров. В кубическом сантиметре 2,5 х
10 98 кубов, сторона которых имеет планковскую длину.
Даже десятой части гугола. Во всей Вселенной, имеющей радиус примерно
10 28 см, следовательно, имеется примерно 10 184 кубов Планка. Это число — число Планка
кубов во Вселенной — это, наверное, самое большое число, которое мы можем дать
сущности в физическом мире. Если отбросить физические
размера и остаются в сфере математической абстракции, мы знаем о некоторых
Простые числа Мерсенна, превышающие гугол, начиная с 2 521 – 1 (включает 157 цифр) и заканчивается 2 43 112 609 – 1 включает 13
миллионов цифр и которое считается самым большим среди известных простых чисел Мерсенна (однако
мы, несомненно, узнаем больше в будущем). Нам удалось
превышают гугол, но мы по-прежнему имеем дело с небольшими числами по сравнению
в гуголплекс.
A googolplex , фактически равно
10 гугол и может быть записан только в
экспоненциальный формат. Гугол, равный 10 9100 ! Не только бы
не хватает бумаги или чернил, но не хватает места или времени, чтобы писать
гуголплекс в полном формате. Даже если вы написали каждую цифру с помощью миниатюры
Даже если вы написали каждую цифру с помощью миниатюры
символов, таких маленьких, что они могли бы поместиться в кубе Планка, во всем пространстве не хватило бы места.
Вселенная, которая, как мы видели, содержит, по максимуму, достаточно места для записи
первые 10 184 цифр. Однако нам нужно много
больше цифр! В свою очередь, гуголплекс, хотя
равно 10 98 больше, чем гугол,
можно считать меньшим числом, например, по сравнению с
то, которое считается самым большим числом, когда-либо использовавшимся в
математический контекст, известный как G, число Грэма. Это число, т.
относительное количество цифр неизвестно, поэтому его нельзя легко записать
даже при использовании экспоненциального формата и необходимо прибегать к
новые форматы, такие как тетрация и последующие экспоненциальные циклы, которые позволяют
его развитие: сложение – умножение – возведение в степень –
тетрация и так далее. Тетрация обозначена двумя стрелками, направленными
вверх, между факторами. Последующие расчеты показаны растущим числом стрелок. Отсюда 3↑3 = 3 93 ). Наконец, 3↑↑↑↑3 = 3↑↑↑(3↑↑↑3).
Отсюда 3↑3 = 3 93 ). Наконец, 3↑↑↑↑3 = 3↑↑↑(3↑↑↑3).
Это представляет собой отправную точку для достижения числа Грэма, которое мы будем называть
г1. Шаг 2 будет g2 = 3↑↑…↑↑3, где количество стрелок равно g1. Следующий шаг
будет g3 = 3↑↑↑↑…↑↑↑↑3, где на этот раз количество стрелок равно a g2. А также
так далее. Это продолжается до 64-го уровня, где мы достигаем g64 = G, числа Грэма ,
очевидно, невообразимое число. Можно, даже легко,
разработать операции, которые привели бы нас к большим числам: можно перейти от простого +1 к экспоненциальному вычислению с
члены даже больше, чем то, что определяет число Грэма (g65), или
которые включают более высокие факторы (например, с использованием 4 вместо 3).
Однако это не
смысл. Суть в том, чтобы найти числа, которые служат определенной цели, содержат определенные
значение, числа, которые получаются в результате операций, из
проблемы ментальной логики, или которые не могут быть, подобно простым числам, выражены в терминах
из меньших чисел. В
В
этот свет, и гугол, и гуголплекс — просто две силы
из 10 названных хорошо известны
и появляются в словарях, энциклопедиях, документации и выдержках. Грэма
число, совершенно иначе, представляет собой верхнюю границу (но не обязательно
наименьший) из «наименьшего числа необходимых измерений» для разработки
свойства гиперкуба (геометрическая фигура с четырьмя или более
пространственные размеры). Вот почему он был назван самым большим номер
среди тех, у кого такой же
значение. я закончу
с какой-то странной информацией о номере Грэма. Его простые числа остаются
неизвестны, и у нас есть веские основания думать, что они никогда не будут обнаружены, так как они исчисляются с самых низов (впрочем, я не хочу
совершить ту же самонадеянную ошибку, о которой я недавно писал, поэтому лучше «никогда
сказать никогда»). Известны последние цифры (на момент
последний счет
было рассчитано 500, и это число растет). Что касается G, которая представляет собой просто уничтожающую последовательность
умножение числа 3, там
7! Наконец, чтобы представить число Грэма в перспективе, давайте не будем забывать
что все цифры гроши по сравнению с бесконечных единиц, описывающих отношения между
длина и диаметр окружности или даже соотношение между
длина диагонали квадрата и его стороны (даже если мы сейчас
говорят о цифрах «после запятой», что существенно не изменит
размер номера). Но даже когда мы говорим о бесконечности, мы должны помнить
Но даже когда мы говорим о бесконечности, мы должны помнить
что существуют как большие, так и меньшие…
Получено из: Le Stelle
нет. 107, июнь 2012 г.
9003
9003
9003 01101111111111110110111111111111110111111101011111110101111111111111111111111111010101010
Никакого спама, поэтому вы можете отменить его в любой момент без щелчка мыши.
Pubblicato il 28/04/2020
В эти дни в газетах и телевизионных программах (и, конечно же, в Интернете) появилось заявление Итальянского общества экологической медицины (SIMA), в котором объявляется о важных открытиях, касающихся связи между взвешенными в воздухе твердыми частицами. и коронавирус, даже описывая их как важные для решений, которые будут приняты в ближайшие недели.
- Показать больше
Самые большие числа в мире
Это здорово!
«Бесконечная среда», арт-инсталляция Дуга Уилера, выставленная в галерее Дуга Цвирнера в Нью-Йорке. (Изображение предоставлено Тимом Найсвандером/IMAGING4ART, любезно предоставлено Дэвидом Цвирнером, Нью-Йорк (c) 2012, Дуг Уилер)
(Изображение предоставлено Тимом Найсвандером/IMAGING4ART, любезно предоставлено Дэвидом Цвирнером, Нью-Йорк (c) 2012, Дуг Уилер)
Большие числа повсюду, от клеток человеческого тела до размеров Вселенной. Но как только числа выходят за пределы физического царства, человеческому разуму становится трудно осознать ужасающий масштаб этих чисел. Даже бесконечность может показаться легче понять по сравнению с ней — она просто продолжается и продолжается. И как только числа становятся достаточно большими, все начинает сливаться воедино, говорит Джон Борвейн, прикладной математик из Университета Ньюкасла в Австралии.
«Мы не понимаем числа на этой шкале, — сказал Борвейн.
От скромного триллиона до числа Грэма — вот некоторые из самых ошеломляющих чисел.
Большое относительно
На этом кадре из анимированного пролета новой карты вселенной, созданной Слоановским цифровым обзором неба-III, показаны положения галактик, нанесенные на карту в трехмерном пространстве. (Изображение предоставлено: Мигель А. Арагон (Университет Джона Хопкинса), Марк СуббаРао (Планетарий Адлера), Алекс Салай (Университет Джона Хопкинса), Юшу Яо (Национальная лаборатория Лоуренса Беркли, NERSC) и сотрудничество SDSS-III)
(Изображение предоставлено: Мигель А. Арагон (Университет Джона Хопкинса), Марк СуббаРао (Планетарий Адлера), Алекс Салай (Университет Джона Хопкинса), Юшу Яо (Национальная лаборатория Лоуренса Беркли, NERSC) и сотрудничество SDSS-III)
Думая о личном бюджете, потолок долга в 16 триллионов долларов кажется невероятным. Но в масштабе атомов во Вселенной это выглядит абсолютно ничтожным по сравнению с этим, сказал Скотт Ааронсон, специалист по информатике из Массачусетского технологического института.
Чтобы понять огромные числа, большинство людей полагаются на масштабные аналогии. Например, Карл Саган классно сравнил возраст Вселенной с календарным годом, когда люди появляются только в последние несколько часов кануна Нового года.
Гипотеза Римана
Торговые номера фондовой биржи. (Изображение предоставлено: Mclek , Shutterstock )
Гипотеза Римана, впервые высказанная в 1859 году, является одной из величайших нерешенных догадок математики, и тот, кто решит ее, получит приз в размере 1 миллиона долларов. «Это самый большой открытый вопрос в математике, который гарантирует, что ваше имя будет известно через 10 000 лет», — сказал Борвейн.
«Это самый большой открытый вопрос в математике, который гарантирует, что ваше имя будет известно через 10 000 лет», — сказал Борвейн.
Гипотеза, если она верна, имеет важное значение для распределения простых чисел, которые не делятся ни на что, кроме самих себя или единицы. По его словам, чтобы проверить гипотезу, математики ищут чрезвычайно большие простые числа — те, которые больше 10, возведенные в степень 30. Это может звучать абстрактно, но это имеет много реальных последствий, сказал Борвейн. «Простые числа встроены во все, что мы используем для шифрования», — сказал он. «Все это зависит от того, что алгоритмы разработаны с использованием свойств простых чисел, которые мы считаем истинными, но не знаем».
Вселенная
(Изображение предоставлено НАСА)
Еще во времена Архимеда философы задавались вопросом, сколько крошечных частиц может поместиться во Вселенной. Архимед подсчитал, что около 10 песчинок в степени 63 могут заполнить Вселенную. Он использовал ряд чрезвычайно грубых оценок — семена мака, из которых состоит песчинка, песчинки, которые покрыли бы длину стадиона, и длины стадий между Землей и Солнцем, — сказал Генри Менделл, историк-классик из Калифорнийский государственный университет, Лос-Анджелес.
Несмотря на его грубые измерения, он был недалеко. По текущим оценкам, общее число атомов во Вселенной составляет примерно 10 к 80.
Квантовый фактор выдумки
Скопление галактик Abell 1689 известно тем, что оно искривляет свет в результате явления, называемого гравитационным линзированием. Новое исследование скопления раскрывает секреты того, как темная энергия формирует вселенную. (Изображение предоставлено: NASA, ESA, E. Jullo (JPL/LAM), P. Natarajan (Yale) и J-P. Kneib (LAM)) постоянна, чтобы объяснить тот факт, что Вселенная неподвижна. Хотя позже он отказался от константы, когда узнал, что Вселенная расширяется, оказалось, что гений, возможно, что-то понял: ученые считают, что космологическая постоянная, которая составляет всего 10, возведенную в степень минус 122, раскрывает ключи к темной энергии. это загадочным образом ускоряет Вселенную, сказал Ааронсон.
Геркулес и Гидра
Этот расписной деревянный флюгер был вырезан американским медником Уорреном Гулдом Роби между 1825 и 1850 годами. выражение женской красоты русалки. (Изображение предоставлено: Shelburne Museum, Shelburne, Vermont)
выражение женской красоты русалки. (Изображение предоставлено: Shelburne Museum, Shelburne, Vermont)
Иногда вещи должны стать большими, прежде чем они станут маленькими. В 1982 году математики Джефф Пэрис и Лори Кирби задали загадку: представьте, что Геракл сражается с гидрой, у которой головы растут, как дерево. Если он отрубит одну голову, мифический монстр просто отрастит определенное количество голов, регулируемое несколькими правилами. Удивительно, но Геракл в конце концов всегда побеждает Гидру и отрубает ей головы.
Но даже если Геракл умен и выберет наиболее эффективную стратегию, Гидра сначала вырастет больше, чем гуголплекс голов (или 10 в 10-й степени в 100-й степени).
Простое число Мерсенна
Найдено самое большое простое число. (Изображение предоставлено Андреасом Гускосом (открывается в новой вкладке) | Shutterstock.com (открывается в новой вкладке))
Простые числа Мерсенна — это класс чисел, которые быстро становятся большими. Эти простые числа равны 2, возведенным в степень простого числа минус 1. Хотя первые несколько начинаются с малого — 3, 7, 31 — они очень быстро становятся невероятно большими. Примерно до 1957 885 161 – 1, содержит более 17 миллионов цифр и был открыт в этом году.
Хотя первые несколько начинаются с малого — 3, 7, 31 — они очень быстро становятся невероятно большими. Примерно до 1957 885 161 – 1, содержит более 17 миллионов цифр и был открыт в этом году.
Триллион треугольников
На этой карте звездного неба показано, как Сатурн, Марс и яркая звезда Спика образуют небесный треугольник в ночь на понедельник (20 августа 2012 г.). На этой карте показано их расположение относительно Луны в 20:30. местное время от средних северных широт. (Изображение предоставлено Starry Night Software)
Около 1000 лет назад персидский математик Аль Караджи впервые задался вопросом, сколько существует конгруэнтных чисел. Но что такое конгруэнтные числа? Цифры представляют собой площади прямоугольных треугольников с целыми или дробными сторонами. Таким образом, треугольник со сторонами 3, 4 и 5 будет иметь площадь ½ * 3 * 4 = 6, что делает 6 конгруэнтным числом.
Потребовалось еще несколько тысячелетий, прежде чем были открыты первые сто конгруэнтных чисел. Однако к 2009 году суперкомпьютеры обнаружили первые 3 148 379 694 совпадающих числа. Некоторые из этих чисел настолько огромны, что если бы их цифры были записаны в десятичной форме, они бы растянулись до Луны и обратно. По словам Борвейна, гигантские числа имеют интересные последствия для хранения данных, потому что они настолько велики, что случайный гамма-луч может разрушить биты в этих числах и сделать их неправильными.
Однако к 2009 году суперкомпьютеры обнаружили первые 3 148 379 694 совпадающих числа. Некоторые из этих чисел настолько огромны, что если бы их цифры были записаны в десятичной форме, они бы растянулись до Луны и обратно. По словам Борвейна, гигантские числа имеют интересные последствия для хранения данных, потому что они настолько велики, что случайный гамма-луч может разрушить биты в этих числах и сделать их неправильными.
Число Грэма
На этом рисунке показана черная дыра, испускающая струи быстро движущейся плазмы над и под собой, когда материя вращается по орбитальному диску. (Изображение предоставлено Центром космических полетов имени Годдарда НАСА)
Все эти числа меркнут по сравнению с числом Грэма, числом настолько большим, что простая попытка вспомнить все цифры превратила бы вашу голову в черную дыру. Число, которое в какой-то момент было самым большим числом, которое когда-либо использовалось в математическом доказательстве, возникло в ответ на простую загадку о том, как распределять людей по определенному набору комитетов с некоторыми ограничениями.
В то время как математики уверены, что для решения задачи требуется не менее 13 человек, в 1970-х годах математик и жонглер Рональд Грэм пришел к выводу, что количество людей должно быть меньше числа Грэма. Простое вычисление числа заняло бы 64 шага и включало бы умножение безумно огромного количества троек.
Невозможно записать число в экспоненциальном представлении, вместо этого оно должно быть записано с помощью ряда стрелок вверх, обозначающих башни показателей. Позже Грэм показал, что верхняя граница для этой загадки намного меньше числа Грэма, но все равно огромна.
TREE(3)
Уравнения не только полезны, но и красивы. (Изображение предоставлено Shutterstock/Fedorov Oleksiy )
Хотя число Грэма было одним из самых больших чисел, предложенных для конкретного математического доказательства, с тех пор математики стали еще больше. В 1998 году логик Харви Фридман из Университета штата Огайо предложил загадку, в которой спрашивалось, насколько длинной последовательности букв должны быть заданы определенные параметры повторяющихся отрезков букв. Хотя ответ не бесконечен, он абсолютно огромен.
Хотя ответ не бесконечен, он абсолютно огромен.
Число, полученное Фридманом, TREE(3), рассчитывается путем создания все более массивных башен из двоек, возведенных в степень двойки, с использованием так называемых функций Аккермана. Чтобы дать представление о масштабе, четвертая функция Аккермана включает в себя возведение двойки в степень 65 536 двоек. Но TREE(3) намного, намного больше — настолько массивно, что по сравнению с ним число Грэма кажется мельчайшей пылинкой.
«Эти более высокие уровни масштаба размываются, когда невозможно отличить один уровень масштаба от другого», — писал Фридман в своей статье.
Тиа — главный редактор, а ранее — старший писатель журнала Live Science. Ее работы публиковались в журналах Scientific American, Wired.com и других изданиях. Она имеет степень магистра биоинженерии Вашингтонского университета, диплом о высшем образовании в области научного письма Калифорнийского университета в Санта-Круз и степень бакалавра машиностроения Техасского университета в Остине. Тиа была частью команды журнала Milwaukee Journal Sentinel, которая опубликовала серию «Пустые колыбели» о преждевременных родах, получившую множество наград, в том числе медаль Кейси 2012 года за заслуги перед журналистикой.
Тиа была частью команды журнала Milwaukee Journal Sentinel, которая опубликовала серию «Пустые колыбели» о преждевременных родах, получившую множество наград, в том числе медаль Кейси 2012 года за заслуги перед журналистикой.
Какое самое большое число? — ПОПУЛЯРНАЯ МИНУТА
http://nonfictionminute.org/nonfictionminute 03.12.2020 142 комментария
Дэвид М. Шварц Можете ли вы выразить словами то, что говорят вам эти уравнения? Задумайте большое число. Как насчет одного миллиона? Это тысяча тысяч. Это много. Если вы считаете без остановки до миллиона, это займет у вас около 23 дней. Конечно, триллион — не самое большое число. Есть квадриллион, квинтиллион, секстиллион, септиллион, октиллион, нониллион, дециллион и другие. Каждый в тысячу раз больше предыдущего. Есть даже огромное число под названием вигинтиллион, состоящее из 63 нулей. Но вигинтиллион — креветка по сравнению с гуголом. Гугол? Обратите внимание, как это пишется: G-O-O-G-O-L, а не G-O-O-G-L-E. Гугол — это единица с сотней нулей. Он получил свое название от девятилетнего мальчика. Гугол — это больше, чем все волосы в мире. Это больше, чем все травинки и все песчинки. Это даже больше, чем количество атомов во Вселенной. Астрофизики оценивают количество атомов как единицу с 82 нулями. Вам нужно добавить еще 18 нулей, чтобы получить гугол. Кстати, несколько лет назад два человека, которые изобрели новый мощный интернет-поисковик, решили назвать свой веб-сайт и компанию гигантским числом гугол. Гугол настолько велик, что практически бесполезен, но мальчик, который назвал его, придумал название для еще большего числа — «гуголплекс». Гуголплекс — это единица с нулями гугола. Во всех ручках мира недостаточно чернил, чтобы написать столько нулей, но не стесняйтесь попробовать. Так значит, гуголплекс — самое большое число? А как насчет гуголплекса и одного? Два гуголплекса? Гуголплекс гуголплекс? Любое число, которое вы говорите, я могу сказать на одно больше. Я слышу, как вы спрашиваете: «А как насчет бесконечности? Разве это не самое большое число?» Извините, но бесконечность не число. Число определяет количество, а бесконечность не является количеством. Это означает «продолжаться и продолжаться вечно». И это то, что делают числа. Они продолжаются и продолжаются вечно. Бесконечность — это не число, но числа бесконечны. Думаете, вы слишком стары для азбуки? Вы подумаете еще раз, если прочитаете отрывок из книги Дэвида М. Шварца: B для двоичных чисел, F для Фибоначчи, P для вероятности… Вы можете видеть, что это книга ABC, не похожая ни на одну другую. Нажмите сюда, для получения дополнительной информации. Дэвид Шварц является участником группы авторов по вызову iNK и доступен для классных программ с помощью FieldTripZoom , потрясающей технологии, для которой требуются только компьютер, Wi-Fi и веб-камера. Нажмите здесь чтобы узнать больше MLA 8 Citation 142 комментария | Новостная лента *НОВОСТИ * Дайан Рэвич, премьер-министр и неутомимый чемпион государственной школы, дала большой отзыв о нас в своем блоге! НОВИНКА! *NEWSFLASH * Категории Все 05 Categories ArchivesMarch 2021 МИНУТА НЕФИКСАЦИИ, Авторы по вызову, и. Для получения дополнительной информации или поддержки обращайтесь по адресу [email protected] Для получения информации о политике конфиденциальности перейдите по адресу . Этот сайт использует файлы cookie, чтобы персонализировать ваш опыт, анализировать использование сайта и предлагать индивидуальные рекламные акции. www.youronlinechoices.eu Архивы сентябрь 2022 г. |
Какое самое большое число и закончатся ли они когда-нибудь?
Это может быть ответом на все вопросы, но мы не думаем, что это самое большое число, которое вы можете придумать (Иллюстрация: Элла Байворт для Metro.co.uk)
Какое самое большое число вы можете придумать?
Миллиард? Триллион? Квадриллион? Секстиллион? Тредециллион? Гугол? Гуголплекс?
На школьном дворе шутят о том, что бесконечность+1 — это самое большое из существующих чисел.
Проблема в том, что бесконечность+1 по-прежнему равна бесконечности.
бесконечность бесконечность ? Еще бесконечность.
Еще большая проблема заключается в том, что бесконечность — это не число, а понятие.
И это самое большое число, которое вы пытаетесь придумать, или это просто название самого большого числа?
В Древней Греции математик Архимед предположил, что самое большое число, которое нам когда-либо понадобится, — это общее количество песчинок во Вселенной.
Большие числа представлены в степенях 10 98
Это единица, за которой следуют 80 квадриллионов нулей.
Для справки: говорят, что в наблюдаемой Вселенной находится где-то от 10 78 до 10 82 атомов, что составляет тредециллион (10 78 ) или чуть больше.
Количество атомов во Вселенной меньше даже 0,1% от числа Зверя.
Несмотря на то, что чисел во Вселенной больше, чем атомов, попытки доказать, что ваше целое число больше любого другого, продолжались веками. 9100 .
9100 .
Чтобы показать, насколько смехотворно это число, математик Вольфганг Нитше начал выпускать книги, пытаясь записать его.
У него было 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 (чуть ниже сексуального затраты) Объем книги, чтобы полностью изобразить количество нулей.
Но он это сделал (хотя мы предполагаем, что у него много автоматизированной помощи, о чем мы просили).
Даже тогда есть большее число, значение которого никто не знает:
Мы не можем себе представить, что он написал все это от руки (Фото: Вольганг Х. Ницше)
Число Грэма занесено в Книгу рекордов Гиннеса как самое большое конкретное целое число, использованное в опубликованном математическом доказательстве.
Решить задачу из теории Рамсея, связанную с n-мерным гиперкубом (если вы хотя бы разбираетесь в этой крошечной части теории, у вас получается лучше, чем у нас).
Число Грэма делится на 3 и оканчивается на 7, его последние 12 цифр — 262464195387, но оно не может быть выражено стандартным образом и слишком велико, чтобы его можно было вычислить полностью.
Но проблема с любым из этих чисел заключается в том, что они не являются «санкционированными» и не очень полезны в повседневной математике или измерениях.
Большой разговор идет о том, какие «полезные» номера следует называть и кто должен отвечать за их присвоение имен.
Имя для гугола (10 100 ) впервые придумал сто лет назад девятилетний племянник математика.
«Вы можете придумывать любые имена, которые вам нравятся, но официальные санкционированы в соответствии с тем, что мы называем соглашением об использовании счетчиков», — говорит Metro.co.uk д-р Ричард Браун, глава отдела метрологии в NPL, Национальном институте измерений Великобритании.
«Это межправительственный договор, в котором государства-члены договариваются о единицах измерения»
Международный комитет мер и весов (CIPM) собирается раз в четыре года и отвечает за то, какой точный ответ может быть на такие вопросы, как «сколько стоит килограмм». взвесить?»
Определение килограмма было изменено на последнем саммите.
Большие числа используются в математике, но CIPM больше ориентирован на практическое использование:
Международная система измерений признает килограммы (1000), мега (1м), гига (1млрд), тера (1тн), пета( 10 15 ), экза (10 18 ), зетта (10 21 ) и йотта (10 24 ) в качестве префиксов.
Эти префиксы могут использоваться перед любыми измерениями — например, километрами, мегаметрами — но большинство понимают их из байтов вычислений (мегабайт, гигабайт).
И, как считает доктор Браун, нам может понадобиться что-то большее:
«Появление таких вещей, как квантовые вычисления, скоро переместит нас на этап, когда нам нужно что-то больше йоттабайта.
‘Исторически эти вещи увеличиваются в десять раз в степени три, так что следующим будет 10 в степени 27’. Шилентнобайт? Домегемегроттебайт? Бронтобайт? Геобайт?
Лучшее из будущего всего
Все они являются подлинными предложениями.
Студент из Калифорнии в 2010 году предложил «hella» в качестве префикса для 10 27 и получил тысячи подписей под онлайн-петицией, но ни эта, ни любая другая из вышеперечисленных так и не попала в CIPM
, с другой стороны, д-р Браун уже представил официальный документ, ожидающий обсуждения.
Используя для вдохновения греческие и латинские сочинения для девятки (ennea, novem) и 10 (deka, decem), он работал в алфавите в обратном порядке ( z etta, y otta, чтобы прийти к буквам, которых не было) t еще не использовался
- Ronna – для обозначения 10 27 или 1000 9
- Quecca — для представления 10 30 или 1000 10
Доктор Браун говорит, что это только начало дискуссии о том, как мы определяем большие числа.
И это не просто разговор о том, как их называть, но и о том, что означает необходимость префиксов для больших значений в повседневной жизни.
Стратег по работе с большими данными Пол Сондереггер назвал всю эту дискуссию «проблемой любого байта» и считает ее неуместной по сравнению с реальной проблемой:
«У нас не только нет названия для этого объема данных, мы не знаем, как говорить о его последствиях», — сказал Зондереггер Forbes.
Подсчитано, как обсуждалось ранее в серии «Будущее всего», что размер мозга составляет до 2,5 петабайт.
Если это так, то в одном йоттабайте достаточно памяти примерно для 400 миллионов мозгов.
В одном роннабайте, или как бы он ни назывался, было бы место для примерно 4 миллиардов мозгов.
В одном кеккабайте более чем достаточно места для всех знаний каждого когда-либо родившегося человека.
«Йоттабайт (10 24 ) по-прежнему является огромной мерой, но она все еще конечна, и мы имеем дело с практическими измерениями, а не с теоретической математикой», — говорит доктор Браун.
‘Нас всегда ограничивает размер вещей, которые мы можем измерить.
«Мы никогда не будем иметь дело с такими большими вещами, как числа Beast, гуголы и тому подобное.»
Хотя дебаты об этта/йотта/что угодно часто ведутся вокруг байтов, CIPM на самом деле не распознает байт как физическое измерение, поскольку оно не имеет размера.
«На самом деле он не входит в международную систему единиц, — говорит доктор Браун.
«Очевидно, что мы должны это учитывать, потому что люди в области вычислений используют наши префиксы, и мы должны помнить об этом.
«Но биты и байты — это не физические единицы, а математические объекты». любой, кто использовал гуголплекс», — говорит д-р Саймон Фостер, физик-солнечник из Имперского колледжа в Лондоне, Metro.co.uk
‘Мои коллеги, изучающие масштабы Вселенной, никогда не имели проблем с числами.
‘Люди, моделирующие галактики, не беспокоятся о том, что их число иссякнет.
Подробнее: Школа
«То, как мы сообщаем о нашей науке, может в конечном итоге стать проблемой, но это не проблема для реальной науки.»
Вместо того, чтобы двигаться к бесконечно большому, доктор Фостер считает, что экспертам лучше искать все меньшие и меньшие числа:
9-3) будет 1/10/10/10 или 0,001.
Но все эти номера существуют уже давно.
Если будут приняты новые термины для 10 27 (ronna) и 10 30 (quecca), они станут первыми новыми префиксами с 1991 года.
Следующей возможностью будет встреча в 2022 году, но Де Браун считает 2026 год более реалистичен.
«Вы не хотите вносить изменения, которыми никто не воспользуется, вы хотите убедиться, что это правильно», — говорит он.
«Большой интерес вызывают названия префиксов, но главное решение: нужно ли вообще расширять систему?»
Если он когда-нибудь пройдет строгие испытания, у доктора Брауна уже есть имя для 10 33 в рукаве: Bundecca, основанное на латыни 11, ундецим.
B — последняя буква, не используемая в качестве префикса.
После этого письма закончились.
Но неужели нам действительно не хватает номеров?
В кодировании действительно можно исчерпать себя.
Если вы используете язык программирования JavaScript, то наибольшее целое число, которое вы можете безопасно использовать в 64-битной системе, равно 2 53 -1 или 9 007 199 254 740 991.
Все, что выше, может отображаться как бесконечность.
В реальном мире имена для чисел могут иссякать, но числа бесконечны, несмотря на то, что говорят вам школьные шутки о бесконечности +1.
Хотя математики разработали теории бесконечности и сложения, до тех пор, пока они не станут общепризнанными, у нас не закончатся числа, а только названия для них.
Будущее всего
Этот фрагмент является частью серии Metro.co.uk «Будущее всего».
От офицеров ордена Британской империи до генеральных директоров, от профессоров до футурологов, от экономистов до социальных теоретиков, от политиков до академиков, получивших множество наград, мы думаем, что у нас есть будущее, вдали от нагнетающих гибель или простых ссылок на отчеты меньшинства.
Каждую неделю мы объясняли, что может (или маловероятно) произойти.
Свяжитесь с нами, используя хэштег #futureofeverthing. Хотя серия больше не выходит еженедельно, если вы считаете, что мы могли пропустить что-то важное для будущего, свяжитесь с нами: hey@metro. co.uk или [email protected]
co.uk или [email protected]
Прочтите каждую историю о Будущем Всего
Это самые большие числа во вселенной
Существуют числа, которые настолько невероятно, невероятно велики, что даже для того, чтобы записать их, понадобилась бы вся Вселенная. Но вот действительно сумасшедшая штука… некоторые из этих непостижимо огромных чисел имеют решающее значение для понимания мира.
Когда я говорю «самое большое число во вселенной», я на самом деле имею в виду самое большое осмысленное 9Число 0079, максимально возможное число, которое может быть полезным. Претендентов на это звание много, но сразу предупрежу: есть вполне реальный риск, что попытка разобраться во всем этом снесет вам крышу. Но тогда, с экстремальной математикой, это половина удовольствия.
Googol и Googolplex
Мы могли бы также начать с двух, вероятно, самых больших чисел, о которых вы когда-либо слышали, и на самом деле это два самых больших числа с общепринятыми определениями в английском языке. (Существует довольно надежная номенклатура, позволяющая называть числа сколь угодно большими, но в настоящее время вы не найдете их в словарях.) Гугол, который с тех пор стал всемирно известным (хотя и с ошибками) в форме Google, начал жизнь в 19100 — или единица с сотней нулей — отныне будет называться гугол.
(Существует довольно надежная номенклатура, позволяющая называть числа сколь угодно большими, но в настоящее время вы не найдете их в словарях.) Гугол, который с тех пор стал всемирно известным (хотя и с ошибками) в форме Google, начал жизнь в 19100 — или единица с сотней нулей — отныне будет называться гугол.
Но юный Милтон не закончил — он предложил еще большее число, гуголплекс. Это число, согласно Мильтону, было единицей, за которой следовало столько нулей, сколько вы могли написать, пока не устанете. Несмотря на очаровательную идею, Каснер решил, что необходимо более техническое определение. Как он объяснил в своей книге 1940 года « Математика и воображение », определение Мильтона оставляет открытой возможность того, что случайный шут может стать более великим математиком, чем Альберт Эйнштейн, просто обладая большей выносливостью. 9100. Чтобы представить это в какой-то умопомрачительной перспективе, Карл Саган однажды заметил, что физически невозможно записать все нули в гуголплексе, потому что во Вселенной просто не хватает места. Если бы вы заполнили весь объем наблюдаемой Вселенной мелкими частицами пыли размером примерно 1,5 микрометра, то количество различных комбинаций , в которых вы могли бы расположить и пронумеровать эти частицы, составило бы примерно один гуголплекс.
Если бы вы заполнили весь объем наблюдаемой Вселенной мелкими частицами пыли размером примерно 1,5 микрометра, то количество различных комбинаций , в которых вы могли бы расположить и пронумеровать эти частицы, составило бы примерно один гуголплекс.
С лингвистической точки зрения, гугол и гуголплекс, вероятно, являются двумя самыми большими значащими числами (по крайней мере, в английском языке), но, как мы сейчас узнаем, способов определить «значащий» бесконечное множество.
Реальный мир
Если мы собираемся говорить о самом большом числе со значением , то есть неплохой аргумент, что это на самом деле означает, что нам нужно найти самое большое число, имеющее какое-либо реальное значение. Мы можем начать торги с нынешней численности населения, которая в настоящее время составляет около 6,92 миллиарда человек. Мировая экономика в 2010 году оценивалась примерно в 61,96 триллиона долларов, но обе эти суммы ничтожны по сравнению с примерно 100 квадриллионами клеток, из которых состоит человеческое тело. 80 — число настолько большое, что в нашем языке нет общепринятого слова для него. 916 конфигураций. На самом деле, — это число , вероятно, самое большое для любого практического применения, если вы не верите во всю идею мультивселенной. Но там все еще скрываются гораздо большие числа. Но для того, чтобы их найти, нам придется углубиться в область чистой математики, и нет лучшего места для начала, чем простые числа.
80 — число настолько большое, что в нашем языке нет общепринятого слова для него. 916 конфигураций. На самом деле, — это число , вероятно, самое большое для любого практического применения, если вы не верите во всю идею мультивселенной. Но там все еще скрываются гораздо большие числа. Но для того, чтобы их найти, нам придется углубиться в область чистой математики, и нет лучшего места для начала, чем простые числа.
Простые числа Мерсенна
Частично трудность здесь заключается в том, чтобы дать хорошее определение тому, что на самом деле представляет собой «значащее» число. Один из способов представить это в терминах простых и составных чисел. Простое число, как вы, вероятно, помните из школьной программы по математике, — это любое число, делителями которого являются только 1 и само себя. Итак, 2, 3 и 5 — простые числа, а 4 (2*2) и 6 (2*3) — составные числа. Это означает, что любое составное число в конечном итоге может быть сведено к его простым делителям. В каком-то смысле такое число, как 5, важнее, чем, скажем, 4, потому что его невозможно выразить в виде меньших чисел.
Очевидно, мы можем расширить это еще немного. 100, например, на самом деле просто 2 * 2 * 5 * 5, а это означает, что в гипотетическом мире, где наши знания о числах достигли только 5, математики все еще могли выразить число 100. Но следующее число 101 простое, это означает, что единственный способ выразить это — иметь прямое знание о его существовании. Это означает, что самые большие известные простые числа важны в том смысле, в каком, скажем, гугол, который в конечном счете представляет собой просто набор 2 и 5, умноженных вместе, на самом деле не так важен. И, поскольку простые числа по существу случайны, нет известного способа предсказать, какое невероятно большое число на самом деле будет простым. По сей день открытие нового простого числа имеет большое значение.
Древнегреческие математики понимали понятие простых чисел, по крайней мере, еще в 500 г. до н. э., но 2000 лет спустя люди все еще знали, какие числа являются простыми, только до 750. Мыслители еще во времена Евклида видели потенциальный короткий путь, но он только в эпоху Возрождения математики могли действительно применить это на практике. 5 — 1 = 32 — 1 = 31,9.43 112 609 — 1, что представляет собой число, состоящее почти из 13 миллионов цифр. Это самое большое известное число, которое не может быть выражено через любые меньшие числа, хотя, если вы хотите помочь найти еще большее простое число Мерсенна , вы (и ваш компьютер) всегда можете присоединиться к поиску.
5 — 1 = 32 — 1 = 31,9.43 112 609 — 1, что представляет собой число, состоящее почти из 13 миллионов цифр. Это самое большое известное число, которое не может быть выражено через любые меньшие числа, хотя, если вы хотите помочь найти еще большее простое число Мерсенна , вы (и ваш компьютер) всегда можете присоединиться к поиску.
Число Скьюза
Давайте на секунду остановимся на простых числах. Как я уже говорил, простые числа принципиально нерегулярны, а это означает, что невозможно предсказать, каким будет следующее простое число. Математикам пришлось приложить немало усилий, чтобы найти число 9.0078 любой способ предсказать будущие простые числа даже в самом расплывчатом смысле. Наиболее успешной из этих попыток, вероятно, является функция подсчета простых чисел, которую придумал легендарный математик Карл Фридрих Гаусс в конце 1700-х годов.
Я избавлю вас от более сложной математики — у нас много еще впереди — но суть функции такова: для любого заданного целого числа x можно оценить, сколько существует простых чисел, которые меньше х. Например, если x = 1000, функция предсказывает, что должно быть 178 простых чисел; если x = 10 000, меньше его на 1 246 простых чисел; а если x = 1 000 000, то существует 78 628 меньших простых чисел. 922, функция подсчета простых чисел немного завышает фактическое количество простых чисел, меньших x. Когда-то математики думали, что это будет иметь место вплоть до бесконечности — это, безусловно, справедливо для некоторых невообразимо огромных величин, — но в 1914 году Джон Эденсор Литтлвуд доказал, что при каком-то неизвестном, непостижимо огромном числе функция счета простых чисел начнет предоставляя оценку ниже числа простых чисел, а затем функция будет переключаться между переоценкой и недооценкой бесконечное количество раз. 934, число, которое затмевает даже могучий гуголплекс? В «Словаре любопытных и интересных чисел пингвинов» Дэвид Уэллс рассказывает об одном из способов, которым математик Г.Х. Харди удалось концептуализировать размер числа Скьюза:
Например, если x = 1000, функция предсказывает, что должно быть 178 простых чисел; если x = 10 000, меньше его на 1 246 простых чисел; а если x = 1 000 000, то существует 78 628 меньших простых чисел. 922, функция подсчета простых чисел немного завышает фактическое количество простых чисел, меньших x. Когда-то математики думали, что это будет иметь место вплоть до бесконечности — это, безусловно, справедливо для некоторых невообразимо огромных величин, — но в 1914 году Джон Эденсор Литтлвуд доказал, что при каком-то неизвестном, непостижимо огромном числе функция счета простых чисел начнет предоставляя оценку ниже числа простых чисел, а затем функция будет переключаться между переоценкой и недооценкой бесконечное количество раз. 934, число, которое затмевает даже могучий гуголплекс? В «Словаре любопытных и интересных чисел пингвинов» Дэвид Уэллс рассказывает об одном из способов, которым математик Г.Х. Харди удалось концептуализировать размер числа Скьюза:
Харди считал его «самым большим числом, которое когда-либо служило какой-либо определенной цели в математике», и предположил, что если играть в шахматы со всеми частицами во Вселенной как штук, один ход представляет собой обмен парой частиц, а игра заканчивается, когда одна и та же позиция повторяется в третий раз, количество возможных игр будет примерно равно числу Скьюза.
9.63.
Вопрос о величине
Прежде чем мы доберемся до числа, по сравнению с которым даже число Скьюза кажется крошечным, нам нужно немного поговорить о масштабе, потому что иначе мы действительно не сможем оценить, куда мы собираемся пойти. . Давайте сначала посмотрим на число 3 — это крошечное число, настолько маленькое, что люди могут интуитивно понять, что оно означает. Под это описание подходит очень мало чисел, поскольку все, что превышает шесть, перестает быть отдельным числом и становится «несколько», «много» и так далее. 9963 — даже с поправкой на то, что все эти числа намного больше, чем 3, это все равно абсолютно ничто по сравнению с экспоненциальной башней с 7,6 триллионами членов.
Очевидно, что невозможно даже начать понимать такое огромное число… и тем не менее, процесс , с помощью которого оно создается, все еще можно понять. Возможно, мы не в состоянии уловить фактическое число , которое создается экспоненциальной башней с 7,6 триллионами 3 в ней, но мы в принципе можем визуализировать экспоненциальную башню с таким количеством членов в ней, и действительно приличный суперкомпьютер был бы в состоянии сохранить башню, даже если он не может начать вычислять ее реальную стоимость.
93. Это число просто непостижимо велико, но, по крайней мере, соответствующие шаги все же можно уловить, если мы будем действовать очень медленно. Мы больше не можем понять число или , представить процедуру, которая его создала бы, но, по крайней мере, мы можем понять основную процедуру, хотя бы в самых расплывчатых выражениях.
Теперь приготовьтесь к тому, что ваш разум будет действительно взорван.
Число Грэма
Вот как вы получаете число Грэма, которое занимает место в Книга рекордов Гиннеса как самое большое число, когда-либо использовавшееся в математическом доказательстве. Совершенно невозможно представить, насколько велико число Грэма, и, честно говоря, не намного проще объяснить, что именно представляет собой . По сути, число Грэма вступает в игру при работе с гиперкубами, которые представляют собой теоретическую геометрическую форму с более чем тремя измерениями. Математик Рональд Грэхем (на фото он устрашающий) хотел выяснить, какое наименьшее количество измерений необходимо для того, чтобы определенные свойства гиперкуба оставались стабильными.
(Извините, что так расплывчато объясняю это, но я почти уверен, что нам всем нужно получить как минимум две ученые степени по математике, прежде чем мы сможем говорить более конкретно.) 93 стрелки между этими двумя тройками. На данный момент мы находимся далеко за пределами даже малейшего возможного понимания того, что такое число, подобное этому, или даже того, как его вычислить.
Теперь повторите этот процесс еще 62 раза.
Это , дамы и господа, это число Грэма, число, которое примерно на 64 порядка выше точки человеческого понимания. Это число намного больше, чем любое число, которое вы могли себе представить, — черт возьми, оно намного больше, чем любая девятка.0078 бесконечность , которую вы когда-либо могли себе представить, что она просто не поддается даже самому абстрактному описанию.
Но вот что странно. Поскольку число Грэма — это просто набор троек, перемноженных вместе, это означает, что мы можем знать некоторые его свойства, не вычисляя их целиком.
Мы не можем представить число Грэма в каких-либо привычных обозначениях — даже если бы мы использовали всю вселенную, чтобы записать его, — но я могу сказать вам прямо сейчас, каковы последние двенадцать цифр числа Грэма: 262 464, 19.5387. И это еще ничего — мы знаем как минимум последние 500 цифр числа Грэма.
Конечно, стоит помнить, что это число — всего лишь верхний предел исходной задачи Грэма. Возможно, фактическое количество измерений, необходимых для хранения свойств, намного меньше. На самом деле, еще в 1980-х большинство экспертов в этой области придерживались мнения, что на самом деле ответ равен шести — число настолько маленькое, что мы можем понять его на интуитивном уровне. С тех пор нижний предел был повышен до 13, но все еще есть очень хороший шанс, что фактическое решение проблемы Грэма находится не где-то в около , такое же большое, как число Грэма.
Навстречу бесконечности
Итак, есть ли числа еще больше, чем число Грэма? Ну конечно есть — есть номер Грэма + 1, для начала.
Что касается осмысленных чисел… ну, есть некоторые чертовски сложные области математики (в частности, область, известная как комбинаторика) и компьютерных наук, которые действительно имеют числа, даже большие, чем число Грэма. Но мы в значительной степени достигли предела того, что я когда-либо мог надеяться разумно объяснить. Для тех, кто достаточно безрассуден, чтобы углубиться еще больше, вы можете проверить некоторые дополнительные материалы на свой страх и риск.
И все же есть еще что-то еще большее, что-то настолько большое, что этот термин теряет всякий смысл: бесконечность. Так что присоединяйтесь к нам на следующей неделе во второй части нашей одиссеи по самым большим числам, которые только можно вообразить, когда мы исследуем все многообразие вкусов бесконечности. А пока я оставлю вас с этой удивительной цитатой, приписываемой Дугласу Рею:
У меня есть это видение скоплений призрачных чисел, таящихся там, во тьме, за маленькой сферой света, отбрасываемой свечой разума.
Они шепчутся друг с другом; придумывать черт знает что. Возможно, они не очень любят нас за то, что мы захватываем их меньших собратьев своим умом. Или, возможно, они просто ведут уникальный образ жизни за пределами нашего понимания.
Дополнительная литература
Большие числа Роберта Мунафо
Словарь любопытных и интересных чисел Penguin Дэвид Уэллс
Самые большие числа во Вселенной Брайан Клер
Кто может назвать большее число? Скотт Ааронсон
1, 2, 3, 4 — четыре цифры, которые затмили вселенную
Насколько велика одна Асамхьея? by Bhikshu Jin Yong
XKCD-Men Origins: Wolverine с Огромным Аккерманом в главной роли by David Morgan-MarВерхнее изображение via DeviantArt . Вселенная через .
Какое самое большое число в мире?
Числа — это математические цифры или значения, используемые в математических операциях, таких как сложение, вычитание, умножение и деление.
Эти значения также известны как числа и обычно используются для определения времени, измерения, маркировки продуктов, продаж, торговли и т. д. в нашей повседневной жизни.
Числа — это математические значения, используемые для счета, измерения и других арифметических вычислений. Некоторыми примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.
Система счисления представляет собой способ представления этих математических цифр в различных формах. Числительные в системе счисления подразделяются на различные типы чисел, например простые числа, нечетные числа, четные числа, рациональные числа, целые числа и т. д. Система определяет, будут ли числа выражаться в виде цифр или слов соответственно.
A Система счисления определяется как способ стандартного представления чисел. Это уникальный способ представления, в котором числа представлены в арифметической и алгебраической структуре.
Типы системы счисления
Как мы узнали, системы счисления представляют собой стандартизированные системы для выражения математических фигур в виде цифр или слов. В зависимости от способа выражения системы счисления подразделяются на четыре распространенных типа.
- Десятичная система счисления: Десятичная система счисления представляет числа в единицах, десятках, сотнях, тысячах по мере продвижения от десятичной точки. Например, 35 — это значение, где 5 соответствует единицам, а 3 — десяткам.
- Двоичная система счисления : Система счисления, состоящая только из двух цифр, 0 и 1, называется двоичной системой счисления. Например, 10011011 — это двоичное число.
- Восьмеричная система счисления : Это система счисления, наиболее применимая в компьютерных приложениях, в которой для представления значений используются числа от 0 до 7. Например, 153 5
- Шестнадцатеричная система: Эта система включает метод представления чисел цифрами, а также буквами.
В шестнадцатеричной двоичной системе числа сначала выражаются в десятичной системе счисления, а затем в алфавитах от A до F.
Типы чисел
Числа — это математические фигуры, которые представляют определенные значения в математических операциях. Существуют различные типы чисел, которые подразделяются на наборы по системе счисления.
- Натуральные числа: Натуральные числа — это набор чисел, считая от 1 до бесконечности. Множество натуральных чисел обозначается буквой «N». Это числа, которые мы обычно используем для счета. Множество натуральных чисел задано N=1,2,.3,4,5,6,7,……………
- Целые числа: Целые числа — это набор натуральных чисел, включая ноль, который считается от 0 до бесконечности. Целые числа не включают дроби или десятичные дроби. Множество целых чисел обозначается буквой «W». Набор целых чисел задается как W=0,1,2,3,4,5,………………
- Целые числа: Целые числа представляют собой набор чисел, включающий все положительные натуральные числа, а также ноль.
как и все отрицательные числа, которые считают от отрицательной бесконечности до положительной бесконечности. В наборе нет дробей и десятичных знаков. Множество целых чисел обозначается Z. Набор целых чисел задается Z=………..,-5.-4,-3,-2,-1,0,1,2,3,4,5,………….
- Десятичные числа: Любое числовое значение, состоящее из десятичной точки, является десятичным числом. Его можно выразить как 2,5,0,567 и т. д.
- Вещественное число: Вещественные числа — это заданные числа, не содержащие мнимых значений. Он включает в себя все положительные целые числа, отрицательные целые числа, дроби и десятичные значения. Обычно обозначается буквой «R».
- Комплексное число : Комплексные числа — это набор чисел, включающий мнимые числа. Его можно выразить как a+bi, где «a» и «b» — действительные числа. Обозначается буквой «С».
- Рациональные числа : Рациональные числа — это числа, которые можно выразить как отношение двух целых чисел.
Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается буквой Q.
- Иррациональные числа : Иррациональные числа — это числа, которые не могут быть выражены дробями или отношениями целых чисел. он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Обозначается буквой «П».
9100 . При записи числа гугол в обычном формате записи числа вероятность потери счета очень высока. Следовательно, его удобнее выразить в виде показателя степени и степени.
Число гуголплекс настолько нелепо велико, что его невозможно записать в формате записи чисел. Следовательно, число остается концепцией, поскольку оно бесполезно в математике для основных вычислений.
Примеры вопросов
Вопрос 1. Какое число в мире является мировым рекордом Гиннесса?
Ответ:
Число Грэма занесено в Книгу рекордов Гиннеса как самое большое конкретное целое число, использованное в опубликованном математическом доказательстве.


