Внедрение математики в биологию вызвало рождение этой науки: Разгадайте кроссворд «История биологии». кроссворд 1.Ткань и одновременно второе имя великого французского… |

Содержание

Тема 1.1. Краткая история развития биологии (Страницы 4,5,6,7,8,9)

1. Дайте определение понятия.

Современная биология – это совокупность естественных наук, изучающих жизнь как особую форму существования материи.

2. Заполните таблицу «Вклад ученых в развитие биологии».

3. Назовите ученых, которые внесли существенный вклад в развитие генетики.

ОТВЕТ: Г. Мендель, Г. де Фриз, Т. Морган, Дж. Уотсон и Ф. Крик.

4. Заполните таблицу «Связь биологии с другими науками».

ОТВЕТ: Сохранение природы, предотвращение экологической катастрофы, создание биологически активных веществ и лекарственных препаратов для лечения смертельных болезней и наследственных болезней, осуществление селекции на клеточном уровне и др.

6. Напишите, что изучают следующие науки.

Ботаника – растения.
Зоология – животных.
Ихтиология – рыб.
Энтомология – насекомых.
Систематика – многообразие живых организмов.

7. Какие естественные науки, составляющие биологию, возникли в конце XX в.?

ОТВЕТ: Биотехнология, генная инженерия

8. Разгадайте кроссворд «История биологии».

1. Ткань и одновременно второе имя великого французского ученого.
2. Вместе с коллегами он открыл структуру ДНК.
3. Он называл человека общественным животным, наделенным разумом.
4. Он создал учение об условных рефлексах.
5. Внедрение математики в биологию вызвало рождение этой науки.
6. Его труды определили появление иммунологии.
7. Наука о поведении.
8. Он вошел в историю как основатель эмбриологии.
9. Для обозначения видов он ввел двойную номенклатуру.
10. Труды Галена заложили фундамент этой науки.
11. Основоположник генетики.
12. Наука о пауках.
13. Создал учение о факторах эволюции.
14. В этой стране зародилась палеонтология.
15. В 9 в. он жил и работал в Азии.

9. Используя дополнительные источники информации, определите, что изучают:

Бриология – наука о мхах.
Микология – наука о грибах.
Палеоботаника – наука об ископаемых растениях.
Альгология – наука о водорослях.

10. Составьте самостоятельно названия наук:

Териология — раздел зоологии, изучающий млекопитающих;
Анатомия — наука о человеке;
Лихенология — наука, изучающая лишайники;
Гистология — раздел морфологии, изучающий ткани многоклеточных животных.

11. Познавательная задача.

Дендрология — раздел ботаники, изучающий древесные растения. Раздел дендрологии, который реконструирует климатические условия прошлого по годичным кольцам, называется дендроклиматологией. Попробуйте дать название научной дисциплине, задача которой — датировка исторических событий и природных явлений путем анализа годичных колец древесины.

Ответ: Дендрохронология.

Имя: Андреас, Жорж, Роберт, Александр, Клавдий, Карл, Уильям, Иван, Грегор, Теодор.
Фамилия: Кювье, Гален, Мендель, Везалий, Гарвей, Сеченов, Флеминг, Кох, Шванн, Линней.
Время жизни: II в. до н. э., XIX в., XVI-XVII вв. , XVIII-XIX вв., XVI в., XIX-XX вв., XIX в., XVIII в., XIX-XX вв., XIX-XX вв.
Страна: Англия, Италия, Германия, Древнеримская империя, Россия, Швеция, Англия, Германия, Франция, Австрия.

13. Сформулируйте и запишите основные идеи § 1.1.

ОТВЕТ:

Современная биология – это совокупность естественных наук, изучающих жизнь как особую форму существования материи. Наука уходит корнями в древность. Большую роль с становлении биологии как науки сыграли следующие выдающиеся ученые
Аристотель, Клавдий Гален, Уильям Гарвей, Карл Линней, Карл Бэр, Жан Батист Ламарк, Жорж Кювье, Т. Шванн и М. Шлейден, Чарлз Дарвин, Г. Мендель, И. Мечников и Л. Пастер, И. Павлов, В. И. Вернадский, Дж. Уотсон и Ф. Крик и многие другие. Эти великие люди жили в разное время (от 2 века до н. э. до наших дней) и сделали открытия, важные для существования человечества.
Сегодня биология представляет собой совокупность наук.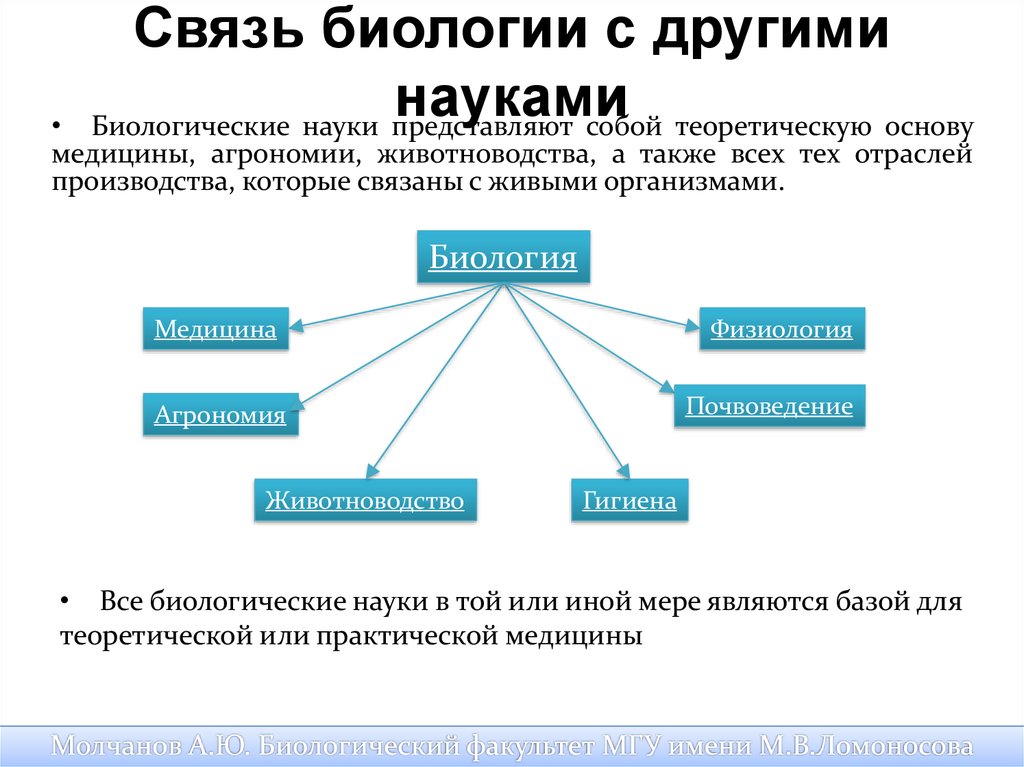 Она разделяется на комплексные науки: ботанику, зоологию, анатомию и физиологию. Затем, сформировались более узкие дисциплины, такие как арахнология, ихтиология, эмбриология, эволюция, генетика и др. В 20 веке на границе смежных дисциплин возникли биохимия, биофизика, биогеография. В конце столетия появились молекулярная биология, биотехнология и клеточная, генная инженерия. Достижения этих наук открывают широкие перспективы для будущего человечества.

Сегодня биология – это производительная сила, по развитию которой можно судить об общем уровне развития человечества.

Оглавление

Тренировочные задания к теме «Организм» — стр. 175-190Тема 1.2. Сущность жизни и свойства живого — стр. 10-12

Сохраните или поделитесь с одноклассниками:

Читать «Биология. Общая биология. Базовый уровень. 10 класс» — Сивоглазов Владислав Иванович, Агафонова Инна Борисовна, Захарова Екатерина Тимофеевна — Страница 2

Каких учёных-биологов вы знаете?

Современная биология уходит корнями в глубокую древность, мы находим её истоки в цивилизациях прошлых тысячелетий: в Древнем Египте, Древней Греции.

Первым учёным, создавшим научную медицинскую школу, был древнегреческий врач Гиппократ (ок. 460 – ок. 370 до н. э.). Он считал, что у каждой болезни есть естественные причины и их можно узнать, изучая строение и жизнедеятельность человеческого организма. С древних времён и по сей день врачи торжественно произносят клятву Гиппократа, обещая хранить врачебную тайну и ни при каких обстоятельствах не оставлять больного без медицинской помощи.

Великий энциклопедист древности Аристотель (384–322 до н. э.) стал одним из основателей биологии как науки, впервые обобщив биологические знания, накопленные до него человечеством. Он разработал систематику животных, определив в ней место и человеку, которого он называл «общественным животным, наделённым разумом». Многие труды Аристотеля были посвящены происхождению жизни.

Древнеримский учёный и врач Клавдий Гален (ок. 130 – ок. 200), изучая строение млекопитающих, заложил основы анатомии человека. В течение следующих пятнадцати веков его труды были основным источником знаний по анатомии.

В Средние века в Европе воцарился период застоя во всех областях знаний. В это время традиции античных авторов нашли своё продолжение в странах Передней и Средней Азии, где жили и творили такие выдающиеся учёные, как Абу Али Ибн Сина (Авиценна) (ок. 980–1037) и Абу Рейхан Мухаммед ибн Ахмет аль-Бируни (973 – ок. 1050). От того времени в современной анатомической номенклатуре сохранилось множество арабских терминов.

Наступление эпохи Возрождения ознаменовало начало нового периода в развитии биологии.

Один из выдающихся людей этой эпохи – Леонардо да Винчи (1452–1519) – описал многие растения, изучал строение человеческого тела, деятельность сердца и зрительную функцию.

После того как был снят церковный запрет на вскрытие человеческого тела, блестящих успехов достигла анатомия человека, что получило отражение в классическом труде Андреаса Везалия (1514–1564) «Строение человеческого тела» (рис. 1). Величайшее научное достижение – открытие кровообращения – совершил в XVII в. английский врач и биолог Уильям Гарвей (1578–1657).

Новую эру в развитии биологии ознаменовало изобретение в конце XVI в. микроскопа. Уже в середине XVII в. была открыта клетка, а позднее обнаружен мир микроскопических существ – простейших и бактерий, изучено развитие насекомых и принципиальное строение сперматозоидов.

В XVIII в. шведский натуралист Карл Линней (1707–1778) предложил систему классификации живой природы и ввёл бинарную (двойную) номенклатуру для наименования видов.

Карл Эрнст Бэр (Карл Максимович Бэр) (1792–1876), профессор Петербургской медико-хирургической академии, изучая внутриутробное развитие, установил, что зародыши всех животных на ранних этапах развития схожи, сформулировал закон зародышевого сходства и вошёл в историю науки как основатель эмбриологии.

Первым биологом, который попытался создать стройную и целостную теорию эволюции живого мира, стал французский учёный Жан Батист Ламарк (1774–1829). Палеонтологию, науку об ископаемых животных и растениях, создал французский зоолог Жорж Кювье (1769–1832).

Огромную роль в понимании единства органического мира сыграла клеточная теория зоолога Теодора Шванна (1810–1882) и ботаника Маттиаса Якоба Шлейдена (1804–1881).

Рис. 1. Титульный лист книги А. Везалия «Строение человеческого тела», напечатанной Иоганном Опорином в 1543 г.

Крупнейшим достижением XIX в. стало эволюционное учение Чарлза Роберта Дарвина (1809–1882), которое имело определяющее значение в формировании современной естественно-научной картины мира (рис. 2).

Основоположником генетики, науки о наследственности и изменчивости, стал Грегор Иоганн Мендель (1822–1884), работы которого настолько опередили своё время, что были не поняты современниками и открыты заново спустя 35 лет.

Одним из основателей современной микробиологии стал немецкий учёный Роберт Кох (1843–1910), а труды Луи Пастера (1822–1895) и Ильи Ильича Мечникова (1845–1916) определили появление иммунологии.

Развитие физиологии связано с именами великих российских учёных Ивана Михайловича Сеченова (1829–1905), заложившего основы изучения высшей нервной деятельности, и Ивана Петровича Павлова (1849–1936), создавшего учение об условных рефлексах.

XX в. ознаменовался бурным развитием биологии. Мутационная теория Гуго де Фриза (1848–1935), хромосомная теория наследственности Томаса Ханта Моргана (1866–1945), учение о факторах эволюции Ивана Ивановича Шмальгаузена (1884–1963), учение о биосфере Владимира Ивановича Вернадского (1863–1945), открытие антибиотиков Александром Флемингом (1881–1955), установление структуры ДНК Джеймсом Уотсоном (р. 1928) и Фрэнсисом Криком (1916–2004) – невозможно перечислить всех тех, кто своим самоотверженным трудом создавал современную биологию, которая в настоящее время является одной из наиболее бурно развивающихся областей человеческого знания.

Система биологических наук. Современная биология – это совокупность естественных наук, изучающих жизнь как особую форму существования материи. Одними из первых в биологии сложились комплексные науки: зоология, ботаника, анатомия и физиология. Позднее внутри них сформировались более узкие дисциплины, например внутри зоологии появилась ихтиология (наука о рыбах), энтомология (о насекомых), арахнология (о пауках) и т. д. Многообразие организмов изучает систематика, историю живого мира – палеонтология. Различные свойства живого являются предметом исследования таких наук, как генетика (закономерности изменчивости и наследственности), этология (поведение), эмбриология (индивидуальное развитие), эволюционное учение (историческое развитие).

Рис. 2. Титульная страница книги Ч. Дарвина «Происхождение видов путём естественного отбора, или Сохранение благоприятствуемых пород в борьбе за жизнь» (издание 1859 г.)

На рубеже XX и XXI вв. с огромной скоростью начала развиваться биотехнология – направление, которому несомненно принадлежит будущее. Последние достижения в этой области открывают широкие перспективы для создания биологически активных веществ и новых лекарственных препаратов, для лечения наследственных заболеваний и осуществления селекции на клеточном уровне.

В настоящее время биология стала реальной производительной силой, по развитию которой можно судить об общем уровне развития человеческого общества.

Вопросы для повторения и задания

1. Расскажите о вкладе в развитие биологии древнегреческих и древнеримских философов и врачей.

2. Охарактеризуйте особенности воззрений на живую природу в Средние века, эпоху Возрождения.

3. Используя знания, полученные на уроках истории, объясните, почему в Средние века в Европе наступил период застоя во всех областях знаний.

4. Какое изобретение XVII в. дало возможность открыть и описать клетку?

5. Каково значение для биологической науки работ Л. Пастера и И. И. Мечникова?

6. Перечислите основные открытия, сделанные в биологии в XX в.

7. Назовите известные вам естественные науки, составляющие биологию. Какие из них возникли в конце XX в.?

Система биологических наук. Современная биология – это совокупность естественных наук, изучающих жизнь как особую форму существования материи

Поделись

Современная биология – это совокупность естественных наук, изучающих жизнь как особую форму существования материи. Одними из первых в биологии сложились комплексные науки: зоология, ботаника, анатомия и физиология. Позднее внутри них сформировались более узкие дисциплины, например внутри зоологии появилась ихтиология (наука о рыбах), энтомология (о насекомых), арахнология (о пауках) и т. д. Многообразие организмов изучает систематика, историю живого мира – палеонтология. Различные свойства живого являются предметом исследования таких наук, как генетика (закономерности изменчивости и наследственности), этология (поведение), эмбриология (индивидуальное развитие), эволюционное учение (историческое развитие).

В середине XX в. в биологию начали активно проникать методы и идеи других естественных наук. На границах смежных дисциплин возникали новые биологические направления: биохимия, биофизика, биогеография, молекулярная биология, космическая биология и многие другие. Широкое внедрение математики в биологию вызвало рождение биометрии. Успехи экологии, а также всё более актуальные проблемы охраны природы способствовали развитию экологического подхода в большинстве отраслей биологии. На рубеже XX и XXI вв. с огромной скоростью начала развиваться биотехнология – направление, которому несомненно принадлежит будущее. Последние достижения в этой области открывают широкие перспективы для создания биологически активных веществ и новых лекарственных препаратов, для лечения наследственных заболеваний и осуществления селекции на клеточном уровне. В настоящее время биология стала реальной производительной силой, по развитию которой можно судить об общем уровне развития человеческого общества.

Вопросы для повторения и задания

1. Расскажите о вкладе в развитие биологии древнегреческих и древнеримских философов и врачей.

2. Охарактеризуйте особенности воззрений на живую природу в Средние века, эпоху Возрождения.

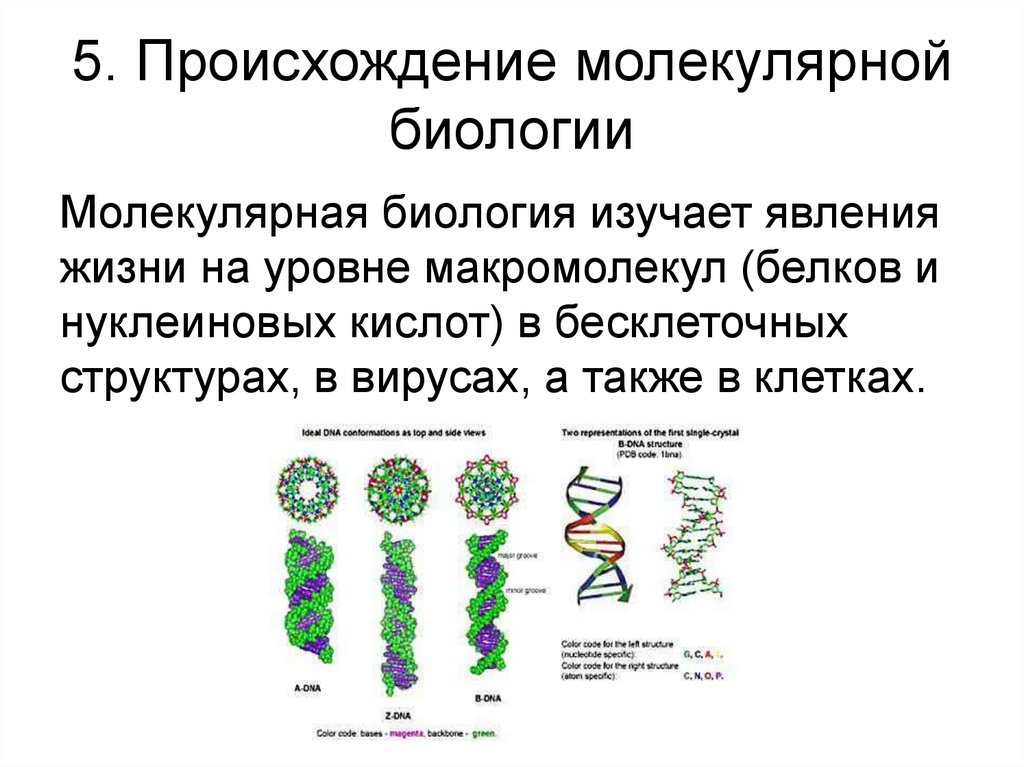
4. Какое изобретение XVII в. дало возможность открыть и описать клетку?

5. Каково значение для биологической науки работ Л. Пастера и И. И. Мечникова?

6. Перечислите основные открытия, сделанные в биологии в XX в.

7. Назовите известные вам естественные науки, составляющие биологию. Какие из них возникли в конце XX в.?

Подумайте! Выполните!

1. Проанализируйте изменения, произошедшие в науке в XVII–XVIII вв. Какие возможности они открыли перед учёными?

2. Как вы понимаете выражение «прикладная биология»?

3. Решение каких проблем человечества зависит от уровня биологических знаний?

4. Проанализируйте материал параграфа. Составьте хронологическую таблицу крупных достижений в области биологии. Какие страны в какие временные периоды были основными «поставщиками» новых идей и открытий? Сделайте вывод о связи между развитием науки и другими характеристиками государства и общества.

5. Приведите примеры современных дисциплин, возникших на стыке биологии и других наук, не упомянутые в параграфе. Что является предметом их изучения? Попробуйте предположить, какие разделы биологии могут возникнуть в будущем.

6. Обобщите информацию о системе биологических наук и представьте её в виде сложной иерархической схемы. Сравните схему, созданную вами, с результатами, которые получились у ваших одноклассников. Одинаковы ли ваши схемы? Если нет, объясните, в чём их принципиальные отличия.

7. Оцените роль биологических знаний в формировании мировоззрения современного человека. Составьте 10–15 тезисов, раскрывающих значимость биологической информации в жизни каждого.

8. Организационный проект. Выберите важное событие в истории биологии, годовщина которого приходится на текущий или следующий год. Разработайте программу вечера (конкурса, викторины), посвящённого этому событию.

Работа с компьютером

Обратитесь к электронному приложению. Изучите материал и выполните задания.

Повторите и вспомните!

Ботаника

В настоящее время ботаническая наука разделилась на ряд самостоятельных, но одновременно взаимосвязанных дисциплин. Морфология в широком смысле слова – это наука о строении растений, в узком смысле – наука о внешнем их строении. Анатомия исследует внутреннее строение растений. Из анатомии растений выделилась цитология, изучающая строение клетки. С изобретением электронного микроскопа возможности цитологических исследований значительно расширились. Особое значение приобрела эмбриология растений, изучающая ранние стадии развития растительных организмов. Физиология растений исследует процессы, происходящие внутри растительного организма. Палеоботаника изучает ископаемые остатки растений, что позволяет восстановить историю растительного мира. Геоботаника – наука о растительном покрове Земли, распространении и закономерностях размещения растительных сообществ. Часто в состав геоботаники включают географию растений. В настоящее время активно развиваются прикладные отрасли ботаники: растениеводство, лесное хозяйство, фармакология и парфюмерная промышленность. Велика роль ботаники в увеличении продуктивности культурных растений, в решении мировой продовольственной проблемы. На первый план выходят такие задачи, как рациональное использование и сохранение растительного мира, защита растений от неблагоприятных факторов

Зоология

Зоология представляет собой сложную науку, состоящую из множества научных дисциплин. Одни из них изучают отдельные группы животных, другие исследуют их строение, развитие, жизнедеятельность. К первой группе зоологических дисциплин относятся такие науки, как, например, энтомология – наука, изучающая насекомых, арахнология – наука о пауках, малакология – наука о моллюсках, герпетология – наука о земноводных и пресмыкающихся и др. Причём все эти науки объединяются в два раздела: зоология позвоночных, изучающая всего один тип – хордовых, и зоология беспозвоночных, исследующая все остальные типы животных. Такое разделение в зоологии возникло ещё во времена Аристотеля и утвердилось при жизни Жана Батиста Ламарка. Вторая группа зоологических дисциплин не менее разнообразна. Морфология и анатомия изучают внешнее и внутреннее строение животных, гистология исследует ткани, а объектом цитологии являются отдельные клетки. Физиология изучает жизнедеятельность животных. Эмбриология исследует индивидуальное развитие. Этология – это наука о поведении животных. Палеозоология – наука об ископаемых животных, она изучает их строение, геологическое распространение, историческое развитие, происхождение, взаимоотношения с современными организмами. В середине XX в. в зоологию начали активно проникать методы и идеи других естественных наук. На границах смежных дисциплин возникали новые биологические направления, например биохимия животных изучает химические процессы, протекающие в животном организме. Многие современные науки, такие как генетика, молекулярная биология, экология, решают свои актуальные задачи, используя для исследования животных. Тесно связана с практической деятельностью человека прикладная зоология, которая включает сельскохозяйственную, лесную, медицинскую зоологию, паразитологию и другие разделы.

Науки о человеке

Зачатки научных знаний о человеке возникли в недрах античной философии. Постепенно, в течение тысячелетий, накопленные знания о различных сторонах человеческого существования складывались в целостную систему общественных, гуманитарных, естественных и технических наук. Среди них одно из самых древних и почётных мест по праву занимает медицина.

Медицина – область науки и практическая деятельность, направленная на сохранение и укрепление здоровья. В медицине выделяют теоретическую и практическую, или клиническую, медицину. Теоретическая медицина изучает организм человека, его строение и работу в норме и при патологиях, заболевания и нарушения состояния, методы их диагностики, коррекции и лечения с теоретической точки зрения. Практическая медицина (медицинская практика) – это применение всех накопленных медицинской наукой знаний для лечения и профилактики заболеваний и патологических состояний человеческого организма.

Анатомия – это наука о строении организма, его систем и органов. Анатомия рассматривает строение тела человека в разные периоды жизни, начиная с эмбрионального развития и до старческого возраста, изучает половые и индивидуальные особенности организма.

Физиология – это наука о функциях организма, его органов и систем, о процессах, протекающих в организме, и о способах их регуляции.

Психология изучает поведение человека, закономерности и механизмы психических процессов.

Гигиена – это один из наиболее древних разделов медицины. Она изучает влияние окружающей среды, условий жизни и труда на организм человека.

https://bio.wikireading.ru/18097

План.

Зарождение научной биологии.

Биология в конце XVIII — первой половины ХIХ в.

Дарвиновская революция.

Особенности биологии XX в.

Заключение

Список литературы.

Биология (от греч. bios — жизнь и logos — учение) — это совокупность наук о живой природе. Об огромном многообразии вымерших и ныне населяющих Землю живых существ, их строении и функциях, происхождении, распространении и развитии, связях друг с другом и с неживой природой. Классическая биология — это биология по преимуществу наблюдательная. В классической биологии эксперимент еще не рассматривался как важный метод эмпирического познания органических объектов.

Таблица по биологии краткая история развития. История развития биологии

Задумывались ли вы о жизни и смерти? Наверное, каждый мыслящий человек рано или поздно это делает. Чаще других думают о жизни ученые-биологи, ведь биология — это и есть наука о жизни, а следовательно, и о смерти. На этом уроке речь пойдет о развитии биологии. Вы познакомитесь с достижениями этой комплексной науки и учеными, которые внесли большой вклад в её развитие за последние две с половиной тысячи лет. Краткий обзор истории биологии включает работы Гиппократа, Аристотеля, Теофраста, Леонардо да Винчи, Антони ван Левенгука, Карла Максимовича Бэра, Жана Батиста Ламарка и великого Чарльза Дарвина, автора основной теории современной биологии — теории эволюции.

Рис. 1. 1. Представители царства Архебактерии, открытые в ХХ веке ()

Эволюционная биология
изучает происхождение живых организмов. В девятнадцатом веке автор теории эволюции, Чарльз Дарвин (рис. 2), начинал свою работу как учёный натуралист: он путешествовал и собирал коллекции животных и растений. Результатом его работы стало создание теории эволюции.

В двадцатом веке соединение идей генетики и теории эволюции (дарвинизма) привело к возникновению синтетической теории эволюции. В основе её лежат труды и идеи Чарльза Дарвина.

Рис. 2. Ч. Дарвин

Физико-химическая биология
исследует строение живых объектов при помощи физических и химических методов. Это быстроразвивающееся направление, которое появилось в конце двадцатого века. К ней относятся два основных направления: биохимия и биофизика, которые изучают соответственно химию и физику жизни.

Таким образом, мы рассмотрели основные направления биологии.

Поговорим теперь об ученых, которые сыграли существенную роль в развитии биологии.

(рис. 3) дал первое подробное описание строения организма человека и животных, указал на роль среды и наследственности в развитии болезней, его называют основоположником, или «отцом» медицины.

Рис. 3. Гиппократ

(рис. 4) первым систематизировал природные объекты и разделил их на 4 царства:

1. Неодушевлённый мир воды, земли и воздуха.

2. Растения

3. Животные

Рис. 4. Аристотель

(рис. 5) — изучал растения, им описаны более 500 новых видов растений, даны сведения о строении и размножении многих из них. Написал трактат по психологии. Его называют основоположником, или «отцом» ботаники.

Рис. 5. Теофраст

Леонардо да Винчи
был ярчайшим представителем эпохи возрождения. Он изучал полёт птиц, рост растений, способы соединения костей в суставах, работу сердца и зрительную функцию глаза, а также обратил внимание на сходство костей человека и животных (рис. 6).

Рис. 6. Рисунки Леонардо да Винчи (XV век)

Антони ван Левенгук
(рис. 7) в семнадцатом веке открыл при помощи микроскопа микроорганизмы.

Рис. 7. А. ван Левенгук

Карл Линней
(рис. 8) предложил в XVIII веке наиболее удачную классификацию живых организмов. В шестнадцатом веке, благодаря Великим географическим открытиям, в Европу хлынуло множество чужеземных животных и растений. Возникла потребность в классификации живых организмов. Система Линнея была признана наиболее удачной, и многими её элементами (бинарными названиями), мы пользуемся до сих пор.

Рис. 8. К. Линней

С середины девятнадцатого века биология стала стремительно развиваться благодаря новым идеям (эволюционизм) и методам исследования (микроскопия, биохимия), и это развитие продолжается до сих пор.

Карл Максимович Бэр
(рис. 9) сформулировал основные положения теории гомологичных органов и законы зародышевого сходства, заложившие научные основы эмбриологии.

Рис. 9. К. Бэр

В 1808 году, в работе «Философия зоологии» Жан Батист Ламарк (рис. 10) поставил вопрос о причинах и механизмах эволюционных преобразований и изложил первую по времени теорию эволюции органического мира.

Рис. 10. Ж.-Б. Ламарк

Зоологом Теодором Шванном
и ботаником Маттиасом Шлейденом
(рис. 11) была предложенная клеточная теория, которая научно подтвердила единство живого мира и послужила одной из предпосылок к созданию теории эволюции Чарльзом Дарвином.

Рис. 11. Т. Шванн и М. Шлейден

Чарльз Дарвин
на основе многочисленных наблюдений создал и опубликовал труд о происхождении видов путём естественного отбора, в котором сформулировал основные идеи теории эволюции, предложил возможные механизмы эволюции и описал пути эволюционных преобразований организмов.

В конце девятнадцатого века микробиология сформировалась в качестве самостоятельной науки благодаря работам Луи Пастера, Роберта Коха, Ильи Ильича Мечникова
.

Рис. 11. Л. Пастер, И. Мечников, П. Эрлих

Кроме этого, работы Ильи Мечникова, Луи Пастера и Пауля Эриха
(рис. 11) послужили началом для образования новой дисциплины — иммунологии.

Двадцатый век начался с повторного открытия законов наследования признаков (законов Менделя
), что ознаменовало появление науки генетики. В 40-50-е годы двадцатого века в биологию стали проникать идеи химии и физики, что значительно её обогатило. В середине двадцатого века благодаря открытию структуры молекулы ДНК (рис. 12), биология вышла на новый молекулярный уровень.

Рис. 12. Структура ДНК

В двадцатом веке оформилось новое прикладное направление биологии — биотехнология. Если говорить о перспективах развития этого направления, то оно, по прогнозам ученых, будет стремительно развиваться в XXI веке.

Антони ван Левенгук

В семнадцатом веке в Голландии жил торговец сукном, которого звали Антони ван Левенгук, у него было увлечение — он шлифовал линзы, его двояковыпуклые линзы давали увеличение в 200-270 раз.

Рис. 13. Микроскоп А. ван Левенгука

С помощью увеличительных стёкол и сконструированного им микроскопа (рис. 13), он рассматривал различные предметы: биологические жидкости, волосы, кожу, насекомых.

Рис. 14. Рисунки А. ван Левенгука — объекты, увиденные под микроскопом

Как гласит легенда, однажды он решил при помощи своих увеличительных стёкол взглянуть на каплю дождевой воды. Там он увидел огромное количество мельчайших организмов. Он стал рассматривать другие жидкости, где наблюдал похожую картину — множество мельчайших организмов, он назвал их «зверюшки» или «анималюсы» (рис. 14).

Первыми микроорганизмами, обнаруженными ван Левенгуком, были инфузории, впоследствии он увидел бактерий, которых обнаружил в зубном налёте.

Бактерии имели различную морфологию: это были извитые формы, кокки, стрептококки. Кроме того, что Левенгук описал эритроциты человека и рыб, движение крови в капиллярах.

Карл Линней

Рис. 15. К. Линней

Карл Линней (рис. 15) — шведский учёный-естествоиспытатель, которого в Швеции ценят как краеведа и путешественника, который открыл для шведов их собственную страну, изучил своеобразие её провинций и увидел, как одна провинция может помочь другой.

Ценность для шведов представляет не только его работа по флоре и фауне Швеции, но и описание им собственных путешествий. Эти дневниковые записи, полные конкретики, богатые противопоставлениями, изложенные ясным языком, до сих пор переиздаются и читаются.

Линней — это один из тех деятелей науки и культуры, с именами которых связано становление современного литературного шведского языка. А для биологов Карл Линней интересен как классификатор живых организмов — ученый-систематик. Всю жизнь он посвятил систематизации живой и неживой природы. Основной труд К. Линнея — «Система природы», в нем он описал огромное, количество видов растений и животных (рис. 16, 17).

Рис. 16. Страницы «Системы природы» Карла Линнея

Историческое значение работы Карла Линней состоит в том, что он выдвинул принцип иерархичности систематических категорий (таксонов).

Рис. 17. Перечень таксонов Линнея

Виды объединяются в Роды, Роды в семейства, Семейства в Отряды, Отряды в Классы. Он впервые выделил классы млекопитающих и птиц, объединил человека и обезьян в Отряд приматов, отметив их несомненное сходство.

Луи Пастер

Человек, который своими работами положил начало современной микробиологии, был выдающийся французский исследователь Луи Пастер. Он открыл бескислородную форму жизнедеятельности — процесс брожения. До Пастера брожение считалось чисто химическим процессом, который возникает вследствие того, что химическое вещество — белок или фермент — передаёт своё «активное начало» молекулам субстрата. Так, в результате спиртового брожения, из сахара образуется спирт.

Пастер показал, что при брожении важную роль играют микроорганизмы, то есть продукты брожения являются продуктами жизнедеятельности микроорганизмов.

Луи Пастер обосновал роль микробов как инфекционных агентов в развитии болезней, разработал метод вакцинации, создал вакцины против сибирской язвы и бешенства, методы стерилизации и дезинфекции.

Список литературы

А.А. Каменский, Е.А. Криксунов, В.В. Пасечник. Общая биология, 10-11 класс. — М.: Дрофа, 2005. ().
Д.К. Беляев. Биология 10-11 класс. Общая биология. Базовый уровень. — 11-е издание, стереотипное. — М.: Просвещение, 2012. — 304 с. ().
В.Б. Захаров, С.Г. Мамонтов, Н.И. Сонин, Е.Т. Захарова. Биология 11 класс. Общая биология. Профильный уровень. — 5-е издание, стереотипное. — М.: Дрофа, 2010. — 388 с. ().
В.И. Сивоглазов, И.Б. Агафонова, Е.Т. Захарова. Биология 10-11 класс. Общая биология. Базовый уровень. — 6-е издание, дополненное. — М.: Дрофа, 2010. — 384 с. ().

Википедия ().
Bio-cat.ru ().
Ishpssb.org ().

Домашнее задание

Какое из направлений биологии самое древнее?
Какие науки возникают на пересечении биологии с другими естественными науками?
Какие направления биологии активно развиваются сейчас?
Как изменило повседневную жизнь людей открытие А. ван Левенгуком микроорганизмов и дальнейшее развитие микробиологии?
В чем значение работ Ч. Дарвина?
Какие понятия ввел в науку К. Линней?
Кто из ученых, описанных в уроке, по вашему мнению, внес наибольший вклад в науку и больше других повлиял на нашу жизнь?
Расскажите друзьям и родным об истории становления и развития биологии. Как наука биология повлияла на жизнь современного человека?

1. Дайте определение понятия.

Современная биология

– это совокупность естественных наук, изучающих жизнь как особую форму существования материи.

2. Заполните таблицу.

Вклад ученых в развитие биологии

3. Назовите ученых, которые внесли существенный вклад в развитие генетики.

Г. Мендель, Г. де Фриз, Т. Морган, Дж. Уотсон и Ф. Крик.

4. Заполните таблицу.

Связь биологии с другими науками

5. Объясните, почему с развитием биологии связывают решение многих современных проблем человечества. Какие проблемы, по вашему мнению, в первую очередь можно решить с помощью биологии?

Сохранение природы, предотвращение экологической катастрофы, создание биологически активных веществ и лекарственных препаратов для лечения смертельных болезней и наследственных болезней, осуществление селекции на клеточном уровне и др.

6. Напишите, что изучают следующие науки.

Ботаника

– растения.

Зоология

– животных.

Ихтиология

– рыб.

Энтомология

– насекомых.

Систематика

– многообразие живых организмов.

7. Какие естественные науки, составляющие биологию, возникли в конце XX в.?

Биотехнология, генная инженерия

8. Разгадайте кроссворд «История биологии».

9. Используя дополнительные источники информации, определите, что изучают:

Бриология

– наука о мхах.

Микология

– наука о грибах.

Палеоботаника

– наука об ископаемых растениях.

Альгология

– наука о водорослях.

10. Составьте самостоятельно названия наук:

Териология

— раздел зоологии, изучающий млекопитающих;

Анатомия

— наука о человеке;

Лихенология

— наука, изучающая лишайники;

Гистология

— раздел морфологии, изучающий ткани многоклеточных животных.

11. Познавательная задача.

Дендрология

— раздел ботаники, изучающий древесные растения. Раздел дендрологии, который реконструирует климатические условия прошлого по годичным кольцам, называется дендроклиматологией. Попробуйте дать название научной дисциплине, задача которой — датировка исторических событий и природных явлений путем анализа годичных колец древесины.

Ответ:

Дендрохронология.

12. Перед вами четыре блока данных: «Имя», «Фамилия», «Время жизни», «Страна». Выбирая по одному элементу из каждого блока, заполните строки в таблице, располагая в хронологическом порядке информацию об учёных, внёсших вклад в развитие биологии.

Имя
: Андреас, Жорж, Роберт, Александр, Клавдий, Карл, Уильям, Иван, Грегор, Теодор.

Фамилия
: Кювье, Гален, Мендель, Везалий, Гарвей, Сеченов, Флеминг, Кох, Шванн, Линней.

Время жизни
: II в. до н. э., XIX в., XVI-XVII вв., XVIII-XIX вв., XVI в., XIX-XX вв., XIX в., XVIII в., XIX-XX вв., XIX-XX вв. Страна: Англия, Италия, Германия, Древнеримская империя, Россия, Швеция, Англия, Германия, Франция, Австрия.

13. Сформулируйте и запишите основные идеи § 1.1.

Современная биология – это совокупность естественных наук, изучающих жизнь как особую форму существования материи. Наука уходит корнями в древность. Большую роль с становлении биологии как науки сыграли следующие выдающиеся ученые

Аристотель, Клавдий Гален, Уильям Гарвей, Карл Линней, Карл Бэр, Жан Батист Ламарк, Жорж Кювье, Т. Шванн и М. Шлейден, Чарлз Дарвин, Г. Мендель, И. Мечников и Л. Пастер, И. Павлов, В. И. Вернадский, Дж. Уотсон и Ф. Крик и многие другие. Эти великие люди жили в разное время (от 2 века до н. э. до наших дней) и сделали открытия, важные для существования человечества.

Сегодня биология представляет собой совокупность наук. Она разделяется на комплексные науки: ботанику, зоологию, анатомию и физиологию. Затем, сформировались более узкие дисциплины, такие как арахнология, ихтиология, эмбриология, эволюция, генетика и др. В 20 веке на границе смежных дисциплин возникли биохимия, биофизика, биогеография. В конце столетия появились молекулярная биология, биотехнология и клеточная, генная инженерия. Достижения этих наук открывают широкие перспективы для будущего человечества.

Сегодня биология – это производительная сила, по развитию которой можно судить об общем уровне развития человечества.

Современная биология уходит корнями в глубокую древность, мы находим ее истоки в цивилизациях прошлых тысячелетий: в Древнем Египте, Древней Греции.

Первым ученым, создавшим научную медицинскую школу, был древнегреческий врач Гиппократ (ок. 460 — ок. 370 до н. э.). Он считал, что у каждой болезни есть естественные причины, и их можно узнать, изучая строение и жизнедеятельность человеческого организма. С древних времен и по сей день врачи торжественно произносят «клятву Гиппократа», обещая хранить врачебную тайну и ни при каких обстоятельствах не оставлять больного без медицинской помощи.

Великий энциклопедист древности Аристотель (384 — 322 до н. э.) стал одним из основателей биологии как науки, впервые обобщив биологические знания, накопленные до него человечеством. Он разработал систематику животных, определив в ней место и человеку, которого он называл «общественным животным, наделенным разумом». Многие труды Аристотеля были посвящены происхождению жизни.

Древнеримский ученый и врач Клавдий Гален (ок. 130 — ок. 200), изучая строение млекопитающих, заложил основы анатомии человека. В течение следующих пятнадцати веков его труды были основным источником знаний по анатомии.

В Средние века в Европе воцарился период застоя во всех областях знаний. В это время традиции античных авторов нашли свое продолжение в странах Передней и Средней Азии, где жили и творили такие выдающиеся ученые, как Абу Али Ибн Сина (Авиценна) (ок. 980-1037) и Абу Рейхан Мухаммед ибн Ахмет аль-Бируни (973—ок. 1050). От того времени в современной анатомической номенклатуре сохранилось множество арабских терминов.

Наступление эпохи Возрождения ознаменовало начало нового периода в развитии биологии.

Один из самых замечательных людей этой эпохи Леонардо да Винчи (1452-1519) описал многие растения, изучал строение человеческого тела, деятельность сердца и зрительную функции.

После того как был снят церковный запрет на вскрытие человеческого тела, блестящих успехов достигла анатомия человека, что получило отражение в классическом труде Андреаса Везалия (1514-1564) «О строении человеческого тела». Величайшее научное достижение — открытие кровообращения — совершил в XVII в. английский врач и биолог Уильям Гарвей (1578-1657).

В XVIII в. шведский натуралист Карл Линней (1707-1778) предложил систему классификации живой природы и ввел бинарную (двойную) номенклатуру для наименования видов.

Карл Эрнст Бэр (Карл Максимович Бэр) (1792-1876), профессор Петербургской медико-хирургической академии, изучая внутриутробное развитие, установил, что зародыши всех животных на ранних этапах развития схожи, сформулировал закон зародышевого сходства и вошел в историю науки как основатель эмбриологии.

Первым биологом, который попытался создать стройную и целостную теорию эволюции живого мира, стал французский ученый Жан Батист Ламарк (1774-1829). Палеонтологию, науку об ископаемых животных и растениях, создал французский зоолог Жорж Кювье (1769-1832).

Огромную роль в понимании единства органического мира сыграла клеточная теория зоолога Теодора Шванна (1810-1882) и ботаника Маттиаса Якоба Шлейдена (1804- 1881).

Крупнейшим достижением XIX в. стало эволюционное учение Чарлза Роберта Дарвина (1809-1882), которое имело определяющее значение в формировании современной естественнонаучной картины мира.

Основоположником генетики, науки о наследственности и изменчивости, стал Грегор Иоганн Мендель (1822-1884), работы которого настолько опередили свое время, что были не поняты современниками и открыты заново спустя 35 лет.

Одним из основателей современной микробиологии стал немецкий ученый Роберт Кох(1843-1910), а труды Луи Пастера (1822-1895) и Ильи Ильича Мечникова (1845-1916) определили появление иммунологии.

Развитие физиологии связано с именами великих российских ученых Ивана Михайловича Сеченова (1829-1905), заложившего основы изучения высшей нервной деятельности, и Ивана Петровича Павлова (1849- 1936), создавшего учение об условных рефлексах.

XX в. ознаменовался бурным развитием биологии. Мутационная теория Гуго де Фриза (1848-1935), хромосомная теория наследственности Томаса Ханта Моргана (1866-1945), учение о факторах эволюции Ивана Ивановича Шмальгаузена (1884-1963), учение о биосфере Владимира Ивановича Вернадского (1863-1945), открытие антибиотиков Александером Флемингом (1881 — 1955), установление структуры ДНК Джеймсом Уотсоном (р. 1928) и Фрэнсисом Криком (1916-2004) — невозможно перечислить всех тех, кто своим самоотверженным трудом создавал современную биологию, которая в настоящее время является одной из наиболее бурно развивающихся областей человеческого знания.

■ Система биологических наук.
Современная биология — это совокупность естественных наук, изучающих жизнь как особую форму существования материи. Одними из первых в биологии сложились комплексные науки: зоология, ботаника, анатомия и физиология. Позднее внутри них сформировались более узкие дисциплины, например внутри зоологии появилась ихтиология (наука о рыбах), энтомология (о насекомых), арахнология (о пауках) и т. д. Многообразие организмов изучает систематика, историю живого мира — палеонтология. Различные свойства живого являются предметом исследования таких наук, как генетика (закономерности изменчивости и наследственности), этология (поведение), эмбриология (индивидуальное развитие), эволюционное учение (историческое развитие).

На рубеже XX и XXI вв. с огромной скоростью начала развиваться биотехнология — направление, которому несомненно принадлежит будущее. Последние достижения в этой области открывают широкие перспективы для создания биологически активных веществ и новых лекарственных препаратов, для лечения наследственных заболеваний и осуществления селекции на клеточном уровне.

Вопросы для самоконтроля.

1. Расскажите о вкладе в развитие биологии древнегреческих и древнеримских философов и врачей.

2. Охарактеризуйте особенности воззрений на живую природу в Средние века, эпоху Возрождения.

3. Какое изобретение XVII в. дало возможность открыть и описать клетку?

4. Каково значение для биологической науки работ Л. Пастера и И. И. Мечникова?

5. Перечислите основные открытия, сделанные в биологии в XX в.

6. Назовите известные вам естественные науки, составляющие биологию. Какие из них возникли в конце XX в.?

Все хорошо знают, что биология — это наука о жизни. В настоящее время она представляет совокупность наук о живой природе. Биология изучает все проявления жизни: строение, функции, развитие и происхождение живых организмов, их взаимоотношения в природных сообществах со средой обитания и с другими живыми организмами.
С тех пор как человек стал осознавать свое отличие от животного мира, он начал изучать окружающий его мир. Сначала от этого зависела его жизнь. Первобытным людям необходимо было знать, какие живые организмы можно употреблять в пищу, использовать в качестве лекарств, для изготовления одежды и жилищ, а какие из них ядовиты или опасны.
С развитием цивилизации человек смог позволить себе такую роскошь, как занятие наукой в познавательных целях.
Исследования культуры древних народов показали, что они имели обширные знания о растениях, животных и широко их применяли в повседневной жизни.?

Современная биология — комплексная наука, для которой характерно взаимопроникновение идей и методов различных биологических дисциплин, а также других наук — прежде всего физики, химии и математики.

Основные направления развития современной биологии. В настоящее время условно можно выделить три направления в биологии.
Во-первых, это классическая биология. Ее представляют учёные-натуралисты, изучающие многообразие живой природы. Они объективно наблюдают и анализируют все, что происходит в живой природе, изучают живые организмы и классифицируют их. Неправильно думать, что в классической биологии все открытия уже сделаны. Во второй половине XX в. не только описано много новых видов, но и открыты крупные таксоны, вплоть до царств (Погонофоры) и даже надцарств (Архебактерии, или Археи). Эти открытия заставили ученых по-новому взглянуть на всю историю развития живой природы, Для настоящих ученых-натуралистов природа — это самоценность. Каждый уголок нашей планеты для них уникален. Именно поэтому они всегда среди тех, кто остро чувствует опасность для окружающей нас природы и активно выступает в ее защиту.
Второе направление — это эволюционная биология. В XIX в, автор теории естественного отбора Чарльз Дарвин начинал как обычный натуралист: он коллекционировал, наблюдал, описывал, путешествовал, раскрывая тайны живой природы. Однако основным результатом его работы, сделавшим его известным ученым, стала теория, объясняющая органическое разнообразие.

В настоящее время изучение эволюции живых организмов активно продолжается. Синтез генетики и эволюционной теории привел к созданию так называемой синтетической теории эволюции. Но и сейчас еще есть много нерешенных вопросов, ответы на которые ищут ученые-эволюционисты.

Созданная в начале XX в. нашим выдающимся биологом Александром Ивановичем Опариным первая научная теория происхождения жизни была чисто теоретической. В настоящее время активно ведутся экспериментальные исследования данной проблемы и благодаря применению передовых физико-химических методов уже сделаны важные открытия и можно ожидать новых интересных результатов.
Новые открытия позволили дополнить теорию антропогенеза. Но переход от животного мира к человеку и сейчас еще остается одной из самых больших загадок биологии.
Третье направление — физико-химическая биология, исследующая строение живых объектов при помощи современных физических и химических методов. Это быстро развивающееся направление биологии, важное как в теоретическом, так и в практическом отношении. Можно с уверенностью говорить, что в физико-химической биологии нас ждут новые открытия, которые позволят решить многие проблемы, стоящие перед человечеством,

Развитие биологии как науки. Современная биология уходит корнями в древность и связана с развитием цивилизации в странах Средиземноморья. Нам известны имена многих выдающихся ученых, внесших вклад в развитие биологии. Назовем лишь некоторых из них.

Гиппократ (460 — ок. 370 до н. э.) дал первое относительно подробное описание строения человека и животных, указал на роль среды и наследственности в возникновении болезней. Его считают основоположником медицины.
Аристотель (384—322 до н. э.) делил окружающий мир на четыре царства: неодушевленный мир земли, воды и воздуха; мир растений; мир животных и мир человека. Он описал многих животных, положил начало систематике. Б написанных им четырех биологических трактатах содержались практически все известные к тому времени сведения о животных. Заслуги Аристотеля настолько велики, что его считают основоположником зоологии.
Теофраст (372—287 до н. э.) изучал растения. Им описано более 500 видов растений, даны сведения о строении и размножении многих из них, введены в употребление многие ботанические термины. Его считают основоположником ботаники.
Гай Плиний Старший (23—79) собрал известные к тому времени сведения о живых организмах и написал 37 томов энциклопедии «Естественная история». Почти до средневековья эта энциклопедия была главным источником знаний о природе.

Клавдий Гален в своих научных исследованиях широко использовал вскрытия млекопитающих. Он первым сделал сравнительно-

анатомическое описание человека и обезьяны. Изучал центральную и периферическую нервную систему. Историки науки считают его последним великим биологом древности.
В средние века господствующей идеологией была религия. Подобно другим наукам, биология в этот период еще не выделилась в самостоятельную область и существовала в общем русле религиозно-философских взглядов. И хотя накопление знаний о живых организмах продолжалось, о биологии как науке в тот период можно говорить лишь условно.
Эпоха Возрождения является переходной от культуры средних веков к культуре нового времени. Коренные социально-экономические преобразования того времени сопровождались новыми открытиями в науке.
Самый известный ученый этой эпохи Леонардо да Винчи (1452— 1519) внес определенный вклад и в развитие биологии.

Он изучал полет птиц, описал многие растения, способы соединения костей в суставах, деятельность сердца и зрительную функцию глаза, сходство костей человека и животных.

Во второй половине XV в. естественнонаучные знания начинают быстро развиваться. Этому способствовали географические открытия, позволившие существенно расширить сведения о животных и растениях. Быстрое накопление научных знаний о живых организмах
вело к разделению биологии на отдельные науки.
В XVI—XVII вв. стали стремительно развиваться ботаника и зоология.
Изобретение микроскопа (начало XVII в.) позволило изучать микроскопическое строение растений и животных. Были открыты невидимые для невооруженного глаза микроскопически малые живые организмы — бактерии и простейшие.
Большой вклад в развитие биологии внес Карл Линней, предложивший систему классификации животных и растений.
Карл Максимович Бэр (1792—1876) в своих работах сформулировал основные положения теории гомологичных органов и закона зародышевого сходства, заложившие научные основы эмбриологии.

В 1808 г. в работе «Философия зоологии» Жан Батист Ламарк поставил вопрос о причинах и механизмах эволюционных преобразований и изложил первую по времени теорию эволюции.

Огромную роль в развитии биологии сыграла клеточная теория, которая научно подтвердила единство живого мира и послужила одной из предпосылок возникновения теории эволюции Чарлза Дарвина. Авторами клеточной теории считают зоолога Теодора Шванна (1818—1882) и ботаника Маттиаса Якоба Шлейдена (1804—1881).

На основе многочисленных наблюдений Ч. Дарвин опубликовал в 1859 г. свой основной труд «О происхождении видов путем естественного отбора или Сохранении благоприятствуемых пород в борьбе за жизнь». В нём он сформулировал основные положения теории эволюции, предложил механизмы эволюции и пути эволюционных преобразований организмов.

XX век начался с переоткрытия законов Грегора Менделя, что ознаменовало собой начало развития генетики как науки.
В 40—50-е годы XX в. в биологии стали широко использоваться идеи и методы физики, химии, математики, кибернетики и других наук, а в качестве объектов исследования — микроорганизмы. В результате возникли и стали бурно развиваться как самостоятельные науки биофизика, биохимия, молекулярная биология, радиационная биология, бионика и др. Исследования в космосе способствовали зарождению и развитию космической биологии.

В XX в. появилось направление прикладных исследований — биотехнология. Это направление, несомненно, будет стремительно развиваться и в XXI в. Более подробно об этом направлении развития биологии вы узнаете при изучении главы «Основы селекции и биотехнологии».

В настоящее время биологические знания используются во всех сферах человеческой деятельности: в промышленности и сельском хозяйстве, медицине и энергетике.
Чрезвычайно важное значение имеют экологические исследования. Мы, наконец, стали осознавать, что хрупкое равновесие, существующее на нашей маленькой планете, легко разрушить. Перед человечеством встала грандиозная задача — сохранение биосферы с целью поддержания условий существования и развития цивилизации. Без биологических знаний и специальных исследований решить ее невозможно. Таким образом, в настоящее время биология стала реальной производительной силой и рациональной научной основой отношений между человеком и природой.

1. Краткая история развития биологии. Биология. Общая биология. 10 класс. Базовый уровень

1. Краткая история развития биологии

Вспомните!

Какие достижения современной биологии вам известны?

Каких учёных-биологов вы знаете?

Наступление эпохи Возрождения ознаменовало начало нового периода в развитии биологии.

Рис. 1. Титульный лист книги А. Везалия «Строение человеческого тела», напечатанной Иоганном Опорином в 1543 г.

Вопросы для повторения и задания

1. Расскажите о вкладе в развитие биологии древнегреческих и древнеримских философов и врачей.

2. Охарактеризуйте особенности воззрений на живую природу в Средние века, эпоху Возрождения.

4. Какое изобретение XVII в. дало возможность открыть и описать клетку?

5. Каково значение для биологической науки работ Л. Пастера и И. И. Мечникова?

6. Перечислите основные открытия, сделанные в биологии в XX в.

7. Назовите известные вам естественные науки, составляющие биологию. Какие из них возникли в конце XX в.?

Подумайте! Выполните!

1. Проанализируйте изменения, произошедшие в науке в XVII–XVIII вв. Какие возможности они открыли перед учёными?

2. Как вы понимаете выражение «прикладная биология»?

3. Решение каких проблем человечества зависит от уровня биологических знаний?

Работа с компьютером

Обратитесь к электронному приложению. Изучите материал и выполните задания.

Повторите и вспомните!

Ботаника

В настоящее время ботаническая наука разделилась на ряд самостоятельных, но одновременно взаимосвязанных дисциплин.

Морфология в широком смысле слова – это наука о строении растений, в узком смысле – наука о внешнем их строении. Анатомия исследует внутреннее строение растений. Из анатомии растений выделилась цитология, изучающая строение клетки. С изобретением электронного микроскопа возможности цитологических исследований значительно расширились. Особое значение приобрела эмбриология растений, изучающая ранние стадии развития растительных организмов. Физиология растений исследует процессы, происходящие внутри растительного организма. Палеоботаника изучает ископаемые остатки растений, что позволяет восстановить историю растительного мира. Геоботаника – наука о растительном покрове Земли, распространении и закономерностях размещения растительных сообществ. Часто в состав геоботаники включают географию растений.

В настоящее время активно развиваются прикладные отрасли ботаники: растениеводство, лесное хозяйство, фармакология и парфюмерная промышленность. Велика роль ботаники в увеличении продуктивности культурных растений, в решении мировой продовольственной проблемы. На первый план выходят такие задачи, как рациональное использование и сохранение растительного мира, защита растений от неблагоприятных факторов.

Зоология

К первой группе зоологических дисциплин относятся такие науки, как, например, энтомология – наука, изучающая насекомых, арахнология – наука о пауках, малакология – наука о моллюсках, герпетология – наука о земноводных и пресмыкающихся и др. Причём все эти науки объединяются в два раздела: зоология позвоночных, изучающая всего один тип – хордовых, и зоология беспозвоночных, исследующая все остальные типы животных. Такое разделение в зоологии возникло ещё во времена Аристотеля и утвердилось при жизни Жана Батиста Ламарка.

Вторая группа зоологических дисциплин не менее разнообразна. Морфология и анатомия изучают внешнее и внутреннее строение животных, гистология исследует ткани, а объектом цитологии являются отдельные клетки. Физиология изучает жизнедеятельность животных. Эмбриология исследует индивидуальное развитие. Этология – это наука о поведении животных. Палеозоология – наука об ископаемых животных, она изучает их строение, геологическое распространение, историческое развитие, происхождение, взаимоотношения с современными организмами.

В середине XX в. в зоологию начали активно проникать методы и идеи других естественных наук. На границах смежных дисциплин возникали новые биологические направления, например биохимия животных изучает химические процессы, протекающие в животном организме.

Многие современные науки, такие как генетика, молекулярная биология, экология, решают свои актуальные задачи, используя для исследования животных. Тесно связана с практической деятельностью человека прикладная зоология, которая включает сельскохозяйственную, лесную, медицинскую зоологию, паразитологию и другие разделы.

Науки о человеке

Медицина – область науки и практическая деятельность, направленная на сохранение и укрепление здоровья. В медицине выделяют теоретическую и практическую, или клиническую, медицину. Теоретическая медицина изучает организм человека, его строение и работу в норме и при патологиях, заболевания и нарушения состояния, методы их диагностики, коррекции и лечения с теоретической точки зрения. Практическая медицина (медицинская практика) – это применение всех накопленных медицинской наукой знаний для лечения и профилактики заболеваний и патологических состояний человеческого организма.

Анатомия – это наука о строении организма, его систем и органов. Анатомия рассматривает строение тела человека в разные периоды жизни, начиная с эмбрионального развития и до старческого возраста, изучает половые и индивидуальные особенности организма.

Физиология – это наука о функциях организма, его органов и систем, о процессах, протекающих в организме, и о способах их регуляции.

Психология изучает поведение человека, закономерности и механизмы психических процессов.

Гигиена – это один из наиболее древних разделов медицины. Она изучает влияние окружающей среды, условий жизни и труда на организм человека.

Данный текст является ознакомительным фрагментом.

I. Краткая история приматологии

I. Краткая история приматологии
Если внимательно приглядеться к истории приматологии, можно обнаружить на протяжении нескольких столетий, включая XX в., недоуменные высказывания разных авторов по поводу какой-то странной недостаточности знаний о приматах. В 1760 г.

Краткая история прививок и вакцинаций

Краткая история прививок и вакцинаций
Научные основы вакцинации были заложены в XVIII—XIX столетиях. В Европе прививка в качестве защитной меры от оспы была впервые предложена леди Мэри Уортли Монтагью (Montagu). Эта женщина в 22-летнем возрасте перенесла жестокую оспу,

Краткая история евгенического движения

Краткая история евгенического движения
Успешное разведение растений и животных отмечает конец периода охоты и собирательства в эволюции человечества. Если говорить о письменных свидетельствах, то «Республику» Платона можно рассматривать как первый теоретический

1. ОПРЕДЕЛЕНИЕ, ОСНОВНЫЕ ПРОБЛЕМЫ И КРАТКАЯ ИСТОРИЯ МЕТОДА ССП

1. ОПРЕДЕЛЕНИЕ, ОСНОВНЫЕ ПРОБЛЕМЫ И КРАТКАЯ ИСТОРИЯ МЕТОДА ССП
1.1. Связанные с событиями потенциалы мозга
ССП представляют собой широкий класс электрофизиологических феноменов, которые специальными методами выделяются из «фоновой», или «сырой», электроэнцефалограммы

Краткая история метода ССП

Краткая история метода ССП
Связь электрической активности мозга с событиями в окружающей среде и поведении впервые была продемонстрирована и описана англичанином Р. Кейтоном (Richard Caton) в 1875–1887 гг. и независимо от него русским учёным В.Я. Данилевским в 1875 г. [Brazier, 1984].

История развития гомеопатии

История развития гомеопатии
Высшее и единственное назначение врача состоит в том, чтобы возвращать здоровье больному — излечивать его. Идеал лечения состоит в том, чтобы восстановить здоровье больного скоро, легко и прочно или устранить и совершенно уничтожить болезнь

4.2. Основные понятия биологии развития

4.2. Основные понятия биологии развития
В конце XX века зародилась новая междисциплинарная наука – биология развития, объединившая достижения эмбриологии, генетики, биохимии, цитологии и ставшая одним из ведущих направлений в познании «феномена жизни». Биологию развития

4.4. Теоретическое значение и проблемы биологии развития

4. 4. Теоретическое значение и проблемы биологии развития
Как уже отмечалось, проблема механизмов развития многоклеточного организма из оплодотворенной яйцеклетки является одной из ключевых проблем биологии. Биология развития в настоящее время находится на «переднем

Глава 1. КРАТКАЯ ИСТОРИЯ ЭКОЛОГИИ

Глава 1. КРАТКАЯ ИСТОРИЯ ЭКОЛОГИИ
Экология – это наука о связях, поддерживающих устойчивость жизни в окружающей среде. Жизнь – самое сложное явление в окружающем нас мире. Ее изучает множество наук, складывающихся в совокупности в дифференцированную и многоплановую

Краткая анекдотичная и недокументированная история

Краткая анекдотичная и недокументированная история
Если, как мы полагаем, существуют обособленные тканевые и организменные интегрирующие системы, то в таком случае их эволюция в процессе возникновения разнообразия Metazoa шла совершенно разными путями. Животные возникли

Естественники и гуманитарии: краткая история подхода

Естественники и гуманитарии: краткая история подхода
Выше я упоминал о различиях естественнонаучного и гуманитарного подхода в изучении поведения человека. Однако пионеры таких исследований не сразу разделились на два этих лагеря; и вопрос о соотношении

Некоторые актуальные вопросы биологии развития поведения[43]

Некоторые актуальные вопросы биологии развития поведения[43]
Введение
Биология развития поведения как научная дисциплина начала развиваться на рубеже XIX и XX вв. Наиболее существенные исследования в этом направлении выполнены Когхиллом (Coghill, 1929), работавшим на

Краткая история психопатии

Краткая история психопатии
Как и Сибрук, я позаимствовал название этой главы – «Страдающие души» – у немецкого психиатра Юлиуса Людвига Августа Коха (1841–1908), который, как считается, изобрел термин psychopatische, то есть психопат, психопатический{7}. В буквальном переводе

Глава II. Краткая история фенетики

Глава II. Краткая история фенетики
Всякое новое есть хорошо забытое старое — гласит известная поговорка. В значительной степени поэтому история науки является не архивом или кладбищем умерших идей, а скорее собранием недостроенных архитектурных ансамблей. И часто

Краткая история развития биологии

Вспомните!

Какие достижения современной биологии вам известны?

рентгенология

аппараты УЗИ, ЭМРТ

установление молекулярной структуры ДНК

расшифровка генома человека и других организмов

генная инженерия

3D-биопринтеры

Электронные сканирующие микроскопы

ГМО

Экстракорпоральное оплодотворение и др.

Каких ученых-биологов вы знаете?

Линней, Ламарк, Дарвин, Мендель, Морган, Павлов, Пастер, Гук, Левенгук, Броун, Пурнинье, Бэр, Мечников, Мичурин, Вернадский, Ивановский, Флеминг, Тенсли, Сукачев, Четвериков, Лайль, Опарин, Шванн, Шлейден, Чаграфф, Навашин, Тимирязев, Мальпиги, Гольджи и др.

Вопросы для повторения и задания

1. Расскажите о вкладе в развитие биологии древнегреческих и древне-римских философов и врачей.

Первым учёным, создавшим научную медицинскую школу, был древнегреческий врач Гиппократ (ок. 460 — ок. 370 до н. э.). Он считал, что у каждой болезни есть естественные причины и их можно узнать, изучая строение и жизнедеятельность человеческого организма. С древних времён и по сей день врачи торжественно произносят клятву Гиппократа, обещая хранить врачебную тайну и ни при каких обстоятельствах не оставлять больного без медицинской помощи. Великий энциклопедист древности Аристотель (384—322 до н. э.). Стал одним из основателей биологии как науки, впервые обобщив биологические знания, накопленные до него человечеством. Он разработал систематику животных, определив в ней место и человеку, которого он называл «общественным животным, наделённым разумом». Многие труды Аристотеля были посвящены происхождению жизни. Древнеримский учёный и врач Клавдий Гален (ок. 130 — ок. 200), изучая строение млекопитающих, заложил основы анатомии человека. В течение следующих пятнадцати веков его труды были основным источником знаний по анатомии.

2. Охарактеризуйте особенности воззрений на живую природу в Средние века, эпоху Возрождения.

Резко возрос интерес к биологии в эпоху Великих географических открытий (XV в.). Открытие новых земель, налаживание торговых отношений между государствами расширяли сведения о животных и растениях. Ботаники и зоологи описывали множество новых, неизвестных ранее видов организмов, принадлежащих к различным царствам живой природы. Один из выдающихся людей этой эпохи — Леонардо да Винчи (1452—1519) — описал многие растения, изучал строение человеческого тела, деятельность сердца и зрительную функцию. После того как был снят церковный запрет на вскрытие человеческого тела, блестящих успехов достигла анатомия человека, что получило отражение в классическом труде Андреаса Везалия (1514—1564) «Строение человеческого тела» (рис. 1). Величайшее научное достижение — открытие кровообращения — совершил в XVII в. английский врач и биолог Уильям Гарвей (1578—1657).

После падения Западной Римской империи в Европе наступил застой в развитии наук и ремесла. Этому способствовали феодальные порядки, установившиеся во всех европейских странах, постоянные войны между феодалами, нашествия полудиких народов с востока, массовые эпидемии, а главное — идеологическое закабаление умов широких народных масс римско-католической церковью. В этот период римско-католическая церковь, несмотря на многие неудачи в борьбе за политическое господство, распространила свое влияние во всей Западной Европе. Имея огромную армию духовенства различных рангов, папство фактически добилось полного господства христианской римско-католической идеологии среди всех западноевропейских народов. Проповедуя смирение и покорность, оправдывая существующие феодальные порядки, римско-католическое духовенство вместе с тем жестоко преследовало все новое и прогрессивное. Естественные науки и вообще так называемое светское образование были полностью подавлены.

4. Какое изобретение XVII в. дало возможность открыть и описать клетку?

5. Каково значение для биологической науки работ Л. Пастера и И. И. Мечникова?

Труды Луи Пастера (1822—1895) и Ильи Ильича Мечникова (1845—1916) определили появление иммунологии. В 1876 г. Пастер полностью посвятил себя иммунологии, окончательно установив специфичность возбудителей сибирской язвы, холеры, бешенства, куриной холеры и других болезней, развил представления об искусственном иммунитете, предложил метод предохранительных прививок, в частности от сибирской язвы, бешенства. Первая прививка против бешенства была сделана Пастером 6 июля 1885 г. В 1888 г. Пастер создал и возглавил научно-исследовательский институт микробиологии (Пастеровский институт), в котором работали многие известные ученые.

Мечников, обнаружив в 1882 г. явление фагоцитоза, разработал на его основе сравнительную патологию воспаления, а в дальнейшем — фагоцитарную теорию иммунитета, за что получил в 1908 г. Нобелевскую премию совместно с П. Эрлихом. Многочисленные работы Мечникова по бактериологии посвящены вопросам эпидемиологии холеры, брюшного тифа, туберкулеза и других инфекционных заболеваний. Мечников создал первую русскую школу микробиологов, иммунологов и патологов; активно участвовал в создании научно-исследовательских учреждений, разрабатывающих различные формы борьбы с инфекционными заболеваниями.

6. Перечислите основные открытия, сделанные в биологии в XX в.

В середине XX в. в биологию начали активно проникать методы и идеи других естественных наук. Достижения современной биологии открывают широкие перспективы для создания биологически активных веществ и новых лекарственных препаратов, для лечения наследственных заболеваний и осуществления селекции на клеточном уровне. В настоящее время биология стала реальной производительной силой, по развитию которой можно судить об общем уровне развития человеческого общества.

– Открытие витаминов

– Открытие пептидных связей в молекулах белков

– Изучение химической природы хлорофилла

– Описали основные ткани растений

– Открытие структуры ДНК

– Исследование фотосинтеза

– Открытие ключевого этапа в дыхании клеток — цикла трикарбоновых кислот, или цикла Кребса

– Исследование физиологии пищеварения

– Наблюдал клеточное строение тканей

– Наблюдал одноклеточных организмов, клетки животных (эритроциты)

– Открытие ядра в клетке

– Открытие аппарата Гольджи — органоида клетки, метод приготовления микроскопических препаратов нервной ткани, исследование строения нервной системы

– Установил, что одни части зародыша имеют влияние на развитие других его частей

– Сформулировал мутационную теорию

– Создание хромосомной теории наследственности

– Сформулировал закон гомологических рядов в наследственной изменчивости

– Обнаружили усиление мутационного процесса под действием радиоактивного излучения

– Открыл сложную структуру гена

– Открыл значение мутационного процесса в процессах, происходящих в популяциях, для эволюции вида

– Установил филогенетический ряд лошадиных как типовой ряд постепенных эволюционных изменений родственных видов

– Разработали теорию зародышевых листков для позвоночных

– Выдвинул теорию происхождения многоклеточных организмов от общего предка — гипотетического организма фагоцителлы

– Обосновывает наличие в прошлом предка многоклеточных — фагоцителлы и предлагает считать его живой моделью многоклеточное животное — трихоплакса

– Обосновали биологический закон «Онтогенез есть краткое повторение филогенеза»

– Написал и опубликовал работу «Географическое распространение животных» — труд, убедительно показавший, как велико значение генетической связи вымершей и современной фауны

– Утверждал, что многие органы многофункциональны; в новых условиях среды одна из второстепенных функций может стать более важной и заменить прежнюю главную функцию органа

– Выдвинул гипотезу возникновения билатеральной симметрии живых организмов

7. Назовите известные вам естественные науки, составляющие биологию. Какие из них возникли в конце XX в.?

На границах смежных дисциплин возникали новые биологические направления: вирусология, биохимия, биофизика, биогеография, молекулярная биология, космическая биология и многие другие. Широкое внедрение математики в биологию вызвало рождение биометрии. Успехи экологии, а также всё более актуальные проблемы охраны природы способствовали развитию экологического подхода в большинстве отраслей биологии. На рубеже XX и XXI вв. с огромной скоростью начала развиваться биотехнология — направление, которому, несомненно, принадлежит будущее.

Подумайте! Вспомните!

1. Проанализируйте изменения, произошедшие в науке в XVII—XVIII вв. Какие возможности они открыли перед учёными?

Новую эру в развитии биологии ознаменовало изобретение в конце XVI в. микроскопа. Уже в середине XVII в. была открыта клетка, а позднее обнаружен мир микроскопических существ — простейших и бактерий, изучено развитие насекомых и принципиальное строение сперматозоидов. В XVIII в. шведский натуралист Карл Линней (1707—1778) предложил систему классификации живой природы и ввёл бинарную (двойную) номенклатуру для наименования видов. Карл Эрнст Бэр (Карл Максимович Бэр) (1792—1876), профессор Петербургской медико-хирургической академии, изучая внутриутробное развитие, установил, что зародыши всех животных на ранних этапах развития схожи, сформулировал закон зародышевого сходства и вошёл в историю науки как основатель эмбриологии. Первым биологом, который попытался создать стройную и целостную теорию эволюции живого мира, стал французский учёный Жан Батист Ламарк (1774—1829). Палеонтологию, науку об ископаемых животных и растениях, создал французский зоолог Жорж Кювье (1769—1832). Огромную роль в понимании единства органического мира сыграла клеточная теория зоолога Теодора Шванна (1810—1882) и ботаника Маттиаса Якоба Шлейдена (1804—1881).

2. Как вы понимаете выражение «прикладная биология»?

Прикладная биология – это отрасль биологии, которая определяется потребностями общества. Из практически важных дисциплин быстро развиваются бионика (изучение технических приложений биологических закономерностей), космическая биология (изучение биологического действия факторов мирового пространства в проблем освоения космоса), астробиология или экзобиология (исследование жизни вне Земли), а также регенеративная биология и медицина. Многие современные науки, такие как генетика, молекулярная биология, экология, решают свои актуальные задачи, используя для исследования животных. Тесно связана с практической деятельностью человека прикладная зоология, которая включает сельскохозяйственную, лесную, медицинскую зоологию, паразитологию и другие разделы. В настоящее время активно развиваются прикладные отрасли ботаники: растениеводство, лесное хозяйство, фармакология и парфюмерная промышленность. Велика роль ботаники в увеличении продуктивности культурных растений, в решении мировой продовольственной проблемы. На первый план выходят такие задачи, как рациональное использование и сохранение растительного мира, защита растений от неблагоприятных факторов.

3. Решение, каких проблем человечества зависит от уровня биологических знаний?

Страны, в которых произошли основные биологические открытия относятся к развитым и активно развивающимся странам.

Примеры современных дисциплин, возникших на стыке биологии и других наук: палеобиология, биомедицина, социобиология, психобиология, бионика, физиология труда, радиобиология.

Разделы биологии могут возникнуть в будущем: биопрограммирование, ИТ-медицина, биоэтика, биоинформатика, биотехнология.

7. Оцените роль биологических знаний в формировании мировоззрения современного человека. Составьте 10—15 тезисов, раскрывающих значимость биологической информации в жизни каждого.

1) Человечество не может существовать без живой природы. Отсюда жизненно необходимо сохранять ее

2) Биология возникла в связи с решением очень важных для людей проблем.

3) Одной из них всегда было более глубокое постижение процессов в живой природе, связанных с получением пищевых продуктов, т. е. знание особенностей жизни растений и животных, их изменение под воздействием человека, способов получения надежного и все более богатого урожая.

4) Человек – продукт развития живой природы. Все процессы нашей жизнедеятельности подобны тем, которые происходят в природе. И поэтому глубокое понимание биологических процессов служит научным фундаментом медицины.

5) Появление сознания, означающее гигантский шаг вперед в самопознании материи, тоже не может быть понято без глубоких исследований живой природы, по крайней мере, в 2-х направлениях – возникновение и развитие мозга как органа мышления (до сих пор загадка мышления остается неразрешенной) и возникновение социальности, общественного образа жизни.

6) Живая природа является источником многих необходимых для человечества материалов и продуктов. Нужно знать их свойства, чтобы правильно использовать, знать, где искать их в природе, как получать.

7) Та вода, которую мы пьем, точнее — чистота этой воды, ее качество тоже определяется в первую очередь живой природой. Наши очистные сооружения лишь завершают тот огромный процесс, который незримо для нас происходит в природе: вода в почве или водоеме многократно проходит через тела мириадов беспозвоночных, фильтруется ими и, освобождаясь от органических и неорганических остатков, становится такой, какой мы знаем ее в реках, озерах и ключах.

8) Проблема качества воздуха и воды – одна из экологических проблем, а экология – биологическая дисциплина, хотя современная экология давно перестала быть только ею и включает в себя много самостоятельных разделов, зачастую принадлежащих к разным научным дисциплинам.

9) В результате освоения человеком всей поверхности планеты, развития сельского хозяйства, промышленности, вырубки лесов, загрязнения материков и океанов все большее число видов растений, грибов, животных исчезает с лица Земли. Исчезнувший вид восстановить невозможно. Он является продуктом миллионов лет эволюции и обладает уникальным генофондом.

10) В данный момент особенно быстро развиваются молекулярная биология, биотехнология и генетика.

Примеры ближайших событий 2016-2017 гг.

Викторина:

– Разделение на группы

– Вступительное слово – описание события, историческая справка события, ученого

– Придумать название команд (по теме викторины)

– 1 раунд – простой: например, закончить предложение: Защитная реакция растений на изменение длины светового дня (листопад).

– 2 раунд – двойной: например, найди пару.

– 3 раунд – сложный: например, изобразить схему процесса, нарисовать явление.

«Секреты жизни: введение математика в молекулярную биологию — катализ исследования на стыке вычислений и биологии»

Университет Южной Калифорнии

Молекулярная биология возникла в результате синтеза двух дополняющих друг друга подходов к изучению жизни — биохимии и генетики — и стала одной из самых захватывающих и ярких научных областей в конце двадцатого века. В этой вводной главе представлена краткая история интеллектуальных основ современной молекулярной биологии и определены ключевые термины и концепции, которые повторяются в последующих главах.

Понятия молекулярной биологии стали нарицательными. ДНК, РНК и ферменты регулярно обсуждаются в газетных статьях, телевизионных шоу в прайм-тайм и деловых еженедельниках. Переход в массовую культуру завершен всего через 40 лет после открытия структуры дезоксирибонуклеиновой кислоты (ДНК) Джеймсом Уотсоном и Фрэнсисом Криком и всего через 20 лет после первых шагов к генной инженерии. С головокружительной скоростью эти фундаментальные научные открытия привели к поразительным научным и практическим выводам: были раскрыты фундаментальные биохимические процессы жизни. Эволюционная летопись жизни может быть прочитана из последовательностей ДНК. Гены таких белков, как инсулин человека, можно встроить в бактерии, которые затем смогут без больших затрат производить большое количество чистого белка. Сельскохозяйственные животные и сельскохозяйственные культуры могут быть модифицированы для производства более здоровых и желанных продуктов. Можно разработать чувствительные и надежные средства диагностики вирусных заболеваний, таких как СПИД, и разработать методы лечения некоторых наследственных заболеваний, таких как муковисцидоз.

Молекулярная биология, несомненно, продолжит свое захватывающее развитие и в следующем столетии. По мере расширения границ меняется и характер поля. С постоянно растущими базами данных последовательностей ДНК и белков и все более мощными методами исследования структуры и функций молекулярная биология становится не только экспериментальной наукой, но и теоретической наукой. Роль теории в молекулярной биологии вряд ли похожа на роль теории в физике, в которой математики могут предлагать теории великого объединения. В биологии ключевые идеи возникают не столько из первых принципов, сколько из интерпретации сумасшедшего набора решений, которые придумала эволюция. Интерпретация зависит от наличия теоретических инструментов и структур. Иногда эти конструкции не математические. Однако все более важную роль играют математические науки — математика, статистика и вычислительная наука.

Эта книга возникла в результате осознания необходимости развивать взаимодействие между молекулярной биологией и математическими науками. В следующих главах различные математики, работающие в области молекулярной биологии, дают представление об этом интерфейсе. Очерки не предназначены для того, чтобы быть всесторонними современными обзорами, а скорее виньетками, которые описывают ровно столько, чтобы соблазнить читателя узнать больше о плодородных областях для исследований в области молекулярной биологии.

В этой вводной главе кратко излагаются интеллектуальные основы молекулярной биологии, вводятся некоторые ключевые термины и концепции, которые повторяются на протяжении всей книги, а также дается предварительный обзор последующих глав.

БИОХИМИЯ

Исторически молекулярная биология выросла из двух дополняющих друг друга экспериментальных подходов к изучению биологических функций: биохимии и генетики (). Биохимия включает фракционирование (расщепление) молекул в живом организме с целью очистки и характеристики химических компонентов, ответственных за выполнение определенной функции. Для этого биохимик разрабатывает анализ для измерения «активности», а затем пробует последовательные процедуры фракционирования, чтобы выделить чистую фракцию, обладающую активностью. Например, биохимик может изучать способность организма усваивать сахар, очищая компонент, способный расщеплять сахар, в тестовом халате.

РИСУНОК 1.1

Генетика и биохимия зародились как независимые способы изучения биологических функций.

Анализы in vitro (буквально, в стекле) проводились еще в те дни, когда биологи все еще боролись с понятием витализма. Первоначально считалось, что жизнь и биохимические реакции не подчиняются известным законам химии и физики. Такой витализм господствовал примерно до 1900 года, когда было показано, что материал из мертвых дрожжевых клеток может сбраживать сахар в этанол, доказывая, что важные процессы живых организмов — это «всего лишь химия». Катализаторы, способствующие этим превращениям, получили название ферментов.

Живые организмы состоят в основном из углерода, водорода, кислорода и азота; они также содержат небольшое количество других ключевых элементов (таких как натрий, калий, магний, сера, марганец и селен). Эти элементы объединены в широкий спектр сложных макромолекул, которые можно разделить на несколько основных типов: белки, нуклеиновые кислоты, липиды (жиры) и углеводы (крахмалы и сахара). Из всех макромолекул белки обладают самым разнообразным набором функций. Человеческое тело производит около 100 000 различных белков, в том числе:

ферменты, катализирующие химические реакции, такие как переваривание пищи;
структурные молекулы, входящие в состав волос, кожи и клеточных стенок;
транспортеры веществ, такие как гемоглобин, который переносит кислород в крови; и
транспортеры информации, такие как рецепторы на поверхности клеток и инсулина и других гормонов.

Короче говоря, работу клетки выполняют белки. Со структурной точки зрения белок представляет собой упорядоченную линейную цепь, состоящую из строительных блоков, известных как аминокислоты (рисунки и ). Существует 20 различных аминокислот, каждая из которых имеет свои химические свойства (включая размер, заряд, полярность и гидрофобность, или склонность избегать упаковки с водой). Каждый белок определяется своей уникальной последовательностью аминокислот; в белке обычно от 50 до 500 аминокислот.

РИСУНОК 1.2

Белки представляют собой линейный полимер, собранный из 20 строительных блоков, называемых аминокислотами, которые различаются своими боковыми цепями. На диаграмме показан сильно стилизованный вид этой линейной структуры.

РИСУНОК 1.3

Примеры различных представлений белковых структур с акцентом на (слева) химические связи и (справа) вторичные структурные особенности, такие как спирали и пластинчатые элементы. Перепечатано с разрешения Ричардсона и Ричардсона (1989). Авторское право (подробнее…)

Аминокислотная последовательность белка заставляет его складываться в определенную трехмерную форму, обладающую наименьшей энергией. Это придает белку его специфические биохимические свойства, то есть его функцию. Как правило, форма белка довольно прочная. Если белок нагреть, он денатурирует (то есть потеряет свою трехмерную структуру), но часто восстанавливает эту структуру (сворачивается) при охлаждении. Предсказание свернутой структуры белка по аминокислотной последовательности остается чрезвычайно сложной задачей математической оптимизации. Проблема создается комбинаторным взрывом правдоподобных форм, каждая из которых представляет локальный минимум сложной невыпуклой функции, глобальный минимум которой ищется.

КЛАССИЧЕСКАЯ ГЕНЕТИКА

Вторым важным подходом к изучению биологических функций была генетика. В то время как биохимики пытаются изучить один единственный компонент, очищенный от организма, генетики изучают мутантные организмы, которые остаются интактными, за исключением одного компонента. Таким образом, биохимик может изучать способность организма метаболизировать сахар, находя мутантов, которые утратили способность расти, используя сахар в качестве источника пищи.

Генетика восходит к новаторским экспериментам Грегора Менделя в 1865 году. Эти ключевые эксперименты элегантно иллюстрируют роль теории и абстракции в биологии. Для своих экспериментов Мендель начал с чистой селекции штаммов гороха, т. е. тех, для которых все потомство, поколение за поколением, последовательно проявляет интересующий признак. Этот выбор был ключом к интерпретации данных.

Одной из особенностей, которую он изучал, было то, какие семена у гороха круглые или морщинистые. Начав с чистого размножения круглых и морщинистых линий, Мендель провел контролируемое скрещивание, чтобы получить поколение F ₁. ( и поколение кросса обозначаются F _i .) Мендель отметил, что все поколение F ₁ состояло из круглых горошин; морщинистая черта полностью исчезла. Однако, когда Мендель скрестил эти сорта гороха F ₁ обратно с чистопородным морщинистым родителем, морщинистый признак снова появился: во втором поколении примерно половина была круглой, а половина морщинистой. Более того, когда Мендель скрещивал между собой горох F ₁, он обнаружил, что второе поколение показало 75 процентов круглых и 25 процентов морщинистых ().

РИСУНОК 1.4

Скрещивания Менделя чисто селекционных сортов гороха с округлыми и морщинистыми семенами выявили характерное биномиальное соотношение 1:2:1 во втором поколении, что привело Менделя к выводу о существовании дискретных частиц наследственности.

На основе этих и других экспериментов Мендель выдвинул гипотезу о том, что на такие черты, как округлость, влияют дискретные факторы, которые сегодня мы называем генами. В частности, Мендель предложил следующее:

Каждый организм наследует две копии гена, по одной от каждого родителя. Каждый родитель передает по одной из двух случайно выбранных копий каждому потомству. (Эти важные постулаты называются первым законом наследственности Менделя.)
Гены могут встречаться в альтернативных формах, называемых аллелями . Например, ген, влияющий на форму семян, встречается в одной форме (аллель A ), вызывающей округлость, и в другой форме (аллель a ), вызывающей морщинистость.
Чистопородные круглые и морщинистые растения несли две копии одного и того же аллеля, AA и аа соответственно. Индивиды, несущие две копии одного и того же гена, называются гомозиготами . Поколение F ₁ состоит из особей с генотипом Аа , с преобладанием округлости над морщинистостью. Такие особи называются гетерозиготами .
При скрещивании поколения F ₁ ( Аа ) с чистопородным морщинистым штаммом ( аа ) потомство представляло собой смесь 1:1 Аа:аа , согласно которой аллель унаследован от родителя F ₁. В помеси двух F ₁ родителей ( Аа ), потомство представляло собой смесь 1:2:1 АА:Аа:аа в соответствии с биномиальным отбором аллелей от двух родителей.

Поразительно осознавать, что существование генов было выведено таким абстрактным математическим путем. Вероятность и статистика были неотъемлемой частью ранней генетики и остались ею. Конечно, в распоряжении Менделя не было формального статистического анализа, но он сумел интуитивно уловить ключевые понятия. Кстати, известный генетик и статистик Р.А. Много лет спустя Фишер проанализировал данные Менделя и пришел к выводу, что они слишком хорошо соответствуют статистическим ожиданиям. Мендель, вероятно, отбросил некоторые выбросы как вероятные экспериментальные ошибки.

Прошло почти 35 лет, прежде чем биологи поняли, где находятся эти гипотетические гены в клетке (в хромосомах), и почти 100 лет, прежде чем они поняли их биохимическую природу.

МОЛЕКУЛЯРНАЯ БИОЛОГИЯ

Как предполагалось в , биохимический и генетический подходы практически не пересекались: биохимик в основном изучал белки, а генетик — гены. Подобно великим объединениям в математике, молекулярная биология возникла из признания того, что две, казалось бы, не связанные между собой области на самом деле являются взаимодополняющими взглядами на один и тот же предмет.

Первые подсказки появились при изучении мутантных микроорганизмов, в которых дефекты генов сделали их неспособными синтезировать определенные ключевые макромолекулы. Биохимическое исследование этих генетических мутантов показало, что у каждого отсутствует определенный фермент. Из этих опытов стала ясной гипотеза, что гены каким-то образом должны «кодировать» ферменты. Эта (нобелевская премия) концепция была названа гипотезой «один ген — один фермент», хотя сегодня она была изменена на «один ген — один белок». Конечно, оставалось загадкой: как гены кодируют белки?

Ответ зависел от обнаружения биохимической природы самого гена, объединяющего поля. Чтобы очистить ген как биохимическую единицу, нужно было провести анализ наследственности в пробирке, что могло показаться невозможным. К счастью, научная интуиция предоставила решение. В знаменитой серии бактериологических исследований Гриффит 50 лет назад показал, что некоторые свойства (например, патогенность) могут передаваться от мертвых бактерий к живым бактериям. Эйвери и др. (1944) смогли последовательно фракционировать мертвые бактерии, чтобы очистить неуловимый «преобразующий принцип», материал, который мог придать бактериям новую наследственность. Неожиданным выводом было то, что ген, по-видимому, состоит из ДНК.

Представление о ДНК как о материале наследственности стало неожиданностью для большинства биохимиков. Известно, что ДНК представляет собой линейный полимер из четырех строительных блоков, называемых нуклеотидами (называемых аденином, тимином, цитозином и гуанином и сокращенно А, Т, С и G), соединенных сахаро-фосфатным остовом. Однако наиболее осведомленные ученые считали, что полимер представляет собой скучную, повторяющуюся структурную молекулу, которая функционирует как своего рода каркас для более важных компонентов. До появления компьютеров было неясно, как линейный полимер может кодировать информацию. Если ДНК содержала гены, ключевым вопросом становилась структура ДНК.

В своей легендарной работе 1953 года Уотсон и Крик правильно определили структуру большинства ДНК и тем самым раскрыли главный секрет наследственности. В то время как некоторые вирусы имеют одноцепочечную ДНК, ДНК человека и большинства других форм жизни состоит из двух антипараллельных цепей (цепей) в форме двойной спирали, в которой основания (нуклеотиды) спариваются, образуя пары оснований определенным образом (), так что последовательность одной цепи полностью определяет последовательность другой: буква А в одной цепи всегда соответствует букве Т в другой, а буква G — букве С. Эти последовательности комплементарны. Избыточность информации объясняет основу репликации живых организмов: две нити двойной спирали раскручиваются, и каждая служит шаблоном для синтеза полной двойной спирали, которая передается дочерней клетке. Этот процесс репликации осуществляется ферментами, называемыми ДНК-полимеразы . Мутации — это изменения в последовательности нуклеотидов в ДНК. Мутации могут быть вызваны внешними силами, такими как солнечный свет и химические вещества, или могут возникать как случайные ошибки копирования во время репликации.

РИСУНОК 1.5

Двойная спираль ДНК состоит из антипараллельных спиральных нитей с комплементарными основаниями (G–C и A–T).

Оставался вопрос, как 4-буквенный алфавит ДНК может «кодировать» инструкции для 20-буквенного алфавита белковых последовательностей. Биохимические исследования, проведенные в течение следующего десятилетия, показали, что гены соответствуют определенным участкам ДНК вдоль хромосомы (во многом подобно отдельным файлам на жестком диске). Эти участки ДНК могут экспрессироваться в определенное время или при определенных обстоятельствах. Как правило, экспрессия гена начинается с транскрипция последовательности ДНК в молекулу-мессенджер, состоящую из рибонуклеиновой кислоты (РНК) (). Этот процесс транскрипции осуществляется ферментами, называемыми РНК-полимеразами . РНК структурно похожа на ДНК и состоит из четырех строительных блоков, нуклеотиды обозначены A, U, C и G, где U (урацил) играет роль T. информационная РНК (мРНК) скопирована с ДНК ген в соответствии с обычными правилами спаривания оснований (U в РНК соответствует A в ДНК, A соответствует T, G соответствует C, а C соответствует G). Матричная РНК, скопированная с гена, является одноцепочечной и является всего лишь нестабильным промежуточным звеном, используемым для передачи информации из ядра клетки (где находится ДНК) в цитоплазму (где происходит синтез белка). Затем мРНК транслируется в белок с помощью замечательной молекулярной машины под названием 9.0003 рибосома .

РИСУНОК 1.6

После транскрипции матричной РНК из последовательности ДНК гена она транслируется в белок с помощью замечательного молекулярного устройства, называемого рибосомой. (A) Рибосомы читают основания РНК и записывают соответствующую последовательность аминокислот. Правильная аминокислота (подробнее…)

Рибосома «читает» линейную последовательность мРНК и «записывает» (т.е. создает) соответствующую линейную последовательность аминокислот кодируемого белка. Перевод осуществляется по трехбуквенному коду: группа из трех букв – это кодон , который определяет конкретную аминокислоту в соответствии с справочной таблицей, называемой генетическим кодом (). Есть 4 ³ различных кодонов. Кодоны считываются непрерывным, неперекрывающимся образом из определенной начальной точки, называемой стартовым сайтом трансляции. Наконец, вновь синтезированная цепь аминокислот спонтанно сворачивается в свою трехмерную структуру. (Недавнее обсуждение фолдинга белков см. в Sali et al., 1994.)

Детали генетического кода были разгаданы с помощью элегантных биохимических приемов, которые были необходимы, поскольку химики могли синтезировать только случайные наборы РНК, имеющие определенные пропорции различных оснований. С некоторыми комбинаторными рассуждениями этого оказалось достаточно. Например, если рибосоме дать мРНК с последовательностью UUUUU…, то она образует белковую цепь, состоящую только из аминокислоты фенилаланина (Phe). Таким образом, UUU должен кодировать фенилаланин. Изучая более сложные смеси, исследователи вскоре разработали весь генетический код.

Молекулярная биология представляет собой третью часть треугольника, связывающую генетику и биохимию ().

РИСУНОК 1.7

Молекулярная биология связала дисциплины генетики и биохимии, показав, как гены кодируют белки.

РЕКОМБИНАТНАЯ ДНК-РЕВОЛЮЦИЯ

К 1965 году молекулярная биология раскрыла основные секреты жизни. Однако без возможности манипулировать генами понимание было скорее теоретическим, чем практическим. В 1970-х эту ситуацию изменила революция рекомбинантных ДНК.

Биохимики открыли множество ферментов, вырабатываемых бактериями, которые позволяют манипулировать ДНК по желанию. Бактерии произвели рестрикционных фермента, , которые разрезают ДНК по определенным последовательностям и служат защитой от вторжения вирусов, и лигазы, которые соединяют фрагменты ДНК. С помощью этих и других инструментов (которые теперь легко доступны у коммерческих поставщиков) стало возможным вырезать и вставлять фрагменты ДНК по желанию и вводить их в живые клетки (). Такие эксперименты по клонированию позволяют ученым воспроизводить неограниченное количество конкретных молекул ДНК и привели к детальному пониманию отдельных генов. Более того, производство молекул рекомбинантной ДНК, содержащих инструкции бактериальной ДНК для создания определенного человеческого белка (например, инсулина), дало начало индустрии биотехнологий.

РИСУНОК 1.8

Путем клонирования чужеродной молекулы ДНК в плазмидном векторе можно размножить ДНК в бактериальной или другой клетке-хозяине.

Ключевым событием стало изобретение секвенирования ДНК, процесса определения точной нуклеотидной последовательности клонированной молекулы ДНК. Благодаря секвенированию ДНК стало возможным считывать последовательность любого гена участками от 300 до 500 нуклеотидов за раз. Секвенирование ДНК выявило поразительное сходство между такими разными живыми существами, как люди и дрожжи, что имеет далеко идущие последствия для нашего понимания молекулярной структуры и эволюции. Секвенирование ДНК также привело к информационному взрыву в биологии, при этом общедоступные базы данных по-прежнему расширяются в геометрической прогрессии. В начале 1993 года в общедоступных базах данных было более 100 миллионов оснований ДНК. Для справки: весь геном кишечной бактерии Escherichia coli ( E. coli ) состоит примерно из 4,6 миллионов оснований, а последовательность генома человека насчитывает примерно 3 миллиарда оснований.

В последние годы к набору инструментов молекулярного биолога был добавлен новый мощный метод, называемый полимеразной цепной реакцией (ПЦР). ПЦР позволяет напрямую амплифицировать определенную последовательность ДНК, не прибегая к клонированию. Для проведения ПЦР используются короткие молекулы ДНК, называемые 9.0003 праймеров (обычно длиной около 20 оснований), которые комплементарны последовательностям, фланкирующим интересующую область. Каждому праймеру дают спариться с основанием в комплементарной области, а затем удлиняют, чтобы он содержал полную последовательность из области, с помощью фермента ДНК-полимеразы. Таким образом, одна копия региона порождает две копии. Повторив этот шаг n раз, можно получить 2 ⁿ копий региона. На практике можно начать с маленькой капли крови или слюны и получить миллионное увеличение участка. Неудивительно, что ПЦР нашла множество применений, особенно в генетической диагностике.

РИСУНОК 1.9

РИСУНОК 1.9 Полимеразная цепная реакция (ПЦР) обеспечивает экспоненциальную амплификацию ДНК. Метод включает последовательные циклы копирования (с использованием фермента ДНК-полимеразы) между двумя синтетическими праймерами, соответствующими соседним последовательностям ДНК. Каждый раунд (подробнее…)

МОЛЕКУЛЯРНАЯ ГЕНЕТИКА В 1990-Х

С помощью инструментов рекомбинации ДНК треугольник знаний (см. ) был преобразован, используя математическую метафору, в коммутативную диаграмму (). Диаграмму можно перемещать в любом направлении — например, чтобы найти гены и белки, лежащие в основе биологической функции, или найти белок и функцию, связанные с данным геном.

РИСУНОК 1.

Рекомбинантная ДНК давала возможность свободно перемещаться в любом направлении между геном, белком и функцией, тем самым превращая треугольник на Рисунке 1.7 в коммутативную диаграмму.

Хорошей иллюстрацией силы методов являются недавние исследования наследственного муковисцидоза (МВ). МВ — рецессивное заболевание, генетика которого формально идентична морщинистости гороха по Менделю: если два непораженных носителя рецессивного гена МВ а (то есть гетерозиготы с генотипом Аа ) вступят в брак, четверть их потомства будет поражена (то есть будет иметь генотип аа ). Частота аллеля, вызывающего заболевание, составляет около 1/42 в европеоидной популяции, поэтому около 1/21 всех европеоидов составляют карьеры. Поскольку в браке между двумя профессиями рождается 1/4 больных детей, частота заболевания в популяции составляет около 1/2000 (≈ 1/4×1/21×1/21).

Несмотря на то, что муковисцидоз был обнаружен относительно рано в этом столетии, молекулярная основа болезни оставалась загадкой до 19 века. 89. Первым прорывом стало генетическое картирование муковисцидоза на хромосому 7 человека в 1985 г. (). Генетическое картирование показало, что модель наследования болезни в семьях тесно коррелирует с моделью наследования определенного полиморфизма ДНК (то есть распространенного варианта написания ДНК), в данном случае на хромосоме 7.

РИСУНОК 1.11

Хромосомный переход от фланкирующих генетических маркеров к гену, ответственному за муковисцидоз. Пройденное расстояние составило более 1 миллиона оснований ДНК.

Корреляция не означает, что полиморфизм вызывает болезнь, а скорее то, что полиморфизм должен быть расположен рядом с участком гена болезни. Конечно, «рядом» — понятие относительное. В этом случае «рядом» означало, что ген CF должен находиться в пределах от 1 до 2 миллионов оснований ДНК вдоль хромосомы. Следующим шагом было физическое картирование и секвенирование ДНК самого гена МВ, на что ушло еще четыре года. Это включало в себя начало от близлежащего полиморфизма и последовательное выделение соседних фрагментов в утомительном процессе, называемом хромосомное хождение до тех пор, пока не будет достигнут ген болезни. Как только ген болезни был обнаружен, была определена его полная последовательность ДНК. (Описание того, как узнать, что обнаружен ген болезни, выходит за рамки этого введения.)

Из последовательности ДНК стало ясно, что ген CF кодирует белок из 1480 аминокислот и что наиболее распространенная ошибка в написании в популяции (составляющей около 70 процентов всех аллелей CF) была трехбуквенная делеция, которая удаляла единственный кодон, определяющий аминокислоту, фенилаланин, в положении 508 белка. На основании этого открытия стало возможным проводить ДНК-диагностику отдельных лиц, чтобы определить, несут ли они распространенную мутацию муковисцидоза.

Еще более интригующе то, что последовательность дала немедленный ключ к пониманию структуры и функции продукта гена. Когда последовательность белка сравнили с общедоступными базами данных предыдущих последовательностей, было обнаружено сильное сходство с классом белков, которые были мембраносвязанными переносчиками — молекулами, которые находятся в клеточной мембране, связывают аденозинтрифосфат (АТФ) и транспортируют вещества. в и из клетки (). По аналогии можно было даже предположить возможную трехмерную форму белка CF (11). Таким образом, компьютерный анализ последовательности пролил существенный свет на структуру и функцию этого важного гена болезни.

. РИСУНОК 1.12. (B) Основываясь на этих сходствах, можно было построить базовую молекулярную модель (подробнее…)

. С недавним появлением генной терапии — способности использовать вирус в качестве челнока для доставки рабочей копии ген в клетки, несущие дефектную версию — начаты клинические испытания, чтобы попытаться вылечить болезнь в клетках легких пациентов с муковисцидозом. Путь от первоначального открытия гена до потенциальных методов лечения в этом случае был ошеломляюще коротким.

ПРОЕКТ «ГЕНОМ ЧЕЛОВЕКА»

С идентификацией гена муковисцидоза, а также рядом других успехов стало ясно, что молекулярная генетика разработала мощную общую парадигму, которая может быть применена ко многим наследственным заболеваниям и будет иметь глубокое значение. влияние на наши представления о здоровье человека. К сожалению, парадигма включает в себя множество утомительных лабораторных шагов: генетическое картирование (обнаружение полиморфизма, тесно связанного с геном болезни), физическое картирование (выделение последовательных фрагментов ДНК вдоль хромосомы) и секвенирование ДНК (обычно выполняемое фрагментами от 300 до 500 писем за раз). Было бы неэффективно повторять эти шаги для каждого из более чем 4000 уже известных генетических признаков и болезней. Для ускорения прогресса молекулярные генетики увидели ценность создания инфраструктуры — общего набора карт, инструментов и информации, — которые можно применять ко всем генетическим проблемам. Это признание привело к созданию проекта «Геном человека» (Национальный исследовательский совет, 1988), международная попытка проанализировать структуру генома человека (а также геномы некоторых ключевых экспериментальных модельных систем, таких как E. coli , дрожжи , нематоды, дрозофилы и мыши).

Поскольку большинство молекулярно-биологических методов применимы только к небольшим фрагментам ДНК, нецелесообразно секвенировать геном человека, просто начав с одного конца и действуя последовательно. Более того, поскольку текущая стоимость секвенирования составляет около 1 доллара за основание, было бы дорого секвенировать 3 × 10 ⁹ оснований хромосом человека общепринятыми методами. Вместо этого разумнее построить карты увеличения, разрешения и разработать более эффективную технологию секвенирования. Текущие цели проекта «Геном человека» включают разработку следующих инструментов:

Генетические карты. Цель состоит в том, чтобы создать генетическую карту, показывающую расположение 5000 полиморфизмов, которые можно использовать для отслеживания наследования болезней в семьях. На момент написания этой статьи цель почти завершена.
Физические карты. Цель состоит в том, чтобы создать коллекцию перекрывающихся фрагментов ДНК, покрывающих все хромосомы человека. Эта цель еще не достигнута, но должна быть достигнута к 1996 году.
Последовательность ДНК. Конечной целью является секвенирование всего генома, но промежуточные этапы включают секвенирование определенных областей, создание более эффективной и автоматизированной технологии и разработку более совершенных аналитических методов для обработки информации о ДНК.

Учитывая огромное количество генерируемой информации, проект «Геном человека» является одной из движущих сил расширения роли математики, статистики и информатики в современной молекулярной биологии.

COMING ATTRACTIONS

Главы этой книги описывают важные применения математических, статистических и вычислительных методов в молекулярной биологии. Эти методы быстро развиваются, и в основном из-за этой ситуации презентации в этой книге предназначены скорее для вводных очерков, чем для научных обзоров. Не претендуя на полноту обзора, эта книга должна познакомить читателей с некоторыми захватывающими примерами использования математики, статистики и вычислений в молекулярной биологии. Другие введения в различные аспекты молекулярной биологии можно найти в Watson et al. (1994), Streyer (1988), Министерство энергетики США (1992), Watson et al. (1987), Левин (1990) и Альбертс и др. (1989).

Глава 2 («Картирование наследственности») описывает, как можно использовать статистические модели для картирования приблизительного расположения генов на хромосомах. Картирование генов упоминалось выше в случае гена муковисцидоза. Проблема становится особенно сложной — и математика играет большую роль — когда болезнь не следует простым менделевским схемам наследования — например, когда она вызвана несколькими генами или когда признак носит количественный, а не качественный характер. Это важная тема для проекта «Геном человека» и его приложений в современной медицинской генетике.

Следующие три главы посвящены анализу последовательностей ДНК и белков. Когда секвенируются новые гены, их регулярно сравнивают с общедоступными базами данных для поиска сходства, которое может указывать на общее эволюционное происхождение, структуру или функцию. Поскольку базы данных расширяются со все возрастающей скоростью, вычислительная эффективность таких сравнений имеет решающее значение. Глава 3 («Наблюдение сохраняющихся сигналов») описывает комбинаторные алгоритмы для этой задачи. Поскольку в таких сравнениях много совпадений, необходим тщательный статистический анализ. В главе 4 («Нагрев далеких эхо-сигналов») обсуждается применение экстремальной статистики к подобию последовательностей. Для близкородственных последовательностей сравнение последовательностей также проливает свет на процесс эволюции. В главе 5 («Калибровка часов») обсуждается применение случайных процессов к такому эволюционному анализу. Открытие и прочтение генетических последовательностей вдохнуло новую жизнь в изучение стохастических процессов эволюции. В этой главе основное внимание уделяется одному из самых захватывающих новых инструментов — использованию коалесцента для оценки времени до самого последнего общего предка.

Геометрические методы, применяемые к структуре и функциям ДНК, находятся в центре внимания следующих трех глав. Знаменитую двойную спираль ДНК Уотсона и Крика можно рассматривать как локальную геометрическую структуру. Есть также много интересной геометрии в более глобальной структуре молекул ДНК. В главе 6 («Скручивание двойной спирали») используются геометрические методы для описания скручивания и упаковки хромосом. В этой главе описывается сверхспирализация двойной спирали в терминах ключевых геометрических величин — связи, закручивания и изгиба — которые связаны фундаментальной теоремой. В главе 7 («Раскручивание двойной спирали») дифференциальная механика используется для изучения того, как нагрузки на молекулу ДНК заставляют ее раскручиваться в определенных областях, тем самым открывая доступ ключевым ферментам, необходимым для экспрессии генов. В главе 8 («Приподнимая занавес») топология используется для вывода о механизме действия ферментов, рекомбинирующих нити ДНК, что дает представление о деталях, которые нельзя увидеть в эксперименте.

Наконец, в главе 9 («Складывание листов») обсуждается один из самых сложных открытых вопросов в вычислительной биологии: проблема свертывания белка, которая касается предсказания трехмерной структуры белка на основе последовательности его аминогрупп. кислоты. Вероятно, для этой центральной проблемы никогда не будет дано простого решения, но было разработано много полезных и интересных приближенных подходов. В заключительной главе рассматриваются различные вычислительные подходы к прогнозированию структуры.

Вместе эти главы дают представление о роли математики, статистики и вычислений в некоторых из наиболее интересных и динамичных областей молекулярной биологии. Если эта книга побудит некоторых математиков, статистиков и ученых-вычислителей узнать больше о молекулярной биологии и внести свой вклад в ее развитие, она достигнет одной из своих целей. Две другие его цели — побудить молекулярных биологов лучше осознавать важность математических и вычислительных наук в молекулярной биологии и побудить научно грамотных людей осознать растущее влияние как молекулярной биологии, так и математических и вычислительных наук на их жизнь. . Если эта книга продвинется к этим трем целям, она стоила затраченных усилий.

ССЫЛКИ

Альбертс Б. , Брей Д., Льюис Дж., Рафт М., Робертс К., Уотсон Дж.Д. Молекулярная биология клетки. 2-е изд. Нью-Йорк: Гарленд; 1989.
Avery OT, McLeod CM, McCarty M. Изучение химической природы вещества, вызывающего трансформацию пневмококкового типа. Дж. Эксп. Мед. 1944; 79: 137–158. [Бесплатная статья PMC: PMC2135445] [PubMed: 19871359]
Левин Б. Гены IV. Оксфорд: Издательство Оксфордского университета; 1990.
Национальный исследовательский совет. Картирование и секвенирование генома человека. Вашингтон, округ Колумбия: Издательство Национальной академии; 1988. [PubMed: 25032310]
Национальный исследовательский совет. Технология ДНК в криминалистике. Вашингтон, округ Колумбия: Издательство Национальной академии; 1992. [PubMed: 25121318]
Ричардсон Дж. С., Ричардсон, округ Колумбия. Принципы и закономерности конформации белков. В: Фасман Джеральд Д., редактор. Предсказание структуры белка и принципы конформации белка. Нью-Йорк: Plenum Publishing Corporation; 1989. стр. 1–98.
Риордан Дж. Р., Ромменс Дж. М., Б. Креме, Алон Н., Розмахель Р., Гжельчак З., Зеленски Дж., Лок С., Плавшич Н., Чоу Дж.-Л., Драмм М. Л., Иннуцци М. С., Коллинз Ф. С., Цуй Л.-К. Идентификация гена муковисцидоза: клонирование и характеристика комплементарной ДНК. Наука. 1989 г., 8 сентября; 245: 1066–1073. [PubMed: 2475911]
Сали А., Шахнович Э., Карплюс М. Как складывается белок? Природа. 1994 г., 19 мая; 369: 248–251. [PubMed: 7710478]
Стрейер Л. Биохимия. Сан-Франциско, Калифорния: WH. Фриман; 1988.
Министерство энергетики США, Программа генома человека. Букварь по молекулярной генетике. Вашингтон, округ Колумбия: Типография правительства США; 1992. Управление энергетических исследований, Управление исследований в области здравоохранения и окружающей среды.
Уотсон Дж. Д., Хопкинс Н., Робертс Дж., Стейц Дж. А., Вайнер А. Молекулярная биология гена. Менло-Парк, Калифорния: Бенджамин-Каммингс; 1987.
Уотсон Дж. Д., Туз Дж., Курц Д. Т. Рекомбинантная ДНК: краткий курс. 2-е изд. Нью-Йорк: WH Фриман и Ко; 1994.

Что такое электрон? Что такое Свет?

Примечание редактора: этот раздел основан на работе из ^[1]

Чтобы стать биологом или медицинским работником, вы должны изучать множество научных дисциплин — биологию, химию, физику и математику. Вы могли заметить, что мир на самом деле не делится таким образом. Скорее, дисциплины исторически были способом выбора подкласса явлений, происходящих в мире, и рассмотрения их определенного аспекта с определенной целью. Различные дисциплины имеют разные наборы инструментов и способов познания. Взгляд на что-то с разных дисциплинарных точек зрения добавляет богатство и глубину нашему пониманию — например, создание двух двухмерных изображений и их слияние в трехмерное изображение.

На вводных занятиях по естествознанию и математике вы часто знакомитесь с некоторыми основами — инструментами, концепциями и словарным запасом — но не даете представления о том, что каждая дисциплина добавляет к тому, что вы изучаете, и как все это сочетается друг с другом. Каждая дисциплина имеет свою направленность и перспективу развития профессионального ученого. Вот краткий (и упрощенный) обзор различных дисциплин, с которыми вы сталкиваетесь при изучении биологии.

Биология

Биология, как вы хорошо знаете, изучает живые организмы. Подход, принятый биологией, руководствуется и ограничивается тем фактом, что предметом изучения являются живые организмы.

Большая часть биологии сложна — Из-за сложности первые шаги в биологии (и в других сложных науках) часто связаны с идентификацией, классификацией и описанием явлений. Всякий раз, когда наука рассматривает сложное явление, она поступает именно так — будь то биология, органическая химия или физика плазмы. В биологии важно описать черты, структуру и поведение биологического явления, прежде чем искать объяснения того, как оно работает. Поэтому было важно заняться линнеевской классификацией и морфологией, прежде чем можно будет разработать идеи эволюции; и понимание природы органической химии и биологических молекул было необходимо, прежде чем можно было распутать молекулярное функционирование биологических систем. Это приводит к тому, что биология имеет огромный словарный запас и множество концепций для изучения.
Биология зависит от истории — Под этим мы подразумеваем не историю развития биологии, а историю развития организмов. Все биологические организмы связаны общей неразрывной историей — цепью или паутиной форм жизни, — которая влияет на то, как обстоят дела сегодня. То, что произошло с течением времени, имеет значение в биологии и влияет на то, как обстоят дела сегодня. Это похоже на геологию и отличается от химии, физики или математики. (Хотя когда биология доходит до механизма того, как все происходит на самом деле, она очень похожа на химию и физику и использует математику.) Свойства живых организмов и их отношения с окружающей средой и друг с другом во многом зависят о том, что случилось с их предками в далеком прошлом. История организма записана в его геноме. Знание эволюционных процессов часто является важным инструментом для «объяснения», почему конкретный организм решает биологическую задачу определенным образом.
Биология ищет механизм — Биология — это не просто «Что такое жизнь?» Это также вопрос «Как это работает?» На одном уровне вы можете посмотреть на органы и части животного или клетки и выяснить, какова их функция для организма. Сегодня, используя инструменты химии и физики (и используя математику), биология спустилась на атомный и молекулярный уровень, выясняя биохимию генов и белков. Сегодня такие количественные измерения можно проводить одновременно на тысячах генов или белков в организме. Это открыло новый рубеж науки, «системной биологии», целью которой является поиск механизмов в этих огромных наборах данных и описание того, как тысячи или миллионы компонентов работают вместе в биологической системе, такой как клетка, организм или популяция.
Биология многомасштабна — организм можно рассматривать во многих масштабах, например, в атомно-молекулярном масштабе (биохимия), с точки зрения внутреннего строения и функционирования его органов и частей (физиология), а также как часть гораздо большей системы как в пространстве (экология), так и во времени (эволюция). Отношение между этими шкалами можно трактовать с точки зрения редукционизма или эмерджентности — перехода к более мелким масштабам для объяснения чего-либо (редукционизм) или наблюдения за возникновением новых явлений по мере перехода к более крупному масштабу (эмерджентность).
Биология является интегративной – Биологические явления возникают и должны соответствовать принципам химии, физики и математики. Другими словами, химия и физика ограничивают то, как организм может вести себя или развиваться. Поэтому биологи должны понимать, как физика и химия проявляются в биологических организмах и системах более высокого порядка. Все чаще биологи, изучающие механизмы сложного биологического поведения, находят полезным использовать в своих исследованиях математические, физические и химические модели.

Химия

Химия начинается с идеи о том, что вся материя состоит из определенных фундаментальных частей — атомов примерно 100 различных видов (элементов) — и о том, как эти элементы объединяются, образуя более сложные структуры — молекулы. Но химия — это не только построение молекул. Речь идет о том, что вы можете сделать с этим знанием в нашем макроскопическом мире.

Химия посвящена тому, как атомы взаимодействуют с образованием молекул — Понимание основных принципов взаимодействия и соединения атомов является фундаментальной отправной точкой для химии.
Химия занимается разработкой принципов и эвристики более высокого уровня — Поскольку существует так много различных типов молекул, химия развивает идеи более высокого уровня, которые помогают вам думать о том, как происходят сложные реакции.
Химия часто пересекает шкалы — соединяя микроскопическое с макроскопическим, пытаясь узнать о молекулярных реакциях из макроскопических наблюдений и выясняя, что возможно макроскопически, исходя из поведения атомов. Связи косвенные, могут быть тонкими и могут включать эмерджентность.
Химия часто предполагает макроскопическую среду — Многое из того, что изучает химия, — это не просто идеализированные атомы, взаимодействующие в вакууме, но множество атомов, взаимодействующих в среде, такой как жидкость, газ или кристалл. В водной среде важную роль играет доступность ионов H+ и OH- в результате диссоциации молекул воды в окружающей среде, в то время как в газовой среде критическое значение имеет баланс парциальных давлений.
Химия часто упрощает — В химии вы часто выбираете доминирующие реакции для рассмотрения, идеализируете ситуации и процессы, чтобы позволить понять наиболее важные особенности.

Для химика большая часть того, что происходит в биологии, является «макроскопическим» — в нем задействовано очень много атомов — даже если для изучения этого вам может понадобиться микроскоп. В вводной химии вы часто предполагаете, что реакции происходят при стандартной температуре и давлении (300 К и 1 атм).

Физика

Цель физики — найти фундаментальные законы и принципы, управляющие всей материей, включая биологические организмы. Эти законы и принципы могут привести ко многим типам сложных и явно различных явлений. Физика, традиционно преподаваемая на вводном уровне, имеет тенденцию явно вводить четыре научных навыка, которые могут показаться отличными от того, что вы видите на вводных уроках биологии и химии, но эти четыре навыка окажутся ценными для вашей карьеры.

Физики часто тратят много времени на разработку простейшего возможного примера («игрушечной модели»), иллюстрирующего принцип — , даже если этот пример кажется не особенно интересным, актуальным или реалистичным. Это позволяет вам ясно и полностью понять, как работает принцип. Затем это понимание может быть вплетено в более сложные ситуации, чтобы лучше понять, что происходит (хотя внедрение простоты в реалистичную, актуальную и сложную ситуацию часто опускается на традиционных вводных уроках физики).
Физики количественно оценивают свое видение реального мира — Хотя в физике много концептуальных и качественных рассуждений, физики, как правило, не удовлетворяются, пока не смогут количественно определить то, о чем они говорят. Это связано с тем, что чисто качественные рассуждения иногда могут вводить в заблуждение. Хотя вы можете придумать аргумент, утверждающий, что происходит А, но если хорошенько подумать, вы также можете прийти к аргументу, утверждающему, что происходит что-то другое — Б. Это произойдет только после того, как вы поймете, что эффект Б в 1000 раз больше, чем эффект. Что вы действительно умеете описывать происходящее. Это так же верно для биологии и химии, как и для физики, но физики склонны вводить количественную оценку в учебную программу раньше и шире, чем химия, которая делает это чаще на вводных занятиях, чем биология.
Физики думают уравнениями — Это больше, чем просто вычисление чисел: физики используют уравнения как для организации своих качественных знаний о том, что на что и как влияет, так и для того, чтобы рассуждать, чтобы определить, как происходят вещи, что важно и насколько . Физики постоянно переключаются между концептуальным размышлением о проблеме и математическим размышлением о проблеме, так что каждый из этих способов мышления проливает свет на другой.
Физики имеют дело с реальными ситуациями путем моделирования и аппроксимации — Это означает определение того, что имеет наибольшее значение в сложной ситуации, и построение довольно простой модели, которая позволит вам получить хорошее представление о том, что происходит. Вот в чем заключается искусство физики: выяснить, что можно игнорировать, не теряя при этом того, на что вы хотите смотреть. Эйнштейн был прав, когда сказал: «Физика должна быть как можно проще, но не проще». Все науки делают это, но поскольку физика занимается «всем и вся», физики часто предполагают, что на вводных занятиях они могут выбрать системы, которые могут показаться упрощенными до неуместности. На этом занятии мы постараемся быть более явными при моделировании сложных примеров, чем на традиционных занятиях по физике.

Этот способ ведения науки немного отличается от того, как часто занимаются биологией, но элементы этого подхода и ограничения, налагаемые на биологию законами физики, становятся все более важными как для биологов-исследователей, так и для медицинских работников. Подробнее об этом читайте на странице Чем физика может быть полезна для биологов.

Математика

Математика немного отличается от естественных наук. По своей сути математика связана с абстрактными отношениями. Поскольку математика связана с абстрактными отношениями и их поведением, она не касается ничего в физическом мире. Но оказывается, что многие отношения в науке могут быть смоделированы отношениями, которые подчиняются математическим правилам, часто очень точно. (Если вы думаете, что это удивительно или странно, вы не одиноки. Ради интереса взгляните на интересную статью лауреата Нобелевской премии по ядерной и математической физике Юджина Вигнера, озаглавленную «Необоснованная эффективность математики в Естественные науки.“)

Математика, которую преподают на уроках математики, часто в первую очередь связана с абстрактными отношениями — изучением того, как использовать математические инструменты. Переход к использованию математики в реальных ситуациях может быть довольно неприятным, поскольку теперь есть дополнительные вещи, на которые следует обратить внимание помимо самой математики, например, на выяснение того, как элементы реальной системы преобразуются в математическую модель. и беспокоясь о том, достаточно ли хороша математическая модель. Мне нравится думать об этом так: на уроке математики вы изучаете «грамматику» языка науки. Здесь и на других ваших научных курсах вам нужно начать изучать «лексику». Объединив грамматику и словарный запас, вы сможете начать описывать Вселенную.

Объединение этих дисциплин

Объединить все это для связного и продуктивного мышления — непростая задача! В этом классе мы ожидаем и призываем вас использовать знания, которые вы получили на других уроках естественных наук, чтобы попытаться увидеть, как они сочетаются друг с другом, поддерживают друг друга и научиться определять, когда конкретный дисциплинарный подход может быть наиболее подходящим и полезным. .

В то время как все эти разные научные дисциплины в конечном итоге работают с одной и той же целью: понять Вселенную. Исторически они развивались полунезависимо. Таким образом, имеется культурные различия между науками так же, как существуют культурные различия между странами (например, правостороннее или левостороннее движение). Эти культурные различия не связаны с «правильными» или «неправильными» способами ведения дел. Они просто разные. На самом деле, эти различия в перспективе — сила! Различные точки зрения между дисциплинами часто приводили ко многим важным открытиям на протяжении всей истории и до сих пор делают многие из самых захватывающих достижений. Однако они могут сбивать с толку. Поэтому мы работали с преподавателями биологии, химии и математики здесь, в Массачусетском университете в Амхерсте. Результатом этих дискуссий стал некоторый общий язык, используемый в этой книге, который поэтому может отличаться от других текстов по физике, которые вы можете просмотреть. Тем не менее, иногда есть места, где нам нужно использовать силу другой точки зрения. Мы укажем на эти различия, используя блоки, подобные приведенному ниже.

Мы будем использовать такие рамки, чтобы указать на важные различия между дисциплинами. Опять же, эти различия не являются «правильными» или «неправильными» способами ведения дел. Это просто артефакты различных наук, которые веками развивались независимо друг от друга под влиянием разных культур со всего земного шара.

Редиш Э. Ф., «Дисциплины: физика, биология, химия и математика», в Introductory Physics for the Life Sciences I — NEXUS Physics , University of Maryland, College Park, 2013. ↵

3 Связь между математическими науками и другими областями

Страница 58

Делиться

Цитировать

Рекомендуемое цитирование: «3 связи между математическими науками и другими областями». Национальный исследовательский совет. 2013. Математические науки в 2025 году . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/15269.

Сохранить

Отменить

Связи между математическими науками и другими областями

ВВЕДЕНИЕ

В дополнение к установлению превосходной внутренней жизнеспособности математических наук, как показано в главе 2, текущее исследование выявило поразительное расширение влияния математических наук в других областях, а также расширение числа подполей математических наук, которые применяются для решения задач вне дисциплины. Это расширение продолжалось десятилетиями, но за последние 10-20 лет оно значительно ускорилось. Некоторые из этих связей развиваются естественным образом, потому что в настоящее время так много науки и техники основано на вычислениях и моделировании, для которых математические науки являются естественным языком. Кроме того, возможности сбора данных значительно расширились и продолжают расти, а математические науки изначально вовлечены в извлечение знаний из всех этих данных. Однако механизмы, облегчающие связи между учеными-математиками и исследователями в других дисциплинах, должны быть усовершенствованы.

В некоторых случаях результаты исследований в области математических наук могут очень сильно распространяться, потому что новое понимание может быть быстро воплощено в программном обеспечении без длительных этапов перевода, которые существуют, скажем, между фундаментальными исследованиями в области химии и использованием утвержденного фармацевтического препарата. Когда исследования в области математических наук создают новый способ сжатия или анализа данных, оценки финансовых продуктов, обработки сигнала от медицинского устройства или военной системы или решения уравнений для инженерного моделирования, выгода может быть реализована быстро. По этой причине даже правительственные учреждения или отрасли промышленности, которые кажутся оторванными от

Страница 59

Делиться

Цитировать

Сохранить

Отменить

Математические науки кровно заинтересованы в поддержании сильного предприятия математических наук в нашей стране. И поскольку это предприятие должно быть здоровым, чтобы способствовать поставке хорошо подготовленных людей в области науки, техники, инженерии и математики (STEM), ясно, что каждый должен заботиться о жизнеспособности математических наук.

В этой главе обсуждается, как растущее взаимодействие с другими областями расширило определение математических наук. Затем он документирует важность математических наук для множества областей. Во многих случаях эту важность можно проиллюстрировать, взглянув на крупные исследования самих дисциплин, в которых проблемы с большим компонентом математических наук часто перечислены как наиболее приоритетные. Обширные примеры этого приведены в Приложении D.

РАСШИРЕНИЕ ОПРЕДЕЛЕНИЯ МАТЕМАТИЧЕСКИХ НАУК

За последнее десятилетие или более произошло быстрое увеличение числа способов использования математических наук и типов применяемых математических идей. Поскольку многим из этих областей роста способствует взрывной рост возможностей для моделирования, вычислений и анализа данных (что само по себе обусловлено ростом сбора данных на порядки), часто предполагается, что соответствующие исследования и их практики попадают под зонтик. информатики. Но на самом деле в эту работу вносят свой вклад люди с разным бэкграундом. Процесс науки и техники, основанный на моделировании, по своей сути очень математический, требующий усовершенствования математических структур, позволяющих моделировать; в разработке алгоритмов; в фундаментальных вопросах вычислительной техники; а также при проверке модели, количественной оценке неопределенности, анализе и оптимизации. Достижения в этих областях необходимы, поскольку ученые и инженеры-вычислители решают все более сложные задачи и используют передовые вычисления. Эти аспекты математической науки требуют значительной интеллектуальной глубины и по своей сути представляют интерес для математических наук.

В настоящее время большая часть работы в этих развивающихся областях — например, биоинформатика, веб-компании, финансовый инжиниринг, анализ данных, вычислительная наука и инженерия — выполняется в основном людьми, которых не обязательно называть «учеными-математиками». ». Но математическое научное содержание такой работы, даже если это не исследование, является значительным, и поэтому крайне важно, чтобы сообщество математических наук играло свою роль посредством образования, исследований и сотрудничества. Люди с математическим образованием сами по себе могут предлагать различные точки зрения, которые дополняют точки зрения компьютерных ученых и других специалистов, а сочетание талантов может быть очень мощным.

Страница 60

Делиться

Цитировать

Сохранить

Отменить

Точного определения «математических наук» не существует. Следующее определение использовалось в XIX в.90 отчет, широко известный как отчет Давида II по имени председателя авторского комитета Эдварда Э. Дэвида:

Дисциплина, известная как математические науки, охватывает базовую (или чистую) и прикладную математику, а также статистику и исследование операций, и распространяется на высшие математические науки. области других областей, таких как теоретическая информатика. Теоретические разделы многих других областей, например биологии, экологии, техники, экономики, органично сливаются с математическими науками. ¹

В отчете Odom 1998 г. неявно использовалось аналогичное определение, представленное на рис. 3-1, адаптированное из этого отчета.

На рис. 3-1 отражена важная характеристика математических наук, а именно то, что они пересекаются со многими другими научными, инженерными и медицинскими дисциплинами, а также с такими областями бизнеса, как финансы и маркетинг. Там, где маленькие эллипсы пересекаются с основным эллипсом (представляющим математические науки), следует предвидеть взаимное переплетение и сцепление, где поля пересекаются и где исследования и люди могут охватывать две или более дисциплины. Некоторые люди, которые явно связаны с математическими науками, могут иметь обширное взаимодействие и глубокое знакомство с одной или несколькими из этих перекрывающихся дисциплин. И некоторые люди в этих других дисциплинах могут чувствовать себя совершенно комфортно в математической или статистической среде, как будет обсуждаться далее. Эти интерфейсы не являются чистыми линиями, а представляют собой области, в которых смешиваются дисциплины. Большая и постоянно растущая часть современной науки и техники в значительной степени «математическая», и любая разделительная линия, разделяющая более центральные и промежуточные области математических наук, несомненно, будет произвольной. Легко указать на работу в теоретической физике или теоретической информатике, которая неотличима от исследований, проводимых математиками, и подобное совпадение происходит с теоретической экологией, математической биологией, биоинформатикой и все большим числом областей. Это не новое явление — например, люди с докторскими степенями по математике, такие как Герберт Гауптман, Джон Попл, Джон Нэш и Уолтер Гилберт, получили Нобелевские премии по химии или экономике, — но оно становится все более распространенным по мере того, как появляется все больше областей. поддается математическим представлениям. Этот взрыв возможностей означает, что большая часть исследований двадцать первого века будет строиться на фундаменте математической науки, и этот фундамент должен продолжать развиваться и расширяться.

______________________

¹ NRC, 1990, Обновление математики в США: план на 1990-е годы . National Academy Press, Вашингтон, округ Колумбия

Страница 61

Делиться

Цитировать

Сохранить

Отменить

РИСУНОК 3-1 Математические науки и их интерфейсы. ИСТОЧНИК: Взято из National Science Foundation, 1998, Report of the Senior Assessment Panel for the International Assessment of the U.S. Mathematical Sciences , NSF, Arlington, VA.

Обратите внимание, что центральный эллипс на рис. 3-1 не разделен. Члены комиссии, как и многие другие, изучавшие математические науки, считают важным рассматривать математические науки как единое целое. Различия между «основной» и «прикладной» математикой все больше кажутся искусственными; в частности, сегодня трудно найти область математики, не имеющую отношения к приложениям. Это правда, что некоторые ученые-математики в основном доказывают теоремы, в то время как другие в основном создают и решают модели, и профессиональные системы вознаграждения должны это учитывать. Но любой конкретный человек может перемещаться между этими видами исследований, и многие области специализации могут включать и включают оба вида работы. В целом, ряд математических наук объединяет общий опыт и мыслительные процессы, и существует долгая история того, как идеи из одной области становились полезными в другой.

Таким образом, комитет соглашается со следующим заявлением, сделанным в Международном обзоре математических наук за 2010 г. (раздел 3.1):

Страница 62

Делиться

Цитировать

Сохранить

Отменить

Давняя практика заключалась в том, чтобы разделить математические науки на категории, которые по смыслу близки к непересекающимся. Два наиболее распространенных различия проводятся между «чистой» и «прикладной» математикой, а также между «математикой» и «статистикой». Эти и другие категории могут быть полезны для передачи реальных различий в стиле, культуре и методологии, но, по мнению Группы, они производят все более негативный эффект, когда математические науки рассматриваются в общем контексте науки и техники, подчеркивая различия, а не различия. чем объединяющие принципы. Кроме того, такие различия могут создавать ненужные барьеры и напряженность в сообществе математических наук, поглощая энергию, которую можно было бы потратить более продуктивно. На самом деле, между различными областями математических наук увеличивается количество совпадений и полезных взаимодействий. . . . [Т] черты, объединяющие математические науки, доминируют над теми, которые их разделяют. ²

В чем заключается эта общность опыта, разделяемого всеми математическими науками? Математические науки стремятся понять мир, выполняя формальные символические рассуждения и вычисления на абстрактных структурах. Один из аспектов математических наук включает раскрытие и понимание глубоких взаимосвязей между этими абстрактными структурами. Другой аспект включает захват определенных характеристик мира абстрактными структурами в процессе моделирования, выполнение формальных рассуждений об этих абстрактных структурах или использование их в качестве основы для вычислений, а затем повторное подключение для прогнозирования мира — часто это итерационный процесс. Связанный аспект заключается в использовании абстрактных рассуждений и структур, чтобы делать выводы о мире на основе данных. Это связано с поиском способов превратить эмпирические наблюдения в средство классификации, упорядочивания и понимания реальности — основное обещание науки. С помощью математических наук исследователи могут построить совокупность знаний, взаимосвязь которых понятна и где можно найти и использовать любое необходимое понимание. Математические науки также служат естественным каналом, по которому концепции, инструменты и лучшие практики могут перемещаться из одной области в другую.

Еще одним аспектом математических наук является исследование того, как сделать процесс рассуждений и вычислений максимально эффективным, а также определить их пределы. Крайне важно понять, что эти различные аспекты математических наук не развиваются изолированно друг от друга. Наоборот, каждый аспект усилий обогащает другие новыми проблемами, новыми инструментами, новыми идеями и, в конечном счете, новыми парадигмами.

Таким образом, нет никакой очевидной причины, по которой такой подход к знаниям позволил бы нам понять физический мир. Но все

______________________

² Исследовательский совет по инженерным и физическим наукам (EPSRC), 2010, International Review of Mathematical Science . EPSRC, Суиндон, Великобритания, с. 10.

Страница 63

Делиться

Цитировать

Сохранить

Отменить

Предприятие по математическим наукам

оказалось не только необычайно эффективным, но и действительно необходимым для понимания нашего мира. Эту загадку часто называют «необоснованной эффективностью математики», упомянутой в главе 2.

В свете этой «необоснованной эффективности» еще более поразительно видеть на рис. 3-1, насколько далеко распространились математические науки с тех пор, как в 19 г.98.

Отражая реальность, лежащую в основе рис. 3-2, в этом отчете используется очень широкое определение «математических наук». Дисциплина охватывает широкий спектр разнообразных действий, связанных с созданием и анализом математических и статистических представлений концепций, систем и процессов, независимо от того, идентифицирует ли лицо, выполняющее эту деятельность, как

Page 64

Делиться

Цитировать

Сохранить

Отменить

ученый-математик. Традиционные области математических наук, безусловно, включены. Но многие другие области науки и техники глубоко связаны с построением и оценкой математических моделей, их вычислительным исследованием и анализом огромных объемов наблюдаемых и вычисляемых данных. Все эти виды деятельности по своей природе являются математическими, и нет четкой границы, разделяющей исследовательские усилия на те, которые являются частью математических наук, и теми, которые являются частью информатики или дисциплины, для которой выполняются моделирование и анализ. ³ Комитет полагает, что здоровье и жизнеспособность дисциплины будут максимальными, если знания и люди смогут легко проникать в этот большой набор усилий.

РИСУНОК 3-2. Математические науки и их интерфейсы в 2013 году. Количество интерфейсов увеличилось со времени, показанного на рис. 3-1, и сами математические науки расширились в ответ. Академическая наука и инженерное предприятие обозначены правой половиной рисунка, а более широкие области человеческой деятельности обозначены левой. В академии математические науки играют более интегрирующую и основополагающую роль, в то время как в обществе их влияние в более широком смысле затрагивает всех нас, хотя это часто недооценивается, потому что остается за кулисами. Эта схема является условной и основана на разнообразном и субъективном опыте комитета, а не на конкретных данных. Он не пытается представить многие другие связи, существующие между академическими дисциплинами и между этими дисциплинами и широкими усилиями левых, только потому, что полное взаимодействие слишком сложно для двухмерной схемы.

Так что же такое «сообщество математических наук»? Это собрание людей, которые продвигают дисциплину математических наук. Некоторые члены этого сообщества могут быть профессионально связаны с двумя или более дисциплинами, одной из которых являются математические науки. (Это выравнивание отражается, например, в том, какие конференции они посещают, в каких журналах публикуются, какие у них ученые степени и к каким академическим факультетам они принадлежат.) Математические науки очень ценны, приветствуя этих «двойных граждан». ; их участие хорошо для математических наук и обогащает способы, которыми другие области могут подходить к их работе.

Скопление людей в зонах перекрытия большое. В нее входят статистики, работающие в области наук о Земле, социальных наук, биоинформатики и других областях, которые по историческим причинам стали специализированными ответвлениями статистики. В него входит некоторая часть исследователей в области научных вычислений, вычислительной науки и техники. В нее входят теоретики чисел, которые вносят свой вклад в криптографию, и настоящие аналитики и статистики, которые вносят свой вклад в машинное обучение. В нее входят исследователи операций, некоторые специалисты по информатике, а также физики, химики, экологи, биологи и экономисты, которые полагаются на сложные математические научные подходы. Также включены некоторые из инженеров, которые продвигают математические модели и вычислительное моделирование. Ясно, что математические науки теперь выходят далеко за рамки определений, подразумеваемых учреждениями — академическими отделами, источниками финансирования, профессиональными обществами и ведущими журналами, — которые поддерживают сердце этой области.

В качестве одной из иллюстраций роли, которую исследователи в других областях играют в математических науках, комитет изучил общедоступные данные ⁴ о грантах Национального научного фонда (NSF), чтобы получить представление о том, какая часть исследований поддерживается другими подразделениями. чем Математический отдел NSF

______________________

³ Большинство других дисциплин, показанных на рис. 3-2, также имеют обширные взаимодействия с другими областями, но полная взаимосвязь этих усилий опущена для ясности.

⁴ Доступно на http://www.nsf.gov/awardssearch/.

Страница 65

Делиться

Цитировать

Сохранить

Отменить

Sciences (DMS) привел к публикациям, которые появились в журналах, легко признанных математическими научными, или которые имеют заголовки, явно предполагающие математическое или статистическое содержание. Хотя это упражнение обязательно было субъективным и далеко не исчерпывающим, оно показало, что поддержка NSF математических наук де-факто шире, чем поддержка DMS. Это также подтвердило аргумент о том, что исследовательская деятельность в области математических наук выходит за рамки группы лиц, которых традиционно называют учеными-математиками. Это упражнение выявило следующую информацию:

• Гранты, присужденные в период 2008-2011 гг. Отделом вычислительной техники и коммуникационных технологий NSF (часть Управления компьютерных и информационных наук и инженерии), привели к 262 публикациям в области графиков и, в меньшей степени, основ алгоритмы.

• Гранты, предоставленные в 2004-2011 гг. Отделением физики, привели к 148 публикациям в общей области теоретической физики.

• Гранты, предоставленные в 2007–2011 годах Отделом инноваций в области строительства, машиностроения и производства Инженерного управления NSF, привели к 107 публикациям по исследованиям операций.

Это беглое исследование также насчитало 15 публикаций по математическим наукам, полученных в результате грантов 2009-2010 годов от Управления биологических наук NSF. (Эти подсчеты публикаций охватывают разные периоды лет, потому что количество публикаций с очевидным содержанием математических наук меняется со временем, вероятно, из-за инициатив по финансированию с ограниченным сроком действия. ) Для сравнения, гранты DMS, которые были активны в 2010 году, привели к 1739 публикациям. Таким образом, в то время как DMS явно является доминирующим сторонником исследований математических наук NSF, другие подразделения вносят нетривиальный вклад.

Аналогичным образом данные о членстве в Обществе промышленной и прикладной математики (SIAM) показывают, что большое количество людей, которые связаны с академическими или промышленными отделами, отличными от математики или статистики, тем не менее связывают себя с этим профессиональным обществом математических наук. Рисунок 3-3 показывает ведомственную принадлежность членов SIAM, не являющихся студентами.

Недавний анализ попытался количественно определить размер этого сообщества на стыке математических наук. ⁵ Выяснилось, что преподаватели 50 ведущих математических факультетов США — которые, следовательно, должны быть на центральном диске на рис. таким образом, можно сделать вывод, что он имеет математическое содержание). За тот же период около 75 000 исследовательских работ, проиндексированных Zentralblatt MATH, были опубликованы преподавателями других факультетов тех же 50 университетов. Подразумевается, что большая часть исследований в области математических наук — почти половина предприятия — проводится за пределами математических факультетов. ⁶ Это также говорит о том, что масштабы большинства математических факультетов могут не отражать истинную широту математических наук.

______________________

⁵ Джозеф Гркар, 2011, Математика, вывернутая наизнанку: интенсивный факультет против экстенсивного факультета. Высшее образование 61(6): 693-720.

Страница 66

Делиться

Цитировать

Сохранить

Отменить

РИСУНОК 3-3 Члены SIAM определяют основной отдел, к которому они относятся. На этом рисунке показана доля 6 269 участников, не являющихся студентами, идентифицирующих себя с определенной категорией.

Этот анализ также создал диаграмму Венна, воспроизведенную здесь как рис. 3-4, которая полезна для представления того, как диапазон областей исследований математических наук соотносится с интеллектуальным пространством, более широким, чем то, которое охватывает большинство факультетов академической математики. (На диаграмме также показано, как фокусы преподавания математических и нематематических факультетов отличаются от их исследовательской направленности.)

ПОСЛЕДСТВИЯ РАСШИРЕНИЯ МАТЕМАТИЧЕСКИХ НАУОК предприятие математической науки — его люди, преподавание и широта исследований. Если наше общее исследовательское предприятие работает хорошо, то исследователи, которые традиционно называют себя учеными-математиками (центральный эллипс на рис. 3.2), в свою очередь, получают стимулы, возникающие с фронтов, где новые типы явлений или данных стимулируют новое мышление в области математики. а статистическое моделирование и новые технические задачи стимулируют более глубокие вопросы для математических наук.

______________________

⁶ Некоторые из этих 75 000 статей относятся к исследователям из отделов статистики или исследований операций, которые мы четко посчитали бы находящимися на центральном диске рис. 3-2. Но в цитируемой статье отмечается, что только около 17 процентов исследований, проиндексированных Zentralblatt MATH, классифицируются как связанные со статистикой, вероятностью или исследованием операций.

Страница 67

Делиться

Цитировать

Сохранить

Отменить

РИСУНОК 3-4 Представление научно-исследовательской и преподавательской деятельности ведущих математических и нематематических факультетов в одних и тех же учебных заведениях. Наиболее публикуемые темы выделены курсивом; наиболее преподаваемые предметы подчеркнуты. ИСТОЧНИК: Джозеф Гркар, 2011 г., «Математика, вывернутая наизнанку: интенсивный факультет против экстенсивного». Высшее образование 61(6):693-720, рисунок 8. Цифры соответствуют следующим классификациям Zentralblatt MATH:

05 Комбинаторика

11 Теория чисел

14 Алгебраическая геометрия

5 9000 15 Алгебра Теория групп.0002 42 Анализ Фурье

46 Функциональный анализ

53 Дифференциальная геометрия

57 Говолны, клеточные комплексы

58 Глобальный анализ

60 Теория вероятности

Статистика

65 Numercal Analysis

68 Computer Science

747 70002. деформируемых твердых тел

76 Механика жидкости

80 Классическая термодинамика

81 Квантовая теория

86 Геофизика

90 Исследование операций

91 Теория игр, экономика

92 Биология

93 Теория систем, управление

94 Информация и коммуникации

Страница 68

Делиться

Цитировать

Сохранить

Отменить

Многие люди с математическим образованием, которые сейчас работают на этих передовых рубежах — исследование операций, компьютерные науки, инженерия, экономика и т. д., — сказали комитету, что они высоко ценят подготовку, обеспечиваемую их математическим образованием, и что для них это важно. Естественно и здорово рассматривать все генеалогическое древо как единое целое. Многие ученые-математики и академические математические факультеты обоснованно сосредоточили внимание на основных областях, и это естественно в том смысле, что никакое другое сообщество не имеет мандата на обеспечение того, чтобы основные области оставались сильными и надежными. Но очень важно, чтобы между всеми математическими науками был легкий поток концепций, результатов, методов и людей. По этой причине важно, чтобы сообщество математических наук активно включало широкое сообщество исследователей, которые вносят интеллектуальный вклад в математические науки, включая людей, которые профессионально связаны с другой дисциплиной.

Неподтвержденная информация свидетельствует о том, что количество аспирантов, обучающихся как математике, так и другим областям — от биологии до инженерии — резко возросло за последние годы. Эта тенденция признается и поощряется, например, программой Math+X Фонда Саймонса, которая предоставляет междисциплинарные профессорские должности и поддержку аспирантам и докторантам, работающим в двух областях. Если это явление так широко распространено, как считает комитет, оно показывает, какой вклад в науку и технику в целом вносит последипломное образование в области математических наук, а также как растет интерес к интерфейсам. Чтобы сообщество могло рационально управлять собой, а финансирующие организации должным образом распределяли свои ресурсы, необходимо начать сбор данных об этой тенденции.

Рекомендация 3-1: Национальному научному фонду следует систематически собирать данные о таких взаимодействиях, например, опрашивая факультеты математических наук о числе зачисленных на курсы повышения квалификации студентов других дисциплин, а также о количестве зачисление аспирантов математических наук на курсы, не относящиеся к математическим наукам. Наиболее эффективным способом сбора этих данных может быть обращение к Американскому обществу с просьбой расширить свои ежегодные анкеты, включив в них такие запросы.

Программисты в NSF/DMS и в других финансирующих организациях осведомлены о многих совпадениях между математическими науками и другими дисциплинами,

Страница 69

Делиться

Цитировать

Сохранить

Отменить

, и есть много примеров гибкости в финансировании — ученые-математики финансируются подразделениями, которые в основном сосредоточены на других дисциплинах, и наоборот. DMS, в частности, работает в той или иной степени с другими подразделениями NSF через формальные механизмы, такие как программы совместного финансирования, и неформальные механизмы, такие как сотрудники программы, перенаправляющие предложения из одного подразделения в другое, подразделения, помогающие друг другу в определении рецензентов, и так далее. Опять же, чтобы сообщество математических наук имело более полное представление о его охвате и помогало финансирующим агентствам лучше ориентировать свои программы, комитет рекомендует более методично собирать небольшой объем данных.

Рекомендация 3-2: Национальному научному фонду следует собирать данные о степени поддержки исследований математического характера в других подразделениях Фонда. (Такой анализ имел бы наибольшую ценность, если бы он был выполнен на уровне выше DMS.) Исследование, направленное на развитие этого понимания в отношении статистических наук в рамках NSF, проводится в настоящее время по запросу помощника директора NSF. для математики и физических наук. Более широкое такое исследование помогло бы сообществу математических наук лучше понять его текущий охват, и это могло бы помочь DMS позиционировать свой собственный портфель, чтобы наилучшим образом дополнить другие источники поддержки для более широкого предприятия математических наук. Это обеспечит основу для выявления изменений в этом предприятии с течением времени. Другие агентства и фонды, поддерживающие математические науки, выиграют от подобной самооценки.

Данные, собранные в соответствии с Рекомендациями 3-1 и 3-2, могут помочь сообществу, возможно, через его профессиональные сообщества, скорректировать обучение выпускников, чтобы оно лучше отражало фактическое поведение учащихся. Например, если значительная часть аспирантов-математиков посещает курсы, не связанные с математикой, либо из интереса, либо из-за беспокойства о будущих возможностях, это то, о чем математические факультеты должны знать и реагировать. Точно так же младшему преподавателю в междисциплинарной области было бы полезно знать, какие подразделения NSF финансировали работу в их области. Хотя такие знания часто можно найти в ходе целенаправленного разговора, видение полной картины было бы полезно для отдельных исследователей и могло бы изменить то, как сообщество математических наук видит себя.

В беседе с лидерами отрасли, описанной в главе 5, комитет был поражен масштабом спроса на работников с математическими навыками всех уровней, независимо от области их обучения. Он услышал о растущем спросе на людей с навыками анализа данных, о сохраняющейся потребности в математических науках в финансовом секторе,

Страница 70

Делиться

Цитировать

Сохранить

Отменить

и множество новых задач для ученых-математиков, работающих в интернет-корпорациях, а также в сфере развлечений и игр. Существует растущий рынок труда, основанный на математических науках. Однако лишь небольшая часть людей, нанятых этими лидерами отрасли, на самом деле имеет ученые степени в области математики и статистики; эти слоты часто заполняются людьми, имеющими образование в области компьютерных наук, инженерии или физических наук. В то время как этот опыт кажется приемлемым для работодателей, этот взрыв рабочих мест, основанных на навыках математических наук, представляет собой прекрасную возможность для математических наук и должен стимулировать сообщество тремя способами:

• Эти растущие области применения создают связанные с ними исследовательские задачи. Это уже хорошо известно в области поисковых технологий, финансовой математики, машинного обучения и анализа данных. Несомненно, новые исследовательские задачи будут по-прежнему возвращаться к исследовательскому сообществу математических наук по мере развития новых приложений;

• Спрос на людей с соответствующими навыками будет ощущаться преподавателями математических наук, которые играют важную роль в обучении этим навыкам учащихся в различных областях; и

• Большое количество карьерных путей, основанных в настоящее время на математических науках, требует внесения изменений в учебные программы для студентов и аспирантов по математике и статистике. Это будет обсуждаться в следующей главе.

Этот поразительный рост потребности в математических навыках у людей, которых можно назвать «практиками математических наук», у людей с передовыми знаниями, но которые могут быть не сосредоточены на исследованиях, представляет большие возможности для сообщества математических наук. В прошлом обучение математическим наукам, конечно же, было необходимо для обучения исследователей в области математики, статистики и многих областей науки и техники. А степень бакалавра по математике или статистике всегда была хорошей базовой степенью, трамплином для многих карьер. Но сообщество математических наук склонно рассматривать себя как состоящее в основном из исследователей и преподавателей математических наук и не расширяющееся в более широком смысле. По мере того, как все больше людей, обученных математическим наукам на всех уровнях, продолжают карьеру, основанную на исследованиях в области математических наук, у сообщества математических наук появляется возможность охватить новые классы профессионалов. В ряде университетов есть возможности для студентов бакалавриата участвовать в исследованиях в неакадемических условиях и программы стажировок для аспирантов в национальных лабораториях и промышленности. В национальных лабораториях доступны некоторые возможности как для постдокторантов, так и для более старших специалистов

Страница 71

Делиться

Цитировать

Сохранить

Отменить

и государственные учреждения. Расширение возможностей такого рода на всех уровнях было бы отрадным событием. Опыт такого рода на уровне факультета может быть особенно ценным.

В идеальном мире сообщество математических наук имело бы более четкое представление о его масштабах и влиянии. В дополнение к шагам, указанным в рекомендациях 3-1 и 3-2, ежегодный сбор следующей информации позволит сообществу лучше понять и улучшить себя:

• Подборка важных областей новых технологий, патентов и начала бизнеса. предприятия, применяющие результаты математических наук, и оценки занятости, связанные с этими разработками;

• Подборка существующих технологических областей, требующих участия и обучения со стороны сообщества математических наук, а также оценки занятости, связанные с этими областями;

• Подборка новых программ бакалавриата и/или магистратуры со значительным содержанием математических наук;

• Отношение количества рабочих мест со значительным содержанием математических наук к количеству новых выпускников (на разных уровнях) в области математических наук;

• Анализ текущей занятости людей, которые в прошлом получали федеральную поддержку в исследованиях или обучении, чтобы определить, работают ли они в настоящее время в университетах США, иностранных университетах, американской или иностранной промышленности, правительстве США или иностранного государства, вооруженных силах и т. д.;

• Подборка и анализ сотрудничества ученых-математиков.

Возможно, профессиональные общества математических наук совместно с некоторыми финансирующими учреждениями могли бы работать над созданием такой информационной базы, которая помогла бы предприятию двигаться вперед. Однако комитет хорошо осведомлен о проблемах сбора таких данных, которые, скорее всего, будут неточными и неполными.

ДВА ОСНОВНЫХ ФАКТОРА РАСШИРЕНИЯ: ВЫЧИСЛЕНИЯ И БОЛЬШИЕ ДАННЫЕ

Сочетание двух факторов привело к значительному расширению роли математических наук: (1) широкая доступность вычислительных мощностей и, как следствие, зависимость от моделирования с помощью математических моделей в сегодняшней науке, технике и технологиях и (2) резкий рост количества собираемых или генерируемых данных, который часто достигает такого масштаба, что его можно оценить только с помощью математических и статистических методов. В результате две области вычислений и «большая

Страница 72

Делиться

Цитировать

Сохранить

Отменить

данных» стали основными движущими силами математических исследований и расширения предприятия. Излишне говорить, что они тесно переплетены, и для крупных исследовательских работ становится все более привычным требовать опыта как в моделировании, так и в крупномасштабном анализе данных.

Перед обсуждением этих двух основных движущих сил важно отметить, что большая часть исследований в области математических наук по-прежнему определяется внутренней логикой предмета, то есть инициируется отдельными исследователями в ответ на их лучшее понимание многообещающих направления. (Часто используемая фраза «движимый любопытством» преуменьшает огромную эффективность этого подхода на протяжении веков.) В беседах комитета со многими учеными-математиками часто слышалось мнение, что невозможно предсказать конкретные области исследований, в которых происходят важные новые разработки. вероятно произойдет. Хотя с годами произошли важные сдвиги в уровне активности по некоторым предметам — например, растущее значение вероятностных методов, подъем дискретной математики и более широкое использование байесовской статистики — комитет не пытался исчерпывающе исследовать такие изменения или прогнозировать предметы, которые, скорее всего, произведут соответствующие прорывы. Главный урок заключается в том, что для источников финансирования по-прежнему важно поддерживать совершенство, где бы оно ни находилось, и продолжать поддерживать весь спектр исследований в области математических наук.

Новое канадское исследование долгосрочного плана развития математики и статистики в этой стране пришло к аналогичному выводу, пояснив его следующим образом: следующие десятилетия. Действительно, все области математических и статистических наук потенциально могут быть важны для инноваций, но временные рамки могут быть очень длинными, а природа связи, вероятно, будет неожиданной. Многие области математических и статистических наук, которые сейчас кажутся нам абстрактными и далекими от очевидного применения, будут полезны так, как мы сейчас не можем себе представить. . . . С одной стороны, нам нужен исследовательский ландшафт, который был бы гибким и не предписывающим с точки зрения поддерживаемых областей. У нас должен быть ландшафт финансирования исследований, способный поддерживать широкий спектр фундаментальных и прикладных исследований и способный учитывать меняющиеся характеристики самого исследовательского предприятия. А с другой стороны, нам необходимо построить и поддерживать инфраструктуру, которая свяжет математические и статистические науки со стратегическими направлениями роста. . . и будет способствовать эффективной передаче технологий и инновациям в науке, промышленности и обществе. ⁷

Вычисления

____________________

⁷ «Решения для сложной эпохи: долгосрочный план математических и статистических исследований в Канаде», Совет по естественным наукам и инженерным исследованиям (Канада), 2012 г. http://longrangeplan.ca/wp-content/uploads/2012/12/3107_MATH_LRP-1212-web.pdf, 28 января 2013 г. Цитируемый текст взят со с. 24.

Страница 73

Делиться

Цитировать

Сохранить

Отменить

Поскольку наука, инженерия, правительство и бизнес все больше полагаются на сложные вычислительные модели, неизбежно укрепляются связи между этими секторами и математическими науками. Это потому, что вычислительное моделирование по своей сути является математическим. Соответственно, эти области зависят — и извлекают выгоду — из достижений в области математических наук и поддержания здорового предприятия математической науки. То же самое верно и в отношении того, что эти сектора все больше полагаются на анализ крупномасштабных объемов данных.

Это не означает, что ученый-математик нужен всякий раз, когда кто-то строит или проводит компьютерную симуляцию или анализирует данные (хотя участие ученого-математика часто полезно, когда работа новая или сложная). Но верно то, что все больше и больше ученых, инженеров и деловых людей нуждаются или получают выгоду от курсовой работы более высокого уровня по математическим наукам, которая укрепляет связи между дисциплинами. Верно также и то, что сложность явлений, которые теперь можно смоделировать in silico, и сложность анализа, ставшего возможным благодаря терамасштабным данным, раздвигают границы исследований в математических науках и бросают вызов тем, кто ранее мог приобрести необходимые навыки по мере их изучения. выполнять свои основные задачи. По мере увеличения этой сложности мы находим все больше и больше случаев, когда требуется или был бы полезен специальный математический и статистический опыт.

Некоторые читатели могут предположить, что многие из тем, упомянутых в этой главе, относятся к области информатики, а не математических наук. На самом деле, многие из этих областей исследований охватывают обе области или могут быть обозначены как угодно. Например, процесс поиска данных, будь то в базе данных или в Интернете, требует как продуктов исследований в области компьютерных наук, так и инструментов моделирования и анализа математических наук. Проблемы теоретической информатики сами по себе на самом деле вполне математические, а области научных вычислений и машинного обучения находятся прямо на стыке математических наук и информатики (во многих случаях с пониманием области применения). Действительно, большая часть моделирования, симуляции и анализа построена на результатах обеих дисциплин, и исследователи с очень похожим опытом можно найти на академических факультетах математики, статистики или компьютерных наук. Конечно, многие исследования в области математических наук имеют не так уж много общего с исследованиями в области компьютерных наук, а также многие исследования в области компьютерных наук не особенно близки к математическим наукам.

Поскольку так много людей, занимающихся наукой, инженерией и медициной, в настоящее время изучают математику и/или статистику, некоторые спрашивают, зачем нам нужны люди, специализирующиеся в математических науках, для участия в меж

Стр.

Делиться

Цитировать

Сохранить

Отменить

дисциплинарных отряда. Причина в том, что исследователи математических наук не только создают инструменты, которые транслируются в приложения в других местах, но также являются творческими партнерами, которые могут соответствующим образом адаптировать результаты математических наук для решения различных задач. Этот последний вид сотрудничества может привести к прорывным возможностям, которые стоят потраченного времени, которое иногда связано с созданием междисциплинарной команды. Не всегда достаточно полагаться на математику и статистику, зафиксированные в учебниках или программном обеспечении, по двум причинам: (1) прогресс постоянно достигается, и готовые методы вряд ли окажутся передовыми, и (2) ) решения, адаптированные к конкретным ситуациям или вопросам, часто могут быть гораздо более эффективными, чем более общие подходы. Это преимущества для членов команды, не занимающихся математическими науками. Для сотрудников математических наук преимущества также двойственны: (1) обнаруживаются новые проблемы, которые могут стимулировать новые результаты, имеющие важное значение для математических наук, и (2) их математические научные методы и идеи могут иметь более широкое влияние.

В прикладных областях с хорошо зарекомендовавшими себя математическими моделями интересующих явлений, таких как физика и инженерия, исследователи могут использовать большие достижения в области вычислений и сбора данных последних десятилетий для исследования более сложных явлений и проведения более точного анализа. И наоборот, там, где отсутствуют математические модели, рост вычислительной мощности и данных теперь позволяет проводить вычислительное моделирование с использованием альтернативных моделей и эмпирически сгенерированных отношений в качестве средства исследования.

Компьютерное моделирование теперь помогает исследователям решать, какие эксперименты проводить, как интерпретировать экспериментальные результаты, какие прототипы создавать, какие медицинские методы лечения могут работать и так далее. Действительно, способность моделировать явление часто рассматривается как проверка нашей способности понять его. За последние 10-15 лет вычислительные возможности достигли порога, при котором стали возможными статистические методы, такие как методы Монте-Карло с цепями Маркова и крупномасштабный сбор и анализ данных, и эти методы доказали свою большую ценность в широком диапазоне задач. ситуации.

Например, на одном из заседаний исследовательский комитет увидел моделирование биохимической активности, разработанное Терренсом Сейновски из Института биологических исследований Солка. Это была демонстрация вычислительного моделирования, основанного на передовых математических и компьютерных науках, которая до недавнего времени была невозможна и которая позволяла проводить новые исследования сложных биологических явлений. В качестве другого примера, за последние 30 лет или около того ультразвук продвинулся от предоставления неподвижных изображений к динамическому показу бьющегося сердца и, совсем недавно, к показу эволюции полного ребенка в утробе матери. Математическая основа УЗИ требует решения обратных задач и рисует

Страница 75

Делиться

Цитировать

Сохранить

Отменить

из методов и результатов в чисто математическом анализе, в теории распространения волн в жидкостях и упругих средах, а также в более практических областях, таких как быстрые численные методы и обработка изображений. По мере совершенствования ультразвуковых технологий необходимо решать и новые математические задачи.

В недавнем документе, подготовленном для Консультативного комитета Управления математики и физических наук (MPS) NSF, определены следующие пять «основных элементов», лежащих в основе вычислительной науки и техники: ⁸

(i) разработка и долгосрочное управление программного обеспечения, включая новые и «основные» коды сообщества, открытые исходные коды и коды для новых или нетрадиционных архитектур;

(ii) разработка моделей, алгоритмов, инструментов и методов проверки, проверки и количественной оценки неопределенности;

(iii) разработка инструментов, методов и лучших практик для сверхбольших наборов данных;

(iv) разработка и внедрение киберинструментов для совместной работы, совместного использования, повторного использования и перепрофилирования программного обеспечения и данных сообществами MPS; и

(v) образование, обучение и развитие кадров следующего поколения ученых-вычислителей.

Математические науки вносят существенный вклад во все пункты этого списка, кроме четвертого.

Подавляющее большинство вычислительной науки и техники могут быть хорошо выполнены исследователями из области исследования: они знают, как создать математическую модель изучаемого явления, и стандартные инструменты численного решения являются адекватными. Однако даже в этих случаях могут потребоваться некоторые специальные математические знания — например, знание того, как и когда добавить «искусственную вязкость» к представлению о потоке жидкости или как справиться с «жесткостью» в системах обыкновенных дифференциальных уравнений, — но это не так. степень мастерства распространилась среди разработчиков численного моделирования во многих дисциплинах. Однако по мере того, как моделируемые явления становятся все более сложными, что, возможно, требует специальной артикуляции между моделями разных масштабов и разных математических типов, все более важными становятся специальные математические научные навыки. Без таких навыков и опыта вычислительные модели могут быть нестабильными или даже давать ненадежные результаты. Валидация таких сложных моделей требует весьма специализированного опыта, и критическая задача количественной оценки их неопределенностей может быть затруднена.0005

______________________

⁸ Шарон Глотцер, Дэвид Киз, Джоэл Толайн и Ежи Лещинский, «Вычислительные науки». 14 мая 2010 г. Доступно по адресу http://www.nsf.gov/attachments/118651/public/Computational_Science_White_Paper.pdf.

Страница 76

Делиться

Цитировать

Сохранить

Отменить

очень сложно. ⁹ А когда модели разрабатываются эмпирически путем поиска закономерностей в крупномасштабных данных — что становится все более распространенным явлением — появляется много возможностей для ложных ассоциаций. Исследовательские группы должны обладать сильными статистическими навыками, чтобы в таких случаях создавать надежные знания.

В ответ на потребность в использовании этой огромной вычислительной мощности сообщество ученых-математиков, являющихся экспертами в области научных вычислений, продолжает расширяться. Эта группа исследователей разрабатывает усовершенствованные методы решения, алгоритмы для схем сетки и вычислительной графики и так далее. В гораздо большей степени эта работа будет стимулироваться появлением новых компьютерных архитектур. И из этой тенденции вытекает гораздо более широкий спектр задач математической науки. Например, перед теорией дифференциальных уравнений стоит задача предоставить структуры, позволяющие нам анализировать аппроксимации многомасштабных моделей; необходимы более надежные методы проверки модели; алгоритмы должны быть разработаны и охарактеризованы; теоретические вопросы информатики нуждаются в разрешении; и так далее. Хотя его часто называют просто «программным обеспечением», этапы представления реальности на компьютере создают множество проблем для математических наук. ¹⁰

Ярким примером того, как расширение вычислительных ресурсов и ресурсов данных привело к «математизации» области науки, является то, как биология стала намного более количественной и зависимой от математического и статистического моделирования после появления геномики. Высокопроизводительные данные в биологии были важной движущей силой новых статистических исследований за последние 10-15 лет. Исследования в области геномики и протеомики в значительной степени опираются на математические науки, часто сложными способами, и поэтому болезни, эволюция, сельское хозяйство и другие темы стали количественными, поскольку геномная и протеомная информация используется в качестве основы для исследований. Возможно, это развитие сделало статистиков центральными игроками в одной из самых горячих областей науки. В течение следующих 10-15 лет получение геномных данных станет довольно простым, и они будут все чаще доступны для освещения биологических процессов. А

______________________

⁹ См. Кристин Сайнани, 2011 г., Ошибка! – Чему биомедицинские вычисления могут научиться на своих ошибках. Biomedical Computation Review , 1 сентября, дает обзор источников ошибок и указывает на некоторые поразительные опубликованные исследования. Доступно по адресу http://biomedicalcomputationreview.org/content/error-%E2%80%93-what-biomedical-computing-can-learn-its-mistakes. См. также Национальный исследовательский совет, 2012 г. Оценка надежности сложных моделей: математические и статистические основы проверки, проверки и количественного определения неопределенности . The National Academies Press, Washington, D.C.

¹⁰ Полный спектр математических задач, связанных с передовыми вычислениями для науки и техники, обсуждается в главе 6 NRC, 2008, The Potential Impact of High-End Computing on Four. Иллюстративные области науки и техники , The National Academies Press, Вашингтон, округ Колумбия

Страница 77

Делиться

Цитировать

Сохранить

Отменить

большая часть этой работы зависит от понимания статистики, но математика также обеспечивает основу: например, методы теории графов необходимы в эволюционной биологии; новые алгоритмы дискретной математики и информатики играют важную роль в поиске, сравнении и извлечении знаний; теория динамических систем играет важную роль в экологии; а более традиционная прикладная математика обычно используется в вычислительной нейробиологии и системной биологии. По мере того как биология переходит от описательной науки к количественной, математические науки будут играть огромную роль.

Социальные науки в разной степени также охватывают инструменты математических наук, особенно статистики, анализа данных и математики, встроенных в симуляции. Например, статистические модели передачи болезней дали очень ценную информацию о закономерностях и путях. Бизнес, особенно финансы и маркетинг, все больше зависит от методов математических наук. Некоторые темы гуманитарных наук также извлекли пользу из методов математических наук, в первую очередь интеллектуального анализа данных, анализа данных и зарождающейся науки о сетях.

Математические науки все больше способствуют принятию решений в здравоохранении на основе данных. Исследование операций применяется для моделирования процессов оказания медицинской помощи, чтобы их можно было методично улучшать. В приложениях используются различные формы моделирования, дискретная оптимизация, марковские процессы принятия решений, динамическое программирование, сетевое моделирование и стохастическое управление. По мере того, как практика здравоохранения переходит на электронные медицинские записи, становятся доступными огромные объемы данных, которые нуждаются в анализе; необходимы новые методы, поскольку эти данные не являются результатом контролируемых испытаний. Новая область исследования сравнительной эффективности, которая в значительной степени опирается на статистику, направлена на то, чтобы опираться на данные такого рода, чтобы охарактеризовать эффективность различных медицинских вмешательств и их ценность для определенных категорий пациентов.

«Большие данные»

В нескольких местах этого обсуждения содержится наблюдение, что объемы данных стремительно растут, предъявляя соразмерные требования к математическим наукам. Эта перспектива упоминалась в большом количестве предыдущих отчетов об этой дисциплине, но она стала вполне реальной за последние 15 лет или около того. Признаком того, что эта область достигла зрелости, является обнародование в марте 2012 года Управлением Белого дома по научно-технической политике (OSTP) Инициативы по исследованию и развитию больших данных. Директор OSTP Джон Холдрен подчеркнул, что «не данные сами по себе создают ценность. Что действительно важно, так это наша способность извлекать из них новые идеи, распознавать взаимосвязи и делать все более точные прогнозы. Наша способность, то есть переход от данных к знаниям и действиям». это точно

Страница 78

Делиться

Цитировать

Сохранить

Отменить

в области перехода от необработанных данных через анализ к знанию того, что математические науки необходимы. Большие, сложные наборы данных и потоки данных играют важную роль в стимулировании новых исследовательских приложений в математических науках, и достижения математических наук необходимы для использования ценности этих данных.

Однако роль математических наук в этой области признается не всегда. Действительно, заявленные цели инициативы OSTP,

, заключаются в продвижении передовых базовых технологий, необходимых для сбора, хранения, сохранения, управления, анализа и обмена огромными объемами данных; использовать эти технологии для ускорения темпов открытий в науке и технике; укрепить нашу национальную безопасность; и преобразовать преподавание и обучение; и расширить штат сотрудников, необходимых для разработки и использования технологий больших данных,

, похоже, недооценивают объем интеллектуальных усилий, необходимых для фактического перехода от данных к знаниям и действиям.

Многочисленные вопросы фундаментальной методологии возникают в контексте больших наборов данных. Некоторые из них возникают из-за основной проблемы масштабируемости — методов, разработанных для небольших или средних наборов данных, не переносятся на современные массивные наборы данных — или из-за проблем с потоковой передачей данных, когда набор данных меняется в процессе анализа. Типичные вопросы включают в себя, как увеличить отношение сигнал-шум в записанных данных, как быстро обнаружить новое или другое состояние (обнаружение аномалий), алгоритмические решения/структуры данных, которые позволяют быстро вычислять привычную статистику, аппаратные решения, которые позволяют эффективно или параллельные вычисления. Многомерные данные создают новые проблемы: новые парадигмы статистического вывода возникают из-за исследовательского характера понимания больших сложных наборов данных, и возникают вопросы о том, как лучше всего моделировать процессы, посредством которых формируются большие и сложные наборы данных. Не все данные являются числовыми — некоторые из них категоричны, некоторые — качественны и т. д., и ученые-математики вносят свой вклад в точки зрения и методы работы как с числовыми, так и с нечисловыми данными, а также с их неопределенностями. Шум в процессе сбора данных необходимо смоделировать, а затем, по возможности, свести к минимуму; новый алгоритм может быть столь же мощным улучшением разрешения, как и новый инструмент. Часто данные, которые можно измерить, не являются теми данными, которые в конечном счете нужны. Это приводит к тому, что известно как обратная задача: процесс сбора данных требует очень сложного преобразования нужных данных, и для обращения процесса требуется вычислительный алгоритм. Классический пример — радар, где форма объекта реконструируется по тому, как от него отражаются радиоволны. Упрощение данных, чтобы найти их базовую структуру, обычно необходимо в больших наборах данных. Общая цель уменьшения размерности — получение данных с большим количеством измерений и поиск комбинаций измерений.0005

Страница 79

Делиться

Цитировать

Сохранить

Отменить

достаточно, чтобы воплотить в себе основные характеристики набора данных, — является всеобъемлющим. Используются и постоянно совершенствуются различные методы, уходящие своими корнями в линейную алгебру и статистику, и в ход идут все более глубокие результаты реального анализа и вероятностных методов, таких как случайные проекции и диффузионная геометрия.

Статистики накопили большой опыт работы со сложностями реальных данных — как обнаружить, когда что-то пойдет не так в процессе сбора данных, как отличить важные выбросы от выбросов, вызванных ошибкой измерения. , как разработать процесс сбора данных, чтобы максимизировать ценность собранных данных, как очистить данные от неизбежных ошибок и пробелов. По мере роста наборов данных до терабайтного и петабайтного диапазона существующих статистических инструментов может уже не хватать, и необходимы постоянные инновации. В сфере массивных данных устоявшиеся парадигмы могут разрушиться — например, ложноположительные результаты могут стать скорее нормой, чем исключением, — и для проведения дополнительных исследований требуется сильный статистический опыт.

Например, в значительной части задач, требующих большого объема данных, наблюдений много, и проблема заключается не столько в том, чтобы избежать обмана из-за небольшого размера выборки, сколько в том, чтобы обнаружить соответствующие закономерности. Как отмечается в New York Times : «Поле за полем компьютеры и Интернет создают новые области данных для изучения сигналов датчиков, записей видеонаблюдения, болтовни в социальных сетях, общедоступных записей и многого другого». ¹¹ Это может потребовать от исследователей в области машинного или статистического обучения разработки алгоритмов, которые прогнозируют результат на основе эмпирических данных, таких как данные датчиков или потоки из Интернета. В этом подходе используется выборка данных для обнаружения взаимосвязей между интересующей величиной и независимыми переменными. Сильные ученые-математики, работающие в этой области, сочетают передовой опыт моделирования данных, управления неопределенностями и статистики с пониманием области применения и вычислительной реализации. Эти проблемы прогнозирования возникают везде: в финансах и медицине, конечно, но они также настолько важны для современной экономики, что такие компании, как Netflix, Google и Facebook, полагаются на прогресс в этой области. Недавняя тенденция заключается в том, что аспиранты-статистики, которые в прошлом часто оказывались в фармацевтических компаниях, где они разрабатывали клинические испытания, все чаще нанимаются компаниями, ориентированными на интернет-торговлю.

Поиск того, что вы ищете в огромном море данных, зависит от поисковых алгоритмов. Это расширяющаяся тема, потому что эти алгоритмы должны искать в базе данных, где данные могут включать слова, числа, изображения и видео, звуки, ответы на вопросы анкеты и другие типы данных, все связанные между собой

____________________

¹¹ Стив Лор, 2009, Для сегодняшнего выпускника всего одно слово: Статистика. New York Times , 5 августа.

Страница 80

Делиться

Цитировать

Сохранить

Отменить

вместе по-разному. Также необходимо, чтобы эти методы становились все более «интеллектуальными» по мере увеличения масштаба данных, потому что недостаточно просто идентифицировать совпадения и предложить упорядоченный список совпадений. Для удовлетворения этой потребности продолжают разрабатываться новые методы машинного обучения. Еще одно новое соображение заключается в том, что данные часто поступают в виде сети; выполнение математического и статистического анализа сетей требует новых методов.

Статистическая теория принятия решений — это раздел статистики, специально посвященный использованию данных для принятия оптимальных решений. Что он добавляет к классической статистике помимо вывода вероятностей, так это то, что он интегрирует в решение информацию о затратах и ценности различных результатов. Это имеет решающее значение для многих проектов, предусмотренных инициативой OSTP по работе с большими данными. Чтобы выбрать два примера из многих, ¹² Центр услуг Medicare и Medicaid (CMS) имеет программу «Использование данных административных требований (Medicare) для улучшения принятия решений, в то время как Управление по санитарному надзору за качеством пищевых продуктов и медикаментов создает виртуальную лабораторную среду, которая будет применять «передовые аналитические и статистические инструменты и возможности, краудсорсинг аналитики для прогнозирования и укрепления общественного здоровья». Лучшее принятие решений было названо одним из наиболее многообещающих способов сократить растущие медицинские расходы при одновременном улучшении результатов лечения пациентов, и статистика лежит в основе этого вопроса.

Идеи из статистики, теоретической информатики и математики обеспечили растущий арсенал методов машинного обучения и статистической теории обучения: анализ главных компонентов, методы ближайших соседей, методы опорных векторов, байесовские и сенсорные сети, регуляризованное обучение, обучение с подкреплением, разреженные оценки, нейронные сети, ядерные методы, древовидные методы, начальная загрузка, бустинг, правила ассоциации, скрытые марковские модели и анализ независимых компонентов — и этот список продолжает расти. Это область, где новые идеи внедряются в быстрой последовательности, где эффективность новых методов часто заметно выше, чем у существующих, и где часто возникают новые классы проблем.

Большие наборы данных требуют высокого уровня вычислительной сложности, поскольку операции, которые легко выполняются в небольших масштабах, например перемещение данных между машинами или в хранилище и из хранилища, визуализация данных или отображение результатов, могут потребовать существенной изобретательности алгоритмов. По мере того, как набор данных становится все более массивным, может оказаться невозможным собрать его в одном месте и проанализировать в целом. Таким образом, может возникнуть потребность в алгоритмах, которые работают распределенным образом, анализируя подмножества данных и агрегируя эти результаты для понимания полного набора. Одним из аспектов этого является

______________________

¹² Информация и цитаты взяты из OSTP, «Информационный бюллетень: Большие данные через федеральное правительство, 29 марта 2012 г. ». Доступно по адресу http://www.whitehouse.gov/sites/default/files/microsites/ostp/big_data_fact_sheet_final.pdf.

Страница 81

Делиться

Цитировать

Сохранить

Отменить

задача усвоения данных, в которой мы хотим использовать новые данные для обновления параметров модели без повторного анализа всего набора данных. Это важно, когда продолжают поступать новые потоки данных или подмножества анализируются изолированно друг от друга, и кто-то стремится улучшить модель и выводы адаптивным образом, например, с помощью потоковых алгоритмов. Математические науки вносят важный вклад в разработку новых алгоритмов и методов анализа, как и другие области.

Упрощение данных для определения их базовой структуры обычно необходимо для больших наборов данных. Общая цель измерения размерности данных с большим количеством измерений и определения того, какие комбинации измерений достаточны для воплощения основных характеристик набора данных, — является всеобъемлющей. Различные методы, уходящие своими корнями в линейную алгебру, статистику и, все чаще, глубокие результаты реального анализа и вероятностные методы, такие как случайные проекции и диффузионная геометрия, используются в различных обстоятельствах, и все еще требуются улучшения. Такие вопросы занимают центральное место в программе NSF «Основные методы и технологии для развития науки и техники больших данных», а также в таких разнообразных данных, как климат, геномика и снижение угроз. С поиском, а также с уменьшением размерности связана проблема обнаружения аномалий — определение того, какие изменения в большой системе являются ненормальными или опасными, что часто называют проблемой «иголки в стоге сена». Агентство перспективных оборонных исследовательских проектов (DARPA) разработало программу «Обнаружение аномалий в различных масштабах» по обнаружению аномалий и характеристике массивных наборов данных, уделяя особое внимание обнаружению внутренней угрозы, в которой аномальные действия человека обнаруживаются на фоне обычной сетевой активности. Для этого можно использовать широкий спектр статистических методов и методов машинного обучения, некоторые из которых выросли из статистических методов, первоначально использовавшихся для контроля качества, другие впервые были разработаны математиками для обнаружения мошенничества с кредитными картами.

Два типа данных, чрезвычайно важных, но чрезвычайно тонких для анализа, — это слова и изображения. Области интеллектуального анализа текста и обработки естественного языка связаны с поиском и извлечением информации и знаний из различных текстовых источников, а также с созданием вероятностных моделей того, как генерируются языковые и грамматические структуры. Обработка изображений, машинное зрение и анализ изображений пытаются восстановить зашумленные данные изображения в форме, которую может обрабатывать человеческий глаз, или полностью обойти человеческий глаз и понять и представить в компьютере то, что происходит на изображении без участия человека. вмешательство.

С анализом изображений связана проблема поиска подходящего языка для описания формы. Появляются различные подходы, от наборов уровней до «собственных форм», при этом центральную роль играет дифференциальная геометрия. В рамках этой проблемы необходимы методы описания малых деформаций форм, обычно использующие какой-либо аспект геометрии пространства

Page 82

Делиться

Цитировать

Сохранить

Отменить

диффеоморфизма. Анализ формы также используется в виртуальной хирургии, где хирургические результаты моделируются на компьютере перед примеркой на пациенте, а также в удаленной хирургии на поле боя. Здесь необходимо сочетать методы математического моделирования, основанные на дифференциальных уравнениях, описывающих механику ткани, с методами описания формы и визуализации.

Поскольку наше общество учится довольно болезненно, данные должны быть защищены. Потребность в конфиденциальности и безопасности привела к появлению областей интеллектуального анализа данных с сохранением конфиденциальности и зашифрованных вычислений, где желательно иметь возможность анализировать набор данных без ущерба для конфиденциальности и иметь возможность выполнять вычисления с зашифрованным набором данных. он остается зашифрованным.

ВКЛАД МАТЕМАТИЧЕСКИХ НАУК В НАУКУ И ТЕХНИКУ

Математические науки имеют долгую историю взаимодействия с другими областями науки и техники. Это взаимодействие предоставляет инструменты и идеи, которые помогут продвинуться в этих других областях; в то же время усилия этих областей по расширению границ исследований обычно ставят новые задачи перед самими математическими науками. Один из способов оценить состояние математических наук — изучить богатство этого взаимодействия. Некоторые взаимодействия между математикой и физикой описаны в главе 2, но их диапазон выходит далеко за пределы физики. Убедительной иллюстрацией того, насколько другие области зависят от математических наук, является изучение собственных оценок перспективных направлений в этих областях и выявление направлений, которые зависят от параллельного прогресса в математических науках. Ряд таких иллюстраций собран в Приложении D.

ВКЛАД МАТЕМАТИЧЕСКИХ НАУК В ПРОМЫШЛЕННОСТЬ

Роль математических наук в промышленности имеет долгую историю, восходящую к временам, когда египтяне использовали прямоугольный треугольник 3-4-5 для восстановления границ ферм после ежегодного разлив Нила. Тем не менее, недавний период характеризуется значительным ростом и диверсификацией. Даже в старых отраслях возросла роль математических наук. Например, в то время как авиационная промышленность долгое время использовала математику при проектировании крыльев самолетов и статистику для обеспечения контроля качества в производстве, теперь математические науки также имеют решающее значение для GPS и навигационных систем, для моделирования структурной надежности конструкции и для оптимизация потока производства. Математические науки используются не только для оптимизации автомобилей и моделирования транспортных потоков, но и для последних разработок, таких как проектирование систем автоматического обнаружения транспортных средств и

Страница 83

Делиться

Цитировать

Сохранить

Отменить

системы предотвращения, которые однажды могут привести к автоматизированному вождению. В то время как статистика долгое время была ключевым элементом медицинских испытаний, теперь математические науки задействованы в разработке лекарств и в моделировании новых способов доставки лекарств к опухолям, и они будут необходимы для выводов в обстоятельствах, которые не допускают двойного действия. слепые рандомизированные клинические испытания. Финансовый сектор, который когда-то полагался на статистику при разработке портфелей, сводящих к минимуму риск при заданном уровне доходности, теперь использует статистику, машинное обучение, стохастическое моделирование, оптимизацию и новую науку о сетях при ценообразовании и разработке ценных бумаг, а также при оценке. риск.

Самое поразительное, однако, это количество новых отраслей, частью которых являются математические науки, часто в качестве ключевого фактора. Индустрия шифрования использует теорию чисел, чтобы сделать возможной интернет-торговлю. Индустрия «поиска» опирается на идеи математических наук, чтобы сделать обширные информационные ресурсы Интернета доступными для поиска. Индустрия социальных сетей использует теорию графов и машинное обучение. В индустрии анимации и компьютерных игр используются такие разнообразные методы, как дифференциальная геометрия и уравнения в частных производных. Биотехнологическая промышленность широко использует математические науки для моделирования действия лекарств, поиска в геномах генов, связанных с человеческими заболеваниями или имеющих отношение к биоинженерным организмам, а также для открытия новых лекарств и понимания того, как они могут действовать. Индустрия визуализации использует идеи дифференциальной геометрии и обработки сигналов для получения минимально инвазивных медицинских и промышленных изображений, а в медицине добавляет методы из обратных задач для разработки целенаправленной лучевой терапии и движется к включению новой области вычислительной анатомии для обеспечения удаленной хирургии. Индустрия онлайн-рекламы использует идеи из теории игр и дискретной математики для определения цены и ставок на онлайн-рекламу, а также методы статистики и машинного обучения, чтобы решить, как настроить таргетинг этой рекламы. Маркетинговая индустрия теперь использует сложные статистические методы и методы машинного обучения, чтобы ориентироваться на клиентов и выбирать места для новых магазинов. Индустрия кредитных карт использует различные методы для обнаружения мошенничества и атак типа «отказ в обслуживании». Политические кампании теперь используют сложные модели электората, а прогнозы в ночь перед выборами полагаются на интеграцию этих моделей с экзит-полами. Полупроводниковая промышленность использует оптимизацию для проектирования компьютерных микросхем и моделирования производства и поведения дизайнерских материалов. Математические науки сейчас присутствуют почти в каждой отрасли, и спектр используемых математических наук был бы невообразимым поколение назад.

Эта точка зрения подтверждается следующим списком тематических исследований, собранных для отчета SIAM Математика в промышленности . ¹³ Этот список носит иллюстративный характер, но его широта поражает:

______________________

¹³ Общество промышленной и прикладной математики, 2012, Математика в промышленности . SIAM, Филадельфия, Пенсильвания

Страница 84

Делиться

Цитировать

Сохранить

Отменить

• Прогнозная аналитика,

• Анализ изображений и интеллектуальный анализ данных,

• Планирование и маршрутизация поставок,

• Математические финансы,

• Алгоритмическая торговля,

• Системная биология,

• Молекулярная динамика,

• Модели цельного пациента,

• Моделирование нефтяного бассейна,

• Виртуальное прототипирование,

• Моликулярная динамика для для проектирование продукции,

• Оптимизация междисциплинарного проектирования и автоматизированное проектирование,

• Робототехника,

• Управление цепочками поставок,

• Логистика,

• Облачные вычисления,

• Моделирование сложных систем,

• Течение вязкой жидкости для проектирования компьютерных и телевизионных экранов,

• Управление инфраструктурой для умных городов и

• Компьютерные системы, программное обеспечение и информационные технологии.

Читатель перенаправляется к отчету SIAM, чтобы ознакомиться с подробностями этих тематических исследований, ¹⁴, в которых приводится множество примеров значительного и рентабельного влияния знаний и исследований в области математических наук на инновации, экономическую конкурентоспособность и национальную безопасность.

В другом недавнем отчете о математических науках в промышленности были сделаны следующие выводы:

Очевидно, что с учетом постоянно растущей сложности реальных приложений способность эффективно использовать математическое моделирование, моделирование, управление и оптимизацию станет основой для технологического и экономического развития Европы и мира. ¹⁵

Только [математические науки] могут помочь промышленности оптимизировать все более и более сложные системы со все большим количеством ограничений. ¹⁶

Однако в этом отчете также указывается на следующую истину:

[Инженерные] дизайнеры используют виртуальные среды проектирования, которые в значительной степени опираются на математику, и производят новые продукты, которые хорошо узнаваемы

___________________

¹⁴ Там же . , стр. 9-24.

¹⁵ Европейский научный фонд, 2010, Математика и промышленность . Страсбург, Франция, с. 8.

¹⁶ Там же, с. 12.

Страница 85

Делиться

Цитировать

Сохранить

Отменить

управление. Однако основные усилия, связанные с созданием надежных, надежных и эффективных виртуальных сред проектирования, не получили признания. В результате математика обычно не считается ключевой технологией в промышленности. Обходной путь для этой проблемы обычно состоит в том, чтобы оставить математику специализированным небольшим компаниям, которые часто используют математические и программные решения, разработанные в академических кругах. К сожалению, уровень связи между этими коммерческими поставщиками и их академическими партнерами в промышленности часто находится на очень низком уровне. Это, в свою очередь, приводит к наблюдению, что можно решить вчерашние проблемы в промышленности, но не проблемы сегодняшнего и завтрашнего дня. Последнее можно адекватно решить только в том случае, если будут предприняты усилия для радикального улучшения связи между промышленными дизайнерами и математиками. ¹⁷

Одним из способов решения этой проблемы коммуникации, конечно же, является привлечение ученых-математиков высокого уровня в корпоративные подразделения по исследованиям и разработкам.

Математические функции, представляющие наибольшую ценность в этих и других успешных приложениях, были охарактеризованы руководителями НИОКР в 1996 году следующим образом:

• Решение проблем,

• Статистический анализ,

• Проверка правильности и

• Анализ точности и надежности.

К этому списку отчет Европейского научного фонда добавляет оптимизацию, отмечая (стр. 12), что «благодаря увеличению вычислительной мощности и достижениям, достигнутым в ускорении алгоритмов. . . оптимизация продуктов [стала] достижимой. Это имеет жизненно важное значение для промышленности». Это очень важное событие, и оно открывает перед математическими науками новые задачи, например, как эффективно исследовать варианты проектирования и как охарактеризовать неопределенности этой вычислительной выборки пространства.

Такого рода возможности были косвенно признаны в отчете Академии наук Китая (CAS), Наука и технологии в Китае: дорожная карта до 2050 года. ¹⁹ В этом отчете определены восемь систем, важных для социально-экономического развития: энергия и ресурсы,

___________________________________

¹⁷ Там же, с. 9.

¹⁸ Общество промышленной и прикладной математики, 1996, Математика в промышленности. Доступно по адресу http://www.siam.org/reports/mii/1996/listtables.php#lt4.

¹⁹ CAS, 2010, Наука и технологии в Китае: план действий до 2050 года . Спрингер. Доступно на сайте http://www.bps.cas.cn/ztzl/cx2050/nrfb/201008/t20100804_22.html.

Страница 86

Делиться

Цитировать

Сохранить

Отменить

передовые материалы и интеллектуальное производство, повсеместные информационные сети, экологическое и ценное сельское хозяйство и биологическая промышленность, обеспечение здоровья, защита окружающей среды и окружающей среды, исследование космоса и океана, а также национальная и общественная безопасность. Чтобы поддержать развитие этих систем, в отчете определены 22 инициативы в области науки и техники. Три из них будут основываться на математических науках: инициатива по созданию «повсеместной информационной производственной системы», еще одна по разработке экзафлопсных вычислительных технологий и третья по базовым междисциплинарным исследованиям в области математики и сложных систем.

Последняя упомянутая инициатива предназначена для исследования «основных принципов, лежащих в основе различных видов сложных систем», и в отчете рекомендуется приложить значительные усилия в следующих направлениях исследований:

• Уравнения математической физики;

• Многомасштабное моделирование и расчет сложных систем;

• Машинный интеллект и механизация математики;

• Теории и методы стохастических структур и данных;

• Коллективное поведение многоагентных сложных систем, их управление и вмешательство; и

• Сложные стохастические сети, сложные адаптивные системы и смежные области.

В частности, в отчете рекомендуется, чтобы из-за фундаментальной важности сложных систем китайское правительство оказывало постоянную и постоянную поддержку исследованиям таких систем, чтобы добиться крупных достижений в этой важной области.

Еще один пример роли математических наук в промышленности взят из отчета NRC Visionary Manufacturing Challenges for 2020, ²⁰, в котором определены НИОКР, которые потребуются для развития национальных производственных возможностей. Ряд этих возможностей основан на исследованиях в области моделирования и симуляции, теории управления и информатики:

• В конечном счете, моделирование производственных систем будет основываться на единой таксономии характеристик процессов, которая включает человеческие характеристики в моделях процессов. Другие области исследований включают общую теорию адаптивных систем, которую можно применить к производственным процессам, системам и производственному предприятию; инструменты для оптимизации выбора конструкции для включения наиболее доступных производственных подходов; и системные исследования взаимодействия между рабочими и производственными процессами для разработки адаптивных, гибких средств управления. (стр. 39)

______________________

²⁰ NRC, 1998, Передовые производственные задачи на 2020 год . National Academy Press, Вашингтон, округ Колумбия

Страница 87

Делиться

Цитировать

Сохранить

Отменить

• Возможности моделирования и симуляции для оценки процессов и сценариев предприятия будут иметь важное значение при разработке реконфигурируемых предприятий. . . . Виртуальное прототипирование производственных процессов и систем позволит производителям оценить ряд вариантов оптимизации своих предприятий. Перспективные области применения технологий моделирования и симуляции для реконфигурируемых систем включают нейронные сети для оптимизации подходов к реконфигурации и искусственный интеллект для принятия решений. . . . Процессы, которые можно адаптировать или легко перенастроить, потребуют гибких датчиков и алгоритмов управления, которые обеспечивают точное управление рядом процессов и сред. (стр. 39-40)

• Исследования в области инструментов моделирования предприятий будут включать «мягкое» моделирование (например, модели, рассматривающие поведение человека как элемент системы, и модели информационных потоков и коммуникаций), оптимизацию и интеграцию смешанных моделей, оптимизацию аппаратных систем, моделей организационных структур и межорганизационного поведения, а также моделей сложных или нелинейных систем и процессов. (стр. 44)

• Информационные системы будущего должны будут собирать и просеивать огромные объемы информации. (стр. 44)

Возобновившийся сегодня акцент на передовое производство, примером которого является недавний отчет «Завоевание отечественного конкурентного преимущества в передовом производстве» , ²¹, также неявно опирается на достижения в области математических наук. 11 сквозных технологических областей, определенных в этом отчете (стр. 18) в качестве основных кандидатов для инвестиций в НИОКР, во многом опираются на моделирование, симуляцию и анализ сложных систем, анализ больших объемов данных, контроль и оптимизацию.

ВКЛАД МАТЕМАТИЧЕСКИХ НАУК В НАЦИОНАЛЬНУЮ БЕЗОПАСНОСТЬ

Национальная безопасность — это еще одна область, которая в значительной степени зависит от математических наук. В Агентстве национальной безопасности (АНБ), например, работает около 1000 ученых-математиков, хотя их число может быть вдвое или вдвое больше, в зависимости от того, как определить таких ученых. ²² В их число входят люди с опытом работы в области базовой и прикладной математики, вероятности и статистики, но люди с опытом работы в области компьютерных наук в этот подсчет не входят. АНБ нанимает около 40-50 математиков в год и старается поддерживать этот показатель на постоянном уровне, чтобы сообщество математических наук0005

______________________

²¹ Белый дом, Управление научно-технической политики, 2012 г.

²² Альфред Хейлз, бывший глава Института оборонного анализа, Центр коммуникационных исследований – Ла-Хойя, презентация комитету в Декабрь 2010 г. Центр IDA в Ла-Холья проводит исследования для АНБ.

Страница 88

Делиться

Цитировать

Сохранить

Отменить

знает, что это может зависеть от такого уровня найма. АНБ заинтересовано в поддержании здорового сообщества математических наук в Соединенных Штатах, включая достаточное количество хорошо подготовленных граждан США. Большая часть найма математических наук в АНБ находится на уровне выпускников, примерно поровну между MS и M. S. и доктор философии уровни. Агентство набирает сотрудников почти во всех областях математических наук, а не в конкретных подобластях, потому что никто не может предсказать сочетание навыков, которые будут важны для карьеры сотрудника в течение десятилетий. Например, несколько десятилетий назад мало кто из математиков мог предположить, что эллиптические кривые будут представлять жизненно важный интерес для АНБ, а теперь они являются важной специальностью, лежащей в основе криптологии.

Хотя криптология явно зависит от математики, существует много других связей между математическими науками и национальной безопасностью. Одним из примеров является анализ сетей (обсуждаемый в следующем разделе), который очень важен для национальной обороны. Другое дело — научные вычисления. Одна из первоначальных причин интереса Джона фон Неймана к созданию одного из первых компьютеров заключалась в том, чтобы иметь возможность выполнять вычисления, необходимые для моделирования того, что произойдет внутри водородной бомбы. Спустя годы, когда атмосферные и подземные ядерные испытания были запрещены, страна снова полагается на моделирование, на этот раз для поддержания готовности своего ядерного арсенала. Поскольку национальная оборона частично зависит от проектирования и производства передового оборудования, она также опирается на математические науки, которые вносят свой вклад в передовые разработки и производство. Уровень сложности этих инструментов неуклонно растет. Математические науки также важны для логистики, моделирования, используемого для обучения и тестирования, военных игр, анализа изображений и сигналов, управления спутниками и самолетами, а также тестирования и оценки нового оборудования. Рисунок 3-5, воспроизведенный с 9В выпуске 0019 «Подпитка инноваций и открытий: математические науки в 21 веке», ²³ представлен широкий спектр способов, которыми математические науки способствуют национальной обороне.

Новые устройства на полях сражений и за их пределами появились в сети и предоставляют ошеломляющее количество данных, больше, чем в настоящее время можно проанализировать. Разработка способов автоматизации анализа этих данных является сложной математической и статистической задачей. Можно ли научить компьютер разбираться в спутниковом изображении, обнаруживать здания и дороги и замечать значительные изменения изображения объекта, не связанные с сезонными колебаниями? Как можно использовать гиперспектральные данные, измеряющие свет, отраженный во всех частотах спектра, для обнаружения дымового шлейфа завода по производству химического оружия? Можно ли идентифицировать технику и корабли противника в загроможденной среде? Эти и многие другие вопросы по своей сути зависят от достижений математических наук.

______________________

²³ Национальный исследовательский совет, 2012 г. The National Academy Press, Вашингтон, округ Колумбия

Страница 89

Делиться

Цитировать

Сохранить

Отменить

Очень серьезной угрозой, которой раньше не существовало, является то, что важные сети постоянно подвергаются изощренным атакам со стороны воров, мошенников и хакеров неизвестного происхождения. Адаптивные методы, основанные на математических науках, необходимы для надежного обнаружения и предотвращения таких атак, которые становятся все более изощренными, чтобы ускользнуть от каждой новой стратегии их предотвращения.

Министерство обороны утвердило семь текущих приоритетных областей для инвестиций в науку и технологии в интересах национальной безопасности.

1. Данные к решениям . Наука и приложения для сокращения времени цикла и потребности в рабочей силе для анализа и использования больших наборов данных.

2. Проектированные устойчивые системы . Инженерные концепции, наука и инструменты проектирования для защиты систем вооружения от злонамеренной компрометации и развития гибкого производства надежных и надежных систем защиты.

3. Кибернаука и технологии . Наука и технологии для эффективных и действенных кибервозможностей во всем спектре совместных операций.

4. Радиоэлектронная борьба/электронная защита . Новые концепции и технологии для защиты систем и расширения возможностей в электромагнитном спектре.

5. Противодействие оружию массового уничтожения (ОМУ) : Расширение возможностей Министерства обороны по обнаружению, обеспечению безопасности, мониторингу, маркировке, отслеживанию, перехвату, уничтожению и атрибутированию оружия и материалов с ОМУ.

6. Автономия . Наука и технологии для создания автономных систем, которые надежно и безопасно выполняют сложные задачи во всех средах.

7. Человеческие системы . Наука и технологии для улучшения интерфейсов человек-машина, повышения производительности и эффективности в широком диапазоне задач. ²⁴

Хотя математические науки явно важны для первой и третьей из этих приоритетных областей, они также играют ключевую роль в поддержке всех остальных. Достижения в математических науках, позволяющие проектировать, тестировать и контролировать сложные системы на основе моделирования, необходимы для создания устойчивых систем. Для развития радиоэлектронной борьбы и защиты необходимы улучшенные методы анализа и обработки сигналов, такие как более быстрые алгоритмы и более чувствительные схемы распознавания образов. Быстро развивающиеся инструменты анализа социальных сетей, основанные на новых методах статистического анализа сетей, применяются в целях

______________________

²⁴ Министерство обороны, 2012 г., Меморандум о Приоритетах науки и техники (S&T) на 2013 финансовый год·17 Планирование. Доступно по адресу http://acq.osd.mil/chieftechnologist/publications/docs/OSD%2002073-11.pdf. По состоянию на 3 мая 2012 г.

Страница 90

Делиться

Цитировать

Сохранить

Отменить

РИСУНОК 3-5 Математические науки на поле боя.

Страница 91

Делиться

Цитировать

Сохранить

Отменить

Страница 92

Делиться

Цитировать

Сохранить

Отменить

, чтобы улучшить наши возможности в борьбе с оружием массового уничтожения. А математические методы машинного обучения необходимы для улучшения наших возможностей в области автономии и человеко-машинных интерфейсов. Вычислительная нейронаука, которая в значительной степени опирается на математические науки, также является многообещающей областью для будущих разработок человеко-машинных интерфейсов.

Область обнаружения угроз в целом требует множества методов математических наук. Как можно наиболее быстро обнаружить закономерности, которые могут указывать на распространение патогена, распространяемого биотерроризмом? Как понять структуру террористической сети? Можно ли спроектировать энергосистему или транспортную сеть таким образом, чтобы она была максимально устойчива к атакам? Новая угроза, кибервойна, становится все более масштабной. Чтобы дать отпор, потребуется комплексный ответ: лучшее шифрование, оптимизированный дизайн сетей и растущая область, требующая больших математических и статистических данных, для обнаружения аномалий.

Что такое математика? | Живая наука

Живая наука поддерживается своей аудиторией. Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот почему вы можете доверять нам.

Математика лежит в основе науки и нашей повседневной жизни.
(Изображение предоставлено: HandmadePictures/Shutterstock.com)

Математика — это наука, изучающая логику формы, количества и расположения. Математика вокруг нас, во всем, что мы делаем. Это строительный блок для всего в нашей повседневной жизни, включая мобильные устройства, компьютеры, программное обеспечение, архитектуру (древнюю и современную), искусство, деньги, инженерию и даже спорт.

С самого начала письменной истории математические открытия были в авангарде каждого цивилизованного общества, и математика использовалась даже в самых примитивных и ранних культурах. Потребность в математике возникла из-за все более сложных требований со стороны обществ во всем мире, которые требовали более продвинутых математических решений, как это изложено математиком Рэймондом Л. Уайлдером в его книге « Эволюция математических концепций » . Дуврские публикации, 2013 г.).

Чем сложнее общество, тем сложнее математические потребности. Первобытным племенам требовалось немного больше, чем умение считать, но они также использовали математику для расчета положения солнца и физики охоты. «Все записи — антропологические и исторические — показывают, что счет и, в конечном счете, системы счисления как устройства для счета образуют начало математического элемента во всех культурах», — писал Уайлдер в 1968 году.

Кто изобрел математику?

Несколько цивилизаций — в Китае, Индии, г. Египет г., Центральная Америка и г. Месопотамия г. — внесли свой вклад в математику, какой мы ее знаем сегодня. По словам Уайлдера, шумеры, жившие в регионе, который сейчас является южным Ираком, были первыми, кто разработал систему счета с основанием 60.

Это было основано на использовании костей пальцев для подсчета, а затем использования в качестве наборов, согласно Жоржу Ифра в его книге « Универсальная история чисел (открывается в новой вкладке)» (John Wiley & Sons, 2000) . Из этих систем мы получаем основу арифметики, которая включает в себя основные операции сложения, умножения, деления, дробей и квадратных корней. Уайлдер объяснил, что шумерская система перешла через Аккадскую империю к вавилонянам около 300 г. до н.э. Шестьсот лет спустя в Центральной Америке Майя разработали сложные календарные системы и были искусными астрономами. Примерно в это же время в Индии была разработана концепция нуля.

По мере развития цивилизации математики начали работать с геометрией, которая вычисляет площади, объемы и углы и имеет множество практических приложений. Геометрия используется во всем: от строительства дома до моды и дизайна интерьера. Как писал Ричард Дж. Гиллингс в своей книге « Математика во времена фараонов » (Dover Publications, 19).82), пирамиды Гизы в Египте являются потрясающими примерами передового использования геометрии древними цивилизациями.

Статуя Мухаммада ибн Мусы аль-Хорезми в Хиве, Узбекистан. (Изображение предоставлено Konstik)

(открывается в новой вкладке)

Геометрия шла рука об руку с алгеброй. По словам Филипа К. Хитти , профессора истории Гарвардский университет. Аль-Хорезми также разработал быстрые методы умножения и деления чисел, которые известны как алгоритмы — искажение его имени, которое на латыни было переведено как Алгоритми.

Алгебра предложила цивилизациям способ разделения наследства и распределения ресурсов. Изучение алгебры означало, что математики могли решать линейные уравнения и системы, а также квадратные уравнения и углубляться в положительные и отрицательные решения. Математики в древности также начали обращаться к теории чисел, которая «имеет дело со свойствами целых чисел, 1, 2, 3, 4, 5,…», — писал Том М. Апостол, профессор Калифорнийского технологического института. в « Введение в аналитическую теорию чисел » (Springer, 1976). Беря начало в построении формы, теория чисел рассматривает фигурные числа, характеристику чисел и теоремы.

Математика в древней Греции

Слово «математика» происходит от древних греков и происходит от слова máthēma, означающего «то, чему учат», согласно Дугласу Р. Харперу, автору «Интернет-словаря этимологии ». математические исследования, и они разработали модель абстрактной математики через геометрию.

Греческие математики были разделены на несколько школ, как отмечает Г. Дональд Аллен, профессор математики Техасского университета A&M в своей статье « Истоки греческой математики »:

В дополнение к перечисленные выше греческие математики, ряд других древних греков оставили неизгладимый след в истории математики, в том числе Архимед , наиболее известный принципом Архимеда относительно выталкивающей силы; Аполлоний, проделавший важную работу с параболы ; Диофант, первый греческий математик, распознавший дроби как числа; Папп, известный своей теоремой о шестиугольнике; и Евклид, впервые описавший золотое сечение .

Золотое сечение — одно из самых известных иррациональных чисел; оно продолжается вечно и не может быть точно выражено без бесконечного пространства. (Изображение предоставлено Shutterstock)

В это время математики начали работать с тригонометрией, которая изучает отношения между сторонами и углами треугольников и вычисляет тригонометрические функции, включая синус, косинус, тангенс и их обратные величины. Тригонометрия опирается на синтетическую геометрию, разработанную греческими математиками, такими как Евклид. В прошлых культурах тригонометрия применялась к астрономии и вычислению углов на небесной сфере.

По словам Уайлдера, развитие математики было взято на вооружение исламскими империями, а затем одновременно в Европе и Китае. Леонардо Фибоначчи был средневековым европейским математиком и был известен своими теориями по арифметике, алгебре и геометрии. Ренессанс привел к достижениям, которые включали десятичные дроби, логарифмы и проективную геометрию. Теория чисел была значительно расширена, и такие теории, как вероятность и аналитическая геометрия, открыли новую эру математики, на переднем плане которой стояло исчисление.

Развитие исчисления

В 17 веке Исаак Ньютон в Англии и Готфрид Лейбниц в Германии независимо друг от друга разработали основы исчисления, объяснил Карл Б. Бойер, историк науки, в « История исчисления и его концептуального развития». (открывается в новой вкладке)» (Dover Publications, 1959). Развитие исчисления прошло через три периода: ожидание, развитие и ригоризацию.

На этапе ожидания математики пытались использовать методы, включающие бесконечные процессы, для нахождения площадей под кривыми или максимизации определенных качеств. На этапе разработки Ньютон и Лейбниц объединили эти методы с помощью производной (кривая математической функции) и интеграла (площадь под кривой). Хотя их методы не всегда были логически обоснованными, математики в 18 веке вступили в стадию ригоризации и смогли обосновать свои методы и создать заключительную стадию исчисления. Сегодня мы определим производную и интеграл с точки зрения пределов.

В отличие от исчисления, которое представляет собой разновидность непрерывной математики (имеющей дело с действительными числами), другие математики придерживаются более теоретического подхода. Дискретная математика — это раздел математики, который имеет дело с объектами, которые могут принимать только отдельные, отдельные значения, как объяснил математик и ученый-компьютерщик Ричард Джонсонбо в « Дискретная математика (открывается в новой вкладке)» (Pearson, 2017). Дискретные объекты можно характеризовать целыми числами, а не действительными числами. Дискретная математика — это математический язык компьютерных наук, поскольку он включает в себя изучение алгоритмов. Области дискретной математики включают комбинаторику, теорию графов и теорию вычислений.

Хотя сложная математика может не казаться важной для повседневной жизни людей, она лежит в основе финансов, путешествий, вычислений и многого другого. (Изображение предоставлено Антоном Белицким/Getty)

Почему математика важна

Люди нередко задаются вопросом, какую роль играет математика в их повседневной жизни. В современном мире такая математика, как прикладная математика, не просто актуальна, она жизненно необходима. Прикладная математика охватывает разделы, изучающие физический, биологический или социологический мир.

«Цель прикладной математики — установить связи между отдельными академическими областями», — написал Ален Гориели в « Прикладная математика: очень краткое введение (открывается в новой вкладке)» (Oxford University Press, 2018). Современные области прикладной математики включают математическую физику, математическую биологию, теорию управления, аэрокосмическую технику и математические финансы. Прикладная математика не только решает проблемы, но и открывает новые проблемы или развивает новые инженерные дисциплины, добавил Гориели. Общий подход в прикладной математике заключается в построении математической модели явления, решении модели и выработке рекомендаций по повышению производительности.

Чистая математика не обязательно является противоположностью прикладной математике, но ею движут абстрактные проблемы, а не проблемы реального мира. Многие предметы, которыми занимаются чистые математики, уходят своими корнями в конкретные физические проблемы, но более глубокое понимание этих явлений приводит к проблемам и техническим аспектам.

Эти абстрактные проблемы и технические детали и есть то, что пытается решить чистая математика, и эти попытки привели к крупным открытиям для человечества, включая универсальную машину Тьюринга, теоретизированную Аланом Тьюрингом в 1919 году. 37. Эта машина, которая начиналась как абстрактная идея, позже заложила основу для разработки современных компьютеров. Чистая математика абстрактна и основана на теории и поэтому не ограничена ограничениями физического мира.

По словам Гориели, «прикладная математика для чистой математики — то же, что поп-музыка для классической музыки». Чистый и прикладной не исключают друг друга, но они уходят корнями в разные области математики и решения задач. Хотя сложная математика, связанная с чистой и прикладной математикой, находится за пределами понимания большинства людей, решения, разработанные на основе процессов, повлияли на жизнь многих и улучшили ее.

Первоначально опубликовано на Live Science .

Глава 2: Природа математики


МОДЕЛИ И ОТНОШЕНИЯ МАТЕМАТИКА, НАУКИ, И ТЕХНИКА МАТЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ Глава 2: ПРИРОДА МАТЕМАТИКИ Математика основывается как на логике, так и на творчестве, и ею занимаются как для различных практических целей, так и для его внутреннего интереса. Для некоторых людей, и не только профессиональных математиков, суть математики заключается в ее красоте и ее интеллектуальной сложности. Для других, включая многих ученых и инженеров, главной ценностью математики, как это применимо к их собственной работе. Потому что математика играет такую центральную роль в современной культуре, некоторое базовое понимание природы математики необходимо для научной грамотности. Для этого учащиеся должны воспринимать математику как часть научное стремление, понять природу математического мышления, и ознакомьтесь с ключевыми математическими идеями и навыками. В этой главе основное внимание уделяется математике как части научной усилия, а затем математику как процесс или способ мышления. Рекомендации, относящиеся к математическим идеям, представлены в главе 9, «Математический мир», и те, которые касаются математических навыков, включены в главе 12 «Привычки ума». МОДЕЛИ И ОТНОШЕНИЯ Математика — это наука о закономерностях и отношениях. В качестве теоретического дисциплина, математика исследует возможные отношения между абстракции, не заботясь о том, есть ли у этих абстракций аналоги в реальном мире. Абстракциями могут быть любые строки числа к геометрическим фигурам к системам уравнений. Обращаясь, скажем: «Формирует ли интервал между простыми числами закономерность?» как теоретический вопрос, математиков интересует только нахождение закономерность или доказательство того, что ее нет, но не в чем польза такая знания могли иметь. При выводе, например, выражения для изменение площади поверхности любого правильного твердого тела в зависимости от его объема приближается к нулю, математиков не интересует никакая переписка между геометрическими телами и физическими объектами в реальном мире. Центральным направлением исследований в теоретической математике является выявление в каждой области исследования небольшой набор основных идей и правил, из которых все другие интересные идеи и правила в этой области могут быть логически выведено. Математики, как и другие ученые, особенно довольны когда обнаруживается, что ранее не связанные части математики могут быть выведены друг от друга или от какой-либо более общей теории. Часть смысла красоты, которую многие люди восприняли в математике, заключается не в в нахождении наибольшей сложности или сложности, а, наоборот, в нахождении наибольшей экономии и простоты представления и доказательство. По мере развития математики все больше и больше соотношений были обнаружены между его частями, которые разрабатывались отдельно — для например, между символическими представлениями алгебры и пространственным представления геометрии. Эти перекрестные связи позволяют получить представление развиваться в различные части; вместе они усиливают вера в правильность и основополагающее единство всей конструкции. Математика также является прикладной наукой. Многие математики обращают внимание их внимание на решении проблем, которые возникают в мире опыт. Они тоже ищут закономерности и отношения, и в процесса они используют методы, аналогичные тем, которые используются в заниматься чисто теоретической математикой. Разница во многом одна намерения. В отличие от математиков-теоретиков, прикладные математики, в примерах, приведенных выше, мог бы изучить шаблон интервала простого чисел для разработки новой системы кодирования числовой информации, а не как абстрактная проблема. Или они могут заняться площадью/объемом проблема как шаг в создании модели для изучения поведения кристалла. Результаты теоретической и прикладной математики часто влияют друг друга. Открытия математиков-теоретиков часто оказываются – иногда спустя десятилетия – иметь непредвиденные практические ценность. Исследования математических свойств случайных событий для например, привели к знаниям, которые впоследствии позволили улучшить планирование экспериментов в социальных и естественных науках. Наоборот, в попытке решить проблему биллинга междугородней телефонной связи пользователей, математики сделали фундаментальные открытия о математика сложных сетей. Теоретическая математика, в отличие от других наук, не стесненных реальным миром, а в длительном запустить его способствует лучшему пониманию этого мира. МАТЕМАТИКА, НАУКИ, И ТЕХНИКА Благодаря своей абстрактности математика в некотором смысле универсальна. что другие области человеческой мысли не являются. Находит полезные применения в бизнесе, промышленности, музыке, исторической науке, политике, спорте, медицина, сельское хозяйство, инженерия, социальные и естественные науки. Отношения между математикой и другими областями фундаментальной и прикладная наука особенно сильна. Это так по нескольким причинам, в том числе: Союз науки и математики имеет долгую историю. датируется многими веками. Наука дает математике интересные проблемы для исследования, а математика дает науке мощные инструменты, которые можно использовать при анализе данных. Часто абстрактные узоры, которые изучались математиками ради самих себя, оказалось, много позже, чтобы быть очень полезным в науке. Наука и математика оба пытаются обнаружить общие закономерности и взаимосвязи, и в этом смысле они являются частью одного и того же усилия. Математика является основным языком науки. Символический язык математики оказалось чрезвычайно ценным для выражения научные идеи однозначно. Утверждение, что a = Ф/м это не просто сокращенный способ сказать, что ускорение объект зависит от приложенной к нему силы и его массы; скорее, это точное определение количественного соотношения между эти переменные. Что еще более важно, математика обеспечивает грамматику наукиправила анализа научных идей и данных строго. Математика и естественные науки имеют много общего. Это включает вера в понятный порядок; игра воображения и строгая логика; идеалы честности и открытости; критическая важность коллегиальной критики; ценность, придаваемая тому, чтобы быть первым, кто сделает ключевое открытие; быть международным по своему охвату; и даже, с разработка мощных электронно-вычислительных машин, способных использовать технологии, открывающие новые области исследований. Математика и технология также установили плодотворные отношения друг с другом. Математика связей и логических цепочек, например, внес большой вклад в разработку компьютерного оборудования. и техники программирования. Математика также вносит более общий вклад инженерии, например, при описании сложных систем, поведение которых затем можно смоделировать на компьютере. В этих симуляциях дизайн особенности и условия эксплуатации могут быть изменены как средство нахождения оптимальные конструкции. Со своей стороны, компьютерные технологии открыли целые новые области математики, даже в самой природе доказательства, и это также продолжает помогать решать ранее сложные проблемы. МАТЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ Использование математики для выражения идей или решения проблем требует как минимум три этапа: (1) абстрактное представление некоторых аспектов вещей, (2) манипулирование абстракциями по правилам логики для поиска новых отношений между ними, и (3) посмотреть, говорят ли новые отношения что-то полезно об оригинальных вещах. Абстракция и символическое представление Математическое мышление часто начинается с процесса абстракции, который то есть замечание сходства между двумя или более объектами или событиями. Аспекты что у них есть общего, будь то конкретное или гипотетическое, может быть представлены такими символами, как цифры, буквы, другие знаки, диаграммы, геометрические конструкции или даже слова. Целые числа — это абстракции. которые представляют размер наборов вещей и событий или порядок вещей в наборе. Круг как понятие является абстракцией полученные из человеческих лиц, цветов, колес или распространяющейся ряби; в буква А может быть абстракцией площади поверхности объектов любой формы, для ускорения всех движущихся объектов или для всех объекты, имеющие определенное свойство; символ + представляет собой процесс добавления, будь то добавление яблок или апельсинов, часов, или миль в час. А абстракции делаются не только из конкретного объекты или процессы; они также могут быть сделаны из других абстракций, например, виды чисел (например, четные числа). Такая абстракция позволяет математикам сосредоточиться на некоторых функциях вещей и избавляет их от необходимости постоянно поддерживать другие функции в уме. Что касается математики, то не имеет значения, треугольник представляет собой площадь поверхности паруса или схождение двух линий визирования на звезду; математики могут работать с понятие таким же образом. Полученная в результате экономия усилий очень полезна при условии, что что при абстракции стараются не игнорировать особенности которые играют существенную роль в определении исхода событий изучается. Манипуляции с математическими выражениями После того, как были сделаны абстракции и символические представления они были выбраны, эти символы можно комбинировать и повторно комбинировать различными способами по четко определенным правилам. Иногда это делается с определенной целью; в других случаях это делается в контекст эксперимента или игры, чтобы увидеть, что происходит. Иногда подходящее манипуляция может быть легко идентифицирована по интуитивному смыслу составляющие слова и символы; в другое время полезная серия манипуляций приходится отрабатывать методом проб и ошибок. Как правило, строки символов объединяются в операторы, выражающие идеи или предложения. Например, символ A для области любого квадрата можно использовать с символом s для длины стороны квадрата, чтобы составить предложение A = s ² . Это уравнение определяет, как площадь связана со стороной и также означает, что он не зависит ни от чего другого. Правила обычного Затем с помощью алгебры можно обнаружить, что если длина сторон площади квадрата удвоится, площадь квадрата увеличится в четыре раза. В более общем плане это знание позволяет выяснить, что происходит с площадью квадрата независимо от длины его сторон изменяется, и наоборот, как любое изменение площади влияет на стороны. Математическое понимание абстрактных отношений выросло тысячи лет, и они до сих пор продлеваются, а иногда и исправлено. Хотя они начинались с конкретного опыта подсчета и измерения, они прошли через многие слои абстракции и теперь гораздо больше зависят от внутренней логики, чем от механической демонстрации. Таким образом, в некотором смысле манипулирование абстракциями очень похоже на игра: начните с некоторых основных правил, а затем делайте любые ходы, соответствующие этим правилав том числе изобретать дополнительные правила и находить новые связи между старыми правилами. Тест на обоснованность новых идей являются ли они непротиворечивыми и связаны ли они логически с остальные правила. Применение Математические процессы могут привести к некой модели вещи, от какое понимание можно получить о самой вещи. Любой математический отношения, полученные путем манипулирования абстрактными утверждениями, могут или может не передать что-то правдивое о моделируемой вещи. За например, если 2 стакана воды добавить к 3 стаканам воды и абстрактный математическая операция 2+3 = 5 используется для вычисления суммы, т.е. правильный ответ 5 стаканов воды. Однако, если 2 стакана сахара добавить к 3 чашкам горячего чая и использовать ту же операцию, 5 — это неверный ответ, так как такое добавление на самом деле приводит лишь к незначительному более 4 чашек очень сладкого чая. Простое добавление томов подходит для первой ситуации, но не для второй что-то можно было бы предсказать, только зная кое-что о физическом различия в двух ситуациях. Чтобы иметь возможность использовать и интерпретировать математика хорошо, поэтому нужно заниматься больше, чем математическая обоснованность абстрактных операций и также учитывать, насколько хорошо они соответствуют свойствам из представленных вещей. Иногда достаточно здравого смысла, чтобы решить, стоит ли результаты математики соответствуют. Например, для оценки рост через 20 лет девушки ростом 5 футов 5 дюймов и растет со скоростью один дюйм в год, здравый смысл подсказывает простой ответ «скорость умножить на время» 7 футов 1 дюйм маловероятно, и вместо этого обращаются к какой-либо другой математической модели, например как кривые, приближающиеся к предельным значениям. Однако иногда может трудно понять, насколько уместны математические результаты для Например, при попытке предсказать цены на фондовом рынке или землетрясения. Часто один раунд математических рассуждений не дает удовлетворительных результатов. выводы и изменения в том, как делается представление или в самих операциях. Действительно, прыжки обычно делаются назад и далее между шагами, и нет никаких правил, определяющих, как продолжать. Процесс обычно протекает рывками, с много неправильных поворотов и тупиков. Этот процесс продолжается до тех пор, пока результаты достаточно хороши. Но какой степени точности достаточно? Ответ зависит от как будет использоваться результат, о последствиях ошибки и о вероятная стоимость моделирования и вычисления более точного ответа. Например, ошибка в 1 процент при расчете количества сахара в рецепте торта может быть неважным, тогда как подобная степень ошибка в вычислении траектории космического зонда может иметь катастрофические последствия. Однако важность «достаточно хорошего» вопроса привела к тому, что к разработке математических процессов для оценки того, насколько далеко от результатов могут быть и сколько вычислений потребуется, чтобы получить желаемую степень точности.

Copyright © 1989, 1990 Американской ассоциации по развитию науки

Математическая биология | исследования | Инженерные науки и прикладная математика

Математическая биология быстро расширяется и развивается по мере того, как ученые в области биологических наук переходят от описательных экспериментов к более количественным экспериментам. Разнообразие и сложность живых организмов означает, что перед математиками стоит гораздо больше задач, связанных с объяснением и предсказанием биологических систем посредством моделирования.

Математическая биология — это широкая тема, которая может охватывать широкий диапазон масштабов длины, от субмикронных длин полимеров ДНК до километровых масштабов схем миграции стад животных.

Биофлюидная механика
Рак
Биология развития
Genomics
Microbiology
Biofluid Mechanics Applydiid
. живые системы. Это область, которая сегодня развивается очень быстро из-за развития новых экспериментальных методов, которые позволили проводить количественные измерения конкретных биологических систем, например движения клетки.
Исследования в рамках ESAM включают разработку математических моделей интересных биологических систем, разработку новых аналитических и вычислительных методов для решения этих моделей и взаимодействие с экспериментальными группами для проверки достоверности исследования. Конкретные области текущих исследований включают биопленки (скопление бактерий на твердых поверхностях, окруженных газом или жидкостью), динамику пузырьков и клеток, а также динамику аневризм.
Факультет
Майкл Дж. Миксис
Петя Влаховска
Вернуться к началу
Рак
Современные экспериментальные методы, используемые для исследования биологических систем, позволяют получать все больше и больше данных. Исследователи все чаще обращаются к математическим и вычислительным моделям, чтобы понять эти данные и сделать количественные прогнозы того, как биологические системы будут вести себя в различных условиях.
Одним из примеров этого является изучение рака. Новые модели, основанные, например, на последней экспрессии генов и высоких данных секвенирования, позволяют по-новому взглянуть на некоторые причины, лежащие в основе этого многогранного заболевания.
Факультет
Уильям Кэт
Вернуться к началу
Биология развития
Соотношение формы и функции организма — одна из центральных тем биологии и результат процесса развития — морфогенеза. Хотя зоопарк форм организмов кажется безграничным, мы ожидаем, что в процессах и механизмах, их порождающих, должно быть единство.
По аналогии с морфогенезом нашей планеты, в то время как детали нынешней формы континентов зависят от времени и исторических случайностей, механизмы, управляющие тектоническими плитами и течениями в ядре Земли, гораздо более общие. Каковы основные принципы и механизмы, лежащие в основе возникновения организменной формы? Это центральный вопрос, лежащий в основе нашего исследования.
Наша работа исследует два направления исследований: 1) решение управляемых данными обратных задач, которые позволяют нам проводить измерения физических сил и химической кинетики, которые эксперименты не дают прямого доступа, и 2) в тесном сотрудничестве с экспериментаторами мы объединить измерения, сделанные в их лабораториях, с нашими, чтобы направить разработку математических моделей, которые носят феноменологический характер, и формализовать нашу интуицию о том, как физические свойства полимеров, клеток и тканей возникают и ограничивают интересующий биологический процесс.
Факультет
Мадхав Мани
Найл Манган
Вернуться к началу
Геномика
Доступ к геному организма подобен примитивному пониманию алфавита языка без понимания значения слов и структуры предложений. Несмотря на то, что нет недостатка в данных, поступающих из экспериментов по секвенированию отдельных клеток, нам не хватает нашего Розеттского камня, чтобы помочь разобраться во всем этом.
Это, пожалуй, самая насущная проблема в количественной биологии и биомедицине, и группы ESAM используют инструменты статистики, машинного обучения и статистической физики для создания управляемых данными математических моделей для ее решения.
Факультет
Мадхав Мани
Вернуться к началу
Микробиология
Микроорганизмы сами по себе являются сложными системами. Они могут проявлять значительную приспособляемость к окружающей среде, вызванную такими стрессами, как голодание, конкуренция со стороны других видов или воздействие антибиотиков. Они способны к передвижению, межклеточному общению и координации как наступательных, так и оборонительных стратегий. Поведение отдельных клеток регулируется экспрессией генов, которые часто моделируются системами обыкновенных дифференциальных уравнений. Часто эти системы включают элементы стохастичности, чтобы объяснить недетерминантный характер этих систем.
Колонии микроорганизмов, взятые в совокупности, можно моделировать с помощью континуальных моделей в виде реакционно-диффузионных систем. Эти системы отслеживают поток питательных веществ и продуктов в более крупной среде.
Понимание микробиологических систем имеет решающее значение для общества. Большинство людей знакомы с распространенными патогенами, вызывающими заболевания, но могут не знать, что бактерии также используются для очистки сточных вод, производства бытовой химии и даже производства энергии. Математическое моделирование может помочь в улучшении лечения заболеваний, чтобы уменьшить вероятность устойчивости к антибиотикам, а также оптимизировать биохимические процессы для улучшения производства энергии или биохимических процессов, полезных для общества.
Факультет
Дэвид Чопп
Найл Манган
Вернуться к началу
Нейронаука
С помощью Periodic Research Animation объем данных, доступных в результате экспериментальных исследований нервной системы, вырос, а математические и вычислительные модели становятся все более важными для понимания функций мозга. Такие модели, например, могут объяснить и предсказать, как поведение отдельных нейронов определяется их морфологической структурой и множеством ионных каналов, присутствующих в клеточных мембранах. Эти модели помогают исследователям изучить, как нейроны обрабатывают различные типы входных данных. Они также обеспечивают основу для подробных моделей, включающих сети нейронов. Для таких сетевых моделей необходимы передовые вычислительные методы.
Однако также возможно изучать многие аспекты больших сетей нейронов, используя модели отдельных нейронов со значительно меньшей сложностью. Например, распространение или отказ активности в нейронных сетях со сложной связностью можно понять, используя относительно простые нейронные элементы.
Подобные проблемы изучаются преподавателями и студентами ESAM, чтобы понять работу структур мозга, участвующих в формировании памяти и обработке зрительной и обонятельной информации.
Факультет
Дэвид Чопп
Уильям Кэт
Герман Рике
Вернуться к началу
Динамика населения
Многие задачи, моделирующие эволюцию населения, связаны с несколькими различными физическими эффектами.

Тема 1.1. Краткая история развития биологии (Страницы 4,5,6,7,8,9)

Читать «Биология. Общая биология. Базовый уровень. 10 класс» — Сивоглазов Владислав Иванович, Агафонова Инна Борисовна, Захарова Екатерина Тимофеевна — Страница 2

Система биологических наук. Современная биология – это совокупность естественных наук, изучающих жизнь как особую форму существования материи

Таблица по биологии краткая история развития. История развития биологии

1. Краткая история развития биологии. Биология. Общая биология. 10 класс. Базовый уровень

I. Краткая история приматологии

Краткая история прививок и вакцинаций

Краткая история евгенического движения

1. ОПРЕДЕЛЕНИЕ, ОСНОВНЫЕ ПРОБЛЕМЫ И КРАТКАЯ ИСТОРИЯ МЕТОДА ССП

Краткая история метода ССП

История развития гомеопатии

4.2. Основные понятия биологии развития

4.4. Теоретическое значение и проблемы биологии развития

Глава 1. КРАТКАЯ ИСТОРИЯ ЭКОЛОГИИ

Краткая анекдотичная и недокументированная история

Естественники и гуманитарии: краткая история подхода

Некоторые актуальные вопросы биологии развития поведения[43]

Краткая история психопатии

Глава II. Краткая история фенетики

Краткая история развития биологии

«Секреты жизни: введение математика в молекулярную биологию — катализ исследования на стыке вычислений и биологии»

БИОХИМИЯ

РИСУНОК 1.1

РИСУНОК 1.2

РИСУНОК 1.3

КЛАССИЧЕСКАЯ ГЕНЕТИКА

РИСУНОК 1.4

МОЛЕКУЛЯРНАЯ БИОЛОГИЯ

РИСУНОК 1.5

РИСУНОК 1.6

РИСУНОК 1.7

РЕКОМБИНАТНАЯ ДНК-РЕВОЛЮЦИЯ

РИСУНОК 1.8

РИСУНОК 1.9

МОЛЕКУЛЯРНАЯ ГЕНЕТИКА В 1990-Х

РИСУНОК 1.

РИСУНОК 1.11

. РИСУНОК 1.12. (B) Основываясь на этих сходствах, можно было построить базовую молекулярную модель (подробнее…)

ПРОЕКТ «ГЕНОМ ЧЕЛОВЕКА»

COMING ATTRACTIONS

ССЫЛКИ

Что такое электрон? Что такое Свет?

Биология

Химия

Физика

Математика

Объединение этих дисциплин

3 Связь между математическими науками и другими областями

Что такое математика? | Живая наука

Кто изобрел математику?

Математика в древней Греции

Развитие исчисления

Почему математика важна

Глава 2: Природа математики

Глава 2: ПРИРОДА МАТЕМАТИКИ

МОДЕЛИ И ОТНОШЕНИЯ

Математическая биология | исследования | Инженерные науки и прикладная математика

Факультет

Рак

Факультет

Биология развития

Факультет

Геномика

Факультет

Микробиология

Факультет

Нейронаука

Факультет

Динамика населения