Содержание
Сколько километров до горизонта? — «Как и Почему»
Главная » Интересные факты
Интересные факты
Автор Вадим Хромов На чтение 3 мин Опубликовано Обновлено
Содержание:
Что такое «горизонт»? Мы часто употребляем это слово, например: солнце скрылось за горизонтом или на горизонте показался автомобиль. Но есть ли научное определение данного термина и можно ли измерять расстояние до горизонта?
Что такое горизонт?
Говоря простым языком, это граница между небом и поверхностью земли или воды. Также иногда можно встретить в определении слово «видимый». Горизонт бывает видимым и истинным.
Видимый горизонт – та часть пространства, которую видит наблюдатель, включая границу между небом и земной поверхностью. Истинный горизонт – воображаемый круг небесной сферы, плоскость которого расположена перпендикулярно относительно вертикальной линии в точке наблюдателя.
Его также называют астрономическим или математическим.
Видимый и астрономический горизонт
Расстояние измеряется до видимого горизонта. Для этого используется теорема Пифагора и несложная формула:
d = √(R + h)2 – R2
Чтобы узнать более-менее точное расстояние, необходимо знать две величины: радиус Земли (R) и высоту, на которой находится наблюдатель (h). Таким образом, очевидно, что чем выше располагается наблюдатель, тем сильнее будет отдаляться линия горизонта.
Примеры расстояния от определенного объекта до горизонта:
- человек ростом 1,75 м, стоящий на земле – 4,7 км;
- крыша 8-этажного дома 25 м – 17,9 км;
- воздушный шар 150 м – 43,8 км;
- самолет 10 км – 357,3 км;
- космический корабль 350 км – 2144 км.
Интересный факт: линия горизонта на Луне выглядит совсем иначе. В связи с отсутствием атмосферы, отдаленные объекты выглядят четче, чем на Земле. Также сложность изучения данного явления связана с тем, что нет привычных объектов, по которым можно было бы оценить масштабы.
В целом лунный горизонт в 2 раза ближе.
Дальность видимости
Если представить, что наблюдатель стоит на ровной поверхности и ничто не загораживает горизонт, то чем ограничен его кругозор? На открытом пространстве линию горизонта ограничивает выпуклость поверхности Земли, связанная с ее геоидной формой.
Предыдущее изображение показывает, что видимость для наблюдателя заканчивается в той точке, где линия горизонта условно пересекается с геоидной формой Земли. Если наблюдатель поднимется выше, его кругозор расширится.
Возникает вопрос, могут ли различные устройства увеличить дальность видимости? Например, способен ли бинокль расширить кругозор в прямом смысле? Поскольку, бинокль – это оптический прибор, он способен лишь увеличить изображение. Для этого он оснащен специальной конструкцией, которая увеличивает отдаленные объекты, делает их более отчетливыми. Но «заглянуть» за линию горизонта при помощи бинокля нельзя.
Конструкция классического бинокля
Горизонт – граница, разделяющая небо и поверхность земли/воды.
Расстояние до видимого горизонта зависит от высоты, на которой находится наблюдатель. Чем выше эта точка, тем сильнее отдаляется горизонт. Например, с высоты среднего человеческого роста (1,75 м) расстояние до горизонта составляет 4,7 км.
Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Поделиться с друзьями
Оцените автора
( 2 оценки, среднее 4 из 5 )
Как измерили расстояние до Солнца / Хабр
Сегодня, когда астрономию вернули в школьную программу, любой старшеклассник (ну, в теории, любой) должен знать: расстояние от нашей планеты до Солнца составляет примерно 149,5 млн километров. Это расстояние еще принято называть астрономической единицей.
Но, понятно, что этот ответ как-то надо было получить и астрономам потребовалось на это несколько шагов, растянувшихся не одно тысячелетие. Ниже — о каждом шаге подробнее.
Шаг первый – безбожник Аристарх и Луна
Аристарх Самосский жил в III веке до нашей эры и был по-настоящему выдающимся астрономом.
Задолго до Коперника он построил гелиоцентрическую модель устройства мира. Довольно точно определил продолжительность года в 365 + (1/4) + (1/1623) дней. Усовершенствовал солнечные часы. А еще он предпринял попытку измерить расстояние от Земли до Солнца и Луны. Этому Аристарх посвятил целый трактат (кстати, единственная письменная работа этого автора, дошедшая до нас).
С Луной у него получилось довольно близко к правильному ответу: 486400 км (по расчетам Аристарха), 380000 км (среднее расстояние по современным данным). Спустя сто лет другой античный астроном Гиппарх, кстати, уточнил эти цифры. А вот с Солнцем у Аристарха получилась нехилая промашка.
Но сначала о том, как вообще древнегреческий астроном измерял это расстояние. Известно, что иногда Солнце и Луну можно наблюдать одновременно. Причем, бывают моменты, когда Солнце освещает ровно половину Луны. Тогда угол «Земля-Луна-Солнце» — прямой, и измеряя угол «Луна-Земля-Солнце» можно с помощью тригонометрических соотношений, зная расстояние Земля-Луна, найти расстояние Земля-Солнце.
Но «гладко было на бумаге». Во-первых, Аристарху надо было поймать момент, когда освещена ровно половина Луны, а сделать это без телескопа было практически невозможно. А во-вторых, опять же без серьезной измерительной аппаратуры, точно измерить все параметры. Не удивительно, что грек ошибся, причем, очень сильно: угол α у него получился целых три градуса (в реальности он равен 10 минутам), а расстояние до Солнца всего 7,5 млн километров. Опираясь на это расстояние, Аристарх пришел к выводу, что Солнце намного больше Земли. Это и стало главным аргументом его гелиоцентризма (в центре мироздания должен быть самый большой объект).
Впрочем, ошибка в определении расстояния большой роли в науке не сыграла, вычисления Аристарха вообще не получили широкой известности (даже среди образованной части населения античных городов). Причина была скорее политической, все дело в его гелиоцентрической модели мироздания. Она противоречила геоцентрической модели, которой придерживался тогдашний научный консенсус.
И есть упоминания, что его даже пытались привлечь к суду как безбожника. Спустя некоторое время сначала Гиппарх подверг критике его взгляды, а позже Птолемей (чья геоцентрическая модель успешно дожила до Коперника) и вовсе проигнорировал результаты Аристарха, способствуя их забвению на долгое время.
Шаг второй — смотрим на Венеру (Кеплер и Хоррокс)
Человечеству потребовалось почти две тысячи лет, чтобы сделать этот следующий шаг к ответу, но будем справедливы, это было нелегкое время и хватало других проблем.
И для начала, надо было выбрать другой объект, на который опираться в своих вычислениях. В 1626 году известный немецкий астроном и математик Иоганн Кеплер предложил в качестве кандидата Венеру. К тому времени астрономы уже знали про одно довольно редкое астрономическое явление – прохождение Венеры по диску Солнца, причем, оно случается дважды с разницей в несколько лет, а потом следует значительный перерыв. Предложенный Кеплером метод заключался в следующем: надо измерить время прохождения Венеры по диску Солнца из разных точек Земли.
И сравнивая эти времена можно найти расстояние от Земли до Венеры и до Солнца.
Впрочем, это только звучит просто. Как минимум, надо было дождаться этого явления. Это удалось британскому астроному Джереми Хороксу, который переписывался с Кеплером и знал про его метод. Сначала британец уточнил частоту этого явления: «дубль» случается с разницей в восемь лет каждые полтора столетия. И ближайшее должно было состояться в 1639 году. Хоррокс подготовился к этому событию, он наблюдал за небом из своего дома в Мач Хул, близ Престона, а его друг делал то же самое из Солфорда, близ Манчестера. Сначала, казалось, что удача от них отвернулась, поскольку в этот день была сильная облачность, но за полчаса до захода Солнца облака разошлись и пара астрономов сумела-таки осуществить свой план. На основании наблюдений, Хоррокс рассчитал, что нашу планету от Солнца отделяет 95,6 млн км. Это было уже гораздо ближе к истине, но все равно неверно.
Шаг третий – смотрим на Марс (Кассини)
До следующего венерианского «дубля» надо было ждать полтора века и пока шло время астрономы тратили его на поиск других способов вычислить искомое расстояние.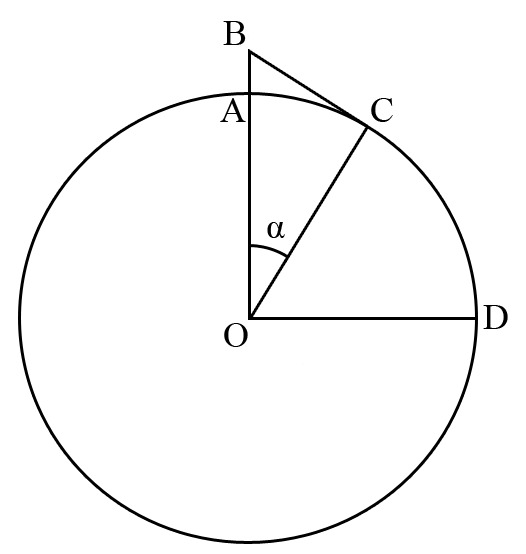
И это удалось французскому астроному итальянского происхождения Джованни Доменико Кассини. Он вообще отметился в астрономии как талантливый наблюдатель (например, это он первым увидел Большое Красное пятно на Юпитере). К тому времени астрономы уже оценили возможности, которые дает одновременное наблюдение за одним и тем же объектом из отдаленных друг от друга мест. В 1672 году Кассини на пару с другим французским астрономом Жаном Рише осуществили такой проект: первый остался в Париже, а второй отправился в Южную Африку, где у Франции были свои колонии. Они одновременно наблюдали Марс и, вычислив параллакс, определили его расстояние от Земли. Параллакс, если кто не знает, это смещение или разница в видимом положении объекта, рассматриваемого на двух разных линиях зрения. Ну а вычислять расстояние до объекта по параллаксу умели уже давно.
И поскольку относительные отношения различных расстояний между Солнцем и планетами уже были известны из геометрии, рассчитав по параллаксу расстояние до Марса, Кассини смог сделать то же самое и для Солнца.
Его результат — 146 млн км – был уже очень близок к современным оценкам. Что интересно, в то время, когда Кассини проводил эти расчеты, он был приверженцем геоцентрической системы, то есть, расстояния он получал близкие к верным, но карту Солнечной системы строил по старинке, с Землей в центре. Позже он признал правоту Коперника, но в ограниченной степени.
Шаг четвертый – снова Венера и астрономы всего мира
Тем временем близился очередной венерианский «дубль» (в 1761 и 1769 годах) и астрономы были намерены выжать из этого события максимум. Чтобы не зависеть от погодных условий и собрать данные с разных точек на Земле, был организован большой международный проект (его считают чуть ли не первым в истории) под эгидой Французской академии наук. Заблаговременно были подготовлены и отправлены научные экспедиции к местам наблюдений. Не все закончилось гладко – экспедиция, отправленная в Новую Гвинею, без вести пропала в джунглях.
Но в целом проект удался.
Кстати, активно в нем участвовала и Россия.
В нашей стране им руководил человек необычайных талантов и энергии – Михайло Ломоносов (это он, кстати, обнаружил атмосферу на Венере).
Ломоносову удалось получить аудиенцию у императрицы Екатерины II и убедить ее в важности этой работы как для науки, так и для государственного престижа. Получив поддержку казны, Ломоносов смог развернуть на территории Российской империи 40 наблюдательных пунктов. На один из них, вблизи Петербурга, приезжала сама Екатерина и с интересом смотрела в телескоп.
Вот в итоге этой большой работы астрономов по всему миру и было получено то число, которое сегодня включено в учебники. Но нет предела совершенству, и еще через сто пятьдесят лет, 8 декабря 1874 года и 6 декабря 1882 года, очередные прохождения Венеры по диску Солнца вновь наблюдали научные экспедиции по всему миру, уточняя полученные данные. А потом еще раз в 2004 и 2012 году. Впрочем, в ходе этих наблюдений получали и другие полезные данные, но это уже другая тема.
«Действительно ли Луна больше, когда она находится на горизонте? Я слышал, что расстояние до Луны не всегда одинаково? Она ближе, когда находится ниже в небе?» | Планетарий
«Действительно ли Луна больше, когда она на горизонте? Я слышал, что расстояние до Луны не всегда одинаково? Она ближе, когда находится ниже в небе?»
— Р.
С., Сако
Приветствую!
Вы имеете в виду известную «лунную иллюзию», когда луна действительно кажется самой большой. На самом деле луна не больше, когда она находится на горизонте, чем когда она находится выше в небе. Вы можете убедиться в этом утверждении сами. Когда вы увидите луну на горизонте, вы обнаружите, что можете прикрыть ее большим пальцем, вытянутым на расстоянии вытянутой руки, точно так же, как вы можете это сделать, когда луна находится выше в небе. Средний угловой диаметр Луны составляет примерно полградуса, такой же, как у Солнца.*
Вы правы в том, что расстояние от Луны до Земли меняется на протяжении всей ее орбиты. Она изменяется от максимума (апогея) до минимума (перигей). Луна в перигее примерно на 13% больше Луны в апогее. Однако перигей данной орбиты отделен от соответствующего апогея примерно на 13-14 дней. (Период между последовательными перигеями, называемый аномальным месяцем, составляет 27,5 дней.) Помните также, что когда мы видим Луну на горизонте, другие люди в других местах видят ее в другом положении на небе.
Многие астрономы пытались объяснить лунную иллюзию. В одном популярном объяснении говорилось, что луна кажется нам больше на горизонте, потому что мы видим ее по отношению к крупным объектам, с которыми мы уже знакомы, таким как деревья, дома и автомобили. Однако эффект увеличенного горизонта Луны также наблюдали жители пустыни и пилоты реактивных самолетов.
Принятая в настоящее время теория включает «иллюзию Понцо».
Эта иллюзия, названная в честь итальянского психолога Марио Понцо (1882-181960), вызвано тем, как ум воспринимает объекты относительно их фона. Луна кажется большой на горизонте, потому что что-то в нашем сознании заставляет такие объекты казаться увеличенными.
Мы должны помнить, что Луна не так близка и не так велика, как многие думают. Диаметр Земли составляет около 7900 миль, а диаметр Луны — около 2150 миль. Его среднее расстояние составляет около 240 000 миль. В масштабной модели, если бы Земля была баскетбольным мячом, Луна была бы размером с теннисный мяч на расстоянии около 24 футов**.
Это расстояние составляет примерно четверть стандартной баскетбольной площадки. Несмотря на то, что Луна является ближайшим небесным объектом к Земле, она отделена от нас довольно большим пространством.
Как обычно, я надеюсь, что этот ответ оказался полезным и не усугубил ситуацию.
*Здравствуйте! Это надоедливое отступление было добавлено, чтобы сообщить вам, что диаметр Луны не всегда будет равен диаметру Солнца. Луна удаляется от Земли примерно на 3,8 см в год. В конце концов видимый угловой диаметр Луны станет настолько мал, что полные солнечные затмения больше не будут происходить: однако мы можем ожидать, что полные солнечные затмения будут продолжаться сотни миллионов лет.
**Мы используем английскую систему единиц в честь сегодняшних всеобщих выборов в Великобритании, а не потому, что мне жалко лень рисовать переводы.
орбита — Каково расстояние Луны от зрителя на горизонте?
На каком расстоянии находится Луна от зрителя на горизонте?
Как отмечают другие, Луна следует по эллиптической орбите, что приведет к наибольшему изменению расстояния независимо от угла наблюдения.
Однако мы можем установить некоторые верхние и нижние границы того, каким должно быть расстояние до горизонта, используя максимальный и минимальный радиусы орбиты (апогей и перигей соответственно) вместе с теоремой Пифагора. 92}$$
Теперь просто подставьте числа. Я использовал следующие значения из вики Orbit of the Moon:
Перигей: 362600 км, Апогей: 405400 км, среднее орбитальное расстояние: 385000 км, радиус Земли: 6371 км
В апогее $x$ = 405349 км
В перигее $x$ = 362544 км
На среднем орбитальном расстоянии $x$ = 384947 км
С точки зрения зрителя Когда луна начинает подниматься над горизонтом, визуально находится ли луна на самом дальнем расстоянии от зрителя?
Как отмечалось выше, угол обзора не является основным фактором при расчете расстояния. Однако для данной точки своей орбиты Луна находится на самых дальних видимых радиусах от Земли на горизонте. Мы можем увидеть это, сравнив расстояние до Луны, когда она находится прямо над наблюдателем.