Орбита планеты с точки зрения геометрии: Геометрия орбиты, 6 (шесть) букв |

Содержание

Какова геометрия Вселенной? / Хабр

Облачные решения хороши тем, что позволяют создавать проекты любой сложности, вплоть до виртуального дата-центра. Если попробовать визуализировать эти структуры, то получится этакая мини-вселенная. Давайте поиграем с геометрией, попробовав визуализировать разные модели нашей вселенной.

В нашем сознании вселенная кажется бесконечной. Но с помощью геометрии мы можем рассмотреть различные трехмерные формы, которые предлагают альтернативу «обычному» бесконечному пространству.

Когда смотришь на ночное небо, кажется, будто пространство расширяется во всех направлениях. Такова наша ментальная модель вселенной, но она не всегда является верной. В конце концов, было время, когда все думали, что Земля плоская, потому что изгибы нашей планеты было чрезвычайно трудно заметить, а уж про сферическую форму Земли и вовсе не думали.

Сегодня мы знаем, что Земля имеет форму сферы. Но мало кто задумывается о форме Вселенной. Подобно тому, как сфера стала альтернативой плоской Земле, другие трехмерные формы предлагают альтернативу «обычному» бесконечному пространству.

Мы можем задать два разных, но все же тесно связанных между собой вопросов о форме Вселенной. Один из них касается её геометрии: мелкозернистых локальных измерений таких элементов, как углы и области. Другой — о топологии: как эти локальные части сшиваются в общую форму.

Космологические данные свидетельствуют о том, что часть Вселенной, которую мы можем видеть, гладкая и однородная, по крайней мере приблизительно. Локальная ткань пространства выглядит одинаково в каждой точке и во всех направлениях. Только три геометрические формы подходят под это описание: плоская, сферическая и гиперболическая. Давайте рассмотрим эти модели, некоторые топологические предположения а также то, что говорят космологические данные о формах лучше всего описывающих нашу вселенную.

Плоская геометрия (планиметрия)

Это геометрия, которую мы изучали в школе. Углы треугольника составляют 180 градусов, а площадь круга — πr2. Самым простым примером плоской трёхмерной формы является обычное бесконечное пространство — то, что математики называют евклидовым пространством, — но есть и другие плоские формы, которые тоже нужно учитывать.

Эти формы сложнее визуализировать, но мы можем попробовать пофантазировать, думая в двух измерениях, а не в трёх. В дополнение к обычной евклидовой плоскости, мы можем создать другие плоские формы, вырезая часть плоскости и скрепляя её края вместе. Например, предположим, что мы вырезаем прямоугольный лист бумаги и скрепляем его противоположными краями. Склеивание верхней и нижней граней даёт нам цилиндр:

Потом мы можем заклеить правый и левый края, чтобы получить пончик (то, что математики называют тором):

Теперь вы, наверное, думаете: «но мне не кажется это плоским». И будете правы. Мы немного сжульничали, описывая, как устроен плоский тор. Если бы вы действительно попытались сделать тор из листа бумаги таким образом, вы бы столкнулись с определенными трудностями.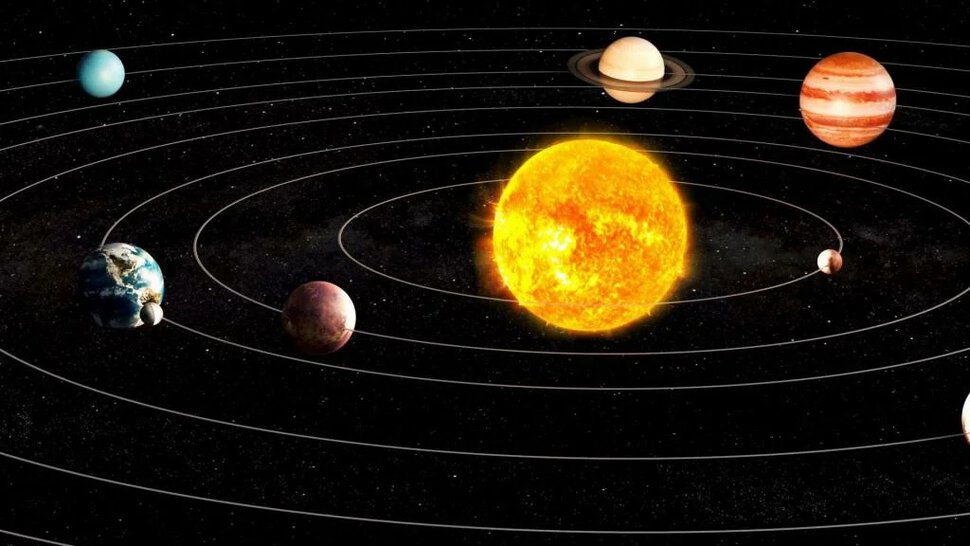 Сделать цилиндр было бы легко, но заклеить концы цилиндра у вас бы не вышло: Бумага сминалась бы по внутреннему кругу тора и не растягивалась бы достаточно далеко по внешнему кругу. Вместо бумаги пришлось бы использовать какой-нибудь растягивающийся материал. Но это растяжение искажает длины и углы, меняя геометрию.

Внутри обычного трёхмерного пространства невозможно построить реальный, гладкий физический тор из плоского материала без искажения его геометрии. Но мы можем отвлечённо порассуждать о том, каково это — жить внутри плоского тора.

Представьте, что вы двумерное существо, чья вселенная — плоский тор. Поскольку геометрия этой вселенной происходит от плоского листа бумаги, все геометрические факты, к которым мы привыкли, такие же, только в маленьком масштабе: углы в треугольнике суммируются до 180 градусов и так далее. Но изменения, которые мы внесли в глобальную топологию путём вырезания и заклеивания, означают, что опыт пребывания в торе будет сильно отличаться от того, к чему мы привыкли.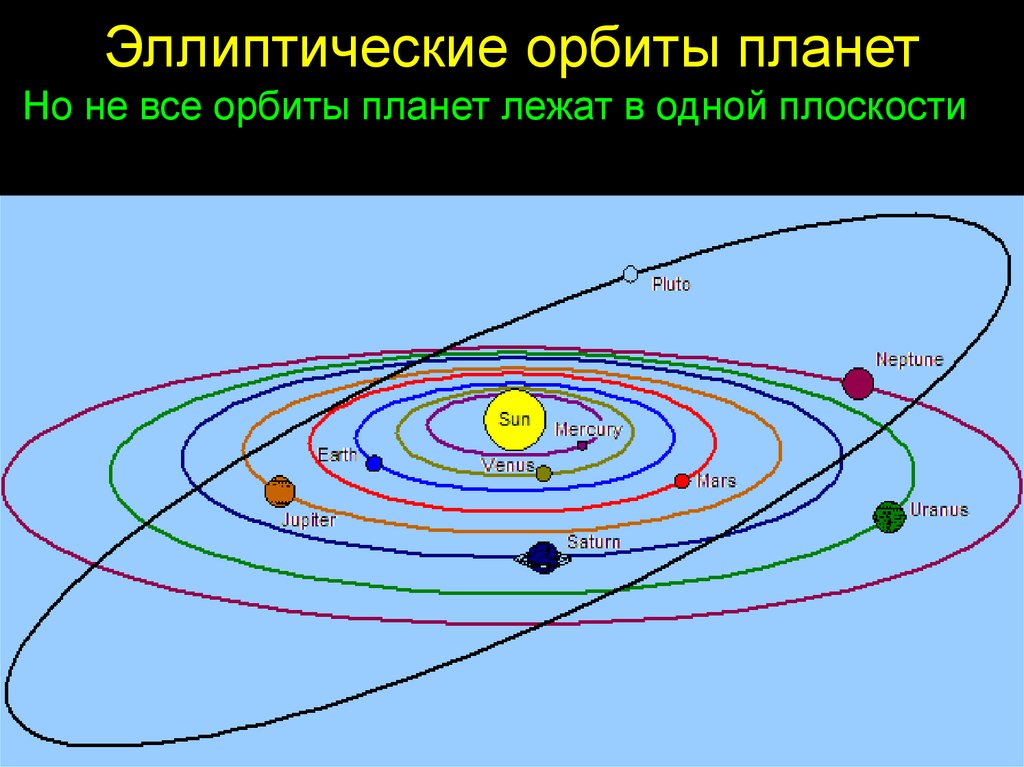

Для начала, на торе есть прямые пути, которые изгибаются и возвращаются туда, откуда начинались:

Эти пути выглядят изогнутыми на искаженном торе, но обитателям плоского тора они кажутся прямыми. А так как свет распространяется по прямым путям, то если посмотрите прямо, то увидите себя сзади:

На листе бумаги свет, который вы видите, проходил сзади, пока не достигал левого края, а затем снова появился справа, как будто в видеоигре:

Можно представить это иначе. Например, вы (или луч света) пересекаете одну из четырёх границ, появляясь в том, что кажется новой «комнатой». Но на самом деле это та же самая комната, только увиденная с новой перспективы.

Это значит, что вы также можете видеть бесконечное множество различных копий себя, глядя в разных направлениях. Это своего рода эффект «Зеркального коридора», за исключением того, что копии вас не являются отражениями:

На пончике они соответствуют множеству различных колец, по которым свет может перемещаться от вас к вам:

Точно так же мы можем построить плоский трехмерный тор, приклеив противоположные стороны куба. Визуализировать это пространство как объект внутри обычного бесконечного пространства не получится, но мы можем абстрактно рассуждать о жизни внутри него.

Подобно тому, как жизнь в двухмерном торе была подобна жизни в бесконечном двухмерном массиве одинаковых прямоугольных комнат, жизнь в трёхмерном торе подобна жизни в бесконечном трёхмерном массиве одинаковых кубических комнат. Вы увидите бесконечно много копий себя:

Трёхмерный тор — всего лишь один из 10 различных плоских конечных миров. Существуют также плоские бесконечные миры, такие как трехмерный аналог бесконечного цилиндра. В каждом из этих миров существует разный набор зеркальных залов.

Является ли наша Вселенная одной из этих плоских форм?

Когда мы смотрим в космос, мы не видим бесконечно много копий себя. Тем не менее, на удивление трудно исключить эти плоские формы. Во-первых, они все имеют одну и ту же локальную геометрию, что и евклидово пространство, поэтому никакое локальное измерение не может различить их.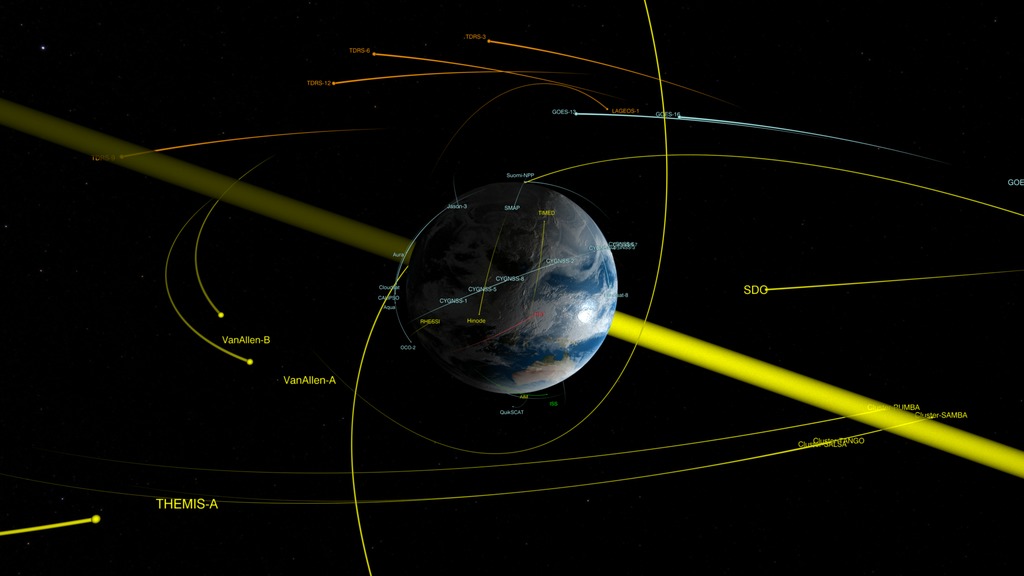

И если бы вы увидели копию себя, то это далёкое изображение показало бы, как вы (или ваша галактика, например) выглядели в далеком прошлом, так как свет должен был долго путешествовать, чтобы добраться до вас. Может быть, мы видим там неузнаваемые копии себя. Что ещё хуже, разные копии себя, как правило, находятся на разных расстояниях от вас, поэтому большинство из них будут выглядеть по-разному. И, возможно, они всё равно слишком далеко, чтобы мы могли их увидеть.

Чтобы обойти эти сложности, астрономы, как правило, ищут не копии самих себя, а повторяющиеся черты в самом дальнем из того, что мы можем видеть: космическое микроволновое фоновое (CMB) излучение, оставшееся после Большого взрыва. На практике это означает поиск пар кругов в реликтовом излучении, которые имеют совпадающие узоры горячих и холодных точек, что позволяет предположить, что это действительно один и тот же круг, который мы видим с двух разных точек.

В 2015 году астрономы провели именно такой анализ, используя данные с космического телескопа Планка. Они прочесали данные о видах совпадающих кругов, которые мы ожидали увидеть внутри плоского трехмерного тора или другой плоской трехмерной формы, называемой пластиной, но им не удалось их найти.

Это означает, что если мы действительно живем в торе, то он, вероятно, настолько велик, что любые повторяющиеся узоры лежат за пределами наблюдаемой вселенной.

Сферическая геометрия

Мы все знакомы с двумерными сферами — поверхностью шара, апельсина, Земли. Но что бы означало для нашей вселенной быть трёхмерной сферой?

Сложно представить себе трёхмерную сферу, но её легко описать с помощью простой аналогии. Подобно тому, как двумерная сфера — это совокупность всех точек на фиксированном расстоянии от некоторой центральной точки в обычном трёхмерном пространстве, так и трёхмерная сфера (или «трехсфера») — это совокупность всех точек на фиксированном расстоянии от некоторой центральной точки в четырёхмерном пространстве.

Жизнь в трёх сферах сильно отличается от жизни в плоском пространстве.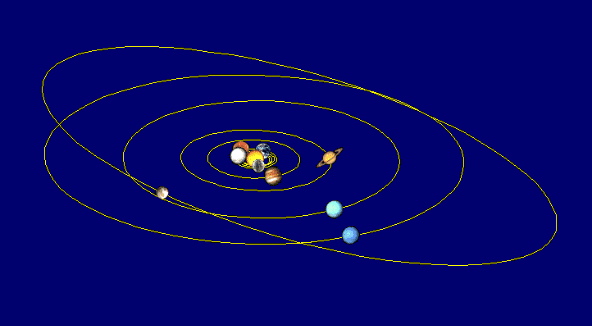 Чтобы почувствовать это, представьте, что вы двухмерное существо, живущее в двухмерной сфере. Двухмерная сфера — это вся Вселенная — вы не можете видеть и не можете получить доступ ни к одному из окружающих трёхмерных пространств. Внутри этой сферической вселенной свет движется по кратчайшим путям: по большим кругам. Для вас эти большие круги кажутся прямыми линиями.

Теперь представьте, что вы и ваш двумерный друг тусуетесь на Северном полюсе, и ваш друг идет на прогулку. В то время как ваш друг прогуливается, вначале он будет становиться все меньше и меньше в вашем зрительном пространстве, так же, как и в нашем обычном мире (хотя он не будет уменьшаться так быстро, как мы привыкли). Это из-за того, что пока ваше зрительное пространство будет увеличиваться, ваш друг будет занимать все меньше и меньше места в нём:

Но как только друг проходит экватор, происходит что-то странное: он начинает казаться всё больше и больше, чем дальше уходит. Это потому, что процент, который он занимает в вашем зрительном пространстве, растёт:

Когда ваш друг будет в трёх метрах от Южного полюса, он будет выглядеть такими же большими, как и в трёх метрах от вас:

А когда он достигнет самого Южного полюса, его можно будет увидеть во всех направлениях, так что он заполнит весь ваш визуальный горизонт:

Если на Южном полюсе никого нет, то ваш визуальный горизонт — это нечто ещё более странное: вы сами.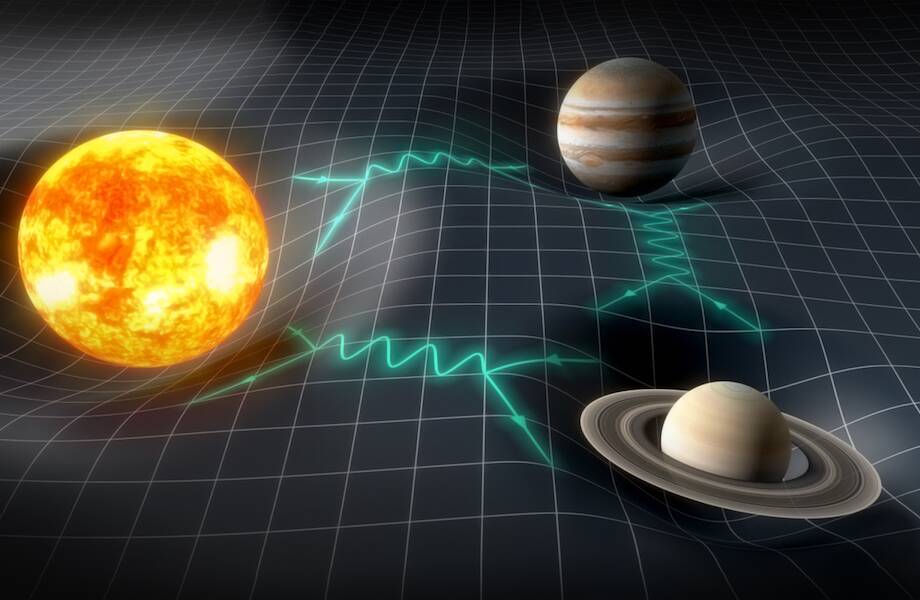 Всё потому, что свет, исходящий от вас, будет идти по всей сфере, пока не вернется к вам.

Это можно соотнести с жизнью в трёхмерной сфере. Каждая точка на трёхсфере имеет противоположную точку, и, если там есть объект, мы увидим его как фон, будто это небо. Если же там ничего нет, то вместо этого мы увидим самих себя в качестве фона – будто наш экстерьер был наложен на воздушный шар, затем вывернут наизнанку и надут, чтобы стать целым горизонтом.

Трёхсфера является фундаментальной моделью сферической геометрии, но это не единственное такое пространство. Подобно тому, как мы строили плоские пространства, вырезая кусок из евклидового пространства и склеивая его, мы можем строить сферические пространства, склеивая подходящий кусок из трех сфер. Каждая из этих склеенных форм, как и в торе, будет иметь эффект «лабиринта отражений», но в этих сферических формах есть только ограниченное количество комнат, через которые можно пройти.

Может ли наша Вселенная быть сферической?

Даже самые самовлюбленные люди не могут представить себя фоном всего ночного неба.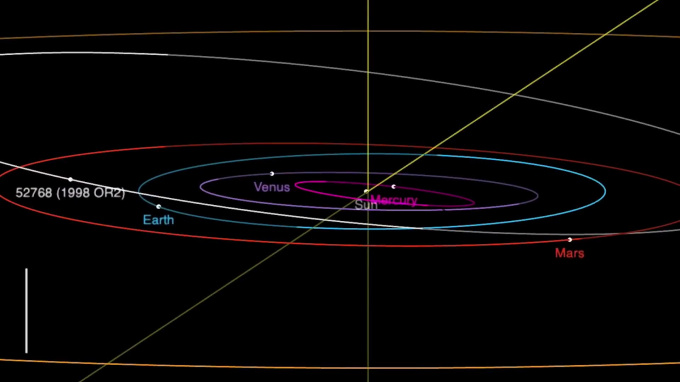 Но, как и в случае с плоским тором, тот факт, что мы не видим какое-либо явление, не означает, что оно не может существовать. Окружность сферической вселенной может быть больше, чем размер обозримой вселенной, что делает фон слишком далёким, чтобы его можно было разглядеть.

Но в отличие от тора, сферическая вселенная может быть обнаружена с помощью чисто локальных измерений. Сферические формы отличаются от бесконечного евклидового пространства не только глобальностью топологии, но и тончайшей геометрией. Например, из-за того, что прямые линии в сферической геометрии представляют собой большие окружности, треугольники получаются более пухлые, чем их евклидовые аналоги, а сумма углов больше 180 градусов:

В сущности, измерение космических треугольников является основным способом, с помощью которого космологи проверяют, является ли Вселенная изогнутой. Для каждой горячей или холодной точки на космическом микроволновом фоне известны ее диаметр по горизонтали и расстояние от Земли, что образует три стороны треугольника. Мы можем измерить угол, под которым пятно скрывается в ночном небе — один из трёх углов треугольника. Затем проверить, подходит ли для плоской, сферической или гиперболической геометрии (в которой сумма углов треугольника больше 180 градусов) комбинация из длины сторон и измеренного угла.

Большинство таких исследований, наряду с другими измерениями кривизны, свидетельствуют о том, что Вселенная либо плоская, либо очень близка к плоской. Но одна исследовательская группа недавно заявила, что часть данных, полученных с помощью космического телескопа Планка в 2018 году, свидетельствуют о существовании сферической вселенной. Другие исследователи возражают против этого утверждения, полагая, что это скорее всего, статистическая случайность.

Гиперболическая геометрия

В отличие от сферы, которая изгибается сама по себе, гиперболическая геометрия раскрывается вовне. Это геометрия гибких шляп, коралловых рифов и седел. Базовая модель гиперболической геометрии – это бесконечное пространство, подобно плоскому евклидовому пространству. Но поскольку гиперболическая геометрия распространяется наружу намного быстрее, чем плоская, не существует способа поместить даже двумерную гиперболическую плоскость внутри обычного евклидового пространства, если только мы не хотим исказить его геометрию. Здесь, например, искажено представление о гиперболической плоскости, известной как диск Пуанкаре:

С нашей точки зрения, треугольники вблизи пограничного круга выглядят намного меньше, чем вблизи центра, но с точки зрения гиперболической геометрии все треугольники одинакового размера. Если бы мы попытались сделать треугольники одинакового размера – например, используя растягивающийся материал для нашего диска и увеличивая каждый треугольник по очереди, выходя наружу из центра, — наш диск стал бы похож на гибкую шляпу и сгибался бы все больше и больше по мере того, как мы прокладывали себе путь наружу. По мере приближения к границе, этот изгиб становился бы все более неконтролируемым.

С точки зрения гиперболической геометрии, граничная окружность бесконечно далека от любой внутренней точки, так как для этого нужно пересечь бесконечно много треугольников. Таким образом, гиперболическая плоскость простирается до бесконечности во всех направлениях, точно так же, как и евклидовая плоскость. Но с точки зрения локальной геометрии жизнь в гиперболической плоскости сильно отличается от того, к чему мы привыкли.

В простой евклидовой геометрии окружность прямо пропорциональна её радиусу, но в гиперболической геометрии окружность растет экспоненциально по сравнению с радиусом. Мы можем видеть экспоненциальное скопление в массах треугольников вблизи границы гиперболического диска.

Из-за этой особенности математики любят говорить, что в гиперболическом пространстве легко заблудиться. Если ваш друг уйдёт от вас в обычном евклидовом пространстве, он начнёт выглядеть меньше, но это будет происходить медленно, потому что ваш визуальный круг растёт не так стремительно. В гиперболическом пространстве ваш зрительный круг растёт в геометрической прогрессии, так что вскоре ваш друг будет выглядеть сжатым до экспоненциально мелкой точки. Если вы внимательно не отследили его маршрут, найти дорогу к нему будет практически невозможно.

А в гиперболической геометрии сумма углов треугольника составляет менее 180 градусов — например, треугольники в нашей плитке диска Пуанкаре имеют углы, составляющие 165 градусов:

Боковые стороны этих треугольников не выглядят прямыми, но это только потому, что мы смотрим на гиперболическую геометрию через искаженную линзу. Для жителя диска Пуанкаре эти кривые являются прямыми линиями, потому что самый быстрый способ добраться из точки A в точку B – срезать путь к центру:

Есть вполне закономерный способ изготовления трехмерного аналога диска Пуанкаре – просто сделайте трехмерный шар и заполните его трехмерными формами, которые становятся меньше по мере приближения к граничной зоне, как треугольники в диске Пуанкаре. И точно так же, как в плоской и сферической геометрии, мы можем сделать ряд других трехмерных гиперболических пространств, вырезая подходящий кусок трехмерного гиперболического шарика и склеивая его грани.

Может ли наша Вселенная быть гиперболической?

Гиперболическая геометрия, с ее узкими треугольниками и экспоненциально растущими кругами, не похожа на геометрию пространства вокруг нас. И действительно, как мы уже видели, большинство космологических измерений указывают на плоскую вселенную.

Но при этом возможность того, что мы живем либо в сферическом, либо в гиперболическом мире, не исключена, так как маленькие кусочки обоих этих миров выглядят почти плоскими. Например, малые треугольники в сферической геометрии имеют углы, которые составляют лишь чуть более 180 градусов, а малые треугольники в гиперболической геометрии имеют углы, которые составляют лишь чуть менее 180 градусов.

Неспроста древние люди считали, что Земля плоская – кривизна Земли была слишком мала, чтобы ее можно было обнаружить. Чем больше сферическая или гиперболическая форма, тем более плоская каждая маленькая деталь. Поэтому, если наша Вселенная имеет чрезвычайно большую сферическую или гиперболическую форму, то та часть, которую мы можем наблюдать, может быть настолько близка к плоской, что ее кривизна может быть обнаружена только с помощью сверхточных приборов, которые нам ещё только предстоит изобрести.

Что ещё полезного можно почитать в блоге Cloud4Y

→ Компьютерные бренды 90-х, ч.3, заключительная

→ Можно ли взломать корабль?

→ Пасхалки на топографических картах Швейцарии

→ Как мама хакера проникла в тюрьму и заразила компьютер начальника

→ Как «сломался» банк

Подписывайтесь на наш Telegram-канал, чтобы не пропустить очередную статью. Пишем не чаще двух раз в неделю и только по делу.

Размышления о красоте движения планет / Хабр

Почему вид Луны притягивает наши взгляды и заставляет умолкнуть? Что такого есть в планетах, этих необычно ярких точках света, движущихся среди звёзд, что нам инстинктивно кажется настолько красивым? Возможно, они заставляют нас мечтать о далёких, недостижимых местах? Возможно, то, что они служат маяками в ночи, природными язычками свечей, позволяют отогнать страх и дают нам надежду во тьме? Или, возможно, то, что они кажутся плывущими в воздухе — а нам нравятся такие вещи, будь то осенние листья, шары, облака или птицы — подвешенные в воздухе, будто бы отрицающие силу гравитации, удерживающую нас на Земле?

Эта последняя мысль содержит в себе интересную иронию, поскольку на самом деле планеты и Луна, путешествуя над нашими головами, подчиняются законам гравитации.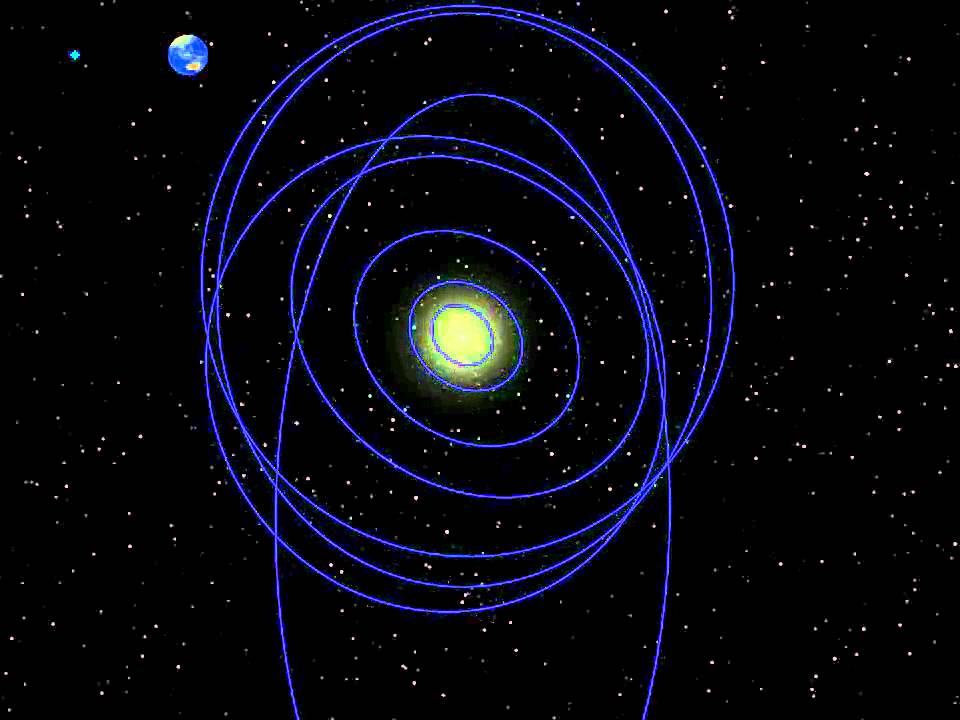

Периодически бывает так, что наш естественный спутник, на своём ежемесячном путешествии вокруг Земли, проходит рядом с тремя яркими планетами в небе, создавая прекрасное зрелище. Естественно, Луна вовсе не проходит физически рядом с этими планетами, точно так же, как ваша вытянутая ладонь, закрывающая Луну, не проходит рядом с Луной. Всё дело в перспективе — или геометрии, игре света и элегантной хореографии нашей Солнечной системы. Но эту перспективу так легко не почувствовать. Наши глаза неспособны воспринимать глубину для объектов, находящихся так далеко, поэтому наш мозг формирует двумерную картинку из трёх измерений Вселенной, и проецирует Луну, планеты, звёзды, находящиеся чрезвычайно далеко друг от друга, на психологически плоский чёрный экран ночного неба. Приходится очень сильно напрягать мозг, чтобы увидеть всё, как оно есть на самом деле, а не так, как кажется. И над этим фактом тоже стоит подумать.

Раз в две недели созерцателей ночного неба ждёт зрелище хрупкой Луны, похожей на кончик ногтя — такой тонкой, будто она готова сломаться от прикосновения. Это происходит дважды за четыре недели, один раз сразу перед восходом, а затем, через два дня, сразу после заката. Почему? Простая геометрия и отражённый свет. [Указанные даты и явления характерны для наблюдателей, находящихся на широте континентальной части США / прим. перев.]

Луна и планеты не светятся самостоятельно; они просто отражают свет Солнца. То, что нам видно, их яркость — всё это определяется тем, сколько солнечного света они отражают в нашу сторону. И это количество — тоже вопрос простой геометрии, следствие того, где находятся Луна и планеты по отношению к Солнцу и Земле. Если вы задумаетесь об этом, и вооружитесь небольшим телескопом, вы даже сможете, к своему полному удовлетворению, узнать, что полученные вами в школе знания истинны: Луна движется по орбите вокруг Земли, а планеты — вокруг Солнца, причём две из них находятся ближе к нему, чем Земля, а остальные — дальше.

Чтобы убедиться, что Луна движется вокруг Земли, и телескопа не надо; нужно лишь повнимательнее присмотреться к нескольким уже известным фактам, которые вы, возможно, не сопоставляли между собой.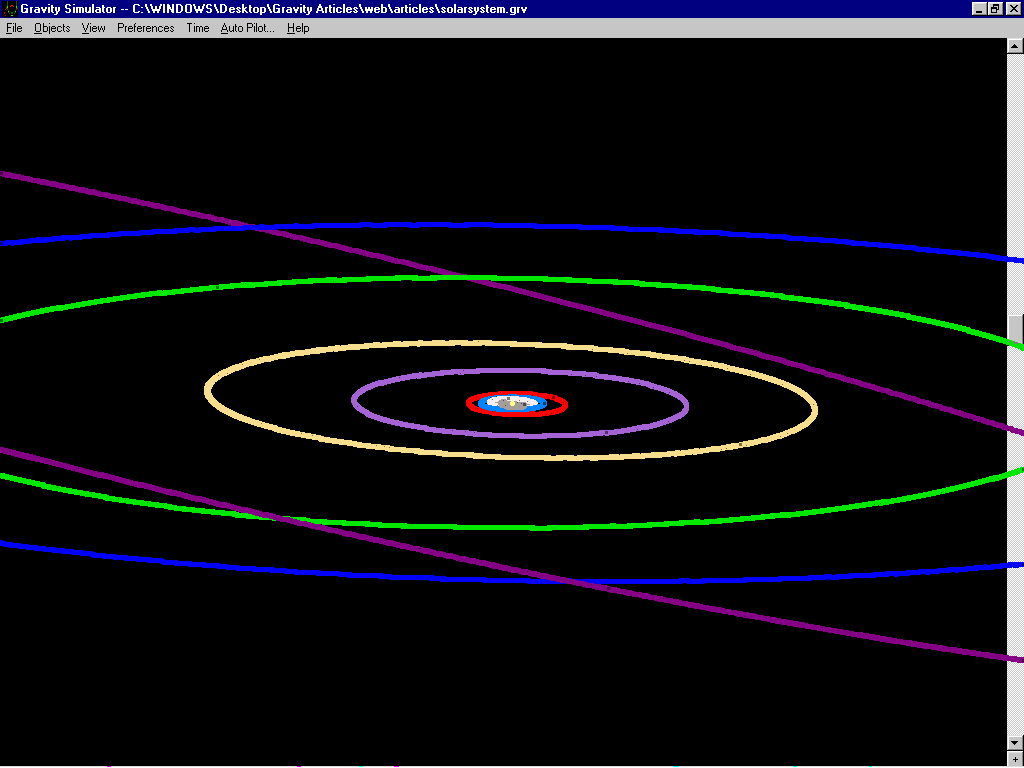 Все мы знаем о «фазах» Луны — периодах в течение четырёх недель лунного цикла, когда она полная, половинчатая или предстаёт в виде серпа. Но замечали ли вы, что эти фазы следуют очень чёткой и простой последовательности? Серп Луны всегда видно сразу после заката, или перед восходом; такой ночью Луна видна всего час или два. Половина луны находится над головой либо на закате, либо на восходе, и видна полночи. Полная Луна видна всю ночь, восходит на закате Солнца, заходит на восходе Солнца, и в полночь находится над головой.

Фазы луны происходят из перекрытия половины Луны, обращённой к Солнцу (освещённой светом и отмеченной более светлым цветом) и половины луны, обращённой к Земле (та часть, что мы можем видеть, к востоку от красных линий). Когда Луна находится примерно между Землёй и Солнцем, можно видеть очень небольшую часть освещённой половины Луны, и Луна выглядит, как серп; когда Земля находится примерно между Луной и Солнцем, подсвеченная и видимая части совпадают, и Луна полная. На рис. расстояния приведены не в масштабе.

А замечали ли вы, что освещённая часть Луны всегда находится на стороне, ближайшей к Солнцу? Если сейчас вечер и Луна видна, то освещённая часть Луны всегда смотрит на запад (по направлению к горизонту, куда садится Луна), а если Луна видна после полуночи, то её освещённая часть всегда смотрит на восток (когда Луна встаёт).

Видимый же размер Луны в небе никогда особо не меняется (за исключением оптической иллюзии, когда она приближается к горизонту, и выглядит больше — если сделать фото, то будет видно, что на самом деле она не больше). Верхняя и нижняя точки серповидной Луны отстоят друг от друга на то же расстояние, как и верх и низ полной Луны. Это также можно подтвердить, если вам повезёт увидеть красивое явление «пепельного света Луны», которое проще всего увидеть до того, как Луна становится слишком яркой — оно происходит в течении нескольких дней после серповидной Луны. Пепельный свет — это свет, отражённый от освещённой части Земли, который добирается до неосвещённой части Луны, а затем — обратно до тёмных частей Земли, где им можно наслаждаться — тусклое свечение тёмной части Луны, по которому видно, что серповидная Луна — всё же сфера, и такого же размера, как и полная Луна.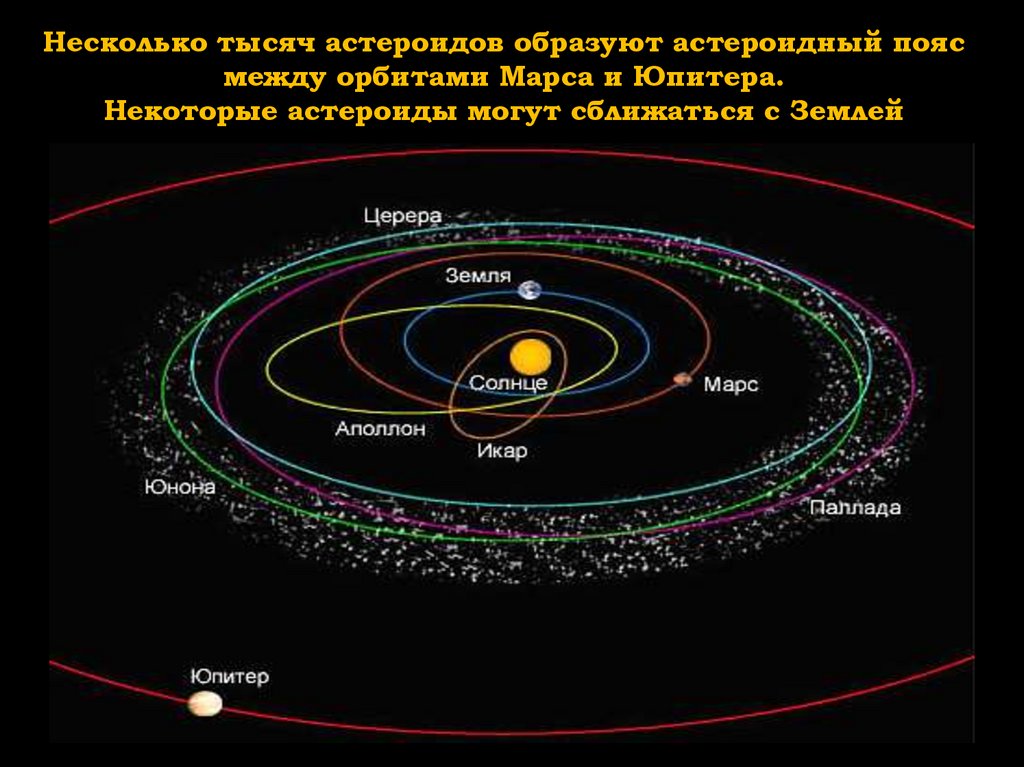

Такие явления могут свидетельствовать о том, что расстояние от Луны до Земли никогда особо не меняется; и что во время полнолуния Земля находится между Луной и Солнцем, а когда Луна имеет вид серпа, она находится между Землёй и Солнцем. Это значит, что Луна двигается по орбите вокруг Земли на почти постоянном расстоянии от Земли с циклом примерно в четыре недели. А то, что узкая полоса освещённой части Луны имеет форму серпа, подтверждает сферичность Луны.

В отличие от этой системы, поведение Венеры и Меркурия в небе поначалу кажется довольно странным. Они никогда не находятся прямо над головой; и вообще, в полночь ни одну из них не будет видно в небе.

Видели ли вы Меркурий? Если только вы не искали его специально, то, вероятно, нет. Чтобы увидеть Меркурий, нужно смотреть на него либо сразу после заката, либо незадолго перед восходом Солнца — но не в один и тот же день, и даже не в один и тот же месяц. Например, 22 февраля [дата вскоре после выхода оригинальной статьи / прим. перев.], если посмотреть вскоре после заката, не дольше 30 минут после него, при чистом горизонте, без заслоняющих его деревьев или зданий, облаков или гор на западе, вы найдёте на расстояние в несколько видимых размеров Луны слева от заходящего серпа Луны маленькую световую точку в одиночестве. Это Меркурий — и он действительно похож на ртуть [Mercury — Меркурий, mercury — ртуть, mercurial — живой, подвижный / прим. перев.], поскольку он довольно тускло виден в сумерках, и очень быстро заходит.

Меркурий и Венера, чьи орбиты ближе к Солнцу, чем орбита Земли, не могут появиться ночью над головой; они заходят вскоре после Солнца, или встают незадолго до него. Угол между ними и горизонтом во время захода или восхода Солнца не бывает больше, чем показано на рисунке (не в масштабе). При самом высоком положении Венера будет находиться гораздо выше Меркурия, что говорит о том, что последний находится ближе к Солнцу. Расстояния и углы даны приблизительно, размеры планет и Солнца — не в масштабе.

Почему Меркурий так сложно увидеть? Его орбита вокруг Солнца гораздо ближе к Солнцу, чем орбита Земли, поэтому он никогда не отходит далеко от Солнца в небе, и должен либо заходить сразу после него, либо вставать как раз перед ним. По своей орбите он (как и Земля) с нашей точки зрения двигается так, что выходит из-за Солнца (где мы его в принципе не увидим) на ту его сторону, которая видна в вечернем небе при закате; затем он проходит между Солнцем и Землёй (и из-за яркости Солнца его нельзя увидеть), а потом появляется в утреннем небе, но недалеко от Солнца, и потом он опять отступает за него и цикл повторяется заново.

Венеру легче увидеть по нескольким причинам. Во-первых, она больше Меркурия, размером сравнима с Землёй. Во-вторых, если Меркурий сероват, Венера ярко-белая; её атмосфера (с чудовищным эффектом от парниковых газов, поддерживающих её температуру на уровне выше, чем в печке), всё время покрытая белыми облаками, обладает хорошо отражающей поверхностью. В-третьих, её орбита отстоит от Солнца дальше, чем орбита Меркурия, и у этого есть два следствия: Венера подходит ближе к Земле, чем Меркурий, из-за чего кажется больше и ярче, и восходит выше в небе, чем Меркурий, что означает, что иногда её можно наблюдать по нескольку часов подряд после заката или до восхода (хотя по тем же причинам, что и Меркурий, не одновременно). Благодаря этому её можно наблюдать без особых усилий. И, неизбежно, каждый раз, когда это яркое пятнышко становится видно, в полицию поступают звонки с жалобами на НЛО — на удивительно яркий неопознанный летающий объект, также известный, как Венера.

Решающим же доводом в пользу того, что Венера и Меркурий двигаются по орбитам вокруг Солнца, а не Земли, состоит в том, что у них, как и у Луны, есть свои фазы — хотя и с ключевыми отличиями. Проходя через фазы они меняют размер, в отличие от Луны, и самыми яркими они бывают не в полной фазе, как Луна, а в фазе широкого серпа. Происходит следующее: сначала Венера появляется в вечернем небе, тусклая, но полностью освещённая. Затем, в последующие недели, она высоко встаёт в вечернем небе, становится больше, ярче, но уже не полностью освещена. Затем она начинает заходить по вечерам за горизонт, но становится всё ярче и крупнее, приближаясь к форме серпа, и затем, с тонким серпом, но большого диаметра, она исчезает в сумраке после заката.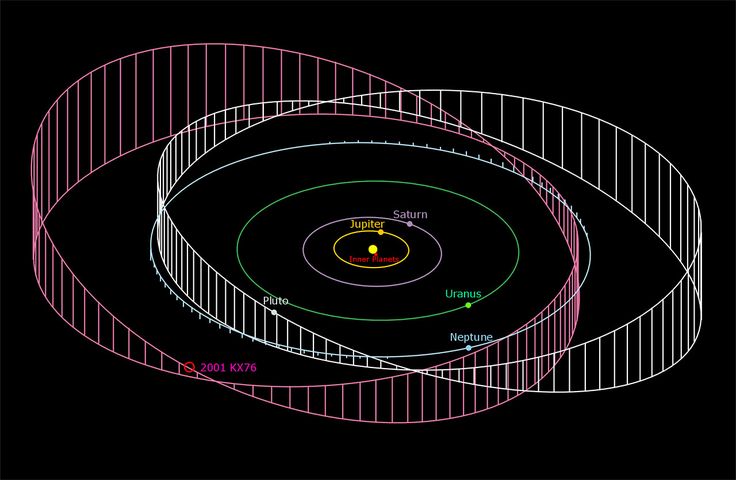

Затем она появляется через несколько дней в сумраке перед восходом в виде тонкого серпа, и происходит вторая половина цикла, когда её видно ранним утром, в обратной по отношению к вечерним торжествам последовательности.

Планета с орбитой меньше земной обладает фазами, похожими на Лунные, но вырастает и сжимается во время движения по орбите из-за изменения расстояния до Земли. Часть планеты, которая видна с Земли, находится слева от пунктирных линий; освещённая часть показана жёлтым.

К несчастью, невооружённым глазом это подтвердить уже нельзя — и вероятно, именно это задержало признание того факта, что Венера движется по орбите вокруг Солнца, на тысячи лет. Только телескоп Галилея, почти 400 лет назад, открыл фазы Венеры, описанные выше.

Из записной книжки Галилея

Телескоп для этого нужен совсем небольшой, такой, что может увеличивать объекты хотя бы в 20 раз, или даже можно обойтись биноклем (если у вас хорошее зрение, небо чистое, и вы способны терпеливо ждать, пока глаза привыкают к темноте.

Фотографии Венеры

21 февраля Венера будет в середине вечерней части цикла. Она будет освещённой больше, чем наполовину, размер её будет расти, Солнце будет освещать её всё меньше, и она будет всё выше забираться по отношению к вечернему горизонту — это зрелище интересно само по себе, и в следующие несколько месяцев станет ещё интереснее. Если следить за ней от недели к неделе, будет видно, как Венера достигнет своей высшей точки по отношению к горизонту примерно за месяц, потом развернётся и будет приближаться к Солнцу с нашей точки зрения. 5-6 июля [2012] Венера пройдёт перед диском Солнца.

25 февраля Луна будет расположена близко к Венере. На той неделе это будет самое интересное зрелище. Когда вы увидите два этих ярких шара в небе, супругу Земли и её сестру, подумайте о том, что ваш мозг не хочет вам сообщать. Несмотря на видимый размер Луны и на то, что Венера кажется небольшой точкой, эта планета на самом деле в пять раз больше Луны (примерно равна Земле), и кажется меньше и тусклее только потому, что сейчас находится в 400 раз дальше.

Ещё подумайте вот о чём. Свет Луны идёт от Солнца (и это занимает у него около 8,5 минут, настолько велико это расстояние), отражается от Луны и приходит на Землю (это занимает примерно 1,5 сек), в то время как свет Венеры должен пройти от Солнца (почти шесть минут), отразиться от Венеры и пройти ещё восемь минут [по расположению планет в феврале 2012] до Земли. Это похоже на задержку эхо; когда вы слышите гром от удара молнии в горах, вы можете сначала услышать его напрямую, а потом снова, когда звук отразится от удалённого пика. Если бы кто-то мог выключить Солнце, вы бы увидели, как Луна погаснет через восемь минут, а Венера будет светить ещё шесть минут сверх того.

Что насчёт Юпитера? Крупнейшая планета Солнечной системы будет продолжать светиться ещё час! Именно столько нужно, чтобы солнечный свет сначала достиг Юпитера (он находится примерно в пять раз дальше от Солнца, чем Земля), а затем отразился от него и достиг Земли (в феврале 2012 это расстояние в пять раз больше, чем от Земли до Венеры).

В конце февраля Юпитер поднимется в небе над Венерой, и будет близко к зениту. 26 февраля Луна пройдёт рядом с ними. Юпитер гораздо больше Земли или Венеры — примерно в 10 раз больше по радиусу — поэтому в телескоп или хороший бинокль (в такой, где видно, что Юпитер — не точка, а диск) он будет выглядеть в два раза большим, чем Венера, несмотря на то, что находится в 10 раз дальше. И всё же, несмотря на то, что он выглядит больше, он кажется тусклее Венеры. Почему? Чем дальше от Солнца, тем сильнее рассеивается его свет, поэтому Солнце на Юпитере будет казаться тусклее и меньше, чем на Земле, а на Венере Солнце будет выглядеть больше и ярче. Это значит, что от поверхности Юпитера света отражается меньше. Но не дайте вашему разуму обмануть себя, когда 26 февраля увидите Юпитер маленьким и тусклым по сравнению с Луной. Помните, что внутри этого газового гиганта Земля может уместиться тысячу раз.

То, что Юпитер движется вокруг Солнца, и что расстояние до него от Солнца гораздо больше, чем до Земли, опять-таки можно убедиться при помощи небольшого телескопа или даже бинокля. В отличие от Венеры и Луны, у Юпитера по сути нет фаз; он всегда почти полностью освещён Солнцем с нашей точки зрения. То же касается Сатурна (а также Урана и Нептуна, которых кроме как в бинокль или телескоп и не увидишь), и, в чуть меньшей степени, Марса. Все эти планеты, в отличие от Венеры и Меркурия, можно видеть в полночь, причём именно в эти ночи они выглядят крупнее и ярче всего. Они наиболее маленькие и тусклые, когда их видно на небе только сразу после заката или незадолго перед восходом.

Почему так происходит? Объект находится в зените в полночь, когда Земля располагается между ним и Солнцем, как в случае полной Луны. А это происходит тогда, когда эти планеты ближе всего к Земле. Когда их видно только после заката, они находятся очень далеко от Земли, а Солнце находится почти между нами и ними, поэтому они довольно тусклые, из-за огромного расстояния между ними и нашей планетой. И поскольку они никогда не проходят между Землёй и Солнцем, они никогда не выглядят в виде серпов, как это происходит с Луной, Меркурием и Венерой.

Изменение видимого размера Юпитера показано в верхнем ряду фотографий

Так что, если вы найдёте телескоп, вы сможете наслаждаться элегантным танцем планет и Луны; наблюдать, как планеты вырастают и уменьшаются в процессе их приближения и удаления; отмечать, как они восходят и заходят в нашем двумерной небе, и как это отражает их движение (и движение Земли) в трёхмерном пространстве; наблюдать за фазами Венеры и за тем, как они подтверждают тот факт, что она вращается вокруг Солнца. И вы можете обдумать тот факт, как небольшой технический прогресс 1609 года усилил зрение Галилея как раз достаточно для того, чтобы позволить ему открыть так много неизвестных ранее свойств Луны, Солнца и планет, и навсегда изменить взгляд человечества на себя и на наших небесных соседей.

Но даже и без телескопа — невооружённым взглядом или при помощи небольшого бинокля — можно насладиться красотой звёздного неба и погрузиться в необъятность нашего дома.

Наблюдая за Луной и Венерой, я буду вспоминать об одной из моих любимых встреч с природой. Случилось это несколько лет назад, во время летнего посещения заповедника, окружающего гору Сент-Хеленс, вулкан на юге штата Вашингтон, взорвавшийся в 1980-м. С северного хребта, стоя лицом к зияющей дыре в склоне горы и к разрушенной долине под ним, я смотрел, как на закате камни окрашиваются в серо-золотистый цвет, и ждал, когда звёзды появятся в небе, ставшем почти чёрным. На запада ярко горела Венера, жемчужина сверху и слева над яркой подвеской лунного полумесяца и пепельно-серой Луны. Затем я услышал сопение, казалось, довольно близко. Я подумал, что это, должно быть, небольшой зверёк в кустах позади меня, но когда я подошёл к кустам, я снова услышал этот звук, уже из другого места. Удивлённый, я посмотрел вверх, и обомлел. На холме, не более, чем в пятидесяти метрах от меня, на фоне последнего оранжевого свечения заката, были видны силуэты трёх величественных рогатых лосей.

Они лениво паслись, пока над ними, за ними, висела Луна, Венера и звёзды, манящие в бездну.

Кеплер, от многогранников к эллипсам, с картины Жана-Пьера Люмине

Введение

Регулярность такой большой активности небесных тел привела многие культуры к тому, чтобы основывать свои модели Вселенной на концепциях порядка и гармонии. Вокруг Средиземноморья именно пифагорейцы первыми высказали идею о том, что вселенная характеризуется пропорциями, ритмом и числовыми закономерностями. Гипотеза Платона была об организованном космосе, законы которого можно было расшифровать и объяснить в терминах геометрии.

История физики есть не что иное, как история стремления человека раскрыть скрытый порядок и гармонию вещей. Наиболее амбициозные физики пытались объединить явно дискретные явления: Галилей с земными и небесными законами; Ньютон с гравитацией и движением небесных тел; Максвелл с магнетизмом и электричеством; Эйнштейн с пространством и временем; сегодняшних физиков с гравитацией и микрофизикой.

Но, как сказал Гераклит еще в 500 г. до н. э., «природа любит прятаться». Действительно, прогресс в геометрии и математике привел к новым теориям космоса, которые мы не в состоянии понять. Они дают только абстрактные образы, которые не позволяют нам визуализировать структуру атомов, динамику пространства-времени или топологию Вселенной в каком-либо прямом смысле.

Именно эта фундаментальная вера в небесную гармонию, для которой последующие поколения находили различные изощренные выражения: справедливая пропорция, уравнение части и целого, симметрия, постоянство, резонанс, теория групп, струны, лежала в основе развития физики за последние 2500 лет.

Меланхолия, или Дух человека в поисках тайны мироздания . На этом офорте, датируемом 1514 годом по цифрам в квадрате в правом верхнем углу, изображен человек, созерцающий природу мира в состоянии меланхолии, которая в средние века ассоциировалась с черной желчью и с планетой Сатурн. Крылатый человек предвосхищает вопросы Иоганна Кеплера, когда он вычисляет, как выразить лежащую в основе гармонию космоса, используя сферы и многогранники. Яркий свет в небе — это большая комета, которую наблюдали зимой 1513–1514 годов. Когда он сияет на весах (изображая астрономический знак Весов), он символизирует конец земного цикла, если не конец самого времени. Лестница с семью ступенями представляет собой веру византийцев в то, что мир не будет существовать более семи тысяч лет. Это конец Средневековья; Дюрер (1471-1528) должен быть одним из первопроходцев Возрождения.

Геометрия и космос

«Геометрия, которая до возникновения вещей была совечна божественному разуму и являлась самим Богом […], снабдила Бога образцами для сотворения мира».
Иоганн Кеплер, Гармония мира, 1619.

Немецкий астроном XVII века Иоганн Кеплер, несомненно, был первым, кто интегрировал человеческое увлечение гармонией в общее видение мира, которое можно с полным правом назвать научным. Для Кеплера, как и для естествоиспытателей Древней Греции, космос представлял собой организованную систему, включающую землю и видимые звезды. Его общепризнанное намерение состояло в том, чтобы исследовать причины количества и размеров планет и почему они движутся именно так. Он считал, что эти причины, а следовательно, и секрет вселенского порядка можно найти в геометрии. Кеплер хотел сделать больше, чем создать простую модель или описать результаты своих экспериментов и наблюдений; он хотел объяснить причины того, что он видел.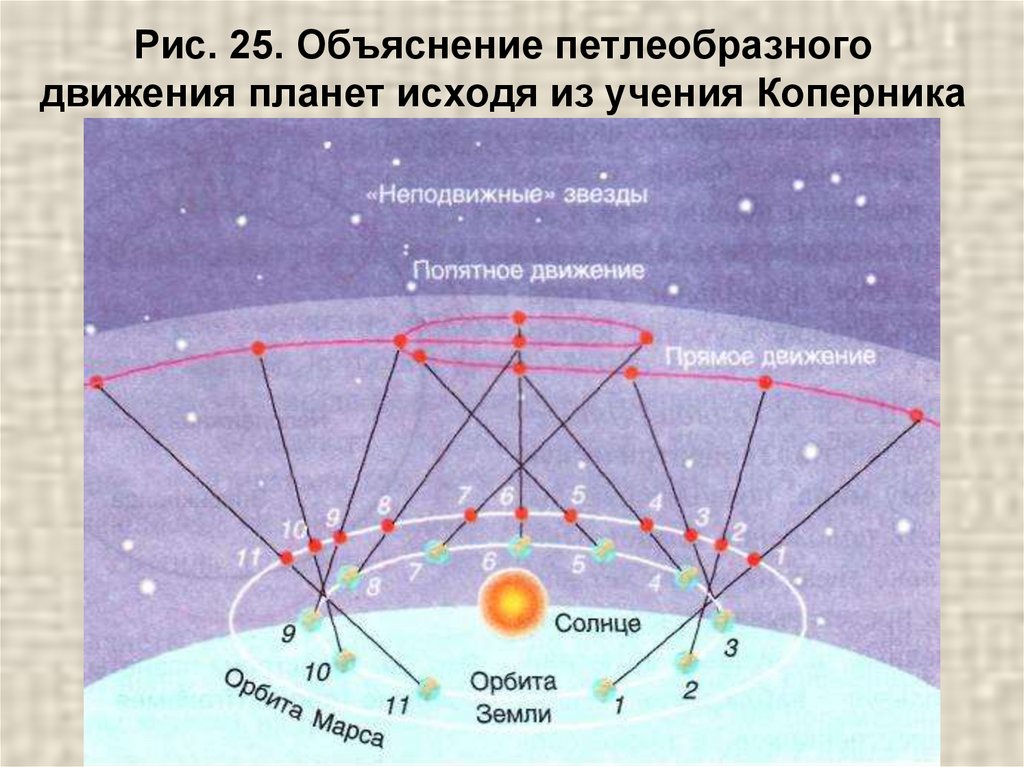 Это делает его одним из величайших новаторов в истории науки и привело его, в частности, к формулировке законов движения планет, которые действуют и сегодня.

Несмотря на свои новаторские методы, Кеплер написал два исследования космоса в стиле древних греков: Mysterium Cosmographicum (Тайна космоса) в 1596 году и Harmonices Mundi (Гармония мира) в 1619. В этот поворотный момент между древним и современным мышлением Кеплер был погружен в традицию, которая явно связывала космологию с понятием божественной гармонии. Но то, что Кеплер пытался выразить, было не числовым мистицизмом пифагорейцев; его отправной точкой были геометрические узоры, которые он рассматривал как «логические элементы». Его глубокое желание разработать рациональное объяснение космоса привело его к установлению процедур, напоминающих методы современной науки.

От многогранников к эллипсам

В 1590-х годах, когда он занимался математикой в Граце (тогда часть Штирии), Кеплер воспринял идеи Коперника. В гелиоцентрической модели, предложенной польским мыслителем пятьдесят лет назад, одновременное движение Земли вокруг Солнца и вокруг собственной оси объясняло наблюдаемое движение планет и звезд. Кеплер задался целью доказать, что эта простая гипотеза, которая была попыткой «сохранить видимость», действительно соответствовала действительности. Однако при этом он заметил, что круговые орбиты планет вокруг Солнца, предложенные Коперником, не соответствовали его точным наблюдениям. Будучи пламенным христианином, Кеплер хотел в то же время прославить Бога, который, по его мнению, был ответственен за гармоничное устройство вселенной (космос, как и Библия, возвещая славу Божию, как книга без слов, тайны которой были человеческими). обязанность обнаружить). Эта цель заявлена в самых первых строках предисловия к Тайна Космоса: «Мое намерение, читатель, показать в этой небольшой книге, что самый великий и добрый Творец при сотворении этой движущейся вселенной и устройстве небес смотрел на эти пять правильных тел.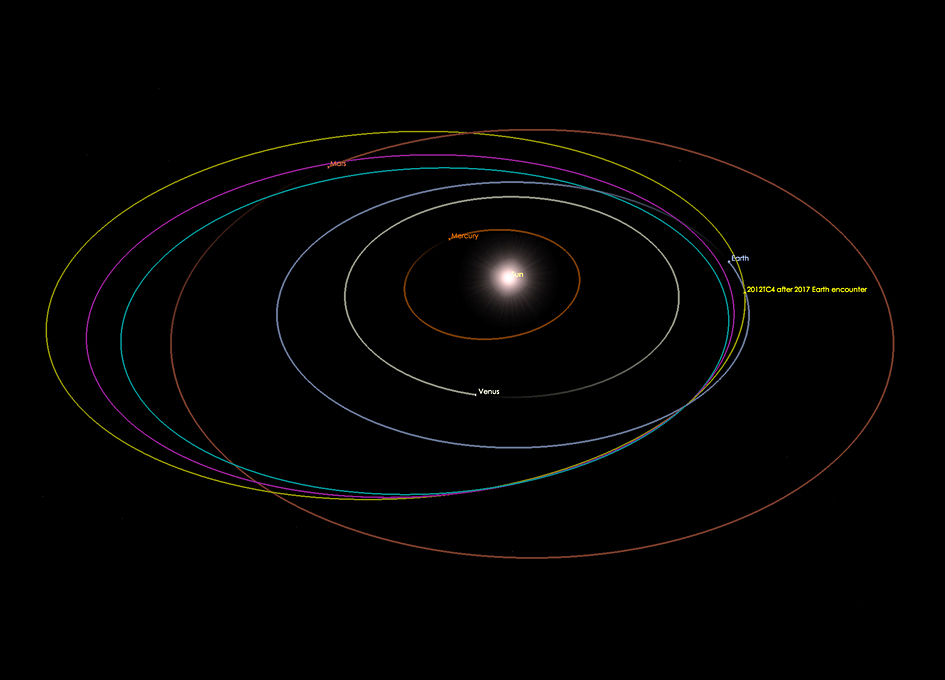 , которые так прославлялись со времен Пифагора и Платона до наших дней, и что он приспособил к природе этих тел число небес, их пропорции и закон их движения». (1)

Космическая Чаша. Эта гравюра, которую Кеплер сделал в возрасте 25 лет, изображает его взгляд на Вселенную, основанный на применении правильных многогранников. Он вставляет октаэдр между орбитами Меркурия и Венеры, икосаэдр между Венерой и Землей, додекаэдр между Землей и Марсом, тетраэдр между Марсом и Юпитером и куб между Юпитером и Сатурном. Обширные расчеты привели Кеплера к выводу, что «симметричные формы могут быть помещены друг в друга настолько точно, чтобы разделить соответствующие орбиты, что если бы неспециалист спросил, как поддерживаются небеса, чтобы предотвратить их падение, ответ был бы простым». Не удовлетворившись этим объяснением небесной гармонии, Кеплер решил превратить его в артефакт и изобрел «космическую чашу», которая фактически разливала бы напитки, представляющие симметрию многогранников и гармонию планет.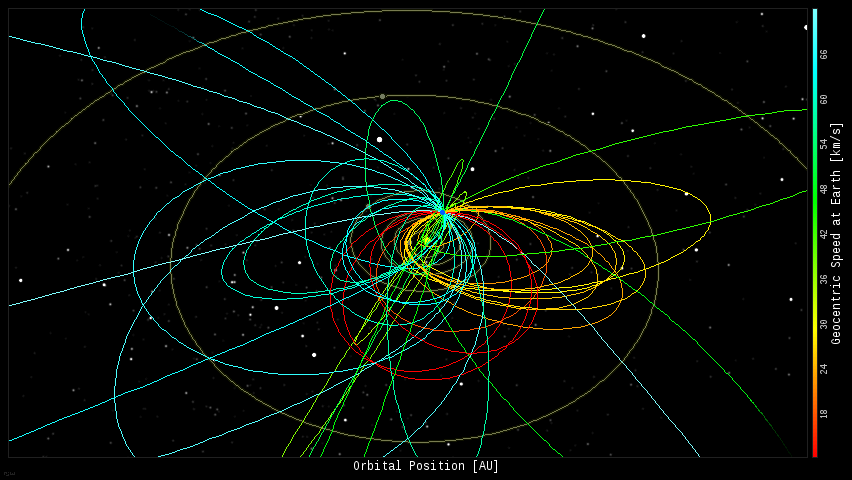 В феврале 159 г.6 он отправился к своему покровителю, герцогу Фридриху Вюртембергскому, чтобы попросить его разрешить строительство модели вселенной в форме чаши. Планеты должны быть сделаны из драгоценных камней — алмаз для Сатурна, сапфир для Юпитера, жемчуг для Луны и т. д. — и напитки, содержащиеся в каждой планетарной сфере, будут подаваться через невидимые трубы в семь кранов по краю круга. чаша. Меркурий давал бренди, Венера — медовуху, Марс — крепкий вермут и так далее. Проект был слишком затратным и так и не был реализован. Иоганн Кеплер, Prodromus Dissertationum Cosmographicarum, Continens Mysterium Cosmographicum de Admirabiii Proportione Orbium Coeslestium, Tubingen, G. Gruppenbach, 1596.

Кеплер наиболее ясно видел эту божественную гармонию в расположении планет и в их относительных расстояниях от Солнца. Все было выражением этой гармонии: поэзия и музыка, а также математика и геометрия, которые, по его словам, имели фундаментальное значение. В этом его можно рассматривать как часть великого движения за восстановление математики в качестве инструмента для изучения природы, движения, которое тогда находилось в зачаточном состоянии, но позже привлекло еще более радикальных последователей, таких как Декарт и Галилей.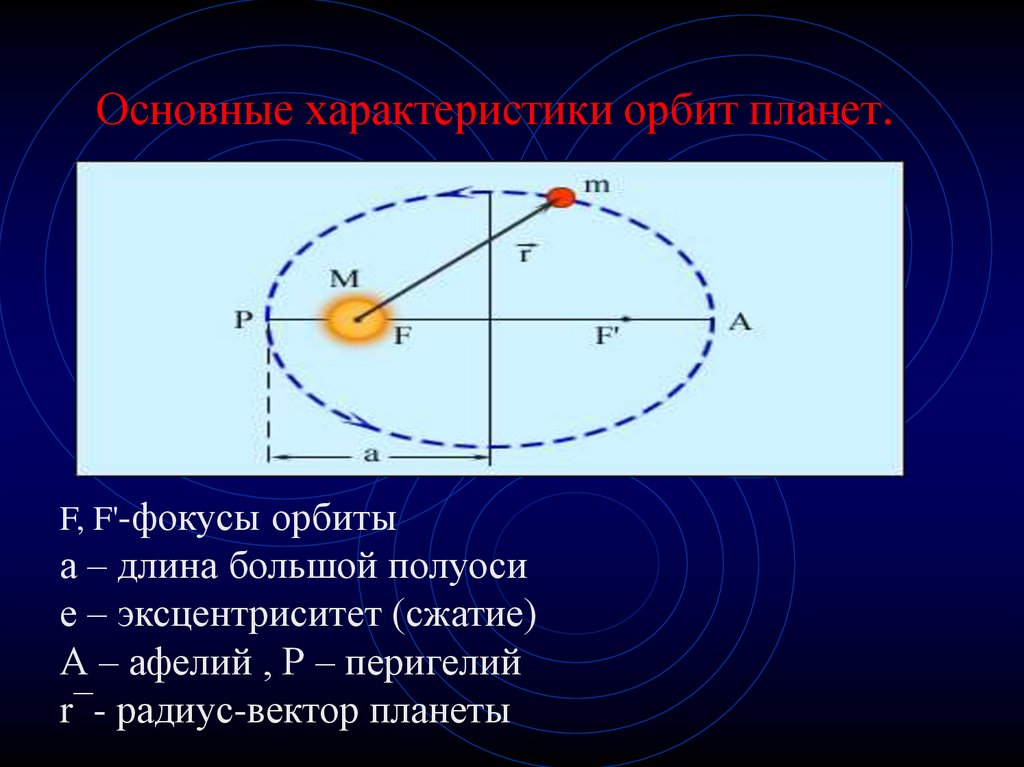 Именно последний должен был заявить в Пробирщик от 1623 года: «Философия написана в этой великой книге — я имею в виду вселенную — которая постоянно открыта нашему взору, но ее нельзя понять, если сначала не научиться понимать язык и интерпретировать символы, в которых он написано. Она написана на языке математики, а ее символы — треугольники, окружности и другие геометрические фигуры, без которых по-человечески невозможно понять ни одно ее слово. Без них человек блуждает в темном лабиринте». (2) Это возрождение математики вскоре сделает нумерологию и числовой мистицизм устаревшими, точно так же, как развитие астрономии и астрофизики должно было привести к упадку астрологии как системы интерпретации Вселенной.

В своей книге «Тайна космоса » Кеплер по-новому применяет геометрию для решения проблемы взаимосвязи орбит планет. Используя правильные многогранники, симметричные геометрические формы, знакомые древним грекам, он доказывает, что пять «совершенных» тел (куб, октаэдр, додекаэдр, тетраэдр и икосаэдр), которые Платон использовал для обозначения пяти элементов (земли, воды, воздуха, огонь и эфир), должны точно соответствовать промежуткам между шестью известными тогда планетами (Меркурий, Венера, Земля, Марс, Юпитер и Сатурн). Далее он математически демонстрирует, как эти платоновские формы могут располагаться одна внутри другой в точном соответствии со структурой солнечной системы. Для Кеплера это не было случайностью: убежденный, что открыл «тайну космоса», он интерпретировал соответствие между планетами и многогранниками как новый и рациональный способ понимания фундаментальной гармонии Вселенной.

В Тайна Космоса Кеплер оправдывал свое использование многогранников, одновременно ставя под сомнение превосходство кривой: «если бы при Сотворении Бог принял во внимание только искривленное, кроме Солнца в центр, который был образом Отца, Сфера Неподвижных Звезд или Моисеевых вод, на окружности, которая была образом Сына, и небесный воздух, который наполняет все части пространства и небесного свода, который был образ Святого Духа — тогда, кроме них, говорю, ничего бы не существовало в этом космическом строении». (3) Но так как существует так много других небесных тел, то «причины всех их мы по необходимости должны искать в прямолинейности» и особенно в правильных многогранниках, совершенство которых синонимично совершенству небесной сферы.

Эксцентриковая орбита Марса . В первом издании «Новой астрономии» Кеплер предложил новый способ описания Солнечной системы, основанный на наблюдениях Тихо Браге. Горячо веря в гелиоцентрический взгляд на космос, Кеплер уделял особое внимание орбите Марса, которую пытался объяснить с точки зрения различных доступных ему систем мира. Он рассчитал ее звездный период (время, необходимое планете, чтобы совершить один оборот вокруг Солнца и вернуться в точную начальную точку) по многочисленным таблицам измерений, составленным Тихо Браге: период составил 687 дней. Сначала он нарисовал круг, изображающий орбиту Земли (какой она фактически и является), и отметил на нем положение Земли — точку наблюдения — в две разные даты. Затем он провел прямую линию через плоскость земной эклиптики, чтобы обозначить наблюдение Марса. Детальный анализ записей Тихо Браге позволил ему найти пять пар наблюдений планеты с интервалом ровно в 687 дней. Некоторые точки, где встречаются пары линий, лежат внутри окружности. Поэтому он искал объяснение, которое удовлетворило бы его стремление к совершенству: эллипс имеет геометрический центр и два фокуса. Его вывод был однозначным: «Идеальный эллипс — единственная возможная форма».
Иоганн Кеплер, Astronomia Nova, 1609.
Париж, BNF, Архив редких книг, gV. 454, с. 149

Кеплер никогда не смог бы полностью отказаться от этого квазимистического взгляда на космос, хотя и отказался от идеи строгого соответствия между формой многогранников и орбитами планет в 1609 г., когда обнаружил, что эти орбиты эллиптические. а не круговой и поэтому не вписывался бы в такую модель. Тем не менее именно его навязчивые поиски лежащей в основе гармонии привели его к законам движения планет, которые более или менее противоречили его первоначальным идеям и произвели революцию в изучении астрономии. В его Astronomia Nova (Новая астрономия) 1609 г. Кеплер модифицировал коперниковскую модель солнечной системы, разрушив веру в совершенство круговых орбит; он даже зашел так далеко, что предположил, что именно влияние солнца заставляет планеты следовать по своим орбитам.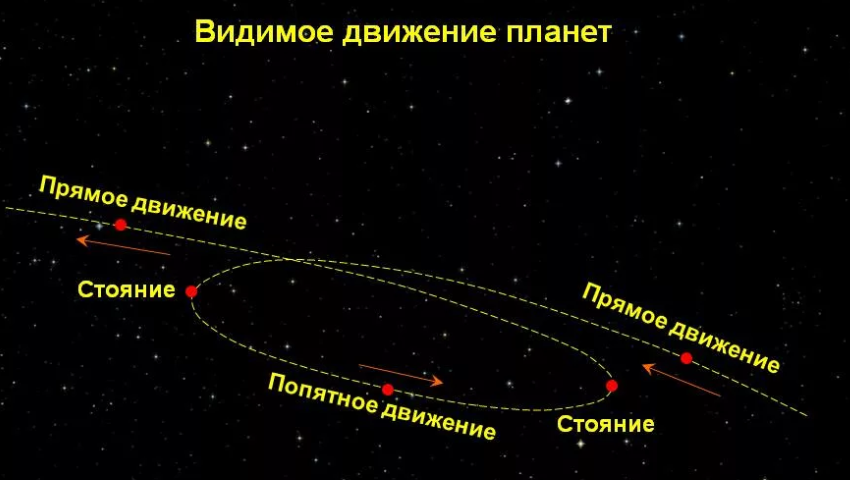

В году Гармония мира года Кеплер завершил свои законы движения планет. Третий из них, известный как закон орбитальных периодов, устанавливает «гармоническую» связь в математическом смысле слова между осью орбиты и орбитальным периодом и позволяет описать и рассчитать движение планет. гораздо легче, однако без объяснения физических причин этих движений. Эта задача выпала на долю Исаака Ньютона, для которого космическая гармония была проявлением универсальных законов притяжения.

Имя Кеплера в основном связано с законами движения планет. Первые два закона были опубликованы в его «Новой астрономии», третий — в «Гармонии мира». Их открытие взволновало его почти до экстаза: «Через несколько дней после того, как засияло чистое Солнце этого чудеснейшего исследования, ничто не удерживает меня; я с удовольствием поддаюсь вдохновенному безумию».
1.Закон эллиптических орбит
Орбита каждой планеты представляет собой эллипс, в одном из фокусов которого находится Солнце.
Эллипс с нулевым эксцентриситетом является окружностью; чем больше эксцентриситет, тем более вытянут эллипс. На орбите с большим эксцентриситетом планета будет проходить очень близко к Солнцу, а затем удаляться от него очень далеко.
2. Закон равных площадей
Планеты движутся таким образом, что их радиус-векторы за равное время охватывают равные площади.
Чем дальше планета от солнца, тем медленнее она движется. Скорость планеты напрямую связана с ее расстоянием от Солнца в том смысле, что площадь сегмента эллипса, очерченного в любой момент времени, постоянна.
3. Закон периодов обращения
Для каждой планеты куб половины большой оси ее орбиты равен квадрату ее периода обращения. Это соотношение применяется независимо от массы планеты.
Законы Кеплера применимы не только к планетам, вращающимся вокруг Солнца, но и к любому телу, вращающемуся вокруг любого другого тела под действием силы тяжести (например, луны, вращающиеся вокруг планет, искусственные спутники, вращающиеся вокруг Земли).

Кеплер и Тихо Браге

На карьеру Кеплера сильно повлияла его встреча с датским астрономом Тихо Браге. В 1576 году покровитель Браге Фридрих II, король Дании, разрешил ему построить великолепный дом и обсерваторию, храм астрономии под названием Ураниборг, на острове Хвен. Браге спроектировал здание в соответствии с теорией «божественной пропорции», разработанной философами итальянского Возрождения и примененной в архитектуре главным образом Палладио.

«Небесный замок»
В своем Большом атласе голландский картограф Джоан Блау опубликовал серию карт Европы, основанных на работах его отца Виллема Блау, который, будучи учеником Тихо Браге, останавливался в Ураниборге. обсерватория. В знак признания влияния Браге Большой Атлас содержит увеличенные изображения серии цветных пластин, которые датский астроном включил в свою книгу Astronomiae Instauratae Mechanica 1598 года. неба, организация которого отражала незаурядную личность его создателя. Помимо самой обсерватории здесь находились мастерские по изготовлению астрономических инструментов, библиотека, лаборатория, бумажная фабрика и печатный станок, огороды, аквариумы, фруктовые сады, ирригационная система, мельница и т. д. Ураниборг был там, где Тихо Браге посвятил себя наблюдению за небом. Там он усовершенствовал знания человека о Луне, изучил преломление света, составил пересмотренный звездный каталог и записал с беспрецедентной точностью положения планет.
Жоан Блау, Большой Атлас, Амстердам, 1662 год.

После смерти покровителя Тихо Браге впал в опалу и покинул Ураниборг. Он восстановил себя под покровительством императора Священной Римской империи Рудольфа II в Богемии, куда пригласил Кеплера работать с ним. Когда Браге умер в 1601 году, именно Кеплер унаследовал записи своих уникальных подробных наблюдений, интенсивно работая над информацией, касающейся орбиты Марса. К 1605 году Кеплер определил его форму: не круг или комбинация кругов, а эллипс с солнцем в одном из фокусов.

Квадрант Фрески Тихо Браге
Тихо Браге, которого Кеплер назвал «принцем астрономов», оставил после себя великолепные гравюры с изображением астрономических инструментов, которые он создал в мастерских в Ураниборге и использовал в Шернеборге, обсерватории, которую он построил недалеко от это четыре года спустя. Самым впечатляющим из них был гигантский квадрант настенной росписи (радиусом 1,8 м), мелко расположенные градуировки которого позволяли проводить самые точные измерения: с точностью до доли угловой минуты. Собранные им данные вскоре вытеснили данные Птолемея, а позже позволили Кеплеру открыть законы движения планет. На рисунке справа изображен сам Тихо Браге, наблюдающий через окно в крыше в левом верхнем углу изображения, в то время как его помощники записывают время наблюдения (внизу справа) и заносят показания в журнал (внизу слева).
Тихо Браге, Astronomiae Instauratae Mechanica,
Wandesburg, 1598.

Литература

(1) Иоганн Кеплер, Тайна космоса, 90 транс. А. М. Дункан, Abaris Books, Нью-Йорк, 1981, с. 63.

(2) Galileo Galilei, The Assayer, в переводе Стиллмана Дрейка и С. Д. О’Мэлли, Univ. Пенсильванской прессы, 1960, стр. 183-84.

(3).Иоганн Кеплер, Тайна космоса, op. цит. п. 95.

Геометрия орбит: эллипсы, параболы и гиперболы

Геометрия орбит: эллипсы, параболы и гиперболы

Орбиты могут иметь три различные формы

Эллипсы: Замкнутые орбиты с периодом: эксцентриситет = от 0 до 0,9999999. Это наиболее распространенные и интересные орбиты, потому что один объект «захвачен» и вращается вокруг другого. Планеты, малые планеты, кометы и двойные звезды имеют такую орбиту. Скорость на орбите всегда меньше той, которая необходима для ухода от центрального объекта.
Гипербола: Открытые орбиты, которые не замыкаются: эксцентриситет > 1. Эти орбиты полезны для описания двух объектов, которые проходят мимо друг друга, но не «захватываются» друг другом. Они используются для объяснения эффекта рогатки. Скорости вдоль гиперболической орбиты всегда больше космической скорости.
Параболы: Тоже открытая орбита, но особый граничный случай с эксцентриситетом = 1 (точно). Эти орбиты описывают случай, когда объект падает на другой объект с очень большого расстояния, когда изначально они имеют очень маленькую скорость. Такой тип орбиты имеют кометы с длинным периодом.

ЭЛЛИПТИЧЕСКИЕ ОРБИТЫ:

На этой диаграмме показаны параметры, которые нам нужны, чтобы говорить об орбитах.

Размер определяется по большой полуоси , а. (Это 1/2 длинного расстояния поперек эллипса.
Форма определяется эксцентриситетом, e = c /a. c = смещение фокуса от центра эллипса.
Две особые точки на орбите (в данном случае орбита вокруг Солнца)
Перигелий: место на ближайшей к Солнцу орбите
Афелий: место на наиболее удаленной от Солнца орбите

Эта диаграмма связывает различные величины, используя уникальные свойства эллипса.

Связь между a, b и c: получается из-за того, что длина линии, проведенной от одного фокуса к эллипсу, а затем обратно к другому фокусу, будет равна большой оси независимо от того, где на эллипсе вы нарисуете линию. Здесь показан частный случай, когда эта точка находится на конце малой полуоси, и теорема Пифагора дает формулу.
Район
Число: эллипса аналогично кругу, за исключением того, что вместо r*r используется a*b. b может быть записано через a и e.
Длина перигелия и афелия: является результатом геометрии вдоль большой оси. Перигелий = а — с, а афелий = а + с

ГИПЕРБОЛИЧЕСКИЕ ОРБИТЫ

Гипербола имеет две ветви, как показано на диаграмме, но орбита использует только одну из них. Существуют отношения между
размеры гиперболы такие же, как и у эллипса. По мере того, как объект движется по гиперболической орбите дальше от фокуса, он приближается к движению прямой линии, асимптоты.