Содержание
Исследовательская работа по математике «Эти непростые «простые числа»
Ленинский район
МБОУ СОШ № 160
Секция «Математика»
Горбунов Александр
4В класс
Эти непростые «простые числа»
Руководитель:
Плешивцева Алёна Николаевна,
учитель начальных классов
Новосибирск
2018
Содержание
I Введение
II Теоритическая часть
- Из истории вопроса
- Алгоритм «решето Эратосфена»
- Моё исследование
- Самое большое простое число
- Узоры простых чисел
III Заключение
Приложение
Всякий, кто изучает простые числа, бывает очарован и одновременно ощущает собственное бессилие. Определение простых чисел так просто и очевидно; найти очередное простое число так легко; разложение на простые сомножители — такое естественное действие. Почему же простые числа столь упорно сопротивляются нашим попыткам постичь порядок и закономерности их расположения? Может быть, в них вообще нет порядка, или же мы так слепы, что не видим его?
Ч. Узерелл «Этюды для программистов»
Узерелл «Этюды для программистов»
Введение
Однажды на уроке мы говорили о «признаках делимости» и я услышал про простые и составные числа. Мне захотелось подробнее изучить эту тему. Какие числа называются простыми? Так ли они просты на самом деле? Простые числа с давних времен привлекают внимание математиков. Простые числа следуют одно за другим по закону, который еще не найден. Хорошо было бы, если все простые числа можно было сосчитать! Но эта проблема до сих пор остается нерешенной.
Цель:
- исследование множества простых чисел.
Задачи:
- исследовать «решето Эратосфена»
- самостоятельно составить таблицу простых чисел до 1000
- выяснить, существует ли самое большое простое число и имеет ли ряд простых чисел конец?
- подробнее узнать о применении простых чисел
Гипотеза: если простые числа так просты, как это кажется, то математики давно их изучили, и тогда про них должно быть все известно.
Методы исследования:
- работа с учебной и научно-популярной литературой, ресурсами сети Интернет
- метод «решето Эратосфена».

- наблюдение, сравнение, анализ
Объект исследования: простые числа
Из истории вопроса
Изучением свойств простых чисел занимается теория чисел.
Просто́е число́ — это натуральное число, которое имеет ровно 2 натуральных делителя (только 1 и самого себя).
Составное число́ — натуральное число большее 1, не являющееся простым.1(единица) – особое число, оно не является ни простым, ни составным.Таким образом, все натуральные числа, за исключением единицы, разбиваются на простые и составные.
Евклид — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Биография, сведения о нем крайне скудны. Его научная деятельность протекала в Александрии в 3 веке до н. э. Евклид — первый математик александрийской школы. Его главная работа «Начала» содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел. В ней он подвёл итог предшествующему развитию греческой математики и создал фундамент дальнейшего развития математики. Евклид — автор работ по математике, астрономии, оптике, музыке и др.
Евклид — автор работ по математике, астрономии, оптике, музыке и др.
Евклид доказал, что простых чисел бесконечно много. Можно также сказать, что среди простых чисел нет самого большого числа.
Эратосфен Киренский — древнегреческий математик (276-194 до нашей эры), заведовал Александрийской библиотекой и заложил основы математической географии, вычислив с большой точностью величину земного шара. Он был первым составителем таблицы простых чисел.
Для нахождения простых чисел Эратосфен придумал следующий способ. Название «решето» метод получил потому, что, согласно легенде, Эратосфен писал числа на дощечке, покрытой воском, и прокалывал дырочки в тех местах, где были написаны составные числа. Поэтому дощечка являлась неким подобием решета, через которое «просеивались» все составные числа, а оставались только числа простые.
Решето́ Эратосфе́на — алгоритм нахождения всех простых чисел до некоторого целого числа n. Как и во многих случаях, здесь название алгоритма говорит о принципе его работы, то есть решето подразумевает фильтрацию, в данном случае фильтрацию всех чисел за исключением простых.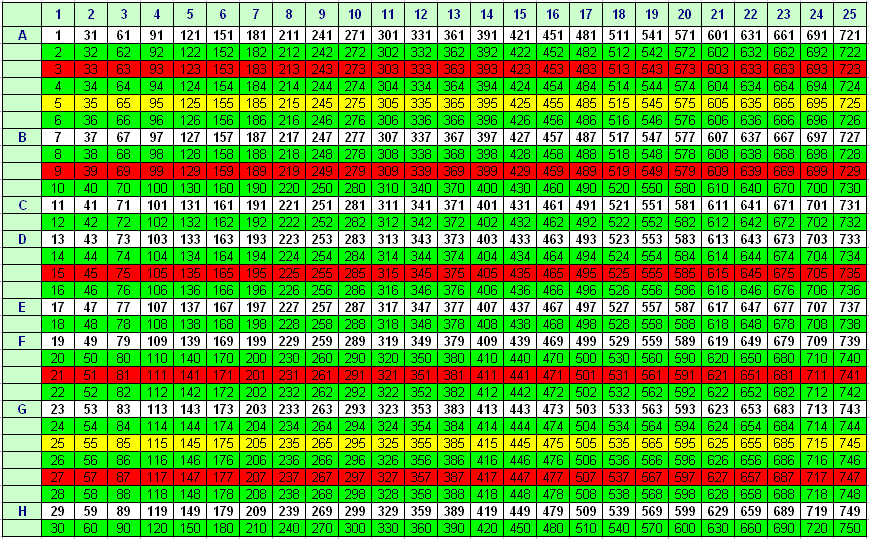 По мере прохождения списка нужные числа остаются, а ненужные исключаются.
По мере прохождения списка нужные числа остаются, а ненужные исключаются.
Алгоритм «Решето Эратосфена»
Эратосфен родился в 276 году до нашей эры, то есть этому методу уже около 2200 лет. Но он настолько прост и изящен,что можно объяснить его любому ребёнку. Итак, в чем суть метода и как его применять.
Предположим для примера,что нужно вычислить все простые числа меньшие 40.
Берем числовую последовательность натуральных чисел, начиная с 2
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
И удаляем все числа кратные 2.
Для этого умножаем числа натурального ряда, по порядку на 2 и результат
умножения вычеркиваем.
2×2=4, вычеркиваем 4,
2х3=6, вычеркиваем 6 и т.д.
Таким образом, исключаем все четные, больше 2.
Два — простое число, так как имеет, всего два натуральных делителя 1 и 2.
Получаем.
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12…
Затем вычеркиваем числа кратные трем (умножаем на 3 все числа, также по
порядку ):
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15…
Потом, вычеркиваем числа кратные пяти и т. д.
д.
В итоге получим последовательность не зачеркнутых чисел, которые и
есть простые.
Сам Эратосфен построил таблицу простых чисел до 1000.
Сейчас, найдены огромные простые числа, но процесс все еще идет.
Моё исследование
Я решил сам составить таблицу простых чисел по методу «решето Эратосфена».
В итоге я составил 10 таблиц и выяснил, что количество простых чисел до 1000 равно 168.
Простые числа от 1 до 100: 25 чисел
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67,71, 73, 79, 83, 89, 97
Простые числа от 101 до 200: 21 число
101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199
Простые числа от 201 до 300: 16 чисел
211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293
Простые числа от 301 до 400: 16 чисел
307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397
Простые числа от 401 до 500: 17 чисел
401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499
Простые числа от 501 до 600: 14 чисел
503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599
Простые числа от 601 до 700: 16 чисел
601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691
Простые числа от 700 до 800: 14 чисел
701,709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797
Простые числа от 800 до 900: 15 чисел
809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887
Простые числа от 900 до 1000: 14 чисел
907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997
Я пришёл к выводу:количество простых чисел постепенно уменьшается.
Самое большое простое число.
Итак, по мере продвижения от малого числа к большему в натуральном ряду простые числа встречаются всё реже. Поэтому одним из первых вопросов был такой: существует ли последнее простое число, то есть, имеет ли ряд простых чисел конец?
Согласно теореме Евклида, количество простых чисел бесконечно. Следовательно, количество простых чисел, превышающих наибольшее известное, тоже бесконечно. Представим, что количество простых чисел конечно. Перемножим их и прибавим единицу. Полученное число не делится ни на одно из конечного набора простых чисел, потому что остаток от деления на любое из них даёт единицу. Значит, число должно делиться на некоторое простое число, не включённое в этот набор.
Многие учёные-математики, а также любители, занимаются поиском рекордных по величине простых чисел, за нахождение которых организацией ElectronicFrontierFoundationбыло предложено несколько наград в зависимости от величины числа. Так, в 2009 году была вручена премия в 100 000 долларов США, назначенная сообществом ElectronicFrontierFoundation за нахождение простого числа, десятичная запись которого содержит не менее 10 миллионов цифр.
Издавна ведутся записи, отмечающие наибольшие известные на то время простые числа. Один из рекордов поставил в 1772 году математик Эйлер, найдя простое число 231 — 1 = 2 147 483 647[2].
26 декабря 2017 года наибольшим известным простым числом стало число 277 232 917 − 1, которое содержит 23 249 425 десятичных цифр[1]. Открытие сделал JonathanPace в рамках проекта GIMPS.
Узоры простых чисел
Иногда своего рода формула возникает как результат наблюдения визуальных закономерностей. Одну из таких закономерностей случайно открыл Станислав Улам, американский математик, поляк по происхождению.
Сидя как-то на скучной лекции, он, ни о чем не думая, начал рисовать решетку из горизонтальных и вертикальных линий. В одной из полученных таким образом клеток он поставил 1 и стал нумеровать остальные клетки по спирали, расходящейся от первой клетки:
5 4 3
6 1 2
7 8 9
Когда спираль совершила уже несколько оборотов, Улам начал обводить кружками простые числа, не преследуя никакой определенной цели. Однако вскоре заметил, как на его глазах возникает довольно любопытная закономерность. Откуда ни возьмись, стали появляться прямые линии. Улам, конечно, сразу понял, что такие линии говорят о закономерности, которую можно облечь в формулу для простых чисел.
Однако вскоре заметил, как на его глазах возникает довольно любопытная закономерность. Откуда ни возьмись, стали появляться прямые линии. Улам, конечно, сразу понял, что такие линии говорят о закономерности, которую можно облечь в формулу для простых чисел.
Компьютерная распечатка, дублирует то, что Улам сделал от руки. На компьютерном графике составные числа представлены маленькими белыми
квадратиками, а простые — черными. Выделяющиеся тёмные линии – это залежи простых чисел.
Улама заинтересовало, как же будет выглядеть его спираль, если её продолжить до нескольких тысяч простых чисел. Разработав программу, Улам получил рисунок для чисел от 1 до 65 000 (иногда его называют «скатертью Улама»), из которого видно, что даже у края картины простые числа продолжают послушно укладываться на прямые.
Фрагмент спирали Улама — простейшая иллюстрация закономерности в распределении простых чисел.
Чтобы отмеченная закономерность проявилась, не обязательно начинать спираль с единицы. Например, простые числа выстраиваются по диагоналям у спирали, начинающейся с числа 41 и заканчивающейся числом 41.
Например, простые числа выстраиваются по диагоналям у спирали, начинающейся с числа 41 и заканчивающейся числом 41.
Заключение
В работе «Эти непростые «простые числа» я изучил историю, закономерности и свойства простых чисел. Убедился, что указать самое большое простое число невозможно, т.к. они бесконечны.
В процессе работы над исследованием, я сделал следующие выводы:
- Можно сказать, что простые числа представляют собой как бы кирпичики, из которых строятся все остальные числа.
- Для простых чисел не существует формулы, по которой их можно вычислить.
- Не существует самого большого простого числа, последовательность простых чисел бесконечна.
- Многие ученые на протяжении многих веков вносили свой вклад в изучение темы «Простые числа»
- В настоящее время исследование темы продолжается, ученые делают и будут делать новые открытия!
Казалось бы, простые числа – чего уж может быть проще. А, оказывается, можно сделать еще столько открытий, и столько проблем ждут своего доказательства.
Математикам всего мира до сих пор хочется найти формулу, позволяющую хотя бы указать точное число простых чисел на любом интервале числовой оси, но, сколько ни бились математики, им так и не удалось найти желанную формулу. Существуют миллионы простых чисел, имеющих ровно 100 цифр, но пока ни одно такое число не обнаружено.
Итак, в наше время изучение простых чисел продолжается… Меня очень заинтересовали вопросы практического применения простых чисел в науке и технике, в криптографии и шифровании. Я думаю, что обязательно в 5 или 6 классе продолжу изучение этой темы.
«Простые числа не так просты,
как это кажется с первого взгляда!»
Фома Евграфович Топорищев,
писатель-философ
Приложение 1
Удивительные сказки
«Сказка о простых числах»
Жил да был на свете один мальчик. Звали его Кирилл. Однажды он в 4 классе со своим учителем поспорил, что простые числа человеку не нужны.
-Ну, есть они и пусть будут, но нам от этого ни какой пользы нет.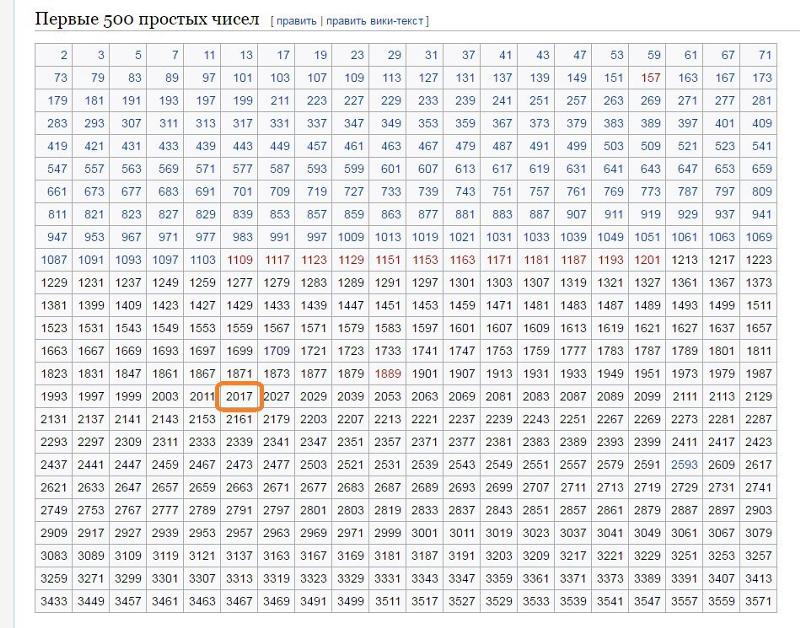
Учитель ему и говорит:
-Раз ты так считаешь то приведи пример.
-Сейчас… ну… эм…
-Ну-ну, молодой человек.
— Я дома найду почему нам от этого нет никакой пользы.
Думал Кирилл, думал и тут, у него дома начались новости. И диктор сказала:
-Срочно — на человека упала надпись с магазина…
И тут Кирилла осенило, что вот они могут убить человека.
Пришёл он в класс и говорит:
-Алена Николаевна, по новостям вчера сказали, что на человека упала надпись с магазина.
-Да-да, было такое!Эх, бедный человек!
-И вот упала цифра 3, это ведь простое число!
— Это работники плохо прикрепили, вот она и упала.
Кирилл продолжал думать, потом пошёл спать. И ему приснился странный сон, как он попал в мир простых чисел. К Кириллу подошла цифра 7 и говорит:
-Добро пожаловать, человек, в наш мир – Мир Простых чисел.
— От вас всё равно нет никакой пользы, — перебил Кирилл.
Подходит к нему учитель и Кирилл подумал, что он заснул на уроке:.
-Так Курочкин к доске! — сказала Алена Николаевна.
Кирилл вышел к доске. Учительница указала на 1.
-Скажи, простое это число или нет?
-Да,- ответил Кирилл.
-Нет. Неправильно, оно не простое и не составное. «2» за урок!
Потом он проснулся, пришёл в школу и сказал:
— Я понял, для чего нужны простые числа.
-Для чего?
-Для того, что бы не получать двойки за урок…
Практическое применение простых чисел.
Поиск простых чисел — по крайней мере, больших простых чисел — довольно сложная задача, потому что еще никому не удалось найти формулу или алгоритм, позволяющий генерировать любые простые числа. Но может возникнуть логичный вопрос: «Для чего нужно генерировать простые числа?»
На этот вопрос можно дать два ответа. Первый из них имеет теоретическое значение. Попытки генерации простых чисел ведут к появлению новых интересных инструментов для расчетов, особенно для компьютерных вычислений. Кроме того, наличие большого списка простых чисел позволяет проверять теоремы, которые еще не доказаны. Если кто-то выдвигает гипотезу относительно простых чисел, но оказывается, что одно из миллионов чисел нарушает ее, то вопрос снимается. Это стимулирует поиск простых чисел различных видов: простых чисел Мерсенна, чисел-близнецов и так далее. Иногда такой поиск превращается в соревнование, в котором устанавливаются мировые рекорды и за победы присуждаются большие призы.
Если кто-то выдвигает гипотезу относительно простых чисел, но оказывается, что одно из миллионов чисел нарушает ее, то вопрос снимается. Это стимулирует поиск простых чисел различных видов: простых чисел Мерсенна, чисел-близнецов и так далее. Иногда такой поиск превращается в соревнование, в котором устанавливаются мировые рекорды и за победы присуждаются большие призы.
Но есть и другая, более практическая причина, связанная с так называемым шифрованием. Электронная почта, банковские операции, кредитные карты и мобильная телефонная связь — все это защищено секретными кодами, непосредственно основанными на свойствах простых чисел.
Криптография и простые числа
В 1975 г. УитфилдуДиффи и Мартину Хеллману, в то время работавшим в Стэнфордском университете, пришла в голову идея асимметричного шифрования, или «шифрования с открытым ключом». Эта система основана на специальных математических функциях, называемых «односторонними функциями с потайным входом», которые позволяют зашифровывать текст, но делают расшифровку практически невозможной без знания используемого кода.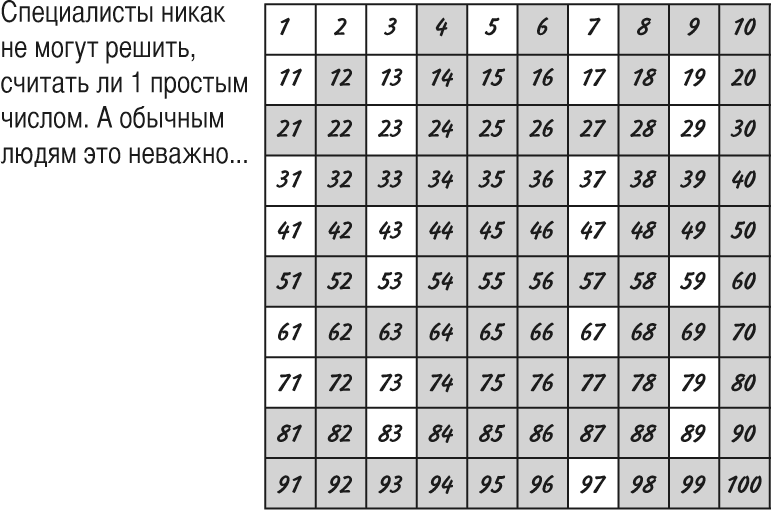 Идея состоит в том, что каждый пользователь имеет пару ключей: открытый и закрытый. Если мы хотим отправить кому-то сообщение, мы зашифровываем это сообщение с помощью открытого ключа — то есть ключа, известного всем. Но только человек, имеющий соответствующий закрытый ключ, может расшифровать это сообщение. Одним из преимуществ такого метода является то, что закрытый ключ никогда не передается и поэтому его не нужно постоянно менять в целях безопасности. Идея метода не совсем проста, но мы можем пояснить ее с помощью аналогии. Представьте себе большой магазин, где продаются сотни тысяч банок с краской разного цвета. Возьмем две любые банки и смешаем краску в разных количествах. Пока все просто. Теперь, если мы покажем кому-нибудь получившийся цвет и попросим «расшифровать», какое количество каких красок использовалось изначально, на такой вопрос будет очень трудно ответить.
Идея состоит в том, что каждый пользователь имеет пару ключей: открытый и закрытый. Если мы хотим отправить кому-то сообщение, мы зашифровываем это сообщение с помощью открытого ключа — то есть ключа, известного всем. Но только человек, имеющий соответствующий закрытый ключ, может расшифровать это сообщение. Одним из преимуществ такого метода является то, что закрытый ключ никогда не передается и поэтому его не нужно постоянно менять в целях безопасности. Идея метода не совсем проста, но мы можем пояснить ее с помощью аналогии. Представьте себе большой магазин, где продаются сотни тысяч банок с краской разного цвета. Возьмем две любые банки и смешаем краску в разных количествах. Пока все просто. Теперь, если мы покажем кому-нибудь получившийся цвет и попросим «расшифровать», какое количество каких красок использовалось изначально, на такой вопрос будет очень трудно ответить.
Именно так работают односторонние функции с потайным входом, которые легко применить в одном направлении, но практически невозможно — в обратном.
Схема, иллюстрирующая алгоритм Диффи — Хеллмана. Имеются два абонента, Алиса и Боб, желающие общаться втайне. Они открыто договариваются о двух числах (простое число р и другое число g, имеющие определенные свойства). И Алиса, и Боб выполняют некоторые операции с этими числами и с еще одним целым числом, которое они держат в секрете, а затем открыто посылают друг другу результаты. Теперь и Алиса, и Боб выполняют с полученным результатом еще одну операцию и получают один и тот же ответ, который будет для них секретным кодом. Потенциальный шпион, перехвативший результаты, посланные Алисой и Бобом, не может сгенерировать секретный код, имея лишь эту информацию.
Предположим теперь, что вместо банок с краской в магазине находятся простые числа. Возьмем любые два, например, 7 и 13, и перемножим их (аналогично смешиванию краски). В результате мы получим 7 х 13 = 91.
Тогда возникает вопрос: можно ли узнать, какие простые числа были перемножены, чтобы в результате получилось 91? Для ответа на него надо взять список простых чисел и проделать несколько проверок. Казалось бы, простое решение, как и в случае определения цвета красок, если в магазине было всего около десятка основных цветов.Но с простыми числами все намного сложнее.
Казалось бы, простое решение, как и в случае определения цвета красок, если в магазине было всего около десятка основных цветов.Но с простыми числами все намного сложнее.
Например, ни у кого не хватит терпения проверить, что число 1409 305 684 859 является результатом умножения простых чисел 705 967 и 1996 277, особенно если учесть, что эти два простых числа взяты из списка простых чисел между 1 и 2000000, а там таких «всего лишь» 148933. Однако мы живем в эпоху высоких технологий, и, конечно, эту задачу можно довольно быстро решить с помощью хорошей программы и мощного компьютера. Хотя все зависит от того, насколько большой этот магазин красок. Не следует также забывать, что количество простых чисел не просто очень большое, а бесконечное.
Пара простых чисел в приведенном выше примере содержит лишь несколько цифр. Если мы возьмем простые числа, каждое из которых содержит сотни цифр, то время, которое потребуется компьютерной программе на простой перебор всех возможных вариантов — метод «грубой силы», как говорят криптографы, — будет больше, чем предполагаемое время существования Земли.
Простые числа повсеместно используются в нашей повседневной жизни, например, в кредитных картах и персональных компьютерах, поэтому постоянно существует потребность в новых простых числах (чем больше, тем лучше) для генерации секретных кодов. Таким образом, имеется спрос на простые числа, но контроль качества так же важен, как и их производство. Чтобы большому числу присвоить статус простого, его должна проверить специальная организация.
Шифр RSA был опубликован в 1978 г., но повсеместно начал использоваться в качестве метода шифрования лишь в конце 1990 гг. в связи с ростом сети интернет. Поиск больших простых чисел прежде требовал специального программного обеспечения, которое, как правило, можно было купить лишь в специализированных фирмах или в университетах, занимающихся такими исследованиями. Однако экспоненциальный рост вычислительных мощностей и появление более совершенных алгоритмов изменили рынок простых чисел и сделали их гораздо более доступными.
Простые числа в науке и технике.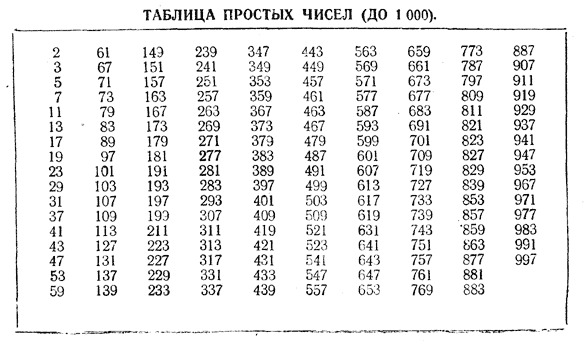
Шифрование – это не единственная область применения простых чисел на практике. Простые числа используются в компьютерном моделировании различных процессов. Так же без них не обойтись и в машиностроении – на пример количество лопаток турбин реактивных самолётов должно составлять простое число. Если этим правилом пренебречь, то возникает резонанс, разрушающий лопатки турбины.
Частые ошибки в дизайне страницы сайта
Частые ошибки дизайна веб-страницы
Простые советы по верстке и оформлению, которые помогут создать красивую страницу сайта
Tilda Education
Никита Обухов
Основатель Tilda Publishing
Тысячи людей во всем мире создают сайты на Тильде. Эта статья основана на большом исследовании, которое мы сделали, анализируя дизайн сайтов, созданных пользователями нашей платформы. Мы выделили частые ошибки и сформулировали простые правила, которые применимы к дизайну любых страниц, независимо от инструмента, с помощью которого они созданы.
Ошибки в дизайне лендинга
1. Нет разделения на смысловые блоки
Информацию проще воспринимать, если она разделена на блоки по смыслу. Чтобы визуально отделить блоки друг от друга, используйте большие отступы (от 120 до 180 px) и отделяйте блоки с помощью разного цвета фона.
Между смысловыми блоками маленькие отступы и нет разделения с помощью цвета — информацию тяжело воспринимать, непонятно, какой текст к чему относится
Отступы достаточно большие и блоки разделены цветом — видно, что это блоки разной информации
2. Разные отступы между элементами
Между смысловыми блоками должны быть одинаковые расстояния. Иначе страница будет выглядеть неаккуратно, и может создаться ощущение, что блоки неравнозначны по смыслу.
| org/ImageObject»> |
Разные отступы —неаккуратно, и есть ощущение, что информация о компании относится к обложке, хотя все блоки равнозначны по смыслу
Одинаковые отступы помогают воспринимать смысловые блоки как равнозначную информацию
3. Маленькие отступы, не позволяющие разделить смысловые блоки сайта
Чтобы разные смысловые части не выглядели как единое целое, важно их разделять и использовать достаточно большое расстояние между ними (не менее 120 px).
Маленькие отступы — блоки сайта прилипают друг к другу. Это перегружает страницу и создает путаницу, как будто это одно целое, а не разные по смыслу части
Отступы достаточно большие, сразу понятно, что блоки разные по смыслу
4. Текст плохо читается на фотографии
Текст плохо читается на фотографии
Текст не должен сливаться с фоновым изображением. Чтобы он хорошо читался, можно наложить на фотографию фильтр контрастного тексту цвета. Чаще всего используют черный, но можно использовать яркие цвета и комбинировать их.
Еще один вариант — использовать изначально контрастную тексту фотографию или располагать текст так, чтобы он был на затемненном участке изображения.
Текст трудно прочитать, фотография слишком светлая
На фотографию наложен фильтр, и текст теперь легко читается
5. Много стилей
Большое количество разных стилей типографики и оформления на одной странице выглядит непрофессионально и затрудняет восприятие информации. Чтобы этого не происходило, ограничьтесь одним шрифтом, одним цветом и двумя видами насыщенности шрифта (например, normal и bold).
| org/ImageObject»> |
Из-за большого количества стилей типографики непонятно, какая информация важная, а какая второстепенная
Использован один шрифт, цвет и два вида насыщенности. Типографика выглядит аккуратно и понятно
6. Узкий цветной блок
Выделение цветом отдельных узких элементов страницы дробит смысловые блоки и выглядит неаккуратно. Например, заголовки уже выделяются среди текста размером, насыщенностью шрифта, а также отступами. Если нужно выделить какую-то информацию на странице — применяйте цветной фон для всего смыслового блока: и для заголовка, и для текста, относящегося к нему.
Заголовки, выделенные цветным фоном дробят смысловые блоки и выглядят отдельными самодостаточными элементами
Заголовок и текст, относящийся к нему, имеют общий фон. За счет этого видно, что это один смысловой блок
7. Много текста в узких колонках
Много текста в узких колонках
Когда в узких колонках много текста, его трудно читать — глазам все время приходится перескакивать с одной строки на другую. К тому же это выглядит некрасиво. Лучше уменьшить количество колонок и сократить текст, иначе его просто никто не будет читать.
Длинный текст в колонках (еще и с выключкой по центру) неудобно читать
Текста в колонках немного, легко прочитать
8. Много текста с выравниванием по центру
Центральная выключка (равнение по центру) текста уместна при небольшом количестве слов, иначе его будет сложно воспринимать. При этом текст стоит сделать покрупнее, от 24 пикселей.
Если вам необходимо большое количество текста, используйте блок с раскрывающимся текстом (в Тильде TX12, TX16N или кнопка BF703).
Текста с центральной выключкой очень много, читается с трудом
Короткий текст под заголовком (все с центральной выключкой) создают хорошую композицию
9. Текст накладывается на важную часть изображения
Не стоит располагать текст на значимых частях фотографии и мелких деталях. Так и изображение не будет видно, и текст будет читаться тяжело. Попробуйте поварьировать выключку текста (равнение по центру или левому краю) и его вертикальное расположение.
Заголовок мешает рассмотреть лицо человека, и текст на фоне мелких деталей сложно читать
Изображение и текст вместе создают хорошую композицию, видно детали фотографии, текст легко прочитать
10. Несоблюдение визуальной иерархии
Несоблюдение визуальной иерархии
Чтобы на странице была видна смысловая иерархия информации, заголовок на обложке должен быть крупнее остальных заголовков на странице либо такого же размера (например, если в заголовке на обложке много слов).
Заголовок на обложке неоправданно меньше, чем последующий заголовок, это создает путаницу. Кажется, что второй заголовок важнее
Заголовок на обложке крупнее, чем в следующем блоке, все выглядит последовательно и гармонично
То же самое относится к визуальной иерархии внутри смыслового блока. Заголовок должен быть самым крупным, а подзаголовок меньше и с меньшей насыщенностью шрифта. Названия преимуществ — заметно меньше, чем заголовок и такой же насыщенности. Описание преимуществ набрано самым мелким текстом.
Таким образом, даже при беглом просмотре страницы посетитель увидит, какая информация самая важная и какая вторичная.
Заголовок меньше, чем названия преимуществ и кажется второстепенным, хотя по смыслу он важнее
Заголовок самый крупный, названия преимуществ меньше, но тоже выделяются среди текста
11. Один смысловой блок визуально распадается на два
Полноэкранное изображение или галерея, расположенные после текста, смотрятся как самостоятельный блок. Если добавить галерее поля, то за счет общего фона текст и изображение будут выглядеть единым смысловым блоком.
Галерея во всю ширину экрана кажется не связанной с заголовком выше и выглядит как самостоятельный блок
Галерея расположена на общем фоне с заголовком — все вместе смотрится единым блоком
12. Слишком крупный длинный заголовок
Слишком крупный длинный заголовок
Очень крупный шрифт хорошо подойдет для короткой фразы. Если заголовок длинный, лучше использовать меньший размер шрифта, так его будет легче читать и всем элементами на обложке не будет тесно.
Слишком крупный заголовок — заслоняет почти всю обложку, элементам тесно, текст тяжело прочитать
Хорошая композиция, все элементы обложки сбалансированны, текст легко читается
13. Неуместное использование обводки в кнопках
Обводка нужна, чтобы сделать прозрачную кнопку. Добавлять обводку к цветной кнопке не нужно — это лишний и бессмысленный элемент интерфейса, который перегружает страницу и усложняет восприятие контента.
14. Слишком много цветов
Большое количество цветовых акцентов создает путаницу на странице: непонятно, что важнее. Достаточно использовать 1−2 цвета, чтобы выделить важные элементы.
Достаточно использовать 1−2 цвета, чтобы выделить важные элементы.
Много ярких цветов, непонятно, на что в первую очередь обратить внимание
Один цветовой акцент создает разнообразие, но не отвлекает от содержания страницы
15. Перегруженное меню
Человек заходит на сайт, чтобы найти решение своей проблемы. Помогите ему в этом. Используйте меню, чтобы посетителю сайта было проще сориентироваться и быстрее найти то, что ему нужно. Не перегружайте меню избыточной информацией. Оптимальное количество пунктов меню — 5-7.
В меню слишком много информации, поэтому в нем сложно сориентироваться
Информации в меню немного, легко сориентироваться
Рекомендации по дизайну меню
Ошибки в дизайне статьи
1. Длинный сплошной текст
Длинный и не разделенный на абзацы текст снижает удобство чтения.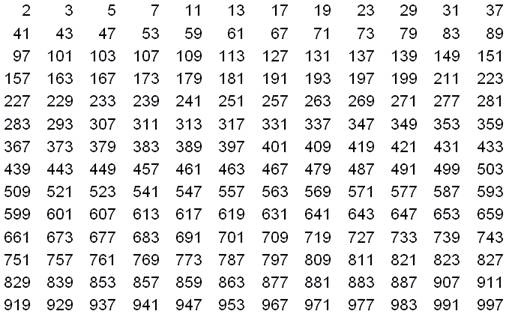 Чтобы в тексте было проще ориентироваться, стоит разделить его на абзацы и разбавить, например, ключевой фразой или изображением.
Чтобы в тексте было проще ориентироваться, стоит разделить его на абзацы и разбавить, например, ключевой фразой или изображением.
Сплошную пелену текста сложно воспринимать глазу
В тексте расставлены акценты, благодаря которым его легче читать
2. Заголовок стоит на равном расстоянии от предыдущего и следующего абзаца
Заголовок не должен «летать» между текстами предыдущей и следующей главы, потому что по смыслу он относится к последующему абзацу. Расстояние над заголовком должно быть раза в 2−3 больше, чем расстояние под ним. А расстояние под заголовком должно быть примерно равным расстоянию между абзацами или немного больше. Так заголовок будет визуально относиться к последующему тексту.
| org/ImageObject»> |
Заголовок находится на равном расстоянии от абзацев снизу и сверху и непонятно, к чему относится
За счет небольшого отступа под заголовком видно, что он относится к последующему тексту
3. Смысловая иерархия не соблюдается
Контраст в типографике помогает визуально разделить уровни текста и четко распределить иерархию. Самыми крупными должны быть заголовки, подзаголовки могут быть заметно меньше, но отчетливо выделяться в тексте.
Заголовок и подзаголовок практически одинакового размера, выглядят как равнозначные уровни текста
Видно, что заголовок важнее по смыслу, чем подзаголовок
4. Разные отступы сверху и снизу одного смыслового блока
Равнозначные по смыслу блоки должны выглядеть соответственно и располагаться на равном расстоянии друг от друга.
Слишком маленький отступ между обложкой и фотографией автора, кажется, что к обложке автор имеет большее отношение, чем к тексту
Отступы одинаковые, блоки выглядят как равнозначные элементы
5. Подпись расположена слишком близко к иллюстрации
Хотя иллюстрация и подпись образуют единую структуру, это два отдельных элемента, и текст не должен вторгаться на территорию изображения.
Подпись приклеилась к изображению и мешает восприятию (и картинки, и текста)
Между картинкой и подписью есть воздух, при этом понятно, что подпись относится к фотографии
6. Между подзаголовком и текстом мало места
Подзаголовок и последующий текст связаны, но если абзацный отступ внутри текста оказывается больше, чем расстояние между всем текстом и подзаголовком, конструкция становится дисгармоничной.
Отступ между заголовком и текстом меньше, чем отступ между абзацами
Отступ после заголовка чуть больше, чем отступ между абзацами
7. Основной текст расположен близко к акценту
Акцент внутри основного текста (например, ключевая фраза или цитата) — самостоятельный объект. И чтобы он действительно выделялся и бросался в глаза, его нужно отделять от основного текста отступами от 75 до 120 px.
Отступ между основным текстом и акцентом слишком маленький
Акцент выделяется в тексте благодаря большим отступам
8. Слабый контраст элементов
Если вы решили сделать акцент на какой-то фразе — будьте смелее, сделайте ключевую фразу крупнее основного текста на 10-15 px, пусть важная мысль действительно выделяется из окружающего текста.
Ключевая фраза как будто притворяется частью текста и не хочет выделяться. Выглядит неаккуратно
Ключевая фраза выделена за счет крупного шрифта и отступов
9. Цветной фон для узкого блока
Чтобы выделить какой-то небольшой блок (например, информацию об авторе), достаточно сделать хороший отступ, это создаст пространство вокруг. Выделять эту информацию на цветном фоне не стоит, это будет выглядеть неуместно.
Подзаголовок также не следует выделять цветом, вполне достаточно того, что он крупнее основного текста и отделен отступами.
10. Между двумя полноэкранными изображениями есть пустое пространство
Расположение нескольких полноэкранных изображений подряд не следует оставлять между ними отступ — граница между фотографиями и так будет видна, незачем добавлять лишний элемент, не несущий никакой смысловой нагрузки.
Пустое пространство между полноэкранными изображениями выглядит бессмысленно и некрасиво
Фотографии выглядят гармонично
11. Много выделений в тексте
Акценты (в данном случае жирное начертание) хорошо работают, когда их мало. Большое количество выделений в тексте затрудняют чтение.
Много выделено жирным, текст рябит в глазах
Небольшое выделение акцентирует внимание на элементе, но не мешает читать весь текст
12. Много стилей типографики
В тексте оформление не должно преобладать над удобочитаемостью. Чем меньше стилей типографики, тем лучше видны акценты в тексте. Достаточно выделять заголовки и подзаголовки, а также делать контрастными ключевые фразы.
| org/ImageObject»> |
В тексте слишком много акцентов и выделений, рябит в глазах и неудобно читать
Стилей типографики немного, четко видны акценты и иерархия в тексте
13. Выравнивание по центру в длинном тексте
Выключку (выравнивание) по центру обычно используют в заголовках и выносах — акцентах в тексте, чтобы выделить элемент из массы. Когда весь текст выровнен по центру, это значительно снижает удобство чтения.
Текст с центральной выключкой выглядит неопрятно, его неудобно читать
Равнение по левому краю лучше всего воспринимается глазом
14. Заголовок прилип к фотографии
Заголовок — самостоятельный элемент. Он не должен быть расположен слишком близко к следующей за ним иллюстрации. Чтобы заголовок хорошо сочетался с изображением, сделайте отступ не менее 60 px и добавьте подзаголовок, он раскроет содержание и правильно расставит акценты.
Заголовок расположен слишком близко к фотографии, нет воздуха
Заголовок отделен от изображения подзаголовком и относится ко всему разделу, а не только к картинке
15. Неуместное использование курсива
Курсив используется для того, чтобы выделить слово или короткую фразу в тексте. Он не так сильно бросается в глаза, как жирное начертание, но позволяет сделать акцент в определенном месте.
Набирать весь текст или заголовки курсивом не следует. В текстах, набранных шрифтами без засечек, курсив лучше не использовать совсем.
Фраза уже выделяется в тексте за счет размера и отступа, курсив уже излишен
Курсив на своем месте — небольшой акцент в основном тексте
16. Смещение блоков относительно центра и друг друга
Этот досадный промах вы легко обнаружите сами, если после всех манипуляций с текстом (изменение размера шрифта, выравнивания, отступов) просто сделаете паузу и посмотрите на то, что получается.
Заголовок и описание смещены влево, а текст вправо
Все элементы текста складываются в гармоничную композицию
Авторы: Ира Смирнова, Маша Белая, Юлия Засс
Дизайн и верстка: Юлия Засс
Если материал вам понравился, расскажите о нем друзьям. Спасибо!
Читайте также:
Как правильно использовать карточки в дизайне сайта
Как делать красивые статьи на Тильде
24 лекции TED для дизайнеров — подборка
Как не облажаться с дизайном
Визуальная иерархия сайта: оформление и организация контента
Персональный сайт личного бренда: как использовать Тильду для развития личного бренда
Флэт (flat) дизайн: лучшие практики плоского дизайна
Навигация по сайту — примеры как сделать навигацию удобной
Белое пространство: способы вёрстки контента на сайте
Обучение веб дизайну: 70+ лучших ресурсов о веб-дизайне
37 лонгридов с отличным дизайном
27 документальных фильмов для дизайнеров
| Показать больше |
Синестеты.
 Они чувствуют иначе. Они среди нас
Они чувствуют иначе. Они среди нас
Регистрация пройдена успешно!
Пожалуйста, перейдите по ссылке из письма, отправленного на
Синестеты
Они чувствуют иначе. Они среди нас
Их менее четырех процентов от всех рожденных на Земле. Часто они не подозревают о том, что иные. Если однажды они расскажут, как выглядит их мир, то рискуют прослыть сумасшедшими или фантазерами. Они — синестеты. Синестезия существует, доказали ученые.
Синестеты — разные. Одни видят в цвете слова и цифры, другие способны различать цветовую ауру настроения человека. Третьи знают вкус каждого цвета. А некоторые видят время как кольцо или бесконечную кривую линию. Мир синестетов устроен сложнее, чем мир обычного человека, но особенности их восприятия не являются психическим расстройством. По одной из исследовательских гипотез, синестетами являются практически все младенцы, но с возрастом мы утрачиваем это феноменальное свойство.
Антенна в голове Нила
В 1984 году в семье ирландки и каталонца родился мальчик, которого назвали Нилом. Он родился с цветовой слепотой и до 20 лет мог различать только оттенки серого. В принципе, глазами он до сих пор видит только серый. Но в 2004 году в его череп смогли имплантировать устройство под названием Eyeborg — специальный гибкий датчик с простой камерой, которая считывает цвета и посылает Нилу звуковой сигнал. И он стал слышать цвет.
Он родился с цветовой слепотой и до 20 лет мог различать только оттенки серого. В принципе, глазами он до сих пор видит только серый. Но в 2004 году в его череп смогли имплантировать устройство под названием Eyeborg — специальный гибкий датчик с простой камерой, которая считывает цвета и посылает Нилу звуковой сигнал. И он стал слышать цвет.
Нил Харбисон мог слышать цвет с помощью устройства Eyeborg
Сначала Нил долго не мог привыкнуть к постоянной какофонии в своей голове. Однако со временем он научился различать цвета по закрепленным за ними нотам. А позже развил и обратную способность: звуки определенной тональности стали вызывать у него ощущения соответствующих цветов.
Так Нил Харбиссон развил синестезию — феномен восприятия, при котором в результате особенностей в работе мозга разные сигналы и чувства смешиваются, дополняют друг друга и сливаются в единое ощущение. А еще Харбиссон стал первым в мире официально признанным киборгом, но это совсем другая история.
Синестезия — малоизученный, но доказанный феномен восприятия, при котором раздражение в одной системе ощущений ведет к автоматическому отклику в другой.
Ваш браузер не поддерживает данный формат видео.
Так Нил Харбиссон «видит» в цвете арию Царицы ночи из оперы Моцарта «Волшебная флейта».
Цвет и звук для Нила теперь взаимосвязаны и неотделимы друг от друга. Свою способность «видеть» звуки в цвете Харбиссон использует в творчестве: например, он пишет картины, на которых в цвете изображает, как для него звучат музыкальные произведения и человеческие голоса.
У Харбиссона синестезия проявилась вследствие использования технологий. Это уникальный случай: у подавляющего большинства синестетов (или синестетиков, оба варианта допустимы) этот феноменальный способ чувствовать — врожденный.
Развить синестезию в себе искусственно нельзя, но люди могут испытывать похожие ощущения при некоторых видах эпилепсии и травмах головы, медитации и сенсорной депривации, а также при употреблении психотропных веществ.
Антон Сидоров-Дорсо, один из авторов программы исследования «Антропология синестезии», руководитель проекта по исследованию синестезии в детском возрасте ЦМИСД МГППУ, сооснователь и член правления Международного сообщества синестетов, деятелей искусства и науки, считает, что отличить синестезию от богатого воображения довольно просто.
Ваш браузер не поддерживает данный формат видео.
Так Нил Харбиссон «видит» в цвете знаменитую речь Мартина Лютера Кинга «I have a dream»
Ваш браузер не поддерживает данный формат видео.
Так Нил Харбиссон «видит» в цвете речь Адольфа Гитлера
Он объясняет, что от простых ассоциаций синестезию отличает непроизвольность связей (чувства «соединяются» непроизвольно, подсознательно) и постоянство ощущений, которые не меняются с течением времени. Чаще всего эти группы чувств включают в себя «материальные» ощущения: осязательные, зрительные, слуховые, вкусовые, обонятельные.
«Кроме того, сам синестет не может объяснить свои реакции: они немотивированны и редко имеют очевидный смысл», — говорит Дорсо.
При синестезии могут «смешиваться» чувства из двух и более систем восприятия.
Например, Анастасия Г. из Москвы, когда пьет не очень хороший, дешевый кофе, помимо вкуса, ощущает его цвет и форму.
Узнать, как Анастасия видит боль, на что для нее похож чай и какого цвета секс, вы можете, послушав цикл «Синестезия. Поразительные истории людей с феноменом восприятия» подкаста «Истории.doc».
Согласно разным исследованиям, врожденной синестезией обладают от одного до четырех процентов населения Земли. От 75 до 300 миллионов человек! Фактически в радиусе двух километров вокруг вас всегда будет хотя бы один синестет. Почему же при таком их количестве мы редко сталкиваемся с ними в жизни? Все просто. Врожденные синестеты воспринимают мир таким образом всю жизнь и считают «смешение» чувств нормой. О том, что ощущения других людей отличаются, синестеты чаще всего узнают случайно. Обычно — в уже зрелом возрасте, порой — не узнают вообще. А те, кто узнает, иногда скрывают свою «инаковость», стесняясь ее или опасаясь непонимания со стороны окружающих.
Вкус плохого дешевого кофе синестет Анастасия Г. из Москвы ощущает примерно вот так
Игорь Дамулин, доктор медицинских наук, профессор кафедры нервных болезней и нейрохирургии Первого МГМУ имени Сеченова, начал изучать синестезию уже состоявшимся ученым.
«Синестеты — люди абсолютно психически нормальные, — говорит Дамулин. — И один из критериев выявления синестезии — это отсутствие психической патологии». В мире синестезию изучают более ста лет, но был период, когда наука «забыла» про этот феномен. Однако современные технологии, такие как функциональная магнитно-резонансная томография, дали возможность изучать синестезию на физиологическом уровне, что породило новую волну интереса со стороны исследователей.
Тем не менее широкая публика о феномене синестезии осведомлена слабо, и синестетов, которые заявляют о себе миру, нередко склонна считать шарлатанами или сумасшедшими. Между тем с любой другой точки зрения синестеты — совершенно обычные люди. Пройдя мимо одного из них, вы даже не заподозрите, что секунду назад разминулись с одним из интереснейших феноменов нейропсихологии.
Разноцветные буквы
Существует более 60 видов синестезии, часто у одного человека может быть сразу несколько проявлений этой особой чувствительности. Самая распространенная форма — графемно-цветовая, при которой синестеты воспринимают в цвете буквы, цифры и их комбинации (слова и числа). При некоторых разновидностях графемы могут также дополняться ощущением объема и текстуры. Например, для Елены А. из Санкт-Петербурга буква «И» похожа на зеленый фикус. А Ангелина К. из Москвы не любит имя Илья, потому что оно черное и склизкое.
Для синестета Елены А. буква «И» по цвету и на ощупь похожа на фикус
Имя «Илья» очень не нравится синестету Ангелине К. Она ощущает это имя черным и склизким.
Тем не менее явление известно ученым и исследователям уже несколько веков. В середине XIX века cинестезия привлекла внимание представителей новой, зарождающейся тогда науки — психологии. Об этом феномене писали многие ученые из разных стран. Быть синестетом в определенных кругах европейского света и богемы стало модным, исследования вызвали интерес, восхищение и даже легкую зависть у людей от мира искусства. В 1871 году французский поэт Артюр Рембо написал стихотворение «Гласные», в котором столь похоже передал ощущения от графемно-цветовой синестезии, что спустя века все ещё существует миф о том, что он сам являлся синестетом.
В 1871 году французский поэт Артюр Рембо написал стихотворение «Гласные», в котором столь похоже передал ощущения от графемно-цветовой синестезии, что спустя века все ещё существует миф о том, что он сам являлся синестетом.
Стихотворение Артюра Рембо «Гласные»
А — черно, бело — Е, У — зелено, О — сине,
И — красно… Я хочу открыть рождение гласных.
А — траурный корсет под стаей мух ужасных,
Роящихся вокруг как в падали иль в тине,
Мир мрака; Е — покой тумана над пустыней,
Дрожание цветов, взлет ледников опасных.
И — пурпур, сгустком кровь, улыбка губ прекрасных
В их ярости иль в их безумье пред святыней.
У — дивные круги морей зеленоватых,
Луг, пестрый от зверья, покой морщин, измятых
Алхимией на лбах задумчивых людей.
О — звона медного глухое окончанье,
Кометой, ангелом пронзенное молчанье,
Омега, луч Ее сиреневых очей.
На самом деле из его поздней переписки стало понятно, что Рембо не был синестетом, но остался впечатленным от общения со знакомыми — носителями синестезии.
Ассоциации, образующие синестетические связи, у каждого человека формируются индивидуально. Поэтому люди с одинаковой формой синестезии могут одни и те же вещи воспринимать и чувствовать по-разному. Так, например, было в семье русского писателя Владимира Набокова.
«Случилось так, что мы обнаружили, что наш сын Дмитрий — тогда он был маленьким мальчиком, одиннадцати или двенадцати лет, — тоже видит буквы в цвете. Тогда мы попросили его перечислить свои цвета, и выяснилось, что в одном случае буква, которую он видит пурпурной или, возможно, розовато-лиловой, является розовой для меня и синей для моей жены. Это буква М. Так комбинация розового и синего дали цвет сирени. Словно гены рисовали акварелью», — писал в мемуарах Набоков.
Набоков был очень близок к истине: синестезию действительно можно унаследовать. Ученые не нашли гены, которые отвечают за развитие этого феномена, но наблюдения показывают, что у синестетов часто рождаются дети с синестезией, причем вероятнее всего — с тем же видом, что у родителей.
Разноцветные звуки
Второй по частоте вид синестезии — цвето-звуковая или хромостезия. При этой форме практически каждый звук, который слышит синестет, окрашивается в его сознании в определенный цвет. Именно этот вид естественно развился у Нила Харбиссона после долгого ношения Eyeborg.
При этой форме практически каждый звук, который слышит синестет, окрашивается в его сознании в определенный цвет. Именно этот вид естественно развился у Нила Харбиссона после долгого ношения Eyeborg.
Признаки хромостезии можно заметить в работах многих известных художников. К сожалению, научные методы, позволяющие однозначно установить наличие синестезии, появились совсем недавно. Поэтому о том, была ли синестезия у мастеров прошлого, судить можно лишь по косвенным признакам: переписке, отзывам современников, общим элементам в их работах. Среди современных художников синестетами точно являются, например, американец Дэвид Хокни и британка Джейн Макей.
Картина американского художника-синестета Дэвида Хокни Pacific Coast Highway And Santa Monica
Картина британской художницы-синестетки Джейн Макей «Prokofiev Piano Sonata No. 7 in B flat major»
Картина американского художника-синестета Дэвида Хокни Pacific Coast Highway And Santa Monica
В прошлом многие знаменитые живописцы умышлено или скорее по эстетическому наитию стремились подражать коллегам-синестетам и передавали свое творческое видение средствами, напоминающими цвето-звуковую синестезию. Например, на своей картине «Крик» норвежец Эдвард Мунк изобразил то, как, по его мнению, синестет воспринимает в цвете человеческий вопль. А русский художник Василий Кандинский, который был прекрасно осведомлен о феномене «цветного слуха», переложил «на цвет» композицию Шенберга, и в результате родилась его картина «Импрессия III (Концерт)».
Например, на своей картине «Крик» норвежец Эдвард Мунк изобразил то, как, по его мнению, синестет воспринимает в цвете человеческий вопль. А русский художник Василий Кандинский, который был прекрасно осведомлен о феномене «цветного слуха», переложил «на цвет» композицию Шенберга, и в результате родилась его картина «Импрессия III (Концерт)».
Антон Сидоров-Дорсо считает, что большую часть своего метода Кандинский черпал из собственной творческой интерпретации значения цвета, абстрактных форм и связей, в том числе звука и цвета. Кандинский называл синестетов «сильно чувствующими людьми» и уподоблял их «обыгранным хорошим скрипкам, звучащим от всякого прикосновения смычком во всех своих частях и жилках». При этом сам прямо и безусловно он себя к синестетам не причислял. У природного синестета реакции (смешения цвета и звуков) немотивированные, они происходят произвольно, без умысла и стараний, объясняет Дорсо. В то же время подражатели синестетам будут «придумывать» сочетания звука и цвета, придавать им некий скрытый смысл.
Ваш браузер не поддерживает данный формат видео.
Когда Эдвард Мунк писал свою знаменитую картину «Крик», он старался изобразить настоящий человеческий вопль так, как его ощущают синестеты (по мнению самого Мунка)
Ваш браузер не поддерживает данный формат видео.
Василий Кандинский был прекрасно осведомлен о феномене «цветного слуха». Отталкиваясь от своих знаний и представлений о синестезии, он переложил «на цвет» композицию Арнольда Шенберга, и в результате родилась картина «Импрессия III (Концерт)»
Для хромостетов каждая нота, каждый голос, каждый звук имеет свой собственный цвет. Хотите узнать, как мог бы видеть вас человек с хромостезией? Составьте свой синестетический цвето-звуковой портрет в формате дополненной реальности с помощью приложения RIA Lab, которое можно скачать в App Store для iOS или Google Play для Android.
Ваш браузер не поддерживает данный формат видео.
Взгляните на мир глазами синестета с «цветным слухом» с помощью приложения
Доказанным синестетом был композитор Римский-Корсаков, который, наоборот, «слышал цвета», превращая музыку у себя в голове в яркие картины.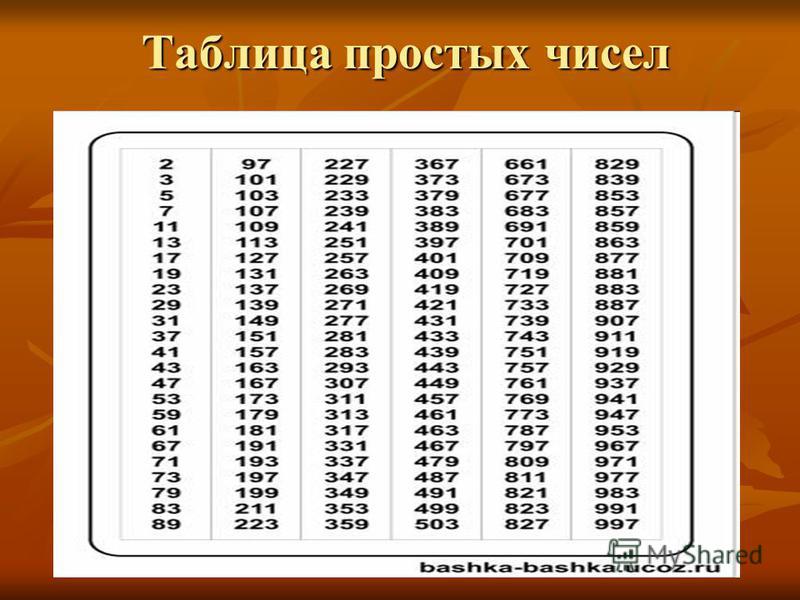 Вот как он описывал свою синестезию: «Все тональности, строи и аккорды, по крайней мере для меня лично, встречаются исключительно в самой природе, в цвете облаков или же в поразительно прекрасном мерцании цветовых столбов и переливах световых лучей северного сияния. Там есть… все, что вы хотите».
Вот как он описывал свою синестезию: «Все тональности, строи и аккорды, по крайней мере для меня лично, встречаются исключительно в самой природе, в цвете облаков или же в поразительно прекрасном мерцании цветовых столбов и переливах световых лучей северного сияния. Там есть… все, что вы хотите».
Мир, в котором каждый цвет, каждый предмет «звучит» по-своему, — мелодия или какофония?
Узнайте сами! Предлагаем взглянуть на мир глазами синестета с «цветным звуком» через приложение RIA Lab в App Store для iOS или Google Play для Android.
Ваш браузер не поддерживает данный формат видео.
Послушайте, как звучит мир в восприятии хромостета
Ангелина К. не только «слышит» цвета — у нее смешаны пять основных чувств. Подробнее о том, как Ангелина ощущает мир, вы можете узнать, послушав цикл «Синестезия. Поразительные истории людей с феноменом восприятия» подкаста «Истории.doc».
А как вы представляете неделю? Большинство ответит, что в виде школьного дневника или календаря в телефоне. Но так не у всех.
Но так не у всех.
Смешиваться могут не только сенсорные ощущения от объективно существующих раздражителей — звука, цвета, запаха, вкуса — но и от субъективно воспринимаемых: букв и цифр, эмоций, имен, характеров, времени.
Синстезия может быть связанной с абстрактными понятиями — скорее с продуктами человеческого мышления, чем с явлениями природы. Например, существуют синестеты, которые воспринимают время исключительно в пространстве. Год для них может выглядеть как кольцо, будущее лежит справа вверху, а день выглядит изогнутой лентой или разбит по часам на колонки. Это одна из разновидностей синестезии локализации последовательностей или «числовых форм». Такие виды синестезии встречаются значительно реже.
Так Наталья Л., синестет числовых форм, условно видит линию года, на самом деле она трёхмерная в сознании синестета
Разноцветные люди
Одни из самых редких видов синестезии включают в себя привязку ощущений к людям, их полу и возрасту, внешности, характеру. Такой тип называется аурическим, поскольку чаще всего такие синестеты воспринимают личность другого человека в виде цветного ореола похожего на ауру. Так «видит» некоторых знаменитостей синестет Елена А. К слову, это у нее буква «И» — зеленый фикус. А время она ощущает в виде винтовой лестницы. Так что у нее как минимум три разных вида синестезии.
Такой тип называется аурическим, поскольку чаще всего такие синестеты воспринимают личность другого человека в виде цветного ореола похожего на ауру. Так «видит» некоторых знаменитостей синестет Елена А. К слову, это у нее буква «И» — зеленый фикус. А время она ощущает в виде винтовой лестницы. Так что у нее как минимум три разных вида синестезии.
Когда Михаил Боярский был моложе, в его «ауре» в восприятии Елены А. преобладал голубой цвет
Так сегодня видит Михаила Боярского синестет «аурического» типа Елена А. из Санкт-Петербурга
«Аура» Дэниела Рэдклиффа в синестетическом восприятии Елены А. преимущественно фиолетовых оттенков
В «ауре» Владимира Путина, как ее «видит» синестет Елена А, преобладает синий цвет
Когда Михаил Боярский был моложе, в его «ауре» в восприятии Елены А. преобладал голубой цвет
«Ауры» разных публичных людей реконструированы в соответствии с описаниями синестета Елены А.
Цвет и структура «ауры», которую видит синестет, зависит не только от физиологии и характера объекта. Эмоции, которые испытывает человек, тоже изменяют цвет и форму его ореола. Антон Сидоров-Дорсо предполагает, что аура, воспринимаемая синестетом, представляет собой воплощение типажей людей как их воспринимает сам синестет. Поэтому по мере знакомства с человеком, изменения впечатлений о нем, развития отношений синестетическая аура меняется и детализируется.
Эмоции, которые испытывает человек, тоже изменяют цвет и форму его ореола. Антон Сидоров-Дорсо предполагает, что аура, воспринимаемая синестетом, представляет собой воплощение типажей людей как их воспринимает сам синестет. Поэтому по мере знакомства с человеком, изменения впечатлений о нем, развития отношений синестетическая аура меняется и детализируется.
Елена считает, что в основе восприятия синестетической ауры лежит интуиция. Дорсо согласен с этим и полагает, что если какой-то черты человеческого типажа нет в интуитивном опыте синестета, то и в цвете «ауры» она не появится.
Посмотрите, если бы вы пообщались с Еленой, она бы видела вас вот так.
Ваш браузер не поддерживает данный формат видео.
Использована эмоционально-цветовая палитра, составленная синестетом Еленой А.
Как Елена использует свою способность в обычной жизни и как синестезия влияет на ее общение с людьми, вы узнаете, послушав цикл «Синестезия. Поразительные истории людей с феноменом восприятия» подкаста «Истории. doc».
doc».
На самом деле среди исследователей есть мнение, что все мы «остаточные» синестеты. Ведь как иначе мы понимали бы такие выражения, как «холодный цвет», «яркая личность», «горячий парень», «красный день календаря»? Кроме того, чтобы легче ориентироваться среди множества на первый взгляд однообразных вещей — лекарств, товаров, документов, химических элементов, спортивных команд, линий метро — мы, совсем как синестеты, интуитивно привязываем к ним более понятные и простые атрибуты — цвета.
Ученые установили, что все мы рождаемся с синестетическим мировосприятием и в младенчестве воспринимаем мир единым чувством. Однако по мере взросления взаимная активация зон мозга, отвечающих за разные ощущения, останавливается. И только нескольким процентам людей повезло сохранить этот прекрасный детский взгляд на наш мир.
В октябре 2019 года в Москве пройдет II Международная конференция Международной ассоциации синестетов, деятелей науки и искусства. В рамках конференции на базе МГППУ и консерватории имени П. И. Чайковского сотни синестетов и исследователей соберутся на симпозиуме «Синестезия: сенсорные аспекты познавательной деятельности в науке и искусстве». Возможно, результаты этой встречи станут крупнейшим прорывом в изучении феномена синестезии.
И. Чайковского сотни синестетов и исследователей соберутся на симпозиуме «Синестезия: сенсорные аспекты познавательной деятельности в науке и искусстве». Возможно, результаты этой встречи станут крупнейшим прорывом в изучении феномена синестезии.
А пока пройдите тест и определите, не синестет ли вы. Возможно, вы входите в те самые один — четыре процента.
Синестезия — малоизученный, но доказанный феномен восприятия, при котором раздражение в одной системе ощущений ведет к автоматическому отклику в другой.
Проект «Синестеты» подготовлен при экспертной и информационной поддержке Первого МГМУ имени Сеченова, Российского синестетического сообщества и Международной ассоциации синестетов, деятелей искусств и науки.
Слушайте три эпизода о феномене синестезии в цикле «Синестезия. Поразительные истории людей с феноменом восприятия» подкаста «Истории.doc», в которых сами синестеты рассказывают о своей жизни и мире, в котором они существуют. Вы также можете скачать и послушать его в мобильных приложениях: для iPhone — iTunes, для Android — Google Podcasts.
Вы также можете скачать и послушать его в мобильных приложениях: для iPhone — iTunes, для Android — Google Podcasts.
11:00 15.11.2018 (обновлено: 13:05 03.03.2020)
диаграмма сотен Prime Climb – чудо математики
Это шестой в серии постов о моем курсе «Развитие математического мышления», факультативе по математике для будущих учителей начального и среднего уровня математики. Все посты из этой серии здесь.
Это последний пост с подробным описанием того, как я представил «Уведомление и удивление» своим учителям до начала работы. Мы использовали его для придания смысла. Затем мы просмотрели фотографии окружающего мира и провели мозговой штурм, увидев и задаваясь вопросом. Студенты позже сделали свои собственные фотографии и идентифицировали математические идеи, которые они видели. (Фотографии и размышления было очень интересно рассматривать!) Затем мы перенесли наши навыки «Замечать и удивляться» в более математические условия, включая одну из математических задач Дэна Мейера в трех действиях, «Зубочистки». Теперь я расскажу вам о консолидирующем задании, в котором я попросил студентов рассказать мне, что они замечают и удивляются в изображении, переполненном математическими идеями.
Теперь я расскажу вам о консолидирующем задании, в котором я попросил студентов рассказать мне, что они замечают и удивляются в изображении, переполненном математическими идеями.
Обновление от 6 августа 2017 г.: В этом посте описывается еще один способ включения «Notice and Wonder» в график сотен Prime Climb.
Примечание. Хотя это выглядит как длинное сообщение, первые 200 слов являются введением; последние 1500 слов представляют собой краткое изложение идей учащихся.
Таблица сотен Prime Climb
Prime Climb — красивая настольная игра, в которой игроки углубляют свое понимание арифметики посредством игрового процесса. Честно говоря, я никогда не играл! Но это не помешало мне оценить великолепную диаграмму сотен, которая сопровождает игру. Версия ниже; вы можете купить это изображение на потрясающем плакате здесь.
Эта таблица сотен заставляет нас замечать и удивляться. Найдите минутку и проведите мозговой штурм для себя. (Дэн Финкель, создатель игры Prime Climb, рассказывает об этом изображении в своем замечательном выступлении на TED «Пять принципов экстраординарного преподавания математики». На просмотр стоит потратить примерно 15 минут.) от моих студентов
На просмотр стоит потратить примерно 15 минут.) от моих студентов
Я попросил свою группу из почти пятидесяти учителей до начала работы рассказать мне о пяти вещах, которые они заметили, и об одной вещи, которая их удивила. Как группа, это потенциально 250 различных вещей, которые они замечают, и 50 вещей, которым они удивляются! Вот сопоставленный список из примерно 100 их идей (с небольшими поправками к неправильной терминологии), небрежно сгруппированных по моим собственным заголовкам разделов. Я попросил их сделать это как индивидуально. Я уверен, что в групповом обсуждении они развили бы и расширили идеи друг друга. В следующий раз!
Приятного чтения; Я, конечно, сделал.
I
уведомление что …
Цвет и структура
- Круги пронумерованы от 1 до 100.
- Диаграмма организована по системе 10×10.
- Числа возрастают.
- Числа в каждом столбце увеличиваются на десять по мере продвижения вниз по списку.

- Цвет как-то связан с числом, и наоборот.
- Есть разные цвета: синий, оранжевый, желтый, красный, зеленый.
- Некоторые круги имеют только один цвет.
- За исключением целых красных кругов, каждый другой цвет появляется как целый круг только один раз.
- Каждый круг состоит из одного или нескольких цветов.
- используется для демонстрации отношений между числами.
- В каждом втором числе есть оранжевый (и аналогичные утверждения о других цветах).
- Все четные числа окрашены в желтый/оранжевый цвет.
- Дружественные числа (5 и 10) выделены синим цветом.
- Круги с синим концом на 5 или 0.
- Много красных кругов/цифр.
- Есть 21 сплошной красный кружок/цифра.
- Красный — самый заметный цвет.
- Purple — наименее используемый цвет.
- Полностью зеленые числа кратны 3 (и аналогичные утверждения о других цветах).
- Кольца разбиты на части, которые варьируются от целого до 1/6.

- В некоторых красных секциях есть маленькие белые цифры.
- Все маленькие белые числа, которые появляются «случайно» в нижней части кругов, являются нечетными числами.
- Красные полные кружки появляются только на нечетных числах.
- Числа с оранжевым цветом (кратные 2) расположены вертикально, как и числа с синим цветом (кратные 5). Но числа с зеленым цветом (кратные 3) расположены по диагонали (справа налево), если смотреть сверху вниз.
- Если вы поместите палец на номер с фиолетовым цветом, затем переместите палец вверх на одну строку, а затем переместите его на три столбца вправо, вы окажетесь на другом номере с фиолетовым цветом (работает с большинством фиолетовых чисел, если только это не слишком близко к край).
- Наибольшее количество цветных секторов вокруг числа равно шести.
- Наибольшее количество различных цветов, содержащихся в секторах, окружающих любое число, равно трем.
- Ни один номер/круг не содержит всех цветов.

- Кажется, что в цветах нет узора.
Цвет
Число 1
- Число 1 не имеет цвета, потому что оно не является ни простым, ни составным числом.
- Число 1 имеет собственный цвет и не является частью какого-либо определенного паттерна на графике. Каждое целое число имеет делитель 1,
- 1 не является простым числом, поэтому оно не окрашено.
Простые числа
- Полноцветные кружки — это простые числа.
- Все простые числа имеют одну сплошную окружность.
- 97 — наибольшее простое число меньше 100.
- Простые числа имеют свой особый цвет до значения 7.
- Числа в красных кружках также являются простыми числами от 11 и выше.
- Все простые числа от 1 до 100, кроме 2, являются нечетными.
- Существует 25 простых чисел от 1 до 100.
- Если внизу круга написано меньшее число, обозначающее большее число, то это означает, что большее число делится на простое число.
 Например, число 92 имеет маленькую цифру 23, написанную внизу круга, это означает, что 92 делится на простое число 23.
Например, число 92 имеет маленькую цифру 23, написанную внизу круга, это означает, что 92 делится на простое число 23. - Существует только одно простое число между 91 и 100. Все остальные блоки из десяти имеют по крайней мере два простых числа.
- В столбце «3» больше всего простых чисел от 1 до 100.
Составные числа
- Числа, не являющиеся простыми, представляют собой смесь цветов. Например, 15 — это 5×3, где 5 — синий, а 3 — зеленый, поэтому 15 — это наполовину синий и наполовину зеленый.
- Все числа, кратные 6, должны быть оранжевого (2) и зеленого (3) цвета.
- Любое число, оканчивающееся на 4,6,8 или 0, не является простым числом.
- Некоторые непростые числа состоят из множителей, которые являются просто (только) простыми числами.
Квадратные числа
- Все квадратные числа состоят из нескольких частей одного цвета.
- Сумма всех квадратных чисел равна 385.

Ориентирован на умножение
- Мы можем использовать цвета вокруг каждого числа и перемножать их «представляющие числа» вместе, чтобы получить число в середине.
- Фрагменты круга символизируют, сколько раз произошло умножение. Например, число 8 состоит из трех фрагментов желтого круга, обозначающих 2×2×2.
- Цвета каждого круга представляют числа, на которые можно разделить большее число. Например, число 95 окрашено в синий и красный цвета. Эти цвета представляют 5 и простое число 19. При умножении их сумма равна 95.
Делитель и множитель
- На этой диаграмме есть только 2 числа, которые представлены кружком, разделенным на шестые. Им 64 и 96.
- Для составления чисел до 100 требуется не более шести множителей.
- Нечетные числа чаще всего имеют делители, являющиеся простыми числами.
- Круги делятся на секции в зависимости от того, сколько у них делителей.

- Множители каждого числа очевидны по раскраске.
- Различные цветные части круга означают, что число делится более чем на одно число.
- Нечетные числа обычно имеют меньше делителей, даже если они не простые.
Простые множители
- Цвета вокруг числа представляют простые множители числа. Например, число 96 состоит из пяти оранжевых сегментов и одного зеленого сегмента, что предполагает, что простые множители числа 96 равны 2×2×2×2×2×3.
Другое
- Все числа, делящиеся на 11, имеют цифру 11 в нижнем индексе и располагаются на диагональной линии.
- Рассмотрите числа с одинаковыми цифрами (11, 22, …). Сумма цифр – все четные числа.
- Нет явных инструкций или «ключа», объясняющего, что на самом деле показывает диаграмма.
- Сумма первых девяти простых чисел равна 100.
- Если вы прищуритесь, вы начнете видеть цветовые узоры, а не замечать числа, как я заметил некоторые из моих предыдущих пунктов.

Интересно…
Цвет и структура
- Почему 1 – единственная цифра серого цвета?
- Почему на некоторых кругах есть лишние цифры белого цвета?
- Что означают сечения кругов?
- Почему разные числа делятся на разные «дроби»? Есть ли в этом основная причина?
- Почему некоторые числа имеют части своего цвета, даже если эти части одного цвета? Например, число 64 состоит из шести частей оранжевого цвета, а оранжевый ассоциируется только с двумя.
- Как им удалось разделить внешний круг числа 24 на четыре сегмента? И почему три из них оранжевые, а один зеленый?
- Какой цвет используется чаще всего?
- Было бы легче читать диаграмму, если бы все простые числа имели свой цвет, а не первые 10?
- Почему числа 96 и 64 имеют больше всего делений?
- Есть ли несколько «решений» этой проблемы?
Выкройки
- Если есть выкройка? А если бы я разобрался?
- Есть ли закономерность между числами и количеством частей в их цветном круге, которую можно использовать для вычисления любого числа?
- Почему они не написали, сколько раз конкретное число входит в большое число внутри соответствующей цветовой секции?
- Почему числа окрашены случайным образом (без определенного шаблона)?
- Можете ли вы использовать эту числовую таблицу и расширить ее, чтобы найти каждое простое число без ручных и утомительных вычислений?
- Существует ли систематический способ определения наибольшего количества секторов или различных цветов, которые могут окружать любое число в наборе (например, от 1 до 1 000 000), без необходимости садиться и умножать простые числа?
Расширение диаграммы
- Если бы получилось 1000, какое число имело бы наибольшее количество разных цветов?
- Если бы это число увеличилось до 1000, начали бы мы видеть все больше и больше красного цвета по сравнению с другими цветами?
- Интересно, как будут выглядеть следующие 100 чисел, разложенные таким образом на простые множители? Я бы предположил, что количество видимого красного уменьшится.

- Как бы это выглядело, если бы увеличилось до 200?
- Если дойдет до 200, будут ли числа иметь больше четырех или пяти цветов?
- Сколько простых чисел будет в следующем наборе из 100 чисел, например, от 101 до 200?
- Когда первая строка из 10 не содержит простых чисел?
Другое
- Для чего можно использовать изучение математики?
- Для чего используются сотни графиков?
- Можно ли использовать подобную таблицу для того, чтобы познакомить детей с математикой до того, как они начнут запоминать наизусть?
- Может ли знание простых и составных чисел помочь в повседневной жизни?
- Как бы это выглядело, если бы мы создали такое изображение на основе сложения?
- Если бы эта диаграмма была так же легко переведена, если бы вместо кругов использовались квадраты, треугольники или какая-либо другая форма?
- Что представляет эта диаграмма? Для кого это было сделано?
- Почему кто-то выбрал это представление?
- Зачем это было создано?
- Сколько времени ушло на создание?
- Кто придумал это представление? Это действительно здорово!
Если вы дочитали до этого места, молодец! Но процитировать последнего студента, это действительно круто, не правда ли?
Нравится:
Нравится Загрузка. ..
..
Картина по простому номеру — Щепотка интеллекта
Две недели назад я наткнулся на концепцию простых портретов. Короче говоря, основные портреты — это изображения, в которых каждому цвету присвоен номер. Когда мы выравниваем каждый пиксель, результатом должно быть простое число. Поскольку я не смог найти код, использованный в статье, я решил воссоздать эти основные портреты в Python — в цвете! Ниже приведен блокнот Jupyter с кодом (также доступным на Github), который я использовал для создания Моны Лизы:
Концепция
Простой портрет представляет собой простое число, отформатированное как матрица с X цифрами в строке. Когда мы выбираем цвет для каждой цифры, мы можем создать изображение.
Вместо того, чтобы делать это для многих простых чисел и цветовых схем, пока вы не найдете что-то похожее на известное изображение, я изменил процесс. Я взял знаковые изображения, такие как Мона Лиза и Звездная ночь, и преобразовал их в изображения всего с 10 цветами. Я присвоил цифру каждому цвету. Затем я сгенерировал много похожих изображений с небольшим добавлением «шума». Шум немного изменил цвета на изображениях и, следовательно, цифры. Если цифры на изображении образуют простое число, я нашел простой портрет!
Я присвоил цифру каждому цвету. Затем я сгенерировал много похожих изображений с небольшим добавлением «шума». Шум немного изменил цвета на изображениях и, следовательно, цифры. Если цифры на изображении образуют простое число, я нашел простой портрет!
импортировать matplotlib.pyplot как plt %matplotlib встроенный импортировать numpy как np импортировать skimage.transform импортировать skimage.io из sklearn.cluster импортировать KMeans импортировать scipy.misc из PIL импортировать изображения, ImageFont, ImageDraw импортировать numpy как np из многопроцессорного пула импорта время импорта импортировать случайный предупреждения об импорте
Проверка на простоту
При работе с очень длинными простыми числами наивный метод проверки каждого делителя займет слишком много времени. Существует много простых чисел, и проверка вашего числа для каждого возможного делителя занимает слишком много времени, чтобы проверить множество простых портретов.
Вместо этого мы применяем вероятностный подход к простым числам. Тест Миллера-Рабина использует эвристику, чтобы определить, является ли число (вероятно) простым или нет. Я загрузил следующий код для теста простоты Миллера-Рабина из кода Rosetta, чтобы проверить простоту:
def try_composite(a, d, n, s):
# проверить базу a, чтобы увидеть, является ли она свидетелем составности n
если pow(a, d, n) == 1:
вернуть ложь
для i в диапазоне (ах):
если pow(a, 2**i * d, n) == n-1:
вернуть ложь
return True # n однозначно составной
def is_probable_prime (n, mrpt_num_trials = 5):
"""
Критерий простоты Миллера-Рабина.
Возвращаемое значение False означает, что n определенно не простое число. Возвращаемое значение
True означает, что n, скорее всего, простое число.
"""
утверждать п >= 2
# частный случай 2
если п == 2:
вернуть Истина
# убедиться, что n нечетно
если n % 2 == 0:
вернуть ложь
# записать n-1 как 2**s * d
# повторно пытаемся разделить n-1 на 2
с = 0
д = п-1
пока верно:
частное, остаток = divmod(d, 2)
если остаток == 1:
ломать
с += 1
д = частное
утверждать(2**s * d == n-1)
для i в диапазоне (mrpt_num_trials):
а = случайный. randrange(2, n)
если try_composite(a, d, n, s):
вернуть ложь
return True # ни одна из проверенных баз не показала n составным
утверждать is_probable_prime(2)
утверждать is_probable_prime (3)
утверждать, что это не is_probable_prime(4)
утверждать is_probable_prime(5)
утверждать, что это не is_probable_prime (123456789)
primes_under_1000 = [i для i в диапазоне (2, 1000), если is_probable_prime(i)]
утверждать len(primes_under_1000) == 168
утверждать, что primes_under_1000[-10:] == [937, 941, 947, 953, 967, 971, 977, 983, 991, 997]
утверждать is_probable_prime(6438080068035544392301298549614926991513861075340134\
32918073439524138264842370630061369715394739134090922937332572039\
71333359695492563226209786633213
randrange(2, n)
если try_composite(a, d, n, s):
вернуть ложь
return True # ни одна из проверенных баз не показала n составным
утверждать is_probable_prime(2)
утверждать is_probable_prime (3)
утверждать, что это не is_probable_prime(4)
утверждать is_probable_prime(5)
утверждать, что это не is_probable_prime (123456789)
primes_under_1000 = [i для i в диапазоне (2, 1000), если is_probable_prime(i)]
утверждать len(primes_under_1000) == 168
утверждать, что primes_under_1000[-10:] == [937, 941, 947, 953, 967, 971, 977, 983, 991, 997]
утверждать is_probable_prime(6438080068035544392301298549614926991513861075340134\
32918073439524138264842370630061369715394739134090922937332572039\
713333596954925632262097866332132966175107096769180017646161\
8515731475963)
утверждать, что это не is_probable_prime (7438080068035544392301298549614926991513861075340134\
32918073439524138264842370630061369715394739134090922937332572039\
713333596954925632262097
866332132966175107096769180017646161\
8515731475963)
Генерация изображений
В основе алгоритма лежит генерация изображений только с 10 возможными цветовыми значениями. Я не знал, каков общий подход к этому, поэтому я подумал, что сработает алгоритм k-средних. Для этого я изменил форму входного изображения (так что каждый пиксель представляет собой точку в трехмерном пространстве), сгруппировал его и использовал 10 созданных кластеров в качестве значений цвета. Побочное примечание: когда ваш молот — машинное обучение, все выглядит как гвоздь…
Я не знал, каков общий подход к этому, поэтому я подумал, что сработает алгоритм k-средних. Для этого я изменил форму входного изображения (так что каждый пиксель представляет собой точку в трехмерном пространстве), сгруппировал его и использовал 10 созданных кластеров в качестве значений цвета. Побочное примечание: когда ваш молот — машинное обучение, все выглядит как гвоздь…
Для основного поколения важно добавить немного шума к исходному изображению, чтобы создать изображения, которые выглядят одинаково, но немного отличаются. Это означает, что вы создали другое число, что дает нам новый шанс найти простое число.
по определению get_k_means (изображение):
pointcloud = np.reshape (изображение, (-1, 3))
kmeans = KMeans (n_clusters = 10).fit (облако точек)
возврат kmeans
def create_numbered_image (изображение, kmeans):
"""
Превращает изображение RGB в изображение с метками кластеров предоставленного классификатора kmeans.
"""
# применяем шум
stdev = np. std(изображение)
random_noise = np.random.random_sample(size=image.shape)*(stdev/3)
изображение = изображение + случайный_шум
orig_shape = изображение.форма
изображение = np.reshape (изображение, (-1, 3))
numbered_image = kmeans.predict(изображение)
numbered_image = np.reshape (numbered_image, orig_shape [: 2])
# убедитесь, что конец неровный
если числовое_изображение[-1,-1]%2==0:
пронумерованное_изображение[-1,-1] += 1
вернуть пронумерованное_изображение
def пронумерованное_изображение_к_нормальному_изображению (нумерованное_изображение, kmeans):
"""
Превращает изображение только со значениями от 0 до 9в цветное изображение, используя центры кластеров
поставляемого классификатора kmeans.
"""
форма = (нумерованное_изображение.форма[0], нумерованное_изображение.форма[1], 3)
изображение = np.zeros (форма)
для метки цвет в zip (диапазон (10), kmeans.cluster_centers_):
изображение[numbered_image==метка] = цвет
вернуть изображение
std(изображение)
random_noise = np.random.random_sample(size=image.shape)*(stdev/3)
изображение = изображение + случайный_шум
orig_shape = изображение.форма
изображение = np.reshape (изображение, (-1, 3))
numbered_image = kmeans.predict(изображение)
numbered_image = np.reshape (numbered_image, orig_shape [: 2])
# убедитесь, что конец неровный
если числовое_изображение[-1,-1]%2==0:
пронумерованное_изображение[-1,-1] += 1
вернуть пронумерованное_изображение
def пронумерованное_изображение_к_нормальному_изображению (нумерованное_изображение, kmeans):
"""
Превращает изображение только со значениями от 0 до 9в цветное изображение, используя центры кластеров
поставляемого классификатора kmeans.
"""
форма = (нумерованное_изображение.форма[0], нумерованное_изображение.форма[1], 3)
изображение = np.zeros (форма)
для метки цвет в zip (диапазон (10), kmeans.cluster_centers_):
изображение[numbered_image==метка] = цвет
вернуть изображение
Примеры пронумерованных изображений
Здесь я создаю несколько примеров небольших пронумерованных изображений Моны Лизы. Если вы присмотритесь, вы увидите, что каждое изображение немного отличается, но вы все равно можете узнать исходное изображение. Это очень важно для нас, так как позволяет нам генерировать несколько пронумерованных изображений, которые мы можем проверить на простоту.
Если вы присмотритесь, вы увидите, что каждое изображение немного отличается, но вы все равно можете узнать исходное изображение. Это очень важно для нас, так как позволяет нам генерировать несколько пронумерованных изображений, которые мы можем проверить на простоту.
В [4]:
def load_and_resize_image(имя файла, resize_factor=18):
изображение = skimage.io.imread (имя файла)
изображение = изображение.astype(np.float64)
изображение = изображение / 255.
старая форма = изображение.форма
с предупреждениями.catch_warnings():
предупреждения.simplefilter("игнорировать")
resized_image = skimage.transform.resize(image, (oldshape[0]//resize_factor, oldshape[1]//resize_factor))
вернуть resized_image
resized_image = load_and_resize_image('input_pictures/monalisa.jpg')
kmeans = get_k_means (resized_image)
N_ИЗОБРАЖЕНИЙ = 3
f, axarr = plt.subplots(1,N_IMAGES)
для индекса в диапазоне (N_IMAGES):
n_image = create_numbered_image (измененное_изображение, kmeans)
normal_image = пронумерованное_изображение_к_нормальному_изображению (n_image, kmeans)
axarr[индекс]. imshow(нормальное_изображение)
imshow(нормальное_изображение)
Вспомогательные функции
Мне пришлось создать несколько вспомогательных функций для возврата строк, целых чисел, а также для загрузки и отображения изображений.
по определению image_to_number(numbered_image):
to_be_number = пронумерованное_изображение.reshape(-1)
as_string = ''.join([str(int(x)) для x в to_be_number])
as_int = int(as_string)
вернуть as_int, as_string
def show_and_save_image (изображение, n_image, имя файла, размер шрифта = 16):
старая форма = изображение.форма
resized_image = scipy.misc.imresize (изображение, (oldshape [0] * размер шрифта, oldshape [1] * размер шрифта), interp = 'ближайший')
img = Image.fromarray(resized_image).convert("RGBA")
txt = Image.new('RGBA', img.size, (255,255,255,0))
рисовать = ImageDraw.Draw(txt)
шрифт = ImageFont.truetype ("pirulen rg.ttf", размер шрифта)
для y_i введите enumerate(n_image):
для x_i, буква в enumerate(totype):
xpos = x_i * размер шрифта + 1
ypos = y_i * размер шрифта
если буква == 1:
xpos += 4
draw. text((xpos, ypos),str(letter),(255,255,255, 128),font=font)
img = Image.alpha_composite(img, txt)
img.save(имя файла)
plt.figure(figsize=(20,20))
plt.imshow (изображение)
plt.show()
def имя_файла_результата (имя файла):
вернуть имя файла.split('.')[0] + "-prime.png"
text((xpos, ypos),str(letter),(255,255,255, 128),font=font)
img = Image.alpha_composite(img, txt)
img.save(имя файла)
plt.figure(figsize=(20,20))
plt.imshow (изображение)
plt.show()
def имя_файла_результата (имя файла):
вернуть имя файла.split('.')[0] + "-prime.png"
Чтобы проверить, является ли что-то хорошим простым портретом, я создал следующие вспомогательные функции:
def is_good_prime_portrait(n_image):
целое число, строка = image_to_number(n_image)
если is_probable_prime (целое число):
возвращаемое целое, строка, n_image
еще:
возврат Нет
def print_result (строка, n_image):
печать (строка)
печать("-"*100)
для строки в n_image:
print(''.join([str(x) для x в строке]))
Многопоточный поиск
Сначала я создал однопоточное решение, которое работало. Однако мой ноутбук имеет несколько ядер и может работать с несколькими числами одновременно, поэтому я переписал свой первоначальный подход в многопоточном режиме:
def print_result(string, n_image):
print("Найден результат: " + "-"*100)
печать (строка)
print("Представляется портретом:" + "-"*100)
для строки в n_image:
print(''. join([str(x) для x в строке]))
def multi_threaded_prime_generator (resized_image, kmeans, имя файла, threads=4, log_process=True):
image_generator = (create_numbered_image (resized_image, kmeans) для _ в диапазоне (1000000))
начало = время.время()
с пулом (потоками) в качестве пула:
результаты = pool.imap_unordered (is_good_prime_portrait, image_generator)
всего_результатов = 0
для результата в результатах:
итог_результатов += 1
# Возможно, записывать время, потраченное на поиск этого простого числа
если log_process и total_results%30==0:
прошедшее = время.время()
прошедшее = прошедшее - начало
print("Секунды, потраченные на (имя функции), составляют {} времени на результат: {}".format(str(истекшее время), str(истекшее время/total_results)))
если результат != Нет:
# Найдено простое число, распечатайте его и сохраните!
целое число, строка, n_image = результат
print_result (строка, n_image)
normal_image = пронумерованное_изображение_к_нормальному_изображению (n_image, kmeans)
plt.
join([str(x) для x в строке]))
def multi_threaded_prime_generator (resized_image, kmeans, имя файла, threads=4, log_process=True):
image_generator = (create_numbered_image (resized_image, kmeans) для _ в диапазоне (1000000))
начало = время.время()
с пулом (потоками) в качестве пула:
результаты = pool.imap_unordered (is_good_prime_portrait, image_generator)
всего_результатов = 0
для результата в результатах:
итог_результатов += 1
# Возможно, записывать время, потраченное на поиск этого простого числа
если log_process и total_results%30==0:
прошедшее = время.время()
прошедшее = прошедшее - начало
print("Секунды, потраченные на (имя функции), составляют {} времени на результат: {}".format(str(истекшее время), str(истекшее время/total_results)))
если результат != Нет:
# Найдено простое число, распечатайте его и сохраните!
целое число, строка, n_image = результат
print_result (строка, n_image)
normal_image = пронумерованное_изображение_к_нормальному_изображению (n_image, kmeans)
plt. imshow (нормальное_изображение)
plt.show()
show_and_save_image (нормальное_изображение, n_image, имя_файла_результата (имя файла))
ломать
def search_prime_portrait (имя файла, resize_factor = 16, log_process = True, threads = 4):
resized_image = load_and_resize_image(имя файла, resize_factor=resize_factor)
print("Работа с размером " + str(resized_image.shape))
kmeans = get_k_means (resized_image)
multi_threaded_prime_generator(resized_image, kmeans, имя файла, log_process=log_process, threads=threads)
imshow (нормальное_изображение)
plt.show()
show_and_save_image (нормальное_изображение, n_image, имя_файла_результата (имя файла))
ломать
def search_prime_portrait (имя файла, resize_factor = 16, log_process = True, threads = 4):
resized_image = load_and_resize_image(имя файла, resize_factor=resize_factor)
print("Работа с размером " + str(resized_image.shape))
kmeans = get_k_means (resized_image)
multi_threaded_prime_generator(resized_image, kmeans, имя файла, log_process=log_process, threads=threads)
Генерация основных портретов
Теперь, когда мы определили все функции, пришло время создать основные портреты! Поэкспериментируйте с ним и попробуйте загрузить свои собственные изображения. Обратите внимание, что вы можете передать переменную resize_factor в функцию «поиск основного портрета». Чем больше resize_factor, тем быстрее вы сможете найти основной портрет. См. ниже дополнительную информацию об экспоненциальном времени, необходимом для создания больших основных портретов.
См. ниже дополнительную информацию об экспоненциальном времени, необходимом для создания больших основных портретов.
папка = 'input_pictures/'
имена файлов = [
папка + 'monalisa.jpg',
#folder + 'подсолнухи.jpg',
#folder + 'звездная ночь.jpg'
]
имя файла = имена файлов[0]
для имени файла в именах файлов:
search_prime_portrait (имя файла, resize_factor = 20, log_process = False, threads = 4)
Работа с размером (19, 13, 3) Нашел результат: ------------------------------------------------------------- -------------------------------------------------- ---- 6666666666662666626266262222222331222222222395146222066685731062280001758180008000853810000006688771802033388995386733331599578182871883701148387881881131880888181181188883118144141011855514411181111757388411111333881144814118814444114111444444441 Представлено в виде портрета:---------------------------------------------------------------------------- -------------------------------------------------- ---- 6666666666662 6666262662622 2222233122222 2222395146222 0666857310622 8000175818000 8000853810000 0066887718020 3338899538673 3331599578182 8718837011483 8788188113188 0888181181188 8831181441410 1185551441118 1111757388411 1113338811448 1411881444411 4111444444441
Как это масштабируется?
По-видимому, самое большое известное простое число состоит из 22338618 цифр. Это позволило бы нам создать прайм-портрет 4726 * 4726, который был бы прайм-портретом в 4K. Мне уже понравились большие изображения «Звездной ночи», и я бы очень хотел получить прайм-портрет этой картины в формате 4K.
Это позволило бы нам создать прайм-портрет 4726 * 4726, который был бы прайм-портретом в 4K. Мне уже понравились большие изображения «Звездной ночи», и я бы очень хотел получить прайм-портрет этой картины в формате 4K.
Однако: я заметил, что нахождение простых чисел на самом деле не масштабируется. Длина простого числа растет квадратично с разрешением ваших изображений, что вызывает большие проблемы. Хотя вероятность того, что вы найдете простое число, уменьшается только линейно с длиной простого числа, она уменьшается квадратично, когда вы получаете большее разрешение изображения. Я изобразил это на этом изображении, чтобы показать эффект до 300×300:
def Trials_expected_img(w,h):
возврат 2,3*ш*ч
необходимо = [trials_expected_img(x,x) для x в диапазоне (1300)]
plt.plot (необходимо)
Но еще хуже то, что время вычислений растет квадратично с длиной простого числа. Я также построил это для своего ноутбука с разрешением изображения 30×30:
def time_expected_img(w,h):
заказ = ш * ч
начало = время. время()
для _ в диапазоне (100):
posprim = random.randrange(10**(порядок-1), 10**порядок)
a = is_probable_prime (posprim)
конец = время.время()
вернуться конец - начало
test_range = диапазон (2,30,4)
time_needed = [time_expected_img(x,x) для x в test_range]
plt.plot (test_range, time_needed)
plt.title("Секунды, ожидаемые для расчета, если изображение XxY является основным портретом")
plt.xlabel("Ширина изображения")
plt.ylabel("Ожидаемые секунды")
время()
для _ в диапазоне (100):
posprim = random.randrange(10**(порядок-1), 10**порядок)
a = is_probable_prime (posprim)
конец = время.время()
вернуться конец - начало
test_range = диапазон (2,30,4)
time_needed = [time_expected_img(x,x) для x в test_range]
plt.plot (test_range, time_needed)
plt.title("Секунды, ожидаемые для расчета, если изображение XxY является основным портретом")
plt.xlabel("Ширина изображения")
plt.ylabel("Ожидаемые секунды")
Комбинируя обе линейные кривые, вы можете легко оценить ожидаемое время, необходимое для поиска портрета определенного размера:
total_needed = [trials_expected_img(x,x)*time_expected_img(x,x) for x in test_range]
plt.plot(test_range, total_needed)
plt.title("Секунды, которые ожидаются для поиска основного портрета XxY")
plt.xlabel("Ширина изображения")
plt.ylabel("Ожидаемые секунды")
Если вы можете найти более эффективную реализацию Python для вероятностной проверки простых чисел или реализовать ее на языке, более подходящем для вычислений с высокими требованиями, вы можете сократить время, необходимое для создания этих портретов. Каждое дополнительное ядро компьютера также немного сокращает это время, но пока мы не можем ожидать первоклассных портретов 4K в ближайшее время.
Каждое дополнительное ядро компьютера также немного сокращает это время, но пока мы не можем ожидать первоклассных портретов 4K в ближайшее время.
Заключение и иллюстрации
Последние пару недель мне очень нравилось позволять компьютеру находить первоклассные портреты. Вот некоторые из работ, найденных моим компьютером:
«Подсолнухи» Ван Гога
«Великая волна» Хокусая
«Девушка с жемчужной сережкой» Вермеера
Картины знаменитостей
довольно сложно создавать красивые портреты людей. Получаемым изображениям часто не хватает контраста, в котором используются только десять цветов. Я решил попробовать сделать несколько портретов людей, за которыми мне нравится следить в Интернете. Изображения, которые нам понравились:
Ионика Смитс
Каждую субботу пишет интересные статьи в голландской газете, а некоторое время назад фигурировала в голландском комиксе под названием «Дональд Дак»:
Брейди Харан
Снимает интересные видеоролики о математических концепциях на канале Numberphile Youtube.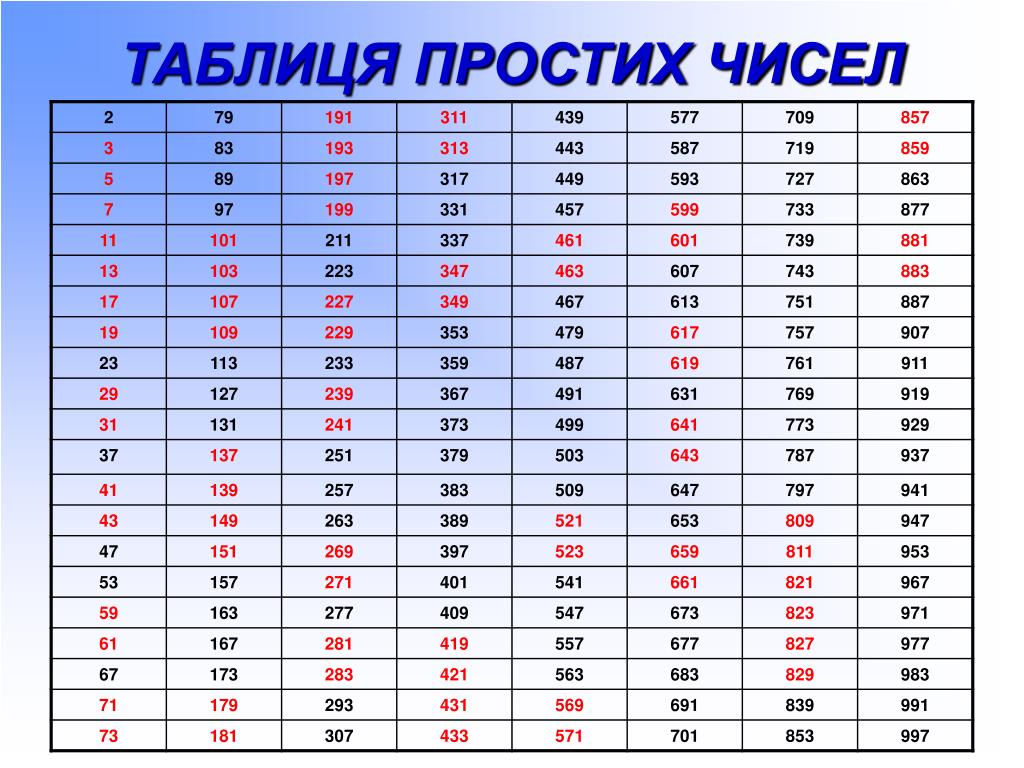 . А еще: есть милая собачка 😉
. А еще: есть милая собачка 😉
Роланд Меертенс
И я.
Запросы
Пока я выкладываю код онлайн, вы можете попробовать создать несколько первоклассных портретов для себя! Если вы действительно думаете, что мне стоит попробовать какое-то произведение искусства, не стесняйтесь обращаться ко мне. Также: если у вас есть хорошая идея, что делать с этими результатами, не стесняйтесь обращаться к нам. Я знаю, что лично я повешу себе на стену прайм-версию «Звездной ночи»!
Share List
Образец «внутри» простых чисел весь пост с более подробной информацией и лучшими определениями.
Осталось доказать наблюдаемую возможную характеристику, а затем завершить ее, найдя последовательности местонахождений «параболических фигур», обитающих в охарактеризованных областях.
Содержание:
Визуализация факторизаций
Внутренние первичные визуализации
Выкройка и вопрос
Параметризация шаблона
Визуализация факторизаций
Здесь я объясню, как мы можем визуализировать положительные целые числа интересным способом, который также обладает тем свойством, что факторизация $n$ закодирована в виде фрактального шаблона.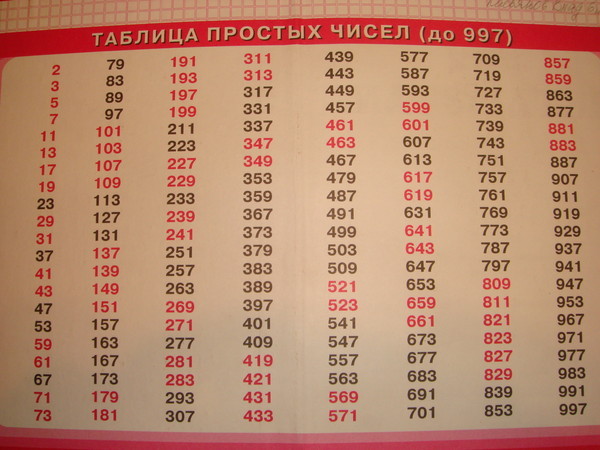 90=a(b+1),a\lt b,a\ge 1$, где в нотации $(n_1,n_2,\dots)_b$ $n_1,n_2,\dots$ обозначают цифры числа $n $ в целочисленной базе $b\ge 2$.
90=a(b+1),a\lt b,a\ge 1$, где в нотации $(n_1,n_2,\dots)_b$ $n_1,n_2,\dots$ обозначают цифры числа $n $ в целочисленной базе $b\ge 2$.
Факторизация натуральных чисел $n$ связана с палиндромами с $2$-значными числами. То есть, если $n$ можно разложить на множители как $n=p\cdot q$, где $p\lt q-1$, это означает, что $n$ — это $2$-значный палиндром в системе счисления $q-1. $, который мы пишем как:
$$ , где $(p,p)$ — цифры числа $n=pq$ в системе счисления $q-1$. Представление $n\in\mathbb N$ в виде суммы $n\times n$ изображений (матриц) Сначала мы определяем «матрицу точек», затем мы определяем «сумму» этих матриц . Пусть $x_0,y_0$ — целые неотрицательные числа. Пусть $P_n(x_0,y_0)$ — матрица $n$ на $n$ «точки $(x_0,y_0)$», левый верхний элемент которой обозначен $P_n(x_0,y_0)(0,0)$ и чья нижняя правая запись обозначена как $P_n(x_0,y_0)(n-1,n-1)$. Он определяется для $x,y\in[0,n)$ как: $$ Чтобы визуализировать $N_n(y_0)$, мы окрасим все записи $0$ в белый цвет, а все остальные — в синий. Эта визуализация остается одинаковой для всех $y_0\ge 1$, за исключением верхней левой записи, которая равна нулю только для $y_0=1$. Если мы выберем $y_0=0$, то визуализация будет «вырожденной». Это побуждает нас писать $N_n=f(N_n(1))$ и называть $N_n$ «образом $n$», где $f$ возвращает ту же матрицу, но все ненулевые элементы устанавливаются в «синие» и все нулевые записи устанавливаются как «белые». Например, ниже показано изображение, показывающее $N_n$ для $n=7,\dots,31$. Обратите внимание, что простых числа представляют собой сплошные синие квадраты без дополнительных деталей, а другие числа имеют визуализацию, соответствующую их разложению на множители.
n=p q=p(q-1)+p=(p, p)_{q-1}, p
P_n(x_0,y_0)(x,y)=
\begin{случаи}
1, & \text{если }x+nx_0\text{ — двузначный палиндром по основанию }y+ny_0\\
0 и \текст{еще}
\end{случаи}
$$ 9{\infty} P_n(k,y_0)$ как «поэлементная сумма $P_n$ вдоль оси $x$ на уровне $y_0$». Обратите внимание, что эта сумма всегда суммирует конечное число матриц, потому что для достаточно больших $k=x_0$ все элементы матрицы равны $0$.
Обратите внимание, что эта сумма всегда суммирует конечное число матриц, потому что для достаточно больших $k=x_0$ все элементы матрицы равны $0$.
Шаблоны в $N_n$ на основе факторизации $n$ 95$ имеют регулярные фрактальные узоры.
Можно спросить, можем ли мы для $n$ вообще вычислить матрицу $N_n$ более эффективно, чем вычислить и суммировать все эти $P_n$. То есть существует ли эффективный тест для прямого получения записи $N_n(x,y)$? $-$ На этот вопрос не нужно отвечать, это просто мои мысли по поводу текущей главы.
Внутри простых визуализаций
$N_p$, где $p$ — простое число, напоминает сплошной синий квадрат и выглядит скучно. Но мы можем «заглянуть внутрь» этот сплошной синий квадрат, заменив нашу функцию $f$.
Напомним, что мы WLOG наблюдаем $y_0=1$, потому что все $y_0\ge 1$ дают эквивалентные изображения.
Матрица «теплового изображения» простого числа $p$
Мы будем писать $\overline{N}_p=h(N_p(1))$ и называть $\overline{N}_p$ » тепловое изображение простого числа $p$», где $h$ присваивает разные цвета различным значениям элементов $N_p(1)$ и возвращает такую матрицу. Пусть нулевое значение будет «черным», наименьшее ненулевое значение будет «красным», а второе наименьшее ненулевое значение будет «желтым».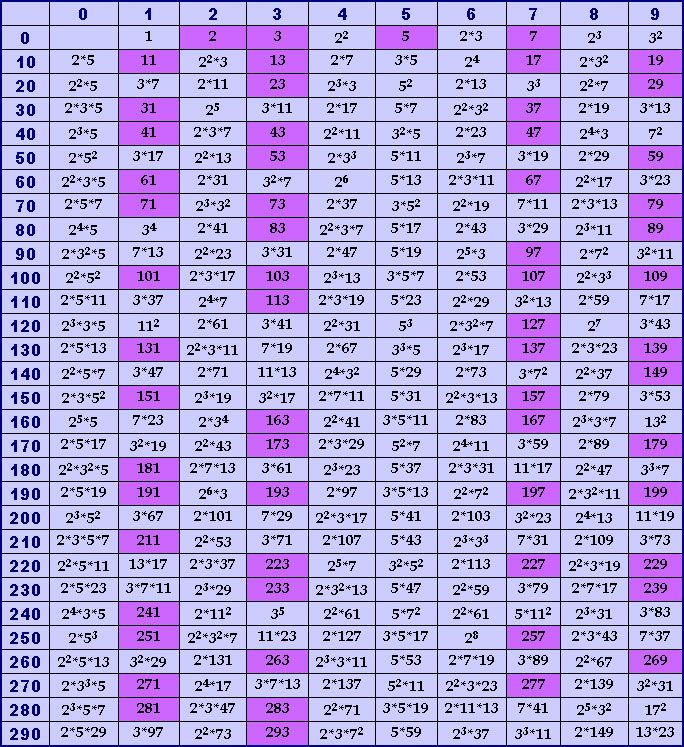 Другие значения могут быть «белыми» или представлены оттенками «серого».
Другие значения могут быть «белыми» или представлены оттенками «серого».
Например, вот $\overline{N}_p$ простых чисел $p=101,103,109$:
На первый взгляд кажется, что это разные размеры одного и того же изображения, но это не так.
В разных $M_p$ мы находим разные шаблоны в определенных областях изображения. Благодаря комментарию Hyperplane мы можем «улучшить» эти области, удалив ненужные детали.
То есть, если мы проигнорируем последнюю строку, то эти $\overline{N}_p$ окажутся симметричными относительно центральной горизонтальной линии. Другими словами, если запись $(x,y)$ красная, то зеркальная запись $(x,|p-y-2|)$ желтая, и наоборот. Однако это верно не для всех записей.
Это побуждает нас наблюдать за «незеркальными» записями и устанавливать для остальных значение $0$.
Образец внутри простого числа $p$
Будем наблюдать неравномерность «теплового изображения». То есть мы определяем новую матрицу $M_p$:
$$
М_р(х,у)=
\begin{случаи}
1, & \text{если} N_p(1)(x,y) = N_p(1)(x,|p-y-2|)\\
0 и \текст{еще}
\end{случаи}
$$
Мы представим эти записи, раскрасив $1$ и $0$ белым и черным цветом соответственно.
Например, вот $M_p$ простых чисел $p=101,103,109$:
Обратите внимание на белые пиксели возле центральной горизонтальной линии. Обратите внимание, что здесь мы можем различать «параболу с толстыми точками» и «параболу с тонкими точками».
Например, увеличение центральной горизонтальной линии $109$ показывает
, что «толстая пунктирная парабола» находится слева, а «тонкая пунктирная парабола» — справа. Это то же самое для простого числа $101$, но не для простого числа $103$, у которого все наоборот.
Оказывается, что простые числа вида $p=4k+1$ «левые» (имеют «толстую» параболу с левой стороны), а простые числа вида $p=4k-1$ «правые» (имеют «толстую» параболу с правой стороны).
Также оказывается, что это не единственные существующие «параболические» группы пикселей. Я попытался отследить простое число $p=101$ из разных групп пикселей и нашел набор из трех различных парабол. Обратите внимание на последнее (четвертое) изображение ниже.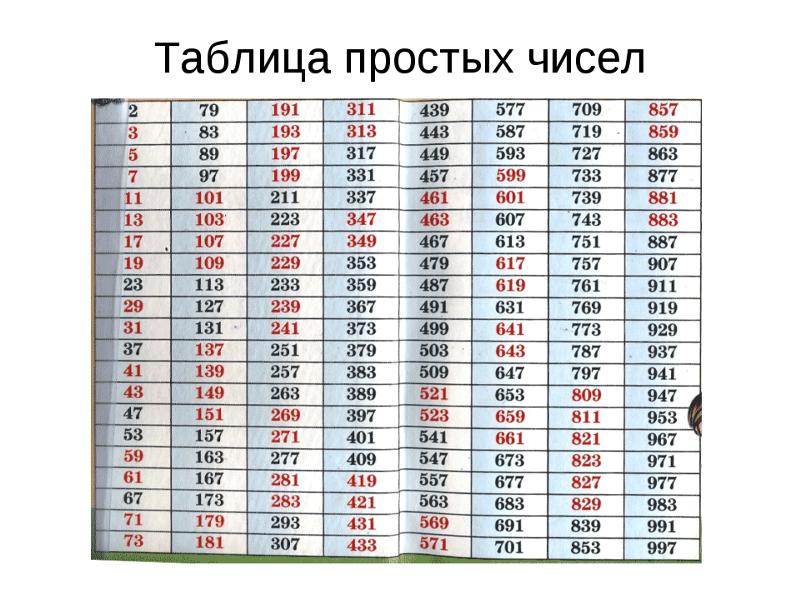
Они имеют одну из следующих «форм» пикселей в «голове»:
- Первая («зеленая парабола») имеет $I_{2}$ — «I-форма высотой 2 пикселя»
- Вторая («синяя парабола») имеет $J_{2,1}$ — «J-образную форму высотой $2+1$ пикселей»
- Третья («красная парабола») имеет $I_{3}$ — «I фигура высотой $3$ пикселей»
Обратите внимание, что эти «фигуры» зеркально отражены ниже/выше центральной горизонтальной линии.
Все $6$ перестановок этих «фигур» могут встречаться в некотором простом числе $p$ (в некотором $M_p$). В зависимости от перестановки, которая появляется на изображении (матрице), мы можем определить, имеет ли простое число форму $p=18k+m$, где $m\in\{-1,1,5,7,11,13 \}$.
Например, все простые числа вида $p=18k+11$ имеют ту же $(I_{2},J_{2,1},I_{3})$ перестановку этих параболических шаблонов, что и простое число $101= 18\cdot 5+11$, в этой области $M_p$.
Чем больше простое число $p$, тем больше таких областей мы можем найти.
Например, в простых числах $p=997$ я выделил четыре из этих областей. Некоторые регионы повторяются несколько раз. Например, обратите внимание, что выделено четыре экземпляра желтой области.
Если изображение выше нечеткое, мы можем альтернативно раскрасить (подсветить) области, соединив пиксели (элементы), которые представляют («принадлежат») соответствующие «параболические» формы:
В каждой области $R $ мы можем наблюдать набор «параболических» фигур. Различные перестановки этих фигур появятся в разных простых числах $p$ (в разных $M_p$), в зависимости от остатка $m$ от деления $p$ на некоторую константу $c_R$.
Вопрос в том, можем ли мы охарактеризовать каждую такую область и ее формы? 9{(s)}_s)$ из $s$ «параболических фигур».
Кажется, что область $R_s$ содержит некоторую перестановку $P_m$ тогда и только тогда, когда $p\equiv m\pmod{c_s}$, где $c_s$ — некоторая константа, связанная с $s$-й областью.
Вопрос.
$1.$ Можем ли мы охарактеризовать все области $R_s$ и их $P_m$ и $c_s$?
«Образец внутри простого числа $p$» будет совокупностью всех областей $R_s$ матрицы $M_p$.
Обратите внимание, что это связано с узором муара, как указал этот пользователь. 9{(3)}_3$. Похоже, что:
$$\begin{align}
R_3 : P=(1,2,3) &\ тогда и только тогда, когда p \equiv 1\pmod{18} \\
R_3 : P=(2,1,3) &\ тогда и только тогда, когда p \equiv 5\pmod{18} \\
R_3 : P=(2,3,1) &\iff p \equiv 7\pmod{18} \\
R_3 : P=(1,3,2) &\iff p \equiv 11\pmod{18} \\
R_3 : P=(3,1,2) &\ тогда и только тогда, когда p \equiv 13\pmod{18} \\
R_3 : P=(3,2,1) &\ тогда и только тогда, когда p \equiv 17\pmod{18} \\
\end{align}$$
Эта область разбивает простые числа на шесть наборов. В отличие от области $R_2$, которая появляется только один раз, эта область $R_3$ появляется на изображении дважды: над и (зеркально) под центральной горизонтальной линией. 9{(4)}_4$. Соответствующие совпадения:
$$\begin{align}
R_4 : P=(1,2,3,4) &\ тогда и только тогда, когда p \equiv 1\pmod{16} \\
R_4 : P=(1,4,3,2) &\ тогда и только тогда, когда p \equiv 3\pmod{16} \\
R_4 : P=(4,1,2,3) &\ тогда и только тогда, когда p \equiv 5\pmod{16} \\
R_4 : P=(2,1,4,3) &\ тогда и только тогда, когда p \equiv 7\pmod{16} \\
R_4 : P=(3,4,1,2) &\ тогда и только тогда, когда p \equiv 9\pmod{16} \\
R_4 : P=(3,2,1,4) &\ тогда и только тогда, когда p \equiv 11\pmod{16} \\
R_4 : P=(2,3,4,1) &\ тогда и только тогда, когда p \equiv 13\pmod{16} \\
R_4 : P=(4,3,2,1) &\ тогда и только тогда, когда p \equiv 15\pmod{16} \\
\end{align}$$
Интересно, что не все сочетания четырех фигур могут появиться в этом регионе. То есть мы видим, что из теоретических $24=4!$ появляется только $8$. Также обратите внимание, что во всех этих перестановках мы чередуем четные и нечетные числа («короткие» и «длинные» фигуры).
То есть мы видим, что из теоретических $24=4!$ появляется только $8$. Также обратите внимание, что во всех этих перестановках мы чередуем четные и нечетные числа («короткие» и «длинные» фигуры).
$$ (s\ge 5) $$
Неожиданно, в отличие от $R_3$ и $R_4$, которые появляются только один раз (на каждой зеркальной стороне), мы можем сказать, что $R_5$ появляется дважды (на каждой зеркальной стороне). сторона). Но в каждой из этих двух зеркальных пар мы имеем разные параболические формы. Следовательно, мы также можем сказать, что существуют две разные области $R_5$.
До сих пор я вручную отслеживал пиксели во многих последовательных простых числах, чтобы наблюдать эти области и их перестановки. Можем ли мы более эффективно охарактеризовать эти регионы?
Я исследовал области $R_5$ и обнаружил, что $c_5=50$, что дает $20$ возможных перестановок. Я также проверил $R_6$ и нашел $c_6=36$, что дает $12$ возможных перестановок.
Обратите внимание, что здесь появляется шаблон. $c_s $ выглядит следующим образом:
$c_s $ выглядит следующим образом:
$$
c_s=2, 4, 18, 16, 50, 36,\точки
$$ 92,2)$. Если это так, то число возможных перестановок равно $s\phi(s)$, что равно A002618.
Другими словами, оказывается, что только перестановки (параболических фигур $\{1, 2, 3, \dots, s\}$), находящиеся «в арифметической прогрессии по модулю $s$», могут существовать внутри $R_s$ регион!
Можем ли мы доказать, что это верно для всех $s$?
Помимо определения того, как отдельные параболические формы переставляются в соответствующих областях, нам также необходимо найти их точное расположение в этих областях, чтобы завершить характеристику.
Разделение пикселей (элементов) на области $R_s$
Интересный вопрос, который мы можем задать: можем ли мы раскрасить каждый пиксель (элемент) $(x,y)$ так, чтобы он принадлежал ровно одному ( или два соседних) региона $R_s$?
То есть $(x,y)$ должен принадлежать региону, если он является частью формы, которая переставляется в этом регионе, или если он «расширяет» одну из этих фигур до границы соседнего область, край.
Я решил раскрасить $R_1,R_2,R_3,R_4$ цветом $\color{purple}{\text{purple}},\color{red}{\text{red}},\color{green} {\text{зеленый}},\color{синий}{\text{синий}}$ соответственно. Я буду использовать белый цвет для окрашивания пикселей, которые «перекрываются» (могут быть в любой области) или те, которые «формируют следующую область».
Простые числа $p=2,3,5$ кажутся слишком маленькими, поэтому мы можем начать с $p=7,11,13,17,19,23$.
Первые три области уже видны в этих маленьких простых числах.
Наблюдая за следующими несколькими простыми числами $p=29,31,37,41$, мы видим, что четвертая область тоже появляется, но все еще пересекает третью область в некоторых частях.
Именно при простых числах $p=43,47,53$ четвертая область должна быть четко видна впервые.
Пятый регион и далее будут отображаться с немного большими штрихами.
Если мы хотим иметь возможность раскрашивать более крупные примеры, нам нужно сначала охарактеризовать регионы (ответьте на мой первый вопрос), а затем мы должны иметь возможность дополнительно определить их точное расположение в соответствующем регионе.
Вопрос. $2.$ Можем ли мы определить расположение параболических фигур для данной области $R_s$?
Я посмотрел на $R_2$ (первая нетривиальная область) и нетрудно увидеть, где именно появятся две соответствующие параболические формы. Это позволило мне придумать параметризацию всего шаблона (матрицы $M_p$), которая представлена в следующей главе.
Параметризация шаблона
Центральная область $R_2$ может использоваться для создания всей матрицы $M_p$. Это намного эффективнее, чем вычисление, и может пролить свет на закономерность.
То есть все регионы $R_s$ возникают в результате следующей параметризации.
Параметризация $M_p$
Для начала найдем начало («голову») «тонкой» и «толстой» параболы. Начальный $y$ будет задан как $y=y_P$ для обоих, где начальный $x=x_L$ самого левого и начальный $x=x_R$ самого правого: 9{(i)}_n)=1$ правильно генерируются последовательностями $i=1,2,3,4,5,6$ и $n$ до тех пор, пока $y$ не выйдет из $[0,p)$ .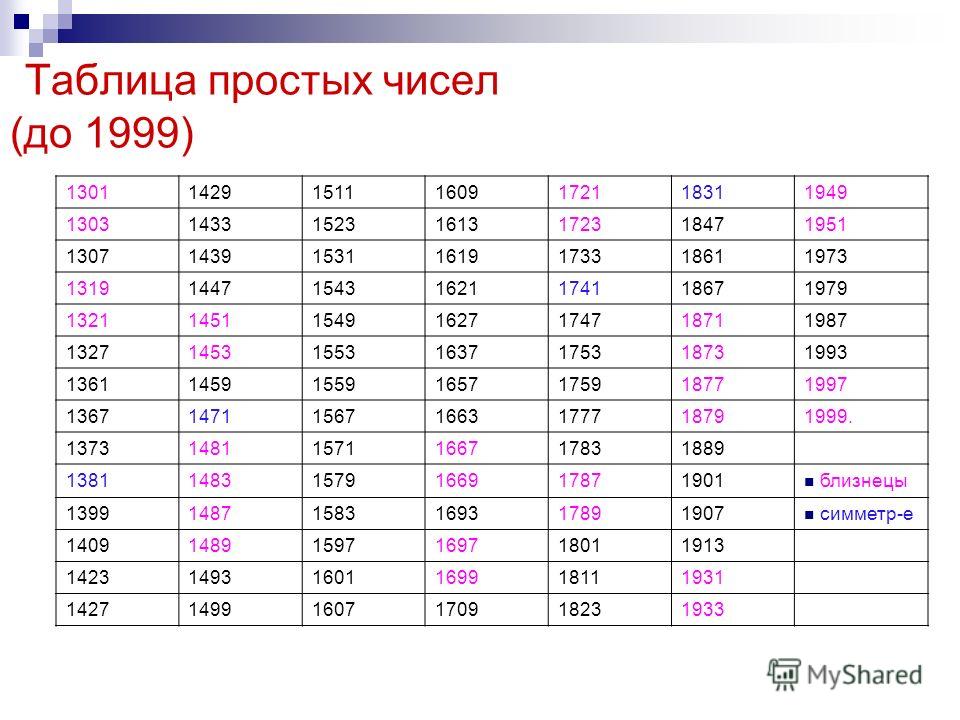





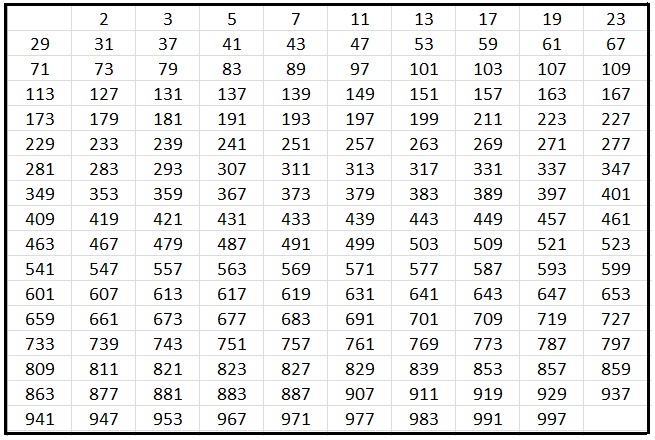 Например, число 92 имеет маленькую цифру 23, написанную внизу круга, это означает, что 92 делится на простое число 23.
Например, число 92 имеет маленькую цифру 23, написанную внизу круга, это означает, что 92 делится на простое число 23.
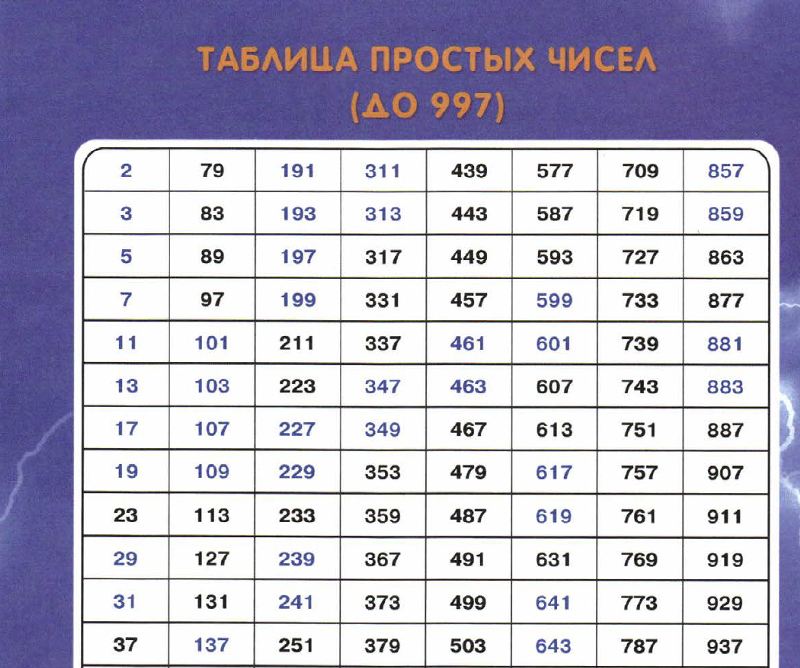

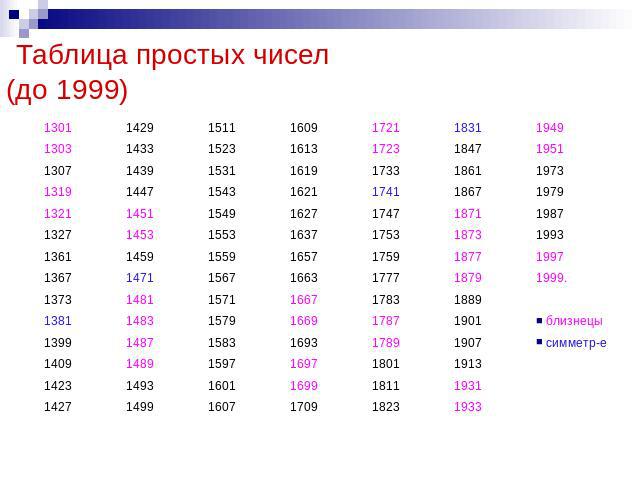
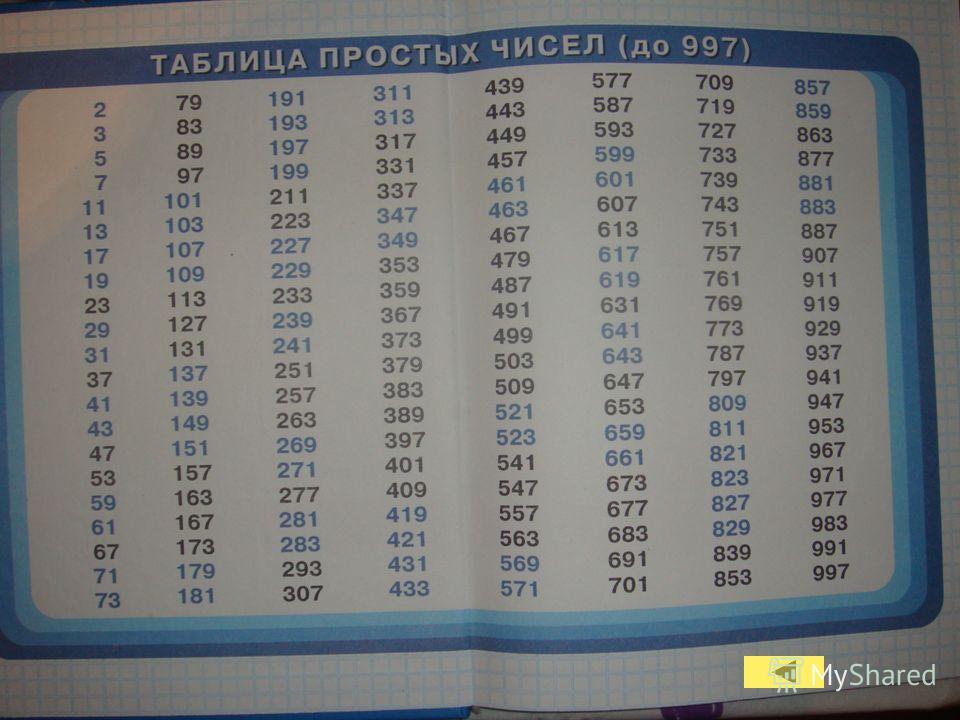 randrange(2, n)
если try_composite(a, d, n, s):
вернуть ложь
return True # ни одна из проверенных баз не показала n составным
утверждать is_probable_prime(2)
утверждать is_probable_prime (3)
утверждать, что это не is_probable_prime(4)
утверждать is_probable_prime(5)
утверждать, что это не is_probable_prime (123456789)
primes_under_1000 = [i для i в диапазоне (2, 1000), если is_probable_prime(i)]
утверждать len(primes_under_1000) == 168
утверждать, что primes_under_1000[-10:] == [937, 941, 947, 953, 967, 971, 977, 983, 991, 997]
утверждать is_probable_prime(6438080068035544392301298549614926991513861075340134\
32918073439524138264842370630061369715394739134090922937332572039\
71333359695492563226209786633213
randrange(2, n)
если try_composite(a, d, n, s):
вернуть ложь
return True # ни одна из проверенных баз не показала n составным
утверждать is_probable_prime(2)
утверждать is_probable_prime (3)
утверждать, что это не is_probable_prime(4)
утверждать is_probable_prime(5)
утверждать, что это не is_probable_prime (123456789)
primes_under_1000 = [i для i в диапазоне (2, 1000), если is_probable_prime(i)]
утверждать len(primes_under_1000) == 168
утверждать, что primes_under_1000[-10:] == [937, 941, 947, 953, 967, 971, 977, 983, 991, 997]
утверждать is_probable_prime(6438080068035544392301298549614926991513861075340134\
32918073439524138264842370630061369715394739134090922937332572039\
71333359695492563226209786633213 std(изображение)
random_noise = np.random.random_sample(size=image.shape)*(stdev/3)
изображение = изображение + случайный_шум
orig_shape = изображение.форма
изображение = np.reshape (изображение, (-1, 3))
numbered_image = kmeans.predict(изображение)
numbered_image = np.reshape (numbered_image, orig_shape [: 2])
# убедитесь, что конец неровный
если числовое_изображение[-1,-1]%2==0:
пронумерованное_изображение[-1,-1] += 1
вернуть пронумерованное_изображение
def пронумерованное_изображение_к_нормальному_изображению (нумерованное_изображение, kmeans):
"""
Превращает изображение только со значениями от 0 до 9в цветное изображение, используя центры кластеров
поставляемого классификатора kmeans.
"""
форма = (нумерованное_изображение.форма[0], нумерованное_изображение.форма[1], 3)
изображение = np.zeros (форма)
для метки цвет в zip (диапазон (10), kmeans.cluster_centers_):
изображение[numbered_image==метка] = цвет
вернуть изображение
std(изображение)
random_noise = np.random.random_sample(size=image.shape)*(stdev/3)
изображение = изображение + случайный_шум
orig_shape = изображение.форма
изображение = np.reshape (изображение, (-1, 3))
numbered_image = kmeans.predict(изображение)
numbered_image = np.reshape (numbered_image, orig_shape [: 2])
# убедитесь, что конец неровный
если числовое_изображение[-1,-1]%2==0:
пронумерованное_изображение[-1,-1] += 1
вернуть пронумерованное_изображение
def пронумерованное_изображение_к_нормальному_изображению (нумерованное_изображение, kmeans):
"""
Превращает изображение только со значениями от 0 до 9в цветное изображение, используя центры кластеров
поставляемого классификатора kmeans.
"""
форма = (нумерованное_изображение.форма[0], нумерованное_изображение.форма[1], 3)
изображение = np.zeros (форма)
для метки цвет в zip (диапазон (10), kmeans.cluster_centers_):
изображение[numbered_image==метка] = цвет
вернуть изображение
 imshow(нормальное_изображение)
imshow(нормальное_изображение)
 text((xpos, ypos),str(letter),(255,255,255, 128),font=font)
img = Image.alpha_composite(img, txt)
img.save(имя файла)
plt.figure(figsize=(20,20))
plt.imshow (изображение)
plt.show()
def имя_файла_результата (имя файла):
вернуть имя файла.split('.')[0] + "-prime.png"
text((xpos, ypos),str(letter),(255,255,255, 128),font=font)
img = Image.alpha_composite(img, txt)
img.save(имя файла)
plt.figure(figsize=(20,20))
plt.imshow (изображение)
plt.show()
def имя_файла_результата (имя файла):
вернуть имя файла.split('.')[0] + "-prime.png"
 join([str(x) для x в строке]))
def multi_threaded_prime_generator (resized_image, kmeans, имя файла, threads=4, log_process=True):
image_generator = (create_numbered_image (resized_image, kmeans) для _ в диапазоне (1000000))
начало = время.время()
с пулом (потоками) в качестве пула:
результаты = pool.imap_unordered (is_good_prime_portrait, image_generator)
всего_результатов = 0
для результата в результатах:
итог_результатов += 1
# Возможно, записывать время, потраченное на поиск этого простого числа
если log_process и total_results%30==0:
прошедшее = время.время()
прошедшее = прошедшее - начало
print("Секунды, потраченные на (имя функции), составляют {} времени на результат: {}".format(str(истекшее время), str(истекшее время/total_results)))
если результат != Нет:
# Найдено простое число, распечатайте его и сохраните!
целое число, строка, n_image = результат
print_result (строка, n_image)
normal_image = пронумерованное_изображение_к_нормальному_изображению (n_image, kmeans)
plt.
join([str(x) для x в строке]))
def multi_threaded_prime_generator (resized_image, kmeans, имя файла, threads=4, log_process=True):
image_generator = (create_numbered_image (resized_image, kmeans) для _ в диапазоне (1000000))
начало = время.время()
с пулом (потоками) в качестве пула:
результаты = pool.imap_unordered (is_good_prime_portrait, image_generator)
всего_результатов = 0
для результата в результатах:
итог_результатов += 1
# Возможно, записывать время, потраченное на поиск этого простого числа
если log_process и total_results%30==0:
прошедшее = время.время()
прошедшее = прошедшее - начало
print("Секунды, потраченные на (имя функции), составляют {} времени на результат: {}".format(str(истекшее время), str(истекшее время/total_results)))
если результат != Нет:
# Найдено простое число, распечатайте его и сохраните!
целое число, строка, n_image = результат
print_result (строка, n_image)
normal_image = пронумерованное_изображение_к_нормальному_изображению (n_image, kmeans)
plt. imshow (нормальное_изображение)
plt.show()
show_and_save_image (нормальное_изображение, n_image, имя_файла_результата (имя файла))
ломать
def search_prime_portrait (имя файла, resize_factor = 16, log_process = True, threads = 4):
resized_image = load_and_resize_image(имя файла, resize_factor=resize_factor)
print("Работа с размером " + str(resized_image.shape))
kmeans = get_k_means (resized_image)
multi_threaded_prime_generator(resized_image, kmeans, имя файла, log_process=log_process, threads=threads)
imshow (нормальное_изображение)
plt.show()
show_and_save_image (нормальное_изображение, n_image, имя_файла_результата (имя файла))
ломать
def search_prime_portrait (имя файла, resize_factor = 16, log_process = True, threads = 4):
resized_image = load_and_resize_image(имя файла, resize_factor=resize_factor)
print("Работа с размером " + str(resized_image.shape))
kmeans = get_k_means (resized_image)
multi_threaded_prime_generator(resized_image, kmeans, имя файла, log_process=log_process, threads=threads)
 время()
для _ в диапазоне (100):
posprim = random.randrange(10**(порядок-1), 10**порядок)
a = is_probable_prime (posprim)
конец = время.время()
вернуться конец - начало
test_range = диапазон (2,30,4)
time_needed = [time_expected_img(x,x) для x в test_range]
plt.plot (test_range, time_needed)
plt.title("Секунды, ожидаемые для расчета, если изображение XxY является основным портретом")
plt.xlabel("Ширина изображения")
plt.ylabel("Ожидаемые секунды")
время()
для _ в диапазоне (100):
posprim = random.randrange(10**(порядок-1), 10**порядок)
a = is_probable_prime (posprim)
конец = время.время()
вернуться конец - начало
test_range = диапазон (2,30,4)
time_needed = [time_expected_img(x,x) для x в test_range]
plt.plot (test_range, time_needed)
plt.title("Секунды, ожидаемые для расчета, если изображение XxY является основным портретом")
plt.xlabel("Ширина изображения")
plt.ylabel("Ожидаемые секунды")
 $1.$ Можем ли мы охарактеризовать все области $R_s$ и их $P_m$ и $c_s$?
$1.$ Можем ли мы охарактеризовать все области $R_s$ и их $P_m$ и $c_s$?